Appendice 2: TEORIA LINEARE della DEFORMAZIONE. ( ),
|
|
|
- Giovanni Savino
- 5 anni fa
- Visualizzazioni
Transcript
1 Capitolo I Cinematica Appendice 2: TEORIA LINEARE della DEFORMAZIONE. Sia C la regione tridimensionale dello spazio occupata da una corpo B nella sua assegnata forma di riferimento. Si assuma che la sostanza costituente il corpo sia distribuita con continuità all interno della regione C e che ogni punto sostanziale p B occupi il posto q C. Si assuma una base ortonormale ij e si istituisca un sistema di riferimento cartesiano ortogonale (o;x,z) ad essa associato. A seguito dell applicazione delle a- zioni esterne che l ambiente circostante esercita sul corpo, quest ultimo subisce un trasporto, assumendo al tempo t la forma attuale o corrente C t ; il generico punto sostanziale p 0, che nella forma di riferimento occupava il posto q 0 di coordinate x,z, viene ora ad occupare il posto p 0. Si definisce spostamento di p 0 il vettore che congiunge q 0 con p 0 : q = q p = : s = sˆ x, z = u i + v j + w le cui componenti ( ), p ( x, z) C, v = vˆ ( x, z) C, w = wˆ ( x, ) C ; ˆ 1 u = u z sono assunte godere di sufficiente regolarità. Le coordinate del posto p 0 C t sono allora date da: x + u, + v, z + w. Si consideri ora un secondo punto sostanziale p 1 occupante il posto q 1 (x+,z) in modo che il segmento referenziale q 0q1 abbia direzione i e lunghezza infinitesima L q =, Fig. 26a. Il punto sostanziale p 1 si porta nel posto p 1, subendo uno 1 = 0q1 spostamento s 1 che, in virtù delle assunzione di distanza infinitesima tra i due posti e di
2 2 Meccanica dei Solidi 3-D continuità delle componenti dello spostamento, differisce da quello di p 0 solo per quantità infinitesime: sˆ 1( x +, z) = s0 + ds = s0 + du i + dv j + dw, con 1 du = u,x + u, + u,z dz, dv = v,x + v, + v,z dz, dw = w,x + w, + w,z dz, che si riducono alle du = u,x, dv = v,x, dw = w,x, in virtù del fatto che al segmento q 0q1 sono state attribuite direzione i e lunghezza 0 (=dz=0). La lunghezza del segmento attuale p 0p1 può allora essere calcolata come: l 1 = p 0 p 1 = {[(x++u+du) (x+u)]2 + [(+v+dv) (+v)] 2 } ½ = = [1 + (u,x ) 2 + 2u,x + (v,x ) 2 ] ½ (1 + 2u,x ) ½, avendo sviluppato i quadrati e trascurato rispetto all unità i quadrati delle derivate spaziali delle componenti di spostamento. L espressione precedente può essere ulteriormente semplificata, sviluppando la radice quadrata in serie di Mac Laurin [18] in funzione dell argomento u/ x: l 1 (1 + 2u,x ) ½ (1 + u,x ). È ora possibile definire la variazione di lunghezza specifica, cioè per unità di lunghezza referenziale, subita dal segmento q 0q1 nella direzione i: ε xx := (l 1 L 1 )/l 1 [(1 + u,x ) - ]/ = u,x come rapporto tra la differenza delle lunghezze del segmento attuale p 0p1 e di quello referenziale q 0q1, e la lunghezza di quest ultimo. La quantità adimensionale ε xx ha il significato di tasso di variazione di lunghezza nella direzione i e prende il nome di deformazione estensionale o assiale nella direzione dell asse x, o anche dilatazione lineare. In maniera formalmente del tutto analoga si possono definire le deformazione assiali nelle altre due direzioni coordinate j e, cioè: 1 La virgola seguita dalla variabile a pedice indica derivazione rispetto alla variabile medesima. Ugo A. Andreaus - SCIENZA DELLE COSTRUZIONI Progetto Leonardo - Editrice Esculapio - Bologna
3 I. Cinematica 3 ε xx = u,x ε = v, ε zz = w,z x x v u p 0 u+du l 1 v+dv p 1 q 2 u α 2 p 2 α 1 p 1 v x x q 0 q 1 q 0 p 0 q 1 a) deformazione assiale, b) variazione angolare; Fig. 26 Piccola deformazione. Si consideri ora un altro punto sostanziale p 2, occupante il posto q 2 (x,+dz) nella forma di riferimento, in modo che il segmento q 0q2 abbia direzione j e la sua lunghezza sia infinitesima e uguale a d Fig. 26b. Il punto sostanziale p 2 subisce uno spostamento s 2 che, in virtù delle assunzioni di distanza infinitesima tra i due posti e di continuità delle componenti dello spostamento, differisce da quello di p 0 ancora solo per quantità infinitesime: con (=dz=0) ( x, + d z) = s + ds = s + du i + dv j + dw, sˆ du = u, dv = v, dw = w, A causa del trasporto, i segmenti referenziali q 0q1 e q 0q2 subiscono una variazione di direzione trasformandosi nei segmenti attuali p 0p1 e p 0p2. La lunghezza del segmento attuale p 0p2 può essere valutata in via approssimata, analogamente a quanto fatto per l 1 : l 2 = p 0 p 2 (1 + v,). Se si indicano con α 1 e α 2 gli angoli che i segmenti attuali formano con quelli referenziali, è possibile valutare tali rotazioni in via approssimata come:
4 4 Meccanica dei Solidi 3-D α 1 Tan α 1 = v,x /l 1 v,x / α 2 Tan α 2 = u, /l 2 u, / dove le lunghezze attuali dei segmenti p 0p1 e p0p2 sono state approssimate con quelle referenziali e rispettivamente, avendo assunto u,x «1 e v, «1. Si definisce allora q1 0 2 π variazione angolare γ x in q 0 e nel piano x la differenza tra l angolo q q = 2 e l angolo p p 1 0p2, cioè: γ x = α 1 + α 2 v,x + u, In maniera formalmente del tutto analoga si possono definire le variazioni angolari tra le altre coppie di direzioni coordinate j e i, cioè: γ x v,x + u, γ z w, + v,z γ zx u,z + w,x Per dare maggiore concisione alle precedenti misure di deformazione e poterle rappresentare mediante la medesima relazione formale, si introducono le semi-variazioni angolari: ε x := γ x /2 = (v,x + u, )/2 ε z := γ z /2 = (w, + v,z )/2 ε zx := γ zx /2 = (u,z + w,x )/2 Le definizioni delle deformazioni assiali e delle semi-variazioni angolari possono essere scritte in forma compatta usando la notazione indiciale: avendo effettuato le seguenti identificazioni: ε ij := (d i,j + d j,i )/2 (1) x 1 =x, x 2 = x 3 =z, d 1 =u, d 2 =v, d 3 =w. Le Eqq. (1) definiscono il tensore della deformazione, che è simmetrico (ε ji =ε ij ) e che può essere rappresentato come una matrice 3 3: ε xx ε x ε xz [ E] = ε x ε ε z. ε zx ε z ε zz Inoltre, le Eqq. (1) correlano le componenti di spostamento d i (i=1,2,3) con le componenti di deformazione ε ij. Se si suppone che gli spostamenti siano funzioni continue derivabili assegnate, allora Eqq. (1) assumono l aspetto di definizione per le componen- Ugo A. Andreaus - SCIENZA DELLE COSTRUZIONI Progetto Leonardo - Editrice Esculapio - Bologna
5 I. Cinematica 5 ti di deformazione: e queste sono ottenibili effettuando le derivazioni indicate nelle Eqq. (1) stesse. Ci si può proporre però il problema inverso: siano assegnate sei funzioni come rappresentative di ε ij. È possibile associare ad esse tre funzioni d i continue e derivabili (delle variabili x,z) che soddisfino le relazioni precedenti? La risposta in generale è negativa. Se le funzioni ε ij non sono opportunamente scelte, le Eqq. (1), intese, questa volta, come sistema di equazioni differenziali nelle incognite d i, non ammettono soluzione. Le Eqq. (1) non esplicano dunque soltanto il ruolo di definizioni delle ε ij, ma indicano anche, implicitamente, che le quantità espressive delle deformazioni non possono essere assegnate arbitrariamente poiché sono legate alla integrabilità delle Eqq. (1). Se le ε ij rendono integrabili le Eqq. (1), si dice che esse sono congruenti e le Eqq. (1) vengono pertanto indicate con la denominazione di equazioni di congruenza. Si consideri ora una porzione di corpo contenuta in un parallelepipedo rettangolare i cui spigoli siano paralleli alle direzioni coordinate e i cui lati abbiano lunghezze infinitesime, d dz, Fig. 27a. La variazione specifica di volume, cioè per unità di volume di riferimento V, di tale elemento sostanziale è detta tasso di variazione di volume o dilatazione cubica, e può essere valutata in via approssimativa come: δv = (v-v)/v = [(1+ε xx ) (1+ε ) (1+ε zz )dz]/( dz) ε xx + ε +ε zz = = u,x + v, + w,z = d 1,1 + d 2,2 + d 3,3 = d i,i = Div d (2) avendo indicato con v il volume attuale, avendo trascurato i termini di 2 grado nel prodotto a numeratore del rapporto precedente e avendo ignorato il contributo delle variazioni angolari alla variazione di lunghezza dei lati dell elemento (approssimazione delle piccole rotazioni). In maniera del tutto analoga si può definire i tassi di variazione areolare di superfici aventi come normali le direzioni, Fig. 27b, j, i come: δa z = [(1+ε xx ) (1+ε )]/( ) ε xx + ε δa ε zz + ε xx, δa x ε + ε zz dove A e a rappresentano l area referenziale e attuale rispettivamente.
6 6 Meccanica dei Solidi 3-D (1+ε zz )dz i dz (1+ε xx ) (1+ε ) j i a) volumico, b) areolare; Fig. 27 Tassi di variazione. (1+ε xx ) (1+ε ) j Ugo A. Andreaus - SCIENZA DELLE COSTRUZIONI Progetto Leonardo - Editrice Esculapio - Bologna
Analisi della deformazione
 3 Analisi della deformazione Tema 3.1 Si consideri un corpo continuo di forma parallelepipedica e di dimensioni a = 15 cm, b = 10 cm, c = 1 cm. Rispetto ad un riferimento centrato nel baricentro del corpo
3 Analisi della deformazione Tema 3.1 Si consideri un corpo continuo di forma parallelepipedica e di dimensioni a = 15 cm, b = 10 cm, c = 1 cm. Rispetto ad un riferimento centrato nel baricentro del corpo
Analisi della Deformazione
 Analisi della Deformazione Tema 1 Si consideri un corpo continuo omogeneo di forma parallelepipedica e lo si riferisca ad un riferimento Cartesiano centrato nel suo baricentro e ad assi paralleli agli
Analisi della Deformazione Tema 1 Si consideri un corpo continuo omogeneo di forma parallelepipedica e lo si riferisca ad un riferimento Cartesiano centrato nel suo baricentro e ad assi paralleli agli
Il teorema dei lavori virtuali, l elasticità lineare ed il problema dell equilibrio elastico
 5 Il teorema dei lavori virtuali, l elasticità lineare ed il problema dell equilibrio elastico Tema 5.1 Si consideri un corpo continuo libero nello spazio, di forma parallelepipedica e di dimensioni a
5 Il teorema dei lavori virtuali, l elasticità lineare ed il problema dell equilibrio elastico Tema 5.1 Si consideri un corpo continuo libero nello spazio, di forma parallelepipedica e di dimensioni a
Teoria dei mezzi continui
 Teoria dei mezzi continui Il modello di un sistema continuo è un modello fenomenologico adatto a descrivere sistemi fisici macroscopici nei casi in cui le dimensione dei fenomeni osservati siano sufficientemente
Teoria dei mezzi continui Il modello di un sistema continuo è un modello fenomenologico adatto a descrivere sistemi fisici macroscopici nei casi in cui le dimensione dei fenomeni osservati siano sufficientemente
Continuo Deformabile: Deformabile cambia forma per effetto dello spostamento dei suoi punti; Continuo gli spostamenti dei punti sono descritti da
 Il Continuo Deformabile Continuo Deformabile: Deformabile cambia forma per effetto dello spostamento dei suoi punti; Continuo gli spostamenti dei punti sono descritti da funzioni continue e differenziabili:
Il Continuo Deformabile Continuo Deformabile: Deformabile cambia forma per effetto dello spostamento dei suoi punti; Continuo gli spostamenti dei punti sono descritti da funzioni continue e differenziabili:
Esempi di domande per scritto e orale
 260 A.Frangi, 208 Appendice D Esempi di domande per scritto e orale D. LE e PLV Risolvere il problema 7.6.6 Risolvere il problema 7.6.7 Nella pagina del docente relativa a Scienza delle Costruzioni allievi
260 A.Frangi, 208 Appendice D Esempi di domande per scritto e orale D. LE e PLV Risolvere il problema 7.6.6 Risolvere il problema 7.6.7 Nella pagina del docente relativa a Scienza delle Costruzioni allievi
Introduzione ai problemi piani in elasticità lineare
 Introduzione ai problemi piani in elasticità lineare 19 novembre 2010 1 Fondamenti dei problemi piani 1.1 Relazioni generali Si consideri un corpo immerso in uno spazio Euclideo tridimensionale R 3 avente
Introduzione ai problemi piani in elasticità lineare 19 novembre 2010 1 Fondamenti dei problemi piani 1.1 Relazioni generali Si consideri un corpo immerso in uno spazio Euclideo tridimensionale R 3 avente
Meccanica dei Fluidi
 POLITECNICO DI MILANO Meccanica dei Fluidi 3. Cinematica dei Fluidi A cura di: Diego Berzi v1.3 Indice 1 Nozioni fondamentali 3 1.1 Velocità e accelerazione..................... 3 1. Moti relativi............................
POLITECNICO DI MILANO Meccanica dei Fluidi 3. Cinematica dei Fluidi A cura di: Diego Berzi v1.3 Indice 1 Nozioni fondamentali 3 1.1 Velocità e accelerazione..................... 3 1. Moti relativi............................
1 Applicazioni lineari
 1 Applicazioni lineari 1 Applicazioni lineari 1.1 Definizione Si considerino lo spazio tridimensionale euclideo E e lo spazio vettoriale V ad esso associato. Definizione. 1.1. Sia A una applicazione di
1 Applicazioni lineari 1 Applicazioni lineari 1.1 Definizione Si considerino lo spazio tridimensionale euclideo E e lo spazio vettoriale V ad esso associato. Definizione. 1.1. Sia A una applicazione di
Elementi finiti solidi
 Esercitazioni del corso di Costruzione di Macchine 2 e Progettazione FEM a cura dell ing. Francesco Villa Elementi finiti solidi Costruzione di Macchine 2 e Progettazione FEM Prof. Sergio Baragetti Dalmine
Esercitazioni del corso di Costruzione di Macchine 2 e Progettazione FEM a cura dell ing. Francesco Villa Elementi finiti solidi Costruzione di Macchine 2 e Progettazione FEM Prof. Sergio Baragetti Dalmine
La trasformazione di camera
 La trasformazione di camera 1 Introduzione Per rappresentare un oggetto tridimensionale nello spazio (scena) in un piano bidimensionale (spazio delle immagini, quale il monitor o un foglio) è necessario
La trasformazione di camera 1 Introduzione Per rappresentare un oggetto tridimensionale nello spazio (scena) in un piano bidimensionale (spazio delle immagini, quale il monitor o un foglio) è necessario
Matematica. Corso integrato di. per le scienze naturali ed applicate. Materiale integrativo.
 Corso integrato di Matematica per le scienze naturali ed applicate Materiale integrativo http://www.dimi.uniud.it/biomat/ Paolo Baiti 1 Lorenzo Freddi 1 1 Dipartimento di Matematica e Informatica, Università
Corso integrato di Matematica per le scienze naturali ed applicate Materiale integrativo http://www.dimi.uniud.it/biomat/ Paolo Baiti 1 Lorenzo Freddi 1 1 Dipartimento di Matematica e Informatica, Università
Il modello di trave adottato dal Saint-Venant si basa sulle seguenti ipotesi:
 IL PROBLEM DEL DE SINT-VENNT Il problema del De Saint-Venant è un particolare problema di equilibrio elastico di notevole interesse applicativo, potendosi considerare alla base della teoria tecnica delle
IL PROBLEM DEL DE SINT-VENNT Il problema del De Saint-Venant è un particolare problema di equilibrio elastico di notevole interesse applicativo, potendosi considerare alla base della teoria tecnica delle
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016
 Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
Meccanica del continuo
 0_Materiali areonautici:layout -07-00 :4 Pagina 5 Meccanica del continuo La meccanica del continuo solido è un argomento estremamente vasto e complesso nell ambito ingegneristico [], [], [3]. Tuttavia
0_Materiali areonautici:layout -07-00 :4 Pagina 5 Meccanica del continuo La meccanica del continuo solido è un argomento estremamente vasto e complesso nell ambito ingegneristico [], [], [3]. Tuttavia
Allora esistono δ > 0 e σ > 0 tali che. f(x, y) = 0; (2) la funzione ϕ : ]x 0 δ, x 0 + δ [ R, y = ϕ(x), è derivabile e.
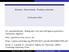
![Allora esistono δ > 0 e σ > 0 tali che. f(x, y) = 0; (2) la funzione ϕ : ]x 0 δ, x 0 + δ [ R, y = ϕ(x), è derivabile e. Allora esistono δ > 0 e σ > 0 tali che. f(x, y) = 0; (2) la funzione ϕ : ]x 0 δ, x 0 + δ [ R, y = ϕ(x), è derivabile e.](/thumbs/96/129204172.jpg) 16 42 Funzioni implicite Il seguente teorema fornisce una condizione sufficiente affinché, data un equazione della forma f(x, ) = 0, sia possibile determinare come funzione della x Teo 11 (Teorema della
16 42 Funzioni implicite Il seguente teorema fornisce una condizione sufficiente affinché, data un equazione della forma f(x, ) = 0, sia possibile determinare come funzione della x Teo 11 (Teorema della
2. ANALISI DELLA DEFORMAZIONE
 . ANALISI DELLA DEFORMAZIONE Un elemento monodimensionale soggetto ad na forza di trazione o compressione sbisce na variazione di lnghezza Δl (rispettivamente n allngamento o n accorciamento) rispetto
. ANALISI DELLA DEFORMAZIONE Un elemento monodimensionale soggetto ad na forza di trazione o compressione sbisce na variazione di lnghezza Δl (rispettivamente n allngamento o n accorciamento) rispetto
Sommario 1 VOLUME CAPITOLO 1 - Matrici 1 VOLUME CAPITOLO 3 - Geometria delle masse 1 VOLUME CAPITOLO 2 - Notazione indiciale
 Sommario CAPITOLO 1 - Matrici...! Definizione! Matrici di tipo particolare Definizioni relative-! Definizioni ed operazioni fondamentali! Somma di matrici (o differenza)! Prodotto di due matrici! Prodotti
Sommario CAPITOLO 1 - Matrici...! Definizione! Matrici di tipo particolare Definizioni relative-! Definizioni ed operazioni fondamentali! Somma di matrici (o differenza)! Prodotto di due matrici! Prodotti
Il teorema dei lavori virtuali applicato alle strutture
 8 Il teorema dei lavori virtuali applicato alle strutture Tema 8.1 Si consideri la struttura riportata in figura 8.1. Si determini la componente di spostamento v S per la sezione S indicata, utilizzando
8 Il teorema dei lavori virtuali applicato alle strutture Tema 8.1 Si consideri la struttura riportata in figura 8.1. Si determini la componente di spostamento v S per la sezione S indicata, utilizzando
ARGOMENTI MATEMATICA PER L INGEGNERIA
 ARGOMENTI DI MATEMATICA PER L INGEGNERIA VOLUME 2 Esercizi proposti Quando non diversamente precisato, nel seguito si intenderà( sempre che nel piano sia stato introdotto un sistema cartesiano ortogonale
ARGOMENTI DI MATEMATICA PER L INGEGNERIA VOLUME 2 Esercizi proposti Quando non diversamente precisato, nel seguito si intenderà( sempre che nel piano sia stato introdotto un sistema cartesiano ortogonale
viene detto il sostegno della curva. Se σ è iniettiva, diciamo che la superficie è semplice. Le equazioni
 Fondamenti di Analisi Matematica 2 - a.a. 2010-11 (Canale 1) Corso di Laurea in Ingegneria Gestionale, Meccanica e Meccatronica Valentina Casarino Appunti sulle superfici 1. Superfici regolari Ricordiamo
Fondamenti di Analisi Matematica 2 - a.a. 2010-11 (Canale 1) Corso di Laurea in Ingegneria Gestionale, Meccanica e Meccatronica Valentina Casarino Appunti sulle superfici 1. Superfici regolari Ricordiamo
FORMULAZIONE DELL ELEMENTO DI TIMOSHENKO
 FORMUAZIONE DE EEMENTO DI TIMOSHENKO Nell analisi strutturale e nel progetto dei telai si utilizza quasi sempre la teoria delle travi sviluppata da Eulero-Bernoulli. Molti manuali usano esclusivamente
FORMUAZIONE DE EEMENTO DI TIMOSHENKO Nell analisi strutturale e nel progetto dei telai si utilizza quasi sempre la teoria delle travi sviluppata da Eulero-Bernoulli. Molti manuali usano esclusivamente
Grandezze: Statiche Cinematiche Idrauliche
 1 Approccio Rigoroso Meccanica mezzi discontinui Solido particellare + Fluido continuo Approccio Ingegneristico Meccanica continuo Solido & Fluido = continui sovrapposti Grandezze: Forze interparticellari
1 Approccio Rigoroso Meccanica mezzi discontinui Solido particellare + Fluido continuo Approccio Ingegneristico Meccanica continuo Solido & Fluido = continui sovrapposti Grandezze: Forze interparticellari
Il Teorema dei Lavori Virtuali Applicato alle Strutture
 Il Teorema dei Lavori Virtuali Applicato alle Strutture Tema 1 Si consideri la struttura riportata in figura 1. Si determini la componente di spostamento v S per la sezione S indicata, utilizzando il teorema
Il Teorema dei Lavori Virtuali Applicato alle Strutture Tema 1 Si consideri la struttura riportata in figura 1. Si determini la componente di spostamento v S per la sezione S indicata, utilizzando il teorema
Corso di Fisica I per Matematica
 Corso di Fisica I per Matematica DOCENTE: Marina COBAL: marina.cobal@cern.ch Tel. 339-2326287 TESTO di RIFERIMENTO: Mazzoldi, Nigro, Voci: Elementi d fisica,meccanica e Termodinamica Ed. EdiSES FONDAMENTI
Corso di Fisica I per Matematica DOCENTE: Marina COBAL: marina.cobal@cern.ch Tel. 339-2326287 TESTO di RIFERIMENTO: Mazzoldi, Nigro, Voci: Elementi d fisica,meccanica e Termodinamica Ed. EdiSES FONDAMENTI
Una approssimazione allo spazio della fisica classica. Spazi affini euclidei.
 Una approssimazione allo spazio della fisica classica. Spazi affini euclidei. Federico Lastaria. Analisi e Geometria 1. Una introduzione allo spazio della fisica classica. 1/20 Lo spazio E 3 (il piano
Una approssimazione allo spazio della fisica classica. Spazi affini euclidei. Federico Lastaria. Analisi e Geometria 1. Una introduzione allo spazio della fisica classica. 1/20 Lo spazio E 3 (il piano
7.4 Massimi e minimi vincolati. Moltiplicatori di Lagrange
 4 7.4 Massimi e minimi vincolati. Moltiplicatori di Lagrange Sia f (,,, n ) una funzione delle n variabili,,, n, supponiamo che esse non siano indipendenti, cioè che siano legate da p < n equazioni: ϕ(,,,
4 7.4 Massimi e minimi vincolati. Moltiplicatori di Lagrange Sia f (,,, n ) una funzione delle n variabili,,, n, supponiamo che esse non siano indipendenti, cioè che siano legate da p < n equazioni: ϕ(,,,
Corso di Matematica B - Ingegneria Informatica Testi di Esercizi. A1. Siano u, v, w vettori. Quali tra le seguenti operazioni hanno senso?
 A. Languasco - Esercizi Matematica B - 4. Geometria 1 A: Vettori geometrici Corso di Matematica B - Ingegneria Informatica Testi di Esercizi A1. Siano u, v, w vettori. Quali tra le seguenti operazioni
A. Languasco - Esercizi Matematica B - 4. Geometria 1 A: Vettori geometrici Corso di Matematica B - Ingegneria Informatica Testi di Esercizi A1. Siano u, v, w vettori. Quali tra le seguenti operazioni
VETTORIALE E PRODOTTO MISTO. PIANI E RETTE DI
 Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA (Edile-Architettura e dell Edilizia) PRODOTTO VETTORIALE E PRODOTTO MISTO. PIANI E RETTE DI R 3. FASCI E STELLE. FORMULE
Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA (Edile-Architettura e dell Edilizia) PRODOTTO VETTORIALE E PRODOTTO MISTO. PIANI E RETTE DI R 3. FASCI E STELLE. FORMULE
Matematica. Corso integrato di. per le scienze naturali ed applicate. Materiale integrativo. Paolo Baiti 1 Lorenzo Freddi 1
 Corso integrato di Matematica per le scienze naturali ed applicate Materiale integrativo Paolo Baiti 1 Lorenzo Freddi 1 1 Dipartimento di Matematica e Informatica, Università di Udine, via delle Scienze
Corso integrato di Matematica per le scienze naturali ed applicate Materiale integrativo Paolo Baiti 1 Lorenzo Freddi 1 1 Dipartimento di Matematica e Informatica, Università di Udine, via delle Scienze
Prefazione... Introduzione... xvii
 Prefazione.......................................................... Introduzione... xvii 1 I concetti di base... 1 1.1 Oggetto e obiettivi.... 1 1.2 Il modello geometrico.............................................
Prefazione.......................................................... Introduzione... xvii 1 I concetti di base... 1 1.1 Oggetto e obiettivi.... 1 1.2 Il modello geometrico.............................................
Il calcolo vettoriale. Marina Cobal - Dipt.di Fisica - Universita' di Udine 1
 Il calcolo vettoriale Universita' di Udine 1 I vettori: definizione Attenzione a definizioni superficiali Del tipo: Definito da modulo, direzione, verso Sono valide a senso, e solo in coordinate cartesiane!
Il calcolo vettoriale Universita' di Udine 1 I vettori: definizione Attenzione a definizioni superficiali Del tipo: Definito da modulo, direzione, verso Sono valide a senso, e solo in coordinate cartesiane!
Il Problema del De Saint Venant
 Il Problema del De Saint Venant Tema 1 Si consideri una trave di acciaio di lunghezza L = m e con sezione retta a corona circolare di raggio esterno R = 30 cm e raggio interno r = 0 cm, che rispetti le
Il Problema del De Saint Venant Tema 1 Si consideri una trave di acciaio di lunghezza L = m e con sezione retta a corona circolare di raggio esterno R = 30 cm e raggio interno r = 0 cm, che rispetti le
Risultati di ANALISI VETTORIALE
 Guida allo studio autonomo in ELETTROMAGNETISMO U Unità Risultati di ANALISI VETTORIALE Introduzione Hai già studiato gran parte della matematica necessaria per questo corso Comunque vale la pena di rivedere
Guida allo studio autonomo in ELETTROMAGNETISMO U Unità Risultati di ANALISI VETTORIALE Introduzione Hai già studiato gran parte della matematica necessaria per questo corso Comunque vale la pena di rivedere
Esonero di Analisi Matematica II (A)
 Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
(i) Determinare l equazione cartesiana dell unica circonferenza C passante per i tre punti dati.
 Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Edile/Architettura Esercizi per il corso di GEOMETRIA - a.a. 7/8 Docente: Prof. F. Flamini - Tutore: Dott. M. Paganin FOGLIO - Esercizi
Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Edile/Architettura Esercizi per il corso di GEOMETRIA - a.a. 7/8 Docente: Prof. F. Flamini - Tutore: Dott. M. Paganin FOGLIO - Esercizi
Introduzione al Metodo agli Elementi Finiti (FEM) (x, y) Γ Tale formulazione viene detta Formulazione forte del problema.
 Introduzione al Metodo agli Elementi Finiti (FEM) Consideriamo come problema test l equazione di Poisson 2 u x 2 + 2 u = f(x, y) u = f y2 definita su un dominio Ω R 2 avente come frontiera la curva Γ,
Introduzione al Metodo agli Elementi Finiti (FEM) Consideriamo come problema test l equazione di Poisson 2 u x 2 + 2 u = f(x, y) u = f y2 definita su un dominio Ω R 2 avente come frontiera la curva Γ,
R è definita infine dall insieme delle curve percorse da ogni singolo punto della corda.
 1. Problema della corda vibrante Si consideri una corda monodimensionale, di sezione nulla avente densità per unità di lunghezza ρ e modulo elastico lineare E. Una corda reale approssima quella ideale
1. Problema della corda vibrante Si consideri una corda monodimensionale, di sezione nulla avente densità per unità di lunghezza ρ e modulo elastico lineare E. Una corda reale approssima quella ideale
; r 0 2 m = l 2 (s 2 θ + c 2 θ) = l 2
 1 Calcolo del momento d inerzia Esercizio I.1 Pendolo semplice Si faccia riferimento alla Figura 1, dove è rappresentato un pendolo semplice; si utilizzeranno diversi sistemi di riferimento: il primo,
1 Calcolo del momento d inerzia Esercizio I.1 Pendolo semplice Si faccia riferimento alla Figura 1, dove è rappresentato un pendolo semplice; si utilizzeranno diversi sistemi di riferimento: il primo,
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009)
 ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009) 1. Sia S = { } (x, y, z) : x 2 + y 2 = 4, 0 z 3 + x. Scrivere le equazioni parametriche di una superficie regolare che abbia S come sostegno. 2. Enunciare
ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009) 1. Sia S = { } (x, y, z) : x 2 + y 2 = 4, 0 z 3 + x. Scrivere le equazioni parametriche di una superficie regolare che abbia S come sostegno. 2. Enunciare
Funzioni. iniettiva se x y = f (x) f (y) o, equivalentemente, f (x) = f (y) = x = y
 Funzioni. Dati due insiemi A e B (non necessariamente distinti) si chiama funzione da A a B una qualunque corrispondenza (formula, regola) che associa ad ogni elemento di A uno ed un solo elemento di B.
Funzioni. Dati due insiemi A e B (non necessariamente distinti) si chiama funzione da A a B una qualunque corrispondenza (formula, regola) che associa ad ogni elemento di A uno ed un solo elemento di B.
3. Metodo degli elementi finiti 3.1 GENERALITÀ
 3. Metodo degli elementi finiti 3.1 GENERALITÀ Si è visto che col metodo degli spostamenti si riesce a risolvere in maniera esatta il problema della determinazione degli spostamenti e degli sforzi in una
3. Metodo degli elementi finiti 3.1 GENERALITÀ Si è visto che col metodo degli spostamenti si riesce a risolvere in maniera esatta il problema della determinazione degli spostamenti e degli sforzi in una
LEZIONE 36. si dice regolare se è. per ogni (u 0, v 0 ) D. Una superficie S R 3 is dice regolare se esiste una sua parametrizzazione regolare.
 LEZIONE 36 36.1. La definizione di superficie. In questo paragrafo iniziamo a dare alcuni esempi di superfici ed a definire alcuni oggetti ad esse naturalmente associati. Come già fatto per le curve, considereremo
LEZIONE 36 36.1. La definizione di superficie. In questo paragrafo iniziamo a dare alcuni esempi di superfici ed a definire alcuni oggetti ad esse naturalmente associati. Come già fatto per le curve, considereremo
SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE
 SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE. Esercizi Esercizio. In R calcolare il modulo dei vettori,, ),,, ) ed il loro angolo. Esercizio. Calcolare una base ortonormale del sottospazio
SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE. Esercizi Esercizio. In R calcolare il modulo dei vettori,, ),,, ) ed il loro angolo. Esercizio. Calcolare una base ortonormale del sottospazio
Argomenti Capitolo 1 Richiami
 Argomenti Capitolo 1 Richiami L insieme dei numeri reali R si rappresenta geometricamente con l insieme dei punti di una retta orientata su cui sia stato fissato un punto 0 e un segmento unitario. L insieme
Argomenti Capitolo 1 Richiami L insieme dei numeri reali R si rappresenta geometricamente con l insieme dei punti di una retta orientata su cui sia stato fissato un punto 0 e un segmento unitario. L insieme
CORSO DI FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA - LAUREA IN INGEGNERIA MECCANICA Padova II prova parziale TEMA n.1
 CORSO DI FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA - LAUREA IN INGEGNERIA MECCANICA Padova 15-06-2010 II prova parziale TEMA n.1 Parte 1. Quesiti preliminari. Stabilire se le seguenti affermazioni sono
CORSO DI FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA - LAUREA IN INGEGNERIA MECCANICA Padova 15-06-2010 II prova parziale TEMA n.1 Parte 1. Quesiti preliminari. Stabilire se le seguenti affermazioni sono
DEFORMAZIONE DI SCORRIMENTO SEMPLICE
 DEFORMAZIONE DI SCORRIMENTO SEMPLICE Prof. Daniele Zaccaria Dipartimento di Ingegneria Civile Università ditrieste Piazzale Europa, Trieste giugno 5 Indice Deformazione Velocità 3 3 Tensori di deformazione
DEFORMAZIONE DI SCORRIMENTO SEMPLICE Prof. Daniele Zaccaria Dipartimento di Ingegneria Civile Università ditrieste Piazzale Europa, Trieste giugno 5 Indice Deformazione Velocità 3 3 Tensori di deformazione
vettore spostamento infinitesimo: ds dr dxi + dyj + dzk
 Appendice A A.1 - istemi di coordinate. 1) Coordinate cartesiane. Il sistema di riferimento è costituito da tre assi perpendicolari uscenti da una comune origine O ed orientati positivamente verso l esterno.
Appendice A A.1 - istemi di coordinate. 1) Coordinate cartesiane. Il sistema di riferimento è costituito da tre assi perpendicolari uscenti da una comune origine O ed orientati positivamente verso l esterno.
Le trasformazioni geometriche nel piano cartesiano. x = ϕ(x', y') τ 1 : G(x', y') = 0. la sua inversa.
 τ : P P' oppure P'=τ(P) P immagine di P trasformato di P secondo τ se α è una figura geometrica α =τ(α) è la figura geometrica trasformata x' = f (x, y) τ : y' = g(x, y) espressione analitica della trasformazione
τ : P P' oppure P'=τ(P) P immagine di P trasformato di P secondo τ se α è una figura geometrica α =τ(α) è la figura geometrica trasformata x' = f (x, y) τ : y' = g(x, y) espressione analitica della trasformazione
Capitolo 8 Forme quadratiche e loro applicazioni Esercizi svolti Tutorato di geometria e algebra lineare. Marco Robutti
 Capitolo 8 Forme quadratiche e loro applicazioni Esercizi svolti Tutorato di geometria e algebra lineare Marco Robutti 5 Ottobre 2017 1 Introduzione Gli esercizi di questo capitolo riguardano i seguenti
Capitolo 8 Forme quadratiche e loro applicazioni Esercizi svolti Tutorato di geometria e algebra lineare Marco Robutti 5 Ottobre 2017 1 Introduzione Gli esercizi di questo capitolo riguardano i seguenti
za Bozza - Appunti di Scienza delle Costruzioni 1, dalle lezioni del prof. P. Podio-Guidugli, a.a. 2007/8 -
 11 Calcolo di spostamenti e rotazioni in travature isostatiche 81 11 Calcolo di spostamenti e rotazioni in travature isostatiche Consideriamo d ora in avanti travature linearmente termoelastiche dello
11 Calcolo di spostamenti e rotazioni in travature isostatiche 81 11 Calcolo di spostamenti e rotazioni in travature isostatiche Consideriamo d ora in avanti travature linearmente termoelastiche dello
Le piastre:classificazione
 Le piastre 1. piastre sottili h/l= 1/50-1/10 : piastre sottili con rigidezza flessionale che portano distribuzioni di carico bidimensionale prevalentemente attraverso momenti flettenti, momenti torcenti
Le piastre 1. piastre sottili h/l= 1/50-1/10 : piastre sottili con rigidezza flessionale che portano distribuzioni di carico bidimensionale prevalentemente attraverso momenti flettenti, momenti torcenti
Appendice 1: CINEMATICA LINEARE della TRAVE ESTENSIBILE e FLESSIBILE
 Capitolo I Cinematica Appendice 1: CINEMATICA LINEARE della TRAVE ETENIBILE e FLEIBILE i assuma la consevazione della nomalità ta la fiba D z a e il vettoe s tangente al suppoto nella foma attuale (tave
Capitolo I Cinematica Appendice 1: CINEMATICA LINEARE della TRAVE ETENIBILE e FLEIBILE i assuma la consevazione della nomalità ta la fiba D z a e il vettoe s tangente al suppoto nella foma attuale (tave
Lezione 13 - Il gradiente di deformazione
 Lezione 3 - Il gradiente di deformazione ü [A.a. 0-03 : ultima revisione 3 ottobre 0] In questa lezione si comincia ad affrontare l'analisi della deformazione, cui compito principale e' rispondere al seguente
Lezione 3 - Il gradiente di deformazione ü [A.a. 0-03 : ultima revisione 3 ottobre 0] In questa lezione si comincia ad affrontare l'analisi della deformazione, cui compito principale e' rispondere al seguente
Domanda Risposta
 Esame di Geometria 18 Maggio 010 Cognome e Nome: Matricola: Corso di Laurea Regolamento della prova. La prova consiste in 7 Domande a risposta multipla chiusa (di cui una soltanto è corretta) e di Esercizi.
Esame di Geometria 18 Maggio 010 Cognome e Nome: Matricola: Corso di Laurea Regolamento della prova. La prova consiste in 7 Domande a risposta multipla chiusa (di cui una soltanto è corretta) e di Esercizi.
Corpo affine elastico vincolato
 Esercizio [5-1] 1 Corpo affine elastico vincolato e 2 e 1 Un corpo a forma di parallelepipedo retto, con spigoli paralleli a e 1 di lunghezza l 1, spigoli paralleli a e 2 di lunghezza l 2 e spigoli paralleli
Esercizio [5-1] 1 Corpo affine elastico vincolato e 2 e 1 Un corpo a forma di parallelepipedo retto, con spigoli paralleli a e 1 di lunghezza l 1, spigoli paralleli a e 2 di lunghezza l 2 e spigoli paralleli
il luogo dei punti in cui un campo scalare assume un valore costante e detto superficie di livello ed e determinato dall equazione u(x,y,z) = c
 Campo scalare e una regione di spazio dove punto per punto sia definibile una funzione scalare continua e derivabile ovunque ( una funzione da a ) n trascurando la dipendenza dal tempo e operando in coordinate
Campo scalare e una regione di spazio dove punto per punto sia definibile una funzione scalare continua e derivabile ovunque ( una funzione da a ) n trascurando la dipendenza dal tempo e operando in coordinate
Piastre sottili: soluzioni esatte. Piastra ellittica incastrata al bordo soggetta a carico distribuito costante
 Piastre sottili: soluzioni esatte Piastra ellittica incastrata al bordo soggetta a carico distribuito costante Piastre sottili: soluzioni esatte Piastra triangolare appoggiata al bordo soggetta a carico
Piastre sottili: soluzioni esatte Piastra ellittica incastrata al bordo soggetta a carico distribuito costante Piastre sottili: soluzioni esatte Piastra triangolare appoggiata al bordo soggetta a carico
MECCANICA COMPUTAZIONALE
 MECCANICA COMPUTAZIONALE Capitolo Metodo diretto della rigidezza Rev. maggio 006 (rev. /05/006) Capitolo : /4 Argomenti trattati nel capitolo Idealizzazione e discretizzazione Rigidezza dell elemento biella
MECCANICA COMPUTAZIONALE Capitolo Metodo diretto della rigidezza Rev. maggio 006 (rev. /05/006) Capitolo : /4 Argomenti trattati nel capitolo Idealizzazione e discretizzazione Rigidezza dell elemento biella
Endomorfismi simmetrici
 Endomorfismi simmetrici Endomorfismo simmetrico: Dato uno spazio vettoriale metrico V e un endomorfismo T appartenente a V. L endomorfismo si definisce simmetrico se e solo se (T(v),v2)=(v,T(v2)) per ogni
Endomorfismi simmetrici Endomorfismo simmetrico: Dato uno spazio vettoriale metrico V e un endomorfismo T appartenente a V. L endomorfismo si definisce simmetrico se e solo se (T(v),v2)=(v,T(v2)) per ogni
Equazioni differenziali
 Equazioni differenziali Antonino Polimeno Università degli Studi di Padova Equazioni differenziali - 1 Un equazione differenziale è un equazione la cui soluzione è costituita da una funzione incognita
Equazioni differenziali Antonino Polimeno Università degli Studi di Padova Equazioni differenziali - 1 Un equazione differenziale è un equazione la cui soluzione è costituita da una funzione incognita
Geometria analitica del piano pag 32 Adolfo Scimone
 Geometria analitica del piano pag 32 Adolfo Scimone CAMBIAMENTI DI SISTEMA DI RIFERIMENTO Consideriamo il piano cartesiano R 2 con un sistema di riferimento (O,U). Se introduciamo in R 2 un secondo sistema
Geometria analitica del piano pag 32 Adolfo Scimone CAMBIAMENTI DI SISTEMA DI RIFERIMENTO Consideriamo il piano cartesiano R 2 con un sistema di riferimento (O,U). Se introduciamo in R 2 un secondo sistema
NUMERI COMPLESSI. Rappresentazione cartesiana dei numeri complessi
 NUMERI COMPLESSI Come sappiamo, non esistono nel campo dei numeri reali le radici di indice pari dei numeri negativi. Ammettiamo pertanto l esistenza della radice quadrata del numero 1. Questo nuovo ente
NUMERI COMPLESSI Come sappiamo, non esistono nel campo dei numeri reali le radici di indice pari dei numeri negativi. Ammettiamo pertanto l esistenza della radice quadrata del numero 1. Questo nuovo ente
Analisi Matematica 2
 Analisi Matematica 2 Differenziabilità per funzioni di due variabili Differenziabilità per funzioni di due variabili CCS Ingegneria Meccanica e Ingegneria Chimica 1 / 26 Differenziabilitá Data la funzione
Analisi Matematica 2 Differenziabilità per funzioni di due variabili Differenziabilità per funzioni di due variabili CCS Ingegneria Meccanica e Ingegneria Chimica 1 / 26 Differenziabilitá Data la funzione
UNIVERSITA DEGLI STUDI DI PAVIA REGISTRO. DELLE LEZIONI ESERCITAZIONI SEMINARI Anno accademico 2016/17
 REGISTRO DELLE LEZIONI ESERCITAZIONI SEMINARI Anno accademico 2016/17 Cognome e Nome: BISI FULVIO Qualifica: PROFESSORE ASSOCIATO MAT/07 DIPARTIMENTO DI MATEMATICA Insegnamento (6 CFU su un totale di 6+3
REGISTRO DELLE LEZIONI ESERCITAZIONI SEMINARI Anno accademico 2016/17 Cognome e Nome: BISI FULVIO Qualifica: PROFESSORE ASSOCIATO MAT/07 DIPARTIMENTO DI MATEMATICA Insegnamento (6 CFU su un totale di 6+3
Discorsi di tensioni e deformazioni
 CHAPTR 1 Discorsi di tensioni e deformazioni 1 Relazioni tra le componenti di tensione Componenti della tensione su un piano generico: S 1 = σ 11 n 1 + σ 1 n + σ31n 3 S = σ 1 n 1 + σ n + σ3n 3 S 3 = σ
CHAPTR 1 Discorsi di tensioni e deformazioni 1 Relazioni tra le componenti di tensione Componenti della tensione su un piano generico: S 1 = σ 11 n 1 + σ 1 n + σ31n 3 S = σ 1 n 1 + σ n + σ3n 3 S 3 = σ
dello spazio architettonico. Assonometria e prospettiva, Napoli,
 PROIEZIONE PARALLELA Riferimento spaziale e riferimento piano; Costruzione dell assonometria obliqua cavaliera con l omologia di ribaltamento; Assonometria obliqua cavaliera militare; Applicazioni grafiche.
PROIEZIONE PARALLELA Riferimento spaziale e riferimento piano; Costruzione dell assonometria obliqua cavaliera con l omologia di ribaltamento; Assonometria obliqua cavaliera militare; Applicazioni grafiche.
v w u O Osserviamo che tale segmento ha la stessa lunghezza del vettore w tale che u+w = v cioe del vettore w = v u. Cosi si ha
 Matematica II, 708 Nel piano sia fissata una unita di misura Dati nel piano due vettori u, v applicati in uno stesso punto O, col termine distanza fra u e v intendiamo e col simbolo d(u, v) indichiamo
Matematica II, 708 Nel piano sia fissata una unita di misura Dati nel piano due vettori u, v applicati in uno stesso punto O, col termine distanza fra u e v intendiamo e col simbolo d(u, v) indichiamo
Spazi vettoriali euclidei.
 Spazi vettoriali euclidei Prodotto scalare, lunghezza e ortogonalità in R n Consideriamo lo spazio vettoriale R n = { =,,, n R}, n con la somma fra vettori e il prodotto di un vettore per uno scalare definiti
Spazi vettoriali euclidei Prodotto scalare, lunghezza e ortogonalità in R n Consideriamo lo spazio vettoriale R n = { =,,, n R}, n con la somma fra vettori e il prodotto di un vettore per uno scalare definiti
Bivettori. Determinanti. Prodotto vettoriale.
 Bivettori. Determinanti. Prodotto vettoriale. 10 Dicembre 2018 Per approfondimenti: bibliografia e siti web sull algebra geometrica (Geometric Algebra): http://geometry.mrao.cam.ac.uk/ https://assets.cambridge.org/052148/0221/sample/0521480221ws.pdf
Bivettori. Determinanti. Prodotto vettoriale. 10 Dicembre 2018 Per approfondimenti: bibliografia e siti web sull algebra geometrica (Geometric Algebra): http://geometry.mrao.cam.ac.uk/ https://assets.cambridge.org/052148/0221/sample/0521480221ws.pdf
Geometria analitica: rette e piani
 Geometria analitica: rette e piani parametriche Allineamento nel piano nello spazio Angoli tra rette e distanza 2 2006 Politecnico di Torino 1 Esempio 2 Sia A = (1, 2). Per l interpretazione geometrica
Geometria analitica: rette e piani parametriche Allineamento nel piano nello spazio Angoli tra rette e distanza 2 2006 Politecnico di Torino 1 Esempio 2 Sia A = (1, 2). Per l interpretazione geometrica
Anno Accademico Corso di Laurea in Scienze biologiche Prova scritta 1 di Istituzioni di Matematiche del 13 febbraio 2007 COMPITO A
 del 13 febbraio 007 COMPITO A 1. Dire per quali valori del parametro reale λ, il seguente sistema lineare x + y = 1 x + y = x y = λ ammette soluzioni e trovarle.. Siano date le rette r : x + 3y + 3 = 0
del 13 febbraio 007 COMPITO A 1. Dire per quali valori del parametro reale λ, il seguente sistema lineare x + y = 1 x + y = x y = λ ammette soluzioni e trovarle.. Siano date le rette r : x + 3y + 3 = 0
1 Schemi alle differenze finite per funzioni di una variabile
 Introduzione In questa dispensa vengono forniti alcuni elementi di base per la soluzione di equazioni alle derivate parziali che governano problemi al contorno. A questo scopo si introducono, in forma
Introduzione In questa dispensa vengono forniti alcuni elementi di base per la soluzione di equazioni alle derivate parziali che governano problemi al contorno. A questo scopo si introducono, in forma
Lezione 5 Geometria Analitica 1
 Lezione 5 Geometria Analitica 1 Donato A Ciampa In questa lezione richiameremo alcune nozioni della geometria analitica, quali le trasformazioni del piano in se stesso e le varie equazioni relative alla
Lezione 5 Geometria Analitica 1 Donato A Ciampa In questa lezione richiameremo alcune nozioni della geometria analitica, quali le trasformazioni del piano in se stesso e le varie equazioni relative alla
M to t d o i d d i d p ro r i o ezion o e n. c rr r i r spo p ndenza z b univo v ca ope p ra r zi z oni d i p r p o r iezi z one e s ezi z one
 Metodi di proiezione. I sistemi di rappresentazione geometrica consentono di rappresentare un oggetto tridimensionale su un piano bidimensionale, mediante un immagine che abbia con l oggetto originale
Metodi di proiezione. I sistemi di rappresentazione geometrica consentono di rappresentare un oggetto tridimensionale su un piano bidimensionale, mediante un immagine che abbia con l oggetto originale
(x B x A, y B y A ) = (4, 2) ha modulo
 GEOMETRIA PIANA 1. Esercizi Esercizio 1. Dati i punti A(0, 4), e B(4, ) trovarne la distanza e trovare poi i punti C allineati con A e con B che verificano: (1) AC = CB (punto medio del segmento AB); ()
GEOMETRIA PIANA 1. Esercizi Esercizio 1. Dati i punti A(0, 4), e B(4, ) trovarne la distanza e trovare poi i punti C allineati con A e con B che verificano: (1) AC = CB (punto medio del segmento AB); ()
2. ANALISI DELLA DEFORMAZIONE 2.1 SCOPO
 Cap. ANALISI DELLA DEFORMAZIONE. ANALISI DELLA DEFORMAZIONE. SCOPO Abbiamo visto nell Introduzione come l'ipotesi di corpo rigido debba essere rimossa qualora si vogliano studiare le strutture iperstatiche.
Cap. ANALISI DELLA DEFORMAZIONE. ANALISI DELLA DEFORMAZIONE. SCOPO Abbiamo visto nell Introduzione come l'ipotesi di corpo rigido debba essere rimossa qualora si vogliano studiare le strutture iperstatiche.
Esercizi di Elementi di Matematica Corso di laurea in Farmacia
 Esercizi di Elementi di Matematica Corso di laurea in Farmacia dott.ssa Marilena Ligabò November 24, 2015 1 Esercizi sulla notazione scientifica Esercizio 1.1. Eseguire il seguente calcolo utilizzando
Esercizi di Elementi di Matematica Corso di laurea in Farmacia dott.ssa Marilena Ligabò November 24, 2015 1 Esercizi sulla notazione scientifica Esercizio 1.1. Eseguire il seguente calcolo utilizzando
1 Geometria analitica nel piano
 Lezioni di Geometria a.a. 2007-2008 cdl SIE prof. C. Franchetti 1 Geometria analitica nel piano 1.1 Distanza di due punti Siano P 1 = (x 1, y 1 ), P 2 = (x 2, y 2 ) due punti del piano, se d(p 1, P 2 )
Lezioni di Geometria a.a. 2007-2008 cdl SIE prof. C. Franchetti 1 Geometria analitica nel piano 1.1 Distanza di due punti Siano P 1 = (x 1, y 1 ), P 2 = (x 2, y 2 ) due punti del piano, se d(p 1, P 2 )
4. Sia Γ la conica che ha fuoco F (1, 1) e direttrice d : x y = 0, e che passa per il punto P (2, 1).
 Geometria Complementi ed esercizi sulle coniche 1 (a) Scrivere l equazione dell ellisse Γ che ha fuochi F 1 ( 1, 1), F (1, 1) e che passa per il punto P (1, 1) (b) Determinare il centro, gli assi e i vertici
Geometria Complementi ed esercizi sulle coniche 1 (a) Scrivere l equazione dell ellisse Γ che ha fuochi F 1 ( 1, 1), F (1, 1) e che passa per il punto P (1, 1) (b) Determinare il centro, gli assi e i vertici
Esercizi per il corso di Algebra e Geometria L.
 Esercizi per il corso di Algebra e Geometria L AA 2006/2007 1 Foglio 1 In tutti gli esercizi che seguiranno lo spazio ambiente sarà il piano cartesiano a valori nel campo dei numeri reali, dove supporremo
Esercizi per il corso di Algebra e Geometria L AA 2006/2007 1 Foglio 1 In tutti gli esercizi che seguiranno lo spazio ambiente sarà il piano cartesiano a valori nel campo dei numeri reali, dove supporremo
INTRODUZIONE ALLA CINEMATICA DEL PUNTO MATERIALE PROF. FRANCESCO DE PALMA
 INTRODUZIONE ALLA CINEMATICA DEL PUNTO MATERIALE PROF. FRANCESCO DE PALMA Sommario MOTO E TRAIETTORIA... 3 PUNTO MATERIALE... 3 TRAIETTORIA... 3 VELOCITÀ... 4 VELOCITÀ MEDIA... 4 VELOCITÀ ISTANTANEA...
INTRODUZIONE ALLA CINEMATICA DEL PUNTO MATERIALE PROF. FRANCESCO DE PALMA Sommario MOTO E TRAIETTORIA... 3 PUNTO MATERIALE... 3 TRAIETTORIA... 3 VELOCITÀ... 4 VELOCITÀ MEDIA... 4 VELOCITÀ ISTANTANEA...
Cinematica ed equilibrio del corpo rigido
 omportamento meccanico dei materiali inematica piana omportamento meccanico dei materiali inematica ed equilibrio del corpo rigido inematica piana Equilibrio esterno aratteristiche di sollecitazione 2
omportamento meccanico dei materiali inematica piana omportamento meccanico dei materiali inematica ed equilibrio del corpo rigido inematica piana Equilibrio esterno aratteristiche di sollecitazione 2
Istituzioni di Matematiche quarta parte
 Istituzioni di Matematiche quarta parte anno acc. 2012/2013 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 22 index Derivate 1 Derivate 2 Teoremi
Istituzioni di Matematiche quarta parte anno acc. 2012/2013 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 22 index Derivate 1 Derivate 2 Teoremi
Trasformazioni - II. Classificazione delle trasformazioni in R 3. Rotazioni in R 3. Lezione 6 Maggio Lezione 6 maggio 2003
 Corso di Laurea in Disegno Industriale Corso di Metodi Numerici per il Design Lezione 6 maggio Trasformazioni - II F. Caliò Classificazione delle trasformazioni in R (TITOLO) Rotazioni in R (TITOLO) Rotazione
Corso di Laurea in Disegno Industriale Corso di Metodi Numerici per il Design Lezione 6 maggio Trasformazioni - II F. Caliò Classificazione delle trasformazioni in R (TITOLO) Rotazioni in R (TITOLO) Rotazione
Matematica e Statistica
 Matematica e Statistica Prova d esame (26/06/203) Università di Verona - Laurea in Biotecnologie - A.A. 202/3 Matematica e Statistica Prova di MATEMATICA (26/06/203) Università di Verona - Laurea in Biotecnologie
Matematica e Statistica Prova d esame (26/06/203) Università di Verona - Laurea in Biotecnologie - A.A. 202/3 Matematica e Statistica Prova di MATEMATICA (26/06/203) Università di Verona - Laurea in Biotecnologie
Capitolo 2. Cenni di geometria analitica nel piano
 Capitolo Cenni di geometria analitica nel piano 1 Il piano cartesiano Il piano cartesiano è una rappresentazione grafica del prodotto cartesiano R = R R La rappresentazione grafica è possibile se si crea
Capitolo Cenni di geometria analitica nel piano 1 Il piano cartesiano Il piano cartesiano è una rappresentazione grafica del prodotto cartesiano R = R R La rappresentazione grafica è possibile se si crea
Introduzione alla Meccanica Teorica ERRATA CORRIGE. Fulvio Bisi, Riccardo Rosso
 Introduzione alla Meccanica Teorica ERRATA CORRIGE Fulvio Bisi, Riccardo Rosso FINO A MARZO 2017 1 Gli errata vengono evidenziati in rosso con una sottolineatura ondulata, le correzioni corrispondenti
Introduzione alla Meccanica Teorica ERRATA CORRIGE Fulvio Bisi, Riccardo Rosso FINO A MARZO 2017 1 Gli errata vengono evidenziati in rosso con una sottolineatura ondulata, le correzioni corrispondenti
CORSO DI FISICA DELLA MATERIA CONDENSATA A. A. 2013/14
 1 CORSO DI FISICA DELLA MATERIA CONDENSATA 3 MODI NORMALI DI VIBRAZIONE DELLE MOLECOLE POLIATOMICHE Appunti dalle Lezioni del Prof. P. Calvani A. A. 2013/14 Queste dispense sono per solo uso interno e
1 CORSO DI FISICA DELLA MATERIA CONDENSATA 3 MODI NORMALI DI VIBRAZIONE DELLE MOLECOLE POLIATOMICHE Appunti dalle Lezioni del Prof. P. Calvani A. A. 2013/14 Queste dispense sono per solo uso interno e
sen n x( tan xn n n=1
 8 Gennaio 2016 Nome (in stampatello): 1) (8 punti) Discutere la convergenza della serie di funzioni al variare di x in [ 1, 1]. n x( tan xn n ) xn sen n 2) (7 punti) Provare che la forma differenziale
8 Gennaio 2016 Nome (in stampatello): 1) (8 punti) Discutere la convergenza della serie di funzioni al variare di x in [ 1, 1]. n x( tan xn n ) xn sen n 2) (7 punti) Provare che la forma differenziale
SISSA Area Matematica Esame di ammissione per il corso di Analisi Matematica, Modelli e Applicazioni 27 marzo 2019
 SISSA Area Matematica Esame di ammissione per il corso di Analisi Matematica, Modelli e Applicazioni 27 marzo 2019 Il candidato risolva CINQUE dei seguenti problemi, e indichi chiaramente sulla prima pagina
SISSA Area Matematica Esame di ammissione per il corso di Analisi Matematica, Modelli e Applicazioni 27 marzo 2019 Il candidato risolva CINQUE dei seguenti problemi, e indichi chiaramente sulla prima pagina
TRASFORMAZIONI GEOMETRICHE E FUNZIONI
 TRASFORMAZIONI GEOMETRICHE E FUNZIONI La trasformazione geometrica del piano in sé è una corrispondenza biunivoca tra i punti di un piano; è indicata con t ed è un applicazione del piano in se che trasforma
TRASFORMAZIONI GEOMETRICHE E FUNZIONI La trasformazione geometrica del piano in sé è una corrispondenza biunivoca tra i punti di un piano; è indicata con t ed è un applicazione del piano in se che trasforma
Geometria analitica - Testo pagina 1 di 5 67
 Geometria analitica - Testo pagina di 5 67 5. GEOMETRI NLITI: Geometria lineare nel piano È fissato nel piano un sistema di coordinate cartesiane ortogonali monometriche Oxy. 50. 502. 503. 504. Scrivere
Geometria analitica - Testo pagina di 5 67 5. GEOMETRI NLITI: Geometria lineare nel piano È fissato nel piano un sistema di coordinate cartesiane ortogonali monometriche Oxy. 50. 502. 503. 504. Scrivere
RICHIAMI SU RETTA, PARABOLA E DISEQUAZIONI. Angela Donatiello 1
 RICHIAMI SU RETTA, PARABOLA E DISEQUAZIONI Angela Donatiello 1 Una funzione del tipo f() = m + q, con m e q numeri reali, è una FUNZIONE LINEARE. Il numero q è detto INTERCETTA o ORDINATA ALL ORIGINE,
RICHIAMI SU RETTA, PARABOLA E DISEQUAZIONI Angela Donatiello 1 Una funzione del tipo f() = m + q, con m e q numeri reali, è una FUNZIONE LINEARE. Il numero q è detto INTERCETTA o ORDINATA ALL ORIGINE,
CAPITOLO III. La cinematica del moto dei fluidi
 Cap.III La cinematica 37 CAPITOLO III La cinematica del moto dei fluidi 1. - Impostazione del problema. Nel descrivere il moto dei fluidi possiamo seguire due schemi, due grandi vie. La prima consiste
Cap.III La cinematica 37 CAPITOLO III La cinematica del moto dei fluidi 1. - Impostazione del problema. Nel descrivere il moto dei fluidi possiamo seguire due schemi, due grandi vie. La prima consiste
Equazione d onda per il campo elettromagnetico
 Equazione d onda per il campo elettromagnetico Leggi fondamentali dell elettromagnetismo. I campi elettrici sono prodotti da cariche elettriche e da campi magnetici variabili. Corrispondentemente l intensità
Equazione d onda per il campo elettromagnetico Leggi fondamentali dell elettromagnetismo. I campi elettrici sono prodotti da cariche elettriche e da campi magnetici variabili. Corrispondentemente l intensità
