Teoria della decisione e della stima. Esercitazioni di laboratorio Anno accademico M.S. Greco
|
|
|
- Violetta Cara
- 5 anni fa
- Visualizzazioni
Transcript
1 Teoria della decisione e della stima Esercitazioni di laboratorio Anno accademico M.S. Greco
2 Laboratorio del 30/09/09 09 Processi AR + Sx() z = Rx( m) z m= m Densità spettrale complessa La regione di convergenza di S () x z è costituita dai valori di z per cui converge la sommatoria La densità spettrale di potenza ( j f Sx e π ) si ottiene valutando Sx() z sul cerchio unitario Im{z} f=1/4 f=1/ f=-1/ f=0 Re{z}
3 Laboratorio del 30/09/09 09 Processi AR AR(1) R ( m) = σ ρ ρ < 1 x x m < m <+ Calcoliamo la densità spettrale complessa: + 1 m m m m m m x() = σx ρ = σx ρ + σx ρ m= m= m= 0 S z z z z σ ρz ρz m m x x ( z) = x z ( z) = m= 1 m= 0 1 σ ρ σ ρ ρ ρ z < 1 z < 1 ρ σ σ m 1 x x ( ρz ) = z > ρ 1 m= 0 1 ρz zona di convergenza 1 ρ ρ S x ( 1 ρ ) σx σxρz σx () z = + = ρz 1 ρz 1 ρz 1 ρz ( )( )
4 Laboratorio del 30/09/09 09 Processi AR Esercizio proposto: Processo reale AR(1) con autocorrelazione R ( m) Rappresentazione di una possibile realizzazione, grafico del coefficiente di autocorrelazione e della densità spettrale di potenza al variare di ρ Uso delle istruzioni: randn, filter, plot e stem x = σ ρ x m
5 Laboratorio del 30/09/09 09 Processi AR Generazione di rumore Gaussiano bianco w=sigmaw*randn(1,n); Generazione sequenziale di dati correlati tramite l istruzione filter a(1)=1; a()=-ro; b(1)=1; x=filter(b,a,w); Generazione di dati correlati tramite le istruzioni toeplitz e chol M=toeplitz(r); L=(chol(M)). ; x=lw;
6 Laboratorio del 30/09/09 09 Processi AR Processo di Markov Realizzazione Processo passa-alto alto
7 Laboratorio del 30/09/09 09 Processi AR Processo di Markov Coefficiente di correlazione Processo passa-alto alto
8 Laboratorio del 30/09/09 09 Processi AR Processo di Markov PSD S x j π f ( e ) = σ W 1 1 ρexp ( j π f ) σw = 1 + ρ ρcos π ( f ) Processo passa-alto alto
9 Laboratorio del 7/10/09 Processi AR Esercizio proposto: Sia dato un processo reale AR() che soddisfa all equazione alle differenze xn ( ) = a xn ( 1) + a xn ( ) + wn ( ),1, Detti p = p i poli del sistema, calcolare la relazione tra tali poli ed i 1 coefficienti dell eq. alle differenze. Verificare tale relazione tramite l istruzione matlab poly per p1 = 0.98 e j 3π 4 continua...
10 Laboratorio del 7/10/09 Processi AR Rappresentare una possibile realizzazione del processo al variare del modulo e della fase dei poli, supponendo che w(n) sia rumore Gaussiano bianco con varianza unitaria. Utilizzare l istruzione filter; Calcolare l espressione della densità spettrale di potenza (DSP) del processo, verificarne l esattezza tramite le istruzione matlab poly e polyval; Fare il grafico della DSP al variare del modulo e della fase dei poli. continua...
11 Laboratorio del 7/10/09 Processi AR Calcolare in forma chiusa l espressione della correlazione del processo; Verificare il risultato tramite IFFT della DSP del processo; Fare il grafico della funzione di autocorrelazione al variare del modulo e della fase dei poli.
12 Laboratorio del 7/10/09 Processi AR Funzione di correlazione R m a R m a R m m m x( ) =,1 x( 1) +, x( ) + σδ w ( ) 0 R ( m) = c p + c p x m m 1 1 Rx(0) = σ x = c + c Rx (1) = c1p1+ cp 1 R (0) a R (1) a R () =σ a,1rx(0) + (1 a,) Rx(1) = 0 a,rx(0) + a,1rx(1) Rx() = 0 x,1 x, x w
13 Laboratorio del 7/10/09 Processi AR Realizzazione 15 realizzazione del processo AR() 10 Processo passa-banda ampiezza 5 0 p1 = 0.98 e j 3π # samples
14 Laboratorio del 7/10/09 Processi AR PSD processo AR() Processo passa-banda DSP 600 p1 = 0.98 e j 3π normalized frequency
15 Laboratorio del 7/10/09 Processi AR Funzione di correlazione Processo passa-banda correlazione processo AR()- IFFT formula teorica p1 = 0.98 e j 3π 4 correlazione m
16 Laboratorio del 7/10/09 Processi AR 3 realizzazione del processo AR() Realizzazione p1 = 0.58 e π j 4 ampiezza # samples
17 Laboratorio del 7/10/09 Processi AR 5 processo AR() PSD p1 = 0.58 e π j 4 DSP normalized frequency
18 Laboratorio del 7/10/09 Processi AR processo AR()- IFFT Funzione di correlazione correlazione p1 = 0.58 e π j 4 correlazione formula teorica m
19 Laboratorio del 14/10/09 Stima ML Esercizio proposto: Stima ML del valor medio di un processo Gaussiano a valor medio μ a varianza nota a partire da una sequenza di N campioni Calcolo dell istogramma della ddp della stima per due valori di N Uso dell istruzione: hist
20 Laboratorio del 14/10/09 Stima ML N=8 N=104
21 Laboratorio del 14/10/09 Stima ML Esercizio proposto: Stima congiunta del valor medio e della varianza di un processo Gaussiano a valor medio μ e varianza unitaria Calcolo della polarizzazione e dell RMSE al variare del numero di campioni N
22 Laboratorio del 14/10/09 Stima ML N 1 1 ˆ μ = xn ( ) N n= 0 RMSE dello stimatore ML del valor medio
23 Laboratorio del 14/10/09 Stima ML N 1 1 ˆ μ = xn ( ) N n= 0 Polarizzazione dello stimatore ML del valor medio
24 Laboratorio del 14/10/09 Stima ML ˆ σ ML N 1 1 = N n= 0 ( xn ( ) ˆ μ ) ML RMSE dello stimatore ML della varianza
25 Laboratorio del 14/10/09 Stima ML ˆ σ ML N 1 1 = N n= 0 ( xn ( ) ˆ μ ) ML Polarizzazione dello stimatore ML della varianza
26 Laboratorio del 1/10/09 ML vs MAP x ( n) = A + w( n) wn N σ ( ) (0, ) 1) A deterministico incognito A N σ ) (0, A) Esercizio proposto: SNR = σ A σ SNR = A σ Grafico della ddp di A, della ddp di X A e del loro prodotto. Commenti Calcolo dell MSE della stima ML e MAP di A al variare del numero di campioni N per SNR=-4 db; Calcolo dell MSE della stima ML e MAP di A al variare del rapporto segnale-rumore SNR per N=4; Grafici di confronto.
27 10 0 ddpa 10 0 ddpa Laboratorio del 1/10/09 ML vs MAP SNR=-4 db 10-1 ddpxca ddpxa 10-1 ddpxca ddpxa N= N=4
28 10 0 ddpa Laboratorio del 1/10/09 ML vs MAP 10-5 ddpxca ddpxa SNR=-4 db N=
29 10 0 ddpa 10 0 ddpa Laboratorio del 1/10/09 ML vs MAP N= ddpxca ddpxa 10-1 ddpxca ddpxa SNR=-4 db SNR=10 db
30 Laboratorio del 1/10/09 ML vs MAP SNR=-4 db 10 0 ML MAP N 1 ˆ 1 AML = xn ( ) N n= 0 ˆ σ AMAP = xn ( ) σ N 1 A + σ AN n= 0 MSE N
31 Laboratorio del 1/10/09 ML vs MAP 10 0 ML MAP N= SNR = A σ MSE SNR = σ A σ SNR (db)
32 Laboratorio del 1/10/09 ML vs MAP Conclusioni All aumentare di N lo stimatore MAP tende allo stimatore ML (informazioni a posteriori dominanti) All aumentare di SNR lo stimatore MAP tende allo stimatore ML (informazioni a posteriori dominanti)
33 Laboratorio del 8/10/09 Stima ML Esercizio proposto: Il segnale osservato è X( n) = B+ V( n) dove B è un parametro deterministico incognito e V(n) è un processo Gaussiano AR(1) con coefficiente di correlazione ad un passo ρ. Si calcoli tramite simulazione Monte Carlo la varianza dello stimatore ML di B che utilizza i soli campioni X(0) e X(1) al variare del valore di ρ da a 0.95 a parità di rapporto segnale rumore SNR = B σ v. Per generare i campioni del processo a partire da rumore bianco si utilizzi la decomposizione di Cholensky della matrice di correlazione. Si commentino i risultati ottenuti
34 Laboratorio del 8/10/09 Stima ML La funzione di verosimiglianza può essere scritta come 1 L( x; B) = exp 1 π M T 1 ( x B1) M ( x B1) dove x x(0) = x(1) 1 1 = 1 ρ 1 e M = σ v ρ 1 Risolvendo l equazione ln L( x; B) B si ottiene Bˆ ML x(0) + x(1) = = 0
35 Laboratorio del 8/10/09 Stima ML Bˆ ML = x(0) + x(1) 10 0 Radice dell errore quadratico medio RMSE var { Bˆ ML } σ = ( + ρ ) v ro
36 Laboratorio del 8/10/09 Stima ML Bˆ ML = x(0) + x(1) Polarizzazione E{ BˆML } = B bias ro
37 Laboratorio del 4/11/09 Stima ML Stima ML dei parametri di una cosinusoide immersa in rumore termico x( n) = Acos(πf 0Tc n φ) + w( n) 1 N 1 ˆ j π ftc n f0ml = arg max x( n) e f N n= 0 N 1 = x n e N ˆ ˆ π 0 ML c ( ) A ML n= 0 j f T n ˆ φ ML = arctg N 1 n= 0 N 1 n= 0 xn ( )sen( π fˆ Tn) 0ML xn ( )cos( π fˆ Tn) 0ML c c
38 Laboratorio del 4/11/09 Stima ML Limiti di Cramér-Rao σ CRLB( A) = N 1 CRLB( f0) = (π ) ηn( N (N 1) CRLB( φ) = ηn( N + 1) 1) dove η = A σ
39 Laboratorio del 4/11/09 Stima ML Esercizio proposto: implementazione della stima ML calcolo degli RMSE al variare di N confronto con i CRLB istruzioni: fft, angle, max
40 Laboratorio del 4/11/09 Stima ML Stima della frequenza A= MSE CRLB σ =1 Frequency MSE N
41 Laboratorio del 4/11/09 Stima ML Stima dell ampiezza 10 MSE CRLB A= σ =1 Amplitude MSE N
42 Laboratorio del 4/11/09 Stima ML Stima della fase 10 0 MSE CRLB A= σ =1 Phase MSE N
43 Laboratorio del 11/11 11/09 /09 Filtro di Wiener Modello del segnale e dell osservato s( n) = αs( n 1) + w( n) xn ( ) = sn ( ) + vn ( ) wn N σ w ( ) (0, = 1) vn N σ v ( ) (0, ) w(n) rumore di generazione v(n) rumore di osservazione indipendente dal s(n)
44 Laboratorio del 11/11 11/09 /09 Filtro di Wiener IIR causale: Si può dimostrare che β n hn ( ) = 1 β un ( ) α dove β = α + γ α + γ (1 ) (1 ) se α = α + > α 0 β = α + γ + α + γ (1 ) (1 ) 1 σ 1 α γ = σ s v 1+ α 1 1 se α = α + < α s SNR = σ σ v 0
45 Laboratorio del 11/11 11/09 /09 Filtro di Wiener FIR a 3 prese sˆ( n) = h(0) x( n) + h(1) x( n 1) + h() x( n ) E necessario risolvere questo sistema Rh x = r xs
46 Laboratorio del 11/11 11/09 /09 Filtro di Wiener Esercizio proposto: implementazione del filtro di Wiener IIR causale implementazione del filtro FIR a tre prese confronto tra le risposte impulsive e in frequenza dei due filtri confronto fra le uscite dei due filtri istruzioni: filter, inv
47 Laboratorio del 11/11 11/09 /09 Filtro di Wiener SNR=10 db α=-0.9
48 Laboratorio del 11/11 11/09 /09 Filtro di Wiener SNR=10 db α=-0.9
49 Laboratorio del 11/11 11/09 /09 Filtro di Wiener SNR=10 db α=-0.9
50 Laboratorio del 11/11 11/09 /09 Filtro di Wiener SNR=10 db α=0.99
51 Laboratorio del 11/11 11/09 /09 Filtro di Wiener SNR=10 db α=0.99
52 Laboratorio del 11/11 11/09 /09 Filtro di Wiener SNR=10 db α=0.99
53 Laboratorio del 11/11 11/09 /09 Filtro di Wiener SNR=0 db α=0.99
54 Laboratorio del 11/11 11/09 /09 Filtro di Wiener SNR=0 db α=0.99
55 Laboratorio del 11/11 11/09 /09 Filtro di Wiener SNR=0 db α=0.99
56 Laboratorio del 11/11 11/09 /09 Filtro di Wiener Conclusioni: β diminuisce all aumentare di SNR Per SNR - (db) β=α, h(n)=0 e sˆ( n ) = 0 cioè pari al suo valor medio All aumentare di SNR β si allontana da α e tende a 0. La banda aumenta e il guadagno del filtro IIR aumenta. Se SNR il polo si sposta nell origine, β=0 e il filtro di Wiener diventa passa-tutto.
57 Laboratorio del 18/11/09 Filtro di Kalman Stima della posizione e della velocità angolare e radiale di un bersaglio radar Equazioni del moto ρ( n+ 1) = ρ( n) + T ρ( n) ρ( n+ 1) ρ( n) = T ρ( n) = u ( n) 1 ρ( n) θ ( n) ρ ( n + 1) Accelerazione radiale θ ( n+ 1) = θ( n) + T θ( n) θ ( n + 1) θ ( n+ 1) θ( n) = T θ( n) = u ( n) Accelerazione angolare
58 Laboratorio del 18/11/09 Filtro di Kalman Esercizio proposto: implementazione del filtro di Kalman vettoriale per la stima di posizione e velocità angolare e radiale di un bersaglio radar grafico del segnale vero, osservato e stimato al variare del tempo
59 Laboratorio del 18/11/09 Filtro di Kalman Stimatore: Sˆ( n) = A( n) Sˆ( n 1) + K( n)[ X( n) C( n) A( n) Sˆ( n 1)] Guadagno del filtro: T T K( n) = P1( n) C ( n) ( n) 1( n) ( n) + ( n) C P C R 1 MSE della stima al passo n: P( n) = P( n) K( n) C( n) P( n) 1 1 con: P( n) = A( n) P( n 1) A T ( n) + Q( n 1) 1
60 Laboratorio del 18/11/09 Filtro di Kalman Modello del segnale ρ( n+ 1) 1 T 0 0 ρ( n) 0 ρ( n+ 1) ρ( n) u1( n) = + θ( n + 1) T θ( n) 0 θ( n+ 1) θ( n) u ( n) S( n+ 1) = AS( n) + W( n) Modello dell osservato x ( n) = ρ( n) + v ( n) 1 1 x ( n) = θ ( n) + v ( n) ρ( n) x1( n) ρ( n) v1( n) x( n) = θ ( n) v( n) θ ( n) X( n) = CS( n) + V( n)
61 Laboratorio del 18/11/09 Filtro di Kalman σ1 0 0 T Q( n) = E{ W( n) W ( n) } = σ Matrice di covarianza del rumore di misura T σ 0 ρ R( n) = E{ V( n) V ( n) } = 0 σθ Matrice di covarianza del rumore di osservazione V(n) e W(n) vettori congiuntamente Gaussiani stazionari
62 Laboratorio del 18/11/09 Filtro di Kalman Inizializzazione del filtro 0 0 S (0) = S(1) = W (1) X(0) = V(0) 0 0 σ ρ x1 (1) σ ρ 0 0 T x1(1) x1(0) σρ σ ρ + σ1 0 0 ˆ (1) T S = P(0) = T T x (1) σθ 0 0 σθ x(1) x(0) T T σθ σθ σ T T
63 Laboratorio del 18/11/09 Filtro di Kalman Parametri di lavoro vera stimata osservato σ σ θ ρ 1 = = 500 m T = 1 s σ = 1 m σ = 0.1 distanza radiale (metri) tempo di osservazione
64 Laboratorio del 18/11/09 Filtro di Kalman Parametri di lavoro vera stimata σ σ θ ρ 1 = = 500 m T = 1 s σ = 1 m σ = 0.1 velocità radiale (metri/s) tempo di osservazione
65 Laboratorio del 18/11/09 Filtro di Kalman Parametri di lavoro vera stimata osservato σ σ θ ρ 1 = = 500 m T = 1 s σ = 1 m σ = 0.1 distanza angolare (gradi) tempo di osservazione
66 Laboratorio del 18/11/09 Filtro di Kalman Parametri di lavoro 0 15 vera stimata σ σ θ ρ 1 = = 500 m T = 1 s σ = 1 m σ = 0.1 velocità radiale (gradi/s) tempo di osservazione
67 Criterio di decisione MAP Laboratorio del 5/11/09 Criterio Segnalazione antipodale P H ) = P( ) ( 0 H1 ntc T H1 : x( ntc) = A rect + w( ntc) T ntc T H0 : x( ntc) = A rect + w( ntc) T dove: n = 0,1,, N 1 in notazione vettoriale: H H 1 0 : : x= As+ w x= As+ w N = T T c
68 Criterio di decisione MAP Laboratorio del 5/11/09 Criterio Esercizio proposto: implementazione del filtro adattato grafico del segnale all ingresso e all uscita del filtro adattato al variare del tempo in presenza di rumore bianco calcolo della probabilità d errore teorica e confronto con quella ottenuta tramite simulazione Monte Carlo in funzione del rapporto segnale-rumore istruzioni: conv, erfc Q ( x) = 0.5* erfc( x ) Strategia di decisione: H1 T sx > < H 0 0
69 Criterio di decisione MAP Laboratorio del 5/11/09 Criterio 4 Segnale osservato nell hp H 1 N=16 SNR=0 db observed data samples
70 Criterio di decisione MAP Laboratorio del 5/11/09 Criterio 1 Filtro adattato N=16 SNR=0 db matched filter output samples
71 Criterio di decisione MAP Laboratorio del 5/11/09 Criterio 6 5 Segnale osservato nell hp H 1 N=16 SNR=10 db observed data samples
72 Criterio di decisione MAP Laboratorio del 5/11/09 Criterio Filtro adattato N=16 SNR=10 db matched filter output samples
73 Criterio di decisione MAP Laboratorio del 5/11/09 Criterio Probabilità d errore N=16 N s =50000 error probability sim Q SNR (db)
74 Criterio di decisione MAP Laboratorio del 5/11/09 Criterio Probabilità d errore N=8 N s =50000 error probability sim Q SNR (db)
75 Laboratorio del 3/1/08 Criterio di decisione NP Segnalazione on-off H H 1 0 : : x( nt x( nt c c ) ) = nt Arect = w( nt c ) in notazione vettoriale: c T T H H 1 0 : : dove: + x x = = w( nt w c ) n = 0,1,, N 1 As + w N = T T c Q ( x) = 0.5* erfc( x )
76 Laboratorio del /1/09 Criterio di decisione NP Esercizio proposto: calcolo della probabilità di falso allarme teorica e confronto con quella ottenuta tramite simulazione Monte Carlo al variare della soglia di decisione calcolo delle caratteristiche operative ROC (in teoria e per simulazione) calcolo della probabilità di rivelazione in funzione del rapporto segnale rumore (in teoria e per simulazione)
77 Laboratorio del /1/09 Criterio di decisione NP ROC per SNR=0 db P FA in funzione della soglia
78 Laboratorio del /1/09 Criterio di decisione NP P D in funzione di SNR, P FA =10-3
79 Laboratorio del 9/1/09 Stima spettrale Sequenza dei dati utili di lunghezza N dn [ ] rumore Gaussiano bianco a varianza unitaria Esercizio proposto: Calcolo del periodogramma dei dati al variare di N. Considerazioni sulla non consistenza dello stimatore istruzioni: periodogram
80 Laboratorio del 9/1/09 Stima spettrale N=64 N=104
81 Laboratorio del 9/1/09 Stima spettrale Sequenza dei dati utili ( ) yn [ ] = Asin( π fn) + Asin( π f + α N n) + dn [ ] dove dn [ ] rumore Gaussiano bianco a varianza =10-3 f 0 = 0.
82 Laboratorio del 9/1/09 Stima spettrale Esercizio proposto: Risoluzione: si supponga A 1 =A =1 e N=64. Calcolare il periodogramma della sequenza di dati per α=0.1, 0.9 e e commentare l abilità del periodogramma a risolvere le righe spettrali. Leakage: si supponga A 1 =1 e N=64 e si vari il valore di A, per es. A =0.5, 0.1, Calcolare il periodogramma per α=4 e commentare l abilità del periodogramma a risolvere le righe spettrali. In entrambi i casi disegnare il periodogramma in scala semilogaritmica istruzioni: periodogram
83 Laboratorio del 9/1/09 Stima spettrale α=0.1 Risoluzione α=
84 Laboratorio del 9/1/09 Stima spettrale Leakage DSP 10-3 α=4 A 1 =1 A = normalized frequency
Processi AR. = σ ρ. Esercizio proposto:
 Laboratorio del 5/10/06 Processi AR Esercizio proposto: Processo reale AR(1) con autocorrelazione R ( m) Rappresentazione di una possibile realizzazione, grafico del coefficiente di autocorrelazione e
Laboratorio del 5/10/06 Processi AR Esercizio proposto: Processo reale AR(1) con autocorrelazione R ( m) Rappresentazione di una possibile realizzazione, grafico del coefficiente di autocorrelazione e
Teoria della decisione e della stima. Esercitazioni di laboratorio Anno accademico M.S. Greco
 Teoria della decisione e della stima Esercitazioni di laboratorio Anno accademico 008-09 M.S. Greco Laboratorio dell 1/10/08 Processi AR + Sx() z = Rx( m) z m= m Densità spettrale complessa La regione
Teoria della decisione e della stima Esercitazioni di laboratorio Anno accademico 008-09 M.S. Greco Laboratorio dell 1/10/08 Processi AR + Sx() z = Rx( m) z m= m Densità spettrale complessa La regione
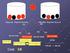
1 = Processi Autoregressivi AR(1) Filtro IIR di ordine 1. (WGN White Gaussian Noise) Eq. alle differenze ricorsiva. w=randn(n,1) MATLAB:
 Processi Autoregressivi AR(1) Filtro IIR di ordine 1 Wn [ ] hn [ ] X[ n] = ρ X[ n 1] + W[ n] (WGN White Gaussian Noise) w=randn(n,1) Eq. alle differenze ricorsiva MATLAB: n hn [ ] = ρ un [ ] y=filter(b,a,x)
Processi Autoregressivi AR(1) Filtro IIR di ordine 1 Wn [ ] hn [ ] X[ n] = ρ X[ n 1] + W[ n] (WGN White Gaussian Noise) w=randn(n,1) Eq. alle differenze ricorsiva MATLAB: n hn [ ] = ρ un [ ] y=filter(b,a,x)
Corso di Elaborazione Numerica dei Segnali Esame del 30 settembre 2005
 Corso di Elaborazione Numerica dei Segnali Esame del 30 settembre 005 TOTALE PUNTI: 44 L allievo é invitato a dare una ragionata e succinta risposta a tutti gli argomenti proposti, per dimostrare il livello
Corso di Elaborazione Numerica dei Segnali Esame del 30 settembre 005 TOTALE PUNTI: 44 L allievo é invitato a dare una ragionata e succinta risposta a tutti gli argomenti proposti, per dimostrare il livello
Esercitazione su Filtraggio Adattativo (17 Giugno 2008)
 Esercitazione su Filtraggio Adattativo 17 Giugno 008) D. Donno Esercizio 1: Stima adattativa in rumore colorato Una sequenza disturbante x n è ottenuta filtrando un processo bianco u n con un filtro FIR
Esercitazione su Filtraggio Adattativo 17 Giugno 008) D. Donno Esercizio 1: Stima adattativa in rumore colorato Una sequenza disturbante x n è ottenuta filtrando un processo bianco u n con un filtro FIR
FENS- ENS esame del 24 febbraio 2006
 FENS- ENS esame del 24 febbraio 26 L allievo é invitato a dare una ragionata e succinta risposta a tutti gli argomenti proposti, per dimostrare il livello di preparazione globale. I calcoli devono essere
FENS- ENS esame del 24 febbraio 26 L allievo é invitato a dare una ragionata e succinta risposta a tutti gli argomenti proposti, per dimostrare il livello di preparazione globale. I calcoli devono essere
Statistica Applicata all edilizia: Stime e stimatori
 Statistica Applicata all edilizia E-mail: orietta.nicolis@unibg.it 15 marzo 2011 Statistica Applicata all edilizia: Indice 1 2 Statistica Applicata all edilizia: Uno dei problemi principali della statistica
Statistica Applicata all edilizia E-mail: orietta.nicolis@unibg.it 15 marzo 2011 Statistica Applicata all edilizia: Indice 1 2 Statistica Applicata all edilizia: Uno dei problemi principali della statistica
Corso di Teoria della Stima Prove Itinere del 01 Luglio 2003
 Corso di eoria della Stima Prove Itinere del 0 Luglio 003 L allievo é invitato a dare una risposta ragionata e succinta a tutti gli argomenti proposti al fine di dimostrare il livello di preparazione globale.
Corso di eoria della Stima Prove Itinere del 0 Luglio 003 L allievo é invitato a dare una risposta ragionata e succinta a tutti gli argomenti proposti al fine di dimostrare il livello di preparazione globale.
Esercitazione ENS su processi casuali (13 e 14 Maggio 2008)
 Esercitazione ES su processi casuali ( e 4 Maggio 2008) D. Donno Esercizio : Calcolo di autovalori e autovettori Si consideri un processo x n somma di un segnale e un disturbo: x n = Ae π 2 n + w n, n
Esercitazione ES su processi casuali ( e 4 Maggio 2008) D. Donno Esercizio : Calcolo di autovalori e autovettori Si consideri un processo x n somma di un segnale e un disturbo: x n = Ae π 2 n + w n, n
Università di Siena. Corso di STATISTICA. Parte seconda: Teoria della stima. Andrea Garulli, Antonello Giannitrapani, Simone Paoletti
 Università di Siena Corso di STATISTICA Parte seconda: Teoria della stima Andrea Garulli, Antonello Giannitrapani, Simone Paoletti Master E 2 C Centro per lo Studio dei Sistemi Complessi Università di
Università di Siena Corso di STATISTICA Parte seconda: Teoria della stima Andrea Garulli, Antonello Giannitrapani, Simone Paoletti Master E 2 C Centro per lo Studio dei Sistemi Complessi Università di
Università di Siena. Teoria della Stima. Lucidi del corso di. Identificazione e Analisi dei Dati A.A
 Università di Siena Teoria della Stima Lucidi del corso di A.A. 2002-2003 Università di Siena 1 Indice Approcci al problema della stima Stima parametrica Stima bayesiana Proprietà degli stimatori Stime
Università di Siena Teoria della Stima Lucidi del corso di A.A. 2002-2003 Università di Siena 1 Indice Approcci al problema della stima Stima parametrica Stima bayesiana Proprietà degli stimatori Stime
Fondamenti di comunicazioni elettriche (Ing. Elettronica - A.A )
 Fondamenti di comunicazioni elettriche (Ing. Elettronica - A.A.-) Es. La variabile aleatoria ha densità di probabilità uniorme nell intervallo [,]. Trovare valor medio e varianza di. La densità di probabilità
Fondamenti di comunicazioni elettriche (Ing. Elettronica - A.A.-) Es. La variabile aleatoria ha densità di probabilità uniorme nell intervallo [,]. Trovare valor medio e varianza di. La densità di probabilità
( e j2π ft 0.9 j) ( e j2π ft j)
 Esercitazione Filtri IIR Es. 1. Si consideri il filtro dato dalla seguente equazione alle differenze y[n]+0.81y[n-2]=x[n]-x[n-2] - Determinare la funzione di trasferimento del filtro Eseguendo la Trasformata
Esercitazione Filtri IIR Es. 1. Si consideri il filtro dato dalla seguente equazione alle differenze y[n]+0.81y[n-2]=x[n]-x[n-2] - Determinare la funzione di trasferimento del filtro Eseguendo la Trasformata
SEGNALI E SISTEMI Proff. L. Finesso, M. Pavon e S. Pinzoni (a.a ) Homework assignment #2 Testo e Soluzione
 SEGNALI E SISTEMI Proff. L. Finesso, M. Pavon e S. Pinzoni (a.a. 00-005) Homework assignment # Testo e Soluzione Esercizio Si consideri l equazione differenziale ordinaria, lineare a coefficienti costanti
SEGNALI E SISTEMI Proff. L. Finesso, M. Pavon e S. Pinzoni (a.a. 00-005) Homework assignment # Testo e Soluzione Esercizio Si consideri l equazione differenziale ordinaria, lineare a coefficienti costanti
FENS (5 crediti) - ENS (10 crediti) Esame del 24 febbraio 2005
 FES (5 crediti) - ES (0 crediti) Esame del 4 febbraio 005 L allievo é invitato a dare una ragionata e succinta risposta a tutti gli argomenti proposti, per dimostrare il livello di preparazione globale.
FES (5 crediti) - ES (0 crediti) Esame del 4 febbraio 005 L allievo é invitato a dare una ragionata e succinta risposta a tutti gli argomenti proposti, per dimostrare il livello di preparazione globale.
Computazione per l interazione naturale: Regressione probabilistica
 Computazione per l interazione naturale: Regressione probabilistica Corso di Interazione Naturale Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it boccignone.di.unimi.it/in_2016.html
Computazione per l interazione naturale: Regressione probabilistica Corso di Interazione Naturale Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it boccignone.di.unimi.it/in_2016.html
Teoria dei segnali terza edizione
 Capitolo 9 Segnali aleatori a tempo continuo e a tempo discreto SOLUZIONI DEGLI ESERCIZI Soluzione dell esercizio 9.3 Si osservi innanzitutto che, essendo il processo () t Gaussiano, anche il processo
Capitolo 9 Segnali aleatori a tempo continuo e a tempo discreto SOLUZIONI DEGLI ESERCIZI Soluzione dell esercizio 9.3 Si osservi innanzitutto che, essendo il processo () t Gaussiano, anche il processo
Esercitazione ENS su periodogramma (27 e 28 Maggio 2008) Esercizio 1: Autocorrelazione e stima della densità spettrale di potenza
 sercitazione S su periodogramma (7 e 8 Maggio 008 D. Donno sercizio : Autocorrelazione e stima della densità spettrale di potenza Si consideri la sequenza x n di lunghezza = 8 campioni. x n è somma di
sercitazione S su periodogramma (7 e 8 Maggio 008 D. Donno sercizio : Autocorrelazione e stima della densità spettrale di potenza Si consideri la sequenza x n di lunghezza = 8 campioni. x n è somma di
Sequenze (Sistemi) di Variabili Aleatorie Se consideriamo un numero di variabili aleatorie, generalmente dipendenti si parla equivalentemente di:
 Teoria dei Fenomeni Aleatori AA 01/13 Sequenze (Sistemi) di Variabili Aleatorie Se consideriamo un numero di variabili aleatorie, generalmente dipendenti si parla equivalentemente di: N-pla o Sequenza
Teoria dei Fenomeni Aleatori AA 01/13 Sequenze (Sistemi) di Variabili Aleatorie Se consideriamo un numero di variabili aleatorie, generalmente dipendenti si parla equivalentemente di: N-pla o Sequenza
FENS - ENS Esame del 9 febbraio 2005
 FENS - ENS Esame del 9 febbraio 005 L allievo é invitato a dare una ragionata e succinta risposta a tutti gli argomenti proposti, per dimostrare il livello di preparazione globale. I calcoli devono essere
FENS - ENS Esame del 9 febbraio 005 L allievo é invitato a dare una ragionata e succinta risposta a tutti gli argomenti proposti, per dimostrare il livello di preparazione globale. I calcoli devono essere
Corso di Elaborazione Numerica dei Segnali Esame del 7 Luglio 2004
 Corso di Elaborazione Numerica dei Segnali Esame del 7 Luglio TOTALE PUNTI: L allievo é invitato a dare una ragionata e succinta risposta a tutti gli argomenti proposti, per dimostrare il livello di preparazione
Corso di Elaborazione Numerica dei Segnali Esame del 7 Luglio TOTALE PUNTI: L allievo é invitato a dare una ragionata e succinta risposta a tutti gli argomenti proposti, per dimostrare il livello di preparazione
Calcolo delle probabilità (3/7/2001) (Ing. Elettronica, Informatica, Telecomunicazioni - Latina)
 Calcolo delle probabilità (3/7/00). La distribuzione di probabilità di un numero aleatorio X non negativo soddisfa la condizione P (X > x + y X > y) = P (X > x), x > 0, y > 0. Inoltre la previsione di
Calcolo delle probabilità (3/7/00). La distribuzione di probabilità di un numero aleatorio X non negativo soddisfa la condizione P (X > x + y X > y) = P (X > x), x > 0, y > 0. Inoltre la previsione di
Stima del valore di una costante in presenza di rumore esponenzialmente correlato. Carlo Fisicaro
 Stima del valore di una costante in presenza di rumore esponenzialmente correlato Carlo Fisicaro OBIETTIVO Stimare il valore della costante β adimensionale per mezzo di misurazioni soggette a rumore stocastico
Stima del valore di una costante in presenza di rumore esponenzialmente correlato Carlo Fisicaro OBIETTIVO Stimare il valore della costante β adimensionale per mezzo di misurazioni soggette a rumore stocastico
1 PROCESSI STOCASTICI... 11
 1 PROCESSI STOCASTICI... 11 Introduzione... 11 Rappresentazione dei dati biomedici... 11 Aleatorietà delle misure temporali... 14 Medie definite sul processo aleatorio... 16 Valore atteso... 16 Esercitazione
1 PROCESSI STOCASTICI... 11 Introduzione... 11 Rappresentazione dei dati biomedici... 11 Aleatorietà delle misure temporali... 14 Medie definite sul processo aleatorio... 16 Valore atteso... 16 Esercitazione
Computazione per l interazione naturale: Regressione probabilistica
 Computazione per l interazione naturale: Regressione probabilistica Corso di Interazione Naturale Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it boccignone.di.unimi.it/in_2018.html
Computazione per l interazione naturale: Regressione probabilistica Corso di Interazione Naturale Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it boccignone.di.unimi.it/in_2018.html
Identificazione dei Modelli e Analisi dei Dati 6/5/1993
 Identificazione dei Modelli e Analisi dei Dati 6/5/1993 3. Siano date due V.C. X e Y, di cui è supposta nota la ddp congiunta. Sia Xˆ (Y) uno stimatore di X basato sull'osservazione di Y. Ci si prefigge
Identificazione dei Modelli e Analisi dei Dati 6/5/1993 3. Siano date due V.C. X e Y, di cui è supposta nota la ddp congiunta. Sia Xˆ (Y) uno stimatore di X basato sull'osservazione di Y. Ci si prefigge
1) Entropia di variabili aleatorie continue. 2) Esempi di variabili aleatorie continue. 3) Canali di comunicazione continui. 4) Canale Gaussiano
 Argomenti della Lezione 1) Entropia di variabili aleatorie continue ) Esempi di variabili aleatorie continue 3) Canali di comunicazione continui 4) Canale Gaussiano 5) Limite di Shannon 1 Entropia di una
Argomenti della Lezione 1) Entropia di variabili aleatorie continue ) Esempi di variabili aleatorie continue 3) Canali di comunicazione continui 4) Canale Gaussiano 5) Limite di Shannon 1 Entropia di una
ANALISI DELLE SERIE STORICHE
 ANALISI DELLE SERIE STORICHE De Iaco S. s.deiaco@economia.unile.it UNIVERSITÀ del SALENTO DIP.TO DI SCIENZE ECONOMICHE E MATEMATICO-STATISTICHE FACOLTÀ DI ECONOMIA 24 settembre 2012 Indice 1 Funzione di
ANALISI DELLE SERIE STORICHE De Iaco S. s.deiaco@economia.unile.it UNIVERSITÀ del SALENTO DIP.TO DI SCIENZE ECONOMICHE E MATEMATICO-STATISTICHE FACOLTÀ DI ECONOMIA 24 settembre 2012 Indice 1 Funzione di
Ripasso segnali e processi casuali. Trasmissione dell Informazione
 Ripasso segnali e processi casuali 1 Breve ripasso di segnali e trasformate Dato un segnale s(t), la sua densità spettrale si calcola come dove S(f) è la trasformata di Fourier. L energia di un segnale
Ripasso segnali e processi casuali 1 Breve ripasso di segnali e trasformate Dato un segnale s(t), la sua densità spettrale si calcola come dove S(f) è la trasformata di Fourier. L energia di un segnale
Elaborazione numerica dei segnali
 POLITECNICO DI TORINO Elaborazione numerica dei segnali Progetto di un filtro FIR Fiandrino Claudio Matricola: 138436 18 giugno 21 Relazione sul progetto di un filtro FIR Descrizione del progetto L obbiettivo
POLITECNICO DI TORINO Elaborazione numerica dei segnali Progetto di un filtro FIR Fiandrino Claudio Matricola: 138436 18 giugno 21 Relazione sul progetto di un filtro FIR Descrizione del progetto L obbiettivo
COMPITO DI IDENTIFICAZIONE DEI MODELLI ED ANALISI DEI DATI 23 luglio 2012
 COMPITO DI IDENTIFICAZIONE DEI MODELLI ED ANALISI DEI DATI 23 luglio 2012 Domanda 1. Si assuma che un sistema fisico di interesse con ingresso u(t) (misurato) ed uscita y(t) si possa modellare tramite
COMPITO DI IDENTIFICAZIONE DEI MODELLI ED ANALISI DEI DATI 23 luglio 2012 Domanda 1. Si assuma che un sistema fisico di interesse con ingresso u(t) (misurato) ed uscita y(t) si possa modellare tramite
01CXGBN Trasmissione numerica. parte 6: calcolo delle probabilità I
 01CXGBN Trasmissione numerica parte 6: calcolo delle probabilità I 1 Probabilità di errore BER e SER Per rappresentare la bontà di un sistema di trasmissione numerica in termini di probabilità di errore
01CXGBN Trasmissione numerica parte 6: calcolo delle probabilità I 1 Probabilità di errore BER e SER Per rappresentare la bontà di un sistema di trasmissione numerica in termini di probabilità di errore
Comunicazioni Elettriche anno accademico Esercitazione 1
 Comunicazioni Elettriche anno accademico 003-004 Esercitazione Esercizio Un processo aleatorio a tempo discreto X(n) è definito nel seguente modo: Viene lanciata una moneta. Se il risultato è testa X(n)=
Comunicazioni Elettriche anno accademico 003-004 Esercitazione Esercizio Un processo aleatorio a tempo discreto X(n) è definito nel seguente modo: Viene lanciata una moneta. Se il risultato è testa X(n)=
Università di Pavia Econometria. Richiami di teoria delle distribuzioni statistiche. Eduardo Rossi
 Università di Pavia Econometria Richiami di teoria delle distribuzioni statistiche Eduardo Rossi Università di Pavia Distribuzione di Bernoulli La variabile casuale discreta Y f Y (y; θ) = 0 θ 1, dove
Università di Pavia Econometria Richiami di teoria delle distribuzioni statistiche Eduardo Rossi Università di Pavia Distribuzione di Bernoulli La variabile casuale discreta Y f Y (y; θ) = 0 θ 1, dove
Teoria dei Fenomeni Aleatori AA 2012/13. Il Modello Lognormale La funzione di densità di probabilità lognormale è data:
 Il Modello Lognormale La funzione di densità di probabilità lognormale è data: ( ln x a) 1 f ( x ) = exp x > 0 X b x b π in cui a e b sono due costanti, con b> 0. Se X è una v.a. lognormale allora Y lnx
Il Modello Lognormale La funzione di densità di probabilità lognormale è data: ( ln x a) 1 f ( x ) = exp x > 0 X b x b π in cui a e b sono due costanti, con b> 0. Se X è una v.a. lognormale allora Y lnx
Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche. Modulazione A.A Alberto Perotti
 Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Modulazione A.A. 8-9 Alberto Perotti DELEN-DAUIN Modello di sistema di comunicazione Il modello di sistema di comunicazione
Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Modulazione A.A. 8-9 Alberto Perotti DELEN-DAUIN Modello di sistema di comunicazione Il modello di sistema di comunicazione
ESERCITAZIONE 21 : VARIABILI ALEATORIE CONTINUE
 ESERCITAZIONE 21 : VARIABILI ALEATORIE CONTINUE e-mail: tommei@dm.unipi.it web: www.dm.unipi.it/ tommei Ricevimento: su appuntamento Dipartimento di Matematica, piano terra, studio 114 7 Maggio 2013 Esercizio
ESERCITAZIONE 21 : VARIABILI ALEATORIE CONTINUE e-mail: tommei@dm.unipi.it web: www.dm.unipi.it/ tommei Ricevimento: su appuntamento Dipartimento di Matematica, piano terra, studio 114 7 Maggio 2013 Esercizio
Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Processi casuali A.A Alberto Perotti, Roberto Garello
 Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Processi casuali A.A. 2006-07 Alberto Perotti, Roberto Garello DELEN-DAUIN Processi casuali Sono modelli probabilistici
Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Processi casuali A.A. 2006-07 Alberto Perotti, Roberto Garello DELEN-DAUIN Processi casuali Sono modelli probabilistici
Fondamenti di elaborazione numerica dei segnali
 Esercizi per la I prova in itinere del corso: Fondamenti di elaborazione numerica dei segnali. Trasformata z di una sequenza illimitata causale Si consideri la sequenza causale ) 3 n x n = e i π 3 n, n
Esercizi per la I prova in itinere del corso: Fondamenti di elaborazione numerica dei segnali. Trasformata z di una sequenza illimitata causale Si consideri la sequenza causale ) 3 n x n = e i π 3 n, n
Frequenza relativa e probabilità
 Frequenza relativa e probabilità La La probabilità e' e' un un numero con con cui cuisi si descrivono i i fenomeni che che possono essere essere pensati come come risultato di di un un esperimento che
Frequenza relativa e probabilità La La probabilità e' e' un un numero con con cui cuisi si descrivono i i fenomeni che che possono essere essere pensati come come risultato di di un un esperimento che
Vettore (o matrice) casuale (o aleatorio): vettore (o matrice) i cui elementi sono variabili aleatorie
 Variabili (vettori e matrici) casuali Variabile casuale (o aleatoria): Variabile che può assumere un insieme di valori ognuno con una certa probabilità La variabile aleatoria rappresenta la popolazione
Variabili (vettori e matrici) casuali Variabile casuale (o aleatoria): Variabile che può assumere un insieme di valori ognuno con una certa probabilità La variabile aleatoria rappresenta la popolazione
VIII Indice 2.6 Esperimenti Dicotomici Ripetuti: Binomiale ed Ipergeometrica Processi Stocastici: Bernoul
 1 Introduzione alla Teoria della Probabilità... 1 1.1 Introduzione........................................ 1 1.2 Spazio dei Campioni ed Eventi Aleatori................ 2 1.3 Misura di Probabilità... 5
1 Introduzione alla Teoria della Probabilità... 1 1.1 Introduzione........................................ 1 1.2 Spazio dei Campioni ed Eventi Aleatori................ 2 1.3 Misura di Probabilità... 5
STATISTICA. Esercitazione 5
 STATISTICA Esercitazione 5 Esercizio 1 Ad un esame universitario sono stati assegnati in modo casuale due compiti diversi con i seguenti risultati: Compito A Compito B Numero studenti 102 105 Media dei
STATISTICA Esercitazione 5 Esercizio 1 Ad un esame universitario sono stati assegnati in modo casuale due compiti diversi con i seguenti risultati: Compito A Compito B Numero studenti 102 105 Media dei
Maria Prandini Dipartimento di Elettronica e Informazione Politecnico di Milano
 Note relative a test di bianchezza rimozione delle componenti deterministiche da una serie temporale a supporto del Progetto di Identificazione dei Modelli e Analisi dei Dati Maria Prandini Dipartimento
Note relative a test di bianchezza rimozione delle componenti deterministiche da una serie temporale a supporto del Progetto di Identificazione dei Modelli e Analisi dei Dati Maria Prandini Dipartimento
Modulazioni di ampiezza
 Modulazioni di ampiezza 1) Si consideri un segnale z(t) modulato in ampiezza con soppressione di portante dal segnale di informazione x(t): z(t) = Ax(t)cos(2πf 0 t) Il canale di comunicazione aggiunge
Modulazioni di ampiezza 1) Si consideri un segnale z(t) modulato in ampiezza con soppressione di portante dal segnale di informazione x(t): z(t) = Ax(t)cos(2πf 0 t) Il canale di comunicazione aggiunge
Stima puntuale di parametri
 Probabilità e Statistica Esercitazioni a.a. 2009/2010 C.d.L.: Ingegneria Elettronica e delle Telecomunicazioni, Ingegneria Informatica Stima puntuale di parametri Ines Campa Probabilità e Statistica -
Probabilità e Statistica Esercitazioni a.a. 2009/2010 C.d.L.: Ingegneria Elettronica e delle Telecomunicazioni, Ingegneria Informatica Stima puntuale di parametri Ines Campa Probabilità e Statistica -
Stima puntuale di parametri
 Probabilità e Statistica Esercitazioni a.a. 006/007 C.d.L.: Ingegneria per l Ambiente ed il Territorio, Ingegneria Civile, Ingegneria Gestionale, Ingegneria dell Informazione C.d.L.S.: Ingegneria Civile
Probabilità e Statistica Esercitazioni a.a. 006/007 C.d.L.: Ingegneria per l Ambiente ed il Territorio, Ingegneria Civile, Ingegneria Gestionale, Ingegneria dell Informazione C.d.L.S.: Ingegneria Civile
I appello di calcolo delle probabilità e statistica
 I appello di calcolo delle probabilità e statistica A.Barchielli, L. Ladelli, G. Posta 8 Febbraio 13 Nome: Cognome: Matricola: Docente: I diritti d autore sono riservati. Ogni sfruttamento commerciale
I appello di calcolo delle probabilità e statistica A.Barchielli, L. Ladelli, G. Posta 8 Febbraio 13 Nome: Cognome: Matricola: Docente: I diritti d autore sono riservati. Ogni sfruttamento commerciale
PROBLEMI SULL IDENTIFICAZIONE COL METODO PEM
 PROBLEMI SULL IDENTIFICAZIONE COL METODO PEM G. Picci 12 gennaio 2012 N.B. : Quando serve la dizione rumore bianco è da interpretare secondo il contesto come processo i.i.d. Il processo di ingresso si
PROBLEMI SULL IDENTIFICAZIONE COL METODO PEM G. Picci 12 gennaio 2012 N.B. : Quando serve la dizione rumore bianco è da interpretare secondo il contesto come processo i.i.d. Il processo di ingresso si
Fondamenti di Elaborazione Numerica dei Segnali Anno Accademico Primo Appello 26/2/2015
 Fondamenti di Elaborazione Numerica dei Segnali Anno Accademico 204-205 Primo Appello 26/2/205 Quesiti relativi alla prima parte del corso (tempo max. 90 min). Calcolare: la trasformata z di x(n) = ( )
Fondamenti di Elaborazione Numerica dei Segnali Anno Accademico 204-205 Primo Appello 26/2/205 Quesiti relativi alla prima parte del corso (tempo max. 90 min). Calcolare: la trasformata z di x(n) = ( )
01CXGBN Trasmissione numerica. parte 11: modulazione 2-PAM
 0CXGBN Trasmissione numerica parte : modulazione 2-PAM PARTE 2: Modulazioni Numeriche 2 Modulazioni: introduzione Per ogni modulazione considereremo: Caratteristiche generali Costellazione (insieme di
0CXGBN Trasmissione numerica parte : modulazione 2-PAM PARTE 2: Modulazioni Numeriche 2 Modulazioni: introduzione Per ogni modulazione considereremo: Caratteristiche generali Costellazione (insieme di
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica ST410 - Statistica 1 - A.A. 2014/2015 II Esonero - 15 Gennaio 2015
 UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica ST410 - Statistica 1 - A.A. 014/015 II Esonero - 15 Gennaio 015 1 3 4 5 6 Tot. Avvertenza: Svolgere ogni esercizio nello spazio assegnato,
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica ST410 - Statistica 1 - A.A. 014/015 II Esonero - 15 Gennaio 015 1 3 4 5 6 Tot. Avvertenza: Svolgere ogni esercizio nello spazio assegnato,
4. Stime & Test. Corso di Simulazione. Anno accademico 2008/09
 Anno accademico 2008/09 Media campionaria X 1, X 2,..., X n v.c. indipendenti con distribuzione F, e: E[X i ] = µ Var[X i ] = σ 2, i = 1,..., n Media campionaria: X n è uno stimatore di µ. È uno stimatore
Anno accademico 2008/09 Media campionaria X 1, X 2,..., X n v.c. indipendenti con distribuzione F, e: E[X i ] = µ Var[X i ] = σ 2, i = 1,..., n Media campionaria: X n è uno stimatore di µ. È uno stimatore
Circuiti a tempo discreto Raffaele Parisi
 Università di Roma La Sapienza Laurea specialistica in Ingegneria Elettronica Circuiti a tempo discreto Raffaele Parisi : Risposta in frequenza dei circuiti TD Rappresentazione nel dominio della frequenza,
Università di Roma La Sapienza Laurea specialistica in Ingegneria Elettronica Circuiti a tempo discreto Raffaele Parisi : Risposta in frequenza dei circuiti TD Rappresentazione nel dominio della frequenza,
Corso di Laurea in Informatica Calcolo delle Probabilità e Statistica (269AA) A.A. 2017/18 - Prova scritta
 Corso di Laurea in Informatica Calcolo delle Probabilità e Statistica (269AA A.A. 2017/18 - Prova scritta 2018-09-12 La durata della prova è di tre ore. Le risposte devono essere adeguatamente giustificate.
Corso di Laurea in Informatica Calcolo delle Probabilità e Statistica (269AA A.A. 2017/18 - Prova scritta 2018-09-12 La durata della prova è di tre ore. Le risposte devono essere adeguatamente giustificate.
Generazione di Numeri Casuali- Parte 2
 Esercitazione con generatori di numeri casuali Seconda parte Sommario Trasformazioni di Variabili Aleatorie Trasformazione non lineare: numeri casuali di tipo Lognormale Trasformazioni affini Numeri casuali
Esercitazione con generatori di numeri casuali Seconda parte Sommario Trasformazioni di Variabili Aleatorie Trasformazione non lineare: numeri casuali di tipo Lognormale Trasformazioni affini Numeri casuali
Analisi della correlazione canonica
 Analisi della correlazione canonica Su un collettivo di unità statistiche si osservano due gruppi di k ed m variabili L analisi della correlazione canonica ha per obiettivo lo studio delle relazioni di
Analisi della correlazione canonica Su un collettivo di unità statistiche si osservano due gruppi di k ed m variabili L analisi della correlazione canonica ha per obiettivo lo studio delle relazioni di
Il metodo delle osservazioni indirette
 Il metodo delle osservazioni indirette Teoria della stima ai minimi quadrati Il criterio di massima verosimiglianza Sia data una grandezza η e si abbiano n osservazioni indipendenti l i (i=1,...,n) di
Il metodo delle osservazioni indirette Teoria della stima ai minimi quadrati Il criterio di massima verosimiglianza Sia data una grandezza η e si abbiano n osservazioni indipendenti l i (i=1,...,n) di
Comunicazioni Elettriche II
 Comunicazioni Elettriche II Laurea Magistrale in Ingegneria Elettronica Università di Roma La Sapienza A.A. 2017-2018 Codifica di canale Il codificatore di canale Bits della sorgente Codificatore di canale
Comunicazioni Elettriche II Laurea Magistrale in Ingegneria Elettronica Università di Roma La Sapienza A.A. 2017-2018 Codifica di canale Il codificatore di canale Bits della sorgente Codificatore di canale
Analisi della Regressione Lineare
 Analisi della Regressione Lineare Master in Tecnologie Bioinformatiche 29/09/06 Adriano Decarli 1 29/09/06 Adriano Decarli 2 29/09/06 Adriano Decarli 3 29/09/06 Adriano Decarli 4 29/09/06 Adriano Decarli
Analisi della Regressione Lineare Master in Tecnologie Bioinformatiche 29/09/06 Adriano Decarli 1 29/09/06 Adriano Decarli 2 29/09/06 Adriano Decarli 3 29/09/06 Adriano Decarli 4 29/09/06 Adriano Decarli
Probabilità e Statistica
 Probabilità e Statistica Stima puntuale di parametri Marco Pietro Longhi C.d.L.: Ingegneria Elettronica e delle Telecomunicazioni, Ingegneria Informatica a.s. 018/019 Marco Pietro Longhi Prob. e Stat.
Probabilità e Statistica Stima puntuale di parametri Marco Pietro Longhi C.d.L.: Ingegneria Elettronica e delle Telecomunicazioni, Ingegneria Informatica a.s. 018/019 Marco Pietro Longhi Prob. e Stat.
Richiami di probabilità e statistica
 Richiami di probabilità e statistica Una variabile casuale (o aleatoria) X codifica gli eventi con entità numeriche x ed è caratterizzata dalla funzione di distribuzione di probabilità P(x) : P(x)=Pr ob[x
Richiami di probabilità e statistica Una variabile casuale (o aleatoria) X codifica gli eventi con entità numeriche x ed è caratterizzata dalla funzione di distribuzione di probabilità P(x) : P(x)=Pr ob[x
Sequenze (Sistemi) di Variabili Aleatorie Se consideriamo un numero di variabili aleatorie, generalmente dipendenti si parla equivalentemente di:
 Teoria dei Fenomeni Aleatori AA 01/13 Sequenze (Sistemi) di Variabili Aleatorie Se consideriamo un numero di variabili aleatorie, generalmente dipendenti si parla equivalentemente di: N-pla o Sequenza
Teoria dei Fenomeni Aleatori AA 01/13 Sequenze (Sistemi) di Variabili Aleatorie Se consideriamo un numero di variabili aleatorie, generalmente dipendenti si parla equivalentemente di: N-pla o Sequenza
Fondamenti di Data Processing
 Fondamenti di Data Processing Vincenzo Suraci Automazione INTRODUZIONE AL DATA PROCESSING ACQUISIZIONE DATI SCHEMA COSTRUTTIVO SCHEDA INPUT OSCILLATORE A FREQUENZA COSTANTE BANDA PASSANTE ACCORDATA AL
Fondamenti di Data Processing Vincenzo Suraci Automazione INTRODUZIONE AL DATA PROCESSING ACQUISIZIONE DATI SCHEMA COSTRUTTIVO SCHEDA INPUT OSCILLATORE A FREQUENZA COSTANTE BANDA PASSANTE ACCORDATA AL
CANALE STAZIONARIO CANALE TEMPO INVARIANTE
 CANALE STAZIONARIO Si parla di un Canale Stazionario quando i fenomeni che avvengono possono essere modellati da processi casuali e le proprietà statistiche di tali processi sono indipendenti dal tempo.
CANALE STAZIONARIO Si parla di un Canale Stazionario quando i fenomeni che avvengono possono essere modellati da processi casuali e le proprietà statistiche di tali processi sono indipendenti dal tempo.
Mattia Zanella. Ferrara, April
 Department of Mathematical Sciences Politecnico di Torino, Italy http://www.mattiazanella.eu Ferrara, April 5 217 Programma della lezione Seminario I Introduzione a Matlab U(, 1): metodo di inversione
Department of Mathematical Sciences Politecnico di Torino, Italy http://www.mattiazanella.eu Ferrara, April 5 217 Programma della lezione Seminario I Introduzione a Matlab U(, 1): metodo di inversione
DIPARTIMENTO DI INGEGNERIA DELL INFORMAZIONE
 U N I V E R S I T À D E G L I S T U D I D I P I S A DIPARTIMENTO DI INGEGNERIA DELL INFORMAZIONE Cmunicazini numeriche Esercizi su sistemi di variabili aleatrie-e sui prcessi stcastici Sistemi di variabili
U N I V E R S I T À D E G L I S T U D I D I P I S A DIPARTIMENTO DI INGEGNERIA DELL INFORMAZIONE Cmunicazini numeriche Esercizi su sistemi di variabili aleatrie-e sui prcessi stcastici Sistemi di variabili
FILTRI NUMERICI. Sistema LTI H (z)
 x [n] FILTRI UMERICI Sistema LTI H (z) y [n] Un sistema numerico LTI è in molti casi descritto con un equazione alle differenze lineare a coefficienti costanti: M [ ] = [ ] a y n k b x n r k k= r= Z {}
x [n] FILTRI UMERICI Sistema LTI H (z) y [n] Un sistema numerico LTI è in molti casi descritto con un equazione alle differenze lineare a coefficienti costanti: M [ ] = [ ] a y n k b x n r k k= r= Z {}
COMUNICAZIONI ELETTRICHE
 COMUNICAZIONI ELERICHE Diploma Universitario Ingegneria Elettronica - Ingegneria Inormatica ESERCIZIO : Si consideri il sistema mostrato in igura. Il iltro ha risposta in requenza H() = j segn (), dove
COMUNICAZIONI ELERICHE Diploma Universitario Ingegneria Elettronica - Ingegneria Inormatica ESERCIZIO : Si consideri il sistema mostrato in igura. Il iltro ha risposta in requenza H() = j segn (), dove
Teoria dei Segnali Trasmissione binaria casuale; somma di processi stocastici
 eoria dei Segnali rasmissione binaria casuale; somma di processi stocastici Valentino Liberali Dipartimento di Fisica Università degli Studi di Milano valentino.liberali@unimi.it eoria dei Segnali rasmissione
eoria dei Segnali rasmissione binaria casuale; somma di processi stocastici Valentino Liberali Dipartimento di Fisica Università degli Studi di Milano valentino.liberali@unimi.it eoria dei Segnali rasmissione
IL CRITERIO DELLA MASSIMA VEROSIMIGLIANZA
 Metodi per l Analisi dei Dati Sperimentali AA009/010 IL CRITERIO DELLA MASSIMA VEROSIMIGLIANZA Sommario Massima Verosimiglianza Introduzione La Massima Verosimiglianza Esempio 1: una sola misura sperimentale
Metodi per l Analisi dei Dati Sperimentali AA009/010 IL CRITERIO DELLA MASSIMA VEROSIMIGLIANZA Sommario Massima Verosimiglianza Introduzione La Massima Verosimiglianza Esempio 1: una sola misura sperimentale
Corso di Fondamenti di Telecomunicazioni Esercizi Teoria dei segnali Prof. Giovanni Schembra
 Corso di Fondamenti di Telecomunicazioni Esercizi Teoria dei segnali Prof. Giovanni Schembra Sommario CARATTERISTICHE DEI SEGNALI DETERMINATI.... ESERCIZIO.... ESERCIZIO... 5.3 ESERCIZIO 3 CONVOLUZIONE...
Corso di Fondamenti di Telecomunicazioni Esercizi Teoria dei segnali Prof. Giovanni Schembra Sommario CARATTERISTICHE DEI SEGNALI DETERMINATI.... ESERCIZIO.... ESERCIZIO... 5.3 ESERCIZIO 3 CONVOLUZIONE...
Argomenti della lezione: Campionamento Stima Distribuzione campionaria Campione Popolazione Sottoinsieme degli elementi (o universo) dell '
 Lezione 2 Argomenti della lezione: La statistica inferenziale: concetti di base Campionamento Stima Distribuzione campionaria Popolazione (o universo) Insieme di tutti gli elementi cui si rivolge il ricercatore
Lezione 2 Argomenti della lezione: La statistica inferenziale: concetti di base Campionamento Stima Distribuzione campionaria Popolazione (o universo) Insieme di tutti gli elementi cui si rivolge il ricercatore
Proprietà asintotiche dello stimatore OLS
 Università di Pavia Proprietà asintotiche dello stimatore OLS Eduardo Rossi Sequenze Consideriamo un infinita sequenza di variabili indicizzate con i numeri naturali: X 1, X 2, X 3,...,X N,... = {X N }
Università di Pavia Proprietà asintotiche dello stimatore OLS Eduardo Rossi Sequenze Consideriamo un infinita sequenza di variabili indicizzate con i numeri naturali: X 1, X 2, X 3,...,X N,... = {X N }
Università degli Studi Roma Tre Anno Accademico 2017/2018 ST410 Statistica 1
 Università degli Studi Roma Tre Anno Accademico 2017/2018 ST410 Statistica 1 Lezione 1 - Mercoledì 27 Settembre 2017 Introduzione al corso. Richiami di probabilità: spazi di probabilità, variabili aleatorie,
Università degli Studi Roma Tre Anno Accademico 2017/2018 ST410 Statistica 1 Lezione 1 - Mercoledì 27 Settembre 2017 Introduzione al corso. Richiami di probabilità: spazi di probabilità, variabili aleatorie,
Analisi statistica classica. Analisi statistica in simulazione. Stima della media. Stima della media
 Analisi statistica in simulazione Analisi statistica classica Aspetto fondamentale in simulazione, a volte sottovalutato Corrette interpretazione dei risultati Analisi dei dati di di input definizione
Analisi statistica in simulazione Analisi statistica classica Aspetto fondamentale in simulazione, a volte sottovalutato Corrette interpretazione dei risultati Analisi dei dati di di input definizione
La modulazione numerica
 La modulazione numerica Mauro Giaconi 26/05/2009 trasmissione numerica 1 Principi di modulazione numerica 26/05/2009 trasmissione numerica 2 Modulazione numerica La modulazione trasla l informazione di
La modulazione numerica Mauro Giaconi 26/05/2009 trasmissione numerica 1 Principi di modulazione numerica 26/05/2009 trasmissione numerica 2 Modulazione numerica La modulazione trasla l informazione di
) $ ' con T0=5s e T=2s. La funzione deve essere
 Metodi per l Analisi dei Segnali Biomedici. Esercitazioni AA 2010/2011 Esercitazione 11/03/2011 " t!t es_1.1. Disegnare la funzione rect 0 % $ ' con T0=5s e T=2s. La funzione deve essere calcolata # T
Metodi per l Analisi dei Segnali Biomedici. Esercitazioni AA 2010/2011 Esercitazione 11/03/2011 " t!t es_1.1. Disegnare la funzione rect 0 % $ ' con T0=5s e T=2s. La funzione deve essere calcolata # T
PROCESSO STOCASTICO I
 PROCESSO STOCASTICO I valori futuri di un segnale aleatorio (stocastico) non possono essere predetti esattamente. I segnali aleatori sono tali per loro natura (meccanismo interno) o rappresentano meccanismi
PROCESSO STOCASTICO I valori futuri di un segnale aleatorio (stocastico) non possono essere predetti esattamente. I segnali aleatori sono tali per loro natura (meccanismo interno) o rappresentano meccanismi
Prestazione e equalizzatori frazionari
 Prestazione e equalizzatori frazionari libro Prestazioni degli equalizzatori ZF Supponendo la situazione ideale (infiniti pesi, step-size piccolo, fase di tracking, decisioni corrette), rimarrebbe solo
Prestazione e equalizzatori frazionari libro Prestazioni degli equalizzatori ZF Supponendo la situazione ideale (infiniti pesi, step-size piccolo, fase di tracking, decisioni corrette), rimarrebbe solo
IDENTIFICAZIONE dei MODELLI e ANALISI dei DATI. Lezione 20: Stima puntuale. Stimatore lineare a MEQM. Esempi. Motivazioni
 IDENTIFICAZIONE dei MODELLI e ANALISI dei DATI Lezione 20: Stima puntuale Motivazioni Stima puntuale Indice di qualitá della stima Stimatore a MEQM Stimatore lineare a MEQM Il caso gaussiano Esempi 20-1
IDENTIFICAZIONE dei MODELLI e ANALISI dei DATI Lezione 20: Stima puntuale Motivazioni Stima puntuale Indice di qualitá della stima Stimatore a MEQM Stimatore lineare a MEQM Il caso gaussiano Esempi 20-1
Pulse Amplitude Modulation (PAM) 2 Scelta delle risposte impulsive dei filtri in trasmissione e ricezione
 Pulse Amplitude Modulation (PAM 1 Definizione La trasmissione di una sequenza di numeri {a k } mediante un onda PAM consiste nel generare, a partire dalla sequenza {a k } il segnale a tempo continuo u(t
Pulse Amplitude Modulation (PAM 1 Definizione La trasmissione di una sequenza di numeri {a k } mediante un onda PAM consiste nel generare, a partire dalla sequenza {a k } il segnale a tempo continuo u(t
1 Serie temporali. 1.1 Processi MA
 1 Serie temporali Un processo stocastico 1 {X t, t T }, dove T = N o T = Z, si dice stazionario se (X 1,..., X n ) e (X k+1,...,x k+n ) hanno la stessa distribuzione per ogni n 1 e per ogni k T. Un processo
1 Serie temporali Un processo stocastico 1 {X t, t T }, dove T = N o T = Z, si dice stazionario se (X 1,..., X n ) e (X k+1,...,x k+n ) hanno la stessa distribuzione per ogni n 1 e per ogni k T. Un processo
Probablità, Statistica e Processi Stocastici
 Probablità, Statistica e Processi Stocastici Franco Flandoli, Università di Pisa Programma del corso vettori gaussiani, PCA ed fpca altri metodi di analisi e previsione di serie storiche catene di Markov
Probablità, Statistica e Processi Stocastici Franco Flandoli, Università di Pisa Programma del corso vettori gaussiani, PCA ed fpca altri metodi di analisi e previsione di serie storiche catene di Markov
Elenco dei simboli 9. Prefazione 10
 Indice Elenco dei simboli 9 Prefazione 10 1 Analisi nel dominio del tempo 11 1.1 Segnali tempo discreto... 11 1.1.1 Segnali notevoli tempo discreto... 13 1.1.2 Alcuni criteri di classificazione di segnali
Indice Elenco dei simboli 9 Prefazione 10 1 Analisi nel dominio del tempo 11 1.1 Segnali tempo discreto... 11 1.1.1 Segnali notevoli tempo discreto... 13 1.1.2 Alcuni criteri di classificazione di segnali
Fin qui si sono considerate le variabili casuali ciascuna per proprio conto. Ora consideriamo la possibilità di relazioni tra variabili.
 Sistemi di variabili casuali Fin qui si sono considerate le variabili casuali ciascuna per proprio conto. Ora consideriamo la possibilità di relazioni tra variabili. Esempi: - il massimo annuale della
Sistemi di variabili casuali Fin qui si sono considerate le variabili casuali ciascuna per proprio conto. Ora consideriamo la possibilità di relazioni tra variabili. Esempi: - il massimo annuale della
Filtraggio Digitale. Alfredo Pironti. Ottobre Alfredo Pironti Univ. di Napoli Federico II Corso Ansaldo Breda 1 / 20
 Filtraggio Digitale Alfredo Pironti Ottobre 2012 Alfredo Pironti Univ. di Napoli Federico II Corso Ansaldo Breda 1 / 20 Filtri Analogici (1) Un filtro analogico è un sistema lineare tempo-invariante (LTI)
Filtraggio Digitale Alfredo Pironti Ottobre 2012 Alfredo Pironti Univ. di Napoli Federico II Corso Ansaldo Breda 1 / 20 Filtri Analogici (1) Un filtro analogico è un sistema lineare tempo-invariante (LTI)
Teoria dell informazione e codici Parte II
 Facoltà di Ingegneria Appunti dalle lezioni del corso di Teoria dell informazione e codici Parte II Prof. Alessandro NERI Anno accademico 008-009 1 Stima di Parametro A differenza del problema di decisione
Facoltà di Ingegneria Appunti dalle lezioni del corso di Teoria dell informazione e codici Parte II Prof. Alessandro NERI Anno accademico 008-009 1 Stima di Parametro A differenza del problema di decisione
Corso di Elaborazione Numerica dei Segnali Esame+Compitino del 24 giugno 2002
 Corso di Elaborazione Numerica dei Segnali Esame+Compitino del giugno 00 TOTALE PUNTI: 38 + 6 opz. L allievo é invitato a dare una ragionata e succinta risposta a tutti gli argomenti proposti, per dimostrare
Corso di Elaborazione Numerica dei Segnali Esame+Compitino del giugno 00 TOTALE PUNTI: 38 + 6 opz. L allievo é invitato a dare una ragionata e succinta risposta a tutti gli argomenti proposti, per dimostrare
Fondamenti di Elaborazione Numerica dei Segnali Anno Accademico Seconda Prova Intermedia 4/2/2013
 Fondamenti di Elaborazione Numerica dei Segnali Anno Accademico 0-0 Seconda Prova Intermedia 4//0 Quesiti relativi alla seconda prova in itinere (tempo max. h). (6 punti) Calcolare la H(z) Y (z)/x(z) associata
Fondamenti di Elaborazione Numerica dei Segnali Anno Accademico 0-0 Seconda Prova Intermedia 4//0 Quesiti relativi alla seconda prova in itinere (tempo max. h). (6 punti) Calcolare la H(z) Y (z)/x(z) associata
Tecniche di sondaggio
 SMID a.a. 2005/2006 Corso di Statistica per la Ricerca Sperimentale Tecniche di sondaggio 24/1/2006 Nomenclatura Indicheremo con P una popolazione, con N la sua numerosità, con k la sua etichetta e con
SMID a.a. 2005/2006 Corso di Statistica per la Ricerca Sperimentale Tecniche di sondaggio 24/1/2006 Nomenclatura Indicheremo con P una popolazione, con N la sua numerosità, con k la sua etichetta e con
RETI DI TELECOMUNICAZIONE
 RETI DI TELECOMUNICAZIONE Modelli delle Sorgenti di Traffico Generalità Per la realizzazione di un modello analitico di un sistema di telecomunicazione dobbiamo tenere in considerazione 3 distinte sezioni
RETI DI TELECOMUNICAZIONE Modelli delle Sorgenti di Traffico Generalità Per la realizzazione di un modello analitico di un sistema di telecomunicazione dobbiamo tenere in considerazione 3 distinte sezioni
Statistica Applicata all edilizia: il modello di regressione
 Statistica Applicata all edilizia: il modello di regressione E-mail: orietta.nicolis@unibg.it 27 aprile 2009 Indice Il modello di Regressione Lineare 1 Il modello di Regressione Lineare Analisi di regressione
Statistica Applicata all edilizia: il modello di regressione E-mail: orietta.nicolis@unibg.it 27 aprile 2009 Indice Il modello di Regressione Lineare 1 Il modello di Regressione Lineare Analisi di regressione
STATISTICA INDUTTIVA: STIMA DI PARAMETRI STIMA PUNTUALE
 S.S.I.S TOSCANA F.I.M. -II anno STATISTICA INDUTTIVA: STIMA DI PARAMETRI STIMA PUNTUALE PROBLEMA 1 Vogliamo valutare la percentuale p di donne fumatrici tra le donne in età fertile. Procediamo all estrazione
S.S.I.S TOSCANA F.I.M. -II anno STATISTICA INDUTTIVA: STIMA DI PARAMETRI STIMA PUNTUALE PROBLEMA 1 Vogliamo valutare la percentuale p di donne fumatrici tra le donne in età fertile. Procediamo all estrazione
Analisi della disponibilità d acqua. Valutazione dell impianto attraverso il calcolo di un indice economico (criterio)
 Analisi della disponibilità d acqua Valutazione dell impianto attraverso il calcolo di un indice economico (criterio) Approccio diverso a seconda del criterio di valutazione Nel caso di criterio statistico
Analisi della disponibilità d acqua Valutazione dell impianto attraverso il calcolo di un indice economico (criterio) Approccio diverso a seconda del criterio di valutazione Nel caso di criterio statistico
Comunicazioni Elettriche II
 Comunicazioni Elettriche II Laurea Magistrale in Ingegneria Elettronica Università di Roma La Sapienza A.A. 2017-2018 Esercitazione 16 Segnali d immagine I Esercizio: Rapporto d aspetto Si calcoli il rapporto
Comunicazioni Elettriche II Laurea Magistrale in Ingegneria Elettronica Università di Roma La Sapienza A.A. 2017-2018 Esercitazione 16 Segnali d immagine I Esercizio: Rapporto d aspetto Si calcoli il rapporto
Statistica Esercitazione. alessandro polli facoltà di scienze politiche, sociologia, comunicazione
 Statistica Esercitazione alessandro polli facoltà di scienze politiche, sociologia, comunicazione Obiettivo I due semplici esercizi seguenti hanno l obiettivo di consolidare le nostre nozioni in tema di
Statistica Esercitazione alessandro polli facoltà di scienze politiche, sociologia, comunicazione Obiettivo I due semplici esercizi seguenti hanno l obiettivo di consolidare le nostre nozioni in tema di
Corso di Identificazione dei Modelli e Analisi dei Dati
 Corso di Identificazione dei Modelli e Analisi dei Dati Prof. Sergio Bittanti Esercitazione di Laboratorio A.A. 2010-11 Sistemi dinamici lineari a tempo discreto 1. Si consideri il sistema dinamico a tempo
Corso di Identificazione dei Modelli e Analisi dei Dati Prof. Sergio Bittanti Esercitazione di Laboratorio A.A. 2010-11 Sistemi dinamici lineari a tempo discreto 1. Si consideri il sistema dinamico a tempo
Costruzione di macchine. Modulo di: Progettazione probabilistica e affidabilità. Marco Beghini. Lezione 7: Basi di statistica
 Costruzione di macchine Modulo di: Progettazione probabilistica e affidabilità Marco Beghini Lezione 7: Basi di statistica Campione e Popolazione Estrazione da una popolazione (virtualmente infinita) di
Costruzione di macchine Modulo di: Progettazione probabilistica e affidabilità Marco Beghini Lezione 7: Basi di statistica Campione e Popolazione Estrazione da una popolazione (virtualmente infinita) di
RICHIAMI SU PROCESSI ALEATORI E DENSITÀ SPETTRALE DI POTENZA
 RICHIAMI SU PROCESSI ALEATORI E DENSITÀ SPETTRALE DI POTENZA Paolo Bestagini Ph.D. Student bestagini@elet.polimi.it http://home.deib.polimi.it/bestagini Sommario 2 Segnali deterministici Continui Discreti
RICHIAMI SU PROCESSI ALEATORI E DENSITÀ SPETTRALE DI POTENZA Paolo Bestagini Ph.D. Student bestagini@elet.polimi.it http://home.deib.polimi.it/bestagini Sommario 2 Segnali deterministici Continui Discreti
