ROBERTO VACCA - BRUNO ARTUSO - CLAUDIA BEZZI. Geometria 2
|
|
|
- Giustina Rosso
- 7 anni fa
- Visualizzazioni
Transcript
1
2 ROBERTO VACCA - BRUNO ARTUSO - CLAUDIA BEZZI Geometria 2 Edizione Direzione Editoriae: Roberto Invernici Coordinamento Editoriae: Progetti di Editoria s.r.. Redazione: Domenico Gesmundo, Mario Scavini Progetto grafico: Ufficio Tecnico Atas Fotocomposizione, impaginazione e disegni: GIERRE, Bergamo Copertina: Vavassori & Vavassori Iustrazioni: Bruno Doif Stampa: Vincenzo Bona - Torino Con a coaborazione dea Redazione e dei Consuenti de'i.i.e.a. L'editore si impegna a mantenere invariato i contenuto di questo voume, secondo e norme vigenti. Si ringraziano e prof.sse Barbara Vanzani ed Eisabetta Zampiceni per a coaborazione editoriae. I materiae iustrativo proviene da'archivio iconografico Atas. L'editore eá a disposizione degi aventi diritto non potuti reperire. Ipresente voume eá conforme ae disposizioni ministeriai in merito ae caratteristiche tecniche e tecnoogiche dei ibri di testo. Ogni riproduzione depresente voume eá vietata. Le fotocopie per uso personae de ettore possono essere effettuate nei imiti de 15% di ciascun voume dietro pagamento aa SIAE de compenso previsto da'art. 68, commi 4 e 5, dea egge 22 aprie 1941 n Le riproduzioni effettuate per finaitaá di carattere professionae, economico o commerciae o comunque per uso diverso da queo personae possono essere effettuate a seguito di specifica autorizzazione riasciata da AIDRO, Corso di Porta Romana n. 108, Miano 20122, e-mai segreteria@aidro.org e sito web I peso di questo voume rientra nei imiti suggeriti da'associazione Itaiana Editori. Q 2011 by ISTITUTO ITALIANO EDIZIONI ATLAS Bergamo - Via Crescenzi, 88 - Te. (035) Fax (035)
3 Presentazione Matematica per obiettivi e competenze Questo nuovo corso di matematica eá un ibro misto che nasce da una puriennae esperienza nea scuoa, sia sotto i profio de'insegnamento che sotto queo dea ricerca e de'aggiornamento. Esso accogie tutte e esigenze didattiche ed editoriai che i nuovo scenario dea Scuoa itaiana esige da'insegnamento dea matematica, che ha assunto oggi ampie finaitaá educative e costituisce un momento importante nea formazione di ogni ragazzo. La scuoa de'autonomia e a didattica per competenze vaorizzano sempre di piuá i ruoo cuturae e formativo dea matematica, ponendoa a centro de curricuum deo studente. Oggi e nefuturo prossimo, infatti, a societaá avraá sempre piuá bisogno di cittadini che siano "competenti" sotto iprofio matematico in termini di capacitaá di matematizzare, per affrontare in modo consapevoe una societaá moto compessa e in rapido cambiamento. L'informazione disponibie, soprattutto in questi utimi anni, eá cresciuta in maniera esponenziae e i cittadini devono essere in grado di decidere come affrontare queste informazioni. In tae contesto, secondo e indicazioni ministeriai e e attese generai, un corso di matematica deve avere acune caratteristiche indispensabii: stimoare a comprensione e per questo deve essere scritto in un inguaggio chiaro, accattivante e soprattutto comprensibie per uno studente di etaá tra gi anni; far capire percheâ e competenze matematiche sono indispensabii ne'affrontare e risovere probemi de mondo reae; essere ricco di esempi, dai piuá sempici, che servono per imparare e formue e i concetti, a quei piuá compessi, nei quai e formue e i concetti "si appicano" a probemi reai; proporre un abbondante repertorio di esercizi, opportunamente graduati e non banai, che stimoino i ragionamento e a rifessione; utiizzare gi strumenti che a tecnoogia informatica mette a disposizione dea didattica: e risorse on ine ealavagna Interattiva Mutimediae; mettere in grado o studente di auto vautare a propria preparazione, di capire gi errori che commette, in modo da rendero consapevoe dee proprie abiitaá e conoscenze. Struttura de'opera In tae prospettiva, i corso Matematica per obiettivi e competenze eá un progetto didattico che favorisce e esigenze egate aa programmazione de Docente, soprattutto aa uce dee nuove disposizioni sua certificazione dee competenze. Icorso tiene inotre conto depeso e detetto di spesa, secondo e norme vigenti. Si compone di due voumi di Aritmetica, tre di Geometria, uno di Agebra e un voume di Informatica. Ai testi deprimo anno eá aegato i voume reativo ae prove Invasi che contiene 19 prove, divise per anno di corso, che possono essere svote a fine anno oppure a'inizio de'anno successivo come test d'ingresso. A queste si aggiungono i testi assegnati come prova d'esame a partire da'anno scoastico 2007/2008. Ogni voume si articoa in piuá aree ognuna dee quai eá suddivisa in capitoi. In ogni area sono espressamente dichiarate e Competenze che ciascun aunno deve padroneggiare per affrontare in modo consapevoe situazioni reai che a quest'etaá possono incontrare sia nea oro vita di studenti, sia a di fuori de'ambito scoastico; i capitoi si aprono con a formuazione dei Prerequisiti necessari per anaizzare consapevomen- 2 PRESENTAZIONE Q ISTITUTO ITALIANO EDIZIONI ATLAS
4 te e con successo gi argomenti contenuti e gi Obiettivi che si vogiono raggiungere, suddivisi in Conoscenze e AbiitaÁ. Ogni capitoo si apre con a rubrica "Perche studiare..." che, attraverso aneddoti e informazioni tratti daa reataá di tutti i giorni, ha o scopo di trovare un coegamento tra i contenuti de capitoo e 'esperienza personae degi aunni. EÁ in questo contesto che si cooca a rubrica Matematica e reataá, che mira a visuaizzare come i inguaggio e i concetti dea matematica si trovano nea reataá che ci circonda: sono, come diceva Gaieo "a ingua de'universo e de reae". La parte di teoria di ogni capitoo si chiude con a presenza di una scheda di ripasso che riprende i "Concetti chiave" studiati. Contenuti e impostazione didattica Nea trattazione teorica si evidenzia a presenza di numerosi Esempi svoti ed esercizi di Controo immediato che, inseriti a termine di ogni paragrafo, sono voutamente di facie comprensione e souzione. I Docente puoá presentari agi aunni subito dopo a spiegazione per 'accertamento dee conoscenze man mano acquisite. Ogni capitoo eá corredato da un vastissimo repertorio di esercizi suddivisi in reazione aa scansione dei paragrafi dea teoria e, per ciascun paragrafo, in due uteriori categorie: Esercizi di Comprensione dea teoria, spesso in forma di test a risposta mutipa, di domande a risposta chiusa o di frasi di competamento: servono per verificare e conoscenze teoriche senza e quai non eá possibie appicare i concetti studiati. Esercizi di Appicazione, inseriti dopo quei di comprensione, sotto forma di esercizi e probemi da svogere: mirano a sviuppare e capacitaá ogiche-deduttive, ad acquisire nuove abiitaá di cacoo e ad appicare e procedure piuá adatte a risovere un probema. Sono esercizi che normamente vengono svoti a casa come studio individuae. Gi esercizi sono stati suddivisi in tre ivei di difficotaá (ben riconoscibii daa grafica) e comunque graduati a'interno di ciascun iveo. Ao scopo di faciitare i processo di apprendimento sono presenti numerosi Esercizi guida, che permettono agi aunni di acquisire e principai tecniche risoutive e sono finaizzati aa comprensione e aa risouzione dee diverse probematiche presenti. A'interno di questa sezione, per ciascun capitoo, eá sempre stato inserito un esercizio di Matematica appicata ae scienze, che mira a favorire i processi di matematizzazione dea reataá che ci circonda. Ogni capitoo si concude con a proposta di una serie di: Esercizi sue Competenze di base: sono esercizi che tendono a verificare e competenze di riproduzione (secondo a terminoogia OCSE-PISA), che prevedono 'esecuzione di procedure di routine, 'appicazione di agoritmi standard e di abiitaá di cacoo e a manipoazione di espressioni e formue. Test Invasi: sono esercizi seezionati dae prove Invasi somministrate negi anni precedenti a'anno scoastico 2007/2008. Possono essere utiizzati per verificare i iveo di preparazione raggiunto dagi aunni in vista dea prova Invasi di fine cico dea scuoa secondaria di primo grado che sta assumendo sempre piuá importanza ai fini dea vautazione finae. Esercizi di Autovautazione suddivisi in due ivei: Verifica dee conoscenze e Verifica dee abiitaá. Tai esercizi possono essere utiizzati dao studente per testare i proprio iveo di apprendimento e diventano un vaido strumento per a preparazione dee prove di verifica. AttivitaÁ di Recupero, sono esercizi che servono per puntuaizzare e chiarire e nozioni minime di base che devono essere possedute da tutti gi aunni, anche quei che presentano maggiori difficotaá ne'apprendimento dei contenuti. A concusione de'attivitaá di recupero eá poi presente una scheda di Vautazione de recupero per 'accertamento dee conoscenze e dee abiitaá. AttivitaÁ di Consoidamento, sono esercizi voti a consoidare e conoscenze in precedenza acquisite e, suddivisi per iveo di difficotaá, rappresentano un utie banco di prova per verificare a propria preparazione. AttivitaÁ di Potenziamento, sono esercizi destinati agi studenti piuá capaci che vogiono mettersi aa prova con esercizi piuá compessi e con proposte piuá creative. Q ISTITUTO ITALIANO EDIZIONI ATLAS PRESENTAZIONE 3
5 Gare di matematica, sono esercizi assegnati nee varie competizioni nazionai ed internazionai di matematica e, suddivisi in reazione ae scansioni dei contenuti dei testi, rappresentano un vaido strumento per a vaorizzazione dee ecceenze. A termine di ogni area sono stati inseriti esercizi proposti nei testi di vautazione eaborati da'ocse (Organizzazione per a cooperazione e o sviuppo economico) a'interno de progetto PISA (Programme for Internationa Student Assessment), che intende vautare i iveo di competenze matematiche in piuá di 60 Nazioni. Gi esercizi proposti richiedono a capacitaá deo studente di pianificare strategie di souzione e di appicare in ambiti matematici piuá compessi e meno famiiari. Tai esercizi possono essere un vaido aiuto per a verifica dee competenze di Connessione edirifessione. Ogni area si chiude con a rubrica Math in Engish con esercizi di matematica in ingua ingese. Informatica per a matematica Aa uce dee moderne tecniche d'insegnamento, un corso di matematica non puoá fare a meno dea presenza paraea, teorica ed appicativa de'informatica. Per questo i corso si competa con un voume di informatica che tratta in modo competo ed articoato software quai Geogebra ed EXCEL, che appicati ai capitoi di geometria e aritmetica, portano progressivamente gi aunni ad integrare e competare i processi di apprendimento. A'interno dee esercitazioni con Exce eá inotre prevista una parte dedicata a inguaggio di programmazione Visua Basic, che consente di creare sempici procedure software ed agoritmi di cacoo, daa fase di scrittura de testo sorgente (editing) fino a'esecuzione de programma. Un'opera mista: Matematica on ine e ibro LIM In piena aderenza con e disposizioni ministeriai, Matematica per obiettivi e competenze eá un'opera mista in quanto propone partendo da sito moti materiai on ine ad integrazione e competamento dei voumi a stampa. In particoare, per ogni capitoo sono disponibii in rete: uteriori esercizi suddivisi per conoscenze e abiitaá; questi utimi sono a oro vota suddivisi per iveo di difficotaá; verifica interattiva dei contenuti per ciascun capitoo; uteriori schede storiche sui principai protagonisti dea storia dea Matematica e su acuni temi affascinanti e interessanti. Non mancheranno, inotre, curiositaá e aneddoti che servono a rendere piuá accattivante 'approccio a sapere matematico; simuazione di atre prove Invasi per iterzo anno; esercitazioni di Informatica con Cabri GeÂomeÁtre. Tutti questi materiai on ine saranno via via aggiornati e potenziati in modo continuativo. Otre ai materiai on ine eá disponibie a versione sfogiabie con a Lavagna Interattiva Mutimediae dei voumi base, con e funzioni di ingrandimento di figure e definizioni, di scrittura e canceazione. Per i Docente sono disponibii anche e animazioni in Power Point che iustrano e principai definizioni, proprietaá e regoe, percheâ i Docente e possa utiizzare durante e ezioni. I testi dei Giochi Matematici che compaiono aa fine di ogni capitoo sotto a rubrica "Gare di Matematica" sono stati gentimente forniti da Centro Pristem-Eeusi de'universitaá Bocconi di Miano e si riferiscono ae competizioni matematiche organizzate dao stesso Centro. 4 PRESENTAZIONE Q ISTITUTO ITALIANO EDIZIONI ATLAS
6 Indice generae AREA 1: L'equivaenza dee figure 1. L'area dee figure piane 1. L'equivaenza dee figure piane Figure equicomposte 11 å Approfondimenti Un atro modo per verificare 'equivaenza L'area derettangoo L'area dequadrato L'area de paraeogrammo L'area detriangoo La formua di Erone L'area derombo e dedetoide L'area detrapezio L'area di un poigono circoscritto ad una circonferenza L'area di un poigono regoare L'area di un poigono regoare e i numeri fissi L'area di un poigono irregoare 25 å Approfondimenti L'area di una figura a contorno curviineo 27 å Concetti Chiave 29 Esercizi 30 Esercizi sue competenze di base 74 Esercizi INVALSI 76 Verifica dee conoscenze 78 Verifica dee abiitaá 79 AttivitaÁdi recupero 80 Scheda di vautazione de recupero 83 AttivitaÁdi consoidamento 84 AttivitaÁdi potenziamento 87 Gare di matematica I teorema di Pitagora 1. Iteorema di Pitagora Iteorema di Pitagora nei poigoni Iteorema di Pitagora e a circonferenza 102 å Matematica e storia Le terne pitagoriche 104 å Concetti Chiave 107 Esercizi 108 Esercizi sue competenze di base 137 Esercizi INVALSI 139 Verifica dee conoscenze 141 Verifica dee abiitaá 142 AttivitaÁdi recupero 143 Scheda di vautazione de recupero 146 AttivitaÁdi consoidamento 147 AttivitaÁdi potenziamento 149 Gare di matematica 150 Materiai on ine Esercizi di conoscenza Esercizi di abiitaá Verifica interattiva Scheda di approfondimento ESERCIZI OCSE PISA - AREA 1 Competenze di iveo avanzato 152 Math in Engish 154 Materiai on ine Laboratorio: attivitaá sue competenze Materiai on ine Esercizi di conoscenza Esercizi di abiitaá Verifica interattiva Scheda di approfondimento Prove Invasi Q ISTITUTO ITALIANO EDIZIONI ATLAS INDICE 5
7 AREA 2: Trasformazioni geometriche 1. Le trasformazioni isometriche 1. Congruenza diretta e inversa La trasazione 159 å Approfondimenti La composizione di trasazioni La rotazione 161 å Approfondimenti La composizione di rotazioni concentriche La simmetria assiae La simmetria centrae 164 å Approfondimenti La composizione di simmetrie assiai La simmetria e i poigoni 167 å Matematica e arte Le trasformazioni isometriche ne'arte 169 å Concetti Chiave 170 Esercizi 171 Esercizi sue competenze di base 194 Esercizi INVALSI 197 Verifica dee conoscenze 199 Verifica dee abiitaá 200 AttivitaÁdi recupero 201 Scheda di vautazione de recupero 204 AttivitaÁdi consoidamento 205 AttivitaÁdi potenziamento 207 Gare di matematica 209 Materiai on ine Esercizi di conoscenza Esercizi di abiitaá Verifica interattiva Scheda di approfondimento 2. Le trasformazioni non isometriche 1. L'omotetia Le proprietaá dee figure omotetiche La simiitudine I poigoni simii I criteri di simiitudine nei triangoi 219 å Approfondimenti Atre trasformazioni non isometriche I teoremi dea simiitudine I teorema dea paraea a ato di un triangoo I teorema dee atezze corrispondenti di due triangoi simii Iteorema dei perimetri di due poigoni simii I teorema dee aree di due poigoni simii I teoremi di Eucide Iprimo teorema di Eucide Isecondo teorema di Eucide Interpretazione geometrica dei teoremi di Eucide 227 å Approfondimenti I frattai 228 å Concetti Chiave 230 Esercizi 231 Esercizi sue competenze di base 252 Esercizi INVALSI 254 Verifica dee conoscenze 255 Verifica dee abiitaá 256 AttivitaÁdi recupero 257 Scheda di vautazione de recupero 262 AttivitaÁdi consoidamento 263 AttivitaÁdi potenziamento 265 Gare di matematica 266 Materiai on ine Esercizi di conoscenza Esercizi di abiitaá Verifica interattiva Scheda di approfondimento ESERCIZI OCSE PISA - AREA 2 Competenze di iveo avanzato 267 Math in Engish 268 Materiai on ine Laboratorio: attivitaá sue competenze å Souzioni prove Invasi 269 å Souzioni schede di verifica 269 å Souzioni schede di vautazione derecupero 271 å Souzioni gare di matematica 272 å Tavoe numeriche 274 å Gossario 286 å Tabea dei simboi 287 å Formuario INDICE Q ISTITUTO ITALIANO EDIZIONI ATLAS
8 Area1 L'equivaenza dee figure Competenze n Saper studiare una situazione probematica sintetizzando e informazioni in un disegno. n Saper dedurre da un probema di diversa natura e informazioni richieste, appicare e formue studiate (anche inerenti ateorema di Pitagora) e giustificare e proprie risposte. L'area dee figure piane Iteorema di Pitagora Capitoi Q ISTITUTO ITALIANO EDIZIONI ATLAS
9 L'AREA DELLE FIGURE PIANE Obiettivi Prerequisiti 3 Operare con e quattro operazioni 3 Eevare un numero a quadrato 3 Estrarre a radice quadrata di un numero 3 Conoscere i sistema internazionae di misura 3 Trasformare una grandezza in un'atra con diversa unitaá di misura 3 Conoscere e figure piane, i oro eementi e e oro proprietaá CONOSCENZE 3 I concetto di equivaenza 3 I concetto di equiscomponibiitaá 3 Le formue per cacoare 'area di un poigono 3 Le formue inverse de'area ABILITA Á 3 Rappresentare figure equivaenti 3 Appicare e formue dirette per i cacoo dee aree dei poigoni 3 Appicare e formue inverse dee aree dei poigoni 3 Cacoare 'area di un poigono quasiasi Ne'opera Omaggio a quadrato di Josef Aberts, e inee diagonai che congiungono i vertici dei quadrati si incontrano in un punto coincidente con i centro di un rettangoo a cui area corrisponde a metaá di quea compessiva. PercheÂstudiare 'area dee figure piane Proviamo a reaizzare una sempice costruzione geometrica: prendiamo un cartoncino a forma quadrata e su di esso tracciamo una dee due diagonai; in uno dei due triangoi rettangoi ottenuti, tracciamo quindi 'atezza reativa a'ipotenusa, otteniamo, cosõá, i triangoi rettangoi isoscei 1 e 2; consideriamo ora i punti medi dei cateti de secondo triangoo rettangoo ed uniamoi con un segmento; otteniamo in questo modo un trapezio isoscee ed un triangoo rettangoo isoscee 3; ne triangoo rettangoo isoscee 3 consideriamo i punto medio de'ipotenusa e ne triangoo rettangoo isoscee 1 i punto medio de cateto; uniamoi con un segmento in modo da ottenere i paraeogrammo 4ed un trapezio isoscee; ne trapezio isoscee che eá rimasto tracciamo e due atezze dai vertici dea base minore in modo da ottenere atri due triangoi rettangoi isoscei 5 e 7 ed un quadrato 6. 8 L'AREA DELLE FIGURE PIANE - AREA 1 - CAPITOLO 1 Q ISTITUTO ITALIANO EDIZIONI ATLAS
10 1 La tecnica de mosaico consiste ne coprire a superficie a disposizione con tessere poigonai di area ridotta. Quanto piuá 'area di ciascuna tessera eá minore tanto maggiore saraá i dettagio dea reaizzazione finae. I gioco de Tangram prevede soamente una regoa: utiizzare tutte e tessere senza acuna sovrapposizione. Componendo in diverso modo e tessere eá possibie reaizzare un'infinitaá di figure. Questa costruzione "apparentemente senza senso" eá a base di un gioco mienario inventato nea ontana Cina che nea denominazione originae si chiama "Le sette pietre dea saggezza" e che in Occidente eá conosciuto con i piuá famoso nome di Tangram. Combinando opportunamente tutti i sette pezzi de Tangram, eá possibie ottenere un numero pressocheâ infinito di figure, acune geometriche, atre che ricordano oggetti d'uso comune. La caratteristica di tutte queste figure eá 'equiscomponibiitaá, concetto che approfondiremo in questo capitoo. Voete mettervi aa prova con tae gioco? Provate a costruire con tutti i sette pezzi un triangoo rettangoo isoscee, un rettangoo con e dimensioni una doppia de'atra, un trapezio isoscee con a base maggiore pari a tre vote 'atezza (a sua vota congruente aa base minore), un esagono schiacciato, un pentagono irregoare. Se ci siete riusciti potete provare a costruire oggetti ed animai come ad esempio un cigno o un gatto (acune souzioni e trovi ne paragrafo 1.1). Q ISTITUTO ITALIANO EDIZIONI ATLAS L'AREA DELLE FIGURE PIANE - AREA 1 - CAPITOLO 1 9
11 1 L'equivaenza dee figure piane Gi esercizi di questo paragrafo sono a pag. 30 Lo scorso anno scoastico abbiamo studiato i poigoni e i abbiamo cassificati in base a numero dei ati esaminandone e reative proprietaá (figura 1a). Inotre, abbiamo considerato figure piane a contorno curviineo (cioeá composte interamente da inee curve, figura 1b) o a contorno mistiineo (cioeá composte da inee rette e inee curve, figura 1c). Figura 1 a. b. c. In tutti i casi, quaunque sia i contorno, e figure piane occupano sempre una parte di piano; possiamo quindi dire che hanno una superficie (o estensione). Tae superficie eá una grandezza misurabie, pertanto: Figura 2 DEFINIZIONE. Per area di una figura piana si intende a misura dea sua superficie. Per misurare a superficie di una figura occorre confrontara con un'unitaá di misura, in modo da stabiire quante vote quest'utima eá contenuta in quea da misurare. Ricordiamo aora che 'unitaá di misura dee superfici eá i metro quadrato (m 2 ) con i suoi mutipi e sottomutipi: km 2 hm 2 dam 2 m 2 dm 2 cm 2 mm 2 e che per trasformare una unitaá in un'atra, mutipa dea prima, occorre dividere per 100, , etc., mentre per trasformare una unitaá in un'atra, sottomutipa dea prima, occorre motipicare per 100, , etc. Chiarito i concetto di area, vogiamo adesso esaminare un atro fondamentae concetto dea geometria piana: 'equivaenza dee superfici. Consideriamo due poigoni congruenti, ad esempio i rettangoi dea figura 2. EÁ evidente che, avendo i ati congruenti, essi occupano a stessa superficie, cioeá hanno a stessa area. Consideriamo adesso piuá poigoni, ad esempio, un triangoo, un quadrato e un rettangoo (in ato nea figura 3). Disponiamo e tre figure in modo da ottenere composizioni aventi forme diverse (figura 3a e 3b). Notiamo che e figure ottenute, pur non avendo a stessa forma, sono peroá composte dagi stessi poi- Figura 3 a. b. i inguaggio dea La paroa area (come pure a paroa perimetro) indica una misura. Quindi si dice «'area dea figura eá (di) 10 cm 2», e non;«'area dea figura misura 10 cm 2», percheâ sarebbe una ripetizione. Ricordiamo invece che i termini ato, atezza, apotema indicano dei segmenti e non e oro misure. Quando ci riferiamo ad essi dobbiamo quindi dire «i ato AB misura 5 cm», oppure «i ato AB eá ungo 5 cm», e non «i ato AB eá (di) 5 cm». matematica 10 L'AREA DELLE FIGURE PIANE - AREA 1 - CAPITOLO 1 Q ISTITUTO ITALIANO EDIZIONI ATLAS
12 goni e occupano quindi a stessa superficie. Possiamo esprimere questo fatto dicendo che e due composizioni di figure sono equivaenti (o equiestese); pertanto: DEFINIZIONE. Due superfici A e B, anche di forma diversa, che occupano a stessa parte di piano, si dicono equivaenti. In simboi: Aˆ: B e si egge: «A equivaente a B» Dae considerazioni fatte possiamo dunque concudere: PROPRIETA Á. n Due figure congruenti sono sempre equivaenti (vedi figura 2) n due figure equivaenti non sono, in generae, congruenti (vedi figura 3). Diremo infine che: DEFINIZIONE. Tra due poigoni con diversa superficie, i poigono con 'estensione maggiore prende inome di prevaente, queo con 'estensione iminore di suvvaente. 1.1 Figure equicomposte Per stabiire se due figure piane sono equivaenti ci basiamo su principio dea equiscomponibiitaá, ovvero sua possibiitaá di scomporre e due figure in atre figure tra oro congruenti a due a due. Ricordando aora quanto detto ne paragrafo precedente eá facie affermare che: PROPRIETA Á. Due figure equicomposte sono necessariamente equivaenti. Per spiegare megio questa proprietaá esaminiamo i casi che si possono presentare. La proprietaá enunciata non eá invertibie cioeá due figure equivaenti non sono necessariamente equicomposte. Primo caso EquiscomponibiitaÁ mediante somma di figure Consideriamo a figura 4 in cui abbiamo rappresentato acune dee costruzioni che si possono ottenere con tutti i pezzi detangram. Figura 4 a. b. c. d. EÁ evidente che e diverse figure sono equivaenti percheâ ottenute mediante a somma degi stessi poigoni. Possiamo quindi dire che: PROPRIETA Á. Figure che sono state ottenute mediante somma di parti rispettivamente congruenti sono equivaenti. Q ISTITUTO ITALIANO EDIZIONI ATLAS L'AREA DELLE FIGURE PIANE - AREA 1 - CAPITOLO 1 11
13 Secondo caso EquiscomponibiitaÁ mediante differenza di figure I poigoni dea figura 5 ottenuti, a partire da quadrato iniziae, eiminando quattro quadrati congruenti sono a oro vota equivaenti. Pertanto: PROPRIETA Á. Figure che sono state ottenute mediante differenza di parti rispettivamente congruenti sono equivaenti. Figura 5 a. b. c. Approfondimenti Un atro modo per verificare 'equivaenza Esaminiamo i quadrato e i cerchio dea figura 6. Figura 6 Ci accorgiamo immediatamente che non eá possibie stabiire con esattezza se e due figure sono equivaenti utiizzando uno dei due procedimenti geometrici anaizzati in precedenza. Ricorriamo quindi ad un metodo indiretto, che consiste nea pesatura dee due figure. Ritagiamo da uno stesso fogio di cartone e due figure da confrontare e, dopo avere appese ai bracci di una biancia di precisione (figura 7), controiamo se hanno o stesso peso. Se i bracci restano in equiibrio, aora abbiamo utiizzato a stessa quantitaá di cartone e quindi e due figure sono equivaenti. Se invece non restano in equiibrio, aora a figura che pesa di piuá saraá quea di maggiore estensione. Figura 7 o ro o o 1 Due figure sono equivaenti quando hanno: a. o stesso perimetro; b. a stessa area; c. o stesso numero di ati. 2 Indica quae dee seguenti affermazioni eá vera: a. per misurare 'estensione di una superficie occorre confrontara con un'unitaá di misura in modo da stabiire quante vote quest'utima eá contenuta in quea da misurare; 12 L'AREA DELLE FIGURE PIANE - AREA 1 - CAPITOLO 1 Q ISTITUTO ITALIANO EDIZIONI ATLAS
14 b. per misurare 'estensione di una superficie occorre confrontara con un'atra superficie, fissata come unitaá di misura, per stabiire quante vote a superficie da misurare eá contenuta nea superficie fissata come unitaá di misura; c. per misurare 'estensione di una superficie occorre confrontara con un'atra superficie. 3 Tra e seguenti figure determina quee tra oro congruenti e quee tra oro equivaenti: 4 Quai fra i seguenti poigoni sono equicomposti? 2 L'area de rettangoo Gi esercizi di questo paragrafo sono a pag. 34 Nea figura 8 eá rappresentato un rettangoo con a base unga 4 cm e 'atezza che misura 5 cm. Per cacoare a sua area dovremo contare quante vote 'unitaá di misura eá contenuta in esso. Se prendiamo come riferimento icm 2 osserviamo che ne rettangoo ci sono 20 quadratini, ciascuno dei quai ha un'area di 1 cm 2 ; possiamo dunque dire che irettangoo ha area di 20 cm 2.EÁ possibie ottenere o stesso risutato motipicando fra oro a misura dea base e de'atezza (in cm): 5cm 4cmˆ20 cm 2. Figura 8 Pertanto possiamo affermare che: REGOLA. L'area de rettangoo si ricava motipicando a misura dea base per quea de'atezza. In simboi: A ˆ b h Da questa formua ricaviamo e seguenti formue inverse che ci permettono di risaire ae misure dea base o de'atezza, note e atre due grandezze: b ˆ A : h h ˆ A : b Q ISTITUTO ITALIANO EDIZIONI ATLAS L'AREA DELLE FIGURE PIANE - AREA 1 - CAPITOLO 1 13
15 CONCETTI 1 CHIAVE Somma di figure si ottiene mediante a somma di parti rispettivamente congruenti Differenza di figure si ottiene mediante a differenza di parti rispettivamente congruenti Figure equicomposte I concetto di equivaenza quando due superfici A e B di forma diversa, occupano a stessa parte di piano a misura dea superficie da esse occupata Rettangoo 'area si ottiene motipicando a misura dea base per quea de'atezza: A ˆ b h Quadrato 'area si ottiene motipicando a misura deato per se stessa: A ˆ `2 Paraeogrammo 'area si ottiene motipicando a misura dea base per quea de'atezza: A ˆ b h Triangoo 'area si ottiene motipicando a misura dea base per quea de'atezza e dividendo i prodotto ottenuto per due: A ˆ b h : 2 Rombo e detoide 'area si ottiene motipicando e misure dee diagonai e dividendo iprodotto ottenuto per due: A ˆ d D : 2 Trapezio 'area si ottiene motipicando a somma dee misure dee basi per quea de'atezza e dividendo iprodotto ottenuto per due: A ˆ b B h : 2 Poigono regoare 'area si ottiene motipicando i semiperimetro per a misura de'apotema A ˆ p a oppure a misura deato aquadrato per inumero fisso A ˆ `2 ' Poigono irregoare 'area si ottiene scomponendo i poigono dato in figure note di cui si conosce a formua per cacoare 'area. Q ISTITUTO ITALIANO EDIZIONI ATLAS L'AREA DELLE FIGURE PIANE - AREA 1 - CAPITOLO 1 29
16 L'AREA DELLE FIGURE PIANE Esercizi 1 1 L'equivaenza dee figure piane teoria a pag. 10 richiami dea teoria n L'area di una figura piana eá a misura dea sua superficie espressa in una certa unitaá di misura; n per misurare una superficie occorre confrontara con un'unitaá di misura, cosõá da stabiire quante vote quest'utima eá contenuta in quea da misurare; n due superfici A e B, anche di forma diversa, si dicono equivaenti se occupano a stessa parte di piano, si indicano con A ˆ: B; n figure che sono state ottenute mediante a somma di parti rispettivamente congruenti sono equivaenti; n figure che sono state ottenute mediante a differenza di parti rispettivamente congruenti sono equivaenti. COMPRENSIONE DELLA TEORIA 1 Competa a seguente affermazione: 'area di una figura piana eá a... dea... occupata daa figura stessa. 2 Due figure si dicono equivaenti se hanno: a. o stesso perimetro; b. a stessa area; c. gi angoi congruenti; d. i ati congruenti. 3 QuaeÁ i simboo di equivaenza? a. ˆ; b. ˆ: ; c. '. 4 Due figure equivaenti: a. sono sempre fra oro congruenti; b. non sono, in generae, congruenti; c. sono sempre equicomposte. 5 Due figure equiscomponibii hanno necessariamente: a. o stesso perimetro; b. a stessa area; c. gi angoi congruenti; d. i ati congruenti. 6 Quai dee seguenti figure sono equivaenti? a. b. c. d. 7 Dee seguenti affermazioni indica quai sono vere e quai fase: a. somme di figure equivaenti sono equivaenti fra oro V F b. differenze di figure equivaenti non sono equivaenti fra oro V F c. due figure equicomposte sono sempre equivaenti V F d. due figure equivaenti non sempre sono equicomposte. V F 30 L'AREA DELLE FIGURE PIANE - AREA 1 - CAPITOLO 1 Q ISTITUTO ITALIANO EDIZIONI ATLAS
17 8 Competa e seguenti affermazioni: a. se due figure hanno a stessa forma e a stessa estensione, sono... e quindi anche...; b. se due figure hanno forma diversa ma uguae estensione aora sono...; c. se due figure sono state ottenute mediante a somma di parti rispettivamente congruenti aora sono...; d. se due figure sono state ottenute mediante a differenza di parti rispettivamente... aora sono equivaenti. 9 Indica quai dee seguenti figure sono congruenti e quai equivaenti. 10 Tra e seguenti figure individua quea prevaente. a. b. 11 Tra e seguenti figure individua quea suvvaente. a. b. APPLICAZIONE 12 Esercizio guida Stabiisci se e seguenti figure sono tra oro equivaenti. a. b. a. Itriangoo ABC eá equivaente a rettangoo A 0 B 0 C 0 D 0 in quanto ottenuto mediante equiscomponibiitaá. b. Itriangoo EFG eá equivaente a paraeogrammo E 0 F 0 H 0 I 0 in quanto ottenuto mediante equiscomponibiitaá. 13 Disegna un rettangoo equivaente aa seguente figura: Q ISTITUTO ITALIANO EDIZIONI ATLAS L'AREA DELLE FIGURE PIANE - AREA 1 - CAPITOLO 1 31
18 14 Esercizio guida Determina una figura equivaente a trapezio ABCD. Consideriamo itriangoo AED ottenuto proungando a base DC di un segmento CE congruente aa base minore AB e congiungendo ivertice A con E. Ipunto O determina due triangoi ABO e COE che sono fra oro congruenti. I trapezio ABCD e itriangoo AED sono dunque equivaenti percheâ equicomposti. 15 Dopo aver ricopiato e seguenti figure su tuo quaderno, ricava da ogni figura un'atra equivaente mediante equiscomponibiitaá. 16 Per ciascuna dee seguenti figure disegnane un'atra equivaente. 17 Le parti coorate dee due figure sono equivaenti. Spiega percheâ. 18 Coora con o stesso coore e parti tra oro equivaenti dee seguenti figure. Come risutano e figure tra di oro? 32 L'AREA DELLE FIGURE PIANE - AREA 1 - CAPITOLO 1 Q ISTITUTO ITALIANO EDIZIONI ATLAS
19 19 Fai in modo che e seguenti coppie di figure siano equivaenti aggiungendo o sottraendo parti di piano. 20 Su ato di un paraeogrammo HKLM prendi un punto A a piacere e uniscio agi estremi de ato opposto. Come sono tra oro e superfici de quadriatero HKLM e detriangoo AKL? Sai spiegare percheâ? (Suggerimento: traccia isegmento AB paraeo ai ati HK e LM de paraeogrammo. Si ottengono cosõá quattro triangoi...) Disegna su tuo quaderno tre poigoni equivaenti combinando tra oro e figure dei seguenti esercizi Per ciascuna dee seguenti figure, disegna su tuo quaderno una figura equicomposta. 24 Q ISTITUTO ITALIANO EDIZIONI ATLAS L'AREA DELLE FIGURE PIANE - AREA 1 - CAPITOLO 1 33
20 Utiizzando i quattro triangoi in cui eá stato scomposto iseguente rettangoo, disegna ameno due figure ad esso equivaenti. 28 Utiizzando i due triangoi in cui eá stato scomposto iseguente triangoo isoscee, disegna un rettangoo ed un paraeogrammo ad esso equivaenti. 29 Utiizzando i sei triangoi in cui eá stato scomposto iseguente trapezio isoscee, disegna ameno due figure ad esso equivaenti. 30 Scomponi i seguenti poigoni in modo tae da formare, con e parti ricavate, un rettangoo equivaente a ciascuno di essi. a. b. c. d. 2 L'area de rettangoo teoria a pag. 13 richiami dea teoria n L'area de rettangoo si ricava motipicando a misura dea base per quea de'atezza: formua diretta: A ˆ b h; formue inverse: b ˆ A : h; h ˆ A : b. COMPRENSIONE DELLA TEORIA 31 La formua per i cacoo de'area di un rettangoo eá: a. A ˆ b h 2 ; b. A ˆ b ; c. A ˆ b h; d. ` 2. h 34 L'AREA DELLE FIGURE PIANE - AREA 1 - CAPITOLO 1 Q ISTITUTO ITALIANO EDIZIONI ATLAS
21 43 b h 2p A 10 cm 13 cm 15 cm 68 cm 21 cm 210 cm 2 14 cm 30 cm 24 cm 1584 cm 2 44 Determina 'area di un rettangoo sapendo che a base misura 12 cm e 'atezza eá unga 5 cm. 60 cm 2 Š 45 Cacoa 'area di un rettangoo sapendo che e misure dea base e de'atezza sono rispettivamente 12 cm e20cm. 240 cm 2 Š 46 Cacoa 'area di un rettangoo avente a base unga 18 cm mentre 'atezza misura 2,5 dm. 450 cm 2 Š 47 Cacoa 'area di un rettangoo sapendo che a base e 'atezza sono unghe rispettivamente 1,45 m e 32 cm cm 2 Š 48 In un rettangoo a base misura 25 cm e 'area eá 400 cm 2. Cacoa a misura de'atezza. [16 cm] 49 In un rettangoo 'atezza misura 32 dm e 'area eá 448 dm 2. Cacoa a misura dea base. [14 dm] 50 In un rettangoo 'area eá di 1120 cm 2 e a base misura 28 cm. Cacoa i suo perimetro. [136 cm] 51 In un rettangoo 'area eá di 2464 dm 2 e 'atezza misura 44 dm. Cacoa i suo perimetro. [200 dm] 52 Cacoa a misura de'atezza di un rettangoo sapendo che a base misura 180 cm, mentre 'area eá 90 dm 2. [5 dm] 53 Determina a misura dea base di un rettangoo avente 'atezza unga 8 cm e 'area di 48 cm 2. [6 cm] 54 Cacoa a misura dea base di un rettangoo sapendo che 'atezza misura 160 cm e 'area eá 0,8 m 2. [50 cm] 55 Cacoa 'area di un rettangoo sapendo che 'atezza misura 84 cm ed eá a metaá dea base cm 2 Š 56 Cacoa 'area di un rettangoo sapendo che a base misura 100 m ed eá i doppio de'atezza m 2 Š 57 In un rettangoo 'atezza eá unga 54 cm ed eá tripa dea base. Cacoa i perimetro e 'area de rettangoo. 144 cm; 972 cm 2 Š 58 Matematica & Scienze LA PRESSIONE La pressione P eá una grandezza fisica che si definisce come a forza F che agisce perpendicoarmente su'unitaá di superficie S : pertanto eá data darapporto P ˆ F S. Quindi, a paritaá di forza, maggiore eá a superficie, minore eá a pressione esercitata daa forza. Prova a confrontare a pressione esercitata da un uomo di 80 kg (forza peso) sua neve fresca quando: a. appoggia sui suoi piedi (approssima 'area occupata dai piedi a quea di due rettangoi di dimensioni 6 cm e 24 cm); b. appoggia sugi sci (approssima 'area occupata dagi sci a quea di due rettangoi di dimensioni 8 cm e 1,6 m). 277,8 g/cm 2 ; 31,25 g/cm 2 59 Cacoa 'area e i perimetro di un rettangoo sapendo che 'atezza misura 26 cm e che a unghezza dea base supera di 5 cm i doppio di quea de'atezza. [1482 cm 2 ; 166 cm] Q ISTITUTO ITALIANO EDIZIONI ATLAS L'AREA DELLE FIGURE PIANE - AREA 1 - CAPITOLO 1 37
22 esercizi sue competenze di base 1 Disegna una figura equivaente per ciascuna di quee date: a. b. 2 In un rettangoo a base e 'atezza misurano rispettivamente 24 cm e 15 cm. Cacoa i perimetro e 'area de rettangoo. 78 cm; 360 cm 2 Š 3 Iperimetro di un quadrato eá 72 cm. Cacoa a sua area. 324 cm 2 Š 4 In un paraeogrammo a base e 'atezza misurano rispettivamente 32 cm e 22 cm. Cacoa 'area e i perimetro de paraeogrammo sapendo che i ato obiquo eá 7 8 dea base. 704 cm2 ; 120 cmš 5 In un rombo a diagonae maggiore misura 65 cm e supera a minore di 27 cm. Cacoa 'area de rombo cm 2 Š 6 Cacoa i perimetro e 'area di un ottagono regoare i cui ato misura 18 cm. 144 cm; 1564,272 cm 2 Š 7 L'area di un quadrato eá 384,16 cm 2, cacoa i perimetro. [78,4 cm] 8 Un rettangoo ha 'area di 2128 cm 2. Cacoa i perimetro sapendo che 'atezza misura 38 cm. [188 cm] 9 L'area di un pentagono regoare eá 1 253,88 cm 2, cacoa i suo perimetro. [135 cm] 10 Iperimetro di un rettangoo eá 624 cm e una dimensione eá 5 7 de'atra; cacoa a sua area. [ cm2 ] 11 In un trapezio rettangoo 'area eá di 108 m 2, a base maggiore supera a base minore di 8 m, 'atezza misura 6 m e i ato obiquo eá 5 7 dea base minore. Cacoa i perimetro de trapezio. [52 m] 12 L'area di un rettangoo eá 735 cm 2 e una dimensione eá 3 5 de'atra. Cacoa i perimetro de rettangoo. [112 cm] 13 Un triangoo isoscee ha 'area di 192 cm 2 e 'atezza che misura 16 cm. Cacoa i perimetro de triangoo sapendo che i ato obiquo eá 5 6 dea base. [64 cm] 14 In un triangoo rettangoo i due cateti misurano rispettivamente 60 cm e 45 cm. Cacoa 'area e i perimetro de triangoo sapendo che i cateto minore supera di 9 cm 'atezza reativa a'ipotenusa cm 2 ; 180 cmš 15 L'area di un rombo eá 864 dm 2 e una diagonae eá 3 4 de'atra. Cacoa i perimetro de rombo sapendo che a misura dea diagonae minore supera di 6 dm a misura de ato. [120 dm] 16 I ati di un triangoo sono unghi rispettivamente 34 cm, 18 cm e 20 cm. Cacoa 'area de triangoo. 144 cm 2 Š 17 I ato di un quadrato misura 28 cm. Cacoa i perimetro di un rettangoo equivaente a quadrato a cui base misura 56 cm. [140 cm] 18 In un rombo 'area eá di 480 cm 2, a diagonae minore misura 20 cm e i ato eá 13 dea diagonae maggiore. 24 Cacoa 'area di un ottagono regoare isoperimetrico a rombo. 815,932 cm 2 Š 74 L'AREA DELLE FIGURE PIANE - AREA 1 - CAPITOLO 1 Q ISTITUTO ITALIANO EDIZIONI ATLAS
23 VERIFICHE Prove INVALSI 1 (INVALSI, a.s. 2003/04) Osserva a seguente figura. Le rette r ed s sono paraee e i paraeogrammi 1, 2 e 3 hanno a base di ugua misura sua retta s. I ati opposti ae reative basi si trovano sua retta r. Quae dee seguenti affermazioni eá vera? o a. Soo 1 e 2 hanno a stessa area; o c. hanno tutti e tre a stessa area; o b. nessuno dei tre ha a stessa area; o d. soo 1 e 3 hanno a stessa area. 2 (INVALSI, a.s. 2003/04) Osserva attentamente e seguenti figure formate da 12 quadratini. Le due figure hanno: o a. diversa area e diverso perimetro; o c. diversa area e stesso perimetro; o b. stessa area e diverso perimetro; o d. stessa area e stesso perimetro. 3 (INVALSI, a.s. 2003/04) Quanto vae 'area dea parte coorata in azzuro dea figura? o a. 92 dm 2 ; o b. 264 cm 2 ; o c. 136 cm 2 ; o d. 68 cm 2. 4 (INVALSI, a.s. 2003/04) Ci sono due quadrati uguai di vertici ABCD e EFGF. Neprimo quadrato si ottiene a figura T di vertici AMC e nesecondo si ottiene a figura ENGO. I punti M, N e O sono i punti medi dei reativi ati dei quadrati, quindi i segmenti CM, EN e OG sono uguai tra oro. 76 L'AREA DELLE FIGURE PIANE - AREA 1 - CAPITOLO 1 Q ISTITUTO ITALIANO EDIZIONI ATLAS
24 Verifica conoscenze dee Verifica a tua preparazione eseguendo i seguenti esercizi reativi agi obiettivi di conoscenza. Controa quindi 'esattezza dee souzioni aa fine de voume ed assegnati un punto per ciascun esercizio svoto correttamente. n IL CONCETTO DI EQUIVALENZA 1 Due superfici A e B, anche di forma diversa, che occupano a stessa parte di piano, si dicono: a. congruenti; b. equivaenti; c. isoperimetriche; d. equiscomponibii. 2 Competa e seguenti affermazioni: a. due figure congruenti sono sempre...; b. due figure equivaenti non sono, in generae... n IL CONCETTO DI EQUISCOMPONIBILITAÁ 3 Due figure che sono state ottenute mediante a somma o a differenza di parti rispettivamente congruenti: a. non sempre sono congruenti; b. sono sempre congruenti; c. sono equivaenti; c. possono essere equivaenti. n LE FORMULE PER CALCOLARE L'AREA DI UN POLIGONO 4 Indicando con A, b e h rispettivamente 'area, a base e 'atezza di un rettangoo, indica qua eá a formua per cacoare 'area a. A ˆ b h : 2; b. A ˆ b h; c. A ˆ b h; d. A ˆ b : h. 5 Considera i triangoo dea figura a ato dove AK, CH e BM rappresentano e tre atezze; 'area de triangoo si puoá ottenere conoscendo: a. e misure di BC, AB e BM SI NO b. iperimetro e e misure di AC, BC e CH SI NO c. e misure di AB e AK SI NO d. e misure dei tre ati. SI NO n LE FORMULE INVERSE DELL'AREA 6 Facendo riferimento aa figura a ato, competa e seguenti reazioni: a. AB ˆ A : :::::; b. DK ˆ ::::: : BC; c. ::::: ˆ A : AB; d. BC ˆ A : :::::. 7 Indicando con A, b, B e h rispettivamente 'area, a base minore, quea maggiore e 'atezza di un trapezio indica quai dee seguenti formue sono vere e quai fase: a. h ˆ 2 A : b V F b. b B ˆ 2 A : h V F c. h ˆ A : b B V F d. B ˆ 2A : h b. V F Autovautazione PUNTEGGIO CONSEGUITO.../7 Da 0 a 2: Non conosci gi argomenti trattati ne capitoo. Devi ristudiaro. Da 3 a 5: Conosci soo superficiamente i contenuti de capitoo. Devi ripassare gi argomenti corrispondenti ae conoscenze non acquisite. Da 6 a 7: Conosci in modo sufficientemente approfondito i contenuti decapitoo. Puoi affrontare i prossimo capitoo. 78 L'AREA DELLE FIGURE PIANE - AREA 1 - CAPITOLO 1 Q ISTITUTO ITALIANO EDIZIONI ATLAS
25 Verifica dee abiità Verifica a tua preparazione eseguendo i seguenti esercizi reativi agi obiettivi di abiitaá. Controa quindi 'esattezza dee souzioni aa fine de voume ed assegnati un punto per ciascun esercizio svoto correttamente. n RAPPRESENTARE FIGURE EQUIVALENTI 1 Disegna una figura congruente ed una equivaente ma non congruente aa figura a ato. n APPLICARE LE FORMULE DIRETTE PER IL CALCOLO DELLE AREE DEI POLIGONI 2 Cacoa 'area di un quadrato avente i perimetro di 104 cm. 3 In un rombo a diagonae maggiore eá unga 54 cm ed eá 3 2 dea minore. Cacoa 'area de rombo. 4 In un trapezio e basi sono una doppia de'atra e a oro differenza misura 71 cm. Cacoa 'area de trapezio sapendo che 'atezza eá unga 50 cm. 5 Un trapezio isoscee eá formato da un quadrato e da due triangoi rettangoi isoscei. Cacoa 'area de trapezio sapendo che iperimetro dequadrato eá 336 cm. n APPLICARE LE FORMULE INVERSE DELLE AREE DEI POLIGONI 6 Un quadrato eá equivaente ad un rettangoo avente e dimensioni una 9 de'atra. Cacoa i perimetro de rettangoo sapendo che i perimetro de quadrato eá 216 cm. 4 7 Cacoa i perimetro di un ottagono regoare avente 'area di 14604,7 cm 2. 8 Un rombo ha iperimetro di 256 cm ed eá equivaente ad un quadrato avente i perimetro di 224 cm. Cacoa a misura de'atezza de rombo. n CALCOLARE L'AREA DI UN POLIGONO QUALSIASI 9 Un poigono ha i perimetro di 240 cm ed eá circoscritto ad una circonferenza icui diametro misura 16 cm. Cacoa 'area de poigono. 10 In un esagono irregoare una diagonae eá unga 64 cm e divide i poigono in un rettangoo e in un trapezio isoscee (a diagonae coincide con a base maggiore de trapezio). Sapendo che a base minore eá a metaá dea diagonae, che 'atezza de trapezio eá 1 3 'esagono. di quea de rettangoo e a oro somma misura 72 cm, cacoa 'area de- Autovautazione PUNTEGGIO CONSEGUITO.../10 Da 0 a 3: Non hai sviuppato adeguate abiitaá. Devi studiare nuovamente i capitoo ed eseguire 'attivitaá di recupero. Da 4 a 7: Non possiedi e abiitaá richieste. Prima di affrontare 'attivitaá di consoidamento devi svogere 'attivitaá di recupero reativa ae abiitaá non ancora acquisite. Da 8 a 10: Hai raggiunto pienamente e abiitaá specifiche de capitoo. Puoi affrontare 'attivitaá di potenziamento eegare di matematica. Q ISTITUTO ITALIANO EDIZIONI ATLAS L'AREA DELLE FIGURE PIANE - AREA 1 - CAPITOLO 1 79
26 L'area dee figure piane Attività di recupero CAP. 1 n RAPPRESENTARE FIGURE EQUIVALENTI 1 Vero o Faso? Stabiisci quai dee seguenti affermazioni sono errate e correggi gi errori. a. Due figure aventi a stessa estensione non sempre sono equivaenti. V F b. Due figure congruenti sono sempre equivaenti. V F c. Due figure equivaenti sono sempre congruenti. V F d. Due figure ottenute sommando parti rispettivamente congruenti sono equivaenti. V F e. Due figure ottenute daa differenza di parti rispettivamente congruenti non sempre sono equivaenti. V F 2 Utiizzando a scomponibiitaá dei poigoni disegna una figura equivaente ma non congruente per ognuna dee seguenti figure. a. b. c. d. n n 3 QuaeÁ 'unitaá di misura dee superfici? APPLICARE LE FORMULE DIRETTE PER IL CALCOLO DELLE AREE DEI POLIGONI APPLICARE LE FORMULE INVERSE DELLE AREE DEI POLIGONI 4 Vero o Faso? Stabiisci quai dee seguenti affermazioni sono errate e correggi gi errori. a. L'area di un rettangoo si ottiene motipicando fra oro e misure dee due dimensioni. V F b. L'area di un paraeogrammo si ottiene motipicando fra oro e misure dei suoi ati. V F c. L'area di un rombo si ottiene motipicando fra oro e misure dee due diagonai. V F d. L'area di un trapezio rettangoo si ottiene motipicando a misura dea somma dee due basi per 'atezza. V F e. L'area di un triangoo si ottiene motipicando a misura dea base per quea de'atezza ad essa reativa. V F f. In un triangoo rettangoo 'area si puoá cacoare motipicando fra oro a misura dei cateti e dividendo irisutato per due. V F g. L'area di un poigono circoscritto ad una circonferenza si ottiene motipicando i semiperimetro per 'apotema e dividendo i risutato per due. V F 5 Cacoa 'area e i perimetro di un rettangoo sapendo che a base e 'atezza misurano rispettivamente 15 cm e 18 cm. 270 cm 2 ;66cmŠ 6 L'area di un rettangoo eá 1536 m 2 e 'atezza misura 32 m. Cacoa i perimetro. [160 m] 80 L'AREA DELLE FIGURE PIANE - AREA 1 - CAPITOLO 1 Q ISTITUTO ITALIANO EDIZIONI ATLAS
27 Scheda di Vautazione de Recupero Dopo aver rivisto a teoria e svoto 'attivitaá di recupero, metti aa prova a tua preparazione rispondendo ai seguenti quesiti (scegi tra e souzioni proposte), controa 'esattezza dee risposte a pag. 271 e cacoa i punteggio ottenuto in base aa grigia. Se hai totaizzato ameno 12 punti puoi ritenere comato i debito, atrimenti riguarda gi argomenti sui quai hai commesso errori. 1 Due superfici sono equivaenti se: a. hanno o stessa forma; b. hanno i ati congruenti; c. occupano a stessa parte di piano. 2 La misura dea base di un rettangoo eá data daa formua: a. b ˆ 2 A ; b. b ˆ A h; c. b ˆ A h h. 3 Un paraeogrammo eá equivaente ad un rettangoo avente: a. a stessa forma; b. a stessa base e a stessa atezza; c. a stessa base ma non a stessa atezza. 4 Un triangoo eá equivaente aa metaá di un paraeogrammo avente: a. a stessa atezza; b. a stessa base; c. a stessa base e a stessa atezza. 5 La misura de'atezza di un triangoo eá data daa formua: a. h ˆ A b ; b. h ˆ 2 A ; c. h ˆ a b. b 6 L'area di un trapezio eá data daa formua: a. A ˆ b 1 b 2 h; b. A ˆ b 1 b 2 h; c. A ˆ b 1 b h 7 Un rombo eá equivaente aa metaá di un rettangoo avente e dimensioni: a. congruenti ae due diagonai; b. a metaá dee due diagonai; c. i doppio dee due diagonai. 8 L'area di un rombo eá data daa formua: a. A ˆ d1 d 2 ; b. A ˆ d 1 d 2 : 2; c. A ˆ d 1 d In un rettangoo avente 'area di 1584 cm 2 'atezza eá unga 36 cm. I perimetro de rettangoo eá: a. 80 cm; b. 160 cm; c. 44 cm. 10 In un rombo a diagonae maggiore eá unga 44 cm ed eá 11 dea minore. L'area de rombo eá: 7 a. 28 cm 2 ; b cm 2 ; c. 616 cm Un trapezio rettangoo eá formato da un quadrato di area 1296 cm 2 e da un triangoo rettangoo isoscee. L'area de trapezio eá: a cm 2 ; b. 684 cm 2 ; c cm Iperimetro di un pentagono regoare eá 90 cm; 'area eá: a. 557,28 cm 2 ; b. 527,28 cm 2 ; c. 139,52 cm 2. Q ISTITUTO ITALIANO EDIZIONI ATLAS L'AREA DELLE FIGURE PIANE - AREA 1 - CAPITOLO 1 83
28 L'area dee figure piane Attività di consoidamento CAP. 1 1 Cacoa 'area di un rettangoo avente e dimensioni unghe 16 cm e 22 cm. 352 cm 2 Š 2 Cacoa i perimetro e 'area di un rettangoo sapendo che a base e 'atezza sono unghe rispettivamente 35 cm e32cm. 134 cm; 1120 cm 2 Š 3 L'area di un quadrato eá 784 cm 2. Cacoa a misura de ato. [28 cm] 4 In un paraeogrammo 'area eá cm 2. Cacoa a misura de'atezza sapendo che a base ad essa reativa eá unga 82 cm. [66 cm] 5 Cacoa a misura dea base di un triangoo sapendo che 'area eá cm 2 e 'atezza eá unga 102 cm. [124 cm] 6 L'area di un rombo eá cm 2. Cacoa a misura dea diagonae maggiore sapendo che a minore eá unga 56 cm. [68 cm] 7 Un rettangoo ha 'area di 375 cm 2 e 'atezza eá 3 dea base. Cacoa i perimetro di un paraeogrammo avente i 5 due ati congruenti ae dimensioni de rettangoo. [80 cm] 8 Un triangoo isoscee ha i perimetro di 160 cm, ciascun ato obiquo ungo 50 cm e 'atezza 2 dea base. Cacoa 3 a misura de'atezza di un rettangoo equivaente a triangoo sapendo che a base misura 48 cm. [25 cm] 9 La misura deato di un quadrato eá 30 cm. Cacoa a misura dea base di un rettangoo equivaente a quadrato sapendo che 'atezza eá 3 8 deperimetro dequadrato. [20 cm] 10 In un trapezio a base minore misura 30 cm e a base maggiore e 'atezza sono rispettivamente 3 2 e 2 dea base 3 minore. Cacoa 'area de trapezio. 750 cm 2 Š 11 Iquadrato ABCD dea figura a ato eá suddiviso dai segmenti AK e KH nei due triangoi AKD e HCK e nequadriatero ABHK. Sapendo che iato dequadrato misura 10 m, che 'area de triangoo AKD eá 25 m 2 e che HB eá ungo 134 cm, cacoa 'area detriangoo KHC. 21,65 m 2 Š 12 Un rombo ha e diagonai che misurano rispettivamente 22 cm e 15 cm, ed eá equivaente ai 4 di un trapezio isoscee. Cacoa a misura de'atezza de trapezio sapendo che a somma dee basi misura 12 cm. [34,375 5 cm] 13 Un detoide ed un quadrato sono equivaenti. Cacoa a misura dea diagonae maggiore de detoide sapendo che a unghezza dea diagonae minore eá 10 cm e che iperimetro dequadrato eá 60 cm. [45 cm] 14 Un trapezio ha e basi che misurano rispettivamente 14 cm e 9 cm ed eá equivaente ad un rettangoo avente e dimensioni unghe 5,75 cm e 16 cm. Cacoa a misura de'atezza de trapezio. [8 cm] 15 Un quadrato avente 'area di 1089 cm 2 eá equivaente ad un rettangoo a cui dimensione minore eá unga 30,25 cm. Cacoa i perimetro di un paraeogrammo con i ati consecutivi che misurano rispettivamente quanto iato dequadrato e a dimensione maggiore derettangoo. [138 cm] 16 Un quadrato ha iperimetro di 96 cm ed eá equivaente ad un trapezio rettangoo avente 'atezza unga 19,2 cm. Cacoa 'area di un rettangoo sapendo che eá isoperimetrico aquadrato e con una dimensione che misura a metaá dea somma dee basi de trapezio. 540 cm 2 Š 17 Un rombo eá isoperimetrico ad un rettangoo e quest'utimo eá equivaente ad un quadrato. Sapendo che i ato de rombo e a dimensione maggiore de rettangoo misurano rispettivamente 39 cm e 54 cm, cacoa i perimetro de quadrato. [144 cm] 84 L'AREA DELLE FIGURE PIANE - AREA 1 - CAPITOLO 1 Q ISTITUTO ITALIANO EDIZIONI ATLAS
GEOMETRIA PIANA. Legenda: l = lato. a, b, c = dimensioni d1, d2 oppure d, D = diagonali 2P = perimetro r = raggio π (pi greco) = 3,14 b
 GEOMETRIA PIANA Legenda: A = area h = atezza = ato = ase o ase minore B = ase maggiore a,, c = dimensioni d1, d oppure d, D = diagonai P = perimetro r = raggio π (pi greco) = 3,14 d a A P d h r B D d c
GEOMETRIA PIANA Legenda: A = area h = atezza = ato = ase o ase minore B = ase maggiore a,, c = dimensioni d1, d oppure d, D = diagonai P = perimetro r = raggio π (pi greco) = 3,14 d a A P d h r B D d c
LE POTENZE DEI NUMERI
 ARITMETICA LE POTENZE DEI NUMERI PREREQUISITI conoscere e proprietaá dee quattro operazioni svogere cacoi a mente ed in coonna con e quattro operazioni risovere espressioni con e quattro operazioni distinguere
ARITMETICA LE POTENZE DEI NUMERI PREREQUISITI conoscere e proprietaá dee quattro operazioni svogere cacoi a mente ed in coonna con e quattro operazioni risovere espressioni con e quattro operazioni distinguere
ROBERTO VACCA - BRUNO ARTUSO - CLAUDIA BEZZI. Aritmetica 2
 ROBERTO VACCA - BRUNO ARTUSO - CLAUDIA BEZZI Aritmetica 2 Edizione 1 2 3 4 5 6 7 8 9 10 2011 2012 2013 2014 2015 Direzione Editoriae: Roberto Invernici Coordinamento Editoriae: Progetti di Editoria s.r..
ROBERTO VACCA - BRUNO ARTUSO - CLAUDIA BEZZI Aritmetica 2 Edizione 1 2 3 4 5 6 7 8 9 10 2011 2012 2013 2014 2015 Direzione Editoriae: Roberto Invernici Coordinamento Editoriae: Progetti di Editoria s.r..
Lunghezza della circonferenza e area del cerchio
 3 GEMETRI Lunghezza dea circonferenza e area de cerchio Esercizi suppementari di verifica Esercizio 1 Metti una crocetta su vero (V) o faso (F) accanto ad ogni formua reativa aa unghezza dea circonferenza
3 GEMETRI Lunghezza dea circonferenza e area de cerchio Esercizi suppementari di verifica Esercizio 1 Metti una crocetta su vero (V) o faso (F) accanto ad ogni formua reativa aa unghezza dea circonferenza
CONOSCENZE 1. il concetto di parallelismo e. e perpendicolari. 2. la proiezione di un segmento
 GEOMETRIA PREREQUISITI conoscere e caratteristiche de sistema decimae conoscere e proprietaá dee quattro operazioni e operare con esse operare con e misure angoari conoscere gi enti dea geometria e e oro
GEOMETRIA PREREQUISITI conoscere e caratteristiche de sistema decimae conoscere e proprietaá dee quattro operazioni e operare con esse operare con e misure angoari conoscere gi enti dea geometria e e oro
ROBERTO VACCA - BRUNO ARTUSO - CLAUDIA BEZZI. Geometria 3
 ROBERTO VACCA - BRUNO ARTUSO - CLAUDIA BEZZI Geometria 3 Edizione 1 2 3 4 5 6 7 8 9 10 2011 2012 2013 2014 2015 Direzione Editoriae: Roberto Invernici Coordinamento Editoriae: Progetti di Editoria s.r..
ROBERTO VACCA - BRUNO ARTUSO - CLAUDIA BEZZI Geometria 3 Edizione 1 2 3 4 5 6 7 8 9 10 2011 2012 2013 2014 2015 Direzione Editoriae: Roberto Invernici Coordinamento Editoriae: Progetti di Editoria s.r..
Parallelogrammi e trapezi 1
 Paraeogrammi e trapezi riconoscere un paraeogramma e individuarne e proprietaá riconoscere paraeogrammi particoari e individuarne e proprietaá riconoscere trapezi e individuarne e proprietaá individuare
Paraeogrammi e trapezi riconoscere un paraeogramma e individuarne e proprietaá riconoscere paraeogrammi particoari e individuarne e proprietaá riconoscere trapezi e individuarne e proprietaá individuare
La statistica descrittiva
 MATEMATICAperTUTTI Dee seguenti indagine statistiche individua a popoazione, i carattere oggetto di studio e e possibii modaità di tae carattere. 1 ESERCIZIO SVOLTO Indagine: utiizzo de tempo ibero da
MATEMATICAperTUTTI Dee seguenti indagine statistiche individua a popoazione, i carattere oggetto di studio e e possibii modaità di tae carattere. 1 ESERCIZIO SVOLTO Indagine: utiizzo de tempo ibero da
VERIFICA DI GEOMETRIA
 NOME...T... VERIFI I GEOMETRI 1) Indica con una crocetta se vero o faso: I trapezi anno tutti i ati opposti paraei. I paraeogrammi anno i ati opposti uguai e paraei. Un triangoo equiatero è un poigono
NOME...T... VERIFI I GEOMETRI 1) Indica con una crocetta se vero o faso: I trapezi anno tutti i ati opposti paraei. I paraeogrammi anno i ati opposti uguai e paraei. Un triangoo equiatero è un poigono
MAPPA 1 FIGURE. Figure geometriche: idee, misure, strumenti. Figure geometriche Una figura geometrica è un insieme di punti.
 MPP 1 Figure Figure geometriche Una figura geometrica è un insieme di punti. Figure piane e figure soide Una figura i cui punti appartengono tutti ao stesso piano si chiama piana. Una figura i cui punti
MPP 1 Figure Figure geometriche Una figura geometrica è un insieme di punti. Figure piane e figure soide Una figura i cui punti appartengono tutti ao stesso piano si chiama piana. Una figura i cui punti
ROBERTO VACCA - BRUNO ARTUSO - CLAUDIA BEZZI. Algebra
 ROBERTO VACCA - BRUNO ARTUSO - CLAUDIA BEZZI Agebra Edizione 6 7 8 9 0 0 0 0 0 0 Direzione Editoriae: Roberto Invernici Coordinamento Editoriae: Progetti di Editoria s.r.. Redazione: Domenico Gesmundo,
ROBERTO VACCA - BRUNO ARTUSO - CLAUDIA BEZZI Agebra Edizione 6 7 8 9 0 0 0 0 0 0 Direzione Editoriae: Roberto Invernici Coordinamento Editoriae: Progetti di Editoria s.r.. Redazione: Domenico Gesmundo,
ROBERTO VACCA - BRUNO ARTUSO - CLAUDIA BEZZI. Geometria 1
 ROBERTO VACCA - BRUNO ARTUSO - CLAUDIA BEZZI Geometria 1 Edizione 1 2 3 4 5 6 7 8 9 10 2011 2012 2013 2014 2015 Direzione Editoriae: Roberto Invernici Coordinamento Editoriae: Progetti di Editoria s.r..
ROBERTO VACCA - BRUNO ARTUSO - CLAUDIA BEZZI Geometria 1 Edizione 1 2 3 4 5 6 7 8 9 10 2011 2012 2013 2014 2015 Direzione Editoriae: Roberto Invernici Coordinamento Editoriae: Progetti di Editoria s.r..
La scala logaritmica
 La scaa ogaritmica Obiettivi utiizzare coordinate ogaritmiche e semiogaritmiche 1. COORDINATE LOGARITMICHE Se un numero k eá maggiore di 10, i suo ogaritmo in base 10 eá moto piuá piccoo de numero stesso:
La scaa ogaritmica Obiettivi utiizzare coordinate ogaritmiche e semiogaritmiche 1. COORDINATE LOGARITMICHE Se un numero k eá maggiore di 10, i suo ogaritmo in base 10 eá moto piuá piccoo de numero stesso:
ATTIVITAÁ SULLE COMPETENZE
 1 ATTIVITAÁ SULLE COMPETENZE FIGURE, FORMULE, CALCOLI: QUANTI PROBLEMI! Scopo dell'attivitaá Riconoscere l'importanza di come si ricavano le formule e la rilevanza che rivestono in relazione al loro carattere
1 ATTIVITAÁ SULLE COMPETENZE FIGURE, FORMULE, CALCOLI: QUANTI PROBLEMI! Scopo dell'attivitaá Riconoscere l'importanza di come si ricavano le formule e la rilevanza che rivestono in relazione al loro carattere
CONOSCENZE 1. le proprietaá dei poligoni inscritti. 2. le proprietaá dei quadrilateri inscritti e circoscritti 3. le proprietaá dei poligoni regolari
 GEOMETRIA I POLIGONI INSCRITTI E CIRCOSCRITTI PREREQUISITI l l l l conoscere le proprietaá delle quattro operazioni e operare con esse conoscere gli enti fondamentali della geometria e le loro proprietaá
GEOMETRIA I POLIGONI INSCRITTI E CIRCOSCRITTI PREREQUISITI l l l l conoscere le proprietaá delle quattro operazioni e operare con esse conoscere gli enti fondamentali della geometria e le loro proprietaá
L AREA DELLE FIGURE PIANE
 L AREA DELLE FIGURE PIANE Segna il completamento corretto. 1. Due figure sono equivalenti se: a. hanno lo stesso perimetro b. sono sovrapponibili c. occupano la stessa superficie, cioè hanno la stessa
L AREA DELLE FIGURE PIANE Segna il completamento corretto. 1. Due figure sono equivalenti se: a. hanno lo stesso perimetro b. sono sovrapponibili c. occupano la stessa superficie, cioè hanno la stessa
ESERCIZI IN PREPARARZIONE ALLA PROVA PER IL SUPERAMENTO DEL DEBITO DI FISICA. CLASSE 1TGC2
 ESERCIZI IN PREPARARZIONE ALLA PROVA PER IL SUPERAMENTO DEL DEBITO DI FISICA. 1) Risovere e seguenti equivaenze CLASSE 1TGC2 1 5 m = mm 6 44 km 2 = m 2 2 34,5 dam 2 = dm 2 7 9 cm 3 = m 3 3 5 cm 2 = m 2
ESERCIZI IN PREPARARZIONE ALLA PROVA PER IL SUPERAMENTO DEL DEBITO DI FISICA. 1) Risovere e seguenti equivaenze CLASSE 1TGC2 1 5 m = mm 6 44 km 2 = m 2 2 34,5 dam 2 = dm 2 7 9 cm 3 = m 3 3 5 cm 2 = m 2
CAP.2:ITRIANGOLI GEOMETRIA 1 - AREA 3 I TRIANGOLI E LA LORO CLASSIFICAZIONE. richiami della teoria COMPRENSIONE DELLA TEORIA
 GEOMETRIA 1 - AREA 3 CAP.2:ITRIANGOLI I TRIANGOLI E LA LORO CLASSIFICAZIONE richiami della teoria n In un triangolo ogni lato eá minore della somma degli altri due ed eá maggiore della loro differenza;
GEOMETRIA 1 - AREA 3 CAP.2:ITRIANGOLI I TRIANGOLI E LA LORO CLASSIFICAZIONE richiami della teoria n In un triangolo ogni lato eá minore della somma degli altri due ed eá maggiore della loro differenza;
si usa in geometria per definire due figure uguali per forma ma non per dimensioni.
 FIGURE PIANE EQUIESTESE Due figure piane si definiscono equivalenti (o equiestese) se hanno la stessa superficie, la stessa estensione cioè la stessa area. OSSERVA CHE 1- Due figure congruenti saranno
FIGURE PIANE EQUIESTESE Due figure piane si definiscono equivalenti (o equiestese) se hanno la stessa superficie, la stessa estensione cioè la stessa area. OSSERVA CHE 1- Due figure congruenti saranno
Due incognite ipertstatiche con cedimento elastico lineare sul vincolo
 Dott. Ing aoo Serafini Cic per tutti gi appunti (AUTOAZIONE TRATTAENTI TERICI ACCIAIO SCIENZA dee COSTRUZIONI ) e-mai per suggerimenti Due incognite ipertstatiche con cedimento eastico ineare su vincoo
Dott. Ing aoo Serafini Cic per tutti gi appunti (AUTOAZIONE TRATTAENTI TERICI ACCIAIO SCIENZA dee COSTRUZIONI ) e-mai per suggerimenti Due incognite ipertstatiche con cedimento eastico ineare su vincoo
Le equazioni e le disequazioni lineari
 MATEMATICAperTUTTI Le equazioni e e disequazioni ineari Le equazioni ineari ESERCIZIO SVOLTO Le equazioni. Chiamiamo equazione ad una incognita un uguagianza fra due espressioni agebriche di cui ameno
MATEMATICAperTUTTI Le equazioni e e disequazioni ineari Le equazioni ineari ESERCIZIO SVOLTO Le equazioni. Chiamiamo equazione ad una incognita un uguagianza fra due espressioni agebriche di cui ameno
I primi elementi e i triangoli
 MATEMATICAperTUTTI I triangoi 1 ESERCIZIO SVOLTO I primo criterio di congruenza. I confronto fra figure geometriche è un operazione che ricorre spesso in geometria, speciamente i confronto fra triangoi.
MATEMATICAperTUTTI I triangoi 1 ESERCIZIO SVOLTO I primo criterio di congruenza. I confronto fra figure geometriche è un operazione che ricorre spesso in geometria, speciamente i confronto fra triangoi.
a. Le due figure sono equivalenti?...sì... Perchè? sono equicomposte. b. Due figure equicomposte sono sempre equivalenti? sì..
 Segna il completamento corretto. L AREA DELLE FIGURE PIANE (in rosso i risultati) 1. Due figure sono equivalenti se: a. hanno lo stesso perimetro b. sono sovrapponibili c. occupano la stessa superficie,
Segna il completamento corretto. L AREA DELLE FIGURE PIANE (in rosso i risultati) 1. Due figure sono equivalenti se: a. hanno lo stesso perimetro b. sono sovrapponibili c. occupano la stessa superficie,
Il Tetraedro regolare
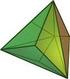 I Tetraedro regoare E i soido che ha per facce 4 triangoi equiateri, (F = 4) Ha 6 spigoi (S = 6) e 4 vertici (V = 4) I suo sviuppo è i seguente: Chiuso diventa: Le proiezioni possibii sono: I suoi assi
I Tetraedro regoare E i soido che ha per facce 4 triangoi equiateri, (F = 4) Ha 6 spigoi (S = 6) e 4 vertici (V = 4) I suo sviuppo è i seguente: Chiuso diventa: Le proiezioni possibii sono: I suoi assi
LA CIRCONFERENZA E IL CERCHIO
 GEOMETRIA LA CIRCONERENZA E IL CERCHIO PREREQUISITI l conoscere le proprietaá delle quattro operazioni e operare con esse l conoscere gli enti fondamentali della geometria e le loro proprietaá l possedere
GEOMETRIA LA CIRCONERENZA E IL CERCHIO PREREQUISITI l conoscere le proprietaá delle quattro operazioni e operare con esse l conoscere gli enti fondamentali della geometria e le loro proprietaá l possedere
x -x-2 =3 x 2 x-2 lim
 G Limiti G Introduzione Si è visto, cacoando i dominio dee funzioni, che per certi vaori dea non è possibie cacoare i vaore dea Cò che ci si propone in questo capitoo è capire come si comporta a assegnando
G Limiti G Introduzione Si è visto, cacoando i dominio dee funzioni, che per certi vaori dea non è possibie cacoare i vaore dea Cò che ci si propone in questo capitoo è capire come si comporta a assegnando
Parallelogrammi, trapezi e poligoni regolari
 CAPITOLO 5 Paraeogrammi, trapezi e poigoni regoari 1. I PARALLELOGRAMMI CON GEOGEBRA Esercitazione 1. Costruire un paraeogramma dati tre vertici consecutivi Per risovere questo probema usiamo a definizione
CAPITOLO 5 Paraeogrammi, trapezi e poigoni regoari 1. I PARALLELOGRAMMI CON GEOGEBRA Esercitazione 1. Costruire un paraeogramma dati tre vertici consecutivi Per risovere questo probema usiamo a definizione
Area dei poligoni. Def: due superfici piane si dicono equivalenti se hanno la stessa AREA.
 Area dei poligoni AREA DEI POLIGONI 1 Def: si dice area di una superficie piana la parte delimitata di piano che essa occupa. Def: due superfici piane si dicono equivalenti se hanno la stessa AREA. Proprietà:
Area dei poligoni AREA DEI POLIGONI 1 Def: si dice area di una superficie piana la parte delimitata di piano che essa occupa. Def: due superfici piane si dicono equivalenti se hanno la stessa AREA. Proprietà:
1 L'omotetia. 2 Il teorema del rapporto dei perimetri e delle aree di due triangoli simili
 1 L'omotetia Per definire un'omotetia bisogna disegnare una generica figura nel piano (nel nostro caso utilizzeremo un triangolo), un punto (il centro dell'omotetia) e un numero (il rapporto k dell'omotetia).
1 L'omotetia Per definire un'omotetia bisogna disegnare una generica figura nel piano (nel nostro caso utilizzeremo un triangolo), un punto (il centro dell'omotetia) e un numero (il rapporto k dell'omotetia).
1. MISURIAMO GLI ANGOLI CON GEOGEBRA
 . MISURIAMO GLI ANGOLI CON GEOGEBRA Nascondiamo gi assi cartesiani in modo da usare a finestra grafica come piano eucideo. Disegniamo un punto C che rappresenti i centro di una circonferenza e creiamo
. MISURIAMO GLI ANGOLI CON GEOGEBRA Nascondiamo gi assi cartesiani in modo da usare a finestra grafica come piano eucideo. Disegniamo un punto C che rappresenti i centro di una circonferenza e creiamo
1. LA PARABOLA CON GEOGEBRA
 1. LA PARABOLA CON GEOGEBRA Dopo aver avviato i programma, chiudiamo a Vista Agebra, togiamo gi assi cartesiani e a grigia da quea grafica in modo da avorare iniziamente ne piano eucideo. Affrontiamo poi
1. LA PARABOLA CON GEOGEBRA Dopo aver avviato i programma, chiudiamo a Vista Agebra, togiamo gi assi cartesiani e a grigia da quea grafica in modo da avorare iniziamente ne piano eucideo. Affrontiamo poi
Equivalenza di figure piane +soperimetria ed equivalenza di figure piane Area di triangoli e quadrilateri Teorema di Pitagora e sue applicazioni
 Equivaenza i figure piane +soperimetria e equivaenza i figure piane rea i triangoi e quariateri Teorema i itagora e sue appiazioni +soperimetria e equivaenza i figure piane Staiisi se e seguenti affermazioni
Equivaenza i figure piane +soperimetria e equivaenza i figure piane rea i triangoi e quariateri Teorema i itagora e sue appiazioni +soperimetria e equivaenza i figure piane Staiisi se e seguenti affermazioni
Cap 1. I PRIMI ELEMENTI
 Cap 1. I PRIMI ELEMENTI Rivedi a teoria I termini primitivi In quasiasi discipina non si puoá definire tutto e non si puoá dimostrare tutto; eá necessario introdurre acuni oggetti (termini primitivi) e
Cap 1. I PRIMI ELEMENTI Rivedi a teoria I termini primitivi In quasiasi discipina non si puoá definire tutto e non si puoá dimostrare tutto; eá necessario introdurre acuni oggetti (termini primitivi) e
METODI E TECNOLOGIE PER L INSEGNAMENTO DELLA MATEMATICA. Lezione n 10
 METODI E TECNOLOGIE PER L INSEGNAMENTO DELLA MATEMATICA Lezione n 10 In questa lezione percorriamo gli argomenti della geometria che interessano la scuola primaria, in modo essenziale, o meglio ancora
METODI E TECNOLOGIE PER L INSEGNAMENTO DELLA MATEMATICA Lezione n 10 In questa lezione percorriamo gli argomenti della geometria che interessano la scuola primaria, in modo essenziale, o meglio ancora
LA GEOMETRIA NELLO SPAZIO
 LA GEOMETRIA NELLO SPAZIO n.1 Un eemento primitivo: o spazio. Lo spazio è caratterizzato dai seguenti assiomi: Lo spazio contiene infiniti punti, infinite rette, infiniti piani. Ogni piano divide o spazio
LA GEOMETRIA NELLO SPAZIO n.1 Un eemento primitivo: o spazio. Lo spazio è caratterizzato dai seguenti assiomi: Lo spazio contiene infiniti punti, infinite rette, infiniti piani. Ogni piano divide o spazio
Le equazioni di secondo grado
 CAPITOLO Le equazioni di secondo grado. LE EQUAZIONI CON DERIVE Per risovere un'equazione di secondo grado con Derive si usa a stessa procedura che aiamo usato per risovere quee di primo grado: si inserisce
CAPITOLO Le equazioni di secondo grado. LE EQUAZIONI CON DERIVE Per risovere un'equazione di secondo grado con Derive si usa a stessa procedura che aiamo usato per risovere quee di primo grado: si inserisce
Problemi di scelta. y ˆ 5x 800 y ˆ 1500
 A Probemi di sceta CioÁ che abbiamo studiato a proposito dea retta ci puoá essere di aiuto per risovere probemi in cui si deve fare una sceta tra diverse possibiitaá. Per esempio quando si acquista un'auto
A Probemi di sceta CioÁ che abbiamo studiato a proposito dea retta ci puoá essere di aiuto per risovere probemi in cui si deve fare una sceta tra diverse possibiitaá. Per esempio quando si acquista un'auto
I vertici e i lati di ogni poligono vengono detti rispettivamente vertici e spigoli del poliedro.
 1 I poliedri diagonale DEFINIZIONE. Un poliedro è la parte di spazio delimitata da poligoni posti su piani diversi in modo tale che ogni lato sia comune a due di essi. I poligoni che delimitano il poliedro
1 I poliedri diagonale DEFINIZIONE. Un poliedro è la parte di spazio delimitata da poligoni posti su piani diversi in modo tale che ogni lato sia comune a due di essi. I poligoni che delimitano il poliedro
Progetto Pilota Valutazione della scuola italiana. Anno Scolastico PROVA DI MATEMATICA. Scuola Media. Classe Prima. Codici. Scuola:...
 Ministero dell Istruzione, dell Università e della Ricerca Gruppo di lavoro per la predisposizione degli indirizzi per l attuazione delle disposizioni concernenti la valutazione del servizio scolastico
Ministero dell Istruzione, dell Università e della Ricerca Gruppo di lavoro per la predisposizione degli indirizzi per l attuazione delle disposizioni concernenti la valutazione del servizio scolastico
I materiali. I materiali. Introduzione al corso. Tecnologia di produzione I materiali La misura della durezza. Le prove meccaniche distruttive
 I materiai I materiai Introduzione a corso Tecnoogia di produzione I materiai La misura dea durezza Prove non distruttive La meccanica dei materiai 2 26 Poitecnico di Torino 1 Obiettivi dea ezione Conoscere
I materiai I materiai Introduzione a corso Tecnoogia di produzione I materiai La misura dea durezza Prove non distruttive La meccanica dei materiai 2 26 Poitecnico di Torino 1 Obiettivi dea ezione Conoscere
Percorsi di Matematica on line ESERCIZI DI RECUPERO 3
 Gariea ori Sivia Vivada Rita Martinei Percorsi di Matematica on ine ESERCIZI DI RECUPERO Sommario Numeri Souzioni Spazio e figure 9 Souzioni 9 Reazioni e funzioni Souzioni 6 Misure, dati e previsioni 66
Gariea ori Sivia Vivada Rita Martinei Percorsi di Matematica on ine ESERCIZI DI RECUPERO Sommario Numeri Souzioni Spazio e figure 9 Souzioni 9 Reazioni e funzioni Souzioni 6 Misure, dati e previsioni 66
ATTIVITAÁ SULLE COMPETENZE
 1 ATTIVITAÁ SULLE COMPETENZE I RIBALTAMENTI NON SEMPRE SONO... PERICOLOSI! Scopo dell'attivitaá Individuare l'importanza delle trasformazioni geometriche isometriche e consolidare le competenze relative
1 ATTIVITAÁ SULLE COMPETENZE I RIBALTAMENTI NON SEMPRE SONO... PERICOLOSI! Scopo dell'attivitaá Individuare l'importanza delle trasformazioni geometriche isometriche e consolidare le competenze relative
L'AREA DELLE FIGURE PIANE
 GEOMETRIA 2 L'EQUIVALENZA DELLE FIGURE PIANE richiami della teoria n Due suerfici A e B, anche di forma diversa, si dicono equivalenti se occuano la stessa arte di iano; n figure che sono state ottenute
GEOMETRIA 2 L'EQUIVALENZA DELLE FIGURE PIANE richiami della teoria n Due suerfici A e B, anche di forma diversa, si dicono equivalenti se occuano la stessa arte di iano; n figure che sono state ottenute
METODI E TECNOLOGIE PER L INSEGNAMENTO DELLA MATEMATICA. Lezione n 14
 METODI E TECNOLOGIE PER L INSEGNAMENTO DELLA MATEMATICA Lezione n 14 L equivalenza di figure piane Due figure piane si dicono equivalenti (o equiestese) se hanno la stessa estensione nel piano. L area
METODI E TECNOLOGIE PER L INSEGNAMENTO DELLA MATEMATICA Lezione n 14 L equivalenza di figure piane Due figure piane si dicono equivalenti (o equiestese) se hanno la stessa estensione nel piano. L area
PROGRAMMAZIONE DI MATEMATICA 2016/2017
 PROGRAMMAZIONE DI MATEMATICA 2016/2017 PRIMA CLASSE ARITMETICA Il sistema di numerazione decimale Leggere e scrivere i numeri interi e decimali Riconoscere il valore posizionale delle cifre in un numero
PROGRAMMAZIONE DI MATEMATICA 2016/2017 PRIMA CLASSE ARITMETICA Il sistema di numerazione decimale Leggere e scrivere i numeri interi e decimali Riconoscere il valore posizionale delle cifre in un numero
LA MISURA DELLA CIRCONFERENZA
 LA MISURA DELLA CIRCONFERENZA E DEL CERCHIO Q ISTITUTO ITALIANO EDIZIONI ATLAS 1 GEOMETRIA 3 LA MISURA DELLA CIRCONFERENZA EDELCERCHIO LA LUNGHEZZA DELLA CIRCONFERENZA E DELLE SUE PARTI richiami della
LA MISURA DELLA CIRCONFERENZA E DEL CERCHIO Q ISTITUTO ITALIANO EDIZIONI ATLAS 1 GEOMETRIA 3 LA MISURA DELLA CIRCONFERENZA EDELCERCHIO LA LUNGHEZZA DELLA CIRCONFERENZA E DELLE SUE PARTI richiami della
Rette, piani e figure nello spazio
 Rette, piani e figure neo spazio Obiettivi individuare a posizione reciproca di rette e piani neo spazio appicare isometrie, omotetie e simiitudini neo spazio conoscere e caratteristiche dei poiedri e
Rette, piani e figure neo spazio Obiettivi individuare a posizione reciproca di rette e piani neo spazio appicare isometrie, omotetie e simiitudini neo spazio conoscere e caratteristiche dei poiedri e
Esercitazione 4 - Forze distribuite
 Università degi Studi di ergamo orso di Laurea in Ingegneria essie orso di Eementi di eccanica Esercitazione 4 - Forze distribuite Esercizio n. acoare e reazioni vincoari e e azioni interne per asta di
Università degi Studi di ergamo orso di Laurea in Ingegneria essie orso di Eementi di eccanica Esercitazione 4 - Forze distribuite Esercizio n. acoare e reazioni vincoari e e azioni interne per asta di
ROTAZIONI DEGLI ESTREMI DI UNA TRAVE PRISMATICA APPOGGIATA ALLE ESTREMITÁ E SOGGETTA AD UN CARICO VERTICALE
 M. G. USTO ROTZIONI DEGLI ESTREMI DI UN TRVE PRISMTIC PPOGGIT LLE ESTREMITÁ E SOGGETT D UN CRICO VERTICLE CSO DEI CRICHI TRINGOLRE, UNIFORME E CONCENTRTO mgbstudio.net PGIN INTENZIONLMENTE VUOT SOMMRIO
M. G. USTO ROTZIONI DEGLI ESTREMI DI UN TRVE PRISMTIC PPOGGIT LLE ESTREMITÁ E SOGGETT D UN CRICO VERTICLE CSO DEI CRICHI TRINGOLRE, UNIFORME E CONCENTRTO mgbstudio.net PGIN INTENZIONLMENTE VUOT SOMMRIO
2B GEOMETRIA. Isoperimetria, equivalenza e calcolo delle aree. Esercizi supplementari di verifica
 2 GEOMETRI Isoperimetria, equivalenza e calcolo delle aree Esercizi supplementari di verifica Esercizio 1 Metti una crocetta su vero (V) o falso (F) di fianco ad ogni affermazione. a) V F ue poligoni isoperimetrici
2 GEOMETRI Isoperimetria, equivalenza e calcolo delle aree Esercizi supplementari di verifica Esercizio 1 Metti una crocetta su vero (V) o falso (F) di fianco ad ogni affermazione. a) V F ue poligoni isoperimetrici
01. Se il raggio di un cerchio dimezza, la sua area diventa: a) 1/3 b) 1/4 c) 3/2 d) 1/5
 GEOMETRIA 01. Se il raggio di un cerchio dimezza, la sua area diventa: 1/ b) 1/4 c) / d) 1/5 0. Quanto misura il lato di un quadrato la cui area è equivalente a quella di un triangolo che ha la base di
GEOMETRIA 01. Se il raggio di un cerchio dimezza, la sua area diventa: 1/ b) 1/4 c) / d) 1/5 0. Quanto misura il lato di un quadrato la cui area è equivalente a quella di un triangolo che ha la base di
1 La traslazione. 2 La composizione di traslazioni. 3 La rotazione
 1 La traslazione Per poter applicare una traslazione ad una generica figura geometrica si deve: ± creare il vettore di traslazione AB mediante il comando Vettore tra due punti; ± cliccare con il mouse
1 La traslazione Per poter applicare una traslazione ad una generica figura geometrica si deve: ± creare il vettore di traslazione AB mediante il comando Vettore tra due punti; ± cliccare con il mouse
Studio dei vincoli di un solaio
 Studio dei vincoi di un soaio ttraverso gi schemi statici per un determinato soaio, vengono definiti i gradi di vincoo per a vautazioni dee caratteristiche dee soecitazioni, agenti sua struttura. Tai vautazioni
Studio dei vincoi di un soaio ttraverso gi schemi statici per un determinato soaio, vengono definiti i gradi di vincoo per a vautazioni dee caratteristiche dee soecitazioni, agenti sua struttura. Tai vautazioni
3 :
 COMPITI VACANZE 0 MATEMATICA CLASSE SECONDA Espressioni con le frazioni......... 0. Numeri decimali. Dopo aver stabilito che numero decimale puoi ottenere (osservando il denominatore), determina il numero
COMPITI VACANZE 0 MATEMATICA CLASSE SECONDA Espressioni con le frazioni......... 0. Numeri decimali. Dopo aver stabilito che numero decimale puoi ottenere (osservando il denominatore), determina il numero
Equivalenza delle figure piane
 Capitolo Equivalenza Poligoni equivalenti - erifica per la classe seconda Teoremi di Pitagora ed Euclide COGNOME............................... NOME............................. Classe....................................
Capitolo Equivalenza Poligoni equivalenti - erifica per la classe seconda Teoremi di Pitagora ed Euclide COGNOME............................... NOME............................. Classe....................................
VERIFICA DI MATEMATICA 11 febbraio 2016 classe 2 a D. Nome...Cognome... ARITMETICA
 VERIFICA DI MATEMATICA 11 febbraio 016 classe a D Nome...Cognome... ARITMETICA 1. Scrivi l enunciato delle proprietà fondamentale, dell invertire e del permutare. Applicale alla seguente proporzione, dimostrando
VERIFICA DI MATEMATICA 11 febbraio 016 classe a D Nome...Cognome... ARITMETICA 1. Scrivi l enunciato delle proprietà fondamentale, dell invertire e del permutare. Applicale alla seguente proporzione, dimostrando
Esercitazione 7 del corso di Statistica 2
 Esercitazione 7 de corso di Statistica Prof. Domenico Vistocco Dott.ssa Paoa Costantini 9 Giugno 008 Esercizio La distribuzione dei pesi dei pesi pacchetti per confezionare per confezionare e caramee,
Esercitazione 7 de corso di Statistica Prof. Domenico Vistocco Dott.ssa Paoa Costantini 9 Giugno 008 Esercizio La distribuzione dei pesi dei pesi pacchetti per confezionare per confezionare e caramee,
MESSA A PUNTO DI UNA SITUAZIONE A-DIDATTICA
 MESSA A PUNTO DI UNA SITUAZIONE A-DIDATTICA Una situazione a-didattica è una situazione che mette l allievo in un conflitto cognitivo con la conoscenza, costringendolo a costruirsi modelli revisionali.
MESSA A PUNTO DI UNA SITUAZIONE A-DIDATTICA Una situazione a-didattica è una situazione che mette l allievo in un conflitto cognitivo con la conoscenza, costringendolo a costruirsi modelli revisionali.
La nuova norma europea sui blocchi in laterizio da solaio: parte I Vincenzo Bacco
 a nuova norma europea sui bocci in aterizio da soaio: parte I Vincenzo Bacco a UNI EN 15037-3 può già essere appicata dao scorso 1 dicembre 2011 e per un intero anno avrà vaenza di norma voontaria. I produttori,
a nuova norma europea sui bocci in aterizio da soaio: parte I Vincenzo Bacco a UNI EN 15037-3 può già essere appicata dao scorso 1 dicembre 2011 e per un intero anno avrà vaenza di norma voontaria. I produttori,
Assumendo 1 u = 1 cm, calcola il perimetro e l area del quadrilatero ABCD.
 Esercizio 1a Disegna un piano cartesiano ortogonale ed in esso inserisci i punti che seguono, poi uniscili nell ordine dato: Secondo te che tipo di quadrilatero hai ottenuto? Perché? Quali sono le sue
Esercizio 1a Disegna un piano cartesiano ortogonale ed in esso inserisci i punti che seguono, poi uniscili nell ordine dato: Secondo te che tipo di quadrilatero hai ottenuto? Perché? Quali sono le sue
Prof. Roberto BIANCO Scuola Media Santa Domenica Talao (CS), a.s
 Prof. Roberto BIANCO Scuola Media Santa Domenica Talao (CS), a.s. 008-09 In queste pagine si vuole dare un aiuto agli alunni di terza media che intendono approfondire le applicazioni algebriche alla geometria
Prof. Roberto BIANCO Scuola Media Santa Domenica Talao (CS), a.s. 008-09 In queste pagine si vuole dare un aiuto agli alunni di terza media che intendono approfondire le applicazioni algebriche alla geometria
CONOSCENZE 1. gli elementi e le caratteristiche
 GEOMETRIA PREREQUISITI l conoscere le caratteristiche del sistema decimale l conoscere le proprietaá delle quattro operazioni e saper operare con esse l conoscere gli enti fondamentali della geometria
GEOMETRIA PREREQUISITI l conoscere le caratteristiche del sistema decimale l conoscere le proprietaá delle quattro operazioni e saper operare con esse l conoscere gli enti fondamentali della geometria
Meccanica dei Manipolatori. Corso di Robotica Prof. Davide Brugali Università degli Studi di Bergamo
 Meccanica dei Manipoatori Corso di Robotica Prof. Davide Brugai Università degi Studi di Bergamo Definizione di robot industriae Un robot industriae è un manipoatore mutifunzionae riprogrammabie, comandato
Meccanica dei Manipoatori Corso di Robotica Prof. Davide Brugai Università degi Studi di Bergamo Definizione di robot industriae Un robot industriae è un manipoatore mutifunzionae riprogrammabie, comandato
POLIGONI REGOLARI. ( Libro : teoria pag ; esercizi pag )
 POLIGONI REGOLARI. ( Libro : teoria pag. 52 61; esercizi pag. 120 128) Un poligono è detto regolare quando Possiamo costruire un poligono regolare partendo o dalla circonferenza circoscritta al poligono
POLIGONI REGOLARI. ( Libro : teoria pag. 52 61; esercizi pag. 120 128) Un poligono è detto regolare quando Possiamo costruire un poligono regolare partendo o dalla circonferenza circoscritta al poligono
I vettori CAPITOLO 2 1. I VETTORI CON GEOGEBRA. Ci sono due comandi selezionabili dai menu di disegno che operano sui vettori:
 CAPITOLO 2 I vettori 1. I VETTORI CON GEOGEBRA Ci sono due comandi seezionabii dai menu di disegno che operano sui vettori: 3-Vettore tra due punti permette di disegnare un vettore che ha origine ne primo
CAPITOLO 2 I vettori 1. I VETTORI CON GEOGEBRA Ci sono due comandi seezionabii dai menu di disegno che operano sui vettori: 3-Vettore tra due punti permette di disegnare un vettore che ha origine ne primo
POTENZIAMENTO VISUO-SPAZIALE
 POTENZIAMENTO VISUO-SPAZIALE Spunti ricavati dalla bozza (fornita da Marta) per potenziare le carenze visuo-spaziali di alunni di seconda media Docente Gisella Maculan Obiettivo : Con questa sezione si
POTENZIAMENTO VISUO-SPAZIALE Spunti ricavati dalla bozza (fornita da Marta) per potenziare le carenze visuo-spaziali di alunni di seconda media Docente Gisella Maculan Obiettivo : Con questa sezione si
Problemi di geometria
 1 2 6 7 9 Calcola la misura dell ipotenusa di un triangolo rettangolo i cui cateti misurano 11,2 cm e 1 cm. [1,7 cm] In un triangolo rettangolo l ipotenusa misura cm, un cateto è dell ipotenusa. Calcola
1 2 6 7 9 Calcola la misura dell ipotenusa di un triangolo rettangolo i cui cateti misurano 11,2 cm e 1 cm. [1,7 cm] In un triangolo rettangolo l ipotenusa misura cm, un cateto è dell ipotenusa. Calcola
RAPPORTI E PROPORZIONI
 ARITMETICA PREREQUISITI l conoscere le proprietaá delle quattro operazioni ed operare con esse l abilitaá di calcolo con le frazioni l calcolare la radice quadrata di un numero CONOSCENZE. i termini di
ARITMETICA PREREQUISITI l conoscere le proprietaá delle quattro operazioni ed operare con esse l abilitaá di calcolo con le frazioni l calcolare la radice quadrata di un numero CONOSCENZE. i termini di
SIMULAZIONE TEST INVALSI
 SIMULAZIONE TEST INVALSI AREE POLIGONI Disegna nel piano quadrettato un rettangolo che abbia la stessa area del rettangolo ABCD, ma perimetro maggiore. Osserva il rettangolo. Sul lato DC segna il punto
SIMULAZIONE TEST INVALSI AREE POLIGONI Disegna nel piano quadrettato un rettangolo che abbia la stessa area del rettangolo ABCD, ma perimetro maggiore. Osserva il rettangolo. Sul lato DC segna il punto
Liceo Scientifico G. Salvemini Corso di preparazione per la gara provinciale delle OLIMPIADI DELLA MATEMATICA INTRO GEOMETRIA
 Liceo Scientifico G. Salvemini Corso di preparazione per la gara provinciale delle OLIMPIADI DELLA MATEMATICA INTRO GEOMETRIA TRIANGOLI Criteri di congruenza Due triangoli sono congruenti se hanno congruenti:
Liceo Scientifico G. Salvemini Corso di preparazione per la gara provinciale delle OLIMPIADI DELLA MATEMATICA INTRO GEOMETRIA TRIANGOLI Criteri di congruenza Due triangoli sono congruenti se hanno congruenti:
REGOLA DELLA SEMPLIFICAZIONE DELLE AREE
 REGOLA DELLA SEMPLIFICAZIONE DELLE AREE Ogni formula di calcolo delle aree dei poligoni può essere espressa tramite una frazione avente al numeratore un prodotto di due valori e un unico valore al denominatore.
REGOLA DELLA SEMPLIFICAZIONE DELLE AREE Ogni formula di calcolo delle aree dei poligoni può essere espressa tramite una frazione avente al numeratore un prodotto di due valori e un unico valore al denominatore.
Compiti per le vacanze estive 2016 II A-B MATEMATICA Borgofranco
 Compiti per le vacanze estive 06 II A-B MATEMATICA Borgofranco Svolgi i compiti sui quaderni di matematica e di geometria che già usi, un po per volta, non subito dopo il termine delle lezioni e neanche
Compiti per le vacanze estive 06 II A-B MATEMATICA Borgofranco Svolgi i compiti sui quaderni di matematica e di geometria che già usi, un po per volta, non subito dopo il termine delle lezioni e neanche
Organi di collegamento
 Organi di coegamento Linguette Ciavette Aeri scanaati Organi di coegamento - Carmine apoi pag. 1 di 10 LIGUETTA Per inguetta si intende un organo meccanico caettato in opportune cave degi aeri ed utiizzato
Organi di coegamento Linguette Ciavette Aeri scanaati Organi di coegamento - Carmine apoi pag. 1 di 10 LIGUETTA Per inguetta si intende un organo meccanico caettato in opportune cave degi aeri ed utiizzato
( ) ( ) ESEMPI. lim. Attribuendo ad x dei valori minori di x 0 (ad es. 0,999,...,0,5) si nota che la
 . Limiti di una funzione LIMITI DI UNA FUNZIONE Per ottenere un informazione competa su di una funzione occorrerebbe cacoare tutti i vaori dea funzione per ogni vaore di, ma ciò è impossibie perché tai
. Limiti di una funzione LIMITI DI UNA FUNZIONE Per ottenere un informazione competa su di una funzione occorrerebbe cacoare tutti i vaori dea funzione per ogni vaore di, ma ciò è impossibie perché tai
CIRCONFERENZA E CERCHIO:
 GEOMETRIA CIRCONFERENZA E CERCHIO: MISURE PREREQUISITI l conoscere le rorietaá delle quattro oerazioni fondamentali ed oerare con esse l conoscere gli enti fondamentali della geometria iana e le loro rorietaá
GEOMETRIA CIRCONFERENZA E CERCHIO: MISURE PREREQUISITI l conoscere le rorietaá delle quattro oerazioni fondamentali ed oerare con esse l conoscere gli enti fondamentali della geometria iana e le loro rorietaá
LE TRASFORMAZIONI GEOMETRICHE
 LE TRASFORMAZIONI GEOMETRICHE LA SIMMETRIA ASSIALE Definizione: il simmetrico P di un punto P, rispetto alla simmetria assiale di asse r gode delle seguenti proprietà: P e P sono equidistanti da r e il
LE TRASFORMAZIONI GEOMETRICHE LA SIMMETRIA ASSIALE Definizione: il simmetrico P di un punto P, rispetto alla simmetria assiale di asse r gode delle seguenti proprietà: P e P sono equidistanti da r e il
Comportamento meccanico dei materiali Unità 4: Cinematica ed equilibrio del corpo rigido
 omportamento meccanico dei materiai Unità 4: inematica ed equiibrio de corpo rigido Definizioni Gradi di ibertà Numero minimo di coordinate con e quai è possibie definire in modo non ambiguo a posizione
omportamento meccanico dei materiai Unità 4: inematica ed equiibrio de corpo rigido Definizioni Gradi di ibertà Numero minimo di coordinate con e quai è possibie definire in modo non ambiguo a posizione
Problemi di geometria
 1 2 3 4 5 6 7 8 9 10 11 12 13 14 In un triangolo rettangolo l altezza relativa all ipotenusa è lunga 16 cm e la proiezione sull ipotenusa di un cateto è lunga 4 cm. Calcola l area del triangolo. [544 cm
1 2 3 4 5 6 7 8 9 10 11 12 13 14 In un triangolo rettangolo l altezza relativa all ipotenusa è lunga 16 cm e la proiezione sull ipotenusa di un cateto è lunga 4 cm. Calcola l area del triangolo. [544 cm
Istruzioni. Ecco gli argomenti che ti chiediamo di ripassare:
 Matematica La matematica rappresenta una delle materie di base dei vari indirizzi del nostro Istituto e, anche se non sarà approfondita come in un liceo scientifico, prevede comunque lo studio di tutte
Matematica La matematica rappresenta una delle materie di base dei vari indirizzi del nostro Istituto e, anche se non sarà approfondita come in un liceo scientifico, prevede comunque lo studio di tutte
PERCORSO 2 Poligoni e triangoli
 PERCORSO 2 Poligoni e triangoli di Elena Ballarin Riferimento al testo base: A. Acquati, Mate.com, volume 1B, capitolo 4, pp. 132-177 Destinatari: scuola secondaria di primo grado, classe 1 a In classe
PERCORSO 2 Poligoni e triangoli di Elena Ballarin Riferimento al testo base: A. Acquati, Mate.com, volume 1B, capitolo 4, pp. 132-177 Destinatari: scuola secondaria di primo grado, classe 1 a In classe
COMPETENZE U.D.A. ABILITA CONTENUTI _ Saper operare con il sistema di numerazione decimale.
 SCUOLA SECONDARIA DI 1 GRADO TOVINI CURRICOLO DI SCIENZE MATEMATICHE PER LA CLASSE PRIMA COMPETENZE U.D.A. ABILITA CONTENUTI _ Saper operare con il sistema di numerazione decimale. _Il concetto di insieme.
SCUOLA SECONDARIA DI 1 GRADO TOVINI CURRICOLO DI SCIENZE MATEMATICHE PER LA CLASSE PRIMA COMPETENZE U.D.A. ABILITA CONTENUTI _ Saper operare con il sistema di numerazione decimale. _Il concetto di insieme.
IL TANGRAM. Il quadrato della saggezza. Il tangram e un' antica invenzione cinese e forse il più antico puzzle di carattere geometrico.
 IL TANGRAM. Il quadrato della saggezza. Il tangram e un' antica invenzione cinese e forse il più antico puzzle di carattere geometrico. Consiste in un quadrato diviso in 7 parti, chiamati tan, come indicate
IL TANGRAM. Il quadrato della saggezza. Il tangram e un' antica invenzione cinese e forse il più antico puzzle di carattere geometrico. Consiste in un quadrato diviso in 7 parti, chiamati tan, come indicate
Geometria euclidea. Alessio del Vigna. Lunedì 15 settembre
 Geometria euclidea Alessio del Vigna Lunedì 15 settembre La geometria euclidea è una teoria fondata su quattro enti primitivi e sulle relazioni che tra essi intercorrono. I quattro enti primitivi in questione
Geometria euclidea Alessio del Vigna Lunedì 15 settembre La geometria euclidea è una teoria fondata su quattro enti primitivi e sulle relazioni che tra essi intercorrono. I quattro enti primitivi in questione
Circonferenze e cerchi
 Alunno/a... Geometria Classe... Sez.... Data... Circonferenze e cerchi 1 Definisci la circonferenza: 2 Definisci il settore circolare: 3 Definisci la figura che nel disegno è colorata in grigio: 4 Osserva
Alunno/a... Geometria Classe... Sez.... Data... Circonferenze e cerchi 1 Definisci la circonferenza: 2 Definisci il settore circolare: 3 Definisci la figura che nel disegno è colorata in grigio: 4 Osserva
PROGRAMMAZIONE ANNUALE MATEMATICA CLASSE SECONDA
 PROGRAMMAZIONE ANNUALE MATEMATICA CLASSE SECONDA AMBITI DI CONTENUTO UNITA DI APPRENDIMENTO OBIETTIVI DI APPRENDIMENTO OBIETTIVI MINIMI DI APPRENDIMENTO Frazioni e razionali assoluti (Q+) Passare dalle
PROGRAMMAZIONE ANNUALE MATEMATICA CLASSE SECONDA AMBITI DI CONTENUTO UNITA DI APPRENDIMENTO OBIETTIVI DI APPRENDIMENTO OBIETTIVI MINIMI DI APPRENDIMENTO Frazioni e razionali assoluti (Q+) Passare dalle
Gli angoli corrispondenti sono congruenti; I lati corrispondenti, che si dicono lati omologhi, sono in rapporto costante:
 ome sai, se vuoi riprodurre una figura, puoi disegnarla perfettamente uguale rispettandone la forma e le dimensioni e cambiandone quindi solo la posizione. In questo caso la riproduci isometricamente,
ome sai, se vuoi riprodurre una figura, puoi disegnarla perfettamente uguale rispettandone la forma e le dimensioni e cambiandone quindi solo la posizione. In questo caso la riproduci isometricamente,
COMPITI PER LE VACANZE ESTIVE
 ISTITUTO SALESIANO «Beata Vergine di San Luca» via Jacopo della Quercia, 1-40128 BOLOGNA tel. 051/41.51.711 www.salesianibologna.net presideme.bolognabv@salesiani.it Il Preside Futura Classe: 3^C (a.s.
ISTITUTO SALESIANO «Beata Vergine di San Luca» via Jacopo della Quercia, 1-40128 BOLOGNA tel. 051/41.51.711 www.salesianibologna.net presideme.bolognabv@salesiani.it Il Preside Futura Classe: 3^C (a.s.
Una figura in due parti
 Una figura in due parti Equiestensione per somma di parti congruenti: triangolo, trapezio Isoperimetria Trasformazioni: Rotazione Argomentazione Indicazioni e note da UMI 2001 - I numeri, - Lo spazio e
Una figura in due parti Equiestensione per somma di parti congruenti: triangolo, trapezio Isoperimetria Trasformazioni: Rotazione Argomentazione Indicazioni e note da UMI 2001 - I numeri, - Lo spazio e
I grafici derivati e la periodicità
 A I grafici derivati e a periodicità A partire dai grafici dee funzioni goniometriche fondamentai possiamo costruire queo di atre funzioni appicando opportune isometrie. Di seguito vediamo acuni esempi.
A I grafici derivati e a periodicità A partire dai grafici dee funzioni goniometriche fondamentai possiamo costruire queo di atre funzioni appicando opportune isometrie. Di seguito vediamo acuni esempi.
1 L omotetia. i punti O, A e A siano allineati
 1 L omotetia DEFINIZIONE. Dato un punto O ed un numero reale k, si dice omotetia di centro O e rapporto k, quella trasformazione del piano che associa ad ogni punto A il corrispondente punto A tale che
1 L omotetia DEFINIZIONE. Dato un punto O ed un numero reale k, si dice omotetia di centro O e rapporto k, quella trasformazione del piano che associa ad ogni punto A il corrispondente punto A tale che
Indice. Unità 1 Frazioni e numeri decimali 1. Unità 2. Il numero. La radice quadrata 22
 Indice Il numero Unità 1 Frazioni e numeri decimali 1 I numeri decimali 2 Dalla frazione al numero decimale 4 Dal numero decimale alla frazione 6 Operazioni con i numeri decimali 7 Le conoscenze essenziali
Indice Il numero Unità 1 Frazioni e numeri decimali 1 I numeri decimali 2 Dalla frazione al numero decimale 4 Dal numero decimale alla frazione 6 Operazioni con i numeri decimali 7 Le conoscenze essenziali
Parallelismo e perpendicolaritaá nel piano
 CAPITOLO 3 Paraeismo e perpendicoaritaá ne piano 1. L'UTILIZZO DEGLI SLIDER E IL PARALLELISMO CON GEOGEBRA Uno sider eá un numero, oppure un angoo, i cui vaore puoá variare in un fissato intervao a, bš
CAPITOLO 3 Paraeismo e perpendicoaritaá ne piano 1. L'UTILIZZO DEGLI SLIDER E IL PARALLELISMO CON GEOGEBRA Uno sider eá un numero, oppure un angoo, i cui vaore puoá variare in un fissato intervao a, bš
RADICE È L OPERAZIONE INVERSA DELLA POTENZA RADICE: 6 RADICANDO: 36 RADICALE: INDICE: 2 ESEMPIO 36 E UN QUADRATO PERFETTO:
 RADICE È L OPERAZIONE INVERSA DELLA POTENZA RADICE: 6 RADICANDO: 36 RADICALE: INDICE: 2 I NUMERI LA CUI RADICE QUADRATA E UN NUMERO NATURALE SI DICONO QUADRATI PERFETTI ESEMPIO 36 E UN QUADRATO PERFETTO:
RADICE È L OPERAZIONE INVERSA DELLA POTENZA RADICE: 6 RADICANDO: 36 RADICALE: INDICE: 2 I NUMERI LA CUI RADICE QUADRATA E UN NUMERO NATURALE SI DICONO QUADRATI PERFETTI ESEMPIO 36 E UN QUADRATO PERFETTO:
OBIETTIVI di APPRENDIMENTO INDICAZIONI (dalle indicazioni Nazionali)
 Curricolo di Matematica - Classe seconda CURRICOLO DI MATEMATICA - SCUOLA SECONDARIA classe seconda TRAGUARDI delle COMPETENZE (dalle indicazioni Nazionali) NUCLEI TEMATICI OBIETTIVI di APPRENDIMENTO INDICAZIONI
Curricolo di Matematica - Classe seconda CURRICOLO DI MATEMATICA - SCUOLA SECONDARIA classe seconda TRAGUARDI delle COMPETENZE (dalle indicazioni Nazionali) NUCLEI TEMATICI OBIETTIVI di APPRENDIMENTO INDICAZIONI
La macroeconomia: il modello di Keynes
 La macroeconomia: i modeo di Keynes Obiettivi comprendere i significato di domanda aggregata comprendere e eggi de modeo economico keynesiano e sapero interpretare 1. LA VISIONE STORICA John Maynard Keynes
La macroeconomia: i modeo di Keynes Obiettivi comprendere i significato di domanda aggregata comprendere e eggi de modeo economico keynesiano e sapero interpretare 1. LA VISIONE STORICA John Maynard Keynes
C8. Teoremi di Euclide e di Pitagora - Esercizi
 C8. Teoremi di Euclide e di Pitagora - Esercizi EQUIVALENZA DI FIGURE GEOMETRICHE E CALCOLO DI AREE 1) Dimostra che ogni mediana divide un triangolo in due triangoli equivalenti. 2) Dato un parallelogramma
C8. Teoremi di Euclide e di Pitagora - Esercizi EQUIVALENZA DI FIGURE GEOMETRICHE E CALCOLO DI AREE 1) Dimostra che ogni mediana divide un triangolo in due triangoli equivalenti. 2) Dato un parallelogramma
Esercizi per le vacanze estive.
 Esercizi per le vacanze estive. ^ A B Controlla il quaderno delle regole: se non è ordinato o se mancano alcune parti, completalo, chiedendo se è possibile ad un compagno. GEOMETRIA A Ripassa le caratteristiche
Esercizi per le vacanze estive. ^ A B Controlla il quaderno delle regole: se non è ordinato o se mancano alcune parti, completalo, chiedendo se è possibile ad un compagno. GEOMETRIA A Ripassa le caratteristiche
CIRCONFERENZA E CERCHIO
 CIRCONFERENZA E CERCHIO Definizione di circonferenza La circonferenza è una linea chiusa i cui punti sono tutti equidistanti da un punto fisso detto CENTRO Definizione di cerchio Si definisce CERCHIO la
CIRCONFERENZA E CERCHIO Definizione di circonferenza La circonferenza è una linea chiusa i cui punti sono tutti equidistanti da un punto fisso detto CENTRO Definizione di cerchio Si definisce CERCHIO la
Si chiamano poligoni regolari quei poligoni che sono equilateri ed equiangoli.
 6.4 I poligoni regolari Si chiamano poligoni regolari quei poligoni che sono equilateri ed equiangoli. Poligoni regolari: triangolo equilatero; quadrato; pentagono regolare; esagono regolare; ettagono
6.4 I poligoni regolari Si chiamano poligoni regolari quei poligoni che sono equilateri ed equiangoli. Poligoni regolari: triangolo equilatero; quadrato; pentagono regolare; esagono regolare; ettagono
Problemi di geometria
 criteri di similitudine sui triangoli 1 Dimostra che le altezze di un triangolo sono inversamente proporzionali ai relativi lati. 2 Dimostra che due triangoli rettangoli sono simili se hanno ordinatamente
criteri di similitudine sui triangoli 1 Dimostra che le altezze di un triangolo sono inversamente proporzionali ai relativi lati. 2 Dimostra che due triangoli rettangoli sono simili se hanno ordinatamente
