Matematica e Statistica per STB A.A. 2017/2018. Foglio 1
|
|
|
- Gilda Sara Genovese
- 8 anni fa
- Visualizzazioni
Transcript
1 Matematica e Statistica per STB A.A. 2017/2018 Foglio 1 1. Siano A e B due insiemi tali che A = 50, A B = 10, A B = 70. Quanto vale B? 2. Un esperimento consiste nel lanciare un dado a 6 facce e successivamente estrarre una pallina da un urna contenente 4 palline rosse e 6 palline verdi. Vengono osservati la faccia del dado e il colore della pallina. a) Descrivere lo spazio dei campioni associato all esperimento. b) Descrivere l evento E 1 = {numero dispari} c) Descrivere l evento E 2 = {esce una pallina verde} d) Descrivere l evento E 3 = {esce un numero minore di 4} e) Gli eventi E 1 ed E 2 sono incompatibili? f) Gli eventi E 1 ed E 3 sono esaustivi? 3. Si hanno due monete di cui la prima ha una testa ed una croce, mentre la seconda ha una testa su entrambi i lati. Si sceglie a caso una moneta (ad esempio mettendo le due monete in un urna ed estraendone una) e si lancia, ottenendo testa come risultato. Qual è la probabilità che si sia scelta la seconda moneta? Suggerimento: Formalizzate il problema considerando preliminarmente i seguenti eventi E 1 = {si è scelta la prima moneta}, E 2 = {si è scelta la seconda moneta}, A = {dopo il lancio si è ottenuta una testa}. 4. Il 20% dei farmaci prodotti da una casa farmaceutica è stato classificato come dannoso. Se consideriamo i farmaci dannosi, la probabilità che essi contengano una certa sostanza S è pari a 0.7, mentre per i farmaci non dannosi tale probabilità risulta pari al Calcolare la probabilità che un farmaco che contiene la sostanza S sia un farmaco dannoso. 5. Supponiamo che il 90% degli studenti sia stato promosso in matematica, il 75% sia stato promosso in chimica e il 70% sia stato promosso sia in matematica che in chimica. Viene scelto uno studente a caso. Se lo studente è stato promosso in chimica, qual è la probabilità che sia stato promosso in matematica? Se lo studente è stato promosso in matematica, qual è la probabilità che sia stato promosso in chimica? Qual è la probabilità che sia stato promosso sia in matematica che in chimica? 6. Siano A e B due eventi tali che P (A) = 0.5, P (A B) = 0.7. Si determini P (B) nei seguenti casi : 1
2 A e B sono incompatibili A e B sono indipendenti P (A B)= Nella mensa di una scuola vengono preparati 4 primi diversi, 3 secondi diversi e 2 contorni diversi. Quanti pasti diversi possono mangiare i bambini? 8. Tre coppie vanno a teatro insieme. In quanti modi diversi possono sedersi se le coppie siedono accanto? 9. Avete un sacchetto di palline (tutte distinguibili). Ci sono 4 palline blu, 5 verdi e 2 rosse. Estraete dal sacchetto 3 palline a caso. In quanti modi possono uscire: a) Esattamente 1 blu o esattamente 2 verdi? b) Almeno 1 rossa? c) Tutte verdi? d) Esattamente 2 verdi o almeno 1 blu? e) Esattamente 2 verdi o tutte blu? 10. Avete a disposizione 3 libri con la copertina verde tutti differenti e 3 libri con la copertina viola tutti differenti. In quanti modi li potete mettere su uno scaffale di modo che i colori si alternino? 11. Il 60% degli studenti di una scuola non indossano nè anello nè collana. Il 20% porta un anello e il 30% una collana. Se scegliamo uno studente a caso, qual è la probabilità che indossi a) un anello o una collana? b) un anello e una collana? 12. Il 28% degli statunitensi fuma sigarette, il 7% sigari e il 5% sia sigarette che sigari. Se scelgo uno statunitense a caso qual è la probabilità che a) non fumi? b) fumi sigari, ma non sigarette? 13. Un urna contiene 3 palline rosse e 7 nere. Due giocatori A e B estraggono uno alla volta una pallina dall urna, finchè non viene estratta la prima pallina rossa. Qual è la probabilità che A (che è il primo a cominciare) estragga per primo una pallina rossa? 14. Una squadra di basket formata da 3 giocatori (guardia, ala e centro). Se scegliamo un giocatore a caso da 3 squadre, qual è la probabilità che a) venga selezionata una nuova squadra con tutti e tre i ruoli? b) giochino tutti e tre nello stesso ruolo? 2
3 15. Il 98% dei neonati sopravvive al parto. Tuttavia il 15% dei parti sono cesarei e quando si realizza un parto cesareo il neonato sopravvive nel 96% dei casi. Qual è la probabilità condizionata che il neonato di una donna scelta a caso tra quelle che non fanno parto cesareo sopravviva al parto? 16. Uno studente ha intenzione di dare un esame universitario sostenendo tre prove intermedie. Se una di queste non viene superata lo studente non può effettuare la prova successiva. La probabilità che lo studente superi la prima prova è 0.9. Se supera la prima prova, la probabilità condizionata che superi la seconda è 0.8 e se supera la prima e la seconda la probabilità condizionata che superi la terza è 0.7. a) Qual è la probabilità che lo studente superi tutte le prove intermedie? b) Sapendo che lo studente non ha passato una delle prove, qual è la probabilità condizionata che abbia fallito la seconda? 17. Si consideri una popolazione Ω. Sia A il sottoinsieme di Ω degli individui con patologia a. L incidenza della patologia è dell 1%. Sia B l insieme degli individui che risultano positivi ad un test di ricerca per a. La sensibilità del test del 95% e la sua specificità è del 99%. Qual è la probabilità che se il test risulta positivo il soggetto sia affetto dalla patologia a? 18. Una compagnia che produce chip usa due fabbriche. A produce il 60% dei chip; questi chip hanno lo di probabilità di essere difettosi, mentre quelli provenienti da B hanno una corrispondente probabilità uguale a Qual è la probabilità che un dato chip difettoso provenga da A? 19. In quanti modi diversi si possono allineare 7 oggetti a 1...a 7 in modo che nè a 1 nè a 2 siano nei primi due posti? 20. Calcolare il numero dei triangoli aventi come vertici quelli di un quadrato assegnato. 21. Una soluzione omogenea è costituita da 70% di A e 30% di B. Si isola un campione di 10 molecole. Calcolare la probabilità di avere a) 5 A e 5 B? b) 7 A e 3 B? c) almeno 7 A? 22. Un sondaggio rivela che il 32% degli studenti di un università crede nell esistenza di forme di vita extra-terrestri. Qual è la probabilità che, in un gruppo selezionato a caso di 12 studenti, i) esattamente 3 di loro credano nell esistenza di forma di vita extraterrestri? ii) meno di 10 credano nell esistenza di forme di vita extra-terrestri? iii) tra 3 e 5 di loro credano nell esistenza di forme di vita extra-terrestri? 3
4 23. A 1000 ospiti di una struttura alberghiera viene chiesto di esprimere un giudizio sui servizi offerti, usando una scala da 0 a 4. Le risposte ottenute sono riportate nela tabella seguente Giudizio Frequenza Trovarne la media, la moda, la mediana e la varianza dei giudizi espressi. 24. Luca e Paolo hanno raccolto e misurato ciascuno cinque aghi di Larix decidua. I dati sono raccolti in tabella. numero ago lunghezza (cm) aghi di Luca lunghezza (cm) aghi di Paolo 1 1, 3 1, 5 2 1, 4 1, 4 3 1, 5 1, 4 4 1, 3 1, 5 5 1, 3 1, 5 Calcolare: mediana, moda, intervallo di varianza, media, varianza, deviazione standard, coefficiente di variazione e media pesata (dando peso 1 ai dati di Luca e 2 ai dati di Paolo) per i dati solo di Luca, solo di Paolo e di Luca e Paolo messi assieme. 25. Attorno all edificio di biologia ci sono cinque gatti. Le loro caratteristiche sono riportate in tabella. nome del gatto colore del pelo lunghezza del pelo Leo rosso lungo Neve nero corto Poldo rosso corto Luna nero lungo Birba rosso, bianco e nero corto Quali sono le mediane e le mode dei nomi, del colore del pelo e della lunghezza del pelo? 26. a) Fare un esempio di cinque numeri x 1 x 2 x 3 x 4 x 5 tali che la loro mediana non sia uno degli x i con i {1, 2, 3, 4, 5}. b) Quali sono gli insiemi di quattro numeri x 1 x 2 x 3 x 4 tali che la loro mediana è uno degli x i? 27. In generale c è differenza fra media e mediana? E fra media e mediana di due numeri? 28. Nel corso degli anni sono stati prodotti alcuni modelli di smartphone. Alcune specifiche sono riportate in tabella. 4
5 anno peso (g) superficie frontale (cm 2 ) a) Qual è la media e la varianza del peso? Qual è l intervallo di variabilità degli anni? b) Calcolare le rette di regressione per le coppie anno-peso e annosuperficie frontale e dire se le interpolazioni sono buone. 29. Qual è il coefficiente di correlazione (o di Pearson) per una retta di regressione calcolata per soli due punti generici (x, y) e (x, y ) con x x? 30. Sia P il coefficiente di correlazione (o di Pearson) di un retta di regressione. In generale esistono rette di regressione con i seguenti coefficienti di correlazione (o di Pearson)? a) 1 P b) 1 P 5
ESERCIZI SULLA PROBABILITA
 PROBABILITA CLASSICA ESERCIZI SULLA PROBABILITA 1) Si estrae una carta da un mazzo di 40 carte ; calcolare la probabilità che la carta sia: a. una figura; b. una carta di danari; c. un asso. 2) Un urna
PROBABILITA CLASSICA ESERCIZI SULLA PROBABILITA 1) Si estrae una carta da un mazzo di 40 carte ; calcolare la probabilità che la carta sia: a. una figura; b. una carta di danari; c. un asso. 2) Un urna
UNIVERSITÀ di ROMA TOR VERGATA
 UNIVERSITÀ di ROMA TOR VERGATA Corso di Statistica, anno 00- P.Baldi Lista di esercizi. Corso di Laurea in Biotecnologie Esercizio Si sa che in una schedina del totocalcio i tre simboli, X, compaiono con
UNIVERSITÀ di ROMA TOR VERGATA Corso di Statistica, anno 00- P.Baldi Lista di esercizi. Corso di Laurea in Biotecnologie Esercizio Si sa che in una schedina del totocalcio i tre simboli, X, compaiono con
p k q n k = p n (k) = n 12 = 1 = 12 1 12 11 10 9 1 0,1208. q = 1 2 e si ha: p 12 (8) = 12 8 4
 CAPITOLO QUARTO DISTRIBUZIONE BINOMIALE (O DI BERNOULLI) Molti degli esempi che abbiamo presentato nei capitoli precedenti possono essere pensati come casi particolari di uno schema generale di prove ripetute,
CAPITOLO QUARTO DISTRIBUZIONE BINOMIALE (O DI BERNOULLI) Molti degli esempi che abbiamo presentato nei capitoli precedenti possono essere pensati come casi particolari di uno schema generale di prove ripetute,
Lo spazio degli eventi del lancio di un dado regolare a sei facce è l insieme U 1. 2. 3. U 4. 5. 6
 EVENTI ALEATORI E LORO RAPPRESENTAZIONE Lo spazio degli eventi del lancio di un dado regolare a sei facce è l insieme U... U.. La definizione classica di probabilità dice che, se gli eventi che si considerano
EVENTI ALEATORI E LORO RAPPRESENTAZIONE Lo spazio degli eventi del lancio di un dado regolare a sei facce è l insieme U... U.. La definizione classica di probabilità dice che, se gli eventi che si considerano
ESERCITAZIONE 20 : VARIABILI ALEATORIE DISCRETE
 ESERCITAZIONE 20 : VARIABILI ALEATORIE DISCRETE e-mail: [email protected] web: www.dm.unipi.it/ tommei Ricevimento: su appuntamento Dipartimento di Matematica, piano terra, studio 114 30 Aprile 2013 Esercizio
ESERCITAZIONE 20 : VARIABILI ALEATORIE DISCRETE e-mail: [email protected] web: www.dm.unipi.it/ tommei Ricevimento: su appuntamento Dipartimento di Matematica, piano terra, studio 114 30 Aprile 2013 Esercizio
ESERCIZI PROBABILITA E CALCOLO COMBINATORIO CON RISULTATI 1. P che estraendo a caso 1 carta da un mazzo di 52 sia una regina?
 ESERCIZI PROBABILITA E CALCOLO COMBINATORIO CON RISULTATI 1. P che estraendo a caso 1 carta da un mazzo di 52 sia una regina? [4/52] 2. Estratta una Q, P che ad una seconda estrazione si presenti ancora
ESERCIZI PROBABILITA E CALCOLO COMBINATORIO CON RISULTATI 1. P che estraendo a caso 1 carta da un mazzo di 52 sia una regina? [4/52] 2. Estratta una Q, P che ad una seconda estrazione si presenti ancora
0.1 Esercizi calcolo combinatorio
 0.1 Esercizi calcolo combinatorio Esercizio 1. Sia T l insieme dei primi 100 numeri naturali. Calcolare: 1. Il numero di sottoinsiemi A di T che contengono esattamente 8 pari.. Il numero di coppie (A,
0.1 Esercizi calcolo combinatorio Esercizio 1. Sia T l insieme dei primi 100 numeri naturali. Calcolare: 1. Il numero di sottoinsiemi A di T che contengono esattamente 8 pari.. Il numero di coppie (A,
L indagine statistica
 1 L indagine statistica DEFINIZIONE. La statistica è quella disciplina che si occupa della raccolta di dati quantitativi relativi a diversi fenomeni, della loro elaborazione e del loro utilizzo a fini
1 L indagine statistica DEFINIZIONE. La statistica è quella disciplina che si occupa della raccolta di dati quantitativi relativi a diversi fenomeni, della loro elaborazione e del loro utilizzo a fini
ITCS Erasmo da Rotterdam. Anno Scolastico 2014/2015. CLASSE 4^ M Costruzioni, ambiente e territorio
 ITCS Erasmo da Rotterdam Anno Scolastico 014/015 CLASSE 4^ M Costruzioni, ambiente e territorio INDICAZIONI PER IL LAVORO ESTIVO DI MATEMATICA e COMPLEMENTI di MATEMATICA GLI STUDENTI CON IL DEBITO FORMATIVO
ITCS Erasmo da Rotterdam Anno Scolastico 014/015 CLASSE 4^ M Costruzioni, ambiente e territorio INDICAZIONI PER IL LAVORO ESTIVO DI MATEMATICA e COMPLEMENTI di MATEMATICA GLI STUDENTI CON IL DEBITO FORMATIVO
STATISTICA DESCRITTIVA. Elementi di statistica medica GLI INDICI INDICI DI DISPERSIONE STATISTICA DESCRITTIVA
 STATISTICA DESCRITTIVA Elementi di statistica medica STATISTICA DESCRITTIVA È quella branca della statistica che ha il fine di descrivere un fenomeno. Deve quindi sintetizzare tramite pochi valori(indici
STATISTICA DESCRITTIVA Elementi di statistica medica STATISTICA DESCRITTIVA È quella branca della statistica che ha il fine di descrivere un fenomeno. Deve quindi sintetizzare tramite pochi valori(indici
nome: classe: data: delle quattro figure sottostanti non risulta in ogni caso congruente a quella sopra?
 Verifica IVPROVA_MAT_Sim_01 nome: classe: data: 1. Osserva la figura. Immaginiamo di spostarla tramite movimenti rigidi: quale delle quattro figure sottostanti non risulta in ogni caso congruente a quella
Verifica IVPROVA_MAT_Sim_01 nome: classe: data: 1. Osserva la figura. Immaginiamo di spostarla tramite movimenti rigidi: quale delle quattro figure sottostanti non risulta in ogni caso congruente a quella
3. Qual è l equazione della retta rappresentata nel piano cartesiano?
 Verifica IVPROVA_MAT_Sim_06 nome: classe: data: Quattro fratelli hanno ciascuno due sorelle. Quante sono le sorelle? La somma delle aree dei due triangoli è di 40 cm 2, ma l area del triangolo grigio è
Verifica IVPROVA_MAT_Sim_06 nome: classe: data: Quattro fratelli hanno ciascuno due sorelle. Quante sono le sorelle? La somma delle aree dei due triangoli è di 40 cm 2, ma l area del triangolo grigio è
Analisi. Calcolo Combinatorio. Ing. Ivano Coccorullo
 Analisi Ing. Ivano Coccorullo Prof. Ivano Coccorullo ü Molti dei problemi classici di calcolo delle probabilità si riducono al calcolo dei casi favorevoli e di quelli possibili. Quando le situazioni diventano
Analisi Ing. Ivano Coccorullo Prof. Ivano Coccorullo ü Molti dei problemi classici di calcolo delle probabilità si riducono al calcolo dei casi favorevoli e di quelli possibili. Quando le situazioni diventano
PROBABILITÀ SCHEDA N. 5 SOMMA E DIFFERENZA DI DUE VARIABILI ALEATORIE DISCRETE
 PROBABILITÀ SCHEDA N. 5 SOMMA E DIFFERENZA DI DUE VARIABILI ALEATORIE DISCRETE 1. Distribuzione congiunta Ci sono situazioni in cui un esperimento casuale non si può modellare con una sola variabile casuale,
PROBABILITÀ SCHEDA N. 5 SOMMA E DIFFERENZA DI DUE VARIABILI ALEATORIE DISCRETE 1. Distribuzione congiunta Ci sono situazioni in cui un esperimento casuale non si può modellare con una sola variabile casuale,
ESAME DI STATO. SIMULAZIONE PROVA NAZIONALE Scuola Secondaria di I grado Classe Terza. Prova 3. Anno Scolastico 20. - 20. Classe:... Data:...
 Prova Nazionale di Matematica: Simulazioni - a cura di M. Zarattini Prova ESAME DI STATO Anno Scolastico 0. - 0. SIMULAZIONE PROVA NAZIONALE Scuola Secondaria di I grado Classe Terza Classe:... Data:...
Prova Nazionale di Matematica: Simulazioni - a cura di M. Zarattini Prova ESAME DI STATO Anno Scolastico 0. - 0. SIMULAZIONE PROVA NAZIONALE Scuola Secondaria di I grado Classe Terza Classe:... Data:...
Unione Matematica Italiana PROGETTO OLIMPIADI DI MATEMATICA. 4. Qual è la cifra delle unità di 3 (87)? (A) 1 (B) 7 (C) 3 (D) 9 (E) 5
 T1 Unione Matematica Italiana PROGETTO OLIMPIADI DI MATEMATICA Ministero dell Istruzione, dell Università e della Ricerca Scuola Normale Superiore I Giochi di Archimede - Gara Biennio 25 novembre 2015
T1 Unione Matematica Italiana PROGETTO OLIMPIADI DI MATEMATICA Ministero dell Istruzione, dell Università e della Ricerca Scuola Normale Superiore I Giochi di Archimede - Gara Biennio 25 novembre 2015
Interpolazione Statistica
 Interpolazione Statistica Come determinare una funzione che rappresenti la relazione tra due grandezze x e y a cura di Roberto Rossi novembre 2008 Si parla di INTERPOLAZIONE quando: Note alcune coppie
Interpolazione Statistica Come determinare una funzione che rappresenti la relazione tra due grandezze x e y a cura di Roberto Rossi novembre 2008 Si parla di INTERPOLAZIONE quando: Note alcune coppie
TEST DI INGRESSO. Al seguente indirizzo puoi trovare il test di matematica di base per scienze biotecnologiche http://www.testingressoscienze.
 TEST DI INGRESSO http://www.smfn.unipi.it/prova_ingresso/verifica2009.aspx Al precedente sito internet puoi trovare un esempio pubblico di test di matematica di base e un test di matematica di base del
TEST DI INGRESSO http://www.smfn.unipi.it/prova_ingresso/verifica2009.aspx Al precedente sito internet puoi trovare un esempio pubblico di test di matematica di base e un test di matematica di base del
Prof.ssa Laura Pagnozzi Prof. Ivano Coccorullo. Calcolo Combinatorio
 Prof.ssa Laura Pagnozzi Prof. Ivano Coccorullo Calcolo Combinatorio Calcolo Combinatorio ü Molti dei problemi classici di calcolo delle probabilità si riducono al calcolo dei casi favorevoli e di quelli
Prof.ssa Laura Pagnozzi Prof. Ivano Coccorullo Calcolo Combinatorio Calcolo Combinatorio ü Molti dei problemi classici di calcolo delle probabilità si riducono al calcolo dei casi favorevoli e di quelli
Esercitazione # 3. Trovate la probabilita che in 5 lanci di un dado non truccato il 3 si presenti
 Statistica Matematica A Esercitazione # 3 Binomiale: Esercizio # 1 Trovate la probabilita che in 5 lanci di un dado non truccato il 3 si presenti 1. mai 2. almeno una volta 3. quattro volte Esercizio #
Statistica Matematica A Esercitazione # 3 Binomiale: Esercizio # 1 Trovate la probabilita che in 5 lanci di un dado non truccato il 3 si presenti 1. mai 2. almeno una volta 3. quattro volte Esercizio #
CORSO DI STATISTICA (parte 1) - ESERCITAZIONE 5
 CORSO DI STATISTICA (parte 1) - ESERCITAZIONE 5 Dott.ssa Antonella Costanzo [email protected] Esercizio 1. Misura dell associazione tra due caratteri Uno store manager è interessato a studiare la relazione
CORSO DI STATISTICA (parte 1) - ESERCITAZIONE 5 Dott.ssa Antonella Costanzo [email protected] Esercizio 1. Misura dell associazione tra due caratteri Uno store manager è interessato a studiare la relazione
Esercizi sulla conversione tra unità di misura
 Esercizi sulla conversione tra unità di misura Autore: Enrico Campanelli Prima stesura: Settembre 2013 Ultima revisione: Settembre 2013 Per segnalare errori o per osservazioni e suggerimenti di qualsiasi
Esercizi sulla conversione tra unità di misura Autore: Enrico Campanelli Prima stesura: Settembre 2013 Ultima revisione: Settembre 2013 Per segnalare errori o per osservazioni e suggerimenti di qualsiasi
Corso di Laurea in Matematica per l Informatica e la Comunicazione Scientifica
 Corso di Laurea in Matematica per l Informatica e la Comunicazione Scientifica Soluzione del compito di Matematica Discreta 1 del 25 luglio 200 1. Qual è il numero di applicazioni f : A = {1,..., 5} B
Corso di Laurea in Matematica per l Informatica e la Comunicazione Scientifica Soluzione del compito di Matematica Discreta 1 del 25 luglio 200 1. Qual è il numero di applicazioni f : A = {1,..., 5} B
Metodi per la risoluzione di sistemi lineari
 Metodi per la risoluzione di sistemi lineari Sistemi di equazioni lineari. Rango di matrici Come è noto (vedi [] sez.0.8), ad ogni matrice quadrata A è associato un numero reale det(a) detto determinante
Metodi per la risoluzione di sistemi lineari Sistemi di equazioni lineari. Rango di matrici Come è noto (vedi [] sez.0.8), ad ogni matrice quadrata A è associato un numero reale det(a) detto determinante
Re = f (A) f. 2 ),,, f (af. n )}
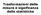 Trasformazioni delle misure e significanza delle statistiche Trasformazione e Significanza delle Statistiche: *) Invarianza assoluta. *) Invarianza di riferimento. *) Invarianza di confronto. *) Schemi
Trasformazioni delle misure e significanza delle statistiche Trasformazione e Significanza delle Statistiche: *) Invarianza assoluta. *) Invarianza di riferimento. *) Invarianza di confronto. *) Schemi
Matematica con il foglio di calcolo
 Matematica con il foglio di calcolo Sottotitolo: Classe: V primaria Argomento: Numeri e operazioni Autore: Guido Gottardi, Alberto Battaini Introduzione: l uso del foglio di calcolo offre l opportunità
Matematica con il foglio di calcolo Sottotitolo: Classe: V primaria Argomento: Numeri e operazioni Autore: Guido Gottardi, Alberto Battaini Introduzione: l uso del foglio di calcolo offre l opportunità
Correlazione. Daniela Valenti, Treccani Scuola 1
 Correlazione 1 I dati di un indagine per riflettere Cominciamo con i dati di un indagine svolta in una quinta classe di scuola superiore. Dopo l Esame di Stato 12 studenti si sono iscritti a corsi di laurea
Correlazione 1 I dati di un indagine per riflettere Cominciamo con i dati di un indagine svolta in una quinta classe di scuola superiore. Dopo l Esame di Stato 12 studenti si sono iscritti a corsi di laurea
Statistica. Esercitazione 10. Alfonso Iodice D Enza [email protected]. Università degli studi di Cassino. Statistica. A. Iodice. V.C.
 uniforme Bernoulli binomiale di Esercitazione 10 Alfonso Iodice D Enza [email protected] Università degli studi di Cassino () 1 / 55 Outline uniforme Bernoulli binomiale di 1 uniforme 2 Bernoulli 3 4
uniforme Bernoulli binomiale di Esercitazione 10 Alfonso Iodice D Enza [email protected] Università degli studi di Cassino () 1 / 55 Outline uniforme Bernoulli binomiale di 1 uniforme 2 Bernoulli 3 4
4) 8 g di idrogeno reagiscono esattamente con 64 g di ossigeno secondo la seguente reazione:
 Esercizi Gli esercizi sulla legge di Lavoisier che seguono si risolvono ricordando che la massa iniziale, prima della reazione, deve equivalere a quella finale, dopo la reazione. L uguaglianza vale anche
Esercizi Gli esercizi sulla legge di Lavoisier che seguono si risolvono ricordando che la massa iniziale, prima della reazione, deve equivalere a quella finale, dopo la reazione. L uguaglianza vale anche
I problemi di questa prova
 I problemi di questa prova Categoria Problemi 3 1-2-3-4-5 4 1-2-3-4-5-6 5 1-2-3-4-5-6-7 6 7-8-9-10-11-12-13 7 8-9-10-11-12-13-14 8 8-9-10-11-12-13-14 9 10-11-12-13-14-15-16 10 10-11-12-13-14-15-16 Correzione
I problemi di questa prova Categoria Problemi 3 1-2-3-4-5 4 1-2-3-4-5-6 5 1-2-3-4-5-6-7 6 7-8-9-10-11-12-13 7 8-9-10-11-12-13-14 8 8-9-10-11-12-13-14 9 10-11-12-13-14-15-16 10 10-11-12-13-14-15-16 Correzione
Esercizi di Probabilità
 Esercizi di Probabilità Annalisa Cerquetti - Sandra Fortini Vai all indice Istituto di Metodi Quantitativi, Viale Isonzo, 25, 2033 Milano, Italy. E-mail: [email protected],[email protected]
Esercizi di Probabilità Annalisa Cerquetti - Sandra Fortini Vai all indice Istituto di Metodi Quantitativi, Viale Isonzo, 25, 2033 Milano, Italy. E-mail: [email protected],[email protected]
ARROTONDANDO FIGURE CON TRIANGOLI EQUILATERI
 ARROTONDANDO Cosa succede ad accostare figure identiche una all altra? Le figure ottenute che proprietà presentano? Posso trovare un qualche tipo di legge generale? Per rispondere a questa ed altre domande
ARROTONDANDO Cosa succede ad accostare figure identiche una all altra? Le figure ottenute che proprietà presentano? Posso trovare un qualche tipo di legge generale? Per rispondere a questa ed altre domande
Esercitazioni di Statistica
 Esercitazioni di Statistica Rappresentazioni grafiche Prof. Livia De Giovanni [email protected] Esercizio 1 Si consideri la seguente distribuzione delle industrie tessili secondo il fatturato
Esercitazioni di Statistica Rappresentazioni grafiche Prof. Livia De Giovanni [email protected] Esercizio 1 Si consideri la seguente distribuzione delle industrie tessili secondo il fatturato
7 Disegni sperimentali ad un solo fattore. Giulio Vidotto Raffaele Cioffi
 7 Disegni sperimentali ad un solo fattore Giulio Vidotto Raffaele Cioffi Indice: 7.1 Veri esperimenti 7.2 Fattori livelli condizioni e trattamenti 7.3 Alcuni disegni sperimentali da evitare 7.4 Elementi
7 Disegni sperimentali ad un solo fattore Giulio Vidotto Raffaele Cioffi Indice: 7.1 Veri esperimenti 7.2 Fattori livelli condizioni e trattamenti 7.3 Alcuni disegni sperimentali da evitare 7.4 Elementi
1 IL LINGUAGGIO MATEMATICO
 1 IL LINGUAGGIO MATEMATICO Il linguaggio matematico moderno è basato su due concetti fondamentali: la teoria degli insiemi e la logica delle proposizioni. La teoria degli insiemi ci assicura che gli oggetti
1 IL LINGUAGGIO MATEMATICO Il linguaggio matematico moderno è basato su due concetti fondamentali: la teoria degli insiemi e la logica delle proposizioni. La teoria degli insiemi ci assicura che gli oggetti
Corso di Psicometria Progredito
 Corso di Psicometria Progredito 4. Esercizi di Inferenza Statistica Gianmarco Altoè Dipartimento di Psicologia Università di Cagliari, Anno Accademico 2011-2012 Esercizio 4.1 - I due esami Nella seguente
Corso di Psicometria Progredito 4. Esercizi di Inferenza Statistica Gianmarco Altoè Dipartimento di Psicologia Università di Cagliari, Anno Accademico 2011-2012 Esercizio 4.1 - I due esami Nella seguente
Esperimento sull ottica
 Esperimento sull ottica Gruppo: Valentina Sotgiu, Irene Sini, Giorgia Canetto, Federica Pitzalis, Federica Schirru, Jessica Atzeni, Martina Putzu, Veronica, Orgiu e Deborah Pilleri. Teoria di riferimento:
Esperimento sull ottica Gruppo: Valentina Sotgiu, Irene Sini, Giorgia Canetto, Federica Pitzalis, Federica Schirru, Jessica Atzeni, Martina Putzu, Veronica, Orgiu e Deborah Pilleri. Teoria di riferimento:
Il test (o i test) del Chi-quadrato ( 2 )
 Il test (o i test) del Chi-quadrato ( ) I dati: numerosità di osservazioni che cadono all interno di determinate categorie Prima di tutto, è un test per confrontare proporzioni Esempio: confronto tra numero
Il test (o i test) del Chi-quadrato ( ) I dati: numerosità di osservazioni che cadono all interno di determinate categorie Prima di tutto, è un test per confrontare proporzioni Esempio: confronto tra numero
Definizione Dati due insiemi A e B, contenuti nel campo reale R, si definisce funzione reale di variabile reale una legge f : A
 Scopo centrale, sia della teoria statistica che della economica, è proprio quello di esprimere ed analizzare le relazioni, esistenti tra le variabili statistiche ed economiche, che, in linguaggio matematico,
Scopo centrale, sia della teoria statistica che della economica, è proprio quello di esprimere ed analizzare le relazioni, esistenti tra le variabili statistiche ed economiche, che, in linguaggio matematico,
Pro memoria per la ripartizione delle spese
 Pro memoria per la ripartizione delle spese Documento di lavoro post incontro del 23 e 24 novembre 2009, Roma, ad uso interno del Gruppo di lavoro Istat-Upi per la sperimentazione della contabilità ambientale
Pro memoria per la ripartizione delle spese Documento di lavoro post incontro del 23 e 24 novembre 2009, Roma, ad uso interno del Gruppo di lavoro Istat-Upi per la sperimentazione della contabilità ambientale
Esercizi sulle affinità - aprile 2009
 Esercizi sulle affinità - aprile 009 Ingegneria meccanica 008/009 Esercizio Sono assegnate nel piano le sei rette r : =, s : =, t : =, r : =, s : =, t : = determinare l affinità che trasforma ordinatamente
Esercizi sulle affinità - aprile 009 Ingegneria meccanica 008/009 Esercizio Sono assegnate nel piano le sei rette r : =, s : =, t : =, r : =, s : =, t : = determinare l affinità che trasforma ordinatamente
Capitolo 9. Esercizio 9.1. Esercizio 9.2
 Capitolo 9 Esercizio 9.1 Considerare lo relazione in figura 9.19 e individuare le proprietà della corrispondente applicazione. Individuare inoltre eventuali ridondanze e anomalie nella relazione. Docente
Capitolo 9 Esercizio 9.1 Considerare lo relazione in figura 9.19 e individuare le proprietà della corrispondente applicazione. Individuare inoltre eventuali ridondanze e anomalie nella relazione. Docente
9 = Soluzione. Soluzione
 Esercizio 1 Un'urna contiene 6 palline rosse, 4 nere, 8 bianche. Si estrae una pallina; calcolare la probabilità di avere a) una pallina bianca; b) una pallina nera; e) una pallina non bianca; d) una pallina
Esercizio 1 Un'urna contiene 6 palline rosse, 4 nere, 8 bianche. Si estrae una pallina; calcolare la probabilità di avere a) una pallina bianca; b) una pallina nera; e) una pallina non bianca; d) una pallina
Onde sonore stazionarie in un tubo risonante
 Onde sonore stazionarie in un tubo risonante Scopo dell esperimento Determinare la velocità del suono analizzando le caratteristiche delle onde sonore stazionarie in un tubo risonante. Richiamo teorico
Onde sonore stazionarie in un tubo risonante Scopo dell esperimento Determinare la velocità del suono analizzando le caratteristiche delle onde sonore stazionarie in un tubo risonante. Richiamo teorico
Errori cognitivi, probabilità e decisioni mediche nella diagnostica di laboratorio. M. Besozzi - IRCCS Istituto Auxologico Italiano
 Errori cognitivi, probabilità e decisioni mediche nella diagnostica di laboratorio M. Besozzi - IRCCS Istituto Auxologico Italiano L argomento... Errori cognitivi Il problema gnoseologico Dati, informazione
Errori cognitivi, probabilità e decisioni mediche nella diagnostica di laboratorio M. Besozzi - IRCCS Istituto Auxologico Italiano L argomento... Errori cognitivi Il problema gnoseologico Dati, informazione
Esercitazioni di Reti Logiche. Lezione 1 Rappresentazione dell'informazione. Zeynep KIZILTAN [email protected]
 Esercitazioni di Reti Logiche Lezione 1 Rappresentazione dell'informazione Zeynep KIZILTAN [email protected] Introduzione Zeynep KIZILTAN Si pronuncia Z come la S di Rose altrimenti, si legge come
Esercitazioni di Reti Logiche Lezione 1 Rappresentazione dell'informazione Zeynep KIZILTAN [email protected] Introduzione Zeynep KIZILTAN Si pronuncia Z come la S di Rose altrimenti, si legge come
Esercitazioni di statistica
 Esercitazioni di statistica Misure di associazione: Indipendenza assoluta e in media Stefania Spina Universitá di Napoli Federico II [email protected] 22 ottobre 2014 Stefania Spina Esercitazioni
Esercitazioni di statistica Misure di associazione: Indipendenza assoluta e in media Stefania Spina Universitá di Napoli Federico II [email protected] 22 ottobre 2014 Stefania Spina Esercitazioni
ESERCIZI SVOLTI Giuliano Bonollo - Michele Bonollo
 ESERCIZI SVOLTI Giuliano Bonollo - Michele Bonollo 1 La seguente tabella riporta le frequenze relative riguardanti gli studenti di un università e gli esiti dell esame da essi sostenuto. Qual è la percentuale
ESERCIZI SVOLTI Giuliano Bonollo - Michele Bonollo 1 La seguente tabella riporta le frequenze relative riguardanti gli studenti di un università e gli esiti dell esame da essi sostenuto. Qual è la percentuale
Quesito 1 Si calcoli. 3 2 2 4 3 3 = 3 2 4 3 = 2 ln3 = 8 81 2,3. 1 = 2 3 2 3 = 2 3 1+1 2 1 = = =ln81. Soluzione 1
 ESAME DI STATO DI LICEO SCIENTIFICO Sessione Ordinaria 0 PIANO NAZIONALE INFORMATICA Questionario Quesito Si calcoli 3 3 è 0 0 Applicando De L Hospital si ha: -,3 3 3 4 3 3 = infatti: 0 = 3 4 3 3 = 3 4
ESAME DI STATO DI LICEO SCIENTIFICO Sessione Ordinaria 0 PIANO NAZIONALE INFORMATICA Questionario Quesito Si calcoli 3 3 è 0 0 Applicando De L Hospital si ha: -,3 3 3 4 3 3 = infatti: 0 = 3 4 3 3 = 3 4
Esercitazioni di statistica
 Esercitazioni di statistica Intervalli di confidenza Stefania Spina Universitá di Napoli Federico II [email protected] 10 Dicembre 2014 Stefania Spina Esercitazioni di statistica 1/43 Stefania Spina
Esercitazioni di statistica Intervalli di confidenza Stefania Spina Universitá di Napoli Federico II [email protected] 10 Dicembre 2014 Stefania Spina Esercitazioni di statistica 1/43 Stefania Spina
10. Quale dei seguenti numeri
 Test d'ingresso di matematica per la secondaria di secondo grado (liceo classico) Il test si basa su alcuni test di ingresso (opportunamente modificati) assegnati al liceo classico e trovati in Rete Nome:
Test d'ingresso di matematica per la secondaria di secondo grado (liceo classico) Il test si basa su alcuni test di ingresso (opportunamente modificati) assegnati al liceo classico e trovati in Rete Nome:
Capitolo 2 Eredità mendeliana
 Capitolo 2 Eredità mendeliana 2.1 Se una cavia nera di sesso femminile è sottoposta a incrocio di prova e produce 2 figli neri, qual è il suo probabile genotipo? Con quale grado di certezza può essere
Capitolo 2 Eredità mendeliana 2.1 Se una cavia nera di sesso femminile è sottoposta a incrocio di prova e produce 2 figli neri, qual è il suo probabile genotipo? Con quale grado di certezza può essere
COMPITO n. 1. 3. Siano X, Y due variabili aleatorie tali che il vettore (X, Y ) sia distribuito uniformemente
 COMPITO n. 1 a) Nel gioco del poker ad ogni giocatore vengono distribuite cinque carte da un normale mazzo di 52. Quant è la probabilità che un giocatore riceva una scala di re (ovvero 9, 10, J, Q, K anche
COMPITO n. 1 a) Nel gioco del poker ad ogni giocatore vengono distribuite cinque carte da un normale mazzo di 52. Quant è la probabilità che un giocatore riceva una scala di re (ovvero 9, 10, J, Q, K anche
EQUAZIONI CON VALORE ASSOLUTO DISEQUAZIONI CON VALORE ASSOLUTO
 EQUAZIONI CON VALORE AOLUTO DIEQUAZIONI CON VALORE AOLUTO Prima di tutto: che cosa è il valore assoluto di un numero? Il valore assoluto è quella legge che ad un numero (positivo o negativo) associa sempre
EQUAZIONI CON VALORE AOLUTO DIEQUAZIONI CON VALORE AOLUTO Prima di tutto: che cosa è il valore assoluto di un numero? Il valore assoluto è quella legge che ad un numero (positivo o negativo) associa sempre
ESERCITAZIONE 3 : PERCENTUALI
 ESERCITAZIONE 3 : PERCENTUALI e-mail: [email protected] web: www.dm.unipi.it/ tommei Ricevimento: Lunedi 14-17 Dipartimento di Matematica, piano terra, studio 114 22 Ottobre 2013 Esercizio 1 Nel 2006,
ESERCITAZIONE 3 : PERCENTUALI e-mail: [email protected] web: www.dm.unipi.it/ tommei Ricevimento: Lunedi 14-17 Dipartimento di Matematica, piano terra, studio 114 22 Ottobre 2013 Esercizio 1 Nel 2006,
Confrontare angoli Indica, colorando il quadratino, quali sono gli angoli retti tra quelli che vedi qui sotto.
 Confrontare angoli Indica, colorando il quadratino, quali sono gli angoli retti tra quelli che vedi qui sotto. R V T P S U Z Colora di verde le caselle corrispondenti agli angoli piatti e di rosso quelle
Confrontare angoli Indica, colorando il quadratino, quali sono gli angoli retti tra quelli che vedi qui sotto. R V T P S U Z Colora di verde le caselle corrispondenti agli angoli piatti e di rosso quelle
Il metodo delle proporzioni crescenti
 Il metodo delle proporzioni crescenti Ulisse Di Corpo Abstract I modelli predittivi, che utilizzano le regressioni multiple, partono dall assunto che le relazioni tra le variabili sono lineari o traducibili
Il metodo delle proporzioni crescenti Ulisse Di Corpo Abstract I modelli predittivi, che utilizzano le regressioni multiple, partono dall assunto che le relazioni tra le variabili sono lineari o traducibili
Variabili aleatorie Parte I
 Variabili aleatorie Parte I Variabili aleatorie Scalari - Definizione Funzioni di distribuzione di una VA Funzioni densità di probabilità di una VA Indici di posizione di una distribuzione Indici di dispersione
Variabili aleatorie Parte I Variabili aleatorie Scalari - Definizione Funzioni di distribuzione di una VA Funzioni densità di probabilità di una VA Indici di posizione di una distribuzione Indici di dispersione
INSIEMI E LOGICA. 2527+2234+1846=6607 6607-6000 = 607 numero individui con entrambi gli antigeni
 In uno studio di gruppi sanguigni ABO, furono sottoposti ad analisi 6000 cinesi. 2527 avevano l antigene A, 2234 l antigene B e 1846 nessun antigene. Quanti individui avevano entrambi gli antigeni? 2527+2234+1846=6607
In uno studio di gruppi sanguigni ABO, furono sottoposti ad analisi 6000 cinesi. 2527 avevano l antigene A, 2234 l antigene B e 1846 nessun antigene. Quanti individui avevano entrambi gli antigeni? 2527+2234+1846=6607
Cromosomi sessuali. Le cellule maschili e femminili differiscono per i cromosomi sessuali o
 Cromosomi sessuali Le cellule maschili e femminili differiscono per i cromosomi sessuali o cromosomi del sesso o eterosomi (cosiddetti perché hanno forma diversa). Nell uomo e in molte altre specie (ma
Cromosomi sessuali Le cellule maschili e femminili differiscono per i cromosomi sessuali o cromosomi del sesso o eterosomi (cosiddetti perché hanno forma diversa). Nell uomo e in molte altre specie (ma
Matematica II: Calcolo delle Probabilità e Statistica Matematica
 Matematica II: Calcolo delle Probabilità e Statistica Matematica ELT A-Z Docente: dott. F. Zucca Esercitazione # 3 1 Distribuzione di Bernoulli e Distribuzione Binomiale Esercizio 1 Sia n un intero maggiore
Matematica II: Calcolo delle Probabilità e Statistica Matematica ELT A-Z Docente: dott. F. Zucca Esercitazione # 3 1 Distribuzione di Bernoulli e Distribuzione Binomiale Esercizio 1 Sia n un intero maggiore
STATISTICA: esercizi svolti sulla MEDIA ARITMETICA
 STATISTICA: esercizi svolti sulla MEDIA ARITMETICA 1 1 MEDIA ARITMETICA 2 1 MEDIA ARITMETICA 1. La seguente tabella riporta il numero di persone divise per sesso che si sono presentate durante l anno 1997
STATISTICA: esercizi svolti sulla MEDIA ARITMETICA 1 1 MEDIA ARITMETICA 2 1 MEDIA ARITMETICA 1. La seguente tabella riporta il numero di persone divise per sesso che si sono presentate durante l anno 1997
INVALSI. u ola. Ministero dell Istruzione dell Università e della Ricerca
 II MATEMATICA_COP_Layout 1 15/03/11 08:12 Pagina 2 Ministero dell Istruzione dell Università e della Ricerca INVALSI Istituto nazionale per la valutazione del sistema educativo di istruzione e di formazione
II MATEMATICA_COP_Layout 1 15/03/11 08:12 Pagina 2 Ministero dell Istruzione dell Università e della Ricerca INVALSI Istituto nazionale per la valutazione del sistema educativo di istruzione e di formazione
Derivate delle funzioni di una variabile.
 Derivate delle funzioni di una variabile. Il concetto di derivata di una funzione di una variabile è uno dei più fecondi della matematica ed è quello su cui si basa il calcolo differenziale. I problemi
Derivate delle funzioni di una variabile. Il concetto di derivata di una funzione di una variabile è uno dei più fecondi della matematica ed è quello su cui si basa il calcolo differenziale. I problemi
Calcolo di una Regressione lineare semplice con Excel
 Calcolo di una Regressione lineare semplice con Excel Inserire i dati In un tabellone vuoto di Excel, inserire i dati di X e di Y. Ad esempio i dati della Tabella 0.1 dovrebbero essere inseriti in Excel
Calcolo di una Regressione lineare semplice con Excel Inserire i dati In un tabellone vuoto di Excel, inserire i dati di X e di Y. Ad esempio i dati della Tabella 0.1 dovrebbero essere inseriti in Excel
GUIDA ALLA PRENOTAZIONE ESAMI PORTALE ISIDATA.NET
 Gestione Esami GUIDA ALLA PRENOTAZIONE ESAMI PORTALE ISIDATA.NET Dalla seguente videata abbiamo con una sola pagina la possibilità di operare sugli esami registrati (modifiche e prenotazioni), rinnovare
Gestione Esami GUIDA ALLA PRENOTAZIONE ESAMI PORTALE ISIDATA.NET Dalla seguente videata abbiamo con una sola pagina la possibilità di operare sugli esami registrati (modifiche e prenotazioni), rinnovare
Manuale per il controllo del materiale delle Prove INVALSI 2015
 Manuale per il controllo del materiale delle Prove 1 A.S. 2014 15 Pubblicato il 10.04.2015 Manuale per il controllo del materiale per le prove 1. Premessa Il controllo del materiale per le prove è molto
Manuale per il controllo del materiale delle Prove 1 A.S. 2014 15 Pubblicato il 10.04.2015 Manuale per il controllo del materiale per le prove 1. Premessa Il controllo del materiale per le prove è molto
VBA è un linguaggio di scripting derivato da Visual Basic, da cui prende il nome. Come ogni linguaggio ha le sue regole.
 Excel VBA VBA Visual Basic for Application VBA è un linguaggio di scripting derivato da Visual Basic, da cui prende il nome. Come ogni linguaggio ha le sue regole. 2 Prima di iniziare. Che cos è una variabile?
Excel VBA VBA Visual Basic for Application VBA è un linguaggio di scripting derivato da Visual Basic, da cui prende il nome. Come ogni linguaggio ha le sue regole. 2 Prima di iniziare. Che cos è una variabile?
ESERCIZI DEL CORSO DI INFORMATICA
 ESERCIZI DEL CORSO DI INFORMTIC Questa breve raccolta di esercizi vuole mettere in luce alcuni aspetti della prima parte del corso e fornire qualche spunto di riflessione. Il contenuto del materiale seguente
ESERCIZI DEL CORSO DI INFORMTIC Questa breve raccolta di esercizi vuole mettere in luce alcuni aspetti della prima parte del corso e fornire qualche spunto di riflessione. Il contenuto del materiale seguente
Capitolo 11 Test chi-quadro
 Levine, Krehbiel, Berenson Statistica II ed. 2006 Apogeo Capitolo 11 Test chi-quadro Insegnamento: Statistica Corsi di Laurea Triennale in Economia Facoltà di Economia, Università di Ferrara Docenti: Dott.
Levine, Krehbiel, Berenson Statistica II ed. 2006 Apogeo Capitolo 11 Test chi-quadro Insegnamento: Statistica Corsi di Laurea Triennale in Economia Facoltà di Economia, Università di Ferrara Docenti: Dott.
Si dice parabola il luogo geometrico dei punti del piano, equidistanti da un punto fisso, detto fuoco, e da una retta fissa, detta direttrice.
 LA PARABOLA Definizione: Si dice parabola il luogo geometrico dei punti del piano, equidistanti da un punto fisso, detto fuoco, e da una retta fissa, detta direttrice. Dimostrazione della parabola con
LA PARABOLA Definizione: Si dice parabola il luogo geometrico dei punti del piano, equidistanti da un punto fisso, detto fuoco, e da una retta fissa, detta direttrice. Dimostrazione della parabola con
Concetti principale della lezione precedente
 Corso di Statistica medica e applicata 9 a Lezione Dott.ssa Donatella Cocca Concetti principale della lezione precedente I concetti principali che sono stati presentati sono: Variabili su scala nominale
Corso di Statistica medica e applicata 9 a Lezione Dott.ssa Donatella Cocca Concetti principale della lezione precedente I concetti principali che sono stati presentati sono: Variabili su scala nominale
2. Variabilità mediante il confronto di valori caratteristici della
 2. Variabilità mediante il confronto di valori caratteristici della distribuzione Un approccio alternativo, e spesso utile, alla misura della variabilità è quello basato sul confronto di valori caratteristici
2. Variabilità mediante il confronto di valori caratteristici della distribuzione Un approccio alternativo, e spesso utile, alla misura della variabilità è quello basato sul confronto di valori caratteristici
Carta di credito standard. Carta di credito business. Esercitazione 12 maggio 2016
 Esercitazione 12 maggio 2016 ESERCIZIO 1 Si supponga che in un sondaggio di opinione su un campione di clienti, che utilizzano una carta di credito di tipo standard (Std) o di tipo business (Bsn), si siano
Esercitazione 12 maggio 2016 ESERCIZIO 1 Si supponga che in un sondaggio di opinione su un campione di clienti, che utilizzano una carta di credito di tipo standard (Std) o di tipo business (Bsn), si siano
Grafico 1: LAUREATI E DIPLOMATI ANNO 2001 PER ETA' E SESSO 16.117 13.482 < = 22 23 24 25 26 27 28 29 > = 30
 Il presente documento fornisce un'analisi grafica dei laureati nel corso dell'anno solare 21 secondo l'età alla laurea. Dati più dettagliati possono essere consultati sul sito dell'ufficio di statistica
Il presente documento fornisce un'analisi grafica dei laureati nel corso dell'anno solare 21 secondo l'età alla laurea. Dati più dettagliati possono essere consultati sul sito dell'ufficio di statistica
Le sezioni piane del cubo
 Le sezioni piane del cubo Versione provvisoria 11 dicembre 006 1 Simmetrie del cubo e sezioni speciali Sezioni speciali si presentano in corrispondenza di piani perpendicolari agli assi di simmetria del
Le sezioni piane del cubo Versione provvisoria 11 dicembre 006 1 Simmetrie del cubo e sezioni speciali Sezioni speciali si presentano in corrispondenza di piani perpendicolari agli assi di simmetria del
Simulazione del comportamento energetico di una turbina eolica: bilanci energetici ed analisi economica
 Università del Salento Facoltà di Ingegneria Corso di Laurea Specialistica in Ingegneria Meccanica a.a 2006/2007 Esame di Energetica industriale Simulazione del comportamento energetico di una turbina
Università del Salento Facoltà di Ingegneria Corso di Laurea Specialistica in Ingegneria Meccanica a.a 2006/2007 Esame di Energetica industriale Simulazione del comportamento energetico di una turbina
ANAGRAFE NAZIONALE CREDITI FORMATIVI. Manuale utente
 ANAGRAFE NAZIONALE CREDITI FORMATIVI Manuale utente Versione 1.0.0 APRILE 2015 1. Registrazione Per accedere al Sistema è necessario avere un nome utente e una password, ottenibili mediante una semplice
ANAGRAFE NAZIONALE CREDITI FORMATIVI Manuale utente Versione 1.0.0 APRILE 2015 1. Registrazione Per accedere al Sistema è necessario avere un nome utente e una password, ottenibili mediante una semplice
SOTTOSPAZI E OPERAZIONI IN SPAZI DIVERSI DA R n
 SPAZI E SOTTOSPAZI 1 SOTTOSPAZI E OPERAZIONI IN SPAZI DIVERSI DA R n Spazi di matrici. Spazi di polinomi. Generatori, dipendenza e indipendenza lineare, basi e dimensione. Intersezione e somma di sottospazi,
SPAZI E SOTTOSPAZI 1 SOTTOSPAZI E OPERAZIONI IN SPAZI DIVERSI DA R n Spazi di matrici. Spazi di polinomi. Generatori, dipendenza e indipendenza lineare, basi e dimensione. Intersezione e somma di sottospazi,
Syllabus: argomenti di Matematica delle prove di valutazione
 Syllabus: argomenti di Matematica delle prove di valutazione abcdef... ABC (senza calcolatrici, senza palmari, senza telefonini... ) Gli Argomenti A. Numeri frazioni e numeri decimali massimo comun divisore,
Syllabus: argomenti di Matematica delle prove di valutazione abcdef... ABC (senza calcolatrici, senza palmari, senza telefonini... ) Gli Argomenti A. Numeri frazioni e numeri decimali massimo comun divisore,
ESERCIZI PER LE VACANZE
 ESERCIZI PER LE VACANZE Tutti gli esercizi devono essere svolti sul quaderno. 1. Trova il quoziente di ciascuna frazione senza usare la calcolatrice (ricorda che puoi ridurre le frazioni ai minimi termini
ESERCIZI PER LE VACANZE Tutti gli esercizi devono essere svolti sul quaderno. 1. Trova il quoziente di ciascuna frazione senza usare la calcolatrice (ricorda che puoi ridurre le frazioni ai minimi termini
Risoluzione di problemi ingegneristici con Excel
 Risoluzione di problemi ingegneristici con Excel Problemi Ingegneristici Calcolare per via numerica le radici di un equazione Trovare l equazione che lega un set di dati ottenuti empiricamente (fitting
Risoluzione di problemi ingegneristici con Excel Problemi Ingegneristici Calcolare per via numerica le radici di un equazione Trovare l equazione che lega un set di dati ottenuti empiricamente (fitting
Progettazione logica
 Progettazione logica Progettazione Logica Il prodotto della progettazione logica è uno schema logico che rappresenta le informazioni contenute nello schema E- R in modo corretto ed efficiente. Richiede
Progettazione logica Progettazione Logica Il prodotto della progettazione logica è uno schema logico che rappresenta le informazioni contenute nello schema E- R in modo corretto ed efficiente. Richiede
Uno spazio per lo spazio.
 Uno spazio per lo spazio. Il gruppo di matematica del Laboratorio Franco Conti ha lavorato quest anno nella direzione di ripensare l insegnamento della geometria dello spazio, unendo la riflessione teorica
Uno spazio per lo spazio. Il gruppo di matematica del Laboratorio Franco Conti ha lavorato quest anno nella direzione di ripensare l insegnamento della geometria dello spazio, unendo la riflessione teorica
Esercitazioni di Statistica
 Esercitazioni di Statistica Indici di posizione e di variabilità Prof. Livia De Giovanni [email protected] Esercizio 1 Data la seguente distribuzione unitaria del carattere X: X : 4 2 4 2 6 4
Esercitazioni di Statistica Indici di posizione e di variabilità Prof. Livia De Giovanni [email protected] Esercizio 1 Data la seguente distribuzione unitaria del carattere X: X : 4 2 4 2 6 4
Prova d esame di Reti Logiche T 10 Giugno 2016
 Prova d esame di Reti Logiche T 10 Giugno 2016 COGNOME:.. NOME:.. MATRICOLA: Si ricorda il divieto di utilizzare qualsiasi dispositivo elettronico (computer, tablet, smartphone,..) eccetto la calcolatrice,
Prova d esame di Reti Logiche T 10 Giugno 2016 COGNOME:.. NOME:.. MATRICOLA: Si ricorda il divieto di utilizzare qualsiasi dispositivo elettronico (computer, tablet, smartphone,..) eccetto la calcolatrice,
Guida Esempi di calcolo del contributo Enasarco
 Guida Esempi di calcolo del contributo Enasarco Questa guida riporta alcuni esempi di calcolo del contributo Enasarco. Sono stati utilizzati i criteri di calcolo validi dal 1 gennaio 2012 al 31 dicembre
Guida Esempi di calcolo del contributo Enasarco Questa guida riporta alcuni esempi di calcolo del contributo Enasarco. Sono stati utilizzati i criteri di calcolo validi dal 1 gennaio 2012 al 31 dicembre
La Prova Invalsi 2014. per la scuola secondaria di 2 grado
 La Prova Invalsi 2014 MATHES - Sezione di Roma per la scuola secondaria di 2 grado Il test che l Invalsi ha utilizzato nell anno 2014 per la rilevazione degli apprendimenti in matematica conseguiti nelle
La Prova Invalsi 2014 MATHES - Sezione di Roma per la scuola secondaria di 2 grado Il test che l Invalsi ha utilizzato nell anno 2014 per la rilevazione degli apprendimenti in matematica conseguiti nelle
Appendice B Esempi di item di matematica
 Appendice B Esempi di item di matematica Esempi di item di matematica Classe quarta primaria 1 Osserva la seguente sequenza di numeri. 100, 1, 99, 2, 98, C, C, C Quali numeri devono andare nei tre riquadri?
Appendice B Esempi di item di matematica Esempi di item di matematica Classe quarta primaria 1 Osserva la seguente sequenza di numeri. 100, 1, 99, 2, 98, C, C, C Quali numeri devono andare nei tre riquadri?
Per capire qual è l altezza media degli italiani è stato intervistato un campione di 1523 cittadini. La media campionaria dell altezza risulta essere:
 PROBABILITÀ E STATISTICA Per capire qual è l altezza media degli italiani è stato intervistato un campione di 1523 cittadini. La media campionaria dell altezza risulta essere: x = 172, 3 cm Possiamo affermare
PROBABILITÀ E STATISTICA Per capire qual è l altezza media degli italiani è stato intervistato un campione di 1523 cittadini. La media campionaria dell altezza risulta essere: x = 172, 3 cm Possiamo affermare
LA VARIANTE PER I PRINCIPIANTI Cocotaki è un gioco pazzo. Quando si gioca per la prima volta, in particolare con bambini piccoli, è bene iniziare con
 HAIM SHAFIR Giocatori: 2 10 Età: a partire dai 5 anni Durata: circa 15 minuti Contenuto: 112 carte da gioco 1 istruzioni per il gioco IDEA DEL GIOCO In questo gioco meravigliosamente turbolento tutto è
HAIM SHAFIR Giocatori: 2 10 Età: a partire dai 5 anni Durata: circa 15 minuti Contenuto: 112 carte da gioco 1 istruzioni per il gioco IDEA DEL GIOCO In questo gioco meravigliosamente turbolento tutto è
ESERCIZIO 1. Confrontare, analiticamente e graficamente, la forma e la variabilità delle due distribuzioni. Commentare i risultati ottenuti.
 ESERCIZIO 1 Una società di ricerche di mercato ha svolto un indagine per conoscere il reddito mensile dalle famiglie residenti nelle regioni Lazio e Campania. I dati in Euro sono riportati nelle due tabelle
ESERCIZIO 1 Una società di ricerche di mercato ha svolto un indagine per conoscere il reddito mensile dalle famiglie residenti nelle regioni Lazio e Campania. I dati in Euro sono riportati nelle due tabelle
FUNZIONE DI UTILITÀ CURVE DI INDIFFERENZA (Cap. 3)
 FUNZIONE DI UTILITÀ CURVE DI INDIFFERENZA (Cap. 3) Consideriamo un agente che deve scegliere un paniere di consumo fra quelli economicamente ammissibili, posto che i beni di consumo disponibili sono solo
FUNZIONE DI UTILITÀ CURVE DI INDIFFERENZA (Cap. 3) Consideriamo un agente che deve scegliere un paniere di consumo fra quelli economicamente ammissibili, posto che i beni di consumo disponibili sono solo
Esercitazione # 6. a) Fissato il livello di significatività al 5% si tragga una conclusione circa l opportunità di avviare la campagna comparativa.
 Statistica Matematica A Esercitazione # 6 DUE MEDIE CON VARIANZE NOTE: Esercizio # Le ditte A e B producono sfere luminose. Una volta attivata la reazione chimica che rende luminosa una di queste sfere,
Statistica Matematica A Esercitazione # 6 DUE MEDIE CON VARIANZE NOTE: Esercizio # Le ditte A e B producono sfere luminose. Una volta attivata la reazione chimica che rende luminosa una di queste sfere,
descrivere le caratteristiche della sfera utilizzare le formule inerenti. Introduzione
 Anno 4 Sfera 1 Introduzione In questa lezione parleremo di un importante solido di rotazione detto sfera. Ne daremo la definizione, ne studieremo le caratteristiche e le formule a essa inerenti. Al termine
Anno 4 Sfera 1 Introduzione In questa lezione parleremo di un importante solido di rotazione detto sfera. Ne daremo la definizione, ne studieremo le caratteristiche e le formule a essa inerenti. Al termine
8 RALLY MATEMATICO TRANSALPINO PROVA II (marzo 2000) 1. 1. IN BICICLETTA (Cat. 3)
 1. IN BICICLETTA (Cat. 3) Claudio, Hans, Alfio, Jacky e Giancarlo partecipano ad una gara di biciclette e passano la linea del traguardo uno dopo l altro. Claudio arriva dopo Hans ma prima di Alfio. Giancarlo
1. IN BICICLETTA (Cat. 3) Claudio, Hans, Alfio, Jacky e Giancarlo partecipano ad una gara di biciclette e passano la linea del traguardo uno dopo l altro. Claudio arriva dopo Hans ma prima di Alfio. Giancarlo
Prontuario degli argomenti di Algebra
 Prontuario degli argomenti di Algebra NUMERI RELATIVI Un numero relativo è un numero preceduto da un segno + o - indicante la posizione rispetto ad un punto di riferimento a cui si associa il valore 0.
Prontuario degli argomenti di Algebra NUMERI RELATIVI Un numero relativo è un numero preceduto da un segno + o - indicante la posizione rispetto ad un punto di riferimento a cui si associa il valore 0.
