Soluzioni f(y)e iyx dy. f(y)e iy( x) dy = 1. = F 1 f( x)
|
|
|
- Gastone Carlucci
- 4 anni fa
- Visualizzazioni
Transcript
1 Soluzioni 8. Allora Quindi Usiamo la convenzione 3 F f(k) = f(k) = F f(x) = f(x) = F f(x) = = = F f( x) f(x)e ikx dx f(k)e ikx dk f(y)e iyx dy f(y)e iy( x) dy F f = F F f( x) = f( x) (a) f pari significa f( x) = f(x). Se f è pari allora F f = f( x) = f(x). Se F f(x) = f(x) allora f(x) = f( x). (b) f dispari significa f( x) = f(x). Come prima, F f(x) = f(x). (c) f = f P +f D (qualunque funzione è decomponibile nella somma di una funzione pari e una dispari). Allora F 4 f = F 4 (f P + f D ) = F (F f P + F f D ) = F (f P f D ) = f P + f D = f 3 f(x)e ikx dx = = = f(x)e ikx dx f( x)e ikx dx f(x)e ikx dx
2 4 f(x)e ikx dx = = = f(x)e ikx dx f( x)e ikx dx f(x)e ikx dx 5 f(k) = = = = f( k) f(x)e ikx dx f( x)e ikx dx f(x)e ikx dx 6 da cui 3 { se x < f(x) = altrimenti e ix dx = e ix ik f(k) = sin k k = eik e ik ik = sin k π k = sin k k 7 Se { se x < a f(x) = altrimenti F sin ak = f(k) = π k
3 3 allora, per la relazione di reciprocità, { sin ax F se k < a f(x) = = f(k) = π x altrimenti 8 k = è una discontinuità: regola dell / della somma di limite destro e sinistro. sin x (cos kx + i sin kx)dx = + π x k= π sin x cos x dx = x sin x cos x dx = π x 4 9 Si usi integrazione per parti e esercizio precedente. Già calcolato sopra. Si usi integrazione per parti e esercizi precedenti. Correzione del testo: Calcolare la trasformata di Fourier della funzione f(x) = e a x dove a >. Risposta: e a x e ikx = a a + k 3 ovvero Dall esercizio precedente segue che e ax = a π a a + k eikx dk = e a x cos kx a + k dk, x >
4 4 che è quanto si chiedeva di dimostrare. 4 In primo luogo si osservi che sin k k dk = π. Questo integrale può essere calcolato con i metodi dell analisi complessa oppure essere ottenuto come conseguenza del fatto che { sin k se x < π k eikx dk = altrimenti (esercizio 6). Ponendo x = si ottiene π sin k k da cui segue il risultato desiderato. Adesso si effettui nell integrale il cambiamento di variabili xt = u e si osservi che, per x >, π sin xt dt = t π e per x <, sin xt dt = π t π che è quanto si voleva dimostrare. = sin u u du = sin u du = u 5 Valgono le risposte e/o aiuti dati nel testo. 6 Valgono le risposte e/o aiuti dati nel testo. 7 Valgono le risposte e/o aiuti dati nel testo. 8 Valgono le risposte e/o aiuti dati nel testo. 9
5 5 Esercizio 6 del foglio 7. (da ricordare a memoria): Dunque, con la convenzione 3 ( ) f(k) = F + x e ikx + x = πe k = e ikx π + x dx = e k g(x) = a ix a + x = a ix (a + ix)(a ix) = a + ix = i x ia ( ) F = ie ikx a + ix x ia dx Metodo dei residui: polo semplice in x = ia. Per k >, chiusura nel semipiano inferiore, ( ) i F = = x ia Per k <, chiusura nel semipiano superiore, ( ) i ĝ(k) = F = (i)( i)e ak = e ak x ia Quindi a ix a + x Per k =, regola dell /: F = ĝ() = { e ak se k < se k > = π Integrale di Fourier della gaussiana (da ricordare a memoria): π e ax e ikx k dx = 4a e ax e ikx dx = per a = si ha la risposta al quesito, e k 4. a e k a e 4a
6 6 3 a = della formula dell esercizio precedente, k e 8. 4 Completare i quadrati e x +x = e (x +x+ 4)+ = e (x+ ) + e usare la proprietà di traslazione della trasformata di Fourier. 5 Banale. 6 Allora da cui Si derivi membro a membro rispetto a k: e x e ikx dx = ( ix)e x e ikx dx = k e 4 ( k ) e k 4, 4 xe x e ikx dx = i k ke 4 7 Come nell esercizio precedente, usando adesso quanto ottenuto nell esercizio : e a x e ikx = a a + k 8 Risposta: ( ik)e k ik
7 9 N. B. Con la convenzione 3, risulta comodo definire il prodotto di convoluzione nel come f g(x) = f(u)g(x u)du L esercizio è inteso con questa convenzione (lo stesso vale per gli esercizi seguenti). 7 f g(x) = = = i = i = sin ax f(u) sin(ax au)du f(u) ei(ax au) e i(ax au) du i ] [e iax f(u)e iau du e iax f(u)e iau du [e iax f(u)e iau du e iax f(u)e iau du f(u)e iau du ] (f è pari) 3 f(k) = ike k ĝ(k) = e k 4 f g(x) = x 3 x 3 e 3 3 Semplice generalizzazione di quanto visto in classe. 3 Usare Cauchy Schwarz.
8 8 33 f(k) = f(x)e ikx dx f(x)e ikx dx = = f L f(x) dx 34 Vedere lezione..
S.9. = f (z). (z + 1)(z + 3) = 1/2. = 1 2z 1. S-50 nino zanghì S.9.1. Se C. f (z)dz = 0 indipendentemente da C, allora ne segue che
 S-5 nino zanghì S.9 S.9.. Se C f (z)dz = indipendentemente da C, allora ne segue che F(z) = z a f (z)dz è indipendente dal percorso che unisce a e z, purché tale percorso si trovi tutto dentro la regione
S-5 nino zanghì S.9 S.9.. Se C f (z)dz = indipendentemente da C, allora ne segue che F(z) = z a f (z)dz è indipendente dal percorso che unisce a e z, purché tale percorso si trovi tutto dentro la regione
Esame di Fisica Matematica 2, a.a (5/6/2012)
 Esame di Fisica Matematica 2, a.a. 2-22 (5/6/22) Tempo a disposizione: TRE ORE. Svolgere tutti gli esercizi. Scrivere chiaramente nome, cognome e numero di matricola. Non e consentito l uso di libri, appunti
Esame di Fisica Matematica 2, a.a. 2-22 (5/6/22) Tempo a disposizione: TRE ORE. Svolgere tutti gli esercizi. Scrivere chiaramente nome, cognome e numero di matricola. Non e consentito l uso di libri, appunti
Metodi Matematici per la Fisica
 Metodi Matematici per la Fisica Prova scritta - 6 settembre Esercizio 6 punti Calcolare l integrale π dx I π + 4 cos x. Con la sostituzione z e ix quindi: x i lnz e dx idz/z l integrale diventa dz/z I
Metodi Matematici per la Fisica Prova scritta - 6 settembre Esercizio 6 punti Calcolare l integrale π dx I π + 4 cos x. Con la sostituzione z e ix quindi: x i lnz e dx idz/z l integrale diventa dz/z I
Metodi Matematici per la Fisica
 Metodi Matematici per la Fisica Prova scritta - 6 ottobre 0 Esercizio (6 punti Si usi il metodo dei residui per calcolare l integrale J (z + sin 3 (/z, z con il cammino d integrazione percorso in senso
Metodi Matematici per la Fisica Prova scritta - 6 ottobre 0 Esercizio (6 punti Si usi il metodo dei residui per calcolare l integrale J (z + sin 3 (/z, z con il cammino d integrazione percorso in senso
7.6 Esercizi svolti Trasformata di Fourier
 78 7 Trasformata di Fourier 7.6 Esercizi svolti Esercizio 7. Determinare la trasformata di Fourier delle seguenti funzioni : a x(t =u(t e t + u(t u(t + ; b x(t =e i3t p (t + ; c x(t =p (t ; ( d x(t =p
78 7 Trasformata di Fourier 7.6 Esercizi svolti Esercizio 7. Determinare la trasformata di Fourier delle seguenti funzioni : a x(t =u(t e t + u(t u(t + ; b x(t =e i3t p (t + ; c x(t =p (t ; ( d x(t =p
METODI MATEMATICI PER L INGEGNERIA - A.A Primo appello del 9/6/2010. e 2ix dx = e ix 2 dx = t e it dt = [ it e it e it ] π/2
![METODI MATEMATICI PER L INGEGNERIA - A.A Primo appello del 9/6/2010. e 2ix dx = e ix 2 dx = t e it dt = [ it e it e it ] π/2 METODI MATEMATICI PER L INGEGNERIA - A.A Primo appello del 9/6/2010. e 2ix dx = e ix 2 dx = t e it dt = [ it e it e it ] π/2](/thumbs/96/130608003.jpg) METODI MATEMATICI PER L INGEGNERIA - A.A. 29- Primo appello del 9/6/2 Risolvere i seguenti esercizi, spiegando il procedimento usato. Calcolare la proiezione in L 2 π 2, π 2 di xt = t sul sottospazio generato
METODI MATEMATICI PER L INGEGNERIA - A.A. 29- Primo appello del 9/6/2 Risolvere i seguenti esercizi, spiegando il procedimento usato. Calcolare la proiezione in L 2 π 2, π 2 di xt = t sul sottospazio generato
u(x, 0) = 0 in R. Soluzioni
 Es. Es. Es. 3 Es. 4 Totale Politecnico di Milano - Ingegneria Energetica Metodi Analitici e Numerici A 6 Giugno 7 Cognome: Nome: Matricola: Esercizio. a. Si consideri la funzione vx, t = e t x e t + e
Es. Es. Es. 3 Es. 4 Totale Politecnico di Milano - Ingegneria Energetica Metodi Analitici e Numerici A 6 Giugno 7 Cognome: Nome: Matricola: Esercizio. a. Si consideri la funzione vx, t = e t x e t + e
ESERCITAZIONE 9: INTEGRALI DEFINITI. CALCOLO DELLE AREE E ALTRE APPLICAZIONI
 ESERCITAZIONE 9: INTEGRALI DEFINITI. CALCOLO DELLE AREE E ALTRE APPLICAZIONI Tiziana Raparelli 5/5/9 CONOSCENZE PRELIMINARI Vogliamo calcolare f ( x, ax + bx + c ) dx. Se a =, allora basta porre bx + c
ESERCITAZIONE 9: INTEGRALI DEFINITI. CALCOLO DELLE AREE E ALTRE APPLICAZIONI Tiziana Raparelli 5/5/9 CONOSCENZE PRELIMINARI Vogliamo calcolare f ( x, ax + bx + c ) dx. Se a =, allora basta porre bx + c
Limitiamoci dapprima a considerare una funzione f di periodo 2π. Cercheremo di approssimarla con polinomi trigonometrici di ordine n della forma
 Serie di Fourier L idea che sta alla base degli sviluppi in serie di Fourier è quella di approssimare, in qualche senso, le funzioni (integrabili periodiche per mezzo di funzioni più regolari e/o più facilmente
Serie di Fourier L idea che sta alla base degli sviluppi in serie di Fourier è quella di approssimare, in qualche senso, le funzioni (integrabili periodiche per mezzo di funzioni più regolari e/o più facilmente
(1) Per ciascuno dei seguenti spazi dire se è o meno uno spazio vettoriale (spiegare)
 1 Spazi vettoriali (1) Per ciascuno dei seguenti spazi dire se è o meno uno spazio vettoriale (spiegare) (a) R 5 (b) [0, ) (c) x R 2 : x 1 + 2x 2 = 0} (d) x R 2 : x 2 1 + 2x 2 = 0} (e) x R 2 : x 1 > x
1 Spazi vettoriali (1) Per ciascuno dei seguenti spazi dire se è o meno uno spazio vettoriale (spiegare) (a) R 5 (b) [0, ) (c) x R 2 : x 1 + 2x 2 = 0} (d) x R 2 : x 2 1 + 2x 2 = 0} (e) x R 2 : x 1 > x
ESERCIZI DI MATEMATICA APPLICATA
 ANTONIO LEACI Analisi Complessa ( È data la funzione: f(z (z2 + e z sin z Si studi l analiticità di f(z nel piano complesso C Si determinino e si classifichino le eventuali singolarità Si calcoli il residuo
ANTONIO LEACI Analisi Complessa ( È data la funzione: f(z (z2 + e z sin z Si studi l analiticità di f(z nel piano complesso C Si determinino e si classifichino le eventuali singolarità Si calcoli il residuo
Metodi Matematici per la Fisica
 Metodi Matematici per la Fisica Prova scritta - giugno 0 Esercizio 8 punti) Si consideri la funzione fz) = z sinz) sin[sinz)], si studino e classifichino le singolarità e, di conseguenza, si stabilisca
Metodi Matematici per la Fisica Prova scritta - giugno 0 Esercizio 8 punti) Si consideri la funzione fz) = z sinz) sin[sinz)], si studino e classifichino le singolarità e, di conseguenza, si stabilisca
Convergenza puntuale ed uniforme delle serie di Fourier
 Convergenza puntuale ed uniforme delle serie di Fourier 8 aprile 009 In questi appunti prendiamo in considerazione funzioni di variabile reale che possono assumere però valori complessi. Una funzione F
Convergenza puntuale ed uniforme delle serie di Fourier 8 aprile 009 In questi appunti prendiamo in considerazione funzioni di variabile reale che possono assumere però valori complessi. Una funzione F
Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1
 Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1 30 Gennaio 2018 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo.
Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1 30 Gennaio 2018 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo.
Dispensa per il modulo METODI MATEMATICI Corso di Laurea in Fisica. La Trasformata Di Fourier
 1 Dispensa per il modlo METODI MATEMATICI Corso di Larea in Fisica La Trasformata Di Forier G. Nisticò 2 1. INTRODUZIONE Sia f na fnzione complessa di variabile reale, integrabile in modlo, cioè tale che
1 Dispensa per il modlo METODI MATEMATICI Corso di Larea in Fisica La Trasformata Di Forier G. Nisticò 2 1. INTRODUZIONE Sia f na fnzione complessa di variabile reale, integrabile in modlo, cioè tale che
f(x) = E chiaro che in questo caso, l integrale di f si puo fare ed e finito: f(x)dx = dx = b a
 1. Lo spazio L 1 Avremo bisogno di calcolare integrali di funzioni definite su tutto R, e quindi ricordiamo brevemente alcuni esempi di funzioni integrabili. Definition 1. Si dice che una funzione f appartiene
1. Lo spazio L 1 Avremo bisogno di calcolare integrali di funzioni definite su tutto R, e quindi ricordiamo brevemente alcuni esempi di funzioni integrabili. Definition 1. Si dice che una funzione f appartiene
Esame di Fisica Matematica III, a.a (8/2/2011)
 Esame di Fisica Matematica III, a.a. 010-011 (8//011) Tempo a disposizione: TRE ORE. Non e consentito l uso di appunti o calcolatrici. Svolgere tutti gli esercizi. Esercizio 1. Determinare la piu generale
Esame di Fisica Matematica III, a.a. 010-011 (8//011) Tempo a disposizione: TRE ORE. Non e consentito l uso di appunti o calcolatrici. Svolgere tutti gli esercizi. Esercizio 1. Determinare la piu generale
Capitolo 4. Trasformate Integrali. 4.1 Trasformata di Fourier
 Capitolo 4 Trasformate Integrali 4. Trasformata di Fourier Nel capitolo abbiamo imparato a risolvere l eq. (3.) nel caso in cui il termine noto sia periodico e abbiamo dovuto poi allargare il discorso
Capitolo 4 Trasformate Integrali 4. Trasformata di Fourier Nel capitolo abbiamo imparato a risolvere l eq. (3.) nel caso in cui il termine noto sia periodico e abbiamo dovuto poi allargare il discorso
3) Enunciare e dimostrare le regole di trasformazione algebriche e analitiche della trasformata di Fourier.
 Lecce, 16/4/2008 1) Calcolare il valor principale del seguente integrale: x + 1 (x 2 + 4)x dx Y (t) 3Y (t) + 2Y (t) = H(t 1) e t t > 0, Y (0) = 0, Y (0) = 1, 3) Enunciare e dimostrare le regole di trasformazione
Lecce, 16/4/2008 1) Calcolare il valor principale del seguente integrale: x + 1 (x 2 + 4)x dx Y (t) 3Y (t) + 2Y (t) = H(t 1) e t t > 0, Y (0) = 0, Y (0) = 1, 3) Enunciare e dimostrare le regole di trasformazione
Esame di Metodi Matematici per l Ingegneria Prima prova in itinere. Novembre 2016 A.A. 2016/2017. Prof. M. Bramanti Tema A
 Esame di Metodi Matematici per l Ingegneria Prima prova in itinere. Novembre 6 A.A. 6/7. Prof. M. Bramanti Tema A Cognome: Nome N matr. o cod. persona: Dom Dom Dom 3 Es Es Es 3 Tot. Punti Domande di teoria
Esame di Metodi Matematici per l Ingegneria Prima prova in itinere. Novembre 6 A.A. 6/7. Prof. M. Bramanti Tema A Cognome: Nome N matr. o cod. persona: Dom Dom Dom 3 Es Es Es 3 Tot. Punti Domande di teoria
Analisi Matematica 3, a.a Scritto del quinto appello, 11 settembre 2019 Testi 1
 Scritto del quinto appello, 11 settembre 019 Testi 1 1. a) Dato u L 1 R), sia vx) := u x); esprimere ˆv in termini di û. b) Caratterizzare le funzioni u L 1 R) tali che û è una funzione dispari a valori
Scritto del quinto appello, 11 settembre 019 Testi 1 1. a) Dato u L 1 R), sia vx) := u x); esprimere ˆv in termini di û. b) Caratterizzare le funzioni u L 1 R) tali che û è una funzione dispari a valori
Complementi di Matematica - Ingegneria Energetica/Elettrica/Sicurezza Prova scritta intermedia del 7 dicembre nx 1 + n α x 2.
 Complementi di Matematica - Ingegneria Energetica/Elettrica/Sicurezza Prova scritta intermedia del 7 dicembre 7. Si consideri la successione di funzioni f n, dove f n : [, [ R è definita da e dove α >
Complementi di Matematica - Ingegneria Energetica/Elettrica/Sicurezza Prova scritta intermedia del 7 dicembre 7. Si consideri la successione di funzioni f n, dove f n : [, [ R è definita da e dove α >
Serie di Fourier - Esercizi svolti
 Serie di Fourier - Esercizi svolti Esercizio 1 È data la funzione f con domf) = R, periodica di periodo, tale che onda quadra) 1 se < x < fx) = se x = e x = 1 se < x < 1) 1 Calcolare i coefficienti di
Serie di Fourier - Esercizi svolti Esercizio 1 È data la funzione f con domf) = R, periodica di periodo, tale che onda quadra) 1 se < x < fx) = se x = e x = 1 se < x < 1) 1 Calcolare i coefficienti di
MODELLI e METODI MATEMATICI della FISICA. Esercizi - A.A
 MODELLI e METODI MATEMATICI della FISICA Esercizi - A.A. 08-9 settimana Esercizi:. Risolvere il problema di Cauchy y (x) = αy (x) + y (x) y (x) = αy (x) + y 3 (x) y 3(x) = αy 3 (x) con condizioni iniziali
MODELLI e METODI MATEMATICI della FISICA Esercizi - A.A. 08-9 settimana Esercizi:. Risolvere il problema di Cauchy y (x) = αy (x) + y (x) y (x) = αy (x) + y 3 (x) y 3(x) = αy 3 (x) con condizioni iniziali
Analisi Matematica I per Ingegneria Gestionale, a.a Scritto del quarto appello, 7 giugno 2018 Testi 1
 Scritto del quarto appello, 7 giugno 28 Testi Prima parte, gruppo.. Trovare le soluzioni della disequazione tan(3x) nell intervallo x π/3. 2. Scrivere l equazione della retta tangente al grafico y = x
Scritto del quarto appello, 7 giugno 28 Testi Prima parte, gruppo.. Trovare le soluzioni della disequazione tan(3x) nell intervallo x π/3. 2. Scrivere l equazione della retta tangente al grafico y = x
Analisi Reale e Complessa - a.a. 2008/2009
 Terzo appello Esercizio Analisi Reale e Complessa - a.a. 8/9 Sia (a) Si provi che f L (R); f(x) eix x i. (b) Si calcoli con metodi di variabile complessa la trasformata di Fourier di f. (a) Si osservi
Terzo appello Esercizio Analisi Reale e Complessa - a.a. 8/9 Sia (a) Si provi che f L (R); f(x) eix x i. (b) Si calcoli con metodi di variabile complessa la trasformata di Fourier di f. (a) Si osservi
Corso di Laurea in Matematica, A.A. 2013/2014 Analisi Reale e Complessa, Esame del y 2 x2 + y 2 2 R 2 ; 1 }
 NOME:................. MATRICOLA:................. Corso di Laurea in Matematica, A.A. 3/ Analisi Reale e Complessa, Esame del 8..5 Si stabilisca se la formula x + y α se f(x, y x + y x + y, x + y se x
NOME:................. MATRICOLA:................. Corso di Laurea in Matematica, A.A. 3/ Analisi Reale e Complessa, Esame del 8..5 Si stabilisca se la formula x + y α se f(x, y x + y x + y, x + y se x
Esame di Fisica Matematica III, a.a (27/9/2011)
 Esame di Fisica Matematica III, a.a. 010-011 (7/9/011) Tempo a disposizione: DUE ORE. Non e consentito l uso di appunti o calcolatrici. Svolgere tutti gli esercizi. Esercizio 1. Si determini, attraverso
Esame di Fisica Matematica III, a.a. 010-011 (7/9/011) Tempo a disposizione: DUE ORE. Non e consentito l uso di appunti o calcolatrici. Svolgere tutti gli esercizi. Esercizio 1. Si determini, attraverso
18.3. Il nucleo del calore e altre applicazioni Il nucleo del calore.
 18.3. Il nucleo del calore e altre applicazioni. 18.3.1. Il nucleo del calore. analisi dimensionale Vogliamo studiare la propagazione del calore in un filo (adiabaticamente isolato) di lunghezza infinita.
18.3. Il nucleo del calore e altre applicazioni. 18.3.1. Il nucleo del calore. analisi dimensionale Vogliamo studiare la propagazione del calore in un filo (adiabaticamente isolato) di lunghezza infinita.
Provetta scritta di Calcolo I Corsi di laurea in Fisica - Scienza e Tecnologia dei Materiali Prova scritta del 7/12/2005 Fila A
 Provetta scritta di Calcolo I Prova scritta del 7/2/25 Fila A ) Calcolare i limiti 3 x 3 x 4 ; b) lim sin(2x) + x2 x( cos(3x)) c) lim + 5 x 7 x 4 x 2 + x. 2) Determinare il massimo di x 3 (2 + x 4 ) 3/2,
Provetta scritta di Calcolo I Prova scritta del 7/2/25 Fila A ) Calcolare i limiti 3 x 3 x 4 ; b) lim sin(2x) + x2 x( cos(3x)) c) lim + 5 x 7 x 4 x 2 + x. 2) Determinare il massimo di x 3 (2 + x 4 ) 3/2,
MODELLI E METODI MATEMATICI DELLA FISICA A.A. 2016/2017 Prof. C. Presilla. Prova A1 27 aprile 2017
 MODELLI E METODI MATEMATICI DELLA FISICA A.A. 206/207 Prof. C. Presilla Prova A 27 aprile 207 Cognome Nome Matricola iscritto al secondo anno iscritto al terzo anno fuoricorso o con più di 55 CFU penalità
MODELLI E METODI MATEMATICI DELLA FISICA A.A. 206/207 Prof. C. Presilla Prova A 27 aprile 207 Cognome Nome Matricola iscritto al secondo anno iscritto al terzo anno fuoricorso o con più di 55 CFU penalità
Esercizio 1. Calcolare per n Z z 2. Soluzione: Per n 0 si ha che l integrale é nullo per il teorema integrale di Cauchy. Per n = 1 si ha che 2
 Sapienza - Università di Roma Facoltà di Ingegneria - A.A. -4 Esercitazione per il corso di Metodi Matematici per l Ingegneria (Docente Daniela Giachetti) a cura di Ida de Bonis Esercizio. Calcolare per
Sapienza - Università di Roma Facoltà di Ingegneria - A.A. -4 Esercitazione per il corso di Metodi Matematici per l Ingegneria (Docente Daniela Giachetti) a cura di Ida de Bonis Esercizio. Calcolare per
METODI MATEMATICI PER LA FISICA
 METODI MATEMATICI PER LA FISICA SECONDO ESONERO - 5 GIUGNO 6 Si svolgano cortesemente i seguenti Problemi. PRIMO PROBLEMA (PUNTEGGIO: 3/3) Dati due operatori hermitiani  and ˆB in uno spazio di Hilbert
METODI MATEMATICI PER LA FISICA SECONDO ESONERO - 5 GIUGNO 6 Si svolgano cortesemente i seguenti Problemi. PRIMO PROBLEMA (PUNTEGGIO: 3/3) Dati due operatori hermitiani  and ˆB in uno spazio di Hilbert
19.1. Il nucleo del calore e altre applicazioni Il nucleo del calore.
 19.1. Il nucleo del calore e altre applicazioni. 19.1.1. Il nucleo del calore. analisi dimensionale Vogliamo studiare la propagazione del calore in un filo (adiabaticamente isolato) di lunghezza infinita.
19.1. Il nucleo del calore e altre applicazioni. 19.1.1. Il nucleo del calore. analisi dimensionale Vogliamo studiare la propagazione del calore in un filo (adiabaticamente isolato) di lunghezza infinita.
Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1
 Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1 27 giugno 2017 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo.
Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1 27 giugno 2017 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo.
3.2 Funzioni periodiche e sviluppi in Serie di Fourier
 3. Funzioni periodiche e sviluppi in Serie di Fourier Una prima classe di funzioni per cui si può effettuare l analisi armonica (3.5 contiene le funzioni periodiche (di periodo, tali cioè che f(t + = f(t,
3. Funzioni periodiche e sviluppi in Serie di Fourier Una prima classe di funzioni per cui si può effettuare l analisi armonica (3.5 contiene le funzioni periodiche (di periodo, tali cioè che f(t + = f(t,
Metodi Matematici per la Fisica
 Si svolgano cortesemente i seguenti esercizi Esercizio (6 punti) Si calcoli l integrale Metodi Matematici per la Fisica Prova scritta - dicembre 03 I = sen (x) cosh 3 (x) Possiamo riscrivere l integrale
Si svolgano cortesemente i seguenti esercizi Esercizio (6 punti) Si calcoli l integrale Metodi Matematici per la Fisica Prova scritta - dicembre 03 I = sen (x) cosh 3 (x) Possiamo riscrivere l integrale
Esercitazione di Metodi Matematici per l Ottica del E. Scoppola. y 1 x, 1 y 1, x > 0, y < log x
 Esercitazione di Metodi Matematici per l Ottica del 6-4 - 7 E. Scoppola Esercizio Determinare gli insiemi di definizione delle funzioni: fx) = x y y ) /4 loge x ) + loglog x y), gx) = x y y Per fx) abbiamo
Esercitazione di Metodi Matematici per l Ottica del 6-4 - 7 E. Scoppola Esercizio Determinare gli insiemi di definizione delle funzioni: fx) = x y y ) /4 loge x ) + loglog x y), gx) = x y y Per fx) abbiamo
Svolgimento degli esercizi N. 3
 Svolgimento degli esercizi N. 3 Prova scritta parziale n. del // Fila. Calcolare il valore del seguente integrale definito: ( x + e x ) dx. ( x + e x ) dx ( x + e 4x + x e x) dx x dx + e 4x dx + x e x
Svolgimento degli esercizi N. 3 Prova scritta parziale n. del // Fila. Calcolare il valore del seguente integrale definito: ( x + e x ) dx. ( x + e x ) dx ( x + e 4x + x e x) dx x dx + e 4x dx + x e x
Metodi Matematici per la Fisica
 Metodi Matematici per la Fisica Prova scritta - 7 febbraio Eserciio (6 punti) Calcolare il valore principale di Cauchy dell integrale con a e b reali e a, b >. J = P.V. Soluione L integrale può essere
Metodi Matematici per la Fisica Prova scritta - 7 febbraio Eserciio (6 punti) Calcolare il valore principale di Cauchy dell integrale con a e b reali e a, b >. J = P.V. Soluione L integrale può essere
Esame di Analisi Funzionale e Trasformate Quinto appello. Febbraio 2018 A.A. 2016/2017. Prof. M. Bramanti
 Esame di Analisi Funzionale e Trasformate Quinto appello. Febbraio 28 A.A. 26/27. Prof. M. Bramanti Cognome: Nome N matr. o cod. persona: Dom Dom 2 Dom 3 Es Es 2 Es 3 Tot. Punti Domande di teoria rispondere
Esame di Analisi Funzionale e Trasformate Quinto appello. Febbraio 28 A.A. 26/27. Prof. M. Bramanti Cognome: Nome N matr. o cod. persona: Dom Dom 2 Dom 3 Es Es 2 Es 3 Tot. Punti Domande di teoria rispondere
Esercizio 1. (i) Si dia la definizione di successione delle somme parziali per una serie di funzioni. (ii) Data la serie n + 1.
 Sapienza - Università di Roma Facoltà di Ingegneria - A.A. 0-04 Esercitazione per il corso di Metodi Matematici per l Ingegneria a cura di Daniela Giachetti Esercizio. (i) Si dia la definizione di successione
Sapienza - Università di Roma Facoltà di Ingegneria - A.A. 0-04 Esercitazione per il corso di Metodi Matematici per l Ingegneria a cura di Daniela Giachetti Esercizio. (i) Si dia la definizione di successione
METODI MATEMATICI DELLA FISICA A.A. 2004/2005 Prof. C. Presilla. Prova di recupero 14 settembre 2005
 METODI MATEMATICI DELLA FISICA A.A. 2004/2005 Prof. C. Presilla Prova di recupero 4 settembre 2005 Cognome Nome Corso di Laurea in sostituzione delle prove in itinere segnare) 2 3 penalità esercizio voto
METODI MATEMATICI DELLA FISICA A.A. 2004/2005 Prof. C. Presilla Prova di recupero 4 settembre 2005 Cognome Nome Corso di Laurea in sostituzione delle prove in itinere segnare) 2 3 penalità esercizio voto
Esame di Metodi Matematici per l Ingegneria Prima prova in itinere. Novembre 2017 A.A. 2017/2018. Prof. M. Bramanti Tema A
 Esame di Metodi Matematici per l Ingegneria Prima prova in itinere. Novembre 2017 A.A. 2017/2018. Prof. M. Bramanti Tema A Cognome: Nome N matr. o cod. persona: Dom 1 Dom 2 Dom 3 Es 1 Es 2 Es 3 Tot. Punti
Esame di Metodi Matematici per l Ingegneria Prima prova in itinere. Novembre 2017 A.A. 2017/2018. Prof. M. Bramanti Tema A Cognome: Nome N matr. o cod. persona: Dom 1 Dom 2 Dom 3 Es 1 Es 2 Es 3 Tot. Punti
Esercizi sulle trasformate di Fourier
 Esercizi sulle trasformate di Fourier Corso di Fisica Matematica, a.a. 3-4 Dipartimento di Matematica, Università di Milano 8 Novembre 3 Questi esercizi richiederanno il calcolo di integrali a volte non
Esercizi sulle trasformate di Fourier Corso di Fisica Matematica, a.a. 3-4 Dipartimento di Matematica, Università di Milano 8 Novembre 3 Questi esercizi richiederanno il calcolo di integrali a volte non
Esame di Fisica Matematica 2, a.a (8/7/2014)
 Esame di Fisica Matematica 2, a.a. 23-24 (8/7/24) Tempo a disposizione: DUE ORE. Svolgere tutti gli esercizi, che hanno lo stesso nel determinare il voto finale. Scrivere chiaramente e a stampatello nome,
Esame di Fisica Matematica 2, a.a. 23-24 (8/7/24) Tempo a disposizione: DUE ORE. Svolgere tutti gli esercizi, che hanno lo stesso nel determinare il voto finale. Scrivere chiaramente e a stampatello nome,
Analisi Matematica 3, a.a Scritto del quarto appello, 10 luglio 2019 Testi 1
 Scritto del quarto appello, luglio 29 Testi. Data f : [ π, π] C di classe C, scrivere i coefficienti di Fourier complessi di f in funzione di quelli di f e del numero mf := fπ f π. 2. Calcolare la Trasformata
Scritto del quarto appello, luglio 29 Testi. Data f : [ π, π] C di classe C, scrivere i coefficienti di Fourier complessi di f in funzione di quelli di f e del numero mf := fπ f π. 2. Calcolare la Trasformata
Reti nel dominio delle frequenze. Lezione 10 2
 Lezione 10 1 Reti nel dominio delle frequenze Lezione 10 2 Introduzione Lezione 10 3 Cosa c è nell Unità 3 In questa sezione si affronteranno Introduzione all Unità Trasformate di Laplace Reti nel dominio
Lezione 10 1 Reti nel dominio delle frequenze Lezione 10 2 Introduzione Lezione 10 3 Cosa c è nell Unità 3 In questa sezione si affronteranno Introduzione all Unità Trasformate di Laplace Reti nel dominio
METODI MATEMATICI PER LA FISICA
 METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 3 FEBBRAIO 6 Si risolvano cortesemente i seguenti problemi. PRIMO PROBLEMA (PUNTEGGIO: 6/3) Si calcoli l integrale SOLUZIONE DEL PRIMO PROBLEMA M=. (+ x
METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 3 FEBBRAIO 6 Si risolvano cortesemente i seguenti problemi. PRIMO PROBLEMA (PUNTEGGIO: 6/3) Si calcoli l integrale SOLUZIONE DEL PRIMO PROBLEMA M=. (+ x
Matematica - Prova d esame (25/06/2004)
 Matematica - Prova d esame (/6/4) Università di Verona - Laurea in Biotecnologie AI - A.A. /4. (a) Disegnare sul piano di Gauss i numeri z = i e w = i, e scriverne la forma trigonometrica. Calcolare z
Matematica - Prova d esame (/6/4) Università di Verona - Laurea in Biotecnologie AI - A.A. /4. (a) Disegnare sul piano di Gauss i numeri z = i e w = i, e scriverne la forma trigonometrica. Calcolare z
Corso di Laurea in Ingegneria Informatica Prova scritta di Analisi Matematica 1
 Corso di Laurea in Ingegneria Informatica Prova scritta di Analisi Matematica 1 16 febbraio 017 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo.
Corso di Laurea in Ingegneria Informatica Prova scritta di Analisi Matematica 1 16 febbraio 017 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo.
z i z + 1 z + 1 3, da cui, ponendo come al solito z 2i z 2i 1, da cui si ricava x y. ln(7) + i(π + 2kπ). sin z = 3.
 METODI MATEMATICI per l INGEGNERIA PRIMA PROVA IN ITINERE del 9 novembre ) Determinare l insieme di convergenza della serie n 3 n ( ) n z i z + precisando se è aperto o chiuso. ( ) z i Soluzione. Ponendo
METODI MATEMATICI per l INGEGNERIA PRIMA PROVA IN ITINERE del 9 novembre ) Determinare l insieme di convergenza della serie n 3 n ( ) n z i z + precisando se è aperto o chiuso. ( ) z i Soluzione. Ponendo
Analisi Matematica I per Ingegneria Gestionale, a.a Scritto del sesto appello, 16 luglio 2018 Testi 1
 Scritto del sesto appello, 6 luglio 208 Testi Prima parte, gruppo.. Trovare α [0, 2π) per cui vale l identità trigonometrica sin(x π/3) = cos(x + α). 2. Trovare il polinomio di Taylor (in 0) di ordine
Scritto del sesto appello, 6 luglio 208 Testi Prima parte, gruppo.. Trovare α [0, 2π) per cui vale l identità trigonometrica sin(x π/3) = cos(x + α). 2. Trovare il polinomio di Taylor (in 0) di ordine
Esame di Metodi Matematici per l Ingegneria Primo appello. Febbraio 2019 A.A. 2018/2019. Prof. M. Bramanti Tema A
 Esame di Metodi Matematici per l Ingegneria Primo appello. Febbraio 9 A.A. 8/9. Prof. M. Bramanti Tema A Cognome: Nome N matr. o cod. persona: Dom Dom Dom 3 Es Es Es 3 Tot. Punti Domande di teoria rispondere
Esame di Metodi Matematici per l Ingegneria Primo appello. Febbraio 9 A.A. 8/9. Prof. M. Bramanti Tema A Cognome: Nome N matr. o cod. persona: Dom Dom Dom 3 Es Es Es 3 Tot. Punti Domande di teoria rispondere
Esercizio III Calcolare la trasformata di Fourier della funzione. Esercizio IV Sviluppare la funzione. Tema d esame. Giugno 2004
 Tema d esame. Giugno 24 Esercizio I Calcolare il seguente integrale col metodo dei residui 2π dφ < a < () + a 2 2a cos φ Esercizio II Trovare la soluzione dell equazione di Laplace nella regione del piano
Tema d esame. Giugno 24 Esercizio I Calcolare il seguente integrale col metodo dei residui 2π dφ < a < () + a 2 2a cos φ Esercizio II Trovare la soluzione dell equazione di Laplace nella regione del piano
f(n)r n e inx lim Se f(x) C(T) allora f S (r) f(x) = lim e inx
 17.1. Analisi di Fourier III. 17.1.1. Teorema di approssimazione di Weierstrass. Un polinomio trigonometrico è una qualunque funzione della forma n
17.1. Analisi di Fourier III. 17.1.1. Teorema di approssimazione di Weierstrass. Un polinomio trigonometrico è una qualunque funzione della forma n
METODI MATEMATICI PER LA FISICA
 Si svolgano cortesemente i seguenti esercizi. ESERCIZIO (5 PUNTI) METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 3 LUGLIO 4 Sia f (z) una funzione analitica nel dominio D = {z : z (, ), > }, con f (z),
Si svolgano cortesemente i seguenti esercizi. ESERCIZIO (5 PUNTI) METODI MATEMATICI PER LA FISICA PROVA SCRITTA - 3 LUGLIO 4 Sia f (z) una funzione analitica nel dominio D = {z : z (, ), > }, con f (z),
Secondo appello 2005/ Tema 1
 Secondo appello 2005/2006 - Tema Esercizio Risolvere l equazione di variabile complessa determinando le soluzioni in forma algebrica. Ponendo z = x + iy con x, y R, si ottiene z 2 + 2iz + 2 z = 0, () (x
Secondo appello 2005/2006 - Tema Esercizio Risolvere l equazione di variabile complessa determinando le soluzioni in forma algebrica. Ponendo z = x + iy con x, y R, si ottiene z 2 + 2iz + 2 z = 0, () (x
Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1
 Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1 5 Giugno 2018 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo.
Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1 5 Giugno 2018 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo.
Esercitazione di riepilogo su serie di funzioni, e in particolare serie di Fourier
 Esercitazione di riepilogo su serie di funzioni, e in particolare serie di Fourier Serie di funzioni e convergenza totale Tenere presente: De nizione di convergenza puntuale e convergenza totale per una
Esercitazione di riepilogo su serie di funzioni, e in particolare serie di Fourier Serie di funzioni e convergenza totale Tenere presente: De nizione di convergenza puntuale e convergenza totale per una
Esame di Analisi Funzionale e Trasformate Secondo appello. Agosto 2018 A.A. 2017/2018. Prof. M. Bramanti
 Esame di Analisi Funzionale e Trasformate Secondo appello. Agosto 08 A.A. 07/08. Prof. M. Bramanti Cognome: Nome N matr. o cod. persona: Dom Dom Dom 3 Es Es Es 3 Tot. Punti Domande di teoria rispondere
Esame di Analisi Funzionale e Trasformate Secondo appello. Agosto 08 A.A. 07/08. Prof. M. Bramanti Cognome: Nome N matr. o cod. persona: Dom Dom Dom 3 Es Es Es 3 Tot. Punti Domande di teoria rispondere
Modelli e Metodi Matematici della Fisica. Scritto 1
 Modelli e Metodi Matematici della Fisica. Scritto 1 Cesi/Presilla A.A. 2 7 Canale 1 Cesi Presilla Nome Cognome Il voto dello scritto rimpiazza gli esoneri 1 2 3 penalità problema voto 1 2 3 4 5 7 8 penalità
Modelli e Metodi Matematici della Fisica. Scritto 1 Cesi/Presilla A.A. 2 7 Canale 1 Cesi Presilla Nome Cognome Il voto dello scritto rimpiazza gli esoneri 1 2 3 penalità problema voto 1 2 3 4 5 7 8 penalità
ANALISI MATEMATICA 1 ESERCIZI ASSEGNATI IN AULA O A CASA Corso di Laurea in Matematica aa 2003/04 01/03/04
 ANALISI MATEMATICA ESERCIZI ASSEGNATI IN AULA O A CASA Corso di Laurea in Matematica aa 2003/04 0/03/04 Esercizio. Calcolare la somma della serie ( 2 k ). 3 k 2 k Esercizio 2. Scrivere sotto forma di frazione
ANALISI MATEMATICA ESERCIZI ASSEGNATI IN AULA O A CASA Corso di Laurea in Matematica aa 2003/04 0/03/04 Esercizio. Calcolare la somma della serie ( 2 k ). 3 k 2 k Esercizio 2. Scrivere sotto forma di frazione
EQUAZIONI DIFFERENZIALI Esercizi svolti. y = xy. y(2) = 1.
 EQUAZIONI DIFFERENZIALI Esercizi svolti 1. Determinare la soluzione dell equazione differenziale (x 2 + 1)y + y 2 =. y + x tan y = 2. Risolvere il problema di Cauchy y() = 1 2 π. 3. Risolvere il problema
EQUAZIONI DIFFERENZIALI Esercizi svolti 1. Determinare la soluzione dell equazione differenziale (x 2 + 1)y + y 2 =. y + x tan y = 2. Risolvere il problema di Cauchy y() = 1 2 π. 3. Risolvere il problema
Es. 1 Es. 2 Es. 3 Es. 4 Totale Teoria
 Es. Es. Es. 3 Es. 4 Totale Teoria Analisi e Geometria Docente: Politecnico di Milano Ingegneria Industriale 5 Settembre Compito A Cognome: Nome: Matricola: Punteggi degli esercizi: Es.: 6 punti; Es.: punti;
Es. Es. Es. 3 Es. 4 Totale Teoria Analisi e Geometria Docente: Politecnico di Milano Ingegneria Industriale 5 Settembre Compito A Cognome: Nome: Matricola: Punteggi degli esercizi: Es.: 6 punti; Es.: punti;
ANALISI MATEMATICA T-B xx Maggio 2019 (tempo 90 minuti)
 ESERCIZIO 1 La lunghezza della curva γ(t) = (e t, 2t, e t ), t [0, 1] è γ F d s =, con F (x, y, z) = (xy 4 z 2, 2x 2 y 3 z 2, x 2 y 4 z) ESERCIZIO 2 Sia x = x(t) la soluzione del problema di Cauchy t 2
ESERCIZIO 1 La lunghezza della curva γ(t) = (e t, 2t, e t ), t [0, 1] è γ F d s =, con F (x, y, z) = (xy 4 z 2, 2x 2 y 3 z 2, x 2 y 4 z) ESERCIZIO 2 Sia x = x(t) la soluzione del problema di Cauchy t 2
EQUAZIONI DIFFERENZIALI Esercizi con soluzione
 EQUAZIONI DIFFERENZIALI Esercizi con soluzione 1. Calcolare l integrale generale delle seguenti equazioni differenziali lineari del primo ordine: (a) y 2y = 1 (b) y + y = e x (c) y 2y = x 2 + x (d) 3y
EQUAZIONI DIFFERENZIALI Esercizi con soluzione 1. Calcolare l integrale generale delle seguenti equazioni differenziali lineari del primo ordine: (a) y 2y = 1 (b) y + y = e x (c) y 2y = x 2 + x (d) 3y
Integrali inde niti. F 2 (x) = x5 3x 2
 Integrali inde niti Abbiamo sinora studiato come ottenere la funzione derivata di una data funzione. Vogliamo ora chiederci, data una funzione f, come ottenerne una funzione, che derivata dia f. Esempio
Integrali inde niti Abbiamo sinora studiato come ottenere la funzione derivata di una data funzione. Vogliamo ora chiederci, data una funzione f, come ottenerne una funzione, che derivata dia f. Esempio
Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1
 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo. Tempo 3 minuti. Durante la prova non si può uscire dall aula. Non si possono consultare
Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo. Tempo 3 minuti. Durante la prova non si può uscire dall aula. Non si possono consultare
f(x)e 2πixy dx g(y)e 2πixy dy
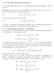 18.2. Il paradiso dell integrale di Fourier. Lo spazio delle funzioni buone è il paradiso dell integrale di Fourier. teorema: Vale il Teorema 1 (teorema di inversione di Fourier per funzioni buone). Se
18.2. Il paradiso dell integrale di Fourier. Lo spazio delle funzioni buone è il paradiso dell integrale di Fourier. teorema: Vale il Teorema 1 (teorema di inversione di Fourier per funzioni buone). Se
x + 2x(e 1 x 1) 4 lim x sinh 1 x E : 0 F :
 ANALISI MATEMATICA 1 - PARTE II 11 gennaio 2010 Compito 1 1. Il limite vale sin 1 lim x sinh 1 x x + 2x(e 1 x 1) 4 Risp.: A : 1 B : e 6 C : e D : 1 6 E : 0 F : 2. Sia y(x) la soluzione del problema di
ANALISI MATEMATICA 1 - PARTE II 11 gennaio 2010 Compito 1 1. Il limite vale sin 1 lim x sinh 1 x x + 2x(e 1 x 1) 4 Risp.: A : 1 B : e 6 C : e D : 1 6 E : 0 F : 2. Sia y(x) la soluzione del problema di
Equazioni differenziali a variabili separabili e lineari del primo ordine. Esercizi.
 Equazioni differenziali a variabili separabili e lineari del primo ordine. Esercizi. Mauro Saita Versione provvisoria. Dicembre 204 Per commenti o segnalazioni di errori scrivere, per favore, a: maurosaita@tiscalinet.it
Equazioni differenziali a variabili separabili e lineari del primo ordine. Esercizi. Mauro Saita Versione provvisoria. Dicembre 204 Per commenti o segnalazioni di errori scrivere, per favore, a: maurosaita@tiscalinet.it
Corso di Metodi Matematici per l Ingegneria A.A. 2016/2017 Esercizi svolti sulla trasformata di Fourier
 Corso di Metodi Matematici per l Ingegneria A.A. 6/7 Esercizi svolti sulla trasformata di Fourier Marco Bramanti Politecnico di Milano December 5, 6 Esercizi A. Esercizi sul calcolo di trasformate Esercizio
Corso di Metodi Matematici per l Ingegneria A.A. 6/7 Esercizi svolti sulla trasformata di Fourier Marco Bramanti Politecnico di Milano December 5, 6 Esercizi A. Esercizi sul calcolo di trasformate Esercizio
Il Principio di Indeterminazione di Heisenberg
 Il Principio di Indeterminazione di Heisenberg Il Principio di Indeterminazione di Heisenberg è uno dei fondamenti della meccanica quantistica, e stabilisce che non è possibile ottenere nello stesso tempo
Il Principio di Indeterminazione di Heisenberg Il Principio di Indeterminazione di Heisenberg è uno dei fondamenti della meccanica quantistica, e stabilisce che non è possibile ottenere nello stesso tempo
Trasformata di Fourier e applicazioni
 Trasformata di Fourier e applicazioni Docente:Alessandra Cutrì Trasformata di Fourier della funzione gaussiana Esempio: Calcoliamo la trasformata di Fourier di f (x) = e x 2 x n f (x) L 1 (R) per ogni
Trasformata di Fourier e applicazioni Docente:Alessandra Cutrì Trasformata di Fourier della funzione gaussiana Esempio: Calcoliamo la trasformata di Fourier di f (x) = e x 2 x n f (x) L 1 (R) per ogni
Prima prova in Itinere Ist. Mat. 1, Prima parte, Tema PIPPO COGNOME: NOME: MATR.: 1) 7; C: x sin(x) dx è A: π ; B:2 ; C: 0 ; D: π/2; E: N.A.
 Prima prova in Itinere Ist. Mat., Prima parte, Tema PIPPO 4 aprile 7 COGNOME: NOME: MATR.: ) Una primitiva di x 5 e x3 è A: e x3 (x 3 ); B: e x3 (x 5 ) 7; C: ex3 (x 3 + ) D: ex3 (x 3 ) + 7; E: N.A. ) Il
Prima prova in Itinere Ist. Mat., Prima parte, Tema PIPPO 4 aprile 7 COGNOME: NOME: MATR.: ) Una primitiva di x 5 e x3 è A: e x3 (x 3 ); B: e x3 (x 5 ) 7; C: ex3 (x 3 + ) D: ex3 (x 3 ) + 7; E: N.A. ) Il
Esercizi di riepilogo 2: soluzioni ( Verifica di analisi funzionale e serie di Fourier)
 Esercizi di riepilogo 2: soluzioni ( Verifica di analisi funzionale e serie di Fourier) Spazi Vettoriali e Funzionali 1. Risposte: (a) Spazio vettoriale complesso. (b) Spazio vettoriale reale. (c) Non
Esercizi di riepilogo 2: soluzioni ( Verifica di analisi funzionale e serie di Fourier) Spazi Vettoriali e Funzionali 1. Risposte: (a) Spazio vettoriale complesso. (b) Spazio vettoriale reale. (c) Non
MODELLI E METODI MATEMATICI DELLA FISICA A.A. 2016/2017 Prof. C. Presilla. Prova A2 18 luglio 2017
 MODELLI E METODI MATEMATICI DELLA FISICA A.A. 6/7 Prof. C. Presilla Prova A 8 luglio 7 Cognome Nome Matricola iscritto al secondo anno iscritto al terzo anno fuoricorso o con più di 55 CFU penalità esercizio
MODELLI E METODI MATEMATICI DELLA FISICA A.A. 6/7 Prof. C. Presilla Prova A 8 luglio 7 Cognome Nome Matricola iscritto al secondo anno iscritto al terzo anno fuoricorso o con più di 55 CFU penalità esercizio
(1) Determinare l integrale generale dell equazione
 FONDAMENTI DI ANALISI MATEMATICA (9 cfu Commissione F. Albertini, V. Casarino, M. Motta Ingegneria Gestionale, Meccanica e Meccatronica, Vicenza Vicenza, 3 settembre 8 Quarto appello Avvertenza: Nella
FONDAMENTI DI ANALISI MATEMATICA (9 cfu Commissione F. Albertini, V. Casarino, M. Motta Ingegneria Gestionale, Meccanica e Meccatronica, Vicenza Vicenza, 3 settembre 8 Quarto appello Avvertenza: Nella
1 Parziale di Studio di Funzioni di Interesse Fisico, 26/02/2009
 Parziale di Studio di Funzioni di Interesse Fisico, 6/0/009. Riconsegnare il testo degli esercizi, firmato, congiuntamente all elaborato scritto.. Firmare e consegnare solo il materiale che si desidera
Parziale di Studio di Funzioni di Interesse Fisico, 6/0/009. Riconsegnare il testo degli esercizi, firmato, congiuntamente all elaborato scritto.. Firmare e consegnare solo il materiale che si desidera
Dispense del corso di Analisi II
 Dispense del corso di Analisi II versione preliminare Paolo Tilli Dipartimento di Matematica Politecnico di Torino email: paolo.tilli@polito.it 8 gennaio 5 Capitolo 6 La trasformata di Fourier 6. Introduzione
Dispense del corso di Analisi II versione preliminare Paolo Tilli Dipartimento di Matematica Politecnico di Torino email: paolo.tilli@polito.it 8 gennaio 5 Capitolo 6 La trasformata di Fourier 6. Introduzione
Integrali doppi. Riccarda Rossi. Università di Brescia. Analisi Matematica B
 Integrali doppi Riccarda Rossi Università di Brescia Analisi Matematica B Riccarda Rossi (Università di Brescia) Integrali doppi Analisi Matematica B 1 / 92 Motivazione per l integrale di Riemann: calcolo
Integrali doppi Riccarda Rossi Università di Brescia Analisi Matematica B Riccarda Rossi (Università di Brescia) Integrali doppi Analisi Matematica B 1 / 92 Motivazione per l integrale di Riemann: calcolo
ANALISI DI FOURIER. 2πk. è periodica di periodo T. Più precisamente, essendo. T x + 2π = cos. s(x) = s x + T ) T +α. f(x) dx
 ANALISI DI FOURIER Sia >. Una funzione f, definita per x R, si dice periodica di periodo, se f(x + = f(x, x R. ( Se una funzione è periodica di periodo, essa è anche periodica di periodo, 3,..., k,....
ANALISI DI FOURIER Sia >. Una funzione f, definita per x R, si dice periodica di periodo, se f(x + = f(x, x R. ( Se una funzione è periodica di periodo, essa è anche periodica di periodo, 3,..., k,....
z n dove γ é la circonferenza di centro l origine e raggio 1.
 . Calcolare ( n= n ) dove é la circonferena di centro l origine e raggio.. Mostrare che n= n l origine e raggio. é analitica nel complementare del cerchio di centro 3. Mostrare che n= e n sen (n) é analitica
. Calcolare ( n= n ) dove é la circonferena di centro l origine e raggio.. Mostrare che n= n l origine e raggio. é analitica nel complementare del cerchio di centro 3. Mostrare che n= e n sen (n) é analitica
UNIVERSITÀ DEGLI STUDI DI PERUGIA Facoltà di Scienze MM. FF. e NN.
 A.A. 213/214 2 Novembre 213 I esercitazione Esercizio 1. Dato il problema di Cauchy ( e y 2 2 1 ) arctan 3y 5 y = 2 sin (1) 2 x 2, 1 + x 2 y() = 1, (b) provare che la soluzione y di (3) è definita in tutto
A.A. 213/214 2 Novembre 213 I esercitazione Esercizio 1. Dato il problema di Cauchy ( e y 2 2 1 ) arctan 3y 5 y = 2 sin (1) 2 x 2, 1 + x 2 y() = 1, (b) provare che la soluzione y di (3) è definita in tutto
Cognome e nome... Firma... Matricola...
 Analisi Matematica B 0 gennaio 2017 COMPITO 1 Cognome e nome................................ Firma................ Matricola................ Corso di Laurea: AMBL; CIVL; GESL. Istruzioni 1. COMPILARE la
Analisi Matematica B 0 gennaio 2017 COMPITO 1 Cognome e nome................................ Firma................ Matricola................ Corso di Laurea: AMBL; CIVL; GESL. Istruzioni 1. COMPILARE la
Metodi Matematici della Fisica. S3
 Metodi Matematici della Fisica. S Filippo Cesi 0 Nome Cognome Devo verbalizzare questo esame come (fare una croce): 6 CFU 8 CFU 4 + 6 CFU altro: problema 4 5 6 7 8 9 0 test totale voto in trentesimi voto
Metodi Matematici della Fisica. S Filippo Cesi 0 Nome Cognome Devo verbalizzare questo esame come (fare una croce): 6 CFU 8 CFU 4 + 6 CFU altro: problema 4 5 6 7 8 9 0 test totale voto in trentesimi voto
ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009)
 ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009) 1. Sia S = { } (x, y, z) : x 2 + y 2 = 4, 0 z 3 + x. Scrivere le equazioni parametriche di una superficie regolare che abbia S come sostegno. 2. Enunciare
ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009) 1. Sia S = { } (x, y, z) : x 2 + y 2 = 4, 0 z 3 + x. Scrivere le equazioni parametriche di una superficie regolare che abbia S come sostegno. 2. Enunciare
Istituzioni di Matematiche Modulo A (ST)
 Istituzioni di Matematice Modulo A ST) II foglio di esercizi Ricordo alcuni iti notevoli: Inoltre, se a > 0 e b > 0 allora = 1, e x 1 1 + x) = 1, = 1 b x x b 1) x + x a = 0, ) x + e ax = 0 ESERCIZIO 1
Istituzioni di Matematice Modulo A ST) II foglio di esercizi Ricordo alcuni iti notevoli: Inoltre, se a > 0 e b > 0 allora = 1, e x 1 1 + x) = 1, = 1 b x x b 1) x + x a = 0, ) x + e ax = 0 ESERCIZIO 1
METODI MATEMATICI PER LA FISICA
 METODI MATEMATICI PER LA FISICA SECONDO ESONERO - 6 GIUGNO 7 Si risolvano cortesemente i seguenti problemi PRIMO PROBLEMA (PUNTEGGIO: 3/3) Facendo uso delle proprietà della matrici di Pauli, si calcoli
METODI MATEMATICI PER LA FISICA SECONDO ESONERO - 6 GIUGNO 7 Si risolvano cortesemente i seguenti problemi PRIMO PROBLEMA (PUNTEGGIO: 3/3) Facendo uso delle proprietà della matrici di Pauli, si calcoli
COGNOME... NOME... Matricola... Corso Prof... Esame di ANALISI MATEMATICA II - 27 Gennaio cos x
 COGNOME... NOME... Matricola... Corso Prof.... Esame di ANALISI MATEMATICA II - 27 Gennaio 25 A ESERCIZIO. 4 punti) Verificare che la serie 7 2 cos x ) n è convergente per ogni x R, e calcolarne la somma.
COGNOME... NOME... Matricola... Corso Prof.... Esame di ANALISI MATEMATICA II - 27 Gennaio 25 A ESERCIZIO. 4 punti) Verificare che la serie 7 2 cos x ) n è convergente per ogni x R, e calcolarne la somma.
Integrali (M.S. Bernabei & H. Thaler)
 Integrali (M.S. Bernabei & H. Thaler) Integrali. Motivazione Che cos é un integrale? Sia f 0 e limitata b a f ( x) dx area f ( x, y) dxdy volume Definizione di integrale: b a dove f ( x) dx lim n n k b
Integrali (M.S. Bernabei & H. Thaler) Integrali. Motivazione Che cos é un integrale? Sia f 0 e limitata b a f ( x) dx area f ( x, y) dxdy volume Definizione di integrale: b a dove f ( x) dx lim n n k b
Esame di Fisica Matematica 2, a.a (8/9/2014)
 Esame di Fisica Matematica 2, a.a. 213-214 (8/9/214) Tempo a disposizione: DUE ORE. Svolgere tutti gli esercizi, che hanno lo stesso nel determinare il voto finale. Scrivere chiaramente e a stampatello
Esame di Fisica Matematica 2, a.a. 213-214 (8/9/214) Tempo a disposizione: DUE ORE. Svolgere tutti gli esercizi, che hanno lo stesso nel determinare il voto finale. Scrivere chiaramente e a stampatello
Corso di Laurea in Matematica Applicata PROVA DI ANALISI MATEMATICA 1 Mod. 1-2/2/2015 Tipologia A
 Corso di Laurea in Matematica Applicata PROVA DI ANALISI MATEMATICA Mod. - 2/2/25 Tipologia A. Si enunci il criterio del rapporto per la convergenza delle serie..2 Se f : R R è una funzione continua e
Corso di Laurea in Matematica Applicata PROVA DI ANALISI MATEMATICA Mod. - 2/2/25 Tipologia A. Si enunci il criterio del rapporto per la convergenza delle serie..2 Se f : R R è una funzione continua e
Appello Straordinario AC
 Appello Straordinario AC 2016-2017 Esercizio I Si consideri la seguente funzione f(z) f(z) = 1 (e z 1) sin(z). 1. Si determini la natura della singolarità di f in z = 0. 2. Nel caso si tratti di una singolarità
Appello Straordinario AC 2016-2017 Esercizio I Si consideri la seguente funzione f(z) f(z) = 1 (e z 1) sin(z). 1. Si determini la natura della singolarità di f in z = 0. 2. Nel caso si tratti di una singolarità
Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1
 Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1 6 giugno 2017 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo.
Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1 6 giugno 2017 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo.
Modelli e Metodi Matematici della Fisica. S1
 Modelli e Metodi Matematici della Fisica S Filippo Cesi 0 Nome Cognome Devo verbalizzare questo esame come (fare una croce): 6 CFU 8 CFU 4 + 6 CFU altro: problema 4 5 6 7 8 9 0 test totale voto in trentesimi
Modelli e Metodi Matematici della Fisica S Filippo Cesi 0 Nome Cognome Devo verbalizzare questo esame come (fare una croce): 6 CFU 8 CFU 4 + 6 CFU altro: problema 4 5 6 7 8 9 0 test totale voto in trentesimi
Esame di Fisica Matematica 2, a.a (8/5/2014)
 Esame di Fisica Matematica, a.a. 03-04 (8/5/04) Tempo a disposizione: DUE ORE E MEZZA. Svolgere tutti gli esercizi. Scrivere chiaramente nome, cognome e numero di matricola. Non è consentito l uso di libri,
Esame di Fisica Matematica, a.a. 03-04 (8/5/04) Tempo a disposizione: DUE ORE E MEZZA. Svolgere tutti gli esercizi. Scrivere chiaramente nome, cognome e numero di matricola. Non è consentito l uso di libri,
Risoluzione del compito n. 2 (Febbraio 2018/1)
 Risoluzione del compito n. Febbraio 18/1 PROBLEMA 1 Dopo averlo scritto in forma trigonometrica, determinate le radiciquadrate complesse del numero +i 3. Determinate tutte le soluzioni w C dell equazione
Risoluzione del compito n. Febbraio 18/1 PROBLEMA 1 Dopo averlo scritto in forma trigonometrica, determinate le radiciquadrate complesse del numero +i 3. Determinate tutte le soluzioni w C dell equazione
Modulo di Matematica
 Università degli Studi di Udine Anno Accademico 05/06 Corso di Laurea in Biotecnologie Modulo di Matematica Esame del 0/0/06 N.B.: scrivere nome, cognome e numero di matricola su ogni foglio consegnato.
Università degli Studi di Udine Anno Accademico 05/06 Corso di Laurea in Biotecnologie Modulo di Matematica Esame del 0/0/06 N.B.: scrivere nome, cognome e numero di matricola su ogni foglio consegnato.
