Fisica Nucleare e Subnucleare
|
|
|
- Ivo Venturi
- 4 anni fa
- Visualizzazioni
Transcript
1 Fisica Nucleare e Subnucleare Prova Scritta, 17 Febbraio 2015 Modulo I 1) Una trasformazione di Lorentz collega le coordinate dello spazio tempo di due sistemi di riferimento inerziali e può essere scritta nella forma x µ = Λ µ νx ν. i) Quali proprietà devono soddisfare le Λ µ ν (le componenti della matrice Λ) affinché la trasformazione appartenga al gruppo di Lorentz? ii) Come si trasformano le componenti del tensore del campo elettromagnetico F µν? iii) Come è definito F µν, il tensore del campo elettromagnetico con gli indici in basso? iv) Come si trasforma la quantità F µν F µν? Calcolarne il valore in termini di E e B. i) Dalla richiesta di invarianza di s 2 = η µν x µ x ν sotto la trasformazione x µ = Λ µ νx ν segue che η µν Λ µ αλ ν β = η αβ dove gli indici µ, ν, α, β assumono i valori 0, 1, 2, 3 (naturalmente due indici ripetuti sono da considerare sommati su tutti i loro possibili valori). Alternativamente, usando l algebra matriciale, possiamo indicare con x il vettore colonna contenente le componenti di x µ, con η la matrice della metrica di Minkowski e con Λ la matrice di una trasformazione di Lorentz. Dall invarianza di s 2 = x T ηx sotto la trasformazione x = Λx, segue che Λ T ηλ = η. ii) Il tensore F µν contiene le componenti dei campi elettrico e magnetico 0 E x E y E z F µν E = x 0 B z B y E y B z 0 B x. (1) E z B y B x 0 e per trasformazioni di Lorentz si trasforma nel modo seguente F µν = Λ µ αλ ν β F αβ. Alternativamente, indicando con F la matrice con componenti F µν si ha F = ΛF Λ T. iii) Gli indici sono abbassati usando la metrica di Minkowski η µν, le cui uniche componenti diverse da zero sono η 00 = 1, η 11 = η 22 = η 33 = 1. In particolare, per il quadrivettore posizione si ha x µ = η µν x ν e quindi x 0 = x 0, x 1 = x 1, x 2 = x 2, x 3 = x 3. Si noti che solo la componente temporale cambia segno. Per il tensore campo elettromagnetico si ha F µν = η µα η νβ F αβ
2 per cui F 0i = F 0i e F ij = F ij con i, j = 1, 2, 3. In forma matriciale iv) Un calcolo diretto produce 0 E x E y E z E F µν = x 0 B z B y E y B z 0 B x. (2) E z B y B x 0 F µν F µν = F 00 F 00 + F 01 F 01 + F 02 F = 0 (E x ) 2 (E y ) = 2( B 2 E 2 ) infatti si devono sommare i prodotti delle componenti che hanno la stessa posizione di riga e colonna in (1) e (2). 2) Dare la corretta definizione di energia ed impulso relativistico per una particella di massa m e velocità v, studiando e commentando il loro limite non-relativistico. Scrivere inoltre l azione per la particella relativistica libera e derivarne le definizioni di energia e impulso descritti precedentemente. La definizione relativistica di energia è Dallo sviluppo in serie di Taylor di E = m γ = valida per x 1, ed identificando x = v2 per v c E = mc2 (1 + x) α = 1 + αx α(α 1)x mc2 e α = 1, si può ottenere il limite non relativistico 2 = m mv mv da cui si riconosce l energia dovuta alla massa m (una sorpresa per la fisica pre-relativistica), l energia cinetica non-relativistica 1 2 mv2, e la prima correzione relativistica. Similmente, il momento relativistico è definito da p = mγ v = m v
3 che nel limite non-relativistico può essere sviluppato come p = m v = m v + m v 2 v c2 da si riconosce la definizione non relativistica di momento m v, e la prima correzione relativistica. L azione relativistica per una particella libera è proporzionale al tempo proprio (così da garantire l invarianza relativistica) dove v = x = d x dt S[ x] = dt L = m dt 1 e l energia (hamiltoniana) da v v, L = m v v 1 descrive la velocità della particella. Il momento coniugato è definito da p L v = m v E = p v L = mc2 definizioni che coincidono con quelle date precedentemente. 3) Nel decadimento di un pione π + a riposo in muone µ + e neutrino ν µ π + µ + + ν µ si osserva il muone con una energia cinetica di 4 MeV. La massa del muone è di 106 MeV/ mentre quella del neutrino è trascurabile. Calcolare la massa del pione. Usiamo unità di misura naturali (c = 1). Il decadimento è visto nel sistema a riposo del pione, per cui il suo quadrimpulso vale P µ π = (m π, 0, 0, 0). Decade in muone e neutrino, ed indichiamo i loro quadrimpulsi con P µ muone = (E µ, p µ ), P µ neutrino = (E ν, p ν ). Dalla conservazione del quadrimpulso totale abbiamo che m π = E µ + E ν p µ + p ν = 0 (3) L energia del muone vale E µ = m µ + K
4 dove m µ indica la massa del muone e K la sua energia cinetica. L energia del neutrino, considerando nulla la sua massa, è e dalla (3) si he che E ν = p ν per cui p ν = p µ = E 2 µ m 2 µ m π = E µ + E ν = m µ + K + (m µ + K) 2 m 2 µ = m µ + K + 2m µ K + K 2 = ( ) MeV 139.4MeV 4) Sia data la rappresentazione definente R(g) di un gruppo G, dove g G è un elemento arbitrario del gruppo. Per definizione questa agisce sui vettori di uno spazio vettoriale le cui componenti indicate con v a (indici in alto) si trasformano come v a v a = [R(g) v] a = [R(g)] a b v b. Cosa sono e come si trasformano i vettori con indici puntati e non puntati in alto ed in basso? Dimostare che il prodotto w a v a è uno scalare. In generale, il prodotto v a t a non lo è, in quali casi anche questo prodotto diventa uno scalare? Data la rappresentazione R(g), se ne possono immediatamente costruire altre tre: la rappresentazione complesso coniugata R(g), la rappresentazione inverso trasposta R(g) 1 T la rappresentazione inverso hermitiana R(g) 1. Infatti se R(g 1 ) R(g 2 ) = R(g 1 g 2 ) e R(e) = 1, prendendo il complesso coniugato di queste relazioni segue che R(g 1 ) R(g 2 ) = R(g 1 g 2 ), come anche R(e) = 1, per cui anche R(g) definisce una rappresentazione del gruppo. Similmente negli altri casi. Queste rappresentazioni matriciali trasformano vettori di opportuni spazi vettoriali, le cui componenti sono per convenzione indicate con indici puntati in alto, indici in basso ed indici puntati in basso, rispettivamente. In formule vȧ v a vȧ vȧ = [R(g) v]ȧ = [R(g) ]ȧḃ vḃ v a = [R(g) 1 T v] a = [R(g) 1 T ] a b v b vȧ = [R(g) 1 v]ȧ = [R(g) 1 ]ȧ ḃ vḃ L invarianza di w a v a segue dal calcolo diretto w a v a w av a = [R(g) 1 T ] a b w b [R(g)] a c v c (si noti uso indici c b)
5 = [R(g) 1 T ] b a [R(g)] a c w b v c (i numeri commutano tra loro) = [R(g) 1 ] b a[r(g)] a c w b v c (relazione tra matrice e sua trasposta) = [I] b c w b v c (prodotto di matrici da la matrice identita I) = δc b w b v c (inseriti i valori della matrice identita ) = w b v b (sommato su indice c) = w a v a (rinominato indice muto da b ad a) Dunque w av a = w a v a, e questo prodotto è invariante (uno scalare). Nei casi in cui R(g) = R(g) 1 T (matrici ortogonali) si ha invarianza di v a t a, in quanto v a = v a e v a t a è invariante (dal calcolo qui sopra!).
Appunti di Relatività Ristretta
 Appunti di Relatività Ristretta (per il corso di Elementi di Fisica Nucleare e Subnucleare 2007/08) Fiorenzo Bastianelli 1 Introduzione Agli inizi del 1900 erano conosciute due grandi teorie fisiche: 1)
Appunti di Relatività Ristretta (per il corso di Elementi di Fisica Nucleare e Subnucleare 2007/08) Fiorenzo Bastianelli 1 Introduzione Agli inizi del 1900 erano conosciute due grandi teorie fisiche: 1)
Relatività Ristretta
 Relatività Ristretta (Appunti per il corso di Teoria dei Campi 1-2010/11) Fiorenzo Bastianelli 1 Introduzione Agli inizi del 1900 erano conosciute due grandi teorie fisiche: 1) la meccanica di Galileo
Relatività Ristretta (Appunti per il corso di Teoria dei Campi 1-2010/11) Fiorenzo Bastianelli 1 Introduzione Agli inizi del 1900 erano conosciute due grandi teorie fisiche: 1) la meccanica di Galileo
Relatività Ristretta
 Relatività Ristretta (Appunti per il corso di Fisica Nucleare e Subnucleare 2011/12) Fiorenzo Bastianelli 1 Introduzione Agli inizi del 1900 erano conosciute due grandi teorie fisiche: 1) la meccanica
Relatività Ristretta (Appunti per il corso di Fisica Nucleare e Subnucleare 2011/12) Fiorenzo Bastianelli 1 Introduzione Agli inizi del 1900 erano conosciute due grandi teorie fisiche: 1) la meccanica
Appunti di relatività ristretta
 Appunti di relatività ristretta (per il corso di Fisica Nucleare e Subnucleare 2014/15) 17.10.2014 Fiorenzo Bastianelli 1 Introduzione Agli inizi del 1900 erano conosciute due grandi teorie fisiche: 1)
Appunti di relatività ristretta (per il corso di Fisica Nucleare e Subnucleare 2014/15) 17.10.2014 Fiorenzo Bastianelli 1 Introduzione Agli inizi del 1900 erano conosciute due grandi teorie fisiche: 1)
1 Trasformazione di vettori e 1-forme per cambiamenti
 Trasformazione di vettori e -forme per cambiamenti di coordinate Consideriamo lo spazio di Minkowski in coordinate cartesiane {x µ } (x,x,x 2,x 3 ). La sua metrica è ds 2 (dx ) 2 +(dx ) 2 +(dx 2 ) 2 +(dx
Trasformazione di vettori e -forme per cambiamenti di coordinate Consideriamo lo spazio di Minkowski in coordinate cartesiane {x µ } (x,x,x 2,x 3 ). La sua metrica è ds 2 (dx ) 2 +(dx ) 2 +(dx 2 ) 2 +(dx
Trasformazioni di Lorentz, Quadrivettori, Impulso ed Angoli
 Trasformazioni di Lorentz, Quadrivettori, Impulso ed Angoli Trasformazioni tra Sistemi di Riferimento Quantita di interesse in un esperimento: sezioni d urto, distribuzioni angolari, polarizzazioni. Confrontabili
Trasformazioni di Lorentz, Quadrivettori, Impulso ed Angoli Trasformazioni tra Sistemi di Riferimento Quantita di interesse in un esperimento: sezioni d urto, distribuzioni angolari, polarizzazioni. Confrontabili
Appunti di relatività ristretta
 Appunti di relatività ristretta (per il corso di Fisica Nucleare e Subnucleare 2016/17) 19.10.2016 Fiorenzo Bastianelli 1 Introduzione Agli inizi del 1900 erano conosciute due grandi teorie fisiche: 1)
Appunti di relatività ristretta (per il corso di Fisica Nucleare e Subnucleare 2016/17) 19.10.2016 Fiorenzo Bastianelli 1 Introduzione Agli inizi del 1900 erano conosciute due grandi teorie fisiche: 1)
Appunti di relatività ristretta
 Appunti di relatività ristretta (per il corso di Fisica Nucleare e Subnucleare 2017/18) 28.9.2017 Fiorenzo Bastianelli 1 Introduzione Agli inizi del 1900 erano conosciute due grandi teorie fisiche: 1)
Appunti di relatività ristretta (per il corso di Fisica Nucleare e Subnucleare 2017/18) 28.9.2017 Fiorenzo Bastianelli 1 Introduzione Agli inizi del 1900 erano conosciute due grandi teorie fisiche: 1)
Appunti di relatività ristretta
 Appunti di relatività ristretta (per il corso di Fisica Nucleare e Subnucleare 2018/19) 25.9.2018 Fiorenzo Bastianelli 1 Introduzione Agli inizi del 1900 erano conosciute due grandi teorie fisiche: 1)
Appunti di relatività ristretta (per il corso di Fisica Nucleare e Subnucleare 2018/19) 25.9.2018 Fiorenzo Bastianelli 1 Introduzione Agli inizi del 1900 erano conosciute due grandi teorie fisiche: 1)
Elettromagnetismo. Prof. Francesco Ragusa Università degli Studi di Milano. Lezione n
 Elettromagnetismo Prof. Francesco Ragusa Università degli Studi di Milano Lezione n. 24 1.04.2019 Quadrivettori e trasformazioni di Lorentz Cinematica e dinamica relativistiche Forza magnetica e relatività
Elettromagnetismo Prof. Francesco Ragusa Università degli Studi di Milano Lezione n. 24 1.04.2019 Quadrivettori e trasformazioni di Lorentz Cinematica e dinamica relativistiche Forza magnetica e relatività
1 Trasformazione di vettori e 1-forme per cambiamenti
 PRIMA ESERCITAZIONE Trasformazione di vettori e -forme per cambiamenti di coordinate Consideriamo lo spazio di Minkowski in coordinate cartesiane {x } (x,x,x 2,x 3 ). La sua metrica è ds 2 (dx ) 2 +(dx
PRIMA ESERCITAZIONE Trasformazione di vettori e -forme per cambiamenti di coordinate Consideriamo lo spazio di Minkowski in coordinate cartesiane {x } (x,x,x 2,x 3 ). La sua metrica è ds 2 (dx ) 2 +(dx
B = 0 E. Usando queste equazioni, ponendo le sorgenti (J e ρ) a zero, si ottengono le equazioni delle onde elettromagnetiche nel vuoto 2 E
 Gruppo di Lorentz Typeset in TEX in date 17 10 2007 1.Introduzione storica Nel 1873 J. C. Maxwell riunisce in A treatise on electricity and magnetism i fenomeni riconducibili all elettricità e al magnetismo
Gruppo di Lorentz Typeset in TEX in date 17 10 2007 1.Introduzione storica Nel 1873 J. C. Maxwell riunisce in A treatise on electricity and magnetism i fenomeni riconducibili all elettricità e al magnetismo
α µ + m δ α ψ β (x) = 0. (2) Equazione di Dirac La relazione relativistica tra energia ed impulso di una particella libera
 1 Spin 1 2 : l equazione di Dirac Storicamente Dirac trovò la corretta equazione per descrivere particelle di spin 1 2 cercando un equazione relativistica che potesse avere un interpretazione probabilistica
1 Spin 1 2 : l equazione di Dirac Storicamente Dirac trovò la corretta equazione per descrivere particelle di spin 1 2 cercando un equazione relativistica che potesse avere un interpretazione probabilistica
Elettromagnetismo. Prof. Francesco Ragusa Università degli Studi di Milano. Lezione n
 Elettromagnetismo Prof. Francesco Ragusa Università degli Studi di Milano Lezione n. 25 6.04.2018 Campo elettrico di una carica accelerata Quadrivettori e trasformazioni di Lorentz Cinematica e dinamica
Elettromagnetismo Prof. Francesco Ragusa Università degli Studi di Milano Lezione n. 25 6.04.2018 Campo elettrico di una carica accelerata Quadrivettori e trasformazioni di Lorentz Cinematica e dinamica
Richiami di algebra lineare
 2 Richiami di algebra lineare 2.1 Prodotto scalare, prodotto vettoriale e prodotto misto Sia V lo spazio vettoriale tridimensionale ordinario, che dotiamo di una base ortonormale (e 1, e 2, e 3 ), e i
2 Richiami di algebra lineare 2.1 Prodotto scalare, prodotto vettoriale e prodotto misto Sia V lo spazio vettoriale tridimensionale ordinario, che dotiamo di una base ortonormale (e 1, e 2, e 3 ), e i
Istituzioni di Fisica Nucleare e Subnucleare
 Istituzioni di Fisica Nucleare e Subnucleare R. Sparvoli-R. Di Salvo-P. Dimopoulos Lezione 3 R. Sparvoli-R. Di Salvo-P. Dimopoulos Istituzioni di Fisica Nucleare e Subnucleare Lezione 3 1 / 38 Libri di
Istituzioni di Fisica Nucleare e Subnucleare R. Sparvoli-R. Di Salvo-P. Dimopoulos Lezione 3 R. Sparvoli-R. Di Salvo-P. Dimopoulos Istituzioni di Fisica Nucleare e Subnucleare Lezione 3 1 / 38 Libri di
Geometria BAER Canale A-K Esercizi 11
 Geometria BAER 6-7 Canale A-K Esercizi Esercizio. Scrivere la matrice delle seguenti trasformazioni ortogonali del piano (a Proiezione ortogonale sulla retta x + y = (b Rotazione di π/4 seguita da riflessione
Geometria BAER 6-7 Canale A-K Esercizi Esercizio. Scrivere la matrice delle seguenti trasformazioni ortogonali del piano (a Proiezione ortogonale sulla retta x + y = (b Rotazione di π/4 seguita da riflessione
3. Si descrivano lo schema di Schroedinger e lo schema di Heisenberg per rappresentare l evoluzione temporale di un sistema quantistico.
 1 Fisica Matematica Avanzata, 11 9 2009 [ ] 1. Sia A = 1 i 1 2 la matrice che rappresenta una osservabile A di i 1 un sistema quantistico nello spazio di Hilbert H = C 2. a) Trovare la risoluzione dell
1 Fisica Matematica Avanzata, 11 9 2009 [ ] 1. Sia A = 1 i 1 2 la matrice che rappresenta una osservabile A di i 1 un sistema quantistico nello spazio di Hilbert H = C 2. a) Trovare la risoluzione dell
LA RELATIVITÀ RISTRETTA
 CAPITOLO LA RELATIVITÀ RISTRETTA L INTERVALLO INVARIANTE Negli intervalli di tipo tempo, la distanza spaziale tra gli eventi è minore della distanza percorsa dalla luce nell intervallo di tempo tra i due
CAPITOLO LA RELATIVITÀ RISTRETTA L INTERVALLO INVARIANTE Negli intervalli di tipo tempo, la distanza spaziale tra gli eventi è minore della distanza percorsa dalla luce nell intervallo di tempo tra i due
α µ + m δ α ψ β (x) = 0. (2) Equazione di Dirac La relazione relativistica tra energia ed impulso di una particella libera
 1 Spin 1 : l equazione di Dirac Storicamente Dirac trovò la corretta equazione per descrivere particelle di spin 1 cercando un equazione relativistica che potesse avere un interpretazione probabilistica
1 Spin 1 : l equazione di Dirac Storicamente Dirac trovò la corretta equazione per descrivere particelle di spin 1 cercando un equazione relativistica che potesse avere un interpretazione probabilistica
Esercizio 1 I mesoni K + possono essere prodotti attraverso la reazione γ + p K + + Λ su protoni fermi.
 Esercizio 1 I mesoni K + possono essere prodotti attraverso la reazione γ + p K + + Λ su protoni fermi. Determinare l energia minima del fotone nel laboratorio per cui la reazione avviene Λ decade in volo
Esercizio 1 I mesoni K + possono essere prodotti attraverso la reazione γ + p K + + Λ su protoni fermi. Determinare l energia minima del fotone nel laboratorio per cui la reazione avviene Λ decade in volo
Trasformazione della metrica per cambiamenti di coordinate
 TERZA ESERCITAZIONE Trasformazione della metrica per cambiamenti di coordinate Consideriamo lo spazio di Minkowski in coordinate cartesiane {x µ } (x, x, x, x 3. La sua metrica è ds (dx + (dx + (dx + (dx
TERZA ESERCITAZIONE Trasformazione della metrica per cambiamenti di coordinate Consideriamo lo spazio di Minkowski in coordinate cartesiane {x µ } (x, x, x, x 3. La sua metrica è ds (dx + (dx + (dx + (dx
Trasformazioni di Lorentz
 Trasformazioni di Lorentz Regole di trasformazione fra un sistema inerziale S (descritto da x, y, z, t) ed uno S (descritto da x, y, z, t ) che viaggia a velocità V lungo x rispetto a S: x = γ(x V t) y
Trasformazioni di Lorentz Regole di trasformazione fra un sistema inerziale S (descritto da x, y, z, t) ed uno S (descritto da x, y, z, t ) che viaggia a velocità V lungo x rispetto a S: x = γ(x V t) y
1 Esercizi di ripasso 4
 Esercizi di ripasso 4. Determinare k in modo che il piano kx + 2y 6z + = 0 sia parallelo al piano x + y z + = 0. Soluzione. La condizione di parallelismo richiede che ( ) k 2 6 rg = Ne segue che k = e
Esercizi di ripasso 4. Determinare k in modo che il piano kx + 2y 6z + = 0 sia parallelo al piano x + y z + = 0. Soluzione. La condizione di parallelismo richiede che ( ) k 2 6 rg = Ne segue che k = e
ESAME DI GEOMETRIA. 6 febbraio 2002 CORREZIONE QUIZ
 ESAME DI GEOMETRIA 6 febbraio CORREZIONE QUIZ. La parte reale di ( + i) 9 è positiva. QUIZ Si può procedere in due modi. Un primo modo è osservare che ( + i) =i, dunque ( + i) 9 =(+i)(i) 4 = 4 ( + i) :
ESAME DI GEOMETRIA 6 febbraio CORREZIONE QUIZ. La parte reale di ( + i) 9 è positiva. QUIZ Si può procedere in due modi. Un primo modo è osservare che ( + i) =i, dunque ( + i) 9 =(+i)(i) 4 = 4 ( + i) :
Possiamo scrivere le tre precedenti espressioni in un'unica equazione matriciale:
 A1. Considerazioni sul cambio di un sistema di riferimento cartesiano ortogonale Sia xyz un sistema di riferimento cartesiano ortogonale di origine O e di riferimento cartesiano pure di origine O. un secondo
A1. Considerazioni sul cambio di un sistema di riferimento cartesiano ortogonale Sia xyz un sistema di riferimento cartesiano ortogonale di origine O e di riferimento cartesiano pure di origine O. un secondo
PROGRAMMA DEL CORSO DI FISICA TEORICA 1 PROF. E. PACE CORSO DI LAUREA TRIENNALE IN FISICA A. A
 PROGRAMMA DEL CORSO DI FISICA TEORICA 1 PROF. E. PACE CORSO DI LAUREA TRIENNALE IN FISICA A. A. 2013-2014 ELETTROSTATICA NEL VUOTO Equazione di Poisson ed equazione di Laplace. Teorema di Green; I e II
PROGRAMMA DEL CORSO DI FISICA TEORICA 1 PROF. E. PACE CORSO DI LAUREA TRIENNALE IN FISICA A. A. 2013-2014 ELETTROSTATICA NEL VUOTO Equazione di Poisson ed equazione di Laplace. Teorema di Green; I e II
FAM. = 5 4 Mc2 = E C = 5 2 Mc2 1 v2. c 2. 2 M 2M) = 1 2 Mc2
 Serie 19: Soluzioni FAM C. Ferrari Esercizio 1 Collisione completamente anelastica Utilizziamo la conservazione dell energia e della quantità di moto (sistema isolato) in cui trattiamo A e B all inizio
Serie 19: Soluzioni FAM C. Ferrari Esercizio 1 Collisione completamente anelastica Utilizziamo la conservazione dell energia e della quantità di moto (sistema isolato) in cui trattiamo A e B all inizio
Equazioni di Maxwell. I campi elettrici e magnetici (nel vuoto) sono descritti dalle equazioni di Maxwell (in unità MKSA)
 Equazioni di Maxwell I campi elettrici e magnetici (nel vuoto) sono descritti dalle equazioni di Maxwell (in unità MKSA) E = ϱ ɛ 0 (1) E = B (2) B = 0 (3) E B = µ 0 j + µ 0 ɛ 0 (4) La forza che agisce
Equazioni di Maxwell I campi elettrici e magnetici (nel vuoto) sono descritti dalle equazioni di Maxwell (in unità MKSA) E = ϱ ɛ 0 (1) E = B (2) B = 0 (3) E B = µ 0 j + µ 0 ɛ 0 (4) La forza che agisce
Scattering Cinematica Relativistica
 Scattering Cinematica Relativistica V Trasformazioni di Lorentz, 4-vettori, imulsi e angoli 3/5/9 E.Menichetti - Univ. di Torino Trasformazioni di Lorentz Per due riferimenti in configurazione tiica: '
Scattering Cinematica Relativistica V Trasformazioni di Lorentz, 4-vettori, imulsi e angoli 3/5/9 E.Menichetti - Univ. di Torino Trasformazioni di Lorentz Per due riferimenti in configurazione tiica: '
Fisica Quantistica III Esercizi Natale 2009
 Fisica Quantistica III Esercizi Natale 009 Philip G. Ratcliffe (philip.ratcliffe@uninsubria.it) Dipartimento di Fisica e Matematica Università degli Studi dell Insubria in Como via Valleggio 11, 100 Como
Fisica Quantistica III Esercizi Natale 009 Philip G. Ratcliffe (philip.ratcliffe@uninsubria.it) Dipartimento di Fisica e Matematica Università degli Studi dell Insubria in Como via Valleggio 11, 100 Como
Le simmetrie nell elettromagnetismo
 Le simmetrie nell elettromagnetismo Adriana Pecoraro N94/56 Lucia Trozzo N94/51 1 Introduzione In questa tesina saranno trattate le simmetrie del campo elettromagnetico libero. Nella prima sezione saranno
Le simmetrie nell elettromagnetismo Adriana Pecoraro N94/56 Lucia Trozzo N94/51 1 Introduzione In questa tesina saranno trattate le simmetrie del campo elettromagnetico libero. Nella prima sezione saranno
Matrici di Dirac. Nicola Cabibbo. 23 Ottobre La dimensionalità delle matrici di Dirac
 Matrici di Dirac Nicola Cabibbo 23 Ottobre 1999 1 La dimensionalità delle matrici di Dirac Dimostriamo che la dimensionalità N delle matrici di Dirac deve essere un multiplo di 4. Partiamo dalle relazioni
Matrici di Dirac Nicola Cabibbo 23 Ottobre 1999 1 La dimensionalità delle matrici di Dirac Dimostriamo che la dimensionalità N delle matrici di Dirac deve essere un multiplo di 4. Partiamo dalle relazioni
CMP-II Equazioni di Hartree-Fock
 CMP-II Equazioni di Hartree-Fock Dipartimento di Fisica, UniTS 9 marzo 019 1 Equazioni di Hartree-Fock 1.1 Funzioni d onda a singolo determinante di Slater (Fermioni) Consideriamo un Hamiltoniana di Fermioni
CMP-II Equazioni di Hartree-Fock Dipartimento di Fisica, UniTS 9 marzo 019 1 Equazioni di Hartree-Fock 1.1 Funzioni d onda a singolo determinante di Slater (Fermioni) Consideriamo un Hamiltoniana di Fermioni
INTRODUZIONE ALLA RELATIVITÀ SPECIALE: Dalla seconda legge di Newton a E = mc 2. 8 marzo 2017
 INTRODUZIONE ALLA RELATIVITÀ SPECIALE: Dalla seconda legge di Newton a E = mc 2 8 marzo 2017 Piano della presentazione Trasformazioni di Lorentz Red Shift Relatività e leggi di Newton Galileo Seconda Legge
INTRODUZIONE ALLA RELATIVITÀ SPECIALE: Dalla seconda legge di Newton a E = mc 2 8 marzo 2017 Piano della presentazione Trasformazioni di Lorentz Red Shift Relatività e leggi di Newton Galileo Seconda Legge
Operatori C, P e T { } Stati Fisici. Osservabili. Osservabili (II) prof. Domenico Galli
 Stati Fisici Operatori C, P e T prof. Domenico Galli Fisica delle Alte Energie agli Acceleratori Dottorato di Ricerca in Fisica Uno stato fisico è rappresentato da un vettore di stato (ket) in uno spazio
Stati Fisici Operatori C, P e T prof. Domenico Galli Fisica delle Alte Energie agli Acceleratori Dottorato di Ricerca in Fisica Uno stato fisico è rappresentato da un vettore di stato (ket) in uno spazio
FAM A+B C. Considera la disintegrazione di una particella A in due particelle B e C: A B +C.
 Serie 19: Relatività VIII FAM C. Ferrari Esercizio 1 Collisione completamente anelastica Considera la collisione frontale di due particelle A e B di massa M A = M B = M e v A = v B = 3/5c, tale che alla
Serie 19: Relatività VIII FAM C. Ferrari Esercizio 1 Collisione completamente anelastica Considera la collisione frontale di due particelle A e B di massa M A = M B = M e v A = v B = 3/5c, tale che alla
Innalzamento e abbassamento di indici
 TERZA ESERCITAZIONE Innalzamento e abbassamento di indici Consideriamo lo spazio di Minkowski in coordinate sferiche {x µ } (t, r, θ, φ). La sua metrica è con ds dt + dr + r dθ + r sin θdφ g µν dx µ dx
TERZA ESERCITAZIONE Innalzamento e abbassamento di indici Consideriamo lo spazio di Minkowski in coordinate sferiche {x µ } (t, r, θ, φ). La sua metrica è con ds dt + dr + r dθ + r sin θdφ g µν dx µ dx
Violazione della Parità
 Violazione della Parità Raffaele Pontrandolfi Corso di Astrosica e Particelle Elementari Motivazione Per spiegare l asimmetria nell universo tra particelle e antiparticelle bisogna trovare dei processi
Violazione della Parità Raffaele Pontrandolfi Corso di Astrosica e Particelle Elementari Motivazione Per spiegare l asimmetria nell universo tra particelle e antiparticelle bisogna trovare dei processi
20 giugno La sezione d urto invariante impolarizzata per il processo (1) è
 20 giugno 2002 e (p 1 ) + e + (p 2 ) γ(k) + Z 0 (q) (1) (i tetra-impulsi delle particelle sono indicati in parentesi). 1. Si scrivano i diagrammi di Feynman rilevanti per il processo, e si scriva l espressione
20 giugno 2002 e (p 1 ) + e + (p 2 ) γ(k) + Z 0 (q) (1) (i tetra-impulsi delle particelle sono indicati in parentesi). 1. Si scrivano i diagrammi di Feynman rilevanti per il processo, e si scriva l espressione
TEORIA DELLE INTERAZIONI FONDAMENTALI PROBLEMI
 TEORIA DELLE INTERAZIONI FONDAMENTALI PROBLEMI Cenni di teoria quantistica dei campi (1) I generatori delle traslazioni P µ e delle trasformazioni di Lorentz J µν soddisfano le relazioni di commutazione
TEORIA DELLE INTERAZIONI FONDAMENTALI PROBLEMI Cenni di teoria quantistica dei campi (1) I generatori delle traslazioni P µ e delle trasformazioni di Lorentz J µν soddisfano le relazioni di commutazione
APPUNTI DI ALGEBRA LINEARE
 APPUNTI DI ALGEBRA LINEARE. Definizione Si dice spazio vettoriale (sul campo dei numeri reali R) un insieme V per il quale siano definite l operazione interna di somma (che ad ogni coppia di vettori e
APPUNTI DI ALGEBRA LINEARE. Definizione Si dice spazio vettoriale (sul campo dei numeri reali R) un insieme V per il quale siano definite l operazione interna di somma (che ad ogni coppia di vettori e
Interazioni Elettrodeboli. Lezione n. 15
 Interazioni Elettrodeboli prof. Francesco Ragusa Università di Milano Lezione n. 15 28.11.2017 Corrente adronica debole Decadimento del mesone π Decadimento del leptone τ: τ π ν τ Proprietà isotopiche
Interazioni Elettrodeboli prof. Francesco Ragusa Università di Milano Lezione n. 15 28.11.2017 Corrente adronica debole Decadimento del mesone π Decadimento del leptone τ: τ π ν τ Proprietà isotopiche
Daniela Lera A.A
 Daniela Lera Università degli Studi di Cagliari Dipartimento di Matematica e Informatica A.A. 2016-2017 Richiami Algebra Lineare Spazio normato Uno spazio lineare X si dice normato se esiste una funzione
Daniela Lera Università degli Studi di Cagliari Dipartimento di Matematica e Informatica A.A. 2016-2017 Richiami Algebra Lineare Spazio normato Uno spazio lineare X si dice normato se esiste una funzione
Interazioni Elettrodeboli. Lezione n. 15
 Interazioni Elettrodeboli prof. Francesco Ragusa Università di Milano Lezione n. 15 22.11.2018 Polarizzazione nel decadimento del mesone π Decadimento del leptone τ: τ π ν τ Proprietà isotopiche della
Interazioni Elettrodeboli prof. Francesco Ragusa Università di Milano Lezione n. 15 22.11.2018 Polarizzazione nel decadimento del mesone π Decadimento del leptone τ: τ π ν τ Proprietà isotopiche della
GEOMETRIA svolgimento di uno scritto del 11 Gennaio 2012
 GEOMETRIA svolgimento di uno scritto del Gennaio ) Trovare una base per lo spazio delle soluzioni del seguente sistema omogeneo: x + y 5z = 3x y + z = x y + 8z =. Il sistema può essere scritto in forma
GEOMETRIA svolgimento di uno scritto del Gennaio ) Trovare una base per lo spazio delle soluzioni del seguente sistema omogeneo: x + y 5z = 3x y + z = x y + 8z =. Il sistema può essere scritto in forma
Campi e Particelle. Prima Parte: Campi. Esercizi e Soluzioni
 Campi e Particelle. Prima Parte: Campi. Esercizi e Soluzioni Alexandre Kamenchtchik Problema No 1 Trovare una soluzione statica (cioè indipendente dal tempo) dell equazione di Klein-Gordon per un campo
Campi e Particelle. Prima Parte: Campi. Esercizi e Soluzioni Alexandre Kamenchtchik Problema No 1 Trovare una soluzione statica (cioè indipendente dal tempo) dell equazione di Klein-Gordon per un campo
VETTORIALE E PRODOTTO MISTO. PIANI E RETTE DI
 Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA (Edile-Architettura e dell Edilizia) PRODOTTO VETTORIALE E PRODOTTO MISTO. PIANI E RETTE DI R 3. FASCI E STELLE. FORMULE
Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA (Edile-Architettura e dell Edilizia) PRODOTTO VETTORIALE E PRODOTTO MISTO. PIANI E RETTE DI R 3. FASCI E STELLE. FORMULE
Algebra lineare. Laboratorio di programmazione e calcolo CdL in Chimica. Pierluigi Amodio
 Algebra lineare Laboratorio di programmazione e calcolo CdL in Chimica Pierluigi Amodio Dipartimento di Matematica Università di Bari pierluigi.amodio@uniba.it http://dm.uniba.it/ amodio A.A. 2016/17 P.
Algebra lineare Laboratorio di programmazione e calcolo CdL in Chimica Pierluigi Amodio Dipartimento di Matematica Università di Bari pierluigi.amodio@uniba.it http://dm.uniba.it/ amodio A.A. 2016/17 P.
Il determinante. Calcolo del determinante di matrici particolari. matrici di ordine 2: sia. a11 a A = allora
 Calcolo del determinante di matrici particolari matrici di ordine 2: sia allora Esempio. [ ] a11 a A = 12, a 21 a 22 det A = a 11 a 22 a 21 a 12. Calcolare il determinante di [ ] 1 2 A =. 3 4 matrici di
Calcolo del determinante di matrici particolari matrici di ordine 2: sia allora Esempio. [ ] a11 a A = 12, a 21 a 22 det A = a 11 a 22 a 21 a 12. Calcolare il determinante di [ ] 1 2 A =. 3 4 matrici di
Cos è un gruppo. A IV) Esiste l elemento inverso di ogni elemento A:
 Cos è un gruppo Con gruppo si intende un insieme G di elementi A, B, C,..., tali che possa essere definita un operazione detta moltiplicazione di gruppo che associa un terzo elemento (uno ed uno solo)
Cos è un gruppo Con gruppo si intende un insieme G di elementi A, B, C,..., tali che possa essere definita un operazione detta moltiplicazione di gruppo che associa un terzo elemento (uno ed uno solo)
Geometria per Fisica e Astrofisica
 Geometria per Fisica e Astrofisica Soluzione esercizi - Foglio 3 Esercizio. Risolvere i seguenti sistemi lineari al variare dei parametri reali α β e k < < (a) x + y z = αx + αy + βz = x + y z = β. (b)
Geometria per Fisica e Astrofisica Soluzione esercizi - Foglio 3 Esercizio. Risolvere i seguenti sistemi lineari al variare dei parametri reali α β e k < < (a) x + y z = αx + αy + βz = x + y z = β. (b)
Esercizi geometria analitica nel piano. Corso di Laurea in Informatica A.A. Docente: Andrea Loi. Correzione
 Esercizi geometria analitica nel piano Corso di Laurea in Informatica A.A. Docente: Andrea Loi Correzione 1. Scrivere le equazioni parametriche delle rette r e s di equazioni cartesiane r : 2x y + = 0
Esercizi geometria analitica nel piano Corso di Laurea in Informatica A.A. Docente: Andrea Loi Correzione 1. Scrivere le equazioni parametriche delle rette r e s di equazioni cartesiane r : 2x y + = 0
Le matrici. Sia K un campo con elemento neutro dell addizione 0 ed elemento neutro della moltiplicazione 1.
 Le matrici Sia K un campo con elemento neutro dell addizione 0 ed elemento neutro della moltiplicazione 1. Siano m, n N\{0}. Una matrice m n a coefficienti in K è una tabella di m n elementi di K disposti
Le matrici Sia K un campo con elemento neutro dell addizione 0 ed elemento neutro della moltiplicazione 1. Siano m, n N\{0}. Una matrice m n a coefficienti in K è una tabella di m n elementi di K disposti
x n i sima pos. x, y = x T y = x i y i R. i=1
 1 Elementi di Algebra Lineare In questo capitolo introduttivo al corso di Calcolo Numerico per la laurea triennale in Informatica, saranno presentate una serie di definizioni e proprietà di matrici e dei
1 Elementi di Algebra Lineare In questo capitolo introduttivo al corso di Calcolo Numerico per la laurea triennale in Informatica, saranno presentate una serie di definizioni e proprietà di matrici e dei
L equazione di Schrödinger
 1 Forma dell equazione L equazione di Schrödinger Postulato - ψ r, t 0 ) definisce completamente lo stato dinamico del sistema al tempo t 0. L equazione che regola l evoluzione di ψ r, t) deve essere:
1 Forma dell equazione L equazione di Schrödinger Postulato - ψ r, t 0 ) definisce completamente lo stato dinamico del sistema al tempo t 0. L equazione che regola l evoluzione di ψ r, t) deve essere:
1 Spin 1: equazioni di Maxwell e Proca
 1 Spin 1: equazioni di Maxwell e Proca Proca Particelle di spin 1 possono essere descritte da un campo vettoriale A µ x). Nel caso di particelle massive di massa m le equazioni libere sono conosciute come
1 Spin 1: equazioni di Maxwell e Proca Proca Particelle di spin 1 possono essere descritte da un campo vettoriale A µ x). Nel caso di particelle massive di massa m le equazioni libere sono conosciute come
Dinamica relativistica
 Dinamica relativistica 111 impulso relativistico Utilizzando semplici problemi d urto, si può far vedere che la conservazione della quantità di moto classica non vale per velocità relativistiche. Es. urto
Dinamica relativistica 111 impulso relativistico Utilizzando semplici problemi d urto, si può far vedere che la conservazione della quantità di moto classica non vale per velocità relativistiche. Es. urto
ESPLICITA DERIVAZIONE DELLA RELAZIONE RELATIVISTICA MASSA-ENERGIA PER UN SISTEMA COMPOSTO CON POTENZIALI INTERNI
 ESPLICITA DERIVAZIONE DELLA RELAZIONE RELATIVISTICA MASSA-ENERGIA PER UN SISTEMA COMPOSTO CON POTENZIALI INTERNI Di Riccardo Messina L espressione dell equivalenza massaenergia che è qui riportata non
ESPLICITA DERIVAZIONE DELLA RELAZIONE RELATIVISTICA MASSA-ENERGIA PER UN SISTEMA COMPOSTO CON POTENZIALI INTERNI Di Riccardo Messina L espressione dell equivalenza massaenergia che è qui riportata non
1 Interazioni tra campi, teorie di Fermi e di Yukawa
 1 Interazioni tra campi, teorie di Fermi e di Yukawa Costanti d accoppiamento Le teorie di campo libere che abbiamo analizzato fin qui descrivono la propagazione di particelle ed antiparticelle relativistiche
1 Interazioni tra campi, teorie di Fermi e di Yukawa Costanti d accoppiamento Le teorie di campo libere che abbiamo analizzato fin qui descrivono la propagazione di particelle ed antiparticelle relativistiche
Teorie di gauge. Note per il corso di Sistemi Dinamici 2 Dipartimento di Matematica, Università di Milano a.a Versione del 14/12/2012
 Teorie di gauge Note per il corso di Sistemi Dinamici 2 Dipartimento di Matematica, Università di Milano a.a. 2012 2013 Versione del 14/12/2012 1 Trasformazioni di gauge Consideriamo una Lagrangiana naturale,
Teorie di gauge Note per il corso di Sistemi Dinamici 2 Dipartimento di Matematica, Università di Milano a.a. 2012 2013 Versione del 14/12/2012 1 Trasformazioni di gauge Consideriamo una Lagrangiana naturale,
p e c = ev Å
 Corso di Introduzione alla Fisica Quantistica (f) Soluzioni Esercizi: Giugno 006 * Quale la lunghezza d onda di de Broglie di un elettrone che ha energia cinetica E 1 = KeV e massa a riposo m 0 = 9.11
Corso di Introduzione alla Fisica Quantistica (f) Soluzioni Esercizi: Giugno 006 * Quale la lunghezza d onda di de Broglie di un elettrone che ha energia cinetica E 1 = KeV e massa a riposo m 0 = 9.11
Brevi Appunti sulla Teoria dei Gruppi di Lie
 Brevi Appunti sulla Teoria dei Gruppi di Lie (Appunti per il corso di Teoria dei Campi 1-010/11) Fiorenzo Bastianelli 1 Definizione di gruppo Un gruppo G = {g} è definito come l insieme di elementi g che
Brevi Appunti sulla Teoria dei Gruppi di Lie (Appunti per il corso di Teoria dei Campi 1-010/11) Fiorenzo Bastianelli 1 Definizione di gruppo Un gruppo G = {g} è definito come l insieme di elementi g che
3. Elementi di Algebra Lineare.
 CALCOLO NUMERICO Francesca Mazzia Dipartimento Interuniversitario di Matematica Università di Bari 3. Elementi di Algebra Lineare. 1 Sistemi lineari Sia A IR m n, x IR n di n Ax = b è un vettore di m componenti.
CALCOLO NUMERICO Francesca Mazzia Dipartimento Interuniversitario di Matematica Università di Bari 3. Elementi di Algebra Lineare. 1 Sistemi lineari Sia A IR m n, x IR n di n Ax = b è un vettore di m componenti.
Brevi Appunti sulla Teoria dei Gruppi
 Brevi Appunti sulla Teoria dei Gruppi (per il corso di Fisica Nucleare e Subnucleare 014/15) 17.10.014 Fiorenzo Bastianelli 1 Definizione di gruppo Consideriamo un gruppo G = {g} visto come insieme di
Brevi Appunti sulla Teoria dei Gruppi (per il corso di Fisica Nucleare e Subnucleare 014/15) 17.10.014 Fiorenzo Bastianelli 1 Definizione di gruppo Consideriamo un gruppo G = {g} visto come insieme di
produzione di particelle in laboratorio
 produzione di particelle in laboratorio In un urto tra due particelle, può essere prodotta una particella pesante a spese dell energia cinetica dello stato iniziale In questo modo possono essere prodotte
produzione di particelle in laboratorio In un urto tra due particelle, può essere prodotta una particella pesante a spese dell energia cinetica dello stato iniziale In questo modo possono essere prodotte
CAPITOLO 16. (nella (16 2) gli indici i, k a secondo membro non possono essere 0 causa l antisimmetria
 CAPITOLO 16 E finalmente torniamo alla fisica Riprendiamo il filo del discorso dal Cap. 1, dove abbiamo visto che in un RIL la fisica è (localmente) lorentziana. Dunque possiamo trovare coordinate {x α
CAPITOLO 16 E finalmente torniamo alla fisica Riprendiamo il filo del discorso dal Cap. 1, dove abbiamo visto che in un RIL la fisica è (localmente) lorentziana. Dunque possiamo trovare coordinate {x α
Collana di Fisica e Astronomia
 Collana di Fisica e Astronomia A cura di: Michele Cini Stefano Forte Massimo Inguscio Guida Montagna Oreste Nicrosini Franco Pacini Luca Peliti Alberto Rotondi Maurizio Gasperini Manuale di Relatività
Collana di Fisica e Astronomia A cura di: Michele Cini Stefano Forte Massimo Inguscio Guida Montagna Oreste Nicrosini Franco Pacini Luca Peliti Alberto Rotondi Maurizio Gasperini Manuale di Relatività
Interazioni Elettrodeboli. Lezione n. 12. Studi sperimentali: Correlazioni angolari Forme bilineari covarianti θ τ puzzle e violazione della parità
 Interazioni Elettrodeboli prof. Francesco Ragusa Università di Milano Lezione n. 12 13.11.2018 Studi sperimentali: Correlazioni angolari Forme bilineari covarianti θ τ puzzle e violazione della parità
Interazioni Elettrodeboli prof. Francesco Ragusa Università di Milano Lezione n. 12 13.11.2018 Studi sperimentali: Correlazioni angolari Forme bilineari covarianti θ τ puzzle e violazione della parità
ALGEBRA LINEARE E GEOMETRIA: ESERCIZI 5. Indice. 2. Esercizi 5
 ALGEBRA LINEARE E GEOMETRIA: ESERCIZI 5 Indice 1. Principali definizioni 1 2. Esercizi 5 Operazioni con le matrici 1. Principali definizioni Ricordiamo le principali definizioni legate alle matrici a coefficienti
ALGEBRA LINEARE E GEOMETRIA: ESERCIZI 5 Indice 1. Principali definizioni 1 2. Esercizi 5 Operazioni con le matrici 1. Principali definizioni Ricordiamo le principali definizioni legate alle matrici a coefficienti
Interazioni Elettrodeboli. Lezione n. 3. Equazione di Dirac 2 invarianza relativistica
 Interazioni Elettrodeboli prof. Francesco Ragusa Università di Milano Lezione n. 3 13.1.216 Equazione di Dirac 2 invarianza relativistica anno accademico 216-217 Interpretazione delle soluzioni con p o
Interazioni Elettrodeboli prof. Francesco Ragusa Università di Milano Lezione n. 3 13.1.216 Equazione di Dirac 2 invarianza relativistica anno accademico 216-217 Interpretazione delle soluzioni con p o
Capitolo IV SPAZI VETTORIALI EUCLIDEI
 Capitolo IV SPAZI VETTORIALI EUCLIDEI È ben noto che in VO 3 si possono considerare strutture più ricche di quella di spazio vettoriale; si pensi in particolare all operazioni di prodotto scalare di vettori.
Capitolo IV SPAZI VETTORIALI EUCLIDEI È ben noto che in VO 3 si possono considerare strutture più ricche di quella di spazio vettoriale; si pensi in particolare all operazioni di prodotto scalare di vettori.
Esame scritto (parte di Meccanica Quantistica) 19/06/2017. Esercizio 1. Si consideri l oscillatore armonico descritto dalla Hamiltoniana
 Corso di Fisica Matematica 3 a.a. 06/7 Esame scritto (parte di Meccanica Quantistica) 9/06/07 Esercizio. Si consideri l oscillatore armonico descritto dalla Hamiltoniana H 0 = p m + mω x, e siano n (n
Corso di Fisica Matematica 3 a.a. 06/7 Esame scritto (parte di Meccanica Quantistica) 9/06/07 Esercizio. Si consideri l oscillatore armonico descritto dalla Hamiltoniana H 0 = p m + mω x, e siano n (n
PARITA. Parità Parità intrinseca Conservazione della Parità
 PARITA Parità Parità intrinseca Conservazione della Parità PARITÀ L operatore di inversione spaziale è una trasformazione discreta che inverte il segno delle tre coordinate spaziali: P x, y, z -x, -y,
PARITA Parità Parità intrinseca Conservazione della Parità PARITÀ L operatore di inversione spaziale è una trasformazione discreta che inverte il segno delle tre coordinate spaziali: P x, y, z -x, -y,
Simmetrie e leggi di conservazione
 Simmetrie e leggi di conservazione (Appunti per il corso di Fisica Nucleare e Subnucleare 00/) Fiorenzo Bastianelli Traccia schematica delle lezioni su simmetrie e leggi di conservazione. NB: questi appunti
Simmetrie e leggi di conservazione (Appunti per il corso di Fisica Nucleare e Subnucleare 00/) Fiorenzo Bastianelli Traccia schematica delle lezioni su simmetrie e leggi di conservazione. NB: questi appunti
Elementi di Algebra Lineare Spazi Vettoriali
 Elementi di Algebra Lineare Spazi Vettoriali Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017) Elementi di Algebra Lineare 1 / 41 index Spazi vettoriali
Elementi di Algebra Lineare Spazi Vettoriali Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017) Elementi di Algebra Lineare 1 / 41 index Spazi vettoriali
Interazioni Elettrodeboli. Lezione n. 2. Equazione di Dirac 1 Introduzione
 Interazioni Elettrodeboli prof. Francesco Ragusa Università di Milano Lezione n. 2 5.10.2017 Equazione di Dirac 1 Introduzione anno accademico 2017-2018 Rappresentazione di Pauli-Dirac Nella Rappresentazione
Interazioni Elettrodeboli prof. Francesco Ragusa Università di Milano Lezione n. 2 5.10.2017 Equazione di Dirac 1 Introduzione anno accademico 2017-2018 Rappresentazione di Pauli-Dirac Nella Rappresentazione
PROBLEMI DI FISICA MODERNA E MECCANICA QUANTISTICA. FISICA MODERNA anno accademico
 PROBLEMI DI FISICA MODERNA E MECCANICA QUANTISTICA FISICA MODERNA anno accademico 2011-2012 Si consideri un sistema che può trovarsi in uno di tre stati esclusivi 1, 2, 3, e si supponga che esso si trovi
PROBLEMI DI FISICA MODERNA E MECCANICA QUANTISTICA FISICA MODERNA anno accademico 2011-2012 Si consideri un sistema che può trovarsi in uno di tre stati esclusivi 1, 2, 3, e si supponga che esso si trovi
Elementi di Algebra Lineare Spazi Vettoriali
 Elementi di Algebra Lineare Spazi Vettoriali Antonio Lanteri e Cristina Turrini UNIMI - 2017/2018 Antonio Lanteri e Cristina Turrini (UNIMI - 2017/2018) Elementi di Algebra Lineare 1 / 37 index Spazi vettoriali
Elementi di Algebra Lineare Spazi Vettoriali Antonio Lanteri e Cristina Turrini UNIMI - 2017/2018 Antonio Lanteri e Cristina Turrini (UNIMI - 2017/2018) Elementi di Algebra Lineare 1 / 37 index Spazi vettoriali
Figura 7.1: Ipotesi di Heisenberg
 Capitolo 7 Isospin nei nuclei Nel 9 Heisenberg scrisse tre articoli sulla forza nucleare, trattando neutrone e protone come due stati della stessa particella, il nucleone, distinti dal valore assunto da
Capitolo 7 Isospin nei nuclei Nel 9 Heisenberg scrisse tre articoli sulla forza nucleare, trattando neutrone e protone come due stati della stessa particella, il nucleone, distinti dal valore assunto da
Capitolo 3 Matrici. Marco Robutti. Facoltà di ingegneria Università degli studi di Pavia. Anno accademico
 Capitolo 3 Matrici Marco Robutti Facoltà di ingegneria Università degli studi di Pavia Anno accademico 2017-2018 Tutorato di geometria e algebra lineare Definizione (Matrice) Una matrice A M R (k, n) è
Capitolo 3 Matrici Marco Robutti Facoltà di ingegneria Università degli studi di Pavia Anno accademico 2017-2018 Tutorato di geometria e algebra lineare Definizione (Matrice) Una matrice A M R (k, n) è
Autovalori ed autovettori di una matrice
 Autovalori ed autovettori di una matrice Lucia Gastaldi Dipartimento di Matematica, http://lucia-gastaldi.unibs.it page 1 Indice 1 Definizioni di autovalori ed autovettori Autovalori ed autovettori 2 Metodo
Autovalori ed autovettori di una matrice Lucia Gastaldi Dipartimento di Matematica, http://lucia-gastaldi.unibs.it page 1 Indice 1 Definizioni di autovalori ed autovettori Autovalori ed autovettori 2 Metodo
Interazioni Elettrodeboli. Lezione n. 3. Equazione di Dirac 2 Descrizione relativistica dello spin Interazione elettromagnetica
 Interazioni Elettrodeboli prof. Francesco Ragusa Università di Milano Lezione n. 3 10.10.2017 Equazione di Dirac 2 Descrizione relativistica dello spin Interazione elettromagnetica anno accademico 2018-2019
Interazioni Elettrodeboli prof. Francesco Ragusa Università di Milano Lezione n. 3 10.10.2017 Equazione di Dirac 2 Descrizione relativistica dello spin Interazione elettromagnetica anno accademico 2018-2019
Prodotto scalare, covarianza e controvarianza, tensore metrico
 Prodotto scalare, covarianza e controvarianza, tensore metrico Marco Bonvini 29 settembre 2005 1 Prodotto scalare Sia V spazio lineare su R; dati u, v V il loro prodotto scalare, indicato con (u, v), è:
Prodotto scalare, covarianza e controvarianza, tensore metrico Marco Bonvini 29 settembre 2005 1 Prodotto scalare Sia V spazio lineare su R; dati u, v V il loro prodotto scalare, indicato con (u, v), è:
Richiami di Algebra Lineare
 Appendice A Richiami di Algebra Lineare In questo capitolo sono presentati alcuni concetti di algebra lineare L algebra lineare è quella branca della matematica che si occupa dello studio di vettori, spazi
Appendice A Richiami di Algebra Lineare In questo capitolo sono presentati alcuni concetti di algebra lineare L algebra lineare è quella branca della matematica che si occupa dello studio di vettori, spazi
Il problema dei due corpi La dinamica planetaria
 Il problema dei due corpi La dinamica planetaria La Meccanica Classica Lagrange Hamilton Jacobi Vettori Per rendere conto della 3-dimensionalità in fisica, e in matematica, si usano delle grandezze più
Il problema dei due corpi La dinamica planetaria La Meccanica Classica Lagrange Hamilton Jacobi Vettori Per rendere conto della 3-dimensionalità in fisica, e in matematica, si usano delle grandezze più
Autovalori ed autovettori di una matrice
 Autovalori ed autovettori di una matrice Lucia Gastaldi Dipartimento di Matematica, http://lucia-gastaldi.unibs.it page 1 Indice 1 Definizioni di autovalori ed autovettori Autovalori ed autovettori 2 Metodo
Autovalori ed autovettori di una matrice Lucia Gastaldi Dipartimento di Matematica, http://lucia-gastaldi.unibs.it page 1 Indice 1 Definizioni di autovalori ed autovettori Autovalori ed autovettori 2 Metodo
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
Matrici g r(g) (1) r : G
 1 Brevi Appunti sulla Teoria dei Gruppi di Lie Consideriamo un gruppo G = {g} visto come insieme di elementi g che soddisfano alle seguenti proprietà: 1) esiste una legge di composizione: presi g 1, g
1 Brevi Appunti sulla Teoria dei Gruppi di Lie Consideriamo un gruppo G = {g} visto come insieme di elementi g che soddisfano alle seguenti proprietà: 1) esiste una legge di composizione: presi g 1, g
Autovalori ed autovettori di una matrice
 Autovalori ed autovettori di una matrice Lucia Gastaldi Dipartimento di Matematica, http://dm.ing.unibs.it/gastaldi/ 24 febbraio 2008 Outline 1 Definizioni di autovalori ed autovettori Autovalori ed autovettori
Autovalori ed autovettori di una matrice Lucia Gastaldi Dipartimento di Matematica, http://dm.ing.unibs.it/gastaldi/ 24 febbraio 2008 Outline 1 Definizioni di autovalori ed autovettori Autovalori ed autovettori
Il prodotto tra matrici non è commutativo. Nelle notazioni precedenti, ponendo n = p e m = q si hanno:
 L anello delle matrici Esempio. Siano A = [ ] 0 1 3 0 2 1, B = 1 2 0 0 1 2 3 4, 1 0 calcolare AB e BA. Osservazioni Siano A Mat m,n (K) e B Mat p,q (K). Il prodotto AB è definito se n = p. Si ha AB Mat
L anello delle matrici Esempio. Siano A = [ ] 0 1 3 0 2 1, B = 1 2 0 0 1 2 3 4, 1 0 calcolare AB e BA. Osservazioni Siano A Mat m,n (K) e B Mat p,q (K). Il prodotto AB è definito se n = p. Si ha AB Mat
Elementi di Algebra Lineare Spazi Vettoriali
 Elementi di Algebra Lineare Spazi Vettoriali Antonio Lanteri e Cristina Turrini UNIMI - 2015/2016 Antonio Lanteri e Cristina Turrini (UNIMI - 2015/2016) Elementi di Algebra Lineare 1 / 37 index Spazi vettoriali
Elementi di Algebra Lineare Spazi Vettoriali Antonio Lanteri e Cristina Turrini UNIMI - 2015/2016 Antonio Lanteri e Cristina Turrini (UNIMI - 2015/2016) Elementi di Algebra Lineare 1 / 37 index Spazi vettoriali
Brevi Appunti sulla Teoria dei Gruppi
 Brevi Appunti sulla Teoria dei Gruppi (per il corso di Fisica Nucleare e Subnucleare 015/16 14.10.015 Fiorenzo Bastianelli 1 Definizione di gruppo Consideriamo un gruppo G = {g} visto come insieme di elementi
Brevi Appunti sulla Teoria dei Gruppi (per il corso di Fisica Nucleare e Subnucleare 015/16 14.10.015 Fiorenzo Bastianelli 1 Definizione di gruppo Consideriamo un gruppo G = {g} visto come insieme di elementi
Problemi per il corso di teoria delle interazioni fondamentali gennaio 2013
 Problemi per il corso di teoria delle interazioni fondamentali gennaio 203 Primo Modulo. Urto Bhabha in QED Considerare il processo e + e e + e nella regione di energia per cui la massa degli elettroni
Problemi per il corso di teoria delle interazioni fondamentali gennaio 203 Primo Modulo. Urto Bhabha in QED Considerare il processo e + e e + e nella regione di energia per cui la massa degli elettroni
Appendice 1. Spazi vettoriali
 Appendice. Spazi vettoriali Indice Spazi vettoriali 2 2 Dipendenza lineare 2 3 Basi 3 4 Prodotto scalare 3 5 Applicazioni lineari 4 6 Applicazione lineare trasposta 5 7 Tensori 5 8 Decomposizione spettrale
Appendice. Spazi vettoriali Indice Spazi vettoriali 2 2 Dipendenza lineare 2 3 Basi 3 4 Prodotto scalare 3 5 Applicazioni lineari 4 6 Applicazione lineare trasposta 5 7 Tensori 5 8 Decomposizione spettrale
Esercizi di geometria affine in 3 dimensioni
 Esercizi di geometria affine in 3 dimensioni Nicola Sansonetto febbraio 009 Esercizio 1. Si consideri nel piano affine A (R) un riferimento cartesiano, la retta τ di equazione affine y + x = 1 e il triangolo
Esercizi di geometria affine in 3 dimensioni Nicola Sansonetto febbraio 009 Esercizio 1. Si consideri nel piano affine A (R) un riferimento cartesiano, la retta τ di equazione affine y + x = 1 e il triangolo
Interazioni Elettrodeboli. Lezione n. 14
 Interazioni Elettrodeboli prof. Francesco Ragusa Università di Milano Lezione n. 14 20.11.2018 Hamiltoniana del decadimento β Chiralità e proiezioni chirali Correnti chirali. Universalità Decadimento π
Interazioni Elettrodeboli prof. Francesco Ragusa Università di Milano Lezione n. 14 20.11.2018 Hamiltoniana del decadimento β Chiralità e proiezioni chirali Correnti chirali. Universalità Decadimento π
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria - Edile ed Edile/Architettura
 Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria - Edile ed Edile/Architettura Primo Appello del corso di Geometria 2 Docente F. Flamini, Roma, 22/02/2007 SVOLGIMENTO COMPITO I APPELLO
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria - Edile ed Edile/Architettura Primo Appello del corso di Geometria 2 Docente F. Flamini, Roma, 22/02/2007 SVOLGIMENTO COMPITO I APPELLO
Esercizi Riepilogativi Svolti
 Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA Edile-Architettura e dell Edilizia SPAZI EUCLIDEI. TRASFORMAZIONI. ORIENTAZIONI. FORMULE DI GEOMETRIA IN R. Docente:
Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA Edile-Architettura e dell Edilizia SPAZI EUCLIDEI. TRASFORMAZIONI. ORIENTAZIONI. FORMULE DI GEOMETRIA IN R. Docente:
sulla massa invariante Consideriamo i due processi per la produzione di antiprotoni
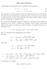 sulla massa invariante Consideriamo i due processi per la produzione di antiprotoni e + + e p + p, (1) p + p p + p + p + p. (2) Per entrambi si calcoli l energia cinetica di soglia del processo sia nel
sulla massa invariante Consideriamo i due processi per la produzione di antiprotoni e + + e p + p, (1) p + p p + p + p + p. (2) Per entrambi si calcoli l energia cinetica di soglia del processo sia nel
