Sistemi lineari. n Nozioni fondamentali
|
|
|
- Antonio Luca Fortunato
- 7 anni fa
- Visualizzazioni
Transcript
1 n n n n n n Nozioni fondamentali Il metodo di eliminazione Matrici e sistemi lineari Sistemi di n equazioni in n incognite Sistemi di m equazioni in n incognite Sistemi lineari parametrici n Nozioni fondamentali Introduzione In questo capitolo approfondiremo lo studio dei sistemi lineari, cioè dei sistemi di equazioni di primo grado, che affronteremo utilizzando le matrici Dopo aver rivisitato il metodo di eliminazione alla luce delle nozioni sulle matrici in nostro possesso, studieremo il metodo della matrice inversa per risolvere sistemi di n equazioni in n incognite e rivedremo la regola di Cramer Infine affronteremo l importante teorema di Rouché-Capelli, che stabilisce una condizione necessaria e sufficiente affinché un sistema lineare ammetta soluzioni Ricordiamo che si dicono lineari le equazioni di primo grado e si dice perciò lineare un sistema di equazioni di primo grado Un sistema lineare di m equazioni nelle n incognite x, x,, x n si dice in forma normale se è scritto nel modo seguente a x þ a x þ þ a n x n ¼ b a x þ a x þ þ a n x n ¼ b > a m x þ a m x þ þ a mn x n ¼ b m SAI GIÀ CHE Forma normale di un sistema i termini con le incognite sono tutti a sinistra del simbolo di uguaglianza e i termini noti a destra Le lettere x, x,, x n indicano le n incognite del sistema; i numeri a ij si dicono coefficienti delle incognite e i numeri b i si chiamano termini noti Scrivendo a ij s intende che il primo indice i ði ¼,,, m) si riferisce alla i-esima equazione e che il secondo indice j ðj ¼,,, n) si riferisce alla j-esima incognita Ad esempio, a indicherà, nella seconda equazione, il coefficiente della terza incognita (ossia x Þ Il sistema h si dice omogeneo se i termini noti sono tutti nulli b ¼ b ¼ ¼ b m ¼ Un sistema omogeneo assume dunque la forma a x þ a x þ þ a n x n ¼ a x þ a x þ þ a n x n ¼ > a m x þ a m x þ þ a mn x n ¼ Se invece almeno uno dei termini b i risulta diverso da zero, il sistema si dirà non omogeneo & De Agostini Scuola SpA Novara
2 Definizioni principali DEFINIZIONE SOLUZIONE DEL SISTEMA Una n-pla ordinata di numeri reali ðc ; c ; ; c n Þ è soluzione del sistema a x þ a x þ þ a n x n ¼ b a x þ a x þ þ a n x n ¼ b > a m x þ a m x þ þ a mn x n ¼ b m se le m equazioni del sistema risultano contemporaneamente verificate quando si operino in esse le sostituzioni x ¼ c, x ¼ c,, x n ¼ c n DEFINIZIONI SISTEMA POSSIBILE, SISTEMA IMPOSSIBILE Un sistema lineare si dice possibile e le sue equazioni si dicono compatibili se esso ammette almeno una soluzione; si dice impossibile e le sue equazioni si dicono incompatibili se esso non ammette alcuna soluzione DEFINIZIONI SISTEMA DETERMINATO, SISTEMA INDETERMINATO Un sistema lineare possibile è determinato se ha una sola soluzione, è indeterminato se ha infinite soluzioni Si potrebbe dimostrare che non vi sono altre possibilità un sistema lineare non può avere un numero di soluzioni finito maggiore di uno È immediato verificare che ogni sistema omogeneo ammette sempre almeno la soluzione x ¼ x ¼ ¼ x n ¼ detta soluzione nulla Dunque i sistemi omogenei sono sempre possibili Introduciamo ora un importante definizione che utilizzeremo spesso in seguito DEFINIZIONE COMBINAZIONE LINEARE DI EQUAZIONI Si dice combinazione lineare di due equazioni ogni equazione che si ottiene sommando membro a membro le due equazioni date, dopo aver eventualmente moltiplicato entrambi i membri di ciascuna di esse per un opportuno numero diverso da zero I due numeri per cui si moltiplicano entrambi i membri delle due equazioni si dicono coefficienti della combinazione lineare Infine, consideriamo il principio di riduzione, che già conosciamo e su cui si basa il metodo di eliminazione, di cui parleremo nel PARAGRAFO Vista la definizione di combinazione lineare, il principio di riduzione può essere riformulato così Sostituendo una combinazione lineare di due equazioni di un sistema al posto di una di esse, si ottiene un sistema equivalente al sistema dato SAI GIÀ CHE Il principio di riduzione afferma che, dato un sistema di due equazioni in due incognite, se a un equazione si sostituisce l equazione che si ottiene sommando o sottraendo membro a membro le due equazioni date, si ottiene un sistema equivalente a quello dato & De Agostini Scuola SpA Novara
3 n Il metodo di eliminazione Definizione e applicazione Il metodo di eliminazione consiste essenzialmente nel procedimento seguente Applicando ripetutamente il principio di riduzione, si cerca di eliminare la prima incognita da tutte le equazioni, eccetto che dalla prima; si cerca poi di eliminare la seconda incognita da tutte le equazioni eccetto che dalla seconda; Per simboleggiare il passaggio che consiste nel sostituire una combinazione lineare di due equazioni al posto di una di esse, scriveremo, a sinistra della parentesi graffa, il numero per cui si moltiplicano entrambi i membri di ciascuna delle equazioni considerate; sotto al sistema tracceremo una linea sotto la quale scriveremo la combinazione lineare così formata ESEMPIO Risolviamo il seguente sistema di tre equazioni in tre incognite < x þ y ¼ x þ z ¼ y þ z ¼ Cominciamo con l eliminare la prima incognita, ossia la x, da tutte le equazioni tranne la prima (cioè in questo caso solo dalla seconda equazione) Per far ciò sostituiremo al posto della seconda equazione una combinazione lineare delle prime due equazioni e, per il principio di riduzione, il nuovo sistema risulterà equivalente al sistema h Affinché nella combinazione lineare non figuri l incognita x, dovremo far in modo che i coefficienti di x, nelle due prime equazioni date, risultino opposti Osserviamo che i coefficienti della x nella prima e nella seconda equazione sono rispettivamente e, ed è mcm ( ; ) ¼ Moltiplicando per entrambi i membri della prima equazione e per entrambi i membri della seconda, tali coefficienti divengono ¼ e ¼ ; perciò, sommando membro a membro le due equazioni così ottenute, si elideranno i termini contenenti la x Sostituiamo perciò al posto della seconda equazione la combinazione della prima e della seconda equazione secondo i coefficienti e (si osservi che avremmo potuto scegliere anche i coefficienti e ) < x þ y ¼ x þ z ¼ y þ z ¼ < == y z ¼ x þ y ¼ y z ¼ y þ z ¼ Procediamo nello stesso modo, eliminando prima la y da tutte le equazioni eccetto che dalla seconda e, dopo, eliminando la z da tutte le equazioni eccetto che dalla terza < x þ y ¼ y z ¼ y þ z ¼ x == þ z ¼ < x þ z ¼ y z ¼ y þ z ¼ // þz ¼ < x þ z ¼ y z ¼ z ¼ & De Agostini Scuola SpA Novara
4 A questo punto si potrebbe facilmente risolvere il sistema h sostituendo z ¼ nella prima e seconda equazione; invece, al fine di completare l esposizione del metodo, noi continueremo nella sua applicazione < x þ z ¼ y z ¼ z ¼ x == ¼ ( x ¼ y z ¼ z ¼ y == ¼ ( x ¼ y ¼ z ¼ Il sistema ottenuto è equivalente al sistema h, perché è stato ottenuto da esso mediante ripetute applicazioni del principio di riduzione Perciò anche il sistema h è determinato e la terna ordinata ð ; ; Þ ne è la soluzione Applicando il metodo di eliminazione si possono presentare le seguenti situazioni Nella prima equazione può non comparire la prima incognita, oppure nella seconda equazione può non comparire la seconda incognita, In tal caso è sufficiente scambiare di posto l equazione considerata con una sottostante contenente l incognita che interessa, oppure, se in nessuna delle equazioni sottostanti compare tale incognita, si sposta tale incognita all ultimo posto in tutte le equazioni che la contengono Nel corso dei calcoli una delle equazioni del sistema può assumere la forma di un uguaglianza del tipo ¼ o un altra forma impossibile, oppure due equazioni del sistema si rivelano palesemente incompatibili In tal caso il sistema dato risulta impossibile e non v è motivo di proseguire i calcoli Nel corso dei calcoli una delle equazioni del sistema può assumere la forma di un identità del tipo ¼ o un altra forma equivalente; tale equazione può allora essere trascurata, eliminandola dal sistema Analogamente possono comparire due o più equazioni formalmente identiche o palesemente equivalenti in tal caso si potranno trascurare tutte queste equazioni tranne una, eliminandole dal sistema Prima di completare l esposizione del metodo d eliminazione, illustriamo quanto detto con alcuni esempi Osserviamo che nel risolvere i sistemi è molto utile, per la chiarezza dei calcoli, incolonnare le incognite di ugual nome che compaiono nelle varie equazioni ESEMPIO Risolviamo il seguente sistema di quattro equazioni in cinque incognite x þ x þ x þ x þ x ¼ x x þ x x x ¼ x x þ x x x ¼ > x þ x x þ x þ x ¼ Si ha x þ x þ x þ x þ x ¼ x x þ x x x ¼ x x þ x x x ¼ > x þ x x þ x þ x ¼ == x == þ x þ x ¼ & De Agostini Scuola SpA Novara
5 x þ x þ x þ x þ x ¼ x þ x þ x ¼ x x þ x x x ¼ > x þ x x þ x þ x ¼ == x == þ x þ x ¼ x þ x þ x þ x ¼ x þ x þ x ¼ x þ x þ x ¼ > x þ x x þ x þ x ¼ La seconda e la terza equazione sono equivalenti infatti la terza si ottiene dalla seconda moltiplicandone per entrambi i membri Possiamo quindi eliminare una di queste due equazioni, per esempio la terza x þ x þ x þ x þ x ¼ x þ x þ x þ x þ x ¼ x þ x þ x ¼! x > þ x þ x ¼ x þ x x þ x þ x ¼ > x þ x þ x ¼ == x == þ x þ x ¼ La seconda e la terza equazione sono evidentemente incompatibili il sistema è quindi impossibile Sistemi determinati e indeterminati Completiamo ora l esposizione del metodo di eliminazione, esaminando i casi che si possono presentare quando l applicazione del procedimento esposto è terminata perché non ci sono più equazioni da cui poter eliminare altre incognite Se il sistema non si è rivelato impossibile, si possono presentare i due seguenti casi A B In ogni equazione compare una sola incognita e il numero delle equazioni rimaste è uguale al numero delle incognite del sistema (ESEMPIO del PARAGRAFO ) In tal caso il sistema è determinato In almeno un equazione compaiono due o più incognite e il numero r delle equazioni rimaste è minore del numero n delle incognite In tal caso il sistema è indeterminato Infatti, posto k ¼ n r, attribuendo alle incognite x rþ, x rþ,, x n valori arbitrari come, per esempio, x rþ ¼ p ; x rþ ¼ p ; ; x n ¼ p k il sistema si può risolvere rispetto alle restanti incognite x ; x ; ; x r I valori così trovati, insieme ai valori h arbitrariamente attribuiti, costituiscono una soluzione del sistema dato Se ora, invece di sostituire al posto di x rþ,, x n dei numeri arbitrari lasciamo indicate le lettere p,, p k (parametri) otteniamo la soluzione generale del sistema dato Ciò significa che le soluzioni del sistema dato sono tutte quelle che si possono ottenere dal sistema attribuendo ai parametri p,, p k dei valori arbitrari Poiché vi sono infiniti modi di attribuire un valore arbitrario a ciascuno di questi k parametri, si dice che il sistema ha k soluzioni ESEMPIO Risolviamo il seguente sistema di quattro equazioni in quattro incognite x þ 9x þ x þ x ¼ x þ x ¼ x þ x þ x þ x ¼ 9 > x þ x þ x þ x ¼ & De Agostini Scuola SpA Novara
6 Eliminiamo l incognita x da tutte le equazioni eccetto che dalla prima x þ 9x þ x þ x ¼ x þ x ¼! x þ x þ x þ x ¼ 9 > x þ x þ x þ x ¼ == x þ x == ¼! x þ 9x þ x þ x ¼ x þ x ¼ x þ x ¼ > x þ x þ x þ x ¼ == x þ 9x == ¼! x þ 9x þ x þ x ¼ x þ x ¼! x þ x ¼ > x þ x ¼ Nel sistema ottenuto vi sono tre equazioni formalmente identiche possiamo perciò trascurarne due; eliminiamo poi l incognita x dalla prima equazione del nuovo sistema così ottenuto 9 ( x þ 9x þ x þ x ¼ x þ x ¼ x == x þ x ¼! ( x x þ x ¼! x þ x ¼ L applicazione del metodo d eliminazione esposto al paragrafo precedente è terminata Abbiamo ottenuto un sistema in ciascuna delle cui equazioni compare più di un incognita (caso B) Il sistema è perciò indeterminato Per ricavare l espressione generale delle soluzioni del sistema h poniamo perciò x ¼ p e x ¼ p nell ultimo dei sistemi h, che risolviamo poi rispetto a x e x ( x p þ p ¼ x þ p ¼! > x ¼ p p x ¼ p L espressione generale delle soluzioni del sistema h è perciò x ¼ p p x ¼ p x ¼ p > x ¼ p Il significato delle h è il seguente comunque si attribuiscano a p e p dei valori arbitrari, i corrispondenti valori di x, x, x, x costituiscono una soluzione del sistema h Ad esempio, se si pone p ¼ p ¼, dalle h si ottiene x ¼, x ¼, x ¼ x ¼ ; se invece si assume p ¼, p ¼ si ottiene x ¼, x ¼, x ¼, x ¼ ; Viceversa, ogni soluzione del sistema h si può ottenere dalle h con opportuni valori di p e p Per tale motivo si dice che le h esprimono la soluzione generale del sistema h Inoltre, poiché tale soluzione generale è espressa mediante parametri, ognuno dei quali può assumere infiniti valori, si dice che il sistema ha soluzioni & De Agostini Scuola SpA Novara
7 OSSERVAZIONI Il precedente esempio ci offre lo spunto per alcune importanti osservazioni L introduzione di parametri non è strettamente necessaria; avremmo potuto trattare direttamente x e x come parametri, risolvendo le h rispetto alle incognite x e x Si sarebbero ottenute le equazioni > x ¼ x x x ¼ x che esprimono, più sinteticamente delle h, la soluzione generale del sistema h La scelta delle variabili da trattare come incognite e di quelle da trattare come parametri in generale non è unica, ma ciò non significa che tale scelta sia del tutto arbitraria Ad esempio, il sistema h non può essere risolto rispetto alle incognite x e x Ritorneremo su tale problema nei prossimi paragrafi; per il momento si tenga presente che l applicazione del metodo di eliminazione, così come l abbiamo esposto, conduce a una corretta scelta delle variabili da trattare come incognite n Matrici e sistemi lineari Applicazione del metodo di eliminazione alla matrice associata a un sistema Consideriamo un generico sistema lineare di m equazioni in n incognite, scritto in forma normale a x þ a x þ þ a n x n ¼ b a x þ a x þ þ a n x n ¼ b > a m x þ a m x þ þ a mn x n ¼ b m La seguente tabella formata dai coefficienti e dai termini noti del sistema h, disposti in m righe e n þ colonne, come vedremo meglio nei prossimi paragrafi, si chiama matrice completa del sistema a a a n b a a a n b a m a m a mn b m In pratica, in tale tabella ogni riga corrisponde a un equazione del sistema, ognuna delle prime n colonne corrisponde a un incognita e nell ultima colonna si trovano i termini noti In ogni riga si trovano dunque i coefficienti delle incognite dell equazione corrispondente e, precisamente, al primo posto si trova il coefficiente della prima incognita, al secondo posto il coefficiente della seconda incognita,, mentre all ultimo posto compare il termine noto Se in qualche equazione non compare qualche incognita, gli elementi corrispondenti della matrice del sistema saranno uguali a zero È importante notare che, nella risoluzione di un sistema lineare, si opera solo sui coefficienti delle incognite e sui termini noti, mentre le incognite non svolgono altro ruolo che quello di inerti segnaposto Questa osservazione suggerisce l idea di risolvere un sistema operando sulla sua matrice anziché sul sistema stesso Premettiamo che per combinazione lineare di due righe di una matrice intendiamo una riga che si ottiene moltiplicando tutti gli elementi di una delle due righe per uno stesso numero diverso da zero, moltiplicando tutti gli elementi dell altra riga per uno stesso numero diverso dal precedente e da zero e sommando gli elementi corrispondenti delle due righe così modificate & De Agostini Scuola SpA Novara
8 Vediamo dunque, con un esempio, come le operazioni su un sistema lineare equivalgano a operazioni sulla sua matrice Scriviamo, su due colonne, a sinistra il sistema e a destra la sua matrice, intestandone le colonne con i simboli delle relative incognite (vedi il successivo punto ) < x þ y þ z ¼ x þ y þ z ¼ x þ y þ z ¼ x y z termini noti Cerchiamo di rendere nulli i coefficienti di x in tutte le equazioni tranne la prima Formiamo una combinazione lineare della prima e della seconda equazione secondo i coefficienti ee sostituiamola alla seconda equazione; formiamo poi una combinazione lineare della prima e della terza equazione, secondo i coefficienti e, e sostituiamola alla terza equazione < x þ y þ z ¼ x þ y þ z ¼ x þ y þ z ¼ == y z ¼? y < x þ y þ z ¼ y z ¼ x þ y þ z ¼ == y þ z ¼? y x þ y þ z ¼ y z ¼ > y þ z ¼ Semplifichiamo la terza equazione dividendone entrambi i membri per < x þ y þ z ¼ y z ¼ y þ z ¼ Cerchiamo di rendere nulli tutti gli elementi della prima colonna eccetto quello della prima riga Formiamo una combinazione lineare della prima e della terza riga secondo i coefficienti e, e sostituiamola alla seconda riga; formiamo poi una combinazione lineare della prima e della terza riga, secondo i coefficienti e, e sostituiamola alla terza riga - - x y z termini noti? y x y z termini noti? y x y z termini noti Dividiamo per ciascun elemento della terza riga x y z termini noti Come si vede, tutte le operazioni che, eseguite su un sistema lineare, lo trasformano in un altro a esso equivalente, corrispondono a operazioni eseguibili direttamente sulla matrice del sistema È quindi possibile, nella matrice del sistema, moltiplicare o dividere tutti gli elementi di una riga per una stessa costante diversa da zero; ciò infatti equivale a moltiplicare o dividere entrambi i membri della corrispondente equazione per una stessa costante non nulla; sostituire la combinazione lineare di due righe al posto di una di esse; ciò infatti equivale a sostituire la combinazione lineare di due equazioni al posto di una di esse; & De Agostini Scuola SpA Novara
9 cambiare l ordine delle righe della matrice, perché ciò equivale a mutare l ordine delle equazioni del sistema dato; cambiare l ordine delle colonne della matrice, eccetto l ultima (colonna dei termini noti), perché ciò equivale a mutare l ordine delle incognite del sistema Le intestazioni delle colonne della matrice permetteranno di riconoscere l ordine in cui si trovano le incognite Si deve inoltre ricordare che, se eseguendo le operazioni descritte compare nella matrice una riga nulla, cioè formata da soli zero, essa si può trascurare, eliminandola dalla matrice Infatti tale riga corrisponde a una equazione nella forma ¼, che è identicamente soddisfatta Invece una riga i cui elementi sono tutti nulli, eccetto l ultimo, equivale a una equazione impossibile del tipo ¼ b, con b ¼ La comparsa di una tale riga sta a indicare che l intero sistema è impossibile ESEMPI Riprendiamo il sistema h o, meglio, la relativa matrice, al punto in cui l avevamo lasciata x y z termini noti Cerchiamo di rendere nulli tutti gli elementi della seconda colonna eccetto il secondo (nelle seguenti tabelle, tn indica i termini noti) x y z tn x y z tn x y z tn! 9! 9 9 Semplifichiamo la prima e la terza riga dividendone tutti gli elementi per e, successivamente, rendiamo nulli tutti gli elementi della terza colonna eccetto il terzo x y z tn x y z tn x y z tn!! Dividiamo per tutti gli elementi della prima riga e per tutti gli elementi della seconda riga x y z tn I numeri che costituiscono la quarta colonna della matrice h sono la terna che è soluzione del sistema h Infatti la matrice h corrisponde al sistema seguente < x þ y þ z ¼ < x ¼ x þ y þ z ¼! y ¼ x þ y þ z ¼ z ¼ Il sistema h è equivalente al sistema h, che pertanto è determinato, e ne esprime la soluzione 9 & De Agostini Scuola SpA Novara
10 Risolviamo il seguente sistema x x x ¼ x þ x þ x x x ¼ x þ x þ x x x ¼ > x þ x þ x x x ¼ Si tratta di un sistema omogeneo di quattro equazioni con cinque incognite Il sistema h è dunque possibile, ammettendo almeno la soluzione nulla x ¼ x ¼ x ¼ x ¼ x ¼ (vedi PARAGRAFO ) Risolviamolo con il metodo di eliminazione, per sapere se tale sistema è determinato (nel qual caso la soluzione nulla sarà l unica) o indeterminato (nel qual caso si dovrà trovare un espressione generale delle soluzioni) Scriviamo la matrice corrispondente al sistema h x x x x x tn Cominciamo con l osservare che nella prima riga è nullo il primo elemento (ossia nella prima equazione non compare la prima incognita) Per poter applicare il metodo di eliminazione è allora necessario scambiare tra loro prima e seconda riga Fatto ciò, procediamo rendendo nulli tutti gli elementi della prima colonna eccetto il primo x x x x x tn x x x x x tn x x x x x tn!! La seconda e la terza riga sono identiche, mentre gli elementi della quarta sono gli opposti dei corrispondenti elementi della seconda e della terza riga Tali righe rappresentano quindi tre equazioni equivalenti; possiamo perciò eliminarne due, ad esempio la terza e la quarta Nella tabella così ottenuta sono nulli il primo e il secondo elemento della seconda riga; per procedere scambiamo tra loro la seconda e terza colonna x x x x x tn x x x x x tn! Non ci resta ora che rendere nullo il secondo elemento della prima riga x x x x x tn x x x x x tn! 9 9 x þ 9x x x ¼ La tabella ottenuta rappresenta il sistema x x x ¼ che equivale al sistema h Per risolverlo questa volta non introdurremo nuovi parametri, ma tratteremo le variabili x e x come incognite e x ; x ; x come parametri; otteniamo x ¼ 9x þ x þ x x ¼ x > þ x Il sistema h esprime la soluzione generale del sistema h, che quindi è indeterminato e ammette soluzioni & De Agostini Scuola SpA Novara
11 Forma matriciale di un sistema lineare Consideriamo un sistema lineare di m equazioni in n incognite a x þ a x þ þ a n x n ¼ b a x þ a x þ þ a n x n ¼ b > a m x þ a m x þ þ a mn x n ¼ b m a a a n a a a n La matrice di tipo ðm; nþ A ¼ a m a m a mn si chiama matrice dei coefficienti o matrice incompleta del sistema, mentre le due matrici colonna, rispettivamente di tipo ðn; Þ e ðm; Þ X ¼ x x n B ¼ si chiamano, rispettivamente, matrice colonna delle incognite e matrice colonna dei termini noti La matrice di tipo ðm; n þ Þ a a a n b A a a a n b ¼ a m a m a mn b m ottenuta dalla matrice A dei coefficienti aggiungendovi, come ultima colonna, la matrice colonna dei termini noti, è detta, come già sappiamo, matrice completa del sistema Ricordando la definizione di prodotto tra matrici, e osservando che le matrici A e X sono conformabili rispetto al prodotto, notiamo che il sistema h può essere riscritto, in forma matriciale, nel modo seguente a a a n x b a a a x n b ¼ a m a m a x mn n b m ovvero, in forma compatta, A X ¼ B b b m ESEMPIO Consideriamo il seguente sistema di tre equazioni nelle quattro incognite x, y, z, w < x þ y z þ w ¼ x þ z w ¼ y þ z w ¼ La matrice dei coefficienti è A ¼ & De Agostini Scuola SpA Novara
12 La matrice colonna delle incognite e la matrice colonna dei termini noti sono, rispettivamente, x y X ¼ B ¼ z w La matrice completa del sistema è A ¼ In forma matriciale, il sistema dato si scrive nel modo seguente x y ¼ z w n Sistemi di n equazioni in n incognite Metodo della matrice inversa Consideriamo il sistema h del paragrafo precedente, nel caso particolare in cui sia m ¼ n, ossia nel caso in cui il numero delle equazioni sia uguale al numero delle incognite a x þ a x þ þ a n x n ¼ b a x þ a x þ þ a n x n ¼ b > a n x þ a n x þ þ a nn x n ¼ b n In forma matriciale, tale sistema sarà La matrice dei coefficienti del sistema risulta quadrata Supponiamo inoltre che il suo determinante non sia nullo, sia cioè jaj ¼ e quindi esista la matrice inversa A A X ¼ B NOTA BENE Come vedremo, se è jaj ¼il sistema può essere impossibile o indeterminato Vogliamo dimostrare che, sotto tali ipotesi, il sistema è possibile e determinato e la sua soluzione è data da X ¼ A B n Dimostrazione Sostituendo nella h, al posto di X, l espressione data dalla h,siha A ða BÞ ¼B che, per la proprietà associativa del prodotto tra matrici, può scriversi ða A ÞB ¼ B Da questa relazione, per le proprietà della matrice inversa e della matrice unità, si ottiene un identità che verifica la h I B ¼ B! B ¼ B & De Agostini Scuola SpA Novara
13 Quindi il sistema dato ammette almeno una soluzione ed è perciò possibile Dimostriamo ora che il sistema è determinato, cioè che non ammette altra soluzione oltre alla h Se vi fosse un altra soluzione, X ¼ A B, si avrebbe A X ¼ B Moltiplicando a sinistra per A entrambi i membri di tale uguaglianza, otteniamo A ðax Þ¼A B! ða AÞX ¼ A B! I X ¼ A B! X ¼ A B contro l ipotesi X ¼ A B cvd OSSERVAZIONE Il risultato ora ottenuto ci permette di affermare che la condizione jaj ¼ èsufficiente affinché il sistema sia possibile e determinato La matrice A B, che per la h è uguale a X, risulta una matrice colonna di tipo ðn; Þ Gli elementi di A B ci forniscono i valori cercati di x, x,, x n, cioè l unica soluzione del sistema dato ESEMPIO < x þ y ¼ Vogliamo risolvere il sistema x þ y þ z ¼ x þ y þ z ¼ La matrice inversa della matrice dei coefficienti di tale sistema si determina con il metodo esposto nel capitolo sulle matrici Si ottiene quindi ¼ Quindi, applicando la h ed eseguendo poi il prodotto, si ottiene x y ¼! z x < x ¼! y ¼! y ¼ z z ¼ 9 9 SAI GIÀ CHE A A A n jaj jaj jaj A A A n A ¼ jaj jaj jaj A n A n A nn jaj jaj jaj dove A ik è il complemento algebrico dell elemento a ik, ossia è il determinante moltiplicato per ð Þ iþk della matrice che si ottiene sopprimendo la riga e la colonna di quell elemento Regola di Cramer Il metodo della matrice inversa, esposto nel paragrafo precedente per la risoluzione di un sistema lineare di n equazioni in n incognite, può essere facilmente tradotto in una comoda regola Sempre supponendo jaj ¼, abbiamo dunque visto che X ¼ A B, cioè x x x n A jaj A ¼ jaj A n jaj A jaj A jaj A n jaj A n jaj A n b b b n jaj A nn jaj & De Agostini Scuola SpA Novara
14 Incominciamo a ricavare x x ¼ A jaj b þ A jaj b þ þ A n jaj b n ¼ b A þ b A þ þ b n A n jaj Il numeratore dell ultimo membro della h è, per definizione, lo sviluppo secondo la prima colonna del determinante della matrice b a a n b a a n b n a n a nn ottenibile dalla matrice A dei coefficienti sostituendo la prima colonna con quella dei termini noti del sistema dato In modo analogo si ottiene a b a a n a b a a n x ¼ A jaj b þ A jaj b þ þ A n b jaj n ¼ b A þ b A þ þ b n A n a ¼ n b n a n a nn jaj jaj e così via per le restanti incognite Possiamo quindi enunciare la regola seguente REGOLA DI CRAMER Un sistema di n equazioni in n incognite x, x,, x n, in cui il determinante della matrice dei coefficienti è diverso da zero, è possibile e ammette una e una sola soluzione data da x ¼ D jaj ; x ¼ D jaj ; ; x i ¼ D i jaj ; ; x n ¼ D n jaj essendo D i il determinante della matrice che si ottiene dalla matrice A dei coefficienti sostituendo alla i-esima colonna (cioè a quella dei coefficienti dell incognita che si vuol determinare) la colonna dei termini noti del sistema ATTENZIONE La regola di Cramer non va applicata a sistemi lineari con un gran numero di equazioni e incognite, perché i calcoli diventano troppo laboriosi ESEMPIO Risolviamo con la regola di Cramer il seguente sistema lineare < x þ x x ¼ x x x ¼ x x þ x ¼ Il determinante della matrice dei coefficienti è jaj ¼ ¼ ¼ Calcoliamo D ¼ ¼ ; D ¼ ¼ ; D ¼ ¼ e pertanto si ottiene x ¼ D jaj ¼ ¼ ; x ¼ D jaj ¼ ¼ ; x ¼ D jaj ¼ ¼ & De Agostini Scuola SpA Novara
15 n Sistemi di m equazioni in n incognite 9 Teorema di Rouché-Capelli Approfondiremo ora la trattazione della risolubilità di un generico sistema lineare, in cui il numero delle equazioni non coincide necessariamente con il numero delle incognite Il teorema di Rouché-Capelli, che enunciamo senza darne la dimostrazione, ci permette di decidere se un dato sistema è possibile o impossibile TEOREMA DI ROUCHÉ-CAPELLI Un sistema lineare è possibile se e soltanto se la matrice dei coefficienti e la matrice completa del sistema hanno lo stesso rango Prima di vedere qualche esempio, osserviamo che se r è il rango di A, matrice dei coefficienti, e r è il rango di A, matrice completa del sistema, risulta sempre r r Infatti, essendo r il rango di A, la matrice A contiene un minore non nullo di ordine r e, poiché A è una sottomatrice di A, tale minore risulta contenuto anche in A Perciò, ricordando la definizione di rango di una matrice, si possono presentare due casi n º caso A contiene un altro minore non nullo di ordine maggiore di r Si ha allora r < r e quindi, essendo r ¼ r, per il teorema di Rouché-Capelli, il sistema è impossibile (cioè le sue equazioni sono incompatibili) n º caso Tutti i minori di A di ordine maggiore di r sono nulli Si ha allora r ¼ r eilsistema è possibile (le sue equazioni risultano compatibili) IN SINTESI n rango ða Þ > rango ðaþ () sistema impossibile n rango ða Þ¼rango ðaþ () sistema possibile Se il sistema dato è omogeneo, ossia se i termini noti sono tutti nulli, esso, come abbiamo già detto nel PARAGRAFO, risulta possibile Tale risultato è coerente con il teorema di Rouché-Capelli infatti la matrice completa del sistema si ottiene dalla matrice dei coefficienti aggiungendovi una colonna di elementi nulli; pertanto le due matrici hanno certamente lo stesso rango Per ricercare eventuali soluzioni diverse dalla soluzione nulla, si procederà come descritto nei paragrafi successivi ESEMPI Verificare se è possibile o no il seguente sistema < x þ x x þ x ¼ x þ x þ x x ¼ x þ x x þ x ¼ La matrice dei coefficienti e la matrice completa del sistema sono, rispettivamente A ¼ A ¼ Il minore di ordine formato con gli elementi della a e a riga e della a e a colonna di A, che è un minore anche di A, risulta non nullo ¼ Poiché la terza riga di entrambe le matrici è la somma delle prime due, qualunque minore di ordine, estratto da una delle due matrici, ha la terza riga uguale alla somma delle prime due e perciò sarà nullo per la proprietà 9 dei determinanti (vedi PARAGRAFO, capitolo sulle matrici) Perciò le due matrici A e A hanno entrambe rango e quindi il sistema risulta possibile & De Agostini Scuola SpA Novara
16 Verificare se è possibile o no il sistema seguente < x þ y þ z ¼ x þ y z ¼ x y þ z ¼ La matrice dei coefficienti e la matrice completa del sistema sono rispettivamente A ¼ A ¼ Com è facile verificare, si ha che jaj ¼ e quindi la matrice A non ha rango ; si ha invece che il minore ¼ 9 è un minore non nullo di ordine La matrice A, perciò, ha rango Invece si ha che ¼ è un minore non nullo di A di ordine A perciò ha rango Il sistema dato è dunque impossibile Risoluzione di un sistema lineare Vediamo ora come si può risolvere un sistema di m equazioni in n incognite, di cui si sia accertata la possibilità Sia r il rango della matrice A dei coefficienti, coincidente dunque con il rango della matrice completa A del sistema Si individua una matrice quadrata con determinante diverso da zero di ordine r, che chiameremo H, sottomatrice di A H deve esistere perché r è il rango di A Se risulta r < m, si considerano le r equazioni del sistema corrispondenti alle righe di H, trascurando le rimanenti m r equazioni Nel caso che sia m ¼ r si conservano tutte le equazioni Si prendono come incognite del sistema le r incognite corrispondenti ai coefficienti che costituiscono le colonne di H; se si desidera ottenere una soluzione particolare del sistema, si attribuiscono alle restanti k ¼ n r incognite valori scelti ad arbitrio Se invece si vuole ottenere la soluzione generale del sistema, si trattano le restanti k incognite come parametri Si è così ottenuto un sistema di r equazioni in r incognite, la cui matrice dei coefficienti è H Essendo per ipotesi jhj ¼, il sistema risulta possibile e determinato; lo si può risolvere con uno dei metodi noti (ad esempio il metodo di Cramer, il metodo di eliminazione, oppure il metodo di sostituzione, ) Nell applicare il procedimento appena visto, occorre tenere presenti le seguenti osservazioni n Nel caso in cui il rango r delle due matrici del sistema risulti minore del numero m di equazioni, le m r equazioni che vengono trascurate risultano certamente soddisfatte dalle soluzioni del sistema formato con le restanti r equazioni Infatti, come si potrebbe dimostrare, le equazioni trascurate non sono che delle combinazioni lineari di quelle considerate n Nel caso in cui il rango r delle due matrici del sistema coincida con il numero n delle incognite, il sistema si riduce a un sistema di n equazioni in n incognite e risulta possibile e determinato In particolare, se il sistema risulta omogeneo, esso ammette solo la soluzione nulla x ¼ x ¼ ¼ x n ¼ n Se invece risulta r < n, posto k ¼ n r, la soluzione del sistema dipende dal valore attribuito a ciascuna delle k incognite declassate Come già detto nel PARAGRAFO, si usa allora dire che il si- & De Agostini Scuola SpA Novara
17 stema ammette k soluzioni, poiché a ogni k pla ordinata di numeri reali (i valori attribuiti arbitrariamente alle k incognite declassate ) corrisponde una soluzione del sistema Evidentemente, in questo caso, poiché le soluzioni del sistema sono infinite, il sistema risulta indeterminato n Nel caso in cui il sistema abbia n equazioni e n incognite ðm ¼ nþ, se il determinante jaj della matrice dei coefficienti è diverso da zero, il rango di tale matrice risulta n, edèn anche il rango della matrice completa Pertanto, per il teorema di Rouché-Capelli, il sistema è possibile e, per quanto osservato nel PARAGRAFO, il sistema è anche determinato Se invece il determinante jaj della matrice dei coefficienti fosse nullo, sempre nel caso m ¼ n, per decidere se il sistema è possibile, si può applicare il teorema di Rouché-Capelli Se si verificano le condizioni di possibilità, essendo sicuramente r < n, varranno in questo caso le osservazioni fatte al punto precedente n Quando si risolve un sistema applicando il metodo di eliminazione, esposto nei PARAGRAFI e, la possibilità del sistema viene accertata nel corso della risoluzione Pertanto, applicando il metodo di eliminazione, è superfluo accertare preventivamente la possibilità del sistema mediante il teorema di Rouché-Capelli IN SINTESI Sistemi possibili di m equazioni in n incognite r ¼ rango ðaþ ¼rango ða Þ¼rango ðhþ (A matrice dei coefficienti; A matrice completa; jhj minore non nullo di A) m ¼ n m ¼ n Se jaj ¼ ðr ¼ m ¼ nþ il sistema è determinato Se jaj ¼ ðr < m ¼ nþ il sistema è indeterminato Se r ¼ n < m si trascurano le m r equazioni non corrispondenti alle righe di H Il sistema è determinato Se r ¼ m < n il sistema è indeterminato len r incognite non corrispondenti alle colonne di H diventano parametri da cui dipendono le n r soluzioni del sistema Se r < m ^ r < n vanno trascurate le m r equazioni non corrispondenti alle righe di H; il sistema è indeterminato ESEMPI Risolviamo il sistema ( x þ y z ¼ x þ y z ¼ x þ z ¼ Le matrici incompleta e completa del sistema sono A ¼ A ¼ Notiamo che, essendo jaj ¼, non è possibile applicare direttamente al sistema h il metodo di Cramer Allo scopo di stabilire se il sistema è possibile o no, determiniamo i ranghi delle due matrici Osserviamo che sia da A sia da A si può estrarre un minore non nullo di ordine e precisamente quello formato con gli elementi delle prime due righe e delle prime due colonne jhj ¼ ¼ L unico minore di A che si può ottenere orlando H è jaj ¼ Perciò A è di rango & De Agostini Scuola SpA Novara
18 I minori di ordine di A che si possono ottenere orlando H sono due, entrambi nulli ¼ ¼ Perciò anche A ha rango e quindi, per il teorema di Rouché-Capelli, il sistema h è possibile e ammette ¼ soluzioni Per risolverlo, consideriamo la prima e la seconda equazione, corrispondenti alle righe di H, e trascuriamo la terza; come già detto, essa risulterà certamente soddisfatta da tutte le soluzioni del sistema formato dalle prime due equazioni Si può osservare che, in questo caso, la terza equazione del sistema si ottiene sommando alla seconda la prima moltiplicata per Prendiamo inoltre come incognite x e y, corrispondenti alle colonne di H, e attribuiamo a z un valore arbitrario, ponendo Si ottiene il sistema ( x þ y p ¼ x þ y p ¼ z ¼ p ( x þ y ¼ þ p! x þ y ¼ þ p Risolviamolo applicando la regola di Cramer Il determinante della matrice dei coefficienti è jhj ¼; si ha poi D x ¼ þ p þ p ¼ þ p D þ p y ¼ ¼ p þ p Perciò è x ¼ D x jhj ¼ þ p ¼ þ p, y ¼ D y p ¼ ¼ p; tenendo presente anche la h, jhj possiamo affermare che la soluzione generale del sistema è x ¼ þ p y ¼ p > z ¼ p A ogni valore reale di p corrisponde una soluzione particolare del sistema poiché i valori che si possono attribuire a p sono infiniti, il sistema h ha infinite soluzioni e quindi, come già osservato, è indeterminato NOTA BENE Come già osservato nel PARAGRAFO, l introduzione di parametri non è strettamente necessaria Avremmo potuto trattare direttamente l incognita z come un parametro, risolvendo il sistema (dopo aver soppresso la terza equazione) rispetto alle incognite x e y ( ( ( x þ y z ¼ x þ y ¼ þ z!! x ¼ þ z x þ y z ¼ x þ y ¼ þ z y ¼ z Il minore H prescelto non è l unico minore di ordine della matrice A Potevamo considerare, ad esempio, il minore K formato dalla prima e terza riga e dalla seconda e terza colonna jkj ¼ ¼ ¼ Considerando tale minore avremmo potuto risolvere il sistema h eliminando la seconda equazione e considerando come incognite y e z x þ y z ¼ y z ¼ x y ¼ x!! x þ z ¼ z ¼ þx z ¼ þx È importante rilevare che le h e le h differiscono solo formalmente in realtà esse esprimono lo stesso insieme di soluzioni ciò significa che, se dalle h, per un particolare valore di z, otteniamo una soluzione ðx ; y ; z, si può ottenere la stessa soluzione dalle h per un opportuno valore di x Ad esempio, dalle h per z ¼ otteniamo x ¼, y ¼ ; la stessa terna ð; ; Þ si ricava dalle h per x ¼ & De Agostini Scuola SpA Novara
19 Determiniamo la soluzione generale del sistema < x þ x x þ x ¼ x þ x þ x x ¼ x þ x x þ x ¼ già considerato all ESEMPIO del PARAGRAFO 9 Come abbiamo già detto, tale sistema risulta possibile e ammette soluzioni; lo possiamo risolvere considerando solo le prime due equazioni e prendendo come incognite x e x Tratteremo perciò x e x come dei parametri e risolveremo il sistema h con uno dei metodi noti ( x x ¼ x x x þ x ¼ x þ x! > x ¼ x þ x x ¼ 9 þ x n Sistemi lineari parametrici Risoluzione di sistemi con discussione Nel caso in cui in un sistema, oltre alle incognite, figurino uno o più parametri, la risoluzione dovrà essere preceduta da un opportuna discussione, il cui scopo sarà quello di stabilire per quali valori dei parametri il sistema risulti determinato, indeterminato o impossibile ESEMPI Risolvere il sistema ða Þx þ ay ¼ x y ¼ a R Consideriamo la matrice dei coefficienti e la matrice completa del sistema dato, che sono rispettivamente " # " # a a a a A ¼ e A ¼ A è una matrice quadrata di ordine, che possiede elementi non nulli; il suo rango è perciò maggiore o uguale a, ed è se e solo se il suo determinante jaj ¼ a è diverso da zero; ciò accade se e solo se si ha a ¼ () a ¼ Dunque per a ¼ = il rango di A è e in tal caso A, avendo un minore non nullo di ordine (jaj stesso) ha anch essa rango e, per quanto detto nel PARAGRAFO 9, il sistema h è determinato Risolvendolo si trova x ¼ ^ y ¼ Per a ¼ = il sistema h si riduce a x þ < y ¼ esiha A ¼ e B ¼ x y ¼ Il rango di A, come già detto, è in questo caso Per determinare il rango di B, anziché applicare il teorema di Kronecker, si può osservare che la seconda riga di B si ottiene moltiplicando per la prima Perciò, qualunque minore di ordine estratto da B, avendo due righe proporzionali, è nullo; dunque anche il rango di B è e quindi il sistema h è possibile La soluzione generale si può trovare considerando una qualsiasi delle due equazioni e trattando ad esempio x come incognita Si ottiene x ¼ y þ Riassumendo a ¼ =! sistema determinato x ¼ ^ y ¼ a ¼ =! sistema indeterminato con soluzioni x ¼ y þ ^ y R 9 & De Agostini Scuola SpA Novara
20 Risolvere il sistema ax þ y þ z ¼ a by z ¼ > ax þðbþþyþða Þz ¼ Cominciamo con il determinare il rango della matrice dei coefficienti, che è a A ¼ b a bþ a In questo caso, essendo A una matrice quadrata, conviene ragionare nel modo seguente Il rango di A è se e solo se il suo determinante, che è a b,èdiverso da Ciò accade se e solo se si ha a ¼ ^ b ¼ Analizziamo ora che cosa accade rispettivamente nel caso in cui sia a ¼ e nel caso b ¼ Se è a ¼ siha A ¼ b b þ Tale matrice ha rango almeno, essendo non nullo, ad esempio, il minore costituito dal secondo elemento della prima riga Orlando tale minore (possiamo trascurare i minori di ordine formati con elementi della prima colonna, che sono certamente nulli), si ottengono i seguenti minori di ordine b ¼ b; ¼ b b þ entrambi si annullano se e solo se è b ¼ = Dunque, nel caso sia a ¼, il rango di A è seèanche b ¼ =, mentre A ha rango se è b ¼ = Analizziamo ora che cosa accade se è b ¼ In tal caso è a A ¼ a a e il minore formato dalle prime due righe e dalla seconda e terza colonna è non nullo, essendo ¼ ¼ Dunque se è b ¼, indipendentemente dal valore di a, il rango di A è Riassumiamo i risultati fin qui ottenuti A a ¼ ^ b ¼! il rango di A è ; B a ¼ ^ b ¼ =! il rango di A è ; C a ¼ ^ b ¼ =! il rango di A è ; D b ¼! il rango di A è Consideriamo ora, in corrispondenza di ciascuno di tali casi, la matrice completa del sistema a a A ¼ b a bþ a A a ¼ ^ b ¼ Essendo il rango di A, la matrice A, che contiene A come sottomatrice, ha anch essa rango Il sistema è quindi determinato Risolvendolo con uno dei metodi noti si trova x ¼, y ¼, z ¼ & De Agostini Scuola SpA Novara
21 B a ¼ ^ b ¼ = Si ha A ¼ b b þ Il rango di A, che non può essere minore di quello di A (PARAGRAFO 9) èalmeno Del resto i minori di ordine estratti da A prendendo la prima colonna sono certamente nulli essendo nulli tutti gli elementi di tale colonna; l unico minore che non contiene tale colonna è quello formato dalla seconda, terza e quarta colonna di A, ma poiché le ultime due di queste colonne sono opposte, anche tale minore è nullo Quindi in questo caso anche il rango di A è e il sistema h risulta possibile Per risolverlo possiamo considerare x come un parametro, ponendo x ¼ p, e risolvere rispetto a y eazil sistema formato dalla prima e dalla seconda equazione, che per a ¼ si riduce a y þ z ¼! y ¼ by z ¼ z ¼ Si osservi che nel sistema ottenuto per a ¼ non compare l incognita x Ciò significa che il sistema h per y ¼ ^ z ¼ èsoddisfatto da qualunque valore di x ed è quindi indeterminato, ammettendo soluzioni L insieme delle soluzioni è quindi formato dalle terne di numeri reali ðp ; ; Þ con p R C a ¼ ^ b ¼ = Si ha A ¼ D Si può osservare che in tale matrice la seconda e la terza riga sono proporzionali alla prima Pertanto, qualunque minore di ordine estratto da A, avendo due righe proporzionali, è nullo e il rango di A è come quello di A Il sistema h è quindi possibile; lo si può risolvere ponendo x ¼ p e y ¼ p e considerando solo la prima equazione che, in questo caso diviene p þ z ¼! z ¼ p þ Il sistema h ammette quindi soluzioni, costituite dalle terne di numeri reali del tipo p ; p ; p þ, con p, p R b ¼ Si ha a a A ¼ a a Orliamo il minore costituito dagli elementi della prima e seconda riga e della seconda e terza colonna con gli elementi della quarta colonna e terza riga (è inutile considerare la prima colonna perché in tal caso si otterrebbe di nuovo jaj che sappiamo già essere nullo) Si ottiene a ¼ a Dunque il rango di A è e coincide con quello di A il sistema è possibile; risolviamolo ponendo x ¼ p e considerando la prima e la seconda equazione nelle incognite y e z < að pþ ap þ y þ z ¼ a y ¼! z ¼ z ¼ Il sistema h è perciò indeterminato, ammettendo come soluzioni le terne di numeri reali nella forma p ; ;, con p R að pþ & De Agostini Scuola SpA Novara
22 Riassumendo A a ¼ ^ b ¼! sistema determinato B a ¼ ^ b ¼! < x ¼ y ¼ z ¼ sistema indeterminato con soluzioni < x ¼ p y ¼ z ¼ C a ¼ ^ b ¼! sistema indeterminato con soluzioni x ¼ p y ¼ p > z ¼ p þ x ¼ p D b ¼! sistema indeterminato con soluzioni að pþ y ¼ > z ¼ & De Agostini Scuola SpA Novara
23 Esercizi n n n n Nozioni fondamentali Il metodo di eliminazione Matrici e sistemi lineari Metodo della matrice inversa Regola di Cramer Teorema di Rouché-Capelli Sistemi parametrici Nozioni fondamentali RICORDIAMO LA TEORIA n Sistema lineare sistema di equazioni di primo grado n Sistema omogeneo i termini noti di tutte le sue equazioni sono nulli n Soluzione di un sistema di m equazioni in n incognite n-upla ordinata che verifica contemporaneamente tutte le equazioni del sistema n Sistema lineare determinato ha un unica soluzione n Sistema indeterminato ha infinite soluzioni n Sistema impossibile non ammette soluzione QUESITI Che cos è un equazione lineare? In quale caso le equazioni di un sistema si dicono incompatibili? Da che cosa dipendono le n r soluzioni di un sistema indeterminato? VERO O FALSO? Un sistema omogeneo può essere impossibile Un sistema omogeneo può essere indeterminato Un sistema lineare determinato, di due equazioni in due incognite, ha due soluzioni In un sistema lineare il numero delle equazioni può essere diverso dal numero delle incognite In un sistema lineare il numero delle soluzioni è uguale al numero delle incognite 9 Se un sistema lineare ha più di una soluzione, allora è indeterminato Se un sistema lineare ha due equazioni incompatibili, allora è impossibile In un sistema lineare indeterminato il numero delle equazioni non equivalenti è minore del numero delle incognite QUESITI A RISPOSTA MULTIPLA x y þ z ¼ Il sistema è x y þ z ¼ &a &b &c indeterminato, perché il numero delle incognite supera il numero delle equazioni impossibile, perché le equazioni sono incompatibili determinato, perché ammette solo la soluzione ð ; Þ & De Agostini Scuola SpA Novara
24 Esercizi Un sistema omogeneo può essere (si può dare più di una risposta) &a impossibile e indeterminato &b possibile e indeterminato &c impossibile e determinato &d possibile e determinato Il metodo di eliminazione Matrici e sistemi lineari RICORDIAMO LA TEORIA n Principio di riduzione sostituendo una combinazione lineare di due equazioni di un sistema al posto di una di esse, si ottiene un sistema equivalente al sistema dato n Metodo di eliminazione applicando ripetutamente il principio di riduzione, si cerca di eliminare la prima incognita da tutte le equazioni, eccetto che dalla prima; si cerca poi di eliminare la seconda incognita da tutte le equazioni eccetto che dalla seconda; Alla fine, se il sistema non è impossibile, può accadere che il sistema sia determinato, se in ogni equazione compare una sola incognita; indeterminato, se in almeno un equazione figurano due o più incognite n Dato il sistema lineare a x þ a x þ þ a n x n ¼ b a x þ a x þ þ a n x n ¼ b > a m x þ a m x þ þ a mn x n ¼ b m la matrice dei coefficienti del sistema è a a a n a a a n A ¼ a m a m a mn Aggiungendo ad A, come colonna ðn þ Þ-esima, la matrice colonna dei termini noti b B ¼ si ottiene la matrice completa A del sistema b m QUESITI Che cos è una combinazione lineare di due equazioni? Quando la matrice dei coefficienti e la matrice completa di un sistema lineare coincidono? VERO O FALSO? Il metodo di eliminazione si può applicare alla risoluzione di qualsiasi sistema lineare Se al termine dell applicazione del metodo di eliminazione in qualche equazione compare più di un incognita, il sistema è impossibile Il metodo di eliminazione si può applicare solo se in ogni equazione compaiono tutte le incognite 9 Applicando il metodo di eliminazione non è necessario assicurarsi che il sistema sia possibile Un sistema in cui il numero delle equazioni supera il numero delle incognite può essere determinato Un sistema in cui il numero delle equazioni supera il numero delle incognite può essere impossibile COMPLETARE Se, applicando il metodo di eliminazione, due delle equazioni del sistema divengono identiche o equivalenti, allora una delle equazioni Se, applicando il metodo di eliminazione, un equazione assume la forma ¼, allora il sistema è & De Agostini Scuola SpA Novara
25 Esercizi Se, al termine dell applicazione del metodo di eliminazione, in ogni equazione compare una sola incognita, il sistema è Forma la combinazione lineare delle equazioni x y þ z ¼ e9x y þ z ¼ secondo i coefficienti e ½z ¼ Š Forma la combinazione lineare delle equazioni x y þ z ¼ exþyþz¼ secondo i coefficienti e ½x þ y þ 9z ¼ Š Forma la combinazione lineare delle equazioni x þ x x þ x ¼ ex þ x x x ¼ secondo i coefficienti e ½x þ x ¼ Š Forma una combinazione lineare delle equazioni x y þ z ¼ ex þ y þ z ¼ in modo che in essa non compaia l incognita x 9 Forma una combinazione lineare delle equazioni x y z ¼ ex þ y z ¼ in modo che in essa non compaia l incognita y Scrivi i seguenti sistemi in forma matriciale ( ( x y þ z þ w ¼ x x þ x ¼ ; x þ y z w ¼ x þ x x ¼ x þ x ¼ x þ y ¼ x x ¼ x y ¼ ; x x ¼ > z þ w ¼ x þ x þ x ¼ z w ¼ > x þ x ¼ ( x x þ x x ¼ x þ x x þ x þ ðx x Þ¼ðx x þ Þþx Risolvi i seguenti sistemi con il metodo di eliminazione ESERCIZIO SVOLTO < x þ x ¼ x x þ x ¼ x þ x ¼ La matrice completa del sistema è Eliminiamo l incognita x dalla seconda e dalla terza equazione, cioè rendiamo nulli gli elementi della prima colonna tranne quello della prima riga Sostituendo alla seconda riga la differenza tra la prima e la seconda, otteniamo e, sostituendo ora alla terza riga la differenza tra la prima e la terza, si ha Rendiamo ora nulli gli elementi della seconda colonna tranne quello della seconda riga sostituendo alla prima riga la differenza tra la prima e la seconda riga e poi alla terza riga la somma tra la seconda e la terza, otteniamo che, dividendo per la terza riga, equivale a & De Agostini Scuola SpA Novara
26 Esercizi Infine, rendiamo nulli tutti gli elementi della terza colonna tranne quello della terza riga sostituiamo alla prima riga la differenza della prima con la terza e alla seconda riga la somma della seconda con la terza, preventivamente moltiplicata per Otteniamo, dapprima e, poi, Abbiamo quindi ottenuto per soluzione la terna x ¼ ; x ¼ ; x ¼ 9 < x þ x x ¼ x x x ¼ x þ x þ x ¼ < x þ x x ¼ x þ x x ¼ x x x ¼ < x þ y z ¼ x þ y þ z ¼ x y þ z ¼ < x þ y þ z ¼ x þ y þ z ¼ x þ y þ z ¼ x þ x þ x ¼ x þ x þ x ¼ > x þ x þ x ¼ < y þ z ¼ x þ x ¼ y þ z z ¼ x y < x þ x ¼ 9 x þ x ¼ x þ x ¼ < x þ x þ x ¼ x þ x þ x ¼ x þ x þ x ¼ < x y ¼ x y þ z ¼ x þ y z ¼ < x y þ z ¼ y z ¼ x þ y ¼ x þ y þ z ¼ x þ y z ¼ > x þ z ¼ x þ y þ z ¼ < x x x ¼ x x þ x ¼ x þ x þ x ¼ < x x þ x ¼ x x ¼ x þ x þ x ¼ < x þ y þ z ¼ x y z ¼ x þ y z ¼ ½x ¼ x ¼ ; x ¼ Š ½x ¼ ; x ¼ ; x ¼ Š ½x ¼ ; y ¼ ; z ¼ Š ½x ¼ ; y ¼ ; z ¼ Š x ¼ ; x ¼ ; x ¼ x ¼ ; y ¼ ; z ¼ ½x ¼ ; x ¼ ; x ¼ 9Š ½x ¼ ; x ¼ ; x ¼ Š ½impossibileŠ ½x ¼ ; y ¼ ; z ¼ Š ½x ¼ ; y ¼ ; z ¼ Š x ¼ ; x ¼ 9 ; x ¼ ½impossibileŠ ½x ¼ ; y ¼ ; z ¼ Š & De Agostini Scuola SpA Novara
Argomento 13 Sistemi lineari
 Sistemi lineari: definizioni Argomento Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto
Sistemi lineari: definizioni Argomento Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto
SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI
 SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI Appunti presi dalle lezioni del prof. Nedo Checcaglini Liceo Scientifico di Castiglion Fiorentino (Classe 4B) January 17, 005 1 SISTEMI LINEARI Se a ik, b i R,
SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI Appunti presi dalle lezioni del prof. Nedo Checcaglini Liceo Scientifico di Castiglion Fiorentino (Classe 4B) January 17, 005 1 SISTEMI LINEARI Se a ik, b i R,
Note sull algoritmo di Gauss
 Note sull algoritmo di Gauss 29 settembre 2009 Generalità Un sistema lineare di m equazioni in n incognite x,..., x n è un espressione del tipo: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n
Note sull algoritmo di Gauss 29 settembre 2009 Generalità Un sistema lineare di m equazioni in n incognite x,..., x n è un espressione del tipo: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA
 UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito C 3/5/25 A. A. 24 25 ) Risolvere il seguente sistema
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito C 3/5/25 A. A. 24 25 ) Risolvere il seguente sistema
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA
 UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito B 3/05/005 A. A. 004 005 ) Risolvere il seguente sistema
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito B 3/05/005 A. A. 004 005 ) Risolvere il seguente sistema
LEZIONE 3. a + b + 2c + e = 1 b + d + g = 0 3b + f + 3g = 2. a b c d e f g
 LEZIONE 3 3.. Matrici fortemente ridotte per righe. Nella precedente lezione abbiamo introdotto la nozione di soluzione di un sistema di equazioni lineari. In questa lezione ci poniamo il problema di descrivere
LEZIONE 3 3.. Matrici fortemente ridotte per righe. Nella precedente lezione abbiamo introdotto la nozione di soluzione di un sistema di equazioni lineari. In questa lezione ci poniamo il problema di descrivere
LEZIONE 2. ( ) a 1 x 1 + a 2 x a n x n = b, ove a j, b R sono fissati.
 LEZIONE 2 2 Sistemi di equazioni lineari Definizione 2 Un equazione lineare nelle n incognite x, x 2,, x n a coefficienti reali, è un equazione della forma (2 a x + a 2 x 2 + + a n x n = b, ove a j, b
LEZIONE 2 2 Sistemi di equazioni lineari Definizione 2 Un equazione lineare nelle n incognite x, x 2,, x n a coefficienti reali, è un equazione della forma (2 a x + a 2 x 2 + + a n x n = b, ove a j, b
Matrici triangolari [Abate, 3.2] Lezioni 05 e 06. Determinante di una matrice triangolare [Abate, es. 9.3] Matrici ridotte per righe.
![Matrici triangolari [Abate, 3.2] Lezioni 05 e 06. Determinante di una matrice triangolare [Abate, es. 9.3] Matrici ridotte per righe. Matrici triangolari [Abate, 3.2] Lezioni 05 e 06. Determinante di una matrice triangolare [Abate, es. 9.3] Matrici ridotte per righe.](/thumbs/100/147138366.jpg) Matrici triangolari [Abate, 32] Definizione Una matrice A = a ij ) R m,n si dice triangolare superiore se a ij = 0 per ogni i > j; triangolare inferiore se a ij = 0 per ogni i < j Lezioni 05 e 06 Una matrice
Matrici triangolari [Abate, 32] Definizione Una matrice A = a ij ) R m,n si dice triangolare superiore se a ij = 0 per ogni i > j; triangolare inferiore se a ij = 0 per ogni i < j Lezioni 05 e 06 Una matrice
A titolo di esempio proponiamo la risoluzione del sistema sia con il metodo della matrice inversa sia con il metodo di Cramer.
 ) Trovare le soluzioni del seguente sistema lineare: x+ y+ z = 3x y + z = 0 x + 5y 4z = 5 Osserviamo in primo luogo che il sistema dato è un sistema quadrato di tre equazioni in tre incognite, precisamente
) Trovare le soluzioni del seguente sistema lineare: x+ y+ z = 3x y + z = 0 x + 5y 4z = 5 Osserviamo in primo luogo che il sistema dato è un sistema quadrato di tre equazioni in tre incognite, precisamente
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI
 CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
Sistemi Lineari. Elisabetta Colombo. Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico
 Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 200-20 2 a di o.0 4 Capelli Rango o Caratterisca : definizioni a di o.0 Un equazione nelle n incognite x,..., x n della forma dove
Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 200-20 2 a di o.0 4 Capelli Rango o Caratterisca : definizioni a di o.0 Un equazione nelle n incognite x,..., x n della forma dove
1. Sistemi di equazioni lineari. 1.1 Considerazioni preliminari
 1. Sistemi di equazioni lineari 1.1 Considerazioni preliminari I sistemi lineari sono sistemi di equazioni di primo grado in più incognite. Molti problemi di matematica e fisica portano alla soluzione
1. Sistemi di equazioni lineari 1.1 Considerazioni preliminari I sistemi lineari sono sistemi di equazioni di primo grado in più incognite. Molti problemi di matematica e fisica portano alla soluzione
Note per il corso di Geometria Corso di laurea in Ing. Edile/Architettura. 4 Sistemi lineari. Metodo di eliminazione di Gauss Jordan
 Note per il corso di Geometria 2006-07 Corso di laurea in Ing. Edile/Architettura Sistemi lineari. Metodo di eliminazione di Gauss Jordan.1 Operazioni elementari Abbiamo visto che un sistema di m equazioni
Note per il corso di Geometria 2006-07 Corso di laurea in Ing. Edile/Architettura Sistemi lineari. Metodo di eliminazione di Gauss Jordan.1 Operazioni elementari Abbiamo visto che un sistema di m equazioni
Esercizi sui sistemi di equazioni lineari.
 Esercizi sui sistemi di equazioni lineari Risolvere il sistema di equazioni lineari x y + z 6 x + y z x y z Si tratta di un sistema di tre equazioni lineari nelle tre incognite x, y e z Poichè m n, la
Esercizi sui sistemi di equazioni lineari Risolvere il sistema di equazioni lineari x y + z 6 x + y z x y z Si tratta di un sistema di tre equazioni lineari nelle tre incognite x, y e z Poichè m n, la
Sistemi lineari. a 11 x 1 + a 12 x a 1n x n = b 1 a 21 x 1 + a 22 x a 2n x n = b 2 : : : a m1 x 1 + a m2 x 2 +..
 Sistemi lineari: definizioni Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto termine
Sistemi lineari: definizioni Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto termine
Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016.
 Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016 Di seguito si riporta il riassunto degli argomenti svolti; i riferimenti sono a parti del Cap8 Elementi di geometria e algebra lineare Par5
Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016 Di seguito si riporta il riassunto degli argomenti svolti; i riferimenti sono a parti del Cap8 Elementi di geometria e algebra lineare Par5
Sistemi lineari. a 11 x 1 + a 12 x a 1n x n = b 1 a 21 x 1 + a 22 x a 2n x n = b 2 : : : a m1 x 1 + a m2 x 2 +..
 Sistemi lineari: definizioni Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto termine
Sistemi lineari: definizioni Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto termine
SISTEMI LINEARI, METODO DI GAUSS
 SISTEMI LINEARI, METODO DI GAUSS Abbiamo visto che un sistema di m equazioni lineari in n incognite si può rappresentare in forma matriciale come A x = b dove: A è la matrice di tipo (m, n) dei coefficienti
SISTEMI LINEARI, METODO DI GAUSS Abbiamo visto che un sistema di m equazioni lineari in n incognite si può rappresentare in forma matriciale come A x = b dove: A è la matrice di tipo (m, n) dei coefficienti
Introduzione soft alla matematica per l economia e la finanza. Marta Cardin, Paola Ferretti, Stefania Funari
 Introduzione soft alla matematica per l economia e la finanza Marta Cardin, Paola Ferretti, Stefania Funari Capitolo Sistemi di equazioni lineari.8 Il Teorema di Cramer Si consideri un generico sistema
Introduzione soft alla matematica per l economia e la finanza Marta Cardin, Paola Ferretti, Stefania Funari Capitolo Sistemi di equazioni lineari.8 Il Teorema di Cramer Si consideri un generico sistema
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof. Fabio Perroni. 3. Sistemi di equazioni lineari
 Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 3 Sistemi di equazioni lineari Siano m, n N \ {}, sia K un campo Definizione a) Un sistema
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 3 Sistemi di equazioni lineari Siano m, n N \ {}, sia K un campo Definizione a) Un sistema
2x 5y +4z = 3 x 2y + z =5 x 4y +6z = A =
 Esercizio 1. Risolvere il sistema lineare 2x 5y +4z = x 2y + z =5 x 4y +6z =10 (1) Soluz. La matrice dei coefficienti è 1 4 6, calcoliamone il rango. Il determinante di A è (applico la regola di Sarrus):
Esercizio 1. Risolvere il sistema lineare 2x 5y +4z = x 2y + z =5 x 4y +6z =10 (1) Soluz. La matrice dei coefficienti è 1 4 6, calcoliamone il rango. Il determinante di A è (applico la regola di Sarrus):
( 5) 2 = = = +1
 1 IDENTITA ED EQUAZIONI Consideriamo la seguente uguaglianza: ( 2x + 3) 2 = 4x 2 +12x + 9 Diamo alcuni valori arbitrari all incognita x e vediamo se l uguaglianza risulta vera. Per x = 1 si avrà: ( 2 1+
1 IDENTITA ED EQUAZIONI Consideriamo la seguente uguaglianza: ( 2x + 3) 2 = 4x 2 +12x + 9 Diamo alcuni valori arbitrari all incognita x e vediamo se l uguaglianza risulta vera. Per x = 1 si avrà: ( 2 1+
MATEMATICA. a.a. 2014/ Sistemi di equazioni lineari
 MATEMATICA a.a. 2014/15 8. Sistemi di equazioni lineari SISTEMI LINEARI Si definisce sistema lineare un sistema di p equazioni di primo grado in q incognite. a11x1 + a12 x2 +... + a1 qxq = k1 a21x1 + a22x2
MATEMATICA a.a. 2014/15 8. Sistemi di equazioni lineari SISTEMI LINEARI Si definisce sistema lineare un sistema di p equazioni di primo grado in q incognite. a11x1 + a12 x2 +... + a1 qxq = k1 a21x1 + a22x2
Sistemi lineari. Lorenzo Pareschi. Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara
 Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
( 5) 2 = = = +1
 1 IDENTITA ED EQUAZIONI Consideriamo la seguente uguaglianza: ( 2x + 3) 2 = 4x 2 +12x + 9 Diamo alcuni valori arbitrari all incognita x e vediamo se l uguaglianza risulta vera. Per x = 1 si avrà: ( 2 1+
1 IDENTITA ED EQUAZIONI Consideriamo la seguente uguaglianza: ( 2x + 3) 2 = 4x 2 +12x + 9 Diamo alcuni valori arbitrari all incognita x e vediamo se l uguaglianza risulta vera. Per x = 1 si avrà: ( 2 1+
Equazioni di primo grado
 Equazioni di primo grado 15 15.1 Identità ed equazioni Analizziamo le seguenti proposizioni: a ) cinque è uguale alla differenza tra sette e due ; b ) la somma di quattro e due è uguale a otto ; c ) il
Equazioni di primo grado 15 15.1 Identità ed equazioni Analizziamo le seguenti proposizioni: a ) cinque è uguale alla differenza tra sette e due ; b ) la somma di quattro e due è uguale a otto ; c ) il
il determinante che si ottiene da A, sopprimendo la i - esima riga e la j - esima colonna. Si definisce complemento algebrico dell'elemento a ij
 Determinanti Sia data la matrice quadrata a... a n a a n =...... a... a n nn Chiamiamo determinante di il numero det o che ad essa viene associato. det = a a... a... a... a n n n... a nn Un generico elemento
Determinanti Sia data la matrice quadrata a... a n a a n =...... a... a n nn Chiamiamo determinante di il numero det o che ad essa viene associato. det = a a... a... a... a n n n... a nn Un generico elemento
Si consideri il sistema a coefficienti reali di m equazioni lineari in n incognite
 3 Sistemi lineari 3 Generalità Si consideri il sistema a coefficienti reali di m equazioni lineari in n incognite ovvero, in forma matriciale, a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x
3 Sistemi lineari 3 Generalità Si consideri il sistema a coefficienti reali di m equazioni lineari in n incognite ovvero, in forma matriciale, a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x
Equazioni lineari con due o più incognite
 Equazioni lineari con due o più incognite Siano date le uguaglianze: k 0; x + y = 6; 3a + b c = 8. La prima ha un termine incognito rappresentato dal simbolo letterale k; la seconda ha due termini incogniti
Equazioni lineari con due o più incognite Siano date le uguaglianze: k 0; x + y = 6; 3a + b c = 8. La prima ha un termine incognito rappresentato dal simbolo letterale k; la seconda ha due termini incogniti
Il teorema di Rouché-Capelli
 Luciano Battaia Questi appunti (1), ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia, campus di Treviso, contengono un
Luciano Battaia Questi appunti (1), ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia, campus di Treviso, contengono un
Un sistema di equazioni lineari ( o brevemente un sistema lineare) di m equazioni in n incognite, si presenta nella forma:
 SISTEMI LINEARI Un sistema di equazioni lineari ( o brevemente un sistema lineare) di m equazioni in n incognite, si presenta nella forma: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x n =
SISTEMI LINEARI Un sistema di equazioni lineari ( o brevemente un sistema lineare) di m equazioni in n incognite, si presenta nella forma: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x n =
APPLICAZIONI. Im f = {b B a A tale che f (a) = b}.
 APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
LE EQUAZIONI LINEARI LE IDENTITA ( )( ) 5. a Cosa hanno in comune le seguenti uguaglianze? Uguaglianza (1) a
 LE EQUAZIONI LINEARI 1 LE IDENTITA a b = ( a + b)( a b) () 1 a = a + a ( ) ( a + b) = a + ab + b () 3 Cosa hanno in comune le seguenti uguaglianze? Uguaglianza (1) a b = ( a+ b)( a b) È sempre vera qualunque
LE EQUAZIONI LINEARI 1 LE IDENTITA a b = ( a + b)( a b) () 1 a = a + a ( ) ( a + b) = a + ab + b () 3 Cosa hanno in comune le seguenti uguaglianze? Uguaglianza (1) a b = ( a+ b)( a b) È sempre vera qualunque
Le equazioni lineari
 Perchè bisogna saper risolvere delle equazioni? Perché le equazioni servono a risolvere dei problemi! Le equazioni lineari Un problema è una proposizione che richiede di determinare i valori di alcune
Perchè bisogna saper risolvere delle equazioni? Perché le equazioni servono a risolvere dei problemi! Le equazioni lineari Un problema è una proposizione che richiede di determinare i valori di alcune
SISTEMI DI DUE EQUAZIONI IN DUE INCOGNITE
 SISTEMI DI DUE EQUAZIONI IN DUE INCOGNITE Un equazione di primo grado in una incognita del tipo, con ha: una sola soluzione (equazione determinata) se nessuna soluzione (equazione impossibile) se tutte
SISTEMI DI DUE EQUAZIONI IN DUE INCOGNITE Un equazione di primo grado in una incognita del tipo, con ha: una sola soluzione (equazione determinata) se nessuna soluzione (equazione impossibile) se tutte
SISTEMI LINEARI MATRICI E SISTEMI 1
 MATRICI E SISTEMI SISTEMI LINEARI Sistemi lineari e forma matriciale (definizioni e risoluzione). Teorema di Rouché-Capelli. Sistemi lineari parametrici. Esercizio Risolvere il sistema omogeneo la cui
MATRICI E SISTEMI SISTEMI LINEARI Sistemi lineari e forma matriciale (definizioni e risoluzione). Teorema di Rouché-Capelli. Sistemi lineari parametrici. Esercizio Risolvere il sistema omogeneo la cui
Federica Gregorio e Cristian Tacelli
 1 Sistemi lineari Federica Gregorio e Cristian Tacelli Un sistema lineare m n (m equazioni in n incognite) è un insieme di equazioni lineari che devono essere soddisfatte contemporaneamente a 11 x 1 +
1 Sistemi lineari Federica Gregorio e Cristian Tacelli Un sistema lineare m n (m equazioni in n incognite) è un insieme di equazioni lineari che devono essere soddisfatte contemporaneamente a 11 x 1 +
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari
 Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017 Elementi di Algebra Lineare
Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017 Elementi di Algebra Lineare
SISTEMI LINEARI. x y + 2t = 0 2x + y + z t = 0 x z t = 0 ; S 3 : ; S 5x 2y z = 1 4x 7y = 3
 SISTEMI LINEARI. Esercizi Esercizio. Verificare se (,, ) è soluzione del sistema x y + z = x + y z = 3. Trovare poi tutte le soluzioni del sistema. Esercizio. Scrivere un sistema lineare di 3 equazioni
SISTEMI LINEARI. Esercizi Esercizio. Verificare se (,, ) è soluzione del sistema x y + z = x + y z = 3. Trovare poi tutte le soluzioni del sistema. Esercizio. Scrivere un sistema lineare di 3 equazioni
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Definizione: Due equazioni si dicono equivalenti se ammettono le stesse soluzioni.
 Facoltà di Medicina e Chirurgia Corso Zero di Matematica Gruppi: MC-MF3 / PS-MF3 II Lezione EQUAZIONI E SISTEMI Dr. E. Modica erasmo@galois.it www.galois.it IDENTITÀ ED EQUAZIONI Si consideri un uguaglianza
Facoltà di Medicina e Chirurgia Corso Zero di Matematica Gruppi: MC-MF3 / PS-MF3 II Lezione EQUAZIONI E SISTEMI Dr. E. Modica erasmo@galois.it www.galois.it IDENTITÀ ED EQUAZIONI Si consideri un uguaglianza
Sistemi II. Sistemi II. Elisabetta Colombo
 Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, http://users.mat.unimi.it/users/colombo/programmabio.html 1 2 3 con R.C.+ o 1.10 Rango massimo e determinante con R.C.+
Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, http://users.mat.unimi.it/users/colombo/programmabio.html 1 2 3 con R.C.+ o 1.10 Rango massimo e determinante con R.C.+
Precorso di Matematica
 UNIVERSITÀ DEGLI STUDI ROMA TRE FACOLTA DI ARCHITETTURA Precorso di Matematica Anna Scaramuzza Anno Accademico 2005-2006 4-10 Ottobre 2005 INDICE 1. ALGEBRA................................. 3 1.1 Equazioni
UNIVERSITÀ DEGLI STUDI ROMA TRE FACOLTA DI ARCHITETTURA Precorso di Matematica Anna Scaramuzza Anno Accademico 2005-2006 4-10 Ottobre 2005 INDICE 1. ALGEBRA................................. 3 1.1 Equazioni
Le equazioni e i sistemi di primo grado
 Le equazioni e i sistemi di primo grado prof. Roberto Boggiani Isiss Marco Minghetti 1 settembre 009 Sommario In questo documento verrà trattato in modo semplice e facilmente comprensibile la teoria delle
Le equazioni e i sistemi di primo grado prof. Roberto Boggiani Isiss Marco Minghetti 1 settembre 009 Sommario In questo documento verrà trattato in modo semplice e facilmente comprensibile la teoria delle
Esercizi svolti. risolvere, se possibile, l equazione xa + B = O, essendo x un incognita reale
 Esercizi svolti 1. Matrici e operazioni fra matrici 1.1 Date le matrici 1 2 1 6 A = B = 5 2 9 15 6 risolvere, se possibile, l equazione xa + B = O, essendo x un incognita reale Osservazione iniziale: qualunque
Esercizi svolti 1. Matrici e operazioni fra matrici 1.1 Date le matrici 1 2 1 6 A = B = 5 2 9 15 6 risolvere, se possibile, l equazione xa + B = O, essendo x un incognita reale Osservazione iniziale: qualunque
Metodi per la risoluzione di sistemi lineari
 Metodi per la risoluzione di sistemi lineari Sistemi di equazioni lineari. Rango di matrici Come è noto (vedi [] sez.0.8), ad ogni matrice quadrata A è associato un numero reale det(a) detto determinante
Metodi per la risoluzione di sistemi lineari Sistemi di equazioni lineari. Rango di matrici Come è noto (vedi [] sez.0.8), ad ogni matrice quadrata A è associato un numero reale det(a) detto determinante
Argomenti trattati nella settimana novembre Il libro cui faccio riferimento, se non specificato altrimenti, è Lang, Algebra lineare
 Argomenti trattati nella settimana 23-27 novembre 2009 Il libro cui faccio riferimento, se non specificato altrimenti, è Lang, Algebra lineare 1 Sistemi lineari; 2 applicazioni lineari; Sistemi lineari;
Argomenti trattati nella settimana 23-27 novembre 2009 Il libro cui faccio riferimento, se non specificato altrimenti, è Lang, Algebra lineare 1 Sistemi lineari; 2 applicazioni lineari; Sistemi lineari;
Soluzioni del Foglio 2 I sistemi lineari
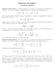 Soluzioni del Foglio 2 I sistemi lineari Soluzione dell esercizio 1 Il sistema assegnato è un sistema di 2 equazioni in 2 incognite non omogeneo Le matrici incompleta e completa associate al sistema sono
Soluzioni del Foglio 2 I sistemi lineari Soluzione dell esercizio 1 Il sistema assegnato è un sistema di 2 equazioni in 2 incognite non omogeneo Le matrici incompleta e completa associate al sistema sono
LEZIONE 5. AX = 0 m,1.
 LEZIONE 5 5 isoluzione di sistemi Supponiamo che AX = B sia un sistema di equazioni lineari Ad esso associamo la sua matrice completa (A B Per quanto visto nella precedente lezione, sappiamo di poter trasformare,
LEZIONE 5 5 isoluzione di sistemi Supponiamo che AX = B sia un sistema di equazioni lineari Ad esso associamo la sua matrice completa (A B Per quanto visto nella precedente lezione, sappiamo di poter trasformare,
I. Foglio di esercizi su vettori linearmente dipendenti e linearmente indipendenti. , v 2 = α v 1 + β v 2 + γ v 3. α v 1 + β v 2 + γ v 3 = 0. + γ.
 ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
( ) TEORIA DELLE MATRICI. A. Scimone a.s pag 1
 . Scimone a.s 1997 98 pag 1 TEORI DELLE MTRICI Dato un campo K, definiamo matrice ad elementi in K di tipo (m, n) un insieme di numeri ordinati secondo righe e colonne in una tabella rettangolare del tipo
. Scimone a.s 1997 98 pag 1 TEORI DELLE MTRICI Dato un campo K, definiamo matrice ad elementi in K di tipo (m, n) un insieme di numeri ordinati secondo righe e colonne in una tabella rettangolare del tipo
1 Ampliamento del piano e coordinate omogenee
 1 Ampliamento del piano e coordinate omogenee Vogliamo dare una idea, senza molte pretese, dei concetti che stanno alla base di alcuni calcoli svolti nella classificazione delle coniche. Supponiamo di
1 Ampliamento del piano e coordinate omogenee Vogliamo dare una idea, senza molte pretese, dei concetti che stanno alla base di alcuni calcoli svolti nella classificazione delle coniche. Supponiamo di
Geometria BAER PRIMO CANALE Foglio esercizi 1
 Geometria BAER PRIMO CANALE Foglio esercizi 1 Esercizio 1. Risolvere le seguenti equazioni lineari nelle variabili indicate trovando una parametrizzazione dell insieme delle soluzioni. a) x + 5y = nelle
Geometria BAER PRIMO CANALE Foglio esercizi 1 Esercizio 1. Risolvere le seguenti equazioni lineari nelle variabili indicate trovando una parametrizzazione dell insieme delle soluzioni. a) x + 5y = nelle
3x 2 = 6. 3x 2 x 3 = 6
 Facoltà di Scienze Statistiche, Algebra Lineare 1 A, GParmeggiani LEZIONE 7 Sistemi lineari Scrittura matriciale di un sistema lineare Def 1 Un sistema di m equazioni ed n incognite x 1, x 2, x n, si dice
Facoltà di Scienze Statistiche, Algebra Lineare 1 A, GParmeggiani LEZIONE 7 Sistemi lineari Scrittura matriciale di un sistema lineare Def 1 Un sistema di m equazioni ed n incognite x 1, x 2, x n, si dice
Sistemi lineari 1 / 12
 Sistemi lineari 1 / 12 Sistemi lineari 2 / 12 Ricordiamo che cosa è un sistema lineare con m equazioni in n incognite (m,n N, m,n 1): a 11 x 1 + +a 1n x n = b 1 a 21 x 1 + +a 2n x n = b 2, (1).. a m1 x
Sistemi lineari 1 / 12 Sistemi lineari 2 / 12 Ricordiamo che cosa è un sistema lineare con m equazioni in n incognite (m,n N, m,n 1): a 11 x 1 + +a 1n x n = b 1 a 21 x 1 + +a 2n x n = b 2, (1).. a m1 x
Lezione del 24 novembre. Sistemi lineari
 Lezione del 24 novembre Sistemi lineari 1 Nelle lezioni scorse abbiamo considerato sistemi di equazioni lineari dei seguenti tipi: un equazione in un incognita; una, due o tre equazioni in due incognite;
Lezione del 24 novembre Sistemi lineari 1 Nelle lezioni scorse abbiamo considerato sistemi di equazioni lineari dei seguenti tipi: un equazione in un incognita; una, due o tre equazioni in due incognite;
Note sui sistemi lineari per il Corso di Geometria per Chimica, Facoltà di Scienze MM.FF.NN., UNICAL (Dott.ssa Galati C.) Rende, 4 Maggio 2010
 Note sui sistemi lineari per il Corso di Geometria per Chimica, Facoltà di Scienze MM.FF.NN., UNICAL (Dott.ssa Galati C.) Rende, 4 Maggio 21 Sistemi lineari. Un sistema lineare di n 1 equazioni in m incognite
Note sui sistemi lineari per il Corso di Geometria per Chimica, Facoltà di Scienze MM.FF.NN., UNICAL (Dott.ssa Galati C.) Rende, 4 Maggio 21 Sistemi lineari. Un sistema lineare di n 1 equazioni in m incognite
MATRICI E SISTEMI LINEARI
 1 Rappresentazione di dati strutturati MATRICI E SISTEMI LINEARI Gli elementi di una matrice, detti coefficienti, possono essere qualsiasi e non devono necessariamente essere omogenei tra loro; di solito
1 Rappresentazione di dati strutturati MATRICI E SISTEMI LINEARI Gli elementi di una matrice, detti coefficienti, possono essere qualsiasi e non devono necessariamente essere omogenei tra loro; di solito
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE. Giovanni Villani
 Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
Sistemi di equazioni lineari
 Sistemi di equazioni lineari I sistemi di equazioni si incontrano in natura in molti problemi di vita reale. Per esempio, prendiamo in considerazione una bevanda a base di uova, latte e succo d arancia.
Sistemi di equazioni lineari I sistemi di equazioni si incontrano in natura in molti problemi di vita reale. Per esempio, prendiamo in considerazione una bevanda a base di uova, latte e succo d arancia.
Ax = b ; b = b 1 b 2. a 11 a 12 a 1n a 21 a 22 a 2n. b m. a m1 a m2 a mn
 SISTEMI LINERI Consideriamo il seguente sistema di m equazioni lineare nelle n incognite,,, n : a + a + + a n n = b >< a + a + + a n n = b = >: a m + a m + + a mn n = b m tale sistema può essere scritto
SISTEMI LINERI Consideriamo il seguente sistema di m equazioni lineare nelle n incognite,,, n : a + a + + a n n = b >< a + a + + a n n = b = >: a m + a m + + a mn n = b m tale sistema può essere scritto
Chi non risolve esercizi non impara la matematica.
 5.5 esercizi 9 Per trovare la seconda equazione ragioniamo così: la parte espropriata del primo terreno è x/00, la parte espropriata del secondo è y/00 e in totale sono stati espropriati 000 m, quindi
5.5 esercizi 9 Per trovare la seconda equazione ragioniamo così: la parte espropriata del primo terreno è x/00, la parte espropriata del secondo è y/00 e in totale sono stati espropriati 000 m, quindi
Lezioni di Algebra Lineare. II. Aritmetica delle matrici e eliminazione di Gauss. versione ottobre 2008
 versione ottobre 2008 Lezioni di Algebra Lineare II. Aritmetica delle matrici e eliminazione di Gauss Contenuto. 1. Somma di matrici e prodotto di una matrice per uno scalare 2. Prodotto di matrici righe
versione ottobre 2008 Lezioni di Algebra Lineare II. Aritmetica delle matrici e eliminazione di Gauss Contenuto. 1. Somma di matrici e prodotto di una matrice per uno scalare 2. Prodotto di matrici righe
Anno 2. Risoluzione di sistemi di primo grado in due incognite
 Anno Risoluzione di sistemi di primo grado in due incognite Introduzione In questa lezione impareremo alcuni metodi per risolvere un sistema di due equazioni in due incognite. Al termine di questa lezione
Anno Risoluzione di sistemi di primo grado in due incognite Introduzione In questa lezione impareremo alcuni metodi per risolvere un sistema di due equazioni in due incognite. Al termine di questa lezione
EQUAZIONI DI II GRADO
 RICHIAMI SULLE EQUAZIONI DI PRIMO E SECONDO GRADO PROF.SSA ROSSELLA PISCOPO Indice 1 EQUAZIONI DI I GRADO --------------------------------------------------------------------------------------------------
RICHIAMI SULLE EQUAZIONI DI PRIMO E SECONDO GRADO PROF.SSA ROSSELLA PISCOPO Indice 1 EQUAZIONI DI I GRADO --------------------------------------------------------------------------------------------------
I sistemi lineari Prof. Walter Pugliese
 I sistemi lineari Prof. Walter Pugliese Le equazioni lineari in due incognite Un equazione nelle incognite x e y del tipo #$ + &' = ) dove *,,, - sono numeri reali è un equazione lineare in due incognite
I sistemi lineari Prof. Walter Pugliese Le equazioni lineari in due incognite Un equazione nelle incognite x e y del tipo #$ + &' = ) dove *,,, - sono numeri reali è un equazione lineare in due incognite
y 5z = 7 y +8z = 10 +3z = 3
 Sistemi lineari Sistemi lineari in tre incognite; esempi tipici Tre equazioni incognite x, y, z Consideriamo il seguente sistema di tre equazioni lineari nelle tre x 2y +6z = 11 x +3y 11z = 18 2x 5y +20z
Sistemi lineari Sistemi lineari in tre incognite; esempi tipici Tre equazioni incognite x, y, z Consideriamo il seguente sistema di tre equazioni lineari nelle tre x 2y +6z = 11 x +3y 11z = 18 2x 5y +20z
1. Consideriamo un sistema lineare. E piuttosto naturale aspettarsi che
 Algebra Lineare (Matematica CI) 151113 1 Consideriamo un sistema lineare E piuttosto naturale aspettarsi che (a) se il numero delle equazioni e minore del numero delle incognite allora il sistema e indeterminato;
Algebra Lineare (Matematica CI) 151113 1 Consideriamo un sistema lineare E piuttosto naturale aspettarsi che (a) se il numero delle equazioni e minore del numero delle incognite allora il sistema e indeterminato;
4 Sistemi di equazioni.
 4 Sistemi di equazioni. Risolvere un sistema significa erminare le soluzioni comuni a tutte le equazioni che lo compongono. Il grado di un sistema è il prodotto dei gradi di tali equazioni. 4. Sistemi
4 Sistemi di equazioni. Risolvere un sistema significa erminare le soluzioni comuni a tutte le equazioni che lo compongono. Il grado di un sistema è il prodotto dei gradi di tali equazioni. 4. Sistemi
Identità ed equazioni
 Matematica e-learning - Identità ed equazioni Prof. erasmo@galois.it A.A. 2009/2010 1 Generalità sulle equazioni Si consideri un uguaglianza tra due espressioni algebriche A = B Se si sostituiscono al
Matematica e-learning - Identità ed equazioni Prof. erasmo@galois.it A.A. 2009/2010 1 Generalità sulle equazioni Si consideri un uguaglianza tra due espressioni algebriche A = B Se si sostituiscono al
Sistemi di equazioni lineari
 Sistemi di equazioni lineari Siano X 1,, X n indeterminate Un equazione lineare (o di primo grado) nelle incognite X 1,, X n a coefficienti nel campo K è della forma a 1 X 1 + + a n X n = b, a i, b K,
Sistemi di equazioni lineari Siano X 1,, X n indeterminate Un equazione lineare (o di primo grado) nelle incognite X 1,, X n a coefficienti nel campo K è della forma a 1 X 1 + + a n X n = b, a i, b K,
Applicazioni eliminazione di Gauss
 Applicazioni eliminazione di Gauss. Premessa Nel seguito supporremo sempre di applicare il metodo di eliminazione di Gauss allo scopo di trasformare la matrice del sistema Ax = b in una matrice triangolare
Applicazioni eliminazione di Gauss. Premessa Nel seguito supporremo sempre di applicare il metodo di eliminazione di Gauss allo scopo di trasformare la matrice del sistema Ax = b in una matrice triangolare
I sistemi lineari di n equazioni in n incognite
 I sistemi lineari I sistemi lineari di n equazioni in n incognite I sistemi lineari di n equazioni in n incognite, sono formati da equazioni di primo grado, in cui le incognite hanno tutte esponente uguale
I sistemi lineari I sistemi lineari di n equazioni in n incognite I sistemi lineari di n equazioni in n incognite, sono formati da equazioni di primo grado, in cui le incognite hanno tutte esponente uguale
Pagine di Algebra lineare. di premessa al testo Pagine di Geometria di Sara Dragotti. Parte terza: SISTEMI LINEARI
 Pagine di Algebra lineare di premessa al testo Pagine di Geometria di Sara Dragotti Parte terza: SISTEMI LINEARI 1. Definizioni Dato un campo K ed m 1 polinomi su K in n indeterminate di grado non superiore
Pagine di Algebra lineare di premessa al testo Pagine di Geometria di Sara Dragotti Parte terza: SISTEMI LINEARI 1. Definizioni Dato un campo K ed m 1 polinomi su K in n indeterminate di grado non superiore
12 - Sistemi di Equazioni Lineari
 Università degli Studi di Palermo Facoltà di Economia Dipartimento SEAS Appunti del corso di Matematica - Sistemi di Equazioni Lineari Anno Accademico 5/6 D. Provenzano, M. Tumminello, V. Lacagnina e A.
Università degli Studi di Palermo Facoltà di Economia Dipartimento SEAS Appunti del corso di Matematica - Sistemi di Equazioni Lineari Anno Accademico 5/6 D. Provenzano, M. Tumminello, V. Lacagnina e A.
Dipendenza e indipendenza lineare
 Dipendenza e indipendenza lineare Luciano Battaia Questi appunti () ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia campus
Dipendenza e indipendenza lineare Luciano Battaia Questi appunti () ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia campus
CENNI SUL CONCETTO DI FUNZIONE
 CENNI SUL CONCETTO DI FUNZIONE Dati due insiemi A e B, una funzione f è una relazione tra gli elementi dell insieme A e gli elementi dell insieme B tale che ad ogni elemento di A corrisponde uno ed un
CENNI SUL CONCETTO DI FUNZIONE Dati due insiemi A e B, una funzione f è una relazione tra gli elementi dell insieme A e gli elementi dell insieme B tale che ad ogni elemento di A corrisponde uno ed un
A =, c d. d = ad cb. c d A =
 Geometria e Algebra (II), 271112 1 Definizione D ora innanzi, al posto di dire matrice quadrata di tipo n n o matrice quadrata n n diremo matrice quadrata di ordine n o in breve matrice di ordine n Il
Geometria e Algebra (II), 271112 1 Definizione D ora innanzi, al posto di dire matrice quadrata di tipo n n o matrice quadrata n n diremo matrice quadrata di ordine n o in breve matrice di ordine n Il
a + 2b + c 3d = 0, a + c d = 0 c d
 SPAZI VETTORIALI 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x,
SPAZI VETTORIALI 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x,
y + P(x) y + Q(x) y = 0 y(x) = c 1y 1(x) + c 2 y 2(x).
 Proposizione 4. Se y 1(x) e y (x) sono soluzioni linearmente indipendenti di y + P(x) y + Q(x) y = 0 ogni altra soluzione della stessa equazione si scrive nella forma per una scelta opportuna delle costanti
Proposizione 4. Se y 1(x) e y (x) sono soluzioni linearmente indipendenti di y + P(x) y + Q(x) y = 0 ogni altra soluzione della stessa equazione si scrive nella forma per una scelta opportuna delle costanti
Rette e piani in R 3
 Rette e piani in R 3 In questa dispensa vogliamo introdurre in modo elementare rette e piani nello spazio R 3 (si faccia riferimento anche al testo Algebra Lineare di S. Lang). 1 Rette in R 3 Vogliamo
Rette e piani in R 3 In questa dispensa vogliamo introdurre in modo elementare rette e piani nello spazio R 3 (si faccia riferimento anche al testo Algebra Lineare di S. Lang). 1 Rette in R 3 Vogliamo
21 - Sistemi di Equazioni Lineari
 Università degli Studi di Palermo Facoltà di Economia Dipartimento di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica - Sistemi di Equazioni Lineari Anno Accademico 5/6 M. Tumminello,
Università degli Studi di Palermo Facoltà di Economia Dipartimento di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica - Sistemi di Equazioni Lineari Anno Accademico 5/6 M. Tumminello,
Equazioni di primo grado ad un incognita
 Equazioni di primo grado ad un incognita Identità Si dice IDENTITÀ un uguaglianza fra due espressioni letterali che è verificata per ogni valore attribuito alle lettere. è un identità. Verificare un identità
Equazioni di primo grado ad un incognita Identità Si dice IDENTITÀ un uguaglianza fra due espressioni letterali che è verificata per ogni valore attribuito alle lettere. è un identità. Verificare un identità
Sistemi di equazioni
 Sistemi di equazioni 19 191 Equazione lineare in due incognite Definizione 191 Una equazione di primo grado (in n incognite) si chiama equazione lineare Problema 191 Determinare due numeri naturali la
Sistemi di equazioni 19 191 Equazione lineare in due incognite Definizione 191 Una equazione di primo grado (in n incognite) si chiama equazione lineare Problema 191 Determinare due numeri naturali la
ESERCIZI PROPOSTI. det A = = per cui il sistema si può risolvere applicando le formule di Cramer, cioè: dove: = =
 ESERCIZI PROPOSTI Risolvere i seguenti sistemi lineari )-0), utilizzando, dove possibile, sia il metodo di Cramer sia quello della matrice inversa, dopo aver analizzato gli esempi a)-d): 2x + + 4z 5 a)
ESERCIZI PROPOSTI Risolvere i seguenti sistemi lineari )-0), utilizzando, dove possibile, sia il metodo di Cramer sia quello della matrice inversa, dopo aver analizzato gli esempi a)-d): 2x + + 4z 5 a)
Soluzioni. Foglio 1. Rette e piani. n x + c = 0. (1)
 Soluzioni Foglio 1. Rette e piani. Esercizio 1. Se n è la normale al piano, sia c = n x 0. Dimostriamo prima che se x π, allora x soddisfa Si ha Sostituendo dentro (1) si ottiene n x + c = 0. (1) x = x
Soluzioni Foglio 1. Rette e piani. Esercizio 1. Se n è la normale al piano, sia c = n x 0. Dimostriamo prima che se x π, allora x soddisfa Si ha Sostituendo dentro (1) si ottiene n x + c = 0. (1) x = x
I sistemi di primo grado
 MATEMATICAperTUTTI 1 ESERCIZIO SVOLTO Un equazione che ha due incognite, x e y, salvo casi particolari, ha sempre infinite soluzioni rappresentate da tutte le coppie ðx, yþ che la soddisfano. Se di equazioni
MATEMATICAperTUTTI 1 ESERCIZIO SVOLTO Un equazione che ha due incognite, x e y, salvo casi particolari, ha sempre infinite soluzioni rappresentate da tutte le coppie ðx, yþ che la soddisfano. Se di equazioni
r 2 r 2 2r 1 r 4 r 4 r 1
 SPAZI R n 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x, y, z)
SPAZI R n 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x, y, z)
Esercitazione 6 - Soluzione
 Anno Accademico 28-29 Corso di Algebra Lineare e Calcolo Numerico per Ingegneria Meccanica Esercitazione 6 - Soluzione Immagine, nucleo. Teorema di Rouché-Capelli. Esercizio Sia L : R 3 R 3 l applicazione
Anno Accademico 28-29 Corso di Algebra Lineare e Calcolo Numerico per Ingegneria Meccanica Esercitazione 6 - Soluzione Immagine, nucleo. Teorema di Rouché-Capelli. Esercizio Sia L : R 3 R 3 l applicazione
Appunti di matematica per le Scienze Sociali Parte 1
 Appunti di matematica per le Scienze Sociali Parte 1 1 Equazioni 1.1 Definizioni preliminari 1.1.1 Monomi Si definisce monomio ogni prodotto indicato di fattori qualsiasi, cioè uguali o diseguali, numerici
Appunti di matematica per le Scienze Sociali Parte 1 1 Equazioni 1.1 Definizioni preliminari 1.1.1 Monomi Si definisce monomio ogni prodotto indicato di fattori qualsiasi, cioè uguali o diseguali, numerici
Argomento 12 Matrici
 Argomento 2 Matrici 2 Vettori di R n eoperazioni I Vettore di R n : x =(x i ) i=n =(x i ) n i=,conx i R componenti di x I R n = spazio dei vettori reali a n componenti = spazio vettoriale reale n-dimensionale
Argomento 2 Matrici 2 Vettori di R n eoperazioni I Vettore di R n : x =(x i ) i=n =(x i ) n i=,conx i R componenti di x I R n = spazio dei vettori reali a n componenti = spazio vettoriale reale n-dimensionale
Matematica II
 Matematica II 29..0. Somma di due matrici. Siano m ed n due interi positivi fissati. Date due matrici A, B R m n di tipo m n, sommando a ciascun elemento di A il corrispondente elemento di B, si ottiene
Matematica II 29..0. Somma di due matrici. Siano m ed n due interi positivi fissati. Date due matrici A, B R m n di tipo m n, sommando a ciascun elemento di A il corrispondente elemento di B, si ottiene
Operazioni tra matrici e n-uple
 CAPITOLO Operazioni tra matrici e n-uple Esercizio.. Date le matrici 0 4 e dati λ = 5, µ =, si calcoli AB, BA, A+B, B A, λa+µb. Esercizio.. Per ognuna delle seguenti coppie di matrici A, B e scalari λ,
CAPITOLO Operazioni tra matrici e n-uple Esercizio.. Date le matrici 0 4 e dati λ = 5, µ =, si calcoli AB, BA, A+B, B A, λa+µb. Esercizio.. Per ognuna delle seguenti coppie di matrici A, B e scalari λ,
0.1 Soluzioni esercitazione IV, del 28/10/2008
 1 0.1 Soluzioni esercitazione IV, del 28/10/2008 Esercizio 0.1.1. Risolvere, usando il teorema di Cramer, i seguenti sistemi lineari 2x + y + z = 0 x + 3z = 1 x y z = 1 kx + y z = 1 x y + 2z = 1 2x + 2y
1 0.1 Soluzioni esercitazione IV, del 28/10/2008 Esercizio 0.1.1. Risolvere, usando il teorema di Cramer, i seguenti sistemi lineari 2x + y + z = 0 x + 3z = 1 x y z = 1 kx + y z = 1 x y + 2z = 1 2x + 2y
ALGEBRA LINEARE PARTE III
 DIEM sez Matematica Finanziaria Università degli studi di Genova Dicembre 200 Indice PREMESSA 2 GENERALITA 2 RAPPRESENTAZIONE DI UN SISTEMA LINEARE IN FORMA MATRI- CIALE 2 3 SOLUZIONE DI SISTEMI LINEARI
DIEM sez Matematica Finanziaria Università degli studi di Genova Dicembre 200 Indice PREMESSA 2 GENERALITA 2 RAPPRESENTAZIONE DI UN SISTEMA LINEARE IN FORMA MATRI- CIALE 2 3 SOLUZIONE DI SISTEMI LINEARI
LEZIONE Equazioni matriciali. Negli Esempi e si sono studiati più sistemi diversi AX 1 = B 1, AX 2 = R m,n, B = (b i,h ) 1 i m
 LEZIONE 4 41 Equazioni matriciali Negli Esempi 336 e 337 si sono studiati più sistemi diversi AX 1 = B 1, AX 2 = B 2,, AX p = B p aventi la stessa matrice incompleta A Tale tipo di problema si presenta
LEZIONE 4 41 Equazioni matriciali Negli Esempi 336 e 337 si sono studiati più sistemi diversi AX 1 = B 1, AX 2 = B 2,, AX p = B p aventi la stessa matrice incompleta A Tale tipo di problema si presenta
Argomento 13 Sistemi lineari
 Sistemi lineari: definizioni Argomento 3 Sistemi lineari I Un equazione nelle n incognite x,,x n della forma c x + + c n x n = b ove c,,c n sono numeri reali (detti coefficienti) eb è un numero reale (detto
Sistemi lineari: definizioni Argomento 3 Sistemi lineari I Un equazione nelle n incognite x,,x n della forma c x + + c n x n = b ove c,,c n sono numeri reali (detti coefficienti) eb è un numero reale (detto
