CHIMICA ORGANICA: IBRIDAZIONE & RISONANZA IBRIDIZZAZIONE. un atomo compie all atto di formazione di un composto al fine di formare un maggior
|
|
|
- Valentina Dolce
- 8 anni fa
- Visualizzazioni
Transcript
1 CHIMICA ORGANICA: IBRIDAZIONE & RISONANZA IBRIDIZZAZIONE L ibridizzazione o ibridazione è una ricombinazione dei propri orbitali atomici che un atomo compie all atto di formazione di un composto al fine di formare un maggior numero di legami covalenti e una distribuzione più simmetrica della densità elettronica e, quindi, una maggiore stabilità nel composto finale. Quando si verifica il fenomeno dell ibridizzazione orbitali di tipo diverso ma con contenuto di energia dello stesso ordine di grandezza, mescolano la loro densità di carica, che poi si ridistribuisce formando un ugual numero di nuovi orbitali detti "ibridi" che sono isoenergetici e di uguale forma. Questi addensamenti di carica, maggiormente localizzati, consentono maggiori ricoperture e gli orbitali ibridi formano, quindi, legami più forti che non gli orbitali semplici da cui provengono. Il processo di ibridazione comporta una certa spesa di energia, largamente compensata però dalla stabilità dei legami che è possibile costruire con gli ibridi: è un vero e proprio investimento energetico! 1
2 Gli orbitali ibridi prendono il nome dagli orbitali atomici usati; ogni combinazione ha una sua conformazione geometrica, generalmente con gli orbitali ibridi alla massima distanza angolare tra loro (per ridurre l'energia di repulsione). Ibridazione sp. Lineare: Esempi: CO 2, BeCl 2. Ibridazione sp 2. Trigonale planare: Esempi: BF 3, SO 2, CO 3, CH 2 CH 2. Ibridazione sp 3. Tetraedrica: 2
3 Esempi: CH 4, NH 3, H 2 O. Ibridazione sp 2 d, sp 3 d ed sp 3 d 2. Quadrata planare, bipiramide trigonale e ottaetrica, rispettivamente. Questi tre tipi di ibridazioni giustificano la cosiddetta espansione dell'ottetto. Esempi: PdCl 4, Ni(CN) 4 PCl 5, CuCl 5 3 Ni(NH 3 ) 6 ++, IF 5, SF 6 3
4 Combinazione Ibridazione degli orbitali atomici sp (s + p) / 2 Conformazione Lineare esempi CO 2, BeCl 2 Trigonale sp 2 (s + p x + p y ) / 3 BF 3, SO 2, CO 3, CH 2 CH 2 Tetraedrica sp 3 (s + p x + p y + p z ) / 4 CH 4, NH 3, H 2 O dsp 2 (s + d x2 y2 + p x + p y ) / 4 planare quadrata PdCl 4, Ni(CN) 4 trigonale bipiramidale 3 PCl 5, CuCl 5 dsp 3 (s + d 2 z + p x + p y + p z ) / 5 (s + d x2 y2 + p x + p y + p z ) / 5 Rara quadrata piramidale Ottaedrica d 2 sp 3 (s + d x2 y2 + d z2 + p x + p y + p z ) / 6 Ni(NH 3 ) ++ 6, IF 5, SF 6 4
5 MESOMERIA O RISONANZA La risonanza è un concetto quantomeccanico introdotto da Pauling per descrivere lo stato di un legame di una molecola, altrimenti non descrivibile con una normale formula di struttura. ossia La risonanza è un fenomeno di delocalizzazione elettronica per cui per un composto non è possibile scrivere un unica formula di struttura che la descriva completamente. quindi Si definisce ibrido di risonanza una molecola (o uno ione molecolare) per la quale non è possibile scrivere un unica formula di struttura che la descriva completamente, ma si scrivono più formule elettroniche (strutture limite o canoniche) che differiscono tra loro solo per la distribuzione degli elettroni π. Ognuna di esse contribuisce alla situazione reale in base alla sua probabilità di esistenza e perciò alla sua energia; maggiore è il numero di strutture limite (soprattutto se equivalenti) più è stabile l ibrido. Esaminando ad esempio la formula dello ione nitrato NO 3 osserviamo che in esso sono presenti due legami singoli e un doppio legame, per cui si potrebbe dedurre una non equivalenza della lunghezza e della energia di legame dato che i legami multipli hanno una lunghezza di legame minore e una energia di legame maggiore dei legami 5
6 semplici. I dati sperimentali però rivelano che tutti i legami N O sono identici. Si deve quindi ammettere che il doppietto elettronico del legame π sia delocalizzato, cioè mobile su tutti i legami N O; anche la carica negativa non è localizzata su un determinato atomo di ossigeno ma è portata dallo ione nel suo complesso. La situazione più aderente alla realtà e quindi quella di rappresentare la formula dello ione NO 3 con tre formule di struttura, che differiscano per la posizione del doppio legame collegate con una freccia a due punte per indicare che la vera struttura è un intermedio tra le tre strutture limite; lo ione è quindi un ibrido di risonanza. il benzene (C 6 H 6 ), è un ibrido di risonanza, cioè può ssere descritto da due formule di risonanza: = in pratica il benzene non è un cicloesantriene, ovvero un ciclo esano con tre doppi legami; le evidenze sperimentali ci dicono che: 1) i legami nel benzene sono tutti della stessa distanza intermedia fra quella di un singolo legame e quella di un doppio legame 2) 2) il benzene non presenta la reattività tipica degli alcheni (che danno reazioni di addizione elettrofila), ma risulta molto più stabile (meno reattivo, infatti viene usato spesso come solvente) 3) il benzene non dà reazioni di addizione poiché queste lo trasformerebbero in un prodotto meno stabile, distruggendo il sistema aromatico dell'anello. Per questo motivo, il benzene tende a dare piuttosto reazioni di sostituzione. 6
7 IL CARBONIO: Il carbonio (C) appartiene al II periodo e al IV gruppo, quindi ha configurazione elettronica 1s 2 2s 2 2p 2 con elettronegatività pari a 2,5. La disposizione elettronica del C allo stato fondamentale comporta il totale riempimento del primo livello energetico, del sottolivello (2s) ed il parziale riempimento del sottolivello (2p) poiché soltanto gli orbitali (2px) e (2py) contengono un elettrone ciascuno, mentre l orbitale (2pz) risulta vuoto. Si possono avere tre tipi di ibridazione: sp 3, sp 2 ed sp: Ibridazione sp 3 L atomo di carbonio ibridato sp 3 è costituito da quattro orbitali ibridi energeticamente equivalenti tra loro ed orientati verso i quattro vertici di un ipotetico tetraedro regolare, nel quale il nucleo dell atomo si trova al centro. Gli angoli di legame che si formano tra i quattro siti di legame sono di 109,5 ciascuno. Nell atomo di carbonio ibrido sp 3 si verificano per ¼ (25%) le caratteristiche dell orbitale s e per ¾ quelle dell orbitale p. Se immaginiamo che due atomi di carbonio ibridato sp 3 sono molto vicini in modo tale che due orbitali ibridi si sovrappongono per formare un nuovo 7
8 orbitale molecolare, con la formazione di un legame covalente stabile di tipo σ. I rimanenti tre orbitali ibridi possono formare dei legami covalenti con altri atomi di carbonio o anche con altri atomi diversi. Questo stato di ibridazione è tipico in una classe di composti organici di fondamentale importanza, che prendono il nome di alcani. Ibridazione sp 2 L atomo di carbonio ibridato sp 2 è costituito da tre orbitali ibridi energeticamente equivalenti tra di loro e complanari, inoltre essi formano angoli di legame di 120 ciascuno, orientati verso i tre vertici di un ipotetico triangolo. Oltre ai tre orbitali ibridi, il carbonio ibridato sp 2 presenta anche un orbitale non ibrido 2p. nell ibrido sp 2 ritroviamo per 1/3 (33%) le caratteristiche di s e per 2/3 le caratteristiche di p. Se immaginiamo che due atomi di carbonio ibridato sp 2 sono molto vicini in modo tale che due orbitali ibridi si sovrappongono, si forma un orbitale molecolare attraverso un legame di tipo σ e, tra i due orbitali p rimasti non ibridi, si forma un legame di tipo π. Tra due atomi di carbonio sp 2 si stabiliscono, quindi, due legami diversi, uno, il legame σ, abbastanza forte, mentre l altro, il legame π, più debole. 8
9 Il doppio legame presenta, per questo motivo, una forza maggiore rispetto al legame singolo tipico dell atomo di carbonio ibridato sp 3 e questo significa che i due nuclei legati insieme da un doppio legame si presentano più vicini rispetto a due nuclei legati da un legame singolo. Questo tipo di ibridazione è tipica di una classe di composti affine agli alcani, la classe degli alcheni. Ibridazione sp L atomo di carbonio ibridato sp presenta due orbitali ibridi energeticamente equivalenti tra di loro e lineari, cioè situati su una retta passante per il nucleo, con gli angoli di legame di 180 ciascuno, e due orbitali non ibridi p situati perpendicolarmente ai due orbitali ibridi. Nell ibridazione sp si verificano per ½ le caratteristiche di s e per altrettanto ½ (50%) le caratteristiche di p. Se immaginiamo che due atomi di carbonio ibridati sp sono molto vicini da poter sovrapporre due orbitali ibridi, si ha la formazione di un nuovo orbitale molecolare con la formazione di un legame di tipo σ e la formazione, tra gli orbitali non ibridi p, di due legami di tipo π. Si stabiliscono, pertanto, tra i due atomi di carbonio tre legami, un σ (forte) e due π (deboli). 9
10 Il tipo di ibridazione appena descritto lo possiamo trovare nella classe degli alchini. TIPI DI LEGAME CARBONIO-CARBONIO: - legame semplice: : è un legame di tipo sigma (σ), cioè ammette libera rotazione degli atomi legati l uno rispetto all altro. - legame doppio: : è caratterizzato dalla presenza di un legame sigma e uno p-greco (π), che non ammette libera rotazione - legame triplo: è costituito da un legame di tipo sigma e due di tipo p-greco. tipo di ibridazione sp numero e tipo di orbitali coinvolti 2s + 1 orbitale 2p numero di atomi legati 2 tipo di legami tra gli atomi 1 1 singolo + 1 triplo angoli di legame entipo di disposizione nello spazio 180 lineare esempi H-C C-H acetilene sp 2 2s + 2 orbitali 2p sp 3 2s + 3 orbitali 2p 3 2 singoli + 1 doppio 4 4 singoli 120 planare 109,5 tridimensionale (tetraedrica) etilene metano 1 Legame singolo = σ,, legame doppio = σ + π, legame triplo = σ + 2π 10
VSEPR Polarità Ibridizzazione
 VSEPR Polarità Ibridizzazione VSEPR VSEPR = Valance-Shell electron-pair repulsion Principio fondamentale: ciascun gruppo di elettroni di valenza attorno ad un atomo centrale è situato il più lontano possibile
VSEPR Polarità Ibridizzazione VSEPR VSEPR = Valance-Shell electron-pair repulsion Principio fondamentale: ciascun gruppo di elettroni di valenza attorno ad un atomo centrale è situato il più lontano possibile
Poniamo il carbonio al centro, tre idrogeni sono legati al carbonio direttamente e uno attraverso l ossigeno
 Strutture di Lewis E un metodo semplice per ottenere le formule di struttura di composti covalenti nota la formula molecolare, la configurazione elettronica del livello di valenza degli atomi e la connettività
Strutture di Lewis E un metodo semplice per ottenere le formule di struttura di composti covalenti nota la formula molecolare, la configurazione elettronica del livello di valenza degli atomi e la connettività
Dalla Chimica Generale
 RISNANZA RISNANZA Vi sono molecole le cui proprietà non sono ben spiegate da una singola struttura di Lewis che tenga conto cioé delle proprietà osservate (contenuto energetico, lunghezza dei legami, comportamento
RISNANZA RISNANZA Vi sono molecole le cui proprietà non sono ben spiegate da una singola struttura di Lewis che tenga conto cioé delle proprietà osservate (contenuto energetico, lunghezza dei legami, comportamento
Formule di Struttura delle Molecole Organiche
 Formule di Struttura delle Molecole Organiche Costituzione L ordine in cui gli atomi di una molecola sono connessi è chiamata costituzione o connettività. La costituzione di una molecola deve essere determinata
Formule di Struttura delle Molecole Organiche Costituzione L ordine in cui gli atomi di una molecola sono connessi è chiamata costituzione o connettività. La costituzione di una molecola deve essere determinata
GEOMETRIA MOLECOLARE
 GEOMETRIA MOLECOLARE Le molecole hanno geometrie spaziali ben definite caratterizzate da distanze di legame ed angoli di legame. Questi possono essere determinati sperimentalmente (es. raggi X). Si vede
GEOMETRIA MOLECOLARE Le molecole hanno geometrie spaziali ben definite caratterizzate da distanze di legame ed angoli di legame. Questi possono essere determinati sperimentalmente (es. raggi X). Si vede
REAZIONI ORGANICHE Variazioni di energia e velocità di reazione
 REAZIONI ORGANICHE Variazioni di energia e velocità di reazione Abbiamo visto che i composti organici e le loro reazioni possono essere suddivisi in categorie omogenee. Per ottenere la massima razionalizzazione
REAZIONI ORGANICHE Variazioni di energia e velocità di reazione Abbiamo visto che i composti organici e le loro reazioni possono essere suddivisi in categorie omogenee. Per ottenere la massima razionalizzazione
Organic Chemistry. 4 th Edition Paula Yurkanis Bruice. Delocalizzazione degli elettroni e risonanza
 Organic Chemistry 4 th Edition Paula Yurkanis Bruice Delocalizzazione degli elettroni e risonanza 1 Elettroni Localizzati contro elettroni delocalizzati localized electrons localized electrons delocalized
Organic Chemistry 4 th Edition Paula Yurkanis Bruice Delocalizzazione degli elettroni e risonanza 1 Elettroni Localizzati contro elettroni delocalizzati localized electrons localized electrons delocalized
LA MOLE : UN UNITA DI MISURA FONDAMENTALE PER LA CHIMICA
 LA MOLE : UN UNITA DI MISURA FONDAMENTALE PER LA CHIMICA Poiché è impossibile contare o pesare gli atomi o le molecole che formano una qualsiasi sostanza chimica, si ricorre alla grandezza detta quantità
LA MOLE : UN UNITA DI MISURA FONDAMENTALE PER LA CHIMICA Poiché è impossibile contare o pesare gli atomi o le molecole che formano una qualsiasi sostanza chimica, si ricorre alla grandezza detta quantità
Le proprietà periodiche degli elementi LA LEZIONE
 Le proprietà periodiche degli elementi LA LEZIONE Le proprietà degli elementi mostrano delle tendenze che possono essere predette usando il sistema periodico ed essere spiegate e comprese analizzando la
Le proprietà periodiche degli elementi LA LEZIONE Le proprietà degli elementi mostrano delle tendenze che possono essere predette usando il sistema periodico ed essere spiegate e comprese analizzando la
1. PRIME PROPRIETÀ 2
 RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
 LEGAME CHIMICO In natura solo i gas nobili si ritrovano allo stato monoatomico. Gli altri atomi tendono a legarsi spontaneamente fra di loro per formare delle MOLECOLE, raggiungendo una condizione di MAGGIORE
LEGAME CHIMICO In natura solo i gas nobili si ritrovano allo stato monoatomico. Gli altri atomi tendono a legarsi spontaneamente fra di loro per formare delle MOLECOLE, raggiungendo una condizione di MAGGIORE
APPUNTI DI MATEMATICA ALGEBRA \ INSIEMISTICA \ TEORIA DEGLI INSIEMI (1)
 ALGEBRA \ INSIEMISTICA \ TEORIA DEGLI INSIEMI (1) Un insieme è una collezione di oggetti. Il concetto di insieme è un concetto primitivo. Deve esistere un criterio chiaro, preciso, non ambiguo, inequivocabile,
ALGEBRA \ INSIEMISTICA \ TEORIA DEGLI INSIEMI (1) Un insieme è una collezione di oggetti. Il concetto di insieme è un concetto primitivo. Deve esistere un criterio chiaro, preciso, non ambiguo, inequivocabile,
IDROCARBURI AROMATICI
 IDROCARBURI AROMATICI Idrocarburi ciclici contenenti un sistema di elettroni delocalizzati su tutto il perimetro dell anello BENZENE C 6 H 6 sp 2 angoli 120 coplanarità struttura simmetrica ad esagono
IDROCARBURI AROMATICI Idrocarburi ciclici contenenti un sistema di elettroni delocalizzati su tutto il perimetro dell anello BENZENE C 6 H 6 sp 2 angoli 120 coplanarità struttura simmetrica ad esagono
Corrispondenze e funzioni
 Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
Il magnetismo nella materia
 Le orbite degli elettroni in atomo di idrogeno Forma spaziale degli Orbitali elettronici di atomo di idrogeno Un solido Il magnetismo nella materia ferrimagnetismo Dr. Daniele Di Gioacchino Istituto Nazionale
Le orbite degli elettroni in atomo di idrogeno Forma spaziale degli Orbitali elettronici di atomo di idrogeno Un solido Il magnetismo nella materia ferrimagnetismo Dr. Daniele Di Gioacchino Istituto Nazionale
isomeria di struttura isomeria di posizione isomeria di catena stereoisomeria isomeria di conformazione isomeria di configurazione 'isomeria ottica
 ISOMERIA L'isomeria di struttura è connessa al diverso modo in cui gli atomi di due o più composti si legano tra loro in sequenza. Ci sono due forme: isomeria di posizione e isomeria di catena. La stereoisomeria
ISOMERIA L'isomeria di struttura è connessa al diverso modo in cui gli atomi di due o più composti si legano tra loro in sequenza. Ci sono due forme: isomeria di posizione e isomeria di catena. La stereoisomeria
Energia nelle reazioni chimiche. Lezioni d'autore di Giorgio Benedetti
 Energia nelle reazioni chimiche Lezioni d'autore di Giorgio Benedetti VIDEO Introduzione (I) L energia chimica è dovuta al particolare arrangiamento degli atomi nei composti chimici e le varie forme di
Energia nelle reazioni chimiche Lezioni d'autore di Giorgio Benedetti VIDEO Introduzione (I) L energia chimica è dovuta al particolare arrangiamento degli atomi nei composti chimici e le varie forme di
Forza. Forza. Esempi di forze. Caratteristiche della forza. Forze fondamentali CONCETTO DI FORZA E EQUILIBRIO, PRINCIPI DELLA DINAMICA
 Forza CONCETTO DI FORZA E EQUILIBRIO, PRINCIPI DELLA DINAMICA Cos è una forza? la forza è una grandezza che agisce su un corpo cambiando la sua velocità e provocando una deformazione sul corpo 2 Esempi
Forza CONCETTO DI FORZA E EQUILIBRIO, PRINCIPI DELLA DINAMICA Cos è una forza? la forza è una grandezza che agisce su un corpo cambiando la sua velocità e provocando una deformazione sul corpo 2 Esempi
La teoria del legame di valenza
 La teoria del legame di valenza La teoria di Lewis (postulata prima dell'avvento della meccanica quantistica) considera gli elettroni di valenza degli atomi che formano legami, ma prescinde totalmente
La teoria del legame di valenza La teoria di Lewis (postulata prima dell'avvento della meccanica quantistica) considera gli elettroni di valenza degli atomi che formano legami, ma prescinde totalmente
Teoria del campo cristallino (CFT)
 Teoria del campo cristallino (CFT) Interazione elettrostatica (non covalente) tra: - leganti anionici cariche elettriche puntiformi - leganti neutri dipoli elettrici con la parte negativa verso il centro
Teoria del campo cristallino (CFT) Interazione elettrostatica (non covalente) tra: - leganti anionici cariche elettriche puntiformi - leganti neutri dipoli elettrici con la parte negativa verso il centro
IDROCARBURI AROMATICI. Scaricato da Sunhope.it
 IDROCARBURI AROMATICI BENZENE E il capostipite degli idrocarburi aromatici. Osservazioni sperimentali: Formula bruta C 6 6 elevato grado di insaturazione (4) I 6 atomi di C sono legati a formare un anello
IDROCARBURI AROMATICI BENZENE E il capostipite degli idrocarburi aromatici. Osservazioni sperimentali: Formula bruta C 6 6 elevato grado di insaturazione (4) I 6 atomi di C sono legati a formare un anello
LA RETTA. Retta per l'origine, rette orizzontali e verticali
 Retta per l'origine, rette orizzontali e verticali LA RETTA Abbiamo visto che l'equazione generica di una retta è del tipo Y = mx + q, dove m ne rappresenta la pendenza e q il punto in cui la retta incrocia
Retta per l'origine, rette orizzontali e verticali LA RETTA Abbiamo visto che l'equazione generica di una retta è del tipo Y = mx + q, dove m ne rappresenta la pendenza e q il punto in cui la retta incrocia
Esempi di funzione. Scheda Tre
 Scheda Tre Funzioni Consideriamo una legge f che associa ad un elemento di un insieme X al più un elemento di un insieme Y; diciamo che f è una funzione, X è l insieme di partenza e X l insieme di arrivo.
Scheda Tre Funzioni Consideriamo una legge f che associa ad un elemento di un insieme X al più un elemento di un insieme Y; diciamo che f è una funzione, X è l insieme di partenza e X l insieme di arrivo.
Trasformazioni materia
 REAZIONI CHIMICHE Trasformazioni materia Trasformazioni fisiche (reversibili) Trasformazioni chimiche (irreversibili) È una trasformazione che non produce nuove sostanze È una trasformazione che produce
REAZIONI CHIMICHE Trasformazioni materia Trasformazioni fisiche (reversibili) Trasformazioni chimiche (irreversibili) È una trasformazione che non produce nuove sostanze È una trasformazione che produce
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Forme molecolari - Teoria VSEPR Teoria della repulsione dei doppietti elettronici di valenza
 Lezione 8 1. Teoria VSEPR 2. Il legame chimico 3. Legame covalente - Valence Bond 4. Legami e 5. Sovrapposizione di orbitali atomici 6. Intro IBRIDAZIONE Forme molecolari - Teoria VSEPR Teoria della repulsione
Lezione 8 1. Teoria VSEPR 2. Il legame chimico 3. Legame covalente - Valence Bond 4. Legami e 5. Sovrapposizione di orbitali atomici 6. Intro IBRIDAZIONE Forme molecolari - Teoria VSEPR Teoria della repulsione
MODELLI ATOMICI. Modello Atomico di Dalton
 MODELLI ATOMICI Gli atomi sono i piccoli mattoni che compongono la materia. Circa 2500 anni fa, il filosofo DEMOCRITO credeva che tutta la materia fosse costituita da piccole particelle che chiamò atomi.
MODELLI ATOMICI Gli atomi sono i piccoli mattoni che compongono la materia. Circa 2500 anni fa, il filosofo DEMOCRITO credeva che tutta la materia fosse costituita da piccole particelle che chiamò atomi.
I NUMERI DECIMALI. che cosa sono, come si rappresentano
 I NUMERI DECIMALI che cosa sono, come si rappresentano NUMERI NATURALI per contare bastano i numeri naturali N i numeri naturali cominciano con il numero uno e vanno avanti con la regola del +1 fino all
I NUMERI DECIMALI che cosa sono, come si rappresentano NUMERI NATURALI per contare bastano i numeri naturali N i numeri naturali cominciano con il numero uno e vanno avanti con la regola del +1 fino all
Le Biomolecole I parte. Lezioni d'autore di Giorgio Benedetti
 Le Biomolecole I parte Lezioni d'autore di Giorgio Benedetti LE BIOMOLECOLE Le biomolecole, presenti in tutti gli esseri viventi, sono molecole composte principalmente da carbonio, idrogeno, azoto e ossigeno.
Le Biomolecole I parte Lezioni d'autore di Giorgio Benedetti LE BIOMOLECOLE Le biomolecole, presenti in tutti gli esseri viventi, sono molecole composte principalmente da carbonio, idrogeno, azoto e ossigeno.
EMISSIONE E ASSORBIMENTO DI LUCE DA PARTE DELLA MATERIA
 EMISSIONE E ASSORBIMENTO DI LUCE DA PARTE DELLA MATERIA Poiché la luce è energia trasportata da oscillazioni del campo elettrico (fotoni) e la materia è fatta di particelle elettricamente cariche (atomi
EMISSIONE E ASSORBIMENTO DI LUCE DA PARTE DELLA MATERIA Poiché la luce è energia trasportata da oscillazioni del campo elettrico (fotoni) e la materia è fatta di particelle elettricamente cariche (atomi
15 febbraio 2010 - Soluzione esame di geometria - 12 crediti Ingegneria gestionale - a.a. 2009-2010 COGNOME... NOME... N. MATRICOLA...
 15 febbraio 010 - Soluzione esame di geometria - 1 crediti Ingegneria gestionale - a.a. 009-010 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura
15 febbraio 010 - Soluzione esame di geometria - 1 crediti Ingegneria gestionale - a.a. 009-010 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura
Processo di rendering
 Processo di rendering Trasformazioni di vista Trasformazioni di vista Il processo di visione in tre dimensioni Le trasformazioni di proiezione 2 Rendering nello spazio 2D Il processo di rendering (visualizzazione)
Processo di rendering Trasformazioni di vista Trasformazioni di vista Il processo di visione in tre dimensioni Le trasformazioni di proiezione 2 Rendering nello spazio 2D Il processo di rendering (visualizzazione)
GEOMETRIA DELLE MASSE
 1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
Gli orbitali: modello atomico probabilistico
 1 Approfondimento 2.1 Gli orbitali: modello atomico probabilistico Modello atomico planetario (o a gusci): gli elettroni ruotano intorno al nucleo percorrendo orbite prefissate. Il modello atomico planetario
1 Approfondimento 2.1 Gli orbitali: modello atomico probabilistico Modello atomico planetario (o a gusci): gli elettroni ruotano intorno al nucleo percorrendo orbite prefissate. Il modello atomico planetario
L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare
 L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare Cap.4 giroscopio, magnetismo e forza di Lorentz teoria del giroscopio Abbiamo finora preso in considerazione le condizionidi equilibrio
L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare Cap.4 giroscopio, magnetismo e forza di Lorentz teoria del giroscopio Abbiamo finora preso in considerazione le condizionidi equilibrio
Consideriamo due polinomi
 Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Com è fatto l atomo ATOMO. UNA VOLTA si pensava che l atomo fosse indivisibile. OGGI si pensa che l atomo è costituito da tre particelle
 STRUTTURA ATOMO Com è fatto l atomo ATOMO UNA VOLTA si pensava che l atomo fosse indivisibile OGGI si pensa che l atomo è costituito da tre particelle PROTONI particelle con carica elettrica positiva e
STRUTTURA ATOMO Com è fatto l atomo ATOMO UNA VOLTA si pensava che l atomo fosse indivisibile OGGI si pensa che l atomo è costituito da tre particelle PROTONI particelle con carica elettrica positiva e
IBRIDAZIONE e GEOMETRIA MOLECOLARE
 IBRIDAZIONE e GEOMETRIA MOLECOLARE Esempio: struttura della molecola del metano CH 4 1s 2s 2p Configurazione elettronica del C Per esempio il carbonio può utilizzare la configurazione in cui un elettrone
IBRIDAZIONE e GEOMETRIA MOLECOLARE Esempio: struttura della molecola del metano CH 4 1s 2s 2p Configurazione elettronica del C Per esempio il carbonio può utilizzare la configurazione in cui un elettrone
Il bilanciamento delle reazioni chimiche
 1 Il bilanciamento delle reazioni chimiche Avete visto che gli atomi hanno diversi modi di unirsi l uno all altro. Si può anche iniziare a capire che una reazione chimica non è nient altro che un cambiamento
1 Il bilanciamento delle reazioni chimiche Avete visto che gli atomi hanno diversi modi di unirsi l uno all altro. Si può anche iniziare a capire che una reazione chimica non è nient altro che un cambiamento
Spettrofotometria. Le onde luminose consistono in campi magnetici e campi elettrici oscillanti, fra loro perpendicolari.
 Spettrofotometria. Con questo termine si intende l utilizzo della luce nella misura delle concentrazioni chimiche. Per affrontare questo argomento dovremo conoscere: Natura e proprietà della luce. Cosa
Spettrofotometria. Con questo termine si intende l utilizzo della luce nella misura delle concentrazioni chimiche. Per affrontare questo argomento dovremo conoscere: Natura e proprietà della luce. Cosa
CHIMICA. Una teoria è scientifica solo se è falsificabile (cioè se è possibile sperimentalmente smentire le sue previsioni)
 CHIMICA SCIENZA SPERIMENTALE: cioè si basa sul metodo sperimentale (Galileo è il precursore). Osservazione dei fenomeni (raccolta e interpretazioni dati) Formulazione ipotesi Verifica sperimentale (eventualmente
CHIMICA SCIENZA SPERIMENTALE: cioè si basa sul metodo sperimentale (Galileo è il precursore). Osservazione dei fenomeni (raccolta e interpretazioni dati) Formulazione ipotesi Verifica sperimentale (eventualmente
Il legame chimico II: la geometria molecolare e l ibridizzazione degli orbitali atomici. Capitolo 10
 Il legame chimico II: la geometria molecolare e l ibridizzazione degli orbitali atomici Capitolo 10 Legame tra un derivato del Buckyball e il sito dell HIV-Protease Repulsione delle coppie di elettroni
Il legame chimico II: la geometria molecolare e l ibridizzazione degli orbitali atomici Capitolo 10 Legame tra un derivato del Buckyball e il sito dell HIV-Protease Repulsione delle coppie di elettroni
TRASFORMAZIONI GEOMETRICHE NEL PIANO. Parte 1
 TRASFORMAZIONI GEOMETRICHE NEL PIANO Parte 1 La geometria è la scienza che studia la forma e l estensione dei corpi e le trasformazioni che questi possono subire. In generale per trasformazione geometrica
TRASFORMAZIONI GEOMETRICHE NEL PIANO Parte 1 La geometria è la scienza che studia la forma e l estensione dei corpi e le trasformazioni che questi possono subire. In generale per trasformazione geometrica
APPUNTI DEL CORSO DI SISTEMI IMPIANTISTICI E SICUREZZA INTRODUZIONE AGLI IMPIANTI ELETTRICI: FONDAMENTI DI ELETTROTECNICA
 APPUNTI DEL CORSO DI SISTEMI IMPIANTISTICI E SICUREZZA INTRODUZIONE AGLI IMPIANTI ELETTRICI: FONDAMENTI DI ELETTROTECNICA Concetti e grandezze fondamentali CAMPO ELETTRICO: è un campo vettoriale di forze,
APPUNTI DEL CORSO DI SISTEMI IMPIANTISTICI E SICUREZZA INTRODUZIONE AGLI IMPIANTI ELETTRICI: FONDAMENTI DI ELETTROTECNICA Concetti e grandezze fondamentali CAMPO ELETTRICO: è un campo vettoriale di forze,
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI
 APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
MATEMATICA 2001. p = 4/6 = 2/3; q = 1-2/3 = 1/3. La risposta corretta è quindi la E).
 MATEMATICA 2001 66. Quale fra le seguenti affermazioni è sbagliata? A) Tutte le funzioni ammettono la funzione inversa B) Una funzione dispari è simmetrica rispetto all origine C) Una funzione pari è simmetrica
MATEMATICA 2001 66. Quale fra le seguenti affermazioni è sbagliata? A) Tutte le funzioni ammettono la funzione inversa B) Una funzione dispari è simmetrica rispetto all origine C) Una funzione pari è simmetrica
Gas perfetti e sue variabili
 Gas perfetti e sue variabili Un gas è detto perfetto quando: 1. è lontano dal punto di condensazione, e quindi è molto rarefatto 2. su di esso non agiscono forze esterne 3. gli urti tra le molecole del
Gas perfetti e sue variabili Un gas è detto perfetto quando: 1. è lontano dal punto di condensazione, e quindi è molto rarefatto 2. su di esso non agiscono forze esterne 3. gli urti tra le molecole del
Sommario Ottica geometrica... 2 Principio di Huygens-Fresnel... 4 Oggetto e immagine... 6 Immagine reale... 7 Immagine virtuale...
 IMMAGINI Sommario Ottica geometrica... 2 Principio di Huygens-Fresnel... 4 Oggetto e immagine... 6 Immagine reale... 7 Immagine virtuale... 9 Immagini - 1/11 Ottica geometrica È la branca dell ottica che
IMMAGINI Sommario Ottica geometrica... 2 Principio di Huygens-Fresnel... 4 Oggetto e immagine... 6 Immagine reale... 7 Immagine virtuale... 9 Immagini - 1/11 Ottica geometrica È la branca dell ottica che
PROTEINE. sono COMPOSTI ORGANICI QUATERNARI
 PROTEINE sono COMPOSTI ORGANICI QUATERNARI Unione di elementi chimici diversi Il composto chimico principale è il C (carbonio) Sono quattro gli elementi chimici principali che formano le proteine : C (carbonio),
PROTEINE sono COMPOSTI ORGANICI QUATERNARI Unione di elementi chimici diversi Il composto chimico principale è il C (carbonio) Sono quattro gli elementi chimici principali che formano le proteine : C (carbonio),
GLI STATI DI AGGREGAZIONE DELLA MATERIA. Lo stato gassoso
 GLI STATI DI AGGREGAZIONE DELLA MATERIA Lo stato gassoso Classificazione della materia MATERIA Composizione Struttura Proprietà Trasformazioni 3 STATI DI AGGREGAZIONE SOLIDO (volume e forma propri) LIQUIDO
GLI STATI DI AGGREGAZIONE DELLA MATERIA Lo stato gassoso Classificazione della materia MATERIA Composizione Struttura Proprietà Trasformazioni 3 STATI DI AGGREGAZIONE SOLIDO (volume e forma propri) LIQUIDO
materia atomi miscugli omogenei e eterogenei sostanze elementari composti
 Elementi e Composti materia miscugli omogenei e eterogenei sostanze elementari composti atomi Gli atomi sono, per convenzione, le unità costituenti le sostanze Le sostanze possono essere costituite da
Elementi e Composti materia miscugli omogenei e eterogenei sostanze elementari composti atomi Gli atomi sono, per convenzione, le unità costituenti le sostanze Le sostanze possono essere costituite da
CORRENTE ELETTRICA Intensità e densità di corrente sistema formato da due conduttori carichi a potenziali V 1 e V 2 isolati tra loro V 2 > V 1 V 2
 COENTE ELETTICA Intensità e densità di corrente sistema formato da due conduttori carichi a potenziali V 1 e V isolati tra loro V > V 1 V V 1 Li colleghiamo mediante un conduttore Fase transitoria: sotto
COENTE ELETTICA Intensità e densità di corrente sistema formato da due conduttori carichi a potenziali V 1 e V isolati tra loro V > V 1 V V 1 Li colleghiamo mediante un conduttore Fase transitoria: sotto
La Programmazione Lineare
 4 La Programmazione Lineare 4.1 INTERPRETAZIONE GEOMETRICA DI UN PROBLEMA DI PROGRAMMAZIONE LINEARE Esercizio 4.1.1 Fornire una rappresentazione geometrica e risolvere graficamente i seguenti problemi
4 La Programmazione Lineare 4.1 INTERPRETAZIONE GEOMETRICA DI UN PROBLEMA DI PROGRAMMAZIONE LINEARE Esercizio 4.1.1 Fornire una rappresentazione geometrica e risolvere graficamente i seguenti problemi
CONCETTO DI LIMITE DI UNA FUNZIONE REALE
 CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
RELAZIONI BINARIE. Proprietà delle relazioni Data una relazione R, definita in un insieme non vuoto U, si hanno le seguenti proprietà :
 RELAZIONI INARIE Dati due insiemi non vuoti, A detto dominio e detto codominio, eventualmente coincidenti, si chiama relazione binaria (o corrispondenza) di A in, e si indica con f : A, (oppure R ) una
RELAZIONI INARIE Dati due insiemi non vuoti, A detto dominio e detto codominio, eventualmente coincidenti, si chiama relazione binaria (o corrispondenza) di A in, e si indica con f : A, (oppure R ) una
COMPOSTI DI COORDINAZIONE (complessi)
 Gli ioni dei metalli di transizione nei sistemi biologici non si presentano come acquoioni [M(H 2 O) n ] x+ ma come. COMPOSTI DI COORDINAZIONE (complessi) derivano dall interazione (coordinazione) tra
Gli ioni dei metalli di transizione nei sistemi biologici non si presentano come acquoioni [M(H 2 O) n ] x+ ma come. COMPOSTI DI COORDINAZIONE (complessi) derivano dall interazione (coordinazione) tra
Appunti sulla Macchina di Turing. Macchina di Turing
 Macchina di Turing Una macchina di Turing è costituita dai seguenti elementi (vedi fig. 1): a) una unità di memoria, detta memoria esterna, consistente in un nastro illimitato in entrambi i sensi e suddiviso
Macchina di Turing Una macchina di Turing è costituita dai seguenti elementi (vedi fig. 1): a) una unità di memoria, detta memoria esterna, consistente in un nastro illimitato in entrambi i sensi e suddiviso
13 La temperatura - 8. Il gas perfetto
 La mole e l equazione del gas perfetto Tutto ciò che vediamo intorno a noi è composto di piccolissimi grani, che chiamiamo «molecole». Per esempio, il ghiaccio, l acqua liquida e il vapore acqueo sono
La mole e l equazione del gas perfetto Tutto ciò che vediamo intorno a noi è composto di piccolissimi grani, che chiamiamo «molecole». Per esempio, il ghiaccio, l acqua liquida e il vapore acqueo sono
DEL LEGAME DI VALENZA
 Chimica Silvia LICOCCIA Professore Ordinario di Fondamenti Chimici per le Tecnologie Dipartimento di Scienze e Tecnologie Chimiche Università di Roma Tor Vergata TEORIA DEL LEGAME DI VALENZA Teoria del
Chimica Silvia LICOCCIA Professore Ordinario di Fondamenti Chimici per le Tecnologie Dipartimento di Scienze e Tecnologie Chimiche Università di Roma Tor Vergata TEORIA DEL LEGAME DI VALENZA Teoria del
Serie completa di Modelli Molecolari per la Chimica Organica
 EdiSES Istruzioni per l utilizzo dei modelli molecolari Serie completa di Modelli Molecolari per la Chimica Organica allegati ai seguenti volumi: Chimica Organica - Paula Y. Bruice Elementi di Chimica
EdiSES Istruzioni per l utilizzo dei modelli molecolari Serie completa di Modelli Molecolari per la Chimica Organica allegati ai seguenti volumi: Chimica Organica - Paula Y. Bruice Elementi di Chimica
È importante quindi conoscere le proprietà chimiche dell acqua. Le reazioni acido base sono particolari esempi di equilibrio chimico in fase acquosa
 Premessa Le nozioni di acido e di base non sono concetti assoluti ma sono relativi al mezzo in cui tale sostanze sono sciolte. L acqua è il solvente per eccellenza, scelto per studiare le caratteristiche
Premessa Le nozioni di acido e di base non sono concetti assoluti ma sono relativi al mezzo in cui tale sostanze sono sciolte. L acqua è il solvente per eccellenza, scelto per studiare le caratteristiche
I semiconduttori Semiconduttori intrinseci
 I semiconduttori Semiconduttori intrinseci I semiconduttori naturali usati per la produzione di dispositivi elettronici sono stati per molti anni il silicio e il germanio. Il germanio è andato, con il
I semiconduttori Semiconduttori intrinseci I semiconduttori naturali usati per la produzione di dispositivi elettronici sono stati per molti anni il silicio e il germanio. Il germanio è andato, con il
CALCOLO COMBINATORIO
 CALCOLO COMBINATORIO 1 Modi di formare gruppi di k oggetti presi da n dati 11 disposizioni semplici, permutazioni Dati n oggetti distinti a 1,, a n si chiamano disposizioni semplici di questi oggetti,
CALCOLO COMBINATORIO 1 Modi di formare gruppi di k oggetti presi da n dati 11 disposizioni semplici, permutazioni Dati n oggetti distinti a 1,, a n si chiamano disposizioni semplici di questi oggetti,
I derivati del benzene e la loro chimica
 I derivati del benzene e la loro chimica Benzene: 6 e- π Questi composti sono chiamati aromatici è hanno 4N + 2 e- π in un anello planare (regola di Hückel). La delocalizzazione di questi e- π stabilizza
I derivati del benzene e la loro chimica Benzene: 6 e- π Questi composti sono chiamati aromatici è hanno 4N + 2 e- π in un anello planare (regola di Hückel). La delocalizzazione di questi e- π stabilizza
Lezioni di Matematica 1 - I modulo
 Lezioni di Matematica 1 - I modulo Luciano Battaia 16 ottobre 2008 Luciano Battaia - http://www.batmath.it Matematica 1 - I modulo. Lezione del 16/10/2008 1 / 13 L introduzione dei numeri reali si può
Lezioni di Matematica 1 - I modulo Luciano Battaia 16 ottobre 2008 Luciano Battaia - http://www.batmath.it Matematica 1 - I modulo. Lezione del 16/10/2008 1 / 13 L introduzione dei numeri reali si può
IBRIDAZIONE. MODELLO DELL ORBITALE di LEGAME
 IBRIDAZIONE MODELLO DELL ORBITALE di LEGAME Approccio più semplice per descrivere la struttura elettronica di una specie sfruttando il concetto di orbitale. METANO Gli atomi nel formare legami usano elettroni
IBRIDAZIONE MODELLO DELL ORBITALE di LEGAME Approccio più semplice per descrivere la struttura elettronica di una specie sfruttando il concetto di orbitale. METANO Gli atomi nel formare legami usano elettroni
ELEMENTI DI GEOMETRIA ANALITICA: LA RETTA.
 ELEMENTI DI GEOMETRIA ANALITICA: LA RETTA. Prerequisiti I radicali Risoluzione di sistemi di equazioni di primo e secondo grado. Classificazione e dominio delle funzioni algebriche Obiettivi minimi Saper
ELEMENTI DI GEOMETRIA ANALITICA: LA RETTA. Prerequisiti I radicali Risoluzione di sistemi di equazioni di primo e secondo grado. Classificazione e dominio delle funzioni algebriche Obiettivi minimi Saper
Slide Cerbara parte1 5. Le distribuzioni teoriche
 Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
( x) ( x) 0. Equazioni irrazionali
 Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
Chimica. Ingegneria Meccanica, Elettrica e Civile Simulazione d'esame
 Viene qui riportata la prova scritta di simulazione dell'esame di Chimica (per meccanici, elettrici e civili) proposta agli studenti alla fine di ogni tutoraggio di Chimica. Si allega inoltre un estratto
Viene qui riportata la prova scritta di simulazione dell'esame di Chimica (per meccanici, elettrici e civili) proposta agli studenti alla fine di ogni tutoraggio di Chimica. Si allega inoltre un estratto
5A un multiplo di 3 5B una potenza di 5 5C divisibile per 7 e per 11 5D. D. 6 Le soluzioni dell equazione 1 + 3x 2x 2 = 0 sono 3 ± 17 6D 3 ± 17
 UNIVERSITÀ DEGLI STUDI DI ROMA LA SAPIENZA 0 Settembre 008 Spnz0000 Ingegneria - Scienze Matematiche Fisiche Naturali - Scienze Statistiche Test di Matematica D. Il numero è uguale a A 5 B 5 C D 0 0 D.
UNIVERSITÀ DEGLI STUDI DI ROMA LA SAPIENZA 0 Settembre 008 Spnz0000 Ingegneria - Scienze Matematiche Fisiche Naturali - Scienze Statistiche Test di Matematica D. Il numero è uguale a A 5 B 5 C D 0 0 D.
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I. 2004
 ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
Epoca k Rata Rk Capitale Ck interessi Ik residuo Dk Ek 0 S 0 1 C1 Ik=i*S Dk=S-C1. n 0 S
 L AMMORTAMENTO Gli ammortamenti sono un altra apllicazione delle rendite. Il prestito è un operazione finanziaria caratterizzata da un flusso di cassa positivo (mi prendo i soldi in prestito) seguito da
L AMMORTAMENTO Gli ammortamenti sono un altra apllicazione delle rendite. Il prestito è un operazione finanziaria caratterizzata da un flusso di cassa positivo (mi prendo i soldi in prestito) seguito da
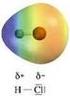
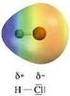
I legami covalenti eteronucleari spostano la carica del legame sull atomo più elettronegativo
 La polarità I legami covalenti eteronucleari spostano la carica del legame sull atomo più elettronegativo L elettronegatività è il parametro di riferimento utilizzato per valutare il trasferimento di carica
La polarità I legami covalenti eteronucleari spostano la carica del legame sull atomo più elettronegativo L elettronegatività è il parametro di riferimento utilizzato per valutare il trasferimento di carica
nei materiali (Inserendo un materiale all interno di un campo magnetico generato da un magnete permanente)
 COMPORTAMENTO MAGNETICO DEI MATERIALI a) nel vuoto B = μ0 H μ0 = 4 π 10-7 H/m b) nei materiali (Inserendo un materiale all interno di un campo magnetico generato da un magnete permanente) Il materiale
COMPORTAMENTO MAGNETICO DEI MATERIALI a) nel vuoto B = μ0 H μ0 = 4 π 10-7 H/m b) nei materiali (Inserendo un materiale all interno di un campo magnetico generato da un magnete permanente) Il materiale
Luigi Piroddi piroddi@elet.polimi.it
 Automazione industriale dispense del corso 10. Reti di Petri: analisi strutturale Luigi Piroddi piroddi@elet.polimi.it Analisi strutturale Un alternativa all analisi esaustiva basata sul grafo di raggiungibilità,
Automazione industriale dispense del corso 10. Reti di Petri: analisi strutturale Luigi Piroddi piroddi@elet.polimi.it Analisi strutturale Un alternativa all analisi esaustiva basata sul grafo di raggiungibilità,
LA CORRENTE ELETTRICA
 L CORRENTE ELETTRIC H P h Prima che si raggiunga l equilibrio c è un intervallo di tempo dove il livello del fluido non è uguale. Il verso del movimento del fluido va dal vaso a livello maggiore () verso
L CORRENTE ELETTRIC H P h Prima che si raggiunga l equilibrio c è un intervallo di tempo dove il livello del fluido non è uguale. Il verso del movimento del fluido va dal vaso a livello maggiore () verso
Teoria VSEPR Geometria molecolare
 Teoria VSEPR Geometria molecolare la teoria VSEPR la forma delle molecole Massima distanza possibile! Teoria della repulsione delle coppie di elettroni di valenza VSEPR Struttura delle molecole Le regioni
Teoria VSEPR Geometria molecolare la teoria VSEPR la forma delle molecole Massima distanza possibile! Teoria della repulsione delle coppie di elettroni di valenza VSEPR Struttura delle molecole Le regioni
Corso di Matematica per la Chimica
 Dott.ssa Maria Carmela De Bonis a.a. 203-4 I sistemi lineari Generalità sui sistemi lineari Molti problemi dell ingegneria, della fisica, della chimica, dell informatica e dell economia, si modellizzano
Dott.ssa Maria Carmela De Bonis a.a. 203-4 I sistemi lineari Generalità sui sistemi lineari Molti problemi dell ingegneria, della fisica, della chimica, dell informatica e dell economia, si modellizzano
RELAZIONI E FUNZIONI. Per ricordare. Figura 1. Figura 2. Figura 3. Figura 4
 RELAZIONI E FUNZIONI 3 Per ricordare H Dati due insiemi A e B e una proposizione aperta px,y, con x 2 A e y 2 B, si dice che x eá in relazione con y, e si scrive x R y, sepx,y eá vera; si parla allora
RELAZIONI E FUNZIONI 3 Per ricordare H Dati due insiemi A e B e una proposizione aperta px,y, con x 2 A e y 2 B, si dice che x eá in relazione con y, e si scrive x R y, sepx,y eá vera; si parla allora
Trasformazioni Geometriche 1 Roberto Petroni, 2011
 1 Trasformazioni Geometriche 1 Roberto etroni, 2011 Trasformazioni Geometriche sul piano euclideo 1) Introduzione Def: si dice trasformazione geometrica una corrispondenza biunivoca che associa ad ogni
1 Trasformazioni Geometriche 1 Roberto etroni, 2011 Trasformazioni Geometriche sul piano euclideo 1) Introduzione Def: si dice trasformazione geometrica una corrispondenza biunivoca che associa ad ogni
Il concetto di valore medio in generale
 Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
GEOMETRIA MOLECOLARE. Ibridazione La teoria VSEPR
 GEOMETRIA MOLECOLARE Ibridazione La teoria VSEPR 1 Ibridazione e geometria molecolare Teoria di Lewis e VB vista finora non sono in grado di descrivere correttamente la geometria di molte molecole anche
GEOMETRIA MOLECOLARE Ibridazione La teoria VSEPR 1 Ibridazione e geometria molecolare Teoria di Lewis e VB vista finora non sono in grado di descrivere correttamente la geometria di molte molecole anche
3 GRAFICI DI FUNZIONI
 3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
Relazioni statistiche: regressione e correlazione
 Relazioni statistiche: regressione e correlazione È detto studio della connessione lo studio si occupa della ricerca di relazioni fra due variabili statistiche o fra una mutabile e una variabile statistica
Relazioni statistiche: regressione e correlazione È detto studio della connessione lo studio si occupa della ricerca di relazioni fra due variabili statistiche o fra una mutabile e una variabile statistica
INDICAZIONI ED ESERCIZI PER LA PREPARAZIONE ALLA PROVA DI VERIFICA DI SETTEMBRE SCIENZE INTEGRATE (CHIMICA)
 ISTITUTO DI ISTRUZIONE SUPERIORE CHINO CHINI Via Pietro Caiani 68-50032 Borgo San Lorenzo (Fi) Tel. 055.8459.268 - Fax 055.8495.131 Sito Web: www.chinochini.it - E-mail: chinochini@tin.it - PEC FIIS02300N@PEC.ISTRUZIONE.IT
ISTITUTO DI ISTRUZIONE SUPERIORE CHINO CHINI Via Pietro Caiani 68-50032 Borgo San Lorenzo (Fi) Tel. 055.8459.268 - Fax 055.8495.131 Sito Web: www.chinochini.it - E-mail: chinochini@tin.it - PEC FIIS02300N@PEC.ISTRUZIONE.IT
Teorie del legame chimico. Teorie del legame chimico
 Teorie del legame chimico Le teorie proposte per la trattazione del legame chimico si prefiggono i seguenti scopi: 1. Prevedere la formazione di un legame tra due elementi 2. Predire la lunghezza del legame
Teorie del legame chimico Le teorie proposte per la trattazione del legame chimico si prefiggono i seguenti scopi: 1. Prevedere la formazione di un legame tra due elementi 2. Predire la lunghezza del legame
ESERCIZI DI ALGEBRA LINEARE E GEOMETRIA
 ESERCIZI DI ALGEBRA LINEARE E GEOMETRIA Francesco Bottacin Padova, 24 febbraio 2012 Capitolo 1 Algebra Lineare 1.1 Spazi e sottospazi vettoriali Esercizio 1.1. Sia U il sottospazio di R 4 generato dai
ESERCIZI DI ALGEBRA LINEARE E GEOMETRIA Francesco Bottacin Padova, 24 febbraio 2012 Capitolo 1 Algebra Lineare 1.1 Spazi e sottospazi vettoriali Esercizio 1.1. Sia U il sottospazio di R 4 generato dai
f : A A = f (A) In altre parole f è una funzione che associa a un punto del piano un altro punto del piano e che si può invertire.
 Consideriamo l insieme P dei punti del piano e una f funzione biiettiva da P in P: f : { P P A A = f (A) In altre parole f è una funzione che associa a un punto del piano un altro punto del piano e che
Consideriamo l insieme P dei punti del piano e una f funzione biiettiva da P in P: f : { P P A A = f (A) In altre parole f è una funzione che associa a un punto del piano un altro punto del piano e che
un legame covalente due legami covalenti? tre legami covalenti due legami covalenti un legame covalente
 e C N un legame covalente due legami covalenti? tre legami covalenti O F Ne 1s 2s 2p due legami covalenti un legame covalente C 1s 2s 2p ibridazione quattro legami covalenti Cariche Formali Usando le strutture
e C N un legame covalente due legami covalenti? tre legami covalenti O F Ne 1s 2s 2p due legami covalenti un legame covalente C 1s 2s 2p ibridazione quattro legami covalenti Cariche Formali Usando le strutture
Risonanza magnetica nucleare protonica (NMR - PMR)
 Risonanza magnetica nucleare protonica (NMR - PMR) Basi fisiche I nuclei degli atomi hanno un movimento di rotazione intorno a se stessi (spin). Posto che ogni carica dotata di moto genera un campo magnetico,
Risonanza magnetica nucleare protonica (NMR - PMR) Basi fisiche I nuclei degli atomi hanno un movimento di rotazione intorno a se stessi (spin). Posto che ogni carica dotata di moto genera un campo magnetico,
FUNZIONE. Si scrive: A B f: A B x y=f(x) (si legge: f funzione da A in B) x f y= f(x)
 1 FUNZIONE Dati gli insiemi A e B, si definisce funzione da A in B una relazione o legge o corrispondenza che ad ogni elemento di A associa uno ed un solo elemento di B. Si scrive: A B f: A B f() (si legge:
1 FUNZIONE Dati gli insiemi A e B, si definisce funzione da A in B una relazione o legge o corrispondenza che ad ogni elemento di A associa uno ed un solo elemento di B. Si scrive: A B f: A B f() (si legge:
9. Urti e conservazione della quantità di moto.
 9. Urti e conservazione della quantità di moto. 1 Conservazione dell impulso m1 v1 v2 m2 Prima Consideriamo due punti materiali di massa m 1 e m 2 che si muovono in una dimensione. Supponiamo che i due
9. Urti e conservazione della quantità di moto. 1 Conservazione dell impulso m1 v1 v2 m2 Prima Consideriamo due punti materiali di massa m 1 e m 2 che si muovono in una dimensione. Supponiamo che i due
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Metodi basati sulla meccanica quantistica
 Metodi basati sulla meccanica quantistica La descrizione più corretta della struttura elettronica delle molecole, come quella degli atomi, è basata sulla meccanica quantistica. Esistono due principali
Metodi basati sulla meccanica quantistica La descrizione più corretta della struttura elettronica delle molecole, come quella degli atomi, è basata sulla meccanica quantistica. Esistono due principali
PIANO DIDATTICO SCIENZA DEI MATERIALI PER LA CONVERSIONE FOTOVOLTAICA
 PIANO DIDATTICO SCIENZA DEI MATERIALI PER LA CONVERSIONE FOTOVOLTAICA Celle solari: dai mirtilli agli spaghetti CONVERSIONE FOTOVOLTAICA: L ENERGIA DEL FUTURO v Energia inesauribile e rinnovabile v Non
PIANO DIDATTICO SCIENZA DEI MATERIALI PER LA CONVERSIONE FOTOVOLTAICA Celle solari: dai mirtilli agli spaghetti CONVERSIONE FOTOVOLTAICA: L ENERGIA DEL FUTURO v Energia inesauribile e rinnovabile v Non
GEOMETRIA MOLECOLARE
 GEOMETRIA MOLECOLARE Ibridazione La teoria VSEPR 1 Ibridazione e geometria molecolare Teoria di Lewis e VB vista finora non sono in grado di descrivere correttamente la geometria di molte molecole anche
GEOMETRIA MOLECOLARE Ibridazione La teoria VSEPR 1 Ibridazione e geometria molecolare Teoria di Lewis e VB vista finora non sono in grado di descrivere correttamente la geometria di molte molecole anche
Corso di Laurea in Farmacia Insegnamento di CHIMICA BIOLOGICA. Angela Chambery Lezione 2
 Corso di Laurea in Farmacia Insegnamento di CHIMICA BIOLOGICA Angela Chambery Lezione 2 Versatilità del carbonio nel formare legami covalenti La chimica degli organismi viventi è organizzata intorno al
Corso di Laurea in Farmacia Insegnamento di CHIMICA BIOLOGICA Angela Chambery Lezione 2 Versatilità del carbonio nel formare legami covalenti La chimica degli organismi viventi è organizzata intorno al
ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA Corso di Laurea Ingegneria Edile-Architettura
 Cognome Nome Matricola ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA Corso di Laurea Ingegneria Edile-Architettura (Primo appello/ii prova parziale 15/6/15 - Chiarellotto-Urbinati) Per la II prova: solo esercizi
Cognome Nome Matricola ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA Corso di Laurea Ingegneria Edile-Architettura (Primo appello/ii prova parziale 15/6/15 - Chiarellotto-Urbinati) Per la II prova: solo esercizi
