Rappresentazione di oggetti 3D
|
|
|
- Lazzaro Ferrario
- 10 anni fa
- Visualizzazioni
Transcript
1 Rappresentazione di oggetti 3D 1
2 Modellazione geometrica La modellazione geometrica riguarda le tecniche di rappresentazione di curve e superfici Surface modeling Rappresentazione della superficie di un oggetto 3D mediante le curve che delimitano tale superficie Volume modeling Rappresentazione del volume delimitato dalle superfici 2
3 Modello geometrico Descrive il metodo o lo schema di rappresentazione utilizzato nel modello geometrico. I principali: Surface modelling: mesh o griglia poligonale, patch parametriche Volume modeling: poliedri, CSG (geometria solida costruttiva), suddivisione spaziale (voxel) Oggetto di studio del CAD 3
4 Elementi base Quadrilatero (o triangolo) Patch parametrica CSG voxel quadrica 4
5 Poliedri Oggetto superfici poligoni spigoli vertici Un oggetto è rappresentato come un insieme di facce- ciascuna faccia è approssimata da un insieme di poligoni ogni poligono è rappresentato da un insieme di spigoli- ogni spigolo è descritto da un insieme di vertici L accuratezza dipende dalla curvatura della superficie Con sistemi automatici si possono generano molti triangoli: problema della decimazione dei triangoli 5
6 Importanza della struttura dati oggetti superfici Poligoni/facce spigoli vertici 6
7 Polygon mesh Polygon mesh: insieme di edges, vertici e poligoni tale che: Un edge connette 2 vertici V 1..V 2 Un poligono è una sequenza chiusa di edge V 1 Ogni edge è parte di un poligono V 3 V 2 7
8 Polygon mesh Polygon mesh: insieme di edges, vertici e poligoni tale che: Un edge è comune al più a 2 poligoni detti adiacenti P 1 P 2 Un vertice è comune ad almeno 2 edge 8
9 Rappresentazione esplicita Ciascun poligono è rappresentato da una lista di vertici P = ( (x 1,y 1,z 1 ), (x 2,y 2,z 2 ), (x n,y n,z n )) V 1 V n I vertici sono memorizzati in senso orario o antiorario Gli edge sono definiti tra 2 vertici successivi della lista e tra l ultimo vertice ed il primo 9
10 Rappresentazione esplicita P = ( P 1, P 2 ) P 1 = ( V 1, V 3, V 4 ) P 2 = ( V 1, V 2, V 3 ) V 1..V 2 P 2 V 4. P 1.V 3 La rappresentazione risulta inefficiente perché i vertici in comune sono ripetuti Non vi è una rappresentazione esplicita degli edge in comune 10
11 Rappresentazione indexed La più semplice rappresentazione indexed è definita da: Una unica lista di vertici ( per tutti i poligoni) Ogni poligono è definito mediante una lista di puntatori alla lista dei vertici 11
12 Rappresentazione indexed P = ( P 1, P 2 ), V=( V 1, V 2, V 3,V 4, ) P 1 = ( 1, 3, 4) P 2 = ( 1 1 2, 3 ) V 1..V 2 P 1 P 2 V 4..V 3 La rappresentazione risulta più efficiente perché ogni vertice è rappresentato una sola volta. Si ha quindi Risparmio di memoria Possibilità di variare facilmente le coordinate di un vertice Non vi è una rappresentazione esplicita degli edge in comune 12
13 Triangolazione Triangolazione o rassellazione è il procedimento che scompone in triangoli una superficie Generalmente si vuole ridurre il numero di triangoli. Il proceso si chiama anche decimazione Vantaggi Considerati 3 vertici V 1, V 2, V 3 la faccia triangolare definita dai vertici (nello spazio) è sempre piana Si ha che per 3 punti nello spazio passa uno ed un solo piano 13
14 Decimazione dei triangoli Perche triangoli Come decimare? Ridurre i triangoli nelle regioni piatte Preservare l aspetto Stimare la curvatura: f u, f v dove f(u,v) è la superficie descritta in forma parametrica 14
15 Triangolazione di Delaunay La triangolazione di Delaunay ha la proprietà che il cerchio circoscritto a un qualunque triangolo non contiene alcun punto della triangolazione 15
16 Diagramma di Voronoi Consideriamo un insieme di punti P e li chiamiamo vertici Il diagramma di Voronoi dei vertici P è una partizione del piano in celle tali che: Ogni cella di Voronoi, generata dal vertice P, contiene tutti i punti che sono più vicini a P che a qualunque altro vertice 16
17 Triangolazione Triangolazione di Delaunay e diagrammi di Voronoi Partizione del piano in celle tali che tutti i punti di una cella sono piu vicini al vertice generatore della cella di ogni altro punto 17
18 Algoritmo di Sibson Data una triangolazione qualsiasi l algoritmo di Sibson genera la triangolazione di Delaunay considerando coppie di triangoli adiacenti Data una coppia di triangoli adiacenti, si esaminano i 2 triangoli e si ridefiniscono se il vertice di un triangolo risulta essere interno al cerchio circoscritto dell altro 18
19 Algoritmo di Sibson Siano t 1 = (P 0, P 1, P 2 ) e t 2 = (P 3, P 1, P 2 ) Il vertice P 3 risulta interno al cerchio circoscritto al triangolo t 1 I 2 triangoli si ridefiniscono come t 1 e t 2 19
Prof. Caterina Rizzi Dipartimento di Ingegneria Industriale
 RUOLO DELLA MODELLAZIONE GEOMETRICA E LIVELLI DI MODELLAZIONE PARTE 2 Prof. Caterina Rizzi... IN QUESTA LEZIONE Modelli 2D/3D Modelli 3D/3D Dimensione delle primitive di modellazione Dimensione dell oggettoy
RUOLO DELLA MODELLAZIONE GEOMETRICA E LIVELLI DI MODELLAZIONE PARTE 2 Prof. Caterina Rizzi... IN QUESTA LEZIONE Modelli 2D/3D Modelli 3D/3D Dimensione delle primitive di modellazione Dimensione dell oggettoy
Introduzione al 3D con Autocad
 2 Introduzione al 3D con Autocad Coso di CAD B condotto da Daniela Sidari a.a. 2012/2013 19.02.2013 Modellazione geometrica 3D wireframe superfici solidi Si distinguono tre tecniche principali di modellazione:
2 Introduzione al 3D con Autocad Coso di CAD B condotto da Daniela Sidari a.a. 2012/2013 19.02.2013 Modellazione geometrica 3D wireframe superfici solidi Si distinguono tre tecniche principali di modellazione:
Creare superfici. Le superfici. Informatica Grafica ][ Le superfici. Le superfici. Le superfici. Le superfici
![Creare superfici. Le superfici. Informatica Grafica ][ Le superfici. Le superfici. Le superfici. Le superfici Creare superfici. Le superfici. Informatica Grafica ][ Le superfici. Le superfici. Le superfici. Le superfici](/thumbs/27/10902677.jpg) Informatica Grafica ][ Creare superfici Come visto nel corso di IG1, gli oggetti 3D vengono memorizzati attraverso le superfici che li delimitano. In Maya esistono 3 diverse classi di superfici: Marco
Informatica Grafica ][ Creare superfici Come visto nel corso di IG1, gli oggetti 3D vengono memorizzati attraverso le superfici che li delimitano. In Maya esistono 3 diverse classi di superfici: Marco
Capitolo 1 La misura di entità geometriche 1. 1.1 Interazione tra misuratore e misurato...1
 Libro_v11b.pdf 9-09-2009 16:34:44-1 - ( ) Indice Capitolo 1 La misura di entità geometriche 1 1.1 Interazione tra misuratore e misurato...1 1.2 Natura della luce...3 Teoria corpuscolare della luce...3
Libro_v11b.pdf 9-09-2009 16:34:44-1 - ( ) Indice Capitolo 1 La misura di entità geometriche 1 1.1 Interazione tra misuratore e misurato...1 1.2 Natura della luce...3 Teoria corpuscolare della luce...3
Parte Seconda. Geometria
 Parte Seconda Geometria Geometria piana 99 CAPITOLO I GEOMETRIA PIANA Geometria: scienza che studia le proprietà delle figure geometriche piane e solide, cioè la forma, l estensione e la posizione dei
Parte Seconda Geometria Geometria piana 99 CAPITOLO I GEOMETRIA PIANA Geometria: scienza che studia le proprietà delle figure geometriche piane e solide, cioè la forma, l estensione e la posizione dei
REVERSE ENGINEERING. Reverse Engineering 22/12/2008. [email protected] 1. Contenuto della lezione. Reverse Engineering
 Corso di Laboratorio Progettuale di Disegno Assistito da Calcolatore Knowledge Aided Engineering Manufacturing and Related Technologies REVERSE ENGINEERING Contenuto della lezione Metodologia Tecnologie
Corso di Laboratorio Progettuale di Disegno Assistito da Calcolatore Knowledge Aided Engineering Manufacturing and Related Technologies REVERSE ENGINEERING Contenuto della lezione Metodologia Tecnologie
INTRODUZIONE AI SISTEMI CAD
 INTRODUZIONE AI SISTEMI CAD 407 Introduzione Il termine CAD sta per Computer-aided Design. L interpretazione corretta del termine è quella di progettazione assistita dal calcolatore (e non di disegno assistito
INTRODUZIONE AI SISTEMI CAD 407 Introduzione Il termine CAD sta per Computer-aided Design. L interpretazione corretta del termine è quella di progettazione assistita dal calcolatore (e non di disegno assistito
ASSIOMI DELLA GEOMETRIA RAZIONALE
 ASSIOMI DELLA GEOMETRIA RAZIONALE ASSIOMI DI APPARTENENZA A1 Per ogni coppia di punti A e B di un piano π esiste ed è unica la retta che li contiene. A2 Data nel piano π una retta r esistono almeno due
ASSIOMI DELLA GEOMETRIA RAZIONALE ASSIOMI DI APPARTENENZA A1 Per ogni coppia di punti A e B di un piano π esiste ed è unica la retta che li contiene. A2 Data nel piano π una retta r esistono almeno due
I Modelli 3D più comuni: Mesh poligonali
 Modellazione 3D 3D Models for interactive applications Marco Tarini I Modelli 3D più comuni: Mesh poligonali Di triangoli, o mista (quadrilateri + triangoli) Struttura dati per modellare oggetti 3D GPU
Modellazione 3D 3D Models for interactive applications Marco Tarini I Modelli 3D più comuni: Mesh poligonali Di triangoli, o mista (quadrilateri + triangoli) Struttura dati per modellare oggetti 3D GPU
DISEGNO TECNICO INDUSTRIALE
 DISEGNO TECNICO INDUSTRIALE COSTRUZIONI GEOMETRICHE Anno Accademico 2014-2015 Le Costruzioni Geometriche Nello studio del disegno tecnico, inteso come linguaggio grafico comune fra i tecnici per la progettazione
DISEGNO TECNICO INDUSTRIALE COSTRUZIONI GEOMETRICHE Anno Accademico 2014-2015 Le Costruzioni Geometriche Nello studio del disegno tecnico, inteso come linguaggio grafico comune fra i tecnici per la progettazione
Modellazione. Dove si delineano le principali tecniche per descrivere e rappresentare oggetti in uno spazio tridimensionale.
 Modellazione Dove si delineano le principali tecniche per descrivere e rappresentare oggetti in uno spazio tridimensionale. Rappresentazione poligonale Curve e superfici Gometria Solida Costruttiva Suddivisione
Modellazione Dove si delineano le principali tecniche per descrivere e rappresentare oggetti in uno spazio tridimensionale. Rappresentazione poligonale Curve e superfici Gometria Solida Costruttiva Suddivisione
Modulo 3. Rappresentazione di solidi mediante forntiera e strutture dati collegate.
 Modulo 3. Rappresentazione di solidi mediante forntiera e strutture dati collegate. Nel precedente modulo abbiamo presentato le modalità di rappresentazione di un solido mediante enumerazione o mediante
Modulo 3. Rappresentazione di solidi mediante forntiera e strutture dati collegate. Nel precedente modulo abbiamo presentato le modalità di rappresentazione di un solido mediante enumerazione o mediante
Applicazioni 3D avanzate
 Azienda Ospedaliera Card. G. Panico Applicazioni 3D avanzate VR e segmentazione delle articolazioni: campi applicativi Indice Applicazioni 3D avanzate Articolazioni e grandi macchine 1. Definizioni 2.
Azienda Ospedaliera Card. G. Panico Applicazioni 3D avanzate VR e segmentazione delle articolazioni: campi applicativi Indice Applicazioni 3D avanzate Articolazioni e grandi macchine 1. Definizioni 2.
MATEMATICA DEL DISCRETO elementi di teoria dei grafi. anno acc. 2009/2010
 elementi di teoria dei grafi anno acc. 2009/2010 Grafi semplici Un grafo semplice G è una coppia ordinata (V(G), L(G)), ove V(G) è un insieme finito e non vuoto di elementi detti vertici o nodi di G, mentre
elementi di teoria dei grafi anno acc. 2009/2010 Grafi semplici Un grafo semplice G è una coppia ordinata (V(G), L(G)), ove V(G) è un insieme finito e non vuoto di elementi detti vertici o nodi di G, mentre
INTEGRALI DEFINITI. Tale superficie viene detta trapezoide e la misura della sua area si ottiene utilizzando il calcolo di un integrale definito.
 INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
Come si indica un punto? Un punto si indica (distingue) con una lettera maiuscola dell alfabeto italiano.
 Il punto Il punto è un elemento geometrico fondamentale privo di dimensioni ed occupa solo una posizione. Come si indica un punto? Un punto si indica (distingue) con una lettera maiuscola dell alfabeto
Il punto Il punto è un elemento geometrico fondamentale privo di dimensioni ed occupa solo una posizione. Come si indica un punto? Un punto si indica (distingue) con una lettera maiuscola dell alfabeto
Argomento interdisciplinare
 1 Argomento interdisciplinare Tecnologia-Matematica Libro consigliato: Disegno Laboratorio - IL MANUALE DI TECNOLOGIA _G.ARDUINO_LATTES studiare da pag.19.da 154 a 162 Unità aggiornata: 7/2012 2 Sono corpi
1 Argomento interdisciplinare Tecnologia-Matematica Libro consigliato: Disegno Laboratorio - IL MANUALE DI TECNOLOGIA _G.ARDUINO_LATTES studiare da pag.19.da 154 a 162 Unità aggiornata: 7/2012 2 Sono corpi
Ricorsione. Rosario Culmone. - p. 1/13
 Ricorsione Rosario Culmone - p. 1/13 Induzione e Ricorsione Spesso utilizzeremo le definizioni induttive. Sono forme di definizione compatte che descrivono un numero infinito di elementi. I contesti di
Ricorsione Rosario Culmone - p. 1/13 Induzione e Ricorsione Spesso utilizzeremo le definizioni induttive. Sono forme di definizione compatte che descrivono un numero infinito di elementi. I contesti di
Gli oggetti 3D di base
 Gli oggetti 3D di base 04 Attraverso gli oggetti 3D di base, AutoCAD dispiega la sua capacità di modellazione per volumi e per superfici per quei modelli che si possono pensare come composizioni di oggetti
Gli oggetti 3D di base 04 Attraverso gli oggetti 3D di base, AutoCAD dispiega la sua capacità di modellazione per volumi e per superfici per quei modelli che si possono pensare come composizioni di oggetti
IR(3): Illuminazione Globale
 IR(3): Illuminazione Globale Alessandro Martinelli [email protected] 21 Dicembre 2011 IR(3): Illuminazione Globale Illuminazione e Rendering: Principi di Illuminazione Rendering Real-Time
IR(3): Illuminazione Globale Alessandro Martinelli [email protected] 21 Dicembre 2011 IR(3): Illuminazione Globale Illuminazione e Rendering: Principi di Illuminazione Rendering Real-Time
PROGRAMMAZIONE di MATEMATICA CLASSE PRIMA
 PROGRAMMAZIONE di MATEMATICA 1.NUMERI CLASSE PRIMA Comprende il significato Comprendere il significato Insiemi numerici NQZ Utilizzare le tecniche e le procedure del calcolo aritmetico e algebrico rappresentandole
PROGRAMMAZIONE di MATEMATICA 1.NUMERI CLASSE PRIMA Comprende il significato Comprendere il significato Insiemi numerici NQZ Utilizzare le tecniche e le procedure del calcolo aritmetico e algebrico rappresentandole
TRASFORMAZIONI GEOMETRICHE NEL PIANO. Parte 1
 TRASFORMAZIONI GEOMETRICHE NEL PIANO Parte 1 La geometria è la scienza che studia la forma e l estensione dei corpi e le trasformazioni che questi possono subire. In generale per trasformazione geometrica
TRASFORMAZIONI GEOMETRICHE NEL PIANO Parte 1 La geometria è la scienza che studia la forma e l estensione dei corpi e le trasformazioni che questi possono subire. In generale per trasformazione geometrica
Indici di dispersione
 Indici di dispersione 1 Supponiamo di disporre di un insieme di misure e di cercare un solo valore che, meglio di ciascun altro, sia in grado di catturare le caratteristiche della distribuzione nel suo
Indici di dispersione 1 Supponiamo di disporre di un insieme di misure e di cercare un solo valore che, meglio di ciascun altro, sia in grado di catturare le caratteristiche della distribuzione nel suo
Dovremmo a questo punto incominciare a vedere la suddivisione della nostra superficie.
 Vediamo ancora come lavorare sulle superfici attraverso la loro parametrizzazione, e suddivisione progressiva. Alcune volte in Grasshopper ci sono diversi modi per fare le stesse cose. Abbiamo visto il
Vediamo ancora come lavorare sulle superfici attraverso la loro parametrizzazione, e suddivisione progressiva. Alcune volte in Grasshopper ci sono diversi modi per fare le stesse cose. Abbiamo visto il
CONVESSITÀ NELLA GEOMETRIA DEL TAXI DI MINKOWSKI
 CONVESSITÀ NELLA GEOMETRIA DEL TAXI DI MINKOWSKI ELISABETTA AVIZZANO NICOLETTA CAPOTORTO CHIARA CEROCCHI GIORGIO CICCARELLA IVAN COLAVITA EMANUELE DI CARO SERENA NUNZIATA AMANDA PISELLI ANDREA PIEPOLI
CONVESSITÀ NELLA GEOMETRIA DEL TAXI DI MINKOWSKI ELISABETTA AVIZZANO NICOLETTA CAPOTORTO CHIARA CEROCCHI GIORGIO CICCARELLA IVAN COLAVITA EMANUELE DI CARO SERENA NUNZIATA AMANDA PISELLI ANDREA PIEPOLI
PointCloud 7.0 Anno 2011
 PointCloud 7.0 Anno 2011 Compatibilità con AutoCAD 2007-2012 ed AutoCAD 2007-2012 Supporto del formato nativo delle nuvole di punti di AutoCAD (PCG) e miglioramento delle performance riguardo la velocità
PointCloud 7.0 Anno 2011 Compatibilità con AutoCAD 2007-2012 ed AutoCAD 2007-2012 Supporto del formato nativo delle nuvole di punti di AutoCAD (PCG) e miglioramento delle performance riguardo la velocità
Sommario. Definizione di informatica. Definizione di un calcolatore come esecutore. Gli algoritmi.
 Algoritmi 1 Sommario Definizione di informatica. Definizione di un calcolatore come esecutore. Gli algoritmi. 2 Informatica Nome Informatica=informazione+automatica. Definizione Scienza che si occupa dell
Algoritmi 1 Sommario Definizione di informatica. Definizione di un calcolatore come esecutore. Gli algoritmi. 2 Informatica Nome Informatica=informazione+automatica. Definizione Scienza che si occupa dell
APPUNTI DI MATEMATICA GEOMETRIA \ GEOMETRIA EUCLIDEA \ GEOMETRIA DEL PIANO (1)
 GEOMETRIA \ GEOMETRIA EUCLIDEA \ GEOMETRIA DEL PIANO (1) Un ente (geometrico) è un oggetto studiato dalla geometria. Per descrivere gli enti vengono utilizzate delle definizioni. Una definizione è una
GEOMETRIA \ GEOMETRIA EUCLIDEA \ GEOMETRIA DEL PIANO (1) Un ente (geometrico) è un oggetto studiato dalla geometria. Per descrivere gli enti vengono utilizzate delle definizioni. Una definizione è una
Sistema Informativo Geografico:
 Sistemi Informativi Geografici Sistema Informativo Geografico: È un sistema informativo che tratta informazioni spaziali georeferenziate, ne consente la gestione e l'analisi. Informazioni spaziali: dati
Sistemi Informativi Geografici Sistema Informativo Geografico: È un sistema informativo che tratta informazioni spaziali georeferenziate, ne consente la gestione e l'analisi. Informazioni spaziali: dati
geometriche. Parte Sesta Trasformazioni isometriche
 Parte Sesta Trasformazioni isometriche In questa sezione di programma di matematica parliamo della geometria delle trasformazioni che studia le figure geometriche soggette a movimenti. Tali movimenti,
Parte Sesta Trasformazioni isometriche In questa sezione di programma di matematica parliamo della geometria delle trasformazioni che studia le figure geometriche soggette a movimenti. Tali movimenti,
Strutturazione logica dei dati: i file
 Strutturazione logica dei dati: i file Informazioni più complesse possono essere composte a partire da informazioni elementari Esempio di una banca: supponiamo di voler mantenere all'interno di un computer
Strutturazione logica dei dati: i file Informazioni più complesse possono essere composte a partire da informazioni elementari Esempio di una banca: supponiamo di voler mantenere all'interno di un computer
CONI, CILINDRI, SUPERFICI DI ROTAZIONE
 CONI, CILINDRI, SUPERFICI DI ROTAZIONE. Esercizi x + z = Esercizio. Data la curva x, calcolare l equazione del cilindro avente γ y = 0 come direttrice e con generatrici parallele al vettore v = (, 0, ).
CONI, CILINDRI, SUPERFICI DI ROTAZIONE. Esercizi x + z = Esercizio. Data la curva x, calcolare l equazione del cilindro avente γ y = 0 come direttrice e con generatrici parallele al vettore v = (, 0, ).
AMBIENTE VIRTUALE. Moduli logici di un Ambiente Virtuale. Modellazione. Management Rendering Interazione. Sintesi. Comportamenti.
 Moduli logici di un Ambiente Virtuale Sintesi Campionamento Comportamenti Proprietà AMBIENTE VIRTUALE Management Rendering Interazione UTENTE È il processo che porta alla descrizione di un oggetto (modello),
Moduli logici di un Ambiente Virtuale Sintesi Campionamento Comportamenti Proprietà AMBIENTE VIRTUALE Management Rendering Interazione UTENTE È il processo che porta alla descrizione di un oggetto (modello),
LA GEOMETRIA NELLE PIASTRELLE
 LA GEOMETRIA NELLE PIASTRELLE Supponiamo di dover pavimentare delle superfici molto estese e vogliamo evitare le classiche composizioni quadrate, rettangolari o a spina di pesce, per rendere meno banale
LA GEOMETRIA NELLE PIASTRELLE Supponiamo di dover pavimentare delle superfici molto estese e vogliamo evitare le classiche composizioni quadrate, rettangolari o a spina di pesce, per rendere meno banale
LEZIONI CON I PAD Docente scuola secondaria IC Moglia Carla Casareggio Classi seconde 2014/2015 Proprietà triangoli e quadrilateri con Sketchometry
 LEZIONI CON I PAD Docente scuola secondaria IC Moglia Carla Casareggio Classi seconde 2014/2015 Proprietà triangoli e quadrilateri con Sketchometry La costruzione di figure geometriche al computer con
LEZIONI CON I PAD Docente scuola secondaria IC Moglia Carla Casareggio Classi seconde 2014/2015 Proprietà triangoli e quadrilateri con Sketchometry La costruzione di figure geometriche al computer con
e l insieme delle soluzioni, dopo le analoghe riduzioni del caso n = 2, si scrive come
 Numeri complessi 9 Da questi esempi si può osservare che, facendo le successive potene di un numero complesso, i punti corrispondenti girano attorno all origine. Se inoltre > allora i punti si allontanano
Numeri complessi 9 Da questi esempi si può osservare che, facendo le successive potene di un numero complesso, i punti corrispondenti girano attorno all origine. Se inoltre > allora i punti si allontanano
La propagazione delle onde luminose può essere studiata per mezzo delle equazioni di Maxwell. Tuttavia, nella maggior parte dei casi è possibile
 Elementi di ottica L ottica si occupa dello studio dei percorsi dei raggi luminosi e dei fenomeni legati alla propagazione della luce in generale. Lo studio dell ottica nella fisica moderna si basa sul
Elementi di ottica L ottica si occupa dello studio dei percorsi dei raggi luminosi e dei fenomeni legati alla propagazione della luce in generale. Lo studio dell ottica nella fisica moderna si basa sul
Cluster. Vicino alla temperatura critica gli spin formano grandi gruppi (cluster)
 Cluster Vicino alla temperatura critica gli spin formano grandi gruppi (cluster) all interno di ogni gruppo è molto improbabile riuscire a flippare uno spin perché ci sarebbe una grande perdita di energia,
Cluster Vicino alla temperatura critica gli spin formano grandi gruppi (cluster) all interno di ogni gruppo è molto improbabile riuscire a flippare uno spin perché ci sarebbe una grande perdita di energia,
Per effettuare la stampa di una cartella di lavoro si accede al comando. Stampa dal menu File o si utilizza il pulsante omonimo sulla barra
 4.5 Stampa 4.5.1 Stampare semplici fogli elettronici 4.5.1.1 Usare le opzioni di base della stampa Per effettuare la stampa di una cartella di lavoro si accede al comando Stampa dal menu File o si utilizza
4.5 Stampa 4.5.1 Stampare semplici fogli elettronici 4.5.1.1 Usare le opzioni di base della stampa Per effettuare la stampa di una cartella di lavoro si accede al comando Stampa dal menu File o si utilizza
V MODELLAZIONE DEGLI OGGETTI A 2 ED A 3 DIMENSIONI. Capitolo 5 MODELLAZIONE DEGLI OGGETTI A 2 ED A 3 DIMENSIONI
 Capitolo 5 MODELLAZIONE DEGLI OGGETTI A 2 ED A 3 DIMENSIONI V MODELLAZIONE DEGLI OGGETTI A 2 ED A 3 DIMENSIONI 5.1 Linee, polilinee, poligoni, tassellazioni 5.2 Superfici, terreni 5.3 Quadtree, Octree
Capitolo 5 MODELLAZIONE DEGLI OGGETTI A 2 ED A 3 DIMENSIONI V MODELLAZIONE DEGLI OGGETTI A 2 ED A 3 DIMENSIONI 5.1 Linee, polilinee, poligoni, tassellazioni 5.2 Superfici, terreni 5.3 Quadtree, Octree
RILIEVO TRIDIMENSIONALE DEL «CONVENTO ROSSO», SOHAG (EGITTO)
 1 RILIEVO TRIDIMENSIONALE DEL «CONVENTO ROSSO», SOHAG (EGITTO) DI MASSIMO SABATINI Lo studio finalizzato ad un interesse di carattere statico e conservativo eseguito sulle volumetrie degli oggetti, ha
1 RILIEVO TRIDIMENSIONALE DEL «CONVENTO ROSSO», SOHAG (EGITTO) DI MASSIMO SABATINI Lo studio finalizzato ad un interesse di carattere statico e conservativo eseguito sulle volumetrie degli oggetti, ha
Università degli Studi Mediterranea di Reggio Calabria.
 Università degli Studi Mediterranea di Reggio Calabria. Laboratorio di Analisi e Pianificazione della città e del territorio Modulo: Pianificazione del territorio prof. Maria Adele Teti Collaboratori:
Università degli Studi Mediterranea di Reggio Calabria. Laboratorio di Analisi e Pianificazione della città e del territorio Modulo: Pianificazione del territorio prof. Maria Adele Teti Collaboratori:
AMBIENTE VIRTUALE UTENTE
 Moduli logici di un Ambiente Virtuale Sintesi Campionamento Comportamenti Proprietà AMBIENTE VIRTUALE Management Rendering Interazione UTENTE È il processo che porta alla descrizione di un oggetto (modello),
Moduli logici di un Ambiente Virtuale Sintesi Campionamento Comportamenti Proprietà AMBIENTE VIRTUALE Management Rendering Interazione UTENTE È il processo che porta alla descrizione di un oggetto (modello),
Costruite un grafo che rappresenti la situazione del torneo (in modo che siano rappresentate le squadre e le partite). Che tipo di grafo ottenete?
 IL TORNEO DI CALCIO Avete un gruppo di sei squadre che devono sfidarsi in un torneo di calcio. Il torneo deve essere circolare e di sola andata, cioè ogni squadra deve giocare una partita contro ciascuna
IL TORNEO DI CALCIO Avete un gruppo di sei squadre che devono sfidarsi in un torneo di calcio. Il torneo deve essere circolare e di sola andata, cioè ogni squadra deve giocare una partita contro ciascuna
Computer Graphics. 3D Rendering. Digital representation of 3D objects. Scena 3D rendering image. Geometry of a 3D object. 3D Model
 Computer Graphics 3D Rendering Università dell Insubria Digital representation of 3D objects Facoltà di Scienze MFN di Varese Corso di Laurea in Informatica Anno Accademico 2014/15 Scena 3D rendering image
Computer Graphics 3D Rendering Università dell Insubria Digital representation of 3D objects Facoltà di Scienze MFN di Varese Corso di Laurea in Informatica Anno Accademico 2014/15 Scena 3D rendering image
SCUOLA PRIMARIA I.C. di CRESPELLANO PROGRAMMAZIONE ANNUALE MATEMATICA
 SCUOLA PRIMARIA I.C. di CRESPELLANO PROGRAMMAZIONE ANNUALE MATEMATICA ANNO SCOLASTICO 2013/2014 INSEGNANTI Gabellone, Silvagni,Damiano TRAGUARDI DELLE COMPETENZE AL TERMINE della CLASSE QUARTA Sviluppa
SCUOLA PRIMARIA I.C. di CRESPELLANO PROGRAMMAZIONE ANNUALE MATEMATICA ANNO SCOLASTICO 2013/2014 INSEGNANTI Gabellone, Silvagni,Damiano TRAGUARDI DELLE COMPETENZE AL TERMINE della CLASSE QUARTA Sviluppa
Tutorial e lavoro su altre caratteristiche di Grasshopper Arch. A. Di Raimo
 Tutorial e lavoro su altre caratteristiche di Grasshopper Arch. A. Di Raimo Abbiamo già introdotto il concetto di parametro: come abbiamo osservato si tratta ancora di una variabile che ci permette di
Tutorial e lavoro su altre caratteristiche di Grasshopper Arch. A. Di Raimo Abbiamo già introdotto il concetto di parametro: come abbiamo osservato si tratta ancora di una variabile che ci permette di
ISTITUTO COMPRENSIVO MONTEGROTTO TERME SCUOLA PRIMARIA DISCIPLINA: MATEMATICA - CLASSE PRIMA OBIETTIVI DI APPRENDIMENTO
 PRIMA DELLA DISCIPLINA: MATEMATICA - CLASSE PRIMA L alunno si muove con sicurezza nel calcolo scritto e mentale con i numeri naturali. Legge e comprende testi che coinvolgono aspetti logici e matematici.
PRIMA DELLA DISCIPLINA: MATEMATICA - CLASSE PRIMA L alunno si muove con sicurezza nel calcolo scritto e mentale con i numeri naturali. Legge e comprende testi che coinvolgono aspetti logici e matematici.
Grafica al calcolatore. Computer Graphics. 4 - Modellazione 21/10/13
 Grafica al calcolatore Computer Graphics 4 - Modellazione 1 Modellazione Definiamo ora possibili strutture dati per modellare gli oggetti nello spazio. Poi vedremo come modellare anche la formazione delle
Grafica al calcolatore Computer Graphics 4 - Modellazione 1 Modellazione Definiamo ora possibili strutture dati per modellare gli oggetti nello spazio. Poi vedremo come modellare anche la formazione delle
Spline Nurbs. IUAV Disegno Digitale. Camillo Trevisan
 Spline Nurbs IUAV Disegno Digitale Camillo Trevisan Spline e Nurbs Negli anni 70 e 80 del secolo scorso nelle aziende si è iniziata a sentire l esigenza di concentrare in un unica rappresentazione gestita
Spline Nurbs IUAV Disegno Digitale Camillo Trevisan Spline e Nurbs Negli anni 70 e 80 del secolo scorso nelle aziende si è iniziata a sentire l esigenza di concentrare in un unica rappresentazione gestita
Osservazioni sulla prima prova intermedia
 Avviso Istituzioni di matematiche 2 Diego Noja ([email protected]) 28 aprile 2009 La seconda prova intermedia si svolgerà martedì 26 maggio 2008, dalle 16.30 alle 18.30 Cognomi dalla A alla L: aula
Avviso Istituzioni di matematiche 2 Diego Noja ([email protected]) 28 aprile 2009 La seconda prova intermedia si svolgerà martedì 26 maggio 2008, dalle 16.30 alle 18.30 Cognomi dalla A alla L: aula
Definizione DEFINIZIONE
 Definizione Funzione reale di due variabili reali Indichiamo con R 2 l insieme di tutti i vettori bidimensionali. Dato un sottoinsiemed R 2, una funzione f: D R è una legge che assegna a ogni punto (x,
Definizione Funzione reale di due variabili reali Indichiamo con R 2 l insieme di tutti i vettori bidimensionali. Dato un sottoinsiemed R 2, una funzione f: D R è una legge che assegna a ogni punto (x,
APPUNTI DI MATEMATICA ALGEBRA \ INSIEMISTICA \ TEORIA DEGLI INSIEMI (1)
 ALGEBRA \ INSIEMISTICA \ TEORIA DEGLI INSIEMI (1) Un insieme è una collezione di oggetti. Il concetto di insieme è un concetto primitivo. Deve esistere un criterio chiaro, preciso, non ambiguo, inequivocabile,
ALGEBRA \ INSIEMISTICA \ TEORIA DEGLI INSIEMI (1) Un insieme è una collezione di oggetti. Il concetto di insieme è un concetto primitivo. Deve esistere un criterio chiaro, preciso, non ambiguo, inequivocabile,
Capitolo 11. Il disegno in 3D
 Capitolo 11 Il disegno in 3D o 11.1 Uso delle coordinate nello spazio o 11.2 Creazione di oggetti in 3D o 11.3 Uso dei piani di disegno in 3D (UCS) o 11.4 Creazione delle finestre di vista o 11.5 Definizione
Capitolo 11 Il disegno in 3D o 11.1 Uso delle coordinate nello spazio o 11.2 Creazione di oggetti in 3D o 11.3 Uso dei piani di disegno in 3D (UCS) o 11.4 Creazione delle finestre di vista o 11.5 Definizione
Modelli 1D/2D Modelli 1D/3D. Modelli 2D/3D Modelli 3D/3D. Spline Bezier B Spline NURBS Nuvole di punti e triangoli. Caterina RIZZI
 RUOLO DELLA MODELLAZIONE GEOMETRICA E LIVELLI DI MODELLAZIONE PARTE 1 Prof. Caterina Rizzi... IN QUESTA LEZIONE Modello di riferimento Modelli 1D/2D Modelli 1D/3D Modelli di solidi Modelli 2D/3D Modelli
RUOLO DELLA MODELLAZIONE GEOMETRICA E LIVELLI DI MODELLAZIONE PARTE 1 Prof. Caterina Rizzi... IN QUESTA LEZIONE Modello di riferimento Modelli 1D/2D Modelli 1D/3D Modelli di solidi Modelli 2D/3D Modelli
Sistema operativo: Gestione della memoria
 Dipartimento di Elettronica ed Informazione Politecnico di Milano Informatica e CAD (c.i.) - ICA Prof. Pierluigi Plebani A.A. 2008/2009 Sistema operativo: Gestione della memoria La presente dispensa e
Dipartimento di Elettronica ed Informazione Politecnico di Milano Informatica e CAD (c.i.) - ICA Prof. Pierluigi Plebani A.A. 2008/2009 Sistema operativo: Gestione della memoria La presente dispensa e
PROGRAMMI PER GLI ESAMI I PATENTE DE MAESTRI E DELLE MAESTRE DELLE SCUOLE PRIMARIE
 Programmi per le Scuole normali e magistrali, e per gli esami di Patente de Maestri e delle Maestre delle Scuole primarie approvati con regio decreto 9 novembre 1861 n. 315 (Raccolta ufficiale delle leggi
Programmi per le Scuole normali e magistrali, e per gli esami di Patente de Maestri e delle Maestre delle Scuole primarie approvati con regio decreto 9 novembre 1861 n. 315 (Raccolta ufficiale delle leggi
GEOGEBRA I OGGETTI GEOMETRICI
 GEOGEBRA I OGGETTI GEOMETRICI PROPRIETA : Finestra Proprietà (tasto destro mouse sull oggetto) Fondamentali: permette di assegnare o cambiare NOME, VALORE, di mostrare nascondere l oggetto, di mostrare
GEOGEBRA I OGGETTI GEOMETRICI PROPRIETA : Finestra Proprietà (tasto destro mouse sull oggetto) Fondamentali: permette di assegnare o cambiare NOME, VALORE, di mostrare nascondere l oggetto, di mostrare
Information Visualization
 Information Visualization Introduzione alla CG Prof. Andrea F. Abate [email protected] http://www.unisa.it/docenti/andreafrancescoabate/index CG e VR: cosa sono e a cosa servono Con il termine Computer Graphics,
Information Visualization Introduzione alla CG Prof. Andrea F. Abate [email protected] http://www.unisa.it/docenti/andreafrancescoabate/index CG e VR: cosa sono e a cosa servono Con il termine Computer Graphics,
Andrea Pagano, Laura Tedeschini Lalli
 3.5 Il toro 3.5.1 Modelli di toro Modelli di carta Esempio 3.5.1 Toro 1 Il modello di toro finito che ciascuno può costruire è ottenuto incollando a due a due i lati opposti di un foglio rettangolare.
3.5 Il toro 3.5.1 Modelli di toro Modelli di carta Esempio 3.5.1 Toro 1 Il modello di toro finito che ciascuno può costruire è ottenuto incollando a due a due i lati opposti di un foglio rettangolare.
La modellazione con le superfici
 Alla fine del capitolo saremo in grado di: Comprendere il significato di B-Spline Rappresentare i diversi tipi di curve piane e nello spazio Creare superfici con metodi differenti Modificare le superfici
Alla fine del capitolo saremo in grado di: Comprendere il significato di B-Spline Rappresentare i diversi tipi di curve piane e nello spazio Creare superfici con metodi differenti Modificare le superfici
GEOMETRIA DELLE MASSE
 1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
Similitudine e omotetia nella didattica della geometria nella scuola secondaria di primo grado di Luciano Porta
 Similitudine e omotetia nella didattica della geometria nella scuola secondaria di primo grado di Luciano Porta Il concetto di similitudine è innato: riconosciamo lo stesso oggetto se è più o meno distante
Similitudine e omotetia nella didattica della geometria nella scuola secondaria di primo grado di Luciano Porta Il concetto di similitudine è innato: riconosciamo lo stesso oggetto se è più o meno distante
2 + (σ2 - ρσ 1 ) 2 > 0 [da -1 ρ 1] b = (σ 2. 2 - ρσ1 σ 2 ) = (σ 1
![2 + (σ2 - ρσ 1 ) 2 > 0 [da -1 ρ 1] b = (σ 2. 2 - ρσ1 σ 2 ) = (σ 1 2 + (σ2 - ρσ 1 ) 2 > 0 [da -1 ρ 1] b = (σ 2. 2 - ρσ1 σ 2 ) = (σ 1](/thumbs/25/5899888.jpg) 1 PORTAFOGLIO Portafoglio Markowitz (2 titoli) (rischiosi) due titoli rendimento/varianza ( μ 1, σ 1 ), ( μ 2, σ 2 ) Si suppone μ 1 > μ 2, σ 1 > σ 2 portafoglio con pesi w 1, w 2 w 1 = w, w 2 = 1- w 1
1 PORTAFOGLIO Portafoglio Markowitz (2 titoli) (rischiosi) due titoli rendimento/varianza ( μ 1, σ 1 ), ( μ 2, σ 2 ) Si suppone μ 1 > μ 2, σ 1 > σ 2 portafoglio con pesi w 1, w 2 w 1 = w, w 2 = 1- w 1
Siamo così arrivati all aritmetica modulare, ma anche a individuare alcuni aspetti di come funziona l aritmetica del calcolatore come vedremo.
 DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
3DE Modeling Professional
 3DE Modeling Professional 3DE Modeling Professional è la parte di 3DE Modeling Suite che si occupa della modellazione 3D automatica di oggetti ed edifici a partire da nuvole di punti ottenute con scanner
3DE Modeling Professional 3DE Modeling Professional è la parte di 3DE Modeling Suite che si occupa della modellazione 3D automatica di oggetti ed edifici a partire da nuvole di punti ottenute con scanner
ALGORITMI e PROGRAMMI Programmazione: Lavoro che si fa per costruire sequenze di istruzioni (operazioni) adatte a svolgere un dato calcolo
 ALGORITMI e PROGRAMMI Programmazione: Lavoro che si fa per costruire sequenze di istruzioni (operazioni) adatte a svolgere un dato calcolo INPUT: dati iniziali INPUT: x,y,z AZIONI esempio: Somma x ed y
ALGORITMI e PROGRAMMI Programmazione: Lavoro che si fa per costruire sequenze di istruzioni (operazioni) adatte a svolgere un dato calcolo INPUT: dati iniziali INPUT: x,y,z AZIONI esempio: Somma x ed y
Qui cade sua altezza
 Qui cade sua altezza Silvia Sbaragli N.R.D. Bologna DFA, SUPSI Locarno (Svizzera) Pubblicato in: Sbaragli S. (2010). Qui cade sua altezza. La Vita Scolastica. 18, 25-27. Nell insegnamento della matematica
Qui cade sua altezza Silvia Sbaragli N.R.D. Bologna DFA, SUPSI Locarno (Svizzera) Pubblicato in: Sbaragli S. (2010). Qui cade sua altezza. La Vita Scolastica. 18, 25-27. Nell insegnamento della matematica
Syllabus delle conoscenze per il modulo: linguaggio matematico di base, modellizzazione e ragionamento. Esempi di domande
 Syllabus delle conoscenze per il modulo: linguaggio matematico di base, modellizzazione e ragionamento Esempi di domande Nelle pagine che seguono sono riportati, come esempio, i venticinque quesiti già
Syllabus delle conoscenze per il modulo: linguaggio matematico di base, modellizzazione e ragionamento Esempi di domande Nelle pagine che seguono sono riportati, come esempio, i venticinque quesiti già
Introduzione. Informatica B. Daniele Loiacono
 Introduzione Informatica B Perchè studiare l informatica? Perchè ha a che fare con quasi tutto quello con cui abbiamo a che fare ogni giorno Perché è uno strumento fondamentale per progettare l innovazione
Introduzione Informatica B Perchè studiare l informatica? Perchè ha a che fare con quasi tutto quello con cui abbiamo a che fare ogni giorno Perché è uno strumento fondamentale per progettare l innovazione
11.2 Software Calcolo Energia di Deformazione
 11.2 Software Calcolo Energia di Deformazione 61 il software calcola l energia di deformazione di un veicolo o di una coppia di veicoli che si sono urtati a partire dalla conoscenza del coefficiente di
11.2 Software Calcolo Energia di Deformazione 61 il software calcola l energia di deformazione di un veicolo o di una coppia di veicoli che si sono urtati a partire dalla conoscenza del coefficiente di
Interpolazione ed approssimazione di funzioni
 Interpolazione ed approssimazione di funzioni Lucia Gastaldi Dipartimento di Matematica, http://dm.ing.unibs.it/gastaldi/ 9 novembre 2007 Outline 1 Polinomi Valutazione di un polinomio Algoritmo di Horner
Interpolazione ed approssimazione di funzioni Lucia Gastaldi Dipartimento di Matematica, http://dm.ing.unibs.it/gastaldi/ 9 novembre 2007 Outline 1 Polinomi Valutazione di un polinomio Algoritmo di Horner
ANALISI NUMERICA. Elementi finiti bidimensionali. a.a. 2014 2015. Maria Lucia Sampoli. ANALISI NUMERICA p.1/23
 ANALISI NUMERICA Elementi finiti bidimensionali a.a. 2014 2015 Maria Lucia Sampoli ANALISI NUMERICA p.1/23 Elementi Finiti 2D Consideriamo 3 aspetti per la descrizione di elementi finiti bidimensionali:
ANALISI NUMERICA Elementi finiti bidimensionali a.a. 2014 2015 Maria Lucia Sampoli ANALISI NUMERICA p.1/23 Elementi Finiti 2D Consideriamo 3 aspetti per la descrizione di elementi finiti bidimensionali:
Gli angoli. In questa dispensa vengono presentati i concetti fondamentali relativi agli angoli.
 Gli angoli In questa dispensa vengono presentati i concetti fondamentali relativi agli angoli. Dopo le prime nozioni riguardanti angoli convessi e concavi, angolo piatto, angolo giro e angolo nullo, si
Gli angoli In questa dispensa vengono presentati i concetti fondamentali relativi agli angoli. Dopo le prime nozioni riguardanti angoli convessi e concavi, angolo piatto, angolo giro e angolo nullo, si
Funzioni funzione dominio codominio legge argomento variabile indipendente variabile dipendente
 Funzioni In matematica, una funzione f da X in Y consiste in: 1. un insieme X detto dominio di f 2. un insieme Y detto codominio di f 3. una legge che ad ogni elemento x in X associa uno ed un solo elemento
Funzioni In matematica, una funzione f da X in Y consiste in: 1. un insieme X detto dominio di f 2. un insieme Y detto codominio di f 3. una legge che ad ogni elemento x in X associa uno ed un solo elemento
Creare primitive solide
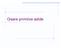 Creare primitive solide I solidi sono caratterizzati dal fatto di avere una massa oltre alle superfici e agli spigoli. Rappresentano l intero volume dell oggetto. Caratteristiche Il solido viene creato:
Creare primitive solide I solidi sono caratterizzati dal fatto di avere una massa oltre alle superfici e agli spigoli. Rappresentano l intero volume dell oggetto. Caratteristiche Il solido viene creato:
Verifica delle tolleranze attraverso Reverse Engineering: sviluppo di algoritmi per l'analisi di superfici cilindriche
 Laurea Magistrale in Ingegneria Meccanica aa 13-14 Verifica delle tolleranze attraverso Reverse Engineering: sviluppo di algoritmi per l'analisi di superfici cilindriche Candidato: Alessio Trifirò Relatore:
Laurea Magistrale in Ingegneria Meccanica aa 13-14 Verifica delle tolleranze attraverso Reverse Engineering: sviluppo di algoritmi per l'analisi di superfici cilindriche Candidato: Alessio Trifirò Relatore:
Laboratorio di Matematica Computazionale A.A. 2007-2008 - Laboratorio nr.8
 Laboratorio di Matematica Computazionale A.A. 2007-2008 - Laboratorio nr.8 Complementi di grafica 2D Un fondo di investimento ventennale frutta il 5% di interessi composti annualmente. Un capitale di 10.000
Laboratorio di Matematica Computazionale A.A. 2007-2008 - Laboratorio nr.8 Complementi di grafica 2D Un fondo di investimento ventennale frutta il 5% di interessi composti annualmente. Un capitale di 10.000
MINIMI QUADRATI. REGRESSIONE LINEARE
 MINIMI QUADRATI. REGRESSIONE LINEARE Se il coefficiente di correlazione r è prossimo a 1 o a -1 e se il diagramma di dispersione suggerisce una relazione di tipo lineare, ha senso determinare l equazione
MINIMI QUADRATI. REGRESSIONE LINEARE Se il coefficiente di correlazione r è prossimo a 1 o a -1 e se il diagramma di dispersione suggerisce una relazione di tipo lineare, ha senso determinare l equazione
Lezione 9: Cambio di base
 Lezione 9: Cambio di base In questa lezione vogliamo affrontare uno degli argomenti piu ostici per lo studente e cioè il cambio di base all interno di uno spazio vettoriale, inoltre cercheremo di capire
Lezione 9: Cambio di base In questa lezione vogliamo affrontare uno degli argomenti piu ostici per lo studente e cioè il cambio di base all interno di uno spazio vettoriale, inoltre cercheremo di capire
Algoritmi di clustering
 Algoritmi di clustering Dato un insieme di dati sperimentali, vogliamo dividerli in clusters in modo che: I dati all interno di ciascun cluster siano simili tra loro Ciascun dato appartenga a uno e un
Algoritmi di clustering Dato un insieme di dati sperimentali, vogliamo dividerli in clusters in modo che: I dati all interno di ciascun cluster siano simili tra loro Ciascun dato appartenga a uno e un
Codifica delle immagini
 Codifica delle immagini Abbiamo visto come la codifica di testi sia (relativamente) semplice Un testo è una sequenza di simboli Ogni simbolo è codificato con un numero Ed ecco che il testo è trasformato
Codifica delle immagini Abbiamo visto come la codifica di testi sia (relativamente) semplice Un testo è una sequenza di simboli Ogni simbolo è codificato con un numero Ed ecco che il testo è trasformato
Algoritmi e diagrammi di flusso
 Algoritmi e diagrammi di flusso Un algoritmo può essere descritto come una sequenza finita ed ordinata di operazioni che descrivono la soluzione di un problema. Per sequenza finita si intende che un algoritmo
Algoritmi e diagrammi di flusso Un algoritmo può essere descritto come una sequenza finita ed ordinata di operazioni che descrivono la soluzione di un problema. Per sequenza finita si intende che un algoritmo
Linguaggi di programmazione
 Linguaggi di programmazione Un calcolatore basato sul modello di von Neumann permette l esecuzione di un programma, cioè di una sequenza di istruzioni descritte nel linguaggio interpretabile dal calcolatore
Linguaggi di programmazione Un calcolatore basato sul modello di von Neumann permette l esecuzione di un programma, cioè di una sequenza di istruzioni descritte nel linguaggio interpretabile dal calcolatore
Processo di rendering
 Processo di rendering Trasformazioni di vista Trasformazioni di vista Il processo di visione in tre dimensioni Le trasformazioni di proiezione 2 Rendering nello spazio 2D Il processo di rendering (visualizzazione)
Processo di rendering Trasformazioni di vista Trasformazioni di vista Il processo di visione in tre dimensioni Le trasformazioni di proiezione 2 Rendering nello spazio 2D Il processo di rendering (visualizzazione)
Esponenziali elogaritmi
 Esponenziali elogaritmi Potenze ad esponente reale Ricordiamo che per un qualsiasi numero razionale m n prendere n>0) si pone a m n = n a m (in cui si può sempre a patto che a sia un numero reale positivo.
Esponenziali elogaritmi Potenze ad esponente reale Ricordiamo che per un qualsiasi numero razionale m n prendere n>0) si pone a m n = n a m (in cui si può sempre a patto che a sia un numero reale positivo.
Capitolo 13. Interrogare una base di dati
 Capitolo 13 Interrogare una base di dati Il database fisico La ridondanza è una cosa molto, molto, molto brutta Non si devono mai replicare informazioni scrivendole in più posti diversi nel database Per
Capitolo 13 Interrogare una base di dati Il database fisico La ridondanza è una cosa molto, molto, molto brutta Non si devono mai replicare informazioni scrivendole in più posti diversi nel database Per
Principi e Metodologie della Progettazione Meccanica
 Principi e Metodologie della Progettazione Meccanica Corso del II anno della laurea magistrale in ingegneria meccanica ing. F. Campana Modellazione di superfici: introduzione Curve parametriche di Hermite
Principi e Metodologie della Progettazione Meccanica Corso del II anno della laurea magistrale in ingegneria meccanica ing. F. Campana Modellazione di superfici: introduzione Curve parametriche di Hermite
Contenimento in UML: alcune linee guida generali. Dr. Andrea Baruzzo [email protected] www.dimi.uniud.it/~baruzzo
 Contenimento in UML: alcune linee guida generali Dr. Andrea Baruzzo [email protected] www.dimi.uniud.it/~baruzzo Sommario La relazione «has-a» Composizione Aggregazione Linee guida object modeling
Contenimento in UML: alcune linee guida generali Dr. Andrea Baruzzo [email protected] www.dimi.uniud.it/~baruzzo Sommario La relazione «has-a» Composizione Aggregazione Linee guida object modeling
1. PRIME PROPRIETÀ 2
 RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
Si sa che la via più breve tra due punti è la linea retta. Ma vi siete mai chiesti, Qual è la via più breve tra tre punti? o tra quattro punti?
 Dov'è Moriart? Cerchiamo la via più breve con Mathcad Potete determinare la distanza più breve da tre punti e trovare Moriart? Si sa che la via più breve tra due punti è la linea retta. Ma vi siete mai
Dov'è Moriart? Cerchiamo la via più breve con Mathcad Potete determinare la distanza più breve da tre punti e trovare Moriart? Si sa che la via più breve tra due punti è la linea retta. Ma vi siete mai
Appunti di Sistemi Elettronici
 Prof.ssa Maria Rosa Malizia 1 LA PROGRAMMAZIONE La programmazione costituisce una parte fondamentale dell informatica. Infatti solo attraverso di essa si apprende la logica che ci permette di comunicare
Prof.ssa Maria Rosa Malizia 1 LA PROGRAMMAZIONE La programmazione costituisce una parte fondamentale dell informatica. Infatti solo attraverso di essa si apprende la logica che ci permette di comunicare
LA RETTA. Retta per l'origine, rette orizzontali e verticali
 Retta per l'origine, rette orizzontali e verticali LA RETTA Abbiamo visto che l'equazione generica di una retta è del tipo Y = mx + q, dove m ne rappresenta la pendenza e q il punto in cui la retta incrocia
Retta per l'origine, rette orizzontali e verticali LA RETTA Abbiamo visto che l'equazione generica di una retta è del tipo Y = mx + q, dove m ne rappresenta la pendenza e q il punto in cui la retta incrocia
CORSO DI FORMAZIONE MODELLAZIONE 3D RENDERING ANIMAZIONE
 RHINOCEROS FLAMINGO PENGUIN BONGO CORSO DI FORMAZIONE MODELLAZIONE 3D RENDERING ANIMAZIONE Gabriele Verducci RHINOCEROS FLAMINGO PENGUIN BONGO INDICE:.01 cenni di informatica differenza tra files bitmap
RHINOCEROS FLAMINGO PENGUIN BONGO CORSO DI FORMAZIONE MODELLAZIONE 3D RENDERING ANIMAZIONE Gabriele Verducci RHINOCEROS FLAMINGO PENGUIN BONGO INDICE:.01 cenni di informatica differenza tra files bitmap
MATEMATICA SCUOLA PRIMARIA CLASSE TERZA TRAGUARDI PER LO SVILUPPO DELLE COMPETENZE RELATIVI A NUMERI
 MATEMATICA SCUOLA PRIMARIA CLASSE TERZA TRAGUARDI PER LO SVILUPPO DELLE COMPETENZE RELATIVI A NUMERI L alunno si muove con sicurezza nel calcolo scritto e mentale con i numeri naturali e sa valutare l
MATEMATICA SCUOLA PRIMARIA CLASSE TERZA TRAGUARDI PER LO SVILUPPO DELLE COMPETENZE RELATIVI A NUMERI L alunno si muove con sicurezza nel calcolo scritto e mentale con i numeri naturali e sa valutare l
Fasi di creazione di un programma
 Fasi di creazione di un programma 1. Studio Preliminare 2. Analisi del Sistema 6. Manutenzione e Test 3. Progettazione 5. Implementazione 4. Sviluppo 41 Sviluppo di programmi Per la costruzione di un programma
Fasi di creazione di un programma 1. Studio Preliminare 2. Analisi del Sistema 6. Manutenzione e Test 3. Progettazione 5. Implementazione 4. Sviluppo 41 Sviluppo di programmi Per la costruzione di un programma
B+Trees. Introduzione
 B+Trees Introduzione B+Trees Il B+Trees e la variante maggiormente utilizzata dei BTrees BTrees e B+trees fanno parte della famiglia degli alberi di ricerca. Nel B+Trees i dati sono memorizzati solo nelle
B+Trees Introduzione B+Trees Il B+Trees e la variante maggiormente utilizzata dei BTrees BTrees e B+trees fanno parte della famiglia degli alberi di ricerca. Nel B+Trees i dati sono memorizzati solo nelle
