AUTOVALORI E AUTOVETTORI
|
|
|
- Gianpaolo Amedeo Manzo
- 6 anni fa
- Visualizzazioni
Transcript
1 Capitolo 4 AUTOVALORI E AUTOVETTORI Abbiamo visto nel paragrafo 2.17 che la matrice associata ad una applicazione lineare f : R n R m dipende dalle basi scelte in R n e R m. Un problema interessante che si presenta quando n = m è il seguente: esiste in R n una base per cui la matrice associata ad f ha forma diagonale? Come vedremo in questo capitolo la risposta, che non è sempre affermativa, dipende da un insieme particolare di vettori legati alla matrice e detti autovettori. 4.1 Definizione. Sia A R n n. Un numero λ per cui esiste un vettore x 0 tale che valga la relazione Ax = λx (1) è detto autovalore di A ed x è detto autovettore corrispondente a λ. L insieme degli autovalori di A costituisce lo spettro di A e il modulo massimo ρ(a) degli autovalori è detto raggio spettrale di A. 4.2 Polinomio caratteristico. Il sistema (1), che si può scrivere anche nella forma ammette soluzioni non nulle se e solo se (A λi)x = 0, (2) det(a λi) = 0. (3) Sviluppando il determinante della matrice a 11 λ a 12 a 1n a A λi = 21 a 22 λ a 2n a n1 a n2 a nn λ
2 Capitolo 4. Autovalori e autovettori 60 con la (1, cap. 3), si vede che det(a λi) è un polinomio p(λ) i cui coefficienti dipendono dagli elementi di A. Uno dei termini dello sviluppo è dato dal prodotto degli elementi principali di A λi ed è uguale a (a 11 λ) (a nn λ) e nessun altro termine dello sviluppo contiene più di n 2 fattori della forma (a ii λ). Quindi il grado di p(λ) è esattamente n e i coefficienti di λ n e di λ n 1 risultano rispettivamente uguali a ( 1) n e ( 1) n 1 (a a nn ). L ultimo coefficiente è dato da p(0) = det A. Si può quindi scrivere p(λ) = det(a λi) = ( 1) n λ n + (1) n 1 tra λ n det A, in cui si è indicata con tra la traccia di A, cioè la somma degli elementi principali di A. Il polinomio p(λ) è detto polinomio caratteristico di A e l equazione p(λ) = 0 è detta equazione caratteristica di A. Gli autovalori di A sono tutte e sole le soluzioni dell equazione caratteristica. Per il teorema fondamentale dell algebra l equazione caratteristica ha nel campo complesso n radici, tenendo conto della loro molteplicità. Quindi una matrice di ordine n ha, tenendo conto della loro molteplicità, n autovalori nel campo complesso. Gli autovettori sono dunque le soluzioni non nulle del sistema lineare omogeneo (2); quindi un autovettore corrispondente ad un autovalore λ risulta determinato a meno di una costante moltiplicativa k 0, cioè se x è autovettore di A, anche kx è autovettore di A, corrispondente allo stesso autovalore. Ad esempio, il polinomio caratteristico della matrice 1 3 A = 3 1 si ricava dal determinante det(a λi) = det L equazione caratteristica corrispondente 1 λ 3 = λ 2 2λ λ λ 2 2λ 8 = 0 ha come radici λ 1 = 2 e λ 2 = 4, che sono gli autovalori di A. L autovettore corrispondente a λ 1 = 2 si calcola risolvendo il sistema (2) che in questo caso diventa 3 3 x1 = x 2
3 61 Capitolo 4. Autovalori e autovettori Dalla prima equazione si ottiene x 1 + x 2 = 0, da cui x 1 = x 2, e ne segue che qualunque vettore della forma x 1 = k 1 1 con k 0, è autovettore di A corrispondente all autovalore λ 1 = 2. L autovettore corrispondente a λ 2 = 4 si determina risolvendo il sistema 3 3 x1 = x 2 Dalla prima equazione si ottiene x 1 + x 2 = 0, da cui x 1 = x 2, e ne segue che qualunque vettore della forma x 1 = k 1 1 con k 0, è autovettore di A corrispondente all autovalore λ 2 = 4. Se ripetiamo lo stesso procedimento con la matrice A = si ricava dall equazione caratteristica 2 1, 1 2 λ 2 4λ + 5 = 0 che gli autovalori sono λ 1 = 2 + i e λ 2 = 2 i. Risolvendo i sistemi (2) si ottengono gli autovalori x 1 corrispondente a λ 1 e x 2 corrispondente a λ 2 dove x 1 = k i 1 e x 2 = k i 1 con k Somma e prodotto degli autovalori. Dalle relazioni che legano i coefficienti e le radici di un equazione algebrica risulta che: n n λ i = tr A e λ i = det A. (4) i=1 i=1
4 4.4 Proprietà degli autovalori. Capitolo 4. Autovalori e autovettori 62 a) Gli autovalori di una matrice A diagonale o triangolare (superiore o inferiore) sono uguali agli elementi principali. Infatti la matrice A λi è ancora diagonale o triangolare e quindi det(a λi) = n (a ii λ). i=1 b) Un autovalore λ di A è anche autovalore di A T. Infatti det(a λi) = det(a λi) T = det(a T λi), e quindi se det(a λi) = 0 è det(a T λi) = 0. Sia λ un autovalore di A e x un autovettore corrispondente. Allora c) λ i è autovalore di A i e x è un autovettore corrispondente. Infatti A i x = A i 1 Ax = A i 1 λx = λa i 1 x = λa i 2 Ax =... = λ i x. d) Se B = b 0 A k + b 1 A k b k I, dove b 0, b 1,..., b k R, allora µ = b 0 λ k + b 1 λ k b k è autovalore di B e x è un autovettore corrispondente. Infatti Bx = b 0 A k x + b 1 A k 1 x + + b k x = b 0 λ k x + b 1 λ k 1 x + + b k x = µx. e) Se A è non singolare, allora λ 0 e 1/λ è autovalore di A 1 con x autovettore corrispondente. Infatti da Ax = λx si ha e quindi x = λa 1 x λ 0 e A 1 x = 1 λ x. Per esempio, la matrice A = (5) 0 1 1
5 63 Capitolo 4. Autovalori e autovettori ha gli autovalori λ 1 = 1 2, λ 2 = 1, λ 3 = e i corrispondenti autovettori sono x 1 = 1 2, x 2 = 1 0, x 3 = La matrice A 1 ha gli autovalori 1/λ 1 = 2 1, 1/λ 2 = 1, 1/λ 3 = 2 1 e gli stessi autovettori di A. La matrice ha gli autovalori 2 1 B = 3A 2 A + 2I = , (6) µ i = 3λ 2 i λ i + 2, per i = 1, 2, 3, cioè µ 1 = , µ 2 = 4, µ 3 = e gli stessi autovettori di A Molteplicità di un autovalore e autospazio corrispondente. Sia λ un autovalore di A. Si chiama molteplicità algebrica di λ, e si indica con σ(λ), la molteplicità di λ come radice dell equazione caratteristica, autospazio di λ l insieme V λ di tutti gli autovettori corrispondenti a λ (è facile verificare che V λ è un sottospazio di R n ), molteplicità geometrica di λ, e si indica con τ(λ), la dimensione di V λ e quindi il massimo numero di autovettori linearmente indipendenti corrispondenti a λ. Se due autovalori sono distinti i corrispondenti autospazi sono disgiunti. Vale infatti il seguente teorema. 4.6 Teorema. Autovettori corrispondenti ad autovalori distinti sono linearmente indipendenti. Dim. Siano λ 1,..., λ m, m n, m autovalori di A a due a due distinti, e siano x 1,..., x m i corrispondenti autovettori. Si procede per induzione su m. Per m = 1, x 1 0, quindi x 1 è linearmente indipendente.
6 Capitolo 4. Autovalori e autovettori 64 Per m > 1, si supponga per assurdo che esista una combinazione lineare dei vettori x 1,..., x m tale che m α i x i = 0, (7) i=1 in cui non tutti gli α i siano nulli e sia j tale che α j 0. In tal caso esiste almeno un altro indice k j, per cui α k 0; altrimenti, se ciò non fosse, seguirebbe che x j = 0. Moltiplicando entrambi i membri della (7) per A, si ottiene m m m 0 = A α i x i = α i Ax i = α i λ i x i, (8) i=1 moltiplicando entrambi i membri della (7) per λ j, si ottiene i=1 i=1 m 0 = λ j α i x i = i=1 m α i λ j x i. (9) i=1 Sottraendo membro a membro la (9) dalla (8), si ha: 0 = m α i (λ i λ j )x i = i=1 m α i (λ i λ j )x i. i=1 i j Si ottiene così una combinazione lineare nulla degli m 1 autovettori x i 0, i = 1,..., m, i j, in cui λ i λ j 0 per i j e gli α i per i j non sono tutti nulli, essendo α k 0, ciò che è assurdo perché per l ipotesi induttiva gli m 1 vettori sono linearmente indipendenti. Dal teorema 4.6 risulta che se A ha n autovalori tutti distinti e quindi tutti di molteplicità algebrica 1, allora A ha n autovettori linearmente indipendenti. Quindi l autospazio corrispondente ad ogni autovalore ha dimensione 1. Se A non ha n autovalori distinti, può avere n autovettori linearmente indipendenti oppure no. Per esempio, la matrice identica I di R n n, che ha il solo autovalore 1, ha tutti i vettori e i della base canonica di R n come autovettori, infatti è Quindi risulta τ(1) = σ(1) = n. I e i = e i, per i = 1,..., n.
7 65 Capitolo 4. Autovalori e autovettori Invece la matrice A = ha 1 come autovalore di molteplicità algebrica n a cui corrispondono solo autovettori della forma x = ke 1, k 0. In questo caso risulta quindi τ(1) = 1 e σ(1) = n. Vale sempre la disuguaglianza 1 τ(λ) σ(λ) n., 4.7 Matrici simili. Ritorniamo al problema che ci eravamo posti all inizio del capitolo: se A è la matrice associata all applicazione lineare f : R n R n, è possibile cambiare la base di R n in modo che la matrice B associata ad f nella nuova base abbia forma diagonale? Dalla (18, cap. 2) segue che, se P è la matrice del cambiamento di base, le due matrici A e B sono legate dalla relazione A = P BP 1. (10) Due matrici A, B R n n si dicono simili se esiste una matrice non singolare P per cui vale la (10). La trasformazione che associa la matrice A alla matrice B viene detta trasformazione per similitudine. Se la matrice P è tale che P T P = I (cioè le colonne di P formano una base ortonormale di R n ) la trasformazione viene detta unitaria. La trasformazione per similitudine è una relazione di equivalenza, in quanto gode delle proprietà riflessiva, simmetrica e transitiva. Le proprietà degli autovalori e autovettori sono proprietà intrinseche dell applicazione lineare e non legate solamente alla matrice che la rappresenta in una particolare base. Vale infatti il seguente teorema. 4.8 Teorema. Due matrici simili hanno gli stessi autovalori con le stesse molteplicità algebriche e geometriche.
8 Capitolo 4. Autovalori e autovettori 66 Dim. Siano A e B matrici simili, cioè tali che A = P BP 1. Si ha: det(a λi) = det(p BP 1 λp P 1 ) = det [P (B λi)p 1 ] = det P det(b λi) det(p 1 ) = det(b λi) per cui le due matrici hanno lo stesso polinomio caratteristico e quindi hanno gli stessi autovalori con le stesse molteplicità algebriche. Se x è autovettore di A corrispondente all autovalore λ, risulta: e quindi P BP 1 x = λx BP 1 x = λp 1 x. Perciò il vettore y = P 1 x è autovettore di B corrispondente a λ. Inoltre, essendo P 1 non singolare, se x i, i = 1,..., τ(λ), sono autovettori linearmente indipendenti di A, anche y i = P 1 x i, i = 1,..., τ(λ) sono linearmente indipendenti. Quindi A e B hanno gli stessi autovalori con le stesse molteplicità geometriche. Da questo teorema risulta che se due matrici sono simili, hanno uguali la traccia e il determinante. 4.9 Matrici diagonalizzabili. Una matrice A simile ad una matrice diagonale D si dice diagonalizzabile Teorema. Una matrice A di ordine n è diagonalizzabile se e solo se ha n autovettori linearmente indipendenti. Inoltre le colonne della matrice P, per cui P 1 AP è diagonale, sono gli autovettori di A. Dim. Si suppone dapprima che A abbia n autovettori linearmente indipendenti x 1,..., x n, corrispondenti agli autovalori λ 1,..., λ n. Siano D la matrice diagonale avente λ i come i-esimo elemento principale, e P la matrice la cui i-esima colonna è uguale a x i. Dalla relazione si ha anche che Ax i = λ i x i, i = 1, 2,..., n, AP = P D. (11) Essendo P non singolare, perché formata da colonne linearmente indipendenti, esiste P 1 ; quindi dalla (11) si ha A = P DP 1.
9 67 Capitolo 4. Autovalori e autovettori Viceversa, sia A = P DP 1, D matrice diagonale con gli autovalori di A come elementi principali. Allora risulta AP = P D. Indicando con p 1,..., p n le colonne di P, si ha: A [p 1 p 2 p n ] = [λ 1 p 1 λ 2 p 2 λ n p n ] e quindi Ap i = λ i p i, i = 1, 2,..., n. Perciò le colonne di P sono n autovettori di A, che risultano linearmente indipendenti, perché P è non singolare. Per esempio, le matrici A definita in (5) e B = 3A 2 A + 2I definita in (6) hanno entrambe tre autovalori distinti e gli stessi tre autovettori linearmente indipendenti. Quindi sono diagonalizzabili dalla stessa trasformazione per similitudine. Posto P = , si ha e P 1 = 1/4 2/4 1/4 1/2 0 1/2 1/4 2/4 1/4 A = P B = P P 1, P 1. 2 Dai teoremi 4.6 e 4.10 segue che se una matrice ha tutti gli autovalori distinti, allora è diagonalizzabile, in quanto ha n autovettori linearmente indipendenti. Se una matrice non ha tutti gli autovalori distinti, può non essere diagonalizzabile e questo accade se per almeno un autovalore di A la molteplicità geometrica è minore della corrispondente molteplicità algebrica. Vi è un importante classe di matrici che sono sicuramente diagonalizzabili anche se hanno autovalori non tutti distinti. Si tratta delle matrici simmetriche.
10 Capitolo 4. Autovalori e autovettori Matrici simmetriche. Una matrice A R n n si dice simmetrica se A T = A. L insieme delle matrici simmetriche è chiuso rispetto all operazione di inversione, mentre non lo è rispetto all operazione di moltiplicazione, infatti se A = A T e A = B T, è (AB) T = B T A T = BA AB Teorema. Gli autovalori delle matrici simmetriche sono reali. Dim. Supponiamo per assurdo che la matrice A simmetrica abbia un autovalore complesso λ = a + ib, con b 0. La matrice A λi è singolare, quindi è singolare anche la matrice B = (A λi)(a λi) = (A ai) 2 + b 2 I. Sia x un autovettore di B relativo all autovalore 0; risulta 0 = x T Bx = x T (A ai) 2 x + b 2 x T x. Posto y = (A ai)x, dalla simmetria di A segue che y T y + b 2 x T x = 0, e questo è assurdo perché y T y 0 e x T x > 0 e b 0. Una matrice simmetrica è sempre diagonalizzabile. Vale infatti il seguente teorema Teorema. Sia A una matrice simmetrica di ordine n e siano λ 1,..., λ n i suoi autovalori. Allora A è diagonalizzabile per trasformazione unitaria. Dim. Si procede per induzione. Per n = 1 la tesi vale con P = [1]. Per n > 1, consideriamo un autovalore λ 1, che è sicuramente reale e un corrispondente autovettore normalizzato x 1 a elementi reali. Sia S lo spazio generato da x 1. Indicata con y 2,..., y n una base ortonormale dello spazio S, la matrice Q = [ x 1 y 2 y n ]
11 69 Capitolo 4. Autovalori e autovettori è tale che Q T Q = I e Q T x 1 = e 1. La matrice B = Q T AQ è simmetrica, infatti si ha B T = (Q T AQ) T = Q T A T Q = Q T AQ = B. Poiché la prima colonna di B è Be 1 = Q T AQe 1 = Q T Ax 1 = Q T λ 1 x 1 = λ 1 Q T x 1 = λ 1 e 1, B può essere partizionata nel modo seguente: B = λ 1 0 T, 0 A 1 dove A 1 R (n 1) (n 1) è ancora simmetrica. Per l ipotesi induttiva A 1 è diagonalizzabile per trasformazione unitaria, cioè esiste una matrice U R (n 1) (n 1) tale che U T U = I e A 1 = UA 2 U T, dove A 2 R (n 1) (n 1) è diagonale. Allora risulta La matrice A = QBQ T = Q λ 1 0 T Q T = Q λ 1 0 T Q T 0 A 1 0 UA 2 U T = Q 1 0T λ 1 0 T 1 0T Q T. 0 U 0 A 1 0 U T P = Q 1 0T 0 U è tale che P T P = 1 0T Q T Q 1 0T = 1 0T 0 U T 0 U 0 U T 1 0T = 0 U 1 0T = I, 0 U T U
12 e Capitolo 4. Autovalori e autovettori 70 A = P λ 1 0 T P T, 0 A 2 da cui la tesi, essendo A 2 matrice diagonale. Poichè le colonne di P sono gli autovettori di A, da questo teorema segue che una matrice simmetrica ha n autovettori ortonormali. Per esempio, la matrice A = è simmetrica. I suoi autovalori sono λ 1 = 9, λ 2 = 9 e λ 3 = 18. I corrispondenti autovettori sono x 1 = 1 2, x 2 = , x 3 = È facile verificare che gli autovettori sono ortogonali. Per ottenere la matrice P occorre però normalizzare gli autovettori, moltiplicandoli per 1/3. Si ottiene così A = P DP T, dove P = , D = Forma quadratica associata ad una matrice simmetrica. Si chiama forma quadratica associata ad una matrice A R n n una espressione della forma x T Ax, dove x R n. Espandendo questa espressione rispetto alle componenti x 1, x 2,..., x n di x, si vede che la forma quadratica è uguale ad un polinomio di secondo grado omogeneo nelle variabili x 1, x 2,..., x n. Se la matrice A è simmetrica, la forma quadratica si può esprimere in modo molto semplice in termini degli autovalori di A. Infatti dal teorema 4.13 si ha
13 71 Capitolo 4. Autovalori e autovettori λ 1 A = P DP T, dove D = λ 2... λn, e quindi avendo posto y = P T x, e quindi x T Ax = x T P DP T x = y T Dy, x T Ax = [y 1,..., y n ] D y 1. y n = λ 1 y λ n y 2 n. (12) 4.15 Teorema. Sia A una matrice simmetrica di ordine n. Allora le due condizioni: a) la forma quadratica x T Ax è positiva per ogni x 0, b) gli autovalori di A sono tutti positivi, sono equivalenti. Dim. a) b) Sia λ un autovalore e x 0 un autovettore corrispondente; da Ax = λx, premoltiplicando per x T, si ottiene x T Ax = λx T x, in cui il primo membro è positivo, ed essendo x T x > 0, risulta λ > 0. b) a) Sia x R n. Dalla (12) segue che x T Ax = λ 1 y λ n y 2 n, dove λ 1,..., λ n sono gli autovalori di A, che per il teorema 4.12 sono reali, e y = P T x. Se x 0, anche y 0, perché P è non singolare. Ne segue che x T Ax > 0 perché λ i > 0 per i = 1,..., n e gli y i non sono tutti nulli Matrici definite positive. Le matrici simmetriche che soddisfano alle condizioni del teorema 4.15 sono dette definite positive e si presentano spesso nelle applicazioni. Poiché il prodotto degli autovalori di una matrice è uguale al determinante, dal teorema 4.15 segue che il determinante di una matrice definita
14 Capitolo 4. Autovalori e autovettori 72 positiva è positivo. Segue inoltre che l inversa di una matrice definita positiva è ancora definita positiva. Infatti l inversa A 1 di una matrice simmetrica A è simmetrica, e gli autovalori di A 1 sono positivi in quanto reciproci di quelli di A. Per esempio, la matrice simmetrica A = è definita positiva, infatti per ogni vettore x = [x 1, x 2, x 3 ] T 0 si ha x T Ax = (2x 1 x 2 ) 2 + (2x 2 + x 3 ) 2 + x x x 2 3 > 0. Il suo polinomio caratteristico è dato da P (λ) = λ λ 2 99λ = (λ 3)(λ 6)(λ 9), e gli autovalori sono tutti positivi Forma canonica o normale di Jordan. Abbiamo visto che una matrice è diagonalizzabile solo se possiede n autovettori linearmente indipendenti Viene allora da chiedersi se non sia possibile trovare una forma abbastanza vicina a quella diagonale a cui ridurre la matrice nel caso più generale in cui vi siano meno di n autovettori linearmente indipendenti. A questa domanda risponde la seguente forma canonica o normale di Jordan. Sia A R n n e siano λ i, i = 1,..., p, i suoi autovalori distinti, con molteplicità algebrica σ(λ i ) e molteplicità geometrica τ(λ i ). Allora A è simile ad una matrice diagonale a blocchi J 1 J J = 2,... Jp in cui il blocco J i, relativo all autovalore λ i, ha ordine σ(λ i ) ed è a sua volta diagonale a blocchi J i = C (1) i C (2) i... C (τ(λi)) i, i = 1, 2,..., p,
15 73 Capitolo 4. Autovalori e autovettori e ognuno dei τ(λ i ) blocchi è della forma λ i C (j) i = λ i 1 λ i Cν(j) i ν (j) i, j = 1, 2,..., τ(λ i ), dove gli interi ν (j) i sono tali che τ(λ i ) j=1 ν (j) i = σ(λ i ). La matrice J è detta forma canonica (o normale) di Jordan della matrice A, ed è unica, a meno dell ordinamento dei blocchi che la compongono. Se gli autovalori λ i di A sono tutti distinti, i blocchi J i hanno tutti ordine 1, e quindi la matrice è diagonalizzabile. Se invece gli autovalori non sono tutti distinti, ma A ha n autovettori linearmente indipendenti, allora i blocchi J i sono diagonali, e anche in questo caso la matrice è diagonalizzabile. È possibile che matrici diverse abbiano gli stessi autovalori con le stesse molteplicità algebriche e geometriche e siano riconducibili alle rispettive forme di Jordan con la stessa trasformazione per similitudine. e Per esempio, le matrici A 1 = A 2 = hanno entrambe l autovalore λ = 2 di molteplicità algebrica 6 e geometrica 3, ma forme di Jordan diverse, come risulta dalle reazioni seguenti:
16 e A 1 = P J P = P A 2 = P J P 1 = P dove P =, P = Localizzazione degli autovalori. Capitolo 4. Autovalori e autovettori P 1 P 1, Il calcolo effettivo degli autovalori di una matrice non è facile, soprattutto quando la matrice è di grandi dimensioni. Si deve ricorrere a metodi numerici, che in generale sono iterativi e quindi richiedono di possedere una stima, magari non molto precisa, dell autovalore che si vuole approssimare. Talvolta la precisione con cui si vogliono calcolare gli autovalori è così bassa che anche una stima un po grossolana può bastare. La stima più semplice si ottiene dal teorema di Gerschgorin Cerchi di Gerschgorin. Sia A R n n. I cerchi del piano complesso K i = { z C : z a ii di centro a ii e raggio r i = n a ij }, i = 1, 2,..., n, j=1 j i n a ij sono detti cerchi di Gerschgorin. j=1 j i
17 75 Capitolo 4. Autovalori e autovettori 4.20 Teorema di Gerschgorin. Gli autovalori della matrice A di ordine n sono tutti contenuti in K i. i=1,...,n Dim. Sia λ un autovalore di A e x un autovettore corrispondente, ossia Allora si ha: da cui Ax = λ x, x 0. n a ij x j = λ x i, i = 1,..., n, j=1 (λ a ii )x i = n j=1 j i a ij x j, i = 1,..., n. (13) Sia x p la componente di x di massimo modulo, cioè quella per cui e, ponendo i = p nella (13), si ha: da cui: e, per la (14), x p = max j=1,...,n x j = 0, (14) (λ a pp )x p = λ a pp x p λ a pp x p infine dividendo per x p > 0, si ottiene λ a pp n j=1 j p n j=1 j p n j=1 j p a pj x j ; a pj x j, a pj x p ; n a pj, j=1 j p
18 Capitolo 4. Autovalori e autovettori 76 e quindi λ K p. Si osservi che, poiché a priori non è noto il valore dell indice p, è possibile solo dire che λ appartiene all unione di tutti i cerchi K i. Poiché il teorema precedente può essere applicato anche alla matrice A T, che ha gli stessi autovalori della matrice A, risulta che gli autovalori di A appartengono anche all unione dei cerchi H i = { z C : z a ii n a ji }, i = 1, 2,..., n, j=1 j i e quindi gli autovalori di A appartengono all insieme ( ) ( ) K i H i. sono i=1,...,n i=1,...,n Per esempio, i cerchi di Gerschgorin della matrice A = K 1 = {z C : z 15 4}, K 2 = {z C : z 10 4}, K 3 = {z C : z 3}. K 3 K 2 K Per il teorema gli autovalori stanno nelle aree grigie. Consideriamo poi i cerchi H 1 = {z C : z 15 3}, associati alla matrice A T. H 2 = {z C : z 10 3}, H 3 = {z C : z 5},
19 77 Capitolo 4. Autovalori e autovettori H 3 H 2 H Quindi gli autovalori di A stanno nell intersezione dei due insiemi di cerchi K 3 H 2 H Si può poi dimostrare che se l unione M 1 di k cerchi di Gerschgorin è disgiunta dall unione M 2 dei rimanenti n k, allora k autovalori appartengono a M 1 e n k autovalori appartengono a M 2. Dei tre autovalori della matrice A dell esempio, uno è contenuto in K 3, mentre gli altri due appartengono ad H 1 H 2. I due autovalori contenuti in H 1 H 2 possono essere reali o complessi e hanno modulo compreso fra 7 e 18. L autovalore contenuto in K 3 è reale; infatti, se avesse parte immaginaria non nulla, anche il suo coniugato dovrebbe essere un autovalore di A, essendo zero di un polinomio a coefficienti reali, e apparterrebbe ancora a K 3, mentre sappiamo che in K 3 c è un solo autovalore Predominanza diagonale. Un altra classe importante di matrici è quella delle matrici a predominanza diagonale, che si presentano spesso nella risoluzione numerica di problemi differenziali.
20 Capitolo 4. Autovalori e autovettori 78 Una matrice A R n n si dice a predominanza diagonale in senso stretto se per ogni i = 1,..., n risulta a ii > j=1 j i a ij. La definizione di predominanza diagonale in senso stretto si può dare anche per colonne, considerando le somme per colonne anziché per righe e in tal caso si specifica che la predominanza diagonale in senso stretto è per colonne Teorema. Una matrice a predominanza diagonale in senso stretto è non singolare. Se inoltre A ha elementi principali tutti reali e positivi, allora gli autovalori di A hanno parte reale positiva e se A è anche simmetrica, allora A è definita positiva. Dim. Se A è a predominanza diagonale in senso stretto i cerchi di Gerschgorin, avendo raggio minore della distanza del centro dall origine del piano complesso, non possono includere l origine, e quindi A non può avere un autovalore nullo. Se inoltre A ha elementi principali tutti positivi, nessun cerchio può contenere numeri complessi a parte reale negativa. Quindi se A è anche simmetrica, cioè con autovalori reali, questi devono essere positivi, e quindi la matrice è definita positiva. Poiché gli autovalori della matrice A sono uguali a quelli della matrice A T, le tesi del teorema 4.22 valgono anche nel caso in cui la predominanza diagonale in senso stretto della matrice sia per colonne Esercizi. 1. Sia A R n n. Si definisce traccia di A la somma dei termini principali di A: n tr A = a ii. i=1 Dimostrare che tr (A + B) = tr A + tr B,, tr (αa) = α tr A, α R, tr (AB) = tr (BA), n tr (AA T ) = tr (A T A) = i,j=1 a 2 ij.
21 79 Capitolo 4. Autovalori e autovettori 2. Dimostrare che l insieme delle matrici simmetriche è uno spazio vettoriale su R di dimensione n(n + 1)/ Dimostrare che una matrice simmetrica e triangolare è diagonale. Dire per quali valori dei parametri α e β la matrice 1 3 A = 2 2 α β è a) simmetrica b) definita positiva. 5. Siano A e B due matrici simmetriche. Far vedere con un esempio che la matrice AB non è sempre simmetrica e dimostrare che lo è se e solo se A e B commutano. 6. Sia A R n n. Dimostrare che se A è simmetrica, anche adja e A 1 sono simmetriche. 7. Sia A R n n. Verificare che le matrici AA T, A T A, e A+A T sono simmetriche e che, se A non è singolare, le matrici A T A e AA T sono definite positive. 8. Sia A R n n una matrice definita positiva. Dimostrare che a) gli elementi principali sono positivi, b) l elemento di massimo modulo è un elemento principale. (Traccia: imporre la condizione che la forma quadratica x T Ax > 0, dove x = e i, per i = 1,..., n nel caso a) e x = e i + e j, x = e i e j, per i, j = 1,..., n nel caso b).) 9. Determinare il polinomio caratteristico delle seguenti matrici , , Calcolare autovalori e autovettori delle matrici ,, 1 1 0,
22 Capitolo 4. Autovalori e autovettori Dire se la matrice A = ha un autovalore maggiore o uguale a 20. (Traccia: verificare che det(a 20I) < 0.) 12. Verificare che il raggio spettrale della matrice A = è maggiore di Sia A R n n la matrice i cui elementi sono dati da a ij = { i per i = j, 1 per i < j, 0 per i > j. Determinare gli autovalori e gli autovettori di A e A T. (Traccia: tenendo presente l esercizio 13 cap. 3, dimostrare che A = XDX 1 e A T = X T DX T, dove X = , D = ) n 14. Siano A, B R n n. Dimostrare che le matrici AB e BA hanno gli stessi autovalori. Se A e B sono singolari, è possibile che AB e BA, pur avendo gli stessi autovalori, non siano simili: esaminare il caso A = 1 0, B = (Traccia: se una delle due matrici, ad esempio A, è non singolare, è AB = A(BA)A 1, e quindi le matrici AB e BA sono simili. In generale, se λ 0 è autovalore di AB, cioè ABx = λx, x 0, allora
23 81 Capitolo 4. Autovalori e autovettori Bx 0 e (BA)Bx = λbx. Quindi λ è autovalore di BA. Se AB è singolare, anche BA lo è.) 15. Dimostrare che gli autovalori della matrice A R n n i cui elementi sono dati da a ij = { αi se i = 1, j = n e j = i 1, per i = 2,..., n, 0 altrimenti, dove α 1 α 2 α n = 1, sono i numeri λ k = cos 2πk n 2πk + i sin, k = 1, 2,..., n. n (Traccia: calcolare il polinomio caratteristico.) 16. Sia A la matrice A = 1 α, 0 1 dove α 0. Verificare che A non può essere diagonalizzata. 17. Sia A la matrice diagonale a blocchi A 11 A A = Ann, con blocchi diagonali quadrati. a) Dimostrare che lo spettro degli autovalori di A è dato dall unione degli spettri dei blocchi A 11, A 22,..., A nn ; b) dimostrare che la stessa proprietà vale se la matrice A è triangolare a blocchi; c) dire come sono fatti gli autovettori di A. Siano x, y R n. Determinare autovalori e autovettori delle ma- 18. trici A = xy T e I + xy T. (Traccia: tenere conto che la matrice xy H ha rango 1 e che xy H x = (y H x)x; quali sono i vettori z 0 tali che xy H z = 0?)
24 Capitolo 4. Autovalori e autovettori Siano A e B R n n. Dimostrare che lo spettro degli autovalori della matrice A B C = B A è costituito dall unione degli spettri delle matrici A + B e A B, e che gli autovettori di C sono i vettori x x e y, y in cui x e y sono gli autovettori di A + B e A B. 20. Dire quante e quali sono le matrici di ordine 6, non simili fra di loro, il cui polinomio caratteristico è dato da P (λ) = (3 λ) 4 (1 λ) 2. (Traccia: due matrici simili hanno la stessa forma normale di Jordan.) 21. Dire se la matrice A = ha autovalori complessi. (Traccia: sfruttare il teorema di Gerschgorin.) 22. Si calcolino gli autovalori della matrice A = Si determinino anche gli autovettori relativi all autovalore di modulo minimo. 23. Sia A la matrice 2n 2n i cui elementi a ij sono definiti nel modo seguente: a i,2n+1 i = 1 per i = 1,..., n, a i,2n+1 i = 1 per i = n+1,..., 2n,
25 83 Capitolo 4. Autovalori e autovettori a ij = 0, altrimenti. Si calcolino il determinante e gli autovalori di A. 24. Per quali valori reali di k la matrice A = k ha un autovalore di molteplicità (algebrica) 2? 25. Data l applicazione lineare f : R 2 R 2 definita dai valori 3 1 f(e 1 ) =, f(e 1 2 ) = 3 che assume sui vettori della base canonica, si consideri la matrice A associata ad f, e si trovi una base di R 2 rispetto alla quale la matrice associata ad f risulta diagonale. 26. Sia A = Si calcolino autovalori e autovettori di A. Si dica se A è diagonalizzabile, e, in tal caso, si indichi una matrice S tale che S 1 AS sia diagonale Si dimostri che la matrice A = non è diagonalizzabile con una trasformazione per similitudine. È data la matrice A = Si dica se è diagonalizzabile per similitudine, e in tal caso si determini una matrice che la diagonalizza. È possibile diagonalizzare A con una trasformazione unitaria? 29. Si dica se la matrice A = [ 0 ] 2 1 3
26 Capitolo 4. Autovalori e autovettori 84 è diagonalizzabile con una trasformazione per similitudine sui reali. Se lo è, si determini una matrice di trasformazione S. Si dica se è possibile scegliere S unitaria. 30. Si calcolino tutti gli autovalori della matrice n n A = Nell ipotesi che n sia pari, si calcolino gli autovettori relativi all autovalore di modulo minimo. 31. Si determinino autovalori e autovettori della matrice 0 1 A =. 4 3 Si dica se A è diagonalizzabile. Senza eseguire altri calcoli, si dica se A 2 è diagonalizzabile. 32. Siano u, v e z tre vettori ortonormali di R n, con n 3. Si dimostri che la matrice A = uv T + vu T è singolare (suggerimento: si consideri il vettore Az). Per n = 3 e u = 1/ 3[1 1 1] T, v = 1/ 2[1 0 1] T, si calcolino gli autovalori di A. 33. Si calcolino autovalori e autovettori della matrice A = A è diagonalizzabile per similitudine? 34. Si calcolino autovettori e autovalori della matrice ( ) 2 1 A = Si dica se la matrice
27 85 Capitolo 4. Autovalori e autovettori 36. è diagonalizzabile per similitudine. Si stabilisca se la matrice è diagonalizzabile per similitudine. 37. Si dica se la matrice A = è diagonalizzabile per similitudine.
CORSO DI ALGEBRA (M-Z) Prof. A. Venezia
 CORSO DI ALGEBRA (M-Z) Prof. A. Venezia 2015-16 Complementi ed Esercizi 1. AUTOVETTORI e AUTOVALORI di ENDOMORFISMI e MATRICI Una applicazione lineare avente per dominio e condominio lo stesso spazio vettoriale
CORSO DI ALGEBRA (M-Z) Prof. A. Venezia 2015-16 Complementi ed Esercizi 1. AUTOVETTORI e AUTOVALORI di ENDOMORFISMI e MATRICI Una applicazione lineare avente per dominio e condominio lo stesso spazio vettoriale
1 Addendum su Diagonalizzazione
 Addendum su Diagonalizzazione Vedere le dispense per le definizioni di autovettorre, autovalore e di trasformazione lineare (o matrice) diagonalizzabile. In particolare, si ricorda che una condizione necessaria
Addendum su Diagonalizzazione Vedere le dispense per le definizioni di autovettorre, autovalore e di trasformazione lineare (o matrice) diagonalizzabile. In particolare, si ricorda che una condizione necessaria
3. Elementi di Algebra Lineare.
 CALCOLO NUMERICO Francesca Mazzia Dipartimento Interuniversitario di Matematica Università di Bari 3. Elementi di Algebra Lineare. 1 Sistemi lineari Sia A IR m n, x IR n di n Ax = b è un vettore di m componenti.
CALCOLO NUMERICO Francesca Mazzia Dipartimento Interuniversitario di Matematica Università di Bari 3. Elementi di Algebra Lineare. 1 Sistemi lineari Sia A IR m n, x IR n di n Ax = b è un vettore di m componenti.
x n i sima pos. x, y = x T y = x i y i R. i=1
 1 Elementi di Algebra Lineare In questo capitolo introduttivo al corso di Calcolo Numerico per la laurea triennale in Informatica, saranno presentate una serie di definizioni e proprietà di matrici e dei
1 Elementi di Algebra Lineare In questo capitolo introduttivo al corso di Calcolo Numerico per la laurea triennale in Informatica, saranno presentate una serie di definizioni e proprietà di matrici e dei
Richiami di Algebra Lineare
 Richiami di Algebra Lineare Eduardo Rossi Università degli Studi di Pavia Corso di Econometria Marzo 2012 Rossi Algebra Lineare 2012 1 / 59 Vettori Prodotto interno a : (n 1) b : (n 1) a b = a 1 b 1 +
Richiami di Algebra Lineare Eduardo Rossi Università degli Studi di Pavia Corso di Econometria Marzo 2012 Rossi Algebra Lineare 2012 1 / 59 Vettori Prodotto interno a : (n 1) b : (n 1) a b = a 1 b 1 +
Elementi di Algebra Lineare
 Elementi di Algebra Lineare Corso di Calcolo Numerico, a.a. 2009/2010 Francesca Mazzia Dipartimento di Matematica Università di Bari 13 Marzo 2006 Francesca Mazzia (Univ. Bari) Elementi di Algebra Lineare
Elementi di Algebra Lineare Corso di Calcolo Numerico, a.a. 2009/2010 Francesca Mazzia Dipartimento di Matematica Università di Bari 13 Marzo 2006 Francesca Mazzia (Univ. Bari) Elementi di Algebra Lineare
Autovalori e autovettori di una matrice quadrata
 Autovalori e autovettori di una matrice quadrata Data la matrice A M n (K, vogliamo stabilire se esistono valori di λ K tali che il sistema AX = λx ammetta soluzioni non nulle. Questo risulta evidentemente
Autovalori e autovettori di una matrice quadrata Data la matrice A M n (K, vogliamo stabilire se esistono valori di λ K tali che il sistema AX = λx ammetta soluzioni non nulle. Questo risulta evidentemente
La forma normale di Schur
 La forma normale di Schur Dario A Bini, Università di Pisa 30 ottobre 2013 Sommario Questo modulo didattico contiene risultati relativi alla forma normale di Schur, alle sue proprietà e alle sue applicazioni
La forma normale di Schur Dario A Bini, Università di Pisa 30 ottobre 2013 Sommario Questo modulo didattico contiene risultati relativi alla forma normale di Schur, alle sue proprietà e alle sue applicazioni
Autovalori, Autovettori, Diagonalizzazione.
 Autovalori Autovettori Diagonalizzazione Autovalori e Autovettori Definizione Sia V uno spazio vettoriale sul campo K = R o C e sia T : V V un endomorfismo Un vettore non nullo v V \ {O} si dice autovettore
Autovalori Autovettori Diagonalizzazione Autovalori e Autovettori Definizione Sia V uno spazio vettoriale sul campo K = R o C e sia T : V V un endomorfismo Un vettore non nullo v V \ {O} si dice autovettore
Algebra lineare. Laboratorio di programmazione e calcolo CdL in Chimica. Pierluigi Amodio
 Algebra lineare Laboratorio di programmazione e calcolo CdL in Chimica Pierluigi Amodio Dipartimento di Matematica Università di Bari pierluigi.amodio@uniba.it http://dm.uniba.it/ amodio A.A. 2016/17 P.
Algebra lineare Laboratorio di programmazione e calcolo CdL in Chimica Pierluigi Amodio Dipartimento di Matematica Università di Bari pierluigi.amodio@uniba.it http://dm.uniba.it/ amodio A.A. 2016/17 P.
APPLICAZIONI LINEARI O OMOMORFISMI
 42 APPLICAZIONI LINEARI O OMOMORFISMI Definizione 9 Dati due spazi vettoriali U e V sullo stesso campo K, una applicazione f : U V è detta lineare o omomorfismo se soddisfa le seguenti due condizioni:
42 APPLICAZIONI LINEARI O OMOMORFISMI Definizione 9 Dati due spazi vettoriali U e V sullo stesso campo K, una applicazione f : U V è detta lineare o omomorfismo se soddisfa le seguenti due condizioni:
Richiami di Algebra Lineare
 Richiami di Algebra Lineare Fabrizio Silvestri December 14, 010 Matrice Sia R il campo dei numeri reali. Si indica con R m n l insieme delle matrici ad elementi reali con m righe ed n colonne. Se A R n
Richiami di Algebra Lineare Fabrizio Silvestri December 14, 010 Matrice Sia R il campo dei numeri reali. Si indica con R m n l insieme delle matrici ad elementi reali con m righe ed n colonne. Se A R n
4 Autovettori e autovalori
 4 Autovettori e autovalori 41 Cambiamenti di base Sia V uno spazio vettoriale tale che dim V n Si è visto in sezione 12 che uno spazio vettoriale ammette basi distinte, ma tutte con la medesima cardinalità
4 Autovettori e autovalori 41 Cambiamenti di base Sia V uno spazio vettoriale tale che dim V n Si è visto in sezione 12 che uno spazio vettoriale ammette basi distinte, ma tutte con la medesima cardinalità
Matrici simili. Matrici diagonalizzabili.
 Matrici simili. Matrici diagonalizzabili. Definizione (Matrici simili) Due matrici quadrate A, B si dicono simili se esiste una matrice invertibile P tale che B = P A P. () interpretazione: cambio di base.
Matrici simili. Matrici diagonalizzabili. Definizione (Matrici simili) Due matrici quadrate A, B si dicono simili se esiste una matrice invertibile P tale che B = P A P. () interpretazione: cambio di base.
Diagonalizzabilità di endomorfismi
 Capitolo 16 Diagonalizzabilità di endomorfismi 16.1 Introduzione Nei capitoli precedenti abbiamo definito gli endomorfismi su uno spazio vettoriale E. Abbiamo visto che, dato un endomorfismo η di E, se
Capitolo 16 Diagonalizzabilità di endomorfismi 16.1 Introduzione Nei capitoli precedenti abbiamo definito gli endomorfismi su uno spazio vettoriale E. Abbiamo visto che, dato un endomorfismo η di E, se
MATRICI ORTOGONALI. MATRICI SIMMETRICHE E FORME QUADRATICHE
 DIAGONALIZZAZIONE 1 MATRICI ORTOGONALI. MATRICI SIMMETRICHE E FORME QUADRATICHE Matrici ortogonali e loro proprietà. Autovalori ed autospazi di matrici simmetriche reali. Diagonalizzazione mediante matrici
DIAGONALIZZAZIONE 1 MATRICI ORTOGONALI. MATRICI SIMMETRICHE E FORME QUADRATICHE Matrici ortogonali e loro proprietà. Autovalori ed autospazi di matrici simmetriche reali. Diagonalizzazione mediante matrici
0 0 c. d 1. det (D) = d 1 d n ;
 Registro Lezione di Algebra lineare del 23 novembre 216 1 Matrici diagonali 2 Autovettori e autovalori 3 Ricerca degli autovalori, polinomio caratteristico 4 Ricerca degli autovettori, autospazi 5 Matrici
Registro Lezione di Algebra lineare del 23 novembre 216 1 Matrici diagonali 2 Autovettori e autovalori 3 Ricerca degli autovalori, polinomio caratteristico 4 Ricerca degli autovettori, autospazi 5 Matrici
Autovalori e autovettori
 Autovalori e autovettori Definizione 1 (per endomorfismi). Sia V uno spazio vettoriale su di un campo K e f : V V un suo endomorfismo. Si dice autovettore per f ogni vettore x 0 tale che f(x) = λx, per
Autovalori e autovettori Definizione 1 (per endomorfismi). Sia V uno spazio vettoriale su di un campo K e f : V V un suo endomorfismo. Si dice autovettore per f ogni vettore x 0 tale che f(x) = λx, per
Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti)
 Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti) April 14, 2011 (alcune note non complete sugli argomenti trattati: eventuali completamenti saranno aggiunti)
Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti) April 14, 2011 (alcune note non complete sugli argomenti trattati: eventuali completamenti saranno aggiunti)
Sistemi lineari. Sia A R m n, x R n Ax = b è un vettore di m componenti. a m,1 x 1 + a m,2 x a m,n x n = b m
 1 Sistemi lineari. Sia A R m n, x R n Ax = b è un vettore di m componenti. Numero di operazioni per calcolare b: m n moltiplicazioni m (n 1) addizioni. a 1,1 x 1 + a 1,2 x 2 +... + a 1,n x n = b 1 a 2,1
1 Sistemi lineari. Sia A R m n, x R n Ax = b è un vettore di m componenti. Numero di operazioni per calcolare b: m n moltiplicazioni m (n 1) addizioni. a 1,1 x 1 + a 1,2 x 2 +... + a 1,n x n = b 1 a 2,1
Richiami di Algebra Lineare
 Università di Pavia Richiami di Algebra Lineare Eduardo Rossi Vettori a : (n 1) b : (n 1) Prodotto interno a b = a 1 b 1 + a 2 b 2 +... + a n b n Modulo (lunghezza): a = a 2 1 +... + a2 n Vettori ortogonali:
Università di Pavia Richiami di Algebra Lineare Eduardo Rossi Vettori a : (n 1) b : (n 1) Prodotto interno a b = a 1 b 1 + a 2 b 2 +... + a n b n Modulo (lunghezza): a = a 2 1 +... + a2 n Vettori ortogonali:
Algebra lineare. {ax 2 + bx + c R 2 [x] : 2a + 3b = 1} a b c d. M(2, 2) : a + c + d = 2. a b. c d
![Algebra lineare. {ax 2 + bx + c R 2 [x] : 2a + 3b = 1} a b c d. M(2, 2) : a + c + d = 2. a b. c d Algebra lineare. {ax 2 + bx + c R 2 [x] : 2a + 3b = 1} a b c d. M(2, 2) : a + c + d = 2. a b. c d](/thumbs/104/162200055.jpg) Algebra lineare 1. Riconoscere se il seguente insieme costituisce uno spazio vettoriale. In caso affermativo trovarne la dimensione e una base. (R n [x] denota lo spazio dei polinomi nell indeterminata
Algebra lineare 1. Riconoscere se il seguente insieme costituisce uno spazio vettoriale. In caso affermativo trovarne la dimensione e una base. (R n [x] denota lo spazio dei polinomi nell indeterminata
Geometria Prova scritta, appello unico, sessione autunnale Corso di laurea in fisica A.A 2017/2018 Canali A C, e L Pa
 Geometria Prova scritta, appello unico, sessione autunnale Corso di laurea in fisica A.A 27/28 Canali A C, e L Pa Durata: 2 ore e 3 minuti Simone Diverio Alessandro D Andrea Paolo Piccinni 7 settembre
Geometria Prova scritta, appello unico, sessione autunnale Corso di laurea in fisica A.A 27/28 Canali A C, e L Pa Durata: 2 ore e 3 minuti Simone Diverio Alessandro D Andrea Paolo Piccinni 7 settembre
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria: Elettronica. Corso di Geometria ed Algebra Docente F. Flamini
 Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria: Elettronica Corso di Geometria ed Algebra Docente F. Flamini Capitolo IV - 3: Teorema Spettrale degli operatori autoaggiunti e Teorema
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria: Elettronica Corso di Geometria ed Algebra Docente F. Flamini Capitolo IV - 3: Teorema Spettrale degli operatori autoaggiunti e Teorema
Richiami di algebra delle matrici a valori reali
 Richiami di algebra delle matrici a valori reali Vettore v n = v 1 v 2. v n Vettore trasposto v n = (v 1, v 2,..., v n ) v n = (v 1, v 2,..., v n ) A. Pollice - Statistica Multivariata Vettore nullo o
Richiami di algebra delle matrici a valori reali Vettore v n = v 1 v 2. v n Vettore trasposto v n = (v 1, v 2,..., v n ) v n = (v 1, v 2,..., v n ) A. Pollice - Statistica Multivariata Vettore nullo o
Applicazioni lineari simmetriche e forme quadratiche reali.
 Applicazioni lineari simmetriche e forme quadratiche reali 1 Applicazioni lineari simmetriche Consideriamo lo spazio IR n col prodotto scalare canonico X Y = t XY = x 1 y 1 + + x n y n Definizione Un applicazione
Applicazioni lineari simmetriche e forme quadratiche reali 1 Applicazioni lineari simmetriche Consideriamo lo spazio IR n col prodotto scalare canonico X Y = t XY = x 1 y 1 + + x n y n Definizione Un applicazione
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof. F.Podestà, a.a
 APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
Soluzione della prova scritta di di Algebra lineare del 10 giugno Esercizio 1
 Soluzione della prova scritta di di Algebra lineare del 0 giugno 05 Esercizio (a) La matrice A che rappresenta f rispetto alle basi assegnate è la seguente: A = 0 0 0 (b) Applicando il metodo di Gauss
Soluzione della prova scritta di di Algebra lineare del 0 giugno 05 Esercizio (a) La matrice A che rappresenta f rispetto alle basi assegnate è la seguente: A = 0 0 0 (b) Applicando il metodo di Gauss
INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 17 SETTEMBRE 2012
 INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 7 SETTEMBRE 202 Esercizio. Sia V = R[X] 2 lo spazio vettoriale dei polinomi ax 2 + bx + c nella variabile X di grado al più 2 a coefficienti
INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 7 SETTEMBRE 202 Esercizio. Sia V = R[X] 2 lo spazio vettoriale dei polinomi ax 2 + bx + c nella variabile X di grado al più 2 a coefficienti
RICHIAMI DI ALGEBRA LINEARE E NORME DI MATRICI E VETTORI. a 11 a 12 a 1n a 21 a 22 a 2n. a m1 a m2 a mn
 RICHIAMI DI ALGEBRA LINEARE E NORME DI MATRICI E VETTORI LUCIA GASTALDI 1. Matrici. Operazioni fondamentali. Una matrice A è un insieme di m n numeri reali (o complessi) ordinati, rappresentato nella tabella
RICHIAMI DI ALGEBRA LINEARE E NORME DI MATRICI E VETTORI LUCIA GASTALDI 1. Matrici. Operazioni fondamentali. Una matrice A è un insieme di m n numeri reali (o complessi) ordinati, rappresentato nella tabella
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA CHIMICA E DEI MATERIALI 27 GIUGNO 2016
 FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA CHIMICA E DEI MATERIALI 7 GIUGNO 06 MATTEO LONGO Ogni versione del compito contiene solo due tra i quattro esercizi 6-7-8-9. Esercizio. Considerare
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA CHIMICA E DEI MATERIALI 7 GIUGNO 06 MATTEO LONGO Ogni versione del compito contiene solo due tra i quattro esercizi 6-7-8-9. Esercizio. Considerare
Applicazioni lineari e diagonalizzazione. Esercizi svolti
 . Applicazioni lineari Esercizi svolti. Si consideri l applicazione f : K -> K definita da f(x,y) = x + y e si stabilisca se è lineare. Non è lineare. Possibile verifica: f(,) = 4; f(,4) = 6; quindi f(,4)
. Applicazioni lineari Esercizi svolti. Si consideri l applicazione f : K -> K definita da f(x,y) = x + y e si stabilisca se è lineare. Non è lineare. Possibile verifica: f(,) = 4; f(,4) = 6; quindi f(,4)
1 Il polinomio minimo.
 Abstract Il polinomio minimo, così come il polinomio caratterisico, è un importante invariante per le matrici quadrate. La forma canonica di Jordan è un approssimazione della diagonalizzazione, e viene
Abstract Il polinomio minimo, così come il polinomio caratterisico, è un importante invariante per le matrici quadrate. La forma canonica di Jordan è un approssimazione della diagonalizzazione, e viene
Algebra Lineare Autovalori
 Algebra Lineare Autovalori Stefano Berrone Sandra Pieraccini Dipartimento di Matematica Politecnico di Torino, Corso Duca degli Abruzzi 24, 10129, Torino, Italy e-mail: sberrone@calvino.polito.it sandra.pieraccini@polito.it
Algebra Lineare Autovalori Stefano Berrone Sandra Pieraccini Dipartimento di Matematica Politecnico di Torino, Corso Duca degli Abruzzi 24, 10129, Torino, Italy e-mail: sberrone@calvino.polito.it sandra.pieraccini@polito.it
ESAME DI GEOMETRIA. 6 febbraio 2002 CORREZIONE QUIZ
 ESAME DI GEOMETRIA 6 febbraio CORREZIONE QUIZ. La parte reale di ( + i) 9 è positiva. QUIZ Si può procedere in due modi. Un primo modo è osservare che ( + i) =i, dunque ( + i) 9 =(+i)(i) 4 = 4 ( + i) :
ESAME DI GEOMETRIA 6 febbraio CORREZIONE QUIZ. La parte reale di ( + i) 9 è positiva. QUIZ Si può procedere in due modi. Un primo modo è osservare che ( + i) =i, dunque ( + i) 9 =(+i)(i) 4 = 4 ( + i) :
Soluzione della seconda prova intermedia di Algebra lineare del 17 maggio Esercizio 1
 Soluzione della seconda prova intermedia di Algebra lineare del 17 maggio 2012 Esercizio 1 (a) Si calcola il polinomio caratteristico λ 2 1 p(λ) = det k 1 2k λ k 1 2 2 λ usando lo sviluppo di Laplace secondo
Soluzione della seconda prova intermedia di Algebra lineare del 17 maggio 2012 Esercizio 1 (a) Si calcola il polinomio caratteristico λ 2 1 p(λ) = det k 1 2k λ k 1 2 2 λ usando lo sviluppo di Laplace secondo
AUTOVALORI, AUTOVETTORI, AUTOSPAZI
 AUTOVALORI, AUTOVETTORI, AUTOSPAZI. Esercizi Esercizio. Sia f : R 3 R 3 l endomorfismo definito da f(x, y, z) = (x+y, y +z, x+z). Calcolare gli autovalori ed una base per ogni autospazio di f. Dire se
AUTOVALORI, AUTOVETTORI, AUTOSPAZI. Esercizi Esercizio. Sia f : R 3 R 3 l endomorfismo definito da f(x, y, z) = (x+y, y +z, x+z). Calcolare gli autovalori ed una base per ogni autospazio di f. Dire se
{Geometria per [Fisica e (Fisica e Astrofisica)]}
![{Geometria per [Fisica e (Fisica e Astrofisica)]} {Geometria per [Fisica e (Fisica e Astrofisica)]}](/thumbs/103/157763717.jpg) {Geometria per [Fisica e (Fisica e Astrofisica)]} Foglio 9 - Soluzioni Esercizio (facoltativo) Un quadrato magico reale di ordine n è una matrice di M n n (R) tale che sommando gli elementi di ogni sua
{Geometria per [Fisica e (Fisica e Astrofisica)]} Foglio 9 - Soluzioni Esercizio (facoltativo) Un quadrato magico reale di ordine n è una matrice di M n n (R) tale che sommando gli elementi di ogni sua
Corso di Geometria Ing. Informatica e Automatica Test 1: soluzioni
 Corso di Geometria Ing. Informatica e Automatica Test : soluzioni k Esercizio Data la matrice A = k dipendente dal parametro k, si consideri il k sistema lineare omogeneo AX =, con X = x x. Determinare
Corso di Geometria Ing. Informatica e Automatica Test : soluzioni k Esercizio Data la matrice A = k dipendente dal parametro k, si consideri il k sistema lineare omogeneo AX =, con X = x x. Determinare
Definizione. Sia f : V V un endomorfismo e λ R. Se esiste v V non nullo tale che
 Autovalori ed autovettori [Abate, 131] Sia f : V V un endomorfismo e λ R Se esiste v V non nullo tale che f(v) = λv, diremo che λ è un autovalore di f e che v è un autovettore di f associato a λ Lezioni
Autovalori ed autovettori [Abate, 131] Sia f : V V un endomorfismo e λ R Se esiste v V non nullo tale che f(v) = λv, diremo che λ è un autovalore di f e che v è un autovettore di f associato a λ Lezioni
Endomorfismi e matrici simmetriche
 CAPITOLO Endomorfismi e matrici simmetriche Esercizio.. [Esercizio 5) cap. 9 del testo Geometria e algebra lineare di Manara, Perotti, Scapellato] Calcolare una base ortonormale di R 3 formata da autovettori
CAPITOLO Endomorfismi e matrici simmetriche Esercizio.. [Esercizio 5) cap. 9 del testo Geometria e algebra lineare di Manara, Perotti, Scapellato] Calcolare una base ortonormale di R 3 formata da autovettori
0.1 Condizione sufficiente di diagonalizzabilità
 0.1. CONDIZIONE SUFFICIENTE DI DIAGONALIZZABILITÀ 1 0.1 Condizione sufficiente di diagonalizzabilità È naturale porsi il problema di sapere se ogni matrice sia o meno diagonalizzabile. Abbiamo due potenziali
0.1. CONDIZIONE SUFFICIENTE DI DIAGONALIZZABILITÀ 1 0.1 Condizione sufficiente di diagonalizzabilità È naturale porsi il problema di sapere se ogni matrice sia o meno diagonalizzabile. Abbiamo due potenziali
Prova scritta di Geometria 1 Docente: Giovanni Cerulli Irelli 15 Febbraio 2017
 Prova scritta di Geometria Docente: Giovanni Cerulli Irelli 5 Febbraio 7 Esercizio. Si considerino i due sottospazi π e π di R dati dalle seguenti equazioni: π : x y + z = ; π : x + y z =.. Trovare una
Prova scritta di Geometria Docente: Giovanni Cerulli Irelli 5 Febbraio 7 Esercizio. Si considerino i due sottospazi π e π di R dati dalle seguenti equazioni: π : x y + z = ; π : x + y z =.. Trovare una
Capitolo 8 Forme quadratiche e loro applicazioni Esercizi svolti Tutorato di geometria e algebra lineare. Marco Robutti
 Capitolo 8 Forme quadratiche e loro applicazioni Esercizi svolti Tutorato di geometria e algebra lineare Marco Robutti 5 Ottobre 2017 1 Introduzione Gli esercizi di questo capitolo riguardano i seguenti
Capitolo 8 Forme quadratiche e loro applicazioni Esercizi svolti Tutorato di geometria e algebra lineare Marco Robutti 5 Ottobre 2017 1 Introduzione Gli esercizi di questo capitolo riguardano i seguenti
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA INDUSTRIALE 27 GENNAIO 2014
 FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA INDUSTRIALE 27 GENNAIO 2014 DOCENTE: MATTEO LONGO Rispondere alle domande di Teoria in modo esauriente e completo. Svolgere il maggior numero di esercizi
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA INDUSTRIALE 27 GENNAIO 2014 DOCENTE: MATTEO LONGO Rispondere alle domande di Teoria in modo esauriente e completo. Svolgere il maggior numero di esercizi
DIARIO DEL CORSO DI MATHEMATICS FOR DATA SCIENCE TRENTO, A.A. 2018/19 DOCENTI: ANDREA CARANTI, SIMONE UGOLINI
 DIARIO DEL CORSO DI MATHEMATICS FOR DATA SCIENCE TRENTO, A.A. 2018/19 DOCENTI: ANDREA CARANTI, SIMONE UGOLINI Nota. La descrizione di lezioni non ancora svolte si deve intendere come una previsione/pianificazione.
DIARIO DEL CORSO DI MATHEMATICS FOR DATA SCIENCE TRENTO, A.A. 2018/19 DOCENTI: ANDREA CARANTI, SIMONE UGOLINI Nota. La descrizione di lezioni non ancora svolte si deve intendere come una previsione/pianificazione.
CORSO DI MATEMATICA II Prof. Paolo Papi ESERCIZI. 1). Stabilire quali dei seguenti sottoinsiemi di V sono sottospazi vettoriali. (a) V = R 3.
 CORSO DI MATEMATICA II Prof Paolo Papi ESERCIZI ) Stabilire quali dei seguenti sottoinsiemi di V sono sottospazi vettoriali (a) V = R 3 () W = {(x,,x 3 ) x,x 3 R} (2) W 2 = {(x,,x 3 ) x,x 3 R} (3) W 3
CORSO DI MATEMATICA II Prof Paolo Papi ESERCIZI ) Stabilire quali dei seguenti sottoinsiemi di V sono sottospazi vettoriali (a) V = R 3 () W = {(x,,x 3 ) x,x 3 R} (2) W 2 = {(x,,x 3 ) x,x 3 R} (3) W 3
(V) (FX) L unione di due basi di uno spazio vettoriale è ancora una base dello spazio vettoriale.
 8 gennaio 2009 - PROVA D ESAME - Geometria e Algebra T NOME: MATRICOLA: a=, b=, c= Sostituire ai parametri a, b, c rispettivamente la terzultima, penultima e ultima cifra del proprio numero di matricola
8 gennaio 2009 - PROVA D ESAME - Geometria e Algebra T NOME: MATRICOLA: a=, b=, c= Sostituire ai parametri a, b, c rispettivamente la terzultima, penultima e ultima cifra del proprio numero di matricola
Applicazioni lineari e diagonalizzazione
 Autovalori e autovettori Matrici associate a applicazioni lineari Endomorfismi semplici e matrici diagonalizzabili Prodotti scalari e Teorema Spettrale nel caso generale 2 2006 Politecnico di Torino 1
Autovalori e autovettori Matrici associate a applicazioni lineari Endomorfismi semplici e matrici diagonalizzabili Prodotti scalari e Teorema Spettrale nel caso generale 2 2006 Politecnico di Torino 1
DIAGONALIZZAZIONE E FORME QUADRATICHE / ESERCIZI PROPOSTI
 M.GUIDA, S.ROLANDO, 204 DIAGONALIZZAZIONE E FORME QUADRATICHE / ESERCIZI PROPOSTI L asterisco contrassegna gli esercizi più difficili o che possono considerarsi meno basilari. Autovalori, autospazi e diagonalizzazione
M.GUIDA, S.ROLANDO, 204 DIAGONALIZZAZIONE E FORME QUADRATICHE / ESERCIZI PROPOSTI L asterisco contrassegna gli esercizi più difficili o che possono considerarsi meno basilari. Autovalori, autospazi e diagonalizzazione
GEOMETRIA 1 Autovalori e autovettori
 GEOMETRIA 1 Autovalori e autovettori Gilberto Bini - Anna Gori - Cristina Turrini 2018/2019 Gilberto Bini - Anna Gori - Cristina Turrini (2018/2019) GEOMETRIA 1 1 / 28 index Matrici rappresentative "semplici"
GEOMETRIA 1 Autovalori e autovettori Gilberto Bini - Anna Gori - Cristina Turrini 2018/2019 Gilberto Bini - Anna Gori - Cristina Turrini (2018/2019) GEOMETRIA 1 1 / 28 index Matrici rappresentative "semplici"
3. Vettori, Spazi Vettoriali e Matrici
 3. Vettori, Spazi Vettoriali e Matrici Vettori e Spazi Vettoriali Operazioni tra vettori Basi Trasformazioni ed Operatori Operazioni tra Matrici Autovalori ed autovettori Forme quadratiche, quadriche e
3. Vettori, Spazi Vettoriali e Matrici Vettori e Spazi Vettoriali Operazioni tra vettori Basi Trasformazioni ed Operatori Operazioni tra Matrici Autovalori ed autovettori Forme quadratiche, quadriche e
ALGEBRA C. MALVENUTO
 ALGEBRA CANALE A-L ESAME SECONDA PARTE SECONDO ESONERO 27 GENNAIO 22 C. MALVENUTO Istruzioni. Completare subito la parte inferiore di questa pagina con il proprio nome, cognome e firma. Scrivere solamente
ALGEBRA CANALE A-L ESAME SECONDA PARTE SECONDO ESONERO 27 GENNAIO 22 C. MALVENUTO Istruzioni. Completare subito la parte inferiore di questa pagina con il proprio nome, cognome e firma. Scrivere solamente
0 1 k. k k k +4. b) Posto k = 0, si calcoli l inversa di A e l inversa di T.
 Esercizi per il Parziale 2, Prof. Fioresi, 2018 1. Cambi di base, determinante e inversa 1. Si trovino le coordinate del vettore v = (1, 1,2) espresso nella base canonica, rispetto alla base B = {(1, 4,3),(5,3,
Esercizi per il Parziale 2, Prof. Fioresi, 2018 1. Cambi di base, determinante e inversa 1. Si trovino le coordinate del vettore v = (1, 1,2) espresso nella base canonica, rispetto alla base B = {(1, 4,3),(5,3,
LEZIONE 16 A = Verifichiamo se qualcuna fra le entrate a di A è suo autovalore. determinare per quale entrata a di A risulta rk(a ai 2 ) 1.
 LEZIONE 16 16.1. Autovalori, autovettori ed autospazi di matrici. Introduciamo la seguente definizione. Definizione 16.1.1. Siano k = R, C e A k n,n. Un numero λ k si dice autovalore di A su k) se rka
LEZIONE 16 16.1. Autovalori, autovettori ed autospazi di matrici. Introduciamo la seguente definizione. Definizione 16.1.1. Siano k = R, C e A k n,n. Un numero λ k si dice autovalore di A su k) se rka
RICHIAMI DI ALGEBRA LINEARE E NORME DI MATRICI E VETTORI. a 11 a 12 a 1n a 21 a 22 a 2n. a m1 a m2 a mn
 RICHIAMI DI ALGEBRA LINEARE E NORME DI MATRICI E VETTORI LUCIA GASTALDI 1. Matrici. Operazioni fondamentali. Una matrice A è un insieme di m n numeri reali (o complessi) ordinati, rappresentato nella tabella
RICHIAMI DI ALGEBRA LINEARE E NORME DI MATRICI E VETTORI LUCIA GASTALDI 1. Matrici. Operazioni fondamentali. Una matrice A è un insieme di m n numeri reali (o complessi) ordinati, rappresentato nella tabella
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA PRIMO APPELLO, 15 GIUGNO 2010 VERSIONE A. 1 a 1. 0 a a 2
 FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA PRIMO APPELLO, 5 GIUGNO 2 VERSIONE A Esercizio Al variare del parametro reale a, si consideri l endomorfismo : R R definito dalle condizioni: a a a 2 a a 2 =,
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA PRIMO APPELLO, 5 GIUGNO 2 VERSIONE A Esercizio Al variare del parametro reale a, si consideri l endomorfismo : R R definito dalle condizioni: a a a 2 a a 2 =,
CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI A.A. 2018/2019 PROF. VALENTINA BEORCHIA
 CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Matrici associate a un applicazione lineare 1 2 Cambiamenti di base 4 3 Diagonalizzazione 6 1 MATRICI ASSOCIATE
CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Matrici associate a un applicazione lineare 1 2 Cambiamenti di base 4 3 Diagonalizzazione 6 1 MATRICI ASSOCIATE
Determinante, autovalori e autovettori
 Determinante, autovalori e autovettori Lorenzo Pareschi Dipartimento di Matematica, Universitá di Ferrara http://wwwlorenzopareschicom lorenzopareschi@unifeit Lorenzo Pareschi (Univ Ferrara) Determinante,
Determinante, autovalori e autovettori Lorenzo Pareschi Dipartimento di Matematica, Universitá di Ferrara http://wwwlorenzopareschicom lorenzopareschi@unifeit Lorenzo Pareschi (Univ Ferrara) Determinante,
INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 19 GIUGNO 2012
 INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 19 GIUGNO 2012 MATTEO LONGO Esercizio 1. Al variare del parametro a R, si consideri l applicazione lineare L a : R R definita dalle
INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 19 GIUGNO 2012 MATTEO LONGO Esercizio 1. Al variare del parametro a R, si consideri l applicazione lineare L a : R R definita dalle
3. Vettori, Spazi Vettoriali e Matrici
 3. Vettori, Spazi Vettoriali e Matrici Vettori e Spazi Vettoriali Operazioni tra vettori Basi Trasformazioni ed Operatori Operazioni tra Matrici Autovalori ed autovettori Forme quadratiche, quadriche e
3. Vettori, Spazi Vettoriali e Matrici Vettori e Spazi Vettoriali Operazioni tra vettori Basi Trasformazioni ed Operatori Operazioni tra Matrici Autovalori ed autovettori Forme quadratiche, quadriche e
Complementi di Algebra e Fondamenti di Geometria
 Complementi di Algebra e Fondamenti di Geometria Capitolo 5 Forme quadratiche inr n M. Ciampa Ingegneria Elettrica, a.a. 2009/2010 Capitolo 5 Forme quadratiche inr n In questo capitolo si definisce la
Complementi di Algebra e Fondamenti di Geometria Capitolo 5 Forme quadratiche inr n M. Ciampa Ingegneria Elettrica, a.a. 2009/2010 Capitolo 5 Forme quadratiche inr n In questo capitolo si definisce la
Diagonalizzazione di matrici: autovalori, autovettori e costruzione della matrice diagonalizzante 1 / 13
 Diagonalizzazione di matrici: autovalori, autovettori e costruzione della matrice diagonalizzante 1 / 13 Matrici diagonali 2 / 13 Ricordiamo che una matrice quadrata si dice matrice diagonale se a ij =
Diagonalizzazione di matrici: autovalori, autovettori e costruzione della matrice diagonalizzante 1 / 13 Matrici diagonali 2 / 13 Ricordiamo che una matrice quadrata si dice matrice diagonale se a ij =
Autovalori e autovettori
 Capitolo 3 Autovalori e autovettori 3. Richiami di teoria Prerequisiti: nozioni elementari di algebra lineare, numeri complessi. Sia A R n n. Un numero λ per cui esiste un vettore x 0 tale che valga la
Capitolo 3 Autovalori e autovettori 3. Richiami di teoria Prerequisiti: nozioni elementari di algebra lineare, numeri complessi. Sia A R n n. Un numero λ per cui esiste un vettore x 0 tale che valga la
Autovalori ed autovettori di un endomorfismo
 Autovalori ed autovettori di un endomorfismo Endomorfismo = applicazione (funzione) lineare da un spazio vettoriale V in sé stesso 1. Data una funzione lineare, scriverne la matrice associata dei coefficienti:
Autovalori ed autovettori di un endomorfismo Endomorfismo = applicazione (funzione) lineare da un spazio vettoriale V in sé stesso 1. Data una funzione lineare, scriverne la matrice associata dei coefficienti:
Autovalori ed autovettori di una matrice
 Autovalori ed autovettori di una matrice Lucia Gastaldi DICATAM http://www.ing.unibs.it/gastaldi/ Indice 1 Definizioni di autovalori ed autovettori Autovalori ed autovettori 2 Metodo delle potenze 3 Calcolo
Autovalori ed autovettori di una matrice Lucia Gastaldi DICATAM http://www.ing.unibs.it/gastaldi/ Indice 1 Definizioni di autovalori ed autovettori Autovalori ed autovettori 2 Metodo delle potenze 3 Calcolo
Esercizi di ripasso: geometria e algebra lineare.
 Esercizi di ripasso: geometria e algebra lineare. Esercizio. Sia r la retta passante per i punti A(2,, 3) e B(,, 2) in R 3. a. Scrivere l equazione cartesiana del piano Π passante per A e perpendicolare
Esercizi di ripasso: geometria e algebra lineare. Esercizio. Sia r la retta passante per i punti A(2,, 3) e B(,, 2) in R 3. a. Scrivere l equazione cartesiana del piano Π passante per A e perpendicolare
CALCOLO NUMERICO. Francesca Mazzia. Calcolo degli autovalori. Dipartimento Interuniversitario di Matematica. Università di Bari
 CALCOLO NUMERICO Francesca Mazzia Dipartimento Interuniversitario di Matematica Università di Bari Calcolo degli autovalori 1 Calcolo degli autovalori Gli autovalore e gli autovettore di una matrice quadrata
CALCOLO NUMERICO Francesca Mazzia Dipartimento Interuniversitario di Matematica Università di Bari Calcolo degli autovalori 1 Calcolo degli autovalori Gli autovalore e gli autovettore di una matrice quadrata
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE110 - Geometria 1 a.a Prova scritta del TESTO E SOLUZIONI
 UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE110 - Geometria 1 a.a. 2011-2012 Prova scritta del 28-1-2013 TESTO E SOLUZIONI 1. Per k R considerare il sistema lineare X 1 X 2 + kx 3 =
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE110 - Geometria 1 a.a. 2011-2012 Prova scritta del 28-1-2013 TESTO E SOLUZIONI 1. Per k R considerare il sistema lineare X 1 X 2 + kx 3 =
LA DIAGONALIZZAZIONE. asdf. Polinomi di matrici. 30 January 2012
 asdf LA DIAGONALIZZAZIONE 30 January 2012 L'intento di questo articolo è di affrontare, si spera sempre nel modo più corretto e chiaro possibile, la trattazione di un argomento importante nell'ambito dell'algebra
asdf LA DIAGONALIZZAZIONE 30 January 2012 L'intento di questo articolo è di affrontare, si spera sempre nel modo più corretto e chiaro possibile, la trattazione di un argomento importante nell'ambito dell'algebra
SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE
 SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE. Esercizi Esercizio. In R calcolare il modulo dei vettori,, ),,, ) ed il loro angolo. Esercizio. Calcolare una base ortonormale del sottospazio
SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE. Esercizi Esercizio. In R calcolare il modulo dei vettori,, ),,, ) ed il loro angolo. Esercizio. Calcolare una base ortonormale del sottospazio
Corso di Laurea in Scienza dei Materiali PROVA SCRITTA DI GEOMETRIA DEL 12/07/2016 SOLUZIONE DEGLI ESERCIZI PROPOSTI
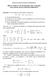 Corso di Laurea in Scienza dei Materiali PROVA SCRITTA DI GEOMETRIA DEL 12/07/2016 SOLUZIONE DEGLI ESERCIZI PROPOSTI Esercizio 1 Si consideri la conica affine d equazione 9x 2 + 6y 2 4xy 6x + 8y = 1 (1)
Corso di Laurea in Scienza dei Materiali PROVA SCRITTA DI GEOMETRIA DEL 12/07/2016 SOLUZIONE DEGLI ESERCIZI PROPOSTI Esercizio 1 Si consideri la conica affine d equazione 9x 2 + 6y 2 4xy 6x + 8y = 1 (1)
=. Il vettore non è della forma λ, dunque non è un. 2. Il vettore 8 2 non è della forma λ 1
 a.a. 2005-2006 Esercizi. Autovalori e autovettori. Soluzioni. Sia A = e sia x =. Dire se x è autovettore di A. Se si dire per quale 8 autovalore. Sol. Si ha =. Il vettore non è della forma λ dunque 8 29
a.a. 2005-2006 Esercizi. Autovalori e autovettori. Soluzioni. Sia A = e sia x =. Dire se x è autovettore di A. Se si dire per quale 8 autovalore. Sol. Si ha =. Il vettore non è della forma λ dunque 8 29
TEORIA DEI SISTEMI ANALISI DEI SISTEMI LTI
 TEORIA DEI SISTEMI Laurea Specialistica in Ingegneria Meccatronica Laurea Specialistica in Ingegneria Gestionale Indirizzo Gestione Industriale TEORIA DEI SISTEMI ANALISI DEI SISTEMI LTI Ing. Cristian
TEORIA DEI SISTEMI Laurea Specialistica in Ingegneria Meccatronica Laurea Specialistica in Ingegneria Gestionale Indirizzo Gestione Industriale TEORIA DEI SISTEMI ANALISI DEI SISTEMI LTI Ing. Cristian
Autovettori e autovalori
 Autovettori e autovalori Definizione 1 Sia A Mat(n, n), matrice a coefficienti reali. Si dice autovalore di A un numero λ R tale che v 0 R n Av = λv. Ogni vettore non nullo v che soddisfa questa relazione
Autovettori e autovalori Definizione 1 Sia A Mat(n, n), matrice a coefficienti reali. Si dice autovalore di A un numero λ R tale che v 0 R n Av = λv. Ogni vettore non nullo v che soddisfa questa relazione
ESEMPIO DI SISTEMA LINEARE CON SOLUZIONE. Esercizio Si consideri il sistema di equazioni lineari dipendente da un parametro λ R:
 ESEMPIO DI SISTEMA LINEARE CON SOLUZIONE Esercizio Si consideri il sistema di equazioni lineari dipendente da un parametro λ R: x 1 + x = 0 6x 1 + (λ + )x + x 3 + x 4 = 1 x 1 4x + (λ + 1)x 3 + 6x 4 = 3
ESEMPIO DI SISTEMA LINEARE CON SOLUZIONE Esercizio Si consideri il sistema di equazioni lineari dipendente da un parametro λ R: x 1 + x = 0 6x 1 + (λ + )x + x 3 + x 4 = 1 x 1 4x + (λ + 1)x 3 + 6x 4 = 3
ESERCIZI DI ALGEBRA LINEARE. Vincenzo Di Gennaro
 ESERCIZI DI ALGEBRA LINEARE Vincenzo Di Gennaro Sono raccolti, in ordine cronologico, gli esercizi di Algebra Lineare proposti nelle prove scritte per i vari corsi di Geometria 1 che ho tenuto presso la
ESERCIZI DI ALGEBRA LINEARE Vincenzo Di Gennaro Sono raccolti, in ordine cronologico, gli esercizi di Algebra Lineare proposti nelle prove scritte per i vari corsi di Geometria 1 che ho tenuto presso la
APPUNTI DI ALGEBRA LINEARE
 APPUNTI DI ALGEBRA LINEARE. Definizione Si dice spazio vettoriale (sul campo dei numeri reali R) un insieme V per il quale siano definite l operazione interna di somma (che ad ogni coppia di vettori e
APPUNTI DI ALGEBRA LINEARE. Definizione Si dice spazio vettoriale (sul campo dei numeri reali R) un insieme V per il quale siano definite l operazione interna di somma (che ad ogni coppia di vettori e
Algebra lineare e geometria AA Esercitazione del 14/6/2018
 Algebra lineare e geometria AA. 2017-2018 Esercitazione del 14/6/2018 1) Siano A, B due matrici n n tali che 0 < rk(a) < rk(b) = n. (a) AB è invertibile. (b) rk(ab) = nrk(b). (c) det(ab) = det(a). (d)
Algebra lineare e geometria AA. 2017-2018 Esercitazione del 14/6/2018 1) Siano A, B due matrici n n tali che 0 < rk(a) < rk(b) = n. (a) AB è invertibile. (b) rk(ab) = nrk(b). (c) det(ab) = det(a). (d)
Calcolo degli Autovalori. Avviso. Spettro di una matrice. Polinomio caratteristico. Data la matrice A:
 M. Annunziato, DMI Università di Salerno - documento provvisorio p. 3/9 M. Annunziato, DMI Università di Salerno - documento provvisorio p. 4/9 Avviso I contenuti di queste slide non sono esaustivi ai
M. Annunziato, DMI Università di Salerno - documento provvisorio p. 3/9 M. Annunziato, DMI Università di Salerno - documento provvisorio p. 4/9 Avviso I contenuti di queste slide non sono esaustivi ai
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA
 Cognome Nome Matricola FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA Ciarellotto, Esposito, Garuti Prova del 21 settembre 2013 Dire se è vero o falso (giustificare le risposte. Bisogna necessariamente rispondere
Cognome Nome Matricola FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA Ciarellotto, Esposito, Garuti Prova del 21 settembre 2013 Dire se è vero o falso (giustificare le risposte. Bisogna necessariamente rispondere
0 1 k. k k k +4. b) Posto k = 0, si calcoli l inversa di A e l inversa di T.
 Esercizi per il Parziale 2, Prof. Fioresi, 2016 1. Cambi di base, determinante e inversa 1. Si trovino le coordinate del vettore v = (1, 1,2) espresso nella base canonica, rispetto alla base B = {(1, 4,3),(5,3,
Esercizi per il Parziale 2, Prof. Fioresi, 2016 1. Cambi di base, determinante e inversa 1. Si trovino le coordinate del vettore v = (1, 1,2) espresso nella base canonica, rispetto alla base B = {(1, 4,3),(5,3,
PreCorso di Matematica - PCM Corso M-Z
 PreCorso di Matematica - PCM Corso M-Z DOCENTE: M. Auteri Outline Docente: Auteri PreCorso di Matematica 2016 2 Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti
PreCorso di Matematica - PCM Corso M-Z DOCENTE: M. Auteri Outline Docente: Auteri PreCorso di Matematica 2016 2 Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti
Corso di Calcolo Numerico
 Corso di Laurea in Ingegneria Gestionale Sede di Fermo Corso di 8 - METODI ITERATIVI PER I SISTEMI LINEARI Norme Una norma in R n è una funzione. : R n R tale che x 0 x R n ; x = 0 x = 0; αx = α x ; x
Corso di Laurea in Ingegneria Gestionale Sede di Fermo Corso di 8 - METODI ITERATIVI PER I SISTEMI LINEARI Norme Una norma in R n è una funzione. : R n R tale che x 0 x R n ; x = 0 x = 0; αx = α x ; x
Prova scritta di Geometria 1 Docente: Giovanni Cerulli Irelli 20 Gennaio 2017
 Prova scritta di Geometria Docente: Giovanni Cerulli Irelli Gennaio 7 Esercizio. Si considerino i seguenti tre punti dello spazio euclideo: P :=, Q :=, R :=.. Dimostrare che P, Q ed R non sono collineari.
Prova scritta di Geometria Docente: Giovanni Cerulli Irelli Gennaio 7 Esercizio. Si considerino i seguenti tre punti dello spazio euclideo: P :=, Q :=, R :=.. Dimostrare che P, Q ed R non sono collineari.
LAUREA IN INGEGNERIA CIVILE ED AMBIENTE-TERRITORIO Corso di Matematica 2 Padova TEMA n.1
 LAUREA IN INGEGNERIA CIVILE ED AMBIENTE-TERRITORIO Corso di Matematica Padova -8-8 TEMA n.1 PARTE 1. Quesiti preliminari Stabilire se le seguenti affermazioni sono vere o false giustificando brevemente
LAUREA IN INGEGNERIA CIVILE ED AMBIENTE-TERRITORIO Corso di Matematica Padova -8-8 TEMA n.1 PARTE 1. Quesiti preliminari Stabilire se le seguenti affermazioni sono vere o false giustificando brevemente
PROVA SCRITTA DEL 10 LUGLIO 2008 e SOLUZIONI. Per ognuno dei seguenti quiz indicare l unica risposta corretta tra le quattro proposte.
 Geometria B1-02efe Geometria - 13bcg PROVA SCRITTA DEL 10 LUGLIO 2008 e SOLUZIONI Per ognuno dei seguenti quiz indicare l unica risposta corretta tra le quattro proposte. Esercizio 1. Sia u, v, w vettori
Geometria B1-02efe Geometria - 13bcg PROVA SCRITTA DEL 10 LUGLIO 2008 e SOLUZIONI Per ognuno dei seguenti quiz indicare l unica risposta corretta tra le quattro proposte. Esercizio 1. Sia u, v, w vettori
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006. Matematica 2 (Analisi)
 Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
- ciascun autovalore di T ha molteplicità geometrica uguale alla moltplicitaà algebrica.
 Lezioni del 14.05 e 17.05 In queste lezioni si sono svolti i seguenti argomenti. Ripresa del teorema generale che fornisce condizioni che implicano la diagonalizzabilità, indebolimento delle ipotesi, e
Lezioni del 14.05 e 17.05 In queste lezioni si sono svolti i seguenti argomenti. Ripresa del teorema generale che fornisce condizioni che implicano la diagonalizzabilità, indebolimento delle ipotesi, e
Esame scritto di Geometria I
 Esame scritto di Geometria I Università degli Studi di Trento Corso di laurea in Fisica A.A. 26/27 Appello di febbraio 27 Esercizio Sia f h : R R l applicazione lineare definita da f h (e ) = 2e + (2 h)e
Esame scritto di Geometria I Università degli Studi di Trento Corso di laurea in Fisica A.A. 26/27 Appello di febbraio 27 Esercizio Sia f h : R R l applicazione lineare definita da f h (e ) = 2e + (2 h)e
Autovalori ed autovettori di una matrice
 Autovalori ed autovettori di una matrice Lucia Gastaldi Dipartimento di Matematica, http://lucia-gastaldi.unibs.it page 1 Indice 1 Definizioni di autovalori ed autovettori Autovalori ed autovettori 2 Metodo
Autovalori ed autovettori di una matrice Lucia Gastaldi Dipartimento di Matematica, http://lucia-gastaldi.unibs.it page 1 Indice 1 Definizioni di autovalori ed autovettori Autovalori ed autovettori 2 Metodo
Parte 8. Prodotto scalare, teorema spettrale
 Parte 8. Prodotto scalare, teorema spettrale A. Savo Appunti del Corso di Geometria 3-4 Indice delle sezioni Prodotto scalare in R n, Basi ortonormali, 4 3 Algoritmo di Gram-Schmidt, 7 4 Matrici ortogonali,
Parte 8. Prodotto scalare, teorema spettrale A. Savo Appunti del Corso di Geometria 3-4 Indice delle sezioni Prodotto scalare in R n, Basi ortonormali, 4 3 Algoritmo di Gram-Schmidt, 7 4 Matrici ortogonali,
Sapienza Università di Roma Corso di laurea in Ingegneria Energetica Geometria A.A ESERCIZI DA CONSEGNARE prof.
 Sapienza Università di Roma Corso di laurea in Ingegneria Energetica Geometria A.A. 2015-2016 ESERCIZI DA CONSEGNARE prof. Cigliola Consegna per Martedì 6 Ottobre Esercizio 1. Una matrice quadrata A si
Sapienza Università di Roma Corso di laurea in Ingegneria Energetica Geometria A.A. 2015-2016 ESERCIZI DA CONSEGNARE prof. Cigliola Consegna per Martedì 6 Ottobre Esercizio 1. Una matrice quadrata A si
Matematica per Chimica, Chimica Industriale e Scienze dei Materiali Primo appello 7/02/2012 Tema A
 Matematica per Chimica, Chimica Industriale e Scienze dei Materiali Primo appello 7/02/202 Tema A NOME:..................................................... COGNOME:.....................................................
Matematica per Chimica, Chimica Industriale e Scienze dei Materiali Primo appello 7/02/202 Tema A NOME:..................................................... COGNOME:.....................................................
INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 25 FEBBRAIO a a. A a = 1 a 0
 INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 5 FEBBRAIO 013 Esercizio 1. Al variare del parametro a R, si consideri la matrice A a = 1 a 0 a 1 0. 1 1 a (1) Si discuta al variare
INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 5 FEBBRAIO 013 Esercizio 1. Al variare del parametro a R, si consideri la matrice A a = 1 a 0 a 1 0. 1 1 a (1) Si discuta al variare
2 Sistemi lineari. Metodo di riduzione a scala.
 Sistemi lineari. Metodo di riduzione a scala. Esercizio.1 Utilizzando il metodo di eliminazione di Gauss, risolvere i seguenti sistemi lineari: 1. 3. x 1 x + 3x 3 = 1 x 1 x x 3 = x 1 + x + 3x 3 = 5 x 1
Sistemi lineari. Metodo di riduzione a scala. Esercizio.1 Utilizzando il metodo di eliminazione di Gauss, risolvere i seguenti sistemi lineari: 1. 3. x 1 x + 3x 3 = 1 x 1 x x 3 = x 1 + x + 3x 3 = 5 x 1
3 Soluzione di sistemi lineari
 3 Soluzione di sistemi lineari Prima di addentrarci nello studio dei metodi numerici, è doveroso introdurre le matrici e alcune strutture particolari di matrici nonchè alcuni concetti fondamentali quali
3 Soluzione di sistemi lineari Prima di addentrarci nello studio dei metodi numerici, è doveroso introdurre le matrici e alcune strutture particolari di matrici nonchè alcuni concetti fondamentali quali
Si deve verificare (sulla brutta copia) che (1 i 3)z dà lo stesso risultato usando l espressione del testo e la soluzione trovata.
 Università degli Studi di Bergamo Corso integrato di Analisi 1 (Geometria e Algebra Lineare 18 febbraio 1 Tema A Tempo a disposizione: ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio
Università degli Studi di Bergamo Corso integrato di Analisi 1 (Geometria e Algebra Lineare 18 febbraio 1 Tema A Tempo a disposizione: ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio
