f : R 2 R, f(x, y) = x(4 x 2 y 2 ).
|
|
|
- Albano Ruggeri
- 4 anni fa
- Visualizzazioni
Transcript
1 ANALISI MATEMATICA ING. AEROSPAZIALE L-Z PROVE SCRITTE VERSIONE PROVVISORIA SI PREGA DI SEGNALARE EVENTUALI ERRORI * Determinare purché esistano i punti critici della seguente funzione e stabilirne la natura: f : R R, fx, y = x4 x y. Facoltativo: stabilire la natura di uno dei punti critici senza utilizzare la matrice hessiana. 6 punti, ± punti di sella, / 3, punto di massimo locale, / 3, punto di minimo locale. Svolgimento. Si ha se e solo se Quindi i punti critici sono Si ha 4 y = x = f x = 4 3x y = f y = xy = oppure 4 3x = y =. P 1 =,, P =,, P 3 = / 3,, P 4 = / 3,. 6x y detd fx, y = det y x = 1x 4y. Quindi P 1 e P sono punti di sella, P 3 è un punto di massimo locale e P 4 è un punto di minimo locale. Si ha f, = e perciò, è un punto di sella. fx, = x 3 x, * Determinare i punti critici della funzione f : R \ {, } R definita da fx, y = logx + y x y e stabilirne la natura. 7 punti, punto di massimo locale, ± 3/, 1/ punti di sella. Svolgimento. Si ha { f x = f y = x x = x x +y y x +y 1 = 1 1 x +y = se e solo se { x = y 1 = } oppure { x + y = 1 y 1 =.
2 Perciò i punti critici sono,, 3, 1/ e 3, 1/. Si ha y x 4xy D x fx, y = +y x +y. 4xy x y x +y x +y Valutandolo nei punti critici si ottiene la risposta. * Determinare il massimo assoluto e il minimo assoluto della funzione f : Ω R definita da fx, y = 1 4 x y + 1 y, Ω = { x, y R : x + y 1 }. 7 punti max f = 3/8, min f = 3/4. Svolgimento. Si ha fx, y = x, y + 1 = x, y =, 1, quindi f non ha punti critici interni. Perciò il massimo e il minimo che esistono per il Teorema di Weierstrass sono assunti su Ω. Posto Lx, y, λ = 1 4 x y + 1 y + λ1 x y, si ha se e solo se Lx, y, λ = x λx, y + 1 λy, 1 x y = Si ha x =, y = ±1 oppure λ = 1/4, y = 1/, x = ± 3/. da cui segue la risposta. f, 1 = 1/4, f, 1 = 3/4, f± 3/, 1/ = 3/8, Per studiare f su Ω si può in alternativa considerare la funzione gy = f1 y, y = y + y, y [ 1, 1] e osservare che g ha massimo assoluto in y = 1/ e minimo assoluto in y = 1, oppure passare in coordinate polari. * Sia f : R R definita da fx, y = 3x 3 + y 3. a Determinare la natura dei punti critici. b Determinare i punti di massimo assoluto e i punti di minimo assoluto di f nel seguente insieme: K = { x, y R : 3x 4 + y 4 1 }.
3 7 punti a, punto di sella; b max K f =, min K f =. a Si verifica facilmente che fx, y =, se e solo se x, y =,. Poiché f, =, si ha fx, y f, = 3 1/3 x + y 3 /3 x 3 1/3 xy + y }{{} 3 1/3 x y, > x,y R quindi, è un punto di sella per esempio, f, y f, se e solo se y. b Sia Risolvendo il sistema si ottiene Lx, y, λ = 3x 3 + y 3 λ3x 4 + y 4 1. L x = 9x 1λx 3 = 3x 3 4λx = L y = 3y 4λy 3 = y 3 4λy = L λ = 1 3x 4 y 4 = x, y = ±1/3 1/4, oppure x, y =, ±1 oppure x, y = ±1, 1/. Valutando la funzione in tali punti si ottiene, rispettivamente, ±3 1/4, ±1, ±, da cui segue la risposta 3 1/4 < 1/ visto che 3 < 4. * Sia f : R R definita da e sia fx, y = 1 x y x + y Ω = {x, y R : x + y 1, x }. Determinare il massimo assoluto e il minimo assoluto di f in Ω. 7 punti max f = f1/ 6, 1/ 6 = Ω 3, min f = f, 1/ 3 = 3 Ω 3. 3 I punti critici interni si determinano risolvendo f = xx + y + 1 x y, yx + y + 1 x y! =,. Sottraendo le due equazioni e svolgendo semplici calcoli, si ottiene che l unico punto critico interno ad Ω è P 1 = 1/ 6, 1/ 6. Per quanto riguarda Ω, si ha f Γ1, Γ 1 = Ω {x + y = 1}
4 mentre su Γ = Ω {x = } si studia la funzione g : [ 1, 1] R, gy := f, y = y1 y e si verifica che y = 1 e y = 1/ 3 sono punti di massimo locale per g in [ 1, 1], mentre y = 1/ 3 e y = 1 sono punti di minimo locale. Confrontando i valori dei candidati ottenuti si ottiene la risposta. * Determinare il massimo assoluto ed il minimo assoluto della funzione f : Ω R definita da fx, y = x x y +, Ω = { x, y R : x y x + 4 }. 7 punti max f = 4, min f = 4. Ω Ω Si ha fx, y =, 3x y +, x =, x, y =,, quindi P :=, è un punto critico interno ad Ω. Si ha inoltre Ω = Γ 1 Γ, dove Γ 1 = {x, y R : x, y = x } Γ = {x, y R : x, y = x + 4} Restringendo la funzione su Γ 1 si ottiene ϕ 1 x := f Γ1 = x x, x [, ] e si verifica che x = ed x = /3 sono punti di massimo locale per ϕ 1, mentre x = /3 ed x = sono punti di minimo locale per ϕ 1. A tali punti corrispondono i candidati P 1 :=, 8 e P := /3, 4/3 possibili punti di massimo locale per f e P 3 := /3, 4/3 e P 4 :=, 8 possibili punti di minimo locale per f. Su Γ si ha invece che ϕ x := f Γ = x, x [, ] da cui segue che x = ed x = sono, rispettivamente, punti di massimo locale e di minimo locale per ϕ x, cui corrispondono i candidati P 1 e P 4. Confrontando i valori dei candidati P,..., P 4 si ottiene la risposta. * Sia f : R R definita da fx, y = x y. Determinare il massimo assoluto ed il minimo assoluto di f su { Ω = x, y R : x + 4y + x, x 3 }. 7 punti
5 min f =, max f = 19/16. Ω Ω Cenno di svolgimento: La funzione ha un punto critico interno 1/,. Su Ω si ottengono i punti critici vincolati,, 1/3, ± 5/6 e 3/,. Inoltre si devono considerare a parte i vertici 3/, ± 3/4. Confrontando i valori si ottiene la risposta. * Sia f : R R definita da fx, y = x 5 x y + 1. Verificare che il Teorema delle funzioni implicite o di Dini è applicabile in un intorno del punto 1, e determinare il polinomio di Taylor di ordine centrato in x = 1 della funzione x gx definita implicitamente da fx, y = f1,. 7 punti 5x 1. Svolgimento. Si ha fx, y = 5x 4 xy, x, f1, = 5, 1, quindi il teorema di Dini è applicabile rispetto a entrambe le variabili. Segue dal Teorema di Dini che quindi g x = 5x4 xgx x da cui segue la risposta. = 5x gx x, g x = 1x g x + gx x x, g1 =, g 1 = 5, g 1 = 1 1 = Si noti che in questo caso g può anche essere ricavata esplicitamente: fx, y = f1, x 5 x y + 1 = y = x5 1 x da cui g x = 3x + x 3, g x = 6x 6 x 4, = x 3 1 =: gx, x e valutando in x = 1 si riottiene la risposta. * Verificare che, in un intorno del punto x, y = 1, π, l equazione sinxy x = 1 individua implicitamente una funzione y = gx oppure x = hy. Determinare lo sviluppo di Taylor del secondo ordine con centro in x = 1 oppure in y = π, rispettivamente della funzione cosí ottenuta.
6 7 punti gx = π 1 + πx πx 1. Lo svolgimento mediante il Teorema di Dini è standard e si rimanda allo svolgimento della prova precedente. Si osservi che, in alternativa, l equazione può essere risolta esplicitamente rispetto a x in un intorno di 1, π, osservando che sinxy = sinxy π: si ottiene y = gx = π + arcsin1 x. x * Disegnare l insieme Ω = { x, y : y 1 x y 1 } e calcolarne il baricentro. 7 punti x b, y b = 7/5, Svolgimento. La rappresentazione di Ω segue dal grafico delle due funzioni elementari y y 1 e y y 1. Per simmetria, y b =. Si ha da cui Ω = x b = 6 5 = y 1 y 1 1 y 1 1 dxdy = 1 y 1 xdxdy = y y dy = = 5 3, 1 y 4y 4 + 9y 3dy = 3 5 y 1 4y 1 dy = 7 5. * Determinare il baricentro del seguente insieme: { Ω = x, y R : x y } x +. 7 punti
7 5, 5. Il dominio è simmetrico rispetto a x = perché le funzioni x x e x x + sono pari. Quindi x b = e dove Ω = Ω 1, y b = 1 Ω 1 Ω 1 ydxdy, Ω 1 = {x, y R : x, x y x + }. Si verifica facilmente che, per x, x x + se e solo se x. Pertanto Ω 1 = {x, y R : x [, ], x y x + } e quindi y b = Ω 1 = 3 x+ 5 x x+ x dydx = 3 5 ydydx = 5 5. * Determinare le coordinate del baricentro del seguente insieme: Ω = { x, y R : y 3 x y }. 7 punti 3/7, 1/5 Per definzione dove Ω è l area di Ω. Poiché x b = 1 x dxdy, y b = 1 y dxdy Ω Ω Ω Ω y 3 y y [, 1], Ω si riscrive come dominio semplice come segue: Ω = { x, y R : y [, 1], y 3 x y }. Pertanto Quindi y b = 1 5 Ω = 1 y 1 y y 3 y 3 dx dy = 1 y dx dy = 1 5 = 1 5 y y 3 dy = y y y 3 dy y 3/ y 4 dy = 1 5,
8 mentre x b = y y 3 x dx dy = = x y y 3 dy y y 6 dy = 3 7. * Calcolare Ω xy dxdy, Ω = { x, y R : y x, 1 x + y 4 }. 7 punti 15/16. * Calcolare I = Ω x + ydxdydz, Ω = {x, y, z R 3 : x + y z x y}. 7 punti Primo metodo. Ponendo u = x + y e v = x y, si ottiene I = 1 ududvdz, T = {u, v, z R 3 1 : u + v z v} T e il risultato segue poiché l integranda è dispari rispetto a u = e il dominio è simmetrico rispetto ad u =. Secondo metodo. Passando in coordinate cilindriche, si ottiene I = r cos φ + sin φdrdφdz, dove Si ha S S = {r, φ, z [, [ π, π] R : r z rcos φ sin φ}. perciò, integrando per fili, r rcos φ sin φ r cos φ sin φ, I = E rcos φ sin φ r cos φ + sin φdz, r
9 dove Si ha Perciò I = = π/4 3π/4 π/4 3π/4 E = {r, φ : φ [ π, π], r cos φ sin φ}. cos φ sin φ cos φ sin φ φ [ 3π/4, π/4]. r 3 cos φ + sin φcos φ sin φ rdr dφ 1 cos φ + sin φcos φ sin φ5 dφ = 1 1 cos φ sin φ6 π/4 3π/4 Naturalmente i due metodi presentati non sono i soli: si può anche integrare per fili prima di passare in coordinate cilindriche, oppure osservare le proprietà di simmetria in qualunque momento del procedimento. =. * Calcolare il volume del solido ottenuto ruotando il triangolo definito sul piano z = di vertici 1, 1,,, 4,, 1, 4, di un angolo π attorno all asse y. 7 punti 4π. Cenno di svolgimento: Si tratta del volume di un solido di rotazione un tronco di cono meno un cilindro, che quindi vale 4 y + π 1 dy = 4π. 3 1 * Data la curva γ : [ π/, π/] R, γt = cos t, cost, calcolare γ x ds. 7 punti 17 3/ 1/4. Cenno di svolgimento: Applicando la definizione di integrale curvilineo di prima specie e ossefvando che l integranda è pari, si ottiene γ x ds = π/ π/ cos t sin t cos t 1/ dt = che si integra con la sostituzione y = cos t. π/ cos t sin t cos t 1/ dt
10 * Sia γ : [, 1] R definita da γt = t, t /. Calcolare xyds. γ 7 punti 1 + /15. * Determinare un insieme connesso E R in cui la forma differenziale y ω = x3x y dx + 1 3x y dy sia esatta; in E determinare una funzione potenziale ovvero una primitiva di ω. 7 punti D 1 = {x, y R : x >, y > 3x}, Ux, y = log x 3x y + C, C R Svolgimento. Il dominio della forma è D = {x, y R : x, y 3x}. Verifichiamo che ω è esatta su ciascuna componente connessa di D determinandone una funzione potenziale: 1 Ux, y = dy = log 3x y + Cx, 3x y da cui se e solo se x Ux, y = 3 3x y + C x =! y x3x y C x= 3 3x y y x3x y = 3x y x3x y = 1 x. Perciò Cx = log x + C, ovvero Ux, y = log x 3x y + C, C R. Si può quindi scegliere qualunque componente connessa di D, per esempio D 1 = {x, y R : x >, y > 3x}. * Disegnare l insieme D = {x, y R : 4x + y 8x 4y + 4 < }
11 e determinare il valore di A R per cui la forma differenziale ω = Ax 1dx + y dy 4x + y 8x 4y + 4 è esatta in D. 7 punti D è l interno dell ellisse di centro 1, e semiassi paralleli agli assi, di lunghezza 1 e ; A = 8. Svolgimento. Si ha 4x + y 8x 4y + 4 = 4x 1 + y 4, da cui segue la caratterizzazione di D. Dalla precedente identità segue anche facilmente che ω è esatta se e solo se A = 8 in tal caso una primitiva di ω è Ux, y = log 4x 1 + y 4. * Sia Calcolare γ : [, 1] R, γt = γ πt 1 t cosπt 3, sin t + 5. e y 1 + x dx + ey arctan x dy. 7 punti πe5 4 Svolgimento. Verifichiamo che la forma differenziale è esatta: e y Ux, y = 1 + x dx = ey arctan x + Cy da cui ovvero U y = e y arctan x + C y! = e y arctan x C y =, Ux, y = e y arctan x + C, C R. Perciò, osservando che γ1 = 1, 5 e γ =, 5, si ottiene e y 1 + x dx + ey arctan x dy = U1, 5 U, 5 = πe5 4. γ * Sia ωx, y = x x + y + 1 dx + y x + y x e sia γ : [, 1] R definita da γt = t 7 t, t. Calcolare ω. γ dy, x, y R
12 7 punti log 4 3. La forma differenziale ω 1 x, y := è esatta in R, con funzione potenziale Perciò γ ω = Uγ1 Uγ + x x + y + 1 dx + y x + y + 1 dy Ux, y = 1 log1 + x + y. γ 3xdy = log t 8 t dt = log 4 3. * Sia ω la forma differenziale definita da y ωx, y = 1 + x y x x dx + dy, x, y 1 + x R y e sia γ : [ 1, 1] R la curva definita da γt = t 4 cos πt 1, t, t [ 1, 1] orientata nel verso delle t crescenti. Calcolare γ + ω. 7 punti. Cenno di svolgimento: La curva è chiusa e la forma è esatta, con funzioni potenziali Ux, y = arctanxy x + C, C R. * Sia γ : [, π] R la curva definita da γt = cos t, sin t, t [, π] orientata nel verso delle t crescenti e sia ω la forma differenziale definita da ωx, y = xy x 1 + x 4 y dx x 4 y + x dy.
13 Calcolare γ + ω. 7 punti π La forma differenziale ω 1 := ω x dy è esatta in R le sue funzioni potenziali sono Ux, y = arctanx y + C, C R. Poiché γ è chiusa, si ottiene π ω = x dy = cos t dt = π. γ + γ + * Sia Ω R il triangolo di vertici,,, 1 e 1,, e sia ω la forma differenziale definita da 4x 3 ωx, y = 1 + x 4 + y dx + 4y x 4 + y + x dy. 4 Calcolare Ω + ω. 7 punti 1/ Si ha dove v = ω = v nds, Ω + Ω + 4y x 4 + y 4 + x, 4x x 4 + y 4 Applicando il Teorema della divergenza, si ottiene ω = div vdxdy = Ω = 1 Ω + Ω. In alternativa, siano ω 1 =. 4x x 4 + y 4 dx + 4y x 4 + y 4 dy, ω = xdy. Si verifica che ω 1 è esatta osservando che è chiusa in R o determinandone un potenziale, quindi ω = xdy Ω + Ω +
14 che si calcola facilmente ponendo attenzione al verso di percorrenza!. * a Determinare A R in modo tale che la forma differenziale ω = 1 Aydx xdy x + y sia chiusa nel suo dominio naturale D; b per tale valore di A calcolare ω, dove γ è una qualunque curva regolare in D γ che parte dal punto, 1 e arriva al punto 1,. 7 punti * Calcolare Ω + xy dy, Ω = {x, y R : y, y 5x, y 7x }. 7 punti log 7. Svolgimento. Segue dalle formule di Green che I = xy dy = ydxdy. Ω + L insieme Ω è semplice rispetto a entrambi gli assi: { Ω = x, y R : x [, 7/], y min {5x, 7x }} { = x, y R : y [, 5], y 5 x 7 }. y + Quindi I = 1 5x ydydx + 7/ 7/x 1 Ω ydydx oppure I = e svolgendo correttamente gli integrali si ottiene la risposta. 5 7/y+ y/5 ydxdy * Sia γ : [, π] R la curva piana definita da γt = sin t, t sin t. a Verificare che γ è una curva di Jordan. b Calcolare l area del suo interno.
15 7 punti π/4 La curva in esame è chiusa in quanto γ =, = γπ, ed è semplice in quanto γt 1 = γt { t1 sin t 1 = t sin t sin t 1 = sin t = t 1 = t sostituendo la seconda nella prima. Quindi è una curva di Jordan. Perciò l area del suo interno, Ω, è, a meno del segno che dipende dall orientazione di γ, π ydx = t sin t cos tdt = π 4, da cui segue il risultato. Ω * Calcolare x + y 3, y + x 6 nds Ω dove Ω = {x, y R : x + y 4y + x + 1 } ed n è la normale esterna ad Ω. 7 punti * Calcolare il flusso del campo vettoriale V = xz, yz, xy uscente da Ω = [, 1] 3. 7 punti 1 * Sia Ω R 3 un dominio di Green di volume 3 e baricentro, 1,, e sia V il seguente campo vettoriale: V : R 3 R 3, Vx, y, z = 3x, y, 5z + z. Calcolare il flusso di V uscente da Ω. 6 punti 9
16 Svolgimento. Applicando il teorema della divergenza, si ottiene V n e ds = 6x + y + 1z + 1dxdydz Ω Ω 6 = Ω xddydz + yddydz + 1 zddydz + 1 Ω Ω Ω Ω Ω Ω = = 9. * Determinare l area della porzione di superficie cilindrica definita da Σ = {x, y, z R 3 : x + y + = 4, z x}. 8 punti 8 Svolgimento. Si parametrizza Σ mediante coordinate cilindriche: σ : D R 3, σφ, z = cos φ, + sin φ, z. Per determinare D si nota che z x z cos φ, quindi D = {φ, z [, π R : z cos φ}. Poiché σ φ = sin φ, cos φ, e σ z =,, 1, si ha σ φ σ z = cos φ, sin φ, =. Quindi dσ = dφdz. Σ D Si riscrive D come dominio semplice osservando che cos φ φ [ π/, π/]. Pertanto Σ dσ = π/ cos φ π/ π/ dzdφ = 4 cos φdφ = 8. π/ * Sia Σ + la superficie ottenuta ruotando il sostegno della curva γt =, e t, t, t [, 1] di un angolo π attorno all asse z, orientata in modo tale che n + e 3. Calcolare il flusso del campo vettoriale Vx, y, z = x, y, attraverso Σ +. 7 punti
17 πe 1. Cenno di svolgimento: La parametrizzazione è σφ, t = e t cos φ, e t sin φ, t e la normale da scegliere è n + = σ φ σ t. Il resto è un calcolo. * Sia Σ la porzione del cono z = x + y compresa tra i piani z = e z = 1. Calcolare zdσ. S 6 punti * Sia v : R 3 R 3 il campo vettoriale definito da e sia Σ + la superficie definita da vx, y, z =, y, z Σ = { x, y, z R 3 : x = 4y + z, x [1, ] } e orientata in modo tale che n + e 1 >. Calcolare il flusso di v attraverso Σ +. 7 punti 7π/1 Si parametrizza la superficie utilizzando coordinate cartesiane o cilindriche. Nel secondo caso σr, φ = r, r cos φ, r sin φ, D = [1/, 1] [, π]. Si ha σ r =, cos φ, sin φ, σ φ =, r sin φ, r cos φ, quindi σ r σ φ = r, r cos φ, r sin φ, la cui orientazione coincide con quella richiesta. Pertanto Φ Σ v = v n + dσ = v σ σ r σ φ drdφ = r drdφ = 7π/1. Σ D D
18 * Determinare una parametrizzazione σ : D R R 3 della superficie Σ = { x, y, z R 3 : x, y, z, x 8 + y + 4z = 6 } e determinare il piano tangente e i due versori normali a Σ in 1, 1, 1. 6 punti Una possibile parametrizzazione è: D = {u, v : u +4v 6}, σu, v = 6 u 4v 1/8, u, v, il piano tangente è x 1 + y 1/4 + z 1 = e i versori normali sono n = ± , 1/4, 1. Svolgimento. Si può parametrizzare Σ come superficie cartesiana rispetto a qualunque asse. Per esempio, poiché x, pertanto x = 6 y 4z 1/8 =: fy, z, 6 y 4z, D = {u, v : u + 4v 6}, σu, v = 6 u 4v 1/8, u, v. Poiché si tratta di una superficie cartesiana, il piano tangente e i versori normali sono dati rispettivamente da 1 x 1 f y 1, 1y 1 f z 1, 1z 1 =, n = ± 1, f 1 + f y + fz y, f z. Poiché f y y, z = y 4z 7/8, f z y, z = 6 y 4z 7/8, si ha f y 1, 1 = 1/4, f z 1, 1 = 1, da cui segue la risposta. * Sia Σ + la superficie definita da { Σ = x, y, z R 3 : z = xy, x + y 1, y } 3x e orientata in modo tale che n + e 3 <. a Calcolare l area di Σ. b Calcolare la circuitazione del vettore v = x,, y lungo Σ +. 7 punti a π 3 1; b 1/3. Σ è una superficie cartesiana parametrizzata da σu, v = u, v, uv, D = {u, v R : u + v 1, v 3u}. Si ha quindi σ u σ v = v, u, 1, σ u σ v = 1 + u + v.
19 Perciò la risposta ad a è Σ = D 1 + u + v dudv = 4π/3 π/3 Per b, si osserva che versori normali sono 1 v, u, 1 ± 1 + u + v e quello tale che il prodotto scalare con e 3 è negativo è Si osserva inoltre che n + := v, u, u + v. rotv = 1,,, rotv n + = ρ 1 + ρ dρdφ = π 3 1. v 1 + u + v. Applicando il teorema del rotore, si conclude che la circuitazione vale D vdudv = 4π/3 1 π/3 ρ sin φdρdφ = 1 3. * Risolvere il seguente problema di Cauchy, specificando l intervallo massimale di esistenza della soluzione: { y x = 3 x 1 1 x yx e y y 1 =. log 3 7 punti yx = log x 3 3x + 1, y 3,. L equazione differenziale è a variabili separabili: yxe y x y x = 3 x 1 e y x = x 3 3x + C. Imponendo la condizione iniziale si ricava C = 1. Quindi yx = ± log x 3 3x + 1, e per soddisfare la condizione iniziale si deve scegliere la soluzione positiva: Tale funzione è definita se yx = log x 3 3x + 1. x 3 3x x x 3 { { x x x 3 x 3 [ x ] 3, [ 3, +,
20 quindi l intervallo aperto massimale che contiene x = 1 è 3,. * Determinare la soluzione del seguente problema di Cauchy, specificandone l intervallo massimale di esistenza: { x y x = yx 1 + yxe x/yx y1 = 1 log 4 si suggerisce di ricondursi a un equazione a variabili separabili mediante un opportuno cambio di variabile. 8 punti yx = x, log3+x x, +. Svolgimento. Ponendo ad esempio si ottiene Quindi ovvero Si ha u1 = 1/y1 = log 4, quindi ux := x yx, u = 1 y xy y = 1 y 1 y 1 + yeu = e u. e u = e u u = 1, e ux = C + x. e u1 = C + 1! = 4 C = 3. Pertanto ux = log3 + x yx = x ux = x log3 + x, x, +. * Determinare l integrale generale della seguente equazione differenziale: x y x xy x + 1 yx = log x, x >. 9 8 punti yx = c + c 1 log x x 1/3 + 9 log x Svolgimento. L equazione assegnata una equazione di Eulero. Ponendo l equazione differenziale per ut diventa x = e t t = log x, ut = ye t, u t 3 u t + 1 ut = t. 9
21 Le radici del polinomio caratteristico sono λ 1 = λ = 1, per cui l integrale generale 3 dell omogenea associata risulta essere u o t = c + c 1 t e t/3. Per determinare una soluzione particolare si utilizza il metodo di somiglianza: da cui segue che u p t = At + B, y pt = A, y pt =, u pt 3 u pt u pt = 3 A At B! = t A = 9, B = 54. Da ci segue che l integrale generale nell incognita ut ut = c + c 1 t e t/3 + 9t + 54 e sostituendo t = log x si ottiene la risposta. * Determinare l integrale generale della seguente equazione differenziale: y x 4y x + 13yx = e x. 7 punti * Determinare purché esistano i valori dei parametri α R e β R per i quali la soluzione del problema di Cauchy y x + yx = β sinx y π = α y π = β. è periodica di periodo π. 7 punti α = β = 4 3. L equazione assegnata è lineare. Le radici del polinomio caratteristico sono λ 1 = i, λ = i. Di conseguenza l integrale generale dell omogenea associata è: y o x = c 1 cos x + c sin x. Per determinare la soluzione particolare si usa il metodo di somiglianza: y p t = A cosx + B sinx + C.
22 Sostituendo nell equazione differenziale si ricava che A =, B = /3 e C = β, per cui l integrale generale risulta essere: y gen x = c 1 cos x + c sin x + sinx + β. 3 Imponendo poi le condizioni iniziali si ha che { c + β = α c = β { c1 = β 4 3 c = α β da cui si ricava che la soluzione del problema di Cauchy è: yx = β 4 cos x + α β sin x sinx + β Annullando infine i coefficienti delle funzioni sin x e cos x, uniche a non essere π- periodiche, si ottiene la risposta. * Risolvere il seguente problema di Cauchy, specificando l intervallo massimale di esistenza della soluzione: y x = yx + 1 y x y = y = 1 7 punti yx = x I =, 1 1 x Cenno di svolgimento: Attraverso il metodo risolutivo per equazioni autonome del secondo ordine oppure, più semplicemente, osservando che si possono integrare una volta entrambi i membri dell equazione. * Risolvere il seguente problema di Cauchy, determinando anche l intervallo massimale di esistenza della soluzione: { y x = x + 3yx 1 3 y = 1. 7 punti * Determinare la soluzione del seguente problema di Cauchy, specificandone l intervallo massimale di esistenza: { y x + x yx = e x3 y 4 x. y = 1
23 si suggerisce di utilizzare la sostituzione ux = yx 3. 7 punti * Determinare la soluzione del seguente problema di Cauchy, specificandone l intervallo massimale di esistenza: y = y sin y cos y y 1/ = π/4. y 1/ = 7 punti yx = arcsin 1 + x, I = 1 1/, 1 1/. * Determinare l integrale generale della seguente equazione differenziale: y + 4y = 1 7 punti C 1 cosx + C sinx + C 3 + C 4 x x. * Dopo aver determinato lo sviluppo in serie di Fourier della funzione fx = sin x, calcolare la somma della seguente serie numerica: k=1 1 4k 1. 7 punti 1/ La funzione é pari e periodica di periodo π. Si ha quindi b n = per ogni n e a n = 4 π π/ sin x cosnxdx.
24 Quindi π/ e, integrando per parti, a = 4 π sin xdx = 4 π 4 π π/ sin x cosnxdx = [sin x sinnx]π/ } nπ {{} nπ ovvero n π quindi π/ = = [ 1 cos x cosnx n π sin x cosnxdx = Si conclude che la serie di Fourier è ] π/ 4 a n = 4n 1π. π 4 4n 1π cosnx. n=1 π/ + 1 n π cos x sinnxdx π/ sin x cosnxdx, [ ] π/ 1 cos x cosnx = 1 n π n π, Valutando la serie in x = e tenendo conto che f =, si ottiene 1 = 1 4n 1. n=1 * Determinare lo sviluppo in serie di Fourier della funzione f : R R, periodica di periodo π, definita in [ π, π] da { 1 se x < π fx = se π x π e utilizzarlo per calcolare la somma della seguente serie: k= 1 k k punti Sia A R e sia ω una forma differenziale di classe C 1 A. Dimostrare che se ω è esatta in A, allora è chiusa in A. Sia x, y R e sia f : R R differenziabile in x, y. Utilizzando la definizione, calcolare d dt fx + t, y e t nel punto t =.
25 Calcolare, purché esista, il seguente limite: y 3 + xy lim x,y, x + y. Dimostrare che per ogni x in un intorno di x = 1 esiste un unico yx in un intorno di y = 1 tale che x, yx risolve l equazione e dimostrare che yx < 1 se x > 1. x 5 y 7 x 8 y 1 = Sia Ω R un dominio regolare a tratti di area 1 e sia u : C 1 R R tale che ux, y = 3 per ogni x, y Ω. Calcolare u n e ds. Sia f una funzione continua π-periodica e sia Ω fx = a + a k coskx + b k sinkx k=1 il suo sviluppo in serie di Fourier. Dimostrare che se f è pari allora b k = per ogni k 1. Sia f : R R di classe C 1 R e sia x, y R. Determinare la direzione di massima pendenza del grafico di f in x, y. Determinare purché esistano le soluzioni dell equazione differenziale y x y x + y x = che posseggono un asintoto orizzontale per x. Siano f : R 3 R ed Ω R 3 definiti rispettivamente da fx, y, z = x + y + z e Ω = {x, y, z R 3 : x + y + z 1}. Calcolare il flusso del campo vettoriale f uscente da Ω. Enunciare e dimostrare la disuguaglianza di Cauchy-Schwarz in R. Dimostrare che se f : R R è differenziabile in x, y, allora. f x x, y = fx, y 1, Fornire l esempio di una forma differenziale chiusa, ma non esatta, in D R. Determinare i valori del parametro α, + per i quali la funzione f : R R definita da fx, y = x 3α y α è differenziabile in x, y =,. Sia f : R 3 R definita da fx, y, z = x 3 y 3 z 3, e sia Ω R 3 un dominio regolare di volume 1 e baricentro in 1,,. Determinare il flusso di f attraverso Ω. Enunciare e dimostrare le formule di Green in R su un dominio semplice rispetto ad esntrambi gli assi.
sen n x( tan xn n n=1
 8 Gennaio 2016 Nome (in stampatello): 1) (8 punti) Discutere la convergenza della serie di funzioni al variare di x in [ 1, 1]. n x( tan xn n ) xn sen n 2) (7 punti) Provare che la forma differenziale
8 Gennaio 2016 Nome (in stampatello): 1) (8 punti) Discutere la convergenza della serie di funzioni al variare di x in [ 1, 1]. n x( tan xn n ) xn sen n 2) (7 punti) Provare che la forma differenziale
DIARIO DELLE LEZIONI DI ANALISI MATEMATICA II Corso di laurea in Ingegneria Clinica Canale PZ A.A. 2017/2018 Codocente: Dott. Salvatore Fragapane
 DIARIO DELLE LEZIONI DI ANALISI MATEMATICA II Corso di laurea in Ingegneria Clinica Canale PZ A.A. 07/08 Codocente: Dott. Salvatore Fragapane Lezione - 09/03/08, dalle 6.00 alle 8.00 in aula 6 Es. Studiare
DIARIO DELLE LEZIONI DI ANALISI MATEMATICA II Corso di laurea in Ingegneria Clinica Canale PZ A.A. 07/08 Codocente: Dott. Salvatore Fragapane Lezione - 09/03/08, dalle 6.00 alle 8.00 in aula 6 Es. Studiare
Analisi Matematica 2 (Corso di Laurea in Informatica)
 COGNOME NOME Matr. Firma dello studente A Tempo: 3 ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
COGNOME NOME Matr. Firma dello studente A Tempo: 3 ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009)
 ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009) 1. Sia S = { } (x, y, z) : x 2 + y 2 = 4, 0 z 3 + x. Scrivere le equazioni parametriche di una superficie regolare che abbia S come sostegno. 2. Enunciare
ANALISI MATEMATICA II PROVA DI TEORIA (23/6/2009) 1. Sia S = { } (x, y, z) : x 2 + y 2 = 4, 0 z 3 + x. Scrivere le equazioni parametriche di una superficie regolare che abbia S come sostegno. 2. Enunciare
Alcuni esercizi risolti da esami di anni passati
 Alcuni esercizi risolti da esami di anni passati Andrea Braides ( x. Calcolare, se esiste, il limite lim (x,y (, x + y log + y + x 3 y. x + y Dato che log( + s = s + o(s per s, abbiamo lim (x,y (, ( x
Alcuni esercizi risolti da esami di anni passati Andrea Braides ( x. Calcolare, se esiste, il limite lim (x,y (, x + y log + y + x 3 y. x + y Dato che log( + s = s + o(s per s, abbiamo lim (x,y (, ( x
Analisi Matematica 2: Secondo Parziale, , Versione A. Cognome e nome:...matricola:...
 Analisi Matematica : Secondo Parziale, 6.6.7, Versione A Cognome e nome:....................................matricola:......... es. es. es.3 es.4 es.5 es.6 es.7 somma 5cr. 6 6 6 6 6 - - 3 9cr. 5 5 5 5
Analisi Matematica : Secondo Parziale, 6.6.7, Versione A Cognome e nome:....................................matricola:......... es. es. es.3 es.4 es.5 es.6 es.7 somma 5cr. 6 6 6 6 6 - - 3 9cr. 5 5 5 5
Facoltà di Scienze MM.FF.NN. Corso di Laurea in Matematica - A.A Prova scritta di Analisi Matematica II del c.1.
 Prova scritta di Analisi Matematica II del 14-07-1999 - c.1 1) Sia (d n ) una successione di numeri reali tali che inf d n > 0. Studiare il carattere della serie + n=1 al variare del parametro reale positivo
Prova scritta di Analisi Matematica II del 14-07-1999 - c.1 1) Sia (d n ) una successione di numeri reali tali che inf d n > 0. Studiare il carattere della serie + n=1 al variare del parametro reale positivo
Esercizi di Analisi Matematica II assegnati nell A.A. 2011/12. Corsi di laurea in Ingegneria Elettronica ed Informatica
 Esercizi di Analisi Matematica II assegnati nell A.A. 2011/12 Corsi di laurea in Ingegneria Elettronica ed Informatica 1) Rappresentare nel piano xy i campi di esistenza delle seguenti funzioni: a) xy
Esercizi di Analisi Matematica II assegnati nell A.A. 2011/12 Corsi di laurea in Ingegneria Elettronica ed Informatica 1) Rappresentare nel piano xy i campi di esistenza delle seguenti funzioni: a) xy
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica 2 del 19/06/2010 A
 Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9/6/ A ) ata la funzione f(x, y) x y log( + x + y ), a) stabilire dove risulta derivabile parzialmente nel suo
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9/6/ A ) ata la funzione f(x, y) x y log( + x + y ), a) stabilire dove risulta derivabile parzialmente nel suo
Esempi di esercizi d esame A.A. 2006/07 Analisi Matematica 2 Ingegneria Elettronica Proff. G. Vergara Caffarelli e L. Giacomelli
 Esempi di esercizi d esame A.A. 6/7 Analisi Matematica Ingegneria Elettronica Proff. G. Vergara Caffarelli e L. Giacomelli versione preliminare, si prega di segnalare eventuali errori *) Determinare e
Esempi di esercizi d esame A.A. 6/7 Analisi Matematica Ingegneria Elettronica Proff. G. Vergara Caffarelli e L. Giacomelli versione preliminare, si prega di segnalare eventuali errori *) Determinare e
Contents. 1. Funzioni di più variabili.
 RACCOLTA DI ESERCIZI PER IL CORSO DI ANALISI MATEMATICA II A.A. 03/04 CORSI DI LAUREA IN INGEGNERIA DELL EDILIZIA, INGEGNERIA EDILE-ARCHITETTURA PROF. D. BARTOLUCCI Contents. Funzioni di più variabili..
RACCOLTA DI ESERCIZI PER IL CORSO DI ANALISI MATEMATICA II A.A. 03/04 CORSI DI LAUREA IN INGEGNERIA DELL EDILIZIA, INGEGNERIA EDILE-ARCHITETTURA PROF. D. BARTOLUCCI Contents. Funzioni di più variabili..
Analisi Matematica II - Ingegneria Meccanica/Energetica - 29 Gennaio 2018
 nalisi Matematica II - Ingegneria Meccanica/Energetica - 29 Gennaio 218 1) ia data la funzione f(x, y, z) = (x 2 + y 2 1) 2 + 8 a) tudiare l esistenza di massimi e minimi assoluti della funzione f nella
nalisi Matematica II - Ingegneria Meccanica/Energetica - 29 Gennaio 218 1) ia data la funzione f(x, y, z) = (x 2 + y 2 1) 2 + 8 a) tudiare l esistenza di massimi e minimi assoluti della funzione f nella
Recupero 1 compitino di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2017/2018. Prof. M. Bramanti.
 Recupero compitino di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 7/8. Prof. M. Bramanti Tema n 3 4 5 6 Tot. Cognome e nome in stampatello codice persona o n di matricola
Recupero compitino di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 7/8. Prof. M. Bramanti Tema n 3 4 5 6 Tot. Cognome e nome in stampatello codice persona o n di matricola
Quesito 1. f(x, y) = xy log (x 2 + y 2 ) Quesito 2. Quesito 3. y = 2y3 +x 3. xy 2 y(1) = 1. Quesito 4
 Corso di laurea in Ing. Meccanica, a.a. 2002/2003 Prova scritta di Analisi Matematica 2 del 7 gennaio 2003 Determinare gli eventuali estremi relativi della funzione f(x, y) = xy log (x 2 + y 2 ) Calcolare
Corso di laurea in Ing. Meccanica, a.a. 2002/2003 Prova scritta di Analisi Matematica 2 del 7 gennaio 2003 Determinare gli eventuali estremi relativi della funzione f(x, y) = xy log (x 2 + y 2 ) Calcolare
Versione preliminare si prega di segnalare eventuali errori
 Analisi matematica (I mod) Ing. Elettronica PROFF. GIACOMELLI e VERGARA CAFFARELLI ESEMPI DI ESERCIZI D ESAME A.A.8/9 Versione preliminare si prega di segnalare eventuali errori *) Determinare (purché
Analisi matematica (I mod) Ing. Elettronica PROFF. GIACOMELLI e VERGARA CAFFARELLI ESEMPI DI ESERCIZI D ESAME A.A.8/9 Versione preliminare si prega di segnalare eventuali errori *) Determinare (purché
Recupero 1 compitino di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2016/2017. Prof. M. Bramanti.
 Recupero 1 compitino di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 16/17. Prof. M. Bramanti 1 Tema n 1 3 4 6 Tot. Cognome e nome in stampatello codice persona o n di
Recupero 1 compitino di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 16/17. Prof. M. Bramanti 1 Tema n 1 3 4 6 Tot. Cognome e nome in stampatello codice persona o n di
Esercizi sull integrazione II
 ANALISI MATEMATICA T-2 (C.d.L. Ing. per l ambiente e il territorio) - COMPL. DI ANALISI MATEMATICA (A-K) (C.d.L. Ing. Civile) A.A.28-29 - Prof. G.Cupini Esercizi sull integrazione II (Grazie agli studenti
ANALISI MATEMATICA T-2 (C.d.L. Ing. per l ambiente e il territorio) - COMPL. DI ANALISI MATEMATICA (A-K) (C.d.L. Ing. Civile) A.A.28-29 - Prof. G.Cupini Esercizi sull integrazione II (Grazie agli studenti
Analisi Matematica 2: Secondo Parziale, , Versione A. Cognome e nome:...matricola:...
 Analisi Matematica : Secondo Parziale, 1.6.17, Versione A Cognome e nome:....................................matricola:......... es.1 es. es.3 es. es.5 es.6 es.7 somma 5cr. 6 6 6 6 6 - - 3 9cr. 5 5 5 5
Analisi Matematica : Secondo Parziale, 1.6.17, Versione A Cognome e nome:....................................matricola:......... es.1 es. es.3 es. es.5 es.6 es.7 somma 5cr. 6 6 6 6 6 - - 3 9cr. 5 5 5 5
Esonero di Analisi Matematica II (A)
 Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
Prima Prova Scritta 18/03/1997
 Prima Prova Scritta 18/03/1997 1 + x y6 f(x, y) = x 6 + y 6, (x, y) (0, 0) k, (x, y) = (0, 0) A 2 Determinare, per k R, l insieme di continuità di f. B 2 Determinare, per k R, l insieme di differenziabilità
Prima Prova Scritta 18/03/1997 1 + x y6 f(x, y) = x 6 + y 6, (x, y) (0, 0) k, (x, y) = (0, 0) A 2 Determinare, per k R, l insieme di continuità di f. B 2 Determinare, per k R, l insieme di differenziabilità
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica 2 del 29 settembre 2012
 Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9 settembre A) Data la funzione f(x, y) = { xy x se (x, y) (, ) se (x, y) = (, ), i) stabilire se risulta continua
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9 settembre A) Data la funzione f(x, y) = { xy x se (x, y) (, ) se (x, y) = (, ), i) stabilire se risulta continua
1) Studiare la natura dei seguenti integrali impropri: 2x2 1. x dx (c) e x + 1. log x. n n + 1 n (a) n=1. (b) n + log n n 2n 2 1.
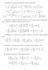 ) Studiare la natura dei seguenti integrali impropri: 0 x 3 dx (b) + 2x2 2 x 2 + 2 dx (c) e x + 0 e x dx (g) (d) + 0 + 0 x( + x) dx x sin x x 2 dx (h) (e) 0 + log x x 2 dx (f) 2 log x dx x + log( + x 2
) Studiare la natura dei seguenti integrali impropri: 0 x 3 dx (b) + 2x2 2 x 2 + 2 dx (c) e x + 0 e x dx (g) (d) + 0 + 0 x( + x) dx x sin x x 2 dx (h) (e) 0 + log x x 2 dx (f) 2 log x dx x + log( + x 2
Corso di Laurea in Ingegneria Gestionale - Sede di Fermo Anno Accademico 2009/2010 Matematica 2 Esercizi d esame
 Corso di Laurea in Ingegneria Gestionale - ede di Fermo Anno Accademico 2009/2010 Matematica 2 Esercizi d esame Nome... N. Matricola... Fermo, gg/mm/aaaa 1. tabilire l ordine di ciascuna delle seguenti
Corso di Laurea in Ingegneria Gestionale - ede di Fermo Anno Accademico 2009/2010 Matematica 2 Esercizi d esame Nome... N. Matricola... Fermo, gg/mm/aaaa 1. tabilire l ordine di ciascuna delle seguenti
Cognome Nome Matricola Codice ESEMPIO 1
 Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di derivata di una funzione in un punto. Sia A R N ; sia a A; sia f : A R M ; sia f differenziabile in a; allora la derivata di f in a è...
Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di derivata di una funzione in un punto. Sia A R N ; sia a A; sia f : A R M ; sia f differenziabile in a; allora la derivata di f in a è...
Analisi Matematica 2. Michele Campiti. Prove scritte di. Ingegneria Industriale a.a
 Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
COMPLEMENTI DI ANALISI MATEMATICA A.A Primo appello del 5/5/2010
 COMPLEMENTI DI ANALISI MATEMATICA A.A. 29- Primo appello del 5/5/2 Qui trovate le tracce delle soluzioni degli esercizi del compito. Ho tralasciato i calcoli da Analisi (che comunque sono parte della risoluzione),
COMPLEMENTI DI ANALISI MATEMATICA A.A. 29- Primo appello del 5/5/2 Qui trovate le tracce delle soluzioni degli esercizi del compito. Ho tralasciato i calcoli da Analisi (che comunque sono parte della risoluzione),
Analisi 4 - SOLUZIONI (compito del 29/09/2011)
 Corso di laurea in Matematica Analisi 4 - SOLUZIONI compito del 9/09/0 Docente: Claudia Anedda Calcolare, tramite uno sviluppo in serie noto, la radice quinta di e la radice cubica di 9 Utilizzando la
Corso di laurea in Matematica Analisi 4 - SOLUZIONI compito del 9/09/0 Docente: Claudia Anedda Calcolare, tramite uno sviluppo in serie noto, la radice quinta di e la radice cubica di 9 Utilizzando la
Risposta La curva r è regolare a tratti per via di quanto succede della sua rappresentazione parametrica nel punto t = 1: pur riuscendo
 ANALISI VETTORIALE OMPITO PER LE VAANZE DI FINE D ANNO Esercizio Sia r(t) la curva regolare a tratti x = t, y = t, t [, ] e x = t, y = t, t [, ]. alcolare la lunghezza di r, calcolare, dove esistono, i
ANALISI VETTORIALE OMPITO PER LE VAANZE DI FINE D ANNO Esercizio Sia r(t) la curva regolare a tratti x = t, y = t, t [, ] e x = t, y = t, t [, ]. alcolare la lunghezza di r, calcolare, dove esistono, i
Facoltà di Scienze MM.FF.NN. Corso di Laurea in Matematica - A.A Prova scritta di Analisi Matematica II del
 Prova scritta di nalisi Matematica II del 12-06-2001. C1 1) Studiare la convergenza semplice, uniforme e totale della serie di funzioni seguente ( 1) [ n 2 ] n x 1 + n 2 x. n=0 2) Data la funzione (x 2
Prova scritta di nalisi Matematica II del 12-06-2001. C1 1) Studiare la convergenza semplice, uniforme e totale della serie di funzioni seguente ( 1) [ n 2 ] n x 1 + n 2 x. n=0 2) Data la funzione (x 2
ESAMI E ESERCITAZIONI A.A. 2010/11. Calcolare la lunghezza del grafico di f. Suggerimento: ricordare che, se h(u) è una funzione continua e.
 ESAMI E ESERCITAZIONI AA 2010/11 ANDREA RATTO Sommario In questo file presentiamo esercitazioni ed esami relativi al Corso Integrato di Matematica per Scienze dell Architettura 1 Esercitazione del 2 Maggio
ESAMI E ESERCITAZIONI AA 2010/11 ANDREA RATTO Sommario In questo file presentiamo esercitazioni ed esami relativi al Corso Integrato di Matematica per Scienze dell Architettura 1 Esercitazione del 2 Maggio
Istituzioni di Matematica II 5 Luglio 2010
 Istituzioni di Matematica II 5 Luglio 010 1. Classificare, al variare del parametro α R, la forma quadratica (1 + α )x + 4xy + αy.. i) Si determinino tutti i punti critici della seguente funzione f(x,
Istituzioni di Matematica II 5 Luglio 010 1. Classificare, al variare del parametro α R, la forma quadratica (1 + α )x + 4xy + αy.. i) Si determinino tutti i punti critici della seguente funzione f(x,
Prove d Esame A.A. 2012/2013
 Complementi di Analisi Polo di Savona Complementi di Analisi Matematica Prove d Esame A.A. 2012/2013 1- PrCam.TEX [] Complementi di Analisi Polo di Savona Prima Prova parziale 23/11/2011 Prima Prova parziale
Complementi di Analisi Polo di Savona Complementi di Analisi Matematica Prove d Esame A.A. 2012/2013 1- PrCam.TEX [] Complementi di Analisi Polo di Savona Prima Prova parziale 23/11/2011 Prima Prova parziale
Soluzioni degli esercizi proposti nella sessione estiva Terni Perugia. F NdS. div F = 2 div F dxdydz = 2volume (V ) = 36π.
 Soluzioni degli esercizi proposti nella sessione estiva 2-2 Terni Perugia ) Sia F = (2x, y, z) e V il volume delimitato dalle superfici: la semisfera S := z = 9 x 2 y 2 ed il disco S 2 di equazione z =,
Soluzioni degli esercizi proposti nella sessione estiva 2-2 Terni Perugia ) Sia F = (2x, y, z) e V il volume delimitato dalle superfici: la semisfera S := z = 9 x 2 y 2 ed il disco S 2 di equazione z =,
Corsi di laurea in ingegneria aerospaziale e ingegneria meccanica Prova scritta di Fondamenti di Analisi Matematica II. Padova, 19.9.
 Corsi di laurea in ingegneria aerospaziale e ingegneria meccanica Prova scritta di Fondamenti di Analisi Matematica II Padova, 19.9.2016 Si svolgano i seguenti esercizi facendo attenzione a giustificare
Corsi di laurea in ingegneria aerospaziale e ingegneria meccanica Prova scritta di Fondamenti di Analisi Matematica II Padova, 19.9.2016 Si svolgano i seguenti esercizi facendo attenzione a giustificare
Prove scritte dell esame di Analisi Matematica II a.a. 2016/2017
 Prove scritte dell esame di Analisi Matematica II a.a. 6/7 C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 5 giugno 7. Assegnati ( l insieme E {(x,
Prove scritte dell esame di Analisi Matematica II a.a. 6/7 C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 5 giugno 7. Assegnati ( l insieme E {(x,
Fondamenti di Analisi Matematica 2 - a.a. 2016/2017 Primo appello
 Fondamenti di Analisi Matematica 2 - a.a. 216/217 Primo appello Esercizi senza svolgimento - Tema 1 Ω = { x, y, z) R 3 : 4x 2 + y 2 + z 2 1, z }. x = ρ/2) sen ϕ cos ϑ, 1. y = ρ sen ϕ sen ϑ, ρ [, 1], ϕ
Fondamenti di Analisi Matematica 2 - a.a. 216/217 Primo appello Esercizi senza svolgimento - Tema 1 Ω = { x, y, z) R 3 : 4x 2 + y 2 + z 2 1, z }. x = ρ/2) sen ϕ cos ϑ, 1. y = ρ sen ϕ sen ϑ, ρ [, 1], ϕ
ANALISI MATEMATICA 2 - INGEGNERIA MECCANICA ED ENERGETICA A.A PROVA SCRITTA DEL 28/1/19
 ANALISI MATEMATICA - INGEGNERIA MECCANICA E ENERGETICA A.A. 8-9 PROVA SCRITTA EL 8//9 Scrivere nome cognome e numero di matricola in stampatello su tutti i fogli da consegnare. Consegnare solo la bella
ANALISI MATEMATICA - INGEGNERIA MECCANICA E ENERGETICA A.A. 8-9 PROVA SCRITTA EL 8//9 Scrivere nome cognome e numero di matricola in stampatello su tutti i fogli da consegnare. Consegnare solo la bella
ESERCIZI DI ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 2006/2007
 ESERCIZI I ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 006/007 1 FUNZIONI IN UE VARIABILI (I parte) Insiemi di definizione eterminare gli insiemi di definizione delle seguenti funzioni in due
ESERCIZI I ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 006/007 1 FUNZIONI IN UE VARIABILI (I parte) Insiemi di definizione eterminare gli insiemi di definizione delle seguenti funzioni in due
PROGRAMMA PROVVISORIO DI ANALISI MATEMATICA 2 INGEGNERIA EDILE -ARCHITETTURA, A.A. 2018/2019 DOCENTE MICHIEL BERTSCH
 PROGRAMMA PROVVISORIO DI ANALISI MATEMATICA 2 INGEGNERIA EDILE -ARCHITETTURA, A.A. 2018/2019 DOCENTE MICHIEL BERTSCH Libro di testo di riferimento: M. Bertsch, R. Dal Passo, L. Giacomelli, Analisi Matematica,
PROGRAMMA PROVVISORIO DI ANALISI MATEMATICA 2 INGEGNERIA EDILE -ARCHITETTURA, A.A. 2018/2019 DOCENTE MICHIEL BERTSCH Libro di testo di riferimento: M. Bertsch, R. Dal Passo, L. Giacomelli, Analisi Matematica,
ANALISI B alcuni esercizi proposti
 ANALISI B alcuni esercizi proposti G.P. Leonardi Parte II 1 Limiti e continuità per funzioni di 2 variabili Esercizio 1.1 Calcolare xy log(1 + x ) lim (x,y) (0,0) 2x 2 + 5y 2 Esercizio 1.2 Studiare la
ANALISI B alcuni esercizi proposti G.P. Leonardi Parte II 1 Limiti e continuità per funzioni di 2 variabili Esercizio 1.1 Calcolare xy log(1 + x ) lim (x,y) (0,0) 2x 2 + 5y 2 Esercizio 1.2 Studiare la
Facoltà di Ingegneria Prova scritta di Analisi Matematica II. Lecce, y y x = x3 y 4. y(1) = 1.
 Lecce, 10.4.2003 1. Risolvere il seguente problema di Cauchy: y y x = x3 y 4 y(1) = 1. 2. Determinare gli estremi della funzione f(x, y) = x 2 y 2 nell insieme } E = {(x, y) R 2 : (x 1) 2 + y2 4 1, y 0.
Lecce, 10.4.2003 1. Risolvere il seguente problema di Cauchy: y y x = x3 y 4 y(1) = 1. 2. Determinare gli estremi della funzione f(x, y) = x 2 y 2 nell insieme } E = {(x, y) R 2 : (x 1) 2 + y2 4 1, y 0.
Analisi Matematica III
 Università di Pisa - Corso di Laurea in Ingegneria Civile dell ambiente e territorio Analisi Matematica III Pisa, 1 giugno 4 (Cognome (Nome (Numero di matricola Esercizio 1 Si consideri la successione
Università di Pisa - Corso di Laurea in Ingegneria Civile dell ambiente e territorio Analisi Matematica III Pisa, 1 giugno 4 (Cognome (Nome (Numero di matricola Esercizio 1 Si consideri la successione
Analisi Matematica 2. Trasformazioni integrali. Trasformazioni integrali 1 / 29
 Analisi Matematica 2 Trasformazioni integrali Trasformazioni integrali 1 / 29 Trasformazioni integrali. 1) Formule di Gauss-Green: nel piano: trasformano un integrale doppio in un integrale curvilineo,
Analisi Matematica 2 Trasformazioni integrali Trasformazioni integrali 1 / 29 Trasformazioni integrali. 1) Formule di Gauss-Green: nel piano: trasformano un integrale doppio in un integrale curvilineo,
Prove scritte dell esame di Analisi Matematica II a.a. 2015/2016
 Prove scritte dell esame di Analisi Matematica II a.a. 5/6 C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 6 giugno 6. Determinare massimi e minimi
Prove scritte dell esame di Analisi Matematica II a.a. 5/6 C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 6 giugno 6. Determinare massimi e minimi
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006. Matematica 2 (Analisi)
 Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
Cognome Nome Matricola Codice ESEMPIO 1
 Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di forma differenziale chiusa. Sia A R N ; sia A aperto; sia ω = N i=1 ω i dx i una forma differenziale su A; sia ω di classe C 1 ; si dice
Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di forma differenziale chiusa. Sia A R N ; sia A aperto; sia ω = N i=1 ω i dx i una forma differenziale su A; sia ω di classe C 1 ; si dice
1 x 2 y 2 dxdy D. 3 (1 ρ2 ) 3/2 = 1 3. = π 12.
 INGEGNERIA CIVILE - AMBIENTE E TERRITORIO ANALISI MATEMATICA II SOLUZIONI DELLA PROVA SCRITTA DEL 19-6-15 ESERCIZIO 1 Calcolare 1 x y dxdy D dove D è il dominio piano delimitato dalla curva x + y x e dalle
INGEGNERIA CIVILE - AMBIENTE E TERRITORIO ANALISI MATEMATICA II SOLUZIONI DELLA PROVA SCRITTA DEL 19-6-15 ESERCIZIO 1 Calcolare 1 x y dxdy D dove D è il dominio piano delimitato dalla curva x + y x e dalle
Compiti d Esame A.A. 2005/2006
 Compiti d Esame A.A. 25/26 UNIVERSITÀ DEGLI STUDI DI PERUGIA A.A. 25/26 I Esercitazione 21 Aprile 26 { y = xy ln(xy) si chiede di dimostrare che: y(1) = 1, (a) ammette un unica soluzione massimale y =
Compiti d Esame A.A. 25/26 UNIVERSITÀ DEGLI STUDI DI PERUGIA A.A. 25/26 I Esercitazione 21 Aprile 26 { y = xy ln(xy) si chiede di dimostrare che: y(1) = 1, (a) ammette un unica soluzione massimale y =
1 x 2 y 2 dxdy D. 3 (1 ρ2 ) 3/2 = 1 3. = π 12.
 INGEGNERIA CIVILE - AMBIENTE E TERRITORIO ANALISI MATEMATICA II SOLUZIONI DELLA PROVA SCRITTA DEL 19-6-15 ESERCIZIO 1 Calcolare 1 x y dxdy D dove D è il dominio piano delimitato dalla curva x + y = x e
INGEGNERIA CIVILE - AMBIENTE E TERRITORIO ANALISI MATEMATICA II SOLUZIONI DELLA PROVA SCRITTA DEL 19-6-15 ESERCIZIO 1 Calcolare 1 x y dxdy D dove D è il dominio piano delimitato dalla curva x + y = x e
Analisi Matematica I
 Università degli Studi di Genova Facoltà di Ingegneria - Polo di Savona via Cadorna 7-7 Savona Tel. +39 9 264555 - Fax +39 9 264558 Analisi Matematica I Testi d esame e Prove parziali Analisi Matematica
Università degli Studi di Genova Facoltà di Ingegneria - Polo di Savona via Cadorna 7-7 Savona Tel. +39 9 264555 - Fax +39 9 264558 Analisi Matematica I Testi d esame e Prove parziali Analisi Matematica
Soluzione della prova scritta di Analisi Matematica II del 15 Aprile 2009 (Ingegneria Edile e Architettura)
 Soluzione della prova scritta di Analisi Matematica II del 5 Aprile 009 Ingegneria Edile e Architettura x. Calcolare J = ds essendo γ la curva ottenuta intersecando γ + y il cilindro di equazione x + y
Soluzione della prova scritta di Analisi Matematica II del 5 Aprile 009 Ingegneria Edile e Architettura x. Calcolare J = ds essendo γ la curva ottenuta intersecando γ + y il cilindro di equazione x + y
Prima prova di verifica in itinere di ANALISI MATEMATICA II. 12 Marzo 2008 Compito A. 1 (punti 3)
 anno accademico 007-008 Prima prova di verifica in itinere di ANALISI MATEMATICA II Marzo 008 Compito A (punti ) y = x + xy + y x. (punti 4) y + y x = ln x x y. (punti ) y = y + y ln y. 4 (punti 6) Determinare
anno accademico 007-008 Prima prova di verifica in itinere di ANALISI MATEMATICA II Marzo 008 Compito A (punti ) y = x + xy + y x. (punti 4) y + y x = ln x x y. (punti ) y = y + y ln y. 4 (punti 6) Determinare
Analisi Matematica 2 per Matematica Esempi di compito, secondo semestre 2012/2013
 Analisi Matematica 2 per Matematica Esempi di compito, secondo semestre 2012/2013 Primo compito. Si consideri la regione stokiana E di R 3 definita dalle disuguaglianze: { + y 2 a 2 0 z tan α)x b) dove
Analisi Matematica 2 per Matematica Esempi di compito, secondo semestre 2012/2013 Primo compito. Si consideri la regione stokiana E di R 3 definita dalle disuguaglianze: { + y 2 a 2 0 z tan α)x b) dove
Analisi Matematica 2 5 febbraio Risposte. (Giusta = 3, non data = 0, sbagliata = 1) Versione Es. 1 Es. 2 Es. 3 Es. 4 Es. 5 Es. 6 Es.
 Analisi Matematica 2 5 febbraio 2013 Nome, Cognome, Matricola: Cognome del Docente: Risposte. (Giusta = 3, non data = 0, sbagliata = 1) Versione Es. 1 Es. 2 Es. 3 Es. 4 Es. 5 Es. 6 Es. 7 1 Esercizio 1.
Analisi Matematica 2 5 febbraio 2013 Nome, Cognome, Matricola: Cognome del Docente: Risposte. (Giusta = 3, non data = 0, sbagliata = 1) Versione Es. 1 Es. 2 Es. 3 Es. 4 Es. 5 Es. 6 Es. 7 1 Esercizio 1.
Analisi Matematica 3
 Testi delle prove d esame del corso di Analisi Matematica 3 presso la Facoltà di Ingegneria Bruno Rubino L Aquila, 2006 Indice 1 Curve 3 2 Superfici 4 3 Teorema di Gauss-Green e formula dell area 4 4 Campi
Testi delle prove d esame del corso di Analisi Matematica 3 presso la Facoltà di Ingegneria Bruno Rubino L Aquila, 2006 Indice 1 Curve 3 2 Superfici 4 3 Teorema di Gauss-Green e formula dell area 4 4 Campi
PROVE SCRITTE DI ANALISI MATEMATICA II(N.O.), ANNO 2006/07
 PROV SCRITT DI ANALISI MATMATICA II(N.O.), ANNO 6/7 Prova scritta del 5//6 Si determini l insieme di convergenza della serie di funzioni n= n( + sin x) n limitatamente all intervallo x π, e si specifichi
PROV SCRITT DI ANALISI MATMATICA II(N.O.), ANNO 6/7 Prova scritta del 5//6 Si determini l insieme di convergenza della serie di funzioni n= n( + sin x) n limitatamente all intervallo x π, e si specifichi
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 2 Secondo compito in itinere 30 Giugno 2016
 Politecnico di Milano Ingegneria Industriale Analisi e Geometria Secondo compito in itinere Giugno 6 Cognome: Nome: Matricola: Es.: 9 punti Es.: 9 punti Es.: 6 punti Es.4: 9 punti Totale. Si consideri
Politecnico di Milano Ingegneria Industriale Analisi e Geometria Secondo compito in itinere Giugno 6 Cognome: Nome: Matricola: Es.: 9 punti Es.: 9 punti Es.: 6 punti Es.4: 9 punti Totale. Si consideri
Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005
 Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005 Prova orale il: Docente: Determinare, se esistono, il massimo ed il minimo assoluto della funzione
Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005 Prova orale il: Docente: Determinare, se esistono, il massimo ed il minimo assoluto della funzione
Analisi 4 - SOLUZIONI (15/07/2015)
 Corso di Laurea in Matematica Analisi 4 - SOLUZIONI (5/7/5) Docente: Claudia Anedda ) Calcolare l area della superficie totale della regione di spazio limitata, interna al paraboloide di equazione x +y
Corso di Laurea in Matematica Analisi 4 - SOLUZIONI (5/7/5) Docente: Claudia Anedda ) Calcolare l area della superficie totale della regione di spazio limitata, interna al paraboloide di equazione x +y
Foglio 3 Esercizi su forme differenziali lineari ed integrali di seconda specie (alcuni con cenno di soluzione).
 Università degli Studi di Padova Facoltà di Ingegneria Laurea in Ingegneria Gestionale e MeccanicaMeccatronica, V. Casarino P. Mannucci (-) Foglio 3 Esercizi su forme differenziali lineari ed integrali
Università degli Studi di Padova Facoltà di Ingegneria Laurea in Ingegneria Gestionale e MeccanicaMeccatronica, V. Casarino P. Mannucci (-) Foglio 3 Esercizi su forme differenziali lineari ed integrali
Cognome Nome Matricola Codice ESEMPIO 1
 Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di sistema fondamentale di soluzioni di un equazione differenziale lineare d ordine n omogenea. Sia I un intervallo non banale di R; siano
Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di sistema fondamentale di soluzioni di un equazione differenziale lineare d ordine n omogenea. Sia I un intervallo non banale di R; siano
ISTITUZIONI DI MATEMATICHE II
 ISTITUZIONI DI MATEMATIHE II SEONDO ESONERO Esercizio 1. Data la funzione f(x, y) = (x + y )(1 y) i) se ne studi il segno. ii) Si trovino i punti critici di f e se ne studi le natura. iii) Sia D = {(x,
ISTITUZIONI DI MATEMATIHE II SEONDO ESONERO Esercizio 1. Data la funzione f(x, y) = (x + y )(1 y) i) se ne studi il segno. ii) Si trovino i punti critici di f e se ne studi le natura. iii) Sia D = {(x,
Analisi Matematica 2: Scritto Generale, Cognome e nome:...matricola:...
 Analisi Matematica 2: Scritto Generale, 21.02.2017 Cognome e nome:....................................matricola:......... es.1 es.2 es.3 es.4 es.5 es.6 es.7 somma 5cr. 6 6 6 6 6 - - 30 6/9cr. 5 5 5 5 5
Analisi Matematica 2: Scritto Generale, 21.02.2017 Cognome e nome:....................................matricola:......... es.1 es.2 es.3 es.4 es.5 es.6 es.7 somma 5cr. 6 6 6 6 6 - - 30 6/9cr. 5 5 5 5 5
5π/2. 3π/2. y = f(x) π π. -5π/2-2π -3π/2 -π -π/2 π/2 π 3π/2 2π 5π/2 3π 7π. -π/2
 Corso di Laurea in Matematica Analisi 4 - SOLUZIONI /9/8) Docente: Claudia Anedda ) Data la funzione yx) x + π, x, π) prolungarla su tutto R in modo tale che sia una funzione π-periodica pari, disegnare
Corso di Laurea in Matematica Analisi 4 - SOLUZIONI /9/8) Docente: Claudia Anedda ) Data la funzione yx) x + π, x, π) prolungarla su tutto R in modo tale che sia una funzione π-periodica pari, disegnare
Es. 1 Es. 2 Es. 3 Es. 4 Totale
 Es. Es. Es. Es. 4 Totale Analisi e Geometria Seconda prova in itinere Docente: luglio Cognome: Nome: Matricola: Ogni risposta dev essere giustificata. Gli esercizi vanno svolti su questi fogli, nello spazio
Es. Es. Es. Es. 4 Totale Analisi e Geometria Seconda prova in itinere Docente: luglio Cognome: Nome: Matricola: Ogni risposta dev essere giustificata. Gli esercizi vanno svolti su questi fogli, nello spazio
Prove scritte dell esame di Analisi Matematica II a.a. 2013/2014
 Prove scritte dell esame di Analisi Matematica II a.a. 3/4 C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 9 giugno 4. (8 punti) Risolvere il problema
Prove scritte dell esame di Analisi Matematica II a.a. 3/4 C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 9 giugno 4. (8 punti) Risolvere il problema
Soluzioni. 152 Roberto Tauraso - Analisi Risolvere il problema di Cauchy. { y (x) + 2y(x) = 3e 2x y(0) = 1
 5 Roberto Tauraso - Analisi Soluzioni. Risolvere il problema di Cauchy y (x) + y(x) = 3e x y() = R. Troviamo la soluzione generale in I = R. Una primitiva di a(x) = è A(x) = a(x) dx = dx = x e il fattore
5 Roberto Tauraso - Analisi Soluzioni. Risolvere il problema di Cauchy y (x) + y(x) = 3e x y() = R. Troviamo la soluzione generale in I = R. Una primitiva di a(x) = è A(x) = a(x) dx = dx = x e il fattore
Analisi Matematica II Corso di Ingegneria Gestionale Compito del xy + 2x + 2y + 2xy + 2x + 2y + sin
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del 9--8 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del 9--8 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del A
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del -7-5 - A Esercizio ( punti Data la funzione f(x, y = x + y + 4xy 8x 4y + 4 i trovare tutti i punti critici e, se possibile, caratterizzarli
Analisi Matematica II Corso di Ingegneria Gestionale Compito del -7-5 - A Esercizio ( punti Data la funzione f(x, y = x + y + 4xy 8x 4y + 4 i trovare tutti i punti critici e, se possibile, caratterizzarli
Prove scritte dell esame di Analisi Matematica II a.a. 2011/2012
 Prove scritte dell esame di Analisi Matematica II a.a. / C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 7 giugno. ( punti) Disegnare l insieme E (x,
Prove scritte dell esame di Analisi Matematica II a.a. / C.d.L. in Ingegneria Informatica ed Elettronica - Università degli Studi di Perugia Prova scritta del 7 giugno. ( punti) Disegnare l insieme E (x,
Per determinare una soluzione particolare descriveremo un metodo che vale solo nel caso in cui la funzione f(x) abbia una forma particolare:
 42 Roberto Tauraso - Analisi 2 Ora imponiamo condizione richiesta: ( lim c e 4x + c 2 + c 3 e 2x cos(2x) + c 4 e 2x sin(2x) ) = 3. x + Il limite esiste se e solo c 3 = c 4 = perché le funzioni e 2x cos(2x)
42 Roberto Tauraso - Analisi 2 Ora imponiamo condizione richiesta: ( lim c e 4x + c 2 + c 3 e 2x cos(2x) + c 4 e 2x sin(2x) ) = 3. x + Il limite esiste se e solo c 3 = c 4 = perché le funzioni e 2x cos(2x)
x(y 2 + 2z 2 ) dxdydz, (1 y 2 z 2 ) 2 (y 2 + 2z 2 ) dydz, 1 ( x(y 2 + 2z 2 ) dydz) dx, 1 x r 3 dr) (
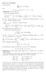 Esame del 5//9. Determinare dove Svolgimento. Due modi diversi. (i) Per fili: l integrale diventa D y z Ω x(y + z ) dxdydz, Ω = {(x, y, z) R 3 ; y + z + x, x }. x(y + z ) dx) dydz = D ( y z ) (y + z )
Esame del 5//9. Determinare dove Svolgimento. Due modi diversi. (i) Per fili: l integrale diventa D y z Ω x(y + z ) dxdydz, Ω = {(x, y, z) R 3 ; y + z + x, x }. x(y + z ) dx) dydz = D ( y z ) (y + z )
si ha La lunghezza L si calcola per ciascun tratto L = (2t)2 + (3t 2 ) dt+ 2 (3t2 ) 2 + (2t) 2 dt = 4t2 + 9t 4 dt = t
 ANALISI VETTORIALE Soluzione esercizi 1 gennaio 211 6.1. Esercizio. Sia Γ la curva regolare a tratti di rappresentazione parametrica x = t 2, y = t, t [, 1] e x = t, y = t 2, t [1, 2] calcolare la lunghezza,
ANALISI VETTORIALE Soluzione esercizi 1 gennaio 211 6.1. Esercizio. Sia Γ la curva regolare a tratti di rappresentazione parametrica x = t 2, y = t, t [, 1] e x = t, y = t 2, t [1, 2] calcolare la lunghezza,
Corsi di laurea in ingegneria aerospaziale e ingegneria meccanica Prova scritta di Fondamenti di Analisi Matematica II. Padova, 26.1.
 Corsi di laurea in ingegneria aerospaziale e ingegneria meccanica Prova scritta di Fondamenti di Analisi Matematica II Padova, 6.1.16 Si svolgano i seguenti esercizi facendo attenzione a giustificare le
Corsi di laurea in ingegneria aerospaziale e ingegneria meccanica Prova scritta di Fondamenti di Analisi Matematica II Padova, 6.1.16 Si svolgano i seguenti esercizi facendo attenzione a giustificare le
Prima prova in itinere di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2017/2018. Prof. M. Bramanti.
 Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 07/08. Prof. M. Bramanti Tema n 4 5 6 Tot. Cognome e nome (in stampatello) codice persona (o n
Prima prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 07/08. Prof. M. Bramanti Tema n 4 5 6 Tot. Cognome e nome (in stampatello) codice persona (o n
Forme differenziali e campi vettoriali: esercizi svolti
 Forme differenziali e campi vettoriali: esercizi svolti 1 Esercizi sul Teorema di Green......................... 2 2 Esercizi sul Teorema di Stokes......................... 4 3 Esercizi sul Teorema di
Forme differenziali e campi vettoriali: esercizi svolti 1 Esercizi sul Teorema di Green......................... 2 2 Esercizi sul Teorema di Stokes......................... 4 3 Esercizi sul Teorema di
y = x y(0) = 0.
 A.A. 2006/2007 I Esercitazione 19 aprile 2007 Esercizio 1. Dato il problema di Cauch = x 2 2 2 + 1 (0) = 0, dimostrare che: (a) ammette un unica soluzione massimale ; (b) tale soluzione è definita globalmente;
A.A. 2006/2007 I Esercitazione 19 aprile 2007 Esercizio 1. Dato il problema di Cauch = x 2 2 2 + 1 (0) = 0, dimostrare che: (a) ammette un unica soluzione massimale ; (b) tale soluzione è definita globalmente;
Analisi Matematica II Corso di Ingegneria Biomedica Compito del
 Analisi Matematica II Corso di Ingegneria Biomedica Compito del 7-- Esercizio. punti Data la funzione fx, y = log x + y x + y + x y i trovare tutti i punti critici; ii trovare massimo e minimo assoluti
Analisi Matematica II Corso di Ingegneria Biomedica Compito del 7-- Esercizio. punti Data la funzione fx, y = log x + y x + y + x y i trovare tutti i punti critici; ii trovare massimo e minimo assoluti
UNIVERSITÀ DI ROMA TOR VERGATA. Analisi Matematica II per Ingegneria Prof. C. Sinestrari
 UNIVERSITÀ DI ROMA TOR VERGATA Analisi Matematica II per Ingegneria Prof. C. Sinestrari Risposte sintetiche) agli esercizi del 15.XII.218 1. NB si ricorda che l equazione del piano passante per un punto
UNIVERSITÀ DI ROMA TOR VERGATA Analisi Matematica II per Ingegneria Prof. C. Sinestrari Risposte sintetiche) agli esercizi del 15.XII.218 1. NB si ricorda che l equazione del piano passante per un punto
Seconda prova in itinere di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2016/2017. Prof. M. Bramanti.
 Seconda prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 16/17. Prof. M. Bramanti 1 Tema n 1 5 6 Tot. Cognome e nome in stampatello codice persona o n
Seconda prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 16/17. Prof. M. Bramanti 1 Tema n 1 5 6 Tot. Cognome e nome in stampatello codice persona o n
Analisi Matematica II 14 Giugno 2019
 Analisi Matematica II 14 Giugno 2019 Cognome: Nome: Matricola: 1. (10 punti) Si determinino i sottoinsiemi del piano in cui valgano, rispettivamente, continuità, derivabilità e differenziabilità della
Analisi Matematica II 14 Giugno 2019 Cognome: Nome: Matricola: 1. (10 punti) Si determinino i sottoinsiemi del piano in cui valgano, rispettivamente, continuità, derivabilità e differenziabilità della
Gruppo esercizi 1: Dominio [E.1] Disegnare nel piano cartesiano il dominio della funzione
![Gruppo esercizi 1: Dominio [E.1] Disegnare nel piano cartesiano il dominio della funzione Gruppo esercizi 1: Dominio [E.1] Disegnare nel piano cartesiano il dominio della funzione](/thumbs/88/116749009.jpg) Gruppo esercizi 1: Dominio [E.1] Disegnare nel piano cartesiano il dominio della funzione [E.2] Disegnare nel piano cartesiano il dominio della funzione ( 4 x 2 y 2) ) (1 x 2 y2 y + x 2. 4 1 y ex y y x
Gruppo esercizi 1: Dominio [E.1] Disegnare nel piano cartesiano il dominio della funzione [E.2] Disegnare nel piano cartesiano il dominio della funzione ( 4 x 2 y 2) ) (1 x 2 y2 y + x 2. 4 1 y ex y y x
Forme differenziali lineari
 Forme differenziali lineari Sia Ω R un insieme aperto e siano A, B, C: Ω R funzioni continue in Ω. Si definisce forma differenziale ω in Ω l espressione ω = A(x, y, z)dx + B(x, y, z)dy + C(x, y, z)dz Data
Forme differenziali lineari Sia Ω R un insieme aperto e siano A, B, C: Ω R funzioni continue in Ω. Si definisce forma differenziale ω in Ω l espressione ω = A(x, y, z)dx + B(x, y, z)dy + C(x, y, z)dz Data
Università di Trieste Facoltà d Ingegneria. Esercizi sulle curve, le superfici, i campi vettoriali. Dott. Franco Obersnel
 Università di Trieste Facoltà d Ingegneria. Esercizi sulle curve, le superfici, i campi vettoriali. Dott. Franco Obersnel Esercizio 1 Sia f : [a, b] IR 2 una funzione di classe C 1 su [a, b]. consideri
Università di Trieste Facoltà d Ingegneria. Esercizi sulle curve, le superfici, i campi vettoriali. Dott. Franco Obersnel Esercizio 1 Sia f : [a, b] IR 2 una funzione di classe C 1 su [a, b]. consideri
Argomenti delle singole lezioni del corso di Analisi Matematica 2 (Ingegneria Edile-Architettura, A.A )
 Argomenti delle singole lezioni del corso di Analisi Matematica 2 (Ingegneria Edile-Architettura, A.A. 2018-19) NB. Le indicazioni bibliografiche si riferiscono al libro di testo. Lezione nr. 1, 24/9/2018.
Argomenti delle singole lezioni del corso di Analisi Matematica 2 (Ingegneria Edile-Architettura, A.A. 2018-19) NB. Le indicazioni bibliografiche si riferiscono al libro di testo. Lezione nr. 1, 24/9/2018.
Estremi. 5. Determinare le dimensioni di una scatola rettangolare di volume v assegnato, che abbia la superficie minima.
 Estremi 1. Determinare gli estremi relativi di f(x, y) = e x (x 1)(y 1) + (y 1).. Determinare gli estremi relativi di f(x, y) = y (y + 1) cos x. 3. Determinare gli estremi relativi di f(x, y) = xye x +y..
Estremi 1. Determinare gli estremi relativi di f(x, y) = e x (x 1)(y 1) + (y 1).. Determinare gli estremi relativi di f(x, y) = y (y + 1) cos x. 3. Determinare gli estremi relativi di f(x, y) = xye x +y..
Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 3 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata, Matematica
 DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 3 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 3 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
Seconda prova in itinere di Analisi Matematica 2 Ingegneria Elettronica. Politecnico di Milano. A.A. 2018/2019. Prof. M. Bramanti.
 Seconda prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 8/9. Prof. M. Bramanti Tema n 4 5 6 Tot. Cognome e nome in stampatello codice persona o n di
Seconda prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 8/9. Prof. M. Bramanti Tema n 4 5 6 Tot. Cognome e nome in stampatello codice persona o n di
Analisi 4 - SOLUZIONI (17/01/2013)
 Corso di Laurea in Matematica Analisi 4 - SOLUZIONI 7//23 Docente: Claudia Anedda Utilizzando uno sviluppo in serie noto, scrivere lo sviluppo in serie di MacLaurin della funzione fx = 32 + x, specificando
Corso di Laurea in Matematica Analisi 4 - SOLUZIONI 7//23 Docente: Claudia Anedda Utilizzando uno sviluppo in serie noto, scrivere lo sviluppo in serie di MacLaurin della funzione fx = 32 + x, specificando
Matematica e Statistica (A-E, F-O, P-Z)
 Matematica e Statistica (A-E, F-O, P-Z) Prova d esame (08/07/20) Università di Verona - Laurea in Biotecnologie - A.A. 200/ Matematica e Statistica (A-E, F-O, P-Z) Prova di MATEMATICA (A-E, F-O, P-Z) (08/07/20)
Matematica e Statistica (A-E, F-O, P-Z) Prova d esame (08/07/20) Università di Verona - Laurea in Biotecnologie - A.A. 200/ Matematica e Statistica (A-E, F-O, P-Z) Prova di MATEMATICA (A-E, F-O, P-Z) (08/07/20)
ARGOMENTI MATEMATICA PER L INGEGNERIA
 ARGOMENTI DI MATEMATICA PER L INGEGNERIA VOLUME 2 Esercizi proposti Quando non diversamente precisato, nel seguito si intenderà( sempre che nel piano sia stato introdotto un sistema cartesiano ortogonale
ARGOMENTI DI MATEMATICA PER L INGEGNERIA VOLUME 2 Esercizi proposti Quando non diversamente precisato, nel seguito si intenderà( sempre che nel piano sia stato introdotto un sistema cartesiano ortogonale
COMPLEMENTI DI ANALISI MATEMATICA II. Prova scritta del 20 gennaio 2014
 Prova scritta del 20 gennaio 2014 Studiare la convergenza puntuale e uniforme della serie di potenze n x 2n 2n + e n. Valutare poi la misurabilità e l integrabilità secondo Lebesgue della funzione somma
Prova scritta del 20 gennaio 2014 Studiare la convergenza puntuale e uniforme della serie di potenze n x 2n 2n + e n. Valutare poi la misurabilità e l integrabilità secondo Lebesgue della funzione somma
Analisi Matematica II Corso di Ingegneria Gestionale Compito del f(x, y) = e (x3 +x) y
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del 8--7 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del 8--7 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Soluzione. Il dominio E consiste nella parte di spazio contenuta nella sfera ma esterna al cono rappresentata in Figura 1. Infatti
 Esercizio 1 (G. Ziglio). (6 punti) Calcolare il volume della porzione di spazio E interna alla sfera di equazione x 2 + y 2 + z 2 = 1 ed esterna al cono di equazione z 2 = x 2 + y 2 E = (x, y, z) R x 2
Esercizio 1 (G. Ziglio). (6 punti) Calcolare il volume della porzione di spazio E interna alla sfera di equazione x 2 + y 2 + z 2 = 1 ed esterna al cono di equazione z 2 = x 2 + y 2 E = (x, y, z) R x 2
Esercizi I : curve piane
 Esercizi I : curve piane. Esercizio Si consideri la curva parametrizzata sin t, t [, 2π]. cos(2t) a) Stabilire per quali valori di t la parametrizzazione è regolare. b) Sia Γ la traccia di α. Descrivere
Esercizi I : curve piane. Esercizio Si consideri la curva parametrizzata sin t, t [, 2π]. cos(2t) a) Stabilire per quali valori di t la parametrizzazione è regolare. b) Sia Γ la traccia di α. Descrivere
A Analisi Matematica 2 (Corso di Laurea in Informatica) Simulazione compito d esame
 COGNOME NOME Matr. Firma dello studente A Analisi Matematica (Corso di Laurea in Informatica) Simulazione compito Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni
COGNOME NOME Matr. Firma dello studente A Analisi Matematica (Corso di Laurea in Informatica) Simulazione compito Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni
Analisi Matematica II Corso di Ingegneria Biomedica Compito A del f(x, y) = x 2 + y 2
 Analisi Matematica II Corso di Ingegneria Biomedica Compito A del -7- - È obbligatorio consegnare tutti i fogli, anche quelli della brutta. - Le risposte senza giustificazione sono considerate nulle. Esercizio.
Analisi Matematica II Corso di Ingegneria Biomedica Compito A del -7- - È obbligatorio consegnare tutti i fogli, anche quelli della brutta. - Le risposte senza giustificazione sono considerate nulle. Esercizio.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del -09-08 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del -09-08 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
