Scomposizione in fattori
|
|
|
- Dante Guglielmi
- 9 anni fa
- Visualizzazioni
Transcript
1 Corso di Laurea: Biologia Tutor: Marta Floris, Max Artizzu PRECORSI DI MATEMATICA 1 Introduzione Scomposizione in fattori La scomposizione in fattori dei polinomi assume un importanza speciale quando si deve risolvere un equazione o una disequazione. Le equazioni di primo e secondo grado sono di trattazione relativamente facile, in quanto è sufficiente limitarsi all applicazione delle formule risolutive per ottenere le soluzioni. Ma per equazioni come x 3 6x x 6 = 0 bisogna servirsi di formule complicate per la risoluzione, che solitamente non vengono insegnate. Tuttavia, sapendo che il polinomio al primo membro si può riscrivere come (x 1)(x 2 5x + 6), il problema si semplifica notevolmente: per trovare le soluzioni dell equazione, dunque, basta (come sempre) trovare i valori di x che annullano l espressione. Per la regola dell annullamento, si tratta di trovare i valori di x che annullano il primo fattore x 1, più quelli che annullano il secondo fattore x 2 5x + 6. Si tratta dunque di trovare le soluzioni dei singoli fattori, i quali sono di primo e secondo grado e pertanto si possono risolvere con i metodi visti in precedenza. Nell esempio, si trovano facilmente le soluzioni x 1 = 1, x 2 = 2 e x 3 = 3. Dunque, la scomposizione in fattori ci consente di ridurre il problema in più problemi ma di più semplice risoluzione. Nella trattazione che segue si darà per scontata una certa pratica col calcolo letterale, e nella seconda parte anche la capacità di apprendere velocemente tramite esempi. 2 Prodotti notevoli Ci sono alcuni casi in cui delle espressioni polinomiali sono di immediata scomposizione, in quanto di forma particolarmente nota. Si tratta dei prodotti notevoli. Di seguito ne verranno elencati di diversi. Siano dunque a e b due espressioni qualsiasi (monomiali o anche polinomiali). Si hanno le seguenti scomposizioni immediate. Differenza di quadrati: a 2 b 2 = (a + b)(a b). Ad esempio, possiamo scomporre l espressione x 2 9 come (x + 3)(x 3). Si badi che anche il binomio x 2 2 si può vedere come differenza di quadrati: basta che si veda 2 come il quadrato di... 2! Dunque si può scrivere x 2 2 = (x + 2)(x 2). Anche un espressione come (x + 7) 2 9 si può immaginare come differenza di quadrati, e scomporre come (x )(x + 7 3) = (x + 10)(x + 4). 1
2 Allo stesso modo, anche una differenza di quarte potenze, o di seste, o in generale di potenze pari si può considerare come differenza di quadrati: x 8 y 6 = (x 4 + y 3 )(x 4 y 3 ). Quadrato di un binomio: a 2 + 2ab + b 2 = (a + b) 2. Per riconoscere che un trinomio in realtà è il quadrato di un binomio occorre una certa pratica. Ad esempio, potrebbe non saltare subito all occhio che x x + 25 è il quadrato di x + 5, mentre è ancora più difficile vedere che x 2 3x + 9 ( 4 = x 2) 3 2. Differenza di cubi: a 3 b 3 = (a b)(a 2 + ab + b 2 ). Come esempio, si consideri o anche 8p 3 q 3 = (2p q)(4p 2 + 2pq + q 2 ), 125x 3 27y 6 = (5x 3y 2 )(25x xy 2 + 9y 4 ). Somma di cubi: a 3 + b 3 = (a + b)(a 2 ab + b 2 ). Come esempio, si consideri o anche 8p 3 + q 3 = (2p + q)(4p 2 2pq + q 2 ), 125x y 6 = (5x + 3y 2 )(25x 2 15xy 2 + 9y 4 ). Sia la somma che la differenza di cubi si possono generalizzare alla somma ed alla differenza di potenze dispari: per ora basti sapere che la somma e la differenza di potenze dispari sono divisibili rispettivamente per a + b e a b (vedere in seguito la parte relativa alla divisione polinomiale). Cubo di un binomio: a 3 + 3a 2 b + 3ab 2 + b 3 = (a + b) 3. Similmente al quadrato di un binomio, anche in questo caso occorre una certa pratica per riconoscere l espressione. La cosa è ancora più difficile dato che di cubi di trinomi se ne incontrano relativamente pochi. Trinomio con somma e prodotto: x 2 + (a + b)x + ab = (x + a)(x + b). Anche in questo caso è necessario avere una certa pratica per riconoscere questo tipo di prodotti notevoli. Ad esempio: x x + 36 = (x + 2)(x + 18). Ancora più sottile è il caso in cui a è positivo e b è negativo (o viceversa). Ad esempio: x 2 x 20 = (x 5)(x + 4). Polinomio di secondo grado: ax 2 + bx + x = a(x x 1 )(x x 2 ). Il metodo precedente si applica solo nel caso in cui il coefficiente di x 2 è 1: nel caso generale è possibile procedere individuando le radici x 1 e x 2 del polinomio di secondo grado, e scomporlo come a(x x 1 )(x x 2 ). Ad esempio, il polinomio 8x 2 + 2x 3 ha come radici 3/4 e 1/2, e pertanto si può scrivere ( 8x 2 + 2x 3 = 8 x )( x 1 2 ). 2
3 3 Raccoglimento a fattor comune Uno dei metodi più semplici per la scomposizione di polinomi, ma che richiede una certa pratica, consiste nel raccoglimento parziale a fattor comune. Si tratta di un metodo utile nel caso di un numero pari di termini del polinomio, o nel caso di un trinomio, ma con una variante. Si prenda ad esempio il polinomio x 3 3x 2 + 2x 6, con quattro termini. Si considerino a gruppi i primi due termini e gli ultimi due: x 3 3x } {{ } 2 +2x } {{ 6 } Ora si considerino i fattori comuni dei due gruppi, e li si raccolga: x 2 (x 3) + 2(x 3). A questo punto si può notare che il fattore x 3 è in comune, e pertanto può essere raccolto a sua volta, completando la scomposizione: x 2 (x 3) + 2(x 3) = (x 3)(x 2 + 2). Uno dei problemi che si possono incontrare con questo tipo di scomposizione è quando non è chiaro se, al primo passaggio, conviene raccogliere il fattore comune con il segno positivo o negativo. Ad esempio, nel polinomio 6x 3 4x 2 9x + 6, si raccoglie 2x 2 nel primo gruppo di due termini, ma poi non conviene raccogliere 3 al secondo gruppo: 6x 3 4x 2 9x + 6 = 2x 2 (3x 2) + 3( 3x + 2), quanto invece è conveniente raccogliere 3, ottenendo la scomposizione 6x 3 4x 2 9x + 6 = 2x 2 (3x 2) 3(3x 2) = (3x 2)(2x 2 3). Il trucco, in questo caso, consiste (oltre alla prova empirica) nell osservare che il coefficiente del primo termine (6) è di segno opposto al coefficiente del terzo termine ( 9), e quindi al secondo gruppo conviene cambiare di segno. Come già accennato, questo procedimento si può generalizzare al caso di polinomi con un numero pari di termini: 4x 5 6x } {{ } 4 2x3 + 3x } {{ } 2 +6x } {{ 9 } = =3x 4 (2x 3) x 2 (2x 3) + 3(2x 3) = =(2x 3)(3x 4 x 2 + 3). Il raccoglimento a fattor comune si può applicare anche in generale, quando il numero di fattori è dispari, previa qualche operazione preliminare. Tuttavia, la cosa è abbastanza semplice giusto quando si ha a che fare con un trinomio. Si consideri ad esempio 4x x + 7. Si può notare come il coefficiente di x, 11, è pari alla somma di 4 e 7, e dunque possiamo scrivere 4x x + 7 = 4x 2 + 4x + 7x
4 Ora è facile raccogliere a fattor comune ed arrivare alla scomposizione (4x+7)(x+1). Tuttavia, la cosa in generale è più difficile. Si consideri la seguente scomposizione: x 2 + 5x + 6 = x 2 + 3x + 2x + 6 = x(x + 3) + 2(x + 3) = (x + 3)(x + 2), o ancora di più la seguente: x 2 x 12 = x 2 4x + 3x 12 = x(x 4) + 3(x 4) = (x 4)(x + 3). Si può notare che non è semplice accorgersi che può convenire scrivere 5x come 3x+2x, o x come 4x + 3x. Come sempre, bisogna fare pratica per assimilare al meglio queste tecniche. 4 Regola di Ruffini La scomposizione tramite la regola di Ruffini è un metodo per la scomposizione di quei polinomi particolari che non rientrano nelle categorie precedenti. Si tratta di un metodo che non sempre va a buon fine e che procede per tentativi, ma è uno dei metodi più semplici per la scomposizione di polinomi. Si consideri ad esempio il polinomio x 3 + 5x 2 + 2x 8. Ora si riportano i coefficienti del polinomio su una griglia di questo tipo, avendo cura di isolare il termine noto: A questo punto si sceglie un valore adeguato da scrivere nella griglia sulla sinistra, e si trascrive in basso il primo coefficiente. 3 1 Ora si moltiplica il valore sulla sinistra per l ultimo valore riportato in basso (che nel nostro caso è 1), e si scrive il risultato nella seconda colonna, sommando poi i due numeri in basso: Si ripete ora il procedimento, moltiplicando 3 per l ultimo numero scritto in basso, cioè 2, si riporta nella terza colonna e poi si somma. Infine si fa lo stesso sino all ultima colonna isolata a destra, ottenendo lo schema finale
5 I valori 1, 2 e 4 diventano rispettivamente i coefficienti di x 2, di x ed il termine noto, ottenendo x 2 + 2x 4: tale polinomio sarà il fattore che moltiplicherà x + 3, cioè x meno il valore scelto 3. Invece 4 è il resto della scomposizione. In definitiva, x 3 + 5x 2 + 2x 8 = (x + 3)(x 2 + 2x 4) + 4. Non si tratta di una buona trasformazione, perché il resto +4 è d intralcio. L ideale sarebbe di trovare 0 come resto, nel qual caso avremmo solo il prodotto di due polinomio. Ad esempio, provando il valore 2 si ottiene lo schema Dunque x 3 +5x 2 +2x 8 = (x+2)(x 2 +3x 4). Ora il problema sta nell individuare un valore adeguato per operare la scomposizione con la regola di Ruffini. Scegliere a caso è un assurdità, ma è possibile restringere l insieme di scelta ai soli divisori del termine noto. Nell esempio il termine noto era 8, ed i divisori sono 1, 2, 4, 8 ed i corrispettivi negativi 1, 2, 4 e 8. Questo è un metodo valido ma sotto particolari condizioni: la prima è che il coefficiente del termine di grado più elevato (detto termine di testa) sia 1; l altra è che tutti i coefficienti siano interi. Era dunque evidente che il valore 3 non sarebbe andato bene. Ci sono dei casi in cui al polinomio può mancare uno dei termini, nel qual caso è opportuno riempire la relativa colonna nella griglia con uno 0. Si consideri ad esempio il polinomio x 3 + x 2 2: x 3 + x 2 2 = (x 1)(x 2 + 2x + 2). Nel caso in cui il coefficiente del termine di testa sia diverso da 1 la faccenda si complica, in quanto i divisori del termine noto potrebbero non andare bene. In questo caso si deve provare con dei valori frazionari, il cui numeratore va scelto ancora tra i divisori del termine noto, ed il denominatore tra i divisori del coefficiente del termine di testa. Ad esempio, il polinomio 2x 3 + x 2 + x + 6 può essere scomposto usando il valore 3/2: ( 2x 3 + x 2 + x + 6 = x + 3 ) (2x 2 2x + 4). 2 Risulta evidente però che il procedimento si allunga. Se qualcuno dei coefficienti dell equazione è frazionario, è bene portare tutto sotto una stessa frazione ed isolare il denominatore, prima di procedere alla scomposizione: x x2 1 4 x = 8x3 2x 2 2x = 1 8 (8x3 2x 2 2x + 3). A questo punto si può procedere alla scomposizione di 8x 3 2x 2 2x + 3 tramite il procedimento già visto: 5
6 x x2 1 4 x = 1 8 ( x + 3 ) (8x 2 8x + 4). 4 5 Divisione polinomiale Oltre a potersi sommare, sottrarre e moltiplicare, i polinomi si possono anche dividere tra loro, tramite un procedimento che per certi versi non è diverso da quello della divisione tra due numeri insegnato alle scuole elementari. Supponiamo dunque di voler dividere il polinomio 2x 4 5x 3 2x 2 + x + 3 per x 3. Scriviamo dunque i due polinomi in una griglia di questo tipo: 2x 4 5x 3 2x 2 x +3 x 3 Ora si considerano i termini di testa del polinomio dividendo e del polinomio divisore, cioè nel nostro caso rispettivamente 2x 4 e x, e si divide l uno per l altro ottenendo 2x 3 : tale valore si scrive come quoziente parziale sotto il divisore: 2x 3 A questo punto si moltiplica 2x 3 cambiando di segno: per il divisore e lo si scrive sotto il dividendo, 2x 4 +6x 3 2x 3 Si esegue la somma a parte e si riporta sotto il risultato, e poi si abbassa il termine successivo del dividendo, cioè 3x 2 (ma si possono abbassare anche più termini, anche tutti, come viene meglio): 2x 4 +6x 3 2x 3 = x 3 2x 2 A questo punto si ripete il procedimento con il resto parziale ottenuto: si divide il termine di testa x 3 per x, e si scrive il risultato nel quoziente parziale, dopodiché lo si moltiplica per il divisore x 3 e lo si scrive sotto il resto parziale dopo aver cambiato di segno: 2x 4 +6x 3 2x 3 + x 2 = x 3 2x 2 x 3 4x 2 Si continua il procedimento fino a che anche il termine noto è stato abbassato: 6
7 2x 4 +6x 3 2x 3 + x 2 + x + 4 = x 3 2x 2 x 3 3x 2 = x 2 +x x 2 +3x = 4x +3 4x +12 = 15 Dunque si ha il quoziente 2x 3 + x 2 + x + 4 ed il resto 15, e si può quindi scrivere 2x 4 5x 3 2x 2 + x + 3 = (x 3)(2x 3 + x 2 + x + 4) Come nel caso della scomposizione tramite la regola di Ruffini, anche in questo caso è opportuno riempire i buchi dei termini nei polinomi con degli zeri: x x 3 x x x x 3 x
Monomi e Polinomi. Monomio Si dice monomio un espressione letterale in cui figurano solo operazioni di moltiplicazione.
 Monomi e Polinomi Monomio Si dice monomio un espressione letterale in cui figurano solo operazioni di moltiplicazione. ) Sono monomi: 5 a 3 b 2 z; 2 3 a2 c 9 ; +7; 8a b 3 a 2. Non sono monomi: a + 2; xyz
Monomi e Polinomi Monomio Si dice monomio un espressione letterale in cui figurano solo operazioni di moltiplicazione. ) Sono monomi: 5 a 3 b 2 z; 2 3 a2 c 9 ; +7; 8a b 3 a 2. Non sono monomi: a + 2; xyz
Le quattro operazioni
 Le quattro operazioni 1. Addizione a + b = c addendi somma Proprietà commutativa Cambiando l ordine degli addendi, la somma non cambia. a + b = b + a Proprietà associativa La somma di tre numeri non cambia,
Le quattro operazioni 1. Addizione a + b = c addendi somma Proprietà commutativa Cambiando l ordine degli addendi, la somma non cambia. a + b = b + a Proprietà associativa La somma di tre numeri non cambia,
( ) ( ) 2 + 3( a + b) = ( ) + b( x 1) = ( ) ( ) b( x + y) = ( ) x 2 ( a + b) y 2 + ( a + b) = ( ) + ( a b) = ( ) a( 4x + 7) = ( ) + 3a( 2 5y) =
 1 Scomposizione in fattori di un polinomio Scomporre in fattori un polinomio significa trasformare il polinomio, che è una somma algebrica di monomi, nel prodotto di fattori con il grado più basso possibile.
1 Scomposizione in fattori di un polinomio Scomporre in fattori un polinomio significa trasformare il polinomio, che è una somma algebrica di monomi, nel prodotto di fattori con il grado più basso possibile.
CALCOLO LETTERALE. Le espressioni letterali sono espressioni contenenti operazioni fra numeri e lettere:
 CALCOLO LETTERALE Le espressioni letterali sono espressioni contenenti operazioni fra numeri e lettere: 5x. x + y ab + c, In generale le lettere rappresentano numeri generici. Ad esempio, se vogliamo convertire
CALCOLO LETTERALE Le espressioni letterali sono espressioni contenenti operazioni fra numeri e lettere: 5x. x + y ab + c, In generale le lettere rappresentano numeri generici. Ad esempio, se vogliamo convertire
1 Fattorizzazione di polinomi
 1 Fattorizzazione di polinomi Polinomio: un polinomio di grado n nella variabile x, è dato da p(x) = a n x n + a n 1 x n 1 + + a 1 x + a 0 con a n 0, a 0 è detto termine noto, a k è detto coefficiente
1 Fattorizzazione di polinomi Polinomio: un polinomio di grado n nella variabile x, è dato da p(x) = a n x n + a n 1 x n 1 + + a 1 x + a 0 con a n 0, a 0 è detto termine noto, a k è detto coefficiente
2 xab ; a2 x 3 y. 3a; 4b 2 ; 0,75y 3 z
 1 Premessa. In questa sezione verranno richiamati alcuni concetti fondamentali dell algebra, quella parte della matematica che si occupa dello studio del cosiddetto calcolo letterale, utili ai fini della
1 Premessa. In questa sezione verranno richiamati alcuni concetti fondamentali dell algebra, quella parte della matematica che si occupa dello studio del cosiddetto calcolo letterale, utili ai fini della
SCOMPOSIZIONE DI UN POLINOMIO IN FATTORI
 SCOMPOSIZIONE DI UN POLINOMIO IN FATTORI BINOMIO RACCOGLIMENTO ax + bx = x ( a + b ) a 2 b 2 = ( a + b ) ( a b ) CUBI a 3 - b 3 = ( a - b ) ( a 2 + ab + b 2 ) SOMMA DI CUBI a 3 + b 3 = ( a + b ) ( a 2
SCOMPOSIZIONE DI UN POLINOMIO IN FATTORI BINOMIO RACCOGLIMENTO ax + bx = x ( a + b ) a 2 b 2 = ( a + b ) ( a b ) CUBI a 3 - b 3 = ( a - b ) ( a 2 + ab + b 2 ) SOMMA DI CUBI a 3 + b 3 = ( a + b ) ( a 2
Calcolo algebrico. Maria Simonetta Bernabei & Horst Thaler
 Calcolo algebrico Maria Simonetta Bernabei & Horst Thaler CALCOLO LETTERALE Perché? E opportuno rappresentare i numeri con lettere dell alfabeto per fare affermazioni che valgono indipendentemente dal
Calcolo algebrico Maria Simonetta Bernabei & Horst Thaler CALCOLO LETTERALE Perché? E opportuno rappresentare i numeri con lettere dell alfabeto per fare affermazioni che valgono indipendentemente dal
Calcolo algebrico. Maria Simonetta Bernabei & Horst Thaler
 Calcolo algebrico Maria Simonetta Bernabei & Horst Thaler CALCOLO LETTERALE Perché? E opportuno rappresentare i numeri con lettere dell alfabeto per fare affermazioni che valgono indipendentemente dal
Calcolo algebrico Maria Simonetta Bernabei & Horst Thaler CALCOLO LETTERALE Perché? E opportuno rappresentare i numeri con lettere dell alfabeto per fare affermazioni che valgono indipendentemente dal
1 Prodotti e potenze notevoli 1. 2 Divisione tra polinomi 2 2.1 Regola di Ruffini... 4. 3 Fattorizzazione di un polinomio 5. 4 Teorema di Ruffini 8
 UNIVR Facoltà di Economia Sede di Vicenza Corso di Matematica 1 Polinomi Indice 1 Prodotti e potenze notevoli 1 2 Divisione tra polinomi 2 2.1 Regola di Ruffini................................................
UNIVR Facoltà di Economia Sede di Vicenza Corso di Matematica 1 Polinomi Indice 1 Prodotti e potenze notevoli 1 2 Divisione tra polinomi 2 2.1 Regola di Ruffini................................................
U.D. N 04 I polinomi
 Unità Didattica N 0 I polinomi U.D. N 0 I polinomi 0) Monomi 0) Somma algebrica di monomi simili 0) Prodotto di due i più monomi 0) Quoziente di due monomi 05) Potenza di un monomio 06) Massimo comune
Unità Didattica N 0 I polinomi U.D. N 0 I polinomi 0) Monomi 0) Somma algebrica di monomi simili 0) Prodotto di due i più monomi 0) Quoziente di due monomi 05) Potenza di un monomio 06) Massimo comune
Equazioni di I e II grado
 Corso di Laurea: Biologia Tutor: Marta Floris, Max Artizzu PRECORSI DI MATEMATICA Equazioni di I e II grado 1 Introduzione ai polinomi Un incognita è un simbolo letterale che sta a simboleggiare un valore
Corso di Laurea: Biologia Tutor: Marta Floris, Max Artizzu PRECORSI DI MATEMATICA Equazioni di I e II grado 1 Introduzione ai polinomi Un incognita è un simbolo letterale che sta a simboleggiare un valore
Le espressioni letterali
 Calcolo letterale Le espressioni letterali Sono espressioni contenenti numeri reali e lettere. A=(B+b)h/2 A=2(b+h) Le lettere rappresentano numeri reali. La stessa lettera assume sempre lo stesso valore.
Calcolo letterale Le espressioni letterali Sono espressioni contenenti numeri reali e lettere. A=(B+b)h/2 A=2(b+h) Le lettere rappresentano numeri reali. La stessa lettera assume sempre lo stesso valore.
DIVISIONE TRA POLINOMI E SCOMPOSIZIONI
 DIVISIONE TRA POLINOMI E SCOMPOSIZIONI Esegui la seguente divisione fra polinomi e scrivi quoziente e resto.. b b 8b b 5 : b 5 5. x x x : x. 6 x x x : x x Q b b R 5; Q x x x ; R x 7 9 Q x x x ; R x Esegui
DIVISIONE TRA POLINOMI E SCOMPOSIZIONI Esegui la seguente divisione fra polinomi e scrivi quoziente e resto.. b b 8b b 5 : b 5 5. x x x : x. 6 x x x : x x Q b b R 5; Q x x x ; R x 7 9 Q x x x ; R x Esegui
Scomposizione di un polinomio in fattori
 Scomposizione di un polinomio in fattori Scomporre in fattori primi un polinomio significa esprimerlo come il prodotto di due più polinomi non più scomponibili. Ad esempio x 2 9 = x 3) x + 3) }{{} fattore
Scomposizione di un polinomio in fattori Scomporre in fattori primi un polinomio significa esprimerlo come il prodotto di due più polinomi non più scomponibili. Ad esempio x 2 9 = x 3) x + 3) }{{} fattore
CORSO ZERO DI MATEMATICA
 UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA CALCOLO LETTERALE Dr. Erasmo Modica [email protected] MONOMI In una formula si dicono variabili le lettere alle quali può
UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA CALCOLO LETTERALE Dr. Erasmo Modica [email protected] MONOMI In una formula si dicono variabili le lettere alle quali può
Un monomio è in forma normale se è il prodotto di un solo fattore numerico e di fattori letterali con basi diverse. Tutto quanto sarà detto di
 DEFINIZIONE Espressione algebrica costituita dal prodotto tra una parte numerica (coefficiente) e una o più variabili e/o costanti (parte letterale). Variabili e costanti possono comparire elevate a potenza
DEFINIZIONE Espressione algebrica costituita dal prodotto tra una parte numerica (coefficiente) e una o più variabili e/o costanti (parte letterale). Variabili e costanti possono comparire elevate a potenza
MATEMATICA EQUAZIONI FRATTE, DI SECONDO GRADO O SUPERIORE GSCATULLO
 MATEMATICA EQUAZIONI FRATTE, DI SECONDO GRADO O SUPERIORE GSCATULLO Equazioni fratte, di secondo grado o superiore Le equazioni di secondo grado Un equazione è di secondo grado se si può scrivere nella
MATEMATICA EQUAZIONI FRATTE, DI SECONDO GRADO O SUPERIORE GSCATULLO Equazioni fratte, di secondo grado o superiore Le equazioni di secondo grado Un equazione è di secondo grado se si può scrivere nella
5) 1 2 essendo x1 e x2 due
 SCOMPOSIZIONE IN FATTORI 1) Raccoglimento a fattore comune ( Applicabile ad un polinomio di un numero qualunque di termini purchè i termini presentino almeno una lettera o un numero che si ripete in tutti)
SCOMPOSIZIONE IN FATTORI 1) Raccoglimento a fattore comune ( Applicabile ad un polinomio di un numero qualunque di termini purchè i termini presentino almeno una lettera o un numero che si ripete in tutti)
Un polinomio è un espressione algebrica data dalla somma di più monomi.
 1 I polinomi 1.1 Terminologia sui polinomi Un polinomio è un espressione algebrica data dalla somma di più monomi. I termini di un polinomio sono i monomi che compaiono come addendi nel polinomio. Il termine
1 I polinomi 1.1 Terminologia sui polinomi Un polinomio è un espressione algebrica data dalla somma di più monomi. I termini di un polinomio sono i monomi che compaiono come addendi nel polinomio. Il termine
U.D. N 04 I polinomi
 8 U.D. N 04 I polinomi 0) Monomi 0) Somma algebrica di monomi simili 0) prodotto di due i più monomi 04) Quoziente di due monomi 05) Potenza di un monomio 06) Massimo comune divisore di due o più monomi
8 U.D. N 04 I polinomi 0) Monomi 0) Somma algebrica di monomi simili 0) prodotto di due i più monomi 04) Quoziente di due monomi 05) Potenza di un monomio 06) Massimo comune divisore di due o più monomi
B3. Scomposizione di polinomi
 B3. Scomposizione di polinomi Quando si calcola una espressione contenente solo prodotti di polinomi si ottiene un polinomio, che è il risultato dell espressione. La scomposizione in fattori di polinomi
B3. Scomposizione di polinomi Quando si calcola una espressione contenente solo prodotti di polinomi si ottiene un polinomio, che è il risultato dell espressione. La scomposizione in fattori di polinomi
DIVISIONE TRA POLINOMI IN UNA VARIABILE
 DIVISIONE TRA POLINOMI E SCOMPOSIZIONE Prof. Erasmo Modica [email protected] DIVISIONE TRA POLINOMI IN UNA VARIABILE L algoritmo della divisione tra polinomi è analogo a quello della divisione ordinaria
DIVISIONE TRA POLINOMI E SCOMPOSIZIONE Prof. Erasmo Modica [email protected] DIVISIONE TRA POLINOMI IN UNA VARIABILE L algoritmo della divisione tra polinomi è analogo a quello della divisione ordinaria
UNITÀ DIDATTICA 11 POLINOMI
 UNITÀ DIDATTICA 11 POLINOMI 11.1 Definizione di polinomio. Grado e ordine di polinomi. Operazioni con i polinomi Si chiama polinomio, un monomio o una somma algebrica di due o Definizione di polinomio
UNITÀ DIDATTICA 11 POLINOMI 11.1 Definizione di polinomio. Grado e ordine di polinomi. Operazioni con i polinomi Si chiama polinomio, un monomio o una somma algebrica di due o Definizione di polinomio
FATTORIZZAZIONE DI UN POLINOMIO
 FATTORIZZAZIONE DI UN POLINOMIO Così come avviene con i numeri ( 0 = 5), la fattorizzazione di un polinomio è la scomposizione di un polinomio in un prodotto di due o più polinomi. Esempio: = + + Un polinomio
FATTORIZZAZIONE DI UN POLINOMIO Così come avviene con i numeri ( 0 = 5), la fattorizzazione di un polinomio è la scomposizione di un polinomio in un prodotto di due o più polinomi. Esempio: = + + Un polinomio
CORSO ZERO DI MATEMATICA per Ing. Chimica e Ing. delle Telecomunicazioni MONOMI E POLINOMI Prof. Erasmo Modica
 CORSO ZERO DI MATEMATICA per Ing. Chimica e Ing. delle Telecomunicazioni MONOMI E POLINOMI Prof. Erasmo Modica [email protected] MONOMI In una formula si dicono variabili le lettere alle quali può essere
CORSO ZERO DI MATEMATICA per Ing. Chimica e Ing. delle Telecomunicazioni MONOMI E POLINOMI Prof. Erasmo Modica [email protected] MONOMI In una formula si dicono variabili le lettere alle quali può essere
Prontuario degli argomenti di Algebra
 Prontuario degli argomenti di Algebra NUMERI RELATIVI Un numero relativo è un numero preceduto da un segno + o - indicante la posizione rispetto ad un punto di riferimento a cui si associa il valore 0.
Prontuario degli argomenti di Algebra NUMERI RELATIVI Un numero relativo è un numero preceduto da un segno + o - indicante la posizione rispetto ad un punto di riferimento a cui si associa il valore 0.
Precorso di Matematica A. A. 2017/2018. Algebra
 Precorso di Matematica A. A. 017/018 Algebra 1 Monomi Monomio: espressione algebrica ottenuta come prodotto di fattori sia numerici sia letterali. Grado di un monomio rispetto ad una sua lettera: esponente
Precorso di Matematica A. A. 017/018 Algebra 1 Monomi Monomio: espressione algebrica ottenuta come prodotto di fattori sia numerici sia letterali. Grado di un monomio rispetto ad una sua lettera: esponente
MATEMATICA SCOMPOSIZIONE E FRAZIONE ALGEBRICHE GSCATULLO
 MATEMATICA SCOMPOSIZIONE E FRAZIONE ALGEBRICHE GSCATULLO 1 Scomposizione e frazioni algebriche Scomposizione in Fattori Scomporre in fattori un polinomio significa scriverlo sotto forma di un prodotto
MATEMATICA SCOMPOSIZIONE E FRAZIONE ALGEBRICHE GSCATULLO 1 Scomposizione e frazioni algebriche Scomposizione in Fattori Scomporre in fattori un polinomio significa scriverlo sotto forma di un prodotto
EQUAZIONI DISEQUAZIONI
 EQUAZIONI DISEQUAZIONI Indice 1 Background 1 1.1 Proprietà delle potenze................................ 1 1.2 Prodotti notevoli................................... 1 2 Equazioni e disequazioni razionali
EQUAZIONI DISEQUAZIONI Indice 1 Background 1 1.1 Proprietà delle potenze................................ 1 1.2 Prodotti notevoli................................... 1 2 Equazioni e disequazioni razionali
espressione letterale valore numerico Monomio: forma normale coefficiente parte letterale Monomi simili: Monomi opposti: Grado di un monomio:
 Calcolo letterale Espressione letterale Un espressione letterale è un insieme di numeri e lettere legati dai simboli delle operazioni. Il valore numerico di un espressione letterale è il risultato numerico
Calcolo letterale Espressione letterale Un espressione letterale è un insieme di numeri e lettere legati dai simboli delle operazioni. Il valore numerico di un espressione letterale è il risultato numerico
Precorso di Matematica Maria Margherita Obertino Università degli Studi di Torino Di.S.A.F.A.
 Precorso di Matematica Maria Margherita Obertino Università degli Studi di Torino Di.S.A.F.A.! Divisione tra polinomi ( 2.2 del testo)! La regola di Ruffini ( 2.3 del testo)! I prodotti notevoli ( 2.3
Precorso di Matematica Maria Margherita Obertino Università degli Studi di Torino Di.S.A.F.A.! Divisione tra polinomi ( 2.2 del testo)! La regola di Ruffini ( 2.3 del testo)! I prodotti notevoli ( 2.3
Scomposizione in fattori dei polinomi
 Scomposizione in fattori dei polinomi Scomporre in fattori un polinomio significa esprimere quel polinomio come prodotto di altri polinomi di grado inferiore ad esso. Questo procedimento può essere visto
Scomposizione in fattori dei polinomi Scomporre in fattori un polinomio significa esprimere quel polinomio come prodotto di altri polinomi di grado inferiore ad esso. Questo procedimento può essere visto
COMPITI DELLE VACANZE DI MATEMATICA CLASSI PRIME A.F.M. A.S. 2016/17 1) Calcola le seguenti espressioni: + = = { : 3 3 } :( =
 COMPITI DELLE VACANZE DI MATEMATICA CLASSI PRIME A.F.M. A.S. 06/7 ) Calcola le seguenti espressioni: 5 7 { } 7 0 8 5 5 5 : 5 :( 5 5 5 ) 5 : 5 : ( 5 ) ( ) 5 + b) 5 ( 6 ) :( 7 ) : ( ) 6 : ( ) ( 6 ) + + +
COMPITI DELLE VACANZE DI MATEMATICA CLASSI PRIME A.F.M. A.S. 06/7 ) Calcola le seguenti espressioni: 5 7 { } 7 0 8 5 5 5 : 5 :( 5 5 5 ) 5 : 5 : ( 5 ) ( ) 5 + b) 5 ( 6 ) :( 7 ) : ( ) 6 : ( ) ( 6 ) + + +
Scomposizione di polinomi. Scomporre un polinomio significa riscriverlo nel PRODOTTO di due o più polinomi di grado inferiore
 Scomposizione di polinomi Scomporre un polinomio significa riscriverlo nel PRODOTTO di due o più polinomi di grado inferiore Raccoglimento a fattor comune Il raccoglimento a fattor comune consiste nel
Scomposizione di polinomi Scomporre un polinomio significa riscriverlo nel PRODOTTO di due o più polinomi di grado inferiore Raccoglimento a fattor comune Il raccoglimento a fattor comune consiste nel
Soluzioni verifica scritta 1A Scientifico 20/01/2009
 Soluzioni verifica scritta 1A Scientifico 0/01/009 Esercizio 1 68 = 3 + ; = 11 + 0 MCD68 ; ) = ultimo resto 0) 68 68 mcm68 ; ) = = =68 11 = 68 10 + 1) = 680 + 68 = 748 MCD68; ) Esercizio Possiamo considerare
Soluzioni verifica scritta 1A Scientifico 0/01/009 Esercizio 1 68 = 3 + ; = 11 + 0 MCD68 ; ) = ultimo resto 0) 68 68 mcm68 ; ) = = =68 11 = 68 10 + 1) = 680 + 68 = 748 MCD68; ) Esercizio Possiamo considerare
Soluzioni delle Esercitazioni I 19-23/09/2016
 Esercitazioni di Matematica Esercitazioni I 9-3/09/06 Soluzioni delle Esercitazioni I 9-3/09/06 A. Polinomi Si ha:. (x+y)(3xy xy) = 6x y x y +3xy 3 xy.. (x y) = 4x 4xy +y. 3. Se non ci si ricorda lo sviluppo
Esercitazioni di Matematica Esercitazioni I 9-3/09/06 Soluzioni delle Esercitazioni I 9-3/09/06 A. Polinomi Si ha:. (x+y)(3xy xy) = 6x y x y +3xy 3 xy.. (x y) = 4x 4xy +y. 3. Se non ci si ricorda lo sviluppo
Insiemi numerici. Alcune definizioni. La retta dei numeri
 Insiemi numerici Q Z N 0 1 1 1 4 4 N = 0,1,,,4, = insieme dei numeri naturali Z = insieme dei numeri interi (formato dall unione dei numeri naturali e dei numeri interi negativi) Q = insieme dei numeri
Insiemi numerici Q Z N 0 1 1 1 4 4 N = 0,1,,,4, = insieme dei numeri naturali Z = insieme dei numeri interi (formato dall unione dei numeri naturali e dei numeri interi negativi) Q = insieme dei numeri
14 : : : : 3 15 : 5. 2) Fra le seguenti espressioni indica, motivando la risposta, i monomi:
 COMPITI DELLE VACANZE DI MATEMATICA CLASSI PRIME A.F.M. A.S. 0/5 ) Calcola le seguenti espressioni: 5 0 : 7 : 8 : : 5 : 5 5 6 0 : : : : : b) 7 9 5 5 5 7 0 5 9 b) 6 66 :6 :6 :6 : : : : 5 d) 7 : 9 6 7 8
COMPITI DELLE VACANZE DI MATEMATICA CLASSI PRIME A.F.M. A.S. 0/5 ) Calcola le seguenti espressioni: 5 0 : 7 : 8 : : 5 : 5 5 6 0 : : : : : b) 7 9 5 5 5 7 0 5 9 b) 6 66 :6 :6 :6 : : : : 5 d) 7 : 9 6 7 8
ESERCIZI IN PIÙ I NUMERI COMPLESSI
 ESERCIZI IN PIÙ I NUMERI COMPLESSI L equazione x x 0 non ha soluzioni nell insieme dei numeri reali; infatti, applicando la formula ridotta, si ottiene x, 3. Interpretando come numero immaginario, cioè
ESERCIZI IN PIÙ I NUMERI COMPLESSI L equazione x x 0 non ha soluzioni nell insieme dei numeri reali; infatti, applicando la formula ridotta, si ottiene x, 3. Interpretando come numero immaginario, cioè
IL PROBLEMA. Somma fra frazioni algebriche. Lezione di matematica Prof Giovanni Ianne
 IL PROBLEMA Somma fra frazioni algebriche Lezione di matematica Prof Giovanni Ianne Come facevi finora? Es: Fra frazioni numeriche: 1 5 = 6 9 Cosa fai?.. = Scomponi in fattori primi i denominatori: 6 =
IL PROBLEMA Somma fra frazioni algebriche Lezione di matematica Prof Giovanni Ianne Come facevi finora? Es: Fra frazioni numeriche: 1 5 = 6 9 Cosa fai?.. = Scomponi in fattori primi i denominatori: 6 =
Scomposizione in fattori di un polinomio. Prof. Walter Pugliese
 Scomposizione in fattori di un polinomio Prof. Walter Pugliese La scomposizione in fattori dei polinomi Scomporre in fattori un polinomio significa scriverlo sotto forma di prodotto di polinomi di grado
Scomposizione in fattori di un polinomio Prof. Walter Pugliese La scomposizione in fattori dei polinomi Scomporre in fattori un polinomio significa scriverlo sotto forma di prodotto di polinomi di grado
Frazioni algebriche. Osserviamo che un espressione di questo tipo si ottiene talvolta quando ci si propone di ottenere il quoziente di due monomi.
 Frazioni algebriche 14 14.1 Definizione di frazione algebrica Diamo la seguente definizione: Definizione 14.1. Si definisce frazione algebrica un espressione del tipo A B polinomi. dove A e B sono Osserviamo
Frazioni algebriche 14 14.1 Definizione di frazione algebrica Diamo la seguente definizione: Definizione 14.1. Si definisce frazione algebrica un espressione del tipo A B polinomi. dove A e B sono Osserviamo
Prodotti Notevoli e Scomposizione. Feo Maurizio
 Prodotti Notevoli e Scomposizione Feo Maurizio August 12, 2013 2 Preambolo Gli appunti che seguono non vogliono sostituire il testo, ma rappresentano solo una bozza per raccogliere in maniera organica
Prodotti Notevoli e Scomposizione Feo Maurizio August 12, 2013 2 Preambolo Gli appunti che seguono non vogliono sostituire il testo, ma rappresentano solo una bozza per raccogliere in maniera organica
Le equazioni di I grado
 Le equazioni di I grado ITIS Feltrinelli anno scolastico 007-008 R. Folgieri 007-008 1 Le equazioni abbiamo una uguaglianza tra due quantità (espressioni algebriche, perché nei due termini ci possono essere
Le equazioni di I grado ITIS Feltrinelli anno scolastico 007-008 R. Folgieri 007-008 1 Le equazioni abbiamo una uguaglianza tra due quantità (espressioni algebriche, perché nei due termini ci possono essere
Esempio B2.1: dire il grado del monomio seguente rispetto ad ogni lettera e il suo grado complessivo:
 B. Polinomi B.1 Cos è un polinomio Un POLINOMIO è la somma di due o più monomi. Se ha due termini, come a+b è detto binomio Se ha tre termini, come a-3b+cx è detto trinomio, eccetera GRADO DI UN POLINOMIO
B. Polinomi B.1 Cos è un polinomio Un POLINOMIO è la somma di due o più monomi. Se ha due termini, come a+b è detto binomio Se ha tre termini, come a-3b+cx è detto trinomio, eccetera GRADO DI UN POLINOMIO
Le frazioni algebriche
 Le frazioni algebriche Le frazioni algebriche, a differenza delle frazioni numeriche, sono frazioni che prevedono al denominatore espressioni polinomiali. Le seguenti, ad esempio, sono frazioni algebriche
Le frazioni algebriche Le frazioni algebriche, a differenza delle frazioni numeriche, sono frazioni che prevedono al denominatore espressioni polinomiali. Le seguenti, ad esempio, sono frazioni algebriche
Il calcolo letterale
 Il calcolo letterale Si dice ESPRESSIONE ALGEBRICA LETTERALE (o semplicemente espressione algebrica) un espressione in cui compaiono lettere che rappresentano numeri. Esempio: 5ab 4a b 3 + b 5a 1 ab 3
Il calcolo letterale Si dice ESPRESSIONE ALGEBRICA LETTERALE (o semplicemente espressione algebrica) un espressione in cui compaiono lettere che rappresentano numeri. Esempio: 5ab 4a b 3 + b 5a 1 ab 3
Liceo Scientifico Statale S. Cannizzaro Palermo Classe III D EQUAZIONI POLINOMIALI Divisione di polinomi, teorema del resto e teorema di Ruffini
 Divisione di polinomi, teorema del resto e teorema di Ruffini Teorema (della divisione con resto tra due polinomi in una variabile). Dati due polinomi A x e B x, con B x 0, esistono sempre, e sono unici,
Divisione di polinomi, teorema del resto e teorema di Ruffini Teorema (della divisione con resto tra due polinomi in una variabile). Dati due polinomi A x e B x, con B x 0, esistono sempre, e sono unici,
UNITÀ FORMATIVA DISCIPLINARE: N. 9 Titolo: SCOMPOSIZIONI POLINOMI
 UNITÀ FORMATIVA DISCIPLINARE: N. 9 Titolo: SCOMPOSIZIONI POLINOMI N. ore previste 35 Periodo di realizzazione SETTEMBRE OTTOBRE 2017 in termini di competenze, abilità e conoscenze Monomi Polinomi Prodotti
UNITÀ FORMATIVA DISCIPLINARE: N. 9 Titolo: SCOMPOSIZIONI POLINOMI N. ore previste 35 Periodo di realizzazione SETTEMBRE OTTOBRE 2017 in termini di competenze, abilità e conoscenze Monomi Polinomi Prodotti
Equazioni. Le equazioni sono relazioni di uguaglianza tra due espressioni algebriche.
 Equazioni Le equazioni sono relazioni di uguaglianza tra due espressioni algebriche. Nelle espressioni compare una lettera, chiamata incognita. Possiamo attribuire un valore a questa incognita, e vedere
Equazioni Le equazioni sono relazioni di uguaglianza tra due espressioni algebriche. Nelle espressioni compare una lettera, chiamata incognita. Possiamo attribuire un valore a questa incognita, e vedere
Prodotti Notevoli. 1. Prodotto della somma di due monomi per la loro differenza
 Prodotti Notevoli I prodotti notevoli sono particolari prodotti o potenze di polinomi, che si sviluppano secondo formule facilmente memorizzabili. Questi consentono di effettuare i calcoli in maniera più
Prodotti Notevoli I prodotti notevoli sono particolari prodotti o potenze di polinomi, che si sviluppano secondo formule facilmente memorizzabili. Questi consentono di effettuare i calcoli in maniera più
Esercizi sulle Disequazioni
 Esercizi sulle Disequazioni Esercizio Trovare le soluzioni delle seguenti disequazioni:.).).).) ).) ) ).).7) 8.8).) Esercizio Trovare le soluzioni delle seguenti disequazioni tratte dal secondo parziale
Esercizi sulle Disequazioni Esercizio Trovare le soluzioni delle seguenti disequazioni:.).).).) ).) ) ).).7) 8.8).) Esercizio Trovare le soluzioni delle seguenti disequazioni tratte dal secondo parziale
Espressioni algebriche: espressioni razionali
 Espressioni algebriche: espressioni razionali definizione: Il rapporto fra due polinomi si dice espressione razionale. Le espressioni razionali in una sola variabile si scrivono nella forma generale esempio:
Espressioni algebriche: espressioni razionali definizione: Il rapporto fra due polinomi si dice espressione razionale. Le espressioni razionali in una sola variabile si scrivono nella forma generale esempio:
Soluzioni della verifica scritta 1 B Scientifico 24/01/2009
 Soluzioni della verifica scritta 1 B Scientifico 4/01/009 Esercizio 1. Il polinomio x +x 4 5 xy + y non èordinatoné rispetto a x nè rispetto a y. E completo rispetto a y ma non rispetto a x. Nonè omogeneo.
Soluzioni della verifica scritta 1 B Scientifico 4/01/009 Esercizio 1. Il polinomio x +x 4 5 xy + y non èordinatoné rispetto a x nè rispetto a y. E completo rispetto a y ma non rispetto a x. Nonè omogeneo.
ALGEBRA. Monomio: In un monomio distinguiamo parte numerica (o coefficiente) e parte letterale. Es.: -7 ax 2 b 3 y. Parte letterale.
 ALGEBRA Monomio: un espressione algebrica dove non figurano operazioni (e non segni) di addizione (+) o sottrazione(-); figurano solo moltiplicazioni e potenze. In un monomio distinguiamo parte numerica
ALGEBRA Monomio: un espressione algebrica dove non figurano operazioni (e non segni) di addizione (+) o sottrazione(-); figurano solo moltiplicazioni e potenze. In un monomio distinguiamo parte numerica
Precorso di Matematica
 UNIVERSITÀ DEGLI STUDI ROMA TRE FACOLTA DI ARCHITETTURA Precorso di Matematica Anna Scaramuzza Anno Accademico 2005-2006 4-10 Ottobre 2005 INDICE 1. ALGEBRA................................. 3 1.1 Equazioni
UNIVERSITÀ DEGLI STUDI ROMA TRE FACOLTA DI ARCHITETTURA Precorso di Matematica Anna Scaramuzza Anno Accademico 2005-2006 4-10 Ottobre 2005 INDICE 1. ALGEBRA................................. 3 1.1 Equazioni
1 Le espressioni algebriche letterali
 1 Le espressioni algebriche letterali DEFINIZIONE. Chiamiamo espressione algebrica letterale un insieme di numeri, rappresentati anche da lettere, legati uno all altro da segni di operazione. ESEMPI 2a
1 Le espressioni algebriche letterali DEFINIZIONE. Chiamiamo espressione algebrica letterale un insieme di numeri, rappresentati anche da lettere, legati uno all altro da segni di operazione. ESEMPI 2a
APPUNTI DI MATEMATICA ALGEBRA \ CALCOLO LETTERALE \ MONOMI (1)
 LGEBR \ CLCOLO LETTERLE \ MONOMI (1) Un monomio è un prodotto di numeri e lettere; gli (eventuali) esponenti delle lettere sono numeri naturali (0 incluso). Ogni numero (reale) può essere considerato come
LGEBR \ CLCOLO LETTERLE \ MONOMI (1) Un monomio è un prodotto di numeri e lettere; gli (eventuali) esponenti delle lettere sono numeri naturali (0 incluso). Ogni numero (reale) può essere considerato come
CORSO ZERO DI MATEMATICA
 UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA EQUAZIONI E DISEQUAZIONI DI SECONDO GRADO Dr. Erasmo Modica [email protected] EQUAZIONI DI SECONDO GRADO Definizione: Dicesi
UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA EQUAZIONI E DISEQUAZIONI DI SECONDO GRADO Dr. Erasmo Modica [email protected] EQUAZIONI DI SECONDO GRADO Definizione: Dicesi
I POLINOMI. La forma normale di un polinomio. Un polinomio è detto in FORMA NORMALE se in esso non compaiono monomi simili.
 I POLINOMI Un polinomio è una somma algebrica tra monomi Sono polinomi le seguenti espressioni 2ab + 4bc -5a 2 b + 2ab - 5c 5x + 2y + 8x in esse infatti troviamo somme o differenze tra monomi La forma
I POLINOMI Un polinomio è una somma algebrica tra monomi Sono polinomi le seguenti espressioni 2ab + 4bc -5a 2 b + 2ab - 5c 5x + 2y + 8x in esse infatti troviamo somme o differenze tra monomi La forma
Programma di matematica classe I sez. B a.s
 Programma di matematica classe I sez. B a.s. 2016-2017 Testi in adozione: Bergamini-Barozzi-TrifoneMatematica.bluSeconda edizione vol.1- primo biennio Ed. Zanichelli MODULO A: I numeri naturali e i numeri
Programma di matematica classe I sez. B a.s. 2016-2017 Testi in adozione: Bergamini-Barozzi-TrifoneMatematica.bluSeconda edizione vol.1- primo biennio Ed. Zanichelli MODULO A: I numeri naturali e i numeri
PROGRAMMAZIONE ANNUALE
 ISTITUTO di ISTRUZIONE SUPERIORE NICOLA MORESCHI SETTORE ECONOMICO Amministrazione, finanza e marketing Relazioni internazionali per il marketing Sistemi informativi aziendali LICEO SCIENTIFICO Viale San
ISTITUTO di ISTRUZIONE SUPERIORE NICOLA MORESCHI SETTORE ECONOMICO Amministrazione, finanza e marketing Relazioni internazionali per il marketing Sistemi informativi aziendali LICEO SCIENTIFICO Viale San
Scomposizioni polinomiali
 Scomposizioni polinomiali Le scomposizioni polinomiali sono uno degli argomenti fondamentali di tutta l'algebra di scuola superiore, essendo utilizzate in ogni altro argomento del programma di seconda
Scomposizioni polinomiali Le scomposizioni polinomiali sono uno degli argomenti fondamentali di tutta l'algebra di scuola superiore, essendo utilizzate in ogni altro argomento del programma di seconda
RECUPERO LE PROPRIETÀ DELLE POTENZE IN Z
 I NUMERI NATURALI E I NUMERI INTERI Recupero LE PROPRIETÀ DELLE POTENZE IN Z [( ) ] {[( ) ] [( ) ] [( ) ] }. [( ) ] {[( ) ] [( ) ] [( ) ] } () {() ( ) ( ) } Applica la proprietà della potenza di potenza.
I NUMERI NATURALI E I NUMERI INTERI Recupero LE PROPRIETÀ DELLE POTENZE IN Z [( ) ] {[( ) ] [( ) ] [( ) ] }. [( ) ] {[( ) ] [( ) ] [( ) ] } () {() ( ) ( ) } Applica la proprietà della potenza di potenza.
Moltiplicazione. Divisione. Multipli e divisori
 Addizione Sottrazione Potenze Moltiplicazione Divisione Multipli e divisori LE QUATTRO OPERAZIONI Una operazione aritmetica è quel procedimento che fa corrispondere ad una coppia ordinata di numeri (termini
Addizione Sottrazione Potenze Moltiplicazione Divisione Multipli e divisori LE QUATTRO OPERAZIONI Una operazione aritmetica è quel procedimento che fa corrispondere ad una coppia ordinata di numeri (termini
Equazioni e disequazioni
 Equazioni e disequazioni Le equazioni Una uguaglianza tra espressioni letterali che risulta vera per ogni valore delle lettere che vi compaiono prende il nome di identità. 2a=2a (a+b)(a-b)=a 2 -b 2 Una
Equazioni e disequazioni Le equazioni Una uguaglianza tra espressioni letterali che risulta vera per ogni valore delle lettere che vi compaiono prende il nome di identità. 2a=2a (a+b)(a-b)=a 2 -b 2 Una
TEOREMA DEL RESTO E REGOLA DI RUFFINI
 TEOREMA DEL RESTO E REGOLA DI RUFFINI ALCUNI TEOREMI IMPORTANTI Prendiamo una divisione intera tra numeri: 6 : 3 = 2. Il resto di questa divisione è 0, e questo significa che moltiplicando il quoziente
TEOREMA DEL RESTO E REGOLA DI RUFFINI ALCUNI TEOREMI IMPORTANTI Prendiamo una divisione intera tra numeri: 6 : 3 = 2. Il resto di questa divisione è 0, e questo significa che moltiplicando il quoziente
Polinomi Prodotti notevoli. Esempi di polinomi
 Pagina 1 Polinomi Definizione: Dicesi polinomio la somma algebrica di due o più monomi. I monomi si dicono i termini del polinomio. Un polinomio formato da due termini dicesi binomio, da tre termini trinomio,
Pagina 1 Polinomi Definizione: Dicesi polinomio la somma algebrica di due o più monomi. I monomi si dicono i termini del polinomio. Un polinomio formato da due termini dicesi binomio, da tre termini trinomio,
Polinomi. Corso di accompagnamento in matematica. Lezione 1
 Polinomi Corso di accompagnamento in matematica Lezione 1 Sommario 1 Insiemi numerici 2 Definizione di polinomio 3 Operazioni tra polinomi 4 Fattorizzazione Corso di accompagnamento Polinomi Lezione 1
Polinomi Corso di accompagnamento in matematica Lezione 1 Sommario 1 Insiemi numerici 2 Definizione di polinomio 3 Operazioni tra polinomi 4 Fattorizzazione Corso di accompagnamento Polinomi Lezione 1
EQUAZIONI BIQUADRATICHE
 EQUAZIONI PARTICOLARI PROF.SSA ROSSELLA PISCOPO Indice 1 EQUAZIONI BIQUADRATICHE ------------------------------------------------------------------------------------------ 3 2 EQUAZIONI RECIPROCHE -----------------------------------------------------------------------------------------------
EQUAZIONI PARTICOLARI PROF.SSA ROSSELLA PISCOPO Indice 1 EQUAZIONI BIQUADRATICHE ------------------------------------------------------------------------------------------ 3 2 EQUAZIONI RECIPROCHE -----------------------------------------------------------------------------------------------
Dott. Marta Ruspa 0321/ /
 FISICA APPLICATA Dott. Marta Ruspa [email protected] 0321/660669 011/6707310 Lezione I 1 CORSO INTEGRATO DI SCIENZE FISICHE e STATISTICHE Discipline: FISICA APPLICATA STATISTICA INFORMATICA Lezione I
FISICA APPLICATA Dott. Marta Ruspa [email protected] 0321/660669 011/6707310 Lezione I 1 CORSO INTEGRATO DI SCIENZE FISICHE e STATISTICHE Discipline: FISICA APPLICATA STATISTICA INFORMATICA Lezione I
per un altro; le più importanti sono quelle di seguito elencate.
 2 Abilità di calcolo I quiz raccolti in questo capitolo sono finalizzati alla valutazione della rapidità e della precisione con cui esegui i calcoli matematici. Prima di cimentarti con i test proposti,
2 Abilità di calcolo I quiz raccolti in questo capitolo sono finalizzati alla valutazione della rapidità e della precisione con cui esegui i calcoli matematici. Prima di cimentarti con i test proposti,
Precorso di Matematica Maria Margherita Obertino Università degli Studi di Torino Di.S.A.F.A.
 Precorso di Matematica Maria Margherita Obertino Università degli Studi di Torino Di.S.A.F.A. Scomposizione dei polinomi in fattori primi ( 2.4 del testo) Equazioni di primo grado ( 3.1 del testo) Equazioni
Precorso di Matematica Maria Margherita Obertino Università degli Studi di Torino Di.S.A.F.A. Scomposizione dei polinomi in fattori primi ( 2.4 del testo) Equazioni di primo grado ( 3.1 del testo) Equazioni
Anno 1. M.C.D. fra polinomi
 Anno 1 M.C.D. fra polinomi 1 Introduzione In questa lezione introdurremo il concetto di Massimo Comune Divisore (M.C.D.) fra polinomi. Al termine di questa lezione sarai in grado di: calcolare il M.C.D.
Anno 1 M.C.D. fra polinomi 1 Introduzione In questa lezione introdurremo il concetto di Massimo Comune Divisore (M.C.D.) fra polinomi. Al termine di questa lezione sarai in grado di: calcolare il M.C.D.
c) ogni numero ha infiniti multipli
 Multipli e divisori Def: Si dice MULTIPLO di un numero naturale ogni numero che si ottiene moltiplicando tale numero per qualsiasi numero naturale. Es: è un multiplo di perché. Osservazioni: Es: b) ogni
Multipli e divisori Def: Si dice MULTIPLO di un numero naturale ogni numero che si ottiene moltiplicando tale numero per qualsiasi numero naturale. Es: è un multiplo di perché. Osservazioni: Es: b) ogni
FRAZIONI ALGEBRICHE: CAMPO DI ESISTENZA
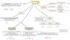 FRAZIONI ALGEBRICHE: CAMPO DI ESISTENZA Frazione Algebrica C.E.: poni il denominatore diverso da zero Risolvo l'equazione 3 2 +2+5 4 5 3 +6+5 4 0 4 12+25 +5 3 7 +5 3 +4 12 5 +8+15 5 6 3 ++12 2+ Frazione
FRAZIONI ALGEBRICHE: CAMPO DI ESISTENZA Frazione Algebrica C.E.: poni il denominatore diverso da zero Risolvo l'equazione 3 2 +2+5 4 5 3 +6+5 4 0 4 12+25 +5 3 7 +5 3 +4 12 5 +8+15 5 6 3 ++12 2+ Frazione
Polinomi. Definizioni. Polinomi a più variabili. Grado di polinomi a più variabili. Operazioni tra polinomi. Somma. Moltiplicazione.
 Polinomi Definizioni Polinomi a più variabili Grado di polinomi a più variabili Operazioni tra polinomi Somma Moltiplicazione Fattorizzazione Polinomi a singola variabile Grado di un polinomio a singola
Polinomi Definizioni Polinomi a più variabili Grado di polinomi a più variabili Operazioni tra polinomi Somma Moltiplicazione Fattorizzazione Polinomi a singola variabile Grado di un polinomio a singola
1. riconoscere la risolubilità di equazioni e disequazioni in casi particolari
 Secondo modulo: Algebra Obiettivi 1. riconoscere la risolubilità di equazioni e disequazioni in casi particolari 2. risolvere equazioni intere e frazionarie di primo grado, secondo grado, grado superiore
Secondo modulo: Algebra Obiettivi 1. riconoscere la risolubilità di equazioni e disequazioni in casi particolari 2. risolvere equazioni intere e frazionarie di primo grado, secondo grado, grado superiore
SCHEMI DI MATEMATICA
 SCHEMI DI MATEMATICA SCHEMA 1: somme algebriche tra numeri ( ci sono sia somme che sottrazioni) Obiettivo dello schema1: saper risolvere espressioni come : -3-6 Metodo: se il segno dei due numeri è uguale
SCHEMI DI MATEMATICA SCHEMA 1: somme algebriche tra numeri ( ci sono sia somme che sottrazioni) Obiettivo dello schema1: saper risolvere espressioni come : -3-6 Metodo: se il segno dei due numeri è uguale
LE EQUAZIONI DI SECONDO GRADO
 LE EQUAZIONI DI SECONDO GRADO Definizione: un equazione è di secondo grado se, dopo aver applicato i principi di equivalenza, si può scrivere nella forma, detta normale: ax + bx + c 0!!!!!con!a 0 Le lettere
LE EQUAZIONI DI SECONDO GRADO Definizione: un equazione è di secondo grado se, dopo aver applicato i principi di equivalenza, si può scrivere nella forma, detta normale: ax + bx + c 0!!!!!con!a 0 Le lettere
radicando. Si ottiene 5 RADICALI Termini a x = indice della radice y = esponente del radicando Esempi: 25 = 5 perché 5 = 25
 RADICALI Termini x y a x = indice della radice y = esponente del radicando 25 = 5 perché 5 = 25 5 indica la radice quadrata di 5, non è un numero intero, è decimale, illimitato e non periodico. 16 = 2
RADICALI Termini x y a x = indice della radice y = esponente del radicando 25 = 5 perché 5 = 25 5 indica la radice quadrata di 5, non è un numero intero, è decimale, illimitato e non periodico. 16 = 2
