IL METODO MO-SCF PER MOLECOLE PO- LIELETTRONICHE

Transcript

1 IL METODO MO-SCF PER MOLECOLE PO- LIELETTRONICHE Vogliamo ora considerare il trattamento con il metodo dell orbitale molecolare (MO) per una molecola polielettronica generica. Si tratta quindi di generalizzare quello che abbiamo visto per la molecola di idrogeno e per le molecole biatomiche oppure per gli atomi polielettronici. La procedura è nota come metodo di Hartree-Fock (HF), come abbiamo già detto per gli atomi polielettronici. Nella trattazione più generale includeremo più esplicitamente termini che sono legati allo spin degli elettroni e che prima non erano stati evidenziati. Consideriamo una molecola generica con 2n elettroni che, nello stato fondamentale, occupano completamente gli n orbitali molecolari di energia più bassa secondo la configurazione elettronica mostrata in Figura. In questa situazione si dice che abbiamo a che fare con un sistema a guscio chiuso (closed shell) dove quindi non sono presenti elettroni spaiati. Tratteremo l argomento con la seguente successione. Prima ridefiniremo l Hamiltoniano del sistema e la forma della funzione d onda polielettronica. Poi calcoleremo l energia (integrale variazionale). Procederemo poi ad applicare il teorema variazionale e cioè minimizzeremo l energia rispetto a eventuali parametri presenti nella funzione d onda: ciò porterà a trovare equazioni di Schrödinger efficaci (equazione di Fock) per ogni singolo elettrone sottoposto alla interazione con i nuclei e con un potenziale medio dovuto a tutti gli altri elettroni. Poi vedremo la forma che assumono le equazioni se decidiamo di sviluppare gli orbitali molecolari in una base di orbitali atomici giungendo a quelle che si chiamano equazioni di Roothan. Faremo infine una serie di esempi su molecole tipiche usando per semplificare il problema e per vedere gli aspetti qualitativi la simmetria molecolare. Nella trattazione del problema ometteremo tutta la parte algebrica cercando solo di generalizzare quanto abbiamo visto già per le molecole biatomiche. L Hamiltoniano e la funzione d onda La forma dell Hamiltoniano elettronico è quella che abbiamo già visto quando abbiamo introdotto l approssimazione di Born-Oppenheimer

2 H = i 2 2 i + αi Z α r iα + ij r ij () Ribadiamo che si tratta del solo Hamiltoniano elettronico e che, nell approssimazione di Born-Oppenheimer, supponiamo di lavorare a nuclei fissi e che quindi non è incluso il termine di repulsione nucle-nucleo V nn = + αβ Z α Z β r αβ (2) che può essere considerato una costante ed essere aggiunto in fondo. L Hamiltoniano elettronico può essere riscritto raggruppando i termini H = i ( 2 2 i + α Z α r iα ) + ij rj = i H c i + ij r ij = H + H 2 (3) In questo modo si mette in evidenza che nell operatore ci sono termini monoelettronici (raggruppati in H ) e termini bielettronici (raggruppati in H 2 ). I termini mono elettronici riguardano l energia cinetica e l interazione con i nuclei di ciascun singolo elettrone, i termini bielettronici sono i termini di repulsione tra coppie di elettroni. Nella notazione quindi stiamo ora usando gli indici i e j per numerare gli elettroni. La funzione d onda polielettronica deve essere antisimmetrica per lo scambio di due elettroni. Scriviamo allora la funzione d onda come determinante di Slater con riferimento alla configurazione elettronica della figura Ψ = (2n)! ϕ () ϕ () ϕ 2 () ϕ n () ϕ n () ϕ n () ϕ (2) ϕ (2) ϕ 2 (2) ϕ 2 () ϕ n (2) ϕ n (2) ϕ (3) ϕ (3) ϕ 2 (3) ϕ 2 (3) ϕ n (3) ϕ n (3) ϕ (2n) ϕ (2n) ϕ 2 (2n) ϕ 2 (2n) ϕ n (2n) ϕ n (2n) (4) dove abbiamo incluso il fattore di normalizzazione il cui calcolo viene omesso. Le funzioni che compaiono nel determinante sono gli orbitali molecolari della configurazione di figura, orbitali molecolari che non conosciamo nella loro forma esatta e che ci proponiamo di determinare (insieme alla loro energia) 2

3 con il metodo variazionale. Scegliamo in partenza gli orbitali molecolari in modo che siano ortogonali e normalizzati < ϕ i ϕ j >= δ ij (5) È necessario che in tutta la procedura l ortonormalità degli orbitali molecolari venga conservata. Notiamo che nella relazione che abbiamo scritto sopra gli indici i e j identificano ora gli orbitali molecolari come sarà nel resto della trattazione. Come abbiamo già visto il determinante può essere sviluppato e la funzione d onda polielettronica può essere scritta più esplicitamente come somma di tutte le permutazioni dell elemento diagonale, prendendo ogni permutazione con il segno positivo o negativo a seconda che la permutazione sia pari (numero pari di scambi di coppie di elettroni) o dispari Ψ = [( ) p p{ϕ ()ϕ (2)ϕ 2 (3) ϕ n (2n)} (6) (2n)! Calcolo degli integrali e dell energia p Il nostro scopo sarebbe di risolvere l equazione di Schrödinger HΨ = EΨ (7) e determinare gli orbitali molecolari (monoelettronici) che costituiscono la funzione d onda. Applicando il metodo variazionale dobbiamo calcolare l integrale E =< Ψ H Ψ > (8) usando una funzione di prova da ottimizzare. In base alla forma dell Hamiltoniano avremo E =< Ψ H Ψ >=< Ψ H Ψ > + < Ψ H 2 Ψ >= = < Ψ Hk c Ψ > + (9) < Ψ Ψ >= E + E 2 r kl k kl dove quindi, per comodità, spezziamo l energia in un contributo mono elettronico ed in un contributo bielettronico che calcoliamo separatamente. 3

4 Per quanto riguarda il primo termine dell energia notiamo che gli elettroni sono indistinguibili e quindi per ogni elettrone otterremo un contributo uguale. Possiamo allora calcolare il contributo monolettronico solo per l elettrone (k= nel primo termine) e moltiplicare il risultato per il numero di elettroni (2n) Si trova facilmente che E = 2n < Ψ H c Ψ > (0) Più esplicitamente E = 2 i < ϕ i () H c ϕ i () >= 2 i H ii () H ii = ϕ i ()Hϕ c i ()dr = ϕ i ()( 2 2 i + α Z α r iα )ϕ i ()dr (2) Il significato dell integrale è semplice: si tratta dell energia cinetica e della interazione elettrone-nucleo per un elettrone nell orbitale molecolare i. E è quindi la somma di queste energie di core per tutti gli elettroni che occupano gli orbitali molecolari. Infatti abbiamo una somma su tutti gli orbitali molecolari ed il fattore 2 compare perché in ogni orbitale molecolare ci sono 2 elettroni con spin opposto. Il calcolo di integrali bielettronici è ovviamente più complicato. In effetti le difficoltà nel trattamento MO di molecole polielettroniche deriva proprio dalla presenza di termini bielettronici. Comunque anche per il calcolo degli integrali bielettronici sfruttiamo l indistinguibilità degli elettroni nel senso che l energia di repulsione sarà sempre la stessa per qualsiasi coppia di elettroni. Perciò è lecito calcolare l energia di repulsione della coppia - 2 e moltiplicheremo poi il risultato per il numero di coppie distinte. A tal fine ricordiamo che un elettrone non interagisce ovviamente con se stesso e quindi l elettrone interagisce con (2n-) elettroni, l elettrone 2 interagisce con (2n-2) elettroni in quanto abbiamo già considerato l interazione 2 - e così via, per cui il numero di coppie indipendenti è 4

5 (2n ) (2n 2) (2n 3). 2 (3) per cui il numero totale di interazioni a coppie sarà (somma dei primi 2n- numeri interi) Avremo allora 2n(2n ) 2 (4) 2n(2n ) E 2 = < Ψ Ψ > (5) 2 r 2 L argomento da usare per calcolare questo integrale è il seguente. Nello sviluppo del determinante evidentemente gli elettroni e 2 si potranno trovare in tutti gli orbitali. Ad esempio, se avessimo un determinante 3x3 nello sviluppo del determinante troveremmo, a parte le costanti e lo spin ϕ () ϕ 2 () ϕ 3 () ϕ (2) ϕ 2 (2) ϕ 3 (2) ϕ (3) ϕ 2 (3) ϕ 3 (3) = = ϕ ()ϕ 2 (2)ϕ 3 (3) + ϕ (3)ϕ 2 ()ϕ 3 (2) + ϕ (2)ϕ 2 (3)ϕ 3 () ϕ (3)ϕ 2 (2)ϕ 3 () ϕ (2)ϕ 2 ()ϕ 3 (3) ϕ ()ϕ 2 (3)ϕ 3 (2) (6) Poiché l operatore contiene le coordinate di due soli elettroni esso agisce su due soli orbitali molecolari e per l ortogonalità degli orbitali molecolari possiamo avere a che fare solo con termini non nulli del tipo < ϕ ()ϕ 2 (2) < ϕ ()ϕ 2 (2) r 2 ϕ ()ϕ 2 (2) >< ϕ 3 (3) ϕ 3 (3) > (7) r 2 ϕ (2)ϕ 2 () >< ϕ 3 (3) ϕ 3 (3) > (8) 5

6 Il secondo tipo di termini ha evidentemente segno negativo e per l ortonormalità sarà < ϕ 3 (3) ϕ 3 (3) >= (9) In generale avremo due tipi di termini e cioè con il segno positivo e con il segno negativo J ij =< ϕ i ()ϕ j (2) K ij =< ϕ i ()ϕ j (2) r 2 ϕ i ()ϕ j (2) > (20) r 2 ϕ i (2)ϕ j () > (2) Nel primo integrale vediamo che l elettrone è nell orbitale i sia a destra che a sinistra mentre l elettrone 2 è in un diverso orbitale j e quindi gli spin dei due elettroni potranno essere come nella tabella seguente ϕ i () ϕ j (2) ϕ i () ϕ j (2) α() α(2) α() α(2) α() β(2) α() β(2) β() α(2) β() α(2) β() β(2) β() β(2) (22) e quindi ci sono 4 possibili aqccoppiamenti di spin. Nell integrale K invece degli accoppiamenti di spin ϕ i () ϕ j (2) ϕ i (2) ϕ j () α() α(2) α(2) α() α() β(2) α(2) β() β() α(2) β(2) α() β() β(2) β(2) β() (23) possibili sono solo il primo ed il quarto in quanto con il secondo e terzo accoppiamento quando andiamo ad integrare sulle variabili di spin otteniamo integrali < α() β() >< β(2) α() >= 0 (24) < β() α() >< α(2) β(2) >= 0 (25) 6

7 che annullano i relativi contributi. Sommando tutti i termini non nulli otterremo il doppio di termini per gli integrali J ed il risultato è E 2 = ij (2J ij Kij) (26) Esaminiamo il significato dei due integrali. L integrale coulombiano ha esplicitamente la forma J ij = ϕ i ()ϕ j(2) ϕ i ()ϕ j (2)dr dr 2 (27) r 2 che possiamo riscrivere nella forma J ij = ϕ i () 2 ϕ j (2) 2 dr dr 2 (28) r 2 da cui si vede che esso rappresenta la repulsione coulombiana tra la distribuzione di carica dell elettrone nell orbitale molecolare i ϕ i () 2 e la distribuzione di carica dell elettrone 2 nell orbitale molecolare j ϕ j (2) 2. Dagli accoppiamenti di spin possibili che abbiamo visto si capisce che il termine coulombiano esiste per tutte le coppie sia che abbiano spin parallelo sia che abbiano spin opposto. L integrale di scambio ha la forma esplicita K ij = ϕ i ()ϕ j(2) ϕ i (2)ϕ j ()dr dr 2 (29) r 2 Non è possibile dare una interpretazione classica dell integrale di scambio: esso viene fuori perché abbiamo imposto che l autofunzione deve essere antisimmetrica per lo scambio di elettroni e va scritta come un determinante di Slater. Da quanto visto sopra, l integrale di scambio si troverà solo per elettroni con spin parallelo. Quindi se abbiamo due elettroni in orbitali i e j ed i due elettroni hanno spin opposto la repulsione elettronica sarà J ij (30) Per gli stessi due elettroni con spin parallelo invece la repulsione sarà J ij K ij (3) Poiché entrambi gli integrali sono positivi si vede che la repulsione tra elettroni con spin opposti è maggiore che tra due elettroni con spin parallello. 7

8 Questo da una giustificazione della regola di Hund per la quale elettroni in orbitali diversi tendono a disporsi con spin paralleli. In conclusione siamo giunti al risultato che l energia elettronica di una molecola polielettronica a shell chiuso è data da E = E + E 2 = 2 i H ii + ij (2J ij K ij ) (32) Minimizzazione dell energia - Equazione di Fock Avendo ottenuto un espressione per l energia elettronica possiamo ora applicare il teorema variazionale e cioè variare gli orbitali molecolari scelti inizialmente in modo da ottenere quelli che danno il valore più basso dell energia: questi costituiranno la migliore approssimazione agli orbitali molecolari esatti. Vogliamo quindi per tutti gli orbitali molecolari trovare la condizione di minimo E ϕ i = 0 (33) Applichiamo il teorema variazionale al differenziale totale δe = 0 (34) Stiamo ora discutendo la procedura in termini generali in quanto non abbiamo ancora fatto nessuna ipotesi concreta sulla forma degli orbitali molecolari: questo verrà fatto nel capitolo prossimo. Ci accingiamo quindi a variare in qualche modo gli orbitali molecolari. Ma questi erano stati scelti originariamente ortonormali ed è necessario mantenere in tutte le fasi del processo variazionale questa condizione e cioè < ϕ i ϕ j >= S ij = δ ij (35) In nostro allora non è un semplice problema di ricerca di un minimo ma di ricerca di un minimo condizionato, un minimo che preservi la condizione di ortonormalità. Si può vedere che questo corrisponde a minimizzare non la funzione E ma una funzione G G = E 2 ij ε ij S ij = 2 i H ii + ij (2J ij K ij ) 2 ij ε ij S ij (36) 8

9 dove gli ε ij sono detti moltiplicatori indeterminati di Lagrange ed il loro significato sarà chiarito al termine del processo di minimizzazione. La condizione di minimo che cerchiamo è allora δg = 2 i δh ii + ij (2δJ ij δk ij ) 2 ij ε ij δs ij = 0 (37) Si tratta ora di esprimere tutti questi differenziali. Guardiamo ad esempio quello che riguarda un termine J. Ricordando l espressione di J avremo δj ij =< δϕ i ()ϕ j (2) ϕ i ()ϕ j (2) > + < ϕ i ()δϕ j (2) ϕ i ()ϕ j (2) > + r 2 r 2 + < ϕ i ()ϕ j (2) δϕ i ()ϕ j (2) > + < ϕ i ()ϕ j (2) ϕ i ()δϕ j (2) > r 2 r 2 (38) scriviamo questo differenziale in forma più compatta definendo un operatore coulombiano Ĵ j () =< ϕ j (2) ϕ j (2) > (39) r 2 Questo operatore ha la proprietà evidente che Usando questo operatore possiamo scrivere < ϕ i () Ĵj() ϕ i () >= J ij (40) δj ij =< δϕ i () Ĵj() ϕ i () > + < δϕ j (2) Ĵi(2) ϕ j (2) > +complesso coniugato (4) Analogamente definiamo un operatore di scambio K j ()ϕ i () =< ϕ j (2) ϕ i (2) > ϕ j () > (42) r 2 Usando questi operatori, raccogliendo i termini e usando alcune proprietà di simmetria degli integrali il differenziale totale assume la forma δg = 2 i [< δϕ i () H c ()+ j (2Ĵj() K j ()) ϕ i () > j ε ij < δϕ i () ϕ j ()] = 0 (43) 9

10 Poiché i differenziali sono arbitrari la condizione di minimo sarà [ H c () + ] (2Ĵj() K j ()) ϕ i () = ε ij ϕ j () (44) j j Se definiamo un operatore di Fock F = H c () + j (2Ĵj() K j ()) (45) la condizione di minimo può essere scritta F ϕ i () = j ε ij ϕ j () (46) Questa è l equazione di Hartree-Fock. La prima cosa importante da notare è che essendo partiti da un equazione di Schrödinger polielettronica l applicazione del metodo variazionale ci permette di arrivare ad una equazione monoelettronica. L operatore di Fock gioca il ruolo di un operatore Hamiltoniano efficace monoelettronico. Nell operatore di Fock compaiono due termini. Il primo è il termine di core che, come abbiamo visto più volte, include l energia cinetica dell elettrone e l interazione con i nuclei. Il secondo termine può essere interpretato come un potenziale efficace di repulsione elettronica v HF eff = j (2Ĵj() K j () (47) cioè come una media della repulsione che l elettrone risente da parte di tutti gli altri elettroni per cui l equazione di Fock equivale a (H c () + v HF eff )ϕ i () = j ε ij ϕ j () (48) Lo spirito del metodo di Hartree-Fock è appunto questo: trasformare un problema a molti elettroni in una equazione monoelettronica in cui l elettrone si muove in un campo creato dai nuclei ed in campo medio efficace dovuto a tutti gli altri elettroni. Tuttavia l equazione di Fock non è una normale equazione agli autovalori in quanto l applicazione dell operatore ad una funzione dà una combinazione di tutte le funzioni. Notiamo però che se scriviamo 0

11 F ϕ j = k ε kj ϕ k (49) abbiamo ϕ i F ϕ j = k ε kj ϕ i ϕ k = ε ij (50) da cui si vede che i moltiplicatori di Lagrange sono gli elementi di matrice dell operatore di Fock. Ora è sempre possibile fare una trasformazione che riduca una matrice in forma diagonale. Nel caso specifico è sempre possibile fare delle combinazioni lineari degli orbitali molecolari in modo da ottenere i cosiddetti orbitali molecolari canonici con i quali la matrice dei moltiplicatori è diagonale e rispetto ai quali abbiamo quindi F ϕ j = ε jj ϕ j (5) cioè una normale equazione agli autovalori. Supponiamo da ora in poi di lavorare sempre con gli orbitali molecolari canonici. Volendo ora risolvere l equazione di Fock per trovare le energie e la forma degli orbitali molecolari, notiamo che l operatore di Fock dipende, come si vede dalla definizione degli operatori coulombiano e di scambio, dagli orbitali che sono soluzioni della equazione di Fock. Si tratta quindi di una complicata equazione integro-differenziale. Per la sua soluzione procediamo allora in modo iterativo attraverso i seguenti stadi. sciegliamo un gruppo iniziale di orbitali molecolari; 2. calcoliamo gli operatori coulombiano e di scambio e l operatore di Fock; 3. risolviamo l equazione di Fock e troviamo le energie e la forma di nuovi orbitali molecolari; 4. con queste nuove funzioni ritorniamo al punto 2); 5. ripetiamo la procedura fino a convergenza e cioè fino a che l energia degli orbitali molecolari non cambia da un ciclo all altro. Il campo allora diventa autoconsistente (Self Consistent Field =SCF ) cioè riproduce se stesso da un ciclo all altro. Lo schema della procedura SCF è illustrato graficamente in figura 2a.

12 Metodo LCAO - Equazioni di Roothan La procedura iterativa di Hartree-Fock e del campo autoconsistente che abbiamo illustrato è chiara nei suoi termini generali. Tuttavia, ai fini di una applicazione pratica ci sono due difficoltà. La prima deriva dalla natura stessa della equazione di Fock che è una equazione integro-differenziale nella quale l operatore dipende dalla soluzioni incognite. Il secondo problema deriva dal fatto che non abbiamo detto nulla sulla forma effettiva delle funzioni (cioè degli orbitali molecolari) e quindi sui parametri variazionali rispetto ai quale l energia deve essere minimizzata. È necessario trovare un espressione degli orbitali molecolari che renda l equazione di Fock di soluzione agevole. L approssimazione usuale è di esprimere gli orbitali molecolari come combinazione lineare di orbitali atomici in modo che i parametri variazionali siano i coefficienti della combinazione. Questo corrisponde all intuizione chimica elementare di ricondure la formazione della molecola agli atomi costituenti. Con questa approssimazione si tratta quindi di applicare il metodo variazionale lineare che abbiamo già visto in generale trattando i metodi di approssimazione ed abbiamo in parte applicato trattando gli atomi polielettronici e la molecola di idrogeno. Conosciamo quindi già quali sono le equazioni che si ottengono. Riguardiamo il procedimento sia per riprendere quanto già fatto sia per adattarlo, se necessario, alla forma degli elementi di matrice che abbiamo visto nel capitolo precedente. Esprimiamo gli orbitali molecolari come combinazione lineare di orbitali atomici degli atomi costituenti la molecola. Usando indici italici per numerare gli orbitali molecolari ed indici greci per gli orbitali atomici avremo φ i = µ c µi ϕ µ (52) Scriviamo ovviamente una analoga equazione per tutti gli orbitali molecolari (i=,2,3,...,n). Mettiamo insieme tutte queste relazioni in una forma matriciale definendo una matrice riga per le due basi degli orbitali molecolari e degli orbitali atomici ed una matrice dei coefficienti dello sviluppo che, nel metodo variazionale sono le incognite (o i parametri variazionali) 2

13 (φ φ 2 φ 3 φ n ) = (ϕ ϕ 2 ϕ 3 ϕ 4 ) che con una scrittura più compatta è c c 2 c 3 c n c 2 c 22 c 23 c 2n c 3 c 32 c 33 c 3n c n c n2 c n3 c nn (53) φ = ϕc (54) Prima di procedere vediamo degli esempi pratici di scelta della base di orbitali atomici per la espansione degli orbitali molecolari. Le scelte più semplici sono a. Base minima (minimal basis set) tutti gli orbitali atomici fino allo shell di valenza b. Base estesa (extended basis set) minimal basis set + orbitali atomici più esterni c. Base di valenza (valence basis set) solo gli orbitali atomici dello strato di valenza Ad esempio nel caso della molecola LiH abbiamo minimal Li s 2s 2p x 2p y 2p z H s extended Li s 2s 2p x 2p y 2p z 3s 3d H s 2s 2p valence Li 2s 2p x 2p y 2p z H s Naturalmente una base estesa può essere ampia quanto si vuole. Definiamo la densità di carica elettronica nella molecola, densità che integrata su tutto lo spazio darà ovviamente il numero di elettroni 2n, occ ρ(r) = 2 φ i (R)φ i (R) (55) i Esprimiamo ora questa densità elettronica in termini degli orbitali atomici usando l espansione definita sopra occ ρ(r) = 2 φ i (R)φ i (R) = 2 i i c µic νi ϕ µ(r)ϕ ν (R) (56) µν 3

14 = µν ϕ µ(r)ϕ ν (R)( i 2c µic νi ) = µν P µν ϕ µ(r)ϕ ν (R) (57) dove abbiamo introdotto P µν = ( i 2c µic νi ) (58) che corrisponde a definire una matrice P Si ha P = C C (59) 2n = drρ(r) = µν P µν < ϕ µ ϕ ν >= µν P µν S µν = T r(ps) (60) dove Tr indica la traccia della matrice prodotto PS (e cioè la somma degli elementi diagonali ). Avendo adottato per gli orbitali molecolari l espansione in orbitali atomici vogliamo ora esprimere l energia elettronica E = 2 i H ii + ij (2J ij K ij ) (6) negli orbitali atomici. Si tratta quindi di esprimere negli orbitali atomici gli integrali di core, coulombiano e di scambio in modo da potere poi minimizzare l integrale variazionale esplicitamente rispetto ai coefficienti della espansione lineare. Per questo definiamo i seguenti integrali (elementi di matrice) in termini di orbitali atomici H µν =< ϕ µ H c ϕ ν > (62) (µν λσ) = ϕ µ () ϕ λ (2) ϕ ν () ϕ σ (2) r 2 (µλ νσ) = ϕ µ () ϕ λ (2) ϕ ν (2) ϕ σ () r 2 (63) (64) 4

15 il cui significato è chiaro per confronto con la definizione degli integrali di core, coulombiano e di scambio. Il primo è un integrale a due centri, gli altri due invece sono integrali potenzialmente a quattro centri nel senso che possono coinvolgere diversi orbitali atomici su quattro diversi atomi. L allocazione degli elettroni negli integrali bielettronici è: (µν λσ) = in µν 2 = in λσ (65) (µλ νσ) = in µσ 2 = in λν (66) La trasformazione degli integrali è semplice: si tratta di sostituire l espansione in orbitali atomici facendo attenzione agli indici. Ad esempio avremo H ii = ϕ i H c ϕ i = µν c µic νi H µν (67) Introducendo nel termine relativo dell energia elettronica avremo 2 i H ii = µν H µν 2c µic νi = P µν H µν (68) µν i Procedendo analogamente con gli altri termini si arriva alla seguente espressione per l energia E = P µν H µν + [ P µν P λσ (µν λσ) ] 2 2 (µλ νσ) (69) µν µν λσ oppure, volendo far comparire esplicitamente i coefficienti per la successiva differenziazione E = 2H µν c µic νi + c µic νi c λjc σj [2 (µν λσ) (µλ νσ)] µν i ij µν λσ (70) Si tratta ora di procedere a fare il differenziale per la condizione di minimo condizionato. Per questo dobbiamo trasformare anche gli integrali di sovrapposizione φ i φ j = δ ij = µν c µic νj S µν (7) 5

16 Dobbiamo ora calcolare il differenziale della funzione δg = δe 2 ij ε ij δs ij (72) Con un poco di algebra e considerando di avere comunque a che fare con gli orbitali molecolari canonici si giunge al seguente sistema di equazioni per i coefficienti dell espansione { c νi H µν + ν λσ P λσ [ (µν λσ) 2 (µλ νσ) ] ε ii S µν } = 0 (73) che possiamo riscrivere in forma più compatta definendo l elemento di matrice F µν = H µν + [ P λσ (µν λσ) ] 2 (µλ νσ) (74) λσ come (F µν ε ii S µν )c νi = 0 (75) ν Queste sono note come equazioni di Roothan. Ripetendo quanto già visto, per l orbitale molecolare i mo si ottiene il seguente sistema di equazioni esplicite (F ε ii S )c i + (F 2 ε ii S 2 )c i2 + (F 3 ε ii S 3 )c i3 + = 0 (F 2 ε ii S 2 )c i + (F 22 ε ii S 22 )c i2 + (F 23 ε ii S 23 )c i3 + = 0 (F 3 ε ii S 3 )c i + (F 32 ε ii S 32 )c i2 + (F 33 ε ii S 33 )c i3 + = 0 (76) ed analogamente per tutti gli altri orbitali molecolari. Questi sistemi di equazioni si possono scrivere in maniera più compatta con una notazione matriciale nella forma FC = SCE (77) Questa è l espressione che avevamo trovato trattando il metodo variazionale lineare in generale. Ripetendo quanto già detto in generale e quanto visto in particolare nella trattazione della molecola di idrogeno, il problema si riduce 6

17 alla ricerca di autovalori ed autovettori della matrice F se si riesce ad ortogonalizzare la base atomica in modo che S=. Ci sono varie procedure di ortogonalizzazione della base, procedure che sono generalizzazioni di quella che abbiamo visto nel caso particolare della molecola di idrogeno. Se supponiamo di lavorare con una base ortogonalizzata le equazioni di Roothan si possono scrivere FC = CE (78) Il problema allora si riduce alla diagonalizzazione della matrice Fcon una trasformazione E E 2 C FC = E = E 3 (79) Gli elementi diagonali di E (E < E 2 < E 3 ) sono le migliori approssimazioni( con la base scelta) per le energie degli orbitali molecolari. Per ciascun orbitale molecolare i, i coefficienti della combinazione lineare sono dati dalla colonna i ma della matrice C. La procedura variazionale nel metodo SCF-LCAO è in sintesi la seguente.. Scelta della base di orbitali atomici per l espansione degli orbitali molecolari; 2. Scelta di un set iniziale di coefficienti della espansione e quindi scelta di una matrice C iniziale o di una matrice P; 3. Calcolo degli integrali monoelettronici H µν e bielettronici (µν λσ) e (µλ νσ), e calcolo della matrice F; 4. Ortogonalizzazione della base e diagonalizzazione della matrice F ed ottenimento delle energie degli MO e di una nuova matrice C o P; 5. Controllo di quanto di quanto è variata l energia e ritorno al punto 3 fino a che non si ha variazione apprezzabile delle energie da un ciclo all altro. Graficamente lo schema della procedura è illustrato nella figura 2b. 7

18 Alcune considerazioni sul metodo SFC-LCAO Possiamo cercare di chiarire lo spirito della procedura SCF-LCAO con alcune considerazioni importanti.. Abbiamo trovato che l energia elettronica di una molecola polielettronica è data dall espressione E = 2 i H ii + ij (2J ij K ij ) (80) dove, ripetendo quello che abbiamo già visto, H ii J ij K ij rappresenta l energia di un elettrone nell orbitale i soggetto al campo nucleare; rappresenta la repulsione che un elettrone nell orbitale i sente da parte di un elettrone nell orbitale j; è la correzione a questa repulsione quando i due elettroni hanno spin parallelo. È evidente quindi che l energia dell orbitale molecolare i sarà data da ε i = H ii + j (2J ij K ij ) (8) Questa espressione può essere ottenuta direttamente come elemento di matrice dell operatore di Fock. L energia totale elettronica non è allora uguale alla somma delle energie degli orbitali molecolari occupati, considerati due volte per la doppia occupazione E 2 i ε i (82) ma sarà E = 2 i ε i j (2J ij K ij ) (83) Infatti sommando semplicemente le energie degli orbitali si verrebbero a considerare due volte i termini di repulsione elettrone elettrone. 8

19 2. Abbiamo trovato l espressione per la energia di ciascun orbitale molecolare. L energia dell orbitale molecolare i mo può essere determinata sperimentalmente (con la spettroscopia di fotoelettroni) estraendo un elettrone dall orbitale i. Questo è quello che afferma il cosiddetto teorema di Koopmans. Il teorema afferma che l energia di un orbitale molecolare è uguale all energia di ionizzazione verticale. La precisazione significa questo: quando un elettrone viene espulso dobbiamo immaginare che gli orbitali molecolari e la loro energia cambino in quanto cambia l insieme delle repulsioni elettroniche. L identificazione ε i = energia di ionizzazione è valida nel limite che l espulsione di un elettrone non cambi la struttura e l energia degli orbitali e quindi non cambi la struttura molecolare. Nella spettroscopia di fotoelettroni gli elettroni vengono espulsi inviando una radiazione sulla molecola e si misura l energia degli elettroni espulsi. Ogni picco nello spettro corrisponde all energia di ionizzazione di un elettrone. Nella Figura 3 è mostrato lo spettro di fotoelettroni della molecola di azoto e si vedono picchi corrispondenti alle energie degli orbitali molecolari della configurazione elettronica che abbiamo gia visto per l azoto. 3. Si si fa una espansione in m orbitali atomici si otterrano m orbitali molecolari. Di questi n sarannpo occupati dai 2n elettroni della molecola ed i rimanenti saranno vuoti e sono detti orbitali virtuali (vedi figura ). L energia del primo orbitale virtuale corrisponde approssimativamente alla affinità elettronica della molecola. 4. Nella procedura LCAO la bontà del risultato (cioè quanto siamo vicini alla energia ed alla struttura vera della molecola) dipende dalla estensione della base usata e cioè dal numero di orbitali atomici che usiamo per espandere gli orbitali molecolari. Se aumentiamo il numero di orbitali atomici (usiamo una base più estesa) i risultati migliorano, come mostrato nella figura 4. Per una base molto estesa (al limite per una base di infiniti orbitali atomici) il risultato converge verso quello che si dice il limite di Hartree-Fock. 5. Poiché abbiamo visto come postulato che una funzione può essere sempre espansa in un set completo di autofunzioni ci si potrebbe aspettare di ottenere nel limite di Hartree Fock un risultato esatto. Non è così se confrontiamo con gli esperimenti. Si trova infatti che l energia vera 9

20 E o dello stato fondamentale è sempre più bassa dell energia di Hartree Fock e la differenza viene detta energia di correlazione E corr = E o E HF (84) Questo è dovuto al fatto che, come già visto per la molecola di idrogeno, nel metodo HF non si tiene conto in modo appropriato della correlazione elettronica, particolarmente per gli elettroni con spin opposto. Ci sono vari metodi per tenere conto della correlazione elettronica. Si può ricorrere alla interazione di configurazione secondo la quale la funzione d onda elettronica viene espressa non come un singolo determinante di Slater corrispondente alla configurazione dello stato fondamentale ma come una combinazione lineare dei determininati di Slater di tutte le possibili configurazioni elettroniche in cui,2,3,... elettroni sono promossi dagli orbitali occupati agli orbitali virtuali. Si prendono quindi tutte le possibili configurazioni come mostrato in figura 5. Computazionalmente l interazione di configurazione porta a calcoli molto pesanti. Si può allora, per tenere conto anche se approssimativamente della interazione di configurazione, applicare il metodo delle perturbazioni. In anni recenti è stata messa a punto una teoria (detta teoria del funzionale della densità DFT ) che è oggi di applicazione molto estesa per fare calcoli includendo la correlazione elettronica anche per molecole molto complesse. 6. Abbiamo detto che nell appprossimazione LCAO gli orbitali molecolari sono espressi come combinazione di orbitali atomici. Per quanto riguarda la forma degli orbitali atomici la scelta più naturale è quella di orbitali tipo Slater (STO = Slater Type Orbitals) che abbiamo già introdotto e nei quali la parte radiale ha la forma e ζr (85) con ζ esponente orbitale efficace a rappresentare una carica nucleare schermata. La forma degli orbitali di Slater rende però molto complicato il calcolo degli integrali. Questo calcolo sarebbe molto semplificato se la parte radiale avesse una forma gaussiana 20 e αr2 (86)

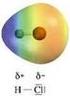
21 Però, come si vede dalla figura 6 una funzione gaussiana è molto diversa da una funzione tipo Slater. Si può ovviare a questa difficoltà esprimendo una funzione tipo Slater a sua volta come combinazione di più funzioni gaussiane. Ad esempio nella opzione denominata STO-3G si usano funzioni tipo Slater (STO) ma ogni orbitale di Slater è espresso come combinazione di 3 funzioni gaussiane (3G). Come si vede dalla figura 7 la combinazione di 3 gaussiane è in grado di approssimare bene un orbitale tipo Slater. 7. L energia che si ottiene con la procedura SCF costituisce l energia puramente elettronica ed è ottenuta nell approssimazione di Born-Oppenheimer a nuclei fissi. A questa energia va quindi aggiunta l energia di interazione nucleo-nucleo per ottenere l energia totale. Il calcolo andrebbe poi ripetuto per varie configurazioni nucleari per ottenere la energia di minimo corrispondente alla geometria di equilibrio. In realtà esistono metodi per la ricerca diretta dei minimi. 8. Abbiamo definito la densità elettronica come ρ(r) = µν P µν ϕ µ(r)ϕ ν (R) (87) È spesso di interesse vedere quale è la distribuzione elettronica risultante sulla molecola attribuendo una carica parziale a ciascun atomo. Per fare questo in maniera razionale ricordiamo che la carica elettronica totale corrisponde ai 2n elettroni 2n = drρ(r) = µν P µν < ϕ µ ϕ ν >= µν P µν S µν = T r(ps) = µ (PS) µµ (88) Per ripartire la carica elettronica attribuiamo a ciascun atomo tutti i termini diagonali (PS) µµ della matrice prodotto che si riferiscono ad indici µ di orbitali atomici che appartengono a quell atomo. Aggiungendo a questa parte della carica elettronica la carica nucleare dell atomo otteniamo la carica risultante su quell atomo. Questa procedura ci da la distribuzione di carica sulla molecola secondo Mulliken, distribuzione che rifletterà la diversa elettronegatività degli atomi. Un esempio 2

22 di distribuzione elettronica calcolata è mostrato in figura 8. Queste cariche atomiche sono molto utili ed importanti ma hanno un valore qualitativo. In effetti esistono altri metodi di ripartire la carica tra i vari atomi che danno risultati diversi dal metodo di Mulliken. 9. Gli orbitali molecolari ottenuti con la trattazione SCF sono orbitali che si estendono su tutta la molecola. La distribuzione elettronica globale sulla molecola sarà la risultante delle distribuzioni elettroniche di tutti gli elettroni negli orbitali occupati. In questa descrizione sembra quindi perdersi la tradizionale descrizione della molecola come giustapposizione di un insieme di legami chimici, localizzati, con una loro definita orientazione spaziale. Tuttavia ricordiamo che la scelta degli orbitali molecolari non è unica. Noi ci riferiamo in generale ad orbitali molecolari canonici. Ma combinazioni di orbitali molecolari canonici sono scelte altrettanto buone per la soluzione delle nostre equazioni. In questa ottica invece di scegliere gli orbitali molecolari canonici estesi su tutta la molecola possiamo scegliere delle combinazioni opportune per ottenere degli orbitali molecolari che siano localizzati, ad esempio in corrispondenza di ogni legame o di ogni doppietto di non legame. In questo modo si recupera la descrizione più semplice e tradizionale delle strutture molecolari. La cosa importante è che la distribuzione elettronica totale sarà la stessa qualsiasi sia la scelta degli orbitali molecolari. In figura 9a sono mostrati gli orbitali canonici delocalizzati della molecola di acqua mentre nella figura 9b sono mostrati orbitali molecolari localizzati. 22