Rappresentazione grafica delle funzioni di trasferimento: diagrammi di Bode
|
|
|
- Marcellina Bucci
- 6 anni fa
- Visualizzazioni
Transcript
1 Capitolo 7 Rappresentazione grafica delle funzioni di trasferimento: diagrammi di Bode 7. Rappresentazione grafica di funzioni di trasferimento razionali La funzione di trasferimento e una funzione di variabile complessa W s), Laplace trasformata della risposta impulsiva, definita per Res > σw), dove σw) è l ascissa di convergenza. Limitandoci al caso di funzioni di trasferimento razionali proprie W s) = i b is i i a is i, quando la rappresentazione è irriducibile si ha σw) = sup{ α : i a i α i = 0} e nel semipiano Res > σw) la W s) è funzione analitica. La funzione W s) è poi unicamente prolungabile su tutto il piano complesso nella funzione meromorfa W s), che a sua volta individua in modo unico la sua restrizione all asse immaginario W jω) = i b i jω) i / i a i jω) i. Viceversa, la restrizione W jω) di W s) all asse immaginario è sufficiente per ottenere in modo unico la W s) Quest ultimo fatto è piuttosto importante quando si intende fornire una rappresentazione grafica della funzione di trasferimento, perché consente di sostituire alla sua rappresentazione sul piano complesso o almeno sul semipiano di convergenza) quella di una funzione a valori complessi della variabile reale ω.
2 CAPITOLO 7. DIAGRAMMI DI BODE Nella rappresentazione grafica di W jω) sovente conviene considerare il logaritmo complesso) di W jω) e assumere come variabile indipendente in luogo di ω il suo logaritmo per ω > 0). Il ricorso a una scala logaritmica offre il vantaggio di - analizzare la funzione per ampie escursioni delle variabili - ottenere i diagrammi di funzioni complicate per sovrapposizione di diagrammi elementari standard su ciò torneremo a lungo nel seguito). Si noti, infine, che nella mappa j W jω) W : ω ReW jω) + jimw jω) = W jω) e e nella mappa ln W : ω ln W jω) + j W jω la fase W jω è individuata solo ameno di multipli interi di π. Ciò è irrilevante nella valutazione del numero complesso W jω) in corrispondenza a uno specifico valore di ω, ma richiede una certaattenzione quando ciò che si intende valutare è la varia zione di fase di W jω) al variare di Ω su un assegnato intervallo di pulsazioni, ossia l angolo con vertice nell origine del piano di Gauss che il vettore W jω) descrive al variare di ω. Figura 7.. Ancora più delicata da valutare è la situazione in cui W jω) si annulla o ha un polo sull asse immaginario, dato che in tal punto la fase non è definita. Ma anche su questo argomento torneremo fra breve. 7. Diagrammi di Bode di una funzione razionale: introduzione Fattorizzando sul campo reale i polinomi a numeratore e a denominatore di W s) in fattori irriducibili del primo e del secondo grado, si può sempre esprimere W s) nella forma ) ν s α ν W s) = K s α ) ) µ s + δ ω n s + ) µ ω n ) s + δ q ω nq s + ω nq ) q ) s ν ) ν ) µ ) µq α s α s + δ ω n s + ω n ) s + δ q ω nq s + ω nq ) 7.)
3 7.. DIAGRAMMI DI BODE DI UNA FUNZIONE RAZIONALE: INTRODUZIONE 3 e quindi anche nella forma di Bode ν + st ) + st p W s) = K s ν 0 Per ottenere 7.) da 7.) ) ν p + δ s + ω n ) ν ) νp + st + st p + δ ω n s + ) µ s + δ ω n q s + ) ω nq ) µ s ω n ) + δq ω nq s + ) µ s q ω nq ) ) µq s ω nq) 7.) si moltiplica ciascun fattore s α, con α 0, per T = /α, ottenendo un fattore del tipo + T s si moltiplica ciascun fattore s + δω n s + ω n per /ω n, ottenendo un fattore del tipo + δ ω n s + s ω n si raccolgono, a compensare le precedenti moltiplicazioni, i prodotti dei reciproci dei T e degli ω n, ottenendo K = K T ν... ω n )µ... T )ν... ω n ) µ... ν 0 può essere positivo, nel qual caso W s) ha un polo nell origine, negativo se W s) ha uno zero nell origine, o nullo. La costante K = [W s)s ν 0 ] 7.3) s+0 è detta guadagno o costante) di Bode e coincide con W 0) quando non vi siano singolarità i.e.poli o zeri) nell origine. È facile constatare che l andamento di W jω) è noto quando sia conosciuto per i soli valori positivi della pulsazione ω; infatti, avendo la funzione razionale W s) coefficienti reali, si ha W š) = W s))ˇ e, in particolare W jω) = W jω)ˇ 7.4) La refsempli) implica, per quanto riguarda modulo e fase di W jω), W jω) = W jω) 7.5) W jω) = W jω) 7.6) I diagrammi di Bode sono due: uno per il modulo o il guadagno ) W jω), ω R +, uno per la fase W jω), ω R +. In entrambi, la pulsazione è riportata in scala logaritmica in base 0, o, o naturale). La scala logaritmica è utilizzata anche per il guadagno, che è abitualmente espresso
4 4 CAPITOLO 7. DIAGRAMMI DI BODE - in decibel : W jω) db = 0 log 0 W jω) - in neper : W jω) np = ln W jω) Per la fase, si utilizzano indifferentemente misure in radianti o in gradi sessagesimali. Infine, pur essendo logaritmiche le scale, si riportano spesso in ascissa i valori effettivi della pulsazione, anziché quelli del suo logaritmo i.e. nel punto di coordinata x = log ω si riporta il valore di ω anziché quello di x) Se W jω) è fattorizzata in forma di Bode ν + jωt ) + jωt p K jω) ν 0 si ha ) ν p + δ jω ω n ) ν ) νp + j + j p + δ ω n jω ) µ ω + δ ω n q jω ) ω nq ) µ ω ω n ) + δq ω nq jω Figura 7.. ) µ ω q ω nq ) ) µq ω ω nq) 7.7) e 0 log 0 W jω) = 0 log 0 K + ν 0 log 0 + jωt µ δ 0 log 0 + ω n jω ω +... ω n ) ν 0 0 log 0 jω ν 0 log 0 + jωt... δ µ0 log 0 + jω ω ) ω n ω n ) W jω) = K ) + ν + jωt µ + δ ω n jω ω ) ω n +... ) ν 0 jω ) ν + jωt...
5 7.3. DIAGRAMMI DI BODE DELLE FUNZIONI ELEMENTARI 5 µ + δ jω ω ) ω n ω n ) ) Pertanto, il guadagno in db o in altra scala logaritmica) si ottiene sommando algebricamente i guadagni corrispondenti ai singoli fattori della funzione di trasferimento, e lo stesso vale per la fase. Ciò consente di ricondurre il tracciamento a quello delle funzioni elementari le costanti e i polinomi di primo e secondo grado) e di ottenere il diagramma finale per somma algebrica dei corrispondenti diagrammi elementari. Il paragrafo seguente sarà dedicato appunto alla determinazione della struttura di tali diagrammi elementari. 7.3 Diagrammi di Bode delle funzioni elementari Si riportano qui di seguito i diagrammi di Bode delle funzioni elementari, ovvero k, jω, + jωt, + δ ω n ω ω n e delle loro reciproche. La scala delle ascisse riporta il logaritmo in base 0 della pulsazione, quella delle ordinate il valore in decibel del guadagno e in radianti della fase. ) funzione costante K Se K = la retta è l asse delle ascisse, se K < la retta sta sotto l asse delle ascisse, e sta sopra se K > Per /K il diagramma del guadagno si riflette rispetto all asse delle ascisse, essendo 0 log 0 K = 0 log 0 K Figura 7.3. La fase è nulla se K > 0, vale π se K < 0. Il passaggio al reciproco non altera la fase. Figura 7.3.
6 6 CAPITOLO 7. DIAGRAMMI DI BODE ) funzioni jω e jω Si ha jω db = 0 log 0 jω = 0 log 0 ω e, per la fase, jω = π/ Per il guadagno della funzione reciproca si ha = 0 log 0 db Per la fase jω = π/ ω. jω jω ω. = 0 log 0 ω Figura Definizione 7.3. [Decade e ottava] Si dice decade un intervallo di pulsazioni che ha ampiezza unitaria nella scala logaritmica in base 0, ovvero un intervallo di pulsazioni comprese fra ω e 0 ω. Un intervallo di un ottava è invece quello compreso fra una pulsazione ω e la pulsazione doppia ω. È chiaro allora che il guadagno della funzione jω di /jω) si accresce diminuisce) di 0 db per decade. 3) la funzione + jωt e la reciproca Per il tracciamento del diagramma del guadagni, si ha + jωt db = 0 log 0 + jωt 7.0) In modo esatto quando ω = 0, e con piccolo errore quando la polsazione ω è piccola, la 7.0) può essere approssimata dalla funzione nulla. Per grandi valori di ω, invece, nella valutazione del guadagno è trascurabile l addendo rispetto a jωt e si ottiene + jωt db 0 log 0 jωt = 0 log 0ω + 0 log 0 T 7.) Nel diagramma logaritmico la 7.) è una retta che attraversa l asse delle ascisse per log 0 ω = log 0 T = log 0 /T e ha pendenza positiva pari a 0 db per decade. La approssimazione asintotica del guadagno consiste di due semirette: - per piccoli ω, inferiori a /T, è la semiretta orizzontale corrispondente a un guadagno di 0 db; - per ω /T è la semiretta di equazione 7.).
7 7.3. DIAGRAMMI DI BODE DELLE FUNZIONI ELEMENTARI 7 Il punto corrispondente alla pulsazione /T si dice punto di spezzamento o di rottura del diagramma asintotico. Figura Si noti che, se la pulsazione raddoppia, ossia se l intervallo fra la pulsazione più bassa e la più alta è di un ottava, l incremento di guadagno nella zona delle alte frequenze è dato da 0 log 0 ωt 0 log 0 = 0 log 0 = 6db Fra la curva esatta del guadagno e la sua approssimazione asintotica il massimo scostamento si ha alla pulsazione di rottura ω = /T e vale 3 db. Infatti 0 log 0 ± j = 0 log 0 = 0 log 0 3 db 7.) Figura Esercizio 7.3. Si verifichi che a distanza di un ottava prima e dopo la pulsazione di spezzamento /T, cioè alle pulsazioni /T ) e /T, l errore del diagramma asintotico rispetto a quello esatto è di circa db. Soluzione. In ω = /T il valore esatto del guadagno è 0 log 0 + j = 0 log mentre il valore previsto dal diagramma asintotico è 0 log 0 T T = 0 log 0 6 Per la fase + jωt ) = arctgωt ), quando ω tende a zero la fase tende a zero, mentre quando ω diverge la fase tende a π/ se T è positivo e a π/ se T è negativo. Inoltre, per T > 0 per T < 0) la fase cresce decresce) monotonicamente e vale π/4 -π/4) nel punto di spezzamento ω = /T.
8 8 CAPITOLO 7. DIAGRAMMI DI BODE L approssimazione più drastica consiste nel rappresentare + jωt ) con due semirette orizzontali, ponendo nulla la fase per ω < /T e pari a π/ o a π/ per ω > /T, a seconda che sia T > 0 o T < 0. Figura La figura fa riferimento al caso T > 0 ed è evidente che l errore è massimo alla pulsazione di spezzamento, dove vale π/4. Un approssimazione meno cruda si ottiene conservando le due semirette asintotiche per ω < 0 T e per ω > 0 T e raccordando linearmente rispetto alla scala logaritmica delle pulsazioni) sull intervallo [ 0 T, 0 T ]. Ció consente, fra l altro, di avere errore nullo in T, dove la fase vale ±π/4. In questo caso, l errore nei punti angolosi della spezzata vale circa /0 di radiante. Un altra approssimazione si basa sulla spezzata ottenuta utilizzando per T > 0) la tangente alla curva esatta nel punto, π/4) e le semirette orizzontali oltre ai punti di intersezione delle stesse con la tangente: Tali punti cadono circa in ω = 5 T e in ω = 5 T. Figura Riportiamo infine i diagrammi asintotici per la funzione reciproca /+jωt ): l andamento delle figure si deduce dai precedenti in modo ovvio. Si lascia come esercizio l approssimazione della funzione reciproca mediante spezzate.
9 7.3. DIAGRAMMI DI BODE DELLE FUNZIONI ELEMENTARI 9 Figura ) funzione + δ jω ω, δ, ) ω n ω n È facile ottenere per il guadagno l espressione + δ jω ω ω ω n ωn = 0 log 0 db ωn ) + jδ ω [ = 0 log0 ω ω n ωn ) + 4δ ω ] ωn [ = 0 log 0 ω ωn ) + 4δ ω ] ωn 7.3) Per piccoli valori di ω il guadagno è prossimo a zero e vale esattamente zero per ω = 0, ovvero per log 0 ω =. Per grandi valori di ω si possono trascurare in 7.3) le potenze di ω inferiori alla quarta, ottenendo l espressione asintotica + δ jω ω ω 4 0 log ω 0 n db ω n ω 4 n = 40 log 0 ω 40 log 0 ω n 7.4) Nel diagramma logaritmico la 7.4) è rappresentata da una retta che attraversa l asse delle ascisse per log 0 ω = log 0 ω n e che ha pendenza positiva pari a 40 db per decade. L approssimazione asintotica più cruda utilizza fino alla pulsazione ω n la semiretta di guadagno nullo, e per ω > ω n la semiretta a pendenza 40 db/decade, associata all equazione 7.4)
10 0 CAPITOLO 7. DIAGRAMMI DI BODE Figura Vogliamo ora valutare quali sono gli scostamenti del diagramma esatto del guadagno dal diagramma asintotico sopra considerato. Si noti che la funzione 7.3) dipende dal parametro δ lo smorzamento, se δ > 0), e perciò gli errori, e le correzioni eventuali, dipenderanno da δ. Per ω = ω n, l espressione 7.3) vale 0 log 0 4δ ) = 0 log 0 δ. Se δ = /, si ha 0 log 0 δ = 0, come nella rappresentazione asintotica Se δ > / si ha 0 log 0 δ > 0 e per δ si arriva al valore 0 log 0 6 db Se δ < / si ha 0 log 0 δ < 0 e per δ 0 l errore del diagramma asintotico tende a Figura 7.3.0
11 7.3. DIAGRAMMI DI BODE DELLE FUNZIONI ELEMENTARI Possiamo quindi concludere che per piccoli valori di δ la deviazione del diagramma esatto rispetto a quello asintotico è assai cospicua, e l uso del diagramma asintotico può indurre errori sensibili di valutazione. Per comprendere meglio l andamento effettivo della funzione + δ jω ω ω n ωn al variare di ω, deriviamone il quadrato rispetto a ω ed eguagliamo la derivata a zero: d dω La derivata si annulla alla pulsazione [[ ω ω n ) + 4δ ω ] ωn = 0 ω = ω n δ, 7.5) che è un numero reale solo se δ, ossia se δ /. In corrispondenza a tale valore ω la curva del modulo ha un minimo, il cui valore è pari a [ δ )) + 4δ δ )] / = [4δ 4δ 4 ] / = δ δ 7.6) Per δ /, la 7.6) fornisce un valore minore di, come ci dovevamo attendere dal momento che il guadagno vale in ω = 0 e ω è il punto in cui il guadagno è minimo. Il guadagno in decibel, nel punto di minimo, vale 0 log 0 δ δ ) = 0 log log 0 δ + 0 log 0 δ ) log 0 δ e tende a quando δ 0. La fase è data da ω ωn + jδ ω δ ) = arctg[ ω ] ω n ω n ω ω n ) = arccos [ ω ω n ω ω n + jδ ω ω n ) ] 7.7) Per δ > 0, ossia quando gli zeri del polinomio appartengono al semipiano Re s < 0, la fase è nulla per ω = 0 ed è funzione crescente di ω per ogni ω R +, raggiungendo il valore π/ in ω = ω n e tendendo a π quando ω. Per δ < 0,la fase, nulla in ω = 0, decresce al crescere di ω, assumendo per ogni ω valori opposti a quelli che assumerebbe in corrispondenza al parametro δ. Figura 7.3.
12 CAPITOLO 7. DIAGRAMMI DI BODE L approssimazione più cruda del diagramma di fase sta nel prendere una coppia di semirette, con un salto di π nel punto ω n : la figura si riferisce al caso δ > 0. Per costruire approssimazioni migliori, conviene osservare che anche lil diagramma di fase dipende da δ. Quanto più δ è prossimo a zero, tanto più accettabile è la approssimazione asintotica costituita dalle due semirette, dal momento che la transizione i fase si verifiva in un piccolo intervallo di pulsazioni intorno ad ω n. Questo fatto può essere compreso ω meglio riportando, in funzione di ω n, gli andamenti della parte reale e del coefficiente ] dell immaginario della funzione [ ω ) + jδ ω ωn ω n Figura 7.3. Se δ è molto prossimo a zero, quando ω/ω n è minore di, anche per piccoli scostamenti di ω/ω n dal valore la parte reale prevale nettamente sulla immaginaria e la fase è conseguentemente prossima a zero. Se invece ω/ω n è maggiore di, la parte reale tende con legge quadratica verso, prevalendo sul coefficiente della parte immaginaria, che cresce linearmente, e se δ è piccolo la fase raggiunge in pratica il valore ±π quando ω supera di poco ω n. Per valori di δ discosti dallo zero, si rinvia alla consultazione di tavole e grafici reperibili, as esempio in [LV] o in [Ma. Infine, notiamo che per δ = il polinomio del secondo grado non è irriducibile, ma fattorizza nella forma + δ ω n s + s ω n = ± s ω n ) Ponendo T = /ω n si ha il quadrato di un fattore del primo ordine del tipo considerato al punto 3 e per il quale il diagramma di fase è fornito dal diagramma riportato nella figura Figura 7.3.3
13 7.4. TRACCIAMENTO DEL DIAGRAMMA DI BODE 3 Infine, per la funzione reciproca si possono ripetere - mutatis mutandis - le considerazioni svolte finora. Nelle figure a seguire si forniscono solamente i diagrammi asintotici di prima approssimazione. Figura Tracciamento del diagramma di Bode Data una funzione razionale W jω) in forma di Bode, i diagrammi di Bode si ottnegono per sovrapposizione dei diagrammi asintotici o non) delle funzioni elementari componenti. Alcune regole pratiche per il tracciamento del diagramma, con riferimento alle 7.8) e 7.9).. Si individuano i punti di rottura sull asse ω, cioè le ascisse dei vertici delle spezzate: log 0, log T 0 i T i, log 0 ω ni, log 0 ω ni,. Nel diagramma asintotico dei moduli, il primo tratto ha pendenza 0ν 0 db/decade [si ricordi che ν 0, se positivo, rappresenta la molteplicità del polo nell origine; se negativo, rappresenta la molteplicità dello zero nell origine] Tenendo conto soltanto dei fattori jω) ν 0 e del guadagno K, al quale corrisponde K db = 0 log 0 K, si traccia una retta che attraversa l asse delle ordinate in K db e ha pendenza 0ν Ad ogni successivo punto di rottura, si varia la pendenza, incrementandola di 0ν db/decade per uno zero reale di molteplicità ν, diminuendola di 0ν db/decade per un polo reale di molteplicità ν, incrementandola di 40µ db/decade per una coppia di zeri complessi coniugati di molteplicità ν, diminuendola di 40µ db/decade per una coppia di poli complessi coniugati di molteplicità µ. 4, Per il diagramma delle fasi, quando ω tende a 0, e quindi il suo logaritmo tende a π la fase è ν 0, cui si aggiunge π se K è una costante negativa.
14 4 CAPITOLO 7. DIAGRAMMI DI BODE 5. Ad ogni punto di rottura si varia la fase di +ν π i negli zeri reali negativi, i.e. se T > 0, ν i π negli zeri reali positivi, i.e. se T < 0 +µ i π nelle coppie di zeri compl.coniugati a parte reale negativa δ > 0), µ i π nelle coppie di zeri compl.coniugati a parte reale positiva δ < 0) π ν i nei poli reali negativi, i.e. se T > 0, π +ν i nei poli reali positivi, i.e. se T < 0 µ i π nelle coppie di poli compl.coniugati a parte reale negativa δ > 0), +µ i π nelle coppie di poli compl.coniugati a parte reale positiva δ < 0) 6. I diagrammi esatti si ottengono da quelli asintotici sommando all ordinata dell asintotico i termini correttivi relativi ai fattori del primo e del secondo ordine. Esempio 7.4. Tracciamento dei diagrammi di Bode di a) Riscriviamo W s) in forma di Bode W s) = 00 + s ) W s) = s s + s 00s + ) ss + 0s + 00) con T =, ω n = 0, δ = /. b) Abbiamo perciò, in ordine di pulsazione crescente, un polo nell origine, con molteplicità, uno zero di modulo /T =, ) ) = 4 + s s + s + s ) = 4 + st ) s + δ ω n s + s una coppia di poli complessi coniugati, con pulsazione naturale ω n = 0 e smorzamento δ = 0, 5: essi si trovano nei punti 5 ± 0j 0, 75 = 5 ± j5 3 del piano complesso. ω n ) Figura 7.4. c) Tracciamento del diagramma di guadagno
15 7.4. TRACCIAMENTO DEL DIAGRAMMA DI BODE 5 si comincia con il fattore 4/jω: si tratta di una retta con pendenza -0 db/decade, che interseca l asse delle ordinate nel punto 0 log 0 4 db; Figura 7.4. per ω = c e una pulsazione di rottura, corrispondente a uno zero della f.d.t.: la pendenza della curva di guadagno cresce di 0 db/decade, quindi nel diagramma asintotico la pendenza si azzera fino alla pulsazione di rottura successiva; alla pulsazione 0 c è una coppia di poli complessi coniugati: nel diagramma asintotico ha inizio una pendenza di -40 db/decade. d) Correzioni: +3db nel punto ω =, + db nel punto ω = 4 un ottava dopo lo spezzamento) e nel punto ω = un ottava prima dello spezzamento) Poiché δ vale /, non si dà luogo a correzione in ω n = 0. e) Per il diagramma di fase, si riporta a tratto continuo nella figura A il diagramma asintotico risultante dalla somma dei diagrammi asintotici dei tre fattori; nella figura B si riportano invece gli andamenti con approssimazione lineare di ciascuno dei tre fattori, la cui somma da luogo all andamento tratteggiato di figura A. Figura 7.4.3
16 6 CAPITOLO 7. DIAGRAMMI DI BODE 7.5 Esempi di tracciamento Esempio 7.5. Figura 7.5. Esempio 7.5. Figura 7.5.
17 7.5. ESEMPI DI TRACCIAMENTO 7 Esempio Figura Esempio Figura 7.5.4
18 8 CAPITOLO 7. DIAGRAMMI DI BODE Esempio Figura Esempio Figura 7.5.6
19 7.6. COMPLEMENTI Complementi 7.6. Stima della funzione di trasferimento Spesso è possibile stimare la funzione di trasferimento dai diagrammi di Bode della risposta in frequenza. Il primo passo consiste nell approssimare con segmenti di retta, di pendenza 0ν db/decade con ν numero intero) il diagramma del guadagno; i valori di frequenza nei quali si hanno i cambiamenti di pendenza sono le pulsazioni di spezzamento; nei poli la pendenza diminuisce, mentre cresce in corrispondenza agli zeri; se l incremento di pendenza è di 40 db/decade, lo spezzamento pu o corrispondere - a un polo reale doppio -a una coppia di poli complessi coniugati con frequenza naturale nel punto di spezzamento Nel secondo caso, lo smorzamento può essere stimato esaminando l andamento del guadagno nell intorno del punto di spezzamento. La curva del guadagno non individua univocamente la W jω) Infatti, moltiplicando W s) per una funzione passatutto del tipo T s + T s oppure δ ω n s + s ωn + δ ω n s + s ωn 7.8) non si altera il diagramma del guadagno, dato che ciascuna funzione ha guadagno di 0 db/decade ad ogni frequenza. Essa peraltro altera la fase. Per la prima delle 7.8), ad esempio, si ha e d altra parte jωt )/ + jωt ) = jωt ) + jωt ) jωt ) = + jωt ) Quindi il diagramma di fase della funzione passatutto, per T > 0 ha l andamento riportato in figura 7.6. / jωt +jωt Figura 7.6.
20 0 CAPITOLO 7. DIAGRAMMI DI BODE e la funzione T s introduce un ritardo di fase di π senza alterare il guadagno della + T s funzione di trasferimento di cui è un fattore. Esercizio 7.6. Dati i diagrammi di Bode di figura 7.6., studiare le proprietà della funzione di trasferimento. Figura 7.6. Cenno di soluzione. ) Si determina il punto di spezzamento / T prolungando i tratti rettilinei : si deve avere un fattore del tipo / + st ); ) sull asse delle ordinate si legge il valore 0 log 0 K, quindi si ricava K ; 3) dalla fase asintotica per ω 0 si conclude che la costante di Bode K è positiva, dal fatto che intorno a /T la fase decresce, si conclude che T è positivo. Quindi W s) = K + st con K, T > 0 Esercizio 7.6. Dai diagrammi do Bode di figura ricavare le proprietà di una funzione di trasferimento del secondo ordine. δ > 0 /W Figura Cenno di soluzione. ) La fase è nulla per ω 0, quindi K è positivo e si può desumere dall intersezione della curva asintotica del guadagno con l asse delle ordinate; ) il fattore del secondo ordine è un denominatore della funzione di trasferimento, dato che per ω grande si ha una pendenza negativa pari a 40 db/decade; 3) dall andamento del diagramma asintotico del guadagno si conclude che in ω n c e uno spezzamento, corrispondente a un polo doppio reale o a una coppia polare complessa coniugata: l andamento intorno a ω 0 giustifica l ipotesi di una coppia complessa coniugata; Per ω = ω n risulta ω + δ jω) ωn db = ω n δ db 4) se ɛ è lo scarto nel punto ω n vedi figura), allora δ = / se ɛ = 0, δ < / se ɛ > 0, δ > / se ɛ < 0; nel nostro caso, ɛ è positivo, quindi vale la seconda ipotesi: se, ad esempio, sul diagramma di
21 7.6. COMPLEMENTI ampiezza si legge ɛ= 5 db, allora 0 log 0 δ = 5 log 0 δ = /4 δ = 0/4 δ = 0 /4 ; 5) per determinare il segno di δ, si osserva che la curva di fase decresce nell intorno di ω 0: quindi deve essere δ > Picco di risonanza Si consideri la funzione W jω) = + δ 7.9) ω n jω ω ωn L andamento del guadagno in db della funzione 7.9) è, ovviamente, l opposto di quello della funzione polinomiale studiata al punto 4) del paragrafo 7.3. Se lo smorzamento δ è inferiore a /, la curva del guadagno ha un massimo per ω = ω n δ Il guadagno corrispondente alla pulsazione ω è /δ δ ) ovvero, in decibel W jω) W j ω) db = 0 log 0 0 log 0 δ 0 log 0 δ ) 6 0 log 0 δ = 0 log 0 δ 6 7.0) Figura dove l approssimazione vale se δ è molto prossimo a zero. La pulsazione ω, il cui valore è sempre inferiore a ω n, si dice pulsazione di risonanza e, quando δ 0, si ha ω ω n e W j ω) db Formula di Bode Nelle considerazioni che seguiranno, useremo in ascisse il logaritmo neperiano della pulsazione e in ordinate il logaritmo neperiano del modulo assumeremo quindi come unità di misura il neper, associato al segmento che congiunge due valori il cui rapporto è pari ad e). Nel diagramma dei moduli abbiamo che jω np = ln jω = ln ω è rappresentato da una retta a pendenza unitaria passante per l origine;
22 CAPITOLO 7. DIAGRAMMI DI BODE + jωt np ha come diagramma asintotico una spezzata costituita da due semirette, ovvero ln = 0 per ω 0: una semiretta orizzontale; + jωt np = ln ω + ln T per ω + : una semiretta con pendenza unitaria e punto di spezzamento in ln /T etc. per le altre funzioni elementari Si noti che, per quanto riguarda le pendenze nel diagramma asintotico di ampiezza, a ± 0 db/decade corrispondono ± np/np e a ±40 db/decade ± np/np. Definizione 7.6. [Funzioni a fase minima] Una funzione di trasferimento razionale W s) si dice a fase minima se è priva di zeri e di poli per Res 0 La formula di Bode, che qui ci limitiamo ad enunciare, consente di esprimere, nel caso di funzioni razionali a fase minima, la fase di W jω) ad un arbitraria pulsazione ω in funzione dell intero andamento del modulo W jω) np. Teorema 7.6. [Formula di Bode] Si ponga x = ln ω, x = ln ω scala delle frequenze : logaritmi naturali) ycot) : x ω ln W jω) scala dei guadagni : logaritmi naturali) z ) : x ω W jω) in radianti Nell ipotesi che la funzione di trasferimento razionale W jω) abbia fase minima e sia K > 0, risulta z x) = W i ω) = π ln cotgh α + dy dx ln cotgh N.B. x x π dx 7.) + ln cotgh α dα = π e α α Figura Si ricorda che la cotangente iperbolica di α, α R, è definita in termini di seno e coseno iperbolico dalla formula cotghα = coshα sinhα = eα + e α e α e α = eα + e α
23 7.6. COMPLEMENTI 3 Come conseguenza del teorema di Bode, la fase alla pulsazione ω è la media pesata della derivata di ln W jω), pensata come funzione di ln ω e assumendo come peso la funzione di figura 7.6.5, con α = ln ω ln ω. La formula ha alcune interessanti conseguenze, che illustreremo brevemente. Se ω è lontano dai punti di spezzamento del diagramma di ampiezza, l andamento di ln W jω) ha pendenza costante rispetto alla variabile ln ω, quindi la funzione dy/dx che compare in 7.) è una costante in ogni intorno di ln ω i cui estremi rimangano abbastanze lontani dai punti di spezzamento. D altra parte, la funzione π ln cotgh α ha ampiezza trascurabile nei punti esterni all intervallo I = [ln 0, ln 0], nel senso che l integrale sull intervallo è molto prossimo a π/, mentre vale π/ l integrale da a +. Conseguentemente, se l intervallo I x = [ x + ln 0, x + ln 0] è contenuto nella regione dove dy/dx è costante, si può scrivere z x) = + dy π dx ln cotgh x x dx dy π dx ln cotgh x x dx I x dy ln cotgh dx x= x I x x x dx π dy dx x= x Poiché la pendenza dy/dx nell intorno di x = ln ω è espressa da un numero intero si usano i neper!), la fase è un multiplo intero di π/. Si ritrova così, come regola generale per le funzioni a fase minima, un risultato già noto dalla costruzione dei diagrammi di Bode Il ricorso alla formula di Bode è particolarmente vantaggioso quando il diagramma di ampiezza non è noto in modo esatto ad esempio, perché lo si è ottenuto per via sperimentale) in quanto consente egualmente di ricavare il diagramma di fase. In queste situazioni si può procedere - approssimando il diagramma di ampiezza con una spezzata, - determinando in corrispondenza la funzione costante a tratti dy/dx Figura Con la notazione in decibel, dove la pendenza è di 0k db/decade, la fase risulta kπ/
24 4 CAPITOLO 7. DIAGRAMMI DI BODE - ricorrendo vedi figura 7.6.7) alla tabulazione della funzione βx) = x ln cotgh α dα, x, + ) π 0 Figura Infatti la fase in x sarà data da + dy ln cotgh x x π dx dx = A x ln cotgh x x π dx + A x ln cotgh x x π x dx A + n ln cotgh x x π x n dx = A x x ln cotgh u du + A x x ln cotgh u du A + n ln cotgh u du π π π x x = A [βx x) β )] + A [βx x) βx x)] +... Osservazione Se W s) non ha fase minima o se K è negativo), la formula di Bode non fornisce risultati corretti. Si consideri ad esempio la funzione W s) = s + s = s + st = + s + st x n x con T =, T =, K = La pendenza del diagramma delle ampiezze in [ln, + ) è 0, ed una applicazione errata!) della formula di Bode darebbe fase nulla per grandi valori di ω. In realtà su [ln, + ) la fase tende a π lo zero in T < 0 induce un decremento di fase). W jω) Figura 7.6.8
25 7.7. RIFERIMENTI BIBLIOGRAFICI Riferimenti bibliografici [Ma ] G.Marro, Controlli Automatici, Zanichelli [LV ] A.Lepschy, U.Viaro Guida allo studio dei controlli automatici, Patron [Si ] N.Sinha, Control systems Wiley, 994
Rappresentazione grafica delle funzioni di trasferimento: diagramma di Nyquist
 Capitolo 8 Rappresentazione grafica delle funzioni di trasferimento: diagramma di Nyquist 8. Proprietà generali del diagramma di Nyquist Il diagramma di Nyquist (o polare ) della funzione W (jω) è definito
Capitolo 8 Rappresentazione grafica delle funzioni di trasferimento: diagramma di Nyquist 8. Proprietà generali del diagramma di Nyquist Il diagramma di Nyquist (o polare ) della funzione W (jω) è definito
Tracciamento dei Diagrammi di Bode
 Tracciamento dei Diagrammi di Bode L. Lanari, G. Oriolo Dipartimento di Ingegneria Informatica, Automatica e Gestionale Sapienza Università di Roma October 24, 24 diagrammi di Bode rappresentazioni grafiche
Tracciamento dei Diagrammi di Bode L. Lanari, G. Oriolo Dipartimento di Ingegneria Informatica, Automatica e Gestionale Sapienza Università di Roma October 24, 24 diagrammi di Bode rappresentazioni grafiche
Stabilità dei sistemi di controllo in retroazione
 Stabilità dei sistemi di controllo in retroazione Risposta in frequenza Rappresentazione grafica naturale Rappresentazione grafica modificata di fdt elementari Esempio 7 Politecnico di Torino 1 Risposta
Stabilità dei sistemi di controllo in retroazione Risposta in frequenza Rappresentazione grafica naturale Rappresentazione grafica modificata di fdt elementari Esempio 7 Politecnico di Torino 1 Risposta
Diagrammi Di Bode. Prof. Laura Giarré https://giarre.wordpress.com/ca/
 Diagrammi Di Bode Prof. Laura Giarré Laura.Giarre@UNIMORE.IT https://giarre.wordpress.com/ca/ Diagrammi di Bode e polari Problema della rappresentazione grafica di funzioni complesse di variabile reale
Diagrammi Di Bode Prof. Laura Giarré Laura.Giarre@UNIMORE.IT https://giarre.wordpress.com/ca/ Diagrammi di Bode e polari Problema della rappresentazione grafica di funzioni complesse di variabile reale
CONTROLLI AUTOMATICI Ingegneria Meccanica e Ingegneria del Veicolo. DIAGRAMMI DI BODE
 CONTROLLI AUTOMATICI Ingegneria Meccanica e Ingegneria del Veicolo http://www.dii.unimore.it/~lbiagiotti/controlliautomatici.html DIAGRAMMI DI BODE Ing. e-mail: luigi.biagiotti@unimore.it http://www.dii.unimore.it/~lbiagiotti
CONTROLLI AUTOMATICI Ingegneria Meccanica e Ingegneria del Veicolo http://www.dii.unimore.it/~lbiagiotti/controlliautomatici.html DIAGRAMMI DI BODE Ing. e-mail: luigi.biagiotti@unimore.it http://www.dii.unimore.it/~lbiagiotti
Diagrammi di Bode. Esempio: j. 1+ s. 1+j ω. Diagrammi di Bode: ω Diagramma dei moduli. Ampiezza [db] Diagramma delle fasi.
![Diagrammi di Bode. Esempio: j. 1+ s. 1+j ω. Diagrammi di Bode: ω Diagramma dei moduli. Ampiezza [db] Diagramma delle fasi. Diagrammi di Bode. Esempio: j. 1+ s. 1+j ω. Diagrammi di Bode: ω Diagramma dei moduli. Ampiezza [db] Diagramma delle fasi.](/thumbs/62/48312755.jpg) .. 3.2 Diagrammi di Bode La funzione di risposta armonica F(ω) = G(jω) può essere rappresentata graficamente in tre modi diversi: i Diagrammi di Bode, i Diagrammi di Nyquist e i Diagrammi di Nichols. I
.. 3.2 Diagrammi di Bode La funzione di risposta armonica F(ω) = G(jω) può essere rappresentata graficamente in tre modi diversi: i Diagrammi di Bode, i Diagrammi di Nyquist e i Diagrammi di Nichols. I
COMPORTAMENTO DI UN SISTEMA IN REGIME SINUSOIDALE
 COMPORTAMENTO DI UN SISTEMA IN REGIME SINUSOIDALE Un sistema risponde ad una sinusoide in ingresso con una sinusoide in uscita della stessa pulsazione. In generale la sinusoide d uscita ha una diversa
COMPORTAMENTO DI UN SISTEMA IN REGIME SINUSOIDALE Un sistema risponde ad una sinusoide in ingresso con una sinusoide in uscita della stessa pulsazione. In generale la sinusoide d uscita ha una diversa
Diagrammi di Bode. Lezione 16 1
 Diagrammi di Bode Lezione 16 1 Funzione di trasferimento da considerare Tracciare il diagramma di Bode (solo spettro di ampiezza) della funzione di trasferimento: H() s = Punti critici: ss ( + 500) ( s+
Diagrammi di Bode Lezione 16 1 Funzione di trasferimento da considerare Tracciare il diagramma di Bode (solo spettro di ampiezza) della funzione di trasferimento: H() s = Punti critici: ss ( + 500) ( s+
Lezione 8. Stabilità dei sistemi di controllo
 Lezione 8 Stabilità dei sistemi di controllo Poli di un sistema di controllo Riprendiamo lo schema a blocchi di un sistema di controllo in retroazione: d y + + + y L(s) + + n Fig. 1 : Sistema di controllo
Lezione 8 Stabilità dei sistemi di controllo Poli di un sistema di controllo Riprendiamo lo schema a blocchi di un sistema di controllo in retroazione: d y + + + y L(s) + + n Fig. 1 : Sistema di controllo
Soluzione degli esercizi del Capitolo 9
 Soluzione degli esercizi del Capitolo 9 Soluzione dell Esercizio 9.1 Il diagramma polare associato alla funzione L(s) = µ/s, µ > comprende l intero semiasse reale negativo. È quindi immediato concludere
Soluzione degli esercizi del Capitolo 9 Soluzione dell Esercizio 9.1 Il diagramma polare associato alla funzione L(s) = µ/s, µ > comprende l intero semiasse reale negativo. È quindi immediato concludere
Funzioni di trasferimento
 1 Funzioni di trasferimento Introduzione 3 Cosa c è nell Unità 4 In questa sezione si affronteranno: introduzione uso dei decibel e delle scale logaritmiche diagrammi di Bode 4 Funzione di trasferimento
1 Funzioni di trasferimento Introduzione 3 Cosa c è nell Unità 4 In questa sezione si affronteranno: introduzione uso dei decibel e delle scale logaritmiche diagrammi di Bode 4 Funzione di trasferimento
Controlli Automatici Compito del - Esercizi
 Compito del - Esercizi. Data la funzione di trasferimento G(s) = s (s +),sicalcoli a) La risposta impulsiva g(t); b) L equazione differenziale associata al sistema G(s); c) Si commenti la stabilità del
Compito del - Esercizi. Data la funzione di trasferimento G(s) = s (s +),sicalcoli a) La risposta impulsiva g(t); b) L equazione differenziale associata al sistema G(s); c) Si commenti la stabilità del
SISTEMI ELEMENTARI DEL 1 o E 2 o ORDINE
 CONTROLLI AUTOMATICI Ingegneria della Gestione Industriale e della Integrazione di Impresa http://www.automazione.ingre.unimore.it/pages/corsi/controlliautomaticigestionale.htm SISTEMI ELEMENTARI DEL o
CONTROLLI AUTOMATICI Ingegneria della Gestione Industriale e della Integrazione di Impresa http://www.automazione.ingre.unimore.it/pages/corsi/controlliautomaticigestionale.htm SISTEMI ELEMENTARI DEL o
UNITÀ DIDATTICA 2 LE FUNZIONI
 UNITÀ DIDATTICA LE FUNZIONI. Le funzioni Definizione. Siano A e B due sottoinsiemi non vuoti di R. Si chiama funzione di A in B una qualsiasi legge che fa corrispondere a ogni elemento A uno ed un solo
UNITÀ DIDATTICA LE FUNZIONI. Le funzioni Definizione. Siano A e B due sottoinsiemi non vuoti di R. Si chiama funzione di A in B una qualsiasi legge che fa corrispondere a ogni elemento A uno ed un solo
Diagrammi di Bode. I Diagrammi di Bode sono due: 1) il diagramma delle ampiezze rappresenta α = ln G(jω) in funzione
 0.0. 3.2 Diagrammi di Bode Possibili rappresentazioni grafiche della funzione di risposta armonica F (ω) = G(jω) sono: i Diagrammi di Bode, i Diagrammi di Nyquist e i Diagrammi di Nichols. I Diagrammi
0.0. 3.2 Diagrammi di Bode Possibili rappresentazioni grafiche della funzione di risposta armonica F (ω) = G(jω) sono: i Diagrammi di Bode, i Diagrammi di Nyquist e i Diagrammi di Nichols. I Diagrammi
Scomposizione in fratti semplici
 0.0.. Scomposizione in fratti semplici La determinazione dell evoluzione libera e dell evoluzione forzata di un sistema lineare stazionario richiedono l antitrasformazione di una funzione razionale fratta
0.0.. Scomposizione in fratti semplici La determinazione dell evoluzione libera e dell evoluzione forzata di un sistema lineare stazionario richiedono l antitrasformazione di una funzione razionale fratta
Nome: Nr. Mat. Firma:
 Fondamenti di Controlli Automatici - A.A. 212/13 9 novembre 212 - Domande Teoriche Nome: Nr. Mat. Firma: Per ciascuno dei test a soluzione multipla segnare con una crocetta tutte le affermazioni che si
Fondamenti di Controlli Automatici - A.A. 212/13 9 novembre 212 - Domande Teoriche Nome: Nr. Mat. Firma: Per ciascuno dei test a soluzione multipla segnare con una crocetta tutte le affermazioni che si
Capitolo. Stabilità dei sistemi di controllo. 8.1 Generalità. 8.2 Criterio generale di stabilità. 8.3 Esercizi - Criterio generale di stabilità
 Capitolo 7 Stabilità dei sistemi di controllo 8.1 Generalità 8. Criterio generale di stabilità 8.3 Esercizi - Criterio generale di stabilità 8.4 Criterio di stabilità di Nyquist 8.5 Esercizi - Criterio
Capitolo 7 Stabilità dei sistemi di controllo 8.1 Generalità 8. Criterio generale di stabilità 8.3 Esercizi - Criterio generale di stabilità 8.4 Criterio di stabilità di Nyquist 8.5 Esercizi - Criterio
Corso di Laurea in Ingegneria Meccatronica SISTEMI ELEMENTARI DEL 1 o E 2 o ORDINE
 Automation Robotics and System CONTROL Università degli Studi di Modena e Reggio Emilia Corso di Laurea in Ingegneria Meccatronica SISTEMI ELEMENTARI DEL o E 2 o ORDINE CA 5 Cesare Fantuzzi (cesare.fantuzzi@unimore.it)
Automation Robotics and System CONTROL Università degli Studi di Modena e Reggio Emilia Corso di Laurea in Ingegneria Meccatronica SISTEMI ELEMENTARI DEL o E 2 o ORDINE CA 5 Cesare Fantuzzi (cesare.fantuzzi@unimore.it)
Stabilità dei sistemi in retroazione. Diagrammi polari e teorema di Nyquist
 Stabilità dei sistemi in retroazione Diagrammi polari e teorema di Nyquist STABILITA DEI SISTEMI IN RETROAZIONE Vogliamo studiare la stabilità del sistema in retroazione a partire della conoscenza di L(s
Stabilità dei sistemi in retroazione Diagrammi polari e teorema di Nyquist STABILITA DEI SISTEMI IN RETROAZIONE Vogliamo studiare la stabilità del sistema in retroazione a partire della conoscenza di L(s
CONTROLLI AUTOMATICI Ingegneria della Gestione Industriale DIAGRAMMI DI BODE
 CONTROLLI AUTOMATICI Ingegneria della Gestione Industriale DIAGRAMMI DI BODE Ing. Luigi Biagiotti Tel. 51 29334 / 51 29368 e-mail: lbiagiotti@deis.unibo.it http://www-lar.deis.unibo.it/~lbiagiotti e polari
CONTROLLI AUTOMATICI Ingegneria della Gestione Industriale DIAGRAMMI DI BODE Ing. Luigi Biagiotti Tel. 51 29334 / 51 29368 e-mail: lbiagiotti@deis.unibo.it http://www-lar.deis.unibo.it/~lbiagiotti e polari
Reti nel dominio delle frequenze. Lezione 10 2
 Lezione 10 1 Reti nel dominio delle frequenze Lezione 10 2 Introduzione Lezione 10 3 Cosa c è nell Unità 3 In questa sezione si affronteranno Introduzione all Unità Trasformate di Laplace Reti nel dominio
Lezione 10 1 Reti nel dominio delle frequenze Lezione 10 2 Introduzione Lezione 10 3 Cosa c è nell Unità 3 In questa sezione si affronteranno Introduzione all Unità Trasformate di Laplace Reti nel dominio
= b ns n + + b 0. (s p i ), l r, A(p i) 0, i = 1,..., r. Y f (s) = G(s)U(s) = H(s) + n i=1. Parte dipendente dai poli di G(s) ( transitorio ).
 RISPOSTA FORZATA SISTEMI LINEARI STAZIONARI u(t) G(s) = B(s) A(s) = b ns n + + b 0 s n + + a 0 y f (t) Classe di funzioni di ingresso. U := l Q(s) u( ) : U(s) = P (s) = i= (s z i ) ri= (s p i ), l r, A(p
RISPOSTA FORZATA SISTEMI LINEARI STAZIONARI u(t) G(s) = B(s) A(s) = b ns n + + b 0 s n + + a 0 y f (t) Classe di funzioni di ingresso. U := l Q(s) u( ) : U(s) = P (s) = i= (s z i ) ri= (s p i ), l r, A(p
Esercizi sul luogo delle radici
 FA Esercizi 6, 1 Esercizi sul luogo delle radici Analisi di prestazioni a ciclo chiuso, progetto di regolatori facendo uso del luogo delle radici. Analisi di prestazioni FA Esercizi 6, 2 Consideriamo il
FA Esercizi 6, 1 Esercizi sul luogo delle radici Analisi di prestazioni a ciclo chiuso, progetto di regolatori facendo uso del luogo delle radici. Analisi di prestazioni FA Esercizi 6, 2 Consideriamo il
FUNZIONI. y Y. Def. L insieme Y è detto codominio di f. Es. Siano X = R, Y = R e f : x y = 1 x associo il suo inverso). (ad un numero reale
 FUNZIONI Siano X e Y due insiemi. Def. Una funzione f definita in X a valori in Y è una corrispondenza (una legge) che associa ad ogni elemento X al più un elemento in Y. X Y Def. L insieme Y è detto codominio
FUNZIONI Siano X e Y due insiemi. Def. Una funzione f definita in X a valori in Y è una corrispondenza (una legge) che associa ad ogni elemento X al più un elemento in Y. X Y Def. L insieme Y è detto codominio
FUNZIONI. y Y. Def. L insieme Y è detto codominio di f. Es. Siano X = R, Y = R e f : x y = 1 x associo il suo inverso). (ad un numero reale
 FUNZIONI Siano X e Y due insiemi. Def. Una funzione f definita in X a valori in Y è una corrispondenza (una legge) che associa ad ogni elemento X al piú un elemento in Y. X Y Def. L insieme Y è detto codominio
FUNZIONI Siano X e Y due insiemi. Def. Una funzione f definita in X a valori in Y è una corrispondenza (una legge) che associa ad ogni elemento X al piú un elemento in Y. X Y Def. L insieme Y è detto codominio
STABILITÀ DEI SISTEMI Metodo di Bode e Nyquist
 I.T.I. Modesto PANETTI B A R I Via Re David, 186-70125 BARI 080-542.54.12 - Fax 080-542.64.32 Internet http://www.itispanetti.it email : BATF05000C@istruzione.it INTRODUZIONE STABILITÀ DEI SISTEMI Metodo
I.T.I. Modesto PANETTI B A R I Via Re David, 186-70125 BARI 080-542.54.12 - Fax 080-542.64.32 Internet http://www.itispanetti.it email : BATF05000C@istruzione.it INTRODUZIONE STABILITÀ DEI SISTEMI Metodo
Prof. Milizia, Liceo Scientifico di Mesagne (BR) 1
 Prof. Milizia, Liceo Scientifico di Mesagne (BR) 1 CAPITOLO 8. LE FUNZIONI. 1. Generalità sulle funzioni.. Le rappresentazioni di una funzione. 3. Le funzioni reali di variabile reale. 4. L espressione
Prof. Milizia, Liceo Scientifico di Mesagne (BR) 1 CAPITOLO 8. LE FUNZIONI. 1. Generalità sulle funzioni.. Le rappresentazioni di una funzione. 3. Le funzioni reali di variabile reale. 4. L espressione
Diagrammi di Nyquist o polari
 0.0. 3.3 1 qualitativa Ampiezza Diagrammi di Nyquist o polari Esempio di diagramma polare senza poli nell origine: 40 20 G(s) = 100(1+ s 50 ) (1+ s 10 )2 (1+ s 20 )(1+ s 100 ) Imag 0 20 15 20 30 80 0.1
0.0. 3.3 1 qualitativa Ampiezza Diagrammi di Nyquist o polari Esempio di diagramma polare senza poli nell origine: 40 20 G(s) = 100(1+ s 50 ) (1+ s 10 )2 (1+ s 20 )(1+ s 100 ) Imag 0 20 15 20 30 80 0.1
I diagrammi di Bode. Corso di Laurea in Ingegneria Meccanica Controlli Automatici L
 Diagrammi di Bode - 1 Corso di Laurea in Ingegneria Meccanica I diagrammi di Bode DEIS-Università di Bologna Tel. 51 2932 Email: crossi@deis.unibo.it URL: www-lar.deis.unibo.it/~crossi Diagrammi di Bode
Diagrammi di Bode - 1 Corso di Laurea in Ingegneria Meccanica I diagrammi di Bode DEIS-Università di Bologna Tel. 51 2932 Email: crossi@deis.unibo.it URL: www-lar.deis.unibo.it/~crossi Diagrammi di Bode
ANTITRASFORMATA DI LAPLACE MODI DI UN SISTEMA
 CONTROLLI AUTOMATICI Ingegneria Gestionale http://www.automazione.ingre.unimore.it/pages/corsi/controlliautomaticigestionale.htm ANTITRASFORMATA DI LAPLACE MODI DI UN SISTEMA Ing. Federica Grossi Tel.
CONTROLLI AUTOMATICI Ingegneria Gestionale http://www.automazione.ingre.unimore.it/pages/corsi/controlliautomaticigestionale.htm ANTITRASFORMATA DI LAPLACE MODI DI UN SISTEMA Ing. Federica Grossi Tel.
Esercizio 1. Si consideri la funzione di trasferimento. G(s) = K 1 + st
 Esercizio. Si consideri la funzione di trasferimento G(s) = K + st + sτ. Si dimostri che, qualunque siano i valori dei parametri reali K, T e τ, il relativo diagramma di Nyquist è una circonferenza. Si
Esercizio. Si consideri la funzione di trasferimento G(s) = K + st + sτ. Si dimostri che, qualunque siano i valori dei parametri reali K, T e τ, il relativo diagramma di Nyquist è una circonferenza. Si
Funzioni e grafici. prof. Andres Manzini
 Università degli studi di Modena e Reggio Emilia Dipartimento di Scienze e Metodi dell Ingegneria Corso MOOC Iscriversi a Ingegneria Reggio Emilia Introduzione Definizione Si dice funzione (o applicazione)
Università degli studi di Modena e Reggio Emilia Dipartimento di Scienze e Metodi dell Ingegneria Corso MOOC Iscriversi a Ingegneria Reggio Emilia Introduzione Definizione Si dice funzione (o applicazione)
Risposta al gradino di un sistema del primo ordine
 0.0..4 Risposta al gradino di un sistema del primo ordine Diagramma Si consideri il seguente sistema lineare del primo ordine: G(s) = +τ s L unico parametro che caratterizza il sistema è la costante di
0.0..4 Risposta al gradino di un sistema del primo ordine Diagramma Si consideri il seguente sistema lineare del primo ordine: G(s) = +τ s L unico parametro che caratterizza il sistema è la costante di
Problema ( ) = 0,!
 Domanda. Problema ( = sen! x ( è! Poiché la funzione seno è periodica di periodo π, il periodo di g x! = 4. Studio di f. La funzione è pari, quindi il grafico è simmetrico rispetto all asse y. È sufficiente
Domanda. Problema ( = sen! x ( è! Poiché la funzione seno è periodica di periodo π, il periodo di g x! = 4. Studio di f. La funzione è pari, quindi il grafico è simmetrico rispetto all asse y. È sufficiente
SISTEMI ELEMENTARI DEL 1 o E 2 o ORDINE
 CONTROLLI AUTOMATICI Ingegneria Meccanica e Ingegneria del Veicolo http://www.dii.unimore.it/~lbiagiotti/controlliautomatici.html SISTEMI ELEMENTARI DEL 1 o E 2 o ORDINE Ing. e-mail: luigi.biagiotti@unimore.it
CONTROLLI AUTOMATICI Ingegneria Meccanica e Ingegneria del Veicolo http://www.dii.unimore.it/~lbiagiotti/controlliautomatici.html SISTEMI ELEMENTARI DEL 1 o E 2 o ORDINE Ing. e-mail: luigi.biagiotti@unimore.it
Stabilità e retroazione
 0.0. 4.1 1 iagramma Stabilità e retroazione Stabilità dei sistemi dinamici lineari: Un sistema G(s) è asintoticamente stabile se tutti i suoi poli sono a parte reale negativa. Un sistema G(s) è stabile
0.0. 4.1 1 iagramma Stabilità e retroazione Stabilità dei sistemi dinamici lineari: Un sistema G(s) è asintoticamente stabile se tutti i suoi poli sono a parte reale negativa. Un sistema G(s) è stabile
Sistemi Elementari. Prof. Laura Giarré https://giarre.wordpress.com/ca/
 Sistemi Elementari Prof. Laura Giarré Laura.Giarre@UNIMORE.IT https://giarre.wordpress.com/ca/ Rappresentazioni di una funzione di trasferimento Una funzione di trasferimento espressa in forma polinomiale
Sistemi Elementari Prof. Laura Giarré Laura.Giarre@UNIMORE.IT https://giarre.wordpress.com/ca/ Rappresentazioni di una funzione di trasferimento Una funzione di trasferimento espressa in forma polinomiale
Funzioni. iniettiva se x y = f (x) f (y) o, equivalentemente, f (x) = f (y) = x = y
 Funzioni. Dati due insiemi A e B (non necessariamente distinti) si chiama funzione da A a B una qualunque corrispondenza (formula, regola) che associa ad ogni elemento di A uno ed un solo elemento di B.
Funzioni. Dati due insiemi A e B (non necessariamente distinti) si chiama funzione da A a B una qualunque corrispondenza (formula, regola) che associa ad ogni elemento di A uno ed un solo elemento di B.
Geometria analitica di base. Equazioni di primo grado nel piano cartesiano Funzioni quadratiche Funzioni a tratti Funzioni di proporzionalità inversa
 Equazioni di primo grado nel piano cartesiano Funzioni quadratiche Funzioni a tratti Funzioni di proporzionalità inversa Equazioni di primo grado nel piano cartesiano Risoluzione grafica di un equazione
Equazioni di primo grado nel piano cartesiano Funzioni quadratiche Funzioni a tratti Funzioni di proporzionalità inversa Equazioni di primo grado nel piano cartesiano Risoluzione grafica di un equazione
FILTRI in lavorazione. 1
 FILTRI 1 in lavorazione. Introduzione Cosa sono i filtri? C o II filtri sono dei quadripoli particolari, che presentano attenuazione differenziata in funzione della frequenza del segnale applicato in ingresso.
FILTRI 1 in lavorazione. Introduzione Cosa sono i filtri? C o II filtri sono dei quadripoli particolari, che presentano attenuazione differenziata in funzione della frequenza del segnale applicato in ingresso.
la somma delle distanze dai due fuochi assume il valore costante 2a.
 Appendice A Le coniche A.1 L ellisse Rappresentazione implicita L ellisse di semiassi a e b (0 < b a) è una curva del piano dotata di due assi di simmetria ortogonali che, nel riferimento individuato da
Appendice A Le coniche A.1 L ellisse Rappresentazione implicita L ellisse di semiassi a e b (0 < b a) è una curva del piano dotata di due assi di simmetria ortogonali che, nel riferimento individuato da
Cognome Nome: Matricola: Corso di Laurea: Fondamenti di Controlli Automatici - A.A. 2011/12 20 settembre Domande Teoriche
 Fondamenti di Controlli Automatici - A.A. / settembre - Domande Teoriche Cognome Nome: Matricola: Corso di Laurea: Per ciascuno dei test a soluzione multipla segnare con una crocetta tutte le affermazioni
Fondamenti di Controlli Automatici - A.A. / settembre - Domande Teoriche Cognome Nome: Matricola: Corso di Laurea: Per ciascuno dei test a soluzione multipla segnare con una crocetta tutte le affermazioni
RICHIAMI MATEMATICI. x( t)
 0.0. 0.1 1 RICHIAMI MATEMATICI Funzioni reali del tempo: (t) : t (t) (t) ( t) Funzioni reali dell ingresso: y() t t y( ) y() : y() Numeri complessi. Un numero complesso è una coppia ordinata di numeri
0.0. 0.1 1 RICHIAMI MATEMATICI Funzioni reali del tempo: (t) : t (t) (t) ( t) Funzioni reali dell ingresso: y() t t y( ) y() : y() Numeri complessi. Un numero complesso è una coppia ordinata di numeri
Elaborazione di segnali e immagini: modulo segnali
 Elaborazione di segnali e immagini: modulo segnali 30 gennaio 014 Esame parziale con soluzioni Esercizio 1 Dato un sistema LTI descritto dalla seguente equazione alle differenze: v(k) + v(k 1) 10v(k )
Elaborazione di segnali e immagini: modulo segnali 30 gennaio 014 Esame parziale con soluzioni Esercizio 1 Dato un sistema LTI descritto dalla seguente equazione alle differenze: v(k) + v(k 1) 10v(k )
04 - Numeri Complessi
 Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 04 - Numeri Complessi Anno Accademico 2013/2014 M. Tumminello, V. Lacagnina e
Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 04 - Numeri Complessi Anno Accademico 2013/2014 M. Tumminello, V. Lacagnina e
Esercizio 1. (s 1) (s 0.5)(s 1) G(s) 28. p1 = -0.5 (sx) p2 = -1 (sx) Tipo: g=0. G(0) = 56 = 20log10(56) ~ 35 db
 Esercizio 1 2 G(s) 28 (s 1) (s.5)(s 1) Poli: p1 = -.5 p2 = -1 zeri: z1 = 1 (dx) Tipo: g= Guadagno: G() = 56 = 2log1(56) ~ 35 db Bode del Modulo 3 Scala 4 6 5 4 3 Magnitude (db) 2 1-1 -2 1.1.2.3 1 1 Piazzamento
Esercizio 1 2 G(s) 28 (s 1) (s.5)(s 1) Poli: p1 = -.5 p2 = -1 zeri: z1 = 1 (dx) Tipo: g= Guadagno: G() = 56 = 2log1(56) ~ 35 db Bode del Modulo 3 Scala 4 6 5 4 3 Magnitude (db) 2 1-1 -2 1.1.2.3 1 1 Piazzamento
Esercitazioni di Analisi Matematica FUNZIONI CUBICHE. Effettuare lo studio completo delle seguenti funzioni di terzo grado intere:
 FUNZIONI CUBICHE Effettuare lo studio completo delle seguenti funzioni di terzo grado intere: 1) y = fx) = x 3 + 2x 2 + x 2) y = fx) = x 3 + x 2 + x + 2 3) y = fx) = x 3 + 2x 2 + x 4 4) y = fx) = x 3 +
FUNZIONI CUBICHE Effettuare lo studio completo delle seguenti funzioni di terzo grado intere: 1) y = fx) = x 3 + 2x 2 + x 2) y = fx) = x 3 + x 2 + x + 2 3) y = fx) = x 3 + 2x 2 + x 4 4) y = fx) = x 3 +
Controlli Automatici L-A - Esercitazione
 Controlli Automatici L-A - Esercitazione 1. Si consideri lo schema a blocchi di figura. d(t) K d x(t) e(t) R(s) u(t) G(s) y(t) - R(s) = K τs + 1 s + 1, G(s) = K d = 2 s(s 2 + 6s + ), a) Considerando gli
Controlli Automatici L-A - Esercitazione 1. Si consideri lo schema a blocchi di figura. d(t) K d x(t) e(t) R(s) u(t) G(s) y(t) - R(s) = K τs + 1 s + 1, G(s) = K d = 2 s(s 2 + 6s + ), a) Considerando gli
Derivata di una funzione
 Derivata di una funzione Prof. E. Modica http://www.galois.it erasmo@galois.it Il problema delle tangenti Quando si effettua lo studio delle coniche viene risolta una serie di esercizi che richiedono la
Derivata di una funzione Prof. E. Modica http://www.galois.it erasmo@galois.it Il problema delle tangenti Quando si effettua lo studio delle coniche viene risolta una serie di esercizi che richiedono la
Capacità parassita. Quindi ci si aspetta che la funzione di trasferimento dipenda dalla frequenza
 Esperienza n. 10 Partitore resistivo e sua compensazione in c.a. Partitore resistivo-capacitivo Partitore resistivo: abbiamo visto che in regime di corrente continua il rapporto di partizione è costante:
Esperienza n. 10 Partitore resistivo e sua compensazione in c.a. Partitore resistivo-capacitivo Partitore resistivo: abbiamo visto che in regime di corrente continua il rapporto di partizione è costante:
Controlli Automatici T. Analisi Armonica. Parte 5 Aggiornamento: Settembre Prof. L. Marconi
 Parte 5 Aggiornamento: Settembre 2010 Parte 5, 1 Analisi Armonica Prof. Lorenzo Marconi DEIS-Università di Bologna Tel. 051 2093788 Email: lmarconi@deis.unibo.it URL: www-lar.deis.unibo.it/~lmarconi Analisi
Parte 5 Aggiornamento: Settembre 2010 Parte 5, 1 Analisi Armonica Prof. Lorenzo Marconi DEIS-Università di Bologna Tel. 051 2093788 Email: lmarconi@deis.unibo.it URL: www-lar.deis.unibo.it/~lmarconi Analisi
Soluzione degli esercizi del Capitolo 7
 Soluzione degli esercizi del Capitolo 7 Soluzione dell Esercizio 7.1 La trasformata di Laplace dell uscita del sistema è da cui, per t, Y(s) = G(s)U(s) = 2 3.2 1+5ss 2 +.16 = = 64 1 5s +12.8 s+.2 s 2 +.16
Soluzione degli esercizi del Capitolo 7 Soluzione dell Esercizio 7.1 La trasformata di Laplace dell uscita del sistema è da cui, per t, Y(s) = G(s)U(s) = 2 3.2 1+5ss 2 +.16 = = 64 1 5s +12.8 s+.2 s 2 +.16
FORMULARIO DI CONTROLLI AUTOMATICI
 FORMULARIO DI CONTROLLI AUTOMATICI Sistema x (t) = A x (t) + B u (t) y (t) = C x (t) + D u (t) Funzione di trasferimento G (s) = y (s) / u (s) = C (si A) -1 B + D Sistema Serie G (s) = i G i (s) prodotto
FORMULARIO DI CONTROLLI AUTOMATICI Sistema x (t) = A x (t) + B u (t) y (t) = C x (t) + D u (t) Funzione di trasferimento G (s) = y (s) / u (s) = C (si A) -1 B + D Sistema Serie G (s) = i G i (s) prodotto
Prof. Milizia, Liceo Scientifico di Mesagne (BR) 1
 Prof. Milizia, Liceo Scientifico di Mesagne (BR) 1 CAPITOLO 8. LE FUNZIONI. 1. Generalità sulle funzioni.. Le rappresentazioni di una funzione.. Funzioni iniettive, suriettive e biiettive.. Le funzioni
Prof. Milizia, Liceo Scientifico di Mesagne (BR) 1 CAPITOLO 8. LE FUNZIONI. 1. Generalità sulle funzioni.. Le rappresentazioni di una funzione.. Funzioni iniettive, suriettive e biiettive.. Le funzioni
Diagrammi di Bode e polari
 Marzo - Giugno Automation Robotics and System CONTROL Corso di laurea in Ingegneria Meccatronica DIAGRAMMI DI BODE Cesare Fantuzzi (cesare.fantuzzi@unimore.it) Cristian Secchi (cristian.secchi@unimore.it)
Marzo - Giugno Automation Robotics and System CONTROL Corso di laurea in Ingegneria Meccatronica DIAGRAMMI DI BODE Cesare Fantuzzi (cesare.fantuzzi@unimore.it) Cristian Secchi (cristian.secchi@unimore.it)
Analisi Matematica 1
 Analisi Matematica 1 Schema provvisorio delle lezioni A. A. 2015/16 1 Distribuzione degli argomenti delle lezioni Argomento ore tot Numeri reali 11 11 Numeri complessi 1 12 Spazio euclideo 2 14 Topologia
Analisi Matematica 1 Schema provvisorio delle lezioni A. A. 2015/16 1 Distribuzione degli argomenti delle lezioni Argomento ore tot Numeri reali 11 11 Numeri complessi 1 12 Spazio euclideo 2 14 Topologia
Risposta armonica Analisi nel dominio del tempo: caratterizzazione del sistema osservando la sua risposta (forzata) ad ingressi significativi
 Risposta armonica Analisi nel dominio del tempo: caratterizzazione del sistema osservando la sua risposta (forzata) ad ingressi significativi Ipotesi: il sistema ha f.d.t. G(s)=N(s)/D(s) e la corrispondente
Risposta armonica Analisi nel dominio del tempo: caratterizzazione del sistema osservando la sua risposta (forzata) ad ingressi significativi Ipotesi: il sistema ha f.d.t. G(s)=N(s)/D(s) e la corrispondente
Geometria analitica di base (seconda parte)
 SAPERE Al termine di questo capitolo, avrai appreso: il concetto di luogo geometrico la definizione di funzione quadratica l interpretazione geometrica di un particolare sistema di equazioni di secondo
SAPERE Al termine di questo capitolo, avrai appreso: il concetto di luogo geometrico la definizione di funzione quadratica l interpretazione geometrica di un particolare sistema di equazioni di secondo
Graficazione qualitativa del luogo delle radici
 .. 1.1 1 Graficazione qualitativa del luogo delle radici Esempio. Si faccia riferimento al seguente sistema retroazionato: d(t) G(s) r(t) e(t) K 1(s 1) s(s+1)(s +8s+5) y(t) Per una graficazione qualitativa
.. 1.1 1 Graficazione qualitativa del luogo delle radici Esempio. Si faccia riferimento al seguente sistema retroazionato: d(t) G(s) r(t) e(t) K 1(s 1) s(s+1)(s +8s+5) y(t) Per una graficazione qualitativa
I DIAGRAMMI DI BODE. B.1 Diagramma del modulo B.2 Diagramma della fase
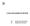 B I DIAGRAMMI DI BODE B. Diagramma del modulo B. Diagramma della fase Appunti del corso Elettronica Analogica Prof. Marco Sampietro - POLIMI La funzione di trasferimento di un circuito elettronico, in
B I DIAGRAMMI DI BODE B. Diagramma del modulo B. Diagramma della fase Appunti del corso Elettronica Analogica Prof. Marco Sampietro - POLIMI La funzione di trasferimento di un circuito elettronico, in
CONCETTO DI STABILITÀ NEI SISTEMI DI CONTROLLO. Sistema in condizioni di equilibrio a t = 0. d(t) = 0. u(t) = 0. y(t) = 0. Sistema
 CONCETTO DI STABILITÀ NEI SISTEMI DI CONTROLLO Sistema in condizioni di equilibrio a t = 0. d(t) = 0 u(t) = 0 Sistema y(t) = 0 Tipi di perturbazione. Perturbazione di durata limitata: u(t) = 0, t > T u
CONCETTO DI STABILITÀ NEI SISTEMI DI CONTROLLO Sistema in condizioni di equilibrio a t = 0. d(t) = 0 u(t) = 0 Sistema y(t) = 0 Tipi di perturbazione. Perturbazione di durata limitata: u(t) = 0, t > T u
Luogo delle Radici. Università degli Studi di Firenze. L. Chisci, P. Falugi
 Università degli Studi di Firenze Luogo delle Radici L. Chisci, P. Falugi Corso di Fondamenti di Automatica per CdL Ing. dell Informazione e Ing. dell Ambiente e delle Risorse Anno Accademico 005/06 Fondamenti
Università degli Studi di Firenze Luogo delle Radici L. Chisci, P. Falugi Corso di Fondamenti di Automatica per CdL Ing. dell Informazione e Ing. dell Ambiente e delle Risorse Anno Accademico 005/06 Fondamenti
un sistema è stabile se, in conseguenza di una sollecitazione esterna limitata, la sua risposta (variazione dell uscita) è limitata (Bounded Input
 un sistema è stabile se, in conseguenza di una sollecitazione esterna limitata, la sua risposta (variazione dell uscita) è limitata (Bounded Input Bounded Output) Un sistema si dice asintoticamente stabile
un sistema è stabile se, in conseguenza di una sollecitazione esterna limitata, la sua risposta (variazione dell uscita) è limitata (Bounded Input Bounded Output) Un sistema si dice asintoticamente stabile
Sistemi non lineari e Funzione Descrittiva
 Sistemi non lineari e Funzione Descrittiva (Complementi di Controlli Automatici: prof. Giuseppe Fusco) Si consideri il sistema a retroazione rappresentato in Figura 1. In un punto generico della catena
Sistemi non lineari e Funzione Descrittiva (Complementi di Controlli Automatici: prof. Giuseppe Fusco) Si consideri il sistema a retroazione rappresentato in Figura 1. In un punto generico della catena
Soluzione esercizi sulle funzioni - 5 a E Liceo Scientifico - 04/11/ 13
 Soluzione esercizi sulle funzioni - 5 a E Liceo Scientifico - 04// 3 Esercizio. Si consideri la funzione ) se 0 f) e se 0. e si verifichi che non è continua in 0. Che tipo di discontinuità presenta in
Soluzione esercizi sulle funzioni - 5 a E Liceo Scientifico - 04// 3 Esercizio. Si consideri la funzione ) se 0 f) e se 0. e si verifichi che non è continua in 0. Che tipo di discontinuità presenta in
Diagrammi asintotici di Bode: esercizi. Tracciare i diagrammi asintotici di Bode della seguente funzione G(s): s 2. s(s 30)(1+ s
 .. 3.2 1 Nyquist: Diagrammi asintotici di Bode: esercizi Tracciare i diagrammi asintotici di Bode della seguente funzione G(s): 6(s2 +.8s+4) s(s 3)(1+ s 2 )2. Pendenza iniziale: -2 db/dec. Pulsazioni critiche:
.. 3.2 1 Nyquist: Diagrammi asintotici di Bode: esercizi Tracciare i diagrammi asintotici di Bode della seguente funzione G(s): 6(s2 +.8s+4) s(s 3)(1+ s 2 )2. Pendenza iniziale: -2 db/dec. Pulsazioni critiche:
rapporto tra ingresso e uscita all equilibrio.
 Sistemi Dinamici: Induttore: Condensatore: Massa: Oscillatore meccanico: Pendolo: Serbatoio cilindrico: Serbatoio cilindrico con valvola d efflusso: Funzione di Trasferimento: Stabilità del sistema: (N.B.
Sistemi Dinamici: Induttore: Condensatore: Massa: Oscillatore meccanico: Pendolo: Serbatoio cilindrico: Serbatoio cilindrico con valvola d efflusso: Funzione di Trasferimento: Stabilità del sistema: (N.B.
a) Determinare il dominio, i limiti agli estremi del dominio e gli eventuali asintoti di f. Determinare inoltre gli zeri di f e studiarne il segno.
 1 ESERCIZI CON SOLUZIONE DETTAGLIATA Esercizio 1. Si consideri la funzione f(x) = e x 3e x +. a) Determinare il dominio, i limiti agli estremi del dominio e gli eventuali asintoti di f. Determinare inoltre
1 ESERCIZI CON SOLUZIONE DETTAGLIATA Esercizio 1. Si consideri la funzione f(x) = e x 3e x +. a) Determinare il dominio, i limiti agli estremi del dominio e gli eventuali asintoti di f. Determinare inoltre
Argomento 7. Studio di funzione
 Argomento 7 Studio di funzione Studiare una funzione significa ottenere, mediante strumenti analitici (iti, derivate, ecc.) informazioni utili a disegnare un grafico qualitativo della funzione data. I
Argomento 7 Studio di funzione Studiare una funzione significa ottenere, mediante strumenti analitici (iti, derivate, ecc.) informazioni utili a disegnare un grafico qualitativo della funzione data. I
5. Per ω = 1/τ il diagramma reale di Bode delle ampiezze della funzione G(jω) =
 Fondamenti di Controlli Automatici - A.A. 211/12 3 luglio 212 - Domande Teoriche Cognome Nome: Matricola: Corso di Laurea: Per ciascuno dei test a soluzione multipla segnare con una crocetta tutte le affermazioni
Fondamenti di Controlli Automatici - A.A. 211/12 3 luglio 212 - Domande Teoriche Cognome Nome: Matricola: Corso di Laurea: Per ciascuno dei test a soluzione multipla segnare con una crocetta tutte le affermazioni
Limite. Se D non è limitato si può fare il limite di f(x) per x che tende
 Appunti sul corso di Complementi di Matematica,mod.Analisi, prof. B.Bacchelli - a.a. 200/20. 05 - Limiti continuità: Riferimenti: R.Adams, Calcolo Differenziale 2. Capitoli 3., 3.2. - Esercizi 3., 3.2.
Appunti sul corso di Complementi di Matematica,mod.Analisi, prof. B.Bacchelli - a.a. 200/20. 05 - Limiti continuità: Riferimenti: R.Adams, Calcolo Differenziale 2. Capitoli 3., 3.2. - Esercizi 3., 3.2.
Studi di funzione. D. Barbieri. Studiare comportamento asintotico e monotonia di. f(x) = 1 x x4 + 4x e x
 Studi di funzione D. Barbieri Esercizi Esercizio Esercizio Studiare comportamento asintotico e monotonia di f(x) = x + x4 + 4x Studiare il comportamento asintotico di f(x) = + x x + + e x Esercizio 3 Determinare
Studi di funzione D. Barbieri Esercizi Esercizio Esercizio Studiare comportamento asintotico e monotonia di f(x) = x + x4 + 4x Studiare il comportamento asintotico di f(x) = + x x + + e x Esercizio 3 Determinare
Campi Elettromagnetici e Circuiti I Risposta in frequenza
 Facoltà di Ingegneria Università degli studi di Pavia Corso di aurea Triennale in Ingegneria Elettronica e Informatica Campi Elettromagnetici e Circuiti I isposta in frequenza Campi Elettromagnetici e
Facoltà di Ingegneria Università degli studi di Pavia Corso di aurea Triennale in Ingegneria Elettronica e Informatica Campi Elettromagnetici e Circuiti I isposta in frequenza Campi Elettromagnetici e
Esercizi- Risposta in frequenza
 esercizi 6, 1 Esercizi- Risposta in frequenza Diagrammi di Nyquist Data una funzione di trasferimento: Vogliamo ottenere la sua rappresentazione nel piano complesso al variare della frequenza. curva parametrizzata
esercizi 6, 1 Esercizi- Risposta in frequenza Diagrammi di Nyquist Data una funzione di trasferimento: Vogliamo ottenere la sua rappresentazione nel piano complesso al variare della frequenza. curva parametrizzata
s + 6 s 3, b) i valori di K per i quali il sistema a ciclo chiuso risulta asintoticamente stabile;
 1 Esercizi svolti Esercizio 1. Con riferimento al sistema di figura, calcolare: ut) + K s s + 6 s 3 yt) a) la funzione di trasferimento a ciclo chiuso tra ut) e yt); b) i valori di K per i quali il sistema
1 Esercizi svolti Esercizio 1. Con riferimento al sistema di figura, calcolare: ut) + K s s + 6 s 3 yt) a) la funzione di trasferimento a ciclo chiuso tra ut) e yt); b) i valori di K per i quali il sistema
Luogo delle radici. Si consideri il seguente schema in retroazione:
 0.0. 5.1 1 Luogo delle radici Si consideri il seguente schema in retroazione: La funzione di trasferimento G 0 (s) del sistema retroazionato è: G 0 (s) = G(s)H(s) 1+G(s)H(s) I poli del sistema retroazionato
0.0. 5.1 1 Luogo delle radici Si consideri il seguente schema in retroazione: La funzione di trasferimento G 0 (s) del sistema retroazionato è: G 0 (s) = G(s)H(s) 1+G(s)H(s) I poli del sistema retroazionato
Diagrammi polari, di Nyquist e di Nichols
 Diagrammi polari, di Nyquist e di Nichols Diagramma polare La risposta in frequenza si analizza tramite G(s) s jω G(jω) M( ω) e G(jω) jϕ( ω) e ω < Un altra rappresentazione grafica di G(jω) si ottiene
Diagrammi polari, di Nyquist e di Nichols Diagramma polare La risposta in frequenza si analizza tramite G(s) s jω G(jω) M( ω) e G(jω) jϕ( ω) e ω < Un altra rappresentazione grafica di G(jω) si ottiene
FUNZIONI GONIOMETRICHE
 FUNZIONI GONIOMETRICHE Misura degli angoli Seno, coseno e tangente di un angolo Relazioni fondamentali tra le funzioni goniometriche Angoli notevoli Grafici delle funzioni goniometriche GONIOMETRIA : scienza
FUNZIONI GONIOMETRICHE Misura degli angoli Seno, coseno e tangente di un angolo Relazioni fondamentali tra le funzioni goniometriche Angoli notevoli Grafici delle funzioni goniometriche GONIOMETRIA : scienza
SISTEMI DIGITALI DI CONTROLLO
 Sistemi Digitali di Controllo A.A. 2009-2010 p. 1/27 SISTEMI DIGITALI DI CONTROLLO Prof. Alessandro De Luca DIS, Università di Roma La Sapienza deluca@dis.uniroma1.it Lucidi tratti dal libro C. Bonivento,
Sistemi Digitali di Controllo A.A. 2009-2010 p. 1/27 SISTEMI DIGITALI DI CONTROLLO Prof. Alessandro De Luca DIS, Università di Roma La Sapienza deluca@dis.uniroma1.it Lucidi tratti dal libro C. Bonivento,
Fondamenti di Automatica
 Fondamenti di Automatica Analisi armonica e metodi grafici Dott. Ing. Marcello Bonfè Dipartimento di Ingegneria - Università di Ferrara Tel. +39 053 974839 E-mail: marcello.bonfe@unife.it pag. Analisi
Fondamenti di Automatica Analisi armonica e metodi grafici Dott. Ing. Marcello Bonfè Dipartimento di Ingegneria - Università di Ferrara Tel. +39 053 974839 E-mail: marcello.bonfe@unife.it pag. Analisi
Diagrammi di Bode. delle
 .. 3.2 delle Diagrammi di Bode La funzione di risposta armonica F(ω) = G(jω) può essere rappresentata graficamente in tre modi diversi: i Diagrammi di Bode, i Diagrammi di Nyquist e i Diagrammi di Nichols.
.. 3.2 delle Diagrammi di Bode La funzione di risposta armonica F(ω) = G(jω) può essere rappresentata graficamente in tre modi diversi: i Diagrammi di Bode, i Diagrammi di Nyquist e i Diagrammi di Nichols.
Stabilità dei sistemi di controllo. Fondamenti di Automatica Prof. Silvia Strada
 Stabilità dei sistemi di controllo Fondamenti di Automatica Prof. Silvia Strada 1 Stabilità Nei sistemi dinamici LTI la stabilità non dipende dagli ingressi. Asintoticamente stabili tutte le FdT attraverso
Stabilità dei sistemi di controllo Fondamenti di Automatica Prof. Silvia Strada 1 Stabilità Nei sistemi dinamici LTI la stabilità non dipende dagli ingressi. Asintoticamente stabili tutte le FdT attraverso
Stabilità BIBO Risposta impulsiva (vedi Marro par. 2.3, vedi Vitelli-Petternella par. III.1, vedi es. in LabView) Poli sull asse immaginario
 Stabilità BIBO Risposta impulsiva (vedi Marro par..3, vedi Vitelli-Petternella par. III., vedi es. in LabView) Poli sull asse immaginario Criteri per la stabilità (vedi Marro Par. 4. a 4., vedi Vitelli-Petternella
Stabilità BIBO Risposta impulsiva (vedi Marro par..3, vedi Vitelli-Petternella par. III., vedi es. in LabView) Poli sull asse immaginario Criteri per la stabilità (vedi Marro Par. 4. a 4., vedi Vitelli-Petternella
Rappresentazioni e parametri della funzione di trasferimento
 FUNZIONE DI TRASFERIMENTO Definizione e proprietà Rappresentazioni e parametri della funzione di trasferimento Risposta allo scalino Illustrazioni dal Testo di Riferimento per gentile concessione degli
FUNZIONE DI TRASFERIMENTO Definizione e proprietà Rappresentazioni e parametri della funzione di trasferimento Risposta allo scalino Illustrazioni dal Testo di Riferimento per gentile concessione degli
Definizione: Dato un sottoinsieme non vuoti di. Si chiama funzione identica o identità di in sé la funzione tale che.
 Esercitazioni di Analisi Matematica Prof.ssa Chiara Broggi Materiale disponibile su www.istitutodefilippi.it/claro Lezione 2: Funzioni reali e loro proprietà Definizione: Siano e due sottoinsiemi non vuoti
Esercitazioni di Analisi Matematica Prof.ssa Chiara Broggi Materiale disponibile su www.istitutodefilippi.it/claro Lezione 2: Funzioni reali e loro proprietà Definizione: Siano e due sottoinsiemi non vuoti
Si considerino i sistemi elettrici RL rappresentati nella seguente figura: L u 1 (t)
 Esercizio Circuiti R in serie). Si considerino i sistemi elettrici R rappresentati nella seguente figura: + + + + u t) R y t) u t) R y t) Si consideri inoltre il sistema ottenuto collegando in serie i
Esercizio Circuiti R in serie). Si considerino i sistemi elettrici R rappresentati nella seguente figura: + + + + u t) R y t) u t) R y t) Si consideri inoltre il sistema ottenuto collegando in serie i
06. Analisi Armonica. Controlli Automatici. Prof. Cesare Fantuzzi Ing. Cristian Secchi Ing. Federica Ferraguti
 Controlli Automatici 6. Analisi Armonica Prof. Cesare Fantuzzi Ing. Cristian Secchi Ing. Federica Ferraguti ARSControl - DISMI - Università di Modena e Reggio Emilia E-mail: {nome.cognome}@unimore.it http://www.arscontrol.org/teaching
Controlli Automatici 6. Analisi Armonica Prof. Cesare Fantuzzi Ing. Cristian Secchi Ing. Federica Ferraguti ARSControl - DISMI - Università di Modena e Reggio Emilia E-mail: {nome.cognome}@unimore.it http://www.arscontrol.org/teaching
Graficazione qualitativa del luogo delle radici
 .. 5.3 1 Graficazione qualitativa del luogo delle radici Esempio. Si faccia riferimento al seguente sistema retroazionato: d(t) G(s) r(t) e(t) K 1(s 1) s(s + 1)(s + 8s + 5) y(t) Per una graficazione qualitativa
.. 5.3 1 Graficazione qualitativa del luogo delle radici Esempio. Si faccia riferimento al seguente sistema retroazionato: d(t) G(s) r(t) e(t) K 1(s 1) s(s + 1)(s + 8s + 5) y(t) Per una graficazione qualitativa
Disequazioni di secondo grado
 Disequazioni di secondo grado. Disequazioni Definizione: una disequazione è una relazione di disuguaglianza tra due espressioni. Detti p() e g() due polinomi definiti in un insieme A, una disequazione
Disequazioni di secondo grado. Disequazioni Definizione: una disequazione è una relazione di disuguaglianza tra due espressioni. Detti p() e g() due polinomi definiti in un insieme A, una disequazione
Soluzioni dei problemi della maturità scientifica A.S. 2012/2013
 Soluzioni dei problemi della maturità scientifica A.S. / Nicola Gigli Sun-Ra Mosconi June, Problema. Il teorema fondamentale del calcolo integrale garantisce che Quindi f (x) = cos x +. f (π) = cos π +
Soluzioni dei problemi della maturità scientifica A.S. / Nicola Gigli Sun-Ra Mosconi June, Problema. Il teorema fondamentale del calcolo integrale garantisce che Quindi f (x) = cos x +. f (π) = cos π +
Funzione di trasferimento
 Funzione ditrasferimento - 1 Corso di Laurea in Ingegneria Meccanica Funzione di trasferimento DEIS-Università di Bologna Tel. 51 2932 Email: crossi@deis.unibo.it URL: www-lar.deis.unibo.it/~crossi Definizione
Funzione ditrasferimento - 1 Corso di Laurea in Ingegneria Meccanica Funzione di trasferimento DEIS-Università di Bologna Tel. 51 2932 Email: crossi@deis.unibo.it URL: www-lar.deis.unibo.it/~crossi Definizione
ANTITRAFORMATE DI LAPLACE MODI DI UN SISTEMA
 FONDAMENTI DI CONTROLLI AUTOMATICI Ingegneria Meccanica http://web.ing.unimo.it/~lbiagiotti/fondamenticontrolli1415.html ANTITRAFORMATE DI LAPLACE MODI DI UN SISTEMA Ing. e-mail: luigi.biagiotti@unimore.it
FONDAMENTI DI CONTROLLI AUTOMATICI Ingegneria Meccanica http://web.ing.unimo.it/~lbiagiotti/fondamenticontrolli1415.html ANTITRAFORMATE DI LAPLACE MODI DI UN SISTEMA Ing. e-mail: luigi.biagiotti@unimore.it
Stabilità e risposte di sistemi elementari
 Parte 4 Aggiornamento: Settembre 2010 Parte 4, 1 Stabilità e risposte di sistemi elementari Prof. Lorenzo Marconi DEIS-Università di Bologna Tel. 051 2093788 Email: lmarconi@deis.unibo.it URL: www-lar.deis.unibo.it/~lmarconi
Parte 4 Aggiornamento: Settembre 2010 Parte 4, 1 Stabilità e risposte di sistemi elementari Prof. Lorenzo Marconi DEIS-Università di Bologna Tel. 051 2093788 Email: lmarconi@deis.unibo.it URL: www-lar.deis.unibo.it/~lmarconi
MODULO 2. Rappresentazioni grafiche: Bode e Nyquist V ITI INFORMATICA CORSO DI SISTEMI. o Cenni sui logaritmi;
 V ITI INFORMATICA CORSO DI SISTEMI a.s. 2012/13 MODULO 2 Rappresentazioni grafiche: Bode e Nyquist o Cenni sui logaritmi; U.D.2.2: o Rappresentazioni della F(s); U.D.2.3: o Diagrammi di Bode del modulo:
V ITI INFORMATICA CORSO DI SISTEMI a.s. 2012/13 MODULO 2 Rappresentazioni grafiche: Bode e Nyquist o Cenni sui logaritmi; U.D.2.2: o Rappresentazioni della F(s); U.D.2.3: o Diagrammi di Bode del modulo:
Argomento 2 IIparte Funzioni elementari e disequazioni
 Argomento IIparte Funzioni elementari e disequazioni Applicazioni alla risoluzione di disequazioni Disequazioni di I grado Per la risoluzione delle disequazioni di primo grado per via algebrica, si veda
Argomento IIparte Funzioni elementari e disequazioni Applicazioni alla risoluzione di disequazioni Disequazioni di I grado Per la risoluzione delle disequazioni di primo grado per via algebrica, si veda
SIMULAZIONE - 29 APRILE QUESITI
 www.matefilia.it SIMULAZIONE - 29 APRILE 206 - QUESITI Q Determinare il volume del solido generato dalla rotazione attorno alla retta di equazione y= della regione di piano delimitata dalla curva di equazione
www.matefilia.it SIMULAZIONE - 29 APRILE 206 - QUESITI Q Determinare il volume del solido generato dalla rotazione attorno alla retta di equazione y= della regione di piano delimitata dalla curva di equazione
COMPENDIO ESPONENZIALI LOGARITMI
 TORINO SETTEMBRE 2010 COMPENDIO DI ESPONENZIALI E LOGARITMI di Bart VEGLIA 1 ESPONENZIALi 1 Equazioni esponenziali Un espressione in cui l incognita compare all esponente di una o più potenze si chiama
TORINO SETTEMBRE 2010 COMPENDIO DI ESPONENZIALI E LOGARITMI di Bart VEGLIA 1 ESPONENZIALi 1 Equazioni esponenziali Un espressione in cui l incognita compare all esponente di una o più potenze si chiama
Condizione di allineamento di tre punti
 LA RETTA L equazione lineare in x e y L equazione: 0 con,,, e non contemporaneamente nulli, si dice equazione lineare nelle due variabili e. Ogni coppia ; tale che: 0 si dice soluzione dell equazione.
LA RETTA L equazione lineare in x e y L equazione: 0 con,,, e non contemporaneamente nulli, si dice equazione lineare nelle due variabili e. Ogni coppia ; tale che: 0 si dice soluzione dell equazione.
3 Equazioni e disequazioni.
 3 Equazioni e disequazioni. 3. Equazioni. Una equazione algebrica è un uguaglianza tra espressioni letterali soddisfatta per alcuni valori attribuiti alle lettere che vi compaiono. Tali valori sono detti
3 Equazioni e disequazioni. 3. Equazioni. Una equazione algebrica è un uguaglianza tra espressioni letterali soddisfatta per alcuni valori attribuiti alle lettere che vi compaiono. Tali valori sono detti
