fig. 1 fig. 2 In base alla figura 1 si definiscono il seno ed il coseno di un angolo come segue:
|
|
|
- Laura Casadei
- 5 anni fa
- Visualizzazioni
Transcript
1 Trigonometria teoria Funzioni goniometriche Premessa Si definiscono funzioni goniometriche quelle la cui variabile risulta un angolo, oppure un arco. Prima di passare alla loro definizione è necessario assegnare un criterio in base al quale fare la lettura degli angoli in un opportuno riferimento. Convenzionalmente si stabilisce di leggere gli angoli, come pure gli archi, in senso antiorario a partire dal semiasse delle ascisse positive, e la seconda. Ovviamente una lettura in senso orario corrisponde ad una lettura negativa degli angoli. fig. 1 fig. sin(x) e cos(x) In base alla figura 1 si definiscono il seno ed il coseno di un angolo come segue: Sin(x) = PQ OP Cos(x) = OQ OP dove P é un punto liberamente scelto sulla semiretta, libera di ruotare al variare dell angolo, e Q é la proiezione ortogonale di P sulla semiretta fissa. Poiché la figura che si viene a formare in seguito alla proiezione ortogonale del punto P é un triangolo rettangolo, in base alle definizioni date si può asserire che il seno di un angolo rappresenta la misura del cateto opposto all angolo rispetto all ipotenusa assunta come campione di unità di misura lineare, mentre il coseno rappresenta la misura del cateto adiacente all angolo, rispetto alla stessa unità di misura. Dalle precedenti definizioni è facile constatare la convenienza di uniformizzare la scelta di P, per ogni angolo ricorrendo alla circonferenza descritta dallo stesso punto P e scegliendo anche che il raggio di quest ultima sia pari al campione unitario (fig. ). Tale circonferenza viene detta: «circonferenza goniometrica». Tenuto conto di quest ultima scelta si può dire che la coppia (cos x, sin x) rappresenta le coordinate del punto P al variare di questo sulla circonferenza goniometrica conseguentemente al variare dell angolo. tan(x) e cot(x) La tangente trigonometrica di un angolo si definisce ricorrendo all uso di una tangente geometrica condotta per il punto di intersezione della circonferenza trigonometrica con il punto di intersezione di questa con il semiasse positivo delle ascisse. Si ha
2 A10 Trigonometria.nb tan(x) = TA OA Dall analisi dei triangoli OPQ ed OTA, simili fra loro, si dimostra la seguente identità: tan(x) = sin(x) cos(x) La cotangente trigonometrica di un angolo si definisce mediante l uso di una tangente geometrica condotta per il punto di intersezione della circonferenza trigonometrica con il punto di intersezione di questa con il semiasse positivo delle ordinate. Si ha cot(x) = BS OB Dall analisi dei triangoli OPQ ed OBS, simili fra loro, si dimostra la seguente identità: cot(x) = cos(x) sin(x) fig. fig. sec(x) e csc(x) Se si conduce, invece, la tangente geometrica, per ogni punto P che il raggio vettore che descrive l angolo ha in comune con la circonferenza, si ha modo di definire ancora due funzioni goniometriche che sono, appunto, sec(x) e cosec(x). Si ha sec(x) = OS OP Dall analisi dei triangoli OPQ ed OPS, simili fra loro, si dimostra la seguente identità: ed ancora sec(x) = 1 cos(x) csc(x) = OT OP Dall analisi dei triangoli OPQ ed OPT, simili fra loro, si dimostra la seguente identità: csc(x) = 1 sin(x) fig. Se si tiene conto della teoria che riguarda i triangoli rettangoli notevoli con angoli di e di 0 e 60 gradi, é possibile calcolare un consistente numero di valori per ognuna delle funzioni sopra definite con i quali formulare una tabella da cui, poi, conseguono i grafici delle stesse funzioni. Con quanto si é studiato fin qui, é facile giustificare la seguente tavola da cui, poi, discendono i relativi grafici riportati nelle successive figure.
3 A10 Trigonometria.nb fig. 6 fig. 7 tabella dei valori notevoli noti i triangoli rett. speciali x x rad Sin x Cos x Tan x Cot x Sec x Csc x tab. 1 Con i valori calcolati nella precedente tabella è possibile stabilire qual'é il grafico e quali sono le proprietà immediate di ciascuna funzione definita. Sinusoide fig. 8
4 A10 Trigonometria.nb Dominio R Codominio [-1;1] Periodo Considerando f : x sin x come funzione operante da R R non è iniettiva ne suriettiva; come funzione operante da R [-1;1] è suriettiva ma non è iniettiva; come funzione da - ; [- 1; 1] è biiettiva e quindi invertibile. Cosinusoide Dominio R Codominio [-1;1] Periodo Considerando f : x cos x come funzione operante da R R non è iniettiva ne suriettiva; come funzione operante da R [-1;1] è suriettiva ma non è iniettiva; come funzione da [0; ] [- 1; 1] è biiettiva e quindi invertibile. Tangentoide Dominio R - {/ + k} con k Z Codominio R Periodo Considerando f : x tg x come funzione operante da R -{/ + k} R è suriettiva; come funzione operante da ]-/;/[ R è biiettiva e quindi invertibile. fig. 9 fig. 10 fig. 11
5 A10 Trigonometria.nb Cotangentoide Dominio R - {k} con k Z Codominio R Periodo Considerando f : x cotg x come funzione operante da R - {k} R è suriettiva; come funzione operante da ]0 ; [ R è biiettiva e quindi invertibile. fig. 1 fig. 1 Determinare il grafico della Secantoide e quello della Cosecantoide come esercizio. Riepilogo delle proprietà fondamentali Archi associati 1) Sin (x) + Cos (x) = 1 ) Tan(x) = sin(x) cos(x) ) Cot(x) = cos(x) sin(x) ) Sec(x) = 1 cos(x) ) Csc(x) = 1 sin(x) a) Angoli complementari: x e (90-x) Sin(90 - x) = Cos x Cos(90 - x) = Sin x Tan(90 - x) = Cot x Cot(90 - x) = Tan x Sec(90 - x) =... Cosec(90 - x) =... tan(x) cot(x) = 1
6 6 A10 Trigonometria.nb fig. 1 fig. 1 b) Angoli che differiscono di 90 : x e (90+x) Sin(90+x) = Cos x Cos(90+x) = - Sin x Tan(90+x) = - Cot x Cot(90+x) = - Tan x Sec(90+x) =... Cosec(90+x) =... c) Angoli supplementari: x e (180-x) Sin(180-x) = Sin x Cos(180-x) = - Cos x Tan(180-x) = - Tan x Cot(180-x) = - Cot x Sec(180-x) =... Cosec(180-x) =... fig. 16 fig. 17 d) Angoli che differiscono di 180 : x e (180+x) Sin(180+x) = - Sin x Cos(180+x) = - Cos x Tan(180+x) = Tan x Cot(180+x) = Cot x Sec(180+x) =... Cosec(180+x) =... e) Angoli che sommati danno 70: x e (70-x) Sin(70-x) = - Cos x Cos(70-x) = - Sin x Tan(70-x) = Cot x Cot(70-x) = Tan x Sec(70-x) =... Cosec(70-x) =...
7 A10 Trigonometria.nb 7 fig. 18 fig. 19 f) Angoli che differiscono di 70 : x e (70+x) Sin(70+x) = - Cox x Cos(70+x) = Sin x Tan(70+x) = - Cot x Cot(70+x) = - Tan x Sec(70+x) =... Cosec(70+x) =... g) Angoli esplementari: x e (60-x) Sin(60-x) = - Sin x Cos(60-x) = Cos x Tan(60-x) = - Tan x Cot(60-x) = - Cot x Sec(60-x) =... Cosec(60-x) =... fig. 0 fig. 1 h) Angoli che differiscono di 60 : x e (60+x) Sin(60+x) = Sin x Cos(60+x) = Cos x Tan(60+x) = Tan x Cot(60+x) = Cot x Sec(60+x) =... Cosec(60+x) =... g) Angoli opposti: x e -x Sin(-x) = - Sin x Cos(-x) = Cos x Tan(-x) = - Tan x
8 8 A10 Trigonometria.nb Cot(-x) = - Cot x Sec(-x) =... Cosec(-x) =... fig. fig. Dimostrazione della formula di sottrazione del coseno Seguendo la figura si conclude che la corda PQ è uguale alla corda AB, risultando uguali per ipotesi i corrispondenti archi. Inoltre i punti A, B, P e Q hanno le seguenti coordinate: Poiché segue e quindi da cui A = (1, 0) B = [Cos(αα - ββ), Sin(αα - ββ)] P = (Cos αα, Sin αα) Q = (Cos ββ, Sin ββ) AB = PQ AB = PQ [Cos(αα - ββ) - 1] + [Sin(αα - ββ)] = (Cos αα - Cos ββ) + (Sin αα - Sin ββ) Cos (αα - ββ) - Cos(αα - ββ) Sin (αα - ββ) = Cos αα - Cos αα Cos ββ + Cos ββ + Sin αα - Sin αα Sin ββ + Sin ββ applicando la relazione fondamentale della trigonometria al primo come al secondo membro della precedente equazione si ottiene: - Cos(αα - ββ) = - Cos αα Cos ββ - Sin αα Sin ββ da cui semplificando e riducendo Cos(αα - ββ) = Cos αα Cos ββ + Sin αα Sin ββ Dalla formula di sottrazione del coseno discendono, ricorrendo, talora, opportunamente alla teoria degli archi associati e ad alcune delle proprietà formali, tutte le seguenti formule di addizione e sottrazione. Formule di addizione Sin(x+y) = Sinx Cosy + Siny Cosx Cos(x+y) = Cosx Cosy - Sinx Siny Tan(x + y) = tan(x)+tan(y) 1- tan(x) tan(y) Cot(x + y) = cot(x) cot(y)- 1 cot(x)+cot(y) Formule di sottrazione Sin(x-y) = Sinx Cosy - Siny Cosx
9 A10 Trigonometria.nb 9 Cos(x-y) = Cosx Cosy + Sinx Siny Tan(x - y) = tan(x)- tan(y) 1+tan(x) tan(y) Cot(x - y) = cot(x) cot(y)+1 cot(x)- cot(y) Formule di duplicazione Sinx= Sinx Cosx Cosx = Cos x - Sin x Tan( x) = tan(x) 1- tan (x) Cot( x) = cot (x)- 1 cot(x) Formule di Bisezione Sin x = ± 1- cos(x) da cui sin x = 1- cos(x) ; Sin x = 1 - cos(x) Cos x = ± 1+cos(x) da cui Cos x = 1+cos(x) ; Cos x = 1 + Cos(x) Tan x = ± 1- cos(x) 1+cos(x) da cui Tan x = 1- cos(x) 1+cos(x) Cot x = ± 1+cos(x) 1- cos(x) da cui Cot x = 1+cos(x) 1- cos(x) Formule di prostaferesi e di Werner Le formule di prostaferesi permettono di trasformare in prodotti la somma o la differenza di due seni o di due coseni e quindi di rendere logaritmica un espressione polinomia. sin(x) + sin(y) = sin x+y sin(x) - sin(y) = sin x- y cos(x) + cos(y) = cos x+y cos(x) - cos(y) = - sin x+y tan(x) ± tan(y) = cot(x) ± cot(y) = sin(x±y) cos x- y cos x+y cos(x) cos(y) sin(y±x) sin(x) sin(y) cos x- y sin x- y con x e y ( k + 1) con x e y k Al contrario le formule di Werner permettono di trasformare in una somma o in una differenza di coseni oppure di seni il prodotto di due coseni, di due seni o di un seno per un coseno sin(x) cos(y) = 1 (sin(x + y) + sin(x - y)) cos(x) cos(y) = 1 (cos(x + y) + cos(x - y))
10 10 A10 Trigonometria.nb sin(x) sin(y) = - 1 (cos(x + y) - cos(x - y)) dimostrazione delle formule di Werner premesse Si pone αα + ββ = p ed αα - ββ = q sommando e sottraendo membro a membro si ottiene: αα = p+q ed ββ = p- q Tenendo presenti le precedenti posizioni si ricava: Sin p = Sin (αα + ββ) = Sin αα Cos ββ + Sin ββ Cosαα Sin q = Sin (αα - ββ) = Sin αα Cos ββ - Sin ββ Cosαα e sommando membro a membro Sin p + Sin q = Sin αα Cos ββ Sin p + Sin q = Sin p+q mentre sottraendo membro a membro Cos p- q Sin p - Sin q = Sin ββ Cos αα Sin p - Sin q = Sin p- q Cos p+q ovvero ovvero La (1) e la (), tenuto conto delle precedenti premesse, dimostrano le formule di Werner (1) () Sin αα Cos ββ = 1 [Sin (αα + ββ) + Sin (αα - ββ)] così come, procedendo analogamente mediante la funzione coseno, si perviene a: Cos αα Cos ββ = 1 [Cos (αα + ββ) + Cos (αα - ββ)] Sin αα Sin ββ = 1 [Cos (αα + ββ) - Cos (αα - ββ)] tabella dei valori notevoli alla luce delle proprietà goniometriche
11 A10 Trigonometria.nb 11 x x rad Sin x Cos x Tan x Cot x Sec x Csc x calcoli notevoli tab =
12 1 A10 Trigonometria.nb = = 10 - costruzioni grafiche Equazioni gonometriche Una equazione goniometrica può essere sempre ricondotta, ad esempio, alla forma Sin(x) = a oppure Cos(x) = a, Tan(x) = a e le sue soluzioni, come si può dedurre anche dal seguente grafico, sono tutti i valori dell arco (angolo) x tali che: Esempio 01 x = Arcsin(a) Per trovare le soluzioni della equazione Sin x = 1 è sufficiente confrontare graficamente le funzioni: y = Sin x ed y = 1 come avviene nel seguente grafico Da qui si evince che: l equazione ammette soluzioni; che le soluzioni sono infinite; fig. che le soluzioni sono cicliche ovvero che l equazioni ammette due souzioni distinte per ogni ciclo della funzione Sin x e dunque che si ripetono per intervalli regolari. Pertanto le soluzioni della precedente equazione si possono così enunciare: x = + k ( ) x = + k ( ) 6 6 fig.
13 A10 Trigonometria.nb 1 Identità Risolvendo una equazione, si dice che essa costituisce una identità allorché risulta soddisfatta da tutti i valori di x che fanno parte dell'insieme di esistenza dell'equazione stessa. Equazione lineare in senx e cosx e sua omogenea associata a Sin x + b Cos x + c = 0 Le equazioni lineari con termine noto si possono risolvere in uno dei seguenti modi: trasformazione di senx e cosx in tg(x/) tenendo presente che qualora l equazione che ne risulta si abbassi di grado rispetto al secondo occorre aggiungere alle soluzioni trovate le soluzioni «x = p + kp» valori per i quali tg(x/) non è definita, mentre l equazione data in sen x e cos x, si. Si ricordi che valgono le seguenti formule parametriche: Sin(x) = t 1- t ; Cos(x) = con t = tan x 1+t 1+t Metodo grafico - Si possono interpretare e quindi porre Sin x = Y e Cos x = X a condizione che Sin x + Cos x = 1 quindi da a Sin x + b Cos x + c = 0 si passa alla risoluzione del sistema: a X + b Y + c = 0 X + Y = 1 Calcolate le eventuali coppie di punti di intersezione fra retta e circonferenza si risale agli angoli soddisfacenti l equazione lineare assegnata. N.B. Le equazioni omogenee associate alle lineari, ossia a Sin x + b Cos x = 0 oltre che con i metodi sopra esposti, si possono risolvere trasformandole in equazioni nella variabile tg(x), oppure nella variabile cotg(x). Equazioni omogenee di secondo grado con (o senza) termine noto a Sin x + b Cos x + c Sin x Cos x + d = 0 Si osservi, innanzitutto, che è sufficiente trasformare d = d 1 = d Sin x + Cos x e l equazione diventa sempre omogenea pura. A tal punto si procederà trasformando in tg(x) per x + k, soluzioni che occorrerà aggiungere in caso di abbassamento di grado durante la trasformazione in tg(x). Ovviamente in quest ultima circostanza l equazione può essere trasformata in cotg(x). Un secondo criterio di risoluzione consiste nell utilizzo del seguente gruppo di trasformazioni Sin (x) = 1 - Cos( x) Cos (x) = 1 + Cos( x) Sin(x) Cos(x) = Sin( x) Mediante il precedente gruppo di trasformazioni l equazione si trasforma in una lineare in Sin( x) e Cos( x). Questo metodo risulta ottimo per la risoluzione dei sistemi misti. Si noti, infatti, l abbassamento di grado che si ha da un punto di vista algebrico e quindi la possibilità di rappresentare l equazione mediante una retta (od una famiglia di rette in caso di equazione parametrica). Equazione biquadratica in Sin(x) e Cos(x) a Sin x + b Sin x Cos x + c Cos x = 0 Per la sua risoluzione è sufficiente dividere ambo i membri per Cosx 0; così facendo l equazione si
14 1 A10 Trigonometria.nb Per la sua risoluzione è sufficiente dividere ambo i membri per Cosx 0; così facendo l equazione si trasforma in una equazione biquadratica in tg(x): a Tan x + b Tan x + c = 0 N.B. Attenzione anche quì agli eventuali abbassamenti di grado rispetto al quarto: in tal caso occorre integrare le soluzioni come per gli altri casi. Equazioni simmetriche Sono le equazioni che risultano della forma: a Sin x + a Cos x + b Sinx Cos x + c = 0 Si risolvono ponendo x = ( + a). Infatti si ottiene: Elementi di trigonometria Premessa Per convezione, si assume che in ogni triangolo i vertici, i lati ( rispettivamente opposti ai vertici) e gli angoli (relativi a vertici) vengano indicati con la stessa lettera: i vertici con lettere italiane e maiuscole, i lati con lettere italiane e minuscole ed i vertici con lettere greche minuscole. A titolo di esempio si osservi la figura 1. fig. 1 fig. Teoremi sui triangoli rettangoli In ogni triangolo rettangolo si possono enunciare quattro teoremi: essi seguono direttamente dalla definizione del seno e del coseno di uno degli angoli acuti del triangolo. Posto, infatti, che il triangolo sia quello rappresentato in figura, si ha: Sin(αα) = a c a = c Sin(αα) (1) Cos(αα) = b c b = c Cos(αα) () Il primo teorema si enuncia dicendo che in ogni triangolo rettangolo un cateto è dato dal prodotto fra l ipotenusa per il seno dell angolo opposto allo stesso cateto. Il secondo si enuncia, invece, come segue: in ogni triangolo rettangolo un cateto è dato dal prodotto fra l ipotenusa per il coseno dell angolo adiacente allo stesso cateto. Ovviamente quanto detto a proposito dell angol αα si può ripetere a favore dell angolo ββ. Dividendo membro a membro la (1) con la (), prima in un senso e poi nell altro si ottengono i rimanenti teoremi. Infatti si ha: a = c sin(αα) = Tan(αα) a = b Tan(αα) () b c cos(αα) b = c cos(αα) = Cot(αα) b = a Cot(αα) () a c sin(αα) La () si enuncia dicendo che: in ogni triangolo rettangolo un cateto è dato dal prodotto dell altro cateto per la tangente dell angolo opposto al primo. La (), invece, si enuncia: in ogni triangolo rettangolo un cateto è dato dal prodotto fra il secondo cateto per la cotangente dell angolo adiacente al primo.
15 A10 Trigonometria.nb 1 Anche la () come la () possono essere enunciati rispetto all angolo ββ. Teorema della corda Come conseguenza dei teoremi sui triangoli rettangoli è semplice dimostrare che: qualunque corda di una circonferenza è data dal prodotto del diametro della circonferenza per il seno dell'angolo sotto cui è vista da un punto qualsiasi della circonferenza la corda stessa. fig. fig. Una facile applicazione del precedente teorema consiste nel fatto che, poiché ogni triangolo ammette sempre anche la circonferenza circoscritta, ogni suo lato può calcolarsi tramite il teorema della corda. Teorema dei seni o di Eulero "In un qualunque triangolo, il rapporto tra la misura di un lato ed il seno dell'angolo ad esso opposto è costante". Si dimostra, in modo molto semplice, che la costante corrisponde al diametro della circonferenza circoscritta al triangolo stesso. In pratica: a Sin αα = b Sin ββ = c Sin δδ = R fig. fig. 6 Teorema delle proiezioni o di Côtes In ogni triangolo ogni lato è dato dalla somma dei prodotti che si ottengono moltiplicando ciascun altro lato per il coseno dell angolo che esso forma con il primo. In pratica: a = b Cos γγ + c Cos ββ b = a Cos γγ + c Cos αα c = a Cos ββ + b Cos αα fig. 7 fig. 8
16 16 A10 Trigonometria.nb Teorema del Coseno o di Carnot Il teorema è detto inpropriamente teorema di Carnot: il vero scopritore è Viète (XVI secolo) In qualsivoglia triangolo, il quadrato della misura di un lato è uguale alla somma dei quadrati delle misure degli altri lati diminuita del doppio prodotto di questi due lati per il coseno dell angolo opposto al primo lato. In pratica: a b c = b + c - b c Cos (αα) = a + c - a c Cos (ββ) = a + b - a b Cos (γγ) Per la dimostrazione si procede a partire dalle formule che traducono il teorema delle proiezioni, scritte per ogni lato, e dopo semplici passaggi si perviene al risultato sopra enunciato. fig. 9 fig. 10 Il teorema sopra riportato traduce in linguaggio trigonometrico il noto teorema di Ippocrate (estensione di quello di Pitagora): «In ogni triangolo, l area del quadrato costruito su un lato è uguale alla somma delle aree dei quadrati costruiti sugli altri due lati diminuita od aumentata (secondo che l angolo opposto al lato considerato sia acuto oppure ottuso) del doppio dell area del rettangolo le cui dimensioni sono: una la lunghezza di uno di questi due lati e l altra quella della proiezione del restante lato sulla retta di quest ultimo». A questi risultati Ippocrate vi perviene mediante la seguente analisi: nel triangolo acutangolo ma da cui a = h + (c - b') = h + c + b' - c b' h = b - b' a = b - b' + c + b' - c b' a = b + c - c b' Per vedere nell ultima equazione il teorema del coseno basta tenere presente che b' = b Cos αα nel triangolo ottusangolo ma da cui a = h + (c + b') = h + c + b' + c b' h = b - b' a = b - b' + c + b' + c b' a = b + c + c b' Per vedere nell ultima equazione il teorema del coseno basta tenere presente che b' = - b Cos αα N.B. Mediante permutazioni circolari si ottengono le rimanenti due relazioni relative agli altri due lati. b = a + c - a c Cos ββ
17 A10 Trigonometria.nb 17 c = b + a - a b Cos γγ Formula di Erone Tenuto conto che p indica il semiperimetro del triangolo e che al solito a, b, c indicano le misure dei lati, l area A del superficie del triangolo vale: A = p(p - a) (p - b) (p - c) Tale formula si riesce facilmente a dimostrare sia per via geometrica che per via trigonometrica. Teorema delle tangenti o di Nepero Il teorema è detto inpropriamente teorema di Nepero: il vero scopritore è Finck (XVI secolo) In un qualunque triangolo: «la somma di due lati sta alla loro differenza come la tangente della somma degli angoli opposti sta alla tangente della loro semidifferenza»: a+b a- b = tan αα+ββ tan αα- ββ a+c a- c = tan αα+γγ tan αα- γγ b+c b- c = tan ββ+γγ tan ββ- γγ ed analogamente Formule di Briggs (Enrico Briggs, matematico inglese ) Associando le formule relative al teorema del coseno o di Carnot a quelle di bisezione degli archi si giunge alle formule di Briggs, le quali sono logaritmiche e consentono di calcolare gli angoli αα, ββ, γγ quando sono noti i lati a, b, c. In pratica si ottiene: Sin αα = (p- b) (p- c) b c Cos αα = p(p- a) bc Tan αα = (p- b) (p- c) p(p- a) ed analogamente Tan ββ = (p- a) (p- c) p(p- b) Tan γγ = (p- a) (p- b) p(p- c) Applicazioni Esercizi
funzioni goniometriche ed elementi di trigonometria Matematica di Base - Ingegneria UniUD
 funzioni goniometriche ed elementi di trigonometria idoro.sciarratta@alice.it Matematica di Base - Ingegneria UniUD y P O α Q x Definizione di Sinα e Cosα O y α Q Sin( α ) = PQ OP Cos( α ) = OQ P x OP
funzioni goniometriche ed elementi di trigonometria idoro.sciarratta@alice.it Matematica di Base - Ingegneria UniUD y P O α Q x Definizione di Sinα e Cosα O y α Q Sin( α ) = PQ OP Cos( α ) = OQ P x OP
GONIOMETRIA. sin (x) = PH OP. ctg (x ) = cos (x) = CB sin (x) cosec (x ) = 1 = ON sin (x)
 GONIOMETRIA sin (x = PH OP cos (x = OH OP tg (x = sin(x = TA cos(x ctg (x = cos (x = CB sin (x sec (x = 1 = OM cos(x cosec (x = 1 = ON sin (x La tangente si calcola sempre sulla retta verticale passante
GONIOMETRIA sin (x = PH OP cos (x = OH OP tg (x = sin(x = TA cos(x ctg (x = cos (x = CB sin (x sec (x = 1 = OM cos(x cosec (x = 1 = ON sin (x La tangente si calcola sempre sulla retta verticale passante
CORSO ZERO DI MATEMATICA
 UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA GONIOMETRIA E TRIGONOMETRIA Dr. Erasmo Modica erasmo@galois.it RADIANTI E CIRCONFERENZA GONIOMETRICA Definizione: Si dice
UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA GONIOMETRIA E TRIGONOMETRIA Dr. Erasmo Modica erasmo@galois.it RADIANTI E CIRCONFERENZA GONIOMETRICA Definizione: Si dice
RADIANTI E CIRCONFERENZA GONIOMETRICA
 Facoltà di Medicina e Chirurgia Corso Zero di Matematica Gruppi: MC-MF / PS-MF IV Lezione TRIGONOMETRIA Dr. E. Modica erasmo@galois.it RADIANTI E CIRCONFERENZA GONIOMETRICA Definizione: Si dice angolo
Facoltà di Medicina e Chirurgia Corso Zero di Matematica Gruppi: MC-MF / PS-MF IV Lezione TRIGONOMETRIA Dr. E. Modica erasmo@galois.it RADIANTI E CIRCONFERENZA GONIOMETRICA Definizione: Si dice angolo
RADIANTI E CIRCONFERENZA GONIOMETRICA
 CORSO ZERO DI MATEMATICA per Ing. Chimica e Ing. delle Telecomunicazioni GONIOMETRIA E TRIGONOMETRIA Prof. Erasmo Modica erasmo@galois.it RADIANTI E CIRCONFERENZA GONIOMETRICA Definizione: Si dice angolo
CORSO ZERO DI MATEMATICA per Ing. Chimica e Ing. delle Telecomunicazioni GONIOMETRIA E TRIGONOMETRIA Prof. Erasmo Modica erasmo@galois.it RADIANTI E CIRCONFERENZA GONIOMETRICA Definizione: Si dice angolo
dove i simboli α gradi ed α radianti indicano rispettivamente la misura dell angolo in gradi ed in radianti. Da qui si ottengono le seguenti formule
 8 Trigonometria 81 Seno, coseno, tangente Un angolo α può essere definito geometricamente come la parte di piano compresa tra due semirette, dette lati dell angolo, aventi origine nello stesso punto O,
8 Trigonometria 81 Seno, coseno, tangente Un angolo α può essere definito geometricamente come la parte di piano compresa tra due semirette, dette lati dell angolo, aventi origine nello stesso punto O,
APPUNTI DI GONIOMETRIA
 APPUNTI DI GONIOMETRIA RADIANTI E CIRCONFERENZA GONIOMETRICA Definizione: Si dice angolo ciascuna delle due parti in cui un piano è diviso da due semirette aventi la stessa origine. Definizione: Dicesi
APPUNTI DI GONIOMETRIA RADIANTI E CIRCONFERENZA GONIOMETRICA Definizione: Si dice angolo ciascuna delle due parti in cui un piano è diviso da due semirette aventi la stessa origine. Definizione: Dicesi
TRIGONOMETRIA. Un angolo si misura in gradi. Un grado è la novantesima parte di un angolo retto.
 TRIGONOMETRIA DA RICORDARE: Due angoli si dicono supplementari quando la loro somma è pari a 80 Due angoli si dicono complementari quando la loro somma è pari a 90 Due angoli si dicono opposti quando la
TRIGONOMETRIA DA RICORDARE: Due angoli si dicono supplementari quando la loro somma è pari a 80 Due angoli si dicono complementari quando la loro somma è pari a 90 Due angoli si dicono opposti quando la
Goniometria e Trigonometria
 Università degli studi di Modena e Reggio Emilia Dipartimento di Scienze e Metodi dell Ingegneria Corso MOOC Iscriversi a Ingegneria Reggio Emilia Introduzione La goniometria è la parte della matematica
Università degli studi di Modena e Reggio Emilia Dipartimento di Scienze e Metodi dell Ingegneria Corso MOOC Iscriversi a Ingegneria Reggio Emilia Introduzione La goniometria è la parte della matematica
TRIGONOMETRIA. Ripasso veloce
 TRIGONOMETRIA Ripasso veloce Definizioni principali Sia u un segmento con un estremo nell origine e l altro sulla circonferenza di centro l origine e raggio (circonferenza goniometrica) che formi un angolo
TRIGONOMETRIA Ripasso veloce Definizioni principali Sia u un segmento con un estremo nell origine e l altro sulla circonferenza di centro l origine e raggio (circonferenza goniometrica) che formi un angolo
Banca Dati Finale Senza Risposte
 Banca Dati Finale Senza Risposte TRG da 5451 a 6100 5451 La tangente di un angolo di 90 : A) è 1 B) è 0 C) non è definita D) è 1 5452 Quanto vale in gradi un angolo di (5/4) π radianti? A) 240 B) 270 C)
Banca Dati Finale Senza Risposte TRG da 5451 a 6100 5451 La tangente di un angolo di 90 : A) è 1 B) è 0 C) non è definita D) è 1 5452 Quanto vale in gradi un angolo di (5/4) π radianti? A) 240 B) 270 C)
Teoria in sintesi 10. Teoria in sintesi 14
 Indice L attività di recupero Funzioni goniometriche Teoria in sintesi 0 Obiettivo Calcolare il valore di espressioni goniometriche in seno e coseno Obiettivo Determinare massimo e minimo di funzioni goniometriche
Indice L attività di recupero Funzioni goniometriche Teoria in sintesi 0 Obiettivo Calcolare il valore di espressioni goniometriche in seno e coseno Obiettivo Determinare massimo e minimo di funzioni goniometriche
HP VP. (rispettivamente seno, coseno e tangente di β)
 Trigonometria Prerequisiti: Nozione di angolo e di arco. Obiettivi convertire le misure degli angoli dai gradi ai radianti e viceversa; sapere le relazioni fra gli elementi (lati, angoli) di un triangolo;
Trigonometria Prerequisiti: Nozione di angolo e di arco. Obiettivi convertire le misure degli angoli dai gradi ai radianti e viceversa; sapere le relazioni fra gli elementi (lati, angoli) di un triangolo;
Capitolo 8: introduzione alla trigonometria
 Capitolo 8: introduzione alla trigonometria 8.1 Trasformare da gradi sessagesimali a radianti o viceversa a 0 0 ; b 70 0 ; c 60 0 ; d 1 0 ; e 5 0 ; f 15 0 ; g 5 0 ; h 15 0 ; i 10 0 0 ; j 1 0 9 ; k 1 0
Capitolo 8: introduzione alla trigonometria 8.1 Trasformare da gradi sessagesimali a radianti o viceversa a 0 0 ; b 70 0 ; c 60 0 ; d 1 0 ; e 5 0 ; f 15 0 ; g 5 0 ; h 15 0 ; i 10 0 0 ; j 1 0 9 ; k 1 0
1 Funzioni trigonometriche
 1 Funzioni trigonometriche 1 1 Funzioni trigonometriche Definizione 1.1. Si definisce circonferenza goniometrica la circonferenza centrata nell origine di un piano cartesiano e raggio unitario. L equazione
1 Funzioni trigonometriche 1 1 Funzioni trigonometriche Definizione 1.1. Si definisce circonferenza goniometrica la circonferenza centrata nell origine di un piano cartesiano e raggio unitario. L equazione
SENO, COSENO E TANGENTE DI UN ANGOLO
 Goniometria e trigonometria Misurare gli angoli nel sistema circolare L unità di misura del sistema circolare è il radiante def. Un radiante è la misura di un angolo alla circonferenza che sottende un
Goniometria e trigonometria Misurare gli angoli nel sistema circolare L unità di misura del sistema circolare è il radiante def. Un radiante è la misura di un angolo alla circonferenza che sottende un
\ 0 1,2,3,4,... P 0,2,4,6,... D 1,3,5,7,... Simboli. Appartenenza ad un insieme. \ Insieme privato di 0,1,2,3,... Insieme dei numeri naturali.
 Simboli Appartenenza ad un insieme. \ Insieme privato di 0,,,,... Insieme dei numeri naturali. 0 \ 0,,,,... Insieme dei numeri naturali privato dello zero. P 0,,,6,... Insieme dei numeri naturali pari.
Simboli Appartenenza ad un insieme. \ Insieme privato di 0,,,,... Insieme dei numeri naturali. 0 \ 0,,,,... Insieme dei numeri naturali privato dello zero. P 0,,,6,... Insieme dei numeri naturali pari.
1. conoscere la terminologia e le proprietà dei logaritmi e saperne utilizzare le regole di calcolo
 Quinto modulo: Funzioni Obiettivi. conoscere la terminologia e le proprietà dei logaritmi e saperne utilizzare le regole di calcolo. saper operare con le funzioni esponenziale e logaritmo per risolvere
Quinto modulo: Funzioni Obiettivi. conoscere la terminologia e le proprietà dei logaritmi e saperne utilizzare le regole di calcolo. saper operare con le funzioni esponenziale e logaritmo per risolvere
 Trigonometria 5451 La tangente di un angolo di 90 : A) è 1 B) è 0 C) non è definita D) è 1 5452 Quanto vale in gradi un angolo di (4/3) π radianti? A) 240 B) 245 C) 230 D) 120 5453 La tangentoide è la
Trigonometria 5451 La tangente di un angolo di 90 : A) è 1 B) è 0 C) non è definita D) è 1 5452 Quanto vale in gradi un angolo di (4/3) π radianti? A) 240 B) 245 C) 230 D) 120 5453 La tangentoide è la
Dato un angolo α e il suo complementare (π/2 α) il seno del complementare equivale a:
 6651 6652 6653 6654 6655 6656 6657 6658 L'equazione 2 senx 1 = 0 per 0 x < 2π ha: A) una soluzione B) quattro soluzioni C) solo due soluzioni D) infinite soluzioni Dato l'angolo α di 90, si può affermare
6651 6652 6653 6654 6655 6656 6657 6658 L'equazione 2 senx 1 = 0 per 0 x < 2π ha: A) una soluzione B) quattro soluzioni C) solo due soluzioni D) infinite soluzioni Dato l'angolo α di 90, si può affermare
Scopo della trigonometria è la risoluzione di un triangolo a partire da un numero minimo di informazioni sul triangolo steso che come sappiamo è 3.
 MODULO 3 LEZIONE 3 parte 2 Trigonometria: La risoluzione dei triangoli. Scopo della trigonometria è la risoluzione di un triangolo a partire da un numero minimo di informazioni sul triangolo steso che
MODULO 3 LEZIONE 3 parte 2 Trigonometria: La risoluzione dei triangoli. Scopo della trigonometria è la risoluzione di un triangolo a partire da un numero minimo di informazioni sul triangolo steso che
Angolo. Si chiama angolo ciascuna delle due parti di piano in cui esso è diviso da due semirette uscenti da uno stesso punto O.
 Angolo Si chiama angolo ciascuna delle due parti di piano in cui esso è diviso da due semirette uscenti da uno stesso punto O. Trigonometria - Corso di matematica - Alessia Ceccato 1 Circonferenza goniometrica
Angolo Si chiama angolo ciascuna delle due parti di piano in cui esso è diviso da due semirette uscenti da uno stesso punto O. Trigonometria - Corso di matematica - Alessia Ceccato 1 Circonferenza goniometrica
che ci permette di passare da un sistema di misura all'altro con le:
 Goniometria Misura degli angoli Gli angoli vengono spesso misurati in gradi sessagesimali (1 = 1/360 dell'angolo giro), anche se una Legge dello Stato italiano del 1960 impone di esprimerli in radianti.
Goniometria Misura degli angoli Gli angoli vengono spesso misurati in gradi sessagesimali (1 = 1/360 dell'angolo giro), anche se una Legge dello Stato italiano del 1960 impone di esprimerli in radianti.
COMPITI PER IL RECUPERO DELLA CARENZA FORMATIVA (E RIPASSO) MATEMATICA III - A PT
 1 COMPITI PER IL RECUPERO DELLA CARENZA FORMATIVA (E RIPASSO) MATEMATICA III - A PT Scheda 1: Fondamenti di geometria analitica 1. Determina il punto P dell asse y che forma con A(; ) e B(; ) un triangolo
1 COMPITI PER IL RECUPERO DELLA CARENZA FORMATIVA (E RIPASSO) MATEMATICA III - A PT Scheda 1: Fondamenti di geometria analitica 1. Determina il punto P dell asse y che forma con A(; ) e B(; ) un triangolo
Liceo Scientifico Severi Salerno
 Liceo Scientifico Severi Salerno VERIFICA DI MATEMATICA Docente: Pappalardo Vincenzo Data: 11/04/019 Classe: 4D 1. Risolvere le seguenti equazioni e disequazioni goniometriche: tg x π 34 = ctg x + π 3
Liceo Scientifico Severi Salerno VERIFICA DI MATEMATICA Docente: Pappalardo Vincenzo Data: 11/04/019 Classe: 4D 1. Risolvere le seguenti equazioni e disequazioni goniometriche: tg x π 34 = ctg x + π 3
COMPITI PER IL RECUPERO DELLA CARENZA FORMATIVA (E RIPASSO) MATEMATICA III - VE
 1 COMPITI PER IL RECUPERO DELLA CARENZA FORMATIVA (E RIPASSO) MATEMATICA III - VE Scheda 1: Fondamenti di geometria analitica 1. Determina il punto P dell asse y che forma con A(; ) e B(; ) un triangolo
1 COMPITI PER IL RECUPERO DELLA CARENZA FORMATIVA (E RIPASSO) MATEMATICA III - VE Scheda 1: Fondamenti di geometria analitica 1. Determina il punto P dell asse y che forma con A(; ) e B(; ) un triangolo
Anno Scolastico:
 LICEO SCIENTIFICO DI STATO "G. BATTAGLINI" TARANTO PROGRAMMA DI MATEMATICA svolto nella Classe III Sezione A. Anno Scolastico: 2012-2013. Docente: Francesco Pantano. 1. Disequazioni. Richiami sulle disequazioni
LICEO SCIENTIFICO DI STATO "G. BATTAGLINI" TARANTO PROGRAMMA DI MATEMATICA svolto nella Classe III Sezione A. Anno Scolastico: 2012-2013. Docente: Francesco Pantano. 1. Disequazioni. Richiami sulle disequazioni
IIS A.Moro Dipartimento di Matematica e Fisica
 IIS A.Moro Dipartimento di Matematica e Fisica Obiettivi minimi per le classi quarte - Matematica UNITA DIDATTICA CONOSCENZE COMPETENZE ABILITA Coniche e luoghi geometrici Le coniche Le coniche e i luoghi
IIS A.Moro Dipartimento di Matematica e Fisica Obiettivi minimi per le classi quarte - Matematica UNITA DIDATTICA CONOSCENZE COMPETENZE ABILITA Coniche e luoghi geometrici Le coniche Le coniche e i luoghi
Gli insiemi, la logica
 Gli insiemi, la logica 1 Dato l insieme A = {x N : x < 5}, quale delle seguenti affermazioni è falsa: (a) 1 A (b) 5 / A (c) A (d) A risp (e) {1, } A Sono dati gli insiemi A = {, 5, 7, 9} e B = {5, 7} Quali
Gli insiemi, la logica 1 Dato l insieme A = {x N : x < 5}, quale delle seguenti affermazioni è falsa: (a) 1 A (b) 5 / A (c) A (d) A risp (e) {1, } A Sono dati gli insiemi A = {, 5, 7, 9} e B = {5, 7} Quali
Programma svolto nell'a.s. 2016/2017 Disciplina: Matematica. Classe: 4D Docente: Prof. Ezio Pignatelli Programma sintetico.
 Programma svolto nell'a.s. 2016/2017 Disciplina: Matematica. Classe: 4D Docente: Prof. Ezio Pignatelli Programma sintetico. 1. Funzione esponenziale e logaritmica. a) Riepilogo delle proprietà delle potenze.
Programma svolto nell'a.s. 2016/2017 Disciplina: Matematica. Classe: 4D Docente: Prof. Ezio Pignatelli Programma sintetico. 1. Funzione esponenziale e logaritmica. a) Riepilogo delle proprietà delle potenze.
Programma di Matematica Liceo Scientifico A. Romita Classe: 4G a.s.:2015 / 2016
 Programma di Matematica Liceo Scientifico A. Romita Classe: 4G a.s.:2015 / 2016 Le funzioni goniometriche La misura degli angoli Gli angoli e la loro ampiezza La misura in gradi La misura i radianti Dai
Programma di Matematica Liceo Scientifico A. Romita Classe: 4G a.s.:2015 / 2016 Le funzioni goniometriche La misura degli angoli Gli angoli e la loro ampiezza La misura in gradi La misura i radianti Dai
2. Calcola, enunciando, descrivendo e applicando la definizione, la derivata della 2
 Domande di matematica per l esame di stato per il liceo classico Analisi matematica 1. Spiega quando una funzione è un infinitesimo e quando è un infinito per x che tende a x 0. Quali sono i possibili
Domande di matematica per l esame di stato per il liceo classico Analisi matematica 1. Spiega quando una funzione è un infinitesimo e quando è un infinito per x che tende a x 0. Quali sono i possibili
FORMULARIO DEI TRIANGOLI
 RISOLUZIONE TRIANGOLI GENERICI Pagina 1 di 15 FORMULARIO DEI TRIANGOLI Teorema di Pitagora OP= 1 PP = sen OP = cos QQ = tan = Definizione seno Definizione coseno Definizione tangente TT = cotan = Consideriano
RISOLUZIONE TRIANGOLI GENERICI Pagina 1 di 15 FORMULARIO DEI TRIANGOLI Teorema di Pitagora OP= 1 PP = sen OP = cos QQ = tan = Definizione seno Definizione coseno Definizione tangente TT = cotan = Consideriano
Goniometria Domande, Risposte & Esercizi
 Goniometria Domande, Risposte & Esercizi Angoli e Archi. Dare la definizione di grado sessagesimale (DMS). Il grado sessagesimale si definisce come la 36ª parte di un angolo giro. Esso viene indicato con
Goniometria Domande, Risposte & Esercizi Angoli e Archi. Dare la definizione di grado sessagesimale (DMS). Il grado sessagesimale si definisce come la 36ª parte di un angolo giro. Esso viene indicato con
Formule Utili Analisi Matematica per Informatici a.a
 Formule Utili Analisi Matematica per Informatici a.a. 006-007 Dott. Simone Zuccher dicembre 006 Nota. Queste pagine potrebbero contenere degli errori: chi li trova è pregato di segnalarli all autore zuccher@sci.univr.it).
Formule Utili Analisi Matematica per Informatici a.a. 006-007 Dott. Simone Zuccher dicembre 006 Nota. Queste pagine potrebbero contenere degli errori: chi li trova è pregato di segnalarli all autore zuccher@sci.univr.it).
FUNZIONI TRIGONOMETRICHE
 FUNZIONI TRIGONOMETRICHE RICHIAMI DI TEORIA Definizione: si dice angolo positivo individuato dalla coppia di semirette r e r' uscenti dal punto O, l'insieme dei punti del piano descritti dai punti di r
FUNZIONI TRIGONOMETRICHE RICHIAMI DI TEORIA Definizione: si dice angolo positivo individuato dalla coppia di semirette r e r' uscenti dal punto O, l'insieme dei punti del piano descritti dai punti di r
TRIGONOMETRIA E COORDINATE
 Y Y () X O (Y Y ) - α X (X X ) 200 c TRIGONOMETRI E OORDINTE ngoli e sistemi di misura angolare Funzioni trigonometriche Risoluzione dei triangoli rettangoli Risoluzione dei poligoni Risoluzione dei triangoli
Y Y () X O (Y Y ) - α X (X X ) 200 c TRIGONOMETRI E OORDINTE ngoli e sistemi di misura angolare Funzioni trigonometriche Risoluzione dei triangoli rettangoli Risoluzione dei poligoni Risoluzione dei triangoli
Risoluzione dei triangoli rettangoli
 Risoluzione dei triangoli rettangoli In questa dispensa esamineremo il problema della risoluzione dei triangoli rettangoli. Riprendendo la definizione di seno e coseno, mostreremo come questi si possano
Risoluzione dei triangoli rettangoli In questa dispensa esamineremo il problema della risoluzione dei triangoli rettangoli. Riprendendo la definizione di seno e coseno, mostreremo come questi si possano
Gli insiemi, la logica
 Gli insiemi, la logica 1 Dato l insieme A = {x N : x < 5}, quale delle seguenti affermazioni è falsa: (a) 1 A (b) 5 / A (c) 2 A (d) A (e) {1, } A 2 Sono dati gli insiemi A = {, 5, 7, 9} e B = {5, 7} Quali
Gli insiemi, la logica 1 Dato l insieme A = {x N : x < 5}, quale delle seguenti affermazioni è falsa: (a) 1 A (b) 5 / A (c) 2 A (d) A (e) {1, } A 2 Sono dati gli insiemi A = {, 5, 7, 9} e B = {5, 7} Quali
Il coseno di un angolo
 Il coseno di un angolo Per capire cos è il coseno di un angolo dobbiamo fare riferimento alla circonferenza goniometrica. Prendiamo un angolo a sulla nostra circonferenza tracciano una linea dall origine.
Il coseno di un angolo Per capire cos è il coseno di un angolo dobbiamo fare riferimento alla circonferenza goniometrica. Prendiamo un angolo a sulla nostra circonferenza tracciano una linea dall origine.
Programma di Matematica Anno Scolastico 2012/2013 Classe III G
 Liceo Scientifico Statale G. BATTAGLINI Corso Umberto I 74100 Taranto Programma di Matematica Anno Scolastico 2012/2013 Classe III G Prof. Paolo Pantano Richiami di Algebra Equazioni e disequazioni Definizioni.
Liceo Scientifico Statale G. BATTAGLINI Corso Umberto I 74100 Taranto Programma di Matematica Anno Scolastico 2012/2013 Classe III G Prof. Paolo Pantano Richiami di Algebra Equazioni e disequazioni Definizioni.
Funzioni elementari: funzioni trigonometriche 1 / 17
 Funzioni elementari: funzioni trigonometriche 1 / 17 La circonferenza di equazione x 2 + y 2 = 1 é detta circonferenza goniometrica. La circonferenza goniometrica 1 P 1 α 0 A 1 2 / 17 La circonferenza
Funzioni elementari: funzioni trigonometriche 1 / 17 La circonferenza di equazione x 2 + y 2 = 1 é detta circonferenza goniometrica. La circonferenza goniometrica 1 P 1 α 0 A 1 2 / 17 La circonferenza
Liceo Scientifico Statale Einstein
 Liceo Scientifico Statale Einstein PROGRAMMA CONSUNTIVO MATEMATICA Classe IV I Anno Scolastico 2017-2018 Docente: prof. Barbara Veronesi Ore di insegnamento: 4 settimanali Funzioni Classificazione delle
Liceo Scientifico Statale Einstein PROGRAMMA CONSUNTIVO MATEMATICA Classe IV I Anno Scolastico 2017-2018 Docente: prof. Barbara Veronesi Ore di insegnamento: 4 settimanali Funzioni Classificazione delle
Liceo Scientifico Statale Leonardo da Vinci Reggio Calabria. PROGRAMMA DI MATEMATICA Per la classe IV sez.d Anno scolastico 2012/13
 Liceo Scientifico Statale Leonardo da Vinci Reggio Calabria PROGRAMMA DI MATEMATICA Per la classe IV sez.d Anno scolastico 2012/13 Modulo 1: Le coniche Geometria elementare retta e circonferenza nel piano
Liceo Scientifico Statale Leonardo da Vinci Reggio Calabria PROGRAMMA DI MATEMATICA Per la classe IV sez.d Anno scolastico 2012/13 Modulo 1: Le coniche Geometria elementare retta e circonferenza nel piano
FUNZIONI GONIOMETRICHE
 FUNZIONI GONIOMETRICHE ANGOLI Col termine angolo indichiamo la parte di piano limitata da due semirette aventi la stessa origine, chiamata vertice. Possiamo definire anche l angolo come la parte di piano
FUNZIONI GONIOMETRICHE ANGOLI Col termine angolo indichiamo la parte di piano limitata da due semirette aventi la stessa origine, chiamata vertice. Possiamo definire anche l angolo come la parte di piano
Formule Utili Analisi Matematica per Bioinformatici a.a
 Formule Utili Analisi Matematica per Bioinformatici a.a. 007-008 Dott. Simone Zuccher settembre 007 Nota. Queste pagine potrebbero contenere degli errori: chi li trova è pregato di segnalarli all autore
Formule Utili Analisi Matematica per Bioinformatici a.a. 007-008 Dott. Simone Zuccher settembre 007 Nota. Queste pagine potrebbero contenere degli errori: chi li trova è pregato di segnalarli all autore
LE FUNZIONI TRIGONOMETRICHE. Prof.ssa CaterinaVespia
 LE FUNZIONI TRIGONOMETRICHE 1 LE FUNZIONI SENO E COSENO Detto P il punto sulla circonferenza che è associato all angolo α, e H il punto della proiezione di P sull asse delle x, si definisce: coseno seno
LE FUNZIONI TRIGONOMETRICHE 1 LE FUNZIONI SENO E COSENO Detto P il punto sulla circonferenza che è associato all angolo α, e H il punto della proiezione di P sull asse delle x, si definisce: coseno seno
Copyright Esselibri S.p.A.
 .2. Risoluzione di triangoli qualsiasi In questo paragrafo estenderemo le funzioni goniometriche anche ad angoli retti ed ottusi, per potere risolvere triangoli qualsiasi. er fare ciò ovviamente vogliamo
.2. Risoluzione di triangoli qualsiasi In questo paragrafo estenderemo le funzioni goniometriche anche ad angoli retti ed ottusi, per potere risolvere triangoli qualsiasi. er fare ciò ovviamente vogliamo
I LICEO CLASSICO. Le equazioni e le disequazioni di II grado e di grado superiore
 CONOSCENZE indirizzo CLASSICO I LICEO CLASSICO Le equazioni e le disequazioni di II grado e di grado superiore Equazioni di secondo grado incomplete; equazioni di secondo grado complete; formula risolutiva
CONOSCENZE indirizzo CLASSICO I LICEO CLASSICO Le equazioni e le disequazioni di II grado e di grado superiore Equazioni di secondo grado incomplete; equazioni di secondo grado complete; formula risolutiva
Liceo Scientifico Severi Salerno
 Liceo Scientifico Severi Salerno VERIFICA DI MATEMATICA Docente: Pappalardo Vincenzo Data: 11/04/019 Classe: 4D 1. Risolvere le seguenti equazioni e disequazioni goniometriche: π sen x = cos x 3 sen x
Liceo Scientifico Severi Salerno VERIFICA DI MATEMATICA Docente: Pappalardo Vincenzo Data: 11/04/019 Classe: 4D 1. Risolvere le seguenti equazioni e disequazioni goniometriche: π sen x = cos x 3 sen x
Note di trigonometria
 Note di trigonometria Daniel Gessuti indice Elementi di Trigonometria Seno, coseno e tangente Relazione fondamentale Secante, cosecante e cotangente 3 Le funzioni seno, coseno e tangente e le loro inverse
Note di trigonometria Daniel Gessuti indice Elementi di Trigonometria Seno, coseno e tangente Relazione fondamentale Secante, cosecante e cotangente 3 Le funzioni seno, coseno e tangente e le loro inverse
Trigonometria angoli e misure
 Trigonometria angoli e misure ITIS Feltrinelli anno scolastico 27-28 R. Folgieri 27-28 1 Angoli e gradi Due semirette che condividono la stessa origine danno luogo ad un angolo. Le due semirette (che si
Trigonometria angoli e misure ITIS Feltrinelli anno scolastico 27-28 R. Folgieri 27-28 1 Angoli e gradi Due semirette che condividono la stessa origine danno luogo ad un angolo. Le due semirette (che si
CLASSI: TerzeMateria: MATEMATICA e COMPLEMENTIOre settimanali previste: 4
 CLASSI: TerzeMateria: MATEMATICA e COMPLEMENTIOre settimanali previste: 4 modulo Titolo Modulo Titolo unità didattiche Ore previste Periodo Competenze Modulo 1 RACCORDO CON IL BIENNIO EQUAZIONI (SISTEMI)
CLASSI: TerzeMateria: MATEMATICA e COMPLEMENTIOre settimanali previste: 4 modulo Titolo Modulo Titolo unità didattiche Ore previste Periodo Competenze Modulo 1 RACCORDO CON IL BIENNIO EQUAZIONI (SISTEMI)
TRIGONOMETRIA PIANA: I TRIANGOLI QUALUNQUE
 TRIGONOMETRIA PIANA: I TRIANGOLI QUALUNQUE IL TEOREMA DEI SENI TEOREMA In un triangolo le misure dei lati sono proporzionali ai seni degli angoli opposti. IL TEOREMA DEI SENI DIMOSTRAZIONE Consideriamo
TRIGONOMETRIA PIANA: I TRIANGOLI QUALUNQUE IL TEOREMA DEI SENI TEOREMA In un triangolo le misure dei lati sono proporzionali ai seni degli angoli opposti. IL TEOREMA DEI SENI DIMOSTRAZIONE Consideriamo
I.S.I.S.S. U. FOSCOLO TEANO
 I.S.I.S.S. U. FOSCOLO TEANO PROGRAMMAZIONE ANNUALE A.S. 2018-19 Materia: matematica Classe 4^A S Docente: Mesolella Giuseppina SITUAZIONE DI PARTENZA Classe vivace dal punto di vista comportamentale, generalmente
I.S.I.S.S. U. FOSCOLO TEANO PROGRAMMAZIONE ANNUALE A.S. 2018-19 Materia: matematica Classe 4^A S Docente: Mesolella Giuseppina SITUAZIONE DI PARTENZA Classe vivace dal punto di vista comportamentale, generalmente
COMPENDIO TRIGONOMETRIA
 TORINO MAGGIO 2011 COMPENDIO DI TRIGONOMETRIA di Bart VEGLIA 1 FUNZIONI GONIOMETRICHE 1 Premessa La trigonometria ha lo scopo, come dice il nome, (dal greco, trigonon = triangolo e metron = misura) di
TORINO MAGGIO 2011 COMPENDIO DI TRIGONOMETRIA di Bart VEGLIA 1 FUNZIONI GONIOMETRICHE 1 Premessa La trigonometria ha lo scopo, come dice il nome, (dal greco, trigonon = triangolo e metron = misura) di
Funzioni. iniettiva se x y = f (x) f (y) o, equivalentemente, f (x) = f (y) = x = y
 Funzioni. Dati due insiemi A e B (non necessariamente distinti) si chiama funzione da A a B una qualunque corrispondenza (formula, regola) che associa ad ogni elemento di A uno ed un solo elemento di B.
Funzioni. Dati due insiemi A e B (non necessariamente distinti) si chiama funzione da A a B una qualunque corrispondenza (formula, regola) che associa ad ogni elemento di A uno ed un solo elemento di B.
ISTITUTO TECNICO INDUSTRIALE G. FERRARIS
 ISTITUTO TECNICO INDUSTRIALE G. FERRARIS EMPOLI PIANO DI LAVORO PROF. BICCI ANDREA CONSIGLIO DI CLASSE 3 SEZ. B Informatica INDIRIZZO INFORMATICO ANNO SCOLASTICO 2015-2016 MATERIE MATEMATICA (tre ore settimanali)
ISTITUTO TECNICO INDUSTRIALE G. FERRARIS EMPOLI PIANO DI LAVORO PROF. BICCI ANDREA CONSIGLIO DI CLASSE 3 SEZ. B Informatica INDIRIZZO INFORMATICO ANNO SCOLASTICO 2015-2016 MATERIE MATEMATICA (tre ore settimanali)
Problemi sulla circonferenza verso l esame di stato
 Problemi sulla circonferenza verso l esame di stato * * * n. 0 pag. 06 a) Scrivi l equazione della circonferenza γ 1 di centro P ; ) e passante per il punto A0; 1). b) Scrivi l equazione della circonferenza
Problemi sulla circonferenza verso l esame di stato * * * n. 0 pag. 06 a) Scrivi l equazione della circonferenza γ 1 di centro P ; ) e passante per il punto A0; 1). b) Scrivi l equazione della circonferenza
ISTITUTO TECNICO TECNOLOGICO STATALE G.
 ISTITUTO TECNICO TECNOLOGICO STATALE G. e M. MONTANI FERMO Anno Scolastico 2015/ 16 PROGRAMMA SVOLTO DI MATEMATICA 3 ore settimanali COMPLEMENTI DI MATEMATICA 1 ora settimanale Classe: 3^ INFORMATICA sez.
ISTITUTO TECNICO TECNOLOGICO STATALE G. e M. MONTANI FERMO Anno Scolastico 2015/ 16 PROGRAMMA SVOLTO DI MATEMATICA 3 ore settimanali COMPLEMENTI DI MATEMATICA 1 ora settimanale Classe: 3^ INFORMATICA sez.
Corso multimediale di matematica
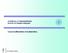 2006 ACCENI ALLA TRIGNMETRIA teoremi sui triangoli rettangoli rof. Calogero Contrino Accenni alla trigonometria: Risoluzione di triangoli Si illustra nel seguito cosa deve intendersi con la locuzione «risolvere
2006 ACCENI ALLA TRIGNMETRIA teoremi sui triangoli rettangoli rof. Calogero Contrino Accenni alla trigonometria: Risoluzione di triangoli Si illustra nel seguito cosa deve intendersi con la locuzione «risolvere
Alcune nozioni di trigonometria 1
 Alcune nozioni di trigonometria. Angoli In un sistema di assi cartesiani ortogonali la misura degli angoli si effettua a partire dal semiasse positivo delle x, assumendo come positivo il verso antiorario.
Alcune nozioni di trigonometria. Angoli In un sistema di assi cartesiani ortogonali la misura degli angoli si effettua a partire dal semiasse positivo delle x, assumendo come positivo il verso antiorario.
GONIOMETRIA E TRIGONOMETRIA
 Dispensa di Matematica per la classe 4. C Anno scolastico 017-018 GONIOMETRIA E TRIGONOMETRIA Nome e Cognome: CIRCONFERENZA GONIOMETRICA In un triangolo rettangolo con ipotenusa 1 e angolo α i due cateti
Dispensa di Matematica per la classe 4. C Anno scolastico 017-018 GONIOMETRIA E TRIGONOMETRIA Nome e Cognome: CIRCONFERENZA GONIOMETRICA In un triangolo rettangolo con ipotenusa 1 e angolo α i due cateti
Silvia Braschi PROGRAMMA SVOLTO 3 i Matematica 2017/2018
 Silvia Braschi PROGRAMMA SVOLTO i Matematica 017/018 Geometria Analitica (vol A) Ripasso delle disequazioni di secondo grado intere e fratte Disequazioni di grado superiore al secondo Sistemi di disequazioni
Silvia Braschi PROGRAMMA SVOLTO i Matematica 017/018 Geometria Analitica (vol A) Ripasso delle disequazioni di secondo grado intere e fratte Disequazioni di grado superiore al secondo Sistemi di disequazioni
formule trigonometria
 1 formule trigonometria circonferenza trigonometrica di raggio 1 Funzioni Trigonometriche Dato un piano cartesiano, costituito da due assi ortogonali, consideriamo una circonferenza di raggio R avente
1 formule trigonometria circonferenza trigonometrica di raggio 1 Funzioni Trigonometriche Dato un piano cartesiano, costituito da due assi ortogonali, consideriamo una circonferenza di raggio R avente
Corso di Analisi: Algebra di Base. 7^ Lezione
 Corso di Analisi: Algebra di Base 7^ Lezione Goniometria.Elementi di trigonometria piana. Unità di misura degli angoli. Misura di angoli orientati. Circonferenza goniometrica. Angoli e archi noti. Le funzioni,
Corso di Analisi: Algebra di Base 7^ Lezione Goniometria.Elementi di trigonometria piana. Unità di misura degli angoli. Misura di angoli orientati. Circonferenza goniometrica. Angoli e archi noti. Le funzioni,
SCHEDA OBIETTIVI MINIMI. Materia:MATEMATICA
 Pag. 1 di 5 SCHEDA OBIETTIVI MINIMI Materia:MATEMATICA Classi QUARTA A e QUARTA B Spec.: LICEO DELLE SCIENZE APPLICATE a.s: 2016 / 2017 4 3 2 1 Presidente di dipartimento 0 DOC DS Maria Grazia Gillone
Pag. 1 di 5 SCHEDA OBIETTIVI MINIMI Materia:MATEMATICA Classi QUARTA A e QUARTA B Spec.: LICEO DELLE SCIENZE APPLICATE a.s: 2016 / 2017 4 3 2 1 Presidente di dipartimento 0 DOC DS Maria Grazia Gillone
MATEMATICA - LEZIONE 5 Goniometria Equazioni e disequazioni trigonometriche. Relatore prof. re CATELLO INGENITO
 MATEMATICA - LEZIONE 5 Goniometria Equazioni e disequazioni trigonometriche Relatore prof. re CATELLO INGENITO Sommario della lezione Angoli goniometrici Funzioni goniometriche Equazioni e disequazioni
MATEMATICA - LEZIONE 5 Goniometria Equazioni e disequazioni trigonometriche Relatore prof. re CATELLO INGENITO Sommario della lezione Angoli goniometrici Funzioni goniometriche Equazioni e disequazioni
Funzioni goniometriche di angoli notevoli
 Funzioni goniometriche di angoli notevoli In questa dispensa calcoleremo il valore delle funzioni goniometriche per gli angoli notevoli di 30, 45 e 60. Dopo aver richiamato il concetto di sezione aurea
Funzioni goniometriche di angoli notevoli In questa dispensa calcoleremo il valore delle funzioni goniometriche per gli angoli notevoli di 30, 45 e 60. Dopo aver richiamato il concetto di sezione aurea
CLASSI: TERZE Materia: MATEMATICA e COMPLEMENTI Ore settimanali previste: 4
 CLASSI: TERZE Materia: MATEMATICA e COMPLEMENTI Ore settimanali previste: 4 N. modulo Titolo Modulo Titolo unità didattiche del modulo Ore previste Periodo mensile Competenze 1 Raccordo con il biennio
CLASSI: TERZE Materia: MATEMATICA e COMPLEMENTI Ore settimanali previste: 4 N. modulo Titolo Modulo Titolo unità didattiche del modulo Ore previste Periodo mensile Competenze 1 Raccordo con il biennio
trasformazione grafico Cosa si deve fare Esempio goniometrico
 trasformazione grafico Cosa si deve fare Esempio goniometrico = cos + b>0 Traslazione verticale b 0 si sposta il grafico verso l alto, oppure l asse orizzontale verso il
trasformazione grafico Cosa si deve fare Esempio goniometrico = cos + b>0 Traslazione verticale b 0 si sposta il grafico verso l alto, oppure l asse orizzontale verso il
RACCOLTA DI ESERCIZI PER I CORSI PRELIMINARI
 RACCOLTA DI ESERCIZI PER I CORSI PRELIMINARI V PARTE: TRIGONOMETRIA MISURE DEGLI ANGOLI IN GRADI E IN RADIANTI Nota; nel seguito per la misura degli angoli in gradi viene utilizzato il sistema "sessadecimale"
RACCOLTA DI ESERCIZI PER I CORSI PRELIMINARI V PARTE: TRIGONOMETRIA MISURE DEGLI ANGOLI IN GRADI E IN RADIANTI Nota; nel seguito per la misura degli angoli in gradi viene utilizzato il sistema "sessadecimale"
Carlo Sintini, Problemi di maturità, 1950 Luglio, matematicamente.it Luglio 1950, primo problema
 Luglio 1950, primo problema Risolvere un trapezio isoscele convesso avente le diagonali perpendicolari ai lati obliqui, sapendo che la somma dei quadrati delle misure dei suoi lati è m e la lunghezza di
Luglio 1950, primo problema Risolvere un trapezio isoscele convesso avente le diagonali perpendicolari ai lati obliqui, sapendo che la somma dei quadrati delle misure dei suoi lati è m e la lunghezza di
MATEMATICA COMPLEMENTI DI MATEMATICA
 ISTITUTO TECNICO TECNOLOGICO STATALE G. e M. MONTANI FERMO Anno Scolastico 2014/ 15 PROGRAMMA SVOLTO DI Disciplina: MATEMATICA Classe di Concorso A047 3 ore settimanali Disciplina: COMPLEMENTI DI MATEMATICA
ISTITUTO TECNICO TECNOLOGICO STATALE G. e M. MONTANI FERMO Anno Scolastico 2014/ 15 PROGRAMMA SVOLTO DI Disciplina: MATEMATICA Classe di Concorso A047 3 ore settimanali Disciplina: COMPLEMENTI DI MATEMATICA
Carlo Sintini, Problemi di maturità, 1949 Settembre, matematicamente.it Settembre 1949, primo problema
 Settembre 199, primo problema In una data circonferenza di centro O, la corda AB è il lato del quadrato inscritto. Condotta nel punto B la semiretta tangente alla circonferenza che giace, rispetto alla
Settembre 199, primo problema In una data circonferenza di centro O, la corda AB è il lato del quadrato inscritto. Condotta nel punto B la semiretta tangente alla circonferenza che giace, rispetto alla
LICEO SCIENTIFICO STATALE G. MARCONI FOGGIA. PROGRAMMA DI Matematica. Classe IVB. Anno Scolastico
 LICEO SCIENTIFICO STATALE G. MARCONI FOGGIA PROGRAMMA DI Matematica Classe IVB Anno Scolastico 2014-2015 Insegnante: Prof.ssa La Salandra Incoronata 1 Le coniche nella discussione dei problemi (Richiami)
LICEO SCIENTIFICO STATALE G. MARCONI FOGGIA PROGRAMMA DI Matematica Classe IVB Anno Scolastico 2014-2015 Insegnante: Prof.ssa La Salandra Incoronata 1 Le coniche nella discussione dei problemi (Richiami)
Registro di Matematica /19 - F. Demontis 2
 Registro delle lezioni di MATEMATICA 1 Corso di Laurea in Chimica 6 CFU - A.A. 2018/2019 docente: Francesco Demontis ultimo aggiornamento: 11 gennaio 2019 1. Mercoledì 03/10/2018, 11 13. ore: 2(2) Linguaggio
Registro delle lezioni di MATEMATICA 1 Corso di Laurea in Chimica 6 CFU - A.A. 2018/2019 docente: Francesco Demontis ultimo aggiornamento: 11 gennaio 2019 1. Mercoledì 03/10/2018, 11 13. ore: 2(2) Linguaggio
Capitolo 3. Le funzioni elementari
 Capitolo 3 Le funzioni elementari Uno degli scopi di questo capitolo è lo studio delle funzioni reali di variabile reale, ossia funzioni che hanno come dominio un sottoinsieme di R e codominio R. Lo studio
Capitolo 3 Le funzioni elementari Uno degli scopi di questo capitolo è lo studio delle funzioni reali di variabile reale, ossia funzioni che hanno come dominio un sottoinsieme di R e codominio R. Lo studio
PROGRAMMAZIONE MODULARE DI MATEMATICA PER LA CLASSE III LICEO DELLE SCIENZE UMANE - LICEO LINGUISTICO LICEO MUSICALE- LICEO COREUTICO L.E.S.
 PROGRAMMAZIONE MODULARE DI MATEMATICA PER LA CLASSE III LICEO DELLE SCIENZE UMANE - LICEO LINGUISTICO LICEO MUSICALE- LICEO COREUTICO L.E.S. Titolo del modulo LA DIVISIONE FRA POLINOMI E LA SCOMPOSIZIONE
PROGRAMMAZIONE MODULARE DI MATEMATICA PER LA CLASSE III LICEO DELLE SCIENZE UMANE - LICEO LINGUISTICO LICEO MUSICALE- LICEO COREUTICO L.E.S. Titolo del modulo LA DIVISIONE FRA POLINOMI E LA SCOMPOSIZIONE
ANGOLI. ANGOLO OTTUSO ( β > 90 ) ANGOLO ACUTO ( β < 90 )
 ANGOLI Angolo è ciascuna delle due parti nelle quali un piano viene diviso da due semirette aventi la stessa origine. Le due semirette sono dette lati dei due angoli e l'origine comune il loro vertice.
ANGOLI Angolo è ciascuna delle due parti nelle quali un piano viene diviso da due semirette aventi la stessa origine. Le due semirette sono dette lati dei due angoli e l'origine comune il loro vertice.
Corso multimediale di matematica
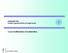 2006 GNIMETRIA rof. Calogero Contrino Sia dato un generico angolo acuto ab di vertice e lati a, b. Si consideri su uno dei suoi lati (p.e. il secondo) una generica sequenza di punti (anche infinita),,.
2006 GNIMETRIA rof. Calogero Contrino Sia dato un generico angolo acuto ab di vertice e lati a, b. Si consideri su uno dei suoi lati (p.e. il secondo) una generica sequenza di punti (anche infinita),,.
UNITÀ DIDATTICA 3 FUNZIONI GONIOMETRICHE
 UNITÀ DIDATTICA FUNZIONI GONIOMETRICHE 1 La misura degli angoli In ogni circonferenza è possibile definire una corrispondenza biunivoca tra angoli al centro e archi: a ogni angolo al centro corrisponde
UNITÀ DIDATTICA FUNZIONI GONIOMETRICHE 1 La misura degli angoli In ogni circonferenza è possibile definire una corrispondenza biunivoca tra angoli al centro e archi: a ogni angolo al centro corrisponde
01 LE FUNZIONI GONIOMETRICHE
 0 LE FUNZIONI GONIOMETRICHE. LA MISURA DEGLI ANGOLI ESERCIZI Esprimi in forma sessadecimale le seguenti misure di angoli. A 4 9 ; 8 56 6 ; 57 59 B 44 ; 78 56 ; 9 4 0.,57 ; 8,97 ; 57,0. 4,4 ; 7,5 ; 9,569
0 LE FUNZIONI GONIOMETRICHE. LA MISURA DEGLI ANGOLI ESERCIZI Esprimi in forma sessadecimale le seguenti misure di angoli. A 4 9 ; 8 56 6 ; 57 59 B 44 ; 78 56 ; 9 4 0.,57 ; 8,97 ; 57,0. 4,4 ; 7,5 ; 9,569
Classe 3 Sezione Indirizzo Liceo delle Scienze Applicate
 Alessandria, Settembre 2016 Anno scolastico 2016/2017 A Classe 3 Sezione C Indirizzo Liceo delle Scienze Applicate Materia Matematica Docente/i Nome e cognome PierCarlo Barbierato Nome e cognome Firma
Alessandria, Settembre 2016 Anno scolastico 2016/2017 A Classe 3 Sezione C Indirizzo Liceo delle Scienze Applicate Materia Matematica Docente/i Nome e cognome PierCarlo Barbierato Nome e cognome Firma
LICEO delle SCIENZE UMANE B. PASCAL
 LICEO delle SCIENZE UMANE B. PASCAL Prof. Loredana Mannarino INDICE 1. FUNZIONI ESPONENZIALI 1.1. Richiami sulle potenze...3 1.2. Il grafico della funzione esponenziale.4 1.3. Equazioni esponenziali...6
LICEO delle SCIENZE UMANE B. PASCAL Prof. Loredana Mannarino INDICE 1. FUNZIONI ESPONENZIALI 1.1. Richiami sulle potenze...3 1.2. Il grafico della funzione esponenziale.4 1.3. Equazioni esponenziali...6
Classe III Aritmetica e Algebra Dati e previsioni Geometria Geometria
 Classe III U. D. 1 Equazioni e disequazioni (ripasso) Aritmetica e Algebra Equazioni algebriche numeriche con δ 2. Disequazioni algebriche numeriche con δ 2. Sistemi di equazioni e/o disequazioni algebriche
Classe III U. D. 1 Equazioni e disequazioni (ripasso) Aritmetica e Algebra Equazioni algebriche numeriche con δ 2. Disequazioni algebriche numeriche con δ 2. Sistemi di equazioni e/o disequazioni algebriche
Corso multimediale di matematica
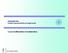 2006 GNIMETRIA rof. Calogero Contrino Sia dato un generico angolo acuto ab di vertice e lati a, b. Si consideri su uno dei suoi lati (p.e. il secondo) una generica sequenza di punti (anche infinita),,.
2006 GNIMETRIA rof. Calogero Contrino Sia dato un generico angolo acuto ab di vertice e lati a, b. Si consideri su uno dei suoi lati (p.e. il secondo) una generica sequenza di punti (anche infinita),,.
- le disequazioni di grado superiore al secondo: disequazioni biquadratiche, binomie e trinomie
 LICEO ARTISTICO STATALE BRUNO MUNARI, CREMONA Anno scolastico 2011-2012 PROGRAMMA SVOLTO DI MATEMATICA CLASSE IV A Ripasso: le disequazioni e le loro proprietà: (pag. 2, Volume SL 1) - gli intervalli limitati
LICEO ARTISTICO STATALE BRUNO MUNARI, CREMONA Anno scolastico 2011-2012 PROGRAMMA SVOLTO DI MATEMATICA CLASSE IV A Ripasso: le disequazioni e le loro proprietà: (pag. 2, Volume SL 1) - gli intervalli limitati
f: x R sen x [0, 1] g: x R cos x [0, 1] 1.Il dominio della funzione sen x è R. 1. Il dominio della funzione cos x è R.
![f: x R sen x [0, 1] g: x R cos x [0, 1] 1.Il dominio della funzione sen x è R. 1. Il dominio della funzione cos x è R. f: x R sen x [0, 1] g: x R cos x [0, 1] 1.Il dominio della funzione sen x è R. 1. Il dominio della funzione cos x è R.](/thumbs/63/48698325.jpg) Le funzioni seno e coseno. Ogni numero reale è la misura in radianti di un angolo goniometrico; pertanto possiamo definire il seno e il coseno di un numero reale ricorrendo al seno e coseno dell angolo
Le funzioni seno e coseno. Ogni numero reale è la misura in radianti di un angolo goniometrico; pertanto possiamo definire il seno e il coseno di un numero reale ricorrendo al seno e coseno dell angolo
Verifica di Topografia
 ISTITUTO TECNICO STATALE COMMERCIALE E PER GEOMETRI " In Memoria dei Morti per la Patria " * CHIAVARI * ANNO SCOLASTICO 2010-2011 Verifica di Topografia classe 4^ Geometri 1) 15 osservazioni sono sufficienti
ISTITUTO TECNICO STATALE COMMERCIALE E PER GEOMETRI " In Memoria dei Morti per la Patria " * CHIAVARI * ANNO SCOLASTICO 2010-2011 Verifica di Topografia classe 4^ Geometri 1) 15 osservazioni sono sufficienti
Repetitorium trigonometriae - per immagini
 Repetitorium trigonometriae - per immagini Regole di base Ipotenusa Opposto Adiacente Tenendo a mente la seguente nomenclatura di un triangolo rettangolo si ha: sin = Opposto Ipotenusa cos = Adiacente
Repetitorium trigonometriae - per immagini Regole di base Ipotenusa Opposto Adiacente Tenendo a mente la seguente nomenclatura di un triangolo rettangolo si ha: sin = Opposto Ipotenusa cos = Adiacente
9) Ricava per quali valori di x è positiva e per quali è negativa la funzione di equazione: > 0 [ 0 < x < ] ; y < 0 se. 1 [ x ] 0 [ x 1 ] + >
![9) Ricava per quali valori di x è positiva e per quali è negativa la funzione di equazione: > 0 [ 0 < x < ] ; y < 0 se. 1 [ x ] 0 [ x 1 ] + > 9) Ricava per quali valori di x è positiva e per quali è negativa la funzione di equazione: > 0 [ 0 < x < ] ; y < 0 se. 1 [ x ] 0 [ x 1 ] + >](/thumbs/96/127193609.jpg) Verifiche 4 C 4 H Anno scolastico 010/011 ESPONENZIALI LOGARITMI 1) Calcola il dominio della funzione: y = log / (5 x) + 1 [ x < 5 ] ) Calcola il dominio della funzione y = 3 log (x 8) [ - 4 x < < x 4
Verifiche 4 C 4 H Anno scolastico 010/011 ESPONENZIALI LOGARITMI 1) Calcola il dominio della funzione: y = log / (5 x) + 1 [ x < 5 ] ) Calcola il dominio della funzione y = 3 log (x 8) [ - 4 x < < x 4
PROGRAMMAZIONE III Geometri. ORGANIZZAZIONE MODULARE (Divisa in unità didattiche) MODULO TITOLO DEL MODULO ORE PREVISTE A Richiami di algebra 30
 PROGRAMMAZIONE III Geometri ORGANIZZAZIONE MODULARE (Divisa in unità didattiche) MODULO TITOLO DEL MODULO ORE PREVISTE A Richiami di algebra 30 B Geometria analitica 32 C Goniometria 30 D Trigonometria
PROGRAMMAZIONE III Geometri ORGANIZZAZIONE MODULARE (Divisa in unità didattiche) MODULO TITOLO DEL MODULO ORE PREVISTE A Richiami di algebra 30 B Geometria analitica 32 C Goniometria 30 D Trigonometria
x + x + 1 < Compiti vacanze classi 4D
 Compiti vacanze classi D Ripassare scomposizioni e prodotti notevoli, metodo di Ruffini, razionalizzazioni, equazioni irrazionali. (Libro di prima e seconda). Recuperare formulario con regole di risoluzione
Compiti vacanze classi D Ripassare scomposizioni e prodotti notevoli, metodo di Ruffini, razionalizzazioni, equazioni irrazionali. (Libro di prima e seconda). Recuperare formulario con regole di risoluzione
Equazioni parametriche goniometriche
 Equazioni parametriche goniometriche Discutere un equazione parametrica significa stabilire, al variare del parametro, il numero di soluzioni dell equazione soddisfacenti le limitazioni assegnate all incognita.
Equazioni parametriche goniometriche Discutere un equazione parametrica significa stabilire, al variare del parametro, il numero di soluzioni dell equazione soddisfacenti le limitazioni assegnate all incognita.
ISTITUTO ISTRUZIONE SUPERIORE
 ISTITUTO ISTRUZIONE SUPERIORE Federico II di Svevia Indirizzi: Liceo Scientifico Classico Linguistico Artistico e Scienze Applicate Via G. Verdi, 1 85025 MELFI (PZ) Tel. 097224434/35 Cod. Min.: PZIS02700B
ISTITUTO ISTRUZIONE SUPERIORE Federico II di Svevia Indirizzi: Liceo Scientifico Classico Linguistico Artistico e Scienze Applicate Via G. Verdi, 1 85025 MELFI (PZ) Tel. 097224434/35 Cod. Min.: PZIS02700B
