Complementi 5 - Le equazioni di Beltrami e l'equilibrio elastico
|
|
|
- Michelina Pagano
- 5 anni fa
- Visualizzazioni
Transcript
1 Complementi 5 - Le equazioni di Beltrami e l'equilibrio elastico [Ultimarevisione: revisione:5 5gennaio gennaio009] In questi complementi vengono dedotte le equazioni dell'equilibrio elastico in termini di tensioni, partendo dalle equazioni di compatibilita' di De Saint-Venant. Introducendo in esse la legge di Hooke le si trasforma in equazioni in termini di tensioni, poi si utilizzando le equazioni indefinite dell'equilibrio, giungendo infine ad un sistema di sei equazioni nelle sei incognite s ij La deduzione delle equazioni di Beltrami Per ottenere le equazioni di equilibrio in termini di tensioni, si parta dalle equazioni di compatibilita' di De saint venant, si utilizzi in esse le leggi di Hooke (equazioni costitutive) e le equazioni indefinite dell'equilibrio. Si giungera' ad un sistema di sei equazioni nelle sei incognite s ij, cui andranno associate le opportune condizioni ai limiti. à Il primo gruppo Si parta allora dall'equazione di compatibilita': e = e e x x x x e si utilizzino le relazioni costitutive nella forma: () Si ha: e ij = E σ ij E δ ij σ kk () H L σ = H L J σ σ J σ σ x x x x x x Si considerino ora le equazioni indefinite dell'equilibrio elastico: () σ σ σ X x x x = 0 σ σ σ X x x x = 0 (4) σ σ σ X x x x = 0
2 44 Complementi 5 - Le equazioni di Beltrami e l'equilibrio elastico.nb Derivando la prima rispetto ad x, la seconda rispetto ad x, e la terza rispetto ad x si ottiene: σ = σ x x x σ X x x x (5) σ = σ σ X x x x x x x σ x x e sommando le prime due: σ σ X = 0 x x x x σ = σ x x x Dalla(6) si ottiene: σ X x x σ σ X x x x x x (6) (7) σ x x e quindi la (7) si scrive: σ = σ X x x x x (8) σ = σ σ σ X X X x x x x x x x x Questa espressione puo' essere sostituita nella (), che cosi' diviene: (9) ossia ancora: H L J σ x σ x σ x X X X = x x x H L J σ x σ x J σ x σ x (0) H L J X X X = x x x H L J σ x σ x σ x σ x σ x () J σ σ x x Aggiungendo e sottraendo si ottiene: H L J X X X = x x x H L J σ x σ x σ x σ x σ x σ x σ x () che puo' scriversi: σ σ x x J σ σ σ σ x x x x
3 Complementi 5 - Le equazioni di Beltrami e l'equilibrio elastico.nb 45 H L J X X X = x x x H L J σ kk σ avendo introdotto l'operatore : σ x J σ kk σ x () = x x x (4) Dalle altre due equzioni di compatibilita' dello stesso gruppo, operando nello stesso modo, si ottengono altre due equazioni: H L J X X X = x x x H L J σ kk σ H L J X X X = x x x H L J σ kk σ Sommando le (-5) si ottiene: σ x J σ kk σ x σ x J σ kk σ x (5) (6) ossia: H L J X X X = H L x x x σ kk σ kk (7) σ kk = J X X X x x x Questa espressione puo' essere sostituita nella (), ottenendo: (8) ed infine: H L J X X X = x x x σ kk H L J σ J X X X x x σ σ x σ kk x σ kk x σ x σ x J X X X = x x x = J X X X X x x x x con due equazioni simili ottenute per permutazione circolare degli indici: σ σ kk x = J X X X X x x x x (9) (0) () ()
4 46 Complementi 5 - Le equazioni di Beltrami e l'equilibrio elastico.nb σ σ kk x = J X X X X x x x x () à Il secondo gruppo Si parta ora da una equazione di compatibilita' del secondo gruppo: e x x = e si introduca la legge di Hooke: J e e e x x x x (4) ossia: H L σ x x σ = H L x x J σ σ σ x x x x (5) σ x x σ = σ x x x σ x x σ x x (6) Aggiungendo e sottraendo: ossia: σ σ σ x x x x x x σ x σ σ x x x x σ σ x x σ = x x x x (7) σ = σ x x σ σ x x x x x σ σ x x x x Si derivi la seconda equazione indefinita dell'equilibrio rispetto ad x, e la terza rispetto ad x : (8) σ x x 0 σ = x x σ σ x x x X = x σ σ x x x X x σ σ x x σ X = x x x x (9) 0 σ = σ σ x x x x X x x e si sostituisca nella (7):
5 Complementi 5 - Le equazioni di Beltrami e l'equilibrio elastico.nb 47 σ kk x x = σ σ x x X x x (0) σ σ x x X σ x x x Semplificando si giunge a scrivere: σ x x σ x x σ con le altre due: σ σ σ = J X x x σ = J X x x σ = J X x x X x x X x x X x x () () () à Le sei equazioni Le sei equazioni (0-) e (0-) si possono scrivere, in termini indiciali: σ ij σ = x i x j δ ij Div HXL J X i X j x j x i (4) e ad esse vanno associate le condizioni ai limiti σ ij n j = p i (5) sulla parte di frontiera dove sono assegnate le forze superficiali. Le eqn.(4) si chiamano equazioni di Beltrami, o anche equazioni di Beltrami-Michell [Beltrami] ote [Beltrami] - In assenza di forze di massa, le equazioni (4) sono state dedotte da Enrico Beltrami in "Osservazioni alla nota del prof.morera", Rendiconti della R.Accademia dei Lincei, serie V, tomo I, 4-4 (89), cfr. anche Opere Vol.IV, pagg.50-5, oppure il sito nella sezione Ricerca. In presenza di forze di massa le equazioni furono dedotte da Luigi Donati, "Ulteriori osservazioni intorno al teorema di Menabrea", Mem. Accad. Sci.Bologna (5), 4, (894) e solo in seguito riscoperte da J.H. Michell in "On the direct determination of stress in an elastic solid, with applications to the theory of plates", Proc.Lond. Math. Soc., 00-4 (900). Un ricordo del pressocche' dimenticato prof. Donati e' riportato nel sito nella sezione Ricerca.
6 48 Complementi 5 - Le equazioni di Beltrami e l'equilibrio elastico.nb Figura - J.H.Michell
Lezione 18 - L'equilibrio elastico
Lezione 18 - L'equilibrio elastico [Ultimarevisione: revisione:14 14gennaio gennaio9] Le prime lezioni sono state dedicate all'analisi della tensione, giungendo ad enunciare le equazioni indefinite dell'equilibrio
Lezione 18 - L'equilibrio elastico
Lezione 18 - L'equilibrio elastico ü [A.a. 1-13 : ultima revisione 5 novembre 1] Le prime lezioni sono state dedicate all'analisi della tensione, giungendo ad enunciare le equazioni indefinite dell'equilibrio
Complementi 7 - Le funzioni di tensione
Complementi 7 - Le funzioni di tensione [Ultimarevisione: revisione:17 17gennaio gennaio2009] In questo notebook si vogliono studiare le equazioni indefinite dell'equilibrio in assenza di forze di massa:
Lezione 9 - Le equazioni indefinite di equilibrio
Lezione 9 - Le equazioni indefinite di equilibrio ü [A.a. 212-213 : ultima revisione 28 ottobre 212] In questa lezione si deducono le cosiddette equazioni indefinite dellequilibrio, e si dimostra limportante
Complementi 9 - Le soluzioni di De Saint-Venant
Complementi 9 - Le soluzioni di De Saint-Venant [Ultimarevisione: revisione: gennaio gennaio009] In questa lezione si illustra un metodo per ottenere le soluzioni per il problema debole di De Saint-Venant.
Lezione 9 - Le equazioni indefinite di equilibrio
Leione 9 - Le equaioni indefinite di equilibrio [Ultimarevisione: revisione:11 11dicembre dicembre8] In questa leione si deducono le cosiddette equaioni indefinite dellequilibrio, e si dimostra limportante
Complementi 11 - Le travature reticolari iperstatiche
Complementi 11 - Le travature reticolari iperstatiche [Ultimarevisione: revisione:1 1febbraio febbraio009] In questa leione si prosegue lo studio delle travature reticolari, affrontando il caso delle travature
Introduzione ai problemi piani in elasticità lineare
Introduzione ai problemi piani in elasticità lineare 19 novembre 2010 1 Fondamenti dei problemi piani 1.1 Relazioni generali Si consideri un corpo immerso in uno spazio Euclideo tridimensionale R 3 avente
Lezione 19 - Stati piani di tensione e deformazione
Lezione 9 - Stati piani di tensione e deformazione [Ultimarevisione: revisione:9 9gennaio gennaio009] Si e' visto, nella lezione precedente, che la soluzione del problema ai limiti dell'elasticita' non
Lezione 19 - Stati piani di tensione e spostamento
Lezione 19 - Stati piani di tensione e spostamento ü [A.a. 01-013 : ultima revisione 5 Novembre 01] Si e' visto, nella lezione precedente, che la soluzione del problema ai limiti dell'elasticita' non sempre
Complementi 3 - Richiami di algebra tensoriale
Complementi 3 - Richiami di algebra tensoriale [Ultimarevisione revisione9gennaio gennaio2009] In questo notebook si richiamano brevemente alcune definizioni ed alcune proprieta di algebra tensoriale,
Verifica n crediti
Verifica n.45-1 crediti aprile 014 - Mercoledi' 9.0-11.0 Si consideri il telaio di Figura 1, vincolato con due appoggi al piede e disconnesso con un bipendolo interno ad asse verticale nella mezzeria del
Aindica la sezione retta della trave, ipotizzata costante lungo tutta la lunghezza,
Capitolo 9 IL PROBLEMA DI SAINT-VENANT (prof. Elio Sacco) 9.1 Posizione del problema Saint-Venant 1 considerò un particolare problema dell equilibrio elastico. 9.1.1 Ipotesi geometriche Il corpo tridimensionale
Lezione 14 - Il tensore di Green- Lagrange
Lezione 14 - Il tensore di Green- Lagrange [Ultimarevisione: revisione:4 4novembre novembre009] In questa lezione si generalizza quanto detto nella lezione precedente, considerando la trasformazione subita
Lezione 8 - Il teorema di Cauchy-Poisson
Lezione 8 - Il teorema di Cauchy-Poisson [Ultimarevisione: revisione:11 11dicembre dicembre2008] Come detto al termine della lezione precedente, occorre ora dare un criterio operativo per poter calcolare
Lezione 8 - Il teorema di Cauchy- Poisson
Lezione 8 - Il teorema di Cauchy- Poisson ü [A.a. 2012-2013 : ultima revisione 28 ottobre 2012] Come detto al termine della lezione precedente, occorre ora dare un criterio operativo per poter calcolare
SISTEMI DI PRODUZIONE
0/0/05 SISTEMI DI PRODUZIONE Dario Antonelli Lezione A7 Introduzione alla lezione Elementi base di meccanica del continuo Legge elastica Legge plastica Casi particolari 0/0/05 Moduli del corso A: I materiali
il determinante che si ottiene da A, sopprimendo la i - esima riga e la j - esima colonna. Si definisce complemento algebrico dell'elemento a ij
Determinanti Sia data la matrice quadrata a... a n a a n =...... a... a n nn Chiamiamo determinante di il numero det o che ad essa viene associato. det = a a... a... a... a n n n... a nn Un generico elemento
Il modello di trave adottato dal Saint-Venant si basa sulle seguenti ipotesi:
IL PROBLEM DEL DE SINT-VENNT Il problema del De Saint-Venant è un particolare problema di equilibrio elastico di notevole interesse applicativo, potendosi considerare alla base della teoria tecnica delle
Sistemi di equazioni lineari
Sistemi di equazioni lineari Siano X 1,, X n indeterminate Un equazione lineare (o di primo grado) nelle incognite X 1,, X n a coefficienti nel campo K è della forma a 1 X 1 + + a n X n = b, a i, b K,
Equazioni simboliche
581 Alcuni quiz riportano lo schema classico di un equazione matematica o di un sistema di equazioni matematiche, utilizzando, tuttavia, in luogo delle comuni lettere, dei simboli come @, #,!, etc. o delle
Sommario 1 VOLUME CAPITOLO 1 - Matrici 1 VOLUME CAPITOLO 3 - Geometria delle masse 1 VOLUME CAPITOLO 2 - Notazione indiciale
Sommario CAPITOLO 1 - Matrici...! Definizione! Matrici di tipo particolare Definizioni relative-! Definizioni ed operazioni fondamentali! Somma di matrici (o differenza)! Prodotto di due matrici! Prodotti
Lezione 17 - Il solido isotropo
Lezione 17 - Il solido isotropo ü [A.a. 2011-2012 : ultima revisione 23 agosto 2011] Si e' visto che le costanti elastiche previste dalla teoria di Green sono, in generale, 21. Non sembra possibile ridurre
21 - La scrittura diretta delle equazioni di congruenza - Parte II
21 - a scrittura diretta delle equazioni di congruenza - Parte II ü [.a. 2011-2012 : ultima revisione 15 aprile 2012] Esercizio n.9 Si calcolino le reazioni e si disegni il diagramma delle c.s.i. per il
Il Problema del De Saint Venant
Il Problema del De Saint Venant Tema 1 Si consideri una trave di acciaio di lunghezza L = m e con sezione retta a corona circolare di raggio esterno R = 30 cm e raggio interno r = 0 cm, che rispetti le
Indice. Prefazione XIII
indice_majorana 9-02-2007 9:26 Pagina V XIII Prefazione 1 Introduzione alla Scienza delle Costruzioni 2 1 Il modello geometrico 5 2 Il modello delle azioni esterne 5 3 Il modello meccanico (reologico)
Complementi 10 - Le travature reticolari isostatiche
Complementi - Le travature reticolari isostatiche [Ultimarevisione: revisione: febbraio febbraio9] In questa lezione si analizza la prima classe strutturale di interesse, costituita da un assemblaggio
Lezione 30 - La teoria di Eulero per la trave snella
ezione 3 - a teoria di Eulero per la trave snella ü [A.a. 211-212 : ultima revisione 11 marzo 212] In questa parte del corso si particolarizzano i risultati della teoria dell'elasticita' e della teoria
Formulazione delle equazioni del moto per un sistema lineare a tre gradi di libertà. Proprietà delle matrici di rigidezza e di flessibilità
Formulazione delle equazioni del moto per un sistema lineare a tre gradi di libertà Proprietà delle matrici di rigidezza e di flessibilità Prof. Adolfo Santini - Dinamica delle Strutture Introduzione In
13 - Le travi soggette a sforzo assiale
13 - e travi soggette a sforzo assiale ü [A.a. 212-213 : ultima revisione 7 febbraio 213] Relazioni fondamentali Si consideri una trave rettilinea soggetta ai carichi assiali th ). Per essa, si hanno le
Lezione 37 - La teoria di Timoshenko per le travi alte
ezione 7 - a teoria di Timoshenko per le travi alte [Ultima revisione: 4 maggio ] Quali sono i limiti della teoria di Eulero-Bernoulli? Come e possibile migliorare la teoria, senza rinunciare alla semplicita
FISICA. Questi problemi si risolvono utilizzando la seconda legge di Newton F = m a che può scriversi, utilizzando le intensità. F = ma.
Serie 9: Soluzioni FISICA I liceo Esercizio 1 Seconda legge di Newton Questi problemi si risolvono utilizzando la seconda legge di Newton F = m a che può scriversi, utilizzando le intensità Ricorda che
Esercizio. di centro l'origine e raggio R nel piano verticale O(x; z). Sia A il punto piu' alto dove la
Esercizio Due punti materiali P 1 e P, di ugual massa m, sono vincolati a muoversi sulla circonferenza di centro l'origine e raggio R nel piano verticale Ox; z). Sia A il punto piu' alto dove la circonferenza
Introduzione. Elenco dei principali simboli
Indice Prefazione Introduzione Elenco dei principali simboli xiii xv xxi 1 L analisi della deformazione 1 1.1 La congruenza dello spostamento..................... 1 1.2 Il vettore deformazione infinitesima....................
Lezione 13 - Il gradiente di deformazione
Lezione 3 - Il gradiente di deformazione ü [A.a. 0-03 : ultima revisione 3 ottobre 0] In questa lezione si comincia ad affrontare l'analisi della deformazione, cui compito principale e' rispondere al seguente
Lezione 37 - La teoria di Timoshenko per le travi alte
ezione 7 - a teoria di Timoshenko per le travi alte ü [A.a. 11-1 : ultima revisione 9 agosto 11] Quali sono i limiti della teoria di Eulero-Bernoulli? Come e' possibile migliorare la teoria, senza rinunciare
Lezione 41 - Il teorema di reciprocita'
ezione 41 - Il teorema di reciprocita' ü [A.a. 212-213 : ultima revisione 25 Aprile 213] In questa ezione si introduce il concetto di distorsione, e si dimostra un principio generale di reciprocita', da
MECCANICA DEL CONTINUO - TENSIONI
MECCANICA DEL CONTINUO - TENSIONI Si consideri un corpo continuo in equilibrio sotto l azione di un sistema di forze esterne (P 1, P,, P N ). Per studiare l effetto di queste sollecitazioni in un generico
Risposta in vibrazioni libere di un sistema lineare viscoso a più gradi di libertà. Prof. Adolfo Santini - Dinamica delle Strutture 1
Risposta in vibrazioni libere di un sistema lineare viscoso a più gradi di libertà Prof. Adolfo Santini - Dinamica delle Strutture 1 Vibrazioni libere non smorzate 1/6 Le equazioni del moto di un sistema
LEZIONE 2. ( ) a 1 x 1 + a 2 x a n x n = b, ove a j, b R sono fissati.
LEZIONE 2 2 Sistemi di equazioni lineari Definizione 2 Un equazione lineare nelle n incognite x, x 2,, x n a coefficienti reali, è un equazione della forma (2 a x + a 2 x 2 + + a n x n = b, ove a j, b
Unità didattica 3. Terza unità didattica (Fisica) 1. Corso integrato di Matematica e Fisica per il Corso di Farmacia
Unità didattica 3 Elasticità dei materiali Deformazione di un solido..2 Legge di Hooke.. 3 Forza elastica.. 4 Deformazione elastica di una molla... 5 Accumulo di energia attraverso la deformazione elastica..6
Note sull algoritmo di Gauss
Note sull algoritmo di Gauss 29 settembre 2009 Generalità Un sistema lineare di m equazioni in n incognite x,..., x n è un espressione del tipo: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n
Sistemi lineari di due equazioni in due incognite
Sistemi lineari di due equazioni in due incognite Incognite Lettere (di solito X e Y) alle quali è possibile sostituire dei valori numerici Coppia ordinata Coppia (X;Y) di valori numerici, per la quale
29. Mezzi elastici RELAZIONE SFORZO-DEFORMAZIONE
29. Mezzi elastici I mezzi continui solidi sono caratterizzati da piccole deformazioni, che consentono di stabilire una relazione lineare tra sforzo e deformazione nota come legge di Hook. Linearizzando
TEOREMA DI BETTI E LINEE DI INFLUENZA (prof. Elio Sacco)
Capitolo 5 TEOEMA DI BETTI E LINEE DI INFLUENZA (prof. Elio Sacco) 5.1 Teorema di Betti Siano S 1 = {b 1, p 1, û 1 } ed S 2 = {b 2, p 2, û 2 } due differenti sistemi di sollecitazioni agenti sul medesimo
Elementi finiti solidi
Esercitazioni del corso di Costruzione di Macchine 2 e Progettazione FEM a cura dell ing. Francesco Villa Elementi finiti solidi Costruzione di Macchine 2 e Progettazione FEM Prof. Sergio Baragetti Dalmine
23 - La scrittura diretta delle equazioni di congruenza - Il metodo misto
3 - a scrittura diretta delle equazioni di congruenza - Il metodo misto ü [.a. 01-013 : ultima revisione 15 aprile 013] ' talvolta conveniente operare una scelta di incognite iperstatiche che rende la
Sistemi di equazioni lineari
Sistemi di equazioni lineari A. Bertapelle 25 ottobre 212 Cos è un sistema lineare? Definizione Un sistema di m equazioni lineari (o brevemente sistema lineare) nelle n incognite x 1,..., x n, a coefficienti
3) DIMENSIONAMENTO DI UNA SEZIONE INFLESSA
3) DIMENSIONAMENTO DI UNA SEZIONE INFLESSA Quanto segue ci consente di dimensionare l altezza di una trave inflessa con un criterio di imporre che la tensione massima agente sulla sezione della trave sia
ESERCITAZIONE RIEPILOGATIVA TECNOLOGIE DELLE COSTRUZIONI AEROSPAZIALI. Prof. Claudio Scarponi Ing. Carlo Andreotti
TECNOLOGIE DELLE COSTRUZIONI AEROSPAZIALI ESERCITAZIONE RIEPILOGATIVA Prof. Claudio Scarponi Ing. Carlo Andreotti Ing. Carlo Andreotti 1 ESERCIZIO N 1 In un componente meccanico è stato determinato il
Enrico Borghi DESCRIZIONI CLASSICHE DEI FENOMENI ELETTROMAGNETICI
Enrico Borghi DESCRIZIONI CLASSICHE DEI FENOMENI ELETTROMAGNETICI La materia ordinaria contiene, fra altre, particelle di due tipi, elettroni e protoni, che interagiscono scambiando fra loro particelle
Es. 1 Es. 2 Es. 3 Es. 4 Totale Teoria. Punteggi degli esercizi: Es.1: 8 punti; Es.2: 8 punti; Es.3: 8 punti; Es.4: 8 punti.
Es. Es. Es. 3 Es. 4 Totale Teoria Analisi e Geometria Terzo appello 8 Settembre 4 Compito B Docente: Politecnico di Milano Ingegneria Industriale Cognome: Nome: Matricola: Punteggi degli esercizi: Es.:
Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016.
Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016 Di seguito si riporta il riassunto degli argomenti svolti; i riferimenti sono a parti del Cap8 Elementi di geometria e algebra lineare Par5
Esercizi Di Geometria 1 (BAER) Canale 1 Da consegnare Lunedi 26 Ottobre
Esercizi Di Geometria 1 (BAER) Canale 1 Da consegnare Lunedi 26 Ottobre SETTIMANA 4 (19 25 Ottobre) Matrici elementari Gli esercizi sono presi dal libro Intorduction to Linear Algebra di Serge Lang. Esercizio
4.11 Massimi e minimi relativi per funzioni di più variabili
5. Determinare, al variare del parametro a R, la natura delle seguenti forme quadratiche: (i) Φ(x, y, z) = x 2 + 2axy + y 2 + 2axz + z 2, (ii) Φ(x, y, z, t) = 2x 2 + ay 2 z 2 t 2 + 2xz + 4yt + 2azt. 4.11
Capitolo 1. Introduzione. 1.1 Argomenti Meccanica del continuo
Capitolo 1 Introduzione La Scienza delle Costruzioni fornisce gli strumenti di base ed i metodi necessari per la determinazione del grado di sicurezza, inteso in senso generale, di una qualsiasi struttura
Meccanica del continuo
0_Materiali areonautici:layout -07-00 :4 Pagina 5 Meccanica del continuo La meccanica del continuo solido è un argomento estremamente vasto e complesso nell ambito ingegneristico [], [], [3]. Tuttavia
Risoluzione delle Piastre Le piastre sottili in regime elastico
Corso di rogetto di Strutture OTENZA, a.a. 1 13 Risoluione delle iastre Le piastre sottili in regime elastico Dott. arco VONA DiSGG, Università di Basilicata marco.vona@unibas.it http://www.unibas.it/utenti/vona/
Lezione 43 - Le linee di influenza delle c.s.i.
Lezione 43 - Le linee di influenza delle c.s.i. ü [.a. 2012-2013 : ultima revisione 8 prile 2014] In questa Lezione si continua lo studio delle linee di influenza, affrontando il secondo gruppo di possibili
Punti di massimo o di minimo per funzioni di n variabili reali
Punti di massimo o di minimo per funzioni di n variabili reali Dati f : A R n R ed X 0 A, X 0 si dice : punto di minimo assoluto se X A, f ( x ) f ( X 0 ) punto di massimo assoluto se X A, f ( x ) f (
Equazioni differenziali. Elisabetta Colombo
Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2018-2019, http://users.mat.unimi.it/users/colombo/programmabio.html Eq. diff. 1 2 Un equazione differenziale e un equazione che
Soluzioni del Foglio 2 I sistemi lineari
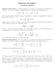Soluzioni del Foglio 2 I sistemi lineari Soluzione dell esercizio 1 Il sistema assegnato è un sistema di 2 equazioni in 2 incognite non omogeneo Le matrici incompleta e completa associate al sistema sono
Integrazione di equazioni differenziali lineari. Il metodo di Cauchy
1 EQUAZIONI DIFFERENZIALI LINEARI OMOGENEE Integrazione di equazioni differenziali lineari. Il metodo di Cauchy Marcello Colozzo 1 Equazioni differenziali lineari omogenee Sia data l equazione differenziale
Sistemi lineari 1 / 12
Sistemi lineari 1 / 12 Sistemi lineari 2 / 12 Ricordiamo che cosa è un sistema lineare con m equazioni in n incognite (m,n N, m,n 1): a 11 x 1 + +a 1n x n = b 1 a 21 x 1 + +a 2n x n = b 2, (1).. a m1 x
Soluzione della prova di Matematica PNI
Soluzione della prova di Matematica PNI Anno Scolastico 2012 2013 Prof. Ing. Luigi Verolino Università Federico II di Napoli Dipartimento di Ingegneria Elettrica e Tecnologie dell Informazione Via Claudio
7.8. Le analogie nella torsione...
Prefazione XIII 1. IL PROBLEMA Dl SAINT-VENANT I 1.1. Generalit I 1.1.1. Modello geometrico I 1.1.2. Modello delle azioni esterne 2 1.1.3. Modello meccanico o reologico del materiale 3 1.1.4. Equazioni
Equazioni di Primo grado
Equazioni di Primo grado Definizioni Si dice equazione di primo grado un uguaglianza tra due espressioni algebriche verificata solo per un determinato valore della variabile x, detta incognita. Si chiama
SCIENZA DELLE COSTRUZIONI: GES L - Z 1 a PROVA 7/05/2007 Tema A : allievo
SCIENZA DELLE COSTRUZIONI: GES L - Z 1 a PROVA 7/05/2007 Tema A : allievo ESERCIZIO 1 (punti 18) - Data la struttura di figura, si chiede di: 1a. effettuare l analisi cinematica (2); 1b. determinare le
Lezione 29 - La teoria approssimata
Lezione 9 - La teoria approssimata [Ultimarevisione: revisione:3 3marzo marzo009] Nella Lezione precedente si e' illustrata la trattazione del quinto e sesto caso di sollecitazione semplice di De Saint-Venant,
Dom. 1 Dom 2 Es. 1 Es. 2 Es. 3 Es. 4 Totale. Cognome: Nome: Matricola:
Dom. Dom 2 Es. Es. 2 Es. Es. 4 Totale Analisi e Geometria Secondo appello 06 luglio 206 Compito B Docente: Numero Alfabetico: Cognome: Nome: Matricola: Prima parte. L insieme (, 0] ammette minimo. F 2.
LEZIONE 3. a + b + 2c + e = 1 b + d + g = 0 3b + f + 3g = 2. a b c d e f g
LEZIONE 3 3.. Matrici fortemente ridotte per righe. Nella precedente lezione abbiamo introdotto la nozione di soluzione di un sistema di equazioni lineari. In questa lezione ci poniamo il problema di descrivere
Argomento 13 Sistemi lineari
Sistemi lineari: definizioni Argomento Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto
Geometria BAER I canale Foglio esercizi 2
Geometria BAER I canale Foglio esercizi 2 Esercizio 1. Calcolare il determinante e l inversa (quando esiste) della matrice ( ) cos θ sin θ R θ =, θ [0, 2π] sin θ cos θ Soluzione: Il determinante ( é cos
La formula riportata rappresenta il valore medio della tensione normale sulla sezione trasversale.
RIEILOGO M. Gobbi ver. 1.0, 6 Novembre 008 Tensioni in elementi strutturali: carico assiale La forza per unità di area si definisce tensione. La tensione normale in un elemento di sezione trasversale soggetto
Progetto di un solaio laterocementizio
1 Prima esercitazione progettuale Progetto di un solaio laterocementizio Lezione del 20/10/2015: Analisi delle sollecitazioni con il Metodo delle Forze 1 Definizione dei coefficienti di deformabilità 2
Corso di Laurea Ingegneria Civile e Ambientale. Moto vario nelle correnti a superficie libera
Corso di Laurea Ingegneria Civile e Ambientale UNIVERSITÀ DEGLI STUDI DI ENNA KORE FACOLTÀ DI INGEGNERIA E ARCHITETTURA Moto vario nelle correnti a superficie libera Complementi di Idraulica Ambientale
Meccanica Vettori, Principio di Saint Venant, Legge di Hooke, fatica
Meccanica Vettori, Principio di Saint Venant, Legge di Hooke, fatica Grandezze scalari e vettoriali Grandezza scalare: numero reale, in fisica associato ad una unità di misura (senza direzione né verso)
Metodo degli Elementi finiti: Formulazione secondo P.L.V. L est = P δf + ½. δf δp
Metodo degli Elementi finiti: Formulazione secondo P.L.V. P Per sistemi linearmente elastici δp L est L est = ½.P.f L est δf f L est = P δf + ½. δf δp Per strutture tridimensionali sottoposte a forze distribuite
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito C 3/5/25 A. A. 24 25 ) Risolvere il seguente sistema
CIRCUITI IN CORRENTE CONTINUA
IUITI IN ONT ONTINUA Un induttanza e tre resistenze 2 J J 2 L Il circuito sta funzionando da t = con l interruttore aperto. Al tempo t = 0 l interruttore viene chiuso. alcolare le correnti. Per t 0 circola
Per equazione lineare nelle incognite x, y intendo un equazione del tipo. ax = b,
Matematica II 161110 1 Equazioni lineari in una incognita Per equazione lineare nell incognita x intendo un equazione del tipo ax = b dove a b sono due costanti reali a e il coefficiente e b e il termine
EQUAZIONI COSTITUTIVE
QUAZIONI COSTITUTIV Macchina per Prova di trazione P P quazioni costitutive Prova di trazione di una barra di acciaio dolce, normalmente utiliato nelle costruzioni civili. Registriamo i valori simultanei
Complementi di Algebra e Fondamenti di Geometria
Complementi di Algebra e Fondamenti di Geometria Capitolo 3 Forma canonica di Jordan M. Ciampa Ingegneria Elettrica, a.a. 29/2 Capitolo 3 Forma canonica di Jordan Nel Capitolo si è discusso il problema
Corso di introduzione all Astrofisica
Corso di introduzione all Astrofisica I modulo Prof. Giuseppe Bertin Anno accademico 9 Indice Il teorema del viriale. Problema....................................... Equazioni del moto e energia per sistemi
Scienza delle costruzioni
Luigi Gambarotta Luciano Nunziante Antonio Tralli Scienza delle costruzioni web site McGraw-Hill IUAV - VENEZIA A 323 BIBLIOTECA CENTRALE Luigi Gambarotta Luciano Nunziante Antonio Tralli \ : Scienza delle
Lezione 34 - I vincoli imperfetti
ezione 34 - I vincoli imperfetti [Ultima revisione: 26 febbraio 29] In quanto si e detto finora, si e sempre ipotizzato che il vincolo sia in grado di svolgere perfettamente la sua funzione, annullando
BOZZA F B C D L/2 L/2 L/2 L/2. Indicando i movimenti indipendenti come componenti di un vettore, si può porre
ezione n. 9 Il metodo dell equilibrio: esempio #3 a matrice di rigidezza a caratterizzazione generale del metodo dell equilibrio per la soluzione di sistemi strutturali iperstatici richiede la definizione
che cosa significa soluzione dei circuiti?
Capitolo 3: dei circuiti elettrici Dipartimento Energia Politecnico di Torino di di di Settembre 2012 di di di che cosa significa dei circuiti? un per la dei circuiti deve fornire i seguenti risultati:
ESERCIZIO SOLUZIONE. 13 Aprile 2011
ESERCIZIO Un corpo di massa m è lasciato cadere da un altezza h sull estremo libero di una molla di costante elastica in modo da provocarne la compressione. Determinare: ) la velocità del corpo all impatto
L ALGORITMO DEL SIMPLESSO REVISIONATO
L ALGORITMO DEL SIMPLESSO REVISIONATO L'algoritmo del simplesso revisionato costituisce una diversa implementazione dell algoritmo standard tesa a ridurre, sotto certe condizioni, il tempo di calcolo e
Lezione 36 - Le travi a piu' campate. Parte II
Lezione 36 - Le travi a piu' campate. Parte II ü [A.a. 011-01 : ultima revisione 0 marzo 01] Nella lezione precedente si sono introdotti i vincoli intermedi, suddividendoli in vincoli esterni, che non
FACOLTÀ DI STUDI INGEGNERIA E ARCHITETTURA A. A Corso di Laurea Magistrale in Architettura
FACOLTÀ DI STUDI INGEGNERIA E ARCHITETTURA A. A. 2015-2016 - Corso di Laurea Magistrale in Architettura TECNICA DELLE COSTRUZIONI (9 CFU) DOCENTE: ING. GIUSEPPE MACALUSO Stati Limite Ultimi Sta9 limite
Determinante. Elisabetta Colombo. Determinante. Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico ,
Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, 1 n=2 2 3 con le 4 n=2 n=2 con le Ad ogni matrice quadrata A = (a ij ) j=1...n i=1...n di ordine n si può associare
Lezione 39 - Le equazioni di congruenza
Lezione 9 - Le equazioni di congruenza ü [.a. 0-0 : ultima revisione 7 agosto 0] Per definizione, in una trave iperstatica non e' possibile calcolare le reazioni vincolari con sole equazioni di equilibrio.
Istituzioni di Matematiche, Integrali fratti. corso di laurea in Scienze geologiche. Mauro Costantini
Istituzioni di Matematiche, Integrali fratti corso di laurea in Scienze geologiche. Mauro Costantini tipo: Il nostro obiettivo è studiare gli integrali (indefiniti e definiti delle funzioni razionali,
1 Applicazioni lineari
1 Applicazioni lineari 1 Applicazioni lineari 1.1 Definizione Si considerino lo spazio tridimensionale euclideo E e lo spazio vettoriale V ad esso associato. Definizione. 1.1. Sia A una applicazione di
Università Politecnica delle Marche Facoltà di Ingegneria Ing. Informatica e Automatica Ing. delle Telecomunicazioni Teledidattica
Università Politecnica delle Marche Facoltà di Ingegneria Ing. Informatica e Automatica Ing. delle Telecomunicazioni Teledidattica ANALISI NUMERICA TEMA B (Prof. A. M. Perdon) Ancona, giugno 006 PARTE
FONDAZIONI DI MACCHINE VIBRANTI: metodologia di analisi ed esempio pratico
FONDAZIONI DI ACCHINE VIBRANTI: metodologia di analisi ed esempio pratico 1. ETODOLOGIA DI ANALISI L azione delle macchine vibranti sul terreno attraverso le fondazioni si traduce sempre nella trasmissione
Sistemi vibranti ad 1 gdl
Sistemi vibranti ad 1 gdl - vibrazioni forzate - 14 novembre 2 Le vibrazioni forzate di un sistema ad 1 gdl sono descritte dall equazione: mẍ + cẋ + x = F sin(ωt) (1) dove, con riferimento alla figura