Esame di stato di istruzione secondaria superiore Indirizzi: Scientifico comunicazione opzione sportiva Tema di matematica
|
|
|
- Adriana Angeli
- 5 anni fa
- Visualizzazioni
Transcript
1 Esame di stato di istruzione secondaria superiore Indirizzi: Scientifico comunicazione opzione sportiva Tema di matematica Il candidato risolva uno dei due problemi e risponda a 5 quesiti del questionario PROBLEMA Sia dato un sistema di assi cartesiani Oxy in cui l unità corrisponde a metro. Una particella puntiforme si muove lungo l asse delle ascisse, nel verso positivo, partendo dall origine, con una velocità di metri al secondo. Quando la particella si trova in un generico punto x = a, costruisci un triangolo prendendo le tangenti alla curva di equazione y = ax x nei punti di ascissa e a.. Determina l area del triangolo in funzione di a; quanto vale l area del triangolo dopo 5 secondi?. Dopo quanti secondi il triangolo diventa equilatero? 3. Esprimi in funzione di a l angolo θ formato dalle due tangenti alla curva di equazione y = ax x nei punti di ascissa e a; utilizzando l espressione di θ in funzione di a, verifica la correttezza della risposta che hai fornito al punto precedente. 4. Quando la particella si trova nel generico punto x = a, determina l area della superficie limitata superiormente dalle due rette tangenti e inferiormente dalla curva di equazione y = ax x.
2 Punto Consideriamo i punti O = (,), A = (a, ). SVOLGIMENTO La tangente alla curva y = ax x in O = (,) ha equazione: y = f () x = [a x] x= x = a x La tangente alla curva y = ax x in A = (a, ) ha equazione: y = f (a) (x a) = [a x] x=a (x a) = a (x a) = ax + a Le due tangenti si intersecano nel punto B = ( a, a ). Di seguito la figura in cui è rappresentato il triangolo OBA di cui calcolare l area. Il triangolo OBA è isoscele e la sua area è:
3 S(OBA) = OA BH = a a = a3 4 Dopo 5 secondi sono stati percorsi a = metri pertanto l area del triangolo è: Punto Il triangolo è equilatero se S() = 5 m OB = OA Essendo OB = a + a4 = a 4 4 a +, il triangolo è equilatero se: a a + = a a + = a + = 4 a = 3 a = ± 3 Scartando la soluzione negativa a = 3, il triangolo è equilatero se a = 3 e lo diventa dopo 3 secondi. Alternativamente il triangolo è equilatero quando gli angoli sono di 6 ovvero quando l angolo formato dalla retta OB con l asse delle ascisse è pari a 6. Considerando che, da un punto di vista geometrico, il coefficiente angolare a della retta OB di equazione y = ax coincide con la tangente dell angolo formato dalla retta OB con l asse delle ascisse, deduciamo che il triangolo è equilatero se: Punto 3 a = tan(6 ) = 3 Consideriamo la figura seguente in cui è raffigurato il triangolo con i relativi angoli.
4 La tangente dell angolo formato dalle due tangenti è pari a: tan( θ) = m OB m AB = a + m OB m AB a Se < a < ovvero < θ < 45 si ha tan( θ) < pertanto a a tan( θ) = a = a θ = tan ( a a ) Se a > ovvero 45 < θ < 9 si ha tan( θ) > pertanto Quindi in conclusione: a a tan( θ) = a = a θ = tan ( a a ) ed il triangolo è equilatero se: θ = tan ( a a ) tan ( a a ) = 3 tan ( a a ) = 3
5 a a = 3 a 3 a 3 = a = ± 3 a =, a = ed il valore accettabile è a = 3 come trovato in precedenza. Punto 4 Di seguito la regione di piano R di cui calcolare l area. E possibile calcolare tale area per differenza tra l area del triangolo OBA e l area sottesa dal segmento parabolico: S(R) = a3 a 4 (ax x ) dx = a3 4 [ax x3 a 3 ] = a3 4 (a3 a3 3 ) = a3 4 a3 6 = a3 Alternativamente l area del segmento parabolico, per il teorema di Archimede, è pari ai 3 dell area del rettangolo circoscritto.
6 Il rettangolo circoscritto ha base a ed altezza pari all ordinata del vertice della parabola ovvero a, di 4 conseguenza l area del rettangolo sarà a3 e l area del segmento parabolico a3 = a
7 PROBLEMA Fissato un numero reale k >, si definiscono le funzioni: f k (x) = k ln(x) e g k (x) = e x k i cui grafici sono indicati, rispettivamente, con F k e G k.. Verifica che, qualunque sia k >, le due funzioni f k e g k sono tra loro inverse; definite inoltre le funzioni: stabilisci se si verifica a(x) = b(x), x R. a(x) = f k (g k (x)) e b(x) = g k (f k (x)). Indicata con r la retta di equazione y = x, determina l'equazione della retta s, parallela a r e tangente al grafico F della funzione f (x) = ln(x). Determina inoltre l'equazione della retta t, parallela a r e tangente al grafico G della funzione g (x) = e x. Rappresenta i grafici F e G insieme alle rette s e t e stabilisci qual è la distanza minima tra un punto di F e un punto di G. 3. Verifica che l'equazione f 3 (x) = g 3 (x) possiede due soluzioni sapendo che, qualunque sia k >, gli eventuali punti d'intersezione tra il grafico F k e il grafico G k coincidono con i punti di intersezione tra uno qualsiasi di tali grafici e la retta di equazione y = x. Stabilisci inoltre per quali valori k > i grafici F k e G k sono secanti, per quali valori sono disgiunti e per quale valore essi sono tangenti. 4. Sia A la regione limitata compresa tra i grafici F e e G e e gli assi cartesiani. Determina l'area di A ed il volume del solido generato ruotando A attorno a uno degli assi cartesiani.
8 SVOLGIMENTO Punto La funzione f k (x) = k ln(x) ha come dominio x > e la derivata prima f k (x) = k è sempre x positiva nel dominio, di conseguenza la funzione è strettamente crescente ed è quindi invertibile. La sua inversa è: y = k ln(x) ln(x) = y k x = ey k Invertendo le variabili x ed y otteniamo che la funzione inversa di f k (x) = k ln(x) è g k (x) = e x k. La funzione g k (x) = e x k ha come dominio R e la derivata prima g k (x) = k ex k è sempre positiva nel dominio, di conseguenza la funzione è strettamente crescente ed è quindi invertibile. La sua inversa è: y = e x k x = ln(y) x = k ln(y) k Invertendo le variabili x ed y otteniamo che la funzione inversa di g k (x) = e x k è f k (x) = k ln(x). Calcoliamo ora a(x) = f k (g k (x)) e b(x) = g k (f k (x)), si ha: a(x) = k ln (e x k) = k x = x, x R k b(x) = e k ln(x) k = e ln (x) = x, x > Di conseguenza a(x) = b(x) solo per x > e non per x R. Punto L equazione della retta s, parallela a r e tangente al grafico F è: y = x + q Detto S = (a, a + q) il punto di tangenza, la condizione di tangenza a f (x) = ln(x) è soddisfatta se f (a) = a = a = Imponendo l uguaglianza tra f (x) e s nel passaggio per il punto di tangenza S = (, + q) si ha: ln() = + q q = ln() Quindi il punto di tangenza è S = (, + ln()) e la retta tangente è: s : y = x + ln()
9 L equazione della retta t, parallela a r e tangente al grafico G è: y = x + q Detto T = (a, a + q) il punto di tangenza, la condizione di tangenza a g (x) = e x è soddisfatta se g (a) = ea = e a = a = ln () Imponendo l uguaglianza tra g (x) e t nel passaggio per il punto di tangenza T = ( ln(), ln() + q) si ha: = ln() + q q = ln () Quindi il punto di tangenza è T = ( ln(), ) e la retta tangente è: Di seguito il grafico. t : y = x + ln () La distanza minima tra un punto di F e un punto di G è la distanza tra i punti di tangenza T ed S: d = ( ln ) + ( ln ) = ( ln ).87 Punto 3 Consideriamo la funzione h(x) = f 3 (x) g 3 (x) = 3 ln(x) e x 3, x > Si ha:
10 h() = 3 ln() e 3 = e 3 < h() = 3 ln() e 3 > h(4) = 3 ln(4) e 4 3 > h(5) = 3 ln(5) e 5 3 < di conseguenza le funzioni f 3 (x) e g 3 (x) si intersecano in punti ad ascisse: α (,) β (4,5) Per verificare che le intersezioni siano solo, verifichiamo che le intersezioni tra f k (x) = k ln(x) e la retta y = x siano al massimo al variare di k. Consideriamo la funzione h (x) = f k (x) x = k ln(x) x, x > La derivata prima è h (x) = k x Se k < la funzione h (x) è strettamente decrescente e poichè lim h (x) = + x + lim h (x) = x si deduce che h (x) ha un unica radice ed appartiene all intervallo (,). Se k > si ha: lim h (x) = x + lim h (x) = x + lim x + k x kx (ln x k ) = lim ( x) = x + Inoltre per k > la funzione h (x) è strettamente crescente in (, k) e strettamente decrescente in (k, + ) pertanto (k, k ln k k) è punto di massimo relativo; in particolare tale massimo relativo avrà ordinata positiva se di conseguenza k ln k k > ln k > k > e
11 se k < e, considerando il comportamento di h (x) nell intorno dello e di +, deduciamo che la funzione h (x) non ha alcuna radice reale; se k = e, considerando il comportamento di h (x) nell intorno dello e di +, deduciamo che la funzione h (x) ha una radice doppia x = e; se k > e, considerando il comportamento di h (x) nell intorno dello e di +, deduciamo che la funzione h(x) ha radici reali. Quindi: se k < e i grafici F k e G k sono disgiunti; se k = e i grafici F k e G k sono tangenti; se k > e i grafici F k e G k sono secanti. Di seguito 3 grafici relativi alle 3 differenti situazioni: k = e, k = e, k = e +.
12 Punto 4 Consideriamo la figura seguente in cui è raffigurata la regione A:
13 L area richiesta è pari a: e S(A) = e x e e dx e ln x dx = [e e x e e] e [x(ln x )] e = = (e e) e( + ) = e e Il volume dato dalla rotazione di A intorno all asse delle ascisse è: e V(A) = e x e e dx (e ln x) = ( e3 e ) e (e ) = ( e3 dx = [ e e ex ] e [x(ln x ln x + )] e = + e e ) = + 4e e ( e3 )
14 QUESTIONARIO. Considerati nel piano cartesiano i punti A(,) e B(, ), sia R la regione piana delimitata dal segmento AB e dall arco di curva avente equazione y = 4 sin x, con x. Calcolare il massimo perimetro che può avere un rettangolo inscritto in R avente un lato contenuto nel segmento AB.. Si consideri la funzione f(x) = nell intervallo [p, p] e, detto Γ il suo grafico, sia t la retta x tangente a Γ nel suo punto di ascissa p. Determinare, al variare di p, le aree delle due parti in cui la retta t divide la regione finita di piano compresa fra Γ e l asse delle ascisse. 3. Determinare l equazione della superficie sferica di centro C(,,) tangente al piano di equazione x y z = e le coordinate del punto di contatto tra la superficie sferica e il piano. 4. Verificare che cos n (x) dx = n n cosn (x) dx per n > e usare questo risultato per calcolare cos 4 (x) dx. 5. Si lancia n volte un dado regolare a sei facce. Qual è il più piccolo valore di n tale che la probabilità che non esca mai il numero 3 sia minore dello,%? 6. Data la funzione y = x ax + b 3, determinare i valori dei coefficienti a e b per i quali il grafico della funzione è tangente nel punto di ascissa x = alla retta di equazione y = 7x Date le curve γ e γ di equazione rispettivamente y = x + e y = x 8x + 9, sia t la retta che è tangente a entrambe. Stabilire l area della regione di piano di area finita che è delimitata da γ, γ e t. 8. Una variabile casuale, a valori nell intervallo [, ], è distribuita secondo la densità di probabilità data dalla funzione f(x) = { 3 4 x, x, < x Stabilire il valore medio e il valore mediano di questa variabile casuale. 9. Determinare il luogo geometrico dei punti P(x, y, z) equidistante dai punti ti A(,,) e B( 3,,).. Verificare che la funzione y(x) = e x sin x è soluzione dell equazione differenziale y + y + y =.
15 SVOLGIMENTO. Consideriamo la figura seguente. Il rettangolo R ha vertici: C = (x, ), D = ( x, ), E = (x, 4 sin x), F = ( x, 4 sin x) Il perimetro del rettangolo è pari a: p(x) = ( x) + 4 sin x = ( x + 4 sin x) La derivata prima della funzione perimetro è: p (x) = ( + 4 cos x) ed è positiva se cos x > x < 3 Di conseguenza la funzione perimentro è strettamente crescente per x < 3 e strettamente decrescente per 3 < x pertanto il perimetro è massimo per x = 3 e misura p ( 3 ) = ( ) =
16 . La retta t ha equazione: dove f (p) = p pertanto la retta diventa: t: y = f (p)(x p) p t: y = p (x p) p = x p p La retta tantente interseca l asse delle ascisse in (p, ). Consideriamo la figura seguente in cui, considerando p >, sono rappresentate le regioni di piano in cui la tangente t divide la regione finita di piano compresa fra Γ e l asse delle ascisse. I punti A, B e C hanno coordinate A = (p, ), B = (p, ), C = (p, ). p L area del triangolo ABC è: S(ABC) = AC CB L area della regione in grigio chiaro è: p S(ABD) = dx x p = p p = = [ln x] p p = ln(p) ln(p) = ln() Quindi al variare di p le aree in cui la tangente t divide la regione finita di piano compresa fra Γ e l asse delle ascisse misurano rispettivamente e ln().
17 3. La retta perpendicolare al piano di eqauzione x y + z = e passante per il centro C(,,) ha equazione parametrica: x = + t { y = t z = + t Sostituendo tale equazione parametrica nell equazione del piano, troviamo il punto di intersezione tra la retta ed il piano: x y + z = + t + + t + + t = 3t = 6 t = pertanto il punto di intersezione è P(3, 3,4). Il raggio della superficie sferica è: RC = (3 ) + ( 3 + ) + (4 ) = 3 Quindi l equazione della sfera è: (x ) + (y + ) + (z ) = 4. Si ha: cos n (x) dx = cos(x) cos n (x) dx ed applicando l integrazione per parti si ricava:
18 cos n (x) dx = cos(x) cos n (x) dx = [sin(x) cos n (x)] = = (n ) sin (x) cos n (x) dx = + (n ) sin (x) cos n (x) dx = = (n ) [ cos (x)] cos n (x) dx = = (n ) cos n (x) dx (n ) cos n (x) dx cos n (x) dx + (n ) cos n (x) dx = (n ) cos n (x) dx n cos n (x) dx = (n ) cos n (x) dx (n cos n ) (x) dx = cos n (x) dx n Applicando il risultato a cos 4 (x) dx si ricava: cos 4 (x) dx = 3 4 cos (x) dx = 3 4 dx = La probabilità che, lanciando una volta un dado regolare a 6 facce, non esca 3 è pari a p = 5 6. Lanciando n volte il dado, la probabilità che non esca mai 3 è p n = ( 5 6 )n. Imponendo che tale probabilità sia minore di, si ha: ( 5 6 )n <, ln [( 5 6 )n ] < ln( 4 ) n ln ( 5 4 ln ) < 4 ln n > ln( 5 6 ) Quindi con n = 5 si ottiene una probabilità inferiore a,%. 6. Il valore assoluto nella funzione y = x ax + b 3 ha senso solo se i coefficienti a e b sono di segno discorde. Assumiamo quindi che a e b siano di segno discorde. E possibile scrivere la funzione y = x ax + b 3 nel seguente modo:
19 y = ax 3 + bx 3 ax 3 bx 3 { se x b a, x b a se b a < x < b a La derivata prima della funzione è: y = 3ax + b 3ax b { se x b a, x b a se b a < x < b a Il passaggio per il punto (, ) implica che: a + b 3 = a + b = Il grafico di y è tangente alla retta y = 7x 9 nel punto (, ) se y () = 7 ovvero se oppure 3a + b = 7 se b a + b a Consideriamo ora a + b a b. 3a + b = 7 se < b a + b < a I coefficienti a e b deve soddisfare il seguente sistema: la cui soluzione è: a + b = { 3a + b = 7 { a = 3 b = ed è accettabile in quanto soddisfa la condizione a + b. In questo caso l equazione della funzione è
20 y = x 3x 3 = x(3x ) 3 = 3x 3 x 3 Consideriamo ora a + b < a < b. I coefficienti a e b devono soddisfare i seguenti sistemi: la cui soluzione è: a + b = { 3a + b = 7 a = 3 { b = ed è accettabile a + b < e corrisponde alla precedente con il segno invertito. In questo caso l equazione della funzione è Quindi i coefficienti a e b sono y = x 3x + 3 = x(3x ) 3 = 3x 3 x 3 { a = 3 = 3 oppure {a b = b = e la funzione richiesta in ambo i casi è y = 3x 3 x 3.
21 7. Sia T = (a, b) il punto di tangenza di t con γ e S = (c, d) il punto di tangenza di t con γ. Il coefficiente angolare della tangente a γ è: m = f (a) = a mentre il coefficiente angolare della tangente a γ è: m = f (c) = c 8 Imponendo l uguaglianza si ricava: a = c 8 c = a + 4 La retta tangente a γ ha equazione: y = a(x a) + a + La retta tangente a γ ha equazione: y = a(x a 4) + (a + 4) 8(a + 4) + 9 Imponendone l uguaglianza si ricava: a(x a) + a + = a(x a 4) + (a + 4) 8(a + 4) + 9 ax a + = ax a 8a + a + 8a + 6 8a a + = a 8a 7 8a = 8 a = L equazione della tangente è quindi: y = (x + ) + + = x ed i punti di tangenza sono rispettivamente: T = (,), S = (3, 6) Di seguito la figura in cui viene raffigurata in grigio la regione di piano delimitata da γ, γ e t.. Le due curve si intersecano nel pinto A = (,). L area richiesta è pari a:
22 S = (x + + x) = (x + ) (x + )3 = [ ] 3 3 dx + (x 8x x) 3 dx + (x 3) dx = (x 3)3 + [ ] 3 3 = = 6 3 dx = 8. Verifichiamo innanzitutto che f(x) è una densità di probabilità ovvero che Si ha: f(x) dx = ( 3 4 x ) f(x) dx = dx + ( ) = ( 3 ) + ( ) = = dx = [ x 3 x3 ] + [ x ] = Il valore medio è pari a: E[X] = xf(x) dx = ( 3 x 4 x3 ) dx + ( x) = ( 6 6 ) + (5 6 4 ) = = 3 48 dx = [ x 6 x4 6 ] + [ x 4 ] = Poichè p( X ) = ( 3 4 x ) dx = [ x 3 x3 ] = 4 p( X ) = ( ) dx = [ x ] = 3 4 deduciamo che il valore mediano appartiene all intervallo [,]. Indichiamo con y il valore mediano, per definizione di valore mediano si ha: y f(x) dx = e + y f(x) dx = Nel caso in esame, ricordando che il valore mediano appartiane all intervallo [,], y è valore mediano se:
23 dx = y y = y = 5 6 y = 3 y = 4 9. Imponendo PA = PB si ha: (x ) + (y ) + (z ) = (x + 3) + (y ) + (z ) x + y y + + z 4z + 4 = x + 6x y 4y z 6x y + 4z + 8 = 3x y + z + 4 = Quindi il luogo dei punti equidistanti è il piano di equazione 3x y + z + 4 =. Alternativamente il luogo geometrico dei punti equidistanti è il piano perpendicolare ad AB passante per il punto medio di AB. Il punto medio di AB è M = ( 3, 3, ) ed il piano ha parametri direttori a = 3 = 3, b = =, c = =, di conseguenza il piano perpendicolare ad AB e passante per M ha equazione: 3 (x + 3 ) + (y 3 ) (z ) = 3x y + z + 4 =. Le derivate prima e seconda della funzione soluzione sono: y (x) = e x sin x + e x cos x y (x) = e x sin x e x cos x e x cos x e x sin x = e x cos x Sostituendo nell equazione differenziale si ricava: e x cos x + ( e x sin x + e x cos x) + e x sin x = = e x cos x e x sin x + e x cos x + e x sin x = Avendo dimostrato l identità deduciamo che y(x) = e x sin x è soluzione dell equazione differenziale y + y + y =.
Il candidato risolva uno dei due problemi e risponda a 5 quesiti del questionario
 Esame di stato di istruzione secondaria superiore Indirizzi: Scientifico, Scientifico opzione scienze applicate e Scientifico ad indirizzo sportivo Tema di matematica Il candidato risolva uno dei due problemi
Esame di stato di istruzione secondaria superiore Indirizzi: Scientifico, Scientifico opzione scienze applicate e Scientifico ad indirizzo sportivo Tema di matematica Il candidato risolva uno dei due problemi
Il candidato risolva uno dei due problemi e risponda a 5 quesiti del questionario
 Esame di stato di istruzione secondaria superiore Indirizzi: Scientifico, Scientifico opzione scienze applicate e Scientifico ad indirizzo sportivo Tema di matematica Il candidato risolva uno dei due problemi
Esame di stato di istruzione secondaria superiore Indirizzi: Scientifico, Scientifico opzione scienze applicate e Scientifico ad indirizzo sportivo Tema di matematica Il candidato risolva uno dei due problemi
SESSIONE SUPPLETIVA QUESTIONARIO QUESITO 1
 www.matefilia.it SESSIONE SUPPLETIVA 8 - QUESTIONARIO QUESITO A = (; ) e B = (; ) ; y = 4 sen(x) con x Rappresentiamo la regione R ed un rettangolo inscritto in R avente un lato contenuto nel segmento
www.matefilia.it SESSIONE SUPPLETIVA 8 - QUESTIONARIO QUESITO A = (; ) e B = (; ) ; y = 4 sen(x) con x Rappresentiamo la regione R ed un rettangolo inscritto in R avente un lato contenuto nel segmento
II Prova - Matematica Classe V Sez. Unica
 Liceo Scientifico Paritario R. Bruni Padova, loc. Ponte di Brenta, 5/7/8 II Prova - Matematica Classe V Sez. Unica Soluzione Problemi. Risolvi uno dei due problemi: Problema. Un artigiano deve realizzare
Liceo Scientifico Paritario R. Bruni Padova, loc. Ponte di Brenta, 5/7/8 II Prova - Matematica Classe V Sez. Unica Soluzione Problemi. Risolvi uno dei due problemi: Problema. Un artigiano deve realizzare
Matematica classe 5 C a.s. 2012/2013
 Matematica classe 5 C a.s. 2012/2013 Asintoti e grafici 1) Una funzione y = f(x) gode delle seguenti caratteristiche: D / 4, y 0 se x 0 x 2, lim, 3. Rappresentare un grafico qualitativo della funzione.
Matematica classe 5 C a.s. 2012/2013 Asintoti e grafici 1) Una funzione y = f(x) gode delle seguenti caratteristiche: D / 4, y 0 se x 0 x 2, lim, 3. Rappresentare un grafico qualitativo della funzione.
Verifica del 8 febbraio 2018
 Verifica del 8 febbraio 018 Esercizio 1 (15 punti) Risolvi le seguenti disequazioni: 1 x 1 a) x + 6x + 8 x 3 b) x + 1 + 1 c) d) Esercizio (0 punti) 3 x 8 x 4 x 3 ax 9 Considera la funzione f ( x) = x 3x
Verifica del 8 febbraio 018 Esercizio 1 (15 punti) Risolvi le seguenti disequazioni: 1 x 1 a) x + 6x + 8 x 3 b) x + 1 + 1 c) d) Esercizio (0 punti) 3 x 8 x 4 x 3 ax 9 Considera la funzione f ( x) = x 3x
1) Ricava il dominio di ciascuna delle due funzioni e scrivilo attraverso intervalli
 1) Ricava il dominio di ciascuna delle due funzioni e scrivilo attraverso intervalli A) 1 2 B) [ A) 2 x 1; B) (-, - 3) ( - 3, 0) ( 0, + ) ] 2) Riferendoti al grafico rappresentato completa a) Il dominio
1) Ricava il dominio di ciascuna delle due funzioni e scrivilo attraverso intervalli A) 1 2 B) [ A) 2 x 1; B) (-, - 3) ( - 3, 0) ( 0, + ) ] 2) Riferendoti al grafico rappresentato completa a) Il dominio
ULTERIORI ESERCIZI SUL CALCOLO DIFFERENZIALE
 ULTERIORI ESERCIZI SUL CALCOLO DIFFERENZIALE 1 Scrivi l equazione della retta tangente al grafico di f(x) = (1 + 2x) 4 nel suo punto di intersezione con l asse y 2 Scrivi l equazione della retta tangente
ULTERIORI ESERCIZI SUL CALCOLO DIFFERENZIALE 1 Scrivi l equazione della retta tangente al grafico di f(x) = (1 + 2x) 4 nel suo punto di intersezione con l asse y 2 Scrivi l equazione della retta tangente
VERIFICA DI MATEMATICA. Classe 3P 02/10/2018
 Non utilizzare matita e bianchetto. Classe 3P 02/10/2018 Il punteggio viene attribuito in base alla correttezza e alla completezza nella risoluzione dei quesiti, al metodo risolutivo adottato e alle caratteristiche
Non utilizzare matita e bianchetto. Classe 3P 02/10/2018 Il punteggio viene attribuito in base alla correttezza e alla completezza nella risoluzione dei quesiti, al metodo risolutivo adottato e alle caratteristiche
di 4, che è l area dell intera mattonella, imponiamo che 5 e quindi a = 7 5
 Problemi Problema 1) 1) Siccome la funzione f(x) è una retta, l espressione cercata è f(x) = 1 x che soddisfa le condizioni a), b) e c) richieste. Per riflessione rispetto all asse y, all asse x e all
Problemi Problema 1) 1) Siccome la funzione f(x) è una retta, l espressione cercata è f(x) = 1 x che soddisfa le condizioni a), b) e c) richieste. Per riflessione rispetto all asse y, all asse x e all
f(x) = sin cos α = k2 2 k
 28 Maggio 2015 Il punteggio viene attribuito in base alla correttezza e completezza nella risoluzione dei quesiti, nonché alle caratteristiche dell esposizione: chiarezza, ordine ed organicità. La sufficienza
28 Maggio 2015 Il punteggio viene attribuito in base alla correttezza e completezza nella risoluzione dei quesiti, nonché alle caratteristiche dell esposizione: chiarezza, ordine ed organicità. La sufficienza
Esame di Stato di Liceo Scientifico Corso di Ordinamento. Soluzione dei Temi di Matematica proposti nella Sessione Ordinaria 2010.
 Corso di Ordinamento Soluzione dei Temi di Matematica proposti nella Sessione Ordinaria 00. Sommario Problema... Punto.... Punto.... Punto.... 4 Punto 4.... 5 Problema... 6 Punto.... 6 Punto.... 7 Punto....
Corso di Ordinamento Soluzione dei Temi di Matematica proposti nella Sessione Ordinaria 00. Sommario Problema... Punto.... Punto.... Punto.... 4 Punto 4.... 5 Problema... 6 Punto.... 6 Punto.... 7 Punto....
CALENDARIO BOREALE 1 EUROPA 2015 QUESITO 1
 www.matefilia.it Indirizzi: LI0, EA0 SCIENTIFICO; LI0 - SCIENTIFICO - OPZIONE SCIENZE APPLICATE CALENDARIO BOREALE EUROPA 05 QUESITO La funzione f(x) è continua per x [ 4; 4] il suo grafico è la spezzata
www.matefilia.it Indirizzi: LI0, EA0 SCIENTIFICO; LI0 - SCIENTIFICO - OPZIONE SCIENZE APPLICATE CALENDARIO BOREALE EUROPA 05 QUESITO La funzione f(x) è continua per x [ 4; 4] il suo grafico è la spezzata
Soluzioni verifica di Matematica 5 a E Liceo Scientifico - 17/10/2013
 Istituto Superiore XXV aprile Pontedera - Prof Francesco Daddi Soluzioni verifica di Matematica 5 a E Liceo Scientifico - 7/0/03 Esercizio Si consideri la funzione e x+ se x < f(x) = 0 se x = x x x se
Istituto Superiore XXV aprile Pontedera - Prof Francesco Daddi Soluzioni verifica di Matematica 5 a E Liceo Scientifico - 7/0/03 Esercizio Si consideri la funzione e x+ se x < f(x) = 0 se x = x x x se
M557 - ESAME DI STATO DI LICEO SCIENTIFICO
 M7 - ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO Tema di: MATEMATICA Il candidato risolva uno dei due problemi e cinque quesiti scelti nel questionario. PROBLEMA 1 Nel primo quadrante del
M7 - ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO Tema di: MATEMATICA Il candidato risolva uno dei due problemi e cinque quesiti scelti nel questionario. PROBLEMA 1 Nel primo quadrante del
CALENDARIO BOREALE 1 EUROPA 2015 QUESITO 1
 www.matefilia.it Indirizzi: LI0, EA0 SCIENTIFICO; LI0 - SCIENTIFICO - OPZIONE SCIENZE APPLICATE CALENDARIO BOREALE EUROPA 05 QUESITO La funzione f(x) è continua per x [ 4; 4] il suo grafico è la spezzata
www.matefilia.it Indirizzi: LI0, EA0 SCIENTIFICO; LI0 - SCIENTIFICO - OPZIONE SCIENZE APPLICATE CALENDARIO BOREALE EUROPA 05 QUESITO La funzione f(x) è continua per x [ 4; 4] il suo grafico è la spezzata
CALENDARIO BOREALE 2 AMERICHE 2015 QUESITO 1
 www.matefilia.it Indirizzi: LI0, EA0 SCIENTIFICO; LI0 - SCIENTIFICO - OPZIONE SCIENZE APPLICATE CALENDARIO BOREALE AMERICHE 0 QUESITO Determinare il volume del solido generato dalla rotazione attorno alla
www.matefilia.it Indirizzi: LI0, EA0 SCIENTIFICO; LI0 - SCIENTIFICO - OPZIONE SCIENZE APPLICATE CALENDARIO BOREALE AMERICHE 0 QUESITO Determinare il volume del solido generato dalla rotazione attorno alla
SIMULAZIONE - 29 APRILE QUESITI
 www.matefilia.it SIMULAZIONE - 29 APRILE 206 - QUESITI Q Determinare il volume del solido generato dalla rotazione attorno alla retta di equazione y= della regione di piano delimitata dalla curva di equazione
www.matefilia.it SIMULAZIONE - 29 APRILE 206 - QUESITI Q Determinare il volume del solido generato dalla rotazione attorno alla retta di equazione y= della regione di piano delimitata dalla curva di equazione
SIMULAZIONE - 29 APRILE QUESITI
 www.matefilia.it SIMULAZIONE - 29 APRILE 206 - QUESITI Q Determinare il volume del solido generato dalla rotazione attorno alla retta di equazione y= della regione di piano delimitata dalla curva di equazione
www.matefilia.it SIMULAZIONE - 29 APRILE 206 - QUESITI Q Determinare il volume del solido generato dalla rotazione attorno alla retta di equazione y= della regione di piano delimitata dalla curva di equazione
QUESITO 1. Lanciando due dadi, qual è il numero che ha maggiore probabilità di uscita? Qual è la probabilità che esca un numero primo?
 www.matefilia.it PNI 29 SESSIONE STRAORDINARIA - QUESITI QUESITO 1 Lanciando due dadi, qual è il numero che ha maggiore probabilità di uscita? Qual è la probabilità che esca un numero primo? Nel lancio
www.matefilia.it PNI 29 SESSIONE STRAORDINARIA - QUESITI QUESITO 1 Lanciando due dadi, qual è il numero che ha maggiore probabilità di uscita? Qual è la probabilità che esca un numero primo? Nel lancio
( ) 2. Determina il resto della divisione fra il polinomio P ( x) 2 2x. 3. Per quale valore del parametro m il polinomio P(
 ALGEBRA E ANALITICA. Determina il resto della divisione fra il polinomio P ( ) e il binomio D ( ). [ R ( ) ] + + + ( ) Detto D() il polinomio divisore, Q() il polinomio quoziente, R() il resto, il polinomio
ALGEBRA E ANALITICA. Determina il resto della divisione fra il polinomio P ( ) e il binomio D ( ). [ R ( ) ] + + + ( ) Detto D() il polinomio divisore, Q() il polinomio quoziente, R() il resto, il polinomio
Problema ( ) = 0,!
 Domanda. Problema ( = sen! x ( è! Poiché la funzione seno è periodica di periodo π, il periodo di g x! = 4. Studio di f. La funzione è pari, quindi il grafico è simmetrico rispetto all asse y. È sufficiente
Domanda. Problema ( = sen! x ( è! Poiché la funzione seno è periodica di periodo π, il periodo di g x! = 4. Studio di f. La funzione è pari, quindi il grafico è simmetrico rispetto all asse y. È sufficiente
SESSIONE SUPPLETIVA QUESTIONARIO QUESITO 1
 www.matefilia.it SESSIONE SUPPLETIVA 015 - QUESTIONARIO x QUESITO 1 Data la funzione integrale ln(t) dt, determinare per quali valori di x il suo grafico 1 incontra la retta di equazione y = x + 1. Calcoliamo
www.matefilia.it SESSIONE SUPPLETIVA 015 - QUESTIONARIO x QUESITO 1 Data la funzione integrale ln(t) dt, determinare per quali valori di x il suo grafico 1 incontra la retta di equazione y = x + 1. Calcoliamo
` Ç áàxüé wxääë\áàüâé ÉÇx? wxääëhç äxüá àõ x wxäät e vxüvt
 ESAME DI STATO DI LICEO SCIENTIFICO Sessione Ordinaria 205 ` Ç áàxüé wxääë\áàüâé ÉÇx? wxääëhç äxüá àõ x wxäät e vxüvt M557 ESAME DI STATO DI ISTRUZIONE SECONDARIA SUPERIORE Indirizzi: LI02, EA02 SCIENTIFICO
ESAME DI STATO DI LICEO SCIENTIFICO Sessione Ordinaria 205 ` Ç áàxüé wxääë\áàüâé ÉÇx? wxääëhç äxüá àõ x wxäät e vxüvt M557 ESAME DI STATO DI ISTRUZIONE SECONDARIA SUPERIORE Indirizzi: LI02, EA02 SCIENTIFICO
Indirizzo: Tema di Il candidato risolva uno dei due problemi e 4 quesiti del questionario. PROBLEMA 1 PROBLEMA 2
 Sessione ordinaria all estero (EUROPA) 8-9 ESAMI DI STATO DI LICEO SCIENTIFICO SCUOLE ITALIANE ALL ESTERO: EUROPA CORSO DI ORDINAMENTO Indirizzo: SCIENTIFICO Tema di: MATEMATICA Il candidato risolva uno
Sessione ordinaria all estero (EUROPA) 8-9 ESAMI DI STATO DI LICEO SCIENTIFICO SCUOLE ITALIANE ALL ESTERO: EUROPA CORSO DI ORDINAMENTO Indirizzo: SCIENTIFICO Tema di: MATEMATICA Il candidato risolva uno
Liceo Scientifico di ordinamento anno ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO anno PROBLEMA 1
 Liceo Scientifico di ordinamento anno 00-00 ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO anno 00-00 PROBLEMA Punto a Indicati rispettivamente con V ed S il volume e l area totale di T e con
Liceo Scientifico di ordinamento anno 00-00 ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO anno 00-00 PROBLEMA Punto a Indicati rispettivamente con V ed S il volume e l area totale di T e con
8 Simulazione di prova d Esame di Stato
 8 Simulazione di prova d Esame di Stato Problema Risolvi uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario Si consideri la famiglia di funzioni f α () = a e a con a parametro reale
8 Simulazione di prova d Esame di Stato Problema Risolvi uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario Si consideri la famiglia di funzioni f α () = a e a con a parametro reale
SYLLABUS DI GEOMETRIA ANALITICA 3A DON BOSCO
 SYLLABUS DI GEOMETRIA ANALITICA 3A DON BOSCO 2014-15 Si precisa che, con questo syllabus, l intenzione non è quella di ridurre l apprendimento della matematica allo studio mnemonico di una serie di procedure.
SYLLABUS DI GEOMETRIA ANALITICA 3A DON BOSCO 2014-15 Si precisa che, con questo syllabus, l intenzione non è quella di ridurre l apprendimento della matematica allo studio mnemonico di una serie di procedure.
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO
 ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO Il candidato risolva uno dei due problemi e 5 dei quesiti in cui si articola il questionario. PROBLEMA In un piano, riferito ad un sistema di assi
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO Il candidato risolva uno dei due problemi e 5 dei quesiti in cui si articola il questionario. PROBLEMA In un piano, riferito ad un sistema di assi
Una circonferenza e una parabola sono disegnate nel piano cartesiano. La circonferenza ha centro nel punto
 La parabola Esercizi Esercizio 368.395 Una circonferenza e una parabola sono disegnate nel piano cartesiano. La circonferenza ha centro nel punto 0 ;5 e raggio, e la parabola ha il suo vertice in 0 ;0.
La parabola Esercizi Esercizio 368.395 Una circonferenza e una parabola sono disegnate nel piano cartesiano. La circonferenza ha centro nel punto 0 ;5 e raggio, e la parabola ha il suo vertice in 0 ;0.
SESSIONE ORDINARIA 2007 CORSO DI ORDINAMENTO SCUOLE ITALIANE ALL ESTERO - AMERICHE
 SESSIONE ORDINARIA 007 CORSO DI ORDINAMENTO SCUOLE ITALIANE ALL ESTERO - AMERICHE PROBLEMA Si consideri la funzione f definita da f ( x) x, il cui grafico è la parabola.. Si trovi il luogo geometrico dei
SESSIONE ORDINARIA 007 CORSO DI ORDINAMENTO SCUOLE ITALIANE ALL ESTERO - AMERICHE PROBLEMA Si consideri la funzione f definita da f ( x) x, il cui grafico è la parabola.. Si trovi il luogo geometrico dei
SIMULAZIONE DEL 25/5/ Seconda prova
 SIMULAZIONE DEL 25/5/2017 - Seconda prova Il candidato risolva uno dei due problemi e risponda a 5 quesiti del questionario. PROBLEMA 1 La lampada da tavolo in figura, dove il sistema di riferimento cartesiano
SIMULAZIONE DEL 25/5/2017 - Seconda prova Il candidato risolva uno dei due problemi e risponda a 5 quesiti del questionario. PROBLEMA 1 La lampada da tavolo in figura, dove il sistema di riferimento cartesiano
1) Qual è il parallelogrammo di area massima tra quelli di lati assegnati? Giustificare la risposta.
 TEMA PROBLEMA k Sono assegnate le funzioni di equazione y = e, essendo k un numero reale. a. stabilire al variare di k il numero di punti stazionari e la loro natura b. stabilire per quali valori di k
TEMA PROBLEMA k Sono assegnate le funzioni di equazione y = e, essendo k un numero reale. a. stabilire al variare di k il numero di punti stazionari e la loro natura b. stabilire per quali valori di k
Ministero dell Istruzione, dell Università e della Ricerca
 Pag. 1/5 Sessione straordinaria 2018 I043 ESAME DI STATO DI ISTRUZIONE SECONDARIA SUPERIORE Indirizzi: LI02, EA02 SCIENTIFICO LI03 - SCIENTIFICO - OPZIONE SCIENZE APPLICATE LI15 - SCIENTIFICO - SEZIONE
Pag. 1/5 Sessione straordinaria 2018 I043 ESAME DI STATO DI ISTRUZIONE SECONDARIA SUPERIORE Indirizzi: LI02, EA02 SCIENTIFICO LI03 - SCIENTIFICO - OPZIONE SCIENZE APPLICATE LI15 - SCIENTIFICO - SEZIONE
1. Indicato con T il punto di tangenza delle due circonferenze e posto TQ = QC = y, applicando il ( ) ( ) ( ) 2. =, con la limitazione 0 x 1.
 PROBLEMA. Indicato con T il punto di tangenza delle due circonferenze e posto TQ = QC = y, applicando il teorema di Pitagora al triangolo rettangolo ABC, si ha: + y = + y, ovvero y = + e, infine, y = f
PROBLEMA. Indicato con T il punto di tangenza delle due circonferenze e posto TQ = QC = y, applicando il teorema di Pitagora al triangolo rettangolo ABC, si ha: + y = + y, ovvero y = + e, infine, y = f
x = t y = t z = t 3 1 A = B = 1 2
 11/1/05 Teoria: Enunciare e discutere il teorema di Lagrange. Esercizio 1. Determinare l equazione cartesiana del piano passante per P 0 = (1,, 1) e contenente i vettori u = (,, ) e v = (1, 5, 4). Risposta
11/1/05 Teoria: Enunciare e discutere il teorema di Lagrange. Esercizio 1. Determinare l equazione cartesiana del piano passante per P 0 = (1,, 1) e contenente i vettori u = (,, ) e v = (1, 5, 4). Risposta
ESAME DI STATO 2016 INDIRIZZO SCIENTIFICO E OPZIONE SCIENZE APPLICATE
 ESAME DI STATO 2016 INDIRIZZO SCIENTIFICO E OPZIONE SCIENZE APPLICATE Il candidato risolva uno dei due problemi e risponda a 5 quesiti del questionario 1. PROBLEMA 1 L amministratore di un piccolo condominio
ESAME DI STATO 2016 INDIRIZZO SCIENTIFICO E OPZIONE SCIENZE APPLICATE Il candidato risolva uno dei due problemi e risponda a 5 quesiti del questionario 1. PROBLEMA 1 L amministratore di un piccolo condominio
Stabilire se il punto di coordinate (1,1) appartiene alla circonferenza centrata nell origine e di raggio 1.
 Definizione di circonferenza e cerchio. Equazione della circonferenza centrata in O e di raggio R. Esercizi. La circonferenza e il cerchio Definizioni: dato un punto C nel piano cartesiano e dato un numero
Definizione di circonferenza e cerchio. Equazione della circonferenza centrata in O e di raggio R. Esercizi. La circonferenza e il cerchio Definizioni: dato un punto C nel piano cartesiano e dato un numero
y = [Sol. y 2x = 4x Verifica n.1
 Verifica n.1 disegnare curve, con valori assoluti e radicali luoghi geometrici (con retta, parabola, circonferenza) funzione omografica parabola aree (ellisse, segmento parabolico) formule goniometriche:
Verifica n.1 disegnare curve, con valori assoluti e radicali luoghi geometrici (con retta, parabola, circonferenza) funzione omografica parabola aree (ellisse, segmento parabolico) formule goniometriche:
Condizione di allineamento di tre punti
 LA RETTA L equazione lineare in x e y L equazione: 0 con,,, e non contemporaneamente nulli, si dice equazione lineare nelle due variabili e. Ogni coppia ; tale che: 0 si dice soluzione dell equazione.
LA RETTA L equazione lineare in x e y L equazione: 0 con,,, e non contemporaneamente nulli, si dice equazione lineare nelle due variabili e. Ogni coppia ; tale che: 0 si dice soluzione dell equazione.
` Ç áàxüé wxääë\áàüâé ÉÇx? wxääëhç äxüá àõ x wxäät e vxüvt
 ESAME DI STATO DI LICEO SCIENTIFICO Sessione Ordinaria 2016 ` Ç áàxüé wxääë\áàüâé ÉÇx? wxääëhç äxüá àõ x wxäät e vxüvt M557 ESAME DI STATO DI ISTRUZIONE SECONDARIA SUPERIORE Indirizzi: LI02, EA02 SCIENTIFICO
ESAME DI STATO DI LICEO SCIENTIFICO Sessione Ordinaria 2016 ` Ç áàxüé wxääë\áàüâé ÉÇx? wxääëhç äxüá àõ x wxäät e vxüvt M557 ESAME DI STATO DI ISTRUZIONE SECONDARIA SUPERIORE Indirizzi: LI02, EA02 SCIENTIFICO
Determinare l altezza del triangolo relativa al lato AB e tracciare la circonferenza k avente centro in C e tangente al lato AB.
 www.matefilia.it PNI 006 SESSIONE STRAORDINARIA - PROBLEMA 1 È dato il triangolo ABC in cui: AB = 5, AC = 5 5, tg A =. Determinare l altezza del triangolo relativa al lato AB e tracciare la circonferenza
www.matefilia.it PNI 006 SESSIONE STRAORDINARIA - PROBLEMA 1 È dato il triangolo ABC in cui: AB = 5, AC = 5 5, tg A =. Determinare l altezza del triangolo relativa al lato AB e tracciare la circonferenza
COMPITI PER IL RECUPERO DELLA CARENZA FORMATIVA (E RIPASSO) MATEMATICA III - A GAT
 1 COMPITI PER IL RECUPERO DELLA CARENZA FORMATIVA (E RIPASSO) MATEMATICA III - A GAT Scheda 1: Fondamenti di geometria analitica 1. Determina il punto P dell asse y che forma con A(; ) e B(; ) un triangolo
1 COMPITI PER IL RECUPERO DELLA CARENZA FORMATIVA (E RIPASSO) MATEMATICA III - A GAT Scheda 1: Fondamenti di geometria analitica 1. Determina il punto P dell asse y che forma con A(; ) e B(; ) un triangolo
LICEO SCIENTIFICO SESSIONE STRAORDINARIA 2016 QUESTIONARIO QUESITO 1. lim. = lim cos(x) = 1 2 QUESITO 2
 www.matefilia.it LICEO SCIENTIFICO SESSIONE STRAORDINARIA 6 QUESTIONARIO QUESITO Calcolare il limite: sen(cos(x) ) lim x ln (cos (x)) Ricordiamo che, se f(x) tende a zero, risulta: senf(x)~f(x) ed ln (
www.matefilia.it LICEO SCIENTIFICO SESSIONE STRAORDINARIA 6 QUESTIONARIO QUESITO Calcolare il limite: sen(cos(x) ) lim x ln (cos (x)) Ricordiamo che, se f(x) tende a zero, risulta: senf(x)~f(x) ed ln (
Il candidato risolva uno dei due problemi e risponda a 5 quesiti del questionario
 Esame di stato di istruzione secondaria superiore Indirizzi: Scientifico, Scientifico opzione scienze applicate e Scientifico ad indirizzo sportivo Tema di matematica Il candidato risolva uno dei due problemi
Esame di stato di istruzione secondaria superiore Indirizzi: Scientifico, Scientifico opzione scienze applicate e Scientifico ad indirizzo sportivo Tema di matematica Il candidato risolva uno dei due problemi
COMPITI PER IL RECUPERO DELLA CARENZA FORMATIVA (E RIPASSO) MATEMATICA III - VE
 1 COMPITI PER IL RECUPERO DELLA CARENZA FORMATIVA (E RIPASSO) MATEMATICA III - VE Scheda 1: Fondamenti di geometria analitica 1. Determina il punto P dell asse y che forma con A(; ) e B(; ) un triangolo
1 COMPITI PER IL RECUPERO DELLA CARENZA FORMATIVA (E RIPASSO) MATEMATICA III - VE Scheda 1: Fondamenti di geometria analitica 1. Determina il punto P dell asse y che forma con A(; ) e B(; ) un triangolo
a) Rappresentiamo il quadrato ABCD e il punto P sul prolungamento del lato AB.
 VERIFICA DI MATEMATICA SIMULAZIONE GLI INTEGRALI DEFINITI - SOLUZIONI Problema : a) Rappresentiamo il quadrato ABCD e il punto P sul prolungamento del lato AB. Per determinare la posizione di P, affinché
VERIFICA DI MATEMATICA SIMULAZIONE GLI INTEGRALI DEFINITI - SOLUZIONI Problema : a) Rappresentiamo il quadrato ABCD e il punto P sul prolungamento del lato AB. Per determinare la posizione di P, affinché
DERIVATE E LORO APPLICAZIONE
 DERIVATE E LORO APPLICAZIONE SIMONE ALGHISI 1. Applicazione del calcolo differenziale 1 Abbiamo visto a lezione che esiste un importante legame tra la continuità di una funzione y = f(x) in un punto x
DERIVATE E LORO APPLICAZIONE SIMONE ALGHISI 1. Applicazione del calcolo differenziale 1 Abbiamo visto a lezione che esiste un importante legame tra la continuità di una funzione y = f(x) in un punto x
1 Funzioni trigonometriche
 1 Funzioni trigonometriche 1 1 Funzioni trigonometriche Definizione 1.1. Si definisce circonferenza goniometrica la circonferenza centrata nell origine di un piano cartesiano e raggio unitario. L equazione
1 Funzioni trigonometriche 1 1 Funzioni trigonometriche Definizione 1.1. Si definisce circonferenza goniometrica la circonferenza centrata nell origine di un piano cartesiano e raggio unitario. L equazione
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 2007 Sessione suppletiva
 ESAME DI STAT DI LIE SIENTIFI RS DI RDINAMENT 7 Sessione suppletiva Il candidato risolva uno dei due problemi e 5 dei quesiti in cui si articola il questionario. PRBLEMA Rispetto a un sistema di assi cartesiani
ESAME DI STAT DI LIE SIENTIFI RS DI RDINAMENT 7 Sessione suppletiva Il candidato risolva uno dei due problemi e 5 dei quesiti in cui si articola il questionario. PRBLEMA Rispetto a un sistema di assi cartesiani
f(x) := 1 10 x g(x) := f(x) x = 1 x + 100
 PROBLEMA. Dal momento che la spesa totale mensile data dalla somma del canone mensile e della spesa dovuta alle telefonate al minuto, indicando con x i minuti di conversazione ed f : R + R + la funzione
PROBLEMA. Dal momento che la spesa totale mensile data dalla somma del canone mensile e della spesa dovuta alle telefonate al minuto, indicando con x i minuti di conversazione ed f : R + R + la funzione
x = x. Si ha quindi: Macerata 6 marzo 2015 classe 3M COMPITO DI MATEMATICA SOLUZIONE QUESITO 1 Considera il fascio di parabole di equazione: ( )
 Macerata 6 marzo 0 classe M COMPITO DI MATEMATICA SOLUZIONE QUESITO Considera il fascio di parabole di equazione: a) Trova eventuali punti base. y = k x + x + P ( 0;) Le curve sostegno del fascio sono
Macerata 6 marzo 0 classe M COMPITO DI MATEMATICA SOLUZIONE QUESITO Considera il fascio di parabole di equazione: a) Trova eventuali punti base. y = k x + x + P ( 0;) Le curve sostegno del fascio sono
Ministero dell Istruzione, dell Università e della Ricerca
 Pag. /5 Sessione ordinaria 27 I43 ESAME DI STATO DI ISTRUZIONE SECONDARIA SUPERIORE Indirizzi: LI2, EA2 SCIENTIFICO LI3 - SCIENTIFICO - OPZIONE SCIENZE APPLICATE (Testo valevole anche per la corrispondente
Pag. /5 Sessione ordinaria 27 I43 ESAME DI STATO DI ISTRUZIONE SECONDARIA SUPERIORE Indirizzi: LI2, EA2 SCIENTIFICO LI3 - SCIENTIFICO - OPZIONE SCIENZE APPLICATE (Testo valevole anche per la corrispondente
Carlo Sintini, Problemi di maturità, 1948 Luglio, matematicamente.it Luglio 1948, primo problema
 Luglio 1948, primo problema In un cerchio di raggio r è condotta una corda AB la cui distanza dal centro è r/. Inscrivere nel segmento circolare che non contiene il centro, un triangolo ABC in modo che
Luglio 1948, primo problema In un cerchio di raggio r è condotta una corda AB la cui distanza dal centro è r/. Inscrivere nel segmento circolare che non contiene il centro, un triangolo ABC in modo che
Esercizi riepilogativi sulle coniche verso l esame di stato
 Esercizi riepilogativi sulle coniche verso l esame di stato n. 9 pag. 55 Sono date le curve α e β definite dalle seguenti relazioni: α : xy x y + 4 = 0 β : luogo dei punti P (k + ; 1 + k ), k R a) Dopo
Esercizi riepilogativi sulle coniche verso l esame di stato n. 9 pag. 55 Sono date le curve α e β definite dalle seguenti relazioni: α : xy x y + 4 = 0 β : luogo dei punti P (k + ; 1 + k ), k R a) Dopo
x 4 4 e il binomio x 2.
 ALGEBRA E ANALITICA. Determina il resto della divisione fra il polinomio P ( ) e il binomio D ( ). [ R ( ) ] Detto D() il polinomio divisore, Q() il polinomio quoziente, R() il resto, il polinomio P()
ALGEBRA E ANALITICA. Determina il resto della divisione fra il polinomio P ( ) e il binomio D ( ). [ R ( ) ] Detto D() il polinomio divisore, Q() il polinomio quoziente, R() il resto, il polinomio P()
COMPITI PER IL RECUPERO DELLA CARENZA FORMATIVA (E RIPASSO) MATEMATICA III - A PT
 1 COMPITI PER IL RECUPERO DELLA CARENZA FORMATIVA (E RIPASSO) MATEMATICA III - A PT Scheda 1: Fondamenti di geometria analitica 1. Determina il punto P dell asse y che forma con A(; ) e B(; ) un triangolo
1 COMPITI PER IL RECUPERO DELLA CARENZA FORMATIVA (E RIPASSO) MATEMATICA III - A PT Scheda 1: Fondamenti di geometria analitica 1. Determina il punto P dell asse y che forma con A(; ) e B(; ) un triangolo
ESAME DI STATO 2017 TEMA DI MATEMATICA. Il candidato risolva uno dei due problemi e risponda a 5 quesiti del questionario.
 ESAME DI STATO 217 TEMA DI MATEMATICA Il candidato risolva uno dei due problemi e risponda a 5 quesiti del questionario. Problema 1 Si può pedalare agevolmente su una bicicletta a ruote quadrate? A New
ESAME DI STATO 217 TEMA DI MATEMATICA Il candidato risolva uno dei due problemi e risponda a 5 quesiti del questionario. Problema 1 Si può pedalare agevolmente su una bicicletta a ruote quadrate? A New
Capitolo 8: introduzione alla trigonometria
 Capitolo 8: introduzione alla trigonometria 8.1 Trasformare da gradi sessagesimali a radianti o viceversa a 0 0 ; b 70 0 ; c 60 0 ; d 1 0 ; e 5 0 ; f 15 0 ; g 5 0 ; h 15 0 ; i 10 0 0 ; j 1 0 9 ; k 1 0
Capitolo 8: introduzione alla trigonometria 8.1 Trasformare da gradi sessagesimali a radianti o viceversa a 0 0 ; b 70 0 ; c 60 0 ; d 1 0 ; e 5 0 ; f 15 0 ; g 5 0 ; h 15 0 ; i 10 0 0 ; j 1 0 9 ; k 1 0
1. (Da Medicina e Odontoiatria 2012) Determinare l'area del triangolo che ha come vertici i punti (0,0), (0,1), (13,12) del piano cartesiano:
 QUESITI 1 PIANO CARTESIANO 1. (Da Medicina e Odontoiatria 2012) Determinare l'area del triangolo che ha come vertici i punti (0,0), (0,1), (13,12) del piano cartesiano: a) 6 b) 13/2 c) 12 d) 13 e) 78 2.
QUESITI 1 PIANO CARTESIANO 1. (Da Medicina e Odontoiatria 2012) Determinare l'area del triangolo che ha come vertici i punti (0,0), (0,1), (13,12) del piano cartesiano: a) 6 b) 13/2 c) 12 d) 13 e) 78 2.
Esame di Stato di Liceo Scientifico Corso di Ordinamento
 Corso di Ordinamento Soluzione dei Temi di Matematica proposti nella Sessione Ordinaria Sommario Problema Punto Punto 4 Punto 5 Punto 4 6 Problema 7 Punto 7 Punto 7 Punto 9 Punto 4 Questionario Quesito
Corso di Ordinamento Soluzione dei Temi di Matematica proposti nella Sessione Ordinaria Sommario Problema Punto Punto 4 Punto 5 Punto 4 6 Problema 7 Punto 7 Punto 7 Punto 9 Punto 4 Questionario Quesito
CLASSE 4^ A/C LICEO SCIENTIFICO 29 Maggio 2014 Simulazione di SECONDA PROVA
 PROBLEMA 1 È data la parabola di equazione +. Rappresentala in un sistema di assi cartesiani ortogonali. a. Determina le equazioni della trasformazione t ottenuta dalla composizione della traslazione di
PROBLEMA 1 È data la parabola di equazione +. Rappresentala in un sistema di assi cartesiani ortogonali. a. Determina le equazioni della trasformazione t ottenuta dalla composizione della traslazione di
` Ç áàxüé wxääë\áàüâé ÉÇx? wxääëhç äxüá àõ x wxäät e vxüvt
 ESAME DI STATO DI LICEO SCIENTIFICO Sessione Ordinaria 2018 ` Ç áàxüé wxääë\áàüâé ÉÇx? wxääëhç äxüá àõ x wxäät e vxüvt M557 ESAME DI STATO DI ISTRUZIONE SECONDARIA SUPERIORE Indirizzi: LI02, EA02 SCIENTIFICO
ESAME DI STATO DI LICEO SCIENTIFICO Sessione Ordinaria 2018 ` Ç áàxüé wxääë\áàüâé ÉÇx? wxääëhç äxüá àõ x wxäät e vxüvt M557 ESAME DI STATO DI ISTRUZIONE SECONDARIA SUPERIORE Indirizzi: LI02, EA02 SCIENTIFICO
Verifiche di matematica classe 3 C 2012/2013
 Verifiche di matematica classe 3 C 2012/2013 1) È assegnato il punto P 1 (3; 1), calcolare le coordinate dei punti: P 2 simmetrico di P 1 rispetto alla bisettrice del primo e terzo quadrante P 3 simmetrico
Verifiche di matematica classe 3 C 2012/2013 1) È assegnato il punto P 1 (3; 1), calcolare le coordinate dei punti: P 2 simmetrico di P 1 rispetto alla bisettrice del primo e terzo quadrante P 3 simmetrico
C I R C O N F E R E N Z A...
 C I R C O N F E R E N Z A... ESERCITAZIONI SVOLTE 3 Equazione della circonferenza di noto centro C e raggio r... 3 Equazione della circonferenza di centro C passante per un punto A... 3 Equazione della
C I R C O N F E R E N Z A... ESERCITAZIONI SVOLTE 3 Equazione della circonferenza di noto centro C e raggio r... 3 Equazione della circonferenza di centro C passante per un punto A... 3 Equazione della
Liceo Einstein Milano. Verifica di matematica 10 ottobre 2018
 Liceo Einstein Milano 3G 10 ottobre 2018 1) Risolvi i seguenti sistemi: 2) A) Nel trapezio rettangolo ABCD la base maggiore AB e la base minore CD misurano rispettivamente 15 e 12 e l altezza AD misura
Liceo Einstein Milano 3G 10 ottobre 2018 1) Risolvi i seguenti sistemi: 2) A) Nel trapezio rettangolo ABCD la base maggiore AB e la base minore CD misurano rispettivamente 15 e 12 e l altezza AD misura
di f '( x ) ; stabilisci infine se la funzione f '( )
 Problema 1 La funzione f ( x ) rappresentata in figura 1 è continua e derivabile in R. Il suo grafico è tangente all asse x nell origine e alla retta t nel punto A. A. Traccia il grafico della funzione
Problema 1 La funzione f ( x ) rappresentata in figura 1 è continua e derivabile in R. Il suo grafico è tangente all asse x nell origine e alla retta t nel punto A. A. Traccia il grafico della funzione
Corso di Geometria BIAR, BSIR Esercizi 8: soluzioni
 Corso di Geometria 2010-11 BIAR, BSIR Esercizi 8: soluzioni Esercizio 1. a) Disegnare la retta r di equazione cartesiana x 2y 4 = 0. b) Determinare l equazione cartesiana della retta r 1 passante per P
Corso di Geometria 2010-11 BIAR, BSIR Esercizi 8: soluzioni Esercizio 1. a) Disegnare la retta r di equazione cartesiana x 2y 4 = 0. b) Determinare l equazione cartesiana della retta r 1 passante per P
Soluzioni dei problemi della maturità scientifica A.S. 2007/2008
 Soluzioni dei problemi della maturità scientifica A.S. 007/008 Nicola Gigli Sunra J.N. Mosconi 19 giugno 008 Problema 1 (a) Determiniamo in funzione di a i lati del triangolo. Essendo l angolo BĈA retto
Soluzioni dei problemi della maturità scientifica A.S. 007/008 Nicola Gigli Sunra J.N. Mosconi 19 giugno 008 Problema 1 (a) Determiniamo in funzione di a i lati del triangolo. Essendo l angolo BĈA retto
a a e coincide quindi con la lunghezza del lato della ruota quadrata. 3) Dalla similitudine dei triangoli ACL e ALM, abbiamo che CL AL CA = AM
 Problemi Problema ) ) Un profilo adeguato f(x) deve essere una funzione concava per garantire che il lato della ruota, che risulta essere tangente nel punto di contatto, sia completamente al di sopra del
Problemi Problema ) ) Un profilo adeguato f(x) deve essere una funzione concava per garantire che il lato della ruota, che risulta essere tangente nel punto di contatto, sia completamente al di sopra del
2 x y x 2 y 2 2p. Le lunghezze dei lati del trapezio sono. BC x y AB 2y y 2 CD 2x x 2 E quindi il suo perimetro è
 Luglio 935 Primo problema Di un trapezio convesso isoscele, le cui diagonali sono perpendicolari fra loro, si conosce il perimetro p e si sa che è equivalente a un quadrato di lato lungo m. Determinare
Luglio 935 Primo problema Di un trapezio convesso isoscele, le cui diagonali sono perpendicolari fra loro, si conosce il perimetro p e si sa che è equivalente a un quadrato di lato lungo m. Determinare
(x B x A, y B y A ) = (4, 2) ha modulo
 GEOMETRIA PIANA 1. Esercizi Esercizio 1. Dati i punti A(0, 4), e B(4, ) trovarne la distanza e trovare poi i punti C allineati con A e con B che verificano: (1) AC = CB (punto medio del segmento AB); ()
GEOMETRIA PIANA 1. Esercizi Esercizio 1. Dati i punti A(0, 4), e B(4, ) trovarne la distanza e trovare poi i punti C allineati con A e con B che verificano: (1) AC = CB (punto medio del segmento AB); ()
Corso di ordinamento- Sessione ordinaria all estero (EUROPA) - a.s Soluzione di De Rosa Nicola
 Corso di ordinamento- Sessione ordinaria all estero (EUROPA - a.s. 007-008 MINISTERO DELLA PUBBLICA ISTRUZIONE SCUOLE ITALIANE ALL ESTERO (EUROPA ESAMI DI STATO DI LICEO SCIENTIFICO Sessione Ordinaria
Corso di ordinamento- Sessione ordinaria all estero (EUROPA - a.s. 007-008 MINISTERO DELLA PUBBLICA ISTRUZIONE SCUOLE ITALIANE ALL ESTERO (EUROPA ESAMI DI STATO DI LICEO SCIENTIFICO Sessione Ordinaria
Risoluzione dei problemi
 Risoluzione dei problemi Il dominio della generica funzione è:! a a) Scriviamo l espressione della funzione in forma di equazione raccogliendo separatamente i termini contenenti il parametro a e quelli
Risoluzione dei problemi Il dominio della generica funzione è:! a a) Scriviamo l espressione della funzione in forma di equazione raccogliendo separatamente i termini contenenti il parametro a e quelli
1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: c) x + 1 d)x sin x.
 Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
Soluzione esercizi sulle funzioni - 5 a E Liceo Scientifico - 04/11/ 13
 Soluzione esercizi sulle funzioni - 5 a E Liceo Scientifico - 04// 3 Esercizio. Si consideri la funzione ) se 0 f) e se 0. e si verifichi che non è continua in 0. Che tipo di discontinuità presenta in
Soluzione esercizi sulle funzioni - 5 a E Liceo Scientifico - 04// 3 Esercizio. Si consideri la funzione ) se 0 f) e se 0. e si verifichi che non è continua in 0. Che tipo di discontinuità presenta in
Esercizi svolti. a 2 x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.
 Esercizi svolti 1. Sia sin(x ) f(x) = x ( 1 + x 1 ) se x > 0 a x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.. Scrivere l equazione della retta tangente nel punto di ascissa
Esercizi svolti 1. Sia sin(x ) f(x) = x ( 1 + x 1 ) se x > 0 a x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.. Scrivere l equazione della retta tangente nel punto di ascissa
QUESITO 1. . Si trovi l equazione della retta normale a γ nel punto (2, 4). (x ) 2 ; f (2) = 30 QUESITO 2
 www.matefilia.it Quesiti QUESITO 1 Sia γ il grafico di y = 10x. Si trovi l equazione della retta normale a γ nel punto (, 4). x +1 Il coefficiente angolare della normale nel punto di ascissa è m = 1 f
www.matefilia.it Quesiti QUESITO 1 Sia γ il grafico di y = 10x. Si trovi l equazione della retta normale a γ nel punto (, 4). x +1 Il coefficiente angolare della normale nel punto di ascissa è m = 1 f
COMPITI DELLE VACANZE A.S. 2015/16 MATEMATICA
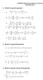 1) Risolvi le seguenti equazioni: COMPITI DELLE VACANZE A.S. 015/1 MATEMATICA 3 3 5 + + 3 5 3 5 3 3 3 1 + + + ( )( ) 5 5 18 1 5 + + 5 1 30 0 + 8 1 1 1 3 1 1 1 1 5 + + 15 30 1 1 3 1 1 + + 18 e) f) + + 3
1) Risolvi le seguenti equazioni: COMPITI DELLE VACANZE A.S. 015/1 MATEMATICA 3 3 5 + + 3 5 3 5 3 3 3 1 + + + ( )( ) 5 5 18 1 5 + + 5 1 30 0 + 8 1 1 1 3 1 1 1 1 5 + + 15 30 1 1 3 1 1 + + 18 e) f) + + 3
LICEO SCIENTIFICO SESSIONE STRAORDINARIA 2017 QUESTIONARIO QUESITO 1. = lim. = lim QUESITO 2
 www.matefilia.it LICEO SCIENTIFICO SESSIONE STRAORDINARIA 217 QUESTIONARIO QUESITO 1 Calcolare la derivata della funzione f(x) = ln(x), adoperando la definizione di derivata. Ricordiamo che la definizione
www.matefilia.it LICEO SCIENTIFICO SESSIONE STRAORDINARIA 217 QUESTIONARIO QUESITO 1 Calcolare la derivata della funzione f(x) = ln(x), adoperando la definizione di derivata. Ricordiamo che la definizione
Corso di Geometria, a.a Ing. Informatica e Automatica Esercizi VII: soluzioni
 Corso di Geometria, a.a. 2009-2010 Ing. Informatica e Automatica Esercizi VII: soluzioni 12 novembre 2009 1 Geometria dello spazio Esercizio 1 Dato il punto P 0 = ( 1, 0, 1) e il piano π : x + y + z 2
Corso di Geometria, a.a. 2009-2010 Ing. Informatica e Automatica Esercizi VII: soluzioni 12 novembre 2009 1 Geometria dello spazio Esercizio 1 Dato il punto P 0 = ( 1, 0, 1) e il piano π : x + y + z 2
Corso di Geometria BIAR, BSIR Esercizi 10: soluzioni
 Corso di Geometria 2010-11 BIAR, BSIR Esercizi 10: soluzioni 1 Geometria dello spazio Esercizio 1. Dato il punto P 0 = ( 1, 0, 1) e il piano π : x + y + z 2 = 0, determinare: a) Le equazioni parametriche
Corso di Geometria 2010-11 BIAR, BSIR Esercizi 10: soluzioni 1 Geometria dello spazio Esercizio 1. Dato il punto P 0 = ( 1, 0, 1) e il piano π : x + y + z 2 = 0, determinare: a) Le equazioni parametriche
Compito di Matematica per Agraria 16/1/ Si disegni il grafico della seguente funzione: 1 x
 16/1/08 f(x) = ln x. Considerata poi la funzione g(x) = 1 x si calcoli dominio ed espressione 2. Si determini il dominio della funzione: 1 x f(x) = + 4 2x 1 + 1 1 + x x 1 3. data la funzione f(x) = 3 +
16/1/08 f(x) = ln x. Considerata poi la funzione g(x) = 1 x si calcoli dominio ed espressione 2. Si determini il dominio della funzione: 1 x f(x) = + 4 2x 1 + 1 1 + x x 1 3. data la funzione f(x) = 3 +
IL PIANO CARTESIANO E LA RETTA
 IL PIANO CARTESIANO E LA RETTA ESERCIZI 1. Le coordinate di un punto su un piano 1 A Scrivi le coordinate dei punti indicati in figura. 1 B Scrivi le coordinate dei punti indicati in figura. Rappresenta
IL PIANO CARTESIANO E LA RETTA ESERCIZI 1. Le coordinate di un punto su un piano 1 A Scrivi le coordinate dei punti indicati in figura. 1 B Scrivi le coordinate dei punti indicati in figura. Rappresenta
4 Simulazione di prova d Esame di Stato
 Simulazione di prova d Esame di Stato Problema Risolvi uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario Si consideri una sfera di centro O e raggio R; sia SS un suo diametro. Un
Simulazione di prova d Esame di Stato Problema Risolvi uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario Si consideri una sfera di centro O e raggio R; sia SS un suo diametro. Un
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 2006 Sessione suppletiva
 ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 006 Sessione suppletiva Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PROBLEMA Nel piano, riferito
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 006 Sessione suppletiva Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PROBLEMA Nel piano, riferito
PIANO DI RECUPERO DI MATEMATICA ANNO SCOLASTICO 2015/2016 CLASSI 3
 PIANO DI RECUPERO DI MATEMATICA ANNO SCOLASTICO 0/0 CLASSI DISEQUAZIONI Risolvi le seguenti disequazioni numeriche intere. ) ) 9 ) ) 9 ( ) ) ) non esiste R non esiste R Risolvi le seguenti disequazioni
PIANO DI RECUPERO DI MATEMATICA ANNO SCOLASTICO 0/0 CLASSI DISEQUAZIONI Risolvi le seguenti disequazioni numeriche intere. ) ) 9 ) ) 9 ( ) ) ) non esiste R non esiste R Risolvi le seguenti disequazioni
PNI SESSIONE SUPPLETIVA QUESITO 1
 www.matefilia.it PNI 010 - SESSIONE SUPPLETIVA QUESITO 1 In cima ad una roccia a picco sulla riva di un fiume è stata costruita una torretta d osservazione alta 11 metri. Le ampiezze degli angoli di depressione
www.matefilia.it PNI 010 - SESSIONE SUPPLETIVA QUESITO 1 In cima ad una roccia a picco sulla riva di un fiume è stata costruita una torretta d osservazione alta 11 metri. Le ampiezze degli angoli di depressione
Esame di maturità scientifica, corso di ordinamento a. s
 Problema 1 Esame di maturità scientifica, corso di ordinamento a. s. -4 Sia f la funzione definita da: f()=- Punto 1 Disegnate il grafico G di f()=-. La funzione f()=- è una funzione polinomiale (una cubica).
Problema 1 Esame di maturità scientifica, corso di ordinamento a. s. -4 Sia f la funzione definita da: f()=- Punto 1 Disegnate il grafico G di f()=-. La funzione f()=- è una funzione polinomiale (una cubica).
ORDINAMENTO 2006 SESSIONE SUPPLETIVA - PROBLEMA 2
 www.matefilia.it ORDINAMENTO 2006 SESSIONE SUPPLETIVA - PROBLEMA 2 Nel piano, riferito ad un sistema monometrico di assi cartesiani ortogonali (Oxy), sono assegnate le curve di equazione: x + k y, dove
www.matefilia.it ORDINAMENTO 2006 SESSIONE SUPPLETIVA - PROBLEMA 2 Nel piano, riferito ad un sistema monometrico di assi cartesiani ortogonali (Oxy), sono assegnate le curve di equazione: x + k y, dove
determinare le coordinate di P ricordando la relazione che permette di calcolare le coordinate del punto medio di un segmento si
 PROBLEMA Determinare il punto simmetrico di P( ;) rispetto alla retta x y =0 Soluzione Il simmetrico di P rispetto ad una retta r è il punto P che appartiene alla retta passante per P, perpendicolare ad
PROBLEMA Determinare il punto simmetrico di P( ;) rispetto alla retta x y =0 Soluzione Il simmetrico di P rispetto ad una retta r è il punto P che appartiene alla retta passante per P, perpendicolare ad
Geometria analitica del piano II (M.S. Bernabei & H. Thaler)
 Geometria analitica del piano II (M.S. Bernabei & H. Thaler) Equazione della retta in forma esplicita Sia data una retta r ax + by + c = 0 con b 0. Svolgendo questa equazione per y otteniamo e ponendo
Geometria analitica del piano II (M.S. Bernabei & H. Thaler) Equazione della retta in forma esplicita Sia data una retta r ax + by + c = 0 con b 0. Svolgendo questa equazione per y otteniamo e ponendo
Analisi Matematica 1 e Matematica 1 Geometria Analitica: Coniche
 Analisi Matematica 1 e Matematica 1 Geometria Analitica: Coniche Annalisa Amadori e Benedetta Pellacci amadori@uniparthenope.it pellacci@uniparthenope.it Università di Napoli Parthenope Contenuti Coniche
Analisi Matematica 1 e Matematica 1 Geometria Analitica: Coniche Annalisa Amadori e Benedetta Pellacci amadori@uniparthenope.it pellacci@uniparthenope.it Università di Napoli Parthenope Contenuti Coniche
ESAME DI STATO 2009/10
 MATEMATICA & FISICA E DINTORNI Pasquale Spiezia ESAME DI STATO 9/ Scientifico Tradizionale PROBLEMI QUESITI 4 5 6 7 8 9 PROBLEMA Sia ABCD un quadrato di lato, P un punto di AB e γ la circonferenza di centro
MATEMATICA & FISICA E DINTORNI Pasquale Spiezia ESAME DI STATO 9/ Scientifico Tradizionale PROBLEMI QUESITI 4 5 6 7 8 9 PROBLEMA Sia ABCD un quadrato di lato, P un punto di AB e γ la circonferenza di centro
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 2005
 ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 5 Il candidato risolva uno dei due problemi e cinque quesiti scelti nel questionario. PROBLEMA Nel primo quadrante del sistema di riferimento Oy,
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 5 Il candidato risolva uno dei due problemi e cinque quesiti scelti nel questionario. PROBLEMA Nel primo quadrante del sistema di riferimento Oy,
La retta nel piano cartesiano
 La retta nel piano cartesiano Se proviamo a disporre, sul piano cartesiano, una retta vediamo che le sue possibili posizioni sono sei: a) Coincidente con l asse delle y; b) Coincidente con l asse delle
La retta nel piano cartesiano Se proviamo a disporre, sul piano cartesiano, una retta vediamo che le sue possibili posizioni sono sei: a) Coincidente con l asse delle y; b) Coincidente con l asse delle
Nicola De Rosa, Liceo della comunicazione sessione ordinaria 2012, matematicamente.it
 Nicola De Rosa, Liceo della comunicazione sessione ordinaria, matematicamente.it PROBLEMA Sia f ( ) ln ( ) ln e sia g ( ) ln ( ) ln. Si determinino i domini di f e di g.. Si disegnino, nel medesimo sistema
Nicola De Rosa, Liceo della comunicazione sessione ordinaria, matematicamente.it PROBLEMA Sia f ( ) ln ( ) ln e sia g ( ) ln ( ) ln. Si determinino i domini di f e di g.. Si disegnino, nel medesimo sistema
SIMULAZIONE DELLA PROVA DI MATEMATICA DELL ESAME DI STATO. Il candidato risolva uno dei problemi e risponda a 5 quesiti del questionario.
 ANNO SCOLASTICO 06/7 SIMULAZIONE DELLA PROVA DI MATEMATICA DELL ESAME DI STATO PER IL LICEO SCIENTIFICO Il candidato risolva uno dei problemi e risponda a 5 quesiti del questionario. Problema Modello in
ANNO SCOLASTICO 06/7 SIMULAZIONE DELLA PROVA DI MATEMATICA DELL ESAME DI STATO PER IL LICEO SCIENTIFICO Il candidato risolva uno dei problemi e risponda a 5 quesiti del questionario. Problema Modello in
