Stato cristallino e simmetria
|
|
|
- Daniella Sassi
- 7 anni fa
- Visualizzazioni
Transcript
1 Corso di laurea triennale in Chimica a.a Stato cristallino e simmetria «Una buona conoscenza della geometria cristallina dovrebbe far parte del bagaglio culturale di chiunque si occuppi dello stato cristallino o che desideri leggere in maniera proficua qualunque pubblicazione si occupi della materia cristallina. L aspetto fondamentale della geometria cristallina è che essa ha a che fare con ripetizioni ordinate. In effetti, la geometria dei cristalli è la geometria dell ordine». Martin J. Buerger, 1971 Docente: Ernesto Mesto ernesto.mesto@uniba.it Website:
2 Stati della materia Staro della materia Volume fisso Forma fissa Ordine Proprietà Aeriforme No No Nessuno Isotrope a Liquido Si No A corto raggio b Isotrope Solido(Amorfo) Si Si A corto raggio b Isotrope Solido (Cristallino) Si Si A lungo raggio b Anisotrope d a Il sistema mostra sempre le stesse proprietà a prescindere dalla direzione. b L ordine a corto raggio si estende per pochi atomi. L ordine a lungo raggio si estende da 10 3 a atomi. c Il sistema mostra proprietà differenti in differenti direzioni.
3 Stato cristallino Un cristallo è un oggetto solido costituito da atomi, molecole e/o ioni aventi una disposizione geometricamente regolare, che si ripete indefinitamente nelle tre dimensioni spaziali. Tale disposizione è rappresentata dal reticolo cristallino o di Bravais. Un materiale è un cristallo se esso ha essenzialmente un pattern di diffrazione. La parola essenzialmente indica che la maggior parte dell intensità diffratta è relativamente concentrata in picchi di Bragg, a prescindere della intensità di scattering diffusa, sempre presente.
4 Solidi cristallini I solidi possono presentarsi in forma di: Monocristalli (periodicità perfetta su tutto il solido). Policristalli (grani di dimensione variabile separati da bordi di grano). I solidi possono anche essere Amorfi o non-cristallini
5 Solidi amorfi Esistono solidi non cristallini: i solidi amorfi nei quali la crescita della fase cristallina è impedita cineticamente. Per esempio: i vetri in cui la struttura disordinata della fase liquida è ritenuta nel solido se i fusi vengono raffreddati rapidamente. Se riscaldati i vetri vanno incontro a cristallizzazione in quanto la fase cristallina è quella più stabile da un punto di vista termodinamico. Solido cristallino anisotropo Solido amorfo isotropo
6 Cosa sono i cristalli? Slide gentilmente concessa dal dott. Michele Zema. Università di Pavia b a La struttura periodica di un cristallo ideale è descritta da un reticolo cristallino (ovvero una griglia di punti). Nel reticolo cristallino, tutte le celle elementari (parallelepipedi) hanno la stessa forma, dimensione e contenuto.
7 Reticolo cristallino L intero cristallo può essere ricostruito dalla traslazione della cella elementare in una, due o tre direzioni, indipendentemente. In genere, l origine del reticolo e l origine della cella elementare può essere scelta arbitrariamente. Nella figura di fianco, forma e contenuto della cella elementare sono gli stessi della figura in alto.
8 In tutti gli esempi mostrati, la cella elementare (o unitaria) conteneva tre oggetti (molecole, atomi,o ioni), uno grande, uno piccolo e l ultimo di dimensioni medie. Posso descrivere la posizione degli oggetti all interno della cella elementare attraverso le coordinate frazionarie (x 1 e y 1, x 2 e y 2, x 3 e y 3 ), cioè come frazioni della lunghezza degli assi cristallografici a, b e c. Gli assi a, b e c sono le lunghezze dei lati della cella. Anche la forma della cella elementare può cambiare. Nella figura di fianco l origine del reticolo reciproco e la forma e dimensione della cella sono cambiate rispetto alle figure precedenti, ma non il contenuto di cella che è rimasto immutato.
9 This image cannot currently be displayed. This image cannot currently be displayed. cross-shaped twins in staurolite Sono considerati cristalli anche i Geminati Due ( o più) individui della stessa fase cristallina relazionati da un operazione geometrica chiamata operazione di gemminazione, che rappresenta un elemento di simmetria per gli edifici geminati ma non per i singoli individui. Il risultato è un intercrescita di due (o più) cristalli distinti. knee-shaped twins in rutile fluorite Carlsbad twinning in orthoclase Esempio di geminazione merohedrica Slide gentilmente concessa dal dott. Michele Zema. Università di Pavia. swallowtail or fishtail twins in gypsum
10 Come scegliere la cella elementare o maglia. esempio 2D - salgemma (cloruro di sodio, NaCl) Na Cl Definiamo i nodi reticolari come punti caratterizzati da intorni identici. La scelta dell origine è arbitraria. I nodi reticolari non devono essere necessariamente atomi - ma le celle devono essere tutte identiche.
11 Come scegliere la cella elementare o maglia. esempio 2D - salgemma (cloruro di sodio, NaCl) Anche questa e una cella elementare - non importa se si parte da Na o Cl o se non si parte da un atomo
12 Come scegliere la cella elementare o maglia. esempio 2D - salgemma (cloruro di sodio, NaCl) Questa NON e una cella elementare. La periodicità traslazionale non è rispettata! Non devono esserci spazi vuoti!
13 Cella elementare Per descrivere completamente un reticolo cristallino o la sua cella elementare (il mattone fondamentale) è necessario utilizzare tre vettori non complanari. Questi vettori (a, b e c), vettori base, coincidano con gli spigoli della cella elementare. Per descrivere completamente la cella elementare devo specificare un totale di sei quantità scalari, che sono chiamati parametri reticolari e si indicano con i simboli: a, b, c lunghezze degli spigoli α, β, γ angoli tra gli spigoli Ogni punto all interno del reticolo cristallino può essere descritto da un vettore q, definito dall equazione: q = ua +vb + wc dove a, b,e c sono i tre vettori base e u, v, w sono numeri interi Tutti i vettori q rappresentano traslazioni all interno del reticolo cristallino
14 Slide gentilmente concessa dal dott. Michele Zema. Università di Pavia Il periodo di ripetizione di questa figura è due barche. Riuscite a trovarlo? Ci sono degli elementi di simmetria che relazionano gli oggetti in figura? Elementi di simmetria posso essere presenti all interno della cella unitaria.
15 Unità asimetrica = Asse binario L unità asimetrica (in verde) è la porzione di cella elementare che contiene il gruppo di atomi indipendenti per simmetria. Raramente la cella elementare è formata da gruppi di atomi indipendenti tra loro. In genere la cella unitaria contiene atomi o gruppi di atomi che possono essere converti li uni negli altri da semplici trasformazioni geometriche chiamate operazioni di simmetria. Le molecole delle celle elementari in figura possono essere convertite le une nelle altre da rotazioni di 180 attorno a gli assi binari mostrati. La presenza di un asse binario nel centro della cella unitaria, combinata con la periodicità del reticolo cristallino genera altri otto assi binari ai vertici e al centro degli spigoli della celle elementare.
16 = enantiomorfo di Per conoscere il numero esatto di elementi di simmetria presenti nella cella elementare è necessario esaminarla nelle tre dimensioni. Una vista prospettica della cella unitaria, dove tutti i centri di simmetria sono mostrati. Gli otto centri di simmetria indipendenti (quelli NON ottenibili per traslazione) sono mostrati in blu.
17 Elementi di simmetria puntuali Oltre alla traslazione esistono altre operazioni di simmetria: Operazioni di simmetria puntuale: lasciano invariato almeno un punto. 1) Inversione rispetto a un punto (lascia invariato il centro di inversione) 2) Rotazione rispetto ad un asse (lascia invariati i punti sull asse) 3) Riflessione rispetto a un piano (lascia invariati i punti sul piano) 4) Rotoinversione combinazione di una rotazione rispetto ad un asse e una inversione rispetto ad un punto (lascia invariato il centro di inversione) 5) Rotoriflessione - combinazione di una rotazione rispetto ad un asse e una riflessione rispetto a un piano (lascia invariato il punto di intersezione tra il piano e l asse)
18 Operazioni di simmetria semplice senza componente traslazionale Un operazione di simmetria non è la stessa cosa di un elemento di simmetria. Un operazione di simmetria esegue una certa trasformazione geometrica (simmetrica) che porta alla formazione di un oggetto addizionale (es. un atomo o una molecola) all interno della cella. Un elemento di simmetria è una rappresentazione grafica di un operazione di simmetria (es. un piano di simmetria, un asse di rotazione o un centro di simmetria) Operazioni di simmetria semplici Rotazione Un asse di rotazione di ordine n, ruota il motivo di un agolo pari a 2π/n. Inversione Inverte l oggetto rispetto ad un punto, il centro di simmetria. Riflessione Riflette l oggetto rispetto ad un piano di simmetria Traslazione Trasla l oggetto di un periodo τ lungo una direzione
19 Operazioni di simmetria complesse senza componente traslazionale Operazione di simmetria semplici Rappresentazione geometrica Elemento di simmetria Rotazione Asse (linea) Asse di rotazione Inversione Punto (centro) Centro di simmetria Riflessione Piano Piano di simmetria Traslazione Vettore Vettore di traslazione La combinazione degli operatori di simmetria semplici porta alla creazione degli operatori di simmetria complessi. Essi sono: L asse di roto-inversione (asse di inversione). Effettua una simultanea rotazione e inversione. Elicogira. Effettua simultaneamente una rotazione e traslazione. Slittopiano. Effettua simultaneamente una riflessione e una traslazione. Gli operatori di simmetra senza componente traslazionale sono sempre evidenziati dalla simmetria morfologica del cristallo
20 Operazioni di simmetria proprie e improprie Gli operatori di simmetria possono anche essere classificati come propri o impropri. Un operatore di simmetria improprio inverte un oggetto in modo da creare il suo enantiomorfo. Gli anagoli dell oggetto enantimorfo saranno uguale in valore, ma di segno opposto rispetto all originale. Gli operatori di simmetria che comportano una riflessione o un inversione sono impropri. Elemento di simmetria Proprio Improprio Elementi puntuali Assi rotazionali Assi di inversione Elementi con componente traslazionale Assi rototraslazionali Slittopiani a b c n d
21 Restrizioni alle simmetrie possibili dovute alla periodicità del reticolo cristallino Sia T un vettore di reticolo passante per l'origine O, e perpendicolarmente a T sia definito un asse di simmetria per rotazione di ordine N (= il cristallo è invariante per rotazioni di ordine n) (punti reticolari in blu) TT = 2OO, mm OO = T cos 2π n, qqqqqq B B 2T cos 2π n = TT dove m numero intero Per n = 1, 2, 3, 4, 6 si hanno gli unici assi di rot. possibili VALORI DEL SENO E DEL COSENO DI ALCUNI ANGOLI PARTICOLARI Il coseno è la 1 a coordinata, ossia l ascissa del punto; il seno è la 2 a coordinata, ossia l ordinata. Per esempio: l angolo di 120 ha come misura in radianti 2 π, e, dato che il punto associato è 3 1, 3, significa che: 2 2 cos 120 = cos 2 π = 1 e che il sssssss = sss 2 π =
22 Restrizioni alle simmetrie possibili dovute alla periodicità del reticolo cristallino Sia T un vettore di reticolo passante per l'origine O, e perpendicolarmente a T sia definito un asse di simmetria per rotazione di ordine N (= il cristallo è invariante per rotazioni di ordine n) (punti reticolari in blu) TT = 2OO, mm OO = T cos 2π n, qqqqqq B B 2T cos 2π n = TT dove m numero intero Per n = 1, 2, 3, 4, 6 si hanno gli unici assi di rot. possibili Quindi gli assi di rotazione di ordine 5, 7, etc. sono proibiti nei cristalli. Ma perchè non posso avere un reticolo cristallino formato da celle elementari con forma di pentagono regolare disposte come in figura? Non avrei diffrazione? I pentagoni regolari non sono una cella elementare accettabile. Non possono esistere spazi vuoti (i parallelogrammi bianchi) tra una cella e l altra. Però questi oggetti diffrangono e sono chiamati quasicristalli.
23 I quasicristalli Sono materiali con un ordine perfetto a lungo raggio, ma senza periodicità traslazionale nelle tre dimensioni. L alto grado di ordine si manifesta in patterns di diffrazione che mostrano picchi stretti e intensi, nei quali compaiono assi di simmetria non cristallografici. Di consequanza i quasicristalli hanno simmetrie cristallografiche proibite e non possono essere considerati cristalli in senso proprio. Esiste una forte analogia tra i quasicristalli e la tassellatura di Penrose, proposta da Roger Penrose. Infatti, alcuni quasicristalli possono essere affettati in modo tale che gli atomi sulla superficie seguano esattamente lo schema di una tassellatura di Penrose. Patterns di diffrazione elettronica del primo quasicristallo naturale scoperto da un ricercatore italiano. Bindi et al. (2009) Science, 324, Slide modificata dall originale del dott. Michele Zema. Università di Pavia. Modello atomico di un quasicristallo di argentoalluminio (Ag-Al). Tassellatura di Penrose con assi di rotazione di ordine 5
24 Motivo, cella elementare e reticolo cristallino I cristalli sono formati dalla ripetizione regolare di un motivo (molegole o gruppi di molecole). Non si deve confondere la simmetria del motivo con quella della cella elementare. bis(dicarbollile)-metallo. Il complesso mostra un asse di rotazione di ordine 5. Un frammento della struttura cristallina del (BEDT-TTF)[8,8'-Br0.75Cl1.25-3,3'-Co(1,2-C2B9H10)2]. La cella elementare è caratterizzata dalla presenza di centri di simmetria, ma di nessun asse di ordine 5. Crystals 2012, 2, 43-55; doi: /cryst
25 Sotto Asse di rotoinversione 1. Asse 1 e 1 L asse di rotazione 1 ruota il motivo di 360 riposizionandolo nella posizione originale. Non genera altri oggetti nella cella unitaria e coincide con l operatore di simmetria indentità (E). Esso è Asse di rotazione 1 sempre presente in ogni cristallo. L asse di rotoinversione unario viene indicato col simbolo 1. Il motivo originale viene ruotato di 360 cossichè ritorna nella posizione originale ed è quindi invertito attraverso il centro. Questa combinazione di operazioni produce lo stesso risultato dell operatore centro di inversione (i). - i (centro di simmetria) i + Sopra Visuale dal polo nord. La circonferenza tratteggiata rappresenta il piano equatoriale della sfera di proiezione. Notazione cristallografica: + e indicano la quota, mentre indica l enatiomorfo.
26 Asse dd rrrrrrrrr bbbbbbb L asse di rotazione 2, chiamato anche asse binario, ruota il motivo di 180. Esso generà un secondo oggetto (equivalente al primo per simmetria). Se si applica nuovamente l operazione di rotazione su quest ultimo si ha l oggetto originale. Simbolo internazionale asse binario + - Asse binario parallelo al foglio Asse binario + + Asse binario perpendicolare al foglio Asse binario perpendicolare al foglio. Due rotazioni di 180
27 Asse dd rrrrrrrrrrrrrr bbbbbbb 2 (Equivalente ad un piano di simmetria) A B Il motivo A superiore e B inferiore si sovrappongono nella visuale dal polo N L asse di rotoinversione 2 ruota il motivo originale di 180 e quindi ne compie l inversione attraverso il centro. Questa combinazione di operazioni produce lo stesso risultato di un piano di simmetra (m). 2 Piano di simmetria perpendicolare al foglio Piano di simmetria + + Piano di simmetria parallelo al foglio m i Simbolo internazionale piano di simmetria - +
28 Asse 3 e 3 Simbolo internazionale asse 3 L asse di rotazione 3, chiamato anche asse ternario, ruota il motivo di 120. Esso generà due oggetti (equivalenti al primo per simmetria). L asse di rotoinversione 3 ruota il motivo originale di 120 e quindi ne compie l inversione attraverso il centro. Questa combinazione di operazioni produce lo stesso risultato dell operatore un asse 3 più l operatore centro di simmetria (i). 3 (Equivalente asse ternario + centro di simmetria) Motivo originale sopra Simbolo internazionale asse 3
29 Asse 4 e 4 L asse di rotazione 4, chiamato anche asse quaterario, ruota il motivo di 90. Esso generà tre oggetti (equivalenti al primo per simmetria). Simbolo internazionale per l asse di rotazione quaternario L asse di rotoinversione 4 ruota il motivo originale di 90 e quindi ne compie l inversione attraverso il centro. 4 Motivo originale sopra Simbolo internazionale per l asse di rotoinversione quaternario -
30 Tutta la verità sull asse 4 4 L asse di rotoinversione 4 non coincide con un asse di rotazione 4 + centro di simmetria (i) 2 Le operazioni di rotazione e inversione 6 5 nell asse 4 sono contemporanee, a ogni 1 rotazione segue l inversione. Questo porta ad avere un totale di quattro oggetti 1 distribuiti nello spazio secondo le figure a 3 sinistra Vista prospetica 4/m Nel caso di asse 4 e un centro di simmetria, l asse quaternario produrà quattro oggetti, ciascuno ruotato di 90 rispetto al precedente. Questi saranno quindi invertiti dal centro di simmetria che genererà per ciascuno di loro un enantiomorfo. Questa operazione coincide con la i = 4/m presenza di un piano di simmetria (m) ortogonale all asse quaternario. In totale si avranno otto oggetti come illustrato a destra. + m
31 Asse dd oooooo 6 e L asse di rotazione 6, chiamato anche asse senario, ruota il motivo di 60. Esso generà cinque oggetti (equivalenti al primo per simmetria) Simbolo internazionale asse 6 L asse di rotoinversione 6 ruota il motivo originale di 60 e quindi ne compie l inversione attraverso il centro. Questa combinazione di operazioni produce lo stesso risultato di un piano di simmetra (m) perpendicolare ad un asse ternario. 6 Equivalente un asse ternario + piano di simemtria perpendicolare all asse (3/m) I motivi superiori e inferiori si sovrappongono Simbolo internazionale asse
32 Elementi di simmetria puntuali Elemento di simmetria SIMBOLI GRAFICI Normale Paralello Inclinato Non esiste un asse di rotazione 5, ciò non vuol dire che non esiste la simmetria di ordine 5 in una oggetto (molecola) ma che con quell oggetto non si può riempire lo spazio. Non tutti gli elementi di simmetria sono necessari: molti assi di rotoriflessione e rotoinversione in realtà corrispondono ad altri elementi di simmetria. Es: l asse di rotoinversione di ordine 1 corrisponde al centro di inversione, quello di ordine 2 ad un piano di riflessione perpendicolare ad esso etc.
33 Combinazione operatori di simmetria senza componenti traslazionali E possibile combinare diversi operatori di simmetria per ottenere modelli tridimensionali. La combinazione non deve portare alla formazione di un nuomero infinito di elementi di simmetria. Se ad esempio combino due assi quaternari inclinati con un angolo acuto, ciascuno opererà sull altro portando alla creazione di infini elementi di simmetria. Per evitare ciò gli assi devono essere orientati a 90 l uno rispetto all altro. Tutti gli operatori di simmetria inoltre devono intersecarsi in un unico punto. y Asse quaternario verticale conbinato con asse binario orientato secondo Est-Ovest. Dalla combinazione dei due (in blu) si generano altri tre assi binari (in nero). Asse senario verticale conbinato con asse binario orientato secondo Est-Ovest. Dalla combinazione dei due (in blu) si generano altri cinque assi binari (in nero).
34 Combinazione operatori di simmetria senza componenti traslazionali Operatori ed elementi di simmetria possono interagire per dar luogo alla formazione di nuovi elementi e operatori di simmetria. Infatti : si assuma che ci sia un operatore di simmetria che converta l oggetto X nell oggetto X 1, si assuma che ci sia un secondo operatore di simmetria che converta l oggetto X1 nell oggetto X2 Allora poichè l oggetto X1 è simmetricamente equivalente a X, e anche l oggetto X2 è simmetricamente equivalente a X, gli oggetti X e X2 devono anche essere simemtricamente equivalenti. Deve esistere un operatore e un elemnto di simmetria che converte l oggetto X in X2. Per esempio: Se A può essere convertito in B dall asse 2 Se B può essere convertito in C dal centro di simmetria (i = 1) Allora: A può essere convertito in C dal piano di simmetria (m)
35 Combinazione operatori di simmetria senza componenti traslazionali Il piano di simmetria quindi deriva dalla combinazione di un asse binario (2) e un centro di simmetria (i) posizionato su di esso. La relazione può essere scritta in forma di equazione usando la notazione internazionale dei corrispondenti elementi di simmetria: 2 1 oo 2 = 1 oo 2 2 = m ( 2 aaaaaaaaaa 1) Dove simboleggia l interazione tra gli elementi di simmetria. Lo stesso risultato si ottiene se parto da una qualunque combinazione di due dei tre elementi di simmetria considerati. Posso cioè scrivere le seguenti equazioni: 2 m 2 = m 2 2 = 1 (ss m 2) m 1 oo m = 1 oo m m = 2 ( m aaaaaaaaaa 1)
36 Gruppi puntuali Come mostrato, l interazione tra due elementi di simmetria porta alla generazione di un terzo elemento di simmetria. Quest ultimo può essere un nuovo elemento di simmetria o uno già esistente. Se nessun nuovo elemento di simmetria compare e quando tutte le interazioni tra gli elementi di simmetria sono state considerate, la generazione di nuovi elementi di simmetria è completa. La somma totale di tutti gli elementi di simmetria è chiamato gruppo puntuale. Il termine puntuale si riferisce al fatto che tutti gli elementi di simmetria del gruppo si intersecano in un punto. Elemento di m simmetria m m m 1 1 m m Elementi di simmetria risultanti dalla combinazionendi 1, 1, 2, m. Nessun ulteriore elemento di simmetria può essere generato dalla combianzione degli elementi di simmetria considerati. Gruppo puntuale 2/m.
37 Derivazione della classi di simmetria Poniamoci il problema di derivare quali sono tutte le combinazioni di operatori di simemtria compatibili con la periodicità di un cristallo. Consideremo solo quelle combinazioni di operatori di simmetria senza componente traslazionale, cioè combinazioni di assi proprio o impropri che si intersecano in un punto (classi di simmetria o gruppi puntuali). Le più semplici combinazioni di operatori sono quelle caratterizzate dalla presenza di un solo asse, che può essere proprio (P), improprio (I) o contemporaneamente proprio e improprio (P/I). P I P/I (= 1) (= m) (= 2 m) (= 3) (= 4 m) (= 6 m) Totale
38 Derivazione della classi di simmetria Il problema della coesistenza di più elementi di simmetria passanti per un punto fu risolto per la prima volta da Eulero. Teorema di Eulero: Supponiamo che esistanto due assi propri l 1 e l 2 che si intersacano in un punto O. L asse l 1 ripete in Q l oggetto originariamente in P, l asse l 2 ripete in R l oggetto in Q. Essendo P direttamente congruente a Q, e R direttamente congruente a Q, allora anche P sarà direttamente congruente a R e cioè, deve esistere un altro operatore proprio,l 3, che ripete l oggetto P direttamente in R. l 1 Q P R O Classi caratterizzanti dalla coesistenza di più assi: PPP, PPP, III, III, P I P P I I l2 Se l asse l 1 è di rotazione proprio (P), mentre l asse l 2 è improprio (I), allora gli oggetto P e Q sono direttamente congruenti, mentre l oggetto R è enantiomorfo rispetto ad essi (ovvero legato da congruenza opposta). Per tanto il terzo operatore di simmetria, l 3, che relazione P a R sarà anch esso improprio. Si conclude che di tre operatori di simmetria, se uno è di inversione lo è almeno un altro. Quindi avremo altri gruppi puntuali caratterizzati da combinazioni del tipo PII, IPI, IIP. Inoltre possimao P P considerare anche gruppi del tipi P. Inoltre se due I I I dei tre assi sono equivalenti per simmetria, non possono essere uno proprio e uno improprio.
39 Derivazione della classi di simmetria PPP PII IPI IIP P I (= 2mm) 222 (= mmm) 2 2 2(= mmm) 2 m ) (= 3mm) 322 (= 3 2 m 3 2 2(= 3 2 m (= 4mm) 422 (= 42m) 4 2 2(= 4mm) (= 6mm) 622 (= 62m) 6 2 2(= 6mm) P I P I (= m 2 ) m (= m (= m (= 2 m 3 3) 233 (= 2 m 3 3) 2 3 3(= 2 m 3 3) 2 2 m 2 (= 3 2 m 2 m 2 m 2 ) m 2 ) m 2 ) m 2 ) m 3 3 (= 2 m 3 3) (= 4 m 3 m) 432 (= 43m) (= 4 m 3 m) (= 4 m 3 m) Tot Abbiamo generato 19 classi di simmetria che sommate alle 13 aventi un solo asse, prima ricavate, fa un totale di 32 classi di simmetria (o gruppi puntuali) compatibili con la periodicità cristallina.
40 Gruppi puntuali Considerando le combinazioni che portano solo alla formazioni di gruppi puntuali con un numero finito di elementi di simmetria si ottengono solo 32 gruppi puntuali. I cristalli afferiranno ad uno di essi. Affinchè le interazioni diano un numero finito di elementi di simmetria solo le combinazioni riportate in tabella sono permesse. Primo elemento Secondo elemento Elemento generato 1 Asse di oridine N Piano di simmetria per N pari Asse di rotoinversione di ordine N per N dispari 2 2 a φ = 30,45, 60 o 90 m 2 a φ = 30,45, 60 o 90 Asse di rotazione di ordine N, con N=180/φ Asse di rotazione di ordine N, con N=180/φ Commenti o esempi 2 = m 3 6,4,3,o 2 assi perpendicolari al 1 e 2 asse 6,4,3,o 2 assi lungo la linea comune m 2 a 90 Centro di simmetria 1 all intersezione tra m e 2
41 Gruppi puntuali In modo equivalente alla tabella precedente, le regole di combinazione degli elementi di simmetria possono essere definite nel modo seguente: a) Un asse di rotazione di ordine pari, un piano di simmetria perpendicolare ad esso ed il centro di simmetria sono elementi di simmetria tali per cui la presenza di due di essi implica la presenza del terzo. b) Se esiste un asse binario normale ad un asse di ordine n, allora esistono altri n-1 assi binari ad angoli pari a 2π\n. c) Se su di un piano di riflessione giace un asse di ordine n, allora esistono altri n-1 piani ad angoli 2π\n. d) Le combinazioni di assi diverse da quelle stabilite al punto b) sono solo di due tipi ed entrambi implicano la presenza di quattro assi ternari disposti ad angoli di ; in un caso essi sono combinati con tre assi binari tra loro perpendicolari e nell altro con tre assi quaternari tra loro perpendicolari e sei assi binari.
42 Esempio: asse binario inclinato a 45 rispetto ad un piano di simmetria L interazione tra un asse binario e un piano di simmetria inclinati a 45 porta alla formazione di una asse di rotazione di ordine 4 (4 per esatezza). Sappiamo che il piano m coincide con un asse 2 (asse di rotoinversione di ordine 2) perpendicolare ad esso. Questo sarò ancora inclinato a 45 rispetto alla asse 2 della figura. Dalla tabella precedente si ricava che si formerà un asse di ordine 180 /45 = 4. Gli altri elementi di simmetria vengono generati di conseguenza dalle interazioni di questi e tre.
43 Esempio: asse binario inclinato a 45 rispetto ad un piano di simmetria B A L asse 2 trasforma A in B A B C A D Il piano m rifletterà anche l asse binario, infatti C e D sono relazionati da una rotazione binaria.
44 Esempio: asse binario inclinato a 45 rispetto ad un piano di simmetria B C B C A D Il nuovo asse 2 trasforma A e B in E e F, rispettivamente A D mm E F A e C, C e E, E e H, H e A sono relazionati da un asse 4, così come B e D, D ef, F e G e G e B. A G B H C F D mm E Il secondo asse binario ruoterà anche il piano di simmetria, infatti D ed E e C e F sono relazionati da una riflessione. Si avrà quindi un secondo piano di simmetria m
45 Gruppi puntuali La simmetria cristallina si conforma ai 32 gruppi puntuali 32 classi cristalline in 7 sistemi cristallini Sistema Cristallino Acentrico Centrato Triclino 1 1 Monoclino 2, 2 (= m) 2/m Ortorombico 222, 2mm 2/m 2/m 2/m Tetragonale 4, 4, 422, 4mm, 42m 4/m, 4/m 2/m 2/m Trigonale Esagonale 3, 32, 3m 3, 3 2/m 6, 6, 622, 6mm, 62m 6/m, 6/m 2/m 2/m Cubico 23, 432, 43m 2/m 3, 4/m 3 2/m I gruppi puntuali indicano il numero minimo di elementi di simmetria che devo opportunamente combinare per ricostruire l intera simmetria morfologica del cristallo. Cristallo con simmetria morfologica afferente al gruppo puntuale 2 I termini triclino, monclino, etc. saranno spieghati nelle prossime slide.
46 Gruppi puntuali Sistema cristallino N. di gruppi puntuali Notazione Herman- Mauguin Notazione Schoenflies Triclino 2 1, 1 C 1, C i Monoclino 3 2, m, 2/m C 2, C s, C 2h Orthorhombico 3 222, mm2, mmm D 2, C 2v, D 2h Trigonale 5 Esagonale 7 Tetragonale 7 Cubico 5 3, 3, 32, 3m, 3m 6, 6, 6/m, 622, 6mm, 62m, 6mm 4, 4, 4/m, 422, 4mm, 42m, 4/mmm 23, m3, 432, 432, m 3m C 3, S 6, D 3, C 3v, D 3d C 6, C 3h, C 4h, D 6, C 6v, D 3h, D 6h C 4, S 4, C 4h, D 4, C 4v, D 2d, D 4h T, T h, O, T d, O h Il sistema Hermann-Mauguin, noto anche come sistema internazionale, è una notazione utilizzata in cristallografia per descrivere i diversi gruppi puntuali. Deve il suo nome al cristallografo tedesco Carl Hermann e al mineralogista francese Charles Victor Mauguin. Il numero indica l'ordine dell'asse di simmetria n-ario, la lettera "m" un piano speculare, la barra indica che il piano speculare è perpendicolare all'asse di simmetria, mentre la lineetta sopra il numero indica che l'elemento di simmetria e combinato con una inversione. Il sistema Schoenflies rappresenta una notazione utilizzata in alternativa e che in genere si usa per classificare la simmetria delle molecole.
47 Notazione Schoenflies Cn Un asse di simmetria di ordine n; Sn Un asse di rotorifelssione di ordine n; Dn Un asse di simmetria di ordine n avente n assi binari ortogonali; Cnh Un asse di simmetria di ordine n normale a un piano di simmetria; Dnh Un asse di simmetria di ordine n aventi n assi binari giacenti in un piano di dimmetria ortogonale; Cnv Un asse di simmetria di ordine n giacente in n piani di simmetria verticali; Dnd Un asse di simmetria di ordine n aventi n assi binari ortogonali e n piani diagonali; T Quattro assi ternari combinati con tre assi binari mutualmente ortogonali; O Quattro assi ternari combinati con tre assi quaternari mutualmente ortogonali e sei assi binari, ciascuno dei quali giacenti tra due di loro; Th Quattro assi ternari combinati cone tre assi binari mutualmente ortogonali, ciascuno avente un piano di simmetria normale a esso; Td Quatrro assi ternari combinati con tra assi binari mutualmente ortogonali e piani di simmetria diagonal; Oh Quattro assi ternari combinati con tre assi quaternari mutualmente ortogonali e sei assi binari, ciascuno dei quali giacenti tra due di loro con un piano di simmetria normale a ciascun asse binario e quaternario.
48 Notazione Hermann- Mauguin n/m Un asse di simmetria di ordine n normale (/) a un piano di simmetria; nm Un asse di simmetria di ordine n giacente in un piano di simmetria verticale; n n Un asse di simmetria di ordine n combinato con un n assi ortogonali se n = 2 (e n > n ), altrimenti si tratta del caso di una simmetria cubica (n = 3).
49 Classi di Laue Radiazioni e particelle (es. raggi-x e neutroni) interagiscono con un cristallo in modo che il pattern di diffrazione risultante sia sempre centrosimmetrico, a dispetto se il centro di simmetria sia o meno realmente presente. Questi patterns di diffrazione, così ottenuti afferiscono a gruppi puntuali speciali, chiamati classi di Laue. La classe di Laue può essere facilmente ottenutaa partire da un gruppo puntuale, aggiungendo ad esso un centro di simmetria. Per esempio, il sistema cristallino monoclino è caratterizzato dalla presenza di un solo asse binario. I gruppi puntuali di questo sistema sono 2, m (= 2) e 2/m, ma la classe di Laue di questo sistema è sempre 2/m. Se ad esempio abbiamo un cristallo monoclino afferente al gruppo puntuale 2. Per ricavare la sua classe di Laue devo aggiungere un centro di simmetria, ma dall interazione dell asse 2 con il centro di simmetria si viene a creare un piano di simmetria perpendicolare all asse 2, quindi la classe di Laue e 2/m. Un risultato analogo è ottenuto se si considera il piano di simmetria.
50 La scelta della maglia unitaria In linea di principio, soddisfatto il criterio di rispettare la periodicità traslazionale del cristallo e quindi non lasciare «spazi vuoti» tra una cella unitaria e quelle attigue, la scelta della cella elementare (maglia unitaria nel piano) è arbitraria. Tuttavia, da un punto di vista matematico, qualora nella struttura cristallina fossere presenti elementi di simmetria, conviene scegliere la cella elementare in modo che gli assi di questa siano rispettivamente coincidenti o perpendicolari agli assi di rotazione e piani di simmetria presenti. Anche qualora si rispettino tale direttive, talvolta è possibile scegliere comunque celle diverse. Tutte le celle rappresentate in figura sono caratterizzate dalla presenza di un asse binario. La due celle superiori sono primitive, le due inferiori sono centrate, ovvero vi un nodo al centro di una faccia (ma nelle 3D questo può anche essere al centro del corpo della cella). Tutte le celle sono compatibili con il sistema monoclino.
51 I reticoli piani Se consideriamo i reticoli di traslazione bidimensionali abbiamo 5 reticoli di Bravais: 1) Obliquo: c è solo un asse di rotazione binario. 2) Rettangolare: due piani di riflessione perpendicolari e un asse di rotazione binario 3) Quadrato: un asse quaternario e quattro piani 4) Esagonale: un asse di ordine sei e sei piani Auguste Bravais ( )
52 Maglie non primitive La maglia obliqua nella figura di sinistra è elementare ma non è rappresentativa della simmetria del reticolo di Bravais (a=b). La maglia che descrive la simmetria del reticolo è quella di destra che però non è primitiva
53 Maglie non primitive La traslazione τ = (ma/2 + nb/2) con n e m interi è una nuova operazione di simmetria chiamata centratura della cella. Nello spazio bidimensionale questo è l unico caso in cui l operazione di centratura origina un nuovo reticolo. In totale quindi nel caso bidimensionale ho 5 possibili reticoli di Bravais. Nel caso di reticoli tridimensionali la situazione è più complessa e si possono avere diversi tipi di centratura.
54 I reticoli di Bravais Le celle elementari illustrare in Figura sono le celle convenzionali dei 14 reticoli di Bravais. Esse hanno le caratteristiche richieste convenzionalmente per una cella: il minore volume possibile, compatibilmente con la massima simmetria del sistema cristallino.
55 Celle non primitive Nel caso di reticoli tridimensionali si possono avere diversi tipi di centratura: Simbolo Tipo traslazione Punti reticolari\ celle P Primitiva Nessuna 1 A Faccia centrata-a τ A = (½nb + ½pc) 2 B Faccia centrata-b τ B = (½ma + ½pc) 2 C Faccia centrata-c τ C = (½ma + ½nb) 2 F Tutte facce centrate τ A ; τ B ; τ C ; 4 I Corpo centrato τ I = (½ma + ½nb + ½pc) 2 R Romboedrica τ R1 = (⅓ma + ⅔nb + ⅔pc); τ R2 = (⅔ma + ⅓nb + ⅓pc) 3
56 Condizioni per i sette sistemi cristallini La presenza di certi assi vincola la geometria del reticolo. Queste restrizioni danno origine ai sette sistemi cristallini. E infatti conveniente raggruppare classi di simmetria che hanno delle somiglianze: in tal modo i cristalli corrispondenti potranno essere descritti con uno stesso tipo di cella elementare. Questa a sua volta potrà essere scelta in modo da evidenziare la simmetria presente. Ad esempio, nei gruppi 1 e 1 non è definito alcun asse di simmetria e quindi non c è vincolo per la cella elementare. I rapporti a:b:c e gli angoli potranno essere liberi. Si dice che le due classi fanno parte del sistema triclino. I gruppi 2, m, 2/m sono riferibili ad un reticolo che presenta solo un asse 2,e una cella elementare con due angoli di 90. I tre gruppi appartengono al sistema monoclino. Assi di simmetria che definiscono il sistema e la loro orientazione E o i 1 o 1 C 2 o σ 2 o 2 (lungo b o c) tre C 2 o σ tre 2 o 2 (perpendicolari) C 4 o S 4 o 4 C 6 o S 3 3 o 3 C 6 o S 3 6 o 6 quattro assi 3 o 3 lungo la diagonle del cubo Sistema cristallino Trimetrici Triclino Monoclino Ortorombico Dimetrici Tetragonale Trigonale (Romboedrico) Esagonale Monometrico Cubico Parametri del reticolo a b c α β γ a b c α = γ = 90 β (1 setting) α = β = 90 γ (2 setting) a b c α = β = γ = 90 a = b c α = β = γ = 90 a = b c α = β = 90, γ = 120 a = b c α = β = 90, γ = 120 a = b = c α = β = γ = 90
57 Condizioni per i sette sistemi cristallini Per esempio se nel sistema monoclino si dispone l asse 2 lungo l asse a, si avrebbe che... a Simbolo per l asse binario parallelo alla pagina c β Per il sistema monoclino: a b c α = γ = 90 β Una rotazione di 180º attorno all asse a, risulta incompatibile con la periodicità della traslazione del reticolo monoclino.
58 Condizioni per i sette sistemi cristallini Se invece si dispone l asse binario coincidente con l asse b, si avrebbe che... b a γ = 90 Per il sistema monoclino: a b c α = γ = 90 β Una rotazione di 180º attorno all asse b, risulta compatibile con la periodicità della traslazione del reticolo monoclino. Risultati analoghi si sarebbero ottenuti se si fosse disposto l asse binario lungo c, utilizzandole relazioni geometriche a b c e α = β = 90 γ
59 Sistema triclino Assi caraterizzanti: 1, 1 a b c α β γ Cella primitiva
60 Sistema monoclino Assi caraterizzanti: un solo asse binario a b c e α = γ = 90 β Cella primitiva Cella a faccia centrata C
61 Sistema ortorombico Assi caraterizzanti: tre assi binari a b c α = β = γ = 90 Cella primitiva Cella a faccia centrata C Cella a corpo centrato I Cella a tutte facce centrate I
62 Sistema tetragonale Assi caraterizzanti: un solo asse quaternario a = b c α = β = γ = 90 Cella primitiva Cella a corpo centrato I
63 Sistema esagonale Sistema trigonale Assi caraterizzanti: un solo asse sernario a = b c α = β = 90, γ = 120 Assi caraterizzanti: un solo asse ternario Cella primitiva Cella romboedrica
64 Assi caraterizzanti: quattro assi ternari Sistema cubico a = b = c α = β = γ = 90 Cella primitiva Cella a tutte facce centrate F Cella a corpo centrato I
65 Proiezioni stereografiche Tutti gli elementi di simmetria appartenenti a uno dei gruppi puntuali (tridimensionali) possono essere rappresentanti nelle due dimensioni attraverso il meccanismo della proiezione stereografica. Piano equatoriale Polo Sud Proiezione stereografica Si abbia una sfera di proiezione, il cui centro coincida con il punto di intersezione degli elementi di simmetria. Si consideri il piano equatoriale della sfera (piano di proiezione). Si prolunghino idealmente gli elementi di simmetria sino a che non incontrino la superfice della emisfera superiore. Si congiungano i punti di contatto tra l elemento di simmetria e la superfice dell emisfera con il polo opposto (polo sud). La regione (punto, linea o arco) del piano di proiezione toccata dal congiungimento dell elemento di simmetria prolungato sulla superficei dell emisfera, rappresenta la proiezione stereografica dell elemento stesso. Si indicano gli elementi di simmetria con il relativo simbolo internazionale.
66 Esempio: Proiezione stereografica Sistema tetragonale Combinazione degli elementi di simmetria Proiezione dei soli elementi di simmetria Il problema è che orientando gli elementi di simmetria in modo diverso (ad esempio orientando l asse 4 lungo Est- Ovest avrei una differente proiezione stereografica. Per ovviare al problema si orientano gli elementi di simmetria all interno della sfera di proiezione in funzione del gruppo puntuale rappresentato.
67 Orientamento del cristallo all interno della sfera di proiezione SISTEMA MONOMETRICO (CUBICO) Caratterizzato da 3 assi di lunghezza uguale e ortogonali tra loro. Il solido deve essere allineato in modo che i tre assi di ordine 4 (classe di simmetria: 432, 43m, 4/m32/m) o di ordine 2 (classe di simmetria: 23, 2/m3) coincidano con la terna di riferimento della sfera di proiezione. +a 3 = +z -a 2 = -y +a 1 = +z -a 1 = -z +a 2 = +y -a 3 = -z
68 Orientamento del cristallo all interno della sfera di proiezione SISTEMA TETRAGONALE Caratterizzato da un asse lungo o corto (c) e due assi di lunghezza uguale (a 1, a 2 ). Tutti gli assi sono ortogonali tra loro. L asse di ordine 4 deve coincidere con l asse z della sfera di proiezione; gli assi di ordine 2 o i piani di simmetria devono rispettivamente coincidere o essere paralleli agli assi x e y della sfera di proiezione.
69 Orientamento del cristallo all interno della sfera di proiezione SISTEMA ORTOROMBICO Caratterizzato da tre assi di lunghezza diversa (a, b, c); tutti ortogonali tra loro. I tre assi devono coincidere con la terna di riferimento della sfera di proiezione; per il gruppo puntuale mm2, l asse z della sfera di proiezione deve coincidere con l asse di ordine 2, mentre gli assi x e y devo essere normali ai piani m.
70 Proiezioni stereografica dei gruppi puntuali ortonormali Proiezione stereografica della distribuzione del motivo e degli elementi di simmetria delle classi di simmetria (gruppi puntuali) ortonormali. I motivi al di sopra della pagina sono equivalenti a quelle al di sotto, ma sono distinte in punti e cerchietti. Simboli degli elementi di simmetria Le 32 classi di simmetria (gruppi puntuali).
71 Tabella dei gruppi puntuali e dei loro elementi di simmetria Nella tabella di fianco sono riportati i gruppi puntuali afferenti ai sette sistemi cristallini con gli elementi di simmetria che li contradistinguono e le loro orientazioni rispetto agli assi cristallografici del sistema cristallino. Esistono due notazioni diverse per indicare convenzionalmente i vari tipi di simmetria: la notazione di Hermann-Mauguin (colonna H-M in tabella) che è usata prevalentemente in campo cristallografico e quella di Schönflies usata in campo molecolare. Il pedice p vicino al simbolo di un asse indica che quell asse è un asse polare. Gli assi che incontrano alle due estremità del cristallo elementi geometrici non equivalenti tra loro o proprietà fisiche diverse si dicono polari (Es. i quattro assi ternari che congiungono i vertici di un tetraedro con il centro della facce opposte).
72 Operazioni di simmetria con componente traslazionale ELICOGIRE: Associano un operazione di traslazione ad una rotazione. La traslazione avviene parallelamente all asse di rotazione; l entità della traslazione è sempre una frazione del periodo di traslazione del reticolo. Il simbolo di un elicogira è del tipo: N K, dove N indica l ordine dell asse di rotazione e K la lunghezza della traslazione (τ = K/N). es. elicodigira (n = 2): p = 1 τ / 2 (si indica con 2 1 ) elicotrigira (n = 3): p = 1, 2 τ / 3 (3 1 ); 2τ / 3 (3 2 )
73 Operazioni di simmetria con componente traslazionale Elicogira. Simmetria di tipo N k : Esegue una rotazione di ordine N (360 /N) e una traslazione di k/n. Per esempio: 2 1 rotazione di ordine 2 (180 ) e traslazione di 1/2 lungo l asse 3 1 rotazione di 120 e traslazione di 1/3 lungo l asse (destrorsa) 3 2 rotazione di 120 e traslazione di 2/3 lungo l asse (sinistrorsa) Traslazione pari a ½ del periodo di ripetizione dell asse Asse binario Elicogira 2 1 Perchè l elicogira 2 1 trasla solo di ½ non potrebbe traslare di un valore x qualunque?
74 Restrizioni alle simmetrie possibili dovute alla periodicità del reticolo cristallino 2 0 = = = 2 1 τ = 3/2 T τ = ½ T τ = 2/2 T T τ = ½ T T T Non ha senso considerare elicogiore N k con K > N, perchè esse sono equivalenti per traslazione reticolare a quelli per K < N.
75 Elicogira: Sia τ la componente traslazionale di un asse elicogira, se l'asse di rototraslazione è di ordine N si deve avere che se lo applico N volte esso deve produrre una posizione equivalente a quella che otterei per un multiplo intero di T (periodo di traslazione) : Nτ = mm, dove T è la periodicità del vettore reticolo e m = 1,2,3.... Dunque: τ = T m N Restrizioni alle simmetrie possibili dovute alla periodicità del reticolo cristallino Per esempio: Se N =2, m= 1 τ = T 1/2 con [m = 0, 1, 2,3... (n-1)]. Se N = 3, m = 1 o m = 2 τ = T m n I valori di m sono limitati a 0 < m < (N-1) perchè per m > N si ottengono movimenti equivalenti per traslazione reticolare a quelli per m < N T Per ogni rotazione di 120 si ha una traslazione di 1/3 del vettore di cella elementare (3 1 ) T Per ogni rotazione di 120 si ha una traslazione di 2/3 del vettore di cella elementare (3 2 )
76 Elicogire 3 1 e 3 2 Traslazione di 1/3 della lunghezza dell asse Asse di rotazione ternario Eligorira 3 1 Se si uniscono gli oggetti generati dalla simmetria 3 1 si ottiene un elica sinistrorsa; Se si uniscono gli oggetti generati dalla simmetria 3 2 si ottiene un elica destrorsa. Le due eliche sono enantiomorfe. Le altre copie di elicogire enantiomorfe sono: 4 1 e 4 3, 6 1 e 6 5, 6 2 e /3 1/3 0 Elicogira 3 1 4/3, (1/3) Elicogira 3 2 2/3
77 Asse 4 e Elicogire e 4 3 Asse 4 Elicogire 4 1 Elicogire 4 2 Elicogire 4 3
78 Asse 6 e Elicogire e 6 5 Asse 6 Elicogira 6 1 Elicogira 6 2 Elicogira 6 3 Elicogira 6 4 Elicogira 6 5
79 Elicogire enantiomorfe Elicogire enantiomorfe
80 Simboli internazionali assi rototraslazionali Ordine Simbolo Simbolo grafico Traslazione lungo l asse * * Dato come frazione di una traslazione completa nella direzione positiva assumendo un verso di rotazione antioraria lungo l asse stesso. Vettore di traslazione, b Rotazione Elicogira 2 1 orizzontale parallela a b. La piramide tratteggiata indica la posizione intermedia dove la prima piramide è ruotata prima di essere traslata lungo l asse di shift di b/2. Elicogira 2 1 parallela a c.
81 Slittopiano SLITTOPIANI: Associano un operazione di traslazione ad una riflessione Le traslazioni associate agli slittopiani avvengono in direzioni parallele ai piani stessi. Poiché le celle elementari che si assumono per descrivere una struttura sono generalmente orientate in maniera semplice rispetto ai piani di simmetria, ne consegue che le traslazioni dovute agli slittopiani hanno luogo in direzioni corrispondenti ai lati o alle diagonali delle facce o della cella stessa a, b, c sono i simboli degli slittopiani con componente traslazionale di mezzo periodo lungo i corrispondenti lati della cella elementare n si riferisce agli slittopiani con componente traslazionale di mezza diagonale di una faccia o della cella d si riferisce agli slittopiani con componente traslazionale di un quarto di diagonale di una faccia o della cella
82 Slittopiano La combinazione di una riflessione con una traslazione, sempre parallela al piano, porta alla definizione di un totale di cinque slittopiani cristallografici. Simbolo Ordine Simbolo grafico Vettore traslazione Vettore di traslazione, b b d è il vettore diagonale. Es. a+b, a-b, a+b+c. Riflessione Slitto piano b, perpendicolare ad a con una traslazione di b/2 Slitto piano c, perpendicolare ad a con una traslazione di c/2
83 a b
84 Gruppi Spaziali I 7 sistemi cristallini, i 14 reticoli di Bravais e le 32 classi cristalline ci consentono di classificare la geometria reticolare e la simmetria di un cristallo. Tuttavia, per comprendere a pieno una struttura cristallina dobbiamo esaminare la distribuzione spaziale della densità elettronica (la disposizione spaziale degli atomi). E necessario descrivere questa distribuzione solo nell ambito della cella elementare perchè le operazioni traslazionali reticolari generano l intero cristallo. Una descrizione della distribuzione elettronica dal punto di vista della simmetria richiede l uso dei gruppi Formalmente, un gruppo spaziale è il gruppo che contiene tutte le operazioni di simmetria spaziale degli atomi nel cristallo. Per la presenza di operazioni di simmetria traslazionali non varrà più, ovviamente, che tutti gli elementi di simmetria devono passare per un punto. Vi sono 230 gruppi spaziali (non magnetici). L associazione dei reticoli di Bravais con le combinazioni di elementi di simmetria senza componente traslazionale dà luogo a 73 gruppi spaziali che vengono chiamati simmorfici.
85 Classificazione dei gruppi spaziali Le convenzioni più rilevanti in accordo con la notazione di Hermann-Mauguin sono: Al primo posto appare sempre il simbolo del reticolo di Bravais. Dopo di questo: a) nei gruppi monoclini appare il simbolo dell'asse di simmetria e, se presente, dopo una barra appare il simbolo del piano o slittopiano normale ad esso; b) nei gruppi ortorombici i simboli degli elementi di simmetria si riferiscono alle direzioni a, b, c nell'ordine (gli elementi sono paralleli ad essi se assi propri, perpendicolari se piani); c) nei gruppi afferenti al sistema tetragonale appare per primo il simbolo dell'asse quaternario e, quando presente, dopo una barra appare il simbolo del piano o slittopiano normale ad esso. Subito dopo appare il simbolo dell'elemento di simmetria che si riferisce alla direzione a (e quindi b) e poi quello dell elemento relativo alle diagonali della maglia normale all asse quaternario; d) nei gruppi afferenti al sistema trigonale ed esagonale appare per primo il simbolo dell asse ternario o senario. Nei gruppi esagonali, quando presente, appare dopo una barra il simbolo del piano normale ad esso. Il primo dei simboli successivi si riferisce all'asse a (e quindi a b e quindi alla diagonale corta della maglia normale all'asse ternario), il secondo alla diagonale lunga della maglia; e) nei gruppi del sistema cubico i simboli degli elementi di simmetria si riferiscono nell'ordine ad a (e quindi a b e a c), alle diagonali principali della cella (asse ternario), alle diagonali delle facce della cella. I 230 gruppi spaziali furono determinati alla fine del secolo scorso, attraverso i lavori matematici di Fedorov (1891) e Schoenflies (1891). Tutte le informazioni sui gruppi spaziali sono contenute nelle International Tables for X-Ray Crystallography.
86 Piani cristallografici, direzioni e indici I nodi di un reticolo t m = m 1 a + m 2 b + m 3 c, sono caratterizzati da numeri razionali (interi se la cella elementare è primitiva). Le proprietà dei reticoli connesse ai nodi sono quindi dette razionali. Si parlerà di direzioni razionali per intendere direzioni definite da due nodi reticolari e di piani razionali per intendere piani definiti da tre nodi reticolari. Direzioni cristallografiche. Come abbiamo visto, i cristalli sono anisotropi: sarà quindi necessario specificare in modo semplice le direzioni nelle quali si manifestano determinate proprietà fisiche. In un reticolo esistono infiniti filari paralleli, ciascuno definito da due punti nodali, che sono caratterizzati da uno stesso periodo di ripetizione. I filari definiscono una direzione cristallografica. Se un filare passa per l origine la sua direzione sarà definita dai valori m i di uno qualunque dei nodi del filare. La direzione viene indicata con [m 1 m 2 m 3 ]. La stessa direzione è indicata anche da un multiplo del tipo [nm 1 nm 2 nm 3 ].
Simmetrie Cristallografiche A.A Marco Nardini Dipartimento di Scienze Biomolecolari e Biotecnologie Università di Milano
 A.A. 2009-2010 Marco Nardini Dipartimento di Scienze Biomolecolari e Biotecnologie Università di Milano Reticolo Cristallino: insieme di punti detti nodi separati da intervalli a, b, e c (reticolo di ripetizione)
A.A. 2009-2010 Marco Nardini Dipartimento di Scienze Biomolecolari e Biotecnologie Università di Milano Reticolo Cristallino: insieme di punti detti nodi separati da intervalli a, b, e c (reticolo di ripetizione)
Materiale didattico: dispense fornite durante il corso
 Struttura e Proprietà dei Materiali 6 crediti lezioni frontali+ 3 crediti di laboratorio Richiami di cristallochimica Reticolo reciproco Diffrazione di raggi X e di Neutroni Produzione Raggi X (Tubi, Sincrotroni)
Struttura e Proprietà dei Materiali 6 crediti lezioni frontali+ 3 crediti di laboratorio Richiami di cristallochimica Reticolo reciproco Diffrazione di raggi X e di Neutroni Produzione Raggi X (Tubi, Sincrotroni)
Corso di Mineralogia 1
 1 DEFINIZIONE DI MINERALE - Corpo solido naturale con composizione chimica definita - Stato Solido Cristallino - Amorfo - Atomi disposti in modo ordinato e periodico - Anisotropia Isotropia Composto chimico
1 DEFINIZIONE DI MINERALE - Corpo solido naturale con composizione chimica definita - Stato Solido Cristallino - Amorfo - Atomi disposti in modo ordinato e periodico - Anisotropia Isotropia Composto chimico
Stato cristallino e simmetria
 Corso di laurea triennale in Scienza dei Materiali a.a. 2018-2019 Stato cristallino e simmetria «Una buona conoscenza della geometria cristallina dovrebbe far parte del bagaglio culturale di chiunque si
Corso di laurea triennale in Scienza dei Materiali a.a. 2018-2019 Stato cristallino e simmetria «Una buona conoscenza della geometria cristallina dovrebbe far parte del bagaglio culturale di chiunque si
Reticoli di Bravais e sistemi cristallini
 Reticoli di Bravais e sistemi cristallini Come in 2D, anche in 3D si individuano un motivo, che si ripete in modo periodico nello spazio e un reticolo (disposizione di punti, ciscuno che possiede lo stesso
Reticoli di Bravais e sistemi cristallini Come in 2D, anche in 3D si individuano un motivo, che si ripete in modo periodico nello spazio e un reticolo (disposizione di punti, ciscuno che possiede lo stesso
Combinazione operatori di simmetria senza componenti traslazionali
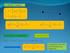 Combinazione operatori di simmetria senza componenti traslazionali E possibile combinare diversi operatori di simmetria per ottenere modelli tridimensionali. La combinazione non deve portare alla formazione
Combinazione operatori di simmetria senza componenti traslazionali E possibile combinare diversi operatori di simmetria per ottenere modelli tridimensionali. La combinazione non deve portare alla formazione
Corso di Mineralogia
 Corso di Mineralogia Scienze Geologiche A.A. 2016 / 2017 Elementi di cristallografia strutturale (pdf # 06) (2) - Mineralogia 2016/2017_cristallografia CRISTALLOGRAFIA STRUTTURALE Cristallografia morfologica
Corso di Mineralogia Scienze Geologiche A.A. 2016 / 2017 Elementi di cristallografia strutturale (pdf # 06) (2) - Mineralogia 2016/2017_cristallografia CRISTALLOGRAFIA STRUTTURALE Cristallografia morfologica
Corso di Mineralogia
 Corso di Mineralogia Scienze Geologiche A.A. 2017 / 2018 Elementi di cristallografia strutturale (pdf # 06) (2) - Mineralogia 2017/2018_cristallografia CRISTALLOGRAFIA STRUTTURALE Cristallografia morfologica
Corso di Mineralogia Scienze Geologiche A.A. 2017 / 2018 Elementi di cristallografia strutturale (pdf # 06) (2) - Mineralogia 2017/2018_cristallografia CRISTALLOGRAFIA STRUTTURALE Cristallografia morfologica
E possibile definire gli indici delle facce di un cristallo come un rapporto di rapporti parametrici.
 INDICIZZAZIONE DELLE FACCE E possibile definire gli indici delle facce di un cristallo come un rapporto di rapporti parametrici. Essi saranno una terna di numeri (h,k,l) primi fra loro (generalmente piccoli).
INDICIZZAZIONE DELLE FACCE E possibile definire gli indici delle facce di un cristallo come un rapporto di rapporti parametrici. Essi saranno una terna di numeri (h,k,l) primi fra loro (generalmente piccoli).
La Cristallografia. 1: la traslazione
 La Cristallografia 1: la traslazione Spiega: Perché i cristalli hanno le facce Come le chiamiamo Come si dividono le celle elementari (e i cristalli macroscopici) La traslazione Reticolo unidimensionale
La Cristallografia 1: la traslazione Spiega: Perché i cristalli hanno le facce Come le chiamiamo Come si dividono le celle elementari (e i cristalli macroscopici) La traslazione Reticolo unidimensionale
Elementi di strutturistica cristallina III
 Chimica fisica superiore Modulo 1 Elementi di strutturistica cristallina III Sergio Brutti Reticoli tri-dimensionali Consideriamo nuovamente i 14 reticoli di Bravais Basi cristalline Analogamente che al
Chimica fisica superiore Modulo 1 Elementi di strutturistica cristallina III Sergio Brutti Reticoli tri-dimensionali Consideriamo nuovamente i 14 reticoli di Bravais Basi cristalline Analogamente che al
LA SIMMETRIA NEI CRISTALLI. Cristallo di berillo varietà acquamarina su quarzo
 LA SIMMETRIA NEI CRISTALLI Cristallo di berillo varietà acquamarina su quarzo Simmetria La simmetria di una figura, o di un sistema molecolare o cristallino, etc. (bidimensionale o tridimensionale) è l
LA SIMMETRIA NEI CRISTALLI Cristallo di berillo varietà acquamarina su quarzo Simmetria La simmetria di una figura, o di un sistema molecolare o cristallino, etc. (bidimensionale o tridimensionale) è l
Struttura e geometria cristallina
 Struttura e geometria cristallina Tecnologia Meccanica RETICOLO SPAZIALE E CELLE UNITARIE Gli atomi, disposti in configurazioni ripetitive 3D, con ordine a lungo raggio (LRO), danno luogo alla struttura
Struttura e geometria cristallina Tecnologia Meccanica RETICOLO SPAZIALE E CELLE UNITARIE Gli atomi, disposti in configurazioni ripetitive 3D, con ordine a lungo raggio (LRO), danno luogo alla struttura
Simmetria nei cristalli
 Simmetria nei cristalli Un operazione di simmetria lascia invariato un cristallo, ovvero il cristallo trasformato è sovrapponibile al cristallo originario. Tali operazioni possono essere classificate in
Simmetria nei cristalli Un operazione di simmetria lascia invariato un cristallo, ovvero il cristallo trasformato è sovrapponibile al cristallo originario. Tali operazioni possono essere classificate in
LA PROIEZIONE STEREOGRAFICA (PARTE I)
 Corso di laurea triennale in Scienze Naturali a.a. 2012-2013 LA PROIEZIONE STEREOGRAFICA (PARTE I) «Una proiezione cristallina è un metodo di rappresentazione dei cristalli tridimensionali su di un piano
Corso di laurea triennale in Scienze Naturali a.a. 2012-2013 LA PROIEZIONE STEREOGRAFICA (PARTE I) «Una proiezione cristallina è un metodo di rappresentazione dei cristalli tridimensionali su di un piano
LA PROIEZIONE STEREOGRAFICA
 Corso di laurea triennale in Scienze Naturali a.a. 2015-2016 LA PROIEZIONE STEREOGRAFICA «Una proiezione cristallina è un metodo di rappresentazione dei cristalli tridimensionali su di un piano bidimensionale.
Corso di laurea triennale in Scienze Naturali a.a. 2015-2016 LA PROIEZIONE STEREOGRAFICA «Una proiezione cristallina è un metodo di rappresentazione dei cristalli tridimensionali su di un piano bidimensionale.
Reticoli, basi e strutture cristalline in 1D
 Reticoli, basi e strutture cristalline in 1D a a vettore primitivo del reticolo diretto (o di Bravais) R = na n=1,2,. vettori principali del reticolo diretto di Bravais, unidimensionale e di parametro
Reticoli, basi e strutture cristalline in 1D a a vettore primitivo del reticolo diretto (o di Bravais) R = na n=1,2,. vettori principali del reticolo diretto di Bravais, unidimensionale e di parametro
Fisica dello Stato Solido
 Fisica dello Stato Solido Lezione n.1 Strutture Cristalline Mara Bruzzi Corso di Laurea Specialistica Ingegneria Elettronica a.a.07-08 Scaricabile al sito: http://www.de.unifi.it/fisica/bruzzi/bruzzi_dida_fss.html
Fisica dello Stato Solido Lezione n.1 Strutture Cristalline Mara Bruzzi Corso di Laurea Specialistica Ingegneria Elettronica a.a.07-08 Scaricabile al sito: http://www.de.unifi.it/fisica/bruzzi/bruzzi_dida_fss.html
Corso di Mineralogia 1
 1 DEFINIZIONE DI MINERALE - Corpo solido naturale con composizione chimica definita - Stato Solido Cristallino - Amorfo - Atomi disposb in modo ordinato e periodico - Anisotropia Isotropia Composto chimico
1 DEFINIZIONE DI MINERALE - Corpo solido naturale con composizione chimica definita - Stato Solido Cristallino - Amorfo - Atomi disposb in modo ordinato e periodico - Anisotropia Isotropia Composto chimico
STRUTTURA DEI SOLIDI
 STRUTTURA DEI SOLIDI I solidi possono essere classificati in funzione della regolarità con cui gli atomi o gli ioni si dispongono nello spazio. Un materiale è detto cristallino se caratterizzato da configuarazioni
STRUTTURA DEI SOLIDI I solidi possono essere classificati in funzione della regolarità con cui gli atomi o gli ioni si dispongono nello spazio. Un materiale è detto cristallino se caratterizzato da configuarazioni
DEFINIZIONE DI MINERALE
 DEFINIZIONE DI MINERALE - Corpo solido naturale - Stato Solido Cristallino - Amorfo - Atomi dispos> in modo ordinato e periodico - Anisotropia Isotropia - Legge Costanza angoli diedri (Romè de l Isle,
DEFINIZIONE DI MINERALE - Corpo solido naturale - Stato Solido Cristallino - Amorfo - Atomi dispos> in modo ordinato e periodico - Anisotropia Isotropia - Legge Costanza angoli diedri (Romè de l Isle,
INDICE CAPITOLO 1 CAPITOLO 1
 INDICE CAPITOLO. Cristalli.. Tipici piani reticolari di un cristallo cubico.2. Reticoli... Reticolo quadrato bidimensionale..2. Reticolo cubico semplice.. Celle unitarie... Primo esempio di arrangiamenti
INDICE CAPITOLO. Cristalli.. Tipici piani reticolari di un cristallo cubico.2. Reticoli... Reticolo quadrato bidimensionale..2. Reticolo cubico semplice.. Celle unitarie... Primo esempio di arrangiamenti
Elettronica dello Stato Solido Lezione 2: I cristalli. Daniele Ielmini DEI Politecnico di Milano
 Elettronica dello Stato Solido Lezione 2: I cristalli Daniele Ielmini DEI Politecnico di Milano ielmini@elet.polimi.it D. Ielmini Elettronica dello Stato Solido 02 2 Outline Definizione del problema Struttura
Elettronica dello Stato Solido Lezione 2: I cristalli Daniele Ielmini DEI Politecnico di Milano ielmini@elet.polimi.it D. Ielmini Elettronica dello Stato Solido 02 2 Outline Definizione del problema Struttura
Lo stato solido. Solido: qualsiasi corpo rigido e incomprimibile che ha forma e volume propri. amorfi. cristallini
 Lo stato solido Solido: qualsiasi corpo rigido e incomprimibile che ha forma e volume propri Solidi amorfi cristallini Cella elementare: la più piccola porzione del reticolo cristallino che ne possiede
Lo stato solido Solido: qualsiasi corpo rigido e incomprimibile che ha forma e volume propri Solidi amorfi cristallini Cella elementare: la più piccola porzione del reticolo cristallino che ne possiede
Sistemi cristallini 1
 Sistemi cristallini Esercizio Calcolare la densità atomica definita come il rapporto tra il numero di atomi e il volume unitario per ) il litio sapendo che la distanza tra i centri dei primi vicini è R
Sistemi cristallini Esercizio Calcolare la densità atomica definita come il rapporto tra il numero di atomi e il volume unitario per ) il litio sapendo che la distanza tra i centri dei primi vicini è R
Tipologie di materiali
 Tipologie di materiali Caratteristiche macroscopiche Lavorazione Microstruttura Formula chimica Legami chimici Struttura atomica Struttura La struttura fisica dei materiali dipende dalla disposizione degli
Tipologie di materiali Caratteristiche macroscopiche Lavorazione Microstruttura Formula chimica Legami chimici Struttura atomica Struttura La struttura fisica dei materiali dipende dalla disposizione degli
POLIEDRI IN CRISTALLOGRAFIA
 POLIEDRI IN CRISTALLOGRAFIA L'universo è composto di materia, ovviamente. E la materia è composta di particelle: elettroni, neutroni e protoni. Dunque l'intero universo è composto di particelle. Ora, di
POLIEDRI IN CRISTALLOGRAFIA L'universo è composto di materia, ovviamente. E la materia è composta di particelle: elettroni, neutroni e protoni. Dunque l'intero universo è composto di particelle. Ora, di
Diffrazione di Raggi X
 Diffrazione di Raggi X 1. Laue, Friedrich, Knipping (Monaco, 1912): diffrazione da reticolo tridimensionale 2. Ewald (Tesi di dottorato, Monaco, 1913): costruzione del reticolo reciproco 3. Bragg and Bragg
Diffrazione di Raggi X 1. Laue, Friedrich, Knipping (Monaco, 1912): diffrazione da reticolo tridimensionale 2. Ewald (Tesi di dottorato, Monaco, 1913): costruzione del reticolo reciproco 3. Bragg and Bragg
Gruppi puntuali. Primo elemento
 Gruppi puntuali Considerando le combinazioni che portano solo alla formazioni di gruppi puntuali con un numero finito di elementi di simmetria si ottengono solo 32 gruppi puntuali. I cristalli afferiranno
Gruppi puntuali Considerando le combinazioni che portano solo alla formazioni di gruppi puntuali con un numero finito di elementi di simmetria si ottengono solo 32 gruppi puntuali. I cristalli afferiranno
Sistemi cristallini - Soluzioni degli esercizi
 Sistemi cristallini - Soluzioni degli esercizi Fisica della Materia Condensata Dipartimento di Matematica e Fisica Università degli Studi Roma Tre A.A. 06/07 Sistemi cristallini Esercizio.........................................
Sistemi cristallini - Soluzioni degli esercizi Fisica della Materia Condensata Dipartimento di Matematica e Fisica Università degli Studi Roma Tre A.A. 06/07 Sistemi cristallini Esercizio.........................................
Elettronica dello Stato Solido Lezione 2: I cristalli. Daniele Ielmini DEI Politecnico di Milano
 Elettronica dello Stato Solido Lezione 2: I cristalli Daniele Ielmini DEI Politecnico di Milano ielmini@elet.polimi.it Outline Definizione del problema Struttura cristallina Diffrazione Conclusioni D.
Elettronica dello Stato Solido Lezione 2: I cristalli Daniele Ielmini DEI Politecnico di Milano ielmini@elet.polimi.it Outline Definizione del problema Struttura cristallina Diffrazione Conclusioni D.
Sistemi cristallini - Soluzioni degli esercizi. Fisica della Materia Condensata
 Sistemi cristallini - Soluzioni degli esercizi Fisica della Materia Condensata A.A. 05/06 Indice Esercizio Esercizio Esercizio 6 Esercizio 9 Esercizio 5 Esercizio 6 Esercizio 7 Esercizio 8 6 Esercizio
Sistemi cristallini - Soluzioni degli esercizi Fisica della Materia Condensata A.A. 05/06 Indice Esercizio Esercizio Esercizio 6 Esercizio 9 Esercizio 5 Esercizio 6 Esercizio 7 Esercizio 8 6 Esercizio
Scienza dei Materiali 1 Esercitazioni
 Scienza dei Materiali 1 Esercitazioni 2. Cristallografia dei materiali ver. 1.1 Reticoli cristallini Reticolo è una griglia tridimensionale di punti possiamo individuare un insieme minimo di punti (cella)
Scienza dei Materiali 1 Esercitazioni 2. Cristallografia dei materiali ver. 1.1 Reticoli cristallini Reticolo è una griglia tridimensionale di punti possiamo individuare un insieme minimo di punti (cella)
Interazione dei raggi X con la materia
 Interazione dei raggi X con la materia Emissione di fotoelettroni Fascio incidente (I 0 ) di raggi X Fluorescenza Scattering coerente e incoerente Assorbimento (I) calore Lo scattering coerente dei raggi
Interazione dei raggi X con la materia Emissione di fotoelettroni Fascio incidente (I 0 ) di raggi X Fluorescenza Scattering coerente e incoerente Assorbimento (I) calore Lo scattering coerente dei raggi
Proprietà fisiche e Anisotropia Gabriella Salviulo Università di Padova
 Proprietà fisiche e Anisotropia Gabriella Salviulo Università di Padova La Fisica dei Minerali: implicazioni geologiche e applicazioni pratiche 2-5 Febbraio 2015 Bressanone OBIETTIVO N 1: ALLINEATI ALLA
Proprietà fisiche e Anisotropia Gabriella Salviulo Università di Padova La Fisica dei Minerali: implicazioni geologiche e applicazioni pratiche 2-5 Febbraio 2015 Bressanone OBIETTIVO N 1: ALLINEATI ALLA
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
MINERALOGIA Corso di Laurea in Scienze Naturali II Anno I Sem. - 9 CFU A.A
 MINERALOGIA Corso di Laurea in Scienze Naturali II Anno I Sem. - 9 CFU A.A. 2008-2009 Prof. Antonio GIANFAGNA Dipartimento di Scienze della Terra Stanza 309, Edificio Mineralogia Tel. 06-49914921 e-mail:
MINERALOGIA Corso di Laurea in Scienze Naturali II Anno I Sem. - 9 CFU A.A. 2008-2009 Prof. Antonio GIANFAGNA Dipartimento di Scienze della Terra Stanza 309, Edificio Mineralogia Tel. 06-49914921 e-mail:
Teorema di Cauchy. a) le azioni sono delle forze che ammettono densità rispetto alla lunghezza della linea ideale di taglio;
 Teorema di Cauchy Cosideriamo un corpo continuo in uno spazio bidimensionale. Esso può essere separato in due parti tracciando una linea (regolare) ideale. Queste parti si scambiano azioni dinamiche. L
Teorema di Cauchy Cosideriamo un corpo continuo in uno spazio bidimensionale. Esso può essere separato in due parti tracciando una linea (regolare) ideale. Queste parti si scambiano azioni dinamiche. L
Corso di Studi di Fisica Corso di Chimica
 Corso di Studi di Fisica Corso di Chimica Luigi Cerruti www.minerva.unito.it Lezioni 17-18 2010 Caratteristiche dei solidi Incompressibilità Proprietà comune con i liquidi (l altro stato condensato della
Corso di Studi di Fisica Corso di Chimica Luigi Cerruti www.minerva.unito.it Lezioni 17-18 2010 Caratteristiche dei solidi Incompressibilità Proprietà comune con i liquidi (l altro stato condensato della
Posizioni Atomiche nelle Celle Unitarie Cubiche
 Posizioni Atomiche nelle Celle Unitarie Cubiche Il sistema di coordinate cartesiane è usato per individuare gli atomi. In una cella unitaria cubica l asse x è la direzione che esce dal foglio. l asse y
Posizioni Atomiche nelle Celle Unitarie Cubiche Il sistema di coordinate cartesiane è usato per individuare gli atomi. In una cella unitaria cubica l asse x è la direzione che esce dal foglio. l asse y
Elementi di strutturistica cristallina iv
 Chimica fisica superiore Modulo Elementi di strutturistica cristallina iv Sergio Brutti Reticoli tri-dimensionali Consideriamo nuovamente i reticoli di Bravais Basi cristalline Analogamente che al caso
Chimica fisica superiore Modulo Elementi di strutturistica cristallina iv Sergio Brutti Reticoli tri-dimensionali Consideriamo nuovamente i reticoli di Bravais Basi cristalline Analogamente che al caso
La composizione di isometrie
 La composizione di isometrie Quello che è più interessante in una trasformazione geometrica è studiare quali effetti ha sulle figure e soprattutto valutare quali proprietà delle figure di partenza si conservano
La composizione di isometrie Quello che è più interessante in una trasformazione geometrica è studiare quali effetti ha sulle figure e soprattutto valutare quali proprietà delle figure di partenza si conservano
Negli esercizi che seguono ci sono alcune cose da specificare:
 DISCLAIMER Negli esercizi che seguono ci sono alcune cose da specificare: ) voi dovete interpretare i simboli V e A (R) sempre come R. Questo oggetto sarà chiamato alle volte piano affine e alle volte
DISCLAIMER Negli esercizi che seguono ci sono alcune cose da specificare: ) voi dovete interpretare i simboli V e A (R) sempre come R. Questo oggetto sarà chiamato alle volte piano affine e alle volte
LA GEOMETRIA DELLO SPAZIO
 LA GEOMETRIA ELLO SPAZIO 1 alcola l area e il perimetro del triangolo individuato dai punti A ; 0; 4, ; 1; 5 e 0; ;. ( ) ( ) ( ) 9 ; + 6 Stabilisci se il punto A ( 1;1; ) appartiene all intersezione dei
LA GEOMETRIA ELLO SPAZIO 1 alcola l area e il perimetro del triangolo individuato dai punti A ; 0; 4, ; 1; 5 e 0; ;. ( ) ( ) ( ) 9 ; + 6 Stabilisci se il punto A ( 1;1; ) appartiene all intersezione dei
Geometria e Topologia I 22 Giugno 2005 (U1-10, 9:00 11:00) [PROVA PARZIALE]1/8
![Geometria e Topologia I 22 Giugno 2005 (U1-10, 9:00 11:00) [PROVA PARZIALE]1/8 Geometria e Topologia I 22 Giugno 2005 (U1-10, 9:00 11:00) [PROVA PARZIALE]1/8](/thumbs/103/157085746.jpg) Geometria e Topologia I 22 Giugno 2005 (U-0, 9:00 :00) [PROVA PARZIALE]/8 Correzione 0 () In A 3 (R) siano dati i tre punti A =, B = 0, C =. 0 (a) A B e C sono allineati? Dipendenti? (b) Dimostrare che
Geometria e Topologia I 22 Giugno 2005 (U-0, 9:00 :00) [PROVA PARZIALE]/8 Correzione 0 () In A 3 (R) siano dati i tre punti A =, B = 0, C =. 0 (a) A B e C sono allineati? Dipendenti? (b) Dimostrare che
Reticoli e Diffrazione - Testi degli esercizi
 Reticoli e Diffrazione - Testi degli esercizi Fisica della Materia Condensata Dipartimento di Matematica e Fisica Università degli Studi Roma Tre A.A. 2016/2017 Reticoli e Diffrazione Esercizio 1....................................
Reticoli e Diffrazione - Testi degli esercizi Fisica della Materia Condensata Dipartimento di Matematica e Fisica Università degli Studi Roma Tre A.A. 2016/2017 Reticoli e Diffrazione Esercizio 1....................................
ESERCIZI DI GEOMETRIA E ALGEBRA LINEARE (II PARTE) In ogni sezione gli esercizi sono tendenzialmente ordinati per difficoltà crescente.
 ESERCIZI DI GEOMETRIA E ALGEBRA LINEARE (II PARTE) versione: 24 maggio 27 In ogni sezione gli esercizi sono tendenzialmente ordinati per difficoltà crescente Autovettori e autovalori Esercizio Trova gli
ESERCIZI DI GEOMETRIA E ALGEBRA LINEARE (II PARTE) versione: 24 maggio 27 In ogni sezione gli esercizi sono tendenzialmente ordinati per difficoltà crescente Autovettori e autovalori Esercizio Trova gli
ELEMENTI DI CALCOLO VETTORIALE
 ELEMENTI DI CALCOLO VETTORIALE Vettori liberi e vettori applicati o Vettore libero: - individuato da una direzione orientata ed una lunghezza - non ha un'ubicazione fissa nello spazio: - puo' essere traslato
ELEMENTI DI CALCOLO VETTORIALE Vettori liberi e vettori applicati o Vettore libero: - individuato da una direzione orientata ed una lunghezza - non ha un'ubicazione fissa nello spazio: - puo' essere traslato
Geometria analitica pagina 1 di 5
 Geometria analitica pagina 1 di 5 GEOMETRIA LINEARE NEL PIANO È fissato nel piano un sistema di coordinate cartesiane ortogonali monometriche Oxy. 01. Scrivere due diverse rappresentazioni parametriche
Geometria analitica pagina 1 di 5 GEOMETRIA LINEARE NEL PIANO È fissato nel piano un sistema di coordinate cartesiane ortogonali monometriche Oxy. 01. Scrivere due diverse rappresentazioni parametriche
Introduzione alla Fisica dello Stato Solido
 Introduzione alla Fisica dello Stato Solido Docente: Paolo Giannozzi, e-mail: paolo.giannozzi@uniud.it Stanza L1-1-BE ai Rizzi, Tel.: 0432-558216 Ricevimento ufficiale Venerdì 10:30-12:30 Orario: Me 17-19,
Introduzione alla Fisica dello Stato Solido Docente: Paolo Giannozzi, e-mail: paolo.giannozzi@uniud.it Stanza L1-1-BE ai Rizzi, Tel.: 0432-558216 Ricevimento ufficiale Venerdì 10:30-12:30 Orario: Me 17-19,
GEOMETRIA ANALITICA NELLO SPAZIO (3D Geometry)
 GEOMETRIA ANALITICA NELLO SPAZIO (3D Geometry) SISTEMA DI RIFERIMENTO NELLO SPAZIO La geometria analitica dello spazio è molto simile alla geometria analitica del piano. Per questo motivo le formule sono
GEOMETRIA ANALITICA NELLO SPAZIO (3D Geometry) SISTEMA DI RIFERIMENTO NELLO SPAZIO La geometria analitica dello spazio è molto simile alla geometria analitica del piano. Per questo motivo le formule sono
Lezione 6 Richiami di Geometria Analitica
 1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
Ricordiamo brevemente come possono essere rappresentate le rette nel piano: 1) mediante un'equazione cartesiana. = ( p 1
 Introduzione Nella computer grafica, gli oggetti geometrici sono definiti a partire da un certo numero di elementi di base chiamati primitive grafiche Possono essere punti, rette e segmenti, curve, superfici
Introduzione Nella computer grafica, gli oggetti geometrici sono definiti a partire da un certo numero di elementi di base chiamati primitive grafiche Possono essere punti, rette e segmenti, curve, superfici
I CRISTALLI DI PIRITE. Gilberto Bini Università degli Studi di Milano Trieste, 19 gennaio 2018
 I CRISTALLI DI PIRITE Gilberto Bini Università degli Studi di Milano Trieste, 19 gennaio 2018 L UNICA REALTÀ Non solo la matematica è reale, ma è l unica realtà. Beh, l universo è composto di materia ovviamente.
I CRISTALLI DI PIRITE Gilberto Bini Università degli Studi di Milano Trieste, 19 gennaio 2018 L UNICA REALTÀ Non solo la matematica è reale, ma è l unica realtà. Beh, l universo è composto di materia ovviamente.
(i) Determinare l equazione cartesiana dell unica circonferenza C passante per i tre punti dati.
 Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Edile/Architettura Esercizi per il corso di GEOMETRIA - a.a. 7/8 Docente: Prof. F. Flamini - Tutore: Dott. M. Paganin FOGLIO - Esercizi
Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Edile/Architettura Esercizi per il corso di GEOMETRIA - a.a. 7/8 Docente: Prof. F. Flamini - Tutore: Dott. M. Paganin FOGLIO - Esercizi
Corso di Matematica B - Ingegneria Informatica Testi di Esercizi. A1. Siano u, v, w vettori. Quali tra le seguenti operazioni hanno senso?
 A. Languasco - Esercizi Matematica B - 4. Geometria 1 A: Vettori geometrici Corso di Matematica B - Ingegneria Informatica Testi di Esercizi A1. Siano u, v, w vettori. Quali tra le seguenti operazioni
A. Languasco - Esercizi Matematica B - 4. Geometria 1 A: Vettori geometrici Corso di Matematica B - Ingegneria Informatica Testi di Esercizi A1. Siano u, v, w vettori. Quali tra le seguenti operazioni
Indici di Miller nei sistemi Trigonali ed Esagonali
 Indici di Miller nei sistemi Trigonali ed Esagonali -a 1 ( 100) (0 10) a 3 c (001) ( 100) -a 2 (0 10) c ( 110) a 2 -a 2 ( 110) -a 1 ( 110) (1 10) (100) (010) a 1 (100) (001) -c (010) -a 3 a 2 a 1 Una croce
Indici di Miller nei sistemi Trigonali ed Esagonali -a 1 ( 100) (0 10) a 3 c (001) ( 100) -a 2 (0 10) c ( 110) a 2 -a 2 ( 110) -a 1 ( 110) (1 10) (100) (010) a 1 (100) (001) -c (010) -a 3 a 2 a 1 Una croce
La matematica del CAD. Vettori e Matrici
 La matematica del CAD Vettori e Matrici IUAV Disegno Digitale Camillo Trevisan I programmi CAD riducono tutti i problemi geometrici in problemi analitici: la proiezione di un punto su un piano viene, ad
La matematica del CAD Vettori e Matrici IUAV Disegno Digitale Camillo Trevisan I programmi CAD riducono tutti i problemi geometrici in problemi analitici: la proiezione di un punto su un piano viene, ad
Corso di Mineralogia per Scienze Geologiche Laurea Triennale - Codice: 096SM CFU: 6+3 II Periodo Didattico - A.A. 2018/2019
 Corso di Mineralogia per Scienze Geologiche Laurea Triennale - Codice: 096SM 1-2 - CFU: 6+3 II Periodo Didattico - A.A. 2018/2019 Docente: prof. Francesco Princivalle (Ricevimento su appuntamento via mail
Corso di Mineralogia per Scienze Geologiche Laurea Triennale - Codice: 096SM 1-2 - CFU: 6+3 II Periodo Didattico - A.A. 2018/2019 Docente: prof. Francesco Princivalle (Ricevimento su appuntamento via mail
Geometria analitica del piano pag 32 Adolfo Scimone
 Geometria analitica del piano pag 32 Adolfo Scimone CAMBIAMENTI DI SISTEMA DI RIFERIMENTO Consideriamo il piano cartesiano R 2 con un sistema di riferimento (O,U). Se introduciamo in R 2 un secondo sistema
Geometria analitica del piano pag 32 Adolfo Scimone CAMBIAMENTI DI SISTEMA DI RIFERIMENTO Consideriamo il piano cartesiano R 2 con un sistema di riferimento (O,U). Se introduciamo in R 2 un secondo sistema
VETTORIALE E PRODOTTO MISTO. PIANI E RETTE DI
 Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA (Edile-Architettura e dell Edilizia) PRODOTTO VETTORIALE E PRODOTTO MISTO. PIANI E RETTE DI R 3. FASCI E STELLE. FORMULE
Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA (Edile-Architettura e dell Edilizia) PRODOTTO VETTORIALE E PRODOTTO MISTO. PIANI E RETTE DI R 3. FASCI E STELLE. FORMULE
Geometria BATR-BCVR Esercizi 9
 Geometria BATR-BCVR 2015-16 Esercizi 9 Esercizio 1. Per ognuna delle matrici A i si trovi una matrice ortogonale M i tale che Mi ta im sia diagonale. ( ) 1 1 2 3 2 A 1 = A 2 1 2 = 1 1 0 2 0 1 Esercizio
Geometria BATR-BCVR 2015-16 Esercizi 9 Esercizio 1. Per ognuna delle matrici A i si trovi una matrice ortogonale M i tale che Mi ta im sia diagonale. ( ) 1 1 2 3 2 A 1 = A 2 1 2 = 1 1 0 2 0 1 Esercizio
M to t d o i d d i d p ro r i o ezion o e n. c rr r i r spo p ndenza z b univo v ca ope p ra r zi z oni d i p r p o r iezi z one e s ezi z one
 Metodi di proiezione. I sistemi di rappresentazione geometrica consentono di rappresentare un oggetto tridimensionale su un piano bidimensionale, mediante un immagine che abbia con l oggetto originale
Metodi di proiezione. I sistemi di rappresentazione geometrica consentono di rappresentare un oggetto tridimensionale su un piano bidimensionale, mediante un immagine che abbia con l oggetto originale
Condizione di allineamento di tre punti
 LA RETTA L equazione lineare in x e y L equazione: 0 con,,, e non contemporaneamente nulli, si dice equazione lineare nelle due variabili e. Ogni coppia ; tale che: 0 si dice soluzione dell equazione.
LA RETTA L equazione lineare in x e y L equazione: 0 con,,, e non contemporaneamente nulli, si dice equazione lineare nelle due variabili e. Ogni coppia ; tale che: 0 si dice soluzione dell equazione.
La Funzione di Patterson A.A Marco Nardini Dipartimento di Scienze Biomolecolari e Biotecnologie Università di Milano
 A.A. 2009-2010 Marco Nardini Dipartimento di Scienze Biomolecolari e Biotecnologie Università di Milano La Funzione di Patterson Sviluppo in serie di Fourier svolto con i quadrati dei moduli dei fattori
A.A. 2009-2010 Marco Nardini Dipartimento di Scienze Biomolecolari e Biotecnologie Università di Milano La Funzione di Patterson Sviluppo in serie di Fourier svolto con i quadrati dei moduli dei fattori
Geometria analitica - Testo pagina 1 di 5 67
 Geometria analitica - Testo pagina di 5 67 5. GEOMETRI NLITI: Geometria lineare nel piano È fissato nel piano un sistema di coordinate cartesiane ortogonali monometriche Oxy. 50. 502. 503. 504. Scrivere
Geometria analitica - Testo pagina di 5 67 5. GEOMETRI NLITI: Geometria lineare nel piano È fissato nel piano un sistema di coordinate cartesiane ortogonali monometriche Oxy. 50. 502. 503. 504. Scrivere
Istituzioni di Matematica per Scienze Ambientali
 per Scienze Ambientali GEOMETRIA ANALITICA - Appunti 1 1 Dipartimento di Matematica Sapienza, Università di Roma Roma, 5 - Novembre 2012 Coordinate La corrispondenza tra numeri reali e punti di una retta
per Scienze Ambientali GEOMETRIA ANALITICA - Appunti 1 1 Dipartimento di Matematica Sapienza, Università di Roma Roma, 5 - Novembre 2012 Coordinate La corrispondenza tra numeri reali e punti di una retta
Elementi di matematica - dott. I. GRASSI
 Gli assi cartesiani e la retta. Il concetto di derivata. È ormai d uso comune nei libri, in televisione, nei quotidiani descrivere fenomeni di varia natura per mezzo di rappresentazioni grafiche. Tali
Gli assi cartesiani e la retta. Il concetto di derivata. È ormai d uso comune nei libri, in televisione, nei quotidiani descrivere fenomeni di varia natura per mezzo di rappresentazioni grafiche. Tali
Strutture solide di simmetria impossibile : I quasicristalli. Lezioni d'autore
 Strutture solide di simmetria impossibile : I quasicristalli Lezioni d'autore VIDEO Introduzione (I) La scoperta alla fine del 1984 di materiali formati dalla consolidazione di vari tipi di leghe metalliche
Strutture solide di simmetria impossibile : I quasicristalli Lezioni d'autore VIDEO Introduzione (I) La scoperta alla fine del 1984 di materiali formati dalla consolidazione di vari tipi di leghe metalliche
Le simmetrie dei poliedri regolari
 Le simmetrie dei poliedri regolari Le isometrie del piano e dello spazio sono state classificate da due illustri matematici. Per quanto riguarda il piano, il teorema di Chasles, del 8, afferma che nel
Le simmetrie dei poliedri regolari Le isometrie del piano e dello spazio sono state classificate da due illustri matematici. Per quanto riguarda il piano, il teorema di Chasles, del 8, afferma che nel
Formulario. Coordinate del punto medio M di un segmento di estremi A(x 1, y 1 ) e B(x 2, y 2 ): x1 + x y 2
 Formulario Componenti di un vettore di estremi A(x 1, y 1 e B(x 2, y 2 B A = AB = (x2 x 1 i + (y 2 y 1 j Distanza tra due punti A(x 1, y 1 e B(x 2, y 2 : AB = (x 2 x 1 2 + (y 2 y 1 2 Coordinate del punto
Formulario Componenti di un vettore di estremi A(x 1, y 1 e B(x 2, y 2 B A = AB = (x2 x 1 i + (y 2 y 1 j Distanza tra due punti A(x 1, y 1 e B(x 2, y 2 : AB = (x 2 x 1 2 + (y 2 y 1 2 Coordinate del punto
Prisma retto. Generatrice. Direttrice. Prisma obliquo. Nel caso le generatrici non siano parallele. Generatrice
 Oggetti (identificati) nello spazio Una porzione di piano delimitata da una linea spezzata chiusa si chiama poligono, un solido delimitato da un numero finito di facce piane si chiama poliedro. In un poliedro
Oggetti (identificati) nello spazio Una porzione di piano delimitata da una linea spezzata chiusa si chiama poligono, un solido delimitato da un numero finito di facce piane si chiama poliedro. In un poliedro
1 Congruenza diretta e inversa
 1 Congruenza diretta e inversa PROPRIETÀ. La congruenza tra due figure piane mantiene inalterata la lunghezza dei segmenti e l ampiezza degli angoli; ciò che cambia è la posizione delle figure nel piano.
1 Congruenza diretta e inversa PROPRIETÀ. La congruenza tra due figure piane mantiene inalterata la lunghezza dei segmenti e l ampiezza degli angoli; ciò che cambia è la posizione delle figure nel piano.
VETTORI E SCALARI DEFINIZIONI. Si definisce scalare una grandezza definita interamente da un solo numero, affiancato dalla sua unità di misura.
 VETTORI E SCALARI DEFINIZIONI Si definisce scalare una grandezza definita interamente da un solo numero, affiancato dalla sua unità di misura. Un vettore è invece una grandezza caratterizzata da 3 entità:
VETTORI E SCALARI DEFINIZIONI Si definisce scalare una grandezza definita interamente da un solo numero, affiancato dalla sua unità di misura. Un vettore è invece una grandezza caratterizzata da 3 entità:
VETTORI. OPERAZIONI CON I VETTORI. RAPPRESENTAZIONE CARTESIANA DEI VETTORI. APPLICAZIONI.
 VETTORI. OPERAZIONI CON I VETTORI. RAPPRESENTAZIONE CARTESIANA DEI VETTORI. APPLICAZIONI. Sia AB un segmento orientato. Ad esso è possibile associare: 1) la direzione, cioè la direzione della retta su
VETTORI. OPERAZIONI CON I VETTORI. RAPPRESENTAZIONE CARTESIANA DEI VETTORI. APPLICAZIONI. Sia AB un segmento orientato. Ad esso è possibile associare: 1) la direzione, cioè la direzione della retta su
Reticoli Cristallini. i tre vettori che individuano la cella elementare, ogni punto del reticolo è individuato da un vettore della forma :
 Reticoli Cristallini Cristallo E costruito affiancando tanti blocchetti identici, senza sovrapposizione e senza vuoti (interstizi). Noi, salvo esplicite affermazioni contrarie, considereremo cristalli
Reticoli Cristallini Cristallo E costruito affiancando tanti blocchetti identici, senza sovrapposizione e senza vuoti (interstizi). Noi, salvo esplicite affermazioni contrarie, considereremo cristalli
( ρ, θ + π ) sono le coordinate dello stesso punto. Pertanto un punto P può essere descritto come
 Coordinate polari Il sistema delle coordinate cartesiane è uno dei possibili sistemi per individuare la posizione di un punto del piano, relativamente ad un punto fisso O, mediante una coppia ordinata
Coordinate polari Il sistema delle coordinate cartesiane è uno dei possibili sistemi per individuare la posizione di un punto del piano, relativamente ad un punto fisso O, mediante una coppia ordinata
Capitolo 1 Vettori applicati e geometria dello spazio
 Capitolo 1 Vettori applicati e geometria dello spazio Marco Robutti Facoltà di ingegneria Università degli studi di Pavia Tutorato di geometria e algebra lineare Anno accademico 2014-2015 Definizione (Vettore
Capitolo 1 Vettori applicati e geometria dello spazio Marco Robutti Facoltà di ingegneria Università degli studi di Pavia Tutorato di geometria e algebra lineare Anno accademico 2014-2015 Definizione (Vettore
NOTE sulle ISOMETRIE a cura di Sara Bacci e Gabriele Cecchin III F 04/11/09
 NOTE sulle ISOMETRIE a cura di Sara Bacci e Gabriele Cecchin III F 04/11/09 Introduzione Prima di analizzare le isometrie è necessario fare una breve introduzione. Bisogna innanzitutto ricordare che due
NOTE sulle ISOMETRIE a cura di Sara Bacci e Gabriele Cecchin III F 04/11/09 Introduzione Prima di analizzare le isometrie è necessario fare una breve introduzione. Bisogna innanzitutto ricordare che due
Geometria BAER Canale I Esercizi 11
 Geometria BAER Canale I Esercizi Esercizio. Scrivere la matrice delle seguenti trasformazioni ortogonali del piano (a Proiezione ortogonale sulla retta x + y = 0 (b Rotazione di π/4 seguita da riflessione
Geometria BAER Canale I Esercizi Esercizio. Scrivere la matrice delle seguenti trasformazioni ortogonali del piano (a Proiezione ortogonale sulla retta x + y = 0 (b Rotazione di π/4 seguita da riflessione
I SOLIDI CRISTALLINI ED IL RETICOLO CRISTALLINO
 I SOLIDI CRISTALLINI ED IL RETICOLO CRISTALLINO A differenza dei solidi amorfi, caratterizzati da disordine spaziale delle particelle (atomi o molecole) e isotropia delle proprietà fisiche, il solido cristallino
I SOLIDI CRISTALLINI ED IL RETICOLO CRISTALLINO A differenza dei solidi amorfi, caratterizzati da disordine spaziale delle particelle (atomi o molecole) e isotropia delle proprietà fisiche, il solido cristallino
Gli esercizi assegnati all esame saranno varianti di alcuni degli esercizi seguenti
 Gli esercizi assegnati all esame saranno varianti di alcuni degli esercizi seguenti 1.1) Su un piano α (trasparente) sia tracciato un triangolo equilatero. Si consideri un piano β parallelo ad α e raggi
Gli esercizi assegnati all esame saranno varianti di alcuni degli esercizi seguenti 1.1) Su un piano α (trasparente) sia tracciato un triangolo equilatero. Si consideri un piano β parallelo ad α e raggi
Un approccio costruttivo alle trasformazioni geometriche del piano
 Un approccio costruttivo alle trasformazioni geometriche del piano Le cosiddette trasformazioni geometriche elementari del piano sono corrispondenze bigettive, del piano su se stesso, caratterizzate dalla
Un approccio costruttivo alle trasformazioni geometriche del piano Le cosiddette trasformazioni geometriche elementari del piano sono corrispondenze bigettive, del piano su se stesso, caratterizzate dalla
EQUAZIONE DELLA RETTA
 EQUAZIONE DELLA RETTA EQUAZIONE DEGLI ASSI L equazione dell asse x è 0. L equazione dell asse y è 0. EQUAZIONE DELLE RETTE PARALLELE AGLI ASSI L equazione di una retta r parallela all asse x è cioè è uguale
EQUAZIONE DELLA RETTA EQUAZIONE DEGLI ASSI L equazione dell asse x è 0. L equazione dell asse y è 0. EQUAZIONE DELLE RETTE PARALLELE AGLI ASSI L equazione di una retta r parallela all asse x è cioè è uguale
PROVA SCRITTA DI GEOMETRIA 2 MATEMATICA, 20/09/2011
 PROVA SCRITTA DI GEOMETRIA 2 MATEMATICA, 20/09/2011 In questo elenco, la presenza di esercizi relativi ai singoli argomenti non è correlata alla loro rilevanza, né alla ricorrenza nella prova scritta.
PROVA SCRITTA DI GEOMETRIA 2 MATEMATICA, 20/09/2011 In questo elenco, la presenza di esercizi relativi ai singoli argomenti non è correlata alla loro rilevanza, né alla ricorrenza nella prova scritta.
Commenti ad alcuni degli esercizi proposti 13. Uso del prodotto scalare: condizioni di perpendicolarità, angoli, distanze.
 Commenti ad alcuni degli esercizi proposti 13. Uso del prodotto scalare: condizioni di perpendicolarità, angoli, distanze. Risposte agli esercizi iniziali. Nello spazio vettoriale euclideo R 2 3, dotato
Commenti ad alcuni degli esercizi proposti 13. Uso del prodotto scalare: condizioni di perpendicolarità, angoli, distanze. Risposte agli esercizi iniziali. Nello spazio vettoriale euclideo R 2 3, dotato
ISTITUTO SAN GABRIELE CLASSI 4 S - 4 SA PROF. ANDREA PUGLIESE GEOMETRIA EUCLIDEA NELLO SPAZIO
 ISTITUTO SAN GABRIELE CLASSI 4 S - 4 SA PROF. ANDREA PUGLIESE GEOMETRIA EUCLIDEA NELLO SPAZIO GEOMETRIA NELLO SPAZIO Gli enti fondamentali sono punto, retta, piano, e spazio. Con le lettere maiuscole (A,B,C,...)
ISTITUTO SAN GABRIELE CLASSI 4 S - 4 SA PROF. ANDREA PUGLIESE GEOMETRIA EUCLIDEA NELLO SPAZIO GEOMETRIA NELLO SPAZIO Gli enti fondamentali sono punto, retta, piano, e spazio. Con le lettere maiuscole (A,B,C,...)
Caratteristiche dei solidi
 Corso di Studi di Fisica Corso di Chimica Luigi Cerruti www.minerva.unito.it Caratteristiche dei solidi Incompressibilità Proprietà comune con i liquidi (l altro stato condensato della materia) Rigidità
Corso di Studi di Fisica Corso di Chimica Luigi Cerruti www.minerva.unito.it Caratteristiche dei solidi Incompressibilità Proprietà comune con i liquidi (l altro stato condensato della materia) Rigidità
Geometria BAER Canale I Esercizi 12
 Geometria BAER Canale I Esercizi Esercizio. x = 0 x = Date le rette r : y = t e s : y = t, si verifichi che sono sghembe e si scrivano le equazioni z = t z = t parametriche di una retta r ortogonale ed
Geometria BAER Canale I Esercizi Esercizio. x = 0 x = Date le rette r : y = t e s : y = t, si verifichi che sono sghembe e si scrivano le equazioni z = t z = t parametriche di una retta r ortogonale ed
Capitolo 2. Cenni di geometria analitica nel piano
 Capitolo Cenni di geometria analitica nel piano 1 Il piano cartesiano Il piano cartesiano è una rappresentazione grafica del prodotto cartesiano R = R R La rappresentazione grafica è possibile se si crea
Capitolo Cenni di geometria analitica nel piano 1 Il piano cartesiano Il piano cartesiano è una rappresentazione grafica del prodotto cartesiano R = R R La rappresentazione grafica è possibile se si crea
Diffrazione di raggi X
 Diffrazione di raggi X Campione radiazione rivelatore tecnica monocromatica pellicole Oscillante Weissenberg Buerger Gandolfi Cristallo singolo Contatore (convenzionale, IP, CCD) Diffrattometro a 4-cerchi
Diffrazione di raggi X Campione radiazione rivelatore tecnica monocromatica pellicole Oscillante Weissenberg Buerger Gandolfi Cristallo singolo Contatore (convenzionale, IP, CCD) Diffrattometro a 4-cerchi
proprietà: comportamento del materiale in determinate condizioni, quindi possibilità di prevedere e progettare
 La struttura dei materiali definizioni e classificazioni Chi è lo scienziato dei materiali? un conoscitore della natura dei materiali e quindi di: struttura: concetto vago perché molte definizioni sono
La struttura dei materiali definizioni e classificazioni Chi è lo scienziato dei materiali? un conoscitore della natura dei materiali e quindi di: struttura: concetto vago perché molte definizioni sono
Corso di Idraulica ed Idrologia Forestale
 Corso di Idraulica ed Idrologia Forestale Docente: Prof. Santo Marcello Zimbone Collaboratori: Dott. Giuseppe Bombino - Ing. Demetrio Zema Lezione n. 1: Cenni al calcolo vettoriale Anno Accademico 2008-2009
Corso di Idraulica ed Idrologia Forestale Docente: Prof. Santo Marcello Zimbone Collaboratori: Dott. Giuseppe Bombino - Ing. Demetrio Zema Lezione n. 1: Cenni al calcolo vettoriale Anno Accademico 2008-2009
