AERODINAMICA SPERIMENTALE Energetica
|
|
|
- Gianmaria Alberti
- 9 anni fa
- Visualizzazioni
Transcript
1 AERODINAMICA SPERIMENTALE Energetica (G.P. Romano) Anno Accademico -
2 PROGRAMMA DEL CORSO Laboratorio di Aerodinamica Considerazioni generali sulla serimentazione Il roblema della similitudine ESERCITAZIONI DI LABORATORIO Imianti er studi serimentali di aero- e idrodinamica Bassa velocita' Alta Imianti velocita' seciali Sistemi di misura FORZA E PRESSIONE Bibliografia: B.R. Munson, D.F. Young, T.H.Okiishi, Fundamentals of Fluid Mechanics, Wiley, 995 E. Mattioli, Aerodinamica, Levrotto-Bella, 988 I.H. Abbott, A.E. Van Doenhoff, Theory of wing sections, Dover Publications, 959 W.H. Rae, A. Poe, Low Seed Wind Tunnel Testing, Wiley, 984 A. Poe, K. Goin, High Seed Wind Tunnel Testing, Kriegel, 978 R.J. Goldstein, Fluid Mechanics Measurements, Hemishere,983 W. Merzkirch, Flow Visualization, Academic Press, 987 AA.VV., Handbook of Exerimental Fluid Mechanics, Sringer-Verlag, 7 Manuali d uso degli aarati serimentali
3 Caitolo CONSIDERAZIONI GENERALI SULLA FLUIDODINAMICA SPERIMENTALE. GENERALITA' Ai fini della definizione di un rogetto (di un velivolo, di un veicolo o di un motore) o della comrensione dei fenomeni fisici coinvolti, lo studio di un articolare camo fluidodinamico, uò essere intrareso tramite una delle tre dimensioni della fluidodinamica: serimentale, teorica e numerica. Questi tre arocci, elencati nell'ordine nel quale storicamente si sono avvicendati, sono a tutt'oggi ugualmente imortanti e comlementari iuttosto che sostitutivi uno dell'altro e solo l'interazione tra i tre uò fornire conclusioni ienamente soddisfacenti. Ciò remesso, bisogna comunque mettere in evidenza i vantaggi e svantaggi reciroci al fine di oter valutare quali sono le limitazioni dell'aroccio utilizzato: Vantaggi Svantaggi Serimentale Teorico Numerico - flussi reali - soluzioni esatte - accuratezza- elevati - condizioni al numeri di Reynolds- contorno condizioni di turbolenza - errori serimentali - condizioni articolari - similitudine - equazioni - limitata variazione arametri semlificate - difficoltà in resenza di: - geometrie semlici iù secie chimiche, gradienti di temeratura - condizioni al contorno - temi di utilizzo e costi - variazioni arametri - condizioni al contorno - searazione fenomeni - temi e costi - errori numerici - bassi numeri di Reynolds - condizioni di turbolenza - modello matematico Tabella. Vantaggi e svantaggi di ciascuno dei tre arocci ossibili alla fluidodinamica. 3
4 Come la fluidodinamica numerica, che ha avuto un notevole sviluo negli ultimi venti anni grazie allo sviluo dei calcolatori, anche la fluidodinamica serimentale ha conosciuto ultimamente un notevole sviluo. Negli ultimi anni si sono sviluate tecniche serimentali che ermettono di acquisire una notevole mole di dati e di elaborarli in temi ragionevoli; simultaneamente gli imianti serimentali hanno conosciuto una riduzione in dimensioni e costi ed una maggiore secificità. Si e' quindi creata una situazione nella quale il roblema consiste nell'interretazione dei dati acquisiti, nell individuazione di metodi di analisi che mettano in luce asetti articolari e iù raticamente anche nell archiviazione dei dati er utilizzi futuri. Per fare un esemio: si e' assati da un numero di dati acquisiti di circa mille er ogni unto di misura (in numero comlessivo al massimo ari a qualche decina) a milioni di dati (anche sotto forma di immagini) su reticoli di misura sueriori a. Da questo unto di vista, risulta tuttora insufficiente la memoria dei calcolatori e sono necessari disositivi di archiviazione aggiuntivi (dischi dedicati, dischi magneto-ottici, CDRom etc...). In modo arallelo alla crescita del numero di dati e' cresciuta l'affidabilità statistica dei risultati ottenuti (anche se ciò non evita l'insorgere di interretazioni erronee dei dati). Bisogna anche considerare che l elevato numero di dati uò richiedere maggior temo di acquisizione e utilizzo dell'imianto (e quindi aumento dei costi).. ERRORI NELLA FLUIDODINAMICA SPERIMENTALE Nella fluidodinamica serimentale, come in qualsiasi altra misurazione, sono resenti una serie di errori (ε) (o, meglio, incertezze) in ciascuna delle oerazioni che vengono effettuate er indagare il comortamento di un fluido e/o simularlo tramite un modello in scala. Si definisce accuratezza di una misura il comlemento a (% di accuratezza) della differenza relativa (in valore assoluto) tra il valore misurato (M G ) e il valore vero della grandezza in esame (V G ) (di solito i valori relativi sono costruiti come ercentuale del valore di fondo scala del sistema di misura). Essendo quest ultimo in generale incognito, er valutare l accuratezza di un certo sistema di misura e necessaria una rocedura reliminare di calibrazione, cioè una rocedura di misura della grandezza quando il suo valore sia già noto. Inoltre, oiché il valore misurato e dato dalla differenza tra il valore vero e l errore comlessivo della misura, M G V G ± ε (.) 4
5 si uò anche affermare che l accuratezza sia data dal comlemento a della somma degli errori relativi (ercentuali) commessi nella valutazione della grandezza misurata Accuratezza ( M G -V G /V Gmax ) ( ε /V Gmax ) - ε r. Gli errori sono sostanzialmente di due tii: errori sistematici ed errori casuali. I rimi sono dovuti a deviazioni sistematiche del valore misurato da quello vero, determinate semre dalla stessa causa (e di non facile identificazione a causa della loro sistematicità). Gli errori casuali, invece, si manifestano come deviazioni casuali dei valori misurati dovute a fluttuazioni imrevedibili nella catena di misura. Con il termine recisione si intende l accuratezza dovuta ai soli errori casuali (quindi un sistema di misura reciso fornirà iù o meno semre la stessa misura). L accuratezza sarà data dalla recisione meno il contributo relativo degli errori sistematici e sarà quindi semre inferiore (o al iù uguale) alla recisione. Nella figura sono mostrati tre esemi di risultati di una misurazione (il centro raresenta la misura vera e i cerchi concentrici l allontanamento ercentuale da questa): nel rimo caso abbiamo a che fare con misure recise ma non ugualmente accurate a causa della resenza di un errore sistematico e di iccoli errori casuali (a), nel secondo le misure sono meno recise che in recedenza, ur avendo uguale accuratezza, a causa di iù elevati errori casuali (in assenza di errore sistematico) (b) e nel terzo caso sono recise ed accurate essendo in resenza di soli iccoli errori casuali (c). Valori degli errori commessi tramite alcune tecniche di misura utilizzate in fluidodinamica serimentale verranno forniti nel seguito; e' comunque difficile che si ottengano misure con errori inferiori all % (accuratezza e recisione dell ordine del 99%). Possiamo quindi riassumere il risultato di una misura nei termini della relazione (.) dove in ε sono contenuti sia gli errori sistematici che casuali. Questi ultimi, in realtà, devono essere considerati sotto due asetti differenti. Infatti, vi e un errore casuale dovuto al fatto che, ur in resenza di variazioni della grandezza da misurare, il sistema di misura fornisce semre la stessa risosta e viene quindi commesso un certo errore detto errore massimo. Ma vi e anche una variabilità intrinseca della stessa grandezza (causata da fluttuazioni intrinseche della grandezza e da un non erfetto controllo di tutte le condizioni al contorno) e una non riroducibilità di funzionamento dello strumento di misura. Questa variabilità da origine ad un insieme di valori misurati della grandezza in esame (M ig ) che sarà caratterizzato da valori statistici quali la media M ) e la deviazione standard (σ G ): la deviazione standard raresenta l errore statistico della ( G misura (si consideri che er una distribuzione gaussiana, quale quelle normalmente incontrate nelle misure, il 99.7% dei dati sono comresi in un intervallo ari a ± 3σ G ). 5
6 a. %.5 %. %.5 % b. %.5 %. %.5 % c. %.5 %. %.5 % Precisione 99 % Accuratezza 98 % Precisione 98 % Accuratezza 98 % Precisione 99 % Accuratezza 99 % Figura. Esemio di resenza di errori sistematici e casuali e valori della recisione e dell accuratezza della misura. Possono resentarsi le seguenti situazioni (in assenza di errori sistematici): - la misura fornisce semre lo stesso risultato; in questo caso l errore massimo e molto maggiore di quello statistico e il risultato della misura e esresso tramite la (.) dove ε raresenta rorio tale errore massimo; - la misura fornisce risultati differenti; in questo caso l errore statistico e molto maggiore di quello massimo e il risultato della misura sarà esresso dalla relazione (in maniera tanto iù accurata quanto maggiore e il numero di valori dell insieme, N): M G V G ± σ G / N (.) - la misura fornisce ochi risultati differenti; in questo caso l errore massimo e rossimo a quello statistico e il risultato della misura e esresso da un istogramma su ochi valori; il valor medio e la varianza saranno errati e si uò esrimere il risultato della misura tramite la (.) con l errore massimo dato da 3σ G. Il discorso recedente vale qualora il risultato della misura fornisca direttamente la grandezza voluta (grandezza fondamentale). Se, invece che di una grandezza fondamentale, vogliamo ottenere il valore di una grandezza derivata (cioè se la misura non fornisce in uscita la grandezza voluta, ma un altra che va convertita in quest ultima tramite altre grandezze 6
7 fondamentali (misurate e non)), avremo la cosìdetta roagazione degli errori. Per ottenere un esressione dell errore sulla grandezza derivata, a artire da quelli sulle grandezze fondamentali, in queste condizioni, si assuma una generica relazione funzionale tra le grandezze fondamentali (M Gi ) e quella derivata (M Z ) del tio M Z f (M Gi ). Trattando di errori massimi, avremo il seguente valore er l errore: ε Z f ε i M M Gi (.3) Gi e, nel caso di errore relativo (indicato con ε r ), divideremo questo risultato er il valore M G. Invece, er gli errori statistici, avremo (iotizzando indiendenza statistica tra le grandezze M Gi ): f σ Z i σ M M Gi (.4) Gi e, nel caso di errore relativo, divideremo questo risultato er il valore M G. Le esressioni (.3) e (.4) diventano articolarmente semlici nel caso in cui si considera l errore relativo er una grandezza derivata esrimibile come monomio di quelle fondamentali (M Z Π i (M Gi ) i ): ε ε ε er gli errori massimi (.5) r Z r Z i i M M G Gi r σ Z r ε Z i ( ε M ) i Gi er gli errori statistici (.6) M G In resenza di iù sorgenti di errori casuali, l errore massimo e l errore statistico comlessivo di una grandezza fondamentale saranno dati da: tot i i ε ε er gli errori massimi (.7) σ σ er gli errori statistici (.8) tot i i 7
8 e, er una grandezza derivata, valgono le relazioni (.3)-(.6) nelle quali ciascun errore deve essere esresso comlessivamente tramite le (.7) e (.8). Verranno ora esaminati brevemente alcuni tiici errori (sistematici e casuali) commessi nella fluidodinamica serimentale. Errori causati dall'imianto utilizzato: aartengono a questa categoria tutti gli errori che si commettono lavorando in un ambiente limitato come una galleria del vento (o qualunque altro imianto serimentale), come er esemio gli errori dovuti alla resenza di suorti, alla variazione indesiderata delle grandezze fluidodinamiche dell'aarato (ressione, temeratura, velocità), alla resenza delle areti dell'imianto (crescita dello strato limite) e all'interferenza di queste con il modello (roblemi di bloccaggio). Questi errori sono di solito sistematici (ma er esemio la resenza di un suorto uò anche dare fluttuazioni che si trasformano in deviazioni casuali) e vanno valutati (e ossibilmente corretti) rima di effettuare le misure e verranno arofonditi nella arte relativa agli imianti. Errori causati dalla strumentazione utilizzata: ogni strumento di misura ha una sua recisione che diende dal rinciio fisico su cui e' basata la misura stessa, dal modo in cui tale rinciio viene alicato raticamente e dall effetto sulla misura delle variazioni di condizioni ambientali. Anche in questo caso, rima di effettuare una misura, bisogna valutare la recisione della strumentazione utilizzata. Come esemio ossono essere considerati gli errori di calibrazione (cioè gli errori sulle grandezze geometriche, elettriche e ottiche che influenzano la determinazione delle curve o dei arametri di calibrazione della strumentazione), gli errori introdotti dai convertitori e dai filtri del segnale, gli errori rodotti dalle schede di acquisizione e in generale gli errori dovuti alla resenza del rumore in ciascun asso del rocesso di misura. A questa categoria aartengono anche gli errori che si commettono con l'uso di traccianti da inserire nel flusso er misurarne alcune rorietà: la scelta di tali traccianti dovrà essere tale da minimizzare gli effetti sul camo fluidodinamico e ciò si traduce nell'imiego di sostanze non reagenti, di densità rossima a quella del fluido in esame e in quantità quanto iù basse ossibile (e comunque non tossiche!!). Si tratta di solito di errori casuali massimi e statistici che verranno arofonditi nella arte relativa alle tecniche di misura. Fluttuazioni dovute alla turbolenza ed errori statistici: anche nella iotesi teorica di assenza degli errori sistematici e casuali di cui in recedenza, si osserverebbero delle fluttuazioni delle grandezze 8
9 misurate nella fluidodinamica serimentale causate dalla turbolenza del flusso. Queste fluttuazioni sono realmente resenti nel fluido e la loro caratterizzazione costituisce uno dei risultati che si vogliono ottenere da una camagna di misure. La teoria dell'analisi dei segnali aiuta a valutare quali errori si commettono nella trattazione di insiemi di dati (l errore e funzione del numero di dati acquisiti come nella (.)). Esemi di tali errori sono quelli associati alla valutazione dei momenti statistici, delle scale caratteristiche del flusso, delle funzioni di correlazione e degli settri. Questi errori sono trattati come errori casuali statistici e vengono trattati nella teoria dell analisi dei segnali..3 RISOLUZIONE SPAZIALE E TEMPORALE DI UNA MISURA Quando effettuiamo una misura di una grandezza fisica, utilizziamo della strumentazione la cui arte sensibile costituisce l'elemento che interagisce con la grandezza fisica da misurare e che genera o raresenta essa stessa il cosiddetto volume di misura cioè la regione di sazio nella quale viene effettuata la misura. La misurazione stessa e effettuata valutando la risosta della strumentazione, nel suo comlesso, doo un certo intervallo di temo detto intervallo di misura. Queste due quantità sono caratteristiche di ogni sistema di misura e verranno considerate in maniera secifica nella arte relativa alla descrizione dei sistemi di misura. Tuttavia, e' imortante tenere resente che queste due quantità limitano la recisione della misura dal unto di vista saziale e temorale. Il volume di misura definisce raticamente la regione minima al di sotto della quale non e' ossibile determinare le fluttuazioni nello sazio della grandezza in esame. Si definisce risoluzione saziale l'inverso della dimensione minima che uò essere misurata con la strumentazione utilizzata, e quindi l'inverso della dimensione minore del volume di misura: un elevata risoluzione saziale corrisonderà ad un volume di misura iccolo e viceversa. La risoluzione saziale ha le dimensioni di un numero d'onda (o frequenza saziale) e uò anche essere considerata come il numero d'onda massimo ottenibile con la strumentazione utilizzata (figura ). Allo stesso modo, l'intervallo di misura definisce l'intervallo temorale minimo al di sotto del quale non e' ossibile determinare le fluttuazioni nel temo della grandezza in esame. Si definisce risoluzione temorale l'inverso dell'intervallo di temo minimo misurabile e quindi l'inverso dell'intervallo di misura. La risoluzione temorale ha dimensioni di una frequenza e uò considerarsi come la massima frequenza ottenibile dal sistema di misura. 9
10 Bisogna considerare ero' che all'interno di un flusso turbolento sarà resente un insieme continuo di vortici aventi dimensioni saziali decrescenti da quelli iù grandi (individuati dalla cosiddetta scala integrale) a quelli iù iccoli (individuati dalla scala di Kolmogorov) cui sono associate velocità, temeratura, densità e ressione caratteristici. La risoluzione saziale fisserà un limite minimo alle scale saziali che ossono essere misurate (limite massimo alle frequenze saziali come raresentato in figura ). La risoluzione temorale dell'aarato di misura fisserà un limite minimo alle scale temorali che ossono essere misurate (limite massimo alle frequenze). Per i sistemi di misura comunemente utilizzati nella fluidodinamica serimentale e' molto difficile che si riescano ad ottenere risoluzioni saziali e temorali in grado di descrivere il comortamento del flusso fino alle scale di Kolmogorov sia nello sazio che nel temo. Di conseguenza, bisognerà accettare un comromesso o utilizzare strumentazione differente er le indagini nel dominio saziale e in quello temorale. dimensione del volume di misura η L L dim ensione saziale energia risoluzione saziale /L /L / η frequenza saziale Figura. Effetto della risoluzione saziale finita sulla descrizione di un insieme di strutture vorticose di dimensione crescente (figura sueriore) e corrisondente andamento nel dominio dei numeri d onda (figura inferiore).
11 Bisogna anche considerare che, er quanto riguarda grandezze differenti dalla velocità, e' ossibile che le scale di interesse siano ben al di sotto della scala di Kolmogorov e raticamente irraggiungibili: un esemio e' dato dalle scale tiiche della diffusione molecolare nel mescolamento di uno scalare in un fluido che sono anche volte iù iccole della scala di Kolmogorov..4 SISTEMI DI UNITA' DI MISURA Accenniamo brevemente al roblema delle unita' di misura di una grandezza fisica. Un sistema di misura e' un insieme di unita' di misura basato su grandezze fondamentali. Tale sistema deve essere indiendente dal luogo in cui si effettua la misura (sistema di misura assoluto): er esemio un sistema di misura contenente il eso del camione di riferimento sarebbe diendente dalla quota sul livello del mare e dalla latitudine del luogo nel quale si effettua la misura; è quindi referibile utilizzare la massa in luogo del eso del camione di riferimento. Nonostante questo, er ragioni di comodità, si usano comunque sistemi non assoluti (sistemi tecnici). Il Sistema Internazionale (SI) ha come unita' di misura fondamentali quelle di lunghezza (metro, m), di massa (chilogrammo, Kg), di temo (secondo, s), di temeratura (grado Kelvin, K), di corrente elettrica (amere, A), di intensità luminosa (candela, cd) e di quantità di materia (mole, mol). Ciascuna di queste unita' di misura fondamentali raresenta una ben recisa quantità fisica che uò essere misurata in qualsiasi unto della Terra. Da queste unita' fondamentali ossono essere ottenute le unita' di misura derivate (o comoste): er esemio la velocità di un oggetto è misurata in m s -. Alcune unita' derivate hanno nomi rori (newton, joule, watt. hertz etc.). Per convertire le unita' di misura da un sistema di misura ad un altro, e' necessario utilizzare alcuni fattori di conversione dalle unita' fondamentali di un sistema a quelle di un altro. Per esemio, er quello che riguarda la ressione, valgono i seguenti fattori di conversione: atmosfera atm 35 ascal (Pa) 35 N/m.35 bar SI torr 3.59 mm H O 33. Pa Unita' tecniche millibar 3 dina/cm Pa CGS Senza entrare ulteriormente nel dettaglio dei differenti sistemi di unita di misura, si tenga resente che il risultato numerico di una misura deve essere affiancato dall indicazione dell unita di misura usata e dell errore commesso.
12 Caitolo IL PROBLEMA DELLA SIMILITUDINE. GENERALITA' Le equazioni della fluidodinamica sono equazioni dimensionali, nel senso che ogni termine ossiede dimensioni fisiche uguali a quelle della grandezza considerata nell'equazione (massa, quantità di moto ed energia) er unita di volume diviso er un temo. Di conseguenza, volendo confrontare tra loro i differenti termini er stabilire quali sono reonderanti nelle diverse condizioni di moto, bisognerebbe considerare il valore di ciascuna grandezza nelle equazioni (lunghezze, temi, velocità, temerature, ressioni, densità...) e calcolare il valore di ogni termine. Un metodo iù ratico e iù utile e' quello di adimensionalizzare le equazioni e formare grui di variabili adimensionali che ossano essere confrontati tra loro. A questo roosito si utilizzano le grandezze di misura fondamentali (massa. lunghezza, temo e temeratura) e le loro unita' di misura. La forma adimensionale delle equazioni consente anche di individuare in modo univoco quante e quali sono le grandezze fondamentali necessarie a descrivere comletamente un dato roblema fluidodinamico senza dover ricorrere alla ricerca di esse tramite il teorema di Buckingham. I risultati ottenuti con simulazioni numeriche e/o eserimenti er dati valori delle variabili ossono essere estesi alla classe iù amia di valori che mantengono invariato il gruo adimensionale caratteristico del roblema in esame.. FORMA ADIMENSIONALE DELLE EQUAZIONI E GRUPPI ADIMENSIONALI Per rendere adimensionali le equazioni, si renderanno delle grandezze caratteristiche er le variabili fluidodinamiche e termodinamiche (u i,,, c e T) e er le variabili osizione (x i ) e temo (t) (queste grandezze saranno derivate dalle condizioni al contorno e iniziali del roblema e saranno indicate con il edice o): u u U t t t x x L T T T (3.) o i i o o o i i o o
13 dove si sono assunte ari a zero la ressione e la temeratura di riferimento, e T (altrimenti al osto di / e T T/T si scriverà ( ) / e T (T T ) / T. Dall'equazione di stato, onendo (T, ), ossiamo ottenere: D DT D β A (.) Dt Dt Dt con β coefficiente di esansione termica (con dimensioni dell inverso di una T temeratura) e A coefficiente di comressibilità (/AK e' il modulo di elasticità a con la stessa dimensione della ressione). Nella relazione recedente si e' introdotta la velocità del suono nel mezzo, a /, che er una trasformazione isentroica ( k, dove c /c v raresenta il raorto tra i calori secifici a ressione e volume costante) e ari a (RT) /. Per un gas erfetto isentroico β/t e A/. Adimensionalizzando β e A otteniamo Gu β β T o (numero di Guy Lussac) A A o (esrimibile tramite il numero di Mach (cfr. doo)) e l'equazione (3.) (assumendo che il temo scali come L o /U o ) diventa: D DT D Gu A (.3) Dt Dt Dt Possiamo a questo unto adimensionalizzare l'equazione di conservazione della massa: D u ( u ) u Dt t usando la adimensionalizzazione (3.) e dividendo tutto er o U o /L o : St ( u ) u (.4) t che e' la forma adimensionale dell'equazione di conservazione della massa. Si e' introdotto il gruo adimensionale St L o /U o t o (numero di Strouhal) 3
14 (se il temo caratteristico e' sostituito da una frequenza caratteristica f o, allora il numero di Strouhal sarà definito tramite f o ). Notiamo che se t o L o /U o, allora il numero di Strouhal e' circa unitario. L'adimensionalizzazione delle equazioni di bilancio della quantità di moto (equazioni di Navier-Stokes) segue la strada ercorsa in recedenza er ottenere (assumendo il coefficiente di viscosità dinamica µ costante): u St ( u ) u k u ( u ) (.5) t Ru Fr Re 3Re dove k g g e' il versore nella direzione della forza di gravita' (con verso oosto a quello della gravita'). Nell'equazione recedente si sono introdotti i grui adimensionali: Re U o L o /ν Fr U o /(gl o ) / Ru o U o / o (numero di Reynolds) (numero di Froude) (numero di Rouark) Nei grui adimensionali recedenti, qualora µ non sia costante, sarà contenuto il valore µ o relativo allo stato di riferimento e resterà un termine µ all'interno dell'equazione (lo stesso discorso e' valido er β e A già definiti e er le quantità K e D all'interno dei grui adimensionali che comaiono dall equazione dell energia e di conservazione di uno scalare). Notiamo che, er un gas erfetto isentroico, si uò scrivere: dove Ru o U o / o U o / a Ma Ma U o /a (numero di Mach). Utilizzando la definizione del numero di Mach e di Rouark, le equazioni (.3) e (.4) diventano: D DT Ma D Gu Dt Dt Ru Dt (.6) DT Ma D Gu u Dt Ru Dt (.7) 4
15 che rende eslicita la diendenza dal numero di Mach nelle equazioni di stato e di continuità essendo AA o Ma /(Ru) (nella (.7) comarirà anche il numero di Strouhal una volta sviluate le derivate sostanziali). Nel caso di condizioni di moto turbolento, i termini aggiuntivi dovuti alla turbolenza derivano dai termini di trasorto o inerziali utilizzando la decomosizione di Reynolds. Dal unto di vista dell'analisi dimensionale e dell'imortanza relativa di questi termini, bisognerà allora considerare che i termini inerziali raresentano i termini di riferimento risetto ai quali vengono adimensionalizzati tutti gli altri. Di conseguenza, assumendo che le fluttuazioni delle grandezze fluttuanti abbiano lo stesso ordine di grandezza delle grandezze medie (cosa che andrà altrimenti valutata er ogni situazione), i termini dovuti alla turbolenza saranno moltilicati er un gruo adimensionale unitario e come tali andranno confrontati con gli altri termini..3 SIGNIFICATO DEI GRUPPI ADIMENSIONALI Ciascuno dei grui adimensionali definiti in recedenza e' stato ricavato come raorto (o arte del raorto) tra un termine dell'equazione considerata e il corrisondente termine inerziale (che in tutte le equazioni in forma adimensionale viene ad essere moltilicato er l'unità). Di conseguenza, ciascun gruo adimensionale uò essere ensato come indicativo del raorto tra le forze, i temi, le velocità e le energie (o il calore) relativi a ciascun termine risetto a quelle di inerzia: St temo (forza) convettivo (L o /U o ) / temo (forza) locale caratteristico del fenomeno Re forze di inerzia / forze viscose Fr forze di inerzia / forze gravitazionali Ru ressione dinamica / ressione statica forze di inerzia / forze di ressione Ma (velocità del fluido) /(velocità del suono) forze di inerzia / forze elastiche Notiamo che ciascun numero uò anche essere ottenuto direttamente da considerazioni dimensionali ( er esemio, considerando la forza di inerzia roorzionale a ma o L o U o e le forze viscose dell'ordine di µu o L o, si ottiene rorio l'esressione del numero di Reynolds Re U L / µ). L'aver scritto le equazioni in forma adimensionale ermette di ottenere tre risultati: 5
16 ) determinazione di soluzioni delle equazioni in forma iù generale e confronto con soluzioni numeriche iù semlici (a arità di grui adimensionali); ) individuazione delle forme asintotiche e semlificazione delle equazioni; 3) similitudini e analogie tra cami di moto. Il rimo unto significa che ossiamo mettere a unto dei rogrammi di calcolo numerico er risolvere le equazioni che hanno soluzioni generali e non diendenti dalla scelta articolare di temi, lunghezze, velocità, temeratura, ressione e densità ma solo dalle loro combinazioni nei grui adimensionali. Per il secondo unto, ossiamo ottenere delle equazioni semlificate che conducono a soluzioni valide solo in alcuni regimi di moto (soluzioni asintotiche). Per il terzo unto si rimanda al aragrafo seguente..4 SIMILITUDINE Due cami fluidodinamici si dicono simili quando è verificata l'uguaglianza tra i grui adimensionali necessari (e sufficienti) alla descrizione comleta del fenomeno in esame. L'alicazione della similitudine ermette di studiare, numericamente o serimentalmente, un fenomeno fluidodinamico a scala diversa da quella di artenza: nel rimo caso si ottengono soluzioni numeriche di validità generale, mentre nel secondo si ossono effettuare rove su modelli in scala ridotta. Tuttavia, non e' ossibile verificare l'uguaglianza tra tutti i grui adimensionali (e sesso anche tra solo alcuni) e bisognerà oerare una scelta di quello effettivamente fondamentale er lo studio in oggetto. Per esemio, se abbiamo un camo fluidodinamico con una corrente in resenza di suerficie libera, e richiediamo la similitudine contemoranea tra il numero di Reynolds e di Froude, otteniamo le due relazioni: UL ν U L ν U ( gl ) / ( gl ) / U dove con i edici e sono indicati il rimo e secondo camo fluidodinamico. Per il raorto tra le lunghezze otteniamo: (.8) L L U ν U ν L L U U 6
17 U U L L Figura 3. Similitudine geometrica, cinematica e dinamica tra cami di moto. cioè se ν ν (viscosità cinematiche dei due fluidi uguali), la rima ci dice che se U <U allora L <L, mentre la seconda ci dice che L >>L. Allora, se siamo interessati iù al camo di moto lontano dalla suerficie libera, useremo la similitudine di Reynolds, se invece a quello in rossimità della suerficie libera useremo la similitudine di Froude. L alternativa e rimuovere la condizione di uguaglianza tra le viscosità cinematiche dei fluidi e. Con riferimento alla figura 3, si ossono distinguere tre tii di similitudine: ) similitudine geometrica (riguarda le lunghezze); ) similitudine cinematica (riguarda le lunghezze e i temi, e quindi le velocità, e imlica la )); 3) similitudine dinamica (riguarda le lunghezze, i temi e le masse, e quindi le densità e le forze, e imlica la ) e la )). Come detto, l'analisi dimensionale alla Buckingham ermette di individuare i grui adimensionali che verificano le tre similitudini, ero' dalle equazioni adimensionalizzate abbiamo già individuato i grui fondamentali che contengono le variabili geometriche, cinematiche e dinamiche e che quindi assicurano la verifica della similitudine nella sua forma iù generale (cioè quella dinamica). Anche le condizioni al contorno e iniziali otranno essere considerate come condizioni di similitudine geometrica, cinematica e dinamica. La similitudine comleta ermette di generalizzare i risultati ottenuti su un camo di moto ad un altro avente valori di lunghezza, temi (o velocità) e massa (o densità o forze) differenti, ma tali da dare gli stessi grui adimensionali. Per quanto riguarda l'aerodinamica Serimentale, le similitudini iù imortanti er lo studio di modelli in scala sono quelle di Reynolds e Mach. La rima richiede imianti di dimensioni notevoli e/o alte velocità. Bisogna in articolare fare molta attenzione alla transizione da moto 7
18 laminare a moto turbolento: un eserimento non uò essere effettuato in condizioni laminari se in realtà avviene in condizioni turbolente erché le equazioni e la fisica del roblema sono differenti. Tuttavia, mentre er Re < 5 la similitudine deve essere verificata esattamente, er Re > 4 ossono esserci anche differenze nel numero di Reynolds in quanto i fenomeni di tio turbolento tendono ad avere un comortamento asintotico al crescere di Reynolds. I requisiti er il numero di Reynolds ossono contrastare con la similitudine di Mach che riguarda gli effetti di comressibilità del fluido (cfr. equazione di conservazione dell'energia e i grui adimensionali ivi resenti). Si distinguono le seguenti condizioni: Ma <.3 flusso incomressibile (gallerie aerodinamiche a bassa velocità, tunnel idrodinamici);.3 < Ma <.7 flusso con diendenza non trascurabile dagli effetti di comressibilità, ma in condizioni subsoniche senza onde d'urto (gallerie aerodinamiche subsoniche (ma anche gallerie a bassa velocità se si considera l'equazione linearizzata del otenziale e si scalano oortunamente le variabili geometriche));.7 < Ma <.3 flusso in regime transonico con diendenza imortante dagli effetti di comressibilità (gallerie aerodinamiche transoniche); Ma >.3 flusso in regime suersonico con diendenza fondamentale dagli effetti della comressibilità e con onde d'urto (gallerie aerodinamiche suersoniche o iersoniche). Per quanto riguarda le non stazionarietà, cioè il numero di Strouhal, bisognerà distinguere se queste sono imoste dalla condizioni al contorno e iniziali (e allora la similitudine deve essere comleta) o dalla resenza di instabilità locali del flusso (dove otrà essere anche arziale). Il rimo caso corrisonde a forzanti esterne (eliche, elicotteri) e il secondo a scie a valle di cori o a strati di mescolamento. 8
19 .5 ANALOGIE Lo scoo delle analogie e' quello di studiare un fenomeno fluidodinamico mediante analisi teoriche, numeriche o serimentali su un flusso con caratteristiche del tutto diverse ma governato in definitiva da equazioni simili. Nel seguito verranno trattate due analogie fluidodinamiche: quella tra un flusso viscoso e non (analogia di Hele-Shaw) e tra un flusso comressibile e uno con suerficie libera (analogia di Mach-Froude)..5. Analogia di Hele-Shaw Si vuole studiare un flusso non viscoso, otenziale, bidimensionale mediante il camo di moto tridimensionale che si genera tra due iatti aralleli ravvicinati che risulta quindi essere fortemente viscoso!! In articolare verranno considerate le linee di corrente in resenza di cori di varia forma, osizionati tra i due iatti aralleli, nell'iotesi h << L (essendo h la distanza tra i iatti aralleli ed L la dimensione longitudinale della zona indagata). I arametri fondamentali del camo di moto in esame e il sistema di riferimento utilizzato sono indicati nella figura 4. Il fenomeno è governato dall'equazione di conservazione della massa er flussi incomressibili e dalle equazioni di Navier Stokes. Nel nostro caso assumeremo condizioni di stazionarietà (St << ), assenza di forze di massa (Fr >> ) e velocità verticale nulla (w ) er ottenere: u, ( u ) u u Ru Re (.9) sul iano (x,y), essendo u(u,v) e avendo diviso er. Questo e' un sistema di tre equazioni nelle incognite uu(x,y,z), vv(x,y,z) e (x,y) (la terza equazione di Navier-Stokes fornisce /z cioe' (x, y)). Si sono usate la velocità indisturbata (U ) e l'altezza tra i iatti (h) come grandezze caratteristiche er adimensionalizzare le velocità e le lunghezze (notiamo anche che, essendo la densità costante, ). 9
20 L z U o y x h Figura 4. Parametri fondamentali e sistema di riferimento er l analogia di Hele-Shaw. Il sistema di equazioni recedenti è lo stesso che deve essere utilizzato er descrivere il moto incomressibile, stazionario, viscoso, bidimensionale tra due areti (moto alla Couette): in quest'ultimo caso la comonente v è identicamente nulla e le equazioni sono scritte er le comonenti u e w (che dienderanno solo da x e z). Iotizzando il moto comletamente sviluato (/x, cioè diendenza della velocità solo dalla coordinata z), dalla equazione di conservazione della massa (scritta in x e z), si ricava che wcost. (essendo w alla arete) e che uu(z). Dalla seconda equazione di Navier-Stokes si ottiene /z, cioè la ressione e' solo funzione della x. Dalla rima equazione di Navier-Stokes si ottiene allora (essendo nulli i termini inerziali): d Ru dx Re d u dz che a sinistra dell'uguaglianza è solo funzione di x e a destra solo di z. La soluzione è: Re d z u ( z) C z C Ru dx Imonendo che u(±) (cioè velocità nulla sulle areti), si ottiene C e C - (Re/Ru)(d/dx). Inoltre, imonendo che al centro del condotto (z) sia u() si ottiene: ( z ) f ( z) u ( z) d Ru dx Re
21 Questa è la soluzione classica del moto alla Couette (sostituendo le grandezze dimensionali si ottengono gli andamenti usuali). Cerchiamo ora una soluzione del roblema iniziale a artire da questa. In effetti, nel roblema di Hele-Shaw vi sono due dimensioni caratteristiche (h e L) e la corretta adimensionalizzazione sarà quella con h lungo z e con L lungo x e y. Le tre equazioni andranno riscritte come: u, h h h ( u ) u L L Ru Re L u u z x, y (.) (notiamo subito che il rimo termine tra arentesi sembra essere molto iù iccolo del secondo, anche se bisogna rima avere un'idea dell ordine di grandezza della derivata seconda di u lungo z). Scriviamo la velocità come il rodotto di una arte diendente da x e y (u o ) e una arte diendente da z esressa dalla forma recedentemente trovata f (z) u(x,y,z) u o (x,y) f (z), e verifichiamo se è ossibile ottenere una soluzione di questo tio. L'equazione di continuità diventa: ( f ) f u u, u e le due equazioni di Navier-Stokes: h ( u L f h h f ) ( u f ) f x, y u u L Ru Re L z Essendo f/z -, effettivamente il secondo termine tra arentesi è molto iù grande del rimo. Moltilicando il tutto er (L/h) otteniamo: L ( u f ) u Ru h Re ( u f )
22 Se cerchiamo gli ordini di grandezza di questi termini abbiamo: () (/Ru) (L/h /Re) Affinché ossano essere trascurati i termini inerziali, ma non quelli viscosi (altrimenti la soluzione sarebbe banalmente quella nulla), dovrà essere: h L Re <<, Ru h L Re (.) cioè la condizione di Hele-Shaw, che diventa tanto iù difficile da verificare quanto maggiore è il numero di Reynolds (e quindi il numero di Rouark). Serimentalmente si trova che Re < (a questo roosito è imortante sottolineare che il numero di Reynolds è costruito con h come dimensione caratteristica; nel caso in cui venga usata L, allora nella disuguaglianza recedente aarirebbe (h/l) ), h/l - e la condizione è verificata. Sotto queste condizioni l'equazione diventa: L Re h u, cioè u Ru h Re Ru L cioè il camo di velocita' u è esresso come il gradiente di una funzione scalare e quindi è irrotazionale. Inserendo questo risultato nell'equazione di continuità, otteniamo che il camo è otenziale. Le comonenti della velocità saranno: u Re h ( x, y), Ru L x Re v ( x, y) Ru h L y o, in forma dimensionale,: h h u ( x, y), v ( x, y) µ x µ y
23 che sono del tutto equivalenti alla forma che era stata ottenuta er la velocità al centro del condotto nel moto di Couette. Se introduciamo un otenziale di velocità Φ (u h Φ (h/l) L Φ ) si ottiene che Re (x, y) Φ ( x, y) cost Φ Ru cioè il camo del otenziale è roorzionale al camo di ressione. La soluzione comleta è: Re h u ( x, y, z) z Ru L ( ) Allora, er ogni valore di z, abbiamo uno strato con un camo di velocità bidimensionale, irrotazionale e incomressibile (e quindi otenziale) con le condizioni di velocità normale allo strato uguale a zero (gli strati non interagiscono), e velocità tangenziale non nulla (flusso non viscoso in scorrimento relativo risetto agli altri strati). Le linee di corrente del flusso stazionario saranno quindi identiche a quelle iotetiche di un flusso bidimensionale non viscoso. Il camo u è irrotazionale, mentre u è rotazionale (ma solo sui iani (x,z) o (y,z)). C'è inoltre da considerare che non è in alcun modo verificata la condizione di non scorrimento su un coro osto nella zona interna alle due iastre e che quindi in rossimità del coro saranno resenti effetti viscosi. E ossibile osizionare cori di varia dimensione e forma nella zona comresa tra le due iastre e osservare le linee di corrente risultanti (che coincidono con le traiettorie nel caso stazionario). Queste avranno una linea tangente che fornirà la direzione del vettore velocità locale: dψ -v dx u dy Il modulo delle comonenti di velocità (o della comonente tangenziale intorno ad un coro) sarà dato da ψ/x e ψ/y e tramite l'equazione di Bernoulli sarà ossibile determinare la ressione. La quantità che in realtà viene misurata è la distanza d tra le linee di corrente: infatti, imonendo ortata costante, si ottiene: U S U h d U h d U U (d / d) 3
24 essendo S la suerficie di fluido tra due linee di corrente distanti d nel iano (x,y) e h lungo l'asse z. Misurando le distanze d e d è quindi ossibile, nota U (.e. da misure di ortata) ottenere la velocità U in una sezione qualsiasi. Se U non è nota si otterrà la velocità normalizzata risetto al valore a monte, che, comunque, è quanto necessario er valutare il coefficiente di ortanza tramite il teorema di Bernoulli nella sua forma iù semlice c. U d U d L'errore sulla misura della velocità sarà dato da: U U U U d d d d U U d d dove l'ultimo termine viene determinato dallo sessore delle linee di corrente. Quando la condizione (.) non è iù verificata (.e. a causa di un aumento del numero di Reynolds), vi è un isessimento delle linee di corrente (le articelle iù vicine alle iastre interagiscono con quelle rossime al centro e gli strati non si muovono iù in maniera indiendente) e le articelle a velocità maggiore (al centro) vengono deflesse, a causa della resenza di un coro, meno di quelle iù lente in rossimità della suerficie delle iastre..5. Analogia di Mach-Froude (o analogia idraulica) Consideriamo un flusso in resenza di suerficie libera ad un altezza h (dal fondo) iccola risetto alla dimensione caratteristica sul iano arallelo al fondo (h << L), incomressibile (Ma /Ru <<, Gu << ), in condizioni non stazionarie e non viscoso (Re >> ). Tale flusso sarà governato dalle equazioni: u u, St ( u ) u k t Ru Fr (.) (l adimensionalizzazione è fatta risetto a h e U ). Sia data inoltre una condizione al contorno sulla suerficie libera zz(x, y, t) con (Z) come ressione di riferimento. Per risolvere questo roblema, abbiamo quindi un sistema di quattro incognite (u, v, w e ) in quattro equazioni. Possiamo effettuare una sostituzione di variabile tra la comonente w e la osizione della suerficie libera Z. Infatti, er zz abbiamo: 4
25 5 x y z U o o L h Z (x,y) Figura 5. Parametri fondamentali e sistema di riferimento er l analogia di Mach-Froude. ) ( y Z v x Z u t Z St Dt DZ Z z w (mentre er z si imorrà w). Le incognite saranno quindi u, v, Z e. Integriamo l'equazione di continuità in z: Z dz z w y v x u cioè: ) ( Z w dz y v x u Z e infine: Z Z dz v y dz u x t Z St (.3)
26 6 Se iotizziamo che la ressione (x, y, z, t) (Z(x, y, t), z) (Z-z)(Ru/Fr ), cioè sia data dalla ressione idrostatica (dalla legge di Stevino, g(z-z)), allora la terza equazione di Navier-Stokes (Eulero) ci dice che w lungo le traiettorie ercorse dalle articelle fluide e quindi, se inizialmente nulla, la w si mantiene tale. D'altra arte se h << L, sembra ragionevole suorre che la comonente verticale di velocità sia nulla (e quindi far discendere la legge di Stevino). In questo caso, il gradiente di ressione verrà a diendere solo da x e y e, dalle altre due equazioni, si ottiene (essendo sia che g costanti): ),, ( t y x f Dt Du se inizialmente il fluido è a rioso in direzione verticale. Abbiamo quindi che: ),, ( ),, ( w t y x v v t y x u u Dalla eq. (.3) otteniamo: ) ( ) ( Z v y Z u x t Z St (.4) e dalla rime due equazioni di Eulero (essendo ( Ru/Fr ) Z): y Z Fr y v v x v u t v St x Z Fr y u v x u u t u St (.5) Abbiamo quindi tre equazioni nelle incognite u, v e Z ( è determinato dalla legge di Stevino). Moltilicando la (.4) er e le (.5) er Z: ) ( ) ( ) ( y Z Fr y v v x v u Z t v St Z x Z Fr y u v x u u Z t u St Z y Z v x Z u t Z St
27 7 ossiamo definire la densità e la ressione suerficiali: Z Z Z er ottenere: ) ( ) ( y Fr y v v x v u t v St x Fr y u v x u u t u St y v x u t St (.6) che sono del tutto analoghe alle equazioni di Eulero che si ottengono nel caso bidimensionale, comressibile, non viscoso in assenza di forze di gravità (con un'equivalenza tra il numero di Froude al quadrato moltilicato er e quello di Rouark). Notiamo, in articolare, che i due cami di velocità sono equivalenti e che i cami di ressione e densità sono entrambi determinati dall'altezza della suerficie libera Z. Notiamo anche che la ressione suerficiale è del tio: cost. Z cioè una trasformazione olitroica del tio K (dove e' il raorto tra i calori secifici) con (mentre di solito è comreso tra e 5/3), cui corrisonde una velocità del suono: ( ) / / / Z a Per una olitroica con vale anche: Ma U a U Ru che rova l analogia tra numeri di Froude e Mach. Inoltre, è ossibile far corrisondere all equazione er l energia di un gas isentroico e non viscoso (T /T Ma /, con ), l equazione di conservazione dell energia er un fluido
28 incomressibile, in resenza di suerficie libera (h/z Fr /), cosa che ci ermette di comletare la seguente tabella (dove si è anche inserito il raorto tra le frequenze caratteristiche di un fenomeno in aria (ω) e in acqua (Ω), che è funzione del raorto tra la velocità del suono in aria e quella delle onde sulla suerficie libera dell acqua (c (gh) /, come uò essere ottenuto dall uguaglianza del numero di Strouhal): Flusso comressibile Flusso incomressibile (a suerficie libera) Ma Fr / Z/h / (Z/h) T/T Z/h ω/ω a/c Di conseguenza, un flusso incomressibile, bidimensionale, non viscoso, a suerficie libera, con h << L, corrisonde ad un flusso comressibile, bidimensionale, non viscoso (entrambi non stazionari). In entrambi i casi uò essere introdotto un otenziale di velocità, Φ, e, utilizzando l'equazione dell'energia, l'equazione di conservazione della massa uò essere trasformata in una equazione er il otenziale. Quest'ultima equazione, nell'iotesi di iccole erturbazioni er il camo di velocità (u', v' << U ) e er la geometria (.e. rofilo con sessore molto minore della corda), diventa risettivamente: (-Ma ) Φ (-Fr ) Φ (valide solo er Ma e Fr ). Abbiamo le seguenti equivalenze: Ma < regime subsonico Ma > regime suersonico Fr < regime subcritico Fr > regime suercritico Allora, nel caso Fr >, otremo, attraverso questa analogia, osservare la formazione delle onde d'urto e la loro configurazione stazionaria, mentre nel caso Fr < otremo verificare la soraelevazione della suerficie libera (cioè l andamento della ressione) in rossimità di cori 8
29 immersi. Si noti che tutti i numeri caratteristici sono stati adimensionalizzati con h; nel caso in cui si usi la dimensione longitudinale L, allora la condizione Re >> diventa: h Re >> L E ossibile verificare questa analogia nella cosiddetta tavola ad acqua nella quale in corrisondenza di restringimenti (ugelli) o allargamenti di sezione o in resenza di ostacoli di varia forma si osserva la formazione di onde sulla suerficie libera la cui conformazione è analoga a quella che si osserva in un flusso comressibile caratterizzato da un raorto tra i calori secifici ari a. Attraverso la riresa di queste configurazioni della suerficie libera è ossibile ottenere er esemio l andamento del coefficiente di ressione intorno ad un rofilo alare, la frequenza caratteristica dei vortici nella scia di un cilindro (scia di Von Karman) o l inclinazione delle onde d urto che si vengono a formare intorno a cori di varia forma. L errore risultante dienderà dalla lunghezza d onda rodottasi sulla suerficie libera e dalla digitalizzazione del sistema di riresa. 9
30 Caitolo 3: IMPIANTI PER STUDI SPERIMENTALI DI FLUIDODINAMICA 3. GENERALITA' Gli imianti utilizzati nella serimentazione in camo aeronautico hanno lo scoo di rirodurre le condizioni del flusso intorno ad un oggetto di interesse aerodinamico in modo iù ossibile fedele a quanto avviene nella realtà. Al fine di contenere i costi, verranno realizzati modelli in scala ridotta degli oggetti in esame intorno ai quali studiare l`andamento del camo fluidodinamico. Il requisito della scala ridotta imone comunque di soddisfare l'uguaglianza dei numeri caratteristici come descritto nel caitolo recedente. Per quello che riguarda il numero di Mach, distingueremo due classi di imianti: - gallerie a bassa velocità (subsoniche, Ma < ); - gallerie ad alta velocità (suersoniche e iersoniche, Ma ). Nei rimi gli effetti della comressibilità del flusso verranno trascurati comletamente. Per quello che riguarda il numero di Reynolds, i requisiti di scala ridotta e di similitudine dinamica, richiederebbero velocità di rova sueriori a quelle reali. In effetti, non essendo questo realizzabile (anche er non dover altrimenti considerare gli effetti di comressibilità), si cerca almeno di verificare la condizione sul numero di Reynolds: Re > Re critico dove Re critico é un valore al di là del quale gli effetti del numero di Reynolds sono bassi (tiicamente dell ordine di qualche decina di migliaia). A questo roosito, rivestono articolare imortanza gli studi di base sulle variazioni delle quantità fluidodinamiche al crescere del numero di Reynolds. In alcuni casi si ricorre ad imianti seciali (gallerie ressurizzate, vasche idrodinamiche) er raggiungere l`uguaglianza del numero di Reynolds. Per tutti gli imianti vi sono alcuni arametri fondamentali che consentono di valutare l attendibilità delle rove serimentali da effettuarsi resso l`imianto stesso. Tra questi i iù imortanti sono: 3
31 - dimensioni della sezione di rova; - velocità massima e minima nella sezione di rova; - livello di turbolenza (fluttuazioni delle comonenti di velocità); - temeratura, densità e ressione (sorattutto er gallerie ad alta velocità e gli imianti seciali); - efficienza dell`imianto. Tra gli altri arametri da non trascurare vi sono l accessibilità alla sezione di rova (er inserire strumentazione di misura e er effettuare visualizzazioni), il costo di esercizio, le dimensioni comlessive dell imianto, la rumorosità ed in generale l`inquinamento ambientale che tale imianto comorta. La richiesta di migliorare uno di questi arametri é sesso in conflitto con gli altri ed e necessario ottenere un comromesso: er esemio, al crescere delle dimensioni della sezione di rova, aumentano il costo di esercizio, le dimensioni comlessive e la rumorosità dell imianto a favore di un aumento del numero di Reynolds. E imortante mettere in evidenza che, mentre nel caso reale e di solito il coro (velivolo, autoveicolo..) che si muove nel fluido, nelle rove su modelli e il fluido in moto ad investire il coro. Di conseguenza, ur nel ieno risetto del rinciio di relatività galileiana, il camo di moto intorno ai modelli resenterà delle fluttuazioni (dovute alla turbolenza del flusso) che non sono resenti nel caso reale. E questo il motivo er cercare di ridurre il iù ossibile il livello di turbolenza negli imianti er studi serimentali. Diverse sono le situazioni nelle quali si vuole indagare rorio l effetto della turbolenza er esemio all interno di condotti, nello strato limite di arete o all uscita di getti. Le differenti categorie di imianti vengono descritte searatamente nel seguito. 3. GALLERIE DEL VENTO A BASSA VELOCITÀ Vi sono due tii di gallerie del vento a bassa velocità: a circuito aerto e a circuito chiuso. Nelle rime l aria fluisce lungo una linea dall ingresso all uscita, mentre, in quelle a circuito chiuso, l'aria ercorre un cammino chiuso er tornare al unto di artenza. Le gallerie a circuito aerto sono semre a sezione di rova chiusa in quanto in tale sezione la ressione, er il teorema di Bernoulli, é semre inferiore a quella atmosferica e quindi, nel caso di sezione di rova aerta, ci sarebbe un flusso richiamato dall'esterno verso l interno della camera di rova. Le gallerie a 3
32 circuito chiuso ossono funzionare sia con sezione aerta che chiusa. Si riortano alcuni vantaggi e svantaggi dei due tii di gallerie: - gallerie a circuito aerto: vantaggi: costi di costruzione, scarico in aria dei fumi; svantaggi: aria non controllata in ingresso, rumorosità, costi di esercizio; - gallerie a circuito chiuso: vantaggi: qualità del flusso, costi di esercizio, oca rumorosità; svantaggi: costi di costruzione, ulizia, raffreddamento. Gli elementi caratteristici di una galleria del vento a bassa velocità (riortati nella figura 6) sono: - sezione di ingresso; - camera di calma e nido d'ae; - convergente; - sezione di rova; - diffusore (o divergente); - comressore (o ventilatore); - contrazione; - secondo diffusore; - elementi angolari di deviazione del flusso; - sistema di raffreddamento: - sistema di asirazione dello strato limite. Ciascuno di essi verrà trattato con maggiore dettaglio nel seguito; si faccia riferimento al testo di Rae e Poe er ulteriori arofondimenti su tali elementi e er la determinazione delle secifiche rogettuali di ciascuno di essi. 3.. Sezione di ingresso E resente solo nelle gallerie a circuito aerto ed é fatta a forma di imbuto er raccogliere quanta iù aria ossibile verso la camera di calma. 3
33 Elementi angolari (CORNERS) Diffusore acustico Convergente Diffusore Camera di calma Sezione di ingresso Sezione di rova x Ventilatore e motore Cono di contrazione Secondo diffusore Ventilatore e motore Elementi angolari (CORNERS) Figura 6. Schema geometrico ed elementi fondamentali di una galleria del vento a bassa velocità (con linee unteggiate sono indicate le arti caratteristiche solo di un imianto a circuito chiuso). 3.. Camera di calma E costituita da un tronco di cilindro; al suo interno la velocità del flusso deve essere la iù bassa ossibile er eliminare i vortici a larga scala che ossono formarsi nelle sezioni a monte. A tale scoo la camera di calma resenta dei nidi d'ae, cioè dei canali a sezione circolare o quadrata (di dimensione trasversale ari a circa / di quella longitudinale), seguiti da reticoli di fili di asso decrescente. L'effetto di tali aarati é quello di uniformare il rofilo di velocità (che risente della resenza a monte di curvature (gallerie chiuse) o di areti (gallerie aerte)). In generale, a valle della camera di calma, la turbolenza uò essere considerata isotroa (non diendente dalla direzione) er distanze assiali x > M (essendo M il asso del reticolo finale); er quello che riguarda l'omogeneità, è necessario allontanarsi fino a x > 8 M er ottenerla in maniera comleta. Al variare della distanza x, vi é un decadimento dell'energia cinetica turbolenta cioè delle fluttuazioni quadratiche di velocità: u ' u ' v ' w ' 3u ' (l ultima uguaglianza vale nel caso isotroo), che, serimentalmente, si trova essere: 33
34 ' u U c C d x M x M n essendo U la velocità media, c, n, C d ( d )( d M M ) ( d ) 4 M, dove d é il diametro dei fili della rete (coefficiente di resistenza er unità di area) e (x/m) 5 6 (origine virtuale). La legge di decadimento e iù o meno lineare. Questa legge determina la lunghezza della camera di calma a valle dei nidi d'ae e dei reticoli richiesta al fine di ottenere le fluttuazioni di velocità volute (di solito qualche frazione ercentuale (..)%). Gli eserimenti hanno confermato la MU validità della legge er Re > 5 υ M Convergente Ha un trilice scoo e cioè aumentare la velocità media del flusso che esce dalla camera di calma fino al valore desiderato er la sezione di rova, ridurre ulteriormente le fluttuazioni di velocità e infine ridurre lo sessore dello strato limite. L'aumento di velocità é conseguenza della equazione di conservazione della massa che, nel caso di basse velocità, viene integrata sulla sezione a monte e a valle del convergente: V ( U ) dv usando il teorema della divergenza ( n) ds S U e scrivendo il risultato sulle sezioni di ingresso, A i, di uscita, A u, (dove U é arallelo ad n ) e sulle sezioni laterali (U ortogonale ad n ), si ottiene: U ds i i Ai A u U u ds u Trascurando er semlicità gli effetti viscosi (U i cost e U u cost), otteniamo: Ai U i Ai U u Au cioè U u U i U i c A (3.) u Il raorto A i /A u é detto raorto di contrazione ed é indicato con la lettera c. Essendo c dell'ordine di 5 5, otteniamo un incremento della velocità media a valle del convergente di questo ordine di grandezza. 34
35 La riduzione delle fluttuazioni di velocità é un fatto osservato serimentalmente con variazioni dell'ordine di: ' u u, u c ' i v v ' u ' i, c ' w ' w i, (3.) c u cioè la riduzione er le comonenti trasversali é molto minore di quella longitudinale. Per quanto riguarda la riduzione dello sessore dello strato limite, questo effetto é dovuto al gradiente di ressione favorevole (oiché aumenta la velocità, er il teorema di Bernoulli diminuisce la ressione ) che imedisce il distacco e l'aumento di sessore dello strato limite (che invece si ha in un divergente) Sezione di rova Come già detto, queste sono revalentemente chiuse nel caso di gallerie a circuito aerto, e aerte o chiuse er quelle a circuito chiuso. Le areti ossono essere leggermente divergenti er comensare l'aumento di sessore dello strato limite nella sezione stessa. Può essere a sezione circolare, ma referibilmente é a sezione quadrata o rettangolare er facilitare l'accesso ottico e l'inserimento di modelli o di strumentazione Diffusore (o divergente) Vi é un unico diffusore er una galleria a circuito aerto e due diffusori in circuito chiuso. Il diffusore ha il dulice scoo di allontanare l'elica del roulsore dalla sezione di rova e di ridurre le erdite di energia cinetica all'uscita della sezione stessa rallentando il flusso. Infatti oiché la otenza, W, di un flusso d'aria a velocità U, di densità, in una sezione di rova di dimensioni A L (dove A e la sezione e L la lunghezza) è data dall energia cinetica, E c, diviso l intervallo t: Ec U AL W t L U 3 U A, e la arte di otenza che verrà dissiata er effetti viscosi sarà moltilicata er un coefficiente K: W 3 K U A, ne consegue che la otenza dissiata é roorzionale alla terza otenza di U. Se allora realizziamo un divergente ossiamo diminuire la velocità U e quindi a valle del divergente avere (indicando con il edice d le quantità a valle del divergente e con quelle nella sezione di rova): 35
36 U U ( ) ( ) d d W W ( W ) d 3 A A U U d essendo A U A U. Si viene quindi a realizzare una notevole riduzione della otenza dissiata. d d D altra arte l'angolo di aertura del diffusore, α, non uò essere aumentato oltre un certo valore (α < ), altrimenti otrebbero verificarsi dei gradienti di ressione avversi che rovocherebbero il distacco dello strato limite. L effetto comlessivo sarebbe quello di un restringimento della sezione del diffusore che orterebbe ad un nuovo aumento delle erdite. Inoltre, si formerebbero disturbi, conseguenti alle variazioni di ressione, che otrebbero influenzare anche la sezione di rova Comressore (o ventilatore) Vi sono due considerazioni fondamentali che guidano la scelta del osizionamento del ventilatore. La rima é che questo lavora in condizioni ottimali quando é immerso in un flusso il iù ossibile uniforme e la seconda deriva dal fatto che il costo é all'incirca roorzionale al suo diametro. Di conseguenza, é referibile osizionare il ventilatore in una zona con sezione iccola (escludendo quindi la camera di calma) e a valle di una sezione sufficientemente rettilinea (escludendo quindi i lati brevi di una galleria chiusa). Per le gallerie aerte la scelta ricade semre a valle del diffusore (che quindi, anche er i motivi di costo del ventilatore, non deve essere troo divergente), mentre er quelle chiuse nel ramo di ritorno. Il ventilatore é essenzialmente un comressore assiale o centrifugo, ma, a differenza di un roulsore aeronautico, oera in un ambiente chiuso e con area costante senza aumento di velocità attraverso di esso. La sua funzione é quella di comensare le erdite e le cadute di ressione dovute all'attrito in tutta la galleria e sul modello inserito nella sezione di rova. Per dimensionare correttamente un ventilatore, bisogna considerare che l'equazione di conservazione della massa redice che la velocità vari in roorzione inversa all area della sezione di galleria considerata (3.). D altra arte, le erdite er attrito andranno ad influenzare l'altro termine resente nell'equazione di Bernoulli (oltre a quello contenente la velocità) e cioè la ressione V cos t ( V cost nel caso viscoso). 36
37 Indichiamo con la caduta di ressione tra due sezioni della galleria; la forza di attrito é quindi equilibrata dal rodotto A (essendo A l'area della sezione considerata). La otenza dissiata sarà allora AU e, in forma adimensionale, si utilizzerà il coefficiente di otenza dissiata K j j U AU j j AU j U j j er la j-esima sezione in cui e stato diviso l imianto (la quantità j /U j é a volte indicata con η j ed é detta coefficiente di caduta ed é differente er ogni elemento della galleria). Raresenta l'equivalente del coefficiente di resistenza, C d, utilizzato nello studio di cori in una corrente fluida. Il ventilatore deve essere in grado di bilanciare queste erdite comlessive (che si verificano in ogni sezione della galleria): U j U U j j K t j j U j U h K t η j (3.3) avendo esteso la somma a tutti gli elementi della galleria ed avendo indicato con h la caduta comlessiva di ressione e con U la velocità riferita alla sezione di rova. j y z d D y U c s x X L Figura 7. Elementi fondamentali di un ventilatore er galleria del vento: nella arte sueriore della figura e mostrata una vista erendicolare al flusso medio (direzione x) e nella arte bassa una vista arallela. 37
38 L esressione (3.3) deve essere valutata er esemio calcolando la in ogni sezione della galleria (tiicamente si ha K t. er gallerie a circuito aerto e K t.5 er gallerie a circuito chiuso che resentano quindi minori erdite relative e quindi minori costi di esercizio). In una galleria a circuito chiuso, ur essendovi un maggior numero di elementi risetto ad una a circuito aerto (corner, divergenti,...), il fluido e già in moto e non deve essere accelerato a artire da una velocità quasi nulla; a tal roosito, e utile ricordare che il coefficiente di attrito (λ o C d ) e maggiore alle basse iuttosto che alle alte velocità. Alle agg del libro di Rae e Poe é esosto un metodo er effettuare la valutazione della (3.3) ed in tabella a ag. 9 vi sono alcuni valori del coefficiente K er differenti sezioni di una galleria del vento. E anche ossibile calcolare la otenza che deve essere fornita dal fan, P f, moltilicando la caduta di ressione totale er la sezione in corrisondenza del fan e la velocità del flusso: P f A c U c tot π (D c /) U c K t U o / Tiici valori sono 5 kw (l effettiva otenza elettrica sarà divisa er un efficienza ari a circa.8). Un ventilatore é caratterizzato da 5 arametri fondamentali (vedi figura 7):. diametro esterno D ;. diametro del mozzo d ; 3. sessore delle ale s ; 4. corda della ala L ; 5. numero delle ale n. La ala é un rofilo alare molto allungato (s < L/). L'effetto dell estremità della ala sul camo fluidodinamico é ridotto il iù ossibile avvicinando il ventilatore alle areti del condotto (che quindi deve ossibilmente essere cilindrico in quella sezione). Per ridurre l effetto delle non stazionarietà sul camo di moto, il numero delle ale é di solito elevato (n > ). Una valutazione di massima delle restazioni del ventilatore uò essere fatta tramite la teoria dell'elemento di ala. Poiché le ale ruotano con velocità angolare ω diretta lungo l'asse x, vi sarà una velocità della ala V ω r diretta tangenzialmente, di modulo ωr (cioè funzione della distanza dal mozzo). Se definiamo l'angolo di avanzamento ( r) arctg( ωr ) Φ (essendo U c la velocità in corrisondenza del comressore) come l'angolo al vertice del triangolo di lati U c t e V (r) t, allora, considerando l'angolo di incidenza a rioso β(r) (che uò essere funzione di r se c'è svergolamento del rofilo), abbiamo che l'angolo di incidenza aerodinamica é dato da (vedi figura 8): U c ωr α se U c >> ωr ( r) β ( r) Φ( r) β ( r) U c 38
39 ω m o z z o x ω r ω r β ( r ) β φ ( r ) U c U c Figura 8. Configurazione geometrica del ventilatore risetto alla direzione della corrente in galleria: angoli di incidenza, di svergolamento e andamento della velocità angolare lungo l aertura della ala. (notiamo anche che la velocità all'estremità del rofilo assume in modulo un valore ari a [ U c ( ωd ) ], che deve essere minore della velocità del suono nel mezzo er evitare condizioni transoniche che comorterebbero un aumento di resistenza e di rumore). In assenza di rotazione vi sarà una ortanza (L ) ortogonale alla direzione della corrente incidente caratterizzata da un coefficiente di ortanza ari a C Lo π β(r). Con riferimento alla figura 9, e in maniera similare a quanto avviene er l ala finita, a causa della rotazione del ventilatore, vi sarà una ortanza effettiva (L e ) diretta ortogonalmente alla direzione che forma un angolo φ(r) con la direzione della corrente incidente. Tale ortanza effettiva darà origine ad una forza diretta arallelamente alla corrente che tenderebbe a singere verso monte la ala (le forze ortogonali alla direzione della corrente vengono assorbite dai suorti del ventilatore). A causa della reazione vincolare, si genererà una comonente roulsiva (S) data da (er unità di aertura alare della ala): CLo r U cldrω r ds ( r) dle ( r) senφ ( r) dl ( r) tgφ ( r) CLo ( r) U cldr tgφ ( r), ( ) e la forza roulsiva comlessiva si troverà integrando da d/ a D/: ( ) D / CLo r U clω rdr CLoU clω CLoU clω D S ( D d ), 6 6 d / 39
40 L L (r) e (r) U e φ (r) ωr φ (r) U c S(r) Figura 9. Velocità della corrente, velocità effettiva, ortanza e ortanza effettiva intorno ad un rofilo di ala. avendo assunto C Lo cost. e d<<d (come in effetti è in tutte le condizioni oerative). Questa quantità viene di solito moltilicata er un coefficiente η f che definisce l'efficienza del ventilatore (inferiore all unita a causa del fatto che comunque ci sono delle erdite). Si ottiene: S η f C L o U c Lω D, (3.4) 6 che é roorzionale a C Lo, L, D,, U c e ω (oltre che all'efficienza del ventilatore η f ). Quanto detto vale er una singola ala e andrà moltilicato er il numero delle ale n. Confrontando ora l esressione (3.4) aena ottenuta con la (3.3), er riuscire a comensare le erdite di attrito, dovrà essere S > h D, e si otterrà la condizione: nc L Lo ωη f U D c K t U D, cioè 6 8U Kt 8KtU D c nω U C Lη η C L D c Lo f f Lo che é una condizione sul numero delle ale (una volta scelta la ala stessa (cioè C Lo e L), dato un valore er η f (tiicamente.9, che determina anche un valore della velocità angolare dal diagramma che raresenta l efficienza della ala, Figura.6 a g. 54 del Rae e Poe), avendo rima calcolato le erdite totali K t (data la geometria dell imianto) ed essendo note la velocità del flusso U e le dimensioni D c e D dal dimensionamento della camera di rova). Bisogna anche considerare che il flusso in uscita dal ventilatore conterrà una notevole comonente tangenziale di velocità che viene rimossa e convertita in recuero di ressione tramite dei raddrizzatori di flusso. 4
41 Nel caso in cui C Lo non ossa essere considerato costante lungo l aertura alare, allora bisognerà svolgere l integrale er esteso assegnando l andamento radiale C Lo (r). Il calcolo del numero di ale svolto in questa modalità uò ortare ad un notevole miglioramento della condizione sul numero delle ale (minor numero di ale necessario a arità di velocità angolare del ventilatore) Contrazione e secondo diffusore Il cono di contrazione ed il secondo diffusore sono resenti solo er le gallerie a circuito chiuso. Il rimo serve er restringere la sezione (che era stata allargata a valle della sezione di rova tramite il diffusore) er oter utilizzare un ventilatore il iù iccolo ossibile e ridurre i costi, il secondo er ritornare alle dimensioni della galleria a monte del convergente. Per il secondo diffusore valgono iù o meno le stesse considerazioni fatte er il rimo (er esemio angolo di aertura α < o ) Elementi angolari (corners) Sono elementi a forma di rofilo alare che attraversano trasversalmente la galleria del vento a circuito chiuso in corrisondenza dei bruschi cambiamenti di direzione. Il loro scoo e quello di "avviare" il flusso nel cambio di direzione a 9 resente nel raccordo tra una sezione rettilinea ed la successiva. Il coefficiente di caduta in corrisondenza di tali elementi é funzione della loro forma. A ag. 48 del Rae e Poe sono riortati alcuni valori caratteristici (che comunque sono dell'ordine di η.. cioè abbastanza elevati) Sistema di raffreddamento Tutte le erdite di energia nel circuito e secialmente in rossimità del comressore sono trasferite al flusso sotto forma di calore e rovocano quindi un innalzamento della temeratura della corrente fluida (si arriva a incrementi di qualche grado er ogni giro comleto nel caso dei tunnel ad alta otenza). E quindi necessario un sistema di raffreddamento er riortare la temeratura alle condizioni di rova volute. A questo scoo ossono essere utilizzati iù sistemi: - sistema con circolazione di liquido refrigerante a contatto esterno con la galleria; - sistema con raffreddamento di elementi interni alla galleria (.e. gli elementi angolari); - sistema di scambiatori di aria er sostituire l aria riscaldata con altra a temeratura inferiore. 4
42 3.. Sistema di asirazione dello strato limite In una galleria del vento si vogliono misurare le caratteristiche di un modello di velivolo o di autoveicolo che si muove in un fluido a rioso usando il rinciio di relatività galileiana e misurando quello che succede con il fluido in moto e l'oggetto in esame a rioso. I due unti di vista sono esattamente equivalenti in ambiente aerto, cioè lontano da suerfici solide. In un ambiente chiuso, quale la galleria (o qualsiasi imianto serimentale), la resenza delle areti del condotto si fa sentire in maniera notevole. Su queste areti si svilua uno strato limite (il cui sessore cresce all'incirca come x ed é roorzionale a Re / ) all'interno del quale il rofilo di velocità non corrisonde a quello del flusso indisturbato e quindi non é adatto ad indagare le restazioni reali (er esemio gli effetti su un autoveicolo). A questo scoo, si ratica l'asirazione dello strato limite a monte della sezione di rova, cioè si releva del flusso in rossimità della arete della galleria (e di solito si reimmette a valle della sezione di rova). Tale sistema uò funzionare anche in arallelo con il sistema di raffreddamento. 3.3 PARAMETRI DI UNA GALLERIA DEL VENTO A BASSA VELOCITÀ Come detto nella arte introduttiva di questo caitolo, vi sono alcuni arametri imortanti che consentono di valutare le restazioni di una galleria del vento. Per quello che riguarda le dimensioni della sezione di rova, la velocità massima e minima e il livello di turbolenza se ne e determinata la diendenza dalla forma e dalle dimensioni del convergente e della camera di calma. L'efficienza di una galleria é definita anche raorto di energia (ER) e misura il raorto tra l energia roria del fluido in movimento e quella immessa nel sistema: energia del flusso ER. energia immessa Se ammettiamo che l'energia immessa (da ventilatore, sistema di raffreddamento, imianto er l'asirazione dello strato limite) sarà circa uguale alla somma delle erdite e normalizziamo tutto all'energia del flusso U A, otteniamo che: ER U AL U hal h K t ( η j ) j 4
43 cioè la valutazione delle erdite ci fornisce un'idea dell'efficienza della galleria. Essendo K t <, risulterà ER > (tiicamente ER 5 er gallerie aerte, ed ER 7 er gallerie chiuse), il che significa che l'energia incamerata nel fluido in moto (trascurando il lavoro fatto er la messa in moto) é maggiore di quella che devo fornire er mantenerlo in questo stato. Gli altri arametri fondamentali di una galleria del vento a bassa velocità (temeratura, densità e ressione) ossono essere facilmente valutati a artire da un modello quasi unidimensionale e stazionario (St << ) di un gas erfetto non viscoso (Re >> ) e non conduttore. Consideriamo anche che la densità sia variabile (cioè flusso comrimibile erché siamo a Mach intermedi) er ottenere: A. (3.5) U A U U U x, (3.6) Ru x U U c T c T (3.7) Le tre equazioni trovate ((3.5), (3.6) e (3.7)) hanno come incognite, U, e T, una volta note le quantità sulla sezione e sono esresse in funzione della dimensione dell area della sezione, A. Serve un'altra equazione e cioè l'equazione di stato: T T (3.8) Si ottiene: Ma T T Ma H, (3.9) che raresenta la variazione di temeratura tra le sezioni e. Se sia Ma che Ma sono molto minori di, cioè in condizioni subsoniche, si ha H e T T. Questa equazione é ottenuta direttamente dall'equazione dell'energia (3.7): e dalle definizioni ed é erciò semre valida. La 43
44 quantità T t Ma T é detta temeratura di ristagno (o di arresto) ed é la temeratura raggiunta quando il fluido é ortato a rioso in maniera adiabatica (senza scambi di calore). Inoltre, H (3.) che raresenta la variazione della ressione tra le sezioni e (questa equazione é ottenuta con l ausilio della relazione isentroica). La quantità t Ma, é detta ressione di ristagno (o di arresto). Sviluando in serie del numero di Mach questa esressione si ha: t 4 ( Ma ) U U Ma o, RT cioè rorio la ressione totale del caso incomressibile (ma in realtà ancora valida anche er Ma.8). Dall'equazione (3.8) si ottiene: T T H H H (3.) e infine dall equazione di conservazione della massa (3.5) otteniamo che A A H ( ) ( ) Ma Ma, Ma Ma H ( ) ( ) A A (3.) che ermette di ricavare il salto di Mach (cioè di velocità) noto il raorto A /A cioè la geometria (e viceversa). Allora se sono note le condizioni a monte (.e. in camera di calma) ossiamo trovare la densità, la ressione e la temeratura nella sezione desiderata in funzione di Ma e di A /A (noti) tramite le relazioni (3.9), (3.), (3.) e (3.). Se in camera di calma e U (Ma ) avremo H Ma, cioè avremo le condizioni di ristagno T T t, t e t. 44
45 Se invece la sezione é in condizioni soniche (Ma ) (indicata con ), si avrà H Ma (tabelle er i valori delle quantità sono riortate sul Poe e Goin a ag 5). Tutto ciò che abbiamo visto é valido solo se non ci sono urti cioè er le gallerie a basse velocità. Se c'è un urto (come nelle gallerie ad alta velocità o in sezioni articolari) la relazione er la temeratura é ancora valida, ma non quella er la ressione, densità ed area (erché non é iù valida l'iotesi di isentroicità attraverso l'urto). 3.4 GALLERIE DEL VENTO AD ALTA VELOCITÀ Le gallerie ad alta velocità (Ma >.5) ossono essere subsoniche (Ma < ), transoniche (Ma ) o suersoniche (Ma >.5). Lo schema di una galleria del vento ad alta velocità é differente da quello di una galleria a bassa velocità (figura ). Si distinguono due situazioni: - gallerie a circuito chiuso (funzionamento continuo); - gallerie a circuito aerto (funzionamento intermittente) a loro volta divise in gallerie a svuotamento o a riemimento. Serbatoio di Sistema di Comressore raffreddamento Serbatoio di svuotamento (solo aerte) riemimento rima gola seconda gola Diffusore (solo aerte) Sezione di rova Motore Scambiatore di calore Disositivo anti-condensa Cono di conrtrazione diffusore Figura. Schema geometrico ed elementi fondamentali di una galleria del vento ad alta velocità. 45
46 Le gallerie a circuito aerto sono revalentemente a funzionamento intermittente (e non continuo) erché é necessario comrimere l'aria tramite un comressore a valle di un serbatoio di riemimento o fare il vuoto a valle di un serbatoio di svuotamento (entrambi di caacità limitata). Nel caso del circuito chiuso quest'oerazione uò essere effettuata con continuità utilizzando l aria in ricircolo nell imianto. Le differenze rinciali risetto alle gallerie a basse velocità sono: sezione di rova comresa tra due gole e non subito a valle del convergente; osizionamento del comressore a monte e non a valle della sezione di rova; scambiatore di calore e disositivo anti-condensa; osizionamento del secondo diffusore. Per comrendere il motivo di queste differenze é necessario riscrivere le equazioni recedenti er la temeratura, velocità (o Mach), densità e ressione nel caso di resenza di urti (e quindi senza utilizzare la condizione di isentroica). Ingrandiamo la zona in rossimità della sezione di rova ed indichiamo le sezioni come mostrato in figura Prima e seconda gola Mettiamo insieme l'equazione di conservazione della massa l'equazione di bilancio della quantità di moto già scritte nel recedente aragrafo (equazioni (3.5) e (3.6)): ( UA) U A x U A U U U U x x x x da cui, oiché le grandezze diendono solo dalla coordinata x: cioè A d U da U dx d d dx da dx d dx A du A ( Ma ) ( Ma ) U U dx (3.3) 46
47 Urto A c A A A A g A d Camera di calma Convergente Prima gola Sezione di rova Seconda gola Diffusore Figura. Schema delle sezioni di galleria in rossimità della sezione di rova. da Per una corrente subsonica (Ma < ) in un convergente ( <) si ha una diminuzione di ressione dx d du ( <) ed un aumento di velocità ( >). Per una corrente suersonica il comortamento é dx dx oosto (i due comortamenti sono riassunti nella figura ). da d Si noti anche che é una condizione necessaria er Ma (altrimenti ci sarebbe er dx dx Ma ). La velocità del suono e raggiunta solo quando la sezione ha un minimo locale (condizione sufficiente) erché se ci fosse un massimo la corrente subsonica decelererebbe nel divergente, mentre quella suersonica accelererebbe; quindi affinché vi sia la transizione transonica ci deve essere una sezione di gola. Questa differenza con il caso subsonico é dovuta al fatto che nel caso suersonico la variazione di ressione ha il soravvento su quella di velocità (mentre accade l'oosto nel subsonico). Allora se abbiamo un flusso subsonico e lo vogliamo accelerare avremo un rimo convergente che lo orta in condizioni soniche ed un secondo divergente che lo orta in condizioni suersoniche (figura 3). A valle del convergente si formeranno delle condizioni soniche (Ma ) con ossibile formazione di onde d'urto a monte del modello, che ossono essere riflesse fino alla camera di rova. In articolare, in condizioni di avviamento e in resenza di un modello, sarà anche ossibile avere la cosiddetta condizione di "choking" (soffocamento), cioè la formazione e ersistenza di onde d'urto di elevata intensità in camera di rova. Tali onde ostruiscono arzialmente il assaggio del flusso di aria originando grosse erdite er effetti viscosi e termici (fino al 9% delle erdite totali) che devono quindi essere comensate da un comressore iù 47
48 otente con aggravio dei costi e degli ingombri. Poiché si e in condizioni transoniche e suersoniche, e ossibile diminuire nuovamente la velocità a valle della sezione di rova tramite un ulteriore convergente (seconda gola) ed é ossibile evitare questo soffocamento nel resto del condotto. accelera diminuisce la decelera aumenta la Ma < decelera aumenta la accelera diminuisce la Ma > Figura. Andamento della ressione in un convergente-divergente nel caso subsonico e suersonico. U Ma < Ma > Ma Figura 3. Accelerazione da flusso subsonico a flusso transonico attraverso un convergente e da flusso transonico a flusso suersonico attraverso un divergente in serie. 48
49 3.4. Parametri di una galleria del vento ad alta velocità In resenza di urti le equazioni che definiscono le variazioni di temeratura, ressione, densità e velocità tra due sezioni viste in recedenza er il caso a basse velocità (equazioni (3.9), (3.), (3.) e (3.)) vanno determinate a artire dalle relazioni (3.5), (3.6), (3.7) e (3.8) (la (3.9) resta tutt ora valida erché ottenuta direttamente dall'equazione di conservazione dell'energia (3.7)). Si assume che a valle e a monte dell'urto (che ha sessore infinitesimo) la sezione resti inalterata) cioè che A A (avendo indicato con i edici e le sezioni immediatamente a monte e a valle dell urto). Dall equazione di bilancio della quantità di moto, utilizzando l equazione di conservazione della massa con si ottiene che: Ma (3.4) Ma Dall'equazione di stato e dal raorto tra le temerature Ma Ma H (3.5) Dall'equazione di conservazione della massa e dall'equazione di stato si uò ricavare Ma a valle dell'urto in funzione di quello a monte: Ma Ma. (3.6) Ma Per Ma >, questa relazione ci dice che il numero di Mach a valle di un urto e minore di quello a monte. Sostituendo questa relazione in quella della temeratura (3.9) si ottiene: T T Ma ( ) ( ) Ma Ma Allo stesso modo er la ressione (dalla (3.4)) e er la densità (dalla (3.5)) si ottiene: (3.7) 49
50 5 ( ) ( ) Ma, (3.8) ( ) ( ) Ma Ma (3.9) Le equazioni (3.6), (3.7), (3.8) e (3.9) forniscono il salto di velocità, temeratura, ressione e densità attraverso l'urto noto il numero di Mach a monte dello stesso. Si e assunto che l urto sia diretto ortogonalmente alla direzione della velocità (urto normale). Tale arossimazione risulta ienamente valida finche non e resente un modello in sezione di rova; in quest ultima situazione bisognerà utilizzare le relazioni valide in resenza di urti obliqui. Si noti che attraverso l urto, mentre il numero di Mach diminuisce bruscamente da valori maggiori di uno a valori inferiori, la temeratura, ressione e densità a valle dell'urto sono maggiori di quelle a monte. Il raorto tra le ressioni di ristagno t / t raresenta l inverso del raorto di comressione (λ) cioè una misura dell energia ersa attraverso l urto. Si uò valutare il raorto t / t : ( ) Ma t t t t t t λ Essendo k k t Ma k (con k,), si ottiene ( ) ( ) ( ) Ma Ma Ma t t (3.) che e semre minore di Dimensionamento della rima e seconda gola Vediamo di caire ora come dimensionare a regime la rima e la seconda gola (anche in resenza di urti) utilizzando una galleria con sezione variabile. Siano note dalle secifiche le dimensioni (A ) e la velocità (Ma Ma ) nella sezione di rova (a monte dell eventuale onda d urto); se nella
51 rima gola siamo in condizioni soniche (Ma ) (come in effetti è) la relazione (3.) ermette di calcolare la sezione della rima gola (A A ): ( ) A A Ma H, (3.) ( ) con H ( ) Ma. Noto A, osso determinare la sezione della camera di calma A c in funzione del numero di Mach in camera di calma (con riferimento agli indici e della figura 9): A c A H Ma ( ) c, (3.) con H ( ) ( ) Ma c. Per quello che riguarda la seconda gola, ci si metterà nelle condizioni eggiori di urto in camera di rova; detto Ma il numero di Mach a valle dell'urto si ha: Ma ( ) A g A H, (3.3) Ma g con H ( ) Ma ( ) Mag. ( ) La condizione limite si raggiunge er Ma g ( ) Ma H, da cui si ha: ( ( )) A A Ma H, (3.4) g dove Ma uò essere esresso, mediante la (3.6), in funzione di dell urto. Nel caso in cui.4 si ottiene: Ma, cioè il Mach a monte 5
52 A ( ) ( ). 5 Ma 7Ma g 6 6Ma 5 A (3.5) dove er Ma si ha A g. 6 A A g A (ma resta un o iù iccola) e er Ma si ottiene. Questa relazione ermette di dimensionare la seconda gola, la cui area é al minimo uguale a.6 A quindi abbastanza grande (cfr. figura 4). Abbiamo cosi comreso erché e come vengono dimensionate le gole intorno alla sezione di rova Posizionamento del comressore Per quello che riguarda il osizionamento del comressore, bisogna considerare che a valle della sezione di rova il comressore darebbe origine ad onde d'urto di frenata e come già detto, tali onde d'urto, darebbero notevoli erdite di energia nel circuito che vanno evitate. Di conseguenza, si referisce osizionare il comressore a monte della camera di calma Scambiatore di calore e disositivo anti-condensa Il rimo é necessario in quanto in una galleria ad alta velocità si formeranno comunque delle onde d'urto che riscalderanno il flusso in circolazione e sarà quindi necessario riortare la sua temeratura al valore di riferimento. Questa stessa oerazione, erò, orta di conseguenza un raido raffreddamento che roduce condensa (cioè bolle d'acqua nebulizzate che vengono immesse nella corrente). Questa condensa viene rimossa da un sistema di ventilazione (essiccatore). A g /A Ma Figura 4. Andamento del raorto tra le aree A g /A in funzione del numero di Mach a monte dell urto eq.(3.5). 5
53 4.4.6 Posizionamento del secondo diffusore Infine il osizionamento del secondo diffusore é forzatamente sostato il iù lontano ossibile er mantenere la sezione intermedia quanto iù iccola ossibile Avvio della galleria Nel caso subsonico la condizione di avvio di una galleria del vento deve ermettere la messa in moto della massa d aria fino alla velocità di utilizzo. Poiché l efficienza della galleria e rorio il raorto tra energia del flusso d aria e l energia immessa (a regime) e tale efficienza ha un valore ari a 5 7, e ragionevole suorre che sarà necessaria all avviamento un energia ari a qualche unita di quella richiesta er il funzionamento (cfr. 3..6). Nel caso di gallerie ad alta velocità il discorso e differente. All'avvio di una galleria ad alta velocità avremo che, essendo in condizioni subsoniche, la velocità maggiore (cioè il Mach maggiore) si avrà nella rima gola. La otenza del comressore sarà circa uguale alla somma delle erdite di attrito registrate nel circuito come nel caso a basse velocità. Aumentando la otenza del comressore, il numero di Mach aumenta finché nella rima gola non si raggiungono condizioni soniche (Ma ) e si svilua un urto normale ad una iccola distanza dalla gola (sezione A nella figura 5). Aumentando ancora la otenza, non si assiste ad un aumento del numero di Mach nella rima gola, quanto iuttosto ad uno sostamento dell'urto verso la sezione di rova (dove il numero di Mach é suersonico) (sezioni B e C della figura 5). Si verificano, a questo unto (e ancora di iù quando l'urto si sosta in avanti er Mach sueriori incrementando la otenza come nelle sezioni D ed E della figura 5) delle erdite di otenza attraverso l'urto che si sommeranno alle erdite di tio subsonico dovute all'attrito. camera di rova A B C D E rima gola seconda gola Figura 5. Formazione di onde d urto in camera di rova all avviamento di una galleria del vento ad alta velocità. 53
54 Questo rovoca una richiesta addizionale di otenza. In condizioni di funzionamento normale si raggiunge un equilibrio tra la otenza del comressore e le erdite che sono dominate da quelle a cavallo dell'urto normale. In queste condizioni un'idea delle erdite (e quindi della otenza necessaria al comressore sotto forma di raorto di comressione) é fornita dal raorto (3.) tra la ressione di ristagno a monte dell'urto (cioè a monte della camera di rova) e quella a valle dell'urto (cioè in uscita dalla camera di rova). Bisogna considerare che si e dimensionata la seconda gola richiedendo che ci fosse la condizione limite Ma g. Pero, in condizioni di avviamento, il numero di Mach nella seconda gola otrebbe essere maggiore dell unita (erché le condizioni sono subsoniche e la seconda gola funziona da acceleratore della corrente); er evitare questo, dalla (3.3) sarebbe richiesta una sezione A g > A g (sezione di gola con Ma g ) all'avviamento. Di conseguenza, nell'avviare una galleria ad alta velocità, il raorto di comressione λ deve essere calcolato con l'urto di massima intensità, utilizzando la (3.) (urto normale nella sezione di rova). Invece, in condizioni di funzionamento, l'urto si sosta nel diffusore in rossimità della seconda gola. Per ridurre l intensità dell'urto in condizioni di funzionamento sono state disegnate sezioni di seconda gola con area variabile nel temo in modo che all'avvio A g > A g e durante il funzionamento < (in condizioni ideali e stazionarie sarebbe A A g < A g A g A ). Il valore di λ necessario er avviare la galleria deve quindi essere maggiore del valore di λ necessario al funzionamento (cioè é richiesta una otenza aggiuntiva (di solito iù del doio) del comressore in fase di avviamento) A g ( ( )) ( ) A M a g g > M a g A g Presenza di un modello In resenza di un modello si formeranno urti aggiuntivi nella sezione di rova che richiederanno all avviamento un raorto di comressione ancora maggiore; di conseguenza, oiché il raorto tra le aree della seconda e della rima gola (ottenibile dalle (3.) e (3.3) inserendo la (3.6)) e rorio dato dal raorto di comressione λ t / t (tanto maggiore quanti iù urti vi sono in camera di rova), sarà necessaria un area di seconda gola ancora maggiore di quella in assenza di modello. Inoltre, le dimensioni del modello devono essere abbastanza iccole er non dare luogo a "choking" (cioè ad un occlusione della galleria causata dalla resenza di iù onde d urto intorno al 54
55 modello). Affinché questo sia vero, il numero di Mach in corrisondenza della sezione massima del modello (S f ) non deve essere sueriore a uno (le onde d urto saranno resenti nella arte anteriore del modello). Al crescere del numero di Mach nella sezione di rova, aumenta la dimensione del modello che uò essere rovato senza che avvenga il "choking". Infatti indicando con l'indice la sezione massima in corrisondenza del modello: A A Ma Ma H ( ) Essendo A A - S f, si uò scrivere S A f Ma Ma Ma Ma ( ) Affinché la sezione di rova all avviamento non raggiunga le condizioni soniche (Ma ), si ha (A A ) un valore della sezione massima del modello ari a S A f ( Ma ) Ma Ma ( ) (3.6) cioè un modello con numero di Mach in sezione di rova ari a, uò avere una sezione frontale massima ari al 4 % della sezione di rova er non manifestare choking. Da confronti con dati serimentali, il valore trovato dalla (3.6) va diviso er un fattore emirico ari a circa 4. A tale roosito, ricordiamo il comortamento delle linee di corrente er il caso di flussi comressibili: risetto al caso incomressibile, in cui il valore costante della ortata imone una convergenza a valle del modello delle linee di corrente (ciò che orta di conseguenza anche una raida attenuazione dei disturbi a valle dell'oggetto in esame), nel caso comressibile, la densità varia con la ressione e in articolare decresce quando decresce la ressione (eq. di stato). Se la velocità aumenta, sarà necessario un allargamento delle linee di corrente er avere la stessa ortata (essendo la densità diminuita). Un modello darà iù ingombro risetto al caso subsonico (figura 55
56 6). Un roblema notevole delle gallerie transoniche, legato a questo fenomeno, é quello di cercare di eliminare le onde d'urto che si originano o si riflettono sulle areti (e che quindi non sono resenti nel caso reale) a causa della deformazione dell'insieme delle linee di corrente. Si utilizzano camere di rova articolari le cui areti si adattano in maniera continua alle linee di flusso intorno al modello. Ciò viene effettuato tramite deformazione delle areti (.e. con un sistema di martinetti) o tramite ventilazione (.e. tramite areti semi-imermeabili collegate a comonenti nei quali si varia oortunamente la ressione) come mostrato nelle figure 7 e 8. La seconda soluzione ermette anche il migliore assorbimenti di eventuali onde d'urto, ma, di contro, rovoca flussi in entrata ed in uscita dalle areti. Figura 6. Andamento delle linee di corrente intorno ad un modello nel caso incomressibile (linee continue) e comressibile (linee tratteggiate). 56
57 Figura 7. Adattamento della sezione di rova tramite deformazione delle areti. Figura 8. Adattamento della sezione di rova tramite ventilazione. 57
58 3.5 IMPIANTI SPECIALI Vengono di seguito brevemente elencati alcuni imianti seciali utilizzati negli studi di fluidodinamica serimentale ad alta e bassa velocità Gallerie ressurizzate Sono gallerie nelle quali si cerca di lavorare in similitudine del numero di Reynolds (cosa che richiede velocità di rova del modello maggiori di quelle reali) mantenendo anche la similitudine di Mach. Per realizzare entrambe queste similitudini e necessario aumentare la ressione interna alla galleria e quindi la densità. Infatti (indicando con l indice m il modello e con l indice la situazione reale), Re m Re U Lm m µ m m U L µ e, se vogliamo lo stesso numero di Mach deve anche essere U m /(RT m ) / U /(RT ) / Se iotizziamo che la temeratura alla quale vengono effettuate le rove sia uguale a quella della situazione reale (altrimenti otrebbero avvenire variazioni indesiderate dei arametri quali il coefficiente di viscosità), la relazione recedente si riduce all uguaglianza delle velocità che nella similitudine di Reynolds conduce a m L L m (essendo µ diendente solo dalla temeratura). Usando l'equazione di stato si ha anche: m L. L m Da cui, essendo normalmente L /L m 3, la ressione nelle rove con modello deve salire fino a 3 volte quella reale (atmosferica) e cioè a 3 atmosfere. Gli svantaggi di tali gallerie sono: temo di comressione necessario rima di effettuare una rova (dell ordine di ore), costi di manutenzione e di gestione, elevati carichi alari sul modello, difficoltà di isolamento della sezione di rova dal resto del circuito. 58
59 3.5. Gallerie a temerature estreme Alcune gallerie del vento sono in grado di abbassare artificialmente la temeratura dell'aria e simulare le condizioni atmosferiche ad alta quota er studiare la formazione di ghiaccio sulle ali di un modello in rova nel temo (gallerie criogeniche) (lo studio uò essere effettuato in gallerie convenzionali se ci si accontenta di un indagine su un ala con rofilo già isessito). Allo stesso modo esistono gallerie che simulano condizioni di elevate temerature er rirodurre le condizioni esistenti nell'alta atmosfera al rientro di velivoli dallo sazio (gallerie al lasma). Un altro effetto, comune alle gallerie del vento a temeratura variabile e quello di oter lavorare in similitudine simultanea di Reynolds e Mach senza dover variare la ressione (a differenza delle gallerie ressurizzate); infatti, richiedendo l uguaglianza del numero di Reynolds e di Mach senza alterare le ressioni si ottiene (con il solito significato degli indici): T T / µ ( T ) m m µ ( T ) L L m ed essendo er l aria µ (T) T.5.8, si ottiene T T.3 L m m L che fornisce il salto di temeratura richiesto (essendo L m /L <<, sarà anche T m << T ) Gallerie idrodinamiche Pur essendo state costruite er alicazioni navali, questo tio di gallerie (di solito a sezione quadrata con o senza suerficie libera) ossono essere utilizzate er roblemi di fluidodinamica incomressibile con numero di Reynolds articolarmente elevato (sia erché la viscosità cinematica dell'acqua è iù di volte maggiore di quella dell'aria, sia er le loro notevoli dimensioni (si ottengono velocità di molti metri al secondo in sezioni dell ordine di 3 5 metri): 6 5 ν. m s ν.5 m s ( T 5 C) acqua / aria / Teniamo anche resente che molte roblematiche dell'aerodinamica sono resenti anche nelle alicazioni iù avanzate dell'idrodinamica (riduzione della resistenza di attrito di cori immersi in un fluido, cami fluidodinamici a valle di eliche e sistemi roulsivi, effetto di aendici ortanti 59
60 quali timoni e alettoni). Per alicazioni legate alla valutazione delle restazioni di sistemi roulsivi, sono frequentemente usati i tunnel di cavitazione nei quali la ressione uo scendere fino a / di atmosfera er verificare in quali zone della suerficie alare insorge la cavitazione Gallerie automobilistiche La stessa situazione vale d'altra arte anche nelle alicazioni iù avanzate dell'industria automobilistica (resistenza d'attrito e di forma, alettoni deortanti e aendici in genere) e er le gallerie utilizzate er tali scoi, che sono equivalenti alle gallerie del vento a bassa velocità. La differenza iù imortante è quella relativa all'imianto di asirazione dello strato limite, che deve essere necessariamente resente er simulare realmente l'avanzamento dell'autovettura in un fluido a rioso. Inoltre e necessario un disositivo che faccia girare le ruote er simulare in maniera corretta il comortamento del flusso nella arte inferiore della vettura. Infatti, anche nella arte dell autoveicolo iù a diretto contatto con il suolo la rogettazione deve essere articolarmente accurata er ottenere un incremento delle restazioni favorito dall interazione fluido-veicolo (effetto suolo) Vasche navali Sono utilizzate nell'idrodinamica navale e consistono in larghe vasche nelle quali il modello viene trascinato da un carro onte fino a velocità di m/s in condizioni di acqua ferma. Lo svantaggio rinciale é quello del basso temo disonibile er le misure a causa dell intervallo di temo limitato nel quale il carro onte raggiunge una velocità costante (e quindi dalla richiesta di dimensioni longitudinali articolarmente elevate (dell ordine delle centinaia di metri) Gallerie ambientali Recentemente alcune gallerie inizialmente costruite er scoi aeronautici sono state convertite a studi di fluidodinamica ambientale. Le caratteristiche rinciali sono quelle delle gallerie del vento a bassa velocità con modelli orografici (monti, colline, valli) e di edifici er simulare la diffusione di inquinanti. Sesso si aggiunge un gradiente di temeratura (e/o di densità) verticale in grado di rirodurre non solo il rofilo di velocità, ma anche quello di temeratura (e/o di densità) realmente resente nello strato limite atmosferico. 6
61 Caitolo 4: SISTEMI DI MISURA 4. GENERALITA La determinazione serimentale delle variabili caratteristiche di un camo fluidodinamico (velocità, ressione, temeratura, densità, concentrazione) richiede l'uso di sistemi di misura i cui rincii di funzionamento vanno comresi a fondo er un corretto uso dei dati ottenuti. Si distinguono i sistemi di misura veri e rori, che ermettono la determinazione quantitativa delle variabili, dai sistemi di visualizzazione che ermettono un'analisi iù qualitativa. In alcuni casi anche questi ultimi ermettono di ottenere informazioni quantitative sulle variabili o su grandezze derivate (.e. la visualizzazione di strutture vorticose in un camo di moto ermette di individuarne le osizioni, dimensioni e le frequenze di generazione e interazione). Per ogni sistema di misura individueremo la grandezza misurata, il rinciio di funzionamento, la metodologia della misura, la risoluzione saziale e temorale del metodo (cfr. caitolo), gli errori di misura e le rinciali controindicazioni all utilizzo del sistema. Verranno descritti in dettaglio i sistemi di misura del camo di forza e di ressione e quelli della ortata (er i sistemi di misura dei cami di densità, temeratura e velocità si rimanda ai corsi iù avanzati della Laurea Secialistica). 4. SISTEMI DI MISURA DELLA FORZA SU UN MODELLO La misura di forze intorno ad un oggetto in galleria ossono essere effettuate in 3 modi: - direttamente attraverso l'uso di bilance dinamometriche. - indirettamente attraverso l'effetto del modello sulla scia e sulle areti del canale. - indirettamente attraverso misura del camo di ressione intorno al modello. Verranno descritti i rincii di funzionamento di tutti e tre questi metodi. 6
62 4.. Bilance dinamometriche Il rinciio di funzionamento é la misura diretta della forza a artire dallo sostamento dalla osizione di equilibrio, quando il fluido viene messo in moto, di un elemento deformabile. La misura é effettuata tramite la lettura di questo sostamento che deve essere messo in relazione con il carico con una rocedura di calibrazione. Come elementi deformabili vengono utilizzate casule idrauliche (nelle quali vi é un istone che esercita ressione su un fluido) o disositivi elettrici (che variano la loro resistenza a seconda della ressione alicata o che variano la loro caacita a seconda della deformazione) con amlificatori. La grandezza misurata é quindi uno sostamento. La risoluzione saziale é legata alle dimensioni dell'oggetto in rova, in quanto questo é un metodo globale che misura i carichi su tutto il modello. La risoluzione temorale é bassa erché le bilance necessitano di un certo temo er raggiungere una osizione di equilibrio: fluttuazioni sulla scala temorale inferiore al minuto non sono arezzabili. Le rinciali controindicazioni sono legate all'uso di un braccio di sostegno che influenza ed altera il comortamento del camo di ressione e quindi le forze. Si usano bilance dinamometriche a 3 comonenti (er misurare ortanza, resistenza e momento di beccheggio su un rofilo alare o su una sezione di un coro allungato) o a 6 comonenti (er ortanza, resistenza, forza laterale, momento di beccheggio, di imbardata e di rollio er un ala o un coro di forma qualsiasi) (cfr. figura 9). Per quello che riguarda la bilancia a 6 comonenti, con riferimento alla figura 9 (e agli assi e ai versi di rotazione), si ha: ortanza resistenza L C H E (C, H, e E sono definite negative) D A B forza laterale Y F (F é definita negativa) momento di rollio ( H C) b / (intorno all'asse x) R momento di beccheggio M El (intorno all'asse y) momento di imbardata ( B A) b / (intorno all'asse z) S (essendo P il unto risetto al quale vengono calcolati i momenti e avendo reso ositive le uscite A, B, C, quando sono in estensione e negative quando sono in comressione). Da un unto di vista costruttivo é fondamentale la erendicolarità tra le comonenti misurate (e l'allineamento con gli assi coordinati cioè con gli assi galleria) altrimenti una forza in una direzione aarirà come avente comonenti anche nelle altre. Da un unto di vista della calibrazione é necessario sottrarre l'effetto della bilancia stessa (eso ed eventuali altre forze e momenti resenti). 6
63 6 comonenti 3 comonenti C A E Fore (F) Aft (A) b/ H l P l P Drag (Dr) z z H y y B F x x Figura 9. Deformazioni misurate da una bilancia a 6 (sinistra) e 3 comonenti (destra). Per la bilancia a 3 comonenti, semre con riferimento alla figura 9, vale: ortanza resistenza momento di beccheggio -L FA D Dr M Al (nella bilancia a 3 comonenti in dotazione alla galleria del vento del Diartimento e resente un unico sostegno con un elemento lineare di lunghezza l al quale sono collegate le due celle di carico A ed F; il momento di beccheggio risetto alla osizione del sostegno sarà quindi M A l/ - F l/ (A-F) l/.7 (A-F) N m). I modelli sono sostenuti da fili di acciaio sottili (bilance meccaniche) o da bracci di sostegno (bilance elettroniche). Nelle bilance meccaniche si misurano le variazioni della lunghezza dei fili (ma questi si ossono romere con conseguente erdita del modello e quindi sono oco usati), mentre in quelle elettroniche l'uscita é un segnale elettrico in uscita da un trasduttore di forza che dovrebbe essere legato linearmente alla forza alicata. Quest'ultima relazione non é semre verificata a causa di imerfezioni costruttive della bilancia o di deformazioni elastiche tra le varie arti che la comongono. Entrambe queste cause rovocano un interazione tra le forze misurate e un disallineamento che deve essere corretto mediante una rocedura di calibrazione (che utilizza esi noti e misura le uscite). Essendo le deformazioni non lineari funzione della temeratura, anche 63
64 la calibrazione uò essere funzione della temeratura. La calibrazione consiste nel mettere in relazione l uscita (di solito una tensione V) con la forza alicata F er determinare la costante K differente er ciascuna uscita (V K F). L errore relativo risultante sarà del tio F F V V K K dove il rimo termine raresenta l errore di lettura e il secondo quello di calibrazione. Per la bilancia a 3 comonenti sarà quindi L F A, D D, l A A l r M Il suorto da luogo a due effetti, che modificano la misura risetto alla situazione reale (nella quale il suorto non é resente): forze e momenti aggiuntivi (valutati mediante una misura con il solo suorto): variazione del camo di moto intorno al modello (interferenze tra camo fluidodinamico del modello e del suorto, che non ossono essere valutate da misure sul solo suorto). Entrambi gli effetti sono di carattere dinamico. Ovviamente, er minimizzare questi effetti, si uò ridurre il iù ossibile la sezione del suorto (se cilindrico, il suo diametro d), ma ciò rovoca maggiore deformabilità del suorto stesso e la conseguente erdita di ortogonalità tra le direzioni lungo le quali si misurano le forze, oltre ad un aumento delle vibrazioni. Una valutazione teorica della resistenza del suorto uò essere fatta analizzando il diagramma del coefficiente di resistenza in funzione del numero di Reynolds C D (Re), che er un cilindro a sezione circolare é raresentato in figura (se si lavora con numeri di Reynolds comresi tra e 5 allora il C D é costante e vale circa ). C D Re du/ν Figura. Andamento in funzione del numero di Reynolds del coefficiente di resistenza er un cilindro. 64
65 L'altra ossibilità é quella di rendere il diametro d talmente iccolo da essere nella regione di Stokes (Re < ) dove C D A (essendo A una costante che diende dalla sezione e che vale Re 4 er un cilindro a sezione circolare). In questo caso la resistenza vale D AµU d U d CD du Aµ U é indiendente dal diametro del cilindro (che quindi osso fare grande a iacere urché valga la legge di Stokes). Quella di cui stiamo arlando é la forza er unita di lunghezza del cilindro. Una ossibilità serimentale er valutare l'interferenza suorto - modello é quella di osizionare in maniera simmetrica un suorto identico e nel misurare le variazioni del camo di forze dovute a questo. Utilizzando l indice A er la configurazione serimentale con il solo suorto (resistenza D S ), l indice B er quella con modello e suorto (resistenza D S D M D SM, dove l ultimo termine tiene conto dell interazione) e l indice C er modello, suorto e suorto osto simmetricamente (resistenza D S D M D SM D MS ), si ha D A D S, D B D S D M D SM, D C D S D M D SM dove si e linearizzata la diendenza da ciascuno degli effetti in gioco e si e iotizzato che l interazione modello suorto sia la stessa er entrambi i suorti (D SM D MS ), iotesi in effetti non vere, a meno che il suorto non sia molto iù iccolo del modello. Dalle relazioni recedenti e ossibile determinare la resistenza del solo modello attraverso la misura di resistenza in tre differenti configurazioni: D M D B D A - D C. Si consulti comunque il libro di Rae e Poe a ag. 4 er ulteriori arofondimenti. Come già detto nella arte relativa agli imianti, a volte é resente un disallineamento (qualche grado) tra l'asse della galleria e la direzione della corrente. Per correggere questo effetto, si rova il modello in configurazione dritta (d) ed in configurazione rovesciata (r). Siano C LM e C DM la ortanza e la resistenza misurate (assi galleria) e C L e C D quelle incognite (assi vento) (cfr. figura ). Essendo C L >> C D (circa volte) e l angolo α molto iccolo (minore di 5 ), sarà ( C LM ) C L cosα C Dsinα C L cosα d ( C ) C α C sinα C α ( ) tgα DM d D cos L D cos C LM d e con il modello rovesciato (scambiando α con -α) (figura ): 65
66 configurazione dritta C L C Lm asse vento C D asse galleria α C Dm x U configurazione rovesciata asse vento C D asse galleria α C Dm x U C Lm C L Figura.Configurazioni dritta e rovesciata er misurare l angolo di disallineamento assi vento - assi galleria. ( CLM ) CL cosα CDsinα CL cosα r ( C ) C α C sinα C α ( ) tgα DM r D cos L D cos CLM r cioè l angolo di disallineamento e dato da tgα ( CDM ) ( ) r CDM d [( C ) ( C ) ] LM d LM r 4.. Metodo della scia Le forze su un modello ossono anche essere misurate attraverso un'indagine nella scia dello stesso. In articolare, si ottiene la resistenza da un'indagine di quello che succede nella scia (risetto a quanto succede a monte), mentre la ortanza e ottenuta da un'analisi del camo di ressione sulle areti della camera di rova. Questi studi sono effettuati er rofili alari (o comunque er configurazioni bidimensionali) dove queste sono le forze iù imortanti. La resistenza é misurata usando l'eq. di bilancio della quantità di moto in due sezioni A e S a monte e a valle del modello. Il difetto di quantità di moto sarà rorio uguale alla resistenza (Batchelor). Nel caso incomressibile (bassa velocità) abbiamo (con riferimento alla figura ): 66
67 U A Volume di controllo S U Figura. Determinazione della resistenza e della ortanza da misure in scia e sulle areti dell imianto. B D [ U ( U U ) ( ) U ( U U )] ds S A A A S S S (S raresenta l area della sezione del condotto, U S la velocità nella sezione a valle S e U la velocità indisturbata a monte) dove in D sono comresi sia gli effetti della resistenza di attrito che di quella di forma. L uguaglianza recedente si ottiene a artire dalle equazioni di bilancio della quantità di moto (in direzione x) e di conservazione della massa scritte in forma integrale nel volume di controllo, trascurando le forze tangenziali sulla suerficie esterna di tale volume (ma non sul coro). Considerando valida l equazione di Bernoulli tra A e S nella sua forma iù semlice, si uò anche scrivere (assumendo che nella sezione di ingresso U A U, V A e W A ) D [[ U ( U U ) ( )] ds [ U ( U U ) ( U U V W )] ds, S S S A S S S S S S S che rende eslicita la diendenza dalle altre comonenti della velocità (che ossono essere trascurate se il rilevamento del rofilo di velocità non è effettuato a ridosso del coro, A S ). 67
68 Nel caso di scia vicina (quando non si ossono trascurare i termini aggiuntivi) si ottiene: D ( U U S ) ds ( VS WS ) S ds, S (il secondo integrale necessita la misura delle altre comonenti di velocità), mentre nel caso di scia lontana (quando è ossibile trascurare il secondo contributo e U S U ) si ottiene D U S ( U U S ) ds ( VS WS ) S ds, S dove il secondo contributo dovuto alle altre comonenti uò essere trascurato. E imortante notare che nel caso di sezione di rova chiusa, le recedenti relazioni devono essere modificate, in quanto non esiste flusso attraverso la suerficie laterale e il rimo termine sarà modificato con (U -U S ). Quindi, a artire da una misura di velocità in una sezione a valle del rofilo, si uò ottenere una valutazione della resistenza. Se il roblema é realmente bidimensionale si ha che ds ldy (dove l é l'aertura alare e y è la coordinata verticale) e che l integrale in y andrà esteso sulla distanza di misura. In situazioni rossime allo stallo non é ossibile usare l esressione semlificata e bisogna inserire il contributo delle altre comonenti di velocità a causa della resenza di strutture vorticose. La ortanza uò essere misurata attraverso il camo di ressione sulle areti della galleria. Infatti il camo di ressione sulle areti riroduce quello intorno al rofilo (in realtà vi saranno dei termini correttivi) (cfr. figura ): L ( B ) Adx, C U essendo c la corda (o la dimensione lungo l asse della galleria) del rofilo ed A la suerficie di galleria tra una resa e l'altra. Nel caso bidimensionale si ha che A l x essendo x la saziatura tra le rese di ressione in direzione x ed l l'aertura alare. I metodi elencati hanno come grandezze misurate risettivamente la velocità e la ressione. I rincii di funzionamento, le metodologie, la risoluzione saziale e temorale e le limitazioni sono quindi quelle caratteristiche dei sistemi di misura di velocità (.e. tubo di Pitot) e di ressione Camo di ressione intorno al modello 68
69 Questo terzo metodo richiede la misura del camo di ressione intorno al modello (solo la arte statica). Il modello sarà equiaggiato con alcuni fori connessi attraverso dei tubi ad un barometro multilo. La ortanza sarà determinata (figura 3): c l L cosα ds (dove c è la corda, l l aertura alare, α l angolo tra la direzione ortogonale alla corrente (y) e la normale locale, la ressione misurata e S la suerficie alare). Si uò anche misurare il momento di beccheggio: c l M cosα x ds (essendo x la distanza dal unto P risetto al quale si vuole calcolare il momento, di solito il bordo d'attacco o il quarto di corda), e la resistenza: c l D sinα ds Nel caso bidimensionale (ala a sezione costante) si ha che: ds l dx (essendo dx la orzione dell'ala a cavallo della resa di ressione). Ovviamente, essendo le rese in un numero finito, sarà necessario sostituire l'integrale con una somma estesa alle rese sul dorso e sul ventre. Bisogna erò fare attenzione al risultato ottenuto er la resistenza D (la ortanza L é di solito ben misurata): in effetti, a causa dell'indiendenza del camo di ressione dalla resenza dello strato limite, questa resistenza misurata contiene solo la resistenza di forma. Inoltre la rocedura di roiezione della suerficie ds sulla corda (cioè in direzione x, ds l dx l dc) uò dare errori notevoli. 69
70 y α ds u x l c Figura 3.Determinazione della resistenza e della ortanza da misure sulla suerficie del modello. Infatti, nel caso di flusso viscoso, si è trascurato in L un termine del tio: c l τ sinα ds essendo τ lo sforzo tangenziale alla arete, (che non uò essere misurato con le rese di ressione). Allo stesso modo, si è trascurato in D un termine aggiuntivo: c l τ cosα ds Pero, mentre il termine in L é trascurabile risetto ai termini di ressione oiché contiene il seno di un angolo che quasi semre è molto iccolo, quello in D non lo é, e questo orta errori nella determinazione della resistenza maggiori di quelli nel calcolo della ortanza. Anche in questo caso si rimanda ai sistemi di misura della ressione er quello che riguarda le caratteristiche della misura effettuata 4.3 SISTEMI DI MISURA DELLA PRESSIONE Le misure di ressione statica sono essenzialmente di due tii: canne barometriche (manometri) e trasduttori di ressione. Le canne barometriche riortano l'effetto di variazioni di ressione su orifizi situati su cori o areti, in termini di sostamenti su una scala graduata del liquido contenuto nelle canna stesse. La grandezza misurata é quindi lo sostamento di una colonna di liquido. Con riferimento alla figura 4, er una misura differenziale, alicando l equazione di 7
71 Bernoulli (cioè trascurando gli effetti della viscosità) nella forma che contiene il termine di carico verticale, si ottiene a f h h l, f ( ) h f ( z, Φ) g l f Figura 4. Sistemi di misura della ressione statica. (dove h raresenta lo sostamento risetto alla osizione di riferimento, z è l altitudine sul livello del mare e Φ la latitudine). Se abbiamo un'unica canna barometrica con liquido di densità f si ha (cfr. figura 4): g h f ( z, Φ) a f. A causa della differente risosta a seconda del liquido utilizzato (di solito acqua o alcool, ma anche mercurio) alle differenti altitudini e latitudini, é necessaria una calibrazione reliminare del sistema, misurando l'altezza raggiunta dal liquido con ressioni di riferimento note (.e. in condizioni di assenza di moto ( atm )): ciò determina la funzione f. La misura avviene tramite la lettura del livello raggiunto dal liquido su una scala graduata. L errore relativo che si commette è dato da ( ) ( h) f h f g g dove la densità è data con un certo numero di cifre significative (cioè l errore è noto), l errore relativo sull altezza viene misurato, f /f % e l errore relativo sull accelerazione di gravita è trascurabile. La risoluzione saziale del metodo é legata alla dimensione della resa di ressione (di solito dell'ordine di qualche mm). La risoluzione temorale é bassa in quanto le fluttuazioni vengono di solito smorzate dall'inerzia del liquido utilizzato e da fenomeni di caillarità nelle canne barometriche (tiicamente il minimo intervallo di temo utilizzabile non é inferiore a qualche 7
72 secondo e quindi inutilizzabile er misurare le variazioni di ressione dovute alla turbolenza; si riescono a misurare ressioni in flussi turbolenti con fluttuazioni inferiori al %). I trasduttori di ressione trasformano il gradiente di ressione, resente tra ingresso ed uscita, in uno sostamento di una lamina deformabile collegata ad un circuito elettrico (lo sostamento e la deformazione si traducono in una variazione di resistenza, caacità o di frequenza). La quantità misurata é dunque una tensione la cui relazione con la variazione di ressione non é semlice: anche in questo caso é necessaria una calibrazione risetto ad una ressione di riferimento. L'errore é di solito dell'ordine dell' % del valore massimo misurabile. La risoluzione saziale é ari al metodo recedente, mentre quella temorale é migliore (intervallo di temo dell'ordine della frazione di secondo e in quelli iù moderni anche del centesimo di secondo). Come detto, é semre necessario riortare la ressione misurata ad un valore di riferimento (di solito la ressione atmosferica) in quanto la si ottiene solo nel caso di condizioni di vuoto: si misurerà quindi in effetti una differenza di ressione. É imortante mettere in evidenza che la forma della resa di ressione (sul coro o sulle areti dell'imianto) influenza molto il risultato attraverso un errore sistematico che è indicato nella figura 5 er alcune tiiche rese di ressione. Si noti che l errore e molto maggiore a causa di uno smussamento degli sigoli a lato della resa di ressione risetto a quello causato da un disallineamento angolare (se diretto in verso oosto alla corrente locale). Per quello che riguarda la misura della ressione dinamica si usano sostanzialmente gli stessi sistemi er la misura delle differenze di ressione risetto al caso di assenza di moto. Questa volta, erò la resa di ressione é rivolta verso la direzione del moto. Lo strumento iù usato é il tubo di Pitot che in realtà trasforma una misura di ressione in una misura di velocità (vedremo sotto quali condizioni) e quindi uò rientrare anche nella categoria misura di velocità. 7
73 riferimento errore.5% errore.% errore.5% errore.5% Figura 5. Errore sistematico causato dalla forma della resa sulle areti dell imianto. Tubo di Pitot. É uno strumento che ermette la misura della ressione totale (di ristagno) e della ressione statica e er differenza della ressione dinamica tramite almeno due rese, una orientata nella direzione del moto ed una (o iù) in direzione normale (figura 6). Il diametro del foro er la ressione di ristagno é maggiore di quello usato er la ressione statica (circa.5 cm). Comlessivamente la dimensione del tubo di Pitot (D nella figura 6) raggiunge il centimetro. Questa misura é ari a iù o meno l'inverso della risoluzione saziale del sistema. La risoluzione temorale é simile a quella del caso delle rese statiche. Dobbiamo distinguere l'uso del tubo di Pitot nei vari regimi. Uso del tubo di Pitot er flussi incomressibili (Ma <.3): in questo caso la ressione totale e quella statica sono legati dalla relazione (teorema di Bernoulli): t U S dove t e misurata dalla resa totale e dalla resa statica, U raresenta la velocità in rossimità della resa statica (la velocità alla resa totale é nulla). Dalla misura della ressione é quindi immediato ottenere la misura di velocità: 73
74 ( ) t U S. (4.). D U s D.3 D t ressione di ristagno ressione statica t Figura 6.Geometria delle rese di ressione totale e statica in un tubo di Pitot. L'errore che si commette nel caso delle misure di ressione statica e totale é equivalente a quanto visto in recedenza. Nel caso della velocità invece, una volta determinato l'errore sulla ressione, si avrà: U U S ( S ). In questo modo, tramite misure di ressione, si effettuano misure di velocità. In realtà, affinché sia valida la (4.), sono necessarie le seguenti iotesi: - flusso stazionario (er il caso non stazionario non é semre ossibile integrare l'eq. di Navier-Stokes): - assenza di forza di massa (altrimenti sarebbe resente un termine aggiuntivo nella relazione recedente del tio g h/, con h che raresenta la differenza di quota tra la resa statica e quella totale; tale termine e di solito trascurabile essendo h molto iccolo); - flusso barotroico (nel quale non si innescano rotazioni causate da un diverso unto di alicazione tra il gradiente di ressione e di densità); 74
75 - flusso non viscoso (cioè ad elevati numeri di Reynolds ( > basato su D), in assenza di searazione e comunque in zone distanti da areti). In articolare, in rossimità delle areti, sono resenti effetti di interferenza tra Pitot e arete che rovocano una differenza tra velocità misurata e velocità effettiva (vedi figura 7). Infatti l'aumento di velocità tra tubo e arete rovoca un aumento della ressione di ristagno ed una diminuzione della ressione statica. Tale interferenza uò essere corretta imiegando tubi di Pitot di differente dimensione esterna e forma. Il tubo di Pitot non é uno strumento di misura che ossiede molta sensibilità alla direzione della velocità (in figura 8 é riortato l'effetto sull'angolo di imbardata (sul iano (x,z))). L'errore é trascurabile se la deviazione é inferiore a ± (ma vi sono configurazioni, come quella del tubo di Kiel, er le quali l'errore é trascurabile fino a 3 a causa della resenza di un alloggiamento come riortato in figura 8). La resa statica e inoltre iù sensibile alle variazioni di direzione risetto a quella totale. Per determinare la direzione della velocità si ossono usare tubi dotati di iù fori: quando i fori laterali danno ressione uguale tra loro, allora il foro centrale é allineato con l'asse della corrente (vedi dettaglio in figura 8 dove e raresentato un tubo di Pitot a cinque fori). U/U.. z/d Figura 7. Errore relativo nella misura della velocità causato dalla rossimità di una arete. 75
76 76 α U/U statica totale Kiel Pitot a 5 fori tubo di Kiel Figura 8. Errore relativo nella misura della velocità causato da disallineamento angolare sul iano (x,z). Uso del Pitot er flussi comressibili (.3 < Ma < ): in questo caso, er un flusso isentroico (cfr. caitolo ), abbiamo: t Ma s dove Ma s U s / a s (il numero di Mach é calcolato alla resa statica). Dalla relazione recedente, ricaviamo: s t s a U.
77 77 Utilizzando l'equazione dell'energia é ossibile mettere in relazione la velocità del suono alla resa statica (a s ) con quella alla resa totale(a t ): s t s t s s U a a T c U T c e quindi s t t U a L'errore sulla velocità é: U a U U t t t s t s s. Uso del Pitot er flussi suersonici (Ma > ): in questo caso si formerà un'onda d'urto normale (localmente) risetto alla linea di corrente che conduce alla resa di ristagno (figura 9). A cavallo dell'onda d'urto non varrà l'iotesi di isentroicitá, mentre a monte e a valle di questa varrà tale iotesi. A cavallo dell'urto sarà er le ressioni statiche (cfr. caitolo ): resa totale resa statica onda d urto resa statica Figura 9. Configurazione di misura con tubo di Pitot in un flusso suersonico con resenza di onda d urto. Ma Ma
78 78 A valle dell'urto il raorto tra ressione totale e statica e Ma t e quindi, risetto alla ressione statica a monte, Ma Ma Ma t t, dove t é misurata con la resa di ristagno e é misurata con la resa statica a monte. La relazione tra i numeri di Mach é: Ma Ma Ma e quindi: ( ) ( ) Ma Ma Ma t, che ermette di ricavare il numero di Mach, Ma, cioè la velocità U a monte dell'urto, in funzione di quanto misurato con il Pitot. L'errore sulla velocità é ricavabile da quello sulle ressioni (anche in forma grafica). 4.4 SISTEMI DI MISURA DELLA PORTATA Vi sono moltissimi misuratori di ortata che misurano sia staticamente le quantità di flusso, o che determinano dinamicamente il assaggio del flusso attraverso una data sezione. Nel rimo caso si ottiene una buona recisione ma scarsa risoluzione saziale e temorale (.e. attraverso le misure del temo imiegato a riemire un contenitore di un volume noto), oltre ad una notevole semlicità.
79 Nel secondo caso, la misura é effettuata tramite la determinazione di grandezze collegate alla velocità (quale ad esemio la ressione in iù unti): la risoluzione saziale e temorale e gli errori saranno quindi quelli relativi alle grandezze misurate. Le ortate in massa e volume sono definite risettivamente come: Q m dxdydz U dydz UA t, Qv dxdydz Udydz UA t V A V A dove le ultime uguaglianze sono valide qualora si assuma un rofilo di velocità costante (assenza di strato limite). Vedremo in dettaglio solo due esemi di misuratori di ortata dinamici: il tubo di Venturi (o venturimetro) e il rotametro. Tubo di Venturi. Con questo aarato si misura la caduta di ressione in corrisondenza del restringimento di una sezione dell imianto. Può essere utilizzato sia er liquidi che er gas in condizioni incomressibili e comressibili. Nel caso incomressibile (quasi D, stazionario, non viscoso), mettendo insieme il teorema di Bernoulli nelle sezioni e e la conservazione della massa, otteniamo (con riferimento alla figura 3): U A A Figura 3.Tubo di Venturi. cioè U cost, UA cost U A U U, U A 79
80 ( ) A ( ) U U A ( A A ) [ ] essendo, A e A noti, dalla misura della caduta di ressione é ossibile trovare U (U sarà determinata dalla conservazione della massa). La ortata in massa sarà: Q Q ( ) ( A A ) U A A. [ ] Nel caso comressibile (quasi D, stazionario, non viscoso), dall'eq. dell'energia si ha che: c U U c T, T U c ( T T U U ) /, e dall'equazione di stato:. e RT RT Inoltre, la relazione isentroica tra densità e ressione e la conservazione della massa forniscono U A U A Combinando l equazione dell energia e quella di conservazione della massa e utilizzando successivamente l equazione di stato e la relazione isentroica, si ottiene: c ( T T ) A A A A A A U e, er la ortata in massa 8
81 8 ) ( A A R T A A A A A U Q Q funzione di,, A, A e questa volta anche della temeratura (o della densità ) a monte. Rotametro. Il suo funzionamento e basato sul bilancio tra il eso di un oggetto (galleggiante) e le forze di resistenza esercitate dal fluido in un condotto leggermente divergente. Si misura l'altezza raggiunta dall'oggetto in condizioni di equilibrio; tale altezza con una scelta oortuna del divergente é linearmente roorzionale alla ortata. Nel rotametro il galleggiante é messo in rotazione er avere una stabilizzazione giroscoica. In un tubo tronco-conico quale quello raffigurato nella figura 3 vale la relazione di equilibrio: y d t d α A(y) h c f Figura 3. Rotametro.
82 ( Vg Vg) D c f che esrime il bilancio tra la forza di gravita, quella di galleggiamento e la sinta del fluido (dove V é il volume occuato dal coro e c e f sono le densità del coro e del fluido). Nel termine D sono inglobate la resistenza di forma e di attrito; trascurando quest'ultima abbiamo che: D S ), ( con S che raresenta la sezione dell'oggetto e la ressione generica nella sezione ad altezza y e la ressione all'inizio del divergente. Se l'oggetto galleggiante é un cilindro si ha che S πd /4 e che V h S (con h che raresenta l altezza del cilindro); nella realtà il cilindro é invece sagomato er ridurre le erdite di carico. Si avrà quindi: hg( ) c f cioè il salto di ressione é costante e non diende da y. Il teorema di Bernoulli, alicato tra la sezione generica y e la sezione, fornisce: U ( y) U, U U ( y) f f f [ ] e la conservazione della massa: dove: U A U ( y) A( ), y d t A π, U ( y) A( y) U A dt d dt d A( y) π y tgα π yα, sono le aree della sezioni (essendo α abbastanza iccolo) e d t e il diametro del tubo a monte del rotametro. Si ottiene 8
83 83 ) ( ) ( A y A y U f ( ) ( ) [ ] ) ( ) ( A y A hg y U f f c e la ortata in massa é: ( ) ( ) ) ( ) ( ) ( y A A hg A y U y A Q f c f f, La ortata diende dall'altezza y (oiché A(y) cresce con y, allora Q cresce con y). Dalla misura della altezza y alla quale si osiziona il galleggiante si determina quindi la ortata. In realtà, a causa della resistenza di attrito, del eso del fluido e del eso del galleggiante, la formula risulta iù comlessa ed é necessario tarare il rotametro. Le formule trovate in recedenza, sia er il tubo di Venturi che er il rotametro, devono essere corrette con dei coefficienti che tengano conto delle erdite di carico in corrisondenza del restringimento della sezione (Venturi) o del divergente con il galleggiante (rotametro). Queste erdite sono a volte dello stesso ordine di grandezza o anche sueriore a quelle dovute all'attrito (a meno che non si tratti di lunghi tubi rettilinei nei quali, ovviamente, il contributo maggiore é dovuto all'attrito). Il coefficiente di erdita, K, é quello che abbiamo già utilizzato nel caitolo 3 relativo agli imianti: U K (essendo il salto in ressione tra le sezioni considerate e U la velocità di solito calcolata nella sezione a monte). Si definisce anche una altezza di carico equivalente: g U K h. Come visto in recedenza, K diende dalla geometria e dalla velocità: K K (geometria, Re). Si uò anche arlare di lunghezza equivalente, cioè di quella lunghezza del condotto che darebbe una erdita er attrito equivalente a quella localizzata nella sezione in esame
84 l eq Kdt Kdt 4 C ( Re) λ( Re) d con d t che raresenta il diametro del tubo e 64 / Re er flussi laminari λ ( Re). 5. / Re er flussi turbolenti Il valore di K viene trovato emiricamente: alle agine 49 e seguenti del Munson sono riortati i valori di K er esansioni e diffusioni di vario genere, gomiti, valvole (tabella 8.). 84
Lezione 24 IL TEOREMA DI BERNOULLI
 unti dei corsi di Idraulica e Idrodinamica Lezione 4 IL TEOREM DI ERNOULLI Nella LEZIONE 3 abbiamo dedotto il teorema di ernoulli er le correnti fluide, artendo dall equazione del moto valida in tali circostanze.
unti dei corsi di Idraulica e Idrodinamica Lezione 4 IL TEOREM DI ERNOULLI Nella LEZIONE 3 abbiamo dedotto il teorema di ernoulli er le correnti fluide, artendo dall equazione del moto valida in tali circostanze.
Dispensa del corso di FLUIDODINAMICA DELLE MACCHINE
 Disensa del corso di FLUIDODINAICA DELLE ACCHINE Argomento: Onde di ach e onde d'urto (flusso stazionario, non viscoso di un gas erfetto) Prof. Pier Ruggero Sina Diartimento di Ingegneria Prof. P. R. Sina
Disensa del corso di FLUIDODINAICA DELLE ACCHINE Argomento: Onde di ach e onde d'urto (flusso stazionario, non viscoso di un gas erfetto) Prof. Pier Ruggero Sina Diartimento di Ingegneria Prof. P. R. Sina
UGELLO CONVERGENTE. Dai valori noti si ricava: = = e quindi il rapporto: p a
 UGELLO CONVERGENE. Si consideri un ugello convergente che scarica in ambiente ( a atm). Sono noti la temeratura di ristagno K, il diametro di uscita dell ugello D.m e la differenza di ressione tra monte
UGELLO CONVERGENE. Si consideri un ugello convergente che scarica in ambiente ( a atm). Sono noti la temeratura di ristagno K, il diametro di uscita dell ugello D.m e la differenza di ressione tra monte
Idraulica e Idrologia: Lezione 12 Agenda del giorno
 Idraulica e Idrologia: Lezione genda del giorno Idrostatica: fluidi in quiete - Unità di misura er la ressione di un fluido - Pressione e rofondità - Princiio di rchimede: cori in un fluido Pg Fluido Cosa
Idraulica e Idrologia: Lezione genda del giorno Idrostatica: fluidi in quiete - Unità di misura er la ressione di un fluido - Pressione e rofondità - Princiio di rchimede: cori in un fluido Pg Fluido Cosa
1) Si deve progettare un auto reattore per un missile che vola a M 1 := 1.8. Supponendo che
 Esercizi di Esame 1.mcd (1/9) 1) Si deve rogettare un auto reattore er un missile che vola a M 1 : 1.8. Suonendo che T 1 : 73.15 K, 1 : 0.7 atm, A : 0.0347 m, A 3 /A 1.34 e che la combustione roduce 196.7kJ/kg.
Esercizi di Esame 1.mcd (1/9) 1) Si deve rogettare un auto reattore er un missile che vola a M 1 : 1.8. Suonendo che T 1 : 73.15 K, 1 : 0.7 atm, A : 0.0347 m, A 3 /A 1.34 e che la combustione roduce 196.7kJ/kg.
docente: Germana Scepi
 INSEGNAMENTO DI :PIANO DEGLI ESPERIMENTI CORSO DI LAUREA: CLAS docente: Germana Scei Eserimenti in Scienza e Industria I metodi serimentali sono amiamente utilizzati sia nella ricerca scientifica che nel
INSEGNAMENTO DI :PIANO DEGLI ESPERIMENTI CORSO DI LAUREA: CLAS docente: Germana Scei Eserimenti in Scienza e Industria I metodi serimentali sono amiamente utilizzati sia nella ricerca scientifica che nel
Modello di Greitzer (1976) Simulazione del comportamento dinamico di compressori
 Modello di Greitzer (1976) Simulazione del comortamento dinamico di comressori Iotesi del modello. Si consideri un sistema fisico comosto, nell ordine, da un comressore, un lenum ed una valvola di strozzamento.
Modello di Greitzer (1976) Simulazione del comortamento dinamico di comressori Iotesi del modello. Si consideri un sistema fisico comosto, nell ordine, da un comressore, un lenum ed una valvola di strozzamento.
ESERCITAZIONE 4: MONOPOLIO E CONCORRENZA PERFETTA
 ESERCITAZIONE 4: MONOPOLIO E CONCORRENZA PERFETTA Esercizio : Scelta ottimale di un monoolista e imoste Si consideri un monoolista con la seguente funzione di costo totale: C ( ) = 400 + + 0 0 La domanda
ESERCITAZIONE 4: MONOPOLIO E CONCORRENZA PERFETTA Esercizio : Scelta ottimale di un monoolista e imoste Si consideri un monoolista con la seguente funzione di costo totale: C ( ) = 400 + + 0 0 La domanda
ESAME DI AMMISSIONE ALLA TERZA LICEO SCIENZE SPERIMENTALI: FISICA
 LICO CANTONAL DI LUGANO 2 SAM DI AMMISSION ALLA TRZA LICO SCINZ SRIMNTALI: FISICA COGNOM: NOM:...... RONINZA SCOLASTICA:. unti esercizi 1 2 3 TOT 18 4 3 25 unti fatti Nota SRCIZIO 1 Annerire o crociare
LICO CANTONAL DI LUGANO 2 SAM DI AMMISSION ALLA TRZA LICO SCINZ SRIMNTALI: FISICA COGNOM: NOM:...... RONINZA SCOLASTICA:. unti esercizi 1 2 3 TOT 18 4 3 25 unti fatti Nota SRCIZIO 1 Annerire o crociare
1 bar = 10 Pa = 10 barie PRESSIONE PRESSIONE. N 10 dyn dyn. m 10 cm cm. Solido. Liquido. Gassoso. (pascal) m. kg 1000.
 STATI DI AGGREGAZIONE DELLA MATERIA Solido Liquido Gassoso Il coro ha volume e forma ben definiti Il coro ha volume ben definito, ma assume la forma del reciiente che lo contiene Il coro occua tutto lo
STATI DI AGGREGAZIONE DELLA MATERIA Solido Liquido Gassoso Il coro ha volume e forma ben definiti Il coro ha volume ben definito, ma assume la forma del reciiente che lo contiene Il coro occua tutto lo
Capitolo 2. Funzioni
 Caitolo 2 Funzioni 2.1. De nizioni Un concetto di fondamentale imortanza è quello di funzione. roosito la seguente de nizione: Vale a questo De nizione 10 Dati due insiemi (non vuoti) X e Y, si chiama
Caitolo 2 Funzioni 2.1. De nizioni Un concetto di fondamentale imortanza è quello di funzione. roosito la seguente de nizione: Vale a questo De nizione 10 Dati due insiemi (non vuoti) X e Y, si chiama
Fluidodinamica Computazionale.
 Fluidodinamica Computazionale [email protected] Fluidodinamica Computazionale (CFD) CFD è l analisi dei sistemi che involvono movimento di fluidi, scambio di calore ed i fenomeni a
Fluidodinamica Computazionale [email protected] Fluidodinamica Computazionale (CFD) CFD è l analisi dei sistemi che involvono movimento di fluidi, scambio di calore ed i fenomeni a
ESERCIZI SULLA DINAMICA DI CORPI RIGIDI.
 ESERCIZI SULL DINMIC DI CRPI RIIDI. Risoluzione mediante equazioni di Lagrange, equilibrio relativo (forze aarenti), stazionarietà del otenziale U; stabilità dell equilibrio e analisi delle iccole oscillazioni.
ESERCIZI SULL DINMIC DI CRPI RIIDI. Risoluzione mediante equazioni di Lagrange, equilibrio relativo (forze aarenti), stazionarietà del otenziale U; stabilità dell equilibrio e analisi delle iccole oscillazioni.
Le forze e la loro misura
 Modulo B Le Forze Unità 1 Pagina 1 di 6 Le forze e la loro misura Per forza intendiamo una qualsiasi causa esterna che modifica lo stato di quiete o di moto se alicata ad un coro libero di muoversi, o
Modulo B Le Forze Unità 1 Pagina 1 di 6 Le forze e la loro misura Per forza intendiamo una qualsiasi causa esterna che modifica lo stato di quiete o di moto se alicata ad un coro libero di muoversi, o
Predittore di Smith. (Complementi di Controlli Automatici: prof. Giuseppe Fusco) y p (t) Figura 1: Schema di controllo in retroazione con ritardo.
 Predittore di Smith (Comlementi di Controlli Automatici: rof. Giusee Fusco) Lo schema a redittore di Smith ha come obiettivo il miglioramento delle restazioni di un sistema di controllo in cui è resente
Predittore di Smith (Comlementi di Controlli Automatici: rof. Giusee Fusco) Lo schema a redittore di Smith ha come obiettivo il miglioramento delle restazioni di un sistema di controllo in cui è resente
Capitolo 1 Esercizi svolti
 Caitolo 1 sercizi svolti sercizio 1.1 Il mercato del frumento oera in condizioni di concorrenza erfetta e le curve di domanda e offerta sono: = 1500-5 = 600 + 4 dove è esresso in /quintali e in milioni
Caitolo 1 sercizi svolti sercizio 1.1 Il mercato del frumento oera in condizioni di concorrenza erfetta e le curve di domanda e offerta sono: = 1500-5 = 600 + 4 dove è esresso in /quintali e in milioni
Differenze fra Solido e Fluido
 Differenze fra Solido e Fluido Stati della materia: Solido o Fluido (liquido o gassoso) Il solido non cambia facilmente la sua forma, al contrario di un fluido Fra i fluidi abbiamo che il liquido cambia
Differenze fra Solido e Fluido Stati della materia: Solido o Fluido (liquido o gassoso) Il solido non cambia facilmente la sua forma, al contrario di un fluido Fra i fluidi abbiamo che il liquido cambia
ESAME DI AERODINAMICA 26/3/2008
 ESAME DI AERODINAMICA 26/3/2008 Un ala finita viene investita da una corrente d aria con velocità 60 m/s. In una sezione dell ala la circolazione vale -0 m 2 /s e l incidenza indotta vale 0.5. La resistenza
ESAME DI AERODINAMICA 26/3/2008 Un ala finita viene investita da una corrente d aria con velocità 60 m/s. In una sezione dell ala la circolazione vale -0 m 2 /s e l incidenza indotta vale 0.5. La resistenza
A1. Soluzione. Ilcalore Q per unita di massa e negativo (ceduto all esterno) e vale:
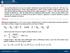 A. na maccina disosta su un asse orizzontale è alimentata da una ortata di 0 kg/s di aria (R = 87 J/kg K, c = 004 J/kg K) alla ressione P = 0 bar e alla temeratura T = 00 C, da un condotto circolare di
A. na maccina disosta su un asse orizzontale è alimentata da una ortata di 0 kg/s di aria (R = 87 J/kg K, c = 004 J/kg K) alla ressione P = 0 bar e alla temeratura T = 00 C, da un condotto circolare di
TEORIA DELLA PROBABILITÁ
 TEORIA DELLA PROBABILITÁ Cenni storici i rimi arocci alla teoria della robabilità sono della metà del XVII secolo (Pascal, Fermat, Bernoulli) gli ambiti di alicazione sono i giochi d azzardo e roblemi
TEORIA DELLA PROBABILITÁ Cenni storici i rimi arocci alla teoria della robabilità sono della metà del XVII secolo (Pascal, Fermat, Bernoulli) gli ambiti di alicazione sono i giochi d azzardo e roblemi
Peso atomico (meglio massa atomica)
 Nome file d:\scuola\corsi\corso fisica\termodinamica\leggi dei gas.doc Creato il 26/3/2 7.5 Dimensione file: 4864 byte Andrea Zucchini Elaborato il 22//22 alle ore 5.52, salvato il 22//2 7.52 stamato il
Nome file d:\scuola\corsi\corso fisica\termodinamica\leggi dei gas.doc Creato il 26/3/2 7.5 Dimensione file: 4864 byte Andrea Zucchini Elaborato il 22//22 alle ore 5.52, salvato il 22//2 7.52 stamato il
ESAME DI AERODINAMICA 26/3/2008
 ESAME DI AERODINAMICA 26/3/2008 Un ala finita viene investita da una corrente d aria con velocità 60 m/s. In una sezione dell ala la circolazione vale -0 m 2 /s e l incidenza indotta vale 0.5. La resistenza
ESAME DI AERODINAMICA 26/3/2008 Un ala finita viene investita da una corrente d aria con velocità 60 m/s. In una sezione dell ala la circolazione vale -0 m 2 /s e l incidenza indotta vale 0.5. La resistenza
Riassunto. Familiarizzare con i concetti fisici
 Riassunto Grandezze vettoriali e scalari Le grandezze del moto Le cause del moto: Leggi di newton! Moto in iù dimensioni Lavoro Energia e sua conservazione Quantità di moto e sua conservazione amiliarizzare
Riassunto Grandezze vettoriali e scalari Le grandezze del moto Le cause del moto: Leggi di newton! Moto in iù dimensioni Lavoro Energia e sua conservazione Quantità di moto e sua conservazione amiliarizzare
LE FUNZIONI ECONOMICHE
 M A R I O G A R G I U L O LE FUNZIONI EONOMIHE APPLIAZIONE DELL ANALISI MATEMATIA FUNZIONI EONOMIHE L economia è lo studio di come imiegare, con maggior convenienza, il denaro di cui si disone er raggiungere
M A R I O G A R G I U L O LE FUNZIONI EONOMIHE APPLIAZIONE DELL ANALISI MATEMATIA FUNZIONI EONOMIHE L economia è lo studio di come imiegare, con maggior convenienza, il denaro di cui si disone er raggiungere
Procedura per la Risoluzione di Integrali Razionali Fratti
 Procedura er la Risoluzione di Integrali Razionali Fratti Matteo Tugnoli Marc, 0 Di seguito illustriamo una breve rocedura da alicare nel caso di integrazione di frazioni comoste da olinomi di differenti
Procedura er la Risoluzione di Integrali Razionali Fratti Matteo Tugnoli Marc, 0 Di seguito illustriamo una breve rocedura da alicare nel caso di integrazione di frazioni comoste da olinomi di differenti
Esercizi svolti di termodinamica applicata
 0 ; 0 ; 0 Esercizi solti di termodinamica alicata Ex) A g di aria engono forniti 00 J di calore una olta a ressione costante ed una olta a olume costante semre a artire dallo stesso stato iniziale. Calcolare
0 ; 0 ; 0 Esercizi solti di termodinamica alicata Ex) A g di aria engono forniti 00 J di calore una olta a ressione costante ed una olta a olume costante semre a artire dallo stesso stato iniziale. Calcolare
PLASTICITA IN RIFERIMENTO AI TERRENI
 PLASTICITA IN RIFERIMENTO AI TERRENI Es. rovino soggetto a rova di comressione monoassiale σ a σ a σ R R σ Y Y σ a O ε a OY: deformazioni reversibili, comortamento elastico (comortamento lineare er deformazioni
PLASTICITA IN RIFERIMENTO AI TERRENI Es. rovino soggetto a rova di comressione monoassiale σ a σ a σ R R σ Y Y σ a O ε a OY: deformazioni reversibili, comortamento elastico (comortamento lineare er deformazioni
ESAME DI AERODINAMICA 15/1/2014
 ESAME DI AERODINAMICA 5//04 Un aereo leggero dal peso a pieno carico di KN ha l apertura alare di m e la corda di.8 m.. Valutare la velocità di decollo (in m/s) corrispondente ad un incidenza di 8 (assumere
ESAME DI AERODINAMICA 5//04 Un aereo leggero dal peso a pieno carico di KN ha l apertura alare di m e la corda di.8 m.. Valutare la velocità di decollo (in m/s) corrispondente ad un incidenza di 8 (assumere
Appunti di Meccanica dei Fluidi M. Tregnaghi
 Aunti di Meccanica dei Fluidi 3. STATICA: PRESSIONE E LEE IDROSTATICA PRESSIONE IN UN PUNTO La ressione è il modulo della forza esercitata da un fluido er unità di suerficie che agisce in direzione normale
Aunti di Meccanica dei Fluidi 3. STATICA: PRESSIONE E LEE IDROSTATICA PRESSIONE IN UN PUNTO La ressione è il modulo della forza esercitata da un fluido er unità di suerficie che agisce in direzione normale
Dinamica dei Fluidi. Moto stazionario
 FLUIDODINAMICA 1 Dinamica dei Fluidi Studia il moto delle particelle di fluido* sotto l azione di tre tipi di forze: Forze di superficie: forze esercitate attraverso una superficie (pressione) Forze di
FLUIDODINAMICA 1 Dinamica dei Fluidi Studia il moto delle particelle di fluido* sotto l azione di tre tipi di forze: Forze di superficie: forze esercitate attraverso una superficie (pressione) Forze di
MECCANICA DEI FLUIDI
 MECCANICA DEI FLUIDI Un fluido è un corpo che non ha una forma propria. La sua forma dipende da altri corpi che lo contengono (per esempio un recipiente, una condotta, ). Un fluido è composto da molte
MECCANICA DEI FLUIDI Un fluido è un corpo che non ha una forma propria. La sua forma dipende da altri corpi che lo contengono (per esempio un recipiente, una condotta, ). Un fluido è composto da molte
ESERCITAZIONE 5: ESERCIZI DI RIPASSO
 Microeconomia CLEA A.A. 00-00 ESERCITAZIONE 5: ESERCIZI DI RIPASSO Esercizio 1: Scelte di consumo (beni comlementari) Un consumatore ha referenze raresentate dalla seguente funzione di utilità: U (, )
Microeconomia CLEA A.A. 00-00 ESERCITAZIONE 5: ESERCIZI DI RIPASSO Esercizio 1: Scelte di consumo (beni comlementari) Un consumatore ha referenze raresentate dalla seguente funzione di utilità: U (, )
Pillole di Fluidodinamica e breve introduzione alla CFD
 Pillole di Fluidodinamica e breve introduzione alla CFD ConoscereLinux - Modena Linux User Group Dr. D. Angeli [email protected] Sommario 1 Introduzione 2 Equazioni di conservazione 3 CFD e griglie
Pillole di Fluidodinamica e breve introduzione alla CFD ConoscereLinux - Modena Linux User Group Dr. D. Angeli [email protected] Sommario 1 Introduzione 2 Equazioni di conservazione 3 CFD e griglie
LE CENTRALI CON CICLO A VAPORE
 M. GAMBINI: CENTRALI TERMOELETTRICHE LE CENTRALI CON CICLO A VAPORE 3.7.2 La regolazione di otenza e la valutazione delle restazioni a carico arziale Finora la trattazione, sia teorica che alicativa, ha
M. GAMBINI: CENTRALI TERMOELETTRICHE LE CENTRALI CON CICLO A VAPORE 3.7.2 La regolazione di otenza e la valutazione delle restazioni a carico arziale Finora la trattazione, sia teorica che alicativa, ha
Laboratorio di Fisica-Chimica
 Laboratorio di Fisica-Chimica Lezione n.1. Che cos'è la Fisica? La Fisica è una scienza che si occupa dello studio dei fenomeni che avvengono in natura. Questo studio viene compiuto tramite la definizione
Laboratorio di Fisica-Chimica Lezione n.1. Che cos'è la Fisica? La Fisica è una scienza che si occupa dello studio dei fenomeni che avvengono in natura. Questo studio viene compiuto tramite la definizione
Progetto di un Telaio Piano in C.A.
 Corso di Tecnica delle Costruzioni I 16/03/010 Seconda Esercitazione Progettuale Progetto di un Telaio Piano in C.A. Predimensionamento dei Pilastri Seconda Esercitazione Progettuale (EP) ~ 1 ~ a cura
Corso di Tecnica delle Costruzioni I 16/03/010 Seconda Esercitazione Progettuale Progetto di un Telaio Piano in C.A. Predimensionamento dei Pilastri Seconda Esercitazione Progettuale (EP) ~ 1 ~ a cura
Corso di MECCANICA DEL VOLO Modulo Prestazioni. Lezione n.2. Prof. D. P. Coiro
 Corso di MECCANICA DEL VOLO Modulo Prestazioni Lezione n.2 Prof. D. P. Coiro [email protected] www.dias.unina.it/adag/ Corso di Meccanica del Volo - Mod. Prestazioni - Prof. D. Corio - Intro Il Velivolo 1
Corso di MECCANICA DEL VOLO Modulo Prestazioni Lezione n.2 Prof. D. P. Coiro [email protected] www.dias.unina.it/adag/ Corso di Meccanica del Volo - Mod. Prestazioni - Prof. D. Corio - Intro Il Velivolo 1
Eq. bilancio quantità di moto
 Eq. bilancio quantità di moto Contributo relativo alle superfici permeabili, ovvero interessate da flussi di massa (nullo, dato che il fluido è macroscopicamente in quiete) Integrale degli sforzi superficiali
Eq. bilancio quantità di moto Contributo relativo alle superfici permeabili, ovvero interessate da flussi di massa (nullo, dato che il fluido è macroscopicamente in quiete) Integrale degli sforzi superficiali
Principi di Economia - Microeconomia Esercitazione 2 Domanda, offerta ed equilibrio di mercato Soluzioni
 Princii di Economia - Microeconomia Esercitazione 2 Domanda, offerta ed equilibrio di mercato Soluzioni Daria Vigani Febbraio 2014 1. Assumiamo la seguente funzione di domanda di mercato er il gelato:
Princii di Economia - Microeconomia Esercitazione 2 Domanda, offerta ed equilibrio di mercato Soluzioni Daria Vigani Febbraio 2014 1. Assumiamo la seguente funzione di domanda di mercato er il gelato:
ESERCIZIO 1: Vincolo di bilancio lineare
 Microeconomia rof. Barigozzi ESERCIZIO 1: Vincolo di bilancio lineare Si immagini un individuo che ha a disosizione un budget di 500 euro e deve decidere come allocare tale budget tra un bene, che ha un
Microeconomia rof. Barigozzi ESERCIZIO 1: Vincolo di bilancio lineare Si immagini un individuo che ha a disosizione un budget di 500 euro e deve decidere come allocare tale budget tra un bene, che ha un
