Lavoro delle forze nei fluidi
|
|
|
- Mauro Chiari
- 9 anni fa
- Visualizzazioni
Transcript
1 aoro delle forze nei fluidi EC P G att est S S C D C D l t h EC P G P S gh t P S gh ρ t ρ B B l t ( P P ) P h ( ρgh ρgh ) - EP att est ( P P ) + ( ρgh ρgh ) + + ρ ρ att est EP + P + + EC
2 Fluidi ideali: Teorea di Bernoulli P G att est EC + att est ( P P ) + ( ρgh ρgh ) + ρ ρ 0 P ρg - P ρg + h h + g g 0 P P + h + + h + ρg g ρg g costante
3 Dinaica dei fluidi reali: iscosità In un condotto di lunghezza 0 F 4πη a M M η coefficiente di iscosità. Diinuisce per T Parete Diensioni [η] [ - ][M][T - ] Unità di isura: [SI] poiseuille; poiseuille N. s/ [CGS] poise (P); P dina. s/c Fattore di ragguaglio poiseuille 0 P sostanza acqua sangue η 0.0 P 0.04 P
4 Fluidi reali: laoro delle forze di attrito P EP att est att 8η 4 πr R resistenza Q EC RQ Per un condotto cilindrico a sezione costante: In un condotto di lunghezza F 8η Q 4 πr 4πη a M 8 EP η Q + est P + + πr 4 EC S r
5 Fluidi reali: legge di Poiseuille 8 EP η Q + est P + + πr 4 EC 8 η πr Q P P P 4 S r 8η P P πr 4 Q legge di Poiseuille
6 Pressione e elocità del sangue e olue dei asi Hg aorta arterie arteriole capillari enule ene caa pressione elocità c/s olue c
7 PPICZIONI
8 Da un aso sanguigno con sezione S di area di 8 si diraano 4 asi più piccoli di sezioni S uguali tra loro. Quale de essere l area di ciascuna di tali sezioni perché la elocità del sangue sia la stessa che nel aso grande? 4S S Un liquido scorre in un condotto di raggio r,5 c, che si suddiide in N condotti tutti uguali. Sapendo che la elocità del liquido nel condotto principale è c/s e che la portata (flusso) di ciascuna diraazione è Q 78,5 c 3 /s, calcolare N. N 3 πr NQ N3.4x6.5x/78.53
9 neurisa e stenosi S S S >S costanza della portata: S < S P P legge di Bernoulli: + ρg g ρg + P g >P Pertanto l aneurisa tende a peggiorare. nalogaente in corrispondenza a un restringiento (stenosi) la elocità auenta e la pressione diinuisce. a stenosi tende a peggiorare.
10 Esepio: Un arteria di raggio r,5 è parzialente bloccata da una placca. Nella regione ostruita il raggio effettio è r,8 e la elocità edia del sangue è 50 c/s. Calcolare la elocità edia del sangue nella regione non ostruita. Soluzione: Chiaando S e S le sezioni dell arteria rispettiaente nelle regione non ostruita e ostruita (, 8 0 ) (, 5 0 ) S πr S S 50 5, 9 S πr c s. Calcolare la differenza tra le pressioni nelle due sezioni Per la legge di Bernoulli: ρ P P 68 ( ) ( ) dine/c 0, Hg
11 Circolazione del sangue Possiao calcolare la caduta di pressione nel sangue quando attraersa un capillare. Un capillare ha una lunghezza tipica di, raggio r. 0-6, <> 0,33/s e η N. s/. P P 8η 8η Q 4 4 πr πr πr P P , N 3 0, ,5 Hg
12 Esepio: ungo un tratto di un condotto cilindrico, inclinato di 30 rispetto ad un piano orizzontale, scorre un liquido ideale in condizione di oto stazionario. Si deterini la differenza di pressione tra due sezioni del condotto che distano 80 c se la densità del liquido è ρ g/c 3. Se la sezione del condotto andasse restringendosi erso l alto, tale differenza di pressione sarebbe aggiore,inore o uguale rispetto al alore 30 deterinato? h Soluzione: ( P P ) + ( ρgh ρgh ) + ρ ρ 0 Il condotto è cilindrico Si può applicare il teorea di Bernoulli h ( P P ) ρg( h h ) 3900 ρg senθ 980 dine/c 9, 4Hg 80 0, 5
13 Esepio: ungo un tratto di un condotto cilindrico erticale, di diaetro d0 e lungo 0, scorre acqua in condizioni di oto stazionario in regie lainare. a elocità edia dell acqua S B in corrispondenza della sezione in basso (S )è <> /s. (a)quanto ale la differenza di pressione P -P B se il liquido scorre erso l alto? (b) Quanto ale la differenza di pressione se il liquido scorre erso il basso? (η 0,0 poise, ρ g/c 3 ). Soluzione: (a) (b) P EP P -RQ - 8η RQ πr 3000 dine/c 4 πr EP 5 ρg ,8 0 dine/c 5 P P RQ + ρg 0, 0 dine/c B P P P RQ + ρg 9,48 0 B 5 S dine/c h B h
14 ungo un tratto erticale di un condotto cilindrico di diaetro D0 scorre erso il basso acqua in condizioni di oto stazionario in regie lainare con elocità edia 50 c/s nella sezione in basso. Qual è la differenza di pressione tra due sezioni del condotto che distano 0? Il coefficiente di iscosità dell'acqua è pari a 0,0 poise e la sua densità è d g/c3 EP P -RQ - h B S B S h B RQ 8η πr 4 πr 4000 dine/c EP 5 ρg ,8 0 dine/c P P P RQ + ρg 9,76 0 P PB 73, Hg 5 dine/c
15 Esepio: Dato il condottoin figura percorso da un fluido ideale, tracciare un grafico che rappresenti in odo qualitatio l andaento della pressione lungo il condotto edesio. Fare questo partendo dalla sezione - ed arriando alla sezione E-E, attraerso le sezioni B-B, C-C e D-D, con S S B S C S D. S S B S C S D S E Soluzione: P + ρgh + ρ costante S costante > B C D E P E P C P B C D E
16 aoro del cuore: Calcolare il laoro cardiaco di ogni pulsazione per un soggetto sotto sforzo in cui la frequenza cardiaca è di 80 pulsazioni al inuto, il olue pulsatorio di 60 c 3, la pressione edia del entricolo sinistro è di 50 Hg e la pressione nella ena caa è uguale a zero. Deterinare la potenza cardiaca edia. Soluzione: Il laoro cardiaco copiuto nel corso di una pulsazione è: ( ) ( 3 50 Hg c ) P 60 7 ( ) 60 3, 0 erg 3,J Questo laoro iene eseguito nel tepo di (60/80) s 0,33 s. W P P Q t t 3, W 9, 7 watt. 0, 33
17 Esepio: Calcolare la resistenza del circolo sisteico sapendo che la gittata cardiaca (portata) ale 6 l/in, la pressione edia nell aorta è di 90 Hg e la pressione nell atrio destro è di 6 Hg. Espriere il risultato in unità [cgs]. Si supponga di oler auentare la gittata cardiaca di 4 olte, senza con ciò iporre al cuore un auento di potenza. Perché ciò accada dee auentare il raggio edio delle arteriole. Supponendo che il resto del circolo presenti resistenza nulla, di quanto dee auentare questo raggio? Soluzione: R.x0 3 dine. s/c 5 R R/6 r r
18 Esepio: Se la iscosità del sangue auenta del 0%, di quanto dee auentare la potenza del cuore per antenere costante la gittata cardiaca? Soluzione: RQ + W Q 0 W RQ Per un condotto cilindrico: 8η R π 4 r W', W
19 Esepio: Tre tubi antincendio sono collegati ad un idrante antincendio. Ciascun tubo ha il raggio r di,0 c. acqua entra nell idrante attraerso un tubo il cui raggio è R8,0 c. In questo tubo l acqua ha la elocità di 3 /s. a) Si troi la elocità dell acqua in ciascuno dei 3 tubi piccoli. b) Quanti litri di acqua engono riersati su un incendio in un ora? Soluzione: Q S cost R r a) b) πr 3πr πr 3πr c/s 6 /s 3 4 ol. πr t 3, litri
20 Esepio: Un liquido fluisce lungo un tubo orizzontale il cui raggio è r,0 c. Il tubo si piega lungo la erticale ascendente per un tratto 0 e si unisce ad un altro tubo orizzontale il cui raggio è R 4,0 c. Si deterini la portata che antiene uguali le pressioni nei due tubi orizzontali. Soluzione: Q S S B B r P PB + ρg B B g h ( ) ( h h + ρ ) 0 R Q πr πr B B 4 r ( ) ( h + 6 ) g 5 B 5 0 g 5 B 9, 8 0 3, 07 3, 7/s R
21 Esepio: Un tratto di aso sanguigno di sezione costante (lunghezza l 0 c e raggio r ) è disposto coe in figura. a differenza di quota tra S e S B è h0c. Si deterini la differenza di pressione P -P B tra le pressioni eatiche esistenti in corrispondenza delle sezioni S e S B se il sangue scorre nel erso indicato con elocità edia 4 c/s in corrispondenza della sezione S. Il coefficiente di iscosità del sangue è η0,04 poise e la sua densità è ρ g/c 3. Soluzione: P EP att est EC S S B h P -P B ( ) dine/c 9,7Hg Se il sangue scorresse erso il basso, si arebbe: P -P B ( ) dine/c 5,43Hg
22 - Una grande arteria ha un raggio di 4 e il sangue i scorre con una portata di.5 c 3 /s. Calcolare: a) la elocità edia del sangue, b) la caduta di pressione, in Hg, in un tratto dell arteria lungo 0 c quando l indiiduo è disteso. (η 0.04 poise) (a:.98 c/s, b: P0.05 Hg). - aorta di un indiiduo ha un raggio di.4 c. Calcolare la resistenza e la caduta di pressione in un tratto lungo 0 c se la portata e di 00 c 3 /s (R5.3 unità CGS, P0.04 Hg). - Un aso sanguigno di raggio R si raifica in nuerosi asi di raggio rr/6. Se la elocità edia del sangue nei asi più piccoli è un terzo di quella del aso più grande, quanti sono i asi secondari? (n08). - Calcolare la pressione idrostatica esercitata da una colonna di sangue alta 80 c. (densità del sangue.06g/c 3 ) (P63.6 Hg).
LEZIONE 17 ESERCIZI-FLUIDI
 LEZIONE 17 ESERCIZI-FLUIDI Qual è, in at, la pressione a 20 di profondità? (densità dell acqua = 1,0 gr/c ) P = 2 at. Sapendo che la densità del ghiaccio è 0,92 g/c e quella dell acqua di are 1,0 g/c,
LEZIONE 17 ESERCIZI-FLUIDI Qual è, in at, la pressione a 20 di profondità? (densità dell acqua = 1,0 gr/c ) P = 2 at. Sapendo che la densità del ghiaccio è 0,92 g/c e quella dell acqua di are 1,0 g/c,
La circolazione del sangue
 La circolazione del sangue elemento caratteristica approssimazione sangue fluido reale e non omogeneo fluido reale omogeneo moto pulsatile (valvola aortica) stazionario condotti distensibili rigidi Fisica
La circolazione del sangue elemento caratteristica approssimazione sangue fluido reale e non omogeneo fluido reale omogeneo moto pulsatile (valvola aortica) stazionario condotti distensibili rigidi Fisica
I fluidi. Alberto Barbisan - Meccanica ITIS FERMI
 I fluidi Esercizio Una stanza ha dimensioni: 3.5 m (larghezza) e 4. m (lunghezza) ed una altezza di.4 m. (a) Quanto pesa l aria nella stanza se la pressione e.0 atm? SOLUZIONE: mg ( ρv)g (. kg / 48 N m
I fluidi Esercizio Una stanza ha dimensioni: 3.5 m (larghezza) e 4. m (lunghezza) ed una altezza di.4 m. (a) Quanto pesa l aria nella stanza se la pressione e.0 atm? SOLUZIONE: mg ( ρv)g (. kg / 48 N m
FISICA DEL SISTEMA CARDIOCIRCOLATORIO
 FISICA DEL SISTEMA CARDIOCIRCOLATORIO Conferenza organizzata dalla Fondazione Livia Tonolini e dalla Sezione Mathesis di Bergamo, a cura di F. Tonolini il 22 aprile 2005 A. Fondamenti di reologia B. Il
FISICA DEL SISTEMA CARDIOCIRCOLATORIO Conferenza organizzata dalla Fondazione Livia Tonolini e dalla Sezione Mathesis di Bergamo, a cura di F. Tonolini il 22 aprile 2005 A. Fondamenti di reologia B. Il
I fluidi Approfondimento I
 I fluidi Approfondimento I statica dei fluidi Legge di Stevino, Principio di Pascal, Principio di Archimede e applicazioni dinamica dei fluidi ideali Flusso di un fluido e continuità Equazione di Bernoulli
I fluidi Approfondimento I statica dei fluidi Legge di Stevino, Principio di Pascal, Principio di Archimede e applicazioni dinamica dei fluidi ideali Flusso di un fluido e continuità Equazione di Bernoulli
Dinamica dei Fluidi. Moto stazionario
 FLUIDODINAMICA 1 Dinamica dei Fluidi Studia il moto delle particelle di fluido* sotto l azione di tre tipi di forze: Forze di superficie: forze esercitate attraverso una superficie (pressione) Forze di
FLUIDODINAMICA 1 Dinamica dei Fluidi Studia il moto delle particelle di fluido* sotto l azione di tre tipi di forze: Forze di superficie: forze esercitate attraverso una superficie (pressione) Forze di
Meccanica dei Fluidi con Fondamenti di Ingegneria Chimica Prova in Itinere Tema A 23 Novembre 2012
 Meccanica dei Fluidi con Fondamenti di Ingegneria Chimica Proa in Itinere Tema A 3 Noembre 01 Esercizio 1 Tubazione scabra in ghisa Si consideri la tubazione in ghisa (indice di scabrezza ε=0.10 mm) disegnata
Meccanica dei Fluidi con Fondamenti di Ingegneria Chimica Proa in Itinere Tema A 3 Noembre 01 Esercizio 1 Tubazione scabra in ghisa Si consideri la tubazione in ghisa (indice di scabrezza ε=0.10 mm) disegnata
Chimica e Tecnologia Farmaceutiche Esercitazioni di Fisica a.a Emanuele Biolcati
 Esercitazione 5 Dr. Monica Casale Chimica e Tecnologia Farmaceutiche Esercitazioni di Fisica a.a. 2010-2011 Emanuele Biolcati Ringraziamenti speciali a Monica Casale per la preparazione delle slides Fluidi
Esercitazione 5 Dr. Monica Casale Chimica e Tecnologia Farmaceutiche Esercitazioni di Fisica a.a. 2010-2011 Emanuele Biolcati Ringraziamenti speciali a Monica Casale per la preparazione delle slides Fluidi
La lezione di oggi. I fluidi reali La viscosità Flussi laminare e turbolento. La resistenza idrodinamica
 1 La lezione di oggi I fluidi reali La viscosità Flussi laminare e turbolento La resistenza idrodinamica 2 La lezione di oggi Forze di trascinamento nei fluidi La legge di Stokes La centrifuga 3 ! Viscosità!
1 La lezione di oggi I fluidi reali La viscosità Flussi laminare e turbolento La resistenza idrodinamica 2 La lezione di oggi Forze di trascinamento nei fluidi La legge di Stokes La centrifuga 3 ! Viscosità!
Meccanica dei FLUIDI
 Meccanica dei FLUIDI Densità Portata Pressione Moto stazionario: equazione di continuità Legge di Stevino Pressione idrostatica Spinta di Archimede Teorema di Bernoulli Viscosità Moto laminare: equazione
Meccanica dei FLUIDI Densità Portata Pressione Moto stazionario: equazione di continuità Legge di Stevino Pressione idrostatica Spinta di Archimede Teorema di Bernoulli Viscosità Moto laminare: equazione
La corrente di un fluido
 La corrente di un fluido 0 La corrente di un fluido è il movimento ordinato di un liquido o di un gas. 0 La portata q è il rapporto tra il volume di fluido V che attraversa una sezione in un tempo t ed
La corrente di un fluido 0 La corrente di un fluido è il movimento ordinato di un liquido o di un gas. 0 La portata q è il rapporto tra il volume di fluido V che attraversa una sezione in un tempo t ed
STATICA E DINAMICA DEI FLUIDI
 STATICA E DINAMICA DEI FLUIDI Pressione Principio di Pascal Legge di Stevino Spinta di Archimede Conservazione della portata Teorema di Bernoulli Legge di Hagen-Poiseuille Moto laminare e turbolento Stati
STATICA E DINAMICA DEI FLUIDI Pressione Principio di Pascal Legge di Stevino Spinta di Archimede Conservazione della portata Teorema di Bernoulli Legge di Hagen-Poiseuille Moto laminare e turbolento Stati
1 bar = 10 Pa = 10 barie PRESSIONE PRESSIONE. N 10 dyn dyn. m 10 cm cm. Solido. Liquido. Gassoso. (pascal) m. kg 1000.
 STATI DI AGGREGAZIONE DELLA MATERIA Solido Liquido Gassoso Il coro ha volume e forma ben definiti Il coro ha volume ben definito, ma assume la forma del reciiente che lo contiene Il coro occua tutto lo
STATI DI AGGREGAZIONE DELLA MATERIA Solido Liquido Gassoso Il coro ha volume e forma ben definiti Il coro ha volume ben definito, ma assume la forma del reciiente che lo contiene Il coro occua tutto lo
Se la curvatura è minore, la tensione totale deve essere più grande per mantenere la stessa componente della tensione verso il basso
 Le Pressioni in emodinamica sono: Pressione di propulsione Pa Pv, responsabile del flusso Pressione transmurale (P tm ). Poiché i vasi sono distensibili la P tm può influenzare il raggio del vaso e per
Le Pressioni in emodinamica sono: Pressione di propulsione Pa Pv, responsabile del flusso Pressione transmurale (P tm ). Poiché i vasi sono distensibili la P tm può influenzare il raggio del vaso e per
Fluidodinamica. Q=V/Δt=costante
 Liquido perfetto o ideale: Fluidodinamica Incomprimibile (densità costante sia nel tempo che nello spazio) Assenza di attrito interno (in un liquido reale si conserva la caratteristica dell incompressibilità
Liquido perfetto o ideale: Fluidodinamica Incomprimibile (densità costante sia nel tempo che nello spazio) Assenza di attrito interno (in un liquido reale si conserva la caratteristica dell incompressibilità
FORMULARIO DI MECCANICA
 Forulario di Meccanica Pagina 1 di 8 FOMULAIO DI MECCANICA NOTA: le grandezze ettoriali sono indicate in neretto. CINEMATICA Vettore posizione del punto ateriale r(t) x i + y j + z k (nel SI etri ) Vettore
Forulario di Meccanica Pagina 1 di 8 FOMULAIO DI MECCANICA NOTA: le grandezze ettoriali sono indicate in neretto. CINEMATICA Vettore posizione del punto ateriale r(t) x i + y j + z k (nel SI etri ) Vettore
La lezione di oggi. La densità La pressione L equazione di continuità Il teorema di Bernoulli. Stenosi e aneurismi
 La lezione di oggi La densità La pressione L equazione di continuità Il teorema di Bernoulli Stenosi e aneurismi ! Densità, pressione! La portata di un condotto! Il teorema di Bernoulli! Applicazioni dell
La lezione di oggi La densità La pressione L equazione di continuità Il teorema di Bernoulli Stenosi e aneurismi ! Densità, pressione! La portata di un condotto! Il teorema di Bernoulli! Applicazioni dell
IL MOTO DEI FLUIDI. con applicazione al sistema circolatorio
 IL MOTO DEI FLUIDI con applicazione al sistema circolatorio Portata Pressione Moto stazionario: equazione di continuità Applicazione al sistema circolatorio: pressione e velocità del sangue Moto laminare
IL MOTO DEI FLUIDI con applicazione al sistema circolatorio Portata Pressione Moto stazionario: equazione di continuità Applicazione al sistema circolatorio: pressione e velocità del sangue Moto laminare
PORTATA DI UN CONDOTTO. Portata Q: volume di fluido che attraversa la sezione di un condotto nell unità di tempo. V v t. = t
 PORTATA DI UN CONDOTTO Portata Q: volume di fluido che attraversa la sezione di un condotto nell unità di tempo. A vt V A v t Q = = = A v t t 1 MOTO STAZIONARIO Un moto si dice stazionario quando le principali
PORTATA DI UN CONDOTTO Portata Q: volume di fluido che attraversa la sezione di un condotto nell unità di tempo. A vt V A v t Q = = = A v t t 1 MOTO STAZIONARIO Un moto si dice stazionario quando le principali
DINAMICA DEI FLUIDI con applicazioni al sistema circolatorio
 CLASSE DELLE LAUREE TRIENNALI DELLE PROFESSIONI SANITARIE DELLA RIABILITAZIONE DINAMICA DEI FLUIDI con applicazioni al sistema circolatorio PORTATA PRESSIONE MOTO STAZIONARIO APPLICAZIONI AL SISTEMA CIRCOLATORIO
CLASSE DELLE LAUREE TRIENNALI DELLE PROFESSIONI SANITARIE DELLA RIABILITAZIONE DINAMICA DEI FLUIDI con applicazioni al sistema circolatorio PORTATA PRESSIONE MOTO STAZIONARIO APPLICAZIONI AL SISTEMA CIRCOLATORIO
Esercitazioni di fisica I fluidi
 Corso di Laurea in Scienze e Tecnologie Biologiche Esercitazioni di fisica I fluidi (pt. 1: fluidostatica e fluidi ideali) Luca Brombal [email protected] 16/11/2017 #1 Legno e granito Un blocco
Corso di Laurea in Scienze e Tecnologie Biologiche Esercitazioni di fisica I fluidi (pt. 1: fluidostatica e fluidi ideali) Luca Brombal [email protected] 16/11/2017 #1 Legno e granito Un blocco
Le resistenze dei singoli segmenti della circolazione sistemica si sommano e determinano la Resistenza vascolare totale del circolo sistemico.
 RESISTENZA VASCOLARE E DISPOSIZIONE DEI VASI: IN SERIE O IN PARALLELO RESISTENZE IN CONDOTTI POSTI IN SERIE R 1 R 2 R 3 Pi F Pu Il flusso F, generato dal P, deve vincere una Resistenza totale, che è la
RESISTENZA VASCOLARE E DISPOSIZIONE DEI VASI: IN SERIE O IN PARALLELO RESISTENZE IN CONDOTTI POSTI IN SERIE R 1 R 2 R 3 Pi F Pu Il flusso F, generato dal P, deve vincere una Resistenza totale, che è la
Applicazione equazione di Bernoulli: stenosi arteriosa(restringimento arteria)
 Applicazione equazione di Bernoulli: stenosi arteriosa(restringimento arteria) Applicazione equazione di Bernoulli: Aneurisma (dilatazione arteria) Liquidi reali attrito interno-viscosita' la velocita'
Applicazione equazione di Bernoulli: stenosi arteriosa(restringimento arteria) Applicazione equazione di Bernoulli: Aneurisma (dilatazione arteria) Liquidi reali attrito interno-viscosita' la velocita'
L apparato cardiocircolatorio. In movimento Marietti Scuola 2010 De Agostini Scuola S.p.A. Novara
 L apparato cardiocircolatorio L apparato cardiocircolatorio La funzione dell apparato circolatorio è di trasportare a tutte le cellule, attraverso il sangue, l ossigeno necessario per l uso delle sostanze
L apparato cardiocircolatorio L apparato cardiocircolatorio La funzione dell apparato circolatorio è di trasportare a tutte le cellule, attraverso il sangue, l ossigeno necessario per l uso delle sostanze
Meccanica dei fluidi
 Programma Parte I Meccanica dei Fluidi Proprietà generali dei Fluidi; Il Principio di Pascal; La legge di Stevino per i liquidi pesanti; Il Principio di Archimede; Il moto dei fluidi; Legge di Bernoulli;
Programma Parte I Meccanica dei Fluidi Proprietà generali dei Fluidi; Il Principio di Pascal; La legge di Stevino per i liquidi pesanti; Il Principio di Archimede; Il moto dei fluidi; Legge di Bernoulli;
IDROSTATICA leggi dell'equilibrio. IDRODINAMICA leggi del movimento
 IDROSTATICA leggi dell'equilibrio IDRODINAMICA leggi del movimento La materia esite in tre stati: SOLIDO volume e forma propri LIQUIDO volume proprio ma non una forma propria (forma del contenitore) AERIFORME
IDROSTATICA leggi dell'equilibrio IDRODINAMICA leggi del movimento La materia esite in tre stati: SOLIDO volume e forma propri LIQUIDO volume proprio ma non una forma propria (forma del contenitore) AERIFORME
MECCANICA DEI FLUIDI
 MECCANICA DEI FLUIDI Un fluido è un corpo che non ha una forma propria. La sua forma dipende da altri corpi che lo contengono (per esempio un recipiente, una condotta, ). Un fluido è composto da molte
MECCANICA DEI FLUIDI Un fluido è un corpo che non ha una forma propria. La sua forma dipende da altri corpi che lo contengono (per esempio un recipiente, una condotta, ). Un fluido è composto da molte
SISTEMA CARDIOVASCOLARE
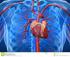 Il sangue circola attraverso l organismo umano pompato dal cuore all interno di una fitta rete di vasi sanguiferi. Il sangue è composto da: v Plasma: prevalentemente acqua, in cui sono disciolte varie
Il sangue circola attraverso l organismo umano pompato dal cuore all interno di una fitta rete di vasi sanguiferi. Il sangue è composto da: v Plasma: prevalentemente acqua, in cui sono disciolte varie
Dinamica dei fluidi. Marina Cobal - Dipt.di Fisica - Universita' di Udine 1
 Dinamica dei fluidi Universita' di Udine 1 Caratteristiche di un fluido In generale: FLUIDO sostanza senza forma propria (assume la forma del recipiente che la contiene) liquido volume limitato dalla superficie
Dinamica dei fluidi Universita' di Udine 1 Caratteristiche di un fluido In generale: FLUIDO sostanza senza forma propria (assume la forma del recipiente che la contiene) liquido volume limitato dalla superficie
ESERCITAZIONE 6. Dr.ssa Valeria Monti Corso di Laurea in Chimica e Tecnologia Farmaceutiche Fisica a.a
 ESERCITAZIONE 6 Dr.ssa Valeria Monti Corso di Laurea in Chimica e Tecnologia Farmaceutiche Fisica a.a. 2016 2017 Fluidi : Esercizio 1 Un arteria di raggio R 1 = 2.5 mm è parzialmente bloccata da una placca.
ESERCITAZIONE 6 Dr.ssa Valeria Monti Corso di Laurea in Chimica e Tecnologia Farmaceutiche Fisica a.a. 2016 2017 Fluidi : Esercizio 1 Un arteria di raggio R 1 = 2.5 mm è parzialmente bloccata da una placca.
Fisica Applicata, Area Infermieristica, M. Ruspa MECCANICA DEI FLUIDI. Fluidostatica: fluidi in quiete Fluidodinamica: fluidi in moto
 MECCANICA DEI FLUIDI Fluidostatica: fluidi in quiete Fluidodinamica: fluidi in moto I diversi stati di aggregazione della materia dipendono dalle forze di legame interatomiche o intermolecolari. SOLIDI
MECCANICA DEI FLUIDI Fluidostatica: fluidi in quiete Fluidodinamica: fluidi in moto I diversi stati di aggregazione della materia dipendono dalle forze di legame interatomiche o intermolecolari. SOLIDI
In un vaso sanguigno si forma un aneurisma dove la sezione aumenta del 15%. Si calcoli la conseguente variazione percentuale della velocita del sangue
 Esercizio In un vaso sanguigno si forma un aneurisma dove la sezione aumenta del 15%. Si calcoli la conseguente variazione percentuale della velocita del sangue 1 MOTO DI FLUIDI REALI 2 MOTO DI UN FLUIDO
Esercizio In un vaso sanguigno si forma un aneurisma dove la sezione aumenta del 15%. Si calcoli la conseguente variazione percentuale della velocita del sangue 1 MOTO DI FLUIDI REALI 2 MOTO DI UN FLUIDO
La corrente di un fluido
 Dinamica dei Fluidi Dinamica dei fluidi La corrente di un fluido La corrente di un fluido è il movimento ordinato di un liquido o di un gas. La portata q è il rapporto tra il volume di fluido ΔV che attraversa
Dinamica dei Fluidi Dinamica dei fluidi La corrente di un fluido La corrente di un fluido è il movimento ordinato di un liquido o di un gas. La portata q è il rapporto tra il volume di fluido ΔV che attraversa
MECCANICA dei FLUIDI nei SISTEMI BIOLOGICI
 MECCANICA dei FLUIDI nei SISTEMI BIOLOGICI parte II a parte I! - EQUAZIONE DI CONTINUITA - PRESSIONE IDROSTATICA Lucidi del Prof. D. Scannicchio MASSA, PESO, DENSITA' m kg massa g massa p = m g kg peso
MECCANICA dei FLUIDI nei SISTEMI BIOLOGICI parte II a parte I! - EQUAZIONE DI CONTINUITA - PRESSIONE IDROSTATICA Lucidi del Prof. D. Scannicchio MASSA, PESO, DENSITA' m kg massa g massa p = m g kg peso
IL MOTO DEI FLUIDI. con applicazione al sistema circolatorio
 IL MOTO DEI FLUIDI con applicazione al sistema circolatorio Portata Pressione Moto stazionario: equazione di continuità Applicazione al sistema circolatorio: pressione e velocità del sangue Moto laminare
IL MOTO DEI FLUIDI con applicazione al sistema circolatorio Portata Pressione Moto stazionario: equazione di continuità Applicazione al sistema circolatorio: pressione e velocità del sangue Moto laminare
DINAMICA DEI FLUIDI G. ROBERTI
 DINAMICA DEI FLUIDI G. ROBERTI Dinamica dei Fluidi Studia il moto delle particelle di fluido* sotto l azione di tre tipi di forze: Forze di superficie: forze esercitate attraverso una superficie (pressione)
DINAMICA DEI FLUIDI G. ROBERTI Dinamica dei Fluidi Studia il moto delle particelle di fluido* sotto l azione di tre tipi di forze: Forze di superficie: forze esercitate attraverso una superficie (pressione)
Un corpo di forma cubica (lato L = 10 cm) e densità ρ = 800 kg/m 3 è immerso in acqua (densità ρ 0
 Un corpo di forma cubica (lato L = 10 cm) e densità ρ = 800 kg/m 3 è immerso in acqua (densità ρ 0 = 1000 kg/m 3 ). Il corpo è tenuto immerso da un filo attaccato al fondo del recipiente. Calcolare: a)la
Un corpo di forma cubica (lato L = 10 cm) e densità ρ = 800 kg/m 3 è immerso in acqua (densità ρ 0 = 1000 kg/m 3 ). Il corpo è tenuto immerso da un filo attaccato al fondo del recipiente. Calcolare: a)la
Il sistema cardio-circolatorio è più complesso: Condotti elastici e non rigidi Tratti (capillari) che consentono la fuoriuscita e l ingresso di
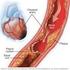 Le leggi dell idrostatica e dell idrodinamica permettono di comprendere i principi fisici che sono alla base del funzionamento del sistema cardio-vascolare, anche se le caratteristiche particolari di questo
Le leggi dell idrostatica e dell idrodinamica permettono di comprendere i principi fisici che sono alla base del funzionamento del sistema cardio-vascolare, anche se le caratteristiche particolari di questo
è completamente immerso in acqua. La sua
 In un tubo scorre in regime stazionario un liquido ideale con densità 1.00 10 3 kg/m 3 ; in un punto A il tubo ha raggio R A = 2.00 cm, la velocità di scorrimento è v A = 5.00 m/se la pressione è P A =
In un tubo scorre in regime stazionario un liquido ideale con densità 1.00 10 3 kg/m 3 ; in un punto A il tubo ha raggio R A = 2.00 cm, la velocità di scorrimento è v A = 5.00 m/se la pressione è P A =
Meccanica dei fluidi. ! definizioni; ! statica dei fluidi (principio di Archimede); ! dinamica dei fluidi (teorema di Bernoulli).
 Meccanica dei fluidi! definizioni;! statica dei fluidi (principio di Archimede);! dinamica dei fluidi (teorema di Bernoulli). [importanti applicazioni in biologia / farmacia : ex. circolazione del sangue]
Meccanica dei fluidi! definizioni;! statica dei fluidi (principio di Archimede);! dinamica dei fluidi (teorema di Bernoulli). [importanti applicazioni in biologia / farmacia : ex. circolazione del sangue]
Eq. bilancio quantità di moto
 Eq. bilancio quantità di moto Contributo relativo alle superfici permeabili, ovvero interessate da flussi di massa (nullo, dato che il fluido è macroscopicamente in quiete) Integrale degli sforzi superficiali
Eq. bilancio quantità di moto Contributo relativo alle superfici permeabili, ovvero interessate da flussi di massa (nullo, dato che il fluido è macroscopicamente in quiete) Integrale degli sforzi superficiali
Meccanica dei fluidi. Fluidostatica (fluidi in quiete) Fluidodinamica (fluidi in movimento) Trasporto in regime viscoso
 Meccanica dei fluidi Fluidostatica (fluidi in quiete) Fluidodinamica (fluidi in movimento) Trasporto in regime viscoso Densità m Unità di misura (S.I.): kg/m d = 3 V Funzione scalare di ogni punto del
Meccanica dei fluidi Fluidostatica (fluidi in quiete) Fluidodinamica (fluidi in movimento) Trasporto in regime viscoso Densità m Unità di misura (S.I.): kg/m d = 3 V Funzione scalare di ogni punto del
Lezione 11. Fluido dinamica
 Lezione 11 Fluido dinamica Equazione di Bernoulli per un fluido ideale L equazione di Bernoulli esprime la legge di conservazione dell energia totale di un fluido ideale che si muove in un condotto: Le
Lezione 11 Fluido dinamica Equazione di Bernoulli per un fluido ideale L equazione di Bernoulli esprime la legge di conservazione dell energia totale di un fluido ideale che si muove in un condotto: Le
Richiami moto circolare uniforme
 Esercizi oto piano Richiai oto circolare unifore an Velocità orbitale: Costante in odulo, a non in direzione e erso = R/T = R Con: R= raggio della traiettoria circolare, T=periodo, = elocità angolare Accelerazione
Esercizi oto piano Richiai oto circolare unifore an Velocità orbitale: Costante in odulo, a non in direzione e erso = R/T = R Con: R= raggio della traiettoria circolare, T=periodo, = elocità angolare Accelerazione
LAVORO DI UNA FORZA (1)
 LAVORO ED ENERGIA INTRODUZIONE L introduzione dei concetto di lavoro, energia cinetica ed energia potenziale ci perettono di affrontare i problei della dinaica in un odo nuovo In particolare enuncereo
LAVORO ED ENERGIA INTRODUZIONE L introduzione dei concetto di lavoro, energia cinetica ed energia potenziale ci perettono di affrontare i problei della dinaica in un odo nuovo In particolare enuncereo
Dall idrostatica alla idrodinamica. Fisica con Elementi di Matematica 1
 Dall idrostatica alla idrodinamica Fisica con Elementi di Matematica 1 Concetto di Campo Insieme dei valori che una certa grandezza fisica assume in ogni punto di una regione di spazio. Esempio: Consideriamo
Dall idrostatica alla idrodinamica Fisica con Elementi di Matematica 1 Concetto di Campo Insieme dei valori che una certa grandezza fisica assume in ogni punto di una regione di spazio. Esempio: Consideriamo
Tratti (capillari) che consentono la fuoriuscita e l ingresso di liquido
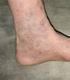 Le leggi dell idrostatica e dell idrodinamica spiegano i principi fisici che sono alla base del funzionamento del sistema cardio circolatorio, ma le caratteristiche particolari di questo sistema impediscono
Le leggi dell idrostatica e dell idrodinamica spiegano i principi fisici che sono alla base del funzionamento del sistema cardio circolatorio, ma le caratteristiche particolari di questo sistema impediscono
Fluidi II. Applicazioni della legge di Bernoulli Viscosità Legge di Poiseuille Regime stazionario Tensione superficiale Capillarità
 Fluidi II Applicazioni della legge di Bernoulli Viscosità Legge di Poiseuille Regime stazionario Tensione superficiale Capillarità Applicazioni della legge di Bernoulli Dilatazione (aneurisma) e restringimento
Fluidi II Applicazioni della legge di Bernoulli Viscosità Legge di Poiseuille Regime stazionario Tensione superficiale Capillarità Applicazioni della legge di Bernoulli Dilatazione (aneurisma) e restringimento
Dinamica dei fluidi viscosi
 a.a. 2005/2006 Laurea Specialistica in Fisica Corso di Fisica Medica 1 Dinamica dei fluidi viscosi 14/3/2006 Ripartizione del sangue portata totale NQ diametro iniziale D diametro d dei rami secondari
a.a. 2005/2006 Laurea Specialistica in Fisica Corso di Fisica Medica 1 Dinamica dei fluidi viscosi 14/3/2006 Ripartizione del sangue portata totale NQ diametro iniziale D diametro d dei rami secondari
Alcuni valori della densita'
 Fluidi Comprendono liquidi e gas La distanza tra le particelle non è fissata Il liquido non è facilmente comprimibile Il gas si può comprimere facilmente e non ha forma propria Solidi, liquidi e gas sono
Fluidi Comprendono liquidi e gas La distanza tra le particelle non è fissata Il liquido non è facilmente comprimibile Il gas si può comprimere facilmente e non ha forma propria Solidi, liquidi e gas sono
Dall idrostatica alla idrodinamica. Fisica con Elementi di Matematica
 Dall idrostatica alla idrodinamica 1 Concetto di Campo Insieme dei valori che una certa grandezza fisica assume in ogni punto di una regione di spazio. Esempio: Consideriamo il valore della pressione atmosferica
Dall idrostatica alla idrodinamica 1 Concetto di Campo Insieme dei valori che una certa grandezza fisica assume in ogni punto di una regione di spazio. Esempio: Consideriamo il valore della pressione atmosferica
ENERGIA DI PRESSIONE TEOREMA DI BERNOULLI PRESSIONE IDROSTATICA SPINTA DI ARCHIMEDE
 CLASSE DELLE LAUREE TRIENNALI DELLE PROFESSIONI SANITARIE DELLA RIABILITAZIONE L ENERGIA NEI FLUIDI ENERGIA DI PRESSIONE TEOREMA DI BERNOULLI PRESSIONE IDROSTATICA SPINTA DI ARCHIMEDE A. A. 014-015 Fabrizio
CLASSE DELLE LAUREE TRIENNALI DELLE PROFESSIONI SANITARIE DELLA RIABILITAZIONE L ENERGIA NEI FLUIDI ENERGIA DI PRESSIONE TEOREMA DI BERNOULLI PRESSIONE IDROSTATICA SPINTA DI ARCHIMEDE A. A. 014-015 Fabrizio
Fluidodinamica applicata Esercizi Finali
 ESERCZO (NS MENSONE CONOTTO) U Condotto infinito di sezione x Usando l analisi diensionale, studiao la dipendenza del gradiente della pressione dagli altri paraetri del flusso: f (,, U, ) dove U velocità
ESERCZO (NS MENSONE CONOTTO) U Condotto infinito di sezione x Usando l analisi diensionale, studiao la dipendenza del gradiente della pressione dagli altri paraetri del flusso: f (,, U, ) dove U velocità
E un sistema efficiente perché consente di mantenere costante il LEC con un basso volume circolatorio ( 5l).
 SISTEMA CIRCOLATORIO Permette il trasporto, attraverso il sangue, di gas, sostanze nutritizie e ormoni a tutte le cellule per mantenere costante la composizione del LEC. E un sistema efficiente perché
SISTEMA CIRCOLATORIO Permette il trasporto, attraverso il sangue, di gas, sostanze nutritizie e ormoni a tutte le cellule per mantenere costante la composizione del LEC. E un sistema efficiente perché
Meccanica dei Fluidi: statica e dinamica
 Meccanica dei Fluidi: statica e dinamica Stati della materia (classificazione assai approssimativa!) Solido: ha una forma propria, poco compressibile, alta densità Liquido: non ha una forma propria, poco
Meccanica dei Fluidi: statica e dinamica Stati della materia (classificazione assai approssimativa!) Solido: ha una forma propria, poco compressibile, alta densità Liquido: non ha una forma propria, poco
PRESSIONE ATMOSFERICA
 PRESSIONE ATMOSFERICA Peso della colonna di aria che ci sovrasta di altezza quindi pari all altezza dell atmosfera p atm = d g h con d densita aria h altezza atmosfera 197 MISURA DELLA PRESSIONE ATMOSFERICA:
PRESSIONE ATMOSFERICA Peso della colonna di aria che ci sovrasta di altezza quindi pari all altezza dell atmosfera p atm = d g h con d densita aria h altezza atmosfera 197 MISURA DELLA PRESSIONE ATMOSFERICA:
V in A? V in B? V in C?
 V in A? V in B? V in C? K + U 0 K + U K + U i i f f 1 e se c è attrito? (forze dissipative) L NC K + U F d att K + U F att d N Riassunto Grandezze vettoriali e scalari Le grandezze del moto Le cause del
V in A? V in B? V in C? K + U 0 K + U K + U i i f f 1 e se c è attrito? (forze dissipative) L NC K + U F d att K + U F att d N Riassunto Grandezze vettoriali e scalari Le grandezze del moto Le cause del
La pressione diminuisce a causa dell ATTRITO
 Il gradiente pressorio generato dal cuore induce il sangue a scorrere nel sistema circolatorio Atrio destro La pressione diminuisce a causa dell ATTRITO PAM = 80 mmhg+1/3(120-80 mmhg) 1 Concetti base di
Il gradiente pressorio generato dal cuore induce il sangue a scorrere nel sistema circolatorio Atrio destro La pressione diminuisce a causa dell ATTRITO PAM = 80 mmhg+1/3(120-80 mmhg) 1 Concetti base di
scaricatoda SISTEMA CIRCOLATORIO
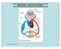 SISTEMA CIRCOLATORIO SISTEMA CIRCOLATORIO Il movimento dei fluidi (liquidi e gas) è stimolato da una differenza di pressione (ΔP). Il fluido si muove da regioni a maggiore P verso regioni a P inferiore.
SISTEMA CIRCOLATORIO SISTEMA CIRCOLATORIO Il movimento dei fluidi (liquidi e gas) è stimolato da una differenza di pressione (ΔP). Il fluido si muove da regioni a maggiore P verso regioni a P inferiore.
Lezione 9. Statica dei fluidi
 Lezione 9 Statica dei fluidi Meccanica dei fluidi Un fluido e un corpo che non ha una forma definita, ma che, se e contenuto da un contenitore solido, tende a occupare (riempire) una parte o tutto il volume
Lezione 9 Statica dei fluidi Meccanica dei fluidi Un fluido e un corpo che non ha una forma definita, ma che, se e contenuto da un contenitore solido, tende a occupare (riempire) una parte o tutto il volume
Esercizi di fisica per Medicina C.Patrignani, Univ. Genova (rev: 9 Ottobre 2003) 1. Idraulica e Fluidi
 Esercizi di fisica per Medicina C.Patrignani, Univ. Genova (rev: 9 Ottobre 2003) 1 Idraulica e Fluidi 1) L acqua di un ruscello cade da una cascata alta 10 m con velocità iniziale praticamente nulla. Quanto
Esercizi di fisica per Medicina C.Patrignani, Univ. Genova (rev: 9 Ottobre 2003) 1 Idraulica e Fluidi 1) L acqua di un ruscello cade da una cascata alta 10 m con velocità iniziale praticamente nulla. Quanto
ESCLUSIVO USO DIDATTICO INTERNO - Meccanica dei fluidi nei sistemi biologici
 UNIVERSITÀ DEGLI STUDI DI PAVIA dip. Fisica nucleare e teorica via Bassi 6, 700 Pavia, Italy - tel. 03898.7905 [email protected] - www.unipv.it/webgiro webgiro elio giroletti fluidi nei sistemi biologici
UNIVERSITÀ DEGLI STUDI DI PAVIA dip. Fisica nucleare e teorica via Bassi 6, 700 Pavia, Italy - tel. 03898.7905 [email protected] - www.unipv.it/webgiro webgiro elio giroletti fluidi nei sistemi biologici
PRESSIONE IN UN FLUIDO IN QUIETE
 PRESSIONE IN UN FLUIDO IN QUIETE P p 0 Quali e quante pressioni in P? 1) pressione esterna (tipicamente pressione atmosferica) 2) pressione idrostatica Pressione totale = p 0 + dgh LEGGE di STEVINO 156
PRESSIONE IN UN FLUIDO IN QUIETE P p 0 Quali e quante pressioni in P? 1) pressione esterna (tipicamente pressione atmosferica) 2) pressione idrostatica Pressione totale = p 0 + dgh LEGGE di STEVINO 156
VISCOSITA. dv dr. P 2 r. η coefficiente di viscosità R P 1 >P 2 P 1. mks kg /(s m) = Pa s. cgs g /(s cm) = poise 1 poise=0.1 Pa s
 FLUIDI EALI Durante lo scorrimento di un fluido reale in un condotto si manifestano forze di attrito interno che ne ostacolano il moto. Esse sono proporzionali alla velocità (piccole velocità) o al quadrato
FLUIDI EALI Durante lo scorrimento di un fluido reale in un condotto si manifestano forze di attrito interno che ne ostacolano il moto. Esse sono proporzionali alla velocità (piccole velocità) o al quadrato
