12. Funzioni numeriche misurabili.
|
|
|
- Gianfranco Maggi
- 5 anni fa
- Visualizzazioni
Transcript
1 12. Funzioni numeriche misurabili Funzioni numeriche misurabili. D ora in avanti, nel corso di questi appunti, adotteremo la seguente terminologia: per far riferimento ad una funzione f : Ω R, per la quale l insieme di arrivo è R, parleremo di funzione numerica; invece, nel caso in cui l insieme di arrivo è R, adopereremo la locuzione funzione reale. Inoltre, poiché le funzioni misurabili che d ora in poi considereremo avranno per lo più come spazio misurabile di arrivo lo spazio (R, B 1 ), è conveniente introdurre una terminologia semplificata per questo caso specifico. Definizione (Funzione numerica misurabile). Se (Ω, A) è uno spazio misurabile e f : Ω R è una funzione numerica su Ω, si dice che la funzione f è A-misurabile per significare che f è A B 1 -misurabile. Osservazione Se f : Ω R è una funzione reale, allora, dato che f può essere pensata anche come funzione numerica, per tale funzione ha senso parlare sia di A B 1 - misurabilità che di A B 1 -misurabilità. Tuttavia, dato che la σ-algebra B 1 è la traccia di B 1 su R, la Proposizione assicura che le due proprietà sono perfettamente equivalenti. Pertanto, nel caso di una funzione reale f : Ω R, possiamo usare tranquillamente l espressione f è A-misurabile, senza alcun pericolo di ambiguità. Definizione (Indicatore di un insieme). Sia Ω un insieme non vuoto (l insieme ambiente ). Per ogni insieme A Ω si chiama indicatore (o funzione indicatrice o funzione caratteristica) dell insieme A la funzione 1l A : Ω R definita nel modo seguente: 1l A (ω) = { 1 se ω A, 0 se ω / A. Nel seguito, occasionalmente, quando sarà necessario evidenziare l insieme ambiente Ω, adotteremo la notazione 1l Ω A invece di 1l A. Proposizione (Proprietà degli indicatori). Siano A, B e A i, i I, arbitrari sottoinsiemi dell insieme ambiente Ω. Valgono le seguenti proprietà: (1) 1l A c = 1 1l A, (2) A B 1l A 1l B, (3) A = B 1l A = 1l B, (4) 1l = sup 1l i I A Ai, (5) 1l = inf i i I i I A 1l i i I A i. 1
2 Dimostrazione. Verifichiamo, a titolo di esempio, la (4) (naturalmente, il significato della funzione che figura al secondo membro è: ( ) sup 1l Ai (ω) = sup{1l Ai (ω) : i I} ω Ω ). i I Fissato ω Ω, si hanno due possibilità: ω i I A i ; in questo caso si ha 1l i I A i (ω) = 1 e, dato che ω appartiene a qualcuno degli insiemi A i, l insieme {1l Ai (ω) : i I} contiene il numero 1, quindi anche il sup{1l Ai (ω) : i I} è uguale a 1; ω / i I A i ; allora 1l i I A i (ω) = 0 e, dato che ω non appartiene a nessuno degli insiemi A i, cioè 1l Ai (ω) = 0 i I, anche il sup{1l Ai (ω) : i I} è uguale a 0. Proposizione (Misurabilità dell indicatore). Sia (Ω, A) uno spazio misurabile e sia A un sottoinsieme di Ω. Vale l equivalenza: 1l A è A-misurabile A A. Dimostrazione. Per ogni insieme B R si ha: se 0, 1 / B ; (12.1.1) 1l 1 (B) = A se 1 B, 0 / B ; A A c se 0 B, 1 / B ; Ω se 0, 1 B. Supponiamo che 1l A sia A-misurabile. Ne segue che l insieme 1l 1 ({1}) (controimmagine di un insieme chiuso, e quindi boreliano) appartiene alla σ-algebra A. Pertanto, grazie A alla (12.1.1) possiamo concludere che A = 1l 1 ({1}) A. A Viceversa, se A A, la (12.1.1) implica che 1l 1 (B) appartiene a A, qualunque sia A l insieme B R; pertanto la funzione 1l A è A B-misurabile, qualunque sia la σ-algebra B in R; in particolare, 1l A è A-misurabile Criteri di misurabilità delle funzioni numeriche. Notazioni. Se Ω è un insieme non vuoto (l insieme ambiente ) e f, g sono due funzioni numeriche su Ω, utlizzeremo, per brevità, la notazione per indicare l insieme {f g} {ω Ω : f(ω) g(ω)}, sempreché tale notazione non dia possibiltà di equivoco. Analogo significato hanno le notazioni {f < g}, {f > g}, {f = g} ecc. ecc. 2
3 Teorema Se f è una funzione numerica su Ω, ognuna delle seguenti quattro condizioni è equivalente alla A-misurabilità di f: (a) {f α} A α R ; (b) {f > α} A α R ; (c) {f α} A α R ; (d) {f < α} A α R. Dimostrazione. Osserviamo che, per ogni α R, si ha {f α} = f 1 ([α, + ]). Di conseguenza, dato che (Proposizione 6.3.2) la famiglia di intervalli {[α, + ] : α R} è un generatore di B 1, l equivalenza (a) la funzione f è A-misurabile discende subito dal criterio generale di misurabilità (Teorema 9.1.1). Dimostriamo adesso l equivalenza delle condizioni (a) - (d). (a) = (b). Per ogni α R si ha {f > α} = {f α + 1 n } (1 ) ; pertanto, dato che ognuno degli insiemi {f α + 1 n }, n N, appartiene per ipotesi alla σ-algebra A, anche {f > α} appartiene a A. (b) = (c). Per ogni α R si ha {f α} = {f > α} c, pertanto, dato che {f > α} A per ipotesi, anche {f α} appartiene alla σ-algebra A. (c) = (d). Segue dall uguaglianza {f < α} = {f α 1 n } α R. (d) = (a). Segue dall uguaglianza {f α} = {f < α} c α R. ( 1 ) Se ω {f > α}, allora è f(ω) > α e quindi, per n sufficientemente grande, si ha pure f(ω) α + n 1, dunque ω {f α + n 1 }; viceversa, se ω {f α + n 1 }, allora f(ω) α + n 1 per qualche n N e quindi, a maggior ragione, f(ω) > α, cioè ω {f > α}. 3
4 Teorema Supponiamo che D sia un sottoinsieme di R denso in R. Se f è una funzione numerica su Ω, ognuna delle seguenti quattro condizioni è equivalente alla A-misurabilità di f: (a ) {f β} A β D ; (b ) {f > β} A β D ; (c ) {f β} A β D ; (d ) {f < β} A β D. Dimostrazione. Dimostriamo che ognuna delle condizioni (a ) - (d ) è equivalente alle condizioni (a) - (d) del precedente teorema. (a) = (a ). Questa implicazione è ovvia. (a ) = (b ). Per ogni β D, denotata con {β n } una successione di elementi di D tale da aversi β < β n < β + 1 n n N (l esistenza di {β n} è assicurata dalla densità di D), si ha l uguaglianza {f > β} = {f β n } ; pertanto, dato che ognuno degli insiemi {f β n }, n N, appartiene per ipotesi alla σ-algebra A, anche {f > β} appartiene a A. (b ) = (c ). Segue dal fatto che {f β} = {f > β} c β D. (c ) = (d ). Segue dal fatto che, per ogni β D, si ha {f < β} = {f β n }, dove {β n } è una qualunque successione di elementi di D tale che β 1 n < β n < β n N. (d ) = (d). Segue dal fatto che, per ogni α R, si ha {f < α} = {f < β n }, dove {β n } è una qualunque successione di elementi di D tale che α 1 n < β n < α n N. 4
5 12.3. Operazioni con le funzioni numeriche misurabili. Proposizione Se f, g sono due funzioni numeriche A-misurabili su Ω, ognuno degli insiemi {f < g}, {f g}, {f = g}, {f g} appartiene alla σ-algebra A. Dimostrazione. Si ha: {f < g} = q Q({f < q} {g > q}) ( 2 ). Pertanto, dato che per ogni q Q gli insiemi {f < q}, {f > q}, e quindi anche la loro intersezione {f < q} {f > q}, appartengono alla σ-algebra A, anche l unione (numerabile) q Q ({f < q} {f > q}) appartiene a A, dunque {f < g} appartiene a A. Da quanto dimostrato, scambiando i ruoli delle due funzioni f e g, segue che l insieme {f > g} appartiene a A. Pertanto anche l insieme complementare {f > g} c, cioè {f g}, appartiene a A. Infine, gli insiemi {f = g} e {f g} appartengono a A in quanto {f = g} = {f g} \ {f < g}, {f g} = {f = g} c. Teorema Se f, g sono due funzioni numeriche A-misurabili su Ω, anche la funzione somma f + g, la funzione differenza f g (se definite in tutto Ω) e la funzione prodotto f g sono A-misurabili. Dimostrazione. Suddividiamo la dimostrazione in vari punti. a) Proviamo che la A-misurabilità di una funzione numerica f implica la A-misurabilità di σf + τ, qualunque siano le costanti σ, τ R. Se σ = 0 la funzione σf + τ è costante e quindi A-misurabile. Se σ > 0 osserviamo che, per ogni α R, per la A-misurabilità di f si ha {σf + τ α} = { } f α τ σ A e quindi σf + τ è A-misurabile per il Teorema Il ragionamento è analogo se σ < 0; infatti, per ogni α R, si ha {σf + τ α} = { } f α τ σ A. b) Da a) segue subito, come caso particolare, che se g è una funzione numerica A- misurabile, allora anche g è A-misurabile. ( 2 ) Infatti, se ω {f < g}, cioè f(ω) < g(ω), esiste q Q tale che f(ω) < q < g(ω); ne segue che ω {f < q} {g > q} e quindi ω q Q ({f < q} {f > q}). Viceversa, se ω q Q ({f < q} {f > q}), allora ω {f < q} {g > q} per qualche q Q e quindi f(ω) < g(ω), cioè ω {f < g}. 5
6 c) Proviamo che se f, g sono due funzioni numeriche A-misurabili su Ω e la loro la funzione somma f +g è definita in tutto Ω, allora f +g è A-misurabile. Infatti, per quanto dimostrato in a) e b) si ha che, per ogni α R, la funzione α g è A-misurabile, pertanto, per la Proposizione , l insieme {f α g} appartiene a A. A questo punto basta osservare che, per ogni α R, risulta {f + g α} = {f α g} ( 3 ) ed invocare il Teorema d) Da c) e b) segue immediatamente che, se f, g sono due funzioni numeriche A- misurabili su Ω e la loro la funzione differenza f g è definita in tutto Ω, allora anche f g è A-misurabile. e) Proviamo adesso che, se f è una funzione numerica A-misurabile su Ω, allora anche f 2 è A-misurabile. Infatti, per ogni α R, si ha {f 2 α} = { Ω se α 0, {f 2 α} {f 2 α} se α > 0, quindi, in ogni caso, {f 2 α} A. f) Dimostriamo che, nel caso in cui le due funzioni numeriche A-misurabili f, g sono reali, allora anche la funzione prodotto f g è A-misurabile. Si ha infatti l identità fg = 1 4 [ (f + g) 2 (f g) 2] e la funzione scritta al secondo membro è A-misurabile per quanto provato in c), d), e) e a). g) Dimostriamo infine che, se f, g sono due funzioni numeriche A-misurabili su Ω, anche f g è una funzione A-misurabile. Consideriamo i seguenti sottoinsiemi di Ω: Ω + = {fg = + }, Ω = {fg = }, Ω 0 = {fg = 0}. ( 3 ) Verifichiamo l uguaglianza insiemistica. Se ω {f + g α}, cioè f(ω) + g(ω) α, vi sono due posssibiltà: o f(ω) + g(ω) R, quindi tutti i termini della precedente disuguaglianza sono numeri reali e pertanto si ha pure f(ω) α g(ω), cioè ω {f α g}; oppure f(ω)+g(ω) = +, cioè almeno uno dei due addendi f(ω) e g(ω) è uguale a +, ma anche in questo caso è ovvio che ω {f α g}. Viceversa, se ω {f α g}, cioè f(ω) α g(ω), si osserva, come prima cosa, che non può essere f(ω) = perché, altrimenti, si avrebbe pure g(ω) = + e la funzione somma f + g non sarebbe definita nel punto ω; a questo punto vi sono due posssibiltà: o f(ω) = + ed allora è chiaro che ω {f + g α}; oppure f(ω) R, ma, anche questa volta, tanto nel caso g(ω) R che in quello g(ω) = +, è evidente che ω {f + g α}. 6
7 Verifichiamo che si tratta di insiemi misurabili. Si ha infatti Ω + = ({f = + } {g > 0}) ({f = } {g < 0}) ({f > 0} {g = + }) ({f < 0} {g = }), Ω = ({f = } {g > 0}) ({f = + } {g < 0}) ({f > 0} {g = }) ({f < 0} {g = + }), Ω 0 = {f = 0} {g = 0} ed i secondi membri delle precedenti uguaglianze sono insiemi che appartengono a A poiché le funzioni f e g sono A-misurabili ( 4 ). Consideriamo l insieme Ω = Ω \ (Ω + Ω Ω 0 ) e indichiamo (se Ω ) con f e g le restrizioni di f e g a Ω. Tali restrizioni sono (Proposizione 9.1.1) Ω A-misurabili e sono funzioni reali per come è stato definito Ω. Pertanto, per il precedente punto f), la funzione f g è Ω A-misurabile, quindi, tenendo presente che Ω appartiene a A, si ha {f g α} Ω A A α R (dove, ovviamente, {f g α} sta per {ω Ω : f (ω)g (ω) α}). A questo punto, per completare la dimostrazione, basta osservare che, fissato un qualsiasi α R, si ha Ω + {f g α} Ω 0 se α 0, {fg α} = Ω + {f g α} se α > 0, (convenendo, naturalmente, che {f g α} = se Ω = ) e quindi {fg α} A in qualunque caso. Teorema Sia {f n } una successione di funzioni numeriche A-misurabili su Ω. Allora anche le funzioni sup f n e inf f n sono A-misurabili. ( 4 ) L appartenenza a A degli insiemi del tipo {f = + } o {f = } si può acquisire, ad esempio, tramite la Proposizione , considerando come funzione g la funzione costante + o. 7
8 Dimostrazione. Per ogni α R si ha, come è immediato verificare, { } sup f n α = {f n α}, pertanto, dato che ognuno degli insiemi {f n α}, n N, appartiene per ipotesi alla σ-algebra A, anche l insieme { } sup f n α appartiene a A. Ciò prova la misurabilità di sup f n. Per dimostrare la misurabilità di inf f n si procede in maniera analoga, osservando che per ogni α R risulta { } inf f n α = {f n α}. Corollario Sia {f n } una successione di funzioni numeriche A-misurabili su Ω. Allora anche le funzioni lim f n e lim f n n n sono A-misurabili. Dimostrazione. Dal Teorema segue che, per ogni n N, la funzione e n = inf m n f m è A-misurabile; di conseguenza, per lo stesso teorema, anche lim n f n = sup e n è A-misurabile. In modo analogo si ragiona per il massimo limite. Corollario Sia {f n } una successione di funzioni numeriche A-misurabili su Ω. Supponiamo inoltre che tale successione di funzioni sia convergente (in R) in ogni punto di Ω. Allora anche la funzione lim n f n è A-misurabile. Corollario Siano f 1,..., f n funzioni numeriche A-misurabili su Ω. Allora anche le funzioni max{f 1,..., f n } e min{f 1,..., f n } sono A-misurabili. 8
9 Dimostrazione. Segue subito dal Teorema scrivendo il massimo ed il minimo come estremo superiore ed inferiore di una successione di funzioni A-misurabili: max{f 1,..., f n } = sup{f 1,..., f n, f 1, f 1, f 1,...} min{f 1,..., f n } = inf{f 1,..., f n, f 1, f 1, f 1,...} Corollario Se f è una funzione numerica A-misurabile su Ω, allora anche la funzione f è A-misurabile. Dimostrazione. Segue dal Teorema e dal Corollario tenendo presente che f = max{f, f}. 9
Geometria Superiore Esercizi 1 (da consegnare entro... )
 Geometria Superiore Esercizi 1 (da consegnare entro... ) In questi esercizi analizziamo il concetto di paracompattezza per uno spazio topologico e vediamo come questo implichi l esistenza di partizioni
Geometria Superiore Esercizi 1 (da consegnare entro... ) In questi esercizi analizziamo il concetto di paracompattezza per uno spazio topologico e vediamo come questo implichi l esistenza di partizioni
10. Insiemi non misurabili secondo Lebesgue.
 10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
5. La teoria astratta della misura.
 5. La teoria astratta della misura. 5.1. σ-algebre. 5.1.1. σ-algebre e loro proprietà. Sia Ω un insieme non vuoto. Indichiamo con P(Ω la famiglia di tutti i sottoinsiemi di Ω. Inoltre, per ogni insieme
5. La teoria astratta della misura. 5.1. σ-algebre. 5.1.1. σ-algebre e loro proprietà. Sia Ω un insieme non vuoto. Indichiamo con P(Ω la famiglia di tutti i sottoinsiemi di Ω. Inoltre, per ogni insieme
Per lo svolgimento del corso risulta particolarmente utile considerare l insieme
 1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
A i è un aperto in E. i=1
 Proposizione 1. A è aperto se e solo se A c è chiuso. Dimostrazione. = : se x o A c, allora x o A = A o e quindi esiste r > 0 tale che B(x o, r) A; allora x o non può essere di accumulazione per A c. Dunque
Proposizione 1. A è aperto se e solo se A c è chiuso. Dimostrazione. = : se x o A c, allora x o A = A o e quindi esiste r > 0 tale che B(x o, r) A; allora x o non può essere di accumulazione per A c. Dunque
Riconoscere e formalizzare le dipendenze funzionali
 Riconoscere e formalizzare le dipendenze funzionali Giorgio Ghelli 25 ottobre 2007 1 Riconoscere e formalizzare le dipendenze funzionali Non sempre è facile indiduare le dipendenze funzionali espresse
Riconoscere e formalizzare le dipendenze funzionali Giorgio Ghelli 25 ottobre 2007 1 Riconoscere e formalizzare le dipendenze funzionali Non sempre è facile indiduare le dipendenze funzionali espresse
FUNZIONI CONTINUE - ESERCIZI SVOLTI
 FUNZIONI CONTINUE - ESERCIZI SVOLTI 1) Verificare che x è continua in x 0 per ogni x 0 0 ) Verificare che 1 x 1 x 0 è continua in x 0 per ogni x 0 0 3) Disegnare il grafico e studiare i punti di discontinuità
FUNZIONI CONTINUE - ESERCIZI SVOLTI 1) Verificare che x è continua in x 0 per ogni x 0 0 ) Verificare che 1 x 1 x 0 è continua in x 0 per ogni x 0 0 3) Disegnare il grafico e studiare i punti di discontinuità
Equazioni differenziali ordinarie
 Equazioni differenziali ordinarie Denis Nardin January 2, 2010 1 Equazioni differenziali In questa sezione considereremo le proprietà delle soluzioni del problema di Cauchy. Da adesso in poi (PC) indicherà
Equazioni differenziali ordinarie Denis Nardin January 2, 2010 1 Equazioni differenziali In questa sezione considereremo le proprietà delle soluzioni del problema di Cauchy. Da adesso in poi (PC) indicherà
Le funzioni reali di variabile reale
 Prof. Michele Giugliano (Gennaio 2002) Le funzioni reali di variabile reale ) Complementi di teoria degli insiemi. A) Estremi di un insieme numerico X. Dato un insieme X R, si chiama maggiorante di X un
Prof. Michele Giugliano (Gennaio 2002) Le funzioni reali di variabile reale ) Complementi di teoria degli insiemi. A) Estremi di un insieme numerico X. Dato un insieme X R, si chiama maggiorante di X un
0.1 Esercizi calcolo combinatorio
 0.1 Esercizi calcolo combinatorio Esercizio 1. Sia T l insieme dei primi 100 numeri naturali. Calcolare: 1. Il numero di sottoinsiemi A di T che contengono esattamente 8 pari.. Il numero di coppie (A,
0.1 Esercizi calcolo combinatorio Esercizio 1. Sia T l insieme dei primi 100 numeri naturali. Calcolare: 1. Il numero di sottoinsiemi A di T che contengono esattamente 8 pari.. Il numero di coppie (A,
5 DERIVATA. 5.1 Continuità
 5 DERIVATA 5. Continuità Definizione 5. Sia < a < b < +, f : (a, b) R e c (a, b). Diciamo che f è continua in c se sono verificate le ue conizioni: (i) c esiste (ii) = f(c) c Si osservi che nella efinizione
5 DERIVATA 5. Continuità Definizione 5. Sia < a < b < +, f : (a, b) R e c (a, b). Diciamo che f è continua in c se sono verificate le ue conizioni: (i) c esiste (ii) = f(c) c Si osservi che nella efinizione
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
Corso di Analisi Matematica. Successioni e serie numeriche
 a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Successioni e serie numeriche Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Successioni e serie numeriche Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8. Cognome:... Nome:... Matricola:...
 Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
SPAZI METRICI. Uno spazio metrico X con metrica d si indica con il simbolo (X, d). METRICI 1
 SPAZI METRICI Nel piano R 2 o nello spazio R 3 la distanza fra due punti è la lunghezza, o norma euclidea, del vettore differenza di questi due punti. Se p = (x, y, z) è un vettore in coordinate ortonormali,
SPAZI METRICI Nel piano R 2 o nello spazio R 3 la distanza fra due punti è la lunghezza, o norma euclidea, del vettore differenza di questi due punti. Se p = (x, y, z) è un vettore in coordinate ortonormali,
19. Inclusioni tra spazi L p.
 19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
16. Vari modi di convergenza delle successioni di funzioni reali misurabili.
 16. Vari modi di convergenza delle successioni di funzioni reali misurabili. L argomento centrale di questa ultima parte del corso è lo studio in generale della convergenza delle successioni negli spazi
16. Vari modi di convergenza delle successioni di funzioni reali misurabili. L argomento centrale di questa ultima parte del corso è lo studio in generale della convergenza delle successioni negli spazi
CONCETTO DI LIMITE DI UNA FUNZIONE REALE
 CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
Lezioni di Matematica 1 - I modulo
 Lezioni di Matematica 1 - I modulo Luciano Battaia 16 ottobre 2008 Luciano Battaia - http://www.batmath.it Matematica 1 - I modulo. Lezione del 16/10/2008 1 / 13 L introduzione dei numeri reali si può
Lezioni di Matematica 1 - I modulo Luciano Battaia 16 ottobre 2008 Luciano Battaia - http://www.batmath.it Matematica 1 - I modulo. Lezione del 16/10/2008 1 / 13 L introduzione dei numeri reali si può
Esistenza di funzioni continue non differenziabili in alcun punto
 UNIVERSITÀ DEGLI STUDI DI CAGLIARI FACOLTÀ DI SCIENZE MATEMATICHE, FISICHE E NATURALI CORSO DI LAUREA IN MATEMATICA Esistenza di funzioni continue non differenziabili in alcun punto Relatore Prof. Andrea
UNIVERSITÀ DEGLI STUDI DI CAGLIARI FACOLTÀ DI SCIENZE MATEMATICHE, FISICHE E NATURALI CORSO DI LAUREA IN MATEMATICA Esistenza di funzioni continue non differenziabili in alcun punto Relatore Prof. Andrea
Una ricetta per il calcolo dell asintoto obliquo. Se f(x) è asintotica a mx+q allora abbiamo f(x) mx q = o(1), da cui (dividendo per x) + o(1), m =
 Una ricetta per il calcolo dell asintoto obliquo Se f() è asintotica a m+q allora abbiamo f() m q = o(1), da cui (dividendo per ) m = f() q + 1 f() o(1) = + o(1), mentre q = f() m = o(1). Dunque si ha
Una ricetta per il calcolo dell asintoto obliquo Se f() è asintotica a m+q allora abbiamo f() m q = o(1), da cui (dividendo per ) m = f() q + 1 f() o(1) = + o(1), mentre q = f() m = o(1). Dunque si ha
Sulla monotonia delle funzioni reali di una variabile reale
 Liceo G. B. Vico - Napoli Sulla monotonia delle funzioni reali di una variabile reale Prof. Giuseppe Caputo Premetto due teoremi come prerequisiti necessari per la comprensione di quanto verrà esposto
Liceo G. B. Vico - Napoli Sulla monotonia delle funzioni reali di una variabile reale Prof. Giuseppe Caputo Premetto due teoremi come prerequisiti necessari per la comprensione di quanto verrà esposto
3 GRAFICI DI FUNZIONI
 3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
Limiti e continuità di funzioni reali di una variabile
 di funzioni reali di una variabile Corso di Analisi Matematica - capitolo VI Facoltà di Economia, UER Maria Caterina Bramati Université Libre de Bruxelles ECARES 22 Novembre 2006 Intuizione di ite di funzione
di funzioni reali di una variabile Corso di Analisi Matematica - capitolo VI Facoltà di Economia, UER Maria Caterina Bramati Université Libre de Bruxelles ECARES 22 Novembre 2006 Intuizione di ite di funzione
G. Pareschi ALGEBRE DI BOOLE. 1. Algebre di Boole
 G. Pareschi ALGEBRE DI BOOLE 1. Algebre di Boole Nel file precedente abbiamo incontrato la definizione di algebra di Boole come reticolo: un algebra di Boole e un reticolo limitato, complementato e distributivo.
G. Pareschi ALGEBRE DI BOOLE 1. Algebre di Boole Nel file precedente abbiamo incontrato la definizione di algebra di Boole come reticolo: un algebra di Boole e un reticolo limitato, complementato e distributivo.
1 Giochi a due, con informazione perfetta e somma zero
 1 Giochi a due, con informazione perfetta e somma zero Nel gioco del Nim, se semplificato all estremo, ci sono due giocatori I, II e una pila di 6 pedine identiche In ogni turno di gioco I rimuove una
1 Giochi a due, con informazione perfetta e somma zero Nel gioco del Nim, se semplificato all estremo, ci sono due giocatori I, II e una pila di 6 pedine identiche In ogni turno di gioco I rimuove una
Successioni di funzioni reali
 E-school di Arrigo Amadori Analisi I Successioni di funzioni reali 01 Introduzione. In questo capitolo applicheremo i concetti di successione e di serie alle funzioni numeriche reali. Una successione di
E-school di Arrigo Amadori Analisi I Successioni di funzioni reali 01 Introduzione. In questo capitolo applicheremo i concetti di successione e di serie alle funzioni numeriche reali. Una successione di
RELAZIONI BINARIE. Proprietà delle relazioni Data una relazione R, definita in un insieme non vuoto U, si hanno le seguenti proprietà :
 RELAZIONI INARIE Dati due insiemi non vuoti, A detto dominio e detto codominio, eventualmente coincidenti, si chiama relazione binaria (o corrispondenza) di A in, e si indica con f : A, (oppure R ) una
RELAZIONI INARIE Dati due insiemi non vuoti, A detto dominio e detto codominio, eventualmente coincidenti, si chiama relazione binaria (o corrispondenza) di A in, e si indica con f : A, (oppure R ) una
Università degli Studi di Catania A.A. 2012-2013. Corso di laurea in Ingegneria Industriale
 Università degli Studi di Catania A.A. 2012-2013 Corso di laurea in Ingegneria Industriale Corso di Analisi Matematica I (A-E) (Prof. A.Villani) Elenco delle dimostrazioni che possono essere richieste
Università degli Studi di Catania A.A. 2012-2013 Corso di laurea in Ingegneria Industriale Corso di Analisi Matematica I (A-E) (Prof. A.Villani) Elenco delle dimostrazioni che possono essere richieste
Studio di funzione. Tutti i diritti sono riservati. E vietata la riproduzione, anche parziale, senza il consenso dell autore. Funzioni elementari 2
 Studio di funzione Copyright c 2009 Pasquale Terrecuso Tutti i diritti sono riservati. E vietata la riproduzione, anche parziale, senza il consenso dell autore. Funzioni elementari 2 Studio di funzione
Studio di funzione Copyright c 2009 Pasquale Terrecuso Tutti i diritti sono riservati. E vietata la riproduzione, anche parziale, senza il consenso dell autore. Funzioni elementari 2 Studio di funzione
La logica modale e la dimostrazione dell esistenza di Dio di Gödel. LOGICA MODALE
 La logica modale e la dimostrazione dell esistenza di Dio di Gödel. In alcuni giornali ho letto che di recente ci sono stati diversi studi che hanno riportato alla ribalta la dimostrazione dell esistenza
La logica modale e la dimostrazione dell esistenza di Dio di Gödel. In alcuni giornali ho letto che di recente ci sono stati diversi studi che hanno riportato alla ribalta la dimostrazione dell esistenza
7 Esercizi e complementi di Elettrotecnica per allievi non elettrici. Circuiti elementari
 7 Esercizi e complementi di Elettrotecnica per allievi non elettrici Circuiti elementari Gli esercizi proposti in questa sezione hanno lo scopo di introdurre l allievo ad alcune tecniche, semplici e fondamentali,
7 Esercizi e complementi di Elettrotecnica per allievi non elettrici Circuiti elementari Gli esercizi proposti in questa sezione hanno lo scopo di introdurre l allievo ad alcune tecniche, semplici e fondamentali,
CAPITOLO IV RISOLUZIONE DEI SISTEMI LINEARI COL METODO DEI DETERMINANTI
 CAPITOLO IV RISOLUZIONE DEI SISTEMI LINEARI COL METODO DEI DETERMINANTI 1. REGOLA DI CRAMER Sia S un sistema lineare di n ( 2) equazioni in n incognite su un campo K : a 11 x 1 + a 12 x 2 + + a 1n x n
CAPITOLO IV RISOLUZIONE DEI SISTEMI LINEARI COL METODO DEI DETERMINANTI 1. REGOLA DI CRAMER Sia S un sistema lineare di n ( 2) equazioni in n incognite su un campo K : a 11 x 1 + a 12 x 2 + + a 1n x n
STRUTTURE ALGEBRICHE
 STRUTTURE ALGEBRICHE Operazioni in un insieme Sia A un insieme non vuoto; una funzione f : A A A si dice operazione binaria (o semplicemente operazione), oppure legge di composizione interna. Per definizione
STRUTTURE ALGEBRICHE Operazioni in un insieme Sia A un insieme non vuoto; una funzione f : A A A si dice operazione binaria (o semplicemente operazione), oppure legge di composizione interna. Per definizione
Lezione 1. Gli Insiemi. La nozione di insieme viene spesso utilizzata nella vita di tutti i giorni; si parla dell insieme:
 Lezione 1 Gli Insiemi La nozione di insieme viene spesso utilizzata nella vita di tutti i giorni; si parla dell insieme: degli iscritti ad un corso di laurea delle stelle in cielo dei punti di un piano
Lezione 1 Gli Insiemi La nozione di insieme viene spesso utilizzata nella vita di tutti i giorni; si parla dell insieme: degli iscritti ad un corso di laurea delle stelle in cielo dei punti di un piano
Corso di Analisi Matematica. Funzioni continue
 a.a. 203/204 Laurea triennale in Informatica Corso di Analisi Matematica Funzioni continue Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti.
a.a. 203/204 Laurea triennale in Informatica Corso di Analisi Matematica Funzioni continue Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti.
COGNOME e NOME: FIRMA: MATRICOLA:
 Anno Accademico 04/ 05 Corsi di Analisi Matematica I Proff. A. Villani, R. Cirmi e F. Faraci) Prova d Esame del giorno 6 febbraio 05 Prima prova scritta compito A) Non sono consentiti formulari, appunti,
Anno Accademico 04/ 05 Corsi di Analisi Matematica I Proff. A. Villani, R. Cirmi e F. Faraci) Prova d Esame del giorno 6 febbraio 05 Prima prova scritta compito A) Non sono consentiti formulari, appunti,
1. Intorni di un punto. Punti di accumulazione.
 1. Intorni di un punto. Punti di accumulazione. 1.1. Intorni circolari. Assumiamo come distanza di due numeri reali x e y il numero non negativo x y (che, come sappiamo, esprime la distanza tra i punti
1. Intorni di un punto. Punti di accumulazione. 1.1. Intorni circolari. Assumiamo come distanza di due numeri reali x e y il numero non negativo x y (che, come sappiamo, esprime la distanza tra i punti
1. I limiti delle funzioni.
 1. I iti delle funzioni. 1.1. Considerazioni introduttive. La nozione di ite di una funzione reale di variabile reale costituisce una naturale generalizzazione della nozione di ite di una successione.
1. I iti delle funzioni. 1.1. Considerazioni introduttive. La nozione di ite di una funzione reale di variabile reale costituisce una naturale generalizzazione della nozione di ite di una successione.
Prodotto elemento per elemento, NON righe per colonne Unione: M R S
 Relazioni binarie Una relazione binaria può essere rappresentata con un grafo o con una matrice di incidenza. Date due relazioni R, S A 1 A 2, la matrice di incidenza a seguito di varie operazioni si può
Relazioni binarie Una relazione binaria può essere rappresentata con un grafo o con una matrice di incidenza. Date due relazioni R, S A 1 A 2, la matrice di incidenza a seguito di varie operazioni si può
ALGEBRA I: CARDINALITÀ DI INSIEMI
 ALGEBRA I: CARDINALITÀ DI INSIEMI 1. CONFRONTO DI CARDINALITÀ E chiaro a tutti che esistono insiemi finiti cioè con un numero finito di elementi) ed insiemi infiniti. E anche chiaro che ogni insieme infinito
ALGEBRA I: CARDINALITÀ DI INSIEMI 1. CONFRONTO DI CARDINALITÀ E chiaro a tutti che esistono insiemi finiti cioè con un numero finito di elementi) ed insiemi infiniti. E anche chiaro che ogni insieme infinito
1 Applicazioni Lineari tra Spazi Vettoriali
 1 Applicazioni Lineari tra Spazi Vettoriali Definizione 1 (Applicazioni lineari) Si chiama applicazione lineare una applicazione tra uno spazio vettoriale ed uno spazio vettoriale sul campo tale che "!$%!
1 Applicazioni Lineari tra Spazi Vettoriali Definizione 1 (Applicazioni lineari) Si chiama applicazione lineare una applicazione tra uno spazio vettoriale ed uno spazio vettoriale sul campo tale che "!$%!
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica.
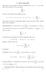 8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
PROVA DI VERIFICA DEL 24/10/2001
 PROVA DI VERIFICA DEL 24/10/2001 [1] Il prodotto di due numeri non nulli è maggiore di zero se: a. il loro rapporto è maggiore di zero, b. il loro rapporto è minore di zero, c. il loro rapporto è uguale
PROVA DI VERIFICA DEL 24/10/2001 [1] Il prodotto di due numeri non nulli è maggiore di zero se: a. il loro rapporto è maggiore di zero, b. il loro rapporto è minore di zero, c. il loro rapporto è uguale
INDICAZIONI PER LA RICERCA DEGLI ASINTOTI VERTICALI
 2.13 ASINTOTI 44 Un "asintoto", per una funzione y = f( ), è una retta alla quale il grafico della funzione "si avvicina indefinitamente", "si avvicina di tanto quanto noi vogliamo", nel senso precisato
2.13 ASINTOTI 44 Un "asintoto", per una funzione y = f( ), è una retta alla quale il grafico della funzione "si avvicina indefinitamente", "si avvicina di tanto quanto noi vogliamo", nel senso precisato
Introduzione alla programmazione lineare. Mauro Pagliacci
 Introduzione alla programmazione lineare Mauro Pagliacci c Draft date 25 maggio 2010 Premessa In questo fascicolo sono riportati gli appunti dalle lezioni del corso di Elaborazioni automatica dei dati
Introduzione alla programmazione lineare Mauro Pagliacci c Draft date 25 maggio 2010 Premessa In questo fascicolo sono riportati gli appunti dalle lezioni del corso di Elaborazioni automatica dei dati
Parte 6. Applicazioni lineari
 Parte 6 Applicazioni lineari A Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Applicazioni fra insiemi, 2 Applicazioni lineari tra spazi vettoriali, 2 3 Applicazioni lineari da R n a R
Parte 6 Applicazioni lineari A Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Applicazioni fra insiemi, 2 Applicazioni lineari tra spazi vettoriali, 2 3 Applicazioni lineari da R n a R
Moto uniforme sul toro bidimensionale
 4/3/06 Luigi Chierchia Moto uniforme sul toro bidimensionale 1. Il toro bidimensionale Denotiamo con R l insieme dei numeri reali e con Z l insieme dei numeri interi (con segno) {..., 2, 1, 0, 1, 2,...};
4/3/06 Luigi Chierchia Moto uniforme sul toro bidimensionale 1. Il toro bidimensionale Denotiamo con R l insieme dei numeri reali e con Z l insieme dei numeri interi (con segno) {..., 2, 1, 0, 1, 2,...};
p k q n k = p n (k) = n 12 = 1 = 12 1 12 11 10 9 1 0,1208. q = 1 2 e si ha: p 12 (8) = 12 8 4
 CAPITOLO QUARTO DISTRIBUZIONE BINOMIALE (O DI BERNOULLI) Molti degli esempi che abbiamo presentato nei capitoli precedenti possono essere pensati come casi particolari di uno schema generale di prove ripetute,
CAPITOLO QUARTO DISTRIBUZIONE BINOMIALE (O DI BERNOULLI) Molti degli esempi che abbiamo presentato nei capitoli precedenti possono essere pensati come casi particolari di uno schema generale di prove ripetute,
Massimi e minimi vincolati in R 2 - Esercizi svolti
 Massimi e minimi vincolati in R 2 - Esercizi svolti Esercizio 1. Determinare i massimi e minimi assoluti della funzione f(x, y) = 2x + 3y vincolati alla curva di equazione x 4 + y 4 = 1. Esercizio 2. Determinare
Massimi e minimi vincolati in R 2 - Esercizi svolti Esercizio 1. Determinare i massimi e minimi assoluti della funzione f(x, y) = 2x + 3y vincolati alla curva di equazione x 4 + y 4 = 1. Esercizio 2. Determinare
TOPOLOGIA ALBERTO SARACCO
 TOPOLOGIA ALBERTO SARACCO Abstract. Le presenti note saranno il più fedeli possibile a quanto detto a lezione. I testi consigliati sono Jänich [1], Kosniowski [2] e Singer- Thorpe [3]. Un ottimo libro
TOPOLOGIA ALBERTO SARACCO Abstract. Le presenti note saranno il più fedeli possibile a quanto detto a lezione. I testi consigliati sono Jänich [1], Kosniowski [2] e Singer- Thorpe [3]. Un ottimo libro
Esercizi sulla conversione tra unità di misura
 Esercizi sulla conversione tra unità di misura Autore: Enrico Campanelli Prima stesura: Settembre 2013 Ultima revisione: Settembre 2013 Per segnalare errori o per osservazioni e suggerimenti di qualsiasi
Esercizi sulla conversione tra unità di misura Autore: Enrico Campanelli Prima stesura: Settembre 2013 Ultima revisione: Settembre 2013 Per segnalare errori o per osservazioni e suggerimenti di qualsiasi
Corso di Analisi Matematica. Polinomi e serie di Taylor
 a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Polinomi e serie di Taylor Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli
a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Polinomi e serie di Taylor Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli
Normalizzazione. Definizione
 Normalizzazione Definizione Le forme normali 2 Una forma normale è una proprietà di una base di dati relazionale che ne garantisce la qualità, cioè l'assenza di determinati difetti Quando una relazione
Normalizzazione Definizione Le forme normali 2 Una forma normale è una proprietà di una base di dati relazionale che ne garantisce la qualità, cioè l'assenza di determinati difetti Quando una relazione
4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale
 4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale Spazi Metrici Ricordiamo che uno spazio metrico è una coppia (X, d) dove X è un insieme e d : X X [0, + [ è una funzione, detta metrica,
4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale Spazi Metrici Ricordiamo che uno spazio metrico è una coppia (X, d) dove X è un insieme e d : X X [0, + [ è una funzione, detta metrica,
Sulle funzioni di W 1,p (Ω) a traccia nulla
 Sulle funzioni di W 1,p () a traccia nulla Sia u W 1,p (R n ) e supponiamo che il supp u, essendo un aperto di R n. Possiamo approssimare u con una successione di funzioni C il cui supporto è contenuto
Sulle funzioni di W 1,p () a traccia nulla Sia u W 1,p (R n ) e supponiamo che il supp u, essendo un aperto di R n. Possiamo approssimare u con una successione di funzioni C il cui supporto è contenuto
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria).
 Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Appunti di Complementi di Matematica. Jacobo Pejsachowicz (a cura di Nathan Quadrio)
 Appunti di Complementi di Matematica Jacobo Pejsachowicz (a cura di Nathan Quadrio) 1 Indice 1 Cenni della teoria degli insiemi 4 1.1 Classi ed insiemi........................... 4 1.2 Operazioni fra gli
Appunti di Complementi di Matematica Jacobo Pejsachowicz (a cura di Nathan Quadrio) 1 Indice 1 Cenni della teoria degli insiemi 4 1.1 Classi ed insiemi........................... 4 1.2 Operazioni fra gli
Il Metodo Scientifico
 Unita Naturali Il Metodo Scientifico La Fisica si occupa di descrivere ed interpretare i fenomeni naturali usando il metodo scientifico. Passi del metodo scientifico: Schematizzazione: modello semplificato
Unita Naturali Il Metodo Scientifico La Fisica si occupa di descrivere ed interpretare i fenomeni naturali usando il metodo scientifico. Passi del metodo scientifico: Schematizzazione: modello semplificato
Siano f e g due funzioni, allora x D f D g, cioè appartenente all intersezione dei loro domini, possiamo definire
 Operazioni tra funzioni Siano f e g due funzioni, allora D f D g, cioè appartenente all intersezione dei loro domini, possiamo definire f() ± g(), f() g(), f () g() se g() 0 Es. f() = 4, g() = 3 + D f
Operazioni tra funzioni Siano f e g due funzioni, allora D f D g, cioè appartenente all intersezione dei loro domini, possiamo definire f() ± g(), f() g(), f () g() se g() 0 Es. f() = 4, g() = 3 + D f
Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata, Matematica
 DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
TEORIA RELAZIONALE: INTRODUZIONE
 TEORIA RELAZIONALE: INTRODUZIONE Tre metodi per produrre uno schema relazionale: a) Partire da un buon schema a oggetti e tradurlo b) Costruire direttamente le relazioni e poi correggere quelle che presentano
TEORIA RELAZIONALE: INTRODUZIONE Tre metodi per produrre uno schema relazionale: a) Partire da un buon schema a oggetti e tradurlo b) Costruire direttamente le relazioni e poi correggere quelle che presentano
Funzioni. Parte prima. Daniele Serra
 Funzioni Parte prima Daniele Serra Nota: questi appunti non sostituiscono in alcun modo le lezioni del prof. Favilli, né alcun libro di testo. Sono piuttosto da intendersi a integrazione di entrambi. 1
Funzioni Parte prima Daniele Serra Nota: questi appunti non sostituiscono in alcun modo le lezioni del prof. Favilli, né alcun libro di testo. Sono piuttosto da intendersi a integrazione di entrambi. 1
21. Studio del grafico di una funzione: esercizi
 1. Studio del grafico di una funzione: esercizi Esercizio 1.6. Studiare ciascuna delle seguenti funzioni in base allo schema di pagina 194, eseguendo anche il computo della derivata seconda e lo studio
1. Studio del grafico di una funzione: esercizi Esercizio 1.6. Studiare ciascuna delle seguenti funzioni in base allo schema di pagina 194, eseguendo anche il computo della derivata seconda e lo studio
Elementi di topologia della retta
 Elementi di topologia della retta nome insieme definizione l insieme è un concetto primitivo che si accetta come intuitivamente noto secondo George Cantor, il padre della teoria degli insiemi: Per insieme
Elementi di topologia della retta nome insieme definizione l insieme è un concetto primitivo che si accetta come intuitivamente noto secondo George Cantor, il padre della teoria degli insiemi: Per insieme
APPENDICE NOZIONI BASE E VARIE
 pag. 131 Appendice: Nozioni base e varie G. Gerla APPENDICE NOZIONI BASE E VARIE 1. Funzioni e relazioni di equivalenza Questi appunti sono rivolti a persone che abbiano già una conoscenza elementare della
pag. 131 Appendice: Nozioni base e varie G. Gerla APPENDICE NOZIONI BASE E VARIE 1. Funzioni e relazioni di equivalenza Questi appunti sono rivolti a persone che abbiano già una conoscenza elementare della
u 1 u k che rappresenta formalmente la somma degli infiniti numeri (14.1), ordinati al crescere del loro indice. I numeri u k
 Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
DOMINI A FATTORIZZAZIONE UNICA
 DOMINI A FATTORIZZAZIONE UNICA CORSO DI ALGEBRA, A.A. 2012-2013 Nel seguito D indicherà sempre un dominio d integrità cioè un anello commutativo con unità privo di divisori dello zero. Indicheremo con
DOMINI A FATTORIZZAZIONE UNICA CORSO DI ALGEBRA, A.A. 2012-2013 Nel seguito D indicherà sempre un dominio d integrità cioè un anello commutativo con unità privo di divisori dello zero. Indicheremo con
Prof. Stefano Capparelli
 APPUNTI PER UN SECONDO CORSO DI ALGEBRA LINEARE Prof. Stefano Capparelli A mia madre Prefazione. Brevi Richiami di Algebra Lineare. Forma Canonica di Jordan.. Blocco di Jordan.. Base di Jordan.. Polinomio
APPUNTI PER UN SECONDO CORSO DI ALGEBRA LINEARE Prof. Stefano Capparelli A mia madre Prefazione. Brevi Richiami di Algebra Lineare. Forma Canonica di Jordan.. Blocco di Jordan.. Base di Jordan.. Polinomio
Corso di Analisi Matematica. Funzioni reali di variabile reale
 a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Funzioni reali di variabile reale Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Funzioni reali di variabile reale Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
Indice. 1 Introduzione alle Equazioni Differenziali 1 1.1 Esempio introduttivo... 1 1.2 Nomenclatura e Teoremi di Esistenza ed Unicità...
 Indice 1 Introduzione alle Equazioni Differenziali 1 1.1 Esempio introduttivo............................. 1 1.2 Nomenclatura e Teoremi di Esistenza ed Unicità.............. 5 i Capitolo 1 Introduzione
Indice 1 Introduzione alle Equazioni Differenziali 1 1.1 Esempio introduttivo............................. 1 1.2 Nomenclatura e Teoremi di Esistenza ed Unicità.............. 5 i Capitolo 1 Introduzione
2 FUNZIONI REALI DI VARIABILE REALE
 2 FUNZIONI REALI DI VARIABILE REALE 2.1 CONCETTO DI FUNZIONE Definizione 2.1 Siano A e B due insiemi. Una funzione (o applicazione) f con dominio A a valori in B è una legge che associa ad ogni elemento
2 FUNZIONI REALI DI VARIABILE REALE 2.1 CONCETTO DI FUNZIONE Definizione 2.1 Siano A e B due insiemi. Una funzione (o applicazione) f con dominio A a valori in B è una legge che associa ad ogni elemento
Lezione 6. Divisibilità e divisori. Teorema di divisione euclidea. Algoritmo delle divisioni successive.
 Lezione 6 Prerequisiti: L'insieme dei numeri interi. Lezione 5. Divisibilità e divisori. Teorema di divisione euclidea. Algoritmo delle divisioni successive. Questa è la prima lezione dedicata all'anello
Lezione 6 Prerequisiti: L'insieme dei numeri interi. Lezione 5. Divisibilità e divisori. Teorema di divisione euclidea. Algoritmo delle divisioni successive. Questa è la prima lezione dedicata all'anello
Lezione 3: Il problema del consumatore: Il
 Corso di Economica Politica prof. Stefano Papa Lezione 3: Il problema del consumatore: Il vincolo di bilancio Facoltà di Economia Università di Roma La Sapienza Il problema del consumatore 2 Applichiamo
Corso di Economica Politica prof. Stefano Papa Lezione 3: Il problema del consumatore: Il vincolo di bilancio Facoltà di Economia Università di Roma La Sapienza Il problema del consumatore 2 Applichiamo
ISTITUTO D'ISTRUZIONE SUPERIORE A. MOTTI
 ISTITUTO D'ISTRUZIONE SUPERIORE A. MOTTI ISTITUTO PROFESSIONALE DI ENOGASTRONOMIA E OSPITALITA ALBERGHIERA CON I PERCORSI: ACCOGLIENZA TURISTICA, CUCINA, SALA-BAR ISTITUTO TECNICO PER IL TURISMO Sede Amministrativa:
ISTITUTO D'ISTRUZIONE SUPERIORE A. MOTTI ISTITUTO PROFESSIONALE DI ENOGASTRONOMIA E OSPITALITA ALBERGHIERA CON I PERCORSI: ACCOGLIENZA TURISTICA, CUCINA, SALA-BAR ISTITUTO TECNICO PER IL TURISMO Sede Amministrativa:
FUNZIONI / ESERCIZI SVOLTI
 ANALISI MATEMATICA I - A.A. 0/0 FUNZIONI / ESERCIZI SVOLTI ESERCIZIO. Data la funzione f () = determinare l insieme f (( +)). Svolgimento. Poiché f (( +)) = { dom f : f () ( +)} = { dom f : f () > } si
ANALISI MATEMATICA I - A.A. 0/0 FUNZIONI / ESERCIZI SVOLTI ESERCIZIO. Data la funzione f () = determinare l insieme f (( +)). Svolgimento. Poiché f (( +)) = { dom f : f () ( +)} = { dom f : f () > } si
VALORE PIÙ CONVENIENTE DEL RENDIMENTO
 VALORE PIÙ CONVENIENTE DEL RENDIENTO In una macchina elettrica ad un rendimento più elevato corrisponde un minor valore delle perdite e quindi un risparmio nelle spese di esercizio (in quanto minori risultano
VALORE PIÙ CONVENIENTE DEL RENDIENTO In una macchina elettrica ad un rendimento più elevato corrisponde un minor valore delle perdite e quindi un risparmio nelle spese di esercizio (in quanto minori risultano
Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R
 Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Syllabus: argomenti di Matematica delle prove di valutazione
 Syllabus: argomenti di Matematica delle prove di valutazione abcdef... ABC (senza calcolatrici, senza palmari, senza telefonini... ) Gli Argomenti A. Numeri frazioni e numeri decimali massimo comun divisore,
Syllabus: argomenti di Matematica delle prove di valutazione abcdef... ABC (senza calcolatrici, senza palmari, senza telefonini... ) Gli Argomenti A. Numeri frazioni e numeri decimali massimo comun divisore,
Funzione reale di variabile reale
 Funzione reale di variabile reale Siano A e B due sottoinsiemi non vuoti di. Si chiama funzione reale di variabile reale, di A in B, una qualsiasi legge che faccia corrispondere, a ogni elemento A x A
Funzione reale di variabile reale Siano A e B due sottoinsiemi non vuoti di. Si chiama funzione reale di variabile reale, di A in B, una qualsiasi legge che faccia corrispondere, a ogni elemento A x A
Liceo Scientifico Statale. Leonardo da Vinci. Fisica. Programma svolto durante l anno scolastico 2012/13 CLASSE I B. DOCENTE Elda Chirico
 Liceo Scientifico Statale Leonardo da Vinci Fisica Programma svolto durante l anno scolastico 2012/13 CLASSE I B DOCENTE Elda Chirico Le Grandezze. Introduzione alla fisica. Metodo sperimentale. Grandezze
Liceo Scientifico Statale Leonardo da Vinci Fisica Programma svolto durante l anno scolastico 2012/13 CLASSE I B DOCENTE Elda Chirico Le Grandezze. Introduzione alla fisica. Metodo sperimentale. Grandezze
Testing: basato su analisi dinamica del codice. Metodi Formali: basato su analisi statica del codice.
 Convalida: attività volta ad assicurare che il SW sia conforme ai requisiti dell utente. Verifica: attività volta ad assicurare che il SW sia conforme alle specifiche dell analista. Goal: determinare malfunzionamenti/anomalie/errori
Convalida: attività volta ad assicurare che il SW sia conforme ai requisiti dell utente. Verifica: attività volta ad assicurare che il SW sia conforme alle specifiche dell analista. Goal: determinare malfunzionamenti/anomalie/errori
Corso di Laurea in Ingegneria Informatica Analisi Numerica
 Corso di Laurea in Ingegneria Informatica Lucio Demeio Dipartimento di Scienze Matematiche 1 2 Analisi degli errori Informazioni generali Libro di testo: J. D. Faires, R. Burden, Numerical Analysis, Brooks/Cole,
Corso di Laurea in Ingegneria Informatica Lucio Demeio Dipartimento di Scienze Matematiche 1 2 Analisi degli errori Informazioni generali Libro di testo: J. D. Faires, R. Burden, Numerical Analysis, Brooks/Cole,
Convessità e derivabilità
 Convessità e derivabilità Definizione 1 (convessità per funzioni derivabili) Sia f : (a, b) R derivabile su (a, b). Diremo che f è convessa o concava su (a, b) se per ogni 0 (a,b) il grafico di f sta tutto
Convessità e derivabilità Definizione 1 (convessità per funzioni derivabili) Sia f : (a, b) R derivabile su (a, b). Diremo che f è convessa o concava su (a, b) se per ogni 0 (a,b) il grafico di f sta tutto
Classificazione Singolarità isolate, Serie di Laurent, Residui, Teorema dei residui e applicazioni
 Classificazione Singolarità isolate, Serie di Laurent, Residui, Teorema dei residui e applicazioni Docente:Alessandra Cutrì Richiamo:Zeri di Funzioni olomorfe (o analitiche) Sia f : A C C A aperto connesso,
Classificazione Singolarità isolate, Serie di Laurent, Residui, Teorema dei residui e applicazioni Docente:Alessandra Cutrì Richiamo:Zeri di Funzioni olomorfe (o analitiche) Sia f : A C C A aperto connesso,
Regola del partitore di tensione
 Regola del partitore di tensione Se conosciamo la tensione ai capi di una serie di resistenze e i valori delle resistenze stesse, è possibile calcolare la caduta di tensione ai capi di ciascuna R resistenza,
Regola del partitore di tensione Se conosciamo la tensione ai capi di una serie di resistenze e i valori delle resistenze stesse, è possibile calcolare la caduta di tensione ai capi di ciascuna R resistenza,
LEZIONE 23. Esempio 23.1.3. Si consideri la matrice (si veda l Esempio 22.2.5) A = 1 2 2 3 3 0
 LEZIONE 23 231 Diagonalizzazione di matrici Abbiamo visto nella precedente lezione che, in generale, non è immediato che, data una matrice A k n,n con k = R, C, esista sempre una base costituita da suoi
LEZIONE 23 231 Diagonalizzazione di matrici Abbiamo visto nella precedente lezione che, in generale, non è immediato che, data una matrice A k n,n con k = R, C, esista sempre una base costituita da suoi
CONTINUITÀ E DERIVABILITÀ Esercizi risolti
 CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
SESSIONE ORDINARIA 2007 CORSO DI ORDINAMENTO SCUOLE ITALIANE ALL ESTERO - AMERICHE
 SESSIONE ORDINARIA 007 CORSO DI ORDINAMENTO SCUOLE ITALIANE ALL ESTERO - AMERICHE PROBLEMA Si consideri la funzione f definita da f ( x) x, il cui grafico è la parabola.. Si trovi il luogo geometrico dei
SESSIONE ORDINARIA 007 CORSO DI ORDINAMENTO SCUOLE ITALIANE ALL ESTERO - AMERICHE PROBLEMA Si consideri la funzione f definita da f ( x) x, il cui grafico è la parabola.. Si trovi il luogo geometrico dei
ALCUNE APPLICAZIONI DEL CALCOLO DIFFERENZIALE
 ALCUNE APPLICAZIONI DEL CALCOLO DIFFERENZIALE Sia I un intervallo di R e siano a = inf(i) R { } e b = sup(i) R {+ }; i punti di I diversi dagli estremi a e b, ( e quindi appartenenti all intervallo aperto
ALCUNE APPLICAZIONI DEL CALCOLO DIFFERENZIALE Sia I un intervallo di R e siano a = inf(i) R { } e b = sup(i) R {+ }; i punti di I diversi dagli estremi a e b, ( e quindi appartenenti all intervallo aperto
3.1 Successioni. R Definizione (Successione numerica) E Esempio 3.1 CAPITOLO 3
 CAPITOLO 3 Successioni e serie 3. Successioni Un caso particolare di applicazione da un insieme numerico ad un altro insieme numerico è quello delle successioni, che risultano essere definite nell insieme
CAPITOLO 3 Successioni e serie 3. Successioni Un caso particolare di applicazione da un insieme numerico ad un altro insieme numerico è quello delle successioni, che risultano essere definite nell insieme
Protocollo dei saperi imprescindibili Ordine di scuola: professionale
 Protocollo dei saperi imprescindibili Ordine di scuola: professionale DISCIPLINA: MATEMATICA RESPONSABILE: CAGNESCHI F. IMPERATORE D. CLASSE: prima servizi commerciali Utilizzare le tecniche e le procedure
Protocollo dei saperi imprescindibili Ordine di scuola: professionale DISCIPLINA: MATEMATICA RESPONSABILE: CAGNESCHI F. IMPERATORE D. CLASSE: prima servizi commerciali Utilizzare le tecniche e le procedure
Corso di Calcolo Numerico
 Corso di Calcolo Numerico Dottssa MC De Bonis Università degli Studi della Basilicata, Potenza Facoltà di Ingegneria Corso di Laurea in Ingegneria Meccanica Corso di Calcolo Numerico - Dottssa MC De Bonis
Corso di Calcolo Numerico Dottssa MC De Bonis Università degli Studi della Basilicata, Potenza Facoltà di Ingegneria Corso di Laurea in Ingegneria Meccanica Corso di Calcolo Numerico - Dottssa MC De Bonis
x log(x) + 3. f(x) =
 Università di Bari, Corso di Laurea in Economia e Commercio Esame di Matematica per l Economia L/Z Dr. G. Taglialatela 03 giugno 05 Traccia dispari Esercizio. Calcolare Esercizio. Calcolare e cos log d
Università di Bari, Corso di Laurea in Economia e Commercio Esame di Matematica per l Economia L/Z Dr. G. Taglialatela 03 giugno 05 Traccia dispari Esercizio. Calcolare Esercizio. Calcolare e cos log d
CRITERI DI CONVERGENZA PER LE SERIE. lim a n = 0. (1) s n+1 = s n + a n+1. (2) CRITERI PER LE SERIE A TERMINI NON NEGATIVI
 Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
1.1. Spazi metrici completi
 SPAZI METRICI: COMPLETEZZA E COMPATTEZZA Note informali dalle lezioni 1.1. Spazi metrici completi La nozione di convergenza di successioni è centrale nello studio degli spazi metrici. In particolare è
SPAZI METRICI: COMPLETEZZA E COMPATTEZZA Note informali dalle lezioni 1.1. Spazi metrici completi La nozione di convergenza di successioni è centrale nello studio degli spazi metrici. In particolare è
COEFFICIENTI BINOMIALI
 COEFFICIENTI BINOMIALI Michele Impedovo micheleimpedovo@uni-bocconiit Una definizione insiemistica Se n è un numero naturale e è un numero naturale compreso tra e n, si indica con il simbolo il coefficiente
COEFFICIENTI BINOMIALI Michele Impedovo micheleimpedovo@uni-bocconiit Una definizione insiemistica Se n è un numero naturale e è un numero naturale compreso tra e n, si indica con il simbolo il coefficiente
Note del corso di Calcolabilità e Linguaggi Formali - Lezione 6
 Note del corso di Calcolabilità e Linguaggi Formali - Lezione 6 Alberto Carraro 30 novembre DAIS, Universitá Ca Foscari Venezia http://www.dsi.unive.it/~acarraro 1 Funzioni Turing-calcolabili Finora abbiamo
Note del corso di Calcolabilità e Linguaggi Formali - Lezione 6 Alberto Carraro 30 novembre DAIS, Universitá Ca Foscari Venezia http://www.dsi.unive.it/~acarraro 1 Funzioni Turing-calcolabili Finora abbiamo
NUMERI COMPLESSI. Test di autovalutazione
 NUMERI COMPLESSI Test di autovalutazione 1. Se due numeri complessi z 1 e z 2 sono rappresentati nel piano di Gauss da due punti simmetrici rispetto all origine: (a) sono le radici quadrate di uno stesso
NUMERI COMPLESSI Test di autovalutazione 1. Se due numeri complessi z 1 e z 2 sono rappresentati nel piano di Gauss da due punti simmetrici rispetto all origine: (a) sono le radici quadrate di uno stesso
Algebra Booleana 1 ALGEBRA BOOLEANA: VARIABILI E FUNZIONI LOGICHE
 Algebra Booleana 1 ALGEBRA BOOLEANA: VARIABILI E FUNZIONI LOGICHE Andrea Bobbio Anno Accademico 2000-2001 Algebra Booleana 2 Calcolatore come rete logica Il calcolatore può essere visto come una rete logica
Algebra Booleana 1 ALGEBRA BOOLEANA: VARIABILI E FUNZIONI LOGICHE Andrea Bobbio Anno Accademico 2000-2001 Algebra Booleana 2 Calcolatore come rete logica Il calcolatore può essere visto come una rete logica
