Basi di spazi vettoriali di polinomi Consideriamo lo spazio vettoriale dei polinomi di grado al più 2 R 2 [x] = {ax 2 + bx + c; a, b, c R},
|
|
|
- Bianca Mariani
- 4 anni fa
- Visualizzazioni
Transcript
1 Lezione del Dopo avere svolto un esercizio in uno spazio vettoriale di polinomi, si è introdotto il concetto di applicazione lineare e l esempio fondamentale di applicazione lineare da uno spazio R n di vettori colonna n 1 ad uno spazio R m di vettori colonna m 1, cioè le moltiplicazione a sinistra per una data matrice m n. Il riferimento è Cap.5 Applicazioni lineari, Par.5.1 Definizione di applicazione lineare (tranne ultima parte dal Th in poi). Di seguito si riporta un resoconto degli argomenti svolti. Basi di spazi vettoriali di polinomi Consideriamo lo spazio vettoriale dei polinomi di grado al più 2 R 2 [x] = {ax 2 + bx + c; a, b, c R}, che possiamo riguardare sia come espressioni formali che come funzioni polinomiali R R; scegliamo di riguardarli come espressioni formali. Indicheremo i polinomi scrivendoli esplicitamente oppure con lettere latine minuscole sottolineate p, q,... Questo spazio ha una base ordinata canonica costituita dai polinomi potenza ordinati per grado decrescente C : x 2, x, 1 (un altra base ordinata canonica è 1, x, x 2 ). Dunque R 2 [x] ha dimensione 3. La scrittura ax 2 + bx + c si può intendere come la scrittura del generico polinomio come combinazione lineare a x 2 + b x + c 1 dei vettori della base canonica C; dunque ax 2 + bx + c ha vettore delle coordinate (ax 2 + bx + c) C = (a, b, c) Di seguito mostriamo come si determinano le coordinate di un polinomio rispetto ad altre basi. Esercizio. Nello spazio vettoriale R 2 [x] si consideri la lista di polinomi B : x 2 x, x 2 + x, x 1 (1) B è una base (ordinata) di R 2 [x]? (2) in caso affermativo, si determinino le coordinate del polinomio p = 2x 2 + 3x + 5 rispetto a B. Svolgimento. (1) Essendo B una linsta di 3 vettori in uno spazio vettoriale di dimensione 3, per verificare che B è una base basta verificare che B è linearmente indipendente. Consideriamo un uguaglianza α(x 2 x) + β(x 2 + x) + γ(x 2 1) = 0 dove 0 è il polinomio nullo; questa uguaglianza si può riscrivere come dunque si deve avere (α + β + γ)x 2 + ( α + γ)x γ = 0; α + β + γ = 0 α + β = 0 γ = 0 da cui α = β = γ = 0. Dunque B è una base di R 2 [x]. 1
2 2 2) La lista α, β, γ delle coordinate del polinomio p rispetto alla base B è definita dall uguaglianza cioè questa uguaglianza vale se e solo se α(x 2 x) + β(x 2 + x) + γ(x 2 1) = 2x 2 + 3x + 5 (α + β + γ)x 2 + ( α + γ)x γ = 2x 2 + 3x + 5; α + β + γ = 2 α + β = 3 γ = 5 cioè α = 2, β = 5, γ = 5. Verifica: deve valere l uguaglianza fra polinomi vera. Sinteticamente, si ha Applicazioni lineari. 2(x 2 x) + 5(x 2 + x) 5(x 2 1) = 2x 2 + 3x + 5; (p) B = (2, 5, 5). Applicazioni. Ricordiamo che una funzione da un insieme dominio ad un insieme codominio è una legge che associa a ciscun elemento del dominio uno ed un solo elemento immagine nel codominio. Se f, A, B indicano la funzione, il dominio ed il codominio, si scrive f : A B, e per ciascun a A l immagine di a si indica con f(a); l insieme delle immagini degli elmenti di A si dice immagine di A e si indica con f(a), in simboli: {f(a); a A} = f(a). Per ogni insieme A, la funzione da A ad A che associa ad ogni elemento se stesso si dice funzione identita e si indica con id A ; in simboli: id A : A A, id A (a) = a per ogni a A. Il termine applicazione è sinonimo di funzione. Introduzione al concetto di applicazione lineare. Abbiamo visto che, fissata in uno spazio vettoriale V una base ordinata B : v 1,..., v n, ciascun vettore di V individua una n pla ordinata di coordinate. Associando a ciascun v in V il vettore (v) B delle sue coordinate si ha un applicazione V R n, ed abbiamo visto che questa applicazione è biunivoca e compatibile con le operazioni in V ed in R n, e dunque permette di identificare lo spazio vettoriale V con lo spazio vettoriale R n. Questo è un primo esempio di applicazione lineare, nel senso della seguente Definizione. Sia F : V W un applicazione fra due spazi vettoriali V, W. Si dice che F è lineare se soddisfa entrambe le condizioni (1) F (u + v) = F (u) + F (v) u, v V ; (1) F (λu) = λf (u) λ R, u V. Esempi ovvi. Per ogni spazio vettoriale V, l applicazione identica id V : V V è lineare. Per ogni due spazi vettoriali V, W, l applicazione V W che manda ciascun v di V nel vettore nullo 0 W di W è lineare.
3 3 Prime proprietà. Sia F : V W un applicazione lineare. Allora F (0 V ) = 0 W, F ( v) = F (v), v V Dimostrazione della prima: F (0 V ) = F (00 V ) = 0F (0 V ) = 0 W. Dimostrazione della seconda: F ( v) = F (( 1)v) = ( 1)F (v) = F (v). Esempi di applicazioni lineari R n R. (A) L applicazione L : R R, L(x) = 2x è lineare in quanto: (1) per ogni x 1, x 2 R, da una parte si ha L(x 1 + x 2 ) = 2(x 1 + x 2 ) e dall altra parte si ha L(x 1 ) + L(x 2 ) = 2x 1 + 2x 2 ; da 2(x 1 + x 2 ) = 2x 1 + 2x 2 (proprietà distributiva del prodotto rispetto alla somma in R) segue L(x 1 + x 2 ) = L(x 1 ) + L(x 2 ) (2) per ogni λ R, x R, da una parte si ha L(λx) = 2(λx) e dall altra parte si ha λl(x) = λ(2x); da 2(λx) = λ(2x) (proprietà associativa e commutativa del prodotto in R) segue L(λx) = λl(x). Allo stesso modo si prova che per ogni fissato a R, l applicazione L : R R, L(x) = ax è lineare. Queste sono le applicazioni che esprimono leggi di proporzionalità diretta fra valori in entrata e valori in uscita. Hanno per grafico le rette passanti per l origine (escluso il secondo asse coordinato). (A ) L applicazione L : R R, L(x) = x + 1 non è lineare in quanto L(0) = 1 0. (A ) L applicazione Q : R R, Q(x) = x 2 non è lineare. Infatti la proprietà e questa proprietà è falsa. Q(x 1 + x 2 ) = Q(x 1 ) + Q(x 2 ), x 1, x 2 R (x 1 + x 2 ) 2 = x x 2 2 x 1, x 2 R (B) L applicazione L : R 2 R, L(x, y) = 2x + 3y è lineare in quanto: (1) la proprietà L((x 1, y 1 ) + (x 2, y 2 )) = L(x 1, y 1 ) + L(x 2, y 2 ), (x 1, y 1 ), (x 2, y 2 ) R 2 che a sua volta L(x 1 + x 2, y 1 + y 2 ) = L(x 1, y 1 ) + L(x 2, y 2 )... 2(x 1 + x 2 ) + 3(y 1 + y 2 ) = 2x 1 + 3y 1 + 2x 2 + 3y 2... proprietà che è vera (per la commutatività della somma e la prorietà distributiva del prodotto rispetto alla somma in R); (2) la proprietà che a sua volta L(λ(x, y)) = λl(x, y), λ R, (x, y) R 2 L(λx, λy) = λl(x, y)... 2(λx) + 3(λy) = λ(2x + 3y)...
4 4 proprietà che è vera (per la associatività e commutatività del prodotto e la prorietà distributiva del prodotto rispetto alla somma in R). In modo simile si prova che per ogni fissata n pla a 1,..., a n R, l applicazione L : R n R, L(x 1,..., x n ) = a 1 x a n x n in breve L((x i ) n ) = a i x i è lineare. Algebra delle matrici. Proprietà del prodotto rispetto alle altre operazioni. Prima di proseguire con gli esempi, completiamo il discorso sulle operazioni sulle matrici. Sull insieme delle matrici ad elementi in R abbiamo definito le operazioni interne parziali di prodotto e somma e l operazione esterna di prodotto per scalari. Abbiamo visto le proprietà del prodotto (in particolare associatività e non commutatività) e le proprietà complessive della somma e del prodotto per scalari (che danno la struttura di spazio vettoriale sugli insiemi di matrici di uno stesso tipo fissato). Vediamo ora le proprietà che legano il prodotto alle altre due operazioni. Proprietà distributive. Partiamo da un esempio; si ha (( ) ( )) ( ) ( ) (2 3) + = (2 3) + (2 3) ; infatti: al primo membro si ha (2 3) ( 10 12) = 56; al secondo membro si ha = 56. Non è un caso infatti vale la Proposizione. Per ogni a, a M 1,n ed ogni b, b M n,1 si ha a(b + b ) = ab + ab (a + a )b = ab + a b Dimostrazione della prima proprietà (la seconda è analoga). Posto a = (a i ) n 1, b = (b i ) n 1, b = (b i) n 1, la prima proprietà a i (b i + b i) = a i b i + a i b i,... proprietà vera (per la commutatività della somma e la prorietà distributiva del prodotto rispetto alla somma in R). Proposizione (proprietà distributiva del prodotto rispetto alla somma). Per ogni A, A M m,n ed ogni B, B M n,p si ha A(B + B ) = AB + AB (A + A )B = AB + A B Dimostrazione della prima proprietà (la seconda è analoga). Per ogni i = 1,..., m e j = 1,..., p si ha: la matrice A(B + B ) ha elemento di posto (i, j) (A(B + B )) ij = A i: (B + B ) :j = A i: (B :j + B :j); la matrice AB + AB ha elemento di posto (i, j) (AB + AB ) ij = (AB) ij + (AB ) ij = A i: B :j + A i: B :j; e le ultime espressioni sono uguali per la proposizione precedente.
5 Si prova anche la Proposizione (proprietà pseudo associativa fra prodotto e prodotto per scalari). Per ogni A M m,n, B M n,p e λ R si ha Applicazioni lineari R n R m. Esempio. Consideriamo l applicazione A(λB) = (λa)b = λ(ab). L : R 2 R 3, L(x, y) = (2x + 3y, 4x + 5y, 6x + 7y). Scrivendo le coppie ordinate e le terne ordinate come matrici colonna, si ha ( ) 2x + 3y x L = 4x + 5y = 2 3 ( ) 4 5 x y y 6x + 7y 6 7 cioè L è l operazione di moltiplicazione a sinistra per la matrice Convenzione: D ora innanzi, salvo avviso contrario, quando identificheremo ennuple di numeri reali con matrici, le identificheremo con matrici colonna ad n componenti. Proposizione. Per ciasuna matrice A M m,n fissata, la moltiplicazione a sinistra per A L : R n R m, L(x) = Ax, è un applicazione lineare. Dimostrazione. L è un applicazione R n R m ; infatti A è di tipo m n, dunque per ogni x di tipo n 1 il prodotto Ax è definito ed ha tipo m 1. L è lineare; infatti ogni x, x R n e λ R si ha (1) L(x + x ) = A(x + x ) = Ax + Ax = L(x) + L(x ) (1) L(λx) = A(λx) = λ(ax) = λl(x) Dunque ogni matrice m n fornisce un applicazione lineare R n R m. Vedremo che non ci sono altre applicazioni lineari al di fuori di queste. 5
- ciascun autovalore di T ha molteplicità geometrica uguale alla moltplicitaà algebrica.
 Lezioni del 14.05 e 17.05 In queste lezioni si sono svolti i seguenti argomenti. Ripresa del teorema generale che fornisce condizioni che implicano la diagonalizzabilità, indebolimento delle ipotesi, e
Lezioni del 14.05 e 17.05 In queste lezioni si sono svolti i seguenti argomenti. Ripresa del teorema generale che fornisce condizioni che implicano la diagonalizzabilità, indebolimento delle ipotesi, e
Di seguito diamo un procedimento generale che separa nettamente gli aspetti concettuali e gli aspetti di calcolo.
 Lezione del 0905 Le basi degli spazi vettoriali permettono di rappresentare vettori con ennuple e applicazioni lineari con matrici Si hanno basi più o meno adatte a rappresentare vettori ed applicazioni
Lezione del 0905 Le basi degli spazi vettoriali permettono di rappresentare vettori con ennuple e applicazioni lineari con matrici Si hanno basi più o meno adatte a rappresentare vettori ed applicazioni
Proposizione (relazione fra V, opposti in R e opposti in V ).
 Lezione del 20.03. Ci sono vari tipi di strutture che conducono al concetto di spazio vettoriale, in particolare quelle sugli insiemi R n di ennuple di numeri reali (n = 1, 2, 3,...) e quelle sugli insiemi
Lezione del 20.03. Ci sono vari tipi di strutture che conducono al concetto di spazio vettoriale, in particolare quelle sugli insiemi R n di ennuple di numeri reali (n = 1, 2, 3,...) e quelle sugli insiemi
Parte I. Algebra lineare teorica
 Parte I Algebra lineare teorica 1 1 Gli spazi vettoriali 11 Definizione ed esempi Consideriamo come esempio di riferimento lo spazio R n, n 1, ossia l insieme delle n uple di numeri reali con n fissato
Parte I Algebra lineare teorica 1 1 Gli spazi vettoriali 11 Definizione ed esempi Consideriamo come esempio di riferimento lo spazio R n, n 1, ossia l insieme delle n uple di numeri reali con n fissato
Richiami di Algebra Lineare
 Appendice A Richiami di Algebra Lineare In questo capitolo sono presentati alcuni concetti di algebra lineare L algebra lineare è quella branca della matematica che si occupa dello studio di vettori, spazi
Appendice A Richiami di Algebra Lineare In questo capitolo sono presentati alcuni concetti di algebra lineare L algebra lineare è quella branca della matematica che si occupa dello studio di vettori, spazi
Elementi di Algebra Lineare Spazi Vettoriali
 Elementi di Algebra Lineare Spazi Vettoriali Antonio Lanteri e Cristina Turrini UNIMI - 2015/2016 Antonio Lanteri e Cristina Turrini (UNIMI - 2015/2016) Elementi di Algebra Lineare 1 / 37 index Spazi vettoriali
Elementi di Algebra Lineare Spazi Vettoriali Antonio Lanteri e Cristina Turrini UNIMI - 2015/2016 Antonio Lanteri e Cristina Turrini (UNIMI - 2015/2016) Elementi di Algebra Lineare 1 / 37 index Spazi vettoriali
0 0 c. d 1. det (D) = d 1 d n ;
 Registro Lezione di Algebra lineare del 23 novembre 216 1 Matrici diagonali 2 Autovettori e autovalori 3 Ricerca degli autovalori, polinomio caratteristico 4 Ricerca degli autovettori, autospazi 5 Matrici
Registro Lezione di Algebra lineare del 23 novembre 216 1 Matrici diagonali 2 Autovettori e autovalori 3 Ricerca degli autovalori, polinomio caratteristico 4 Ricerca degli autovettori, autospazi 5 Matrici
Elementi di Algebra Lineare Spazi Vettoriali
 Elementi di Algebra Lineare Spazi Vettoriali Antonio Lanteri e Cristina Turrini UNIMI - 2017/2018 Antonio Lanteri e Cristina Turrini (UNIMI - 2017/2018) Elementi di Algebra Lineare 1 / 37 index Spazi vettoriali
Elementi di Algebra Lineare Spazi Vettoriali Antonio Lanteri e Cristina Turrini UNIMI - 2017/2018 Antonio Lanteri e Cristina Turrini (UNIMI - 2017/2018) Elementi di Algebra Lineare 1 / 37 index Spazi vettoriali
Elementi di Algebra Lineare Spazi Vettoriali
 Elementi di Algebra Lineare Spazi Vettoriali Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017) Elementi di Algebra Lineare 1 / 41 index Spazi vettoriali
Elementi di Algebra Lineare Spazi Vettoriali Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017) Elementi di Algebra Lineare 1 / 41 index Spazi vettoriali
1 Cenni di teoria degli insiemi
 1 Cenni di teoria degli insiemi 1.1. Siano A, B, C,... insiemi. Scriveremo a A, a / A per affermare rispettivamente che l elemento a appartiene all insieme A e che l elemento a non appartiene ad A. Diremo
1 Cenni di teoria degli insiemi 1.1. Siano A, B, C,... insiemi. Scriveremo a A, a / A per affermare rispettivamente che l elemento a appartiene all insieme A e che l elemento a non appartiene ad A. Diremo
Algebra lineare. Laboratorio di programmazione e calcolo CdL in Chimica. Pierluigi Amodio
 Algebra lineare Laboratorio di programmazione e calcolo CdL in Chimica Pierluigi Amodio Dipartimento di Matematica Università di Bari pierluigi.amodio@uniba.it http://dm.uniba.it/ amodio A.A. 2016/17 P.
Algebra lineare Laboratorio di programmazione e calcolo CdL in Chimica Pierluigi Amodio Dipartimento di Matematica Università di Bari pierluigi.amodio@uniba.it http://dm.uniba.it/ amodio A.A. 2016/17 P.
Lezione 5: Applicazioni Lineari. 1 Definizione di applicazione lineare
 Lezione 5: Applicazioni Lineari Le applicazioni lineari sono funzioni tra spazi vettoriali che ne rispettano la struttura, cioe che conservano le operazioni di somma tra vettori e moltiplicazione di un
Lezione 5: Applicazioni Lineari Le applicazioni lineari sono funzioni tra spazi vettoriali che ne rispettano la struttura, cioe che conservano le operazioni di somma tra vettori e moltiplicazione di un
Elementi di Algebra Lineare Spazi Vettoriali
 Elementi di Algebra Lineare Spazi Vettoriali Cristina Turrini UNIMI - 2018/2019 Cristina Turrini (UNIMI - 2018/2019) Elementi di Algebra Lineare 1 / 32 index Spazi vettoriali 1 Spazi vettoriali 2 Sottospazi
Elementi di Algebra Lineare Spazi Vettoriali Cristina Turrini UNIMI - 2018/2019 Cristina Turrini (UNIMI - 2018/2019) Elementi di Algebra Lineare 1 / 32 index Spazi vettoriali 1 Spazi vettoriali 2 Sottospazi
GEOMETRIA 1 terza parte
 GEOMETRIA 1 terza parte Cristina Turrini C. di L. in Fisica - 2014/2015 Cristina Turrini (C. di L. in Fisica - 2014/2015) GEOMETRIA 1 1 / 32 index Applicazioni lineari 1 Applicazioni lineari 2 Nucleo e
GEOMETRIA 1 terza parte Cristina Turrini C. di L. in Fisica - 2014/2015 Cristina Turrini (C. di L. in Fisica - 2014/2015) GEOMETRIA 1 1 / 32 index Applicazioni lineari 1 Applicazioni lineari 2 Nucleo e
0.1 Coordinate in uno spazio vettoriale
 0.. COORDINATE IN UNO SPAZIO VETTORIALE 0. Coordinate in uno spazio vettoriale Sia V uno spazio vettoriale di dimensione finita n costruito sul campo K. D ora in poi, ogni volta che sia fissata una base
0.. COORDINATE IN UNO SPAZIO VETTORIALE 0. Coordinate in uno spazio vettoriale Sia V uno spazio vettoriale di dimensione finita n costruito sul campo K. D ora in poi, ogni volta che sia fissata una base
Lezione del dove a 1, a n e b sono numeri reali assegnati, detti coefficienti e termine noto dell equazione;
 Le lezioni del 60 e 010 si riferiscono al Capitolo 1 Introduzione ai sistemi lineari Di seguito si elencano gli argomenti svolti, descrivendoli sinteticamente dando i riferimenti a tale capitolo, oppure
Le lezioni del 60 e 010 si riferiscono al Capitolo 1 Introduzione ai sistemi lineari Di seguito si elencano gli argomenti svolti, descrivendoli sinteticamente dando i riferimenti a tale capitolo, oppure
Algebra Lineare. a.a Gruppo A-H. Prof. P. Piazza Soluzioni del compito pomeridiano del 6/12/2004
 Algebra Lineare. a.a. 004-05. Gruppo A-H. Prof. P. Piazza Soluzioni del compito pomeridiano del 6/1/004 Esercizio 1. Siano V e W due spazi vettoriali e sia F : V W un isomorfismo (quindi F è lineare e
Algebra Lineare. a.a. 004-05. Gruppo A-H. Prof. P. Piazza Soluzioni del compito pomeridiano del 6/1/004 Esercizio 1. Siano V e W due spazi vettoriali e sia F : V W un isomorfismo (quindi F è lineare e
3. Elementi di Algebra Lineare.
 CALCOLO NUMERICO Francesca Mazzia Dipartimento Interuniversitario di Matematica Università di Bari 3. Elementi di Algebra Lineare. 1 Sistemi lineari Sia A IR m n, x IR n di n Ax = b è un vettore di m componenti.
CALCOLO NUMERICO Francesca Mazzia Dipartimento Interuniversitario di Matematica Università di Bari 3. Elementi di Algebra Lineare. 1 Sistemi lineari Sia A IR m n, x IR n di n Ax = b è un vettore di m componenti.
Corso di Geometria Lezione II: Spazi vettoriali
 .. Corso di Geometria Lezione II: Spazi vettoriali F. Baldassarri 8 ottobre 2013 Definizione di spazio vettoriale Uno spazio vettoriale su un campo C (ad es. Q,R,C,{0, 1}) è un insieme V dotato di due
.. Corso di Geometria Lezione II: Spazi vettoriali F. Baldassarri 8 ottobre 2013 Definizione di spazio vettoriale Uno spazio vettoriale su un campo C (ad es. Q,R,C,{0, 1}) è un insieme V dotato di due
Analisi dei dati corso integrato - Algebra lineare, e a b c 0. le soluzioni del sistema lineare omogeneo x d e f 2. a b c.
 Analisi dei dati corso integrato - Algebra lineare 4.3.8 e 5.3.8-1 1. Nella lezione precedente abbiamo definito lo spazio nullo e lo spazio delle colonne di una matrice; ora definiamo lo spazio delle righe
Analisi dei dati corso integrato - Algebra lineare 4.3.8 e 5.3.8-1 1. Nella lezione precedente abbiamo definito lo spazio nullo e lo spazio delle colonne di una matrice; ora definiamo lo spazio delle righe
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
APPUNTI DI ALGEBRA LINEARE
 APPUNTI DI ALGEBRA LINEARE. Definizione Si dice spazio vettoriale (sul campo dei numeri reali R) un insieme V per il quale siano definite l operazione interna di somma (che ad ogni coppia di vettori e
APPUNTI DI ALGEBRA LINEARE. Definizione Si dice spazio vettoriale (sul campo dei numeri reali R) un insieme V per il quale siano definite l operazione interna di somma (che ad ogni coppia di vettori e
Anno Accademico 2015/2016
 Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2015/2016 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2015/2016 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
GEOMETRIA 1 seconda parte
 GEOMETRIA 1 seconda parte Cristina Turrini C. di L. in Fisica - 2014/2015 Cristina Turrini (C. di L. in Fisica - 2014/2015) GEOMETRIA 1 1 / 40 index Spazi vettoriali 1 Spazi vettoriali 2 Sottospazi 3 Sistemi
GEOMETRIA 1 seconda parte Cristina Turrini C. di L. in Fisica - 2014/2015 Cristina Turrini (C. di L. in Fisica - 2014/2015) GEOMETRIA 1 1 / 40 index Spazi vettoriali 1 Spazi vettoriali 2 Sottospazi 3 Sistemi
Richiami di Algebra Lineare
 Richiami di Algebra Lineare Eduardo Rossi Università degli Studi di Pavia Corso di Econometria Marzo 2012 Rossi Algebra Lineare 2012 1 / 59 Vettori Prodotto interno a : (n 1) b : (n 1) a b = a 1 b 1 +
Richiami di Algebra Lineare Eduardo Rossi Università degli Studi di Pavia Corso di Econometria Marzo 2012 Rossi Algebra Lineare 2012 1 / 59 Vettori Prodotto interno a : (n 1) b : (n 1) a b = a 1 b 1 +
Elementi di Algebra Lineare
 Elementi di Algebra Lineare Corso di Calcolo Numerico, a.a. 2009/2010 Francesca Mazzia Dipartimento di Matematica Università di Bari 13 Marzo 2006 Francesca Mazzia (Univ. Bari) Elementi di Algebra Lineare
Elementi di Algebra Lineare Corso di Calcolo Numerico, a.a. 2009/2010 Francesca Mazzia Dipartimento di Matematica Università di Bari 13 Marzo 2006 Francesca Mazzia (Univ. Bari) Elementi di Algebra Lineare
LEZIONE 11. s V : V V V (v 1, v 2 ) v 1 + v 2 = s V (v 1, v 2 ), p V : k V V. per cui valgono:
 LEZIONE 11 11.1. Spazi vettoriali ed esempi. La nozione di spazio vettoriale generalizza quanto visto nelle lezioni precedenti: l insieme k m,n delle matrici m n a coefficienti in k = R, C, l insieme V
LEZIONE 11 11.1. Spazi vettoriali ed esempi. La nozione di spazio vettoriale generalizza quanto visto nelle lezioni precedenti: l insieme k m,n delle matrici m n a coefficienti in k = R, C, l insieme V
Matematica per Analisi dei Dati,
 Matematica per Analisi dei Dati, 230209 1 Spazio vettoriale R n Sia n un intero positivo fissato Lo spazio vettoriale R n e l insieme delle n ple ordinate di numeri reali, che rappresenteremo sempre come
Matematica per Analisi dei Dati, 230209 1 Spazio vettoriale R n Sia n un intero positivo fissato Lo spazio vettoriale R n e l insieme delle n ple ordinate di numeri reali, che rappresenteremo sempre come
3. Determinare le soluzioni del sistema lineare Σ α interpretato ora come sistema lineare nelle 4 incognite x 1, x 2, x 3, x 4.
 Corsi di Laurea in INGEGNERIA INDUSTRIALE Canali 1-2-5 Corso di Fondamenti di Algebra Lineare e Geometria Padova 21 Aprile 2012 I prova parziale Tema n.1 PARTE A. Risolvere i seguenti esercizi: Esercizio
Corsi di Laurea in INGEGNERIA INDUSTRIALE Canali 1-2-5 Corso di Fondamenti di Algebra Lineare e Geometria Padova 21 Aprile 2012 I prova parziale Tema n.1 PARTE A. Risolvere i seguenti esercizi: Esercizio
Sistemi lineari e spazi vettoriali 1 / 14
 Sistemi lineari e spazi vettoriali 1 / 14 Sistemi lineari 2 / 14 Studieremo sistemi lineari costituiti da m equazioni in n incognite (m,n N, m,n 1): cioè a 11 x 1 + +a 1n x n = b 1 a 21 x 1 + +a 2n x n
Sistemi lineari e spazi vettoriali 1 / 14 Sistemi lineari 2 / 14 Studieremo sistemi lineari costituiti da m equazioni in n incognite (m,n N, m,n 1): cioè a 11 x 1 + +a 1n x n = b 1 a 21 x 1 + +a 2n x n
LEZIONE 12. v = α 1 v α n v n =
 LEZIONE 12 12.1. Combinazioni lineari. Definizione 12.1.1. Sia V uno spazio vettoriale su k = R, C e v 1,..., v n V vettori fissati. Un vettore v V si dice combinazione lineare di v 1,..., v n se esistono
LEZIONE 12 12.1. Combinazioni lineari. Definizione 12.1.1. Sia V uno spazio vettoriale su k = R, C e v 1,..., v n V vettori fissati. Un vettore v V si dice combinazione lineare di v 1,..., v n se esistono
Terminiamo gli ultimi due esercizi della lezione 4 SPAZI E SOTTOSPAZI VETTORIALI
 Terminiamo gli ultimi due esercizi della lezione 4 SPAZI E SOTTOSPAZI VETTORIALI Dato un campo K e (V) gruppo abeliano se è definita la legge di composizione tra gli scalari λ di K e gli elementi v di
Terminiamo gli ultimi due esercizi della lezione 4 SPAZI E SOTTOSPAZI VETTORIALI Dato un campo K e (V) gruppo abeliano se è definita la legge di composizione tra gli scalari λ di K e gli elementi v di
Elementi di Algebra Lineare. Spazio Vettoriale (lineare)
 Elementi di Algebra Lineare Spazio Vettoriale (lineare) Uno spazio vettoriale su un corpo F è una quadrupla (X, F, +, ) costituita da: un insieme di elementi X, detti vettori, un corpo F, i cui elementi
Elementi di Algebra Lineare Spazio Vettoriale (lineare) Uno spazio vettoriale su un corpo F è una quadrupla (X, F, +, ) costituita da: un insieme di elementi X, detti vettori, un corpo F, i cui elementi
Funzioni reali di variabile reale
 Lezione 10.1, Analisi, 03.10.2017 Funzioni reali di variabile reale Funzioni polinomiali Rette nel piano e funzioni polinomiali di I grado Sia fissato un sistema di riferimento cartesiano ortogonale monometrico
Lezione 10.1, Analisi, 03.10.2017 Funzioni reali di variabile reale Funzioni polinomiali Rette nel piano e funzioni polinomiali di I grado Sia fissato un sistema di riferimento cartesiano ortogonale monometrico
ed un operazione di moltiplicazione per scalari reali u u 2u
 Geometria e Algebra (II), 0... Consideriamo il piano della geometria euclidea, intuitivamente inteso, e sia un punto fissato in esso. Sull insieme P dei vettori del piano applicati nel punto sono definite
Geometria e Algebra (II), 0... Consideriamo il piano della geometria euclidea, intuitivamente inteso, e sia un punto fissato in esso. Sull insieme P dei vettori del piano applicati nel punto sono definite
Analisi dei dati corso integrato - Algebra lineare,
 Analisi dei dati corso integrato - Algebra lineare, 26.2.8-27.2.8. Un sottinsieme non vuoto = V R n dello spaio vettoriale R n che sia chiuso rispetto alle operaioni sui vettori, cioe tale che per ogni
Analisi dei dati corso integrato - Algebra lineare, 26.2.8-27.2.8. Un sottinsieme non vuoto = V R n dello spaio vettoriale R n che sia chiuso rispetto alle operaioni sui vettori, cioe tale che per ogni
MATRICI E SISTEMI LINEARI
 MATRICI E SISTEMI LINEARI - PARTE I - Felice Iavernaro Dipartimento di Matematica Università di Bari 27 Febbraio 2006 Felice Iavernaro (Univ. Bari) Matrici e Sistemi lineari 27/02/2006 1 / 1 Definizione
MATRICI E SISTEMI LINEARI - PARTE I - Felice Iavernaro Dipartimento di Matematica Università di Bari 27 Febbraio 2006 Felice Iavernaro (Univ. Bari) Matrici e Sistemi lineari 27/02/2006 1 / 1 Definizione
x 1 Fig.1 Il punto P = P =
 Geometria di R 2 In questo paragrafo discutiamo le proprietà geometriche elementari del piano Per avere a disposizione delle coordinate nel piano, fissiamo un punto, che chiamiamo l origine Scegliamo poi
Geometria di R 2 In questo paragrafo discutiamo le proprietà geometriche elementari del piano Per avere a disposizione delle coordinate nel piano, fissiamo un punto, che chiamiamo l origine Scegliamo poi
25 - Funzioni di più Variabili Introduzione
 Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 25 - Funzioni di più Variabili Introduzione Anno Accademico 2013/2014 M. Tumminello
Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 25 - Funzioni di più Variabili Introduzione Anno Accademico 2013/2014 M. Tumminello
Anno Accademico 2017/2018
 Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2017/2018 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2017/2018 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
Esempi. In R 2, le coppia (2, 5) è combinazione lineare dei vettori (0, 1) e (1, 1). Infatti:
 Combinazioni lineari [Abate, 4.2] Sia V uno spazio vettoriale e v 1, v 2,..., v n dei vettori di V. Diremo che un vettore w V è combinazione lineare dei vettori v 1,..., v n se esistono a 1, a 2,..., a
Combinazioni lineari [Abate, 4.2] Sia V uno spazio vettoriale e v 1, v 2,..., v n dei vettori di V. Diremo che un vettore w V è combinazione lineare dei vettori v 1,..., v n se esistono a 1, a 2,..., a
Algebra Lineare. a.a Gruppo A-H. Prof. P. Piazza Soluzioni compito pomeridiano del 20/12/2004
 Algebra Lineare. a.a. 2004-05. Gruppo A-H. Prof. P. Piazza Soluzioni compito pomeridiano del 20/12/2004 Esercizio 1. Consideriamo una retta r dello spazio affine. Diremo che le equazioni cartesiane di
Algebra Lineare. a.a. 2004-05. Gruppo A-H. Prof. P. Piazza Soluzioni compito pomeridiano del 20/12/2004 Esercizio 1. Consideriamo una retta r dello spazio affine. Diremo che le equazioni cartesiane di
Algebra lineare. {ax 2 + bx + c R 2 [x] : 2a + 3b = 1} a b c d. M(2, 2) : a + c + d = 2. a b. c d
![Algebra lineare. {ax 2 + bx + c R 2 [x] : 2a + 3b = 1} a b c d. M(2, 2) : a + c + d = 2. a b. c d Algebra lineare. {ax 2 + bx + c R 2 [x] : 2a + 3b = 1} a b c d. M(2, 2) : a + c + d = 2. a b. c d](/thumbs/104/162200055.jpg) Algebra lineare 1. Riconoscere se il seguente insieme costituisce uno spazio vettoriale. In caso affermativo trovarne la dimensione e una base. (R n [x] denota lo spazio dei polinomi nell indeterminata
Algebra lineare 1. Riconoscere se il seguente insieme costituisce uno spazio vettoriale. In caso affermativo trovarne la dimensione e una base. (R n [x] denota lo spazio dei polinomi nell indeterminata
Lezione 2: Spazi Vettoriali
 Lezione 2: Spazi Vettoriali In questa lezione vogliamo introdurre il vero protagonista dell algebra lineare: lo spazio vettoriale. Si tratta di una astrazione che comprende concetti che già ben conosciamo;
Lezione 2: Spazi Vettoriali In questa lezione vogliamo introdurre il vero protagonista dell algebra lineare: lo spazio vettoriale. Si tratta di una astrazione che comprende concetti che già ben conosciamo;
Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016.
 Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016 Di seguito si riporta il riassunto degli argomenti svolti; i riferimenti sono a parti del Cap8 Elementi di geometria e algebra lineare Par5
Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016 Di seguito si riporta il riassunto degli argomenti svolti; i riferimenti sono a parti del Cap8 Elementi di geometria e algebra lineare Par5
Esercizi di geometria per Fisica / Fisica e Astrofisica
 Esercizi di geometria per Fisica / Fisica e Astrofisica Foglio 3 - Soluzioni Esercizio. Stabilire se i seguenti sottoinsiemi di R 3 sono sottospazi vettoriali: (a) S = {(x y z) R 3 : x + y + z = }. (b)
Esercizi di geometria per Fisica / Fisica e Astrofisica Foglio 3 - Soluzioni Esercizio. Stabilire se i seguenti sottoinsiemi di R 3 sono sottospazi vettoriali: (a) S = {(x y z) R 3 : x + y + z = }. (b)
Algebra delle matrici
 Algebra delle matrici Metodo di Gauss-Jordan per l inversione di una matrice. Nella lezione scorsa abbiamo visto che un modo per determinare l eventuale inversa di una matrice quadrata A consiste nel risolvere
Algebra delle matrici Metodo di Gauss-Jordan per l inversione di una matrice. Nella lezione scorsa abbiamo visto che un modo per determinare l eventuale inversa di una matrice quadrata A consiste nel risolvere
Sistemi lineari. Sia A R m n, x R n Ax = b è un vettore di m componenti. a m,1 x 1 + a m,2 x a m,n x n = b m
 1 Sistemi lineari. Sia A R m n, x R n Ax = b è un vettore di m componenti. Numero di operazioni per calcolare b: m n moltiplicazioni m (n 1) addizioni. a 1,1 x 1 + a 1,2 x 2 +... + a 1,n x n = b 1 a 2,1
1 Sistemi lineari. Sia A R m n, x R n Ax = b è un vettore di m componenti. Numero di operazioni per calcolare b: m n moltiplicazioni m (n 1) addizioni. a 1,1 x 1 + a 1,2 x 2 +... + a 1,n x n = b 1 a 2,1
ALGEBRA E GEOMETRIA Esercizi Corso di Laurea in Chimica - anno acc. 2015/2016 docente: Elena Polastri,
 ALGEBRA E GEOMETRIA Esercizi Corso di Laurea in Chimica - anno acc. 05/06 docente: Elena Polastri, plslne@unife.it Esercizi 3: SPAZI VETTORIALI e MATRICI Combinazioni lineari di vettori.. Scrivere il vettore
ALGEBRA E GEOMETRIA Esercizi Corso di Laurea in Chimica - anno acc. 05/06 docente: Elena Polastri, plslne@unife.it Esercizi 3: SPAZI VETTORIALI e MATRICI Combinazioni lineari di vettori.. Scrivere il vettore
Elementi di Algebra Lineare Applicazioni lineari
 Elementi di Algebra Lineare Applicazioni lineari Cristina Turrini UNIMI - 2015/2016 Cristina Turrini (UNIMI - 2015/2016) Elementi di Algebra Lineare 1 / 18 index Applicazioni lineari 1 Applicazioni lineari
Elementi di Algebra Lineare Applicazioni lineari Cristina Turrini UNIMI - 2015/2016 Cristina Turrini (UNIMI - 2015/2016) Elementi di Algebra Lineare 1 / 18 index Applicazioni lineari 1 Applicazioni lineari
Facoltà di Scienze. Appello A
 Facoltà di Scienze Appello -2-28-A SOLUZIONI Esercizio. Discutere e risolvere almeno 3 dei seguenti esercizi. Giustificare sempre le risposte, fornendo una dimostrazione nel caso l affermazione sia vera
Facoltà di Scienze Appello -2-28-A SOLUZIONI Esercizio. Discutere e risolvere almeno 3 dei seguenti esercizi. Giustificare sempre le risposte, fornendo una dimostrazione nel caso l affermazione sia vera
b = p + q l q Diciamo che p e la proiezione ortogonale di b su l, e che q e la proiezione ortogonale di b su l.
 Matematica II, 4... rtogonalita nel piano. Fissato nel piano un punto, consideriamo il piano vettoriale P. Diamo per intuitivamente nota la nozione di ortogonalita fra due vettori non nulli. Per convenzione,
Matematica II, 4... rtogonalita nel piano. Fissato nel piano un punto, consideriamo il piano vettoriale P. Diamo per intuitivamente nota la nozione di ortogonalita fra due vettori non nulli. Per convenzione,
Richiami di Algebra Lineare
 Università di Pavia Richiami di Algebra Lineare Eduardo Rossi Vettori a : (n 1) b : (n 1) Prodotto interno a b = a 1 b 1 + a 2 b 2 +... + a n b n Modulo (lunghezza): a = a 2 1 +... + a2 n Vettori ortogonali:
Università di Pavia Richiami di Algebra Lineare Eduardo Rossi Vettori a : (n 1) b : (n 1) Prodotto interno a b = a 1 b 1 + a 2 b 2 +... + a n b n Modulo (lunghezza): a = a 2 1 +... + a2 n Vettori ortogonali:
ALGEBRA LINEARE E GEOMETRIA: ESERCIZI 5. Indice. 2. Esercizi 5
 ALGEBRA LINEARE E GEOMETRIA: ESERCIZI 5 Indice 1. Principali definizioni 1 2. Esercizi 5 Operazioni con le matrici 1. Principali definizioni Ricordiamo le principali definizioni legate alle matrici a coefficienti
ALGEBRA LINEARE E GEOMETRIA: ESERCIZI 5 Indice 1. Principali definizioni 1 2. Esercizi 5 Operazioni con le matrici 1. Principali definizioni Ricordiamo le principali definizioni legate alle matrici a coefficienti
Daniela Lera A.A
 Daniela Lera Università degli Studi di Cagliari Dipartimento di Matematica e Informatica A.A. 2016-2017 Richiami Algebra Lineare Spazio normato Uno spazio lineare X si dice normato se esiste una funzione
Daniela Lera Università degli Studi di Cagliari Dipartimento di Matematica e Informatica A.A. 2016-2017 Richiami Algebra Lineare Spazio normato Uno spazio lineare X si dice normato se esiste una funzione
Spazi vettoriali euclidei.
 Spazi vettoriali euclidei Prodotto scalare, lunghezza e ortogonalità in R n Consideriamo lo spazio vettoriale R n = { =,,, n R}, n con la somma fra vettori e il prodotto di un vettore per uno scalare definiti
Spazi vettoriali euclidei Prodotto scalare, lunghezza e ortogonalità in R n Consideriamo lo spazio vettoriale R n = { =,,, n R}, n con la somma fra vettori e il prodotto di un vettore per uno scalare definiti
A = e 1 = e 2 + e 3, e 2 = e 1 + e 3, e 3 = e 1, ; e 3 =
 aa -6 Soluzioni Esercizi Applicazioni lineari Sia data l applicazione lineare F : R R, F X A X, dove A i Sia {e, e, e } la base canonica di R Far vedere che i vettori e e + e, e e + e, e e, formano una
aa -6 Soluzioni Esercizi Applicazioni lineari Sia data l applicazione lineare F : R R, F X A X, dove A i Sia {e, e, e } la base canonica di R Far vedere che i vettori e e + e, e e + e, e e, formano una
Esercizi geometria analitica nel piano. Corso di Laurea in Informatica A.A. Docente: Andrea Loi. Correzione
 Esercizi geometria analitica nel piano Corso di Laurea in Informatica A.A. Docente: Andrea Loi Correzione 1. Scrivere le equazioni parametriche delle rette r e s di equazioni cartesiane r : 2x y + = 0
Esercizi geometria analitica nel piano Corso di Laurea in Informatica A.A. Docente: Andrea Loi Correzione 1. Scrivere le equazioni parametriche delle rette r e s di equazioni cartesiane r : 2x y + = 0
CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI A.A. 2018/2019 PROF. VALENTINA BEORCHIA
 CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Matrici associate a un applicazione lineare 1 2 Cambiamenti di base 4 3 Diagonalizzazione 6 1 MATRICI ASSOCIATE
CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Matrici associate a un applicazione lineare 1 2 Cambiamenti di base 4 3 Diagonalizzazione 6 1 MATRICI ASSOCIATE
Note di Matematica Generale Elementi di Teoria degli Spazi Vettoriali. Roberto Monte
 Note di Matematica Generale Elementi di Teoria degli Spazi Vettoriali Roberto Monte December 5, 23 Abstract These notes are still a work in progress and are intended to be for internal use. Please, don
Note di Matematica Generale Elementi di Teoria degli Spazi Vettoriali Roberto Monte December 5, 23 Abstract These notes are still a work in progress and are intended to be for internal use. Please, don
CORSO DI ALGEBRA (M-Z) Prof. A. Venezia
 CORSO DI ALGEBRA (M-Z) Prof. A. Venezia 2015-16 Complementi ed Esercizi 1. AUTOVETTORI e AUTOVALORI di ENDOMORFISMI e MATRICI Una applicazione lineare avente per dominio e condominio lo stesso spazio vettoriale
CORSO DI ALGEBRA (M-Z) Prof. A. Venezia 2015-16 Complementi ed Esercizi 1. AUTOVETTORI e AUTOVALORI di ENDOMORFISMI e MATRICI Una applicazione lineare avente per dominio e condominio lo stesso spazio vettoriale
21 settembre Soluzione esame di geometria - 12 crediti Ingegneria gestionale - a.a COGNOME... NOME... N. MATRICOLA...
 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
CORSO DI ALGEBRA (M-Z) Prof. A. Venezia
 CORSO DI ALGEBRA (M-Z) Prof. A. Venezia 2018-19 Complementi ed Esercizi APPLICAZIONI LINEARI Siano V e V spazi vettoriali sul campo K. Una applicazione L: V V si dice lineare se: 1 AL. L(v+w) = L(v) +
CORSO DI ALGEBRA (M-Z) Prof. A. Venezia 2018-19 Complementi ed Esercizi APPLICAZIONI LINEARI Siano V e V spazi vettoriali sul campo K. Una applicazione L: V V si dice lineare se: 1 AL. L(v+w) = L(v) +
Matrici e sistemi. Geometria. Matrici e operazioni tra matrici. Operazioni elementari e riduzione Sistemi lineari Matrici invertibili Determinante
 Geometria Matrici e sistemi Operazioni elementari e riduzione Sistemi lineari Matrici invertibili Determinante 2 2006 Politecnico di Torino 1 Matrici e sistemi Matrici: definizione e notazioni Somma e
Geometria Matrici e sistemi Operazioni elementari e riduzione Sistemi lineari Matrici invertibili Determinante 2 2006 Politecnico di Torino 1 Matrici e sistemi Matrici: definizione e notazioni Somma e
Lezioni di Algebra Lineare V. Autovalori e autovettori
 Lezioni di Algebra Lineare V. Autovalori e autovettori Versione novembre 2008 Contenuto 1. Cambiamenti di base 2. Applicazioni lineari, matrici e cambiamenti di base 3. Autovalori e autovettori 2 1. Cambiamenti
Lezioni di Algebra Lineare V. Autovalori e autovettori Versione novembre 2008 Contenuto 1. Cambiamenti di base 2. Applicazioni lineari, matrici e cambiamenti di base 3. Autovalori e autovettori 2 1. Cambiamenti
Capitolo IV SPAZI VETTORIALI EUCLIDEI
 Capitolo IV SPAZI VETTORIALI EUCLIDEI È ben noto che in VO 3 si possono considerare strutture più ricche di quella di spazio vettoriale; si pensi in particolare all operazioni di prodotto scalare di vettori.
Capitolo IV SPAZI VETTORIALI EUCLIDEI È ben noto che in VO 3 si possono considerare strutture più ricche di quella di spazio vettoriale; si pensi in particolare all operazioni di prodotto scalare di vettori.
UNIVERSITA DEGLI STUDI DI PAVIA REGISTRO DELLE LEZIONI-ESERCITAZIONI- SEMINARI. Corso di laurea INGEGNERIA ELETTRONICA/INFORMATICA.
 REGISTRO DELLE LEZIONI-ESERCITAZIONI- SEMINARI Anno accademico 2018/19 Cognome e Nome BISI FULVIO Qualifica PROFESSORE ASSOCIATO MAT/07 DIPARTIMENTO DI MATEMATICA Insegnamento di GEOMETRIA E ALGEBRA (500473)
REGISTRO DELLE LEZIONI-ESERCITAZIONI- SEMINARI Anno accademico 2018/19 Cognome e Nome BISI FULVIO Qualifica PROFESSORE ASSOCIATO MAT/07 DIPARTIMENTO DI MATEMATICA Insegnamento di GEOMETRIA E ALGEBRA (500473)
a 1n. a nn + + x n vale solo per x 1 = = x n = 0. Ciò si può fare risolvendo fino a un certo punto il sistema di equazioni
 Lezione del 30 Alcuni argomenti in taglio Problema Stabilire se n vettori a a n,, a n a nn R n sono linearmente indipendenti, cioè se l uguaglianza a a n + + x n x a n a nn = vale solo per x = = x n =
Lezione del 30 Alcuni argomenti in taglio Problema Stabilire se n vettori a a n,, a n a nn R n sono linearmente indipendenti, cioè se l uguaglianza a a n + + x n x a n a nn = vale solo per x = = x n =
CORSO DI LAUREA IN INGEGNERIA DELLE TELECOMUNICAZIONI
 CORSO DI LAUREA IN INGEGNERIA DELLE TELECOMUNICAZIONI FOGLIO DI ESERCIZI # GEOMETRIA E ALGEBRA 009/0 Esercizio.. Dati i vettori di R : v (,, ), v (, 4, 6), v (,, 5), v 4 (,, 0) determinare se v 4 è combinazione
CORSO DI LAUREA IN INGEGNERIA DELLE TELECOMUNICAZIONI FOGLIO DI ESERCIZI # GEOMETRIA E ALGEBRA 009/0 Esercizio.. Dati i vettori di R : v (,, ), v (, 4, 6), v (,, 5), v 4 (,, 0) determinare se v 4 è combinazione
Esempio. L immagine di f è l insieme dei vettori w = (w 1, w 2 ) R 2 che hanno w 1 = w 2. Quindi:
 Nucleo, immagine e loro proprietà [Abate, 5.2] Data una applicazione lineare f : V W, chiamiamo nucleo di f l insieme N(f) := { v V : f(v) = 0 W } Se S V è un sottoinsieme del dominio, indichiamo con f(s)
Nucleo, immagine e loro proprietà [Abate, 5.2] Data una applicazione lineare f : V W, chiamiamo nucleo di f l insieme N(f) := { v V : f(v) = 0 W } Se S V è un sottoinsieme del dominio, indichiamo con f(s)
AL220 - Gruppi, Anelli e Campi
 AL220 - Gruppi, Anelli e Campi Prof. Stefania Gabelli - a.a. 2013-2014 Settimana 1 - Traccia delle Lezioni Funzioni tra insiemi Ricordiamo che una funzione o applicazione di insiemi f : A B è una corrispondenza
AL220 - Gruppi, Anelli e Campi Prof. Stefania Gabelli - a.a. 2013-2014 Settimana 1 - Traccia delle Lezioni Funzioni tra insiemi Ricordiamo che una funzione o applicazione di insiemi f : A B è una corrispondenza
Esercizi del tutoraggio - algebra lineare
 Esercizi del tutoraggio - algebra lineare 13 Novembre 2008 6 Ottobre 2008 Esercizio 1. Siano dati i seguenti punti nel piano. Dire se i vettori geometrici pq e p q sono equipollenti. p = (1, 2) q = (3,
Esercizi del tutoraggio - algebra lineare 13 Novembre 2008 6 Ottobre 2008 Esercizio 1. Siano dati i seguenti punti nel piano. Dire se i vettori geometrici pq e p q sono equipollenti. p = (1, 2) q = (3,
4. Richiami: sistemi lineari e matrici
 4 Richiami: sistemi lineari e matrici Vettori 4a Combinazioni lineari Indichiamo con R n l insieme delle n-uple ordinate di elementi di R, { } R n := x = (x 1, x 2,, x n ) x i R, i = 1,,n Si dice che x
4 Richiami: sistemi lineari e matrici Vettori 4a Combinazioni lineari Indichiamo con R n l insieme delle n-uple ordinate di elementi di R, { } R n := x = (x 1, x 2,, x n ) x i R, i = 1,,n Si dice che x
ESERCIZI DI ALGEBRA LINEARE E COMPLEMENTI DI GEOMETRIA
 ESERCIZI DI ALGEBRA LINEARE E COMPLEMENTI DI GEOMETRIA Foglio 4 Esempio. Sia V = P 5 (R) lo spazio dei polinomi di grado strettamente minore di 5. Si considerino i seguenti sottoinsiemi di V (i) Dimostrare
ESERCIZI DI ALGEBRA LINEARE E COMPLEMENTI DI GEOMETRIA Foglio 4 Esempio. Sia V = P 5 (R) lo spazio dei polinomi di grado strettamente minore di 5. Si considerino i seguenti sottoinsiemi di V (i) Dimostrare
VETTORIALE E PRODOTTO MISTO. PIANI E RETTE DI
 Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA (Edile-Architettura e dell Edilizia) PRODOTTO VETTORIALE E PRODOTTO MISTO. PIANI E RETTE DI R 3. FASCI E STELLE. FORMULE
Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA (Edile-Architettura e dell Edilizia) PRODOTTO VETTORIALE E PRODOTTO MISTO. PIANI E RETTE DI R 3. FASCI E STELLE. FORMULE
Spazi vettoriali. Vettori geometrici. Spazi vettoriali R n. Spazi vettoriali.
 Spazi vettoriali Vettori geometrici. Spazi vettoriali R n. Spazi vettoriali. Piano vettoriale geometrico G 2 Il contesto del discorso che svolgiamo in questa parte e il piano della geometria elementare,
Spazi vettoriali Vettori geometrici. Spazi vettoriali R n. Spazi vettoriali. Piano vettoriale geometrico G 2 Il contesto del discorso che svolgiamo in questa parte e il piano della geometria elementare,
Corso di Laurea in Fisica. Geometria. a.a Prof. P. Piazza Soluzione compito a casa del 24/10/09
 Corso di Laurea in Fisica. Geometria. a.a. 29-. Prof. P. Piazza Soluzione compito a casa del 24//9 Soluzione esercizio. Siano A e B due matrici simmetriche e λ un numero reale. Dobbiamo mostrare che anche
Corso di Laurea in Fisica. Geometria. a.a. 29-. Prof. P. Piazza Soluzione compito a casa del 24//9 Soluzione esercizio. Siano A e B due matrici simmetriche e λ un numero reale. Dobbiamo mostrare che anche
Lezione 4: Base e dimensione
 Lezione 4: Base e dimensione 1 Base: definizione ed esempi Come la parola stessa suggerisce, il concetto di base di uno spazio vettoriale e fondamentale e racchiude tutte le informazioni necessarie a ricostruire
Lezione 4: Base e dimensione 1 Base: definizione ed esempi Come la parola stessa suggerisce, il concetto di base di uno spazio vettoriale e fondamentale e racchiude tutte le informazioni necessarie a ricostruire
3 Soluzione di sistemi lineari
 3 Soluzione di sistemi lineari Prima di addentrarci nello studio dei metodi numerici, è doveroso introdurre le matrici e alcune strutture particolari di matrici nonchè alcuni concetti fondamentali quali
3 Soluzione di sistemi lineari Prima di addentrarci nello studio dei metodi numerici, è doveroso introdurre le matrici e alcune strutture particolari di matrici nonchè alcuni concetti fondamentali quali
Definizione 1 Un insieme (V, +, ) dotato delle due operazioni: - + somma di elementi v 1 V, v 2 V ;
 Spazi vettoriali Definizione Un insieme (V, +, ) dotato delle due operazioni: - + somma di elementi v V, v V ; - prodotto per uno scalare λ K, (K campo); e chiuso rispetto ad esse, è uno spazio vettoriale
Spazi vettoriali Definizione Un insieme (V, +, ) dotato delle due operazioni: - + somma di elementi v V, v V ; - prodotto per uno scalare λ K, (K campo); e chiuso rispetto ad esse, è uno spazio vettoriale
1.1 Coordinate sulla retta e nel piano; rette nel piano
 1 Sistemi lineari 11 Coordinate sulla retta e nel piano; rette nel piano Coordinate sulla retta Scelti su una retta un primo punto O (origine) ed un diverso secondo punto U (unita ), l identificazione
1 Sistemi lineari 11 Coordinate sulla retta e nel piano; rette nel piano Coordinate sulla retta Scelti su una retta un primo punto O (origine) ed un diverso secondo punto U (unita ), l identificazione
Analisi dei dati corso integrato - Algebra lineare,
 Analisi dei dati corso integrato - Algebra lineare, 050308-2 1 Ortogonalita nel piano Sia fissato nel piano un sistema di riferimento cartesiano ortogonale monometrico, con origine in O Tranne avviso contrario,
Analisi dei dati corso integrato - Algebra lineare, 050308-2 1 Ortogonalita nel piano Sia fissato nel piano un sistema di riferimento cartesiano ortogonale monometrico, con origine in O Tranne avviso contrario,
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof. F.Podestà, a.a
 APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
Algebra Lineare e Geometria, a.a. 2012/2013
 Diario delle esercitazioni e lezioni per il corso di Algebra Lineare e Geometria, a.a. 2012/2013 (solo la parte per Fisici e Matematici, non ci sono le lezioni del Modulo B) Lidia Stoppino Lezione 1 9
Diario delle esercitazioni e lezioni per il corso di Algebra Lineare e Geometria, a.a. 2012/2013 (solo la parte per Fisici e Matematici, non ci sono le lezioni del Modulo B) Lidia Stoppino Lezione 1 9
Capitolo 8 Forme quadratiche e loro applicazioni Esercizi svolti Tutorato di geometria e algebra lineare. Marco Robutti
 Capitolo 8 Forme quadratiche e loro applicazioni Esercizi svolti Tutorato di geometria e algebra lineare Marco Robutti 5 Ottobre 2017 1 Introduzione Gli esercizi di questo capitolo riguardano i seguenti
Capitolo 8 Forme quadratiche e loro applicazioni Esercizi svolti Tutorato di geometria e algebra lineare Marco Robutti 5 Ottobre 2017 1 Introduzione Gli esercizi di questo capitolo riguardano i seguenti
Corso di Matematica 2 (mod.a) per la Laurea in Matematica - esercizi per casa del 6 ottobre Cognome... Nome... Matricola...
 6.1.25-M2A-E1 Corso di Matematica 2 (mod.a per la Laurea in Matematica - esercizi per casa del 6 ottobre 25 Lo studente è tenuto a consegnare l elaborato svolto e firmato non più tardi di Lunedì 1 ottobre
6.1.25-M2A-E1 Corso di Matematica 2 (mod.a per la Laurea in Matematica - esercizi per casa del 6 ottobre 25 Lo studente è tenuto a consegnare l elaborato svolto e firmato non più tardi di Lunedì 1 ottobre
Numeri reali. Funzioni reali di variabile reale
 Numeri reali. Funzioni reali di variabile reale Composizione di funzioni. Per semplicita, da ora in poi fino ad avviso contrario, useremo la seguente nozione di composizione di funzioni (che assume una
Numeri reali. Funzioni reali di variabile reale Composizione di funzioni. Per semplicita, da ora in poi fino ad avviso contrario, useremo la seguente nozione di composizione di funzioni (che assume una
Gruppi, spazi e sottospazi vettoriali
 CAPITOLO 3 Gruppi, spazi e sottospazi vettoriali Esercizio 3.1. Dimostrare che l insieme { a G = b forma un gruppo rispetto al prodotto tra matrici. a,b R, a,b Esercizio 3.2. Sia R[x] l insieme dei polinomi
CAPITOLO 3 Gruppi, spazi e sottospazi vettoriali Esercizio 3.1. Dimostrare che l insieme { a G = b forma un gruppo rispetto al prodotto tra matrici. a,b R, a,b Esercizio 3.2. Sia R[x] l insieme dei polinomi
Algebra lineare e geometria AA Soluzioni della simulazione
 Algebra lineare e geometria AA. 2018-2019 Soluzioni della simulazione QUIZ Q1. Sia A R nn una matrice che ammette l autovalore λ 0 con molteplicità algebrica k. Quale delle seguenti affermazioni è vera?
Algebra lineare e geometria AA. 2018-2019 Soluzioni della simulazione QUIZ Q1. Sia A R nn una matrice che ammette l autovalore λ 0 con molteplicità algebrica k. Quale delle seguenti affermazioni è vera?
Esercizi su applicazioni lineari. Per tutto il seguito, se non specificato esplicitamente K indicherà un campo e V,W,U spazi vettoriali su K.
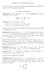 Esercizi su applicazioni lineari Per tutto il seguito, se non specificato esplicitamente K indicherà un campo e V,W,U spazi vettoriali su K. 1. Cose da ricordare Definizione 1.1. Una funzione f : V W si
Esercizi su applicazioni lineari Per tutto il seguito, se non specificato esplicitamente K indicherà un campo e V,W,U spazi vettoriali su K. 1. Cose da ricordare Definizione 1.1. Una funzione f : V W si
1 Rette nel piano ordinario. Rette e piani nello spazio ordinario
 1 Rette nel piano ordinario. Rette e piani nello spazio ordinario 1.1 Vettori applicati Nel seguito denotiamo con P l insieme dei punti del piano ordinario, e con S l insieme dei punti dello spazio ordinario.
1 Rette nel piano ordinario. Rette e piani nello spazio ordinario 1.1 Vettori applicati Nel seguito denotiamo con P l insieme dei punti del piano ordinario, e con S l insieme dei punti dello spazio ordinario.
x n i sima pos. x, y = x T y = x i y i R. i=1
 1 Elementi di Algebra Lineare In questo capitolo introduttivo al corso di Calcolo Numerico per la laurea triennale in Informatica, saranno presentate una serie di definizioni e proprietà di matrici e dei
1 Elementi di Algebra Lineare In questo capitolo introduttivo al corso di Calcolo Numerico per la laurea triennale in Informatica, saranno presentate una serie di definizioni e proprietà di matrici e dei
TEMA 1. Tempo a disposizione: 35 minuti per le domande teoriche e 40 minuti per l esercizio.
 TEMA 1 Teoria 1: 6 punti. Definire il modulo e l argomento di un numero complesso. Teoria 2: 6 punti. Enunciare il teorema delle dimensioni (senza dimostrazione). Teoria 3: 6 punti. Sia K un campo. Dimostrare
TEMA 1 Teoria 1: 6 punti. Definire il modulo e l argomento di un numero complesso. Teoria 2: 6 punti. Enunciare il teorema delle dimensioni (senza dimostrazione). Teoria 3: 6 punti. Sia K un campo. Dimostrare
1.1 Esempio. Siano A = {11, f, β,,, } e B = {x, 11,,,, α, γ} e le seguenti leggi:
 1. Relazioni. 1 Dati due insiemi possiamo stabilire in modo del tutto arbitrario una legge che associ elementi di un insieme ad elementi dell altro insieme. Ovviamente, data la totale arbitrarietà di tale
1. Relazioni. 1 Dati due insiemi possiamo stabilire in modo del tutto arbitrario una legge che associ elementi di un insieme ad elementi dell altro insieme. Ovviamente, data la totale arbitrarietà di tale
17 luglio Soluzione esame di geometria - 12 crediti Ingegneria gestionale - a.a ISTRUZIONI
 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
(VX) (F) Se A e B sono due matrici simmetriche n n allora anche A B è una matrice simmetrica.
 5 luglio 010 - PROVA D ESAME - Geometria e Algebra T NOME: MATRICOLA: a=, b=, c= Sostituire ai parametri a, b, c rispettivamente la terzultima, penultima e ultima cifra del proprio numero di matricola
5 luglio 010 - PROVA D ESAME - Geometria e Algebra T NOME: MATRICOLA: a=, b=, c= Sostituire ai parametri a, b, c rispettivamente la terzultima, penultima e ultima cifra del proprio numero di matricola
Anno Accademico 2016/2017
 Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2016/2017 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2016/2017 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
UN BREVE VIAGGIO ATTRAVERSO GLI SPAZI VETTORIALI 1
 asdf UN BREVE VIAGGIO ATTRAVERSO GLI SPAZI VETTORIALI 4 November 2011 Con questo articolo, stavolta, proviamo a compiere un "viaggetto" attraverso gli spazi vettoriali. Come sempre avremo a che fare con
asdf UN BREVE VIAGGIO ATTRAVERSO GLI SPAZI VETTORIALI 4 November 2011 Con questo articolo, stavolta, proviamo a compiere un "viaggetto" attraverso gli spazi vettoriali. Come sempre avremo a che fare con
Politecnico di Torino Facoltà di Architettura. Raccolta di esercizi proposti nelle prove scritte
 Politecnico di Torino Facoltà di Architettura Raccolta di esercizi proposti nelle prove scritte relativi a: algebra lineare, vettori e geometria analitica Esercizio. Determinare, al variare del parametro
Politecnico di Torino Facoltà di Architettura Raccolta di esercizi proposti nelle prove scritte relativi a: algebra lineare, vettori e geometria analitica Esercizio. Determinare, al variare del parametro
