Analisi 3. a.a Giovanni Alberti. Università di Pisa Corso di laurea in Matematica. Testi e soluzioni degli scritti d esame di
|
|
|
- Anna Massari
- 4 anni fa
- Visualizzazioni
Transcript
1 Versione: 4 settembre 29 Università di Pisa Corso di laurea in Matematica Testi e soluzioni degli scritti d esame di Analisi 3 a.a Giovanni Alberti Giovanni Alberti Dipartimento di Matematica Università di Pisa largo Pontecorvo Pisa
2 Avvertenze. Gli scritti d esame per il corso di Analisi 3 consistono di otto domande a cui dare una risposta articolata. Di queste, le prime quattro sono solitamente più semplici, nel senso che a possono essere facilmente ricondotte a fatti e/o calcoli noti. Il tempo a disposizione è di tre ore. La prima sezione di questa raccolta contiene i testi di tutti gli scritti, incluse le prove in itinere, mentre la seconda parte contiene una traccia delle soluzioni. Programma del corso [versione: 23 dicembre 28]. Sono riportati in corsivo gli argomenti non fondamentali.. Teoria dell integrazione.. Misure σ-additive su σ-algebre. sempio fundamentale: la misura di Lebesgue e la σ-algebra degli insiemi misurabili secondo Lebesgue su R d. Altro esempio: la misura che conta i punti..2. Funzioni misurabili (rispetto ad una data σ-algebra). Proprietà delle funzioni misurabili. Costruzione dell integrale delle funzioni misurabile positive partendo delle funzioni semplici. Integrale delle funzioni misurabili a segno variabile..3. Teorema di convergenza monotona (o di Beppo Levi), lemma di Fatou, teorema di convergenza dominata (o di Lebesgue). Teorema di Fubini-Tonelli. 2. Spazi L p e convoluzione 2.. Disuguaglianze di Jensen, Hölder e Minkowski Spazi L p. Completezza degli spazi L p Prodotto di convoluzione di funzioni su R d e disuguaglianze collegate alle norme L p. Regolarità del prodotto di convoluzione in funzione della regolarità dei fattori. Approssimazione e regolarizzazione per convoluzione delle funzioni in L p (R d ). 3. Spazi di Hilbert 3.. Spazi di Hilbert reali; basi di Hilbert (sistemi ortonormali massimali). Rappresentazione di un elemento dello spazio in termini di una base Proiezione di un vettore su un sottospazio chiuso, e caratterizzazione in termini di distanza. Rappresentazione di un funzionale lineare e continuo tramite prodotto scalare (Teorema di Riesz) Spazi di Hilbert sul campo complesso. 4. Serie di Fourier ed applicazioni 4.. Le funzioni esponenziali e inx (opportunamente rinormalizzate) formano una base di Hilbert di L 2 ( π, π). Serie di Fourier per le funzioni complesse in L 2 ( π, π). Convergenza della serie di Fourier in L 2. Convergenza uniforme per le funzioni 2π-periodiche di classe C. Regolarità delle funzione e comportamento asintotico dei coefficienti. Rappresentazione delle somme parziali della serie di Fourier come convoluzione e ulteriori risultati sulla convergenza puntuale della serie di Fourier Derivazione dell equazione del calore e delle onde in una dimensione spaziale. Soluzione dell equazione del calore e delle onde con condizioni di periodicità agli estremi tramite la serie di Fourier. Disuguaglianza isoperimetrica nel piano Varianti della serie di Fourier: rappresentazione in serie di seni e coseni per le funzioni reali in L 2 ( π, π) (serie di Fourier reale); rappresentazione in serie di seni per le funzioni reali in L 2 (, π); rappresentazione in serie di esponanziali di due variabili per le funzioni complesse in L 2( [ π, π] d) (serie di Fourier in d variabili) Basi ortonormali e autovettori di operatori autoaggiunti. 5. Trasformata di Fourier e applicazioni 5.. Derivazione euristica della trasformata di Fourier a partire dalla serie di Fourier. Trasformata di Fourier delle funzioni (complesse) in L (R). Proprietà elementari della trasformata di Fourier Dimostrazione della formula di inversione. La trasformata di Fourier preserva il prodotto scalare e la norma L 2. Trasformata di Fourier delle funzioni in L 2 (R).
3 5.3. Risoluzione dell equazione del calore tramite trasformata di Fourier e rappresentazione della soluzione tramite il nucleo del calore. 6. Funzioni armoniche 6.. Le funzioni armoniche come soluzioni dell equazione di Laplace. Caratterizzazione in termini di proprietà della media. Principio del massimo e unicità della soluzione dell equazione di Laplace con dato al bordo assegnato Funzioni armoniche e funzioni olomorfe. Risoluzione dell equazione di Laplace nel disco unitario tramite la serie di Fourier, rappresentazione della soluzione tramite nucleo di Poisson.
4 T S T I
5 Primo compitino, 6 dicembre 28 Testi 5. Sia g : R d R una funzione limitata e α-hölderiana per un certo α (, ]. Dimostrare che f g è una funzione α-hölderiana per ogni f L (R d ). 2. Dire per quali p la funzione f(x, x 2 ) := (x 2 + x 4 2) / appartiene a L p (Q) dove Q è il quadrato [, ] 2 in R In L 2 (, ) consideriamo il sottospazio X generato dalle funzioni x, x 2, x 3. Determinare le proiezioni della funzione su X e su X. 4. a) Sia f : R C una funzione 2π-periodica appartenente a L 2 ( π, π). Dato h R, calcolare i coefficienti di Fourier della traslazione f(x h) in termini dei coefficienti c n di f. b) Dato un intero N 2, dimostrare che f 2π/N-periodica se e solo se c n = per ogni n che non è multiplo di N. 5. a) Dimostrare la seguente generalizzazione della disuguaglianza di Hölder: date f, f 2 funzioni misurabili su insieme misurabile in R d e dati p, p, p 2 in [, + ] tali che /p = /p + /p 2, allora f f 2 p f p f 2 p2. [Suggerimento: ricondursi alla disuguaglianza di Hölder.] b) Sia la mappa T che ad ogni coppia di funzioni f, f 2 su associa la funzione prodotto f f 2. Far vedere che T porta L p L p2 in L p. c) Dire se la mappa T è iniettiva / surgettiva / continua. 6. Consideriamo il problema (P ) dato dall equazione u t = cos t u xx con u = u(t, x) definita su [, T ) [ π, π], le condizioni al bordo u(, π) = u(, π) e u x (, π) = u x (, π), e la condizione iniziale u(, ) = u ( ), dove u è una funzione con coefficienti di Fourier c n. Dimostrare che: a) per ogni T > esiste al più una soluzione; 2 b) se n co n < + allora esiste una soluzione per T = π; c) la soluzione al punto b) è di classe C per t > ; d) in generale se T > π non esistono soluzioni, neanche assumendo che u sia C. 7. Dato p [, + ), sia X l insieme delle successioni (x, x 2,... ) l p tali che x n /n per ogni n. Dimostrare che: a) X è chiuso (in l p ) per ogni p. b) X è compatto per p >. c) X non è compatto per p =. 8. Sia f : R d (, + ) una funzione di classe C tale che il rapporto f /f è limitato. a) Far vedere che per ogni δ > esiste m tale che y x δ f(y)/f(x) m. b) Dimostrare che f(n) < + se e solo se f(x) dx < +. n Z d R d c) Dire per quali a > la serie + n a è finita. n Z d In questo contesto si dice che f è h-periodica se f(x) = f(x h) per quasi ogni x R. 2 Al solito si richiede che u sia continua, C 2 in x per t >, C in t per t >.
6 6 Secondo compitino, 8 gennaio 29 Testi. Sia M una matrice d d invertibile e sia u una funzione in L (R d ), e sia v la funzione su R d definita da v(x) := u(mx). a) Dimostrare che v L (R d ) ed scrivere v in termini di u. b) Scrivere la trasformata di Fourier ˆv in termini di û. 2. Calcolare la trasformata di Fourier della funzione u(x) := x 2 + 2x Sia u (x) := 6x 2 x 2 2 per ogni x = (x, x 2 ) R 2. Risolvere l equazione u = sul disco D di centro e raggio con la condizione al bordo u = u su D. 4. Sia Ω un aperto limitato in R d con bordo regolare e sia X il sottospazio di L 2 (Ω) composto dalle funzioni u : Ω R di classe C 2 con supporto compatto. a) Dimostrare che l operatore T : X L 2 (Ω) definito da T : u u è autoaggiunto. b) Cosa si può dire sulla segnatura di T? c) Cosa succede se invece X è il sottospazio delle funzioni che sono restrizioni di funzioni di classe C 2 definite su tutto R d? 5. a) Data m : R C funzione misurabile limitata, dimostrare che esiste uno (ed un solo) operatore lineare T da L 2 C (R) in sé tale che T u = m û per ogni u L 2 C (R). b) Dire per quali m l operatore T è autoaggiunto, e per quali è anche definito positivo. 6. Sia u : R C una funzione di classe C tale che u L C e u L2 C. a) Dimostrare che u = iy û. b) Dimostrare che û L C. 7. Consideriamo il problema (P ) dato dall equazione u t = u xx sull intervallo spaziale [, π] con le condizioni al bordo u(, ) = u(, π) = e la condizione iniziale u(, x) = 8 cos 2 x sin x. a) Trovare una soluzione di (P ). b) Dimostrare che la soluzione di (P ) è unica. c) Dimostrare che l unicità viene meno se si rimuove la condizione al bordo u(, π) =. 8. a) Sia Ω un aperto in R d con Ω, e per ogni x Ω sia d(x) la distanza di x da Ω. a) Dimostrare che esiste una costante C che dipende solo da d tale che per ogni u funzione armonica su Ω vale u(x) C d(x) u per ogni x Ω; b) Dimostrare che ogni funzione armonica u su R d tale che u(x) = o( x ) per x è costante. c) Trovare una stima per k u(x) analoga a quella nel punto a). d) Dimostrare che ogni funzione armonica u su R d tale che u(x) = o( x k ) per x è un polinomio con grado minore di k.
7 Scritto del primo appello, 7 gennaio 29 Testi 7. Sia X il sottospazio delle funzioni u in L 2 ([, 2]) tali che u(x) = per q.o. x [, ]. Determinare X e le proiezioni ortogonali di una generica u L 2 ([, 2]) su X e su X. 2. Calcolare la trasformata di Fourier della funzione u(x) := xe x. 3. Detto X lo spazio delle funzioni f : [, ] R limitate e misurabili, dotato della norma L, consideriamo l applicazione T : X X R data da T (f, f 2 ) = f f 2 dx. a) Dimostrare che T è ben definita e separatamente continua in ciascuna variabile. b) Dimostrare che T non è continua. 4. a) Trovare una funzione v su R 2 tale che v(x) = 4. b) Risolvere l equazione u(x) = 4 sul disco D di centro e raggio in R 2, con la condizione al bordo u(e it ) = t per π t π. 5. a) Scrivere la funzione u (x) := 2 6 cos 2 x sin 2 x in serie di Fourier. b) Risolvere il problema (P ) dato dall equazione alle derivate parziali u tt + 4u t = u xx sull intervallo spaziale [ π, π] con le condizioni di periodicità u(t, π) = u(t, π) e u x (t, π) = u x (t, π), e le condizioni iniziali u(, ) = u e u t (, ) =. c) Dire per quali dati iniziali u la soluzione di (P ) esiste per ogni t, e per quali tende uniformemente a per t Fissato a > consideriamo la funzione f a : R R definita da f a (x) := / x a se x e x, e f a (x) := altrimenti. a) Dire per quali p [, ) si ha che f a L p (R). b) Dire per quali a la funzione f a f a è continua e limitata. (Notare che siccome f a è positiva, f a f a è ben definita per ogni x R, e ha valori in [, + ].) 7. Dato insieme misurabile in R n e p p 2 +, per ogni funzione misurabile u su poniamo u X := inf { } u p + u 2 p2 : u = u + u 2, ed indichiamo con X = X(, p, p 2 ) lo spazio delle u tali che u X < +. Nel caso p 2 < + consideriamo inoltre la funzione g : R R data da g(t) := t p t p2 dove a b := min{a, b}. Dimostrare quanto segue (supponendo p 2 < + tranne che per a)): a) X è una norma su X (avendo identificato le funzioni che coincidono q.o.); b) esiste una costante C tale che g(t + t 2 ) C ( t p + t 2 p2 ) per ogni t, t 2 R; c) u X se e solo se g(u(x)) dx < + ; d) se < allora X = L p e la una norma X equivale alla norma p ; e) lo spazio X con la norma X è completo. 8. a) Far vedere che è possibile definire la Trasformata di Fourier come applicazione lineare e continua da X := X(R,, 2) in X := X(R, 2, ) che coincide con le definizioni già viste su L e su L 2. b) Dire per quali a > si ha che u(x) := x a X(R,, 2). c) Per gli a come sopra, dimostrare che û(y) = b y c per opportuni b, c.
8 8 Scritto del secondo appello, 2 febbraio 29 Testi. Dire per quali p e a la funzione f(x, x 2 ) := xa x quadrato Q := (, ) x4 2 appartiene a L p (Q) dove Q è il 2. Calcolare la serie di Fourier di f(x) := 2 e ix. 3. Sia u : R d C d una funzione di classe C tale che u e u appartengono a L (R d ). sprimere le trasformate di Fourier di u e div u in funzione della trasformata di u. 4. Sia X l insieme delle funzioni u in C c (R) con integrale. a) Dimostrare che la chiusura di X in L (R) è il sottospazio Y delle funzioni con integrale. b) Qual è la chiusura di X in L 2 (R)? 5. Consideriamo il problema (P ) dato dall equazione u t = u xx sull intervallo spaziale [, π] con le condizioni al bordo u(t, ) = e u(t, π) = πt 2 e la condizione iniziale u(, x) =. a) Discutere l unicità della soluzione. b) Discutere l esistenza della soluzione. 6. Consideriamo lo spazio di Hilbert complesso L 2 = L 2 C ([, π]), il sottospazio X delle funzioni u : [, π] C di classe C tali che u() = u(π), e l operatore T : X L 2 dato da T : u i u. a) Dimostrare che T è autoaggiunto. b) Discutere la segnatura di T. c) Trovare una base di Hilbert di L 2 composta di autovettori di T. 7. Fissata una funzione pari g L (R) considero la forma quadratica F su L 2 (R) data da F (u) := g(h) u(x h) u(x) dx dh. R 2 a) Dimostrare che F (u) è ben definita per ogni u L 2 (R); b) Scrivere F (u) in funzione della trasformata di Fourier di u; c) Trovare ipotesi su g che garantiscono che F è definita positiva. 8. In R 2 sia D la corona circolare (chiusa) con centro l origine, raggio interno e raggio esterno 2, e siano S ed S 2 le circonferenze con centro l origine e raggi e 2 rispettivamente, vale a dire le due componenti connesse di D. Date u e u 2 funzioni di classe C definite su S e S 2 rispettivamente, trovare la funzione continua u : D R tale che u = u su S, u = u 2 su S 2, e u è armonica all interno di D. Per le funzioni a valori vettori o matrici la trasformata di Fourier viene calcolata componente per componente.
9 Scritto del terzo appello, 9 giugno 29 Testi 9. Calcolare la trasformata di Fourier di u(x) := sin(2x) + x Tra tutti i polinomi p di grado minore o uguale a due trovare quello che minimizza la distanza dalla funzione sin x in L 2 ( π, π). 3. Sia Ω l insieme del punti (x, y) tali che x > e < y < x 2. Dire per quali p [, + ) la funzione f(x, y) := / x 2 + y 2 appartiene a L p (Ω). 4. Dire per quali a la funzione f : R d \ {} R definita da f(x) := x a è armonica. 5. Sia u : R C una funzione tale che x k u L per ogni k =,, 2,... Dimostrare che la TdF û è una funzione di classe C e calcolarne la serie di Taylor (formale) in. 6. Consideriamo il problema (P ) dato dall equazione u t = 4t 3 u xx, dalle condizioni al bordo u(, ) = u(, π) = e dalla la condizione iniziale u(, ) = u. a) Dimostrare che (P ) ammette al più una soluzione su [, T ) [, π] per ogni T >. b) Dire sotto quali ipotesi (su u ) (P ) ammette una soluzione, e discuterne le regolarità. c) Cosa si può dire sulla risolubilità nel passato di (P )? 7. Dimostrare la seguente variante del teorema di convergenza dominata: sia un insieme misurabile in R d e siano u n : R e v n : [, + ) due successioni di funzioni misurabili tali che u n converge q.o. a u, v n converge a v in L (), e u n v n q.o. per ogni n; allora lim n u n dx = u dx. 8. Sia I := [, ], sia f : R R una funzione continua, e sia T l operatore che ad ogni funzione misurabile u : I R associa la funzione composta f u. Dimostrare quanto segue: a) Se f(t) = O( t ) per t ± allora T porta L p (I) in sé per ogni p [, + ). b) Se f è Lipschitziana allora T porta L p (I) in sé ed è Lipschitziana. c) Se non vale l ipotesi al punto a) allora T non porta L p (I) in sé per alcun p [, + ). d) Se vale l ipotesi al punto a) allora T : L p (I) L p (I) è continua. Al solito, per soluzione intendo una funzione u continua che sia anche di classe C in t e C 2 in x per t >, e che risolve l equazione per t >.
10 Scritto del quarto appello, luglio 29 Testi. Data f : [ π, π] C di classe C, scrivere i coefficienti di Fourier (complessi) di f in funzione di quelli di f e del numero m(f) := f(π) f( π). 2. Calcolare la Trasformata di Fourier della funzione u(x) := x2 x Detto D il disco chiuso (in C) con raggio e centro nell origine, trovare la funzione u : D R continua e armonica all interno di D che soddisfa la condizione al bordo u(e it ) = t Sia I := [, ] e sia X il sottospazio di L 2 (I) dato dalle funzioni u : I R di classe C 2 tali che u() =. Data a : I R funzione di classe C, consideriamo l operatore T : X L 2 (I) dato da T u := (a u). a) Dire per quali funzioni a l operatore T è autoaggiunto. b) Tra le funzioni a del punto a), dire per quali T è semi-definito positivo. c) Tra le funzioni a del punto a), dire per quali T è definito positivo. 5. Sia f : R d R una funzione misurabile, siano, 2,... una successione di insiemi misurabili contenuti in R d e a due a due disgiunti, e sia l unione di questi insiemi. Dimostrare che l uguaglianza ( ) f dx = f dx n n= vale nei seguenti casi: a) f ; b) f L (); c) f è integrabile su. 6. Data una funzione u : R C di classe C 3 e 2π-periodica, consideriamo il problema u tt = u xx + 3u u(, π) = u(, π), u x (, π) = u x (, π) u(, ) = u ( ), u t (, ) = a) Risolvere il problema ( ) per u (x) := cos(x). b) Dire per quali u la soluzione del problema ( ) è definita su tutto R [ π, π] ed è limitata. 7. a) Usando la trasformata di Fourier, trovare una funzione u L (R) che risolve l equazione u u = + x 2. b) Quante soluzioni u in L (R) ammette di quest equazione? c) quante in L 2 (R)? 8. Sia f : R 3 R la funzione data f(x) := / x per x (e f() := ), sia u una funzione in L (R 3 ) e sia A un aperto in R 3 tale che u = q.o. su A; sia infine B := B(, ) la palla chiusa con centro l origine e raggio. a) Dire per quali p la funzione f appartiene agli spazi L p (R 3 ), L p (B), L p (R 3 \ B). b) Dimostrare che il prodotto di convoluzione u f(x) è ben definito per quasi ogni x R 3. c) Dimostrare che u f(x) è ben definito e finito per ogni x A, e che u f è continua su A. d) Dimostrare che u f è armonica su A. (*)
11 Scritto del quinto appello, settembre 29 Testi. a) Dato u L (R), sia v(x) := u( x); esprimere ˆv in termini di û. b) Caratterizzare le funzioni u L (R) tali che û è una funzione dispari a valori reali. 2. a) Scrivere la serie di Fourier della funzione u (x) := 4 sin 3 x. b) Scrivere u come combinazione lineare delle funzioni sin(nx) con n =, 2, Sia u una funzione misurabile su R che è limitata sugli insiemi limitati (ma non necessariamente limitata su tutto R) e sia v una funzione in L (R) con supporto compatto. Dimostrare che: a) u v(x) è ben definito per ogni x R; b) la funzione u v è continua; c) se u(x) = O( x a ) per x + per qualche a R allora u v(x) = O( x a ) per x Sia l insieme dei punti (x, y) R 2 tali che y 2 ( + x 8 ) 2. Dire per quali a e p la funzione f(x) := ( + x 2 + y 2 ) a appartiene a L p (). 5. Trovare una soluzione u = u(t, x) definita su [, + ) [, π] del problema (P ) dato dall equazione differenziale u t = u xx + 3t 2 u, le condizioni al bordo u(, ) = u(, π) = e la condizione iniziale u(, ) = u ( ), dove u è la funzione definita nell esercizio a) Data una funzione armonica u su R d ed un aperto limitato A in R d con frontiera di classe C, dimostrare che il flusso di u uscente da A è zero. b) Far vedere con un esempio che quanto affermato al punto a) non vale se si suppone che u sia una funzione armonica su R d \ {x } con x A. c) Nel contesto del punto b), far vedere che il flusso di u uscente da A non dipende da A. 7. Sia u una funzione radiale di classe C 2 su R d \ {} con d 2, vale a dire una funzione della forma u(x) := v( x ) con v funzione di classe C 2 su (, + ). a) Scrivere u e u in funzione di v. b) Trovare tutte le funzioni armoniche radiali su R d \ {}. 8. Consideriamo una successione di funzioni f n in L (R d ) tali che f n converge a in L (B) per ogni palla B centrata nell origine. a) Far vedere che f n converge a in L () per ogni insieme in R d misurabile e limitato. b) Dare un esempio di f n tale che f n non converge a in L (R d ). c) Caratterizzare gli insiemi misurabili per cui vale sempre che f n converge a in L ().
12 S O L U Z I O N I
13 Primo compitino, 6 dicembre 28 Soluzioni 3. Osservo innanzitutto che il prodotto di convoluzione f g è una funzione limitata ben definita perché f appartiene a L mentre g è limitata. Dati x, x R d, usando la definizione del prodotto di convoluzione ottengo f g(x) f g(x ) = (g(x y) g(x y)) f(y) dy. R d Detta quindi L la costante di α-hölderianità di g ottengo f g(x) f g(x ) g(x y) g(x y) f(y) dy R d L (x y) (x y) α f(y) dy = L x x α f, R d da cui segue che f g è α-hölderiana di costante L := L f. 2. Per capire per quali p la norma f p è finita la devo stimare sia dall alto che dal basso (visto che non la posso calcolare esattamente). Per fare entrambe le stime spezzo il dominio di integrazione Q in due sottoinsiemi Q + e Q definiti come segue: Q è l insieme degli x tali che x Q e x 4 2 x 2, ovvero x e x 2 x /2 ; Q + è l insieme degli x tali che x Q e x 4 2 > x 2, ovvero x 2 e x < x 2 2. L idea di questa suddivisione è che in Q la quantità x 2 + x 4 2 può essere stimata dall alto e dal basso con x 2, mentre in Q + può essere stimata dall alto e dal basso con x 4 2. Per la precisione vale che x Q x 2 x 2 + x 4 2 2x 2 x Q + x 4 2 x 2 + x 4 2 2x p/ x p/5 2 p/ x 2p/5 2 Quindi stimo l integrale f p dall alto e dal basso con Q ( dx /2 ) x dx 2 = dx Q x p/5 x p/5 = f(x) p x p/5 f(x) p dx, x p/5 /2, x 2p/5 2 e quest ultimo integrale è finito se e solo se p/5 /2 <, vale a dire p < 5/2. Analogamente stimo l integrale f p dall alto e dal basso con Q + ( dx ) x 2 2 dx dx 2 = dx Q + x 2p/5 2 x 2p/5 2 =, 2 x 2p/5 2 2 e quest ultimo integrale è finito se e solo se 2p/5 2 <, vale a dire p < 5/2. Sulla base di quanto fatto deduco che la norma f p è finita se e solo se p < 5/2. 3. Siccome X è un sottospazio chiuso di L 2 (, ), so che esiste la proiezione di su X, ed è una funzione della forma f(x) = a x + a 2 x 2 + a 3 x 3, inoltre la proiezione di su X è f. Il fatto f è ortogonale a X si traduce nel seguente sistema di equazioni lineari nei coefficienti a i : = f ; x = x a x 2 a 2 x 3 a 3 x 4 dx = 2 3 a 2 5 a 3 = f ; x 2 = x 2 a x 3 a 2 x 4 a 3 x 5 dx = a 2 = f ; x 3 = x 3 a x 4 a 2 x 5 a 3 x 6 dx = 2 5 a 2 7 a 3 da cui si ricava facilmente che a = a 3 = e a 2 = 5/3. Quindi la proiezione di su X è f = 5 3 x2 e la proiezione su X è f = 5 3 x2..
14 4 Primo compitino, 6 dicembre 28 Soluzioni 4. a) Detta τ h f(x) := f(x h) la traslata di f, per ogni n Z vale che c n (τ h f) = 2π = 2π π π π h f(x h) e inx dx π h π = e inh 2π f(t) e in(t+h) dt π f(t) e int dt = e inh c n. (Nel secondo passaggio ho usato il cambio di variabile x = t + h, nel terzo ho usato il fatto che l integrale di una funzione 2π-periodica su ogni intervallo di lunghezza 2π è lo stesso.) b) Posto h := 2π/N, i seguenti fatti sono equivalenti: (i) f è 2π/N-periodica; (ii) f(x) = τ h f(x) = per q.o. x; (iii) ( e inh )c n = per ogni n Z; (iv) c n = per ogni n Z tale che N non divide n. (L equivalenza (i) (ii) è ovvia, (ii) (iii) segue dal punto a), e infine (iii) (iv) segue dal fatto che e inh se e solo se N non divide n.) 5. a) La condizione /p = /p + /p 2 equivale a = p p + p p 2, (.) il che significa che p /p e p 2 /p sono esponenti coniugati. Posso allora applicare la disuguaglianza di Hölder come segue: f f 2 p = f p p f 2 p dx f p p/p f 2 p = f p f2 p p2/p p p 2. (Il caso p = p = p 2 = + va considerato a parte, ma è immediato.) b) Basta applicare a). c) T non è iniettiva. Infatti posso scrivere la funzione (che appartiene a L p per ogni p) sia come prodotto di per che come prodotto di g per, dove g è una qualunque funzione in L p che non sia quasi ovunque nulla. T è surgettiva. Ricordando la (.) posso infatti scrivere ogni funzione f L p come dove ho posto f = sgn(f) f p/p p f 2/p }{{}}{{} f f 2 + se t >, sgn(t) := se t =, se t <. Si verifica facilmente che f appartiene a L p ed f 2 appartiene a L p2. T è Lipschitziana su ogni sottoinsieme limitato di L p L p2, ed in particolare è continua. Osservo infatti che date due coppie (f, f 2 ) e (f, f 2) in L p L p2 si ha che f f 2 f f p 2 = f (f 2 f 2 ) + (f f )f p 2 f (f 2 f 2 ) p + (f f )f p 2 f p f 2 f p2 2 + f2 p2 f f p. 6. a) Data u soluzione del problema (P ) definita su [, T ) [ π, π], per ogni t [, T ) e n Z indico con c n (t) i coefficienti di Fourier di u(t, ). Allora c n è una funzione continua su [, T ) perché u è continua su [, T ) [ π, π]; c n è una funzione derivabile per ogni t (, T ) perché u è di classe C in t su (, T ) [ π, π], e ċ n (t) sono i coefficienti di Fourier di u t (t, );
15 Primo compitino, 6 dicembre 28 Soluzioni 5 n 2 c n (t) sono i coefficienti di Fourier di u xx (t, ) per ogni t (, T ) perché u(t, ) è di classe C 2 e soddisfa le condizioni al bordo u(, π) = u(, π) e u x (, π) = u x (, π); per ogni t (, T ) vale l identità u t (t, ) = cos t u xx (t, ) da cui segue l identità dei rispettivi coefficienti di Fourier, vale a dire ċ n (t) = n 2 cos t c n (t); c n () = c n perché u(u, ) = u ( ); la funzione c n risolve dunque l equazione differenziale lineare omogenea ẏ = n 2 cos t y con la condizione iniziale y() = c n, e pertanto è univocamente determinata; per la precisione vale che c n (t) = c n e n2 sin t. (.2) Siccome i coefficienti di Fourier di u(t, ) sono univocamente determinati per ogni t [, T ), ho che anche la funzione u(t, ) è univocamente determinata. b) e c) La formula (.2) suggerisce di considerare la soluzione u data da u(t, x) = c n e n2 sin t e inx. (.3) }{{} n Z u n Faccio vedere quanto segue: La serie delle funzioni u n in (.3) converge totalmente su [, π] R, da cui segue che u è ben definita e continua su [, π] R, e 2π-periodica nella variabile x. Infatti, tenuto conto che n 2 sin t per t [, π], ho che u n L ([,π] R) c n, e sappiamo che n c n < + per ipotesi. La serie delle derivate parziali di ogni ordine delle funzioni u n converge totalmente su [δ, π δ] R per ogni δ >, da cui segue che u è di classe C su (, π) R. Si può infatti dimostrare per induzione che per ogni intero h =,... esiste un polinomio P h = P h (y, y 2 ) di grado h tale ( e n 2 sin t ) = c n P h (n 2 sin t, n 2 cos t) e n2 sin t, D h t e quindi per ogni intero k =,,... vale che D k xd h t u n = c n P h (n 2 sin t, n 2 cos t) e n2 sin t (in) k e inx. Usando questa formula, per ogni h =,,... possiamo trovare una costante M h tale che D k xd h t u n L ([δ,π δ] R) M h c n n 2h+k e n2 sin δ, e dunque la serie delle derivate parziali DxD k t h u n converge totalmente perché la successione c n è limitata, e n2 sin δ tende a più che esponenzialmente in n, mentre n 2h+k tende a infinito polinomialmente. Siccome ciascuna funzione u n risolve l equazione in (P ), che è lineare, grazie ai punti precedenti ottengo che anche u risolve tale equazione. Inoltre u è 2π-periodica in x e quindi soddisfa la condizione al bordo in (P ). Infine le funzioni u(, ) e u ( ) coincidono perché hanno gli stessi coefficienti di Fourier. d) Considero la funzione u con coefficienti c n := e n. Siccome c n tende a più che polinomialmente per n ± ho che c n n k < + per k =,,..., n e quindi u è una funzione 2π-periodica su R di classe C. Supponiamo per assurdo che esista una soluzione u di (P ) definita su [, T ) [ π, π]. Preso allora t con π < t < min{t, 2π}, si ha che sin t < e quindi la formula (.2) implica che i coefficienti c n (t) tendono a ± per n ±. Ma questo contraddice il fatto che questi coefficienti sono in l 2, e quindi devono tendere a. 7. a) Sia x (k) una successione di elementi di X che converge a x in l p per k +. Devo mostrare che x appartiene a X. Osservo che per ogni n =, 2... si ha che x (k) n x n x (k) x l p
16 6 Primo compitino, 6 dicembre 28 Soluzioni e quindi x (k) n converge a x n per k +. Inoltre x (k) n /n (perché x (k) appartiene a X) e quindi anche x n soddisfa x n /n, e dunque x appartiene a X. b) Data una successione x (k) di elementi di X, voglio trovare una sotto-successione che converge ad un qualche elemento di X. Fissato n, ho che (k) x n /n per ogni k e quindi posso estrarre da k una sotto-successione k h tale che x (k h) n converge ad un certo x n, che a sua volta soddisfa x n /n. (.4) Usando un procedimento diagonale posso inoltre fare in modo che la successione k h sia la stessa per ogni n. Pongo allora x := (x, x 2,... ), e osservo che x appartiene a X per via della (.4). Mi resta da dimostrare che x (kh) converge a x in l p. Osservo che per ogni n vale x (k h) n x n x (k h) n + x n 2 n, e dunque, fissato un qualunque intero N, vale che x (k h ) x p l p N n= x (k h ) n x n p + 2 p + n=n n p. (.5) Siccome la serie di /n p converge, per ogni ε > posso trovare N tale che la seconda somma in (.5) vale meno di ε; siccome la prima somma in (.5) tende a per h + ho che lim sup x (kh) x p 2 p ε, l h + p e dall arbitrarietà di ε segue che 8. a) Osservo che lim h + x (k h ) x p =. l p (log f) = f f. Dunque l ipotesi fatta su f implica che la funzione log f ha gradiente limitato, ed in particolare è una funzione Lipschitziana su R d. In altre parole esiste una costante L tale che per ogni x, y R d vale L y x log(f(y)) log(f(x)) ( ) = f(y) log, f(x) e dunque exp( L x y ) f(y) exp(l x y ). f(x) In particolare presa δ > e posto m := exp(lδ) si ha che x y δ m f(y) f(x) m. (.6) b) Per ogni vettore n Z d indico con Q(n) il cubo di centro n e lato con lati paralleli agli assi. Osservo che i cubi Q(n) ricoprono R d e l intersezione di due di questi cubi ha misura nulla. Pertanto f(x) dx = f(x) dx. (.7) R d n Z d Q(n) D altra parte il diametro di ciascun Q(n) è d, e posto quindi m := exp ( L d ) la (.6) implica f(n) f(x) m f(n) per ogni x Q(n), m e dunque, ricordando che ogni Q(n) ha volume, m f(n) f(x) dx m f(n). (.8) Q(n) Mettendo insieme (.7) e (.8) ottengo che f(n) f(x) dx m f(n), m n Z d R d n Z d
17 Primo compitino, 6 dicembre 28 Soluzioni 7 da cui segue la tesi. c) Voglio vedere se posso applicare quanto fatto al punto b). Pongo dunque ed osservo che e quindi f(x) := f(x) = f(x) f(x) + x a (.9) ax x a 2 ( + x a ) 2, = a x a + x a, e questa funzione è limitata perché è continua e tende a per x +. Pertanto grazie a quanto fatto al punto b) ho che + n a + n Z d R + x a dx t d + d + t a dt dt dt. ta d+ (L espressione a b sta per a si comporta come b, cioè a è finito se e solo se b è finito.) Siccome l ultimo integrale è finito se e solo se a d + >, cioè a > d, lo stesso vale per la serie. Commenti sercizio. Un passaggio preliminare che molti dei presenti hanno omesso è verificare che il prodotto di convoluzione f g sia effettivamente ben definito, cosa che peraltro segue da un risultato visto a lezione. Alcuni, nel tentativo di farlo vedere, hanno scritto che f g è ben definito perché f g(x) g(x y) f(y) dy g f. Ma questa disuguaglianza non ha molto senso, visto che presuppone l esistenza di f g(x), che è proprio quella che si vorrebbe dimostrare. sercizio 2. Mi scuso perché il suggerimento dato durante lo scritto non era ottimale. Seguendo quel suggerimento, infatti, è facile arrivare alla conclusione che f L p per p < 5 e f / L p for p, ma non è facile arrivare al risultato completo. sercizio 2. Un approccio alternativo (seguito da veri dei presenti) è il seguente: si calcola l integrale di f(x) p su Q usando il cambio di variabili Si noti infatti che f(x) = /ρ /5 ; x = ρ cos θ, x 2 = ρ sin θ. il determinante Jacobiano del cambio di variabili è 2 ρ/ sin θ; Q contiene l insieme B dei punti x tali che ρ e θ π/2; l integrale di f(x) p su Q si comporta come quello su B perché f è limitata su Q \ B e quindi l integrale di f(x) p su Q \ B è finito per ogni p. Ne consegue che f(x) p dx f(x) p dx Q = B π/2 ( = ρ p/5 dρ ρ p/5 /2 ρ 2 dθ dρ sin θ )( π/2 ) dθ 2 sin θ dρ ρ p/5 /2, e dunque f appartiene a L p (Q) se e solo se p/5 /2 <, cioè p < 5/2.
18 8 Primo compitino, 6 dicembre 28 Soluzioni sercizio 3. Noto che le funzioni dispari e quelle pari sono mutuamente ortogonali in L 2 (, ). Usando questa osservazione ed un po di algebra lineare si dimostra che allora la proiezione della funzione pari su X è uguale alla proiezione di sulla retta generata da x 2, che è data dalla formula ; x 2 x 2 2 x 2 = 2/3 2 2/5 x2 = 5 3 x2. sercizio 5c): continuità della mappa T. Diversi gli errori e le dimostrazioni incomplete, cioè basate su enunciati non sono stati dimostrati né a lezione, né dallo studente che li ha usati. Per cominciare, alcuni dei presenti hanno scritto che la mappa T : L p L p2 L p è lineare, mentre invece è bilineare (come ogni prodotto che si rispetti). Altri invece hanno scritto che T è continua perché è separatamente continua nelle due variabili. Il problema è che questa affermazione in generale è falsa, persino nel caso in cui T è una funzione bilineare sul prodotto di due spazi normati (anche a valori in R). Tuttavia è vera se T è una mappa bilineare tra spazi di Banach (come in questo esercizio); però questo enunciato è tutt altro che ovvio, e non può essere dato per buono. Qualcuno ha scritto che T è continua perchè è continua in (, ): questa affermazione è corretta ma non immediata, e non può essere data per buona. Stesso discorso vale l asserzione che la stima T (f, f 2 ) p f p f 2 p2 implica la continuità di T. sercizio 5c): surgettività della mappa T. Alcuni dei presenti hanno dimostrato che T ha immagine densa in L p, e ne hanno dedotto che allora l immagine è tutto L p. Non vedo alcuna ragione per cui debba essere così, e certamente non basta la continuità di T. (Per esempio, dato un insieme di misura nulla, l immersione di L 2 () in L () è una mappa lineare continua con immagine densa, ma non surgettiva.) sercizio 6. Questo esercizio è stato particolarmente difficile da correggere, perché molti hanno dato risposte lunghe e allo stesso tempo vaghe e imprecise, in particolare per quanto riguarda i punti b) e c), dando spesso l impressione di non essere in grado di scriverne di precise. Tuttavia alcuni (ma solo alcuni) hanno anche dato tutte le idee e le formule necessarie, cosa che è stata valutata positivamente. Diverse persone hanno dedicato tempo a raccontare la procedura formale usata per trovare la soluzione del problema. In un esame scritto questo passo può essere ridotto al minimo o anche omesso, e sopratutto deve essere chiaro che non sostituisce le dimostrazioni rigorose. Infine molti dei presenti hanno ridimostrato formule viste e riviste a lezione, come quelle che legano i coefficienti di Fourier di una funzione u(t, ) con quelli di u t (t, ) e di u xx (t, ). Questo non era ovviamente necessario. sercizio 6b). Diversi dei presenti hanno mostrato che la serie delle funzioni u n in (.3) converge totalmente, e da questo hanno dedotto che la funzione u definita da questa serie è una soluzione del problema (P ). In realtà la convergenza totale della serie mostra solo che u è una funzione ben definita e continua su [, π] R, mentre per dimostrare che è una soluzione dell equazione in (P ) bisogna far vedere perlomeno che le serie delle derivate parziali D t u n, D x u n e D xx u n convergono totalmente sui sottoinsiemi compatti di (, π) R. sercizio 6b) e c). Molti dei presenti hanno scritto che le derivate parziali delle funzioni u n di un certo ordine convergono totalmente su (, π) [ π, π], ma questo è falso: convergono totalmente solo in (δ, π δ) [ π, π] per ogni δ >. (L errore è in parte dovuto al tipo di stime scritte, vedere il commento successivo.) sercizio 6b). Per dimostrare la convergenza totale della serie n u n che definisce u, o della serie delle derivate parziali di u n di un certo ordine, molti dei presenti hanno scritto delle stime dipendenti da t, del tipo D t u n n 2 c n e n2 sin t < +, n n dove quindi D t u n non può che essere la norma del sup della funzione D t u n (t, ) a t fissato. Il problema è che questa stima mostra la convergenza totale della serie delle funzioni D t u n (t, )
19 Primo compitino, 6 dicembre 28 Soluzioni 9 per ogni t, che però non implica la convergenza totale delle funzioni D t u n in t e x. In particolare questa convergenza implica che v := D t u n è una funzione continua nella variabile x per ogni t, ma non che v è continua nelle variabili t, x. Inoltre non implica che v coincida con la derivata parziale D t u, né che questa esista. Ovviamente dalla stima data sopra è possibile ricavare una stima della norma del sup delle funzioni D t u n nelle due variabili, ma questa stima andava scritta esplicitamente. sercizio 6d). Alcuni dei presenti hanno fatto vedere che la serie delle funzioni u n non converge totalmente e ne hanno dedotto che quindi la soluzione u non esiste. Scritta così questa inferenza non è corretta. Ma può essere resa corretta osservando che per ogni t la soluzione u(t, ) è per ipotesi una funzione di classe C 2 (nella variabile x) e quindi è anche di classe C, cosa che implica la convergenza totale della serie di Fourier c n (t) e inx (a t fissato). sercizio 7. Gli enunciati a) e b) valgono anche per p = +, ma questo caso è stato escluso per semplificare lo svolgimento dell esercizio. sercizio 7a). Diversi dei presenti hanno dato la seguente dimostrazione: sia p n : l p R la mappa lineare che ad ogni successione x associa il termine n-esimo x n. Si dimostra facilmente che questa mappa è continua e che X = n= p ( ) n [ /n, /n], e dunque X è chiuso in quanto intersezione di chiusi. Attenzione: la continuità della mappa p n non può essere data per scontata, come invece hanno fatto alcuni. sercizio 7b). Molti dei presenti hanno scritto che la compattezza di X segue dal fatto che X è chiuso e limitato, ma questa affermazione è sbagliata. In effetti gli insiemi compatti in uno spazio metrico completo sono caratterizzati dall essere chiusi e totalmente limitati, ma negli spazi normati di dimensione infinita, come ad esempio l p, i limitati non sono sempre totalmente limitati. Un esempio di insieme limitato ma non totalmente limitato è proprio la palla chiusa in l p (con centro l origine e raggio r) che infatti non è compatta. Alcuni dei presenti hanno scritto che sotto opportune ipotesi di numerabilità sulla topologia dello spazio, la compattezza equivale a chiusura e limitatezza (confondendosi, credo, con le ipotesi per l equivalenza di compattezza e compattezza sequenziale). Infine alcuni dei presenti hanno usato la corretta caratterizzazione dei compatti, ma poi hanno usato definizioni non corrette della totale limitatezza. sercizio 7b). Per quanto detto sopra si può dimostrare che X è compatto facendo vedere che è totalmente limitato. La dimostrazione di questo fatto si basa su due osservazioni: la prima è che per ogni ε > esiste N tale che n p < εp, n>n e pertanto, detta p : X X la mappa che ad ogni successione x associa la successione troncata p(x) definita da { x n se n N, p(x) n := se n > N, allora e dunque ( ) /p ( x p(x) l p = x n p dist(x, p(x)) := n>n n>n ) /p n p < ε, inf x y lp < ε per ogni x X. (.) y p(x) La seconda osservazione è che p(x) è un insieme chiuso e limitato in p(l p ), che è uno spazio normato di dimensione finita, quindi p(x) è compatto ed in particolare è totalmente limitato.
20 2 Primo compitino, 6 dicembre 28 Soluzioni Pertanto per ogni ε > posso trovare un insieme finito F p(x) tale che Mettendo insieme le stime (.) e (.) ottengo che dist(x, F ) < ε per ogni x p(x). (.) dist(x, F ) < 2ε per ogni x X. e siccome ε è arbitrario ho dimostrato che X è totalmente limitato. sercizio 7b). La dimostrazione data sopra segue questo schema: data una successione di elementi x (k) di X si estrae una sottosuccessione x (kh) che converge puntualmente ad un qualche x X (nel senso che x (k h) n x n per ogni n) e quindi si dimostra poi che x (kh) converge a x in l p. Alcuni dei presenti hanno proposto una diversa dimostrazione di quest ultimo fatto: detta µ la misura che conta i punti su N := {, 2,... }, hanno osservato che x (kh) x p = x (k h) l p n x n p = x (k h) n x n p dµ(n), N n= e questo integrale tende a per il teorema di convergenza dominata. Per la precisione hanno usato la seguente dominazione: x (k h ) m x m p 2 n p (la successione 2/n p sta in l = L (N, µ) perché p > ). sercizio 8a). Diversi dei presenti hanno dimostrato che una funzione di classe C su R d con gradiente limitato è Lipschitziana. Questo fatto poteva essere dato per buono (come anche detto durante lo scritto). sercizio 8. La versione originale del punto c) chiedeva di considerare a >. Il risultato non cambia, ma la dimostrazione è più complicata perchè la funzione f definita in (.9) non è di classe C su tutto R d per a (non è differenziabile nell origine). Per includere il caso < a basta osservare separatamente che la serie in oggetto vale + perché è sempre maggiore della somma di /( + n a ) con n intero positivo, che vale +. In alternativa si può notare che il criterio di convergenza enunciato al punto b) vale in realtà per tutte le funzioni continue f : R d (, + ) che sono di classe C nel complementare A di una qualche palla chiusa, e tali che il rapporto f /f è limitato su A. sercizio 8a). In diversi hanno dato dimostrazioni sbagliate di questo punto, e spesso l errore è consistito nel dire che il rapporto f /f è limitato anche se f e f non sono calcolate nello stesso punto.
21 Secondo compitino, 8 gennaio 29 Soluzioni 2. a) Usando il cambio di variabile z = Mx (e quindi x = M z, dx = det M dx) ottengo dz v := u(mx) dx = u(z) R d R det M = u det M < +. d b) Usando lo stesso cambio di variabile ottengo anche ˆv(y) = u(mx) e i x ; y dx R d = u(z) e i M x ; y dz R det M d i x ; (M = u(z) e ) T y) dz R det M = M û( (M ) T y ). det d 2. Calcolo la trasformata di u riconducendomi a quella di della funzione w(x) := +x, già calcolata 2 a lezione. Osservo infatti che posso scrivere in u in termini di v usando l operatore di traslazione τ h dato da τ h v(x) := v(x h) e l operatore di riscalamento σ δ dato da σ δ v(x) := δ v(x/δ), e per la precisione u(x) = Pertanto, ricordando che τ h v(y) = e ihyˆv(y), σ δ v(y) = ˆv(δy), ŵ(y) = πe y, ottengo x 2 + 2x + 5 = (x + ) = 4 ( x+ 2 ) 2 = τ σ 2 w + 2( ) (x). û(y) = τ 2 (σ 2 w)(y) = 2 eiy σ 2 w(y) = 2 eiy ˆv(2y) = π 2 eiy e 2y = π 2 e 2 y +iy. 3. Come visto a lezione, conviene identificare il piano R 2 con il piano complesso C. Osservo ora che per ogni punto x = e it del bordo di D vale che ( e u (x) = 6 cos 2 t sin 2 it + e it ) 2 ( e it e it ) 2 t = 6 2 2i = ( e it + e it) 2( e it e it) 2 e quindi l estensione armonica di u all interno di D è = ( e 2it e 2it) 2 = 2 (e it ) 4 (e it ) 4, u(x) = 2 x 4 x 4 = 2 ( Re(x 4 ) ) = 2 ( + 6x 2 x 2 2 x 4 x 4 2). 4. a) Devo far vedere che per ogni u, v X vale T u ; v = u ; T v. stendo u e v a tutto R d ponendole uguali a fuori da Ω. Usando l identità ottengo div(v u) = v div( u) + v u = v u + v u T u ; v = Ω v u dx = Ω div(v u) v u dx, Ω ed applicando il teorema della divergenza ottengo T u ; v = (v u) η dσ(x) v u dx = Ω Ω Ω v u dx, (2.) dove η è la normale esterna a Ω, e l integrale su Ω vale zero perché v = su Ω. Applicando la formula (2.) sia a T u ; v che a T v ; u ottengo infine T u ; v = v u dx = T v ; u = u ; T v. b) Usando di nuovo la formula (2.) ottengo che per ogni u X vale T u ; u = u 2 dx, Ω Ω
22 22 Secondo compitino, 8 gennaio 29 Soluzioni e questo dimostra che T è semidefinito negativo. Inoltre se T u ; u = allora u = quasi ovunque, e quindi ovunque (perché u è una funzione continua). Quindi la funzione u è costante su ogni componente connessa di Ω, ma siccome è anche nulla in un intorno del bordo di ogni componente connessa, deve essere identicamente nulla. Ho quindi dimostrato che T è definito negativo. c) In questo caso la dimostrazione fatta al punto a) non funziona perché l integrale su Ω nella formula (2.) in generale non vale zero, e dunque mi aspetto T non sia autoaggiunto. Per dimostrarlo prendo per esempio u(x) := x 2 e v(x) := e verifico che T u ; v u ; T v = v u u v dx = (2 x 2 ) dx = 2 Ω. Ω Si vede anche che T non è né semidefinito positivo né semidefinito negativo. Il punto a) basta ad escludere la prima possibilità, per escludere la seconda basta osservare che per u(x) := x 2 si ha T u ; u = u u dx = 2x 2 dx >. Ω 5. a) È facile verificare per ogni v L2 C (R) il prodotto mv è una funzione in L2 C (R), e dunque la mappa U : v mv è un operatore lineare da L 2 C (R) in sé. Inoltre U è continuo perché Ω Ω Uv 2 m v 2. Detta F la trasformata di Fourier, intesa come operatore da L 2 C (R) in sé, ho che T := F UF è un operatore continuo da L 2 C (R) in sé che soddisfa T u = m û per ogni u. (L unicità di T u segue dal fatto che la trasformata di Fourier di è invertibile su L 2.) b) Per quali m l operatore T è autoaggiunto? Grazie all identità di Plancherel ho che per ogni u, v L 2 vale T u ; v u ; T v = [ ] T u ; ˆv û ; T v 2π = m) û ˆv dy = 2π R(m i (2.2) (Im m) û ˆv dy. π R Questa identità mostra chiaramente che T è autoaggiunto se m ha valori reali q.o. Faccio ora vedere che vale anche il viceversa, cioè che se T è autoaggiunto allora m ha valori reali q.o. Partendo dalla (2.2) ottengo che per ogni u, v L 2 vale = (Im m) û ˆv dy = (Im m) û ; ˆv, R e siccome la trasformata di Fourier è surgettiva su L 2, questo significa che (Im m) û = q.o. per ogni u L 2, ed in particolare per una u tale che û q.o. (per esempio u(x) = e x ), da cui segue che Im m = q.o. Per quali m l operatore T è definito positivo? Suppongo adesso che T sia autoaggiunto, cioè che m abbia valori reali q.o. Sempre usando l identità di Plancherel ottengo T u ; u = 2π T u ; û = m û 2 dy, (2.3) 2π da cui segue che T è definito positivo se m > q.o. Faccio ora vedere che vale anche il viceversa, cioè che se T è definito positivo allora l insieme dei punti dove m ha misura nulla. Supponendo per assurdo che così non sia trovo un sottoinsieme F con < F <, e siccome l indicatrice F appartiene a L 2, trovo anche u L 2 tale che û = F. Quindi la formula (2.3) dà = T u ; u = 2π R R m ( F ) 2 dy = 2π e questo contraddice il fatto che T sia definito positivo. F Im m dy 6. a) So già che la formula u = iy û vale se invece di u L 2 avessi u L. Suppongo dunque di avere una successione di funzioni u n in C (R) tali che (a) u n L e u n L 2 L per ogni n;
23 Secondo compitino, 8 gennaio 29 Soluzioni 23 (b) u n u in L e u n u in L 2. Allora (c) u n = iy û n per ogni n per via di (a); (d) û n û uniformemente per via di (b); (e) u n u in L 2 per via di (b), e quindi esiste una sottosuccessione tale che u nk u q.o. Passando al limite nella (c) e usando (d) ed (e) ottengo che u = iy û q.o. (non posso dire di più, visto che so solo che u sta in L 2 ). Per completare la dimostrazione devo trovare una successione di funzioni u n che soddisfano (a) e (b). Si verifica facilmente che presa una funzione σ : R [, ] di classe C tale che σ(x) = per x e σ(x) = per x allora le funzioni u n (x) := u(x) σ(x n) soddisfano (a) e (b). b) Siccome û è una funzione continua e limitata, mi basta dimostrare che û appartiene a L () con := R \ [, ]. In effetti û L () = û dy = yû /y dy yû L2 () /y L2 () < +. Nel terzo passaggio ho usato la disuguaglianza di Hölder, nel quarto ho usato che yû appartiene a L 2 (R) (per via del punto (a)) e che /y appartiene a L 2 (), cosa che si verifica con un semplice calcolo. 7. Date le condizioni al bordo, conviene risolvere il problema (P ) scrivendo la soluzione u come combinazione lineare delle funzioni sin(nx) con coefficienti che dipendono da t, vale a dire u(t, x) = b n (t) sin(nx) con b n (t) := 2 π u(t, x) sin(nx) dx. (2.4) π n= Derivando in t e in x ottengo, almeno a livello formale, u t (t, x) = ḃ n (t) sin(nx), u xx (t, x) = n 2 ḃ n (t) sin(nx), (2.5) n= e dunque l equazione u t = u xx si riscrive come uguaglianza dei coefficienti delle due derivate parziali, ovvero ḃn(t) = n 2 b n (t). Scrivendo inoltre il dato u (x) := 8 cos 2 x sin x come combinazione lineare di sin(nx), cioè u (x) = 4 cos x sin(2x) ( e ix + e ix )( e 2ix e 2ix ) = 4 2 2i = 2 eix e ix + e 3ix e 3ix = 2 sin x + 2 sin(3x), 2i ottengo che la condizione iniziale u(, ) = u si riscrive come b n () = 2 per n =, 3 e b n () = altrimenti. Pertanto b n (t) risolve il problema di Cauchy { ẏ = n 2 2 se n =, 3, y, y() = (2.6) altrimenti. da cui segue che b n (t) = La soluzione di (P ) dovrebbe dunque essere n= { 2e n2 t se n =, 3, altrimenti. u(t, x) = 2e t sin x + 2e 9t sin(3x). (2.7) a) Non essendoci sono problemi di convergenza, verificare che la funzione u data in (2.7) è effettivamente una soluzione di (P ) definita per t R e x [, π] è immediato: ogni addendo risolve l equazione di partenza con le giuste condizioni al bordo, e quindi lo stesso vale per u (per linearità dell equazione e delle condizioni al bordo), e chiaramente la condizione iniziale è soddisfatta.
24 24 Secondo compitino, 8 gennaio 29 Soluzioni b) Supponiamo di avere una soluzione u di (P ) definita su I [, π] dove I è un intervallo di tempi che contiene (all interno o come estremo), e per la precisione supponiamo che u sia continua sull insieme di definizione, C nella variabile t e C 2 nella variabile x su (I \{}) [, π]. Per far vedere che tale soluzione è unica (e dunque coincide con la funzione in (2.7)) la scrivo in serie come in (2.4) e mostro che i coefficienti b n (t) sono funzioni continue su I e derivabili per t che risolvono il problema di Cauchy (2.6), e sono pertanto univocamente determinati per tutti i tempi t. Per la precisione osservo che, per via della formula in (2.4) che la definisce, la funzione b n è continua su I, e per il teorema di derivazione sotto il segno di integrale è derivabile in I \ {} e ḃn(t) è il coefficiente n-esimo di u t (t, ). Inoltre integrando due volte per parti l integrale che definisce b n ottengo che n 2 b n (t) è il coefficiente n-esimo di u xx (t, ) (in questo passaggio è essenziale che u(t, ) = u(t, π) = ). Siccome u t e u xx sono uguali, anche i loro coefficienti devono essere uguali, il che significa che b n soddisfa l equazione in (2.6) per t. Che valga la condizione iniziale in (2.6) è ovvio. c) È chiaro il ruolo di entrambe le condizioni al bordo nella dimostrazione dell unicità: servono a garantire che i coefficienti di u xx sono quelli che ci si aspetta. Per mostrare la mancanza di unicità scelgo una funzione g non identicamente nulla, e cerco una soluzione v del problema (P ) dato dall equazione v t = v xx, le condizioni al bordo v(, ) = e v(, π) = g, e la condizione iniziale v(, ) =. Se u è la soluzione di (P ), allora la funzione ũ = u + v risolve l equazione u t = u xx con le condizioni al bordo u(, ) = e u(, π) = g e la condizione iniziale u(, ) = u, ma differisce da u perché non soddisfa le stesse condizioni al bordo. In mancanza di teoremi di esistenza generali, la difficoltà è trovare una funzione g per cui si riesce a risolvere (P ). Una possibilità è prendere g(t) := πt. Per risolvere (P ) uso il cambio di variabile v(t, x) = w(t, x) + 6 (x3 π 2 x) + tx ed ottengo che la nuova incognita w deve risolvere il problema (P ) dato dall equazione w t = w xx, le condizioni al bordo w(, ) = w(, π) =, e la condizione iniziale w(, ) = w con w := 6 (π2 x x 3 ). Trovo una soluzione di (P ) come ho fatto per (P ): usando il fatto che i coefficienti di w per la rappresentazione come serie di sin(nx) sono b n := 2 n ( ) n ottengo che i coefficienti b 3 n (t) della soluzione w(t, ) sono b n (t) = 2 n ( ) n e n2t. 3 Dunque w dovrebbe essere w(t, x) := n= 2 n 3 ( )n e n 2t sin(nx). È facile vedere che questa serie definisce una funzione continua su [, + ) [, π] e di classe C su (, + ) [, π] che risolve (P ). 8. Prendo x Ω e r = d(x)/2, e osservo che la chiusura della palla B(x, r) di centro x e raggio r è contenuta in Ω. Inoltre ogni derivata parziale D i u è pure una funzione armonica e quindi, usando la proprietà della media, D i u(x) = D i u(y) dy = D i u(x + h) dh = a d r d div v(h) dh B(x,r) B(,r) B(,r) dove v è il campo di vettori v(h) := u(x + h) e i, la divergenza è calcolata rispetto alla variabile h, e a d è il volume della palla unitaria in R d. Applicando quindi il teorema della divergenza ottengo D i u(x) = a d r d v(h) η(h) dσ(h) = a d r d u(x + h) e η(h) dσ(h), B(,r) B(,r) dove η(h) è la normale esterna a B(, r) nel punto h. Usando questa formula ottengo la stima u (x) x i a d r d u(x + h) e η(h) dσ(h) B(,r) a d r d u dσ(h) = vol d ( B(, r)) a d r d u = 2d d(x) u. B(,r)
Analisi Matematica 3, a.a Scritto del quinto appello, 11 settembre 2019 Testi 1
 Scritto del quinto appello, 11 settembre 019 Testi 1 1. a) Dato u L 1 R), sia vx) := u x); esprimere ˆv in termini di û. b) Caratterizzare le funzioni u L 1 R) tali che û è una funzione dispari a valori
Scritto del quinto appello, 11 settembre 019 Testi 1 1. a) Dato u L 1 R), sia vx) := u x); esprimere ˆv in termini di û. b) Caratterizzare le funzioni u L 1 R) tali che û è una funzione dispari a valori
Analisi Matematica 3, a.a Secondo compitino, 8 gennaio 2019 Testi 1
 Secondo compitino, 8 gennaio 019 Testi 1 1. Sia M una matrice d d invertibile e sia u una funzione in L 1 ( d ), e sia v la funzione su d definita da v(x) := u(mx). a) Dimostrare che v L 1 ( d ) ed scrivere
Secondo compitino, 8 gennaio 019 Testi 1 1. Sia M una matrice d d invertibile e sia u una funzione in L 1 ( d ), e sia v la funzione su d definita da v(x) := u(mx). a) Dimostrare che v L 1 ( d ) ed scrivere
Analisi Matematica 3, a.a Scritto del quarto appello, 10 luglio 2019 Testi 1
 Scritto del quarto appello, luglio 29 Testi. Data f : [ π, π] C di classe C, scrivere i coefficienti di Fourier complessi di f in funzione di quelli di f e del numero mf := fπ f π. 2. Calcolare la Trasformata
Scritto del quarto appello, luglio 29 Testi. Data f : [ π, π] C di classe C, scrivere i coefficienti di Fourier complessi di f in funzione di quelli di f e del numero mf := fπ f π. 2. Calcolare la Trasformata
Analisi Matematica 3, a.a Scritto del primo appello, 17 gennaio 2019 Testi 1
 Scritto del primo appello, 17 gennaio 219 Testi 1 1. Sia X il sottospazio delle funzioni u in L 2 ([, 2] tali che u(x = per q.o. x [, 1]. Determinare X e le proiezioni ortogonali di una generica u L 2
Scritto del primo appello, 17 gennaio 219 Testi 1 1. Sia X il sottospazio delle funzioni u in L 2 ([, 2] tali che u(x = per q.o. x [, 1]. Determinare X e le proiezioni ortogonali di una generica u L 2
Esercizi del Corso di Istituzioni di Analisi Superiore, I modulo
 sercizi del Corso di Istituzioni di Analisi Superiore, I modulo 1. sercizi su massimo e minimo limite 1. lim inf a n lim sup a n 2. Se a n b n per ogni n N, allora lim inf a n lim inf b n. Vale anche lim
sercizi del Corso di Istituzioni di Analisi Superiore, I modulo 1. sercizi su massimo e minimo limite 1. lim inf a n lim sup a n 2. Se a n b n per ogni n N, allora lim inf a n lim inf b n. Vale anche lim
Anno accademico
 Scuola Normale Superiore Ammissione al 4 anno della Classe di Scienze Prova di Analisi per l ammissione alla Laurea Specialistica in Fisica applicata, Informatica, Matematica, Scienze fisiche, Tecnologie
Scuola Normale Superiore Ammissione al 4 anno della Classe di Scienze Prova di Analisi per l ammissione alla Laurea Specialistica in Fisica applicata, Informatica, Matematica, Scienze fisiche, Tecnologie
Esercizi per il corso di Analisi 6.
 Esercizi per il corso di Analisi 6. 1. Si verifichi che uno spazio normato (X, ) è uno spazio vettoriale topologico con la topologia indotta dalla norma. Si verifichi poi che la norma è una funzione continua
Esercizi per il corso di Analisi 6. 1. Si verifichi che uno spazio normato (X, ) è uno spazio vettoriale topologico con la topologia indotta dalla norma. Si verifichi poi che la norma è una funzione continua
ANALISI MATEMATICA 4. Prova scritta del 24 gennaio 2013
 Prova scritta del 24 gennaio 2013 Esercizio 1. Sia Ω R 3 un insieme misurabile secondo Lebesgue e di misura finita. Sia {f n } n N una successione di funzioni f n : Ω R misurabili e tali che 1) f n (x)
Prova scritta del 24 gennaio 2013 Esercizio 1. Sia Ω R 3 un insieme misurabile secondo Lebesgue e di misura finita. Sia {f n } n N una successione di funzioni f n : Ω R misurabili e tali che 1) f n (x)
ANALISI MATEMATICA 4. Prova scritta del 24 gennaio 2013
 Prova scritta del 24 gennaio 2013 Esercizio 1. Sia Ω R 3 un insieme misurabile secondo Lebesgue e di misura finita. Sia {f n } n N una successione di funzioni f n : Ω R misurabili e tali che 1) f n (x)
Prova scritta del 24 gennaio 2013 Esercizio 1. Sia Ω R 3 un insieme misurabile secondo Lebesgue e di misura finita. Sia {f n } n N una successione di funzioni f n : Ω R misurabili e tali che 1) f n (x)
Registro delle lezioni
 Complementi di Analisi Matematica - a.a. 2006-07 Corso di Laurea Specialistica in Ingegneria Civile (CIS) Registro delle lezioni Laura Poggiolini e Gianna Stefani 2 ottobre 2006, 2 ore, LP Il campo dei
Complementi di Analisi Matematica - a.a. 2006-07 Corso di Laurea Specialistica in Ingegneria Civile (CIS) Registro delle lezioni Laura Poggiolini e Gianna Stefani 2 ottobre 2006, 2 ore, LP Il campo dei
ANALISI C & Complementi di Analisi Matematica di Base. Prova scritta del 23 gennaio 2007
 Prova scritta del 23 gennaio 2007 Esercizio 1. Sia f : R R una funzione misurabile e non negativa; si consideri la successione di funzioni f n (x) = max3f(x) 2n, 0}, x R, n N. Provare che se f è integrabile
Prova scritta del 23 gennaio 2007 Esercizio 1. Sia f : R R una funzione misurabile e non negativa; si consideri la successione di funzioni f n (x) = max3f(x) 2n, 0}, x R, n N. Provare che se f è integrabile
COMPLEMENTI DI ANALISI MATEMATICA DI BASE. Prova scritta del 26 gennaio 2005
 Prova scritta del 26 gennaio 2005 Esercizio 1. Posto B = x R 2 : x 2 2}, sia f n } una successione di funzioni (misurabili e) integrabili in B tali che f n f q.o. in B e, per ogni n N, f n (x) 2 x 3 per
Prova scritta del 26 gennaio 2005 Esercizio 1. Posto B = x R 2 : x 2 2}, sia f n } una successione di funzioni (misurabili e) integrabili in B tali che f n f q.o. in B e, per ogni n N, f n (x) 2 x 3 per
Matematica II prof. C.Mascia
 Corso di laurea in CHIMICA INDUSTRIALE Sapienza, Università di Roma Matematica II prof CMascia alcuni esercizi, parte, 7 marzo 25 Indice Testi degli esercizi 2 Svolgimento degli esercizi 4 Testi degli
Corso di laurea in CHIMICA INDUSTRIALE Sapienza, Università di Roma Matematica II prof CMascia alcuni esercizi, parte, 7 marzo 25 Indice Testi degli esercizi 2 Svolgimento degli esercizi 4 Testi degli
Analisi Matematica 2. Michele Campiti. Prove scritte di. Ingegneria Industriale a.a
 Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
Analisi Matematica I per Ingegneria Gestionale, a.a Scritto del sesto appello, 16 luglio 2018 Testi 1
 Scritto del sesto appello, 6 luglio 208 Testi Prima parte, gruppo.. Trovare α [0, 2π) per cui vale l identità trigonometrica sin(x π/3) = cos(x + α). 2. Trovare il polinomio di Taylor (in 0) di ordine
Scritto del sesto appello, 6 luglio 208 Testi Prima parte, gruppo.. Trovare α [0, 2π) per cui vale l identità trigonometrica sin(x π/3) = cos(x + α). 2. Trovare il polinomio di Taylor (in 0) di ordine
Analisi a più variabili: Integrale di Lebesgue
 Analisi a più variabili: Integrale di Lebesgue 1 Ripasso delle definizioni di Algebre, σ-algebre, misure additive, misure σ-additive, Proprietà della misura astratta, misura esterna. Definizione (Insieme
Analisi a più variabili: Integrale di Lebesgue 1 Ripasso delle definizioni di Algebre, σ-algebre, misure additive, misure σ-additive, Proprietà della misura astratta, misura esterna. Definizione (Insieme
Analisi 2. Roberto Monti. Appunti del Corso - Versione 5 Ottobre 2012
 Analisi 2 Roberto Monti Appunti del Corso - Versione 5 Ottobre 212 Indice Capitolo 1. Programma 5 Capitolo 2. Convergenza uniforme 7 1. Convergenza uniforme e continuità 7 2. Criterio di Abel Dirichlet
Analisi 2 Roberto Monti Appunti del Corso - Versione 5 Ottobre 212 Indice Capitolo 1. Programma 5 Capitolo 2. Convergenza uniforme 7 1. Convergenza uniforme e continuità 7 2. Criterio di Abel Dirichlet
Si dimostri che la (*) possiede un unica soluzione (u n ) limitata.
 Scuola Normale Superiore, ammissione al IV anno del corso ordinario Prova scritta di Analisi Matematica per Fisica, Informatica, Matematica 26 Agosto 2 Esercizio. Siano (a n ) e (b n ) successioni di numeri
Scuola Normale Superiore, ammissione al IV anno del corso ordinario Prova scritta di Analisi Matematica per Fisica, Informatica, Matematica 26 Agosto 2 Esercizio. Siano (a n ) e (b n ) successioni di numeri
ANALISI VETTORIALE COMPITO IN CLASSE DEL 8/11/2013
 ANALISI VETTORIALE COMPITO IN CLASSE DEL 8//3 Premessa (Cfr. gli Appunti di Analisi Vettoriale / del Prof. Troianiello) Nello studio degli integrali impropri il primo approccio all utilizzo del criterio
ANALISI VETTORIALE COMPITO IN CLASSE DEL 8//3 Premessa (Cfr. gli Appunti di Analisi Vettoriale / del Prof. Troianiello) Nello studio degli integrali impropri il primo approccio all utilizzo del criterio
Analisi Matematica I per Ingegneria Gestionale, a.a Scritto del secondo appello, 5 febbraio 2018 Testi 1
 Analisi Matematica I per Ingegneria Gestionale, a.a. 7-8 Scritto del secondo appello, 5 febbraio 8 Testi Prima parte, gruppo.. Trovare r > e α [ π, π] per cui vale l identità 3 sin 3 cos = r sin( + α)..
Analisi Matematica I per Ingegneria Gestionale, a.a. 7-8 Scritto del secondo appello, 5 febbraio 8 Testi Prima parte, gruppo.. Trovare r > e α [ π, π] per cui vale l identità 3 sin 3 cos = r sin( + α)..
2. Si esponga il problema della migliore approssimazione in norma, e si dica in quali spazi esso ha certamente soluzione, e quale è questa soluzione.
 COMPLEMENTI DI MATEMATICA Corso di Laurea Magistrale in Ingegneria Elettrotecnica CM98sett.tex 6..2009 - lunedì (2 ore) Esercitazione del 6..2009 Risolvere tre esercizi per pagina, a scelta.. Si definisca
COMPLEMENTI DI MATEMATICA Corso di Laurea Magistrale in Ingegneria Elettrotecnica CM98sett.tex 6..2009 - lunedì (2 ore) Esercitazione del 6..2009 Risolvere tre esercizi per pagina, a scelta.. Si definisca
f n (x) 3 1. x Essendo g(x) = 3 1
 Secondo esonero di Analisi eale 6//9 a.a. 8-9 ) Studiare la convergenza in L p ((, )), p +, della successione di funzioni cos(nx) e nx f n (x) = 3. x Si vede facilmente che la successione f n converge
Secondo esonero di Analisi eale 6//9 a.a. 8-9 ) Studiare la convergenza in L p ((, )), p +, della successione di funzioni cos(nx) e nx f n (x) = 3. x Si vede facilmente che la successione f n converge
Esonero di Analisi Matematica II (A)
 Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
Il teorema di Ascoli-Arzelà
 Il teorema di Ascoli-Arzelà Alcuni risultati sugli spazi metrici Spazi metrici (e topologici) compatti Richiamiamo le definizioni di compattezza negli spazi metrici. Sia (X, d) una spazio metrico e sia
Il teorema di Ascoli-Arzelà Alcuni risultati sugli spazi metrici Spazi metrici (e topologici) compatti Richiamiamo le definizioni di compattezza negli spazi metrici. Sia (X, d) una spazio metrico e sia
Esame di Analisi Funzionale e Trasformate Prima prova in itinere. Maggio 2017 A.A. 2016/2017. Prof. M. Bramanti Tema A
 Esame di Analisi Funzionale e Trasformate Prima prova in itinere. Maggio 7 A.A. 6/7. Prof. M. Bramanti Tema A Cognome: Nome N matr. o cod. persona: Dom Dom Dom 3 Es Es Es 3 Tot. Punti Domande di teoria
Esame di Analisi Funzionale e Trasformate Prima prova in itinere. Maggio 7 A.A. 6/7. Prof. M. Bramanti Tema A Cognome: Nome N matr. o cod. persona: Dom Dom Dom 3 Es Es Es 3 Tot. Punti Domande di teoria
Definizione 1.1. Dato un insieme non vuoto X, si dice distanza una funzione d : X X R tale che
 1 Spazi metrici Definizione 1.1. Dato un insieme non vuoto X, si dice distanza una funzione d : X X R tale che 1) d(x, y) 0, x, y X; d(x, y) = 0 x = y, ) d(x, y) = d(y, x), x, y X, 3) d(x, z) d(x, y) +
1 Spazi metrici Definizione 1.1. Dato un insieme non vuoto X, si dice distanza una funzione d : X X R tale che 1) d(x, y) 0, x, y X; d(x, y) = 0 x = y, ) d(x, y) = d(y, x), x, y X, 3) d(x, z) d(x, y) +
Modelli e Metodi Matematici della Fisica. Scritto 1
 Modelli e Metodi Matematici della Fisica. Scritto 1 Cesi/Presilla A.A. 2 7 Canale 1 Cesi Presilla Nome Cognome Il voto dello scritto rimpiazza gli esoneri 1 2 3 penalità problema voto 1 2 3 4 5 7 8 penalità
Modelli e Metodi Matematici della Fisica. Scritto 1 Cesi/Presilla A.A. 2 7 Canale 1 Cesi Presilla Nome Cognome Il voto dello scritto rimpiazza gli esoneri 1 2 3 penalità problema voto 1 2 3 4 5 7 8 penalità
( 1 π. (a n cos nt + b n sin nt) t R (3)
 7. SERIE TRIGONOMETRICHE E SERIE DI FOURIER Definizione 1. L p (R), p [1, + ), denota la classe di tutte le funzioni f : R C, misurabili secondo Lebesgue, periodiche con periodo per le quali il funzionale
7. SERIE TRIGONOMETRICHE E SERIE DI FOURIER Definizione 1. L p (R), p [1, + ), denota la classe di tutte le funzioni f : R C, misurabili secondo Lebesgue, periodiche con periodo per le quali il funzionale
ANALISI MATEMATICA 4. Prova scritta del 24 gennaio 2013
 Prova scritta del 24 gennaio 2013 Esercizio 1. Sia Ω R 3 un insieme misurabile secondo Lebesgue e di misura finita. Sia {f n } n N una successione di funzioni f n : Ω R misurabili e tali che 1) f n (x)
Prova scritta del 24 gennaio 2013 Esercizio 1. Sia Ω R 3 un insieme misurabile secondo Lebesgue e di misura finita. Sia {f n } n N una successione di funzioni f n : Ω R misurabili e tali che 1) f n (x)
Analisi Matematica I per Ingegneria Gestionale, a.a Scritto del secondo appello, 1 febbraio 2017 Testi 1
 Analisi Matematica I per Ingegneria Gestionale, a.a. 206-7 Scritto del secondo appello, febbraio 207 Testi Prima parte, gruppo.. Trovare le [0, π] che risolvono la disequazione sin(2) 2. 2. Dire se esistono
Analisi Matematica I per Ingegneria Gestionale, a.a. 206-7 Scritto del secondo appello, febbraio 207 Testi Prima parte, gruppo.. Trovare le [0, π] che risolvono la disequazione sin(2) 2. 2. Dire se esistono
AM2: Tracce delle lezioni- IX Settimana INSIEMI DI LIVELLO, MINIMI VINCOLATI PRINCIPIO DEI MOLTIPLICATORI DI LAGRANGE
 AM2: Tracce delle lezioni- IX Settimana INSIEMI DI LIVELLO, MINIMI VINCOLATI PRINCIPIO DEI MOLTIPLICATORI DI LAGRANGE Sia g C 1 R 2 ), c R. L insieme γ = γ c := {x, y) R 2 : gx, y) = c} si chiama insieme
AM2: Tracce delle lezioni- IX Settimana INSIEMI DI LIVELLO, MINIMI VINCOLATI PRINCIPIO DEI MOLTIPLICATORI DI LAGRANGE Sia g C 1 R 2 ), c R. L insieme γ = γ c := {x, y) R 2 : gx, y) = c} si chiama insieme
I teoremi della funzione inversa e della funzione implicita
 I teoremi della funzione inversa e della funzione implicita Appunti per il corso di Analisi Matematica 4 G. Mauceri Indice 1 Il teorema della funzione inversa 1 Il teorema della funzione implicita 3 1
I teoremi della funzione inversa e della funzione implicita Appunti per il corso di Analisi Matematica 4 G. Mauceri Indice 1 Il teorema della funzione inversa 1 Il teorema della funzione implicita 3 1
Modelli e Metodi Matematici della Fisica. S1/AC
 Modelli e Metodi Matematici della Fisica. S1/AC Cesi A.A. 9 1 Nome Cognome 6 CFU (AA 9-1) 8 CFU 4 CFU (solo analisi complessa) 4 + 6 CFU altro: problema voto 1 4 6 7 8 9 Test totale coeff. voto in trentesimi
Modelli e Metodi Matematici della Fisica. S1/AC Cesi A.A. 9 1 Nome Cognome 6 CFU (AA 9-1) 8 CFU 4 CFU (solo analisi complessa) 4 + 6 CFU altro: problema voto 1 4 6 7 8 9 Test totale coeff. voto in trentesimi
ANALISI MATEMATICA 4. Prova scritta del 24 gennaio 2013
 Prova scritta del 24 gennaio 2013 Esercizio 1. Sia Ω R 3 un insieme misurabile secondo Lebesgue e di misura finita. Sia {f n } n N una successione di funzioni f n : Ω R misurabili e tali che 1) f n (x)
Prova scritta del 24 gennaio 2013 Esercizio 1. Sia Ω R 3 un insieme misurabile secondo Lebesgue e di misura finita. Sia {f n } n N una successione di funzioni f n : Ω R misurabili e tali che 1) f n (x)
Corso di Metodi Matematici per l Ingegneria A.A. 2015/2016 Esercizi su teoria della misura e dell integrazione di Lebesgue
 Corso di Metodi Matematici per l Ingegneria A.A. 5/6 Esercizi su teoria della misura e dell integrazione di Lebesgue Marco Bramanti Politecnico di Milano December 3, 5 A. Esercizi su spazi di misura Esercizio
Corso di Metodi Matematici per l Ingegneria A.A. 5/6 Esercizi su teoria della misura e dell integrazione di Lebesgue Marco Bramanti Politecnico di Milano December 3, 5 A. Esercizi su spazi di misura Esercizio
Serie trigonometriche e di Fourier Ci occuperemo di serie le cui ridotte N-esime sono polinomi trigonometrici di grado (o ordine) N:
 Serie trigonometriche e di Fourier Ci occuperemo di serie le cui ridotte N-esime sono polinomi trigonometrici di grado (o ordine) N: S N (x) = N n=0 (a n cos (nx) + b n sin (nx)), a n, b n R (periodiche
Serie trigonometriche e di Fourier Ci occuperemo di serie le cui ridotte N-esime sono polinomi trigonometrici di grado (o ordine) N: S N (x) = N n=0 (a n cos (nx) + b n sin (nx)), a n, b n R (periodiche
Il problema della migliore approssimazione. Teorema 3.2 Il problema 3.1 ammette sempre almeno una soluzione.
 3. Spazi di Hilbert Wir müssen wissen. Wir werden wissen. Noi abbiamo il dovere di conoscere. Alla fine conosceremo.) David Hilbert 1862-1943) Il problema della migliore approssimazione Problema 3.1 Migliore
3. Spazi di Hilbert Wir müssen wissen. Wir werden wissen. Noi abbiamo il dovere di conoscere. Alla fine conosceremo.) David Hilbert 1862-1943) Il problema della migliore approssimazione Problema 3.1 Migliore
Serie e Trasformata di Fourier
 Serie e Trasformata di Fourier Corso di Analisi Funzionale Prof. Paolo Nistri Cancelli, D Angelo, Giannetti Polinomio di Fourier Si consideri la successione costituita dalle restrizioni delle funzioni
Serie e Trasformata di Fourier Corso di Analisi Funzionale Prof. Paolo Nistri Cancelli, D Angelo, Giannetti Polinomio di Fourier Si consideri la successione costituita dalle restrizioni delle funzioni
ANALISI MATEMATICA 3. esercizi assegnati per la prova scritta del 31 gennaio 2011
 esercizi assegnati per la prova scritta del 31 gennaio 2011 Esercizio 1. Per x > 0 e n N si ponga f n (x) = ln ( n 5 x ) a) Provare l integrabilità delle funzioni f n in (0, + ). 3 + n 4 x 2. b) Studiare
esercizi assegnati per la prova scritta del 31 gennaio 2011 Esercizio 1. Per x > 0 e n N si ponga f n (x) = ln ( n 5 x ) a) Provare l integrabilità delle funzioni f n in (0, + ). 3 + n 4 x 2. b) Studiare
METODI MATEMATICI PER L INGEGNERIA - A.A Primo appello del 9/6/2010. e 2ix dx = e ix 2 dx = t e it dt = [ it e it e it ] π/2
![METODI MATEMATICI PER L INGEGNERIA - A.A Primo appello del 9/6/2010. e 2ix dx = e ix 2 dx = t e it dt = [ it e it e it ] π/2 METODI MATEMATICI PER L INGEGNERIA - A.A Primo appello del 9/6/2010. e 2ix dx = e ix 2 dx = t e it dt = [ it e it e it ] π/2](/thumbs/96/130608003.jpg) METODI MATEMATICI PER L INGEGNERIA - A.A. 29- Primo appello del 9/6/2 Risolvere i seguenti esercizi, spiegando il procedimento usato. Calcolare la proiezione in L 2 π 2, π 2 di xt = t sul sottospazio generato
METODI MATEMATICI PER L INGEGNERIA - A.A. 29- Primo appello del 9/6/2 Risolvere i seguenti esercizi, spiegando il procedimento usato. Calcolare la proiezione in L 2 π 2, π 2 di xt = t sul sottospazio generato
Problemi di topologia metrica.
 Problemi di topologia metrica. 1.) Sia X un insieme, munito di una distanza d : X X R +. Siano x 1 ;x ;x 3 ;x 4 quattro punti qualsiasi di X. Verificare che: d (x 1 ; x 4 ) d (x 1 ; x ) + d (x ; x 3 )
Problemi di topologia metrica. 1.) Sia X un insieme, munito di una distanza d : X X R +. Siano x 1 ;x ;x 3 ;x 4 quattro punti qualsiasi di X. Verificare che: d (x 1 ; x 4 ) d (x 1 ; x ) + d (x ; x 3 )
Corso di Metodi Matematici per l Ingegneria A.A. 2017/2018 Domande-tipo di teoria sulla seconda metà del corso
 Corso di Metodi Matematici per l Ingegneria A.A. 2017/2018 Domande-tipo di teoria sulla seconda metà del corso Marco Bramanti Politecnico di Milano December 20, 2017 Parte 3. Teoria della misura e dell
Corso di Metodi Matematici per l Ingegneria A.A. 2017/2018 Domande-tipo di teoria sulla seconda metà del corso Marco Bramanti Politecnico di Milano December 20, 2017 Parte 3. Teoria della misura e dell
Analisi di Fourier e alcune equazioni della fisica matematica 1. TERZA LEZIONE Serie di funzioni Serie di potenze
 Analisi di Fourier e alcune equazioni della fisica matematica 1 TERZA LEZIONE Serie di funzioni Serie di potenze 1 prof. Claudio Saccon, Dipartimento di Matematica Applicata, Via F. Buonarroti 1/C email:
Analisi di Fourier e alcune equazioni della fisica matematica 1 TERZA LEZIONE Serie di funzioni Serie di potenze 1 prof. Claudio Saccon, Dipartimento di Matematica Applicata, Via F. Buonarroti 1/C email:
Le derivate parziali
 Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
Esame di Analisi Funzionale e Trasformate Prima prova in itinere. Aprile 2018 A.A. 2017/2018. Prof. M. Bramanti Tema A
 Esame di Analisi Funzionale e Trasformate Prima prova in itinere. Aprile 018 A.A. 017/018. Prof. M. Bramanti Tema A Cognome: Nome N matr. o cod. persona: Dom 1 Dom Dom 3 Es 1 Es Es 3 Tot. Punti Domande
Esame di Analisi Funzionale e Trasformate Prima prova in itinere. Aprile 018 A.A. 017/018. Prof. M. Bramanti Tema A Cognome: Nome N matr. o cod. persona: Dom 1 Dom Dom 3 Es 1 Es Es 3 Tot. Punti Domande
Analisi Matematica I per Ingegneria Gestionale, a.a Secondo compitino e primo appello, 12 gennaio 2017 Testi 1
 Secondo compitino e primo appello, gennaio 7 Testi Prima parte, gruppo.. Determinare l insieme di definizione della funzione arcsin(e ).. Determinare lo sviluppo di Taylor di ordine 4 (in ) della funzione
Secondo compitino e primo appello, gennaio 7 Testi Prima parte, gruppo.. Determinare l insieme di definizione della funzione arcsin(e ).. Determinare lo sviluppo di Taylor di ordine 4 (in ) della funzione
Appendice B ANALISI FUNZIONALE. 1 Spazi di Banach
 Appendice B ANALISI FUNZIONALE In questo capitolo si introducono gli spazi di Banach e di Hilbert, gli operatori lineari e loro spettro. Inoltre si discutono gli operatori compatti su uno spazio di Hilbert.
Appendice B ANALISI FUNZIONALE In questo capitolo si introducono gli spazi di Banach e di Hilbert, gli operatori lineari e loro spettro. Inoltre si discutono gli operatori compatti su uno spazio di Hilbert.
Analisi Matematica I per Ingegneria Gestionale, a.a Scritto del terzo appello, 19 febbraio 2018 Testi 1
 Scritto del terzo appello, 9 febbraio 208 Testi Prima parte, gruppo.. Per ciascuno dei seguenti punti dare le coordinate (polari o cartesiane) che mancano: a) = 0, = ; r = α = b) = 3, = 3; r = α = c) r
Scritto del terzo appello, 9 febbraio 208 Testi Prima parte, gruppo.. Per ciascuno dei seguenti punti dare le coordinate (polari o cartesiane) che mancano: a) = 0, = ; r = α = b) = 3, = 3; r = α = c) r
3. Successioni di insiemi.
 3. Successioni di insiemi. Per evitare incongruenze supponiamo, in questo capitolo, che tutti gli insiemi considerati siano sottoinsiemi di un dato insieme S (l insieme ambiente ). Quando occorrerà considerare
3. Successioni di insiemi. Per evitare incongruenze supponiamo, in questo capitolo, che tutti gli insiemi considerati siano sottoinsiemi di un dato insieme S (l insieme ambiente ). Quando occorrerà considerare
Argomento della Lezione N. 1 Argomento della Lezione N. 2 Argomento della Lezione N. 11 Argomento della Lezione N. 12 Introduzione al corso.
 Argomento della Lezione N. 1 Argomento della Lezione N. 2 Argomento della Lezione N. 11 Argomento della Lezione N. 12 Introduzione al corso. Il campo C dei numeri complessi. Fondamenti assiomatici del
Argomento della Lezione N. 1 Argomento della Lezione N. 2 Argomento della Lezione N. 11 Argomento della Lezione N. 12 Introduzione al corso. Il campo C dei numeri complessi. Fondamenti assiomatici del
Esercizi sulla trasformata di Fourier di distribuzioni raccolti dai temi d esame
 Esercizi sulla trasformata di Fourier di distribuzioni raccolti dai temi d esame Esercizio Sia T > 0 e f : R R la funzione reale T -periodica la cui restrizione all intervallo [0, T ] vale f(t) := t(t
Esercizi sulla trasformata di Fourier di distribuzioni raccolti dai temi d esame Esercizio Sia T > 0 e f : R R la funzione reale T -periodica la cui restrizione all intervallo [0, T ] vale f(t) := t(t
Esercizi 8 12 gennaio 2009
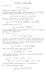 Sia α > e Esercizi 8 2 gennaio 29 f(x, y = ( + x 2 + y 2 α. Dimostrare che f appartiene a L p ( 2, con α p >. Osserviamo innanzitutto che, essendo f continua, l integrale di f p su 2 è uguale all integrale
Sia α > e Esercizi 8 2 gennaio 29 f(x, y = ( + x 2 + y 2 α. Dimostrare che f appartiene a L p ( 2, con α p >. Osserviamo innanzitutto che, essendo f continua, l integrale di f p su 2 è uguale all integrale
Analisi Matematica A e B Soluzioni prova scritta parziale n. 4
 Analisi Matematica A e B Soluzioni prova scritta parziale n. Corso di laurea in Fisica, 08-09 7 aprile 09. Determinare le soluzioni u(x) dell equazione differenziale u + u u = sin x + ex + e x. Soluzione.
Analisi Matematica A e B Soluzioni prova scritta parziale n. Corso di laurea in Fisica, 08-09 7 aprile 09. Determinare le soluzioni u(x) dell equazione differenziale u + u u = sin x + ex + e x. Soluzione.
Soluzione dei problemi assegnati
 ANALISI MATEMATICA 3 Soluzione dei problemi assegnati anno accademico 2018/19 prof. Antonio Greco http://people.unica.it/antoniogreco Dipartimento di Matematica e Informatica Università di Cagliari 23-5-2019
ANALISI MATEMATICA 3 Soluzione dei problemi assegnati anno accademico 2018/19 prof. Antonio Greco http://people.unica.it/antoniogreco Dipartimento di Matematica e Informatica Università di Cagliari 23-5-2019
COMPLEMENTI DI ANALISI MATEMATICA II. Prova scritta del 20 gennaio 2014
 Prova scritta del 2 gennaio 214 Studiare la convergenza puntuale e uniforme della serie di potenze n=1 n x 2n 2n + e n. Valutare poi la misurabilità e l integrabilità secondo Lebesgue della funzione somma
Prova scritta del 2 gennaio 214 Studiare la convergenza puntuale e uniforme della serie di potenze n=1 n x 2n 2n + e n. Valutare poi la misurabilità e l integrabilità secondo Lebesgue della funzione somma
Esercitazione di Analisi Matematica I Esercizi e soluzioni 19/04/2013 TOPOLOGIA
 Esercitazione di Analisi Matematica I Esercizi e soluzioni 9/04/203 TOPOLOGIA Mostrare che uno spazio infinito con la metrica discreta non può essere compatto Soluzione: Per la metrica discreta d : X X
Esercitazione di Analisi Matematica I Esercizi e soluzioni 9/04/203 TOPOLOGIA Mostrare che uno spazio infinito con la metrica discreta non può essere compatto Soluzione: Per la metrica discreta d : X X
ANALISI UNO (A.A. 2008/2009, Docente: S. Finzi Vita) Programma svolto settimanalmente
 ANALISI UNO (A.A. 2008/2009, Docente: S. Finzi Vita) Programma svolto settimanalmente 2-6 Marzo (8 ore) Gli assiomi dei numeri reali. Osservazioni sull assioma di continuità: altre formulazioni e loro
ANALISI UNO (A.A. 2008/2009, Docente: S. Finzi Vita) Programma svolto settimanalmente 2-6 Marzo (8 ore) Gli assiomi dei numeri reali. Osservazioni sull assioma di continuità: altre formulazioni e loro
Corso di Elementi di Analisi Funzionale e Trasformate A.A. 2016/2017 Domande-tipo di teoria sulla prima metà del corso
 Corso di Elementi di Analisi Funzionale e Trasformate A.A. 2016/2017 Domande-tipo di teoria sulla prima metà del corso Marco Bramanti Politecnico di Milano April 20, 2017 Cap. 1. Elementi di analisi funzionale
Corso di Elementi di Analisi Funzionale e Trasformate A.A. 2016/2017 Domande-tipo di teoria sulla prima metà del corso Marco Bramanti Politecnico di Milano April 20, 2017 Cap. 1. Elementi di analisi funzionale
Analisi IV - esercizi. G.P.Leonardi 2008
 Analisi IV - esercizi G.P.Leonardi 2008 1 1 Esercizi settimana n.1 1.1 Siano (X, d) e (X, d ) due spazi metrici. Dimostrare che la funzione d : (X X ) (X X ) [0, ) definita da d((x, x ), (y, y )) = d(x,
Analisi IV - esercizi G.P.Leonardi 2008 1 1 Esercizi settimana n.1 1.1 Siano (X, d) e (X, d ) due spazi metrici. Dimostrare che la funzione d : (X X ) (X X ) [0, ) definita da d((x, x ), (y, y )) = d(x,
Convergenza per funzioni tra spazi metrici. Funzioni uniformemente continue e Lipschitz continue. Esempi. somma e prodotto, il campo C dei numeri
 Argomento della Lezione N. 1 Argomento della Lezione N. 2 Argomento della Lezione N. 11 Argomento della Lezione N. 12 Fondamenti assiomatici del sistema di numeri L unita immaginaria. Convergenza per funzioni
Argomento della Lezione N. 1 Argomento della Lezione N. 2 Argomento della Lezione N. 11 Argomento della Lezione N. 12 Fondamenti assiomatici del sistema di numeri L unita immaginaria. Convergenza per funzioni
Matematica A Corso di Laurea in Chimica. Prova scritta del Tema A
 Matematica A Corso di Laurea in Chimica Prova scritta del 7..6 Tema A P) Data la funzione f(x) = ex+ x determinarne (a) campo di esistenza; (b) zeri e segno; (c) iti agli estremi del campo di esistenza
Matematica A Corso di Laurea in Chimica Prova scritta del 7..6 Tema A P) Data la funzione f(x) = ex+ x determinarne (a) campo di esistenza; (b) zeri e segno; (c) iti agli estremi del campo di esistenza
19. L integrale di Lebesgue: un breve riassunto, I
 156 19. L integrale di Lebesgue: un breve riassunto, I Il problema di caratterizzare la classe delle funzioni integrabili secondo Riemann e di capire per quali funzioni vale il teorema fondamentale del
156 19. L integrale di Lebesgue: un breve riassunto, I Il problema di caratterizzare la classe delle funzioni integrabili secondo Riemann e di capire per quali funzioni vale il teorema fondamentale del
Corso di Metodi Matematici per l Ingegneria A.A. 2016/2017 Domande-tipo di teoria sulla seconda metà del corso
 Corso di Metodi Matematici per l Ingegneria A.A. 2016/2017 Domande-tipo di teoria sulla seconda metà del corso Marco Bramanti Politecnico di Milano January 23, 2017 Parte 3. Teoria della misura e dell
Corso di Metodi Matematici per l Ingegneria A.A. 2016/2017 Domande-tipo di teoria sulla seconda metà del corso Marco Bramanti Politecnico di Milano January 23, 2017 Parte 3. Teoria della misura e dell
Generalizzazioni del Teorema di Weierstrass
 Capitolo 2 Generalizzazioni del Teorema di Weierstrass Il principale riferimento bibliografico per questa lezione è il testo di Checcucci, Tognoli, Vesentini [1]. Introduzione Supponiamo che X = R n. È
Capitolo 2 Generalizzazioni del Teorema di Weierstrass Il principale riferimento bibliografico per questa lezione è il testo di Checcucci, Tognoli, Vesentini [1]. Introduzione Supponiamo che X = R n. È
Studio qualitativo. Emanuele Paolini 2 luglio 2002
 Studio qualitativo Emanuele Paolini 2 luglio 2002 Non sempre è possibile determinare esplicitamente le soluzione di una equazione differenziale. Ci proponiamo quindi di trovare dei metodi per determinare
Studio qualitativo Emanuele Paolini 2 luglio 2002 Non sempre è possibile determinare esplicitamente le soluzione di una equazione differenziale. Ci proponiamo quindi di trovare dei metodi per determinare
LA TRASFORMATA DI FOURIER
 LA TASFOMATA DI FOUIE 1. Definizione della trasformata di Fourier Definizione 1.1. Sia u in L 1 ( e sia ξ in. La trasformata di Fourier di u è la funzione (1.1 F(u(ξ = e iξ x u(x dx. Ovviamente, non è
LA TASFOMATA DI FOUIE 1. Definizione della trasformata di Fourier Definizione 1.1. Sia u in L 1 ( e sia ξ in. La trasformata di Fourier di u è la funzione (1.1 F(u(ξ = e iξ x u(x dx. Ovviamente, non è
x(y + z)dx dy dz y(x 2 + y 2 + z 2 )dx dy dz y 2 zdx dy dz Esempio di insieme non misurabile secondo Lebesgue.
 /3/23 Calcolare dove x(y + z)dx dy dz = {(x, y, z) R 3 : x, y, z, x + y + z }. Calcolare y(x 2 + y 2 + z 2 )dx dy dz dove = {(x, y, z) R 3 : x 2 + y 2 + z 2 z, x 2 + y 2 + z 2 3zx y }. Calcolare dove y
/3/23 Calcolare dove x(y + z)dx dy dz = {(x, y, z) R 3 : x, y, z, x + y + z }. Calcolare y(x 2 + y 2 + z 2 )dx dy dz dove = {(x, y, z) R 3 : x 2 + y 2 + z 2 z, x 2 + y 2 + z 2 3zx y }. Calcolare dove y
non solo otteniamo il valore cercato per la validità della (1.4), ma anche che tale valore non dipende da
 NOTE INTEGRATIVE PER IL CORSO DI ANALISI MATEMATICA 2 ANNO ACCADEMICO 2012/13 NOTE SULLA CONTINUITÀ UNIFORME D.BARTOLUCCI, D.GUIDO Sia f(x) = x 3, x [ 1, 1]. Si ha 1. La continuità uniforme x 3 y 3 = x
NOTE INTEGRATIVE PER IL CORSO DI ANALISI MATEMATICA 2 ANNO ACCADEMICO 2012/13 NOTE SULLA CONTINUITÀ UNIFORME D.BARTOLUCCI, D.GUIDO Sia f(x) = x 3, x [ 1, 1]. Si ha 1. La continuità uniforme x 3 y 3 = x
0.1 Spazi Euclidei in generale
 0.1. SPAZI EUCLIDEI IN GENERALE 1 0.1 Spazi Euclidei in generale Sia V uno spazio vettoriale definito su R. Diremo, estendendo una definizione data in precedenza, che V è uno spazio vettoriale euclideo
0.1. SPAZI EUCLIDEI IN GENERALE 1 0.1 Spazi Euclidei in generale Sia V uno spazio vettoriale definito su R. Diremo, estendendo una definizione data in precedenza, che V è uno spazio vettoriale euclideo
SISSA Area Matematica Esame di ammissione per il corso di Analisi Matematica, Modelli e Applicazioni 27 marzo 2019
 SISSA Area Matematica Esame di ammissione per il corso di Analisi Matematica, Modelli e Applicazioni 27 marzo 2019 Il candidato risolva CINQUE dei seguenti problemi, e indichi chiaramente sulla prima pagina
SISSA Area Matematica Esame di ammissione per il corso di Analisi Matematica, Modelli e Applicazioni 27 marzo 2019 Il candidato risolva CINQUE dei seguenti problemi, e indichi chiaramente sulla prima pagina
D Analisi Matematica 1 (Corso di Laurea in Informatica e Bioinformatica)
 COGNOME NOME Matr. D Firma dello studente Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
COGNOME NOME Matr. D Firma dello studente Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
Corso di Metodi Matematici per l Ingegneria A.A. 2016/2017 Esercizi svolti su misura e integrale di Lebesgue, spazi L p, operatori lineari continui
 Corso di Metodi Matematici per l Ingegneria A.A. 26/27 Esercizi svolti su misura e integrale di Lebesgue, spazi L p, operatori lineari continui Marco Bramanti Politecnico di Milano December 4, 26 Esercizi
Corso di Metodi Matematici per l Ingegneria A.A. 26/27 Esercizi svolti su misura e integrale di Lebesgue, spazi L p, operatori lineari continui Marco Bramanti Politecnico di Milano December 4, 26 Esercizi
(ln 5)i 1 i. (c) (d) Scriviamo il numero complesso assegnato in forma algebrica:
 Primo parziale Test. L argomento principale del numero complesso (ln 5)i i è (a) 4 π (b) (c) (d) Scriviamo il numero complesso assegnato in forma algebrica: Risposta esatta a) ln 5 i i = ln 5 i( + i) i
Primo parziale Test. L argomento principale del numero complesso (ln 5)i i è (a) 4 π (b) (c) (d) Scriviamo il numero complesso assegnato in forma algebrica: Risposta esatta a) ln 5 i i = ln 5 i( + i) i
Analisi Matematica 3/Analisi 4 - SOLUZIONI (20/01/2016)
 Corso di Laurea in Matematica Docente: Claudia Anedda Analisi Matematica 3/Analisi 4 - SOLUZIONI (//6) ) i) Dopo averla classificata, risolvere l equazione differenziale tẋ x = t cos(t), t >. ii) Scrivere
Corso di Laurea in Matematica Docente: Claudia Anedda Analisi Matematica 3/Analisi 4 - SOLUZIONI (//6) ) i) Dopo averla classificata, risolvere l equazione differenziale tẋ x = t cos(t), t >. ii) Scrivere
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016
 Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
Esercizi di Complementi di Matematica (L-Z) a.a. 2015/2016 Prodotti scalari e forme bilineari simmetriche (1) Sia F : R 2 R 2 R un applicazione definita da F (x, y) = x 1 y 1 + 3x 1 y 2 5x 2 y 1 + 2x 2
6.3 Equazioni lineari del secondo ordine
 si supponga di conoscerne una soluzione ψ(x). Si verifichi che con la sostituzione y(x) = ψ(x) + 1, l equazione diventa lineare nell incognita v(x) v(x). Utilizzando questo metodo, si risolva l equazione
si supponga di conoscerne una soluzione ψ(x). Si verifichi che con la sostituzione y(x) = ψ(x) + 1, l equazione diventa lineare nell incognita v(x) v(x). Utilizzando questo metodo, si risolva l equazione
Soluzione della Prova Scritta di Analisi Matematica 4-25/06/13. C.L. in Matematica e Matematica per le Applicazioni. Proff. K. R. Payne e E.
 Soluzione della Prova Scritta di Analisi Matematica 4-5/6/ C.L. in Matematica e Matematica per le Applicazioni Proff. K. R. Payne e E. Terraneo Esercizio. a. Le funzioni f n (x) sono continue e quindi
Soluzione della Prova Scritta di Analisi Matematica 4-5/6/ C.L. in Matematica e Matematica per le Applicazioni Proff. K. R. Payne e E. Terraneo Esercizio. a. Le funzioni f n (x) sono continue e quindi
Analisi II, a.a Soluzioni 1. j j + 1 ; ( 1)j
 Analisi II, a.a. 7-8 Soluzioni Calcolare le seguenti distanze e norme: (i d (x, y dove x = {x j } e y = {y j } sono le successioni di l definite da x j = ( j, y j = j/(j + ; (ii d (f, g dove f, g sono
Analisi II, a.a. 7-8 Soluzioni Calcolare le seguenti distanze e norme: (i d (x, y dove x = {x j } e y = {y j } sono le successioni di l definite da x j = ( j, y j = j/(j + ; (ii d (f, g dove f, g sono
Complementi di Analisi Matematica. Foglio di esercizi n.8 3/5/2019
 Complementi di Analisi Matematica Foglio di esercizi n8 3/5/2019 Esercizi su successioni e serie di funzioni Esercizio 1 Definita g k (x) = e kx2, provare che g k : R R converge puntualmente alla funzione
Complementi di Analisi Matematica Foglio di esercizi n8 3/5/2019 Esercizi su successioni e serie di funzioni Esercizio 1 Definita g k (x) = e kx2, provare che g k : R R converge puntualmente alla funzione
ANALISI MATEMATICA I, Compito scritto del 5/07/2016 Corso di Laurea in Matematica. COGNOME e NOME... MATR T
 ANALISI MATEMATICA I, Compito scritto del 5/7/6 Corso di Laurea in Matematica COGNOME e NOME... MATR... 3 4 T Nelle risposte devono essere riportati anche i conti principali e le motivazioni principali.
ANALISI MATEMATICA I, Compito scritto del 5/7/6 Corso di Laurea in Matematica COGNOME e NOME... MATR... 3 4 T Nelle risposte devono essere riportati anche i conti principali e le motivazioni principali.
SPAZI COMPATTI. Proposizione 2 Sia (X, d) uno spazio metrico. Se esso è sequenzialmente compatto allora è completo.
 SPAZI COMPATTI D ora in poi tutti gli spazi topologici sono di Hausdorff. Definizione 1 Uno spazio topologico (X, τ) si dice sequenzialmente compatto, o compatto per successioni, se ogni successione di
SPAZI COMPATTI D ora in poi tutti gli spazi topologici sono di Hausdorff. Definizione 1 Uno spazio topologico (X, τ) si dice sequenzialmente compatto, o compatto per successioni, se ogni successione di
11. Misure con segno.
 11. Misure con segno. 11.1. Misure con segno. Sia Ω un insieme non vuoto e sia A una σ-algebra in Ω. Definizione 11.1.1. (Misura con segno). Si chiama misura con segno su A ogni funzione ϕ : A R verificante
11. Misure con segno. 11.1. Misure con segno. Sia Ω un insieme non vuoto e sia A una σ-algebra in Ω. Definizione 11.1.1. (Misura con segno). Si chiama misura con segno su A ogni funzione ϕ : A R verificante
Analisi Matematica 3 prof. Antonio Greco
 Analisi Matematica 3 prof. Antonio Greco Alcune domande da rivolgere agli studenti in sede d esame ( ) 18 giugno 2018 Equazioni differenziali 1. Spiegare che cosa si intende per equazione differenziale
Analisi Matematica 3 prof. Antonio Greco Alcune domande da rivolgere agli studenti in sede d esame ( ) 18 giugno 2018 Equazioni differenziali 1. Spiegare che cosa si intende per equazione differenziale
26 - Funzioni di più Variabili Limiti e Derivate
 Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 26 - Funzioni di più Variabili Limiti e Derivate Anno Accademico 2013/2014 M.
Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 26 - Funzioni di più Variabili Limiti e Derivate Anno Accademico 2013/2014 M.
Analisi Matematica 3 (Fisica) Prova scritta del 17 febbraio 2012 Un breve svolgimento delle versioni A
 Analisi Matematica 3 (Fisica) Prova scritta del 7 febbraio Un breve svolgimento delle versioni A Vi sarò grato per la segnalazione di eventuali errori. Esercizio. (a) Dimostrare che l equazione () (3 +
Analisi Matematica 3 (Fisica) Prova scritta del 7 febbraio Un breve svolgimento delle versioni A Vi sarò grato per la segnalazione di eventuali errori. Esercizio. (a) Dimostrare che l equazione () (3 +
Corso di Laurea in Matematica Geometria 2. Foglio di esercizi n. 1 a.a Soluzioni
 Corso di Laurea in Matematica Geometria 2 Foglio di esercizi n. 1 a.a. 2015-16 Soluzioni Gli esercizi sono presi dal libro di Manetti. Per svolgere questi esercizi, studiare con cura i paragrafi 3.1, 3.2,
Corso di Laurea in Matematica Geometria 2 Foglio di esercizi n. 1 a.a. 2015-16 Soluzioni Gli esercizi sono presi dal libro di Manetti. Per svolgere questi esercizi, studiare con cura i paragrafi 3.1, 3.2,
Corso di Geometria III - A.A. 2016/17 Esercizi
 Corso di Geometria III - A.A. 216/17 Esercizi (ultimo aggiornamento del file: 2 ottobre 215) Esercizio 1. Calcolare (1 + 2i) 3, ( ) 2 + i 2, (1 + i) n + (1 i) n. 3 2i Esercizio 2. Sia z = x + iy. Determinare
Corso di Geometria III - A.A. 216/17 Esercizi (ultimo aggiornamento del file: 2 ottobre 215) Esercizio 1. Calcolare (1 + 2i) 3, ( ) 2 + i 2, (1 + i) n + (1 i) n. 3 2i Esercizio 2. Sia z = x + iy. Determinare
Corso di Laurea in Matematica Prova di Analisi in più variabili 2
 orso di Laurea in Matematica Prova di Analisi in più variabili 1 febbraio 15 1. Sia f : R una funzione π-periodica e tale che f L 1 π, π. Dimostrare la seguente formula fn = 1 [ft ft π ] 4π n e int dt
orso di Laurea in Matematica Prova di Analisi in più variabili 1 febbraio 15 1. Sia f : R una funzione π-periodica e tale che f L 1 π, π. Dimostrare la seguente formula fn = 1 [ft ft π ] 4π n e int dt
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA CHIMICA E DEI MATERIALI GENNAIO 2015 DOCENTE: M. LONGO
 FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA CHIMICA E DEI MATERIALI GENNAIO 2015 DOCENTE: M. LONGO 1. Domande Domanda 1. Dire quando una funzione f : X Y tra dee insiemi X ed Y si dice iniettiva.
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA CHIMICA E DEI MATERIALI GENNAIO 2015 DOCENTE: M. LONGO 1. Domande Domanda 1. Dire quando una funzione f : X Y tra dee insiemi X ed Y si dice iniettiva.
COMPLEMENTI DI ANALISI MATEMATICA A.A Primo appello del 5/5/2010
 COMPLEMENTI DI ANALISI MATEMATICA A.A. 29- Primo appello del 5/5/2 Qui trovate le tracce delle soluzioni degli esercizi del compito. Ho tralasciato i calcoli da Analisi (che comunque sono parte della risoluzione),
COMPLEMENTI DI ANALISI MATEMATICA A.A. 29- Primo appello del 5/5/2 Qui trovate le tracce delle soluzioni degli esercizi del compito. Ho tralasciato i calcoli da Analisi (che comunque sono parte della risoluzione),
SOLUZIONI DELLA PRIMA PROVA IN ITINERE DEL CORSO GE220
 SOLUZIONI DELLA PRIMA PROVA IN ITINERE DEL CORSO GE220 ESERCIZIO 1 (6 punti) Sia X uno spazio topologico. Dimostrare che: (i) (3 punti) X è uno spazio T 1 se e solo se per ogni x X l intersezione di tutti
SOLUZIONI DELLA PRIMA PROVA IN ITINERE DEL CORSO GE220 ESERCIZIO 1 (6 punti) Sia X uno spazio topologico. Dimostrare che: (i) (3 punti) X è uno spazio T 1 se e solo se per ogni x X l intersezione di tutti
Equazioni differenziali
 Equazioni differenziali Hynek Kovarik Università di Brescia Analisi Matematica 2 Hynek Kovarik (Università di Brescia) Equazioni differenziali Analisi Matematica 2 1 / 42 Equazioni differenziali Un equazione
Equazioni differenziali Hynek Kovarik Università di Brescia Analisi Matematica 2 Hynek Kovarik (Università di Brescia) Equazioni differenziali Analisi Matematica 2 1 / 42 Equazioni differenziali Un equazione
Esistenza ed unicità per equazioni differenziali
 Esistenza ed unicità per equazioni differenziali Per concludere queste lezioni sulle equazioni differenziali vogliamo dimostrare il teorema esistenza ed unicità per il problema di Cauchy. Faremo la dimostrazione
Esistenza ed unicità per equazioni differenziali Per concludere queste lezioni sulle equazioni differenziali vogliamo dimostrare il teorema esistenza ed unicità per il problema di Cauchy. Faremo la dimostrazione
ANALISI B alcuni esercizi proposti
 ANALISI B alcuni esercizi proposti G.P. Leonardi Parte II 1 Limiti e continuità per funzioni di 2 variabili Esercizio 1.1 Calcolare xy log(1 + x ) lim (x,y) (0,0) 2x 2 + 5y 2 Esercizio 1.2 Studiare la
ANALISI B alcuni esercizi proposti G.P. Leonardi Parte II 1 Limiti e continuità per funzioni di 2 variabili Esercizio 1.1 Calcolare xy log(1 + x ) lim (x,y) (0,0) 2x 2 + 5y 2 Esercizio 1.2 Studiare la
Corso di Laurea in Matematica Geometria 2. Esercizi di preparazione allo scritto a.a Topologia
 Corso di Laurea in Matematica Geometria 2 Esercizi di preparazione allo scritto a.a. 2015-16 Esercizio 1. Dimostrare che Topologia 1. d(x, y) = max 1 i n x i y i definisce una distanza su R n. 2. d(x,
Corso di Laurea in Matematica Geometria 2 Esercizi di preparazione allo scritto a.a. 2015-16 Esercizio 1. Dimostrare che Topologia 1. d(x, y) = max 1 i n x i y i definisce una distanza su R n. 2. d(x,
Alcuni complementi di teoria dell integrazione.
 Alcuni complementi di teoria dell integrazione. In ciò che segue si suppone di avere uno spazio di misura (,, µ) 1 Sia f una funzione misurabile su un insieme di misura positiva tale che f 0. Se fdµ =
Alcuni complementi di teoria dell integrazione. In ciò che segue si suppone di avere uno spazio di misura (,, µ) 1 Sia f una funzione misurabile su un insieme di misura positiva tale che f 0. Se fdµ =
Equazione di Laplace
 Equazione di Laplace. Introduzione Si da il nome di operatore di Laplace o laplaciano all operatore differenziale u = u xx + u yy + u zz in tre dimensioni, o agli analoghi in dimensioni diverse. L operatore
Equazione di Laplace. Introduzione Si da il nome di operatore di Laplace o laplaciano all operatore differenziale u = u xx + u yy + u zz in tre dimensioni, o agli analoghi in dimensioni diverse. L operatore
COMPATTEZZA. i) X è compatto, cioè ogni ricoprimento aperto ammette un sottoricoprimento finito.
 1 COMPATTEZZA Sia X un sottoinsieme di R. Una famiglia A di sottoinsiemi aperti di R si dice ricoprimento aperto di X se X A, cioè se X è contenuto nell unione degli elementi di A. Una sottofamiglia di
1 COMPATTEZZA Sia X un sottoinsieme di R. Una famiglia A di sottoinsiemi aperti di R si dice ricoprimento aperto di X se X A, cioè se X è contenuto nell unione degli elementi di A. Una sottofamiglia di
