G.M.Troianiello ANALISI FUNZIONALE
|
|
|
- Luisa Berti
- 7 anni fa
- Visualizzazioni
Transcript
1 G.M.Troianiello ANALISI FUNZIONALE [Testo di riferimento: Haim Brézis Analisi funzionale: teoria e applicazioni - Napoli: Liguori Editore, 1986 (Serie di matematica e fisica 9)] 1 La norma e il prodotto scalare Indichiamo con E uno spazio vettoriale su K = R o su K = C. Una norma E, o più concisamente, è una funzione E R dotata delle seguenti proprietà: (1.1) x 0 per x E, (1.2) αx = α x per α K e x E, (1.3) x + y x + y per x, y E, (1.4) x = 0 = x = 0 in E. Dalla (1.2) segue subito che x = 0 (in E) = x = 0: scrivendo lo 0 di E come prodotto dello 0 di K e di un qualunque vettore x E otteniamo infatti 0 = 0x = 0 x = 0. Se una funzione gode di tutte le proprietà della norma tranne la (1.4), per cui esiste un vettore x 0 0 con x 0 = 0, diciamo che è una seminorma; tutti i vettori αx 0 con α K hanno ancora seminorma nulla grazie alla (1.2), e per ogni x E si ha x x = 0 quale che sia x = x + αx 0. Le seguenti nozioni hanno senso anche quando è solo una seminorma. Fissato un centro x 0 E ed un raggio r > 0 chiamiamo palla aperta l insieme B r (x 0 ) = {x E x x 0 < r}, superficie sferica o sfera l insieme Σ r (x 0 ) = {x E x x 0 = r} e palla chiusa l insieme B r (x 0 ) Σ r (x 0 ) = {x E x x 0 r}; diciamo che un sottoinsieme di E è limitato se esiste una palla che lo contiene. La (1.3) è la disuguaglianza triangolare. Da essa segue subito che (1.5) x y x y per x, y E. 1
2 Se è una norma su E si dice che E, o per essere più precisi (E, ), è uno spazio normato (su K); il simbolo viene spesso convenientemente modificato per distinguere più facilmente un caso dall altro. La dimensione di (E, ) è quella di E in quanto spazio vettoriale. Siano date due seminorme e su E. Se esiste una costante reale C > 0 tale che x C x per x E diciamo che è più debole di, oppure che è più forte di. In tal caso, ogni x E tale che x x 0 < r verifica anche x x 0 < Cr e quindi ogni palla aperta di (E, ) è contenuta in una palla aperta (con lo stesso centro, ma non necessariamente con lo stesso raggio) di (E, ). Se è sia più debole che più forte di diciamo che le due seminorme sono equivalenti; in tal caso ogni palla di (E, ) è contenuta in una palla di (E, ) e viceversa. Un prodotto scalare ( ) in E è una funzione X E K dotata delle cinque proprietà seguenti: (1.6) (x y) = (y x) per x, y E, (1.7) (αx y) = α(x y) per α K e x, y E, (1.8) (x + y z) = (x z) + (y z) per x, y, z E, (1.9) (x x) 0 per x E, (1.10) (x x) = 0 = x = 0 in E. Quando K = R la sopralineatura del segno di coniugio nella (1.6) è come se non ci fosse o, se si preferisce, va eliminata e la proprietà in questione diventa la simmetria, o commutatività. L ordinario prodotto di numeri reali ha tutte le proprietà di un prodotto scalare. Tuttavia già il prodotto di numeri complessi non è un prodotto scalare in E = K = C perché è commutativo e quindi non soddisfa la (1.6). Se poi E non coincide con K il prodotto scalare, diversamente dalla somma di due vettori, non è il risultato un operazione E E E perché il suo risultato non è un vettore. Dalla (1.7) si ottiene (αy x) = α(y x) = α(y x), e la (1.6) applicata al primo ed al terzo membro dà (1.11) (x αy) = α(x y) per α K e x, y E. 2
3 Dalle (1.7) e (1.8) segue che il prodotto scalare dello 0 di E per un qualunque altro vettore di E è nullo (cioè uguale allo 0 di K): prendendo y = x si ottiene infatti (0 z) = (x x z) = (x z) + ( x z) = (x z) (x z) = 0. Dalle (1.6) e (1.8) segue poi, banalmente, che (x y + z) = (x y) + (x z) per x, y, z E. La (1.9) non può suscitare nessuna perplessità quando K = R. Quando K = C il prodotto scalare di due vettori E e y è in generale un numero complesso, per cui non ha senso parlare del suo segno; però il prodotto scalare di un vettore x per se stesso è sempre, grazie alla (1.6), uguale al suo coniugato e quindi reale. Teorema 1.1 Dalle proprietà (1.6) (1.9), cioè da tutte quelle del prodotto scalare tranne eventualmente la (1.10), segue la disuguaglianza (1.12) (x y) (x x) (y y). DIM. Supponiamo (x y) 0, altrimenti la (1.12) è banale. Siano λ K e x, y E. Risulta (1.13) 0 (x + λy x + λy) = (x x) + λ(x y) + λ(y x) + λ 2 (y y). Scegliamo dapprima λ = r (x y) /(y x), r R, ricordando che siamo nell ipotesi del denominatore 0. Innanzitutto λ 2 = r 2. Inoltre, poichè λ(y x) = r (x y) è reale e dunque = λ(x y) anche quando K è uguale a C e non a R, otteniamo λ(y x) + λ(x y) = 2r (x y) per cui 2r (x y) (x x) + r 2 (y y) grazie alla (1.13). Ora, (y x) 0 implica (y y) > 0: ciò è immediato se si aggiunge l ipotesi (1.10), mentre in assenza di quest ultima si ottiene dalla disuguaglianza precedente, che per (y y) = 0 diventa 2r (x y) (x x) e di conseguenza conduce ad un assurdo quando r. r = (x y) /(y y) e ottenere la (1.12). Possiamo dunque prendere La (1.12) è chiamata disuguaglianza di Cauchy Schwarz. 3
4 Corollario Sotto le ipotesi precedenti la funzione reale x (x x) è una seminorma su E, ed anzi una norma se si aggiunge la (1.10). DIM. Grazie alla (1.12) abbiamo (x + y x + y) = (x x) + 2Re (x y) + (y y) (x x) + 2 (x y) + (y y) (x x) + 2 (x x) ( ) 2 (y y) + ( y y) = (x x) + (y y) e da qui segue la disuguaglianza triangolare. Le altre proprietà sono di verifica immediata. Fa comodo disporre di una terminologia succinta per indicare i casi (come quello cui accenneremo con l Esempio 3.3) in cui valgono tutte le proprietà di un prodotto scalare tranne la (1.10). Noi conveniamo di dire che allora ( ) è un prodotto scalare semidefinito positivo. Quando (x y) ha tutte le proprietà di un prodotto scalare, e di conseguenza x = (x x) è una norma, diciamo che due vettori non nulli x e y di E sono ortogonali se (x y) = 0. In tal caso l identità diventa l identità di Pitagora (x + y x + y) = (x x) + 2Re (x y) + (y y) x + y 2 = x 2 + y 2. 2 Esempi di spazi normati di dimensione finita Esempio 2.1 Per x = (x 1,..., x N ) E = R N (spazio vettoriale su R) poniamo x = max i=1,...,n xi, x 1 = N x i, x 2 = N (x i ) 2 (ma per essere più precisi dovremmo scrivere k;r N al posto di k ). E immediato verificare che e 1 hanno tutte le proprietà di una norma, e sono equivalenti tra di loro: N max i=1,...,n xi x i N max i=1,...,n xi. i=1 4 i=1 i=1
5 Anche 2 è una norma, anzi la più importante delle tre, ed è detta norma euclidea; (R N, 2 ) è lo spazio euclideo di dimensione N. La sola verifica non banale è quella della proprietà triangolare, che si ottiene tenendo conto che la funzione x y = N x i y i i=1 ( y = (y 1,..., y N )) è un prodotto scalare (a valori in K = R) e che x 2 2 = x x. In R N le tre norme k, k = 1, 2, sono equivalenti l una all altra: dell equivalenza tra e 1 abbiamo già detto, per cui basta tener conto che max i=1,...,n xi N (x i ) 2 i=1 N x i. Generalizziamo le norme 1 e 2 fissando un p [1, [ e ponendo i=1 ( N ) 1/p x p = x k p. k=1 La verifica che p ha le proprietà di una norma richiede un solo passaggio non banale quando 1 < p < : la disuguaglianza triangolare, cioè (2.1) ( N ) 1/p ( N ) 1/p ( N ) 1/p x k + y k p x k p + y k p k=1 k=1 k=1 che è detta disuguaglianza di Minkowski. Per dimostrare la (2.1) facciamo innanzitutto vedere che vale la disuguaglianza di Hœlder (2.2) ( N N ) 1/p ( N ) 1/q x k y k x k p y k q k=1 k=1 k=1 (che per p = q = 2 è la disuguaglianza di Cauchy Schwarz) dove indichiamo con q l esponente coniugato di p, dato da 1/p + 1/q = 1. Applichiamo la convessità della funzione esponenziale: e a/p e b/q = e a/p+b/q 1 p ea + 1 q eb. Per ξ h η h 0 poniamo e a = ξ h p, e b = η h q e ricaviamo la disuguaglianza ξ h η h 1 p ξh p + 1 q ηh q, 5
6 che per ξ h η h = 0 è banalmente verificata. Se N ξh p = N ηh q = 1 arriviamo alla N ξ h η h 1 p N ξ h p + 1 q N η h q = 1 e da qui alla (2.2) quando non vale il caso banale che il secondo membro di quest ultima sia nullo ponendo ξ h = x h / ( N k=1 xk p ) 1/p, η h = y h / ( N k=1 yk q ) 1/q. A questo punto otteniamo la (2.1) applicando la disuguaglianza di Hœlder: N x k + y k p k=1 N x k x k + y k p 1 + k=1 N y k x k + y k p 1 k=1 ( N ) 1/p ( N ) 1 1/p ( N ) 1/p ( N ) 1 1/p x k p x k + y k p + y k p x k + y k p. k=1 k=1 k=1 k=1 Esempio 2.2 Dall esempio precedente si ricava subito che, se E 1,..., E N sono spazi normati su K, tutte le funzioni (x 1,..., x N ) max k=1,...,n x k Ek, ( N ) 1/p (x 1,..., x N ) x k p E k i=k per 1 p < sono norme (equivalenti) sul prodotto cartesiano E = E 1 E N : esse infatti non sono altro che le norme p, 1 p dei vettori ( x 1 E1,..., x N EN ) R N. In questo ambito rientra il caso E = C N. (Cfr. l Esercizio 2.2.) Esempio 2.3 Sia E un qualunque spazio vettoriale (su K) di dimensione finita N, sia B = {e 1,..., e N } una sua base, e sia Λ (o più precisamente Λ B ) l isomorfismo E K N definito da (2.1) Λx = (x 1,..., x N ) per x = N x k e k. Data una qualunque norma su K N si definisce una norma su E ponendo x E = Λx 6 k=1
7 per x E (ma dovremmo scrivere x E;B al posto di x E ). Viceversa, se è data una qualunque norma E su E le associamo una norma su K N fissando una base B e ponendo x = Λ 1 x E con Λ = Λ B, stavolta per x K N. Questo mostra che tutte le proprietà legate alla struttura vettoriale e ad una fissata norma su K N valgono tali e quali in E rispetto ad una fissata base B ed alla corrispondente norma E. Naturalmente Λ e Λ 1 trasformano limitati in limitati, e palle aperte (o chiuse) in palle aperte (o chiuse). In particolare si definiscono le norme (2.2) E x x p;e = Λx p per 1 p (ma dovremmo scrivere p;e;b al posto di x p;e ), dove le p sono le norme su K N introdotte nell Esempio 2.1 (se K = R) o 2.2 (se K = C). Una qualunque altra norma E su E è più debole della ;E: x N E = x k e k k=1 E N N x k e k E C 0 x k C x ;E k=1 con C 0 = k e k E. Più in là vedremo che negli spazi normati di dimensione finita tutte le norme sono equivalenti tra di loro. k=1 Esercizi 2.1 Sia f : t (f 1 (t),..., f N (t)) una funzione [a, b] R N, < a < b <, dove ogni f k : [a, b] R è continua. Dimostrare che l integrale b a f(t) dt = ( b a ) b f 1 (t) dt,..., f N (t) dt a verifica la disuguaglianza b a f(t) dt 2 b a f(t) 2 dt. [Suggerimento: Applicare la disuguaglianza di Cauchy Schwarz a y f(t), dove y è l integrale di f.] 2.2 Esplicitare i dettagli dell Esempio
8 3 Esempi di spazi normati di dimensione infinita Esempio 3.1 Per m = 0, 1,... e < a < b < si indica con C m ([a, b]) lo spazio vettoriale delle funzioni (reali o complesse) dotate in [a, b] di derivate continue fino all ordine m. La sua dimensione è infinita: per il Teorema Fondamentale dell Algebra una qualunque combinazione lineare delle potenze t k (tutte elementi dello spazio) non può essere lo zero dello spazio, cioè la funzione identicamente nulla, a meno che i coefficienti della combinazione lineare non siano tutti nulli. Per f C 0 ([a, b]) poniamo b f = max 1 = t [a,b] a f(t) dt, f 2 = b f(t) 2 dt (ma per essere più precisi dovremmo scrivere f p;c 0 ([a,b]) al posto di f p ); il segno di modulo nell ultimo integrale può essere omesso nel caso reale. Abbiamo di nuovo tre diverse norme su uno stesso spazio vettoriale. Se infatti f non è identicamente nulla in [a, b], e quindi ha modulo positivo in un punto t 0 [a, b], essa soddisfa anche la disuguaglianza f(t) > f(t 0 ) /2 in un intervallo non degenere contenente t 0, e ciò implica f p > 0 per k = 1, 2 oltre che (caso ovvio) per p =. Quanto alla disuguaglianza triangolare, essa è banale per la e per la 1, mentre per ciò che riguarda la 2 si deve tener conto della f 2 = (f f) con (f g) = b a f(t)g(t) dt prodotto scalare in C 0 ([a, b]) (la barra di coniugio è inutile nel caso reale). Inoltre valgono le disuguaglianze b b f(t) dt f(t) 2 dt (b a) max f(t) (b a) t [a,b] a a (la prima come conseguenza della disuguaglianza di Cauchy Schwarz applicata alle funzioni f(t) e 1). Quindi (3.1) f 1 (b a) f 2 (b a) f, il che è come dire che la 1 è più debole della 2 e quest ultima della. Generalizziamo le norme 1 e 2 ponendo ( b f p = f(t) p dt a ) 1/p per 1 p <. E qui, di nuovo, quando 1 < p < si pone il problema di dimostrare la disuguaglianza triangolare, cioè la disuguaglianza di Minkowski a (3.2) ( 1/p ( b 1/p ( b b f(t) + g(t) dt) p f(t) dt) p + g(t) p dt a a a ) 1/p 8
9 deducendola dalla disuguaglianza di Hœlder ( b ) 1/p ( b b (3.3) f(t)g(t) dt f(t) p dt g(t) q dt a a (ovvero dalla disuguaglianza di Cauchy Schwarz quando p = q = 2) dove 1/p + 1/q = 1. Le dimostrazioni della (3.3) e, grazie ad essa, della (3.2) procedono nel presente caso degli integrali esattamente come in quello delle somme considerato nell esempio 2.1. a ) 1/q Esempio 3.2 Se J è un qualunque insieme la quantità f B(J) = sup f(t) t J è una norma sulla famiglia B(J) delle funzioni limitate f : J R o f : J C. Esempio 3.3 Se J è un intervallo limitato [a, b] di R ed f vi è integrabile secondo Riemann (senza necessariamente essere continua) sono definite le quantità ( 1/p b f p = f(t) dt) p, 1 p <. a Non si tratta di norme basta pensare che valgono 0 se f è la funzione caratteristica di un punto bensì di seminorme, e nel caso p = 2 il prodotto scalare associato (cfr. l Esempio 3.1) è semidefinito positivo. Esempio 3.4 Introduciamo gli spazi normati c 0, l e l p, 1 p <, di successioni complesse nella maniera seguente: x = {x k } appartiene a c 0 se è infinitesima, a l se è limitata, a l p se verifica n xk p <, con norme sia in c 0 che in l, e invece x = sup x h h ( ) 1/p x p = x k p n in l p. È solo in quest ultimo caso che le proprietà della norma non sono tutte di verifica proprio banale: la disuguaglianza triangolare richiede il passaggio da N ad peraltro immediato nella disuguaglianza di Minkowski (2.1). Segnaliamo che può far comodo disporre di una notazione, nella fattispecie c 00, per il sottospazio di c 0 costituito dalle successioni definitivamente nulle. 9
10 Esercizi 3.1 Dimostrare che la u u + u e la u u(0) + u sono norme equivalenti in C 1 ([0, 1]). 3.2 Dimostrare che nello spazio c delle successioni complesse x = {x h } h N convergenti la x x 0 + x, dove x 0 = lim n x n, è una norma equivalente alla x x. 3.3 Dimostrare che per 1 p < q vale l inclusione propria l p l q. 3.4 (i) Fissati arbitrariamente y [0, 1/3] e t [2/3, 1], dimostrare che ogni u C 2 ([0, 1]) verifica u (x) 3( u(y) + u(t) ) u (s) ds per x [0, 1]. [Suggerimento: Associare all incremento u(t) u(y) un punto ξ ]y, t[ come nel Teorema di Lagrange, e passare all integrale x ξ u (s) ds.] (ii) Dimostrare che in C 2 ([0, 1]) la norma u u 2; = max [0,1] u + max [0,1] u + max [0,1] u è equivalente allla norma u u 2; = max [0,1] u + max [0,1] u. (iii) Dimostrare che in C 2 ([0, 1]) la norma u u 2;1 = 1 0 u ds+ 1 0 u ds+ 1 0 u ds è equivalente allla norma u u 2;1 = 1 0 u ds+ 1 0 u ds. 4 Successioni negli spazi normati Sia data una successione {x n } di elementi di uno spazio vettoriale E dotato di una seminorma. Se esiste un x E tale che x n x 0 (nel senso delle successioni reali), cioè se ad ogni ε > 0 si può associare un ν = ν ε tale che x n x < ε per ogni n > ν diciamo che {x n } è convergente ad x in E; si noti che in tal caso x n x. Fintanto che è solo una seminorma non possiamo affatto affermare che x è determinato univocamente. Se, infatti, x E è diverso da x ma x x = 0, la disuguaglianza triangolare mostra che x n x x n x + x x = x n x e quindi che {x n } converge anche ad x. Quando è una norma, {x n } può converge al più ad un vettore x perché x x x n x + x n x e quindi se {x n } converge anche ad x risulta x x = 0, ovvero x = x per la (1.4). Allora chiamiamo il limite di {x n } (e qui dovremmo aggiungere: per n ), e scriviamo x n x (di nuovo, per n ), oppure lim n x n = x, o addirittura, sbrigativamente, lim n x n = x. 10
11 Affinché una successione {x n } in uno spazio normato E sia convergente è necessario che essa sia limitata (ovvio) e inoltre che verifichi la condizione di Cauchy, cioè che per ogni ε > 0 esista un ν = ν ε tale che x n x n+p < ε per ogni n > ν e per ogni p N : questo lo si vede, come nei casi E = R e E = C, scrivendo x n x n+p x n x + x n+p x con x = lim n x n. Diciamo che E è completo se la condizione di Cauchy, oltre ad essere necessaria, è anche sufficiente affinché una successione {x n } E sia convergente. Come sappiamo tanto R che C sono completi, e grazie alla disuguaglianza triangolare questo implica, per cominciare, che la successione { x n } delle norme è convergente in R se {x n } è di Cauchy in E. Uno spazio normato completo è uno spazio di Banach, e in particolare è uno spazio di Hilbert se la norma è associata ad un prodotto scalare. Se una successione {x n } E è limitata, o di Cauchy, o convergente a x 0 rispetto ad una norma lo anche rispetto ad ogni altra norma più debole, e quindi E è completo rispetto ad una norma se e solo se lo è rispetto ad ogni altra norma equivalente. Sia E uno spazio normato, sia {x n } E e sia {s n } la successione delle ridotte s n = n k=1 x k della serie k=1 x k. Se {s n } converge si dice che la serie è convergente (e che s = lim n s n è la sua somma). Supponiamo che in E esista una famiglia numerabile {u h } tale che ad ogni x E si possa associare una successione di scalari {α h } con la proprietà x n αh u h 0 per n : allora diciamo che E possiede una base di Schauder data da {u h }, e scriviamo anche x = α h u h. Esempio 4.1 Per h N sia e h la successione coi termini tutti nulli tranne l h esimo che vale 1. La famiglia {e h } è una base di Schauder in c 0 ed in l p, 1 p < : per x = {x k } k N la differenza x n xh e h è la successione {x k } k>n, che tende a 0 in norma se x c 0 e in norma p se x l p, 1 p <. Esempio 4.2 Rispetto alla norma le considerazioni dell esempio precedente non valgono con c 0 sostituito da l. In quest ultimo spazio {e h } non è una base di Schauder: la successione 1 con tutti i termini uguali ad 1 verifica 1 n αh e h 1 quale che sia {α h }. Il prossimo risultato si ottiene esattamente come per E = R ed E = C. 11
12 Teorema 4.1 Se è una norma su E e {x n } converge in E a x, allora { x n } non solo è limitata, ma a sua volta converge in R a x. Inoltre ogni sottosuccessione {x kn } di {x n } converge a x. Se poi {y n } E converge a y in E e α, β K, allora anche {αx n + βy n } converge, con lim (αx n + βy n ) = αx + βy. n Teorema 4.2 In K N, munito della norma, ogni successione limitata {x n } ammette una sottosuccessione convergente. DIM. Indichiamo con x 1 n,..., x N n le coordinate di x n. Siccome x 1 n x n la limitatezza della successione vettoriale {x n } implica quella della successione scalare {x 1 n}. Dunque esiste una sottosuccessione {x 1 k n } convergente. Passiamo a {x 2 k n }. Poiché x 2 k n x kn sup n x n si tratta di un altra successione limitata, che di conseguenza ammette una sottosuccessione {x 2 h k } convergente, e quando N = 2 abbiamo già concluso la dimostrazione. n Il passaggio ad un N qualunque si fa a questo punto senza difficoltà. Teorema 4.3 Se (E, E ) è uno spazio normato di dimensione finita ogni altra norma E su E è equivalente a E. DIM. Prendiamo come E la ;E. Già sappiamo che ogni altra E è più debole di E. Supponiamo per assurdo che E non sia più debole di E, cioè che non si possa trovare nessuna costante C > 0 tale che x E C x E per x E. Allora si può associare ad ogni n N un vettore (necessariamente non nullo) x n E tale che (4.1) x n E > n x n E. Poniamo y n = x n / x n E. Siccome y n E = 1 il Teorema 4.2 ci consente di estrarre da {y n } una successione {y kn } convergente ad un vettore y 0 rispetto alla norma E, quindi anche rispetto alla norma più debole E. Da una parte y 0 E = lim n y kn E = 1; dall altra la (4.1) implica x kn E > k n x kn E, ovvero y k n E < 1/k n, e quindi y 0 E = lim n y kn E = 0, cioè y 0 = 0, il che è incompatibile con y 0 E = 1. Grazie al Teorema 4.3 il Teorema 4.2 si estende così: Teorema (di Bolzano Weierstrass) 4.4 In uno spazio normato di dimensione finita ogni successione limitata {x n } ammette una sottosuccessione convergente. 12
13 Dall equivalenza, in uno spazio normato E di dimensione finita, tra ;E ed ogni altra norma E segue subito che una successione {x n } E è limitata, o di Cauchy, o convergente (a x 0 ) rispetto a E se e solo se, fissata una base di E e indicata con x j m la j esima coordinata di x m in tale base, m = 0, 1, 2,..., ciascuna successione {x j n} K, j = 1,..., N è, rispettivamente, limitata, o di Cauchy, o convergente (a x j 0 ). In particolare: Teorema 4.5 Ogni spazio normato E su K di dimensione finita è completo. DIM. Sia {x n } E di Cauchy: anche ogni {x j n} è di Cauchy in K, dunque convergente per la completezza di K = R o K = C. Ma allora anche {x n } è convergente. Uno spazio normato di dimensione infinita può benissimo non essere completo. Esempio 4.3 A ciascun n N associamo una f n continua in [0, 1], lineare in [1/2, 1/2 + 1/n], uguale a 1 in [1, 1/2] e a 0 in [1/2 + 1/n, 1]. Rispetto alle norme 1 e 2 dell Esempio 3.1 la successione delle f n è di Cauchy, ma non non esiste nessuna funzione di C 0 ([0, 1]) tale che f n f 1 0 o f n f 2 0 perché f dovrebbe allora essere uguale a 1 in [1, 1/2] e a 0 in ]1/2, 1]. Ne segue che non sono completi né (C 0 ([0, 1]), 1 ) né (C 0 ([0, 1]), 2 ). Invece (C 0 ([0, 1]), ) è completo. Esempio 4.4 Mostriamo che tutti gli spazi l p, 1 p, sono completi. Fissiamo {x n } n l p di Cauchy ed associamo ad ogni ε > 0 un ν = ν ε N tale che x m x n p ε per m, n ν. Dato comunque h N, dalla disuguaglianza x h m x h n x m x n p segue che {x h n} n C è di Cauchy e quindi converge ad un numero x h. Quando p = si sfrutta la x h x h n = lim m xh m x h n ε per ottenere sup h x h x h n ε, dunque x x n l e di conseguenza x = (x x n ) + x n l, con x x n 0. Sia 1 p <. Per ogni N N vale la N x h x h n p = lim m N x h m x h n p ε p da cui segue che xh x h n p ε p, quindi x x n l p, e x = (x x n ) + x n l p con x x n p 0. 13
14 Esercizi 4.1 Dimostrare che x 2 x 1 per x l 1 (cominciando da x definitivamente nulla). 4.2 Sia E uno spazio normato. Far vedere che ogni successione di Cauchy {x n } E ammette una sottosuccessione {x kn } che verifica x kn+1 x kn < 2 n. 4.3 Servendosi dell esercizio precedente, far vedere che uno spazio normato E è completo se e solo se ogni serie k=1 x k con k=1 x k < è convergente. 4.4 (i) Sia {x n } l 1 tale che: (*) x k n y k per ogni n ed ogni k, dove y = {y k } l 1. Mostrare che {x n } converge ad una x di l 1 se converge ad x componente per componente. (ii) Mostrare con un esempio che la conclusione di (i) viene meno se (*) è sostituita da: x n 1 y 1 per ogni n. (iii) Sia {x n } l 1 convergente componente per componente ad una x l 1, con x n 1 x 1. Mostrare che allora x n x 1 0. [Suggerimento: Per ogni k risulta 0 x k n x k + x k x k n 2 x k.] 5 Gli spazi metrici Sia X un qualunque insieme. Una metrica su X è una funzione X X R, che dovremmo indicare sempre con d X e invece indichiamo quasi sempre con d, dotata delle seguenti proprietà: d(x, y) 0 per x, y X, d(x, y) = d(y, x) per x, y X, d(x, t) d(x, y) + d(y, t) per x, y, t X, d(x, x) = 0 per x X, d(x, y) = 0 = x = y; se si lascia cadere l ultima proprietà della metrica, cioè se non si esclude che d(x, y) possa annullarsi anche per qualche x y, si parla di pseudometrica invece che di metrica. Le proprietà di una metrica non presuppongono nessuna proprietà algebrica dell insieme sostegno: basta pensare che su ogni insieme X è sempre definita almeno la metrica banale (x, y) 0 se x y, (x, x) 1 per ogni x X. Se d è una metrica su X diciamo che (X, d), o più brevemente X, è uno spazio metrico. Ogni sottoinsieme S di X è a sua volta uno spazio metrico nella metrica d S (ma dovremmo scrivere qualcosa come d X;S ) indotta da d X : molti enunciati metrici ma non tutti! basta darli su (X, d X ) perché valgano automaticamente in (S, d S ) quale che sia S X. Fissati un centro x 0 X ed un raggio r > 0 chiamiamo palla aperta l insieme B r (x 0 ) = {x X d(x, x 0 ) < r}, sfera l insieme Σ r (x 0 ) = {x X d(x, x 0 ) = r} e palla chiusa la loro unione {x X d(x, x 0 ) r}; diciamo che un sottoinsieme di X è limitato se esiste una palla che lo contiene. Si noti che per S X una palla di (S, d S ) non è (in generale) una palla di (X, d X ), bensì l intersezione di S e di una palla di (X, d X ). 14
15 Sia data una successione {x n } di elementi di X. Se esiste un x X tale che d(x n, x) 0 (nel senso delle successioni reali), cioè se per ogni ε > 0 è possibile trovare un ν ε tale che d(x n, x) < ε per ogni n > ν ε, diciamo che {x n } è convergente, più precisamente ad x. Siccome d è una metrica, e non solo una pseudometrica, {x n } può converge al più ad un vettore x, perché d(x, x ) d(x n, x) + d(x n, x ), e quindi se {x n } converge anche ad x risulta d(x, x ) = 0, ovvero x = x. Allora chiamiamo x il limite di {x n } (e qui dovremmo aggiungere: per n ), e scriviamo x n x (di nuovo, per n ), oppure lim n x n = x, o anche, sbrigativamente, lim n x n = x. Affinché {x n } sia convergente è necessario che sia limitata (ovvio) e inoltre che verifichi la condizione di Cauchy: per ogni ε > 0 esista un ν = ν ε tale che Questo lo si vede scrivendo d(x n, x n+p ) < ε per ogni n > ν e per ogni p N. d(x n, x n+p ) d(x n, x) + d(x n+p, x) con x = lim n x n. La condizione di Cauchy implica a sua volta la limitatezza ma non, in generale, la convergenza: diciamo che X è completo se questo accade, cioè se la condizione di Cauchy, oltre che necessaria, è anche sufficiente affinché {x n } sia convergente. Osservazione 5.1 Siano {x n }, {y n } successioni (che verificano la condizione) di Cauchy in X. Dalla disuguaglianza triangolare segue che d(x n, y n ) d(x n, x p ) + d(x p, y p ) + d(y p, y n ) e da qui si conclude (dopo aver scambiato tra loro n e p) che la successione reale delle distanze d(x n, y n ) è di Cauchy, dunque convergente grazie alla completezza di R. Se X e Y sono spazi metrici la continuità in un punto x 0 X di una funzione X Y si esprime attraverso la solita formulazione cogli ε e i δ. Si vede subito che, se (E, E ) è uno spazio normato e X E, la funzione X X (x, y) x y E determina su X una struttura di spazio metrico. Riprendiamo in questo ambito una considerazione precedente: una palla di X non è una palla di E, bensì l intersezione di X e di una palla di E. Un isometria di due spazi metrici (X, d) e ( X, d) è un applicazione iniettiva e suriettiva ϕ : X X tale che d(ϕ(x), ϕ(y)) = d(x, y) per x, y X. Un isomorfismo isometrico di due spazi normati è, non sorprendentemente, un isomorfismo che è anche un isometria e quindi conserva le norme. 15
16 Alla nozione di isometria non bisogna far dire più di quello che dice. Basti pensare che uno spazio metrico può essere isometrico ad un suo sottospazio proprio, com è il caso sia di c 0 che di un qualunque l p rispetto all isometria ϕ : {x 1, x 2,...} {0, x 1, x 2,...}; altri esempi appariranno più in là. Pur tenendo conto di questa premessa, sono comunque significative le seguenti considerazioni. Fissiamo un punto a X ed associamo ad ogni x X la funzione t f x (t) = d(x, t) d(a, t), che su X è limitata (perché f x (t) d(x, a) al variare comunque di t) e continua (perché f x (s) f x (t) 2d(s, t) al variare comunque di t e s). Indicando con Cb 0 (X) lo spazio delle funzioni limitate e continue X R dotato della norma del sup è immediato constatare che d(x, y) = f x f y C 0 b (X) : infatti il secondo membro è l estremo superiore della quantità d(x, t) d(y, t), che è maggiorata da d(x, y) per ogni t X e vale proprio d(x, y) quando t = x o t = y. Dunque le proprietà di X legate alla sua struttura metrica si formulano come proprietà, rispetto alla norma C 0 b (X), del sottoinsieme ι(x) di C 0 b (X) costituito dalle funzioni t f x(t) al variare di x X. Ciò detto, in tanti casi è opportuno studiare direttamente le proprietà degli spazi metrici presi in esame piuttosto che ricondursi preliminarmente a spazi normati. Esercizi 5.1 Data la metrica banale d su un insieme X, caratterizzare la successioni convergenti in (X, d) ed il sottoinsieme ι(x) di Cb 0 (X) isometrico ad (X, d). 5.2 Dimostrare che, se (X, d) è un qualunque spazio metrico, Cb 0 (X) è completo. 5.3 Tenendo conto delle proprietà della funzione [0, [ t t/(1 + t) dimostrare che d : (x, y) x y /(1 + x y ) è una metrica su R. 5.4 Dimostrare che d : (x, y) k=1 x k y k /[k!(1 + x k y k )] è una metrica sulla famiglia X delle successioni complesse x = {x k }. 6 Spazi topologici Una topologia su un insieme X è una famiglia U di sottoinsiemi U di X, detti aperti, caratterizzata delle seguenti tre proprietà: (a) tanto X che sono aperti; (b) l unione di una qualunque famiglia di aperti è ancora un aperto; (c) l intersezione di una famiglia finita di aperti è ancora un aperto. 16
17 Insistiamo: in (b) la famiglia di aperti è qualunque, mentre in (c) è finita. Diciamo che (X, U), o più brevemente X, è uno spazio topologico. Una famiglia B U è una base della topologia U se gli aperti sono le unioni di elementi di B. Se S è un qualunque sottoinsieme di X gli aperti di S nella topologia indotta da X sono le intersezioni di S con gli aperti di X. Non è affatto detto che un aperto di S ad esempio S stesso sia un aperto di X. Un intorno di un punto x 0 di X è un qualunque sottoinsieme di X che contiene un aperto U x 0. Dalla (b) segue subito che un sottoinsieme di X è aperto se e solo se è un intorno di ogni suo punto. I chiusi sono i complementari degli aperti. Ecco le proprietà dei chiusi (ovvie conseguenze della definizione dei chiusi e degli assiomi degli aperti): (a ) tanto X che sono chiusi; (b ) l unione di una famiglia finita di chiusi è ancora un chiuso; (c ) l intersezione di una qualunque famiglia di chiusi è ancora un chiuso. X e sono sia aperti che chiusi. Se non sono i soli sottoinsiemi di X con questa proprietà, cioè se esistono aperti U e V tali che U V = e X = U V, diciamo che X è sconnesso, altrimenti che è connesso. Sia S X. Diciamo che x 0 X è un punto interno a S se S è un intorno di x 0, cioè se esiste un aperto x 0 contenuto in S; l interno S (ma per certi versi sarebbe meglio scrivere S) di S è l insieme dei punti interni ad S, cioè l unione di tutti gli aperti contenuti in S. Dunque S è aperto (assioma (b)), e si ottiene immediatamente la Proposizione 6.1 Un sottoinsieme proprio S di uno spazio topologico X è aperto se e solo se coincide col proprio interno S. La chiusura S di S X è l intersezione di tutti i chiusi di X che contengono S. Dunque S è chiuso (assioma (c )), e si ottiene immediatamente la Proposizione 6.2 Un sottoinsieme proprio S di uno spazio topologico X è chiuso se e solo se coincide con la propria chiusura S. Se S = X diciamo che S è denso in X. Quando ciò accade con S discreto (cioè finito o numerabile) diciamo che X è separabile. Diciamo che x 0 X, appartenente o no ad S, è un punto di aderenza per S se in ogni aperto che contiene x 0 cadono dei punti di S, un punto di accumulazione per S se ogni intorno di x 0 contiene almeno un punto x S \ {x 0 }, un punto isolato di S se esiste un aperto U tale che S U = {x 0 }. I punti di aderenza per S sono o di accumulazione o isolati, e la loro totalità non è altro che la chiusura di S, come segue dal prossimo risultato. Proposizione 6.3 Un sottoinsieme proprio S di uno spazio topologico X è chiuso se e solo se contiene tutti i propri punti di accumulazione. 17
18 DIM. Implicazione se : dire che un qualunque punto x 0 X \ S ha un intorno dove non cadono punti di S (poiché altrimenti x 0 sarebbe di accumulazione per S) significa dire che X \ S è aperto, dunque che S è chiuso. Implicazione solo se : dire che S è chiuso, cioè che X \ S è aperto, significa dire che un qualunque punto di X \ S è un punto interno di X \ S, e quindi non può essere di accumulazione per S. Sottolineiamo che, se non esistono punti di accumulazione di S, quest ultimo è chiuso. Una successione {x n } X converge nella topologia U di X se esiste x X tale che ogni suo intorno in U contenga tutti i punti x n a partire da un certo indice (dipendente dall intorno). Date due distinte topologie U 1, U 2 su X diciamo che U 1 è più debole di U 2 se ogni elemento (=aperto) di U 1 è anche un aperto di U 2. In tal caso ogni successione convergente in U 2 converge anche in U 1, e ciò giustifica la terminologia adottata: la convergenza in U 2 è una proprietà più forte della convergenza in U 1. Il seguente risultato è immediato. Proposizione 6.4 Un punto x di uno spazio topologico X è di aderenza per un sottoinsieme proprio S di X se esiste una successione {x n } S convergente ad x. Nella proposizione precedente non si può sostituire se con solo se, come mostra il seguente Esempio 6.1 Siano X = [0, 1] e S = [0, 1[. Definiamo una topologia su X prendendo come chiusi [0, 1], e i sottoinsiemi finiti o numerabili. S coincide con X: l insieme {1} non è un aperto, e di conseguenza 1 è di accumulazione per S. Però una qualunque successione di punti di S costituisce un chiuso e quindi ha per complementare un aperto contenente 1, sicché non può esistere una {x n } X convergente ad 1. L esempio precedente fa vedere come in un generico spazio topologico X le successioni non bastino a caratterizzare (i punti di accumulazione per i sottoinsiemi di X, e quindi) i chiusi di X. La situazione cambia in una opportuna classe di spazi topologici, come vedremo con la Proposizione 7.1. Diciamo che x 0 X è un punto di frontiera per S se non è interno né ad S né al complementare X \ S di S, ovvero se ogni intorno di x 0 ha intersezione non vuota tanto con S che con X \ S; la frontiera S di S è l insieme dei punti di frontiera di S. Dunque S = (X \ S) = S X \ S, per cui S è chiusa, e siccome vale la seguente catena di equivalenze: S è chiuso X \ S è aperto tutti i punti di X \ S sono interni a X \ S, otteniamo subito la Proposizione 6.5 La chiusura di un sottoinsieme proprio S di uno spazio topologico X è l unione di S e della sua frontiera S; S è chiuso se e solo se contiene S. 18
19 Siano X e Y spazi topologici. Una funzione f : X Y è continua in un punto x 0 di X se, dato comunque un aperto V di Y contenente f(x 0 ), esiste un aperto U di X contenente x 0 tale che f(u) V, e dunque f è continua in (ogni punto di) X se la controimmagine in f di un qualunque aperto di Y è un aperto di X. Esercizi 6.1 Siano X un insieme, Y uno spazio topologico e F una famiglia di funzioni X Y. Dimostrare che la famiglia B delle intersezioni finite di insiemi f 1 (V ) con f F e V aperto di X costituisce una base per una topologia di X, detta topologia debole (relativamente a F), che è la meno fine tra quelle che rendono continue tutte le funzioni di F. [Suggerimento: Siano A, B famiglie di indici, U = α A U α, U = β B U β con gli U α e U β presi in B. Allora U U = α,β (U α U β ).] 6.2 Caratterizzare le successioni convergenti dell intervallo [0, 1] munito della topologia definita nell esempio (i) Mostrare che la famiglia B degli intervalli chiusi di R costituisce la base di una topologia, oppure no, a seconda che in B si includano, oppure no, gli intervalli degeneri. (ii) Descrivere la topologia generata da B nel primo dei due casi di (i). 6.4 Mostrare che in Q il sottoinsieme dei punti x tali che 2 < x 2 < 3 è chiuso. 6.5 Mostrare che ogni funzione f : N R è continua. 6.6 Mostrare che ogni funzione continua f : R N è costante. 6.7 Dare un esempio non banalissimo di spazio topologico dotato di punti che non sono dei chiusi. 7 Topologia negli spazi metrici Sia (X, d), o più brevemente X, uno spazio metrico. Le proprietà degli aperti sono soddisfatte dai sottoinsiemi di X che, se contengono un punto x 0, contengono anche tutta una palla aperta di centro x 0. Questo significa che la metrica determina, o, come anche si dice, induce su X una struttura di spazio topologico. Ogni palla aperta B R (x 0 ) è un aperto: se x 1 B R (x 0 ), cioè d(x 1, x 0 ) < R, basta prendere r R d(x 1, x 0 ) per avere B r (x 1 ) B R (x 0 ). Con un ragionamento analogo si vede che il complementare della palla chiusa B R (x 0 ) è un aperto: infatti se d(x 1, x 0 ) > R e 0 < r < d(x 1, x 0 ) R la disuguaglianza d(x, x 1 ) < r implica la d(x, x 0 ) > R. Di conseguenza sono chiusi la palla chiusa e il complementare d(x, x 0 ) R della palla aperta, così come l intersezione dei due 19
20 chiusi, cioè la sfera Σ R (x 0 ); quest ultima è la frontiera della palla aperta, di cui la palla chiusa è la chiusura. Un isometria tra X e un altro spazio metrico Y trasforma aperti in aperti (ovvero chiusi in chiusi); se poi X è separabile lo è anche Y. Proposizione 7.1 Un punto x 0 di uno spazio metrico X è di aderenza per un sottoinsieme S di X se e solo se esiste una successione {x n } S convergente ad x 0. DIM. L implicazione che rimane da dimostrare è la solo se. La palla di centro x 0 e raggio 1/n contiene almeno un punto x n di S, e facendo tendere n all otteniamo x n x 0. Corollario Sia (X, d) uno spazio metrico. S X è chiuso se e solo se il limite di ogni successione convergente {x n } S è a sua volta un punto di S; se X è completo, allora S, preso con la metrica indotta da d, è a sua volta uno spazio metrico completo se e solo se è chiuso come sottoinsieme di X. Diciamo che S X è compatto per successioni se ogni successione di punti di S ammette una sottosuccessione convergente a un punto di S. In tal caso, procedendo esattamente come nel caso unidimensionale S = [a, b], < a < b <, si dimostra che una funzione continua S R è dotata in S di massimo e minimo assoluti (Teorema di Weierstrass: cfr. anche l Esercizio 7.3), il che consente di dotare della norma f = max t S f(t) lo spazio C 0 (S) delle funzioni continue f : S C. Teorema 7.2 limitato. Un sottoinsieme S X è compatto per successioni solo se è chiuso e DIM. Supponiamo S compatto per successioni. Se S non fosse chiuso esisterebbe una successione convergente {x n } S tale che x 0 = lim x n / S, e ogni sottosuccessione di {x n } convergerebbe a x 0, dunque non a un punto di S. Se S non fosse limitato esisterebbero un punto x e una successione {x n } S tale che d(x n, x) > n per ogni n N, sicché nessuna sottosuccessione di {x n } potrebbe essere limitata né tantomeno convergente. Possiamo invertire il Teorema 6.3, cioè sostituire nell enunciato solo se con se? Nella prossima sezione vedremo che, nel caso di uno spazio normato, la risposta è affermativa in dimensione finita, mentre in dimensione infinita la palla unitaria chiusa non è compatta per successioni. Uno spazio metrico non completo X può sempre essere completato, ossia identificato, mediante un isometria, ad un sottoinsieme denso di uno spazio metrico completo X. Per mostrare questo si prenda come X la chiusura in Cb 0 (X) del sottoinsieme ι(x) introdotto nella Sezione 5 o, alternativamente, si utilizzi il 20
21 Teorema (del completamento) 7.3 Siano (X, d) uno spazio metrico non completo, S(X) la famiglia delle successioni di Cauchy in X ed R la relazione di equivalenza tra elementi {x n }, {ξ n } di S(X) così definita: {x n }R{ξ n } se d(x n, ξ n ) 0. L insieme quoziente S(X)/R può essere dotato della struttura di uno spazio metrico completo in cui un sottospazio denso è isometrico a (X, d). DIM. Siano {x n }, {ξ n } S(X) tali che {x n }R{ξ n }, e poi {y n }, {η n } S(X) tali che {y n }R{η n }. Grazie all Osservazione 5.1 sappiamo che le successioni reali delle d(x n, y n ) e delle d(ξ n, η n ) sono convergenti, per cui utilizzando la disuguaglianza triangolare otteniamo d(ξ n, η n ) d(ξ n, x n ) + d(x n, y n ) + d(y n, η n ) e concludiamo (dopo aver scambiato tra loro {x n }, {ξ n } e {y n }, {η n }) che lim n d(x n, y n ) = lim n d(ξ n, η n ). Dunque il limite delle distanze d(x n, y n ) è un numero che non dipende dalle particolari successioni di Cauchy {x n } e {y n }, ma solo dalle loro rispettive classi di equivalenza, diciamo x e y. Ne segue che sul prodotto cartesiano dell insieme quoziente X = S(X)/R per se stesso è ben definita l applicazione (x, y ) d (x, y ) = lim n d(x n, y n ). Si verifica senza difficoltà che d è una metrica. Che X sia isometrico ad un sottospazio di X lo si vede subito associando ad x X l elemento ϕ(x) di X rappresentato dalla successione di termini tutti uguali ad x: dato un altro ϕ(y), y X, risulta d (ϕ(x), ϕ(y)) = d(x, y). Siano x un qualunque elemento di X e {x n } S(X) un rappresentante di x. La quantità d (x, ϕ(x p )) = lim n d(x n, x p ) risulta minore di un ε > 0 prefissato purché p sia sufficientemente grande, e questo mostra che ϕ(x) è denso in X. Per far vedere che (X, d ) è completo fissiamo una successione di Cauchy {x n} X e per ogni n determiniamo uno ξ n X tale che d (ϕ(ξ n ), x n) < 1/n (densità di ϕ(x)). La {ξ n } così ottenuta è di Cauchy, come si vede tenendo conto che d(ξ n, ξ p ) = d (ϕ(ξ n ), ϕ(ξ p )) d (ϕ(ξ n ), x n) + d (x n, x p) + d (x p, ϕ(ξ p )). Sia x l elemento di X rappresentato da {ξ n }: siccome d (x, x p) d (x, ϕ(ξ p )) + d (ϕ(ξ p ), x p) < lim n d(ξ n, ξ p ) + 1/p possiamo concludere che d (x, x p) 0 per p. R è il completamento di Q nella metrica indotta dal valore assoluto. Per la dimostrazione del prossimo risultato cfr. ad esempio [Brézis, Lemma II.1]. Teorema (di Baire) 7.4 Siano X uno spazio metrico completo e {X n } una successione di sottoinsiemi chiusi di X tutti privi di punti interni. Allora è priva di punti interni anche l unione degli X n. 21
22 È utile avere presenti altre due formulazioni del Teorema di Baire. Ecco la prima: Sia X uno spazio metrico completo non vuoto. Se X è unione di una successione {X n } di suoi sottoinsiemi chiusi, allora almeno uno di essi deve possedere punti interni. La seconda formulazione si ottiene dal Teorema 7.4 prendendo G n = X \ X n : Siano X uno spazio metrico completo e {G n } una successione di sottoinsiemi aperti e densi di X. Allora è densa anche l intersezione dei G n. Esercizi 7.1 Mostrare che in uno spazio metrico ogni punto è un chiuso. 7.2 Sia U i la topologia su R costituita dalle semirette aperte ]a, [ (R e compresi) e sia (X, d) uno spazio metrico. Dimostrare che per una f : X R le seguenti tre proprietà sono equivalenti: (i) f è semicontinua inferiormente, cioè ad ogni ε > 0 si può associare un δ ε > 0 tale che f(x) > f(x 0 ) ε per d(x, x 0 ) < δ ε ; (ii) f è continua da (X, d) a R munito della topologia U i ; (iii) data comunque {x n } X convergente risulta f(lim n x n ) lim inf f(x n ). 7.3 Dimostrare il Teorema di Weierstrass nella seguente formulazione: Se (X, d) è compatto per successioni ogni f : X R semicontinua inferiormente è dotata di minimo. 7.4 Mostrare con un esempio che nel Teorema di Baire l ipotesi di completezza dello spazio metrico è essenziale. 8 Topologia negli spazi normati Passiamo al caso di uno spazio normato (E, ) cominciando col Teorema 8.1 Se è un altra norma su E, equivalente a, gli aperti di (E, ) sono gli stessi di (E, ). DIM. Come abbiamo visto nella Sezione 1 ogni palla aperta di (E, ) contiene una palla aperta di (E, ) e viceversa. Osservazione 8.1 Se E è uno spazio normato su K di dimensione finita N in cui è stata fissata una base, l isomorfismo E K N ed il suo inverso trasformano chiusi in chiusi, ovvero aperti in aperti; la topologia in questione è indipendente dalla scelta della norma. Per ciò che riguarda in particolare C N si vede subito che i suoi aperti sono identificabili con quelli di R 2N (cfr. l Esempio 2.2). 22
23 Il completamento metrico di uno spazio normato (E, E ) non completo, ottenuto applicando il procedimento del Teorema 7.3 con d(x, y) = x y E, è uno spazio di Banach: le classi di equivalenza delle successioni di Cauchy in E costituiscono uno spazio vettoriale Ẽ su cui la distanza x d(x, 0) fornisce una norma x x E, e (E, E ) è uno spazio normato completo. Un esempio sofisticato è il completamento di C 0 ([0, 1]) (spazio sui reali) rispetto alla norma 1, detto spazio di Lebesgue e indicato con L 1 (0, 1): i suoi elementi possono venire rappresentati, attraverso un certo numero di passaggi che nella Sezione 16 proporremo come esercizi, da vere e proprie funzioni definite in [0, 1]. Teorema 8.2 Un sottoinsieme di uno spazio normato E di dimensione finita è compatto per successioni se e solo se è chiuso e limitato. DIM. L implicazione solo se l abbiamo già dimostrata (Teorema 7.1) in un qualunque spazio metrico. Per dimostrare l implicazione se fissiamo S E ed una qualunque successione {x n } di vettori di S. Se S è limitato anche {x n } lo è, e siccome qui siamo in dimensione finita possiamo applicare il Teorema 4.4: esiste una sottosuccessione convergente {x kn }. Se S è chiuso il corollario della Proposizione 7.1 garantisce che lim n x kn S. Adesso sappiamo che in uno spazio normato di dimensione finita le palle chiuse sono compatte per successioni, e ci proponiamo di dimostrare che questa è in effetti una caratterizzazione degli spazi normati di dimensione finita. A tal fine utilizzeremo la seguente Proposizione 8.1 Se E è uno spazio normato e G un suo sottospazio proprio esiste x 0 E tale che x 0 = 1 e y x 0 1/2 per y G. DIM. Fissato x E \ G, il numero m = inf y G y x è > 0 grazie alla chiusura di G. Dato comunque y 0 G risulta y + y 0 x y 0 x = y y 0 x + y 0 x y 0 x m y 0 x al variare di y, e di conseguenza anche di y y 0 x + y 0, nel sottospazio G. Scegliendo un y 0 tale che y 0 x < 2m otteniamo il punto x 0 = (x y 0 )/ y 0 x con le proprietà richieste. Teorema 8.3 In uno spazio normato di dimensione infinita le palle chiuse (non degeneri) non sono compatte per successioni. DIM. Sia E di dimensione infinita e sia {x n } E una famiglia numerabile tale che ogni suo sottoinsieme finito sia costituito da vettori linearmente indipendenti. Per q > 1 il sottospazio lineare E q 1 generato da {x 1,..., x q 1 } è chiuso e contenuto propriamente in 23
24 E q, per cui la Proposizione 8.1 garantisce l esistenza di y q E q con le proprietà y q = 1 e y y q 1/2 per y E q 1, quindi per y E p con p < q. Siccome y p y q 1/2 per p q, i vettori y q costituiscono una successione, contenuta nella palla unitaria chiusa di E, da cui non si può estrarre nessuna successione convergente. Nel trasporto agli spazi normati delle nozioni di densità e separabilità si rende utile la seguente osservazione. Supponiamo che E possegga una base di Schauder {u h }. Allora E è separabile: ogni coefficiente complesso α h dello sviluppo in serie n αh u h di un elemento di E è a sua volta limite di una successione di numeri complessi con parti reali e immaginarie in Q. Esempio 8.1 La famiglia {e h } è una base di Schauder in tutti gli spazi c 0 ed in l p, 1 p <, che di conseguenza sono separabili. Invece l non è separabile: la famiglia F delle successioni x α di 0 e di 1 ha la potenza del continuo e per x α x α la distanza di x α e x α vale 1, sicché esiste un infinità non numerabile di palle di centri x α F e raggio 1/3 tutte disgiunte tra loro. Esempio 8.2 Le funzioni continue su un intervallo compatto [a, b] sono (uniformemente continue e quindi) approssimate uniformemente da successioni di funzioni continue lineari a tratti cogli spigoli a coordinate razionali. Conclusione: nella norma del massimo C 0 ([a, b]) è separabile. Esercizi 8.1 Dimostrare che se E è più debole di E ogni chiuso di (E, E ) è anche un chiuso di (E, E ). 8.2 Sia S la successione delle funzioni a triangolo di altezza 1 su [0, 1/n]. Far vedere che S è un chiuso di (C 0 ([0, 1]), ) ma non è un chiuso di (C 0 ([0, 1]), 1 ). 8.3 Dimostrare che in uno spazio normato di dimensione finita una successione decrescente di chiusi e limitati C n non può verificare n N C n = a meno che non risulti C n = definitivamente. 8.4 Dimostrare il Teorema di Dini: Se {f n } C 0 ([0, 1]) converge decrescendo ad una f C 0 ([0, 1]), allora f n f C0 ([0,1]) 0. [Suggerimento: Ricondursi al caso di f identicamente nulla, fissare arbitrariamente ε > 0 e tener conto che, siccome gli insiemi 24
25 chiusi e limitati C n;ε = {x U f n ε} non possono avere intersezione vuota a meno che non risulti C n;ε = definitivamente, è questa seconda eventualità che si deve verificare.] 8.5 Perché la continuità di f = lim n f n non può essere rimossa dalle ipotesi del Teorema di Dini (fermo restando che sarebbe comunque contenuta nella tesi)? 8.6 (i) Dimostrare che ogni famiglia dei vettori e h è un chiuso di l 1. (ii) Sia X uno spazio metrico completo. Dimostrare che una successione decrescente di chiusi e limitati C n può verificare n N C n =, a meno che non risulti diam C n 0, nel qual caso n N C n è un singolo punto. 8.7 (i) Dimostrare che c 0 è la chiusura in l del sottospazio delle successioni definitivamente nulle. (ii) Dimostrare che c è la chiusura in l del sottospazio delle successioni definitivamente costanti. 9 Operatori lineari limitati Se E ed F sono spazi vettoriali (e sottintendiamo: sullo stesso campo K) indichiamo con T x il valore assunto in x E da un operatore lineare T : E F. Quando E ha dimensione finita e F è un qualunque spazio normato, ogni T : E F lineare è automaticamente continuo: data una base {e 1,..., e N } di E il valore di T su un vettore x = x 1 e x N e N è x 1 f x N f N con f k = T e k, e questa è una funzione continua di x. Quando invece dim E è infinita, esistono operatori lineari T : E F che non sono continui: si trovano esempi facili se (Esercizio 10.1), e solo se, non si richiede la completezza di E... A questo riguardo vanno segnalati il Corollario del Teorema 9.4 ed il Teorema 9.5. Teorema 9.1 Siano E, F spazi normati e T un operatore lineare E F. Le seguenti proprietà sono equivalenti: (i) T è continuo in E; (ii) il sup x E =1 T x F è finito; (iii) esiste una costante reale positiva M tale che T x F M x E per x E. DIM. Mostriamo l implicazione (i) = (iii). Sia δ > 0 tale che T y F 1 per y E δ (continuità di T in 0): fissando arbitrariamente x 0 ed applicando la linearità otteniamo T x F = x ( ) E δx F δ T M x E x E con M = 1/δ. Viceversa, la (iii) implica la lipschitzianità T (x y) F M x y E per x, y E, quindi la (i). Che valga la (iii) = (ii) è ovvio, mentre viceversa si vede subito, fissando arbitrariamente x 0 ed applicando la linearità, che se vale la (ii) risulta ( ) x F T x F = x E T M x E x E 25
26 con M = sup x E =1 T x F. La (ii) del teorema si esprime dicendo che T è limitato. La famiglia degli operatori lineari E F continui, ovvero limitati, si indica con L(E, F ). È immediato verificare che L(E, F ) è uno spazio vettoriale su cui l applicazione T sup x E 1 T x F definisce una norma T L(E,F ). Teorema 9.2 L(E, F ) è completo se F è completo. DIM. Data {T n } di Cauchy in L(E, F ) sia ε > 0, e sia ν = ν ε N tale che T m T n L(E,F ) < ε per m, n ν. Allora {T n x} con x E è di Cauchy, dunque convergente ad un vettore T x di F. T è banalmente lineare, e inoltre T x T n x F T x T m x F + T m T n L(E,F ) x E < T x T m x F + ε x E per m, n ν. Facendo tendere m all otteniamo T T n L(E, F ) con T T n L(E,F ) ε : dunque T è continuo, e T T n L(E,F ) 0. Lemma 9.1 Siano E uno spazio normato, F uno spazio di Banach, {T n } una successione di operatori lineari e continui E F con sup n T n L(E,F ) <. Se converge (in F ) ogni successione {T n x} con x D, dove D è un sottoinsieme denso di E, allora esiste T : E F lineare e continuo tale che T n x T x (in F ) per ogni x E. Inoltre T L(E,F ) lim inf n T n L(E,F ). DIM. Per ipotesi T n z C z con C > 0 indipendente tanto da n N che da z E. Sia ε > 0. Fissato arbitrariamente un vettore x E, determiniamo prima y D con la proprietà x y < ε/c, poi ν = ν ε N tale che T m y T n y < ε per m, n ν. Allora {T n x} è di Cauchy: T m x T n x T m (x y) + T m y T n y + T n (y x) < 3ε. Dunque (completezza di F ) per ogni x E esiste in F il vettore T x = lim n T n x. L applicazione x T x è banalmente lineare, e per concludere la dimostrazione basta passare al minimo limite nelle disuguaglianze T n x T n L(E,F ) x, x E. Teorema (di Banach Steinhaus, o dell uniforme limitatezza) 9.3 Siano E uno spazio di Banach, F uno spazio normato, {T α } α A una famiglia di operatori lineari e 26
4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale
 4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale Spazi Metrici Ricordiamo che uno spazio metrico è una coppia (X, d) dove X è un insieme e d : X X [0, + [ è una funzione, detta metrica,
4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale Spazi Metrici Ricordiamo che uno spazio metrico è una coppia (X, d) dove X è un insieme e d : X X [0, + [ è una funzione, detta metrica,
SPAZI METRICI. Uno spazio metrico X con metrica d si indica con il simbolo (X, d). METRICI 1
 SPAZI METRICI Nel piano R 2 o nello spazio R 3 la distanza fra due punti è la lunghezza, o norma euclidea, del vettore differenza di questi due punti. Se p = (x, y, z) è un vettore in coordinate ortonormali,
SPAZI METRICI Nel piano R 2 o nello spazio R 3 la distanza fra due punti è la lunghezza, o norma euclidea, del vettore differenza di questi due punti. Se p = (x, y, z) è un vettore in coordinate ortonormali,
Geometria Superiore Esercizi 1 (da consegnare entro... )
 Geometria Superiore Esercizi 1 (da consegnare entro... ) In questi esercizi analizziamo il concetto di paracompattezza per uno spazio topologico e vediamo come questo implichi l esistenza di partizioni
Geometria Superiore Esercizi 1 (da consegnare entro... ) In questi esercizi analizziamo il concetto di paracompattezza per uno spazio topologico e vediamo come questo implichi l esistenza di partizioni
Per lo svolgimento del corso risulta particolarmente utile considerare l insieme
 1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
10. Insiemi non misurabili secondo Lebesgue.
 10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
Equazioni differenziali ordinarie
 Equazioni differenziali ordinarie Denis Nardin January 2, 2010 1 Equazioni differenziali In questa sezione considereremo le proprietà delle soluzioni del problema di Cauchy. Da adesso in poi (PC) indicherà
Equazioni differenziali ordinarie Denis Nardin January 2, 2010 1 Equazioni differenziali In questa sezione considereremo le proprietà delle soluzioni del problema di Cauchy. Da adesso in poi (PC) indicherà
A i è un aperto in E. i=1
 Proposizione 1. A è aperto se e solo se A c è chiuso. Dimostrazione. = : se x o A c, allora x o A = A o e quindi esiste r > 0 tale che B(x o, r) A; allora x o non può essere di accumulazione per A c. Dunque
Proposizione 1. A è aperto se e solo se A c è chiuso. Dimostrazione. = : se x o A c, allora x o A = A o e quindi esiste r > 0 tale che B(x o, r) A; allora x o non può essere di accumulazione per A c. Dunque
INDICAZIONI PER LA RICERCA DEGLI ASINTOTI VERTICALI
 2.13 ASINTOTI 44 Un "asintoto", per una funzione y = f( ), è una retta alla quale il grafico della funzione "si avvicina indefinitamente", "si avvicina di tanto quanto noi vogliamo", nel senso precisato
2.13 ASINTOTI 44 Un "asintoto", per una funzione y = f( ), è una retta alla quale il grafico della funzione "si avvicina indefinitamente", "si avvicina di tanto quanto noi vogliamo", nel senso precisato
Studio di funzione. Tutti i diritti sono riservati. E vietata la riproduzione, anche parziale, senza il consenso dell autore. Funzioni elementari 2
 Studio di funzione Copyright c 2009 Pasquale Terrecuso Tutti i diritti sono riservati. E vietata la riproduzione, anche parziale, senza il consenso dell autore. Funzioni elementari 2 Studio di funzione
Studio di funzione Copyright c 2009 Pasquale Terrecuso Tutti i diritti sono riservati. E vietata la riproduzione, anche parziale, senza il consenso dell autore. Funzioni elementari 2 Studio di funzione
Esistenza di funzioni continue non differenziabili in alcun punto
 UNIVERSITÀ DEGLI STUDI DI CAGLIARI FACOLTÀ DI SCIENZE MATEMATICHE, FISICHE E NATURALI CORSO DI LAUREA IN MATEMATICA Esistenza di funzioni continue non differenziabili in alcun punto Relatore Prof. Andrea
UNIVERSITÀ DEGLI STUDI DI CAGLIARI FACOLTÀ DI SCIENZE MATEMATICHE, FISICHE E NATURALI CORSO DI LAUREA IN MATEMATICA Esistenza di funzioni continue non differenziabili in alcun punto Relatore Prof. Andrea
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8. Cognome:... Nome:... Matricola:...
 Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
Massimi e minimi vincolati in R 2 - Esercizi svolti
 Massimi e minimi vincolati in R 2 - Esercizi svolti Esercizio 1. Determinare i massimi e minimi assoluti della funzione f(x, y) = 2x + 3y vincolati alla curva di equazione x 4 + y 4 = 1. Esercizio 2. Determinare
Massimi e minimi vincolati in R 2 - Esercizi svolti Esercizio 1. Determinare i massimi e minimi assoluti della funzione f(x, y) = 2x + 3y vincolati alla curva di equazione x 4 + y 4 = 1. Esercizio 2. Determinare
Classificazione Singolarità isolate, Serie di Laurent, Residui, Teorema dei residui e applicazioni
 Classificazione Singolarità isolate, Serie di Laurent, Residui, Teorema dei residui e applicazioni Docente:Alessandra Cutrì Richiamo:Zeri di Funzioni olomorfe (o analitiche) Sia f : A C C A aperto connesso,
Classificazione Singolarità isolate, Serie di Laurent, Residui, Teorema dei residui e applicazioni Docente:Alessandra Cutrì Richiamo:Zeri di Funzioni olomorfe (o analitiche) Sia f : A C C A aperto connesso,
Università degli Studi di Catania A.A. 2012-2013. Corso di laurea in Ingegneria Industriale
 Università degli Studi di Catania A.A. 2012-2013 Corso di laurea in Ingegneria Industriale Corso di Analisi Matematica I (A-E) (Prof. A.Villani) Elenco delle dimostrazioni che possono essere richieste
Università degli Studi di Catania A.A. 2012-2013 Corso di laurea in Ingegneria Industriale Corso di Analisi Matematica I (A-E) (Prof. A.Villani) Elenco delle dimostrazioni che possono essere richieste
19. Inclusioni tra spazi L p.
 19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
1.1. Spazi metrici completi
 SPAZI METRICI: COMPLETEZZA E COMPATTEZZA Note informali dalle lezioni 1.1. Spazi metrici completi La nozione di convergenza di successioni è centrale nello studio degli spazi metrici. In particolare è
SPAZI METRICI: COMPLETEZZA E COMPATTEZZA Note informali dalle lezioni 1.1. Spazi metrici completi La nozione di convergenza di successioni è centrale nello studio degli spazi metrici. In particolare è
+ P a n n=1 + X. a n = a m 3. n=1. m=4. Per poter dare un significato alla somma (formale) di infiniti termini, ricorriamo al seguente procedimento:
 Capitolo 3 Serie 3. Definizione Sia { } una successione di numeri reali. Ci proponiamo di dare significato, quando possibile, alla somma a + a 2 +... + +... di tutti i termini della successione. Questa
Capitolo 3 Serie 3. Definizione Sia { } una successione di numeri reali. Ci proponiamo di dare significato, quando possibile, alla somma a + a 2 +... + +... di tutti i termini della successione. Questa
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 2011/2012
 Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
CAPITOLO IV RISOLUZIONE DEI SISTEMI LINEARI COL METODO DEI DETERMINANTI
 CAPITOLO IV RISOLUZIONE DEI SISTEMI LINEARI COL METODO DEI DETERMINANTI 1. REGOLA DI CRAMER Sia S un sistema lineare di n ( 2) equazioni in n incognite su un campo K : a 11 x 1 + a 12 x 2 + + a 1n x n
CAPITOLO IV RISOLUZIONE DEI SISTEMI LINEARI COL METODO DEI DETERMINANTI 1. REGOLA DI CRAMER Sia S un sistema lineare di n ( 2) equazioni in n incognite su un campo K : a 11 x 1 + a 12 x 2 + + a 1n x n
Appunti di Analisi convessa. Paolo Acquistapace
 Appunti di Analisi convessa Paolo Acquistapace 6 dicembre 2012 Indice 1 Spazi vettoriali topologici 4 1.1 Insiemi convessi.......................... 4 1.2 Funzionale di Minkowski..................... 6
Appunti di Analisi convessa Paolo Acquistapace 6 dicembre 2012 Indice 1 Spazi vettoriali topologici 4 1.1 Insiemi convessi.......................... 4 1.2 Funzionale di Minkowski..................... 6
RICHIAMI SULLE MATRICI. Una matrice di m righe e n colonne è rappresentata come
 RICHIAMI SULLE MATRICI Una matrice di m righe e n colonne è rappresentata come A = a 11 a 12... a 1n a 21 a 22... a 2n............ a m1 a m2... a mn dove m ed n sono le dimensioni di A. La matrice A può
RICHIAMI SULLE MATRICI Una matrice di m righe e n colonne è rappresentata come A = a 11 a 12... a 1n a 21 a 22... a 2n............ a m1 a m2... a mn dove m ed n sono le dimensioni di A. La matrice A può
TOPOLOGIA ALBERTO SARACCO
 TOPOLOGIA ALBERTO SARACCO Abstract. Le presenti note saranno il più fedeli possibile a quanto detto a lezione. I testi consigliati sono Jänich [1], Kosniowski [2] e Singer- Thorpe [3]. Un ottimo libro
TOPOLOGIA ALBERTO SARACCO Abstract. Le presenti note saranno il più fedeli possibile a quanto detto a lezione. I testi consigliati sono Jänich [1], Kosniowski [2] e Singer- Thorpe [3]. Un ottimo libro
Dipendenza dai dati iniziali
 Dipendenza dai dati iniziali Dopo aver studiato il problema dell esistenza e unicità delle soluzioni dei problemi di Cauchy, il passo successivo è vedere come le traiettorie di queste ultime dipendono
Dipendenza dai dati iniziali Dopo aver studiato il problema dell esistenza e unicità delle soluzioni dei problemi di Cauchy, il passo successivo è vedere come le traiettorie di queste ultime dipendono
5. La teoria astratta della misura.
 5. La teoria astratta della misura. 5.1. σ-algebre. 5.1.1. σ-algebre e loro proprietà. Sia Ω un insieme non vuoto. Indichiamo con P(Ω la famiglia di tutti i sottoinsiemi di Ω. Inoltre, per ogni insieme
5. La teoria astratta della misura. 5.1. σ-algebre. 5.1.1. σ-algebre e loro proprietà. Sia Ω un insieme non vuoto. Indichiamo con P(Ω la famiglia di tutti i sottoinsiemi di Ω. Inoltre, per ogni insieme
Parte 2. Metodi Matematici per la Meccanica Quantistica. Spazi di pre-hilbert e spazi di Hilbert. Gianpiero CATTANEO
 Parte Metodi Matematici per la Meccanica Quantistica Spazi di pre-hilbert e spazi di Hilbert Gianpiero CATTANEO 10 giugno 008 Indice I - Spazi con Prodotto Interno e Spazi di Hilbert 5 1 Spazi con Prodotto
Parte Metodi Matematici per la Meccanica Quantistica Spazi di pre-hilbert e spazi di Hilbert Gianpiero CATTANEO 10 giugno 008 Indice I - Spazi con Prodotto Interno e Spazi di Hilbert 5 1 Spazi con Prodotto
SIMULAZIONE TEST ESAME - 1
 SIMULAZIONE TEST ESAME - 1 1. Il dominio della funzione f(x) = log (x2 + 1)(4 x 2 ) (x 2 2x + 1) è: (a) ( 2, 2) (b) ( 2, 1) (1, 2) (c) (, 2) (2, + ) (d) [ 2, 1) (1, 2] (e) R \{1} 2. La funzione f : R R
SIMULAZIONE TEST ESAME - 1 1. Il dominio della funzione f(x) = log (x2 + 1)(4 x 2 ) (x 2 2x + 1) è: (a) ( 2, 2) (b) ( 2, 1) (1, 2) (c) (, 2) (2, + ) (d) [ 2, 1) (1, 2] (e) R \{1} 2. La funzione f : R R
Facoltà di Dipartimento di Ingegneria Elettrica e dell'informazione anno accademico 2014/15 Registro lezioni del docente SPORTELLI LUIGI
 Facoltà di Dipartimento di Ingegneria Elettrica e dell'informazione anno accademico 2014/15 Registro lezioni del docente SPORTELLI LUIGI Attività didattica ANALISI MATEMATICA [2000] Periodo di svolgimento:
Facoltà di Dipartimento di Ingegneria Elettrica e dell'informazione anno accademico 2014/15 Registro lezioni del docente SPORTELLI LUIGI Attività didattica ANALISI MATEMATICA [2000] Periodo di svolgimento:
Informatica Grafica. Un introduzione
 Informatica Grafica Un introduzione Rappresentare la Geometria Operabile da metodi di calcolo automatici Grafica Vettoriale Partiamo dalla rappresentazione di un punto... Spazi Vettoriale SPAZI VETTORIALI
Informatica Grafica Un introduzione Rappresentare la Geometria Operabile da metodi di calcolo automatici Grafica Vettoriale Partiamo dalla rappresentazione di un punto... Spazi Vettoriale SPAZI VETTORIALI
Quesiti di Analisi Matematica A
 Quesiti di Analisi Matematica A Presentiamo una raccolta di quesiti per la preparazione alla prova orale del modulo di Analisi Matematica A. Per una buona preparazione é consigliabile rispondere ad alta
Quesiti di Analisi Matematica A Presentiamo una raccolta di quesiti per la preparazione alla prova orale del modulo di Analisi Matematica A. Per una buona preparazione é consigliabile rispondere ad alta
I appello - 24 Marzo 2006
 Facoltà di Ingegneria - Corso di Laurea in Ing. Energetica e Gestionale A.A.2005/2006 I appello - 24 Marzo 2006 Risolvere gli esercizi motivando tutte le risposte. I.) Studiare la convergenza puntuale,
Facoltà di Ingegneria - Corso di Laurea in Ing. Energetica e Gestionale A.A.2005/2006 I appello - 24 Marzo 2006 Risolvere gli esercizi motivando tutte le risposte. I.) Studiare la convergenza puntuale,
2.1 Definizione di applicazione lineare. Siano V e W due spazi vettoriali su R. Un applicazione
 Capitolo 2 MATRICI Fra tutte le applicazioni su uno spazio vettoriale interessa esaminare quelle che mantengono la struttura di spazio vettoriale e che, per questo, vengono dette lineari La loro importanza
Capitolo 2 MATRICI Fra tutte le applicazioni su uno spazio vettoriale interessa esaminare quelle che mantengono la struttura di spazio vettoriale e che, per questo, vengono dette lineari La loro importanza
NUMERI COMPLESSI. Test di autovalutazione
 NUMERI COMPLESSI Test di autovalutazione 1. Se due numeri complessi z 1 e z 2 sono rappresentati nel piano di Gauss da due punti simmetrici rispetto all origine: (a) sono le radici quadrate di uno stesso
NUMERI COMPLESSI Test di autovalutazione 1. Se due numeri complessi z 1 e z 2 sono rappresentati nel piano di Gauss da due punti simmetrici rispetto all origine: (a) sono le radici quadrate di uno stesso
TOPOLOGIE. Capitolo 2. 2.1 Spazi topologici
 Capitolo 2 TOPOLOGIE Ogni spazio che si considera in gran parte della matematica e delle sue applicazioni è uno spazio topologico di qualche tipo: qui introduciamo in generale le nozioni di base della
Capitolo 2 TOPOLOGIE Ogni spazio che si considera in gran parte della matematica e delle sue applicazioni è uno spazio topologico di qualche tipo: qui introduciamo in generale le nozioni di base della
5 DERIVATA. 5.1 Continuità
 5 DERIVATA 5. Continuità Definizione 5. Sia < a < b < +, f : (a, b) R e c (a, b). Diciamo che f è continua in c se sono verificate le ue conizioni: (i) c esiste (ii) = f(c) c Si osservi che nella efinizione
5 DERIVATA 5. Continuità Definizione 5. Sia < a < b < +, f : (a, b) R e c (a, b). Diciamo che f è continua in c se sono verificate le ue conizioni: (i) c esiste (ii) = f(c) c Si osservi che nella efinizione
x log(x) + 3. f(x) =
 Università di Bari, Corso di Laurea in Economia e Commercio Esame di Matematica per l Economia L/Z Dr. G. Taglialatela 03 giugno 05 Traccia dispari Esercizio. Calcolare Esercizio. Calcolare e cos log d
Università di Bari, Corso di Laurea in Economia e Commercio Esame di Matematica per l Economia L/Z Dr. G. Taglialatela 03 giugno 05 Traccia dispari Esercizio. Calcolare Esercizio. Calcolare e cos log d
7. SINGOLARITA E RESIDUI. 7.1 Punti Singolari Isolati.
 7. SINGOLARITA E RESIDUI. 7. Punti Singolari Isolati. Definizione 55: Si dice che a C é un punto singolare isolato per una funzione f(z), se essa non é olomorfa in a, ma esiste δ > 0 tale che essa sia
7. SINGOLARITA E RESIDUI. 7. Punti Singolari Isolati. Definizione 55: Si dice che a C é un punto singolare isolato per una funzione f(z), se essa non é olomorfa in a, ma esiste δ > 0 tale che essa sia
Programma definitivo Analisi Matematica 2 - a.a. 2005-06 Corso di Laurea Triennale in Ingegneria Civile (ICI)
 1 Programma definitivo Analisi Matematica 2 - a.a. 2005-06 Corso di Laurea Triennale in Ingegneria Civile (ICI) Approssimazioni di Taylor BPS, Capitolo 5, pagine 256 268 Approssimazione lineare, il simbolo
1 Programma definitivo Analisi Matematica 2 - a.a. 2005-06 Corso di Laurea Triennale in Ingegneria Civile (ICI) Approssimazioni di Taylor BPS, Capitolo 5, pagine 256 268 Approssimazione lineare, il simbolo
MINISTERO DELL'ISTRUZIONE, DELL'UNIVERSITÀ, DELLA RICERCA SCUOLE ITALIANE ALL ESTERO
 Sessione Ordinaria in America 4 MINISTERO DELL'ISTRUZIONE, DELL'UNIVERSITÀ, DELLA RICERCA SCUOLE ITALIANE ALL ESTERO (Americhe) ESAMI DI STATO DI LICEO SCIENTIFICO Sessione Ordinaria 4 SECONDA PROVA SCRITTA
Sessione Ordinaria in America 4 MINISTERO DELL'ISTRUZIONE, DELL'UNIVERSITÀ, DELLA RICERCA SCUOLE ITALIANE ALL ESTERO (Americhe) ESAMI DI STATO DI LICEO SCIENTIFICO Sessione Ordinaria 4 SECONDA PROVA SCRITTA
LEZIONE 14. a 1,1 v 1 + a 1,2 v 2 + a 1,3 v 3 + + a 1,n 1 v n 1 + a 1,n v n = w 1
 LEZIONE 14 141 Dimensione di uno spazio vettoriale Abbiamo visto come l esistenza di una base in uno spazio vettoriale V su k = R, C, permetta di sostituire a V, che può essere complicato da trattare,
LEZIONE 14 141 Dimensione di uno spazio vettoriale Abbiamo visto come l esistenza di una base in uno spazio vettoriale V su k = R, C, permetta di sostituire a V, che può essere complicato da trattare,
Introduzione alla programmazione lineare. Mauro Pagliacci
 Introduzione alla programmazione lineare Mauro Pagliacci c Draft date 25 maggio 2010 Premessa In questo fascicolo sono riportati gli appunti dalle lezioni del corso di Elaborazioni automatica dei dati
Introduzione alla programmazione lineare Mauro Pagliacci c Draft date 25 maggio 2010 Premessa In questo fascicolo sono riportati gli appunti dalle lezioni del corso di Elaborazioni automatica dei dati
FUNZIONI CONTINUE - ESERCIZI SVOLTI
 FUNZIONI CONTINUE - ESERCIZI SVOLTI 1) Verificare che x è continua in x 0 per ogni x 0 0 ) Verificare che 1 x 1 x 0 è continua in x 0 per ogni x 0 0 3) Disegnare il grafico e studiare i punti di discontinuità
FUNZIONI CONTINUE - ESERCIZI SVOLTI 1) Verificare che x è continua in x 0 per ogni x 0 0 ) Verificare che 1 x 1 x 0 è continua in x 0 per ogni x 0 0 3) Disegnare il grafico e studiare i punti di discontinuità
16. Vari modi di convergenza delle successioni di funzioni reali misurabili.
 16. Vari modi di convergenza delle successioni di funzioni reali misurabili. L argomento centrale di questa ultima parte del corso è lo studio in generale della convergenza delle successioni negli spazi
16. Vari modi di convergenza delle successioni di funzioni reali misurabili. L argomento centrale di questa ultima parte del corso è lo studio in generale della convergenza delle successioni negli spazi
Corso di Analisi Matematica. Successioni e serie numeriche
 a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Successioni e serie numeriche Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Successioni e serie numeriche Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
Prof. Stefano Capparelli
 APPUNTI PER UN SECONDO CORSO DI ALGEBRA LINEARE Prof. Stefano Capparelli A mia madre Prefazione. Brevi Richiami di Algebra Lineare. Forma Canonica di Jordan.. Blocco di Jordan.. Base di Jordan.. Polinomio
APPUNTI PER UN SECONDO CORSO DI ALGEBRA LINEARE Prof. Stefano Capparelli A mia madre Prefazione. Brevi Richiami di Algebra Lineare. Forma Canonica di Jordan.. Blocco di Jordan.. Base di Jordan.. Polinomio
1 Applicazioni Lineari tra Spazi Vettoriali
 1 Applicazioni Lineari tra Spazi Vettoriali Definizione 1 (Applicazioni lineari) Si chiama applicazione lineare una applicazione tra uno spazio vettoriale ed uno spazio vettoriale sul campo tale che "!$%!
1 Applicazioni Lineari tra Spazi Vettoriali Definizione 1 (Applicazioni lineari) Si chiama applicazione lineare una applicazione tra uno spazio vettoriale ed uno spazio vettoriale sul campo tale che "!$%!
OGNI SPAZIO VETTORIALE HA BASE
 1 Mimmo Arezzo OGNI SPAZIO VETTORIALE HA BASE CONVERSAZIONE CON ALCUNI STUDENTI DI FISICA 19 DICEMBRE 2006 2 1 Preliminari Definizione 1.0.1 Un ordinamento parziale (o una relazione d ordine parziale)
1 Mimmo Arezzo OGNI SPAZIO VETTORIALE HA BASE CONVERSAZIONE CON ALCUNI STUDENTI DI FISICA 19 DICEMBRE 2006 2 1 Preliminari Definizione 1.0.1 Un ordinamento parziale (o una relazione d ordine parziale)
ITCS Erasmo da Rotterdam. Anno Scolastico 2014/2015. CLASSE 4^ M Costruzioni, ambiente e territorio
 ITCS Erasmo da Rotterdam Anno Scolastico 014/015 CLASSE 4^ M Costruzioni, ambiente e territorio INDICAZIONI PER IL LAVORO ESTIVO DI MATEMATICA e COMPLEMENTI di MATEMATICA GLI STUDENTI CON IL DEBITO FORMATIVO
ITCS Erasmo da Rotterdam Anno Scolastico 014/015 CLASSE 4^ M Costruzioni, ambiente e territorio INDICAZIONI PER IL LAVORO ESTIVO DI MATEMATICA e COMPLEMENTI di MATEMATICA GLI STUDENTI CON IL DEBITO FORMATIVO
ELEMENTI DI ANALISI SPETTRALE 1 I DUE DOMINI
 Lezioni di Fisica della Terra Solida, Università di Chieti, a.a. 999/. Docente A. De Santis ELEMENTI DI ANALISI SPETTRALE I DUE DOMINI È spesso utile pensare alle unzioni ed alle loro trasormate di Fourier
Lezioni di Fisica della Terra Solida, Università di Chieti, a.a. 999/. Docente A. De Santis ELEMENTI DI ANALISI SPETTRALE I DUE DOMINI È spesso utile pensare alle unzioni ed alle loro trasormate di Fourier
Syllabus: argomenti di Matematica delle prove di valutazione
 Syllabus: argomenti di Matematica delle prove di valutazione abcdef... ABC (senza calcolatrici, senza palmari, senza telefonini... ) Gli Argomenti A. Numeri frazioni e numeri decimali massimo comun divisore,
Syllabus: argomenti di Matematica delle prove di valutazione abcdef... ABC (senza calcolatrici, senza palmari, senza telefonini... ) Gli Argomenti A. Numeri frazioni e numeri decimali massimo comun divisore,
ESERCIZI DEL CORSO DI INFORMATICA
 ESERCIZI DEL CORSO DI INFORMTIC Questa breve raccolta di esercizi vuole mettere in luce alcuni aspetti della prima parte del corso e fornire qualche spunto di riflessione. Il contenuto del materiale seguente
ESERCIZI DEL CORSO DI INFORMTIC Questa breve raccolta di esercizi vuole mettere in luce alcuni aspetti della prima parte del corso e fornire qualche spunto di riflessione. Il contenuto del materiale seguente
ISTITUTO D'ISTRUZIONE SUPERIORE A. MOTTI
 ISTITUTO D'ISTRUZIONE SUPERIORE A. MOTTI ISTITUTO PROFESSIONALE DI ENOGASTRONOMIA E OSPITALITA ALBERGHIERA CON I PERCORSI: ACCOGLIENZA TURISTICA, CUCINA, SALA-BAR ISTITUTO TECNICO PER IL TURISMO Sede Amministrativa:
ISTITUTO D'ISTRUZIONE SUPERIORE A. MOTTI ISTITUTO PROFESSIONALE DI ENOGASTRONOMIA E OSPITALITA ALBERGHIERA CON I PERCORSI: ACCOGLIENZA TURISTICA, CUCINA, SALA-BAR ISTITUTO TECNICO PER IL TURISMO Sede Amministrativa:
Piano di lavoro di Matematica
 ISTITUTO DI ISTRUZIONE SUPERIORE Liceo Scientifico ALDO MORO Istituto to Tecnico Via Gallo Pecca n. 4/6-10086 Rivarolo Canavese Tel 0124 454511 - Fax 0124 454545 - Cod. Fiscale 85502120018 E-mail: segreteria@istitutomoro.it
ISTITUTO DI ISTRUZIONE SUPERIORE Liceo Scientifico ALDO MORO Istituto to Tecnico Via Gallo Pecca n. 4/6-10086 Rivarolo Canavese Tel 0124 454511 - Fax 0124 454545 - Cod. Fiscale 85502120018 E-mail: segreteria@istitutomoro.it
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica.
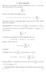 8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
Proprietà metriche di R. Funzioni da R in R. Funzioni continue da R in R. Limiti di funzioni da R in R.
 Università di Trieste - Facoltà d'ingegneria Corsi di Laurea in Ingegneria Chimica, Elettrica, Elettronica, dei Materiali Programma del corso di Analisi Matematica I Anno Accademico 1999-2000 Prof. Pierpaolo
Università di Trieste - Facoltà d'ingegneria Corsi di Laurea in Ingegneria Chimica, Elettrica, Elettronica, dei Materiali Programma del corso di Analisi Matematica I Anno Accademico 1999-2000 Prof. Pierpaolo
1 Serie di Taylor di una funzione
 Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Parte 6. Applicazioni lineari
 Parte 6 Applicazioni lineari A Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Applicazioni fra insiemi, 2 Applicazioni lineari tra spazi vettoriali, 2 3 Applicazioni lineari da R n a R
Parte 6 Applicazioni lineari A Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Applicazioni fra insiemi, 2 Applicazioni lineari tra spazi vettoriali, 2 3 Applicazioni lineari da R n a R
ALGEBRA I: CARDINALITÀ DI INSIEMI
 ALGEBRA I: CARDINALITÀ DI INSIEMI 1. CONFRONTO DI CARDINALITÀ E chiaro a tutti che esistono insiemi finiti cioè con un numero finito di elementi) ed insiemi infiniti. E anche chiaro che ogni insieme infinito
ALGEBRA I: CARDINALITÀ DI INSIEMI 1. CONFRONTO DI CARDINALITÀ E chiaro a tutti che esistono insiemi finiti cioè con un numero finito di elementi) ed insiemi infiniti. E anche chiaro che ogni insieme infinito
Appunti di Complementi di Matematica. Jacobo Pejsachowicz (a cura di Nathan Quadrio)
 Appunti di Complementi di Matematica Jacobo Pejsachowicz (a cura di Nathan Quadrio) 1 Indice 1 Cenni della teoria degli insiemi 4 1.1 Classi ed insiemi........................... 4 1.2 Operazioni fra gli
Appunti di Complementi di Matematica Jacobo Pejsachowicz (a cura di Nathan Quadrio) 1 Indice 1 Cenni della teoria degli insiemi 4 1.1 Classi ed insiemi........................... 4 1.2 Operazioni fra gli
COGNOME e NOME: FIRMA: MATRICOLA:
 Anno Accademico 203/ 204 Corsi di Analisi Matematica I (Proff A Villani e F Faraci) Prova d Esame del giorno 6 febbraio 204 Prima prova scritta (compito A) Non sono consentiti formulari, appunti, libri
Anno Accademico 203/ 204 Corsi di Analisi Matematica I (Proff A Villani e F Faraci) Prova d Esame del giorno 6 febbraio 204 Prima prova scritta (compito A) Non sono consentiti formulari, appunti, libri
0.1 Esercizi calcolo combinatorio
 0.1 Esercizi calcolo combinatorio Esercizio 1. Sia T l insieme dei primi 100 numeri naturali. Calcolare: 1. Il numero di sottoinsiemi A di T che contengono esattamente 8 pari.. Il numero di coppie (A,
0.1 Esercizi calcolo combinatorio Esercizio 1. Sia T l insieme dei primi 100 numeri naturali. Calcolare: 1. Il numero di sottoinsiemi A di T che contengono esattamente 8 pari.. Il numero di coppie (A,
Richiami su norma di un vettore e distanza, intorni sferici in R n, insiemi aperti, chiusi, limitati e illimitati.
 PROGRAMMA di Fondamenti di Analisi Matematica 2 (DEFINITIVO) A.A. 2010-2011, Paola Mannucci, Canale 2 Ingegneria gestionale, meccanica e meccatronica, Vicenza Testo Consigliato: Analisi Matematica, M.
PROGRAMMA di Fondamenti di Analisi Matematica 2 (DEFINITIVO) A.A. 2010-2011, Paola Mannucci, Canale 2 Ingegneria gestionale, meccanica e meccatronica, Vicenza Testo Consigliato: Analisi Matematica, M.
Esercitazioni di statistica
 Esercitazioni di statistica Misure di associazione: Indipendenza assoluta e in media Stefania Spina Universitá di Napoli Federico II stefania.spina@unina.it 22 ottobre 2014 Stefania Spina Esercitazioni
Esercitazioni di statistica Misure di associazione: Indipendenza assoluta e in media Stefania Spina Universitá di Napoli Federico II stefania.spina@unina.it 22 ottobre 2014 Stefania Spina Esercitazioni
Chiusura lineare. N.B. A può essere indifferentemente un insieme, finito o no, o un sistema. Es.1. Es.2
 Chiusura lineare Def. Sia A V (K) con A. Si dice copertura lineare (o chiusura lineare) di A, e si indica con L(A), l insieme dei vettori di V che risultano combinazioni lineari di un numero finito di
Chiusura lineare Def. Sia A V (K) con A. Si dice copertura lineare (o chiusura lineare) di A, e si indica con L(A), l insieme dei vettori di V che risultano combinazioni lineari di un numero finito di
Durata della prova: 3h. 2 +y 4. tan y sin y lim = 1. (x 4 +y 2 )y 3
 Università degli Studi di Napoli Federico II Corso di Laurea in Matematica Analisi Matematica II (Gruppo ), A.A. 22/3 Prova scritta del 28 gennaio 23 Durata della prova: 3h. sercizio (8 punti). Si consideri
Università degli Studi di Napoli Federico II Corso di Laurea in Matematica Analisi Matematica II (Gruppo ), A.A. 22/3 Prova scritta del 28 gennaio 23 Durata della prova: 3h. sercizio (8 punti). Si consideri
ESERCIZI DI ALGEBRA LINEARE E GEOMETRIA
 ESERCIZI DI ALGEBRA LINEARE E GEOMETRIA Francesco Bottacin Padova, 24 febbraio 2012 Capitolo 1 Algebra Lineare 1.1 Spazi e sottospazi vettoriali Esercizio 1.1. Sia U il sottospazio di R 4 generato dai
ESERCIZI DI ALGEBRA LINEARE E GEOMETRIA Francesco Bottacin Padova, 24 febbraio 2012 Capitolo 1 Algebra Lineare 1.1 Spazi e sottospazi vettoriali Esercizio 1.1. Sia U il sottospazio di R 4 generato dai
1 Numeri Complessi, Formula di Eulero, Decomposizioni Notevoli,... ecc.
 Classi Numeriche 1 1 Numeri Complessi, Formula di Eulero, Decomposizioni Notevoli,... ecc. In questo breve capitolo richiamiamo le definizioni delle classi numeriche fondamentali, già note al lettore,
Classi Numeriche 1 1 Numeri Complessi, Formula di Eulero, Decomposizioni Notevoli,... ecc. In questo breve capitolo richiamiamo le definizioni delle classi numeriche fondamentali, già note al lettore,
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
Richiami sulle derivate parziali e definizione di gradiente di una funzione, sulle derivate direzionali. Regola della catena per funzioni composte.
 PROGRAMMA di Fondamenti di Analisi Matematica 2 (che sarà svolto fino al 7 gennaio 2013) A.A. 2012-2013, Paola Mannucci e Claudio Marchi, Canali 1 e 2 Ingegneria Gestionale, Meccanica-Meccatronica, Vicenza
PROGRAMMA di Fondamenti di Analisi Matematica 2 (che sarà svolto fino al 7 gennaio 2013) A.A. 2012-2013, Paola Mannucci e Claudio Marchi, Canali 1 e 2 Ingegneria Gestionale, Meccanica-Meccatronica, Vicenza
Serie numeriche. 1 Definizioni e proprietà elementari
 Serie numeriche Definizioni e proprietà elementari Sia { } una successione, definita per ogni numero naturale n n. Per ogni n n, consideriamo la somma s n degli elementi della successione di posto d s
Serie numeriche Definizioni e proprietà elementari Sia { } una successione, definita per ogni numero naturale n n. Per ogni n n, consideriamo la somma s n degli elementi della successione di posto d s
Capitolo 1 ANALISI COMPLESSA
 Capitolo 1 ANALISI COMPLESSA 1 1.4 Serie in campo complesso 1.4.1 Serie di potenze Una serie di potenze è una serie del tipo a k (z z 0 ) k. Per le serie di potenze in campo complesso valgono teoremi analoghi
Capitolo 1 ANALISI COMPLESSA 1 1.4 Serie in campo complesso 1.4.1 Serie di potenze Una serie di potenze è una serie del tipo a k (z z 0 ) k. Per le serie di potenze in campo complesso valgono teoremi analoghi
Funzioni in più variabili
 Funzioni in più variabili Corso di Analisi 1 di Andrea Centomo 27 gennaio 2011 Indichiamo con R n, n 1, l insieme delle n-uple ordinate di numeri reali R n4{(x 1, x 2,,x n ), x i R, i =1,,n}. Dato X R
Funzioni in più variabili Corso di Analisi 1 di Andrea Centomo 27 gennaio 2011 Indichiamo con R n, n 1, l insieme delle n-uple ordinate di numeri reali R n4{(x 1, x 2,,x n ), x i R, i =1,,n}. Dato X R
3. Sia g(x) = 4. Si calcoli l area del triangolo mistilineo ROS, ove l arco RS appartiene al grafico di f(x) o, indifferentemente, di g(x).
 Esame liceo Scientifico : ordinamento Il candidato risolva uno dei due problemi e risponda a 5 quesiti del questionario. PROBLEMI Problema. Sia ABCD un quadrato di lato, P un punto di AB e γ la circonferenza
Esame liceo Scientifico : ordinamento Il candidato risolva uno dei due problemi e risponda a 5 quesiti del questionario. PROBLEMI Problema. Sia ABCD un quadrato di lato, P un punto di AB e γ la circonferenza
Elementi di matematica finanziaria
 Elementi di matematica finanziaria 1. Percentuale Si dice percentuale di una somma di denaro o di un altra grandezza, una parte di questa, calcolata in base ad un tanto per cento, che si chiama tasso percentuale.
Elementi di matematica finanziaria 1. Percentuale Si dice percentuale di una somma di denaro o di un altra grandezza, una parte di questa, calcolata in base ad un tanto per cento, che si chiama tasso percentuale.
Sulla monotonia delle funzioni reali di una variabile reale
 Liceo G. B. Vico - Napoli Sulla monotonia delle funzioni reali di una variabile reale Prof. Giuseppe Caputo Premetto due teoremi come prerequisiti necessari per la comprensione di quanto verrà esposto
Liceo G. B. Vico - Napoli Sulla monotonia delle funzioni reali di una variabile reale Prof. Giuseppe Caputo Premetto due teoremi come prerequisiti necessari per la comprensione di quanto verrà esposto
Problemi al contorno per equazioni e sistemi di equazioni ellittiche, paraboliche ed iperboliche in domini a frontiera non regolare.
 Prof.ssa Diomeda Lorenza Maria Professore Ordinario Dipartimento di Scienze Economiche Area Matematica Facoltà di Economia, Via C.Rosalba 53- Bari Tel. 080-5049169 Fax 080-5049207 E-mail diomeda@matfin.uniba.it
Prof.ssa Diomeda Lorenza Maria Professore Ordinario Dipartimento di Scienze Economiche Area Matematica Facoltà di Economia, Via C.Rosalba 53- Bari Tel. 080-5049169 Fax 080-5049207 E-mail diomeda@matfin.uniba.it
CONCETTO DI LIMITE DI UNA FUNZIONE REALE
 CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
Successioni e serie di funzioni
 Successioni e serie di funzioni A. Albanese, A. Leaci, D. Pallara In questa dispensa generalizzeremo la trattazione delle successioni e delle serie al caso in cui i termini delle stesse siano non numeri
Successioni e serie di funzioni A. Albanese, A. Leaci, D. Pallara In questa dispensa generalizzeremo la trattazione delle successioni e delle serie al caso in cui i termini delle stesse siano non numeri
LEZIONE 16. Proposizione 16.1.2. Siano V e W spazi vettoriali su k = R, C. Se f: V W
 LEZIONE 16 16.1. Applicazioni lineari iniettive e suriettive. Ricordo le seguenti due definizioni valide per applicazioni di qualsiasi tipo ϕ: X Y fra due insiemi. L applicazione ϕ si dice iniettiva se
LEZIONE 16 16.1. Applicazioni lineari iniettive e suriettive. Ricordo le seguenti due definizioni valide per applicazioni di qualsiasi tipo ϕ: X Y fra due insiemi. L applicazione ϕ si dice iniettiva se
SESSIONE ORDINARIA 2007 CORSO DI ORDINAMENTO SCUOLE ITALIANE ALL ESTERO - AMERICHE
 SESSIONE ORDINARIA 007 CORSO DI ORDINAMENTO SCUOLE ITALIANE ALL ESTERO - AMERICHE PROBLEMA Si consideri la funzione f definita da f ( x) x, il cui grafico è la parabola.. Si trovi il luogo geometrico dei
SESSIONE ORDINARIA 007 CORSO DI ORDINAMENTO SCUOLE ITALIANE ALL ESTERO - AMERICHE PROBLEMA Si consideri la funzione f definita da f ( x) x, il cui grafico è la parabola.. Si trovi il luogo geometrico dei
Illustrazione 1: Telaio. Piantanida Simone 1 G Scopo dell'esperienza: Misura di grandezze vettoriali
 Piantanida Simone 1 G Scopo dell'esperienza: Misura di grandezze vettoriali Materiale utilizzato: Telaio (carrucole,supporto,filo), pesi, goniometro o foglio con goniometro stampato, righello Premessa
Piantanida Simone 1 G Scopo dell'esperienza: Misura di grandezze vettoriali Materiale utilizzato: Telaio (carrucole,supporto,filo), pesi, goniometro o foglio con goniometro stampato, righello Premessa
Note del corso di SISTEMI DINAMICI. Massimiliano Berti
 Note del corso di SISTEMI DINAMICI Massimiliano Berti 16 Dicembre 2011 Versione preliminare Introduzione Va sotto il nome Sistemi Dinamici la teoria delle equazioni differenziali ordinarie, cioè di equazioni
Note del corso di SISTEMI DINAMICI Massimiliano Berti 16 Dicembre 2011 Versione preliminare Introduzione Va sotto il nome Sistemi Dinamici la teoria delle equazioni differenziali ordinarie, cioè di equazioni
Online Gradient Descent
 F94 Metodi statistici per l apprendimento Online Gradient Descent Docente: Nicolò Cesa-Bianchi versione 9 aprile 06 L analisi del Perceptrone ha rivelato come sia possibile ottenere dei maggioranti sul
F94 Metodi statistici per l apprendimento Online Gradient Descent Docente: Nicolò Cesa-Bianchi versione 9 aprile 06 L analisi del Perceptrone ha rivelato come sia possibile ottenere dei maggioranti sul
Appunti del corso di Probabilità e Processi Stocastici
 Appunti del corso di Probabilità e Processi Stocastici in continua revisione e aggiornamento Michele Gianfelice Dipartimento di Matematica Università della Calabria Campus di Arcavacata Ponte Pietro Bucci
Appunti del corso di Probabilità e Processi Stocastici in continua revisione e aggiornamento Michele Gianfelice Dipartimento di Matematica Università della Calabria Campus di Arcavacata Ponte Pietro Bucci
Ottimizazione vincolata
 Ottimizazione vincolata Ricordiamo alcuni risultati provati nella scheda sulla Teoria di Dini per una funzione F : R N+M R M di classe C 1 con (x 0, y 0 ) F 1 (a), a = (a 1,, a M ), punto in cui vale l
Ottimizazione vincolata Ricordiamo alcuni risultati provati nella scheda sulla Teoria di Dini per una funzione F : R N+M R M di classe C 1 con (x 0, y 0 ) F 1 (a), a = (a 1,, a M ), punto in cui vale l
Note integrative ed Esercizi consigliati
 - a.a. 2006-07 Corso di Laurea Specialistica in Ingegneria Civile (CIS) Note integrative ed consigliati Laura Poggiolini e Gianna Stefani Indice 0 1 Convergenza uniforme 1 2 Convergenza totale 5 1 Numeri
- a.a. 2006-07 Corso di Laurea Specialistica in Ingegneria Civile (CIS) Note integrative ed consigliati Laura Poggiolini e Gianna Stefani Indice 0 1 Convergenza uniforme 1 2 Convergenza totale 5 1 Numeri
CAPITOLO V. DATABASE: Il modello relazionale
 CAPITOLO V DATABASE: Il modello relazionale Il modello relazionale offre una rappresentazione matematica dei dati basata sul concetto di relazione normalizzata. I principi del modello relazionale furono
CAPITOLO V DATABASE: Il modello relazionale Il modello relazionale offre una rappresentazione matematica dei dati basata sul concetto di relazione normalizzata. I principi del modello relazionale furono
Se x* e punto di minimo (locale) per la funzione nell insieme Ω, Ω = { x / g i (x) 0 i I, h j (x)= 0 j J } lo e anche per F(x) = f o (x) + c x x 2
 NLP -OPT 1 CONDIZION DI OTTIMO [ Come ricavare le condizioni di ottimo. ] Si suppone x* sia punto di ottimo (minimo) per il problema min f o (x) con vincoli g i (x) 0 i I h j (x) = 0 j J la condizione
NLP -OPT 1 CONDIZION DI OTTIMO [ Come ricavare le condizioni di ottimo. ] Si suppone x* sia punto di ottimo (minimo) per il problema min f o (x) con vincoli g i (x) 0 i I h j (x) = 0 j J la condizione
Integrali di Riemann e di Cauchy
 Integrali di Riemann e di Cauchy Gianni Gilardi Pavia, 14 novembre 1997 L integrale nell ambito delle teorie di Riemann e di Cauchy, fra loro equivalenti, può essere introdotto in vari modi e queste pagine
Integrali di Riemann e di Cauchy Gianni Gilardi Pavia, 14 novembre 1997 L integrale nell ambito delle teorie di Riemann e di Cauchy, fra loro equivalenti, può essere introdotto in vari modi e queste pagine
Lezione 12 Argomenti
 Lezione 12 Argomenti Costi di produzione: differenza tra costo economico e costo contabile I costi nel breve periodo Relazione di breve periodo tra funzione di produzione, produttività del lavoro e costi
Lezione 12 Argomenti Costi di produzione: differenza tra costo economico e costo contabile I costi nel breve periodo Relazione di breve periodo tra funzione di produzione, produttività del lavoro e costi
Autovalori e Autovettori
 Daniela Lera Università degli Studi di Cagliari Dipartimento di Matematica e Informatica A.A. 2008-2009 Autovalori e Autovettori Definizione Siano A C nxn, λ C, e x C n, x 0, tali che Ax = λx. (1) Allora
Daniela Lera Università degli Studi di Cagliari Dipartimento di Matematica e Informatica A.A. 2008-2009 Autovalori e Autovettori Definizione Siano A C nxn, λ C, e x C n, x 0, tali che Ax = λx. (1) Allora
2/4 OPERATORI NEGLI SPAZI DI HILBERT INFINITODIMENSIONALI 08/09 1 INTRODUZIONE
 2/4 OPERATORI NEGLI SPAZI DI HILBERT INFINITODIMENSIONALI 08/09 INTRODUZIONE Il problema agli autovalori di un operatore La trattazione del problema agli autovalori di un operatore fatta negli spazi finitodimensionali
2/4 OPERATORI NEGLI SPAZI DI HILBERT INFINITODIMENSIONALI 08/09 INTRODUZIONE Il problema agli autovalori di un operatore La trattazione del problema agli autovalori di un operatore fatta negli spazi finitodimensionali
F (x) = f(x) per ogni x I. Per esempio:
 Funzioni Primitive (Integrali Indefiniti) (l.v.) Pur essendo un argomento che fa parte del Calcolo Differenziale, molti autori inseriscono funzioni primitive nel capitolo sul Calcolo Integrale, in quanto
Funzioni Primitive (Integrali Indefiniti) (l.v.) Pur essendo un argomento che fa parte del Calcolo Differenziale, molti autori inseriscono funzioni primitive nel capitolo sul Calcolo Integrale, in quanto
Banchi ortogonali Casi importanti
 anchi ortogonali anchi ortogonali Casi importanti Trasformata a blocchi (JPEG, MPEG) anchi a due canali (JPEG 000) anchi modulati Trasformata di Fourier a blocchi (OFDM) anchi coseno-modulati (AC3, MUSICAM)
anchi ortogonali anchi ortogonali Casi importanti Trasformata a blocchi (JPEG, MPEG) anchi a due canali (JPEG 000) anchi modulati Trasformata di Fourier a blocchi (OFDM) anchi coseno-modulati (AC3, MUSICAM)
Richiami di algebra lineare e geometria di R n
 Richiami di algebra lineare e geometria di R n combinazione lineare, conica e convessa spazi lineari insiemi convessi, funzioni convesse rif. BT.5 Combinazione lineare, conica, affine, convessa Un vettore
Richiami di algebra lineare e geometria di R n combinazione lineare, conica e convessa spazi lineari insiemi convessi, funzioni convesse rif. BT.5 Combinazione lineare, conica, affine, convessa Un vettore
OFFERTA DI LAVORO. p * C = M + w * L
 1 OFFERTA DI LAVORO Supponiamo che il consumatore abbia inizialmente un reddito monetario M, sia che lavori o no: potrebbe trattarsi di un reddito da investimenti, di donazioni familiari, o altro. Definiamo
1 OFFERTA DI LAVORO Supponiamo che il consumatore abbia inizialmente un reddito monetario M, sia che lavori o no: potrebbe trattarsi di un reddito da investimenti, di donazioni familiari, o altro. Definiamo
Riconoscere e formalizzare le dipendenze funzionali
 Riconoscere e formalizzare le dipendenze funzionali Giorgio Ghelli 25 ottobre 2007 1 Riconoscere e formalizzare le dipendenze funzionali Non sempre è facile indiduare le dipendenze funzionali espresse
Riconoscere e formalizzare le dipendenze funzionali Giorgio Ghelli 25 ottobre 2007 1 Riconoscere e formalizzare le dipendenze funzionali Non sempre è facile indiduare le dipendenze funzionali espresse
Definizione Dati due insiemi A e B, contenuti nel campo reale R, si definisce funzione reale di variabile reale una legge f : A
 Scopo centrale, sia della teoria statistica che della economica, è proprio quello di esprimere ed analizzare le relazioni, esistenti tra le variabili statistiche ed economiche, che, in linguaggio matematico,
Scopo centrale, sia della teoria statistica che della economica, è proprio quello di esprimere ed analizzare le relazioni, esistenti tra le variabili statistiche ed economiche, che, in linguaggio matematico,
Prova scritta di Geometria 2 Prof. M. Boratynski
 10/9/2008 Es. 1: Si consideri la forma bilineare simmetrica b su R 3 associata, rispetto alla base canonica {e 1, e 2, e 3 } alla matrice 3 2 1 A = 2 3 0. 1 0 1 1) Provare che (R 3, b) è uno spazio vettoriale
10/9/2008 Es. 1: Si consideri la forma bilineare simmetrica b su R 3 associata, rispetto alla base canonica {e 1, e 2, e 3 } alla matrice 3 2 1 A = 2 3 0. 1 0 1 1) Provare che (R 3, b) è uno spazio vettoriale
SERIE NUMERICHE. prof. Antonio Greco 6-11-2013
 SERIE NUMERICHE prof. Antonio Greco 6--203 Indice Motivazioni........... 3 Definizione........... 3 Errore tipico........... 3 Un osservazione utile...... 3 Condizione necessaria...... 4 Serie armonica.........
SERIE NUMERICHE prof. Antonio Greco 6--203 Indice Motivazioni........... 3 Definizione........... 3 Errore tipico........... 3 Un osservazione utile...... 3 Condizione necessaria...... 4 Serie armonica.........
Operatori non limitati con domini densi in spazi di Hilbert.
 Capitolo 5 Operatori non limitati con domini densi in spazi di Hilbert. In questo capitolo estenderemo la teoria degli operatori in spazi di Hilbert considerando operatori non limitati (in particolare
Capitolo 5 Operatori non limitati con domini densi in spazi di Hilbert. In questo capitolo estenderemo la teoria degli operatori in spazi di Hilbert considerando operatori non limitati (in particolare
