FONDAMENTI DI SEGNALI E TRASMISSIONE 5 Laboratorio
|
|
|
- Giordano Grilli
- 4 anni fa
- Visualizzazioni
Transcript
1 FONDAMENTI DI SEGNALI E TRASMISSIONE 5 Laboratorio Paolo Mazzucchelli mazzucch@elet.polimi.it MATLAB: generazione di numeri casuali Il comando che permette di generare una matrice (n r,n c ) composta da numeri casuali, con distribuzione di probabilità uniforme nell intervallo 0 1 è: U=rand(nr,nc); (dove nr e nc rappresentano il numero di righe e di colonne della matrice). Esiste un analogo comando per generare una matrice (n r,n c ) composta da numeri casuali, con distribuzione di probabilità gaussiana, a media nulla e varianza unitaria: N=randn(nr,nc); Per generare una matrice (n r,n c ) composta da numeri casuali, con distribuzione di probabilità gaussiana, a media m e varianza v: N=m+randn(nr,nc)*sqrt(v); MATLAB: stima e visualizzazione di distribuzioni di probabilità Data un insieme di numeri casuali, la distribuzione di probabilità da cui sono generati si può approssimare calcolando l istogramma della sequenza di realizzazioni. Il comando MATLAB per calcolare l istogramma di un vettore x è: H=hist(x,b); (dove b è un vettore che contiene i centri delle celle rispetto alle quali è calcolato l istogramma). Per poter calcolare correttamente la frequenza relativa frr delle estrazioni x, è necessario scalare il risultato per il numero di prove N, e per la dimensione della cella dell istogramma (una variabile casuale continua): frr=hist(x,b)/n/bin; L istogramma della frequenza relativa così calcolata, che approssima la distribuzione di probabilità, può essere visualizzata con il comando: bar(b,frr); Si generi una sequenza di N=10000 numeri casuali che simulino il lancio di un dado. Si simuli poi il lancio di due dadi. Si visualizzino nei due casi le frequenze relative. N=10000; % numero di prove x=rand(1,n); % distribuzione uniforme dado=floor(x*6)+1; frr=hist(dado,[1:6])/n; subplot(1,2,1), bar([1:6],frr); dadi=floor(rand(2,n)*6)+1; frr=hist(sum(dadi),[2:12])/n; % somma per colonne subplot(1,2,2), bar([2:12],frr); 1
2 Si generi una sequenza di N= numeri casuali estratti da una distribuzione gaussiana a media nulla, con varianza σ 2 =100. Si confronti la distribuzione di probabilità stimata con la distribuzione di probabilità gaussiana. N=100000; % numero di prove y=randn(1,n)*sqrt(100); % distribuzione gaussiana frr=hist(y,[-40:40])/n; % attenzione, scalare per la dim. della cella dell istogramma x=[-40:.1:40]; ddp=1/sqrt(2*pi*100)*exp(-x.^2/(2*100)); bar([-40:40],frr); hold on, plot(x,ddp, r ); 2
3 Calcolo di media e varianza La funzione MATLAB che calcola la media di una sequenza di numeri casuali è: m=mean(x); La funzione MATLAB che calcola la varianza di una sequenza di numeri casuali è: v=var(x); E anche possibile calcolare la deviazione standard di un vettore di numeri casuali: s=std(x) Si ricorda che vale la relazione s=sqrt(v)! Se i numeri casuali x sono generati da una distribuzione di probabilità, i valori stimati m e v approssimano media e varianza vere all aumentare del numero di realizzazioni (lunghezza del vettore x) Si stimino media e varianza della distribuzione di probabilità uniforme nell intervallo 0 1, al variare del numero N di prove a disposizione. Si confronti con il risultato noto dalla teoria. Si utilizzi: N=[10:50:10000]; N=[10:50:10000]; t=length(n); varianza=zeros(1,t); media=zeros(1,t); for m=1:t, x=rand(1,n(m)); varianza(m)=var(x); media(m)=mean(x); end, subplot(2,1,1), plot(n,varianza, r,n,ones(1,t)/12, --b ); subplot(2,1,2), plot(n,media, r,n,ones(1,t)*0.5, --b ); 3
4 Teorema del limite centrale Si vuole verificare sperimentalmente il teorema del limite centrale. Si sommino 50 variabili indipendenti con distribuzione uniforme (N=10000 prove) e si confronti la frequenza relativa della distribuzione somma, con il risultato teorico (distribuzione gaussiana con media e varianza note dalla teoria). Quante variabili indipendenti è necessario sommare per approssimare la distribuzione gaussiana? Np=10000; % numero di prove Nv=50; % numero di variabili indipendenti y=rand(nv,np); % distribuzione uniforme Sy=sum(y); % distr. somma media =Nv*.5; varianza=nv*1/12; x=[-4*sqrt(varianza):.5:4*sqrt(varianza)]+media; frr=hist(sy,x)/np/.5; ddp=1/sqrt(2*pi*varianza)*exp(-(x-media).^2/(2*varianza)); bar(x,frr); hold on; plot(x,ddp,'r'); Processo casuale attraverso un filtro lineare Un processo casuale stazionario x(t), può essere descritto nel dominio delle frequenze dalla densità spettrale di potenza S x (f), definita come trasformata di Fourier della funzione di autocorrelazione del processo x(t). La densità spettrale di potenza può essere stimata come: S x (f)=p x (f)/ f X(f) 2 / Ν t La densità spettrale di un processo bianco è una costante di ampiezza σ 2 (autocorrelazione impulsiva). Questo non significa che la S x (f) stimata sia costante per una realizzazione, anzi! È una costante la media di infinite realizzazioni della densità spettrale di potenza! Se il processo casuale x(t) viene filtrato da un filtro con risposta in frequenza H(f), La densità spettrale di potenza in uscita sarà: 4
5 S y (f)= H(f) 2 S x (f) Si generi una realizzazione (N=1000 campioni) di un processo casuale bianco (discretizzato con passo dt=1 ms), con distribuzione gaussiana (di varianza σ 2 =50 ). Si stimi la densità spettrale di potenza. Si stimi nuovamente la densità spettrale di potenza mediando 50 realizzazioni. Si filtrino ora le diverse realizzazioni con un filtro con risposta impulsiva h(t) rettangolare (durata T=0.05 sec). Si stimi la densità spettrale di potenza in uscita, e la si confronti con il risultato teorico noto. N=1000; dt=0.001; t=[0:n-1]*dt; x=randn(1,n)*sqrt(50); % processo casuale Sx=fftshift(abs(fft(x)).^2)/N; % stima della d.s. di pot. df=1/(n*dt); f=[-n/2+[0:n-1]]*df; Sm=zeros(1,N); for k=1:50, x=randn(1,n)*sqrt(50); Sm=Sm+(fftshift(abs(fft(x)).^2)/N)/50; % stima della d.s.p. mediata end, subplot(2,1,1); plot(f,sx,'b'); axis([ ]); subplot(2,1,2); plot(f,sm,'b'); axis([ ]); xlabel('frequenza [Hz]') 5
6 Si vuole ora costruire il filtro rettangolare (T=0.05 sec.). Si stimerà la densità spettrale di potenza S y (f) sempre come media di 50 realizzazioni. Si consiglia di visualizzare il risultato in scala logaritmica (comando semilogy) T= 0.05; M= T/dt; h=ones(1,m)/t; Sy=zeros(1,N); for k=1:50, x=randn(1,n)*sqrt(50); y=conv(x,h)*dt; Sy=Sy+(fftshift(abs(fft(y(1:N))).^2)/N)/50; end, Hf=(1/M*sin(pi*f*dt*M)./sin(pi*f*dt)); % trasformata del rettangolo % discreto di durata M camp. Hf(find(f==0))=1; % -> H(f)=sinc.Per.(f) semilogy(f,abs(hf).^2*50,'-r'); % Sy(f) teorica hold on; semilogy(f,sy,'.b'); % Sy(f) stimata axis([ e-3 1e2]); grid; xlabel('frequenza [Hz]'); 6
FONDAMENTI DI SEGNALI E TRASMISSIONE 4 Laboratorio
 FONDAMENTI DI SEGNALI E TRASMISSIONE 4 Laboratorio Paolo Mazzucchelli mazzucch@elet.polimi.it MATLAB: generazione di numeri casuali Il comando che permette di generare una matrice (n r,n c ) composta da
FONDAMENTI DI SEGNALI E TRASMISSIONE 4 Laboratorio Paolo Mazzucchelli mazzucch@elet.polimi.it MATLAB: generazione di numeri casuali Il comando che permette di generare una matrice (n r,n c ) composta da
Fondamenti di Segnali e Trasmissione Quarto laboratorio
 Fondamenti di Segnali e Trasmissione Quarto laboratorio MATLAB: generazione di numeri casuali Il comando che permette di generare una matrice (nr,nc) composta da numeri casuali, con distribuzione di probabilità
Fondamenti di Segnali e Trasmissione Quarto laboratorio MATLAB: generazione di numeri casuali Il comando che permette di generare una matrice (nr,nc) composta da numeri casuali, con distribuzione di probabilità
FONDAMENTI DI SEGNALI E TRASMISSIONE 4 Laboratorio
 FONDAMENTI DI SEGNALI E TRASMISSIONE 4 Laboratorio Paolo Mazzucchelli mazzucch@elet.polimi.it Campionamento di segnali In MATLAB, qualunque segnale continuo è approssimato da una sequenza campionata. Si
FONDAMENTI DI SEGNALI E TRASMISSIONE 4 Laboratorio Paolo Mazzucchelli mazzucch@elet.polimi.it Campionamento di segnali In MATLAB, qualunque segnale continuo è approssimato da una sequenza campionata. Si
Generazione di Numeri Casuali- Parte 2
 Esercitazione con generatori di numeri casuali Seconda parte Sommario Trasformazioni di Variabili Aleatorie Trasformazione non lineare: numeri casuali di tipo Lognormale Trasformazioni affini Numeri casuali
Esercitazione con generatori di numeri casuali Seconda parte Sommario Trasformazioni di Variabili Aleatorie Trasformazione non lineare: numeri casuali di tipo Lognormale Trasformazioni affini Numeri casuali
FONDAMENTI DI SEGNALI E TRASMISSIONE 2 Laboratorio
 FONDAMENTI DI SEGNALI E TRASMISSIONE 2 Laboratorio Paolo Mazzucchelli mazzucch@elet.polimi.it MATLAB: linguaggio di programmazione L ambiente MATLAB possiede un completo linguaggio di programmazione. Vediamo
FONDAMENTI DI SEGNALI E TRASMISSIONE 2 Laboratorio Paolo Mazzucchelli mazzucch@elet.polimi.it MATLAB: linguaggio di programmazione L ambiente MATLAB possiede un completo linguaggio di programmazione. Vediamo
FONDAMENTI DI SEGNALI E TRASMISSIONE 6 Laboratorio
 FONDAMENTI DI SEGNALI E TRASMISSIONE 6 Laboratorio Paolo Mazzucchelli mazzucch@elet.polimi.it Quantizzazione Il segnale y(t) non solo è campionato sull asse dei tempi, ma anche i valori di ordinata sono
FONDAMENTI DI SEGNALI E TRASMISSIONE 6 Laboratorio Paolo Mazzucchelli mazzucch@elet.polimi.it Quantizzazione Il segnale y(t) non solo è campionato sull asse dei tempi, ma anche i valori di ordinata sono
FONDAMENTI DI SEGNALI E TRASMISSIONE 5 Laboratorio
 FONDAMENTI DI SEGNALI E TRASMISSIONE 5 Laboratorio Paolo Mazzucchelli mazzucch@elet.polimi.it Campionamento di segnali In MATLAB, qualunque segnale continuo è approssimato da una sequenza campionata. Si
FONDAMENTI DI SEGNALI E TRASMISSIONE 5 Laboratorio Paolo Mazzucchelli mazzucch@elet.polimi.it Campionamento di segnali In MATLAB, qualunque segnale continuo è approssimato da una sequenza campionata. Si
1 = Processi Autoregressivi AR(1) Filtro IIR di ordine 1. (WGN White Gaussian Noise) Eq. alle differenze ricorsiva. w=randn(n,1) MATLAB:
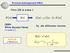 Processi Autoregressivi AR(1) Filtro IIR di ordine 1 Wn [ ] hn [ ] X[ n] = ρ X[ n 1] + W[ n] (WGN White Gaussian Noise) w=randn(n,1) Eq. alle differenze ricorsiva MATLAB: n hn [ ] = ρ un [ ] y=filter(b,a,x)
Processi Autoregressivi AR(1) Filtro IIR di ordine 1 Wn [ ] hn [ ] X[ n] = ρ X[ n 1] + W[ n] (WGN White Gaussian Noise) w=randn(n,1) Eq. alle differenze ricorsiva MATLAB: n hn [ ] = ρ un [ ] y=filter(b,a,x)
Ripasso segnali e processi casuali. Trasmissione dell Informazione
 Ripasso segnali e processi casuali 1 Breve ripasso di segnali e trasformate Dato un segnale s(t), la sua densità spettrale si calcola come dove S(f) è la trasformata di Fourier. L energia di un segnale
Ripasso segnali e processi casuali 1 Breve ripasso di segnali e trasformate Dato un segnale s(t), la sua densità spettrale si calcola come dove S(f) è la trasformata di Fourier. L energia di un segnale
Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Processi casuali A.A Alberto Perotti, Roberto Garello
 Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Processi casuali A.A. 2006-07 Alberto Perotti, Roberto Garello DELEN-DAUIN Processi casuali Sono modelli probabilistici
Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Processi casuali A.A. 2006-07 Alberto Perotti, Roberto Garello DELEN-DAUIN Processi casuali Sono modelli probabilistici
Corso di Fondamenti di Segnali e Trasmissione - Recupero del 10 Settembre 2004
 Corso di Fondamenti di Segnali e Trasmissione - Recupero del 10 Settembre 2004 Gli esercizi devono essere risolti solo sui ogli dei colori indicati. Per esiti e soluzioni si veda il sito web del corso:
Corso di Fondamenti di Segnali e Trasmissione - Recupero del 10 Settembre 2004 Gli esercizi devono essere risolti solo sui ogli dei colori indicati. Per esiti e soluzioni si veda il sito web del corso:
Esercitazione ENS su processi casuali (13 e 14 Maggio 2008)
 Esercitazione ES su processi casuali ( e 4 Maggio 2008) D. Donno Esercizio : Calcolo di autovalori e autovettori Si consideri un processo x n somma di un segnale e un disturbo: x n = Ae π 2 n + w n, n
Esercitazione ES su processi casuali ( e 4 Maggio 2008) D. Donno Esercizio : Calcolo di autovalori e autovettori Si consideri un processo x n somma di un segnale e un disturbo: x n = Ae π 2 n + w n, n
Probabilità e Processi casuali Laboratorio 5 Segnali per le
 Probabilità e Processi casuali Laboratorio 5 Segnali per le Telecomunicazioni Prof. Prati Claudio Maria Autore: Federico Borra Politecnico di Milano, DEIB Email: federico.borra@polimi.it Aprile 17, Ultima
Probabilità e Processi casuali Laboratorio 5 Segnali per le Telecomunicazioni Prof. Prati Claudio Maria Autore: Federico Borra Politecnico di Milano, DEIB Email: federico.borra@polimi.it Aprile 17, Ultima
RICHIAMI SU PROCESSI ALEATORI E DENSITÀ SPETTRALE DI POTENZA
 RICHIAMI SU PROCESSI ALEATORI E DENSITÀ SPETTRALE DI POTENZA Paolo Bestagini Ph.D. Student bestagini@elet.polimi.it http://home.deib.polimi.it/bestagini Sommario 2 Segnali deterministici Continui Discreti
RICHIAMI SU PROCESSI ALEATORI E DENSITÀ SPETTRALE DI POTENZA Paolo Bestagini Ph.D. Student bestagini@elet.polimi.it http://home.deib.polimi.it/bestagini Sommario 2 Segnali deterministici Continui Discreti
Corso di Fondamenti di Telecomunicazioni Esercizi Teoria dei segnali Prof. Giovanni Schembra
 Corso di Fondamenti di Telecomunicazioni Esercizi Teoria dei segnali Prof. Giovanni Schembra Sommario CARATTERISTICHE DEI SEGNALI DETERMINATI.... ESERCIZIO.... ESERCIZIO... 5.3 ESERCIZIO 3 CONVOLUZIONE...
Corso di Fondamenti di Telecomunicazioni Esercizi Teoria dei segnali Prof. Giovanni Schembra Sommario CARATTERISTICHE DEI SEGNALI DETERMINATI.... ESERCIZIO.... ESERCIZIO... 5.3 ESERCIZIO 3 CONVOLUZIONE...
Teorema del limite centrale TCL Questo importante teorema della statistica inferenziale si applica a qualsiasi variabile aleatoria che sia combinazion
 Teorema del limite centrale TCL Questo importante teorema della statistica inferenziale si applica a qualsiasi variabile aleatoria che sia combinazione lineare di N variabili aleatorie le cui funzioni
Teorema del limite centrale TCL Questo importante teorema della statistica inferenziale si applica a qualsiasi variabile aleatoria che sia combinazione lineare di N variabili aleatorie le cui funzioni
2.2.5 Approssimazione di un segnale in una base biortogonale (segnali rettangolari) Esercizi proposti... 46
 Indice 1 Operazioni elementari, convoluzione, correlazione 1 1.1 Operazioni elementari........................ 1 1.1.1 Ribaltamento, traslazione, scalatura............ 1 1.2 Convoluzione.............................
Indice 1 Operazioni elementari, convoluzione, correlazione 1 1.1 Operazioni elementari........................ 1 1.1.1 Ribaltamento, traslazione, scalatura............ 1 1.2 Convoluzione.............................
Prova scritta di Teoria dei Segnali: nuovo ordinamento
 Prova scritta di Teoria dei Segnali: nuovo ordinamento 1. Dati i segnali x(t) = rect[(t-2)/2] e y(t) = 2rect[(t+3)/2], si calcoli il prodotto di convoluzione tra x(t) e y(t), 2. Si calcoli la trasformata
Prova scritta di Teoria dei Segnali: nuovo ordinamento 1. Dati i segnali x(t) = rect[(t-2)/2] e y(t) = 2rect[(t+3)/2], si calcoli il prodotto di convoluzione tra x(t) e y(t), 2. Si calcoli la trasformata
RICHIAMI DI CALCOLO DELLE PROBABILITÀ
 UNIVERSITA DEL SALENTO INGEGNERIA CIVILE RICHIAMI DI CALCOLO DELLE PROBABILITÀ ing. Marianovella LEONE INTRODUZIONE Per misurare la sicurezza di una struttura, ovvero la sua affidabilità, esistono due
UNIVERSITA DEL SALENTO INGEGNERIA CIVILE RICHIAMI DI CALCOLO DELLE PROBABILITÀ ing. Marianovella LEONE INTRODUZIONE Per misurare la sicurezza di una struttura, ovvero la sua affidabilità, esistono due
Campionamento e quantizzazione
 Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Campionamento e quantizzazione A.A. 2008-09 Alberto Perotti DELEN-DAUIN Conversione analogico-digitale L elaborazione
Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Campionamento e quantizzazione A.A. 2008-09 Alberto Perotti DELEN-DAUIN Conversione analogico-digitale L elaborazione
CAMPIONAMENTO E RICOSTRUZIONE. Y(f) Y(f-15) Y(f+15) f[hz] Yc(f) Y(f) Y(f-17.5) Y(f+17.5) Yc(f) Esercizio 1
![CAMPIONAMENTO E RICOSTRUZIONE. Y(f) Y(f-15) Y(f+15) f[hz] Yc(f) Y(f) Y(f-17.5) Y(f+17.5) Yc(f) Esercizio 1 CAMPIONAMENTO E RICOSTRUZIONE. Y(f) Y(f-15) Y(f+15) f[hz] Yc(f) Y(f) Y(f-17.5) Y(f+17.5) Yc(f) Esercizio 1](/thumbs/71/64538047.jpg) CAMPIONAMENTO E RICOSTRUZIONE Esercizio 1 Dato il segnale y(t), con trasformata di Fourier Y(f) rappresentata in figura, rappresentare lo spettro del segnale ottenuto campionando idealmente y(t) con a)
CAMPIONAMENTO E RICOSTRUZIONE Esercizio 1 Dato il segnale y(t), con trasformata di Fourier Y(f) rappresentata in figura, rappresentare lo spettro del segnale ottenuto campionando idealmente y(t) con a)
Corso di Fondamenti di Segnali e Trasmissione - Esame del 21 Febbraio 2006
 Corso di Fondamenti di Segnali e Trasmissione - Esame del Febbraio 006 Gli esercizi devono essere risolti solo sui ogli dei colori indicati. Per esiti e soluzioni si veda il sito web del corso: http://www.elet.polimi.polimi.it/dsp/courses/st.
Corso di Fondamenti di Segnali e Trasmissione - Esame del Febbraio 006 Gli esercizi devono essere risolti solo sui ogli dei colori indicati. Per esiti e soluzioni si veda il sito web del corso: http://www.elet.polimi.polimi.it/dsp/courses/st.
Segnali (processi) aleatori (casuali)
 Segnali (processi) aleatori (casuali) Definizione di processo aleatorio Descrizione statistica di un processo aleatorio Media, potenza, varianza Autocorrelazione e autocovarianza Filtraggio di un processo
Segnali (processi) aleatori (casuali) Definizione di processo aleatorio Descrizione statistica di un processo aleatorio Media, potenza, varianza Autocorrelazione e autocovarianza Filtraggio di un processo
Teoria dei Segnali Trasmissione binaria casuale; somma di processi stocastici
 eoria dei Segnali rasmissione binaria casuale; somma di processi stocastici Valentino Liberali Dipartimento di Fisica Università degli Studi di Milano valentino.liberali@unimi.it eoria dei Segnali rasmissione
eoria dei Segnali rasmissione binaria casuale; somma di processi stocastici Valentino Liberali Dipartimento di Fisica Università degli Studi di Milano valentino.liberali@unimi.it eoria dei Segnali rasmissione
Laboratorio di Calcolo B 68
 Generazione di numeri casuali Abbiamo già accennato all idea che le tecniche statistiche possano essere utili per risolvere problemi di simulazione di processi fisici e di calcoli numerici. Dobbiamo però
Generazione di numeri casuali Abbiamo già accennato all idea che le tecniche statistiche possano essere utili per risolvere problemi di simulazione di processi fisici e di calcoli numerici. Dobbiamo però
PROCESSI CASUALI 1 Fondamenti di segnf a o lin d e a t m ra e s n mtii s T si L o C ne
 PROCESSI CASUALI Fondamenti di segnali Fondamenti e trasmissione TLC Segnali deterministici Un segnale (t) si dice deterministico se è una funzione nota di t, cioè se ad un qualsiasi istante di tempo t
PROCESSI CASUALI Fondamenti di segnali Fondamenti e trasmissione TLC Segnali deterministici Un segnale (t) si dice deterministico se è una funzione nota di t, cioè se ad un qualsiasi istante di tempo t
Laboratorio di Calcolo Paola Gallo
 Studio di una funzione Dopo aver calcolato limiti, massimi, minimi e flessi siamo in grado di stabilire noi quali estremi di variabilità e che passo dare alle mie x per poter visualizzare bene nel grafico
Studio di una funzione Dopo aver calcolato limiti, massimi, minimi e flessi siamo in grado di stabilire noi quali estremi di variabilità e che passo dare alle mie x per poter visualizzare bene nel grafico
Corso di Fondamenti di Segnali e Trasmissione - Esame del 7 Febbraio 2006
 Corso di Fondamenti di Segnali e Trasmissione - Esame del 7 Febbraio 6 Gli esercizi devono essere risolti solo sui ogli dei colori indicati. Per esiti e soluzioni si veda il sito web del corso: http://www.elet.polimi.polimi.it/dsp/courses/st.
Corso di Fondamenti di Segnali e Trasmissione - Esame del 7 Febbraio 6 Gli esercizi devono essere risolti solo sui ogli dei colori indicati. Per esiti e soluzioni si veda il sito web del corso: http://www.elet.polimi.polimi.it/dsp/courses/st.
Segnali analogici. Segnali aleatori. Segnali determinati Trasmissione ideale Trasmissione perfetta. Trasmissione imperfetta
 Segnali determinati Trasmissione ideale Trasmissione perfetta Segnali analogici 40 20 Segnali aleatori Trasmissione imperfetta Laboratorio di Segnali Segnali modulati Segnali tempo discreto e segnali in
Segnali determinati Trasmissione ideale Trasmissione perfetta Segnali analogici 40 20 Segnali aleatori Trasmissione imperfetta Laboratorio di Segnali Segnali modulati Segnali tempo discreto e segnali in
Laboratorio 4 G. Bernasconi,
 Laboratorio 4 G. Bernasconi, bernasco@elet.polimi.it Crosscorrelazione e Autocorrelazione (filtro adattato) La funzione crosscorrelazione tra due segnali continui x(t) ed y(t) è definita come: + R xy (
Laboratorio 4 G. Bernasconi, bernasco@elet.polimi.it Crosscorrelazione e Autocorrelazione (filtro adattato) La funzione crosscorrelazione tra due segnali continui x(t) ed y(t) è definita come: + R xy (
Trasmissione numerica: Compito del 22/07/2008
 Trasmissione numerica: Compito del /07/008 1 Esercizio1 Sia dato un sistema di trasmissione numerica che utilizza un impulso di trasmissione g(t) a radice di coseno rialzato, e una costellazione PAM con
Trasmissione numerica: Compito del /07/008 1 Esercizio1 Sia dato un sistema di trasmissione numerica che utilizza un impulso di trasmissione g(t) a radice di coseno rialzato, e una costellazione PAM con
Trasformata discreta di Fourier diunasequenzafinita: algoritmifft
 diunasequenzafinita: algoritmifft La TDF di una sequenza finita può essere calcolata utilizzando algoritmi, computazionalmente efficienti, quali gli algoritmi Fast Fourier Transform (FFT). L efficienza
diunasequenzafinita: algoritmifft La TDF di una sequenza finita può essere calcolata utilizzando algoritmi, computazionalmente efficienti, quali gli algoritmi Fast Fourier Transform (FFT). L efficienza
MASB AA10/11 21/01/11 test #1 1
 MASB 0/06/11 AA010011test #1. Esercizio 1. Illustrare lo schema generale di un apparecchiatura per l acquisizione di segnali spontanei, descrivendo brevemente i diversi componenti. Fornire una descrizione
MASB 0/06/11 AA010011test #1. Esercizio 1. Illustrare lo schema generale di un apparecchiatura per l acquisizione di segnali spontanei, descrivendo brevemente i diversi componenti. Fornire una descrizione
Vedi: Probabilità e cenni di statistica
 Vedi: http://www.df.unipi.it/~andreozz/labcia.html Probabilità e cenni di statistica Funzione di distribuzione discreta Istogrammi e normalizzazione Distribuzioni continue Nel caso continuo la probabilità
Vedi: http://www.df.unipi.it/~andreozz/labcia.html Probabilità e cenni di statistica Funzione di distribuzione discreta Istogrammi e normalizzazione Distribuzioni continue Nel caso continuo la probabilità
Teoria dei Segnali Processo di Poisson e rumore granulare
 Teoria dei Segnali Processo di Poisson e rumore granulare Valentino Liberali Dipartimento di Fisica Università degli Studi di Milano valentino.liberali@unimi.it Teoria dei Segnali Processo di Poisson e
Teoria dei Segnali Processo di Poisson e rumore granulare Valentino Liberali Dipartimento di Fisica Università degli Studi di Milano valentino.liberali@unimi.it Teoria dei Segnali Processo di Poisson e
) $ ' con T0=5s e T=2s. La funzione deve essere
 Metodi per l Analisi dei Segnali Biomedici. Esercitazioni AA 2010/2011 Esercitazione 11/03/2011 " t!t es_1.1. Disegnare la funzione rect 0 % $ ' con T0=5s e T=2s. La funzione deve essere calcolata # T
Metodi per l Analisi dei Segnali Biomedici. Esercitazioni AA 2010/2011 Esercitazione 11/03/2011 " t!t es_1.1. Disegnare la funzione rect 0 % $ ' con T0=5s e T=2s. La funzione deve essere calcolata # T
FENS- ENS esame del 24 febbraio 2006
 FENS- ENS esame del 24 febbraio 26 L allievo é invitato a dare una ragionata e succinta risposta a tutti gli argomenti proposti, per dimostrare il livello di preparazione globale. I calcoli devono essere
FENS- ENS esame del 24 febbraio 26 L allievo é invitato a dare una ragionata e succinta risposta a tutti gli argomenti proposti, per dimostrare il livello di preparazione globale. I calcoli devono essere
Conversione analogico-digitale
 Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Campionamento e quantizzazione A.A. 2004-05 Alberto Perotti DELEN-DAUIN Conversione analogico-digitale L elaborazione
Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Campionamento e quantizzazione A.A. 2004-05 Alberto Perotti DELEN-DAUIN Conversione analogico-digitale L elaborazione
Utilizzando la terminologia generica di prima, la variabile standardizzata X si calcola quindi
 La variabile standardizzata Utilizzando la terminologia generica di prima, la variabile standardizzata X si calcola quindi X'= X Media(X ) DS(X ) Visto l ampio uso in statistica di questa procedura, la
La variabile standardizzata Utilizzando la terminologia generica di prima, la variabile standardizzata X si calcola quindi X'= X Media(X ) DS(X ) Visto l ampio uso in statistica di questa procedura, la
Corso di Fondamenti di Segnali e Trasmissione - Esame del 14 Febbraio 2007
 Corso di Fondamenti di Segnali e Trasmissione - Esame del 4 Febbraio 007 Gliesercizidevonoessererisoltisolosuifoglideicoloriindicati,indicandoNOME,COGNOMEeMATRI- COLA in testa ad ogni foglio. Per esiti
Corso di Fondamenti di Segnali e Trasmissione - Esame del 4 Febbraio 007 Gliesercizidevonoessererisoltisolosuifoglideicoloriindicati,indicandoNOME,COGNOMEeMATRI- COLA in testa ad ogni foglio. Per esiti
Corso di Elaborazione Numerica dei Segnali Esame del 30 settembre 2005
 Corso di Elaborazione Numerica dei Segnali Esame del 30 settembre 005 TOTALE PUNTI: 44 L allievo é invitato a dare una ragionata e succinta risposta a tutti gli argomenti proposti, per dimostrare il livello
Corso di Elaborazione Numerica dei Segnali Esame del 30 settembre 005 TOTALE PUNTI: 44 L allievo é invitato a dare una ragionata e succinta risposta a tutti gli argomenti proposti, per dimostrare il livello
Laboratorio di Calcolo B 67
 Generazione di numeri casuali Abbiamo già accennato all idea che le tecniche statistiche possano essere utili per risolvere problemi di simulazione di processi fisici e di calcoli numerici. Dobbiamo però
Generazione di numeri casuali Abbiamo già accennato all idea che le tecniche statistiche possano essere utili per risolvere problemi di simulazione di processi fisici e di calcoli numerici. Dobbiamo però
Esercitazione ENS su periodogramma (27 e 28 Maggio 2008) Esercizio 1: Autocorrelazione e stima della densità spettrale di potenza
 sercitazione S su periodogramma (7 e 8 Maggio 008 D. Donno sercizio : Autocorrelazione e stima della densità spettrale di potenza Si consideri la sequenza x n di lunghezza = 8 campioni. x n è somma di
sercitazione S su periodogramma (7 e 8 Maggio 008 D. Donno sercizio : Autocorrelazione e stima della densità spettrale di potenza Si consideri la sequenza x n di lunghezza = 8 campioni. x n è somma di
Laboratorio II, modulo
 Laboratorio II, modulo 2 206-207 Banda di un segnale e filtri (cfr. http://wpage.unina.it/verdoliv/tds/appunti/appunti_03.pdf e http://wpage.unina.it/verdoliv/tds/appunti/appunti_04.pdf e http://wpage.unina.it/verdoliv/tds/appunti/appunti_05.pdf
Laboratorio II, modulo 2 206-207 Banda di un segnale e filtri (cfr. http://wpage.unina.it/verdoliv/tds/appunti/appunti_03.pdf e http://wpage.unina.it/verdoliv/tds/appunti/appunti_04.pdf e http://wpage.unina.it/verdoliv/tds/appunti/appunti_05.pdf
Programma della parte introduttiva: Lezione 5
 Programma della parte introduttiva: Lezione 5 Cap. 3 Presentazione e confronto tra misure Cap. 4 Propagazione delle incertezze Cap 5 Misure ripetute e stimatori Cap.6 Organizzazione e presentazione dei
Programma della parte introduttiva: Lezione 5 Cap. 3 Presentazione e confronto tra misure Cap. 4 Propagazione delle incertezze Cap 5 Misure ripetute e stimatori Cap.6 Organizzazione e presentazione dei
Ulteriori Conoscenze di Informatica e Statistica
 Ulteriori Conoscenze di Informatica e Statistica Carlo Meneghini Dip. di fisica via della Vasca Navale 84, st. 83 (I piano) tel.: 06 55 17 72 17 meneghini@fis.uniroma3.it Indici di forma Descrivono le
Ulteriori Conoscenze di Informatica e Statistica Carlo Meneghini Dip. di fisica via della Vasca Navale 84, st. 83 (I piano) tel.: 06 55 17 72 17 meneghini@fis.uniroma3.it Indici di forma Descrivono le
Corso di Fondamenti di Telecomunicazioni
 Corso di Fondamenti di Telecomunicazioni Prof. Mario Barbera [parte ] Variabili aleatorie Esempio: sia dato l esperimento: Scegliere un qualunque giorno non festivo della settimana, per verificare casualmente
Corso di Fondamenti di Telecomunicazioni Prof. Mario Barbera [parte ] Variabili aleatorie Esempio: sia dato l esperimento: Scegliere un qualunque giorno non festivo della settimana, per verificare casualmente
DISTRIBUZIONI DI PROBABILITA (parte 2) 1 / 27
 DISTRIBUZIONI DI PROBABILITA (parte 2) 1 / 27 Funzione di ripartizione per variabili casuali discrete 2 / 27 Data una variabile casuale discreta possiamo calcolare, analogamente al caso continuo, la probabilità
DISTRIBUZIONI DI PROBABILITA (parte 2) 1 / 27 Funzione di ripartizione per variabili casuali discrete 2 / 27 Data una variabile casuale discreta possiamo calcolare, analogamente al caso continuo, la probabilità
MASB AA10/11 21/01/11 test #1 1
 MASB 20/06/11 AA20102011test #1. Esercizio 1. Illustrare lo schema generale di un apparecchiatura per l acquisizione di segnali spontanei, descrivendo brevemente i diversi componenti. Fornire una descrizione
MASB 20/06/11 AA20102011test #1. Esercizio 1. Illustrare lo schema generale di un apparecchiatura per l acquisizione di segnali spontanei, descrivendo brevemente i diversi componenti. Fornire una descrizione
Prova di AUTOVALUTAZIONE (novembre 2009). nota: l esame ha validità solo se incluso nel piano degli studi per l anno accademico corrente.
 UNIVERSITA DEGLI STUDI ROMA TRE CdS in Ingegneria Informatica corso di FONDAMENTI DI TELECOMUNICAZIONI Prova di AUTOVALUTAZIONE (novembre 2009). COMPITO A nota: l esame ha validità solo se incluso nel
UNIVERSITA DEGLI STUDI ROMA TRE CdS in Ingegneria Informatica corso di FONDAMENTI DI TELECOMUNICAZIONI Prova di AUTOVALUTAZIONE (novembre 2009). COMPITO A nota: l esame ha validità solo se incluso nel
Elaborazione statistica di dati
 Elaborazione statistica di dati 1 CONCETTI DI BASE DI STATISTICA ELEMENTARE 2 Taratura strumenti di misura IPOTESI: grandezza da misurare identica da misura a misura Per la presenza di errori casuali,
Elaborazione statistica di dati 1 CONCETTI DI BASE DI STATISTICA ELEMENTARE 2 Taratura strumenti di misura IPOTESI: grandezza da misurare identica da misura a misura Per la presenza di errori casuali,
PROBABILITA. Distribuzione di probabilità
 DISTRIBUZIONI di PROBABILITA Distribuzione di probabilità Si definisce distribuzione di probabilità il valore delle probabilità associate a tutti gli eventi possibili connessi ad un certo numero di prove
DISTRIBUZIONI di PROBABILITA Distribuzione di probabilità Si definisce distribuzione di probabilità il valore delle probabilità associate a tutti gli eventi possibili connessi ad un certo numero di prove
IL PALLINOMETRO SCOPO
 IL PALLINOMETRO SCOPO Verifica del fatto che gli errori casuali nella misura di una grandezza fisica ripetuta molte volte nelle stesse condizioni sperimentali seguono la distribuzione normale di Gauss.
IL PALLINOMETRO SCOPO Verifica del fatto che gli errori casuali nella misura di una grandezza fisica ripetuta molte volte nelle stesse condizioni sperimentali seguono la distribuzione normale di Gauss.
Segnali e Sistemi Laboratorio Matlab
 Segnali e Sistemi Laboratorio Matlab Irene Pappalardo irene.pappalardo@gmail.com Corso di Laurea in Ingegneria dell Informazione May 05-12-14, 2014 Segnali e Sistemi Laboratorio Matlab 05-12-14.05.2014
Segnali e Sistemi Laboratorio Matlab Irene Pappalardo irene.pappalardo@gmail.com Corso di Laurea in Ingegneria dell Informazione May 05-12-14, 2014 Segnali e Sistemi Laboratorio Matlab 05-12-14.05.2014
Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche. Modulazione A.A Alberto Perotti
 Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Modulazione A.A. 8-9 Alberto Perotti DELEN-DAUIN Modello di sistema di comunicazione Il modello di sistema di comunicazione
Corso di Laurea a Distanza in Ingegneria Elettrica Corso di Comunicazioni Elettriche Modulazione A.A. 8-9 Alberto Perotti DELEN-DAUIN Modello di sistema di comunicazione Il modello di sistema di comunicazione
IL PALLINOMETRO SCOPO
 IL PALLINOMETRO SCOPO Verifica del fatto che gli errori casuali nella misura di una grandezza fisica ripetuta molte volte nelle stesse condizioni sperimentali seguono la distribuzione normale di Gauss.
IL PALLINOMETRO SCOPO Verifica del fatto che gli errori casuali nella misura di una grandezza fisica ripetuta molte volte nelle stesse condizioni sperimentali seguono la distribuzione normale di Gauss.
Ulteriori Conoscenze di Informatica e Statistica
 ndici di forma Ulteriori Conoscenze di nformatica e Statistica Descrivono le asimmetrie della distribuzione Carlo Meneghini Dip. di fisica via della Vasca Navale 84, st. 83 ( piano) tel.: 06 55 17 72 17
ndici di forma Ulteriori Conoscenze di nformatica e Statistica Descrivono le asimmetrie della distribuzione Carlo Meneghini Dip. di fisica via della Vasca Navale 84, st. 83 ( piano) tel.: 06 55 17 72 17
Corso di Fondamenti di Segnali e Trasmissione - Appello del 07 Settembre 2005
 Corso di Fondamenti di Segnali e Trasmissione - Appello del 07 Settembre 2005 Gli esercizi devono essere risolti solo sui fogli dei colori indicati Per esiti e soluzioni si veda il sito web del corso:
Corso di Fondamenti di Segnali e Trasmissione - Appello del 07 Settembre 2005 Gli esercizi devono essere risolti solo sui fogli dei colori indicati Per esiti e soluzioni si veda il sito web del corso:
Statistica Inferenziale
 Statistica Inferenziale Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Riepilogo lezione 4 Abbiamo visto: Distribuzioni discrete Modelli probabilistici nel discreto Distribuzione uniforme
Statistica Inferenziale Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Riepilogo lezione 4 Abbiamo visto: Distribuzioni discrete Modelli probabilistici nel discreto Distribuzione uniforme
Ulteriori conoscenze di informatica Elementi di statistica Esercitazione3
 Ulteriori conoscenze di informatica Elementi di statistica Esercitazione3 Sui PC a disposizione sono istallati diversi sistemi operativi. All accensione scegliere Windows. Immettere Nome utente b## (##
Ulteriori conoscenze di informatica Elementi di statistica Esercitazione3 Sui PC a disposizione sono istallati diversi sistemi operativi. All accensione scegliere Windows. Immettere Nome utente b## (##
COMUNICAZIONI ELETTRICHE A
 COMUNICAZIONI ELERICHE A Laurea riennale in Ingegneria Elettronica e delle elecomunicazioni Prova del 10/1/007 empo a disposizione: ore 1. Si illustri il funzionamento di un ricevitore supereterodina,
COMUNICAZIONI ELERICHE A Laurea riennale in Ingegneria Elettronica e delle elecomunicazioni Prova del 10/1/007 empo a disposizione: ore 1. Si illustri il funzionamento di un ricevitore supereterodina,
Teorema del limite centrale TCL
 Teorema del limite centrale TCL Questo importante teorema della statistica inferenziale si applica a qualsiasi variabile aleatoria che sia combinazione lineare di N variabili aleatorie le cui funzioni
Teorema del limite centrale TCL Questo importante teorema della statistica inferenziale si applica a qualsiasi variabile aleatoria che sia combinazione lineare di N variabili aleatorie le cui funzioni
PRBS. Pseudo Random Binary Sequence
 PRBS Pseudo Random Binary Sequence MARTINA FAVARO Dipartimento di Ingegneria dell Informazione, Università di Padova Lezione n.2 Che cosa é una PRBS? É noto che il segnale di input in un processo di identificazione
PRBS Pseudo Random Binary Sequence MARTINA FAVARO Dipartimento di Ingegneria dell Informazione, Università di Padova Lezione n.2 Che cosa é una PRBS? É noto che il segnale di input in un processo di identificazione
Elaborazione statistica di dati
 Elaborazione statistica di dati CONCETTI DI BASE DI STATISTICA ELEMENTARE Taratura strumenti di misura IPOTESI: grandezza da misurare identica da misura a misura Collaudo sistemi di produzione IPOTESI:
Elaborazione statistica di dati CONCETTI DI BASE DI STATISTICA ELEMENTARE Taratura strumenti di misura IPOTESI: grandezza da misurare identica da misura a misura Collaudo sistemi di produzione IPOTESI:
Gli intervalli di confidenza. Intervallo di confidenza per la media (σ 2 nota) nel caso di popolazione Gaussiana
 Statistica Lez. 1 Gli intervalli di confidenza Intervallo di confidenza per la media (σ nota) nel caso di popolazione Gaussiana Sia X una v.c Gaussiana di media µ e varianza σ. Se X 1, X,..., X n è un
Statistica Lez. 1 Gli intervalli di confidenza Intervallo di confidenza per la media (σ nota) nel caso di popolazione Gaussiana Sia X una v.c Gaussiana di media µ e varianza σ. Se X 1, X,..., X n è un
Laboratorio di Elaborazione di Dati, Segnali e Immagini Biomediche (Parte 5)
 Università degli Studi di Padova - Facoltà di Ingegneria Corso di Laurea in Ingegneria Biomedica A.A. 7-8 Laboratorio di Elaborazione di Dati, Segnali e Immagini Biomediche (Parte 5) Prof. Giovanni Sparacino
Università degli Studi di Padova - Facoltà di Ingegneria Corso di Laurea in Ingegneria Biomedica A.A. 7-8 Laboratorio di Elaborazione di Dati, Segnali e Immagini Biomediche (Parte 5) Prof. Giovanni Sparacino
esperimento casuale: è un esperimento condotto sotto l effetto del caso; evento elementare: ciascuno dei possibili esiti di un esperimento casuale;
 Capitolo 15 Suggerimenti agli esercizi a cura di Elena Siletti Esercizio 15.1: Suggerimento Si ricordi che: esperimento casuale: è un esperimento condotto sotto l effetto del caso; evento elementare: ciascuno
Capitolo 15 Suggerimenti agli esercizi a cura di Elena Siletti Esercizio 15.1: Suggerimento Si ricordi che: esperimento casuale: è un esperimento condotto sotto l effetto del caso; evento elementare: ciascuno
Laboratorio di Statistica 1 con R Esercizi per la Relazione. I testi e/o i dati degli esercizi contassegnati da sono tratti dai libri consigliati
 Laboratorio di Statistica 1 con R Esercizi per la Relazione I testi e/o i dati degli esercizi contassegnati da sono tratti dai libri consigliati nel corso. Esercizio 1. 1. Facendo uso dei comandi
Laboratorio di Statistica 1 con R Esercizi per la Relazione I testi e/o i dati degli esercizi contassegnati da sono tratti dai libri consigliati nel corso. Esercizio 1. 1. Facendo uso dei comandi
Indice. 1 Vibrazioni libere e forzate di oscillatori elementari 1
 Indice Prefazione xiii 1 Vibrazioni libere e forzate di oscillatori elementari 1 1.1 Vibrazioni libere non smorzate l 1.2 Vibrazioni libere smorzate 7 1.3 Vibrazioni forzate per forzante sinusoidale 12
Indice Prefazione xiii 1 Vibrazioni libere e forzate di oscillatori elementari 1 1.1 Vibrazioni libere non smorzate l 1.2 Vibrazioni libere smorzate 7 1.3 Vibrazioni forzate per forzante sinusoidale 12
Processi AR. = σ ρ. Esercizio proposto:
 Laboratorio del 5/10/06 Processi AR Esercizio proposto: Processo reale AR(1) con autocorrelazione R ( m) Rappresentazione di una possibile realizzazione, grafico del coefficiente di autocorrelazione e
Laboratorio del 5/10/06 Processi AR Esercizio proposto: Processo reale AR(1) con autocorrelazione R ( m) Rappresentazione di una possibile realizzazione, grafico del coefficiente di autocorrelazione e
Prova di esame di Teoria dei Segnali
 10 aprile 2018 Prova di esame di Teoria dei Segnali Parte quantitativa Candidato: Esercizio A Un canale binario simmetrico è caratterizzato { da una probabilità di errore p (x1 ) = 0.1 P e = 0.2 e probabilità
10 aprile 2018 Prova di esame di Teoria dei Segnali Parte quantitativa Candidato: Esercizio A Un canale binario simmetrico è caratterizzato { da una probabilità di errore p (x1 ) = 0.1 P e = 0.2 e probabilità
Comunicazioni Elettriche anno accademico Esercitazione 1
 Comunicazioni Elettriche anno accademico 003-004 Esercitazione Esercizio Un processo aleatorio a tempo discreto X(n) è definito nel seguente modo: Viene lanciata una moneta. Se il risultato è testa X(n)=
Comunicazioni Elettriche anno accademico 003-004 Esercitazione Esercizio Un processo aleatorio a tempo discreto X(n) è definito nel seguente modo: Viene lanciata una moneta. Se il risultato è testa X(n)=
Introduzione al modello Uniforme
 Introduzione al modello Uniforme Esempio: conversione Analogico/Digitale Errore di quantizzazione Ampiezza Continua Discreta x () t x ( t ) q Tempo Discreto Continuo Segnale Analogico ( ) x t k t t Segnale
Introduzione al modello Uniforme Esempio: conversione Analogico/Digitale Errore di quantizzazione Ampiezza Continua Discreta x () t x ( t ) q Tempo Discreto Continuo Segnale Analogico ( ) x t k t t Segnale
DISTRIBUZIONI DI CAMPIONAMENTO
 DISTRIBUZIONI DI CAMPIONAMENTO 12 DISTRIBUZIONE DI CAMPIONAMENTO DELLA MEDIA Situazione reale Della popolazione di tutti i laureati in odontoiatria negli ultimi 10 anni, in tutte le Università d Italia,
DISTRIBUZIONI DI CAMPIONAMENTO 12 DISTRIBUZIONE DI CAMPIONAMENTO DELLA MEDIA Situazione reale Della popolazione di tutti i laureati in odontoiatria negli ultimi 10 anni, in tutte le Università d Italia,
Esercitazione 5 del corso di Statistica 2 Prof. Domenico Vistocco
 Esercitazione del corso di Statistica Prof. Domenico Vistocco Alfonso Iodice D Enza May 30, 007 1 Esercizio Si consideri una popolazione caratterizzata dai numeri, 3, 6, 8, 11. Si considerino tutti i possibili
Esercitazione del corso di Statistica Prof. Domenico Vistocco Alfonso Iodice D Enza May 30, 007 1 Esercizio Si consideri una popolazione caratterizzata dai numeri, 3, 6, 8, 11. Si considerino tutti i possibili
Basi matematiche per il Machine Learning
 Basi matematiche per il Machine Learning Corso di AA, anno 2017/18, Padova Fabio Aiolli 04 Ottobre 2017 Fabio Aiolli Basi matematiche per il Machine Learning 04 Ottobre 2017 1 / 14 Probabilità Un esperimento
Basi matematiche per il Machine Learning Corso di AA, anno 2017/18, Padova Fabio Aiolli 04 Ottobre 2017 Fabio Aiolli Basi matematiche per il Machine Learning 04 Ottobre 2017 1 / 14 Probabilità Un esperimento
Teoria dei Segnali Densità spettrale di energia e di potenza; campionamento e teorema di Shannon
 Teoria dei Segnali Densità spettrale di energia e di potenza; campionamento e teorema di Shannon Valentino Liberali Dipartimento di Fisica Università degli Studi di Milano valentino.liberali@unimi.it Teoria
Teoria dei Segnali Densità spettrale di energia e di potenza; campionamento e teorema di Shannon Valentino Liberali Dipartimento di Fisica Università degli Studi di Milano valentino.liberali@unimi.it Teoria
Pulse Amplitude Modulation (PAM) 2 Scelta delle risposte impulsive dei filtri in trasmissione e ricezione
 Pulse Amplitude Modulation (PAM 1 Definizione La trasmissione di una sequenza di numeri {a k } mediante un onda PAM consiste nel generare, a partire dalla sequenza {a k } il segnale a tempo continuo u(t
Pulse Amplitude Modulation (PAM 1 Definizione La trasmissione di una sequenza di numeri {a k } mediante un onda PAM consiste nel generare, a partire dalla sequenza {a k } il segnale a tempo continuo u(t
Questa viene trasmessa sul canale (wireless o wired). In questo corso, modellizzeremo il canale di trasmissione come un canale Gaussiano bianco
 Canale di trasmissione Dati una costellazione M un labeling binario e è possibile associare alle sequenze binarie di informazione u da trasmettere una forma d onda s(t). Questa viene trasmessa sul canale
Canale di trasmissione Dati una costellazione M un labeling binario e è possibile associare alle sequenze binarie di informazione u da trasmettere una forma d onda s(t). Questa viene trasmessa sul canale
Teoria della decisione e della stima. Esercitazioni di laboratorio Anno accademico M.S. Greco
 Teoria della decisione e della stima Esercitazioni di laboratorio Anno accademico 008-09 M.S. Greco Laboratorio dell 1/10/08 Processi AR + Sx() z = Rx( m) z m= m Densità spettrale complessa La regione
Teoria della decisione e della stima Esercitazioni di laboratorio Anno accademico 008-09 M.S. Greco Laboratorio dell 1/10/08 Processi AR + Sx() z = Rx( m) z m= m Densità spettrale complessa La regione
Teoria dei Segnali (19 dicembre 2002)
 Teoria dei Segnali (9 dicembre ) II Provetta Esercizio N. (per gli studenti della laurea quinquennale) All ingresso del modulatore in figura c è il segnale m() t cos( Ωt) l inviluppo complesso del segnale
Teoria dei Segnali (9 dicembre ) II Provetta Esercizio N. (per gli studenti della laurea quinquennale) All ingresso del modulatore in figura c è il segnale m() t cos( Ωt) l inviluppo complesso del segnale
Verifica delle ipotesi
 Statistica inferenziale Stima dei parametri Verifica delle ipotesi Concetti fondamentali POPOLAZIONE o UNIVERSO Insieme degli elementi cui si rivolge il ricercatore per la sua indagine CAMPIONE Un sottoinsieme
Statistica inferenziale Stima dei parametri Verifica delle ipotesi Concetti fondamentali POPOLAZIONE o UNIVERSO Insieme degli elementi cui si rivolge il ricercatore per la sua indagine CAMPIONE Un sottoinsieme
LABORATORIO DI INFORMATICA ESERCITAZIONE VIII
 LABORATORIO DI INFORMATICA ESERCITAZIONE VIII Cercate di eseguire gli esercizi da soli. Se non ci riuscite, cercate di capire i messaggi di errore. Se non ci riuscite, provateci di nuovo. Poi chiamate
LABORATORIO DI INFORMATICA ESERCITAZIONE VIII Cercate di eseguire gli esercizi da soli. Se non ci riuscite, cercate di capire i messaggi di errore. Se non ci riuscite, provateci di nuovo. Poi chiamate
PROBABILITÀ - SCHEDA N. 3 VARIABILI ALEATORIE CONTINUE E SIMULAZIONE
 PROBABILITÀ - SCHEDA N. 3 VARIABILI ALEATORIE CONTINUE E SIMULAZIONE (da un idea di M. Impedovo Variabili aleatorie continue e simulazione Progetto Alice n. 15, ) 1. La simulazione Nelle schede precedenti
PROBABILITÀ - SCHEDA N. 3 VARIABILI ALEATORIE CONTINUE E SIMULAZIONE (da un idea di M. Impedovo Variabili aleatorie continue e simulazione Progetto Alice n. 15, ) 1. La simulazione Nelle schede precedenti
IL CRITERIO DELLA MASSIMA VEROSIMIGLIANZA
 Metodi per l Analisi dei Dati Sperimentali AA009/010 IL CRITERIO DELLA MASSIMA VEROSIMIGLIANZA Sommario Massima Verosimiglianza Introduzione La Massima Verosimiglianza Esempio 1: una sola misura sperimentale
Metodi per l Analisi dei Dati Sperimentali AA009/010 IL CRITERIO DELLA MASSIMA VEROSIMIGLIANZA Sommario Massima Verosimiglianza Introduzione La Massima Verosimiglianza Esempio 1: una sola misura sperimentale
COMUNICAZIONI ELETTRICHE
 COMUNICAZIONI ELERICHE Diploma Universitario Ingegneria Elettronica - Ingegneria Inormatica ESERCIZIO : Si consideri il sistema mostrato in igura. Il iltro ha risposta in requenza H() = j segn (), dove
COMUNICAZIONI ELERICHE Diploma Universitario Ingegneria Elettronica - Ingegneria Inormatica ESERCIZIO : Si consideri il sistema mostrato in igura. Il iltro ha risposta in requenza H() = j segn (), dove
ELABORAZIONE NUMERICA DEI SEGNALI 1 Laboratorio
 ELABORAZIONE NUMERICA DEI SEGNALI 1 Laboratorio Paolo Mazzucchelli mazzucch@elet.polimi.it Quantizzazione Il segnale tempo continuo y(t), campionato con passo di campionamento temporale dt, è quantizzato
ELABORAZIONE NUMERICA DEI SEGNALI 1 Laboratorio Paolo Mazzucchelli mazzucch@elet.polimi.it Quantizzazione Il segnale tempo continuo y(t), campionato con passo di campionamento temporale dt, è quantizzato
Statistica Corso di laurea in Biotecnologie I esonero - 19 aprile 2010
 Statistica Corso di laurea in Biotecnologie I esonero - 9 aprile 00 Esercizio Determinare, a P X ; b PX < /; c il terzo quartile della distribuzione, nei casi ix N, ; iix variabile aleatoria continua con
Statistica Corso di laurea in Biotecnologie I esonero - 9 aprile 00 Esercizio Determinare, a P X ; b PX < /; c il terzo quartile della distribuzione, nei casi ix N, ; iix variabile aleatoria continua con
ESERCIZI DI TEORIA. MEMO I: Una variabile casuale gaussiana ha densita : MEMO II: Date n misure: x1, x2,, xn con relative incertezze: σ1, σ2,, σn
 MEMO I: Una variabile casuale gaussiana ha densita : MEMO II: Date n misure: x1, x2,, xn con relative incertezze: σ1, σ2,, σn La media pesata vale: dove: ESERCIZI DI TEORIA ESERCIZIO 1 Sei su un computer
MEMO I: Una variabile casuale gaussiana ha densita : MEMO II: Date n misure: x1, x2,, xn con relative incertezze: σ1, σ2,, σn La media pesata vale: dove: ESERCIZI DI TEORIA ESERCIZIO 1 Sei su un computer
Variabili casuali. - di Massimo Cristallo -
 Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 16 e 27 maggio 2013 - di Massimo Cristallo - Variabili casuali
Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 16 e 27 maggio 2013 - di Massimo Cristallo - Variabili casuali
Laboratorio di Chimica Fisica. Analisi Statistica
 Università degli Studi di Bari Dipartimento di Chimica 9 giugno F.Mavelli- Laboratorio Chimica Fisica - a.a. 3-4 F.Mavelli Laboratorio di Chimica Fisica a.a. 3-4 Analisi Statistica dei Dati Analisi Statistica
Università degli Studi di Bari Dipartimento di Chimica 9 giugno F.Mavelli- Laboratorio Chimica Fisica - a.a. 3-4 F.Mavelli Laboratorio di Chimica Fisica a.a. 3-4 Analisi Statistica dei Dati Analisi Statistica
DISTRIBUZIONI DI PROBABILITA
 PSICOMETRIA Corso di laurea triennale (classe 34) DISTRIBUZIONI DI PROBABILITA DISTRIBUZIONE DI PROBABILITA I possibili risultati di un esperimento costituiscono uno spazio campionario di n eventi A ciascun
PSICOMETRIA Corso di laurea triennale (classe 34) DISTRIBUZIONI DI PROBABILITA DISTRIBUZIONE DI PROBABILITA I possibili risultati di un esperimento costituiscono uno spazio campionario di n eventi A ciascun
In realtà i segnali con i quali dobbiamo confrontarci più frequentemente sono limitati nel tempo
 Segnali trattati sino ad ora: continui, durata infinita,.. Su essi sono stati sviluppati strumenti per analizzare output di circuiti e caratteristiche del segnale: Risposta all impulso, prodotto di convoluzione,
Segnali trattati sino ad ora: continui, durata infinita,.. Su essi sono stati sviluppati strumenti per analizzare output di circuiti e caratteristiche del segnale: Risposta all impulso, prodotto di convoluzione,
Alcune v.a. discrete notevoli
 Alcune v.a. discrete notevoli Variabile aleatoria Bernoulliana Il risultato X di un esperimento aleatorio può essere classificato nel modo che segue: successo oppure insuccesso. Indichiamo: Successo =
Alcune v.a. discrete notevoli Variabile aleatoria Bernoulliana Il risultato X di un esperimento aleatorio può essere classificato nel modo che segue: successo oppure insuccesso. Indichiamo: Successo =
Esercizi di Calcolo delle Probabilità
 Esercizi di Calcolo delle Probabilità Versione del 1/05/005 Corso di Statistica Anno Accademico 00/05 Antonio Giannitrapani, Simone Paoletti Calcolo delle probabilità Esercizio 1. Un dado viene lanciato
Esercizi di Calcolo delle Probabilità Versione del 1/05/005 Corso di Statistica Anno Accademico 00/05 Antonio Giannitrapani, Simone Paoletti Calcolo delle probabilità Esercizio 1. Un dado viene lanciato
MASB AA10/11 21/01/11 test #1 1
 MASB 20/06/11 AA20102011test #1. Esercizio 1. Illustrare lo schema generale di un apparecchiatura per l acquisizione di segnali spontanei, descrivendo brevemente i diversi componenti. Fornire una descrizione
MASB 20/06/11 AA20102011test #1. Esercizio 1. Illustrare lo schema generale di un apparecchiatura per l acquisizione di segnali spontanei, descrivendo brevemente i diversi componenti. Fornire una descrizione
E S E R C I Z I T U T O R
 E S E R C I Z I T U T O R ESERCIZIO Applicazione del Metodo Montecarlo per calcolare p. Si calcola il rapporto fra l area del cerchio di diametro r e l area del quadrato circoscritto, di lato r. Area del
E S E R C I Z I T U T O R ESERCIZIO Applicazione del Metodo Montecarlo per calcolare p. Si calcola il rapporto fra l area del cerchio di diametro r e l area del quadrato circoscritto, di lato r. Area del
Tutorato di Complementi di Analisi Matematica e Statistica 26 maggio 2016
 Tutorato di Complementi di Analisi Matematica e Statistica 26 maggio 2016 Esercizi possibili di probabilità e statistica Notazioni: U(a, b) è la distribuzione di probabilità uniforma nell intervallo (a,
Tutorato di Complementi di Analisi Matematica e Statistica 26 maggio 2016 Esercizi possibili di probabilità e statistica Notazioni: U(a, b) è la distribuzione di probabilità uniforma nell intervallo (a,
1! 4! = 5. Quindi la probabilità di ottenere 1 successo su 5 lanci sarà 5 2 = 5! 2! 3! = 10
 Note sulla Distribuzione Binomiale La distribuzione binomiale è relativa ad una variabile aleatoria discreta, che descrive i possibili risultati di un esperimento composto da n prove. In particolare, definisce
Note sulla Distribuzione Binomiale La distribuzione binomiale è relativa ad una variabile aleatoria discreta, che descrive i possibili risultati di un esperimento composto da n prove. In particolare, definisce
ESAME. 9 Gennaio 2017 COMPITO B
 ESAME 9 Gennaio 2017 COMPITO B Cognome Nome Numero di matricola 1) Approssimare tutti i calcoli alla quarta cifra decimale. 2) Ai fini della valutazione si terrà conto solo ed esclusivamente di quanto
ESAME 9 Gennaio 2017 COMPITO B Cognome Nome Numero di matricola 1) Approssimare tutti i calcoli alla quarta cifra decimale. 2) Ai fini della valutazione si terrà conto solo ed esclusivamente di quanto
