Appunti sull algebra dei limiti
|
|
|
- Federico Abbate
- 5 anni fa
- Visualizzazioni
Transcript
1 Appunti sull algebra dei iti Emanuele Biolcati I.S. Monti Asti classe V UC 21 gennaio 2016 Emanuele Biolcati 1
2 la pena dell uomo nel provare un piacere è di veder subito i iti della sua estensione G. Leopardi, Zibaldone, 169 Emanuele Biolcati 2
3 Cos è il ite di una funzione? Partiamo da una definizione non rigorosa, ma intuitiva: Data una funzione, supponiamo che x 0 ed l rappresentino due numeri reali oppure che siano + o, si dice che il ite della funzione per x che tende a x 0 vale l se la funzione assume valori vicino quanto si vuole a l, ogniqualvolta i valori di x sono sufficientemente vicini a x 0. Definizione generale rigorosa Siano x 0, l R e sia f(x) funzione reale definita in un intorno di x 0 (escluso al più x 0 ), il ite della funzione per x che tende a x 0 è l e si scrive: x x 0 f(x) = l se per ogni intorno U di l, esiste un intorno V di x 0, tale che per ogni x V (con x x 0 ) risulta f(x) U. Emanuele Biolcati 3
4 Quattro tipologie di ite Nella definizione di ite abbiamo detto che x 0 e l possono essere finiti o infiniti. Ne seguono, dunque, quattro possibili combinazioni. Limite finito, avvicinandosi ad un valore finito x x 0 f(x) = l Limite finito, andando all infinito f(x) = l x ± asintoto orizzontale di equazione y = l Limite infinito, avvicinandosi ad un valore finito x x 0 f(x) = ± asintoto verticale di equazione x = x 0 Limite infinito, andando all infinito f(x) = ± x ± Emanuele Biolcati 4
5 Proprietà algebriche dei iti I iti si comportano bene con le funzioni, intendendo che: ite della somma = somma dei iti ite del prodotto = prodotto dei iti Per calcolare il ite di una qualsiasi funzione, per quanto sia complessa, è allora sufficiente scomporla in somme e prodotti di funzioni elementari di cui siano noti i iti. Diventa pertanto necessario conoscere il comportamento delle funzioni elementari sia in prossimità di alcuni punti (come quelli non appartenenti al dominio) sia per valori tendenti a (più o meno) infinito. Emanuele Biolcati 5
6 Un modo difficile per dire niente salti Ricondursi alle funzioni elementari è possibile perché queste non presentano salti, più formalmente si dice che sono continue nei punti in cui sono definite. Continuità in un punto Una funzione f si dice continua in x 0 se x x0 f(x) = f(x 0 ), ovvero se il ite l coincide con il valore assunto dalla funzione in quel punto. continua non continua Emanuele Biolcati 6
7 La funzione elementare quasi banale: la retta Come prima funzione guardiamo la più semplice in assoluto, l equazione di una retta: f(x) = x di cui ci interessa ricordare il segno: negativa per x < 0, positiva per x > 0. I soli iti utili da calcolare sono per valori molto grandi (x + ) o molto piccoli (x ). E intuitivo vedere che: x = + e x = x + x Emanuele Biolcati 7
8 Una funzione elementare per eccellenza: l iperbole (I) Grande importanza acquista la seguente funzione: f(x) = 1 x per cui sappiamo: dominio: ogni x tranne lo zero (D = R/{0}) nessuna intersezione con gli assi funzione negativa per x < 0, positiva per x > 0 In questo caso ci sono almeno 4 iti utili: infinito e meno infinito, ma anche per valori che si avvicinano a zero, sia da destra che da sinistra. Emanuele Biolcati 8
9 Una funzione elementare per eccellenza: l iperbole (II) La funzione, per valori di x molto grandi (o molto piccoli, verso numeri negativi) si avvicina all asse delle ascisse, quindi al valore di y uguale a 0. Ecco trovato un asintoto orizzontale di equazione y = 0 e infatti: 1 x + x = 0 e 1 x x = 0 A questa conclusione si poteva anche giungere con un ragionamento aritmetico (sempre molto importante nel calcolo dei iti!): se dividiamo il numero 1 per valori sempre più grandi, otteniamo valori sempre più vicini allo zero: 1 2 = 0, = 0, = 0, etc Emanuele Biolcati 9
10 Una funzione elementare per eccellenza: l iperbole (III) Vediamo cosa succede per valori di x molto vicini allo zero. Dal grafico è evidente che la funzione assume valori molto piccoli se ci avviciniamo da sinistra (precipita nel baratro del meno infinito) e valori molto grandi se ci avviciniamo da destra (decolla con vigore verso l infinito e oltre). Ma è naturale pensare che non taglierà mai l asse delle ordinate. Ecco trovato un asintoto verticale di equazione x = 0 e infatti: 1 1 = e x 0 x x 0 + x = + Anche in questo caso funziona l approccio dell aritmetica: se dividiamo il numero 1 per valori sempre più vicini a zero positivi, otteniamo valori sempre più grandi: 1 0, 1 = , 001 = = etc. 0, Emanuele Biolcati 10
11 Funzioni simili alle prime due Con opportune accortezze, è possibile intuire i iti delle funzioni simili alla retta e all iperbole. Dovremo tenere conto del segno, della parità e delle intersezioni con gli assi. Ad esempio f(x) = x 3 e f(x) = x 5 si comporteranno allo stesso modo della retta, perché con stesso segno e dispari. La funzione f(x) = x 2 è pari, sempre positiva, quindi si intuisce che i iti per x ± saranno sempre + e allo stesso modo f(x) = x 4, f(x) = x 6, etc. Discorso analogo per f(x) = 1 x che essendo pari e sempre positiva 2 avrà tutti i iti positivi, mentre f(x) = 1 x tutti negativi. 2 Traslazioni delle funzioni rispetteranno i iti, come f(x + 1) per valori di x molto grandi (perché sommare 1 a infinito non fa molto effetto!). Emanuele Biolcati 11
12 Altre funzioni elementari Sul libro o direttamente giocando con Geogebra prova tu a intuire gli andamenti per le seguenti funzioni elementari: f(x) = ln x f(x) = e x f(x) = x f(x) = sin x E poi prova ad immaginare cosa accade per le funzioni trasformate, come f(x + 2), f(x) + 2, f( x ), etc. Ricorda: si dice che un ite non esiste quando il ite destro è diverso da quello sinistro o quando la funzione oscilla attorno ad un valore (come per le goniometriche). Emanuele Biolcati 12
13 Giocando con il lemniscata Prima di applicare l algebra dei iti, dobbiamo familiarizzare con l aritmetica dell infinito, ovvero dobbiamo capire che risultano diano somme e prodotti tra infinito e infinito o tra infinito e altri valori finiti (l). Ecco i seguenti casi validi in generale: l + = + e l = + + = + e = (l) (± ) = ± e (± ) (± ) = ± (regola dei segni) Mentre i seguenti sono detti forme di indecisione perché non esite una regola valida a priori, ma è necessario studiare i iti caso per caso: Emanuele Biolcati 13
14 Esempi a) x 0 (sin 2 x cos x) = x 0 sin x x 0 sin x x 0 cos x = = 0 ln x b) x 1 x 2 = x 1 ln x x 1 x 2 = 0 1 = 0 ( c) ln x 1 ) ( = ln x + 1 ) = 1 + ( ) = x 1 x 1 x 1 x 1 x 1 d) x 0 [ (x 2 1) ln x ] = x 0 (x 2 1) x 0 ln x = 1 ( ) = + cos x e) = x 0 cos x = 1 x 0 x x 0 x 0 = + Emanuele Biolcati 14
15 Forme di indecisione per funzioni polinomiali Le funzioni polinomiali presentano forme di indecisione solo per x ± e sono facilmente risolvibili sfruttando il raccogento del termine di grado massimo. Esempio: [x (1 3 1x + 1x 2 + 1x )] 3 x + (x3 x 2 + x + 1) = x + = x + x3 ecco che nel secondo membro tutte le frazioni dentro le parentesi tonde per x + tendono a 0, di conseguenza rimane soltanto x 3 (terzo membro). Regola per funzioni polinomiali Per calcolare il ite di un polinomio per x ± è sufficiente calcolare il ite del suo termine di grado massimo. Emanuele Biolcati 15
16 Forme di indecisione per funzioni razionali fratte (I) Le funzioni razionali fratte possono presentare forme di indecisione per x ±, ma anche 0 0 per x x 0 con x 0 punto in cui la funzione non è definita. Nel primo caso si procede analogamente alle polinomiali: x 3 x x ( x x + x 2 = + ) 1 x x + x ( ) = x 2 x 3 = x + x 2 = x = + x + perché nuovamente le frazioni nelle parentesi tonde si annullano. Prima regola per funzioni razionali fratte Per calcolare il ite del rapporto di due polinomi per x ± è sufficiente calcolare il ite del rapporto dei termini di grado massimo. Emanuele Biolcati 16
17 Forme di indecisione per funzioni razionali fratte (II) Per le forme di indecisione 0 0 per x x 0 con x 0, invece, dobbiamo einare l indeterminazione attraverso la scomposizione in polinomi (che è sempre possibile perché x 0 è soluzione sia del denominatore che del numeratore): x 2 + 3x 4 (x 1)(x + 4) x 1 x 2 = 1 x 1 (x 1)(x + 1) = x + 4 = x 1 x + 1 = 5 2 Seconda regola per funzioni razionali fratte Per calcolare il ite del rapporto di due polinomi per x x 0 con x 0 radice di numeratore e denominatore, è sufficiente scomporre denominatore e numeratore, semplificare i polinomi comuni, calcolare il ite rimanente. Emanuele Biolcati 17
18 Gerarchia degli infiniti (I) La rapidità con cui le funzioni crescono (o decrescono) non è sempre la stessa. Ci sono funzioni che crescono molto velocemente (come l esponenziale) o, in altre parole, che aumentando di poco i valori di x, i corrispondenti valori di y schizzano a valori elevatissimi. Al contrario, alcune funzioni (come il logaritmo) impiegano molto tempo a raggiungere valori grandi. Vediamo qualche esempio numerico, confrontando i valori di tre funzioni per x + : x e x x ln(x) 2,3 3,9 4,6 5,3 Si può quindi stabilire una gerarchia tra gli infiniti, ovvero tra le funzioni in base a quanto rapidamente si muovono verso ±. Emanuele Biolcati 18
19 Gerarchia degli infiniti (II) Teorema sulla gerarchia degli infiniti L esponenziale cresce più rapidamente di qualsiasi potenza. La potenza cresce più velocemente di qualsiasi logaritmo. Pertanto si avrà sempre: x + x + a x = + a > 1, b > 0 xb x a = + a > 0, b > 1 log b (x) E questo ci permette di risolvere molte forme di indecisione. Ad esempio: x + x + x 4 2 3x ln(2x) = (vince il denominatore) = 0 ex = (vince il numeratore) = + Emanuele Biolcati 19
20 Limiti notevoli Esistono alcune funzioni particolari i cui iti sono calcolabili mediante teoremi o definizioni. Diventa utile conoscerli (per questo detti notevoli) perché altre funzioni si possono ricondurre a queste. I più celebri sono: Principali iti notevoli ( x sin(x) 1 cos(x) = e = 1 x ± x) x 0 x x 0 x 2 = 1 Emanuele Biolcati 20
21 Cambio di variabile (un trucco) Per sfruttare i iti notevoli o comunque ricondursi a calcoli più semplici, può essere utile cambiare la variabile che si fa tendere ad un certo valore. Per funzioni composte f(g(x)) complicate, infatti, si può definire t = g(x) e calcolare i ite di f(t), con questa volta t che tende ad un nuovo valore. x x 0 f(g(x)) = t t0 f(t) [avendo posto t = g(x)] Esempio: per calcolare x 0 e 1/x, pongo t = 1/x, in modo da avere una funzione semplice e t ; scopro allora che per x 0, t (ricordando la funzione iperbole f(x) = 1/x); quindi calcolo il nuovo ite nella sola variabile t: e 1 x = x 0 t et = 0 [avendo posto t = 1 x ] Emanuele Biolcati 21
22 Teoremi (I) Ci itiamo ad enunciare i tre teoremi più importanti alla base dell algebra dei iti. Teorema di esistenza per funzioni monotone Sia f(x) funzione monotona in un intervallo (a, b), allora esistono sempre, finiti o infiniti, i iti di f(x) per x a + e per x b Teorema di unicità del ite Se una funzione ammette ite, questo ite è unico Emanuele Biolcati 22
23 Teoremi (II) Teorema dei due carabinieri (o del confronto) Date tre funzioni f, g, h : X R definite sul dominio X R, dato x 0 X, se (ipotesi 1) f(x) = h(x) = l x x 0 x x 0 e (ipotesi 2) I f(x) g(x) h(x) x I X \ {x 0 } allora (tesi) g(x) = l. x x 0 In altre parole, se esistono i iti per x che tende a x 0 di due funzioni f e h (ipotesi 1) e se esiste un intorno di x 0 in cui una terza funzione g è contenuta tra le prime due (ipotesi 2), allora il ite di g coincide con quello delle prime due funzioni (tesi). Emanuele Biolcati 23
24 Conclusione Gli appunti qui riportati non vogliono sostituirsi al manuale di testo che si distingue per maggior rigorosità, esaustività e correttezza. Lo scopo è quello di fornire una visione sintetica e semplificata dell argomento, ma questa acquista significato solo se accompagnata da uno studio approfondito e dallo svolgimento degli esercizi. A tal fine si riporta una bibliografia essenziale. Bibliografia: Sasso, Nuova Matematica a Colori, Petrini (2016), vol. 5, pagg Dodero, Baroncini, Manfredi, Nuovi elementi di matematica Ghisetti e Corvi Editori (1997), vol. B, pagg Emanuele Biolcati 24
Studio qualitativo del grafico di una funzione
 Studio qualitativo del grafico di una funzione Obiettivo: ottenere informazioni per descrivere qualitativamente l andamento del grafico di una funzione f campo di esistenza (cioè, l insieme di definizione)
Studio qualitativo del grafico di una funzione Obiettivo: ottenere informazioni per descrivere qualitativamente l andamento del grafico di una funzione f campo di esistenza (cioè, l insieme di definizione)
SOLUZIONE DEGLI ESERCIZI DEL FOGLIO N. 7
 SOLUZIONE DEGLI ESERCIZI DEL FOGLIO N. 7 Esercizio. Funzione da studiare: log( 3).. Dominio: dobbiamo richiedere che il denominatore non si annulli e che il logaritmo sia ben definito. Quindi le condizioni
SOLUZIONE DEGLI ESERCIZI DEL FOGLIO N. 7 Esercizio. Funzione da studiare: log( 3).. Dominio: dobbiamo richiedere che il denominatore non si annulli e che il logaritmo sia ben definito. Quindi le condizioni
Studio Qualitativo di Funzione
 Studio Qualitativo di Funzione Reperire un certo numero di informazioni per descrivere a livello qualitativo l andamento del grafico di una funzione f 1. campo di esistenza (cioè, l insieme di definizione)
Studio Qualitativo di Funzione Reperire un certo numero di informazioni per descrivere a livello qualitativo l andamento del grafico di una funzione f 1. campo di esistenza (cioè, l insieme di definizione)
Limiti di funzioni 1 / 39
 Limiti di funzioni 1 / 39 Comportamento agli estremi: operazione di ite 2 / 39 Sia f (x) una funzione definita su R e supponiamo di voler studiare l andamento della funzione agli estremi del dominio: x
Limiti di funzioni 1 / 39 Comportamento agli estremi: operazione di ite 2 / 39 Sia f (x) una funzione definita su R e supponiamo di voler studiare l andamento della funzione agli estremi del dominio: x
Corso di Analisi Matematica Limiti di funzioni
 Corso di Analisi Matematica Limiti di funzioni Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 39 1 Definizione di ite 2 Il calcolo dei
Corso di Analisi Matematica Limiti di funzioni Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 39 1 Definizione di ite 2 Il calcolo dei
Limiti di funzioni 1 / 41
 Limiti di funzioni 1 / 41 Comportamento agli estremi: operazione di ite 2 / 41 Sia f (x) una funzione definita su R e supponiamo di voler studiare l andamento della funzione agli estremi del dominio: x
Limiti di funzioni 1 / 41 Comportamento agli estremi: operazione di ite 2 / 41 Sia f (x) una funzione definita su R e supponiamo di voler studiare l andamento della funzione agli estremi del dominio: x
Calcolo di limiti. = e il limite. La funzione non è definita in La funzione è definita in. La funzione è continua a destra in
 LIMITI Calcolo di limiti FUNZIONE CONTINUA Definizione Una funzione si dice continua in un punto quando il limite = La funzione non è definita in La funzione è definita in La funzione è definita in ma
LIMITI Calcolo di limiti FUNZIONE CONTINUA Definizione Una funzione si dice continua in un punto quando il limite = La funzione non è definita in La funzione è definita in La funzione è definita in ma
Matematica A Corso di Laurea in Chimica. Prova scritta del Tema A
 Matematica A Corso di Laurea in Chimica Prova scritta del 7..6 Tema A P) Data la funzione f(x) = ex+ x determinarne (a) campo di esistenza; (b) zeri e segno; (c) iti agli estremi del campo di esistenza
Matematica A Corso di Laurea in Chimica Prova scritta del 7..6 Tema A P) Data la funzione f(x) = ex+ x determinarne (a) campo di esistenza; (b) zeri e segno; (c) iti agli estremi del campo di esistenza
Istituzioni di Matematiche terza parte
 Istituzioni di Matematiche terza parte anno acc. 2013/2014 Univ. degli Studi di Milano D.Bambusi, C.Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 45 index Il concetto di ite 1 Il
Istituzioni di Matematiche terza parte anno acc. 2013/2014 Univ. degli Studi di Milano D.Bambusi, C.Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 45 index Il concetto di ite 1 Il
Istituzioni di Matematiche seconda parte
 Istituzioni di Matematiche seconda parte anno acc. 2010/2011 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 26 index 1 2 Continuità Cristina Turrini
Istituzioni di Matematiche seconda parte anno acc. 2010/2011 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 26 index 1 2 Continuità Cristina Turrini
APPUNTI DI MATEMATICA: I limiti e la continuità Le derivate. Prof. ssa Prenol R.
 APPUNTI DI MATEMATICA: I iti e la continuità Le derivate Prof. ssa Prenol R. INTERVALLI e INTORNI Definizione di intervallo: è un sottoinsieme di numeri reali e può essere - ilitato: graficamente viene
APPUNTI DI MATEMATICA: I iti e la continuità Le derivate Prof. ssa Prenol R. INTERVALLI e INTORNI Definizione di intervallo: è un sottoinsieme di numeri reali e può essere - ilitato: graficamente viene
Esercizi sui limiti. lim. lim. lim. lim. log(x 4) + 5x = + + = + 6) x2 4 = 2 =
 Limiti e continuità Risoluzione di forme indeterminate con polinomi Ordine di infinito e confronto di infiniti Alcuni iti notevoli Funzioni continue Esercizi sui iti ( 3 + 3) = (10 + 3 32 ) = 57 ( + 2
Limiti e continuità Risoluzione di forme indeterminate con polinomi Ordine di infinito e confronto di infiniti Alcuni iti notevoli Funzioni continue Esercizi sui iti ( 3 + 3) = (10 + 3 32 ) = 57 ( + 2
tele limite è unico. Ciò significa che se non può accadere che una funzione abbia limiti diversi per x. Se per assurdo si avesse che lim f ( x)
 Calcolo dei iti (C. DIMAURO) Per il calcolo dei iti ci serviamo di alcuni teoremi. Tali teoremi visti nel caso in cui, valgono anche quando Teorema dell unicità del ite: se una funzione ammette ite per
Calcolo dei iti (C. DIMAURO) Per il calcolo dei iti ci serviamo di alcuni teoremi. Tali teoremi visti nel caso in cui, valgono anche quando Teorema dell unicità del ite: se una funzione ammette ite per
Limiti di funzioni e continuità
 Limiti di funzioni e continuità Paolo Montanari Appunti di Matematica Limiti di funzioni e continuità 1 Funzioni limitate La funzione f(x) è limitata superiormente se esiste un numero reale M tale che
Limiti di funzioni e continuità Paolo Montanari Appunti di Matematica Limiti di funzioni e continuità 1 Funzioni limitate La funzione f(x) è limitata superiormente se esiste un numero reale M tale che
Esercitazioni di Analisi Matematica FUNZIONI CUBICHE. Effettuare lo studio completo delle seguenti funzioni di terzo grado intere:
 FUNZIONI CUBICHE Effettuare lo studio completo delle seguenti funzioni di terzo grado intere: 1) y = fx) = x 3 + 2x 2 + x 2) y = fx) = x 3 + x 2 + x + 2 3) y = fx) = x 3 + 2x 2 + x 4 4) y = fx) = x 3 +
FUNZIONI CUBICHE Effettuare lo studio completo delle seguenti funzioni di terzo grado intere: 1) y = fx) = x 3 + 2x 2 + x 2) y = fx) = x 3 + x 2 + x + 2 3) y = fx) = x 3 + 2x 2 + x 4 4) y = fx) = x 3 +
Istituzioni di Matematiche terza parte
 Istituzioni di Matematiche terza parte anno acc. 2011/2012 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 35 index Il concetto di limite 1 Il
Istituzioni di Matematiche terza parte anno acc. 2011/2012 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 35 index Il concetto di limite 1 Il
LICEO LINGUISTICO NINNI CASSARÁ. Classe VA. Studio di Funzioni. prof. Alessio Cangemi
 LICEO LINGUISTICO NINNI CASSARÁ Classe VA Studio di Funzioni prof. Alessio Cangemi Di seguito saranno schematizzati gli step fondamentali per tracciare il grafico probabile di una funzione f(x). 1 Ricerca
LICEO LINGUISTICO NINNI CASSARÁ Classe VA Studio di Funzioni prof. Alessio Cangemi Di seguito saranno schematizzati gli step fondamentali per tracciare il grafico probabile di una funzione f(x). 1 Ricerca
IIID Matematica Aprile ) Cosa significa dire che una funzione reale di variabile reale è continua?
 1) Cosa significa dire che una funzione reale di variabile reale è continua? 2) Dire se la funzione f(x) = x x 2 5 è a continua per x = 5 ; b continua per x = 3 ; c continua per x = π 2 ; 3) Cosa si intente
1) Cosa significa dire che una funzione reale di variabile reale è continua? 2) Dire se la funzione f(x) = x x 2 5 è a continua per x = 5 ; b continua per x = 3 ; c continua per x = π 2 ; 3) Cosa si intente
Metodi Matematici per l Economia A-K Corso di Laurea in Economia - anno acc. 2012/2013 docente: Elena Polastri,
 Metodi Matematici per l Economia A-K Corso di Laurea in Economia - anno acc. 202/203 docente: Elena Polastri, plslne@unife.it Studio di funzione con indicazione degli asintoti e grafico probabile Studiare
Metodi Matematici per l Economia A-K Corso di Laurea in Economia - anno acc. 202/203 docente: Elena Polastri, plslne@unife.it Studio di funzione con indicazione degli asintoti e grafico probabile Studiare
ANALISI MATEMATICA I per Ingegneria Aerospaziale - A.A Diario delle lezioni. Mercoledì 2 ottobre 2013 (2 ore)
 c Andrea Dall Aglio - Analisi Matematica: Diario delle lezioni - 8 novembre 0 ANALISI MATEMATICA I per Ingegneria Aerospaziale - A.A. 0-04 Diario delle lezioni Questo è un indice degli argomenti trattati
c Andrea Dall Aglio - Analisi Matematica: Diario delle lezioni - 8 novembre 0 ANALISI MATEMATICA I per Ingegneria Aerospaziale - A.A. 0-04 Diario delle lezioni Questo è un indice degli argomenti trattati
CAPITOLO VI LIMITI DI FUNZIONI
 CAPITOLO VI LIMITI DI FUNZIONI. CONCETTO DI LIMITE Esula dallo scopo di questo libro la trattazione della teoria sui iti. Tuttavia, pensando di fare cosa gradita allo studente, che deve possedere questa
CAPITOLO VI LIMITI DI FUNZIONI. CONCETTO DI LIMITE Esula dallo scopo di questo libro la trattazione della teoria sui iti. Tuttavia, pensando di fare cosa gradita allo studente, che deve possedere questa
Lezione 18 (8 gennaio) Limiti
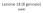 Lezione 18 (8 gennaio) Limiti Ripasso f x = ln 3 x 1 D = (1, + ) ln 3 x 1 + x 1 = ln 3 1 + 1 = ln 3 = ln(+ ) = + 0 + ln 3 x + x 1 = ln 3 + 1 = ln 3 + = ln(0+ ) = 1 Esempi di forme indeterminate x + x3
Lezione 18 (8 gennaio) Limiti Ripasso f x = ln 3 x 1 D = (1, + ) ln 3 x 1 + x 1 = ln 3 1 + 1 = ln 3 = ln(+ ) = + 0 + ln 3 x + x 1 = ln 3 + 1 = ln 3 + = ln(0+ ) = 1 Esempi di forme indeterminate x + x3
= l. x x 0. In realtà può aversi una casistica più amplia potendo sia x che f ( x) tendere ad un elemento dell insieme
 LIMITI DI FUNZIONI. CONCETTO DI LIMITE Esula dallo scopo del presente capitolo la trattazione della teoria sui iti. Tuttavia, pensando di fare cosa gradita allo studente, che deve possedere questa nozione
LIMITI DI FUNZIONI. CONCETTO DI LIMITE Esula dallo scopo del presente capitolo la trattazione della teoria sui iti. Tuttavia, pensando di fare cosa gradita allo studente, che deve possedere questa nozione
Studio Qualitativo di Funzione
 Studio Qualitativo di Funzione Reperire un certo numero di informazioni, per descrivere a livello qualitativo l andamento di una funzione y = f() : 1. campo di esistenza ( insieme di definizione ) 2. segno:
Studio Qualitativo di Funzione Reperire un certo numero di informazioni, per descrivere a livello qualitativo l andamento di una funzione y = f() : 1. campo di esistenza ( insieme di definizione ) 2. segno:
Esercitazioni di Matematica
 Università degli Studi di Udine Anno Accademico 009/00 Facoltà di Agraria Corsi di Laurea in VIT e STAL Esercitazioni di Matematica novembre 009 Trovare le soluzioni della seguente disequazione: x + +
Università degli Studi di Udine Anno Accademico 009/00 Facoltà di Agraria Corsi di Laurea in VIT e STAL Esercitazioni di Matematica novembre 009 Trovare le soluzioni della seguente disequazione: x + +
Funzioni continue. quando. se è continua x I.
 Funzioni continue Definizione: f() si dice continua in 0 D f quando (*) 0 f () f ( 0 ) Definizione: f() si dice continua in I D f se è continua I. Avevamo già dato questa definizione parlando del f ().
Funzioni continue Definizione: f() si dice continua in 0 D f quando (*) 0 f () f ( 0 ) Definizione: f() si dice continua in I D f se è continua I. Avevamo già dato questa definizione parlando del f ().
Esercitazioni di Matematica Generale A.A. 2016/2017 Pietro Pastore Lezione del 2 Dicembre Dominio di Funzioni
 Esercitazioni di Matematica Generale A.A. 06/07 Pietro Pastore Lezione del Dicembre 06 Dominio di Funzioni Determinare il dominio delle seguenti funzioni ) x +3x. fx) =. Il dominio si trova considerando
Esercitazioni di Matematica Generale A.A. 06/07 Pietro Pastore Lezione del Dicembre 06 Dominio di Funzioni Determinare il dominio delle seguenti funzioni ) x +3x. fx) =. Il dominio si trova considerando
Funzioni Continue. se (e solo se) 0
 f : A R R A ' Funzioni Continue La funzione f si dice continua in f ( f ( se (e solo se A Ne seguono tre proprietà affinché f( sia continua in :. Devono esistere finiti il ite destro e sinistro di f( in.
f : A R R A ' Funzioni Continue La funzione f si dice continua in f ( f ( se (e solo se A Ne seguono tre proprietà affinché f( sia continua in :. Devono esistere finiti il ite destro e sinistro di f( in.
CALCOLO DEI LIMITI = =
 CALCOLO DEI LIMITI Tenendo conto dei teoremi dei iti e delle proprietà simboliche dell infinito è possibile calcolare il risultato di diversi tipi di ite. Negli esercizi di questo tipo si sostituisce alla
CALCOLO DEI LIMITI Tenendo conto dei teoremi dei iti e delle proprietà simboliche dell infinito è possibile calcolare il risultato di diversi tipi di ite. Negli esercizi di questo tipo si sostituisce alla
Calcolo infinitesimale
 Calcolo infinitesimale L operazione di limite L operazione di limite ha lo scopo di descrivere il comportamento di una funzione nei pressi di un punto di accumulazione per il suo dominio. Limite finito
Calcolo infinitesimale L operazione di limite L operazione di limite ha lo scopo di descrivere il comportamento di una funzione nei pressi di un punto di accumulazione per il suo dominio. Limite finito
Limiti e continuità. Teoremi sui limiti. Teorema di unicità del limite Teorema di permanenza del segno Teoremi del confronto Algebra dei limiti
 Limiti e continuità Teorema di unicità del ite Teorema di permanenza del segno Teoremi del confronto Algebra dei iti 2 2006 Politecnico di Torino 1 Se f(x) =` ` è unico Per assurdo, siano ` 6= `0 con f(x)
Limiti e continuità Teorema di unicità del ite Teorema di permanenza del segno Teoremi del confronto Algebra dei iti 2 2006 Politecnico di Torino 1 Se f(x) =` ` è unico Per assurdo, siano ` 6= `0 con f(x)
MATEMATICA MATEMATICA FINANZIARIA
 MATEMATICA e MATEMATICA FINANZIARIA a.a. 7-8 Corso di laurea in Economia Aziendale Fascicolo n. Limite di funzioni e applicazioni. Limite di una funzione Funzioni continue Calcolo dei iti Asintoti Prof.ssa
MATEMATICA e MATEMATICA FINANZIARIA a.a. 7-8 Corso di laurea in Economia Aziendale Fascicolo n. Limite di funzioni e applicazioni. Limite di una funzione Funzioni continue Calcolo dei iti Asintoti Prof.ssa
Derivate e studio di funzioni di una variabile
 Derivate e studio di funzioni di una variabile Paolo Montanari Appunti di Matematica Derivate e studio di funzioni 1 Rapporto incrementale e derivata Sia f(x) una funzione definita in un intervallo X R
Derivate e studio di funzioni di una variabile Paolo Montanari Appunti di Matematica Derivate e studio di funzioni 1 Rapporto incrementale e derivata Sia f(x) una funzione definita in un intervallo X R
Teorema sul limite di una somma. ( x) l2. allora
 Teorema sul ite di una somma Se f ( ) l e g( ) l allora [ f ( ) g( ) ] l l Il teorema vale anche per i casi in cui tende a più infinito oppure a infinito. La dimostrazione è analoga a quella vista qui
Teorema sul ite di una somma Se f ( ) l e g( ) l allora [ f ( ) g( ) ] l l Il teorema vale anche per i casi in cui tende a più infinito oppure a infinito. La dimostrazione è analoga a quella vista qui
Studi di funzione. D. Barbieri. Studiare comportamento asintotico e monotonia di. f(x) = 1 x x4 + 4x e x
 Studi di funzione D. Barbieri Esercizi Esercizio Esercizio Studiare comportamento asintotico e monotonia di f(x) = x + x4 + 4x Studiare il comportamento asintotico di f(x) = + x x + + e x Esercizio 3 Determinare
Studi di funzione D. Barbieri Esercizi Esercizio Esercizio Studiare comportamento asintotico e monotonia di f(x) = x + x4 + 4x Studiare il comportamento asintotico di f(x) = + x x + + e x Esercizio 3 Determinare
ESERCIZI DI METODI MATEMATICI PER L ECONOMIA FACOLTÀ DI ECONOMIA DI FERRARA A.A. 2011/2012
 ESERCIZI DI METODI MATEMATICI PER L ECONOMIA FACOLTÀ DI ECONOMIA DI FERRARA A.A. 20/202. Esercizi: lezione 8 novembre 20 Studio di funzione con indicazione degli asintoti e grafico probabile Studiare completamente
ESERCIZI DI METODI MATEMATICI PER L ECONOMIA FACOLTÀ DI ECONOMIA DI FERRARA A.A. 20/202. Esercizi: lezione 8 novembre 20 Studio di funzione con indicazione degli asintoti e grafico probabile Studiare completamente
Abbiamo già visto nel capitolo sulle funzioni che, negli estremi del suo dominio, una funzione può avere degli asintoti.
 Capitolo 7 Limiti di funzioni Abbiamo già visto nel capitolo sulle funzioni che, negli estremi del suo dominio, una funzione può avere degli asintoti. Ricordiamo che un asintoto verticale = a si presenta
Capitolo 7 Limiti di funzioni Abbiamo già visto nel capitolo sulle funzioni che, negli estremi del suo dominio, una funzione può avere degli asintoti. Ricordiamo che un asintoto verticale = a si presenta
f(x) lim x c g(x) = lim x c f(x) lim x c g(x)
 Matematica I, 10.10.2012 Limiti di funzioni (II) 1. Limiti e Operazioni Algebriche L operazione di ite di successioni si comporta bene rispetto alle operazioni algebriche di somma (e sottrazione), prodotto
Matematica I, 10.10.2012 Limiti di funzioni (II) 1. Limiti e Operazioni Algebriche L operazione di ite di successioni si comporta bene rispetto alle operazioni algebriche di somma (e sottrazione), prodotto
f(x) = 1 x 2 Per determinare il dominio di f(x) dobbiamo imporre che il determinante sia diverso da zero
 . Data la funzione approssimarne il grafico. f() = 2 Per determinare il dominio di f() dobbiamo imporre che il determinante sia diverso da zero 2 0 = 2 = ± perciò il dominio ` D = R \ {, } =], [ ], [ ],
. Data la funzione approssimarne il grafico. f() = 2 Per determinare il dominio di f() dobbiamo imporre che il determinante sia diverso da zero 2 0 = 2 = ± perciò il dominio ` D = R \ {, } =], [ ], [ ],
MATEMATICA MATURITA LINGUISTICA. Istituto Paritario A.Ruiz Istituto Paritario A.Ruiz
 MATEMATICA MATURITA LINGUISTICA Istituto Paritario A.Ruiz Istituto Paritario A.Ruiz 1 MATEMATICA MATURITA LINGUISTICA 1. CLASSIFICAZIONE FUNZIONI FUNZIONI ALGEBRICHE (in cui compaiono le quattro operazioni):
MATEMATICA MATURITA LINGUISTICA Istituto Paritario A.Ruiz Istituto Paritario A.Ruiz 1 MATEMATICA MATURITA LINGUISTICA 1. CLASSIFICAZIONE FUNZIONI FUNZIONI ALGEBRICHE (in cui compaiono le quattro operazioni):
Studio Qualitativo di Funzione
 Studio Qualitativo di Funzione Reperire un certo numero di informazioni per descrivere a livello qualitativo l andamento del grafico di una funzione f 1. campo di esistenza (cioè, l insieme di definizione)
Studio Qualitativo di Funzione Reperire un certo numero di informazioni per descrivere a livello qualitativo l andamento del grafico di una funzione f 1. campo di esistenza (cioè, l insieme di definizione)
D Analisi Matematica 1 (Corso di Laurea in Informatica e Bioinformatica)
 COGNOME NOME Matr. D Firma dello studente Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
COGNOME NOME Matr. D Firma dello studente Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
QUINTO APPELLO DEL CORSO DI ANALISI MATEMATICA CORSO DI LAURA IN INFORMATICA, A.A. 2017/18 23 LUGLIO 2018 CORREZIONE. x 4 f(x) = x 2 + x 2
 QUINTO APPELLO DEL CORSO DI ANALISI MATEMATICA CORSO DI LAURA IN INFORMATICA, A.A. 27/8 23 LUGLIO 28 CORREZIONE Esercizio ) Considerate la funzione f definita da f(x) = x 2 + x 2. Trovatene il dominio
QUINTO APPELLO DEL CORSO DI ANALISI MATEMATICA CORSO DI LAURA IN INFORMATICA, A.A. 27/8 23 LUGLIO 28 CORREZIONE Esercizio ) Considerate la funzione f definita da f(x) = x 2 + x 2. Trovatene il dominio
Analisi Matematica I Primo Appello ( ) - Fila 1
 Analisi Matematica I Primo Appello (4-11-003) - Fila 1 1. Determinare la retta tangente alla funzione f() = (1 + ) 1+ in = 0. R. f(0) = 1, mentre la derivata è f () = ( e (1+) log(1+)) ( ) = e (1+) log(1+)
Analisi Matematica I Primo Appello (4-11-003) - Fila 1 1. Determinare la retta tangente alla funzione f() = (1 + ) 1+ in = 0. R. f(0) = 1, mentre la derivata è f () = ( e (1+) log(1+)) ( ) = e (1+) log(1+)
Teorema degli zeri. Essendo f continua in a e in b, per il teorema della
 Teorema degli zeri Una funzione reale f continua nell intervallo chiuso e itato [a; b] che assuma valori di segno opposto negli estremi di tale intervallo, si annulla in almeno un punto ad esso interno
Teorema degli zeri Una funzione reale f continua nell intervallo chiuso e itato [a; b] che assuma valori di segno opposto negli estremi di tale intervallo, si annulla in almeno un punto ad esso interno
Corso di Laurea in Informatica Applicata Esame di Analisi Matematica Secondo test di verifica a. a. 2006/2007
 Corso di Laurea in Informatica Applicata Esame di Analisi Matematica Secondo test di verifica a. a. 2006/2007 Risolvere esattamente due tra gli esercizi seguenti. Le risposte non motivate non saranno prese
Corso di Laurea in Informatica Applicata Esame di Analisi Matematica Secondo test di verifica a. a. 2006/2007 Risolvere esattamente due tra gli esercizi seguenti. Le risposte non motivate non saranno prese
francesca fattori speranza - bozza febbraio 2018 LIMITI applicati allo studio di funzione
 francesca fattori speranza - bozza febbraio 2018 LIMITI applicati allo studio di funzione In questa trattazione si affrontano solo alcuni esempi di funzioni: polinomiali, fratte irrazionale con argomento
francesca fattori speranza - bozza febbraio 2018 LIMITI applicati allo studio di funzione In questa trattazione si affrontano solo alcuni esempi di funzioni: polinomiali, fratte irrazionale con argomento
8. LIMITI. Definizioni e primi teoremi Calcolo di limiti
 ISTITUZIONI DI MATEMATICHE E FONDAMENTI DI BIOSTATISTICA 8. LIMITI Definizioni e primi teoremi Calcolo di limiti A. A. 213-214 1 IDEA INTUITIVA DI LIMITE I Caso Sia f una funzione definita in ogni punto
ISTITUZIONI DI MATEMATICHE E FONDAMENTI DI BIOSTATISTICA 8. LIMITI Definizioni e primi teoremi Calcolo di limiti A. A. 213-214 1 IDEA INTUITIVA DI LIMITE I Caso Sia f una funzione definita in ogni punto
lim f(x) lim In questo caso, lim Una funzione è continua in un punto x 0 se valgono le seguenti condizioni:
 Definizioni fondamentali Un intorno di un punto = 0 è un intervallo I che contiene 0. Un intorno destro per semplicità lo chiamiamo + 0 ) di 0 è un intervallo in cui l estremo sinistro è 0 : tutti i punti
Definizioni fondamentali Un intorno di un punto = 0 è un intervallo I che contiene 0. Un intorno destro per semplicità lo chiamiamo + 0 ) di 0 è un intervallo in cui l estremo sinistro è 0 : tutti i punti
ESERCIZI DI METODI MATEMATICI PER L ECONOMIA FACOLTÀ DI ECONOMIA DI FERRARA A.A. 2011/2012
 ESERCIZI DI METODI MATEMATICI PER L ECONOMIA FACOLTÀ DI ECONOMIA DI FERRARA A.A. 2011/2012 1. Esercizi 3 1. Studiare la seguente funzione FINO alla derivata prima, con tracciamento di grafico ed indicazione
ESERCIZI DI METODI MATEMATICI PER L ECONOMIA FACOLTÀ DI ECONOMIA DI FERRARA A.A. 2011/2012 1. Esercizi 3 1. Studiare la seguente funzione FINO alla derivata prima, con tracciamento di grafico ed indicazione
 LICEO SCIENTIFICO ESEDRA SCUOLA PARITARIA Classe V LS Prof. Francesco Marchi Appunti su: algebra dei iti Introduzione Abbiamo studiato i iti delle funzioni elementari, ad esempio abbiamo visto che: ln
LICEO SCIENTIFICO ESEDRA SCUOLA PARITARIA Classe V LS Prof. Francesco Marchi Appunti su: algebra dei iti Introduzione Abbiamo studiato i iti delle funzioni elementari, ad esempio abbiamo visto che: ln
y = x 3 infinitesimo per x 3 lim = l 0 allora f(x) è dello stesso ordine di g(x), ossia tendono a DEF. Una funzione y = f(x) si dice infinitesimo per
 INFINITI ED INFINITESIMI. ASINTOTI DI UNA FUNZIONE. GRAFICO PROBABILE DI UNA FUNZIONE. TEOREMI SULLE FUNZIONI CONTINUE ESERCIZI SULLA CONTINUITA E SULLA CLASSIFICAZIONE DELLE DISCONTINUITA DI UNA FUNZIONE
INFINITI ED INFINITESIMI. ASINTOTI DI UNA FUNZIONE. GRAFICO PROBABILE DI UNA FUNZIONE. TEOREMI SULLE FUNZIONI CONTINUE ESERCIZI SULLA CONTINUITA E SULLA CLASSIFICAZIONE DELLE DISCONTINUITA DI UNA FUNZIONE
13 LIMITI DI FUNZIONI
 3 LIMITI DI FUNZIONI Estendiamo la nozione di ite a funzioni reali di variabile reale. Definizione caratterizzazione per successioni) Si ha fx) = L x 0, L R) se e solo se per ogni successione a n x 0 con
3 LIMITI DI FUNZIONI Estendiamo la nozione di ite a funzioni reali di variabile reale. Definizione caratterizzazione per successioni) Si ha fx) = L x 0, L R) se e solo se per ogni successione a n x 0 con
UNITÀ DIDATTICA 2 LE FUNZIONI
 UNITÀ DIDATTICA LE FUNZIONI. Le funzioni Definizione. Siano A e B due sottoinsiemi non vuoti di R. Si chiama funzione di A in B una qualsiasi legge che fa corrispondere a ogni elemento A uno ed un solo
UNITÀ DIDATTICA LE FUNZIONI. Le funzioni Definizione. Siano A e B due sottoinsiemi non vuoti di R. Si chiama funzione di A in B una qualsiasi legge che fa corrispondere a ogni elemento A uno ed un solo
Soluzioni delle Esercitazioni V 15-19/10/ x 1 = = /x + = 0. 1+e x = 1. lnx 1+1/x = = = +.
 Soluzioni delle Esercitazioni V 5-9/0/208 A. Limiti I iti che seguono si possono calcolare con l algebra dei iti. 2 3 4 5 6 7 8 9 0 +2 3 = +2 3 = 3 2. e = ) e = e. / + = 0 + = 0 + = 0. +e = +0 = = 0. +/
Soluzioni delle Esercitazioni V 5-9/0/208 A. Limiti I iti che seguono si possono calcolare con l algebra dei iti. 2 3 4 5 6 7 8 9 0 +2 3 = +2 3 = 3 2. e = ) e = e. / + = 0 + = 0 + = 0. +e = +0 = = 0. +/
Programmazione disciplinare: Matematica 4 anno
 Programmazione disciplinare: Matematica 4 anno CONTENUTI RISULTATI DI APPRENDIMENTO (Competenze) CONOSCENZE ABILITA TEMPI (settimane) Intervalli limitati e illimitati in R Saper riconoscere intervalli
Programmazione disciplinare: Matematica 4 anno CONTENUTI RISULTATI DI APPRENDIMENTO (Competenze) CONOSCENZE ABILITA TEMPI (settimane) Intervalli limitati e illimitati in R Saper riconoscere intervalli
Programmazione disciplinare: Matematica 4 anno
 Programmazione disciplinare: Matematica 4 anno CONTENUTI Intervalli limitati e illimitati in R RISULTATI DI APPRENDIMENTO (Competenze) CONOSCENZE ABILITA TEMPI (settimane) Saper riconoscere intervalli
Programmazione disciplinare: Matematica 4 anno CONTENUTI Intervalli limitati e illimitati in R RISULTATI DI APPRENDIMENTO (Competenze) CONOSCENZE ABILITA TEMPI (settimane) Saper riconoscere intervalli
Prefazione LUCIANO ROMANO
 3 Prefazione Il testo, rivolto agli studenti universitari che si apprestano ad affrontare l esame di Analisi Matematica, propone un iniziale parte teorica e suggerimenti sulla risoluzione della vasta gamma
3 Prefazione Il testo, rivolto agli studenti universitari che si apprestano ad affrontare l esame di Analisi Matematica, propone un iniziale parte teorica e suggerimenti sulla risoluzione della vasta gamma
Programma svolto a.s. 2017/2018 Classe 1H Materia: Matematica Docente: De Rossi Francesco
 Classe 1H Materia: Matematica Docente: De Rossi Francesco - Matematica multimediale. bianco Vol 1 Autori: M. Bergamini, G. Barozzi Casa Editrice: Zanichelli codice ISBN 978888334671 Capitolo 1 Insiemi
Classe 1H Materia: Matematica Docente: De Rossi Francesco - Matematica multimediale. bianco Vol 1 Autori: M. Bergamini, G. Barozzi Casa Editrice: Zanichelli codice ISBN 978888334671 Capitolo 1 Insiemi
Concavità verso il basso (funzione concava) Si dice che in x0 il grafico della funzione f(x) abbia la concavità rivolta verso il basso, se esiste
 CONCAVITA E CONVESSITA DI UNA FUNZIONE. FLESSI. SCHEMA GENERALE PER LO STUDIO DI FUNZIONE. FUNZIONI RAZIONALI E IRRAZIONALI INTERE E FRATTE. TEOREMA DI DE L HOSPITAL CON APPLICAZIONI AI LIMITI. 1 Concavit{
CONCAVITA E CONVESSITA DI UNA FUNZIONE. FLESSI. SCHEMA GENERALE PER LO STUDIO DI FUNZIONE. FUNZIONI RAZIONALI E IRRAZIONALI INTERE E FRATTE. TEOREMA DI DE L HOSPITAL CON APPLICAZIONI AI LIMITI. 1 Concavit{
(g(x) = 0 vicino a c)
 Lezione del 15 ottobre. Limiti di funzioni. Calcolo di iti. 1. Sia dato un punto c R; per ciascun numero reale positivo δ > 0, l insieme dei punti che distano da c per meno di δ, cioe l intervallo ]c δ,
Lezione del 15 ottobre. Limiti di funzioni. Calcolo di iti. 1. Sia dato un punto c R; per ciascun numero reale positivo δ > 0, l insieme dei punti che distano da c per meno di δ, cioe l intervallo ]c δ,
Limiti. Limite di una funzione per x che tende a +,.
 Limiti. Limite di una funzione per che tende a +,. Semiintorni. Fissati su una retta un primo ed un diverso secondo punto, consideriamo l identificazione sopra descritta dei numeri reali con punti sulla
Limiti. Limite di una funzione per che tende a +,. Semiintorni. Fissati su una retta un primo ed un diverso secondo punto, consideriamo l identificazione sopra descritta dei numeri reali con punti sulla
STUDIO DEL GRAFICO DI UNA FUNZIONE
 STUDIO DEL GRAFICO DI UNA FUNZIONE PROF.SSA ROSSELLA PISCOPO 2 di 35 Indice 1 SCHEMA PER LO STUDIO DEL GRAFICO DI FUNZIONE... 4 2 ESEMPI... 11 2.1 2.2 2.3 2.4 2.5 2.6 FUNZIONE ESPONENZIALE... 11 FUNZIONE
STUDIO DEL GRAFICO DI UNA FUNZIONE PROF.SSA ROSSELLA PISCOPO 2 di 35 Indice 1 SCHEMA PER LO STUDIO DEL GRAFICO DI FUNZIONE... 4 2 ESEMPI... 11 2.1 2.2 2.3 2.4 2.5 2.6 FUNZIONE ESPONENZIALE... 11 FUNZIONE
CLASSE III D Programmi svolti
 A.S. 2014/2015 CLASSE III D Programmi svolti ************ MATEMATICA INSIEMI NUMERICI: Insiemi numerici e insiemi di punti; intervalli ed intorni; insiemi numerici limitati ed illimitati; estremo superiore
A.S. 2014/2015 CLASSE III D Programmi svolti ************ MATEMATICA INSIEMI NUMERICI: Insiemi numerici e insiemi di punti; intervalli ed intorni; insiemi numerici limitati ed illimitati; estremo superiore
6. LIMITI. Definizione - Funzioni continue - Calcolo dei limiti
 ISTITUZIONI DI MATEMATICHE E FONDAMENTI DI BIOSTATISTICA 6. LIMITI Definizione - Funzioni continue - Calcolo dei limiti A. A. 2014-2015 L.Doretti 1 IDEA INTUITIVA DI LIMITE I Caso: comportamento di una
ISTITUZIONI DI MATEMATICHE E FONDAMENTI DI BIOSTATISTICA 6. LIMITI Definizione - Funzioni continue - Calcolo dei limiti A. A. 2014-2015 L.Doretti 1 IDEA INTUITIVA DI LIMITE I Caso: comportamento di una
LO STUDIO DI FUNZIONE ESERCIZI CON SOLUZIONI
 Autore: Enrico Manfucci - 6/05/0 LO STUDIO DI FUNZIONE ESERCIZI CON SOLUZIONI PREMESSA Per Studio di funzione si intende disegnare il grafico di una funzione data la sua espressione analitica. Questo significa
Autore: Enrico Manfucci - 6/05/0 LO STUDIO DI FUNZIONE ESERCIZI CON SOLUZIONI PREMESSA Per Studio di funzione si intende disegnare il grafico di una funzione data la sua espressione analitica. Questo significa
ESERCIZI DI METODI MATEMATICI PER L ECONOMIA FACOLTÀ DI ECONOMIA DI FERRARA A.A. 2011/2012
 ESERCIZI DI METODI MATEMATICI PER L ECONOMIA FACOLTÀ DI ECONOMIA DI FERRARA A.A. 2011/2012 1. Esercizi: lezione 2 novembre 2011 Studio di funzioni Studiare le seguenti funzioni FINO alla derivata prima,
ESERCIZI DI METODI MATEMATICI PER L ECONOMIA FACOLTÀ DI ECONOMIA DI FERRARA A.A. 2011/2012 1. Esercizi: lezione 2 novembre 2011 Studio di funzioni Studiare le seguenti funzioni FINO alla derivata prima,
Calcolare un limite significa determinare quale sia il suo valore quando al posto dell incognita si sostituisce il valore cui essa tende.
 Infiniti, infinitesimi e forme indeterminate Calcolare un ite significa determinare quale sia il suo valore quando al posto dell incognita si sostituisce il valore cui essa tende. Cioè calcolare 5 4 significa
Infiniti, infinitesimi e forme indeterminate Calcolare un ite significa determinare quale sia il suo valore quando al posto dell incognita si sostituisce il valore cui essa tende. Cioè calcolare 5 4 significa
Elenco moduli Argomenti Strumenti / Testi Letture / Metodi. partecipazione degli alunni. 2 Completamento equazioni e disequazioni.
 Pagina 1 di 5 DISCIPLINA: MATEMATICA E LABORATORIO INDIRIZZO: IGEA CLASSE: IV FM DOCENTE : Cornelio Terreni Elenco moduli Argomenti Strumenti / Testi Letture / Metodi 1 Matematica RIPASSO e COMPLETAMENTO:
Pagina 1 di 5 DISCIPLINA: MATEMATICA E LABORATORIO INDIRIZZO: IGEA CLASSE: IV FM DOCENTE : Cornelio Terreni Elenco moduli Argomenti Strumenti / Testi Letture / Metodi 1 Matematica RIPASSO e COMPLETAMENTO:
Esercitazioni di Matematica Generale A.A. 2016/2017 Pietro Pastore Lezione del 25 Gennaio Studio di Funzione
 Esercitazioni di Matematica Generale A.A. 2016/2017 Pietro Pastore Lezione del 25 Gennaio 2017 Studio di Funzione 1. Si consideri la funzione reale di variabile reale così definita f() = 2 + 4. (a) Determinare
Esercitazioni di Matematica Generale A.A. 2016/2017 Pietro Pastore Lezione del 25 Gennaio 2017 Studio di Funzione 1. Si consideri la funzione reale di variabile reale così definita f() = 2 + 4. (a) Determinare
Esercizio 1. f(x) = 4 5x2 x 2 +x 2. Esercizio 2. f(x) = x2 16. Esercizio 3. f(x) = x2 1 9 x 2
 Matematica ed Informatica+Fisica ESERCIZI Modulo di Matematica ed Informatica Corso di Laurea in CTF - anno acc. 2013/2014 docente: Giulia Giantesio, gntgli@unife.it Esercizi 8: Studio di funzioni Studio
Matematica ed Informatica+Fisica ESERCIZI Modulo di Matematica ed Informatica Corso di Laurea in CTF - anno acc. 2013/2014 docente: Giulia Giantesio, gntgli@unife.it Esercizi 8: Studio di funzioni Studio
Matematica con elementi di statistica ESERCIZI sui limiti Corso di Laurea in Biotecnologie - anno acc. 2014/2015
 Calcolare i seguenti iti. Esercizio 1. Esercizio 2. Esercizio 3. Esercizio 4. Matematica con elementi di statistica ESERCIZI sui iti Corso di Laurea in Biotecnologie - anno acc. 2014/2015 Esercizi 6: iti
Calcolare i seguenti iti. Esercizio 1. Esercizio 2. Esercizio 3. Esercizio 4. Matematica con elementi di statistica ESERCIZI sui iti Corso di Laurea in Biotecnologie - anno acc. 2014/2015 Esercizi 6: iti
Mauro Saita Grafici qualitativi di funzioni reali di variabile reale
 Mauro Saita Grafici qualitativi di funzioni reali di variabile reale Per commenti o segnalazioni di errori scrivere, per favore, a: maurosaita@tiscalinet.it Ottobre 2017 1 Indice 1 Qual è il grafico della
Mauro Saita Grafici qualitativi di funzioni reali di variabile reale Per commenti o segnalazioni di errori scrivere, per favore, a: maurosaita@tiscalinet.it Ottobre 2017 1 Indice 1 Qual è il grafico della
R. Capone Analisi Matematica Limiti di una funzione reale di variabile reale ESERCIZI SUI LIMITI DI FUNZIONE ( )
 Esercizio proposto N 1 Verificare che ESERCIZI SUI LIMITI DI FUNZIONE Si ricordi la definizione di ite finito in un punto: Pertanto, applicando la definizione al caso concreto, si ha: o, ciò che è lo stesso:
Esercizio proposto N 1 Verificare che ESERCIZI SUI LIMITI DI FUNZIONE Si ricordi la definizione di ite finito in un punto: Pertanto, applicando la definizione al caso concreto, si ha: o, ciò che è lo stesso:
Programmazione disciplinare: Matematica 5 anno
 Programmazione disciplinare: Matematica 5 anno Modulo 1/Ripasso: Funzione reale di variabile reale CONTENUTI Funzione fra due insiemi. Funzione reale di variabile reale: definizione e classificazione.
Programmazione disciplinare: Matematica 5 anno Modulo 1/Ripasso: Funzione reale di variabile reale CONTENUTI Funzione fra due insiemi. Funzione reale di variabile reale: definizione e classificazione.
Esercizi di Matematica. Studio di Funzioni
 Esercizi di Matematica Studio di Funzioni CONSIDERAZIONI GENERALI Ad ogni funzione corrisponde un grafico, quindi studiare una funzione significa determinare il suo grafico. Per le conoscenze fin qui acquisite,
Esercizi di Matematica Studio di Funzioni CONSIDERAZIONI GENERALI Ad ogni funzione corrisponde un grafico, quindi studiare una funzione significa determinare il suo grafico. Per le conoscenze fin qui acquisite,
x x ' La funzione f si dice continua in x 0 se (e solo se) 0
 : A R R A ' Funzioni Continue La unzione si dice continua in ( ( se (e solo se A Ne seguono tre proprietà ainché ( sia continua in :. Devono esistere initi il ite destro e sinistro di ( in. Tali iti devono
: A R R A ' Funzioni Continue La unzione si dice continua in ( ( se (e solo se A Ne seguono tre proprietà ainché ( sia continua in :. Devono esistere initi il ite destro e sinistro di ( in. Tali iti devono
Concetto intuitivo di limite di una funzione
 Concetto intuitivo di limite di una funzione I limiti di funzioni sono valori a cui le funzioni si avvicinano in certi punti particolari, ossia in punti in cui non è possibile definire le funzioni stesse
Concetto intuitivo di limite di una funzione I limiti di funzioni sono valori a cui le funzioni si avvicinano in certi punti particolari, ossia in punti in cui non è possibile definire le funzioni stesse
Definizioni di limite mediante intorni
 Definizioni di limite mediante intorni Rispetto all approccio intuitivo, nelle definizioni ufficiali si parte dalle y. Per spiegarvi perché ho chiesto aiuto al mio amico matematico Domenico Fiorenza, che
Definizioni di limite mediante intorni Rispetto all approccio intuitivo, nelle definizioni ufficiali si parte dalle y. Per spiegarvi perché ho chiesto aiuto al mio amico matematico Domenico Fiorenza, che
3. CALCOLO DIFFERENZIALE PER FUNZIONI DI UNA VARIABILE REALE.
 3. CALCOLO DIFFERENZIALE PER FUNZIONI DI UNA VARIABILE REALE. Molto spesso y = f(x) rappresenta l evoluzione di un fenomeno al passare del tempo x.se siamo interessati a sapere con che rapidità il fenomeno
3. CALCOLO DIFFERENZIALE PER FUNZIONI DI UNA VARIABILE REALE. Molto spesso y = f(x) rappresenta l evoluzione di un fenomeno al passare del tempo x.se siamo interessati a sapere con che rapidità il fenomeno
Università degli Studi di Palermo Facoltà di Economia. Dipartimento di Scienze Economiche, Aziendali e Statistiche. Appunti del corso di Matematica
 Università degli Studi di Palermo Facoltà di Economia Dipartimento di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica 06 - Limiti Anno Accademico 2015/2016 M. Tumminello, V.
Università degli Studi di Palermo Facoltà di Economia Dipartimento di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica 06 - Limiti Anno Accademico 2015/2016 M. Tumminello, V.
MATEMATICA I LIMITI E LO STUDIO DELLE FUNZIONI GSCATULLO
 MATEMATICA I LIMITI E LO STUDIO DELLE FUNZIONI GSCATULLO I Limiti e lo Studio delle Funzioni Definizione e calcolo dei iti. Definizione di Limite Possiamo dare una definizione intuitiva, grazie al lavoro
MATEMATICA I LIMITI E LO STUDIO DELLE FUNZIONI GSCATULLO I Limiti e lo Studio delle Funzioni Definizione e calcolo dei iti. Definizione di Limite Possiamo dare una definizione intuitiva, grazie al lavoro
ESERCITAZIONE 16 : STUDIO DI FUNZIONI
 ESERCITAZIONE 16 : STUDIO DI FUNZIONI e-mail: tommei@dm.unipi.it web: www.dm.unipi.it/ tommei Ricevimento: su appuntamento Dipartimento di Matematica, piano terra, studio 114 19 Marzo 2013 Esercizio 1
ESERCITAZIONE 16 : STUDIO DI FUNZIONI e-mail: tommei@dm.unipi.it web: www.dm.unipi.it/ tommei Ricevimento: su appuntamento Dipartimento di Matematica, piano terra, studio 114 19 Marzo 2013 Esercizio 1
Esercitazioni di ISTITUZIONI di MATEMATICA 1 Facoltà di Architettura Anno Accademico 2005/2006
 Esercitazioni di ISTITUZIONI di MATEMATICA 1 Facoltà di Architettura Anno Accademico 005/006 Antonella Ballabene SOLUZIONI -14 marzo 006- SCHEMA per lo STUDIO di FUNZIONI 1. Dominio della funzione f)..
Esercitazioni di ISTITUZIONI di MATEMATICA 1 Facoltà di Architettura Anno Accademico 005/006 Antonella Ballabene SOLUZIONI -14 marzo 006- SCHEMA per lo STUDIO di FUNZIONI 1. Dominio della funzione f)..
ESERCIZI SUI PUNTI DI DISCONTINUITÀ TRATTI DA TEMI D ESAME
 ESERCIZI SUI PUNTI DI DISCONTINUITÀ TRATTI DA TEMI D ESAME a cura di Michele Scaglia FUNZIONI CONTINUE Sia f : domf R una funzione e sia x 0 domf (esista cioè f(x 0 ) R) Possono verificarsi due casi: il
ESERCIZI SUI PUNTI DI DISCONTINUITÀ TRATTI DA TEMI D ESAME a cura di Michele Scaglia FUNZIONI CONTINUE Sia f : domf R una funzione e sia x 0 domf (esista cioè f(x 0 ) R) Possono verificarsi due casi: il
Esercizi sul dominio di funzioni e limiti
 Esercizi sul dominio di funzioni e iti Esercizio 1. Determinare il dominio D, studiare il segno e calcolare il ite ai suoi estremi delle seguenti funzioni: (a) y = e ; (b) y = 4 2 + 9; (c) y = 16 4 ; 2
Esercizi sul dominio di funzioni e iti Esercizio 1. Determinare il dominio D, studiare il segno e calcolare il ite ai suoi estremi delle seguenti funzioni: (a) y = e ; (b) y = 4 2 + 9; (c) y = 16 4 ; 2
ESERCIZI SUL DOMINIO DI UNA FUNZIONE A UNA VARIABILE REALE. Le FUNZIONI RAZIONALI INTERE (i polinomi) hanno come insieme di definizione R.
 ESERCIZI SUL DOMINIO DI UNA FUNZIONE A UNA VARIABILE REALE PREMESSA Ai fini dello studio di una funzione la prima operazione da compiere è quella di determinare il suo dominio, ovvero l' insieme valori
ESERCIZI SUL DOMINIO DI UNA FUNZIONE A UNA VARIABILE REALE PREMESSA Ai fini dello studio di una funzione la prima operazione da compiere è quella di determinare il suo dominio, ovvero l' insieme valori
Istituto Tecnico Statale per il Turismo "Francesco Algarotti" Classe: 3 Sez. A A. S. 2018/19 PROGRAMMA DI MATEMATICA
 Classe: 3 Sez. A A. S. 2018/19 Libro di testo: Bergamini Trifone Barozzi Matematica.bianco (2 vol.) Bergamini Trifone Barozzi Matematica.rosso (vol. 3s) Volume 2 Ripasso. Scomposizione in fattori primi
Classe: 3 Sez. A A. S. 2018/19 Libro di testo: Bergamini Trifone Barozzi Matematica.bianco (2 vol.) Bergamini Trifone Barozzi Matematica.rosso (vol. 3s) Volume 2 Ripasso. Scomposizione in fattori primi
15. Funzioni continue: esercizi
 15. Funzioni continue: esercizi Esercizio 15.7. Data la funzione f : R f(r) con legge α se 0 f() = β 2 se > 0, 1. dire se per α = β = 1 la funzione è invertibile e, in caso affermativo, determinare dominio,
15. Funzioni continue: esercizi Esercizio 15.7. Data la funzione f : R f(r) con legge α se 0 f() = β 2 se > 0, 1. dire se per α = β = 1 la funzione è invertibile e, in caso affermativo, determinare dominio,
Corso di Analisi Matematica. Comportamenti asintotici
 a.a. 2013/2014 Laurea triennale in Informatica Corso di Analisi Matematica Comportamenti asintotici Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli
a.a. 2013/2014 Laurea triennale in Informatica Corso di Analisi Matematica Comportamenti asintotici Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli
Esercitazioni di Matematica Generale A.A. 2016/2017 Pietro Pastore Lezione del 19 Dicembre Studio di Funzione.
 Esercitazioni di Matematica Generale A.A. 2016/2017 Pietro Pastore Lezione del 19 icembre 2016 Studio di Funzione 1. Si consideri la funzione f : R R così definita f(x) 1 2 log x x 2. (a) eterminare il
Esercitazioni di Matematica Generale A.A. 2016/2017 Pietro Pastore Lezione del 19 icembre 2016 Studio di Funzione 1. Si consideri la funzione f : R R così definita f(x) 1 2 log x x 2. (a) eterminare il
SECONDO TEST DI ANALISI 1 per i CdL in FISICA e MATEMATICA, a.a. 2016/17 assegnato in data lim
 SECONDO TEST DI ANALISI per i CdL in FISICA e MATEMATICA, a.a. 06/7 assegnato in data 5..06. Sia f : R \ {(0, 0)} R 3 la funzione definita da ( ( 4 ) f(x, y) = x + y sin, + arctan(x y), x + y Si calcoli
SECONDO TEST DI ANALISI per i CdL in FISICA e MATEMATICA, a.a. 06/7 assegnato in data 5..06. Sia f : R \ {(0, 0)} R 3 la funzione definita da ( ( 4 ) f(x, y) = x + y sin, + arctan(x y), x + y Si calcoli
x + 1 x = x2 1 x 2 = 1 1 x 2., l equazione equivale a ln(1 + 3x) < 1 ; 1 + 3x < e ; x < e 1 3
 A. Peretti Svolgimento dei temi d esame di Matematica A.A. 08/9 PROVA INTERMEDIA DI MATEMATICA I parte Vicenza, 05//08 Domanda. Trovare quoziente e resto della divisione di 3 + per + Possiamo usare la
A. Peretti Svolgimento dei temi d esame di Matematica A.A. 08/9 PROVA INTERMEDIA DI MATEMATICA I parte Vicenza, 05//08 Domanda. Trovare quoziente e resto della divisione di 3 + per + Possiamo usare la
ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classi 5A-5B PROGRAMMA DI MATEMATICA
 ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classi 5A-5B PROGRAMMA DI MATEMATICA PRIMA PARTE Intervallo limitato di numeri reali Dati due numeri reali a e b, con a
ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classi 5A-5B PROGRAMMA DI MATEMATICA PRIMA PARTE Intervallo limitato di numeri reali Dati due numeri reali a e b, con a
LEZIONE 5. Esercizio 5.1. Calcolare il limite per x ± delle seguenti funzioni. lim. lim. lim. lim. lim. e x ) x. per x. lim
 5 LEZIONE 5 Esercizio 5.1. Calcolare il ite per x ± delle seguenti funzioni. 2x3 3x 2 = x3 (2 3/x) =±. x2 sin x 2 x 4 = x4 (sin x 2 /x 2 1) =. ex x = ex (1 x/e x )=. sin 1 x cos x2 =0, infatti all infinito
5 LEZIONE 5 Esercizio 5.1. Calcolare il ite per x ± delle seguenti funzioni. 2x3 3x 2 = x3 (2 3/x) =±. x2 sin x 2 x 4 = x4 (sin x 2 /x 2 1) =. ex x = ex (1 x/e x )=. sin 1 x cos x2 =0, infatti all infinito
Programma svolto a.s. 2018/2019 Classe 1H Materia: Matematica Docente: De Rossi Francesco
 Programma svolto a.s. 2018/2019 Classe 1H Materia: Matematica Docente: De Rossi Francesco - Matematica multimediale. bianco Vol 1 Autori: M. Bergamini, G. Barozzi Casa Editrice: Zanichelli codice ISBN
Programma svolto a.s. 2018/2019 Classe 1H Materia: Matematica Docente: De Rossi Francesco - Matematica multimediale. bianco Vol 1 Autori: M. Bergamini, G. Barozzi Casa Editrice: Zanichelli codice ISBN
10 - Applicazioni del calcolo differenziale
 Università degli Studi di Palermo Facoltà di Economia CdS Sviuppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 10 - Applicazioni del calcolo differenziale Anno Accademico 2015/2016
Università degli Studi di Palermo Facoltà di Economia CdS Sviuppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 10 - Applicazioni del calcolo differenziale Anno Accademico 2015/2016
