MATEMATICA I LIMITI E LO STUDIO DELLE FUNZIONI GSCATULLO
|
|
|
- Nicolina Greco
- 6 anni fa
- Visualizzazioni
Transcript
1 MATEMATICA I LIMITI E LO STUDIO DELLE FUNZIONI GSCATULLO
2 I Limiti e lo Studio delle Funzioni Definizione e calcolo dei iti. Definizione di Limite Possiamo dare una definizione intuitiva, grazie al lavoro del matematico Augustin-Louis Cauchy, dei iti come di una tendenza: l avvicinarsi ad un determinato numero senza mai toccarlo. Esempio I iti vengono utilizzati nello studio delle funzioni. Il ite di una funzione f(x) ci permette di capire quali valori assume la funzione f(x), ovvero la y, in prossimità di un determinato valore n cui tende la x. Il ite si legge: ite per x tendente ad n di f(x) è uguale ad l. Il ite chiede di individuare a quale valore si avvicina l ordinata, quando l ascissa tende a. Quando la x tende a, la funzione f(x), ovvero + tende a. Questa particolare operazione, che per le funzioni più semplice può apparire superflua, torna utilissima per studiare il comportamento delle funzioni in prossimità dei valori delle ascisse per cui non sono definite. Ad esempio nello studiare ci rendiamo conto che f(x) assume il valore impossibile : [ 8 ], ma che la 0 funzione più si avvicina al valore x= più assumerà un comportamento particolare tendendo all infinito. 3x x x
3 Calcolare un ite? Come si calcola un ite? Per calcolare un ite è sufficiente seguire un procedimento molto semplice: x + x x x + [] + x 3 x [] + = Consideriamo un caso semplicissimo. Per calcolare il ite sarà sufficiente ipotizzare di sostituire alla x della funzione f(x) il valore cui la x tende. Eseguiamo ora il calcolo della funzione ottenuta e risolviamo il ite. Ricordiamoci che risolvendo il ite ci stiamo implicitamente ponendo la domanda: a quale numero tenderà la funzione se la x tende a n?. Questo può aiutarci ad organizzare e strutturare i calcoli. Limiti per x È possibile calcolare il ite di una funzione supponendo che la x tenda ad infinito. Quando questo accade bisogna, per risolvere correttamente il ite, porsi una domanda: dove si trova, nella funzione, l incognita? Se l incognita si trova solo al numeratore (o la funzione non è fratta, cioè ha denominatore = ), la funzione tenderà ad infinito. Infatti qualsiasi numero si trovasse al denominatore non riuscirebbe a dividere l infinito! Se l incognita si trova solo al denominatore, la funzione tenderà a zero. Infatti qualsiasi numero, si trovasse al numeratore, per quanto grande sarebbe diviso in infinite parti piccolissime, tendendo così a zero! Il caso particolare in cui l incognita si trova sia al numeratore che al denominatore lo analizzeremo più avanti. x x 4 Consideriamo un caso in cui la x tende all infinito e l incognita si trova solo al numeratore. 3
4 [ ] x 4 [ ] x 4 = Per calcolare il ite sarà sufficiente ipotizzare di sostituire alla x della funzione f(x) il valore cui la x tende, cioè infinito. Un numero infinito può essere diviso da qualsiasi numero ma, per quanto grande, la funzione tenderà sempre ad. Proviamo anche un altro caso. x x Consideriamo un caso in cui la x tende all infinito e l incognita si trova solo al numeratore. x [ ] x [ ] = 0 Ipotizziamo di sostituire all incognita della funzione il valore cui la x tende, cioè. Un numero qualsiasi, per quanto grande, se diviso per infinito porterà la funzione a 0. Limiti per x 0 È anche possibile supporre di calcolare il ite di una funzione per x tendente a zero. Anche in questo caso per risolverlo dovremmo anzitutto domandarci dove si trova l incognita: Se l incognita si trova solo al numeratore (o la funzione non è fratta, cioè ha denominatore = ), la funzione tenderà ad zero. Infatti qualsiasi numero si trovasse al denominatore dividendo lo zero otterrebbe sempre quello come risultato. Se l incognita si trova solo al denominatore, la funzione tenderà a infinito. Infatti qualsiasi numero, si trovasse al numeratore, per quanto piccolo, sarebbe diviso in parti da zero, cioè in infinite parti. Il caso particolare in cui l incognita si trova sia al numeratore che al denominatore lo analizzeremo più avanti. x x 0 4 Consideriamo un caso in cui la x tende a zero e l incognita si trova solo al numeratore. [0] x 0 4 [0] x 0 4 = 0 Ipotizziamo che l incognita della funzione, al numeratore, tenda a zero, tutta la funzione tenderà allora a 0. Analizziamo un secondo caso. x 0 x Consideriamo un caso in cui la x tende a zero e l incognita si trova solo al denominatore. x 0 [0] Ipotizziamo che l incognita della funzione, al denominatore, tenda a zero, dividendo 4
5 x 0 [0] = in infinite parti il numeratore: la funzione tenderà ad infinito. Casi particolari Esistono alcuni casi particolari che può capitarti di incontrare nello studio delle funzioni, sono presenti nel momento in cui l incognita si trova sia al nominatore che al denominatore, infatti la funzione dovrebbe tendere, secondo quanto quello che abbiamo detto, sia ad infinito che a zero contemporaneamente, e questo non è possibile! Un caso particolare ha come possibili soluzioni: ; 0 o un numero finito. Può però anche non esistere. Caso indeterminato Uno dei casi indeterminati più semplice è quello in cui la funzione presenta l incognita sia al numeratore che al denominatore e la x tenda ad infinito. In questi casi il ite si risolve considerando la posizione (numeratore/denominatore) dell incognita di grado maggiore. Se la x di grado maggiore si trova al numeratore la funzione tenderà ad infinito, se si trova al denominatore a zero. Le altre incognite non dovranno essere considerate. Questo perché l incognita elevata ad una potenza maggiore delle altre tenderà all infinito più velocemente. x + x + x 8x + Consideriamo un caso in cui l incognita si trovi sia al numeratore che al denominatore. x + x + x 8x + [ ] + x + = x 8x + L incognita di grado maggiore si trova al numeratore, per tanto dovrò risolvere il ite ipotizzando che essa tenda all infinito. Essendo al numeratore porterà l intera funzione all infinito. Qualora la funzione presenti incognite dello stesso grado massimo sia al numeratore che al denominatore, si considererà come ite cui la funzione tende il numero ottenuto dal coefficiente dell incognita al numeratore, fratto quello dell incognita al denominatore. x + x x 8x + 3 Consideriamo un caso in cui l incognita si trovi sia al numeratore che al denominatore. x + x x 8x + 3 x + x x 8x + 3 Le due incognite di grado massimo si trovano una al numeratore, l altra al denominatore. Consideriamo allora i coefficienti delle due incognite. 3 x + x x 8x + 3 = 8 = 4 Da essi otteniamo un numero finito cui tende la funzione. Per verificare questi casi esiste anche un altro procedimento, più lungo, ma che mostra con chiarezza i diversi passaggi sottesi dal nostro ragionamento:
6 x 7x x x 3 x + 4 Consideriamo un caso in cui l incognita si trovi sia al numeratore che al denominatore. x x ( 7x x ) x 3 ( x x x 3) Raccogliamo l incognita di grado massimo. 3 x ( 7 x ) x x 3 ( x + 4 x 3) Semplifichiamo. 4 x x ( 7 [ ] ) x 3 ( [ ] + 4 [ ] 3) Ipotizziamo che l incognita tenda ad infinito. x ( 0) x x 3 ( 0 + 0) Poiché se l incognita che tende all infinito si trova al denominatore porta l intera frazione a zero possiamo eseguire questi calcoli. 6 x x x 3 Semplifichiamo. x x 7 x [ ] = 0 Risolviamo il ite. Caso indeterminato 0 0 Nel caso in cui l incognita si trovi sia al numeratore che al denominatore e la x tenda a 0, per risolvere il ite sarà necessario scomporre il numeratore o il denominatore in elementi semplificabili. Per nessuna ragione è possibile applicare la regola del grado massimo imparata per il caso! 4x 3x x 0 x Consideriamo un caso in cui l incognita si trovi sia al numeratore che al denominatore. x(4x 3) x 0 x Raccogliamo l incognita del numeratore. 3 x(4x 3) x 0 x Semplifichiamo 4x 3 x 0 6
7 4 4 [0] 3 = 3 x 0 Risolviamo il ite. Verifichiamo un altro caso. x 4 x x Consideriamo un caso in cui l incognita si trovi sia al numeratore che al denominatore. (x + )(x ) x x Ci si accorge subito che è possibile scomporre il numeratore come prodotto notevole. 3 (x + )(x ) x x È allora possibile semplificare. x + x 4 [] + = 4 x Risolviamo il ite Caso indeterminato 0 con 0 Uno dei iti più importanti, detto per questo ite notevole, è un particolare caso indeterminato 0/0: x 0 x = Il risultato di questo ite, e di tutti i iti che presentano il seno di x e l incognita dello stesso grado in posizioni opposte (numeratore-denominatore), è sempre che la funzione tende ad. Questo è dimostrabile: Riportiamo alla mente alcuni elementi della teoria goniometrica. sin0 = 0 cos0 = tg0 = sin0 cos0 = 0 = 0 3 < x < tgx < x < tgx Ricordiamo inoltre le seguenti equivalenze. Considerata la disequazione di base, evidente anche dal grafico, dividiamo tutti i termini per uno stesso valore. 7
8 4 Se x 0 tende a < x < cosx < x < cosx < x < cosx Eseguiamo alcune semplificazioni Ipotizziamo che x tenda a zero e svolgiamo i calcoli. 6 cosx tende a, poiché cos0 = e = < x < Ottenuti i risultati per il teorema del confronto possiamo affermare che x quando x 0 allora =. 7 x = = Così anche il suo reciproco. x 0 x 0 x Potrebbe essere necessario talvolta eseguire alcune operazioni perché la funzione sia riducibile al ite notevole, ad esempio: sin 4 x Consideriamo un caso in cui sia presente x 0 x 3 il seno di x ma le incognite abbiano gradi diversi. 3 sin 4 x x 0 x 3 sin 4 x x 0 x 3 x4 x 4 sin 4 x x 0 x 3 x4 x 4 sin 4 x x 0 x 4 x4 x 3 Per riportare il caso al ite notevole moltiplichiamo la funzione per. Ma moltiplicare per significa anche moltiplicare per un numero che abbia numeratore e denominatore uguali, quindi anche x4 x 4. Portiamo la funzione ad assumere la forma del ite notevole, essendo una moltiplicazione è possibile modificare l ordine dei fattori. 4 x 0 x Semplifichiamo e risolviamo il ite. x = 0 x 0 8
9 Lo Studio delle Funzioni e i Limiti Propedeutica Prima di poter applicare lo studio dei iti alle funzioni, per trovare gli asintoti, è necessario ribadire come si individuano il dominio, il segno e le intersezioni con gli assi dei diversi tipi di funzioni che possiamo affrontare. Di seguito verranno proposte alcune funzioni generiche per poter ripassare lo studio dei vari casi. Funzione razionale fratta f(x) = x x + 3 Data una funzione razionale fratta. x x 3 Dominio: x ( ; 3) ( 3; ) 3 x x + 3 > 0 Studio N. x > 0 x > Studio D. x + 3 > 0 x > 3 Rappresento su un grafico Determiniamo il dominio. Determiniamo il segno. 4 Intersezione con l asse delle ascisse. y = 0 { x = 0 { y = 0 y = 0 x = 0 x = x+3 Determiniamo le intersezioni con gli assi. Intersezione con l asse delle ordinate x = 0 y = = 3 Rappresentiamo sul piano cartesiano, einando le aree dove la funzione sicuramente non può esistere per il dominio o per il segno. 9
10 Funzione irrazionale f(x) = x 7x + 0 Data una funzione irrazionale. x 7x x ; = 7 ± 3 x = x = Determiniamo il dominio. Il radicando deve essere maggiore o uguale a zero. Consideriamo l equazione della parabola. Dominio ( ; ] [; ) 3 Sempre positivo. Il segno nelle radici è sempre positivo. 4 Rappresento sul piano cartesiano. Funzione logaritmica f(x) = ln (x + ) Data una funzione logaritmica. x + > 0 Dominio ( ; ) x > 3 f(x) > 0 x + > x > 0 x > 0 Determiniamo il dominio. L argomento deve essere maggiore di zero. Consideriamo l equazione della parabola. Determiniamo il segno. Poiché la base è maggiore di, il logaritmo sarà positivo quando l argomento è >. 0
11 4 Rappresento sul piano cartesiano. Gli asintoti È molto interessante nello studio delle funzioni verificare il comportamento delle stesse in prossimità dei confini del loro dominio. Questa verifica è possibile attraverso i iti che ci permettono di individuare gli asintoti: delle rette cui il grafico della funzione si avvicina sempre più senza mai toccarli. Di seguito i casi possibili casi ed i relativi iti: Le linee azzurre sono i possibili modi in cui la funzione si avvicina all asintoto, quale di esse sia corretta lo si può dedurre dal segno e dal dominio. Come si evince dal secondo grafico è possibile porsi la domanda del comportamento della funzione quando si avvicina ad un certo valore sia che la funzione si avvicini da sinistra x k che da destra x k +. I due segni ci permettono di porci le due domande in maniera distinta. È anche possibile unire le due domande sovrapponendo i segni x k ma sarà importante nello scrivere il risultato rispettare lo stesso ordine! Quindi, ad esempio, significa Esempi x k f(x) = ± x k ± f(x) = + e f(x) = + x k
12 f(x) = x x + 3 Riprendiamo la funzione già svolta nel capitolo precedente. Dominio: x ( ; 3) ( 3; ) Segno: Ricapitoliamo le informazioni che possediamo sulla funzione. Intersezione con gli assi: A (; 0) B (0; 3 ) 3 Rappresentiamo la funzione sul piano cartesiano x x 3 ± x + 3 [ 3] x 3 ± [ 3] + 3 = [ 3] x 3 ± [ 3] + 3 = x ± x x + 3 Cerchiamo di individuare gli eventuali asintoti. Iniziamo con lo scrivere il ite per x 3 ovvero il punto escluso dal dominio. Se le x tendono a -3, il denominatore tenderà a zero, portando la funzione all infinito. Rispettando dominio e segno, anche guardando il grafico, è chiaro che quando la funzione si avvicina a 3 da destra potrà scendere solo a, perché non può assumere valori positivi; e quando si avvicina a 3 da sinistra potrà scendere solo a. Completiamo dunque il risultato con queste indicazioni. Verifichiamo ora il comportamento della funzione per x ±, per constatare l eventuale presenza di asintoti orizzontali.
13 8 x ± 9 Asintoto orizzontale y = Asintoto verticale x = 3 x x + 3 = Poiché si verifica il caso particolare, e le incognite sono dello stesso grado, ne consideriamo i coefficienti. Scriviamo le equazioni degli asintoti che abbiamo trovato. 0 Rappresentiamo sul piano cartesiano e disegniamo un grafico qualitativo. Un altra funzione d esempio. f(x) = 7x x 7x + 0 Data una funzione. x 7x x ; = 7 ± 3 x = x = Dominio: ( ; ) (; ) (; ) 3 Studio N. 7x > 0 Studiamo il dominio. Risolviamo come fosse l equazione di una parabola. Studiamo il segno. Studio D. x 7x + 0 > 0 x ; = 7 ± 3 x = x = Studio con il grafico. x > 7 4 Intersezione con l asse delle ascisse y = 0 { 7x = 0 { y = 0 x = x 7x+0 7 Intersezione con l asse delle ordinate Trovo le intersezioni con gli assi. 3
14 x = 0 { 0 = Rappresento quanto abbiamo trovato sul piano cartesiano: potrebbe esserci utile per orientarci negli asintoti x x ± x 7x + 0 = 7x x ± x 7x + 0 = 7x x ± x 7x + 0 = 7x x ± x 7x + 0 = ± x ± 7x x 7x + 0 = 0 Cerco il ite per x ±. Dal grafico verifico il segno dell infinito: quando provengo da destra è negativo, perché la funzione non esiste positiva in quel punto, da sinistra positivo perché non esiste negativa. Cerco il ite per x ±. Verifico il segno dell infinito. Cerco eventuali asintoti orizzontali. Con x siamo nella situazione, consideriamo l incognita con il grado maggiore, sta al denominatore, quindi porta la funzione a zero. Ciò è valido sia verso + che verso. 9 Asintoti verticali: x = x = Scriviamo l equazione degli asintoti. Asintoto orizzontale: y = 0 0 Rappresentiamo sul piano cartesiano e cerchiamo di descrivere un grafico qualitativo della funzione. Realizzato da Paolo Franchi, VBC (A.S. 0/06), l /0/06. AMDG 4
Esercitazioni di Matematica Generale A.A. 2016/2017 Pietro Pastore Lezione del 2 Dicembre Dominio di Funzioni
 Esercitazioni di Matematica Generale A.A. 06/07 Pietro Pastore Lezione del Dicembre 06 Dominio di Funzioni Determinare il dominio delle seguenti funzioni ) x +3x. fx) =. Il dominio si trova considerando
Esercitazioni di Matematica Generale A.A. 06/07 Pietro Pastore Lezione del Dicembre 06 Dominio di Funzioni Determinare il dominio delle seguenti funzioni ) x +3x. fx) =. Il dominio si trova considerando
Metodi Matematici per l Economia A-K Corso di Laurea in Economia - anno acc. 2012/2013 docente: Elena Polastri,
 Metodi Matematici per l Economia A-K Corso di Laurea in Economia - anno acc. 202/203 docente: Elena Polastri, plslne@unife.it Studio di funzione con indicazione degli asintoti e grafico probabile Studiare
Metodi Matematici per l Economia A-K Corso di Laurea in Economia - anno acc. 202/203 docente: Elena Polastri, plslne@unife.it Studio di funzione con indicazione degli asintoti e grafico probabile Studiare
MATEMATICA PROPEDEUTICA PER LO STUDIO DELLE FUNZIONI GSCATULLO
 MATEMATICA PROPEDEUTICA PER LO STUDIO DELLE FUNZIONI GSCATULLO 1 Propedeutica alle Funzioni Premessa Questo documento vuole essere una preparazione per lo studio delle funzioni, comprendendo tutte quelle
MATEMATICA PROPEDEUTICA PER LO STUDIO DELLE FUNZIONI GSCATULLO 1 Propedeutica alle Funzioni Premessa Questo documento vuole essere una preparazione per lo studio delle funzioni, comprendendo tutte quelle
LICEO LINGUISTICO NINNI CASSARÁ. Classe VA. Studio di Funzioni. prof. Alessio Cangemi
 LICEO LINGUISTICO NINNI CASSARÁ Classe VA Studio di Funzioni prof. Alessio Cangemi Di seguito saranno schematizzati gli step fondamentali per tracciare il grafico probabile di una funzione f(x). 1 Ricerca
LICEO LINGUISTICO NINNI CASSARÁ Classe VA Studio di Funzioni prof. Alessio Cangemi Di seguito saranno schematizzati gli step fondamentali per tracciare il grafico probabile di una funzione f(x). 1 Ricerca
IIID Matematica Aprile ) Cosa significa dire che una funzione reale di variabile reale è continua?
 1) Cosa significa dire che una funzione reale di variabile reale è continua? 2) Dire se la funzione f(x) = x x 2 5 è a continua per x = 5 ; b continua per x = 3 ; c continua per x = π 2 ; 3) Cosa si intente
1) Cosa significa dire che una funzione reale di variabile reale è continua? 2) Dire se la funzione f(x) = x x 2 5 è a continua per x = 5 ; b continua per x = 3 ; c continua per x = π 2 ; 3) Cosa si intente
ESERCIZI DI METODI MATEMATICI PER L ECONOMIA FACOLTÀ DI ECONOMIA DI FERRARA A.A. 2011/2012
 ESERCIZI DI METODI MATEMATICI PER L ECONOMIA FACOLTÀ DI ECONOMIA DI FERRARA A.A. 20/202. Esercizi: lezione 8 novembre 20 Studio di funzione con indicazione degli asintoti e grafico probabile Studiare completamente
ESERCIZI DI METODI MATEMATICI PER L ECONOMIA FACOLTÀ DI ECONOMIA DI FERRARA A.A. 20/202. Esercizi: lezione 8 novembre 20 Studio di funzione con indicazione degli asintoti e grafico probabile Studiare completamente
~ 1 ~ CALCOLO DEI LIMITI
 ~ ~ CALCOLO DEI LIMITI ) Limiti che si presentano nella forma l. Pur non essendo forme indeterminate (il risultato è indicato convenzionalmente con i, nel senso che la funzione tende, in valore assoluto,
~ ~ CALCOLO DEI LIMITI ) Limiti che si presentano nella forma l. Pur non essendo forme indeterminate (il risultato è indicato convenzionalmente con i, nel senso che la funzione tende, in valore assoluto,
Esercizio 1. f(x) = 4 5x2 x 2 +x 2. Esercizio 2. f(x) = x2 16. Esercizio 3. f(x) = x2 1 9 x 2
 Matematica ed Informatica+Fisica ESERCIZI Modulo di Matematica ed Informatica Corso di Laurea in CTF - anno acc. 2013/2014 docente: Giulia Giantesio, gntgli@unife.it Esercizi 8: Studio di funzioni Studio
Matematica ed Informatica+Fisica ESERCIZI Modulo di Matematica ed Informatica Corso di Laurea in CTF - anno acc. 2013/2014 docente: Giulia Giantesio, gntgli@unife.it Esercizi 8: Studio di funzioni Studio
Concetto intuitivo di limite di una funzione
 Concetto intuitivo di limite di una funzione I limiti di funzioni sono valori a cui le funzioni si avvicinano in certi punti particolari, ossia in punti in cui non è possibile definire le funzioni stesse
Concetto intuitivo di limite di una funzione I limiti di funzioni sono valori a cui le funzioni si avvicinano in certi punti particolari, ossia in punti in cui non è possibile definire le funzioni stesse
lim f(x) lim In questo caso, lim Una funzione è continua in un punto x 0 se valgono le seguenti condizioni:
 Definizioni fondamentali Un intorno di un punto = 0 è un intervallo I che contiene 0. Un intorno destro per semplicità lo chiamiamo + 0 ) di 0 è un intervallo in cui l estremo sinistro è 0 : tutti i punti
Definizioni fondamentali Un intorno di un punto = 0 è un intervallo I che contiene 0. Un intorno destro per semplicità lo chiamiamo + 0 ) di 0 è un intervallo in cui l estremo sinistro è 0 : tutti i punti
Esercitazioni di ISTITUZIONI di MATEMATICA 1 Facoltà di Architettura Anno Accademico 2005/2006
 Esercitazioni di ISTITUZIONI di MATEMATICA 1 Facoltà di Architettura Anno Accademico 005/006 Antonella Ballabene SOLUZIONI -14 marzo 006- SCHEMA per lo STUDIO di FUNZIONI 1. Dominio della funzione f)..
Esercitazioni di ISTITUZIONI di MATEMATICA 1 Facoltà di Architettura Anno Accademico 005/006 Antonella Ballabene SOLUZIONI -14 marzo 006- SCHEMA per lo STUDIO di FUNZIONI 1. Dominio della funzione f)..
Funzioni continue. quando. se è continua x I.
 Funzioni continue Definizione: f() si dice continua in 0 D f quando (*) 0 f () f ( 0 ) Definizione: f() si dice continua in I D f se è continua I. Avevamo già dato questa definizione parlando del f ().
Funzioni continue Definizione: f() si dice continua in 0 D f quando (*) 0 f () f ( 0 ) Definizione: f() si dice continua in I D f se è continua I. Avevamo già dato questa definizione parlando del f ().
R. Capone Analisi Matematica Limiti di una funzione reale di variabile reale ESERCIZI SUI LIMITI DI FUNZIONE ( )
 Esercizio proposto N 1 Verificare che ESERCIZI SUI LIMITI DI FUNZIONE Si ricordi la definizione di ite finito in un punto: Pertanto, applicando la definizione al caso concreto, si ha: o, ciò che è lo stesso:
Esercizio proposto N 1 Verificare che ESERCIZI SUI LIMITI DI FUNZIONE Si ricordi la definizione di ite finito in un punto: Pertanto, applicando la definizione al caso concreto, si ha: o, ciò che è lo stesso:
Gli asintoti. Richiami ed esempi
 Gli asintoti Richiami ed esempi Scheda asintoti Definizioni generali di asintoto orizzontale, verticale e obliquo Scrivere l equazione di una funzione di una variabile dotata di due asintoti, uno orizzontale
Gli asintoti Richiami ed esempi Scheda asintoti Definizioni generali di asintoto orizzontale, verticale e obliquo Scrivere l equazione di una funzione di una variabile dotata di due asintoti, uno orizzontale
ESERCIZI DI METODI MATEMATICI PER L ECONOMIA FACOLTÀ DI ECONOMIA DI FERRARA A.A. 2011/2012
 ESERCIZI DI METODI MATEMATICI PER L ECONOMIA FACOLTÀ DI ECONOMIA DI FERRARA A.A. 2011/2012 1. Esercizi 3 1. Studiare la seguente funzione FINO alla derivata prima, con tracciamento di grafico ed indicazione
ESERCIZI DI METODI MATEMATICI PER L ECONOMIA FACOLTÀ DI ECONOMIA DI FERRARA A.A. 2011/2012 1. Esercizi 3 1. Studiare la seguente funzione FINO alla derivata prima, con tracciamento di grafico ed indicazione
Esercizi svolti sui limiti
 Esercizi svolti sui iti Esercizio. Calcolare sin(). Soluzione. Moltiplichiamo e dividiamo per : sin() sin() sin() a questo punto, ponendo y, dato che otteniamo y sin y y sin() y sin y y. Esercizi svolti
Esercizi svolti sui iti Esercizio. Calcolare sin(). Soluzione. Moltiplichiamo e dividiamo per : sin() sin() sin() a questo punto, ponendo y, dato che otteniamo y sin y y sin() y sin y y. Esercizi svolti
ESERCIZI SUL DOMINIO DI UNA FUNZIONE A UNA VARIABILE REALE. Le FUNZIONI RAZIONALI INTERE (i polinomi) hanno come insieme di definizione R.
 ESERCIZI SUL DOMINIO DI UNA FUNZIONE A UNA VARIABILE REALE PREMESSA Ai fini dello studio di una funzione la prima operazione da compiere è quella di determinare il suo dominio, ovvero l' insieme valori
ESERCIZI SUL DOMINIO DI UNA FUNZIONE A UNA VARIABILE REALE PREMESSA Ai fini dello studio di una funzione la prima operazione da compiere è quella di determinare il suo dominio, ovvero l' insieme valori
Esercitazioni di Matematica Generale A.A. 2016/2017 Pietro Pastore Lezione del 19 Dicembre Studio di Funzione.
 Esercitazioni di Matematica Generale A.A. 2016/2017 Pietro Pastore Lezione del 19 icembre 2016 Studio di Funzione 1. Si consideri la funzione f : R R così definita f(x) 1 2 log x x 2. (a) eterminare il
Esercitazioni di Matematica Generale A.A. 2016/2017 Pietro Pastore Lezione del 19 icembre 2016 Studio di Funzione 1. Si consideri la funzione f : R R così definita f(x) 1 2 log x x 2. (a) eterminare il
STUDIO DEL GRAFICO DI UNA FUNZIONE
 STUDIO DEL GRAFICO DI UNA FUNZIONE PROF.SSA ROSSELLA PISCOPO 2 di 35 Indice 1 SCHEMA PER LO STUDIO DEL GRAFICO DI FUNZIONE... 4 2 ESEMPI... 11 2.1 2.2 2.3 2.4 2.5 2.6 FUNZIONE ESPONENZIALE... 11 FUNZIONE
STUDIO DEL GRAFICO DI UNA FUNZIONE PROF.SSA ROSSELLA PISCOPO 2 di 35 Indice 1 SCHEMA PER LO STUDIO DEL GRAFICO DI FUNZIONE... 4 2 ESEMPI... 11 2.1 2.2 2.3 2.4 2.5 2.6 FUNZIONE ESPONENZIALE... 11 FUNZIONE
CLASSIFICAZIONE DELLE FUNZIONI - TEORIA
 CLASSIFICAZIONE DELLE FUNZIONI - TEORIA Razionali Intere Fratte 9 9 6 Intere Algebriche indice pari Fratte Irrazionali Intere Funzioni indice dispari Fratte log( 1 logaritmiche ) Goniometriche sen cos
CLASSIFICAZIONE DELLE FUNZIONI - TEORIA Razionali Intere Fratte 9 9 6 Intere Algebriche indice pari Fratte Irrazionali Intere Funzioni indice dispari Fratte log( 1 logaritmiche ) Goniometriche sen cos
Correzione del compitino del giorno 13 Dicembre 2012
 Correzione del compitino del giorno 3 Dicembre 0 Davide Boscaini Questa è una soluzione del compitino del giorno 8 febbraio 0. Invito chi trovasse eventuali errori a segnalarli presso davide.boscaini@studenti.univr.it.
Correzione del compitino del giorno 3 Dicembre 0 Davide Boscaini Questa è una soluzione del compitino del giorno 8 febbraio 0. Invito chi trovasse eventuali errori a segnalarli presso davide.boscaini@studenti.univr.it.
3 5 x 25 5 x = 1 5 x (3 25) = x = 1. 5 x = x 8x 8 = 0 2 x (23 ) x. = x (2x ) 3. = x (2 x ) 3 = 0.
 Anno Scolastico 014/15 - Classe 3B Soluzioni della verifica di matematica del 9 Maggio 015 Risolvere le seguenti equazioni esponenziali o logaritmiche. Dove è necessario, scrivere le condizioni di esistenza
Anno Scolastico 014/15 - Classe 3B Soluzioni della verifica di matematica del 9 Maggio 015 Risolvere le seguenti equazioni esponenziali o logaritmiche. Dove è necessario, scrivere le condizioni di esistenza
Mutue posizioni della parabola con gli assi cartesiani
 Mutue posizioni della parabola con gli assi cartesiani L equazione di una parabola generica è data da: Consideriamo l equazione che definisce i punti di intersezione della parabola con l asse delle ascisse
Mutue posizioni della parabola con gli assi cartesiani L equazione di una parabola generica è data da: Consideriamo l equazione che definisce i punti di intersezione della parabola con l asse delle ascisse
LO STUDIO DI FUNZIONE ESERCIZI CON SOLUZIONI
 Autore: Enrico Manfucci - 6/05/0 LO STUDIO DI FUNZIONE ESERCIZI CON SOLUZIONI PREMESSA Per Studio di funzione si intende disegnare il grafico di una funzione data la sua espressione analitica. Questo significa
Autore: Enrico Manfucci - 6/05/0 LO STUDIO DI FUNZIONE ESERCIZI CON SOLUZIONI PREMESSA Per Studio di funzione si intende disegnare il grafico di una funzione data la sua espressione analitica. Questo significa
DISEQUAZIONI DI SECONDO GRADO
 DISEQUAZIONI DI SECONDO GRADO Esercizio - -8 - - - - - - Esercizio L equazione non ha soluzioni e quindi la parabola non interseca l asse delle ascisse - - - - - Pertanto la parabola, avendo la concavità
DISEQUAZIONI DI SECONDO GRADO Esercizio - -8 - - - - - - Esercizio L equazione non ha soluzioni e quindi la parabola non interseca l asse delle ascisse - - - - - Pertanto la parabola, avendo la concavità
Disequazioni. 3 Liceo Scientifico 3 Liceo Scientifico sez. Scienze Applicate A.S. 2016/2017 Prof. Andrea Pugliese
 Disequazioni 3 Liceo Scientifico 3 Liceo Scientifico sez. Scienze Applicate A.S. 2016/2017 Prof. Andrea Pugliese Definizione ed esempi Date due espressioni algebriche A e B contenenti numeri e lettere
Disequazioni 3 Liceo Scientifico 3 Liceo Scientifico sez. Scienze Applicate A.S. 2016/2017 Prof. Andrea Pugliese Definizione ed esempi Date due espressioni algebriche A e B contenenti numeri e lettere
MATEMATICA MATURITA LINGUISTICA. Istituto Paritario A.Ruiz Istituto Paritario A.Ruiz
 MATEMATICA MATURITA LINGUISTICA Istituto Paritario A.Ruiz Istituto Paritario A.Ruiz 1 MATEMATICA MATURITA LINGUISTICA 1. CLASSIFICAZIONE FUNZIONI FUNZIONI ALGEBRICHE (in cui compaiono le quattro operazioni):
MATEMATICA MATURITA LINGUISTICA Istituto Paritario A.Ruiz Istituto Paritario A.Ruiz 1 MATEMATICA MATURITA LINGUISTICA 1. CLASSIFICAZIONE FUNZIONI FUNZIONI ALGEBRICHE (in cui compaiono le quattro operazioni):
Recupero primo quadrimestre CLASSE QUARTA FUNZIONE REALE IN UNA VARIABILE REALE IL CAMPO DI ESITENZA
 Recupero primo quadrimestre CLASSE QUARTA FUNZIONE REALE IN UNA VARIABILE REALE IL CAMPO DI ESITENZA Si dice campo di esistenza (C.E.) di una funzione = f(), l'insieme di tutti i valori reali che assegnati
Recupero primo quadrimestre CLASSE QUARTA FUNZIONE REALE IN UNA VARIABILE REALE IL CAMPO DI ESITENZA Si dice campo di esistenza (C.E.) di una funzione = f(), l'insieme di tutti i valori reali che assegnati
Calcolare un limite significa determinare quale sia il suo valore quando al posto dell incognita si sostituisce il valore cui essa tende.
 Infiniti, infinitesimi e forme indeterminate Calcolare un ite significa determinare quale sia il suo valore quando al posto dell incognita si sostituisce il valore cui essa tende. Cioè calcolare 5 4 significa
Infiniti, infinitesimi e forme indeterminate Calcolare un ite significa determinare quale sia il suo valore quando al posto dell incognita si sostituisce il valore cui essa tende. Cioè calcolare 5 4 significa
SOLUZIONE DEGLI ESERCIZI DEL FOGLIO N. 7
 SOLUZIONE DEGLI ESERCIZI DEL FOGLIO N. 7 Esercizio. Funzione da studiare: log( 3).. Dominio: dobbiamo richiedere che il denominatore non si annulli e che il logaritmo sia ben definito. Quindi le condizioni
SOLUZIONE DEGLI ESERCIZI DEL FOGLIO N. 7 Esercizio. Funzione da studiare: log( 3).. Dominio: dobbiamo richiedere che il denominatore non si annulli e che il logaritmo sia ben definito. Quindi le condizioni
Esercitazioni di Matematica Generale A.A. 2016/2017 Pietro Pastore Lezione del 25 Gennaio Studio di Funzione
 Esercitazioni di Matematica Generale A.A. 2016/2017 Pietro Pastore Lezione del 25 Gennaio 2017 Studio di Funzione 1. Si consideri la funzione reale di variabile reale così definita f() = 2 + 4. (a) Determinare
Esercitazioni di Matematica Generale A.A. 2016/2017 Pietro Pastore Lezione del 25 Gennaio 2017 Studio di Funzione 1. Si consideri la funzione reale di variabile reale così definita f() = 2 + 4. (a) Determinare
Esercizi sullo studio di funzione
 Esercizi sullo studio di funzione Seconda parte Come visto nella prima parte, per poter descrivere una curva, data la sua equazione cartesiana esplicita y f () occorre procedere secondo l ordine seguente:
Esercizi sullo studio di funzione Seconda parte Come visto nella prima parte, per poter descrivere una curva, data la sua equazione cartesiana esplicita y f () occorre procedere secondo l ordine seguente:
FUNZIONE REALE IN UNA VARIABILE REALE IL CAMPO DI ESITENZA
 FUNZIONE REALE IN UNA VARIABILE REALE IL CAMPO DI ESITENZA Si dice campo di esistenza (C.E.) di una funzione f(x), l'insieme di tutti i valori reali che assegnati alla variabile indipendente x permettono
FUNZIONE REALE IN UNA VARIABILE REALE IL CAMPO DI ESITENZA Si dice campo di esistenza (C.E.) di una funzione f(x), l'insieme di tutti i valori reali che assegnati alla variabile indipendente x permettono
ESERCIZI DI METODI MATEMATICI PER L ECONOMIA FACOLTÀ DI ECONOMIA DI FERRARA A.A. 2011/2012
 ESERCIZI DI METODI MATEMATICI PER L ECONOMIA FACOLTÀ DI ECONOMIA DI FERRARA A.A. 20/202. Esercizi: lezione 2 dicembre 20 Studio di funzioni. Studiare la seguente funzione FINO alla derivata seconda, con
ESERCIZI DI METODI MATEMATICI PER L ECONOMIA FACOLTÀ DI ECONOMIA DI FERRARA A.A. 20/202. Esercizi: lezione 2 dicembre 20 Studio di funzioni. Studiare la seguente funzione FINO alla derivata seconda, con
ASINTOTI. Si chiama ASINTOTO di una funzione una retta alla quale la funzione si avvicina senza mai toccarla.
 ASINTOTI Si chiama ASINTOTO di una funzione una retta alla quale la funzione si avvicina senza mai toccarla. Ad esempio: La funzione y=e x ha un asintoto orizzontale: l asse x, cioè la retta y=0. La funzione
ASINTOTI Si chiama ASINTOTO di una funzione una retta alla quale la funzione si avvicina senza mai toccarla. Ad esempio: La funzione y=e x ha un asintoto orizzontale: l asse x, cioè la retta y=0. La funzione
Studio Qualitativo di Funzione
 Studio Qualitativo di Funzione Reperire un certo numero di informazioni per descrivere a livello qualitativo l andamento del grafico di una funzione f 1. campo di esistenza (cioè, l insieme di definizione)
Studio Qualitativo di Funzione Reperire un certo numero di informazioni per descrivere a livello qualitativo l andamento del grafico di una funzione f 1. campo di esistenza (cioè, l insieme di definizione)
Esercizi di Matematica. Studio di Funzioni
 Esercizi di Matematica Studio di Funzioni CONSIDERAZIONI GENERALI Ad ogni funzione corrisponde un grafico, quindi studiare una funzione significa determinare il suo grafico. Per le conoscenze fin qui acquisite,
Esercizi di Matematica Studio di Funzioni CONSIDERAZIONI GENERALI Ad ogni funzione corrisponde un grafico, quindi studiare una funzione significa determinare il suo grafico. Per le conoscenze fin qui acquisite,
3. Asintoti e grafico probabile
 1 3. Asintoti e grafico probabile Introduzione Ricordiamo le definizioni di asintoti verticali e orizzontali del grafico di una funzione, che abbiamo già incontrato nel capitolo precedente. La retta di
1 3. Asintoti e grafico probabile Introduzione Ricordiamo le definizioni di asintoti verticali e orizzontali del grafico di una funzione, che abbiamo già incontrato nel capitolo precedente. La retta di
Esercizi sui limiti. lim. lim. lim. lim. log(x 4) + 5x = + + = + 6) x2 4 = 2 =
 Limiti e continuità Risoluzione di forme indeterminate con polinomi Ordine di infinito e confronto di infiniti Alcuni iti notevoli Funzioni continue Esercizi sui iti ( 3 + 3) = (10 + 3 32 ) = 57 ( + 2
Limiti e continuità Risoluzione di forme indeterminate con polinomi Ordine di infinito e confronto di infiniti Alcuni iti notevoli Funzioni continue Esercizi sui iti ( 3 + 3) = (10 + 3 32 ) = 57 ( + 2
ESERCIZI DI METODI MATEMATICI PER L ECONOMIA FACOLTÀ DI ECONOMIA DI FERRARA A.A. 2011/2012
 ESERCIZI DI METODI MATEMATICI PER L ECONOMIA FACOLTÀ DI ECONOMIA DI FERRARA A.A. 2011/2012 1. Esercizi: lezione 2 novembre 2011 Studio di funzioni Studiare le seguenti funzioni FINO alla derivata prima,
ESERCIZI DI METODI MATEMATICI PER L ECONOMIA FACOLTÀ DI ECONOMIA DI FERRARA A.A. 2011/2012 1. Esercizi: lezione 2 novembre 2011 Studio di funzioni Studiare le seguenti funzioni FINO alla derivata prima,
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA
 UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA III Parziale - Compito C 6/5/5 A. A. 4 5 ) Studiare la seguente funzione polinomiale:
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA III Parziale - Compito C 6/5/5 A. A. 4 5 ) Studiare la seguente funzione polinomiale:
Scheda elaborata dalla prof.ssa Biondina Galdi Docente di Matematica
 Tutorial - Studio di una funzione reale di variabile reale f : x R y = f (x) R Una funzione può essere: - 1 - algebrica ( razionale o irrazionale, intera o fratta) Classificare la trascendentale ( esponenziale,
Tutorial - Studio di una funzione reale di variabile reale f : x R y = f (x) R Una funzione può essere: - 1 - algebrica ( razionale o irrazionale, intera o fratta) Classificare la trascendentale ( esponenziale,
Conoscenze. L operazione di divisione (la divisione di due polinomi) - La divisibilità fra polinomi (la regola di Ruffini, il teorema. del resto.
 Classe: TERZA (Liceo Artistico) Pagina 1 / 2 della Matematica La scomposizione dei polinomi in fattori primi L operazione di divisione (la divisione di due polinomi) - La divisibilità fra polinomi (la
Classe: TERZA (Liceo Artistico) Pagina 1 / 2 della Matematica La scomposizione dei polinomi in fattori primi L operazione di divisione (la divisione di due polinomi) - La divisibilità fra polinomi (la
Programmazione disciplinare: Matematica 4 anno
 Programmazione disciplinare: Matematica 4 anno CONTENUTI RISULTATI DI APPRENDIMENTO (Competenze) CONOSCENZE ABILITA TEMPI (settimane) Intervalli limitati e illimitati in R Saper riconoscere intervalli
Programmazione disciplinare: Matematica 4 anno CONTENUTI RISULTATI DI APPRENDIMENTO (Competenze) CONOSCENZE ABILITA TEMPI (settimane) Intervalli limitati e illimitati in R Saper riconoscere intervalli
Programmazione disciplinare: Matematica 4 anno
 Programmazione disciplinare: Matematica 4 anno CONTENUTI Intervalli limitati e illimitati in R RISULTATI DI APPRENDIMENTO (Competenze) CONOSCENZE ABILITA TEMPI (settimane) Saper riconoscere intervalli
Programmazione disciplinare: Matematica 4 anno CONTENUTI Intervalli limitati e illimitati in R RISULTATI DI APPRENDIMENTO (Competenze) CONOSCENZE ABILITA TEMPI (settimane) Saper riconoscere intervalli
QUINTO APPELLO DEL CORSO DI ANALISI MATEMATICA CORSO DI LAURA IN INFORMATICA, A.A. 2017/18 23 LUGLIO 2018 CORREZIONE. x 4 f(x) = x 2 + x 2
 QUINTO APPELLO DEL CORSO DI ANALISI MATEMATICA CORSO DI LAURA IN INFORMATICA, A.A. 27/8 23 LUGLIO 28 CORREZIONE Esercizio ) Considerate la funzione f definita da f(x) = x 2 + x 2. Trovatene il dominio
QUINTO APPELLO DEL CORSO DI ANALISI MATEMATICA CORSO DI LAURA IN INFORMATICA, A.A. 27/8 23 LUGLIO 28 CORREZIONE Esercizio ) Considerate la funzione f definita da f(x) = x 2 + x 2. Trovatene il dominio
Esercizi 2016/17 - Analisi I - Ing. Edile Architettura Esponenziali e logaritmi
 Esercizi 06/7 - Analisi I - Ing. Edile Architettura Esponenziali e logaritmi Esercizio. Risolvere la seguente equazione: Soluzione. ) x+ ) x 7 x = 0 7 L equazione è definita per ogni x 0, valore in cui
Esercizi 06/7 - Analisi I - Ing. Edile Architettura Esponenziali e logaritmi Esercizio. Risolvere la seguente equazione: Soluzione. ) x+ ) x 7 x = 0 7 L equazione è definita per ogni x 0, valore in cui
Calcola il valore dei seguenti limiti precisando quando si tratta di una forma indeterminata di quale forma si tratta:
 Calcola il valore dei seguenti iti precisando quando si tratta di una forma indeterminata di quale forma si tratta: 2x 2 5x 3 1. x 3 x 2 + 4 x 3 2x 2 5x 3 x 2 + 4 non e una forma indeterminata, basta sostituire
Calcola il valore dei seguenti iti precisando quando si tratta di una forma indeterminata di quale forma si tratta: 2x 2 5x 3 1. x 3 x 2 + 4 x 3 2x 2 5x 3 x 2 + 4 non e una forma indeterminata, basta sostituire
Istituto d Istruzione Superiore A. Tilgher Ercolano (Na)
 LO STUDIO DI FUNZIONE Lo studio di funzione è una delle parti più interessanti dell analisi perché permette di utilizzare le numerose conoscenze acquisite nel corso degli anni in un unico elaborato. Se
LO STUDIO DI FUNZIONE Lo studio di funzione è una delle parti più interessanti dell analisi perché permette di utilizzare le numerose conoscenze acquisite nel corso degli anni in un unico elaborato. Se
ANALISI MATEMATICA I (Versione A) - 24 Novembre 2000 RISOLUZIONE. = 4x 2 + 8x 3 + o(x 3 )
 ANALISI MATEMATICA I (Versione A) - 4 Novembre 000 RISOLUZIONE ESERCIZIO 1. Data la funzione = (e x 1) log(1 + 4x ) : 1. Calcolare lo sviluppo di ordine 3 di MacLaurin di. Scriviamo gli sviluppi di ordine
ANALISI MATEMATICA I (Versione A) - 4 Novembre 000 RISOLUZIONE ESERCIZIO 1. Data la funzione = (e x 1) log(1 + 4x ) : 1. Calcolare lo sviluppo di ordine 3 di MacLaurin di. Scriviamo gli sviluppi di ordine
CONCETTO DI ASINTOTO. Asintoto verticale Asintoto orizzontale Asintoto obliquo
 CONCETTO DI ASINTOTO Asintoto e' una parola che deriva dal greco: a privativo che significa no e sympìptein che significa congiungere cioe' significa che non tocca, in pratica si tratta di una retta che
CONCETTO DI ASINTOTO Asintoto e' una parola che deriva dal greco: a privativo che significa no e sympìptein che significa congiungere cioe' significa che non tocca, in pratica si tratta di una retta che
In tutti i casi giungo alla stessa conclusione che posso rappresentare nel piano cartesiano:
 Funzione polinomiale di 1 grado y = ax + b y = x 6 (coefficiente di x positivo) D = R Determino dove la funzione si annulla (cioè troviamo gli zeri della funzione) risolvendo l equazione x 6 = 0 che, essendo
Funzione polinomiale di 1 grado y = ax + b y = x 6 (coefficiente di x positivo) D = R Determino dove la funzione si annulla (cioè troviamo gli zeri della funzione) risolvendo l equazione x 6 = 0 che, essendo
Università di Pisa - Corso di Laurea in Informatica Analisi Matematica. Pisa, 20 giugno (log x)x 1
 Università di Pisa - Corso di Laurea in Informatica Analisi Matematica Pisa, 0 giugno 019 e 1 se 0 Domanda 1 La funzione f : R R definita da 1 se = 0 A) ha minimo ma non ha massimo ) ha massimo ma non
Università di Pisa - Corso di Laurea in Informatica Analisi Matematica Pisa, 0 giugno 019 e 1 se 0 Domanda 1 La funzione f : R R definita da 1 se = 0 A) ha minimo ma non ha massimo ) ha massimo ma non
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 2007 Sessione suppletiva
 ESAME DI STAT DI LIE SIENTIFI RS DI RDINAMENT 7 Sessione suppletiva Il candidato risolva uno dei due problemi e 5 dei quesiti in cui si articola il questionario. PRBLEMA Rispetto a un sistema di assi cartesiani
ESAME DI STAT DI LIE SIENTIFI RS DI RDINAMENT 7 Sessione suppletiva Il candidato risolva uno dei due problemi e 5 dei quesiti in cui si articola il questionario. PRBLEMA Rispetto a un sistema di assi cartesiani
Appunti sull algebra dei limiti
 Appunti sull algebra dei iti Emanuele Biolcati I.S. Monti Asti classe V UC 21 gennaio 2016 Emanuele Biolcati 1 la pena dell uomo nel provare un piacere è di veder subito i iti della sua estensione G. Leopardi,
Appunti sull algebra dei iti Emanuele Biolcati I.S. Monti Asti classe V UC 21 gennaio 2016 Emanuele Biolcati 1 la pena dell uomo nel provare un piacere è di veder subito i iti della sua estensione G. Leopardi,
Disequazioni goniometriche
 Appunti di Matematica Disequazioni goniometriche Disequazioni goniometriche elementari a) Riprendiamo gli esempi che abbiamo fatto per le equazioni trasformandoli in disequazioni: sen Le soluzioni saranno:
Appunti di Matematica Disequazioni goniometriche Disequazioni goniometriche elementari a) Riprendiamo gli esempi che abbiamo fatto per le equazioni trasformandoli in disequazioni: sen Le soluzioni saranno:
Esercizi con soluzioni dell esercitazione del 31/10/17
 Esercizi con soluzioni dell esercitazione del 3/0/7 Esercizi. Risolvere graficamente la disequazione 2 x 2 2 cos(πx). 2. Determinare l insieme di definizione della funzione arcsin(exp( x 2 )). 3. Trovare
Esercizi con soluzioni dell esercitazione del 3/0/7 Esercizi. Risolvere graficamente la disequazione 2 x 2 2 cos(πx). 2. Determinare l insieme di definizione della funzione arcsin(exp( x 2 )). 3. Trovare
Argomento 7. Studio di funzione
 Argomento 7 Studio di funzione Studiare una funzione significa ottenere, mediante strumenti analitici (iti, derivate, ecc.) informazioni utili a disegnare un grafico qualitativo della funzione data. I
Argomento 7 Studio di funzione Studiare una funzione significa ottenere, mediante strumenti analitici (iti, derivate, ecc.) informazioni utili a disegnare un grafico qualitativo della funzione data. I
Limiti di una funzione
 Limiti di una funzione Definizioni I) Cominciamo a studiare il comportamento di una funzione quando la diventa sempre più grande. Scriveremo che leggeremo: limite per che tende a di. Osservazione: naturalmente
Limiti di una funzione Definizioni I) Cominciamo a studiare il comportamento di una funzione quando la diventa sempre più grande. Scriveremo che leggeremo: limite per che tende a di. Osservazione: naturalmente
MATEMATICA EQUAZIONI FRATTE, DI SECONDO GRADO O SUPERIORE GSCATULLO
 MATEMATICA EQUAZIONI FRATTE, DI SECONDO GRADO O SUPERIORE GSCATULLO Equazioni fratte, di secondo grado o superiore Le equazioni di secondo grado Un equazione è di secondo grado se si può scrivere nella
MATEMATICA EQUAZIONI FRATTE, DI SECONDO GRADO O SUPERIORE GSCATULLO Equazioni fratte, di secondo grado o superiore Le equazioni di secondo grado Un equazione è di secondo grado se si può scrivere nella
Soluzione Traccia A. 14 febbraio 2013
 Soluzione Traccia A 1 febbraio 21 ESERCIZIO 1. Dopo aver disegnato il grafico della circonferenza di equazione x 2 + y 2 2x = trovare le eventuali intersezioni con la retta di equazione 2x y + 2 =. Per
Soluzione Traccia A 1 febbraio 21 ESERCIZIO 1. Dopo aver disegnato il grafico della circonferenza di equazione x 2 + y 2 2x = trovare le eventuali intersezioni con la retta di equazione 2x y + 2 =. Per
Lezione 18 (8 gennaio) Limiti
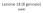 Lezione 18 (8 gennaio) Limiti Ripasso f x = ln 3 x 1 D = (1, + ) ln 3 x 1 + x 1 = ln 3 1 + 1 = ln 3 = ln(+ ) = + 0 + ln 3 x + x 1 = ln 3 + 1 = ln 3 + = ln(0+ ) = 1 Esempi di forme indeterminate x + x3
Lezione 18 (8 gennaio) Limiti Ripasso f x = ln 3 x 1 D = (1, + ) ln 3 x 1 + x 1 = ln 3 1 + 1 = ln 3 = ln(+ ) = + 0 + ln 3 x + x 1 = ln 3 + 1 = ln 3 + = ln(0+ ) = 1 Esempi di forme indeterminate x + x3
Esercitazioni di Matematica
 Università degli Studi di Udine Anno Accademico 009/00 Facoltà di Agraria Corsi di Laurea in VIT e STAL Esercitazioni di Matematica novembre 009 Trovare le soluzioni della seguente disequazione: x + +
Università degli Studi di Udine Anno Accademico 009/00 Facoltà di Agraria Corsi di Laurea in VIT e STAL Esercitazioni di Matematica novembre 009 Trovare le soluzioni della seguente disequazione: x + +
CLASSE QUARTA RECUPERO PRIMO QUADRIMESTRE ANN
 CLASSE QUARTA RECUPERO PRIMO QUADRIMESTRE ANN0 011-01 FUNZIONE REALE IN UNA VARIABILE REALE IL CAMPO DI ESITENZA Si dice campo di esistenza (C.E.) di una funzione y= f(x), l'insieme di tutti i valori reali
CLASSE QUARTA RECUPERO PRIMO QUADRIMESTRE ANN0 011-01 FUNZIONE REALE IN UNA VARIABILE REALE IL CAMPO DI ESITENZA Si dice campo di esistenza (C.E.) di una funzione y= f(x), l'insieme di tutti i valori reali
Studio qualitativo del grafico di una funzione
 Studio qualitativo del grafico di una funzione Obiettivo: ottenere informazioni per descrivere qualitativamente l andamento del grafico di una funzione f campo di esistenza (cioè, l insieme di definizione)
Studio qualitativo del grafico di una funzione Obiettivo: ottenere informazioni per descrivere qualitativamente l andamento del grafico di una funzione f campo di esistenza (cioè, l insieme di definizione)
Elenco moduli Argomenti Strumenti / Testi Letture / Metodi. partecipazione degli alunni. 2 Completamento equazioni e disequazioni.
 Pagina 1 di 5 DISCIPLINA: MATEMATICA E LABORATORIO INDIRIZZO: IGEA CLASSE: IV FM DOCENTE : Cornelio Terreni Elenco moduli Argomenti Strumenti / Testi Letture / Metodi 1 Matematica RIPASSO e COMPLETAMENTO:
Pagina 1 di 5 DISCIPLINA: MATEMATICA E LABORATORIO INDIRIZZO: IGEA CLASSE: IV FM DOCENTE : Cornelio Terreni Elenco moduli Argomenti Strumenti / Testi Letture / Metodi 1 Matematica RIPASSO e COMPLETAMENTO:
Calcolo di limiti. = e il limite. La funzione non è definita in La funzione è definita in. La funzione è continua a destra in
 LIMITI Calcolo di limiti FUNZIONE CONTINUA Definizione Una funzione si dice continua in un punto quando il limite = La funzione non è definita in La funzione è definita in La funzione è definita in ma
LIMITI Calcolo di limiti FUNZIONE CONTINUA Definizione Una funzione si dice continua in un punto quando il limite = La funzione non è definita in La funzione è definita in La funzione è definita in ma
UNITÀ DIDATTICA 5 LA RETTA
 UNITÀ DIDATTICA 5 LA RETTA 5.1 - La retta Equazione generica della retta Dalle considerazioni emerse nel precedente capitolo abbiamo compreso come una funzione possa essere rappresentata da un insieme
UNITÀ DIDATTICA 5 LA RETTA 5.1 - La retta Equazione generica della retta Dalle considerazioni emerse nel precedente capitolo abbiamo compreso come una funzione possa essere rappresentata da un insieme
LIMITI. Sia c D. Sia y=f(x) funzione definita in un dominio D. Tutorial di Paola Barberis - agg Ord =limite
 LIMITI Ord =ite Sia =f() funzione definita in un dominio D. Sia c D c Cercare il LIMITE della funzione per c ( che tende a c) significa trovare, man mano che la TENDE a c, l ORDINATA a cui SI AVVICINA
LIMITI Ord =ite Sia =f() funzione definita in un dominio D. Sia c D c Cercare il LIMITE della funzione per c ( che tende a c) significa trovare, man mano che la TENDE a c, l ORDINATA a cui SI AVVICINA
Disequazioni di secondo grado
 Disequazioni di secondo grado.1 Risoluzione delle disequazioni di secondo grado Una disequazione di secondo grado si presenta in una delle seguenti forme: a + b + c > 0; a + b + c 0; a + b + c < 0; a +
Disequazioni di secondo grado.1 Risoluzione delle disequazioni di secondo grado Una disequazione di secondo grado si presenta in una delle seguenti forme: a + b + c > 0; a + b + c 0; a + b + c < 0; a +
3. Segni della funzione (positività e negatività)
 . Segni della funzione (positività e negatività) Questo punto, qualora sia possibile algebricamente, ci permette di stabilire il segno che assume la variabile dipendente y (che esprime il valore della
. Segni della funzione (positività e negatività) Questo punto, qualora sia possibile algebricamente, ci permette di stabilire il segno che assume la variabile dipendente y (che esprime il valore della
Regole, Esempi, Esercizi. 1. Se nella funzione compare una x al denominatore, bisogna porre il denominatore diverso da zero;
 Lo studio del graco di una funzione Regole, Esempi, Esercizi Ripasso delle regole principali Punto 1: Il calcolo del dominio: Per calcolare il dominio di una funzione, bisogna seguire le tre regole seguenti:
Lo studio del graco di una funzione Regole, Esempi, Esercizi Ripasso delle regole principali Punto 1: Il calcolo del dominio: Per calcolare il dominio di una funzione, bisogna seguire le tre regole seguenti:
rapporto tra l'incremento della funzione e l' incremento corrispondente della
 DERIVATA Sia y f() una funzione reale definita in un intorno di. Si consideri un incremento (positivo o negativo) di : h; la funzione passerà allora dal valore f( ) a quello di f( +h), subendo così un
DERIVATA Sia y f() una funzione reale definita in un intorno di. Si consideri un incremento (positivo o negativo) di : h; la funzione passerà allora dal valore f( ) a quello di f( +h), subendo così un
Teorema sul limite di una somma. ( x) l2. allora
 Teorema sul ite di una somma Se f ( ) l e g( ) l allora [ f ( ) g( ) ] l l Il teorema vale anche per i casi in cui tende a più infinito oppure a infinito. La dimostrazione è analoga a quella vista qui
Teorema sul ite di una somma Se f ( ) l e g( ) l allora [ f ( ) g( ) ] l l Il teorema vale anche per i casi in cui tende a più infinito oppure a infinito. La dimostrazione è analoga a quella vista qui
DEFINIZIONE DI LIMITE
 DEFINIZIONE DI LIMITE LIMITE FINITO PER x CHE TENDE A UN VALORE FINITO Sia y = f(x) una funzione definita in un intorno completo I del punto x 0, escluso al più il punto x 0 (x 0 è un punto di accumulazione)
DEFINIZIONE DI LIMITE LIMITE FINITO PER x CHE TENDE A UN VALORE FINITO Sia y = f(x) una funzione definita in un intorno completo I del punto x 0, escluso al più il punto x 0 (x 0 è un punto di accumulazione)
Programma svolto a.s. 2017/2018 Classe 1H Materia: Matematica Docente: De Rossi Francesco
 Classe 1H Materia: Matematica Docente: De Rossi Francesco - Matematica multimediale. bianco Vol 1 Autori: M. Bergamini, G. Barozzi Casa Editrice: Zanichelli codice ISBN 978888334671 Capitolo 1 Insiemi
Classe 1H Materia: Matematica Docente: De Rossi Francesco - Matematica multimediale. bianco Vol 1 Autori: M. Bergamini, G. Barozzi Casa Editrice: Zanichelli codice ISBN 978888334671 Capitolo 1 Insiemi
Esercizi svolti sui limiti
 Francesco Daddi - dicembre 9 Esercizi svolti sui iti Esercizio. Calcolare sin). Soluzione. Moltiplichiamo e dividiamo per : sin) = sin) = sin) a questo punto, ponendo y =, dato che otteniamo y siny y =
Francesco Daddi - dicembre 9 Esercizi svolti sui iti Esercizio. Calcolare sin). Soluzione. Moltiplichiamo e dividiamo per : sin) = sin) = sin) a questo punto, ponendo y =, dato che otteniamo y siny y =
Lo studio di funzione. 18 febbraio 2013
 Lo studio di funzione 18 febbraio 2013 1 Indice 1 Lo studio di funzione 3 1.1 Dominio di funzioni......................... 3 1.1.1 Domini di funzioni elementari............... 3 1.1.2 Funzioni composte,
Lo studio di funzione 18 febbraio 2013 1 Indice 1 Lo studio di funzione 3 1.1 Dominio di funzioni......................... 3 1.1.1 Domini di funzioni elementari............... 3 1.1.2 Funzioni composte,
Esercizi sul dominio di funzioni e limiti
 Esercizi sul dominio di funzioni e iti Esercizio 1. Determinare il dominio D, studiare il segno e calcolare il ite ai suoi estremi delle seguenti funzioni: (a) y = e ; (b) y = 4 2 + 9; (c) y = 16 4 ; 2
Esercizi sul dominio di funzioni e iti Esercizio 1. Determinare il dominio D, studiare il segno e calcolare il ite ai suoi estremi delle seguenti funzioni: (a) y = e ; (b) y = 4 2 + 9; (c) y = 16 4 ; 2
8. Il teorema dei due carabinieri
 8. Il teorema dei due carabinieri Teorema del confronto (o dei due carabinieri) Consideriamo due funzioni f( ), g( ) per le quali risulti, in un punto di accumulazione per i loro domini : f ( ) g( ) Se
8. Il teorema dei due carabinieri Teorema del confronto (o dei due carabinieri) Consideriamo due funzioni f( ), g( ) per le quali risulti, in un punto di accumulazione per i loro domini : f ( ) g( ) Se
UNITÀ DIDATTICA 2 LE FUNZIONI
 UNITÀ DIDATTICA LE FUNZIONI. Le funzioni Definizione. Siano A e B due sottoinsiemi non vuoti di R. Si chiama funzione di A in B una qualsiasi legge che fa corrispondere a ogni elemento A uno ed un solo
UNITÀ DIDATTICA LE FUNZIONI. Le funzioni Definizione. Siano A e B due sottoinsiemi non vuoti di R. Si chiama funzione di A in B una qualsiasi legge che fa corrispondere a ogni elemento A uno ed un solo
Disequazioni fratte. Una disequazione in cui l'incognita compare a denominatore si chiama fratta o frazionaria.
 1 Disequazioni fratte Una disequazione in cui l'incognita compare a denominatore si chiama fratta o frazionaria. Prima di affrontare le disequazioni fratte, ricordiamo il procedimento che utilizziamo per
1 Disequazioni fratte Una disequazione in cui l'incognita compare a denominatore si chiama fratta o frazionaria. Prima di affrontare le disequazioni fratte, ricordiamo il procedimento che utilizziamo per
Programma svolto a.s. 2018/2019 Classe 1H Materia: Matematica Docente: De Rossi Francesco
 Programma svolto a.s. 2018/2019 Classe 1H Materia: Matematica Docente: De Rossi Francesco - Matematica multimediale. bianco Vol 1 Autori: M. Bergamini, G. Barozzi Casa Editrice: Zanichelli codice ISBN
Programma svolto a.s. 2018/2019 Classe 1H Materia: Matematica Docente: De Rossi Francesco - Matematica multimediale. bianco Vol 1 Autori: M. Bergamini, G. Barozzi Casa Editrice: Zanichelli codice ISBN
Ricevimento del 2 Febbraio 2011
 Ricevimento del 2 Febbraio 20 Davide Boscaini Queste sono le note del ricevimento del 2 Febbraio. Ho scelto di scrivere queste poche pagine per una maggior chiarezza e per chi non fosse stato presente
Ricevimento del 2 Febbraio 20 Davide Boscaini Queste sono le note del ricevimento del 2 Febbraio. Ho scelto di scrivere queste poche pagine per una maggior chiarezza e per chi non fosse stato presente
Prof. Milizia, Liceo Scientifico di Mesagne (BR) 1
 Prof. Milizia, Liceo Scientifico di Mesagne (BR) 1 CAPITOLO 8. LE FUNZIONI. 1. Generalità sulle funzioni.. Le rappresentazioni di una funzione. 3. Le funzioni reali di variabile reale. 4. L espressione
Prof. Milizia, Liceo Scientifico di Mesagne (BR) 1 CAPITOLO 8. LE FUNZIONI. 1. Generalità sulle funzioni.. Le rappresentazioni di una funzione. 3. Le funzioni reali di variabile reale. 4. L espressione
MATEMATICA SCOMPOSIZIONE E FRAZIONE ALGEBRICHE GSCATULLO
 MATEMATICA SCOMPOSIZIONE E FRAZIONE ALGEBRICHE GSCATULLO 1 Scomposizione e frazioni algebriche Scomposizione in Fattori Scomporre in fattori un polinomio significa scriverlo sotto forma di un prodotto
MATEMATICA SCOMPOSIZIONE E FRAZIONE ALGEBRICHE GSCATULLO 1 Scomposizione e frazioni algebriche Scomposizione in Fattori Scomporre in fattori un polinomio significa scriverlo sotto forma di un prodotto
( 5) 2 = = = +1
 1 IDENTITA ED EQUAZIONI Consideriamo la seguente uguaglianza: ( 2x + 3) 2 = 4x 2 +12x + 9 Diamo alcuni valori arbitrari all incognita x e vediamo se l uguaglianza risulta vera. Per x = 1 si avrà: ( 2 1+
1 IDENTITA ED EQUAZIONI Consideriamo la seguente uguaglianza: ( 2x + 3) 2 = 4x 2 +12x + 9 Diamo alcuni valori arbitrari all incognita x e vediamo se l uguaglianza risulta vera. Per x = 1 si avrà: ( 2 1+
SECONDO APPELLO DEL CORSO DI ANALISI MATEMATICA CORSO DI LAURA IN INFORMATICA, A.A. 2017/18 20 FEBBRAIO 2018 CORREZIONE
 SECONDO APPELLO DEL CORSO DI ANALISI MATEMATICA CORSO DI LAURA IN INFORMATICA, A.A. 207/8 20 FEBBRAIO 208 CORREZIONE Esercizio Considerate la funzione f(x = log + x. Tracciate un grafico approssimativo
SECONDO APPELLO DEL CORSO DI ANALISI MATEMATICA CORSO DI LAURA IN INFORMATICA, A.A. 207/8 20 FEBBRAIO 208 CORREZIONE Esercizio Considerate la funzione f(x = log + x. Tracciate un grafico approssimativo
Le disequazioni di primo grado. Prof. Walter Pugliese
 Le disequazioni di primo grado Prof. Walter Pugliese Concetto di disequazione Consideriamo la seguente disuguaglianza: 2x 3 < 5 + x Procedendo per tentativi, attribuiamo alla lettera x alcuni valori e
Le disequazioni di primo grado Prof. Walter Pugliese Concetto di disequazione Consideriamo la seguente disuguaglianza: 2x 3 < 5 + x Procedendo per tentativi, attribuiamo alla lettera x alcuni valori e
Studiamo adesso il comportamento di f(x) alla frontiera del dominio. Si. x 0 lim f(x) = lim. x 2 +
 Esercizi del 2//09. Data la funzione f(x) = ln(x 2 2x) (a) trovare il dominio, gli eventuali asintoti e gli intervalli in cui la funzione cresce o decresce. Disegnare il grafico della funzione. (b) Scrivere
Esercizi del 2//09. Data la funzione f(x) = ln(x 2 2x) (a) trovare il dominio, gli eventuali asintoti e gli intervalli in cui la funzione cresce o decresce. Disegnare il grafico della funzione. (b) Scrivere
Anno Scolastico 2014/15 - Classe 1D Verifica di matematica dell 11 Maggio Soluzioni degli esercizi. 2(x 2) 2(x 1) + 2 = 3x
 Anno Scolastico 2014/15 - Classe 1D Verifica di matematica dell 11 Maggio 2015 - Soluzioni degli esercizi Risolvere le seguenti equazioni. Dove è necessario, scrivere le condizioni di accettabilità e usarle
Anno Scolastico 2014/15 - Classe 1D Verifica di matematica dell 11 Maggio 2015 - Soluzioni degli esercizi Risolvere le seguenti equazioni. Dove è necessario, scrivere le condizioni di accettabilità e usarle
Programmazione modulare
 Programmazione modulare Indirizzo: Informatica Disciplina: MATEMATICA Classi: 3A SIRIO Prof.ssa Clara Di Giacinto Ore settimanali previste: 3 N. Titolo Modulo Titolo unità didattiche in cui è diviso il
Programmazione modulare Indirizzo: Informatica Disciplina: MATEMATICA Classi: 3A SIRIO Prof.ssa Clara Di Giacinto Ore settimanali previste: 3 N. Titolo Modulo Titolo unità didattiche in cui è diviso il
Derivate e studio di funzioni di una variabile
 Derivate e studio di funzioni di una variabile Paolo Montanari Appunti di Matematica Derivate e studio di funzioni 1 Rapporto incrementale e derivata Sia f(x) una funzione definita in un intervallo X R
Derivate e studio di funzioni di una variabile Paolo Montanari Appunti di Matematica Derivate e studio di funzioni 1 Rapporto incrementale e derivata Sia f(x) una funzione definita in un intervallo X R
Esercizi riguardanti limiti di successioni e di funzioni
 Esercizi riguardanti iti di successioni e di funzioni Davide Boscaini Queste sono le note da cui ho tratto le esercitazioni del giorno 0 Novembre 20. Come tali sono ben lungi dall essere esenti da errori,
Esercizi riguardanti iti di successioni e di funzioni Davide Boscaini Queste sono le note da cui ho tratto le esercitazioni del giorno 0 Novembre 20. Come tali sono ben lungi dall essere esenti da errori,
Matematica 2. Derivate Esercizi. y=sen( x 4 3x) y' =cos(x 4 3x)(4x 3 3) y=logsen( x x) y' = sen(x 4 +3x) cos(x4 +3x)(4x 3 +3)
 Matematica 2 Derivate Esercizi y=sen( 4 3) y' =cos( 4 3)(4 3 3) y=logsen( 4 1 3) y' = sen( 4 +3) cos(4 +3)(4 3 +3) y=sen 2 ( 4 3) y' =2sen( 4 3 )cos( 4 3)(4 3 3) Funzioni ad una sola variabile y=f() è
Matematica 2 Derivate Esercizi y=sen( 4 3) y' =cos( 4 3)(4 3 3) y=logsen( 4 1 3) y' = sen( 4 +3) cos(4 +3)(4 3 +3) y=sen 2 ( 4 3) y' =2sen( 4 3 )cos( 4 3)(4 3 3) Funzioni ad una sola variabile y=f() è
Esame di Matematica Generale 7 Febbraio Soluzione Traccia E
 Esame di Matematica Generale 7 Febbraio 013 - Soluzione Traccia E ESERCIZIO 1. Si consideri la funzione f : R R f(x) = x + 1 x. (a) Determinare il dominio di f ed eventuali simmetrie (3 punti). Dominio.
Esame di Matematica Generale 7 Febbraio 013 - Soluzione Traccia E ESERCIZIO 1. Si consideri la funzione f : R R f(x) = x + 1 x. (a) Determinare il dominio di f ed eventuali simmetrie (3 punti). Dominio.
Equazioni di primo grado ad un incognita
 Equazioni di primo grado ad un incognita Identità Si dice IDENTITÀ un uguaglianza fra due espressioni letterali che è verificata per ogni valore attribuito alle lettere. è un identità. Verificare un identità
Equazioni di primo grado ad un incognita Identità Si dice IDENTITÀ un uguaglianza fra due espressioni letterali che è verificata per ogni valore attribuito alle lettere. è un identità. Verificare un identità
1 Funzioni algebriche fratte
 1 Funzioni algebriche fratte 1.1 Esercizio svolto y = x 1 x 11x + 10 (generalizzazione) La funzione è del tipo y = f(x) g(x) con f(x) e g(x) polinomi reali in x. Per determinare il dominio D della funzione
1 Funzioni algebriche fratte 1.1 Esercizio svolto y = x 1 x 11x + 10 (generalizzazione) La funzione è del tipo y = f(x) g(x) con f(x) e g(x) polinomi reali in x. Per determinare il dominio D della funzione
