1.1 Matrici a coefficienti in R. Vi sono alcuni casi particolari che vale la pena evidenziare:
|
|
|
- Aurelia Corso
- 5 anni fa
- Visualizzazioni
Transcript
1 Lezione Matrici a coefficienti in R Definizione Siano m, n Z numeri interi positivi Una matrice m n acoefficientiinrèuninsiemedimn numeri reali disposti su m righe ed n colonne circondata da parentesi tonde Tali numeri sono detti entrate, coefficienti, ocomponenti della matrice L insieme di tutte le matrici m n acoefficientiinr si indica con R m,n Vi sono alcuni casi particolari che vale la pena evidenziare: la matrice m,n R m,n avente tutte le entrate nulle viene detta matrice nulla; se m = n, cioèseilnumerodellerigheèugualealnumerodellecolonne,la matrice è detta matrice quadrata; se m =la matrice è detta matrice riga, mentresen =matrice colonna; se m = n =,cioèquandocisonounasolarigaeunasolacolonna(e,quindi, anche una sola entrata), si preferisce identificare R, con R Esempio Diamo alcuni esempi 3/9 p A R 3,, p 3/9 R,3 R, (matrice quadrata) A R 3, (matrice colonna), R, (matrice riga) 3 Le matrici nulle e 3 sono, = e,3 = 5
2 6 La tabella 3 7 non èunamatrice B Testi diversi utilizzano notazioni diverse per indicare una matrice! Ad esempio la matrice dell Esempio può essere scritta 3/9 p A, La notazione 8 < 4 : A 3 3/9 p 5, 9 3/9 p = ; 3/9 p èdaevitare,perchépuòcreareconfusioneconquellausatapergliinsiemi Sia A R m,n una matrice Ad ogni sua entrata a rimangono associati due numeri interi positivi, gli indici i e j della riga e della colonna al cui incrocio si trova a: i e j vengono detti rispettivamente indice di riga e indice di colonna dell entrata a e a si dice entrata in posizione (i, j) Spesso, per indicare nelle formule l entrata in posizione (i, j) si scrive a i,j Similmente la matrice A si può indicare con la notazione A =(a i,j ) 6i6m 6j6n Tale notazione significa che A èlamatricelecuientratesonoinumeria i,j con gli indici i e j che variano da a m eda a n rispettivamente Se A èquadrataconm = n si può scrivere anche A =(a i,j ) 6i,j6n Quando le dimensioni della matrice sono fissate, a volte conviene indicare le entrate con lettere distinte Per esempio, una matrice generica può essere indifferentemente indicata con a, a (a i,j ) 6i6, (a i,j ) 6j6 6i,j6,, a b, a, a, c d Esempio 3 Si considerino le prime due matrici dell Esempio A 3/9 p A R 3,, B = p 3/9 R,3 L entrata (, ) di A è a, = Leentrate(3, ) e (3, ) di A sono a 3, = a 3, = Invece le entrate (3, 3) e (, 3) non esistono Analogamente, le entrate (3, ), (3, ), (3, 3) di B non esistono Invece le entrate (, ) e (, 3) di B sono b, = 3/9 e b,3 =
3 Definizione 4 (Opposto di una matrice) Sia A R m,n una matrice L opposto di A èlamatricedir m,n,indicatacon A, lacuientrata(i, j) coincide con l opposto dell entrata (i, j) della matrice A, peri =,,m e j =,,n Se A =(a i,j ) 6i6m 6j6n R m,n si scrive in simboli A =( a i,j ) 6i6m 6j6n R m,n Esempio 5 Per le matrici A e B degli Esempi e 3, vale che p A 3/9 A 3/9 R 3, B = p R,3 7 Definizione 6 (Uguaglianza tra matrici) Due matrici A =(a i,j ) 6i6m 6j6n R m,n e B =(b i,j ) 6i6p 6j6q si dicono uguali se valgono le seguenti proprietà: R p,q (U) A e B hanno lo stesso numero di righe e colonne, cioè se m = p ed n = q; (U) le entrate di A e B aventi la stessa posizione nelle due matrici coincidono, cioè se a i,j = b i,j per ogni i =,,m= p e j =,,n= q Le due matrici A e B dell Esempio 3 sono, perciò, diverse Ciononostante, sono legate da un ovvia relazione: l entrata (i, j) di A coincide con l entrata (j, i) di B Definizione 7 (Matrice trasposta) Sia A R m,n La trasposta di A èlamatricedir n,m, indicata con t A, la cui entrata (j, i) coincide con l entrata (i, j) della matrice A per i =,,m e j =,,n Se A =(a i,j ) 6i6m 6j6n R m,n scriveremo in simboli t A =(a j,i ) 6j6n 6i6m R n,m Esempio 8 Per le matrici A e B dell Esempio 3 vale B = t A e A = t B La trasposta di una matrice riga è una matrice colonna e viceversa: C = /3 R,4 ) t C = B A R4, /3 Può accadere che la trasposta di una matrice coincida con la matrice stessa, per esempio e e D e 5 5 p A R 3,3 ) t D e 5 5 p A = D Nel prossimo paragrafo studieremo meglio questo caso
4 8 B Testi diversi utilizzano notazioni diverse per denotare la trasposta Non solo t A, ma anche A t, > A, A > ;piùraramentesitrovaanchea Proposizione 9 (Proprietà della trasposta) Valgono le seguenti proprietà: (T) per ogni matrice A, sihachea R m,n se e solo se t A R n,m ; (T) per ogni A R m,n si ha che t ( t A)=A (la trasposta è un operazione involutiva); (T3) per ogni A R m,n si ha che t ( A) = ( t A) (la trasposta è compatibile con l opposto) Dimostrazione Dimostriamo separatamente le varie proprietà Per le uguaglianze tra matrici usiamo la Definizione 6 Osserviamo innanzitutto che in tutte le uguaglianze da dimostrare le dimensioni delle matrici a destra e a sinistra dell uguale coincidono, quindi dobbiamo solo controllare che anche le entrate al posto (i, j) coincidano (T) Èunaconseguenzadirettadelladefinizione: ilnumerodirighedia èugualealnumerodi colonne di t A esimilmenteilnumerodicolonnediaèugualealnumerodirighedi t A (T) L entrata in posizione (i, j) di t ( t A) coincide per definizione con l entrata in posizione (j, i) di t A,cheasuavoltacoincideconl entratainposizione(i, j) di A Le due matrici quindi coincidono (T3) L entrata in posizione (i, j) di t ( A) coincide con l entrata (j, i) di A, quindiè a j,i D altra parte l entrata (i, j) di ( t A) coincide con l opposto dell entrata (i, j) di t A,cioè a i,j Matrici quadrate In questo paragrafo descriveremo alcune classi notevoli di matrici quadrate Definizione (Diagonale di una matrice quadrata) Sia A =(a i,j ) 6i,j6n R n,n una matrice quadrata La diagonale di A èl insiemeordinatodelleentratediposizione(i, i) di A Esempio Si consideri la matrice 7 4 A 8 A R 3,3 3/4 e La diagonale di A èlasuccessioneordinata(,, e) (e non (, e) o ( e,, ) o altro) Definizione (Matrici diagonali) Sia A =(a i,j ) 6i,j6n R n,n una matrice quadrata A si dice diagonale se tutte le entrate al di fuori della diagonale sono nulle, cioè se a i,j =per ogni i 6= j Esempio 3 Le matrici 7 A A, B A e sono rispettivamente diagonale e non diagonale
5 Osserviamo che una matrice diagonale può essere descritta indicando solo la sua diagonale: per esempio la matrice A dell Esempio 3 si può indicare come A =diag(,, e) Vi sono due casi particolari di matrici diagonali che vale la pena evidenziare: La matrice nulla n,n èdiagonale La matrice diagonale n n avente tutte le entrate diagonali uguali ad è detta matrice identità di ordine n esiindicaconi n In simboli, l entrata in posizione (i, j) di I n coincide con i,j,ilcosiddettodelta di Kronecker, cioè se i = j i,j =, se i 6= j 9 Ad esempio, le matrici identità I n,conn64, sono I =(), I =, I 3 A, I 4 = B A Definizione 4 (Matrici triangolari) Una matrice quadrata A =(a i,j ) 6i,j6n R n,n si dice triangolare superiore se tutte le entrate al di sotto della diagonale sono nulle, cioè se a i,j =quando i>j Similmente A si dice triangolare inferiore se le sue entrate al di sopra della diagonale si annullano, ovvero se a i,j =quando i<j A si dice strettamente triangolare superiore se è triangolare superiore e inoltre le sue entrate sulla diagonale si annullano, ovvero se a i,j =quando i > j Infine, A si dice strettamente triangolare inferiore se è triangolare inferiore e inoltre le sue entrate sulla diagonale si annullano, ovvero se a i,j =quando i 6 j Osserviamo che ogni matrice strettamente triangolare superiore (inferiore) è anche triangolare superiore (inferiore), ma non vale il viceversa Si noti anche che la matrice nulla n,n èsia(strettamente)triangolaresuperiorecheinferiore Esempio 5 Si considerino le due matrici 7 4 A 8 A, B A e 3/4 A è triangolare superiore, ma non lo è strettamente, mentre B è strettamente triangolare inferiore
6 Definizione 6 (Matrici simmetriche e antisimmetriche) Una matrice quadrata A =(a i,j ) 6i,j6n R n,n si dice simmetrica se coincide con la sua trasposta, cioè se t A = A equindia i,j = a j,i per ogni i, j =,,n Una matrice quadrata A =(a i,j ) 6i,j6n R n,n si dice antisimmetrica se coincide con l opposto della sua trasposta, cioè se t A = A equindia i,j = a j,i per ogni i, j =,,n Esempio 7 In R 3,3 si considerino le matrici 7 4 A 7 8 A, B 4 8 e A 7 8 e A èsimmetrica,mentreb non lo è perché b, = 7 6= 4=b, Consideriamo adesso C 7 8A, D 7 8A C èantisimmetrica,mentred non lo è perché d, =6= Si noti che in una matrice simmetrica le entrate in posizione simmetrica al di fuori della diagonale sono uguali; in una matrice antisimmetrica invece le entrate al di fuori della diagonale sono opposte e le entrate diagonali sono necessariamente nulle, dal momento che devono soddisfare l uguaglianza a i,i = a i,i Ogni matrice diagonale, in particolare la matrice nulla n,n,èsimmetrica Invece non possono essere simmetriche le matrici triangolari superiori ed inferiori che non siano diagonali L unica matrice diagonale, o triangolare (superiore ed inferiore), o simmetrica che sia anche antisimmetrica è la matrice nulla n,n 3 Somma e prodotto per scalare In questo paragrafo definiremo due importanti operazioni sulle matrici Definizione 8 (Somma di matrici) Siano A =(a i,j ) 6i6m 6j6n e B =(b i,j ) 6i6m 6j6n due matrici in R m,n Definiamo somma di A e B la matrice di R m,n,indicatacona+b, lacuientrata in posizione (i, j) è a i,j + b i,j B La somma è definita solo per matrici aventi le stesse dimensioni! Esempio 9 In R 3, si 5 7 A 3 3 4A 8 3A / 5/
7 La somma di matrici è quindi un operazione che associa a due matrici delle stesse dimensioni una terza matrice, ancora delle stesse dimensioni Tale operazione soddisfa una serie di proprietà che ora elencheremo Proposizione (Proprietà della somma di matrici) Valgono le seguenti proprietà: (S) per ogni A, B R m,n,sihaa + B = B + A (proprietà commutativa); (S) per ogni A, B, C R m,n, si ha A +(B + C) = (A + B) +C (proprietà associativa); (S3) la matrice nulla è l unico elemento neutro per la somma, cioè è l unica matrice tale che m,n + A = A + m,n = A per ogni A R m,n (esistenza e unicità dell elemento neutro); (S4) per ogni A R m,n, A èl unicoelementooppostodia, cioèèl unicamatrice tale che A +( A) = m,n (esistenza e unicità dell opposto) Inoltre: (ST) per ogni A, B R m,n,siha t (A + B) = t A+ t B (compatibilità con la trasposta) Dimostrazione Per dimostrare le uguaglianze tra matrici usiamo la Definizione 6; come in precedenza, in tutte le uguaglianze da dimostrare le dimensioni delle matrici a destra e a sinistra dell uguale coincidono, quindi dobbiamo solo controllare che anche le entrate al posto (i, j) coincidano (S) Lelemento in posizione (i, j) di A + B è a i,j + b i,j Latesiseguedalfattochel elementoin posizione (i, j) di B + A è b i,j + a i,j = a i,j + b i,j (la somma tra numeri è commutativa!) (S) L elemento in posizione (i, j) di A+(B +C) è a i,j +(b i,j +c i,j ) esihachea i,j +(b i,j +c i,j )= (a i,j + b i,j )+c i,j (la somma tra numeri è associativa!), che è l elemento in posizione (i, j) di (A + B)+C (S3) La verifica che m,n + A = A + m,n = A èimmediata Supponiamoquindicheesistaun secondo elemento neutro, ovvero che esista una matrice X R m,n tale che X + A = A per ogni matrice A R m,n Questo significa che per ogni entrata (i, j) vale l uguaglianza x i,j + a i,j = a i,j equindichex i,j =per ogni I =,,m e j =,,n ecioèx = m,n (S4) Di nuovo, la verifica che A +( A) = m,n èimmediata Supponiamoquindicheesistaun secondo elemento opposto, ovvero che esista una matrice Y R m,n tale che A + Y = m,n Questo significa che per ogni entrata (i, j) vale l uguaglianza a i,j + y i,j =equindiche y i,j = a i,j per ogni i =,,m e j =,,n ecioèy = A (ST) Al posto (i, j) di t (A + B) troviamo l elemento in posizione (j, i) di A + B, cioèa j,i + b j,i, che coincide con la somma dell elemento in posizione (i, j) di t A più l elemento in posizione (i, j) di t B equindiconl elementoinposizione(i, j) di t A + t B Se A, B R m,n,siscrivea B invece di A +( B) Passiamo ora a definire il prodotto di una matrice per un numero reale Definizione (Prodotto per scalare) Siano R un numero (detto anche scalare), A =(a i,j ) 6i6m R m,n una matrice 6j6n Definiamo prodotto dello scalare per la matrice A la matrice di R m,n,indicata con A, lacuientratainposizione(i, j) è a i,j
8 Esempio Si ha 3 5 = Il prodotto per scalare è, quindi, un operazione che associa ad una coppia formata da uno scalare e una matrice m n un altra matrice che ha le stesse dimensioni m n Anche tale operazione soddisfa una serie di proprietà Proposizione 3 (Proprietà del prodotto per scalare) Valgono le seguenti proprietà: (P) per ogni A R m,n,sihaa = A (esistenza dell elemento neutro); (P) per ogni A R m,n eperogni, R, siha ( A)=( )A (proprietà associativa); (SP) per ogni A R m,n e, R, siha( + )A = A + A (proprietà distributiva rispetto alla somma di scalari); (SP) per ogni A, B R m,n e R, si ha (A + B) = A + B (proprietà distributiva rispetto alla somma di matrici) Inoltre: (PT) per ogni A R m,n e R, si ha t ( A) = ( t A) (compatibilità con la trasposta); (LP) per ogni A R m,n e R, risulta A = m,n se e solo se vale =oppure A = m,n (legge di annullamento del prodotto per scalare) Dimostrazione Per dimostrare le uguaglianze tra matrici usiamo la Definizione 6; come in precedenza, in tutte le uguaglianze da dimostrare le dimensioni delle matrici a destra e a sinistra dell uguale coincidono, quindi dobbiamo solo controllare che le entrate al posto (i, j) coincidano Come nella dimostrazione della Proposizione, molte proprietà del prodotto per scalare si basano su proprietà simili a quelle della somma e del prodotto tra numeri (P) L entrata (i, j) di A è a i,j = a i,j (P) Si ha che ( a i,j )=( )a i,j,cheèl elementoinposizione(i, j) della matrice a destra (SP) L entrata (i, j) di ( + )A è ( + )a i,j = a i,j + a i,j,cheèl elemento(i, j) di A + A (SP) Si ha che (a i,j + b i,j )= a i,j + b i,j,dacuil uguaglianzadellematrici (PT) L elemento in posizione (i, j) di t ( A) è a j,i elostessovaleper ( t A) (LP) Se il prodotto A = m,n significa che tutte le entrate della matrice A sono nulle, cioè che per ogni (i, j) il prodotto a i,j =; per la legge di annullamento del prodotto tra numeri questo implica che o =,oppurea i,j =per ogni indice (i, j) equindiaè necessariamente la matrice nulla In generale possiamo dire che le operazioni di somma tra matrici e prodotto per scalare si comportano in modo non troppo diverso dalla somma e dal prodotto tra due numeri cui siamo abituati Nella prossima lezione descriveremo una terza operazione, detta prodotto tra matrici, cheinvecenonavràtalicaratteristiche
LEZIONE 1 C =
 LEZIONE 1 11 Matrici a coefficienti in R Definizione 111 Siano m, n Z positivi Una matrice m n a coefficienti in R è un insieme di mn numeri reali disposti su m righe ed n colonne circondata da parentesi
LEZIONE 1 11 Matrici a coefficienti in R Definizione 111 Siano m, n Z positivi Una matrice m n a coefficienti in R è un insieme di mn numeri reali disposti su m righe ed n colonne circondata da parentesi
Terminiamo gli esercizi dell ultima lezione. (LUCIDI) Calcolare, se possibile, AC, CA, CH e HC. (LUCIDI)
 Terminiamo gli esercizi dell ultima lezione. (LUCIDI) Esempi Calcolare, se possibile, AC, CA, CH e HC. (LUCIDI) Osservazioni per le matrici quadrate a) Data A M n (K) è possibile definire ricorsivamente
Terminiamo gli esercizi dell ultima lezione. (LUCIDI) Esempi Calcolare, se possibile, AC, CA, CH e HC. (LUCIDI) Osservazioni per le matrici quadrate a) Data A M n (K) è possibile definire ricorsivamente
Esercitazioni di Algebra e Geometria
 Esercitazioni di Algebra e Geometria Anno Accademico 2011 2012 Dott.ssa Elisa Pelizzari e-mail elisa.peli@libero.it Esercitazioni: lunedì 14.30 16.30 venerdì 14.30 16.30 Ricevimento studenti: venerdì 13.00
Esercitazioni di Algebra e Geometria Anno Accademico 2011 2012 Dott.ssa Elisa Pelizzari e-mail elisa.peli@libero.it Esercitazioni: lunedì 14.30 16.30 venerdì 14.30 16.30 Ricevimento studenti: venerdì 13.00
ALGEBRA LINEARE E GEOMETRIA: ESERCIZI 5. Indice. 2. Esercizi 5
 ALGEBRA LINEARE E GEOMETRIA: ESERCIZI 5 Indice 1. Principali definizioni 1 2. Esercizi 5 Operazioni con le matrici 1. Principali definizioni Ricordiamo le principali definizioni legate alle matrici a coefficienti
ALGEBRA LINEARE E GEOMETRIA: ESERCIZI 5 Indice 1. Principali definizioni 1 2. Esercizi 5 Operazioni con le matrici 1. Principali definizioni Ricordiamo le principali definizioni legate alle matrici a coefficienti
Le matrici. Sia K un campo con elemento neutro dell addizione 0 ed elemento neutro della moltiplicazione 1.
 Le matrici Sia K un campo con elemento neutro dell addizione 0 ed elemento neutro della moltiplicazione 1. Siano m, n N\{0}. Una matrice m n a coefficienti in K è una tabella di m n elementi di K disposti
Le matrici Sia K un campo con elemento neutro dell addizione 0 ed elemento neutro della moltiplicazione 1. Siano m, n N\{0}. Una matrice m n a coefficienti in K è una tabella di m n elementi di K disposti
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof. Fabio Perroni 2. MATRICI
 Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 2 MATRICI Siano m, n N \ {0}, sia K un campo Una matrice m n a coefficienti in K è una
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 2 MATRICI Siano m, n N \ {0}, sia K un campo Una matrice m n a coefficienti in K è una
Matrici e sistemi. Geometria. Matrici e operazioni tra matrici. Operazioni elementari e riduzione Sistemi lineari Matrici invertibili Determinante
 Geometria Matrici e sistemi Operazioni elementari e riduzione Sistemi lineari Matrici invertibili Determinante 2 2006 Politecnico di Torino 1 Matrici e sistemi Matrici: definizione e notazioni Somma e
Geometria Matrici e sistemi Operazioni elementari e riduzione Sistemi lineari Matrici invertibili Determinante 2 2006 Politecnico di Torino 1 Matrici e sistemi Matrici: definizione e notazioni Somma e
= elemento che compare nella seconda riga e quinta colonna = -4 In generale una matrice A di m righe e n colonne si denota con
 Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti su m righe e n colonne. I numeri che compaiono nella tabella si dicono elementi della matrice. La loro individuazione
Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti su m righe e n colonne. I numeri che compaiono nella tabella si dicono elementi della matrice. La loro individuazione
APPLICAZIONI. Im f = {b B a A tale che f (a) = b}.
 APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
1 PRELIMINARI 1.1 NOTAZIONI. denota l insieme vuoto. a A si legge a appartiene a A oppure a è elemento di A.
 1 PRELIMINARI 1.1 NOTAZIONI denota l insieme vuoto. a A si legge a appartiene a A oppure a è elemento di A. B A si legge B è un sottoinsieme di A e significa che ogni elemento di B è anche elemento di
1 PRELIMINARI 1.1 NOTAZIONI denota l insieme vuoto. a A si legge a appartiene a A oppure a è elemento di A. B A si legge B è un sottoinsieme di A e significa che ogni elemento di B è anche elemento di
LEZIONE 2. ( ) a 1 x 1 + a 2 x a n x n = b, ove a j, b R sono fissati.
 LEZIONE 2 2 Sistemi di equazioni lineari Definizione 2 Un equazione lineare nelle n incognite x, x 2,, x n a coefficienti reali, è un equazione della forma (2 a x + a 2 x 2 + + a n x n = b, ove a j, b
LEZIONE 2 2 Sistemi di equazioni lineari Definizione 2 Un equazione lineare nelle n incognite x, x 2,, x n a coefficienti reali, è un equazione della forma (2 a x + a 2 x 2 + + a n x n = b, ove a j, b
STRUTTURE ALGEBRICHE. Francesca Benanti. Novembre : A A A (a, b) a b, a, b A
 STRUTTURE ALGEBRICHE Francesca Benanti Novembre 2018 1 Semigruppi Definizione 1 Sia A un insieme non vuoto, A. Una operazione (o operazione binaria o legge di composizione interna) su A è un applicazione
STRUTTURE ALGEBRICHE Francesca Benanti Novembre 2018 1 Semigruppi Definizione 1 Sia A un insieme non vuoto, A. Una operazione (o operazione binaria o legge di composizione interna) su A è un applicazione
Matematica II
 Matematica II 29..0. Somma di due matrici. Siano m ed n due interi positivi fissati. Date due matrici A, B R m n di tipo m n, sommando a ciascun elemento di A il corrispondente elemento di B, si ottiene
Matematica II 29..0. Somma di due matrici. Siano m ed n due interi positivi fissati. Date due matrici A, B R m n di tipo m n, sommando a ciascun elemento di A il corrispondente elemento di B, si ottiene
Algebra delle matrici
 Algebra delle matrici Metodo di Gauss-Jordan per l inversione di una matrice. Nella lezione scorsa abbiamo visto che un modo per determinare l eventuale inversa di una matrice quadrata A consiste nel risolvere
Algebra delle matrici Metodo di Gauss-Jordan per l inversione di una matrice. Nella lezione scorsa abbiamo visto che un modo per determinare l eventuale inversa di una matrice quadrata A consiste nel risolvere
LEZIONE 11. s V : V V V (v 1, v 2 ) v 1 + v 2 = s V (v 1, v 2 ), p V : k V V. per cui valgono:
 LEZIONE 11 11.1. Spazi vettoriali ed esempi. La nozione di spazio vettoriale generalizza quanto visto nelle lezioni precedenti: l insieme k m,n delle matrici m n a coefficienti in k = R, C, l insieme V
LEZIONE 11 11.1. Spazi vettoriali ed esempi. La nozione di spazio vettoriale generalizza quanto visto nelle lezioni precedenti: l insieme k m,n delle matrici m n a coefficienti in k = R, C, l insieme V
Lezione Determinanti
 Lezione 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
Lezione 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Lezione Sistemi di equazioni lineari
 Lezione. Sistemi di equazioni lineari Definizione. (Sistemi di equazioni lineari e loro soluzioni). Un equazione lineare nelle n incognite x,,...,x n acoefficientiink = R, èun equazionedellaforma a x +
Lezione. Sistemi di equazioni lineari Definizione. (Sistemi di equazioni lineari e loro soluzioni). Un equazione lineare nelle n incognite x,,...,x n acoefficientiink = R, èun equazionedellaforma a x +
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Lezione 4 - Esercitazioni di Algebra e Geometria - Anno accademico
 Trasformazioni elementari sulle matrici Data una matrice A K m,n definiamo su A le seguenti tre trasformazioni elementari: T : scambiare tra loro due righe (o due colonne) di A; T : sommare ad una riga
Trasformazioni elementari sulle matrici Data una matrice A K m,n definiamo su A le seguenti tre trasformazioni elementari: T : scambiare tra loro due righe (o due colonne) di A; T : sommare ad una riga
Vettori e matrici. Lorenzo Pareschi. Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara
 Vettori e matrici Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utentiunifeit/lorenzopareschi/ lorenzopareschi@unifeit Lorenzo Pareschi Univ Ferrara
Vettori e matrici Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utentiunifeit/lorenzopareschi/ lorenzopareschi@unifeit Lorenzo Pareschi Univ Ferrara
Equivalentemente, le colonne di A sono linearmente indipendenti se e solo se
 Lezioni di Algebra Lineare. Versione novembre 2008 VI. Il determinante Il determinante det A di una matrice A, reale e quadrata, è un numero reale associato ad A. Dunque det è una funzione dall insieme
Lezioni di Algebra Lineare. Versione novembre 2008 VI. Il determinante Il determinante det A di una matrice A, reale e quadrata, è un numero reale associato ad A. Dunque det è una funzione dall insieme
ALGEBRA DELLE MATRICI
 ALGEBRA DELLE MATRICI March 8, 2015 1 Definizioni e notazioni Una matrice è una tabella rettangolare le cui entrate sono numeri organizzati in righe orizzontali e colonne verticali. Esempio 1 2 A = 4 0
ALGEBRA DELLE MATRICI March 8, 2015 1 Definizioni e notazioni Una matrice è una tabella rettangolare le cui entrate sono numeri organizzati in righe orizzontali e colonne verticali. Esempio 1 2 A = 4 0
LEZIONE i 0 3 Le sottomatrici 2 2 di A sono. 1 2 i i 3. Invece (
 LEZIONE 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
( ) TEORIA DELLE MATRICI. A. Scimone a.s pag 1
 . Scimone a.s 1997 98 pag 1 TEORI DELLE MTRICI Dato un campo K, definiamo matrice ad elementi in K di tipo (m, n) un insieme di numeri ordinati secondo righe e colonne in una tabella rettangolare del tipo
. Scimone a.s 1997 98 pag 1 TEORI DELLE MTRICI Dato un campo K, definiamo matrice ad elementi in K di tipo (m, n) un insieme di numeri ordinati secondo righe e colonne in una tabella rettangolare del tipo
Corso di Matematica e Statistica 3 Algebra delle matrici. Una tabella rettangolare: la matrice. Una tabella rettangolare: la matrice
 Pordenone Corso di Matematica e Statistica 3 Algebra delle UNIVERSITAS STUDIORUM UTINENSIS Giorgio T. Bagni Facoltà di Scienze della Formazione Dipartimento di Matematica e Informatica Università di Udine
Pordenone Corso di Matematica e Statistica 3 Algebra delle UNIVERSITAS STUDIORUM UTINENSIS Giorgio T. Bagni Facoltà di Scienze della Formazione Dipartimento di Matematica e Informatica Università di Udine
LEZIONE i i 3
 LEZIONE 5 51 Determinanti In questo lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 5 51 Determinanti In questo lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
A =, c d. d = ad cb. c d A =
 Geometria e Algebra (II), 271112 1 Definizione D ora innanzi, al posto di dire matrice quadrata di tipo n n o matrice quadrata n n diremo matrice quadrata di ordine n o in breve matrice di ordine n Il
Geometria e Algebra (II), 271112 1 Definizione D ora innanzi, al posto di dire matrice quadrata di tipo n n o matrice quadrata n n diremo matrice quadrata di ordine n o in breve matrice di ordine n Il
Strutture Algebriche
 Strutture Algebriche Docente: Francesca Benanti 21 gennaio 2008 1 Operazioni Definizione Sia A un insieme non vuoto, A. Una operazione (o operazione binaria o legge di composizione interna) su A è un applicazione
Strutture Algebriche Docente: Francesca Benanti 21 gennaio 2008 1 Operazioni Definizione Sia A un insieme non vuoto, A. Una operazione (o operazione binaria o legge di composizione interna) su A è un applicazione
Geometria BAER I canale Foglio esercizi 2
 Geometria BAER I canale Foglio esercizi 2 Esercizio 1. Calcolare il determinante e l inversa (quando esiste) della matrice ( ) cos θ sin θ R θ =, θ [0, 2π] sin θ cos θ Soluzione: Il determinante ( é cos
Geometria BAER I canale Foglio esercizi 2 Esercizio 1. Calcolare il determinante e l inversa (quando esiste) della matrice ( ) cos θ sin θ R θ =, θ [0, 2π] sin θ cos θ Soluzione: Il determinante ( é cos
Elementi di Algebra Matriciale. (richiami)
 Elementi di Algebra Matriciale Definizione di matrice (richiami) Matrice quadrata, diagonale, identità, triangolare, simmetrica Matrice trasposta Principali operazioni su matrici e vettori: somma, sottrazione,
Elementi di Algebra Matriciale Definizione di matrice (richiami) Matrice quadrata, diagonale, identità, triangolare, simmetrica Matrice trasposta Principali operazioni su matrici e vettori: somma, sottrazione,
Esercitazioni di Algebra e Geometria
 Esercitazioni di Algebra e Geometria Anno Accademico 2010 2011 Dott.ssa Elisa Pelizzari e-mail elisa.peli@libero.it Esercitazioni: lunedì 14.30 16.30 venerdì 14.30 16.30 Ricevimento studenti: venerdì 13.30
Esercitazioni di Algebra e Geometria Anno Accademico 2010 2011 Dott.ssa Elisa Pelizzari e-mail elisa.peli@libero.it Esercitazioni: lunedì 14.30 16.30 venerdì 14.30 16.30 Ricevimento studenti: venerdì 13.30
Operazioni tra matrici. Moltiplicazione per uno Scalare Moltiplicare ogni elemento della matrice per lo scalare. Sia c = 3
 Operazioni tra matrici Definizione di matrice a ij è un elemento di A a ij è detto l elemento ij-esimo di A Moltiplicazione per uno Scalare Moltiplicare ogni elemento della matrice per lo scalare. Sia
Operazioni tra matrici Definizione di matrice a ij è un elemento di A a ij è detto l elemento ij-esimo di A Moltiplicazione per uno Scalare Moltiplicare ogni elemento della matrice per lo scalare. Sia
Argomento 12 Matrici
 Argomento 2 Matrici 2 Vettori di R n eoperazioni I Vettore di R n : x =(x i ) i=n =(x i ) n i=,conx i R componenti di x I R n = spazio dei vettori reali a n componenti = spazio vettoriale reale n-dimensionale
Argomento 2 Matrici 2 Vettori di R n eoperazioni I Vettore di R n : x =(x i ) i=n =(x i ) n i=,conx i R componenti di x I R n = spazio dei vettori reali a n componenti = spazio vettoriale reale n-dimensionale
CORSO DI LAUREA IN INGEGNERIA DELLE TELECOMUNICAZIONI
 CORSO DI LAUREA IN INGEGNERIA DELLE TELECOMUNICAZIONI FOGLIO DI ESERCIZI # GEOMETRIA E ALGEBRA 009/0 Esercizio.. Dati i vettori di R : v (,, ), v (, 4, 6), v (,, 5), v 4 (,, 0) determinare se v 4 è combinazione
CORSO DI LAUREA IN INGEGNERIA DELLE TELECOMUNICAZIONI FOGLIO DI ESERCIZI # GEOMETRIA E ALGEBRA 009/0 Esercizio.. Dati i vettori di R : v (,, ), v (, 4, 6), v (,, 5), v 4 (,, 0) determinare se v 4 è combinazione
Algebra lineare. Laboratorio di programmazione e calcolo CdL in Chimica. Pierluigi Amodio
 Algebra lineare Laboratorio di programmazione e calcolo CdL in Chimica Pierluigi Amodio Dipartimento di Matematica Università di Bari pierluigi.amodio@uniba.it http://dm.uniba.it/ amodio A.A. 2016/17 P.
Algebra lineare Laboratorio di programmazione e calcolo CdL in Chimica Pierluigi Amodio Dipartimento di Matematica Università di Bari pierluigi.amodio@uniba.it http://dm.uniba.it/ amodio A.A. 2016/17 P.
Lezione del dove a 1, a n e b sono numeri reali assegnati, detti coefficienti e termine noto dell equazione;
 Le lezioni del 60 e 010 si riferiscono al Capitolo 1 Introduzione ai sistemi lineari Di seguito si elencano gli argomenti svolti, descrivendoli sinteticamente dando i riferimenti a tale capitolo, oppure
Le lezioni del 60 e 010 si riferiscono al Capitolo 1 Introduzione ai sistemi lineari Di seguito si elencano gli argomenti svolti, descrivendoli sinteticamente dando i riferimenti a tale capitolo, oppure
Matrici e sistemi. Sistemi lineari. Invertibilità Matrici elementari Criteri di invertibilità Sistemi quadrati e Teorema di Cramer
 Sistemi lineari Invertibilità Matrici elementari Criteri di invertibilità Sistemi quadrati e Teorema di Cramer 2 2006 Politecnico di Torino 1 Prodotto tra matrici quadrate Date comunque A e B matrici quadrate
Sistemi lineari Invertibilità Matrici elementari Criteri di invertibilità Sistemi quadrati e Teorema di Cramer 2 2006 Politecnico di Torino 1 Prodotto tra matrici quadrate Date comunque A e B matrici quadrate
3 Soluzione di sistemi lineari
 3 Soluzione di sistemi lineari Prima di addentrarci nello studio dei metodi numerici, è doveroso introdurre le matrici e alcune strutture particolari di matrici nonchè alcuni concetti fondamentali quali
3 Soluzione di sistemi lineari Prima di addentrarci nello studio dei metodi numerici, è doveroso introdurre le matrici e alcune strutture particolari di matrici nonchè alcuni concetti fondamentali quali
Somma diretta di sottospazi vettoriali
 Capitolo 8 Somma diretta di sottospazi vettoriali 8.1 Introduzione Introduciamo un caso particolare di somma di due sottospazi vettoriali: la somma diretta. Anche questo argomento è stato visto nel corso
Capitolo 8 Somma diretta di sottospazi vettoriali 8.1 Introduzione Introduciamo un caso particolare di somma di due sottospazi vettoriali: la somma diretta. Anche questo argomento è stato visto nel corso
1 Introduzione alle matrici quadrate 2 2 a coefficienti in R.
 1 Introduzione alle matrici quadrate 2 2 a coefficienti in R Per introdurre il concetto di matrice, a 2 righe e 2 colonne, iniziamo col considerare griglie o tabelle di numeri Gli elementi della griglia,
1 Introduzione alle matrici quadrate 2 2 a coefficienti in R Per introdurre il concetto di matrice, a 2 righe e 2 colonne, iniziamo col considerare griglie o tabelle di numeri Gli elementi della griglia,
MATRICI E SISTEMI LINEARI
 MATRICI E SISTEMI LINEARI - PARTE I - Felice Iavernaro Dipartimento di Matematica Università di Bari 27 Febbraio 2006 Felice Iavernaro (Univ. Bari) Matrici e Sistemi lineari 27/02/2006 1 / 1 Definizione
MATRICI E SISTEMI LINEARI - PARTE I - Felice Iavernaro Dipartimento di Matematica Università di Bari 27 Febbraio 2006 Felice Iavernaro (Univ. Bari) Matrici e Sistemi lineari 27/02/2006 1 / 1 Definizione
Sistemi lineari e spazi vettoriali 1 / 14
 Sistemi lineari e spazi vettoriali 1 / 14 Sistemi lineari 2 / 14 Studieremo sistemi lineari costituiti da m equazioni in n incognite (m,n N, m,n 1): cioè a 11 x 1 + +a 1n x n = b 1 a 21 x 1 + +a 2n x n
Sistemi lineari e spazi vettoriali 1 / 14 Sistemi lineari 2 / 14 Studieremo sistemi lineari costituiti da m equazioni in n incognite (m,n N, m,n 1): cioè a 11 x 1 + +a 1n x n = b 1 a 21 x 1 + +a 2n x n
Il prodotto tra matrici non è commutativo. Nelle notazioni precedenti, ponendo n = p e m = q si hanno:
 L anello delle matrici Esempio. Siano A = [ ] 0 1 3 0 2 1, B = 1 2 0 0 1 2 3 4, 1 0 calcolare AB e BA. Osservazioni Siano A Mat m,n (K) e B Mat p,q (K). Il prodotto AB è definito se n = p. Si ha AB Mat
L anello delle matrici Esempio. Siano A = [ ] 0 1 3 0 2 1, B = 1 2 0 0 1 2 3 4, 1 0 calcolare AB e BA. Osservazioni Siano A Mat m,n (K) e B Mat p,q (K). Il prodotto AB è definito se n = p. Si ha AB Mat
Introduzione all algebra delle matrici. Appunti a cura di Lara Ercoli
 Introduzione all algebra delle matrici ppunti a cura di Lara Ercoli Indice Definizioni 3. Matrici particolari............................ 4 2 Operazioni con le matrici 8 2. Somma di matrici.............................
Introduzione all algebra delle matrici ppunti a cura di Lara Ercoli Indice Definizioni 3. Matrici particolari............................ 4 2 Operazioni con le matrici 8 2. Somma di matrici.............................
Matematica II
 Matematica II 241110 Matrice inversa 1 Per n 1, l insieme R n n delle matrici quadrate di ordine n diventa l insieme R dei numeri reali, e la moltiplicazione di matrici diventa la moltiplicazione di numeri
Matematica II 241110 Matrice inversa 1 Per n 1, l insieme R n n delle matrici quadrate di ordine n diventa l insieme R dei numeri reali, e la moltiplicazione di matrici diventa la moltiplicazione di numeri
Operazioni tra matrici e n-uple
 CAPITOLO Operazioni tra matrici e n-uple Esercizio.. Date le matrici 0 4 e dati λ = 5, µ =, si calcoli AB, BA, A+B, B A, λa+µb. Esercizio.. Per ognuna delle seguenti coppie di matrici A, B e scalari λ,
CAPITOLO Operazioni tra matrici e n-uple Esercizio.. Date le matrici 0 4 e dati λ = 5, µ =, si calcoli AB, BA, A+B, B A, λa+µb. Esercizio.. Per ognuna delle seguenti coppie di matrici A, B e scalari λ,
Introduzione allo Scilab Parte 4: matrici; esempi.
 Introduzione allo Scilab Parte 4: matrici; esempi. Felice Iavernaro Dipartimento di Matematica Università di Bari http://dm.uniba.it/ iavernaro felix@dm.uniba.it 20 Giugno 2007 Felice Iavernaro (Univ.
Introduzione allo Scilab Parte 4: matrici; esempi. Felice Iavernaro Dipartimento di Matematica Università di Bari http://dm.uniba.it/ iavernaro felix@dm.uniba.it 20 Giugno 2007 Felice Iavernaro (Univ.
Richiami di algebra delle matrici a valori reali
 Richiami di algebra delle matrici a valori reali Vettore v n = v 1 v 2. v n Vettore trasposto v n = (v 1, v 2,..., v n ) v n = (v 1, v 2,..., v n ) A. Pollice - Statistica Multivariata Vettore nullo o
Richiami di algebra delle matrici a valori reali Vettore v n = v 1 v 2. v n Vettore trasposto v n = (v 1, v 2,..., v n ) v n = (v 1, v 2,..., v n ) A. Pollice - Statistica Multivariata Vettore nullo o
@. A = r 1,1c 1,1 + r 1,2 c 2,1 + + r 1,p c p,1 2 R 1,1. c p,1
 Lezione 2 2 Prodotto di matrici In questo paragrafo introdurremo una nuova operazione detta prodotto tra matrici, oancheprodotto righe per colonne Procederemo per gradi: definiremo prima il prodotto di
Lezione 2 2 Prodotto di matrici In questo paragrafo introdurremo una nuova operazione detta prodotto tra matrici, oancheprodotto righe per colonne Procederemo per gradi: definiremo prima il prodotto di
Geometria BAER I canale Foglio esercizi 3
 Geometria BAER I canale Foglio esercizi 3 Esercizio. Discutere le soluzioni del seguente sistema lineare nelle incognite,, z al variare del parametro k. 3 + kz = k k + 3z = k k + z = Soluzione: Il determinante
Geometria BAER I canale Foglio esercizi 3 Esercizio. Discutere le soluzioni del seguente sistema lineare nelle incognite,, z al variare del parametro k. 3 + kz = k k + 3z = k k + z = Soluzione: Il determinante
4 0 = 4 2 = 4 4 = 4 6 = 0.
 Elementi di Algebra e Logica 2008. Esercizi 4. Gruppi, anelli e campi. 1. Determinare la tabella additiva e la tabella moltiplicativa di Z 6. (a) Verificare dalla tabella moltiplicativa di Z 6 che esistono
Elementi di Algebra e Logica 2008. Esercizi 4. Gruppi, anelli e campi. 1. Determinare la tabella additiva e la tabella moltiplicativa di Z 6. (a) Verificare dalla tabella moltiplicativa di Z 6 che esistono
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof. Fabio Perroni. 3. Sistemi di equazioni lineari
 Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 3 Sistemi di equazioni lineari Siano m, n N \ {}, sia K un campo Definizione a) Un sistema
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 3 Sistemi di equazioni lineari Siano m, n N \ {}, sia K un campo Definizione a) Un sistema
APPUNTI DI ALGEBRA LINEARE
 APPUNTI DI ALGEBRA LINEARE. Definizione Si dice spazio vettoriale (sul campo dei numeri reali R) un insieme V per il quale siano definite l operazione interna di somma (che ad ogni coppia di vettori e
APPUNTI DI ALGEBRA LINEARE. Definizione Si dice spazio vettoriale (sul campo dei numeri reali R) un insieme V per il quale siano definite l operazione interna di somma (che ad ogni coppia di vettori e
LEZIONE 3. a + b + 2c + e = 1 b + d + g = 0 3b + f + 3g = 2. a b c d e f g
 LEZIONE 3 3.. Matrici fortemente ridotte per righe. Nella precedente lezione abbiamo introdotto la nozione di soluzione di un sistema di equazioni lineari. In questa lezione ci poniamo il problema di descrivere
LEZIONE 3 3.. Matrici fortemente ridotte per righe. Nella precedente lezione abbiamo introdotto la nozione di soluzione di un sistema di equazioni lineari. In questa lezione ci poniamo il problema di descrivere
i) la somma e il prodotto godano delle proprietà associativa, commutativa e distributiva;
 1 Spazi vettoriali 11 Definizioni ed assiomi Definizione 11 Un campo è un insieme K dotato di una operazione somma K K K, (x, y) x + y e di una operazione prodotto K K K, (x, y) xy tali che i) la somma
1 Spazi vettoriali 11 Definizioni ed assiomi Definizione 11 Un campo è un insieme K dotato di una operazione somma K K K, (x, y) x + y e di una operazione prodotto K K K, (x, y) xy tali che i) la somma
x n i sima pos. x, y = x T y = x i y i R. i=1
 1 Elementi di Algebra Lineare In questo capitolo introduttivo al corso di Calcolo Numerico per la laurea triennale in Informatica, saranno presentate una serie di definizioni e proprietà di matrici e dei
1 Elementi di Algebra Lineare In questo capitolo introduttivo al corso di Calcolo Numerico per la laurea triennale in Informatica, saranno presentate una serie di definizioni e proprietà di matrici e dei
Lezione Operazioni elementari di riga
 Lezione 4 4. Operazioni elementari di riga Nella lezione precedente abbiamo visto un metodo per risolvere un sistema lineare la cui matrice dei coefficienti sia fortemente ridotta per righe, o anche solo
Lezione 4 4. Operazioni elementari di riga Nella lezione precedente abbiamo visto un metodo per risolvere un sistema lineare la cui matrice dei coefficienti sia fortemente ridotta per righe, o anche solo
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE. Giovanni Villani
 Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
Relazioni e Principio di Induzione
 Relazioni e Principio di Induzione Giovanna Carnovale October 12, 2011 1 Relazioni Dato un insieme S, un sottoinsieme fissato R del prodotto cartesiano S S definisce una relazione ρ tra gli elementi di
Relazioni e Principio di Induzione Giovanna Carnovale October 12, 2011 1 Relazioni Dato un insieme S, un sottoinsieme fissato R del prodotto cartesiano S S definisce una relazione ρ tra gli elementi di
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof. Fabio Perroni. 5. Rango
 Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 5 Rango Definizione 1 Sia A M m,n (K) una matrice m n a coefficienti nel campo K Il rango
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 5 Rango Definizione 1 Sia A M m,n (K) una matrice m n a coefficienti nel campo K Il rango
MATRICI e DETERMINANTI. Prof.ssa Maddalena Dominijanni
 MATRICI e DETERMINANTI Le matrici non sono altro che tabelle di elementi ordinati per righe e colonne. Se m = n la matrice si dice quadrata Matrice quadrata di ordine 3 Matrice rettangolare di tipo 2 3
MATRICI e DETERMINANTI Le matrici non sono altro che tabelle di elementi ordinati per righe e colonne. Se m = n la matrice si dice quadrata Matrice quadrata di ordine 3 Matrice rettangolare di tipo 2 3
Sottospazi vettoriali
 Capitolo 6 Sottospazi vettoriali 6.1 Introduzione Riprendiamo un argomento già studiato ampiamente nel corso di Geometria, i sottospazi vettoriali di uno spazio vettoriale. Ci limiteremo a darne la definizione,
Capitolo 6 Sottospazi vettoriali 6.1 Introduzione Riprendiamo un argomento già studiato ampiamente nel corso di Geometria, i sottospazi vettoriali di uno spazio vettoriale. Ci limiteremo a darne la definizione,
Fattorizzazione QR e matrici di Householder
 Fattorizzazione QR e matrici di Householder ottobre 009 In questa nota considereremo un tipo di fattorizzazione che esiste sempre nel caso di matrici quadrate non singolari ad entrate reali. Definizione
Fattorizzazione QR e matrici di Householder ottobre 009 In questa nota considereremo un tipo di fattorizzazione che esiste sempre nel caso di matrici quadrate non singolari ad entrate reali. Definizione
MATRICI E OPERAZIONI
 MATRICI E SISTEMI MATRICI E OPERAZIONI Matrici, somma e prodotto (definizioni, esempi, non commutatività del prodotto, legge di annullamento del prodotto Potenze e inverse di matrici quadrate (definizioni
MATRICI E SISTEMI MATRICI E OPERAZIONI Matrici, somma e prodotto (definizioni, esempi, non commutatività del prodotto, legge di annullamento del prodotto Potenze e inverse di matrici quadrate (definizioni
R 2 e i numeri complessi
 L. Chierchia. Dipartimento di Matematica e Fisica, Università Roma Tre 1 R e i numeri complessi 1. R come spazio vettoriale R, ossia l insieme delle coppie ordinate x, y con x e y in R è uno spazio vettoriale
L. Chierchia. Dipartimento di Matematica e Fisica, Università Roma Tre 1 R e i numeri complessi 1. R come spazio vettoriale R, ossia l insieme delle coppie ordinate x, y con x e y in R è uno spazio vettoriale
Lezione Diagonalizzazione di matrici
 Lezione 2 2. Diagonalizzazione di matrici Come visto nella precedente lezione, in generale, data una matrice A 2 K n,n con K = R, C,nonèimmediatocheesistasempreunabasecostituitadasuoiautovettori. Definizione
Lezione 2 2. Diagonalizzazione di matrici Come visto nella precedente lezione, in generale, data una matrice A 2 K n,n con K = R, C,nonèimmediatocheesistasempreunabasecostituitadasuoiautovettori. Definizione
MATRICI. Matrici Una matrice A con n-righe e m-colonne, ad elementi reali, è una tabella con la seguente forma: a 2 m. a n m) i j R, 1 i n, 1 j m.
 MATRICI Matrici Una matrice A con n-righe e m-colonne, ad elementi reali, è una tabella con la seguente forma: 11 a 12 a 1 3 a 1m A=(a a 21 a 2 3 a 2m con a a n1 a n2 a n 3 a nm i j R, 1 i n, 1 j m. per
MATRICI Matrici Una matrice A con n-righe e m-colonne, ad elementi reali, è una tabella con la seguente forma: 11 a 12 a 1 3 a 1m A=(a a 21 a 2 3 a 2m con a a n1 a n2 a n 3 a nm i j R, 1 i n, 1 j m. per
LEZIONE 4. Le sottomatrici 2 2 di A sono. Invece ( 1 3 non è sottomatrice di A.
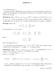 LEZIONE 4 4 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 4 4 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari
 Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017 Elementi di Algebra Lineare
Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017 Elementi di Algebra Lineare
CORSO DI GEOMETRIA DETERMINANTE A.A. 2018/2019 PROF. VALENTINA BEORCHIA
 CORSO DI GEOMETRIA DETERMINANTE AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Definizione induttiva di determinante 1 2 Caratterizzazione delle matrici quadrate di rango massimo 5 3 Regole di Laplace 6
CORSO DI GEOMETRIA DETERMINANTE AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Definizione induttiva di determinante 1 2 Caratterizzazione delle matrici quadrate di rango massimo 5 3 Regole di Laplace 6
Possiamo scrivere le tre precedenti espressioni in un'unica equazione matriciale:
 A1. Considerazioni sul cambio di un sistema di riferimento cartesiano ortogonale Sia xyz un sistema di riferimento cartesiano ortogonale di origine O e di riferimento cartesiano pure di origine O. un secondo
A1. Considerazioni sul cambio di un sistema di riferimento cartesiano ortogonale Sia xyz un sistema di riferimento cartesiano ortogonale di origine O e di riferimento cartesiano pure di origine O. un secondo
MATRICI E SISTEMI LINEARI
 1 Rappresentazione di dati strutturati MATRICI E SISTEMI LINEARI Gli elementi di una matrice, detti coefficienti, possono essere qualsiasi e non devono necessariamente essere omogenei tra loro; di solito
1 Rappresentazione di dati strutturati MATRICI E SISTEMI LINEARI Gli elementi di una matrice, detti coefficienti, possono essere qualsiasi e non devono necessariamente essere omogenei tra loro; di solito
PreCorso di Matematica - PCM Corso M-Z
 PreCorso di Matematica - PCM Corso M-Z DOCENTE: M. Auteri Outline Docente: Auteri PreCorso di Matematica 2016 2 Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti
PreCorso di Matematica - PCM Corso M-Z DOCENTE: M. Auteri Outline Docente: Auteri PreCorso di Matematica 2016 2 Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti
Analisi dei dati corso integrato - Algebra lineare, e a b c 0. le soluzioni del sistema lineare omogeneo x d e f 2. a b c.
 Analisi dei dati corso integrato - Algebra lineare 4.3.8 e 5.3.8-1 1. Nella lezione precedente abbiamo definito lo spazio nullo e lo spazio delle colonne di una matrice; ora definiamo lo spazio delle righe
Analisi dei dati corso integrato - Algebra lineare 4.3.8 e 5.3.8-1 1. Nella lezione precedente abbiamo definito lo spazio nullo e lo spazio delle colonne di una matrice; ora definiamo lo spazio delle righe
AL220 - Gruppi, Anelli e Campi
 AL220 - Gruppi, Anelli e Campi Prof. Stefania Gabelli - a.a. 2013-2014 Settimana 1 - Traccia delle Lezioni Funzioni tra insiemi Ricordiamo che una funzione o applicazione di insiemi f : A B è una corrispondenza
AL220 - Gruppi, Anelli e Campi Prof. Stefania Gabelli - a.a. 2013-2014 Settimana 1 - Traccia delle Lezioni Funzioni tra insiemi Ricordiamo che una funzione o applicazione di insiemi f : A B è una corrispondenza
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
Indice. NUMERI REALI Mauro Saita Versione provvisoria. Ottobre 2017.
 NUMERI REALI Mauro Saita e-mail: maurosaita@tiscalinet.it Versione provvisoria. Ottobre 2017. Indice 1 Numeri reali 2 1.1 Il lato e la diagonale del quadrato sono incommensurabili: la scoperta dei numeri
NUMERI REALI Mauro Saita e-mail: maurosaita@tiscalinet.it Versione provvisoria. Ottobre 2017. Indice 1 Numeri reali 2 1.1 Il lato e la diagonale del quadrato sono incommensurabili: la scoperta dei numeri
Applicazioni lineari simmetriche e forme quadratiche reali.
 Applicazioni lineari simmetriche e forme quadratiche reali 1 Applicazioni lineari simmetriche Consideriamo lo spazio IR n col prodotto scalare canonico X Y = t XY = x 1 y 1 + + x n y n Definizione Un applicazione
Applicazioni lineari simmetriche e forme quadratiche reali 1 Applicazioni lineari simmetriche Consideriamo lo spazio IR n col prodotto scalare canonico X Y = t XY = x 1 y 1 + + x n y n Definizione Un applicazione
1. Proprietà della somma di matrici. 1. (A + B) + C = A + (B + C) qualunque. 2. A + B = B + A qualunque siano le matrici
 Matrici R. Notari 1 1. Proprietà della somma di matrici 1. (A + B) + C = A + (B + C) qualunque siano le matrici A, B, C Mat(m, n; K). 2. A + B = B + A qualunque siano le matrici A, B Mat(m, n; K). 3. Sia
Matrici R. Notari 1 1. Proprietà della somma di matrici 1. (A + B) + C = A + (B + C) qualunque siano le matrici A, B, C Mat(m, n; K). 2. A + B = B + A qualunque siano le matrici A, B Mat(m, n; K). 3. Sia
Lezioni di Algebra Lineare. II. Aritmetica delle matrici e eliminazione di Gauss. versione ottobre 2008
 versione ottobre 2008 Lezioni di Algebra Lineare II. Aritmetica delle matrici e eliminazione di Gauss Contenuto. 1. Somma di matrici e prodotto di una matrice per uno scalare 2. Prodotto di matrici righe
versione ottobre 2008 Lezioni di Algebra Lineare II. Aritmetica delle matrici e eliminazione di Gauss Contenuto. 1. Somma di matrici e prodotto di una matrice per uno scalare 2. Prodotto di matrici righe
1.1 Esempio. Siano A = {11, f, β,,, } e B = {x, 11,,,, α, γ} e le seguenti leggi:
 1. Relazioni. 1 Dati due insiemi possiamo stabilire in modo del tutto arbitrario una legge che associ elementi di un insieme ad elementi dell altro insieme. Ovviamente, data la totale arbitrarietà di tale
1. Relazioni. 1 Dati due insiemi possiamo stabilire in modo del tutto arbitrario una legge che associ elementi di un insieme ad elementi dell altro insieme. Ovviamente, data la totale arbitrarietà di tale
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof. F.Podestà, a.a
 APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
Complemento 10 Numeri complessi
 Analisi Matematica I CL Fisica, Università Roma Tre AA 2008/09 L. Chierchia Complemento 0 Numeri complessi. Il campo complesso Il campo complesso C è, per definizione, la terna R 2, +,, cioè R 2 equipaggiato
Analisi Matematica I CL Fisica, Università Roma Tre AA 2008/09 L. Chierchia Complemento 0 Numeri complessi. Il campo complesso Il campo complesso C è, per definizione, la terna R 2, +,, cioè R 2 equipaggiato
Qualche informazione su gruppi e anelli
 Qualche informazione su gruppi e anelli 1. Gruppi e sottogruppi: prime proprietà Cominciamo subito scrivendo la definizione formale di gruppo. Definizione 0.1. Un gruppo G è un insieme non vuoto dotato
Qualche informazione su gruppi e anelli 1. Gruppi e sottogruppi: prime proprietà Cominciamo subito scrivendo la definizione formale di gruppo. Definizione 0.1. Un gruppo G è un insieme non vuoto dotato
TEMPUS PECUNIA EST COLLANA DI MATEMATICA PER LE SCIENZE ECONOMICHE FINANZIARIE E AZIENDALI
 TEMPUS PECUNIA EST COLLANA DI MATEMATICA PER LE SCIENZE ECONOMICHE FINANZIARIE E AZIENDALI 2 Direttore Beatrice VENTURI Università degli Studi di Cagliari Comitato scientifico Umberto NERI University of
TEMPUS PECUNIA EST COLLANA DI MATEMATICA PER LE SCIENZE ECONOMICHE FINANZIARIE E AZIENDALI 2 Direttore Beatrice VENTURI Università degli Studi di Cagliari Comitato scientifico Umberto NERI University of
1 Relazione di congruenza in Z
 1 Relazione di congruenza in Z Diamo ora un esempio importante di relazione di equivalenza: la relazione di congruenza modn in Z. Definizione 1 Sia X = Z, a,b Z ed n un intero n > 1. Si dice a congruo
1 Relazione di congruenza in Z Diamo ora un esempio importante di relazione di equivalenza: la relazione di congruenza modn in Z. Definizione 1 Sia X = Z, a,b Z ed n un intero n > 1. Si dice a congruo
Matrici quadrate particolari
 Matrici quadrate particolari Sia A Mn(K) una matrice quadrata. Gli elementi (a 1,1, a 2,2,, a n,n ) costituiscono la diagonale principale di A. Gli elementi (a 1,n, a 2,n-1,, a n-1,2, a n,1 ) costituiscono
Matrici quadrate particolari Sia A Mn(K) una matrice quadrata. Gli elementi (a 1,1, a 2,2,, a n,n ) costituiscono la diagonale principale di A. Gli elementi (a 1,n, a 2,n-1,, a n-1,2, a n,1 ) costituiscono
1 Linguaggio degli insiemi
 Lezione 1, Analisi, 18.09.2017 1 Linguaggio degli insiemi Ricordiamo di seguito in modo informale le prime notazioni e nozioni sugli insiemi. Il discorso sugli insiemi si sviluppa a partire dai termini
Lezione 1, Analisi, 18.09.2017 1 Linguaggio degli insiemi Ricordiamo di seguito in modo informale le prime notazioni e nozioni sugli insiemi. Il discorso sugli insiemi si sviluppa a partire dai termini
LEZIONE 5. AX = 0 m,1.
 LEZIONE 5 5 isoluzione di sistemi Supponiamo che AX = B sia un sistema di equazioni lineari Ad esso associamo la sua matrice completa (A B Per quanto visto nella precedente lezione, sappiamo di poter trasformare,
LEZIONE 5 5 isoluzione di sistemi Supponiamo che AX = B sia un sistema di equazioni lineari Ad esso associamo la sua matrice completa (A B Per quanto visto nella precedente lezione, sappiamo di poter trasformare,
Spazi vettoriali euclidei.
 Spazi vettoriali euclidei Prodotto scalare, lunghezza e ortogonalità in R n Consideriamo lo spazio vettoriale R n = { =,,, n R}, n con la somma fra vettori e il prodotto di un vettore per uno scalare definiti
Spazi vettoriali euclidei Prodotto scalare, lunghezza e ortogonalità in R n Consideriamo lo spazio vettoriale R n = { =,,, n R}, n con la somma fra vettori e il prodotto di un vettore per uno scalare definiti
Determinante, autovalori e autovettori
 Determinante, autovalori e autovettori Lorenzo Pareschi Dipartimento di Matematica, Universitá di Ferrara http://wwwlorenzopareschicom lorenzopareschi@unifeit Lorenzo Pareschi (Univ Ferrara) Determinante,
Determinante, autovalori e autovettori Lorenzo Pareschi Dipartimento di Matematica, Universitá di Ferrara http://wwwlorenzopareschicom lorenzopareschi@unifeit Lorenzo Pareschi (Univ Ferrara) Determinante,
Corso di Matematica per la Chimica. Dott.ssa Maria Carmela De Bonis a.a
 Dott.ssa Maria Carmela De Bonis a.a. 2013-14 Spazio dei vettori Il primo oggetto matematico che definiamo sarà il vettore. Partendo dai numeri reali come rappresentazione dei punti della retta reale R,
Dott.ssa Maria Carmela De Bonis a.a. 2013-14 Spazio dei vettori Il primo oggetto matematico che definiamo sarà il vettore. Partendo dai numeri reali come rappresentazione dei punti della retta reale R,
2.1 Numeri naturali, interi relativi, razionali
 2.1 Numeri naturali, interi relativi, razionali Definizione L insieme N = {0, 1, 2, 3,...} costituito dallo 0 e dai numeri interi positivi è l insieme dei numeri naturali. Se a, b 2 N, allora mentre non
2.1 Numeri naturali, interi relativi, razionali Definizione L insieme N = {0, 1, 2, 3,...} costituito dallo 0 e dai numeri interi positivi è l insieme dei numeri naturali. Se a, b 2 N, allora mentre non
