GEOMETRIA 1 seconda parte
|
|
|
- Adelina Ranieri
- 4 anni fa
- Visualizzazioni
Transcript
1 GEOMETRIA 1 seconda parte Cristina Turrini C. di L. in Fisica /2016 Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 1 / 52
2 index Applicazioni lineari 1 Applicazioni lineari 2 Nucleo e immagine di un applicazione 3 Isomorfismo di spazi vettoriali 4 La matrice rappresentativa 5 Il determinante 6 Sottomatrici e minori Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 2 / 52
3 Applicazioni lineari Applicazioni lineari Siano V, W spazi vettoriali sullo stesso campo K. Consideriamo un applicazione f : V W. Si dice che f è lineare (o K-lineare) se u, v V, λ, µ K è: 1) f (u + v) = f (u) + f (v), cioè f conserva la somma o f è additiva; 2) f (λu) = λ f (u), cioè f è omogenea di I grado; (1) + 2)) è equivalente a ciascuna delle seguenti: 3) f (λu + µv) = λ f (u) + µ f (v), 3 ) f ( n i=1 λ iu i ) = n i=1 λ i f (u i ) u 1,..., u n, λ 1,..., λ n K. cioè f conserva le combinazioni lineari. Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 3 / 52
4 Applicazioni lineari Esempi di applicazioni lineari V spazio vettoriale, si può considerare l applicazione identica id V : V V; l applicazione identica è lineare. V, W, si può considerare 0 : V W, v 0 W. L applicazione nulla è lineare. sia V uno spazio vettoriale su K e B = {b 1,..., b n } una sua base (ordinata: qui e nel seguito parlando di base sottointenderemo sempre che lo sia); l applicazione definita da Φ B : V K n Φ B (v) = λ 1 λ λ n se v = λ 1 b 1 + λ 2 b λ n b n, è lineare. Φ B associa ad ogni vettore le sue componenti rispetto alla base B (dette anche coordinate nella base B). Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 4 / 52
5 Applicazioni lineari V = K n, W = K m, A Mat m,n (K), L A : K n K m, (prodotto riga per colonna) x A x L applicazione L A viene detta applicazione associata alla matrice A e, per le proprietà del prodotto riga per colonna, è lineare. Se A Mat m,n (K) e B Mat n,p (K), allora si hanno le applicazioni L A : K n K m e L B : K p K n per cui si può considerare la composizione L A L B : K p K m. Risulta L A L B = L A B cioè l applicazione composta L A L B è l applicazione associata alla matrice A B Mat m,p prodotto riga per colonna di A per B. Se I = I m Mat m è la matrice identica, allora L I : K m K m è l applicazione identica. Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 5 / 52
6 Applicazioni lineari Lo spazio delle applicazioni lineari Siano V e W spazi vettoriali sul campo K. Denotiamo con L(V, W) (o con Hom K (V, W) o Hom(V, W)) l insieme delle applicazioni lineari da V a W. Poniamo L(V, W) = {f : V W f è lineare} + : L(V, W) L(V, W) L(V, W) (f, g) f + g (f + g)(v) = f (v) + g(v) : K L(V, W) L(V, W) (λ, f ) λf (λf )(v) = λf (v) (definizioni puntuali di somma e di prodotto per uno scalare) L(V, W) con queste leggi di composizione è uno spazio vettoriale su K. Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 6 / 52
7 Applicazioni lineari Propriet`à elementari delle applicazioni lineari Siano V, W, Z spazi vettoriali sul campo K. 1) f (0 V ) = 0 W (infatti f (0 V ) = f (0 v) = 0 f (v) = 0 W ). 2) g : W Z. Se f, g sono lineari g f : V Z è lineare. (infatti g f (λu + µv) = g(f (λu + µv)) = g(λf (u) + µf (v)) = λg(f (u) + µg(f (v)) = λ g f (u) + µ g f (v)). 3) Se f è biunivoca, l applicazione inversa di f, f 1 : W V è lineare. (infatti si verifica che il vettore λf 1 (u ) + µf 1 (v ) è l inverso di λu + µv infatti f (λf 1 (u ) + µf 1 (v )) = λf (f 1 (u )) + µf (f 1 (v )) = λu + µv ). Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 7 / 52
8 Applicazioni lineari Teorema di esistenza e unicità TEOREMA - Siano V e W spazi vettoriali su K. Sia B = {b 1,..., b n } una base di V e siano w 1,..., w n W vettori comunque presi. Allora esiste una ed una sola applicazione lineare φ : V W tale che φ(b i ) = w i, i = 1,..., n Dimostrazione - Unicità. v V = B, v = α 1 b α n b n ( la scrittura è unica). Dobbiamo costruire f : V W con le condizioni richieste. Deve necessariamente essere: f (v) = f (α 1 b α n b n ) = α 1 f (b 1 ) + + α n f (b n ) = α 1 w α n w n. L unica possibile definizione è allora ( ) se v = α 1 b α n b n. f (v) = α 1 w α n w n Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 8 / 52
9 Applicazioni lineari Esistenza Si deve mostrare che l applicazione f definita in ( ) soddisfa le condizioni richieste dall enunciato. f è lineare. Infatti (ad esempio per l additività) se e allora quindi v = α 1 b α n b n. u = β 1 b β n b n, v + u = α 1 b α n b n + β 1 b β n b n = = (α 1 + β 1 )b (α n + β n )b n ; f (v + u) = (α 1 + β 1 )w (α n + β n )w n = f (v) + f (u). E analogamente per l omogeneità. f (b i ) = w i, i. Infatti b i = 0b b i + + 0b n f (b i ) = 1w i. Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 9 / 52
10 Applicazioni lineari Siano sempre V e W spazi vettoriali su K, con V f.g., dim V = n, e siano v 1,..., v k V, e w 1,..., w k W. PROBLEMA - Un applicazione lineare f : V W tale che v i w i i = 1,..., k esiste? È unica? Occorre distinguere due casi 1) Se {v 1,..., v k } è l.i., allora l applicazione f esiste, ma in generale non è unica. Infatti l insieme {v 1,..., v k } si può completare a una base, cioè v k+1,..., v n t.c. {v 1,..., v k, v k+1,..., v n } sia base di V. Presi arbitrariamente w k+1,... w n W, per il teorema di esistenza e unicità!f t.c. f (v 1 ) = w 1,... f (v k ) = w k, f (v k+1 ) = w k+1..., f (v n ) = w n Quest applicazione soddisfa le nostre richieste, ma i vettori w k+1,... w n possono essere scelti arbitrariamente in W quindi in generale f. Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 10 / 52
11 Applicazioni lineari 2) Se {v 1,..., v k } è l.d. allora l applicazione f in generale non esiste. Infatti, può esistere un applicazione lineare tale che f (v i ) = w i solo se le relazioni di dipendenza lineare tra i v i sussistono (con gli stessi coefficienti!) tra i w i. Ad esempio, se v 3 = v 1 v 2 f (v 3 ) = f (v 1 v 2 ) = f (v 1 ) f (v 2 ), cioè w 3 = w 1 w 2. Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 11 / 52
12 index Nucleo e immagine di un applicazione 1 Applicazioni lineari 2 Nucleo e immagine di un applicazione 3 Isomorfismo di spazi vettoriali 4 La matrice rappresentativa 5 Il determinante 6 Sottomatrici e minori Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 12 / 52
13 Nucleo e immagine di un applicazione Nucleo e immagine di un applicazione lineare Siano V, W spazi vettoriali su un campo K e sia f : V W lineare. Si dice nucleo di f e si indica con ker(f ) l insieme dei vettori di V che hanno per immagine il vettore nullo. ker(f ) = {v V f (v) = 0 W } Si dice immagine di f e si indica con Im(f ) l usuale immagine dell applicazione. Im(f ) = {w W v V : f (v) = w} Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 13 / 52
14 Nucleo e immagine di un applicazione Proprietà a) ker(f ) V è un sottospazio. Infatti f (0 V ) = 0 W 0 V ker(f ); Inoltre, presi λ, µ K, u, v ker(f ) si ha f (λu+µv) = λf (u)+µf (v) = λ 0 W +µ 0 W = 0 W λu+µv ker(f ). b) Im(f ) W è un sottospazio (verificarlo). TEOREMA (caratterizzazione delle applicazioni lineari iniettive)- Siano V, W spazi vettoriali f.g. su un campo K, f : V W lineare. Sono equivalenti: i) f è iniettiva; ii) ker(f ) = {0 V } (ossia dim(ker(f )) = 0; iii) v 1,..., v n l.i. f (v 1 ),..., f (v n ) l.i. Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 14 / 52
15 Nucleo e immagine di un applicazione Dimostrazione i) ii) Se esistesse v 0 V tale che v ker(f ), si avrebbe f (v) = 0 W. Poichè però f (0 V ) = 0 W, verrebbe contraddetta l iniettività di f. ii) iii) v 1,..., v n V l.i. Dobbiamo dimostrare f (v 1 ),..., f (v n ) l.i. λ 1 f (v 1 ) + + λ n f (v n ) = 0 W f (λ 1 v λ n v n ) = 0 W λ 1 v λ n v n ker(f ) = {0 V } λ 1 v λ n v n = 0 V λ 1 = = λ n = 0 f (v 1 ),..., f (v n ) l.i. iii) i) Dobbiamo dimostrare che se f (v 1 ) = f (v 2 ) = w allora v 1 = v 2. f (v 1 v 2 ) = f (v 1 ) f (v 2 ) = w w = 0 W Se fosse v 1 v 2 0 V, sarebbe v 1 v 2 l.i. e f (v 1 v 2 ) = 0 W l.d.. Contro l ipotesi iii). Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 15 / 52
16 Nucleo e immagine di un applicazione TEOREMA (caratterizzazione delle applicazioni lineari suriettive)- Siano V, W spazi vettoriali f.g. su un campo K, f : V W lineare. Sono equivalenti: i) f è suriettiva; ii) dim(im(f )) = dim(w); iii) < v 1,..., v n >= V < f (v 1 ),..., f (v n ) >= W. (dimostrazione per esercizio). OSSERVAZIONE - In generale (se anche f non è suriettiva) si ha < v 1,..., v n >= V < f (v 1 ),..., f (v n ) >= Im(f ). OSSERVAZIONE - Abbiamo visto che le applicazioni lineari iniettive sono quelle che mutano insiemi di vettori l.i. in insiemi di vettori l.i. e che le applicazioni lineari suriettive sono quelle che mutano generatori di V in generatori di W. Ne segue che le applicazioni lineari biunivoche sono caratterizzate dal mutare basi in basi. Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 16 / 52
17 Nucleo e immagine di un applicazione Teorema della nullità + rango TEOREMA - Siano V, W spazi vettoriali f.g. su un campo K, e sia f : V W lineare. Si ha: ( ) dim(v) = dim(ker(f )) + dim(im(f )). Dimostrazione Anzitutto osserviamo che tutti gli spazi coinvolti dalla ( ) sono f.g. perchè sottospazi di spazi f.g.. Se Im(f ) = {0}, allora f è l applicazione nulla (f (v) = 0, v V) e quindi ker(f ) = V, per cui ( ) è verificata. Possiamo quindi supporre che Im(f ) {0}. Allora Im(f ) ammette una base. Sia {c 1,..., c k } una base di Im(f ). Si prendano (arbitrariamente) vettori b 1,..., b k in V tali che f (b i ) = c i, i = 1,..., k. Se ker(f ) {0}, si prende una base {a 1,..., a r } di ker(f ). Altrimenti non si prende nessun altro vettore. Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 17 / 52
18 Nucleo e immagine di un applicazione Dimostriamo che B = {a 1,..., a r, b 1,..., b k } è una base di V. Questo prova la ( ) perchè si ha dim(v) = r + k = dim(ker(f )) + dim(im(f )). B è l.i. Infatti sia ( ) α 1 a α r a r + β 1 b β k b k = 0. ( ) implica f (α 1 a α r a r + β 1 b β k b k ) = f (0) = 0, quindi 0 = f (α 1 a α r a r + β 1 b β k b k ) = α 1 f (a 1 ) + + α r f (a r ) + β 1 f (b 1 ) + + β k f (b k ) = β 1 c β k c k. Ma c 1,..., c k sono l.i. (base di Im(f )), quindi β 1 = = β k = 0, per cui diventa α 1 a α r a r = 0. Ma a 1,..., a r sono l.i. (base di ker(f )), per cui α 1 = = α r = 0. Pertanto tutti i coefficienti di ( ) sono necessariamente nulli, e quindi B è l.i.. Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 18 / 52
19 Nucleo e immagine di un applicazione < B >= V Sia v V. Dobbiamo mostrare che v si può scrivere come combinazione lineare dei vettori di B. Si ha f (v) Im(f ) =< c 1,..., c k >, quindi f (v) = γ 1 c 1 + +γ k c k = γ 1 f (b 1 )+ +γ k f (b k ) = f (γ 1 b 1 + +γ k b k ). Quindi f (v) f (γ 1 b γ k b k ) = f (v γ 1 b 1 γ k b k ) = 0. Pertanto v γ 1 b 1 γ k b k ker(f ) =< a 1,..., a r > e perciò v γ 1 b 1 γ k b k = δ 1 a δ r a r. In conclusione v = γ 1 b γ k b k + δ 1 a δ r a r. COROLLARIO - Sia f : V W lineare, con V, W f.g. e dim(v) = dim(w). Allora f è iniettiva se e solo se è suriettiva se e solo se è biunivoca. Dimostrazione f iniettiva se e solo se dim(ker(f )) = 0 se e solo se dim(v) = dim(im(f )) se e solo se dim(w) = dim(im(f )) se e solo se f suriettiva. Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 19 / 52
20 index Isomorfismo di spazi vettoriali 1 Applicazioni lineari 2 Nucleo e immagine di un applicazione 3 Isomorfismo di spazi vettoriali 4 La matrice rappresentativa 5 Il determinante 6 Sottomatrici e minori Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 20 / 52
21 Isomorfismo di spazi vettoriali Endomorfismi, isomorfismi, automorfismi ESEMPI Un applicazione lineare biunivoca si dice isomorfismo. Un applicazione lineare da uno spazio in se stesso si dice endomorfismo. Un applicazione isomorfismo ed endomorfismo si dice automorfismo. 1 id V : V V è un automorfismo. 2 se A è una matrice quadrata m m, allora L A : K m K m è un endomorfismo. 3 se A è una matrice quadrata m m invertibile, allora L A : K m K m è un isomorfismo e l applicazione inversa di L A è (L A ) 1 = L A 1 (infatti si ha L A 1 L A = L A 1 A = L I = id). Siano V, W spazi vettoriali su un campo K. Si dice che V e W sono isomorfi, e si scrive V W, se esiste un isomorfismo f : V W. La relazione di isomorfismo è di equivalenza (verificarlo). Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 21 / 52
22 Isomorfismo di spazi vettoriali TEOREMA - Due spazi vettoriali f.g. V e W sullo stesso campo K sono isomorfi se e solo se hanno la stessa dimensione. Dimostrazione Se esiste un isomorfismo f : V W allora f trasforma una base di V in una base di W, quindi dim(v) = dim(w). Se dim(v) = dim(w) = n, allora, fissata una base B = {b 1, b 2,..., b n } l applicazione Φ B : V K n definita da Φ B (v) = λ 1 λ λ n se v = λ 1 b 1 + λ 2 b λ n b n, è un isomorfismo, da cui si deduce che V è isomorfo a K n. Analogamente si costruisce un isomorfismo Φ C : W K n. Di conseguenza (Φ C ) 1 Φ B : V W è pure un isomorfismo. Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 22 / 52
23 index La matrice rappresentativa 1 Applicazioni lineari 2 Nucleo e immagine di un applicazione 3 Isomorfismo di spazi vettoriali 4 La matrice rappresentativa 5 Il determinante 6 Sottomatrici e minori Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 23 / 52
24 La matrice rappresentativa Proprietà della trasformazione L A Sia A Mat m,n (K), siano K n, K m spazi vettoriali. Abbiamo visto che si può costruire L A : K n K m lineare, x A x = y. Si ha: ker L A = {x K n : L A (x) = 0 K m } = {x K n : A x = 0} = {soluzioni del sistema omogeneo A x = 0}. α 11 x α 1n x n = 0. α m1 x α mn x n = 0 ImL A = {y K m : x K n : y = L A (x)} = {y K m : x : A x = y} = {termini noti che rendono risolubile il sistema riportato qui sotto} α 11 x α 1n x n = y 1. α m1 x α mn x n = y m Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 24 / 52
25 La matrice rappresentativa Sia {e 1,..., e n } la base standard di K n. Calcoliamo L A (e i ) Per esempio, per i = 1, α 11 α 1n α L A (e 1 ) = 21 α 2n..... α m1 α mn di A = Analogamente, L A (e i ) = i-esima colonna di A. α 11 α 21. α m1 e 1,..., e n = K n quindi L A (e 1 ),..., L A (e n ) = ImL A (generatori di K n sono mutati da L A in generatori di ImL A ), pertanto i vettori colonna di A sono generatori di ImL A. = A (1) = I colonna Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 25 / 52
26 La matrice rappresentativa Costruzione della matrice rappresentativa Siano V, W spazi vettoriali sul campo K, con dim V = n, dim W = m, e siano A = {a 1,..., a n } una base (ordinata) di V, e B = {b 1,..., b m } una base (ordinata) di W. Sia f : V W lineare; f è univocamente determinata da f (a 1 ),..., f (a n ) (teorema di esistenza e unicità): noti f (a 1 ),..., f (a n ) si può ricostruire f. Scriviamo i vettori f (a 1 ),..., f (a n ) W come combinazioni lineari dei vettori della base B : f (a 1 ) = α 11 b 1 + α 21 b α m1 b m f (a 2 ) = α 12 b 1 + α 22 b α m2 b m. f (a n ) = α 1n b 1 + α 2n b α mn b m Gli α ij sono univocamente determinati da f e la determinano univocamente. Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 26 / 52
27 La matrice rappresentativa Costruiamo la matrice A Mat m,n (K) le cui colonne sono le coordinate dei vettori f (a 2 ) nella base B: α 11 α 12 α 1n α A = 21 α 22 α 2n α m1 α m2 α mn Vogliamo dimostrare che f = L A. Consideriamo il diagramma f V W Φ A Φ B ( ) K n L A K m in cui Φ A denota l applicazione che ad ogni vettore di V associa le sue coordinate nella base A e Φ B quella che ad ogni vettore di W associa le sue coordinate nella base B. Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 27 / 52
28 La matrice rappresentativa Il quadrato ( ) commuta, ossia si ha ( ) L A Φ A = Φ B f. Trattandosi di applicazioni lineari, (per il teorema di esistenza e unicità) basta verificare l uguaglianza ( ) sui vettori di una base. Verifichiamola sui vettori della base A = {a 1,..., a n }. Ad esempio, per a 1, L A Φ A (a 1 ) = L A (e 1 ) = I colonna di A = α 11 α 21. α m1 Φ B f (a 1 ) = Φ B (α 11 b 1 + α 21 b α m1 b m ) = α 11 α 21. α m1. Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 28 / 52
29 La matrice rappresentativa In generale, L A (Φ A (a i )) = A (i) = i esima colonna di A Φ B (f (a i )) = A (i) = i esima colonna di A quindi L A Φ A = Φ B f. Ricapitolando: tutti gli spazi vettoriali f.g. sono del tipo K n ; tutte le applicazioni lineari tra spazi vettoriali f.g. sono del tipo L A. Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 29 / 52
30 La matrice rappresentativa L applicazione M A B Abbiamo visto che, dati due spazi vettoriali V e W di dimensioni rispettive n e m, e date le basi (ordinate) A e B di V e W rispett., ad una applicazione lineare f : V W può essere associata una matrice A tale che essenzialmente si abbia f = L A. La matrice A si dice associata ad f rispetto alle basi A e B o rappresentativa di f rispetto alle basi A e B e si scrive Abbiamo costruito un applicazione A = M A B (f ). M A B : L(V, W) Mat m,n, f A Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 30 / 52
31 La matrice rappresentativa Siano V, W e Z spazi vettoriali (su K) di dimensioni rispettive n, m e l, con basi rispettive A, B e C e siano f : V W e g : W Z applicazioni lineari. PROPRIETÀ (si omettono le dimostrazioni) M A B è un isomorfismo tra gli spazi vettoriali L(V, W) e Mat m,n. M A C (g f ) = M B C (g) M A B (f ), cioè alla composizione di applicazioni lineari corrisponde il prodotto riga per colonna delle matrici rappresentative. Nel caso m = n, V = W, A = B si ha M A B (id V ) = I m. Nel caso m = n, se f : V W è un isomorfismo, e f 1 : W V è l isomorfismo inverso, allora la matrice M A B (f ) è invertibile e si ha M A B (f ) 1 = M B A(f 1 ). Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 31 / 52
32 La matrice rappresentativa Conseguenza: se V è uno spazio vettoriale e A, B sono due sue basi, e f : V V è un endomorfismo, allora esiste una matrice invertibile N tale che ( ) M A A(f ) = N 1 M B B(f ) N. Infatti basta prendere N = M B A (id V) (verificarlo). Due matrici quadrate A, B Mat n si dicono simili se esiste una matrice invertibile N GL(n) tale che B = N 1 A N. La formula ( ) mostra che le matrici rapprentative rispetto a basi diverse di uno stesso endomorfismo sono matrici simili (si noti però che in entrambi i casi la base deve essere la stessa in dominio e codominio!). OSSERVAZIONE - Nel caso V = K n, W = K m e f = L A, con A Mat m,n, la matrice rappresentativa rispetto alle basi canoniche di L A è proprio A. Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 32 / 52
33 index Il determinante 1 Applicazioni lineari 2 Nucleo e immagine di un applicazione 3 Isomorfismo di spazi vettoriali 4 La matrice rappresentativa 5 Il determinante 6 Sottomatrici e minori Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 33 / 52
34 Il determinante Definizione di determinante In questo e nel prossimo capitolo saranno omesse molte dimostrazioni. Ricordo che una permutazione su n elementi è un applicazione biunivoca σ : J n J n, ove J n = {1, 2, 3,..., n}. ( ) n σ : σ(1) σ(2) σ(3) σ(n). Si dice che σ è di classe pari (rispett. dispari) se si passa da (σ(1), σ(2),..., σ(n)) a (1, 2,..., n) con un numero pari (rispett. dispari) di scambi. ESEMPI dispari. ( ) è di classe pari, ( ) è di classe Si dimostra che la definizione di classe pari e dispari è ben posta, ovvero non dipende dal modo con cui σ si ottiene come composizione di scambi. Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 34 / 52
35 Il determinante Data σ S n (gruppo simmetrico su n elementi), definiamo { +1 se σ è pari, ε(σ) = 1 se σ è dispari. Sia A Mat n,n (K), A = (α ij ) i=1,...,n. Si definisce determinante di A: j=1,...,n ( ) det A = σ S n ε(σ)α 1σ(1) α 2σ(2) α nσ(n). Esso è composto da n! addendi. Ciascun addendo contiene uno ed un solo fattore preso da ciascuna riga e ciascuna colonna (σ è biunivoca). Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 35 / 52
36 Il determinante Caso n = 1. A = (α 11 ) S 1 = {σ = id} ε(σ) = +1 ( ) 11 σ = det A = +α 11. Caso n = 2. ( ) α11 α A = 12 α 21 α 22 S 2 = {σ 1 = id, σ 2 = ( ) } ε(σ 1 ) = 1 ε det A = +α 1σ1 (1) α 2σ1 (2) α 1σ2 (1) α 2σ2 (2) = α 11 α 22 α 12 α 21. Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 36 / 52
37 Il determinante Caso n = 3. ( α11 α 12 α 13 ) A = α 21 α 22 α 23 α 31 α 32 α 33 σ 4 = σ 1 = id σ 2 = ( 1 2 ) #S 3 = 3! = 6 ( 1 2 ) σ 5 = ε(σ 1 ) = ε(σ 2 ) = ε(σ 3 ) = +1 ( 1 2 ) σ 3 = ( 1 2 ) σ 6 = ( 1 2 ) ε(σ 4 ) = ε(σ 5 ) = ε(σ 6 ) = 1 det(a) = α 11 α 22 α 33 + α 12 α 23 α 31 + α 13 α 21 α 32 α 12 α 21 α 33 α 13 α 22 α 31 α 11 α 23 α 32. Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 37 / 52
38 Il determinante Data la matrice A Mat n,n (K), indichiamo con A (1),..., A (n) le colonne di A e con A (1),..., A (n) le righe di A : A (1) A = ( A (1),..., A (n)) =.. A (n) Il determinante può essere interpretato in vari modi; a) det : Mat n,n (K) K A det A; b) det : K n K n K n K c) det : K n K n K n K ( A (1), A (2),..., A (n)) det A; A (1) A (2). det A. A (n) Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 38 / 52
39 Il determinante Proprietà del determinante D ora in poi supporremo sempre che sia K = Q, R, oppure C. Siano A, B Mat n,n (K). 1) det( t A) = det A; 2) scambiando tra loro due colonne, il determinante cambia (solo) il segno (idem per le righe) (il determinante è alternante) det( (..., A (i),..., A (j)... ) ) = det( (... A (j),..., A (i),..., ) ); 3) il determinante è lineare in ogni colonna, fissate le altre n 1 colonne (idem per le righe) (il determinante è multilineare); det((..., λb + µc...)) = λ det((..., B,...,)) + µ det((..., C,...,)); Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 39 / 52
40 Il determinante 4) sia I = I n la matrice identica, det I = 1; 5) (teorema di Binet) det(a B) = det A det B; 6) le colonne di A sono l.d. se e solo se det A = 0 (idem per le righe); 7) det(λa) = λ n det A (λ K); 8) A ammette inversa A 1 se e solo se det(a) 0, e inoltre, se det(a) 0, si ha det(a 1 ) = 1 det(a). Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 40 / 52
41 Il determinante Cenno alla dimostrazione di alcune tra le proprietà del determinante viste sopra. La 2) segue dalla definizione di ɛ(σ); la 3) segue dal fatto che in ogni addendo del determinante ( ) compare uno e un solo fattore preso da ciascuna colonna (idem per le righe); la 4) è di verifica immediata; la 7) segue dalla 3) tenendo conto del fatto che moltiplicare una matrice per uno scalare equivale a moltiplicare ciascuna colonna (o riga) per lo stesso scalare; per la 8) si veda dopo. Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 41 / 52
42 Il determinante Per la dimostrazione della 6), si osservi anzitutto che LEMMA - Se A ha due colonne uguali allora det(a) = 0 (idem per le righe). Infatti, per la proprietà 2), scambiando tra loro le due colonne uguali, la matrice non cambia eppure il determinante cambia segno. Verifichiamo ora proprietà 6). Anzitutto, se le colonne di A sono l.i., almeno una di esse è combinazione delle altre. Per la proprietà 3) il determinante di A può essere allora scritto come combinazione lineare di determinanti di matrici con due colonne uguali. Dal Lemma segue quindi che det(a) = 0. Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 42 / 52
43 Il determinante Viceversa, sia det(a) = 0. Se per assurdo le colonne A (1),..., A (n) di A fossero l.i., esse costituirebbero una base di K n, quindi anche i vettori della base canonica potrebbero essere scritti come combinazione lineare di tali colonne: e i = β 1i A (1) + + β ni A (n). Consideriamo la matrice B = (β ji ) e la matrice prodotto C = A B. La colonna C (i) è C (i) = β 1i A (1) + + β ni A (n) = e i, pertanto C è la matrice identica e 1 = det(c) = det(a) det(b) = 0, assurdo. OSSERVAZIONE - Si potrebbe dimostrare che det è l unica applicazione multilineare alternante det : K n K n K n K tale che det I = 1. Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 43 / 52
44 index Sottomatrici e minori 1 Applicazioni lineari 2 Nucleo e immagine di un applicazione 3 Isomorfismo di spazi vettoriali 4 La matrice rappresentativa 5 Il determinante 6 Sottomatrici e minori Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 44 / 52
45 Sottomatrici e minori Sia M Mat m,n una matrice con m righe e n colonne. Si dice sottomatrice di M una qualsiasi matrice che si ottiene cancellando da M alcune righe (eventualmente nessuna) e alcune colonne (eventualmente nessuna). Si dice minore di M il determinante di una sua qualsiasi sottomatrice quadrata. Se A = (a ij ) Mat n,n è una matrice quadrata, si dice minore complementare dell elemento a hk il determinante della sottomatrice M ij di A che si ottiene cancellando la righa h esima e la colonna k esima. Si dice complemento algebrico (o cofattore) dell elemento a hk il numero A ij = ( 1) i+j det M ij K. Si dice matrice dei cofattori di A la matrice cof (A) = (A ij ) Mat n,n ( ) ( ) a b d c Se A = c d, allora cof (A) = b a. Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 45 / 52
46 Sottomatrici e minori TEOREMA (I teorema di Laplace - Data A Mat n,n (K), è (per la i-esima riga): (per la j-esima colonna): det A = α i1 A i1 + α i2 A i2 + + α in A in ; det A = α 1j A 1j + α 2j A 2j + + α nj A nj. TEOREMA II teorema di Laplace - Data A Mat n,n (K), è (per le righe): (per le colonne): se i j, α i1 A j1 + α i2 A j2 + + α in A jn = 0; se i j, α 1i A 1j + α 2i A 2j + + α ni A nj = 0. Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 46 / 52
47 Sottomatrici e minori Il I teorema di Laplace fornisce una metodo (di tipo ricorsivo) per il calcolo del determinante. Ad esempio, nel caso n = 3, per la prima riga si ha: ( ) a11 a 12 a 13 det a 21 a 22 a 23 = a 31 a 32 a ( 33 ) ( ) ( ) a22 a a 11 det 23 a21 a a 32 a a 12 det 23 a21 a 33 a 31 a + a 13 det a 31 a. 32 (il calcolo di determinanati k k viene ridotto a quello di determinanti (k 1) (k 1)). Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 47 / 52
48 Sottomatrici e minori La matrice dei cofattori cof (A) può essere utile per il calcolo della matrice inversa. Si ha LEMMA - A (cof (A)) T = det A I. Infatti, ad esempio ( per n = 3, a11 a 12 a 13 ) A (cof (A)) T = a 21 a 22 a 23 a 31 a 32 a ( ) 33 det(a) det(a) 0, 0 0 det(a) ( A11 A 21 A 31 A 12 A 22 A 32 A 13 A 23 A 33 e l ultima uguaglianza segue dal I teorema di Laplace (per gli elementi della diagonale) e dal II teorema di Laplace per gli elementi fuori dalla diagonale. Ne segue il TEOREMA - Sia A Mat n,n (K) con det A 0. Allora si ha A 1 = 1 det A (cof (A)) T. ) = Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 48 / 52
49 Sottomatrici e minori Spazio delle righe e spazio delle colonne Data una matrice M Mat m,n, si dice rango per righe di M la dimensione del sottospazio R(M) =< t M (1),..., t M (n) > K n generato dalle righe di M (più precisamente si tratta del sottospazio di K n generato dai vettori colonna che si ottengono trasponendo le righe di M). Analogamente si dice rango per colonne di A la dimensione del sottospazio C(M) =< M (1),..., M (m) > K n generato dalle colonne di M. Nella parte quarta di queste note vedremo che: il rango per colonne dim(c(m)) e il rango per righe dim(r(m)) di una matrice M sono uguali tra loro e coincidono con la caratteristica (o rango) r(m) di A (numero di righe non nulle di una riduzione a scalini di M) dim(r(m) = dim(c(m)) = r(m). Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 49 / 52
50 Sottomatrici e minori Reinterpretazione del TEOREMA (di Rouché Capelli) - Il sistema lineare Mx = b ha soluzioni se e solo se la caratteristica della matrice dei coefficienti M coincide con la caratteristica della matrice completa [M b]. Dimostrazione Mx = b ha soluzioni se e solo b Im(L M ) se e solo se b C(M) =< M (1),..., M (n) > se e solo se < M (1),..., M (n) >=< M (1),..., M (n), b > se e solo se dim(< M (1),..., M (n) >) = dim(< M (1),..., M (n), b >) se e solo se il rango per colonne di M è uguale al rango per colonne di [M b]. Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 50 / 52
51 Minori e rango Sottomatrici e minori L uguaglianza "rango per righe = rango per colonne" avrebbe potuto essere mostrata direttamente, come conseguenza di un ulteriore significato della nozione di rango: il rango r di una matrice M è il massimo ordine µ(m) di minori non nulli estratti dalla matrice M, ossia M ha rango r se e solo se esiste un minore non nullo r r di M e tutti i minori s s di M, con s > r, sono nulli. La relazione µ(m) dim(c(m)) è semplice conseguenza della proprietà 6) del determinante (idem per dim(r(m)). Infatti, se in M esiste un minore µ µ non nullo, le colonne di M corrispondenti a quel minore sono l.i.: le colonne del minore sono costituite dagli elementi delle colonne della matrice presi da righe fissate e quindi una relazione di dipendenza lineare tra le colonne di M indurrebbe, in particolare, la medesima relazione tra le colonne del minore. Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 51 / 52
52 Sottomatrici e minori Metodo di Kronecker (o dei minori orlati) per il calcolo della caratteristica. Si cerca un minore non nullo, diciamo h h, di M. Si considerano tutti i minori (h + 1) (h + 1) che "orlano" il minore h h di cui sopra. Se tutti questi minori sono nulli, il rango di A è h, altrimenti il rango è almeno h + 1 ed esiste un minore (h + 1) (h + 1) non nullo. Si considerano tutti i minori (h + 2) (h + 2) che "orlano" il minore (h + 1) (h + 1) di cui sopra,... Cristina Turrini (C. di L. in Fisica /2016) GEOMETRIA 1 52 / 52
GEOMETRIA 1 terza parte
 GEOMETRIA 1 terza parte Cristina Turrini C. di L. in Fisica - 2014/2015 Cristina Turrini (C. di L. in Fisica - 2014/2015) GEOMETRIA 1 1 / 32 index Applicazioni lineari 1 Applicazioni lineari 2 Nucleo e
GEOMETRIA 1 terza parte Cristina Turrini C. di L. in Fisica - 2014/2015 Cristina Turrini (C. di L. in Fisica - 2014/2015) GEOMETRIA 1 1 / 32 index Applicazioni lineari 1 Applicazioni lineari 2 Nucleo e
GEOMETRIA 1 seconda parte
 GEOMETRIA 1 seconda parte Gilberto Bini - Cristina Turrini 2017/2018 Gilberto Bini - Cristina Turrini (2017/2018) GEOMETRIA 1 1 / 62 index Applicazioni lineari 1 Applicazioni lineari 2 Nucleo e immagine
GEOMETRIA 1 seconda parte Gilberto Bini - Cristina Turrini 2017/2018 Gilberto Bini - Cristina Turrini (2017/2018) GEOMETRIA 1 1 / 62 index Applicazioni lineari 1 Applicazioni lineari 2 Nucleo e immagine
Elementi di Algebra Lineare Applicazioni lineari
 Elementi di Algebra Lineare Applicazioni lineari Cristina Turrini UNIMI - 2016/2017 Cristina Turrini (UNIMI - 2016/2017) Elementi di Algebra Lineare 1 / 50 index Applicazioni lineari 1 Applicazioni lineari
Elementi di Algebra Lineare Applicazioni lineari Cristina Turrini UNIMI - 2016/2017 Cristina Turrini (UNIMI - 2016/2017) Elementi di Algebra Lineare 1 / 50 index Applicazioni lineari 1 Applicazioni lineari
Elementi di Algebra Lineare Il determinante
 Elementi di Algebra Lineare Cristina Turrini UNIMI - 2015/2016 Cristina Turrini (UNIMI - 2015/2016) Elementi di Algebra Lineare 1 / 17 index 1 2 Sottomatrici e minori Cristina Turrini (UNIMI - 2015/2016)
Elementi di Algebra Lineare Cristina Turrini UNIMI - 2015/2016 Cristina Turrini (UNIMI - 2015/2016) Elementi di Algebra Lineare 1 / 17 index 1 2 Sottomatrici e minori Cristina Turrini (UNIMI - 2015/2016)
Elementi di Algebra Lineare Applicazioni lineari
 Elementi di Algebra Lineare Applicazioni lineari Cristina Turrini UNIMI - 2015/2016 Cristina Turrini (UNIMI - 2015/2016) Elementi di Algebra Lineare 1 / 18 index Applicazioni lineari 1 Applicazioni lineari
Elementi di Algebra Lineare Applicazioni lineari Cristina Turrini UNIMI - 2015/2016 Cristina Turrini (UNIMI - 2015/2016) Elementi di Algebra Lineare 1 / 18 index Applicazioni lineari 1 Applicazioni lineari
CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI A.A. 2018/2019 PROF. VALENTINA BEORCHIA
 CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Matrici associate a un applicazione lineare 1 2 Cambiamenti di base 4 3 Diagonalizzazione 6 1 MATRICI ASSOCIATE
CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Matrici associate a un applicazione lineare 1 2 Cambiamenti di base 4 3 Diagonalizzazione 6 1 MATRICI ASSOCIATE
GEOMETRIA 1 Autovalori e autovettori
 GEOMETRIA 1 Autovalori e autovettori Gilberto Bini - Anna Gori - Cristina Turrini 2018/2019 Gilberto Bini - Anna Gori - Cristina Turrini (2018/2019) GEOMETRIA 1 1 / 28 index Matrici rappresentative "semplici"
GEOMETRIA 1 Autovalori e autovettori Gilberto Bini - Anna Gori - Cristina Turrini 2018/2019 Gilberto Bini - Anna Gori - Cristina Turrini (2018/2019) GEOMETRIA 1 1 / 28 index Matrici rappresentative "semplici"
APPLICAZIONI. Im f = {b B a A tale che f (a) = b}.
 APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
PROGRAMMA del corso di. GEOMETRIA 1 - Algebra Lineare. Laurea Triennale in Matematica. Anno Accademico 2007/08. docente : Bruno Zimmermann
 PROGRAMMA del corso di GEOMETRIA 1 - Algebra Lineare Laurea Triennale in Matematica Anno Accademico 2007/08 docente : Bruno Zimmermann (Il presente programma è stato redatto sulla base degli appunti del
PROGRAMMA del corso di GEOMETRIA 1 - Algebra Lineare Laurea Triennale in Matematica Anno Accademico 2007/08 docente : Bruno Zimmermann (Il presente programma è stato redatto sulla base degli appunti del
Anno Accademico 2016/2017
 Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2016/2017 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2016/2017 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
GEOMETRIA 1 quarta parte
 GEOMETRIA 1 quarta parte Cristina Turrini C. di L. in Fisica - 2014/2015 Cristina Turrini (C. di L. in Fisica - 2014/2015) GEOMETRIA 1 1 / 36 index Forme bilineari 1 Forme bilineari 2 Il caso reale: spazi
GEOMETRIA 1 quarta parte Cristina Turrini C. di L. in Fisica - 2014/2015 Cristina Turrini (C. di L. in Fisica - 2014/2015) GEOMETRIA 1 1 / 36 index Forme bilineari 1 Forme bilineari 2 Il caso reale: spazi
Esempio. L immagine di f è l insieme dei vettori w = (w 1, w 2 ) R 2 che hanno w 1 = w 2. Quindi:
 Nucleo, immagine e loro proprietà [Abate, 5.2] Data una applicazione lineare f : V W, chiamiamo nucleo di f l insieme N(f) := { v V : f(v) = 0 W } Se S V è un sottoinsieme del dominio, indichiamo con f(s)
Nucleo, immagine e loro proprietà [Abate, 5.2] Data una applicazione lineare f : V W, chiamiamo nucleo di f l insieme N(f) := { v V : f(v) = 0 W } Se S V è un sottoinsieme del dominio, indichiamo con f(s)
APPUNTI DI ALGEBRA LINEARE
 APPUNTI DI ALGEBRA LINEARE. Definizione Si dice spazio vettoriale (sul campo dei numeri reali R) un insieme V per il quale siano definite l operazione interna di somma (che ad ogni coppia di vettori e
APPUNTI DI ALGEBRA LINEARE. Definizione Si dice spazio vettoriale (sul campo dei numeri reali R) un insieme V per il quale siano definite l operazione interna di somma (che ad ogni coppia di vettori e
Anno Accademico 2017/2018
 Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2017/2018 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2017/2018 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
Elementi di Algebra Lineare Spazi Vettoriali
 Elementi di Algebra Lineare Spazi Vettoriali Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017) Elementi di Algebra Lineare 1 / 41 index Spazi vettoriali
Elementi di Algebra Lineare Spazi Vettoriali Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017) Elementi di Algebra Lineare 1 / 41 index Spazi vettoriali
GEOMETRIA 1 seconda parte
 GEOMETRIA 1 seconda parte Cristina Turrini C. di L. in Fisica - 2014/2015 Cristina Turrini (C. di L. in Fisica - 2014/2015) GEOMETRIA 1 1 / 40 index Spazi vettoriali 1 Spazi vettoriali 2 Sottospazi 3 Sistemi
GEOMETRIA 1 seconda parte Cristina Turrini C. di L. in Fisica - 2014/2015 Cristina Turrini (C. di L. in Fisica - 2014/2015) GEOMETRIA 1 1 / 40 index Spazi vettoriali 1 Spazi vettoriali 2 Sottospazi 3 Sistemi
APPLICAZIONI LINEARI O OMOMORFISMI
 42 APPLICAZIONI LINEARI O OMOMORFISMI Definizione 9 Dati due spazi vettoriali U e V sullo stesso campo K, una applicazione f : U V è detta lineare o omomorfismo se soddisfa le seguenti due condizioni:
42 APPLICAZIONI LINEARI O OMOMORFISMI Definizione 9 Dati due spazi vettoriali U e V sullo stesso campo K, una applicazione f : U V è detta lineare o omomorfismo se soddisfa le seguenti due condizioni:
CORSO DI ALGEBRA (M-Z) Prof. A. Venezia
 CORSO DI ALGEBRA (M-Z) Prof. A. Venezia 2015-16 Complementi ed Esercizi 1. AUTOVETTORI e AUTOVALORI di ENDOMORFISMI e MATRICI Una applicazione lineare avente per dominio e condominio lo stesso spazio vettoriale
CORSO DI ALGEBRA (M-Z) Prof. A. Venezia 2015-16 Complementi ed Esercizi 1. AUTOVETTORI e AUTOVALORI di ENDOMORFISMI e MATRICI Una applicazione lineare avente per dominio e condominio lo stesso spazio vettoriale
Elementi di Algebra Lineare Spazi Vettoriali
 Elementi di Algebra Lineare Spazi Vettoriali Antonio Lanteri e Cristina Turrini UNIMI - 2015/2016 Antonio Lanteri e Cristina Turrini (UNIMI - 2015/2016) Elementi di Algebra Lineare 1 / 37 index Spazi vettoriali
Elementi di Algebra Lineare Spazi Vettoriali Antonio Lanteri e Cristina Turrini UNIMI - 2015/2016 Antonio Lanteri e Cristina Turrini (UNIMI - 2015/2016) Elementi di Algebra Lineare 1 / 37 index Spazi vettoriali
4. Richiami: sistemi lineari e matrici
 4 Richiami: sistemi lineari e matrici Vettori 4a Combinazioni lineari Indichiamo con R n l insieme delle n-uple ordinate di elementi di R, { } R n := x = (x 1, x 2,, x n ) x i R, i = 1,,n Si dice che x
4 Richiami: sistemi lineari e matrici Vettori 4a Combinazioni lineari Indichiamo con R n l insieme delle n-uple ordinate di elementi di R, { } R n := x = (x 1, x 2,, x n ) x i R, i = 1,,n Si dice che x
Elementi di Algebra Lineare Spazi Vettoriali
 Elementi di Algebra Lineare Spazi Vettoriali Antonio Lanteri e Cristina Turrini UNIMI - 2017/2018 Antonio Lanteri e Cristina Turrini (UNIMI - 2017/2018) Elementi di Algebra Lineare 1 / 37 index Spazi vettoriali
Elementi di Algebra Lineare Spazi Vettoriali Antonio Lanteri e Cristina Turrini UNIMI - 2017/2018 Antonio Lanteri e Cristina Turrini (UNIMI - 2017/2018) Elementi di Algebra Lineare 1 / 37 index Spazi vettoriali
Contenuti aggiuntivi su matrici e determinanti, Dimostrazioni del Capitolo 3
 Contenuti aggiuntivi su matrici e determinanti, Dimostrazioni del Capitolo 3 Dimostrazione 310 Sia W = L(C A ) K Osserviamo che S è una base di W Infatti S è indipendente, inoltre ogni vettore di W dipende
Contenuti aggiuntivi su matrici e determinanti, Dimostrazioni del Capitolo 3 Dimostrazione 310 Sia W = L(C A ) K Osserviamo che S è una base di W Infatti S è indipendente, inoltre ogni vettore di W dipende
1 2 1 x = Quando sapremo calcolare i determinanti potremo ricavare:
 5 NOVEMBRE 2009 Esempio: Risolviamo il sistema: 3x + 2y + 4z = 1 2x y + z = 0 x + 2y + 3z = 1 1 2 4 3 1 4 3 2 1 0 1 1 2 0 1 2 1 0 1 2 3 1 1 3 1 2 1 x =, y =, z = 3 2 4 3 2 4 3 2 4 2 1 1 2 1 1 2 1 1 1 2
5 NOVEMBRE 2009 Esempio: Risolviamo il sistema: 3x + 2y + 4z = 1 2x y + z = 0 x + 2y + 3z = 1 1 2 4 3 1 4 3 2 1 0 1 1 2 0 1 2 1 0 1 2 3 1 1 3 1 2 1 x =, y =, z = 3 2 4 3 2 4 3 2 4 2 1 1 2 1 1 2 1 1 1 2
GEOMETRIA 1 prima parte
 GEOMETRIA 1 prima parte Cristina Turrini C. di L. in Fisica - 2014/2015 Cristina Turrini (C. di L. in Fisica - 2014/2015) GEOMETRIA 1 1 / 44 index Relazioni in un insieme 1 Relazioni in un insieme 2 Gruppi,
GEOMETRIA 1 prima parte Cristina Turrini C. di L. in Fisica - 2014/2015 Cristina Turrini (C. di L. in Fisica - 2014/2015) GEOMETRIA 1 1 / 44 index Relazioni in un insieme 1 Relazioni in un insieme 2 Gruppi,
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof. Fabio Perroni. 5. Rango
 Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 5 Rango Definizione 1 Sia A M m,n (K) una matrice m n a coefficienti nel campo K Il rango
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 5 Rango Definizione 1 Sia A M m,n (K) una matrice m n a coefficienti nel campo K Il rango
A =, c d. d = ad cb. c d A =
 Geometria e Algebra (II), 271112 1 Definizione D ora innanzi, al posto di dire matrice quadrata di tipo n n o matrice quadrata n n diremo matrice quadrata di ordine n o in breve matrice di ordine n Il
Geometria e Algebra (II), 271112 1 Definizione D ora innanzi, al posto di dire matrice quadrata di tipo n n o matrice quadrata n n diremo matrice quadrata di ordine n o in breve matrice di ordine n Il
Determinante. Sia M(n, n, K) lo spazio delle matrici quadrate n n a coefficienti in un campo K, vogliamo provare il seguente Teorema:
 Determinante 1 Proprieta Sia M(n, n, K) lo spazio delle matrici quadrate n n a coefficienti in un campo K, vogliamo provare il seguente Teorema: Theorem 1.1 Esiste un unica mappa F dallo spazio delle matrici
Determinante 1 Proprieta Sia M(n, n, K) lo spazio delle matrici quadrate n n a coefficienti in un campo K, vogliamo provare il seguente Teorema: Theorem 1.1 Esiste un unica mappa F dallo spazio delle matrici
Elementi di Algebra Lineare Spazi Vettoriali
 Elementi di Algebra Lineare Spazi Vettoriali Cristina Turrini UNIMI - 2018/2019 Cristina Turrini (UNIMI - 2018/2019) Elementi di Algebra Lineare 1 / 32 index Spazi vettoriali 1 Spazi vettoriali 2 Sottospazi
Elementi di Algebra Lineare Spazi Vettoriali Cristina Turrini UNIMI - 2018/2019 Cristina Turrini (UNIMI - 2018/2019) Elementi di Algebra Lineare 1 / 32 index Spazi vettoriali 1 Spazi vettoriali 2 Sottospazi
APPLICAZIONI LINEARI
 APPLICAZIONI LINEARI Fra le applicazioni definite tra spazi vettoriali sono particolarmente significative quelle che conservano le operazioni, dette applicazioni lineari. Definizione Siano V, W due k-s.v.
APPLICAZIONI LINEARI Fra le applicazioni definite tra spazi vettoriali sono particolarmente significative quelle che conservano le operazioni, dette applicazioni lineari. Definizione Siano V, W due k-s.v.
Matrici simili, invarianti e decomposizione di matrici 1 / 14
 Matrici simili, invarianti e decomposizione di matrici 1 / 14 Applicazioni lineari 2 / 14 Se X = t [x 1,...,x n ] sono le coordinate di un generico vettore rispetto alla base canonica, possiamo assumere
Matrici simili, invarianti e decomposizione di matrici 1 / 14 Applicazioni lineari 2 / 14 Se X = t [x 1,...,x n ] sono le coordinate di un generico vettore rispetto alla base canonica, possiamo assumere
ENDOMORFISMI. NOTE DI ALGEBRA LINEARE
 ENDOMORFISMI. NOTE DI ALGEBRA LINEARE 2010-11 MARCO MANETTI: 15 GENNAIO 2011 1. Endomorfismi e sottospazi invarianti Definizione 1.1. Sia V uno spazio vettoriale su K. Un endomorfismo di V è una qualsiasi
ENDOMORFISMI. NOTE DI ALGEBRA LINEARE 2010-11 MARCO MANETTI: 15 GENNAIO 2011 1. Endomorfismi e sottospazi invarianti Definizione 1.1. Sia V uno spazio vettoriale su K. Un endomorfismo di V è una qualsiasi
Matematica discreta 1 [145016]
![Matematica discreta 1 [145016] Matematica discreta 1 [145016]](/thumbs/94/119285443.jpg) Facoltà di Scienze Matematiche, Fisiche e Naturali anno accademico 2008/09 Registro dell'attività didattica Matematica discreta 1 [145016] Attività didattica: Attività didattica [codice] Corso di studio
Facoltà di Scienze Matematiche, Fisiche e Naturali anno accademico 2008/09 Registro dell'attività didattica Matematica discreta 1 [145016] Attività didattica: Attività didattica [codice] Corso di studio
Capitolo 3 Matrici. Marco Robutti. Facoltà di ingegneria Università degli studi di Pavia. Anno accademico
 Capitolo 3 Matrici Marco Robutti Facoltà di ingegneria Università degli studi di Pavia Anno accademico 2017-2018 Tutorato di geometria e algebra lineare Definizione (Matrice) Una matrice A M R (k, n) è
Capitolo 3 Matrici Marco Robutti Facoltà di ingegneria Università degli studi di Pavia Anno accademico 2017-2018 Tutorato di geometria e algebra lineare Definizione (Matrice) Una matrice A M R (k, n) è
Anno Accademico 2015/2016
 Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2015/2016 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2015/2016 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
Nozioni e notazioni: concetti primitivi di insieme, elemento ed appartenenza.
 Geometria I lezione del 30 settembre 2013 Presentazione del corso. Nozioni e notazioni: concetti primitivi di insieme, elemento ed appartenenza. Insiemi numerici: i numeri naturali, gli interi, i numeri
Geometria I lezione del 30 settembre 2013 Presentazione del corso. Nozioni e notazioni: concetti primitivi di insieme, elemento ed appartenenza. Insiemi numerici: i numeri naturali, gli interi, i numeri
Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari
 Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017 Elementi di Algebra Lineare
Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017 Elementi di Algebra Lineare
CORSO DI GEOMETRIA DETERMINANTE A.A. 2018/2019 PROF. VALENTINA BEORCHIA
 CORSO DI GEOMETRIA DETERMINANTE AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Definizione induttiva di determinante 1 2 Caratterizzazione delle matrici quadrate di rango massimo 5 3 Regole di Laplace 6
CORSO DI GEOMETRIA DETERMINANTE AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Definizione induttiva di determinante 1 2 Caratterizzazione delle matrici quadrate di rango massimo 5 3 Regole di Laplace 6
Rango di una matrice e teorema di Rouché-Capelli
 Rango di una matrice e teorema di Rouché-Capelli Sappiamo che a una matrice m n, A, è associata l applicazione lineare L A : R n R m, L A (X) = AX, X R n. Definizione 1. Lo spazio nullo di A, N (A), è
Rango di una matrice e teorema di Rouché-Capelli Sappiamo che a una matrice m n, A, è associata l applicazione lineare L A : R n R m, L A (X) = AX, X R n. Definizione 1. Lo spazio nullo di A, N (A), è
LEZIONE 12. Y = f(x) = f( x j,1 f(e j ) = x j,1 A j = AX = µ A (X),
 LEZIONE 1 1.1. Matrice di un applicazione lineare. Verifichiamo ora che ogni applicazione lineare f: R n R m è della forma µ A per un unica A R m,n. Definizione 1.1.1. Per ogni j 1,..., n indichiamo con
LEZIONE 1 1.1. Matrice di un applicazione lineare. Verifichiamo ora che ogni applicazione lineare f: R n R m è della forma µ A per un unica A R m,n. Definizione 1.1.1. Per ogni j 1,..., n indichiamo con
Autovalori e autovettori
 Autovalori e autovettori Definizione 1 (per endomorfismi). Sia V uno spazio vettoriale su di un campo K e f : V V un suo endomorfismo. Si dice autovettore per f ogni vettore x 0 tale che f(x) = λx, per
Autovalori e autovettori Definizione 1 (per endomorfismi). Sia V uno spazio vettoriale su di un campo K e f : V V un suo endomorfismo. Si dice autovettore per f ogni vettore x 0 tale che f(x) = λx, per
MATRICI E SISTEMI LINEARI
 MATRICI E SISTEMI LINEARI - PARTE I - Felice Iavernaro Dipartimento di Matematica Università di Bari 27 Febbraio 2006 Felice Iavernaro (Univ. Bari) Matrici e Sistemi lineari 27/02/2006 1 / 1 Definizione
MATRICI E SISTEMI LINEARI - PARTE I - Felice Iavernaro Dipartimento di Matematica Università di Bari 27 Febbraio 2006 Felice Iavernaro (Univ. Bari) Matrici e Sistemi lineari 27/02/2006 1 / 1 Definizione
MATRICI. Matrici Una matrice A con n-righe e m-colonne, ad elementi reali, è una tabella con la seguente forma: a 2 m. a n m) i j R, 1 i n, 1 j m.
 MATRICI Matrici Una matrice A con n-righe e m-colonne, ad elementi reali, è una tabella con la seguente forma: 11 a 12 a 1 3 a 1m A=(a a 21 a 2 3 a 2m con a a n1 a n2 a n 3 a nm i j R, 1 i n, 1 j m. per
MATRICI Matrici Una matrice A con n-righe e m-colonne, ad elementi reali, è una tabella con la seguente forma: 11 a 12 a 1 3 a 1m A=(a a 21 a 2 3 a 2m con a a n1 a n2 a n 3 a nm i j R, 1 i n, 1 j m. per
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE. Giovanni Villani
 Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
Federica Gregorio e Cristian Tacelli
 1 Sistemi lineari Federica Gregorio e Cristian Tacelli Un sistema lineare m n (m equazioni in n incognite) è un insieme di equazioni lineari che devono essere soddisfatte contemporaneamente a 11 x 1 +
1 Sistemi lineari Federica Gregorio e Cristian Tacelli Un sistema lineare m n (m equazioni in n incognite) è un insieme di equazioni lineari che devono essere soddisfatte contemporaneamente a 11 x 1 +
Sui determinanti e l indipendenza lineare di vettori
 Sui determinanti e l indipendenza lineare di vettori 1 Si dice che m vettori v 1, v 2,,v m di R n sono linearmente indipendenti, se una loro combinazione lineare può dare il vettore nullo solo se i coefficienti
Sui determinanti e l indipendenza lineare di vettori 1 Si dice che m vettori v 1, v 2,,v m di R n sono linearmente indipendenti, se una loro combinazione lineare può dare il vettore nullo solo se i coefficienti
Equivalentemente, le colonne di A sono linearmente indipendenti se e solo se
 Lezioni di Algebra Lineare. Versione novembre 2008 VI. Il determinante Il determinante det A di una matrice A, reale e quadrata, è un numero reale associato ad A. Dunque det è una funzione dall insieme
Lezioni di Algebra Lineare. Versione novembre 2008 VI. Il determinante Il determinante det A di una matrice A, reale e quadrata, è un numero reale associato ad A. Dunque det è una funzione dall insieme
Corso introduttivo pluridisciplinare Matrici e sistemi lineari
 Corso introduttivo pluridisciplinare Matrici e sistemi lineari anno acc. 2013/2014 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano Corso introduttivo pluridisciplinare 1 / 30
Corso introduttivo pluridisciplinare Matrici e sistemi lineari anno acc. 2013/2014 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano Corso introduttivo pluridisciplinare 1 / 30
Fattorizzazione QR e matrici di Householder
 Fattorizzazione QR e matrici di Householder ottobre 009 In questa nota considereremo un tipo di fattorizzazione che esiste sempre nel caso di matrici quadrate non singolari ad entrate reali. Definizione
Fattorizzazione QR e matrici di Householder ottobre 009 In questa nota considereremo un tipo di fattorizzazione che esiste sempre nel caso di matrici quadrate non singolari ad entrate reali. Definizione
Esercizi di Geometria
 UNIVERSITÀ DEGLI STUDI DI TRENTO FACOLTÀ DI INGEGNERIA Marco Andreatta Luca Migliorini Gianluca Occhetta Davide Panizzolo Lorenza Tonetto Marina Avitabile Esercizi di Geometria Luglio 2000 2 1. Programma
UNIVERSITÀ DEGLI STUDI DI TRENTO FACOLTÀ DI INGEGNERIA Marco Andreatta Luca Migliorini Gianluca Occhetta Davide Panizzolo Lorenza Tonetto Marina Avitabile Esercizi di Geometria Luglio 2000 2 1. Programma
Lo scopo della teoria dei determinanti è di definire una funzione. det : M n R. sia calcolabile facendo somme e prodotti delle entrate delle matrici
 Determinanti 1 / 44 Lo scopo della teoria dei determinanti è di definire una funzione det : M n R chiamata determinante tale che: sia calcolabile facendo somme e prodotti delle entrate delle matrici det(a)
Determinanti 1 / 44 Lo scopo della teoria dei determinanti è di definire una funzione det : M n R chiamata determinante tale che: sia calcolabile facendo somme e prodotti delle entrate delle matrici det(a)
Soluzione degli esercizi di algebra lineare (del 26 ottobre 2018)
 Soluzione degli esercizi di algebra lineare (del 26 ottobre 28) Esercizio. Siano V un K-spazio vettoriale con base B = (v,..., v n ) e W un K-spazio vettoriale con base C = (w,..., w m ), e sia f : V W
Soluzione degli esercizi di algebra lineare (del 26 ottobre 28) Esercizio. Siano V un K-spazio vettoriale con base B = (v,..., v n ) e W un K-spazio vettoriale con base C = (w,..., w m ), e sia f : V W
CORSO DI ALGEBRA (M-Z) Prof. A. Venezia
 CORSO DI ALGEBRA (M-Z) Prof. A. Venezia 2018-19 Complementi ed Esercizi APPLICAZIONI LINEARI Siano V e V spazi vettoriali sul campo K. Una applicazione L: V V si dice lineare se: 1 AL. L(v+w) = L(v) +
CORSO DI ALGEBRA (M-Z) Prof. A. Venezia 2018-19 Complementi ed Esercizi APPLICAZIONI LINEARI Siano V e V spazi vettoriali sul campo K. Una applicazione L: V V si dice lineare se: 1 AL. L(v+w) = L(v) +
ESAME DI GEOMETRIA. 6 febbraio 2002 CORREZIONE QUIZ
 ESAME DI GEOMETRIA 6 febbraio CORREZIONE QUIZ. La parte reale di ( + i) 9 è positiva. QUIZ Si può procedere in due modi. Un primo modo è osservare che ( + i) =i, dunque ( + i) 9 =(+i)(i) 4 = 4 ( + i) :
ESAME DI GEOMETRIA 6 febbraio CORREZIONE QUIZ. La parte reale di ( + i) 9 è positiva. QUIZ Si può procedere in due modi. Un primo modo è osservare che ( + i) =i, dunque ( + i) 9 =(+i)(i) 4 = 4 ( + i) :
10. Il gruppo Speciale Lineare SL(V )
 1 2 3 4 5 6 7 8 9 1 10. Il gruppo Speciale Lineare SL(V ) Siano F un campo e V uno spazio vettoriale di dimensione n su F. Indichiamo con GL(V ) l insieme delle applicazioni lineari biiettive di V in sé.
1 2 3 4 5 6 7 8 9 1 10. Il gruppo Speciale Lineare SL(V ) Siano F un campo e V uno spazio vettoriale di dimensione n su F. Indichiamo con GL(V ) l insieme delle applicazioni lineari biiettive di V in sé.
Definizione 1. Una matrice n m a coefficienti in K é una tabella del tipo. ... K m, detto vettore riga i-esimo, ed a im
 APPUNTI ed ESERCIZI su matrici, rango e metodo di eliminazione di Gauss Corso di Laurea in Chimica, Facoltà di Scienze MM.FF.NN., UNICAL (Dott.ssa Galati C.) Rende, 23 Aprile 2010 Matrici, rango e metodo
APPUNTI ed ESERCIZI su matrici, rango e metodo di eliminazione di Gauss Corso di Laurea in Chimica, Facoltà di Scienze MM.FF.NN., UNICAL (Dott.ssa Galati C.) Rende, 23 Aprile 2010 Matrici, rango e metodo
Argomento 12 Matrici
 Argomento 2 Matrici 2 Vettori di R n eoperazioni I Vettore di R n : x =(x i ) i=n =(x i ) n i=,conx i R componenti di x I R n = spazio dei vettori reali a n componenti = spazio vettoriale reale n-dimensionale
Argomento 2 Matrici 2 Vettori di R n eoperazioni I Vettore di R n : x =(x i ) i=n =(x i ) n i=,conx i R componenti di x I R n = spazio dei vettori reali a n componenti = spazio vettoriale reale n-dimensionale
ALGEBRA LINEARE E GEOMETRIA: ESERCIZI 5. Indice. 2. Esercizi 5
 ALGEBRA LINEARE E GEOMETRIA: ESERCIZI 5 Indice 1. Principali definizioni 1 2. Esercizi 5 Operazioni con le matrici 1. Principali definizioni Ricordiamo le principali definizioni legate alle matrici a coefficienti
ALGEBRA LINEARE E GEOMETRIA: ESERCIZI 5 Indice 1. Principali definizioni 1 2. Esercizi 5 Operazioni con le matrici 1. Principali definizioni Ricordiamo le principali definizioni legate alle matrici a coefficienti
Spazi affini e combinazioni affini.
 Spazi affini e combinazioni affini. Morfismi affini. Giorgio Ottaviani Abstract Introduciamo il concetto di combinazione affine in uno spazio affine, e in base a questo, ne caratterizziamo i sottospazi.
Spazi affini e combinazioni affini. Morfismi affini. Giorgio Ottaviani Abstract Introduciamo il concetto di combinazione affine in uno spazio affine, e in base a questo, ne caratterizziamo i sottospazi.
Calendario delle lezioni di Geometria e Algebra
 Calendario delle lezioni di Geometria e Algebra 28 settembre 2016 Lezione 28/09, 11-13 aula EF1 1. Insieme. Elementi di un insieme. 2. Sottoinsiemi di un insieme: A B. Uguaglianza di insiemi. 3. A = B
Calendario delle lezioni di Geometria e Algebra 28 settembre 2016 Lezione 28/09, 11-13 aula EF1 1. Insieme. Elementi di un insieme. 2. Sottoinsiemi di un insieme: A B. Uguaglianza di insiemi. 3. A = B
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof. F.Podestà, a.a
 APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria Edile ed Edile/Architettura. Complementi di Geometria Proiettiva Docente F.
 Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria Edile ed Edile/Architettura Complementi di Geometria Proiettiva Docente F. Flamini POLARITA DEFINITA DA UNA CONICA 1 Spazio vettoriale duale.
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria Edile ed Edile/Architettura Complementi di Geometria Proiettiva Docente F. Flamini POLARITA DEFINITA DA UNA CONICA 1 Spazio vettoriale duale.
Lezione 4 - Esercitazioni di Algebra e Geometria - Anno accademico
 Trasformazioni elementari sulle matrici Data una matrice A K m,n definiamo su A le seguenti tre trasformazioni elementari: T : scambiare tra loro due righe (o due colonne) di A; T : sommare ad una riga
Trasformazioni elementari sulle matrici Data una matrice A K m,n definiamo su A le seguenti tre trasformazioni elementari: T : scambiare tra loro due righe (o due colonne) di A; T : sommare ad una riga
Note per le esercitazioni di Geometria 1 a.a. 2007/08 A. Lotta. Metodi per il calcolo del rango di una matrice
 Note per le esercitazioni di Geometria 1 a.a. 2007/08 A. Lotta Versione del 21/12/07 Metodi per il calcolo del rango di una matrice Sia A M m,n (K). Denotiamo con A (i) la riga i-ma di A, i {1,..., m}.
Note per le esercitazioni di Geometria 1 a.a. 2007/08 A. Lotta Versione del 21/12/07 Metodi per il calcolo del rango di una matrice Sia A M m,n (K). Denotiamo con A (i) la riga i-ma di A, i {1,..., m}.
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI
 CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
Introduzione soft alla matematica per l economia e la finanza. Marta Cardin, Paola Ferretti, Stefania Funari
 Introduzione soft alla matematica per l economia e la finanza Marta Cardin, Paola Ferretti, Stefania Funari Capitolo Sistemi di equazioni lineari.8 Il Teorema di Cramer Si consideri un generico sistema
Introduzione soft alla matematica per l economia e la finanza Marta Cardin, Paola Ferretti, Stefania Funari Capitolo Sistemi di equazioni lineari.8 Il Teorema di Cramer Si consideri un generico sistema
Soluzioni primi compitini - Geometria 1
 Soluzioni primi compitini - Geometria Caterina Vernieri Ottobre 7 Le soluzioni proposte non sono state riviste dai professori Soluzioni Primi Compitini - G I compitino 7//3 Esercizio Al variare di α R
Soluzioni primi compitini - Geometria Caterina Vernieri Ottobre 7 Le soluzioni proposte non sono state riviste dai professori Soluzioni Primi Compitini - G I compitino 7//3 Esercizio Al variare di α R
Note per il corso di Geometria Corso di laurea in Ing. Edile/Architettura. 4 Sistemi lineari. Metodo di eliminazione di Gauss Jordan
 Note per il corso di Geometria 2006-07 Corso di laurea in Ing. Edile/Architettura Sistemi lineari. Metodo di eliminazione di Gauss Jordan.1 Operazioni elementari Abbiamo visto che un sistema di m equazioni
Note per il corso di Geometria 2006-07 Corso di laurea in Ing. Edile/Architettura Sistemi lineari. Metodo di eliminazione di Gauss Jordan.1 Operazioni elementari Abbiamo visto che un sistema di m equazioni
Geometria e Algebra. Ingegneria dell Informazione
 Geometria e Algebra Ingegneria dell Informazione 2013 2014 Rocco Chirivì Dipartimento di Matematica e Fisica Università del Salento rocco.chirivi@unisalento.it www.dmf.unisalento.it/persone/chirivi Modalità
Geometria e Algebra Ingegneria dell Informazione 2013 2014 Rocco Chirivì Dipartimento di Matematica e Fisica Università del Salento rocco.chirivi@unisalento.it www.dmf.unisalento.it/persone/chirivi Modalità
Esercizi su applicazioni lineari. Per tutto il seguito, se non specificato esplicitamente K indicherà un campo e V,W,U spazi vettoriali su K.
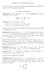 Esercizi su applicazioni lineari Per tutto il seguito, se non specificato esplicitamente K indicherà un campo e V,W,U spazi vettoriali su K. 1. Cose da ricordare Definizione 1.1. Una funzione f : V W si
Esercizi su applicazioni lineari Per tutto il seguito, se non specificato esplicitamente K indicherà un campo e V,W,U spazi vettoriali su K. 1. Cose da ricordare Definizione 1.1. Una funzione f : V W si
INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 19 GIUGNO 2012
 INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 19 GIUGNO 2012 MATTEO LONGO Esercizio 1. Al variare del parametro a R, si consideri l applicazione lineare L a : R R definita dalle
INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 19 GIUGNO 2012 MATTEO LONGO Esercizio 1. Al variare del parametro a R, si consideri l applicazione lineare L a : R R definita dalle
( ) TEORIA DELLE MATRICI. A. Scimone a.s pag 1
 . Scimone a.s 1997 98 pag 1 TEORI DELLE MTRICI Dato un campo K, definiamo matrice ad elementi in K di tipo (m, n) un insieme di numeri ordinati secondo righe e colonne in una tabella rettangolare del tipo
. Scimone a.s 1997 98 pag 1 TEORI DELLE MTRICI Dato un campo K, definiamo matrice ad elementi in K di tipo (m, n) un insieme di numeri ordinati secondo righe e colonne in una tabella rettangolare del tipo
1. [15 punti] Calcolare il rango della seguente matrice a coefficienti reali: ( 1/2) 1 (1/2)
![1. [15 punti] Calcolare il rango della seguente matrice a coefficienti reali: ( 1/2) 1 (1/2) 1. [15 punti] Calcolare il rango della seguente matrice a coefficienti reali: ( 1/2) 1 (1/2)](/thumbs/101/152415317.jpg) Università di Modena e Reggio Emilia Facoltà di Scienze MM.FF.NN. PROVA DI ALGEBRA LINEARE del 17 febbraio 011 ISTRUZIONI PER LO SVOLGIMENTO. Scrivere cognome, nome, numero di matricola in alto a destra
Università di Modena e Reggio Emilia Facoltà di Scienze MM.FF.NN. PROVA DI ALGEBRA LINEARE del 17 febbraio 011 ISTRUZIONI PER LO SVOLGIMENTO. Scrivere cognome, nome, numero di matricola in alto a destra
GEOMETRIA 1 prima parte
 GEOMETRIA 1 prima parte Gilberto Bini - Cristina Turrini 2016/2017 Gilberto Bini - Cristina Turrini (2016/2017) GEOMETRIA 1 1 / 89 index Relazioni in un insieme 1 Relazioni in un insieme 2 Gruppi, anelli,
GEOMETRIA 1 prima parte Gilberto Bini - Cristina Turrini 2016/2017 Gilberto Bini - Cristina Turrini (2016/2017) GEOMETRIA 1 1 / 89 index Relazioni in un insieme 1 Relazioni in un insieme 2 Gruppi, anelli,
0.1 Coordinate in uno spazio vettoriale
 0.. COORDINATE IN UNO SPAZIO VETTORIALE 0. Coordinate in uno spazio vettoriale Sia V uno spazio vettoriale di dimensione finita n costruito sul campo K. D ora in poi, ogni volta che sia fissata una base
0.. COORDINATE IN UNO SPAZIO VETTORIALE 0. Coordinate in uno spazio vettoriale Sia V uno spazio vettoriale di dimensione finita n costruito sul campo K. D ora in poi, ogni volta che sia fissata una base
ENDOMORFISMI. ove B := (v 1,v 2,v 3 ). (1) Determinare gli autovalori di f e le relative molteplicità algebriche e geometriche.
 ENDOMORFISMI Esercizi Esercizio 1 Siano v 1 := T (1, 1, 1, 0), v 2 := T (0, 1, 2, 1), v 3 := T (0, 0, 1, 1) Consideriamo V := L(v 1,v 2,v 3 ) R 4 e sia f End R (V ) associato alla matrice A := MB B (f)
ENDOMORFISMI Esercizi Esercizio 1 Siano v 1 := T (1, 1, 1, 0), v 2 := T (0, 1, 2, 1), v 3 := T (0, 0, 1, 1) Consideriamo V := L(v 1,v 2,v 3 ) R 4 e sia f End R (V ) associato alla matrice A := MB B (f)
REGISTRO DELLE LEZIONI
 UNIVERSITA DEGLI STUDI DI GENOVA FACOLTA DI SCIENZE MATEMATICHE, FISICHE E NATURALI REGISTRO DELLE LEZIONI del Corso UFFICIALE di GEOMETRIA B tenute dal prof. Domenico AREZZO nell anno accademico 2006/2007
UNIVERSITA DEGLI STUDI DI GENOVA FACOLTA DI SCIENZE MATEMATICHE, FISICHE E NATURALI REGISTRO DELLE LEZIONI del Corso UFFICIALE di GEOMETRIA B tenute dal prof. Domenico AREZZO nell anno accademico 2006/2007
DIARIO DEL CORSO DI MATHEMATICS FOR DATA SCIENCE TRENTO, A.A. 2018/19 DOCENTI: ANDREA CARANTI, SIMONE UGOLINI
 DIARIO DEL CORSO DI MATHEMATICS FOR DATA SCIENCE TRENTO, A.A. 2018/19 DOCENTI: ANDREA CARANTI, SIMONE UGOLINI Nota. La descrizione di lezioni non ancora svolte si deve intendere come una previsione/pianificazione.
DIARIO DEL CORSO DI MATHEMATICS FOR DATA SCIENCE TRENTO, A.A. 2018/19 DOCENTI: ANDREA CARANTI, SIMONE UGOLINI Nota. La descrizione di lezioni non ancora svolte si deve intendere come una previsione/pianificazione.
Appunti del corso di geometria 1. G. Bande
 Appunti del corso di geometria 1 G. Bande 21 febbraio 2011 2 Indice 1 Spazi vettoriali 5 1.0.1 Esempi di spazi vettoriali.................. 6 1.1 Sottospazi vettoriali......................... 7 1.1.1
Appunti del corso di geometria 1 G. Bande 21 febbraio 2011 2 Indice 1 Spazi vettoriali 5 1.0.1 Esempi di spazi vettoriali.................. 6 1.1 Sottospazi vettoriali......................... 7 1.1.1
(V) (FX) L unione di due basi di uno spazio vettoriale è ancora una base dello spazio vettoriale.
 8 gennaio 2009 - PROVA D ESAME - Geometria e Algebra T NOME: MATRICOLA: a=, b=, c= Sostituire ai parametri a, b, c rispettivamente la terzultima, penultima e ultima cifra del proprio numero di matricola
8 gennaio 2009 - PROVA D ESAME - Geometria e Algebra T NOME: MATRICOLA: a=, b=, c= Sostituire ai parametri a, b, c rispettivamente la terzultima, penultima e ultima cifra del proprio numero di matricola
Testi consigliati e contatti
 Testi consigliati e contatti P.Bonacini, M. G. Cinquegrani, L. Marino, Algebra lineare: esercizi svolti, Cavallotto Edizioni, Catania P. Bonacini, M. G. Cinquegrani, L. Marino, Geometria analitica: esercizi
Testi consigliati e contatti P.Bonacini, M. G. Cinquegrani, L. Marino, Algebra lineare: esercizi svolti, Cavallotto Edizioni, Catania P. Bonacini, M. G. Cinquegrani, L. Marino, Geometria analitica: esercizi
LEZIONE i i 3
 LEZIONE 5 51 Determinanti In questo lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 5 51 Determinanti In questo lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
Sistemi II. Sistemi II. Elisabetta Colombo
 Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, http://users.mat.unimi.it/users/colombo/programmabio.html 1 2 3 con R.C.+ o 1.10 Rango massimo e determinante con R.C.+
Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, http://users.mat.unimi.it/users/colombo/programmabio.html 1 2 3 con R.C.+ o 1.10 Rango massimo e determinante con R.C.+
Forme bilineari simmetriche
 Forme bilineari simmetriche Qui il campo dei coefficienti è sempre R Definizione 1 Sia V uno spazio vettoriale Una forma bilineare su V è una funzione b: V V R tale che v 1, v 2, v 3 V b(v 1 + v 2, v 3
Forme bilineari simmetriche Qui il campo dei coefficienti è sempre R Definizione 1 Sia V uno spazio vettoriale Una forma bilineare su V è una funzione b: V V R tale che v 1, v 2, v 3 V b(v 1 + v 2, v 3
Matematica Discreta I
 Matematica Discreta I 5 Febbraio 8 TEMA A Esercizio Sia data la matrice A M (R) A = (i) Calcolare gli autovalori di A (ii) Determinare una base di R composta di autovettori di A (iii) Diagonalizzare la
Matematica Discreta I 5 Febbraio 8 TEMA A Esercizio Sia data la matrice A M (R) A = (i) Calcolare gli autovalori di A (ii) Determinare una base di R composta di autovettori di A (iii) Diagonalizzare la
LEZIONE i 0 3 Le sottomatrici 2 2 di A sono. 1 2 i i 3. Invece (
 LEZIONE 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
x n i sima pos. x, y = x T y = x i y i R. i=1
 1 Elementi di Algebra Lineare In questo capitolo introduttivo al corso di Calcolo Numerico per la laurea triennale in Informatica, saranno presentate una serie di definizioni e proprietà di matrici e dei
1 Elementi di Algebra Lineare In questo capitolo introduttivo al corso di Calcolo Numerico per la laurea triennale in Informatica, saranno presentate una serie di definizioni e proprietà di matrici e dei
Applicazioni lineari tra spazi euclidei. Cambi di base.
 pplicazioni lineari tra spazi euclidei. Cambi di base. Esercizio. Data la seguente applicazione lineare f : R R : f(x, y, z) = (x z, x + y, y + z), scrivere la matrice B, rappresentativa di f rispetto
pplicazioni lineari tra spazi euclidei. Cambi di base. Esercizio. Data la seguente applicazione lineare f : R R : f(x, y, z) = (x z, x + y, y + z), scrivere la matrice B, rappresentativa di f rispetto
Esempi. In R 2, le coppia (2, 5) è combinazione lineare dei vettori (0, 1) e (1, 1). Infatti:
 Combinazioni lineari [Abate, 4.2] Sia V uno spazio vettoriale e v 1, v 2,..., v n dei vettori di V. Diremo che un vettore w V è combinazione lineare dei vettori v 1,..., v n se esistono a 1, a 2,..., a
Combinazioni lineari [Abate, 4.2] Sia V uno spazio vettoriale e v 1, v 2,..., v n dei vettori di V. Diremo che un vettore w V è combinazione lineare dei vettori v 1,..., v n se esistono a 1, a 2,..., a
Il Teorema Spettrale. 0.1 Applicazioni lineari simmetriche ed hermitiane
 0.1. APPLICAZIONI LINEARI SIMMETRICHE ED HERMITIANE 1 Il Teorema Spettrale In questa nota vogliamo esaminare la dimostrazione del Teorema Spettrale e studiare le sue conseguenze per quanto riguarda i prodotti
0.1. APPLICAZIONI LINEARI SIMMETRICHE ED HERMITIANE 1 Il Teorema Spettrale In questa nota vogliamo esaminare la dimostrazione del Teorema Spettrale e studiare le sue conseguenze per quanto riguarda i prodotti
Geometria BAER I canale Foglio esercizi 2
 Geometria BAER I canale Foglio esercizi 2 Esercizio 1. Calcolare il determinante e l inversa (quando esiste) della matrice ( ) cos θ sin θ R θ =, θ [0, 2π] sin θ cos θ Soluzione: Il determinante ( é cos
Geometria BAER I canale Foglio esercizi 2 Esercizio 1. Calcolare il determinante e l inversa (quando esiste) della matrice ( ) cos θ sin θ R θ =, θ [0, 2π] sin θ cos θ Soluzione: Il determinante ( é cos
Registro dell insegnamento
 Registro dell insegnamento Anno accademico 2016/17 Prof. Settore inquadramento Gabriele Vezzosi MAT-03 Scuola di Ingegneria Dipartimento DIMAI U. Dini Insegnamento Geometria Moduli Settore insegnamento
Registro dell insegnamento Anno accademico 2016/17 Prof. Settore inquadramento Gabriele Vezzosi MAT-03 Scuola di Ingegneria Dipartimento DIMAI U. Dini Insegnamento Geometria Moduli Settore insegnamento
Definizione 1 Una applicazione f : V W, con V, W spazi vettoriali sul campo K si dice lineare se conserva le combinazioni lineari:
 Applicazioni lineari Definizione Una applicazione f : V W, con V, W spazi vettoriali sul campo K si dice lineare se conserva le combinazioni lineari: f(αv + βv 2 ) = αf(v ) + βf(v 2 ) v, v 2 V, α, β K.
Applicazioni lineari Definizione Una applicazione f : V W, con V, W spazi vettoriali sul campo K si dice lineare se conserva le combinazioni lineari: f(αv + βv 2 ) = αf(v ) + βf(v 2 ) v, v 2 V, α, β K.
Si consideri il sistema a coefficienti reali di m equazioni lineari in n incognite
 3 Sistemi lineari 3 Generalità Si consideri il sistema a coefficienti reali di m equazioni lineari in n incognite ovvero, in forma matriciale, a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x
3 Sistemi lineari 3 Generalità Si consideri il sistema a coefficienti reali di m equazioni lineari in n incognite ovvero, in forma matriciale, a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof. Fabio Perroni. 3. Sistemi di equazioni lineari
 Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 3 Sistemi di equazioni lineari Siano m, n N \ {}, sia K un campo Definizione a) Un sistema
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 3 Sistemi di equazioni lineari Siano m, n N \ {}, sia K un campo Definizione a) Un sistema
Autovalori, Autovettori, Diagonalizzazione.
 Autovalori Autovettori Diagonalizzazione Autovalori e Autovettori Definizione Sia V uno spazio vettoriale sul campo K = R o C e sia T : V V un endomorfismo Un vettore non nullo v V \ {O} si dice autovettore
Autovalori Autovettori Diagonalizzazione Autovalori e Autovettori Definizione Sia V uno spazio vettoriale sul campo K = R o C e sia T : V V un endomorfismo Un vettore non nullo v V \ {O} si dice autovettore
