Indice. IL METODO DELLE COORDINATE NEL PIANO Mauro Saita Versione provvisoria. Giugno 2019.
|
|
|
- Mariana Fontana
- 4 anni fa
- Visualizzazioni
Transcript
1 IL METODO DELLE COORDINATE NEL PIANO Versione provvisoria. Giugno Indice 1 Il piano euclideo La rivoluzione cartesiana: fare geometria con l algebra Il piano secondo Cartesio Somma di vettori. Moltiplicazione di un vettore per un numero Prodotto scalare Vettori ortogonali, lunghezza, distanza Proiezione di un vettore lungo un altro Angoli Teorema di Pitagora Equivalenza delle due definizioni di prodotto scalare Rette nel piano Equazioni parametriche della retta Retta per due punti Rette parallele e rette ortogonali Equazione cartesiana della retta Da equazioni parametriche a equazioni cartesiane (e viceversa): il caso di rette in R Distanza di un punto da una retta Fasci di rette Esercizi 21 0 File tex: metodo delle coordinate 2019.tex 1
2 1 Il piano euclideo Quando si studia la geometria euclidea prima si definiscono enti geometrici quali punti, segmenti, rette, poligoni, circonferenze, eccetera e poi si acquisiscono conoscenze su di essi mediante teoremi, cioè mediante proprietà che richiedono dimostrazioni rigorose. In questo contesto interessa solamente ricordare che lo spazio in cui collocare idealmente tutti gli oggetti geometrici fin qui incontrati è il piano euclideo: un piano formato da punti geometrici (un punto, per Euclide, è ciò che non ha parti). In questo piano ha senso, per esempio, parlare di distanza tra due punti e di angolo tra due rette, così come ha senso parlare di rette parallele e di rette ortogonali, di triangoli, di poligoni e così via. Figura 1: Punti, segmenti, rette, vettori, angoli, circonferenze, eccetera stanno nel piano euclideo. Nel corso di fisica, invece, si sono introdotti i vettori: si è imparato a sommarli (con la regola del parallelogramma o con il metodo punta coda ) e a moltiplicare un vettore per un numero. Inoltre si è definito il prodotto scalare nel seguente modo Definizione 1.1. Il prodotto scalare di due vettori A, B è il numero (positivo, negativo, nullo) dato da A B = A B cos ϑ dove A, B indicano le lunghezze di A, B e ϑ l angolo compreso tra di essi Anche i vettori vanno idealmente collocati nel piano euclideo. 1.1 La rivoluzione cartesiana: fare geometria con l algebra. René Descartes (Cartesio ( )) è stato colui che ha avuto il merito di collegare il mondo della geometria con quello dell algebra. L essenza della sua idea si può concettualizzare nel seguente modo: sia π il piano della geometria euclidea (costituito da punti geometrici ) e R 2 l isieme di tutte le coppie ordinate di numeri reali, cioè R 2 = {(x, y) x R, y R} 2
3 Figura 2: Il piano secondo Cartesio L idea su cui si fonda la geometria analitica consiste nell identificare i punti del piano π con le coppie ordinate di numeri reali. Per fare questo occorre dapprima fissare un sistema di riferimento (ortogonale) in π, cioè occorre: - fissare un punto O detto origine del sistema di riferimento; - fissare una coppia di vettori E 1, E 2 di lunghezza unitaria e tra loro ortogonali E 1 E 2 = 0 Le due rette ortogonali, passanti per l origine e dirette come E 1, E 2 si chiamano assi coordinati (oppure, asse x, asse y; oppure asse delle ascisse, asse delle ordinate). P = xe 1 + ye 2 E 2 = (0, 1) E 1 = (1, 0) Figura 3: Sistema di riferimento cartesiano (ortogonale) nel piano. Ogni punto P del piano si identifica con la coppia ordinata di numeri reali così definita P = xe 1 + ye 2 = (x, y) In questo modo, si è stabilita una corrispondenza biunivoca π R 2 che a ogni punto del piano associa una (e una sola) coppia (x, y) ordinata di numeri reali, e viceversa. 3
4 D ora in poi se, ad esempio, si scrive P = (2, 7) si intende indicare l unico punto del piano che (nel sistema di riferimento prescelto) ha esattamente quelle coordinate. Punti del piano e vettori spiccati dall origine. Fissato un sistema di riferimento xoy nel piano π, la coppia ordinata P = (x, y) di numeri reali può essere interpretata geometricamente come vettore spiccato dall origine. Quindi, a seconda delle necessità potremo pensare R 2 come un insieme di punti del piano ordinario, oppure, come un insieme di vettori spiccati dall origine; solo il contesto ci dirà qual è l interpretazione migliore. 4
5 2 Il piano secondo Cartesio 2.1 Somma di vettori. Moltiplicazione di un vettore per un numero. Si consideri l insieme costituito da tutte le coppie ordinate di numeri reali, ossia R 2 = {(x, y) x R, y R} Si ricordi che gli elementi di R 2 si possono identificare con vettori spiccati dall origine. Somma di vettori. Siano P = (p 1, p 2 ) e Q = (q 1, q 2 ) due vettori di R 2. Si chiama somma di P e Q il vettore P + Q = (p 1 + q 1, p 2 + q 2 ) Per esempio, se P = (1, 2) e Q = (3, 4) allora P + Q = (1 + 3, 2 + 4). Osservando la figura qui sotto riportata è facile convincersi che il vettore P + Q è lo stesso che si trova utilizzando la regola del parallelogramma introdotta in fisica. P + Q = (p 1 + q 1, p 2 + q 2 ) Q = (q 1, q 2 ) P = (p 1, p 2 ) Figura 4: Il vettore P + Q = (p 1 + q 1, p 2 + q 2 ) è lo stesso che si trova con la regola del parallelogramma. Per l operazione somma di vettori appena definita in R 2 valgono le seguenti proprietà (la verifica è lasciata per esercizio). (a) La somma è commutativa: per ogni P, Q in R 2 P + Q = Q + P (b) La somma è associativa: per ogni P, Q, R in R 2 (P + Q) + R = P + (Q + R) (c) Esiste un vettore in R 2, il vettore nullo 0, che è elemento neutro rispetto all operazione di somma, nel senso che P + 0 = P per ogni vettore P. 5
6 (d) Per ogni vettore P R 2 esiste un vettore, l opposto di P, denotato P, che sommato a P dà il vettore nullo: P + ( P) = 0. Poichè valgono le proprietà qui sopra enunciate, si dice che R 2, con l operazione di somma, è un gruppo abeliano. Moltiplicazione di un vettore per uno scalare. Sia P = (p 1, p 2 ) R 2 un vettore spiccato dall origine e k un numero reale. Allora si chiama moltiplicazione del vettore P per il numero k il vettore kp = (kp 1, kp 2 ) Per esempio, se P = (1, 2) e k = 3 allora kp = (3 1, 3 2) = (3, 6). Moltiplicare il vettore P per il numero reale k significa dilatare (contrarre) il vettore P del fattore k. P = (p 1, p 2 ) k P = (k p 1, k p 2 ) Figura 5: Il vettore k P è il vettore P dilatato del fattore k. Per la moltiplicazione di un vettore per un numero valgono le seguenti proprietà (e) h(kp) = (hk)p, per ogni P R 2, per ogni h, k R. (f) (h + k)p = hp + kp, per ogni P R 2, per ogni h, k R. (g) h(p + Q) = hp + hq, per ogni P, P R 2, per ogni h R. (h) 1P = P Riassumendo, sono state introdotte in R 2 due operazioni: la somma di vettori (spiccati dall origine) per la quale valgono le proprietà (a),(b),(c),(d), e la moltiplicazione di un vettore per un numero reale per la quale valgono le proprietà (e),(f),(g),(h). Si può sintetizzare tutto ciò dicendo che R 2 è uno spazio vettoriale reale rispetto alle due operazioni introdotte. 6
7 2.2 Prodotto scalare Definizione 2.1. Siano A = (a 1, a 2 ) e B = (b 1, b 2 ) due vettori di R 2. Chiamiamo prodotto scalare di A e B il numero A B = (a 1 b 1 + a 2 b 2 ) (A B si legge: A scalare B ) Per il prodotto scalare valgono le seguenti proprietà (la cui verifica è lasciata per esercizio) (a) Bilinearità. Per ogni fissato A, B, C R 2 e per ogni k R, (A + B) C = (A C) + (B C) e A (B + C) = (A B) + (A C) ka B = k(a B) e A kb = k(a B) (b) Simmetria. Per ogni A, B in R 2 A B = B A (c) Definita positività. Per ogni A 0 A A > Vettori ortogonali, lunghezza, distanza Definizione 2.2 (Vettori ortogonali). Per ogni A, B R 2, si dice che A e B sono ortogonali se A B = 0 Per esempio se A = (1, 2) e B = (3, 4) si ottiene A B = = 11 0; quindi i due vettori non sono ortogonali. Se invece A = (1, 2) e B = ( 2, 1), A B = = 0; i due vettori sono ortogonali. Infine si osservi che, in base alla definizione appena data, il vettore nullo O = (0, 0) risulta ortogonale a ogni vettore A di R 2 perchè A O = 0. Dalla definizione di prodotto scalare si ricava subito che A A = a a2 2 = A 2. Questo fatto giustifica la seguente definizione Definizione 2.3 (Lunghezza di un vettore). La lunghezza di un vettore A di R 2 è il numero reale A = A A = a a2 2 7
8 a 2 A = (a 1, a 2 ) A A a 1 Figura 6: La lunghezza del vettore A è A A = a a2 2 Un vettore U R 2 si dice unitario se U = 1. Definizione 2.4 (Distanza tra due punti). La distanza d(a, B) fra due punti A, B R 2 è il numero d(a, B) = A B = (a 1 b 1 ) 2 + (a 2 b 2 ) 2 B B A A Figura 7: La distanza di A da B è la lunghezza del vettore B A. 2.4 Proiezione di un vettore lungo un altro. Teorema 2.5 (Proiezione di un vettore lungo un altro). Sia B R 2, B 0. Ogni vettore A R 2, si scrive in modo unico come con A parallelo a B e A ortogonale a B. A = A + A (2.1) 8
9 A A B A Figura 8: Il vettore A è la proiezione ortogonale di A lungo B. Si ha: e, di conseguenza, A = A B B B B (2.2) Dimostrazione. A = A A B B B B (2.3) La dimostrazione consiste nel trovare un vettore A che sia parallelo a B e tale che la differenza A A sia ortogonale a B. In altri termini, un vettore A che sia parallelo a B è un vettore multiplo di B, cioè del tipo tb (t R); tale vettore ha la proprietà che A tb è ortogonale a B se e solo se ossia (A tb) B = 0 A B t(b B) = 0 L ultima uguaglianza è un equazione di primo grado in t nella quale B B 0 perchè, per ipotesi, B 0. L unica soluzione di questa equazione è Quindi, e, per differenza, t = A B B B A = tb = A B B B B A = A A = A A B B B B 9
10 Quindi per ogni A in R 2 e per ogni B O, il teorema appena dimostrato permette di calcolare con un semplice conto la proiezione ortogonale di A su B, si scrive P B (A): P B (A) = A B B B B (2.4) Esempio. Se A = (0, 1) e B = (1, 1), la proiezione ortogonale di A sul vettore B è Osservazione 1. P B (A) = A B B B B = 1 ( 1 (1, 1) = 2 2, 1 ) 2 Se al posto di B si sostituisce un suo qualunque multiplo (non nullo) k B (k R), la proiezione P B (A) non cambia. Infatti, A k B k B k B k B = A B B B B Dunque, si può pensare la proiezione P B (A) come la proiezione di A lungo la retta orientata del vettore B. Osservazione 2. Per un vettore U unitario (U U = 1), la proiezione di A lungo U assume la seguente forma (più semplice): P U (A) = (A U) U (2.5) 2.5 Angoli Sia U un vettore unitario. Ricordando che la proiezione di A lungo U (la componente di A lungo U è il prodotto della lunghezza di A per il coseno ϑ dell angolo compreso tra A e U si ottiene: ossia (A U) U = ( A cos ϑ) U cos ϑ = A U A Esempio. Trovare il coseno dell angolo α formato dai vettori A = (2, 0) e B = (1, 1). ( ) Soluzione. Il vettore unitario parallelo a B e orientato come B è U = B B = 2 1 1, 2 cos ϑ = A U A = =
11 2.6 Teorema di Pitagora Teorema 2.6 ( Teorema di Pitagora ). Siano A e B vettori di R 2. ortogonali, allora A + B 2 = A 2 + B 2 Se A e B sono Dimostrazione. A + B 2 = (A + B) (A + B) = A A + 2(A B) + B B = A 2 + 2(A B) + B 2 = A 2 + B 2 (perchè A, B sono ortogonali per ipotesi, cioè A B = 0) 11
12 2.7 Equivalenza delle due definizioni di prodotto scalare In questa sezione si mostra che la definizione di prodotto scalare in termini di componenti, A B = a 1 b 1 + a 2 b 2, è equivalente a quella introdotta nel corso di fisica, A B = A B cos ϑ, (dove ϑ è l angolo compreso tra i due vettori). A α β α β B Figura 9: A B = a 1 b 1 + a 2 b 2 = ( A cos α) ( B cos β) + ( A sin α) ( B sin β) = ( A B cos α cos β) + ( A B sin α sin β) = A B (cos α cos β + sin α sin β) = A B cos(α β) = A B cos ϑ 12
13 3 Rette nel piano 3.1 Equazioni parametriche della retta Si osservi la seguente figura: P = A + Vt r A Vt V Figura 10: L equazione parametrica (vettoriale) della retta r passante per A e parallela al vettore non nullo V è Il vettore V si chiama vettore di direzione della retta. P = A + Vt t R (3.1) L equazione (3.1) si può scrivere in termini di coordinate; se A = (a 1, a 2 ), V = (v 1, v 2 ) e P = (x, y) si ottiene 1 { x = a1 + v 1 t y = a 2 + v 2 t t R (3.2) 1 L equazione parametrica di una retta nel piano R 2 è una funzione R r R 2 t (a 1 + v 1t, a 2 + v 2t) In linea di principio, è bene distinguere la funzione R r R 2 dalla sua immagine, cioè dall insieme dei punti r(t) = A + Vt nel piano, ottenuti al variare del parametro t in R. Distinguere i due concetti è importante, ad esempio, in cinematica: la funzione R r R 2 è (la legge oraria di) un moto rettilineo uniforme, di velocità vettoriale V, passante per A all istante t = 0; invece la sua immagine Im (r) = {P R 2 P = A + V t, t R } è la traiettoria (o orbita) del moto. Naturalmente, una stessa traiettoria può essere percorsa in infiniti modo diversi. In termini geometrici: una retta, intesa come insieme di punti dello spazio, può essere parametrizzata in infiniti modi diversi. 13
14 Esempi 1) Equazioni parametriche per la retta passante per P 0 = (3, 5) e con vettore di direzione V = (1, 2, ) sono: { x = 3 + t y = 5 + 2t t R 2) Equazioni parametriche per l asse delle x sono: { x = t t R y = Retta per due punti L equazione parametrica, in forma vettoriale, per la retta che passa per i due punti (distinti) A e B è : P = A + (B A)t, t R In componenti, se A = (a 1, a 2 ), B = (b 1, b 2 ), equazioni parametriche sono: { x = a1 + (b 1 a 1 )t t R y = a 2 + (b 2 a 2 )t (Spiegare facendo una figura). 3.3 Rette parallele e rette ortogonali Rette parallele. Due rette r e r di equazioni parametriche r : { x = a1 + v 1 t y = a 2 + v 2 t t R r : { x = a 1 + v 1 u y = a 2 + v 2 u u R (3.3) sono parallele se e solo se i loro vettori di direzione (v 1, v 2 ) e (v 1, v 2 ) sono proporzionali, cioè se esiste un numero reale k per il quale v 1 = kv 1, v 2 = kv 2 Rette ortogonali. Due rette r e r di equazioni parametriche r : { x = x0 + lt y = y 0 + mt t R r : { x = a 1 + v 1 u y = a 2 + v 2 u u R (3.4) sono ortogonali se e solo se i loro vettori di direzione (v 1, v 2 ) e (v 1, v 2 ) sono ortogonali, cioè se e solo se v 1 v 1 + v 2 v 2 = 0 14
15 3.4 Equazione cartesiana della retta Sia N = (a, b) un qualunque vettore non nullo ortogonale alla retta r e sia P 0 = (x 0, y 0 ) un punto (qualunque) appartenente alla retta. N P P 0 P P 0 r N O Figura 11: Un punto P = (x, y) appartiene alla retta se, e solo se, il vettore P P 0 è ortogonale a N. Quindi l equazione della retta, in forma vettoriale, è N (P P 0 ) = 0 (3.5) In coordinate cartesiane ortogonali, l equazione vettoriale (3.5) della retta r si scrive Posto c = ax 0 by 0 e con facili calcoli si ottiene: a(x x 0 ) + b(y y 0 ) = 0 (3.6) ax + by + c = 0 (3.7) Riassumendo: ogni retta r è rappresentata da un equazione di primo grado in x, y, ax + by + c = 0 (3.8) dove almeno uno dei due coefficienti a, b è diverso da zero. La (3.8) si chiama equazione cartesiana della retta. Il vettore non nullo V = (a, b) ha una interpretazione geometrica: è un vettore ortogonale alla retta r. Viceversa, sia ax + by + c = 0 (3.9) 15
16 una qualunque equazione di primo grado in x, y con almeno uno dei due coefficienti a, b non nullo. Bisogna dimostrare che l insieme delle soluzioni dell equazione (3.9), cioè l insieme dei punti P = (x, y) in R 2 le cui coordinate soddisfano (3.9), è una retta nel piano. Infatti, sia P 0 = (x 0, y 0 ) un punto (qualunque) del piano le cui coordinate soddisfino l equazione (3.9): ax 0 + by 0 + c = 0 (3.10) (Un tale punto (x 0, y 0 ) esiste sicuramente. Ad esempio, se b 0, basta dare a x un valore arbitrario x 0 e poi ricavare il valore y 0 : si ottiene y 0 = ax 0 c b ). Da questa uguaglianza si ricava c = ax 0 by 0. Sostituendo questo valore di c in (3.9), si ricava: oppure, in forma vettoriale, a(x x 0 ) + b(y y 0 ) + c = 0 (3.11) V (P P 0 ) = 0 (3.12) dove V = (a, b) e P P 0 = (x x 0, y y 0 ). Quest ultima equazione (3.12) ha un evidente significato geometrico: rappresenta il luogo dei punti P del piano per i quali il vettore P P 0 è ortogonale al fissato vettore V. Dunque, anche l equazione (3.9), equivalente a (3.12), rappresenta una retta: precisamente la retta passante per P 0 = (x 0, y 0 ) e ortogonale al vettore V = (a, b). 3.5 Da equazioni parametriche a equazioni cartesiane (e viceversa): il caso di rette in R 2 Spesso è utile saper passare dalle equazioni parametriche di una retta a una sua equazione cartesiana e vicersa. Da equazioni parametriche a equazioni cartesiane. Se si conoscono le equazioni parametriche della retta r { x = x0 + at y = y 0 + bt si può sempre ricavare t da almeno una delle due equazioni; per esempio, se a 0 dalla prima equazione si ottiene: t = x x 0 a e sostituendo il valore trovato di t nella seconda equazione si trova y = y 0 + b x x 0 a che rappresenta una equazione cartesiana di r. (3.13) (3.14) 16
17 Da equazioni cartesiane a equazioni parametriche Se si conosce una equazione cartesiana della retta r ax + by + c = 0 (3.15) almeno uno dei due coefficienti a, b è diverso da zero. Se, per esempio a 0, si sostituisce y = t nell equazione (3.16) Quindi, equazioni parametriche di r sono ax + bt + c = 0 (3.16) { x = c a b a t y = t Esempio. Trovare un equazione cartesiana per la retta di equazioni parametriche { x = 1 3t y = 2 + t Soluzione. Dalla seconda equazione si ricava t = y 2 e sostituendo nella prima: x = 1 3(y 2), x + 3y 7 = 0. Esempio. Trovare equazioni parametriche per la retta r di equazione cartesiana: 2x 7y + 1 = 0 Soluzione. Dall equazione cartesiana, posto y = t si ottiene: ossia { 2x 7t + 1 = 0 y = t { x = t y = t che fornisce equazioni parametriche della retta r. 17
18 3.6 Distanza di un punto da una retta La distanza di P 0 = (x 0, y 0 ) dalla retta r di equazione ax + by + c = 0 è d = ax 0 + by 0 + c a 2 + b 2 La distanza di P 0 = (x 0, y 0 ) dalla retta r di equazione y = mx + q è d = mx 0 y 0 + q m Prima dimostrazione. Sia r la retta di equazione ax + by + c = ( 0 e R = (x 1, y 1 ) un punto qualsiasi di tale retta. Un a b vettore unitario ortogonale a r è N =, a 2 +b 2 a ). 2 +b 2 P 0 = (x 0, y 0 ) d P N (P 0 R) N R = (x 1, y 1 ) P 0 R r Figura 12: La distanza di P 0 da r coincide con la lunghezza del vettore P N (P 0 R) (proiezione di P 0 R lungo N). Si osservi la figura 12: la proiezione P N (P 0 R) di P 0 R lungo N coincide con la distanza cercata. Si ha P N (P 0 R) = (P 0 R) N = = (x 0 x 1, y 0 y 1 ) a(x 0 x 1 )+b(y 0 y 1 ) a 2 +b 2 ( a, a 2 +b 2 ) b a 2 +b 2 Infine, osservando che ax 1 + by 1 + c = 0 (R = (x 1, y 1 ) sta sulla retta r) si ottiene d = P N (P 0 R) = ax 0 + by 0 + c a 2 + b 2 18
19 Seconda dimostrazione Si osservi la figura 13. I due triangoli grigi sono simili (perchè?). Dalla proporzione si ricava 1 : m = d : mx 0 + q y 0 d = mx 0 + q y 0 m r 1 m d mx 0 + q y 0 P 0 = (x 0, y 0 ) 1 x 0 Figura 13: 19
20 3.7 Fasci di rette Siano r e r due rette distinte del piano di equazione, nell ordine, ax + by + c = 0 a x + b y + c = 0. L equazione del fascio di rette aventi per generatrici r e r è e λ(ax + by + c) + µ(a x + b y + c ) = 0 (3.17) dove λ, µ R. Per ogni coppia (λ, µ) l uguaglianza (3.17) individua una retta di equazione (λa + µa )x + (λb + µb )y + λc + µc = 0 Se le rette generatrici r, r sono incidenti e T è il punto di intersezione allora le rette del fascio (3.17) sono tutte e sole le rette passanti per T mentre se r, r sono parallele (e distinte) le rette del fascio sono tutte e sole le rette parallele a r (r ). È possibile descrivere il fascio di rette utilizzando un solo parametro anzichè due. Infatti, dividendo l equazione (3.17) per λ 0 si ottiene ovvero (ax + by + c) + µ λ (a x + b y + c ) = 0 (ax + by + c) + k(a x + b y + c ) = 0 (3.18) dove k = µ λ. Si tenga presente che in questo caso NON esiste alcun valore di k che permetta di determinare la retta r. In altre parole, l equazione (3.18) fornisce, per ogni k R, una retta del fascio meno una: la retta r. Esempi 1. L equazione del fascio di rette di centro (sostegno) P 0 = (x 0, y 0 ) si scrive spesso nel seguente modo y y 0 = m(x x 0 ) 2. (Fascio di rette parallele a una retta data.) Se la retta r ha equazione y = 2x 3 allora il fascio di rette parallele a r ha equazione y = 2x + q 20
21 4 Esercizi Esercizio 4.1. Vero o Falso? Motivare le risposte per iscritto, sul quaderno. 1. V F Se A = ( 2 3, 1) e Se B = (+ 5 3, 2) allora A + B = ( 7 3, 3) 2. V F Se A = ( 5 2, 0) e Se B = ( 2 3, 1) allora 2A + 3B = (3, 3) 3. V F I vettori A = (2, 5) e B = (6, 15) sono paralleli. 4. V F Se A = (2, 3) e B = ( 4, 5) allora A B = 23. (A B = prodotto scalare di A e B). 5. V F I vettori A = ( 3, 2) e B = (4, 6) sono ortogonali. 6. V F La lunghezza del vettore A = (3, 4) è A = V F Siano A = ( 1, 3) è B = (+2, 2). La distanza d(a, B) = A B = V F Il punto P = ( 1, 2) appartiene alla retta r di equazioni parametriche { x = 2 3t y = 1 t 9. V F Le rette r e s rispettivamente di equazioni parametriche r : { x = t y = t t R s : { x = 2 3u y = 1 + 2u u R sono parallele. 10. V F Le rette r e s rispettivamente di equazioni parametriche r : { x = 1 3 t y = t t R s : { x = 2 6u y = u u R sono ortogonali. Esercizio 4.2. Siano X = (x 1, x 2 ) e Y = (y 1, y 2 ) due vettori di R 2. Scrivere: a) il prodotto scalare X Y ; b) la norma di X e il coseno dell angolo tra X e Y (supponendo X, Y 0); c) l espressione della distanza di X da Y. Esercizio 4.3. Quando due vettori X = (x 1, x 2 ) e Y = (y 1, y 2 ) di R 2 di dicono ortogonali? Stabilire per quali eventuali valori di h R i vettori (2 h, 1) e ( 1, 1 + h) sono ortogonali. 21
22 Esercizio 4.4. Scrivere tutti i vettori che sono multipli del vettore (1, 1) e che hanno lunghezza 1. Esercizio 4.5. Trovare le equazioni parametriche per la retta r che contiene i punti A = (1, 0) e B = (2, 4). Esercizio 4.6. Si considerino i punti A = (1, 4) e B = ( 2 3, 2). parametriche dell asse del segmento AB. Scrivere le equazioni Esercizio 4.7. Le rette r e s di equazioni parametriche r : { x = t y = 2 + t t R s : { x = 2 2u y = u u R sono incidenti? In caso affermativo, trovare le coordinate del punto di intersezione. Esercizio 4.8. Trovare i punti di intersezione della retta r di equazioni parametriche con gli assi cartesiani. { x = 5t y = 2 3t Da equazioni parametriche a equazioni cartesiane (e viceversa): il caso di rette in R 2 Esercizio 4.9. Trovare un equazione cartesiana per la retta di equazioni parametriche { x = 1 3t y = 2 + t Esercizio Trovare equazioni parametriche per la retta r di equazione cartesiana: 2x 7y + 1 = 0 22
Metodo delle coordinate. Rette nel piano. Mauro Saita. Versione provvisoria. Novembre 2015.
 . Rette nel piano. maurosaita@tiscalinet.it Versione provvisoria. Novembre 2015. Indice 1 Cartesio (1596-1650). 2 2 Lo spazio vettoriale R 2 2 2.1 Prodotto scalare. Distanza.............................
. Rette nel piano. maurosaita@tiscalinet.it Versione provvisoria. Novembre 2015. Indice 1 Cartesio (1596-1650). 2 2 Lo spazio vettoriale R 2 2 2.1 Prodotto scalare. Distanza.............................
Note di geometria analitica nel piano
 Note di geometria analitica nel piano e-mail: maurosaita@tiscalinet.it Versione provvisoria. Novembre 2015. 1 Indice 1 Punti e vettori spiccati dall origine 3 1.1 Coordinate......................................
Note di geometria analitica nel piano e-mail: maurosaita@tiscalinet.it Versione provvisoria. Novembre 2015. 1 Indice 1 Punti e vettori spiccati dall origine 3 1.1 Coordinate......................................
1 Rette e piani in R 3
 POLITECNICO DI MILANO. FACOLTÀ DI INGEGNERIA INDUSTRIALE. Analisi e Geometria 1. Sez. D - G. Docenti: Federico G. Lastaria, Mauro Saita, Nadir Zanchetta,. 1 1 Rette e piani in R 3 Una retta parametrizzata
POLITECNICO DI MILANO. FACOLTÀ DI INGEGNERIA INDUSTRIALE. Analisi e Geometria 1. Sez. D - G. Docenti: Federico G. Lastaria, Mauro Saita, Nadir Zanchetta,. 1 1 Rette e piani in R 3 Una retta parametrizzata
Mauro Saita Gennaio Equazioni cartesiane di rette e equazioni parametriche di piani Esempi...
 ette e piani in ette e piani in. Esercizi e-mail: maurosaita@tiscalinet.it Gennaio 2016. Indice 1 Equazioni parametriche della retta 2 1.1 Esempi........................................ 2 2 Equazione cartesiana
ette e piani in ette e piani in. Esercizi e-mail: maurosaita@tiscalinet.it Gennaio 2016. Indice 1 Equazioni parametriche della retta 2 1.1 Esempi........................................ 2 2 Equazione cartesiana
Rette e piani nello spazio Federico Lastaria, Analisi e Geometria 1. Politecnico di Milano Corso di Analisi e Geometria 1
 ette e piani nello spazio Federico Lastaria, Analisi e Geometria 1 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it ette e piani nello spazio. 9 Gennaio
ette e piani nello spazio Federico Lastaria, Analisi e Geometria 1 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it ette e piani nello spazio. 9 Gennaio
Prodotto scalare. Piani nello spazio Federico Lastaria, Analisi e Geometria 1. Politecnico di Milano Corso di Analisi e Geometria 1
 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it Prodotto scalare in R n. Piani nello spazio. 19 Dicembre 2016 Indice 1 Prodotto scalare nello spazio 2
Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it Prodotto scalare in R n. Piani nello spazio. 19 Dicembre 2016 Indice 1 Prodotto scalare nello spazio 2
Prodotto scalare. Piani e rette nello spazio. Federico Lastaria, Analisi e Geometria 1. Politecnico di Milano Corso di Analisi e Geometria 1
 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it Prodotto scalare in n. Piani e rette nello spazio. 17 Gennaio 2016 Indice 1 Prodotto scalare nello spazio
Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it Prodotto scalare in n. Piani e rette nello spazio. 17 Gennaio 2016 Indice 1 Prodotto scalare nello spazio
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
Rette nel piano. Esercizi. Mauro Saita. Versione provvisoria. Novembre { x = 2 + 3t y = 1 2t
 Rette nel piano. Esercizi. e-mail: maurosaita@tiscalinet.it Versione provvisoria. Novembre 205. Esercizi Esercizio.. Nel piano R 2 si considerino i vettori A = ( 2, ) e B = ( 5 2, 3 ). A è parallelo a
Rette nel piano. Esercizi. e-mail: maurosaita@tiscalinet.it Versione provvisoria. Novembre 205. Esercizi Esercizio.. Nel piano R 2 si considerino i vettori A = ( 2, ) e B = ( 5 2, 3 ). A è parallelo a
Geometria analitica: rette e piani
 Geometria analitica: rette e piani parametriche Allineamento nel piano nello spazio Angoli tra rette e distanza 2 2006 Politecnico di Torino 1 Esempio 2 Sia A = (1, 2). Per l interpretazione geometrica
Geometria analitica: rette e piani parametriche Allineamento nel piano nello spazio Angoli tra rette e distanza 2 2006 Politecnico di Torino 1 Esempio 2 Sia A = (1, 2). Per l interpretazione geometrica
Algebra Lineare e Geometria, a.a. 2012/2013
 Diario delle esercitazioni e lezioni per il corso di Algebra Lineare e Geometria, a.a. 2012/2013 (solo la parte per Fisici e Matematici, non ci sono le lezioni del Modulo B) Lidia Stoppino Lezione 1 9
Diario delle esercitazioni e lezioni per il corso di Algebra Lineare e Geometria, a.a. 2012/2013 (solo la parte per Fisici e Matematici, non ci sono le lezioni del Modulo B) Lidia Stoppino Lezione 1 9
GEOMETRIA ANALITICA NELLO SPAZIO (3D Geometry)
 GEOMETRIA ANALITICA NELLO SPAZIO (3D Geometry) SISTEMA DI RIFERIMENTO NELLO SPAZIO La geometria analitica dello spazio è molto simile alla geometria analitica del piano. Per questo motivo le formule sono
GEOMETRIA ANALITICA NELLO SPAZIO (3D Geometry) SISTEMA DI RIFERIMENTO NELLO SPAZIO La geometria analitica dello spazio è molto simile alla geometria analitica del piano. Per questo motivo le formule sono
Una approssimazione allo spazio della fisica classica. Spazi affini euclidei.
 Una approssimazione allo spazio della fisica classica. Spazi affini euclidei. Federico Lastaria. Analisi e Geometria 1. Una introduzione allo spazio della fisica classica. 1/20 Lo spazio E 3 (il piano
Una approssimazione allo spazio della fisica classica. Spazi affini euclidei. Federico Lastaria. Analisi e Geometria 1. Una introduzione allo spazio della fisica classica. 1/20 Lo spazio E 3 (il piano
Corso di Geometria BIAR, BSIR Esercizi 8: soluzioni
 Corso di Geometria 2010-11 BIAR, BSIR Esercizi 8: soluzioni Esercizio 1. a) Disegnare la retta r di equazione cartesiana x 2y 4 = 0. b) Determinare l equazione cartesiana della retta r 1 passante per P
Corso di Geometria 2010-11 BIAR, BSIR Esercizi 8: soluzioni Esercizio 1. a) Disegnare la retta r di equazione cartesiana x 2y 4 = 0. b) Determinare l equazione cartesiana della retta r 1 passante per P
Piano passante per un punto e ortogonale a un vettore (1) Piano passante per un punto e ortogonale a un vettore (2)
 Piano passante per un punto e ortogonale a un vettore (1) Equazione vettoriale del piano passante per un punto e ortogonale a un vettore Un punto X appartiene al piano P passante per il punto X 0 e ortogonale
Piano passante per un punto e ortogonale a un vettore (1) Equazione vettoriale del piano passante per un punto e ortogonale a un vettore Un punto X appartiene al piano P passante per il punto X 0 e ortogonale
x 1 Fig.1 Il punto P = P =
 Geometria di R 2 In questo paragrafo discutiamo le proprietà geometriche elementari del piano Per avere a disposizione delle coordinate nel piano, fissiamo un punto, che chiamiamo l origine Scegliamo poi
Geometria di R 2 In questo paragrafo discutiamo le proprietà geometriche elementari del piano Per avere a disposizione delle coordinate nel piano, fissiamo un punto, che chiamiamo l origine Scegliamo poi
Prodotto interno (prodotto scalare definito positivo)
 Contenuto Prodotto scalare. Lunghezza, ortogonalità. Sistemi e basi ortonormali. Somma diretta: V = U U. Proiezioni. Teorema di Pitagora, disuguaglianza di Cauchy-Schwarz. Angoli. Federico Lastaria. Analisi
Contenuto Prodotto scalare. Lunghezza, ortogonalità. Sistemi e basi ortonormali. Somma diretta: V = U U. Proiezioni. Teorema di Pitagora, disuguaglianza di Cauchy-Schwarz. Angoli. Federico Lastaria. Analisi
Vettori. Capitolo Vettori applicati e vettori liberi
 apitolo 3 Vettori 3.1 Vettori applicati e vettori liberi In questo numero introduciamo il concetto di vettore geometrico su una retta, nel piano e nello spazio che ci consentirà di sviluppare un linguaggio
apitolo 3 Vettori 3.1 Vettori applicati e vettori liberi In questo numero introduciamo il concetto di vettore geometrico su una retta, nel piano e nello spazio che ci consentirà di sviluppare un linguaggio
Corso di Geometria, a.a Ing. Informatica e Automatica Esercizi VI: soluzioni
 Corso di Geometria, a.a. 2009-2010 Ing. Informatica e Automatica Esercizi VI: soluzioni 5 novembre 2009 1 Geometria del piano e prodotto scalare Richiami. Il prodotto scalare di due vettori del piano v,
Corso di Geometria, a.a. 2009-2010 Ing. Informatica e Automatica Esercizi VI: soluzioni 5 novembre 2009 1 Geometria del piano e prodotto scalare Richiami. Il prodotto scalare di due vettori del piano v,
P z. OP x, OP y, OP z sono le proiezioni ortogonali di v sugli assi x, y, z, per cui: OP x = ( v i) i. k j. P x. OP z = ( v k) k
 Richiami di calcolo vettoriale Consideriamo il vettore libero v = OP. Siano P x, P y, P z le proiezioni ortogonali di P sui tre assi cartesiani. v è la diagonale del parallelepipedo costruito su OP x,
Richiami di calcolo vettoriale Consideriamo il vettore libero v = OP. Siano P x, P y, P z le proiezioni ortogonali di P sui tre assi cartesiani. v è la diagonale del parallelepipedo costruito su OP x,
Esercizi geometria analitica nello spazio. Corso di Laurea in Informatica. Docente: Andrea Loi. Correzione
 Esercizi geometria analitica nello spazio Corso di Laurea in Informatica Docente: Andrea Loi Correzione 1. Denotiamo con P 1, P 13, P 3, P 1, P, P 3, P i simmetrici di un punto P rispetto ai piani coordinati
Esercizi geometria analitica nello spazio Corso di Laurea in Informatica Docente: Andrea Loi Correzione 1. Denotiamo con P 1, P 13, P 3, P 1, P, P 3, P i simmetrici di un punto P rispetto ai piani coordinati
Esercitazione di Analisi Matematica II
 Esercitazione di Analisi Matematica II Barbara Balossi 06/04/2017 Esercizi di ripasso Esercizio 1 Sia data l applicazione lineare f : R 3 R 3 definita come f(x, y, z) = ( 2x + y z, x 2y + z, x y). a) Calcolare
Esercitazione di Analisi Matematica II Barbara Balossi 06/04/2017 Esercizi di ripasso Esercizio 1 Sia data l applicazione lineare f : R 3 R 3 definita come f(x, y, z) = ( 2x + y z, x 2y + z, x y). a) Calcolare
Matematica Domande di Algebra e Geometria Analitica
 Matematica Domande di Algebra e Geometria Analitica prof. Vincenzo De Felice 2015 O studianti, studiate le matematiche, e non edificate sanza fondamenti. Leonardo da Vinci (1452-1519). 1 2 Tutto per la
Matematica Domande di Algebra e Geometria Analitica prof. Vincenzo De Felice 2015 O studianti, studiate le matematiche, e non edificate sanza fondamenti. Leonardo da Vinci (1452-1519). 1 2 Tutto per la
Esercizi su curvatura e torsione.
 Esercizi su curvatura e torsione. e-mail: maurosaita@tiscalinet.it Versione provvisoria, gennaio 016. 1 Indice 1 Curvatura e torsione 1.1 Curve parametrizzate alla lunghezza d arco................... 1.
Esercizi su curvatura e torsione. e-mail: maurosaita@tiscalinet.it Versione provvisoria, gennaio 016. 1 Indice 1 Curvatura e torsione 1.1 Curve parametrizzate alla lunghezza d arco................... 1.
ax 1 + bx 2 + c = 0, r : 2x 1 3x = 0.
 . Rette in R ; circonferenze. In questo paragrafo studiamo le rette e le circonferenze in R. Ci sono due modi per descrivere una retta in R : mediante una equazione cartesiana oppure mediante una equazione
. Rette in R ; circonferenze. In questo paragrafo studiamo le rette e le circonferenze in R. Ci sono due modi per descrivere una retta in R : mediante una equazione cartesiana oppure mediante una equazione
Corso di Geometria, a.a Ing. Informatica e Automatica Esercizi VI
 Corso di Geometria, a.a. 009-010 Ing. Informatica e Automatica Esercizi VI 5 novembre 009 Leggere i Capitoli 1-18, 0-4 del libro di testo. Tralasciare il Capitolo 19 (Sottospazi affini). 1 Geometria del
Corso di Geometria, a.a. 009-010 Ing. Informatica e Automatica Esercizi VI 5 novembre 009 Leggere i Capitoli 1-18, 0-4 del libro di testo. Tralasciare il Capitolo 19 (Sottospazi affini). 1 Geometria del
Geometria analitica: rette e piani
 Geometria analitica: rette e piani Equazioni del piano Intersezioni di piani. Rette nello spazio Fasci di piani e rette Intersezioni fra piani e rette Piani e rette ortogonali Piani di forma parametrica
Geometria analitica: rette e piani Equazioni del piano Intersezioni di piani. Rette nello spazio Fasci di piani e rette Intersezioni fra piani e rette Piani e rette ortogonali Piani di forma parametrica
PIANO CARTESIANO e RETTE classi 2 A/D 2009/2010
 PIANO CARTESIANO e RETTE classi 2 A/D 2009/2010 1) PIANO CARTESIANO serve per indicare, identificare, chiamare... ogni PUNTO del piano (ente geometrico) con una coppia di valori numerici (detti COORDINATE).
PIANO CARTESIANO e RETTE classi 2 A/D 2009/2010 1) PIANO CARTESIANO serve per indicare, identificare, chiamare... ogni PUNTO del piano (ente geometrico) con una coppia di valori numerici (detti COORDINATE).
Appunti di geometria analitica dello spazio. di Fabio Maria Antoniali
 Appunti di geometria analitica dello spazio di Fabio Maria Antoniali versione del 23 maggio 2017 1 Un po di teoria 1.1 Vettori e punti 1.1.1 Componenti cartesiane e vettoriali Fissato nello spazio un riferimento
Appunti di geometria analitica dello spazio di Fabio Maria Antoniali versione del 23 maggio 2017 1 Un po di teoria 1.1 Vettori e punti 1.1.1 Componenti cartesiane e vettoriali Fissato nello spazio un riferimento
Capitolo 1 Vettori applicati e geometria dello spazio
 Capitolo 1 Vettori applicati e geometria dello spazio Marco Robutti Facoltà di ingegneria Università degli studi di Pavia Tutorato di geometria e algebra lineare Anno accademico 2014-2015 Definizione (Vettore
Capitolo 1 Vettori applicati e geometria dello spazio Marco Robutti Facoltà di ingegneria Università degli studi di Pavia Tutorato di geometria e algebra lineare Anno accademico 2014-2015 Definizione (Vettore
21. (cenni di) Geometria analitica del piano.
 . (cenni di) Geometria analitica del piano... Definizione. Sia π un piano e sia O un suo punto. Siano i e j due versori ortogonali tra loro e paralleli al piano π. Diremo che la terna ordinata (O, i, j)
. (cenni di) Geometria analitica del piano... Definizione. Sia π un piano e sia O un suo punto. Siano i e j due versori ortogonali tra loro e paralleli al piano π. Diremo che la terna ordinata (O, i, j)
GEOMETRIA ANALITICA 1 IL PIANO CARTESIANO
 GEOMETRI NLITIC 1 IL PINO CRTESINO Il piano cartesiano è costituito da due rette orientate e tra loro perpendicolari chiamate assi cartesiani, generalmente una orizzontale e l altra verticale, sulle quali
GEOMETRI NLITIC 1 IL PINO CRTESINO Il piano cartesiano è costituito da due rette orientate e tra loro perpendicolari chiamate assi cartesiani, generalmente una orizzontale e l altra verticale, sulle quali
Geometria analitica del piano pag 25 Adolfo Scimone. Equazione della retta perpendicolare ad una retta data passante per un punto
 Geometria analitica del piano pag 5 Adolfo Scimone Equazione della retta perpendicolare ad una retta data passante per un punto Consideriamo una retta r di equazione r: ax by sia P ( x y), un punto del
Geometria analitica del piano pag 5 Adolfo Scimone Equazione della retta perpendicolare ad una retta data passante per un punto Consideriamo una retta r di equazione r: ax by sia P ( x y), un punto del
Capitolo 2. Cenni di geometria analitica nel piano
 Capitolo Cenni di geometria analitica nel piano 1 Il piano cartesiano Il piano cartesiano è una rappresentazione grafica del prodotto cartesiano R = R R La rappresentazione grafica è possibile se si crea
Capitolo Cenni di geometria analitica nel piano 1 Il piano cartesiano Il piano cartesiano è una rappresentazione grafica del prodotto cartesiano R = R R La rappresentazione grafica è possibile se si crea
Coordinate cartesiane e coordinate omogenee
 Coordinate cartesiane e coordinate omogenee Fissiamo nel piano un sistema di riferimento cartesiano ortogonale O, x, y, u. Ad ogni punto P del piano possiamo associare le coordinate cartesiane (x, y),
Coordinate cartesiane e coordinate omogenee Fissiamo nel piano un sistema di riferimento cartesiano ortogonale O, x, y, u. Ad ogni punto P del piano possiamo associare le coordinate cartesiane (x, y),
Geometria BAER Canale I Esercizi 11
 Geometria BAER Canale I Esercizi 11 Esercizio 1. Data la retta x = t r : y = t z = 1 si trovi il punto A di r tale che l angolo di r con il vettore AO sia π/2, e il punto B di r tale che l angolo di r
Geometria BAER Canale I Esercizi 11 Esercizio 1. Data la retta x = t r : y = t z = 1 si trovi il punto A di r tale che l angolo di r con il vettore AO sia π/2, e il punto B di r tale che l angolo di r
La retta nel piano. Supponiamo che la retta r sia assegnata attraverso un suo punto P 0 (x 0, y 0 ) e un vettore v (l, m) che ne indichi la direzione.
 La retta nel piano Equazioni vettoriale e parametriche di una retta Supponiamo che la retta r sia assegnata attraverso un suo punto P 0 (x 0, y 0 ) e un vettore v (l, m) che ne indichi la direzione. Condizione
La retta nel piano Equazioni vettoriale e parametriche di una retta Supponiamo che la retta r sia assegnata attraverso un suo punto P 0 (x 0, y 0 ) e un vettore v (l, m) che ne indichi la direzione. Condizione
Analisi Matematica 1 e Matematica 1 Geometria Analitica: Rette
 Analisi Matematica 1 e Matematica 1 Geometria Analitica: Rette Annalisa Amadori e Benedetta Pellacci amadori@uniparthenope.it pellacci@uniparthenope.it Università di Napoli Parthenope Contenuti Nel Piano
Analisi Matematica 1 e Matematica 1 Geometria Analitica: Rette Annalisa Amadori e Benedetta Pellacci amadori@uniparthenope.it pellacci@uniparthenope.it Università di Napoli Parthenope Contenuti Nel Piano
Piano cartesiano e retta
 Piano cartesiano e retta Il punto, la retta e il piano sono concetti primitivi di cui non si da una definizione rigorosa, essi sono i tre enti geometrici fondamentali della geometria euclidea. Osservazione
Piano cartesiano e retta Il punto, la retta e il piano sono concetti primitivi di cui non si da una definizione rigorosa, essi sono i tre enti geometrici fondamentali della geometria euclidea. Osservazione
2 Sistemi lineari. Metodo di riduzione a scala.
 Sistemi lineari. Metodo di riduzione a scala. Esercizio.1 Utilizzando il metodo di eliminazione di Gauss, risolvere i seguenti sistemi lineari: 1. 3. x 1 x + 3x 3 = 1 x 1 x x 3 = x 1 + x + 3x 3 = 5 x 1
Sistemi lineari. Metodo di riduzione a scala. Esercizio.1 Utilizzando il metodo di eliminazione di Gauss, risolvere i seguenti sistemi lineari: 1. 3. x 1 x + 3x 3 = 1 x 1 x x 3 = x 1 + x + 3x 3 = 5 x 1
Lezione 6 Richiami di Geometria Analitica
 1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
Note per il corso di Geometria e algebra lineare Laurea in Ing.Inform. e Com., Ing.Info.Gest.Imp., Informatica. 1 Vettori geometrici 1.
 1 Note per il corso di Geometria e algebra lineare 2016-17 Laurea in Ing.Inform. e om., Ing.Info.Gest.Imp., Informatica 1 Vettori geometrici 1.1 I prodotti cartesiani R R = R 2 e R R R = R 3, costituiti
1 Note per il corso di Geometria e algebra lineare 2016-17 Laurea in Ing.Inform. e om., Ing.Info.Gest.Imp., Informatica 1 Vettori geometrici 1.1 I prodotti cartesiani R R = R 2 e R R R = R 3, costituiti
1.1 Coordinate sulla retta e nel piano; rette nel piano
 1 Sistemi lineari 11 Coordinate sulla retta e nel piano; rette nel piano Coordinate sulla retta Scelti su una retta un primo punto O (origine) ed un diverso secondo punto U (unita ), l identificazione
1 Sistemi lineari 11 Coordinate sulla retta e nel piano; rette nel piano Coordinate sulla retta Scelti su una retta un primo punto O (origine) ed un diverso secondo punto U (unita ), l identificazione
VETTORI. OPERAZIONI CON I VETTORI. RAPPRESENTAZIONE CARTESIANA DEI VETTORI. APPLICAZIONI.
 VETTORI. OPERAZIONI CON I VETTORI. RAPPRESENTAZIONE CARTESIANA DEI VETTORI. APPLICAZIONI. Sia AB un segmento orientato. Ad esso è possibile associare: 1) la direzione, cioè la direzione della retta su
VETTORI. OPERAZIONI CON I VETTORI. RAPPRESENTAZIONE CARTESIANA DEI VETTORI. APPLICAZIONI. Sia AB un segmento orientato. Ad esso è possibile associare: 1) la direzione, cioè la direzione della retta su
Argomenti Capitolo 1 Richiami
 Argomenti Capitolo 1 Richiami L insieme dei numeri reali R si rappresenta geometricamente con l insieme dei punti di una retta orientata su cui sia stato fissato un punto 0 e un segmento unitario. L insieme
Argomenti Capitolo 1 Richiami L insieme dei numeri reali R si rappresenta geometricamente con l insieme dei punti di una retta orientata su cui sia stato fissato un punto 0 e un segmento unitario. L insieme
Corso di Geometria BIAR, BSIR Esercizi 9: soluzioni
 Corso di Geometria 2010-11 BIAR, BSIR Esercizi 9: soluzioni Esercizio 1. Nello spazio sono dati i punti A = (1, 2, 3), B = (2, 4, 5), C = (1, 1, 4). a) Scrivere equazioni parametriche della retta r 1 passante
Corso di Geometria 2010-11 BIAR, BSIR Esercizi 9: soluzioni Esercizio 1. Nello spazio sono dati i punti A = (1, 2, 3), B = (2, 4, 5), C = (1, 1, 4). a) Scrivere equazioni parametriche della retta r 1 passante
Simmetria assiale. Siano a una retta e v = (l, m) un vettore in A 2 (R) (direzione di a non sia proporzionale a v).
 Simmetria assiale Siano a una retta e v = (l, m) un vettore in A 2 (R) (direzione di a non sia proporzionale a v). Definizione La simmetria assiale di asse a e direzione v è la funzione: σ a : { A2 (R)
Simmetria assiale Siano a una retta e v = (l, m) un vettore in A 2 (R) (direzione di a non sia proporzionale a v). Definizione La simmetria assiale di asse a e direzione v è la funzione: σ a : { A2 (R)
Geometria Analitica nello Spazio
 Geometria Analitica nello Spazio Andrea Damiani 4 marzo 2015 Equazione della retta - forma parametrica Se sono dati il punto A(x 0, y 0, z 0 ) e il vettore v (v x, v y, v z ), il generico punto P (x, y,
Geometria Analitica nello Spazio Andrea Damiani 4 marzo 2015 Equazione della retta - forma parametrica Se sono dati il punto A(x 0, y 0, z 0 ) e il vettore v (v x, v y, v z ), il generico punto P (x, y,
Vettori e geometria analitica in R 3 1 / 25
 Vettori e geometria analitica in R 3 1 / 25 Sistemi di riferimento in R 3 e vettori 2 / 25 In fisica, grandezze fondamentali come forze, velocità, campi elettrici e magnetici vengono convenientemente descritte
Vettori e geometria analitica in R 3 1 / 25 Sistemi di riferimento in R 3 e vettori 2 / 25 In fisica, grandezze fondamentali come forze, velocità, campi elettrici e magnetici vengono convenientemente descritte
1. conoscere le nozioni fondamentali della geometria analitica del piano e dello spazio
 Terzo modulo: Geometria analitica Obiettivi 1 conoscere le nozioni fondamentali della geometria analitica del piano e dello spazio interpretare geometricamente equazioni e sistemi algebrici di primo e
Terzo modulo: Geometria analitica Obiettivi 1 conoscere le nozioni fondamentali della geometria analitica del piano e dello spazio interpretare geometricamente equazioni e sistemi algebrici di primo e
= (cioè le due terne di numeri direttori ( devono essere ) proporzionali). Tale uguaglianza non è verificata, poiché risulta ρ
 Alcuni esercizi sullo spazio euclideo R Nel seguito R indicherà lo spazio euclideo tridimensionale standard, dotato del riferimento cartesiano naturale (pag 56-57 del libro Nota: gli esercizi proposti
Alcuni esercizi sullo spazio euclideo R Nel seguito R indicherà lo spazio euclideo tridimensionale standard, dotato del riferimento cartesiano naturale (pag 56-57 del libro Nota: gli esercizi proposti
Corso di Geometria, a.a Ing. Informatica e Automatica Esercizi VII: soluzioni
 Corso di Geometria, a.a. 2009-2010 Ing. Informatica e Automatica Esercizi VII: soluzioni 12 novembre 2009 1 Geometria dello spazio Esercizio 1 Dato il punto P 0 = ( 1, 0, 1) e il piano π : x + y + z 2
Corso di Geometria, a.a. 2009-2010 Ing. Informatica e Automatica Esercizi VII: soluzioni 12 novembre 2009 1 Geometria dello spazio Esercizio 1 Dato il punto P 0 = ( 1, 0, 1) e il piano π : x + y + z 2
Spazi vettoriali euclidei.
 Spazi vettoriali euclidei Prodotto scalare, lunghezza e ortogonalità in R n Consideriamo lo spazio vettoriale R n = { =,,, n R}, n con la somma fra vettori e il prodotto di un vettore per uno scalare definiti
Spazi vettoriali euclidei Prodotto scalare, lunghezza e ortogonalità in R n Consideriamo lo spazio vettoriale R n = { =,,, n R}, n con la somma fra vettori e il prodotto di un vettore per uno scalare definiti
VETTORIALE E PRODOTTO MISTO. PIANI E RETTE DI
 Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA (Edile-Architettura e dell Edilizia) PRODOTTO VETTORIALE E PRODOTTO MISTO. PIANI E RETTE DI R 3. FASCI E STELLE. FORMULE
Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA (Edile-Architettura e dell Edilizia) PRODOTTO VETTORIALE E PRODOTTO MISTO. PIANI E RETTE DI R 3. FASCI E STELLE. FORMULE
Geometria BATR-BCVR Esercizi 9
 Geometria BATR-BCVR 2015-16 Esercizi 9 Esercizio 1. Per ognuna delle matrici A i si trovi una matrice ortogonale M i tale che Mi ta im sia diagonale. ( ) 1 1 2 3 2 A 1 = A 2 1 2 = 1 1 0 2 0 1 Esercizio
Geometria BATR-BCVR 2015-16 Esercizi 9 Esercizio 1. Per ognuna delle matrici A i si trovi una matrice ortogonale M i tale che Mi ta im sia diagonale. ( ) 1 1 2 3 2 A 1 = A 2 1 2 = 1 1 0 2 0 1 Esercizio
Capitolo 1 Vettori applicati e geometria dello spazio
 Capitolo 1 Vettori applicati e geometria dello spazio Marco Robutti Facoltà di ingegneria Università degli studi di Pavia Anno accademico 2017-2018 Tutorato di geometria e algebra lineare Definizione (Vettore
Capitolo 1 Vettori applicati e geometria dello spazio Marco Robutti Facoltà di ingegneria Università degli studi di Pavia Anno accademico 2017-2018 Tutorato di geometria e algebra lineare Definizione (Vettore
CORSO DI LAUREA IN INGEGNERIA MECCANICA A.A PROVA SCRITTA DI GEOMETRIA DEL Corsi dei Proff. M. BORDONI, A.
 CORSO DI LAUREA IN INGEGNERIA MECCANICA A.A. - PROVA SCRITTA DI GEOMETRIA DEL -- Corsi dei Proff. M. BORDONI, A. FOSCHI Esercizio. E data l applicazione lineare L : R 4 R 3 definita dalla matrice A = 3
CORSO DI LAUREA IN INGEGNERIA MECCANICA A.A. - PROVA SCRITTA DI GEOMETRIA DEL -- Corsi dei Proff. M. BORDONI, A. FOSCHI Esercizio. E data l applicazione lineare L : R 4 R 3 definita dalla matrice A = 3
1 Geometria analitica nel piano
 Lezioni di Geometria a.a. 2007-2008 cdl SIE prof. C. Franchetti 1 Geometria analitica nel piano 1.1 Distanza di due punti Siano P 1 = (x 1, y 1 ), P 2 = (x 2, y 2 ) due punti del piano, se d(p 1, P 2 )
Lezioni di Geometria a.a. 2007-2008 cdl SIE prof. C. Franchetti 1 Geometria analitica nel piano 1.1 Distanza di due punti Siano P 1 = (x 1, y 1 ), P 2 = (x 2, y 2 ) due punti del piano, se d(p 1, P 2 )
Prodotto scalare e norma
 Capitolo 7 Prodotto scalare e norma Riprendiamo ora lo studio dei vettori da un punto di vista più geometrico. È noto, per esempio dalla Fisica, che spesso è comodo visualizzare un vettore del piano o
Capitolo 7 Prodotto scalare e norma Riprendiamo ora lo studio dei vettori da un punto di vista più geometrico. È noto, per esempio dalla Fisica, che spesso è comodo visualizzare un vettore del piano o
LEZIONE 9. Figura 9.1.1
 LEZIONE 9 9.1. Equazioni cartesiane di piani. Abbiamo visto come rappresentare parametricamente un piano. Un altro interessante metodo di rappresentazione di un piano nello spazio è tramite la sua equazione
LEZIONE 9 9.1. Equazioni cartesiane di piani. Abbiamo visto come rappresentare parametricamente un piano. Un altro interessante metodo di rappresentazione di un piano nello spazio è tramite la sua equazione
Corso Integrato: Matematica e Statistica. Corso di Matematica (6 CFU)
 Corso di Laurea in Scienze e Tecnologie Agrarie Corso Integrato: Matematica e Statistica Modulo: Matematica (6 CFU) (4 CFU Lezioni + CFU Esercitazioni) Corso di Laurea in Tutela e Gestione del territorio
Corso di Laurea in Scienze e Tecnologie Agrarie Corso Integrato: Matematica e Statistica Modulo: Matematica (6 CFU) (4 CFU Lezioni + CFU Esercitazioni) Corso di Laurea in Tutela e Gestione del territorio
Esercizi geometria analitica nel piano. Corso di Laurea in Informatica A.A. Docente: Andrea Loi. Correzione
 Esercizi geometria analitica nel piano Corso di Laurea in Informatica A.A. Docente: Andrea Loi Correzione 1. Scrivere le equazioni parametriche delle rette r e s di equazioni cartesiane r : 2x y + = 0
Esercizi geometria analitica nel piano Corso di Laurea in Informatica A.A. Docente: Andrea Loi Correzione 1. Scrivere le equazioni parametriche delle rette r e s di equazioni cartesiane r : 2x y + = 0
Corso di Geometria BIAR, BSIR Esercizi 10: soluzioni
 Corso di Geometria 2010-11 BIAR, BSIR Esercizi 10: soluzioni 1 Geometria dello spazio Esercizio 1. Dato il punto P 0 = ( 1, 0, 1) e il piano π : x + y + z 2 = 0, determinare: a) Le equazioni parametriche
Corso di Geometria 2010-11 BIAR, BSIR Esercizi 10: soluzioni 1 Geometria dello spazio Esercizio 1. Dato il punto P 0 = ( 1, 0, 1) e il piano π : x + y + z 2 = 0, determinare: a) Le equazioni parametriche
Esercizi di geometria analitica negli spazi affini Giorgio Ottaviani
 Esercizi di geometria analitica negli spazi affini Giorgio Ottaviani Percorse a cavallo duemila chilometri di steppa russa, superó gli Urali, entró in Siberia, viaggió per quaranta giorni fino a raggiungere
Esercizi di geometria analitica negli spazi affini Giorgio Ottaviani Percorse a cavallo duemila chilometri di steppa russa, superó gli Urali, entró in Siberia, viaggió per quaranta giorni fino a raggiungere
Facsimile di prova d esame Esempio di svolgimento
 Geometria analitica 18 marzo 009 Facsimile di prova d esame Esempio di svolgimento 1 Nello spazio, riferito a coordinate cartesiane ortogonali e monometriche x,y,z, è assegnata la retta r di equazioni
Geometria analitica 18 marzo 009 Facsimile di prova d esame Esempio di svolgimento 1 Nello spazio, riferito a coordinate cartesiane ortogonali e monometriche x,y,z, è assegnata la retta r di equazioni
Geometria BAER Canale A-K Esercizi 9
 Geometria BAER 2016-2017 Canale A-K Esercizi 9 Esercizio 1. Si considerino i punti del piano A (1, 1), B (4, 1), C ( 1/2, 2) (a) Si determini se i punti A, B, C sono allineati e, in caso affermativo, si
Geometria BAER 2016-2017 Canale A-K Esercizi 9 Esercizio 1. Si considerino i punti del piano A (1, 1), B (4, 1), C ( 1/2, 2) (a) Si determini se i punti A, B, C sono allineati e, in caso affermativo, si
ALGEBRA VETTORIALE Corso di Fisica per la Facoltà di Farmacia, Università Gabriele D Annunzio, Chieti-Pescara, Cosimo Del Gratta 2008
 LGER VETTORILE DEFINIZIONE DI VETTORE (1) Sia E lo spazio tridimensionale della geometria euclidea. Consideriamo due punti e appartenenti a E Si chiama segmento orientato, e si indica con (,) il segmento
LGER VETTORILE DEFINIZIONE DI VETTORE (1) Sia E lo spazio tridimensionale della geometria euclidea. Consideriamo due punti e appartenenti a E Si chiama segmento orientato, e si indica con (,) il segmento
Parte 9. Geometria del piano
 Parte 9. Geometria del piano A. Savo Appunti del Corso di Geometria 2013-14 Indice delle sezioni 1 Vettori geometrici del piano, 1 2 Lo spazio vettoriale VO 2, 3 3 Sistemi di riferimento, 8 4 Equazioni
Parte 9. Geometria del piano A. Savo Appunti del Corso di Geometria 2013-14 Indice delle sezioni 1 Vettori geometrici del piano, 1 2 Lo spazio vettoriale VO 2, 3 3 Sistemi di riferimento, 8 4 Equazioni
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria - Edile ed Edile/Architettura
 Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria - Edile ed Edile/Architettura Primo Appello del corso di Geometria 2 Docente F. Flamini, Roma, 22/02/2007 SVOLGIMENTO COMPITO I APPELLO
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria - Edile ed Edile/Architettura Primo Appello del corso di Geometria 2 Docente F. Flamini, Roma, 22/02/2007 SVOLGIMENTO COMPITO I APPELLO
Esercizi Riepilogativi Svolti Esercizio 1: Si consideri R 3 come spazio cartesiano, con riferimento cartesiano standard (O; x
 Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA (Edile-Architettura e dell Edilizia) - a.a. 00/0 I Semestre Docente: Prof. F. Flamini Esercizi Riepilogativi Svolti
Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA (Edile-Architettura e dell Edilizia) - a.a. 00/0 I Semestre Docente: Prof. F. Flamini Esercizi Riepilogativi Svolti
CORSO DI LAUREA IN INGEGNERIA MECCANICA A.A PROVA SCRITTA DI GEOMETRIA DEL Compito A Corso del Prof.
 CORSO DI LAUREA IN INGEGNERIA MECCANICA A.A. 202-203 PROVA SCRITTA DI GEOMETRIA DEL 8-02-3 Compito A Corso del Prof. Manlio BORDONI Esercizio. Sia W il sottospazio vettoriale di R 4 generato dai vettori
CORSO DI LAUREA IN INGEGNERIA MECCANICA A.A. 202-203 PROVA SCRITTA DI GEOMETRIA DEL 8-02-3 Compito A Corso del Prof. Manlio BORDONI Esercizio. Sia W il sottospazio vettoriale di R 4 generato dai vettori
CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA
 CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA FOGLIO DI ESERCIZI 1 GEOMETRIA 2009/10 Esercizio 1.1 (2.2). Determinare l equazione parametrica e Cartesiana della retta dello spazio (a) Passante per i
CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA FOGLIO DI ESERCIZI 1 GEOMETRIA 2009/10 Esercizio 1.1 (2.2). Determinare l equazione parametrica e Cartesiana della retta dello spazio (a) Passante per i
1. LA GEOMETRIA ANALITICA
 LA GEOMETRIA ANALITICA IL PIANO CARTESIANO Coordinate cartesiane Due rette orientate nel piano perpendicolari tra loro, aventi come punto d intersezione il punto O, costituiscono un sistema di riferimento
LA GEOMETRIA ANALITICA IL PIANO CARTESIANO Coordinate cartesiane Due rette orientate nel piano perpendicolari tra loro, aventi come punto d intersezione il punto O, costituiscono un sistema di riferimento
Indice. NUMERI REALI Mauro Saita Versione provvisoria. Ottobre 2017.
 NUMERI REALI Mauro Saita e-mail: maurosaita@tiscalinet.it Versione provvisoria. Ottobre 2017. Indice 1 Numeri reali 2 1.1 Il lato e la diagonale del quadrato sono incommensurabili: la scoperta dei numeri
NUMERI REALI Mauro Saita e-mail: maurosaita@tiscalinet.it Versione provvisoria. Ottobre 2017. Indice 1 Numeri reali 2 1.1 Il lato e la diagonale del quadrato sono incommensurabili: la scoperta dei numeri
Formulario. Coordinate del punto medio M di un segmento di estremi A(x 1, y 1 ) e B(x 2, y 2 ): x1 + x y 2
 Formulario Componenti di un vettore di estremi A(x 1, y 1 e B(x 2, y 2 B A = AB = (x2 x 1 i + (y 2 y 1 j Distanza tra due punti A(x 1, y 1 e B(x 2, y 2 : AB = (x 2 x 1 2 + (y 2 y 1 2 Coordinate del punto
Formulario Componenti di un vettore di estremi A(x 1, y 1 e B(x 2, y 2 B A = AB = (x2 x 1 i + (y 2 y 1 j Distanza tra due punti A(x 1, y 1 e B(x 2, y 2 : AB = (x 2 x 1 2 + (y 2 y 1 2 Coordinate del punto
Lezione 5 Geometria Analitica 1
 Lezione 5 Geometria Analitica 1 Donato A Ciampa In questa lezione richiameremo alcune nozioni della geometria analitica, quali le trasformazioni del piano in se stesso e le varie equazioni relative alla
Lezione 5 Geometria Analitica 1 Donato A Ciampa In questa lezione richiameremo alcune nozioni della geometria analitica, quali le trasformazioni del piano in se stesso e le varie equazioni relative alla
Rette e piani: eq. parametriche di rette
 In A 3 (R) fissiamo un riferimento affine [O, B], con B = ( e 1, e 2, e 3 ). Assi coordinati: asse delle ascisse: [O, < e 1 >], asse delle ordinate: [O, < e 2 >], asse delle quote: [O, < e 3 >]. Piani
In A 3 (R) fissiamo un riferimento affine [O, B], con B = ( e 1, e 2, e 3 ). Assi coordinati: asse delle ascisse: [O, < e 1 >], asse delle ordinate: [O, < e 2 >], asse delle quote: [O, < e 3 >]. Piani
Esercizi complementari
 Esercizi complementari (tratti dagli esercizi del prof. Alberto Del Fra) Relazioni 1) Quali delle seguenti relazioni sono di equivalenza? x, y R {0} xry x/y Q x, y Z xry x + y è divisibile per 17 x, y
Esercizi complementari (tratti dagli esercizi del prof. Alberto Del Fra) Relazioni 1) Quali delle seguenti relazioni sono di equivalenza? x, y R {0} xry x/y Q x, y Z xry x + y è divisibile per 17 x, y
Curve parametrizzate. Esercizi. 1 Curve parametrizzate con parametri arbitrari. Curvatura. Torsione
 Curve parametrizzate. Esercizi Mauro Saita e-mail: maurosaita@tiscalinet.it Versione provvisoria, gennaio 014. 1 1 Curve parametrizzate con parametri arbitrari. Curvatura. Torsione Qui di seguito si riporta
Curve parametrizzate. Esercizi Mauro Saita e-mail: maurosaita@tiscalinet.it Versione provvisoria, gennaio 014. 1 1 Curve parametrizzate con parametri arbitrari. Curvatura. Torsione Qui di seguito si riporta
Esercizi Riepilogativi Svolti
 Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA Edile-Architettura e dell Edilizia SPAZI EUCLIDEI. TRASFORMAZIONI. ORIENTAZIONI. FORMULE DI GEOMETRIA IN R. Docente:
Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA Edile-Architettura e dell Edilizia SPAZI EUCLIDEI. TRASFORMAZIONI. ORIENTAZIONI. FORMULE DI GEOMETRIA IN R. Docente:
RELAZIONI e CORRISPONDENZE
 RELAZIONI e CORRISPONDENZE Siano X e Y due insiemi non vuoti si chiama relazione tra X e Y un qualunque sottoinsieme del prodotto cartesiano: X x Y = {(x,y): x X, y Y} L insieme costituito dai primi (secondi)
RELAZIONI e CORRISPONDENZE Siano X e Y due insiemi non vuoti si chiama relazione tra X e Y un qualunque sottoinsieme del prodotto cartesiano: X x Y = {(x,y): x X, y Y} L insieme costituito dai primi (secondi)
Bivettori. Determinanti. Prodotto vettoriale.
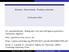 Bivettori. Determinanti. Prodotto vettoriale. 10 Dicembre 2018 Per approfondimenti: bibliografia e siti web sull algebra geometrica (Geometric Algebra): http://geometry.mrao.cam.ac.uk/ https://assets.cambridge.org/052148/0221/sample/0521480221ws.pdf
Bivettori. Determinanti. Prodotto vettoriale. 10 Dicembre 2018 Per approfondimenti: bibliografia e siti web sull algebra geometrica (Geometric Algebra): http://geometry.mrao.cam.ac.uk/ https://assets.cambridge.org/052148/0221/sample/0521480221ws.pdf
Sommario lezioni di geometria
 Sommario lezioni di geometria C. Franchetti November 12, 2006 1 Geometria analitica nel piano 1.1 Distanza di due punti Siano P 1 = (x 1, y 1 ), P 2 = (x 2, y 2 ) due punti del piano, se d(p 1, P 2 ) indica
Sommario lezioni di geometria C. Franchetti November 12, 2006 1 Geometria analitica nel piano 1.1 Distanza di due punti Siano P 1 = (x 1, y 1 ), P 2 = (x 2, y 2 ) due punti del piano, se d(p 1, P 2 ) indica
LEZIONE 9. k, tenendo conto delle formule che permettono di calcolare il prodotto scalare ed il prodotto vettoriale, otteniamo
 LEZIONE 9 9.1. Prodotto misto. Siano dati i tre vettori geometrici u, v, w V 3 (O) definiamo prodotto misto di u, v e w il numero u, v w. Fissiamo un sistema di riferimento O ı j k in S 3. Se u = u x ı
LEZIONE 9 9.1. Prodotto misto. Siano dati i tre vettori geometrici u, v, w V 3 (O) definiamo prodotto misto di u, v e w il numero u, v w. Fissiamo un sistema di riferimento O ı j k in S 3. Se u = u x ı
Proprietà focali delle coniche.
 roprietà focali delle coniche. Mauro Saita e-mail: maurosaita@tiscalinet.it Versione provvisoria, gennaio 2014 Indice 1 Coniche 1 1.1 arabola....................................... 1 1.1.1 roprietà focale
roprietà focali delle coniche. Mauro Saita e-mail: maurosaita@tiscalinet.it Versione provvisoria, gennaio 2014 Indice 1 Coniche 1 1.1 arabola....................................... 1 1.1.1 roprietà focale
Esercizi di Geometria e Algebra per Ingegneria Aerospaziale (nuovo ordinamento)
 Esercizi di Geometria e Algebra per Ingegneria Aerospaziale (nuovo ordinamento) Relazioni 1) Quali delle seguenti relazioni sono di equivalenza? x, y R {0} xry x/y Q x, y Z xry x + y è divisibile per 17
Esercizi di Geometria e Algebra per Ingegneria Aerospaziale (nuovo ordinamento) Relazioni 1) Quali delle seguenti relazioni sono di equivalenza? x, y R {0} xry x/y Q x, y Z xry x + y è divisibile per 17
Esercizi di Geometria Affine
 Esercizi di Geometria Affine Sansonetto Nicola dicembre 01 Geometria Affine nel Piano Esercizio 1. Nel piano affine standard A (R) dotato del riferimento canonico, si consideri la retta τ di equazione
Esercizi di Geometria Affine Sansonetto Nicola dicembre 01 Geometria Affine nel Piano Esercizio 1. Nel piano affine standard A (R) dotato del riferimento canonico, si consideri la retta τ di equazione
Geometria BAER Canale I Esercizi 10
 Geometria BAER Canale I Esercizi 10 Esercizio 1. Data la retta x = t r : y = t z = 1 si trovi il punto A di r tale che l angolo di r con il vettore AO sia π/2, e il punto B di r tale che l angolo di r
Geometria BAER Canale I Esercizi 10 Esercizio 1. Data la retta x = t r : y = t z = 1 si trovi il punto A di r tale che l angolo di r con il vettore AO sia π/2, e il punto B di r tale che l angolo di r
Politecnico di Torino Facoltà di Architettura. Raccolta di esercizi proposti nelle prove scritte
 Politecnico di Torino Facoltà di Architettura Raccolta di esercizi proposti nelle prove scritte relativi a: algebra lineare, vettori e geometria analitica Esercizio. Determinare, al variare del parametro
Politecnico di Torino Facoltà di Architettura Raccolta di esercizi proposti nelle prove scritte relativi a: algebra lineare, vettori e geometria analitica Esercizio. Determinare, al variare del parametro
Lezione 10 27/11/09. = 0 = x y + 2z = 0. Le componenti del vettore v devono essere quindi soluzione del sistema linere omogeneo. { x y +2z = 0 x z = 0
 Lezione 10 7/11/09 Esercizio 1 Nello spazio vettoriale euclideo V 3 sia W il sottospazio generato dai vettori v 1 = 1, 1, 1), v = 0,, 1) Determinare un vettore di W di modulo 3 ortogonale al vettore v
Lezione 10 7/11/09 Esercizio 1 Nello spazio vettoriale euclideo V 3 sia W il sottospazio generato dai vettori v 1 = 1, 1, 1), v = 0,, 1) Determinare un vettore di W di modulo 3 ortogonale al vettore v
a.a MG.VETTORI E RETTE
 a.a. 2013-2014 MG.VETTORI E RETTE Definizione 0.1. Un vettore applicato o segmento orientato dello spazio ordinario è il dato di una coppia ordinata di punti dello spazio, il primo detto punto iniziale
a.a. 2013-2014 MG.VETTORI E RETTE Definizione 0.1. Un vettore applicato o segmento orientato dello spazio ordinario è il dato di una coppia ordinata di punti dello spazio, il primo detto punto iniziale
Condizione di allineamento di tre punti
 LA RETTA L equazione lineare in x e y L equazione: 0 con,,, e non contemporaneamente nulli, si dice equazione lineare nelle due variabili e. Ogni coppia ; tale che: 0 si dice soluzione dell equazione.
LA RETTA L equazione lineare in x e y L equazione: 0 con,,, e non contemporaneamente nulli, si dice equazione lineare nelle due variabili e. Ogni coppia ; tale che: 0 si dice soluzione dell equazione.
GEOMETRIA PIANA. 1) sia verificata l uguaglianza di segmenti AC = CB (ossia C è punto medio del segmento AB);
 VETTORI E GEOMETRIA ANALITICA 1 GEOMETRIA PIANA Segmenti e distanza tra punti. Rette in forma cartesiana e parametrica. Posizioni reciproche di due rette, parallelismo e perpendicolarità. Angoli e distanze.
VETTORI E GEOMETRIA ANALITICA 1 GEOMETRIA PIANA Segmenti e distanza tra punti. Rette in forma cartesiana e parametrica. Posizioni reciproche di due rette, parallelismo e perpendicolarità. Angoli e distanze.
RETTE E PIANI. ove h R. Determinare i valori di h per cui (1) r h e α sono incidenti ed, in tal caso, determinare l angolo ϑ h da essi formato;
 RETTE E PIANI Esercizi Esercizio 1. Nello spazio con riferimento cartesiano ortogonale Oxyz si considerino la retta r h ed il piano α rispettivamente di equazioni x = 1 + t r h : y = 1 t α : x + y + z
RETTE E PIANI Esercizi Esercizio 1. Nello spazio con riferimento cartesiano ortogonale Oxyz si considerino la retta r h ed il piano α rispettivamente di equazioni x = 1 + t r h : y = 1 t α : x + y + z
x + 2y = 0 Soluzione. La retta vettoriale di equazione cartesiana x + 2y = 0.
 Algebra Lineare. a.a. 4-5. Gruppo A-H. Prof. P. Piazza Soluzioni del compito pomeridiano del //5 Esercizio. Sia V = R il piano vettoriale euclideo con base ortonormale standard {e, e }. Determinare le
Algebra Lineare. a.a. 4-5. Gruppo A-H. Prof. P. Piazza Soluzioni del compito pomeridiano del //5 Esercizio. Sia V = R il piano vettoriale euclideo con base ortonormale standard {e, e }. Determinare le
DEFINIZIONE Un vettore (libero) è un ente geometrico rappresentato da un segmento orientato caratterizzato da tre parametri:
 DEFINIZIONE Un vettore (libero) è un ente geometrico rappresentato da un segmento orientato caratterizzato da tre parametri: 1. modulo: la lunghezza del segmento 2. direzione: coincidente con la direzione
DEFINIZIONE Un vettore (libero) è un ente geometrico rappresentato da un segmento orientato caratterizzato da tre parametri: 1. modulo: la lunghezza del segmento 2. direzione: coincidente con la direzione
Soluzioni esercizi complementari
 Soluzioni esercizi complementari Relazioni 1) Quali delle seguenti relazioni sono di equivalenza? x, y R {0} xry x/y Q x, y Z xry x + y è divisibile per 17 x, y Z xry x y X, Y sottoinsiemi di un insieme
Soluzioni esercizi complementari Relazioni 1) Quali delle seguenti relazioni sono di equivalenza? x, y R {0} xry x/y Q x, y Z xry x + y è divisibile per 17 x, y Z xry x y X, Y sottoinsiemi di un insieme
