Equazioni differenziali lineari e oscillatori
|
|
|
- Gastone Neri
- 4 anni fa
- Visualizzazioni
Transcript
1 Equazioni differenziali lineari e oscillatori A.Gaudillière 1 Equazioni differenziali lineari 1.1 Equazione oogenea Un e.d.l. è un equazione d incognita x : I E = K n I intervallo di R, K = R o C della fora ẋt = Atxt + bt t I 1.1 dove A e b sono delle funzioni su I a valori in M n K e K n. Se A e b sono continue il teorea di Cauchy-Lipschitz lineare dà, per ogni t I e x in E, l esistenza e l unicità di souluzioni globali definite sull intero intervallo I del problea di Cauchy { ẋ = Ax + b xt = x Supponiao adesso che x sia una soluzione particolare di 1.1. soluzioni di 1.1 è l insiee delle funzioni x + y con L insiee S delle i.e., y soluzione di x + ẏ = A x + Ay + b ẋ = Ax è chiaata equazione oogenea associata a 1.1. In altre parole, se S è lo spazio vettoriale delle soluzioni di 1.2, allora S = x + S. Per risolvere 1.1 si tratta quindi di trovare una soluzione particolare x e di risolvere l equazione oogenea Equazioni in diensione 1 o a coefficienti costanti Se n = 1 o A è costante, l equazione 1.1 con condizione iniziale xt = x dà, per ogni t I: ẋt Atxt = bt e At ẋt e At Atxt }{{} d dte At xt 1 = e At bt
2 con At := t e, integrando tra t e t, t Asds se A è costante allora At = t t A e At xt x = t xt = e At x + e At t Osservazione: Nel caso A costante ritroviao t e As bsds t e As bsds. 1.3 S = { t e t t A x : x E } e S = x + S. Esepio: Il problea di Cauchy in R { ẋ = x t + 1 t 2 x1 = x 1 ha per unica soluzione su R + la funzione che a ogni t > associa xt = e ln t x 1 + e ln t t 1 e ln s s 2 ds = x 1 + ln t t Osservazione: la forula può anche essere utilizzata coe seplice guida nella ricerca delle soluzioni. 2 Oscillatore aronico forzato e sorzato 2.1 Equazione del oto Si considera un punto ateriale di assa che si uove orizzontalente sotto l azione di tre forze al punto x: i una forza di richiao kx con k >, ii una forza periodica f di periodo T, iii una forza d attrito fluido αẋ con α.. oppure L equazione del oto è ẍ = kx αẋ + f ẍ + α ẋ + ω2 x = f 2.1 2
3 k ẋ con ω :=, o ancora, con x := x, 1 ẋ = ω 2 α x + f }{{}}{{} A costante b periodica 2.2 Abbiao x = x + y dove x è una soluzione particolare e y una soluzione dell equazione oogenea. 2.2 Soluzione dell equazione oogenea La soluzione di ẏ = Ay che vale y in t = è t e ta y. Gli autovalori di A sono le soluzioni di deta XI = X 1 α X = X2 + α X + ω2 =. ω 2 Con := α 2 4ω 2 abbiao tre casi: i se <, i.e., α < 2ω, allora gli autovalori di A sono λ ± := α ± i ω 2 2 α le coponenti y e ẏ di e ta y sono cobinazioni lineari di e tλ + e e tλ, sicché yt = e α α 2 2 t.c cos t ω 2 + ϕ 2 per qualche C e ϕ in R +, 2 2, ii se =, i.e., α = 2ω, allora gli autovalori di A coincidono in α, le coponenti 2 di e ta y sono cobinazioni lineari di e α 2 t e te α 2 t, e per qualche C 1 e C 2 in R, yt = e α 2 t C 1 + C 2 t iii se >, i.e., α > 2ω, allora gli autovalori di A sono α 2 ± α 2 2 ω 2, e per qualche C 1 e C 2 in R. yt = C 1 e α α ω 2 t + C 2 e α + α ω 2 t 3
4 2.3 Ricerca della soluzione particolare Cerchiao una soluzione di con f periodica. Utiliziao: ẋ = Ax + f Teorea 1 Fourier Sia g una funzione T-periodica di classe C k con k 2. Con, per ogni n Z, abbiao e, per ogni t, ĝ n := 1 T con convergenza norale della seria. T gte 2iπ T nt dt li n k ĝ n = n + gt = n Z ĝ n e 2iπ T nt Da ora in poi supporeo che f è C 2. Se troviao, per ogni n Z, x n t.c. allora per linearità avreo x n = A x n + ˆf n e 2iπ T nt } {{ } b nt x := n Z x n t R 2.3 soluzione di x = Ax + b purché x n converga uniforaente. Siccoe b n converge noralente e A è continua, basterà la convergenza unifore di x n vedi dà, per ogni t t x n t = e ta x n + e ta e sa ˆf n e 2iπ T ns ds. Riscrivendo quest equazione in una base dove A trigonalizza si vede al eno nel caso che se α > o ω 2πn esiste una soluzione della fora c T ne 2iπ T nt, entre se α = e ω = 2πn esiste una soluzione della fora c T nte 2iπ T nt. Nel prio caso caso non risonante si trova, risolvendo 2.1: c n := ˆf n ω 2 + α 2iπ n 2π n 2 T T 4
5 e il teorea di Fourier assicura la convergenza della seria che definisce la soluzione particolare xt := c n e 2iπ T nt t R. n Z Se α = ed esiste n N t.c. ω = 2πn T caso risonante si trova, risolvendo 2.1: ˆf n c n = ω 2 per n ±n 2π n 2 T e sicché xt := c n = n Z\{ n ;n } ˆf n 4iπ T n per n = ±n c n e 2iπ T nt + 2tRe { ˆfn 2iω eiω T } t R è una soluzione particolare. Nel caso risonante la soluzione diverge nel tepo. 3 La forula di Liouville Consideriao un sistea lineare su R n ẋt = Atxt e denotiao t Φ t x la soluzione del problea di Cauchy { ẋt = Atxt x = x È iediato verificare che, per ogni λ, µ in R e x, x in R n Φ t λx + µx = λφ t x + µφ t x t. Per ogni t, Φ t è quindi un applicazione lineare su R n a valori in R n. È anche iniettiva e quindi biettiva visto che opera su uno spazio di diensione finita: se Φ t1 x = Φ t1 x = x 1 R n allora x = x per unicità della soluzione del problea di Cauchy { ẋt = Atxt xt 1 = x 1 Per ogni t, Φ t appartienne a gl n R, l insiee degli autoorfisi di R n. Definiao adesso W t := detφ t. Proposizione 3..1 Liouville { t W t = exp 5 } tr Asds
6 Prova: Calcoliao la derivata di W. Abbiao D t W = D t det Φ = D Φt det D t Φ e quindi due differenziali da calcolare. Iniziao con D t Φ. Per ogni x in R n, per ogni h in R, abbiao, in R n : Φ t+h x = Φ t x + hatφ t x + h ɛ x h con li h ɛ x h =. Applicando la forula a x = e 1, e 2,..., e n i vettori di una base di R n otteniao, in LR n : con li h ɛh =. Sicché: Φ t+h = Φ t + hatφ t + h ɛh D t Φ : h R hatφ t LR n. 3.1 Calcoliao adesso, per A GL n R il differenziale del deterinante in A. Per ogni H M n R deta + H = detai + A 1 H = deta deti + A 1 H Scrivendo l ultio deterinante coe soa sulle perutazioni in S n si ottienne deta + H = deta1 + tr A 1 H + H ɛh con li H ɛh = li H ɛ H =. Sicché = deta + detatr A 1 H + H ɛ H D A det : H M n R detatr A 1 H R. 3.2 Quindi, per h R D t W h = detφ t tr Φ 1 t hatφ t = detφ t tr hatφ t Φ 1 t = detφ t tr hat = htr At detφ t = htr AtW t In altre parole dw = tr AtW t. dt La risoluzione di quest equazione differenziale lineare in diensione 1 dà, per ogni t: { t } W t = exp tr Asds W 6
7 Siccoe arriviao a W = detφ = detid = 1 { t } W t = exp tr Asds In particolare, se tr At allora detφ t 1. 4 Risonanza paraetrica: l altalena 4.1 Equazione del oto Se il conducente di un altalena non si uove rispetto all altalena, il oviento è governato dall equazione del pendolo g θ + l sin θ = con θ l angolo tra le corde e la verticale e l la distanza dell asse al centro di assa. L equazione si approssia per θ piccolo in g θ + l θ =. Se il conducente sposta il suo centro di assa piegando e stendendo le gabe il sistea si può odellizzare con l equazione: i.e., introducendo x := θ θ, Supponiao ω periodica di periodo T. θ + ω 2 tθ = 1 ẋt = ω 2 x. t }{{} At 4.2 Applicazione su un periodo Se a t = il sistea è in x, dopo il tepo T sarà in Φ T x. Siccoe A è T -periodico dopo il tepo 2T sarà in Φ T Φ T x, e dopo nt in Φ n T x. Φ T si chiaa applicazione su un periodo. Coe evolve Φ n T n? Gli autovalori di Φ T hanno soa tr Φ T e prodotto detφ T = 1 per la forula di Liouville. Sono soluzioni di X 2 tr Φ T X + 1 = equazione di discriinante := tr Φ T
8 Se <, i.e. tr Φ T < 2, gli autovalori sono coplessi distinti e coniugati. Φ T è equivalente a una rotazione. Se >, i.e. tr Φ T > 2, Φ T ha due autovalori reali distinti. Uno di questi ha quindi un odulo strettaente aggiore di 1, e Φ n T n diverge. Esiste ω : t ωt tale che tr Φ T > 2? 4.3 ω quasi costante Cerchiao di rispondere alla doanda nel caso ωt = ω + ɛat t con a data periodica di periodo T e tale che Calcolo di Φ T nel caso ɛ = sup at = 1. t [;T ] Per dare una rappresentazione atriciale di Φ T basta calcolare le iagini via Φ T dei vettori della base canonica, i.e. calcolare Φ T x per x = θ θ = 1, 1. La soluzione del problea di Cauchy { θ + ω 2 = θ = 1 θ = è t cos ω t, e la soluzione di { θ + ω 2 = θ = θ = 1 è t 1 ω o sin ω T. Sicché, nella base canonica, e φ T = È possibile tr Φ T > 2 per ɛ >? L insiee cos ω T 1 ω o sin ω T ω sin ω T cos ω { = 2 se ω π tr Φ T = 2 cos ω T N, T < 2 altrienti. U := { ω, ɛ R 2 + : tr Φ T < 2 } è un aperto di R 2 +. Quindi, se ω π N, i.e. se T non è un ultiplo del ezzo-periodo T del sistea non perturbato ɛ =, non c è speranza che delle piccole oscillazioni rendino instabile la posizione d equilibrio dell altalena. Invece se ω = ω k := k π 4.1 T 8
9 per k N allora siao sulla frontiera di U. E si può ostrare che V := { ω, ɛ R 2 + : tr Φ T > 2 } va a sfiorare l asse ɛ = in ω k, k = 1, 2,... ad esepio con a costante a tratti di lunghezza T/2 e a valori in { 1; 1} vedi Arnold. Delle piccole oscillazioni del conducente andano l altalena fuori dal regie θ piccolo se 4.1 è soddisfatta. 9
Fisica 1, a.a : Oscillatore armonico
 Fisica 1, a.a. 2014-2015: Oscillatore aronico Anna M. Nobili 1 Oscillatore aronico in una diensione senza dissipazione e in assenza di forze esterne Ad una olla di assa trascurabile, costante elastica
Fisica 1, a.a. 2014-2015: Oscillatore aronico Anna M. Nobili 1 Oscillatore aronico in una diensione senza dissipazione e in assenza di forze esterne Ad una olla di assa trascurabile, costante elastica
Oscillazioni. Definizione Moto circolare uniforme Moto armonico
 Oscillazioni Definizione Moto circolare unifore Moto aronico Moto aronico e oto circolare unifore sinωt La curva a destra dello schizzo è una sinusoide. Abbiao diviso l asse x in parti uguali di angoli
Oscillazioni Definizione Moto circolare unifore Moto aronico Moto aronico e oto circolare unifore sinωt La curva a destra dello schizzo è una sinusoide. Abbiao diviso l asse x in parti uguali di angoli
Prova Scritta di di Meccanica Analitica. 3 luglio Un punto di massa unitaria si muove soggetto al potenziale. V (x) = k 2 x2 + l2 2x 2 x > 0
 Prova Scritta di di Meccanica Analitica 3 luglio 015 Problea 1 Un punto di assa unitaria si uove soggetto al potenziale V (x) = k x + l x x > 0 a) disegnare lo spazio delle fasi e calcolare la frequenza
Prova Scritta di di Meccanica Analitica 3 luglio 015 Problea 1 Un punto di assa unitaria si uove soggetto al potenziale V (x) = k x + l x x > 0 a) disegnare lo spazio delle fasi e calcolare la frequenza
2. calcolare l energia cinetica del corpo e tracciare il suo andamento nel tempo;
 1 Esercizio (tratto dal Problea 4.29 del Mazzoldi 2) Un corpo di assa = 1.5 Kg è agganciato ad una olla di costante elastica k = 2 N/, di lunghezza a riposo = 50 c, fissata ad una parete verticale in x
1 Esercizio (tratto dal Problea 4.29 del Mazzoldi 2) Un corpo di assa = 1.5 Kg è agganciato ad una olla di costante elastica k = 2 N/, di lunghezza a riposo = 50 c, fissata ad una parete verticale in x
Strumenti matematici. La forza intermolecolare. Introduzione al problema fisico Base di uno spazio vettoriale Serie di Fourier
 Struenti ateatici Struenti ateatici Introduzione al problea fisico Base di uno spazio vettoriale Serie di Fourier Serie di Taylor Nueri coplessi Stru. at. Stru. at. Forza di attrazione Forza di repulsione
Struenti ateatici Struenti ateatici Introduzione al problea fisico Base di uno spazio vettoriale Serie di Fourier Serie di Taylor Nueri coplessi Stru. at. Stru. at. Forza di attrazione Forza di repulsione
Fisica 1, a.a : Oscillatore armonico
 Fisica 1, a.a. 2014-2015: Oscillatore aronico Anna M. Nobili 1 Oscillatore aronico in una diensione senza dissipazione e in assenza di forze esterne Ad una olla di assa trascurabile, costante elastica
Fisica 1, a.a. 2014-2015: Oscillatore aronico Anna M. Nobili 1 Oscillatore aronico in una diensione senza dissipazione e in assenza di forze esterne Ad una olla di assa trascurabile, costante elastica
Di seguito, per semplicità, mostreremo esempi in cui il termine di destra della (*) f è costante nel tempo. %%%%%%%
 Note su uso delle equazioni differenziali in eccanica Spesso la risoluzione delle equazioni del oto si ottiene attraverso la risoluzione di equazioni differenziali lineari a coefficienti costanti. L uso
Note su uso delle equazioni differenziali in eccanica Spesso la risoluzione delle equazioni del oto si ottiene attraverso la risoluzione di equazioni differenziali lineari a coefficienti costanti. L uso
LAVORO DI UNA FORZA (1)
 LAVORO ED ENERGIA INTRODUZIONE L introduzione dei concetto di lavoro, energia cinetica ed energia potenziale ci perettono di affrontare i problei della dinaica in un odo nuovo In particolare enuncereo
LAVORO ED ENERGIA INTRODUZIONE L introduzione dei concetto di lavoro, energia cinetica ed energia potenziale ci perettono di affrontare i problei della dinaica in un odo nuovo In particolare enuncereo
Esercizio (tratto dal Problema 2.6 del Mazzoldi)
 1 Esercizio (tratto dal Problea 2.6 del Mazzoldi) Un punto ateriale di assa è sospeso traite un filo verticale ed è collegato al suolo da una olla, di costante elastica 70 N/, che si trova alla lunghezza
1 Esercizio (tratto dal Problea 2.6 del Mazzoldi) Un punto ateriale di assa è sospeso traite un filo verticale ed è collegato al suolo da una olla, di costante elastica 70 N/, che si trova alla lunghezza
1 Oscillazioni libere (oscillatore armonico)
 C. d. L. Ingegneria Inforatica e delle Telecounicazioni A.A. / Fisica Generale PROCESSI OSCILLATORI Oscillazioni liere (oscillatore aronico) Siao in presenza di un sistea la cui equazione che esprie il
C. d. L. Ingegneria Inforatica e delle Telecounicazioni A.A. / Fisica Generale PROCESSI OSCILLATORI Oscillazioni liere (oscillatore aronico) Siao in presenza di un sistea la cui equazione che esprie il
m O Esercizio (tratto dal Problema 4.29 del Mazzoldi 2)
 Esercizio tratto dal Problea 4.29 del Mazzoldi 2) Un corpo di assa 0.5 Kg è agganciato ad un supporto fisso traite una olla di costante elastica 2 N/; il corpo è in quiete nel punto O di un piano orizzontale,
Esercizio tratto dal Problea 4.29 del Mazzoldi 2) Un corpo di assa 0.5 Kg è agganciato ad un supporto fisso traite una olla di costante elastica 2 N/; il corpo è in quiete nel punto O di un piano orizzontale,
Oscillazioni. Definizioni Mo/ armonici Propagazione delle onde
 Oscillazioni Definizioni Mo/ aronici Propagazione delle onde Il oto aronico e il oto circolare unifore sinωt La curva a destra dello schizzo è una sinusoide. Abbiao diviso l asse x in parti uguali di angoli
Oscillazioni Definizioni Mo/ aronici Propagazione delle onde Il oto aronico e il oto circolare unifore sinωt La curva a destra dello schizzo è una sinusoide. Abbiao diviso l asse x in parti uguali di angoli
Esercizio (tratto dal Problema 4.7 del Mazzoldi 2)
 1 Esercizio (tratto dal Problea 4.7 del Mazzoldi 2) Un punto ateriale di assa è sospeso traite un filo verticale ed è collegato al suolo da una olla, di costante elastica = 70 N/, che si trova alla lunghezza
1 Esercizio (tratto dal Problea 4.7 del Mazzoldi 2) Un punto ateriale di assa è sospeso traite un filo verticale ed è collegato al suolo da una olla, di costante elastica = 70 N/, che si trova alla lunghezza
Esercizio (tratto dal Problema 2.6 del Mazzoldi)
 Esercizio (tratto dal Problea 2.6 del Mazzoldi) Un punto ateriale di assa è sospeso traite un filo verticale ed è collegato al suolo da una olla, di costante elastica 70 N/, che si trova alla lunghezza
Esercizio (tratto dal Problea 2.6 del Mazzoldi) Un punto ateriale di assa è sospeso traite un filo verticale ed è collegato al suolo da una olla, di costante elastica 70 N/, che si trova alla lunghezza
Esame 20 Luglio 2017
 Esae 0 Luglio 07 Roberto Bonciani e Paolo Dore Corso di Fisica Generale Dipartiento di ateatica Università degli Studi di Roa La Sapienza Anno Accadeico 06-07 Esae - Fisica Generale I 0 Luglio 07 R. Bonciani,
Esae 0 Luglio 07 Roberto Bonciani e Paolo Dore Corso di Fisica Generale Dipartiento di ateatica Università degli Studi di Roa La Sapienza Anno Accadeico 06-07 Esae - Fisica Generale I 0 Luglio 07 R. Bonciani,
Soluzioni Esonero di Fisica I - Meccanica Anno Accademico
 Soluzioni Esonero di Fisica I - Meccanica Anno Accadeico 2008-2009 Esercizio n.1: Un punto ateriale di assa è inizialente fero su di un piano orizzontale scabro. Siano µ s e µ d i coefficienti di attrito
Soluzioni Esonero di Fisica I - Meccanica Anno Accadeico 2008-2009 Esercizio n.1: Un punto ateriale di assa è inizialente fero su di un piano orizzontale scabro. Siano µ s e µ d i coefficienti di attrito
Lezione 5: Sistemi ad un grado di libertà: l oscillatore elementare (5)
 Lezione 5: Sistei ad un grado di libertà: l oscillatore eleentare (5) Federico Cluni 7 arzo 25 Risposta sotto forzante qualsiasi - Integrale di Duhael. Sovrapposizione degli effetti L equazione del oto
Lezione 5: Sistei ad un grado di libertà: l oscillatore eleentare (5) Federico Cluni 7 arzo 25 Risposta sotto forzante qualsiasi - Integrale di Duhael. Sovrapposizione degli effetti L equazione del oto
Meccanica Dinamica del punto materiale
 Meccanica 17-18 8 Legge fondaentale della dinaica (II legge di Newton) Nota la forza possiao deterinare l equazione del oto d r F a dt al oviento (accelerazione) risaliao alla forza che lo produce Tipi
Meccanica 17-18 8 Legge fondaentale della dinaica (II legge di Newton) Nota la forza possiao deterinare l equazione del oto d r F a dt al oviento (accelerazione) risaliao alla forza che lo produce Tipi
si ottiene (come si può facilmente verificare sostituendo la soluzione proposta nell equazione): 1
 Prisa: legge di Cauchy Per deterinare la relazione tra l indice di rifrazione e la lunghezza d onda delle onde e- si utilizza un odello classico olto seplice, valido per atoi in un gas a che è counque
Prisa: legge di Cauchy Per deterinare la relazione tra l indice di rifrazione e la lunghezza d onda delle onde e- si utilizza un odello classico olto seplice, valido per atoi in un gas a che è counque
LAVORO ED ENERGIA Corso di Fisica per Farmacia, Facoltà di Farmacia, Università G. D Annunzio, Cosimo Del Gratta 2006
 LAVORO ED ENERGIA INTRODUZIONE L introduzione dei concetto di lavoro, energia cinetica ed energia potenziale ci perettono di affrontare i problei della dinaica in un odo nuovo In particolare enuncereo
LAVORO ED ENERGIA INTRODUZIONE L introduzione dei concetto di lavoro, energia cinetica ed energia potenziale ci perettono di affrontare i problei della dinaica in un odo nuovo In particolare enuncereo
Nome Cognome Numero di matricola Coordinata posizione. Quarto compito di Fisica Generale 1 + Esercitazioni, a.a Settembre 2018
 Noe Cognoe Nuero di atricola Coordinata posizione Quarto copito di isica Generale + Esercitazioni, a.a. 207-208 3 Settebre 208 ===================================================================== Preesse
Noe Cognoe Nuero di atricola Coordinata posizione Quarto copito di isica Generale + Esercitazioni, a.a. 207-208 3 Settebre 208 ===================================================================== Preesse
Compito di Analisi Matematica II del 28 giugno 2006 ore 11
 Compito di Analisi Matematica II del 28 giugno 26 ore Esercizio. ( punti) Calcolare il flusso del campo vettoriale F (,, z) = (z, z 2, z 2 ) } uscente dalla frontiera di D = (,, z) R 3 : 2 + z 2, z,. Svolgimento
Compito di Analisi Matematica II del 28 giugno 26 ore Esercizio. ( punti) Calcolare il flusso del campo vettoriale F (,, z) = (z, z 2, z 2 ) } uscente dalla frontiera di D = (,, z) R 3 : 2 + z 2, z,. Svolgimento
# $$ % % # & ' # $ $$ % ( # ( % % $
 !" # $$% % # & ' # $$$% # % %$ !" # X F = f x ˆ ι F = f = f x x F x F x >, f x < F = k xιˆ F = k r F = k r r # * +*,-+. /, $! x k k x + x = pongo ω = > Equazione oraria x t = l cos ωt + φ +l -l
!" # $$% % # & ' # $$$% # % %$ !" # X F = f x ˆ ι F = f = f x x F x F x >, f x < F = k xιˆ F = k r F = k r r # * +*,-+. /, $! x k k x + x = pongo ω = > Equazione oraria x t = l cos ωt + φ +l -l
Meccanica Dinamica del punto materiale
 Meccanica 07-08 7 VARIAZIOE DELLA VELOCITA accelerazione Principio d inerzia Un corpo perane nel suo stato di oto rettilineo unifore (o di quiete) a eno che non intervenga una forza esterna (I Legge di
Meccanica 07-08 7 VARIAZIOE DELLA VELOCITA accelerazione Principio d inerzia Un corpo perane nel suo stato di oto rettilineo unifore (o di quiete) a eno che non intervenga una forza esterna (I Legge di
Oscillazioni e Onde Forza elastica
 Oscillazioni e Onde Forza elastica Riprendiao la legge oraria di una assa attaccata a una olla vincolata in un estreo. Per fare ciò occorre scriverne la legge del oto: ka da cui k d dt d dt k d dt Per
Oscillazioni e Onde Forza elastica Riprendiao la legge oraria di una assa attaccata a una olla vincolata in un estreo. Per fare ciò occorre scriverne la legge del oto: ka da cui k d dt d dt k d dt Per
Forze Centrali e Problema dei Due Corpi
 Forze Centrali e Problea dei Due Corpi In questo capitolo studiao il oto di un punto ateriale sottoposto ad una forza centrale. Uno dei risultati più iportanti che verrà presentato è la derivazione delle
Forze Centrali e Problea dei Due Corpi In questo capitolo studiao il oto di un punto ateriale sottoposto ad una forza centrale. Uno dei risultati più iportanti che verrà presentato è la derivazione delle
Lezione 12. Sottogruppi finiti di ordine fissato. I Teoremi di Sylow.
 Lezione 1 Prerequisiti: Lezioni, 7. ruppi di perutazioni. Riferienti ai testi: [Fd] Sezione.1; [H] Sezione.7; [PC] Sezione 5.1 Sottogruppi finiti di ordine fissato. I Teorei di Sylow. Dal Teorea di Lagrange
Lezione 1 Prerequisiti: Lezioni, 7. ruppi di perutazioni. Riferienti ai testi: [Fd] Sezione.1; [H] Sezione.7; [PC] Sezione 5.1 Sottogruppi finiti di ordine fissato. I Teorei di Sylow. Dal Teorea di Lagrange
Sistemi differenziali 2 2: esercizi svolti. 1 Sistemi lineari Stabilità nei sistemi lineari
 Sistemi differenziali : esercizi svolti 1 Sistemi lineari Stabilità nei sistemi lineari 14 1 Sistemi differenziali : esercizi svolti 1 Sistemi lineari Gli esercizi contrassegnati con il simbolo * presentano
Sistemi differenziali : esercizi svolti 1 Sistemi lineari Stabilità nei sistemi lineari 14 1 Sistemi differenziali : esercizi svolti 1 Sistemi lineari Gli esercizi contrassegnati con il simbolo * presentano
2. Fissato nello spazio un punto O, consideriamo lo spazio vettoriale geometrico
 Algebra lineare (Mateatica C.I.) 0.2.3. Fissato nello spazio un punto O, consideriao lo spazio vettoriale geoetrico S O dei vettori dello spazio con origine nel punto O. Sia π un piano passante per il
Algebra lineare (Mateatica C.I.) 0.2.3. Fissato nello spazio un punto O, consideriao lo spazio vettoriale geoetrico S O dei vettori dello spazio con origine nel punto O. Sia π un piano passante per il
Equazioni differenziali
 Equazioni differenziali Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Equazioni differenziali Analisi Matematica 1 1 / 30 Formulazione del problema In generale
Equazioni differenziali Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Equazioni differenziali Analisi Matematica 1 1 / 30 Formulazione del problema In generale
COGNOME: NOME: MATR.: 1. Si consideri la serie di Fourier data da n 2
 COGNOME: NOME: MATR.: Ingegneria Aerospaziale. Analisi Matematica 2. Compito del 16 febbraio 2019 - PARTE A 1. Si consideri la serie di Fourier data da n 2 sin(2nt). Diamo per buono che esiste il limite
COGNOME: NOME: MATR.: Ingegneria Aerospaziale. Analisi Matematica 2. Compito del 16 febbraio 2019 - PARTE A 1. Si consideri la serie di Fourier data da n 2 sin(2nt). Diamo per buono che esiste il limite
A. Teta APPUNTI DI MECCANICA RAZIONALE. Sistemi unidimensionali. a.a. 2016/17
 A. Teta APPUNTI DI MECCANICA RAZIONALE Sistei unidiensionali a.a. 16/17 1 INDICE 1. Introduzione pag. 3. Conservazione dell energia e riduzione alle quadrature 4 3. Equilibrio e stabilitá 6 4. Moti periodici
A. Teta APPUNTI DI MECCANICA RAZIONALE Sistei unidiensionali a.a. 16/17 1 INDICE 1. Introduzione pag. 3. Conservazione dell energia e riduzione alle quadrature 4 3. Equilibrio e stabilitá 6 4. Moti periodici
Prova Scritta di Fondamenti di Automatica del 21 Giugno 2006 B
 Prova Scritta di Fondaenti di Autoatica del Giugno 6 Studente: Matricola: I F G( Motore Carico ) Per il sistea gru scheatizzato in figura, si assua che il otore sia descritto da una fdt G () s I( (.s +.8s
Prova Scritta di Fondaenti di Autoatica del Giugno 6 Studente: Matricola: I F G( Motore Carico ) Per il sistea gru scheatizzato in figura, si assua che il otore sia descritto da una fdt G () s I( (.s +.8s
Facoltà di Ingegneria Prova scritta di Fisica I
 Facoltà di Ingegneria Prova scritta di Fisica I 6..6 CMPIT C Esercizio n. Un blocco, assiilabile ad un punto ateriale di assa = kg, partendo da fero, scivola da un altezza h = 7 lungo una guida priva di.
Facoltà di Ingegneria Prova scritta di Fisica I 6..6 CMPIT C Esercizio n. Un blocco, assiilabile ad un punto ateriale di assa = kg, partendo da fero, scivola da un altezza h = 7 lungo una guida priva di.
FM1 - Equazioni differenziali e meccanica. Il metodo di variazione delle costanti (Livia Corsi)
 Corso di laurea in Matematica - Anno Accademico 009/010 FM1 - Equazioni differenziali e meccanica Il metodo di variazione delle costanti (Livia Corsi Il metodo di variazione delle costanti è una tecnica
Corso di laurea in Matematica - Anno Accademico 009/010 FM1 - Equazioni differenziali e meccanica Il metodo di variazione delle costanti (Livia Corsi Il metodo di variazione delle costanti è una tecnica
y = cos x y = (y ) 2 + c : giustifichino le due affermazioni. y = y y = y 2 y = y(1 y) y = xy Applicazioni Equazioni delle cinetica chimica:
 Corso di laurea in Chimica Industriale Matematica II A.A. 2015/2016 Argomenti delle lezioni Giovedí 3 marzo - 2 ore. Richiami sulle equazioni e sui metodi utilizzati nel risolverle. Equazioni differenziali.
Corso di laurea in Chimica Industriale Matematica II A.A. 2015/2016 Argomenti delle lezioni Giovedí 3 marzo - 2 ore. Richiami sulle equazioni e sui metodi utilizzati nel risolverle. Equazioni differenziali.
Compito di febbraio 2004
 Copito di febbraio 004 Una laina oogenea di assa, avente la fora di un disco di raggio da cui è stato asportato il triangolo equilatero inscritto ABC, rotola senza strisciare lungo l asse delle ascisse
Copito di febbraio 004 Una laina oogenea di assa, avente la fora di un disco di raggio da cui è stato asportato il triangolo equilatero inscritto ABC, rotola senza strisciare lungo l asse delle ascisse
Foglio di Esercizi 7 Meccanica Razionale a.a. 2018/19 Canale A-L (P. Buttà)
 Foglio di Esercizi 7 Meccanica Razionale a.a. 018/19 Canale A-L P. Buttà Esercizio 1. Sia {O; x, y, z} un sistema di riferimento ortonormale con l asse z diretto secondo la verticale ascendente. Un punto
Foglio di Esercizi 7 Meccanica Razionale a.a. 018/19 Canale A-L P. Buttà Esercizio 1. Sia {O; x, y, z} un sistema di riferimento ortonormale con l asse z diretto secondo la verticale ascendente. Un punto
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 2
 Politecnico di Milano Ingegneria Industriale Analisi e Geometria Preparazione al primo compito in itinere. (a) Mostrare che l insieme B = {b, b, b 3 }, formato dai vettori b = (,, ), b = (,, ) e b 3 =
Politecnico di Milano Ingegneria Industriale Analisi e Geometria Preparazione al primo compito in itinere. (a) Mostrare che l insieme B = {b, b, b 3 }, formato dai vettori b = (,, ), b = (,, ) e b 3 =
Esercizi svolti di Statica e Dinamica
 Esercizi svolti di Statica e Dinaica 1. La assa è sospesa coe in figura. Nota la costante elastica k della olla, deterinarne l allungaento in condizioni di equilibrio. 1.6 Kg ; θ 30 ; k 10 N -1 θ Il diagraa
Esercizi svolti di Statica e Dinaica 1. La assa è sospesa coe in figura. Nota la costante elastica k della olla, deterinarne l allungaento in condizioni di equilibrio. 1.6 Kg ; θ 30 ; k 10 N -1 θ Il diagraa
Prova Scritta di Fondamenti di Automatica del 21 Giugno 2006 A
 Prova Scritta di Fondaenti di Autoatica del Giugno 6 A Studente: Matricola: I F G( Motore Carico ) Per il sistea gru scheatizzato in figura, si assua che il otore sia descritto da una fdt F( G () s I(
Prova Scritta di Fondaenti di Autoatica del Giugno 6 A Studente: Matricola: I F G( Motore Carico ) Per il sistea gru scheatizzato in figura, si assua che il otore sia descritto da una fdt F( G () s I(
ANALISI MATEMATICA 3. esercizi assegnati per la prova scritta del 31 gennaio 2011
 esercizi assegnati per la prova scritta del 31 gennaio 2011 Esercizio 1. Per x > 0 e n N si ponga f n (x) = ln ( n 5 x ) a) Provare l integrabilità delle funzioni f n in (0, + ). 3 + n 4 x 2. b) Studiare
esercizi assegnati per la prova scritta del 31 gennaio 2011 Esercizio 1. Per x > 0 e n N si ponga f n (x) = ln ( n 5 x ) a) Provare l integrabilità delle funzioni f n in (0, + ). 3 + n 4 x 2. b) Studiare
Soluzioni Prova Scritta di di Meccanica Analitica. 17 aprile Un punto di massa unitaria si muove lungo una retta soggetto al potenziale
 Soluzioni Prova Scritta di di Meccanica Analitica 17 aprile 15 Problema 1 Un punto di massa unitaria si muove lungo una retta soggetto al potenziale V x = exp x / a Tracciare il grafico del potenziale
Soluzioni Prova Scritta di di Meccanica Analitica 17 aprile 15 Problema 1 Un punto di massa unitaria si muove lungo una retta soggetto al potenziale V x = exp x / a Tracciare il grafico del potenziale
Equazioni Differenziali
 Università degli Studi di Udine Anno Accademico 2015/2016 Dipartimento di Scienze Matematiche, Informatiche e Fisiche Corso di Laurea in Matematica Equazioni Differenziali Appello del 26 gennaio 2016 N.B.:
Università degli Studi di Udine Anno Accademico 2015/2016 Dipartimento di Scienze Matematiche, Informatiche e Fisiche Corso di Laurea in Matematica Equazioni Differenziali Appello del 26 gennaio 2016 N.B.:
Meccanica Dinamica del punto materiale
 Meccanica 8-9 inaica del punto ateriale 7 Legge fondaentale della dinaica ota la forza possiao deterinare l equazione del oto d r a dt al oviento (accelerazione) risaliao alla forza che lo produce rincipio
Meccanica 8-9 inaica del punto ateriale 7 Legge fondaentale della dinaica ota la forza possiao deterinare l equazione del oto d r a dt al oviento (accelerazione) risaliao alla forza che lo produce rincipio
FM210 - Fisica Matematica 1 Tutorato V - Martha Faraggiana e Enzo Livrieri (soluzioni degli esercizi)
 Corso di laurea in Mateatica - Anno Accadeico 01/013 FM10 - Fisica Mateatica 1 Tutorato V - Martha Faraggiana e Enzo Livrieri (soluzioni degli esercizi) Esercizio 1. Abbiao il sistea eccanico ẍ = dv d
Corso di laurea in Mateatica - Anno Accadeico 01/013 FM10 - Fisica Mateatica 1 Tutorato V - Martha Faraggiana e Enzo Livrieri (soluzioni degli esercizi) Esercizio 1. Abbiao il sistea eccanico ẍ = dv d
SISTEMI DI EQUAZIONI DIFFERENZIALI- ESERCIZI SVOLTI
 SISTEMI DI EQUAZIONI DIFFERENZIALI- ESERCIZI SVOLTI Generalità sui sistemi Sia xt, yt la soluzione del problema di Cauchy Posto vt = e xtyt, calcolare v x = 3x x = y = x y = 0 Sia x = 3x y y = x + y Scrivere
SISTEMI DI EQUAZIONI DIFFERENZIALI- ESERCIZI SVOLTI Generalità sui sistemi Sia xt, yt la soluzione del problema di Cauchy Posto vt = e xtyt, calcolare v x = 3x x = y = x y = 0 Sia x = 3x y y = x + y Scrivere
Equazioni differenziali lineari del secondo ordine a coefficienti costanti
 Equazioni differenziali lineari del secondo ordine a coefficienti costanti 0.1 Introduzione Una equazione differenziale del secondo ordine è una relazione del tipo F (t, y(t), y (t), y (t)) = 0 (1) Definizione
Equazioni differenziali lineari del secondo ordine a coefficienti costanti 0.1 Introduzione Una equazione differenziale del secondo ordine è una relazione del tipo F (t, y(t), y (t), y (t)) = 0 (1) Definizione
Soluzione del compito di Fisica 2. 2 febbraio 2012 (Udine)
 del copito di isica febbraio 1 (Udine) Elettrodinaica E` data una spira conduttrice quadrata di lato L e resistenza R, vincolata sul piano xy, in oto lungo x con velocita` iniziale v. Nel punto x la spira
del copito di isica febbraio 1 (Udine) Elettrodinaica E` data una spira conduttrice quadrata di lato L e resistenza R, vincolata sul piano xy, in oto lungo x con velocita` iniziale v. Nel punto x la spira
Esame di Calcolo delle Probabilità del 7 gennaio 2008 (Corso di Laurea Triennale in Matematica, Università degli Studi di Padova).
 Esae di Calcolo delle Probabilità del 7 gennaio 2008 (Corso di Laurea Triennale in Mateatica, Università degli Studi di Padova). Cognoe Noe Matricola Es. 1 Es. 2 Es. 3 Es. 4 Soa Voto finale Attenzione:
Esae di Calcolo delle Probabilità del 7 gennaio 2008 (Corso di Laurea Triennale in Mateatica, Università degli Studi di Padova). Cognoe Noe Matricola Es. 1 Es. 2 Es. 3 Es. 4 Soa Voto finale Attenzione:
Analisi Matematica I per Ingegneria Gestionale, a.a Scritto del terzo appello, 19 febbraio 2018 Testi 1
 Scritto del terzo appello, 9 febbraio 208 Testi Prima parte, gruppo.. Per ciascuno dei seguenti punti dare le coordinate (polari o cartesiane) che mancano: a) = 0, = ; r = α = b) = 3, = 3; r = α = c) r
Scritto del terzo appello, 9 febbraio 208 Testi Prima parte, gruppo.. Per ciascuno dei seguenti punti dare le coordinate (polari o cartesiane) che mancano: a) = 0, = ; r = α = b) = 3, = 3; r = α = c) r
Compiti d Esame A.A. 2005/2006
 Compiti d Esame A.A. 25/26 UNIVERSITÀ DEGLI STUDI DI PERUGIA A.A. 25/26 I Esercitazione 21 Aprile 26 { y = xy ln(xy) si chiede di dimostrare che: y(1) = 1, (a) ammette un unica soluzione massimale y =
Compiti d Esame A.A. 25/26 UNIVERSITÀ DEGLI STUDI DI PERUGIA A.A. 25/26 I Esercitazione 21 Aprile 26 { y = xy ln(xy) si chiede di dimostrare che: y(1) = 1, (a) ammette un unica soluzione massimale y =
Prova Scritta di di Meccanica Analitica. 12 Gennaio 2017
 Prova Scritta di di Meccanica Analitica 1 Gennaio 017 Problema 1 Si studi il sistema meccanico costituito da un punto materiale di massa unitaria soggetto al potenziale V x) = a lnx) x > 0 x a) Scrivere
Prova Scritta di di Meccanica Analitica 1 Gennaio 017 Problema 1 Si studi il sistema meccanico costituito da un punto materiale di massa unitaria soggetto al potenziale V x) = a lnx) x > 0 x a) Scrivere
Prova Scritta di di Meccanica Analitica. 8 Giugno Problema 1. Si consideri un punto materiale di massa unitaria soggetto ad un potenziale
 Prova Scritta di di Meccanica Analitica 8 Giugno 018 Problema 1 Si consideri un punto materiale di massa unitaria soggetto ad un potenziale V (x) = x x4 Schematizzare lo spazio delle fasi calcolando i
Prova Scritta di di Meccanica Analitica 8 Giugno 018 Problema 1 Si consideri un punto materiale di massa unitaria soggetto ad un potenziale V (x) = x x4 Schematizzare lo spazio delle fasi calcolando i
Equazioni differenziali
 Equazioni differenziali In un equazione differenziale l incognita da trovare è una funzione, di cui è data, dall equazione, una relazione con le sue derivate (fino ad un certo ordine) e la variabile libera:
Equazioni differenziali In un equazione differenziale l incognita da trovare è una funzione, di cui è data, dall equazione, una relazione con le sue derivate (fino ad un certo ordine) e la variabile libera:
Frequenze proprie di una catena unidimensionale
 UNIVERSITA DEGLI STUDI DI CATANIA Dipartiento di Scienze MM FF NN Corso di Laurea di prio livello in Fisica Frequenze proprie di una catena unidiensionale Cristalli e quasicristalli Oscillazioni e onde
UNIVERSITA DEGLI STUDI DI CATANIA Dipartiento di Scienze MM FF NN Corso di Laurea di prio livello in Fisica Frequenze proprie di una catena unidiensionale Cristalli e quasicristalli Oscillazioni e onde
8.4 Calcolo di tensori di inerzia
 1 CAPITL 8. IL CRP RIGID Infatti B I ( u) (P )(P ) [ u (P )] dτ(p ) B (P )(P ) [ u (P )] dτ(p ) B 1 + ρ(p )(P ) [ u (P )] dτ(p ) B B = 1 B I + I Analoga proprietà vale per i oenti di inerzia. 8. Calcolo
1 CAPITL 8. IL CRP RIGID Infatti B I ( u) (P )(P ) [ u (P )] dτ(p ) B (P )(P ) [ u (P )] dτ(p ) B 1 + ρ(p )(P ) [ u (P )] dτ(p ) B B = 1 B I + I Analoga proprietà vale per i oenti di inerzia. 8. Calcolo
Gli strumenti necessari per lo studio
 La potenza di un fucile a olla Sunto E possibile deterinare la potenza di un fucile a olla quando sono note la costante elastica K della olla, la isura d della copressione e la assa del proiettile sparato?
La potenza di un fucile a olla Sunto E possibile deterinare la potenza di un fucile a olla quando sono note la costante elastica K della olla, la isura d della copressione e la assa del proiettile sparato?
6.3 Equazioni lineari del secondo ordine
 si supponga di conoscerne una soluzione ψ(x). Si verifichi che con la sostituzione y(x) = ψ(x) + 1, l equazione diventa lineare nell incognita v(x) v(x). Utilizzando questo metodo, si risolva l equazione
si supponga di conoscerne una soluzione ψ(x). Si verifichi che con la sostituzione y(x) = ψ(x) + 1, l equazione diventa lineare nell incognita v(x) v(x). Utilizzando questo metodo, si risolva l equazione
Autovalori e autovettori
 Autovalori e autovettori Equazione caratteristica Molti problei interessanti in un gran nuero di discipline scientifiche si possono ricondurre alla seguente relazione atriciale Ax = λx dove A è una atrice
Autovalori e autovettori Equazione caratteristica Molti problei interessanti in un gran nuero di discipline scientifiche si possono ricondurre alla seguente relazione atriciale Ax = λx dove A è una atrice
Sistemi di Equazioni Differenziali
 Sistemi di Equazioni Differenziali Nota introduttiva: Lo scopo di queste dispense non è trattare la teoria riguardo ai sistemi di equazioni differenziali, ma solo dare un metodo risolutivo pratico utilizzabile
Sistemi di Equazioni Differenziali Nota introduttiva: Lo scopo di queste dispense non è trattare la teoria riguardo ai sistemi di equazioni differenziali, ma solo dare un metodo risolutivo pratico utilizzabile
Eserciziario di Fisica
 Eserciziario di Fisica Matteo Parriciatu Problea 1 In uno spettroetro di Depster dei fasci colliati di ioni con carica q = 1 18 C attraversano un selettore di velocitá costituito da due piastre etalliche
Eserciziario di Fisica Matteo Parriciatu Problea 1 In uno spettroetro di Depster dei fasci colliati di ioni con carica q = 1 18 C attraversano un selettore di velocitá costituito da due piastre etalliche
Equazioni differenziali del 2 ordine Prof. Ettore Limoli. Sommario. Equazione differenziale omogenea a coefficienti costanti
 Equazioni differenziali del 2 ordine Prof. Ettore Limoli Sommario Equazione differenziale omogenea a coefficienti costanti... 1 Equazione omogenea di esempio... 2 Equazione differenziale non omogenea a
Equazioni differenziali del 2 ordine Prof. Ettore Limoli Sommario Equazione differenziale omogenea a coefficienti costanti... 1 Equazione omogenea di esempio... 2 Equazione differenziale non omogenea a
2) Scrivere la soluzione generale del seguente sistema di equazioni differenziali lineari del primo ordine. y 1 = 2y 1 5y 3 y 2
 Corso di Laurea in Matematica Analisi Matematica 3/Analisi 4 - SOLUZIONI (8/6/5) Docente: Claudia Anedda ) Trovare il limite puntuale della successione di funzioni f k (t) = cos(kt), t R. Stabilire se
Corso di Laurea in Matematica Analisi Matematica 3/Analisi 4 - SOLUZIONI (8/6/5) Docente: Claudia Anedda ) Trovare il limite puntuale della successione di funzioni f k (t) = cos(kt), t R. Stabilire se
1. Quale delle seguenti affermazioni è corretta? (riscrivere la risposta corretta per esteso e solo sul foglio protocollo, non qui sotto): [4 punti]
![1. Quale delle seguenti affermazioni è corretta? (riscrivere la risposta corretta per esteso e solo sul foglio protocollo, non qui sotto): [4 punti] 1. Quale delle seguenti affermazioni è corretta? (riscrivere la risposta corretta per esteso e solo sul foglio protocollo, non qui sotto): [4 punti]](/thumbs/70/63070055.jpg) Problea Un uoo di assa si trova sul bordo estreo di una piattafora di assa, a fora di disco di raggio, che ruota attorno al suo asse verticale con velocità angolare costante ω i. L uoo è inizialente fero
Problea Un uoo di assa si trova sul bordo estreo di una piattafora di assa, a fora di disco di raggio, che ruota attorno al suo asse verticale con velocità angolare costante ω i. L uoo è inizialente fero
Esercizi sulla trasformata di Fourier di distribuzioni raccolti dai temi d esame
 Esercizi sulla trasformata di Fourier di distribuzioni raccolti dai temi d esame Esercizio Sia T > 0 e f : R R la funzione reale T -periodica la cui restrizione all intervallo [0, T ] vale f(t) := t(t
Esercizi sulla trasformata di Fourier di distribuzioni raccolti dai temi d esame Esercizio Sia T > 0 e f : R R la funzione reale T -periodica la cui restrizione all intervallo [0, T ] vale f(t) := t(t
Complementi di Analisi Matematica. Foglio di esercizi n.9 10/04/2017 (Aggiornamento del 26/04/2017)
 Complementi di Analisi Matematica. Foglio di esercizi n.9 0/04/207 (Aggiornamento del 26/04/207) Esercizi su equazioni differenziali Esercizio Tracciare i grafici qualitativi delle soluzioni dell equazione
Complementi di Analisi Matematica. Foglio di esercizi n.9 0/04/207 (Aggiornamento del 26/04/207) Esercizi su equazioni differenziali Esercizio Tracciare i grafici qualitativi delle soluzioni dell equazione
FM210 - Fisica Matematica I
 Corso di laurea in Matematica - Anno Accademico 2/4 FM2 - Fisica Matematica I Prima Prova di Esonero [--2]. (2 punti). Si consideri il sistema lineare ẋ = αx + x 2 + α, ẋ 2 = x + 2α, ẋ = α 2 x 2 con α
Corso di laurea in Matematica - Anno Accademico 2/4 FM2 - Fisica Matematica I Prima Prova di Esonero [--2]. (2 punti). Si consideri il sistema lineare ẋ = αx + x 2 + α, ẋ 2 = x + 2α, ẋ = α 2 x 2 con α
Cognome Nome Matricola Codice ESEMPIO 1
 Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Teorema sulla condizione affinchè φ(t) = e λt sia una soluzione di un equazione differenziale lineare d ordine n a coefficienti costanti. Siano a 1, a
Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Teorema sulla condizione affinchè φ(t) = e λt sia una soluzione di un equazione differenziale lineare d ordine n a coefficienti costanti. Siano a 1, a
GRAFICA E COMPUTER. 19 giugno () PLS-Grafica 19 giugno / 32
 GRAFICA E COMPUTER 19 giugno 2013 3 2 1 0 1 2 3 3 2 1 0 1 2 3 () PLS-Grafica 19 giugno 2013 1 / 32 Equazioni differenziali modellizzano fenomeni (fisici e non) che variano nel tempo partendo da dati noti,
GRAFICA E COMPUTER 19 giugno 2013 3 2 1 0 1 2 3 3 2 1 0 1 2 3 () PLS-Grafica 19 giugno 2013 1 / 32 Equazioni differenziali modellizzano fenomeni (fisici e non) che variano nel tempo partendo da dati noti,
LA RETTA DI REGRESSIONE LINEARE E SISTEMI SOVRADETERMINATI
 LA RETTA DI REGRESSIONE LINEARE E SISTEMI SOVRADETERMINATI MAURIZIO PAOLINI - CORSO PAS CLASSE A048 Dipartiento di Mateatica e Fisica, Università Cattolica, sede di Brescia. paolini@df.unicatt.it E-ail
LA RETTA DI REGRESSIONE LINEARE E SISTEMI SOVRADETERMINATI MAURIZIO PAOLINI - CORSO PAS CLASSE A048 Dipartiento di Mateatica e Fisica, Università Cattolica, sede di Brescia. paolini@df.unicatt.it E-ail
Equazioni Differenziali
 Università degli Studi di Udine Anno Accademico 2012/2013 Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Matematica Equazioni Differenziali Appello del 5 febbraio 2013 N.B.: scrivere
Università degli Studi di Udine Anno Accademico 2012/2013 Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Matematica Equazioni Differenziali Appello del 5 febbraio 2013 N.B.: scrivere
FM210 - Fisica Matematica I
 FM21 - Fisica Matematica I Seconda Prova Scritta [16-2-212] Soluzioni Problema 1 1. Chiamiamo A la matrice del sistema e cerchiamo anzitutto gli autovalori della matrice: l equazione secolare è (λ + 2β)λ
FM21 - Fisica Matematica I Seconda Prova Scritta [16-2-212] Soluzioni Problema 1 1. Chiamiamo A la matrice del sistema e cerchiamo anzitutto gli autovalori della matrice: l equazione secolare è (λ + 2β)λ
Esercitazione 09: Forze d inerzia e oscillatore armonico
 Meccanica e Tecnica delle Costruzioni Meccaniche Esercitazioni del corso. Periodo II Prof. Leonardo BERTINI Ing. Ciro SANTUS Esercitazione 09: Forze d inerzia e oscillatore aronico Indice 1 Moto relativo
Meccanica e Tecnica delle Costruzioni Meccaniche Esercitazioni del corso. Periodo II Prof. Leonardo BERTINI Ing. Ciro SANTUS Esercitazione 09: Forze d inerzia e oscillatore aronico Indice 1 Moto relativo
Traiettorie nello spazio degli stati
 . Traiettorie nello spazio degli stati Per mostrare i tipici andamenti delle traiettorie nello spazio degli stati in funzione della posizione dei poli del sistema si farà riferimento ad un esempio: un
. Traiettorie nello spazio degli stati Per mostrare i tipici andamenti delle traiettorie nello spazio degli stati in funzione della posizione dei poli del sistema si farà riferimento ad un esempio: un
TEMI D ESAME DI ANALISI MATEMATICA I
 TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
Dalla dinamica alla normativa sismica
 Dalla dinaica alla norativa sisica Sistei a più gradi di libertà: analisi statica e analisi odale Catania, 4 arzo 004 Aurelio Ghersi Possibili approcci per valutare la risposta elastica Analisi dinaica,
Dalla dinaica alla norativa sisica Sistei a più gradi di libertà: analisi statica e analisi odale Catania, 4 arzo 004 Aurelio Ghersi Possibili approcci per valutare la risposta elastica Analisi dinaica,
1 Note sulle equazioni differenziali ordinarie
 1 Note sulle equazioni differenziali ordinarie La ricerca di una primitiva su un intervallo, y = f(x), è l esempio più semplice di equazione differenziale cioè la ricerca di una funzione con assegnata
1 Note sulle equazioni differenziali ordinarie La ricerca di una primitiva su un intervallo, y = f(x), è l esempio più semplice di equazione differenziale cioè la ricerca di una funzione con assegnata
y = A(t)y + b(t) (37)
 II-1 Equazioni differenziali lineari. Introduzione Sia M n lo spazio delle matrici quadrate reali di ordine n. In questo paragrafo tratteremo la classe particolare delle equazioni differenziali lineari,
II-1 Equazioni differenziali lineari. Introduzione Sia M n lo spazio delle matrici quadrate reali di ordine n. In questo paragrafo tratteremo la classe particolare delle equazioni differenziali lineari,
R = Esercizio n.6 di pagina 154. calcoliamo f: In quanto. quindi. Calcoliamo l accelerazione alle estremità; questa in generale è:
 Esercizio n.6 di pagina 154. V t = 3100 /s R = 4. 10 7 a =? v ax =? calcoliao f: In quanto velocità del satellite (tangenziale) raggio dell orbita del satellite frequenza del oto del punto accelerazione
Esercizio n.6 di pagina 154. V t = 3100 /s R = 4. 10 7 a =? v ax =? calcoliao f: In quanto velocità del satellite (tangenziale) raggio dell orbita del satellite frequenza del oto del punto accelerazione
COGNOME... NOME... Matricola... Corso Prof... Esame di ANALISI MATEMATICA II - 27 Gennaio cos x
 COGNOME... NOME... Matricola... Corso Prof.... Esame di ANALISI MATEMATICA II - 27 Gennaio 25 A ESERCIZIO. 4 punti) Verificare che la serie 7 2 cos x ) n è convergente per ogni x R, e calcolarne la somma.
COGNOME... NOME... Matricola... Corso Prof.... Esame di ANALISI MATEMATICA II - 27 Gennaio 25 A ESERCIZIO. 4 punti) Verificare che la serie 7 2 cos x ) n è convergente per ogni x R, e calcolarne la somma.
AM2: Tracce delle lezioni- Settimana 12 SISTEMI DI EQUAZIONI DIFFERENZIALI LINEARI
 AM2: Tracce delle lezioni- Settimana 12 SISTEMI DI EQUAZIONI DIFFERENZIALI LINEARI Sia A = (a ij ), i, j = 1,..., n matrice n n. Le soluzioni del sistema differenziale lineare di n equazioni nelle n incognite
AM2: Tracce delle lezioni- Settimana 12 SISTEMI DI EQUAZIONI DIFFERENZIALI LINEARI Sia A = (a ij ), i, j = 1,..., n matrice n n. Le soluzioni del sistema differenziale lineare di n equazioni nelle n incognite
DIARIO DELLE LEZIONI DEL CORSO DI FISICA MATEMATICA A.A. 2013/2014 CORSO DI LAUREA MAGISTRALE IN INGEGNERIA MECCANICA
 DIARIO DELLE LEZIONI DEL CORSO DI FISICA MATEMATICA A.A. 2013/2014 CORSO DI LAUREA MAGISTRALE IN INGEGNERIA MECCANICA DANIELE ANDREUCCI DIP. SCIENZE DI BASE E APPLICATE PER L INGEGNERIA UNIVERSITÀ LA SAPIENZA
DIARIO DELLE LEZIONI DEL CORSO DI FISICA MATEMATICA A.A. 2013/2014 CORSO DI LAUREA MAGISTRALE IN INGEGNERIA MECCANICA DANIELE ANDREUCCI DIP. SCIENZE DI BASE E APPLICATE PER L INGEGNERIA UNIVERSITÀ LA SAPIENZA
FM210 - Fisica Matematica 1 Tutorato 11 ( )
 Corso di laurea in atematica - Anno Accademico 3/4 F - Fisica atematica Tutorato (--) Esercizio. Si calcolino i momenti principali di inerzia dei seguenti corpi rigidi rispetto al loro centro di massa:.
Corso di laurea in atematica - Anno Accademico 3/4 F - Fisica atematica Tutorato (--) Esercizio. Si calcolino i momenti principali di inerzia dei seguenti corpi rigidi rispetto al loro centro di massa:.
2.1 Osservazioni sull esercitazione del
 ¾ ½¾º¼ º¾¼½ Queste note (attualmente, e probabilmente per un bel po ) sono altamente provvisorie e (molto probabilmente) non prive di errori. 2.1 Osservazioni sull esercitazione del 5.3.214 2.1.1 Equazione
¾ ½¾º¼ º¾¼½ Queste note (attualmente, e probabilmente per un bel po ) sono altamente provvisorie e (molto probabilmente) non prive di errori. 2.1 Osservazioni sull esercitazione del 5.3.214 2.1.1 Equazione
Esercizi di preparazione alla PFB
 Università degli Studi Roma Tre - Corso di Laurea in Matematica Esercizi di preparazione alla PFB A.A. 0-03 - Docenti: A. Bruno e G. Gentile Tutori: Sara Lamboglia e Maria Chiara Timpone Parte : Analisi
Università degli Studi Roma Tre - Corso di Laurea in Matematica Esercizi di preparazione alla PFB A.A. 0-03 - Docenti: A. Bruno e G. Gentile Tutori: Sara Lamboglia e Maria Chiara Timpone Parte : Analisi
Appello di Sistemi Dinamici Prova scritta del 22 settembre 2017
 Appello di Sistemi Dinamici Prova scritta del 22 settembre 2017 ẋ = x(µ x 2 )(x µ + 2) 2. Si calcoli la matrice esponenziale della matrice [ ] 2 4. 0 2 3. Dato il sistema differenziale lineare non omogeneo
Appello di Sistemi Dinamici Prova scritta del 22 settembre 2017 ẋ = x(µ x 2 )(x µ + 2) 2. Si calcoli la matrice esponenziale della matrice [ ] 2 4. 0 2 3. Dato il sistema differenziale lineare non omogeneo
meccanica delle vibrazioni laurea magistrale ingegneria meccanica parte 4 modelli matematici per sistemi MDOF
 E vietato ogni utilizzo diverso da quello inerente la preparazione dell esae del corso di @Units eccanica delle vibrazioni laurea agistrale ingegneria eccanica!! parte 4 odelli ateatici per sistei MDOF
E vietato ogni utilizzo diverso da quello inerente la preparazione dell esae del corso di @Units eccanica delle vibrazioni laurea agistrale ingegneria eccanica!! parte 4 odelli ateatici per sistei MDOF
Onde. Fisica Generale - L.Venturelli
 Onde Per descriere olti fenoeni fisici si ricorre a concetti (antitetici): particella onda Utili soprattutto per descriere i diersi odi in cui l energia iene trasferita: particella La ptc è pensata coe
Onde Per descriere olti fenoeni fisici si ricorre a concetti (antitetici): particella onda Utili soprattutto per descriere i diersi odi in cui l energia iene trasferita: particella La ptc è pensata coe
Esercizi 2: Curve dello spazio Soluzioni
 Esercizi 2: Curve dello spazio Soluzioni. Esercizio Si consideri la curva (elica circolare): a α(t) = a sin t, t R, bt dove a >. a) Calcolare curvatura e torsione di α nel generico punto t. b) Determinare
Esercizi 2: Curve dello spazio Soluzioni. Esercizio Si consideri la curva (elica circolare): a α(t) = a sin t, t R, bt dove a >. a) Calcolare curvatura e torsione di α nel generico punto t. b) Determinare
Oscillazioni. Si produce un oscillazione quando un sistema viene perturbato rispetto a una posizione di equilibrio stabile
 Oscillazioni Si produce un oscillazione quando un sistema viene perturbato rispetto a una posizione di equilibrio stabile Caratteristica più evidente del moto oscillatorio è di essere un moto periodico,
Oscillazioni Si produce un oscillazione quando un sistema viene perturbato rispetto a una posizione di equilibrio stabile Caratteristica più evidente del moto oscillatorio è di essere un moto periodico,
Facoltà di Scienze MM.FF.NN. Corso di Laurea in Matematica - A.A Prova scritta di Analisi Matematica II del
 Prova scritta di nalisi Matematica II del 12-06-2001. C1 1) Studiare la convergenza semplice, uniforme e totale della serie di funzioni seguente ( 1) [ n 2 ] n x 1 + n 2 x. n=0 2) Data la funzione (x 2
Prova scritta di nalisi Matematica II del 12-06-2001. C1 1) Studiare la convergenza semplice, uniforme e totale della serie di funzioni seguente ( 1) [ n 2 ] n x 1 + n 2 x. n=0 2) Data la funzione (x 2
11.1. Esercizio. Dato il numero complesso z = 2 + i 2, calcolare z, z, scrivere la rappresentazione trigonometrica di z, calcolare z 8.
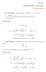 ANALISI Soluzione esercizi gennaio 0.. Esercizio. Dato il numero complesso z = + i, calcolare z, z, scrivere la rappresentazione trigonometrica di z, calcolare z 8. z = i ( ) + ( ) =, π z = arg(z) = 4
ANALISI Soluzione esercizi gennaio 0.. Esercizio. Dato il numero complesso z = + i, calcolare z, z, scrivere la rappresentazione trigonometrica di z, calcolare z 8. z = i ( ) + ( ) =, π z = arg(z) = 4
Esercizi di Fisica Generale Foglio 3. Forze
 31.01.11 Esercizi di Fisica Generale Foglio 3. Forze 1. Un corpo di assa viene sospeso da una olla con costante elastica k, coe in figura (i). La olla si allunga di 0.1. Se ora due corpi identici di assa
31.01.11 Esercizi di Fisica Generale Foglio 3. Forze 1. Un corpo di assa viene sospeso da una olla con costante elastica k, coe in figura (i). La olla si allunga di 0.1. Se ora due corpi identici di assa
I PROVA SCRITTA DI ANALISI MATEMATICA A Ing. [Informatica, Telecomunicazioni](L-Z)
 I PROVA SCRITTA DI ANALISI MATEMATICA A Ing. [Informatica, Telecomunicazioni](L-Z)](/thumbs/75/72088693.jpg) I PROVA SCRITTA DI ANALISI MATEMATICA A Ing. [Informatica, Telecomunicazioni](L-Z) (Alberto PARMEGGIANI) A.A. 1999/2000: 22 Ottobre 1999 (1) COGNOME e NOME (Stampatello): MATRICOLA: N.B. Ogni risposta
I PROVA SCRITTA DI ANALISI MATEMATICA A Ing. [Informatica, Telecomunicazioni](L-Z) (Alberto PARMEGGIANI) A.A. 1999/2000: 22 Ottobre 1999 (1) COGNOME e NOME (Stampatello): MATRICOLA: N.B. Ogni risposta
EQUAZIONI DIFFERENZIALI
 EQUAZIONI DIFFERENZIALI 1 Primo ordine - variabili separabili Sia dato il problema di Cauchy seguente: { y = a(x)b(y) Si proceda come segue y(x 0 ) = y 0 (1) Si calcolino le radici dell equazione b(y)
EQUAZIONI DIFFERENZIALI 1 Primo ordine - variabili separabili Sia dato il problema di Cauchy seguente: { y = a(x)b(y) Si proceda come segue y(x 0 ) = y 0 (1) Si calcolino le radici dell equazione b(y)
se si perturba la corda spostandola in direzione verticale
 1 Onde trasversali in una corda tesa all equilibrio la corda e tesa lungo l asse delle Corda tesa quindi ( t, ) = 0 0 per ogni e per ogni t se si perturba la corda spostandola in direzione verticale t
1 Onde trasversali in una corda tesa all equilibrio la corda e tesa lungo l asse delle Corda tesa quindi ( t, ) = 0 0 per ogni e per ogni t se si perturba la corda spostandola in direzione verticale t
n=1 c n <. Data la seguente serie di trigonometrica + sin cn 1 cos 2 c2 n sin 2nx, n 2a + 3
 Facoltà di Scienze MM. FF. e NN. A.A. 013/014 I Esercitazione 30 Aprile 014 Esercizio 1. Dato il problema di Cauchy x = 3 + cos 3 x, x(0) = 0, studiare esistenza e unicità locale e globale. Provare che
Facoltà di Scienze MM. FF. e NN. A.A. 013/014 I Esercitazione 30 Aprile 014 Esercizio 1. Dato il problema di Cauchy x = 3 + cos 3 x, x(0) = 0, studiare esistenza e unicità locale e globale. Provare che
La lezione di oggi. Equilibrio statico e dinamico. Leve. L elasticità in un solido e la legge di Hooke
 1 La lezione di oggi Equilibrio statico e dinaico Leve L elasticità in un solido e la legge di Hooke Corpo rigido Si definisce corpo rigido un corpo che non si può deforare, qualunque sia l entità delle
1 La lezione di oggi Equilibrio statico e dinaico Leve L elasticità in un solido e la legge di Hooke Corpo rigido Si definisce corpo rigido un corpo che non si può deforare, qualunque sia l entità delle
