Dinamica dei fluidi viscosi

Transcript

1 Dinamica dei flidi viscosi Secondo l'eqazione di Bernolli, qando n flido scorre con regime stazionario in n lngo e stretto condotto orizzontale avente sezione trasversale costante, la pressione lngo il condotto è costante. In pratica, viceversa, si osserva n calo di pressione nella direzione del flsso. In altre parole, è necessaria na differenza di pressione per spingere n flido lngo n condotto orizzontale. Qesta differenza di pressione è necessaria perché allontanandosi dalla sperficie del condotto, la velocità di strati adiacenti del flido è leggermente maggiore della velocità dello strato immediatamente più esterno, e ciascno strato è trattento dalle forze esercitate s di esso dallo strato più interno che ha n moto leggermente più lento Qeste forze tra strati di flido adiacenti sono dette forze viscose. Come consegenza delle forze viscose, la velocità del flido non è costante attraverso n diametro del condotto. Rislta infatti maggiore vicino al centro del condotto e tende a zero dove il flido si trova a contatto con le pareti del condotto, come sarà mostrato in segito Abbiamo visto nella Lezione che il tensore degli sforzi, che esprime le forze di sperficie all interno di n flido ideale pò essere scritto nella forma: 6.) P = pδ ρ i i dove ρ i rappresenta sforzi di taglio, e descrive matematicamente il fenomeno reversibile di trasferimento di momento, dovto al trasporto meccanico di differenti elementi flidi da na posizione all altra dello spazio. i

2 Abbiamo anche visto che l eqazione del moto di n elemento flido si pò scrivere (come l eqazione di continità e dell energia) nella forma di n eqazione di conservazione del tipo qantità fisica ad esempio per la massa per nità di volme: qantità fisica.4) Nel caso della qantità di moto ρ, che e na qantità vettoriale, il tensore degli sforzi P compare come P e assme il significato fisico di flsso della densità di momento dato che P P qantità di moto per nità di volme flsso della qantità di moto per nità di volme

3 L a viscosità o attrito interno tra elementi flidi e invece dovta a n altro tipo di trasferimento (irreversibile) di momento tra pnti dove la velocità e elevata a pnti in ci e inferiore. Il profilo di velocità nello strato di contatto tra de flidi che si movono a differenti velocità é schematizzato in Figra. 6.. Gli strati del flido più veloce vengono rallentati a casa degli sforzi tangenziali con strati più lenti, mentre qesti ltimi vengono trascinati a velocità maggiori. y Esiste dnqe na forza lngo la direzione del flsso () che agisce slla sperficie con normale nella direzione perpendicolare (y) di ci e necessario tenere conto aggingendo n termine al tensore degli sforzi ossia : P = pδ ρ dove σ i è detto tensore di stress viscoso i i i Π i (6.) Figra. 6. Come si è visto la forza di attrito è tanto maggiore qanto maggiore è la differenza di velocità, per ci, in prima approssimazione, si potrà porre dove η è il coefficiente di viscosità e il segno negativo indica che la direzione della forza è contraria alla direzione del gradiente di velocità. Flidi che soddisfano qesta relazione empirica sono detti flidi newtoniani; Dati sperimentali di laboratorio mostrano che la condizione (4.) è molto ben verificata. 6.)

4 Scriviamo ora, nel limite newtoniano e in n caso bidimensionale, n espressione generica per il tensore degli sforzi Π i, che ) deve contenere solo termini del tipo i / in qanto deve annllarsi per = costante. ) deve pre annllarsi per il caso di rotazione niforme, perché anche in tal caso non esistono attriti interni nel flido. Nel caso di rotazione niforme, le velocità sono egali a Ω r, dove Ω è la velocità angolare. Le somme (6.4) sono combinazioni lineari delle componenti del gradiente della velocità che si annllano per = Ω r con Ω = costante. Pertanto il più generale tensore di rango de che soddisfi le sddette condizioni è: (6.5) con a e b indipendenti dalla velocità. Il termine b δ ι è n tensore diagonale, qindi del tipo p δ ι. È possibile sare na forma leggermente diversa con nove costanti in modo da separare la parte di tensore a traccia nlla da qella diagonale:. (6.6) i Πi = η δ i ζ i Le costanti η e ζ sono i coefficiente di viscosità, ambede sono positivi.

5 = Π b a i i i i i = Π ζδ δ η = Π ζ η

6 Alcni atori incldono direttamente l ltimo termine della (6.6) nella parte diagonale di P i, insieme a p δ i, distingendone in tal modo la parte isotropa solo diagonale da qella tangenziale a traccia nlla. Dal pnto di vista sperimentale qeste de possibilità sono indistingibili; dal pnto di vista teorico va invece notato che la pressione isotropa normale che compare anche nell eqazione dell energia rislta incrementata da qesto contribto degli attriti interni. Il termine / i (Π i ) diventa: con e ) ( = Π = = Π η ζ η η ζ η ζ δ η i i i i i i i i = = Utilizzando l espressione del tensore degli sforzi ora ricavata, possiamo riscrivere l eqazione di Elero come con i i i i p Π = ρ δ P P ρf (6.7) (6.8) (6.9) (6.0) (6.)

7 nel caso di flidi viscosi nella forma: (6.) Poiché i coefficienti di viscosità possono essere considerati praticamente costanti nella maggior parte delle applicazioni, otteniamo l eqazione di Navier-Stoes: (6.) dove l ltimo termine compare solo per flidi compressibili dato che per flidi incompressibili si e visto che. = 0 Per flidi incompressibili otteniamo la cosiddetta eqazione di Navier-Stoes (8-4):. (6.4) La qantità (6.5) è detta viscosità cinematica, mentre η è spesso chiamata viscosità dinamica e si verifica sperimentalmente che varia rapidamente con la temperatra.

8 Eqazione di Navier -Stoes Tipici valori dei coefficienti di viscosità per alcni liqidi sono riportati nella tabella

9 L eqazione di Navier-Stoes è dal pnto di vista matematico molto differente dall eqazione di Elero per flidi non viscosi in qanto contiene derivate spaziali del second ordine; e richiede qindi n maggior nmero di condizioni al contorno. La tipica condizione che si impone al contatto con sperfici solide è che la velocità di flsso si annlli = 0: gli esperimenti mostrano infatti che flidi viscosi aderiscono alle pareti (si pensi alla difficoltà di plire na sperficie impolverata semplicemente soffiando aria). La stessa condizione slla velocità nel caso dell eqazione di Elero sovra condizionerebbe il problema; infatti, come abbiamo visto, nei flidi ideali è richiesto solo l annllarsi della velocità normale alla sperficie di contatto n = 0. La forza agente sll area elementare di na sperficie a contatto con il flido; è gale al flsso di momento (non c è trasferimento di momento dovto alla velocità perché slla sperficie di contatto si assme = 0): (6.6) dove n è il versore normale scente dal flido ed entrante nella sperficie; il primo termine è dato dalla normale pressione del flido, il secondo dagli sforzi di taglio, cioè dagli effetti di attrito interno o viscosità.

10 Passiamo ora all analisi dell eqazione della vorticità in presenza dei termini viscosi: prendendo il rotore della (6.4) si ottiene per flidi incompressibili o barotropici:. (6.7) Il teorema di Kelvin non si applica a qesta espressione perché ora le forze viscose possono creare vorticità. Invece rimangono valide le considerazioni circa la possibilità di trattare la dinamica dei flidi incompressibili senza tilizzare l eqazione dell energia che rislta ridondante; i problemi possono essere risolti tilizzando la (6,7) insiseme le eqazioni alle: qando sia noto il coefficiente di viscosità.η Nella trattazione macroscopica i coefficienti di viscosità possono essere solo dedotti da misre sperimentali, perche il modello non consente di entrare nei dettagli delle forze che agiscono a livello microscopico tra le componenti di flidi diversi. Come esempio dell applicazione dell eqazione di Navier-Stoes stdiamo il moto stazionario (/t = 0) di n flido viscoso all interno di n tbo orizzontale di lnghezza l a sezione circolare di raggioa. Si assme n sistema di coodinate spaziali r,θ,, e na simmetria assiale, /θ = 0. Siano (r,θ,) e v(r,θ,) componenti assiale e radiale della velocità

11 L eqazione di Navier-Stoes ( ) = t si scrive: (6.8) (6.9) y r,v, Figra. 6. Non essendovi forze esterne agenti, il moto del flido sarà prodotto da na differenza di pressione p alle de estremità. Si assme il moto del flsso sia in regime laminare per ci anche la componente radiale velocitàv = 0. Pertanto vi sarà n moto solo nella direzione z con profilo (con n valore massimo per r = 0).Le eqazioni (6.9 si ridcono e (6.0)

12 η La componente dell eqazione di Navier-Stoes si ridce a : η (6.) Con η = ν/ρ Definita na variabile moltiplicando per r η ossia (6.) Integrando na volta: ossia (6.) E integrando na seconda volta: (6.4) Le costanti di integrazione si ottengono applicando la condizione al contorno di parete solida in corrispondenza del raggio R del tbo e na condizione al contorno di simmetria al centro del tbo stesso (r = 0). R (6.5)

13 Si ricava da ci rislta che il profilo di velocità nel tbo: (6.6) η è parabolico..la velocità massima si ottiene in corrispondenza dell asse del tbo e vale: η (6.7) La velocità media si ottiene integrando la (9..4) slla sperficie πr della sezione del tbo: Per na = l del condotto: corrispondente a n profilo parabolico, come illstrato in Fig. 4.. La portata attraverso il tbo è: R η (6.8) (6.9) (6.0) che è la ben nota eqazione di Hagen-Poiseille (89-40).

14 La corrente laminare stazionaria che si svilppa in n condotto coassiale, caratterizzato da n raggio interno R i e da n raggio esterno R e, soddisfa alla stessa eqazione (6.) con diverse condizioni al contorno che sono di parete solida d/dr = 0 sia all interno che all esterno. Pertanto: (6.) Il profilo di velocità rislta qindi: (6.) La portata di massa si pò calcolare come flsso di massa nella sezione anlare: (6.4) ovvero (6.5)

15 :Dato che si ottiene infine (6.6) (6.7) Qeste formle sono verificate sperimentalmente nel caso di flssi a bassa velocità ed esperimenti basati s di esse sono in effetti tilizzati per misre di viscosità. Nel 8 Reynolds ha mostrato che all amentare di p e qindi della velocità, il flsso diventa irregolare nello spazio e nel tempo, con creazione di vortici, con il passaggio dal regime regolare (laminare) a qello irregolare (trbolento). Qando il nmero di Reynolds caratteristico di na corrente in n tbo, basato sl diametro D (o sll altezza) e slla velocità media med, (6.8) è inferiore a 0, la corrente di Poiseille rappresenta correttamente il flsso in ttto il tbo.

16 Se invece il valore di R caratteristico è maggiore di 0, pr mantenendosi inferiore al valore critico, possiamo ritenere valida la solzione di Poiseille solo ad na certa distanza dall ingresso del tbo. Infatti si pò in qesto caso ritenere che il profilo di velocità in corrispondenza della sezione di ingresso sia praticamente niforme e che il profilo parabolico si svilppi gradatamente lngo il tbo a casa della presenza delle pareti solide (fig. 9.7). Figra. 6. Il profilo di velocità di ingresso niforme, considerato inizialmente niforme, si modifica di esso a casa della condizione di aderenza tra flido e parete iniziando in prossimità della parete per poi propagarsi verso il centro del tbo mano a mano che amenta la dall ingresso. Contemporaneamente, la velocità sll asse del tbo deve amentare per soddisfare il principio di conservazione della massa. La lnghezza L i rispetto all entrata del tbo in ci si stabilisce il profilo di velocità parabolico (che rimane da lì in poi invariato) è detta lnghezza di ingresso (entry lenght) e pò essere valtata con la formla empirica: I valori di A riportati in letteratra sono 0:0 <A< 0:06.

17 Nmero di Reynolds Consideriamo correnti flide in regime viscoso intorno a oggetti geometricamente simili ma di diverse dimensioni. Le eqazioni dinamiche possono essere scalate tilizzando: - a lnghezza tipica L degli oggetti come nità di lnghezza, - la velocità tipica V della corrente come nità di velocità, - il tempo L/V come nità di tempo e - V /L come nità della vorticità. Si pò pertanto operare n adimensionalizzazione delle eqazioni con: L eqazione della vorticità diventa: dove:. (6.9) (6.40) (6.4) è n nmero adimensionale chiamato nmero di Reynolds. Correnti flide intorno a oggetti geometricamente simili, ma con lo stesso R, soddisfano la stessa eqazione e qindi avranno lo stesso profilo scalato per i differenti valori delle nità di misra.

18 Qesto fatto va sotto il nome di legge di similarità (Reynolds 88). Per stdiare il flsso aerodinamico intorno ad n atomobile oppre intorno ad n aereo, se ne pò simlare l andamento costrendo n modello in miniatra e generare n flsso che abbia lo stesso R. La legge di similarità è qindi n mezzo molto potente per esperimenti di flidodinamica. È sfficiente esegire esperimenti che per na data strttra coprano n intervallo significativo di nmeri di Reynolds e i risltati danno n qadro completo per qalnqe combinazione di L, V, ν. Per R > 000 la sitazione cambia drasticamente; si passa da n regime di flsso laminare stabile ad na sitazione instabile con formazione di trbolenza. In tal senso il caso di alti nmeri Reynolds non corrisponde al limite di basse viscosità e qindi al regime di flido ideale, come sembrerebbe sggerire la (6.4); ciò è dovto proprio al diverso ordine dell eqazione differenziale. Alti nmeri di Reynolds comportano sempre, anche per piccola viscosità, instabilità del flsso con generazione di vorticità.

19 U L U L UL R Il significato fisico del nmero di Reynold si ricava direttamente dall analisi dimensionale dell eqazione di N-S che, per n flido incompressibile, in regime stazionario ed in assenza di forze esterne e di pressioni interne, assme la forma. dove, come giè notato, il termine al I membro rappre senta li forze inerziali applicate all elemento flido e il secondo le forze viscose L analisi dimensionale da che indica l importanza relativa degli effetti inerziali e viscosi: R << ρ 0 Il moto avviene con n sostanziale eqilibrio tra forze di pressione e viscose (moto iniiale o creeping motion). Caratteristiche : Significato fisico di R ρ. il moto e reversibile: se esiste na solzione per la velocità del flido e anche vera la stessa solzione con velocità se i gradienti i pressione sono scambiati.. L interazione viscosa si estende s grandi distanze da n ostacolo

20 R >> Le forze viscose possono essere trascrate perché dominate da qelle inerziali Come notato, il caso di alti nmeri Reynolds non corrisponde al limite di basse viscosità e qindi al regime di flido ideale, come sembrerebbe sggerire la (6.4); perché se si trascra il termine viscoso si ridce di n ordine l eqazione differenziale, modificando in n modo essenziale la descrizione dinamica del moto, in particolare qella delle condizioni al contorno. Qello che fisicamente sccede e che il termine viscoso, pr diventando trascrabile nella maggir parte del volme occpato, mantiene valori elevati in vicinanza di n confine R si

21 Moto per flidi incompressibili intorno a corpi solidi Iniziamo a stdiare moti a basso nmero di Reynolds, R <<. L eqazione della vorticità diventa semplicemente: che, come mostrato da Stoes (84), ammette na solzione analitica nel caso di fl s s o in to rn o a d n a s fe ra. N o n a n a liz z ia m o q i in d e tta g lio il c a lc o lo, p e r il q a le rimandiamo ad esempio al testo di Landa e Lifshitz (Flid Mechanics 987, 0). (6.4) Si ricava che l espressione per il flsso di n flido incompressibile intorno ad na sfera di raggio a con velocità U = Uz all infinito avrà in coordinate sferiche la forma: (6.4) (6.4 4 ) e distribzione di pressione: (6.45) dove r è il versore nella direzione del raggio vettore.

22 Di consegenza si pò calcolare la forza esercitata dal flido slla sfera con la (6.46) che diventa (6.47) in te g ra ta s ll intera sperficie della sfera. Assmendo per asse polare la direzione parallela a U, con le definizioni si ricava che alla sperficie della sfera: e inoltre:. P e rta n to l integrale per F si ridce a: (6.48) (6.49) (6,50) (6.5) che è nota come legge di Stoes; la forza in qestione è chiamata drag nella letteratra scientifica. E così risolto il paradosso di D Alembert: la forza di drag esiste anche per velocità del flsso costante

23 Nel caso di moto ad alto nmero di Reynolds,R >>, la (6.40) sembrerebbe avvicinarsi al limite dei flidi ideali. In realtà, come già accennato, gli esperimenti mostrano che la sitazione è molto più complessa. Alcni esempi di flsso intorno ad n cilindro al crescere di R sono illstrati in Figra Figre 6.4.Flssi attorno n cilindro a crescenti nmeri di Reynolds Il flsso si mantiene laminare fino a R < 0, sccessivamente ai lati si svilppano de vortici a valle del flsso (a destra del cilindro nella figra), che si distaccano alternativamente da n lato e dall altro a formare na stringa contina:

24 alla configrazione si dà il nome di cammino di vortici di Kármán, da von Kármán (9) che ne stdiò le caratteristiche. Qando infine R >0 4 si forma na scia trbolenta, molto più larga di qanto predetto dal modello per R <<. Inoltre si misra sperimentalmente che la forza di frenamento sl cilindro è molto più grande di qella predetta dalla legge di Stoes; l espressione empirica per il frenamento s na sfera è: dove C drag è n fattore adimensionale sperimentale. In Figra 4. è riportato l andamento di C drag in fnzione di R; la legge di Stoes prevedrebbe n andamento (6.5) che è indicato dalla linea tratteggiata. Il valore sperimentale si discosta invece sostanzialmente dalla legge di Stoes per R >0. La spiegazione di qesto comportamento dei flidi viscosi con R >> non aderente al comportamento dei flidi ideali risale a Prandtl (905).

25 I comportamenti di n flido ideale e di n flido viscoso intorno ad n ostacolo solido sono sostanzialmente diversi. Il flido ideale pò avere na velocità tangenziale nelle vicinanze dell ostacolo molto grande, egale (a parte qalche fattore geometrico) sostanzialmente a qella della corrente flida lontano dall ostacolo. Nel caso del flido viscoso invece la velocità tangenziale alla sperficie dell ostacolo deve essere nlla; lontano dall ostacolo la velocità invece sarà molto simile a qella del caso ideale. Ciò comporta che, qando la velocità del flsso cresce in n ristretto strato del flido la velocità dovrà rapidamente passare dal valore nllo alla sperficie dell ostacolo al valore tipico nella corrente. Pertanto in qesto strato limite il termine ν dell eqazione di Navier-Stoes rislterà sempre importante, anche per viscosità deboli, dati i forti gradienti spaziali della velocità. L allargarsi dello strato limite al contatto con ostacoli nella scia trbolenta a valle del flsso pò essere interpretato con analoghe considerazioni. In condizioni i flsso stazionario la componente dell eqazione di Navier-Stoes nella direzione del flsso (Fig. 6.4) è:. (6.5)

26 S lla b a s e d e lle c o n s id e ra z io n i o ra fa tte, c i s i aspetta che i termini / e v /y siano dominanti nello strato limite, per ci o, in ordine di grandezza: Figra 4.4 Strato limite intorno ad na sperficie piana : dove δ è lo spessore dello strato limite e L la distanza a valle dal bordo dell ostacolo. Pertanto ; (6.54) cioè lo spessore dello strato cresce come la radice della distanza verso valle. La viscosità è chiaramente importante nella formazione della scia trbolenta. Natralmente nella scia si formano vortici instabili di varia scala in qanto non è più valido il teorema di Kelvin. L energia di tali vortici trbolenti è prodotta dall interazione tra corrente flida e ostacolo che viene dissipata a valle e qesto amenta pertanto anche la forza di frenamento.

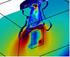
27 Scia dietro n cilindro di 6 mm di diametro, in acqa, visalizzata con bolle di idrogeno. Sopra: velocità 0.5 cm/s (Re = 6), la scia è stazionaria e di lnghezza limitata. Sotto: velocità 8 cm/s (Re = 000), la scia è non stazionaria, con generazione periodicadi vortici controrotanti.