Sistemi lineari a due Equazioni
|
|
|
- Adriano Calo
- 6 anni fa
- Visualizzazioni
Transcript
1 Sistemi lineari a due Equazioni Significato Grafico Posizioni reciproche Tecniche Risolutive: I Metodo Metodo del Confronto diretto (Transitivo) II Metodo Metodo di Sostituzione III Metodo Metodo di Riduzione (Addizione e Sottrazione) IV Metodo Metodo di Cramer - 0
2 Sistemi lineari a due Equazioni Quando due o più equazioni valgono contemporaneamente, si parla si sistema di equazioni. Un sistema di equazioni è risolvibile se il numero delle incognite è uguale (o inferiore) al numero delle equazioni indipendenti. Se il numero delle incognite supera il numero di equazioni, allora il sistema non è risolvibile, ossia, non è possibile attribuire dei valori univoci per le incognite, che quindi, per definizione non sono delle incognite ma bensì delle variabili. L esempio più semplice è quello della retta cartesiana, dove è presente una sola equazione ma contenente due variabili, la e la, che non assumono quindi un valore specifico ma hanno la caratteristica di disporsi lungo una retta. Significato Grafico Intersezione Retta Retta Intersezione Retta Parabola Sistema lineare Sistema non lineare Posizioni Reciproche Due rette possono essere reciprocamente: Incidenti Sistema Determinato Due rette incidenti sono complanari, la loro intersezione genera un punto e il sistema ha una soluzione reale. Parallele Sistema Impossibile Due rette parallele sono complanari, non hanno nessun punto in comune e il sistema non ha alcuna soluzione, si parla di equazioni linearmente dipendenti la cui risoluzione non è possibile. Coincidenti Sistema Indeterminato Due rette coincidenti sono collineari, hanno tutti i loro punti in comune e il sistema non ha una soluzione determinata - 1
3 TECNICHE RISOLUTIVE I Metodo Metodo del Confronto (Proprietà Transitiva) Questo metodo è indicato quando le due rette sono date in forma esplicita Consiste nel risolvere entrambe le equazioni rispetto ad una incognita. In virtù della proprietà transitiva possiamo eguagliare i membri delle due equazioni. Es. Dato il seguente sistema di equazioni rappresentante due rette date nella loro forma esplicita: =4 2 =3 +3 possiamo eguagliare tra loro i membri destri delle equazione ottenendo un equazione polinomiale di primo grado: 4 2 = che si risolve portando a sinistra dell uguale i monomi con l incognita e a destra i termini noti 4 3 = per poi giungere al valore dell incognita = una volta trovato il valore dell incognita x il sistema non è ancora risolto, occorre trovare anche il valore dell altra incognita. A tale scopo occorre prendere il valore della appena trovato ed inserirlo in una delle due equazioni iniziali. È importante considerare che sia una che l altra equazione dovranno portare allo stesso valore per, dunque, si sceglie di considerare la più semplice delle due equazioni, ed eventualmente, si può utilizzare l altra come verifica. con la prima equazione =4 2 h =5 =4 5 2 =18 oppure con la seconda =3 +3 h =5 =3 5+3 =18 le due rette di equazione rispettivamente =4 2, e =3 +3, si incontrano nel punto = 5,18 la soluzione del sistema può quindi essere espressa nel modo seguente: = 5,18-2
4 II Metodo Metodo di Sostituzione Questo metodo è indicato quando una retta è data in forma esplicita e una in forma implicita Consiste nel risolvere un equazione rispetto a una delle due incognite e sostituire l incognita ricavata nell altra equazione. Rimane solo un equazione ad una incognita, si risolve e si ottiene il valore. Sostituendo nel risultato parziale precedente, si ottiene il valore dell altra incognita. Es. = =3 si inserisce la prima equazione nella seconda: = 3 ottenendo un equazione con una incognita, e si risolve: dunque: = 3 ; 3 = 3 6 ; 3 = 3 = Si trova poi l altra incognita inserendo il valore trovato nell equazione ricavata precedentemente: dunque: = 5 2 ; = ; = 5 2 = le due rette si incontrano nel punto: = 1, 7 si esprime quindi la soluzione: = 1, 7-3
5 III Metodo Metodo di Riduzione (Addizione e Sottrazione) Questo metodo è indicato quando le due rette sono date in forma implicita Questa tecnica consiste nel sommare i termini simili tra loro, in modo da ottenere l annullamento di uno dei due termini con l incognita. Es = =3 si può moltiplicare la prima equazione per = = = 5 sommando membro a membro, la sparisce e rimane l equazione ad una incognita: = 5 = per ricavare la seconda incognita, partendo nuovamente dal sistema iniziale 3 +2 = =3 moltiplichiamo la prima per 3 e la seconda per = = =6 sommando membro a membro, la y sparisce e rimane 3 = 6 = 2 le due rette si incontrano nel punto = 2,5 per cui, la soluzione del sistema = 2,5-4
6 IV Metodo Metodo di Cramer Questo metodo è indicato quando le due rette sono date in forma implicita Il metodo di Cramer, nome dato in onore dell omonimo matematico del 700 (Gabriel Cramer ) dà una soluzione esplicita del sistema, attraverso una tecnica che sfrutta le proprietà delle matrice e dei determinati. Questa tecnica ha il vantaggio di essere molto meccanica ed è particolarmente facile da programmare al calcolatore, ad esempio con un foglio elettronico. Dato il seguente sistema di equazioni: + = + = lo si risolve col modo seguente: costruzione delle matrici e calcolo del determinante: = = = = = = si ricavano le incognite x e y nel seguente modo = = Es. Dato il seguente sistema di due equazioni lineari 8 +7 = = 1 si costruiscono le seguenti matrici = = =25 = = =35 = = =15 = = la soluzione è dunque = 5 3,7 3-5
SISTEMI DI DUE EQUAZIONI IN DUE INCOGNITE
 SISTEMI DI DUE EQUAZIONI IN DUE INCOGNITE Un equazione di primo grado in una incognita del tipo, con ha: una sola soluzione (equazione determinata) se nessuna soluzione (equazione impossibile) se tutte
SISTEMI DI DUE EQUAZIONI IN DUE INCOGNITE Un equazione di primo grado in una incognita del tipo, con ha: una sola soluzione (equazione determinata) se nessuna soluzione (equazione impossibile) se tutte
Unità Didattica N 08 I sistemi di primo grado a due incognite 1. U.D. N 08 I sistemi di primo grado a due incognite
 Unità Didattica N 08 I sistemi di primo grado a due incognite 1 U.D. N 08 I sistemi di primo grado a due incognite 01) Coordinate cartesiane 0) I sistemi di primo grado a due incognite 03) Metodo di sostituzione
Unità Didattica N 08 I sistemi di primo grado a due incognite 1 U.D. N 08 I sistemi di primo grado a due incognite 01) Coordinate cartesiane 0) I sistemi di primo grado a due incognite 03) Metodo di sostituzione
SISTEMI LINEARI: Prof.ssa Maddalena Dominijanni
 SISTEMI LINEARI: Prof.ssa Maddalena Dominijanni 1 PERCORSO Cos è un sistema lineare? Come si risolve un sistema lineare Regola di Cramer Metodo di sostituzione Metodo del confronto Metodo di riduzione
SISTEMI LINEARI: Prof.ssa Maddalena Dominijanni 1 PERCORSO Cos è un sistema lineare? Come si risolve un sistema lineare Regola di Cramer Metodo di sostituzione Metodo del confronto Metodo di riduzione
Prof. I. Savoia. SISTEMI LINEARI E RETTA (VERSIONE PROVVISORIA NON ULTIMATA)
 SISTEMI LINEARI E RETTA 1 Proprietà e rappresentazione grafica dei sistemi lineari. I sistemi lineari in due incognite sono insiemi di due equazioni di primo grado, nei qualiciascuna di esse rappresenta
SISTEMI LINEARI E RETTA 1 Proprietà e rappresentazione grafica dei sistemi lineari. I sistemi lineari in due incognite sono insiemi di due equazioni di primo grado, nei qualiciascuna di esse rappresenta
Vettori nel Piano e nello Spazio
 Vettori nel Piano e nello Spazio Caratteristiche di un vettore Componenti di un vettore e Vettore applicato all origine Vettore definito da due punti Operazioni unarie sul vettore Lunghezza di un vettore
Vettori nel Piano e nello Spazio Caratteristiche di un vettore Componenti di un vettore e Vettore applicato all origine Vettore definito da due punti Operazioni unarie sul vettore Lunghezza di un vettore
+2 3 = = =3 + =3 + =8 =15. Sistemi lineari. nelle stesse due incognite. + = + = = = Esempi + =5. Il sistema è determinato
 Sistemi di equazioni SISTEMI LINEARI Un sistema di equazioni è un insieme di equazioni per le quali si cercano eventuali soluzioni comuni. +=7 =1 Ognuna delle due equazioni ha infinite soluzioni. La coppia
Sistemi di equazioni SISTEMI LINEARI Un sistema di equazioni è un insieme di equazioni per le quali si cercano eventuali soluzioni comuni. +=7 =1 Ognuna delle due equazioni ha infinite soluzioni. La coppia
Sistemi di equazioni di primo grado (sistemi lineari)
 Sistemi di equazioni di primo grado (sistemi lineari) DEFINIZIONE Un sistema di equazioni è un insieme di due o più equazioni, tutte nelle stesse incognite, di cui cerchiamo soluzioni comuni. Esempi 1.
Sistemi di equazioni di primo grado (sistemi lineari) DEFINIZIONE Un sistema di equazioni è un insieme di due o più equazioni, tutte nelle stesse incognite, di cui cerchiamo soluzioni comuni. Esempi 1.
B6. Sistemi di primo grado
 B6. Sistemi di primo grado Nelle equazioni l obiettivo è determinare il valore dell incognita che verifica l equazione. Tale valore, se c è, è detto soluzione. In un sistema di equazioni l obiettivo è
B6. Sistemi di primo grado Nelle equazioni l obiettivo è determinare il valore dell incognita che verifica l equazione. Tale valore, se c è, è detto soluzione. In un sistema di equazioni l obiettivo è
Sistemi di 1 grado in due incognite
 Sistemi di 1 grado in due incognite Problema In un cortile ci sono polli e conigli: in totale le teste sono 7 e zampe 18. Quanti polli e quanti conigli ci sono nel cortile? Soluzione Indichiamo con e con
Sistemi di 1 grado in due incognite Problema In un cortile ci sono polli e conigli: in totale le teste sono 7 e zampe 18. Quanti polli e quanti conigli ci sono nel cortile? Soluzione Indichiamo con e con
Programma di Matematica Anno Scolastico 2014/2015 Classe 3M
 Programma di Matematica Anno Scolastico 204/205 Classe 3M Modulo : Richiami calcolo letterale Il prodotto notevole di una somma per una di erenza (a+b)(a (a + b) 2 : Cubo di un binomio (a + b) 3 : b):
Programma di Matematica Anno Scolastico 204/205 Classe 3M Modulo : Richiami calcolo letterale Il prodotto notevole di una somma per una di erenza (a+b)(a (a + b) 2 : Cubo di un binomio (a + b) 3 : b):
GEOMETRIA ANALITICA ESERCIZI CON SOLUZIONI
 utore: Enrico Manfucci - 0/0/0 GEOMETRI NLITIC ESERCIZI CON SOLUZIONI. Posizionare nel piano cartesiano e calcolare la distanza delle seguenti coppie di punti: a. (, ) e (, ) I due punti hanno la stessa
utore: Enrico Manfucci - 0/0/0 GEOMETRI NLITIC ESERCIZI CON SOLUZIONI. Posizionare nel piano cartesiano e calcolare la distanza delle seguenti coppie di punti: a. (, ) e (, ) I due punti hanno la stessa
Esercizi sulla retta. Gruppo 1 (4A TSS SER, 4B TSS SER, 4A AM )
 Esercizi sulla retta. Gruppo 1 (4A TSS SER, 4B TSS SER, 4A AM ) 1. Scrivere l'equazione della retta passante per i punti P1(-3,1), P2(2,-2). Dobbiamo applicare l'equazione di una retta passante per due
Esercizi sulla retta. Gruppo 1 (4A TSS SER, 4B TSS SER, 4A AM ) 1. Scrivere l'equazione della retta passante per i punti P1(-3,1), P2(2,-2). Dobbiamo applicare l'equazione di una retta passante per due
Le equazioni e i sistemi di primo grado
 Le equazioni e i sistemi di primo grado prof. Roberto Boggiani Isiss Marco Minghetti 1 settembre 009 Sommario In questo documento verrà trattato in modo semplice e facilmente comprensibile la teoria delle
Le equazioni e i sistemi di primo grado prof. Roberto Boggiani Isiss Marco Minghetti 1 settembre 009 Sommario In questo documento verrà trattato in modo semplice e facilmente comprensibile la teoria delle
LE EQUAZIONI LINEARI LE IDENTITA ( )( ) 5. a Cosa hanno in comune le seguenti uguaglianze? Uguaglianza (1) a
 LE EQUAZIONI LINEARI 1 LE IDENTITA a b = ( a + b)( a b) () 1 a = a + a ( ) ( a + b) = a + ab + b () 3 Cosa hanno in comune le seguenti uguaglianze? Uguaglianza (1) a b = ( a+ b)( a b) È sempre vera qualunque
LE EQUAZIONI LINEARI 1 LE IDENTITA a b = ( a + b)( a b) () 1 a = a + a ( ) ( a + b) = a + ab + b () 3 Cosa hanno in comune le seguenti uguaglianze? Uguaglianza (1) a b = ( a+ b)( a b) È sempre vera qualunque
Università di Pisa - Ingegneria Meccanica Geometria e Algebra Lineare 2009/2010. Soluzioni esercitazione 11/11/2009
 Università di Pisa - Ingegneria Meccanica Geometria e Algebra Lineare 29/2 Soluzioni esercitazione //29 Esercizio. Risolvere, al variare del parametro reale λ, il seguente sistema lineare: x 2 y z = λ
Università di Pisa - Ingegneria Meccanica Geometria e Algebra Lineare 29/2 Soluzioni esercitazione //29 Esercizio. Risolvere, al variare del parametro reale λ, il seguente sistema lineare: x 2 y z = λ
PROGRAMMAZIONE DISCIPLINARE INDIVIDUALE a. s. 2013/2014. Elenco moduli Argomenti Strumenti / Testi / Letture
 Pagina 1 di 6 DISCIPLINA: MATEMATICA CLASSE: II TU DOCENTE : Cornelio Terreni Elenco moduli Argomenti Strumenti / Testi / Letture 1 Equazioni numeriche. RIPASSO di: equazioni e Testo classe Prima. principi
Pagina 1 di 6 DISCIPLINA: MATEMATICA CLASSE: II TU DOCENTE : Cornelio Terreni Elenco moduli Argomenti Strumenti / Testi / Letture 1 Equazioni numeriche. RIPASSO di: equazioni e Testo classe Prima. principi
Geometria Analitica Domande e Risposte
 Geometria Analitica Domande e Risposte La Retta. Qual è l equazione della retta in forma nel piano cartesiano? L equazione della generica retta nel piano cartesiano in forma esplicita è y mx q, mentre
Geometria Analitica Domande e Risposte La Retta. Qual è l equazione della retta in forma nel piano cartesiano? L equazione della generica retta nel piano cartesiano in forma esplicita è y mx q, mentre
Geometria Analitica Domande e Risposte
 Geometria Analitica Domande e Risposte A. Il Piano Cartesiano. Qual è la formula della distanza tra due punti nel piano cartesiano? Per calcolare la formula della distanza tra due punti nel piano cartesiano
Geometria Analitica Domande e Risposte A. Il Piano Cartesiano. Qual è la formula della distanza tra due punti nel piano cartesiano? Per calcolare la formula della distanza tra due punti nel piano cartesiano
PROGRAMMA DI MATEMATICA APPLICATA
 PROGRAMMA DI MATEMATICA APPLICATA Classe II A Turismo A.S. 2014/2015 Prof.ssa RUGGIERO ANGELA ISABELLA I NUMERI REALI Radicali: - Riduzione allo stesso indice e semplificazione - Alcune operazioni fra
PROGRAMMA DI MATEMATICA APPLICATA Classe II A Turismo A.S. 2014/2015 Prof.ssa RUGGIERO ANGELA ISABELLA I NUMERI REALI Radicali: - Riduzione allo stesso indice e semplificazione - Alcune operazioni fra
Appunti: il piano cartesiano. Distanza tra due punti
 ppunti: il piano cartesiano Distanza tra due punti Come determinare la distanza tra i punti ( ; ) e ( ; ): Se i due punti e hanno la stessa ascissa = allora (-3;1) (-3; 5) d()= d()= 1 5 4 4 Se i due punti
ppunti: il piano cartesiano Distanza tra due punti Come determinare la distanza tra i punti ( ; ) e ( ; ): Se i due punti e hanno la stessa ascissa = allora (-3;1) (-3; 5) d()= d()= 1 5 4 4 Se i due punti
Condizione di allineamento di tre punti
 LA RETTA L equazione lineare in x e y L equazione: 0 con,,, e non contemporaneamente nulli, si dice equazione lineare nelle due variabili e. Ogni coppia ; tale che: 0 si dice soluzione dell equazione.
LA RETTA L equazione lineare in x e y L equazione: 0 con,,, e non contemporaneamente nulli, si dice equazione lineare nelle due variabili e. Ogni coppia ; tale che: 0 si dice soluzione dell equazione.
Esercizio 8: Siano dati l equazione della parabola e i due punti e.
 Esercizio 8: Siano dati l equazione della parabola e i due punti e. tracciare dal punto A le tangenti r ed s alla parabola ottenendo i punti di contatto P e Q; tracciare dal punto B le tangenti t ed u
Esercizio 8: Siano dati l equazione della parabola e i due punti e. tracciare dal punto A le tangenti r ed s alla parabola ottenendo i punti di contatto P e Q; tracciare dal punto B le tangenti t ed u
Soluzioni. Foglio 1. Rette e piani. n x + c = 0. (1)
 Soluzioni Foglio 1. Rette e piani. Esercizio 1. Se n è la normale al piano, sia c = n x 0. Dimostriamo prima che se x π, allora x soddisfa Si ha Sostituendo dentro (1) si ottiene n x + c = 0. (1) x = x
Soluzioni Foglio 1. Rette e piani. Esercizio 1. Se n è la normale al piano, sia c = n x 0. Dimostriamo prima che se x π, allora x soddisfa Si ha Sostituendo dentro (1) si ottiene n x + c = 0. (1) x = x
Per equazione lineare nelle incognite x, y intendo un equazione del tipo. ax = b,
 Matematica II 161110 1 Equazioni lineari in una incognita Per equazione lineare nell incognita x intendo un equazione del tipo ax = b dove a b sono due costanti reali a e il coefficiente e b e il termine
Matematica II 161110 1 Equazioni lineari in una incognita Per equazione lineare nell incognita x intendo un equazione del tipo ax = b dove a b sono due costanti reali a e il coefficiente e b e il termine
Chi non risolve esercizi non impara la matematica.
 5.5 esercizi 9 Per trovare la seconda equazione ragioniamo così: la parte espropriata del primo terreno è x/00, la parte espropriata del secondo è y/00 e in totale sono stati espropriati 000 m, quindi
5.5 esercizi 9 Per trovare la seconda equazione ragioniamo così: la parte espropriata del primo terreno è x/00, la parte espropriata del secondo è y/00 e in totale sono stati espropriati 000 m, quindi
Quaderno per il recupero del debito MATEMATICA ANNO SCOLASTICO 2016/2017 Prof.ssa Migliaccio Gabriella CLASSE III
 Quaderno per il recupero del debito MATEMATICA ANNO SCOLASTICO 016/017 Prof.ssa Migliaccio Gabriella CLASSE III Gli esercizi vanno svolti e consegnati, anche su un quaderno, il giorno dell esame per il
Quaderno per il recupero del debito MATEMATICA ANNO SCOLASTICO 016/017 Prof.ssa Migliaccio Gabriella CLASSE III Gli esercizi vanno svolti e consegnati, anche su un quaderno, il giorno dell esame per il
Sistema di due equazioni di primo grado in due incognite
 Sistema di due equazioni di primo grado in due incognite Problema Un trapezio rettangolo di area cm ha altezza di 8 cm. Sapendo che il triplo della base minore è inferiore di cm al doppio della base maggiore
Sistema di due equazioni di primo grado in due incognite Problema Un trapezio rettangolo di area cm ha altezza di 8 cm. Sapendo che il triplo della base minore è inferiore di cm al doppio della base maggiore
Ricordiamo. 1. Tra le equazioni delle seguenti rette individua e disegna quelle parallele all asse delle ascisse:
 La retta Retta e le sue equazioni Equazioni di rette come luogo geometrico y = h h R equazione di una retta parallela all asse delle ascisse x = 0 equazione dell asse delle ordinate y = h h R equazione
La retta Retta e le sue equazioni Equazioni di rette come luogo geometrico y = h h R equazione di una retta parallela all asse delle ascisse x = 0 equazione dell asse delle ordinate y = h h R equazione
RETTE E PIANI NELLO SPAZIO
 VETTORI E GEOMETRIA ANALITICA 1 RETTE E PIANI NELLO SPAZIO Rette e piani in forma cartesiana e parametrica. Parallelismo e perpendicolarità, posizioni reciproche tra rette e piani, distanze. Esercizio
VETTORI E GEOMETRIA ANALITICA 1 RETTE E PIANI NELLO SPAZIO Rette e piani in forma cartesiana e parametrica. Parallelismo e perpendicolarità, posizioni reciproche tra rette e piani, distanze. Esercizio
RIPASSO PROPEDEUTICO AL V ANNO. Disciplina: MATEMATICA
 RIPASSO PROPEDEUTICO AL V ANNO Disciplina: MATEMATICA Testi consigliati : - BOOK IN PROGRESS MATEMATICA, ALGEBRA PRIMO ANNO, tomo n http://www.itistulliobuzzi.it/buzziwebsite/studenti/matematica/tomo%0_algebra%0buzzi%
RIPASSO PROPEDEUTICO AL V ANNO Disciplina: MATEMATICA Testi consigliati : - BOOK IN PROGRESS MATEMATICA, ALGEBRA PRIMO ANNO, tomo n http://www.itistulliobuzzi.it/buzziwebsite/studenti/matematica/tomo%0_algebra%0buzzi%
LA RETTA
 EQUAZIONE DEL Ogni equazione di I grado in due variabili x e y rappresenta nel piano cartesiano una retta, per cui si dice che a x + b y + c = 0 è l equazione di una retta in forma implicita. OSSERVAZIONE:
EQUAZIONE DEL Ogni equazione di I grado in due variabili x e y rappresenta nel piano cartesiano una retta, per cui si dice che a x + b y + c = 0 è l equazione di una retta in forma implicita. OSSERVAZIONE:
IIS Via Silvestri 301. Plesso Volta. Programma di Matematica Indirizzo Elettronica ed Elettrotecnica a.s. 2016/17
 IIS Via Silvestri 301. Plesso Volta. Programma di Matematica Indirizzo Elettronica ed Elettrotecnica a.s. 2016/17 Classe 1A MODULO 1: I NUMERI NATURALI 1. Le operazioni definite nell insieme dei numeri
IIS Via Silvestri 301. Plesso Volta. Programma di Matematica Indirizzo Elettronica ed Elettrotecnica a.s. 2016/17 Classe 1A MODULO 1: I NUMERI NATURALI 1. Le operazioni definite nell insieme dei numeri
Definizione: Due equazioni si dicono equivalenti se ammettono le stesse soluzioni.
 Facoltà di Medicina e Chirurgia Corso Zero di Matematica Gruppi: MC-MF3 / PS-MF3 II Lezione EQUAZIONI E SISTEMI Dr. E. Modica erasmo@galois.it www.galois.it IDENTITÀ ED EQUAZIONI Si consideri un uguaglianza
Facoltà di Medicina e Chirurgia Corso Zero di Matematica Gruppi: MC-MF3 / PS-MF3 II Lezione EQUAZIONI E SISTEMI Dr. E. Modica erasmo@galois.it www.galois.it IDENTITÀ ED EQUAZIONI Si consideri un uguaglianza
Algebra Lineare (Matematica C.I.), 12.11.13. Sistemi di equazioni lineari. 1. Un equazione lineare in una incognita reale x e un equazione del tipo
 Algebra Lineare (Matematica C.I.), 12.11.13 Sistemi di equazioni lineari 1. Un equazione lineare in una incognita reale x e un equazione del tipo ax = b, dove a e b sono numeri reali dati; a e il coefficiente
Algebra Lineare (Matematica C.I.), 12.11.13 Sistemi di equazioni lineari 1. Un equazione lineare in una incognita reale x e un equazione del tipo ax = b, dove a e b sono numeri reali dati; a e il coefficiente
Capitolo 1 Vettori applicati e geometria dello spazio
 Capitolo 1 Vettori applicati e geometria dello spazio Marco Robutti Facoltà di ingegneria Università degli studi di Pavia Tutorato di geometria e algebra lineare Anno accademico 2014-2015 Definizione (Vettore
Capitolo 1 Vettori applicati e geometria dello spazio Marco Robutti Facoltà di ingegneria Università degli studi di Pavia Tutorato di geometria e algebra lineare Anno accademico 2014-2015 Definizione (Vettore
4 Sistemi di equazioni.
 4 Sistemi di equazioni. Risolvere un sistema significa erminare le soluzioni comuni a tutte le equazioni che lo compongono. Il grado di un sistema è il prodotto dei gradi di tali equazioni. 4. Sistemi
4 Sistemi di equazioni. Risolvere un sistema significa erminare le soluzioni comuni a tutte le equazioni che lo compongono. Il grado di un sistema è il prodotto dei gradi di tali equazioni. 4. Sistemi
Istituto di Istruzione Secondaria Superiore Statale «Via Silvestri 301» Programma di MATEMATICA
 1. MODULO 1: RICHIAMI DI CALCOLO LETTERALE La scomposizione di polinomi e le operazioni con le frazioni algebriche 2. MODULO 2: LE EQUAZIONI Istituto di Istruzione Secondaria Superiore Statale Classe 1
1. MODULO 1: RICHIAMI DI CALCOLO LETTERALE La scomposizione di polinomi e le operazioni con le frazioni algebriche 2. MODULO 2: LE EQUAZIONI Istituto di Istruzione Secondaria Superiore Statale Classe 1
Capitolo 2. Cenni di geometria analitica nel piano
 Capitolo Cenni di geometria analitica nel piano 1 Il piano cartesiano Il piano cartesiano è una rappresentazione grafica del prodotto cartesiano R = R R La rappresentazione grafica è possibile se si crea
Capitolo Cenni di geometria analitica nel piano 1 Il piano cartesiano Il piano cartesiano è una rappresentazione grafica del prodotto cartesiano R = R R La rappresentazione grafica è possibile se si crea
UNITÀ DIDATTICA 5 LA RETTA
 UNITÀ DIDATTICA 5 LA RETTA 5.1 - La retta Equazione generica della retta Dalle considerazioni emerse nel precedente capitolo abbiamo compreso come una funzione possa essere rappresentata da un insieme
UNITÀ DIDATTICA 5 LA RETTA 5.1 - La retta Equazione generica della retta Dalle considerazioni emerse nel precedente capitolo abbiamo compreso come una funzione possa essere rappresentata da un insieme
Esercitazione: 16 novembre 2009 SOLUZIONI
 Esercitazione: 16 novembre 009 SOLUZIONI Esercizio 1 Scrivere [ ] equazione vettoriale, parametrica [ ] e cartesiana della retta passante 1 per il punto P = e avente direzione d =. 1 x 1 Soluzione: Equazione
Esercitazione: 16 novembre 009 SOLUZIONI Esercizio 1 Scrivere [ ] equazione vettoriale, parametrica [ ] e cartesiana della retta passante 1 per il punto P = e avente direzione d =. 1 x 1 Soluzione: Equazione
Quadro riassuntivo di geometria analitica
 Quadro riassuntivo di geometria analitica IL PIANO CARTESIANO (detta ascissa o coordinata x) e y quella dall'asse x (detta ordinata o coordinata y). Le coordinate di un punto P sono: entrambe positive
Quadro riassuntivo di geometria analitica IL PIANO CARTESIANO (detta ascissa o coordinata x) e y quella dall'asse x (detta ordinata o coordinata y). Le coordinate di un punto P sono: entrambe positive
Autovalori ed autovettori di un endomorfismo
 Autovalori ed autovettori di un endomorfismo Endomorfismo = applicazione (funzione) lineare da un spazio vettoriale V in sé stesso 1. Data una funzione lineare, scriverne la matrice associata dei coefficienti:
Autovalori ed autovettori di un endomorfismo Endomorfismo = applicazione (funzione) lineare da un spazio vettoriale V in sé stesso 1. Data una funzione lineare, scriverne la matrice associata dei coefficienti:
IPSSEOA "PiETRO PIAZZA" - PALERMO. Programma svolto di Matematica. Anno scolastico 2016/2017
 IPSSEOA "PiETRO PIAZZA" - PALERMO Programma svolto di Matematica Classe: 1 A_ 1 Periodo Didattico )t. s;. - :,., 4 " - 4.UDA1: INSIEMINUMERICI L'insieme dei numeri naturali : Operazioni, proprieta delle
IPSSEOA "PiETRO PIAZZA" - PALERMO Programma svolto di Matematica Classe: 1 A_ 1 Periodo Didattico )t. s;. - :,., 4 " - 4.UDA1: INSIEMINUMERICI L'insieme dei numeri naturali : Operazioni, proprieta delle
Programma svolto a.s. 2017/2018 Classe 1H Materia: Matematica Docente: De Rossi Francesco
 Classe 1H Materia: Matematica Docente: De Rossi Francesco - Matematica multimediale. bianco Vol 1 Autori: M. Bergamini, G. Barozzi Casa Editrice: Zanichelli codice ISBN 978888334671 Capitolo 1 Insiemi
Classe 1H Materia: Matematica Docente: De Rossi Francesco - Matematica multimediale. bianco Vol 1 Autori: M. Bergamini, G. Barozzi Casa Editrice: Zanichelli codice ISBN 978888334671 Capitolo 1 Insiemi
Facsimile di prova d esame Esempio di svolgimento
 Geometria analitica 18 marzo 009 Facsimile di prova d esame Esempio di svolgimento 1 Nello spazio, riferito a coordinate cartesiane ortogonali e monometriche x,y,z, è assegnata la retta r di equazioni
Geometria analitica 18 marzo 009 Facsimile di prova d esame Esempio di svolgimento 1 Nello spazio, riferito a coordinate cartesiane ortogonali e monometriche x,y,z, è assegnata la retta r di equazioni
Programma di MATEMATICA
 Classe 3B Indirizzo ELETTRONICA ED ELETTROTECNICA 1. MODULO 1: GEOMETRIA ANALITICA La parabola: la parabola come luogo geometrico del piano. Rappresentazione della parabola nel piano cartesiano e ricerca
Classe 3B Indirizzo ELETTRONICA ED ELETTROTECNICA 1. MODULO 1: GEOMETRIA ANALITICA La parabola: la parabola come luogo geometrico del piano. Rappresentazione della parabola nel piano cartesiano e ricerca
Sistemi lineari (di I grado)
 Sistemi lineari (di I grado) Un sistema lineare è un insieme di equazioni lineari (di I grado), che devono essere verificate tutte contemporaneamente. Risolvere un sistema di equazioni vuol dire trovare
Sistemi lineari (di I grado) Un sistema lineare è un insieme di equazioni lineari (di I grado), che devono essere verificate tutte contemporaneamente. Risolvere un sistema di equazioni vuol dire trovare
Equazioni lineari con due o più incognite
 Equazioni lineari con due o più incognite Siano date le uguaglianze: k 0; x + y = 6; 3a + b c = 8. La prima ha un termine incognito rappresentato dal simbolo letterale k; la seconda ha due termini incogniti
Equazioni lineari con due o più incognite Siano date le uguaglianze: k 0; x + y = 6; 3a + b c = 8. La prima ha un termine incognito rappresentato dal simbolo letterale k; la seconda ha due termini incogniti
Il teorema di Rouché-Capelli
 Luciano Battaia Questi appunti (1), ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia, campus di Treviso, contengono un
Luciano Battaia Questi appunti (1), ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia, campus di Treviso, contengono un
LEZIONE DI MATEMATICA PROF : GIOVANNI IANNE. I sistemi di equazioni di I grado
 LEZIONE DI MATEMATICA PROF : GIOVANNI IANNE I sistemi di equazioni di I grado Diamo la seguente definizione: Un sistema di equazioni è un insieme di due o più equazioni, tutte nelle stesse incognite, di
LEZIONE DI MATEMATICA PROF : GIOVANNI IANNE I sistemi di equazioni di I grado Diamo la seguente definizione: Un sistema di equazioni è un insieme di due o più equazioni, tutte nelle stesse incognite, di
MATEMATICA. a.a. 2014/ Sistemi di equazioni lineari
 MATEMATICA a.a. 2014/15 8. Sistemi di equazioni lineari SISTEMI LINEARI Si definisce sistema lineare un sistema di p equazioni di primo grado in q incognite. a11x1 + a12 x2 +... + a1 qxq = k1 a21x1 + a22x2
MATEMATICA a.a. 2014/15 8. Sistemi di equazioni lineari SISTEMI LINEARI Si definisce sistema lineare un sistema di p equazioni di primo grado in q incognite. a11x1 + a12 x2 +... + a1 qxq = k1 a21x1 + a22x2
Precorso di Matematica
 Precorso di Matematica Lezione 3 Andrea Susa OPERATORE DI PRODOTTO Π 2 1 Operatore di prodotto Π Consideriamo un insieme numerico ={ =1, }. Definiamo prodotto degli elementi in, = Esempio: ={ =1, =2, =3,
Precorso di Matematica Lezione 3 Andrea Susa OPERATORE DI PRODOTTO Π 2 1 Operatore di prodotto Π Consideriamo un insieme numerico ={ =1, }. Definiamo prodotto degli elementi in, = Esempio: ={ =1, =2, =3,
Equazioni di Primo grado
 Equazioni di Primo grado Definizioni Si dice equazione di primo grado un uguaglianza tra due espressioni algebriche verificata solo per un determinato valore della variabile x, detta incognita. Si chiama
Equazioni di Primo grado Definizioni Si dice equazione di primo grado un uguaglianza tra due espressioni algebriche verificata solo per un determinato valore della variabile x, detta incognita. Si chiama
EQUAZIONE DELLA RETTA
 EQUAZIONE DELLA RETTA EQUAZIONE DEGLI ASSI L equazione dell asse x è 0. L equazione dell asse y è 0. EQUAZIONE DELLE RETTE PARALLELE AGLI ASSI L equazione di una retta r parallela all asse x è cioè è uguale
EQUAZIONE DELLA RETTA EQUAZIONE DEGLI ASSI L equazione dell asse x è 0. L equazione dell asse y è 0. EQUAZIONE DELLE RETTE PARALLELE AGLI ASSI L equazione di una retta r parallela all asse x è cioè è uguale
Sistemi di equazioni
 Sistemi di equazioni 19 191 Equazione lineare in due incognite Definizione 191 Una equazione di primo grado (in n incognite) si chiama equazione lineare Problema 191 Determinare due numeri naturali la
Sistemi di equazioni 19 191 Equazione lineare in due incognite Definizione 191 Una equazione di primo grado (in n incognite) si chiama equazione lineare Problema 191 Determinare due numeri naturali la
Rette e piani in R 3
 Rette e piani in R 3 In questa dispensa vogliamo introdurre in modo elementare rette e piani nello spazio R 3 (si faccia riferimento anche al testo Algebra Lineare di S. Lang). 1 Rette in R 3 Vogliamo
Rette e piani in R 3 In questa dispensa vogliamo introdurre in modo elementare rette e piani nello spazio R 3 (si faccia riferimento anche al testo Algebra Lineare di S. Lang). 1 Rette in R 3 Vogliamo
GE110 Soluzioni Tutorato 7 a cura di Giordano Agostini, Giulia Salustri e Andrea Cattaneo
 GE110 Soluzioni Tutorato 7 a cura di Giordano Agostini, Giulia Salustri e Andrea Cattaneo Università degli studi Roma Tre, Corso di Laurea in Matematica Anno Accademico 2011/2012 1 Si determinino esplicitamente
GE110 Soluzioni Tutorato 7 a cura di Giordano Agostini, Giulia Salustri e Andrea Cattaneo Università degli studi Roma Tre, Corso di Laurea in Matematica Anno Accademico 2011/2012 1 Si determinino esplicitamente
[ RITORNA ALLE DOMANDE] 2) Definisci la parabola come luogo geometrico. 1) Che cos è una conica?
![[ RITORNA ALLE DOMANDE] 2) Definisci la parabola come luogo geometrico. 1) Che cos è una conica? [ RITORNA ALLE DOMANDE] 2) Definisci la parabola come luogo geometrico. 1) Che cos è una conica?](/thumbs/57/41170353.jpg) Matematica 1) Che cos è una conica? 2) Definisci la parabola come luogo geometrico. 3) Qual è l equazione di una parabola con asse di simmetria parallelo all asse delle y? 4) Qual è l equazione di una
Matematica 1) Che cos è una conica? 2) Definisci la parabola come luogo geometrico. 3) Qual è l equazione di una parabola con asse di simmetria parallelo all asse delle y? 4) Qual è l equazione di una
Anno 2. Risoluzione di sistemi di primo grado in due incognite
 Anno Risoluzione di sistemi di primo grado in due incognite Introduzione In questa lezione impareremo alcuni metodi per risolvere un sistema di due equazioni in due incognite. Al termine di questa lezione
Anno Risoluzione di sistemi di primo grado in due incognite Introduzione In questa lezione impareremo alcuni metodi per risolvere un sistema di due equazioni in due incognite. Al termine di questa lezione
Programma di Matematica. Classe 1 B odont / d anno scolastico 2009/10 Insegnante: Maria Teresa DI PRIZIO IL CALCOLO NUMERICO IL CALCOLO LETTERALE
 Programma di Matematica Classe 1 B odont / d anno scolastico 2009/10 Insegnante: Maria Teresa DI PRIZIO IL CALCOLO NUMERICO I numeri naturali e numeri razionali Definizione di numero naturale e le quattro
Programma di Matematica Classe 1 B odont / d anno scolastico 2009/10 Insegnante: Maria Teresa DI PRIZIO IL CALCOLO NUMERICO I numeri naturali e numeri razionali Definizione di numero naturale e le quattro
Istituto Tecnico Nautico San Giorgio - Genova - Anno scolastico PROGRAMMA SVOLTO DI MATEMATICA
 Classe: 1 a C Libro di testo: Bergamini Trifone Barozzi Matematica verde vol. 1 ed. Zanichelli Insiemi Definizione di insieme, rappresentazione grafica, tabulare, caratteristica di un insieme Gli insiemi
Classe: 1 a C Libro di testo: Bergamini Trifone Barozzi Matematica verde vol. 1 ed. Zanichelli Insiemi Definizione di insieme, rappresentazione grafica, tabulare, caratteristica di un insieme Gli insiemi
PROGRAMMA DI MATEMATICA
 Classe 2^ sez. A 1. Ripasso Operazioni tra polinomi, prodotti notevoli, equazioni di primo grado intere e frazionarie. Problemi risolvibili con le equazioni di primo grado. 2. Sistemi Sistemi di equazioni
Classe 2^ sez. A 1. Ripasso Operazioni tra polinomi, prodotti notevoli, equazioni di primo grado intere e frazionarie. Problemi risolvibili con le equazioni di primo grado. 2. Sistemi Sistemi di equazioni
Dipendenza e indipendenza lineare
 Dipendenza e indipendenza lineare Luciano Battaia Questi appunti () ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia campus
Dipendenza e indipendenza lineare Luciano Battaia Questi appunti () ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia campus
Complementi di algebra
 Complementi di algebra Equazioni di grado superiore al secondo Come per le equazioni di grado, esistono formule risolutive anche per le equazioni di e grado ma non le studieremo perché sono troppo complesse,mentre
Complementi di algebra Equazioni di grado superiore al secondo Come per le equazioni di grado, esistono formule risolutive anche per le equazioni di e grado ma non le studieremo perché sono troppo complesse,mentre
Geometria BAER Canale I Esercizi 11
 Geometria BAER Canale I Esercizi 11 Esercizio 1. Data la retta x = t r : y = t z = 1 si trovi il punto A di r tale che l angolo di r con il vettore AO sia π/2, e il punto B di r tale che l angolo di r
Geometria BAER Canale I Esercizi 11 Esercizio 1. Data la retta x = t r : y = t z = 1 si trovi il punto A di r tale che l angolo di r con il vettore AO sia π/2, e il punto B di r tale che l angolo di r
SISTEMI DI EQUAZIONI IN DUE INCOGNITE
 ESERCIZI SVOLTI SISTEMI DI EQUAZIONI IN DUE INCOGNITE Il metodo di sostituzione Esercizio 1. Risolvere il seguente sistema di primo grado nelle incognite x e y: x y x + y 1 Quando il sistema da risolvere
ESERCIZI SVOLTI SISTEMI DI EQUAZIONI IN DUE INCOGNITE Il metodo di sostituzione Esercizio 1. Risolvere il seguente sistema di primo grado nelle incognite x e y: x y x + y 1 Quando il sistema da risolvere
Sistemi lineari di due equazioni in due incognite
 Sistemi lineari di due equazioni in due incognite Incognite Lettere (di solito X e Y) alle quali è possibile sostituire dei valori numerici Coppia ordinata Coppia (X;Y) di valori numerici, per la quale
Sistemi lineari di due equazioni in due incognite Incognite Lettere (di solito X e Y) alle quali è possibile sostituire dei valori numerici Coppia ordinata Coppia (X;Y) di valori numerici, per la quale
ISTITUTO PROFESSIONALE PER I SERVIZI ALBERGHIERI E DELLA RISTORAZIONE B.BUONTALENTI,V. DE BRUNI, FIRENZE ANNO SCOLASTICO 2015/2016.
 B.BUONTALENTI,V. DE BRUNI, 6-50133 FIRENZE Classe 1 A Richiami di matematica: formazione degli insiemi numerici i numeri naturali, interi, razionali, irrazionali i numeri reali proprietà delle quattro
B.BUONTALENTI,V. DE BRUNI, 6-50133 FIRENZE Classe 1 A Richiami di matematica: formazione degli insiemi numerici i numeri naturali, interi, razionali, irrazionali i numeri reali proprietà delle quattro
(x B x A, y B y A ) = (4, 2) ha modulo
 GEOMETRIA PIANA 1. Esercizi Esercizio 1. Dati i punti A(0, 4), e B(4, ) trovarne la distanza e trovare poi i punti C allineati con A e con B che verificano: (1) AC = CB (punto medio del segmento AB); ()
GEOMETRIA PIANA 1. Esercizi Esercizio 1. Dati i punti A(0, 4), e B(4, ) trovarne la distanza e trovare poi i punti C allineati con A e con B che verificano: (1) AC = CB (punto medio del segmento AB); ()
CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA
 CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA FOGLIO DI ESERCIZI 1 GEOMETRIA 2009/10 Esercizio 1.1 (2.2). Determinare l equazione parametrica e Cartesiana della retta dello spazio (a) Passante per i
CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA FOGLIO DI ESERCIZI 1 GEOMETRIA 2009/10 Esercizio 1.1 (2.2). Determinare l equazione parametrica e Cartesiana della retta dello spazio (a) Passante per i
ITIS - BAGNOLI IRPINO
 LICEO SCIENTIFICO RINALDO.D AQUINO MONTELLA ITIS - BAGNOLI IRPINO PROGRAMMA SVOLTO A.S. 2017-18 Materia: COMPLEMENTI DI MATEMATICA Classe : 3 A BAGNOLI IRPINO Prof. PARENTI Luigi INSIEMI Gli insiemi: Concetto
LICEO SCIENTIFICO RINALDO.D AQUINO MONTELLA ITIS - BAGNOLI IRPINO PROGRAMMA SVOLTO A.S. 2017-18 Materia: COMPLEMENTI DI MATEMATICA Classe : 3 A BAGNOLI IRPINO Prof. PARENTI Luigi INSIEMI Gli insiemi: Concetto
ESERCITAZIONE 9 : FUNZIONI QUADRATICHE
 ESERCITAZIONE 9 : FUNZIONI QUADRATICHE e-mail: tommei@dm.unipi.it web: www.dm.unipi.it/ tommei Ricevimento: Martedi 16-18 Dipartimento di Matematica, piano terra, studio 126 4 Dicembre 2012 L espressione
ESERCITAZIONE 9 : FUNZIONI QUADRATICHE e-mail: tommei@dm.unipi.it web: www.dm.unipi.it/ tommei Ricevimento: Martedi 16-18 Dipartimento di Matematica, piano terra, studio 126 4 Dicembre 2012 L espressione
La Retta Ogni funzione di primo grado rappresenta, graficamente, una retta. L equazione della retta può essere scritta in due modi
 La Retta Ogni funzione di primo grado rappresenta, graficamente, una retta. L equazione della retta può essere scritta in due modi Forma implicita Forma esplicita a x b y c 0 y m x q a c y x b b Esempio
La Retta Ogni funzione di primo grado rappresenta, graficamente, una retta. L equazione della retta può essere scritta in due modi Forma implicita Forma esplicita a x b y c 0 y m x q a c y x b b Esempio
Università Carlo Cattaneo Ingegneria gestionale Analisi matematica a.a. 2016/2017 RETTE E PIANI NELLO SPAZIO
 Università Carlo Cattaneo Ingegneria gestionale Analisi matematica a.a. 2016/2017 RETTE E PIANI NELLO SPAZIO ESERCIZI CON SOLUZIONE 1) Date le rette : 2 0 32 0 e : 2 5 0 5 2 1 0 a) verificare che sono
Università Carlo Cattaneo Ingegneria gestionale Analisi matematica a.a. 2016/2017 RETTE E PIANI NELLO SPAZIO ESERCIZI CON SOLUZIONE 1) Date le rette : 2 0 32 0 e : 2 5 0 5 2 1 0 a) verificare che sono
Esercizi svolti. risolvere, se possibile, l equazione xa + B = O, essendo x un incognita reale
 Esercizi svolti 1. Matrici e operazioni fra matrici 1.1 Date le matrici 1 2 1 6 A = B = 5 2 9 15 6 risolvere, se possibile, l equazione xa + B = O, essendo x un incognita reale Osservazione iniziale: qualunque
Esercizi svolti 1. Matrici e operazioni fra matrici 1.1 Date le matrici 1 2 1 6 A = B = 5 2 9 15 6 risolvere, se possibile, l equazione xa + B = O, essendo x un incognita reale Osservazione iniziale: qualunque
1 Introduzione alla geometria analitica
 1.1 Il piano cartesiano 1 Introduzione alla geometria analitica Se R è l'insieme di tutti i numeri reali (rappresentabile su una retta), allora R R = R rappresenta il piano euclideo; infatti ciascun punto
1.1 Il piano cartesiano 1 Introduzione alla geometria analitica Se R è l'insieme di tutti i numeri reali (rappresentabile su una retta), allora R R = R rappresenta il piano euclideo; infatti ciascun punto
Matematica II,
 Matematica II, 171110 1 processo di triangolarizzazione, esempio I Consideriamo il sistema lineare di tre equazioni nelle incognite x, y, z 2x + 3y + 4z = 8 4x + 9y + 16z = 14 8x + 27y + 64z = 14 Primo
Matematica II, 171110 1 processo di triangolarizzazione, esempio I Consideriamo il sistema lineare di tre equazioni nelle incognite x, y, z 2x + 3y + 4z = 8 4x + 9y + 16z = 14 8x + 27y + 64z = 14 Primo
Unità Didattica N 9 : La parabola
 0 Matematica Liceo \ Unità Didattica N 9 La parabola Unità Didattica N 9 : La parabola ) La parabola ad asse verticale ) La parabola ad asse orizzontale 5) Intersezione di una parabola con una retta 6)
0 Matematica Liceo \ Unità Didattica N 9 La parabola Unità Didattica N 9 : La parabola ) La parabola ad asse verticale ) La parabola ad asse orizzontale 5) Intersezione di una parabola con una retta 6)
I.T.C. Abba-Ballini Brescia a.s classe 2 a
 MODULO 2 : LA RETTA Competenze Saper formalizzare e rappresentare le funzioni di 1 grado Saper interpretare geometricamente i modelli algebrici di primo grado UD 1.1 LA RETTA Prerequisiti Insiemi numerici
MODULO 2 : LA RETTA Competenze Saper formalizzare e rappresentare le funzioni di 1 grado Saper interpretare geometricamente i modelli algebrici di primo grado UD 1.1 LA RETTA Prerequisiti Insiemi numerici
Equazioni e disequazioni
 Equazioni e disequazioni Le equazioni Una uguaglianza tra espressioni letterali che risulta vera per ogni valore delle lettere che vi compaiono prende il nome di identità. 2a=2a (a+b)(a-b)=a 2 -b 2 Una
Equazioni e disequazioni Le equazioni Una uguaglianza tra espressioni letterali che risulta vera per ogni valore delle lettere che vi compaiono prende il nome di identità. 2a=2a (a+b)(a-b)=a 2 -b 2 Una
Geometria BATR-BCVR Esercizi 9
 Geometria BATR-BCVR 2015-16 Esercizi 9 Esercizio 1. Per ognuna delle matrici A i si trovi una matrice ortogonale M i tale che Mi ta im sia diagonale. ( ) 1 1 2 3 2 A 1 = A 2 1 2 = 1 1 0 2 0 1 Esercizio
Geometria BATR-BCVR 2015-16 Esercizi 9 Esercizio 1. Per ognuna delle matrici A i si trovi una matrice ortogonale M i tale che Mi ta im sia diagonale. ( ) 1 1 2 3 2 A 1 = A 2 1 2 = 1 1 0 2 0 1 Esercizio
LICEO SCIENTIFICO RINALDO.D AQUINO MONTELLA ITIS BAGNOLI IRPINO PROGRAMMA SVOLTO A.S Materia: MATEMATICA Classe : 3 A Prof.
 LICEO SCIENTIFICO RINALDO.D AQUINO MONTELLA ITIS BAGNOLI IRPINO PROGRAMMA SVOLTO A.S. 2017-18 Materia: MATEMATICA Classe : 3 A Prof. PARENTI Luigi LA RETTA SUL PIANO CARTESIANO - Coordinate cartesiane.
LICEO SCIENTIFICO RINALDO.D AQUINO MONTELLA ITIS BAGNOLI IRPINO PROGRAMMA SVOLTO A.S. 2017-18 Materia: MATEMATICA Classe : 3 A Prof. PARENTI Luigi LA RETTA SUL PIANO CARTESIANO - Coordinate cartesiane.
Università degli Studi del Piemonte Orientale Facoltà di Scienze M.F.N. Precorso di Matematica APPUNTI (preparati da Pier Luigi Ferrari)
 Università degli Studi del Piemonte Orientale Facoltà di Scienze M.F.N. Precorso di Matematica APPUNTI (preparati da Pier Luigi Ferrari). Piano cartesiano Per piano cartesiano si intende un piano dotato
Università degli Studi del Piemonte Orientale Facoltà di Scienze M.F.N. Precorso di Matematica APPUNTI (preparati da Pier Luigi Ferrari). Piano cartesiano Per piano cartesiano si intende un piano dotato
x + b! y + c! Osservazione: poiché ci sono infiniti piani ai quali appartiene una retta r, le equazioni non sono univocamente determinate.
 4 La retta in R 3 4 Le equazioni cartesiane di una retta Dati due piani Γ :ax +by +cz +d = 0 e Γ!: a! x + b! y + c! z + d! = 0 non paralleli tra loro, il luogo geometrico dei punti di intersezione tra
4 La retta in R 3 4 Le equazioni cartesiane di una retta Dati due piani Γ :ax +by +cz +d = 0 e Γ!: a! x + b! y + c! z + d! = 0 non paralleli tra loro, il luogo geometrico dei punti di intersezione tra
Programma svolto a.s. 2015/1016 Classe 1G Materia: Matematica Docente: De Rossi Francesco
 Classe 1G Materia: Matematica Docente: De Rossi Francesco - Matematica multimediale. Bianco Vol 1 Autori: M. Bergamini, G. Barozzi Casa Editrice: Zanichelli codice ISBN 978-88-08-53467-5 Capitolo 1 Insiemi
Classe 1G Materia: Matematica Docente: De Rossi Francesco - Matematica multimediale. Bianco Vol 1 Autori: M. Bergamini, G. Barozzi Casa Editrice: Zanichelli codice ISBN 978-88-08-53467-5 Capitolo 1 Insiemi
asse fuoco vertice direttrice Fig. D3.1 Parabola.
 D3. Parabola D3.1 Definizione di parabola come luogo di punti Definizione: una parabola è formata dai punti equidistanti da un punto detto fuoco e da una retta detta direttrice. L equazione della parabola
D3. Parabola D3.1 Definizione di parabola come luogo di punti Definizione: una parabola è formata dai punti equidistanti da un punto detto fuoco e da una retta detta direttrice. L equazione della parabola
 http://www.appuntielettro.altervista.org Possiamo associare a ogni punto di una retta orientata un numero reale Il piano cartesiano associamo a ogni punto del piano una coppia di numeri reali Un piano
http://www.appuntielettro.altervista.org Possiamo associare a ogni punto di una retta orientata un numero reale Il piano cartesiano associamo a ogni punto del piano una coppia di numeri reali Un piano
Corso multimediale di matematica
 2006 GEMETRIA ANALITICA la retta rof. Calogero Contrino equazione della retta passante per due punti Si pone il seguente: problema assegnati due punti ( 1, 1 ) e ( 2, 2 ) sul piano cartesiano, essi individuano
2006 GEMETRIA ANALITICA la retta rof. Calogero Contrino equazione della retta passante per due punti Si pone il seguente: problema assegnati due punti ( 1, 1 ) e ( 2, 2 ) sul piano cartesiano, essi individuano
Studio di rette sghembe
 Studio di rette sghembe V. Alberini, M. Buzzi, L. Cantoni, L. Grignaffini, G. Montis, G. Palù gennaio 17 Problema Stabilisci se le due rette r e s di equazioni: x = 1 + t x = r : y = t e s : z = z = t
Studio di rette sghembe V. Alberini, M. Buzzi, L. Cantoni, L. Grignaffini, G. Montis, G. Palù gennaio 17 Problema Stabilisci se le due rette r e s di equazioni: x = 1 + t x = r : y = t e s : z = z = t
PROGRAMMA MATEMATICA Classe 1 A AFM anno scolastico
 Classe 1 A AFM anno scolastico 2014-2015 I numeri naturali rappresentazione dei numeri naturali, le quattro operazioni, multipli e divisori di un numero. Criteri di divisibilità, le potenze, le espressioni
Classe 1 A AFM anno scolastico 2014-2015 I numeri naturali rappresentazione dei numeri naturali, le quattro operazioni, multipli e divisori di un numero. Criteri di divisibilità, le potenze, le espressioni
y 5z = 7 y +8z = 10 +3z = 3
 Sistemi lineari Sistemi lineari in tre incognite; esempi tipici Tre equazioni incognite x, y, z Consideriamo il seguente sistema di tre equazioni lineari nelle tre x 2y +6z = 11 x +3y 11z = 18 2x 5y +20z
Sistemi lineari Sistemi lineari in tre incognite; esempi tipici Tre equazioni incognite x, y, z Consideriamo il seguente sistema di tre equazioni lineari nelle tre x 2y +6z = 11 x +3y 11z = 18 2x 5y +20z
Come orientarsi nel libro 573 SISTEMI LINEARI. Metodo di riduzione Metodo di Cramer. e inoltre 7 animazioni e 42 esercizi in più
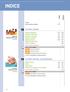 INDICE Il Tutor X Come orientarsi nel libro 573 Un'equazione in due incognite, a pagina 585 100 animali, 100 denari, a pagina 644 18 19 SISTEMI LINEARI 1. Sistemi di equazioni 574 584 2. Metodo di sostituzione
INDICE Il Tutor X Come orientarsi nel libro 573 Un'equazione in due incognite, a pagina 585 100 animali, 100 denari, a pagina 644 18 19 SISTEMI LINEARI 1. Sistemi di equazioni 574 584 2. Metodo di sostituzione
Appunti per la classe terza. Geometria Analitica
 Istituto Professionale L. Lagrange Torino A.S. 008-009 Appunti per la classe terza Geometria Analitica Autore: Di Liscia Francesca Indice 1 Piano cartesiano 1.1 Punto medio......................................
Istituto Professionale L. Lagrange Torino A.S. 008-009 Appunti per la classe terza Geometria Analitica Autore: Di Liscia Francesca Indice 1 Piano cartesiano 1.1 Punto medio......................................
Argomento 13 Sistemi lineari
 Sistemi lineari: definizioni Argomento Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto
Sistemi lineari: definizioni Argomento Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto
EQUAZIONI DI II GRADO
 RICHIAMI SULLE EQUAZIONI DI PRIMO E SECONDO GRADO PROF.SSA ROSSELLA PISCOPO Indice 1 EQUAZIONI DI I GRADO --------------------------------------------------------------------------------------------------
RICHIAMI SULLE EQUAZIONI DI PRIMO E SECONDO GRADO PROF.SSA ROSSELLA PISCOPO Indice 1 EQUAZIONI DI I GRADO --------------------------------------------------------------------------------------------------
Esercitazione di Matematica sui sistemi lineari 2 2 e 3 3
 Esercitazione di Matematica sui sistemi lineari e Esercizio 1. Risolvere i seguenti sistemi lineari : { 5x + y = 6 (a) x + y = 8 ; { x + 5y = 4 4x 7y =. Esercizio. sistemi: (a) { x + y = 6 x y = 1 ; {
Esercitazione di Matematica sui sistemi lineari e Esercizio 1. Risolvere i seguenti sistemi lineari : { 5x + y = 6 (a) x + y = 8 ; { x + 5y = 4 4x 7y =. Esercizio. sistemi: (a) { x + y = 6 x y = 1 ; {
FUNZIONI REALI DI DUE VARIABILI REALI
 FUNZIONI REALI DI DUE VARIABILI REALI DEFINIZIONE VARIABILI Una funione f, associa ad ogni una coppia ordinata di numeri reali,, appartenente ad un sottoinsieme S del piano, uno e un solo numero reale.
FUNZIONI REALI DI DUE VARIABILI REALI DEFINIZIONE VARIABILI Una funione f, associa ad ogni una coppia ordinata di numeri reali,, appartenente ad un sottoinsieme S del piano, uno e un solo numero reale.
il determinante che si ottiene da A, sopprimendo la i - esima riga e la j - esima colonna. Si definisce complemento algebrico dell'elemento a ij
 Determinanti Sia data la matrice quadrata a... a n a a n =...... a... a n nn Chiamiamo determinante di il numero det o che ad essa viene associato. det = a a... a... a... a n n n... a nn Un generico elemento
Determinanti Sia data la matrice quadrata a... a n a a n =...... a... a n nn Chiamiamo determinante di il numero det o che ad essa viene associato. det = a a... a... a... a n n n... a nn Un generico elemento
