LA STRUTTURA DELLE MOLECOLE
|
|
|
- Lucia Viola
- 6 anni fa
- Visualizzazioni
Transcript
1 LA STRUTTURA DELLE MOLECOLE Per studiare la struttura delle molecole procederemo con lo stesso schema utilizzato per gli atomi. Cominceremo con la molecola più semplice, cioè la molecola-ione idrogeno, avente un solo elettrone. Questa molecola è utile perché ci permette di introdurre tutti i concetti fondamentali che poi saranno applicati a molecole di struttura più generale. Lo schema generale della procedura è simile a quello visto nel caso degli atomi. Come gli orbitali dell atomo di idrogeno sono utili per discutere, da un punto di vista qualitativo, la struttura elettronica e le proprietà degli atomi più complessi usando per il riempimento degli orbitali il principio di esclusione di Pauli, analogamente gli orbitali, in questo caso molecolari, della molecola di H + 2 sono una buona base di partenza per discutere la struttura delle molecole biatomiche, sempre sulla base del principio di esclusione di Pauli. Tratteremo la molecola di H + 2 prima in modo completo risolvendo l equazione di Schrödinger in modo esatto. Poi tratteremo la molecola con metodi approssimati, che saranno gli unici possibili nel caso di molecole più complesse, e cioè la tratteremo con il metodo degli orbitali molecolari (MO) che è il metodo oggi più usato per studiare la struttura delle molecole. Successivamente tratteremo la molecola di idrogeno (e le molecole biatomiche omonucleari ed eteronucleari) prima con il metodo MO e poi con il metodo del legame di valenza (VB) confrontando i risultati che si ottengono con i due metodi. Infine tratteremo le molecole poliatomiche generiche con il metodo ab initio ed esattamente con il metodo degli orbitali molecolari nell approccio del campo autoconsistente di Hartree-Fock (HF-SCF) trattando particolarmente lo sviluppo degli orbitali molecolari come combinazioni lineari di orbitali atomici (MO-LCAO) vedendo anche i limiti di questo approccio e descrivendo il concetto di correlazione elettronica e di interazione di configurazione. Poi le molecole poliatomiche saranno anche trattate con il metodo del legame di valenza. Infine illustreremo i concetti fondamentali che entrano nei metodi semiempirici descrivendo, a titolo esemplificativo, i principali. In tutta questa trattazione cercheremo di usare estensivamente la simmetria delle molecole e la teoria dei gruppi per semplificare i problemi ed ottenere informazioni anche di tipo qualitativo. Nella nostra trattazione consideremo sempre molecole con nuclei fissi, e quindi studieremo solo il moto e le autofunzioni per gli elettroni. È quindi necessario giustificare preliminarmente questa approssimazione. 1
2 Approssimazione di Born-Oppenheimer Va sotto questo nome la approssimazione che consente di considerare in una molecola separatamente il moto elettronico ed il moto nucleare: di essa si può dare una giustificazione qualitativa o anche quantitativa. Consideriamo una molecola e per essa scriviamo l Hamiltoniano che conterrà i seguenti termini H = T n + T e + V ne + V ee + V nn (1) che nell ordine si riferiscono a energia cinetica dei nuclei (T n ), energia cinetica degli elettroni (T e ), interazione elettroni-nuclei (V ne ), interazione elettroneelettrone (V ee ) ed interazione nucleo-nucleo (V nn ). Indicando gli elettroni con gli indici i e j ed i nuclei con gli indici α e β i vari termini possono essere scritti esplicitamente in unità atomiche come T n = α 1 2m α 2 α T e = i i V ne = αi V ee = ij Z α r iα 1 r ij (2) V nn = αβ Z α Z β r αβ L equazione di Schrödinger che vogliamo risolvere è allora HΨ(q i q α ) = EΨ(q i q α ) (3) dove q i e q α sono genericamente le coordinate di elettroni e nuclei, E è l energia totale della molecola e l autofunzione dipende dalle coordinate degli elettroni e dei nuclei. Qualitativamente possiamo dire quanto segue. La massa dell elettrone è molto più piccola di quella dei nuclei (almeno 1840 volte più piccola, cioè quattro ordini di grandezza più piccola) per cui possiamo dire che gli elettroni si muovono molto più velocemente e nel tempo in cui gli elettroni hanno compiuto molti cicli del loro movimento i nuclei non si sono 2
3 quasi mossi dallo loro posizione iniziale. Possiamo quindi pensare di risolvere l equazione di Schrödinger per i soli elettroni considerando i nuclei fissi. Naturalmente è chiaro che se fissiamo una certa configurazione dei nuclei l energia e l autofunzione elettronica dipenderanno da questa configurazione nel senso che se cambiamo la configurazione nucleare otterremo un energia ed un autofunzione diverse. Diciamo che la funzione elettronica dipende parametricamente dalla configurazione nucleare per intendere che le coordinate nucleari non compaiono esplicitamente nella funzione elettronica. Seguendo questo ragionamento scriviamo la funzione totale come un prodotto di una funzione elettronica e di una funzione nucleare Ψ(q i q α ) = Ψ e Ψ n = Ψ e (q i q α )Ψ n (q α ) (4) in cui la funzione d onda elettronica è autofunzione di un equazione di Schrödinger puramente elettronica con un Hamiltoniano e con H e = T e + V ne + V ee (5) H e ψ e = E e ψ e (6) Se vogliamo conoscere l energia totale corrispondente alla configurazione nucleare prescelta dovremo aggiungere all energia elettronica l interazione nucleonucleo U tot = E e + V nn = E e + αβ Z α Z β r αβ (7) Se calcoliamo l energia elettronica e l energia totale per tutte le configurazioni nucleari possiamo costruire una curva (o in generale una superficie) dell energia totale, come rappresentata in modo schematico nella figura 1. Nella figura sono indicati anche la energia del minimo e la energia di dissociazione. Dall andamento della curva vedremo quale è la struttura di equilibrio della molecola, struttura che corrisponderà al minimo della energia totale. Secondo questo approccio quindi l equazione per il moto degli elettroni va risolta separatamente per ogni configurazione dei nuclei, per giungere a definire una struttura di minimo. Ovviamente l energia nucleo-nucleo costituisce una costante nell equazione elettronica. Ritornando ora all equazione totale abbiamo 3
4 (T n ψ n )ψ e + (T e + V ne + V ee + V nn )ψ e ψ n = Eψ e ψ n (8) e tenendo conto delle due equazioni precedenti possiamo scrivere (T n ψ n )ψ e + (U tot ψ n )ψ e = (Eψ n )ψ e (9) ed infine dividendo per ψ e otteniamo l equazione per il movimento dei nuclei (T n + U tot ) ψ n = Eψ n (10) Da questa si vede che il potenziale sotto il quale si muovono i nuclei, U tot, contiene due termini e cioè la repulsione nucleo-nucleo e l energia elettronica. In parole povere se immaginiamo di essere nella posizione di minimo e spostiamo i nuclei dalla posizione di equilibrio l energia totale (somma di repulsioni nucleari e di energia elettronica) genera una forza di richiamo che farà oscillare i nuclei intorno alle posizioni di equilibrio. In conclusione quindi le coordinate nucleari compaiono come un parametro nell equazione di Schrödinger per gli elettroni e l energia elettronica determina il movimento dei nuclei. Per capire meglio l essenza della approssimazione di Born-Oppenheimer possiamo considerare la equazione di Schrödinger in modo più esplicito supponendo che la funzione d onda elettronica sia una funzione lentamente variabile delle coordinate nucleari ottenendo le equazioni viste sopra. Il significato della approssimazione di Born-Oppenheimer è in sostanza equivalente a dire che se variamo la energia nucleare (dando ad esempio alla nostra molecola energia vibrazionale e salendo quindi nella curva della energia totale nella figura 1 vista sopra) restiamo sempre nello stesso stato elettronico. Ci sono anche situazioni in cui questa approssimazione non è valida. Ma noi assumeremo di muoverci sempre nei limiti di validità dell approssimazione di Born-Oppenheimer e da ora in poi ci interesseremo solo dell Hamiltoniano elettronico delle molecole che scriviamo esplicitamente H = i i αi Z α r iα + ij 1 r ij (11) Per ottenere l energia della molecola aggiungeremo alla energia elettronica ottenuta dalla risoluzione della equazione di Schrödinger elettronica la repulsione nucleo-nucleo. 4
5 V nn = αβ Z α Z β r αβ (12) La molecola-ione idrogeno La molecola ione idrogeno H + 2 è costituita da due protoni e da un elettrone: la struttura e le coordinate necessarie a descriverla sono mostrate nella figura 2. Si tratta di una molecola osservata in scariche elettriche e che è stata caratterizzata spettroscopicamente. L Hamiltoniano elettronico in unità atomiche è e l equazione di Schrödinger H = r a 1 r b (13) dove ψ 1 r a ψ 1 r b ψ = Eψ (14) ψ = ψ(xyz) (15) è funzione delle tre coordinate dell unico elettrone. Volendo risolvere quest equazione è necessario procedere come visto ormai in molti casi e cioè scegliere un sistema di coordinate che consenta di separare l equazione in tre equazioni in una singola variabile. Il sistema di coordinate più adatto in questo caso è quello di coordinate ellittiche confocali definito con riferimento alla figura 2 dalle coordinate ξ = r a + r b R η = r a r b R φ (16) con limiti di variazione 1 ξ 1 η 1 0 φ 2π (17) 5
6 Il primo passo a questo punto è trasformare l Hamiltoniano nelle nuove coordinate e scrivere la nostra funzione nella forma ψ(ξηφ) = ψ(φ)ψ(ξ)ψ(η) (18) È importante notare che in questo caso, a differenza che negli atomi, non abbiamo una simmetria sferica e quindi L 2 non commuta con H. Tuttavia esiste una simmetria assiale ed L z commuterà con H come si vedrebbe chiaramente dalla forma di H nelle coordinate scelte. Pertanto le autofunzioni saranno anche autofunzioni di L z. D altra parte sappiamo che con L z ψ(φ) = mψ(φ) (19) ψ(φ) = 1 2π e imφ (20) e m=0, ±1, ±2 e quindi possiamo scrivere 1 1 ψ = F (ξη) e imφ = ψ(ξ)ψ(η) e imφ (21) 2π 2π Procedendo ora alla soluzione delle equazioni per ξ e per η non si trova una espressione algebrica, chiusa per E, ma l energia deve essere calcolata numericamente per ogni valore di R. L andamento dell energia elettronica e della energia totale per lo stato elettronico fondamentale e per il primo stato eccitato è riportato in Figure 3 e 4. Si vede che nello stato fondamentale la energia totale ha un minimo, per cui la molecola è stabile rispetto ad un protone ed un atomo di idrogeno separati. Dalla soluzione dell equazione si trova che la energia dipende da m 2 e quindi gli stati con m 0 sono doppiamente degeneri. Gli stati vengono classificati con un simbolo che indica il valore della componente del momento angolare lungo z (asse molecolare) nel modo seguente λ = m λ simbolo σ π δ ϕ (22) Poiché il potenziale è centrale (cambiare di segno a tutte le coordinate equivale a cambiare r a con r b ) le autofunzioni devono essere pari o dispari (per 6
7 essere autofunzioni dell operatore parità). Quindi le autofunzioni e gli stati possono essere classificati come pari (g = gerade) o dispari (u = ungerade). Più semplicemente, la molecola possiede il centro di inversione, per cui gli stati devono necessariamente essere simmetrici o antisimmetrici per inversione al centro. L energia elettronica e l energia totale dei vari stati elettronici della molecola ione idrogeno sono riportate in funzione di R nelle figure 6 e 7. I primi due stati sono classificati allora σ g e σ u rispettivamente. Poiché gli stati con questa simmetria sono molti si numerano con un indice progressivo davanti, indice che giuoca il ruolo del numero quantico principale nel caso atomico, e cioè 1σ g, 2σ g, 3σ g 1σ u, 2σ u, 3σ u (23) Gli stati possono anche essere classificati indicando lo stato dell atomo di idrogeno che si ottiene per R = (cioè con la dissociazione): i primi due stati sono allora classificati come σ g 1s e σ u1s (sul significato di * torneremo in seguito). Molecola H + 2 : trattazione con orbitale molecolare (MO) Come già abbiamo detto molecole complesse possono essere trattate solo con metodi approssimati. Introduciamo i concetti fondamentali trattando la molecola ione idrogeno con il metodo degli orbitali molecolari. In sostanza useremo il metodo variazionale per ottenere l approssimazione migliore alla funzione d onda molecolare minimizzando l energia rispetto ad opportuni parametri variazionali. Il concetto di partenza del metodo MO è che le funzioni d onda che descrivono un elettrone in una molecola sono funzioni estese a tutta la molecola (orbitali molecolari appunto) che in via di principio potrebbero non avere niente a che fare con gli orbitali degli atomi di partenza. Questo del resto è il risultato che abbiamo ottenuto nel paragrafo precedente, dove non c è alcun riferimento agli atomi costituenti, se non nell analisi dei risultati. Avendo già scritto l Hamiltoniano nella forma vista sopra preoccupiamoci di trovare una funzione variazionale. Come funzione variazionale scegliamo una combinazione di funzioni in modo da rientrare nella applicazione del metodo variazionale lineare che abbiamo già trattato in termini generali. La prima cosa da fare è scegliere una combinazione di funzioni adatte. Per questo notiamo che se allontaniamo i nuclei evidentemente arriveremo ad avere un protone più un atomo di idrogeno e quindi in 7
8 questo limite l elettrone sarà descritto dalla funzione d onda per l atomo di idrogeno. D altra parte nella dissociazione l elettrone potrà andare con l uno o l altro dei due nuclei: perciò la combinazione più adatta per descrivere il sistema sarà una combinazione lineare di due funzioni di tipo 1s centrate una sull atomo a ed una sull atomo b ψ = c 1 1 π k 3/2 e kra + c 2 1 π k 3/2 e kr b = c 1 ϕ a + c 2 ϕ b = c 1 1s a + c 2 1s b (24) Con questo abbiamo fatto una combinazione lineare di orbitali atomici (LCAO: Linear Combination of Atomic Orbitals). Nella funzione che abbiamo scritto i parametri variazionali da aggiustare sono i coefficienti c 1 e c 2, tuttavia abbiamo introdotto nelle due funzioni anche il parametro k come esponente orbitale. Infatti notiamo che quando la distanza internucleare si riduce a zero otteniamo uno ione elio ed in questo limite l elettrone sarà descritto dall orbitale 1s dell elio e cioè da ψ = 1 π 2 3/2 e 2r (25) in cui abbiamo un esponente orbitale k = 2. Nel limite invece di R tendente ad infinito le funzioni saranno genuinamente funzioni dell atomo di idrogeno e quindi con esponente orbitale k = 1. Quindi in conclusione dobbiamo aspettarci che l esponente orbitale dipenda dalla separazione internucleare e che in ogni modo sia compreso tra 1 e 2. Ciò premesso applicando il metodo variazionale lineare troviamo, come abbiamo visto, per i coefficienti c il sistema di equazioni lineari omogenee (equazione secolare) dove (H aa W S aa ) c 1 + (H ab W S ab ) c 2 = 0 (H ba W S ba ) c 1 + (H bb W S bb ) c 2 = 0 (26) H aa =< ϕ a H ϕ a >=< 1s a H 1s a > H ab =< ϕ a H ϕ b >=< 1s a H 1s b >= H ba H bb =< ϕ b H ϕ b >=< 1s b H 1s b > S aa =< ϕ a ϕ a >=< 1s a 1s a >= 1 = S bb S ab =< ϕ a ϕ b >=< 1s a 1s a >= S ba (27) 8
9 In particolare S ab è l integrale di sovrapposizione: dalla figura 8 si vede come il valore dell integrale di sovrapposizione vari al variare della distanza. L equazione secolare ha soluzioni non nulle se il determinante dei coefficienti (determinante secolare) è uguale a zero (H aa W S aa ) (H ab W S ab ) (H ba W S ba ) (H bb W S bb ) = 0 (28) A questo punto possiamo procedere in tre modi diversi: o risolviamo direttamente il determinante e le equazioni (cosa che è possibile fare in maniera semplice in questo caso di dimensioni 2x2) oppure usiamo la procedura generale che si deve necessariamente usare nel caso multidimensionale oppure, infine, cerchiamo di sfruttare considerazioni di simmetria. Procedura 1 Gli integrali che dobbiamo considerare nel nostro caso specifico sono H aa = H bb =< ϕ a H ϕ a > H ab = H ba =< ϕ a H ϕ b > S ab = S ba =< ϕ a ϕ b > integrale coulombiano integrale di risonanza integrale di sovrapposizione (29) per cui il determinante secolare, tenendo conto che le funzioni sono normalizzate S aa = S bb = 1 assume la forma specifica (H aa W ) (H ab W S ab ) (H ab W S ab ) (H aa W ) = 0 (30) Sviluppandolo abbiamo e quindi (H aa W ) 2 (H ab W S ab ) 2 = 0 (31) e le due soluzioni sono H aa W = ±(H ab W S ab ) (32) W 1 = H aa + H ab 1 + S ab W 2 = H (33) aa H ab 1 S ab 9
10 Questi sono i possibili valori per l energia dei due orbitali molecolari. In corrispondenza di questi due valori dell energia possiamo trovare i coefficienti c. Per la prima soluzione, cioè usando l autovalore W 1 abbiamo e quindi (H aa W 1 ) c 1 + (H ab W 1 S ab ) c 2 = 0 (34) c 1 = (H ab W 1 S ab ) c 2 (H aa W 1 ) che sostituendo l espressione di W 1 dà (35) Quindi avremo c 1 c 2 = 1 = c 1 = c 2 (36) considerando la condizione di normalizzazione ψ 1 = c 1 (ϕ a + ϕ b ) (37) < ψ 1 ψ 1 >=1 = c 2 1 (< ϕ a ϕ a > + < ϕ a ϕ b > + < ϕ b ϕ a > + < ϕ b ϕ b >) = otteniamo = c 2 1( S ab ) ψ 1 = (38) Sab (ϕ a + ϕ b ) (39) Procediamo analogamente per la soluzione W 2 ed otteniamo, tenendo conto che l integrale H ab è negativo stato fondamentale ψ 1 = 1 2+2Sab (ϕ a + ϕ b ) stato eccitato ψ 2 = 1 2 2Sab (ϕ a ϕ b ) W 1 = Haa+H bb 1+S ab W 2 = Haa H bb 1 S ab (40) Possiamo arrivare allo stesso risultato procedendo in modo più generale secondo la stada alternativa illustrata nel seguito. 10
11 Procedura 2 Come abbiamo visto illustrando il metodo variazionale lineare l equazione secolare può essere scritta con una notazione matriciale dove HC = CSW (41) ( ) Haa H H = ab H ab H bb ( ) 1 Sab S = S ab 1 ( ) W1 0 W = 0 W 2 ( ) c11 c C = 21 c 12 c 22 (42) Questa è la forma del problema agli autovalori che si ottiene nella base prescelta ϕ b ϕ = (ϕ a ϕ b ) (43) per la quale abbiamo in notazione matriciale ( ) ( ) ϕa 1 Sab ϕϕ = (ϕ a ϕ b ) = = S (44) S ab 1 Per semplificare il problema e ridurlo ad una problema agli autovalori di una matrice dobbiamo passare dalla base (ϕ a ϕ b ) ad una nuova base che sia ortogonale nel senso che ) (ϕ aϕ b) = ( ϕ ϕ ϕ = a ϕ b A questo fine per prima cosa scegliamo ϕ a = ϕ = (ϕ aϕ b) (45) ( ) 1 0 = E = matrice unità (46) Sab (ϕ a + ϕ b ) (47) 11
12 ϕ b = 1 2 2Sab (ϕ a ϕ b ) (48) che ha la proprietà desiderata. La procedura è equivalente a diagonalizzare la matrice S con la trasformazione di similarità ( ) (1 S S 1 che definisce una nuova base ) ( ) = ( 1 + S 0 ) 0 1 S (49) ψ a = 1 2 (ϕ a + ϕ b ) (50) ψ b = 1 2 (ϕ a ϕ b ) (51) che una volta normalizzata dà la base (ϕ aϕ b ). Ottenuta questa base ortonormale dobbiamo trasformare in questa nuova base ortonormale la matrice dell Hamiltoniano, cosa che si realizza con la trasformazione ( Sab 2+2Sab 1 2 2Sab 1 2 2Sab ( Haa+Hab = 1+S ab 0 0 H aa H ab 1 S ab ) (Haa ) ( 1 H ab H ab H bb 1 2+2Sab 2 2Sab 1 2+2Sab 1 2 2Sab ) (52) In questa nuova base vediamo quindi che la matrice dell Hamiltoniano è diagonale e gli elementi diagonali sono gli autovalori, cioè le energie degli orbitali molecolari, identiche a quelle trovate con la prima procedura diretta che abbiamo usato prima. Le colonne della matrice di trasformazione a destra della matrice Hamiltoniano (autovettori) sono i coefficienti che definiscono i due orbitali molecolari, come abbiamo già visto con la prima procedura. Si giunge quindi sia per gli autovalori che per gli autovettori alla stessa soluzione cui si era giunti per soluzione diretta dell equazione secolare. Questa seconda procedura è quella da usare nel caso generale con i seguenti stadi: 1. scegliere una base di funzioni in cui espandere gli orbitali molecolari e calcolare gli integrali che definiscono le matrici H ed S; 12 ) =
13 2. trasformare la base in una base ortogonale in cui S è una matrice unità; 3. trasformare la matrice H nella nuova base ottenendo H ; 4. diagonalizzare la matrice H per ottenere le energie ( autovalori ) e gli autovettori nella base ortogonale; 5. ottenere le combinazioni lineari nella base originale. Nell esempio attuale la procedura si ferma allo stadio 3 in quanto per la semplicità del problema si ottiene una matrice H già diagonale, cosa che non avviene nel caso generale. In riferimento ai punti 1 e 2 si può notare che la base iniziale comprende sempre orbitali atomici di atomi diversi che quindi non hanno nessun motivo per essere ortogonali. Anzi per la formazione del legame è essenziale che l integrale di sovrapposizione di orbitali di atomi diversi non sia nullo. Procedura 3 Possiamo procedere in un altro modo ancora usando la simmetria. Limitandoci a considerare che la molecola possiede il centro di inversione, le autofunzioni devono possedere una definita simmetria rispetto a questa operazione e cioè essere simmetriche o antisimmetriche rispetto alla inversione al centro (più esattamente le autofunzioni devono comportarsi come una rappresentazione irriducibile del gruppo di simmetria: in questo caso è sufficiente limitarsi a considerare il solo centro di inversione). Allora le sole funzioni che dobbiamo considerare saranno combinazioni lineari del tipo ψ 1 = c(ϕ a + ϕ b ) (53) ψ 2 = c(ϕ a ϕ b ) (54) che hanno la giusta simmetria. In questo modo si giunge direttamente alla forma delle funzioni già trovata come somma e differenza degli orbitali atomici. Si procede, come già visto, alla normalizzazione delle funzioni di simmetria. Dopo di che sappiamo, sempre per proprietà di simmetria, che in queste funzioni di simmetria la matrice dell Hamiltoniano sarà in forma diagonale (come avevamo già trovato in precedenza) in quanto gli integrali del tipo 13
14 < ψ 1 H ψ 2 > (55) sono nulli se le funzioni sono di simmetria diversa, come nel caso presente. Giunti comunque, per una strada o per l altra, alla forma delle autofunzioni ed alla energia per i primi due stati elettronici della molecola possiamo fare una serie di osservazioni che sono di validità generale. 1. L integrale di risonanza H ab (o integrale di scambio) risulta essere di segno negativo: questo determina la successione per energia crescente dei livelli, come riportata in precedenza. Si vede quindi che l integrale di risonanza è di importanza fondamentale, in questa trattazione, nel determinare la stabilità della molecola e la formazione del legame chimico. Non dobbiamo però attribuire un significato fisico eccessivo a questa osservazione. Infatti questa relazione tra stabilità e segno e valore dell integrale di risonanza è legata al metodo di trattazione usato ed in particolare al fatto che abbiamo espresso la funzione variazionale come una combinazione di funzioni. Notiamo infatti che nella trattazione esatta presentata nel paragrafo precedente non c era traccia di un analogo dell integrale di risonanza. Nella Figura 9 è riportato per lo stato fondamentale il contributo alla stabilità del legame dell integrale coulombiano e di quello di scambio. 2. Interessanti conclusioni possiamo ottenere confrontando la densità elettronica (cioè la probabilità di trovare l elettrone) mentre ci spostiamo lungo la direzione dell asse internucleare. L andamento per le due autofunzioni dell orbitale di legame e di quello di antilegame è mostrato in figura 10. Per la funzione dello stato fondamentale notiamo che al centro tra i due nuclei la densità elettronica è maggiore della somma delle densità elettroniche delle due funzioni separate, mentre la densità elettronica all esterno dei due nuclei diminuisce rispetto alle singole funzioni della combinazione lineare. Questo addensamento della densità elettronica al centro del legame ed il conseguente aumento della interazione attrattiva elettrone-nuclei (l elettrone al centro è soggetto ad una attrazione più efficace da parte di entrambi i nuclei) è essenziale per spiegare la formazione del legame. Possiamo generalizzare questo risultato dicendo che maggiore sarà l addensamento della densità elettronica al centro tra i due atomi più forte sarà il legame (principio 14
15 della massima sovrapposizione). Al contrario come si vede dalla figura 10, per lo stato eccitato la densità elettronica diminuisce fortemente al centro tra i due nuclei rispetto alla somma delle due densità delle funzioni di base, mentre aumenta all esterno. Anzi al centro tra i due nuclei la densità è nulla e la funzione ha un piano nodale. Tutto questo si apprezza meglio guardando le curve di densità elettronica costante per le due funzioni riportate ugualmente in figura 11. Queste caratteristiche spiegano la denominazione delle due funzioni come orbitali di legame e di antilegame, rispettivamente. Questa denominazione, che useremo in generale, risulta ovviamente anche evidente dall esame delle energie associate agli orbitali della molecola rispetto a quelle degli atomi o nuclei separati come si vede ancora in figura. 3. Volendo quantificare la stabilizzazione della molecola rispetto agli atomi dissociati è necessario calcolare gli integrali coulombiano e di risonanza e per questo bisogna scegliere il valore dell esponente orbitale. Trattando k come un parametro variazionale si trova che il valore ottimale alla distanza di legame è k = Con questo valore dell esponente orbitale si ottiene un valore della energia di dissociazione di 2.35 ev rispetto ad una valore sperimentale di Ci sono quindi margini per migliorare ancora la funzione variazionale. Per questo invece di considerare combinazioni di due orbitali di tipo s sui due nuclei consideriamo combinazioni di due orbitali che hanno carattere parzialmente s e parzialmente p o e cioe consideriamo funzioni del tipo ϕ a = k3/2 π e kra + c ζ5/2 4 2π r ae ζra/2 cos θ α (56) dove compare l angolo θ α definito nella figura vista all inizio della trattazione. Con la introduzione di orbitali ibridi del tipo definito sopra si ha un aumento ulteriore della densità elettronica al centro del legame con una conseguente maggiore stabilità. In questo modo si ottiene una energia di dissociazione di 2.73 ev. 4. Avendo fatto una combinazione di due orbitali atomici (uno per atomo) siamo giunti ad una equazione secolare e ad un determinante secolare di dimensioni due e quindi abbiamo ottenuto due orbitali molecolari e due energie relative (vedi la parte inferiore della figura 12). Abbiamo visto che è possibile espandere una funzione in un set completo 15
16 di autofunzioni. In questo caso abbiamo fatto una espansione in due sole funzioni (1s a e 1s b ) e quindi le soluzioni e le energie ottenute sono approssimate. Un confronto con la soluzione esatta è riportato in figura 13. È evidente che gli orbitali molecolari sono molti di più (infiniti): se vogliamo ottenere anche questi orbitali dobbiamo combinare più orbitali atomici di ciascun atomo. Ad esempio se per ogni atomo prendiamo gli orbitali 1s, 2s, 2p x, 2p y e 2p z facciamo una combinazione di 10 orbitali atomici ed otterremo 10 orbitali molecolari. I primi due in questa situazione saranno diversi da quelli che abbiamo ottenuti con la combinazione più semplice. Del resto abbiamo già visto come l energia dello stato fondamentale migliori quando si considerino orbitali ibridi. Tuttavia, nell ambito di una descrizione sostanzialmente qualitativa e tenendo conto che le energie degli orbitali atomici sono nettamente separate possiamo più semplicemente combinare a coppie gli orbitali atomici corrispondenti ed ottenere coppie di orbitali molecolari, come mostrato in figura 12. Le varie combinazioni, la forma approssimata degli orbitali molecolari risultanti e la successione dei livelli sono mostrate in modo schematico e senza alcuna pretesa di precisione nelle figure 14 e 15 e nella tabella 1. I livelli in ordine di energia crescente sono σ g 1s < σ u1s < σ g 2s < σ u2s < < π u 2p +1 = π u 2p 1 < σ g 2p < π g2p +1 = π g2p 1 < σ u2p (57) È necessario solo precisare che, come già detto, i livelli e gli stati che si originano da orbitali atomici con numero quantico m = 0 sono singoli (non degeneri) mentre quelli che si originano da orbitali atomici con m = 1 sono doppiamente degeneri 5. Nella descrizione grafica e nello schema mostrato gli orbitali molecolari sono identificati con dei simboli. Abbiamo già detto del significato di questi simboli. Riepiloghiamo e precisiamo ulteriormente il loro significato. σ identifica il valore m = 0 della componente z del momento angolare; significa anche che l orbitale ha simmetria assiale cioè è simmetrico rispetto ad una rotazione intorno all asse molecolare. 16
17 π identifica il valore m = 1 della componente z del momento angolare. L orbitale è doppiamente degenere. L orbitale derivante dagli orbitali atomici p x è antisimmetrico per una riflessione rispetto al piano yz. g identifica orbitali simmetrici rispetto alla inversione al centro u identifica orbitali antisimmetrici rispetto alla inversione al centro. identifica orbitali antisimmetrici per una riflessione rispetto ad un piano perpendicolare all asse di legame. 6. Nella classificazione degli orbitali molecolari vista sopra abbiamo considerato cosa avviene quando gli atomi costituenti si separano (limite degli atomi separati) e l orbitale molecolare si trasforma in un orbitale atomico degli atomi costituenti (in questo caso di un atomo di idrogeno): il simbolo dell orbitale molecolare è seguito dal simbolo dell orbitale atomico corrispondente. Una ulteriore classificazione degli orbitali molecolari si può avere indicando cosa accade nel limite di distanza interatomica nulla (limite dell atomo unito) cioè quando i due nuclei si fondono in un unico nucleo. Allora si antepone al simbolo dell orbitale molecolare quello dell orbitale risultante nell atomo unito. Nella tabella che segue sono indicate queste corrispondenze. Si noti, a titolo di esempio, che l orbitale σu1s va a finire in un orbitale 2p z : ciò è evidente dalla forma dell orbitale molecolare e dal fatto che la simmetria della funzione deve conservarsi a qualsiasi distanza internucleare. Si può fare di più cercando di stabilire una corrispondenza tra quello che succede nell atomo unito, negli atomi separati e nelle situazioni intermedie. Il diagramma di correlazione è mostrato in figura 16: è interessante notare che l ordine dei livelli cambia con la separazione internucleare. La correlazione atomo unito - atomo separato è illustrata anche in figura 17. Si nota anche nel diagramma che alcuni livelli si intersecano al variare della distanza internucleare : questo non può mai accadere per livelli della stessa simmetria (regola di non crossing ). Questa descrizione sia pure qualitativa è utilissima dal punto di vista generale perché si può utilizzare per descrivere la struttura di molecole omonucleari a molti elettroni. Ad esempio dallo schema di livelli considerati possiamo subito ottenere la struttura elettronica della molecola di azoto, da cui si vede la formazione di un triplo legame (6 elettroni in orbitali di legame con i corrispondenti orbitali di antilegame vuoti) 17
18 costituito da un legame σ e da due legami π o anche la struttura della molecola di ossigeno, mostrata anch essa in figura 15 e 18 che mostra la presenza di due elettroni spaiati e quindi il carattere paramagnetico di questo elemento. Riempiendo in questo modo gli orbitali molecolari, in analogia a quanto visto nel caso degli atomi, si ottiene la configurazione elettronica della molecola biatomica omonucleare. Ad esempio nel caso dell azoto e dell ossigeno si ha N 2 (σ g 1s) 2 (σu1s) 2 (σ g 2s) 2 (σu2s) 2 (π u 2p +1 ) 2 (π u 2p 1 ) 2 (σ g 2p) 2 O 2 (σ g 1s) 2 (σu1s) 2 (σ g 2s) 2 (σu2s) 2 (π u 2p +1 ) 2 (π u 2p 1 ) 2 (σ g 2p) 2 (πg2p) 2 oppure considerando a parte gli shell completamente pieni (orbitali di legame e di antilegame corrispondenti riempiti) N 2 KK(σ g 2s) 2 (σu2s) 2 (π u 2p +1 ) 2 (π u 2p 1 ) 2 (σ g 2p) 2 O 2 KK(σ g 2s) 2 (σu2s) 2 (π u 2p +1 ) 2 (π u 2p 1 ) 2 (σ g 2p) 2 (πg2p) 2 La conformazione e l ordine di legame nelle molecole biatomiche omonucleari sono riportati nella tabella 2 e nelle figure 19, 20a e 20b. È necessario caratterizzare completamente questi stati elettronici globali della molecola in termini della componente z totale del momento angolare e della molteplicità di spin. La componente z del momento angolare totale sarà la somma delle componenti dei singoli elettroni: il fatto importante è che la componente z del momento angolare totale commuta con l Hamiltoniano e quindi esso dovrà avere i seguenti valori M z = M L ħ M L = 0, ±1, ±2, (58) Se indichiamo con Λ = M L il valore assoluto della componente z momento angolare totale possiamo caratterizzare gli stati associando i seguenti simboli ( Λ ) simbolo Σ Π Φ Γ (59) 18
19 In aggiunta possiamo specificare la molteplicità di spin ricordando che lo spin totale avrà valore S = ħ S(S + 1) (60) e che il numero quantico di spin deriverà come al solito dalla composizione degli spin dei singoli elettroni. La molteplicità di spin 2S + 1 viene indicata con un soprascritto posto davanti al simbolo per L z. Ad esempio nellla configurazione per lo stato fondamentale e per lo stato eccitato di H 2 avremo stato fondamentale (σ g 1s) 2 M L = 0 S = 0 = 1 Σ stato eccitato σ g 1sσu1s M L = 0 S = 0 = 1 Σ σ g 1sσu1s M L = 0 S = 1 = 3 Σ (61) e quindi per lo stato eccitato possiamo avere uno stato di singoletto ed uno stato di tripletto. Ovviamente quando un sottostrato è completamente pieno i momenti orbitali si sommano per dare zero (Σ) ed analogamente per gli spin in modo da avere 2S + 1 =1. Quando 2 elettroni occupano 2 orbitali non equivalenti si ottengono configurazioni che danno i seguenti termini σσ M L = 0 S = 0 1 Σ S = 1 3 Σ σπ M L = 1 S = 0 1 Π S = 1 3 Π πδ M L = 3 S = 0 1 Φ S = 1 3 Φ ππ M L = 2 S = 0 1 S = 1 3 M L = 0 S = 0 1 Σ S = 1 3 Σ M L = 0 S = 0 1 Σ S = 1 3 Σ (62) Nell ultimo caso gli stati compaiono due volte in quanto si possono avere gli accoppiamenti di spin e. 19
Le molecole ed il legame chimico
 La meccanica quantistica è in grado di determinare esattamente i livelli energetici dell atomo di idrogeno e con tecniche matematiche più complesse è anche in grado di descrivere l atomo di elio trovando
La meccanica quantistica è in grado di determinare esattamente i livelli energetici dell atomo di idrogeno e con tecniche matematiche più complesse è anche in grado di descrivere l atomo di elio trovando
Lezione 3. Legame Chimico. Teoria degli Orbitali Molecolari
 Lezione 3 Legame Chimico Teoria degli Orbitali Molecolari 1 Perchè si formano i legami? Un diagramma di energia mostra che un legame fra due atomi si forma se l energia del sistema diminuisce quando i
Lezione 3 Legame Chimico Teoria degli Orbitali Molecolari 1 Perchè si formano i legami? Un diagramma di energia mostra che un legame fra due atomi si forma se l energia del sistema diminuisce quando i
Le molecole ed il legame chimico
 TEORIA DELL ORBITALE MOLECOLARE PER MOLECOLE COMPLESSE Per predire molte delle proprietà delle molecole biatomiche si può eleborare una teoria semplice che ricalca il modello della teoria dell elettrone
TEORIA DELL ORBITALE MOLECOLARE PER MOLECOLE COMPLESSE Per predire molte delle proprietà delle molecole biatomiche si può eleborare una teoria semplice che ricalca il modello della teoria dell elettrone
Esercizio 1. CF 2 CS 2 CCl 4 ClF 3
 Esercizio 1 Determinare in base al metodo del legame di valenza la forma delle seguenti molecole, tenendo conto delle repulsioni coulombiane tra le coppie elettroniche di valenza CF 2 CS 2 CCl 4 ClF 3
Esercizio 1 Determinare in base al metodo del legame di valenza la forma delle seguenti molecole, tenendo conto delle repulsioni coulombiane tra le coppie elettroniche di valenza CF 2 CS 2 CCl 4 ClF 3
Le molecole ed il legame chimico
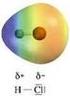 LA MOLECOLA DI IDROGENO X r A2 e 2 r A1 r 12 r B2 e 1 r B1 È il primo caso di molecola bielettronica da noi incontrato ed è la base per lo studio di ogni altra molecola. A R AB B Z Y Se si applica l approssimazione
LA MOLECOLA DI IDROGENO X r A2 e 2 r A1 r 12 r B2 e 1 r B1 È il primo caso di molecola bielettronica da noi incontrato ed è la base per lo studio di ogni altra molecola. A R AB B Z Y Se si applica l approssimazione
La struttura elettronica degli atomi
 1 In unità atomiche: a 0 me 0,59A unità di lunghezza e H 7, ev a H=Hartree unità di energia L energia dell atomo di idrogeno nello stato fondamentale espresso in unità atomiche è: 4 0 me 1 e 1 E H 13,
1 In unità atomiche: a 0 me 0,59A unità di lunghezza e H 7, ev a H=Hartree unità di energia L energia dell atomo di idrogeno nello stato fondamentale espresso in unità atomiche è: 4 0 me 1 e 1 E H 13,
IL LEGAME COVALENTE SECONDO LA MECCANICA ONDULATORIA L
 IL LEGAME COVALENTE SECONDO LA MECCANICA ONDULATORIA L elettrone è dissolto in una nube di carica, ovvero il concetto di orbitale sostituisce il di Lewis LEGAME DI VALENZA (VB) Sviluppo quantomeccanico
IL LEGAME COVALENTE SECONDO LA MECCANICA ONDULATORIA L elettrone è dissolto in una nube di carica, ovvero il concetto di orbitale sostituisce il di Lewis LEGAME DI VALENZA (VB) Sviluppo quantomeccanico
LEGAME COVALENTE: TEORIA DEGLI ORBITALI MOLECOLARI
 LEGAME COVALENTE: TEORIA DEGLI ORBITALI MOLECOLARI Il legame covalente e la geometria delle molecole possono essere descritti dalla teoria del legame di valenza: i legami risultano dalla condivisione di
LEGAME COVALENTE: TEORIA DEGLI ORBITALI MOLECOLARI Il legame covalente e la geometria delle molecole possono essere descritti dalla teoria del legame di valenza: i legami risultano dalla condivisione di
Struttura del sistema periodico Stato fondamentale degli elementi
 Struttura del sistema periodico Stato fondamentale degli elementi Singolo elettrone: 1)Numero quantico principale n 2)Numero quantico del momento angolare orbitale l = 0, 1,, n-1 3)Numero quantico magnetico
Struttura del sistema periodico Stato fondamentale degli elementi Singolo elettrone: 1)Numero quantico principale n 2)Numero quantico del momento angolare orbitale l = 0, 1,, n-1 3)Numero quantico magnetico
TEORIA DEGLI ORBITALI MOLECOLARI
 TEORIA DEGLI ORBITALI MOLECOLARI La teoria VB è la teoria più semplice basata sulla meccanica quantistica. Essa riesce a descrivere correttamente la geometria di moltissime molecole ma non permette di
TEORIA DEGLI ORBITALI MOLECOLARI La teoria VB è la teoria più semplice basata sulla meccanica quantistica. Essa riesce a descrivere correttamente la geometria di moltissime molecole ma non permette di
ATOMI MONOELETTRONICI
 ATOMI MONOELETTRONICI L equazione di Schrödinger per gli atomi contenenti un solo elettrone (atomo di idrogeno, ioni He +, Li 2+ ) può essere risolta in maniera esatta e le soluzioni ottenute permettono
ATOMI MONOELETTRONICI L equazione di Schrödinger per gli atomi contenenti un solo elettrone (atomo di idrogeno, ioni He +, Li 2+ ) può essere risolta in maniera esatta e le soluzioni ottenute permettono
Consideriamo un sistema composto da due particelle identiche. Due particelle sono identiche se hanno le stesse proprietà intrinseche (massa, carica,
 Consideriamo un sistema composto da due particelle identiche. Due particelle sono identiche se hanno le stesse proprietà intrinseche (massa, carica, spin, ). Esempi: due elettroni, due protoni, due neutroni,
Consideriamo un sistema composto da due particelle identiche. Due particelle sono identiche se hanno le stesse proprietà intrinseche (massa, carica, spin, ). Esempi: due elettroni, due protoni, due neutroni,
Con riferimento alla figura 1, l Hamiltoniano della molecola di idrogeno in unità atomiche ha la forma. r a1 r b
 Molecola di idrogeno Nel capitolo precedente, partendo dagli orbitali molecolari della molecolaione idrogeno, è stata possibile una trattazione qualitativa delle molecole biatomiche e quindi anche della
Molecola di idrogeno Nel capitolo precedente, partendo dagli orbitali molecolari della molecolaione idrogeno, è stata possibile una trattazione qualitativa delle molecole biatomiche e quindi anche della
Funzione d onda dello stato fondamentale (trascurando l interazione elettrone-elettrone)
 -e -e +2e ATOMO DI ELIO. Considero il nucleo fisso (sistema di riferimento del centro di massa, circa coincidente col nucleo). I due elettroni vanno trattati come indistinguibili. -e -e +2e SENZA il termine
-e -e +2e ATOMO DI ELIO. Considero il nucleo fisso (sistema di riferimento del centro di massa, circa coincidente col nucleo). I due elettroni vanno trattati come indistinguibili. -e -e +2e SENZA il termine
Elettrone fortemente legato
 Elettrone fortemente legato Introduzione Vogliamo studiare un altra strada, cioè un altra approssimazione per ottenere le bande elettroniche, e cioè quella del metodo dell elettrone fortemente legato.
Elettrone fortemente legato Introduzione Vogliamo studiare un altra strada, cioè un altra approssimazione per ottenere le bande elettroniche, e cioè quella del metodo dell elettrone fortemente legato.
GLI ORBITALI ATOMICI
 GLI ORBITALI ATOMICI Orbitali atomici e loro rappresentazione Le funzioni d onda Ψ n che derivano dalla risoluzione dell equazione d onda e descrivono il moto degli elettroni nell atomo si dicono orbitali
GLI ORBITALI ATOMICI Orbitali atomici e loro rappresentazione Le funzioni d onda Ψ n che derivano dalla risoluzione dell equazione d onda e descrivono il moto degli elettroni nell atomo si dicono orbitali
Esercizi sulle coniche (prof.ssa C. Carrara)
 Esercizi sulle coniche prof.ssa C. Carrara Alcune parti di un esercizio possono ritrovarsi in un altro esercizio, insieme a parti diverse. È un occasione per affrontarle da un altra angolazione.. Determinare
Esercizi sulle coniche prof.ssa C. Carrara Alcune parti di un esercizio possono ritrovarsi in un altro esercizio, insieme a parti diverse. È un occasione per affrontarle da un altra angolazione.. Determinare
Metodi Pseudopotenziale
 Oltre HF Metodi Pseudopotenziale Il moto degli elettroni interni è poco influenzato dall'intorno molecolare Il calcolo può essere semplificato modificando lo hamiltonano: limitandosi a calcolare solo il
Oltre HF Metodi Pseudopotenziale Il moto degli elettroni interni è poco influenzato dall'intorno molecolare Il calcolo può essere semplificato modificando lo hamiltonano: limitandosi a calcolare solo il
L atomo di idrogeno (1) H T = p2 1 2m 1. + p2 2 2m 2. + V ( r 1 r 2 ) (2) Definiamo le nuove variabili: 1. La massa totale M M = m 1 + m 2 (3)
 L atomo di idrogeno Il problema dell atomo di idrogeno é un problema esattamente risolubili ed i suoi risultati possono essere estesi agli atomi idrogenoidi, in cui solo c é solo un elettrone sottoposto
L atomo di idrogeno Il problema dell atomo di idrogeno é un problema esattamente risolubili ed i suoi risultati possono essere estesi agli atomi idrogenoidi, in cui solo c é solo un elettrone sottoposto
Esercizi sulle coniche (prof.ssa C. Carrara)
 Esercizi sulle coniche prof.ssa C. Carrara Alcune parti di un esercizio possono ritrovarsi in un altro esercizio, insieme a parti diverse. È un occasione per affrontarle più volte.. Stabilire il tipo di
Esercizi sulle coniche prof.ssa C. Carrara Alcune parti di un esercizio possono ritrovarsi in un altro esercizio, insieme a parti diverse. È un occasione per affrontarle più volte.. Stabilire il tipo di
Dalle configurazioni ai termini
 Dalle configurazioni ai termini Introduzione Nello sviluppare i metodi di Thomas - Fermi, di Hartree e di Hartree - Fock, abbiamo sempre rappresentato gli autostati di un sistema costituito da due o più
Dalle configurazioni ai termini Introduzione Nello sviluppare i metodi di Thomas - Fermi, di Hartree e di Hartree - Fock, abbiamo sempre rappresentato gli autostati di un sistema costituito da due o più
LA STRUTTURA ELETTRONICA DEGLI ATOMI
 LA STRUTTURA ELETTRONICA DEGLI ATOMI 127 Possiamo trattare insieme l atomo di idrogeno e gli atomi idrogenoidi He +, Li 2+, ecc., in quanto differiscono l uno dall altro solo per la carica nucleare. Protone
LA STRUTTURA ELETTRONICA DEGLI ATOMI 127 Possiamo trattare insieme l atomo di idrogeno e gli atomi idrogenoidi He +, Li 2+, ecc., in quanto differiscono l uno dall altro solo per la carica nucleare. Protone
Molecole. 04/09/13 3-MOL-0.doc 0
 Molecole 04/09/13 3-MOL-0.doc 0 Legame covalente H 2 + Il potenziale cui è soggetto l elettrone ha 2 minimi equivalenti 1) H + si avvicina a H 2) Se la barriera diventa abbastanza sottile la probabilità
Molecole 04/09/13 3-MOL-0.doc 0 Legame covalente H 2 + Il potenziale cui è soggetto l elettrone ha 2 minimi equivalenti 1) H + si avvicina a H 2) Se la barriera diventa abbastanza sottile la probabilità
in cui le sommatorie sono fatte sugli elettroni dell atomo. Le componenti z di L e S sono date dalle somme scalari N
 Termini atomici (o termini spettroscopici) e loro determinazione a partire dalla configurazione elettronica Le configurazioni elettroniche degli atomi sono ambigue nel senso che esiste un certo numero
Termini atomici (o termini spettroscopici) e loro determinazione a partire dalla configurazione elettronica Le configurazioni elettroniche degli atomi sono ambigue nel senso che esiste un certo numero
Lezione n. 19. L equazione. di Schrodinger L atomo. di idrogeno Orbitali atomici. 02/03/2008 Antonino Polimeno 1
 Chimica Fisica - Chimica e Tecnologia Farmaceutiche Lezione n. 19 L equazione di Schrodinger L atomo di idrogeno Orbitali atomici 02/03/2008 Antonino Polimeno 1 Dai modelli primitivi alla meccanica quantistica
Chimica Fisica - Chimica e Tecnologia Farmaceutiche Lezione n. 19 L equazione di Schrodinger L atomo di idrogeno Orbitali atomici 02/03/2008 Antonino Polimeno 1 Dai modelli primitivi alla meccanica quantistica
LA STRUTTURA DELLE MOLECOLE. Orbitali molecolari e legame chimico
 LA STRUTTURA DELLE MOLECOLE Orbitali molecolari e legame chimico GLI ORBITALI MOLECOLARI Quando degli atomi collidono tra di loro i loro nuclei ed elettroni vengono a trovarsi in prossimità influenzandosi
LA STRUTTURA DELLE MOLECOLE Orbitali molecolari e legame chimico GLI ORBITALI MOLECOLARI Quando degli atomi collidono tra di loro i loro nuclei ed elettroni vengono a trovarsi in prossimità influenzandosi
Esercitazioni di Meccanica Quantistica I
 Esercitazioni di Meccanica Quantistica I Sistema a due stati Consideriamo come esempio di sistema a due stati l ammoniaca. La struttura del composto è tetraedrico : alla sommità di una piramide con base
Esercitazioni di Meccanica Quantistica I Sistema a due stati Consideriamo come esempio di sistema a due stati l ammoniaca. La struttura del composto è tetraedrico : alla sommità di una piramide con base
Risultati della teoria di Hartree
 Risultati della teoria di Hartree Il potenziale è a simmetria sferica, come nell atomo di idrogeno, quindi: ψ n, l, m = Rn, l ( r) Θ l, m ( θ ) Φ m ( ϕ ) l l l La dipendenza angolare delle autofunzioni
Risultati della teoria di Hartree Il potenziale è a simmetria sferica, come nell atomo di idrogeno, quindi: ψ n, l, m = Rn, l ( r) Θ l, m ( θ ) Φ m ( ϕ ) l l l La dipendenza angolare delle autofunzioni
Legame e struttura molecolare
 2016 2017 CCS Biologia CCS-Scienze Geologiche 1 Legame e struttura molecolare Orbitali atomici Molecole Cap 9. 1-3, 15-16, 18, 21-23, 40 CONSIDERAZIONI PRELIMINARI 2 Le strutture di Lewis e la teoria VSEPR
2016 2017 CCS Biologia CCS-Scienze Geologiche 1 Legame e struttura molecolare Orbitali atomici Molecole Cap 9. 1-3, 15-16, 18, 21-23, 40 CONSIDERAZIONI PRELIMINARI 2 Le strutture di Lewis e la teoria VSEPR
L atomo di idrogeno. R. Dovesi, M. De La Pierre, C. Murace. Chimica Fisica II. Corso di Laurea in Chimica A.A. 2012/2013
 L atomo di idrogeno R. Dovesi, M. De La Pierre, C. Murace Corso di Laurea in Chimica A.A. 2012/2013 Chimica Fisica II Modello per l atomo di idrogeno Modello: protone fisso nell origine ed elettrone in
L atomo di idrogeno R. Dovesi, M. De La Pierre, C. Murace Corso di Laurea in Chimica A.A. 2012/2013 Chimica Fisica II Modello per l atomo di idrogeno Modello: protone fisso nell origine ed elettrone in
Università degli Studi di Roma La Sapienza. Approssimazione di M. Born & R. Oppenheimer.
 Università degli Studi di Roma La Sapienza Facoltà di Scienze Matematiche, Fisiche, e Naturali. (Appunti di Fisica Nucleare) Approssimazione di M. Born & R. Oppenheimer. F. López (Pancho) pako.lopez@virgilio.it
Università degli Studi di Roma La Sapienza Facoltà di Scienze Matematiche, Fisiche, e Naturali. (Appunti di Fisica Nucleare) Approssimazione di M. Born & R. Oppenheimer. F. López (Pancho) pako.lopez@virgilio.it
Legame covalente: la teoria del legame di valenza
 Legame covalente: la teoria del legame di valenza La teoria di Lewis, un legame è costituito da una coppia di elettroni (postulata prima della meccanica quantistica), considera gli elettroni di valenza
Legame covalente: la teoria del legame di valenza La teoria di Lewis, un legame è costituito da una coppia di elettroni (postulata prima della meccanica quantistica), considera gli elettroni di valenza
Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA (Edile-Architettura e dell Edilizia) CONICHE DI
 Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA (Edile-Architettura e dell Edilizia) CONICHE DI R. Docente: Prof. F. Flamini Esercizi Riepilogativi Svolti Esercizio
Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA (Edile-Architettura e dell Edilizia) CONICHE DI R. Docente: Prof. F. Flamini Esercizi Riepilogativi Svolti Esercizio
SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE
 SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE. Esercizi Esercizio. In R calcolare il modulo dei vettori,, ),,, ) ed il loro angolo. Esercizio. Calcolare una base ortonormale del sottospazio
SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE. Esercizi Esercizio. In R calcolare il modulo dei vettori,, ),,, ) ed il loro angolo. Esercizio. Calcolare una base ortonormale del sottospazio
La forma delle molecole
 La forma delle molecole Geometria molecolare: disposizione relativa nello spazio degli atomi costituenti una molecola o un composto covalente a struttura infinita La geometria delle molecole si esprime
La forma delle molecole Geometria molecolare: disposizione relativa nello spazio degli atomi costituenti una molecola o un composto covalente a struttura infinita La geometria delle molecole si esprime
numeri quantici orbitale spin
 La funzione d onda ψ definisce i diversi stati in cui può trovarsi l elettrone nell atomo. Nella sua espressione matematica, essa contiene tre numeri interi, chiamati numeri quantici, indicati con le lettere
La funzione d onda ψ definisce i diversi stati in cui può trovarsi l elettrone nell atomo. Nella sua espressione matematica, essa contiene tre numeri interi, chiamati numeri quantici, indicati con le lettere
CORSO DI FISICA DELLA MATERIA CONDENSATA A. A. 2013/14
 1 CORSO DI FISICA DELLA MATERIA CONDENSATA 3 MODI NORMALI DI VIBRAZIONE DELLE MOLECOLE POLIATOMICHE Appunti dalle Lezioni del Prof. P. Calvani A. A. 2013/14 Queste dispense sono per solo uso interno e
1 CORSO DI FISICA DELLA MATERIA CONDENSATA 3 MODI NORMALI DI VIBRAZIONE DELLE MOLECOLE POLIATOMICHE Appunti dalle Lezioni del Prof. P. Calvani A. A. 2013/14 Queste dispense sono per solo uso interno e
IL LEGAME SIGMA σ E IL LEGAME PI- GRECO π
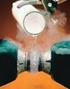 IL LEGAME SIGMA σ E IL LEGAME PI- GRECO π La teoria di Lewis considera gli elettroni di valenza degli atomi che formano legami,ma prescinde totalmente dal fatto che tali elettroni sono descritti da orbitali
IL LEGAME SIGMA σ E IL LEGAME PI- GRECO π La teoria di Lewis considera gli elettroni di valenza degli atomi che formano legami,ma prescinde totalmente dal fatto che tali elettroni sono descritti da orbitali
Enrico Silva - diritti riservati - Non è permessa, fra l altro, l inclusione anche parziale in altre opere senza il consenso scritto dell autore
 Particelle della presente identiche. opera. Principio di Pauli. 1 Particelle identiche: sommario Finora: proprietà di particella singola. Volendo ottenere il comportamento di più particelle, è necessario
Particelle della presente identiche. opera. Principio di Pauli. 1 Particelle identiche: sommario Finora: proprietà di particella singola. Volendo ottenere il comportamento di più particelle, è necessario
Comune ordine di riempimento degli orbitali di un atomo
 Comune ordine di riempimento degli orbitali di un atomo Le energie relative sono diverse per differenti elementi ma si possono notare le seguenti caratteristiche: (1) La maggior differenza di energia si
Comune ordine di riempimento degli orbitali di un atomo Le energie relative sono diverse per differenti elementi ma si possono notare le seguenti caratteristiche: (1) La maggior differenza di energia si
LEZIONE 23. ax 2 + bxy + cy 2 + dx + ey + f
 LEZIONE 23 23.1. Riduzione delle coniche a forma canonica. Fissiamo nel piano un sistema di riferimento Oxy e consideriamo un polinomio di grado 2 in x, y a meno di costanti moltiplicative non nulle, diciamo
LEZIONE 23 23.1. Riduzione delle coniche a forma canonica. Fissiamo nel piano un sistema di riferimento Oxy e consideriamo un polinomio di grado 2 in x, y a meno di costanti moltiplicative non nulle, diciamo
Valitutti, Falasca, Tifi, Gentile. Chimica. concetti e modelli.blu
 Valitutti, Falasca, Tifi, Gentile Chimica concetti e modelli.blu 2 Capitolo 14 Le nuove teorie di legame 3 Sommario 1. I limiti della teoria di Lewis 2. Il legame chimico secondo la meccanica quantistica
Valitutti, Falasca, Tifi, Gentile Chimica concetti e modelli.blu 2 Capitolo 14 Le nuove teorie di legame 3 Sommario 1. I limiti della teoria di Lewis 2. Il legame chimico secondo la meccanica quantistica
Appello di Meccanica Quantistica I
 Appello di Meccanica Quantistica I Facoltà di Scienze M.F.N. Università degli Studi di Pisa gennaio 007 (A.A. 06/07) Tempo a disposizione: 3 ore. Problemi e per il recupero Compitino I; problemi e 3 per
Appello di Meccanica Quantistica I Facoltà di Scienze M.F.N. Università degli Studi di Pisa gennaio 007 (A.A. 06/07) Tempo a disposizione: 3 ore. Problemi e per il recupero Compitino I; problemi e 3 per
E. SCHRODINGER ( )
 E. SCHRODINGER (1887-1961) Elettrone = onda le cui caratteristiche possono essere descritte con un equazione simile a quella delle onde stazionarie le cui soluzioni, dette funzioni d onda ψ, rappresentano
E. SCHRODINGER (1887-1961) Elettrone = onda le cui caratteristiche possono essere descritte con un equazione simile a quella delle onde stazionarie le cui soluzioni, dette funzioni d onda ψ, rappresentano
ATOMO POLIELETTRONICO. Numero quantico di spin m s
 ATOMO POLIELETTRONICO La teoria fisico-matematica che ha risolto esattamente il problema dell atomo di idrogeno non è in grado di descrivere con uguale precisione l atomo polielettronico. Problema: interazioni
ATOMO POLIELETTRONICO La teoria fisico-matematica che ha risolto esattamente il problema dell atomo di idrogeno non è in grado di descrivere con uguale precisione l atomo polielettronico. Problema: interazioni
Compito di Meccanica Razionale M-Z
 Compito di Meccanica Razionale M-Z 11 giugno 213 1. Tre piastre piane omogenee di massa m aventi la forma di triangoli rettangoli con cateti 4l e 3l sono saldate lungo il cateto più lungo come in figura
Compito di Meccanica Razionale M-Z 11 giugno 213 1. Tre piastre piane omogenee di massa m aventi la forma di triangoli rettangoli con cateti 4l e 3l sono saldate lungo il cateto più lungo come in figura
1 Coniche. s (x, y, t ) (1) 1 (x, y, t )F r 2
 1 Coniche Studieremo le curve nel piano euclideo, cioè nel piano con un sistema di riferimento cartesiano ortogonale fissato, oppure nel completamento proiettivo di questo piano, ottenuto con l introduzione
1 Coniche Studieremo le curve nel piano euclideo, cioè nel piano con un sistema di riferimento cartesiano ortogonale fissato, oppure nel completamento proiettivo di questo piano, ottenuto con l introduzione
Esercizi sui sistemi di equazioni lineari.
 Esercizi sui sistemi di equazioni lineari Risolvere il sistema di equazioni lineari x y + z 6 x + y z x y z Si tratta di un sistema di tre equazioni lineari nelle tre incognite x, y e z Poichè m n, la
Esercizi sui sistemi di equazioni lineari Risolvere il sistema di equazioni lineari x y + z 6 x + y z x y z Si tratta di un sistema di tre equazioni lineari nelle tre incognite x, y e z Poichè m n, la
CAPITOLO 14. Quadriche. Alcuni esercizi di questo capitolo sono ripetuti in quanto risolti in maniera differente.
 CAPITOLO 4 Quadriche Alcuni esercizi di questo capitolo sono ripetuti in quanto risolti in maniera differente. Esercizio 4.. Stabilire il tipo di quadrica corrispondente alle seguenti equazioni. Se si
CAPITOLO 4 Quadriche Alcuni esercizi di questo capitolo sono ripetuti in quanto risolti in maniera differente. Esercizio 4.. Stabilire il tipo di quadrica corrispondente alle seguenti equazioni. Se si
0.1 Numeri complessi C
 0.1. NUMERI COMPLESSI C 1 0.1 Numeri complessi C Abbiamo visto sopra come l introduzione dei numeri irrazionali può essere motivata dalla necessità di trovare soluzione all equazione x = 0 che non ha soluzioni
0.1. NUMERI COMPLESSI C 1 0.1 Numeri complessi C Abbiamo visto sopra come l introduzione dei numeri irrazionali può essere motivata dalla necessità di trovare soluzione all equazione x = 0 che non ha soluzioni
Ma se dobbiamo trattare l elettrone come un onda occorre una funzione (che dobbiamo trovare) che ne descriva esaurientemente queste proprietà.
 Ma se dobbiamo trattare l elettrone come un onda occorre una funzione (che dobbiamo trovare) che ne descriva esaurientemente queste proprietà. Nell atomo l energia associata ad un elettrone (trascurando
Ma se dobbiamo trattare l elettrone come un onda occorre una funzione (che dobbiamo trovare) che ne descriva esaurientemente queste proprietà. Nell atomo l energia associata ad un elettrone (trascurando
I NUMERI QUANTICI. per l = orbitale: s p d f
 I NUMERI QUANTICI I numeri quantici sono quattro. I primi tre servono a indicare e a distinguere i diversi orbitali. Il quarto numero descrive una proprietà tipica dell elettrone. Esaminiamo in dettaglio
I NUMERI QUANTICI I numeri quantici sono quattro. I primi tre servono a indicare e a distinguere i diversi orbitali. Il quarto numero descrive una proprietà tipica dell elettrone. Esaminiamo in dettaglio
GLI ORBITALI ATOMICI
 GLI ORBITALI ATOMICI I numeri quantici Le funzioni d onda Ψ n, soluzioni dell equazione d onda, sono caratterizzate da certe combinazioni di numeri quantici: n, l, m l, m s n = numero quantico principale,
GLI ORBITALI ATOMICI I numeri quantici Le funzioni d onda Ψ n, soluzioni dell equazione d onda, sono caratterizzate da certe combinazioni di numeri quantici: n, l, m l, m s n = numero quantico principale,
Interazione luce- atomo
 Interazione luce- atomo Descrizione semiclassica L interazione predominante è quella tra il campo elettrico e le cariche ASSORBIMENTO: Elettrone e protone formano un dipolo che viene messo in oscillazione
Interazione luce- atomo Descrizione semiclassica L interazione predominante è quella tra il campo elettrico e le cariche ASSORBIMENTO: Elettrone e protone formano un dipolo che viene messo in oscillazione
CLASSIFICAZIONE DELLE CONICHE AFFINI
 CLASSIFICAZIONE DELLE CONICHE AFFINI Pre-requisiti necessari. Elementi di geometria analitica punti e rette nel piano cartesiano, conoscenza delle coniche in forma canonica). Risoluzione di equazioni e
CLASSIFICAZIONE DELLE CONICHE AFFINI Pre-requisiti necessari. Elementi di geometria analitica punti e rette nel piano cartesiano, conoscenza delle coniche in forma canonica). Risoluzione di equazioni e
Lezione n. 22. Molecole poliatomiche Metodo VSEPR Orbitali ibridi Coniugazione π. 02/03/2008 Antonino Polimeno 1
 Chimica Fisica - Chimica e Tecnologia Farmaceutiche Lezione n. 22 Molecole poliatomiche Metodo VSEPR Orbitali ibridi Coniugazione π 02/03/2008 Antonino Polimeno 1 Molecole poliatomiche (1) - Siamo ora
Chimica Fisica - Chimica e Tecnologia Farmaceutiche Lezione n. 22 Molecole poliatomiche Metodo VSEPR Orbitali ibridi Coniugazione π 02/03/2008 Antonino Polimeno 1 Molecole poliatomiche (1) - Siamo ora
Prodotto scalare e ortogonalità
 Prodotto scalare e ortogonalità 12 Novembre 1 Il prodotto scalare 1.1 Definizione Possiamo estendere la definizione di prodotto scalare, già data per i vettori del piano, ai vettori dello spazio. Siano
Prodotto scalare e ortogonalità 12 Novembre 1 Il prodotto scalare 1.1 Definizione Possiamo estendere la definizione di prodotto scalare, già data per i vettori del piano, ai vettori dello spazio. Siano
Molecola Idrogeno (struttura elettronica) R P 2. P r 1 b
 Molecola Idrogeno (struttura elettronica) (vedi Slater e Bransden) r b r a rp r rb a rp a R P r a P r + R P P r a P r + R P b P r b P r R P P r b P r R P L Hamiltoniana del sistema è H L L r a r b r a
Molecola Idrogeno (struttura elettronica) (vedi Slater e Bransden) r b r a rp r rb a rp a R P r a P r + R P P r a P r + R P b P r b P r R P P r b P r R P L Hamiltoniana del sistema è H L L r a r b r a
2 2 2 A = Il Det(A) = 2 quindi la conica è non degenere, di rango 3.
 Studio delle coniche Ellisse Studiare la conica di equazione 2x 2 + 4xy + y 2 4x 2y + 2 = 0. Per prima cosa dobbiamo classificarla. La matrice associata alla conica è: 2 2 2 A = 2 2 2 Il DetA = 2 quindi
Studio delle coniche Ellisse Studiare la conica di equazione 2x 2 + 4xy + y 2 4x 2y + 2 = 0. Per prima cosa dobbiamo classificarla. La matrice associata alla conica è: 2 2 2 A = 2 2 2 Il DetA = 2 quindi
Oscillatore armonico in più dimensioni
 Oscillatore armonico in più dimensioni 1 Oscillatore in D dimensioni La teoria dell oscillatore armonico si può generalizzare facilmente da una a più dimensioni. Infatti la hamiltoniana di un oscillatore
Oscillatore armonico in più dimensioni 1 Oscillatore in D dimensioni La teoria dell oscillatore armonico si può generalizzare facilmente da una a più dimensioni. Infatti la hamiltoniana di un oscillatore
4 Autovettori e autovalori
 4 Autovettori e autovalori 41 Cambiamenti di base Sia V uno spazio vettoriale tale che dim V n Si è visto in sezione 12 che uno spazio vettoriale ammette basi distinte, ma tutte con la medesima cardinalità
4 Autovettori e autovalori 41 Cambiamenti di base Sia V uno spazio vettoriale tale che dim V n Si è visto in sezione 12 che uno spazio vettoriale ammette basi distinte, ma tutte con la medesima cardinalità
LEZIONE 3. a + b + 2c + e = 1 b + d + g = 0 3b + f + 3g = 2. a b c d e f g
 LEZIONE 3 3.. Matrici fortemente ridotte per righe. Nella precedente lezione abbiamo introdotto la nozione di soluzione di un sistema di equazioni lineari. In questa lezione ci poniamo il problema di descrivere
LEZIONE 3 3.. Matrici fortemente ridotte per righe. Nella precedente lezione abbiamo introdotto la nozione di soluzione di un sistema di equazioni lineari. In questa lezione ci poniamo il problema di descrivere
1 Cambiamenti di riferimento nel piano
 1 Cambiamenti di riferimento nel piano Siano date due basi ortonormali ordinate di V : B = ( i, j) e B = ( i, j ) e supponiamo che i = a i + b j j = c i + d j allora per un generico vettore v V abbiamo
1 Cambiamenti di riferimento nel piano Siano date due basi ortonormali ordinate di V : B = ( i, j) e B = ( i, j ) e supponiamo che i = a i + b j j = c i + d j allora per un generico vettore v V abbiamo
UNITÀ DIDATTICA 5 LA RETTA
 UNITÀ DIDATTICA 5 LA RETTA 5.1 - La retta Equazione generica della retta Dalle considerazioni emerse nel precedente capitolo abbiamo compreso come una funzione possa essere rappresentata da un insieme
UNITÀ DIDATTICA 5 LA RETTA 5.1 - La retta Equazione generica della retta Dalle considerazioni emerse nel precedente capitolo abbiamo compreso come una funzione possa essere rappresentata da un insieme
Vettori applicati. Capitolo Richiami teorici. Definizione 1.1 Un sistema di vettori applicati Σ è un insieme
 Capitolo 1 Vettori applicati 1.1 Richiami teorici Definizione 1.1 Un sistema di vettori applicati Σ è un insieme {(P i,v i ), P i E, v i V, i = 1,...,N}, (1.1) dove P i è detto punto di applicazione del
Capitolo 1 Vettori applicati 1.1 Richiami teorici Definizione 1.1 Un sistema di vettori applicati Σ è un insieme {(P i,v i ), P i E, v i V, i = 1,...,N}, (1.1) dove P i è detto punto di applicazione del
Corso di Laurea in Fisica. Geometria. a.a Canale 3 Prof. P. Piazza Magiche notazioni
 Corso di Laurea in Fisica. Geometria. a.a. 23-4. Canale 3 Prof. P. Piazza Magiche notazioni Siano V e W due spazi vettoriali e sia T : V W un applicazione lineare. Fissiamo una base B per V ed una base
Corso di Laurea in Fisica. Geometria. a.a. 23-4. Canale 3 Prof. P. Piazza Magiche notazioni Siano V e W due spazi vettoriali e sia T : V W un applicazione lineare. Fissiamo una base B per V ed una base
X = x + 1. X = x + 1
 CONICHE. Esercizi Esercizio. Classificare, ridurre a forma canonica (completando i quadrati), e disegnare le seguenti coniche: γ : x y + x = 0; γ : x + 4x y + = 0; γ 3 : x + y + y + 0 = 0; γ 4 : x + y
CONICHE. Esercizi Esercizio. Classificare, ridurre a forma canonica (completando i quadrati), e disegnare le seguenti coniche: γ : x y + x = 0; γ : x + 4x y + = 0; γ 3 : x + y + y + 0 = 0; γ 4 : x + y
LEZIONE 27. C = { P = (x, y) x 2 /a 2 y 2 /b 2 = 1 }. C si dice iperbole di semiassi a e b (in forma canonica). L equazione
 LEZIONE 27 27.1. Ellisse, iperbole, parabola. Nelle prossime lezioni illustreremo come la teoria delle forme quadratiche e della riduzione ortogonale si applichi allo studio di alcuni oggetti geometrici
LEZIONE 27 27.1. Ellisse, iperbole, parabola. Nelle prossime lezioni illustreremo come la teoria delle forme quadratiche e della riduzione ortogonale si applichi allo studio di alcuni oggetti geometrici
Parte 8. Prodotto scalare, teorema spettrale
 Parte 8. Prodotto scalare, teorema spettrale A. Savo Appunti del Corso di Geometria 3-4 Indice delle sezioni Prodotto scalare in R n, Basi ortonormali, 4 3 Algoritmo di Gram-Schmidt, 7 4 Matrici ortogonali,
Parte 8. Prodotto scalare, teorema spettrale A. Savo Appunti del Corso di Geometria 3-4 Indice delle sezioni Prodotto scalare in R n, Basi ortonormali, 4 3 Algoritmo di Gram-Schmidt, 7 4 Matrici ortogonali,
Atomi a più elettroni
 Chapter 7 Atomi a più elettroni 7.1 Lo spin Gli esperimenti indicano che alle particelle si deve associare un momento angolare intrinseco, o spin, indipendentemente dalla loro natura (particelle elementari
Chapter 7 Atomi a più elettroni 7.1 Lo spin Gli esperimenti indicano che alle particelle si deve associare un momento angolare intrinseco, o spin, indipendentemente dalla loro natura (particelle elementari
Meccanica quantistica (5)
 Meccanica quantistica (5) 0/7/14 1-MQ-5.doc 0 Oscillatore armonico Se una massa è sottoposta ad una forza di richiamo proporzionale allo spostamento da un posizione di equilibrio F = kx il potenziale (
Meccanica quantistica (5) 0/7/14 1-MQ-5.doc 0 Oscillatore armonico Se una massa è sottoposta ad una forza di richiamo proporzionale allo spostamento da un posizione di equilibrio F = kx il potenziale (
Programma della I parte
 Programma della I parte Cenni alla meccanica quantistica: il modello dell atomo Dall atomo ai cristalli: statistica di Fermi-Dirac il modello a bande di energia popolazione delle bande livello di Fermi
Programma della I parte Cenni alla meccanica quantistica: il modello dell atomo Dall atomo ai cristalli: statistica di Fermi-Dirac il modello a bande di energia popolazione delle bande livello di Fermi
I 4 NUMERI QUANTICI. I numeri quantici consentono di definire forma, dimensioni ed energia degli orbitali.
 I 4 NUMERI QUANTICI I numeri quantici consentono di definire forma, dimensioni ed energia degli orbitali. n, numero quantico principale, indica il livello energetico e le dimensioni degli orbitali. Può
I 4 NUMERI QUANTICI I numeri quantici consentono di definire forma, dimensioni ed energia degli orbitali. n, numero quantico principale, indica il livello energetico e le dimensioni degli orbitali. Può
LEZIONE 2. ( ) a 1 x 1 + a 2 x a n x n = b, ove a j, b R sono fissati.
 LEZIONE 2 2 Sistemi di equazioni lineari Definizione 2 Un equazione lineare nelle n incognite x, x 2,, x n a coefficienti reali, è un equazione della forma (2 a x + a 2 x 2 + + a n x n = b, ove a j, b
LEZIONE 2 2 Sistemi di equazioni lineari Definizione 2 Un equazione lineare nelle n incognite x, x 2,, x n a coefficienti reali, è un equazione della forma (2 a x + a 2 x 2 + + a n x n = b, ove a j, b
1 Geometria analitica nel piano
 Lezioni di Geometria a.a. 2007-2008 cdl SIE prof. C. Franchetti 1 Geometria analitica nel piano 1.1 Distanza di due punti Siano P 1 = (x 1, y 1 ), P 2 = (x 2, y 2 ) due punti del piano, se d(p 1, P 2 )
Lezioni di Geometria a.a. 2007-2008 cdl SIE prof. C. Franchetti 1 Geometria analitica nel piano 1.1 Distanza di due punti Siano P 1 = (x 1, y 1 ), P 2 = (x 2, y 2 ) due punti del piano, se d(p 1, P 2 )
I. Foglio di esercizi su vettori linearmente dipendenti e linearmente indipendenti. , v 2 = α v 1 + β v 2 + γ v 3. α v 1 + β v 2 + γ v 3 = 0. + γ.
 ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
II Università degli Studi di Roma
 Versione preliminare gennaio TOR VERGATA II Università degli Studi di Roma Dispense di Geometria. Capitolo 3. 7. Coniche in R. Nel Capitolo I abbiamo visto che gli insiemi di punti P lineare di primo grado
Versione preliminare gennaio TOR VERGATA II Università degli Studi di Roma Dispense di Geometria. Capitolo 3. 7. Coniche in R. Nel Capitolo I abbiamo visto che gli insiemi di punti P lineare di primo grado
Esercizio 2. Consideriamo adesso lo spazio di funzioni V = {f : [0, 1] R}. Dire quali dei seguenti insiemi di funzioni sono sottospazi.
![Esercizio 2. Consideriamo adesso lo spazio di funzioni V = {f : [0, 1] R}. Dire quali dei seguenti insiemi di funzioni sono sottospazi. Esercizio 2. Consideriamo adesso lo spazio di funzioni V = {f : [0, 1] R}. Dire quali dei seguenti insiemi di funzioni sono sottospazi.](/thumbs/70/63345059.jpg) 1 Esercizi 1.1 Spazi vettoriali Studiare gli insiemi definiti di seguito, e verificare quali sono spazi vettoriali e quali no. Per quelli che non lo sono, dire quali assiomi sono violati. x 1, x 2, x 3
1 Esercizi 1.1 Spazi vettoriali Studiare gli insiemi definiti di seguito, e verificare quali sono spazi vettoriali e quali no. Per quelli che non lo sono, dire quali assiomi sono violati. x 1, x 2, x 3
1 Ampliamento del piano e coordinate omogenee
 1 Ampliamento del piano e coordinate omogenee Vogliamo dare una idea, senza molte pretese, dei concetti che stanno alla base di alcuni calcoli svolti nella classificazione delle coniche. Supponiamo di
1 Ampliamento del piano e coordinate omogenee Vogliamo dare una idea, senza molte pretese, dei concetti che stanno alla base di alcuni calcoli svolti nella classificazione delle coniche. Supponiamo di
Struttura dell atomo atomo particelle sub-atomiche - protoni positiva - neutroni } nucleoni - elettroni negativa elemento
 Struttura dell atomo L atomo è la più piccola parte dell elemento che conserva le proprietà dell elemento Negli atomi ci sono tre diverse particelle sub-atomiche: - protoni (con carica positiva unitaria)
Struttura dell atomo L atomo è la più piccola parte dell elemento che conserva le proprietà dell elemento Negli atomi ci sono tre diverse particelle sub-atomiche: - protoni (con carica positiva unitaria)
Rappresentazione matriciale del Gruppo puntuale di simmetria C3v (ammoniaca)
 Rappresentazione matriciale del Gruppo puntuale di simmetria C3v (ammoniaca) La prima cosa da fare è scegliere una BASE. Per l ammoniaca sceglieremo gli orbitali s di valenza dell azoto e degli atomi di
Rappresentazione matriciale del Gruppo puntuale di simmetria C3v (ammoniaca) La prima cosa da fare è scegliere una BASE. Per l ammoniaca sceglieremo gli orbitali s di valenza dell azoto e degli atomi di
ψ = Il carbonio (Z=6) - 2 elettroni equivalenti nello stato 2p - la funzione d onda globale deve essere antisimmetrica tripletto di spin, S=1
 s 1s s 1s p + p o p - configurazione elettronica del C nello stato fondamentale di tripletto di spin [He] (s) (p) p + p o p - configurazione elettronica del C nello stato eccitato di singoletto di spin
s 1s s 1s p + p o p - configurazione elettronica del C nello stato fondamentale di tripletto di spin [He] (s) (p) p + p o p - configurazione elettronica del C nello stato eccitato di singoletto di spin
Struttura molecolare
 Struttura molecolare Nella discussione sulle teorie del legame covalente dobbiamo ternere in considerazione che le teorie che abbiamo discusso rappresentano un tentativo di spiegare e organizzare quello
Struttura molecolare Nella discussione sulle teorie del legame covalente dobbiamo ternere in considerazione che le teorie che abbiamo discusso rappresentano un tentativo di spiegare e organizzare quello
MATRICI ORTOGONALI. MATRICI SIMMETRICHE E FORME QUADRATICHE
 DIAGONALIZZAZIONE 1 MATRICI ORTOGONALI. MATRICI SIMMETRICHE E FORME QUADRATICHE Matrici ortogonali e loro proprietà. Autovalori ed autospazi di matrici simmetriche reali. Diagonalizzazione mediante matrici
DIAGONALIZZAZIONE 1 MATRICI ORTOGONALI. MATRICI SIMMETRICHE E FORME QUADRATICHE Matrici ortogonali e loro proprietà. Autovalori ed autospazi di matrici simmetriche reali. Diagonalizzazione mediante matrici
Risposta in vibrazioni libere di un sistema lineare viscoso a più gradi di libertà. Prof. Adolfo Santini - Dinamica delle Strutture 1
 Risposta in vibrazioni libere di un sistema lineare viscoso a più gradi di libertà Prof. Adolfo Santini - Dinamica delle Strutture 1 Vibrazioni libere non smorzate 1/6 Le equazioni del moto di un sistema
Risposta in vibrazioni libere di un sistema lineare viscoso a più gradi di libertà Prof. Adolfo Santini - Dinamica delle Strutture 1 Vibrazioni libere non smorzate 1/6 Le equazioni del moto di un sistema
un legame covalente due legami covalenti? tre legami covalenti due legami covalenti un legame covalente
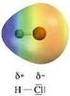 e C N un legame covalente due legami covalenti? tre legami covalenti O F Ne 1s 2s 2p due legami covalenti un legame covalente C 1s 2s 2p ibridazione quattro legami covalenti Cariche Formali Usando le strutture
e C N un legame covalente due legami covalenti? tre legami covalenti O F Ne 1s 2s 2p due legami covalenti un legame covalente C 1s 2s 2p ibridazione quattro legami covalenti Cariche Formali Usando le strutture
Applicazioni eliminazione di Gauss
 Applicazioni eliminazione di Gauss. Premessa Nel seguito supporremo sempre di applicare il metodo di eliminazione di Gauss allo scopo di trasformare la matrice del sistema Ax = b in una matrice triangolare
Applicazioni eliminazione di Gauss. Premessa Nel seguito supporremo sempre di applicare il metodo di eliminazione di Gauss allo scopo di trasformare la matrice del sistema Ax = b in una matrice triangolare
Nell'atomo l'energia dell'elettrone varia per quantità discrete (quanti).
 4. ORBITALI ATOMICI Energia degli orbitali atomici Nell'atomo l'energia dell'elettrone varia per quantità discrete (quanti). Il diagramma energetico dell'atomo di idrogeno: i livelli (individuati da n)
4. ORBITALI ATOMICI Energia degli orbitali atomici Nell'atomo l'energia dell'elettrone varia per quantità discrete (quanti). Il diagramma energetico dell'atomo di idrogeno: i livelli (individuati da n)
ORBITA ORBIT LI ALI MOLECOLARI
 ORBITALI MOLECOLARI Una molecola è dotata di una serie di orbitali detti orbitali molecolari Gli elettroni risiedono negli orbitali molecolari che, in molti casi, sono distribuiti (delocalizzati) su tutta
ORBITALI MOLECOLARI Una molecola è dotata di una serie di orbitali detti orbitali molecolari Gli elettroni risiedono negli orbitali molecolari che, in molti casi, sono distribuiti (delocalizzati) su tutta
Particelle Subatomiche
 GLI ATOMI Particelle Subatomiche ELEMENTI I diversi atomi sono caratterizzati da un diverso numero di protoni e neutroni; il numero di elettroni è sempre uguale al numero dei protoni (negli atomi neutri)
GLI ATOMI Particelle Subatomiche ELEMENTI I diversi atomi sono caratterizzati da un diverso numero di protoni e neutroni; il numero di elettroni è sempre uguale al numero dei protoni (negli atomi neutri)
Teorie del legame chimico. Teorie del legame chimico
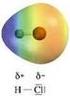 Teorie del legame chimico Le teorie proposte per la trattazione del legame chimico si prefiggono i seguenti scopi: 1. Prevedere la formazione di un legame tra due elementi 2. Predire la lunghezza del legame
Teorie del legame chimico Le teorie proposte per la trattazione del legame chimico si prefiggono i seguenti scopi: 1. Prevedere la formazione di un legame tra due elementi 2. Predire la lunghezza del legame
Parte 12b. Riduzione a forma canonica
 Parte 2b. Riduzione a forma canonica A. Savo Appunti del Corso di Geometria 202-3 Indice delle sezioni. Coniche, 2. Esempio di riduzione, 4 3. Teoremi fondamentali, 6 4. Come determinare l equazione canonica,
Parte 2b. Riduzione a forma canonica A. Savo Appunti del Corso di Geometria 202-3 Indice delle sezioni. Coniche, 2. Esempio di riduzione, 4 3. Teoremi fondamentali, 6 4. Come determinare l equazione canonica,
Transizioni elettroniche per uno ione. Transizioni elettroniche per uno ione metallico in campo dei leganti
 Transizioni elettroniche per uno ione metallico in campo dei leganti d 2 ion Electron-electron repulsion Transizioni elettroniche per uno ione Applichiamo i concetti del modello del campo dei leganti ad
Transizioni elettroniche per uno ione metallico in campo dei leganti d 2 ion Electron-electron repulsion Transizioni elettroniche per uno ione Applichiamo i concetti del modello del campo dei leganti ad
Corso di Chimica Inorganica II (A-L) Laurea Triennale in Chimica (L-27)
 Corso di Chimica Inorganica II (A-L) Laurea Triennale in Chimica (L-7) Dr. Andrea G. Marrani TEORIA DEI GRUPPI E MECCANICA QUANTISTICA Per arrivare a descrivere, seppur approssimativamente, la struttura
Corso di Chimica Inorganica II (A-L) Laurea Triennale in Chimica (L-7) Dr. Andrea G. Marrani TEORIA DEI GRUPPI E MECCANICA QUANTISTICA Per arrivare a descrivere, seppur approssimativamente, la struttura
Risoluzione di sistemi lineari
 Risoluzione di sistemi lineari Teorema (Rouché-Capelli) Dato il sistema di m equazioni in n incognite Ax = b, con A M at(m, n) b R n x R n [A b] si ha che: matrice dei coefficienti, vettore dei termini
Risoluzione di sistemi lineari Teorema (Rouché-Capelli) Dato il sistema di m equazioni in n incognite Ax = b, con A M at(m, n) b R n x R n [A b] si ha che: matrice dei coefficienti, vettore dei termini
Applicazioni del metodo MO-LCAO
 Applicazioni del metodo MO-LCAO Classificazione di stati molecolari Per classificare le funzioni d onda ed i livelli molecolari possiamo procedere come visto in precedenza cercando gli operatori che commutano
Applicazioni del metodo MO-LCAO Classificazione di stati molecolari Per classificare le funzioni d onda ed i livelli molecolari possiamo procedere come visto in precedenza cercando gli operatori che commutano
ε(r) Moti vibrazionali e rotazionali dei nuclei molecolari Introduzione
 oti vibrazionali e rotazionali dei nuclei molecolari (è utile andarsi a ripassare le piccole oscillazioni attorno a posizioni di equilibrio (modi normali) studiate in meccanica razionale) Introduzione
oti vibrazionali e rotazionali dei nuclei molecolari (è utile andarsi a ripassare le piccole oscillazioni attorno a posizioni di equilibrio (modi normali) studiate in meccanica razionale) Introduzione
Operazioni tra matrici e n-uple
 CAPITOLO Operazioni tra matrici e n-uple Esercizio.. Date le matrici 0 4 e dati λ = 5, µ =, si calcoli AB, BA, A+B, B A, λa+µb. Esercizio.. Per ognuna delle seguenti coppie di matrici A, B e scalari λ,
CAPITOLO Operazioni tra matrici e n-uple Esercizio.. Date le matrici 0 4 e dati λ = 5, µ =, si calcoli AB, BA, A+B, B A, λa+µb. Esercizio.. Per ognuna delle seguenti coppie di matrici A, B e scalari λ,
La circonferenza nel piano cartesiano
 6 La circonferenza nel piano cartesiano onsideriamo la circonferenza in figura in cui il centro è ; e il raggio 5 r : se indichiamo con P ; un punto della circonferenza avremo, per definizione, che la
6 La circonferenza nel piano cartesiano onsideriamo la circonferenza in figura in cui il centro è ; e il raggio 5 r : se indichiamo con P ; un punto della circonferenza avremo, per definizione, che la
Dipendenza e indipendenza lineare (senza il concetto di rango)
 CAPITOLO 5 Dipendenza e indipendenza lineare (senza il concetto di rango) Esercizio 5.1. Scrivere un vettore w R 3 linearmente dipendente dal vettore v ( 1, 9, 0). Esercizio 5.2. Stabilire se i vettori
CAPITOLO 5 Dipendenza e indipendenza lineare (senza il concetto di rango) Esercizio 5.1. Scrivere un vettore w R 3 linearmente dipendente dal vettore v ( 1, 9, 0). Esercizio 5.2. Stabilire se i vettori
