DIAGRAMMA DELLE VELOCITA ESERCITAZIONE
|
|
|
- Marianna Biagi
- 8 anni fa
- Visualizzazioni
Transcript
1 PROGETTI DI INFRSTRUTTURE VIRIE DIGRMM DELLE VELOCIT ESERCITZIONE Il capitolo 5.4 del Decreto Ministeriale del 5/11/2001 prevede che per la verifica della correttezza della progettazione si debba redigere il diagramma di velocità per ogni senso di circolazione. Con tale elaborato si vuole rappresentare in forma grafica l andamento della velocità lungo la strada in funzione della progressiva dell asse stradale per pervenire ad una corretta valutazione della velocità lungo il tracciato già in fase di progetto e non solo nella fase di esercizio dell infrastruttura. 1
2 PROGETTI DI INFRSTRUTTURE VIRIE Planimetria di tracciamento (non riferita all esercitazione numerica). 2
3 PROGETTI DI INFRSTRUTTURE VIRIE Finalità: 1. Valutazione dell omogeneità del tracciato in termini di verifica dei gradienti di velocità tra tratti adiacenti (Vp i -Vp i+1 < Vp); 2. Definizione dei valori di velocità di progetto da utilizzare per la verifica delle distanze di sicurezza e visibilità; 3. Progettazione di elementi geometrici particolari (segnaletica, barriere, intersezioni, ecc.). È evidente che maggiore risulta essere il V tra due elementi consecutivi, peggiore è il risultato della progettazione. Il diagramma di velocità, per pendenze delle livellette 6%, si costruisce sulla base del tracciato planimetrico calcolando per ogni elemento di esso l andamento della velocità di progetto. 3
4 PROGETTI DI INFRSTRUTTURE VIRIE Ipotesi: In rettifilo, sugli archi di cerchio con raggio R 2,5 e nelle clotoidi, la velocità di progetto tende al limite superiore dell intervallo; gli spazi di accelerazione conseguenti all uscita di una curva circolare e quelli di decelerazione per l ingresso in curva, ricadono nei detti elementi; La velocità è costante lungo tutto lo sviluppo delle curve con raggio inferiore a R 2.5 L accelerazione e la decelerazione in pieno tracciato si fissano pari a 0.8 m/s 2 L accelerazione e la decelerazione da intersezioni si possono fissare pari a 1.2 m/s 2 * Si assume che le pendenze longitudinali non influenzino la Vp degli autoveicoli (fino ai limiti del punto 4.2) NB: La nuova norma indica con i termini R * ed R 2.5 rispettivamente il R min per la V max (R * ) ed il R max per la V max (R 2.5 ). * In corrispondenza delle zone di estremità ove il tracciato in progetto si connette alle altre strade, la velocità di progetto dipende dalle caratteristiche delle intersezioni (tipologia, geometria, regole di precedenza) e a tal fine si deve fare riferimento al D.M ( Norme funzionali e geometriche per la costruzione delle intersezioni stradali ). In particolare il D.M al punto 4.2 per gli elementi dell intersezione da dimensionare longitudinalmente con criteri dinamici mediante la nota relazione 4
5 PROGETTI DI INFRSTRUTTURE VIRIE indica per l accelerazione a i valori seguenti L = 2 v1 v 2a 2 2 strade tipo CORSIE DI DECELERZIONE e B 3 m/s 2 altre strade 2 m/s 2 TRTTI DI DECELERZIONE NELLE CORSIE DI CCUMULO E SVOLT SINISTR 2 m/s 2 TRTTO DI CCELERZIONE NELLE CORSIE DI ENTRT 1 m/s 2 Rinviando gli opportuni approfondimenti ai corsi della laurea magistrale, in questa sede, per un primo approccio al problema e in modo semplificativo, è possibile adottare il valore a = 1.2 m/s 2 sia per l accelerazione che per la decelerazione nei tratti estremi del progetto didattico.. 5
6 PROGETTI DI INFRSTRUTTURE VIRIE Costruzione del diagramma delle velocità di progetto: Il primo passo è quello di individuare quei punti del tracciato in cui la velocità assume un prefissato valore: 1. punti singolari; 2. punti estremi; 3. curve circolari, lungo le quali si ipotizza che la V p sia costante; Dati dell esercitazione (vd. schema planimetrico pag. 10): Raggio circonferenza 1: 150 m (V= 66 km/h) Raggio circonferenza 2: 155 m (V= 67 km/h) Raggio circonferenza 3: 160 m (V= 68 km/h) Raggio circonferenza 4: 155 m (V= 67 km/h) Raggio circonferenza 5: 150 m (V= 66 km/h) Con f t (V): f t (V)= V V V
7 PROGETTI DI INFRSTRUTTURE VIRIE Preiliminarmente occorre rappresentare l andamento delle curvature e delle livellette: Lunghezza di transizione: E la lunghezza in cui la velocità passa dal valore Vp 1 al valore Vp 2 competenti a due elementi che si succedono D T = 2 V1 V 26 a 2 2 = V Vm a dove: D t :distanza di transizione [m] V:differenza di velocità (Vp 1 -Vp 2 ) [Km/h] V m :velocità media tra i due elementi [Km/h] a :accelerazione o decelerazione [m/s 2 ] 7
8 PROGETTI DI INFRSTRUTTURE VIRIE Distanza di riconoscimento: E la lunghezza massima del tratto di strada entro il quale il conducente può riconoscere eventuali ostacoli ed avvenimenti. D r = t v p con : t= 12 s dove v p (m/s) è riferita all elemento di raggio maggiore. Secondo questo modello l apprezzamento di una variazione di curvatura dell asse, che consente al conducente di modificare la sua velocità, può avvenire solo all interno della distanza di riconoscimento, e quindi per garantire la sicurezza della circolazione: in caso di decelerazioni deve essere: D T D r (cioè devo potere riconoscere un pericolo nello spazio di decelerazione) e comunque, affinché la variazione di curvatura sia effettivamente percepita D T D v dove D v è la distanza di visuale libera nel tratto che precede la curva circolare. 8
9 PROGETTI DI INFRSTRUTTURE VIRIE Foglio Excel (Strada tipo F) Distanza di transizione in pieno tracciato V1 V2 DV Vm a Dt Distanza di transizione in corrispondenza di intersezioni a V(in)=20 Km/h V1 V2 DV Vm a Dt Distanza di transizione in corrispondenza di intersezioni a V(in)=0 Km/h V1 V2 DV Vm a Dt Distanza di riconoscimento t V(Rmax) v(rmax) Dr
10 PROGETTI DI INFRSTRUTTURE VIRIE Dopo aver predisposto il diagramma delle curvature, si associa la velocità di progetto agli elementi a curvatura costante: 1. Si individuano i punti di inizio delle manovre di accelerazione e quelli finali per le decelerazioni L R R L R L R L R L 10
11 PROGETTI DI INFRSTRUTTURE VIRIE 2. Si effettuano i calcoli delle D T relative alle manovre di accelerazione o decelerazione dai rispettivi punti di inizio o fine ; 3. Si paragonano la D T1-2 (che gestisce la transizione della velocità da Vp 1 a Vp 2 ) e la D T2-3 (che gestisce la transizione della velocità da Vp 2 a Vp 3 ) con le distanze disponibili D disp, vale a dire con gli sviluppi di tracciato su cui è possibile variare la velocità; Il pedice 2 rappresenta la sezione teorica in cui si raggiunge la Vp max. 4. Se D disp (D T1-2 +D T2-3 ) allora si raggiunge la velocità massima, altrimenti questa sarà limitata in funzione del tratto D disp ; 5. In quest ultimo caso, D disp (D T1-2 +D T2-3 ), la velocità risultante (V eff ) sarà determinata dall intersezione delle due equazioni che gestiscono la variazione di velocità tra i tre elementi. 6. Dato che in genere la variazione di velocità si rappresenta con una retta, l intersezione tra le due rette determina una velocità che potrebbe essere scelta come V eff. 11
12 PROGETTI DI INFRSTRUTTURE VIRIE D disp =(D T1-2 +D T2-3 ) 12
13 PROGETTI DI INFRSTRUTTURE VIRIE D disp (D T1-2 +D T2-3 ), D disp (D T1-2 +D T2-3 ) 13
14 PROGETTI DI INFRSTRUTTURE VIRIE In realtà, determinando la Veff come intersezione di rette, si commette un errore, anche se piccolo, in quanto l equazione che descrive la D T non è lineare ma quadrata e va gestita tramite le: V eff 2 Vp1 Vp = a Ddisp Veff Vp1 d1 = a d = D d 2 disp dove d 1 è la distanza tra il punto iniziale con Vp 1 e il punto finale con V eff. Errato! Corretto TTENZIONE!!! Occorre utilizzare la procedura analitica per trovare l intersezione tra le distanze di transizione!! 14
15 PROGETTI DI INFRSTRUTTURE VIRIE N.B. rigore, nei punti singolari di estremità di un tracciato, il calcolo della V eff, andrebbe eseguito tenendo conto dei diversi valori di accelerazione (1,2(o 1,5) e 0,8 m/s 2 ) nei due rami del diagramma. Facendo riferimento alla figura seguente si avrà un primo ramo in cui l accelerazione da adottare sarà a 1 =1,2 (o 1,5) m/s 2, e un secondo ramo in cui l accelerazione sarà invece a 1 =0,8 m/s 2. 15
16 PROGETTI DI INFRSTRUTTURE VIRIE ppare chiaro che sia la lunghezza d 1 lungo la quale la velocità aumenterà da V p1 a V eff, che la lunghezza d 2 lungo la quale la velocità diminuirà da V eff a V p3, dovranno rispettare l espressione della distanza di transizione : D t = DV* Vm 12,96 a pplicando tale espressione ai due rami del diagramma, e tenendo conto che la somma delle d 1 e d 2 è pari alla distanza disponibile, è possibile risolvere un sistema di tre equazioni nelle tre incognite d 1, d 2 e V eff : d 1 = (V eff Vp 1 ) (V eff + Vp 1 )/2 12,96 a 1 d 2 = (V p 3 V eff ) (V eff + Vp 3 )/2 12,96(- a 2 ) d 1 + d 2 =D d 16
17 PROGETTI DI INFRSTRUTTURE VIRIE Risolvendo il sistema si arriva all espressione di V eff, valida per due tratti del diagramma con valori diversi di accelerazione: V eff =[[25,92 (a 1 a 2 )/(a 1 +a 2 ) D d ] + [(V 2 p1 a 2 + V 2 p 3 a 1 )/(a 1 +a 2 )]] 1/2 Dove: a 1 : accelerazione del primo tratto di diagramma; a 2 : accelerazione del primo tratto di diagramma; D d : Distanza disponibile; V p1 :Velocità del primo elemento; V p3 :velocità del secondo elemento. Si può facilmente vedere che l espressione della V eff, nel caso a 1 =a 2 si riduce all espressione precedentemente vista, valida per tratti con accelerazioni uguali: V eff =[12,96 a D d + V 2 p1 /2 + V 2 p3 /2] ½ 17
18 PROGETTI DI INFRSTRUTTURE VIRIE $$$$$$$$Esempio: (Si fa riferimento ai valori (R, V) di pag. 6, ai valori Dt, Dr di pag. 9 e a allo schema planimetrico di pag.10). 1) Tratto iniziale rettifilo clotoide curva Schema planimetrico (valori non riferiti all esercitazione). 18
19 PROGETTI DI INFRSTRUTTURE VIRIE Velocità iniziale: 20 km/h Velocità rettifilo: 100 km/h Velocità curva R 150 : 66 km/h Differenza di velocità tra il punto iniziale ed il rettifilo: 80km/h Velocità media: 60 km/h ccelerazione: 1,2 m/s 2 *** Distanza di transizione: (80x60)/(12,96x1,2)=308,642 m Differenza di velocità tra il rettifilo e la curva: 34 km/h Velocità media: 83 km/h ccelerazione: 0,8 m/s 2 Distanza di transizione: (34x83)/(12,96x0,8)=272,184 m Somma delle due distanze di transizione: 580,826 m Distanza di riconoscimento: (12x66)/3,6=220 m Distanza disponibile (clotoide + rettifilo): 207,500 m Cioè la distanza disponibile non è sufficiente alla transizione fino alla massima velocità, per cui si raggiungerà una velocità inferiore(v eff ). Nelle ipotesi semplificative di un unico valore di accelerazione (a=0,8 m/s 2 ) si avrebbe: V eff : ((12,96x0,8x207,5)+20 2 / /2) 0,5 =67,3 km/h Distanza dal punto iniziale di accelerazione: d 1 =(67, )/(2x12,96x0,8)= 199,14 m 19
20 PROGETTI DI INFRSTRUTTURE VIRIE In realtà essendo a 1 =1,2m/s 2 e a 2 =0,8m/s 2 si avrà: Ripetendo i calcoli: Velocità iniziale: 20 km/h Velocità rettifilo: 100 km/h Velocità curva R 150 : 66 km/h Differenza di velocità tra il punto iniziale ed il rettifilo: 80 km/h Velocità media: 60 km/h ccelerazione: 1,2 m/s 2 Distanza di transizione: 308,642 m Differenza di velocità tra il rettifilo e la curva: 34 km/h Velocità media: 83 km/h ccelerazione: 0,8 m/s 2 Distanza di transizione: 272,184 m Somma delle due distanze di transizione: 580,526 m Distanza di riconoscimento: 220 m Distanza disponibile (clotoide + rettifilo): 207,500 m Cioè la distanza disponibile non è sufficiente alla transizione fino alla massima velocità, per cui si raggiungerà una velocità inferiore Veff che va calcolata con l espressione V eff =[[25,92 (a 1 a 2 )/(a 1 +a 2 ) D d ] + [(V 2 p1 a 2 + V 2 p 3 a 1 )/(a 1 +a 2 )]] 1/2 Si ottiene così: V eff =[[25,92 (1,2* 0,8)/(1,2+0,8) 207,5 ] + [(20 2 *0, *1,2)/(1,2+0,8)]] 1/2 = 67,5 Km/h Distanza dal punto iniziale di accelerazione : d 1 =(67, )/(2x12,96x1,2)= 146,48 20
21 PROGETTI DI INFRSTRUTTURE VIRIE 2) Tratto curva 1 clotoide clotoide curva 2 Schema planimetrico (valori non riferiti all esercitazione). 21
22 PROGETTI DI INFRSTRUTTURE VIRIE Velocità curva R 150 : 66 km/h Velocità flesso: 100 km/h Velocità curva R 155 : 67 km/h Differenza di velocità tra la curva 1 ed il flesso: 34 km/h Velocità media: 83 km/h ccelerazione: 0.8 m/s 2 Distanza di transizione: (34x83)/(12,96x0,8)= m Differenza di velocità tra il flesso e la curva 2: 33 km/h Velocità media: 83.5 km/h ccelerazione: 0.8 m/s 2 Distanza di transizione: (33x83,5)/(12,96x0,8)= m Somma delle due distanze di transizione: m Distanza di riconoscimento: (12x67)/3,6=224 m Distanza disponibile (clotoide + clotoide): m Cioè la distanza disponibile non è sufficiente alla transizione: V eff :(12,96x0,8x146, / /2) 0,5 =77.1 km/h Distanza dal punto iniziale di accelerazione: d 1 =(77, )/(2x12,96x0,8)= m 22
23 PROGETTI DI INFRSTRUTTURE VIRIE In modo analogo va definito il diagramma per l altro senso di marcia.. Per poter esprimere un giudizio relativo alla omogeneità del tracciato vanno verificati i gradienti di velocità Vp. La NORMTIV ITLIN stabilisce i valori Vp per le diverse tipologie stradali e per le differenti situazioni presenti all interno del tracciato: Vp 20, 15, 10, 5 Per la nostra tipologia di strada: Nei tratti in cui si passa da Vpmax a Vp inferiori Vp 10 Km/h Fra due curve successive Vp 20 km/h Consigliabile Vp 15 Km/h 23
24 PROGETTI DI INFRSTRUTTURE VIRIE Da un punto di vista generale il livello progettuale può essere cosi definito in relazione alla verifica dei gradienti di velocità ( Vp) fra elementi adiacenti: Livello Progettuale BUONO CCETTBILE SCDENTE Vp < > 20 24
25 PROGETTI DI INFRSTRUTTURE VIRIE Fase 1: L Fase 2: R R L R L R L R L L R R L R L R L R L 25
26 PROGETTI DI INFRSTRUTTURE VIRIE PGIN 26 Commenti: Il diagramma consente di valutare positivamente l omogeneità della strada, come risultato delle scelte progettuali per la definizione dl tracciato planimetrico (successione dei valori dei raggi, sviluppo dei raccordi clotoidici e dei rettifili). Complessivamente, inoltre, si deduce che la lunghezza di tracciato è insufficiente per sviluppare le velocità di progetto massime. N.B.: Completando il diagramma, può anche verificarsi che in curva non si raggiunga il valore di Vp calcolato nella prima fase, e che la V di progetto risulti più ridotta. 26
27 PROGETTI DI INFRSTRUTTURE VIRIE PGIN 27 DIGRMM DI VELOCIT MEZZI PESNTI Tutto quanto fatto fin qui si riferisce ai mezzi leggeri ma per una verifica corretta dell andamento altimetrico dobbiamo tenere conto anche degli eventuali mezzi pesanti e verificare la necessità dell inserimento di una corsia per i veicoli lenti come disposto dal cap. 4.2 della normativa. 27
28 PROGETTI DI INFRSTRUTTURE VIRIE PGIN 28 Il grafico serve alla determinazione delle velocità dei mezzi pesanti (di caratteristiche di potenza e peso assegnate) in funzione delle livellette. Si è ipotizzata una velocità iniziale di 20 km/h e sono state ricavate: 1. V 1 = 40 km/h al termine della prima livelletta 2. V 2 = 43 km/h al termine della seconda livelletta 3. V 3 = 67 km/h al termine della terza livelletta 28
29 PROGETTI DI INFRSTRUTTURE VIRIE PGIN 29 ttenzione!! Il diagramma delle velocità dei mezzi pesanti viene completato anche per illustrare la procedura grafica complessiva. Si osservi che in alcuni casi (ad. es. tratti completamente in discesa) la costruzione può risultare superflua. Queste velocità devono essere comparate con quelle dei mezzi leggeri, ridotte del 50%, per indagare su eccessivi condizionamenti 29
30 PROGETTI DI INFRSTRUTTURE VIRIE PGIN 30 Commenti: Il tratto rosso e quello blu indicano i due versi di percorrenza Il tratto magenta rappresenta quello blu (verso V0-V1 nella planimetria di tracciamento) ridotto al 50% Il tratto ciano tratteggiato indica le velocità dei mezzi pesanti Quando il tratto ciano sta al di sotto di quello magenta, vuol dire che vi è un eccessiva interazione tra queste due tipologie di veicoli e, pertanto, se non vi sono condizioni particolari (distanze opportune per il sorpasso, ) si potrebbe ipotizzare la costruzione di una corsia supplementare per i mezzi pesanti verificandone, però, l effettiva utilità anche dal punto di vista economico. 30
31 PROGETTI DI INFRSTRUTTURE VIRIE PGIN 31 Procedimento 1. Sull asse delle ordinate individuo il valore della velocità che assumo in entrata sulla prima livelletta (es. 20 km/h, se vengo da un intersezione su cui ho la precedenza). 2. Lo prolungo fino ad incontrare la curva (che sarà in accelerazione se V=20 km/h) contrassegnata dalla pendenza della prima livelletta ed abbasso la verticale da questo punto fino ad incontrare l asse delle ascisse. 3. Da questo punto stacco, sempre sull asse delle ascisse, un segmento pari alla lunghezza della livelletta che sto esaminando e, quindi, traccio la verticale fino ad incontrare la precedente curva avente come parametro la pendenza della livelletta. Il punto così individuato mi permette di leggere sull asse delle ordinate il nuovo valore della velocità modificata dalla percorrenza sulla livelletta esaminata. (Nel caso dell esercitazione V 1 =40km/h) 4. Da questo nuovo valore della velocità, si ricomincia il procedimento. 31
32 PROGETTI DI INFRSTRUTTURE VIRIE PGIN 32 Curve a tratto continuo:curve di decelerazione Curve a tratto discontinuo:curve di accelerazione 32
33 PROGETTI DI INFRSTRUTTURE VIRIE PGIN 33 Slide del corso di Strade 33
Insegnamento di Fondamenti di Infrastrutture viarie
 Insegnamento di Fondamenti di Infrastrutture viarie Territorio ed infrastrutture di trasporto La meccanica della locomozione: questioni generali Il fenomeno dell aderenza e l equazione generale del moto
Insegnamento di Fondamenti di Infrastrutture viarie Territorio ed infrastrutture di trasporto La meccanica della locomozione: questioni generali Il fenomeno dell aderenza e l equazione generale del moto
Insegnamento di Fondamenti di Infrastrutture viarie
 Insegnamento di Fondamenti di Infrastrutture viarie Territorio ed infrastrutture di trasporto La meccanica della locomozione: questioni generali Il fenomeno dell aderenza e l equazione generale del moto
Insegnamento di Fondamenti di Infrastrutture viarie Territorio ed infrastrutture di trasporto La meccanica della locomozione: questioni generali Il fenomeno dell aderenza e l equazione generale del moto
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
SOLUZIONE DEL PROBLEMA 1 TEMA DI MATEMATICA ESAME DI STATO 2015
 SOLUZIONE DEL PROBLEMA 1 TEMA DI MATEMATICA ESAME DI STATO 015 1. Indicando con i minuti di conversazione effettuati nel mese considerato, la spesa totale mensile in euro è espressa dalla funzione f()
SOLUZIONE DEL PROBLEMA 1 TEMA DI MATEMATICA ESAME DI STATO 015 1. Indicando con i minuti di conversazione effettuati nel mese considerato, la spesa totale mensile in euro è espressa dalla funzione f()
~ Copyright Ripetizionando - All rights reserved ~ http://ripetizionando.wordpress.com STUDIO DI FUNZIONE
 STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
Basi di matematica per il corso di micro
 Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R
 Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
PLANIMETRIA E PROFILO INSIEME
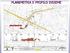 PLANIMETRIA E PROFILO INSIEME planimetria profili 11 RELAZIONE TRA PLANIMETRIA E PROFILO La correlazione tra andamento planimetrico e altimetrico è molto stretta; variazioni del primo incidono subito sul
PLANIMETRIA E PROFILO INSIEME planimetria profili 11 RELAZIONE TRA PLANIMETRIA E PROFILO La correlazione tra andamento planimetrico e altimetrico è molto stretta; variazioni del primo incidono subito sul
Il concetto di valore medio in generale
 Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Soluzione degli esercizi sul moto rettilineo uniformemente accelerato
 Liceo Carducci Volterra - Classe 3 a B Scientifico - Francesco Daddi - 8 novembre 00 Soluzione degli esercizi sul moto rettilineo uniformemente accelerato Esercizio. Un corpo parte da fermo con accelerazione
Liceo Carducci Volterra - Classe 3 a B Scientifico - Francesco Daddi - 8 novembre 00 Soluzione degli esercizi sul moto rettilineo uniformemente accelerato Esercizio. Un corpo parte da fermo con accelerazione
Insegnamento di Fondamenti di Infrastrutture viarie
 Insegnamento di Fondamenti di Infrastrutture viarie Territorio ed infrastrutture di trasporto La meccanica della locomozione: questioni generali Il fenomeno dell aderenza e l equazione Dall equazione alle
Insegnamento di Fondamenti di Infrastrutture viarie Territorio ed infrastrutture di trasporto La meccanica della locomozione: questioni generali Il fenomeno dell aderenza e l equazione Dall equazione alle
Esercizi sul moto rettilineo uniformemente accelerato
 Liceo Carducci Volterra - Classe 3 a B Scientifico - Francesco Daddi - 8 novembre 010 Esercizi sul moto rettilineo uniformemente accelerato Esercizio 1. Un corpo parte da fermo con accelerazione pari a
Liceo Carducci Volterra - Classe 3 a B Scientifico - Francesco Daddi - 8 novembre 010 Esercizi sul moto rettilineo uniformemente accelerato Esercizio 1. Un corpo parte da fermo con accelerazione pari a
Consideriamo due polinomi
 Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
CONTINUITÀ E DERIVABILITÀ Esercizi risolti
 CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I. 2004
 ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
a) Il campo di esistenza di f(x) è dato da 2x 0, ovvero x 0. Il grafico di f(x) è quello di una iperbole -1 1
 LE FUNZIONI EALI DI VAIABILE EALE Soluzioni di quesiti e problemi estratti dal Corso Base Blu di Matematica volume 5 Q[] Sono date le due funzioni: ) = e g() = - se - se = - Determina il campo di esistenza
LE FUNZIONI EALI DI VAIABILE EALE Soluzioni di quesiti e problemi estratti dal Corso Base Blu di Matematica volume 5 Q[] Sono date le due funzioni: ) = e g() = - se - se = - Determina il campo di esistenza
LEZIONE 7. Esercizio 7.1. Quale delle seguenti funzioni è decrescente in ( 3, 0) e ha derivata prima in 3 che vale 0? x 3 3 + x2. 2, x3 +2x +3.
 7 LEZIONE 7 Esercizio 7.1. Quale delle seguenti funzioni è decrescente in ( 3, 0) e ha derivata prima in 3 che vale 0? x 3 3 + x2 2 6x, x3 +2x 2 6x, 3x + x2 2, x3 +2x +3. Le derivate sono rispettivamente,
7 LEZIONE 7 Esercizio 7.1. Quale delle seguenti funzioni è decrescente in ( 3, 0) e ha derivata prima in 3 che vale 0? x 3 3 + x2 2 6x, x3 +2x 2 6x, 3x + x2 2, x3 +2x +3. Le derivate sono rispettivamente,
Capitolo 2. Operazione di limite
 Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
2 Argomenti introduttivi e generali
 1 Note Oltre agli esercizi di questa lista si consiglia di svolgere quelli segnalati o assegnati sul registro e genericamente quelli presentati dal libro come esercizio o come esempio sugli argomenti svolti
1 Note Oltre agli esercizi di questa lista si consiglia di svolgere quelli segnalati o assegnati sul registro e genericamente quelli presentati dal libro come esercizio o come esempio sugli argomenti svolti
Procedura di iscrizione alla Piattaforma On Line
 PUNTO 1 Procedura di iscrizione alla Piattaforma On Line Accedere dal proprio browser internet al sito: http://www.qeselearning.it/ NOTA: è preferibile utilizzare Chrome o Firefox La schermata che le apparirà
PUNTO 1 Procedura di iscrizione alla Piattaforma On Line Accedere dal proprio browser internet al sito: http://www.qeselearning.it/ NOTA: è preferibile utilizzare Chrome o Firefox La schermata che le apparirà
2. Leggi finanziarie di capitalizzazione
 2. Leggi finanziarie di capitalizzazione Si chiama legge finanziaria di capitalizzazione una funzione atta a definire il montante M(t accumulato al tempo generico t da un capitale C: M(t = F(C, t C t M
2. Leggi finanziarie di capitalizzazione Si chiama legge finanziaria di capitalizzazione una funzione atta a definire il montante M(t accumulato al tempo generico t da un capitale C: M(t = F(C, t C t M
Studio di funzioni ( )
 Studio di funzioni Effettuare uno studio qualitativo e tracciare un grafico approssimativo delle seguenti funzioni. Si studi in particolare anche la concavità delle funzioni e si indichino esplicitamente
Studio di funzioni Effettuare uno studio qualitativo e tracciare un grafico approssimativo delle seguenti funzioni. Si studi in particolare anche la concavità delle funzioni e si indichino esplicitamente
La propagazione delle onde luminose può essere studiata per mezzo delle equazioni di Maxwell. Tuttavia, nella maggior parte dei casi è possibile
 Elementi di ottica L ottica si occupa dello studio dei percorsi dei raggi luminosi e dei fenomeni legati alla propagazione della luce in generale. Lo studio dell ottica nella fisica moderna si basa sul
Elementi di ottica L ottica si occupa dello studio dei percorsi dei raggi luminosi e dei fenomeni legati alla propagazione della luce in generale. Lo studio dell ottica nella fisica moderna si basa sul
Anno 4 Grafico di funzione
 Anno 4 Grafico di funzione Introduzione In questa lezione impareremo a disegnare il grafico di una funzione reale. Per fare ciò è necessario studiare alcune caratteristiche salienti della funzione che
Anno 4 Grafico di funzione Introduzione In questa lezione impareremo a disegnare il grafico di una funzione reale. Per fare ciò è necessario studiare alcune caratteristiche salienti della funzione che
Matematica 1 - Corso di Laurea in Ingegneria Meccanica
 Matematica 1 - Corso di Laurea in Ingegneria Meccanica Esercitazione su massimi e minimi vincolati 9 dicembre 005 Esercizio 1. Considerare l insieme C = {(x,y) R : (x + y ) = x } e dire se è una curva
Matematica 1 - Corso di Laurea in Ingegneria Meccanica Esercitazione su massimi e minimi vincolati 9 dicembre 005 Esercizio 1. Considerare l insieme C = {(x,y) R : (x + y ) = x } e dire se è una curva
LE SEZIONI TRASVERSALI
 LE SEZIONI TRASVERSALI Rappresentano l intersezione del corpo stradale e del terreno con un piano verticale e normale all asse stradale. Vengono eseguite in corrispondenza di ciascun picchetto d asse.
LE SEZIONI TRASVERSALI Rappresentano l intersezione del corpo stradale e del terreno con un piano verticale e normale all asse stradale. Vengono eseguite in corrispondenza di ciascun picchetto d asse.
ANNO ACCADEMICO 2010-2011 CORSO DI LAUREA IN INGEGNERIA CIVILE
 ANNO ACCADEMICO 2010-2011 CORSO DI LAUREA IN INGEGNERIA CIVILE CORSO DI STRADE FERROVIE AEROPORTI Studente: Gaetano Passaro Matricola: 278723 ANNO ACCADEMICO 2010-2011 CORSO DI LAUREA IN INGEGNERIA CIVILE
ANNO ACCADEMICO 2010-2011 CORSO DI LAUREA IN INGEGNERIA CIVILE CORSO DI STRADE FERROVIE AEROPORTI Studente: Gaetano Passaro Matricola: 278723 ANNO ACCADEMICO 2010-2011 CORSO DI LAUREA IN INGEGNERIA CIVILE
Relazioni statistiche: regressione e correlazione
 Relazioni statistiche: regressione e correlazione È detto studio della connessione lo studio si occupa della ricerca di relazioni fra due variabili statistiche o fra una mutabile e una variabile statistica
Relazioni statistiche: regressione e correlazione È detto studio della connessione lo studio si occupa della ricerca di relazioni fra due variabili statistiche o fra una mutabile e una variabile statistica
Vademecum studio funzione
 Vademecum studio funzione Campo di Esistenza di una funzione o dominio: Studiare una funzione significa determinare gli elementi caratteristici che ci permettono di disegnarne il grafico, a partire dalla
Vademecum studio funzione Campo di Esistenza di una funzione o dominio: Studiare una funzione significa determinare gli elementi caratteristici che ci permettono di disegnarne il grafico, a partire dalla
Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 2014
 Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 14 Problema 1 Punto a) Osserviamo che g (x) = f(x) e pertanto g () = f() = in quanto Γ è tangente all asse delle ascisse,
Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 14 Problema 1 Punto a) Osserviamo che g (x) = f(x) e pertanto g () = f() = in quanto Γ è tangente all asse delle ascisse,
I documenti di www.mistermanager.it. Gli ingredienti per l allenamento per la corsa LE RIPETUTE
 I documenti di www.mistermanager.it Gli ingredienti per l allenamento per la corsa LE RIPETUTE Le Ripetute sono una delle forme di allenamento che caratterizzano i corridori più evoluti, in quanto partono
I documenti di www.mistermanager.it Gli ingredienti per l allenamento per la corsa LE RIPETUTE Le Ripetute sono una delle forme di allenamento che caratterizzano i corridori più evoluti, in quanto partono
La pista del mio studio Riflettiamo sulla pista. Guida per l insegnante
 Riflettiamo sulla pista Guida per l insegnante Obiettivi educativi generali Compito di specificazione - possiede capacità progettuale - è in grado di organizzare il proprio tempo e di costruire piani per
Riflettiamo sulla pista Guida per l insegnante Obiettivi educativi generali Compito di specificazione - possiede capacità progettuale - è in grado di organizzare il proprio tempo e di costruire piani per
La distribuzione Normale. La distribuzione Normale
 La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
LA RETTA. Retta per l'origine, rette orizzontali e verticali
 Retta per l'origine, rette orizzontali e verticali LA RETTA Abbiamo visto che l'equazione generica di una retta è del tipo Y = mx + q, dove m ne rappresenta la pendenza e q il punto in cui la retta incrocia
Retta per l'origine, rette orizzontali e verticali LA RETTA Abbiamo visto che l'equazione generica di una retta è del tipo Y = mx + q, dove m ne rappresenta la pendenza e q il punto in cui la retta incrocia
( x) ( x) 0. Equazioni irrazionali
 Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
ISTRUZIONI PER LA GESTIONE BUDGET
 ISTRUZIONI PER LA GESTIONE BUDGET 1) OPERAZIONI PRELIMINARI PER LA GESTIONE BUDGET...1 2) INSERIMENTO E GESTIONE BUDGET PER LA PREVISIONE...4 3) STAMPA DIFFERENZE CAPITOLI/BUDGET.10 4) ANNULLAMENTO BUDGET
ISTRUZIONI PER LA GESTIONE BUDGET 1) OPERAZIONI PRELIMINARI PER LA GESTIONE BUDGET...1 2) INSERIMENTO E GESTIONE BUDGET PER LA PREVISIONE...4 3) STAMPA DIFFERENZE CAPITOLI/BUDGET.10 4) ANNULLAMENTO BUDGET
Teoria in sintesi 10. Attività di sportello 1, 24 - Attività di sportello 2, 24 - Verifica conclusiva, 25. Teoria in sintesi 26
 Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
Soluzione di equazioni quadratiche
 Soluzione di equazioni quadratiche Soluzione sulla Retta Algebrica Inseriamo sulla Retta Algebrica le seguenti espressioni polinomiali x e x 3 e cerchiamo di individuare i valori di x per i quali i punti
Soluzione di equazioni quadratiche Soluzione sulla Retta Algebrica Inseriamo sulla Retta Algebrica le seguenti espressioni polinomiali x e x 3 e cerchiamo di individuare i valori di x per i quali i punti
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 2011/2012
 Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
Indicando con x i minuti di conversazione effettuati in un mese, con la spesa totale nel mese e con il costo medio al minuto:
 PROBLEMA 1. Il piano tariffario proposto da un operatore telefonico prevede, per le telefonate all estero, un canone fisso di 10 euro al mese, più 10 centesimi per ogni minuto di conversazione. Indicando
PROBLEMA 1. Il piano tariffario proposto da un operatore telefonico prevede, per le telefonate all estero, un canone fisso di 10 euro al mese, più 10 centesimi per ogni minuto di conversazione. Indicando
G6. Studio di funzione
 G6 Studio di funzione G6 Come tracciare il grafico di una funzione data Nei capitoli precedenti si sono svolti tutti gli argomenti necessari per tracciare il grafico di una funzione In questo capitolo
G6 Studio di funzione G6 Come tracciare il grafico di una funzione data Nei capitoli precedenti si sono svolti tutti gli argomenti necessari per tracciare il grafico di una funzione In questo capitolo
3 GRAFICI DI FUNZIONI
 3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
1. Limite finito di una funzione in un punto
 . Limite finito di una funzione in un punto Consideriamo la funzione: f ( ) = il cui dominio risulta essere R {}, e quindi il valore di f ( ) non è calcolabile in =. Quest affermazione tuttavia non esaurisce
. Limite finito di una funzione in un punto Consideriamo la funzione: f ( ) = il cui dominio risulta essere R {}, e quindi il valore di f ( ) non è calcolabile in =. Quest affermazione tuttavia non esaurisce
CONTINUITÀ E DERIVABILITÀ Esercizi proposti. 1. Determinare lim M(sinx) (M(t) denota la mantissa di t)
 CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
REALTÀ E MODELLI SCHEDA DI LAVORO
 REALTÀ E MDELLI SCHEDA DI LAVR 1 La mansarda Per ultimare l edificazione di una villetta occorre costruire il tetto a due spioventi sopra la mansarda Come dato di progetto è noto quanto segue: considerata
REALTÀ E MDELLI SCHEDA DI LAVR 1 La mansarda Per ultimare l edificazione di una villetta occorre costruire il tetto a due spioventi sopra la mansarda Come dato di progetto è noto quanto segue: considerata
Esponenziali elogaritmi
 Esponenziali elogaritmi Potenze ad esponente reale Ricordiamo che per un qualsiasi numero razionale m n prendere n>0) si pone a m n = n a m (in cui si può sempre a patto che a sia un numero reale positivo.
Esponenziali elogaritmi Potenze ad esponente reale Ricordiamo che per un qualsiasi numero razionale m n prendere n>0) si pone a m n = n a m (in cui si può sempre a patto che a sia un numero reale positivo.
SymCAD/C.A.T.S. modulo Canali Schema
 SymCAD/C.A.T.S. modulo Canali Schema Il modulo Ventilazione Standard permette di effettuare la progettazione integrata (disegno e calcoli) in AutoCAD di reti di canali aria (mandata e ripresa). Il disegno
SymCAD/C.A.T.S. modulo Canali Schema Il modulo Ventilazione Standard permette di effettuare la progettazione integrata (disegno e calcoli) in AutoCAD di reti di canali aria (mandata e ripresa). Il disegno
Aprile (recupero) tra una variazione di velocità e l intervallo di tempo in cui ha luogo.
 Febbraio 1. Un aereo in volo orizzontale, alla velocità costante di 360 km/h, lascia cadere delle provviste per un accampamento da un altezza di 200 metri. Determina a quale distanza dall accampamento
Febbraio 1. Un aereo in volo orizzontale, alla velocità costante di 360 km/h, lascia cadere delle provviste per un accampamento da un altezza di 200 metri. Determina a quale distanza dall accampamento
SEZIONI. Introduzione
 SEIONI 128 Introduzione Sezionare un solido significa tagliarlo secondo una superficie ideale in modo da mostrare il volume interno del solido stesso. Nella maggior parte dei casi l elemento secante è
SEIONI 128 Introduzione Sezionare un solido significa tagliarlo secondo una superficie ideale in modo da mostrare il volume interno del solido stesso. Nella maggior parte dei casi l elemento secante è
SCRUTINIO ON LINE 2 PERIODO
 SCRUTINIO ON LINE 2 PERIODO MANUALE OPERATIVO PER IL DOCENTE COORDINATORE Pagina 1 Accesso al sistema Per entrare nel registro elettronico, il docente apre il browser di accesso ad Internet e può accedere
SCRUTINIO ON LINE 2 PERIODO MANUALE OPERATIVO PER IL DOCENTE COORDINATORE Pagina 1 Accesso al sistema Per entrare nel registro elettronico, il docente apre il browser di accesso ad Internet e può accedere
(Esercizi Tratti da Temi d esame degli ordinamenti precedenti)
 (Esercizi Tratti da Temi d esame degli ordinamenti precedenti) Esercizio 1 L'agenzia viaggi GV - Grandi Viaggi vi commissiona l'implementazione della funzione AssegnaVolo. Tale funzione riceve due liste
(Esercizi Tratti da Temi d esame degli ordinamenti precedenti) Esercizio 1 L'agenzia viaggi GV - Grandi Viaggi vi commissiona l'implementazione della funzione AssegnaVolo. Tale funzione riceve due liste
Polli e conigli. problemi Piano cartesiano. Numeri e algoritmi Sistemi e loro. geometrica. Relazioni e funzioni Linguaggio naturale e
 Polli e conigli Livello scolare: primo biennio Abilità Interessate Calcolo di base - sistemi Risolvere per via grafica e algebrica problemi che si formalizzano con equazioni. Analizzare semplici testi
Polli e conigli Livello scolare: primo biennio Abilità Interessate Calcolo di base - sistemi Risolvere per via grafica e algebrica problemi che si formalizzano con equazioni. Analizzare semplici testi
Fondamenti e didattica di Matematica Finanziaria
 Fondamenti e didattica di Matematica Finanziaria Silvana Stefani Piazza dell Ateneo Nuovo 1-20126 MILANO U6-368 silvana.stefani@unimib.it 1 Unità 9 Contenuti della lezione Operazioni finanziarie, criterio
Fondamenti e didattica di Matematica Finanziaria Silvana Stefani Piazza dell Ateneo Nuovo 1-20126 MILANO U6-368 silvana.stefani@unimib.it 1 Unità 9 Contenuti della lezione Operazioni finanziarie, criterio
G3. Asintoti e continuità
 G3 Asintoti e continuità Un asintoto è una retta a cui la funzione si avvicina sempre di più senza mai toccarla Non è la definizione formale, ma sicuramente serve per capire il concetto di asintoto Nei
G3 Asintoti e continuità Un asintoto è una retta a cui la funzione si avvicina sempre di più senza mai toccarla Non è la definizione formale, ma sicuramente serve per capire il concetto di asintoto Nei
Definisci il Campo di Esistenza ( Dominio) di una funzione reale di variabile reale e, quindi, determinalo per la funzione:
 Verso l'esame di Stato Definisci il Campo di Esistenza ( Dominio) di una funzione reale di variabile reale e, quindi, determinalo per la funzione: y ln 5 6 7 8 9 0 Rappresenta il campo di esistenza determinato
Verso l'esame di Stato Definisci il Campo di Esistenza ( Dominio) di una funzione reale di variabile reale e, quindi, determinalo per la funzione: y ln 5 6 7 8 9 0 Rappresenta il campo di esistenza determinato
f(x) = 1 x. Il dominio di questa funzione è il sottoinsieme proprio di R dato da
 Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
PERCORSO DIDATTICO SULLE SUCCESSIONI NUMERICHE
 PERCORSO DIDATTICO SULLE SUCCESSIONI NUMERICHE Nuclei Fondanti: Relazioni e Funzioni, Geometria Tipo di scuola e classe: Liceo Scientifico, classe II Riferimenti alle Indicazioni Nazionali: OBIETTIVI SPECIFICI
PERCORSO DIDATTICO SULLE SUCCESSIONI NUMERICHE Nuclei Fondanti: Relazioni e Funzioni, Geometria Tipo di scuola e classe: Liceo Scientifico, classe II Riferimenti alle Indicazioni Nazionali: OBIETTIVI SPECIFICI
Matematica e Statistica
 Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
Siamo così arrivati all aritmetica modulare, ma anche a individuare alcuni aspetti di come funziona l aritmetica del calcolatore come vedremo.
 DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
VERIFICA DI MATEMATICA. CLASSI TERZE (3AS, 3BS, 3CS, 3DS, 3ES) 2 settembre 2013 COGNOME E NOME.. CLASSE.
 VERIFIC DI MTEMTIC CLSSI TERZE (S, BS, CS, DS, ES) settembre COGNOME E NOME.. CLSSE. Esercizio In un piano cartesiano ortogonale determinare: a) l equazione della parabola con asse parallelo all asse,
VERIFIC DI MTEMTIC CLSSI TERZE (S, BS, CS, DS, ES) settembre COGNOME E NOME.. CLSSE. Esercizio In un piano cartesiano ortogonale determinare: a) l equazione della parabola con asse parallelo all asse,
Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in
 Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in Solitamente si fa riferimento ad intorni simmetrici =, + + Definizione: dato
Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in Solitamente si fa riferimento ad intorni simmetrici =, + + Definizione: dato
GUIDA ALLA PREDISPOSIZIONE E ALLA GESTIONE DELLA NOTA INFORMATIVA SUI RISCHI (NIR) DEL CENTRO DI RACCOLTA
 QUADERNO RAEE 5 GUIDA ALLA PREDISPOSIZIONE E ALLA GESTIONE DELLA NOTA INFORMATIVA SUI RISCHI (NIR) DEL CENTRO DI RACCOLTA Ai sensi dell Accordo di Programma tra ANCI e CdC RAEE del 28 marzo 2012, modificato
QUADERNO RAEE 5 GUIDA ALLA PREDISPOSIZIONE E ALLA GESTIONE DELLA NOTA INFORMATIVA SUI RISCHI (NIR) DEL CENTRO DI RACCOLTA Ai sensi dell Accordo di Programma tra ANCI e CdC RAEE del 28 marzo 2012, modificato
Esercitazione di Laboratorio - Leve di 1-2 - 3 genere TITOLO ESERCITAZIONE: VERIFICA DELLE LEGGI DELLE LEVE
 TITOLO ESERCITAZIONE: VERIFICA DELLE LEGGI DELLE LEVE PREREQUISITI RICHIESTI PER LO SVOLGIMENTO DELL ATTIVITÀ DI LABORATORIO L alunno deve conoscere la definizione di forza, la definizione di momento.
TITOLO ESERCITAZIONE: VERIFICA DELLE LEGGI DELLE LEVE PREREQUISITI RICHIESTI PER LO SVOLGIMENTO DELL ATTIVITÀ DI LABORATORIO L alunno deve conoscere la definizione di forza, la definizione di momento.
Composizione dell asse. geometrie di transizione
 Composizione dell asse geometrie di transizione Principali criteri di composizione dell asse La lunghezza massima dei rettifili è limitata dalla normativa ad un valore pari a 22 V p max ; le ragioni di
Composizione dell asse geometrie di transizione Principali criteri di composizione dell asse La lunghezza massima dei rettifili è limitata dalla normativa ad un valore pari a 22 V p max ; le ragioni di
Verranno descritti di seguito brevemente gli algoritmi di calcolo utilizzati per l interpretazione nei tre metodi inseriti all interno del programma.
 3. Teoria Verranno descritti di seguito brevemente gli algoritmi di calcolo utilizzati per l interpretazione nei tre metodi inseriti all interno del programma. 3.1 Metodo convenzionale (metodo del tempo
3. Teoria Verranno descritti di seguito brevemente gli algoritmi di calcolo utilizzati per l interpretazione nei tre metodi inseriti all interno del programma. 3.1 Metodo convenzionale (metodo del tempo
GIROSCOPIO. Scopo dell esperienza: Teoria fisica. Verificare la relazione: ω p = bmg/iω
 GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
Parte I: Meccanica della locomozione ed armamento
 Parte I: Meccanica della locomozione ed armamento 1) Meccanica della locomozione: equazione del moto, resistenze al moto, dinamica del veicolo, andamento planoaltimetrico, sopraelevazione in curva, accelerazione
Parte I: Meccanica della locomozione ed armamento 1) Meccanica della locomozione: equazione del moto, resistenze al moto, dinamica del veicolo, andamento planoaltimetrico, sopraelevazione in curva, accelerazione
CAPACITÀ DI PROCESSO (PROCESS CAPABILITY)
 CICLO DI LEZIONI per Progetto e Gestione della Qualità Facoltà di Ingegneria CAPACITÀ DI PROCESSO (PROCESS CAPABILITY) Carlo Noè Università Carlo Cattaneo e-mail: cnoe@liuc.it 1 CAPACITÀ DI PROCESSO Il
CICLO DI LEZIONI per Progetto e Gestione della Qualità Facoltà di Ingegneria CAPACITÀ DI PROCESSO (PROCESS CAPABILITY) Carlo Noè Università Carlo Cattaneo e-mail: cnoe@liuc.it 1 CAPACITÀ DI PROCESSO Il
Studio di una funzione ad una variabile
 Studio di una funzione ad una variabile Lo studio di una funzione ad una variabile ha come scopo ultimo quello di pervenire a un grafico della funzione assegnata. Questo grafico non dovrà essere preciso
Studio di una funzione ad una variabile Lo studio di una funzione ad una variabile ha come scopo ultimo quello di pervenire a un grafico della funzione assegnata. Questo grafico non dovrà essere preciso
Database 1 biblioteca universitaria. Testo del quesito
 Database 1 biblioteca universitaria Testo del quesito Una biblioteca universitaria acquista testi didattici su indicazione dei professori e cura il prestito dei testi agli studenti. La biblioteca vuole
Database 1 biblioteca universitaria Testo del quesito Una biblioteca universitaria acquista testi didattici su indicazione dei professori e cura il prestito dei testi agli studenti. La biblioteca vuole
Le funzioni continue. A. Pisani Liceo Classico Dante Alighieri A.S. 2002-03. A. Pisani, appunti di Matematica 1
 Le funzioni continue A. Pisani Liceo Classico Dante Alighieri A.S. -3 A. Pisani, appunti di Matematica 1 Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato
Le funzioni continue A. Pisani Liceo Classico Dante Alighieri A.S. -3 A. Pisani, appunti di Matematica 1 Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato
FASCI DI RETTE. scrivere la retta in forma esplicita: 2y = 3x + 4 y = 3 2 x 2. scrivere l equazione del fascio di rette:
 FASCI DI RETTE DEFINIZIONE: Si chiama fascio di rette parallele o fascio improprio [erroneamente data la somiglianza effettiva con un fascio!] un insieme di rette che hanno tutte lo stesso coefficiente
FASCI DI RETTE DEFINIZIONE: Si chiama fascio di rette parallele o fascio improprio [erroneamente data la somiglianza effettiva con un fascio!] un insieme di rette che hanno tutte lo stesso coefficiente
UNO STUDIO DI FUNZIONE CON DERIVE a cura del prof. Guida. 4 x
 UNO STUDIO DI FUNZIONE CON DERIVE a cura del prof. Guida Con questa guida si vuol proporre un esempio di studio di funzione con Derive. La versione che ho utilizzato per questo studio è la 6.0. Consideriamo
UNO STUDIO DI FUNZIONE CON DERIVE a cura del prof. Guida Con questa guida si vuol proporre un esempio di studio di funzione con Derive. La versione che ho utilizzato per questo studio è la 6.0. Consideriamo
Fondamenti di Infrastrutture Viarie
 Politecnico di Torino Fondamenti di Infrastrutture Viarie Relazione esercitazioni. Anno Accademico 2011/2012 Corso di Fondamenti di Infrastrutture Viarie Professore: Marco Bassani Esercitatore: Pier Paolo
Politecnico di Torino Fondamenti di Infrastrutture Viarie Relazione esercitazioni. Anno Accademico 2011/2012 Corso di Fondamenti di Infrastrutture Viarie Professore: Marco Bassani Esercitatore: Pier Paolo
Usando il pendolo reversibile di Kater
 Usando il pendolo reversibile di Kater Scopo dell esperienza è la misurazione dell accelerazione di gravità g attraverso il periodo di oscillazione di un pendolo reversibile L accelerazione di gravità
Usando il pendolo reversibile di Kater Scopo dell esperienza è la misurazione dell accelerazione di gravità g attraverso il periodo di oscillazione di un pendolo reversibile L accelerazione di gravità
ESAMI DI QUALIFICA PROFESSIONALE
 ESAMI DI QUALIFICA PROFESSIONALE La procedura per lo svolgimento degli esami di qualifica professionale, per le classi terze inizia nel primo Consiglio di classe successivo agli scrutini di febbraio, con
ESAMI DI QUALIFICA PROFESSIONALE La procedura per lo svolgimento degli esami di qualifica professionale, per le classi terze inizia nel primo Consiglio di classe successivo agli scrutini di febbraio, con
COMPLEMENTI SULLE LEGGI FINANZIARIE
 COMPLEMENI SULLE LEGGI FINANZIARIE asso di rendimento di operazioni finanziarie in valuta estera La normativa vigente consente di effettuare operazioni finanziarie, sia di investimento che di finanziamento,
COMPLEMENI SULLE LEGGI FINANZIARIE asso di rendimento di operazioni finanziarie in valuta estera La normativa vigente consente di effettuare operazioni finanziarie, sia di investimento che di finanziamento,
risulta (x) = 1 se x < 0.
 Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
1. PRIME PROPRIETÀ 2
 RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
Elementi di topologia della retta
 Elementi di topologia della retta nome insieme definizione l insieme è un concetto primitivo che si accetta come intuitivamente noto secondo George Cantor, il padre della teoria degli insiemi: Per insieme
Elementi di topologia della retta nome insieme definizione l insieme è un concetto primitivo che si accetta come intuitivamente noto secondo George Cantor, il padre della teoria degli insiemi: Per insieme
Nel seguito sono riportati due esercizi che si possono risolvere con la formula di Erlang e le relative risoluzioni.
 Nel seguito sono riportati due esercizi che si possono risolvere con la formula di Erlang e le relative risoluzioni. Al fine di risolvere questo tipo di esercizi, si fa in genere riferimento a delle tabelle
Nel seguito sono riportati due esercizi che si possono risolvere con la formula di Erlang e le relative risoluzioni. Al fine di risolvere questo tipo di esercizi, si fa in genere riferimento a delle tabelle
Insegnamento di Fondamenti di Infrastrutture viarie
 Insegnamento di Fondamenti di Infrastrutture viarie Territorio ed infrastrutture di trasporto La meccanica della locomozione: questioni generali Il fenomeno dell aderenza e l equazione generale del moto
Insegnamento di Fondamenti di Infrastrutture viarie Territorio ed infrastrutture di trasporto La meccanica della locomozione: questioni generali Il fenomeno dell aderenza e l equazione generale del moto
Guida Compilazione Piani di Studio on-line
 Guida Compilazione Piani di Studio on-line SIA (Sistemi Informativi d Ateneo) Visualizzazione e presentazione piani di studio ordinamento 509 e 270 Università della Calabria (Unità organizzativa complessa-
Guida Compilazione Piani di Studio on-line SIA (Sistemi Informativi d Ateneo) Visualizzazione e presentazione piani di studio ordinamento 509 e 270 Università della Calabria (Unità organizzativa complessa-
PRINCIPIO ESPLICATIVO DEL FUNZIONAMENTO DEI CILINDRI CROCIATI Prof. Luciano Pietropaolo
 PRINCIPIO ESPLICATIVO DEL FUNZIONAMENTO DEI CILINDRI CROCIATI Prof. Luciano Pietropaolo Viene esposto il principio su cui si basa il funzionamento dei cilindri crociati, per l analisi dell astigmatismo
PRINCIPIO ESPLICATIVO DEL FUNZIONAMENTO DEI CILINDRI CROCIATI Prof. Luciano Pietropaolo Viene esposto il principio su cui si basa il funzionamento dei cilindri crociati, per l analisi dell astigmatismo
INTEGRALI DEFINITI. Tale superficie viene detta trapezoide e la misura della sua area si ottiene utilizzando il calcolo di un integrale definito.
 INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
Corso di formazione assicurativa - 60 ore. (a norma Reg. IVASS n.6/2014) Guida all utilizzo
 Corso di formazione assicurativa - 60 ore (a norma Reg. IVASS n.6/2014) Guida all utilizzo La piattaforma e-learning: la pagina iniziale del corso NAVIGAZIONE: Accesso alle diverse aree del corso e alla
Corso di formazione assicurativa - 60 ore (a norma Reg. IVASS n.6/2014) Guida all utilizzo La piattaforma e-learning: la pagina iniziale del corso NAVIGAZIONE: Accesso alle diverse aree del corso e alla
PARTICOLARI COSTRUTTIVI MURATURA ARMATA POROTON
 PARTICOLARI COSTRUTTIVI MURATURA ARMATA POROTON La muratura armata rappresenta un sistema costruttivo relativamente nuovo ed ancora non molto conosciuto e le richieste di chiarimenti sulle modalità di
PARTICOLARI COSTRUTTIVI MURATURA ARMATA POROTON La muratura armata rappresenta un sistema costruttivo relativamente nuovo ed ancora non molto conosciuto e le richieste di chiarimenti sulle modalità di
Politecnico di Torino. Esercitazioni di Protezione idraulica del territorio
 Politecnico di Torino Esercitazioni di Protezione idraulica del territorio a.a. 2012-2013 ESERCITAZIONE 1 VALUTAZIONE DELLA RARITÀ DI UN EVENTO PLUVIOMETRICO ECCEZIONALE 1. Determinazione del periodo di
Politecnico di Torino Esercitazioni di Protezione idraulica del territorio a.a. 2012-2013 ESERCITAZIONE 1 VALUTAZIONE DELLA RARITÀ DI UN EVENTO PLUVIOMETRICO ECCEZIONALE 1. Determinazione del periodo di
13. Campi vettoriali
 13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
Capitolo 3. L applicazione Java Diagrammi ER. 3.1 La finestra iniziale, il menu e la barra pulsanti
 Capitolo 3 L applicazione Java Diagrammi ER Dopo le fasi di analisi, progettazione ed implementazione il software è stato compilato ed ora è pronto all uso; in questo capitolo mostreremo passo passo tutta
Capitolo 3 L applicazione Java Diagrammi ER Dopo le fasi di analisi, progettazione ed implementazione il software è stato compilato ed ora è pronto all uso; in questo capitolo mostreremo passo passo tutta
Facoltà di Scienze Politiche Corso di Economia Politica. Macroeconomia sui capitoli 21, 22 e 23. Dott.ssa Rossella Greco
 Facoltà di Scienze Politiche Corso di Economia Politica Esercitazione di Macroeconomia sui capitoli 21, 22 e 23 Dott.ssa Rossella Greco Domanda 1 (Problema 4. dal Cap. 21 del Libro di Testo) a) Gregorio,
Facoltà di Scienze Politiche Corso di Economia Politica Esercitazione di Macroeconomia sui capitoli 21, 22 e 23 Dott.ssa Rossella Greco Domanda 1 (Problema 4. dal Cap. 21 del Libro di Testo) a) Gregorio,
Premessa: Nella traccia non è specificato cosa accade se si effettuano per esempio 2,3 minuti di conversazione.
 Esame di stato 5 - Proposta di risoluzione del problema Il piano tariffario proposto da un operatore telefonico prevede, per le telefonate all estero, un canone fisso di euro al mese, più centesimi per
Esame di stato 5 - Proposta di risoluzione del problema Il piano tariffario proposto da un operatore telefonico prevede, per le telefonate all estero, un canone fisso di euro al mese, più centesimi per
PROBLEMI TRADIZIONALI SIMULAZIONE DELLA PROVA DI MATEMATICA
 Simulazione 01/15 ANNO SCOLASTICO 01/15 PROBLEMI TRADIZIONALI SIMULAZIONE DELLA PROVA DI MATEMATICA DELL ESAME DI STATO PER IL LICEO SCIENTIFICO Il candidato risolva uno dei due problemi Problema 1 Nella
Simulazione 01/15 ANNO SCOLASTICO 01/15 PROBLEMI TRADIZIONALI SIMULAZIONE DELLA PROVA DI MATEMATICA DELL ESAME DI STATO PER IL LICEO SCIENTIFICO Il candidato risolva uno dei due problemi Problema 1 Nella
ESEMPIO 1: eseguire il complemento a 10 di 765
 COMPLEMENTO A 10 DI UN NUMERO DECIMALE Sia dato un numero N 10 in base 10 di n cifre. Il complemento a 10 di tale numero (N ) si ottiene sottraendo il numero stesso a 10 n. ESEMPIO 1: eseguire il complemento
COMPLEMENTO A 10 DI UN NUMERO DECIMALE Sia dato un numero N 10 in base 10 di n cifre. Il complemento a 10 di tale numero (N ) si ottiene sottraendo il numero stesso a 10 n. ESEMPIO 1: eseguire il complemento
Progetto La fisica nelle attrazioni Attrazione NIAGARA Dati Utili
 Progetto La fisica nelle attrazioni Attrazione NIAGARA Dati Utili Angolo di risalita = 25 Altezza massima della salita = 25,87 m Altezza della salita nel tratto lineare (fino all ultimo pilone di metallo)
Progetto La fisica nelle attrazioni Attrazione NIAGARA Dati Utili Angolo di risalita = 25 Altezza massima della salita = 25,87 m Altezza della salita nel tratto lineare (fino all ultimo pilone di metallo)
Deducibilità dei canoni di leasing
 Circolare Monografica 11 giugno 2014 n. 1989 DICHIARAZIONI Deducibilità dei canoni di leasing Modifiche normative e gestione in UNICO 2014 di Marianna Annicchiarico, Giuseppe Mercurio La Legge 27 dicembre
Circolare Monografica 11 giugno 2014 n. 1989 DICHIARAZIONI Deducibilità dei canoni di leasing Modifiche normative e gestione in UNICO 2014 di Marianna Annicchiarico, Giuseppe Mercurio La Legge 27 dicembre
Regolamento di attribuzione del codice ISBN e di erogazione dei servizi dell Agenzia ISBN
 Regolamento di attribuzione del codice ISBN e di erogazione dei servizi dell Agenzia ISBN Compilando l apposito form web di adesione il richiedente formula all Agenzia ISBN una proposta per l attribuzione
Regolamento di attribuzione del codice ISBN e di erogazione dei servizi dell Agenzia ISBN Compilando l apposito form web di adesione il richiedente formula all Agenzia ISBN una proposta per l attribuzione
LA TRASMISSIONE DELLE INFORMAZIONI QUARTA PARTE 1
 LA TRASMISSIONE DELLE INFORMAZIONI QUARTA PARTE 1 I CODICI 1 IL CODICE BCD 1 Somma in BCD 2 Sottrazione BCD 5 IL CODICE ECCESSO 3 20 La trasmissione delle informazioni Quarta Parte I codici Il codice BCD
LA TRASMISSIONE DELLE INFORMAZIONI QUARTA PARTE 1 I CODICI 1 IL CODICE BCD 1 Somma in BCD 2 Sottrazione BCD 5 IL CODICE ECCESSO 3 20 La trasmissione delle informazioni Quarta Parte I codici Il codice BCD
Interesse, sconto, ratei e risconti
 TXT HTM PDF pdf P1 P2 P3 P4 293 Interesse, sconto, ratei e risconti Capitolo 129 129.1 Interesse semplice....................................................... 293 129.1.1 Esercizio per il calcolo dell
TXT HTM PDF pdf P1 P2 P3 P4 293 Interesse, sconto, ratei e risconti Capitolo 129 129.1 Interesse semplice....................................................... 293 129.1.1 Esercizio per il calcolo dell
Calcolo del Valore Attuale Netto (VAN)
 Calcolo del Valore Attuale Netto (VAN) Il calcolo del valore attuale netto (VAN) serve per determinare la redditività di un investimento. Si tratta di utilizzare un procedimento che può consentirci di
Calcolo del Valore Attuale Netto (VAN) Il calcolo del valore attuale netto (VAN) serve per determinare la redditività di un investimento. Si tratta di utilizzare un procedimento che può consentirci di
