Appunti di Laboratorio

Transcript

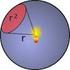
1 Appuni di Laboaoio Sensibilià. E la quanià più piccola che uno sumeno può misuae. Poaa. E la quanià più gande che uno sumeno può misuae. Si noi che un conomeo ha una sensibilià ma non ha una poaa. Misue diee. Misua che si oiene amie l applicazione diea di uno sumeno di misua. Misue indiee. Misua che si oiene uilizzando una elazione maemaica. Esempio. Si vuole misuae l aea di un eangolo. Uilizzando un meo, si misua la base b e l alezza h del eangolo (misue diee). Tamie la elazione A (misua indiea). = b h si deemina l aea Valoe misuao. Il valoe oenuo con una misua diea o indiea (d oa in poi lo indicheemo con VM). Esso in geneale non coincide con il valoe veo. Eoe massimo di misua. Consideiamo un inevallo I di valoi all ineno del quale siamo sicui che si ovi il valoe veo. Il VM occupeà il puno cenale di ale inevallo (fig.1). Vediamo oa quale eoe si commee se consideiamo il VM al poso del valoe veo. Il caso peggioe che VM può capiae è quando il valoe veo cade in coispondenza di uno dei bodi di I. In al caso l eoe è appesenao in figua da. Esso quindi appesena l eoe massimo che si può commeee quando si sosiuisce il valoe veo con il VM. Pe ale agione viene deo eoe massimo di misua (più semplicemene: eoe massimo o eoe di misua ). Il valoe di dipende dalle caaeisiche dello sumeno. Esso non può essee più piccolo della sensibilià (la sensibilià sessa pedeebbe di senso in al caso). In geneale, se non c è nessuna indicazione da pae del cosuoe dello sumeno, si assume pai alla sensibilià. Si noi che l ampiezza dell inevallo è il doppio di. I VM Fig. 1 VM+ Se con un conomeo digiale cenesimale (sensibilià pai a 0,01s ) viene misuao un inevallo empoale pai a 7,5s esso dovà essee ipoao nel seguene modo: T = (7,50± 0,01) s. Con 7,5 7,50 quesa sciua si sa dicendo che il valoe veo è compeso a 7,9s e 7,51s. Si noi che 7,5 e 7,50 appesenano cife affee da eoe Fig. maemaicamene lo sesso numeo ma speimenalmene hanno un significao diveso. La pima, infai, appesena una misua meno Aicolo di Mauizio Schiaulini Pag. 01

2 pecisa della seconda in quano si iiene che l ulima cifa sia sempe affea da eoe (vedi fig.). In moli casi anche la penulima cifa può essee affea da eoe, ma essa poà vaiae al massimo di una unià, come si vede dall esempio. Vale la seguene egola: se l eoe massimo è minoe di 10 1, il VM va sempe scio con un numeo di cife dopo la vigola pai a quello dell eoe massimo. (ovviamene ciò è veo quando VM ed eoe massimo sono espessi nella sessa unià di misua). Consideiamo oa un conomeo con sensibilià pai ad 1s. Supponiamo inole che un ossevaoe abbia misuao un empo pai a 3s, ma che abbia avuo la sensazione di ave soppao il conomeo mezzo secondo dopo la compasa di 3 su display. Tale ossevaoe poebbe essee enao di ipoae il valoe speimenale come T = (3,5± 1) s, in disaccodo con la egola suddea. Ma quesa maggio pecisione ispeo alla sensibilià è solo illusoia. Il di 3 è infai, affeo da eoe ed è quindi inuile aggiungee ale cife ad un numeo già impeciso, non ha semplicemene senso. D ala pae se il cosuoe ha deciso di fa scaae le cife ogni secondo invece che ogni mezzo secondo, significa che il meccanismo del conomeo non gli pemeeva di supeae quesa pecisione. Tuo ciò è valido igoosamene pe sumeni digiali. Pe moli sumeni analogici invece, la pecisione ininseca può anche andae al di là delle caaeisiche cosuive e quindi si può aumenae a occhio la sensibilià di uno sumeno. Consideiamo ad esempio un ighello millimeico. A pima visa la sensibilià di queso sumeno è pai a 0,1cm (un millimeo). Si può peò appezzae ad occhio la mezza-acca ; in queso caso la sensibilià saà di 0,05cm (mezzo millimeo). Consideiamo la fig. 3. In a), viso che l esemo si ova vicino ad una linea ideale che passa a meà a i millimei 01 e 0, la misua saà daa da (0,15± 0,05)cm. In b), viso che l esemo si ova vicino al millimeo 0, la misua saà (0,0± 0,05)cm. Si noi che in quesa siuazione il VM deve sempe finie o con uno 0 oppue con un 5. Queso peché nelle misue diee, il VM deve essee sempe un muliplo della sensibilià. Se avessimo consideao la sensibilià pai a 0,1cm, avemmo avuo (0, 0,1)cm ± pe enambe le misue. In ealà pe il caso a) saebbe sao l opeaoe a decidee se l esemo ea più vicino al millimeo 0 oppue al millimeo Vedi l ulima pagina pe l alo caso. Aicolo di Mauizio Schiaulini Pag. 0

3 Se egli avesse opao pe ques ulimo alloa avebbe dao la misua nel seguene modo: (0,1± 0,1)cm. Se l opeaoe non iesce a decidee a causa del fao che l esemo si ova oppo vicino alla meà, alloa poà consideae una delle due possibilià indiffeenemene. L aumeno a occhio della sensibilià di uno sumeno analogico non è possibile quando la sensibilià è molo piccola; vedi pe esempio il calibo. Bisogna fae aenzione ad alcuni sumeni che sembano analogici ma che in ealà sono digiali. Si considei ad esempio, un conomeo a lancea che pocede pe scai di secondo in secondo. Cife significaive. Il numeo di cife significaive di un valoe speimenale si calcola a paie dall ulima cifa affea da eoe e pocedendo veso sinisa fino ad aivae alla pima cifa divesa da, senza ene cono della vigola. Esempi. 0, ha 5 cife significaive. 3,57 ha cife significaive. 0,600 ha 3 cife significaive. Se si chiede di appossimae i segueni numei 3,00956; 56787; 0,005; 3; con cife significaive, si avà ispeivamene: 3,010; 5675; 0,00500; 3,00. Si deve ene sempe pesene che è l eoe di misua che deemina le cife significaive di un numeo. Infai pe sapee qual è l ulima cifa affea da eoe dobbiamo pima conoscee l eoe di misua. Quando inconiamo dei valoi senza la specifica dell eoe, volendo calcolane il numeo di cife significaive, dobbiamo pesuppoe che essi siano scii nel modo coeo. Ci poebbeo essee peò dei casi ambigui. Pe il numeo,0356 non ci sono poblemi (6 cife significaive); mene un numeo che pesena ambiguià è Infai, se non conosciamo l eoe non possiamo sapee se gli zei finali sono significaivi oppue no. Nel pimo caso si hanno 5 cife significaive, nel secondo se ne hanno. Pe isolvee l ambiguià i valoi andebbeo scii in noazione scienifica almeno nel caso in cui gli zei finali non sono significaivi: pesena ambiguià ( cife significaive). Se scivo gli ulimi non sono significaivi.,3 10 non,30 10, vuol die che dei e zei finali solo Ancoa sull eoe di misua. Concludiamo il discoso sull eoe massimo con la seguene consideazione: come vedemo in seguio, pe le misue indiee l eoe di misua si icava amie un calcolo. Si oeanno quindi eoi di misua con più di una cifa significaiva. Se ci si iflee bene peò, quesa siuazione è piva di significao. Infai la pima cifa significaiva dell eoe ci dice di quano sbagliamo sulla coispondene cifa del VM; che senso ha quindi, meesi a specificae gli eoi sulle ale cife? Possiamo peciò enunciae la seguene egola: Un eoe poveniene da un calcolo e che sia minoe di 10 va sempe appossimao ad una cifa significaiva e sempe pe eccesso. Così gli eoi 1= 0,00385; Aicolo di Mauizio Schiaulini Pag. 03

4 = 8,193; 3= 0,00963; = 0,0058; andanno appossimai come segue: 1= 0,005; = 9; 3= 0,01; = 0,003. ( ) Eoi casuali. Se misuiamo con un egolo millimeico la lunghezza di un oggeo, è molo pobabile che ipeendo la misua più vole si oenga sempe lo sesso isulao. Immaginiamo oa di dove fae la sessa misua, mene l oggeo in movimeno. Quesa vola difficilmene oeemo lo sesso VM. Cosa è successo? Non avevamo deo che l eoe di misua ci gaaniva un inevallo eno cui sicuamene cadeva il valoe veo? Come mai adesso ci sono più valoi? Evidenemene è enao in gioco un alo ipo di eoe: l eoe casuale. Nel caso dell oggeo in movimeno le difficolà dell opeaoe sono aumenae e quindi ineviabilmene egli inoduce degli eoi che si aggiungono all eoe di misua. Quesi eoi peò si aggiungono in modo casuale: una misua poà essee un po più gande, un ala un po più piccola. Toniamo al caso dell oggeo femo. In ealà anche in queso caso l opeaoe inoduce nella misua degli eoi casuali (ogni misua ichiede un abilià più o meno spina), egli infai deve fa coincidee un esemo dell oggeo con la acca dello zeo e non lo fa sempe allo sesso modo. Inole si enga pesene che le acche del ighello hanno uno spessoe e queso influisce nella misua. In ale paole l eoe casuale è pesene in ogni misua, esso è quindi ineliminabile. E evidene comunque che nel caso dell oggeo femo, gli eoi casuali sono molo più piccoli dell eoe di misua e quindi non escono fuoi. Nel caso dell oggeo in movimeno, invece, l eoe casuale è maggioe dell eoe di misua e la cosa appae evidene quando si ipee più vole la sessa misua. Un alo esempio in cui possono compaie eoi casuali consise nel misuae la lunghezza di un oggeo più lungo del ighello. Si invia lo sudene a povae ipeendo la misua più vole. Il paagafo elaivo ai valoi medi illuseà un modo elemenae di aae gli eoi casuali. Eoe elaivo. E un paameo che indica la qualià della misua ed è definio nel seguene modo: =. Tano più l eoe elaivo è piccolo ano più la misua è buona. L eoe VM elaivo, essendo deeminao da un appoo di gandezze omogenee, è un numeo adimensionale (numeo puo). Esempio: misuiamo due disanze con il conachilomei della macchina che ha una sensibilià pai a 100. m ( 0, 0,1 ) ; ( 950,0 0,1) L = ± Km L = ± Km. Pu avendo due misue con lo sesso 1 eoe isula evidene che L è più pecisa di L 1 (sbagliae di ceno mei su novecenocinquana chilomei è paicamene ascuabile; ma sbagliae di ceno mei su una disanza di quaoceno Esise una scuola di pensieo che appossima pe difeo gli eoi del ipo 0,01 0,. Aicolo di Mauizio Schiaulini Pag. 0

5 mei divena ilevane). Queso esempio ci fa vedee che l eoe di misua non è sufficiene a deeminae la qualià della misua. Calcoliamo gli eoi elaivi. ( L) ( L) 0,1 Km 1 1 = = = 0,5 0,3 L1 0,3 Km ( L ) ( L ) 0,1 Km = = = 0, ,000= 10 L 950 Km da cui isula evidene la diffeenza di qualià delle due misue. Noiamo che pe l appossimazione degli eoi elaivi valgono le sesse egole iguadani gli eoi assolui. L eoe elaivo ci dice quana pae dell unià è affea da eoe. Così L 1 0,3 = significa che ho 0,3 pai di eoe pe ogni pae misuaa. E usanza comune ifeisi a 100 pai invece che all unià, usando la noazione pecenuale: misuae. 30 = 0,3= = 30% ; cioè si hanno 30 pai di eoe ogni 100 pai 100 Valoi medi e semidispesione massima. Quando la sensibilià è molo piccola può succedee che ipeendo più vole la misua di una sessa gandezza si oengano isulai divesi (,,,,,...) VM VM VM VM VM. Ciò avviene quando ci sono in gioco dei ipi di eoe che supeano l eoe di misua (eoi casuali; iegolaià della gandezza da misuae). In queso caso esise una pocedua pe simae l eoe casuale e pe avee un VM effeivo. Illusiamo quesa pocedua con un esempio. Esempio: Con un conomeo cenesimale (sensibilià pai a 0,01s ) è sao misuao il peiodo di un pendolo. Ripeendo vole la misua si sono oenui i segueni isulai: (, 5 0,01 ), (,30 0,01 ), (,8 0,01 ), (, 6 0,01) = ± s = ± s = ± s = ± s. 1 3 L eoe casuale, in queso caso, è dovuo al iflesso dell opeaoe nel pemee il pulsane del conomeo quando il pendolo iona al puno di paenza. E noo che il empo di eazione di un essee umano è supeioe al cenesimo di secondo. Come VM (valoe misuao) definiivo si pendeà la media aimeica dei valoi oenui; ale valoe lo indicheemo con la seguene noazione: VM. Nel noso caso avemo:,5+,30+, 8+, 6 = =,75 s. Pe quanificae l eoe casuale possiamo ossevae che se si fa la diffeenza a il valoe più gande e quello più piccolo oeniamo un inevallo abbasanza ampio da conenee ui i valoi misuai e quindi anche il valoe veo. D ala pae sappiamo che come eoe si pende la meà di un ale inevallo (vedi figua 1). Chiameemo quesa gandezza semidispesione massima. Pe il noso Aicolo di Mauizio Schiaulini Pag. 05

6 esempio avemo: Max Min,3,5 d = = = 0,05 s. Queso valoe, adeguaamene appossimao, saà l eoe su (vedi figua ): ( ) 0,03 s. = A queso puno poemo scivee Max min d + d il isulao finale (, 7 0,03) = ± s. Si noi che è sao appossimao con le sesse cife dopo la vigola del suo eoe. Qualche vola può succedee che d sia più piccolo dell eoe di misua dello sumeno, in al caso si pendeà ques ulimo come eoe su. Quindi se nel noso esempio fosse uscio d 0.00 s, = Ricapiolando: = si saebbe faa la seguene scela: ( ) 0,01 s. Quando, effeuando più misue di una sessa gandezza, si oengono valoi misuai divesi VM, VM, VM, VM, VM, ui oenui con un eoe di misua pai a : a) Come VM definiivo si pende la media aimeica dei valoi oenui: VM. b) Si calcola la semidispesione massima appossimandola pe eccesso a una cifa significaiva. c) Si confona d con e, come eoe su VM, si pende il valoe massimo: ( VM) = Max{ d, }. Fig. d== Pe compleezza finiamo di aae l esempio del pendolo. Calcoliamo oa gli eoi elaivi: 0,01 0,01 ( 1) = = 0,00 0,005; ( ) = = 0,003 0,005;, 5,30 0,01 0,01 ( 3) = = 0,003 0,005; ( ) = = 0,00 0,005;,8, 6 0,05 ( ) = = 0,011 0,0., 75 Ripoiamo su una abella i dai speimenali elaivi all esempio: Max min Aicolo di Mauizio Schiaulini Pag. 06

7 ( ) ( ) ( ) ( ) s s \ s s \,5 0,005,30 0,005,8 0,01 0,005,7 0,03 %,6 0,005 Si enga pesene che può essee inseio solo dopo ave calcolao ( ). Si noi che abbiamo ipoao l eoe elaivo in due modi divesi. Popagazione degli eoi. Nelle misue indiee il VM si oiene dall applicazione di una fomula. L eoe assoluo non può, quindi, essee dedoo dalla sensibilià di uno sumeno che non esise. Esisono delle egole che ci danno l eoe assoluo a seconda della foma della fomula. 3 a) Espessioni monomiali semplici. Consideeemo solo quei monomi i cui elemeni sono o delle leee o dei numei o delle poenze; pe esempio: d v M1M T F ma a F G 1) v = ; ) = ; 3) = ; ) = ; 5) =. R 10 La egola, che pe queso ipo di espessioni ci fa icavae l eoe elaivo, è la seguene: L eoe elaivo è dao dalla somma degli eoi elaivi di ui gli elemeni che compongono il monomio. Così pe l esempio 1) si avà: ( v ) = ( d) + ( ). Pe l esempio ) si avà: ( F) ( m) ( a) = +. L esempio 3) ci cea qualche appaene difficolà nell applicazione della egola, ma se isciviamo l espessione nel seguene modo: a v v, cui: ( a) R = non c è più nessuna difficolà: ( a) = v + v +, da = v +. Possiamo opeae nello sesso modo con l esempio ), iscivendo = R R. Avemo: ( F) = ( G) ( M ) ( M ) ( R) ( R) da cui: 1, ( F) ( M ) ( M ) ( R) = In ealà quese egole deivano dal diffeenziale di una funzione a più vaiabili; ma queso è un agomeno che non può essee affonao in quesa sede. Aicolo di Mauizio Schiaulini Pag. 07

8 Abbiamo eliminao ( G) poiché G è una cosane deeminaa speimenalmene con un numeo di cife significaive abbasanza elevao e quindi possiamo endee l eoe di G ascuabile ispeo agli ali eoi usando semplicemene un adeguao numeo di cife significaive. Passiamo all esempio 5). ( ) = ( T) + ( 10 ), da cui ( ) = ( T). Abbiamo eliminao ( 10) peché non ci può essee eoe su un numeo. Quindi quando si sommano gli eoi elaivi, non vanno pesi in consideazione i numei. Vogliamo esaminae ancoa un esempio. Consideiamo il volume di un cubo: V l 3, = abbiamo: ( V) = ( l) + ( l) + ( l), cioè ( V) ( l) = 3. Da queso esempio e dagli esempi 3) e ) capiamo che gli esponeni divenano dei coefficieni nella fomula della popagazione degli eoi. A queso puno imane il poblema della deeminazione degli eoi assolui. Pe fa queso consideiamo la definizione dell eoe elaivo:. essa possiamo icavae conoscendo il VM e l eoe elaivo. Abbiamo l esempio ) avemo ; F = F F analogamene pe gli ali esempi. = Da VM = VM. Pe b) Espessioni polinomiali semplici. Consideeemo solo quei polinomi i cui elemeni sono o dei numei o delle leee o dei monomi fomai da un numeo e da una leea; pe esempio: 1) P= b+ h; ) M = m + m + m ; 3) L= E E ; ) = La egola, che in queso caso ci da dieamene l eoe assoluo, è la seguene: L espessione dell eoe assoluo si oiene dalla fomula sosiuendo alle gandezze, i loo eoi assolui e alle soazioni (se sono peseni), le addizioni. Pe i e esempi sopascii avemo ispeivamene: ( P) ( b) ( h) ( M) ( m ) ( m ) ( m ) 1) = + ; ) = + + ; 1 3 ( T) 3) ( L) = ( E) +( E1) ; ) ( ) =. 10 L esempio ) l abbiamo già inconao nel caso a), ma si può fa ienae anche in quesa ipologia. Pe quano iguada l eoe elaivo, si icoeà semplicemene alla sua definizione. Consideando l esempio 3) avemo peano: ( L) ( L) ; = analogamene pe gli ali esempi 5. L T 10 Avemmo pouo scivee l eoe assoluo anche nel seguene modo: = M M R ( F) G ( M ) ( M ) ( R) 1. Sapee die peché? 5 Avemmo pouo scivee l eoe elaivo anche nel seguene modo: Aicolo di Mauizio Schiaulini Pag. 08

9 A queso puno poponiamo un esempio iassunivo di quano deo sopa. Di un eangolo è saa misuaa la base, b= ( 37,15± 0,05) cm e l alezza, h l aea ed il peimeo. ( b) = 3,70± 0,05 cm. Si deemini 0,05 0,05 ( b) = = = 0,0013 0,00; ( h) = = = 0,001 0,003 b 37,15 h 3,7 ( h) A= bh= 37,15 3,7= 880, 55 cm ; P= b+ h= 7,3+ 7, = 11,7 cm ( A) ( b) ( h) 0,0013 0,001 0,003 0,00 = + = + = ( A) A ( A) 880, 55 0,003,99cm 3cm = = = ( p) 0, ( P) = ( b) + ( h) = 0,1+ 0,1= 0, cm; ( P) = = = 0,0016 0,00 P 11,7 In Definiiva si avà: = ( ± ) = ( ± ) Inseiamo oa i dai oenui in abelle speimenali: A cm ; P 11,7 0, cm. b ( b) ( b) ( b) h ( h) ( h) ( h) cm cm \ \ cm cm \ \ 37,15 0,05 0,00 0,% 3,70 0,05 0,003 0,3% A ( A) ( A) ( A) P ( P) ( P) ( P) cm cm \ \ cm cm \ \ 880 * 3 0,00 0,% 11,7 * 0, 0,00 0,% c) Casi più complicai. Se ci oviamo davani a fomule che non icadono nei casi a) e b), possiamo opeae con delle sosiuzioni in modo ale da ienae nei casi suddei. Consideiamo, pe esempio, l aea di un apezio: A ( B+ ) b h =. Abbiamo davani un monomio, ma uno dei faoi è un polinomio, non icadiamo quindi nel caso a). Facciamo la seguene sosiuzione: s= ( B+ b) e oviamo gli eoi pe s. Quesa fomula icade nel caso b). ( E ) ( E ) + ( L) = E E 1 1. Sapee die peché? * Si noi che quesi valoi possono essee inseii in abella solo dopo avee calcolao gli eoi assolui. Aicolo di Mauizio Schiaulini Pag. 09

10 ( s) ( s) = ( B) +( b) ; ( s) =. s Adesso che conosciamo l eoe assoluo e elaivo di s, possiamo icavaci gli eoi pe A, che oa possiamo scivee nel seguene modo: A= ; quindi ci oviamo davani al caso a). sh ( A) ( s) ( h) ( A) A ( A) = + ; =. Finoa abbiamo sempe eviao di dae egole nel caso in cui l eoe poveniene da un calcolo isuli maggioe o uguale a 10. In queso caso l eoe va appossimao in modo ale che sia divesa da zeo solo la pima cifa e sempe pe eccesso. Il VM invece deve essee appossimao in modo che agli zei dell eoe coispondano degli zei. Diamo alcuni esempi: VM = 157,567 = 13,967 VM = 1570± 0 VM = 1567,189 = 59,67 VM = 1600± 300. Pe finie diamo degli esempi nel caso in cui l eoe sia minoe di 10. Ricodiamo che in al caso l eoe va appossimao pe eccesso e con una cifa significaiva, mene il VM si appossima in modo che abbia le sesse cife dopo la vigola dell eoe. Ciò vuol die che pima bisogna conoscee l eoe appossimao e poi si poà scivee il coeo VM. Esempi: VM = 5,56783 = 0,00867 VM = 5,568± 0,009 VM = 3, = 0,00139 VM = 3, 00± 0,00 VM = 35,739 = 0,0967 VM = 35,7± 0,1 VM = 6,5 =,3 VM = 7± 3. Mauizio Schiaulini Aicolo di Mauizio Schiaulini Pag. 10