vettore spostamento infinitesimo: ds dr dxi + dyj + dzk
|
|
|
- Floriana Landi
- 5 anni fa
- Visualizzazioni
Transcript
1 Appendice A A.1 - istemi di coordinate. 1) Coordinate cartesiane. Il sistema di riferimento è costituito da tre assi perpendicolari uscenti da una comune origine O ed orientati positivamente verso l esterno. Gli assi sono convenzionalmente indicati come asse x, y e z; su ciascuno di essi si sceglie un versore (vettore di modulo unitario) indicato rispettivamente con i, j e k. In una terna destrorsa il verso positivo di rotazione è quello antiorario, e ad essa si fa riferimento. La posizione di un punto P nello spazio è individuata tramite le tre coordinate cartesiane (x,y,z) corrispondenti alla lunghezza della proiezione del segmento OP lungo i tre assi coordinati. z x = OL, y = OM, z = PN elemento di volume: dv d 3 r = dxdydz x L i P vettore posizione : k O j M (P-O) r xi + yj + zk y vettore spostamento infinitesimo: N ds dr dxi + dyj + dzk 2) Coordinate cilindriche. La posizione di un punto P nello spazio è individuata tramite le tre coordinate (r,φ,z): z corrisponde alla lunghezza della proiezione del segmento OP lungo un asse opportunamente scelto, e convenzionalmente indicato con z, su cui è stata fissata un origine O; r corrisponde alla lunghezza della proiezione di OP nel piano perpendicolare a z, φ all angolo che il raggio ON r forma rispetto ad un asse polare, opportunamente scelto nel piano perpendicolare a z e indicato convenzionalmente con x (φ è misurato positivamente in verso antiorario per una terna destrorsa). I versori, fra loro perpendicolari, che costituiscono la base del sistema di riferimento sono indicati con u r = r/r diretto lungo il raggio r ed orientato positivamente verso l esterno, k diretto lungo
2 l asse z e u φ formante con gli altri due una terna ortogonale destrorsa. A differenza del riferimento cartesiano in cui i tre versori mantengono inalterate le loro direzioni nello spazio, in questo caso l orientazione di u r ed u φ cambia a seconda del punto P considerato. r = ON, φ = LON, z = PN vettore posizione: (P-O) r r u r + z vettore spostamento infinitesimo: P ds dr dru r + rdφu φ + dzk z elemento di volume: O k M L φ r u φ dv d 3 r = rdφdrdz N x u r relazione fra coordinate cartesiane e cilindriche: OL = x = rcosφ OM = y = rsinφ PN = z = z 3) Coordinate sferiche. La posizione di un punto P nello spazio è individuata tramite le tre coordinate (r,θ,φ): fissato il punto O come origine ed un asse polare, convenzionalmente indicato con z, r corrisponde alla distanza di P da O, θ all angolo che OP r forma rispetto all asse z, φ all angolo che il raggio ON, proiezione di r nel piano perpendicolare a z, forma rispetto ad un asse polare, opportunamente scelto nel piano perpendicolare a z e indicato convenzionalmente con x (φ e θ sono misurati positivamente in verso antiorario per una terna destrorsa). I versori, fra loro perpendicolari, che costituiscono la base del sistema di riferimento sono indicati con u r = r/r diretto lungo il raggio r ed orientato positivamente verso l esterno, u θ nel piano individuato da OP e dall asse z e perpendicolare ad OP e u φ formante con gli altri due una terna ortogonale destrorsa. A differenza del riferimento cartesiano in cui i tre versori mantengono inalterate le loro direzioni nello spazio, in questo caso l orientazione dei tre versori cambia a seconda del punto P considerato.
3 u z r = OP, φ = LON, θ = QOP Q r vettore posizione: (P-O) r r u r P u φ θ u θ vettore spostamento infinitesimo: O M ds dr dru r + rdθu θ + rsinθdφu φ L φ elemento di volume: x N dv d 3 r = r 2 sinθdrdφdθ relazione fra coordinate cartesiane e sferiche: OL = x = r sinθ cosφ OM = y = r sinθ sinφ PN = z = r cosθ A.2 - Operazioni di prodotto fra vettori. Prodotto scalare: a b Il risultato del prodotto scalare di due vettori a e b è un numero s (scalare) dato dal prodotto dei moduli dei vettori per il coseno dell angolo compreso fra di essi. a A a b = s = abcosθ = b(oh) a b = 0 a b θ O B a = a x i + a y j + a z k b = b x i + b y j + b z k H b a b = s = a x b x + a y b y + a z b z Prodotto vettoriale: a b Il risultato del prodotto vettoriale di due vettori a e b è un vettore v (propriamente un vettore assiale) il cui modulo è dato dal prodotto dei moduli dei vettori per il modulo del seno dell angolo compreso fra di essi, la cui direzione è quella della perpendicolare al piano individuato da a e b e il cui verso è fissato dalla regola della
4 mano destra ( pollice nella direzione di a, indice nella direzione di b, medio nella direzione di v ). a b = - b a = v v v = absinθ = area parallelogrammo individuato da a e b θ b a a b = 0 a // b a = a x i + a y j + a z k b = b x i + b y j + b z k v = (a y b z - a z b y )i + (a z b x - a x b z )j + (a x b y - a y b x )k Doppio prodotto misto: a (b c) Il risultato del doppio prodotto misto è uno scalare il cui valore corrisponde al volume del parallelepipedo individuato dai tre vettori a, b e c. Ne consegue immediatamente l invarianza del prodotto per permutazioni cicliche dei fattori. a c a (b c) = b (c a) = c (a b) a (b c) = 0 a, b, c complanari b Doppio prodotto vettoriale: a (b c) Vale la seguente relazione di decomposizione : a (b c) = (a c)b (a b)c A.3 - Operatori differenziali L operatore differenziale (nabla) in un sistema di coordinate cartesiane è definito come:
5 x i + y j + z k Esso è un operatore differenziale vettoriale che opera su una o più funzioni delle coordinate x,y e z e dà luogo a risultati diversi a seconda di come esso viene applicato alle funzioni ed alle loro caratteristiche. Ad esso si applicano molte delle regole e proprietà che caratterizzano le operazioni fra vettori. Il gradiente di una funzione scalare φ = φ(x,y,z) è definito come: gradφ φ ( x i + y j + φ k)φ = z x i + φ y j + φ z k Dato uno spostamento infinitesimo ds dxi + dyj + dzk risulta immediatamente: φ ds = φ x dx + φ y φ dy + dz = dφ z Quindi il gradiente di una funzione determina la sua variazione nella direzione individuata dal vettore ds ; inoltre esso è sempre perpendicolare alle superfici φ(x,y,z) = cost dato che per uno spostamento ds lungo di esse risulta dφ = 0 e quindi nullo il prodotto scalare (.). La divergenza di una funzione vettoriale v = v(x,y,z) è definita come: div v v = v x x + v y y + v z z Il rotore di una funzione vettoriale è infine definito come: rot v = v = ( v z y v y z )i + ( v x z v z x )j + ( v y x v x y )k L operatore laplaciano è un operatore differenziale del secondo ordine (che coinvolge quindi le derivate seconde) ed definito come: 2 2 x y Trattandosi di un operatore scalare agisce indifferentemente su funzioni scalari o vettoriali e risulta: z 2 φ 2 φ 2 φ x + 2 φ 2 y + 2 φ 2 z 2 v 2 v 2 v x i + 2 v y j + 2 v z k
6 i noti che nella definizione del lapalciano (. ) l operatore nabla segue le regole di un ordinario prodotto scalare fra vettori. Oltre il laplaciano si possono definire altri operatori differenziali del secondo ordine partendo dai prodotti fra vettori precedentemente definiti. i ha quindi: ( v) = 0 come risulta per il doppio prodotto misto ( ) in cui due vettori sono uguali. La condizione, valida in tutti i punti dello spazio, B = 0 definisce un vettore solenoidale (per es. il Campo di induzione magnetica) e la precedente relazione ci dice immediatamente che un tale campo può essere sempre espresso come il rotore di un vettore, ossia B = v. imilmente risulta : φ = 0 come nel caso del prodotto vettoriale di un vettore con sè stesso. L Eq. () esprime la condizione di irrotazionalità di un campo vettoriale v = φ, ossia che v è un campo conservativo derivabile dal potenziale scalare φ. i ha infine l operatore differenziale ottenibile per mezzo del doppio prodotto vettoriale per il quale vale la relazione di decomposizione analoga alla Eq. (): ( v) = ( v) 2 v Riportiamo infine le seguenti relazioni di uso corrente (φv) = v φ + φ v (v w) = w ( v) v ( w) Per il vettore posizione (P-O) r xi + yj + zk, il cui modulo viene indicato con r, si dimostrano facilmente, per derivazione diretta, le seguenti relazioni: r = r r = vers r r = 3 r = 0 r r 3 = ( 1 r 2 r) = 1 r = 2 1 r = δ(r) Risulta utile considerare l effetto dell applicazione dell operatore nabla ad un termine esponenziale di onda piana del tipo φ = e ik r = e i(k x x + k y y + k z z) ; si ha in questo caso:
7 e ik r = e i(k x x + k y y + k z z) = ( x i + y j + z k)ei(kx x + ky y + kz z) = i(k x i + k y j + k z k)e i(kx x + ky y + kz z) = ike ik r Il risultato come si vede è quello di moltiplicare l esponenziale per il vettore ik e pertanto vale in questo caso la regola di sostituzione: Pertanto risultano verificate le relazioni: dove v è un vettore costante. ik e ik r = ike ik r ve ik r = ik ve ik r ve ik r = ik ve ik r Valgono infine le seguenti relazioni integrali: a) per un volume V delimitato dalla superficie chiusa, detti dv l elemento infinitesimo di volume, d l elemento infinitesimo di superfice e n la normale all elemento di superficie d orientata positivamente verso l esterno: φ n d = v n d = v n d = V V φ dv V v dv v dv (Teorema di Gauss) b) per una superficie aperta che si appoggia ad una linea chiusa γ (bordo di ) il cui elemento di linea sia dγ, scelto il verso della normale alla superficie n in relazione al verso di percorrenza di γ secondo la regola della vite destra: φdγ = n φd γ v dγ = ( v) nd γ (Teorema di tokes) i fornisce infine per successiva utilità l espressione dell operatore laplaciano in coordinate sferiche:
8 2 = 1 r 2 r (r 2 r ) + 1 r 2 sinθ θ (sinθ θ ) r 2 sin 2 θ φ 2
Premesse matematiche. 2.1 Gradiente
 Premesse matematiche 2.1 Gradiente ia f(x, y, z) : R 3 una funzione scalare delle coordinate spaziali (x, y, z). L ampiezza della funzione f(x, y, z) dipende dal punto di osservazione e risulta in genere
Premesse matematiche 2.1 Gradiente ia f(x, y, z) : R 3 una funzione scalare delle coordinate spaziali (x, y, z). L ampiezza della funzione f(x, y, z) dipende dal punto di osservazione e risulta in genere
VETTORI GEOMETRICI / RICHIAMI
 M.GUIDA, S.ROLANDO, 2016 1 VETTORI GEOMETRICI / RICHIAMI Chiamiamo vettore un qualsiasi segmento orientato del piano o dello spazio. Orientare un segmento significa scegliere un verso per percorrerlo,
M.GUIDA, S.ROLANDO, 2016 1 VETTORI GEOMETRICI / RICHIAMI Chiamiamo vettore un qualsiasi segmento orientato del piano o dello spazio. Orientare un segmento significa scegliere un verso per percorrerlo,
Risultati di ANALISI VETTORIALE
 Guida allo studio autonomo in ELETTROMAGNETISMO U Unità Risultati di ANALISI VETTORIALE Introduzione Hai già studiato gran parte della matematica necessaria per questo corso Comunque vale la pena di rivedere
Guida allo studio autonomo in ELETTROMAGNETISMO U Unità Risultati di ANALISI VETTORIALE Introduzione Hai già studiato gran parte della matematica necessaria per questo corso Comunque vale la pena di rivedere
Calcolo vettoriale. Versore: vettore u adimensionale di modulo unitario (rapporto tra un vettore e il suo modulo)
 Grandezze scalari: caratterizzate da un valore numerico in una unità di misura scelta (ex: massa, temperatura, ecc) Grandezze vettoriali: oltre al valore numerico necessitano della definizione di una direzione
Grandezze scalari: caratterizzate da un valore numerico in una unità di misura scelta (ex: massa, temperatura, ecc) Grandezze vettoriali: oltre al valore numerico necessitano della definizione di una direzione
Calcolo vettoriale. Grandezze scalari: caratterizzate da un valore numerico in una unità di misura scelta (ex: massa, temperatura, ecc)
 Grandezze scalari: caratterizzate da un valore numerico in una unità di misura scelta (ex: massa, temperatura, ecc) Grandezze vettoriali: oltre al valore numerico necessitano della definizione di una direzione
Grandezze scalari: caratterizzate da un valore numerico in una unità di misura scelta (ex: massa, temperatura, ecc) Grandezze vettoriali: oltre al valore numerico necessitano della definizione di una direzione
Meccanica. 3. Elementi di Analisi Vettoriale. Domenico Galli. Dipartimento di Fisica e Astronomia.
 Meccanica 3. Elementi di Analisi Vettoriale http://campus.cib.unibo.it/246981/ Domenico Galli Dipartimento di Fisica e Astronomia 5 maggio 2017 Traccia 1. Vettori Variabili 2. Derivate e Integrali 3. Derivate
Meccanica 3. Elementi di Analisi Vettoriale http://campus.cib.unibo.it/246981/ Domenico Galli Dipartimento di Fisica e Astronomia 5 maggio 2017 Traccia 1. Vettori Variabili 2. Derivate e Integrali 3. Derivate
Operatori vettoriali su R ³
 Operatori vettoriali su R ³ Sui campi scalari e vettoriali tridimensionali è possibile definire degli operatori vettoriali che giocano un ruolo importantissimo anche per le applicazioni nel campo fisico
Operatori vettoriali su R ³ Sui campi scalari e vettoriali tridimensionali è possibile definire degli operatori vettoriali che giocano un ruolo importantissimo anche per le applicazioni nel campo fisico
Grandezze scalari e vettoriali-esempi
 Grandezze scalari e vettoriali-esempi Massa Tempo Temperatura Pressione Posizione lungo un asse (linea) Volume Lavoro Energia Posizione nel piano Posizione nello spazio Velocità Accelerazione Forza Quantità
Grandezze scalari e vettoriali-esempi Massa Tempo Temperatura Pressione Posizione lungo un asse (linea) Volume Lavoro Energia Posizione nel piano Posizione nello spazio Velocità Accelerazione Forza Quantità
UNIVERSITÀ DI ROMA TOR VERGATA. Analisi Matematica II per Ingegneria Prof. C. Sinestrari
 UNIVERSITÀ DI ROMA TOR VERGATA Analisi Matematica II per Ingegneria Prof. C. Sinestrari Risposte (sintetiche) agli esercizi del 27.XI.217 1. (NB si ricorda che l equazione del piano passante per un punto
UNIVERSITÀ DI ROMA TOR VERGATA Analisi Matematica II per Ingegneria Prof. C. Sinestrari Risposte (sintetiche) agli esercizi del 27.XI.217 1. (NB si ricorda che l equazione del piano passante per un punto
Calcolo 2B - Analisi III dicembre 2004
 Calcolo 2B - Analisi III dicembre 2. Verificare esplicitamente il teorema di Stokes in R 2 : dω = ω per la -forma: nella regione piana data da: ω = x 2 + y 2 dx = x, y x 2 + y 2 ª x, y y 2x 2ª 2. Considerato
Calcolo 2B - Analisi III dicembre 2. Verificare esplicitamente il teorema di Stokes in R 2 : dω = ω per la -forma: nella regione piana data da: ω = x 2 + y 2 dx = x, y x 2 + y 2 ª x, y y 2x 2ª 2. Considerato
Gradiente, divergenza e rotore
 Gradiente, divergenza e rotore Gradiente di una funzione scalare della posizione Sia f(x,y,z) una funzione scalare continua e derivabile delle coordinate costruiamo in ogni punto dello spazio un vettore
Gradiente, divergenza e rotore Gradiente di una funzione scalare della posizione Sia f(x,y,z) una funzione scalare continua e derivabile delle coordinate costruiamo in ogni punto dello spazio un vettore
Teoremi di Stokes, della divergenza e di Gauss Green.
 Matematica 3 Esercitazioni eoremi di tokes, della divergenza e di Gauss Green. Esercizio 1 : Calcolare l area del dominio avente per frontiera la linea chiusa γ di equazioni parametriche x (1 t) t γ :,
Matematica 3 Esercitazioni eoremi di tokes, della divergenza e di Gauss Green. Esercizio 1 : Calcolare l area del dominio avente per frontiera la linea chiusa γ di equazioni parametriche x (1 t) t γ :,
Analisi Matematica II Politecnico di Milano Ingegneria Industriale
 Analisi Matematica II Politecnico di Milano Ingegneria Industriale Autovalutazione #. Sia P l insieme di tutti i parallelepipedi che giacciono nel primo ottante con tre facce sui piani coordinati e un
Analisi Matematica II Politecnico di Milano Ingegneria Industriale Autovalutazione #. Sia P l insieme di tutti i parallelepipedi che giacciono nel primo ottante con tre facce sui piani coordinati e un
Esercizi di Analisi Matematica 3. Prima parte
 Esercizi di Analisi Matematica 3 per le Facoltà di Ingegneria Prima parte Corrado Lattanzio e Bruno Rubino Versione preliminare L Aquila, ottobre 5 Indice 1 Curve, superfici e campi vettoriali 3 1.1 Curve
Esercizi di Analisi Matematica 3 per le Facoltà di Ingegneria Prima parte Corrado Lattanzio e Bruno Rubino Versione preliminare L Aquila, ottobre 5 Indice 1 Curve, superfici e campi vettoriali 3 1.1 Curve
UNIVERSITÀ DI ROMA TOR VERGATA. Analisi Matematica II per Ingegneria Prof. C. Sinestrari
 UNIVERSITÀ DI ROMA TOR VERGATA Analisi Matematica II per Ingegneria Prof. C. Sinestrari Risposte sintetiche) agli esercizi del 15.XII.218 1. NB si ricorda che l equazione del piano passante per un punto
UNIVERSITÀ DI ROMA TOR VERGATA Analisi Matematica II per Ingegneria Prof. C. Sinestrari Risposte sintetiche) agli esercizi del 15.XII.218 1. NB si ricorda che l equazione del piano passante per un punto
ANALISI VETTORIALE ESERCIZI SULLE SUPERFICI
 ANALII VETTORIALE EERCIZI ULLE UPERFICI Esercizio Calcolare l area della superficie dove Σ {(x, y, z) (x, y) E, z 2 + x 2 + y 2 } E {(x, y) x 2 + y 2 4}. Essendo la superficie Σ data come grafico di una
ANALII VETTORIALE EERCIZI ULLE UPERFICI Esercizio Calcolare l area della superficie dove Σ {(x, y, z) (x, y) E, z 2 + x 2 + y 2 } E {(x, y) x 2 + y 2 4}. Essendo la superficie Σ data come grafico di una
e la lunghezza della proiezione del vettore B sul vettore A. s = A B =A b
 8) Prodotto scalare o prodotto interno Si definisce prodotto scalare s di due vettori A e B, l area del rettangolo che ha per lati il modulo del vettore A e la lunghezza della proiezione del vettore B
8) Prodotto scalare o prodotto interno Si definisce prodotto scalare s di due vettori A e B, l area del rettangolo che ha per lati il modulo del vettore A e la lunghezza della proiezione del vettore B
Superfici e integrali di superficie. 1. Scrivere una parametrizzazione per le seguenti superfici
 Superfici e integrali di superficie 1. Scrivere una parametrizzazione per le seguenti superfici (a) Il grafico della funzione f(x, y) = x 2 y 3 (b) La superficie laterale di un cilindro di raggio R e altezza
Superfici e integrali di superficie 1. Scrivere una parametrizzazione per le seguenti superfici (a) Il grafico della funzione f(x, y) = x 2 y 3 (b) La superficie laterale di un cilindro di raggio R e altezza
VETTORI E SCALARI DEFINIZIONI. Si definisce scalare una grandezza definita interamente da un solo numero, affiancato dalla sua unità di misura.
 VETTORI E SCALARI DEFINIZIONI Si definisce scalare una grandezza definita interamente da un solo numero, affiancato dalla sua unità di misura. Un vettore è invece una grandezza caratterizzata da 3 entità:
VETTORI E SCALARI DEFINIZIONI Si definisce scalare una grandezza definita interamente da un solo numero, affiancato dalla sua unità di misura. Un vettore è invece una grandezza caratterizzata da 3 entità:
Flusso, divergenza e rotore. Mauro Saita. Versione provvisoria. Giugno
 Flusso, divergenza e rotore. Esercizi maurosaita@tiscalinet.it ersione provvisoria. Giugno 216. 1 Indice 1 Teorema della divergenza (di Gauss). 2 1.1 Flusso di un campo di forze attraverso un cubo di dimensioni
Flusso, divergenza e rotore. Esercizi maurosaita@tiscalinet.it ersione provvisoria. Giugno 216. 1 Indice 1 Teorema della divergenza (di Gauss). 2 1.1 Flusso di un campo di forze attraverso un cubo di dimensioni
si ha La lunghezza L si calcola per ciascun tratto L = (2t)2 + (3t 2 ) dt+ 2 (3t2 ) 2 + (2t) 2 dt = 4t2 + 9t 4 dt = t
 ANALISI VETTORIALE Soluzione esercizi 1 gennaio 211 6.1. Esercizio. Sia Γ la curva regolare a tratti di rappresentazione parametrica x = t 2, y = t, t [, 1] e x = t, y = t 2, t [1, 2] calcolare la lunghezza,
ANALISI VETTORIALE Soluzione esercizi 1 gennaio 211 6.1. Esercizio. Sia Γ la curva regolare a tratti di rappresentazione parametrica x = t 2, y = t, t [, 1] e x = t, y = t 2, t [1, 2] calcolare la lunghezza,
CALCOLO VETTORIALE ELEMENTI DI ANALISI MATEMATICA
 ELEMENTI DI ANALISI MATEMATICA CALCOLO VETTORIALE - DEFINIZIONE DI VETTORE - COMPONENTI DI UN VETTORE - SOMMA E DIFFERENZA - PRODOTTO SCALARE - PRODOTTO VETTORIALE - VETTORE GRADIENTE - FLUSSO DI UN VETTORE
ELEMENTI DI ANALISI MATEMATICA CALCOLO VETTORIALE - DEFINIZIONE DI VETTORE - COMPONENTI DI UN VETTORE - SOMMA E DIFFERENZA - PRODOTTO SCALARE - PRODOTTO VETTORIALE - VETTORE GRADIENTE - FLUSSO DI UN VETTORE
Dispense dei corsi di Idrodinamica (prof.ssa Giovanna Vittori) e Meccanica dei Fluidi (prof. Paolo Blondeaux)
 Dispense dei corsi di Idrodinamica (prof.ssa Giovanna Vittori e Meccanica dei Fluidi (prof. Paolo Blondeaux Dipartimento di Ingegneria ivile, himica e Ambientale Universitá di Genova a.a. 2013-2014 apitolo
Dispense dei corsi di Idrodinamica (prof.ssa Giovanna Vittori e Meccanica dei Fluidi (prof. Paolo Blondeaux Dipartimento di Ingegneria ivile, himica e Ambientale Universitá di Genova a.a. 2013-2014 apitolo
Risposta La curva r è regolare a tratti per via di quanto succede della sua rappresentazione parametrica nel punto t = 1: pur riuscendo
 ANALISI VETTORIALE OMPITO PER LE VAANZE DI FINE D ANNO Esercizio Sia r(t) la curva regolare a tratti x = t, y = t, t [, ] e x = t, y = t, t [, ]. alcolare la lunghezza di r, calcolare, dove esistono, i
ANALISI VETTORIALE OMPITO PER LE VAANZE DI FINE D ANNO Esercizio Sia r(t) la curva regolare a tratti x = t, y = t, t [, ] e x = t, y = t, t [, ]. alcolare la lunghezza di r, calcolare, dove esistono, i
Integrali di superficie
 Integrali di superficie Hynek Kovarik Università di Brescia Analisi Matematica 2 Hynek Kovarik (Università di Brescia) Integrali curvilinei Analisi Matematica 2 1 / 27 Superfici in forma parametrica Procediamo
Integrali di superficie Hynek Kovarik Università di Brescia Analisi Matematica 2 Hynek Kovarik (Università di Brescia) Integrali curvilinei Analisi Matematica 2 1 / 27 Superfici in forma parametrica Procediamo
Appunti sul corso di Complementi di Matematica (modulo Analisi)
 Appunti sul corso di Complementi di Matematica (modulo Analisi) prof. B.Bacchelli. 04 - Vettori topologia in R n : Riferimenti: R.Adams, Calcolo Differenziale 2. Cap. 1.2: In R n : vettori, somma, prodotto
Appunti sul corso di Complementi di Matematica (modulo Analisi) prof. B.Bacchelli. 04 - Vettori topologia in R n : Riferimenti: R.Adams, Calcolo Differenziale 2. Cap. 1.2: In R n : vettori, somma, prodotto
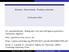
Sia ϕ una funzione continua definita su un rettangolo R = [a, b] [c, d] di R 2 e a valori in R 3 : ϕ : R R 2 R 3
![Sia ϕ una funzione continua definita su un rettangolo R = [a, b] [c, d] di R 2 e a valori in R 3 : ϕ : R R 2 R 3 Sia ϕ una funzione continua definita su un rettangolo R = [a, b] [c, d] di R 2 e a valori in R 3 : ϕ : R R 2 R 3](/thumbs/69/60553365.jpg) 1 uperfici ia ϕ una funzione continua definita su un rettangolo R = [a, b] [c, d] di R 2 e a valori in R 3 : ϕ : R R 2 R 3 (u, v) R ϕ(u, v) = (x(u, v), y(u, v), z(u, v)), cioè tale che le componenti x(u,
1 uperfici ia ϕ una funzione continua definita su un rettangolo R = [a, b] [c, d] di R 2 e a valori in R 3 : ϕ : R R 2 R 3 (u, v) R ϕ(u, v) = (x(u, v), y(u, v), z(u, v)), cioè tale che le componenti x(u,
Richiami di analisi vettoriale. Gradiente, divergenza, rotore Teoremi della divergenza e di Stokes Relazioni campi-sorgenti
 Richiami di analisi vettoriale Gradiente, divergenza, rotore Teoremi della divergenza e di Stokes Relazioni campi-sorgenti Derivate parziali - Gradiente = ( f) dx i i Esercizio Esempi Esempio C 1 b (1,1)
Richiami di analisi vettoriale Gradiente, divergenza, rotore Teoremi della divergenza e di Stokes Relazioni campi-sorgenti Derivate parziali - Gradiente = ( f) dx i i Esercizio Esempi Esempio C 1 b (1,1)
Argomenti Capitolo 1 Richiami
 Argomenti Capitolo 1 Richiami L insieme dei numeri reali R si rappresenta geometricamente con l insieme dei punti di una retta orientata su cui sia stato fissato un punto 0 e un segmento unitario. L insieme
Argomenti Capitolo 1 Richiami L insieme dei numeri reali R si rappresenta geometricamente con l insieme dei punti di una retta orientata su cui sia stato fissato un punto 0 e un segmento unitario. L insieme
CAMPI VETTORIALI (Note)
 CAMPI VETTORIALI (Note) Sia v(x,y,z) il vettore che definisce la grandezza fisica del campo: il problema che ci si pone è di caratterizzare il campo vettoriale sia in termini locali, cioè validi punto
CAMPI VETTORIALI (Note) Sia v(x,y,z) il vettore che definisce la grandezza fisica del campo: il problema che ci si pone è di caratterizzare il campo vettoriale sia in termini locali, cioè validi punto
Vettori e Calcolo vettoriale
 Vettori e Calcolo vettoriale Ci poniamo nello spazio ordinario S, in cui valgono gli assiomi della geometria euclidea. I vettori vengono rappresentati mediante frecce, con un punto iniziale e un punto
Vettori e Calcolo vettoriale Ci poniamo nello spazio ordinario S, in cui valgono gli assiomi della geometria euclidea. I vettori vengono rappresentati mediante frecce, con un punto iniziale e un punto
il luogo dei punti in cui un campo scalare assume un valore costante e detto superficie di livello ed e determinato dall equazione u(x,y,z) = c
 Campo scalare e una regione di spazio dove punto per punto sia definibile una funzione scalare continua e derivabile ovunque ( una funzione da a ) n trascurando la dipendenza dal tempo e operando in coordinate
Campo scalare e una regione di spazio dove punto per punto sia definibile una funzione scalare continua e derivabile ovunque ( una funzione da a ) n trascurando la dipendenza dal tempo e operando in coordinate
Grandezze scalari e vettoriali
 Grandezze scalari e vettoriali Per caratterizzare completamente una grandezza fisica, a volte è sufficiente dare soltanto un numero (scalare), mentre altre volte questo non è sufficiente. Massa, lunghezza,
Grandezze scalari e vettoriali Per caratterizzare completamente una grandezza fisica, a volte è sufficiente dare soltanto un numero (scalare), mentre altre volte questo non è sufficiente. Massa, lunghezza,
I.T.I.S «G. MARCONI» - PADOVA Via Manzoni, 80 Tel.: Fax
 I.T.I.S «G. MARCONI» - PADOVA Via Manzoni, 80 Tel.: 049.80.40.211 Fax 049.80.40.277 marconi@provincia.padova.it www.itismarconipadova.it Settore tecnologico Indirizzo meccanica meccatronica ed energia
I.T.I.S «G. MARCONI» - PADOVA Via Manzoni, 80 Tel.: 049.80.40.211 Fax 049.80.40.277 marconi@provincia.padova.it www.itismarconipadova.it Settore tecnologico Indirizzo meccanica meccatronica ed energia
Provadiprova 2 - aggiornamento 7 giugno 2013
 Università di Trento - Corso di Laurea in Ingegneria Civile e Ambientale Analisi matematica 2 - a.a. 2012-13 - Prof. Gabriele Anzellotti Provadiprova 2 - aggiornamento 7 giugno 2013 La seconda provetta
Università di Trento - Corso di Laurea in Ingegneria Civile e Ambientale Analisi matematica 2 - a.a. 2012-13 - Prof. Gabriele Anzellotti Provadiprova 2 - aggiornamento 7 giugno 2013 La seconda provetta
I tensori ed il calcolo tensoriale... 1
 Appunti di Campi lettromagnetici Capitolo Richiami di calcolo vettoriale e tensoriale I tensori ed il calcolo tensoriale... IL CALCOLO VTTORIAL... Introduzione... Operatore immaginario j... 4 Operatore
Appunti di Campi lettromagnetici Capitolo Richiami di calcolo vettoriale e tensoriale I tensori ed il calcolo tensoriale... IL CALCOLO VTTORIAL... Introduzione... Operatore immaginario j... 4 Operatore
Prodotto scalare e prodotto vettoriale. Elisabetta Colombo
 Corso di Approfondimenti di Matematica Biotecnologie, Anno Accademico 2010-2011, http://users.mat.unimi.it/users/colombo/programmabio.html Vettori Vettori 1 2 3 4 di di Ricordiamo il in R n Dati a = (a
Corso di Approfondimenti di Matematica Biotecnologie, Anno Accademico 2010-2011, http://users.mat.unimi.it/users/colombo/programmabio.html Vettori Vettori 1 2 3 4 di di Ricordiamo il in R n Dati a = (a
Calcolare l area di una superficie. 2. Calcolare l area della porzione del piano 3x + 2y + z = 7 all interno al cilindro x 2 + y 2 = 1.
 Calcolare l area di una superficie. Calcolare l area della porzione del piano x + 2y + z = 5 sopra il cono z = 3(x 2 + y 2 ). 2. Calcolare l area della porzione del piano 3x + 2y + z = 7 all interno al
Calcolare l area di una superficie. Calcolare l area della porzione del piano x + 2y + z = 5 sopra il cono z = 3(x 2 + y 2 ). 2. Calcolare l area della porzione del piano 3x + 2y + z = 7 all interno al
Analisi Vettoriale A.A Soluzioni del Foglio 4
 Analisi Vettoriale A.A. 26-27 - Soluzioni del Foglio 4 Esercizio 4.1. Sia Σ la superficie cartesiana z = 1 x y, (x, y) = {x 2 + y 2 1}, determinare in ogni punto di Σ il versore normale diretto nel verso
Analisi Vettoriale A.A. 26-27 - Soluzioni del Foglio 4 Esercizio 4.1. Sia Σ la superficie cartesiana z = 1 x y, (x, y) = {x 2 + y 2 1}, determinare in ogni punto di Σ il versore normale diretto nel verso
ARGOMENTI MATEMATICA PER L INGEGNERIA
 ARGOMENTI DI MATEMATICA PER L INGEGNERIA VOLUME 2 Esercizi proposti Quando non diversamente precisato, nel seguito si intenderà( sempre che nel piano sia stato introdotto un sistema cartesiano ortogonale
ARGOMENTI DI MATEMATICA PER L INGEGNERIA VOLUME 2 Esercizi proposti Quando non diversamente precisato, nel seguito si intenderà( sempre che nel piano sia stato introdotto un sistema cartesiano ortogonale
Elettromagnetismo Formulazione differenziale
 Elettromagnetismo Formulazione differenziale 1. Legge di Gauss 2. Legge di Ampere 3. Equazioni di Maxwell statiche V - 0 Legge di Gauss Campo elettrico Carica contenuta all interno della superficie A Flusso
Elettromagnetismo Formulazione differenziale 1. Legge di Gauss 2. Legge di Ampere 3. Equazioni di Maxwell statiche V - 0 Legge di Gauss Campo elettrico Carica contenuta all interno della superficie A Flusso
Campi vettoriali. 1. Sia F (x, y) = ye x i + (e x cos y) j un campo vettoriale. Determinare un potenziale per F, se esiste.
 Campi vettoriali. Sia F (x, y = ye x i + (e x cos y j un campo vettoriale. Determinare un potenziale per F, se esiste.. Sia F (x, y = xy i + x j un campo vettoriale. Determinare un potenziale per F, se
Campi vettoriali. Sia F (x, y = ye x i + (e x cos y j un campo vettoriale. Determinare un potenziale per F, se esiste.. Sia F (x, y = xy i + x j un campo vettoriale. Determinare un potenziale per F, se
(x) = F 1 x 1. (x)+ F 2. cioè è la traccia (cioè la somma degli elementi della diagonale principale) della matrice jacobiana J F (x).
 Teorema della divergenza Richiami di teoria Operatori divergenza e di Laplace R n un insieme aperto, x = (x 1, x 2,..., x n ). Divergenza Consideriamo un campo vettoriale F : R n R n differenziabile in
Teorema della divergenza Richiami di teoria Operatori divergenza e di Laplace R n un insieme aperto, x = (x 1, x 2,..., x n ). Divergenza Consideriamo un campo vettoriale F : R n R n differenziabile in
CAPITOLO 3 LA LEGGE DI GAUSS
 CAPITOLO 3 LA LEGGE DI GAUSS Elisabetta Bissaldi (Politecnico di Bari) - A.A. 2017-2018 2 Premesse TEOREMA DI GAUSS Formulazione equivalente alla legge di Coulomb Trae vantaggio dalle situazioni nelle
CAPITOLO 3 LA LEGGE DI GAUSS Elisabetta Bissaldi (Politecnico di Bari) - A.A. 2017-2018 2 Premesse TEOREMA DI GAUSS Formulazione equivalente alla legge di Coulomb Trae vantaggio dalle situazioni nelle
Forme differenziali e campi vettoriali: esercizi svolti
 Forme differenziali e campi vettoriali: esercizi svolti 1 Esercizi sul Teorema di Green......................... 2 2 Esercizi sul Teorema di Stokes......................... 4 3 Esercizi sul Teorema di
Forme differenziali e campi vettoriali: esercizi svolti 1 Esercizi sul Teorema di Green......................... 2 2 Esercizi sul Teorema di Stokes......................... 4 3 Esercizi sul Teorema di
Vettori e geometria analitica in R 3 1 / 25
 Vettori e geometria analitica in R 3 1 / 25 Sistemi di riferimento in R 3 e vettori 2 / 25 In fisica, grandezze fondamentali come forze, velocità, campi elettrici e magnetici vengono convenientemente descritte
Vettori e geometria analitica in R 3 1 / 25 Sistemi di riferimento in R 3 e vettori 2 / 25 In fisica, grandezze fondamentali come forze, velocità, campi elettrici e magnetici vengono convenientemente descritte
Analisi Matematica III (Fisica) 07 Gennaio 2016
 Analisi Matematica III (Fisica 7 Gennaio 16 1. (1 punti Calcolare l area della sezione del cilindro x + y 4 determinata dal piano di equazione z x + y. (Possibilmente in due modi differenti Ci sono vari
Analisi Matematica III (Fisica 7 Gennaio 16 1. (1 punti Calcolare l area della sezione del cilindro x + y 4 determinata dal piano di equazione z x + y. (Possibilmente in due modi differenti Ci sono vari
1- Geometria dello spazio. Vettori
 1- Geometria dello spazio. Vettori I. Generalità (essenziali) sui vettori. In matematica e fisica, un vettore è un segmento orientato nello spazio euclideo tridimensionale. Gli elementi che caratterizzano
1- Geometria dello spazio. Vettori I. Generalità (essenziali) sui vettori. In matematica e fisica, un vettore è un segmento orientato nello spazio euclideo tridimensionale. Gli elementi che caratterizzano
INTRODUZIONE ALLA FISICA PROF. FRANCESCO DE PALMA
 INTRODUZIONE ALLA FISICA PROF. FRANCESCO DE PALMA Sommario GRANDEZZE FISICHE... 3 UNITÀ DI MISURA... 3 PREFISSI... 5 ANALISI DIMENSIONALE... 5 CONVERSIONI DI UNITÀ... 6 SISTEMI DI COORDINATE... 7 I VETTORI...
INTRODUZIONE ALLA FISICA PROF. FRANCESCO DE PALMA Sommario GRANDEZZE FISICHE... 3 UNITÀ DI MISURA... 3 PREFISSI... 5 ANALISI DIMENSIONALE... 5 CONVERSIONI DI UNITÀ... 6 SISTEMI DI COORDINATE... 7 I VETTORI...
Esercitazione di Analisi Matematica II
 Esercitazione di Analisi Matematica II Barbara Balossi 06/04/2017 Esercizi di ripasso Esercizio 1 Sia data l applicazione lineare f : R 3 R 3 definita come f(x, y, z) = ( 2x + y z, x 2y + z, x y). a) Calcolare
Esercitazione di Analisi Matematica II Barbara Balossi 06/04/2017 Esercizi di ripasso Esercizio 1 Sia data l applicazione lineare f : R 3 R 3 definita come f(x, y, z) = ( 2x + y z, x 2y + z, x y). a) Calcolare
Analisi Matematica 2. Forme differenziali lineari. Forme differenziali lineari 1 / 26
 Analisi Matematica 2 Forme differenziali lineari Forme differenziali lineari 1 / 26 Forme differenziali lineari Sia F(x, y, z) = F 1 (x, y, z)i + F 2 (x, y, z)j + F 3 (x, y, z)k un campo vettoriale di
Analisi Matematica 2 Forme differenziali lineari Forme differenziali lineari 1 / 26 Forme differenziali lineari Sia F(x, y, z) = F 1 (x, y, z)i + F 2 (x, y, z)j + F 3 (x, y, z)k un campo vettoriale di
La matematica del CAD. Vettori e Matrici
 La matematica del CAD Vettori e Matrici IUAV Disegno Digitale Camillo Trevisan I programmi CAD riducono tutti i problemi geometrici in problemi analitici: la proiezione di un punto su un piano viene, ad
La matematica del CAD Vettori e Matrici IUAV Disegno Digitale Camillo Trevisan I programmi CAD riducono tutti i problemi geometrici in problemi analitici: la proiezione di un punto su un piano viene, ad
ELEMENTI DI CALCOLO VETTORIALE
 ELEMENTI DI CALCOLO VETTORIALE Vettori liberi e vettori applicati o Vettore libero: - individuato da una direzione orientata ed una lunghezza - non ha un'ubicazione fissa nello spazio: - puo' essere traslato
ELEMENTI DI CALCOLO VETTORIALE Vettori liberi e vettori applicati o Vettore libero: - individuato da una direzione orientata ed una lunghezza - non ha un'ubicazione fissa nello spazio: - puo' essere traslato
Le soluzioni del foglio 3
 Le soluzioni del foglio 3 1. Esercizio Consideriamo la famiglia di elicoidi, vedi Figura 1, x = u cos(v), y = u sin(v), z = kv, u 1, v π Quella proposta nell esercizio corrisponde alla scelta k = 1 Matrice
Le soluzioni del foglio 3 1. Esercizio Consideriamo la famiglia di elicoidi, vedi Figura 1, x = u cos(v), y = u sin(v), z = kv, u 1, v π Quella proposta nell esercizio corrisponde alla scelta k = 1 Matrice
E e B sono inscindibili tra loro e vale la
 Onde elettromagnetiche nel vuoto le onde e.m. sono costituite da un campo elettrico e da uno magnetico variabili nel tempo che si propagano in fase tra loro obbediscono al principio di sovrapposizione
Onde elettromagnetiche nel vuoto le onde e.m. sono costituite da un campo elettrico e da uno magnetico variabili nel tempo che si propagano in fase tra loro obbediscono al principio di sovrapposizione
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
Soluzione della Prova Parziale di Analisi Matematica III - 17/02/04. C.L. in Matematica e Matematica per le Applicazioni. Prof. Kevin R.
 Soluzione della Prova Parziale di Analisi Matematica III - 7//4 C.L. in Matematica e Matematica per le Applicazioni Prof. Kevin R. Payne Esercizio. a. Ricordiamo inanzitutto la seguente: efinizione: Si
Soluzione della Prova Parziale di Analisi Matematica III - 7//4 C.L. in Matematica e Matematica per le Applicazioni Prof. Kevin R. Payne Esercizio. a. Ricordiamo inanzitutto la seguente: efinizione: Si
Corso di FISICA II Prof. Umberto del Pennino
 Contenuti del Corso: Elettricità Magnetismo Ottica Corso di FISICA II Prof. Umberto del Pennino Elettromagnetismo Testo: Mazzoldi, Nigro, Voci:" Elementi di Fisica: Elettromagnetismo e Onde EdiSES Operatori
Contenuti del Corso: Elettricità Magnetismo Ottica Corso di FISICA II Prof. Umberto del Pennino Elettromagnetismo Testo: Mazzoldi, Nigro, Voci:" Elementi di Fisica: Elettromagnetismo e Onde EdiSES Operatori
Prodotto Scalare e Prodotto Vettore I
 Prodotto Scalare e Prodotto Vettore I Prodotto Scalare: pplicaione che va dallo spaio prodotto R 3 R 3 in R tale che: 3 B B B, = j = 1 j j Norma di un Vettore: pplicaione che va dallo spaio dei vettori
Prodotto Scalare e Prodotto Vettore I Prodotto Scalare: pplicaione che va dallo spaio prodotto R 3 R 3 in R tale che: 3 B B B, = j = 1 j j Norma di un Vettore: pplicaione che va dallo spaio dei vettori
Coordinate e Sistemi di Riferimento
 Coordinate e Sistemi di Riferimento Sistemi di riferimento Quando vogliamo approcciare un problema per risolverlo quantitativamente, dobbiamo per prima cosa stabilire in che sistema di riferimento vogliamo
Coordinate e Sistemi di Riferimento Sistemi di riferimento Quando vogliamo approcciare un problema per risolverlo quantitativamente, dobbiamo per prima cosa stabilire in che sistema di riferimento vogliamo
1 Sistemi di riferimento
 Università di Bologna - Corsi di Laurea Triennale in Ingegneria, II Facoltà - Cesena Esercitazioni del corso di Fisica Generale L-A Anno accademico 2006-2007 1 Sistemi di riferimento Le grandezze usate
Università di Bologna - Corsi di Laurea Triennale in Ingegneria, II Facoltà - Cesena Esercitazioni del corso di Fisica Generale L-A Anno accademico 2006-2007 1 Sistemi di riferimento Le grandezze usate
Si definisce un operatore vettoriale (nabla) in coordinate cartesiane nella maniera seguente:
 APPENDICE A.1 Operatori differeniali e relativi teoremi Si definisce un operatore vettoriale (nabla) in coordinate cartesiane nella maniera seguente: xˆ yˆ ˆ. x y E possibile provare che tale operatore
APPENDICE A.1 Operatori differeniali e relativi teoremi Si definisce un operatore vettoriale (nabla) in coordinate cartesiane nella maniera seguente: xˆ yˆ ˆ. x y E possibile provare che tale operatore
Geometria 3 primo semestre a.a
 Geometria 3 primo semestre a.a. 2014-2015 Esercizi Forme differenziali Ricordiamo alcune definizioni date a lezione. s-forma definite da Siano ω una k-forma e φ una ω = I a I dx I, φ = J b J dx J Definizione
Geometria 3 primo semestre a.a. 2014-2015 Esercizi Forme differenziali Ricordiamo alcune definizioni date a lezione. s-forma definite da Siano ω una k-forma e φ una ω = I a I dx I, φ = J b J dx J Definizione
Il Corso di Fisica per Scienze Biologiche
 Il Corso di Fisica per Scienze Biologiche Ø Prof. Attilio Santocchia Ø Ufficio presso il Dipartimento di Fisica (Quinto Piano) Tel. 075-585 2708 Ø E-mail: attilio.santocchia@pg.infn.it Ø Web: http://www.fisica.unipg.it/~attilio.santocchia/
Il Corso di Fisica per Scienze Biologiche Ø Prof. Attilio Santocchia Ø Ufficio presso il Dipartimento di Fisica (Quinto Piano) Tel. 075-585 2708 Ø E-mail: attilio.santocchia@pg.infn.it Ø Web: http://www.fisica.unipg.it/~attilio.santocchia/
VETTORI. OPERAZIONI CON I VETTORI. RAPPRESENTAZIONE CARTESIANA DEI VETTORI. APPLICAZIONI.
 VETTORI. OPERAZIONI CON I VETTORI. RAPPRESENTAZIONE CARTESIANA DEI VETTORI. APPLICAZIONI. Sia AB un segmento orientato. Ad esso è possibile associare: 1) la direzione, cioè la direzione della retta su
VETTORI. OPERAZIONI CON I VETTORI. RAPPRESENTAZIONE CARTESIANA DEI VETTORI. APPLICAZIONI. Sia AB un segmento orientato. Ad esso è possibile associare: 1) la direzione, cioè la direzione della retta su
Università di Trieste Facoltà d Ingegneria. Esercizi sulle curve, le superfici, i campi vettoriali. Dott. Franco Obersnel
 Università di Trieste Facoltà d Ingegneria. Esercizi sulle curve, le superfici, i campi vettoriali. Dott. Franco Obersnel Esercizio 1 Sia f : [a, b] IR 2 una funzione di classe C 1 su [a, b]. consideri
Università di Trieste Facoltà d Ingegneria. Esercizi sulle curve, le superfici, i campi vettoriali. Dott. Franco Obersnel Esercizio 1 Sia f : [a, b] IR 2 una funzione di classe C 1 su [a, b]. consideri
ALCUNI RICHIAMI GENERALI
 ALCUNI RICHIAMI GENERALI 0.1 SUL CONCETTO DI VETTORE La direzione Data una linea retta, è possibile muoversi su questa in due versi opposti: si possono distinguere assegnando a ciascuno di essi un segno
ALCUNI RICHIAMI GENERALI 0.1 SUL CONCETTO DI VETTORE La direzione Data una linea retta, è possibile muoversi su questa in due versi opposti: si possono distinguere assegnando a ciascuno di essi un segno
1) ELETTROSTATICA NEL VUOTO riassunto Gauss
 1) ELETTROSTATICA NEL VUOTO riassunto Gauss - flusso di un vettore attraverso una superficie: ϕ(v) 6 = 8 v n9 ds 6 - teorema di Gauss: ϕ(e) 6 = 8 E n9 ds =??FG q? 6 ε =>?@AB I utile solo se per motivi
1) ELETTROSTATICA NEL VUOTO riassunto Gauss - flusso di un vettore attraverso una superficie: ϕ(v) 6 = 8 v n9 ds 6 - teorema di Gauss: ϕ(e) 6 = 8 E n9 ds =??FG q? 6 ε =>?@AB I utile solo se per motivi
Funzioni di più variabili a valori vettoriali n t m
 Funzioni di più variabili a valori vettoriali n t m Definizione f(x 1, x 2,...x n )=[f 1 (x 1, x 2,...x n ), f 2 (x 1, x 2,...x n ),...f m (x 1, x 2,...x n )] Funzione definita n d m Dove: n = dominio
Funzioni di più variabili a valori vettoriali n t m Definizione f(x 1, x 2,...x n )=[f 1 (x 1, x 2,...x n ), f 2 (x 1, x 2,...x n ),...f m (x 1, x 2,...x n )] Funzione definita n d m Dove: n = dominio
CINEMATICA DEL PUNTO MATERIALE
 CINEMATICA DEL PUNTO MATERIALE Regole di derivazione per il prodotto scalare e per il prodotto vettore Sia v funzione di un parametro reale t, t.c. 5 v : R R 3 t 7 v (t). (1) Proprietà: 1. Limite. Il concetto
CINEMATICA DEL PUNTO MATERIALE Regole di derivazione per il prodotto scalare e per il prodotto vettore Sia v funzione di un parametro reale t, t.c. 5 v : R R 3 t 7 v (t). (1) Proprietà: 1. Limite. Il concetto
Corso di Geometria Lezione II: Spazi vettoriali
 .. Corso di Geometria Lezione II: Spazi vettoriali F. Baldassarri 8 ottobre 2013 Definizione di spazio vettoriale Uno spazio vettoriale su un campo C (ad es. Q,R,C,{0, 1}) è un insieme V dotato di due
.. Corso di Geometria Lezione II: Spazi vettoriali F. Baldassarri 8 ottobre 2013 Definizione di spazio vettoriale Uno spazio vettoriale su un campo C (ad es. Q,R,C,{0, 1}) è un insieme V dotato di due
POLITECNICO DI MILANO. FACOLTÀ DI INGEGNERIA INDUSTRIALE. Analisi e Geometria 2. Giugno Docenti: F. Lastaria, M. Citterio, M.
 POLITECNICO I MILANO. FACOLTÀ I INGEGNERIA INUTRIALE. Analisi e Geometria 2. Giugno 2. ocenti: F. Lastaria, M. Citterio, M. aita Indice Integrali di superficie. Parte prima. Integrali di superficie. Parte
POLITECNICO I MILANO. FACOLTÀ I INGEGNERIA INUTRIALE. Analisi e Geometria 2. Giugno 2. ocenti: F. Lastaria, M. Citterio, M. aita Indice Integrali di superficie. Parte prima. Integrali di superficie. Parte
ELETTROMAGNETISMO APPLICATO ALL'INGEGNERIA ELETTRICA ED ENERGETICA_2b (ultima modifica 30/09/2015)
 ELETTROMGNETISMO PPLICTO LL'INGEGNERI ELETTRIC ED ENERGETIC_2b (ultima modifica 30/09/2015) M. Usai ELETTROMGNETISMO PPLICTO LL'INGEGNERI ELETTRIC ED ENERGETIC 27 L integrale S d s è un integrale superficiale
ELETTROMGNETISMO PPLICTO LL'INGEGNERI ELETTRIC ED ENERGETIC_2b (ultima modifica 30/09/2015) M. Usai ELETTROMGNETISMO PPLICTO LL'INGEGNERI ELETTRIC ED ENERGETIC 27 L integrale S d s è un integrale superficiale
TEOREMA DI GREEN ( ) D ; C è il contorno orientato del dominio D considerato
 Le formule f d dy = f (, y ) dy TEOEMA I GEEN [] f d dy = f (, y ) d [] note come formule di Green sono due relazioni semplici ma molto importanti fra gli integrali estesi ad un dominio piano e gli integrali
Le formule f d dy = f (, y ) dy TEOEMA I GEEN [] f d dy = f (, y ) d [] note come formule di Green sono due relazioni semplici ma molto importanti fra gli integrali estesi ad un dominio piano e gli integrali
Dipolo Elettrico: due cariche (puntiformi) +q e q (stesso modulo, segno opposto) a distanza a. Momento di Dipolo, P: Vettore di modulo
 Il Dipolo Elettrico Dipolo Elettrico: due cariche (puntiformi) q e q (stesso modulo, segno opposto) a distanza a. Momento di Dipolo, P: Vettore di modulo qa che va da qq a q Dato un punto P molto distante
Il Dipolo Elettrico Dipolo Elettrico: due cariche (puntiformi) q e q (stesso modulo, segno opposto) a distanza a. Momento di Dipolo, P: Vettore di modulo qa che va da qq a q Dato un punto P molto distante
Due vettori si dicono opposti se hanno stessa direzione, stesso modulo ma direzione opposte, e si indica con.
 Vettori. Il vettore è un ente geometrico rappresentato da un segmento orientato, che è caratterizzato da una direzione, da un verso e da un modulo. Il punto di partenza si chiama coda (o punto di applicazione),
Vettori. Il vettore è un ente geometrico rappresentato da un segmento orientato, che è caratterizzato da una direzione, da un verso e da un modulo. Il punto di partenza si chiama coda (o punto di applicazione),
Integrali multipli - Esercizi svolti
 Integrali multipli - Esercizi svolti Integrali di superficie. Si calcoli l integrale di superficie Σ z +y +4(x +y ) dσ, dove Σ è la parte di superficie di equazione z = x y che si proietta in = {(x,y)
Integrali multipli - Esercizi svolti Integrali di superficie. Si calcoli l integrale di superficie Σ z +y +4(x +y ) dσ, dove Σ è la parte di superficie di equazione z = x y che si proietta in = {(x,y)
Esercitazioni di Fisica. venerdì 10:00-11:00 aula T4. Valeria Malvezzi
 Esercitazioni di Fisica venerdì 10:00-11:00 aula T4 Valeria Malvezzi E-mail: valeria.malvezzi@roma2.infn.it Richiami di trigonometria Definizioni goniometriche )α Relazione goniometrica fondamentale I
Esercitazioni di Fisica venerdì 10:00-11:00 aula T4 Valeria Malvezzi E-mail: valeria.malvezzi@roma2.infn.it Richiami di trigonometria Definizioni goniometriche )α Relazione goniometrica fondamentale I
, 3x y = a 2 = b 2 + c 2 2bc cos α.
 Esercizi. Soluzioni. (.A ) Siano x = e y =. 2 (i) Calcolare e disegnare i vettori x, 2x, x, 0x. (ii) Calcolare e disegnare i vettori x + y, x y, y e x y. (iii) Calcolare x, y, x + y e x y. Sol. 2 0 (i)
Esercizi. Soluzioni. (.A ) Siano x = e y =. 2 (i) Calcolare e disegnare i vettori x, 2x, x, 0x. (ii) Calcolare e disegnare i vettori x + y, x y, y e x y. (iii) Calcolare x, y, x + y e x y. Sol. 2 0 (i)
Corso di Fisica. Lezione 2 Scalari e vettori Parte 1
 Corso di Fisica Lezione 2 Scalari e vettori Parte 1 Scalari e vettori Consideriamo una libreria. Per determinare quanti libri ci sono su uno scaffale basta individuare lo scaffale in questione e contare
Corso di Fisica Lezione 2 Scalari e vettori Parte 1 Scalari e vettori Consideriamo una libreria. Per determinare quanti libri ci sono su uno scaffale basta individuare lo scaffale in questione e contare
Funzioni vettoriali di variabile scalare
 Capitolo 11 Funzioni vettoriali di variabile scalare 11.1 Curve in R n Abbiamo visto (capitolo 2) come la posizione di un punto in uno spazio R n sia individuata mediante le n coordinate di quel punto.
Capitolo 11 Funzioni vettoriali di variabile scalare 11.1 Curve in R n Abbiamo visto (capitolo 2) come la posizione di un punto in uno spazio R n sia individuata mediante le n coordinate di quel punto.
Terzo esonero. 21 marzo Esercizio
 Terzo esonero 2 marzo 27. Esercizio Disegnare l insieme D : x, y) : x y 2 x, 2x 2 y 2x} e calcolarne l area. Determinare una trasformazione lineare che mandi D in un rettangolo. Calcolare l integale doppio
Terzo esonero 2 marzo 27. Esercizio Disegnare l insieme D : x, y) : x y 2 x, 2x 2 y 2x} e calcolarne l area. Determinare una trasformazione lineare che mandi D in un rettangolo. Calcolare l integale doppio
Prodotto scalare. numero pari al modulo del vettore b a. la grandezza. si definisce prodotto scalare di due vettori
 Moltiplicaione tra vettori Prodotto scalare si definisce prodotto scalare di due vettori θ e ab = abcosϑ= abcosϑ la grandea l operaione prodotto scalare tra due vettori produce un numero pari al modulo
Moltiplicaione tra vettori Prodotto scalare si definisce prodotto scalare di due vettori θ e ab = abcosϑ= abcosϑ la grandea l operaione prodotto scalare tra due vettori produce un numero pari al modulo
Lezioni L3.a. 5. Teorema dei Campi Conservativi; 7. Teorema di Stokes; 9. Rot E=0. FISICA GENERALE II, Cassino A.A
 Lezioni L3.a 1. Flusso attraverso una superficie;. Scalari, Pseudoscalari, Vettori e Pseudovettori; 3. Campi Scalari e Campi Vettoriali ed operatori; 4. Gradiente, Divergenza, Rotore, Laplaciano; 5. Teorema
Lezioni L3.a 1. Flusso attraverso una superficie;. Scalari, Pseudoscalari, Vettori e Pseudovettori; 3. Campi Scalari e Campi Vettoriali ed operatori; 4. Gradiente, Divergenza, Rotore, Laplaciano; 5. Teorema
Analisi Matematica 2. Superfici e integrali superficiali. Superfici e integrali superficiali 1 / 27
 Analisi Matematica 2 Superfici e integrali superficiali Superfici e integrali superficiali 1 / 27 Superficie Sia D un dominio connesso di R 2 (per def. un dominio connesso é la chiusura di un aperto connesso).
Analisi Matematica 2 Superfici e integrali superficiali Superfici e integrali superficiali 1 / 27 Superficie Sia D un dominio connesso di R 2 (per def. un dominio connesso é la chiusura di un aperto connesso).
Bivettori. Determinanti. Prodotto vettoriale.
 Bivettori. Determinanti. Prodotto vettoriale. 10 Dicembre 2018 Per approfondimenti: bibliografia e siti web sull algebra geometrica (Geometric Algebra): http://geometry.mrao.cam.ac.uk/ https://assets.cambridge.org/052148/0221/sample/0521480221ws.pdf
Bivettori. Determinanti. Prodotto vettoriale. 10 Dicembre 2018 Per approfondimenti: bibliografia e siti web sull algebra geometrica (Geometric Algebra): http://geometry.mrao.cam.ac.uk/ https://assets.cambridge.org/052148/0221/sample/0521480221ws.pdf
Onde elettromagnetiche e gravitazionali, equazioni di Maxwell e significato fisico di rotore e divergenza I S. J ds. dj y. div J dv S.
 estratto da : L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare Onde elettromagnetiche e gravitazionali, equazioni di Maxwell e significato fisico di rotore e divergenza Ricordiamo che,
estratto da : L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare Onde elettromagnetiche e gravitazionali, equazioni di Maxwell e significato fisico di rotore e divergenza Ricordiamo che,
Roberto Capone Esercizi di Analisi Matematica 2 Superfici e Integrali superficiali. Superfici
 uperfici i calcoli la matrice jacobiana delle seguenti funzioni: f(x, y) = e x+y i + cos (x + y)j f(x, y, z) = (x + y + 3z 3 )i + (x + sin3y + e z )j i calcoli la divergenza dei seguenti campi vettoriali
uperfici i calcoli la matrice jacobiana delle seguenti funzioni: f(x, y) = e x+y i + cos (x + y)j f(x, y, z) = (x + y + 3z 3 )i + (x + sin3y + e z )j i calcoli la divergenza dei seguenti campi vettoriali
DEFINIZIONE Un vettore (libero) è un ente geometrico rappresentato da un segmento orientato caratterizzato da tre parametri:
 DEFINIZIONE Un vettore (libero) è un ente geometrico rappresentato da un segmento orientato caratterizzato da tre parametri: 1. modulo: la lunghezza del segmento 2. direzione: coincidente con la direzione
DEFINIZIONE Un vettore (libero) è un ente geometrico rappresentato da un segmento orientato caratterizzato da tre parametri: 1. modulo: la lunghezza del segmento 2. direzione: coincidente con la direzione
6. Integrali curvilinei
 6. Integrali curvilinei Davide Catania davide.catania@unibs.it Esercitazioni di Analisi Matematica 2 A.A. 2016/17 Integrali curvilinei di campi scalari Integrali curvilinei di campi vettoriali Campi vettoriali
6. Integrali curvilinei Davide Catania davide.catania@unibs.it Esercitazioni di Analisi Matematica 2 A.A. 2016/17 Integrali curvilinei di campi scalari Integrali curvilinei di campi vettoriali Campi vettoriali
Capitolo 10. Appendice GlioperatoriGRAD,DIV,ROT Significato del Gradiente
 Capitolo 10 Appendice 1 10.1 GlioperatoriGRAD,DIV,ROT 10.1.1 ignificato del Gradiente iadatalafunzionef : D R 3 R, D insieme aperto, f C 2 (D). Tale funzione è anche detta campo scalare. celto un sistema
Capitolo 10 Appendice 1 10.1 GlioperatoriGRAD,DIV,ROT 10.1.1 ignificato del Gradiente iadatalafunzionef : D R 3 R, D insieme aperto, f C 2 (D). Tale funzione è anche detta campo scalare. celto un sistema
x 1 Fig.1 Il punto P = P =
 Geometria di R 2 In questo paragrafo discutiamo le proprietà geometriche elementari del piano Per avere a disposizione delle coordinate nel piano, fissiamo un punto, che chiamiamo l origine Scegliamo poi
Geometria di R 2 In questo paragrafo discutiamo le proprietà geometriche elementari del piano Per avere a disposizione delle coordinate nel piano, fissiamo un punto, che chiamiamo l origine Scegliamo poi
I VETTORI. Definizione Sistemi di riferimento Componenti e modulo Somma e differenza Prodotto scalare Prodotto vettoriale Versori. Vettori. pag.
 I VETTORI Definizione Sistemi di riferimento Componenti e modulo Somma e differenza Prodotto scalare Prodotto vettoriale Versori pag.1 Grandezze scalari e vettoriali Per una descrizione completa del fenomeno
I VETTORI Definizione Sistemi di riferimento Componenti e modulo Somma e differenza Prodotto scalare Prodotto vettoriale Versori pag.1 Grandezze scalari e vettoriali Per una descrizione completa del fenomeno
Elettromagnetismo. Campo elettrico come gradiente del potenziale. Lezione n Prof. Francesco Ragusa Università degli Studi di Milano
 Elettromagnetismo Prof. Francesco Ragusa Università degli Studi di Milano Lezione n. 4 12.10.2017 Campo elettrico come gradiente del potenziale Anno Accademico 2017/2018 Il campo elettrico come gradiente
Elettromagnetismo Prof. Francesco Ragusa Università degli Studi di Milano Lezione n. 4 12.10.2017 Campo elettrico come gradiente del potenziale Anno Accademico 2017/2018 Il campo elettrico come gradiente
Algebra dei vettori OPERAZIONI FRA VETTORI SOMMA DI VETTORI
 Algebra dei vettori Il vettore è un oggetto matematico che è caratterizzato da modulo, direzione e verso. Si indica graficamente con una freccia. Un vettore è individuato da una lettera minuscola con sopra
Algebra dei vettori Il vettore è un oggetto matematico che è caratterizzato da modulo, direzione e verso. Si indica graficamente con una freccia. Un vettore è individuato da una lettera minuscola con sopra
RICHIAMI DI ELETTROMAGNETISMO
 RICHIAMI DI ELETTROMAGNETISMO Equazioni di Maxwell I fenomeni elettrici e magnetici a livello del mondo macroscopico sono descritti da due campi vettoriali, in generale dipendenti dal tempo, E(x, t), H(x,
RICHIAMI DI ELETTROMAGNETISMO Equazioni di Maxwell I fenomeni elettrici e magnetici a livello del mondo macroscopico sono descritti da due campi vettoriali, in generale dipendenti dal tempo, E(x, t), H(x,
