FUNZIONI DI DUE VARIABILI REALI. f(x, y) = ax + by + c. f(x, y) = x 2 + y 2
|
|
|
- Agnolo Garofalo
- 5 anni fa
- Visualizzazioni
Transcript
1 0.1 FUNZIONI DI DUE VARIABILI REALI Sia A R 2. Una applicazione f : A R si chiama funzione reale di due variabili reali ESEMPI: 1. La funzione affine di due variabili reali: 2. f(x, y) = ax + by + c f(x, y) = x 2 + y Come per le funzioni di una sola variabile reale, una funzione di due variabili reali é definita su un dominio di definizione Esempio. Le funzioni precedenti sono definite per qualsiasi valore di x e di y e quindi per qualsiasi coppia (x, y) La funzione f(x, y) = (x 1)(y 1) non é definita per x = 1 e neppure per y = 1, mentre é definita per ogni coppia (x, y) tale che x 1 e y Data una funzione di due variabili f(x, y) definita in un insieme A R 2, possiamo definire due funzioni parziali ottenute considerando fissando un valore della x = x 0 oppure un valore della y = y 0, ovvero: f(x, y 0 ) e f(x 0, y) Ovviamente, per ogni scelta del valore y 0 otteniamo una funzione della sola variabile y e per ogni scelta del valore x 0 otteniamo una funzione della sola variabile y. 0.4 Esempio: f(x, y) = 4x + 3y + 2 Se fissiamo y = 1 otteniamo la funzione della sola variabile x: f(x, 1) = 4x Se fissiamo x = 2 otteniamo la funzione della sola variabile y: f(2, y) = y + 2 1
2 0.5 Piú in generale, se indichiamo con y 0 un qualsiasi valore prescelto per y, otteniamo la funzione della sola variabile x: f(x, y 0 ) = 4x + 3y Se indichiamo con x 0 un qualsiasi valore prescelto per x, otteniamo la funzione della sola variabile y: f(x 0, y) = 4x 0 + 3y Una funzione di due variabili f(x, y) associa ad ogni coppia di numeri reali (x, y) il valore z = f(x, y). Esempio. 1 f(x, y) = (x 1)(y 1) 1 f(2, 3) = (2 1)(3 1) = = 1 2 Analogamente alle funzioni di una variabile reale, il grafico di una funzione di due variabile reale sará costituito dai punti (x, y, z) dello spazio tridimensionale tali che z = f(x, y). 0.7 Esempio. Il punto (x, y, z) = (2, 3, 1 2 ) appartiene al grafico della funzione 1 (x 1)(y 1) perché (2 1)(3 1) = = 1 2 Curve di livello. Data una funzione f(x, y) e un valore z possiamo chiederci quali sono le coppie di valori (x, y) tali che f(x, y) = z. L insieme delle (x, y) che verificano f(x, y) = z costituisce una curva di livello. 0.9 Funzione di produzione. F (K, L) = 12 K 1 4 L 3 4 Se si impiegano 2 unitá di capitale e 3 unitá di lavoro si ottengono 12 ( ) unitá di prodotto. 2
3 Se desideriamo produrre 100 unitá di prodotto, quali combinazioni di capitale e lavoro danno il risultato cercato? L insieme delle coppie (K, L) tali che F (K, L) = 100 é una curva di livello della funzione F, che prende il nome di isoquanto Funzione di utilitá. U(x, y) = x 1 2 y 1 2 Se si consumano 1 unitá del bene x e 1 unitá del bene y si ottiene un livello di utilitá pari a Se desideriamo raggiungere un livello di soddisfazione pari a 10, quali combinazioni di consumo danno il risultato cercato? L insieme delle coppie (x, y) tali che U(x, y) = 10 é una curva di livello della funzione U, che prende il nome di isoutilitá o curva di indifferenza Distanza nel piano. La distanza di due punti P e Q di coordinate rispettivamente (x p, y p ) e (x q, y q ) é data da d(p, Q) = (x q x p ) 2 + (y q y p ) Sulla retta, l intorno di semi-ampiezza δ di un punto x 0 é definito come l insieme dei punti che distano da x 0 meno di δ. La stessa definizione si puó applicare nel piano, ottenendo degli intorni circolari di raggio δ, indicato con I δ (x 0, y 0 ) Consideriamo un insieme A R 2. Un punto (x 0, y 0 ) A si dice - interno ad A se esiste un intorno I δ (x 0, y 0 ) tutto contenuto in A - esterno ad A se esiste un intorno I δ (x 0, y 0 ) non contenente nessun punto di A - di frontiera se qualsiasi intorno I δ (x 0, y 0 ) contiene sia punti di A che punti che non appartengono ad A. Un insieme costituito di soli punti interni si definisce aperto. 3
4 0.14 Limite di funzioni di due variabili. Prendiamo una funzione f(x, y) definita in A R 2. Consideriamo un punto (x 0, y 0 ) di accumulazione per l insieme A. Si dice che f(x, y) tende al limite l R per (x, y) che tende a (x 0, y 0 ) e si scrive lim f(x, y) = l (x,y) (x 0,y 0) se, per ogni ɛ > 0 é possibile trovare un intorno I δ (x 0, y 0 ) di centro (x 0, y 0 ) e semi-ampiezza δ tale che per ogni punto (x, y) A I δ (x 0, y 0 ) si abbia f(x, y) l < ɛ 0.15 Attenzione Se la funzione f(x, y) ammette un limite per (x, y) che tende (x 0, y 0 ) allora le funzioni parziali f(x, y 0 ) e f(x 0, y) convergono allo stesso limite, ma se le due fuzioni parziali convergono ad uno stesso limite non é detto che la funzione f(x, y) ammette limite Data una funzione f(x, y), le sue derivate parziali nel punto (x 0, y 0 ) sono definite come le derivate delle funzioni parziali f(x, y 0 ) e f(x 0, y). Le derivate parziali si indicano con f x oppure f x, f y f y Esempio: f(x, y) = ln x+2y x 3y f x (x, y) = x 3y x+2y x 3y (x+2y) (x 3y) 2 = 5y (x+2y)(x 3y) f y (x, y) = x 3y x+2y 2(x 3y)+3(x+2y) (x 3y) 2 = 5x (x+2y)(x 3y) Il vettore costituito dalle due derivate parziali prime si chiama gradiente e si indica con f(x, y) 0.17 f(x, y) = (x 2 + xy 2 ) f x = 2x + y 2 f y = 2xy 4
5 0.18 f(x, y) = x ln y f x = ln y f y = x y 0.19 f(x, y) = 3x 2 y 5xy 3 + 2x 3y f x = 6xy 5y f y = 3x 2 15xy f(x, y) = x 2 + 4xy + y 2 f x(x, y) = 2x + 4y f y(x, y) = 4x + 2y 0.21 f(x, y) = e x f x(x, y) = e x f y(x, y) = f(x, y) = e x ln y f x(x, y) = e x f x(x, y) = 1 y 0.23 f(x, y) = e x ln(x y) f x(x, y) = e x ln(x y) + e x 1 x f y(x, y) = e x 1 y 0.24 Le derivate delle funzioni parziali si chiamano derivate prime. Il vettore formato dalle due derivate parziali f x(x, y), f y(x, y) si chiama gradiente della funzione o derivata prima e si indica con f(x, y) Esempio. x 2 + y 2 = (2x, 2y) 5
6 0.25 La funzione di due variabili di primo grado é la funzione affine f(x, y) = ax + by + c Analogamente a quanto visto per le funzioni di una variabile con la retta, cosí per le funzioni di due variabili ci interessiamo a quelle funzioni che sono bene approssimabili da una funzione di primo grado. Se una funzione f(x, y) e approssimabile in un punto (x 0, y 0 ) da una funzione di primo grado, diciamo che essa é differenziabile in quel punto e la funzione di primo grado prende nome di piano tangente Attenzione! L esistenza delle due derivate parziali prime é condizione solamente necessaria per la differenziabilitá. Una condizione sufficiente é che le derivate parziali prime siano continue. Nel caso in cui la funzione sia differenziabile, l espressione del piano tangente é Il termine f(x 0, y 0 ) + f x (x 0, y 0 )(x x 0 ) + f y (x 0, y 0 )(y y 0 ) 0.27 f x (x 0, y 0 )(x x 0 ) + f y (x 0, y 0 )(y y 0 ) si indica con df e prende il nome di differenziale totale della funzione Esempio 1. Calcolare il differenziale totale df della funzione f(x, y) = x 2 + y 2 nel punto (x 0, y 0 ) = (2, 3). df = 2x 0 (x x 0 ) + 2y 0 (y y 0 ) = 2 2(x 2) + 2 3(y 3) Esempio 2. Calcolare il differenziale totale df della funzione f(x, y) = x 2 + xy y 2 nel punto (x 0, y 0 ) = (2, 1). df = (2x 0 + y 0 ) (x x 0 ) + (x 0 2y 0 ) (y y 0 ) = ( )(x 2) + (2 2 1) (y 3) 0.28 Esempio 3. Calcolare il differenziale totale df della funzione f(x, y) = x 2 + y 2 punto (x 0, y 0 ) = ( 2, 1). df = x0 (x x 0 ) + y0 (y y 0 ) = x 2 0 +y 2 0 x 2 0 +y 2 0 nel 6
7 2 (x ( 2)) + 1 (y 1) = ( 2)2 +(1) 2 ( 2)2 +(1) (x + 2) (y 1) 0.29 I punti del dominio della funzione in cui le due derivate prime si annullano f x = f y = 0 si chiamano punti stazionari della funzione. Esempio 1: Trovare i punti stazionari della funzione f(x, y) = x 2 + y 2 Soluzione: f x (x, y) = 2x, f y (x, y) = 2y Basta { risolvere il sistema: 2x = 0 2y = 0 quindi l unico punto stazionario é l origine (0, 0) 0.30 Esempio 2: Trovare i punti stazionari della funzione f(x, y) = x 2 + xy + y 2 x Soluzione: f x (x, y) = 2x + y 1, f y (x, y) = 2y + x Basta risolvere il sistema: 2x + y 1 = 0 2y + x = 0 l unico punto stazionario é ( 2 3, 1 3 ) 0.31 Poiché le derivate parziali prime sono delle funzioni di due variabili reali, possiamo definire le loro derivate parziali e cosí via. Quante sono le derivate parziali seconde? Le derivate parziali prime sono due f x e f y A partire da ciascuna di queste si possono definire le due derivate parziali seconde. In totale quindi avremo quattro derivate parziali seconde: f xx, f xy, f yx, f yy 0.32 Esempio 1. f(x, y) = x 2 + y 2 f x = 2x f y = 2y 7
8 0.33 xx = 2 xy = 0 yx = 0 yy = 2 Esempio 2. f(x, y) = 2xy + y 2 f x y = f y = xx = xy = yx = yy = xy+y 2 x+y 2xy+y 2 y 2 2xy+y 2 xy (2xy+y 2 ) 3 2 xy (2xy+y 2 ) 3 2 2xy+y 2 (x+y) 2 (2xy+y 2 ) Domanda: f xy = f yx? Risposta, in generale NO, ma se le due derivate parziali seconde sono continue, allora sono uguali Le derivate parziali seconde di una funzione di due variabili formano la cosidetta matrice hessiana: ( fxx f xy f yx f yy ) che risulta una matrice simmetrica se le derivate parziali miste sono continue. Il determinante della matrice hessiana f xx f yy 2f xy si chiama semplicemente hessiano della funzione f e si indica con H(x, y) Esempio. f(x, y) = x 3 4x y 2y 2 f x = 3x 2 4y f y = 4x 4y 8
9 xx = 6x xy = 4 yy = 4 H(x, y) = 24x Estremi di funzioni di due variabili. Definizione. Un punto (x 0, y 0 ) é un punto di massimo locale per la funzione f(x, y) se esiste un intorno I δ (x 0, y 0 ) tale che f(x, y) < f(x 0, y 0 ) per ogni (x, y) I δ (x 0, y 0 ) \ {(x 0, y 0 )}. Un punto (x 0, y 0 ) é un punto di minimo locale per la funzione f(x, y) se esiste un intorno I δ (x 0, y 0 ) tale che f(x, y) > f(x 0, y 0 ) per ogni (x, y) I δ (x 0, y 0 ) \ {(x 0, y 0 )} Teorema. Sia f(x, y) una funzione di due variabili definita su un insieme A R 2. Se (x 0, y 0 ) é un punto interno ad A, se f(x 0, y 0 ) esiste se (x 0, y 0 ) é un estremo della funzione f ALLORA f(x 0, y 0 ) = (0, 0) 0.39 Attenzione! Il contrario non é vero. I punti stazionari non sono tutti punti di massimo o di minimo! In particolare pu capitare che il punto (x 0, y 0 ) sia un punto di massimo se ci si avvicina secondo una certa direzione e sia invece un punto di minimo se ci si avvicina secondo un altra direzione. In questo caso si parla di punto di sella. Esempio: f(x, y) = x 2 y 2 L unico punto stazionario é (0, 0). Tuttavia se consideriamo la funzione parziale f(x, 0) = x 2 il punto (0, 0) é un punto di minimo, se invece consideriamo la funzione parziale f(0, y) = y 2 il punto (0, 0) é un punto di massimo Come determinare se un punto stazionario é un punto di massimo, di minimo o di sella? Consideriamo le tre derivate parziali seconde f xx, f yy e f xy. 9
10 Consideriamo l espressione H(x, y) = f xx f yy f 2 xy Se H(x, y) > 0 e f xx < 0 allora si ha un massimo locale Se H(x, y) > 0 e f xx > 0 allora si ha un minimo locale Se H(x, y) < 0 si ha un punto di sella. Se H(x, y) = 0 allora questo metodo non permette di arrivare a delle conclusioni Consideriamo una curva di livello di una funzione di due variabili reali F (x, y) = k. Per definizione, la curva di livello é l insieme dei punti del piano di coordinate (x, y) tali che F (x, y) abbia un valore costante k, ovvero: F (x, y) k = 0 Un insieme di punti del piano puó essere descritto da una curva nel piano. Come facciamo a esprimere la y in funzione della x ovvero a trovare l equazione y = φ(x) della curva nel piano? 0.42 Esempio. Consideriamo due beni e indichiamo con x la quantitá del primo bene e con y la quantitá del secondo bene. Indichiamo con p x e p y i rispettivi prezzi unitari. La funzione che associa il costo ad ogni paniere di consumo (x, y) é data da: 0.43 F (x, y) = p x x + p y y La curva di livello di questa funzione é data dalle equazioni del tipo F (x, y) = p x x + p y y = k Ad esempio: p x x + p y y = 1000 Cosa indicano le coppie x e y che risolvono questa equazione? Le soluzioni della precedente equazione indicano le combinazioni di consumo che costano esattamente
11 0.44 Cosa indica la funzione che esprime il valore di y che corrisponde ad ogni valore di x tra le soluzioni della precedente equazione? y = φ(x) Indica la quantitá che possiamo acquistare del bene y quando acquistiamo una quantitá x del primo bene, mantenendo costante la spesa al livello Come fare a trovare questa equazione in forma esplicita? In questo caso é semplice: 0.46 y = 1000 p y p x p y x In altri casi é piú difficile, se non a volte impossibile. Esempio: x 2 + y 2 1 = 0 In generale, questa equazione non puó essere esplicitata, puó esserlo localmente, ovvero nell intorno di un punto (x 0, y 0 ) che risolve l equazione. Un teorema permette di calcolare la derivata della y in funzione della x senza passare per la esplicitazione della funzione Teorema della funzione implicita Data una funzione in forma implicita F (x, y) = 0, se esiste un punto (x 0, y 0 ) che risolve l equazione, ovvero se se in tale punto si ha F (x 0, y 0 ) = 0 F y(x 0, y 0 ) 0 allora é possibile esplicitare localmente la funzione ottenendo una funzione y = φ(x) e si ha 11
12 y (x) = F x F y 0.48 Estremi vincolati. Supponiamo di voler cercare il massimo (o il minimo) di una funzione non su tutto il suo insieme di definizione, ma su un sottoinsieme definito da una equazione, ovvero sul sottoinsieme dell insieme di definzione individuato dai punti (x, y) tale che φ(x, y) = 0 Esempio: min f(x, y) = x 2 + y 2 sotto il vincolo φ(x, y) = x + y 1 = In questo caso, si puó risolvere il problema esplicitando il vincolo, ovvero scrivendo: y = 1 x e sostituendo nella funzione obiettivo f(x, y(x)) = x 2 + (1 x) 2 = 2x 2 2x + 1 Riportando il problema della massimizzazione vincolata di una funzione di due variabili alla massimizzazione libera di una funzione di una variabile Cosa fare quando non é possibile esplicitare il vincolo? Metodo dei moltiplicatori di Lagrange Si voglia massimizzare/minimizzare la funzione sotto il vincolo f(x, y) φ(x, y) = 0 1. Consideriamo la funzione lagrangiana L(x, y, λ) = f(x, y) + λφ(x, y) 12
13 Cerchiamo i punti stazionari della funzione lagrangiana, ovvero scriviamo e risolviamo il sistema: L x(x, y, λ) = 0 L y(x, y, λ) = 0 φ(x, y) = 0 ovvero f x(x, y) + λφ x(x, y) = 0 f y(x, y) + λφ y(x, y) = 0 φ(x, y) = 0 Le soluzioni (x 0, y 0, λ 0 ) di questo sistema rappresentano dei possibili estremanti per la funzione f condizionata al vincolo φ Si ha inoltre Se f e φ sono dotate di derivate seconde continue, per decidere se i punti stazionari della funzione lagrangiana corrispondono a un massimo o un minimo della f(x, y) sulla curva φ(x, y) = 0 si puó studiare il segno del determinante hessiano orlato 0 φ x(x 0, y 0 ) φ y(x 0, y 0 ) H(x 0, y 0 ) = φ x(x 0, y 0 ) L xx (x 0, y 0 ) L xy (x 0, y 0 ) φ y(x 0, y 0 ) L yx (x 0, y 0 ) L yy (x 0, y 0 ) 0.53 Esempio. Cerchiamo gli estremi della funzione f(x, y) = x 2 +y 2 sotto il vincolo x+y = Scriviamo la funzione lagrangiana: L(x, y, λ) = x 2 + y 2 + λ(x + y 1) 2. Scriviamo il sistema L x(x, y, λ) = 0 L y(x, y, λ) = 0 φ(x, y) = 0 ovvero 2x + λ = 0 2y + λ = 0 x + y 1 = 0 che risolviamo ottenendo la soluzione (x, y) = ( 1 2, 1 2 ). 13
14 0.54 Per verificare se l estremante ottenuto corrisponde a un minimo o a un massimo, calcoliamo il determinante hessiano orlato nel punto (x, y) = ( 1 2, 1 2 ): 0 φ x(x 0, y 0 ) φ y(x 0, y 0 ) H(x 0, y 0 ) = φ x(x 0, y 0 ) L xx (x 0, y 0 ) L xy (x 0, y 0 ) φ y(x 0, y 0 ) L yx (x 0, y 0 ) L yy (x 0, y 0 ) φ. ovvero H( 1 2, ) = ovvero H( 1 2, 1 2 ) = 4 e quindi il punto (x, y) = ( 1 2, 1 2 ) é un minimo della f condizionata al vincolo 14
Esercitazione n 6. Esercizio 1: Determinare i punti di massimo e minimo relativo delle seguenti funzioni: (b)f(x, y) = 4y 4 16x 2 y + x
 Esercitazione n 6 1 Massimi e minimi di funzioni di più variabili Esercizio 1: Determinare i punti di massimo e minimo relativo delle seguenti funzioni: (a)f(x, y) = x 3 + y 3 + xy (b)f(x, y) = 4y 4 16x
Esercitazione n 6 1 Massimi e minimi di funzioni di più variabili Esercizio 1: Determinare i punti di massimo e minimo relativo delle seguenti funzioni: (a)f(x, y) = x 3 + y 3 + xy (b)f(x, y) = 4y 4 16x
Modulo 5 Funzioni di piú variabili. A. Scanu
 Modulo 5 Funzioni di piú variabili A. Scanu 1 1 Generalitá In questo modulo studieremo funzioni di piú di una variabile cioé del tipo f : R n R m con n, m 1. In particolare prenderemo in considerazione
Modulo 5 Funzioni di piú variabili A. Scanu 1 1 Generalitá In questo modulo studieremo funzioni di piú di una variabile cioé del tipo f : R n R m con n, m 1. In particolare prenderemo in considerazione
Estremi. 5. Determinare le dimensioni di una scatola rettangolare di volume v assegnato, che abbia la superficie minima.
 Estremi 1. Determinare gli estremi relativi di f(x, y) = e x (x 1)(y 1) + (y 1).. Determinare gli estremi relativi di f(x, y) = y (y + 1) cos x. 3. Determinare gli estremi relativi di f(x, y) = xye x +y..
Estremi 1. Determinare gli estremi relativi di f(x, y) = e x (x 1)(y 1) + (y 1).. Determinare gli estremi relativi di f(x, y) = y (y + 1) cos x. 3. Determinare gli estremi relativi di f(x, y) = xye x +y..
Analisi 4 - SOLUZIONI (compito del 29/09/2011)
 Corso di laurea in Matematica Analisi 4 - SOLUZIONI compito del 9/09/0 Docente: Claudia Anedda Calcolare, tramite uno sviluppo in serie noto, la radice quinta di e la radice cubica di 9 Utilizzando la
Corso di laurea in Matematica Analisi 4 - SOLUZIONI compito del 9/09/0 Docente: Claudia Anedda Calcolare, tramite uno sviluppo in serie noto, la radice quinta di e la radice cubica di 9 Utilizzando la
I teoremi della funzione inversa e della funzione implicita
 I teoremi della funzione inversa e della funzione implicita Appunti per il corso di Analisi Matematica 4 G. Mauceri Indice 1 Il teorema della funzione inversa 1 Il teorema della funzione implicita 3 1
I teoremi della funzione inversa e della funzione implicita Appunti per il corso di Analisi Matematica 4 G. Mauceri Indice 1 Il teorema della funzione inversa 1 Il teorema della funzione implicita 3 1
g(x, y) = b y = h 1 (x), x I 1 oppure x = h 2 (y), y I 2 riconducendosi alla ricerca degli estremanti di una funzione in una sola variabile:
 Estremi vincolati Un problema di ottimizzazione vincolata consiste nella ricerca degli estremanti di una funzione in presenza di un vincolo, cioè limitatamente ad un certo sottoinsieme del dominio di f:
Estremi vincolati Un problema di ottimizzazione vincolata consiste nella ricerca degli estremanti di una funzione in presenza di un vincolo, cioè limitatamente ad un certo sottoinsieme del dominio di f:
Massimi e minimi vincolati
 Massimi e minimi vincolati Sia f una funzione differenziabile, definita su un aperto A di R N. Se K è un sottoinsieme chiuso e limitato di A, per il teorema di Weierstrass f assume massimo e minimo su
Massimi e minimi vincolati Sia f una funzione differenziabile, definita su un aperto A di R N. Se K è un sottoinsieme chiuso e limitato di A, per il teorema di Weierstrass f assume massimo e minimo su
Corso di Laurea in Informatica/Informatica Multimediale Esercizi Analisi Matematica 2
 a.a 2005/06 Corso di Laurea in Informatica/Informatica Multimediale Esercizi Analisi Matematica 2 Funzioni di due variabili a cura di Roberto Pagliarini Vediamo prima di tutto degli esercizi sugli insiemi
a.a 2005/06 Corso di Laurea in Informatica/Informatica Multimediale Esercizi Analisi Matematica 2 Funzioni di due variabili a cura di Roberto Pagliarini Vediamo prima di tutto degli esercizi sugli insiemi
Esercizi su Funzioni di più variabili. - Parte II. Derivate parziali, derivate direzionali, piano tangente
 Esercizi su Funzioni di più variabili. - Parte II Derivate parziali, derivate direzionali, piano tangente 1. Data la funzione f(x, y, z) = e x2 y 3 sin(x + z) calcolarne il gradiente e la derivata direzionale
Esercizi su Funzioni di più variabili. - Parte II Derivate parziali, derivate direzionali, piano tangente 1. Data la funzione f(x, y, z) = e x2 y 3 sin(x + z) calcolarne il gradiente e la derivata direzionale
ESERCIZI MATEMATICA GENERALE - Canale III Prof. A. Fabretti 1 A.A. 2009/2010
 ESERCIZI MATEMATICA GENERALE - Canale III Prof. A. Fabretti 1 A.A. 2009/2010 Individuare il dominio e i punti stazionari delle seguenti funzioni a due variabili 1) f(x, y) = x 3 + 8y 3 3xy 2) f(x, y) =
ESERCIZI MATEMATICA GENERALE - Canale III Prof. A. Fabretti 1 A.A. 2009/2010 Individuare il dominio e i punti stazionari delle seguenti funzioni a due variabili 1) f(x, y) = x 3 + 8y 3 3xy 2) f(x, y) =
Le derivate parziali
 Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
Esercizi su estremi vincolati e assoluti
 Esercizi su estremi vincolati e assoluti Esercizio 1. di sul quadrato Determinare i punti di minimo e di massimo (e i relativi valori di minimo e massimo) assoluto f(x, y) = x cos(πy) Q = [0, 1] [0, 1].
Esercizi su estremi vincolati e assoluti Esercizio 1. di sul quadrato Determinare i punti di minimo e di massimo (e i relativi valori di minimo e massimo) assoluto f(x, y) = x cos(πy) Q = [0, 1] [0, 1].
Analisi Matematica II Corso di Ingegneria Gestionale Compito del xy + 2x + 2y + 2xy + 2x + 2y + sin
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del 9--8 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del 9--8 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica 2 (Corso di Laurea in Informatica)
 COGNOME NOME Matr. Firma dello studente A Tempo: 3 ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
COGNOME NOME Matr. Firma dello studente A Tempo: 3 ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
ESERCITAZIONE SUI PUNTI STAZIONARI DI FUNZIONI LIBERE E SULLE FUNZIONI OMOGENEE
 ESERCITAZIONE SUI PUNTI STAZIONARI DI FUNZIONI LIBERE E SULLE FUNZIONI OMOGENEE 1 Funzioni libere I punti stazionari di una funzione libera di più variabili si ottengono risolvendo il sistema di equazioni
ESERCITAZIONE SUI PUNTI STAZIONARI DI FUNZIONI LIBERE E SULLE FUNZIONI OMOGENEE 1 Funzioni libere I punti stazionari di una funzione libera di più variabili si ottengono risolvendo il sistema di equazioni
Alcune nozioni di calcolo differenziale
 Alcune nozioni di calcolo differenziale G. Mastroeni, M. Pappalardo 1 Limiti per funzioni di piu variabili Supporremo noti i principali concetti algebrici e topologici relativi alla struttura dello spazio
Alcune nozioni di calcolo differenziale G. Mastroeni, M. Pappalardo 1 Limiti per funzioni di piu variabili Supporremo noti i principali concetti algebrici e topologici relativi alla struttura dello spazio
,, con 2. S oppure se x
 Deinizioni preliminari Alcuni elementi sull ottimizzazione di unzioni in due variabili Si deinisce intorno di raggio centro in r un punto S con e si indica con I r R / S R il cerchio di raggio r e r con
Deinizioni preliminari Alcuni elementi sull ottimizzazione di unzioni in due variabili Si deinisce intorno di raggio centro in r un punto S con e si indica con I r R / S R il cerchio di raggio r e r con
ISTITUZIONI DI MATEMATICHE II
 ISTITUZIONI DI MATEMATIHE II SEONDO ESONERO Esercizio 1. Data la funzione f(x, y) = (x + y )(1 y) i) se ne studi il segno. ii) Si trovino i punti critici di f e se ne studi le natura. iii) Sia D = {(x,
ISTITUZIONI DI MATEMATIHE II SEONDO ESONERO Esercizio 1. Data la funzione f(x, y) = (x + y )(1 y) i) se ne studi il segno. ii) Si trovino i punti critici di f e se ne studi le natura. iii) Sia D = {(x,
Teorema delle Funzioni Implicite
 Teorema delle Funzioni Implicite Sia F una funzione di due variabili definita in un opportuno dominio D di R 2. Consideriamo l equazione F (x, y) = 0, questa avrà come soluzioni coppie di valori (x, y)
Teorema delle Funzioni Implicite Sia F una funzione di due variabili definita in un opportuno dominio D di R 2. Consideriamo l equazione F (x, y) = 0, questa avrà come soluzioni coppie di valori (x, y)
Università di Bari - Dipartimento di Economia - Prova scritta di Matematica per l Economia L-Z- 19 Dicembre Traccia A
 Università di Bari - Dipartimento di Economia - Prova scritta di Matematica per l Economia L-Z- 9 Dicembre 07 - Traccia A Cognome e nome................................ Numero di matricola............
Università di Bari - Dipartimento di Economia - Prova scritta di Matematica per l Economia L-Z- 9 Dicembre 07 - Traccia A Cognome e nome................................ Numero di matricola............
Matematica. Corso integrato di. per le scienze naturali ed applicate. Materiale integrativo.
 Corso integrato di Matematica per le scienze naturali ed applicate Materiale integrativo http://www.dimi.uniud.it/biomat/ Paolo Baiti 1 Lorenzo Freddi 1 1 Dipartimento di Matematica e Informatica, Università
Corso integrato di Matematica per le scienze naturali ed applicate Materiale integrativo http://www.dimi.uniud.it/biomat/ Paolo Baiti 1 Lorenzo Freddi 1 1 Dipartimento di Matematica e Informatica, Università
Analisi Matematica II Corso di Ingegneria Gestionale Compito del y 2
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del 15--18 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del 15--18 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Università di Trieste Facoltà d Ingegneria. Esercitazioni per la preparazione della prova scritta di Matematica 3 Dott.
 Università di Trieste Facoltà d Ingegneria Esercitazioni per la preparazione della prova scritta di Matematica Dott Franco Obersnel Lezione 8: estremi vincolati Esercizio 1 Scomporre il numero 411 nella
Università di Trieste Facoltà d Ingegneria Esercitazioni per la preparazione della prova scritta di Matematica Dott Franco Obersnel Lezione 8: estremi vincolati Esercizio 1 Scomporre il numero 411 nella
Analisi Matematica II Corso di Ingegneria Gestionale Compito A del f(x, y) = x 2 + 2y 2 x 3 y 3
 Analisi Matematica II Corso di Ingegneria Gestionale Compito A del 7-7-8 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito A del 7-7-8 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Soluzione. Il dominio E consiste nella parte di spazio contenuta nella sfera ma esterna al cono rappresentata in Figura 1. Infatti
 Esercizio 1 (G. Ziglio). (6 punti) Calcolare il volume della porzione di spazio E interna alla sfera di equazione x 2 + y 2 + z 2 = 1 ed esterna al cono di equazione z 2 = x 2 + y 2 E = (x, y, z) R x 2
Esercizio 1 (G. Ziglio). (6 punti) Calcolare il volume della porzione di spazio E interna alla sfera di equazione x 2 + y 2 + z 2 = 1 ed esterna al cono di equazione z 2 = x 2 + y 2 E = (x, y, z) R x 2
ANALISI B alcuni esercizi proposti
 ANALISI B alcuni esercizi proposti G.P. Leonardi Parte II 1 Limiti e continuità per funzioni di 2 variabili Esercizio 1.1 Calcolare xy log(1 + x ) lim (x,y) (0,0) 2x 2 + 5y 2 Esercizio 1.2 Studiare la
ANALISI B alcuni esercizi proposti G.P. Leonardi Parte II 1 Limiti e continuità per funzioni di 2 variabili Esercizio 1.1 Calcolare xy log(1 + x ) lim (x,y) (0,0) 2x 2 + 5y 2 Esercizio 1.2 Studiare la
ESERCIZI SU MASSIMI E MINIMI DI FUNZIONI IN PIÙ VARIABILI. m(x, y, z) = (2x 2 + y 2 )e x2 y 2, f(x, y) = (y x 2 )(y x2. f(x, y) = x 3 + (x y) 2,
 ESERCIZI SU MASSIMI E MINIMI DI FUNZIONI IN PIÙ VARIABILI VALENTINA CASARINO Esercizi per il corso di Analisi Matematica, (Ingegneria Gestionale, dell Innovazione del Prodotto, Meccanica e Meccatronica,
ESERCIZI SU MASSIMI E MINIMI DI FUNZIONI IN PIÙ VARIABILI VALENTINA CASARINO Esercizi per il corso di Analisi Matematica, (Ingegneria Gestionale, dell Innovazione del Prodotto, Meccanica e Meccatronica,
Esercizi geometria analitica nello spazio. Corso di Laurea in Informatica. Docente: Andrea Loi. Correzione
 Esercizi geometria analitica nello spazio Corso di Laurea in Informatica Docente: Andrea Loi Correzione 1. Denotiamo con P 1, P 13, P 3, P 1, P, P 3, P i simmetrici di un punto P rispetto ai piani coordinati
Esercizi geometria analitica nello spazio Corso di Laurea in Informatica Docente: Andrea Loi Correzione 1. Denotiamo con P 1, P 13, P 3, P 1, P, P 3, P i simmetrici di un punto P rispetto ai piani coordinati
LUISS Laurea specialistica in Economia e Finanza Anno Accademico 2010/2011
 LUISS Laurea specialistica in Economia e Finanza Anno Accademico 1/11 Corso di Metodi Matematici per la Finanza Prof. Fausto Gozzi, Dr. Davide Vergni Soluzioni esercizi 4,5,6 esame scritto del 13/9/11
LUISS Laurea specialistica in Economia e Finanza Anno Accademico 1/11 Corso di Metodi Matematici per la Finanza Prof. Fausto Gozzi, Dr. Davide Vergni Soluzioni esercizi 4,5,6 esame scritto del 13/9/11
Esercizi di ottimizzazione vincolata
 Esercizi di ottimizzazione vincolata A. Agnetis, P. Detti Esercizi svolti 1 Dato il seguente problema di ottimizzazione vincolata max x 1 + x 2 x 1 4x 2 3 x 1 + x 2 2 0 x 1 0 studiare l esistenza di punti
Esercizi di ottimizzazione vincolata A. Agnetis, P. Detti Esercizi svolti 1 Dato il seguente problema di ottimizzazione vincolata max x 1 + x 2 x 1 4x 2 3 x 1 + x 2 2 0 x 1 0 studiare l esistenza di punti
Analisi Matematica 2
 Analisi Matematica 2 Differenziabilità per funzioni di due variabili Differenziabilità per funzioni di due variabili CCS Ingegneria Meccanica e Ingegneria Chimica 1 / 26 Differenziabilitá Data la funzione
Analisi Matematica 2 Differenziabilità per funzioni di due variabili Differenziabilità per funzioni di due variabili CCS Ingegneria Meccanica e Ingegneria Chimica 1 / 26 Differenziabilitá Data la funzione
Massimi e minimi vincolati
 Massimi e minimi vincolati Vedremo tra breve un metodo per studiare il problema di trovare il minimo e il massimo di una funzione su di un sottoinsieme dello spazio ambiente che non sia un aperto. Abbiamo
Massimi e minimi vincolati Vedremo tra breve un metodo per studiare il problema di trovare il minimo e il massimo di una funzione su di un sottoinsieme dello spazio ambiente che non sia un aperto. Abbiamo
Massimi e minimi assoluti vincolati: esercizi svolti
 Massimi e minimi assoluti vincolati: esercizi svolti Gli esercizi contrassegnati con il simbolo * presentano un grado di difficoltà maggiore. Esercizio 1. Determinare i punti di massimo e minimo assoluti
Massimi e minimi assoluti vincolati: esercizi svolti Gli esercizi contrassegnati con il simbolo * presentano un grado di difficoltà maggiore. Esercizio 1. Determinare i punti di massimo e minimo assoluti
= 2x 2λx = 0 = 2y 2λy = 0
 ESERCIZI SULLA OTTIMIZZAZIONE VINCOLATA ESERCIZIO Determinare i punti di massimo e minimo di f x, y = x y soggetta al vincolo x + y = Il vincolo è chiuso e limitato (circonferenza di raggio ) e la funzione
ESERCIZI SULLA OTTIMIZZAZIONE VINCOLATA ESERCIZIO Determinare i punti di massimo e minimo di f x, y = x y soggetta al vincolo x + y = Il vincolo è chiuso e limitato (circonferenza di raggio ) e la funzione
Matematica. Corso integrato di. per le scienze naturali ed applicate. Materiale integrativo. Paolo Baiti 1 Lorenzo Freddi 1
 Corso integrato di Matematica per le scienze naturali ed applicate Materiale integrativo Paolo Baiti 1 Lorenzo Freddi 1 1 Dipartimento di Matematica e Informatica, Università di Udine, via delle Scienze
Corso integrato di Matematica per le scienze naturali ed applicate Materiale integrativo Paolo Baiti 1 Lorenzo Freddi 1 1 Dipartimento di Matematica e Informatica, Università di Udine, via delle Scienze
Funzioni implicite - Esercizi svolti
 Funzioni implicite - Esercizi svolti Esercizio. È data la funzione di due variabili F (x, y) = y(e y + x) log x. Verificare che esiste un intorno I in R del punto di ascissa x 0 = sul quale è definita
Funzioni implicite - Esercizi svolti Esercizio. È data la funzione di due variabili F (x, y) = y(e y + x) log x. Verificare che esiste un intorno I in R del punto di ascissa x 0 = sul quale è definita
Estremi vincolati, Teorema del Dini.
 Estremi vincolati, Teorema del Dini. 1. Da un cartone di 1m si deve ricavare una scatola rettangolare senza coperchio. Trovare il massimo volume possibile della scatola.. Trovare gli estremi assoluti di
Estremi vincolati, Teorema del Dini. 1. Da un cartone di 1m si deve ricavare una scatola rettangolare senza coperchio. Trovare il massimo volume possibile della scatola.. Trovare gli estremi assoluti di
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 2 Secondo compito in itinere 30 Giugno 2016
 Politecnico di Milano Ingegneria Industriale Analisi e Geometria Secondo compito in itinere Giugno 6 Cognome: Nome: Matricola: Es.: 9 punti Es.: 9 punti Es.: 6 punti Es.4: 9 punti Totale. Si consideri
Politecnico di Milano Ingegneria Industriale Analisi e Geometria Secondo compito in itinere Giugno 6 Cognome: Nome: Matricola: Es.: 9 punti Es.: 9 punti Es.: 6 punti Es.4: 9 punti Totale. Si consideri
Polinomio di Taylor del secondo ordine per funzioni di due variabili
 Esercitazioni del 15 aprile 2013 Polinomio di Taylor del secondo ordine per funzioni di due variabili Sia f : A R 2 R una funzione di classe C 2. Fissato un p unto (x 0, y 0 A consideriamo il seguente
Esercitazioni del 15 aprile 2013 Polinomio di Taylor del secondo ordine per funzioni di due variabili Sia f : A R 2 R una funzione di classe C 2. Fissato un p unto (x 0, y 0 A consideriamo il seguente
Soluzioni del compito di Istituzioni di Matematiche/Matematica per Chimica F45 e F5X (10/2/11)
 Soluzioni del compito di Istituzioni di Matematiche/Matematica per Chimica F5 e F5X (//). La funzione f(x) = x 3x x + (a) èdefinita purché l argomento della radice sia non negativo cioè perx 3x : quindi
Soluzioni del compito di Istituzioni di Matematiche/Matematica per Chimica F5 e F5X (//). La funzione f(x) = x 3x x + (a) èdefinita purché l argomento della radice sia non negativo cioè perx 3x : quindi
Analisi II, a.a Soluzioni 4
 Analisi II, a.a. 17-18 Soluzioni 4 1) Consideriamo le curve in forma parametrica in R φ : R R, φ(t) = (cos t, cos(t)), φ : R R, φ(t) = (1 + cos t, sen t) φ :], π/[ R, φ(t) = (sen t, cos t) φ : R R, φ(t)
Analisi II, a.a. 17-18 Soluzioni 4 1) Consideriamo le curve in forma parametrica in R φ : R R, φ(t) = (cos t, cos(t)), φ : R R, φ(t) = (1 + cos t, sen t) φ :], π/[ R, φ(t) = (sen t, cos t) φ : R R, φ(t)
ESERCIZIO SVOLTO N 1 ESERCIZIO SVOLTO N 2. Determinare e rappresentare graficamente il dominio della funzione
 ESERCIZIO SVOLTO N 1 Determinare e rappresentare graficamente il dominio della funzione f(x, y) = y 2 x 2 Trovare gli eventuali punti stazionari e gli estremi di f Il dominio della funzione è dato da dom
ESERCIZIO SVOLTO N 1 Determinare e rappresentare graficamente il dominio della funzione f(x, y) = y 2 x 2 Trovare gli eventuali punti stazionari e gli estremi di f Il dominio della funzione è dato da dom
Tutorato di AM220. Universitá degli Studi Roma Tre - Corso di Laurea in Matematica
 Universitá degli Studi Roma Tre - Corso di Laurea in atematica Tutorato di A220 1 arzo 2012 AA 2011-2012 - Docente: Prof Luigi Chierchia Tutori: Daniele Dimonte e Sara Lamboglia Tutorato 4 1 Esercizio
Universitá degli Studi Roma Tre - Corso di Laurea in atematica Tutorato di A220 1 arzo 2012 AA 2011-2012 - Docente: Prof Luigi Chierchia Tutori: Daniele Dimonte e Sara Lamboglia Tutorato 4 1 Esercizio
Allora esistono δ > 0 e σ > 0 tali che. f(x, y) = 0; (2) la funzione ϕ : ]x 0 δ, x 0 + δ [ R, y = ϕ(x), è derivabile e.
![Allora esistono δ > 0 e σ > 0 tali che. f(x, y) = 0; (2) la funzione ϕ : ]x 0 δ, x 0 + δ [ R, y = ϕ(x), è derivabile e. Allora esistono δ > 0 e σ > 0 tali che. f(x, y) = 0; (2) la funzione ϕ : ]x 0 δ, x 0 + δ [ R, y = ϕ(x), è derivabile e.](/thumbs/96/129204172.jpg) 16 42 Funzioni implicite Il seguente teorema fornisce una condizione sufficiente affinché, data un equazione della forma f(x, ) = 0, sia possibile determinare come funzione della x Teo 11 (Teorema della
16 42 Funzioni implicite Il seguente teorema fornisce una condizione sufficiente affinché, data un equazione della forma f(x, ) = 0, sia possibile determinare come funzione della x Teo 11 (Teorema della
Estremi vincolati, Teorema del Dini.
 Estremi vincolati, Teorema del Dini. 1. Da un cartone di 1m si deve ricavare una scatola rettangolare senza coperchio. Trovare il massimo volume possibile della scatola.. Trovare gli estremi assoluti di
Estremi vincolati, Teorema del Dini. 1. Da un cartone di 1m si deve ricavare una scatola rettangolare senza coperchio. Trovare il massimo volume possibile della scatola.. Trovare gli estremi assoluti di
Svolgimento. f y (x, y) = 8 y 2 x. 1 x 2 y = 0. y 2 x = 0. (si poteva anche ricavare la x dalla seconda equazione e sostituire nella prima)
 Università degli Studi della Basilicata Corsi di Laurea in Chimica / Scienze Geologiche Matematica II A. A. 2013-2014 (dott.ssa Vita Leonessa) Esercizi svolti: Ricerca di massimi e minimi di funzioni a
Università degli Studi della Basilicata Corsi di Laurea in Chimica / Scienze Geologiche Matematica II A. A. 2013-2014 (dott.ssa Vita Leonessa) Esercizi svolti: Ricerca di massimi e minimi di funzioni a
FUNZIONI DI DUE VARIABILI
 Una unzione di più variabili viene indicata come: : A B con A R Se n la unzione presenta due variabili indipendenti e viene normalmente scritta come: z La sua rappresentazione graica si realizza introducendo
Una unzione di più variabili viene indicata come: : A B con A R Se n la unzione presenta due variabili indipendenti e viene normalmente scritta come: z La sua rappresentazione graica si realizza introducendo
4.11 Massimi e minimi relativi per funzioni di più variabili
 5. Determinare, al variare del parametro a R, la natura delle seguenti forme quadratiche: (i) Φ(x, y, z) = x 2 + 2axy + y 2 + 2axz + z 2, (ii) Φ(x, y, z, t) = 2x 2 + ay 2 z 2 t 2 + 2xz + 4yt + 2azt. 4.11
5. Determinare, al variare del parametro a R, la natura delle seguenti forme quadratiche: (i) Φ(x, y, z) = x 2 + 2axy + y 2 + 2axz + z 2, (ii) Φ(x, y, z, t) = 2x 2 + ay 2 z 2 t 2 + 2xz + 4yt + 2azt. 4.11
Alcuni esercizi risolti da esami di anni passati
 Alcuni esercizi risolti da esami di anni passati Andrea Braides ( x. Calcolare, se esiste, il limite lim (x,y (, x + y log + y + x 3 y. x + y Dato che log( + s = s + o(s per s, abbiamo lim (x,y (, ( x
Alcuni esercizi risolti da esami di anni passati Andrea Braides ( x. Calcolare, se esiste, il limite lim (x,y (, x + y log + y + x 3 y. x + y Dato che log( + s = s + o(s per s, abbiamo lim (x,y (, ( x
Massimi e minimi relativi in R n
 Massimi e minimi relativi in R n Si consideri una funzione f : A R, con A R n, e sia x A un punto interno ad A. Definizione: si dice che x è un punto di massimo relativo per f se B(x, r) A tale che f(y)
Massimi e minimi relativi in R n Si consideri una funzione f : A R, con A R n, e sia x A un punto interno ad A. Definizione: si dice che x è un punto di massimo relativo per f se B(x, r) A tale che f(y)
Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler)
 Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler) Studio di una funzione Funzioni crescenti e decrescenti Una funzione f è crescente nell intervallo (a, b) se
Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler) Studio di una funzione Funzioni crescenti e decrescenti Una funzione f è crescente nell intervallo (a, b) se
Soluzione della prova scritta di Analisi Matematica II del 15 Aprile 2009 (Ingegneria Edile e Architettura)
 Soluzione della prova scritta di Analisi Matematica II del 5 Aprile 009 Ingegneria Edile e Architettura x. Calcolare J = ds essendo γ la curva ottenuta intersecando γ + y il cilindro di equazione x + y
Soluzione della prova scritta di Analisi Matematica II del 5 Aprile 009 Ingegneria Edile e Architettura x. Calcolare J = ds essendo γ la curva ottenuta intersecando γ + y il cilindro di equazione x + y
1. Riconoscere la natura delle coniche rappresentate dalle seguenti equazioni e disegnarle:
 Università degli Studi della Basilicata Corsi di Laurea in Chimica / Scienze Geologiche Matematica II A. A. 204-205 (dott.ssa Vita Leonessa) Esercizi proposti n. 3: Funzioni a due variabili. Riconoscere
Università degli Studi della Basilicata Corsi di Laurea in Chimica / Scienze Geologiche Matematica II A. A. 204-205 (dott.ssa Vita Leonessa) Esercizi proposti n. 3: Funzioni a due variabili. Riconoscere
Massimi e minimi vincolati
 Massimi e minimi vincolati Data una funzione G C 1 (D), dove D è un aperto di R 2, sappiamo bene dove andare a cercare gli eventuali punti di massimo e minimo relativi. Una condizione necessaria affinché
Massimi e minimi vincolati Data una funzione G C 1 (D), dove D è un aperto di R 2, sappiamo bene dove andare a cercare gli eventuali punti di massimo e minimo relativi. Una condizione necessaria affinché
7.4 Massimi e minimi vincolati. Moltiplicatori di Lagrange
 4 7.4 Massimi e minimi vincolati. Moltiplicatori di Lagrange Sia f (,,, n ) una funzione delle n variabili,,, n, supponiamo che esse non siano indipendenti, cioè che siano legate da p < n equazioni: ϕ(,,,
4 7.4 Massimi e minimi vincolati. Moltiplicatori di Lagrange Sia f (,,, n ) una funzione delle n variabili,,, n, supponiamo che esse non siano indipendenti, cioè che siano legate da p < n equazioni: ϕ(,,,
Cognome Nome Matricola Codice ESEMPIO 1
 Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di derivata di una funzione in un punto. Sia A R N ; sia a A; sia f : A R M ; sia f differenziabile in a; allora la derivata di f in a è...
Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di derivata di una funzione in un punto. Sia A R N ; sia a A; sia f : A R M ; sia f differenziabile in a; allora la derivata di f in a è...
Analisi Matematica II Corso di Ingegneria Gestionale Compito del f(x, y) = log 1 + (x y 2 ) x 2.
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del 7-7-6 - È obbligatorio consegnare tutti i fogli, anche la brutta. - Le risposte senza giustificazione sono considerate nulle. Esercizio.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del 7-7-6 - È obbligatorio consegnare tutti i fogli, anche la brutta. - Le risposte senza giustificazione sono considerate nulle. Esercizio.
La ricerca di punti di estremo assoluto
 La ricerca di punti di estremo assoluto Riccarda Rossi Università di Brescia Analisi Matematica B Riccarda Rossi (Università di Brescia) Estremi assoluti (I) Analisi Matematica B 1 / 29 Richiami di teoria
La ricerca di punti di estremo assoluto Riccarda Rossi Università di Brescia Analisi Matematica B Riccarda Rossi (Università di Brescia) Estremi assoluti (I) Analisi Matematica B 1 / 29 Richiami di teoria
10 - Applicazioni del calcolo differenziale
 Università degli Studi di Palermo Facoltà di Economia CdS Sviuppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 10 - Applicazioni del calcolo differenziale Anno Accademico 2015/2016
Università degli Studi di Palermo Facoltà di Economia CdS Sviuppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 10 - Applicazioni del calcolo differenziale Anno Accademico 2015/2016
FM1 - Equazioni differenziali e meccanica
 Corso di laurea in Matematica - Anno Accademico 2006/2007 FM1 - Equazioni differenziali e meccanica Prima prova d esonero (03-04-2006) CORREZIONE Esercizio 1. Lo spettro Σ(A) della matrice A si trova risolvendo
Corso di laurea in Matematica - Anno Accademico 2006/2007 FM1 - Equazioni differenziali e meccanica Prima prova d esonero (03-04-2006) CORREZIONE Esercizio 1. Lo spettro Σ(A) della matrice A si trova risolvendo
1 Note ed esercizi risolti a ricevimento
 1 Note ed esercizi risolti a ricevimento Nota 1. Il polinomio di Taylor della funzione f x, y) due variabili), del secondo ordine, nel punto x 0, y 0 ), è P 2 x, y) = f x 0, y 0 ) + f x x 0, y 0 ) x x
1 Note ed esercizi risolti a ricevimento Nota 1. Il polinomio di Taylor della funzione f x, y) due variabili), del secondo ordine, nel punto x 0, y 0 ), è P 2 x, y) = f x 0, y 0 ) + f x x 0, y 0 ) x x
Analisi Matematica II Corso di Ingegneria Gestionale Compito del
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del 30-0-08 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del 30-0-08 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
ANALISI VETTORIALE COMPITO IN CLASSE DEL 24/10/2012
 ANALISI VETTORIALE COMPITO IN CLASSE DEL 4/10/01 Esercizio 1 Dimostrare che l equazione F (x, y) =e tan(x+y) x 3y 1 = 0 definisce implicitamente in un intorno di (0, 0) una funzione y = f(x) tale che F
ANALISI VETTORIALE COMPITO IN CLASSE DEL 4/10/01 Esercizio 1 Dimostrare che l equazione F (x, y) =e tan(x+y) x 3y 1 = 0 definisce implicitamente in un intorno di (0, 0) una funzione y = f(x) tale che F
Analisi II, a.a Soluzioni 5
 Analisi II, a.a. 2017-2018 Soluzioni 5 1) Sia E un sottoinsieme chiuso e limitato di R n e x R n un punto qualunque. Chiamiamo d(x, E) = inf{d(x, y): y E} la distanza di x da E. Dimostrare che esiste un
Analisi II, a.a. 2017-2018 Soluzioni 5 1) Sia E un sottoinsieme chiuso e limitato di R n e x R n un punto qualunque. Chiamiamo d(x, E) = inf{d(x, y): y E} la distanza di x da E. Dimostrare che esiste un
Analisi Matematica II - Ingegneria Meccanica/Energetica - 7 Lulgio a) Studiare l esistenza e la natura degli estremi liberi della funzione.
 Analisi Matematica II - Ingegneria Meccanica/Energetica - 7 Lulgio 218 1) Data la funzione f(, ) = 4 + 4 4 2 7 a) Studiare l esistenza e la natura degli estremi liberi della funzione. b) Trovare il massimo
Analisi Matematica II - Ingegneria Meccanica/Energetica - 7 Lulgio 218 1) Data la funzione f(, ) = 4 + 4 4 2 7 a) Studiare l esistenza e la natura degli estremi liberi della funzione. b) Trovare il massimo
R. Capone Analisi Matematica Calcolo Differenziale Funzioni di due variabili
 Richiami teorici Sia una funzione di due variabili definita in un insieme A e sia un punto interno ad A. Se R è un dominio regolare di centro e di dimensioni e la funzione della sola variabile x, risulta
Richiami teorici Sia una funzione di due variabili definita in un insieme A e sia un punto interno ad A. Se R è un dominio regolare di centro e di dimensioni e la funzione della sola variabile x, risulta
Analisi Matematica II - INGEGNERIA Gestionale - B 20 luglio 2017 Cognome: Nome: Matricola:
 Analisi Matematica II - INGEGNERIA Gestionale - B luglio 7 Cognome: Nome: Matricola: IMPORTANTE: Giustificare tutte le affermazioni e riportare i calcoli essenziali Esercizio [8 punti] Data la matrice
Analisi Matematica II - INGEGNERIA Gestionale - B luglio 7 Cognome: Nome: Matricola: IMPORTANTE: Giustificare tutte le affermazioni e riportare i calcoli essenziali Esercizio [8 punti] Data la matrice
FUNZIONI REALI DI DUE VARIABILI REALI
 FUNZIONI REALI DI DUE VARIABILI REALI DEFINIZIONE VARIABILI Una funione f, associa ad ogni una coppia ordinata di numeri reali,, appartenente ad un sottoinsieme S del piano, uno e un solo numero reale.
FUNZIONI REALI DI DUE VARIABILI REALI DEFINIZIONE VARIABILI Una funione f, associa ad ogni una coppia ordinata di numeri reali,, appartenente ad un sottoinsieme S del piano, uno e un solo numero reale.
Esericizi Quadriche e Coniche nello spazio
 Esericizi Quadriche e Coniche nello spazio 1. In R 3 sia A = (1, 1, 0) e sia r la retta passante per A, parallela al piano x + y + z = 0 e complanare alla retta s di equazione cartesiana x + y z = 0 =
Esericizi Quadriche e Coniche nello spazio 1. In R 3 sia A = (1, 1, 0) e sia r la retta passante per A, parallela al piano x + y + z = 0 e complanare alla retta s di equazione cartesiana x + y z = 0 =
Università di Bari - Dipartimento di Economia - Prova scritta di Matematica per l Economia L-Z- 19 Dicembre Traccia A
 Università di Bari - Dipartimento di Economia - Prova scritta di Matematica per l Economia L-Z- 9 Dicembre 06 - Traccia A Cognome e nome................................ Numero di matricola............
Università di Bari - Dipartimento di Economia - Prova scritta di Matematica per l Economia L-Z- 9 Dicembre 06 - Traccia A Cognome e nome................................ Numero di matricola............
Cognome Nome Matricola Codice ESEMPIO 1
 Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di sistema fondamentale di soluzioni di un equazione differenziale lineare d ordine n omogenea. Sia I un intervallo non banale di R; siano
Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di sistema fondamentale di soluzioni di un equazione differenziale lineare d ordine n omogenea. Sia I un intervallo non banale di R; siano
Analisi Matematica III modulo Soluzioni della prova scritta preliminare n. 2
 Analisi Matematica III modulo Soluzioni della prova scritta preliminare n. Corso di laurea in Matematica, a.a. 003-004 17 dicembre 003 1. Si consideri la funzione f : R R definita da f(x, y) = x 4 y arctan
Analisi Matematica III modulo Soluzioni della prova scritta preliminare n. Corso di laurea in Matematica, a.a. 003-004 17 dicembre 003 1. Si consideri la funzione f : R R definita da f(x, y) = x 4 y arctan
Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler)
 Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler) Studio di una funzione Funzioni crescenti e decrescenti Una funzione f é crescente nell intervallo (a, b) se
Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler) Studio di una funzione Funzioni crescenti e decrescenti Una funzione f é crescente nell intervallo (a, b) se
1 Esercitazioni di Matematica
 CORSO DI LAUREA IN SPTUPA Corso di Matematica e Statistica applicata anno accademico 2013/2014 Secondo l Eneide, all origine della fondazione di Cartagine sta la soluzione di un problema di natura matematica.
CORSO DI LAUREA IN SPTUPA Corso di Matematica e Statistica applicata anno accademico 2013/2014 Secondo l Eneide, all origine della fondazione di Cartagine sta la soluzione di un problema di natura matematica.
Corso di Laurea in Chimica e Tecnologia Farmaceutiche Matematica con Elementi di Informatica COMPITO 19 Febbraio 2016
 Corso di Laurea in Chimica e Tecnologia Farmaceutiche Matematica con Elementi di Informatica COMPITO 19 Febbraio 2016 Nome Cognome Matricola Punteggi 10 cfu Teoria Ex.1 Ex.2 Ex.3 Ex. 4 Ex.5 /6 /5 /5 /5
Corso di Laurea in Chimica e Tecnologia Farmaceutiche Matematica con Elementi di Informatica COMPITO 19 Febbraio 2016 Nome Cognome Matricola Punteggi 10 cfu Teoria Ex.1 Ex.2 Ex.3 Ex. 4 Ex.5 /6 /5 /5 /5
AM2: Tracce delle lezioni- IX Settimana INSIEMI DI LIVELLO, MINIMI VINCOLATI PRINCIPIO DEI MOLTIPLICATORI DI LAGRANGE
 AM2: Tracce delle lezioni- IX Settimana INSIEMI DI LIVELLO, MINIMI VINCOLATI PRINCIPIO DEI MOLTIPLICATORI DI LAGRANGE Sia g C 1 R 2 ), c R. L insieme γ = γ c := {x, y) R 2 : gx, y) = c} si chiama insieme
AM2: Tracce delle lezioni- IX Settimana INSIEMI DI LIVELLO, MINIMI VINCOLATI PRINCIPIO DEI MOLTIPLICATORI DI LAGRANGE Sia g C 1 R 2 ), c R. L insieme γ = γ c := {x, y) R 2 : gx, y) = c} si chiama insieme
Esercizi V settimana
 Esercizi V settimana 6 ottobre 018 1. Dire se e dove la funzione F (x, y) = ( xy, y ) x definisce un diffeomorfismo localmente. Determinare quindi gli insiemi A, B R tali che F : A B sia un diffeomorfismo
Esercizi V settimana 6 ottobre 018 1. Dire se e dove la funzione F (x, y) = ( xy, y ) x definisce un diffeomorfismo localmente. Determinare quindi gli insiemi A, B R tali che F : A B sia un diffeomorfismo
2. FUNZIONI REALI DI n VARIABILI REALI
 FUNZIONI REALI DI n VARIABILI REALI Determinaione del dominio Y Sia D un sottoinsieme dell insieme R R indicato anche con R Graficamente possiamo pensare a D come ad una ona del piano cartesiano secondo
FUNZIONI REALI DI n VARIABILI REALI Determinaione del dominio Y Sia D un sottoinsieme dell insieme R R indicato anche con R Graficamente possiamo pensare a D come ad una ona del piano cartesiano secondo
Alcuni esercizi: funzioni di due variabili e superfici
 ANALISI MATEMATICA T- (C.d.L. Ing. per l ambiente e il territorio) - COMPL. DI ANALISI MATEMATICA (A-K) (C.d.L. Ing. Civile) A.A.008-009 - Prof. G.Cupini Alcuni esercizi: funzioni di due variabili e superfici
ANALISI MATEMATICA T- (C.d.L. Ing. per l ambiente e il territorio) - COMPL. DI ANALISI MATEMATICA (A-K) (C.d.L. Ing. Civile) A.A.008-009 - Prof. G.Cupini Alcuni esercizi: funzioni di due variabili e superfici
Analisi Matematica II Corso di Ingegneria Gestionale Compito del f(x, y) = e (x3 +x) y
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del 8--7 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del 8--7 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Esempio di grafico di una funzione reale di due variabili reali
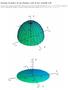 Esempio di grafico di una funzione reale di due variabili reali In questo lucido è rappresentato il grafico della funzione reale di due variabili reali definita da: f(x, y) = 1 x y, in particolare in alto
Esempio di grafico di una funzione reale di due variabili reali In questo lucido è rappresentato il grafico della funzione reale di due variabili reali definita da: f(x, y) = 1 x y, in particolare in alto
Corso di Laurea in Chimica e Tecnologia Farmaceutiche Matematica con Elementi di Informatica COMPITO 29 Gennaio 2016
 Corso di Laurea in Chimica e Tecnologia Farmaceutiche Matematica con Elementi di Informatica COMPITO 29 Gennaio 2016 Nome Cognome Matricola Punteggi 10 cfu Teoria Ex.1 Ex.2 Ex.3 Ex. 4 Ex.5 /6 /5 /5 /5
Corso di Laurea in Chimica e Tecnologia Farmaceutiche Matematica con Elementi di Informatica COMPITO 29 Gennaio 2016 Nome Cognome Matricola Punteggi 10 cfu Teoria Ex.1 Ex.2 Ex.3 Ex. 4 Ex.5 /6 /5 /5 /5
A Analisi Matematica 2 (Corso di Laurea in Informatica) Simulazione compito d esame
 COGNOME NOME Matr. Firma dello studente A Analisi Matematica (Corso di Laurea in Informatica) Simulazione compito Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni
COGNOME NOME Matr. Firma dello studente A Analisi Matematica (Corso di Laurea in Informatica) Simulazione compito Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni
Capitolo 5: funzioni reali a due variabili reali FUNZIONI REALI A DUE VARIABILI REALI
 Capitolo 5 FUNZIONI REALI A DUE VARIABILI REALI Come l insieme R dei numeri reali è in corrispondenza biunivoca con i punti di una retta, così l insieme R delle coppie di numeri reali è in corrispondenza
Capitolo 5 FUNZIONI REALI A DUE VARIABILI REALI Come l insieme R dei numeri reali è in corrispondenza biunivoca con i punti di una retta, così l insieme R delle coppie di numeri reali è in corrispondenza
Esonero di Analisi Matematica II (A)
 Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
Appunti sul corso di Complementi di Matematica mod. Analisi prof. B.Bacchelli - a.a. 2010/2011.
 Appunti sul corso di Complementi di Matematica mod. Analisi prof. B.Baccelli - a.a. 2010/2011. 06 - Derivate, differenziabilità, piano tangente, derivate di ordine superiore. Riferimenti: R.Adams, Calcolo
Appunti sul corso di Complementi di Matematica mod. Analisi prof. B.Baccelli - a.a. 2010/2011. 06 - Derivate, differenziabilità, piano tangente, derivate di ordine superiore. Riferimenti: R.Adams, Calcolo
Istituzioni di Analisi 2 (programma, domande ed esercizi)
 Istituzioni di Analisi programma, domande ed esercizi) nona settimana Argomenti trattati Dal libro di testo: 3. punti critici vincolati), 3.3. estremi assoluti), 0.3. e 0.3. solo la definizione di compatto
Istituzioni di Analisi programma, domande ed esercizi) nona settimana Argomenti trattati Dal libro di testo: 3. punti critici vincolati), 3.3. estremi assoluti), 0.3. e 0.3. solo la definizione di compatto
FUNZIONI SCALARI DI PIU VARIABILI
 FUNZIONI SCALARI DI PIU VARIABILI Stefano Patrì seriegeo@yahoo.it Novembre 2008 1 Introduzione In questa nota analizzeremo le proprietà delle funzioni scalari f : R n R (1) e in particolare discuteremo
FUNZIONI SCALARI DI PIU VARIABILI Stefano Patrì seriegeo@yahoo.it Novembre 2008 1 Introduzione In questa nota analizzeremo le proprietà delle funzioni scalari f : R n R (1) e in particolare discuteremo
Estremi liberi. (H x, x) x 2 (1) F (x) =
 Estremi liberi Allo scopo di ottenere delle condizioni sufficienti affinchè un punto stazionario sia un estremante, premettiamo alcuni risultati riguardanti le proprietà delle forme quadratiche. Sia H
Estremi liberi Allo scopo di ottenere delle condizioni sufficienti affinchè un punto stazionario sia un estremante, premettiamo alcuni risultati riguardanti le proprietà delle forme quadratiche. Sia H
LA STRUTTURA DEI PROBLEMI DI OTTIMIZZAZIONE. L'ipotesi di razionalità implica che un decisore cerchi di
 LA STRUTTURA DEI PROBLEMI DI OTTIMIZZAZIONE L'ipotesi di razionalità implica che un decisore cerchi di individuare la migliore tra tutte le alternative a sua disposizione. Problemi di ottimizzazione =
LA STRUTTURA DEI PROBLEMI DI OTTIMIZZAZIONE L'ipotesi di razionalità implica che un decisore cerchi di individuare la migliore tra tutte le alternative a sua disposizione. Problemi di ottimizzazione =
Analisi Matematica IV modulo Soluzioni prova scritta preliminare n. 1
 Analisi Matematica IV modulo Soluzioni prova scritta preliminare n. 1 Corso di laurea in Matematica, a.a. 2005-2006 27 aprile 2006 1. Disegnare approssimativamente nel piano (x, y) l insieme x 4 6xy 2
Analisi Matematica IV modulo Soluzioni prova scritta preliminare n. 1 Corso di laurea in Matematica, a.a. 2005-2006 27 aprile 2006 1. Disegnare approssimativamente nel piano (x, y) l insieme x 4 6xy 2
UNIVERSITÀ DI ROMA TOR VERGATA. Analisi Matematica II per Ingegneria Prof. C. Sinestrari
 UNIVERSITÀ DI ROMA TOR VERGATA Analisi Matematica II per Ingegneria Prof. C. Sinestrari Risposte (sintetiche) ai quesiti degli esercizi del 12.X.2018 1. (a) Ω è aperto, Ω = {0, 1, 2}, Ω = Ω, Ω = [0, 1]
UNIVERSITÀ DI ROMA TOR VERGATA Analisi Matematica II per Ingegneria Prof. C. Sinestrari Risposte (sintetiche) ai quesiti degli esercizi del 12.X.2018 1. (a) Ω è aperto, Ω = {0, 1, 2}, Ω = Ω, Ω = [0, 1]
1. Funzioni implicite
 1. Funzioni implicite 1.1 Il caso scalare Sia X R 2 e sia f : X R. Una funzione y : (a, b) R si dice definita implicitamente dall equazione f(x, y) = 0 in (a, b) quando: 1. (x, y(x)) X x (a, b); 2. f(x,
1. Funzioni implicite 1.1 Il caso scalare Sia X R 2 e sia f : X R. Una funzione y : (a, b) R si dice definita implicitamente dall equazione f(x, y) = 0 in (a, b) quando: 1. (x, y(x)) X x (a, b); 2. f(x,
Analisi Matematica II Corso di Ingegneria Biomedica Compito A del f(x, y) = x 2 + y 2
 Analisi Matematica II Corso di Ingegneria Biomedica Compito A del -7- - È obbligatorio consegnare tutti i fogli, anche quelli della brutta. - Le risposte senza giustificazione sono considerate nulle. Esercizio.
Analisi Matematica II Corso di Ingegneria Biomedica Compito A del -7- - È obbligatorio consegnare tutti i fogli, anche quelli della brutta. - Le risposte senza giustificazione sono considerate nulle. Esercizio.
Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler)
 Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler) Studio di una funzione Funzioni crescenti e decrescenti Una funzione f é crescente nell intervallo (a, b) se
Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler) Studio di una funzione Funzioni crescenti e decrescenti Una funzione f é crescente nell intervallo (a, b) se
COMPLEMENTI DI ANALISI MATEMATICA A.A Primo appello del 5/5/2010
 COMPLEMENTI DI ANALISI MATEMATICA A.A. 29- Primo appello del 5/5/2 Qui trovate le tracce delle soluzioni degli esercizi del compito. Ho tralasciato i calcoli da Analisi (che comunque sono parte della risoluzione),
COMPLEMENTI DI ANALISI MATEMATICA A.A. 29- Primo appello del 5/5/2 Qui trovate le tracce delle soluzioni degli esercizi del compito. Ho tralasciato i calcoli da Analisi (che comunque sono parte della risoluzione),
DERIVATE SUCCESSIVE E MATRICE HESSIANA
 FUNZIONI DI DUE VARIABILI 1 DERIVATE SUCCESSIVE E MATRICE HESSIANA Derivate parziali seconde e matrice hessiana. Sviluppo di Taylor del secondo ordine. Punti stazionari. Punti di massimo o minimo (locale
FUNZIONI DI DUE VARIABILI 1 DERIVATE SUCCESSIVE E MATRICE HESSIANA Derivate parziali seconde e matrice hessiana. Sviluppo di Taylor del secondo ordine. Punti stazionari. Punti di massimo o minimo (locale
Esame di Analisi Matematica 2 24/7/2013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 2012/2013
 Esame di Analisi Matematica 4/7/013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 01/013 A Cognome (in STAMPATELLO):... Nome (in STAMPATELLO):... CFU:... Esercizio 1. Sia f : R R una funzione
Esame di Analisi Matematica 4/7/013 Corsi di Laurea in Ingegneria Meccanica e Energetica A.A. 01/013 A Cognome (in STAMPATELLO):... Nome (in STAMPATELLO):... CFU:... Esercizio 1. Sia f : R R una funzione
