162 Capitolo 5. Equazioni di grado superiore al secondo. c ) x x 2 7x 196; e ) x x x 2; f ) x x x
|
|
|
- Stefano Stella
- 4 anni fa
- Visualizzazioni
Transcript
1 6 Capitolo Equazioni di grado superiore al secondo 7 Esercizi 7 Esercizi dei singoli paragrafi - Equazioni riconducibili al prodotto di due o più fattori ) Trovare gli zeri dei seguenti polinomi + ; b ) ; c ) ; ; e ) + 7 ; ) Trovare gli zeri dei seguenti polinomi 9 + ; b ) 9 9 ; c ) ; 8 ; e ) 0 + 8; ) Trovare gli zeri dei seguenti polinomi + 9 6; b ) + 6 ; c ) + ; ; e ) ; + ) Trovare gli zeri dei seguenti polinomi ; b ) ; c ) ; ; e ) ; 8 a a + a Trovare gli zeri dei seguenti polinomi ; b ) ; c ) ; a a + a) a + a) + a 6 ) Determinare l insieme soluzione delle seguenti equazioni + = 0; b ) = 0; c ) = 0; + = 0; e ) + = 0; = 0 7 ) Determinare l insieme soluzione delle seguenti equazioni = 0; b ) = 0; c ) = 0; + = + ) ; e ) + +) = 0; + ) = )
2 Sezione 7 Esercizi 6 8 ) Determinare l insieme soluzione delle seguenti equazioni + ) = ) ; b ) + ) ) = + ) + ) ; c ) ) + + ) = ) + ; + + = ; e ) 7 = 0; + ) ) = 8 9 ) Determinare l insieme soluzione delle seguenti equazioni ) = 0; b ) 6 7 = 7 ; c ) ) 0 = ) 0 ; ) 0 = ) 0 ; e ) = 0; = 0 0 ) Determinare l insieme soluzione delle seguenti equazioni b ) c ) = + ; ++ + ) = 0; = 0; ) + = ++ ; e ) = = 0; ) Determinare l insieme soluzione delle seguenti equazioni +9 + = ; b ) ) + 7 = ) ) ; c ) = 0 - Equazioni binomie ) Determinare l insieme soluzione delle seguenti equazioni binomie + 6 = 0; b ) + = 0; c ) + 6 = 0; + 6 = 0; e ) 6 + = 0; 8 = 0 ) Determinare l insieme soluzione delle seguenti equazioni binomie 7 + = 0; b ) 8 + = 0; c ) 8 8 = 0; 6 = 0; e ) 6 = 0; 8 7 = 0 ) Determinare l insieme soluzione delle seguenti equazioni binomie = 0; b ) + 8 = 0; c ) = 0; + 96 = 0; e ) 9 6 = 0; = 7
3 6 Capitolo Equazioni di grado superiore al secondo ) Determinare l insieme soluzione delle seguenti equazioni binomie = 0; b ) = 0; c ) = 0; + 6 = 0; e ) 8 7 = 0; = 0; g ) 8 6 = 0; h ) 6 9 = 0; i ) 8 = 0; j ) 8 = 7; k ) 8 = ; l ) 7 = 0 6 Determinare l insieme soluzione delle seguenti equazioni binomie 6 6 = 0; b ) 6 6 = ; c ) 6 = 6; = 0; e ) 00 = 0; 0 0 = 0; g ) 8 = 0; h ) 8 = 0; i ) 6 = ; j ) = 9 ; k ) 8 6 = 0; l ) + = 0 7 ) Determinare l insieme soluzione delle seguenti equazioni binomie + = 0; b ) + = 0; c ) 6 = 0; = 0; e ) = 0; 9 9 = 0; g ) ) = 6; h ) ) 7 = 0; i ) = + - Equazioni trinomie 8 ) Determinare l insieme soluzione delle seguenti equazioni biquadratiche + 6 = 0; b ) = 0; c ) = 0; + = 0; e ) + 7 = 0; = 0; g ) = 0; h ) + 8 = 0; i ) = 0; j ) = 0; k ) = 0; l ) = 0 9 ) Determinare l insieme soluzione delle seguenti equazioni biquadratiche = 0; b ) = 0; c ) + 6 = 0; + = 0; e ) + 08 = 0; + 9 = 0 0 ) Determinare l insieme soluzione delle seguenti equazioni biquadratiche = + ) ) ; b ) ) = 9 8) + ); c ) 6 = + ) ) 9; ) + = + ) ) + ; e ) + ) + = ) ; 8 ) = ) Determinare l insieme soluzione delle seguenti equazioni biquadratiche = 0; b ) + = 0; c ) = 0; = 0; e ) = 0; = 0
4 Sezione 7 Esercizi 6 ) Determinare l insieme soluzione delle seguenti equazioni biquadratiche ) + 0 = + 6; b ) = + + ; c ) + +) + 9 = + 8; + ) + = + ) ; e ) = + + ; +) = 0 ) Determinare l insieme soluzione delle seguenti equazioni biquadratiche b + a b ) = a + ; b ) b a b + 6 ) + 6a = 0; c ) + 9a ) a a a + a) ; +a a = 6a ; +a e ) + m ) + m ) = 7m m ) ; mm+n) m+n) +mm+n) = m m+n) + n m m È vero che l equazione = 0 ha quattro soluzioni reali a due a due coincidenti? Rispondi senza risolvere l equazione È vero che l equazione + = 0 ha quattro soluzioni reali a due a due coincidenti? Rispondi senza risolvere l equazione 6 Senza risolvere le seguenti equazioni dire se ammettono soluzioni reali: 0 + 9; b ) = 0; c ) = 0; + = 0; e ) = 0; + = 0; g ) + = 0; h ) + = 0; i ) + = 0 7 ) Data l equazione a + ) = a a) determinare per quali valori del parametro a si hanno quattro soluzioni reali 8 È vero che la somma delle radici dell equazione a + b + c = 0 è nulla? 9 Data l equazione a + b + c = 0 verifica le seguenti uguaglianze relative alle soluzioni reali: A = b a B = a c - Equazioni che si risolvono con sostituzioni 0 ) Determinare l insieme soluzione delle seguenti equazioni trinomie = 0; b ) 8 + = 0; c ) = 0; 0 + = 0; e ) = 0; = 0
5 66 Capitolo Equazioni di grado superiore al secondo ) Determinare l insieme soluzione delle seguenti equazioni trinomie = 0; b ) = 0; c ) = 0; = 0 ) Risolvi con le opportune sostituzioni le seguenti equazioni + ) 8 = 0; b ) ) + + ) = 0; c ) + ) 6 + ) + 8 = 0; e ) ) + = 6 9 ; ) + ) 6 + = 0; ) ) + 7 = 0 ) Risolvi con le opportune sostituzioni le seguenti equazioni ) = 8; b ) + ) ) + ) 0 = 0; c ) + ) + ) 9 + ) = 0; + +) = 0; e ) ) + + = +6 ; ) ) ) + ) + = 0 Risolvi con le opportune sostituzioni le seguenti equazioni + ) = ; b ) ) ) + 6 = 0; c ) + ) ) e ) = 0; ) 6 ) + = 0; + ) 0 + ) + = 0; ) ) = 0 Risolvi con le opportune sostituzioni le seguenti equazioni b ) c ) + + = + ) ; ) + 8 = 9; ) ) ) ) + = Equazioni reciproche 6 ) Risolvi le seguenti equazioni reciproche di prima specie = 0; b ) + = 0; c ) + = 0; = 0; e ) = 0; = 0
6 Sezione 7 Esercizi 67 7 ) Risolvi le seguenti equazioni reciproche di prima specie + = ; b ) = ; c ) 9 7 = 0 + ) + ); + ) + ) + = 0 8 ) Risolvi le seguenti equazioni reciproche di prima specie + + ) + + ) + = 0; b ) + = 0; c ) a + a + a + ) + a + a + ) + = 0 9 Dopo aver verificato che = è radice dell equazione + = 0 verificate che l equazione ammette come soluzione = 0 Determina il valore di verità delle seguenti proposizioni: l equazione a + b + c + d = 0 ammette sempre = come soluzione; b ) se nell equazione a + b + c + d = 0 si ha a = d e b = c allora = è una soluzione; c ) in una equazione reciproca di terzo grado la somma dei coefficienti è nulla; se in a + b + c + d = 0 si ha a + d = 0 e b + c = 0 allora = appartiene all I S ) Risolvi le seguenti equazioni reciproche di seconda specie = 0; b ) = 0; c ) = 0; + = 0; e ) = 0; + = 0 ) Risolvi le seguenti equazioni reciproche di seconda specie = ); b ) + 6 ) + 6 ) = 0; c ) + = 0; + ) + ) = Data l equazione a 0 t ) + a t + a = 0 a 0 t + a t + a a 0 = 0 stabilire quale condizione deve sussistere tra i coefficienti affinché esistano valori reali dell incognita t ) Risolvi le seguenti equazioni di quarto grado reciproche di prima specie = 0; b ) = 0; c ) = 0; = 0 ) Risolvi le seguenti equazioni di quarto grado reciproche di seconda specie + = 0; b ) + = 0; c ) = 0; = 0
7 68 Capitolo Equazioni di grado superiore al secondo 6 ) Risolvi le seguenti equazioni di quarto grado reciproche di seconda specie + = 0; b ) = 0; c ) = 0; ) = 7 ) Risolvi le seguenti equazioni reciproche + = 0; b ) = 0; c ) = 0; = 0 8 ) Risolvi le seguenti equazioni reciproche + = 0; b ) + = 0; c ) = 0; = 0 9 ) Risolvi le seguenti equazioni reciproche + = 0; b ) = 0; c ) = 0; + + = 0; e ) = 0; = 0 0 Quale condizione deve sussistere tra i coefficienti dell equazione a 0 + a + a 0 = 0 affinché siano reali le sue soluzioni? ) Determinare per quale valore di k l equazione k ) + = 0 è reciproca È vero che I S = +? 7 Esercizi riepilogativi ) Risolvi le seguenti equazioni di grado superiore al secondo = 0; b ) = 0; c ) + = 0; + = 0; e ) + = 0; + + = 0 ) Risolvi le seguenti equazioni di grado superiore al secondo + + = 0; b ) = 0; c ) + = 0; = 0; e ) = 0; = 0 ) Risolvi le seguenti equazioni di grado superiore al secondo + = 0; b ) = 0; c ) = 0; + = 0; e ) = 0; = 0
8 Sezione 7 Esercizi 69 ) Risolvi le seguenti equazioni di grado superiore al secondo = 0; b ) = 0; c ) + + = 0; + = 0; e ) = 0; + + = 0 6 ) Risolvi le seguenti equazioni di grado superiore al secondo + = 0; b ) + = 0; c ) + + = 0; + + = 0; e ) = 0; = 0 7 ) Risolvi le seguenti equazioni di grado superiore al secondo = 0; b ) = 0; c ) = 0; = 0; e ) + = 0; + + = 0 8 ) Risolvi le seguenti equazioni di grado superiore al secondo + + = 0; b ) + + = 0; c ) + = 0; + + = 0; e ) = 0; = 0 9 ) Risolvi le seguenti equazioni di grado superiore al secondo = 0; b ) = 0; c ) = 0; = 0; e ) = 0; = 0 60 ) Risolvi le seguenti equazioni di grado superiore al secondo 6 + = 0; b ) = 0; c ) = 0; ) + 0 ) = 0; e ) 6 + = ; ) + ) + ) = 0; g ) 9 +) = ; h ) +) 8+ + = 0 6 ) Nell equazione a) + + a) + b + + b = 0 determinare a e b in modo che l equazione sia reciproca 7 Risposte a) ; ; b) ; ; c) ; ; d) ; 7 e) ; ; + f) ; + 7 ; + a) 0; ; b) c) d) ; e) ; ; f) ; ; a) ; b) c) ; d) ; ; e) ; 9 f) ; ;
9 70 Capitolo Equazioni di grado superiore al secondo a) ; ; b) ; 6; 6 a) ; b) c) d) ; e) ; ; f) ; ; 7 a) ; ; b) 0; c) ; ; d) ; + e) ; ; f) 8 a) ; b) ; c) ; d) e) ; 0; + 9 a) 0; ) ; + b) 0; c) R d) 0; ; e) 0 f) 0; ; 0 a) b) ; c) 0; d) b) + c) ; 9 d) 0; ; a) b) c) d) ; + e) 6 f) e) f) ; a) b) c) ; + d) ; + e) ; f) a) b) c) ; d) e) 7 ; 7 f) a) 0 b) 0 c) 0 d) e) f) IS = 9 g) h) 6 i) 9 8 j) 7 e) 8 f) 8 a) ; b) ; c) ; d) i) g) ; h) ; ; ; j) ; 6 k) e) ; f) ; ; l) ; 9 a) 0; b) ; c) ; d) ; e) ; f) ; 0 a) 0; b) ; c) ; d) ; e) ; f) ; a) b) c) d) e) f)
10 Sezione 7 Esercizi 7 a) ; b) f) ; 9 c) ; d) ; e) ; a) a ; b a b) b ; a c) 9a ; a d) m; m e) 7m; m 7 f) m + n 7 a > 0 a) ; b) ; c) ; d) ; e) f) a) b) ; c) ; d) ; 7 a) b) 7 c) ; d) e) 8 7 f) ; 0 a) b) 6; ; c) 6 d) ; 0; e) f) 0; ; 6 a) ; ; b) ; ; c) ; ; d) ; ; e) ; ; f) ; ; 7 a) ; ; b) ; ; c) ; d) ; ; 8 a) ; ; + b) ; + ; c) ; a; a a) ; ; b) ; 7; 7 c) ; ; d) ; ; e) ; ; f) ; a) a) a) 6 a) ; 6 8 ; ; ; 0 b) ; ; c) ; 7 d) ; ; b) c) ; d) ; ; b) c) ; 7 6 b) ; ; c) d) ; 9 ; 7 d) ; 7 a) b) ; ; c) ; ; d) 8 a) ; b) c) ; d) ; ; ;
11 7 Capitolo Equazioni di grado superiore al secondo 9 a) ; ; b) ; ; ; c) ; ; d) ; ; e) ; ; ; ; f) ; ; ; ; a) k = a) ; ; b) c) d) e) ; ; f) a) b) ; c) f) = ; = ; 7 d) ; e) a) b) c) ; d) e) ; f) ; ; a) b) ; c) d) e) ; f) 6 a) 7 a) f) ; ; 7 8 a) b) c) b) c) ; d) e) ; 7 6 f) b) ; c) ; +6; 6 d) e) ; ; d) ; e) f) ; 9 a) b) c) ; ; ; ; d) ; ; e) ; = f) ; 60 a) b) ; c) d) ; ; e) ; ; ; f) g) 7 ; h) 6 a = 7 e b = 7
Equazioni di secondo grado parametriche
 Equazioni di secondo grado parametriche Data un equazione parametrica di secondo grado, determinare per quali valori di k:. l equazione ha due soluzioni reali; Porre 0. da ora in poi, nei punti seguenti,
Equazioni di secondo grado parametriche Data un equazione parametrica di secondo grado, determinare per quali valori di k:. l equazione ha due soluzioni reali; Porre 0. da ora in poi, nei punti seguenti,
EQUAZIONI BIQUADRATICHE
 EQUAZIONI PARTICOLARI PROF.SSA ROSSELLA PISCOPO Indice 1 EQUAZIONI BIQUADRATICHE ------------------------------------------------------------------------------------------ 3 2 EQUAZIONI RECIPROCHE -----------------------------------------------------------------------------------------------
EQUAZIONI PARTICOLARI PROF.SSA ROSSELLA PISCOPO Indice 1 EQUAZIONI BIQUADRATICHE ------------------------------------------------------------------------------------------ 3 2 EQUAZIONI RECIPROCHE -----------------------------------------------------------------------------------------------
LE EQUAZIONI DI SECONDO GRADO
 LE EQUAZIONI DI SECONDO GRADO Definizione: un equazione è di secondo grado se, dopo aver applicato i principi di equivalenza, si può scrivere nella forma, detta normale: ax + bx + c 0!!!!!con!a 0 Le lettere
LE EQUAZIONI DI SECONDO GRADO Definizione: un equazione è di secondo grado se, dopo aver applicato i principi di equivalenza, si può scrivere nella forma, detta normale: ax + bx + c 0!!!!!con!a 0 Le lettere
Identità ed equazioni
 Matematica e-learning - Identità ed equazioni Prof. erasmo@galois.it A.A. 2009/2010 1 Generalità sulle equazioni Si consideri un uguaglianza tra due espressioni algebriche A = B Se si sostituiscono al
Matematica e-learning - Identità ed equazioni Prof. erasmo@galois.it A.A. 2009/2010 1 Generalità sulle equazioni Si consideri un uguaglianza tra due espressioni algebriche A = B Se si sostituiscono al
1 Fattorizzazione di polinomi
 1 Fattorizzazione di polinomi Polinomio: un polinomio di grado n nella variabile x, è dato da p(x) = a n x n + a n 1 x n 1 + + a 1 x + a 0 con a n 0, a 0 è detto termine noto, a k è detto coefficiente
1 Fattorizzazione di polinomi Polinomio: un polinomio di grado n nella variabile x, è dato da p(x) = a n x n + a n 1 x n 1 + + a 1 x + a 0 con a n 0, a 0 è detto termine noto, a k è detto coefficiente
Matematica per le scienze sociali Equazioni e disequazioni. Domenico Cucina
 Matematica per le scienze sociali Equazioni e disequazioni Domenico Cucina University of Roma Tre D. Cucina (domenico.cucina@uniroma3.it) 1 / 19 Outline 1 Equazioni algebriche 2 Equazioni di primo grado
Matematica per le scienze sociali Equazioni e disequazioni Domenico Cucina University of Roma Tre D. Cucina (domenico.cucina@uniroma3.it) 1 / 19 Outline 1 Equazioni algebriche 2 Equazioni di primo grado
Matematica per le scienze sociali Equazioni e disequazioni. Francesco Lagona
 Matematica per le scienze sociali Equazioni e disequazioni Francesco Lagona University of Roma Tre F. Lagona (francesco.lagona@uniroma3.it) 1 / 19 Outline 1 Equazioni algebriche 2 Equazioni di primo grado
Matematica per le scienze sociali Equazioni e disequazioni Francesco Lagona University of Roma Tre F. Lagona (francesco.lagona@uniroma3.it) 1 / 19 Outline 1 Equazioni algebriche 2 Equazioni di primo grado
DIPARTIMENTO DI MATEMATICA A.S EQUAZIONI DI GRADO SUPERIORE AL 2
 DIPARTIMENTO DI MATEMATICA A.S. 00-05 EQUAZIONI DI GRADO SUPERIORE AL 1. EQUAZIONI RISOLVIBILI MEDIANTE SCOMPOSIZIONE. EQUAZIONI BINOMIE. EQUAZIONI TRINOMIE. EQUAZIONI RECIPROCHE 1. EQUAZIONI RISOLVIBILI
DIPARTIMENTO DI MATEMATICA A.S. 00-05 EQUAZIONI DI GRADO SUPERIORE AL 1. EQUAZIONI RISOLVIBILI MEDIANTE SCOMPOSIZIONE. EQUAZIONI BINOMIE. EQUAZIONI TRINOMIE. EQUAZIONI RECIPROCHE 1. EQUAZIONI RISOLVIBILI
ESERCITAZIONE 10 : EQUAZIONI E DISEQUAZIONI
 ESERCITAZIONE 10 : EQUAZIONI E DISEQUAZIONI e-mail: tommei@dm.unipi.it web: www.dm.unipi.it/ tommei Ricevimento: Martedi 16-18 Dipartimento di Matematica, piano terra, studio 126 11 Dicembre 2012 Esercizio
ESERCITAZIONE 10 : EQUAZIONI E DISEQUAZIONI e-mail: tommei@dm.unipi.it web: www.dm.unipi.it/ tommei Ricevimento: Martedi 16-18 Dipartimento di Matematica, piano terra, studio 126 11 Dicembre 2012 Esercizio
Disequazioni razionali (in una variabile)
 5 settembre 8 Disequazioni razionali (in una variabile) Forma normale: f f f < f > Disequazioni razionali intere Nelle disequazioni razionali intere la funzione f è un polinomio. Disequazioni di grado
5 settembre 8 Disequazioni razionali (in una variabile) Forma normale: f f f < f > Disequazioni razionali intere Nelle disequazioni razionali intere la funzione f è un polinomio. Disequazioni di grado
EQUAZIONI. Prendiamo in considerazione le funzioni reali in una variabile reale
 EQUAZIONI Prendiamo in considerazione le funzioni reali in una variabile reale Una equazione è una uguaglianza tra due funzioni eventualmente verificata per particolari valori attribuiti alla variabile
EQUAZIONI Prendiamo in considerazione le funzioni reali in una variabile reale Una equazione è una uguaglianza tra due funzioni eventualmente verificata per particolari valori attribuiti alla variabile
Definizione: Due equazioni si dicono equivalenti se ammettono le stesse soluzioni.
 Facoltà di Medicina e Chirurgia Corso Zero di Matematica Gruppi: MC-MF3 / PS-MF3 II Lezione EQUAZIONI E SISTEMI Dr. E. Modica erasmo@galois.it www.galois.it IDENTITÀ ED EQUAZIONI Si consideri un uguaglianza
Facoltà di Medicina e Chirurgia Corso Zero di Matematica Gruppi: MC-MF3 / PS-MF3 II Lezione EQUAZIONI E SISTEMI Dr. E. Modica erasmo@galois.it www.galois.it IDENTITÀ ED EQUAZIONI Si consideri un uguaglianza
CORSO ZERO DI MATEMATICA
 UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA EQUAZIONI E DISEQUAZIONI DI SECONDO GRADO Dr. Erasmo Modica erasmo@galois.it EQUAZIONI DI SECONDO GRADO Definizione: Dicesi
UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA EQUAZIONI E DISEQUAZIONI DI SECONDO GRADO Dr. Erasmo Modica erasmo@galois.it EQUAZIONI DI SECONDO GRADO Definizione: Dicesi
Espressioni algebriche: espressioni razionali
 Espressioni algebriche: espressioni razionali definizione: Il rapporto fra due polinomi si dice espressione razionale. Le espressioni razionali in una sola variabile si scrivono nella forma generale esempio:
Espressioni algebriche: espressioni razionali definizione: Il rapporto fra due polinomi si dice espressione razionale. Le espressioni razionali in una sola variabile si scrivono nella forma generale esempio:
Sistemi lineari (di I grado)
 Sistemi lineari (di I grado) Un sistema lineare è un insieme di equazioni lineari (di I grado), che devono essere verificate tutte contemporaneamente. Risolvere un sistema di equazioni vuol dire trovare
Sistemi lineari (di I grado) Un sistema lineare è un insieme di equazioni lineari (di I grado), che devono essere verificate tutte contemporaneamente. Risolvere un sistema di equazioni vuol dire trovare
Equazioni. Istituto San Gabriele 3 Liceo Scientifico 3 Liceo Scientifico sez. Scienze Applicate A.S. 2016/2017 Prof.
 Equazioni Istituto San Gabriele 3 Liceo Scientifico 3 Liceo Scientifico sez. Scienze Applicate A.S. 2016/2017 Prof. Andrea Pugliese Definizione ed esempi Un equazione è un uguaglianza tra due espressioni
Equazioni Istituto San Gabriele 3 Liceo Scientifico 3 Liceo Scientifico sez. Scienze Applicate A.S. 2016/2017 Prof. Andrea Pugliese Definizione ed esempi Un equazione è un uguaglianza tra due espressioni
Equazioni di secondo grado
 Equazioni di secondo grado www.competenzamatematica.it E. Modica A.S. 018/019 1 Equazioni di secondo grado Definizione 1. Dicesi equazione di secondo grado, un equazione del tipo: ax + bx + c = 0 con a,
Equazioni di secondo grado www.competenzamatematica.it E. Modica A.S. 018/019 1 Equazioni di secondo grado Definizione 1. Dicesi equazione di secondo grado, un equazione del tipo: ax + bx + c = 0 con a,
3 Equazioni e disequazioni.
 3 Equazioni e disequazioni. 3. Equazioni. Una equazione algebrica è un uguaglianza tra espressioni letterali soddisfatta per alcuni valori attribuiti alle lettere che vi compaiono. Tali valori sono detti
3 Equazioni e disequazioni. 3. Equazioni. Una equazione algebrica è un uguaglianza tra espressioni letterali soddisfatta per alcuni valori attribuiti alle lettere che vi compaiono. Tali valori sono detti
Equazioni di secondo grado Prof. Walter Pugliese
 Equazioni di secondo grado Prof. Walter Pugliese La forma normale di un equazione di secondo grado Un equazione è di secondo grado se, dopo aver applicato i principi di equivalenza già studiati per le
Equazioni di secondo grado Prof. Walter Pugliese La forma normale di un equazione di secondo grado Un equazione è di secondo grado se, dopo aver applicato i principi di equivalenza già studiati per le
3. EQUAZIONI DI GRADO SUPERIORE AL SECONDO
 www.matematicamente.it Matematica C3 Algebra 3. Equazioni di grado superiore al secondo MATEMATICA C 3 -ALGEBRA 3. EQUAZIONI DI GRADO SUPERIORE AL SECONDO Alvaro Tapia, Skateboard http://www.flickr.com/photos/foto_saiker/308790/
www.matematicamente.it Matematica C3 Algebra 3. Equazioni di grado superiore al secondo MATEMATICA C 3 -ALGEBRA 3. EQUAZIONI DI GRADO SUPERIORE AL SECONDO Alvaro Tapia, Skateboard http://www.flickr.com/photos/foto_saiker/308790/
3. EQUAZIONI DI GRADO SUPERIORE AL SECONDO
 MATEMATICA C 3 -ALGEBRA 3. EQUAZIONI DI GRADO SUPERIORE AL SECONDO Alvaro Tapia, Skateboard http://www.flickr.com/photos/foto_saiker/30879011/ 1. Equazioni riconducibili al prodotto di due o più fattori....
MATEMATICA C 3 -ALGEBRA 3. EQUAZIONI DI GRADO SUPERIORE AL SECONDO Alvaro Tapia, Skateboard http://www.flickr.com/photos/foto_saiker/30879011/ 1. Equazioni riconducibili al prodotto di due o più fattori....
1 Disquazioni di primo grado
 1 Disquazioni di primo grado 1 1 Disquazioni di primo grado Si assumono assodate le regole per la risoluzione delle equazioni lineari Ricordando che una disuguaglianza è una scrittura tra due espressioni
1 Disquazioni di primo grado 1 1 Disquazioni di primo grado Si assumono assodate le regole per la risoluzione delle equazioni lineari Ricordando che una disuguaglianza è una scrittura tra due espressioni
LICEO SCIENTIFICO STATALE Enrico Fermi Anno Scolastico 2008/09. Scomposizioni in fattori dei polinomi. Frazioni algebriche
 LICEO SCIENTIFICO STATALE Enrico Fermi Anno Scolastico 2008/09 Classe II E - corso Tecnologico Scomposizioni in fattori dei polinomi Scomposizione di un polinomio in fattori Concetto di scomposizione Raccoglimento
LICEO SCIENTIFICO STATALE Enrico Fermi Anno Scolastico 2008/09 Classe II E - corso Tecnologico Scomposizioni in fattori dei polinomi Scomposizione di un polinomio in fattori Concetto di scomposizione Raccoglimento
COMPITI DELLE VACANZE A.S. 2015/16 MATEMATICA
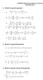 1) Risolvi le seguenti equazioni: COMPITI DELLE VACANZE A.S. 015/1 MATEMATICA 3 3 5 + + 3 5 3 5 3 3 3 1 + + + ( )( ) 5 5 18 1 5 + + 5 1 30 0 + 8 1 1 1 3 1 1 1 1 5 + + 15 30 1 1 3 1 1 + + 18 e) f) + + 3
1) Risolvi le seguenti equazioni: COMPITI DELLE VACANZE A.S. 015/1 MATEMATICA 3 3 5 + + 3 5 3 5 3 3 3 1 + + + ( )( ) 5 5 18 1 5 + + 5 1 30 0 + 8 1 1 1 3 1 1 1 1 5 + + 15 30 1 1 3 1 1 + + 18 e) f) + + 3
Equazioni di grado superiore al secondo
 Equazioni di grado superiore al secondo 5 51 L equazione di terzo grado, un po di storia Trovare un numero il cui cubo, insieme con due suoi quadrati e dieci volte il numero stesso, dia come somma 0 Il
Equazioni di grado superiore al secondo 5 51 L equazione di terzo grado, un po di storia Trovare un numero il cui cubo, insieme con due suoi quadrati e dieci volte il numero stesso, dia come somma 0 Il
Liceo Scientifico Statale S. Cannizzaro Palermo Classe III D EQUAZIONI POLINOMIALI Divisione di polinomi, teorema del resto e teorema di Ruffini
 Divisione di polinomi, teorema del resto e teorema di Ruffini Teorema (della divisione con resto tra due polinomi in una variabile). Dati due polinomi A x e B x, con B x 0, esistono sempre, e sono unici,
Divisione di polinomi, teorema del resto e teorema di Ruffini Teorema (della divisione con resto tra due polinomi in una variabile). Dati due polinomi A x e B x, con B x 0, esistono sempre, e sono unici,
EQUAZIONI DI II GRADO
 RICHIAMI SULLE EQUAZIONI DI PRIMO E SECONDO GRADO PROF.SSA ROSSELLA PISCOPO Indice 1 EQUAZIONI DI I GRADO --------------------------------------------------------------------------------------------------
RICHIAMI SULLE EQUAZIONI DI PRIMO E SECONDO GRADO PROF.SSA ROSSELLA PISCOPO Indice 1 EQUAZIONI DI I GRADO --------------------------------------------------------------------------------------------------
Unità Didattica N 12 Le equazioni ad una incognita 1. Unità Didattica N 12 Le equazioni ad una incognita
 Unità Didattica N Le equazioni ad una incognita Unità Didattica N Le equazioni ad una incognita ) Equazioni risolubili mediante la decomposizione in fattori ) Equazione biquadratica ) Equazioni irrazionali
Unità Didattica N Le equazioni ad una incognita Unità Didattica N Le equazioni ad una incognita ) Equazioni risolubili mediante la decomposizione in fattori ) Equazione biquadratica ) Equazioni irrazionali
Complementi di algebra
 Complementi di algebra Equazioni di grado superiore al secondo Come per le equazioni di grado, esistono formule risolutive anche per le equazioni di e grado ma non le studieremo perché sono troppo complesse,mentre
Complementi di algebra Equazioni di grado superiore al secondo Come per le equazioni di grado, esistono formule risolutive anche per le equazioni di e grado ma non le studieremo perché sono troppo complesse,mentre
UNITÀ FORMATIVA DISCIPLINARE: N. 9 Titolo: SCOMPOSIZIONI POLINOMI
 UNITÀ FORMATIVA DISCIPLINARE: N. 9 Titolo: SCOMPOSIZIONI POLINOMI N. ore previste 35 Periodo di realizzazione SETTEMBRE OTTOBRE 2017 in termini di competenze, abilità e conoscenze Monomi Polinomi Prodotti
UNITÀ FORMATIVA DISCIPLINARE: N. 9 Titolo: SCOMPOSIZIONI POLINOMI N. ore previste 35 Periodo di realizzazione SETTEMBRE OTTOBRE 2017 in termini di competenze, abilità e conoscenze Monomi Polinomi Prodotti
Equazioni. Le equazioni sono relazioni di uguaglianza tra due espressioni algebriche.
 Equazioni Le equazioni sono relazioni di uguaglianza tra due espressioni algebriche. Nelle espressioni compare una lettera, chiamata incognita. Possiamo attribuire un valore a questa incognita, e vedere
Equazioni Le equazioni sono relazioni di uguaglianza tra due espressioni algebriche. Nelle espressioni compare una lettera, chiamata incognita. Possiamo attribuire un valore a questa incognita, e vedere
Fila A 1. Determina l insieme delle soluzioni reali per ciascuna delle seguenti equazioni:
 LS Fila A Determina l insieme delle soluzioni reali per ciascuna delle seguenti equazioni: NB Ciascun procedimento risolutivo si deve concludere con la frase L'insieme delle soluzioni è a) Trasformando
LS Fila A Determina l insieme delle soluzioni reali per ciascuna delle seguenti equazioni: NB Ciascun procedimento risolutivo si deve concludere con la frase L'insieme delle soluzioni è a) Trasformando
raggruppiamo il quadrato di binomio dividiamo per 0 effettuiamo i calcoli a secondo membro Distinguiamo i tre casi: 2 ± 2 ; 2 = 0 ; + si ottiene, =
 Equazioni di II grado Equazione di II grado completa Un equazione di II grado è un equazione che, ridotta a forma normale, è del tipo ++=0 con 0. Per risolverla occorre calcolare il discriminante dell
Equazioni di II grado Equazione di II grado completa Un equazione di II grado è un equazione che, ridotta a forma normale, è del tipo ++=0 con 0. Per risolverla occorre calcolare il discriminante dell
Prima prova in itinere di Geometria (Corso di laurea in Fisica, Canali A-C e D-O) Prof. Barucci e Piccinni 29 novembre 2011
 Prima prova in itinere di Geometria (Corso di laurea in Fisica, Canali A-C e D-O) Prof Barucci e Piccinni 29 novembre 2011 a Scrivere subito canale, cognome e nome b Utilizzare questi fogli per le risposte
Prima prova in itinere di Geometria (Corso di laurea in Fisica, Canali A-C e D-O) Prof Barucci e Piccinni 29 novembre 2011 a Scrivere subito canale, cognome e nome b Utilizzare questi fogli per le risposte
Liceo Scientifico Statale G. Stampacchia Tricase Tempo di lavoro 80 minuti
 Oggetto: compito in Classe D/PNI Liceo Scientifico Statale G. Stampacchia Tricase Tempo di lavoro 8 minuti Argomenti- Geometria: Risoluzione di problemi di secondo grado con applicazione del teorema di
Oggetto: compito in Classe D/PNI Liceo Scientifico Statale G. Stampacchia Tricase Tempo di lavoro 8 minuti Argomenti- Geometria: Risoluzione di problemi di secondo grado con applicazione del teorema di
ALGEBRA ARGOMENTI COMUNI - INTEGRAZIONI. Pag.1 di 10
 1_ALGECOMUNE Quale tra i seguenti numeri 1 2/5. -4 ¾ appartiene all'insieme N? 2_ALGECOMUNE Dire qual è il grado del 8 3 5 15 seguente monomio: x^3 y^5. 3_ALGECOMUNE L equazione 3 x^2 + 3 x = 0 ammette:
1_ALGECOMUNE Quale tra i seguenti numeri 1 2/5. -4 ¾ appartiene all'insieme N? 2_ALGECOMUNE Dire qual è il grado del 8 3 5 15 seguente monomio: x^3 y^5. 3_ALGECOMUNE L equazione 3 x^2 + 3 x = 0 ammette:
Un monomio è in forma normale se è il prodotto di un solo fattore numerico e di fattori letterali con basi diverse. Tutto quanto sarà detto di
 DEFINIZIONE Espressione algebrica costituita dal prodotto tra una parte numerica (coefficiente) e una o più variabili e/o costanti (parte letterale). Variabili e costanti possono comparire elevate a potenza
DEFINIZIONE Espressione algebrica costituita dal prodotto tra una parte numerica (coefficiente) e una o più variabili e/o costanti (parte letterale). Variabili e costanti possono comparire elevate a potenza
MATEMATICA - LEZIONE 1 ALGEBRA. Relatore prof. re CATELLO INGENITO
 MATEMATICA - LEZIONE ALGEBRA Relatore prof. re CATELLO INGENITO Torna al SOMMARIO Torna al SOMMARIO Sommario della lezione Insiemi numerici e potenze Espressioni algebriche Scomposizione e frazioni algebriche
MATEMATICA - LEZIONE ALGEBRA Relatore prof. re CATELLO INGENITO Torna al SOMMARIO Torna al SOMMARIO Sommario della lezione Insiemi numerici e potenze Espressioni algebriche Scomposizione e frazioni algebriche
Stampa Preventivo. A.S Pagina 1 di 11
 Stampa Preventivo A.S. 2009-2010 Pagina 1 di 11 Insegnante MARINO CRISTINA Classe 2AT Materia matematica preventivo consuntivo 124 0 21. RIPASSO 22. LE EQUAZ. E LE DIS. LINEARI 23. I SISTEMI LINEARI 24.
Stampa Preventivo A.S. 2009-2010 Pagina 1 di 11 Insegnante MARINO CRISTINA Classe 2AT Materia matematica preventivo consuntivo 124 0 21. RIPASSO 22. LE EQUAZ. E LE DIS. LINEARI 23. I SISTEMI LINEARI 24.
Elenco degli argomenti svolti
 Elenco degli argomenti svolti Classi prima A, prima B, prima C, seconda B Giorgio Follo (follogio@libero.it) Istituto Tecnico Agrario G. Penna, Località Viatosto, 54, 14100 Asti - AT Sommario. Vengono
Elenco degli argomenti svolti Classi prima A, prima B, prima C, seconda B Giorgio Follo (follogio@libero.it) Istituto Tecnico Agrario G. Penna, Località Viatosto, 54, 14100 Asti - AT Sommario. Vengono
Equazioni di 2 grado
 Equazioni di grado Tipi di equazioni: Un equazione (ad una incognita) è di grado se può essere scritta nella forma generale (o forma tipica o ancora forma canonica): a b c con a, b e c numeri reali (però
Equazioni di grado Tipi di equazioni: Un equazione (ad una incognita) è di grado se può essere scritta nella forma generale (o forma tipica o ancora forma canonica): a b c con a, b e c numeri reali (però
Esercitazione di Matematica sulle equazioni di secondo grado (o ad esse riconducibili) nel campo reale
 Esercitazione di Matematica sulle equazioni di secondo grado (o ad esse riconducibili) nel campo reale 1. Risolvere, nel campo reale, le seguenti equazioni di secondo grado: (a) 81x 0; (b) (x 1) 7x ; (c)
Esercitazione di Matematica sulle equazioni di secondo grado (o ad esse riconducibili) nel campo reale 1. Risolvere, nel campo reale, le seguenti equazioni di secondo grado: (a) 81x 0; (b) (x 1) 7x ; (c)
UNITÀ 4. DISEQUAZIONI E SISTEMI DI DISEQUAZIONI 1. Generalità e definizioni sulle disequazioni. 2. I principi di equivalenza delle disequazioni. 3.
 UNITÀ. DISEQUAZIONI E SISTEMI DI DISEQUAZIONI. Generalità e definizioni sulle diquazioni.. I principi di equivalenza delle diquazioni.. Diquazioni di primo grado.. Diquazioni con più fattori di primo grado..
UNITÀ. DISEQUAZIONI E SISTEMI DI DISEQUAZIONI. Generalità e definizioni sulle diquazioni.. I principi di equivalenza delle diquazioni.. Diquazioni di primo grado.. Diquazioni con più fattori di primo grado..
Gli insiemi, la logica
 Gli insiemi, la logica 1 Dato l insieme A = {x N : x < 5}, quale delle seguenti affermazioni è falsa: (a) 1 A (b) 5 / A (c) 2 A (d) A (e) {1, } A 2 Sono dati gli insiemi A = {, 5, 7, 9} e B = {5, 7} Quali
Gli insiemi, la logica 1 Dato l insieme A = {x N : x < 5}, quale delle seguenti affermazioni è falsa: (a) 1 A (b) 5 / A (c) 2 A (d) A (e) {1, } A 2 Sono dati gli insiemi A = {, 5, 7, 9} e B = {5, 7} Quali
MATEMATICA A Commissione Albertini, Mannucci, Motta, Zanella Ingegneria Gestionale, Meccanica, Meccatronica, Vicenza
 TEMA ( ) f() = log (determinare il dominio D; calcolare i limiti per che tende agli estremi finiti o infiniti z 4 + (3 + 6i)z + 5 + i = 0. ( + 3 ) α α (log + log + ) d. y = e y, y() = α. TEMA ( ) f() =
TEMA ( ) f() = log (determinare il dominio D; calcolare i limiti per che tende agli estremi finiti o infiniti z 4 + (3 + 6i)z + 5 + i = 0. ( + 3 ) α α (log + log + ) d. y = e y, y() = α. TEMA ( ) f() =
MODULO 3 TITOLO EQUAZIONI E DISEQUAZIONI ALGEBRICHE DI PRIMO GRADO FINALITA OBIETTIVI
 MODULO TITOLO FINALITA EQUAZIONI E DISEQUAZIONI ALGEBRICHE DI PRIMO GRADO Risoluzione delle equazioni e delle disequazioni algebriche di primo grado con una o più incognite e loro applicazioni PREREQUISITI
MODULO TITOLO FINALITA EQUAZIONI E DISEQUAZIONI ALGEBRICHE DI PRIMO GRADO Risoluzione delle equazioni e delle disequazioni algebriche di primo grado con una o più incognite e loro applicazioni PREREQUISITI
= 1 4 = 3. Esempio 2 = 2. Esempio 3. x x. Esempio 4. x x. a. scomporre l equazione in fattori b. applicare la legge dell annullamento del prodotto.
 Equazioni di grado superiore al II Equazioni binomie Un equazione binomia è un equazione che, ridotta a forma normale, è del tipo a n + b 0 Per risolvere una tale equazione, volendo cercare anche le soluzioni
Equazioni di grado superiore al II Equazioni binomie Un equazione binomia è un equazione che, ridotta a forma normale, è del tipo a n + b 0 Per risolvere una tale equazione, volendo cercare anche le soluzioni
RIPASSO PROPEDEUTICO AL V ANNO. Disciplina: MATEMATICA
 RIPASSO PROPEDEUTICO AL V ANNO Disciplina: MATEMATICA Testi consigliati : - BOOK IN PROGRESS MATEMATICA, ALGEBRA PRIMO ANNO, tomo n http://www.itistulliobuzzi.it/buzziwebsite/studenti/matematica/tomo%0_algebra%0buzzi%
RIPASSO PROPEDEUTICO AL V ANNO Disciplina: MATEMATICA Testi consigliati : - BOOK IN PROGRESS MATEMATICA, ALGEBRA PRIMO ANNO, tomo n http://www.itistulliobuzzi.it/buzziwebsite/studenti/matematica/tomo%0_algebra%0buzzi%
1 1, { x1 2x 2 + x 3 = 0 2x 2 8x 3 = 1 x 1 x 4 = = 0
 a.a. 5-6 Esercizi. Sistemi lineari. Soluzioni.. Determinare quali delle quaterne, 3,, sono soluzioni del sistema di tre equazioni in 4 incognite { x x + x 3 = x 8x 3 = x x 4 =. Sol. Sostituendo ad x, x,
a.a. 5-6 Esercizi. Sistemi lineari. Soluzioni.. Determinare quali delle quaterne, 3,, sono soluzioni del sistema di tre equazioni in 4 incognite { x x + x 3 = x 8x 3 = x x 4 =. Sol. Sostituendo ad x, x,
Studio del segno di un prodotto
 Studio del segno di un prodotto Consideriamo una disequazione costituita dal prodotto di più binomi, ad esempio: ( x 1 )( 4 x)( x + 3) > 0 Per risolverla possiamo studiare il segno del prodotto al variare
Studio del segno di un prodotto Consideriamo una disequazione costituita dal prodotto di più binomi, ad esempio: ( x 1 )( 4 x)( x + 3) > 0 Per risolverla possiamo studiare il segno del prodotto al variare
INSIEMI. INSIEME = gruppo di oggetti di tipo qualsiasi detti elementi dell insieme.
 INSIEMI INSIEME = gruppo di oggetti di tipo qualsiasi detti elementi dell insieme. Un insieme è definito quando viene dato un criterio non ambiguo che permette di stabilire se l oggetto appartiene o no
INSIEMI INSIEME = gruppo di oggetti di tipo qualsiasi detti elementi dell insieme. Un insieme è definito quando viene dato un criterio non ambiguo che permette di stabilire se l oggetto appartiene o no
Dr. Erasmo Modica
 UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA EQUAZIONI E DISEQUAZIONI DI PRIMO GRADO Dr. Erasmo Modica erasmo@galois.it IDENTITÀ ED EQUAZIONI Si consideri un uguaglianza
UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA EQUAZIONI E DISEQUAZIONI DI PRIMO GRADO Dr. Erasmo Modica erasmo@galois.it IDENTITÀ ED EQUAZIONI Si consideri un uguaglianza
Ripasso delle matematiche elementari: esercizi proposti
 Ripasso delle matematiche elementari: esercizi proposti I Equazioni e disequazioni algebriche Esercizi sui polimoni.............................. Esercizi sulle equazioni di grado superiore al secondo............
Ripasso delle matematiche elementari: esercizi proposti I Equazioni e disequazioni algebriche Esercizi sui polimoni.............................. Esercizi sulle equazioni di grado superiore al secondo............
LE EQUAZIONI LINEARI LE IDENTITA ( )( ) 5. a Cosa hanno in comune le seguenti uguaglianze? Uguaglianza (1) a
 LE EQUAZIONI LINEARI 1 LE IDENTITA a b = ( a + b)( a b) () 1 a = a + a ( ) ( a + b) = a + ab + b () 3 Cosa hanno in comune le seguenti uguaglianze? Uguaglianza (1) a b = ( a+ b)( a b) È sempre vera qualunque
LE EQUAZIONI LINEARI 1 LE IDENTITA a b = ( a + b)( a b) () 1 a = a + a ( ) ( a + b) = a + ab + b () 3 Cosa hanno in comune le seguenti uguaglianze? Uguaglianza (1) a b = ( a+ b)( a b) È sempre vera qualunque
risoluzione di problemi da risolvere tramite la risoluzione di sistemi ed equazioni di 1^ grado. 5 R ed i Radicali
 ORD. MODULO MODULO ARGOMENTO 1 Disequazioni disequazioni di 1^ grado disequazioni fratte disequazioni di grado superiore da risolvere con la scomposizione in fattori sistemi di disequazioni 2 Geometria
ORD. MODULO MODULO ARGOMENTO 1 Disequazioni disequazioni di 1^ grado disequazioni fratte disequazioni di grado superiore da risolvere con la scomposizione in fattori sistemi di disequazioni 2 Geometria
PROGRAMMA MATEMATICA Classe 1 A AFM anno scolastico
 Classe 1 A AFM anno scolastico 2014-2015 I numeri naturali rappresentazione dei numeri naturali, le quattro operazioni, multipli e divisori di un numero. Criteri di divisibilità, le potenze, le espressioni
Classe 1 A AFM anno scolastico 2014-2015 I numeri naturali rappresentazione dei numeri naturali, le quattro operazioni, multipli e divisori di un numero. Criteri di divisibilità, le potenze, le espressioni
Esercitazione di Matematica per la Classe 3AE - RIPASSO
 Esercitazione di Matematica per la Classe AE - RIPASSO LE EQUAZIONI LINEARI Stabilisci se l equazione assegnata è determinata, indeterminata o impossibile ) ) 8 [indeterminata] [impossibile] Risolvi l
Esercitazione di Matematica per la Classe AE - RIPASSO LE EQUAZIONI LINEARI Stabilisci se l equazione assegnata è determinata, indeterminata o impossibile ) ) 8 [indeterminata] [impossibile] Risolvi l
Programma di Matematica Anno Scolastico 2014/2015 Classe 3M
 Programma di Matematica Anno Scolastico 204/205 Classe 3M Modulo : Richiami calcolo letterale Il prodotto notevole di una somma per una di erenza (a+b)(a (a + b) 2 : Cubo di un binomio (a + b) 3 : b):
Programma di Matematica Anno Scolastico 204/205 Classe 3M Modulo : Richiami calcolo letterale Il prodotto notevole di una somma per una di erenza (a+b)(a (a + b) 2 : Cubo di un binomio (a + b) 3 : b):
3. Equazioni biquadratiche. Il polinomio al primo membro contiene un termine con l incognita elevata al quadrato, un termine con
 UNITÀ EQUAZIONI E SISTEMI DI GRADO SUPERIORE AL SECONDO.. Generalità sulle equazioni di grado superiore al secondo.. Equazioni inomie.. Equazioni iquadratiche.. Equazioni trinomie.. Equazioni che si risolvono
UNITÀ EQUAZIONI E SISTEMI DI GRADO SUPERIORE AL SECONDO.. Generalità sulle equazioni di grado superiore al secondo.. Equazioni inomie.. Equazioni iquadratiche.. Equazioni trinomie.. Equazioni che si risolvono
Equazioni e disequazioni algebriche. Soluzione. Si tratta del quadrato di un binomio. Si ha pertanto. (x m y n ) 2 = x 2m 2x m y n + y 2n
 Si tratta del quadrato di un binomio. Si ha pertanto (x m y n ) 2 = x 2m 2x m y n + y 2n 4. La divisione (x 3 3x 2 + 5x 2) : (x 2) ha Q(x) = x 2 x + 3 e R = 4 Dalla divisione tra i polinomi risulta (x
Si tratta del quadrato di un binomio. Si ha pertanto (x m y n ) 2 = x 2m 2x m y n + y 2n 4. La divisione (x 3 3x 2 + 5x 2) : (x 2) ha Q(x) = x 2 x + 3 e R = 4 Dalla divisione tra i polinomi risulta (x
PROGRAMMA MATEMATICA Classe 1 A AFM anno scolastico
 PROGRAMMA MATEMATICA Classe 1 A AFM anno scolastico 2015-2016 I numeri naturali rappresentazione dei numeri naturali, le quattro operazioni, multipli e divisori di un numero. Criteri di divisibilità, le
PROGRAMMA MATEMATICA Classe 1 A AFM anno scolastico 2015-2016 I numeri naturali rappresentazione dei numeri naturali, le quattro operazioni, multipli e divisori di un numero. Criteri di divisibilità, le
Precorso di Matematica Maria Margherita Obertino Università degli Studi di Torino Di.S.A.F.A.
 Precorso di Matematica Maria Margherita Obertino Università degli Studi di Torino Di.S.A.F.A. Scomposizione dei polinomi in fattori primi ( 2.4 del testo) Equazioni di primo grado ( 3.1 del testo) Equazioni
Precorso di Matematica Maria Margherita Obertino Università degli Studi di Torino Di.S.A.F.A. Scomposizione dei polinomi in fattori primi ( 2.4 del testo) Equazioni di primo grado ( 3.1 del testo) Equazioni
ISTITUTO PROFESSIONALE PER I SERVIZI ALBERGHIERI E DELLA RISTORAZIONE B.BUONTALENTI,V. DE BRUNI, FIRENZE ANNO SCOLASTICO 2015/2016.
 B.BUONTALENTI,V. DE BRUNI, 6-50133 FIRENZE Classe 1 A Richiami di matematica: formazione degli insiemi numerici i numeri naturali, interi, razionali, irrazionali i numeri reali proprietà delle quattro
B.BUONTALENTI,V. DE BRUNI, 6-50133 FIRENZE Classe 1 A Richiami di matematica: formazione degli insiemi numerici i numeri naturali, interi, razionali, irrazionali i numeri reali proprietà delle quattro
Gli insiemi, la logica
 Gli insiemi, la logica 1 Dato l insieme A = {x N : x < 5}, quale delle seguenti affermazioni è falsa: (a) 1 A (b) 5 / A (c) A (d) A risp (e) {1, } A Sono dati gli insiemi A = {, 5, 7, 9} e B = {5, 7} Quali
Gli insiemi, la logica 1 Dato l insieme A = {x N : x < 5}, quale delle seguenti affermazioni è falsa: (a) 1 A (b) 5 / A (c) A (d) A risp (e) {1, } A Sono dati gli insiemi A = {, 5, 7, 9} e B = {5, 7} Quali
Equazioni di secondo grado
 Equazioni di secondo grado Un equazione di secondo grado può sempre essere ridotta nella forma: a + bx + c 0 forma normale con a 0. Le lettere a, b, c sono rappresentano i coefficienti. Solo b e c possono
Equazioni di secondo grado Un equazione di secondo grado può sempre essere ridotta nella forma: a + bx + c 0 forma normale con a 0. Le lettere a, b, c sono rappresentano i coefficienti. Solo b e c possono
Chi non risolve esercizi non impara la matematica.
 60 equazioni di secondo grado Esercizio 7. Scomponi + +. Soluzione. Poiché = = = < 0, l equazione associata è impossibile e il trinomio è irriducibile (tabella )..5 esercizi hi non risolve esercizi non
60 equazioni di secondo grado Esercizio 7. Scomponi + +. Soluzione. Poiché = = = < 0, l equazione associata è impossibile e il trinomio è irriducibile (tabella )..5 esercizi hi non risolve esercizi non
Equazioni di primo grado
 Equazioni di primo grado 15 15.1 Identità ed equazioni Analizziamo le seguenti proposizioni: a ) cinque è uguale alla differenza tra sette e due ; b ) la somma di quattro e due è uguale a otto ; c ) il
Equazioni di primo grado 15 15.1 Identità ed equazioni Analizziamo le seguenti proposizioni: a ) cinque è uguale alla differenza tra sette e due ; b ) la somma di quattro e due è uguale a otto ; c ) il
01) Identità ed equazioni 02) Equazione di primo grado ad una incognita 03) Equazione di primo grado frazionarie
 Unità Didattica N 07 Le equazioni di primo grado ad una incognita 6 U.D. N 07 Le equazioni di primo grado ad una incognita 0) Identità ed equazioni 0) Equazione di primo grado ad una incognita 0) Equazione
Unità Didattica N 07 Le equazioni di primo grado ad una incognita 6 U.D. N 07 Le equazioni di primo grado ad una incognita 0) Identità ed equazioni 0) Equazione di primo grado ad una incognita 0) Equazione
Liceo scientifico Leonardo da Vinci PROGRAMMA DI MATEMATICA ANNO SCOLASTICO 2013/2014 II A LE EQUAZIONI LINEARI
 Liceo scientifico Leonardo da Vinci PROGRAMMA DI MATEMATICA ANNO SCOLASTICO 2013/2014 II A LE EQUAZIONI LINEARI Le identità; Le equazioni; Le equazioni equivalenti; I principi di equivalenza; Le equazioni
Liceo scientifico Leonardo da Vinci PROGRAMMA DI MATEMATICA ANNO SCOLASTICO 2013/2014 II A LE EQUAZIONI LINEARI Le identità; Le equazioni; Le equazioni equivalenti; I principi di equivalenza; Le equazioni
LICEO STATALE G. MAZZINI
 LICEO STATALE G. MAZZINI LICEO LINGUISTICO LICEO DELLE SCIENZE UMANE LICEO DELLE SCIENZE UMANE OPZIONE ECONOMICO-SOCIALE Viale Aldo Ferrari, 37 Tel. 0187 743000 19122 La Spezia Fax 0187 743208 C.F. 80011230119
LICEO STATALE G. MAZZINI LICEO LINGUISTICO LICEO DELLE SCIENZE UMANE LICEO DELLE SCIENZE UMANE OPZIONE ECONOMICO-SOCIALE Viale Aldo Ferrari, 37 Tel. 0187 743000 19122 La Spezia Fax 0187 743208 C.F. 80011230119
Disequazioni. 3 Liceo Scientifico 3 Liceo Scientifico sez. Scienze Applicate A.S. 2016/2017 Prof. Andrea Pugliese
 Disequazioni 3 Liceo Scientifico 3 Liceo Scientifico sez. Scienze Applicate A.S. 2016/2017 Prof. Andrea Pugliese Definizione ed esempi Date due espressioni algebriche A e B contenenti numeri e lettere
Disequazioni 3 Liceo Scientifico 3 Liceo Scientifico sez. Scienze Applicate A.S. 2016/2017 Prof. Andrea Pugliese Definizione ed esempi Date due espressioni algebriche A e B contenenti numeri e lettere
Prerequisiti di Matematica Espressioni algebriche
 Prerequisiti di Matematica Espressioni algebriche Annalisa Amadori e Benedetta Pellacci amadori@uniparthenope.it pellacci@uniparthenope.it Università di Napoli Parthenope Un' espressione in cui uno o più
Prerequisiti di Matematica Espressioni algebriche Annalisa Amadori e Benedetta Pellacci amadori@uniparthenope.it pellacci@uniparthenope.it Università di Napoli Parthenope Un' espressione in cui uno o più
Titolo: CALCOLO LETTERALE: SCOMPOSIZIONI E FRAZIONI ALGEBRICHE. N. ore previste 35 Periodo di realizzazione: settembre /novembre
 ISTITUTO DI ISTRUZIONE SUPERIORE I.P.S.I.A. INVERUNO Via G. Marcora,109 20010 INVERUNO (MI) C. F. 93018890157 - c.c.postale n. 24295248 - cod. mec. MIIS016005 + 39 02 97288182 + 39 02 97285314 fax + 39
ISTITUTO DI ISTRUZIONE SUPERIORE I.P.S.I.A. INVERUNO Via G. Marcora,109 20010 INVERUNO (MI) C. F. 93018890157 - c.c.postale n. 24295248 - cod. mec. MIIS016005 + 39 02 97288182 + 39 02 97285314 fax + 39
Studi di funzione. D. Barbieri. Studiare comportamento asintotico e monotonia di. f(x) = 1 x x4 + 4x e x
 Studi di funzione D. Barbieri Esercizi Esercizio Esercizio Studiare comportamento asintotico e monotonia di f(x) = x + x4 + 4x Studiare il comportamento asintotico di f(x) = + x x + + e x Esercizio 3 Determinare
Studi di funzione D. Barbieri Esercizi Esercizio Esercizio Studiare comportamento asintotico e monotonia di f(x) = x + x4 + 4x Studiare il comportamento asintotico di f(x) = + x x + + e x Esercizio 3 Determinare
Equazioni differenziali
 Equazioni differenziali In un equazione differenziale l incognita da trovare è una funzione, di cui è data, dall equazione, una relazione con le sue derivate (fino ad un certo ordine) e la variabile libera:
Equazioni differenziali In un equazione differenziale l incognita da trovare è una funzione, di cui è data, dall equazione, una relazione con le sue derivate (fino ad un certo ordine) e la variabile libera:
Dott. Marta Ruspa 0321/ /
 FISICA APPLICATA Dott. Marta Ruspa ruspa@med.unipmn.it 0321/660669 011/6707310 Lezione I 1 CORSO INTEGRATO DI SCIENZE FISICHE e STATISTICHE Discipline: FISICA APPLICATA STATISTICA INFORMATICA Lezione I
FISICA APPLICATA Dott. Marta Ruspa ruspa@med.unipmn.it 0321/660669 011/6707310 Lezione I 1 CORSO INTEGRATO DI SCIENZE FISICHE e STATISTICHE Discipline: FISICA APPLICATA STATISTICA INFORMATICA Lezione I
Indice. Prefazione. Fattorizzazione di A + B Fattorizzazione di trinomi particolari 22 2
 Prefazione XI Test di ingresso 1 Capitolo 1 Insiemi numerici, intervalli e intorni 5 1.1 Introduzione 5 1.2 Insiemi generici 5 1.2.1 Relazioni e operazioni tra insiemi 7 1.3 Insiemi numerici 8 1.3.1 Rappresentazione
Prefazione XI Test di ingresso 1 Capitolo 1 Insiemi numerici, intervalli e intorni 5 1.1 Introduzione 5 1.2 Insiemi generici 5 1.2.1 Relazioni e operazioni tra insiemi 7 1.3 Insiemi numerici 8 1.3.1 Rappresentazione
SCOMPOSIZIONE IN FATTORI PRIMI Di un Polinomio
 SCOMPOSIZIONE IN FATTORI PRIMI Di un Polinomio 1 Ripassiamo i prodotti notevoli NOME TIPO SVILUPPO Quadrato di un binomio ( a + b ) 2 a 2 + 2ab + b 2 Cubo di un binomio ( a + b ) 3 a 3 + 3a 2 b +3ab 2
SCOMPOSIZIONE IN FATTORI PRIMI Di un Polinomio 1 Ripassiamo i prodotti notevoli NOME TIPO SVILUPPO Quadrato di un binomio ( a + b ) 2 a 2 + 2ab + b 2 Cubo di un binomio ( a + b ) 3 a 3 + 3a 2 b +3ab 2
2.3 Risposte commentate
 2.3 Risposte commentate 2.1.1 A = 7 4. Nota. Il calcolo poteva essere effettuato mediante sostituzione diretta nell espressione data, oppure osservando preliminarmente che l espressione può essere semplificata
2.3 Risposte commentate 2.1.1 A = 7 4. Nota. Il calcolo poteva essere effettuato mediante sostituzione diretta nell espressione data, oppure osservando preliminarmente che l espressione può essere semplificata
PROGRAMMAZIONE DIPARTIMENTO MATEMATICA CLASSI SECONDE A.S
 Progettazione Disciplinare PROGRAMMAZIONE di DIPARTIMENTO di MATEMATICA CLASSI SECONDE A.S. 2018 2019 Rev. 0 del 08-03-04 pag. 1 di 11 Progettazione Disciplinare SCOMPORRE POLINOMI E RISOLVERE EQUAZIONI
Progettazione Disciplinare PROGRAMMAZIONE di DIPARTIMENTO di MATEMATICA CLASSI SECONDE A.S. 2018 2019 Rev. 0 del 08-03-04 pag. 1 di 11 Progettazione Disciplinare SCOMPORRE POLINOMI E RISOLVERE EQUAZIONI
Liceo Scientifico Statale G. Stampacchia Tricase
 Liceo Scientifico Statale G. Stampacchia Tricase Oggetto: Test di ingresso Conoscenze e competenze sul programma previsto nella classe seconda del Liceo Scientifico. Algebra Q) Ordinare in forma crescente
Liceo Scientifico Statale G. Stampacchia Tricase Oggetto: Test di ingresso Conoscenze e competenze sul programma previsto nella classe seconda del Liceo Scientifico. Algebra Q) Ordinare in forma crescente
Il concetto delle equazioni reciproche risale ad A. De Moivre ( ) ed il nome è dovuto a L. Euler ( ).
 Il concetto delle equazioni reciproche risale ad A. De Moivre (1667-1754) ed il nome è dovuto a L. Euler (1707-1783). Girard nel 1629 enunciò, e Gauss poi dimostrò rigorosamente nel 1799, che un equazione
Il concetto delle equazioni reciproche risale ad A. De Moivre (1667-1754) ed il nome è dovuto a L. Euler (1707-1783). Girard nel 1629 enunciò, e Gauss poi dimostrò rigorosamente nel 1799, che un equazione
PROGRAMMA DIDATTICO CONSUNTIVO CLASSE 2GL
 Anno Scolastico 2018/2019 PROGRAMMA DIDATTICO CONSUNTIVO CLASSE 2GL Docente/i MARIANGELA MASSELLA Disciplina MATEMATICA Unità di Lavoro 0: Ripasso - le equazioni di primo grado fratte e letterali : Settembre-ottobre
Anno Scolastico 2018/2019 PROGRAMMA DIDATTICO CONSUNTIVO CLASSE 2GL Docente/i MARIANGELA MASSELLA Disciplina MATEMATICA Unità di Lavoro 0: Ripasso - le equazioni di primo grado fratte e letterali : Settembre-ottobre
I sistemi di secondo grado sono dunque composti da un equazione di secondo grado e da una di primo grado.
 Sistemi non lineari Sistemi di secondo grado Ricordiamo che un sistema di equazioni non è altro che l insieme di più equazioni con le stesse incognite L insieme delle soluzioni è dato dall intersezione
Sistemi non lineari Sistemi di secondo grado Ricordiamo che un sistema di equazioni non è altro che l insieme di più equazioni con le stesse incognite L insieme delle soluzioni è dato dall intersezione
Esercizi sulle Disequazioni
 Esercizi sulle Disequazioni Esercizio Trovare le soluzioni delle seguenti disequazioni:.).).).) ).) ) ).).7) 8.8).) Esercizio Trovare le soluzioni delle seguenti disequazioni tratte dal secondo parziale
Esercizi sulle Disequazioni Esercizio Trovare le soluzioni delle seguenti disequazioni:.).).).) ).) ) ).).7) 8.8).) Esercizio Trovare le soluzioni delle seguenti disequazioni tratte dal secondo parziale
LICEO SCIENTIFICO STATALE G. GALILEI - SIENA
 LICEO SCIENTIFICO STATALE G. GALILEI - SIENA PROGRAMMA DI MATEMATICA SVOLTO NELLA CLASSE 2 sez.e RICHIAMI DI ALGEBRA * prodotti notevoli * scomposizione di un polinomio in fattori * frazioni algebriche
LICEO SCIENTIFICO STATALE G. GALILEI - SIENA PROGRAMMA DI MATEMATICA SVOLTO NELLA CLASSE 2 sez.e RICHIAMI DI ALGEBRA * prodotti notevoli * scomposizione di un polinomio in fattori * frazioni algebriche
Liceo G.B. Vico Corsico a.s
 Liceo G.B. Vico Corsico a.s. 2018-19 Programma svolto durante l anno scolastico Classe: 2^B Materia: Matematica Insegnante: Tommaseo Paola Testo utilizzato: Matematica multimediale.blu con TUTOR vol. 1
Liceo G.B. Vico Corsico a.s. 2018-19 Programma svolto durante l anno scolastico Classe: 2^B Materia: Matematica Insegnante: Tommaseo Paola Testo utilizzato: Matematica multimediale.blu con TUTOR vol. 1
SISTEMI DI EQUAZIONI LINEARI
 SISTEMI DI EQUAZIONI LINEARI Date le rette di equazioni ax + by + c = 0 e a x + b y + c = 0 quanti punti hanno in comune? Per rispondere devo risolvere il sistema ax + by + c = 0 ቊ a x + b y + c = 0 e
SISTEMI DI EQUAZIONI LINEARI Date le rette di equazioni ax + by + c = 0 e a x + b y + c = 0 quanti punti hanno in comune? Per rispondere devo risolvere il sistema ax + by + c = 0 ቊ a x + b y + c = 0 e
Elementi sulle diseguaglianze tra numeri relativi
 Elementi sulle diseguaglianze tra numeri relativi Dati due numeri disuguali a e b risulta a>b oppure ao oppure a-b
Elementi sulle diseguaglianze tra numeri relativi Dati due numeri disuguali a e b risulta a>b oppure ao oppure a-b
P R O G R A M M A ANNO SCOLASTICO 2016/2017 SEDE: I.T.I. MARCONI. materia: MATEMATICA. classe: 1 elettronici sezione P. professori : Gallo Raffaelina
 P R O G R A M M A ANNO SCOLASTICO 2016/2017 SEDE: I.T.I. MARCONI materia: MATEMATICA classe: 1 elettronici sezione P professori : Gallo Raffaelina ALGEBRA DEI NUMERI NOZIONI FONDAMENTALI -nozioni fondamentali
P R O G R A M M A ANNO SCOLASTICO 2016/2017 SEDE: I.T.I. MARCONI materia: MATEMATICA classe: 1 elettronici sezione P professori : Gallo Raffaelina ALGEBRA DEI NUMERI NOZIONI FONDAMENTALI -nozioni fondamentali
Precorso di Matematica
 UNIVERSITÀ DEGLI STUDI ROMA TRE FACOLTA DI ARCHITETTURA Precorso di Matematica Anna Scaramuzza Anno Accademico 2005-2006 4-10 Ottobre 2005 INDICE 1. ALGEBRA................................. 3 1.1 Equazioni
UNIVERSITÀ DEGLI STUDI ROMA TRE FACOLTA DI ARCHITETTURA Precorso di Matematica Anna Scaramuzza Anno Accademico 2005-2006 4-10 Ottobre 2005 INDICE 1. ALGEBRA................................. 3 1.1 Equazioni
CLASSE 1 SEZIONE A PROGRAMMA DI MATEMATICA DOCENTE ENRICO PILI
 ISTITUTO D ISTRUZIONE SECONDARIA SUPERIORE I.T.C.G. L. EINAUDI LICEO SCIENTIFICO G. BRUNO CLASSE 1 SEZIONE A PROGRAMMA DI MATEMATICA DOCENTE ENRICO PILI ANNO SCOLASTICO 2016/2017 RICHIAMI DI ARITMETICA
ISTITUTO D ISTRUZIONE SECONDARIA SUPERIORE I.T.C.G. L. EINAUDI LICEO SCIENTIFICO G. BRUNO CLASSE 1 SEZIONE A PROGRAMMA DI MATEMATICA DOCENTE ENRICO PILI ANNO SCOLASTICO 2016/2017 RICHIAMI DI ARITMETICA
EQUAZIONI E SISTEMI DI 2 GRADO
 EQUAZIONI E SISTEMI DI GRADO Prof. Domenico RUGGIERO In questa breve trattazione vengono esposti la formula risolutiva di equazioni di secondo grado ed il procedimento risolutivo, per sotituzione, di sistemi
EQUAZIONI E SISTEMI DI GRADO Prof. Domenico RUGGIERO In questa breve trattazione vengono esposti la formula risolutiva di equazioni di secondo grado ed il procedimento risolutivo, per sotituzione, di sistemi
Esercizio 1. Per quali valori di h e k le seguenti funzione sono derivabili? x 3 sin 1 x 0. 0 x = 0. x cos 1 x > 0
 Sapienza Università di Roma - Facoltà I3S Corso di Laurea in Statistica Economia Finanza e Assicurazioni Corso di Laurea in Statistica Economia e Società Corso di Laurea in Statistica gestionale Matematica
Sapienza Università di Roma - Facoltà I3S Corso di Laurea in Statistica Economia Finanza e Assicurazioni Corso di Laurea in Statistica Economia e Società Corso di Laurea in Statistica gestionale Matematica
P R O G R A M M A ANNO SCOLASTICO 2017/18 SEDE: I.T.I. MARCONI. materia: MATEMATICA. classe: 1 elettronici sezione P. professori : Gallo Raffaelina
 P R O G R A M M A ANNO SCOLASTICO 2017/18 SEDE: I.T.I. MARCONI materia: MATEMATICA classe: 1 elettronici sezione P professori : Gallo Raffaelina ALGEBRA DEI NUMERI NOZIONI FONDAMENTALI -nozioni fondamentali
P R O G R A M M A ANNO SCOLASTICO 2017/18 SEDE: I.T.I. MARCONI materia: MATEMATICA classe: 1 elettronici sezione P professori : Gallo Raffaelina ALGEBRA DEI NUMERI NOZIONI FONDAMENTALI -nozioni fondamentali
PROGRAMMAZIONE DISCIPLINARE INDIVIDUALE a. s. 2013/2014. Elenco moduli Argomenti Strumenti / Testi / Letture
 Pagina 1 di 6 DISCIPLINA: MATEMATICA CLASSE: II TU DOCENTE : Cornelio Terreni Elenco moduli Argomenti Strumenti / Testi / Letture 1 Equazioni numeriche. RIPASSO di: equazioni e Testo classe Prima. principi
Pagina 1 di 6 DISCIPLINA: MATEMATICA CLASSE: II TU DOCENTE : Cornelio Terreni Elenco moduli Argomenti Strumenti / Testi / Letture 1 Equazioni numeriche. RIPASSO di: equazioni e Testo classe Prima. principi
Dunque l equazione ammette le soluzioni:
 Risolubilità delle equazioni algebriche in campo complesso Es.1 (tema d esame 10 gennaio 2013). Determinare le soluzioni dell equazione algebrica (z 3 + 2 3 i)(z 2 2iz) = 0. È un equazione algebrica di
Risolubilità delle equazioni algebriche in campo complesso Es.1 (tema d esame 10 gennaio 2013). Determinare le soluzioni dell equazione algebrica (z 3 + 2 3 i)(z 2 2iz) = 0. È un equazione algebrica di
