LEZIONE 20. è lineare. Per la commutatività del prodotto scalare segue anche la linearità dell applicazione
|
|
|
- Elvira Boni
- 7 anni fa
- Visualizzazioni
Transcript
1 LEZIONE Prodotti sclri. Definizione Si V uno spzio vettorile su R. Un prodotto sclre su V è un ppliczione tle che:, : V V R (v 1, v 2 ) v 1, v 2 (PS1) per ogni v 1, v 2 V si h v 1, v 2 = v 2, v 1 (il prodotto sclre è commuttivo); (PS2) per ogni v 1, v 2, v 3 V si h v 1, v 2 + v 3 = v 1, v 2 + v 1, v 3 (il prodotto sclre è distributivo rispetto ll somm); (PS3) per ogni α R e v 1, v 2 V si h α v 1, v 2 = αv 1, v 2 ; (PS4) per ogni v V \ { 0 V } si h v, v > 0 (il prodotto sclre è definito positivo). Osservzione Si V uno spzio vettorile su R. lcune ovvie proprietà dei prodotti sclri su V. i) Si v 0 V fissto. Allor l ppliczioni Elenchimo di seguito, v 0 : V R v v, v 0 è linere. Per l commuttività del prodotto sclre segue nche l linerità dell ppliczione v 0, : V R v v 0, v. Per quest doppi proprietà di linerità si dice spesso che il prodotto sclre è un ppliczione bilinere. ii) Si h llor che 0, v = v, 0 = 0 per ogni v V : in prticolre v, v = 0 se e solo se v = 0. iii) Chirmente se W V è un sottoinsieme h senso considerre l restrizione, W W, che è un prodotto sclre su W. 1 Typeset by AMS-TEX
2 PRODOTTI SCALARI Definizione Si V uno spzio vettorile su R munito di prodotto sclre,. Per ogni v V il numero v = v, v si dice modulo di v: i vettori di modulo 1 si dicono versori. Esempio Nello spzio V 3 (O) dei vettori pplicti in O si può definire un prodotto sclre in V 3 (O) ponendo ( ) v, w = v w cos( v w) per ogni coppi di vettori v, w V 3 (O) non nulli. Se O ı j k è un fissto sistem di riferimento nello spzio e v = v x ı + v y j + v z k, w = wx ı + w y j + w z k, è noto che v, w = v x w x + v y w y + v z w z. Esempio Si V = R n. Se x = (x 1,..., x n ) e y = (y 1,..., y n ) si definisce prodotto sclre stndrd Si noti che in tl cso risult x, y = x 1 y x n y n. x, y = x t y = xi n t y come prodotto di mtrici. Il ftto che tle ppliczione soddisfi le prorietà (PS1), (PS2) e (PS3) è evidente dll definizione. Per qunto rigurd l proprietà (PS4) si noti che x, x = x x 2 n : m un somm di numeri reli non negtivi, come lo sono i qudrti di numeri reli, è non negtiv ed è null se e solo se tutti gli ddendi sono nulli. Si noti che questo non è l unico possibile prodotto sclre che possimo definire su R n. Per esempio si verifichi che l ppliczione ((x 1, x 2 ), (y 1, y 2 )) 3x 1 y 1 + x 2 y 2 /2 è un prodotto sclre in R 2 diverso dl prodotto stndrd. Si noti che ( ) ( ) 3 0 y1 3x 1 y 1 + x 2 y 2 /2 = ( x 1 x 2 ). 0 1/4 Si V uno spzio vettorile su R munito di prodotto sclre,. Se v, w V \ { 0 V }, per ogni t R si h v 2 2t v, w + t 2 w 2 = v tw, v tw 0. Il primo membro di tle trinomio non può vere rdici distinte, dovendo ltrimenti cmbire di segno, quindi v, w 2 v 2 w 2 0: essendo v, w > 0 segue llor l cosiddett disuguglinz di Cuchy Schwrtz. y 2
3 LEZIONE 20 3 Proposizione Si V uno spzio vettorile su R munito di prodotto sclre,. Per ogni v, w V ( ) v, w v w Inoltre vle l uguglinz in ( ) se e solo se v e w sono proporzionli. Dimostrzione. Rimne d dimostrre l second ffermzione. Vle l uguglinz in ( ) se e solo se l equzione v 2 2t v, w +t 2 w 2 = 0 h soluzione, ovvero se e solo se v tw, v tw = 0 h soluzione, cioè se e solo se v = tw. Osservzione Si V uno spzio vettorile su R munito di prodotto sclre,. i) Se v, w V \ { 0 V } llor 1 v, w v w 1 : possimo perciò definire l ngolo fr v e w come ( ) v, w vw = rccos. v w Si h quindi v, w = v w cos( vw) che generlizz l ( ) prodotti sclri qulsisi. ii) Sempre d ricvimo l disuguglinz tringolre: v + w 2 = v + w, v + w = v 2 + v, w + w, v + w 2 = = v v, w + w 2 v v, w + w 2 v v w + w 2 = ( v + w ) 2, quindi v + w v + w. In modo nlogo verificre che v w v w. Esempio Si I = [, b] R non vuoto e si consideri nello spzio C 0 (I) l ppliczione f, g = b f(x)g(x)dx. Che le proprietà di prodotto sclre (PS1), (PS2), (PS3) sino soddisftte è ovvio. Inoltre il teorem dell permnenz del segno per funzioni continue ci ssicur che nche l condizione (PS4) è soddisftt. In questo cso l disuguglinz di Cuchy Schwrtz diviene b b b f(x)g(x)dx f(x) 2 dx g(x) 2 dx.
4 BASI ORTONORMALI Per ogni f C 0 (I) l quntità b f 2 = f(x) 2 dx viene dett norm L 2 di f Bsi ortonormli. Definizione Si V uno spzio vettorile su R munito di prodotto sclre,. I vettori v 1, v 2 V si dicono ortogonli (o perpendicolri) se v 1, v 2 = 0 ed in tl cso si scrive v 1 v 2. L insieme { v 1,..., v n } V si dice ortogonle se v i v j per i, j I con i j. L insieme { v 1,..., v n } V si dice ortonormle se è ortogonle ed i v i sono versori. Se V è finitmente generto, un bse ortonormle B = (v 1,..., v n ) è un bse di V tle che l insieme { v 1,..., v n } si ortonormle. In bse ll definizione concludimo che l insieme { v 1,..., v n } V è ortonormle se per ogni i, j = 1,..., n { 1 i = j, v i, v j = δ i,j = 0 i j. Esempio Si fissi un sistem di riferimento O ı j k nello spzio. Allor l insieme { ı, j, k } è ortonormle in V 3 (O) rispetto l prodotto sclre geometrico (si ved l Esempio ). Si noti che B = ( ı, j, k ) viene quindi d essere un bse ortonormle di V 3 (O). Esempio Si consideri lo spzio R n munito del prodotto sclre, definito nell Esempio Allor i vettori dell bse cnonic formno un insieme { e 1,..., e n } ortonormle: perciò l bse cnonic C = (e 1,..., e n ) è un bse ortonormle. Invece { e 1, e 2 } non è ortonormle rispetto l prodotto sclre ((x 1, x 2 ), (y 1, y 2 )) 3x 1 y 1 + x 2 y 2 /2 introdotto nello stesso esempio. Inftti è vero che e 1 e 2 m e 1 = 3 e e 2 = 1/ 2. Concludimo che, rispetto tle prodotto sclre, { e 1 / 3, 2e 2 } è ortonormle.
5 LEZIONE 20 5 Esempio Si consideri lo spzio V delle funzioni continue e periodiche di periodo 2π. Per esempio 1, cos px, sin px V per ogni p N (si noti che sin px e cos px hnno periodo minimo 2π/p). In V definimo f, g = 1 π π π f(x)g(x)dx : è fcile verificre che, è un prodotto sclre. Inoltre dll nlisi è noto che 1/ 2, 1/ 2 = 1 { 1 se p = q 0, cos px, cos qx = 0 se p q, sin px, cos qx = 0 { 1 se p = q 0, sin px, sin qx = 0 se p q, quindi, per ogni N N, l insieme { 1/ 2, cos px, sin qx } p,q=1,...,n è ortonormle. Abbimo visto che in tutti gli esempi trttti è sempre possibile determinre un bse ortonormle. Di ftto questo è un risultto generle che si può dimostrre in modo lgoritmico con il metodo di ortonormlizzzione di Grm Schmidt. Ci limiteremo d enuncire il seguente risultto. Proposizione Si V { 0 V } uno spzio vettorile finitmente generto su R munito di prodotto sclre,. Allor esistono in V bsi ortonormli. L importnz ed utilità delle bsi ortonormli è dt dll seguente Proposizione Si V uno spzio vettorile su R munito di prodotto sclre,. Si { v 1,..., v n } V è un insieme ortonormle. Allor: i) v 1,..., v n sono linermente indipendenti; ii) se V è finitmente generto e dim R (V ) = n, llor B = (v 1..., v n ) è un bse ortonormle di V e si h v = v, v 1 v v, v n v n per ogni v V. Dimostrzione. Per definizione { v 1,..., v n } V è un insieme di vettori ortonormli se e solo se { 0 se i j, v i, v j = 1 se i = j, quindi, se α 1 v α n v n = 0 è un relzione di dipendenz linere, si h 0 = 0, v j = α 1 v α n v n, v j = α 1 v 1, v j + + α n v n, v j = α j. In prticolre v 1,..., v n sono linermente indipendenti. Se V è finitmente generto e dim R (V ) = n, per l Proposizione , segue che B è un bse di V.
6 BASI ORTONORMALI In prticolre per ogni v V esistono α 1,..., α n R tli che v = α 1 v α n v n. Quindi v, v j = α 1 v α n v n, v j = α 1 v 1, v j + + α n v n, v j = α j per ogni j = 1,..., n. Il coefficiente v, v j viene spesso detto coefficiente di Fourier (di v rispetto v j ). Esempio Si consideri lo spzio R 3 munito del prodotto sclre, definito nell Esempio I tre vettori v 1 = 1/3(2, 2, 1), v 2 = 1/3(1, 2, 2) e v 3 = 1/3( 2, 1, 2) formno un insieme { v 1, v 2, v 3 } ortonormle, quindi B = (v 1, v 2, v 3 ) è un bse di R 3. Si v = (1, 1, 1) R 3. Allor v, v 1 = 5/3, v, v 2 = v, v 3 = 1/3: quindi, come è nche fcile verificre direttmente, risult v = 5 3 v v v Mtrici ortogonli. Fccimo un breve digressione su un importnte fmigli di mtrici, quelle ortogonli. Definizione P R n,n si dice ortogonle se t P P = I n. Prim di dre esempi di mtrici ortogonli, fccimo lcune osservzioni. Osservzione Si noti che l mtrice identità I n è ortogonle in bse ll definizione dt: nche ogni mtrice ottenut d I n cmbindo segno d un o più delle sue entrte è ortogonle. Si P R n,n ortogonle. i) Poiché t P P = I n, segue che P è invertibile e P 1 = t P : in prticolre si h nche P t P = I n. In mnier nlog si dimostr che se P t P = I n llor nche t P P = I n, cioè P è ortogonle se e solo se P t P = I n. ii) Si h 1 = det(i n ) = det( t P P ) = det( t P ) det(p ) = det(p ) 2, dunque det(p ) = ±1: qunto sopr osservto sull mtrice identità ci permette di ffermre che esistono mtrici di entrmbe i tipi. iii) Poiché l rig i esim di t P è l colonn i esim P i di P, l condizione t P P = I n si può leggere dicendo che il prodotto sclre stndrd (si ved l Esempio con l solit identificzione di R n con R n,1 ) delle colonne P i e P j di P è δ i,j : in ltre prole un mtrice è ortogonle se e solo se le sue colonne sono un insieme ortonormle, rispetto l prodotto sclre stndrd, di n vettori di R n,1. iv) In mnier simile, poiché nche P t P = I n, nche le righe di P formno un insieme ortonormle, rispetto l prodotto sclre stndrd, di n vettori di R 1,n.
7 LEZIONE 20 7 Le mtrici ortogonli si dividono, quindi, in due clssi non vuote, quelle con determinnte 1 e quelle con determinnte 1. H senso dre un nome questi due tipi di mtrici. Definizione Si P R n,n ortogonle. P si dice specile se det(p ) = 1 non specile det(p ) = 1. Grzie qunto osservto sopr, simo perciò in grdo di dre esempi non bnli di mtrici ortogonli. Esempio Le mtrici di R 3,3 P 1 = , P 2 = , sono ortogonli. L prim è non specile, l second specile. Esempio Determinimo tutte le mtrici ortogonli d ordine 2. Si ( ) p1,1 p P = 1,2 R 2,2 p 2,1 p 2,2 ortogonle. L condizione P t P = I 2 si trduce llor nel sistem p 2 1,1 + p 2 1,2 = 1 p 1,1 p 2,1 + p 1,2 p 2,2 = 0 p 2 2,1 + p 2 2,2 = 1. L prim e l terz equzione implicno l esistenz di ϑ, ϕ [0, 2π] tli che p 1,1 = cos ϑ, p 1,2 = sin ϑ, p 2,1 = sin ϕ, p 2,2 = cos ϕ. L second equzione è llor equivlente 0 = cos ϑ sin ϕ sin ϑ cos ϕ = sin(ϕ ϑ). In prticolre, meno di multipli di 2π, si deve vere o ϕ = ϑ ovvero ϕ = ϑ + π. Nel primo cso ( ) cos ϑ sin ϑ P =, sin ϑ cos ϑ (in tl cso P è ortogonle specile) nel secondo ( ) cos ϑ sin ϑ P = sin ϑ cos ϑ (in tl cso P è ortogonle non specile). Ricordimo un interpretzione geometric delle mtrici ortogonli specili già vist ll inizio del corso. Considerimo nel pino due sistemi di riferimento O ı j,
8 MATRICI ORTOGONALI O ı j e si ψ l ngolo misurto in senso ntiorrio fr i versori ı e ı. Allor si deve vere ı = ı + b j, j = c ı + d j e si h, per l Proposizione ii), = ı, ı = cos ψ, b = ı, j = sin ψ, c = j, ı = sin ψ, d = j, j = cos ψ. Se or considero v = x ı + y j = x ı + y j, sostituendo le espressioni ottenute sopr di ı e j in funzione di ı e j, tenendo conto che ( ı, j ) è un bse di V 2 (O), si ottiene ( ) ( ) ( ) x cos ψ sin ψ x y =. sin ψ cos ψ y Concludimo che le mtrici ortogonli specili corrispondono lle rotzioni nel pino. Per questo spesso indichimo con R ψ l mtrice ( cos ψ sin ψ sin ψ cos ψ Un nlog interpretzione può essere dt per mtrici ortogonli in R n,n con n 3. ).
LEZIONE 24. è lineare. Per la commutatività del prodotto scalare segue anche la linearità dell applicazione
 LEZIONE 24 24.1. Prodotti sclri. Definizione 24.1.1. Si V uno spzio vettorile su R. un ppliczione Un prodotto sclre su V è tle che:, : V V R (v 1, v 2 ) v 1, v 2 (PS1) per ogni v 1, v 2 V si h v 1, v 2
LEZIONE 24 24.1. Prodotti sclri. Definizione 24.1.1. Si V uno spzio vettorile su R. un ppliczione Un prodotto sclre su V è tle che:, : V V R (v 1, v 2 ) v 1, v 2 (PS1) per ogni v 1, v 2 V si h v 1, v 2
11. Rango di una matrice.
 Rngo di un mtrice Considerimo un mtrice di tipo m n d elementi reli rppresentt nel modo seguente: A = (m-) m (m-) m (m-) m (m-) m (n-) (n-) (n-) (m-),(n-) m(n-) n n n (m-)n mn Per ogni i =,,,, (m-), m,
Rngo di un mtrice Considerimo un mtrice di tipo m n d elementi reli rppresentt nel modo seguente: A = (m-) m (m-) m (m-) m (m-) m (n-) (n-) (n-) (m-),(n-) m(n-) n n n (m-)n mn Per ogni i =,,,, (m-), m,
8. Prodotto scalare, Spazi Euclidei.
 8. Prodotto sclre, Spzi Euclidei. Ricordimo l definizione di prodotto sclre di due vettori del pino VO 2 (vle in modo del tutto nlogo nche in VO 3 ). Definizione: Sino v, w VO 2 e si θ l ngolo convesso
8. Prodotto sclre, Spzi Euclidei. Ricordimo l definizione di prodotto sclre di due vettori del pino VO 2 (vle in modo del tutto nlogo nche in VO 3 ). Definizione: Sino v, w VO 2 e si θ l ngolo convesso
SPAZI VETTORIALI. 1. Spazi e sottospazi vettoriali
 SPAZI VETTORIALI 1. Spzi e sottospzi vettorili Definizione: Dto un insieme V non vuoto e un corpo K di sostegno si dice che V è un K-spzio vettorile o uno spzio vettorile su K se sono definite un operzione
SPAZI VETTORIALI 1. Spzi e sottospzi vettorili Definizione: Dto un insieme V non vuoto e un corpo K di sostegno si dice che V è un K-spzio vettorile o uno spzio vettorile su K se sono definite un operzione
2 Generalità sulle matrici
 2 Generlità sulle mtrici 21 Definizione e csi prticolri Definizione 21 Mtrice n m Un mtrice n m è un tbell rettngolre di n righe e m colonne i cui elementi sono numeri reli (o complessi) indicizzti con
2 Generlità sulle mtrici 21 Definizione e csi prticolri Definizione 21 Mtrice n m Un mtrice n m è un tbell rettngolre di n righe e m colonne i cui elementi sono numeri reli (o complessi) indicizzti con
15. Cambiamenti di base in uno spazio vettoriale.
 5 Cmbimenti di bse in uno spzio vettorile 5 Esempio Si VR uno spzio vettorile di dimensione e si B = (u, u, u ) un su bse Sino v = 5u + 6u, v = u u + 5u, v = u + u + u, v = u 4u 7u Si M l mtrice vente
5 Cmbimenti di bse in uno spzio vettorile 5 Esempio Si VR uno spzio vettorile di dimensione e si B = (u, u, u ) un su bse Sino v = 5u + 6u, v = u u + 5u, v = u + u + u, v = u 4u 7u Si M l mtrice vente
11. Rango di una matrice.
 Rngo di un mtrice Considerimo un mtrice di tipo m n d elementi reli rppresentt nel modo seguente: A = (m-) m (m-) m (m-) m (m-) m (n-) (n-) (n-) (m-),(n-) m(n-) n n n (m-)n mn Per ogni i =,,,, (m-), m,
Rngo di un mtrice Considerimo un mtrice di tipo m n d elementi reli rppresentt nel modo seguente: A = (m-) m (m-) m (m-) m (m-) m (n-) (n-) (n-) (m-),(n-) m(n-) n n n (m-)n mn Per ogni i =,,,, (m-), m,
riferimento (assi coordinati) monodimensionale (retta orientata, x), bidimensionale (piano, xy) tridimensionale (spazio tridim.
 I vettori rppresentti come segmenti orientti (rppresentzione geometric) si intendono con l origine coincidente con l origine del sistem di riferimento (ssi coordinti) eccetto nei csi in cui si prli di
I vettori rppresentti come segmenti orientti (rppresentzione geometric) si intendono con l origine coincidente con l origine del sistem di riferimento (ssi coordinti) eccetto nei csi in cui si prli di
Ortogonalità di funzioni
 Cpitolo 0 Ortogonlità di funzioni 01 Funzioni linermente indipendenti e funzioni ortogonli Si (, b) un intervllo dell sse rele Si dice le n + 1 funzioni φ 0 (x), φ 1 (x),, φ n (x), definite in (, b), sono
Cpitolo 0 Ortogonlità di funzioni 01 Funzioni linermente indipendenti e funzioni ortogonli Si (, b) un intervllo dell sse rele Si dice le n + 1 funzioni φ 0 (x), φ 1 (x),, φ n (x), definite in (, b), sono
(da dimostrare); (da dimostrare).
 Proprietà delle trsposte Sino, K m,n e si K, llor vlgono le seguenti relzioni: 1) ( )= 2) (+)= + 3) ()= (d dimostrre); (d dimostrre). (dimostrt di seguito); DIM. 2): Devo dimostrre che l mtrice ugule ll
Proprietà delle trsposte Sino, K m,n e si K, llor vlgono le seguenti relzioni: 1) ( )= 2) (+)= + 3) ()= (d dimostrre); (d dimostrre). (dimostrt di seguito); DIM. 2): Devo dimostrre che l mtrice ugule ll
Geometria I. Prova scritta del 2 marzo 2016
 Geometri I Anno ccdemico 0/06 Prov scritt del mrzo 06 Esercizio. Si E il pino euclideo numerico munito delle coordinte cnoniche (x, y). Si consideri il tringolo T con vertici P = (0, 0), P = (, 0), P =
Geometri I Anno ccdemico 0/06 Prov scritt del mrzo 06 Esercizio. Si E il pino euclideo numerico munito delle coordinte cnoniche (x, y). Si consideri il tringolo T con vertici P = (0, 0), P = (, 0), P =
Determinanti e caratteristica di una matrice (M.S. Bernabei & H. Thaler
 Determinnti e crtteristic di un mtrice (M.S. Bernbei & H. Thler Determinnte Il determinnte può essere definito solmente nel cso di mtrici qudrte Per un mtrice qudrt 11 (del primo ordine) il determinnte
Determinnti e crtteristic di un mtrice (M.S. Bernbei & H. Thler Determinnte Il determinnte può essere definito solmente nel cso di mtrici qudrte Per un mtrice qudrt 11 (del primo ordine) il determinnte
Lezioni di Ricerca Operativa. Corso di Laurea in Informatica ed Informatica Applicata. Università di Salerno. Lezione n 3
 Lezioni di Ricerc Opertiv Corso di Lure in Informtic ed Informtic pplict Richimi di lgebr vettorile: - Mtrici ed Operzioni tr mtrici - Invers di un mtrice Lezione n - Risoluzione di un sistem di equzioni
Lezioni di Ricerc Opertiv Corso di Lure in Informtic ed Informtic pplict Richimi di lgebr vettorile: - Mtrici ed Operzioni tr mtrici - Invers di un mtrice Lezione n - Risoluzione di un sistem di equzioni
Laurea triennale in Scienze della Natura a.a. 2009/2010. Regole di Calcolo
 Lure triennle in Scienze dell Ntur.. 2009/200 Regole di Clcolo In queste note esminimo lcune conseguenze degli ssiomi reltivi lle operzioni e ll ordinmento nell insieme R dei numeri reli. L obiettivo principle
Lure triennle in Scienze dell Ntur.. 2009/200 Regole di Clcolo In queste note esminimo lcune conseguenze degli ssiomi reltivi lle operzioni e ll ordinmento nell insieme R dei numeri reli. L obiettivo principle
3) Sia (X, d) uno spazio metrico. Dimostrare che è una distanza su X la funzione
 Anlisi Rele Esercizi 3 ottobre 2008 ) Tutte le distnze introdotte lezione sono invrinti per trslzioni; ovvero d(x y) = d(x + z y + z) per ogni x y e z. Definire su X = R un metric non invrinte per trslzioni.
Anlisi Rele Esercizi 3 ottobre 2008 ) Tutte le distnze introdotte lezione sono invrinti per trslzioni; ovvero d(x y) = d(x + z y + z) per ogni x y e z. Definire su X = R un metric non invrinte per trslzioni.
, x 2. , x 3. è un equazione nella quale le incognite appaiono solo con esponente 1, ossia del tipo:
 Sistemi lineri Un equzione linere nelle n incognite x 1, x 2, x,, x n è un equzione nell qule le incognite ppiono solo con esponente 1, ossi del tipo: 1 x 1 + 2 x 2 + x +!+ n x n = b con 1, 2,,, n numeri
Sistemi lineri Un equzione linere nelle n incognite x 1, x 2, x,, x n è un equzione nell qule le incognite ppiono solo con esponente 1, ossi del tipo: 1 x 1 + 2 x 2 + x +!+ n x n = b con 1, 2,,, n numeri
Operazioni sulle Matrici
 Corso di Lure in Disegno Industrile Corso di Metodi Numerici per il Design Lezione 9 Ottore Operzioni sulle Mtrici F. Cliò Addizione e Sottrzione Lezione 9 Ottore Operzioni sulle Mtrici Pgin Addizione
Corso di Lure in Disegno Industrile Corso di Metodi Numerici per il Design Lezione 9 Ottore Operzioni sulle Mtrici F. Cliò Addizione e Sottrzione Lezione 9 Ottore Operzioni sulle Mtrici Pgin Addizione
AUTOVALORI ED AUTOVETTORI. Sia V uno spazio vettoriale di dimensione finita n.
 AUTOVALORI ED AUTOVETTORI Si V uno spzio vettorile di dimensione finit n. Dicesi endomorfismo di V ogni ppliczione linere f : V V dello spzio vettorile in sé. Se f è un endomorfismo di V in V, considert
AUTOVALORI ED AUTOVETTORI Si V uno spzio vettorile di dimensione finit n. Dicesi endomorfismo di V ogni ppliczione linere f : V V dello spzio vettorile in sé. Se f è un endomorfismo di V in V, considert
APPLICAZIONI LINEARI e MATRICI ASSOCIATE
 APPLICAZIONI LINEARI e MATRICI ASSOCIATE Dt un ppliczione f: V W con V e W spzi vettorili si dice che f è un ppliczione linere o omomorfismo f(v + v 2 ) = f(v ) + f(v 2 ) v, v 2 V f(αv) = α f(v) v V e
APPLICAZIONI LINEARI e MATRICI ASSOCIATE Dt un ppliczione f: V W con V e W spzi vettorili si dice che f è un ppliczione linere o omomorfismo f(v + v 2 ) = f(v ) + f(v 2 ) v, v 2 V f(αv) = α f(v) v V e
Alcune note introduttive alle serie di Fourier.
 Alcune note introduttive lle serie di Fourier. Definizione. Si f : IR IR periodic di periodo e integrbile su [, ]. Diremo coefficienti di Fourier di f i numeri reli = f dx, = IN f cos dx, b = IN e serie
Alcune note introduttive lle serie di Fourier. Definizione. Si f : IR IR periodic di periodo e integrbile su [, ]. Diremo coefficienti di Fourier di f i numeri reli = f dx, = IN f cos dx, b = IN e serie
Algebra delle Matrici
 lgebr delle Mtrici Definizione di un mtrice Un mtrice esempio: è definit d m righe e d n colonne come d 8 9 8 In questo cso l mtrice è compost d righe e colonne Se il numero delle righe è ugule l numero
lgebr delle Mtrici Definizione di un mtrice Un mtrice esempio: è definit d m righe e d n colonne come d 8 9 8 In questo cso l mtrice è compost d righe e colonne Se il numero delle righe è ugule l numero
= det b, a, b, c R 3. In quest ottica, il determinante del terzo ordine e caratterizzato dalle seguenti proprieta : a a. c c
 Determinnti n = 3. Propriet Possimo rigurdre il determinnte di un mtrie del terzo ordine ome un funzione delle sue olonne: det b = det [, b,,, b, R 3. In quest otti, il determinnte del terzo ordine e rtterizzto
Determinnti n = 3. Propriet Possimo rigurdre il determinnte di un mtrie del terzo ordine ome un funzione delle sue olonne: det b = det [, b,,, b, R 3. In quest otti, il determinnte del terzo ordine e rtterizzto
0.1 Teorema di Lax-Milgram
 0. Teorem di Lx-Milgrm Definizione. (Form sesquilinere) Si H uno spzio di Hilbert su C. Un form sesquilinere sul cmpo C è un ppliczione : H H C linere nell prim componente e ntilinere nell second (cioè
0. Teorem di Lx-Milgrm Definizione. (Form sesquilinere) Si H uno spzio di Hilbert su C. Un form sesquilinere sul cmpo C è un ppliczione : H H C linere nell prim componente e ntilinere nell second (cioè
h, i: V V! R (v 1,v 2 ) 7! hv 1,v 2 i ! R v 7! hv, v 0 i èlineare. Perlacommutativitàdelprodottoscalaresegueanchelalinearità dell applicazione
 Lezione. Prodotti scalari Definizione. (Prodotto scalare). Sia V uno spazio vettoriale su R. Un prodotto scalare su V è un applicazione tale che valgono i seguenti assiomi: h, i: V V! R (v,v ) 7! hv,v
Lezione. Prodotti scalari Definizione. (Prodotto scalare). Sia V uno spazio vettoriale su R. Un prodotto scalare su V è un applicazione tale che valgono i seguenti assiomi: h, i: V V! R (v,v ) 7! hv,v
a 0 n a 1 n... a n n 2a i j x i x j + 1 i<j n
 Coniche e qudriche Un qudric è il luogo degli zeri in E n, lo spzio euclideo di dimensione n, di un polinomio di grdo nelle vribili,, n Polinomi proporzionli dnno luogo ll stess qudric Se n = un qudric
Coniche e qudriche Un qudric è il luogo degli zeri in E n, lo spzio euclideo di dimensione n, di un polinomio di grdo nelle vribili,, n Polinomi proporzionli dnno luogo ll stess qudric Se n = un qudric
5. Autovalori e autovettori di matrici reali.
 5 Autovlori e utovettori di mtrici reli Definizione 5 Dt un mtrice A M n si dice utovlore di A un numero rele tle che X per cui n, n, AX = λ X L mtrice X si dice utovettore reltivo ll'utovlore λ λ Vicevers
5 Autovlori e utovettori di mtrici reli Definizione 5 Dt un mtrice A M n si dice utovlore di A un numero rele tle che X per cui n, n, AX = λ X L mtrice X si dice utovettore reltivo ll'utovlore λ λ Vicevers
AM : Tracce delle lezioni- IV Settimana
 AM0 04-5: Trcce delle lezioni- IV Settimn SUCCESSIONI CONVERGENTI in uno SPAZIO NORMATO Si (E,. ) spzio normto. Sino x k, x E. Allor x k k x x k x k 0 (i) u k, v k E, u k u, v k v tu k + sv k tu + sv t,
AM0 04-5: Trcce delle lezioni- IV Settimn SUCCESSIONI CONVERGENTI in uno SPAZIO NORMATO Si (E,. ) spzio normto. Sino x k, x E. Allor x k k x x k x k 0 (i) u k, v k E, u k u, v k v tu k + sv k tu + sv t,
Polinomi ortogonali. Alvise Sommariva. Università degli Studi di Padova Dipartimento di Matematica. 20 marzo 2017
 Polinomi ortogonli Alvise Sommriv Università degli Studi di Pdov Diprtimento di Mtemtic 20 mrzo 2017 Alvise Sommriv Polinomi ortogonli 1/ 22 Il problem i minimi qudrti Definizione (Spzio di Hilbert) Uno
Polinomi ortogonli Alvise Sommriv Università degli Studi di Pdov Diprtimento di Mtemtic 20 mrzo 2017 Alvise Sommriv Polinomi ortogonli 1/ 22 Il problem i minimi qudrti Definizione (Spzio di Hilbert) Uno
Struttura dello spazio della geometria euclidea e della fisica classica. Spazio affine euclideo
 Struttur dello spzio dell geometri euclide e dell fisic clssic. Spzio ffine euclideo Descrizione dell struttur del pino E 2 (e dello spzio E 3 ) dell geometri e dell fisic clssic come Spzio Affine Euclideo.
Struttur dello spzio dell geometri euclide e dell fisic clssic. Spzio ffine euclideo Descrizione dell struttur del pino E 2 (e dello spzio E 3 ) dell geometri e dell fisic clssic come Spzio Affine Euclideo.
LEZIONE 25. P si dice speciale se det(p ) = 1 non
 LEZIONE 5 5.. Matrici ortogonali. Facciamo una breve digressione su un importante famiglia di matrici, quelle ortogonali. Definizione 5... P R n,n si dice ortogonale se t P I n. Prima di dare esempi di
LEZIONE 5 5.. Matrici ortogonali. Facciamo una breve digressione su un importante famiglia di matrici, quelle ortogonali. Definizione 5... P R n,n si dice ortogonale se t P I n. Prima di dare esempi di
Si noti che da questa definizione segue che il punto C è il punto medio del segmento PP'. Figura 1
 APITOLO 3 LE SIMMETRIE 3. Richimi di teori Definizione. Si dto un punto del pino; si chim simmetri centrle di centro (che si indic con il simbolo s ) l corrispondenz dl pino in sé che d ogni punto P del
APITOLO 3 LE SIMMETRIE 3. Richimi di teori Definizione. Si dto un punto del pino; si chim simmetri centrle di centro (che si indic con il simbolo s ) l corrispondenz dl pino in sé che d ogni punto P del
POTENZA CON ESPONENTE REALE
 PRECORSO DI MATEMATICA VIII Lezione ESPONENZIALI E LOGARITMI E. Modic mtemtic@blogscuol.it www.mtemtic.blogscuol.it POTENZA CON ESPONENTE REALE Definizione: Dti un numero rele > 0 ed un numero rele qulunque,
PRECORSO DI MATEMATICA VIII Lezione ESPONENZIALI E LOGARITMI E. Modic mtemtic@blogscuol.it www.mtemtic.blogscuol.it POTENZA CON ESPONENTE REALE Definizione: Dti un numero rele > 0 ed un numero rele qulunque,
Integrali impropri in R
 Integrli impropri in Flvino Bttelli Diprtimento di Scienze Mtemtiche Università Politecnic delle Mrche Ancon Integrli impropri Indichimo con = {1, 2, 3,...} l insieme dei numeri nturli, con 0 = {0, 1,
Integrli impropri in Flvino Bttelli Diprtimento di Scienze Mtemtiche Università Politecnic delle Mrche Ancon Integrli impropri Indichimo con = {1, 2, 3,...} l insieme dei numeri nturli, con 0 = {0, 1,
Integrale di Riemann
 Integrle di Riemnn Hynek Kovrik Università di Bresci Anlisi Mtemtic Hynek Kovrik (Università di Bresci) Integrle di Riemnn Anlisi Mtemtic / 50 Motivzione: clcolo di re Hynek Kovrik (Università di Bresci)
Integrle di Riemnn Hynek Kovrik Università di Bresci Anlisi Mtemtic Hynek Kovrik (Università di Bresci) Integrle di Riemnn Anlisi Mtemtic / 50 Motivzione: clcolo di re Hynek Kovrik (Università di Bresci)
Esercizi di Geometria - Foglio 2 Corso di Laurea in Matematica
 Esercizi di Geometri - Foglio Corso di Lure in Mtemtic A. Sottospzi ffini. Esercizio A.1 Esempi e non-esempi di sottospzi ffini Determinre quli dei seguenti insiemi sono sottospzi ffini (precisndo di qule
Esercizi di Geometri - Foglio Corso di Lure in Mtemtic A. Sottospzi ffini. Esercizio A.1 Esempi e non-esempi di sottospzi ffini Determinre quli dei seguenti insiemi sono sottospzi ffini (precisndo di qule
13 - Integrali Impropri
 Università degli Studi di Plermo Fcoltà di Economi Diprtimento di Scienze Economiche, Aziendli e Sttistiche Appunti del corso di Mtemtic 3 - Integrli Impropri Accdemico 25/26 M. Tumminello, V. Lcgnin,
Università degli Studi di Plermo Fcoltà di Economi Diprtimento di Scienze Economiche, Aziendli e Sttistiche Appunti del corso di Mtemtic 3 - Integrli Impropri Accdemico 25/26 M. Tumminello, V. Lcgnin,
Richiami sulle matrici (TITOLO)
 Corso di Lure in Disegno Industrile Corso di Metodi Numerici per il Design Lezione prile Introduzione lle trsformzioni F. Cliò Richimi sulle mtrici (TITOLO) Lezione prile Trsformzioni Mtrici: Definizioni
Corso di Lure in Disegno Industrile Corso di Metodi Numerici per il Design Lezione prile Introduzione lle trsformzioni F. Cliò Richimi sulle mtrici (TITOLO) Lezione prile Trsformzioni Mtrici: Definizioni
Minimi quadrati e problemi di distanza minima
 Minimi qudrti e problemi di distnz minim Considerimo un mtrice rettngolre B, con elementi b ij, i 1,..., n, j 1,..., m, con m < n (quindi, più righe che colonne. Voglimo risolvere il sistem linere (1 Bx
Minimi qudrti e problemi di distnz minim Considerimo un mtrice rettngolre B, con elementi b ij, i 1,..., n, j 1,..., m, con m < n (quindi, più righe che colonne. Voglimo risolvere il sistem linere (1 Bx
CORSO ZERO DI MATEMATICA
 UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA ESPONENZIALI E LOGARITMI Dr. Ersmo Modic ersmo@glois.it www.glois.it POTENZA CON ESPONENTE REALE Definizione: Dti un numero
UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA ESPONENZIALI E LOGARITMI Dr. Ersmo Modic ersmo@glois.it www.glois.it POTENZA CON ESPONENTE REALE Definizione: Dti un numero
Integrali su intervalli illimitati Criteri di convergenza 1 Integrali di funzioni non limitate Criteri di convergenza 2 Altri integrali impropri
 Clcolo integrle Integrli su intervlli illimitti Criteri di convergenz Integrli di funzioni non limitte Criteri di convergenz 2 Altri integrli impropri 2 2006 Politecnico di Torino Definizione Considerimo
Clcolo integrle Integrli su intervlli illimitti Criteri di convergenz Integrli di funzioni non limitte Criteri di convergenz 2 Altri integrli impropri 2 2006 Politecnico di Torino Definizione Considerimo
Capitolo 5. Integrali. 5.1 Integrali di funzioni a gradinata
 Cpitolo 5 Integrli 5.1 Integrli di funzioni grdint Un concetto molto semplice m di fondmentle importnz per l trttzione dell integrle di Riemnn è quello di divisione di un intervllo [, b]. In sostnz si
Cpitolo 5 Integrli 5.1 Integrli di funzioni grdint Un concetto molto semplice m di fondmentle importnz per l trttzione dell integrle di Riemnn è quello di divisione di un intervllo [, b]. In sostnz si
; c. ; d nessuna delle precedenti In R 5 [x] distanza tra x e x 2 rispetto al prodotto scalare p, q = 1
![; c. ; d nessuna delle precedenti In R 5 [x] distanza tra x e x 2 rispetto al prodotto scalare p, q = 1 ; c. ; d nessuna delle precedenti In R 5 [x] distanza tra x e x 2 rispetto al prodotto scalare p, q = 1](/thumbs/94/119130474.jpg) Ing. erospzile e meccnic. Geometri e lgebr T. Prov del 08/01/2018 cod. 701385 Nome Cognome Mtricol 1. L conic definit d x 2 + y 2 4xy = 1 è: ellisse iperbole prbol; d un punto. 2. Le coordinte di rispetto
Ing. erospzile e meccnic. Geometri e lgebr T. Prov del 08/01/2018 cod. 701385 Nome Cognome Mtricol 1. L conic definit d x 2 + y 2 4xy = 1 è: ellisse iperbole prbol; d un punto. 2. Le coordinte di rispetto
Erasmo Modica. : K K K
 L insieme dei numeri reli L INSIEME DEI NUMERI REALI Ersmo Modic helthinsurnce@tin.it www.glois.it Per introdurre l insieme dei numeri reli si hnno disposizione diversi modi. Generlmente l iennio si preferisce
L insieme dei numeri reli L INSIEME DEI NUMERI REALI Ersmo Modic helthinsurnce@tin.it www.glois.it Per introdurre l insieme dei numeri reli si hnno disposizione diversi modi. Generlmente l iennio si preferisce
Un polinomio trigonometrico di grado N nell intervallo [ π, π] è una funzione g(x), periodica di periodo 2π, della forma. c n e inx.
![Un polinomio trigonometrico di grado N nell intervallo [ π, π] è una funzione g(x), periodica di periodo 2π, della forma. c n e inx. Un polinomio trigonometrico di grado N nell intervallo [ π, π] è una funzione g(x), periodica di periodo 2π, della forma. c n e inx.](/thumbs/74/71411974.jpg) Cpitolo 6 Serie di Fourier 6.1. Introduzione Un polinomio trigonometrico di grdo N nell intervllo [, π] è un funzione g(x), periodic di periodo, dell form g(x) = N n= N c n e inx per un qulche scelt delle
Cpitolo 6 Serie di Fourier 6.1. Introduzione Un polinomio trigonometrico di grdo N nell intervllo [, π] è un funzione g(x), periodic di periodo, dell form g(x) = N n= N c n e inx per un qulche scelt delle
Il lemma di ricoprimento di Vitali
 Il lemm di ricoprimento di Vitli Si I = {I} un fmigli di intervlli ciusi contenuti in R. Diremo ce l fmigli I ricopre l insieme E nel senso di Vitli (oppure ce I è un ricoprimento di Vitli di E) se per
Il lemm di ricoprimento di Vitli Si I = {I} un fmigli di intervlli ciusi contenuti in R. Diremo ce l fmigli I ricopre l insieme E nel senso di Vitli (oppure ce I è un ricoprimento di Vitli di E) se per
1. Elementi di analisi funzionale Esercizi
 . Elementi di nlisi funzionle Esercizi http://www.cirm.unibo.it/~brozzi/mi/pdf/mi-cp.-ese.pdf.. Spzi vettorili.. Spzi vettorili normti.-. Dimostrre l diseguglinz tringolre in C n reltivmente ll norm (
. Elementi di nlisi funzionle Esercizi http://www.cirm.unibo.it/~brozzi/mi/pdf/mi-cp.-ese.pdf.. Spzi vettorili.. Spzi vettorili normti.-. Dimostrre l diseguglinz tringolre in C n reltivmente ll norm (
Questa successione è tale, per la disuguaglianza di Bessel, c n 2. n=1
 14.1. ABC di nlisi funzionle II. 14.1.1. Un ltro teorem sulle serie di Fourier. Nell lezione 13.1.5 si è visto che, fissto un sistem ortonormle {e n }, d un vettore u è ssocit l successione delle sue coordinte
14.1. ABC di nlisi funzionle II. 14.1.1. Un ltro teorem sulle serie di Fourier. Nell lezione 13.1.5 si è visto che, fissto un sistem ortonormle {e n }, d un vettore u è ssocit l successione delle sue coordinte
Algebra lineare. Capitolo VETTORI
 Cpitolo Algebr linere.. VETTORI In generle, nell geometri elementre un segmento AB è introdotto come l prte di rett compres tr i due punti A, B fissti su di ess, senz specificre un ordine tr gli estremi
Cpitolo Algebr linere.. VETTORI In generle, nell geometri elementre un segmento AB è introdotto come l prte di rett compres tr i due punti A, B fissti su di ess, senz specificre un ordine tr gli estremi
MATRICI E DETERMINANTI CENNI SUI SISTEMI LINEARI. Angela Donatiello 1
 MTRICI E DETERMINNTI CENNI SUI SISTEMI LINERI ngel Dontiello Considerimo un insieme di numeri reli rppresentti tr prentesi qudre o tonde n n ij m m mn ( ) [ ] ij i,,m j,,n Si definisce mtrice un tbell
MTRICI E DETERMINNTI CENNI SUI SISTEMI LINERI ngel Dontiello Considerimo un insieme di numeri reli rppresentti tr prentesi qudre o tonde n n ij m m mn ( ) [ ] ij i,,m j,,n Si definisce mtrice un tbell
ESPONENZIALI E LOGARITMI
 ESPONENZIALI E LOGARITMI RICHIAMI DI TEORIA dom f Im f grfico Funzioni esponenzili y=^ con > Funzioni esponenzili y=^ con
ESPONENZIALI E LOGARITMI RICHIAMI DI TEORIA dom f Im f grfico Funzioni esponenzili y=^ con > Funzioni esponenzili y=^ con
Politecnico di Milano Corso di Analisi e Geometria 1. Federico Lastaria
 Politecnico di Milno Corso di Anlisi e Geometri Federico Lstri federico.lstri@polimi.it Teoremi per l second prov. Dimostrzioni. 8 Dicembre 208 Indice Teoremi per l second prov in itinere. Dimostrzioni.
Politecnico di Milno Corso di Anlisi e Geometri Federico Lstri federico.lstri@polimi.it Teoremi per l second prov. Dimostrzioni. 8 Dicembre 208 Indice Teoremi per l second prov in itinere. Dimostrzioni.
Algebra lineare. Algebra. Vettori. Vettori. Vettori: uguaglianza. Vettori: elementi corrispondenti
 Algebr linere Algebr Un lgebr è un sistem di segni in cui sono definite delle operzioni Algebr sclre Algebr dei vettori Algebr mtricile In lgebr mtricile un numero è chimto sclre Vettori Vettori vettore
Algebr linere Algebr Un lgebr è un sistem di segni in cui sono definite delle operzioni Algebr sclre Algebr dei vettori Algebr mtricile In lgebr mtricile un numero è chimto sclre Vettori Vettori vettore
corrispondenza dal piano in sé, che ad ogni punto P del piano fa corrispondere il punto P' in
 Cpitolo 5 Le omotetie 5. Richimi di teori Definizione Sino fissti un punto C del pino ed un numero rele. Si chim omoteti di centro C e rpporto ( che si indic con il simolo O, ) l corrispondenz dl pino
Cpitolo 5 Le omotetie 5. Richimi di teori Definizione Sino fissti un punto C del pino ed un numero rele. Si chim omoteti di centro C e rpporto ( che si indic con il simolo O, ) l corrispondenz dl pino
Geometria BAER Canale I Esercizi 13
 Geometri BAER Cnle I Esercizi Alcuni di questi esercizi forse sono un po difficili visto che bbimo ftto quest prte un po in frett, m si può sempre provre. Esercizio. Si scrivno le equzioni delle prbole
Geometri BAER Cnle I Esercizi Alcuni di questi esercizi forse sono un po difficili visto che bbimo ftto quest prte un po in frett, m si può sempre provre. Esercizio. Si scrivno le equzioni delle prbole
G. Parmeggiani, 23/11/2018 Algebra Lineare, a.a. 2018/2019, numero di MATRICOLA PARI. Svolgimento degli Esercizi per casa 6 (seconda parte)
 G. Prmeggini, 3//08 Algebr Linere,.. 08/09, Scuol di Scienze - Corsi di lure: Studenti: Sttistic per l economi e l impres Sttistic per le tecnologie e le scienze numero di MATRICOLA PARI Svolgimento degli
G. Prmeggini, 3//08 Algebr Linere,.. 08/09, Scuol di Scienze - Corsi di lure: Studenti: Sttistic per l economi e l impres Sttistic per le tecnologie e le scienze numero di MATRICOLA PARI Svolgimento degli
Le Matrici. 001 ( matrice unità)
 Le Mtrici Un mtrice è un tbell di numeri o più in generle di elementi disposti quindi secondo righe e colonne. Le mtrici si indicno con le lettere miuscole dell lfbeto, gli elementi con quelle minuscole
Le Mtrici Un mtrice è un tbell di numeri o più in generle di elementi disposti quindi secondo righe e colonne. Le mtrici si indicno con le lettere miuscole dell lfbeto, gli elementi con quelle minuscole
Equazioni 1 grado. Definizioni Classificazione Risoluzione Esercizi
 Equzioni grdo Definizioni Clssificzione Risoluzione Esercizi Mteri: Mtemtic Autore: Mrio De Leo Definizioni Prendimo in esme le due espressioni numeriche 8 entrmbe sono uguli 7, e l scrittur si chim uguglinz
Equzioni grdo Definizioni Clssificzione Risoluzione Esercizi Mteri: Mtemtic Autore: Mrio De Leo Definizioni Prendimo in esme le due espressioni numeriche 8 entrmbe sono uguli 7, e l scrittur si chim uguglinz
f(x) f(x 0 ) lim (x) := f(x) f(x 0)
 Cpitolo 3 Derivte 31 Definizione **Definizione 31 (Punto di derivilità) Si f :[, ]! R un funzione e si 2 [, ] Allor f si dice derivile in se esiste finito il In questo cso si dice punto di derivilità per
Cpitolo 3 Derivte 31 Definizione **Definizione 31 (Punto di derivilità) Si f :[, ]! R un funzione e si 2 [, ] Allor f si dice derivile in se esiste finito il In questo cso si dice punto di derivilità per
Politecnico di Milano Corso di Analisi e Geometria 1. Federico Lastaria
 Teoremi per l second prov. Dimostrzioni. Federico Lstri, Anlisi e Geometri Politecnico di Milno Corso di Anlisi e Geometri Federico Lstri federico.lstri@polimi.it Teoremi per l second prov. Dimostrzioni.
Teoremi per l second prov. Dimostrzioni. Federico Lstri, Anlisi e Geometri Politecnico di Milno Corso di Anlisi e Geometri Federico Lstri federico.lstri@polimi.it Teoremi per l second prov. Dimostrzioni.
SUGLI INSIEMI. 1.Insiemi e operazioni su di essi
 SUGLI INSIEMI 1.Insiemi e operzioni su di essi Il concetto di insieme è primitivo ed è sinonimo di clsse, totlità. Si A un insieme di elementi qulunque. Per indicre che è un elemento di A scriveremo A.
SUGLI INSIEMI 1.Insiemi e operzioni su di essi Il concetto di insieme è primitivo ed è sinonimo di clsse, totlità. Si A un insieme di elementi qulunque. Per indicre che è un elemento di A scriveremo A.
Sistemi principali di normali ad una varietà giacenti nel suo o 2. Nota di
 Sistemi principli di normli d un vrietà gicenti nel suo o 2. Not di Giuseppe Vitli Pdov. In un mio recente lvoro *) ho considerto, per ogni superficie il cui j si di 2 k dimensioni (k 2, 3), un sistem
Sistemi principli di normli d un vrietà gicenti nel suo o 2. Not di Giuseppe Vitli Pdov. In un mio recente lvoro *) ho considerto, per ogni superficie il cui j si di 2 k dimensioni (k 2, 3), un sistem
ESERCITAZIONE N.3 DETERMINANTI. il determinante di una matrice 1x1 è l elemento stesso det (a) = a. il determinante di una matrice 2x2 è :
 DETERMINANTI ESERCITAZIONE N 5 mrzo Ad ogni mtrice qudrt coefficienti in R ( o C o un qulsisi K cmpo) è ssocito un numero rele che or definimo,detto det(a),(d(a)) determinnte di A il determinnte di un
DETERMINANTI ESERCITAZIONE N 5 mrzo Ad ogni mtrice qudrt coefficienti in R ( o C o un qulsisi K cmpo) è ssocito un numero rele che or definimo,detto det(a),(d(a)) determinnte di A il determinnte di un
Dimostrazione del teorema di Gauss Green nel piano
 imostrzione del teorem di Guss Green nel pino Gli eventuli lettori sono pregti di segnlrmi gli eventuli errori di stmp. Grzie! L.V. Ricordimo che: dominio è l chiusur di un perto; dominio normle regolre
imostrzione del teorem di Guss Green nel pino Gli eventuli lettori sono pregti di segnlrmi gli eventuli errori di stmp. Grzie! L.V. Ricordimo che: dominio è l chiusur di un perto; dominio normle regolre
Corso di Analisi Matematica. Calcolo integrale
 .. 2011/12 Lure triennle in Informtic Corso di Anlisi Mtemtic Clcolo integrle Avvertenz Questi sono ppunti informli delle lezioni, che vengono resi disponibili per comodità degli studenti. Prte del mterile
.. 2011/12 Lure triennle in Informtic Corso di Anlisi Mtemtic Clcolo integrle Avvertenz Questi sono ppunti informli delle lezioni, che vengono resi disponibili per comodità degli studenti. Prte del mterile
Integrali definiti (nel senso di Riemann)
 Integrli definiti (nel senso di Riemnn) Problem: cos è l re di un figur pin? come clcolrl? Grficmente concetto intuitivo ed evidente. Tecnicmente ci sono definizioni e formule d hoc per le figure elementri.
Integrli definiti (nel senso di Riemnn) Problem: cos è l re di un figur pin? come clcolrl? Grficmente concetto intuitivo ed evidente. Tecnicmente ci sono definizioni e formule d hoc per le figure elementri.
ANALISI 1 1 VENTIDUESIMA LEZIONE Integrali impropri
 ANALISI 1 1 VENTIDUESIMA LEZIONE Integrli impropri 1 prof. Cludio Sccon, Diprtimento di Mtemtic Applict, Vi F. Buonrroti 1/C emil: sccon@mil.dm.unipi.it web: http://www2.ing.unipi.it/ d6081/index.html
ANALISI 1 1 VENTIDUESIMA LEZIONE Integrli impropri 1 prof. Cludio Sccon, Diprtimento di Mtemtic Applict, Vi F. Buonrroti 1/C emil: sccon@mil.dm.unipi.it web: http://www2.ing.unipi.it/ d6081/index.html
Proiettività della Retta e del Piano.
 Introduzione. In queste note proponimo l clssificzione delle proiettività per l rett proiettiv ed il pino proiettivo su un corpo lgebricmente chiuso. Nel cso dell rett studieremo nche il cso del corpo
Introduzione. In queste note proponimo l clssificzione delle proiettività per l rett proiettiv ed il pino proiettivo su un corpo lgebricmente chiuso. Nel cso dell rett studieremo nche il cso del corpo
Equazioni. Definizioni e concetti generali. Incognita: Lettera (di solito X) alla quale e possibile sostituire dei valori numerici
 Equzioni Prerequisiti Scomposizioni polinomili Clcolo del M.C.D. e del m.c.m. tr polinomi P(X) = 0, con P(X) polinomio di grdo qulsisi Definizioni e concetti generli Incognit: Letter (di solito X) ll qule
Equzioni Prerequisiti Scomposizioni polinomili Clcolo del M.C.D. e del m.c.m. tr polinomi P(X) = 0, con P(X) polinomio di grdo qulsisi Definizioni e concetti generli Incognit: Letter (di solito X) ll qule
Integrale Improprio. f(x) dx =: Osserviamo che questa definizione ha senso dal momento che per ogni y è ben definito l integrale b
 Integrle Improprio In queste lezioni riprendimo l teori dell integrzione in un vribile, l ide è di estendere l integrle definito nche in csi in cui l funzione integrnd o l intervllo di integrzione non
Integrle Improprio In queste lezioni riprendimo l teori dell integrzione in un vribile, l ide è di estendere l integrle definito nche in csi in cui l funzione integrnd o l intervllo di integrzione non
Integrali impropri di funzioni di una variabile
 Integrli impropri di funzioni di un vribile. Le funzioni continue Considerimo nel seguito un delle piú importnti ppliczioni del teorem di uniforme continuitá delle funzioni continue su intervlli chiusi
Integrli impropri di funzioni di un vribile. Le funzioni continue Considerimo nel seguito un delle piú importnti ppliczioni del teorem di uniforme continuitá delle funzioni continue su intervlli chiusi
{ 3 x y=4. { x=2. Sistemi di equazioni
 Sistemi di equzioni Definizione Un sistem è un insieme di equzioni che devono essere verificte contempornemente, cioè devono vere contempornemente le stesse soluzioni. Definimo grdo di un sistem il prodotto
Sistemi di equzioni Definizione Un sistem è un insieme di equzioni che devono essere verificte contempornemente, cioè devono vere contempornemente le stesse soluzioni. Definimo grdo di un sistem il prodotto
Introduzione alle disequazioni algebriche
 Introduzione lle disequzioni lgebriche Giovnni decide di fre ttività fisic e chiede informzioni due plestre. Un plestr privt chiede un quot d iscrizione nnu di 312, più 2 per ogni ingresso. L plestr comunle
Introduzione lle disequzioni lgebriche Giovnni decide di fre ttività fisic e chiede informzioni due plestre. Un plestr privt chiede un quot d iscrizione nnu di 312, più 2 per ogni ingresso. L plestr comunle
5. Quanti blocchi ha la forma di Jordan di f(x, y, z, s, t) = (0, y + z, y + z, t, 0)?
 Ing. erospzile e meccnic. Geometri e lgebr T. Prov del 24/01/2018 cod. 8919280 Nome Cognome Mtricol 1. Il rngo di 1 2 0 0 2 0 è: 2 4 3 ; d 5. 1 2 0 2. Le coordinte di 1, 1, 0 rispetto ll bse di C 3 formt
Ing. erospzile e meccnic. Geometri e lgebr T. Prov del 24/01/2018 cod. 8919280 Nome Cognome Mtricol 1. Il rngo di 1 2 0 0 2 0 è: 2 4 3 ; d 5. 1 2 0 2. Le coordinte di 1, 1, 0 rispetto ll bse di C 3 formt
Basi di Algebra Lineare. Ivan Zivko
 Bsi di Algebr Linere Ivn Zivko Trigonometri Rdinti Nelle scienze l unità di misur più ust per glingoli non sono i grdi, bensì i rdinti. Vle l seguente relzione: 36 o = π rd Per trovre qulsisi ngolo in
Bsi di Algebr Linere Ivn Zivko Trigonometri Rdinti Nelle scienze l unità di misur più ust per glingoli non sono i grdi, bensì i rdinti. Vle l seguente relzione: 36 o = π rd Per trovre qulsisi ngolo in
Serie di Potenze. Introduciamo il concetto di convergenza puntuale ed uniforme per successioni. { 0 se 1 < x < 1
 Serie di Potenze Introducimo il concetto di convergenz puntule ed uniforme per successioni di funzioni. Definizione 1 Si I un intervllo di R. Si dt l vrire di n N l funzione f n : I R. Dicimo che l successione
Serie di Potenze Introducimo il concetto di convergenz puntule ed uniforme per successioni di funzioni. Definizione 1 Si I un intervllo di R. Si dt l vrire di n N l funzione f n : I R. Dicimo che l successione
1 Espressioni polinomiali
 1 Espressioni polinomili Un monomio è un espressione letterle in un vribile x che contiene un potenz inter (non negtiv, cioè mggiori o uguli zero) di x moltiplict per un numero rele: x n AD ESEMPIO: sono
1 Espressioni polinomili Un monomio è un espressione letterle in un vribile x che contiene un potenz inter (non negtiv, cioè mggiori o uguli zero) di x moltiplict per un numero rele: x n AD ESEMPIO: sono
Calcolare l area di una regione piana
 Integrli Integrle definito e re con segno Primitiv di un funzione e integrle indefinito Teorem fondmentle del clcolo integrle Clcolo di ree Metodi di integrzione: per prti e per sostituzione Clcolre l
Integrli Integrle definito e re con segno Primitiv di un funzione e integrle indefinito Teorem fondmentle del clcolo integrle Clcolo di ree Metodi di integrzione: per prti e per sostituzione Clcolre l
Meccanica dei Solidi. Vettori
 Meccnic dei Solidi Prof. Ing. Stefno Avers Università di Npoli Prthenope.. 2005-06 Lezione 2 Vettori Definizione: Un grndezz vettorile (o un vettore) è un grndezz fisic crtterizzt oltre che d un numero
Meccnic dei Solidi Prof. Ing. Stefno Avers Università di Npoli Prthenope.. 2005-06 Lezione 2 Vettori Definizione: Un grndezz vettorile (o un vettore) è un grndezz fisic crtterizzt oltre che d un numero
(somma inferiore n esima), (somma superiore n esima).
 Clcolo integrle Appunti integrtivi lle dispense di Mtemtic ssistit rgomento 9 (Integrli definiti) e rgomento (Integrli impropri) cur di C.Znco (Il contenuto di questi ppunti f prte del progrmm d esme)
Clcolo integrle Appunti integrtivi lle dispense di Mtemtic ssistit rgomento 9 (Integrli definiti) e rgomento (Integrli impropri) cur di C.Znco (Il contenuto di questi ppunti f prte del progrmm d esme)
Calcolo integrale in due e più variabili
 Clcolo integrle in due e più vribili 9 dicembre 2010 1 Definizione di integrle Il primo psso st nell definizione e determinzione dell integrle per funzioni due vribili prticolrmente semplici: le funzioni
Clcolo integrle in due e più vribili 9 dicembre 2010 1 Definizione di integrle Il primo psso st nell definizione e determinzione dell integrle per funzioni due vribili prticolrmente semplici: le funzioni
Matematica I, Funzione integrale
 Mtemtic I, 24.0.2. Funzione integrle Definizione Sino f : A R, funzione continu su A intervllo, e c in A. L funzione che ssoci d ogni in A l integrle di f sull intervllo [c, ], viene dett funzione integrle
Mtemtic I, 24.0.2. Funzione integrle Definizione Sino f : A R, funzione continu su A intervllo, e c in A. L funzione che ssoci d ogni in A l integrle di f sull intervllo [c, ], viene dett funzione integrle
Matematica A, Area dell Informazione. Complementi al testo
 1 Preinri Mtemtic A, Are dell Informzione.. 2001-2002, corso prof. Brdi Complementi l testo Proposizione 1 (Proprietà crtteristiche di sup e inf) Si A R un insieme non vuoto e si x R. Allor x = sup A se
1 Preinri Mtemtic A, Are dell Informzione.. 2001-2002, corso prof. Brdi Complementi l testo Proposizione 1 (Proprietà crtteristiche di sup e inf) Si A R un insieme non vuoto e si x R. Allor x = sup A se
Chapter 1. Integrali doppi
 Chpter 1 Integrli doppi Nelle presenti note esporremo un pproccio semplificto ll teori degli integrli doppi. efiniremo tli integrli direttmente su domini normli, come limiti di opportune somme integrli.
Chpter 1 Integrli doppi Nelle presenti note esporremo un pproccio semplificto ll teori degli integrli doppi. efiniremo tli integrli direttmente su domini normli, come limiti di opportune somme integrli.
Matematica II. Un sistema lineare è un sistema di m equazioni lineari (cioè di primo grado) in n incognite x 1,, x n :
 Mtemtic II. Generlità sui sistemi lineri Un sistem linere è un sistem di m equzioni lineri (cioè di primo grdo) in n incognite,, n : n n b b m mn n m (*) Un soluzione del sistem linere è un n-upl di numeri
Mtemtic II. Generlità sui sistemi lineri Un sistem linere è un sistem di m equzioni lineri (cioè di primo grdo) in n incognite,, n : n n b b m mn n m (*) Un soluzione del sistem linere è un n-upl di numeri
Nome.Cognome. 18 Dicembre 2008 Classe 4G. VERIFICA di MATEMATICA
 Nome.Cognome. 8 Dicembre 008 Clsse G VERIFICA di MATEMATICA A) Risolvi le seguenti disequzioni goniometriche sin ) sin + ) 0 6 tn cos + sin ) 0 (punti:0,5) ) tn + tn > 0 sin 5) sin > cos (punti: ) 6) sin
Nome.Cognome. 8 Dicembre 008 Clsse G VERIFICA di MATEMATICA A) Risolvi le seguenti disequzioni goniometriche sin ) sin + ) 0 6 tn cos + sin ) 0 (punti:0,5) ) tn + tn > 0 sin 5) sin > cos (punti: ) 6) sin
1 Equazioni e disequazioni di secondo grado
 UNIVERSITÀ DEGLI STUDI DI ROMA LA SAPIENZA - Fcoltà di Frmci e Medicin - Corso di Lure in CTF 1 Equzioni e disequzioni di secondo grdo Sino 0, b e c tre numeri reli noti, risolvere un equzione di secondo
UNIVERSITÀ DEGLI STUDI DI ROMA LA SAPIENZA - Fcoltà di Frmci e Medicin - Corso di Lure in CTF 1 Equzioni e disequzioni di secondo grdo Sino 0, b e c tre numeri reli noti, risolvere un equzione di secondo
Le equazioni di grado superiore al secondo
 Le equzioni di grdo superiore l secondo ITIS Feltrinelli nno scolstico 007-008 R. Folgieri 007-008 1 Teorem fondmentle dell lger Ogni equzione lgeric di grdo n h sempre n soluzioni, che possono essere
Le equzioni di grdo superiore l secondo ITIS Feltrinelli nno scolstico 007-008 R. Folgieri 007-008 1 Teorem fondmentle dell lger Ogni equzione lgeric di grdo n h sempre n soluzioni, che possono essere
Università del Sannio
 Università del Snnio Corso di Fisic 1 Leione 2 Vettori Prof.ss Stefni Petrcc Corso di Fisic 1 - Le. 02 - Vettori 1 Definiione dei vettori I vettori rppresentno grndee per le quli il vlore, misurto con
Università del Snnio Corso di Fisic 1 Leione 2 Vettori Prof.ss Stefni Petrcc Corso di Fisic 1 - Le. 02 - Vettori 1 Definiione dei vettori I vettori rppresentno grndee per le quli il vlore, misurto con
Definizione opposto: Somma. Definizione vettore 0:
 Somm Operzioni in R n : somm :... n n Definizione ettore : Definizione opposto: :... :... n Rispetto tle operzione R n risult un gruppo elino. Cioè l somm h le seguenti proprietà: S5) Commutti S) Intern
Somm Operzioni in R n : somm :... n n Definizione ettore : Definizione opposto: :... :... n Rispetto tle operzione R n risult un gruppo elino. Cioè l somm h le seguenti proprietà: S5) Commutti S) Intern
Norme, distanze e convegenza. Definizione. Sia V uno spazio vettoriale sul campo reale o complesso. Una funzione
 Norme, distnze e convegenz. Definizione. Si V uno spzio vettorile sul cmpo rele o complesso. Un funzione. : V R si dice norm di v V se soddisf lle seguenti proprietà : Per ogni v V bbimo v 0e v =0 v =
Norme, distnze e convegenz. Definizione. Si V uno spzio vettorile sul cmpo rele o complesso. Un funzione. : V R si dice norm di v V se soddisf lle seguenti proprietà : Per ogni v V bbimo v 0e v =0 v =
LEGGI DELLA DINAMICA
 1) Nel SI l unità di misur dell forz è il Newton (N); 1 N è quell forz che: [A] pplict su un oggetto dell mss di 1 kg lo spost di 1m; [B] pplict su un oggetto che h l mss di 1g lo cceler di 1m/s 2 nell
1) Nel SI l unità di misur dell forz è il Newton (N); 1 N è quell forz che: [A] pplict su un oggetto dell mss di 1 kg lo spost di 1m; [B] pplict su un oggetto che h l mss di 1g lo cceler di 1m/s 2 nell
Se però perdo una delle tre coordinate posso ancora determinare la posizione. Se A = B (ossia, n x,φ n 2 = A x 2 per ogni x) il frame si dice stretto
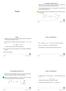 L roustezz dei frme (2) Supponimo or di mndre le componenti rispetto d un insieme di tre vettori (necessrimente linermente dipendenti tr loro) A cus dell dipendenz linere, un componente è inutile, dto
L roustezz dei frme (2) Supponimo or di mndre le componenti rispetto d un insieme di tre vettori (necessrimente linermente dipendenti tr loro) A cus dell dipendenz linere, un componente è inutile, dto
Definiamo ora alcuni vettori particolarmente importanti detti versori.
 Prof. A. Di Mro I versori Definimo or lcni vettori prticolrmente importnti detti versori. Un versore è semplicemente n vettore di modlo nitrio. Normlmente gli ssi, e z vengono ssociti i versori i ˆ, ˆj,
Prof. A. Di Mro I versori Definimo or lcni vettori prticolrmente importnti detti versori. Un versore è semplicemente n vettore di modlo nitrio. Normlmente gli ssi, e z vengono ssociti i versori i ˆ, ˆj,
Numerica e aritmetica dei calcolatori. Introduzione
 NUC Cpitolo Ivn Zivko Introduzione Un mtrice si può descrivere come un tbell ordint di elementi, ognuno dei quli h un posizione ben precis. M 4 7 5 8 3 6 9 NUC Docente: Ivn Zivko Introduzione Se il numero
NUC Cpitolo Ivn Zivko Introduzione Un mtrice si può descrivere come un tbell ordint di elementi, ognuno dei quli h un posizione ben precis. M 4 7 5 8 3 6 9 NUC Docente: Ivn Zivko Introduzione Se il numero
P (a,a) PROBLEMA 10 . C
 PROBLEMA 10 4 FILI LUNGHI CONDUTTORI SONO TRA LORO PARALLELI E DISPOSTI AI VERTICI DI UN QUADRATO DI LATO = 0 cm; IN OGNI FILO CIRCOLA LA CORRENTE i = 0 A, CON I VERSI MOSTRATI IN FIGURA A) CALCOLARE IL
PROBLEMA 10 4 FILI LUNGHI CONDUTTORI SONO TRA LORO PARALLELI E DISPOSTI AI VERTICI DI UN QUADRATO DI LATO = 0 cm; IN OGNI FILO CIRCOLA LA CORRENTE i = 0 A, CON I VERSI MOSTRATI IN FIGURA A) CALCOLARE IL
PNI SESSIONE SUPPLETIVA QUESITO 1
 www.mtefili.it PNI 2005 - SESSIONE SUPPLETIVA QUESITO È dto un trpezio rettngolo, in cui le bisettrici degli ngoli dicenti l lto obliquo si intersecno in un punto del lto perpendicolre lle bsi. Dimostrre
www.mtefili.it PNI 2005 - SESSIONE SUPPLETIVA QUESITO È dto un trpezio rettngolo, in cui le bisettrici degli ngoli dicenti l lto obliquo si intersecno in un punto del lto perpendicolre lle bsi. Dimostrre
Matrici. (Tabelle di elementi disposti su m righe e n colonne) Di particolare interesse le matrici quadrate (m=n): Es. (m=n=3):
 Mtrici (Tbelle di elementi disposti su m righe e n colonne) Di prticolre interesse le mtrici qudrte (m=n): Es. (m=n=3): V = 11 21 31 12 22 32 13 23 33 Mtrici Un vettore n componenti (coordinte), cioè pprtenente
Mtrici (Tbelle di elementi disposti su m righe e n colonne) Di prticolre interesse le mtrici qudrte (m=n): Es. (m=n=3): V = 11 21 31 12 22 32 13 23 33 Mtrici Un vettore n componenti (coordinte), cioè pprtenente
Spazi ed operatori lineari
 Spzi ed opertori lineri Corso di Fisic Mtemtic 2,.. 2013-2014 Diprtimento di Mtemtic, Università di Milno 28/10/2013 1 Spzi lineri Nel seguito dovremo considerre degli spzi lineri, che possono essere pensti
Spzi ed opertori lineri Corso di Fisic Mtemtic 2,.. 2013-2014 Diprtimento di Mtemtic, Università di Milno 28/10/2013 1 Spzi lineri Nel seguito dovremo considerre degli spzi lineri, che possono essere pensti
Esercizi su spazi ed operatori lineari
 Esercizi su spzi ed opertori lineri Corso di Fisic Mtemtic,.. 011-01 Diprtimento di Mtemtic, Università di Milno 9 Novembre 01 1 Spzio L Esercizio 1. Per = 0, b = 1, dire quli delle seguenti funzioni pprtengono
Esercizi su spzi ed opertori lineri Corso di Fisic Mtemtic,.. 011-01 Diprtimento di Mtemtic, Università di Milno 9 Novembre 01 1 Spzio L Esercizio 1. Per = 0, b = 1, dire quli delle seguenti funzioni pprtengono
