h, i: V V! R (v 1,v 2 ) 7! hv 1,v 2 i ! R v 7! hv, v 0 i èlineare. Perlacommutativitàdelprodottoscalaresegueanchelalinearità dell applicazione
|
|
|
- Biaggio Ferrari
- 5 anni fa
- Visualizzazioni
Transcript
1 Lezione. Prodotti scalari Definizione. (Prodotto scalare). Sia V uno spazio vettoriale su R. Un prodotto scalare su V è un applicazione tale che valgono i seguenti assiomi: h, i: V V! R (v,v ) 7! hv,v i (PS) per ogni v,v V,sihahv,v i = hv,v i (il prodotto scalare è commutativo); (PS) per ogni v,v,v 3 V,sihahv,v +v 3 i = hv,v i+hv,v 3 i (il prodotto scalare èdistributivorispettoallasomma); (PS3) per ogni R e v,v V,siha hv,v i = h v,v i; (PS4) per ogni v V \{ 0 V },sihahv, vi > 0 (il prodotto scalare è definito positivo). Osservazione.. Elenchiamo alcune immediate conseguenze degli assiomi della definizione precedente.. Sia v 0 V fissato. Allora l applicazione h,v 0 i: V! R v 7! hv, v 0 i èlineare. Perlacommutativitàdelprodottoscalaresegueanchelalinearità dell applicazione hv 0, i: V! R v 7! hv 0,vi. Per questa doppia proprietà di linearità si dice spesso che il prodotto scalare èun applicazione bilineare.. Per linearità, si ha che h0,vi = hv, 0i =0per ogni v V : in particolare hv, vi =0se e solo se v =0. 3. Se W V èunsottospazio,hasensoconsiderarelarestrizioneh, i W W,che èunprodottoscalaresuw. 3
2 4 Definizione.3 (Modulo di un vettore). Sia V uno spazio vettoriale su R munito di prodotto scalare h, i. Per ogni v V,ilnumero v = p hv, vi si dice modulo di v. Ivettoridimodulo si dicono versori. Si noti che in uno spazio vettoriale V su R munito di prodotto scalare l unico vettore di modulo zero è il vettore nullo ~0 V. Esempio.4. Nello spazio V 3 (O) dei vettori applicati si può definire un prodotto scalare ponendo h~v, ~w i = ~v ~w cos( c ~v ~w ) (..) per ogni coppia di vettori ~v, ~w V 3 (O) non nulli, come avevamo visto nella Lezione 8. Fissato un sistema di riferimento O~ı~ ~ k,se~v = v x ~ı +v y ~ +v z ~ k e w = wx ~ı +w y ~ +w z ~ k, ènotoche h~v, ~w i = v x w x + v y w y + v z w z. Esempio.5. Dati x =(x,...,x n ) e y =(y,...,y n ) in V = R n,sidefinisce prodotto scalare standard il prodotto scalare Si noti che in tal caso risulta hx, yi = x y + + x n y n. (..) hx, yi = t xy= t xi n y come prodotto di matrici. Il fatto che tale applicazione soddisfi gli assiomi (PS), (PS) e (PS3) è evidente dalla definizione. Per quanto riguarda l assioma (PS4), si noti che hx, xi = x + + x n èunasommadinumerirealinonnegativi,comelosonoiquadratidinumerireali, quindi è non negativa ed è nulla se e solo se tutti gli addendi sono nulli. B Quello standard non è l unico possibile prodotto scalare che possiamo definire su R n! Per esempio si verifichi che l applicazione ((x,x ), (y,y )) 7! 3x y + x y / èunprodottoscalareinr diverso dal prodotto standard. Si noti che 3 0 y 3x y + x y /= x x. 0 /4 Sia V uno spazio vettoriale su R munito di prodotto scalare h, i. vettori v, w V \{0 V },perognitr si ha v thv, wi + t w = hv tw, v twi > 0. y Dati due Il primo membro di tale trinomio non può avere radici distinte, dovendo altrimenti cambiare di segno, quindi hv, wi v w 6 0: essendo v, w > 0, segueallorala cosiddetta disuguaglianza di auchy Schwartz (si veda l Osservazione 8.9).
3 Proposizione.6 (Disuguaglianza di auchy Schwartz). Sia V uno spazio vettoriale su R munito di prodotto scalare h, i. Perogniv, w V si ha 5 hv, wi 6 v w (..3) Inoltre vale l uguaglianza in (..3) se e solo se v e w sono proporzionali. Dimostrazione. Rimane da dimostrare solo la seconda affermazione. Vale l uguaglianza in (..3) se e solo se l equazione v thv, wi+t w =0ha soluzione, ovvero se e solo se hv tw, v twi =0 ha soluzione, cioè se e solo se v = tw. Osservazione.7. Sia V uno spazio vettoriale su R munito di prodotto scalare h, i. Sev, w V \{0 V },allora hv, wi 6 v w 6 : possiamo perciò definire l angolo fra v e w come hv, wi cvw =arccos. v w Si ha quindi hv, wi = v w cos(cvw), chegeneralizzalaformula(..)aprodotti scalari qualsiasi. Osservazione.8. Sia V uno spazio vettoriale su R munito di prodotto scalare h, i. Dalladisuguaglianza(..3)ricaviamoancheladisuguaglianza triangolare (si veda di nuovo l Osservazione 8.9): v + w = hv + w, v + wi = v + hv, wi + hw, vi + w = v +hv, wi + w 6 v + hv, wi + w 6 v + v w + w =( v + w ), quindi v +w 6 v + w. In modo analogo il lettore verifichi che v w > v w. Esempio.9. Sia I = [a, b] R non vuoto e si consideri nello spazio 0 (I) l applicazione hf,gi = Z b a f(x)g(x)dx. È immediato verificare che gli assiomi di prodotto scalare (PS), (PS), (PS3) sono soddisfatti; inoltre il teorema della permanenza del segno per funzioni continue ci assicura che lo stesso vale per l assioma (PS4). In questo caso la disuguaglianza di auchy Schwartz diviene s s Z b Z b Z b f(x)g(x)dx 6 f(x) dx g(x) dx. Per ogni f 0 (I) la quantità a a s Z b a viene detta norma L di f. f = a f(x) dx
4 6. Basi ortonormali Definizione.0. Sia V uno spazio vettoriale su R munito di prodotto scalare h, i. Ivettoriv,v V si dicono ortogonali (o perpendicolari) sehv,v i =0ein tal caso si scrive v? v. L insieme { v,...,v n } V si dice ortogonale se v i? v j per i, j I con i 6= j. L insieme { v,...,v n } V si dice ortonormale se è ortogonale e i v i sono versori. Se V èfinitamentegenerato,unabase ortonormale B =(v,...,v n ) èunabase di V tale che l insieme { v,...,v n } sia ortonormale. Dalla definizione sopra possiamo dedurre che un insieme { v,...,v n } V è ortonormale se per ogni i, j =,...,n ( i = j, hv i,v j i = i,j = 0 i 6= j. Esempio.. Si fissi un sistema di riferimento O~ı~ ~ k nello spazio. Allora l insieme { ~ı, ~, ~ k } èortonormaleinv 3 (O) rispetto al prodotto scalare geometrico definito nell Esempio.4. Quindi B =(~ı, ~, ~ k) èunabaseortonormalediv 3 (O). Esempio.. Si consideri lo spazio R n munito del prodotto scalare standard h, i definito nell Esempio.5. I vettori { e,...,e n } formano un insieme ortonormale: perciò la base canonica =(e,...,e n ) èunabaseortonormalerispettoalprodotto scalare standard. Invece {e,e } non è ortonormale rispetto al prodotto scalare ((x,x ), (y,y )) 7! 3x y + x y / introdotto nello stesso Esempio. Infatti è vero che e? e, ma e = p 3 e e =/ p. oncludiamo che, rispetto a tale prodotto scalare, {e / p 3, p e } èortonormale. Esempio.3. Si consideri lo spazio V delle funzioni continue e periodiche di periodo : per esempio, cos px, sin px V per ogni p N (si noti che sin px e cos px hanno periodo minimo /p). In V definiamo l applicazione hf,gi = Z f(x)g(x)dx;
5 7 èfacileverificarecheh, i èunprodottoscalare.inoltredall analisiènotoche hp, p i = hcos px, cos qxi = ( se p = q 6= 0, 0 se p 6= q, hsin px, cos qxi =0 ( se p = q 6= 0, hsin px, sin qxi = 0 se p 6= q, quindi, per ogni N N, l insieme p, cos px, sin qx p,q=,...,n èortonormale. Osserviamo che in tutti gli esempi trattati è stato possibile determinare una base ortonormale. Questo è un risultato generale che si può dimostrare in modo algoritmico, come spiegato nel seguente risultato. Proposizione.4 (Metodo di ortonormalizzazione di Gram Schmidt). Sia V 6= { 0 V } uno spazio vettoriale finitamente generato su R munito di prodotto scalare h, i. AlloraesistonoinV basi ortonormali. Dimostrazione. Sia B =(v,...,v n ) una base di V ;vogliamocostruireunabaseortonormalea partire da B. Procediamonelmodoseguente. Passo (). Il vettore u èsemplicementeugualeav : u = v. Passo (). Il vettore u è v meno la proiezione ortogonale di v nella direzione di u,si veda l Osservazione 8.0: hv,u i u = v u u. Si noti che, per costruzione, hu,u i = 0 e L(u,u ) = L(v,v ), quindi u e u sono linearmente indipendenti. Passo (3). Il vettore u 3 è v 3 cui vengono sottratte le proiezioni ortogonali di v 3 nelle direzioni di u e u : u 3 = v 3 hv 3,u i u u hv 3,u i u u. Si noti che, per costruzione, hu 3,u i = hu 3,u i =0e L(u,u,u 3 )=L(v,v,v 3 ),quindi u,u,u 3 sono linearmente indipendenti.. Passo (i). Il vettore u i è v i cui vengono sottratte le proiezioni ortogonali di v i nelle direzioni di tutti i vettori precedenti u,...,u i : u i = v i hv i,u i u u hv i,u i u u hv i,u i i u i u i. Si noti che, per costruzione, hu i,u i i = = hu i,u i =0e L(u,...,u i )=L(v,...,v i ), quindi u,...,u i sono linearmente indipendenti.
6 8 Alla fine otteniamo una base ortogonale (u,...,u n ). Normalizzando i vettori ricaviamo la base ortonormale cercata. Esempio.5. Data la matrice 0 4 A = B 4 A R4,3, 0 vogliamo trovare una base ortonormale per lo spazio W generato dalle sue colonne. Èimmediatoverificarecheletrecolonnesonolinearmenteindipendenti,quindicome base B di partenza possiamo prendere B =(v,v,v 3 ) con v = A, v = 4 4 A, v 3 = 4 A. 0 Seguendo l algoritmo di Gram Schmidt costruiamo la nuova base ortonormale B 0 = (w,w,w 3 ) nel modo seguente. Passo (). Si ha che 0 u = v = A Passo (). alcoliamo il prodotto scalare hv,u i = +4+4 =6. Definiamo poi il vettore / hv,u i u = v u u = B A = B 5/ A. 5/ Passo (3). alcoliamo i due prodotti scalari hv 3,u i =0e hv 3,u i = definiamo il vettore / hv 3,u i hv 3,u i u 3 = v 3 u u u u 3 = A 0 A + 4 B 5/ 5/ A = 0 5/ oncludiamo normalizzando i 3 vettori, quindi la base ortonormale di W cercata è / / / p w = u u = /A, w = u u = B / A, w 3 = u 3 u 3 = B 0 / / / p A Il lettore verifichi che la base B 0 così ottenuta è effettivamente ortonormale. 0 e 0 0 A.
7 L importanza e utilità delle basi ortonormali è data dalla seguente proposizione. Proposizione.6. Sia V uno spazio vettoriale su R munito di prodotto scalare h, i. Se{ v,...,v n } V èuninsiemeortonormale,allora: (i) v,...,v n sono linearmente indipendenti; (ii) se V èfinitamentegeneratoedim R (V )=n, allorab =(v...,v n ) èunabase ortonormale di V esihav = hv, v iv + + hv, v n iv n per ogni v V. Dimostrazione. Per definizione { v,...,v n } V èuninsiemedivettoriortonormaliseesolose ( 0 se i 6= j, hv i,v j i = se i = j, quindi, se v + + n v n =0èunarelazionedidipendenzalineare,siha 0=h0,v j i = h v + + n v n,v j i = hv,v j i + + n hv n,v j i = j. 9 In particolare v,...,v n sono linearmente indipendenti. Se V èfinitamentegeneratoedim R (V )=n, perlaproposizione6.7,seguecheb èunabase di V. In particolare per ogni v V esistono,..., n R tali che v = v + + n v n.quindi per ogni j =,...,n. hv, v j i = h v + + n v n,v j i = hv,v j i + + n hv n,v j i = j Il coefficiente hv, v j i viene detto coefficiente di Fourier (di v rispetto a v j ). Esempio.7. Si consideri lo spazio R 3 munito del prodotto scalare h, i definito nell Esempio.5. I tre vettori v = (,, ), v 3 = (,, ), v 3 3 = (,, ) 3 formano un insieme { v,v,v 3 } ortonormale, quindi B =(v,v,v 3 ) èunabasedi R 3. Sia v =(,, ) R 3.Allorahv, v i =5/3, hv, v i = hv, v 3 i =/3: quindi,come èanchefacileverificaredirettamente,risulta v = 5 3 v + 3 v + 3 v 3..3 Matrici ortogonali In questo paragrafo introduciamo un importante famiglia di matrici quadrate invertibili. Definizione.8 (Matrici ortogonali). Una matrice P R n,n si dice ortogonale se vale l uguaglianza t PP = I n. Osservazione.9. Sia P R n,n ortogonale.. La matrice identità I n èortogonale;ancheognimatriceottenutadai n cambiando segno a una o più delle sue entrate è ortogonale.
8 0. Poiché t PP = I n,seguechep èinvertibileep = t P : in particolare si ha anche P t P = I n.inmanieraanalogasidimostrachesep t P = I n allora anche t PP = I n,cioèp èortogonaleseesolosep t P = I n. 3. Si ha =det(i n )=det( t PP)=det( t P )det(p )=det(p ),dunque det(p )=± : quanto osservato sulla matrice identità ci permette di affermare che esistono matrici di entrambi i tipi. 4. Poiché la riga i esima di t P èlacolonnai esima P i di P,lacondizione t PP = I n si può leggere dicendo che il prodotto scalare standard dell Esempio.5 delle colonne P i e P j di P è i,j :inaltreparoleunamatriceèortogonalesee solo se le sue colonne sono un insieme ortonormale, rispetto al prodotto scalare standard, di n vettori di R n. 5. Identificando R,n con R n tramite la trasposta, si verifica in maniera simile che la condizione P t P = I n equivale a dire che le righe di P formano un insieme ortonormale di n vettori di R n rispetto al prodotto scalare standard. Le matrici ortogonali si dividono, quindi, in due classi non vuote, quelle con determinante e quelle con determinante. Definizione.0 (Matrici ortogonali speciali e non speciali). Una matrice ortogonale P R n,n si dice speciale se det(p )=, non speciale se det(p )=. Esempio.. Le matrici di R 3,3 0 0 P A, P 3 3 A, sono ortogonali. La prima è non speciale, la seconda speciale. Esempio.. Determiniamo tutte le matrici ortogonali di ordine due; sia p, p P =, R, p, p, ortogonale. La condizione P t P = I si traduce nel sistema 8 >< p, + p, = p, p, + p, p, =0 >: p, + p, =. La prima e la terza equazione implicano l esistenza di #, [0, ] tali che p, =cos#, p, = sin #, p, =sin, p, =cos.
9 La seconda equazione è allora equivalente a 0=cos# sin sin # cos =sin( #). In particolare, a meno di multipli di, sideveavereo = # ovvero = # +. Nel primo caso cos # sin # P =, sin # cos # (e P èortogonalespeciale);nelsecondo P = cos # sin # sin # cos # (e P èortogonalenonspeciale). oncludiamo l esempio con un interpretazione geometrica delle matrici ortogonali speciali: consideriamo nel piano due sistemi di riferimento O~ı~ e O~ı 0 ~ 0 esia l angolo misurato in senso antiorario fra i versori ~ı e ~ı 0. Allora si deve avere ~ı 0 = a~ı + b~, ~ 0 = c~ı + d~ e si ha, per la Proposizione.6, a = h~ı 0,~ıi =cos', b = h~ı 0,~ i =sin', c = h~ 0,~ıi = sin ', d = h~ 0,~ i =cos'. Se ora consideriamo ~v = x 0 ~ı 0 + y 0 ~ 0 = x~ı + y~, sostituendoleespressioniottenute sopra di ~ı 0 e ~ 0 in funzione di ~ı e ~,tenendocontoche(~ı, ~ ) èunabasediv (O), si ottiene x 0 cos ' sin ' x y 0 =. sin ' cos ' y oncludiamo che le matrici ortogonali speciali di ordine due corrispondono alle rotazioni nel piano. Per questo spesso indichiamo con R ' la matrice cos ' sin ' sin '. cos ' Nella figura. qui sotto vediamo un sistema Ox 0 y 0 ottenuto da Oxy con una rotazione.
10 y x' y' v O ϕ x Figura. Un analoga interpretazione può essere data per matrici ortogonali in R n,n con n > 3.
LEZIONE 25. P si dice speciale se det(p ) = 1 non
 LEZIONE 5 5.. Matrici ortogonali. Facciamo una breve digressione su un importante famiglia di matrici, quelle ortogonali. Definizione 5... P R n,n si dice ortogonale se t P I n. Prima di dare esempi di
LEZIONE 5 5.. Matrici ortogonali. Facciamo una breve digressione su un importante famiglia di matrici, quelle ortogonali. Definizione 5... P R n,n si dice ortogonale se t P I n. Prima di dare esempi di
Spazi vettoriali euclidei.
 Spazi vettoriali euclidei Prodotto scalare, lunghezza e ortogonalità in R n Consideriamo lo spazio vettoriale R n = { =,,, n R}, n con la somma fra vettori e il prodotto di un vettore per uno scalare definiti
Spazi vettoriali euclidei Prodotto scalare, lunghezza e ortogonalità in R n Consideriamo lo spazio vettoriale R n = { =,,, n R}, n con la somma fra vettori e il prodotto di un vettore per uno scalare definiti
Fattorizzazione QR e matrici di Householder
 Fattorizzazione QR e matrici di Householder ottobre 009 In questa nota considereremo un tipo di fattorizzazione che esiste sempre nel caso di matrici quadrate non singolari ad entrate reali. Definizione
Fattorizzazione QR e matrici di Householder ottobre 009 In questa nota considereremo un tipo di fattorizzazione che esiste sempre nel caso di matrici quadrate non singolari ad entrate reali. Definizione
0.1 Spazi Euclidei in generale
 0.1. SPAZI EUCLIDEI IN GENERALE 1 0.1 Spazi Euclidei in generale Sia V uno spazio vettoriale definito su R. Diremo, estendendo una definizione data in precedenza, che V è uno spazio vettoriale euclideo
0.1. SPAZI EUCLIDEI IN GENERALE 1 0.1 Spazi Euclidei in generale Sia V uno spazio vettoriale definito su R. Diremo, estendendo una definizione data in precedenza, che V è uno spazio vettoriale euclideo
1 Prodotti scalari e forme bilineari
 orso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 9 Prodotti scalari, forme bilineari, spazi Euclidei Prodotti scalari e forme bilineari
orso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 9 Prodotti scalari, forme bilineari, spazi Euclidei Prodotti scalari e forme bilineari
Lezione Il metodo degli scarti
 Lezione 15 15.1 Il metodo degli scarti Sia dato uno spazio vettoriale V su un campo K = R, C esianov 1,...,v n 2 V vettori fissati. Quanto visto nella lezione precedente ci suggerisce il seguente algoritmo
Lezione 15 15.1 Il metodo degli scarti Sia dato uno spazio vettoriale V su un campo K = R, C esianov 1,...,v n 2 V vettori fissati. Quanto visto nella lezione precedente ci suggerisce il seguente algoritmo
Parte 8. Prodotto scalare, teorema spettrale
 Parte 8. Prodotto scalare, teorema spettrale A. Savo Appunti del Corso di Geometria 3-4 Indice delle sezioni Prodotto scalare in R n, Basi ortonormali, 4 3 Algoritmo di Gram-Schmidt, 7 4 Matrici ortogonali,
Parte 8. Prodotto scalare, teorema spettrale A. Savo Appunti del Corso di Geometria 3-4 Indice delle sezioni Prodotto scalare in R n, Basi ortonormali, 4 3 Algoritmo di Gram-Schmidt, 7 4 Matrici ortogonali,
Prodotto scalare e matrici < PX,PY >=< X,Y >
 Prodotto scalare e matrici Matrici ortogonali Consideriamo in R n il prodotto scalare canonico < X,Y >= X T Y = x 1 y 1 + +x n y n. Ci domandiamo se esistono matrici P che conservino il prodotto scalare,
Prodotto scalare e matrici Matrici ortogonali Consideriamo in R n il prodotto scalare canonico < X,Y >= X T Y = x 1 y 1 + +x n y n. Ci domandiamo se esistono matrici P che conservino il prodotto scalare,
Esempi. In R 2, le coppia (2, 5) è combinazione lineare dei vettori (0, 1) e (1, 1). Infatti:
 Combinazioni lineari [Abate, 4.2] Sia V uno spazio vettoriale e v 1, v 2,..., v n dei vettori di V. Diremo che un vettore w V è combinazione lineare dei vettori v 1,..., v n se esistono a 1, a 2,..., a
Combinazioni lineari [Abate, 4.2] Sia V uno spazio vettoriale e v 1, v 2,..., v n dei vettori di V. Diremo che un vettore w V è combinazione lineare dei vettori v 1,..., v n se esistono a 1, a 2,..., a
La lunghezza dei vettori e legata alle operazioni sui vettori nel modo seguente: Consideriamo due vettori v, w e il vettore v + w loro somma.
 Matematica II, 20.2.. Lunghezza di un vettore nel piano Consideriamo il piano vettoriale geometrico P O. Scelto un segmento come unita, possiamo parlare di lunghezza di un vettore v P O rispetto a tale
Matematica II, 20.2.. Lunghezza di un vettore nel piano Consideriamo il piano vettoriale geometrico P O. Scelto un segmento come unita, possiamo parlare di lunghezza di un vettore v P O rispetto a tale
Lezione Diagonalizzazione ortogonale per matrici simmetriche
 Lezione 22 22. Diagonalizzazione ortogonale per matrici simmetriche La Proposizione 2. afferma che ogni matrice simmetrica reale è diagonalizzabile su R: ilrisultatoprincipalediquestasezioneèchelamatricechediagonalizzapuò
Lezione 22 22. Diagonalizzazione ortogonale per matrici simmetriche La Proposizione 2. afferma che ogni matrice simmetrica reale è diagonalizzabile su R: ilrisultatoprincipalediquestasezioneèchelamatricechediagonalizzapuò
LEZIONE 8. k e w = wx ı + w y j + w z. k di R 3 definiamo prodotto scalare di v e w il numero
 LEZINE 8 8.1. Prodotto scalare. Dati i vettori geometrici v = v x ı + v y j + v z k e w = wx ı + j + k di R 3 definiamo prodotto scalare di v e w il numero v, w = ( v x v y v z ) w x = v x + v y + v z.
LEZINE 8 8.1. Prodotto scalare. Dati i vettori geometrici v = v x ı + v y j + v z k e w = wx ı + j + k di R 3 definiamo prodotto scalare di v e w il numero v, w = ( v x v y v z ) w x = v x + v y + v z.
~ k. Il prodotto scalare di ~v e ~w èilnumero. Confrontando la definizione di prodotto scalare con la Formula (7.3.1) otteniamo
 Lezione 8 8.1 Prodotto scalare Definizione 8.1 (Prodotto scalare). Sia fissato un sistema di riferimento O~ı~ ~ k in S 3 esiano~v, ~w 2 V 3 (O) due vettori, ~v = v x ~ı + v y ~ + v z ~ k e ~w = wx ~ı +
Lezione 8 8.1 Prodotto scalare Definizione 8.1 (Prodotto scalare). Sia fissato un sistema di riferimento O~ı~ ~ k in S 3 esiano~v, ~w 2 V 3 (O) due vettori, ~v = v x ~ı + v y ~ + v z ~ k e ~w = wx ~ı +
APPUNTI DI ALGEBRA LINEARE
 APPUNTI DI ALGEBRA LINEARE. Definizione Si dice spazio vettoriale (sul campo dei numeri reali R) un insieme V per il quale siano definite l operazione interna di somma (che ad ogni coppia di vettori e
APPUNTI DI ALGEBRA LINEARE. Definizione Si dice spazio vettoriale (sul campo dei numeri reali R) un insieme V per il quale siano definite l operazione interna di somma (che ad ogni coppia di vettori e
Capitolo IV SPAZI VETTORIALI EUCLIDEI
 Capitolo IV SPAZI VETTORIALI EUCLIDEI È ben noto che in VO 3 si possono considerare strutture più ricche di quella di spazio vettoriale; si pensi in particolare all operazioni di prodotto scalare di vettori.
Capitolo IV SPAZI VETTORIALI EUCLIDEI È ben noto che in VO 3 si possono considerare strutture più ricche di quella di spazio vettoriale; si pensi in particolare all operazioni di prodotto scalare di vettori.
SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE
 SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE. Esercizi Esercizio. In R calcolare il modulo dei vettori,, ),,, ) ed il loro angolo. Esercizio. Calcolare una base ortonormale del sottospazio
SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE. Esercizi Esercizio. In R calcolare il modulo dei vettori,, ),,, ) ed il loro angolo. Esercizio. Calcolare una base ortonormale del sottospazio
LEZIONE 12. v = α 1 v α n v n =
 LEZIONE 12 12.1. Combinazioni lineari. Definizione 12.1.1. Sia V uno spazio vettoriale su k = R, C e v 1,..., v n V vettori fissati. Un vettore v V si dice combinazione lineare di v 1,..., v n se esistono
LEZIONE 12 12.1. Combinazioni lineari. Definizione 12.1.1. Sia V uno spazio vettoriale su k = R, C e v 1,..., v n V vettori fissati. Un vettore v V si dice combinazione lineare di v 1,..., v n se esistono
1. Complemento ortogonale di un vettore non nullo Abbiamo visto che nel piano
 Geometria e Algebra (II), 11.12.12 1. Complemento ortogonale di un vettore non nullo Abbiamo visto che nel piano P O i vettori ortogonali ad un dato vettore non nullo descrivono una retta per O, e nello
Geometria e Algebra (II), 11.12.12 1. Complemento ortogonale di un vettore non nullo Abbiamo visto che nel piano P O i vettori ortogonali ad un dato vettore non nullo descrivono una retta per O, e nello
Prodotto scalare, ortogonalitá e basi ortonormali
 CAPITOLO 0 Prodotto scalare, ortogonalitá e basi ortonormali Esercizio 0.. Dati i seguenti vettori di R si calcoli il prodotto scalare (v i,v j per i,j =,,...,6: v = (6,3 v = (,0 v 3 = (, v 4 = (,0 v 5
CAPITOLO 0 Prodotto scalare, ortogonalitá e basi ortonormali Esercizio 0.. Dati i seguenti vettori di R si calcoli il prodotto scalare (v i,v j per i,j =,,...,6: v = (6,3 v = (,0 v 3 = (, v 4 = (,0 v 5
B = (e 1,..., e n ) di V, e una sequenza C = ( f 1,..., f n ) di vettori di. Lezione del 21 maggio.
 Lezione del maggio. Il riferimento principale di questa lezione e costituito da parti di: 3 Trasformazioni ortogonali, 4 Complemento ortogonale, 5 Matrici di Gram e proiezioni ortogonali, 6 Orientazione
Lezione del maggio. Il riferimento principale di questa lezione e costituito da parti di: 3 Trasformazioni ortogonali, 4 Complemento ortogonale, 5 Matrici di Gram e proiezioni ortogonali, 6 Orientazione
Per capire meglio il concetto di combinazione lineare prendiamo in considerazione alcuni esempi.
 Lezione 14 14.1 Combinazioni lineari Definizione 14.1. Sia V uno spazio vettoriale su un campo K = R, C esiano v 1,...,v n 2 V vettori fissati. Un vettore v 2 V si dice combinazione lineare di v 1,...,v
Lezione 14 14.1 Combinazioni lineari Definizione 14.1. Sia V uno spazio vettoriale su un campo K = R, C esiano v 1,...,v n 2 V vettori fissati. Un vettore v 2 V si dice combinazione lineare di v 1,...,v
LEZIONE 4. Le sottomatrici 2 2 di A sono. Invece ( 1 3 non è sottomatrice di A.
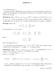 LEZIONE 4 4 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 4 4 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 13. v =α 1 v α i 1 v i 1 + α i v i = =α 1 v α i 1 v i 1 + α i (λ 1 v λ i 1 v i 1 ) =
 LEZIONE 13 13.1. Il metodo degli scarti. Sia dato uno spazio vettoriale V su k = R, C e siano v 1,..., v n V. Quanto visto nella lezione precedente ci suggerisce il seguente algoritmo per stabilire se
LEZIONE 13 13.1. Il metodo degli scarti. Sia dato uno spazio vettoriale V su k = R, C e siano v 1,..., v n V. Quanto visto nella lezione precedente ci suggerisce il seguente algoritmo per stabilire se
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
2 Sistemi lineari. Metodo di riduzione a scala.
 Sistemi lineari. Metodo di riduzione a scala. Esercizio.1 Utilizzando il metodo di eliminazione di Gauss, risolvere i seguenti sistemi lineari: 1. 3. x 1 x + 3x 3 = 1 x 1 x x 3 = x 1 + x + 3x 3 = 5 x 1
Sistemi lineari. Metodo di riduzione a scala. Esercizio.1 Utilizzando il metodo di eliminazione di Gauss, risolvere i seguenti sistemi lineari: 1. 3. x 1 x + 3x 3 = 1 x 1 x x 3 = x 1 + x + 3x 3 = 5 x 1
LeLing12: Ancora sui determinanti.
 LeLing2: Ancora sui determinanti. Ārgomenti svolti: Sviluppi di Laplace. Prodotto vettoriale e generalizzazioni. Rango e determinante: i minori. Il polinomio caratteristico. Ēsercizi consigliati: Geoling
LeLing2: Ancora sui determinanti. Ārgomenti svolti: Sviluppi di Laplace. Prodotto vettoriale e generalizzazioni. Rango e determinante: i minori. Il polinomio caratteristico. Ēsercizi consigliati: Geoling
Geometria e Topologia I (U1-4) 2006-mag-10 61
 Geometria e Topologia I (U1-4) 2006-mag-10 61 (15.9) Teorema. Consideriamo il piano affine. Se A A 2 (K) è un punto e r una retta che non passa per A, allora esiste unica la retta per A che non interseca
Geometria e Topologia I (U1-4) 2006-mag-10 61 (15.9) Teorema. Consideriamo il piano affine. Se A A 2 (K) è un punto e r una retta che non passa per A, allora esiste unica la retta per A che non interseca
Algebra delle matrici
 Algebra delle matrici Metodo di Gauss-Jordan per l inversione di una matrice. Nella lezione scorsa abbiamo visto che un modo per determinare l eventuale inversa di una matrice quadrata A consiste nel risolvere
Algebra delle matrici Metodo di Gauss-Jordan per l inversione di una matrice. Nella lezione scorsa abbiamo visto che un modo per determinare l eventuale inversa di una matrice quadrata A consiste nel risolvere
Esercizi di Geometria - 1
 Esercizi di Geometria - Samuele Mongodi - smongodi@snsit Di seguito si trovano alcuni esercizi assai simili a quelli che vi troverete ad affrontare nei test e negli scritti dell esame Non è detto che vi
Esercizi di Geometria - Samuele Mongodi - smongodi@snsit Di seguito si trovano alcuni esercizi assai simili a quelli che vi troverete ad affrontare nei test e negli scritti dell esame Non è detto che vi
Esempio. L immagine di f è l insieme dei vettori w = (w 1, w 2 ) R 2 che hanno w 1 = w 2. Quindi:
 Nucleo, immagine e loro proprietà [Abate, 5.2] Data una applicazione lineare f : V W, chiamiamo nucleo di f l insieme N(f) := { v V : f(v) = 0 W } Se S V è un sottoinsieme del dominio, indichiamo con f(s)
Nucleo, immagine e loro proprietà [Abate, 5.2] Data una applicazione lineare f : V W, chiamiamo nucleo di f l insieme N(f) := { v V : f(v) = 0 W } Se S V è un sottoinsieme del dominio, indichiamo con f(s)
Facoltà di Scienze Statistiche, Algebra Lineare 1 A, G. Parmeggiani - Programma
 Facoltà di Scienze Statistiche, Algebra Lineare 1 A, G. Parmeggiani - Programma Il testo di riferimento è: Appunti di Algebra Lineare, Gregorio, Parmeggiani, Salce 06/12/04 Matrici. Esempi. Tipi particolari
Facoltà di Scienze Statistiche, Algebra Lineare 1 A, G. Parmeggiani - Programma Il testo di riferimento è: Appunti di Algebra Lineare, Gregorio, Parmeggiani, Salce 06/12/04 Matrici. Esempi. Tipi particolari
vettori V Sia inoltre l angolo che il primo vettore deve percorrere per sovrapporsi al secondo. * **
 Prodotto scalare di vettori. Consideriasmo due vettori u e v e siano O e O due rappresentanti applicati in O. Indichiamo come al solito con u = O la norma (cioè l intensità) del vettore u Sia inoltre l
Prodotto scalare di vettori. Consideriasmo due vettori u e v e siano O e O due rappresentanti applicati in O. Indichiamo come al solito con u = O la norma (cioè l intensità) del vettore u Sia inoltre l
LEZIONE 24. è lineare. Per la commutatività del prodotto scalare segue anche la linearità dell applicazione
 LEZIONE 24 24.1. Prodotti sclri. Definizione 24.1.1. Si V uno spzio vettorile su R. un ppliczione Un prodotto sclre su V è tle che:, : V V R (v 1, v 2 ) v 1, v 2 (PS1) per ogni v 1, v 2 V si h v 1, v 2
LEZIONE 24 24.1. Prodotti sclri. Definizione 24.1.1. Si V uno spzio vettorile su R. un ppliczione Un prodotto sclre su V è tle che:, : V V R (v 1, v 2 ) v 1, v 2 (PS1) per ogni v 1, v 2 V si h v 1, v 2
Geometria BAER Canale A-K Esercizi 8
 Geometria BAER 6-7 Canale A-K Esercizi 8 Esercizio Si consideri il sottospazio (a) Si trovi una base ortonormale di U (b) Si trovi una base ortonormale di U U = L v =, v, v 3 = (c) Si scriva la matrice
Geometria BAER 6-7 Canale A-K Esercizi 8 Esercizio Si consideri il sottospazio (a) Si trovi una base ortonormale di U (b) Si trovi una base ortonormale di U U = L v =, v, v 3 = (c) Si scriva la matrice
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof. F.Podestà, a.a
 APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
Geometria BAER Canale A-K Esercizi 9
 Geometria BAER Canale A-K Esercizi 9 Esercizio Sia (V,, ) uno spazio metrico Si mostri che se U V, v V, p U la proiezione ortogonale su U, allora v p U (v) U Soluzione: Il vettore v si scrive in modo unico
Geometria BAER Canale A-K Esercizi 9 Esercizio Sia (V,, ) uno spazio metrico Si mostri che se U V, v V, p U la proiezione ortogonale su U, allora v p U (v) U Soluzione: Il vettore v si scrive in modo unico
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
Spazi euclidei, endomorfismi simmetrici, forme quadratiche. R. Notari
 Spazi euclidei, endomorfismi simmetrici, forme quadratiche R. Notari 14 Aprile 2006 1 1. Proprietà del prodotto scalare. Sia V = R n lo spazio vettoriale delle n-uple su R. Il prodotto scalare euclideo
Spazi euclidei, endomorfismi simmetrici, forme quadratiche R. Notari 14 Aprile 2006 1 1. Proprietà del prodotto scalare. Sia V = R n lo spazio vettoriale delle n-uple su R. Il prodotto scalare euclideo
GEOMETRIA 1 quarta parte
 GEOMETRIA 1 quarta parte Cristina Turrini C. di L. in Fisica - 2014/2015 Cristina Turrini (C. di L. in Fisica - 2014/2015) GEOMETRIA 1 1 / 36 index Forme bilineari 1 Forme bilineari 2 Il caso reale: spazi
GEOMETRIA 1 quarta parte Cristina Turrini C. di L. in Fisica - 2014/2015 Cristina Turrini (C. di L. in Fisica - 2014/2015) GEOMETRIA 1 1 / 36 index Forme bilineari 1 Forme bilineari 2 Il caso reale: spazi
Appunti di Geometria - 2
 Appunti di Geometria - Samuele Mongodi - s.mongodi@sns.it Cambi di base e applicazioni lineari Richiami Sia V uno spazio vettoriale di dimensione n sul campo K, con base assegnata e,..., e n } (ad esempio
Appunti di Geometria - Samuele Mongodi - s.mongodi@sns.it Cambi di base e applicazioni lineari Richiami Sia V uno spazio vettoriale di dimensione n sul campo K, con base assegnata e,..., e n } (ad esempio
Geometria BAER Canale A-K Esercizi 8
 Geometria BAER Canale A-K Esercizi 8 Esercizio. Si consideri il sottospazio U = L v =, v, v 3 =. (a) Si trovino le equazioni cartesiane ed una base ortonormale di U. (b) Si trovi una base ortonormale di
Geometria BAER Canale A-K Esercizi 8 Esercizio. Si consideri il sottospazio U = L v =, v, v 3 =. (a) Si trovino le equazioni cartesiane ed una base ortonormale di U. (b) Si trovi una base ortonormale di
3. Vettori, Spazi Vettoriali e Matrici
 3. Vettori, Spazi Vettoriali e Matrici Vettori e Spazi Vettoriali Operazioni tra vettori Basi Trasformazioni ed Operatori Operazioni tra Matrici Autovalori ed autovettori Forme quadratiche, quadriche e
3. Vettori, Spazi Vettoriali e Matrici Vettori e Spazi Vettoriali Operazioni tra vettori Basi Trasformazioni ed Operatori Operazioni tra Matrici Autovalori ed autovettori Forme quadratiche, quadriche e
PROGRAMMA DEL CORSO DI GEOMETRIA E ALGEBRA. A.A
 PROGRAMMA DEL CORSO DI GEOMETRIA E ALGEBRA. A.A. 2011-12 DOCENTE TITOLARE: FRANCESCO BONSANTE 1. Geometria analitica dello spazio (1) vettori applicati e lo spazio E 3 O: operazioni su vettori e proprietà.
PROGRAMMA DEL CORSO DI GEOMETRIA E ALGEBRA. A.A. 2011-12 DOCENTE TITOLARE: FRANCESCO BONSANTE 1. Geometria analitica dello spazio (1) vettori applicati e lo spazio E 3 O: operazioni su vettori e proprietà.
Note per il corso di Geometria Corso di laurea in Ing. Elettronica e delle Telecomunicazioni
 Note per il corso di Geometria 9- Corso di laurea in Ing. Elettronica e delle Telecomunicazioni Prodotto scalare e matrici simmetriche. Il prodotto scalare consente di introdurre in uno spazio vettoriale
Note per il corso di Geometria 9- Corso di laurea in Ing. Elettronica e delle Telecomunicazioni Prodotto scalare e matrici simmetriche. Il prodotto scalare consente di introdurre in uno spazio vettoriale
a + 2b + c 3d = 0, a + c d = 0 c d
 SPAZI VETTORIALI 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x,
SPAZI VETTORIALI 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x,
SPAZI VETTORIALI CON PRODOTTO SCALARE A =
 SPAZI VETTORIALI CON PRODOTTO SCALARE Esercizi Esercizio. Nello spazio euclideo standard (R 2,, ) sia data la matrice 2 3 A = 3 2 () Determinare una base rispetto alla quale A sia la matrice di un endomorfismo
SPAZI VETTORIALI CON PRODOTTO SCALARE Esercizi Esercizio. Nello spazio euclideo standard (R 2,, ) sia data la matrice 2 3 A = 3 2 () Determinare una base rispetto alla quale A sia la matrice di un endomorfismo
y + P(x) y + Q(x) y = 0 y(x) = c 1y 1(x) + c 2 y 2(x).
 Proposizione 4. Se y 1(x) e y (x) sono soluzioni linearmente indipendenti di y + P(x) y + Q(x) y = 0 ogni altra soluzione della stessa equazione si scrive nella forma per una scelta opportuna delle costanti
Proposizione 4. Se y 1(x) e y (x) sono soluzioni linearmente indipendenti di y + P(x) y + Q(x) y = 0 ogni altra soluzione della stessa equazione si scrive nella forma per una scelta opportuna delle costanti
Sistemi Lineari. Rango di una matrice. Lezione 21, Algebra Lineare,
 Lezione 21, Algebra Lineare, 15.11.2017 Sistemi Lineari Rango di una matrice Esempio principale, I Considerata una matrice, ci poniamo il problema di determinare il massimo numero di colonne linearmente
Lezione 21, Algebra Lineare, 15.11.2017 Sistemi Lineari Rango di una matrice Esempio principale, I Considerata una matrice, ci poniamo il problema di determinare il massimo numero di colonne linearmente
AUTOVALORI, AUTOVETTORI, AUTOSPAZI
 AUTOVALORI, AUTOVETTORI, AUTOSPAZI. Esercizi Esercizio. Sia f : R 3 R 3 l endomorfismo definito da f(x, y, z) = (x+y, y +z, x+z). Calcolare gli autovalori ed una base per ogni autospazio di f. Dire se
AUTOVALORI, AUTOVETTORI, AUTOSPAZI. Esercizi Esercizio. Sia f : R 3 R 3 l endomorfismo definito da f(x, y, z) = (x+y, y +z, x+z). Calcolare gli autovalori ed una base per ogni autospazio di f. Dire se
NOTE DI ALGEBRA LINEARE v = a 1 v a n v n, w = b 1 v b n v n
 NOTE DI ALGEBRA LINEARE 2- MM 9 NOVEMBRE 2 Combinazioni lineari e generatori Sia K un campo e V uno spazio vettoriale su K Siano v,, v n vettori in V Definizione Un vettore v V si dice combinazione lineare
NOTE DI ALGEBRA LINEARE 2- MM 9 NOVEMBRE 2 Combinazioni lineari e generatori Sia K un campo e V uno spazio vettoriale su K Siano v,, v n vettori in V Definizione Un vettore v V si dice combinazione lineare
Esercizi di geometria per Fisica / Fisica e Astrofisica
 Esercizi di geometria per Fisica / Fisica e Astrofisica Foglio 3 - Soluzioni Esercizio. Stabilire se i seguenti sottoinsiemi di R 3 sono sottospazi vettoriali: (a) S = {(x y z) R 3 : x + y + z = }. (b)
Esercizi di geometria per Fisica / Fisica e Astrofisica Foglio 3 - Soluzioni Esercizio. Stabilire se i seguenti sottoinsiemi di R 3 sono sottospazi vettoriali: (a) S = {(x y z) R 3 : x + y + z = }. (b)
LEZIONE 16 A = Verifichiamo se qualcuna fra le entrate a di A è suo autovalore. determinare per quale entrata a di A risulta rk(a ai 2 ) 1.
 LEZIONE 16 16.1. Autovalori, autovettori ed autospazi di matrici. Introduciamo la seguente definizione. Definizione 16.1.1. Siano k = R, C e A k n,n. Un numero λ k si dice autovalore di A su k) se rka
LEZIONE 16 16.1. Autovalori, autovettori ed autospazi di matrici. Introduciamo la seguente definizione. Definizione 16.1.1. Siano k = R, C e A k n,n. Un numero λ k si dice autovalore di A su k) se rka
Esercizi Di Geometria 1 (BAER) Canale 1
 Esercizi Di Geometria 1 (BAER) Canale 1 SETTIMANA 9 (23 29 Novembre 2015) da consegnare Mercoledi 2 Dicembre. Esercizio 1. Sia E = (V,, ) uno spazio metrico finito dimensionale. sottospazio vettoriale
Esercizi Di Geometria 1 (BAER) Canale 1 SETTIMANA 9 (23 29 Novembre 2015) da consegnare Mercoledi 2 Dicembre. Esercizio 1. Sia E = (V,, ) uno spazio metrico finito dimensionale. sottospazio vettoriale
Federica Gregorio e Cristian Tacelli
 1 Sistemi lineari Federica Gregorio e Cristian Tacelli Un sistema lineare m n (m equazioni in n incognite) è un insieme di equazioni lineari che devono essere soddisfatte contemporaneamente a 11 x 1 +
1 Sistemi lineari Federica Gregorio e Cristian Tacelli Un sistema lineare m n (m equazioni in n incognite) è un insieme di equazioni lineari che devono essere soddisfatte contemporaneamente a 11 x 1 +
Prodotti scalari e matrici
 Prodotti scalari e matrici 1 Forme bilineari e matrici In questa sezione vogliamo studiare la corrispondenza biunivoca che esiste tra l insieme delle forme bilineari su di un certo spazio vettoriale V
Prodotti scalari e matrici 1 Forme bilineari e matrici In questa sezione vogliamo studiare la corrispondenza biunivoca che esiste tra l insieme delle forme bilineari su di un certo spazio vettoriale V
Definizione. Sia f : V V un endomorfismo e λ R. Se esiste v V non nullo tale che
 Autovalori ed autovettori [Abate, 131] Sia f : V V un endomorfismo e λ R Se esiste v V non nullo tale che f(v) = λv, diremo che λ è un autovalore di f e che v è un autovettore di f associato a λ Lezioni
Autovalori ed autovettori [Abate, 131] Sia f : V V un endomorfismo e λ R Se esiste v V non nullo tale che f(v) = λv, diremo che λ è un autovalore di f e che v è un autovettore di f associato a λ Lezioni
Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti)
 Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti) April 14, 2011 (alcune note non complete sugli argomenti trattati: eventuali completamenti saranno aggiunti)
Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti) April 14, 2011 (alcune note non complete sugli argomenti trattati: eventuali completamenti saranno aggiunti)
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof. Fabio Perroni. 3. Sistemi di equazioni lineari
 Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 3 Sistemi di equazioni lineari Siano m, n N \ {}, sia K un campo Definizione a) Un sistema
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 3 Sistemi di equazioni lineari Siano m, n N \ {}, sia K un campo Definizione a) Un sistema
(V) (FX) L unione di due basi di uno spazio vettoriale è ancora una base dello spazio vettoriale.
 8 gennaio 2009 - PROVA D ESAME - Geometria e Algebra T NOME: MATRICOLA: a=, b=, c= Sostituire ai parametri a, b, c rispettivamente la terzultima, penultima e ultima cifra del proprio numero di matricola
8 gennaio 2009 - PROVA D ESAME - Geometria e Algebra T NOME: MATRICOLA: a=, b=, c= Sostituire ai parametri a, b, c rispettivamente la terzultima, penultima e ultima cifra del proprio numero di matricola
Il Teorema Spettrale. 0.1 Applicazioni lineari simmetriche ed hermitiane
 0.1. APPLICAZIONI LINEARI SIMMETRICHE ED HERMITIANE 1 Il Teorema Spettrale In questa nota vogliamo esaminare la dimostrazione del Teorema Spettrale e studiare le sue conseguenze per quanto riguarda i prodotti
0.1. APPLICAZIONI LINEARI SIMMETRICHE ED HERMITIANE 1 Il Teorema Spettrale In questa nota vogliamo esaminare la dimostrazione del Teorema Spettrale e studiare le sue conseguenze per quanto riguarda i prodotti
Matrici simili. Matrici diagonalizzabili.
 Matrici simili. Matrici diagonalizzabili. Definizione (Matrici simili) Due matrici quadrate A, B si dicono simili se esiste una matrice invertibile P tale che B = P A P. () interpretazione: cambio di base.
Matrici simili. Matrici diagonalizzabili. Definizione (Matrici simili) Due matrici quadrate A, B si dicono simili se esiste una matrice invertibile P tale che B = P A P. () interpretazione: cambio di base.
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
PROGRAMMA DEL CORSO DI GEOMETRIA E ALGEBRA. A.A
 PROGRAMMA DEL CORSO DI GEOMETRIA E ALGEBRA. A.A. 2010-11 DOCENTE TITOLARE: FRANCESCO BONSANTE 1. Geometria analitica dello spazio (1) vettori applicati e lo spazio E 3 O: operazioni su vettori e proprietà.
PROGRAMMA DEL CORSO DI GEOMETRIA E ALGEBRA. A.A. 2010-11 DOCENTE TITOLARE: FRANCESCO BONSANTE 1. Geometria analitica dello spazio (1) vettori applicati e lo spazio E 3 O: operazioni su vettori e proprietà.
Trapani. Dispensa di Geometria, x 1 x 2.x n. (x 1 y 1 ) (x n y n ) 2.
 2006 Trapani Dispensa di Geometria, 1 Distanze Siano P e Q punti di R n con P di coordinate allora la distanza tra P e Q e P Q = x 1 x 2 x n (x 1 y 1 ) 2 + (x n y n ) 2 e Q di coordinate Siano Σ 1 e Σ
2006 Trapani Dispensa di Geometria, 1 Distanze Siano P e Q punti di R n con P di coordinate allora la distanza tra P e Q e P Q = x 1 x 2 x n (x 1 y 1 ) 2 + (x n y n ) 2 e Q di coordinate Siano Σ 1 e Σ
Note sull algoritmo di Gauss
 Note sull algoritmo di Gauss 29 settembre 2009 Generalità Un sistema lineare di m equazioni in n incognite x,..., x n è un espressione del tipo: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n
Note sull algoritmo di Gauss 29 settembre 2009 Generalità Un sistema lineare di m equazioni in n incognite x,..., x n è un espressione del tipo: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n
3. Vettori, Spazi Vettoriali e Matrici
 3. Vettori, Spazi Vettoriali e Matrici Vettori e Spazi Vettoriali Operazioni tra vettori Basi Trasformazioni ed Operatori Operazioni tra Matrici Autovalori ed autovettori Forme quadratiche, quadriche e
3. Vettori, Spazi Vettoriali e Matrici Vettori e Spazi Vettoriali Operazioni tra vettori Basi Trasformazioni ed Operatori Operazioni tra Matrici Autovalori ed autovettori Forme quadratiche, quadriche e
Similitudine (ortogonale) e congruenza (ortogonale) di matrici.
 Lezione del 4 giugno. Il riferimento principale di questa lezione e costituito da parti di: 2 Forme bilineari, quadratiche e matrici simmetriche associate, 3 Congruenza di matrici simmetriche, 5 Forme
Lezione del 4 giugno. Il riferimento principale di questa lezione e costituito da parti di: 2 Forme bilineari, quadratiche e matrici simmetriche associate, 3 Congruenza di matrici simmetriche, 5 Forme
Università degli Studi di Bergamo Modulo di Geometria e Algebra Lineare (vecchio programma) 2 settembre 2013 Tema A
 Università degli Studi di Bergamo Modulo di Geometria e Algebra Lineare (vecchio programma) settembre 013 Tema A Tempo a disposizione: ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio
Università degli Studi di Bergamo Modulo di Geometria e Algebra Lineare (vecchio programma) settembre 013 Tema A Tempo a disposizione: ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI
 CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
A =, c d. d = ad cb. c d A =
 Geometria e Algebra (II), 271112 1 Definizione D ora innanzi, al posto di dire matrice quadrata di tipo n n o matrice quadrata n n diremo matrice quadrata di ordine n o in breve matrice di ordine n Il
Geometria e Algebra (II), 271112 1 Definizione D ora innanzi, al posto di dire matrice quadrata di tipo n n o matrice quadrata n n diremo matrice quadrata di ordine n o in breve matrice di ordine n Il
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA INDUSTRIALE 27 GENNAIO 2014
 FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA INDUSTRIALE 27 GENNAIO 2014 DOCENTE: MATTEO LONGO Rispondere alle domande di Teoria in modo esauriente e completo. Svolgere il maggior numero di esercizi
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA INDUSTRIALE 27 GENNAIO 2014 DOCENTE: MATTEO LONGO Rispondere alle domande di Teoria in modo esauriente e completo. Svolgere il maggior numero di esercizi
Complemento ortogonale e proiezioni
 Complemento ortogonale e proiezioni Dicembre 9 Complemento ortogonale di un sottospazio Sie E un sottospazio di R n Definiamo il complemento ortogonale di E come l insieme dei vettori di R n ortogonali
Complemento ortogonale e proiezioni Dicembre 9 Complemento ortogonale di un sottospazio Sie E un sottospazio di R n Definiamo il complemento ortogonale di E come l insieme dei vettori di R n ortogonali
ATTENZIONE: : giustificate le vostre argomentazioni! Geometria Canale 3. Lettere J-PE (Prof P. Piazza) Esame scritto del 12/02/2014. Compito A.
 Geometria Canale. Lettere J-PE (Prof P. Piazza) Esame scritto del 12/02/2014. Compito A. Nome e Cognome: Numero di Matricola: Esercizio Punti totali Punteggio 1 7 2 6 6 4 6+1 5 6+2 Totale 1+ ATTENZIONE:
Geometria Canale. Lettere J-PE (Prof P. Piazza) Esame scritto del 12/02/2014. Compito A. Nome e Cognome: Numero di Matricola: Esercizio Punti totali Punteggio 1 7 2 6 6 4 6+1 5 6+2 Totale 1+ ATTENZIONE:
Prodotto scalare. Piani nello spazio Federico Lastaria, Analisi e Geometria 1. Politecnico di Milano Corso di Analisi e Geometria 1
 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it Prodotto scalare in R n. Piani nello spazio. 19 Dicembre 2016 Indice 1 Prodotto scalare nello spazio 2
Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it Prodotto scalare in R n. Piani nello spazio. 19 Dicembre 2016 Indice 1 Prodotto scalare nello spazio 2
Autovalori e autovettori di una matrice quadrata
 Autovalori e autovettori di una matrice quadrata Data la matrice A M n (K, vogliamo stabilire se esistono valori di λ K tali che il sistema AX = λx ammetta soluzioni non nulle. Questo risulta evidentemente
Autovalori e autovettori di una matrice quadrata Data la matrice A M n (K, vogliamo stabilire se esistono valori di λ K tali che il sistema AX = λx ammetta soluzioni non nulle. Questo risulta evidentemente
Rango di una matrice e teorema di Rouché-Capelli
 Rango di una matrice e teorema di Rouché-Capelli Sappiamo che a una matrice m n, A, è associata l applicazione lineare L A : R n R m, L A (X) = AX, X R n. Definizione 1. Lo spazio nullo di A, N (A), è
Rango di una matrice e teorema di Rouché-Capelli Sappiamo che a una matrice m n, A, è associata l applicazione lineare L A : R n R m, L A (X) = AX, X R n. Definizione 1. Lo spazio nullo di A, N (A), è
APPLICAZIONI. Im f = {b B a A tale che f (a) = b}.
 APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
VETTORI. 1. Si dimostri con un esempio che il prodotto vettoriale non è associativo. u = u u
 VETTORI 1. Si dimostri con un esempio che il prodotto vettoriale non è associativo. Consideriamo i vettori i (1,0,0), j (0,1,0) i ( j j)= i o= o ( i j) j = k j= j k= i il prodotto vettoriale non è associativo
VETTORI 1. Si dimostri con un esempio che il prodotto vettoriale non è associativo. Consideriamo i vettori i (1,0,0), j (0,1,0) i ( j j)= i o= o ( i j) j = k j= j k= i il prodotto vettoriale non è associativo
Le matrici. Sia K un campo con elemento neutro dell addizione 0 ed elemento neutro della moltiplicazione 1.
 Le matrici Sia K un campo con elemento neutro dell addizione 0 ed elemento neutro della moltiplicazione 1. Siano m, n N\{0}. Una matrice m n a coefficienti in K è una tabella di m n elementi di K disposti
Le matrici Sia K un campo con elemento neutro dell addizione 0 ed elemento neutro della moltiplicazione 1. Siano m, n N\{0}. Una matrice m n a coefficienti in K è una tabella di m n elementi di K disposti
0 0 c. d 1. det (D) = d 1 d n ;
 Registro Lezione di Algebra lineare del 23 novembre 216 1 Matrici diagonali 2 Autovettori e autovalori 3 Ricerca degli autovalori, polinomio caratteristico 4 Ricerca degli autovettori, autospazi 5 Matrici
Registro Lezione di Algebra lineare del 23 novembre 216 1 Matrici diagonali 2 Autovettori e autovalori 3 Ricerca degli autovalori, polinomio caratteristico 4 Ricerca degli autovettori, autospazi 5 Matrici
ESERCIZI GEOMETRIA FILE N. 7: FORMA NORMALE DI JORDAN. PRODOTTI SCALARI. SPAZI VETTORIALI EUCLIDEI, I. 1. Forma normale di Jordan
 ESERCIZI GEOMETRIA 2 207-8. FILE N. 7: FORMA NORMALE DI JORDAN. PRODOTTI SCALARI. SPAZI VETTORIALI EUCLIDEI, I. Forma normale di Jordan Es... Esercizi da n. 7 a n. 20 alla fine della Sezione 3 del libro
ESERCIZI GEOMETRIA 2 207-8. FILE N. 7: FORMA NORMALE DI JORDAN. PRODOTTI SCALARI. SPAZI VETTORIALI EUCLIDEI, I. Forma normale di Jordan Es... Esercizi da n. 7 a n. 20 alla fine della Sezione 3 del libro
Punti di massimo o di minimo per funzioni di n variabili reali
 Punti di massimo o di minimo per funzioni di n variabili reali Dati f : A R n R ed X 0 A, X 0 si dice : punto di minimo assoluto se X A, f ( x ) f ( X 0 ) punto di massimo assoluto se X A, f ( x ) f (
Punti di massimo o di minimo per funzioni di n variabili reali Dati f : A R n R ed X 0 A, X 0 si dice : punto di minimo assoluto se X A, f ( x ) f ( X 0 ) punto di massimo assoluto se X A, f ( x ) f (
Spazi vettoriali. Indipendenza lineare.
 Spazi vettoriali Indipendenza lineare Nel piano vettoriale G 2, fissato un punto O ed identificati i vettori con i segmenti orientati con origine in O, informalmente si puo dire che che due vettori sono
Spazi vettoriali Indipendenza lineare Nel piano vettoriale G 2, fissato un punto O ed identificati i vettori con i segmenti orientati con origine in O, informalmente si puo dire che che due vettori sono
Endomorfismi simmetrici
 Endomorfismi simmetrici Endomorfismo simmetrico: Dato uno spazio vettoriale metrico V e un endomorfismo T appartenente a V. L endomorfismo si definisce simmetrico se e solo se (T(v),v2)=(v,T(v2)) per ogni
Endomorfismi simmetrici Endomorfismo simmetrico: Dato uno spazio vettoriale metrico V e un endomorfismo T appartenente a V. L endomorfismo si definisce simmetrico se e solo se (T(v),v2)=(v,T(v2)) per ogni
{Geometria per [Fisica e (Fisica e Astrofisica)]}
![{Geometria per [Fisica e (Fisica e Astrofisica)]} {Geometria per [Fisica e (Fisica e Astrofisica)]}](/thumbs/103/157763717.jpg) {Geometria per [Fisica e (Fisica e Astrofisica)]} Foglio 9 - Soluzioni Esercizio (facoltativo) Un quadrato magico reale di ordine n è una matrice di M n n (R) tale che sommando gli elementi di ogni sua
{Geometria per [Fisica e (Fisica e Astrofisica)]} Foglio 9 - Soluzioni Esercizio (facoltativo) Un quadrato magico reale di ordine n è una matrice di M n n (R) tale che sommando gli elementi di ogni sua
Equivalentemente, le colonne di A sono linearmente indipendenti se e solo se
 Lezioni di Algebra Lineare. Versione novembre 2008 VI. Il determinante Il determinante det A di una matrice A, reale e quadrata, è un numero reale associato ad A. Dunque det è una funzione dall insieme
Lezioni di Algebra Lineare. Versione novembre 2008 VI. Il determinante Il determinante det A di una matrice A, reale e quadrata, è un numero reale associato ad A. Dunque det è una funzione dall insieme
Prova scritta di Geometria 1 Docente: Giovanni Cerulli Irelli 20 Gennaio 2017
 Prova scritta di Geometria Docente: Giovanni Cerulli Irelli Gennaio 7 Esercizio. Si considerino i seguenti tre punti dello spazio euclideo: P :=, Q :=, R :=.. Dimostrare che P, Q ed R non sono collineari.
Prova scritta di Geometria Docente: Giovanni Cerulli Irelli Gennaio 7 Esercizio. Si considerino i seguenti tre punti dello spazio euclideo: P :=, Q :=, R :=.. Dimostrare che P, Q ed R non sono collineari.
Formulario sui Prodotti Hermitiani Marcello Mamino Pisa, 24 v 2010
 Formulario sui Prodotti Hermitiani Marcello Mamino Pisa, 24 v 2010 In quetsa dispensa: V è uno spazio vettoriale di dimensione d sul campo complesso C generato dai vettori v 1,..., v d. Le variabili m,
Formulario sui Prodotti Hermitiani Marcello Mamino Pisa, 24 v 2010 In quetsa dispensa: V è uno spazio vettoriale di dimensione d sul campo complesso C generato dai vettori v 1,..., v d. Le variabili m,
Facoltà di Anno Accademico 2018/19 Registro lezioni del docente PINTUS NICOLA
 Facoltà di Anno Accademico 2018/19 Registro lezioni del docente PINTUS NICOLA Attività didattica GEOMETRIA E ALGEBRA [IN/0079] Partizionamento: Periodo di svolgimento: Docente titolare del corso: PINTUS
Facoltà di Anno Accademico 2018/19 Registro lezioni del docente PINTUS NICOLA Attività didattica GEOMETRIA E ALGEBRA [IN/0079] Partizionamento: Periodo di svolgimento: Docente titolare del corso: PINTUS
Algebra lineare e geometria AA Esercitazione del 14/6/2018
 Algebra lineare e geometria AA. 2017-2018 Esercitazione del 14/6/2018 1) Siano A, B due matrici n n tali che 0 < rk(a) < rk(b) = n. (a) AB è invertibile. (b) rk(ab) = nrk(b). (c) det(ab) = det(a). (d)
Algebra lineare e geometria AA. 2017-2018 Esercitazione del 14/6/2018 1) Siano A, B due matrici n n tali che 0 < rk(a) < rk(b) = n. (a) AB è invertibile. (b) rk(ab) = nrk(b). (c) det(ab) = det(a). (d)
Richiami di algebra delle matrici a valori reali
 Richiami di algebra delle matrici a valori reali Vettore v n = v 1 v 2. v n Vettore trasposto v n = (v 1, v 2,..., v n ) v n = (v 1, v 2,..., v n ) A. Pollice - Statistica Multivariata Vettore nullo o
Richiami di algebra delle matrici a valori reali Vettore v n = v 1 v 2. v n Vettore trasposto v n = (v 1, v 2,..., v n ) v n = (v 1, v 2,..., v n ) A. Pollice - Statistica Multivariata Vettore nullo o
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
SOTTOSPAZI E OPERAZIONI IN SPAZI DIVERSI DA R n
 SPAZI E SOTTOSPAZI 1 SOTTOSPAZI E OPERAZIONI IN SPAZI DIVERSI DA R n Spazi di matrici. Spazi di polinomi. Generatori, dipendenza e indipendenza lineare, basi e dimensione. Intersezione e somma di sottospazi,
SPAZI E SOTTOSPAZI 1 SOTTOSPAZI E OPERAZIONI IN SPAZI DIVERSI DA R n Spazi di matrici. Spazi di polinomi. Generatori, dipendenza e indipendenza lineare, basi e dimensione. Intersezione e somma di sottospazi,
Applicazioni lineari e diagonalizzazione pagina 1 di 5
 pplicazioni lineari e diagonalizzazione pagina 1 di 5 PPLIZIONI LINERI 01. Dire quali delle seguenti applicazioni tra IR-spazi vettoriali sono lineari a. f :IR 2 IR 3 f(x y =(x y πy b. f :IR 3 IR 3 f(x
pplicazioni lineari e diagonalizzazione pagina 1 di 5 PPLIZIONI LINERI 01. Dire quali delle seguenti applicazioni tra IR-spazi vettoriali sono lineari a. f :IR 2 IR 3 f(x y =(x y πy b. f :IR 3 IR 3 f(x
Analisi dei dati corso integrato - Algebra lineare,
 Analisi dei dati corso integrato - Algebra lineare, 050308-2 1 Ortogonalita nel piano Sia fissato nel piano un sistema di riferimento cartesiano ortogonale monometrico, con origine in O Tranne avviso contrario,
Analisi dei dati corso integrato - Algebra lineare, 050308-2 1 Ortogonalita nel piano Sia fissato nel piano un sistema di riferimento cartesiano ortogonale monometrico, con origine in O Tranne avviso contrario,
