Lezione Diagonalizzazione ortogonale per matrici simmetriche
|
|
|
- Gianfranco Poli
- 4 anni fa
- Visualizzazioni
Transcript
1 Lezione Diagonalizzazione ortogonale per matrici simmetriche La Proposizione 2. afferma che ogni matrice simmetrica reale è diagonalizzabile su R: ilrisultatoprincipalediquestasezioneèchelamatricechediagonalizzapuò essere scelta ortogonale, cioè tale che P = t P. Sia A 2 Sim n (R) esiano,..., h 2 R isuoiautovaloriadueaduedistinti. In ciascuno degli autospazi E A ( j ) fissiamo una base, diciamo B j =(P j,,...,p j,mj ), dove m j = m a ( j,a)=m g ( j,a). Per la Proposizione 2.4, B j può essere supposta ortonormale rispetto al prodotto scalare standard di R n. Osserviamo che autovettori di A relativi ad autovalori distinti sono fra loro ortogonali. Infatti, se P i 2 E A ( i ) e P j 2 E A ( j ) con i 6= j,allora j t P i P j = t P i ( j P j )= t P i (AP j )= t P i AP j = t P i t AP j = t (AP i )P j = i t P i P j, quindi ( j i ) t P i P j =. Poiché j 6= i,segue j i 6=,dunquedevevalere t P i P j =. Queste considerazioni ci permettono di affermare che è sempre possibile trovare una base ortonormale di autovettori di A, ovverounamatriceortogonalep 2 R n,n tale che P AP sia diagonale. Proposizione 22.. Sia A 2 Sim n (R) una matrice simmetrica reale. Allora esiste una matrice ortogonale P 2 R n,n tale che P AP = t P AP sia diagonale. La matrice P può essere scelta speciale. Illustriamo quanto detto con un esempio. Esempio Si consideri la matrice A A. Come già visto nell Esempio 2., gli autovalori di A sono E A ( ) = L((,, ), (,, )), E A (2) = L((,, )). 22 e 2, conautospazi
2 224 Per ottenere una matrice ortogonale P che diagonalizzi A ènecessariodeterminare tre autovettori P,P 2,P ortonormali. A tale scopo basta determinare basi ortonormali in E A ( ) e E A (2). Per quanto riguarda E A (2), èsufficientescegliereinesso un versore, ad esempio consideriamo P = p (,, ). Per l autospazio E A ( ) invece il discorso è un po più complicato. Iniziamo a determinare un versore, per esempio P 2 = p 2 (,, ). Per determinare P cerchiamo 2 R tale che i vettori P 2 e X =(,, ) + (,, ) siano ortogonali. Si ha che hp 2,X i =(2+ )/ p 2. Affiché hp 2,X i =si deve avere che = 2, dunquepossiamoscegliere P = p 6 (,, 2). Si noti che questo procedimento è, in realtà, equivalente a trovare una base qualsiasi di E A ( ) ed applicare l algoritmo di ortonormalizzazione di Gram-Schmidt visto nella Proposizione 2.4. Quindi la matrice ortogonale cercata è B P p p2 p6 p p2 p6 p 2 p6 C A. P ènonspecialeerisulta 2 P AP = t P AP A. Per esercizio si verifichi invece che P B p p2 p6 p p2 p6 p 2 p6 C A èspecialeecheancorarisulta 2 P AP = t P AP A.
3 Forme quadratiche reali Nella Lezione 2 abbiamo visto due esempi di prodotto scalare h, i su R n ein entrambi i casi abbiamo verificato l esistenza di una matrice A =(a i,j ) 6i,j6n 2 R n,n simmetrica tale che hx, yi = t xay (22.2.) per ogni x, y 2 R n. Viceversa, data una matrice simmetrica A 2 R n,n,siconsideril applicazione h, i: R n R n! R definita dalla formula (22.2.): per le proprietà dei prodotti di matrici le proprietà (PS2) e (PS) della Definizione 2. sono banalmente soddisfatte. Per quanto riguarda (PS) si noti che, poiché t xay 2 R ed A èsimmetrica,segue hx, yi = t xay= t ( t xay)= t y t Ax= t yax= hy, xi. L unica condizione di non immediata verifica è (PS4), cioè che vale t xax > per ogni x 2 R n \{ R n }. Si noti che t xax èunpolinomiodigrado2 omogeneo nelle entrate di x =(x,...,x n ) della forma x x 2... x n a, x + + a,n x n a 2, x + + a 2,n x n B A = a n, x + + a n,n x n = a, x a,n x x n + a 2, x 2 x + + a 2,n x 2 x n + + a n,n x 2 n. Poiché a i,j = a j,i e x i x j = x j x i per i, j =,...,n,segueche t xax = a, x 2 +2a,2 x x a,n x x n + a 2,2 x a 2, x 2 x + + a n,n x 2 n. Quindi determinare se l applicazione (x, y) 7! t xay èunprodottoscalareequivalea studiare il segno del polinomio q(x) = t xax al variare di x 2 R n. Definizione 22. (Forme quadratiche reali). Una forma quadratica reale q nelle variabili x,...,x n èunpolinomioq(x,...,x n ) 2 R[x,...,x n ] omogeneo di grado due. Possiamo riformulare quanto abbiamo visto sopra dicendo che ogni matrice simmetrica A 2 R n,n definisce una forma quadratica reale q(x) = t xax in n variabili. Vale anche il viceversa: infatti, data la forma quadratica q(x,...,x n )=q, x 2 + q,2 x x q,n x x n + q 2,2 x q 2, x 2 x + + q n,n x 2 n, consideriamo la matrice A =(a i,j ) 6i,j6n 2 R n,n definita da
4 226 8 >< q i,i se i = j, a i,j = q i,j /2 se i<j, >: q j,i /2 se i>j. (22.2.2) Ovviamente A èsimmetricaedèimmediatoverificarechexa t x = q(x): inoltrea è l unica matrice simmetrica con tale proprietà. Definizione 22.4 (Matrice associata ad una forma quadratica reale). Sia q una forma quadratica reale nelle variabili x,...,x n. La matrice simmetrica A 2 Sim n (R) definita dalla formula (22.2.2) viene detta la matrice associata a q. Esempio Si consideri la forma quadratica q(t, x, y, z) =2t 2 y 2 +tx + tz xy +2xz +9yz. La matrice associata a q è 2 /2 /2 A = B/2 /2 /2 9/2A. /2 9/2 22. Forme quadratiche definite Definizione 22.6 (Forme quadratiche definite). Sia q una forma quadratica reale in n variabili e sia A 2 Sim n (R) la sua matrice associata. Allora: (DP) q ed A si dicono definite positive se q(x) = t xax > per ogni x 2 R n \{ R n}; (SDP) q ed A si dicono semidefinite positive se q(x) = t xax > per ogni x 2 R n ; (DN) q ed A si dicono definite negative se q(x) = t xax < per ogni x 2 R n \{ R n}; (SDN) q ed A si dicono semidefinite negative se q(x) = t xax 6 per ogni x 2 R n ; (ID) q ed A si dicono indefinite nei rimanenti casi, cioè se esistono x,x 2 R n tali che q(x )= t x Ax > e q(x )= t x Ax <. Èchiarochelaformaquadraticaq elasuamatricea sono definite o semidefinite negative se e solo se q elasuamatrice A sono definite o semidefinite positive rispettivamente. Osserviamo che alla luce della Definizione 22.6 il problema di stabilire se l applicazione (x, y) 7! t xay èunprodottoscalareèequivalenteaquellodistabiliresea èdefinitapositivaomeno. Esempio In R 2,2 si considerino le matrici I 2 =, E, =, E 2,2 =, E, E 2,2 =.
5 227 Si ha che I 2 èdefinitapositiva,e, èsemidefinitapositiva, E, èsemidefinita negativa, E, E 2,2 è indefinita. L affermazione per I 2 èovvia. Perquantoriguarda E, si ha che q(x) = xe t, x = x 2 : dunque q(, ) =. In maniera simile si procede per E 2,2. Infine q(x) =x(e, E 2,2 ) t x = x 2 x 2 2:dunqueq(, ) > e q(, ) <. Più in generale si ha il seguente ovvio risultato. Proposizione Sia data la matrice diagonale D 2 R n,n con entrate diagonali,..., n. Allora: (i) D èdefinitapositivaseesolose i > per ogni i =,...,n; (ii) D èsemidefinitapositivaseesolose i > per ogni i =,...,n; (iii) D èdefinitanegativaseesolose i < per ogni i =,...,n; (iv) D èsemidefinitanegativaseesolose i 6 per ogni i =,...,n; (v) D èindefinitaseesoloseesistonoi, j =,...,n tali che i > e j <. B Per una matrice simmetrica qualsiasi non è possibile determinare il segno a partire dal segno dei suoi coefficienti come nel caso delle matrici diagonali. Per esempio, vedremo in seguito che la matrice 2 2 èdefinitapositiva,mentre 2 2 èindefinita. Per determinare il segno di una matrice simmetrica A procediamo con cambiamenti di variabili. Più in dettaglio, sia P 2 R n,n una matrice invertibile e si consideri la trasformazione in R n definita da o, equivalentemente, x = P x x = P x. Definiamo la nuova forma quadratica q(x) =q(p x) nella variabile x. Il segno delle forme quadratiche q e q èlostesso: infattix 2 R n soddisfa q(x) > se e solo se x = P x soddisfa q(x) >, poichéperdefinizione q(x) =q(p x) =q(x). Un ragionamento simile si può fare per dimostrare che q(x) =(rispettivamente q(x) < ) se e solo se q(x) =(rispettivamente q(x) < ). Studiamo l azione di un tale cambiamento di variabili sulla matrice A di q. Dal momento che x = P x e, quindi, t x = t x t P,siha
6 228 t xax = t (P x)a(p x) = t x t P AP x = t x ( t P AP ) x. La matrice t P AP èsimmetrica:infatti t ( t P AP )= t P t AP= t PAP, in forza della simmetria di A. Concludiamo, quindi, che la matrice di q è A = t P AP. Definizione 22.9 (Matrici congruenti). Siano A, A 2 Sim n (R). Le matrici A e A si dicono congruenti, esiscrivea A, seesistep 2 R n,n invertibile tale che A = t P AP. Esempio 22.. Si consideri la forma quadratica La sua matrice associata è q(x, y, z) =2xy +2xz +2yz. A A. Per capire se q e A sono o meno definite, si consideri la matrice /2 P /2 A. ÈfacileverificarecheP èinvertibile:inoltre /2 2 A = t P AP /2 /2 /2 A /2 A. 2 In particolare q ed A non sono definite perché per la Proposizione 22.8 A non è definita. L esempio precedente mostra quanto sia semplice stabilire il segno di una matrice A 2 Sim n (R) se si è in grado di determinare una matrice P 2 R n,n invertibile tale che t P AP sia diagonale. Sono vari gli algoritmi che si possono utilizzare a tale scopo. Uno di essi si basa sulla Proposizione 22.. Infatti sappiamo che ogni matrice simmetrica reale A èdiagonalizzabilemediante una matrice ortogonale P : poiché, per una tale matrice P = t P,seguechele matrici A e A = P AP = t P AP sono congruenti. In particolare A ècongruentead una matrice diagonale avente sulla diagonale gli autovalori di A ciascuno ripetuto con la sua molteplicità algebrica. Quindi il problema della determinazione del segno di A si può ridurre alla determinazione del segno dei suoi autovalori. Esempio 22.. Consideriamo la matrice 2 A =. 2
7 229 Il suo polinomio caratteristico è p A (t) = 2 t 2 t = t2 4t +=(t )(t ), quindi A ha autovalori e : inparticolare,inbaseaquantoosservatosopra,a èdefinitapositiva. Se invece consideriamo la matrice essa ha polinomio caratteristico A 2 = 2, 2 p A2 (t) = t 2 2 t = t2 2t =(t )(t +), quindi autovalori indefinita. e. In particolare, in base a quanto osservato sopra, A 2 è Abbiamo avuto modo di osservare che il calcolo degli autovalori di una matrice può essere particolarmente complicato poiché non vi sono modi semplici per calcolare le radici di un polinomio generale di grado n. Inrealtà,però,perdeterminareseuna matrice simmetrica reale è definita o meno a noi non interessa il valore numerico degli autovalori ma solo il loro segno e questo può essere facilmente determinato utilizzando la cosiddetta regola dei segni di Cartesio. Per illustrare tale metodo dobbiamo introdurre la nozione di variazione di una successione di numeri reali. Definizione Sia (a,a,...,a n,a n ) una successione di numeri reali. Il numero di variazioni v(a,a,...,a n,a n ) èilnumerodellecoppiediinteri (i, i + k) con k > tali che. a i a i+k < ; 2. a i+h =per h =,k. Per ogni polinomio a coefficienti reali p(t) =a t n + a t n + + a n t + a n 2 R[t] poniamo v(p(t)) = v(a,a,...,a n,a n ). Esempio 22.. Per esempio, v( t 6 +t 5 t 2 +t+) = v(,,,,,, ) =. Siamo pronti per enunciare la regola dei segni di Cartesio, di cui omettiamo la dimostrazione. Proposizione 22.4 (Regola dei segni di Cartesio). Se tutte le radici di un polinomio p(t) =a t n + a t n + + a n t + a n 2 R[t] sono reali, allora v(p(t)) è il numero delle sue radici positive contate con la loro molteplicità.
8 2 Si osservi che tale proposizione non ci permette di dire nulla sul segno delle radici del polinomio dell Esempio 22., perchè non sappiamo a priori che le sue radici sono tutte reali. Se però consideriamo il polinomio caratteristico di una matrice simmetrica reale, sappiamo che esso ha tutte le radici in R, grazie alla Proposizione 2.. Esempio Riprendiamo la matrice A dell Esempio 22. A A. Il suo polinomio caratteristico è p A (t) = t +t +2,dunqueilnumerodiradici positive di p A (t) è v(,,, 2) = : poiché p A (t) non ha la radice nulla ed ha tre radici reali (perché è polinomio caratteristico di una matrice simmetrica che è diagonalizzabile!), segue che p A (t) ha =2radici negative: infatti gli autovalori di A sono 2 e con m a (2,A)=e m a (,A)=2(si veda l Esempio 2.).
LEZIONE 25. P si dice speciale se det(p ) = 1 non
 LEZIONE 5 5.. Matrici ortogonali. Facciamo una breve digressione su un importante famiglia di matrici, quelle ortogonali. Definizione 5... P R n,n si dice ortogonale se t P I n. Prima di dare esempi di
LEZIONE 5 5.. Matrici ortogonali. Facciamo una breve digressione su un importante famiglia di matrici, quelle ortogonali. Definizione 5... P R n,n si dice ortogonale se t P I n. Prima di dare esempi di
LEZIONE 16 A = Verifichiamo se qualcuna fra le entrate a di A è suo autovalore. determinare per quale entrata a di A risulta rk(a ai 2 ) 1.
 LEZIONE 16 16.1. Autovalori, autovettori ed autospazi di matrici. Introduciamo la seguente definizione. Definizione 16.1.1. Siano k = R, C e A k n,n. Un numero λ k si dice autovalore di A su k) se rka
LEZIONE 16 16.1. Autovalori, autovettori ed autospazi di matrici. Introduciamo la seguente definizione. Definizione 16.1.1. Siano k = R, C e A k n,n. Un numero λ k si dice autovalore di A su k) se rka
Applicazioni lineari simmetriche e forme quadratiche reali.
 Applicazioni lineari simmetriche e forme quadratiche reali 1 Applicazioni lineari simmetriche Consideriamo lo spazio IR n col prodotto scalare canonico X Y = t XY = x 1 y 1 + + x n y n Definizione Un applicazione
Applicazioni lineari simmetriche e forme quadratiche reali 1 Applicazioni lineari simmetriche Consideriamo lo spazio IR n col prodotto scalare canonico X Y = t XY = x 1 y 1 + + x n y n Definizione Un applicazione
MATRICI ORTOGONALI. MATRICI SIMMETRICHE E FORME QUADRATICHE
 DIAGONALIZZAZIONE 1 MATRICI ORTOGONALI. MATRICI SIMMETRICHE E FORME QUADRATICHE Matrici ortogonali e loro proprietà. Autovalori ed autospazi di matrici simmetriche reali. Diagonalizzazione mediante matrici
DIAGONALIZZAZIONE 1 MATRICI ORTOGONALI. MATRICI SIMMETRICHE E FORME QUADRATICHE Matrici ortogonali e loro proprietà. Autovalori ed autospazi di matrici simmetriche reali. Diagonalizzazione mediante matrici
Lezione Diagonalizzazione di matrici
 Lezione 2 2. Diagonalizzazione di matrici Come visto nella precedente lezione, in generale, data una matrice A 2 K n,n con K = R, C,nonèimmediatocheesistasempreunabasecostituitadasuoiautovettori. Definizione
Lezione 2 2. Diagonalizzazione di matrici Come visto nella precedente lezione, in generale, data una matrice A 2 K n,n con K = R, C,nonèimmediatocheesistasempreunabasecostituitadasuoiautovettori. Definizione
Complemento ortogonale e proiezioni
 Complemento ortogonale e proiezioni Dicembre 9 Complemento ortogonale di un sottospazio Sie E un sottospazio di R n Definiamo il complemento ortogonale di E come l insieme dei vettori di R n ortogonali
Complemento ortogonale e proiezioni Dicembre 9 Complemento ortogonale di un sottospazio Sie E un sottospazio di R n Definiamo il complemento ortogonale di E come l insieme dei vettori di R n ortogonali
Punti di massimo o di minimo per funzioni di n variabili reali
 Punti di massimo o di minimo per funzioni di n variabili reali Dati f : A R n R ed X 0 A, X 0 si dice : punto di minimo assoluto se X A, f ( x ) f ( X 0 ) punto di massimo assoluto se X A, f ( x ) f (
Punti di massimo o di minimo per funzioni di n variabili reali Dati f : A R n R ed X 0 A, X 0 si dice : punto di minimo assoluto se X A, f ( x ) f ( X 0 ) punto di massimo assoluto se X A, f ( x ) f (
Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti)
 Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti) April 14, 2011 (alcune note non complete sugli argomenti trattati: eventuali completamenti saranno aggiunti)
Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti) April 14, 2011 (alcune note non complete sugli argomenti trattati: eventuali completamenti saranno aggiunti)
Capitolo 8 Forme quadratiche e loro applicazioni Esercizi svolti Tutorato di geometria e algebra lineare. Marco Robutti
 Capitolo 8 Forme quadratiche e loro applicazioni Esercizi svolti Tutorato di geometria e algebra lineare Marco Robutti 5 Ottobre 2017 1 Introduzione Gli esercizi di questo capitolo riguardano i seguenti
Capitolo 8 Forme quadratiche e loro applicazioni Esercizi svolti Tutorato di geometria e algebra lineare Marco Robutti 5 Ottobre 2017 1 Introduzione Gli esercizi di questo capitolo riguardano i seguenti
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria: Elettronica. Corso di Geometria ed Algebra Docente F. Flamini
 Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria: Elettronica Corso di Geometria ed Algebra Docente F. Flamini Capitolo IV - 3: Teorema Spettrale degli operatori autoaggiunti e Teorema
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria: Elettronica Corso di Geometria ed Algebra Docente F. Flamini Capitolo IV - 3: Teorema Spettrale degli operatori autoaggiunti e Teorema
SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE
 SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE. Esercizi Esercizio. In R calcolare il modulo dei vettori,, ),,, ) ed il loro angolo. Esercizio. Calcolare una base ortonormale del sottospazio
SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE. Esercizi Esercizio. In R calcolare il modulo dei vettori,, ),,, ) ed il loro angolo. Esercizio. Calcolare una base ortonormale del sottospazio
{Geometria per [Fisica e (Fisica e Astrofisica)]}
![{Geometria per [Fisica e (Fisica e Astrofisica)]} {Geometria per [Fisica e (Fisica e Astrofisica)]}](/thumbs/103/157763717.jpg) {Geometria per [Fisica e (Fisica e Astrofisica)]} Foglio 9 - Soluzioni Esercizio (facoltativo) Un quadrato magico reale di ordine n è una matrice di M n n (R) tale che sommando gli elementi di ogni sua
{Geometria per [Fisica e (Fisica e Astrofisica)]} Foglio 9 - Soluzioni Esercizio (facoltativo) Un quadrato magico reale di ordine n è una matrice di M n n (R) tale che sommando gli elementi di ogni sua
Il Teorema Spettrale. 0.1 Applicazioni lineari simmetriche ed hermitiane
 0.1. APPLICAZIONI LINEARI SIMMETRICHE ED HERMITIANE 1 Il Teorema Spettrale In questa nota vogliamo esaminare la dimostrazione del Teorema Spettrale e studiare le sue conseguenze per quanto riguarda i prodotti
0.1. APPLICAZIONI LINEARI SIMMETRICHE ED HERMITIANE 1 Il Teorema Spettrale In questa nota vogliamo esaminare la dimostrazione del Teorema Spettrale e studiare le sue conseguenze per quanto riguarda i prodotti
Applicazioni bilineari e matrici.
 Il caso reale Applicazioni bilineari e matrici Sia g un prodotto scalare su R n Ricordo che un prodotto scalare su R n è un applicazione g : R n R n R che soddisfa le seguenti condizioni: Per ogni v ;
Il caso reale Applicazioni bilineari e matrici Sia g un prodotto scalare su R n Ricordo che un prodotto scalare su R n è un applicazione g : R n R n R che soddisfa le seguenti condizioni: Per ogni v ;
2. Fra tutti i rettangoli inscritti in una circonferenza, determinare quello di area massima.
 2. Fra tutti i rettangoli inscritti in una circonferenza, determinare quello di area massima. 3. Fra tutti i cilindri a base rotonda inscritti in una sfera, determinare quello di volume massimo. 4. Dimostrare
2. Fra tutti i rettangoli inscritti in una circonferenza, determinare quello di area massima. 3. Fra tutti i cilindri a base rotonda inscritti in una sfera, determinare quello di volume massimo. 4. Dimostrare
DIAGONALIZZAZIONE E FORME QUADRATICHE / ESERCIZI PROPOSTI
 M.GUIDA, S.ROLANDO, 204 DIAGONALIZZAZIONE E FORME QUADRATICHE / ESERCIZI PROPOSTI L asterisco contrassegna gli esercizi più difficili o che possono considerarsi meno basilari. Autovalori, autospazi e diagonalizzazione
M.GUIDA, S.ROLANDO, 204 DIAGONALIZZAZIONE E FORME QUADRATICHE / ESERCIZI PROPOSTI L asterisco contrassegna gli esercizi più difficili o che possono considerarsi meno basilari. Autovalori, autospazi e diagonalizzazione
SPAZI VETTORIALI CON PRODOTTO SCALARE A =
 SPAZI VETTORIALI CON PRODOTTO SCALARE Esercizi Esercizio. Nello spazio euclideo standard (R 2,, ) sia data la matrice 2 3 A = 3 2 () Determinare una base rispetto alla quale A sia la matrice di un endomorfismo
SPAZI VETTORIALI CON PRODOTTO SCALARE Esercizi Esercizio. Nello spazio euclideo standard (R 2,, ) sia data la matrice 2 3 A = 3 2 () Determinare una base rispetto alla quale A sia la matrice di un endomorfismo
Applicazioni lineari e diagonalizzazione
 Autovalori e autovettori Matrici associate a applicazioni lineari Endomorfismi semplici e matrici diagonalizzabili Prodotti scalari e Teorema Spettrale nel caso generale 2 2006 Politecnico di Torino 1
Autovalori e autovettori Matrici associate a applicazioni lineari Endomorfismi semplici e matrici diagonalizzabili Prodotti scalari e Teorema Spettrale nel caso generale 2 2006 Politecnico di Torino 1
Autovalori e autovettori di una matrice quadrata
 Autovalori e autovettori di una matrice quadrata Data la matrice A M n (K, vogliamo stabilire se esistono valori di λ K tali che il sistema AX = λx ammetta soluzioni non nulle. Questo risulta evidentemente
Autovalori e autovettori di una matrice quadrata Data la matrice A M n (K, vogliamo stabilire se esistono valori di λ K tali che il sistema AX = λx ammetta soluzioni non nulle. Questo risulta evidentemente
Geometria 1 a.a. 2011/12 Esonero del 15/11/11
 Geometria a.a. 0/ Esonero del 5// () Determinare una base ortonormale del piano π di R 3 di equazione x + y z 0 (rispetto al prodotto scalare standard di R 3 ). Soluzioni. È sufficiente determinare una
Geometria a.a. 0/ Esonero del 5// () Determinare una base ortonormale del piano π di R 3 di equazione x + y z 0 (rispetto al prodotto scalare standard di R 3 ). Soluzioni. È sufficiente determinare una
0.1 Forme quadratiche
 0.1. FORME QUADRATICHE 1 0.1 Forme quadratiche In questa sezione possiamo applicare il Teorema degli Assi Principali per giustificare alcune fatti che sono stati utilizzati nella riduzione a forma canonica
0.1. FORME QUADRATICHE 1 0.1 Forme quadratiche In questa sezione possiamo applicare il Teorema degli Assi Principali per giustificare alcune fatti che sono stati utilizzati nella riduzione a forma canonica
Similitudine (ortogonale) e congruenza (ortogonale) di matrici.
 Lezione del 4 giugno. Il riferimento principale di questa lezione e costituito da parti di: 2 Forme bilineari, quadratiche e matrici simmetriche associate, 3 Congruenza di matrici simmetriche, 5 Forme
Lezione del 4 giugno. Il riferimento principale di questa lezione e costituito da parti di: 2 Forme bilineari, quadratiche e matrici simmetriche associate, 3 Congruenza di matrici simmetriche, 5 Forme
AUTOVALORI, AUTOVETTORI, AUTOSPAZI
 AUTOVALORI, AUTOVETTORI, AUTOSPAZI. Esercizi Esercizio. Sia f : R 3 R 3 l endomorfismo definito da f(x, y, z) = (x+y, y +z, x+z). Calcolare gli autovalori ed una base per ogni autospazio di f. Dire se
AUTOVALORI, AUTOVETTORI, AUTOSPAZI. Esercizi Esercizio. Sia f : R 3 R 3 l endomorfismo definito da f(x, y, z) = (x+y, y +z, x+z). Calcolare gli autovalori ed una base per ogni autospazio di f. Dire se
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof. F.Podestà, a.a
 APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
Applicazioni lineari e diagonalizzazione
 Applicazioni lineari e diagonalizzazione Autospazi Autovettori e indipendenza lineare Diagonalizzabilità e autovalori 2 2006 Politecnico di Torino 1 Esempio (1/6) Utilizzando un esempio già studiato, cerchiamo
Applicazioni lineari e diagonalizzazione Autospazi Autovettori e indipendenza lineare Diagonalizzabilità e autovalori 2 2006 Politecnico di Torino 1 Esempio (1/6) Utilizzando un esempio già studiato, cerchiamo
Prova scritta di Geometria 1 Docente: Giovanni Cerulli Irelli 20 Gennaio 2017
 Prova scritta di Geometria Docente: Giovanni Cerulli Irelli Gennaio 7 Esercizio. Si considerino i seguenti tre punti dello spazio euclideo: P :=, Q :=, R :=.. Dimostrare che P, Q ed R non sono collineari.
Prova scritta di Geometria Docente: Giovanni Cerulli Irelli Gennaio 7 Esercizio. Si considerino i seguenti tre punti dello spazio euclideo: P :=, Q :=, R :=.. Dimostrare che P, Q ed R non sono collineari.
DIAGONALIZZAZIONE. M(f) =
 DIAGONALIZZAZIONE Esercizi Esercizio 1. Sia f End(R 3 ) associato alla matrice M(f) = 0 1 2 0. 2 (1) Determinare gli autovalori di f e le relative molteplicità. (2) Determinare gli autospazi di f e trovare,
DIAGONALIZZAZIONE Esercizi Esercizio 1. Sia f End(R 3 ) associato alla matrice M(f) = 0 1 2 0. 2 (1) Determinare gli autovalori di f e le relative molteplicità. (2) Determinare gli autospazi di f e trovare,
Matrici simili. Matrici diagonalizzabili.
 Matrici simili. Matrici diagonalizzabili. Definizione (Matrici simili) Due matrici quadrate A, B si dicono simili se esiste una matrice invertibile P tale che B = P A P. () interpretazione: cambio di base.
Matrici simili. Matrici diagonalizzabili. Definizione (Matrici simili) Due matrici quadrate A, B si dicono simili se esiste una matrice invertibile P tale che B = P A P. () interpretazione: cambio di base.
1 Addendum su Diagonalizzazione
 Addendum su Diagonalizzazione Vedere le dispense per le definizioni di autovettorre, autovalore e di trasformazione lineare (o matrice) diagonalizzabile. In particolare, si ricorda che una condizione necessaria
Addendum su Diagonalizzazione Vedere le dispense per le definizioni di autovettorre, autovalore e di trasformazione lineare (o matrice) diagonalizzabile. In particolare, si ricorda che una condizione necessaria
0.1 Condizione sufficiente di diagonalizzabilità
 0.1. CONDIZIONE SUFFICIENTE DI DIAGONALIZZABILITÀ 1 0.1 Condizione sufficiente di diagonalizzabilità È naturale porsi il problema di sapere se ogni matrice sia o meno diagonalizzabile. Abbiamo due potenziali
0.1. CONDIZIONE SUFFICIENTE DI DIAGONALIZZABILITÀ 1 0.1 Condizione sufficiente di diagonalizzabilità È naturale porsi il problema di sapere se ogni matrice sia o meno diagonalizzabile. Abbiamo due potenziali
Endomorfismi e matrici simmetriche
 CAPITOLO Endomorfismi e matrici simmetriche Esercizio.. [Esercizio 5) cap. 9 del testo Geometria e algebra lineare di Manara, Perotti, Scapellato] Calcolare una base ortonormale di R 3 formata da autovettori
CAPITOLO Endomorfismi e matrici simmetriche Esercizio.. [Esercizio 5) cap. 9 del testo Geometria e algebra lineare di Manara, Perotti, Scapellato] Calcolare una base ortonormale di R 3 formata da autovettori
Diagonalizzazione di matrici: autovalori, autovettori e costruzione della matrice diagonalizzante 1 / 13
 Diagonalizzazione di matrici: autovalori, autovettori e costruzione della matrice diagonalizzante 1 / 13 Matrici diagonali 2 / 13 Ricordiamo che una matrice quadrata si dice matrice diagonale se a ij =
Diagonalizzazione di matrici: autovalori, autovettori e costruzione della matrice diagonalizzante 1 / 13 Matrici diagonali 2 / 13 Ricordiamo che una matrice quadrata si dice matrice diagonale se a ij =
Fondamenti di Algebra Lineare e Geometria - DII - Ingegneria Aerospaziale Test di preparazione alla seconda prova parziale del
 Fondamenti di Algebra Lineare e Geometria - DII - Ingegneria Aerospaziale Test di preparazione alla seconda prova parziale del 66 Problema Si consideri la trasformazione lineare L: R 4 R 3 la cui matrice
Fondamenti di Algebra Lineare e Geometria - DII - Ingegneria Aerospaziale Test di preparazione alla seconda prova parziale del 66 Problema Si consideri la trasformazione lineare L: R 4 R 3 la cui matrice
Algebra lineare e geometria AA Esercitazione del 14/6/2018
 Algebra lineare e geometria AA. 2017-2018 Esercitazione del 14/6/2018 1) Siano A, B due matrici n n tali che 0 < rk(a) < rk(b) = n. (a) AB è invertibile. (b) rk(ab) = nrk(b). (c) det(ab) = det(a). (d)
Algebra lineare e geometria AA. 2017-2018 Esercitazione del 14/6/2018 1) Siano A, B due matrici n n tali che 0 < rk(a) < rk(b) = n. (a) AB è invertibile. (b) rk(ab) = nrk(b). (c) det(ab) = det(a). (d)
25 - Funzioni di più Variabili Introduzione
 Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 25 - Funzioni di più Variabili Introduzione Anno Accademico 2013/2014 M. Tumminello
Università degli Studi di Palermo Facoltà di Economia CdS Statistica per l Analisi dei Dati Appunti del corso di Matematica 25 - Funzioni di più Variabili Introduzione Anno Accademico 2013/2014 M. Tumminello
Algebra lineare e geometria AA Appunti sul cambio di base in uno spazio vettoriale
 Algebra lineare e geometria AA. -7 Appunti sul cambio di base in uno spazio vettoriale Matrice di un applicazione lineare Siano V e W due spazi vettoriali su un campo K {R, C}, entrambi finitamente generati,
Algebra lineare e geometria AA. -7 Appunti sul cambio di base in uno spazio vettoriale Matrice di un applicazione lineare Siano V e W due spazi vettoriali su un campo K {R, C}, entrambi finitamente generati,
Geometria A. Università degli Studi di Trento Corso di laurea in Matematica A.A. 2017/ Maggio 2018 Prova Intermedia
 Geometria A Università degli Studi di Trento Corso di laurea in Matematica A.A. 7/8 Maggio 8 Prova Intermedia Il tempo per la prova è di ore. Durante la prova non è permesso l uso di appunti e libri. Esercizio
Geometria A Università degli Studi di Trento Corso di laurea in Matematica A.A. 7/8 Maggio 8 Prova Intermedia Il tempo per la prova è di ore. Durante la prova non è permesso l uso di appunti e libri. Esercizio
Prodotto scalare e matrici < PX,PY >=< X,Y >
 Prodotto scalare e matrici Matrici ortogonali Consideriamo in R n il prodotto scalare canonico < X,Y >= X T Y = x 1 y 1 + +x n y n. Ci domandiamo se esistono matrici P che conservino il prodotto scalare,
Prodotto scalare e matrici Matrici ortogonali Consideriamo in R n il prodotto scalare canonico < X,Y >= X T Y = x 1 y 1 + +x n y n. Ci domandiamo se esistono matrici P che conservino il prodotto scalare,
Autovalori, Autovettori, Diagonalizzazione.
 Autovalori Autovettori Diagonalizzazione Autovalori e Autovettori Definizione Sia V uno spazio vettoriale sul campo K = R o C e sia T : V V un endomorfismo Un vettore non nullo v V \ {O} si dice autovettore
Autovalori Autovettori Diagonalizzazione Autovalori e Autovettori Definizione Sia V uno spazio vettoriale sul campo K = R o C e sia T : V V un endomorfismo Un vettore non nullo v V \ {O} si dice autovettore
ENDOMORFISMI. ove B := (v 1,v 2,v 3 ). (1) Determinare gli autovalori di f e le relative molteplicità algebriche e geometriche.
 ENDOMORFISMI Esercizi Esercizio 1 Siano v 1 := T (1, 1, 1, 0), v 2 := T (0, 1, 2, 1), v 3 := T (0, 0, 1, 1) Consideriamo V := L(v 1,v 2,v 3 ) R 4 e sia f End R (V ) associato alla matrice A := MB B (f)
ENDOMORFISMI Esercizi Esercizio 1 Siano v 1 := T (1, 1, 1, 0), v 2 := T (0, 1, 2, 1), v 3 := T (0, 0, 1, 1) Consideriamo V := L(v 1,v 2,v 3 ) R 4 e sia f End R (V ) associato alla matrice A := MB B (f)
Algebra lineare e geometria AA Appunti sul cambio di base in uno spazio vettoriale
 Algebra lineare e geometria AA. 8-9 Appunti sul cambio di base in uno spazio vettoriale Matrice di un applicazione lineare Siano V e W due spazi vettoriali su un campo K {R, C}, entrambi finitamente generati,
Algebra lineare e geometria AA. 8-9 Appunti sul cambio di base in uno spazio vettoriale Matrice di un applicazione lineare Siano V e W due spazi vettoriali su un campo K {R, C}, entrambi finitamente generati,
Soluzione. (a) L insieme F 1 e linearmente indipendente; gli insiemi F 2 ed F 3 sono linearmente
 1. Insiemi di generatori, lineare indipendenza, basi, dimensione. Consideriamo nello spazio vettoriale R 3 i seguenti vettori: v 1 = (0, 1, ), v = (1, 1, 1), v 3 = (, 1, 0), v 4 = (3, 3, ). Siano poi F
1. Insiemi di generatori, lineare indipendenza, basi, dimensione. Consideriamo nello spazio vettoriale R 3 i seguenti vettori: v 1 = (0, 1, ), v = (1, 1, 1), v 3 = (, 1, 0), v 4 = (3, 3, ). Siano poi F
CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI A.A. 2018/2019 PROF. VALENTINA BEORCHIA
 CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Matrici associate a un applicazione lineare 1 2 Cambiamenti di base 4 3 Diagonalizzazione 6 1 MATRICI ASSOCIATE
CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Matrici associate a un applicazione lineare 1 2 Cambiamenti di base 4 3 Diagonalizzazione 6 1 MATRICI ASSOCIATE
(2) Dato il vettore w = (1, 1, 1), calcolare T (w). (3) Determinare la matrice A associata a T rispetto alla base canonica.
 1. Applicazioni lineari Esercizio 1.1. Sia T : R 2 R 3 l applicazione lineare definita sulla base canonica di R 2 nel seguente modo: T (e 1 ) = (1, 2, 1), T (e 2 ) = (1, 0, 1). a) Esplicitare T (x, y).
1. Applicazioni lineari Esercizio 1.1. Sia T : R 2 R 3 l applicazione lineare definita sulla base canonica di R 2 nel seguente modo: T (e 1 ) = (1, 2, 1), T (e 2 ) = (1, 0, 1). a) Esplicitare T (x, y).
Formulario sui Prodotti Hermitiani Marcello Mamino Pisa, 24 v 2010
 Formulario sui Prodotti Hermitiani Marcello Mamino Pisa, 24 v 2010 In quetsa dispensa: V è uno spazio vettoriale di dimensione d sul campo complesso C generato dai vettori v 1,..., v d. Le variabili m,
Formulario sui Prodotti Hermitiani Marcello Mamino Pisa, 24 v 2010 In quetsa dispensa: V è uno spazio vettoriale di dimensione d sul campo complesso C generato dai vettori v 1,..., v d. Le variabili m,
Parte 8. Prodotto scalare, teorema spettrale
 Parte 8. Prodotto scalare, teorema spettrale A. Savo Appunti del Corso di Geometria 3-4 Indice delle sezioni Prodotto scalare in R n, Basi ortonormali, 4 3 Algoritmo di Gram-Schmidt, 7 4 Matrici ortogonali,
Parte 8. Prodotto scalare, teorema spettrale A. Savo Appunti del Corso di Geometria 3-4 Indice delle sezioni Prodotto scalare in R n, Basi ortonormali, 4 3 Algoritmo di Gram-Schmidt, 7 4 Matrici ortogonali,
24.1 Coniche e loro riduzione a forma canonica
 Lezione 24 24. Coniche e loro riduzione a forma canonica Fissiamo nel piano un sistema di riferimento Oxy e consideriamo un polinomio di grado 2 in x, y amenodicostantimoltiplicativenonnulle,diciamo ax
Lezione 24 24. Coniche e loro riduzione a forma canonica Fissiamo nel piano un sistema di riferimento Oxy e consideriamo un polinomio di grado 2 in x, y amenodicostantimoltiplicativenonnulle,diciamo ax
LEZIONE i i 3
 LEZIONE 5 51 Determinanti In questo lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 5 51 Determinanti In questo lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE i 0 3 Le sottomatrici 2 2 di A sono. 1 2 i i 3. Invece (
 LEZIONE 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
Corso di Laurea in Matematica - Esame di Geometria 1. Prova scritta del 7 settembre 2015
 Corso di Laurea in Matematica - Esame di Geometria 1 Prova scritta del 7 settembre 215 Cognome Nome Numero di matricola Voto ATTENZIONE. Riportare lo svolgimento completo degli esercizi. corretti, non
Corso di Laurea in Matematica - Esame di Geometria 1 Prova scritta del 7 settembre 215 Cognome Nome Numero di matricola Voto ATTENZIONE. Riportare lo svolgimento completo degli esercizi. corretti, non
Esempio con n = 2. f(x) = x x2 2 x 1x 2
 Forme quadratiche Definizione 40. Una forma quadratica di n variabili è un polinomio omogeneo di grado 2 in n variabili. Si tratta quindi di una funzione f : R n R somma di monomi di grado 2 nelle n variabili.
Forme quadratiche Definizione 40. Una forma quadratica di n variabili è un polinomio omogeneo di grado 2 in n variabili. Si tratta quindi di una funzione f : R n R somma di monomi di grado 2 nelle n variabili.
Endomorfismi simmetrici
 Endomorfismi simmetrici Endomorfismo simmetrico: Dato uno spazio vettoriale metrico V e un endomorfismo T appartenente a V. L endomorfismo si definisce simmetrico se e solo se (T(v),v2)=(v,T(v2)) per ogni
Endomorfismi simmetrici Endomorfismo simmetrico: Dato uno spazio vettoriale metrico V e un endomorfismo T appartenente a V. L endomorfismo si definisce simmetrico se e solo se (T(v),v2)=(v,T(v2)) per ogni
1. Sia L: R 3 R 3 l applicazione lineare definita dalla matrice. (a) Calcolare: dimkerl = dimiml = (b) Scrivere una base per KerL e una per ImL:
 . Sia L: R 3 R 3 l applicazione lineare definita dalla matrice 3 A =. (a) Calcolare: dimkerl = dimiml = (b) Scrivere una base per KerL e una per ImL: (c) Trovare le equazioni cartesiane per KerL e ImL:
. Sia L: R 3 R 3 l applicazione lineare definita dalla matrice 3 A =. (a) Calcolare: dimkerl = dimiml = (b) Scrivere una base per KerL e una per ImL: (c) Trovare le equazioni cartesiane per KerL e ImL:
DIAGONALIZZAZIONE / ESERCIZI SVOLTI
 M.GUIDA, S.ROLANDO, 015 1 DIAGONALIZZAZIONE / ESERCIZI SVOLTI L asterisco contrassegna gli esercizi meno basilari (perché più difficili o di approfondimento). Stabilire se la matrice A = 1 1 0 0 R 3,3
M.GUIDA, S.ROLANDO, 015 1 DIAGONALIZZAZIONE / ESERCIZI SVOLTI L asterisco contrassegna gli esercizi meno basilari (perché più difficili o di approfondimento). Stabilire se la matrice A = 1 1 0 0 R 3,3
Appunti di Geometria - 5
 Appunti di Geometria - 5 Samuele Mongodi - s.mongodi@sns.it Segnatura di un prodotto scalare Richiami Sia V uno spazio vettoriale reale di dimensione n; sia, : V V R un prodotto scalare. Data una base
Appunti di Geometria - 5 Samuele Mongodi - s.mongodi@sns.it Segnatura di un prodotto scalare Richiami Sia V uno spazio vettoriale reale di dimensione n; sia, : V V R un prodotto scalare. Data una base
GEOMETRIA. 25 GENNAIO ore. Istruzioni: Scrivere cognome, nome, numero di matricola in stampatello negli appositi spazi.
 GEOMETRIA 25 GENNAIO 2008 2 ore Istruzioni: Scrivere cognome, nome, numero di matricola in stampatello negli appositi spazi. Trascrivere i risultati dei quiz della prima parte nella tabella in questa pagina.
GEOMETRIA 25 GENNAIO 2008 2 ore Istruzioni: Scrivere cognome, nome, numero di matricola in stampatello negli appositi spazi. Trascrivere i risultati dei quiz della prima parte nella tabella in questa pagina.
6. Spazi euclidei ed hermitiani
 6. Spazi euclidei ed hermitiani 6.1 In [GA] 5.4 abbiamo definito il prodotto scalare fra vettori di R n (che d ora in poi chiameremo prodotto scalare standard su R n ) e abbiamo considerato le seguenti
6. Spazi euclidei ed hermitiani 6.1 In [GA] 5.4 abbiamo definito il prodotto scalare fra vettori di R n (che d ora in poi chiameremo prodotto scalare standard su R n ) e abbiamo considerato le seguenti
Note per il corso di Geometria Corso di laurea in Ing. Elettronica e delle Telecomunicazioni
 Note per il corso di Geometria 9- Corso di laurea in Ing. Elettronica e delle Telecomunicazioni Prodotto scalare e matrici simmetriche. Il prodotto scalare consente di introdurre in uno spazio vettoriale
Note per il corso di Geometria 9- Corso di laurea in Ing. Elettronica e delle Telecomunicazioni Prodotto scalare e matrici simmetriche. Il prodotto scalare consente di introdurre in uno spazio vettoriale
Prova scritta di Geometria 1 Docente: Giovanni Cerulli Irelli 15 Febbraio 2017
 Prova scritta di Geometria Docente: Giovanni Cerulli Irelli 5 Febbraio 7 Esercizio. Si considerino i due sottospazi π e π di R dati dalle seguenti equazioni: π : x y + z = ; π : x + y z =.. Trovare una
Prova scritta di Geometria Docente: Giovanni Cerulli Irelli 5 Febbraio 7 Esercizio. Si considerino i due sottospazi π e π di R dati dalle seguenti equazioni: π : x y + z = ; π : x + y z =.. Trovare una
Parte 7. Autovettori e autovalori
 Parte 7. Autovettori e autovalori A. Savo Appunti del Corso di Geometria 23-4 Indice delle sezioni Endomorfismi, 2 Cambiamento di base, 3 3 Matrici simili, 6 4 Endomorfismi diagonalizzabili, 7 5 Autovettori
Parte 7. Autovettori e autovalori A. Savo Appunti del Corso di Geometria 23-4 Indice delle sezioni Endomorfismi, 2 Cambiamento di base, 3 3 Matrici simili, 6 4 Endomorfismi diagonalizzabili, 7 5 Autovettori
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria Edile ed Edile/Architettura. Geometria Proiettiva Docente F.
 Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria Edile ed Edile/Architettura Geometria Proiettiva Docente F. Flamini CONICHE PROIETTIVE: Classificazione e forme canoniche proiettive Si
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria Edile ed Edile/Architettura Geometria Proiettiva Docente F. Flamini CONICHE PROIETTIVE: Classificazione e forme canoniche proiettive Si
Forme bilineari e prodotti scalari
 Forme bilineari e prodotti scalari Il prodotto scalare standard di R n può anche essere scritto come un prodotto riga per colonna u, v R n = u t Iv dove I è la matrice identità. Possiamo generalizzare
Forme bilineari e prodotti scalari Il prodotto scalare standard di R n può anche essere scritto come un prodotto riga per colonna u, v R n = u t Iv dove I è la matrice identità. Possiamo generalizzare
Algebra e Geometria 2 per Informatica Primo Appello 23 giugno 2006 Tema A W = { A M 2 (R) A T = A }
 Algebra e Geometria per Informatica Primo Appello 3 giugno 6 Tema A Sia M (R lo spazio vettoriale delle matrici a coefficienti reali Sia W = { A M (R A T = A } il sottospazio vettoriale delle matrici simmetriche
Algebra e Geometria per Informatica Primo Appello 3 giugno 6 Tema A Sia M (R lo spazio vettoriale delle matrici a coefficienti reali Sia W = { A M (R A T = A } il sottospazio vettoriale delle matrici simmetriche
Università degli Studi Roma Tre - Corso di Laurea in Matematica Tutorato di Geometria 1
 Università degli Studi Roma Tre - Corso di Laurea in Matematica Tutorato di Geometria 1 A.A. 28-29 - Docente: Prof. E. Sernesi Tutori: Andrea Abbate e Matteo Acclavio Soluzioni del tutorato numero 1 14
Università degli Studi Roma Tre - Corso di Laurea in Matematica Tutorato di Geometria 1 A.A. 28-29 - Docente: Prof. E. Sernesi Tutori: Andrea Abbate e Matteo Acclavio Soluzioni del tutorato numero 1 14
Corso di Laurea in Fisica. Geometria. a.a Prof. P. Piazza Diagonalizzazione delle forme bilineari simmetriche
 Corso di Laurea in Fisica. Geometria. a.a. 2009-10. Prof. P. Piazza Diagonalizzazione delle forme bilineari simmetriche Sia V uno spazio vettoriale reale. Sia 1. Osservazioni preliminari. : V V R un
Corso di Laurea in Fisica. Geometria. a.a. 2009-10. Prof. P. Piazza Diagonalizzazione delle forme bilineari simmetriche Sia V uno spazio vettoriale reale. Sia 1. Osservazioni preliminari. : V V R un
ESAME DI GEOMETRIA. 6 febbraio 2002 CORREZIONE QUIZ
 ESAME DI GEOMETRIA 6 febbraio CORREZIONE QUIZ. La parte reale di ( + i) 9 è positiva. QUIZ Si può procedere in due modi. Un primo modo è osservare che ( + i) =i, dunque ( + i) 9 =(+i)(i) 4 = 4 ( + i) :
ESAME DI GEOMETRIA 6 febbraio CORREZIONE QUIZ. La parte reale di ( + i) 9 è positiva. QUIZ Si può procedere in due modi. Un primo modo è osservare che ( + i) =i, dunque ( + i) 9 =(+i)(i) 4 = 4 ( + i) :
Complementi di Algebra e Fondamenti di Geometria
 Complementi di Algebra e Fondamenti di Geometria Capitolo 5 Forme quadratiche inr n M. Ciampa Ingegneria Elettrica, a.a. 2009/2010 Capitolo 5 Forme quadratiche inr n In questo capitolo si definisce la
Complementi di Algebra e Fondamenti di Geometria Capitolo 5 Forme quadratiche inr n M. Ciampa Ingegneria Elettrica, a.a. 2009/2010 Capitolo 5 Forme quadratiche inr n In questo capitolo si definisce la
Il Teorema Spettrale e le sue conseguenze
 Il Teorema Spettrale e le sue conseguenze In questa nota vogliamo esaminare la dimostrazione del Teorema Spettrale e studiare le sue conseguenze per quanto riguarda i prodotti scalari e le forme quadratiche.
Il Teorema Spettrale e le sue conseguenze In questa nota vogliamo esaminare la dimostrazione del Teorema Spettrale e studiare le sue conseguenze per quanto riguarda i prodotti scalari e le forme quadratiche.
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA INDUSTRIALE 27 GENNAIO 2014
 FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA INDUSTRIALE 27 GENNAIO 2014 DOCENTE: MATTEO LONGO Rispondere alle domande di Teoria in modo esauriente e completo. Svolgere il maggior numero di esercizi
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA INDUSTRIALE 27 GENNAIO 2014 DOCENTE: MATTEO LONGO Rispondere alle domande di Teoria in modo esauriente e completo. Svolgere il maggior numero di esercizi
Corso di Laurea in Matematica - Esame di Geometria 1. Prova scritta del 20 settembre 2013 Versione 1
 Corso di Laurea in Matematica - Esame di Geometria 1 Prova scritta del 20 settembre 2013 Versione 1 Cognome Nome Numero di matricola Corso (A o B) Voto ATTENZIONE. Riportare lo svolgimento completo degli
Corso di Laurea in Matematica - Esame di Geometria 1 Prova scritta del 20 settembre 2013 Versione 1 Cognome Nome Numero di matricola Corso (A o B) Voto ATTENZIONE. Riportare lo svolgimento completo degli
ATTENZIONE: : giustificate le vostre argomentazioni! Geometria Canale 3. Lettere J-PE (Prof P. Piazza) Esame scritto del 12/02/2014. Compito A.
 Geometria Canale. Lettere J-PE (Prof P. Piazza) Esame scritto del 12/02/2014. Compito A. Nome e Cognome: Numero di Matricola: Esercizio Punti totali Punteggio 1 7 2 6 6 4 6+1 5 6+2 Totale 1+ ATTENZIONE:
Geometria Canale. Lettere J-PE (Prof P. Piazza) Esame scritto del 12/02/2014. Compito A. Nome e Cognome: Numero di Matricola: Esercizio Punti totali Punteggio 1 7 2 6 6 4 6+1 5 6+2 Totale 1+ ATTENZIONE:
Capitolo IX DIAGONALIZZAZIONE DI MATRICI SIMMETRICHE
 Capitolo IX DIAGONALIZZAZIONE DI MATRICI SIMMETRICHE 1. Matrici ortogonali Ricordiamo che, nel Cap. VII, abbiamo studiato le matrici di cambio di base in un R spazio vettoriale. In tale occasione, abbiamo
Capitolo IX DIAGONALIZZAZIONE DI MATRICI SIMMETRICHE 1. Matrici ortogonali Ricordiamo che, nel Cap. VII, abbiamo studiato le matrici di cambio di base in un R spazio vettoriale. In tale occasione, abbiamo
LEZIONE 23. ax 2 + bxy + cy 2 + dx + ey + f
 LEZIONE 23 23.1. Riduzione delle coniche a forma canonica. Fissiamo nel piano un sistema di riferimento Oxy e consideriamo un polinomio di grado 2 in x, y a meno di costanti moltiplicative non nulle, diciamo
LEZIONE 23 23.1. Riduzione delle coniche a forma canonica. Fissiamo nel piano un sistema di riferimento Oxy e consideriamo un polinomio di grado 2 in x, y a meno di costanti moltiplicative non nulle, diciamo
Geometria analitica: curve e superfici
 Geometria analitica: curve e superfici geometriche algebriche e matrici e isometrie Riduzione Invarianti Studio di coniche Intersezione con rette e tangenti in forma parametrica 006 Politecnico di Torino
Geometria analitica: curve e superfici geometriche algebriche e matrici e isometrie Riduzione Invarianti Studio di coniche Intersezione con rette e tangenti in forma parametrica 006 Politecnico di Torino
0 0 c. d 1. det (D) = d 1 d n ;
 Registro Lezione di Algebra lineare del 23 novembre 216 1 Matrici diagonali 2 Autovettori e autovalori 3 Ricerca degli autovalori, polinomio caratteristico 4 Ricerca degli autovettori, autospazi 5 Matrici
Registro Lezione di Algebra lineare del 23 novembre 216 1 Matrici diagonali 2 Autovettori e autovalori 3 Ricerca degli autovalori, polinomio caratteristico 4 Ricerca degli autovettori, autospazi 5 Matrici
Salvo avviso contrario V denota un k-spazio spazio vettoriale (di dimensione finita).
 a.a. 010-011 15.4.011 FORME BILINEARI Salvo avviso contrario V denota un k-spazio spazio vettoriale (di dimensione finita). Data una base F = {f 1,..., f n } di V = v, w V si ha v = n x i f i, w = n y
a.a. 010-011 15.4.011 FORME BILINEARI Salvo avviso contrario V denota un k-spazio spazio vettoriale (di dimensione finita). Data una base F = {f 1,..., f n } di V = v, w V si ha v = n x i f i, w = n y
LEZIONE 4. Le sottomatrici 2 2 di A sono. Invece ( 1 3 non è sottomatrice di A.
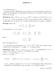 LEZIONE 4 4 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 4 4 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
ESERCIZI GEOMETRIA FILE N. 7: FORMA NORMALE DI JORDAN. PRODOTTI SCALARI. SPAZI VETTORIALI EUCLIDEI, I. 1. Forma normale di Jordan
 ESERCIZI GEOMETRIA 2 207-8. FILE N. 7: FORMA NORMALE DI JORDAN. PRODOTTI SCALARI. SPAZI VETTORIALI EUCLIDEI, I. Forma normale di Jordan Es... Esercizi da n. 7 a n. 20 alla fine della Sezione 3 del libro
ESERCIZI GEOMETRIA 2 207-8. FILE N. 7: FORMA NORMALE DI JORDAN. PRODOTTI SCALARI. SPAZI VETTORIALI EUCLIDEI, I. Forma normale di Jordan Es... Esercizi da n. 7 a n. 20 alla fine della Sezione 3 del libro
Spazi euclidei, endomorfismi simmetrici, forme quadratiche. R. Notari
 Spazi euclidei, endomorfismi simmetrici, forme quadratiche R. Notari 14 Aprile 2006 1 1. Proprietà del prodotto scalare. Sia V = R n lo spazio vettoriale delle n-uple su R. Il prodotto scalare euclideo
Spazi euclidei, endomorfismi simmetrici, forme quadratiche R. Notari 14 Aprile 2006 1 1. Proprietà del prodotto scalare. Sia V = R n lo spazio vettoriale delle n-uple su R. Il prodotto scalare euclideo
3. Determinare dimensione a basi per l annullatore ker(f) e per il complemento. Esercizio 2. Sia V uno spazio vettoriale reale di dimensione finita d.
 Esercizi --- 5-- Esercizio. Sia f =: L A : R 4 R 4, ove A = 3 e sia B =:.. Dimostrare che B è una base di R 4.. Determinare la matrice di L A nella base B. 3. Determinare dimensione a basi per l annullatore
Esercizi --- 5-- Esercizio. Sia f =: L A : R 4 R 4, ove A = 3 e sia B =:.. Dimostrare che B è una base di R 4.. Determinare la matrice di L A nella base B. 3. Determinare dimensione a basi per l annullatore
GEOMETRIA 1 ottava parte
 GEOMETRIA 1 ottava parte Cristina Turrini C. di L. in Fisica - 214/215 Cristina Turrini (C. di L. in Fisica - 214/215) GEOMETRIA 1 1 / 15 index 1 Cristina Turrini (C. di L. in Fisica - 214/215) GEOMETRIA
GEOMETRIA 1 ottava parte Cristina Turrini C. di L. in Fisica - 214/215 Cristina Turrini (C. di L. in Fisica - 214/215) GEOMETRIA 1 1 / 15 index 1 Cristina Turrini (C. di L. in Fisica - 214/215) GEOMETRIA
formano una base B di R 3. Scrivere la matrice di passaggio dalla base B alla base canonica e dire se tale matrice è ortogonale.
 ) Mostrare che i 3 vettori v=, u=, w= 3 formano una base B di R 3. Scrivere la matrice di passaggio dalla base B alla base canonica e dire se tale matrice è ortogonale. ) Sia f : R 4 R 4 la seguente applicazione
) Mostrare che i 3 vettori v=, u=, w= 3 formano una base B di R 3. Scrivere la matrice di passaggio dalla base B alla base canonica e dire se tale matrice è ortogonale. ) Sia f : R 4 R 4 la seguente applicazione
LA DIAGONALIZZAZIONE. asdf. Polinomi di matrici. 30 January 2012
 asdf LA DIAGONALIZZAZIONE 30 January 2012 L'intento di questo articolo è di affrontare, si spera sempre nel modo più corretto e chiaro possibile, la trattazione di un argomento importante nell'ambito dell'algebra
asdf LA DIAGONALIZZAZIONE 30 January 2012 L'intento di questo articolo è di affrontare, si spera sempre nel modo più corretto e chiaro possibile, la trattazione di un argomento importante nell'ambito dell'algebra
LEZIONE 5. AX = 0 m,1.
 LEZIONE 5 5 isoluzione di sistemi Supponiamo che AX = B sia un sistema di equazioni lineari Ad esso associamo la sua matrice completa (A B Per quanto visto nella precedente lezione, sappiamo di poter trasformare,
LEZIONE 5 5 isoluzione di sistemi Supponiamo che AX = B sia un sistema di equazioni lineari Ad esso associamo la sua matrice completa (A B Per quanto visto nella precedente lezione, sappiamo di poter trasformare,
Capitolo Diagonalizzazione e Triangolazione. Esercizio Diagonalizzare la matrice A =
 Capitolo 8 8 Diagonalizzazione e Triangolazione Esercizio 8 Diagonalizzare la matrice A = 3 3 Svolgimento Il polinomio caratteristico della matrice è dato da ( + t) p A (t) = ( + t) = (t + 3) (t 3) 3 3
Capitolo 8 8 Diagonalizzazione e Triangolazione Esercizio 8 Diagonalizzare la matrice A = 3 3 Svolgimento Il polinomio caratteristico della matrice è dato da ( + t) p A (t) = ( + t) = (t + 3) (t 3) 3 3
Tempo a disposizione. 120 minuti. 1 Sia dato l endomorfismo f : R 3 R 3 la cui matrice rispetto alla base canonica di R 3 è.
 Dipartimento di Matematica e Informatica Anno Accademico 2015-2016 Corso di Laurea in Informatica (L-31) Prova in itinere di Matematica Discreta (12 CFU) 13 Giugno 2016 B2 Tempo a disposizione. 120 minuti
Dipartimento di Matematica e Informatica Anno Accademico 2015-2016 Corso di Laurea in Informatica (L-31) Prova in itinere di Matematica Discreta (12 CFU) 13 Giugno 2016 B2 Tempo a disposizione. 120 minuti
LAUREA IN INGEGNERIA CIVILE ED AMBIENTE-TERRITORIO Corso di Matematica 2 Padova TEMA n.1
 LAUREA IN INGEGNERIA CIVILE ED AMBIENTE-TERRITORIO Corso di Matematica Padova -8-8 TEMA n.1 PARTE 1. Quesiti preliminari Stabilire se le seguenti affermazioni sono vere o false giustificando brevemente
LAUREA IN INGEGNERIA CIVILE ED AMBIENTE-TERRITORIO Corso di Matematica Padova -8-8 TEMA n.1 PARTE 1. Quesiti preliminari Stabilire se le seguenti affermazioni sono vere o false giustificando brevemente
GEOMETRIA 28 Giugno minuti
 GEOMETRIA 28 Giugno 2017 90 minuti A Istruzioni: Scrivere cognome, nome, matricola in STAMPATELLO negli appositi spazi. Per ogni quiz nella prima parte, indicare l affermazione giudicata corretta nella
GEOMETRIA 28 Giugno 2017 90 minuti A Istruzioni: Scrivere cognome, nome, matricola in STAMPATELLO negli appositi spazi. Per ogni quiz nella prima parte, indicare l affermazione giudicata corretta nella
Richiami di algebra delle matrici a valori reali
 Richiami di algebra delle matrici a valori reali Vettore v n = v 1 v 2. v n Vettore trasposto v n = (v 1, v 2,..., v n ) v n = (v 1, v 2,..., v n ) A. Pollice - Statistica Multivariata Vettore nullo o
Richiami di algebra delle matrici a valori reali Vettore v n = v 1 v 2. v n Vettore trasposto v n = (v 1, v 2,..., v n ) v n = (v 1, v 2,..., v n ) A. Pollice - Statistica Multivariata Vettore nullo o
Esame di Geometria - 9 CFU (Appello del 14 gennaio A)
 Esame di Geometria - 9 CFU (Appello del 4 gennaio 24 - A) Cognome: Nome: Nr.matricola: Corso di laurea: Esercizio. Si considerino le rette s : { x x 2 2x 3 = 2 3x x 2 =, { x + x s 2 : 2 x 3 = x 2 =.. Stabilire
Esame di Geometria - 9 CFU (Appello del 4 gennaio 24 - A) Cognome: Nome: Nr.matricola: Corso di laurea: Esercizio. Si considerino le rette s : { x x 2 2x 3 = 2 3x x 2 =, { x + x s 2 : 2 x 3 = x 2 =.. Stabilire
ESAMI E ESERCITAZIONI A.A Esempio di Prova d Esame Tempo a disposizione: 60 minuti. Esercizio 1.1. (8 punti) Si consideri la matrice
 ESAMI E ESERCITAZIONI A.A. 2011-12 ANDREA RATTO Sommario. In questo file presentiamo prove d esame, esercitazioni ed esami relativi al Corso di Geometria e Algebra per Ingegneria Biomedica e Meccanica.
ESAMI E ESERCITAZIONI A.A. 2011-12 ANDREA RATTO Sommario. In questo file presentiamo prove d esame, esercitazioni ed esami relativi al Corso di Geometria e Algebra per Ingegneria Biomedica e Meccanica.
Facoltà di Anno Accademico 2018/19 Registro lezioni del docente PINTUS NICOLA
 Facoltà di Anno Accademico 2018/19 Registro lezioni del docente PINTUS NICOLA Attività didattica GEOMETRIA E ALGEBRA [IN/0079] Partizionamento: Periodo di svolgimento: Docente titolare del corso: PINTUS
Facoltà di Anno Accademico 2018/19 Registro lezioni del docente PINTUS NICOLA Attività didattica GEOMETRIA E ALGEBRA [IN/0079] Partizionamento: Periodo di svolgimento: Docente titolare del corso: PINTUS
h, i: V V! R (v 1,v 2 ) 7! hv 1,v 2 i ! R v 7! hv, v 0 i èlineare. Perlacommutativitàdelprodottoscalaresegueanchelalinearità dell applicazione
 Lezione. Prodotti scalari Definizione. (Prodotto scalare). Sia V uno spazio vettoriale su R. Un prodotto scalare su V è un applicazione tale che valgono i seguenti assiomi: h, i: V V! R (v,v ) 7! hv,v
Lezione. Prodotti scalari Definizione. (Prodotto scalare). Sia V uno spazio vettoriale su R. Un prodotto scalare su V è un applicazione tale che valgono i seguenti assiomi: h, i: V V! R (v,v ) 7! hv,v
Esercizi 3, 1. Prof. Thomas Parisini. Esercizi 3, 3 Regola:
 Esercizi 3, 1 Esercizi 3, 2 Esercizi Stabilità per sistemi a tempo continuo Analisi degli autovalori Analisi del polinomio caratteristico, criterio di Routh-Hurwitz Stabilità per sistemi a tempo continuo
Esercizi 3, 1 Esercizi 3, 2 Esercizi Stabilità per sistemi a tempo continuo Analisi degli autovalori Analisi del polinomio caratteristico, criterio di Routh-Hurwitz Stabilità per sistemi a tempo continuo
Stabilità per sistemi a tempo continuo
 Esercizi 3, 1 Stabilità per sistemi a tempo continuo Analisi degli autovalori Analisi del polinomio caratteristico, criterio di Routh-Hurwitz Calcolo di Esercizi 3, 2 Esercizi Stabilità per sistemi a tempo
Esercizi 3, 1 Stabilità per sistemi a tempo continuo Analisi degli autovalori Analisi del polinomio caratteristico, criterio di Routh-Hurwitz Calcolo di Esercizi 3, 2 Esercizi Stabilità per sistemi a tempo
05. Determinare una base ortonormale per ognuno dei seguenti spazi vettoriali.
 T.1 BASI ORTONORMALI, MATRICI ORTOGONALI 01. Sia V il sottospazio di IR 3 generato dalla base B : (1, 0, 2), (0, 2, 1). Verificare che anche C : (1, 2, 1), (1, 4, 0) è base per V e ortonormalizzare le
T.1 BASI ORTONORMALI, MATRICI ORTOGONALI 01. Sia V il sottospazio di IR 3 generato dalla base B : (1, 0, 2), (0, 2, 1). Verificare che anche C : (1, 2, 1), (1, 4, 0) è base per V e ortonormalizzare le
Applicazioni lineari e diagonalizzazione. Esercizi svolti
 . Applicazioni lineari Esercizi svolti. Si consideri l applicazione f : K -> K definita da f(x,y) = x + y e si stabilisca se è lineare. Non è lineare. Possibile verifica: f(,) = 4; f(,4) = 6; quindi f(,4)
. Applicazioni lineari Esercizi svolti. Si consideri l applicazione f : K -> K definita da f(x,y) = x + y e si stabilisca se è lineare. Non è lineare. Possibile verifica: f(,) = 4; f(,4) = 6; quindi f(,4)
25.1 Quadriche e loro riduzione a forma canonica
 Lezione 25 25.1 Quadriche e loro riduzione a forma canonica Fissiamo nello spazio un sistema di riferimento Oxyz e consideriamo un polinomio q(x, y, z) di grado 2 nelle tre variabili x, y, z amenodicostantimoltiplicativenon
Lezione 25 25.1 Quadriche e loro riduzione a forma canonica Fissiamo nello spazio un sistema di riferimento Oxyz e consideriamo un polinomio q(x, y, z) di grado 2 nelle tre variabili x, y, z amenodicostantimoltiplicativenon
