Verifica classe II liceo scientifico: equazioni, disequazioni, problemi di 2 grado 1
|
|
|
- Lorenza Marino
- 7 anni fa
- Visualizzazioni
Transcript
1 Verifica classe II liceo scientifico: equazioni, disequazioni, problemi di grado 1 Verifica di matematica, classe II liceo scientifico Equazioni di secondo grado, equazioni frazionarie, equazioni con moduli, disequazioni, sistemi di disequazioni, disequazioni frazionarie, discussione di equazioni parametriche, applicazioni dei teoremi di Pitagora e Euclide, problemi risolvibili con equazioni di grado. 1. ; ; ; x x x x x x x x 1 0 x 3 x x 0 7. I coefficienti a e b di un'equazione di secondo grado sono a=3 e b=5 e una soluzione è. Determina l'altra soluzione e il coefficiente c. 8. Per quali valori di k l equazione ha: a. soluzioni reali; b. la somma delle radici è c. la somma dei reciproci delle radici è 1; d. Una soluzione è 0 e. la somma delle radici sia uguale al loro prodotto. 9. Disegna una semicirconferenza di diametro AB che misura r (r è una misura assegnata). Sia M un punto della semicirconferenza, indica con H il piede della perpendicolare condotta per M ad AB. Determina la posizione di M (per esempio calcola AH) in modo che si abbia BM AH. 10. In un triangolo equilatero ABC di lato l conduci un segmento di lunghezza x parallelo ad AB e con gli estremi sugli altri due lati, in modo che il triangolo isoscele che ha per vertice il punto medio di AB e per base il segmento di lunghezza x sia i 4/5 del triangolo dato. Determina il valore di x. 11. Il perimetro di un triangolo rettangolo è 1cm. Sapendo che l ipotenusa è uguale ai 5/7 della somma dei cateti, calcola l area del triangolo. 1. Un capitale di 1000 è depositato in banca a un certo tasso di interesse annuale. Alla scadenza del primo anno gli interessi maturati vengono reinvestiti sullo stesso conto allo stesso tasso. Alla scadenza del secondo anno si ritira la somma di 1854,70 euro. Qual è stato il tasso di interesse?
2 Verifica classe II liceo scientifico: equazioni, disequazioni, problemi di grado 1. ; ; ; a) x 49 0 x 49 Poiché sappiamo che un numero elevato al quadrato sarà sempre positivo, questa equazione è impossibile, non ha soluzioni. x 49 impossibile b) x 3 x 313 Moltiplichiamo: poiché abbiamo una somma per un prodotto, calcoleremo direttamente il quadrato del primo meno il quadrato del secondo applicando il prodotto notevole somma per differenza: x 3 13 x 13 3 x 16 x 4 c) x 3x 4 0 Risolviamo con la formula ridotta: b x b ac a x d) 5x x 0 Raccogliamo la x: x5 x 0 Risolviamo con la legge dell annullamento del prodotto: x 0 5 x 0 x 5
3 Verifica classe II liceo scientifico: equazioni, disequazioni, problemi di grado 3. Impostiamo le condizioni di esistenza: C.E. x 3 0 x 3 x 9 0 x 9 Portiamo tutto a sinistra e calcoliamo il minimo comune multiplo, togliendo poi il denominatore. x 9 x 3 x 3 x 9 0 x 9 x 9 x 3 x 9 x 3 x 3 x 9 x 3 0 x 9 x 3 x 9 x 3 x 3 x 9 0 x 8118x x 18x 6x 54 x 9 6x x impossibile x 9 0
4 Verifica classe II liceo scientifico: equazioni, disequazioni, problemi di grado 4 3. Scomponiamo in fattori: x ax a x a x a x a x a a x Cambiamo segno all ultima frazione, affinché il minimo comune multiplo sia uguale: x ax a x a x a x ax a x a x a x a x a a x x a x a a x 0 Impostiamo le condizioni di esistenza: C.E. x a 0 x a x a 0 x a Procediamo con il minimo comune multiplo, eliminando poi il denominatore: x ax a x a x ax a x ax a 0 x ax a x a x ax ax a 0 x a x ax 0 x x ax a 0 x 1a x a 0 Notiamo che il trinomio è un trinomio notevole, cioè della forma x sx p 0. Il coefficiente della x di primo grado è formato dalla somma di due valori, il cui prodotto costituisce il termine noto: x 1 x a 0 Eseguiamo la legge dell annullamento del prodotto: x 1 0 x 1 x a 0 x a
5 Verifica classe II liceo scientifico: equazioni, disequazioni, problemi di grado 5 4. x x x x 8 Per risolvere questa equazione, dobbiamo studiare il caso in cui l argomento del valore assoluto è minore di zero e quello in cui non è minore di zero: x x 0 x x x x 8 o x x 0 (x x) x x 8 Partiamo dal primo sistema: x x 0 x x x x 8 Studiamo il segno: x 0 x x1 0 x x 0 x 1 0 x 1 Risolviamo l equazione: x x x x 8 x x x x 8 0 x 8 0 x 4 x 0 x 1 Il primo sistema sarà quindi x 0 x 1 S : x 4 x 4
6 Verifica classe II liceo scientifico: equazioni, disequazioni, problemi di grado 6 Passiamo ora al secondo sistema: x x 0 (x x) x x 8 x x 0 xx 1 0 Studiamo il segno: x 0 x 1 0 x 1 Prendiamo l intervallo in cui è negativo: Risolviamo l equazione: x x x x 8 x x x x 8 0 4x 8 0 x 8 4 x Il secondo sistema sarà quindi 0 x 1 x 1 0 x Poiché vale circa 1,41 il sistema è impossibile. I due sistemi erano legati dall unione, quindi le soluzioni che soddisfano l equazione di partenza saranno solo quelle del primo sistema, cioè x=4.
7 Verifica classe II liceo scientifico: equazioni, disequazioni, problemi di grado 7 5. a) x x x x Calcoliamo il minimo comune multiplo, togliendo poi il denominatore, poiché è un numero positivo e diverso da zero: x 3x 4 0 x 6x 8 0 Passiamo all equazione associata: x 6x 8 0 Troviamo le soluzioni con la formula x 1 b x b ac a x 4 x Poiché la disequazione è maggiore di zero, sarà risolta per valori esterni all intervallo delle radici: S : x x 4 b) x 4 0 Passiamo all equazione associata e troviamo le soluzioni: x 4 0 x 4 x 4 Poiché la disequazione è minore di zero, sarà risolta per valori interni all intervallo delle radici: S : x
8 Verifica classe II liceo scientifico: equazioni, disequazioni, problemi di grado 8 c) 4x 4x 10 Notiamo che il polinomio è il quadrato di un binomio: x 1 0 x Qualsiasi numero elevato al quadrato è sempre positivo, cioè sempre maggiore o uguale a zero. d) 3x x 0 Passiamo all equazione associata, poi procediamo con il raccoglimento della x: 3x x 0 0 x 3x Risolviamo con la legge dell annullamento del prodotto: x 0 3x 0 x 3 Poiché la disequazione è minore di zero, sarà risolta per valori interni all intervallo delle radici: S : 0 x 3
9 Verifica classe II liceo scientifico: equazioni, disequazioni, problemi di grado 9 6. x x 1 0 x 3 x 3 4x 0 Cominciamo dalla prima disequazione, ponendo numeratore maggiore o uguale a zero e denominatore maggiore di zero, poi studiamo il segno: x x 1 0 x 3 x N 0 x x 1 0 Passiamo all equazione associata e troviamo le soluzioni: x x 1 0 x L equazione è impossibile, poiché 0. La disequazione corrispondente, quindi, sarà risolta D 0 x 3 x 0 Raccogliamo la x: xx 1 0 Studiamo il segno: x 0 x 1 0 x 1 0 x 1 x 1 x 1 x 1 x. Poiché la disequazione è maggiore di zero, prendiamo gli intervalli positivi: 1 x 0 x 1 Studiamo ora il segno fra numeratore e denominatore:
10 Verifica classe II liceo scientifico: equazioni, disequazioni, problemi di grado 10 Ecco quindi le soluzioni della prima disequazione: S : 1 x 0 x 1 Passiamo ora alla seconda: 3 4x 0 3 4x 0 Equazione associata: 3 4x 0 4x 3 x 3 4 x Poiché la disequazione è maggiore di zero, sarà risolta per valori esterni all intervallo delle radici: S : x 3 x 3 Ecco quindi il sistema: 1 x 0 x 1 x 3 x 3 Troviamo le soluzioni: S : 1 x 3 x 1
11 Verifica classe II liceo scientifico: equazioni, disequazioni, problemi di grado I coefficienti a e b di un'equazione di secondo grado sono a=3 e b=5 e una soluzione è. Determina l'altra soluzione e il coefficiente c. Sapendo che a=3 e b=5, possiamo scrivere l equazione in questo modo: ax bx c 0 3x 5x c 0 Inoltre, poiché una delle soluzioni è il valore del termine noto: x 1, possiamo sostituire 3 1 alla x, per poter trovare c c c c c 0 3c 6 c L equazione diventa quindi così: 3x 5x 0 Troviamo le sue soluzioni: x x x 1 3
12 Verifica classe II liceo scientifico: equazioni, disequazioni, problemi di grado 1 8. Per quali valori di k l equazione ha: a. soluzioni reali; b. la somma delle radici è c. la somma dei reciproci delle radici è 1; d. La somma dei quadrati delle radici è 0 e. la somma delle radici sia maggiore del loro prodotto. kx k 1x k 5 0 ax bx c 0 Per prima cosa, troviamo il delta dell equazione: b 4ac k 1 4 k k 5 4k 1 4k 4k 0k 14k a. Affinché l equazione abbia soluzioni reali, è necessario che il suo sia maggiore o uguale a zero. Imponiamo quindi che 0 b 4ac 0 k 1 4 k k 5 0 4k 1 4k 4k 0k 0 14k 0 k 1 4 b. Per far sì che la somma delle radici sia, è necessario porre che x 1 x b a k 1 k Poniamo k 0. Risolviamo l equazione: k 1 k k 1 0 k k 1 k 0 k 1 0 IMPOSSIBILE Non esistono quindi valori di k affinché la somma delle radici dell equazione sia.
13 Verifica classe II liceo scientifico: equazioni, disequazioni, problemi di grado 13 c. Poiché il reciproco di un numero x è 1, la somma dei reciproci delle radici sarà x 1 Abbiamo quindi che: 1 1 x 1 x x x1 x1 x Minimo comune multiplo: x1 x x1 x Togliamo il denominatore: x 1 x x 1 x la somma delle radici è data da b, mentre il loro prodotto da a c a, quindi: 1 x 1 1 x. b a c a k 1 k 5 k k Poniamo k 0 k 1 k 5 k 6 Considerando il segno del discriminante, non possiamo accettare le soluzioni che siano minori di 1 4. k 6 non è accettabile. Di conseguenza, la soluzione d. x 1 x 0 Per poter calcolare questa somma di quadrati, passiamo per il quadrato del binomio costituito dalla somma delle radici, al quale sottrarremo il doppio prodotto del primo per il secondo termine: x 1 x x 1 x x 1 x Se svolgessimo il quadrato avremmo infatti: x 1 x x 1 x x 1 x x 1 x x 1 x x 1 x Procediamo ora sostituendo alla somma b e al prodotto a x 1 x x 1 x 0 b c a a 0 b c a a 0 k 1 k 5 0 k k Poniamo le condizioni di esistenza e risolviamo l equazione: C.E. k 0 k 1 k 10 0 k k 4k 1 4k k 10 0 k k c a :
14 Verifica classe II liceo scientifico: equazioni, disequazioni, problemi di grado 14 Calcoliamo il minimo comune multiplo e togliamo il denominatore: 4k 1 4k k k 10 0 k 4k 1 4k k 10k k k 5 4k 1 4k k 10k 0 0 k k 5 k 14k 1 0 b Troviamo le soluzioni con la formula k b ac a : k Considerando il segno del discriminante, non possiamo accettare le soluzioni che siano minori di La soluzione k, che corrisponde a circa -0,07, non è accettabile, 1 poiché 4 0,04. Dobbiamo scartare anche la soluzione e. x 1 x x 1 x La somma delle radici è data da b a c a k 1 k 5 k k Risolviamo la disequazione: k 1 k 5 0 k k k 1 k 5 0 k k 6 0 k N 0 k 6 0 k 6 Dal grafico stabiliamo il segno: k ,9. b, mentre il loro prodotto da a D 0 k 0 c a, quindi: Dato che la disequazione è maggiore di zero, prendiamo gli intervalli positivi: k 6 k 0
15 Verifica classe II liceo scientifico: equazioni, disequazioni, problemi di grado Disegna una semicirconferenza di diametro AB che misura r. Sia M un punto della semicirconferenza, indica con H il piede della perpendicolare condotta per M ad AB. Determina la posizione di M in modo che si abbia BM AH. Poni AH=x e determina il valore di x. Se M fosse situato nella metà destra della Semicirconferenza, AH sarebbe maggiore del raggio. Di conseguenza, BM, che vale AH, sarebbe più grande del raggio e più grande di AH. Dalla figura a fianco si può notare che ciò non è possibile; quindi M sarà situato per forza nella parte sinistra della semicirconferenza. Per trovare il valore di x sfruttiamo le proprietà dei triangoli rettangoli, ai quali applicheremo il teorema di Euclide. Prendiamo in considerazione il triangolo AMB, rettangolo poiché inscritto in una semicirconferenza. Di esso conosciamo l ipotenusa, che coincide con il diametro e quindi vale r; il lato MB, che per ipotesi vale AH, cioè trovare la misura di HB sfruttando il primo teorema di Euclide: x. Possiamo quindi AB : MB MB : HB HB MB HB x r x r x r Sapendo ora che il diametro vale r e che esso è dato dalla somma di impostiamo l equazione: HB più AH,
16 Verifica classe II liceo scientifico: equazioni, disequazioni, problemi di grado 16 AB AH HB r x x r Risolviamo l equazione, senza porre le condizioni di esistenza, perché sappiamo già che r, essendo la misura di un segmento, non può essere nullo. r x x r 0 r r x r x r 0 r rx x 0 Cambiamo segno e ordiniamo, poi troviamo le soluzioni con la formula x b b 4ac a x rx r 0 x r r 4 r r r 8r r 9r Possiamo tranquillamente portare sicuramente positivo: 9r fuori dalla radice, perché sappiamo che r è x r 9r r 3r r 3r x r 3r x r r 4r r Abbiamo trovato due risultati, dei quali però solo uno è accettabile. Sappiamo infatti che, poiché r è positivo, -r è sicuramente negativo, cosa che per la misura di un segmento non è possibile. Di conseguenza possiamo accettare come valore della x solo r
17 Verifica classe II liceo scientifico: equazioni, disequazioni, problemi di grado In un triangolo equilatero ABC di lato l conduci un segmento di lunghezza x parallelo ad AB e con gli estremi sugli altri due lati, in modo che il triangolo isoscele che ha per vertice il punto medio di AB e per base il segmento x sia i 4/5 del triangolo dato. Determina il valore di x. Per ipotesi sappiamo che A 4 EMD 5 A. Cerchiamo quindi di determinare le aree di ABC questi due triangoli. Prendiamo in considerazione il triangolo ABC : essendo equilatero, la sua altezza CM cade perpendicolare nel punto medio del lato opposto. Sappiamo quindi che MB AB l CB l Con il teorema di Pitagora possiamo quindi determinare l altezza del triangolo ABC : CM CB MB l l l l 4 4l l 4 3l 4 Possiamo portare fuori radice, tenendo conto che in ogni caso il valore di l, essendo il lato di un triangolo, è sempre positivo: CM 3l 4 3l
18 Verifica classe II liceo scientifico: equazioni, disequazioni, problemi di grado 18 Ora consideriamo il triangolo EDC : possiamo affermare che esso è simile al triangolo ABC, in quanto si ha che CED CAB, poiché angoli corrispondenti generati dalle parallele ED e AB tagliate dalla trasversale AC. = Quindi anche il triangolo EDC è equilatero, di lato x. Possiamo quindi determinare la sua altezza CH come abbiamo fatto in precedenza: CH CD DH x x x x 4 4x x 4 3x 4 3x Troviamo ora l altezza HM del triangolo ABC e quella del triangolo : EDC EDM come differenza fra l altezza del triangolo MH CM CH 3l 3x 3l 3x A questo punto, abbiamo sia la base che l altezza del triangolo la sua area: EDM e possiamo calcolare A EDM ED HM x 3l 3x x 3l 3x 1 x 3l 3x 4 : Determiniamo anche l area del triangolo ABC A ABC AB CM 3l l 3l 1 3l 4 Sapendo che A 4 EMD 5 A, sostituiamo alle aree i rispettivi valori e risolviamo ABC l equazione, trovando il valore di x in funzione di l: x 3l 3x 4 x 3l 3x l 5 3l 4
19 Verifica classe II liceo scientifico: equazioni, disequazioni, problemi di grado 19 5 x 3l 3x 4 3l 5 3lx 5 3x 4 3l 5 3lx 5 3x 4 3l 0 5 3x 5 3lx 4 3l 0 Risolviamo con la formula x b b 4ac a : 5 3l x l 5 3l l 1875l 100l l 675l 50 3 Possiamo scomporre 675 come 5*3, cioè come 15 3 e portare fuori dalla radice 15: 5 3l 15 3l 50 3 x 5 3l 15 3l 50 3 x 5 3l 15 3l 50 3 x 40 3l l x 10 3l l
20 Verifica classe II liceo scientifico: equazioni, disequazioni, problemi di grado Il perimetro di un triangolo rettangolo è 1cm. Sapendo che l ipotenusa è uguale ai 5/7 della somma dei cateti, calcola l area del triangolo. Chiamiamo i tre lati del triangolo a,b,c, dove b e c sono i cateti, mentre a è l ipotenusa. Sappiamo che: P 1cm abc 1cm a 5 7 b c Possiamo impostare un sistema, così da trovare il valore di indicheremo con k: a b c 1 a 5 7 b c a k 1 a 5 7 k b c, che per comodità Risolviamo con in metodo della sostituzione: 5 7 k k 1 5k 7k 1 7 a 5 7 k a 5 1k 84 7 k a 5 7 k k a 5 7 k Sostituiamo ora all altra equazione e troviamo il valore di a: k k 7 b c 7 a a 5 a 5
21 Verifica classe II liceo scientifico: equazioni, disequazioni, problemi di grado 1 A questo punto possiamo sfruttare il fatto che il triangolo sia rettangolo e impostare il teorema di Pitagora: a b c a b c Tuttavia, questa scrittura non ci è utile, perché abbiamo trovato in precedenza il valore della somma di b+c, ma non il valore della somma dei loro quadrati. Possiamo però modificare l equazione in questo modo: a b c bc Se svolgessimo il quadrato avremmo infatti che: a b c bc bc b c Sostituiamo quindi i valori trovati in precedenza e ricaviamo dall equazione il prodotto di b per c: a b c bc 5 7 bc 5 49 bc 5 49 bc bc 4 bc 4 1 Avendo il prodotto dei cateti possiamo facilmente determinare l area del triangolo: A bc 1 6cm
22 Verifica classe II liceo scientifico: equazioni, disequazioni, problemi di grado 1. Un capitale di 1000 è depositato in banca a un certo tasso di interesse annuale. Alla scadenza del primo anno gli interessi maturati vengono ridepositati sullo stesso conto. Alla scadenza del secondo anno si ritira la somma di 1854,70 euro. Qual è stato il tasso di interesse? Chiamiamo con x il tasso di interesse annuale. Poiché si partiva da un capitale di 1000, alla scadenza del primo anno, considerando gli interessi, si avrà sul conto un ammontare di 1000 x% 1000 cioè 1000 x x Alla fine del secondo anno si avrà una soma che corrisponde a quella dell anno precedente x più gli interessi sulla stessa soma, quindi: x x x x% x x x 100 x 100 1x 10 10x 100 1x x 100 Ora, sapendo che questa soma, alla fine dei due anni, è uguale a 1854,70 euro, possiamo impostare l equazione: x x x x 100 1x 10 x 100 1x 10 x 100 1x , Calcoliamo il minimo comune multiplo: x 10 x 100 1x x 100x 1x x 400x b Risolviamo con la formula x b ac a
23 Verifica classe II liceo scientifico: equazioni, disequazioni, problemi di grado x x ,5 V x Poiché il tasso di interesse è positivo, possiamo accettare solo il valore della x positivo; quindi il tasso di interesse sarà pari al 3,5 %.
4. Determina le misure dei tre lati x, y, z di un triangolo sapendo che il perimetro è 53cm, inoltre
 www.matematicamente.it Verifica II liceo scientifico: Sistemi, Radicali, Equiestensione 1 Verifica di matematica, classe II liceo scientifico Sistemi, problemi con sistemi, radicali, equiestensione 1.
www.matematicamente.it Verifica II liceo scientifico: Sistemi, Radicali, Equiestensione 1 Verifica di matematica, classe II liceo scientifico Sistemi, problemi con sistemi, radicali, equiestensione 1.
Verifica di matematica, classe II liceo scientifico sistemi, problemi con sistemi, radicali, equiestensione. risolvere con il metodo di Cramer
 Verifica di matematica, classe II liceo scientifico sistemi, problemi con sistemi, radicali, equiestensione 1. 5 x y x 3y 1 risolvere con il metodo di Cramer. x 1 3 y y x 3 risolvere con il metodo di riduzione
Verifica di matematica, classe II liceo scientifico sistemi, problemi con sistemi, radicali, equiestensione 1. 5 x y x 3y 1 risolvere con il metodo di Cramer. x 1 3 y y x 3 risolvere con il metodo di riduzione
k l equazione diventa 2 x + 1 = 0 e ha unica soluzione
 a B 3 Compito del Q 8 maggio 009 A) Equazioni con parametro. Data l equazione ( k + k ) + k + 0 determinare il valore di k in ciascuno dei seguenti casi. L equazione si abbassa di grado (risolvere l equazione
a B 3 Compito del Q 8 maggio 009 A) Equazioni con parametro. Data l equazione ( k + k ) + k + 0 determinare il valore di k in ciascuno dei seguenti casi. L equazione si abbassa di grado (risolvere l equazione
Applicazioni dei teoremi di Pitagora ed Euclide
 Utilizzando le misure di segmenti e superfici si possono riscrivere i teoremi di Pitagora ed Euclide per il triangolo rettangolo: Teorema di Pitagora: 1 + c i c = 1 Teorema di Euclide: c p i 1 = 1 c =
Utilizzando le misure di segmenti e superfici si possono riscrivere i teoremi di Pitagora ed Euclide per il triangolo rettangolo: Teorema di Pitagora: 1 + c i c = 1 Teorema di Euclide: c p i 1 = 1 c =
LE EQUAZIONI DI SECONDO GRADO
 LE EQUAZIONI DI SECONDO GRADO Definizione: un equazione è di secondo grado se, dopo aver applicato i principi di equivalenza, si può scrivere nella forma, detta normale: ax + bx + c 0!!!!!con!a 0 Le lettere
LE EQUAZIONI DI SECONDO GRADO Definizione: un equazione è di secondo grado se, dopo aver applicato i principi di equivalenza, si può scrivere nella forma, detta normale: ax + bx + c 0!!!!!con!a 0 Le lettere
Liceo Scientifico Statale G. Stampacchia Tricase Tempo di lavoro 80 minuti
 Oggetto: compito in Classe D/PNI Liceo Scientifico Statale G. Stampacchia Tricase Tempo di lavoro 8 minuti Argomenti- Geometria: Risoluzione di problemi di secondo grado con applicazione del teorema di
Oggetto: compito in Classe D/PNI Liceo Scientifico Statale G. Stampacchia Tricase Tempo di lavoro 8 minuti Argomenti- Geometria: Risoluzione di problemi di secondo grado con applicazione del teorema di
Problema Un triangolo rettangolo ha l angolo =60. La bisettrice dell angolo msura 6. Calcola il perimetro del triangolo.
 SIMILITUDINE Problemi Problema 8.179 Un triangolo rettangolo ha l angolo =60. La bisettrice dell angolo msura 6. Calcola il perimetro del triangolo. La bisettrice divide l angolo =60 in due angoli di 30,
SIMILITUDINE Problemi Problema 8.179 Un triangolo rettangolo ha l angolo =60. La bisettrice dell angolo msura 6. Calcola il perimetro del triangolo. La bisettrice divide l angolo =60 in due angoli di 30,
Complementi di algebra
 Complementi di algebra Equazioni di grado superiore al secondo Come per le equazioni di grado, esistono formule risolutive anche per le equazioni di e grado ma non le studieremo perché sono troppo complesse,mentre
Complementi di algebra Equazioni di grado superiore al secondo Come per le equazioni di grado, esistono formule risolutive anche per le equazioni di e grado ma non le studieremo perché sono troppo complesse,mentre
Problemi sui teoremi di Euclide e Pitagora
 Appunti di Matematica GEOMETRIA EUCLIDEA Problemi sui teoremi di Euclide e Pitagora Utilizzando le misure di segmenti e superfici si possono riscrivere i teoremi di Pitagora ed Euclide per il triangolo
Appunti di Matematica GEOMETRIA EUCLIDEA Problemi sui teoremi di Euclide e Pitagora Utilizzando le misure di segmenti e superfici si possono riscrivere i teoremi di Pitagora ed Euclide per il triangolo
Verifica di Matematica sommativa durata della prova : 2 ore. Punt. attr. Problema
 Liceo Scientifico Statale M. Curie Classe D aprile Verifica di Matematica sommativa durata della prova : ore Nome Cognome Voto N.B. Il punteggio massimo viene attribuito in base alla correttezza e alla
Liceo Scientifico Statale M. Curie Classe D aprile Verifica di Matematica sommativa durata della prova : ore Nome Cognome Voto N.B. Il punteggio massimo viene attribuito in base alla correttezza e alla
soluzione in 7 step Es n 208
 soluzione in 7 soluzione in 7 soluzione in 7 AH 5 CA CH 5 6 4,8 5 36 3,04 5,96 5 cm soluzione in 7 AH 5 CA CH 5 6 4,8 5 36 3,04 5,96 5 cm 3 : 4,8 5 4,8 : HB 4,8 soluzione in 7 AH 5 CA CH 5 6 4,8 5 36 3,04
soluzione in 7 soluzione in 7 soluzione in 7 AH 5 CA CH 5 6 4,8 5 36 3,04 5,96 5 cm soluzione in 7 AH 5 CA CH 5 6 4,8 5 36 3,04 5,96 5 cm 3 : 4,8 5 4,8 : HB 4,8 soluzione in 7 AH 5 CA CH 5 6 4,8 5 36 3,04
Esercizi 2016/17 - Analisi I - Ing. Edile Architettura Esponenziali e logaritmi
 Esercizi 06/7 - Analisi I - Ing. Edile Architettura Esponenziali e logaritmi Esercizio. Risolvere la seguente equazione: Soluzione. ) x+ ) x 7 x = 0 7 L equazione è definita per ogni x 0, valore in cui
Esercizi 06/7 - Analisi I - Ing. Edile Architettura Esponenziali e logaritmi Esercizio. Risolvere la seguente equazione: Soluzione. ) x+ ) x 7 x = 0 7 L equazione è definita per ogni x 0, valore in cui
ALCUNE LINEE GUIDA PER LA DIMOSTRAZIONE DEI TEOREMI
 ALCUNE LINEE GUIDA PER LA DIMOSTRAZIONE DEI TEOREMI LE RELAZIONI FRA GLI ELEMENTI DI UN TRIANGOLO 1) La somma degli angoli interni di un triangolo è 180 γ Consideriamo il triangolo ABC. Tracciamo la parallela
ALCUNE LINEE GUIDA PER LA DIMOSTRAZIONE DEI TEOREMI LE RELAZIONI FRA GLI ELEMENTI DI UN TRIANGOLO 1) La somma degli angoli interni di un triangolo è 180 γ Consideriamo il triangolo ABC. Tracciamo la parallela
Equazioni e disequazioni algebriche. Soluzione. Si tratta del quadrato di un binomio. Si ha pertanto. (x m y n ) 2 = x 2m 2x m y n + y 2n
 Si tratta del quadrato di un binomio. Si ha pertanto (x m y n ) 2 = x 2m 2x m y n + y 2n 4. La divisione (x 3 3x 2 + 5x 2) : (x 2) ha Q(x) = x 2 x + 3 e R = 4 Dalla divisione tra i polinomi risulta (x
Si tratta del quadrato di un binomio. Si ha pertanto (x m y n ) 2 = x 2m 2x m y n + y 2n 4. La divisione (x 3 3x 2 + 5x 2) : (x 2) ha Q(x) = x 2 x + 3 e R = 4 Dalla divisione tra i polinomi risulta (x
Anno 4 Superficie e volume dei solidi
 Anno 4 Superficie e volume dei solidi Introduzione In questa lezione parleremo del volume e della superficie dei solidi, imparando a trattare con semplicità il loro calcolo tramite le formule Al termine
Anno 4 Superficie e volume dei solidi Introduzione In questa lezione parleremo del volume e della superficie dei solidi, imparando a trattare con semplicità il loro calcolo tramite le formule Al termine
Triangolo rettangolo
 Dato il triangolo rettangolo Possiamo perciò utilizzare angoli). Progetto Matematica in Rete Triangolo rettangolo OPA sappiamo che: PA cateto sen OP cos tg OA cateto OP PA cateto OA cateto opposto ad ipotenusa
Dato il triangolo rettangolo Possiamo perciò utilizzare angoli). Progetto Matematica in Rete Triangolo rettangolo OPA sappiamo che: PA cateto sen OP cos tg OA cateto OP PA cateto OA cateto opposto ad ipotenusa
x 2 + (x+4) 2 = 20 Alle equazioni di secondo grado si possono applicare i PRINCIPI di EQUIVALENZA utilizzati per le EQUAZIONI di PRIMO GRADO.
 EQUAZIONI DI SECONDO GRADO Un'equazione del tipo x 2 + (x+4) 2 = 20 è un'equazione DI SECONDO GRADO IN UNA INCOGNITA. Alle equazioni di secondo grado si possono applicare i PRINCIPI di EQUIVALENZA utilizzati
EQUAZIONI DI SECONDO GRADO Un'equazione del tipo x 2 + (x+4) 2 = 20 è un'equazione DI SECONDO GRADO IN UNA INCOGNITA. Alle equazioni di secondo grado si possono applicare i PRINCIPI di EQUIVALENZA utilizzati
2. Rappresenta graficamente la regione di piano soluzione del seguente sistema di disequazioni: 4<0
 Liceo Scientifico G. Galilei Trebisacce Anno Scolastico 2010-2011 Prova di Matematica : T. Pitagora T. Euclide Disequazioni Alunno: Classe: 2 C 14.04.2011 prof. Mimmo Corrado 1. Risolvi le seguenti disequazioni:
Liceo Scientifico G. Galilei Trebisacce Anno Scolastico 2010-2011 Prova di Matematica : T. Pitagora T. Euclide Disequazioni Alunno: Classe: 2 C 14.04.2011 prof. Mimmo Corrado 1. Risolvi le seguenti disequazioni:
MATEMATICA LA CIRCONFERENZA GSCATULLO
 MATEMATICA LA CIRCONFERENZA GSCATULLO La Circonferenza La circonferenza e la sua equazione Introduzione e definizione La circonferenza è una conica, ovvero quella figura ottenuta tagliando un cono con
MATEMATICA LA CIRCONFERENZA GSCATULLO La Circonferenza La circonferenza e la sua equazione Introduzione e definizione La circonferenza è una conica, ovvero quella figura ottenuta tagliando un cono con
Formule goniometriche
 Appunti di Matematica Formule goniometriche Come possiamo calcolare ( + β )? E chiaro che non può risultare ( β ) + β + : se infatti fosse così e per esempio β avremo + + +! Dobbiamo ricavare delle relazioni
Appunti di Matematica Formule goniometriche Come possiamo calcolare ( + β )? E chiaro che non può risultare ( β ) + β + : se infatti fosse così e per esempio β avremo + + +! Dobbiamo ricavare delle relazioni
Determina il terzo vertice A di un triangolo di cui. l ortocentro
 La Retta Esercizi Esercizio 6. Determina il terzo vertice A di un triangolo di cui sono noti due vertici ; 1, 1; e l ortocentro ;. Soluzione 1 Analizziamo il problema ragionando, per semplicità, su un
La Retta Esercizi Esercizio 6. Determina il terzo vertice A di un triangolo di cui sono noti due vertici ; 1, 1; e l ortocentro ;. Soluzione 1 Analizziamo il problema ragionando, per semplicità, su un
Liceo Scientifico Severi Salerno
 Liceo Scientifico Severi Salerno VERIFICA DI MATEMATICA Docente: Pappalardo Vincenzo Data: 11/04/019 Classe: 4D 1. Risolvere le seguenti equazioni e disequazioni goniometriche: π sen x = cos x 3 sen x
Liceo Scientifico Severi Salerno VERIFICA DI MATEMATICA Docente: Pappalardo Vincenzo Data: 11/04/019 Classe: 4D 1. Risolvere le seguenti equazioni e disequazioni goniometriche: π sen x = cos x 3 sen x
PROBLEMI DI SECONDO GRADO: ESEMPI
 PROBLEMI DI SECONDO GRADO: ESEMPI Problema 1 Sommando al triplo di un numero intero il quadrato del suo consecutivo si ottiene il numero 9. Qual è il numero? Il campo di accettabilità delle soluzioni è,
PROBLEMI DI SECONDO GRADO: ESEMPI Problema 1 Sommando al triplo di un numero intero il quadrato del suo consecutivo si ottiene il numero 9. Qual è il numero? Il campo di accettabilità delle soluzioni è,
Appunti di Matematica 3 - Ripasso - Ripasso di algebra. Equazioni. Equazioni di primo grado
 Ripasso di algebra Equazioni Equazioni di primo grado Un equazione di primo grado può essere sempre ridotta alla forma Se a la soluzione è Se a allora ci sono due casi: a b b e l equazione si dice determinata.
Ripasso di algebra Equazioni Equazioni di primo grado Un equazione di primo grado può essere sempre ridotta alla forma Se a la soluzione è Se a allora ci sono due casi: a b b e l equazione si dice determinata.
3 5 x 25 5 x = 1 5 x (3 25) = x = 1. 5 x = x 8x 8 = 0 2 x (23 ) x. = x (2x ) 3. = x (2 x ) 3 = 0.
 Anno Scolastico 014/15 - Classe 3B Soluzioni della verifica di matematica del 9 Maggio 015 Risolvere le seguenti equazioni esponenziali o logaritmiche. Dove è necessario, scrivere le condizioni di esistenza
Anno Scolastico 014/15 - Classe 3B Soluzioni della verifica di matematica del 9 Maggio 015 Risolvere le seguenti equazioni esponenziali o logaritmiche. Dove è necessario, scrivere le condizioni di esistenza
GEOMETRIA EUCLIDEA I teoremi di Euclide e Pitagora
 GEOMETRIA EUCLIDEA I teoremi di Euclide e Pitagora Vediamo tre importanti teoremi che riguardano i triangoli rettangoli e che si dimostrano utilizzando l equivalenza delle superfici piane. Primo teorema
GEOMETRIA EUCLIDEA I teoremi di Euclide e Pitagora Vediamo tre importanti teoremi che riguardano i triangoli rettangoli e che si dimostrano utilizzando l equivalenza delle superfici piane. Primo teorema
Soluzioni dei quesiti della maturità scientifica A.S. 2009/2010
 Soluzioni dei quesiti della maturità scientifica AS 009/010 Nicola Gigli Sun-Ra Mosconi giugno 010 Quesito 1 Un generico polinomio di grado n si può scrivere nella forma p(x) a 0 + a 1 x + + a n x n dove
Soluzioni dei quesiti della maturità scientifica AS 009/010 Nicola Gigli Sun-Ra Mosconi giugno 010 Quesito 1 Un generico polinomio di grado n si può scrivere nella forma p(x) a 0 + a 1 x + + a n x n dove
2. EQUAZIONI DI SECONDO GRADO
 www.matematicamente.it Matematica C3 Algebra. Equazioni secondo grado MATEMATICA C 3 -ALGEBRA. EQUAZIONI DI SECONDO GRADO Stuartpilbrow, 5/365 Z is for Zzzzzzzzzzz http://www.flickr.com/photos/stuartpilbrow/33674996/.
www.matematicamente.it Matematica C3 Algebra. Equazioni secondo grado MATEMATICA C 3 -ALGEBRA. EQUAZIONI DI SECONDO GRADO Stuartpilbrow, 5/365 Z is for Zzzzzzzzzzz http://www.flickr.com/photos/stuartpilbrow/33674996/.
Equazioni di secondo grado
 Equazioni di secondo grado 3 3.1 Le equazioni di secondo grado in una incognita Consideriamo il seguente problema: in un triangolo rettangolo l ipotenusa è più lunga del cateto minore di 4cm, mentre l
Equazioni di secondo grado 3 3.1 Le equazioni di secondo grado in una incognita Consideriamo il seguente problema: in un triangolo rettangolo l ipotenusa è più lunga del cateto minore di 4cm, mentre l
3x + x 5x = x = = 4 + 3x ; che equivale, moltiplicando entrambi i membri per 2, a risolvere. 4x + 6 x = 4 + 3x.
 1 Soluzioni esercizi 1.1 Equazioni di 1 e grado Risolvere le seguenti equazioni di 1 grado: 1) 3x 5x = 1 x. Abbiamo: 3x + x 5x = 1 + x = 1 + 4 x = 5. ) x + 3 x = + 3x. Facciamo il m.c.m. : 4x + 6 x = 4
1 Soluzioni esercizi 1.1 Equazioni di 1 e grado Risolvere le seguenti equazioni di 1 grado: 1) 3x 5x = 1 x. Abbiamo: 3x + x 5x = 1 + x = 1 + 4 x = 5. ) x + 3 x = + 3x. Facciamo il m.c.m. : 4x + 6 x = 4
Equazioni di secondo grado Prof. Walter Pugliese
 Equazioni di secondo grado Prof. Walter Pugliese La forma normale di un equazione di secondo grado Un equazione è di secondo grado se, dopo aver applicato i principi di equivalenza già studiati per le
Equazioni di secondo grado Prof. Walter Pugliese La forma normale di un equazione di secondo grado Un equazione è di secondo grado se, dopo aver applicato i principi di equivalenza già studiati per le
Esercizi sulle Disequazioni
 Esercizi sulle Disequazioni Esercizio Trovare le soluzioni delle seguenti disequazioni:.).).).) ).) ) ).).7) 8.8).) Esercizio Trovare le soluzioni delle seguenti disequazioni tratte dal secondo parziale
Esercizi sulle Disequazioni Esercizio Trovare le soluzioni delle seguenti disequazioni:.).).).) ).) ) ).).7) 8.8).) Esercizio Trovare le soluzioni delle seguenti disequazioni tratte dal secondo parziale
Una circonferenza e una parabola sono disegnate nel piano cartesiano. La circonferenza ha centro nel punto
 La parabola Esercizi Esercizio 368.395 Una circonferenza e una parabola sono disegnate nel piano cartesiano. La circonferenza ha centro nel punto 0 ;5 e raggio, e la parabola ha il suo vertice in 0 ;0.
La parabola Esercizi Esercizio 368.395 Una circonferenza e una parabola sono disegnate nel piano cartesiano. La circonferenza ha centro nel punto 0 ;5 e raggio, e la parabola ha il suo vertice in 0 ;0.
CORSO ZERO DI MATEMATICA
 UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA EQUAZIONI E DISEQUAZIONI DI SECONDO GRADO Dr. Erasmo Modica erasmo@galois.it EQUAZIONI DI SECONDO GRADO Definizione: Dicesi
UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA EQUAZIONI E DISEQUAZIONI DI SECONDO GRADO Dr. Erasmo Modica erasmo@galois.it EQUAZIONI DI SECONDO GRADO Definizione: Dicesi
Liceo Scientifico Severi Salerno
 Liceo Scientifico Severi Salerno VERIFICA DI MATEMATICA Docente: Pappalardo Vincenzo Data: 11/04/019 Classe: 4D 1. Risolvere le seguenti equazioni e disequazioni goniometriche: tg x π 34 = ctg x + π 3
Liceo Scientifico Severi Salerno VERIFICA DI MATEMATICA Docente: Pappalardo Vincenzo Data: 11/04/019 Classe: 4D 1. Risolvere le seguenti equazioni e disequazioni goniometriche: tg x π 34 = ctg x + π 3
Triangolo rettangolo
 Dato il triangolo rettangolo Possiamo perciò utilizzare angoli). Progetto Matematica in Rete Triangolo rettangolo OPA sappiamo che: PA cateto senα OP OA cateto cos α OP PA cateto tgα OA cateto opposto
Dato il triangolo rettangolo Possiamo perciò utilizzare angoli). Progetto Matematica in Rete Triangolo rettangolo OPA sappiamo che: PA cateto senα OP OA cateto cos α OP PA cateto tgα OA cateto opposto
SOLUZIONE DEL PROBLEMA 1 CORSO DI ORDINAMENTO 2014
 SOLUZIONE DEL PROBLEMA 1 CORSO DI ORDINAMENTO 214 1. Per determinare f() e f(k), applichiamo il teorema fondamentale del calcolo integrale, che si può applicare essendo f continua per ipotesi: g() = f(t)dt
SOLUZIONE DEL PROBLEMA 1 CORSO DI ORDINAMENTO 214 1. Per determinare f() e f(k), applichiamo il teorema fondamentale del calcolo integrale, che si può applicare essendo f continua per ipotesi: g() = f(t)dt
Test sui teoremi di Euclide e di Pitagora
 Test sui teoremi di Euclide e di Pitagora I test proposti in questa dispensa riguardano il teorema di Pitagora e i due teoremi di Euclide, con le applicazioni alle varie figure geometriche. Vengono presentate
Test sui teoremi di Euclide e di Pitagora I test proposti in questa dispensa riguardano il teorema di Pitagora e i due teoremi di Euclide, con le applicazioni alle varie figure geometriche. Vengono presentate
Liceo Scientifico Statale G. Stampacchia Tricase
 Oggetto: compito in Classe D/PNI Liceo Scientifico Statale G. Stampacchia Tricase Tempo di lavoro minuti Argomenti: Radicali Sistema di equazioni e disequazioni a coefficienti irrazionali - Disequazioni
Oggetto: compito in Classe D/PNI Liceo Scientifico Statale G. Stampacchia Tricase Tempo di lavoro minuti Argomenti: Radicali Sistema di equazioni e disequazioni a coefficienti irrazionali - Disequazioni
Disequazioni di secondo grado
 Disequazioni di secondo grado Una disequazione di secondo grado è una disequazione del tipo (oppure a b c o a b c ) a b c oppure a b c I) Cominciamo considerando disequazioni in cui a Esempio Consideriamo
Disequazioni di secondo grado Una disequazione di secondo grado è una disequazione del tipo (oppure a b c o a b c ) a b c oppure a b c I) Cominciamo considerando disequazioni in cui a Esempio Consideriamo
B7. Problemi di primo grado
 B7. Problemi di primo grado B7.1 Problemi a una incognita Per la risoluzione di problemi è possibile usare le equazioni di primo grado. Il procedimento può essere solo indicativo; è fondamentale fare molta
B7. Problemi di primo grado B7.1 Problemi a una incognita Per la risoluzione di problemi è possibile usare le equazioni di primo grado. Il procedimento può essere solo indicativo; è fondamentale fare molta
MATEMATICA EQUAZIONI FRATTE, DI SECONDO GRADO O SUPERIORE GSCATULLO
 MATEMATICA EQUAZIONI FRATTE, DI SECONDO GRADO O SUPERIORE GSCATULLO Equazioni fratte, di secondo grado o superiore Le equazioni di secondo grado Un equazione è di secondo grado se si può scrivere nella
MATEMATICA EQUAZIONI FRATTE, DI SECONDO GRADO O SUPERIORE GSCATULLO Equazioni fratte, di secondo grado o superiore Le equazioni di secondo grado Un equazione è di secondo grado se si può scrivere nella
COMPITI DELLE VACANZE A.S. 2015/16 MATEMATICA
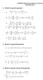 1) Risolvi le seguenti equazioni: COMPITI DELLE VACANZE A.S. 015/1 MATEMATICA 3 3 5 + + 3 5 3 5 3 3 3 1 + + + ( )( ) 5 5 18 1 5 + + 5 1 30 0 + 8 1 1 1 3 1 1 1 1 5 + + 15 30 1 1 3 1 1 + + 18 e) f) + + 3
1) Risolvi le seguenti equazioni: COMPITI DELLE VACANZE A.S. 015/1 MATEMATICA 3 3 5 + + 3 5 3 5 3 3 3 1 + + + ( )( ) 5 5 18 1 5 + + 5 1 30 0 + 8 1 1 1 3 1 1 1 1 5 + + 15 30 1 1 3 1 1 + + 18 e) f) + + 3
Problemi di massimo e minimo
 Problemi di massimo e minimo Supponiamo di avere una funzione continua in Per il teorema di Weierstrass esistono il massimo assoluto M e il minimo assoluto m I problemi di massimo e minimo sono problemi
Problemi di massimo e minimo Supponiamo di avere una funzione continua in Per il teorema di Weierstrass esistono il massimo assoluto M e il minimo assoluto m I problemi di massimo e minimo sono problemi
= r.(porre AH=x, dove H è la proiezione di P su AB)
 Liceo Scientifico Statale M. Curie Classe A Scienze Applicate aprile Verifica di Matematica: sommativa durata della prova : ore ome Cognome Leggete attentamente le seguenti istruzioni: Anche i disegni
Liceo Scientifico Statale M. Curie Classe A Scienze Applicate aprile Verifica di Matematica: sommativa durata della prova : ore ome Cognome Leggete attentamente le seguenti istruzioni: Anche i disegni
1 Funzioni algebriche fratte
 1 Funzioni algebriche fratte 1.1 Esercizio svolto y = x 1 x 11x + 10 (generalizzazione) La funzione è del tipo y = f(x) g(x) con f(x) e g(x) polinomi reali in x. Per determinare il dominio D della funzione
1 Funzioni algebriche fratte 1.1 Esercizio svolto y = x 1 x 11x + 10 (generalizzazione) La funzione è del tipo y = f(x) g(x) con f(x) e g(x) polinomi reali in x. Per determinare il dominio D della funzione
Problemi di geometria
 1 2 3 4 5 6 7 8 9 10 11 12 13 14 In un triangolo rettangolo l altezza relativa all ipotenusa è lunga 16 cm e la proiezione sull ipotenusa di un cateto è lunga 4 cm. Calcola l area del triangolo. [544 cm
1 2 3 4 5 6 7 8 9 10 11 12 13 14 In un triangolo rettangolo l altezza relativa all ipotenusa è lunga 16 cm e la proiezione sull ipotenusa di un cateto è lunga 4 cm. Calcola l area del triangolo. [544 cm
PROGRAMMA DI MATEMATICA PER LA CLASSE 1^A DEL LICEO SCIENTIFICO MALPIGHI SEZIONE ASSOCIATA DELL I.I.S
 PROGRAMMA DI MATEMATICA PER LA CLASSE 1^A DEL LICEO SCIENTIFICO MALPIGHI SEZIONE ASSOCIATA DELL I.I.S. VIA SILVESTRI 301 ANNO SCOLASTICO 2016-2017 INSEGNANTE: MASCI ORNELLA ALGEBRA NUMERI NATURALI: - Ripetizione
PROGRAMMA DI MATEMATICA PER LA CLASSE 1^A DEL LICEO SCIENTIFICO MALPIGHI SEZIONE ASSOCIATA DELL I.I.S. VIA SILVESTRI 301 ANNO SCOLASTICO 2016-2017 INSEGNANTE: MASCI ORNELLA ALGEBRA NUMERI NATURALI: - Ripetizione
Stabilire se il punto di coordinate (1,1) appartiene alla circonferenza centrata nell origine e di raggio 1.
 Definizione di circonferenza e cerchio. Equazione della circonferenza centrata in O e di raggio R. Esercizi. La circonferenza e il cerchio Definizioni: dato un punto C nel piano cartesiano e dato un numero
Definizione di circonferenza e cerchio. Equazione della circonferenza centrata in O e di raggio R. Esercizi. La circonferenza e il cerchio Definizioni: dato un punto C nel piano cartesiano e dato un numero
Don Bosco, A.S. 2013/14 Compiti per le vacanze - 2A
 Don Bosco, A.S. 0/ Compiti per le vacanze - A. Risolvi le seguenti espressioni: [( ) ( ) ] [( ) 5 ] + : ( ) ( ) ( ( ) 5 ) 9 ( 5 ) ( 5 ) ( 7 5 ). Scomponi i seguenti polinomi: a b ax+bx+ay+6by c) x +x d)
Don Bosco, A.S. 0/ Compiti per le vacanze - A. Risolvi le seguenti espressioni: [( ) ( ) ] [( ) 5 ] + : ( ) ( ) ( ( ) 5 ) 9 ( 5 ) ( 5 ) ( 7 5 ). Scomponi i seguenti polinomi: a b ax+bx+ay+6by c) x +x d)
Risoluzione dei problemi
 Risoluzione dei problemi Il dominio della generica funzione è:! a a) Scriviamo l espressione della funzione in forma di equazione raccogliendo separatamente i termini contenenti il parametro a e quelli
Risoluzione dei problemi Il dominio della generica funzione è:! a a) Scriviamo l espressione della funzione in forma di equazione raccogliendo separatamente i termini contenenti il parametro a e quelli
Equazioni frazionarie e letterali
 Equazioni frazionarie e letterali 17 17.1 Equazioni di grado superiore al primo riducibili al primo grado Nel capitolo 15 abbiamo affrontato le equazioni di primo grado. Adesso consideriamo le equazioni
Equazioni frazionarie e letterali 17 17.1 Equazioni di grado superiore al primo riducibili al primo grado Nel capitolo 15 abbiamo affrontato le equazioni di primo grado. Adesso consideriamo le equazioni
TRIGONOMETRIA PIANA: I TRIANGOLI QUALUNQUE
 TRIGONOMETRIA PIANA: I TRIANGOLI QUALUNQUE IL TEOREMA DEI SENI TEOREMA In un triangolo le misure dei lati sono proporzionali ai seni degli angoli opposti. IL TEOREMA DEI SENI DIMOSTRAZIONE Consideriamo
TRIGONOMETRIA PIANA: I TRIANGOLI QUALUNQUE IL TEOREMA DEI SENI TEOREMA In un triangolo le misure dei lati sono proporzionali ai seni degli angoli opposti. IL TEOREMA DEI SENI DIMOSTRAZIONE Consideriamo
Problemi di massimo e minimo
 Problemi di massimo e minimo Supponiamo di avere una funzione continua in. Per il teorema di Weierstrass esistono il massimo assoluto M e il minimo assoluto m. I problemi di massimo e minimo sono problemi
Problemi di massimo e minimo Supponiamo di avere una funzione continua in. Per il teorema di Weierstrass esistono il massimo assoluto M e il minimo assoluto m. I problemi di massimo e minimo sono problemi
Disequazioni di II grado
 Disequazioni di II grado Scomposizione di un trinomio di 2 grado La scomposizione del trinomio di 2 grado ax 2 + bx + c dipende dal discriminante. Se questo è positivo esistono radici reali e distinte
Disequazioni di II grado Scomposizione di un trinomio di 2 grado La scomposizione del trinomio di 2 grado ax 2 + bx + c dipende dal discriminante. Se questo è positivo esistono radici reali e distinte
2. EQUAZIONI DI SECONDO GRADO
 www.matematicamente.it Matematica C3 Algebra. Equazioni secondo grado MATEMATICA C3 -ALGEBRA. EQUAZIONI DI SECONDO GRADO Indice Stuartpilbrow, 5/365 Z is for Zzzzzzzzzzz http://www.flickr.com/photos/stuartpilbrow/33674996/.
www.matematicamente.it Matematica C3 Algebra. Equazioni secondo grado MATEMATICA C3 -ALGEBRA. EQUAZIONI DI SECONDO GRADO Indice Stuartpilbrow, 5/365 Z is for Zzzzzzzzzzz http://www.flickr.com/photos/stuartpilbrow/33674996/.
PROGRAMMA DI MATEMATICA PER LA CLASSE 1^A DEL LICEO SCIENTIFICO MALPIGHI SEZIONE ASSOCIATA DELL I.I.S
 PROGRAMMA DI MATEMATICA PER LA CLASSE 1^A DEL LICEO SCIENTIFICO MALPIGHI SEZIONE ASSOCIATA DELL I.I.S. VIA SILVESTRI 301 ANNO SCOLASTICO 2017-20178 INSEGNANTE: MASCI ORNELLA ALGEBRA NUMERI NATURALI: -
PROGRAMMA DI MATEMATICA PER LA CLASSE 1^A DEL LICEO SCIENTIFICO MALPIGHI SEZIONE ASSOCIATA DELL I.I.S. VIA SILVESTRI 301 ANNO SCOLASTICO 2017-20178 INSEGNANTE: MASCI ORNELLA ALGEBRA NUMERI NATURALI: -
Come risolvere i quesiti dell INVALSI - primo
 Come risolvere i quesiti dell INVALSI - primo Soluzione: Se mancano di 90 significa mancano a 90. Saranno presenti 90 9 = 81 litri. Soluzione: Se il trapezio è isoscele allora l angolo, inoltre l angolo
Come risolvere i quesiti dell INVALSI - primo Soluzione: Se mancano di 90 significa mancano a 90. Saranno presenti 90 9 = 81 litri. Soluzione: Se il trapezio è isoscele allora l angolo, inoltre l angolo
Liceo Classico e Internazionale C. Botta Ivrea LAVORI ESTIVI
 Liceo Classico e Internazionale C. Botta Ivrea LAVORI ESTIVI Anno scolastico: 0-05 Classe: M Docente: Enrica Menaldo Disciplina Matematica Ripassare tutto il programma preparando un formulario per i principali
Liceo Classico e Internazionale C. Botta Ivrea LAVORI ESTIVI Anno scolastico: 0-05 Classe: M Docente: Enrica Menaldo Disciplina Matematica Ripassare tutto il programma preparando un formulario per i principali
LA MATEMATICA DEI POLIEDRI REGOLARI
 LA MATEMATICA DEI POLIEDRI REGOLARI Essi simbolizzano il desiderio di Armonia e di ordine dell uomo, ma nello stesso tempo la loro perfezione desta in noi il senso della nostra impotenza. I poliedri regolari
LA MATEMATICA DEI POLIEDRI REGOLARI Essi simbolizzano il desiderio di Armonia e di ordine dell uomo, ma nello stesso tempo la loro perfezione desta in noi il senso della nostra impotenza. I poliedri regolari
Esercitazioni di Matematica Generale A.A. 2016/2017 Pietro Pastore Lezione del 4 Novembre Trinomi di secondo grado
 Esercitazioni di Matematica Generale AA 016/017 Pietro Pastore Lezione del 4 Novembre 016 Trinomi di secondo grado Possiamo usare le soluzioni dell equazione di secondo grado per scomporre il trinomio
Esercitazioni di Matematica Generale AA 016/017 Pietro Pastore Lezione del 4 Novembre 016 Trinomi di secondo grado Possiamo usare le soluzioni dell equazione di secondo grado per scomporre il trinomio
I sistemi di secondo grado sono dunque composti da un equazione di secondo grado e da una di primo grado.
 Sistemi non lineari Sistemi di secondo grado Ricordiamo che un sistema di equazioni non è altro che l insieme di più equazioni con le stesse incognite L insieme delle soluzioni è dato dall intersezione
Sistemi non lineari Sistemi di secondo grado Ricordiamo che un sistema di equazioni non è altro che l insieme di più equazioni con le stesse incognite L insieme delle soluzioni è dato dall intersezione
2. Determina l equazione della circonferenza passante per i punti A ( 2; 4), B ( 1; 3) ed avente centro sulla retta di equazione 2x 3y + 2 = 0.
 CLASSE 3^ C LICEO SCIENTIFICO Novembre 01 La circonferenza 1. Ricava l equazione di ciascuna delle circonferenze rappresentate, spiegando in maniera esauriente il procedimento che seguirai, prima di svolgere
CLASSE 3^ C LICEO SCIENTIFICO Novembre 01 La circonferenza 1. Ricava l equazione di ciascuna delle circonferenze rappresentate, spiegando in maniera esauriente il procedimento che seguirai, prima di svolgere
IIS Via Silvestri 301. Plesso Volta. Programma di Matematica Opzione Sc. Applicate a.s. 2018/19
 IIS Via Silvestri 301. Plesso Volta. Programma di Matematica Opzione Sc. Applicate a.s. 2018/19 Classe 1L MODULO 1: I NUMERI NATURALI. Cap 1. 1. Le operazioni definite nell insieme dei numeri naturali
IIS Via Silvestri 301. Plesso Volta. Programma di Matematica Opzione Sc. Applicate a.s. 2018/19 Classe 1L MODULO 1: I NUMERI NATURALI. Cap 1. 1. Le operazioni definite nell insieme dei numeri naturali
Fila A 1. Determina l insieme delle soluzioni reali per ciascuna delle seguenti equazioni:
 LS Fila A Determina l insieme delle soluzioni reali per ciascuna delle seguenti equazioni: NB Ciascun procedimento risolutivo si deve concludere con la frase L'insieme delle soluzioni è a) Trasformando
LS Fila A Determina l insieme delle soluzioni reali per ciascuna delle seguenti equazioni: NB Ciascun procedimento risolutivo si deve concludere con la frase L'insieme delle soluzioni è a) Trasformando
Questo teorema era già noto ai babilonesi, ma fu il matematico greco Pitagora, intorno al 500 a.c., a darne una descrizione precisa.
 IL TEOREMA DI PITAGORA Questo teorema era già noto ai babilonesi, ma fu il matematico greco Pitagora, intorno al 500 a.c., a darne una descrizione precisa. ENUNCIATO: la somma dei quadrati costruiti sui
IL TEOREMA DI PITAGORA Questo teorema era già noto ai babilonesi, ma fu il matematico greco Pitagora, intorno al 500 a.c., a darne una descrizione precisa. ENUNCIATO: la somma dei quadrati costruiti sui
Liceo Scientifico G. Galilei Trebisacce Anno Scolastico Prova di Matematica : La retta + Pitagora e Euclide Alunno: Classe: 2 C
 Liceo Scientifico G. Galilei Trebisacce Anno Scolastico 011-01 Prova di Matematica : La retta + Pitagora e Euclide Alunno: Classe: C 8.0.01 prof. Mimmo Corrado A. Dato il triangolo di vertici: 7, 1, 65
Liceo Scientifico G. Galilei Trebisacce Anno Scolastico 011-01 Prova di Matematica : La retta + Pitagora e Euclide Alunno: Classe: C 8.0.01 prof. Mimmo Corrado A. Dato il triangolo di vertici: 7, 1, 65
Carlo Sintini, Problemi di maturità, 1948 Luglio, matematicamente.it Luglio 1948, primo problema
 Luglio 1948, primo problema In un cerchio di raggio r è condotta una corda AB la cui distanza dal centro è r/. Inscrivere nel segmento circolare che non contiene il centro, un triangolo ABC in modo che
Luglio 1948, primo problema In un cerchio di raggio r è condotta una corda AB la cui distanza dal centro è r/. Inscrivere nel segmento circolare che non contiene il centro, un triangolo ABC in modo che
PIANO DI RECUPERO DI MATEMATICA ANNO SCOLASTICO 2015/2016 CLASSI 2 I SISTEMI LINEARI
 PIANO DI RECUPERO DI MATEMATICA ANNO SCOLASTICO 0/0 CLASSI I SISTEMI LINEARI Stabilisci se il sistema è determinato, indeterminato o impossibile senza risolverlo [determinato] [impossibile] Determina per
PIANO DI RECUPERO DI MATEMATICA ANNO SCOLASTICO 0/0 CLASSI I SISTEMI LINEARI Stabilisci se il sistema è determinato, indeterminato o impossibile senza risolverlo [determinato] [impossibile] Determina per
Disequazioni. 3 Liceo Scientifico 3 Liceo Scientifico sez. Scienze Applicate A.S. 2016/2017 Prof. Andrea Pugliese
 Disequazioni 3 Liceo Scientifico 3 Liceo Scientifico sez. Scienze Applicate A.S. 2016/2017 Prof. Andrea Pugliese Definizione ed esempi Date due espressioni algebriche A e B contenenti numeri e lettere
Disequazioni 3 Liceo Scientifico 3 Liceo Scientifico sez. Scienze Applicate A.S. 2016/2017 Prof. Andrea Pugliese Definizione ed esempi Date due espressioni algebriche A e B contenenti numeri e lettere
Soluzioni delle Esercitazioni II 24 28/09/2018 = 1 2 = 1±3 4. t = 1± 1 4
 oluzioni delle Esercitazioni II 4 8/09/08 A Equazioni intere i ha: + = 3 4 Portando a sinistra le e a destra le costanti diventa 6 =, = 3 + = 0 Raccogliendo si può riscrivere come ( + ) = 0, che ha per
oluzioni delle Esercitazioni II 4 8/09/08 A Equazioni intere i ha: + = 3 4 Portando a sinistra le e a destra le costanti diventa 6 =, = 3 + = 0 Raccogliendo si può riscrivere come ( + ) = 0, che ha per
Liceo Scientifico Statale G. Stampacchia Tricase
 Liceo Scientifico Statale G. Stampacchia Tricase Oggetto: Test di ingresso Conoscenze e competenze sul programma previsto nella classe seconda del Liceo Scientifico. Algebra Q) Ordinare in forma crescente
Liceo Scientifico Statale G. Stampacchia Tricase Oggetto: Test di ingresso Conoscenze e competenze sul programma previsto nella classe seconda del Liceo Scientifico. Algebra Q) Ordinare in forma crescente
CORSO DI TECNOLOGIE E TECNICHE DI RAPPRESENTAZIONI GRAFICHE
 CORSO DI TECNOLOGIE E TECNICHE DI RAPPRESENTAZIONI GRAFICHE PER L ISTITUTO TECNICO SETTORE TECNOLOGICO Agraria, Agroalimentare e Agroindustria classe seconda PARTE PRIMA Disegno del rilievo Unità Didattica:
CORSO DI TECNOLOGIE E TECNICHE DI RAPPRESENTAZIONI GRAFICHE PER L ISTITUTO TECNICO SETTORE TECNOLOGICO Agraria, Agroalimentare e Agroindustria classe seconda PARTE PRIMA Disegno del rilievo Unità Didattica:
PNI 2004 QUESITO 1. Il grado sessagesimale è definito come la novantesima parte dell angolo retto.
 www.matefilia.it PNI 2004 QUEITO 1 Il grado sessagesimale è definito come la novantesima parte dell angolo retto. Il grado centesimale è definito come la centesima parte dell angolo retto. La misura in
www.matefilia.it PNI 2004 QUEITO 1 Il grado sessagesimale è definito come la novantesima parte dell angolo retto. Il grado centesimale è definito come la centesima parte dell angolo retto. La misura in
ax 1 + bx 2 + c = 0, r : 2x 1 3x 2 + 1 = 0.
 . Rette in R ; circonferenze. In questo paragrafo studiamo le rette e le circonferenze in R. Ci sono due modi per descrivere una retta in R : mediante una equazione cartesiana oppure mediante una equazione
. Rette in R ; circonferenze. In questo paragrafo studiamo le rette e le circonferenze in R. Ci sono due modi per descrivere una retta in R : mediante una equazione cartesiana oppure mediante una equazione
Disequazioni di secondo grado
 Disequazioni di secondo grado.1 Risoluzione delle disequazioni di secondo grado Una disequazione di secondo grado si presenta in una delle seguenti forme: a + b + c > 0; a + b + c 0; a + b + c < 0; a +
Disequazioni di secondo grado.1 Risoluzione delle disequazioni di secondo grado Una disequazione di secondo grado si presenta in una delle seguenti forme: a + b + c > 0; a + b + c 0; a + b + c < 0; a +
Compito di matematica Classe III ASA 23 aprile 2015
 Compito di matematica Classe III ASA 3 aprile 015 A. Descrivere mediante un opportuno sistema di disequazioni nelle variabili x e y la parte di piano colorata: A1 A A1: y 1 x + x 1 4 x y 0 A: x 4 + y 9
Compito di matematica Classe III ASA 3 aprile 015 A. Descrivere mediante un opportuno sistema di disequazioni nelle variabili x e y la parte di piano colorata: A1 A A1: y 1 x + x 1 4 x y 0 A: x 4 + y 9
Chi non risolve esercizi non impara la matematica.
 60 equazioni di secondo grado Esercizio 7. Scomponi + +. Soluzione. Poiché = = = < 0, l equazione associata è impossibile e il trinomio è irriducibile (tabella )..5 esercizi hi non risolve esercizi non
60 equazioni di secondo grado Esercizio 7. Scomponi + +. Soluzione. Poiché = = = < 0, l equazione associata è impossibile e il trinomio è irriducibile (tabella )..5 esercizi hi non risolve esercizi non
(x B x A, y B y A ) = (4, 2) ha modulo
 GEOMETRIA PIANA 1. Esercizi Esercizio 1. Dati i punti A(0, 4), e B(4, ) trovarne la distanza e trovare poi i punti C allineati con A e con B che verificano: (1) AC = CB (punto medio del segmento AB); ()
GEOMETRIA PIANA 1. Esercizi Esercizio 1. Dati i punti A(0, 4), e B(4, ) trovarne la distanza e trovare poi i punti C allineati con A e con B che verificano: (1) AC = CB (punto medio del segmento AB); ()
I teoremi di Euclide e Pitagora
 GEOMETRIA EUCLIDEA Vediamo tre importanti teoremi che riguardano i triangoli rettangoli e che si dimostrano utilizzando l equivalenza delle superfici piane. 44 Primo teorema di Euclide In un triangolo
GEOMETRIA EUCLIDEA Vediamo tre importanti teoremi che riguardano i triangoli rettangoli e che si dimostrano utilizzando l equivalenza delle superfici piane. 44 Primo teorema di Euclide In un triangolo
PROGRAMMA SVOLTO II LB Matematica 2015/2016
 PROGRAMMA SVOLTO II LB Matematica 2015/2016 Sistemi di equazioni lineari: metodo di sostituzione, metodo del confronto, riduzione e Cramer. Cenni a matrici e operazioni con esse. Interpretazione grafica
PROGRAMMA SVOLTO II LB Matematica 2015/2016 Sistemi di equazioni lineari: metodo di sostituzione, metodo del confronto, riduzione e Cramer. Cenni a matrici e operazioni con esse. Interpretazione grafica
Precorso di Matematica
 UNIVERSITÀ DEGLI STUDI ROMA TRE FACOLTA DI ARCHITETTURA Precorso di Matematica Anna Scaramuzza Anno Accademico 2005-2006 4-10 Ottobre 2005 INDICE 1. ALGEBRA................................. 3 1.1 Equazioni
UNIVERSITÀ DEGLI STUDI ROMA TRE FACOLTA DI ARCHITETTURA Precorso di Matematica Anna Scaramuzza Anno Accademico 2005-2006 4-10 Ottobre 2005 INDICE 1. ALGEBRA................................. 3 1.1 Equazioni
Soluzione verifica scritta dell 8/10/2013
 Soluzione verifica scritta dell 8/10/013 * * * Problema n. 1 a) Determinare l equazione della parabola con asse parallelo all asse y, avente il vertice nel punto V ; ) e passante per l origine degli assi
Soluzione verifica scritta dell 8/10/013 * * * Problema n. 1 a) Determinare l equazione della parabola con asse parallelo all asse y, avente il vertice nel punto V ; ) e passante per l origine degli assi
ESAME DI STATO DI LICEO SCIENTIFICO Sessione suppletiva
 ESAME DI STATO DI LICEO SCIENTIFICO Sessione suppletiva PROBLEMA Il candidato risolva uno dei due problemi e 5 dei quesiti in cui si articola il questionario. Si consideri la funzione reale f m di variabile
ESAME DI STATO DI LICEO SCIENTIFICO Sessione suppletiva PROBLEMA Il candidato risolva uno dei due problemi e 5 dei quesiti in cui si articola il questionario. Si consideri la funzione reale f m di variabile
Teorema di Pitagora. Triangoli con angoli di 45, 30 e 60. Eserciziario con soluzioni. - 1
 Teorema di Pitagora. Triangoli con angoli di 45, 30 e 60. Eserciziario con soluzioni. - 1 Raccolta di problemi di geometra piana sul teorema di Pitagora applicato ai triangolo con angoli di 45, 30 e 60
Teorema di Pitagora. Triangoli con angoli di 45, 30 e 60. Eserciziario con soluzioni. - 1 Raccolta di problemi di geometra piana sul teorema di Pitagora applicato ai triangolo con angoli di 45, 30 e 60
Problemi di geometria
 1 2 5 6 7 8 9 10 11 12 1 1 In un triangolo rettangolo l ipotenusa misura 60 cm e la proiezione del cateto maggiore sull ipotenusa misura 55,29 cm. Calcola la misura dei due cateti. [57,6 cm; 16,8 cm] In
1 2 5 6 7 8 9 10 11 12 1 1 In un triangolo rettangolo l ipotenusa misura 60 cm e la proiezione del cateto maggiore sull ipotenusa misura 55,29 cm. Calcola la misura dei due cateti. [57,6 cm; 16,8 cm] In
Esempio 1 In una circonferenza sono date due corde AB e CD, che si incontrano in P.
 TEOREMI DELLE CORDE, DELLE SECANTI E DELLA TANGENTE Esempio 1 In una circonferenza sono date due corde AB e CD, che si incontrano in P. Sapendo che PA 6 cm, PB cm, PC cm, determina la lunghezza di PD.
TEOREMI DELLE CORDE, DELLE SECANTI E DELLA TANGENTE Esempio 1 In una circonferenza sono date due corde AB e CD, che si incontrano in P. Sapendo che PA 6 cm, PB cm, PC cm, determina la lunghezza di PD.
PROGRAMMA DI MATEMATICA SVOLTO NELL A.S. 2016/2017 ALGEBRA
 LICEO SCIENTIFICO STATALE «CARLO CATTANEO» Sede: Via Sostegno 41/10-10146 TORINO Tel. 011 773 2013 fax: 011 7732014 Succursale: via Postumia 57/60 10142 TORINO Tel. 011 7071984 fax 011 7078256 PROGRAMMA
LICEO SCIENTIFICO STATALE «CARLO CATTANEO» Sede: Via Sostegno 41/10-10146 TORINO Tel. 011 773 2013 fax: 011 7732014 Succursale: via Postumia 57/60 10142 TORINO Tel. 011 7071984 fax 011 7078256 PROGRAMMA
1. Risolvi in R le seguenti disequazioni: 1.a) ( x ) ( x ) b) 2x. 1.e) 2x 1. 1.g)
 LICEO PEDAGOGICO-ARTISTICO GPascoli di Bolzano PROVA SCRITTA DI MATEMATICA-ALUNNI CON GIUDIZIO SOSPESO CLASSE a B /9/9- Tempo h Ogni risposta ai quesiti va opportunamente motivata (con calcoli, grafici,
LICEO PEDAGOGICO-ARTISTICO GPascoli di Bolzano PROVA SCRITTA DI MATEMATICA-ALUNNI CON GIUDIZIO SOSPESO CLASSE a B /9/9- Tempo h Ogni risposta ai quesiti va opportunamente motivata (con calcoli, grafici,
Disequazioni fratte. Una disequazione in cui l'incognita compare a denominatore si chiama fratta o frazionaria.
 1 Disequazioni fratte Una disequazione in cui l'incognita compare a denominatore si chiama fratta o frazionaria. Prima di affrontare le disequazioni fratte, ricordiamo il procedimento che utilizziamo per
1 Disequazioni fratte Una disequazione in cui l'incognita compare a denominatore si chiama fratta o frazionaria. Prima di affrontare le disequazioni fratte, ricordiamo il procedimento che utilizziamo per
Le equazioni di primo grado
 Le equazioni di primo grado Definiamo prima di tutto cosa è una identità. Definizione : un identità è un uguaglianza, dove compaiono espressioni letterali, verificata per qualunque valore attribuito alle
Le equazioni di primo grado Definiamo prima di tutto cosa è una identità. Definizione : un identità è un uguaglianza, dove compaiono espressioni letterali, verificata per qualunque valore attribuito alle
Chi non risolve esercizi non impara la matematica.
 . esercizi Chi non risolve esercizi non impara la matematica.. esercizi + = + = + = 0 = + = 8 + = 0 = 8 8 = + 9 = 0 = + = = + = 0 = = + = 0 = 0 8 0 = 9 = 0 + = + = = 8 = 0 = = = + = 8 = 0 9 = 0 = = + 8
. esercizi Chi non risolve esercizi non impara la matematica.. esercizi + = + = + = 0 = + = 8 + = 0 = 8 8 = + 9 = 0 = + = = + = 0 = = + = 0 = 0 8 0 = 9 = 0 + = + = = 8 = 0 = = = + = 8 = 0 9 = 0 = = + 8
Liceo G.B. Vico Corsico a.s
 Liceo G.B. Vico Corsico a.s. 2018-19 Programma svolto durante l anno scolastico Classe: 2^B Materia: Matematica Insegnante: Tommaseo Paola Testo utilizzato: Matematica multimediale.blu con TUTOR vol. 1
Liceo G.B. Vico Corsico a.s. 2018-19 Programma svolto durante l anno scolastico Classe: 2^B Materia: Matematica Insegnante: Tommaseo Paola Testo utilizzato: Matematica multimediale.blu con TUTOR vol. 1
Le equazioni di primo grado
 Le equazioni di primo grado Definiamo prima di tutto cosa è una identità. Definizione : un identità è un uguaglianza, dove compaiono espressioni letterali, verificata per qualunque valore attribuito alle
Le equazioni di primo grado Definiamo prima di tutto cosa è una identità. Definizione : un identità è un uguaglianza, dove compaiono espressioni letterali, verificata per qualunque valore attribuito alle
I quadrati sono 5. Esercizio pagina 198 numero 119 Calcola la misura del perimetro dell'area del trapezio in figura
 Considera il piano cartesiano. Quanti sono i quadrati aventi un vertice in (-1;-1) e tali che uno degli assi coordinati sia asse di simmetria del quadrato stesso? I quadrati sono 5 Esercizio pagina 198
Considera il piano cartesiano. Quanti sono i quadrati aventi un vertice in (-1;-1) e tali che uno degli assi coordinati sia asse di simmetria del quadrato stesso? I quadrati sono 5 Esercizio pagina 198
Liceo Scientifico G. Galilei Trebisacce Anno Scolastico Prova di Matematica : La retta + Pitagora e Euclide Alunno: Classe: 2 B
 Liceo Scientifico G. Galilei Trebisacce Anno Scolastico 011-01 Prova di Matematica : La retta + Pitagora e Euclide Alunno: Classe: B 9.03.01 prof. Mimmo Corrado A. Dato il triangolo di vertici: 3, 1 4,
Liceo Scientifico G. Galilei Trebisacce Anno Scolastico 011-01 Prova di Matematica : La retta + Pitagora e Euclide Alunno: Classe: B 9.03.01 prof. Mimmo Corrado A. Dato il triangolo di vertici: 3, 1 4,
Macerata 6 febbraio 2015 classe 3M COMPITO DI MATEMATICA RECUPERO ASSENTI. 3 3 < x.
 Macerata 6 febbraio 05 classe 3M COMPITO DI MATEMATICA RECUPERO ASSENTI SOLUZIONE QUESITO a) Rappresenta graficamente la curva descritta dalla seguente equazione: x y x y + + + 4 = 0 Per la presenza del
Macerata 6 febbraio 05 classe 3M COMPITO DI MATEMATICA RECUPERO ASSENTI SOLUZIONE QUESITO a) Rappresenta graficamente la curva descritta dalla seguente equazione: x y x y + + + 4 = 0 Per la presenza del
il discriminante uguale a zero; sviluppando i calcoli si ottiene che deve essere
 Macerata maggio 0 classe M COMPITO DI MATEMATICA RECUPERO ASSENTI QUESITO Considera il fascio di curve di equazione: x y (.) = k + k 6 a) Trova per quali valori di k si hanno delle ellissi. Deve essere
Macerata maggio 0 classe M COMPITO DI MATEMATICA RECUPERO ASSENTI QUESITO Considera il fascio di curve di equazione: x y (.) = k + k 6 a) Trova per quali valori di k si hanno delle ellissi. Deve essere
246 PROBLEMI GEOMETRICI DI 2 GRADO - ESEMPI SVOLTI In un triangolo isoscele la somma di base e altezza è 10 cm, e l area è di 12 cm
 46 PROBLEMI GEOMETRICI DI GRADO - ESEMPI SVOLTI In un triangolo isoscele la somma di base e altezza è 10 cm, e l area è di 1 cm. Trovare il perimetro. Disegno Dati e richieste del problema CA CB CH AB
46 PROBLEMI GEOMETRICI DI GRADO - ESEMPI SVOLTI In un triangolo isoscele la somma di base e altezza è 10 cm, e l area è di 1 cm. Trovare il perimetro. Disegno Dati e richieste del problema CA CB CH AB
Geometria euclidea. Alessio del Vigna. Lunedì 15 settembre
 Geometria euclidea Alessio del Vigna Lunedì 15 settembre La geometria euclidea è una teoria fondata su quattro enti primitivi e sulle relazioni che tra essi intercorrono. I quattro enti primitivi in questione
Geometria euclidea Alessio del Vigna Lunedì 15 settembre La geometria euclidea è una teoria fondata su quattro enti primitivi e sulle relazioni che tra essi intercorrono. I quattro enti primitivi in questione
