ROTTURA SPONTANEA DI SIMMETRIA: DAL FERROMAGNETISMO ALLA FISICA DELLE PARTICELLE
|
|
|
- Isabella Donati
- 7 anni fa
- Visualizzazioni
Transcript
1 ROTTURA SPONTANEA DI SIMMETRIA: DAL FERROMAGNETISMO ALLA FISICA DELLE PARTICELLE
2 2 Indice Indice Indice... 2 Introduzione... 3 Bosoni massivi in fisica della particelle... 3 Correnti schermanti: la massa del fotone... 6 Risoluzione del problema... 7 Diamagnetismo e Superconduttività... 7 Modello di Higgs U(1) Rottura spontanea di simmetria: il caso del ferromagnetismo Rottura spontanea di simmetria: il modello di Higgs U(1) Dove finisce la Gauge invarianza quando la simmetria è rotta? Modello di Higgs SU(2)xU(1) e verifica sperimentale Bibliografia... 18
3 Bosoni massivi in fisica della particelle 3 Introduzione Bosoni massivi in fisica della particelle All epoca della formulazione della meccanica quantistica, l unico bosone mediatore conosciuto era il fotone. Esso è il mediatore del campo elettromagnetico. Le equazioni di Maxwell prevedono che esso sia una particella a massa nulla, e di ciò si hanno evidenze sperimentali. In seguito, con lo studio delle interazioni forti, è stato ipotizzato, e poi confermato indirettamente dai dati sperimentali, che anche l interazione forte è descrivibile con una teoria di gauge e che essa possiede 8 bosoni mediatori, anche essi a massa nulla. Ci si può dunque chiedere se l assenza di massa sia una caratteristica di tutti i bosoni mediatori di un campo di gauge. Tuttavia, quando analizziamo i dati sperimentali di processi dovuti ad interazioni deboli, vediamo che essi non sono compatibili con bosoni mediatori a massa nulla, anzi i bosoni mediatori di tale interazione devono avere una massa molto maggiore di quella del protone! Nasce allora il problema dell invarianza di gauge. In meccanica quantistica una particella elementare è descrivibile con una funzione d onda, che associa ad ogni punto dello spazio un numero complesso. Tale funzione d onda deve soddisfare l equazione di Schrödinger. In assenza di altre particelle o campi però l unica osservabile è la densità di probabilità di osservare la particella in un dato punto, ovvero il modulo di tale funzione d onda. Nasce allora spontanea la domanda: posso scegliere la fase della funzione d onda arbitrariamente in ogni punto dello spazio tempo, se essa non contiene nessuna informazione fisica? Deve continuare a valere è l equazione di Schrödinger: la nuova funzione d onda dovrà sempre essere soluzione dell equazione di Schrödinger. Tuttavia si osserva subito che se è soluzione, allora non lo è, infatti e i termini aggiuntivi che compaiono fanno si che l equazione di Schrödinger scritta in questa forma non sia soddisfatta. Possiamo allora introdurre un campo di gauge, per esempio quello elettromagnetico. In questo
4 4 Bosoni massivi in fisica della particelle caso l Hamiltoniana cambia, e il suo cambiamento rende covariante l equazione di S. sotto trasformazioni arbitrarie di fase: Infatti se allora la funzione d onda trasformata soddisfa l equazione di S. trasformata in modo covariante se i campi trasformano in questo modo: Infatti: In quanto:
5 Bosoni massivi in fisica della particelle 5 L equazione diventa allora che è equivalente a quella di partenza. La stessa cosa avviene in una teoria di gauge come la QED: Se partiamo dalla densità lagrangiana di Dirac: e cambiamo la fase del campo spinoriale allora Se introduciamo però un campo di gauge (campo elettromagnetico) con l accoppiamento minimale la densità lagrangiana diventa: che è invariante sotto trasformazioni del tipo: Infatti Il ruolo di tale campo di gauge sembra quello di riconciliare i cambiamenti di fase che possono riferirsi, in linea di principio, a particelle molto distanti nello spazio. Tuttavia solitamente c è una connessione fra il raggio di azione di un campo e la massa del suo mediatore. Nel caso dei campi di gauge la riconciliazione della fase deve essere fatta su distanze spazio-temporali arbitrariamente grandi, e quindi sembrerebbe allora necessario richiedere che i quanti mediatori siano a massa nulla.
6 6 Correnti schermanti: la massa del fotone Si può vedere matematicamente che i quanti di gauge dovrebbero essere a massa nulla nel modo seguente. L equazione di Maxwell per il campo elettromagnetico è ed è invariante sotto la trasformazione Invece l equazione per un bosone massivo è manifestamente non invariante sotto la trasformazione precedente, e il termine di rottura è proprio quello di massa. Sembra quindi che abbiamo raggiunto un vicolo cieco nel tentativo di applicare una teoria di gauge alle interazioni deboli. Correnti schermanti: la massa del fotone L unico modo per cui le due equazioni possono essere fra loro consistenti è il seguente: prendendo la divergenza dell equazione per il bosone massivo otteniamo la condizione per cui le due equazioni diventano e possono essere consistenti se e solo se cosa che ovviamente non è una condizione gauge invariante. Ciò era presumibile: siamo partiti dall equazione per il bosone massivo che non era gauge invariante, e la condizione che abbiamo trovato sulla divergenza di può essere interpretata come una scelta di gauge per il campo. Vediamo ora perché questa condizione è chiamata di corrente schermante partendo dalle equazioni di Maxwell. Considerando il caso statico dato che si ottiene (usando la corrente schermante):
7 Diamagnetismo e Superconduttività 7 che ha come soluzione accettabile solo l esponenziale decrescente con lunghezza di decadimento, detta lunghezza di schermaggio. Questo significa che in un mezzo in cui valgono le precedenti equazioni, il campo magnetico può penetrare sol per una lunghezza pari a. Cos è che scherma il campo? È il campo stesso che genera correnti indotte le quali generano a loro volta un campo indotto che cancella quello esterno. Risoluzione del problema Diamagnetismo e Superconduttività Consideriamo il problema del Diamagnetismo in meccanica quantistica. Dobbiamo usare la corrente di probabilità quantistica modificata per la presenza del campo elettromagnetico (in unità naturali) corrente ottenuta da quella standard costituendo l operatore con la derivata covariante. La funzione d onda è ovviamente la funzione d onda dell elettrone. Ponendo otteniamo una corrente effettivamente invariante per trasformazioni del tipo Abbiamo allora da risolvere le seguenti equazioni accoppiate dove ci siamo ridotti al caso statico e alla gauge trasversa. Osserviamo che esiste una soluzione dove la funzione d onda è costante:
8 8 Diamagnetismo e Superconduttività da cui risulta che la lunghezza di schermaggio è (andando a ripristinare le costanti universali con l analisi dimensionale): Se consideriamo poi una distribuzione uniforme di elettroni allora dove è il raggio di Bohr, e risulta Questo effetto và applicato singolarmente ad ogni atomo, il quale avendo dimensioni di circa sentirà un attenuazione massima pari a e pertanto il Diamagnetismo è un effetto molto debole. Alcune note: nella soluzione del sistema, per la prima equazione basta considerare l approssimazione di campo debole, per cui si vede che trascurando il termine in la funzione d onda rimane imperturbata e l energia subisce uno schift dovuto a, che non è altro che il contributo orbitale al paramagnetismo. Per questa ragione una seconda semplificazione sta nel porre, ottenendo che così anche l energia non cambia di valore. Un ultima approssimazione necessaria per risolvere solo la seconda equazione consiste nel supporre il modulo della funzione d onda ovunque costante. Questa approssimazione non cambia il risultato finale, cioè che l effetto è molto debole. Consideriamo ora il fenomeno della superconduttività e l effetto Meissner. L effetto del diamagnetismo è piccolo perché è grande rispetto alle dimensioni atomiche. Gli orbitali degli elettroni di conduzione nei metalli si estendono su regioni più ampie, quindi potremmo pensare che l effetto del Diamagnetismo in questo caso sarebbe più grande, ma le funzioni d onda sono fortemente perturbate dal campo e quindi la nostra approssimazione non vale. Se però il metallo viene raffreddato al di sotto di una certa temperatura, il flusso magnetico che lo attraversa viene espulso repentinamente, perché vengono a formarsi correnti superficiali che cancellano esattamente il contributo del campo esterno all interno del conduttore. Nella superconduttività valgono esattamente le stesse equazioni che per il Diamagnetismo, dove però bisogna reinterpretare il significato di ogni singolo termine. La funzione d onda diventa una funzione d onda macroscopica, cioè di tutte le particelle, che vengono quindi considerate coerenti fra loro, cioè aventi la stessa fase. Insomma tutte le particelle stanno nello stesso stato. Qui sorge una domanda: se le particelle sono elettroni, che sono fermioni, come possono stare
9 Diamagnetismo e Superconduttività 9 tutte nello stesso stato? La risposta è che a tale temperatura gli elettroni vanno a formare delle coppie dette coppie di Cooper che sono bosoni e quindi possono stare tutte nello stesso stato. Per quanto riguarda gli altri termini: diventa la carica di una coppia di Cooper, la massa di una coppia di Cooper, e la densità delle coppie di Cooper per unità di volume. Vediamo che si ottiene una praticamente uguale alla precedente: e ponendo Adesso però cambia un altra cosa: prima l elemento a cui andava applicato il singolo effetto di schermaggio era l atomo, ora invece è un oggetto macroscopico di dimensione Quindi lo schermaggio è pressoché totale all interno; infatti già a c è uno schermaggio pari a: Alcune note: Stiamo assumendo che una parte degli elettroni formino coppie di Cooper (bosoni): questa è un assunzione non perturbativa. Usando invece la teoria delle perturbazioni non saremmo mai potuti arrivare a uno stato dove gli elettroni formino coppie di Cooper. Inoltre queste coppie si trovano tutte nello stesso stato quantistico. Si tratta quindi di una condensazione nello spazio degli impulsi: tutte le coppie hanno lo stesso momento del centro di massa. Non tutti gli elettroni di conduzione che si convertono in coppie cadono in questo stato fondamentale, ma solo una frazione, che varia da nessuno (alla temperatura critica) alla totalità (allo zero assoluto). Quindi quando abbiamo posto la densità delle coppie di Cooper pari a metà di quella degli elettroni di conduzione abbiamo fatto l approssimazione di essere vicini a temperatura nulla. Infine notiamo che siamo giunti a un equazione che dà massa alle sole componenti trasverse del campo. Infatti ci siamo messi nella gauge trasversa e abbiamo assunto che la funzione d onda fosse stabile per variazioni del campo : e questo può essere vero solo per variazioni della parte trasversa, in quanto la parte longitudinale può variare di un termine di gradiente che non ha nessun effetto sulla situazione fisica (non modifica né il campo, né altro). Manca allora da capire come si fa a far assumere massa anche alla componente longitudinale, massa che deve essere la stessa di quella delle componenti trasverse.
10 10 Modello di Higgs U(1) Modello di Higgs U(1) Vediamo ora un modello analogo in teoria dei campi. Mettendoci sempre nella gauge trasversa scriviamo l equazione covariante per il campo (ovviamente non possiamo più ridurci al caso statico): Aggiungiamo al modello la presenza di un campo bosonico scalare carico, la cui corrente è: che si ottiene come in M. Q. partendo dalla corrente standard e sostituendo la derivata normale con quella covariante. Assumendo quindi l esistenza di un bosone scalare carico in aggiunta al campo diventa:, l equazione precedente Ponendo poi si ottiene: da cui si può osservare che la seconda parte dell equazione è gauge invariante mentre la prima parte non lo è, avendo scelto la gauge trasversa. Scegliendo poi si ottiene: che dà al campo una massa. Ora vedremo come questo è possibile, ma prima apriamo una piccola parentesi. Rottura spontanea di simmetria: il caso del ferromagnetismo Un semplice esempio di rottura spontanea di simmetria è il modello di un ferromagnete dove l Hamiltoniana che descrive le interazioni spin-spin è invariante per rotazioni. In assenza di campi esterni non ci sono altre interazioni significative e quindi tutta l Hamiltoniana è invariante per rotazioni. Tuttavia, se raffreddiamo il ferromagnete al di sotto della temperatura critica, il ferromagnete presenta una magnetizzazione spontanea non nulla. Il vettore magnetizzazione sceglie a caso una delle possibili direzioni, il fatto che la sceglie fa si che lo stato fondamentale non sia rotazionalmente invariante. Il vettore magnetizzazione può però scegliere qualsiasi direzione, ed è qui che la simmetria dell Hamiltoniana si ripresenta, nascosta. Per questo alcuni libri indicano questo fenomeno come simmetria nascosta invece che rotta, perché in realtà esiste ancora, ma non si vede. Come si può facilmente capire che può esistere uno stato fondamentale con magnetizzazione non nulla? Prendiamo il modello di Landau.
11 Modello di Higgs U(1) 11 Il potenziale termodinamico rilevante è l energia libera di Gibbs che può essere approssimata da: Prendendo configurazioni uniformi l ultimo termine si annulla e il minimo del potenziale si può avere quando vale (abbiamo indicato con il modulo della magnetizzazione, essendo la direzione arbitraria): I punti stazionari sono quindi dove abbiamo scartato la soluzione col segno meno in quanto significherebbe solo un cambio di verso del vettore. Inoltre la seconda soluzione è ammissibile solo se in quanto il modello assume che si ha sempre. Andando a considerare la derivata seconda si vede che il primo caso corrisponde a un minimo se, mentre il secondo è un minimo se. Pertanto riassumendo: Se esiste solo un punto stazionario che è di minimo e corrisponde a magnetizzazione spontanea nulla; questo sarà il caso in cui siamo sopra la temperatura critica Se esistono due punti stazionari, che è di massimo e quindi instabile, ed un altro punto con che è di minimo e quindi stabile; questo sarà invece il caso in cui siamo al di sotto della temperatura critica Ecco di seguito un grafico dell energia di Gibbs in funzione del modulo della magnetizzazione a temperatura maggiore e minore di quella critica. Energia libera di Gibbs a temperatura superiore a quella critica (blu) ed inferiore (viola). Scale arbitrarie.
12 12 Modello di Higgs U(1) Rottura spontanea di simmetria: il modello di Higgs U(1) Il modello di Higgs assume l esistenza di un campo bosonico scalare carico: Dove e sono campi reali per i quali vale lo sviluppo standard in onde piane del tipo che trasforma in questo modo: La scelta della forma del potenziale è il passaggio che determina se c è o meno rottura spontanea di simmetria. Per ragioni dimensionali, perché la teoria sia rinormalizzabile è necessario che il potenziale abbia la forma di un polinomio del campo di grado non superiore a 4. La scelta più ovvia allora ricade su un analogo dell energia di Gibbs del paragrafo precedente: dove abbiamo preso il modulo del campo invece del campo stesso in quanto il potenziale deve essere anche gauge invariante. Se ora scegliessimo avremmo un potenziale con minimo in e quindi valore di aspettazione sul vuoto nullo: Plot 3D del potenziale del campo di Higgs, caso a>0
13 Modello di Higgs U(1) 13 Se scegliessimo invece Il minimo del potenziale si avrà per un valore del campo non nullo, e sarà quello il punto attorno al quale si dovrà sviluppare il campo per applicare la teoria delle perturbazioni: Plot del potenziale del campo di Higgs, caso a<0 Come si può vedere dal plot abbiamo un insieme continuo di minimi, costituito da una circonferenza di raggio. Una volta fissata la gauge, ogni punto della circonferenza è uno stato di vuoto differente; tuttavia a noi è necessario un solo stato fondamentale da cui fare lo sviluppo perturbativo. La scelta dello stato di vuoto da usare è indifferente dato che l intero modello è invariante anche globalmente, ed è quindi sempre possibile fare una trasformazione globale che renda il valore di aspettazione del campo sul vuoto reale. Tuttavia la scelta di uno stato fondamentale fra gli infiniti possibili sulla circonferenza rompe l invarianza del modello. Nel caso di simmetria rotta l equazione per il campo diventa: Alcune note: Quanto detto inizialmente ha quindi valore se siamo nel caso di rottura di simmetria, infatti se il potenziale ha minimo per campo nullo si ha e il campo non acquista massa Per far apparire la massa al campo abbiamo dovuto supporre l esistenza di un altro campo. Questo è detto modello di Higgs minimale in quanto lo abbiamo fatto col numero minimo di campi
14 14 Dove finisce la Gauge invarianza quando la simmetria è rotta? possibile (2 campi scalari reali). È possibile ottenere risultati analoghi usando più campi e complicando il modello. I campi aggiunti devono comunque essere campi bosonici, in quanto campi mediatori di una interazione, e scalari: infatti se esistesse un campo vettoriale con valore di aspettazione sul vuoto non nullo, avremmo una direzione privilegiata nello spazio-tempo e perderemmo quindi l isotropia di quest ultimo. Considerazioni analoghe escludono di poter usare campi tensoriali di ordine superiore. La rottura di simmetria modifica la situazione fisica in modo non perturbativo: cambia infatti lo stato di vuoto della teoria, che passa da uno con valore di aspettazione di tutti i campi nullo a uno dove c è un campo con valore di aspettazione diverso da zero. Non avremmo quindi potuto ottenere questi risultati usando la teoria delle perturbazioni, in quanto cambia il punto attorno a cui sviluppare il potenziale. Dove finisce la Gauge invarianza quando la simmetria è rotta? Per rispondere a questa domanda dobbiamo ricostruire tutte le equazioni in modo che siano gauge invarianti, il modo migliore è scrivere la lagrangiana che abbiamo ottenuto includendo tutti i campi che abbiamo preso in considerazione. Tale Lagrangiana finale risulta essere: dove così scritta è ovvia la gauge invarianza ma si visualizzano male i singoli termini. Sviluppando attorno al minimo del potenziale, facendo varie sostituzioni e ponendo otteniamo: Vediamo che se facciamo la trasformazione di gauge Essendo invariante per trasformazioni di gauge la lagrangiana assume la forma Dove è scomparso il grado di libertà associato a. Se scriviamo le equazioni del moto per il campo otteniamo l equazione Che, con la stessa trasformazione di gauge proposta in precedenza, diventa
15 Modello di Higgs SU(2)xU(1) e verifica sperimentale 15 che è l equazione che avevamo scritto nella gauge trasversa per cui. La trasformazione di gauge presa in considerazione cambia la divergenza di, che non sarà quindi più trasverso, ma avrà una componente longitudinale. Tale componente è acquisita tramite trasformazione di gauge perdendo il grado di libertà di fase. Analizziamo ora i rimanenti termini della lagrangiana (abbiamo tralasciato il termine costante): I primi due termini sono quelli di un campo bosonico massivo libero per il fotone, come abbiamo appena detto, con massa Il terzo e il quarto sono termini di un campo bosonico massivo scalare, con massa accoppiato in modo minimale con il campo elettromagnetico del fotone. Questo è il campo di Higgs per il modello. Gli ultimi due termini sono termini di auto-interazione del campo di Higgs con sè stesso. Andiamo a trarre le conclusioni: Il cambio di gauge che abbiamo mostrato rende possibile scegliere un reale. Il grado di libertà apparentemente perso (dato che era inizialmente complesso) viene in realtà trasformato nel terzo grado di libertà del campo del fotone che, essendo ora massivo, ha tre componenti indipendenti invece di due Se scegliamo di lavorare in altre gauge, dove non scompare, le equazioni del moto, le regole e i diagrammi di Feynmann sono differenti, includendo anche propagatori e vertici per il campo non fisico dovuto al grado di libertà aggiuntivo contenuto in. La rottura di simmetria si è potuta verificare solo grazie a un insieme di precise relazioni fra i parametri della lagrangiana. Attraverso la verifica sperimentale che tali relazioni valgono effettivamente possiamo capire la veridicità del modello e della presenza della rottura di simmetria Modello di Higgs SU(2)xU(1) e verifica sperimentale Il modello di Higgs per il gruppo di isospin debole non ha concettualmente nessuna differenza rispetto a quello : Il campo da scalare complesso diventa un doppietto di isospin debole complesso, la fase matrice hermitiana: diventa una
16 16 Modello di Higgs SU(2)xU(1) e verifica sperimentale e il campo di gauge diventa un campo a 3 componenti dove le sono le matrici di Pauli. Di conseguenza si ridefinisce e il potenziale diventa Di conseguenza si ottiene che la parte di gauge per il modello elettrodebole è Una prima relazione fra i coefficienti si ottiene quando si va ad imporre che la rottura di simmetria sia esattamente per la parte e che la simmetria rimanga quindi esatta: mentre dalla lagrangiana così scritta ricaviamo altre relazioni con dati misurabili: Queste sono 5 equazioni in 5 incognite:. Se conoscessimo i valori di tutte le altre costanti che compaiono nelle equazioni potremmo trovare i valori di tutte le incognite, ma non sarebbe una verifica in quanto per ogni set di dati misurati posso trovare una soluzione al sistema. Aggiungiamo allora anche un altro vincolo, ottenibile confrontando gli accoppiamenti con i leptoni: Usando questo ulteriore vincolo calcoliamo le masse previste dei bosoni:
17 Modello di Higgs SU(2)xU(1) e verifica sperimentale 17 e dai risultati sperimentali risulta: L accordo dei dati migliora andando a fare il calcolo delle masse dei bosoni a 2 loop*: Purtroppo non conosciamo né né (e nemmeno se tale particella effettivamente esiste!), altrimenti potremmo andare a fare anche un confronto ulteriore sul valore della sua massa. I risultati sperimentali finora ottenuti sono comunque in buon accorto con tale modello teorico, infatti le correzioni dalle sezioni d urto dovute ai diagrammi contenenti il bosone di Higgs migliorano l accordo fra previsioni teoriche e dati sperimentali se attribuiamo a tale bosone una massa compresa fra e. Per concludere riporto alcuni dati sul range delle possibili masse del bosone di Higgs: da argomenti teorici (Lee et al 1977) deve valere mentre un risultato del assicura un limite inferiore, a livello di confidenza del, pari a *Poiché a questo livello la massa dei bosoni e dipende dalla massa del bosone di Higgs, riporto dati per il caso
18 18 Modello di Higgs SU(2)xU(1) e verifica sperimentale Bibliografia I.J.R. Aitchison, A.J.G. Hey, Gauge Theories in Particle Physics Vol 2: QCD and the Electroweak Theory, 1989 Taylor and Francis Group I.J.R. Aitchison, A.J.G. Hey, Gauge Theories in Particle Physics Vol 2: QCD and the Electroweak Theory, 2004 Taylor and Francis Group Enore Guadagnini, Fisica Teorica: Lezioni per il corso di Dottorato in Fisica, Cap. 13, 1999 ETS F.Mandl, G. Shaw, Quantum Field Theory, 1993, John Wiley & Sons Georg Weiglein, Precise Predictions for the W-Boson Mass, 1997 Grafici realizzati con il software Wolfram Mathematica 7
ROTTURA SPONTANEA DI SIMMETRIA: DAL FERROMAGNETISMO ALLA FISICA DELLE PARTICELLE
 ROTTURA SPONTANEA DI SIMMETRIA: DAL FERROMAGNETISMO ALLA FISICA DELLE PARTICELLE 2 Indice Indice Indice... 2 Introduzione... 3 Bosoni massivi in fisica della particelle... 3 Correnti schermanti: la massa
ROTTURA SPONTANEA DI SIMMETRIA: DAL FERROMAGNETISMO ALLA FISICA DELLE PARTICELLE 2 Indice Indice Indice... 2 Introduzione... 3 Bosoni massivi in fisica della particelle... 3 Correnti schermanti: la massa
La struttura elettronica degli atomi
 1 In unità atomiche: a 0 me 0,59A unità di lunghezza e H 7, ev a H=Hartree unità di energia L energia dell atomo di idrogeno nello stato fondamentale espresso in unità atomiche è: 4 0 me 1 e 1 E H 13,
1 In unità atomiche: a 0 me 0,59A unità di lunghezza e H 7, ev a H=Hartree unità di energia L energia dell atomo di idrogeno nello stato fondamentale espresso in unità atomiche è: 4 0 me 1 e 1 E H 13,
Misura del momento magnetico dell elettrone
 FACOLTÀ Università degli Studi di Roma Tre DI SCIENZE MATEMATICHE, FISICHE E NATURALI Corso di Laurea in Fisica Misura del momento magnetico dell elettrone Candidato: Andrea Sciandra Matricola 4480 Relatore:
FACOLTÀ Università degli Studi di Roma Tre DI SCIENZE MATEMATICHE, FISICHE E NATURALI Corso di Laurea in Fisica Misura del momento magnetico dell elettrone Candidato: Andrea Sciandra Matricola 4480 Relatore:
Bosone. Particella a spin intero, che obbedisce alla statistica di Bose-Einstein, che è opposta a quella di Fermi-Dirac.
 Particelle ed Interazioni fondamentali Fermione. Particella a spin semintero, che obbedisce alla statistica di Fermi-Dirac, cioè due fermioni con gli stessi numeri quantici non possono coesistere in uno
Particelle ed Interazioni fondamentali Fermione. Particella a spin semintero, che obbedisce alla statistica di Fermi-Dirac, cioè due fermioni con gli stessi numeri quantici non possono coesistere in uno
Consideriamo un sistema composto da due particelle identiche. Due particelle sono identiche se hanno le stesse proprietà intrinseche (massa, carica,
 Consideriamo un sistema composto da due particelle identiche. Due particelle sono identiche se hanno le stesse proprietà intrinseche (massa, carica, spin, ). Esempi: due elettroni, due protoni, due neutroni,
Consideriamo un sistema composto da due particelle identiche. Due particelle sono identiche se hanno le stesse proprietà intrinseche (massa, carica, spin, ). Esempi: due elettroni, due protoni, due neutroni,
L ATOMO SECONDO LA MECCANICA ONDULATORIA IL DUALISMO ONDA-PARTICELLA. (Plank Einstein)
 L ATOMO SECONDO LA MECCANICA ONDULATORIA IL DUALISMO ONDA-PARTICELLA POSTULATO DI DE BROGLIÈ Se alla luce, che è un fenomeno ondulatorio, sono associate anche le caratteristiche corpuscolari della materia
L ATOMO SECONDO LA MECCANICA ONDULATORIA IL DUALISMO ONDA-PARTICELLA POSTULATO DI DE BROGLIÈ Se alla luce, che è un fenomeno ondulatorio, sono associate anche le caratteristiche corpuscolari della materia
Introduzione: Concetti fondamentali della Fisica delle Particelle e Modello Standard
 Corso di Astroparticelle - Univ. di Roma Tor Vergata Anno Accademico 2010-2011 Introduzione: Concetti fondamentali della Fisica delle Particelle e Modello Standard Dott. Carlotta Pittori Lezione I Richiami.
Corso di Astroparticelle - Univ. di Roma Tor Vergata Anno Accademico 2010-2011 Introduzione: Concetti fondamentali della Fisica delle Particelle e Modello Standard Dott. Carlotta Pittori Lezione I Richiami.
Metodi per la risoluzione di sistemi lineari
 Metodi per la risoluzione di sistemi lineari Sistemi di equazioni lineari. Rango di matrici Come è noto (vedi [] sez.0.8), ad ogni matrice quadrata A è associato un numero reale det(a) detto determinante
Metodi per la risoluzione di sistemi lineari Sistemi di equazioni lineari. Rango di matrici Come è noto (vedi [] sez.0.8), ad ogni matrice quadrata A è associato un numero reale det(a) detto determinante
Esercitazioni di Meccanica Quantistica I
 Esercitazioni di Meccanica Quantistica I Sistema a due stati Consideriamo come esempio di sistema a due stati l ammoniaca. La struttura del composto è tetraedrico : alla sommità di una piramide con base
Esercitazioni di Meccanica Quantistica I Sistema a due stati Consideriamo come esempio di sistema a due stati l ammoniaca. La struttura del composto è tetraedrico : alla sommità di una piramide con base
SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI
 SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI Appunti presi dalle lezioni del prof. Nedo Checcaglini Liceo Scientifico di Castiglion Fiorentino (Classe 4B) January 17, 005 1 SISTEMI LINEARI Se a ik, b i R,
SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI Appunti presi dalle lezioni del prof. Nedo Checcaglini Liceo Scientifico di Castiglion Fiorentino (Classe 4B) January 17, 005 1 SISTEMI LINEARI Se a ik, b i R,
I POSTULATI DELLA MECCANICA QUANTISTICA
 68 I POSTULATI DELLA MECCANICA QUANTISTICA Si intende per postulato una assunzione da accettarsi a priori e non contraddetta dall esperienza. I postulati trovano la loro unica giustificazione nella loro
68 I POSTULATI DELLA MECCANICA QUANTISTICA Si intende per postulato una assunzione da accettarsi a priori e non contraddetta dall esperienza. I postulati trovano la loro unica giustificazione nella loro
Secondo parziale di Matematica per l Economia (esempio)
 Corso di Laurea in Economia e Management Secondo parziale di Matematica per l Economia (esempio) lettere E-Z, a.a. 206 207 prof. Gianluca Amato Regole generali Si svolga il primo esercizio e, a scelta
Corso di Laurea in Economia e Management Secondo parziale di Matematica per l Economia (esempio) lettere E-Z, a.a. 206 207 prof. Gianluca Amato Regole generali Si svolga il primo esercizio e, a scelta
Funzioni implicite - Esercizi svolti
 Funzioni implicite - Esercizi svolti Esercizio. È data la funzione di due variabili F (x, y) = y(e y + x) log x. Verificare che esiste un intorno I in R del punto di ascissa x 0 = sul quale è definita
Funzioni implicite - Esercizi svolti Esercizio. È data la funzione di due variabili F (x, y) = y(e y + x) log x. Verificare che esiste un intorno I in R del punto di ascissa x 0 = sul quale è definita
Dinamica: Forze e Moto, Leggi di Newton
 Dinamica: Forze e Moto, Leggi di Newton La Dinamica studia il moto dei corpi in relazione il moto con le sue cause: perché e come gli oggetti si muovono. La causa del moto è individuata nella presenza
Dinamica: Forze e Moto, Leggi di Newton La Dinamica studia il moto dei corpi in relazione il moto con le sue cause: perché e come gli oggetti si muovono. La causa del moto è individuata nella presenza
1 Polinomio di Taylor 1. 2 Formula di Taylor 2. 3 Alcuni sviluppi notevoli 2. 4 Uso della formula di Taylor nel calcolo dei limiti 4
 1 POLINOMIO DI TAYLOR 1 Formula di Taylor Indice 1 Polinomio di Taylor 1 Formula di Taylor 3 Alcuni sviluppi notevoli 4 Uso della formula di Taylor nel calcolo dei iti 4 5 Soluzioni degli esercizi 6 La
1 POLINOMIO DI TAYLOR 1 Formula di Taylor Indice 1 Polinomio di Taylor 1 Formula di Taylor 3 Alcuni sviluppi notevoli 4 Uso della formula di Taylor nel calcolo dei iti 4 5 Soluzioni degli esercizi 6 La
SISTEMI LINEARI. x y + 2t = 0 2x + y + z t = 0 x z t = 0 ; S 3 : ; S 5x 2y z = 1 4x 7y = 3
 SISTEMI LINEARI. Esercizi Esercizio. Verificare se (,, ) è soluzione del sistema x y + z = x + y z = 3. Trovare poi tutte le soluzioni del sistema. Esercizio. Scrivere un sistema lineare di 3 equazioni
SISTEMI LINEARI. Esercizi Esercizio. Verificare se (,, ) è soluzione del sistema x y + z = x + y z = 3. Trovare poi tutte le soluzioni del sistema. Esercizio. Scrivere un sistema lineare di 3 equazioni
QUANTITA DI MOTO Corso di Fisica per Farmacia, Facoltà di Farmacia, Università G. D Annunzio, Cosimo Del Gratta 2006
 QUANTITA DI MOTO DEFINIZIONE(1) m v Si chiama quantità di moto di un punto materiale il prodotto della sua massa per la sua velocità p = m v La quantità di moto è una grandezza vettoriale La dimensione
QUANTITA DI MOTO DEFINIZIONE(1) m v Si chiama quantità di moto di un punto materiale il prodotto della sua massa per la sua velocità p = m v La quantità di moto è una grandezza vettoriale La dimensione
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
ax 1 + bx 2 + c = 0, r : 2x 1 3x 2 + 1 = 0.
 . Rette in R ; circonferenze. In questo paragrafo studiamo le rette e le circonferenze in R. Ci sono due modi per descrivere una retta in R : mediante una equazione cartesiana oppure mediante una equazione
. Rette in R ; circonferenze. In questo paragrafo studiamo le rette e le circonferenze in R. Ci sono due modi per descrivere una retta in R : mediante una equazione cartesiana oppure mediante una equazione
Massimi e minimi vincolati
 Massimi e minimi vincolati Data una funzione G C 1 (D), dove D è un aperto di R 2, sappiamo bene dove andare a cercare gli eventuali punti di massimo e minimo relativi. Una condizione necessaria affinché
Massimi e minimi vincolati Data una funzione G C 1 (D), dove D è un aperto di R 2, sappiamo bene dove andare a cercare gli eventuali punti di massimo e minimo relativi. Una condizione necessaria affinché
Test 1 - Teoria dei Campi 2010
 Test - Teoria dei Campi 200 Discutere il path-integral della QCD in gauge assiale (nell Euclideo) n µ A a µ = 0, a =,..., 8, () dove n µ e un vettore assegnato. Derivare: - regole di Feynman; - identitaà
Test - Teoria dei Campi 200 Discutere il path-integral della QCD in gauge assiale (nell Euclideo) n µ A a µ = 0, a =,..., 8, () dove n µ e un vettore assegnato. Derivare: - regole di Feynman; - identitaà
Il Metodo Scientifico
 Unita Naturali Il Metodo Scientifico La Fisica si occupa di descrivere ed interpretare i fenomeni naturali usando il metodo scientifico. Passi del metodo scientifico: Schematizzazione: modello semplificato
Unita Naturali Il Metodo Scientifico La Fisica si occupa di descrivere ed interpretare i fenomeni naturali usando il metodo scientifico. Passi del metodo scientifico: Schematizzazione: modello semplificato
Le molecole ed il legame chimico
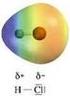 LA MOLECOLA DI IDROGENO X r A2 e 2 r A1 r 12 r B2 e 1 r B1 È il primo caso di molecola bielettronica da noi incontrato ed è la base per lo studio di ogni altra molecola. A R AB B Z Y Se si applica l approssimazione
LA MOLECOLA DI IDROGENO X r A2 e 2 r A1 r 12 r B2 e 1 r B1 È il primo caso di molecola bielettronica da noi incontrato ed è la base per lo studio di ogni altra molecola. A R AB B Z Y Se si applica l approssimazione
Elettromagnetismo Formulazione differenziale
 Elettromagnetismo Formulazione differenziale 1. Legge di Faraday 2. Estensione della legge di Ampere 3. Equazioni di Maxwell 4. Onde elettromagnetiche VI - 0 Legge di Faraday Campo elettrico Campo di induzione
Elettromagnetismo Formulazione differenziale 1. Legge di Faraday 2. Estensione della legge di Ampere 3. Equazioni di Maxwell 4. Onde elettromagnetiche VI - 0 Legge di Faraday Campo elettrico Campo di induzione
15/04/2014. Serway, Jewett Principi di Fisica IV Ed. Capitolo 8. Generalizziamo, considerando due particelle interagenti.
 Serway, Jewett Principi di Fisica IV Ed. Capitolo 8 Esempio arciere su una superficie ghiacciata che scocca la freccia: l arciere (60 kg) esercita una forza sulla freccia 0.5 kg (che parte in avanti con
Serway, Jewett Principi di Fisica IV Ed. Capitolo 8 Esempio arciere su una superficie ghiacciata che scocca la freccia: l arciere (60 kg) esercita una forza sulla freccia 0.5 kg (che parte in avanti con
Esercizi sui sistemi di equazioni lineari.
 Esercizi sui sistemi di equazioni lineari Risolvere il sistema di equazioni lineari x y + z 6 x + y z x y z Si tratta di un sistema di tre equazioni lineari nelle tre incognite x, y e z Poichè m n, la
Esercizi sui sistemi di equazioni lineari Risolvere il sistema di equazioni lineari x y + z 6 x + y z x y z Si tratta di un sistema di tre equazioni lineari nelle tre incognite x, y e z Poichè m n, la
Introduzione al Metodo agli Elementi Finiti (FEM) (x, y) Γ Tale formulazione viene detta Formulazione forte del problema.
 Introduzione al Metodo agli Elementi Finiti (FEM) Consideriamo come problema test l equazione di Poisson 2 u x 2 + 2 u = f(x, y) u = f y2 definita su un dominio Ω R 2 avente come frontiera la curva Γ,
Introduzione al Metodo agli Elementi Finiti (FEM) Consideriamo come problema test l equazione di Poisson 2 u x 2 + 2 u = f(x, y) u = f y2 definita su un dominio Ω R 2 avente come frontiera la curva Γ,
Esercizi per Geometria II Geometria euclidea e proiettiva
 Esercizi per Geometria II Geometria euclidea e proiettiva Filippo F. Favale 8 aprile 014 Esercizio 1 Si consideri E dotato di un riferimento cartesiano ortonormale di coordinate (x, y) e origine O. Si
Esercizi per Geometria II Geometria euclidea e proiettiva Filippo F. Favale 8 aprile 014 Esercizio 1 Si consideri E dotato di un riferimento cartesiano ortonormale di coordinate (x, y) e origine O. Si
LE EQUAZIONI DI SECONDO GRADO
 LE EQUAZIONI DI SECONDO GRADO Definizione: un equazione è di secondo grado se, dopo aver applicato i principi di equivalenza, si può scrivere nella forma, detta normale: ax + bx + c 0!!!!!con!a 0 Le lettere
LE EQUAZIONI DI SECONDO GRADO Definizione: un equazione è di secondo grado se, dopo aver applicato i principi di equivalenza, si può scrivere nella forma, detta normale: ax + bx + c 0!!!!!con!a 0 Le lettere
Particelle Subatomiche
 GLI ATOMI Particelle Subatomiche ELEMENTI I diversi atomi sono caratterizzati da un diverso numero di protoni e neutroni; il numero di elettroni è sempre uguale al numero dei protoni (negli atomi neutri)
GLI ATOMI Particelle Subatomiche ELEMENTI I diversi atomi sono caratterizzati da un diverso numero di protoni e neutroni; il numero di elettroni è sempre uguale al numero dei protoni (negli atomi neutri)
Problemi per il corso di teoria delle interazioni fondamentali giugno 2005
 Problemi per il corso di teoria delle interazioni fondamentali giugno 2005 Primo Modulo 1. Urto Bhabha Determinare la sezione d urto differenziale per l urto e + e e + e, nel limite di alta energia in
Problemi per il corso di teoria delle interazioni fondamentali giugno 2005 Primo Modulo 1. Urto Bhabha Determinare la sezione d urto differenziale per l urto e + e e + e, nel limite di alta energia in
Sistemi lineari. Lorenzo Pareschi. Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara
 Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
Esercitazione 6 - Soluzione
 Anno Accademico 28-29 Corso di Algebra Lineare e Calcolo Numerico per Ingegneria Meccanica Esercitazione 6 - Soluzione Immagine, nucleo. Teorema di Rouché-Capelli. Esercizio Sia L : R 3 R 3 l applicazione
Anno Accademico 28-29 Corso di Algebra Lineare e Calcolo Numerico per Ingegneria Meccanica Esercitazione 6 - Soluzione Immagine, nucleo. Teorema di Rouché-Capelli. Esercizio Sia L : R 3 R 3 l applicazione
Elementi di Teoria dei Sistemi. Definizione di sistema dinamico. Cosa significa Dinamico? Sistema dinamico a tempo continuo
 Parte 2, 1 Parte 2, 2 Elementi di Teoria dei Sistemi Definizione di sistema dinamico Parte 2, 3 Sistema dinamico a tempo continuo Cosa significa Dinamico? Parte 2, 4? e` univocamente determinata? Ingresso
Parte 2, 1 Parte 2, 2 Elementi di Teoria dei Sistemi Definizione di sistema dinamico Parte 2, 3 Sistema dinamico a tempo continuo Cosa significa Dinamico? Parte 2, 4? e` univocamente determinata? Ingresso
I. Foglio di esercizi su vettori linearmente dipendenti e linearmente indipendenti. , v 2 = α v 1 + β v 2 + γ v 3. α v 1 + β v 2 + γ v 3 = 0. + γ.
 ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
LUISS Laurea specialistica in Economia e Finanza Anno Accademico 2010/2011
 LUISS Laurea specialistica in Economia e Finanza Anno Accademico 1/11 Corso di Metodi Matematici per la Finanza Prof. Fausto Gozzi, Dr. Davide Vergni Soluzioni esercizi 4,5,6 esame scritto del 13/9/11
LUISS Laurea specialistica in Economia e Finanza Anno Accademico 1/11 Corso di Metodi Matematici per la Finanza Prof. Fausto Gozzi, Dr. Davide Vergni Soluzioni esercizi 4,5,6 esame scritto del 13/9/11
Dipendenza e indipendenza lineare (senza il concetto di rango)
 CAPITOLO 5 Dipendenza e indipendenza lineare (senza il concetto di rango) Esercizio 5.1. Scrivere un vettore w R 3 linearmente dipendente dal vettore v ( 1, 9, 0). Esercizio 5.2. Stabilire se i vettori
CAPITOLO 5 Dipendenza e indipendenza lineare (senza il concetto di rango) Esercizio 5.1. Scrivere un vettore w R 3 linearmente dipendente dal vettore v ( 1, 9, 0). Esercizio 5.2. Stabilire se i vettori
Il Modello Standard delle particelle
 Il Modello Standard delle particelle Vittorio Del Duca INFN LNF Stages Estivi 12 giugno 2012 Elementi La materia è fatta di elementi con definite proprietà chimiche Atomi Ciascun elemento ha come mattone
Il Modello Standard delle particelle Vittorio Del Duca INFN LNF Stages Estivi 12 giugno 2012 Elementi La materia è fatta di elementi con definite proprietà chimiche Atomi Ciascun elemento ha come mattone
I Neutrini e l'asimmetria tra la materia e l'antimateria nell'universo
 I Neutrini e l'asimmetria tra la materia e l'antimateria nell'universo Journal Club 20 marzo 2015 Serena Palazzo Il Modello Standard Teoria fisica che descrive le componenti prime della materia e le loro
I Neutrini e l'asimmetria tra la materia e l'antimateria nell'universo Journal Club 20 marzo 2015 Serena Palazzo Il Modello Standard Teoria fisica che descrive le componenti prime della materia e le loro
Struttura Elettronica degli Atomi Meccanica quantistica
 Prof. A. Martinelli Struttura Elettronica degli Atomi Meccanica quantistica Dipartimento di Farmacia 1 Il comportamento ondulatorio della materia 2 1 Il comportamento ondulatorio della materia La diffrazione
Prof. A. Martinelli Struttura Elettronica degli Atomi Meccanica quantistica Dipartimento di Farmacia 1 Il comportamento ondulatorio della materia 2 1 Il comportamento ondulatorio della materia La diffrazione
Lezione n. 19. L equazione. di Schrodinger L atomo. di idrogeno Orbitali atomici. 02/03/2008 Antonino Polimeno 1
 Chimica Fisica - Chimica e Tecnologia Farmaceutiche Lezione n. 19 L equazione di Schrodinger L atomo di idrogeno Orbitali atomici 02/03/2008 Antonino Polimeno 1 Dai modelli primitivi alla meccanica quantistica
Chimica Fisica - Chimica e Tecnologia Farmaceutiche Lezione n. 19 L equazione di Schrodinger L atomo di idrogeno Orbitali atomici 02/03/2008 Antonino Polimeno 1 Dai modelli primitivi alla meccanica quantistica
UNITÀ DIDATTICA 5 LA RETTA
 UNITÀ DIDATTICA 5 LA RETTA 5.1 - La retta Equazione generica della retta Dalle considerazioni emerse nel precedente capitolo abbiamo compreso come una funzione possa essere rappresentata da un insieme
UNITÀ DIDATTICA 5 LA RETTA 5.1 - La retta Equazione generica della retta Dalle considerazioni emerse nel precedente capitolo abbiamo compreso come una funzione possa essere rappresentata da un insieme
8.1 Problema della diffusione in meccanica quantistica
 8.1 Problema della diffusione in meccanica quantistica Prima di procedere oltre nello studio dell interazione puntuale, in questo paragrafo vogliamo dare un breve cenno alle nozioni di base della teoria
8.1 Problema della diffusione in meccanica quantistica Prima di procedere oltre nello studio dell interazione puntuale, in questo paragrafo vogliamo dare un breve cenno alle nozioni di base della teoria
Struttura del sistema periodico Stato fondamentale degli elementi
 Struttura del sistema periodico Stato fondamentale degli elementi Singolo elettrone: 1)Numero quantico principale n 2)Numero quantico del momento angolare orbitale l = 0, 1,, n-1 3)Numero quantico magnetico
Struttura del sistema periodico Stato fondamentale degli elementi Singolo elettrone: 1)Numero quantico principale n 2)Numero quantico del momento angolare orbitale l = 0, 1,, n-1 3)Numero quantico magnetico
Lezioni di Meccanica Quantistica
 Luigi E. Picasso Lezioni di Meccanica Quantistica seconda edizione Edizioni ETS www.edizioniets.com Copyright 2015 EDIZIONI ETS Piazza Carrara, 16-19, I-56126 Pisa info@edizioniets.com www.edizioniets.com
Luigi E. Picasso Lezioni di Meccanica Quantistica seconda edizione Edizioni ETS www.edizioniets.com Copyright 2015 EDIZIONI ETS Piazza Carrara, 16-19, I-56126 Pisa info@edizioniets.com www.edizioniets.com
2x 5y +4z = 3 x 2y + z =5 x 4y +6z = A =
 Esercizio 1. Risolvere il sistema lineare 2x 5y +4z = x 2y + z =5 x 4y +6z =10 (1) Soluz. La matrice dei coefficienti è 1 4 6, calcoliamone il rango. Il determinante di A è (applico la regola di Sarrus):
Esercizio 1. Risolvere il sistema lineare 2x 5y +4z = x 2y + z =5 x 4y +6z =10 (1) Soluz. La matrice dei coefficienti è 1 4 6, calcoliamone il rango. Il determinante di A è (applico la regola di Sarrus):
Esercizi svolti. risolvere, se possibile, l equazione xa + B = O, essendo x un incognita reale
 Esercizi svolti 1. Matrici e operazioni fra matrici 1.1 Date le matrici 1 2 1 6 A = B = 5 2 9 15 6 risolvere, se possibile, l equazione xa + B = O, essendo x un incognita reale Osservazione iniziale: qualunque
Esercizi svolti 1. Matrici e operazioni fra matrici 1.1 Date le matrici 1 2 1 6 A = B = 5 2 9 15 6 risolvere, se possibile, l equazione xa + B = O, essendo x un incognita reale Osservazione iniziale: qualunque
Forme differenziali lineari e loro integrazione
 Forme differenziali lineari e loro integrazione Integrazione di una forma differenziale in due variabili Siano L(, ) e ( ) consideriamo l espressione M, due funzioni definite e continue in un insieme connesso
Forme differenziali lineari e loro integrazione Integrazione di una forma differenziale in due variabili Siano L(, ) e ( ) consideriamo l espressione M, due funzioni definite e continue in un insieme connesso
Il teorema di Rouché-Capelli
 Luciano Battaia Questi appunti (1), ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia, campus di Treviso, contengono un
Luciano Battaia Questi appunti (1), ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia, campus di Treviso, contengono un
La lunghezza dei vettori e legata alle operazioni sui vettori nel modo seguente: Consideriamo due vettori v, w e il vettore v + w loro somma.
 Matematica II, 20.2.. Lunghezza di un vettore nel piano Consideriamo il piano vettoriale geometrico P O. Scelto un segmento come unita, possiamo parlare di lunghezza di un vettore v P O rispetto a tale
Matematica II, 20.2.. Lunghezza di un vettore nel piano Consideriamo il piano vettoriale geometrico P O. Scelto un segmento come unita, possiamo parlare di lunghezza di un vettore v P O rispetto a tale
Enrico Silva - diritti riservati - Non è permessa, fra l altro, l inclusione anche parziale in altre opere senza il consenso scritto dell autore
 Particelle della presente identiche. opera. Principio di Pauli. 1 Particelle identiche: sommario Finora: proprietà di particella singola. Volendo ottenere il comportamento di più particelle, è necessario
Particelle della presente identiche. opera. Principio di Pauli. 1 Particelle identiche: sommario Finora: proprietà di particella singola. Volendo ottenere il comportamento di più particelle, è necessario
Interferenza di elettroni e! Principio di Indeterminazione
 Interferenza di elettroni e! Principio di Indeterminazione Paolo Pendenza Corso PAS, 10 luglio 2014 Anche nelle scienze non si possono scoprire nuove terre se non si è pronti a lasciarsi indietro il porto
Interferenza di elettroni e! Principio di Indeterminazione Paolo Pendenza Corso PAS, 10 luglio 2014 Anche nelle scienze non si possono scoprire nuove terre se non si è pronti a lasciarsi indietro il porto
Si consideri il sistema a coefficienti reali di m equazioni lineari in n incognite
 3 Sistemi lineari 3 Generalità Si consideri il sistema a coefficienti reali di m equazioni lineari in n incognite ovvero, in forma matriciale, a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x
3 Sistemi lineari 3 Generalità Si consideri il sistema a coefficienti reali di m equazioni lineari in n incognite ovvero, in forma matriciale, a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x
Lezione 1: Introduzione alle grandezze magnetiche
 Lezione 1: Introduzione alle grandezze magnetiche 1 Campi Magnetici Il campo magnetico è un campo vettoriale: associa, cioè, ad ogni punto nello spazio un vettore. Un campo magnetico si puo misurare per
Lezione 1: Introduzione alle grandezze magnetiche 1 Campi Magnetici Il campo magnetico è un campo vettoriale: associa, cioè, ad ogni punto nello spazio un vettore. Un campo magnetico si puo misurare per
Note sull implementazione in virgola fissa di filtri numerici
 Note sull implementazione in virgola fissa di filtri numerici 4 settembre 2006 1 Introduction Nonostante al giorno d oggi i processori con aritmetica in virgola mobili siano molto comuni, esistono contesti
Note sull implementazione in virgola fissa di filtri numerici 4 settembre 2006 1 Introduction Nonostante al giorno d oggi i processori con aritmetica in virgola mobili siano molto comuni, esistono contesti
L atomo di idrogeno (1) H T = p2 1 2m 1. + p2 2 2m 2. + V ( r 1 r 2 ) (2) Definiamo le nuove variabili: 1. La massa totale M M = m 1 + m 2 (3)
 L atomo di idrogeno Il problema dell atomo di idrogeno é un problema esattamente risolubili ed i suoi risultati possono essere estesi agli atomi idrogenoidi, in cui solo c é solo un elettrone sottoposto
L atomo di idrogeno Il problema dell atomo di idrogeno é un problema esattamente risolubili ed i suoi risultati possono essere estesi agli atomi idrogenoidi, in cui solo c é solo un elettrone sottoposto
Indice. Elettrostatica in presenza di dielettrici Costante dielettrica Interpretazione microscopica 119. capitolo. capitolo.
 Indice Elettrostatica nel vuoto. Campo elettrico e potenziale 1 1. Azioni elettriche 1 2. Carica elettrica e legge di Coulomb 5 3. Campo elettrico 8 4. Campo elettrostatico generato da sistemi di cariche
Indice Elettrostatica nel vuoto. Campo elettrico e potenziale 1 1. Azioni elettriche 1 2. Carica elettrica e legge di Coulomb 5 3. Campo elettrico 8 4. Campo elettrostatico generato da sistemi di cariche
La riduzione a gradini e i sistemi lineari (senza il concetto di rango)
 CAPITOLO 4 La riduzione a gradini e i sistemi lineari (senza il concetto di rango) Esercizio 4.1. Risolvere il seguente sistema non omogeneo: 2x+4y +4z = 4 x z = 1 x+3y +4z = 3 Esercizio 4.2. Risolvere
CAPITOLO 4 La riduzione a gradini e i sistemi lineari (senza il concetto di rango) Esercizio 4.1. Risolvere il seguente sistema non omogeneo: 2x+4y +4z = 4 x z = 1 x+3y +4z = 3 Esercizio 4.2. Risolvere
LEZIONE 9. k, tenendo conto delle formule che permettono di calcolare il prodotto scalare ed il prodotto vettoriale, otteniamo
 LEZIONE 9 9.1. Prodotto misto. Siano dati i tre vettori geometrici u, v, w V 3 (O) definiamo prodotto misto di u, v e w il numero u, v w. Fissiamo un sistema di riferimento O ı j k in S 3. Se u = u x ı
LEZIONE 9 9.1. Prodotto misto. Siano dati i tre vettori geometrici u, v, w V 3 (O) definiamo prodotto misto di u, v e w il numero u, v w. Fissiamo un sistema di riferimento O ı j k in S 3. Se u = u x ı
Sulla nascita di questo libro. Introduzione 1
 Indice Sulla nascita di questo libro V Introduzione 1 1 Luce e materia 7 Che cos è veramente la luce? 7 Ma qui che cosa oscilla? 9 Che cosa sono la frequenza e la lunghezza d onda della luce? 11 Che cos
Indice Sulla nascita di questo libro V Introduzione 1 1 Luce e materia 7 Che cos è veramente la luce? 7 Ma qui che cosa oscilla? 9 Che cosa sono la frequenza e la lunghezza d onda della luce? 11 Che cos
Pagine di Algebra lineare. di premessa al testo Pagine di Geometria di Sara Dragotti. Parte terza: SISTEMI LINEARI
 Pagine di Algebra lineare di premessa al testo Pagine di Geometria di Sara Dragotti Parte terza: SISTEMI LINEARI 1. Definizioni Dato un campo K ed m 1 polinomi su K in n indeterminate di grado non superiore
Pagine di Algebra lineare di premessa al testo Pagine di Geometria di Sara Dragotti Parte terza: SISTEMI LINEARI 1. Definizioni Dato un campo K ed m 1 polinomi su K in n indeterminate di grado non superiore
Meccanica quantistica (5)
 Meccanica quantistica (5) 0/7/14 1-MQ-5.doc 0 Oscillatore armonico Se una massa è sottoposta ad una forza di richiamo proporzionale allo spostamento da un posizione di equilibrio F = kx il potenziale (
Meccanica quantistica (5) 0/7/14 1-MQ-5.doc 0 Oscillatore armonico Se una massa è sottoposta ad una forza di richiamo proporzionale allo spostamento da un posizione di equilibrio F = kx il potenziale (
SISTEMI LINEARI MATRICI E SISTEMI 1
 MATRICI E SISTEMI SISTEMI LINEARI Sistemi lineari e forma matriciale (definizioni e risoluzione). Teorema di Rouché-Capelli. Sistemi lineari parametrici. Esercizio Risolvere il sistema omogeneo la cui
MATRICI E SISTEMI SISTEMI LINEARI Sistemi lineari e forma matriciale (definizioni e risoluzione). Teorema di Rouché-Capelli. Sistemi lineari parametrici. Esercizio Risolvere il sistema omogeneo la cui
Appunti su Indipendenza Lineare di Vettori
 Appunti su Indipendenza Lineare di Vettori Claudia Fassino a.a. Queste dispense, relative a una parte del corso di Matematica Computazionale (Laurea in Informatica), rappresentano solo un aiuto per lo
Appunti su Indipendenza Lineare di Vettori Claudia Fassino a.a. Queste dispense, relative a una parte del corso di Matematica Computazionale (Laurea in Informatica), rappresentano solo un aiuto per lo
Modello Standard e oltre. D. Babusci MasterClass 2007
 Modello Standard e oltre D. Babusci MasterClass 2007 Fisica delle Particelle Elementari (FdP) Si interessa del comportamento fisico dei costituenti fondamentali del mondo, i.e. di oggetti al contempo molto
Modello Standard e oltre D. Babusci MasterClass 2007 Fisica delle Particelle Elementari (FdP) Si interessa del comportamento fisico dei costituenti fondamentali del mondo, i.e. di oggetti al contempo molto
Struttura fine dei livelli dell idrogeno
 Struttura fine dei livelli dell idrogeno. Introduzione Consideriamo un atomo idrogenoide di massa m N e carica atomica Z. Dall equazione di Schrödinger si ottengono per gli stati legati i seguenti autovalori
Struttura fine dei livelli dell idrogeno. Introduzione Consideriamo un atomo idrogenoide di massa m N e carica atomica Z. Dall equazione di Schrödinger si ottengono per gli stati legati i seguenti autovalori
Sulla superficie interna del guscio sferico (induzione totale) si avrà la carica indotta q distribuita uniformemente, quindi
 1) Una sfera conduttrice di raggio r = 5 cm possiede una carica q = 10 8 C ed è posta nel centro di un guscio sferico conduttore, di raggio interno R = 20 cm, posto in contatto con la terra (a massa).
1) Una sfera conduttrice di raggio r = 5 cm possiede una carica q = 10 8 C ed è posta nel centro di un guscio sferico conduttore, di raggio interno R = 20 cm, posto in contatto con la terra (a massa).
TEORIA DEI SISTEMI SISTEMI LINEARI
 TEORIA DEI SISTEMI Laurea Specialistica in Ingegneria Meccatronica Laurea Specialistica in Ingegneria Gestionale Indirizzo Gestione Industriale TEORIA DEI SISTEMI SISTEMI LINEARI Ing. Cristian Secchi Tel.
TEORIA DEI SISTEMI Laurea Specialistica in Ingegneria Meccatronica Laurea Specialistica in Ingegneria Gestionale Indirizzo Gestione Industriale TEORIA DEI SISTEMI SISTEMI LINEARI Ing. Cristian Secchi Tel.
Grandezze e Misure 1
 Grandezze e Misure 1 Grandezze e Misure Introduzione Il Metodo Sperimentale Unità di Misura Grandezze Fondamentali e Derivate Massa e Densità Misure dirette e indirette Strumenti di misura Errori nelle
Grandezze e Misure 1 Grandezze e Misure Introduzione Il Metodo Sperimentale Unità di Misura Grandezze Fondamentali e Derivate Massa e Densità Misure dirette e indirette Strumenti di misura Errori nelle
Appunti ed esercizi sulle coniche
 1 LA CIRCONFERENZA 1 Appunti ed esercizi sulle coniche Versione del 1 Marzo 011 1 La circonferenza Nel piano R, fissati un punto O = (a, b) e un numero r > 0, la circonferenza (o cerchio) C di centro O
1 LA CIRCONFERENZA 1 Appunti ed esercizi sulle coniche Versione del 1 Marzo 011 1 La circonferenza Nel piano R, fissati un punto O = (a, b) e un numero r > 0, la circonferenza (o cerchio) C di centro O
Esercitazione 1. Invece, essendo il mezzo omogeneo, il vettore sarà espresso come segue
 1.1 Una sfera conduttrice di raggio R 1 = 10 cm ha una carica Q = 10-6 C ed è circondata da uno strato sferico di dielettrico di raggio (esterno) R 2 = 20 cm e costante dielettrica relativa. Determinare
1.1 Una sfera conduttrice di raggio R 1 = 10 cm ha una carica Q = 10-6 C ed è circondata da uno strato sferico di dielettrico di raggio (esterno) R 2 = 20 cm e costante dielettrica relativa. Determinare
8. Completamento di uno spazio di misura.
 8. Completamento di uno spazio di misura. 8.1. Spazi di misura. Spazi di misura completi. Definizione 8.1.1. (Spazio misurabile). Si chiama spazio misurabile ogni coppia ordinata (Ω, A), dove Ω è un insieme
8. Completamento di uno spazio di misura. 8.1. Spazi di misura. Spazi di misura completi. Definizione 8.1.1. (Spazio misurabile). Si chiama spazio misurabile ogni coppia ordinata (Ω, A), dove Ω è un insieme
24.1. Ritorno al gruppo delle trasformazioni di Möbius Lo spazio proiettivo degli stati di un qubit.
 4.1. Ritorno al gruppo delle trasformazioni di Möbius. 4.1.1. Lo spazio proiettivo degli stati di un qubit. Il qubit è il sistema quantistico più semplice che esista: un sistema i cui stati possibili possono
4.1. Ritorno al gruppo delle trasformazioni di Möbius. 4.1.1. Lo spazio proiettivo degli stati di un qubit. Il qubit è il sistema quantistico più semplice che esista: un sistema i cui stati possibili possono
1 Definizione di sistema lineare omogeneo.
 Geometria Lingotto. LeLing1: Sistemi lineari omogenei. Ārgomenti svolti: Definizione di sistema lineare omogeneo. La matrice associata. Concetto di soluzione. Sistemi equivalenti. Operazioni elementari
Geometria Lingotto. LeLing1: Sistemi lineari omogenei. Ārgomenti svolti: Definizione di sistema lineare omogeneo. La matrice associata. Concetto di soluzione. Sistemi equivalenti. Operazioni elementari
3. Le coordinate geografiche: latitudine e longitudine
 Introduzione 3. Le coordinate geografiche: latitudine e longitudine Ogni volta che vogliamo individuare un punto sulla superficie terrestre gli associamo due numeri, le coordinate geografiche: la latitudine
Introduzione 3. Le coordinate geografiche: latitudine e longitudine Ogni volta che vogliamo individuare un punto sulla superficie terrestre gli associamo due numeri, le coordinate geografiche: la latitudine
Fisica Quantistica III Esercizi Natale 2009
 Fisica Quantistica III Esercizi Natale 009 Philip G. Ratcliffe (philip.ratcliffe@uninsubria.it) Dipartimento di Fisica e Matematica Università degli Studi dell Insubria in Como via Valleggio 11, 100 Como
Fisica Quantistica III Esercizi Natale 009 Philip G. Ratcliffe (philip.ratcliffe@uninsubria.it) Dipartimento di Fisica e Matematica Università degli Studi dell Insubria in Como via Valleggio 11, 100 Como
Sviluppi e derivate delle funzioni elementari
 Sviluppi e derivate delle funzioni elementari In queste pagine dimostriamo gli sviluppi del prim ordine e le formule di derivazioni delle principali funzioni elementari. Utilizzeremo le uguaglianze lim
Sviluppi e derivate delle funzioni elementari In queste pagine dimostriamo gli sviluppi del prim ordine e le formule di derivazioni delle principali funzioni elementari. Utilizzeremo le uguaglianze lim
x 2 + (x+4) 2 = 20 Alle equazioni di secondo grado si possono applicare i PRINCIPI di EQUIVALENZA utilizzati per le EQUAZIONI di PRIMO GRADO.
 EQUAZIONI DI SECONDO GRADO Un'equazione del tipo x 2 + (x+4) 2 = 20 è un'equazione DI SECONDO GRADO IN UNA INCOGNITA. Alle equazioni di secondo grado si possono applicare i PRINCIPI di EQUIVALENZA utilizzati
EQUAZIONI DI SECONDO GRADO Un'equazione del tipo x 2 + (x+4) 2 = 20 è un'equazione DI SECONDO GRADO IN UNA INCOGNITA. Alle equazioni di secondo grado si possono applicare i PRINCIPI di EQUIVALENZA utilizzati
ESERCIZI SVOLTI SUL CALCOLO INTEGRALE
 ESERCIZI SVOLTI SUL CALCOLO INTEGRALE * Tratti dagli appunti delle lezioni del corso di Matematica Generale Dipartimento di Economia - Università degli Studi di Foggia Prof. Luca Grilli Dott. Michele Bisceglia
ESERCIZI SVOLTI SUL CALCOLO INTEGRALE * Tratti dagli appunti delle lezioni del corso di Matematica Generale Dipartimento di Economia - Università degli Studi di Foggia Prof. Luca Grilli Dott. Michele Bisceglia
DEDUZIONE DEL TEOREMA DELL'ENERGIA CINETICA DELL EQUAZIONE SIMBOLICA DELLA DINAMICA
 DEDUZIONE DEL TEOREMA DELL'ENERGIA CINETICA DELL EQUAZIONE SIMBOLICA DELLA DINAMICA Sia dato un sistema con vincoli lisci, bilaterali e FISSI. Ricaviamo, dall equazione simbolica della dinamica, il teorema
DEDUZIONE DEL TEOREMA DELL'ENERGIA CINETICA DELL EQUAZIONE SIMBOLICA DELLA DINAMICA Sia dato un sistema con vincoli lisci, bilaterali e FISSI. Ricaviamo, dall equazione simbolica della dinamica, il teorema
2 2 2 A = Il Det(A) = 2 quindi la conica è non degenere, di rango 3.
 Studio delle coniche Ellisse Studiare la conica di equazione 2x 2 + 4xy + y 2 4x 2y + 2 = 0. Per prima cosa dobbiamo classificarla. La matrice associata alla conica è: 2 2 2 A = 2 2 2 Il DetA = 2 quindi
Studio delle coniche Ellisse Studiare la conica di equazione 2x 2 + 4xy + y 2 4x 2y + 2 = 0. Per prima cosa dobbiamo classificarla. La matrice associata alla conica è: 2 2 2 A = 2 2 2 Il DetA = 2 quindi
Esercizi sulle coniche (prof.ssa C. Carrara)
 Esercizi sulle coniche prof.ssa C. Carrara Alcune parti di un esercizio possono ritrovarsi in un altro esercizio, insieme a parti diverse. È un occasione per affrontarle più volte.. Stabilire il tipo di
Esercizi sulle coniche prof.ssa C. Carrara Alcune parti di un esercizio possono ritrovarsi in un altro esercizio, insieme a parti diverse. È un occasione per affrontarle più volte.. Stabilire il tipo di
APPENDICE 1 CAMPI CONSERVATIVI CIRCUITAZIONE DI UN VETTORE LUNGO UNA LINEA CHIUSA CORRENTE DI SPOSTAMENTO
 APPENDICE 1 CAMPI CONSERVATIVI CIRCUITAZIONE DI UN VETTORE LUNGO UNA LINEA CHIUSA CORRENTE DI SPOSTAMENTO Quando un punto materiale P si sposta di un tratto s per effetto di una forza F costante applicata
APPENDICE 1 CAMPI CONSERVATIVI CIRCUITAZIONE DI UN VETTORE LUNGO UNA LINEA CHIUSA CORRENTE DI SPOSTAMENTO Quando un punto materiale P si sposta di un tratto s per effetto di una forza F costante applicata
Analisi Matematica 1 e Matematica 1 Geometria Analitica: Rette
 Analisi Matematica 1 e Matematica 1 Geometria Analitica: Rette Annalisa Amadori e Benedetta Pellacci amadori@uniparthenope.it pellacci@uniparthenope.it Università di Napoli Parthenope Contenuti Nel Piano
Analisi Matematica 1 e Matematica 1 Geometria Analitica: Rette Annalisa Amadori e Benedetta Pellacci amadori@uniparthenope.it pellacci@uniparthenope.it Università di Napoli Parthenope Contenuti Nel Piano
Applicazioni lineari tra spazi euclidei. Cambi di base.
 pplicazioni lineari tra spazi euclidei. Cambi di base. Esercizio. Data la seguente applicazione lineare f : R R : f(x, y, z) = (x z, x + y, y + z), scrivere la matrice B, rappresentativa di f rispetto
pplicazioni lineari tra spazi euclidei. Cambi di base. Esercizio. Data la seguente applicazione lineare f : R R : f(x, y, z) = (x z, x + y, y + z), scrivere la matrice B, rappresentativa di f rispetto
SECONDO METODO DI LYAPUNOV
 SECONDO METODO DI LYAPUNOV Il Secondo Metodo di Lyapunov permette di studiare la stabilità degli equilibri di un sistema dinamico non lineare, senza ricorrere alla linearizzazione delle equazioni del sistema.
SECONDO METODO DI LYAPUNOV Il Secondo Metodo di Lyapunov permette di studiare la stabilità degli equilibri di un sistema dinamico non lineare, senza ricorrere alla linearizzazione delle equazioni del sistema.
Esercizi svolti sui sistemi lineari
 Francesco Daddi - www.webalice.it/francesco.daddi Esercizi svolti sui sistemi lineari Esercizio 1. Risolvere il seguente sistema lineare al variare del parametro reale t: tx+(t 1)y + z =1 (t 1)y + tz =1
Francesco Daddi - www.webalice.it/francesco.daddi Esercizi svolti sui sistemi lineari Esercizio 1. Risolvere il seguente sistema lineare al variare del parametro reale t: tx+(t 1)y + z =1 (t 1)y + tz =1
Introduciamo il sistema di riferimento indicato in figura b) con F 1 = ( f, 0) ed F 2 = (f, 0). Se P = (x, y) la condizione (1) fornisce
 1 L ellisse 1.1 Definizione Consideriamo due punti F 1 ed F 2 e sia 2f la loro distanza. L ellisse è il luogo dei punti P tali che la somma delle distanze PF 1 e PF 2 da F 1 ed F 2 è costante. Se indichiamo
1 L ellisse 1.1 Definizione Consideriamo due punti F 1 ed F 2 e sia 2f la loro distanza. L ellisse è il luogo dei punti P tali che la somma delle distanze PF 1 e PF 2 da F 1 ed F 2 è costante. Se indichiamo
Corso di Analisi Numerica
 Corso di Laurea in Ingegneria Informatica Corso di 3 - PROBLEMI DI INTERPOLAZIONE Lucio Demeio Dipartimento di Scienze Matematiche 1 Interpolazione: Polinomio di Lagrange 2 3 Introduzione Problemi di interpolazione
Corso di Laurea in Ingegneria Informatica Corso di 3 - PROBLEMI DI INTERPOLAZIONE Lucio Demeio Dipartimento di Scienze Matematiche 1 Interpolazione: Polinomio di Lagrange 2 3 Introduzione Problemi di interpolazione
Università degli studi di Catania. Corso di laurea in fisica
 Università degli studi di Catania Corso di laurea in fisica Esame di meccanica uantistica I Analisi numerica del potenziale anarmonico Agata Trovato Enrica Trovato Oscillatore armonico Trattazione uantistica
Università degli studi di Catania Corso di laurea in fisica Esame di meccanica uantistica I Analisi numerica del potenziale anarmonico Agata Trovato Enrica Trovato Oscillatore armonico Trattazione uantistica
Derivazione numerica. Introduzione al calcolo numerico. Derivazione numerica (II) Derivazione numerica (III)
 Derivazione numerica Introduzione al calcolo numerico Il calcolo della derivata di una funzione in un punto implica un processo al limite che può solo essere approssimato da un calcolatore. Supponiamo
Derivazione numerica Introduzione al calcolo numerico Il calcolo della derivata di una funzione in un punto implica un processo al limite che può solo essere approssimato da un calcolatore. Supponiamo
(x B x A, y B y A ) = (4, 2) ha modulo
 GEOMETRIA PIANA 1. Esercizi Esercizio 1. Dati i punti A(0, 4), e B(4, ) trovarne la distanza e trovare poi i punti C allineati con A e con B che verificano: (1) AC = CB (punto medio del segmento AB); ()
GEOMETRIA PIANA 1. Esercizi Esercizio 1. Dati i punti A(0, 4), e B(4, ) trovarne la distanza e trovare poi i punti C allineati con A e con B che verificano: (1) AC = CB (punto medio del segmento AB); ()
Esercizi sulle affinità - aprile 2009
 Esercizi sulle affinità - aprile 009 Ingegneria meccanica 008/009 Esercizio Sono assegnate nel piano le sei rette r : =, s : =, t : =, r : =, s : =, t : = determinare l affinità che trasforma ordinatamente
Esercizi sulle affinità - aprile 009 Ingegneria meccanica 008/009 Esercizio Sono assegnate nel piano le sei rette r : =, s : =, t : =, r : =, s : =, t : = determinare l affinità che trasforma ordinatamente
2.6 Calcolo degli equilibri di Nash
 92 2 Giochi non Cooperativi Per queste estensioni di giochi non finiti si possono provare risultati analoghi a quelli visti per i giochi finiti. Rimandiamo alla bibliografia per uno studio più approfondito
92 2 Giochi non Cooperativi Per queste estensioni di giochi non finiti si possono provare risultati analoghi a quelli visti per i giochi finiti. Rimandiamo alla bibliografia per uno studio più approfondito
TEMI D ESAME DI ANALISI MATEMATICA I
 TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
Atomi a più elettroni
 Chapter 7 Atomi a più elettroni 7.1 Lo spin Gli esperimenti indicano che alle particelle si deve associare un momento angolare intrinseco, o spin, indipendentemente dalla loro natura (particelle elementari
Chapter 7 Atomi a più elettroni 7.1 Lo spin Gli esperimenti indicano che alle particelle si deve associare un momento angolare intrinseco, o spin, indipendentemente dalla loro natura (particelle elementari
Sistemi di 1 grado in due incognite
 Sistemi di 1 grado in due incognite Problema In un cortile ci sono polli e conigli: in totale le teste sono 7 e zampe 18. Quanti polli e quanti conigli ci sono nel cortile? Soluzione Indichiamo con e con
Sistemi di 1 grado in due incognite Problema In un cortile ci sono polli e conigli: in totale le teste sono 7 e zampe 18. Quanti polli e quanti conigli ci sono nel cortile? Soluzione Indichiamo con e con
Sistemi di Equazioni Differenziali
 Sistemi di Equazioni Differenziali Nota introduttiva: Lo scopo di queste dispense non è trattare la teoria riguardo ai sistemi di equazioni differenziali, ma solo dare un metodo risolutivo pratico utilizzabile
Sistemi di Equazioni Differenziali Nota introduttiva: Lo scopo di queste dispense non è trattare la teoria riguardo ai sistemi di equazioni differenziali, ma solo dare un metodo risolutivo pratico utilizzabile
Risoluzione di problemi ingegneristici con Excel
 Risoluzione di problemi ingegneristici con Excel Problemi Ingegneristici Calcolare per via numerica le radici di un equazione Trovare l equazione che lega un set di dati ottenuti empiricamente (fitting
Risoluzione di problemi ingegneristici con Excel Problemi Ingegneristici Calcolare per via numerica le radici di un equazione Trovare l equazione che lega un set di dati ottenuti empiricamente (fitting
Esercizi svolti. Geometria analitica: rette e piani
 Esercizi svolti. Sistemi di riferimento e vettori. Dati i vettori v = i + j k, u =i + j + k determinare:. il vettore v + u ;. gli angoli formati da v e u;. i vettore paralleli alle bisettrici di tali angoli;
Esercizi svolti. Sistemi di riferimento e vettori. Dati i vettori v = i + j k, u =i + j + k determinare:. il vettore v + u ;. gli angoli formati da v e u;. i vettore paralleli alle bisettrici di tali angoli;
