LA PROIEZIONE STEREOGRAFICA (PARTE II)
|
|
|
- Camillo Giovannini
- 7 anni fa
- Visualizzazioni
Transcript
1 Corso di laurea triennale in Scienze Naturali a.a LA PROIEZIONE STEREOGRAFICA (PARTE II) «Una proiezione cristallina è un metodo di rappresentazione dei cristalli tridimensionali su di un piano bidimensionale. Sono possibili diversi tipi di proiezioni, tali che per ognuna sono definite regole precise e riproducibili rispetto al cristallo. Il metodo migliore per esprimere la forma di un cristallo ed è generalmente migliore di qualsiasi immagine fotografica di cristalli reali è la proiezione clinografica» Docente: Ernesto Mesto ernesto.mesto@uniba.it Website: Gruppo facebook:
2 INDICIZZAZIONE DELLE FACCE E possibile definire gli indici delle facce di un cristallo come un rapporto di rapporti parametrici. Essi saranno una terna di numeri (h,k,l) primi fra loro (generalmente piccoli). Siano A, B e C i lati di cella della maglia fondamentale o parametrica, mentre A, B e C siano i parametri staccati da una qualunque altra faccia dello stesso cristallo. E allora possibile definire gli indice di una faccia generica come:
3 Quindi, gli indici saranno inversamente proporzionali alle intercette della faccia (o piano cristallografico) con gli assi. INDICIZZAZIONE DELLE FACCE C c a b c C A B B b A B C : : = h : k : l A' B' C' a A Se ad esempio come in figura A =2, B =3 e C =4 allora avremo: 1 2 : 1 3 : 1 4 x y z Si preferisce, però usare numeri interi, ottenibili tramite il minimo comune multiplo. 1 2 : 1 3 : 1 4 = 6 : 4 : 3 h : k : l
4 Sistema Monometrico c C a = b = c Nel caso del sistema cubico, poiché il periodo di ripetizione degli assi cristallografici è lo stesso, dall inclinazione della faccia possiamo avere idea dei rapporti degli indici h, k, l, A C B B b 1 2 : 1 3 : 1 4 = 6 : 4 : 3 h : k : l A a Anche se gli indici sono uguali in valore a quelli del caso precedente, il fatto che a=b=c, ci dice che la faccia (643) del cristallo dovrà per forza avere l inclinazione riportata in figura. (Questo tipo di valutazione è possibile solo quando almeno due dei tre periodi di ripetizione sono uguali tra loro.)
5 Sistema Monometrico Solo per il sistema cubico vale la regola: h > k > l Gli indici sono inversamente proporzionali all intercetta sull asse, quindi: chiamerò h l indice sul cui asse la faccia stacca l intercetta più piccola Chiamerò l l indice sul cui asse la faccia stacca l intercetta più grande Assegnerà l indice k all ultimo asse (QUESTO VALE SOLO PER IL SISTEMA MONOMETRICO)
6 Piani cristallografici, direzioni e indici I nodi di un reticolo t m = m 1 a + m 2 b + m 3 c, sono caratterizzati da numeri razionali (interi se la cella elementare è primitiva). Le proprietà dei reticoli connesse ai nodi sono quindi dette razionali. Si parlerà di direzioni razionali per intendere direzioni definite da due nodi reticolari e di piani razionali per intendere piani definiti da tre nodi reticolari. Direzioni cristallografiche. Come abbiamo visto, i cristalli sono anisotropi: sarà quindi necessario specificare in modo semplice le direzioni nelle quali si manifestano determinate proprietà fisiche. In un reticolo esistono infiniti filari paralleli, ciascuno definito da due punti nodali, che sono caratterizzati da uno stesso periodo di ripetizione. I filari definiscono una direzione cristallografica. Se un filare passa per l origine la sua direzione sarà definita dai valori m i di uno qualunque dei nodi del filare. La direzione viene indicata con [m 1 m 2 m 3 ]. La stessa direzione è indicata anche da un multiplo del tipo [nm 1 nm 2 nm 3 ].
7 Direzioni cristallografiche Per una cella primitiva la direzione [222] è quella della diagonale di corpo, ma lo è anche [111]. Per convenzione si dividono i valori m i per il massimo comune divisore, ottenendo così sempre il set più piccolo. La direzione [936] diventa quindi [312]. Filari che non passano per l origine hanno sempre un filare parallelo centrale, passante cioè per l origine. Se la cella non è primitiva i valori m i sono numeri razionali, esprimibili cioè come rapporti di numeri interi. La direzione corrispondente ad una diagonale di faccia in un reticolo F può essere [½½0].
8 Piani cristallografici L orientazione di un piano cristallografico è definita in termini di indici di Miller (hkl). Tre nodi individuano un piano cristallografico. Se un piano incontra i tre assi cristallografici nei tre nodi (m 1, 0, 0), (0, m 2, 0) e (0, 0, m 3 ), gli indici (m 1, m 2, m 3 ) forniscono l orientazione del piano. Si preferiscono però gli indici di Miller del piano, che sono numeri interi e primi fra loro, inversamente proporzionali alle intercette del piano con gli assi, cioè: h : k : l = m 1-1 : m 2-1 : m 3-1 Esempi di famiglie di piani cristallografici Spesso con la terna di Miller si indica una famiglia di piani. I piani di una stessa famiglia sono: 1. Paralleli tra lori 2. Equalmente spazialti
9 Piani cristallografici Esiste una interpretazione semplice degli indici di Miller h, k e l. I piani della famiglia (hkl) dividono i lati della cella elementare: a in h parti uguali, b in k parti uguali e c in l parti uguali. L equazione della famiglia di piani è h(x/a) + k(y/b) + l(z/c) = n. Gli indici di Miller (hkl) specificano l orientazione del piano ed n la sua posizione rispetto all origine. Famiglia di piani (2 3 6) a è diviso in 2 parti uguali b è diviso in 3 parti uguali c è diviso in 6 parti uguali Famiglia di piani (100) Famiglia di piani (200)
10 Piani cristallografici
11 Determinazione degli indici (hkl) di Gli indici di Miller di un piano cristallino sono definiti come i reciproci delle intersezioni frazionarie (con le frazioni normalizzate a numeri interi) del piano con gli assi cristallografici x, y, z. 1. Scegliere un piano che non passa per l origine (0,0,0) 2. Determinare le intersezioni del piano rispetto agli assi cristallografici, tali intersezioni potrebbero essere anche delle frazioni. 3. Fare i reciproci di queste intersezioni 4. Normalizzare le frazioni agli interi e determinare gli interi più piccoli Miller
12 Piani cristallografici /3 1/2 100
13 Famiglie di piani cristallografici 230
14 Famiglie di piani cristallografici 230
15 Famiglie di piani cristallografici 23 0
16 Facce in posizione speciale Per quanto detto sino ad ora è possibile individuare alcune zone all interno del piano di proiezione dove andranno a cadere facce con indici particolari.
17 Polo della faccia coincidente con l asse x x z y Quando il polo della faccia è attraversata dall asse x, nel caso dei sistemi ortonormali (cubico, tetragonale e ortorombico) si ha che la faccia stessa sarà parallela agli assi y e z (ossia li interceterrà all infinito). Poiché gli indici sono inversamente proporzionali alle intercette della faccia sugli assi, ne risulta che la faccia in questione sia del tipo (h00). A noi comunque interessa il rapporto tra gli indici è possibile quindi divere tutto per h in modo da ottenere: (h/h 0/h 0/h) = (100) Analogamente quando il polo della faccia sarà attraversata dall asse y o z avremo le facce del tipo (010) e (001).
18 x z y x X (100) y X (010) x y X (001)
19 Faccia parallela all asse z z y Se immaginiamo di inclinare leggermente la faccia verso l asse y in modo che rimanga ancora parallela all asse z avremo al situazione seguente: x z In questo caso la faccia non sarà più parallela a y ma la sua intercetta con z sarà ancora infinito. Quindi potremo assegnarle i seguenti indici: α<45 y (hk0) o (kh0) Ricordiamo che nel caso del sistema cubico vale la regola h>k>l. L indice h va assegnato all asse su cui la faccia stacca l intercetta minore, in questo caso l asse x. Quindi gli indici giusti saranno (hk0) x
20 Faccia parallela all asse z z y Se avviciniamo di molto la faccia all asse y in modo che rimanga comunque sempre parallela all asse z avremo al situazione seguente: x z La faccia potrà avere sempre indici del tipo: (hk0) o (kh0) Ma solo nel caso del sistema cubico poiché l indice h va assegnato all asse che ha l intercetta minore con la faccia, che in questo caso è l asse y, dovremo assegnare alla faccia gli indici (kh0) α>45 x y
21 Faccia parallela all asse z z Se il polo della faccia cade su una linea equidistante dall asse x e y: y x z In questo caso la faccia staccherà le stesse intercette su x e y mentre continuerà ad avere intercetta infinito su z. Quindi essa avrà indici del tipo (hh0) che potremo anche scrivere come: (h/h h/h 0/h) = (110) α=45 x y
22 z y x z x z y y X (hk0) X (kh0) Da quanto detto è facile capire che la circonferenza del cerchio rappresenta il luogo dove trovare le facce parallele all asse z. Con un analogo ragionamento si può comprendere che sull asse x troveremo le facce parallele all asse y, mentre sull asse y quelle parallele all asse x. X (110)
23 Altre posizioni speciali Nel caso del sistema monometrico è possibile individuare altre posizioni speciali nella proiezione stereografica. La circonferenza è il luogo dei punti delle facce che hanno il terzo indice uguale a zero (es. hk0, kh0, etc.). L asse X è il luogo dei punti con il secondo indice uguale a zero (es. h0l, l0h, etc.) L asse Y è il luogo dei punti con il primo indice uguale a zero (es. 0kl, 0kl, etc.) I piani a 45 tra due assi saranno le zone dove trovare le faccie con due indici uguali. Ad es. sul piano a 45 tra x e y le facce saranno del tipo (hhk) o (kkh), sul piano a 45 tra x e z le facce saranno del tipo (hkh) o (khk), infine sul piano a 45 tra y e z le facce saranno del tipo (hkk) o (kkh). Se il polo della faccia è attraversato da un asse ternario essa staccherà la stessa intercetta su i tre assi XYZ, quindi sarà del tipo (111).
24 Sistema Monometrico Regole di permutazioni degli indici per l asse ternario X {klh} X {lhk} X {hkl} {hkl} {lhk} {klh} {hkl} Solo per le facce nel quadrante sud-est ruotate in senso antiorario
25 Permutazione piano di simmetria a 45 tra l asse X e Y X Y a X {lhk} 2 Y X X {hlk} a 1 Il piano di simmetria a 45 tra l asse X e l asse Y scambia gli indici relativi all asse x e y (il primo e il secondo indice).
26 Permutazione piani di simmetria obliqui Il piano a 45 tra l asse X e l asse Y scambia gli indici relativi all asse X e all asse Y (il primo e il secondo indice) Il piano a 45 tra l asse Y e l asse Z scambia gli indici relativi all asse Y e all asse Z (il secondo e il terzo indice) Il piano a 45 tra l asse X e l asse Z scambia gli indici relativi all asse X e all asse Z (il primo e il terzo indice)
27 Permutazione piani di simmetria perpendicolare ad un asse cristallografico Il piano perpendicolare all asse X invertirà il segno dell indice relativo all asse X (il primo indice) Il piano perpendicolare all asse Y invertirà il segno dell indice relativo all asse Y (il secondo indice) Il piano perpendicolare all asse Z invertirà il segno dell indice relativo all asse Z (il terzo indice)
28 Operazioni per eseguire correttamente una proiezione stereografica 1. Identificare tutti gli elementi di simmetria del solido 2. Determinare la classe di simmetria e quindi il sistema cristallino. Per es. 4 assi ternari = cubico Solo 1 asse quaternario = tetragonale 3 assi binari o piani di simmetria ortogonali tra loro = ortorombico 3. Disegnare il piano di proiezione. Nel caso del sistema cubico riportare tutti i piani di simmetria fittizi (a tratto intermittente). 4. Orientare in maniera opportuna il solido nel piano di proiezione. (N.B. stare attenti a non cambiare l orientazione del solido durante l esercizio) 5. Proiettare gli elementi di simmetria (assi a tratto intermittente e piani a tratto continuo) 6. Proiettare la prima faccia (di solito nel quadrante sud-est) 7. Usare gli elementi di simmetria per ricavare le altre facce 8. Verificare che il numero delle facce proiettate e la loro posizione coincida con quelle del solido correttamente orientato. 9. Indicizzare le facce. Utilizzando le regole di permutazione e gli elementi di simmetria. Per il sistema cubico verificare le intercette delle facce con gli assi per capire quale è l indice maggiore, intermedio e minore in modo da poter correttamente assegnare nel giusto ordine gli indici h,k,l.
29 Regole di coesistenza degli elementi di simmetria morfologica Un asse di rotazione di ordine pari, un piano di simmetria perpendicolare ad esso ed il centro di simmetria sono elementi di simmetria tali per cui la presenza di due di essi implica la presenza del terzo. Se esiste un asse binario normale ad un asse di ordine N, allora esistono altri N-1 assi binari ad angoli pari a 2p\n. Se su di un piano di riflessione giace un asse di ordine N, allora esistono altri N-1 piani ad angoli 2π\N. Le combinazioni di assi diverse da quelle stabilite al punto b) sono solo di due tipi ed entrambi implicano la presenza di quattro assi ternari disposti ad angoli di ; in un caso essi sono combinati con tre assi binari tra loro perpendicolari e nell altro con tre assi quaternari tra loro perpendicolari e sei assi binari.
30 Permutazione asse ternario su piani di simmetria perpendicolari agli assi a 1, a 2, a 3
31 Permutazione asse ternario su assi di rotazione coincidenti con agli assi a 1, a 2, a 3
32 (001) Permutazione asse ternario su facce perpendicolari a due degli assi a 1, a 2, a 3 (100) (001) (010) (010) (100)
33 Permutazione asse ternario su facce perpendicolari a uno degli assi a 1, a 2, a 3 (0lh) (h0l) (lh0)
34 Permutazione asse ternario su piani di simmetria obliqui agli assi a 1, a 2, a 3
35 Permutazione asse ternario su assi di rotazione obliqui agli assi a 1, a 2, a 3
36 Permutazione asse ternario su alcune facce in posizione speciale (011) (101) (110)
37 Permutazione asse ternario su alcune facce in posizione speciale (lhh) (hlh) (hhl)
38 Permutazione asse ternario su facce in posizione generale (khl) (lhk) (hkl)
39 FORMA CRISTALLINA Una forma semplice consiste di un gruppo di facce di un cristallo tra loro tutte equivalenti (su cui si misurano identici valori di una proprietà fisica), cioè tutte le facce che vengono generate dalla combinazione degli elementi di simmetria presenti nel cristallo. Un cristallo è delimitato da facce appartenenti a forme geometriche semplici: CHIUSE - cubo, ottaedro, rombododecaedro, APERTE - prisma, pinacoide, piramide,.. Un cristallo può essere costituito da una sola o dalla combinazione di più forme semplici Forma semplice + Forma semplice = Forma complessa + =
40 Sviluppo di una forma semplice nelle classi cristalline 1 e m3m 1 m3m c + +a 2 b a a + +a 1 a b a 2 c a Pinacoide {111} a Ottaedro {111}
41 Forma semplice Il numero delle facce (molteplicità) che appartengono ad una forma semplice viene determinato dalla simmetria della classe Gli indici di Miller vengono anche usati come simboli delle forma semplice, in questo caso sono inclusi tra parentesi graffe come {hkl}, {111}... etc. (si preferisce avere tutti gli indici positivi!). In ognuna delle classi cristalline è presente almeno una forma che tagli tutti gli assi cristallografici con lunghezze differenti, questa è la forma generale {hkl}. Tutte le altre sono forme speciali. Nel sistema triclino, monoclino e ortorombico la forma generale è la {111}, perchè tutti gli assi cristallografici hanno lunghezza differente.
42 Forma semplice Una faccia (hkl) non sarà mai parallela o perpendicolare ad un asse o ad un piano di simmetria, indipendentemente dalla classe di simmetria. Una forma speciale, invece consisite in facce che sono parallele o perpendicolari a qualcuno degli elementi di simmetria.
43 I 33 tipi di forme non cubiche Nome* N. Di Facce Nome N. Di Facce Pedione 1 Bipiramide rombica 8 Pinacoide 2 Bipiramide trigonale 3 Doma 2 Bipiramide ditrigonale 6 Sfenoide 2 Bipiramide tetragonale 8 Prisma rombico 4 Bipiramide ditetragonale 16 Prisma trigonale 3 Bipiramide esagonale 12 Prisma ditrigonale 6 Bipiramide diesagonale 24 Prisma tetragonale 4 Trapezoedro trigonale 6 Prisma ditetragonale 4 Trapezoedro tetragonale 8 Prisma esagonale 6 Trapezoedro esagonale 12 Prisma diesagonale 12 Scalenoedro tetragonale 8 Piramide rombica 4 Scalenoedri esagonale 12 Piramide trigonale 3 Romboedro 6 Piramide ditrigonale 6 Bisfenoide rombico 4 Piramide tetragonale 4 Bisfenoide tetragonale 4 Piramide ditetragonale 8 Piramide esagonale 6 Piramide diesagonale 12 *Secondo il sistema di Groth-Rogers
44 Forme semplici non cubiche Pedione: forma aperta costituita da una sola faccia Pinacoide: forma apera costituita da due facce parallele
45 Forme semplici non cubiche Doma: forma aperta costituita da due facce non parallele, simmetriche rispetto ad un piano m Sfenoide: forma aperta costituita da due facce non parallele, simmetriche rispetto ad asse binario
46 Forme semplici non cubiche Prisma: forma aperta composta da 3, 4, 6, 8 o 12 facce, tutte parallele allo stesso asse.
47 Forme semplici non cubiche Prisma: forma aperta composta da 3, 4, 6, 8 o 12 facce, tutte parallele allo stesso asse.
48 Forme semplici non cubiche Piramide: forma aperta composta da 3, 4, 6, 8 o 12 facce, non parallele fra loro che si incontrano in un punto.
49 Forme semplici non cubiche Bipiramide: forma chiusa composta da 6, 8, 12, 16 o 24 facce, non parallele. Si può considerare formata da due piramidi simmetriche rispetto ad un piano di riflessione orizzontale
50 Forme semplici non cubiche Trapezoedro: forma chiusa costituita da 6, 8 o 12 facce, con le 3, 4, o 6 facce superiori spostate rispetto alla 3, 4, o 6 facce inferiori.
51 Nome dell forme Scalenoedro: forma chiusa composta da 8 o 12 facce raggruppate in coppie simmetriche.
52 Forme semplici non cubiche Romboedro: forma chiusa composta da 6 facce, con tre nella parte superiore che si alternano con altre 3 nella parte inferiore. Le due serie sono rotate di 60.
53 Forme semplici non cubiche Bisfenoide: forma chiusa costituita da due facce superiore alternate rispetto a due facce inferiori, ruotate di 90.
54
55 L ABITO di un cristallo è dato dalla forma semplice più sviluppata
56 Habitus cristallino e aggregati Il primo si riferisce all aspetto che assume il minerale in base allo sviluppo delle forme cristalline che lo compongono. Sappiamo però che i minerali sono quasi sempre costituiti da aggregati di cristalli con morfologia da euedrale a subedrale fino ad anedrale. Se le facce sono ben definite, l'abito è ben riconoscibile e si parla di abito euedrale (o idiomorfo); se le facce, invece, sono parzialmente sviluppate e l'abito è ancora riconoscibile si tratta di abito subedrale (o ipidiomorfo); se, infine, le facce non sono ben sviluppate e l'abito è completamente irregolare, l'abito prende il nome di anedrale (o allotriomorfo).
57 Ci sono vari tipi di abiti: ABITO CRISTALLINO - abito equidimensionale (o equante, o isometrico): se il minerale ha simmetria cubica (es. granato); - abito colonnare (o prismatico): se il minerale è abbastanza allungato in una dimensione (es. pirosseni, anfiboli, tormalina); - abito aciculare: se il minerale è esageratamente allungato in una dimensione (es. tormalina, anfiboli); - abito tabulare (o "a libro"): se il minerale è abbastanza appiattito in una dimensione (es. feldspati); - abito lamellare: se l'abito è esageratamente appiattito in una dimensione (es. miche); - abito fibroso (o asbestiforme): è una variante dell'abito tabulare (es. Serpentino); - abito a forma di lama (es. cianite); - abito "a barilotto": è poco comune (es. corindone); - abito bipiramidale (es. zolfo): consiste in due piramidi, una sopra l'altra; - cristalli "a tramoggia": quando la velocità di crescita del minerale è molto marcata (es. quarzo); - abito spatico: è caratterizzato da un'ottima sfaldatura, cioè la capacità del minerale di rompersi lungo superfici nette (es. calcite)
58
59
60 Letture consigliate Trattato di mineralogia Carobbi - 3 a edizione Assi Cristallografici Proiezione dei cristalli La simmetria nei cristalli Leggere: pag 21-85
61 Letture consigliate C. KLEIN - Mineralogia, Zanichelli 2004 Morfologia cristallina Notazione cristallografica per i piani Abito cristallino Forma Nomi delle forme Pag:
Indici di Miller nei sistemi Trigonali ed Esagonali
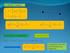
 Indici di Miller nei sistemi Trigonali ed Esagonali -a 1 ( 100) (0 10) a 3 c (001) ( 100) -a 2 (0 10) c ( 110) a 2 -a 2 ( 110) -a 1 ( 110) (1 10) (100) (010) a 1 (100) (001) -c (010) -a 3 a 2 a 1 Una croce
Indici di Miller nei sistemi Trigonali ed Esagonali -a 1 ( 100) (0 10) a 3 c (001) ( 100) -a 2 (0 10) c ( 110) a 2 -a 2 ( 110) -a 1 ( 110) (1 10) (100) (010) a 1 (100) (001) -c (010) -a 3 a 2 a 1 Una croce
LA PROIEZIONE STEREOGRAFICA (PARTE I)
 Corso di laurea triennale in Scienze Naturali a.a. 2012-2013 LA PROIEZIONE STEREOGRAFICA (PARTE I) «Una proiezione cristallina è un metodo di rappresentazione dei cristalli tridimensionali su di un piano
Corso di laurea triennale in Scienze Naturali a.a. 2012-2013 LA PROIEZIONE STEREOGRAFICA (PARTE I) «Una proiezione cristallina è un metodo di rappresentazione dei cristalli tridimensionali su di un piano
Corso di Mineralogia
 Corso di Mineralogia Scienze Geologiche A.A. 2016 / 2017 Lab # 2 Cristallografia morfologica: le forme dei cristalli (pdf Lab#2) ALCUNE NOZIONI DI GEOMETRIA ELEMENTARE Un "cristallo" è riconducibile ad
Corso di Mineralogia Scienze Geologiche A.A. 2016 / 2017 Lab # 2 Cristallografia morfologica: le forme dei cristalli (pdf Lab#2) ALCUNE NOZIONI DI GEOMETRIA ELEMENTARE Un "cristallo" è riconducibile ad
LA PROIEZIONE STEREOGRAFICA
 Corso di laurea triennale in Scienze Naturali a.a. 2015-2016 LA PROIEZIONE STEREOGRAFICA «Una proiezione cristallina è un metodo di rappresentazione dei cristalli tridimensionali su di un piano bidimensionale.
Corso di laurea triennale in Scienze Naturali a.a. 2015-2016 LA PROIEZIONE STEREOGRAFICA «Una proiezione cristallina è un metodo di rappresentazione dei cristalli tridimensionali su di un piano bidimensionale.
Simmetrie Cristallografiche A.A Marco Nardini Dipartimento di Scienze Biomolecolari e Biotecnologie Università di Milano
 A.A. 2009-2010 Marco Nardini Dipartimento di Scienze Biomolecolari e Biotecnologie Università di Milano Reticolo Cristallino: insieme di punti detti nodi separati da intervalli a, b, e c (reticolo di ripetizione)
A.A. 2009-2010 Marco Nardini Dipartimento di Scienze Biomolecolari e Biotecnologie Università di Milano Reticolo Cristallino: insieme di punti detti nodi separati da intervalli a, b, e c (reticolo di ripetizione)
Reticoli di Bravais e sistemi cristallini
 Reticoli di Bravais e sistemi cristallini Come in 2D, anche in 3D si individuano un motivo, che si ripete in modo periodico nello spazio e un reticolo (disposizione di punti, ciscuno che possiede lo stesso
Reticoli di Bravais e sistemi cristallini Come in 2D, anche in 3D si individuano un motivo, che si ripete in modo periodico nello spazio e un reticolo (disposizione di punti, ciscuno che possiede lo stesso
Corso di Mineralogia
 Corso di Mineralogia Scienze Geologiche A.A. 2016 / 2017 Elementi di cristallografia strutturale (pdf # 06) (2) - Mineralogia 2016/2017_cristallografia CRISTALLOGRAFIA STRUTTURALE Cristallografia morfologica
Corso di Mineralogia Scienze Geologiche A.A. 2016 / 2017 Elementi di cristallografia strutturale (pdf # 06) (2) - Mineralogia 2016/2017_cristallografia CRISTALLOGRAFIA STRUTTURALE Cristallografia morfologica
Struttura e geometria cristallina
 Struttura e geometria cristallina Tecnologia Meccanica RETICOLO SPAZIALE E CELLE UNITARIE Gli atomi, disposti in configurazioni ripetitive 3D, con ordine a lungo raggio (LRO), danno luogo alla struttura
Struttura e geometria cristallina Tecnologia Meccanica RETICOLO SPAZIALE E CELLE UNITARIE Gli atomi, disposti in configurazioni ripetitive 3D, con ordine a lungo raggio (LRO), danno luogo alla struttura
INDICE CAPITOLO 1 CAPITOLO 1
 INDICE CAPITOLO. Cristalli.. Tipici piani reticolari di un cristallo cubico.2. Reticoli... Reticolo quadrato bidimensionale..2. Reticolo cubico semplice.. Celle unitarie... Primo esempio di arrangiamenti
INDICE CAPITOLO. Cristalli.. Tipici piani reticolari di un cristallo cubico.2. Reticoli... Reticolo quadrato bidimensionale..2. Reticolo cubico semplice.. Celle unitarie... Primo esempio di arrangiamenti
Materiale didattico: dispense fornite durante il corso
 Struttura e Proprietà dei Materiali 6 crediti lezioni frontali+ 3 crediti di laboratorio Richiami di cristallochimica Reticolo reciproco Diffrazione di raggi X e di Neutroni Produzione Raggi X (Tubi, Sincrotroni)
Struttura e Proprietà dei Materiali 6 crediti lezioni frontali+ 3 crediti di laboratorio Richiami di cristallochimica Reticolo reciproco Diffrazione di raggi X e di Neutroni Produzione Raggi X (Tubi, Sincrotroni)
Posizioni Atomiche nelle Celle Unitarie Cubiche
 Posizioni Atomiche nelle Celle Unitarie Cubiche Il sistema di coordinate cartesiane è usato per individuare gli atomi. In una cella unitaria cubica l asse x è la direzione che esce dal foglio. l asse y
Posizioni Atomiche nelle Celle Unitarie Cubiche Il sistema di coordinate cartesiane è usato per individuare gli atomi. In una cella unitaria cubica l asse x è la direzione che esce dal foglio. l asse y
Scienza dei Materiali 1 Esercitazioni
 Scienza dei Materiali 1 Esercitazioni 2. Cristallografia dei materiali ver. 1.1 Reticoli cristallini Reticolo è una griglia tridimensionale di punti possiamo individuare un insieme minimo di punti (cella)
Scienza dei Materiali 1 Esercitazioni 2. Cristallografia dei materiali ver. 1.1 Reticoli cristallini Reticolo è una griglia tridimensionale di punti possiamo individuare un insieme minimo di punti (cella)
Lezione 6 Richiami di Geometria Analitica
 1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
EQUAZIONE DELLA RETTA
 EQUAZIONE DELLA RETTA EQUAZIONE DEGLI ASSI L equazione dell asse x è 0. L equazione dell asse y è 0. EQUAZIONE DELLE RETTE PARALLELE AGLI ASSI L equazione di una retta r parallela all asse x è cioè è uguale
EQUAZIONE DELLA RETTA EQUAZIONE DEGLI ASSI L equazione dell asse x è 0. L equazione dell asse y è 0. EQUAZIONE DELLE RETTE PARALLELE AGLI ASSI L equazione di una retta r parallela all asse x è cioè è uguale
TIPI DI LINEA E LORO APPLICAZIONI
 TIPI DI LINEA E LORO APPLICAZIONI Tipo di Linea Descrizione Applicazione A B D E Continua grossa Continua fine Continua fine irregolare Tratteggiata grossa Contorni e spigoli in vista Linee di costruzione
TIPI DI LINEA E LORO APPLICAZIONI Tipo di Linea Descrizione Applicazione A B D E Continua grossa Continua fine Continua fine irregolare Tratteggiata grossa Contorni e spigoli in vista Linee di costruzione
DEFINIZIONE DI MINERALE
 DEFINIZIONE DI MINERALE - Corpo solido naturale - Stato Solido Cristallino - Amorfo - Atomi dispos> in modo ordinato e periodico - Anisotropia Isotropia - Legge Costanza angoli diedri (Romè de l Isle,
DEFINIZIONE DI MINERALE - Corpo solido naturale - Stato Solido Cristallino - Amorfo - Atomi dispos> in modo ordinato e periodico - Anisotropia Isotropia - Legge Costanza angoli diedri (Romè de l Isle,
Gruppi puntuali. Primo elemento
 Gruppi puntuali Considerando le combinazioni che portano solo alla formazioni di gruppi puntuali con un numero finito di elementi di simmetria si ottengono solo 32 gruppi puntuali. I cristalli afferiranno
Gruppi puntuali Considerando le combinazioni che portano solo alla formazioni di gruppi puntuali con un numero finito di elementi di simmetria si ottengono solo 32 gruppi puntuali. I cristalli afferiranno
Condizione di allineamento di tre punti
 LA RETTA L equazione lineare in x e y L equazione: 0 con,,, e non contemporaneamente nulli, si dice equazione lineare nelle due variabili e. Ogni coppia ; tale che: 0 si dice soluzione dell equazione.
LA RETTA L equazione lineare in x e y L equazione: 0 con,,, e non contemporaneamente nulli, si dice equazione lineare nelle due variabili e. Ogni coppia ; tale che: 0 si dice soluzione dell equazione.
Piano cartesiano e retta
 Piano cartesiano e retta Il punto, la retta e il piano sono concetti primitivi di cui non si da una definizione rigorosa, essi sono i tre enti geometrici fondamentali della geometria euclidea. Osservazione
Piano cartesiano e retta Il punto, la retta e il piano sono concetti primitivi di cui non si da una definizione rigorosa, essi sono i tre enti geometrici fondamentali della geometria euclidea. Osservazione
POLIEDRI IN CRISTALLOGRAFIA
 POLIEDRI IN CRISTALLOGRAFIA L'universo è composto di materia, ovviamente. E la materia è composta di particelle: elettroni, neutroni e protoni. Dunque l'intero universo è composto di particelle. Ora, di
POLIEDRI IN CRISTALLOGRAFIA L'universo è composto di materia, ovviamente. E la materia è composta di particelle: elettroni, neutroni e protoni. Dunque l'intero universo è composto di particelle. Ora, di
1. (Da Medicina e Odontoiatria 2012) Determinare l'area del triangolo che ha come vertici i punti (0,0), (0,1), (13,12) del piano cartesiano:
 QUESITI 1 PIANO CARTESIANO 1. (Da Medicina e Odontoiatria 2012) Determinare l'area del triangolo che ha come vertici i punti (0,0), (0,1), (13,12) del piano cartesiano: a) 6 b) 13/2 c) 12 d) 13 e) 78 2.
QUESITI 1 PIANO CARTESIANO 1. (Da Medicina e Odontoiatria 2012) Determinare l'area del triangolo che ha come vertici i punti (0,0), (0,1), (13,12) del piano cartesiano: a) 6 b) 13/2 c) 12 d) 13 e) 78 2.
misura. Adesso, ad un arbitrario punto P dello spazio associamo una terna di numeri reali x
 4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
4. Geometria di R 3. Questo paragrafo è molto simile al paragrafo : tratta infatti delle proprietà geometriche elementari dello spazio R 3. Per assegnare delle coordinate nello spazio, fissiamo innanzitutto
Stabilire se il punto di coordinate (1,1) appartiene alla circonferenza centrata nell origine e di raggio 1.
 Definizione di circonferenza e cerchio. Equazione della circonferenza centrata in O e di raggio R. Esercizi. La circonferenza e il cerchio Definizioni: dato un punto C nel piano cartesiano e dato un numero
Definizione di circonferenza e cerchio. Equazione della circonferenza centrata in O e di raggio R. Esercizi. La circonferenza e il cerchio Definizioni: dato un punto C nel piano cartesiano e dato un numero
GEOMETRIA ANALITICA
 GEOMETRIA ANALITICA matematica@blogscuola.it LE COORDINATE CARTESIANE Quando si vuole fissare un sistema di coordinate cartesiane su una retta r, è necessario considerare: un punto O detto origine; un
GEOMETRIA ANALITICA matematica@blogscuola.it LE COORDINATE CARTESIANE Quando si vuole fissare un sistema di coordinate cartesiane su una retta r, è necessario considerare: un punto O detto origine; un
Piano cartesiano e Retta
 Piano cartesiano e Retta 1 Piano cartesiano e Retta 1. Richiami sul piano cartesiano 2. Richiami sulla distanza tra due punti 3. Richiami punto medio di un segmento 4. La Retta (funzione lineare) 5. L
Piano cartesiano e Retta 1 Piano cartesiano e Retta 1. Richiami sul piano cartesiano 2. Richiami sulla distanza tra due punti 3. Richiami punto medio di un segmento 4. La Retta (funzione lineare) 5. L
PIANO CARTESIANO. NB: attenzione ai punti con una coordinata nulla: si trovano sugli assi
 PIANO CARTESIANO Il piano cartesiano è individuato da due rette perpendicolari (ortogonali) che si incontrano in un punto O detto origine del piano cartesiano. Si fissa sulla retta orizzontale il verso
PIANO CARTESIANO Il piano cartesiano è individuato da due rette perpendicolari (ortogonali) che si incontrano in un punto O detto origine del piano cartesiano. Si fissa sulla retta orizzontale il verso
Descrittori quantitativi della geometria cristallina: assi, piani ed indici.
 Descrittori quantitativi della geometria cristallina: assi, piani ed indici. Assi di cella (con angoli interassiali) Reticolo di Bravais Simmetria puntuale (classi) Simmetria spaziale Come individuare
Descrittori quantitativi della geometria cristallina: assi, piani ed indici. Assi di cella (con angoli interassiali) Reticolo di Bravais Simmetria puntuale (classi) Simmetria spaziale Come individuare
Rette e piani nello spazio Federico Lastaria, Analisi e Geometria 1. Politecnico di Milano Corso di Analisi e Geometria 1
 ette e piani nello spazio Federico Lastaria, Analisi e Geometria 1 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it ette e piani nello spazio. 9 Gennaio
ette e piani nello spazio Federico Lastaria, Analisi e Geometria 1 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it ette e piani nello spazio. 9 Gennaio
Corso di Laurea in Scienze dell Architettura. Corso di Fondamenti e Applicazioni di Geometria Descrittiva
 Università degli Studi di Roma Facoltà di Architettura Ludovico Quaroni - AA 2014-2015 Corso di Laurea in Scienze dell Architettura Corso di Fondamenti e Applicazioni di Geometria Descrittiva Riccardo
Università degli Studi di Roma Facoltà di Architettura Ludovico Quaroni - AA 2014-2015 Corso di Laurea in Scienze dell Architettura Corso di Fondamenti e Applicazioni di Geometria Descrittiva Riccardo
Esercitazione di Analisi Matematica II
 Esercitazione di Analisi Matematica II Barbara Balossi 06/04/2017 Esercizi di ripasso Esercizio 1 Sia data l applicazione lineare f : R 3 R 3 definita come f(x, y, z) = ( 2x + y z, x 2y + z, x y). a) Calcolare
Esercitazione di Analisi Matematica II Barbara Balossi 06/04/2017 Esercizi di ripasso Esercizio 1 Sia data l applicazione lineare f : R 3 R 3 definita come f(x, y, z) = ( 2x + y z, x 2y + z, x y). a) Calcolare
PROIEZIONI ASSONOMETRICHE E PROIEZIONI ORTOGONALI
 PROIEZIONI ASSONOMETRICHE E PROIEZIONI ORTOGONALI Le Proiezioni Assonometriche (o Assonometrie), costituiscono un metodo sintetico del disegno tecnico che permette di avere una visione generale di un oggetto
PROIEZIONI ASSONOMETRICHE E PROIEZIONI ORTOGONALI Le Proiezioni Assonometriche (o Assonometrie), costituiscono un metodo sintetico del disegno tecnico che permette di avere una visione generale di un oggetto
Geometria Analitica Domande e Risposte
 Geometria Analitica Domande e Risposte A. Il Piano Cartesiano. Qual è la formula della distanza tra due punti nel piano cartesiano? Per calcolare la formula della distanza tra due punti nel piano cartesiano
Geometria Analitica Domande e Risposte A. Il Piano Cartesiano. Qual è la formula della distanza tra due punti nel piano cartesiano? Per calcolare la formula della distanza tra due punti nel piano cartesiano
Combinazione operatori di simmetria senza componenti traslazionali
 Combinazione operatori di simmetria senza componenti traslazionali E possibile combinare diversi operatori di simmetria per ottenere modelli tridimensionali. La combinazione non deve portare alla formazione
Combinazione operatori di simmetria senza componenti traslazionali E possibile combinare diversi operatori di simmetria per ottenere modelli tridimensionali. La combinazione non deve portare alla formazione
1.4 Geometria analitica
 1.4 Geometria analitica IL PIANO CARTESIANO Per definire un riferimento cartesiano nel piano euclideo prendiamo: Un punto detto origine i Due rette orientate passanti per. ii Due punti e per definire le
1.4 Geometria analitica IL PIANO CARTESIANO Per definire un riferimento cartesiano nel piano euclideo prendiamo: Un punto detto origine i Due rette orientate passanti per. ii Due punti e per definire le
LA RETTA NEL PIANO CARTESIANO
 LA RETTA NEL PIANO CARTESIANO LE COORDINATE CARTESIANE Quando si vuole fissare un sistema di coordinate cartesiane su una retta r, è necessario considerare: un punto O detto origine; un verso di percorrenza;
LA RETTA NEL PIANO CARTESIANO LE COORDINATE CARTESIANE Quando si vuole fissare un sistema di coordinate cartesiane su una retta r, è necessario considerare: un punto O detto origine; un verso di percorrenza;
Corso multimediale di matematica
 2006 GEOMETRIA ANALITICA Il piano cartesiano rof. Calogero Contrino iano cartesiano Su un piano, si considerino due rette incidenti, sulle quali siano fissati due sistemi di ascisse. Si trasli una delle
2006 GEOMETRIA ANALITICA Il piano cartesiano rof. Calogero Contrino iano cartesiano Su un piano, si considerino due rette incidenti, sulle quali siano fissati due sistemi di ascisse. Si trasli una delle
Ricordiamo. 1. Tra le equazioni delle seguenti rette individua e disegna quelle parallele all asse delle ascisse:
 La retta Retta e le sue equazioni Equazioni di rette come luogo geometrico y = h h R equazione di una retta parallela all asse delle ascisse x = 0 equazione dell asse delle ordinate y = h h R equazione
La retta Retta e le sue equazioni Equazioni di rette come luogo geometrico y = h h R equazione di una retta parallela all asse delle ascisse x = 0 equazione dell asse delle ordinate y = h h R equazione
Corso di Geometria BIAR, BSIR Esercizi 8: soluzioni
 Corso di Geometria 2010-11 BIAR, BSIR Esercizi 8: soluzioni Esercizio 1. a) Disegnare la retta r di equazione cartesiana x 2y 4 = 0. b) Determinare l equazione cartesiana della retta r 1 passante per P
Corso di Geometria 2010-11 BIAR, BSIR Esercizi 8: soluzioni Esercizio 1. a) Disegnare la retta r di equazione cartesiana x 2y 4 = 0. b) Determinare l equazione cartesiana della retta r 1 passante per P
ASSONOMETRIA E PROSPETTIVA
 ASSONOMETRIA E PROSPETTIVA 2 Assonometria: trasformazione di uno spazio vettoriale a tre dimensioni in uno a due, in modo che i raggi di proiezione siano paralleli tra loro. Prospettiva: trasformazione
ASSONOMETRIA E PROSPETTIVA 2 Assonometria: trasformazione di uno spazio vettoriale a tre dimensioni in uno a due, in modo che i raggi di proiezione siano paralleli tra loro. Prospettiva: trasformazione
Insiemistica. Capitolo 1. Prerequisiti. Obiettivi. Gli insiemi numerici di base Divisibilità e fattorizzazione nei numeri interi
 Capitolo 1 Insiemistica Prerequisiti Gli insiemi numerici di base Divisibilità e fattorizzazione nei numeri interi Obiettivi Sapere utilizzare opportunamente le diverse rappresentazioni insiemistiche Sapere
Capitolo 1 Insiemistica Prerequisiti Gli insiemi numerici di base Divisibilità e fattorizzazione nei numeri interi Obiettivi Sapere utilizzare opportunamente le diverse rappresentazioni insiemistiche Sapere
Le simmetrie dei poliedri regolari
 Le simmetrie dei poliedri regolari Le isometrie del piano e dello spazio sono state classificate da due illustri matematici. Per quanto riguarda il piano, il teorema di Chasles, del 8, afferma che nel
Le simmetrie dei poliedri regolari Le isometrie del piano e dello spazio sono state classificate da due illustri matematici. Per quanto riguarda il piano, il teorema di Chasles, del 8, afferma che nel
STRUTTURA DEI SOLIDI
 STRUTTURA DEI SOLIDI I solidi possono essere classificati in funzione della regolarità con cui gli atomi o gli ioni si dispongono nello spazio. Un materiale è detto cristallino se caratterizzato da configuarazioni
STRUTTURA DEI SOLIDI I solidi possono essere classificati in funzione della regolarità con cui gli atomi o gli ioni si dispongono nello spazio. Un materiale è detto cristallino se caratterizzato da configuarazioni
Geometria euclidea. Alessio del Vigna. Lunedì 15 settembre
 Geometria euclidea Alessio del Vigna Lunedì 15 settembre La geometria euclidea è una teoria fondata su quattro enti primitivi e sulle relazioni che tra essi intercorrono. I quattro enti primitivi in questione
Geometria euclidea Alessio del Vigna Lunedì 15 settembre La geometria euclidea è una teoria fondata su quattro enti primitivi e sulle relazioni che tra essi intercorrono. I quattro enti primitivi in questione
1 Rette e piani in R 3
 POLITECNICO DI MILANO. FACOLTÀ DI INGEGNERIA INDUSTRIALE. Analisi e Geometria 1. Sez. D - G. Docenti: Federico G. Lastaria, Mauro Saita, Nadir Zanchetta,. 1 1 Rette e piani in R 3 Una retta parametrizzata
POLITECNICO DI MILANO. FACOLTÀ DI INGEGNERIA INDUSTRIALE. Analisi e Geometria 1. Sez. D - G. Docenti: Federico G. Lastaria, Mauro Saita, Nadir Zanchetta,. 1 1 Rette e piani in R 3 Una retta parametrizzata
LE COORDINATE CARTESIANE
 CORSO ZERO DI MATEMATICA per Ing. Chimica e Ing. delle Telecomunicazioni GEOMETRIA ANALITICA Prof. Erasmo Modica erasmo@galois.it LE COORDINATE CARTESIANE Quando si vuole fissare un sistema di coordinate
CORSO ZERO DI MATEMATICA per Ing. Chimica e Ing. delle Telecomunicazioni GEOMETRIA ANALITICA Prof. Erasmo Modica erasmo@galois.it LE COORDINATE CARTESIANE Quando si vuole fissare un sistema di coordinate
LA GEOMETRIA DELLO SPAZIO
 LA GEOMETRIA ELLO SPAZIO 1 alcola l area e il perimetro del triangolo individuato dai punti A ; 0; 4, ; 1; 5 e 0; ;. ( ) ( ) ( ) 9 ; + 6 Stabilisci se il punto A ( 1;1; ) appartiene all intersezione dei
LA GEOMETRIA ELLO SPAZIO 1 alcola l area e il perimetro del triangolo individuato dai punti A ; 0; 4, ; 1; 5 e 0; ;. ( ) ( ) ( ) 9 ; + 6 Stabilisci se il punto A ( 1;1; ) appartiene all intersezione dei
1 Nozioni utili sul piano cartesiano
 Nozioni utili sul piano cartesiano Nozioni utili sul piano cartesiano Il piano cartesiano è un sistema di riferimento costituito da due rette perpendicolari (una orizzontale detta asse delle ascisse x
Nozioni utili sul piano cartesiano Nozioni utili sul piano cartesiano Il piano cartesiano è un sistema di riferimento costituito da due rette perpendicolari (una orizzontale detta asse delle ascisse x
Rette e piani in R 3
 Rette e piani in R 3 In questa dispensa vogliamo introdurre in modo elementare rette e piani nello spazio R 3 (si faccia riferimento anche al testo Algebra Lineare di S. Lang). 1 Rette in R 3 Vogliamo
Rette e piani in R 3 In questa dispensa vogliamo introdurre in modo elementare rette e piani nello spazio R 3 (si faccia riferimento anche al testo Algebra Lineare di S. Lang). 1 Rette in R 3 Vogliamo
Punti nel piano cartesiano
 Punti nel piano cartesiano In un piano consideriamo due rette perpendicolari che chiamiamo x e. Solitamente, disegniamo la retta x (ascisse) orizzontalmente e orientata da sinistra a destra, la retta e
Punti nel piano cartesiano In un piano consideriamo due rette perpendicolari che chiamiamo x e. Solitamente, disegniamo la retta x (ascisse) orizzontalmente e orientata da sinistra a destra, la retta e
Elementi di matematica - dott. I. GRASSI
 Gli assi cartesiani e la retta. Il concetto di derivata. È ormai d uso comune nei libri, in televisione, nei quotidiani descrivere fenomeni di varia natura per mezzo di rappresentazioni grafiche. Tali
Gli assi cartesiani e la retta. Il concetto di derivata. È ormai d uso comune nei libri, in televisione, nei quotidiani descrivere fenomeni di varia natura per mezzo di rappresentazioni grafiche. Tali
CURRICOLO DELLA SCUOLA SECONDARIA DI PRIMO GRADO DISCIPLINA: MATEMATICA CLASSE 1^
 CURRICOLO DELLA SCUOLA SECONDARIA DI PRIMO GRADO DISCIPLINA: MATEMATICA CLASSE 1^ Nucleo fondante 1: IL NUMERO Argomento 1: Sistemi di numerazione Sa rappresentare graficamente numeri, ordinarli e confrontarli.
CURRICOLO DELLA SCUOLA SECONDARIA DI PRIMO GRADO DISCIPLINA: MATEMATICA CLASSE 1^ Nucleo fondante 1: IL NUMERO Argomento 1: Sistemi di numerazione Sa rappresentare graficamente numeri, ordinarli e confrontarli.
1 Prodotto cartesiano di due insiemi 1. 5 Soluzioni degli esercizi 6
 1 PRODOTTO CARTESIANO DI DUE INSIEMI 1 I-4 R 2 ed R 3 Piano e spazio cartesiani Indice 1 Prodotto cartesiano di due insiemi 1 2 Rappresentazione di R 2 sul piano cartesiano 2 3 Sottoinsiemi di R 2 e regioni
1 PRODOTTO CARTESIANO DI DUE INSIEMI 1 I-4 R 2 ed R 3 Piano e spazio cartesiani Indice 1 Prodotto cartesiano di due insiemi 1 2 Rappresentazione di R 2 sul piano cartesiano 2 3 Sottoinsiemi di R 2 e regioni
Circonferenze del piano
 Circonferenze del piano 1 novembre 1 Circonferenze del piano 1.1 Definizione Una circonferenza è il luogo dei punti equidistanti da un punto fisso, detto centro. La distanza di un qualunque punto della
Circonferenze del piano 1 novembre 1 Circonferenze del piano 1.1 Definizione Una circonferenza è il luogo dei punti equidistanti da un punto fisso, detto centro. La distanza di un qualunque punto della
CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA
 CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA FOGLIO DI ESERCIZI 1 GEOMETRIA 2009/10 Esercizio 1.1 (2.2). Determinare l equazione parametrica e Cartesiana della retta dello spazio (a) Passante per i
CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA FOGLIO DI ESERCIZI 1 GEOMETRIA 2009/10 Esercizio 1.1 (2.2). Determinare l equazione parametrica e Cartesiana della retta dello spazio (a) Passante per i
Geometria BATR-BCVR Esercizi 9
 Geometria BATR-BCVR 2015-16 Esercizi 9 Esercizio 1. Per ognuna delle matrici A i si trovi una matrice ortogonale M i tale che Mi ta im sia diagonale. ( ) 1 1 2 3 2 A 1 = A 2 1 2 = 1 1 0 2 0 1 Esercizio
Geometria BATR-BCVR 2015-16 Esercizi 9 Esercizio 1. Per ognuna delle matrici A i si trovi una matrice ortogonale M i tale che Mi ta im sia diagonale. ( ) 1 1 2 3 2 A 1 = A 2 1 2 = 1 1 0 2 0 1 Esercizio
UNITÀ DIDATTICA 5 LA RETTA
 UNITÀ DIDATTICA 5 LA RETTA 5.1 - La retta Equazione generica della retta Dalle considerazioni emerse nel precedente capitolo abbiamo compreso come una funzione possa essere rappresentata da un insieme
UNITÀ DIDATTICA 5 LA RETTA 5.1 - La retta Equazione generica della retta Dalle considerazioni emerse nel precedente capitolo abbiamo compreso come una funzione possa essere rappresentata da un insieme
STRUTTURA E GEOMETRIA CRISTALLINA
 STRUTTURA E GEOMETRIA CRISTALLINA La struttura fisica dei materiali solidi dipende dalla disposizione degli atomi, ioni o molecole che compongono il solido e dalle forze che li legano fra loro. Quando
STRUTTURA E GEOMETRIA CRISTALLINA La struttura fisica dei materiali solidi dipende dalla disposizione degli atomi, ioni o molecole che compongono il solido e dalle forze che li legano fra loro. Quando
Cerchio di Mohr. n y. n x
 t nm m t n P n s n Sia P un punto generico del continuo e z una generica retta passante per esso. Fissato un riferimento cartesiano {,, z}, siano n=[n n 0] T ed m=[m m 0] T due versori ortogonali nel piano
t nm m t n P n s n Sia P un punto generico del continuo e z una generica retta passante per esso. Fissato un riferimento cartesiano {,, z}, siano n=[n n 0] T ed m=[m m 0] T due versori ortogonali nel piano
Geometria euclidea. Alessio del Vigna
 Geometria euclidea Alessio del Vigna La geometria euclidea è una teoria fondata su quattro enti primitivi e sulle relazioni che tra essi intercorrono. I quattro enti primitivi in questione sono il punto,
Geometria euclidea Alessio del Vigna La geometria euclidea è una teoria fondata su quattro enti primitivi e sulle relazioni che tra essi intercorrono. I quattro enti primitivi in questione sono il punto,
MINERALOGIA Corso di Laurea in Scienze Naturali II Anno I Sem. - 9 CFU A.A
 MINERALOGIA Corso di Laurea in Scienze Naturali II Anno I Sem. - 9 CFU A.A. 2008-2009 Prof. Antonio GIANFAGNA Dipartimento di Scienze della Terra Stanza 309, Edificio Mineralogia Tel. 06-49914921 e-mail:
MINERALOGIA Corso di Laurea in Scienze Naturali II Anno I Sem. - 9 CFU A.A. 2008-2009 Prof. Antonio GIANFAGNA Dipartimento di Scienze della Terra Stanza 309, Edificio Mineralogia Tel. 06-49914921 e-mail:
Proiezioni Stereografiche in Geologia Strutturale. Chiara Frassi, Rodolfo Carosi e Chiara Montomoli
 Proiezioni Stereografiche in Geologia Strutturale Chiara Frassi, Rodolfo Carosi e Chiara Montomoli Sommario Prefazione 3 1. Orientazione di piani e linee 7 1. Elementi lineari e planari 7 1.1. Misura di
Proiezioni Stereografiche in Geologia Strutturale Chiara Frassi, Rodolfo Carosi e Chiara Montomoli Sommario Prefazione 3 1. Orientazione di piani e linee 7 1. Elementi lineari e planari 7 1.1. Misura di
I vertici e i lati di ogni poligono vengono detti rispettivamente vertici e spigoli del poliedro.
 1 I poliedri diagonale DEFINIZIONE. Un poliedro è la parte di spazio delimitata da poligoni posti su piani diversi in modo tale che ogni lato sia comune a due di essi. I poligoni che delimitano il poliedro
1 I poliedri diagonale DEFINIZIONE. Un poliedro è la parte di spazio delimitata da poligoni posti su piani diversi in modo tale che ogni lato sia comune a due di essi. I poligoni che delimitano il poliedro
REGISTRO DELLE ESERCITAZIONI
 UNIVERSITA DEGLI STUDI DI GENOVA FACOLTA DI SCIENZE MATEMATICHE, FISICHE E NATURALI REGISTRO DELLE ESERCITAZIONI del Corso UFFICIALE di GEOMETRIA A tenute dal prof. Domenico AREZZO nell anno accademico
UNIVERSITA DEGLI STUDI DI GENOVA FACOLTA DI SCIENZE MATEMATICHE, FISICHE E NATURALI REGISTRO DELLE ESERCITAZIONI del Corso UFFICIALE di GEOMETRIA A tenute dal prof. Domenico AREZZO nell anno accademico
Esercizi svolti. Geometria analitica: rette e piani
 Esercizi svolti. Sistemi di riferimento e vettori. Dati i vettori v = i + j k, u =i + j + k determinare:. il vettore v + u ;. gli angoli formati da v e u;. i vettore paralleli alle bisettrici di tali angoli;
Esercizi svolti. Sistemi di riferimento e vettori. Dati i vettori v = i + j k, u =i + j + k determinare:. il vettore v + u ;. gli angoli formati da v e u;. i vettore paralleli alle bisettrici di tali angoli;
B6. Sistemi di primo grado
 B6. Sistemi di primo grado Nelle equazioni l obiettivo è determinare il valore dell incognita che verifica l equazione. Tale valore, se c è, è detto soluzione. In un sistema di equazioni l obiettivo è
B6. Sistemi di primo grado Nelle equazioni l obiettivo è determinare il valore dell incognita che verifica l equazione. Tale valore, se c è, è detto soluzione. In un sistema di equazioni l obiettivo è
Esercizi Riepilogativi Svolti. = 1 = Or(v, w)
 Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA (Edile-Architettura e dell Edilizia FORMULE DI GEOMETRIA IN R TRASFORMAZIONI DI R CIRCONFERENZE Docente: Prof F Flamini
Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA (Edile-Architettura e dell Edilizia FORMULE DI GEOMETRIA IN R TRASFORMAZIONI DI R CIRCONFERENZE Docente: Prof F Flamini
Diffrazione di Raggi X
 Diffrazione di Raggi X 1. Laue, Friedrich, Knipping (Monaco, 1912): diffrazione da reticolo tridimensionale 2. Ewald (Tesi di dottorato, Monaco, 1913): costruzione del reticolo reciproco 3. Bragg and Bragg
Diffrazione di Raggi X 1. Laue, Friedrich, Knipping (Monaco, 1912): diffrazione da reticolo tridimensionale 2. Ewald (Tesi di dottorato, Monaco, 1913): costruzione del reticolo reciproco 3. Bragg and Bragg
Il valore assoluto (lunghezza, intensita )
 Il valore assoluto (lunghezza, intensita ) = se 0 - se < 0 = 5 5-0, = 0 3, = 3 Il valore assoluto di un numero reale è quindi sempre un numero positivo. Geometricamente rappresenta la misura della distanza
Il valore assoluto (lunghezza, intensita ) = se 0 - se < 0 = 5 5-0, = 0 3, = 3 Il valore assoluto di un numero reale è quindi sempre un numero positivo. Geometricamente rappresenta la misura della distanza
GEOMETRIA ANALITICA Prof. Erasmo Modica
 ISTITUTO PROVINCIALE DI CULTURA E LINGUE NINNI CASSARÀ SEZIONE DISTACCATA DI CEFALÙ CLASSE V C GEOMETRIA ANALITICA Prof. Erasmo Modica LE COORDINATE CARTESIANE Quando si vuole fissare un sistema di coordinate
ISTITUTO PROVINCIALE DI CULTURA E LINGUE NINNI CASSARÀ SEZIONE DISTACCATA DI CEFALÙ CLASSE V C GEOMETRIA ANALITICA Prof. Erasmo Modica LE COORDINATE CARTESIANE Quando si vuole fissare un sistema di coordinate
1. conoscere i concetti fondamentali della geometria sintetica del piano (poligoni, circonferenza
 Terzo modulo: Geometria Obiettivi 1. conoscere i concetti fondamentali della geometria sintetica del piano (poligoni, circonferenza e cerchio, ecc.). calcolare perimetri e aree di figure elementari nel
Terzo modulo: Geometria Obiettivi 1. conoscere i concetti fondamentali della geometria sintetica del piano (poligoni, circonferenza e cerchio, ecc.). calcolare perimetri e aree di figure elementari nel
GEOMETRIA ANALITICA 1 IL PIANO CARTESIANO
 GEOMETRI NLITIC 1 IL PINO CRTESINO Il piano cartesiano è costituito da due rette orientate e tra loro perpendicolari chiamate assi cartesiani, generalmente una orizzontale e l altra verticale, sulle quali
GEOMETRI NLITIC 1 IL PINO CRTESINO Il piano cartesiano è costituito da due rette orientate e tra loro perpendicolari chiamate assi cartesiani, generalmente una orizzontale e l altra verticale, sulle quali
II Università degli Studi di Roma
 Versione preliminare gennaio TOR VERGATA II Università degli Studi di Roma Dispense di Geometria. Capitolo 3. 7. Coniche in R. Nel Capitolo I abbiamo visto che gli insiemi di punti P lineare di primo grado
Versione preliminare gennaio TOR VERGATA II Università degli Studi di Roma Dispense di Geometria. Capitolo 3. 7. Coniche in R. Nel Capitolo I abbiamo visto che gli insiemi di punti P lineare di primo grado
Insiemi di numeri reali
 Capitolo 1 1.1 Elementi di teoria degli insiemi Se S è una totalità di oggetti x, si dice che S è uno spazio avente gli elementi x. Se si considerano alcuni elementi di S si dice che essi costituiscono
Capitolo 1 1.1 Elementi di teoria degli insiemi Se S è una totalità di oggetti x, si dice che S è uno spazio avente gli elementi x. Se si considerano alcuni elementi di S si dice che essi costituiscono
Seconda gara matematica ( ) Soluzioni
 Seconda gara matematica (9..00) Soluzioni 1. Dato un parallelepipedo solido cioè senza buchi al suo interno formato da 180 cubetti e avente spigoli di lunghezza a, b, c, il numero N di cubetti visibili
Seconda gara matematica (9..00) Soluzioni 1. Dato un parallelepipedo solido cioè senza buchi al suo interno formato da 180 cubetti e avente spigoli di lunghezza a, b, c, il numero N di cubetti visibili
( ρ, θ + π ) sono le coordinate dello stesso punto. Pertanto un punto P può essere descritto come
 Coordinate polari Il sistema delle coordinate cartesiane è uno dei possibili sistemi per individuare la posizione di un punto del piano, relativamente ad un punto fisso O, mediante una coppia ordinata
Coordinate polari Il sistema delle coordinate cartesiane è uno dei possibili sistemi per individuare la posizione di un punto del piano, relativamente ad un punto fisso O, mediante una coppia ordinata
Esercitazione struttura
 Esercitazione struttura 1/5. DENSITÀ DI VOLUME Per un elemento, avente peso atomico 106.400, sono stati misurati il suo raggio atomico (r0.176 nm) e la sua densità (ρ1.2 10 4 kg/m ). Verificare se la cella
Esercitazione struttura 1/5. DENSITÀ DI VOLUME Per un elemento, avente peso atomico 106.400, sono stati misurati il suo raggio atomico (r0.176 nm) e la sua densità (ρ1.2 10 4 kg/m ). Verificare se la cella
Fisica dello Stato Solido
 Fisica dello Stato Solido Lezione n.1 Strutture Cristalline Mara Bruzzi Corso di Laurea Specialistica Ingegneria Elettronica a.a.07-08 Scaricabile al sito: http://www.de.unifi.it/fisica/bruzzi/bruzzi_dida_fss.html
Fisica dello Stato Solido Lezione n.1 Strutture Cristalline Mara Bruzzi Corso di Laurea Specialistica Ingegneria Elettronica a.a.07-08 Scaricabile al sito: http://www.de.unifi.it/fisica/bruzzi/bruzzi_dida_fss.html
OBIETTIVI DI APPRENDIMENTO DI MATEMATICA-SCUOLA SECONDARIA DI PRIMO GRADO
 OBIETTIVI DI APPRENDIMENTO DI MATEMATICA-SCUOLA SECONDARIA DI PRIMO GRADO OBIETTIVI DELLE INDICAZIONI PER IL CURRICOLO OBIETTIVI DI APPRENDIMENTO ANNUALI Classe prima- secondaria Classe seconda secondaria
OBIETTIVI DI APPRENDIMENTO DI MATEMATICA-SCUOLA SECONDARIA DI PRIMO GRADO OBIETTIVI DELLE INDICAZIONI PER IL CURRICOLO OBIETTIVI DI APPRENDIMENTO ANNUALI Classe prima- secondaria Classe seconda secondaria
L P R P OIEZI Z ONI N A S A S S O S NO N METRICHE
 LE PROIEZIONI ASSONOMETRICHE La proiezione assonometrica fa parte delle proiezioni parallele, o cilindriche. Essa è caratterizzata quindi dall avere il centro di proiezione all infinito (S ), per cui è
LE PROIEZIONI ASSONOMETRICHE La proiezione assonometrica fa parte delle proiezioni parallele, o cilindriche. Essa è caratterizzata quindi dall avere il centro di proiezione all infinito (S ), per cui è
x 1 Fig.1 Il punto P = P =
 Geometria di R 2 In questo paragrafo discutiamo le proprietà geometriche elementari del piano Per avere a disposizione delle coordinate nel piano, fissiamo un punto, che chiamiamo l origine Scegliamo poi
Geometria di R 2 In questo paragrafo discutiamo le proprietà geometriche elementari del piano Per avere a disposizione delle coordinate nel piano, fissiamo un punto, che chiamiamo l origine Scegliamo poi
La retta nel piano cartesiano
 La retta nel piano cartesiano note a cura di Luigi Carlo Oldani - novembre 9 A technique ceases to be a trick and becomes a method only when it has been encountered enough times to seem natural. W.J.LeVeque,
La retta nel piano cartesiano note a cura di Luigi Carlo Oldani - novembre 9 A technique ceases to be a trick and becomes a method only when it has been encountered enough times to seem natural. W.J.LeVeque,
Costruzioni geometriche. (Teoria pag , esercizi )
 Costruzioni geometriche. (Teoria pag. 81-96, esercizi 141-153 ) 1) Costruzione con squadra e riga. a) Rette parallele. Ricorda: due rette sono parallele quando.... oppure quando hanno la stessa. Matematicamente
Costruzioni geometriche. (Teoria pag. 81-96, esercizi 141-153 ) 1) Costruzione con squadra e riga. a) Rette parallele. Ricorda: due rette sono parallele quando.... oppure quando hanno la stessa. Matematicamente
LAVORO ESTIVO di MATEMATICA Classi Terze Scientifico Moderno N.B. DA CONSEGNARE ALLA PRIMA LEZIONE DI MATEMATICA DI SETTEMBRE
 LAVORO ETIVO di MATEMATICA Classi Terze cientifico Moderno N.B. A CONEGNARE ALLA PRIMA LEZIONE I MATEMATICA I ETTEMBRE PROBLEMI I ALGEBRA APPLICATA ALLA GEOMETRIA ) In un cerchio di raggio r si determini
LAVORO ETIVO di MATEMATICA Classi Terze cientifico Moderno N.B. A CONEGNARE ALLA PRIMA LEZIONE I MATEMATICA I ETTEMBRE PROBLEMI I ALGEBRA APPLICATA ALLA GEOMETRIA ) In un cerchio di raggio r si determini
COMPETENZE U.D.A. ABILITA CONTENUTI _ Saper operare con il sistema di numerazione decimale.
 SCUOLA SECONDARIA DI 1 GRADO TOVINI CURRICOLO DI SCIENZE MATEMATICHE PER LA CLASSE PRIMA COMPETENZE U.D.A. ABILITA CONTENUTI _ Saper operare con il sistema di numerazione decimale. _Il concetto di insieme.
SCUOLA SECONDARIA DI 1 GRADO TOVINI CURRICOLO DI SCIENZE MATEMATICHE PER LA CLASSE PRIMA COMPETENZE U.D.A. ABILITA CONTENUTI _ Saper operare con il sistema di numerazione decimale. _Il concetto di insieme.
PROIEZIONI ASSONOMETRICHE
 1 ci permettono di disegnare un solido, che ha 3 dimensioni, su un foglio che ha 2 dimensioni PROIEZIONI ORTOGONALI PROIEZIONI ASSONOMETRICHE PROIEZIONI PROSPETTICHE Libro consigliato: Disegno Laboratorio
1 ci permettono di disegnare un solido, che ha 3 dimensioni, su un foglio che ha 2 dimensioni PROIEZIONI ORTOGONALI PROIEZIONI ASSONOMETRICHE PROIEZIONI PROSPETTICHE Libro consigliato: Disegno Laboratorio
Testi verifiche 3 C 3 I a. s. 2008/2009
 Testi verifiche 3 C 3 I a. s. 2008/2009 1) Sono assegnati i punti A(- 1; 3) C(3; 0) M ;1 a) Ricavare le coordinate del simmetrico di A rispetto a M e indicarlo con B. Verificare che il segmento congiungente
Testi verifiche 3 C 3 I a. s. 2008/2009 1) Sono assegnati i punti A(- 1; 3) C(3; 0) M ;1 a) Ricavare le coordinate del simmetrico di A rispetto a M e indicarlo con B. Verificare che il segmento congiungente
Sistemi cristallini 1
 Sistemi cristallini Esercizio Calcolare la densità atomica definita come il rapporto tra il numero di atomi e il volume unitario per ) il litio sapendo che la distanza tra i centri dei primi vicini è R
Sistemi cristallini Esercizio Calcolare la densità atomica definita come il rapporto tra il numero di atomi e il volume unitario per ) il litio sapendo che la distanza tra i centri dei primi vicini è R
Geometria analitica piana
 Geometria analitica piana 1. La geometria analitica Il metodo della geometria analitica consiste nell applicare gli strumenti dell algebra allo studio della geometria. Il legame tra enti algebrici ed enti
Geometria analitica piana 1. La geometria analitica Il metodo della geometria analitica consiste nell applicare gli strumenti dell algebra allo studio della geometria. Il legame tra enti algebrici ed enti
Corso di Geometria BIAR, BSIR Esercizi 10: soluzioni
 Corso di Geometria 2010-11 BIAR, BSIR Esercizi 10: soluzioni 1 Geometria dello spazio Esercizio 1. Dato il punto P 0 = ( 1, 0, 1) e il piano π : x + y + z 2 = 0, determinare: a) Le equazioni parametriche
Corso di Geometria 2010-11 BIAR, BSIR Esercizi 10: soluzioni 1 Geometria dello spazio Esercizio 1. Dato il punto P 0 = ( 1, 0, 1) e il piano π : x + y + z 2 = 0, determinare: a) Le equazioni parametriche
Test di Matematica di base
 Test di Matematica di base Geometria Il rapporto tra la superficie di un quadrato e quella di un triangolo equilatero di eguale lato è a. 4 b. 4 d. [ ] Quali sono le ascisse dei punti della curva di equazione
Test di Matematica di base Geometria Il rapporto tra la superficie di un quadrato e quella di un triangolo equilatero di eguale lato è a. 4 b. 4 d. [ ] Quali sono le ascisse dei punti della curva di equazione
Le coniche: circonferenza, parabola, ellisse e iperbole.
 Le coniche: circonferenza, parabola, ellisse e iperbole. Teoria in sintesi Queste curve si chiamano coniche perché sono ottenute tramite l intersezione di una superficie conica con un piano. Si possono
Le coniche: circonferenza, parabola, ellisse e iperbole. Teoria in sintesi Queste curve si chiamano coniche perché sono ottenute tramite l intersezione di una superficie conica con un piano. Si possono
Geometria analitica del piano II (M.S. Bernabei & H. Thaler)
 Geometria analitica del piano II (M.S. Bernabei & H. Thaler) Equazione della retta in forma esplicita Sia data una retta r ax + by + c = 0 con b 0. Svolgendo questa equazione per y otteniamo e ponendo
Geometria analitica del piano II (M.S. Bernabei & H. Thaler) Equazione della retta in forma esplicita Sia data una retta r ax + by + c = 0 con b 0. Svolgendo questa equazione per y otteniamo e ponendo
Francesco Zumbo
 La retta - Teorema di Talete - Equazione della retta: passante per due punti, implicita, esplicita - Parallele e Perpendicolari - Fascio Propio e improprio - Intersezione tra rette Francesco Zumbo www.francescozumbo.it
La retta - Teorema di Talete - Equazione della retta: passante per due punti, implicita, esplicita - Parallele e Perpendicolari - Fascio Propio e improprio - Intersezione tra rette Francesco Zumbo www.francescozumbo.it
D3. Parabola - Esercizi
 D3. Parabola - Esercizi Traccia il grafico delle seguenti parabole e trova i punti d incontro con l asse e con l asse graficamente e/o algebricamente. 1) = ++ (0;)] ) = -+1 ( + 3 ;0), ( 3 ;0), (0;1)] 3)
D3. Parabola - Esercizi Traccia il grafico delle seguenti parabole e trova i punti d incontro con l asse e con l asse graficamente e/o algebricamente. 1) = ++ (0;)] ) = -+1 ( + 3 ;0), ( 3 ;0), (0;1)] 3)
Funzioni goniometriche
 Funzioni goniometriche In questa dispensa vengono introdotte le definizioni delle funzioni goniometriche. Preliminarmente si introducono le convenzioni sull orientazione degli angoli e sulla loro rappresentazione
Funzioni goniometriche In questa dispensa vengono introdotte le definizioni delle funzioni goniometriche. Preliminarmente si introducono le convenzioni sull orientazione degli angoli e sulla loro rappresentazione
Nozioni introduttive e notazioni
 Nozioni introduttive e notazioni 1.1 Insiemi La teoria degli insiemi è alla base di tutta la matematica, in quanto ne fornisce il linguaggio base e le notazioni. Definiamo un insieme come una collezione
Nozioni introduttive e notazioni 1.1 Insiemi La teoria degli insiemi è alla base di tutta la matematica, in quanto ne fornisce il linguaggio base e le notazioni. Definiamo un insieme come una collezione
Proprietà fisiche e Anisotropia Gabriella Salviulo Università di Padova
 Proprietà fisiche e Anisotropia Gabriella Salviulo Università di Padova La Fisica dei Minerali: implicazioni geologiche e applicazioni pratiche 2-5 Febbraio 2015 Bressanone OBIETTIVO N 1: ALLINEATI ALLA
Proprietà fisiche e Anisotropia Gabriella Salviulo Università di Padova La Fisica dei Minerali: implicazioni geologiche e applicazioni pratiche 2-5 Febbraio 2015 Bressanone OBIETTIVO N 1: ALLINEATI ALLA
Minicorso Regole di Disegno Meccanico
 Parte 2 Minicorso Regole di Disegno Meccanico di Andrea Saviano Linee di misura e linee di riferimento Linee per indicazioni particolari Quote e relativa disposizione Sistemi di quotatura Conicità, inclinazione
Parte 2 Minicorso Regole di Disegno Meccanico di Andrea Saviano Linee di misura e linee di riferimento Linee per indicazioni particolari Quote e relativa disposizione Sistemi di quotatura Conicità, inclinazione
g. Ferrari M. Cerini D. giallongo Piattaforma informatica geometria 3 trevisini EDITORE
 g. Ferrari M. Cerini D. giallongo Piattaforma Ma Pia a tematica informatica geometria 3 trevisini EDITORE unità 14 2 UNITÀ14 LE MISURE DI CIRCONFERENZA, CERCHIO E LORO PARTI 1. Relazione tra circonferenza
g. Ferrari M. Cerini D. giallongo Piattaforma Ma Pia a tematica informatica geometria 3 trevisini EDITORE unità 14 2 UNITÀ14 LE MISURE DI CIRCONFERENZA, CERCHIO E LORO PARTI 1. Relazione tra circonferenza
Matematica classe 5 C a.s. 2012/2013
 Matematica classe 5 C a.s. 2012/2013 Asintoti e grafici 1) Una funzione y = f(x) gode delle seguenti caratteristiche: D / 4, y 0 se x 0 x 2, lim, 3. Rappresentare un grafico qualitativo della funzione.
Matematica classe 5 C a.s. 2012/2013 Asintoti e grafici 1) Una funzione y = f(x) gode delle seguenti caratteristiche: D / 4, y 0 se x 0 x 2, lim, 3. Rappresentare un grafico qualitativo della funzione.
