Algoritmi per la Visualizzazione. Disegno 2D ortogonale. Disegno ortogonale 2D (1) Disegno ortogonale 2D (2)
|
|
|
- Sergio Colella
- 8 anni fa
- Visualizzazioni
Transcript
1 Algoritmi per la visualizzazione DISEGNO DI GRAFI: ALCUNI CASI PARTICOLARI Disegno 2D ortogonale Disegno ortogonale 2D () Disegno ortogonale 2D (2) Punto di vista umano: primo criterio per giudicare la qualità di una visualizzazione: leggibilità Punto di vista algoritmico: catturare la qualità tramite funzioni obiettivo: evitare! massimizzare il min angolo (risoluzione angolare) caso particolare: tutti gli angoli sono multipli di "/2 (disegno ortogonale) ma diventa inevitabile ricorrere alle svolte! minimizzare il numero di svolte Il problema è complesso un esempio: minimizzare il # di svolte è NP-arduo [Forman et al. 90] punto cruciale della riduzione: trovare l esatto ordinamento degli archi intorno ai nodi se una rappresentazione è fissata: polinomiale 3 4
2 Disegno ortogonale 2D (3) DEF. Un disegno ortogonale su griglia di un grafo G=(V,E) è una funzione biunivoca che mappa vertici v"v in punti a coordinate intere #(v) ed archi (v,w) " E in cammini che non si sovrappongono tali che le immagini dei loro estremi #(v) e #(w) siano connesse dai cammini corrispondenti. Tali cammini sono costituiti da segmenti orizzontali o verticali con le eventuali svolte a coordinate intere. Possibile visualizzare solo grafi con grado # 4! Codifiche di rappresentazioni di grafi () Codifica di un grafo: elenco dei nodi+elenco degli archi Codifica di una rappresentazione piana di un grafo: elenco dei nodi+elenco degli archi+elenco delle facce+verso di percorrenza (convenzionale) F= {f,, f 5 }; P(f ) = (e,e 3,e 5,e 9,e 0,e 4,e 3,e 2 ); P(f 2 ) = (e 2,e ); P(f 3 ) = (e 5,e 6,e 8 ); P(f 4 ) = (e 6,e 4,e 7 ); P(f 5 ) = (e 8,e 7,e 0,e 9 ); v e f 2 e2 v 2 e 3 v 3 f e 4 e 5 e 6 f 4 f 3 v 6 e 7 v 5 f 5 e 0 e8 e9 v 7 v Codifiche di rappresentazioni di grafi (2) Codifica di una rappresentazione ortogonale di un grafo: elenco dei nodi+elenco degli archi+elenco delle facce+info sulla direzione di partenza degli archi+info sulle svolte F= {f,, f 3 }; H(f ) = ((e,!,3),(e 5,,),(e 4,!,3),(e 2 )0,)); H(f 2 ) = ((e,!, ),(e 6,!,2),(e 5,00,)); H(f 3 ) = ((e 2,000,),(e 4,!,),(e 6,!,), (e 3,0,4),(e 3,,)); 3 e f 2 e 5 2 e 6 e 2 e 3 e 4 4 f f Codifiche di rappresentazioni di grafi (3) regole di consistenza: deve esistere un grafo 4-planare a cui la rappresentazione si riferisce; ogni arco deve essere memorizzato due volte, una per ciascuna faccia a cui appartiene, e le due memorizzazioni devono essere consistenti; la somma degli angoli lungo il perimetro di una faccia deve essere consistente col fatto che la faccia sia un poligono chiuso; per ogni vertice, la somma degli angoli che insistono su quel vertice deve essere 4. N.B. non si parla di lunghezza di archi! si può calcolare la rappr. su griglia di area minima [Tamassia 87] 8
3 st-grafi rappresentazione di visibilità DEF. Un st-grafo G=(V,E) è un grafo diretto aciclico che gode delle seguenti proprietà:.ogni vertice v"v è su un cammino da s a t; 2.per ogni vertice v"v, gli archi entranti appaiono consecutivamente intorno a v, e così gli archi uscenti; in questo modo è sempre possibile distinguere in maniera univoca due facce distinte, quella a sinistra di v (tra il primo arco entrante e il primo arco uscente) e quella a destra di v (tra l ultimo arco entrante e l ultimo arco uscente); 3.per ogni faccia f di G, i confini di f sono delimitati da due cammini distinti con origine e destinazione comune 4.tutti i cammini sono orientati da s a t, ossia G ammette sempre un disegno upward. 0 rappresentazione di visibilità () DEF. : Il duale G* di un grafo orientato G è il grafo orientato così definito :.i vertici di G* sono le facce di G, dove s* e t* sono rispettivamente la faccia a destra dell arco (s, t) e la faccia esterna; 2.un arco (f,g) è in G* se la faccia f condivide con la faccia g un arco (v,w) $ (s, t); 3.l arco (f,g) è orientato da f verso g se f si trova a sinistra dell arco orientato (v,w); 4.G* contiene l arco (s*,t*). N.B. il duale di un grafo planare è ancora planare, ed è mantenuto l orientamento (upward$rightward e downward$leftward). rappresentazione di visibilità (2) Dato un qualunque vertice v di G, il valore %(v) è definito come la lunghezza del più lungo cammino per andare da s a v. Per ogni vertice f di G* il valore &(f) è definito come la lunghezza del più lungo cammino per andare da s* a f. &(f)=2 %(v)=2 2
4 rappresentazione di visibilità (3) DEF. [Otten & van Wijk 78]: La rappresentazione di visibilità #(G) di un grafo G=(V,E) è una sua rappresentazione che disegna ogni vertice v"v come un segmento orizzontale #(v), ed ogni arco (v,w)"e come un segmento verticale le cui estremità giacciono su #(v) e #(w) e non interseca nessun altro segmento vertice #(u) con u$v,w. Inoltre, ne i segmenti orizzontali ne i segmenti verticali si sovrappongono. rappresentazione di visibilità (4) TH. [Rosenthal & Tarjan 86] Sia G un st-grafo planare con n vertici. Allora esiste una rappresentazione di visibilità #(G) per G tale che #(G) ha esattamente una sorgente #(s) ed esattamente un pozzo #(t). DIM. Costruttiva. Algoritmo che determini una rappr. di visibilità di G: Input: st-grafo planare G Output: Una rappresentazione di visibilità # del grafo G..costruisci il grafo duale G* di G; 2.calcola, per ogni v di G il valore %(v); 3.calcola, per ogni vertice f di G* il valore &(f); 3 4 rappresentazione di visibilità (5) (segue DIM.) 4.per ogni arco (u,v) di G do disegna un segmento verticale con ascissa x(u,v) = & (Right(u,v)) tra le ordinate %(u) e %(v); 5.per ogni vertice v do disegna un segmento orizzontale con ordinata y(v) = %(v) tra le ascisse più a sinistra e più a destra dei segmenti verticali associati agli archi incidenti su v. CVD rappresentazione di visibilità (6) TH. Sia G un st-grafo planare con n vertici ed f facce. L area della sua rappresentazione di visibilità #(G) è al più (n-) x (2n-5). DIM. La larghezza e l altezza di #(G) sono limitate dal max valore di %(v) e &(f). Il caso peggiore per entrambi è quando il grafo è un cammino!a ' (n-) x (f-). Per dim. che f- ' 2n-5: Def. grafo planare massimale: non è possibile aggiungere archi senza perdere la planarità!grafo triangolato!3f=2m. Per grafi planari qualunque: 3f ' 2m + formula di Eulero: n-m+f=2 2n-2m+2f=4 ( 2n-3f+2f'4 ( 2n-4'f ( f- ' 2n-5 CVD 5 6
5 rappresentazione di visibilità (7) Algoritmo: INPUT: un st-grafo planare OUTPUT: un disegno ortogonale su griglia piano. creazione rappr. di visibilità (tempo O(n)) 2. creazione disegno ortogonale su griglia piano (tempo O(n)) rappresentazione di visibilità (8) segue Algoritmo 3. riduzione delle svolte (tempo O(n)) arco con svolte sia concave che convesse tutti gli archi intorno ad un nodo con svolte dello stesso tipo due archi e ed e 2 formano 90 ed uno ha una svolta convessa 7 8 rappresentazione di visibilità (9) Un esempio passo 2. N.B. il disegno NON è ottimo, ne in termini di area ne di num. di svolte! passo 3. trasf. T passo 3. trasf. T3 9 rappresentazione di visibilità (0) TH. Dato un st-grafo G, l algoritmo precedente ne calcola un disegno ortogonale su griglia piano con O(n 2 ) area in O(n) tempo. Attenzione: se il grafo non è 2-connesso, lo possiamo partizionare nelle sue componenti 2-connesse, costruire le rappresentazioni, e poi riconnetterle in modo che il grafo finale abbia una sola sorgente e t pozzi. O(n) tempo numero di svolte? 20
6 rappresentazione di visibilità () TH. Se la rappr. di visibilità ha t i pozzi ed n i nodi non sorg. di grado i=2,3,4, allora il numero di svolte del disegno è al più n 3 +2n 4 +t 2 +4t 4 +), dove )=0,,2,4, a seconda che la sorgente abbia grado, 2, 3, 4. DIM. t t 2 n 2 t 3 n 3 t 4 n 4 n 4 rappresentazione di visibilità (2) segue dim. Dopo il passo 2. il # di svolte è t 2 +2t 3 +n 3 +4n 4 +6n 4 +4t 4 +) t t 2 n 2 t 3 n 3 t 4 n 4 n #svolte: applicata volta a g e ad h e 2 volte ad i elimino almeno n 4 +2n 4 svolte. CVD 2 22 st-numerazione () Un algoritmo basato sulla st-numerazione Def. dato G 2-connesso, una st-numerazione di G è un etichettatura dei nodi con, 2,, n tale che ogni nodo etichettato j (2 ' j ' n-) abbia almeno un vicino etichettato i<j ed almeno un vicino etichettato con k>j. I nodi etichettati con ed n sono collegati. E immediato indurre un verso agli archi dalle etichette minori a quelle maggiori. Il grafo risultante, con un unica sorgente () ed un unico pozzo (n) è un st-grafo. 24
7 st-numerazione (2) st-numerazione (3) TH. (Even & Tarjan 76) Sia G un grafo 2-connesso, s e t due suoi nodi adiacenti. Allora, esiste una st-numerazione di G che etichetta s con e t con n, che si può determinare in O(n) tempo. Prima di dimostrare il th. osserviamo che se G non è 2-connesso, non è possibile trovare una st-numerazione. Per assurdo è stata trovata una st-numerazione: s C. s e t sono in comp. distinte t C 2 t C C x 2 s 2. s e t sono nella stessa comp. y e z hanno etichette max e min in C 2 y z DIM. Costruttiva: forniamo l algoritmo. Definiamo le funzioni: DFN(v): num. di visita in profondità FATH(v): padre di v c LOW(v): min{dfn(v), DFN(w) t.c. * un arco all indietro (u,w) con u discendente di v (o v stesso) e w antenato di v}. Definizione ricorsiva: LOW(v): min{dfn(v), DFN(x) con x figlio di v, DFN(w) con (v, w) arco all indietro} e a b Un grafo e l'albero determinato dalla visita in profonfità. Nell'albero, per ogni nodo, sono indicati: DFN tra parentesi quadre; LOW tra parentesi tonde. f d f [4](2) a = t[]() c = s[2]() d[3]() b[6]() e[5](2) st-numerazione (4) st-numerazione (5) segue dim. PATH(v) inizialmente marca t,s, ed (s,t); poi, per ogni v restituisce un cammino non marcato da v ad un nodo marcato, marcando tutti i nodi e gli archi sul cammino. 4 casi:. * (v,w) di riporto non marcato! marca (v,w) e PATH(v)=vw segue dim. 2. * (v,w) dell albero non marcato! considera tutti i nodi aventi LOW=DFN(u) con u antenato di v. PATH(v)=vw 0 w k u e marca tutti i nodi e gli archi sul cammino u v w v (...) w 0 = w w k 27 28
8 st-numerazione (6) segue dim. 3. * (w,v) di riporto non marcato! PATH(v)=vw 0 w k e marca tutti i nodi e gli archi sul cammino (N.B. qui serve la funzione FATH) (...) v w k w w = w 0 4. tutti gli archi incidenti a v sono marcati! PATH(v)=% st-numerazione (7) ALGORITMO ST-NUMBER(G) INPUT: G 2-connesso con s,t nodi adiacenti di G OUTPUT: una st-numerazione di G esegui una visita in prof. e calcola DFN, FATH e LOW di ogni nodo marca s, t ed (s,t) PUSH(PILA, t); PUSH(PILA, s); cont= v=pop(pila) WHILE (v$t) DO IF PATH(v)=% THEN STN(v)=cont; cont++; ELSE (suppondnedo che PATH(v)=vv v k w) PUSH(PILA, v k,,v,v) v=pop(pila) END WHILE STN(t)=n un esempio. n=dfn 6 a =t n=low n=stn 2 c =s 3 d 5 3 f4 6 b e 2 st-numerazione (8) PATH(c): PATH(c)=cda (2) PATH(c)=cbd (3) PATH(c)=cefd (3) PATH(c)=cf (3) PATH(c)=% PATH(e)=% PATH(f)=% PATH(b)=ba () PATH(b)=% PATH(d)=% Ricorda:. & arco di riporto da v 2. & arco dell albero da v 3. & arco di riporto in v e c cf bc cd a st-numerazione (9) TH. L algoritmo precedente trova una st-numerazione di G 2- connesso in O(n+m) tempo. DIM. Ogni nodo riceve un numero: ciò accade quando esso viene rimosso definitivamente dalla pila, cioè quando tutti i suoi archi incidenti sono marcati. Questo accade sempre perché G è 2-connesso! si può sempre arrivare da s ad ogi nodo senza passare per t. La numeraz. è proprio st: STN(s)= e STN(t)=n per l algoritmo. Ogni nodo viene messo in pila per la prima volta come nodo intermedio di un PATH! ha almeno un vicino prima e uno dopo nella pila. Tempo lineare: ogni nodo ed arco non viene più toccato dopo essere stato marcato. CVD 3 32
9 Algoritmo di Biedl-Kant () L algoritmo calcola una st-numerazione ed inserisce i nodi secondo questo ordine sulla griglia, aggiungendo gli archi tra il nodo corrente e la parte del disegno già esistente. Per fare questo aggiunge una nuova riga per ogni nodo da inserire ed una nuova colonna per ogni arco uscente (gli archi entranti non richiedono spazio aggiuntivo). N.B. Il grafo in input deve essere 2-connesso Attenzione: funziona anche per grafi non planari. Se il grafo è planare NON garantisce una visualizzazione piana. Algoritmo di Biedl-Kant (2) ALGORTIMO calcola una st-numerazione metti e 2 così (N.B. per ogni arco uscente è allocata col.) FOR 3#i#n- DO metti i su una nuova riga e su una col. già allocata disegna gli archi entranti sulle col. già allocate alloca col. per ogni arco uscente metti n su una nuova riga su una col. già allocata così Algoritmo di Biedl-Kant (2) Algoritmo di Biedl-Kant (3) un esempio TH. L algoritmo di Biedl-Kant determina un disegno ortogonale su griglia di un grafo 2-connesso con area al più (m-n+) x n. DIM. riga outdeg(v )-+ outdeg(v 2 )- col. riga outdeg(v i )- col. # righe=+(n-3)+2=n #col=! i= n (outdeg(v i )-)+=m-n+ riga se ha indeg!3, 2 righe se ha indeg 4 outdeg(v n )-+ col
10 Algoritmo di Biedl-Kant (4) TH. L algoritmo di Biedl-Kant determina un disegno ortogonale su griglia di un grafo 2-connesso con al più 2m-2n+4 svolte, e tutti gli archi hanno al più 2 svolte, tranne un arco che può averne 3. DIM. deg(v )-+ deg(v 2 )- deg(v i )-2 deg(v n ) se =4 deg(v n )- altrimenti Algoritmo di Biedl-Kant (5) TH. L arco con 3 svolte si può sempre evitare. DIM. Se G ha meno di 2n archi, scegliamo come nodo t un nodo con grado minore di 4. Se il grafo è 4-regolare,lasciamo l arco senza svolte per ultimo ad ogni passo. CVD #svolte=deg(v )+deg(v 2 )-2+! i=3 n- (deg(v i )-2)+deg(v n )= m-2n+4. CVD Algoritmo di Biedl-Kant (6) Algoritmo di Biedl-Kant (7) E facile convincersi che l area può essere migliorata, perché ogni nodo viene posizionato su una nuova riga: Algoritmo di Papakostas-Tollis ( 97). L algoritmo è simile al precedente, ma cerca di diminuire il # di righe e colonne usate IDEA: formare coppie di nodi che possano stare sulla stessa riga o sulla stessa colonna: coppie di riga coppie di colonna ALGORITMO PAPAKOSTAS-TOLLIS calcola una ST-numerazione calcola un accoppiamento di nodi FOR i= TO n DO IF i non è stato già inserito THEN IF i non è accoppiato THEN inserisci come Biedl-Kant ELSE (i e j, i<j, sono nella stessa coppia) inserisci i e j nella stessa riga/colonna AREA: 0.77n 2 (contro n 2 +o(n 2 ) di Biedl-Kant) # SVOLTE: 2n+4 (=Biedl-Kant) COMPLESSITA : O(n) ma usando una struttura dati sofisticata (Dietz-Sleator 87) 39 40
MATEMATICA DEL DISCRETO elementi di teoria dei grafi. anno acc. 2009/2010
 elementi di teoria dei grafi anno acc. 2009/2010 Grafi semplici Un grafo semplice G è una coppia ordinata (V(G), L(G)), ove V(G) è un insieme finito e non vuoto di elementi detti vertici o nodi di G, mentre
elementi di teoria dei grafi anno acc. 2009/2010 Grafi semplici Un grafo semplice G è una coppia ordinata (V(G), L(G)), ove V(G) è un insieme finito e non vuoto di elementi detti vertici o nodi di G, mentre
Sono casi particolari di MCF : SPT (cammini minimi) non vi sono vincoli di capacità superiore (solo x ij > 0) (i, j) A : c ij, costo di percorrenza
 Il problema di flusso di costo minimo (MCF) Dati : grafo orientato G = ( N, A ) i N, deficit del nodo i : b i (i, j) A u ij, capacità superiore (max quantità di flusso che può transitare) c ij, costo di
Il problema di flusso di costo minimo (MCF) Dati : grafo orientato G = ( N, A ) i N, deficit del nodo i : b i (i, j) A u ij, capacità superiore (max quantità di flusso che può transitare) c ij, costo di
PROVA FINALE V. AULETTA G. PERSIANO ALGORITMI II - -MAGIS INFO
 PROVA FINALE V. AULETTA G. PERSIANO ALGORITMI II - -MAGIS INFO 1. Load Balancing Un istanza del problema del load balancing consiste di una sequenza p 1,..., p n di interi positivi (pesi dei job) e un
PROVA FINALE V. AULETTA G. PERSIANO ALGORITMI II - -MAGIS INFO 1. Load Balancing Un istanza del problema del load balancing consiste di una sequenza p 1,..., p n di interi positivi (pesi dei job) e un
Metodi e Modelli per l Ottimizzazione Combinatoria Il problema del flusso di costo minimo
 Metodi e Modelli per l Ottimizzazione Combinatoria Il problema del flusso di costo minimo L. De Giovanni G. Zambelli 1 Problema del flusso a costo minimo Il problema del flusso a costo minimo é definito
Metodi e Modelli per l Ottimizzazione Combinatoria Il problema del flusso di costo minimo L. De Giovanni G. Zambelli 1 Problema del flusso a costo minimo Il problema del flusso a costo minimo é definito
Kangourou della Matematica 2014 finale nazionale italiana Mirabilandia, 12 maggio 2014
 Kangourou della Matematica 2014 finale nazionale italiana Mirabilandia, 12 maggio 2014 LIVELLO STUDENT K,M N CD BC A S1. (5 punti ) In figura si vede una circonferenza della quale i segmenti AB, BC e CD
Kangourou della Matematica 2014 finale nazionale italiana Mirabilandia, 12 maggio 2014 LIVELLO STUDENT K,M N CD BC A S1. (5 punti ) In figura si vede una circonferenza della quale i segmenti AB, BC e CD
Trasformazioni Geometriche 1 Roberto Petroni, 2011
 1 Trasformazioni Geometriche 1 Roberto etroni, 2011 Trasformazioni Geometriche sul piano euclideo 1) Introduzione Def: si dice trasformazione geometrica una corrispondenza biunivoca che associa ad ogni
1 Trasformazioni Geometriche 1 Roberto etroni, 2011 Trasformazioni Geometriche sul piano euclideo 1) Introduzione Def: si dice trasformazione geometrica una corrispondenza biunivoca che associa ad ogni
Rette e piani con le matrici e i determinanti
 CAPITOLO Rette e piani con le matrici e i determinanti Esercizio.. Stabilire se i punti A(, ), B(, ) e C(, ) sono allineati. Esercizio.. Stabilire se i punti A(,,), B(,,), C(,, ) e D(4,,0) sono complanari.
CAPITOLO Rette e piani con le matrici e i determinanti Esercizio.. Stabilire se i punti A(, ), B(, ) e C(, ) sono allineati. Esercizio.. Stabilire se i punti A(,,), B(,,), C(,, ) e D(4,,0) sono complanari.
Programmazione dinamica
 Capitolo 6 Programmazione dinamica 6.4 Il problema della distanza di edit tra due stringhe x e y chiede di calcolare il minimo numero di operazioni su singoli caratteri (inserimento, cancellazione e sostituzione)
Capitolo 6 Programmazione dinamica 6.4 Il problema della distanza di edit tra due stringhe x e y chiede di calcolare il minimo numero di operazioni su singoli caratteri (inserimento, cancellazione e sostituzione)
4. Proiezioni del piano e dello spazio
 4. Proiezioni del piano e dello spazio La visualizzazione di oggetti tridimensionali richiede di ottenere una vista piana dell'oggetto. Questo avviene mediante una sequenza di operazioni. Innanzitutto,
4. Proiezioni del piano e dello spazio La visualizzazione di oggetti tridimensionali richiede di ottenere una vista piana dell'oggetto. Questo avviene mediante una sequenza di operazioni. Innanzitutto,
CORSO DI LAUREA IN INGEGNERIA.
 CORSO DI LAUREA IN INGEGNERIA. FOGLIO DI ESERCIZI 4 GEOMETRIA E ALGEBRA LINEARE 2010/11 Esercizio 4.1 (2.2). Determinare l equazione parametrica e Cartesiana della retta dello spazio (a) Passante per i
CORSO DI LAUREA IN INGEGNERIA. FOGLIO DI ESERCIZI 4 GEOMETRIA E ALGEBRA LINEARE 2010/11 Esercizio 4.1 (2.2). Determinare l equazione parametrica e Cartesiana della retta dello spazio (a) Passante per i
Intelligenza Artificiale
 Intelligenza Artificiale Esercizi e Domande di Esame Tecniche di Ricerca e Pianificazione Esercizi Griglia Si consideri un ambiente costituito da una griglia n n in cui si muove un agente che può spostarsi
Intelligenza Artificiale Esercizi e Domande di Esame Tecniche di Ricerca e Pianificazione Esercizi Griglia Si consideri un ambiente costituito da una griglia n n in cui si muove un agente che può spostarsi
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Università degli Studi di Ferrara - A.A. 2014/15 Dott. Valerio Muzzioli ORDINAMENTO DEI DATI
 ORDINAMENTO DEI DATI Quando si ordina un elenco (ovvero una serie di righe contenenti dati correlati), le righe sono ridisposte in base al contenuto di una colonna specificata. Distinguiamo due tipi di
ORDINAMENTO DEI DATI Quando si ordina un elenco (ovvero una serie di righe contenenti dati correlati), le righe sono ridisposte in base al contenuto di una colonna specificata. Distinguiamo due tipi di
Algoritmi e Strutture Dati & Laboratorio di Algoritmi e Programmazione
 Algoritmi e Strutture Dati & Laboratorio di Algoritmi e Programmazione Esercizi II parte Esercizio 1 Discutere la correttezza di ciascuna delle seguenti affermazioni. Dimostrare formalmente la validità
Algoritmi e Strutture Dati & Laboratorio di Algoritmi e Programmazione Esercizi II parte Esercizio 1 Discutere la correttezza di ciascuna delle seguenti affermazioni. Dimostrare formalmente la validità
Algoritmi e Strutture Dati
 Elementi di Programmazione Dinamica Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino Il problema La CMC produce automobili in uno stabilimento
Elementi di Programmazione Dinamica Maria Rita Di Berardini, Emanuela Merelli 1 1 Dipartimento di Matematica e Informatica Università di Camerino Il problema La CMC produce automobili in uno stabilimento
Algoritmi e strutture dati. Codici di Huffman
 Algoritmi e strutture dati Codici di Huffman Memorizzazione dei dati Quando un file viene memorizzato, esso va memorizzato in qualche formato binario Modo più semplice: memorizzare il codice ASCII per
Algoritmi e strutture dati Codici di Huffman Memorizzazione dei dati Quando un file viene memorizzato, esso va memorizzato in qualche formato binario Modo più semplice: memorizzare il codice ASCII per
CONTINUITÀ E DERIVABILITÀ Esercizi proposti. 1. Determinare lim M(sinx) (M(t) denota la mantissa di t)
 CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
IGiochidiArchimede-SoluzioniBiennio 22 novembre 2006
 PROGETTO OLIMPII I MTEMTI U.M.I. UNIONE MTEMTI ITLIN SUOL NORMLE SUPERIORE IGiochidirchimede-Soluzioniiennio novembre 006 Griglia delle risposte corrette Problema Risposta corretta E 4 5 6 7 8 9 E 0 Problema
PROGETTO OLIMPII I MTEMTI U.M.I. UNIONE MTEMTI ITLIN SUOL NORMLE SUPERIORE IGiochidirchimede-Soluzioniiennio novembre 006 Griglia delle risposte corrette Problema Risposta corretta E 4 5 6 7 8 9 E 0 Problema
Misure di base su una carta. Calcoli di distanze
 Misure di base su una carta Calcoli di distanze Per calcolare la distanza tra due punti su una carta disegnata si opera nel modo seguente: 1. Occorre identificare la scala della carta o ricorrendo alle
Misure di base su una carta Calcoli di distanze Per calcolare la distanza tra due punti su una carta disegnata si opera nel modo seguente: 1. Occorre identificare la scala della carta o ricorrendo alle
Corrispondenze e funzioni
 Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
RETTE, PIANI, SFERE, CIRCONFERENZE
 RETTE, PIANI, SFERE, CIRCONFERENZE 1. Esercizi Esercizio 1. Dati i punti A(1, 0, 1) e B(, 1, 1) trovare (1) la loro distanza; () il punto medio del segmento AB; (3) la retta AB sia in forma parametrica,
RETTE, PIANI, SFERE, CIRCONFERENZE 1. Esercizi Esercizio 1. Dati i punti A(1, 0, 1) e B(, 1, 1) trovare (1) la loro distanza; () il punto medio del segmento AB; (3) la retta AB sia in forma parametrica,
Alberi binari di ricerca
 Alberi binari di ricerca Definizione Visita dell albero inorder Ricerca Ricerca minimo, massimo e successore. Inserimento ed eliminazione di un nodo Problema del bilanciamento dell albero Albero binario
Alberi binari di ricerca Definizione Visita dell albero inorder Ricerca Ricerca minimo, massimo e successore. Inserimento ed eliminazione di un nodo Problema del bilanciamento dell albero Albero binario
Esercizi per il corso di Algoritmi e Strutture Dati
 1 Esercizi per il corso di Algoritmi e Strutture Dati Esercizi sulla Tecnica Divide et Impera N.B. Tutti gli algoritmi vanno scritti in pseudocodice (non in Java, né in C++, etc. ). Di tutti gli algoritmi
1 Esercizi per il corso di Algoritmi e Strutture Dati Esercizi sulla Tecnica Divide et Impera N.B. Tutti gli algoritmi vanno scritti in pseudocodice (non in Java, né in C++, etc. ). Di tutti gli algoritmi
Progetto di Reti di Telecomunicazione Modelli in Programmazione Lineare Problemi di flusso
 Progetto di Reti di Telecomunicazione Modelli in Programmazione Lineare Problemi di flusso Flusso di costo minimo È dato un grafo direzionato G = (N, A). Ad ogni arco (i, j) A è associato il costo c ij
Progetto di Reti di Telecomunicazione Modelli in Programmazione Lineare Problemi di flusso Flusso di costo minimo È dato un grafo direzionato G = (N, A). Ad ogni arco (i, j) A è associato il costo c ij
A intervalli regolari ogni router manda la sua tabella a tutti i vicini, e riceve quelle dei vicini.
 Algoritmi di routing dinamici (pag.89) UdA2_L5 Nelle moderne reti si usano algoritmi dinamici, che si adattano automaticamente ai cambiamenti della rete. Questi algoritmi non sono eseguiti solo all'avvio
Algoritmi di routing dinamici (pag.89) UdA2_L5 Nelle moderne reti si usano algoritmi dinamici, che si adattano automaticamente ai cambiamenti della rete. Questi algoritmi non sono eseguiti solo all'avvio
per immagini guida avanzata Uso delle tabelle e dei grafici Pivot Geometra Luigi Amato Guida Avanzata per immagini excel 2000 1
 Uso delle tabelle e dei grafici Pivot Geometra Luigi Amato Guida Avanzata per immagini excel 2000 1 Una tabella Pivot usa dati a due dimensioni per creare una tabella a tre dimensioni, cioè una tabella
Uso delle tabelle e dei grafici Pivot Geometra Luigi Amato Guida Avanzata per immagini excel 2000 1 Una tabella Pivot usa dati a due dimensioni per creare una tabella a tre dimensioni, cioè una tabella
Luigi Piroddi piroddi@elet.polimi.it
 Automazione industriale dispense del corso 10. Reti di Petri: analisi strutturale Luigi Piroddi piroddi@elet.polimi.it Analisi strutturale Un alternativa all analisi esaustiva basata sul grafo di raggiungibilità,
Automazione industriale dispense del corso 10. Reti di Petri: analisi strutturale Luigi Piroddi piroddi@elet.polimi.it Analisi strutturale Un alternativa all analisi esaustiva basata sul grafo di raggiungibilità,
Seconda Prova di Ricerca Operativa. Cognome Nome Numero Matricola A 1/12 A 2/12
 A / A / Seconda Prova di Ricerca Operativa Cognome Nome Numero Matricola Nota: LA RISOLUZIONE CORRETTA DEGLI ESERCIZI CONTRADDISTINTI DA UN ASTERISCO È CONDIZIONE NECESSARIA PER IL RAGGIUNGIMENTO DELLA
A / A / Seconda Prova di Ricerca Operativa Cognome Nome Numero Matricola Nota: LA RISOLUZIONE CORRETTA DEGLI ESERCIZI CONTRADDISTINTI DA UN ASTERISCO È CONDIZIONE NECESSARIA PER IL RAGGIUNGIMENTO DELLA
Esercizi Capitolo 6 - Alberi binari di ricerca
 Esercizi Capitolo 6 - Alberi binari di ricerca Alberto Montresor 23 settembre 200 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente, è possibile
Esercizi Capitolo 6 - Alberi binari di ricerca Alberto Montresor 23 settembre 200 Alcuni degli esercizi che seguono sono associati alle rispettive soluzioni. Se il vostro lettore PDF lo consente, è possibile
Alberi binari. Ilaria Castelli castelli@dii.unisi.it A.A. 2009/2010. Università degli Studi di Siena Dipartimento di Ingegneria dell Informazione
 Alberi binari Ilaria Castelli castelli@dii.unisi.it Università degli Studi di Siena Dipartimento di Ingegneria dell Informazione A.A. 2009/2010 I. Castelli Alberi binari, A.A. 2009/2010 1/20 Alberi binari
Alberi binari Ilaria Castelli castelli@dii.unisi.it Università degli Studi di Siena Dipartimento di Ingegneria dell Informazione A.A. 2009/2010 I. Castelli Alberi binari, A.A. 2009/2010 1/20 Alberi binari
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Interpolazione ed approssimazione di funzioni
 Interpolazione ed approssimazione di funzioni Lucia Gastaldi Dipartimento di Matematica, http://dm.ing.unibs.it/gastaldi/ 9 novembre 2007 Outline 1 Polinomi Valutazione di un polinomio Algoritmo di Horner
Interpolazione ed approssimazione di funzioni Lucia Gastaldi Dipartimento di Matematica, http://dm.ing.unibs.it/gastaldi/ 9 novembre 2007 Outline 1 Polinomi Valutazione di un polinomio Algoritmo di Horner
GEOGEBRA I OGGETTI GEOMETRICI
 GEOGEBRA I OGGETTI GEOMETRICI PROPRIETA : Finestra Proprietà (tasto destro mouse sull oggetto) Fondamentali: permette di assegnare o cambiare NOME, VALORE, di mostrare nascondere l oggetto, di mostrare
GEOGEBRA I OGGETTI GEOMETRICI PROPRIETA : Finestra Proprietà (tasto destro mouse sull oggetto) Fondamentali: permette di assegnare o cambiare NOME, VALORE, di mostrare nascondere l oggetto, di mostrare
SOLUZIONE DEL PROBLEMA 1 TEMA DI MATEMATICA ESAME DI STATO 2015
 SOLUZIONE DEL PROBLEMA 1 TEMA DI MATEMATICA ESAME DI STATO 015 1. Indicando con i minuti di conversazione effettuati nel mese considerato, la spesa totale mensile in euro è espressa dalla funzione f()
SOLUZIONE DEL PROBLEMA 1 TEMA DI MATEMATICA ESAME DI STATO 015 1. Indicando con i minuti di conversazione effettuati nel mese considerato, la spesa totale mensile in euro è espressa dalla funzione f()
Uso delle tabelle e dei grafici Pivot
 Uso delle tabelle e dei grafici Pivot 1 Una tabella Pivot usa dati a due dimensioni per creare una tabella a tre dimensioni, cioè una tabella riassuntiva basata su condizioni multiple che hanno punti di
Uso delle tabelle e dei grafici Pivot 1 Una tabella Pivot usa dati a due dimensioni per creare una tabella a tre dimensioni, cioè una tabella riassuntiva basata su condizioni multiple che hanno punti di
Ottimizzazione Multi Obiettivo
 Ottimizzazione Multi Obiettivo 1 Ottimizzazione Multi Obiettivo I problemi affrontati fino ad ora erano caratterizzati da una unica (e ben definita) funzione obiettivo. I problemi di ottimizzazione reali
Ottimizzazione Multi Obiettivo 1 Ottimizzazione Multi Obiettivo I problemi affrontati fino ad ora erano caratterizzati da una unica (e ben definita) funzione obiettivo. I problemi di ottimizzazione reali
APPUNTI DI MATEMATICA GEOMETRIA \ GEOMETRIA EUCLIDEA \ GEOMETRIA DEL PIANO (1)
 GEOMETRIA \ GEOMETRIA EUCLIDEA \ GEOMETRIA DEL PIANO (1) Un ente (geometrico) è un oggetto studiato dalla geometria. Per descrivere gli enti vengono utilizzate delle definizioni. Una definizione è una
GEOMETRIA \ GEOMETRIA EUCLIDEA \ GEOMETRIA DEL PIANO (1) Un ente (geometrico) è un oggetto studiato dalla geometria. Per descrivere gli enti vengono utilizzate delle definizioni. Una definizione è una
la restituzione prospettica da singolo fotogramma
 la restituzione prospettica da singolo fotogramma arch. francesco guerini francesco.guerini@gmail.com politecnico di Milano, Facoltà di Architettura e Società Laboratorio di Rappresentazione 1 Prof. Andrea
la restituzione prospettica da singolo fotogramma arch. francesco guerini francesco.guerini@gmail.com politecnico di Milano, Facoltà di Architettura e Società Laboratorio di Rappresentazione 1 Prof. Andrea
Quando A e B coincidono una coppia ordinata é determinata anche dalla loro posizione.
 Grafi ed Alberi Pag. /26 Grafi ed Alberi In questo capitolo richiameremo i principali concetti di due ADT che ricorreranno puntualmente nel corso della nostra trattazione: i grafi e gli alberi. Naturale
Grafi ed Alberi Pag. /26 Grafi ed Alberi In questo capitolo richiameremo i principali concetti di due ADT che ricorreranno puntualmente nel corso della nostra trattazione: i grafi e gli alberi. Naturale
Politecnico di Milano Facoltà di Ingegneria dell Informazione AGENTI AUTONOMI E SISTEMI MULTIAGENTE Appello COGNOME E NOME
 Politecnico di Milano Facoltà di Ingegneria dell Informazione AGENTI AUTONOMI E SISTEMI MULTIAGENTE Appello COGNOME E NOME 5 luglio 2006 RIGA COLONNA MATRICOLA Il presente plico pinzato, composto di quattro
Politecnico di Milano Facoltà di Ingegneria dell Informazione AGENTI AUTONOMI E SISTEMI MULTIAGENTE Appello COGNOME E NOME 5 luglio 2006 RIGA COLONNA MATRICOLA Il presente plico pinzato, composto di quattro
Capitolo 13: L offerta dell impresa e il surplus del produttore
 Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Plate Locator Riconoscimento Automatico di Targhe
 Progetto per Laboratorio di Informatica 3 - Rimotti Daniele, Santinelli Gabriele Plate Locator Riconoscimento Automatico di Targhe Il programma plate_locator.m prende come input: l immagine della targa
Progetto per Laboratorio di Informatica 3 - Rimotti Daniele, Santinelli Gabriele Plate Locator Riconoscimento Automatico di Targhe Il programma plate_locator.m prende come input: l immagine della targa
2 Formulazione dello shortest path come problema di flusso
 Strumenti della Teoria dei Giochi per l Informatica A.A. 2009/10 Lecture 20: 28 Maggio 2010 Cycle Monotonicity Docente: Vincenzo Auletta Note redatte da: Annibale Panichella Abstract In questa lezione
Strumenti della Teoria dei Giochi per l Informatica A.A. 2009/10 Lecture 20: 28 Maggio 2010 Cycle Monotonicity Docente: Vincenzo Auletta Note redatte da: Annibale Panichella Abstract In questa lezione
MATEMATICA. { 2 x =12 y 3 y +8 x =0, si pone il problema di trovare, se esistono, un numero x ed un numero y che risolvano entrambe le equazioni.
 MATEMATICA. Sistemi lineari in due equazioni due incognite. Date due equazioni lineari nelle due incognite x, y come ad esempio { 2 x =12 y 3 y +8 x =0, si pone il problema di trovare, se esistono, un
MATEMATICA. Sistemi lineari in due equazioni due incognite. Date due equazioni lineari nelle due incognite x, y come ad esempio { 2 x =12 y 3 y +8 x =0, si pone il problema di trovare, se esistono, un
1. PRIME PROPRIETÀ 2
 RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
Appunti di Algoritmi e Strutture Dati. Grafi. Gianfranco Gallizia
 Appunti di Algoritmi e Strutture Dati Grafi Gianfranco Gallizia 12 Dicembre 2004 2 Indice 1 Grafi 5 1.1 Definizione.............................. 5 1.2 Implementazione........................... 5 1.2.1
Appunti di Algoritmi e Strutture Dati Grafi Gianfranco Gallizia 12 Dicembre 2004 2 Indice 1 Grafi 5 1.1 Definizione.............................. 5 1.2 Implementazione........................... 5 1.2.1
INTEGRALI DEFINITI. Tale superficie viene detta trapezoide e la misura della sua area si ottiene utilizzando il calcolo di un integrale definito.
 INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
Android. Implementare una interfaccia utente
 Android Implementare una interfaccia utente Introduzione In questa lezione vedremo come implementare una interfaccia utente sullo schermo di Android. Vedremo gli elementi di base visualizzabili sullo schermo
Android Implementare una interfaccia utente Introduzione In questa lezione vedremo come implementare una interfaccia utente sullo schermo di Android. Vedremo gli elementi di base visualizzabili sullo schermo
PROGRAMMA GESTIONE TURNI MANUALE UTENTE. Programma Gestione Turni Manuale Utente versione 1.1
 PROGRAMMA GESTIONE TURNI MANUALE UTENTE INDICE 1 PREMESSA 3 2 COMANDI COMUNI 3 3 SEDI 3 4 FESTIVITÀ 4 5 PERIODI TURNI 4 6 COD. TURNI 6 7 TURNI SPORTIVI 9 8 COD. EQUIPAGGI 9 9 DISPONIBILITÀ 10 10 INDISPONIBILITÀ
PROGRAMMA GESTIONE TURNI MANUALE UTENTE INDICE 1 PREMESSA 3 2 COMANDI COMUNI 3 3 SEDI 3 4 FESTIVITÀ 4 5 PERIODI TURNI 4 6 COD. TURNI 6 7 TURNI SPORTIVI 9 8 COD. EQUIPAGGI 9 9 DISPONIBILITÀ 10 10 INDISPONIBILITÀ
1 Applicazioni Lineari tra Spazi Vettoriali
 1 Applicazioni Lineari tra Spazi Vettoriali Definizione 1 (Applicazioni lineari) Si chiama applicazione lineare una applicazione tra uno spazio vettoriale ed uno spazio vettoriale sul campo tale che "!$%!
1 Applicazioni Lineari tra Spazi Vettoriali Definizione 1 (Applicazioni lineari) Si chiama applicazione lineare una applicazione tra uno spazio vettoriale ed uno spazio vettoriale sul campo tale che "!$%!
Grandezze scalari e vettoriali
 Grandezze scalari e vettoriali Esempio vettore spostamento: Esistono due tipi di grandezze fisiche. a) Grandezze scalari specificate da un valore numerico (positivo negativo o nullo) e (nel caso di grandezze
Grandezze scalari e vettoriali Esempio vettore spostamento: Esistono due tipi di grandezze fisiche. a) Grandezze scalari specificate da un valore numerico (positivo negativo o nullo) e (nel caso di grandezze
Capitolo 3. L applicazione Java Diagrammi ER. 3.1 La finestra iniziale, il menu e la barra pulsanti
 Capitolo 3 L applicazione Java Diagrammi ER Dopo le fasi di analisi, progettazione ed implementazione il software è stato compilato ed ora è pronto all uso; in questo capitolo mostreremo passo passo tutta
Capitolo 3 L applicazione Java Diagrammi ER Dopo le fasi di analisi, progettazione ed implementazione il software è stato compilato ed ora è pronto all uso; in questo capitolo mostreremo passo passo tutta
Sistemi Operativi mod. B. Sistemi Operativi mod. B A B C A B C P 1 2 0 0 P 1 1 2 2 3 3 2 P 2 3 0 2 P 2 6 0 0 P 3 2 1 1 P 3 0 1 1 < P 1, >
 Algoritmo del banchiere Permette di gestire istanze multiple di una risorsa (a differenza dell algoritmo con grafo di allocazione risorse). Ciascun processo deve dichiarare a priori il massimo impiego
Algoritmo del banchiere Permette di gestire istanze multiple di una risorsa (a differenza dell algoritmo con grafo di allocazione risorse). Ciascun processo deve dichiarare a priori il massimo impiego
LIVELLO STUDENT S1. S2. S3. S4. S5. S6.
 LIVELLO STUDENT S1. (5 punti ) La figura mostra due quadrati uguali che hanno in comune esattamente un vertice. È possibile precisare la misura dell'angolo ABC? S2. (7 punti ) Negli usuali fogli (rettangolari)
LIVELLO STUDENT S1. (5 punti ) La figura mostra due quadrati uguali che hanno in comune esattamente un vertice. È possibile precisare la misura dell'angolo ABC? S2. (7 punti ) Negli usuali fogli (rettangolari)
DOMINIO E LIMITI. Esercizio 3 Studiare gli insiemi di livello della funzione f, nei seguenti casi: 1) f(x,y) = y2 x 2 + y 2.
 FUNZIONI DI DUE VARIABILI 1 DOMINIO E LIMITI Domini e disequazioni in due variabili. Insiemi di livello. Elementi di topologia (insiemi aperti, chiusi, limitati, convessi, connessi per archi; punti di
FUNZIONI DI DUE VARIABILI 1 DOMINIO E LIMITI Domini e disequazioni in due variabili. Insiemi di livello. Elementi di topologia (insiemi aperti, chiusi, limitati, convessi, connessi per archi; punti di
B-Tree. Struttura dati usata in applicazioni che necessitano di gestire insiemi di chiavi ordinate Una variante (B+-Tree) è diffusa in:
 B-Tree Prof. Rudolf Bayer Struttura dati usata in applicazioni che necessitano di gestire insiemi di chiavi ordinate Una variante (B+-Tree) è diffusa in: Filesystem: btrfs, NTFS, ReiserFS, NSS, XFS, JFS
B-Tree Prof. Rudolf Bayer Struttura dati usata in applicazioni che necessitano di gestire insiemi di chiavi ordinate Una variante (B+-Tree) è diffusa in: Filesystem: btrfs, NTFS, ReiserFS, NSS, XFS, JFS
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI
 APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
PROIEZIONI ORTOGONALI
 PROIEZIONI ORTOGONALI 104 Il metodo della doppia proiezione ortogonale Il metodo attualmente conosciuto come metodo delle proiezioni ortogonali (o proiezioni ortografiche) inizialmente nacque come metodo
PROIEZIONI ORTOGONALI 104 Il metodo della doppia proiezione ortogonale Il metodo attualmente conosciuto come metodo delle proiezioni ortogonali (o proiezioni ortografiche) inizialmente nacque come metodo
La struttura dati ad albero binario
 La struttura dati ad albero binario L albero è una struttura dati nella quale le informazioni sono organizzate in modo gerarchico, dall alto verso il basso. Gli elementi di un albero si chiamano nodi,
La struttura dati ad albero binario L albero è una struttura dati nella quale le informazioni sono organizzate in modo gerarchico, dall alto verso il basso. Gli elementi di un albero si chiamano nodi,
Indice. pagina 2 di 10
 LEZIONE PROGETTAZIONE ORGANIZZATIVA DOTT.SSA ROSAMARIA D AMORE Indice PROGETTAZIONE ORGANIZZATIVA---------------------------------------------------------------------------------------- 3 LA STRUTTURA
LEZIONE PROGETTAZIONE ORGANIZZATIVA DOTT.SSA ROSAMARIA D AMORE Indice PROGETTAZIONE ORGANIZZATIVA---------------------------------------------------------------------------------------- 3 LA STRUTTURA
Informatica 3. Informatica 3. LEZIONE 10: Introduzione agli algoritmi e alle strutture dati. Lezione 10 - Modulo 1. Importanza delle strutture dati
 Informatica 3 Informatica 3 LEZIONE 10: Introduzione agli algoritmi e alle strutture dati Modulo 1: Perchè studiare algoritmi e strutture dati Modulo 2: Definizioni di base Lezione 10 - Modulo 1 Perchè
Informatica 3 Informatica 3 LEZIONE 10: Introduzione agli algoritmi e alle strutture dati Modulo 1: Perchè studiare algoritmi e strutture dati Modulo 2: Definizioni di base Lezione 10 - Modulo 1 Perchè
Per effettuare la stampa di una cartella di lavoro si accede al comando. Stampa dal menu File o si utilizza il pulsante omonimo sulla barra
 4.5 Stampa 4.5.1 Stampare semplici fogli elettronici 4.5.1.1 Usare le opzioni di base della stampa Per effettuare la stampa di una cartella di lavoro si accede al comando Stampa dal menu File o si utilizza
4.5 Stampa 4.5.1 Stampare semplici fogli elettronici 4.5.1.1 Usare le opzioni di base della stampa Per effettuare la stampa di una cartella di lavoro si accede al comando Stampa dal menu File o si utilizza
Introduzione al 3D con Autocad
 2 Introduzione al 3D con Autocad Coso di CAD B condotto da Daniela Sidari a.a. 2012/2013 19.02.2013 Modellazione geometrica 3D wireframe superfici solidi Si distinguono tre tecniche principali di modellazione:
2 Introduzione al 3D con Autocad Coso di CAD B condotto da Daniela Sidari a.a. 2012/2013 19.02.2013 Modellazione geometrica 3D wireframe superfici solidi Si distinguono tre tecniche principali di modellazione:
SPECTER OPS. L'obiettivo del giocatore agente è quello che il suo agente completi 3 su 4 missioni obiettivo qualsiasi
 SPECTER OPS REGOLE 2-3 giocatori: 1 agente e 2 cacciatori - Le 4 missioni obiettivo sono conosciute dai giocatori: si lancia il dado e si segnano col relativo gettone sul lato verde sulla plancia e sul
SPECTER OPS REGOLE 2-3 giocatori: 1 agente e 2 cacciatori - Le 4 missioni obiettivo sono conosciute dai giocatori: si lancia il dado e si segnano col relativo gettone sul lato verde sulla plancia e sul
Ricerca Operativa Esercizi sul metodo del simplesso. Luigi De Giovanni, Laura Brentegani
 Ricerca Operativa Esercizi sul metodo del simplesso Luigi De Giovanni, Laura Brentegani 1 1) Risolvere il seguente problema di programmazione lineare. ma + + 3 s.t. 2 + + 2 + 2 + 3 5 2 + 2 + 6,, 0 Soluzione.
Ricerca Operativa Esercizi sul metodo del simplesso Luigi De Giovanni, Laura Brentegani 1 1) Risolvere il seguente problema di programmazione lineare. ma + + 3 s.t. 2 + + 2 + 2 + 3 5 2 + 2 + 6,, 0 Soluzione.
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE
 LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
Gestione della memoria centrale
 Gestione della memoria centrale Un programma per essere eseguito deve risiedere in memoria principale e lo stesso vale per i dati su cui esso opera In un sistema multitasking molti processi vengono eseguiti
Gestione della memoria centrale Un programma per essere eseguito deve risiedere in memoria principale e lo stesso vale per i dati su cui esso opera In un sistema multitasking molti processi vengono eseguiti
CONTROLLO ORTOGRAFICO E GRAMMATICALE
 CONTROLLO ORTOGRAFICO E GRAMMATICALE Quando una parola non è presente nel dizionario di Word, oppure nello scrivere una frase si commettono errori grammaticali, allora si può eseguire una delle seguenti
CONTROLLO ORTOGRAFICO E GRAMMATICALE Quando una parola non è presente nel dizionario di Word, oppure nello scrivere una frase si commettono errori grammaticali, allora si può eseguire una delle seguenti
Architettura degli Elaboratori I Esercitazione 1 - Rappresentazione dei numeri
 Architettura degli Elaboratori I Esercitazione 1 - Rappresentazione dei numeri 1 Da base 2 a base 10 I seguenti esercizi richiedono di convertire in base 10 la medesima stringa binaria codificata rispettivamente
Architettura degli Elaboratori I Esercitazione 1 - Rappresentazione dei numeri 1 Da base 2 a base 10 I seguenti esercizi richiedono di convertire in base 10 la medesima stringa binaria codificata rispettivamente
Sequenziamento a minimo costo di commutazione in macchine o celle con costo lineare e posizione home (In generale il metodo di ottimizzazione
 Sequenziamento a minimo costo di commutazione in macchine o celle con costo lineare e posizione home (In generale il metodo di ottimizzazione presentato in questo file trova la seq. a costo minimo per
Sequenziamento a minimo costo di commutazione in macchine o celle con costo lineare e posizione home (In generale il metodo di ottimizzazione presentato in questo file trova la seq. a costo minimo per
Lezione 8. La macchina universale
 Lezione 8 Algoritmi La macchina universale Un elaboratore o computer è una macchina digitale, elettronica, automatica capace di effettuare trasformazioni o elaborazioni su i dati digitale= l informazione
Lezione 8 Algoritmi La macchina universale Un elaboratore o computer è una macchina digitale, elettronica, automatica capace di effettuare trasformazioni o elaborazioni su i dati digitale= l informazione
Excel. A cura di Luigi Labonia. e-mail: luigi.lab@libero.it
 Excel A cura di Luigi Labonia e-mail: luigi.lab@libero.it Introduzione Un foglio elettronico è un applicazione comunemente usata per bilanci, previsioni ed altri compiti tipici del campo amministrativo
Excel A cura di Luigi Labonia e-mail: luigi.lab@libero.it Introduzione Un foglio elettronico è un applicazione comunemente usata per bilanci, previsioni ed altri compiti tipici del campo amministrativo
INdAM QUESITI A RISPOSTA MULTIPLA
 INdAM Prova scritta per il concorso a 40 borse di studio, 2 borse aggiuntive e a 40 premi per l iscrizione ai Corsi di Laurea in Matematica, anno accademico 2011/2012. Piano Lauree Scientifiche. La prova
INdAM Prova scritta per il concorso a 40 borse di studio, 2 borse aggiuntive e a 40 premi per l iscrizione ai Corsi di Laurea in Matematica, anno accademico 2011/2012. Piano Lauree Scientifiche. La prova
Introduzione agli Algoritmi Genetici Prof. Beatrice Lazzerini
 Introduzione agli Algoritmi Genetici Prof. Beatrice Lazzerini Dipartimento di Ingegneria della Informazione Via Diotisalvi, 2 56122 PISA ALGORITMI GENETICI (GA) Sono usati per risolvere problemi di ricerca
Introduzione agli Algoritmi Genetici Prof. Beatrice Lazzerini Dipartimento di Ingegneria della Informazione Via Diotisalvi, 2 56122 PISA ALGORITMI GENETICI (GA) Sono usati per risolvere problemi di ricerca
LA RETTA. Retta per l'origine, rette orizzontali e verticali
 Retta per l'origine, rette orizzontali e verticali LA RETTA Abbiamo visto che l'equazione generica di una retta è del tipo Y = mx + q, dove m ne rappresenta la pendenza e q il punto in cui la retta incrocia
Retta per l'origine, rette orizzontali e verticali LA RETTA Abbiamo visto che l'equazione generica di una retta è del tipo Y = mx + q, dove m ne rappresenta la pendenza e q il punto in cui la retta incrocia
Iniziamo con un esercizio sul massimo comun divisore: Esercizio 1. Sia d = G.C.D.(a, b), allora:
 Iniziamo con un esercizio sul massimo comun divisore: Esercizio 1. Sia d = G.C.D.(a, b), allora: G.C.D.( a d, b d ) = 1 Sono state introdotte a lezione due definizioni importanti che ricordiamo: Definizione
Iniziamo con un esercizio sul massimo comun divisore: Esercizio 1. Sia d = G.C.D.(a, b), allora: G.C.D.( a d, b d ) = 1 Sono state introdotte a lezione due definizioni importanti che ricordiamo: Definizione
Analisi di una Rete Sociale
 2012 Analisi di una Rete Sociale Alessandro Lovati Matricola 626053 Comunicazione Digitale ord. F47 26/01/2012 Indice : 1. Obiettivo del progetto 2. Realizzazione 3. Analisi dei risultati 3.1. Numero di
2012 Analisi di una Rete Sociale Alessandro Lovati Matricola 626053 Comunicazione Digitale ord. F47 26/01/2012 Indice : 1. Obiettivo del progetto 2. Realizzazione 3. Analisi dei risultati 3.1. Numero di
2 - Modifica. 2.1 - Annulla 2.2 - ANNULLA TOPOGRAFICO 2.3 - ANNULLA TOPOGRAFICO MULTIPLO FIGURA 2.1
 2 - Modifica FIGURA 2.1 Il menu a tendina Modifica contiene il gruppo di comandi relativi alla selezione e alla gestione delle proprietà delle entità del disegno e alla gestione dei layer. I comandi sono
2 - Modifica FIGURA 2.1 Il menu a tendina Modifica contiene il gruppo di comandi relativi alla selezione e alla gestione delle proprietà delle entità del disegno e alla gestione dei layer. I comandi sono
STRUTTURE NON LINEARI
 PR1 Lezione 13: STRUTTURE NON LINEARI Michele Nappi mnappi@unisa.it www.dmi.unisa.it/people/nappi Per la realizzazione della presentazione è stato utilizzato in parte materiale didattico prodotto da Oronzo
PR1 Lezione 13: STRUTTURE NON LINEARI Michele Nappi mnappi@unisa.it www.dmi.unisa.it/people/nappi Per la realizzazione della presentazione è stato utilizzato in parte materiale didattico prodotto da Oronzo
8.9 CREARE UNA TABELLA PIVOT
 8.9 CREARE UNA TABELLA PIVOT Utilizziamo la tabella del foglio di Excel Consumo di energia elettrica in Italia del progetto Aggiungere subtotali a una tabella di dati, per creare una Tabella pivot: essa
8.9 CREARE UNA TABELLA PIVOT Utilizziamo la tabella del foglio di Excel Consumo di energia elettrica in Italia del progetto Aggiungere subtotali a una tabella di dati, per creare una Tabella pivot: essa
TSP con eliminazione di sottocicli
 TSP con eliminazione di sottocicli Un commesso viaggiatore deve visitare 7 clienti in modo da minimizzare la distanza percorsa. Le distanze (in Km) tra ognuno dei clienti sono come segue: 7-8 9 7 9-8 79
TSP con eliminazione di sottocicli Un commesso viaggiatore deve visitare 7 clienti in modo da minimizzare la distanza percorsa. Le distanze (in Km) tra ognuno dei clienti sono come segue: 7-8 9 7 9-8 79
A destra è delimitata dalla barra di scorrimento verticale, mentre in basso troviamo una riga complessa.
 La finestra di Excel è molto complessa e al primo posto avvio potrebbe disorientare l utente. Analizziamone i componenti dall alto verso il basso. La prima barra è la barra del titolo, dove troviamo indicato
La finestra di Excel è molto complessa e al primo posto avvio potrebbe disorientare l utente. Analizziamone i componenti dall alto verso il basso. La prima barra è la barra del titolo, dove troviamo indicato
Esponenziali elogaritmi
 Esponenziali elogaritmi Potenze ad esponente reale Ricordiamo che per un qualsiasi numero razionale m n prendere n>0) si pone a m n = n a m (in cui si può sempre a patto che a sia un numero reale positivo.
Esponenziali elogaritmi Potenze ad esponente reale Ricordiamo che per un qualsiasi numero razionale m n prendere n>0) si pone a m n = n a m (in cui si può sempre a patto che a sia un numero reale positivo.
1 Estensione in strategia mista di un gioco
 AVVERTENZA: Di seguito trovate alcuni appunti, poco ordinati e poco formali, che uso come traccia durante le lezioni. Non sono assolutamente da considerarsi sostitutivi del materiale didattico. Riferimenti:
AVVERTENZA: Di seguito trovate alcuni appunti, poco ordinati e poco formali, che uso come traccia durante le lezioni. Non sono assolutamente da considerarsi sostitutivi del materiale didattico. Riferimenti:
Ricorsione in SQL-99. Introduzione. Idea di base
 Ricorsione in SQL-99 Introduzione In SQL2 non è possibile definire interrogazioni che facciano uso della ricorsione Esempio Voli(lineaAerea, da, a, parte, arriva) non è possibile esprimere l interrogazione
Ricorsione in SQL-99 Introduzione In SQL2 non è possibile definire interrogazioni che facciano uso della ricorsione Esempio Voli(lineaAerea, da, a, parte, arriva) non è possibile esprimere l interrogazione
RICERCA OPERATIVA GRUPPO B prova scritta del 22 marzo 2007
 RICERCA OPERATIVA GRUPPO B prova scritta del 22 marzo 2007 Rispondere alle seguenti domande marcando a penna la lettera corrispondente alla risposta ritenuta corretta (una sola tra quelle riportate). Se
RICERCA OPERATIVA GRUPPO B prova scritta del 22 marzo 2007 Rispondere alle seguenti domande marcando a penna la lettera corrispondente alla risposta ritenuta corretta (una sola tra quelle riportate). Se
Grafi. Moreno Marzolla Dip. di Informatica Scienza e Ingegneria Università di Bologna. moreno.marzolla@unibo.it http://www.moreno.marzolla.
 Grafi Moreno Marzolla ip. di Informatica Scienza e Ingegneria Università di ologna moreno.marzolla@unibo.it http://www.moreno.marzolla.name/ opyright lberto Montresor, Università di Trento, Italy (http://www.dit.unitn.it/~montreso/asd/index.shtml)
Grafi Moreno Marzolla ip. di Informatica Scienza e Ingegneria Università di ologna moreno.marzolla@unibo.it http://www.moreno.marzolla.name/ opyright lberto Montresor, Università di Trento, Italy (http://www.dit.unitn.it/~montreso/asd/index.shtml)
Guida all uso di Java Diagrammi ER
 Guida all uso di Java Diagrammi ER Ver. 1.1 Alessandro Ballini 16/5/2004 Questa guida ha lo scopo di mostrare gli aspetti fondamentali dell utilizzo dell applicazione Java Diagrammi ER. Inizieremo con
Guida all uso di Java Diagrammi ER Ver. 1.1 Alessandro Ballini 16/5/2004 Questa guida ha lo scopo di mostrare gli aspetti fondamentali dell utilizzo dell applicazione Java Diagrammi ER. Inizieremo con
TSP con eliminazione di sottocicli
 TSP con eliminazione di sottocicli Un commesso viaggiatore deve visitare 7 clienti in modo da minimizzare la distanza percorsa. Le distanze (in Km) tra ognuno dei clienti sono come segue: 3 5 7-8 9 57
TSP con eliminazione di sottocicli Un commesso viaggiatore deve visitare 7 clienti in modo da minimizzare la distanza percorsa. Le distanze (in Km) tra ognuno dei clienti sono come segue: 3 5 7-8 9 57
5.3 TABELLE 5.3.1 RECORD 5.3.1.1 Inserire, eliminare record in una tabella Aggiungere record Eliminare record
 5.3 TABELLE In un sistema di database relazionali le tabelle rappresentano la struttura di partenza, che resta poi fondamentale per tutte le fasi del lavoro di creazione e di gestione del database. 5.3.1
5.3 TABELLE In un sistema di database relazionali le tabelle rappresentano la struttura di partenza, che resta poi fondamentale per tutte le fasi del lavoro di creazione e di gestione del database. 5.3.1
Modelli di Programmazione Lineare e Programmazione Lineare Intera
 Modelli di Programmazione Lineare e Programmazione Lineare Intera 1 Azienda Dolciaria Un azienda di cioccolatini deve pianificare la produzione per i prossimi m mesi. In ogni mese l azienda ha a disposizione
Modelli di Programmazione Lineare e Programmazione Lineare Intera 1 Azienda Dolciaria Un azienda di cioccolatini deve pianificare la produzione per i prossimi m mesi. In ogni mese l azienda ha a disposizione
Matematica in laboratorio
 Unità 1 Attività guidate Attività 1 Foglio elettronico Divisibilità tra numeri naturali Costruisci un foglio di lavoro per determinare se a è divisibile per b, essendo a e b due numeri naturali, con a
Unità 1 Attività guidate Attività 1 Foglio elettronico Divisibilità tra numeri naturali Costruisci un foglio di lavoro per determinare se a è divisibile per b, essendo a e b due numeri naturali, con a
Macchine sequenziali
 Corso di Calcolatori Elettronici I A.A. 2010-2011 Macchine sequenziali Lezione 14 Università degli Studi di Napoli Federico II Facoltà di Ingegneria Automa a Stati Finiti (ASF) E una prima astrazione di
Corso di Calcolatori Elettronici I A.A. 2010-2011 Macchine sequenziali Lezione 14 Università degli Studi di Napoli Federico II Facoltà di Ingegneria Automa a Stati Finiti (ASF) E una prima astrazione di
Rendering air show e verifica della sincronizzazione
 Capitolo 5 Rendering air show e verifica della sincronizzazione 5.1 Introduzione Il Rendering 3D dell evoluzioni acrobatiche costituisce uno degli aspetti cruciali dell applicazione realizzata. L ambiente
Capitolo 5 Rendering air show e verifica della sincronizzazione 5.1 Introduzione Il Rendering 3D dell evoluzioni acrobatiche costituisce uno degli aspetti cruciali dell applicazione realizzata. L ambiente
RUOTE DENTATE. Introduzione
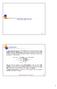 RUOTE DENTATE 362 Introduzione Le ruote dentate costituiscono un sistema affidabile per la trasmissione del moto tra assi paralleli, incidenti e sghembi. La trasmissione avviene per spinta dei denti della
RUOTE DENTATE 362 Introduzione Le ruote dentate costituiscono un sistema affidabile per la trasmissione del moto tra assi paralleli, incidenti e sghembi. La trasmissione avviene per spinta dei denti della
Un esempio di applicazione della programmazione lineare intera all ingegneria del software: stima del worst-case execution time di un programma
 Un esempio di applicazione della programmazione lineare intera all ingegneria del software: stima del worst-case execution time di un programma Corso di Ricerca Operativa per il Corso di Laurea Magistrale
Un esempio di applicazione della programmazione lineare intera all ingegneria del software: stima del worst-case execution time di un programma Corso di Ricerca Operativa per il Corso di Laurea Magistrale
Tabelle 3.4. Unità didattica. Copyright 2009 Apogeo. Obiettivi. Prerequisiti
 Unità didattica 3.4 In questa unità realizzerai un annuncio da appendere in una bacheca per la vendita del tuo lettore MP3. Il tuo annuncio deve essere gradevole e armonioso in modo che, tra tanti altri
Unità didattica 3.4 In questa unità realizzerai un annuncio da appendere in una bacheca per la vendita del tuo lettore MP3. Il tuo annuncio deve essere gradevole e armonioso in modo che, tra tanti altri
3 CENNI DI TEORIA DELLA COMPLESSITA COMPUTAZIONALE. E. Amaldi Fondamenti di R.O. Politecnico di Milano 1
 3 CENNI DI TEORIA DELLA COMPLESSITA COMPUTAZIONALE E. Amaldi Fondamenti di R.O. Politecnico di Milano 1 Scopo: Stimare l onere computazionale per risolvere problemi di ottimizzazione e di altra natura
3 CENNI DI TEORIA DELLA COMPLESSITA COMPUTAZIONALE E. Amaldi Fondamenti di R.O. Politecnico di Milano 1 Scopo: Stimare l onere computazionale per risolvere problemi di ottimizzazione e di altra natura
Capitolo 6. 6.1 TOTALI PARZIALI E COMPLESSIVI Aprire la cartella di lavoro Lezione2 e inserire la tabella n 2 nel Foglio1 che chiameremo Totali.
 Capitolo 6 GESTIONE DEI DATI 6.1 TOTALI PARZIALI E COMPLESSIVI Aprire la cartella di lavoro Lezione2 e inserire la tabella n 2 nel Foglio1 che chiameremo Totali. Figura 86. Tabella Totali Si vuole sapere
Capitolo 6 GESTIONE DEI DATI 6.1 TOTALI PARZIALI E COMPLESSIVI Aprire la cartella di lavoro Lezione2 e inserire la tabella n 2 nel Foglio1 che chiameremo Totali. Figura 86. Tabella Totali Si vuole sapere
