Modelli reologici. Romano Lapasin. Dipartimento di Ingegneria e Architettura Università di Trieste
|
|
|
- Mirella Ferretti
- 5 anni fa
- Visualizzazioni
Transcript
1 Modell reologc Romano Lapasn Dparmeno d Ingegnera e Archeura
2 Approcc fenomenologc e approcc molecolar/mcroreologc Problema cenrale della reologa: defnzone dell equazone cosuva (relazone ra ensore degl sforz e uno o pù ensor cnemac approcc fenomenologc approcc molecolar o mcroreologc Approcco fenomenologco: l obevo prmaro è la defnzone d un modello capace d descrvere nel modo mglore possble l comporameno reologco d un ssema prescndendo dalla sua naura e dalle sue condzon sruural (n emp successv l evenuale rcerca delle correlazon paramer reologc e paramer molecolar o mcroscopc Approcco molecolare o mcroreologco: l obevo è la defnzone d un modello capace d correlare l comporameno reologco d un ssema con paramer che ne caraerzzano la sruura su scala molecolare o superore
3 Approcc e modell fenomenologc Comporameno shear-dpendene Modello d fludo Newonano generalzzao Comporameno shear- e empo-dpendene Approcc ssoropc e approcc vscoelasc Approcco ssoropco anelasco Approcc vscoelasc Modell vscoelasc lnear Modell coroazonal quas-lnear Modell coroazonal non lnear Modell codeformazonal
4 Modello d fludo Newonano generalzzao L approcco fenomenologco pù semplce è basao sulla generalzzazone della relazone valda per flud Newonan D ( ( II D D ( ( La vscosà è una grandezza scalare che può dpendere solano da alre grandezze scalar (componen del ensore I II j j j III j k j jk k Per un fludo ncomprmble n condzon d flusso a aglo: I III v II (
5 Modello d fludo Newonano generalzzao ( equazon ( ( ( ( m n / dfferen k modell ada a descrvere comporamen pseudoplasc, plasc o dlaan k n - n- modell ada alla soluzone d problem rguardan condzon sazonare d flusso a aglo, qual l calcolo d DP nel moo lamnare n ub, o alre condzon approssmabl ad esse non a condzon non sazonare e dverse da quelle a aglo
6 Modello CEF (Crmnale Ercksen Flbey Le dverse verson del modello d fludo Newonano generalzzao possono essere consdera cas parcolar d un modello pù generale valdo per una classe esesa d flud D D D D,, f u nzon : dervaa d Jaumann o dervaa coroazonale rspeo al empo D D D D Omeendo ermn conenen, dall equazone CEF e s rcava l modello d fludo Newonano generalzzao d v D D
7 dal modello CEF al modello d fludo Newonano generalzzao v condzon d flusso a aglo sazonaro ra pan parallel T v = - D D yx xy yy xx zz yy
8 Approcc ssoropc e vscoelasc I modell d fludo Newonano generalzzao sono nada all anals del comporameno empo-dpendene d flud non Newonan Occorre dsporre d un modello n grado d ener cono della memora che l fludo ha della sora cnemaca precedene, ovvero degl effe che essa produce sulla sruura del fludo. Approcc ssoropc Approcc vscoelasc anelasc elasc lnear non lnear Negl approcc ssoropc anelasc (o elasc la empo-dpendenza è dovua solano (o prncpalmene alle varazon sruural prodoe da varazon delle condzon d campo (sforz, graden d velocà alle qual è sooposo l ssema.
9 Approcco fenomenologco al comporameno ssoropco anelasco (Cheng-Evans Il comporameno vscoso shear- e empo-dpendene n condzon d flusso d aglo è descro da : d d f (, g (, equazone d sao equazone cneca Esempo d modello adao a descrvere l comporameno ssoropco d sospenson d caolno e arglla d d k p f (, ( K ( q g (, ( b q p k d ( k n : paramero sruurale arbraro, (,, K K K ( K n condzon sazonare (d equlbro d k d ( d k d eq k b d b eq eq p e r p e r
10 Approcco fenomenologco al comporameno ssoropco anelasco (Cheng-Evans f (, equazone d sao curva d equlbro mappa d curve a cosane (
11 Clay-kaoln suspensons A. Alessandrn, R. Lapasn, F. Surz, Chem. Eng. Commun., 98
12
13 Modell vscoelasc lnear j modello d Maxwell per rapde varazon d / G n condzon sazonare comporameno Newonano a deformazone cosane exp / j j j ' G ( ' j( ' d' exp j( ' d' ' j exp ( ' d' j verson ensoral: n
14 Modell vscoelasc lnear modello d Jeffreys ' ' ( ' ( ' exp d j j j j j j G G / G / ' ' ( ' ( ' exp d j j exp lm ( nx n x n funzone dela d Drac modello d Jeffreys: puno d parenza per lo svluppo d modell vscoelasc non lnear
15 Modell vscoelasc lnear modello d Burgers (modello d Maxwell + modello d Vog-Kelvn rlassameno a deformazone cosane G G creep exp G G G p er recovery ' p er ' ( exp exp G G G exp G G G p er
16 Modell vscoelasc lnear modello d Maxwell generalzzao G ( G exp( G ( G exp( j G k k G ' exp k j G G ( ' d' G G N N spero meccanco G' N G G' ' N G spero de emp d rlassameno G G, : valor da fng, problemache d fng e crer d vncolo (scalng, scalng eorc
17 Modell vscoelasc lnear modello d Maxwell generalzzao meod dfferen d regressone de da spermenal e d regolarzzazone crero emprco d scalng de emp: rduzone del grado d correlazone ra paramer d fng rduzone del numero d paramer aggusabl crer d scalng basa su approcc eorc: eora d Rouse per soluzon polmerche e fus a basso peso molecolare k ( k k k G k k k k
18 Modell vscoelasc lnear modello d Maxwell generalzzao: mplemenazone per esenderne l applcazone a comporamen sold-lke G ( G e G exp( G ( G e p e r j G e G exp G e ' j G ( ' d' G G G N N spero meccanco G' G e N G G' ' N G G ' G e p e r
19 Modell vscoelasc a dervae frazonare Modell vscoelasc basa sull uso d dervae frazonare (operaor maemac negrodfferenzal al poso d funzon e dervae nere d funzon defnzone d dervaa frazonara secondo Remann - Louvlle D corpo elasco d ( G d d f ( d ( d d f ( ( f ( d ( exp( x x dea orgnara d Sco Blar: comporamen vscoelasc compres ra due esrem corpo vscoelasco dx funzone gamma corpo vscoso d ( d funzone d araverso operaore maemaco nermedo ra funzone e dervaa prma
20 Modell vscoelasc a dervae frazonare modfca d modell convenzonal (sosuzone d elemen elasco e vscoso con elemen frazonar d ( d fraconal elemen G sprng dashpo = = FMM (fraconal Maxwell model b b FZM (fraconal Zener model modfca delle equazon cosuve de modell convenzonal (sosuzone con dervae frazonare
21 Modell vscoelasc a dervae frazonare G D G G D FZM ( = b Modello d Fredrch c c c c d d e D [ ] G { D [ ] D [ ]} D G D [ ] (d =, c = - b spero meccanco d ( d c cos( ( cos( d c G' ( = G DG e ( c cos( c ( c d c ( sn( d ( sn( d c G' '( = DG ( c cos( c ( c
22 Modell vscoelasc a dervae frazonare FZM ( = b Modello d Fredrch c c c c d d e D [ ] G { D [ ] D [ ]} D G D [ ] (d =, c = - b Modello d Maxwell (d =, c = (, b, G e G '( = ( DG ( ( G' '( = DG (
23 Modell vscoelasc a dervae frazonare G', G'' [Pa] 5 C 45 C 65 C descrzone della ranszone sol/gel araverso l modello d Fredrch 85 C,,, [rad/s] DG G e X-LBG : d.75 xanhan-locus bean gum (: KCl mm, % 5-85 C G e DG (Pa T ( C c.5.5 (s c, d
24 Modell vscoelasc a dervae frazonare spero meccanco d un polmero assocavo
25 Modell vscoelasc a dervae frazonare spero meccanco d un polmero assocavo
26 G'. G'' Modell vscoelasc a dervae frazonare spero meccanco d un polmero assocavo descrzone con modello FMM G G daa from R.D. Groo, W.G.M. Agerof, Macromolecules, 995, 8,
27 Modell vscoelasc coroazonal Modell vscoelasc lnear rformula scambando l ssema fsso d coordnae con un ssema coroazonale ( 3 ( ( rfermeno fsso ( ' ( 3 ' ( ' ( 3 ( rfermeno moble coroazonale ( rfermeno fsso rfermeno moble coroazonale rformulazone del modello d Jeffreys j j j j j j j j modello lneare modello lneare
28 Modell vscoelasc coroazonal rscrura del modello d Jeffreys nel ssema fsso D D j D D j j D D modello coroazonale d Jeffreys j modello non lneare flusso d aglo sazonaro avvameno spegnmeno, / /
29 Modell vscoelasc coroazonal non lnear per agguna d ermn non lnear al modello d Oldroyd (8 cosan 3 3 ( ( ( ( ( ( ( E kι j j j j j dal modello d Jeffreys coroazonale rscrura nel ssema fsso
30 percors d svluppo de modell lnearà ra fludo Newonano e combnazone d due elemen lnear fludo Newonano generalzzao rascurando ermn conenen gl sforz normal equazone CEF sao sazonaro modello d Maxwell combnazone d pù elemen lnear modello vscoelasco lneare generalzzao rformulazone n ssema coroozonale modell coroazonal quas lnear agguna d ermn non lnear modell coroazonal non lnear
31 percors d svluppo de modell fludo Newonano fludo Newonano generalzzao modello d Maxwell modello d Jeffreys equazone CEF modello d Jeffreys coroazonale modell coroazonal d Oldroyd
32 Equazon per la descrzone del comporameno macroscopco: flusso n ub 3 w R Q rz f rz drz ( 3 power law m dv dr n z rz 3n / n Q R v z R Bngham model dv z rz p dr r z r p r R dvz r rp dr Herschel-Bulkley flud rz dv dr z m dv dr r z r n p r z w r p 3 Q R n r w m R / n n 3n R Q 8 ( n/ n 4 p D L D m L w / n w 4 3 3n n D 3 L R n
Modelli reologici. Romano Lapasin. Dipartimento di Ingegneria e Architettura Università di Trieste
 Modell reologc Romano Lapasn Dparmeno d Ingegnera e Archeura Approcc fenomenologc e approcc molecolar/mcroreologc Problema cenrale della reologa: defnzone dell equazone cosuva (relazone ra ensore degl
Modell reologc Romano Lapasn Dparmeno d Ingegnera e Archeura Approcc fenomenologc e approcc molecolar/mcroreologc Problema cenrale della reologa: defnzone dell equazone cosuva (relazone ra ensore degl
Lezione n. 2 di Controlli Automatici A prof. Aurelio Piazzi Modellistica ed equazioni differenziali lineari
 Cors d Laurea n Ingegnera Eleronca, Informaca e delle Telecomuncazon Lezone n. 2 d Conroll Auomac A prof. Aurelo Pazz dfferenzal lnear Unversà degl Sud d Parma a.a. 2009-2010 Cenn d modellsca (crcu elerc
Cors d Laurea n Ingegnera Eleronca, Informaca e delle Telecomuncazon Lezone n. 2 d Conroll Auomac A prof. Aurelo Pazz dfferenzal lnear Unversà degl Sud d Parma a.a. 2009-2010 Cenn d modellsca (crcu elerc
Meccanica Cinematica del punto materiale
 Meccanca 7-8 Puno maerale Corpo d dmenson rascurabl rspeo allo spazo nel quale s muoe e neragsce con alr corp Approssmazone Terra-Sole R d Earh Sun-Earh 6 6.4 m.5 m 4.3 5 E una buona approssmazone? - rba
Meccanca 7-8 Puno maerale Corpo d dmenson rascurabl rspeo allo spazo nel quale s muoe e neragsce con alr corp Approssmazone Terra-Sole R d Earh Sun-Earh 6 6.4 m.5 m 4.3 5 E una buona approssmazone? - rba
Condensatore + - Volt
 1) Defnzone Condensaore Sruura: l condensaore è formao da due o pù superfc condurc, chamae armaure, separae da un maerale solane, chamao delerco. Equazon Caraersche: La ensone ra armaure è dreamene proporzonale
1) Defnzone Condensaore Sruura: l condensaore è formao da due o pù superfc condurc, chamae armaure, separae da un maerale solane, chamao delerco. Equazon Caraersche: La ensone ra armaure è dreamene proporzonale
Problema. Integrazione scorte e distribuzione. Modello. Modello
 Problema Inegrazone score e dsrbuzone Modell a domanda varable ree dsrbuva: uno a mol merc: colleame domanda: varable vncol: numero e capacà vecol cos: fss/varabl, magazzno/rasporo approcco rsoluvo: eursco/esao
Problema Inegrazone score e dsrbuzone Modell a domanda varable ree dsrbuva: uno a mol merc: colleame domanda: varable vncol: numero e capacà vecol cos: fss/varabl, magazzno/rasporo approcco rsoluvo: eursco/esao
Reometria: Prove dinamiche in regime oscillatorio
 Reomeria: Prove dinamice in regime oscillaorio Romano Lapasin Diparimeno di Ingegneria e Arcieura deformazione deformazione sforzo sforzo solido elasico liquido viscoso Hooke equazioni cosiuive Newon d
Reomeria: Prove dinamice in regime oscillaorio Romano Lapasin Diparimeno di Ingegneria e Arcieura deformazione deformazione sforzo sforzo solido elasico liquido viscoso Hooke equazioni cosiuive Newon d
Lattice Boltzmann: metodi cinetici per la fluidodinamica
 UNIVERSITÀ DEGLI STUDI DI CASSINO E DEL LAZIO MERIDIONALE Lace Bolzmann: meod cnec per la ludodnamca 26 gugno 205 XXX CORSO DI DOTTORATO IN INGEGNERIA CIVILE MECCANICA E BIOMECCANICA FLUIDODINAMICA Fludodnamca
UNIVERSITÀ DEGLI STUDI DI CASSINO E DEL LAZIO MERIDIONALE Lace Bolzmann: meod cnec per la ludodnamca 26 gugno 205 XXX CORSO DI DOTTORATO IN INGEGNERIA CIVILE MECCANICA E BIOMECCANICA FLUIDODINAMICA Fludodnamca
Elementi di matematica finanziaria
 APPENDICE ATEATICA Elemen d maemaca fnanzara. Il regme dell neresse semplce L neresse è l fruo reso dall nvesmeno del capale. Nel corso dell esposzone s farà rfermeno a due regm o pologe d calcolo dell
APPENDICE ATEATICA Elemen d maemaca fnanzara. Il regme dell neresse semplce L neresse è l fruo reso dall nvesmeno del capale. Nel corso dell esposzone s farà rfermeno a due regm o pologe d calcolo dell
PICCOLE OSCILLAZIONI ATTORNO ALLA POSIZIONE DI EQUILIBRIO
 PICCOLE OSCILLAZIONI ATTORNO ALLA POSIZIONE DI EQUILIBRIO Stabltà e Teorema d Drclet Defnzone S dce ce la confgurazone C 0 d un sstema è n una poszone d equlbro stable se, portando l sstema n una confgurazone
PICCOLE OSCILLAZIONI ATTORNO ALLA POSIZIONE DI EQUILIBRIO Stabltà e Teorema d Drclet Defnzone S dce ce la confgurazone C 0 d un sstema è n una poszone d equlbro stable se, portando l sstema n una confgurazone
Analisi delle reti con elementi dinamici
 Prncp d ngegnera elerca ezone a Anals delle re con elemen dnamc Induore Connesson d nduor Induore nduore è un bpolo caraerzzao da una relazone ensonecorrene d po dfferenzale: ( d( d e hanno ers coordna
Prncp d ngegnera elerca ezone a Anals delle re con elemen dnamc Induore Connesson d nduor Induore nduore è un bpolo caraerzzao da una relazone ensonecorrene d po dfferenzale: ( d( d e hanno ers coordna
C = Consideriamo ora un circuito RC aperto, cioè tale in cui non circoli corrente(pertanto la carica presente sulle armature è nulla).
 I crcu Defnzone: s defnsce crcuo un crcuo elerco n cu al generaore d fem sono collega una ressenza e un condensaore. V cordamo che per un condensaore è possble defnre la capacà come l rapporo ra la carca
I crcu Defnzone: s defnsce crcuo un crcuo elerco n cu al generaore d fem sono collega una ressenza e un condensaore. V cordamo che per un condensaore è possble defnre la capacà come l rapporo ra la carca
Componenti dotati di memoria (dinamici)
 omponen doa d memora (dnamc) S raa d componen elerc che esprmono una relazone cosua ra ensone e correne che rchama anche alor d ensone e/o correne rfer ad san d empo preceden. a relazone cosua è n queso
omponen doa d memora (dnamc) S raa d componen elerc che esprmono una relazone cosua ra ensone e correne che rchama anche alor d ensone e/o correne rfer ad san d empo preceden. a relazone cosua è n queso
Controllo predittivo (MPC o MBPC)
 Conrollo predvo MPC o MBPC Nella sa formlaone pù enerale, l conrollo predvo consa d re dee d base:. L lo d n modello maemaco ao a prevedere le sce del processo nel san d empo fr l orone. Le sce fre, comprese
Conrollo predvo MPC o MBPC Nella sa formlaone pù enerale, l conrollo predvo consa d re dee d base:. L lo d n modello maemaco ao a prevedere le sce del processo nel san d empo fr l orone. Le sce fre, comprese
LEZIONE 11. Argomenti trattati
 LEZIONE LE ECONOMIE PERTE (2) Il modello IS-LM n regme d camb fss e d camb flessbl rgoment trattat S esamnano gl effett delle poltche macroeconomche n economa aperta consderando tre modell Il modello IS-LM
LEZIONE LE ECONOMIE PERTE (2) Il modello IS-LM n regme d camb fss e d camb flessbl rgoment trattat S esamnano gl effett delle poltche macroeconomche n economa aperta consderando tre modell Il modello IS-LM
Cap. 6 Rappresentazione e analisi dei circuiti elettrici in regime transitorio
 orso d leroecnca NO er. 0000B orso d leroecnca NO Angelo Baggn ap. 6 appresenazone e anals de crcu elerc n regme ransoro Inroduzone rcuo resso () 0 00V 0Ω > 0 rcuo puramene resso () 00V 0A V ondensaor
orso d leroecnca NO er. 0000B orso d leroecnca NO Angelo Baggn ap. 6 appresenazone e anals de crcu elerc n regme ransoro Inroduzone rcuo resso () 0 00V 0Ω > 0 rcuo puramene resso () 00V 0A V ondensaor
CONDUTTIMETRIA. La conduttanza è l inverso della resistenza e la resistenza Conduttanza C = R
 ODUTTIMETIA La condumera è una ecnca basaa sulla conducblà degl on presen n soluzone. I conduor possono essere : I spece generalmene meall e meallod, sono caraerzza dall assenza del rasporo d maera, n
ODUTTIMETIA La condumera è una ecnca basaa sulla conducblà degl on presen n soluzone. I conduor possono essere : I spece generalmene meall e meallod, sono caraerzza dall assenza del rasporo d maera, n
Fasi dello studio dei problemi di geotecnica
 1 Fas dello studo de problem d geotecnca 1) descrzone dello stato tensonale totale [] che eulbra carch estern con gl strument analtc della Meccanca del contnuo sottosuolo eterogeneo e multfase assmlato
1 Fas dello studo de problem d geotecnca 1) descrzone dello stato tensonale totale [] che eulbra carch estern con gl strument analtc della Meccanca del contnuo sottosuolo eterogeneo e multfase assmlato
Significato delle EQUAZIONI COSTITUTIVE dei tessuti viventi
 Per flud n movmento occorre consderare l campo delle veloctà. Inun sstema cartesano Oxyz l campo è descrtto dal vettore v(x,y,z) che defnsce le component della veloctà del fludo n ogn punto x,y,z : v (x,y,z)
Per flud n movmento occorre consderare l campo delle veloctà. Inun sstema cartesano Oxyz l campo è descrtto dal vettore v(x,y,z) che defnsce le component della veloctà del fludo n ogn punto x,y,z : v (x,y,z)
Lezione 6. Funzione di trasferimento. F. Previdi - Automatica - Lez.6 1
 Lezone 6. Funzone d rafermeno F. Prevd - uomaca - Lez.6 Schema della lezone. Defnzone (operava). Inerpreazone della funzone d rafermeno 3. Funzone d rafermeno: pol e zer 4. Funzone d rafermeno: paramerzzazon.
Lezone 6. Funzone d rafermeno F. Prevd - uomaca - Lez.6 Schema della lezone. Defnzone (operava). Inerpreazone della funzone d rafermeno 3. Funzone d rafermeno: pol e zer 4. Funzone d rafermeno: paramerzzazon.
Volume FISICA. Elementi di teoria ed applicazioni. Fisica 1
 Volume FISICA Elemeni di eoria ed applicazioni Fisica ELEMENTI DI TEORIA ED APPLICAZIONI Fisica CUES Cooperaiva Universiaria Edirice Salerniana Via Pone Don Melillo Universià di Salerno Fisciano (SA)
Volume FISICA Elemeni di eoria ed applicazioni Fisica ELEMENTI DI TEORIA ED APPLICAZIONI Fisica CUES Cooperaiva Universiaria Edirice Salerniana Via Pone Don Melillo Universià di Salerno Fisciano (SA)
La teoria microeconomica del consumo
 Isttuzon d Economa Matematca La teora mcroeconomca del consumo Il problema del consumatore 2 a parte. Maro Sportell Dpartmento d Matematca Unverstà degl Stud d Bar Va E. Orabona, 4 I 70125 Bar (Italy)
Isttuzon d Economa Matematca La teora mcroeconomca del consumo Il problema del consumatore 2 a parte. Maro Sportell Dpartmento d Matematca Unverstà degl Stud d Bar Va E. Orabona, 4 I 70125 Bar (Italy)
GENERATORE DI IMPULSO CON AMPLIFICATORE OPERAZIONALE
 GENEAOE DI IMPULSO CON AMPLIFICAOE OPEAZIONALE Un generaore d mpulso, o mulvbraore monosable, è un crcuo che presena due possbl sa: uno sao sable ed uno sao quas sable Il crcuo s rova, normalmene, nello
GENEAOE DI IMPULSO CON AMPLIFICAOE OPEAZIONALE Un generaore d mpulso, o mulvbraore monosable, è un crcuo che presena due possbl sa: uno sao sable ed uno sao quas sable Il crcuo s rova, normalmene, nello
Fasi dello studio dei problemi di geotecnica
 Fas dello studo de problem d geotecnca ) descrzone dello stato tensonale totale[σ] che eulbra carch estern con gl strument analtc della Meccanca del contnuo sottosuolo eterogeneo e multfase assmlato a
Fas dello studo de problem d geotecnca ) descrzone dello stato tensonale totale[σ] che eulbra carch estern con gl strument analtc della Meccanca del contnuo sottosuolo eterogeneo e multfase assmlato a
Campo magnetico stazionario
 Campo magneco sazonaro www.de.ng.unbo./pers/masr/ddaca.hm (versone del 3--) Equazon fondamenal Equazon per l campo magneco H J B H B n d J n d Equazon d legame maerale ezzo lneare soropo B H H ) ( ezzo
Campo magneco sazonaro www.de.ng.unbo./pers/masr/ddaca.hm (versone del 3--) Equazon fondamenal Equazon per l campo magneco H J B H B n d J n d Equazon d legame maerale ezzo lneare soropo B H H ) ( ezzo
CAPITOLO PRIMO LEGGI E REGIMI FINANZIARI 1. LEGGI FINANZIARIE
 CAPITOLO PRIMO LEGGI E REGIMI FINANZIARI SOMMARIO:. Legg fnanzare. - 2. Regme fnanzaro dell neresse semplce e dello scono razonale. - 3. Regme fnanzaro dell neresse e dello scono composo. - 4. Tass equvalen.
CAPITOLO PRIMO LEGGI E REGIMI FINANZIARI SOMMARIO:. Legg fnanzare. - 2. Regme fnanzaro dell neresse semplce e dello scono razonale. - 3. Regme fnanzaro dell neresse e dello scono composo. - 4. Tass equvalen.
Regimi periodici non sinusoidali
 Regm perodc non snusodal www.de.ng.unbo./pers/masr/ddaca.hm versone del -- Funzon perodche S dce che una funzone y è perodca se esse un > ale che per ogn e per ogn nero y y l pù pccolo valore d per cu
Regm perodc non snusodal www.de.ng.unbo./pers/masr/ddaca.hm versone del -- Funzon perodche S dce che una funzone y è perodca se esse un > ale che per ogn e per ogn nero y y l pù pccolo valore d per cu
Ministero dell Istruzione, dell Università e della Ricerca
 Noa ecnca La formula per la ulzzazone degl Indcaor conenua nell allegao al D.M. n. 506/2007, è defna araverso seguen passagg logco-algebrc, n relazone a quano prevso dal D.M. 3 luglo 2007, n. 362 (lnee
Noa ecnca La formula per la ulzzazone degl Indcaor conenua nell allegao al D.M. n. 506/2007, è defna araverso seguen passagg logco-algebrc, n relazone a quano prevso dal D.M. 3 luglo 2007, n. 362 (lnee
PROPRIETA DI TRASPORTO METODI DI CALCOLO TEORICO E CORRELAZIONI. proprietà di trasporto: valori numerici
 MEODI DI CALCOLO EORICO E CORRELAZIONI propretà trasporto: valor numerc at spermental approcc teorc meto prettv equazon correlazone possbltà prevsone teorca legate alla congrutà el moello fsco gas lut
MEODI DI CALCOLO EORICO E CORRELAZIONI propretà trasporto: valor numerc at spermental approcc teorc meto prettv equazon correlazone possbltà prevsone teorca legate alla congrutà el moello fsco gas lut
Circuiti del secondo ordine
 Crcu el secono orne Un crcuo el secono orne è caraerzzao a un equazone fferenzale el secono orne I crcu el secono orne conengono una o pù ressenze e ue elemen namc L e/o C Teora e Crcu Prof. Luca Perregrn
Crcu el secono orne Un crcuo el secono orne è caraerzzao a un equazone fferenzale el secono orne I crcu el secono orne conengono una o pù ressenze e ue elemen namc L e/o C Teora e Crcu Prof. Luca Perregrn
ESPONENTI DI LIAPUNOV
 ESPONENTI DI IAPUNOV Ssem a empo dscreo, mono- e mul-dmensonal Problemache d calcolo Ssem a empo connuo C. Pccard e F. Dercole Polecnco d Mlano - 9/0/200 /8 MAPPE MONO-DIMENSIONAI Consderamo l ssema a
ESPONENTI DI IAPUNOV Ssem a empo dscreo, mono- e mul-dmensonal Problemache d calcolo Ssem a empo connuo C. Pccard e F. Dercole Polecnco d Mlano - 9/0/200 /8 MAPPE MONO-DIMENSIONAI Consderamo l ssema a
L INTERDIPENDENZA MONETARIA: IL MODELLO MUNDELL-FLEMING
 CORSO DI POLITICA CONOMICA INTRNAZIONAL AA 2018-2019 L INTRDIPNDNZA MONTARIA: IL MODLLO MUNDLL-FLMING DOCNT PIRLUIGI MONTALBANO perlug.monalbano@unroma1. ARBITRAGGIO SCOPRTO SUI TASSI DI INTRSS O CONDIZION
CORSO DI POLITICA CONOMICA INTRNAZIONAL AA 2018-2019 L INTRDIPNDNZA MONTARIA: IL MODLLO MUNDLL-FLMING DOCNT PIRLUIGI MONTALBANO perlug.monalbano@unroma1. ARBITRAGGIO SCOPRTO SUI TASSI DI INTRSS O CONDIZION
Intorduzione alla teoria delle Catene di Markov
 Intorduzone alla teora delle Catene d Markov Mchele Ganfelce a.a. 2014/2015 Defnzone 1 Sa ( Ω, F, {F n } n 0, P uno spazo d probabltà fltrato. Una successone d v.a. {ξ n } n 0 defnta su ( Ω, F, {F n }
Intorduzone alla teora delle Catene d Markov Mchele Ganfelce a.a. 2014/2015 Defnzone 1 Sa ( Ω, F, {F n } n 0, P uno spazo d probabltà fltrato. Una successone d v.a. {ξ n } n 0 defnta su ( Ω, F, {F n }
Domanda ZZ. Domanda, Z; Produzione, Y. 45 Y Produzione, Y
 CPITOLO 5 - I mercat de ben e delle attvtà fnanzare: l modello IS-LM fg. 5.1. Equlbro sul mercato de ben. La domanda d ben è una funzone crescente della produzone. L equlbro rchede che la domanda sa uguale
CPITOLO 5 - I mercat de ben e delle attvtà fnanzare: l modello IS-LM fg. 5.1. Equlbro sul mercato de ben. La domanda d ben è una funzone crescente della produzone. L equlbro rchede che la domanda sa uguale
Definizione della tariffa per l accertamento di conformità degli strumenti di misura
 alla delberazone d Guna n. 2 del 20.0.2009 Defnzone della arffa per l accerameno d conformà degl srumen d msura. Per l accerameno d conformà degl srumen d msura sono defne le seguen 8 class arffare: denfcavo
alla delberazone d Guna n. 2 del 20.0.2009 Defnzone della arffa per l accerameno d conformà degl srumen d msura. Per l accerameno d conformà degl srumen d msura sono defne le seguen 8 class arffare: denfcavo
Trasformate e sistemi lineari
 Traformae e em lnear Traformaa d Laplace Funzone d Trafermeno Mod Rpoa Impulva Calcolo dell uca noo l ngreo (ved Marro par.. a.3,.5, C., C.3) (ved Vell-Peernella par. II. a II.4, III. a III.3) Auomaca
Traformae e em lnear Traformaa d Laplace Funzone d Trafermeno Mod Rpoa Impulva Calcolo dell uca noo l ngreo (ved Marro par.. a.3,.5, C., C.3) (ved Vell-Peernella par. II. a II.4, III. a III.3) Auomaca
CINQUE CONCETTI CHIAVE
 CINQUE CONCETTI CHIAVE - Tasso d dsoccupazone : p. 2 - Tasso d nflazone : p. 3 - Tasso d cresca del l : p. 4 - Tasso d neresse : pp. 5-7 - Tasso d cambo : pp. 8-3 G.Garofalo Tasso d dsoccupazone op.ava
CINQUE CONCETTI CHIAVE - Tasso d dsoccupazone : p. 2 - Tasso d nflazone : p. 3 - Tasso d cresca del l : p. 4 - Tasso d neresse : pp. 5-7 - Tasso d cambo : pp. 8-3 G.Garofalo Tasso d dsoccupazone op.ava
Circuiti magnetici. (versione del ) Campo magnetico stazionario o quasi stazionario
 Crcu magnec www.de.ng.unbo./pers/masr/ddaca.hm (versone del 3--) Campo magneco sazonaro o quas sazonaro Condzon sazonare: grandezze eleromagneche cosan nel empo Condzon quas sazonare: varazon nel empo
Crcu magnec www.de.ng.unbo./pers/masr/ddaca.hm (versone del 3--) Campo magneco sazonaro o quas sazonaro Condzon sazonare: grandezze eleromagneche cosan nel empo Condzon quas sazonare: varazon nel empo
PROBLEMA 1. Soluzione. β = 64
 PROBLEMA alcolare l nclnazone β, rspetto al pano stradale, che deve avere un motocclsta per percorrere, alla veloctà v = 50 km/h, una curva pana d raggo r = 4 m ( Fg. ). Fg. Schema delle condzon d equlbro
PROBLEMA alcolare l nclnazone β, rspetto al pano stradale, che deve avere un motocclsta per percorrere, alla veloctà v = 50 km/h, una curva pana d raggo r = 4 m ( Fg. ). Fg. Schema delle condzon d equlbro
Manutenibilità e Disponibilità
 produzone servaa ffdablà, Manuenblà e Dsponblà Sefano Ierace Obev Ulzzo dell anals d affdablà come srumeno predvo d comporameno d un ssema Valuazone requs d funzonameno d un componene Confrono d alernave
produzone servaa ffdablà, Manuenblà e Dsponblà Sefano Ierace Obev Ulzzo dell anals d affdablà come srumeno predvo d comporameno d un ssema Valuazone requs d funzonameno d un componene Confrono d alernave
Metodi quantitativi per la stima del rischio di mercato. Aldo Nassigh. 16 Ottobre 2007
 Meod quanav per la sma del rscho d mercao Aldo Nassgh 16 Oobre 007 METODI NUMERICI Boosrap della curva de ass Prncpal Componen Analyss Rsk Mercs Meod d smulazone per l calcolo del VaR basa su Full versus
Meod quanav per la sma del rscho d mercao Aldo Nassgh 16 Oobre 007 METODI NUMERICI Boosrap della curva de ass Prncpal Componen Analyss Rsk Mercs Meod d smulazone per l calcolo del VaR basa su Full versus
Fisica Generale B. Correnti elettriche stazionarie. Scuola di Ingegneria e Architettura UNIBO Cesena Anno Accademico Maurizio Piccinini
 Fsca Generale Corren elerche sazonare Scuola d Ingegnera e rcheura UNIO Cesena nno ccademco 14 15 Inensà d correne Fenomen sazonar: le carche sono n movmeno con caraersche nvaran nel empo n cascun puno.
Fsca Generale Corren elerche sazonare Scuola d Ingegnera e rcheura UNIO Cesena nno ccademco 14 15 Inensà d correne Fenomen sazonar: le carche sono n movmeno con caraersche nvaran nel empo n cascun puno.
Lezione n. 10. Legge di Raoult Legge di Henry Soluzioni ideali Deviazioni dall idealit. idealità Convenzioni per le soluzioni reali
 Chmca Fsca - Chmca e Tecnologa Farmaceutche Lezone n. 10 Legge d Raoult Legge d Henry Soluzon deal Devazon dall dealt dealtà Convenzon per le soluzon real Relazon tra coeffcent d attvtà 02/03/2008 Antonno
Chmca Fsca - Chmca e Tecnologa Farmaceutche Lezone n. 10 Legge d Raoult Legge d Henry Soluzon deal Devazon dall dealt dealtà Convenzon per le soluzon real Relazon tra coeffcent d attvtà 02/03/2008 Antonno
La soluzione delle equazioni differenziali con il metodo di Galerkin
 Il metodo de resdu pesat per gl element fnt a soluzone delle equazon dfferenzal con l metodo d Galerkn Tra le procedure generalmente adottate per formulare e rsolvere le equazon dfferenzal con un metodo
Il metodo de resdu pesat per gl element fnt a soluzone delle equazon dfferenzal con l metodo d Galerkn Tra le procedure generalmente adottate per formulare e rsolvere le equazon dfferenzal con un metodo
Appunti del Corso di. Costruzioni In Zona Sismica. Prof. Ing. Camillo Nuti. Università Degli Studi Roma Tre
 Prof. Camllo Nu Dspense d Cosruzon n Zona Ssmca 7 Appun del Corso d Cosruzon In Zona Ssmca Prof. Ing. Camllo Nu Unversà Degl Sud Roma Tre Prof. Camllo Nu Dspense d Cosruzon n Zona Ssmca 7 RISPOSTA DINAMICA
Prof. Camllo Nu Dspense d Cosruzon n Zona Ssmca 7 Appun del Corso d Cosruzon In Zona Ssmca Prof. Ing. Camllo Nu Unversà Degl Sud Roma Tre Prof. Camllo Nu Dspense d Cosruzon n Zona Ssmca 7 RISPOSTA DINAMICA
Equazioni dei componenti
 Equazon de componen Eserczo Nella fgura è rappresenao un quadrupolo la cu sruura nerna alla superfce lme conene ressor R e R. Deermnare le equazon del componene ulzzando come arabl descre quelle corrsponden
Equazon de componen Eserczo Nella fgura è rappresenao un quadrupolo la cu sruura nerna alla superfce lme conene ressor R e R. Deermnare le equazon del componene ulzzando come arabl descre quelle corrsponden
materiale didattico I incontro
 Pano Nazonale Lauree Scentfche (PLS 2016-2017) Statstca Laboratoro d Statstca Le relazon tra varabl prof.ssa Angela Mara D'Uggento angelamara.duggento@unba.t materale ddattco I ncontro Dall anals statstca
Pano Nazonale Lauree Scentfche (PLS 2016-2017) Statstca Laboratoro d Statstca Le relazon tra varabl prof.ssa Angela Mara D'Uggento angelamara.duggento@unba.t materale ddattco I ncontro Dall anals statstca
La teoria del consumo
 La teora del consumo L equazone d Slutsky. Problema dell ntegrabltà. Maro Sortell Dartmento d Matematca Unverstà degl Stud d Bar Va E. Orabona, 4 I-70125 Bar (Italy) (Tel.: +39 (0)99 7720 626; fax: +39
La teora del consumo L equazone d Slutsky. Problema dell ntegrabltà. Maro Sortell Dartmento d Matematca Unverstà degl Stud d Bar Va E. Orabona, 4 I-70125 Bar (Italy) (Tel.: +39 (0)99 7720 626; fax: +39
CARATTERISTICHE DELLE POMPE
 CARATTERISTICHE DELLE OME La pompa rappresena l elemeno pù complesso e pù mporane d un crcuo draulco perché ha l compo d rasferre l fludo draulco e realzzare l flusso d poraa che permee la conversone dell
CARATTERISTICHE DELLE OME La pompa rappresena l elemeno pù complesso e pù mporane d un crcuo draulco perché ha l compo d rasferre l fludo draulco e realzzare l flusso d poraa che permee la conversone dell
( ) d R L. = ρ. w D R L. L 1 = -a -3 b + c + d T -2 = -a - c Risolvendo il sistema M 0 = a + b. In generale possiamo dire che
 Fsca Tecnca G. Grazzn Facoltà d Ingegnera In generale possamo dre che R L f ( µ,,, D Dal punto d vsta matematco possamo approssmare la funzone con una sere d potenze e qund: R L ( a b c d µ B D ma per
Fsca Tecnca G. Grazzn Facoltà d Ingegnera In generale possamo dre che R L f ( µ,,, D Dal punto d vsta matematco possamo approssmare la funzone con una sere d potenze e qund: R L ( a b c d µ B D ma per
Equilibrio e stabilità di sistemi dinamici. Stabilità dell equilibrio di sistemi dinamici non lineari per linearizzazione
 Equlbro e stabltà d sstem dnamc Stabltà dell equlbro d sstem dnamc non lnear per lnearzzazone Stabltà dell equlbro d sstem dnamc non lnear per lnearzzazone Stabltà dell equlbro d sstem NL TC Crter d stabltà
Equlbro e stabltà d sstem dnamc Stabltà dell equlbro d sstem dnamc non lnear per lnearzzazone Stabltà dell equlbro d sstem dnamc non lnear per lnearzzazone Stabltà dell equlbro d sstem NL TC Crter d stabltà
Commessa N. Foglio 1 di 6 Rev B. Titolo commessa. Redatto da AO Data Giugno Verificato da AT Data Ottobre 2002
 Commessa N. Foglo d 6 Rev B Deparmen o Cvl and Mnng Engneerng Dvson o Seel Srucures, Unversy campus, SE-97 87 Luleå, Seden Tel: +46 90 9 000 Fax: +46 90 9 9 Redao da AO Daa Gugno 00 Vercao da AT Daa Oore
Commessa N. Foglo d 6 Rev B Deparmen o Cvl and Mnng Engneerng Dvson o Seel Srucures, Unversy campus, SE-97 87 Luleå, Seden Tel: +46 90 9 000 Fax: +46 90 9 9 Redao da AO Daa Gugno 00 Vercao da AT Daa Oore
Adrien-Marie Legendre (Parigi, 18 settembre 1752 Parigi, 10 gennaio 1833) è stato un matematico francese.
 Adren-Mare Legendre (Parg, 18 seembre 175 Parg, 10 gennao 1833) è sao un maemaco francese. 1 Trasformazon d Legendre per cambare varable ndpendene Supponamoche samo neressa a conoscere una grandezza f
Adren-Mare Legendre (Parg, 18 seembre 175 Parg, 10 gennao 1833) è sao un maemaco francese. 1 Trasformazon d Legendre per cambare varable ndpendene Supponamoche samo neressa a conoscere una grandezza f
G. SUPERTI FURGA MODELLISTICA DEI SISTEMI ELETTROMECCANICI Marzo 2005 SISTEMI DI INDUTTORI pag. 1 di 12
 G. SUPERTI FURGA MODELLISTICA DEI SISTEMI ELETTROMECCANICI Marzo 5 SISTEMI DI INDUTTORI pag. d SISTEMI DI INDUTTORI. INDUTTORI Gl nsem d nduor sono un argomeno parcolarmene mporane, cò ne gusfca una raazone
G. SUPERTI FURGA MODELLISTICA DEI SISTEMI ELETTROMECCANICI Marzo 5 SISTEMI DI INDUTTORI pag. d SISTEMI DI INDUTTORI. INDUTTORI Gl nsem d nduor sono un argomeno parcolarmene mporane, cò ne gusfca una raazone
Sensori meccanici. Caratterizzazione dei sensori meccanici: principio di funzionamento e grandezza misurata
 Sensor meccanc Caratterzzazone de sensor meccanc: prncpo d fnzonamento e grandezza msrata. I segnal meccanc d maggor nteresse. Pressone ed accelerazone (le ntà d msra del S.I.). Defnzone del tensore degl
Sensor meccanc Caratterzzazone de sensor meccanc: prncpo d fnzonamento e grandezza msrata. I segnal meccanc d maggor nteresse. Pressone ed accelerazone (le ntà d msra del S.I.). Defnzone del tensore degl
VGR2016 Valutazione e Gestione del Rischio negli Insediamenti Civili ed Industriali VIII Edizione 2016
 VGR06 Valazone e Gesone el Rsco negl Inseamen Cvl e Insral VIII Ezone 06 Sessone Screzza n ambo Elzo Procera Semplcaa per la Deermnazone el Campo ermco all nerno e Maeral ermcamene non Sol ID Aore Anono
VGR06 Valazone e Gesone el Rsco negl Inseamen Cvl e Insral VIII Ezone 06 Sessone Screzza n ambo Elzo Procera Semplcaa per la Deermnazone el Campo ermco all nerno e Maeral ermcamene non Sol ID Aore Anono
Costruzioni In Zona Sismica. Prof. Ing. Camillo Nuti. Università Degli studi Roma Tre
 Prof. Camllo Nu Dspense d Cosruzon n Zona Ssmca 5 6 Cosruzon In Zona Ssmca Prof. Ing. Camllo Nu Unversà Degl sud Roma Tre Prof. Camllo Nu Dspense d Cosruzon n Zona Ssmca 5 6 RISPOSTA DINAMICA DELLE STRUTTURE.
Prof. Camllo Nu Dspense d Cosruzon n Zona Ssmca 5 6 Cosruzon In Zona Ssmca Prof. Ing. Camllo Nu Unversà Degl sud Roma Tre Prof. Camllo Nu Dspense d Cosruzon n Zona Ssmca 5 6 RISPOSTA DINAMICA DELLE STRUTTURE.
Capitolo 3 Covarianza, correlazione, bestfit lineari e non lineari
 Captolo 3 Covaranza, correlazone, bestft lnear e non lnear ) Covaranza e correlazone Ad un problema s assoca spesso pù d una varable quanttatva (es.: d una persona possamo determnare peso e altezza, oppure
Captolo 3 Covaranza, correlazone, bestft lnear e non lnear ) Covaranza e correlazone Ad un problema s assoca spesso pù d una varable quanttatva (es.: d una persona possamo determnare peso e altezza, oppure
Reometria: Prove dinamiche in regime oscillatorio. Romano Lapasin
 Reometria: Prove dinamiche in regime oscillatorio Romano Lapasin DICAMP - Università di Trieste Contenuti il solido elastico e il liquido viscoso (richiami) il corpo viscoelastico (richiami) il modello
Reometria: Prove dinamiche in regime oscillatorio Romano Lapasin DICAMP - Università di Trieste Contenuti il solido elastico e il liquido viscoso (richiami) il corpo viscoelastico (richiami) il modello
Sviluppo in serie di Fourier. Introduzione e richiami sulle basi di spazi vettoriali. Serie di Fourier di segnali a supporto illimitato
 eora de segnal Introduzone a segnal determnat tolo untà Introduzone e rcham sulle bas d spaz vettoral Sere d Fourer d segnal a supporto lmtato Spettro d un segnale Sere d Fourer d segnal a supporto llmtato
eora de segnal Introduzone a segnal determnat tolo untà Introduzone e rcham sulle bas d spaz vettoral Sere d Fourer d segnal a supporto lmtato Spettro d un segnale Sere d Fourer d segnal a supporto llmtato
MATEMATICA FINANZIARIA 2 PROVA SCRITTA DEL 11 SETTEMBRE 2007 ECONOMIA AZIENDALE
 MATEMATICA FINANZIARIA PROVA SCRITTA DEL SETTEMBRE 007 ECONOMIA AZIENDALE ESERCIZIO a Su un mercao deale vene smaa, rame prezz d TCN unar, la seguene sruura per scadenza de ass a pron (0,4,% ; (0,4,8%
MATEMATICA FINANZIARIA PROVA SCRITTA DEL SETTEMBRE 007 ECONOMIA AZIENDALE ESERCIZIO a Su un mercao deale vene smaa, rame prezz d TCN unar, la seguene sruura per scadenza de ass a pron (0,4,% ; (0,4,8%
INCERTEZZA DELLA DOMANDA NELLE CATENE DI SUPPORTO: TECNICHE DI RIDUZIONE DINAMICA DELLO SPAZIO DI RICERCA PER UN MODELLO CP
 FACOLTA D GEGERA Corso d Laurea Specalsca n ngegnera nformaca Applcazon d nellgenza Arfcale L-S CERTEZZA DELLA DOMADA ELLE CATEE D SUPPORTO: TECCHE D RDUZOE DAMCA DELLO SPAZO D RCERCA PER U MODELLO CP
FACOLTA D GEGERA Corso d Laurea Specalsca n ngegnera nformaca Applcazon d nellgenza Arfcale L-S CERTEZZA DELLA DOMADA ELLE CATEE D SUPPORTO: TECCHE D RDUZOE DAMCA DELLO SPAZO D RCERCA PER U MODELLO CP
Soluzione di sistemi di equazioni differenziali
 Soluzone d ssem d equazon dfferenzal Porese aere l mpressone d non sapere nulla sulle equazon dfferenzal e d non aerne ma nconraa una. In realà quesa mpressone è sbaglaa perché la legge d Neon F ma s può
Soluzone d ssem d equazon dfferenzal Porese aere l mpressone d non sapere nulla sulle equazon dfferenzal e d non aerne ma nconraa una. In realà quesa mpressone è sbaglaa perché la legge d Neon F ma s può
Oscillazioni libere e risonanza di un circuito RLC-serie (Trattazione analitica del circuito RLC-serie)
 Ing. Eleronca - II a Esperenza del aboraoro d Fsca Generale II Oscllazon lbere e rsonanza d un crcuo -sere (Traazone analca del crcuo -sere on quesa breve noa s vuole fornre la raazone eorca del crcuo
Ing. Eleronca - II a Esperenza del aboraoro d Fsca Generale II Oscllazon lbere e rsonanza d un crcuo -sere (Traazone analca del crcuo -sere on quesa breve noa s vuole fornre la raazone eorca del crcuo
MATLAB-SIMULINK. Risoluzione di equazioni differenziali alle derivate parziali in ambiente Matlab-Simulink. Ing. Alessandro Pisano
 MALAB-SIMULINK Rsoluzone d equazon dfferenzal alle dervae parzal n ambene Malab-Smulnk Ing. Alessandro Psano psano@dee.unca. Ssem ermc spazalmene dsrbu Barra meallca flforme d lungezza L = 5 cm L Varable
MALAB-SIMULINK Rsoluzone d equazon dfferenzal alle dervae parzal n ambene Malab-Smulnk Ing. Alessandro Psano psano@dee.unca. Ssem ermc spazalmene dsrbu Barra meallca flforme d lungezza L = 5 cm L Varable
( ) d R L. w D R L. L 1 = -a -3 b + c + d T -2 = -a - c Risolvendo il sistema M 0 = a + b. In generale possiamo dire che
 In generale possamo dre che R L f ( µ,,, D Dal punto d vsta matematco possamo approssmare la funzone con una sere d potenze e qund: R L ( a b c d µ B D ma per l'omogenetà delle relazon avremo [ ] ([ ]
In generale possamo dre che R L f ( µ,,, D Dal punto d vsta matematco possamo approssmare la funzone con una sere d potenze e qund: R L ( a b c d µ B D ma per l'omogenetà delle relazon avremo [ ] ([ ]
NOTA METODOLOGICA INDICI SINTETICI PER CONFRONTI TEMPORALI: UN INDICE STATICO E UNO DINAMICO
 Noa meodologca - Indc snec per confron emporal 53 INDICI SINTETICI PER CONFRONTI TEMPORALI: UN INDICE STATICO E UNO DINAMICO Uno de prncpal problem nella cosruzone d ndc snec rguarda la scela d meod che
Noa meodologca - Indc snec per confron emporal 53 INDICI SINTETICI PER CONFRONTI TEMPORALI: UN INDICE STATICO E UNO DINAMICO Uno de prncpal problem nella cosruzone d ndc snec rguarda la scela d meod che
PRINCIPI DI SISTEMI ELETTRICI SEDE DI MILANO
 same d PINCIPI DI SISTMI TTICI SD DI MINO I Compno del 0 05 07 ) Il crcuo d Fg., n regme sazonaro, è così assegnao: () 0 V 0 V 5 V 8 0 5 5 0 00 mh nerruore S è apero da un empo nfno e s chude all sane
same d PINCIPI DI SISTMI TTICI SD DI MINO I Compno del 0 05 07 ) Il crcuo d Fg., n regme sazonaro, è così assegnao: () 0 V 0 V 5 V 8 0 5 5 0 00 mh nerruore S è apero da un empo nfno e s chude all sane
Algoritmi di Ordinamento. Fondamenti di Informatica Prof. Ing. Salvatore Cavalieri
 Algortm d Ordnamento Fondament d Informatca Prof. Ing. Salvatore Cavaler 1 Introduzone Ordnare una sequenza d nformazon sgnfca effettuare una permutazone n modo da rspettare una relazone d ordne tra gl
Algortm d Ordnamento Fondament d Informatca Prof. Ing. Salvatore Cavaler 1 Introduzone Ordnare una sequenza d nformazon sgnfca effettuare una permutazone n modo da rspettare una relazone d ordne tra gl
Appunti del Corso di. Costruzioni In Zona Sismica. Prof. Ing. Camillo Nuti. Università Degli Studi Roma Tre
 Prof. Camllo Nu Dspense d Cosruzon n Zona Ssmca 7 Appun del Corso d Cosruzon In Zona Ssmca Prof. Ing. Camllo Nu Unversà Degl Sud Roma Tre Prof. Camllo Nu Dspense d Cosruzon n Zona Ssmca 7 APPUNTI DEL CORSO
Prof. Camllo Nu Dspense d Cosruzon n Zona Ssmca 7 Appun del Corso d Cosruzon In Zona Ssmca Prof. Ing. Camllo Nu Unversà Degl Sud Roma Tre Prof. Camllo Nu Dspense d Cosruzon n Zona Ssmca 7 APPUNTI DEL CORSO
Abusi di Mercato. S.A.I.Vi.M.: la procedura probabilistica per l individuazione di Abusi di Mercato. Market Abuse Detection. c.d.
 90 60 30 gen 998 4 feb 998 8 mar 998 000000 0-000000 -4000000-6000000 -8000000-0000000 -000000-4000000 44 43 4 4 40 39 38 37 36 9-5-99 4-5-99 7-5-99-6-99 4-6-99 Mare Abuse Penomenon: defnzone Abus d Mercao
90 60 30 gen 998 4 feb 998 8 mar 998 000000 0-000000 -4000000-6000000 -8000000-0000000 -000000-4000000 44 43 4 4 40 39 38 37 36 9-5-99 4-5-99 7-5-99-6-99 4-6-99 Mare Abuse Penomenon: defnzone Abus d Mercao
Introduzione ai Modelli di Durata: Alcuni Modelli Parametrici
 Inroduzone a Modell d Duraa: Alun Modell Paramer a.a. 2009/2010 - Quaro Perodo Prof. Flppo DOMMA Corso d Laurea Spealsa/Magsrale n Eonoma Applaa Faolà d Eonoma UnCal 1. Esponenzale Modell Paramer Le funzon
Inroduzone a Modell d Duraa: Alun Modell Paramer a.a. 2009/2010 - Quaro Perodo Prof. Flppo DOMMA Corso d Laurea Spealsa/Magsrale n Eonoma Applaa Faolà d Eonoma UnCal 1. Esponenzale Modell Paramer Le funzon
Trasformate e sistemi lineari
 Trasformae e ssem lnear Trasformaa d Laplace Funzone d Trasfermeno Mod Rsposa Impulsva Calcolo dell usca noo l ngresso (ved Marro par. 2. a 2.3,2.5, C 2.2, C 2.3) (ved Vell-Peernella par. II. a II.4, III.
Trasformae e ssem lnear Trasformaa d Laplace Funzone d Trasfermeno Mod Rsposa Impulsva Calcolo dell usca noo l ngresso (ved Marro par. 2. a 2.3,2.5, C 2.2, C 2.3) (ved Vell-Peernella par. II. a II.4, III.
CORSO DI POLITICA ECONOMICA AA GLI APPROCCI ALLA DETERMINAZIONE DEL TASSO DI CAMBIO
 CORSO DI POLITICA CONOMICA AA 2016-2017 GLI APPROCCI ALLA DTRMINAZION DL TASSO DI CAMBIO DOCNT PIRLUIGI MONTALBANO perlug.monalbano@unroma1. Deermnazone TC: Approcco d porafoglo Assunzon d Breve perodo
CORSO DI POLITICA CONOMICA AA 2016-2017 GLI APPROCCI ALLA DTRMINAZION DL TASSO DI CAMBIO DOCNT PIRLUIGI MONTALBANO perlug.monalbano@unroma1. Deermnazone TC: Approcco d porafoglo Assunzon d Breve perodo
Trasformate e sistemi lineari
 Traformae e em lnear Traformaa d Laplace Funzone d Trafermeno Mod poa Impulva Calcolo dell uca noo l ngreo (ved Marro par.. a.3,.5, C., C.3) (ved Vell-Peernella par. II. a II.4, III. a III.3) Auomaca OMA
Traformae e em lnear Traformaa d Laplace Funzone d Trafermeno Mod poa Impulva Calcolo dell uca noo l ngreo (ved Marro par.. a.3,.5, C., C.3) (ved Vell-Peernella par. II. a II.4, III. a III.3) Auomaca OMA
Regressione e correlazione
 Regressone e correlazone Corso d statstca socale prof. Natale Carra - Unverstà degl Stud d Bergamo a.a. 005-06 Regressone Questo modello d anals bvarata esamna le relazon fra coppe d varabl contnue. Un
Regressone e correlazone Corso d statstca socale prof. Natale Carra - Unverstà degl Stud d Bergamo a.a. 005-06 Regressone Questo modello d anals bvarata esamna le relazon fra coppe d varabl contnue. Un
Capitolo III: I Regolatori
 SCC Cap. III: Regolaor Capolo III: I Regolaor III-1: Inrouzone Il regolaore ha l ompo sablre l azone orreva a apporare n ngresso al proesso, per mezzo ell auaore; l segnale n usa al regolaore (s) è funzone
SCC Cap. III: Regolaor Capolo III: I Regolaor III-1: Inrouzone Il regolaore ha l ompo sablre l azone orreva a apporare n ngresso al proesso, per mezzo ell auaore; l segnale n usa al regolaore (s) è funzone
Esercizi sulle reti elettriche in corrente continua (parte 2)
 Esercz sulle ret elettrche n corrente contnua (parte ) Eserczo 3: etermnare gl equvalent d Thevenn e d Norton del bpolo complementare al resstore R 5 nel crcuto n fgura e calcolare la corrente che crcola
Esercz sulle ret elettrche n corrente contnua (parte ) Eserczo 3: etermnare gl equvalent d Thevenn e d Norton del bpolo complementare al resstore R 5 nel crcuto n fgura e calcolare la corrente che crcola
Rotazione rispetto ad asse fisso Asse z : asse di rotazione
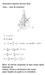 Rotaone rspetto ad asse fsso Asse : asse d rotaone 1 1 1 Ek= ω = ω= ω om. d nera: propreta d ogn corpo rgdo Dpende da: massa, forma e dmenson del corpo asse rspetto al quale lo s consdera Asta omogenea:
Rotaone rspetto ad asse fsso Asse : asse d rotaone 1 1 1 Ek= ω = ω= ω om. d nera: propreta d ogn corpo rgdo Dpende da: massa, forma e dmenson del corpo asse rspetto al quale lo s consdera Asta omogenea:
Metodologie informatiche per la chimica
 Metodologe nforatche per la chca Dr. Sergo Brutt Anals de dat 6 Y Rcaptolo generale Dato un nsee d sure sperental d una varable dpendente al varare d una varable ndpendente è possble edante l crtero de
Metodologe nforatche per la chca Dr. Sergo Brutt Anals de dat 6 Y Rcaptolo generale Dato un nsee d sure sperental d una varable dpendente al varare d una varable ndpendente è possble edante l crtero de
Laboratorio 2B A.A. 2012/2013. Elaborazione Dati. Lab 2B CdL Fisica
 Laboratoro B A.A. 01/013 Elaborazone Dat Lab B CdL Fsca Lab B CdL Fsca Elaborazone dat spermental Prncpo della massma verosmglanza Quando eseguamo una sere d msure relatve ad una data grandezza fsca, quanto
Laboratoro B A.A. 01/013 Elaborazone Dat Lab B CdL Fsca Lab B CdL Fsca Elaborazone dat spermental Prncpo della massma verosmglanza Quando eseguamo una sere d msure relatve ad una data grandezza fsca, quanto
1 Le equazioni per le variabili macroscopiche: i momenti dell equazione di Boltzmann
 FISICA DEI FLUIDI Lezone 5-5 Maggo 202 Le equazon per le varabl macroscopche: moment dell equazone d Boltzmann Teorema H a parte, non è facle estrarre altre consderazon general sulla funzone denstà d probabltà
FISICA DEI FLUIDI Lezone 5-5 Maggo 202 Le equazon per le varabl macroscopche: moment dell equazone d Boltzmann Teorema H a parte, non è facle estrarre altre consderazon general sulla funzone denstà d probabltà
Note: 11 esercitazioni relative ai modelli presentati a lezione. Esercitatori: Ing. Piegari, Ing. Merlo
 Noe: esercazon relae a moell presena a lezone Esercaor: Ing. Pegar, Ing. erlo cemeno: ogn mercole opo le esercazon ermen: el. 376-45 E-mal: marco.merlo@polm., lug.pegar@polm. So: hp://www.eec.polm. DINAICA
Noe: esercazon relae a moell presena a lezone Esercaor: Ing. Pegar, Ing. erlo cemeno: ogn mercole opo le esercazon ermen: el. 376-45 E-mal: marco.merlo@polm., lug.pegar@polm. So: hp://www.eec.polm. DINAICA
Criteri metodologici per la valutazione dei titoli obbligazionari standard e dei contratti derivati non quotati
 Crer meodologc per la valuazone de ol obblgazonar sandard e de conra derva non quoa Adoao con delbera del Consglo d ammnsrazone del /0/20 Modfcao con delbera del Consglo d Ammnsrazone del 28//20 Aggornao
Crer meodologc per la valuazone de ol obblgazonar sandard e de conra derva non quoa Adoao con delbera del Consglo d ammnsrazone del /0/20 Modfcao con delbera del Consglo d Ammnsrazone del 28//20 Aggornao
MODELLISTICA DI SISTEMI DINAMICI
 CONTROLLI AUTOMATICI Ingegnera Gestonale http://www.automazone.ngre.unmore.t/pages/cors/controllautomatcgestonale.htm MODELLISTICA DI SISTEMI DINAMICI Ing. Federca Gross Tel. 059 2056333 e-mal: federca.gross@unmore.t
CONTROLLI AUTOMATICI Ingegnera Gestonale http://www.automazone.ngre.unmore.t/pages/cors/controllautomatcgestonale.htm MODELLISTICA DI SISTEMI DINAMICI Ing. Federca Gross Tel. 059 2056333 e-mal: federca.gross@unmore.t
Amplificatori operazionali
 Amplfcator operazonal Parte 3 www.de.ng.unbo.t/pers/mastr/ddattca.htm (versone del 9-5-) Confgurazone nvertente generalzzata Se nella confgurazone nvertente s sosttuscono le resstenze R e R con due mpedenze
Amplfcator operazonal Parte 3 www.de.ng.unbo.t/pers/mastr/ddattca.htm (versone del 9-5-) Confgurazone nvertente generalzzata Se nella confgurazone nvertente s sosttuscono le resstenze R e R con due mpedenze
PONTE DELLA MUSICA - ROMA Analisi modale operazionale
 g 0.01 g 0.04 g 5.00e-3 g 0.08 g 8.00e-3 g -9.00e-3 20:VACALE:14:+Y 0.00 s 2200.00-0.08 21:VACALE:14:+Z 0.00 s 2200.00-7.00e-3 22:VACALE:12:+Y 0.00 s 2200.00-0.05 23:VACALE:12:+Z 0.00 s 2200.00-0.01 24:VACALE:13:+X
g 0.01 g 0.04 g 5.00e-3 g 0.08 g 8.00e-3 g -9.00e-3 20:VACALE:14:+Y 0.00 s 2200.00-0.08 21:VACALE:14:+Z 0.00 s 2200.00-7.00e-3 22:VACALE:12:+Y 0.00 s 2200.00-0.05 23:VACALE:12:+Z 0.00 s 2200.00-0.01 24:VACALE:13:+X
Esercitazioni di Elettrotecnica: circuiti in evoluzione dinamica
 Unersà degl Sud d assno sercazon d leroecnca: crcu n eoluzone dnamca nono Maffucc maffucc@uncas er oobre 7 rcu dnamc del prmo ordne S Nel seguene crcuo è assegnaa la correne nell nduore all sane caare
Unersà degl Sud d assno sercazon d leroecnca: crcu n eoluzone dnamca nono Maffucc maffucc@uncas er oobre 7 rcu dnamc del prmo ordne S Nel seguene crcuo è assegnaa la correne nell nduore all sane caare
EVOLUZIONE DI UN SISTEMA ROBOTICO COMANDATO IN TELEMANIPOLAZIONE E RETROAZIONATO IN POSIZIONE E FORZA
 EVOLUZIONE DI UN SISTEMA ROBOTICO COMANDATO IN TELEMANIPOLAZIONE E RETROAZIONATO IN POSIZIONE E FORZA Tuor: Prof. Robero Caraccolo 1 INDICE 1. Inroduzone 1.1 Aspe general d elemanpolazone va Inerne 1.2
EVOLUZIONE DI UN SISTEMA ROBOTICO COMANDATO IN TELEMANIPOLAZIONE E RETROAZIONATO IN POSIZIONE E FORZA Tuor: Prof. Robero Caraccolo 1 INDICE 1. Inroduzone 1.1 Aspe general d elemanpolazone va Inerne 1.2
Stabilità dei Sistemi Dinamici. Stabilità Semplice. Stabilità Asintotica. Stabilità: concetto intuitivo che può essere formalizzato in molti modi
 Gustavo Belforte Stabltà de Sstem Dnamc Gustavo Belforte Stabltà de Sstem Dnamc Stabltà de Sstem Dnamc Il Pendolo Stabltà: concetto ntutvo che può essere formalzzato n molt mod Intutvamente: Un oggetto
Gustavo Belforte Stabltà de Sstem Dnamc Gustavo Belforte Stabltà de Sstem Dnamc Stabltà de Sstem Dnamc Il Pendolo Stabltà: concetto ntutvo che può essere formalzzato n molt mod Intutvamente: Un oggetto
LA CALIBRAZIONE NELL ANALISI STRUMENTALE
 LA CALIBRAZIONE NELL ANALISI STRUMENTALE La maggor parte delle anals chmche sono ogg condotte medante metod strumental (spettrometra d assorbmento ed emssone a dverse λ, metod elettrochmc, spettrometra
LA CALIBRAZIONE NELL ANALISI STRUMENTALE La maggor parte delle anals chmche sono ogg condotte medante metod strumental (spettrometra d assorbmento ed emssone a dverse λ, metod elettrochmc, spettrometra
Laboratorio di Didattica della Fisica I
 Laboraoro d Ddaca della Fsca I Daa Oraro Aula Tpo 08-mar 5-7:5 A Lezone 3-mar 5-7:5 A Lezone 5-mar 5-7:5 Lab. MM e Dd. Laboraoro 0-mar 5-7:5 A Lezone -mar 5-7:5 Lab. MM e Dd. Laboraoro 7-mar 5-7:5 A Lezone
Laboraoro d Ddaca della Fsca I Daa Oraro Aula Tpo 08-mar 5-7:5 A Lezone 3-mar 5-7:5 A Lezone 5-mar 5-7:5 Lab. MM e Dd. Laboraoro 0-mar 5-7:5 A Lezone -mar 5-7:5 Lab. MM e Dd. Laboraoro 7-mar 5-7:5 A Lezone
26/08/2010. segnali deterministici. segnali casuali o random. stazionario. periodico. Non stazionario. transitorio
 Cap 5: ANALISI DEI SEGNALI E ARAURA DINAMICA Un segnale è defnto come una qualsas varable fsca che camba nel tempo, nello spazo, o rspetto a altre varabl e che trasporta nformazon segnal determnstc segnal
Cap 5: ANALISI DEI SEGNALI E ARAURA DINAMICA Un segnale è defnto come una qualsas varable fsca che camba nel tempo, nello spazo, o rspetto a altre varabl e che trasporta nformazon segnal determnstc segnal
Ripartizione stati tensionali tra le fasi di un terreno
 1 Rpartzone stat tensonal tra le fas d un terreno I carch estern e le forze d massa agent sul mezzo soldo contnuo deale sono eulbrat dalle tenson defnte con t δ F = lm δ A 0 δ A δf Nel terreno (mezzo granulare
1 Rpartzone stat tensonal tra le fas d un terreno I carch estern e le forze d massa agent sul mezzo soldo contnuo deale sono eulbrat dalle tenson defnte con t δ F = lm δ A 0 δ A δf Nel terreno (mezzo granulare
IMPIANTI E PROCESSI CHIMICI. Tema A 13 Giugno 2011 Colonna binaria
 IMPINTI E PROCESSI CHIMICI Tema 3 Gugno 0 Colonna bnara Soluzone Inzalmente s svolge un calcolo d lash al fne d caratterzzare lo stato della corrente almentata. V z ( K ) defnto e s ottene f ( ) + ( K
IMPINTI E PROCESSI CHIMICI Tema 3 Gugno 0 Colonna bnara Soluzone Inzalmente s svolge un calcolo d lash al fne d caratterzzare lo stato della corrente almentata. V z ( K ) defnto e s ottene f ( ) + ( K
CARATTERISTICHE DEI SEGNALI RANDOM
 CARATTERISTICHE DEI SEGNALI RANDOM I segnal random o stocastc rvestono una notevole mportanza poché sono present, pù che segnal determnstc, nella maggor parte de process fsc real. Esempo d segnale random:
CARATTERISTICHE DEI SEGNALI RANDOM I segnal random o stocastc rvestono una notevole mportanza poché sono present, pù che segnal determnstc, nella maggor parte de process fsc real. Esempo d segnale random:
Ettore Limoli. Lezioni di Matematica Prof. Ettore Limoli. Sommario. Calcoli di regressione
 Sto Personale d Ettore Lmol Lezon d Matematca Prof. Ettore Lmol Sommaro Calcol d regressone... 1 Retta d regressone con Ecel... Uso della funzone d calcolo della tendenza... 4 Uso della funzone d regressone
Sto Personale d Ettore Lmol Lezon d Matematca Prof. Ettore Lmol Sommaro Calcol d regressone... 1 Retta d regressone con Ecel... Uso della funzone d calcolo della tendenza... 4 Uso della funzone d regressone
Funzione di matrice. c i λ i. i=0. i=0. m 1. γ i A i. i=0. Moltiplicando entrambi i membri di questa equazione per A si ottiene. α i 1 A i α m 1 A m
 Captolo INTRODUZIONE Funzone d matrce Sa f(λ) una generca funzone del parametro λ svluppable n sere d potenze f(λ) Sa A una matrce quadrata d ordne n La funzone d matrce f(a) èdefnta nel modo seguente
Captolo INTRODUZIONE Funzone d matrce Sa f(λ) una generca funzone del parametro λ svluppable n sere d potenze f(λ) Sa A una matrce quadrata d ordne n La funzone d matrce f(a) èdefnta nel modo seguente
Dipartimento di Economia Aziendale e Studi Giusprivatistici. Università degli Studi di Bari Aldo Moro. Corso di Macroeconomia 2014
 Dpartmento d Economa Azendale e Stud Gusprvatstc Unverstà degl Stud d Bar Aldo Moro Corso d Macroeconoma 2014 1.Consderate l seguente grafco: LM Partà de tass d nteresse LM B A IS IS Y E E E Immagnate
Dpartmento d Economa Azendale e Stud Gusprvatstc Unverstà degl Stud d Bar Aldo Moro Corso d Macroeconoma 2014 1.Consderate l seguente grafco: LM Partà de tass d nteresse LM B A IS IS Y E E E Immagnate
17. Le soluzioni dell equazione di Schrödinger approfondimento
 7. soluzon dll quazon d Scrödngr approfondmno Gl sa ms Il gao d Scrödngr è l pù famoso sao mso dlla MQ. E una parclla un po spcal, prcé è un oggo macroscopco d cu s dscu l comporamno quansco. E anc una
7. soluzon dll quazon d Scrödngr approfondmno Gl sa ms Il gao d Scrödngr è l pù famoso sao mso dlla MQ. E una parclla un po spcal, prcé è un oggo macroscopco d cu s dscu l comporamno quansco. E anc una
