5.1 Definizione della misura in R 2
|
|
|
- Luigi Franchini
- 5 anni fa
- Visualizzazioni
Transcript
1 Capitolo 5 Misure prodotto 5.1 Definizione della misura in 2 Nell introdurre la misura secondo Lebesgue in, abbiamo definito la misura esterna di un sottoinsieme qualsiasi E come m famiglia numerabile (E) = inf l(i j ), {I j } j J di intervalli aperti : E j J I j, j J essendo l(i) la lunghezza di un intervallo (definita in maniera naturale). Per definire la misura esterna di un sottoinsieme di N è allora sufficiente definire la lunghezza di un intervallo I di N :se con gli I j intervalli di, allora I = I 1... I N l N (I) =l(i 1 )... l(i N ). Una volta definita la lunghezza di un intervallo, la misura esterna N-dimensionale di un sottoinsieme E di N è data da m famiglia numerabile N(E) = inf l N (I j ), {I j } j J di intervalli aperti : E j J I j. j J Una volta definita m N, si dimostra che essa gode di tutte le proprietà dimostrate a suo tempo per m : che è monotona, regolare, che coincide con l n 113
2 CAPITOLO 5. MISUE PODOTTO 114 sugli intervalli di N,è σ-subadditiva ed invariante per traslazioni. Detto misurabile un sottoinsieme E di N tale che m N(A) =m N(A E)+m N(A E c ), A N, la famiglia M N degli insiemi misurabili secondo Lebesgue è una σ-algebra che contiene gli intervalli, gli aperti ed i chiusi, e che verifica tutte le proprietà dimostrate a suo tempo per la famiglia degli insiemi misurabili su. Sudi essa è definita la misura di Lebesgue N-dimensionale m N. In altre parole, una volta scelti i mattoni base (gli intervalli), e definita la misura su di essi, quasi tutte le proprietà della misura esterna (e, di conseguenza, della misura e degli insiemi misurabili) discendono solo dalla sua definizione. Quasi tutte le proprietà, tranne una: il fatto che, sugli intervalli, coincida con la lunghezza; ovvero, che m N sia un estensione di l N. Questo fatto è conseguenza della struttura particolare della famiglia degli intervalli di N, e delle proprietà della lunghezza relativamente alle unioni di intervalli. Definizione Un sottoinsieme C di P( N ) si dice una semi-algebra se i) per ogni C 1, C 2 in C, sihac 1 C 2 C; ii) per ogni C in C, C c è unione disgiunta e finita di elementi di C. La famiglia C degli intervalli di N è una semi-algebra, come si verifica facilmente; in particolare, se N =2,eI è un intervallo di 2, I = I 1 I 2 e I c =( I 2 c ) (I 1 c I 2 )=(I 1 c ) (I 1 I 2 c ), e l unione è disgiunta (si noti che il complementare di I non si scrive in modo unico come unione disgiunta). Come si verifica facilmente, la funzione lunghezza, definita sulla semialgebra degli intervalli, è σ-subadditiva: se I è un intervallo di N, unione di una famiglia numerabile di intervalli {I n }, allora l N (I) + n=1 l N (I n ).
3 CAPITOLO 5. MISUE PODOTTO 115 Questo fatto fa sì che la misura esterna di un intervallo coincida con la sua lunghezza. Infatti, se I è un intervallo, per ogni ε>0 esiste I ε intervallo aperto contenente I e tale che l N (I ε ) l N (I)+ε; pertanto m N(I) l N (I ε ) l N (I)+ε. D altra parte, per ogni ε>0 esiste una famiglia al più numerabile di intervalli aperti {I n } che ricopre I e tale che l N (I n ) m N(I)+ε. Ma allora {I n I} è una famiglia al più numerabile di intervalli la cui unione è I, e quindi m N(I) ε l N (I) l N (I n I) l N (I n ) m N(I)+ε, da cui (per l arbitrarietà diε) l N (I) =m N(I). Il fatto che la misura esterna di un intervallo sia la sua lunghezza (assieme alla σ-subadditività della misura esterna) implica poi che gli intervalli siano misurabili (si veda la dimostrazione del Teorema ). icapitolando, siamo partiti dalla semi-algebra degli intervalli e dalla funzione lunghezza (che è σ-subadditiva), e abbiamo costruito una misura esterna (e quindi la famiglia degli insiemi misurabili), ottenendo che la misura esterna coincide con la lunghezza sugli intervalli, e che gli intervalli sono misurabili. L unico punto di tutto il discorso nel quale è stato usato il fatto che avevamo a che fare proprio con la semi-algebra degli intervalli e con la lunghezza è stato nell usare il fatto che la lunghezza era monotona e σ-subadditiva. In altre parole, è valido il seguente teorema. Teorema Sia C una semi-algebra di sottoinsiemi di N, e sia µ : C [0, + ] una funzione di insieme monotona e σ-subadditiva su C; ovvero, se C in C è unione numerabile di una famiglia {C n } di insiemi di C, allora µ(c) µ(c n ).
4 CAPITOLO 5. MISUE PODOTTO 116 Definiamo, per ogni E sottoinsieme di N, µ famiglia numerabile (E) = inf µ(c j ), {C j } j J di insiemi di C : E j J C j. j J Allora µ è una misura esterna (ovvero, è monotona e σ-subadditiva) tale che µ (C) =µ(c) per ogni C in C. Inoltre, detto misurabile un insieme E tale che µ (A) =µ (A E)+µ (A E c ), A N, la famiglia degli insiemi misurabili è una σ-algebra che contiene C. È allora possibile definire una misura esterna su N in un altra maniera: non partendo dagli intervalli, ma partendo da una semi-algebra più raffinata. Definizione Un rettangolo di N è il prodotto cartesiano di N insiemi misurabili secondo Lebesgue di : = E 1... E N, E i M. La misura di un rettangolo di N è definita in maniera naturale come il prodotto delle misure degli E i : µ() =m(e 1 )... m(e N ). Teorema Sia la famiglia dei rettangoli di N. Allora è una semi-algebra; inoltre, la funzione µ è monotona e σ-subadditiva su. Dimostrazione. Il fatto che sia una semi-algebra è di dimostrazione immediata, così come lo è la monotonia di µ. imane pertanto da verificare la σ-subadditività di µ. Per semplicità, limitamoci al caso N = 2. Sia allora un rettangolo di 2, unione di una famiglia numerabile di rettangoli di 2 : A B = = n = A n B n. Sia x in A fissato; allora x appartiene ad alcuni degli A n ; sia N x = {n N : x A n }. Si ha allora B = x B n.
5 CAPITOLO 5. MISUE PODOTTO 117 Infatti, sia y in B; allora (x, y) èina B e quindi esiste m in N tale che (x, y) èina m B m. Poiché x èina m, m èinn x e quindi y è nell unione dei B n con n in N x (essendo y in B m ). Viceversa, se y è nell unione dei B n con n in N x, allora y èinb m per qualche m in N x e quindi (x, y) èina m B m, ovvero in A B. Essendo i B n misurabili, si ha m(b) m(b n ). x Osserviamo ora che m(b n )è uno degli addendi della somma precdente se e solo se x èina n, e che quindi si può scrivere (ricordiamo che x è fissato) m(b) m(b n )= m(b n ) χ An (x). x Consideriamo ora la funzione caratteristica χ A (x). χ An (x) χ A (x) =χ An (x), Si ha allora, essendo m(b) χ A (x) m(b n ) χ An (x) χ A (x) = m(b n ) χ An (x). Per uno dei corollari del teorema di convergenza monotona, si ha m(b n ) χ An (x) dx = m(b n ) χ An (x) dx = m(a n ) m(b n ), da cui la tesi per la monotonia dell integrale e per definizione di µ, essendo m(b) χ A (x) dx = m(a) m(b). Possiamo allora definire µ N sui sottoinsiemi di N nel seguente modo: µ N(E) = inf j J µ N ( j ), { j } j J famiglia numerabile di insiemi di : E j J j. La funzione d insieme così definita è una misura esterna, e coincide con µ N su. Inoltre, definiti gli insiemi misurabili nella maniera usuale, i rettangoli di N risultano essere misurabili. Ovviamente, dal momento che l insieme
6 CAPITOLO 5. MISUE PODOTTO 118 degli intervalli di N è un sottoinsieme di echeµ N e l N coincidono sugli intervalli, ogni intervallo è misurabile rispetto a µ N, e µ N(I) = l N (I) = m N (I). A questo punto ci si può chiedere se la misura µ N costruita a partire dai rettangoli sia più fine della misura m N costruita a partire dagli intervalli; ovvero se si riescano a misurare più insiemi partendo da ricoprimenti costituiti da rettangoli piuttosto che da intervalli. Teorema Per ogni E sottoinsieme di N si ha µ N(E) =m N(E). Dimostrazione. I, e pertanto Detto I l insieme degli intervalli di N, si ha ovviamente µ N(E) m N(E), E N. Se µ N(E) =+, dalla disuguaglianza precedente segue che m N(E) =+ e quindi si ha la tesi. Supponiamo ora che µ N(E) < +. Sia ε>0 e sia { n } una famiglia al più numerabile di intervalli che ricoprono E e tali che µ N ( n ) µ N(E)+ε. Ognuno degli n ha misura finita, e si scrive come n = A n 1... A n N, con A n j misurabili in e di misura finita. Per ogni j in {1,...,N} esiste allora (si veda il Teorema 2.2.5) una famiglia al più numerabile di intervalli aperti {Im n j } la cui unione contiene A n j e tale che m j N l(i n m j ) m(a n j )+ Definiamo ora, per m =(m 1,...,m N ) N N, I n m = I n m 1... I n m N, ε 2 n (1 + µ N (A n )).
7 CAPITOLO 5. MISUE PODOTTO 119 in modo tale che {I n m, m N N } sia un ricoprimento di n. Inoltre, m N N l N (I n m)= N j=1 m j N l(i n m j ) m(a n )... m(a n N)+ ε 2 n = µ N( n )+ ε 2 n. In definitiva, {I n m, m N N,n N} è una famiglia al più numerabile di intervalli aperti che ricopre E, e si ha Pertanto, m N N da cui la tesi per l arbitrarietà di ε. l N (Im) n µ N ( n )+ε µ N(E)+2ε. m N(E) µ N(E)+2ε, A questo punto, essendo µ N e m N numericamente uguali, ne segue che E è misurabile per µ N se e solo se lo èperm N. Pertanto, la σ-algebra degli insiemi misurabili secondo µ N èlaσ-algebra degli insiemi misurabili secondo m N (ovvero, quella che abbiamo definito come la σ-algebra degli insiemi misurabili secondo Lebesgue). Cosa abbiamo guadagnato? Una sola cosa: adesso possiamo affermare che i rettangoli di N sono misurabili secondo Lebesgue e che m N () =m N() =µ N() =m(a 1 )... m(a n ), ovvero che la misura N-dimensionale del prodotto cartesiano di N insiemi misurabili secondo Lebesgue in è il prodotto delle loro misure. 5.2 Il teorema di Fubini-Tonelli A partire dalla misura N-dimensionale, è possibile definire il concetto di misurabilità per una funzione, e successivamente dare la definizione di integrale. Ancora una volta, tutte le proprietà dimostrate nel caso unidimensionale continuano a valere in dimensione qualsiasi, compresi i teoremi di passaggio al limite sotto il segno di integrale. Per semplicità di esposizione, a partire da ora ci limiteremo a considerare 2. Sia allora f : 2 una funzione sommabile; ovvero, una funzione
8 CAPITOLO 5. MISUE PODOTTO 120 misurabile e tale che f(x, y) dx dy < +. 2 Ci chiediamo ora se per analogia con quanto accade per l integrazione secondo iemann per funzioni continue l integrale precedente possa essere spezzato in due integrali su, ovvero se f(x, y) dx dy = 2 ( ) ( ) f(x, y) dx dy = f(x, y) dy dx. A prescindere dall uguaglianza, affinché la formula precedente sia esatta, devono verificarsi due fatti: i) per ogni fissato ȳ in la funzione x f(x, ȳ) deve essere misurabile e sommabile su ; ii) la funzione y f(x, y) dx deve essere misurabile e sommabile su. Esempio Sia P un insieme non misurabile di contenuto in [0, 1], e sia E = P Q. Allora E (che non è un rettangolo) è misurabile in 2. Infatti, E [0, 1] Q, che è un rettangolo di misura nulla, e pertanto m 2(E) =0, da cui segue (si veda il Teorema 2.3.2), che E è misurabile (e ha misura nulla). Consideriamo ora f(x, y) =χ E (x, y) =χ P (x) χ Q (y). Ovviamente f è misurabile (come funzione caratteristica di un insieme misurabile), e il suo integrale su 2 vale zero (essendo f nulla quasi ovunque). Sia ora ȳ fissato in ; allora f(x, ȳ) =χ P (x) sey è razionale, e zero altrimenti. Pertanto, se ȳ è in Q, f(x, ȳ) non è misurabile e non ha dunque senso scrivere f(x, ȳ) dx. Il che vuol dire che non è (apparentemente) possibile spezzare l integrale di f su tutto 2 come due integrali. In realtà, la funzione f(x, ȳ) è sia misurabile che sommabile su per quasi tutti gli ȳ in : tutti, tranne i razionali, che formano un insieme di misura nulla. Pertanto, possiamo definire, per quasi ogni y in, la funzione y f(x, y) dx, che è la funzione identicamente nulla, definire arbitrariamente la stessa funzione per y razionale (dal momento che siamo interessati ad integrare tale
9 CAPITOLO 5. MISUE PODOTTO 121 funzione su, modificarla o definirla su un insieme di misura nulla non modifica il valore dell integrale), ed ottenere una funzione misurabile (perché quasi ovunque nulla), sommabile, e con integrale zero. La validità della seconda formula è ancora più evidente, dal momento che, per ogni x in la funzione f( x, y) è la funzione quasi ovunque nulla, e pertanto x f(x, y) dy, è nuovamente la funzione ovunque nulla, il cui integrale è zero. L esempio precedente mostra che, nonostante la funzione ottenuta da f(x, y) congelando una delle due variabili possa non essere misurabile, i valori di x (o di y) per i quali si ottiene una funzione non misurabile formano un insieme di misura di nulla, e sono quindi trascurabili quando si parla di integrali. Questo fatto accade non solo nell esempio precedente, ma per ogni funzione misurabile. Per dimostrare questo fatto, abbiamo bisogno di alcuni risultati preliminari. Definizione Sia la famiglia dei rettangoli di 2 : Definiamo e = {A B, A, B M}. = {E = = {E = n, n }, n, n }. Ovviamente, si ha M 2, e le inclusioni sono strette. Alcune delle proprietà di e sono riassunte nel teorema che segue. Teorema Si ha 1) è chiuso rispetto all unione numerabile e all intersezione finita; 2) è chiuso rispetto all unione numerabile e all intersezione numerabile;
10 CAPITOLO 5. MISUE PODOTTO 122 3) per ogni E misurabile in 2 con m 2 (E) < +, e per ogni ε>0, esiste ε in, con E ε,em 2 ( ε ) m 2 (E)+ε; 4) per ogni E misurabile in 2 con m 2 (E) < +, esiste in, con E, em 2 () =m 2 (E); 5) se E èin, esiste una famiglia al più numerabile di rettangoli {Q n } a due a due disgiunti e tali che E = Q n ; 6) se E èin e m 2 (E) < +, esiste una famiglia al più numerabile di insiemi {Q n } in tali che m 2 (Q 1 ) < +, Q n+1 Q n per ogni n in N, ee = Q n. Dimostrazione. Il fatto che sia chiuso rispetto all unione numerabile discende direttamente dalla definizione di.seeefappartengono a, allora E = n, F = Q m, con n e Q m rettangoli. Allora E F = m N m N n Q m, e quindi E F èin dal momento che n Q m è un rettangolo per ogni n e m. Dalla definizione segue poi in maniera evidente che è chiuso rispetto alle unioni numerabili ed alle intersezioni numerabili. Sia ora E misurabile e di misura finita. Essendo m 2 (E) =m 2(E) = µ 2(E), per definizione di µ 2, fissato ε>0 esiste una famiglia { n } al più numerabile di rettangoli la cui unione ricopre E e m 2 ( n ) m 2 (E)+ε. Se definiamo ε = n, allora ε èin, E è contenuto in ε,ed essendo m 2 σ-subadditiva, si ha m 2 ( ε ) m 2 ( n ) m 2 (E)+ε, che è la tesi di 3).
11 CAPITOLO 5. MISUE PODOTTO 123 A partire da 3), sia ε = 1 n, e sia n in tale che E n e m 2 ( n ) m 2 (E)+ 1 n. Definiamo = n. Allora èin, contiene E esi ha, per ogni n in N, m 2 (E) m 2 () m 2 ( n ) m 2 (E)+ 1 n, da cui segue 4). Sia ora E in ; allora E è l unione di una famiglia al più numerabile di rettangoli { n }. Sia P 1 = 1, P 2 = 2 \ 1, P n = n \( n 1 j=1 j ). Gli insiemi P j sono evidentemente a due a due disgiunti, e la loro unione è ancora E. Si verifica facilmente che ognuno dei P j è unione finita di rettangoli a due a due disgiunti: P j = n j i=1 Q j i. Pertanto, E è l unione dei {Q n j }, che sono rettangoli a due a due disgiunti. Infine, sia E in, con m 2 (E) < +. Allora E = n, con n in. Definiamo P 1 = 1, P 2 = 1 2 e P n = n j=1 j. Allora i P j sono ancora in (per 1)), verificano P n+1 P n, e la loro intersezione è ovviamente E; l unica cosa che P 1 potrebbe non verificare è m 2 (P 1 ) < +. In questo caso, siccome m 2 (E) è finita, per il punto 3) esiste in tale che E e m 2 () m 2 (E) + 1; in particolare, ha misura finita. Ma allora {P n } soddisfa tutte le richieste del punto 6). Definizione Sia E un sottoinsieme di 2, e sia x in. Definiamo la sezione di E secondo x l insieme E x = {y :(x, y) E}. Se E è un insieme di 2,ex èin, siha χ Ex (y) =χ E (x, y). Inoltre, se {E n } è una famiglia qualsiasi di insiemi, allora E n = x (E n ) x, E n = x (E n ) x. Teorema Sia x in e sia E in. Allora E x è misurabile in.
12 CAPITOLO 5. MISUE PODOTTO 124 Dimostrazione. Sia E in. Allora E = A B, e quindi { E x = se x A, B se x A. In entrambi i casi, E x è misurabile. Se E èin, allora E x = ( n ) x, dove { n } sono i rettangoli la cui unione è E. Ma allora E x è misurabile come unione numerabile di insiemi misurabili. Infine, se E èin, allora E x = ( n ) x, dove { n } sono gli insiemi di la cui intersezione è E. Ma allora E x è misurabile come intersezione numerabile di insiemi misurabili. Teorema Sia E in con m 2 (E) < +, e sia g(x) =m(e x ). Allora g è misurabile su esiha g(x) dx = m 2 (E). Dimostrazione. Se E è un rettangolo, allora E = A B, E x è B oppure l insieme vuoto a seconda se x appartiene o meno ad A, e quindi g(x) =m(b) χ A (x). Essendo A misurabile, g lo è, e il suo integrale è proprio m(a) m(b) che è m 2 (E). Se E èin, per il Teorema 5.2.2, 5), E è unione al più numerabile di una famiglia { n } di rettangoli a due a due disgiunti. Definiamo g n (x) = m(( n ) x ). Allora g n è misurabile (per quanto appena dimostrato), e si ha g(x) = g n (x), da cui segue che g è misurabile. Infine, essendo g n 0 per ogni n, il corollario del Teorema di convergenza monotona, ed il fatto che gli n sono disgiunti, implica che g(x) dx = g n (x) dx = m 2 ( n )=m 2 (E).
13 CAPITOLO 5. MISUE PODOTTO 125 Sia ora E in. Allora, per il Teorema 5.2.2, 6), E è l intersezione di una famiglia { n } numerabile di insiemi in, con m 2 ( 1 ) < + e n+1 n. Detta g n (x) =m(( n ) x ), si ha che g 1 èinl 1 () eche0 g n+1 (x) g n (x) g 1 (x). Essendo g 1 in L 1 (), g 1 è finita quasi ovunque, e quindi m(( 1 ) x ) < + per quasi ogni x in. Per questi x, dal momento che la successione {( n ) x } è monotona decrescente e la sua intersezione è E x, si ha, per il Teorema 2.3.7, ii), g(x) =m(e x ) = lim m(( n) x ) = lim g n(x). n + n + Pertanto, g n converge a g quasi ovunque e quindi g è misurabile. Essendo 0 g n g 1, dal Teorema di Lebesgue segue g(x) dx = lim n + g n (x) dx = lim m 2( n )=m 2 (E), n + dove nell ultimo passaggio si è usato ancora una volta il Teorema 2.3.7, ii). Finora ci siamo occupati solo degli insiemi di, ma per trattare gli insiemi misurabili qualsiasi ci viene in aiuto il punto 4) del Teorema Teorema Sia E un sottoinsieme misurabile in 2, con m 2 (E) =0. Allora E x è misurabile in per quasi ogni x in esiham(e x )=0. Dimostrazione. Per il Teorema 5.2.2, 4), esiste F in contenente E e con m 2 (F ) = 0. Dal teorema precedente segue allora che 0=m 2 (F )= m(f x ) dx. Essendo m(f x ) una funzione misurabile e non negativa, ne segue che m(f x )= 0 per quasi ogni x in. Essendo E F,sihaE x F x e quindi, per quasi ogni x, E x è misurabile ed ha misura zero. Teorema Sia E un sottoinsieme misurabile di 2, con m 2 (E) < +. Allora per quasi ogni x in l insieme E x è misurabile in ; la funzione, definita quasi ovunque, g(x) =m(e x ) è misurabile in, sommabile su e tale che g(x) dx = m 2 (E).
14 CAPITOLO 5. MISUE PODOTTO 126 Dimostrazione. Sempre per il Teorema 5.2.2, 4), esiste F in tale che E F e m 2 (E) =m 2 (F ). Sia G = F \ E. Allora G ha misura nulla e quindi, per il teorema precedente, G x è misurabile per quasi ogni x in (con m(g x ) = 0). Dal momento che E x = F x \G x, E x è misurabile per quasi ogni x in, em(e x )=m(f x ) per tali x. Pertanto, g(x) =m(f x ) quasi ovunque; per il Teorema 5.2.6, g è dunque misurabile essendo quasi ovunque uguale ad una funzione misurabile. Inoltre, sempre per il Teorema 5.2.6, g(x) dx = m(f x ) dx = m 2 (F )=m 2 (E), come volevasi dimostrare. Osservazione Sia ora E un insieme misurabile di 2, con m 2 (E) < +, e sia f(x, y) =χ E (x, y), cosicché f è sommabile su 2. Dal momento che χ E (x, y) =χ Ex (y) il teorema precedente si può così interpretare: a) per quasi ogni x fissato in, la funzione y f( x, y) = χ E x (y) è misurabile e sommabile su (dal momento che il suo integrale vale m(e x )); b) la funzione (definita per quasi ogni x in ) x f(x, y) dy è misurabile (dato che f(x, y) dy = m(e x)) e sommabile su ; c) si ha ( ) f(x, y) dy dx = m 2 (E) = f(x, y) dx dy. 2 Un discorso analogo si può fare considerando sezioni di E secondo y, ottenendo lo stesso risultato. In altre parole, almeno per le funzioni caratteristiche di insiemi misurabili di misura finita è possibile spezzare un integrale doppio come due integrali semplici, integrando prima rispetto ad una qualsiasi delle due variabili, e poi rispetto all altra. In realtà, la stessa operazione si può effettuare qualsiasi sia la funzione sommabile su 2 ; prima di dimostrare questo fatto, abbiamo bisogno di un ulteriore risultato di approssimazione.
15 CAPITOLO 5. MISUE PODOTTO 127 Teorema Sia f una funzione non negativa e misurabile su 2. Allora esiste una successione crescente di funzioni semplici {ϕ n }, ognuna nulla fuori da un insieme misurabile di misura finita, tale che ϕ n converge a f ovunque in 2. Dimostrazione. L idea di questa dimostrazione è la stessa usata per dimostrare il Teorema Innanzitutto, siano n in N e F n =[ n, n] [ n, n]; definiamo, per k =0,...,n2 n 1, { } k k +1 E n,k = x F n : f(x, y) <,E 2n 2 n n = {(x, y) F n : f(x, y) n}. Gli insiemi E n e E n,k sono ovviamente misurabili (perché loè f), e, se k n 2 n 1, E n,k = E n+1,2k E n+1,2k+1, (2.1) l unione essendo disgiunta. Definiamo ϕ n (x, y) =n χ En (x, y)+ n 2 n 1 k=0 k 2 n χ E n,k (x, y). Per costruzione, ϕ n è una funzione semplice, nulla fuori da F n (ovvero, da un insieme di misura finita). Inoltre, per ogni (x, y) inf n {(x, y) 2 :0 f(x, y) <n} si ha ϕ n (x, y) f(x, y) 1 2. (2.2) n Da (2.1) (e dalla definizione di ϕ n su E n ) segue anche che, su F n,siha ϕ n ϕ n+1 ; dal momento che ϕ n è nulla fuori da F n, mentre ϕ n+1 è non negativa, si ha ϕ n ϕ n+1 su 2. Sia ora (x, y)in 2 tale che f(x, y) < + (quasi ogni (x, y)in 2 soddisfa tale proprietà). Allora esiste n (x,y) in N tale che (x, y) èinf n {(x, y) 2 :0 f(x, y) <n} per ogni n n (x,y) ; per (2.2) si ha allora che ϕ n (x, y) converge a f(x, y). Se, invece, f(x, y) =+, allora esiste n (x,y) in N tale che (x, y) èin F n E n per ogni n n (x,y). Ma allora ϕ n (x, y) =n definitivamente, e quindi tende a + = f(x, y). Possiamo ora enunciare e dimostrare il teorema di spezzamento degli integrali.
16 CAPITOLO 5. MISUE PODOTTO 128 Teorema (Fubini, Tonelli) Sia f : 2 una funzione misurabile e non negativa. Allora (teorema di Tonelli) 1) per quasi ogni x in la funzione f x definita da f x (y) = f( x, y) è misurabile in ; 2) per quasi ogni ȳ in la funzione fȳ definita da fȳ(x) = f(x, ȳ) è misurabile in ; 3) la funzione (definita quasi ovunque) x f(x, y) dy è misurabile su ; 4) la funzione (definita quasi ovunque) y f(x, y) dx è misurabile su ; 5) si ha ( ) ( ) f(x, y) dy dx = f(x, y) dx dy = f(x, y) dx dy. 2 Se f è sommabile (di segno qualsiasi), allora (teorema di Fubini) le funzioni definite nei punti 1) 4) sono sommabili. Dimostrazione. Data la simmetria dell enunciato rispetto ad x e y, è sufficiente dimostrare 1), 3) e 5). Iniziamo con l osservare che il teorema è già provato se f(x, y) è la funzione caratteristica di un insieme misurabile e di misura finita: questo è infatti il contenuto dell Osservazione 5.2.9, la 1), 3) e 5) essendo rispettivamente la a), b) e c). Pertanto, per linearità, il teorema è vero per ogni funzione semplice nulla fuori da un insieme di misura finita. A questo punto utilizziamo il Teorema , e costruiamo una successione {ϕ n } monotona crescente di funzioni semplici convergente ad f ovunque, con ϕ n nulla fuori da un insieme di misura finita. Ovviamente, per ogni x in si ha f x (y) = lim (ϕ n) x (y), n + Sia ora E n contenuto in tale che m(e n )=0e(ϕ n ) x è misurabile in per ogni x in \E n. Detta E l unione degli E n,siham(e) =0,ef x è misurabile
17 CAPITOLO 5. MISUE PODOTTO 129 su per ogni x in \E, essendo limite puntuale di funzioni misurabili. Per x in \E, inoltre, dal Teorema di convergenza monotona segue che f( x, y) dy = lim ϕ n ( x, y) dy, n + cosicché, essendo misurabile per tali x la funzione x ϕ n ( x, y) dy, si ha che è misurabile. Dal momento che x x è limite della successione crescente x f( x, y) dy, f( x, y) dy, ϕ n ( x, y) dy, una seconda applicazione del Teorema della convergenza monotona, ed il fatto che il teorema è vero per funzioni semplici, implica che ( ) f(x, y) dy dx = lim n + = lim n + = ( 2 ) ϕ n (x, y) dy dx ϕ n (x, y) dx dy f(x, y) dx dy, 2 dove nell ultimo passaggio si è usato ancora una volta il Teorema di convergenza monotona. Pertanto, 5) è dimostrata. Supponiamo ora che f sia sommabile; per linearità dell integrale, èsuffi- ciente dimostrare 1), 3) e 5) per f + (x, y) ef (x, y), ovvero dimostrarle per una funzione sommabile non negativa. Essendo una tale funzione misurabile, otteniamo 1), 3) e 5); inoltre, essendo finito l integrale su di x f( x, y) dy,
18 CAPITOLO 5. MISUE PODOTTO 130 ne segue che tale funzione è sommabile, cosicché la funzione definita in 3) è sommabile; essendo sommabile, è finita quasi ovunque, e quindi è sommabile per quasi ogni x. x f( x, y), Osservazione Lo spazio ambiente delle dimostrazioni svolte finora è stato 2, ma il Teorema di Fubini-Tonelli è valido anche in N,che possiamo spezzare come k N k. Analogamente, possiamo spezzare gli integrali come vogliamo, ed effettuarli nell ordine che vogliamo. Osservazione Il teorema precedente è un buon test di sommabilità, nel senso che per dimostrare che una funzione misurabile è sommabile su 2 la si può integrare prima rispetto ad una variabile, poi rispetto all altra; se il risultato è finito, la funzione di partenza è sommabile, altrimenti no. Esempio Sia f in L p (). Allora è finito l integrale su di f(x) p. Pertanto, per il Teorema di Fubini-Tonelli, ( ) f(x) p dx = py p 1 dy dx [0, f(x) ] ( ) = p y p 1 χ [0, f(x) ] (y) dy dx ( ) = p χ {(x,y) 2 :0 y f(x) }(x, y) dx y p 1 dy = p m({x : f(x) y}) χ [0,+ ) (y) y p 1 dy = p y p 1 m({x : f(x) y}) dy, [0,+ ] che dà una formula per il calcolo dell integrale di una funzione di L p () in termini della misura dei sopralivelli. In maniera analoga si dimostra che, se E è un insieme misurabile e f èinl p (E), allora f(x) p dx = p m({x E : f(x) y}) y p 1 dy. E [0,+ ) In modo simile, si ha, per ogni k 0, f(x) p dx = p {x E: f(x) k} [k,+ ) m({x E : f(x) y}) y p 1 dy.
19 CAPITOLO 5. MISUE PODOTTO 131 Ad esempio, se f(x) = 1 x χ [1,+ )(x), dal momento che si ha m({x : f(x) y} = f(x) p dx = p [0,1] { 1 y y p 1 ( 1 y 1 ) 1 se 0 <y 1, 0 altrimenti, dy = 1 p 1. Inoltre, se m(e) < +, esef è tale che esiste una costante C>0tale che m({x E : f(x) > y} C (ovvero, f appartiene allo spazio di t q Marcinkiewicz M q (E)), allora f èinl p (E) per ogni p<q. Infatti E f(x) p dx = {x E: f(x) <1} m(e)+p m(e)+pc f(x) p dx + [1,+ ) [1,+ ) {x E: f(x) 1} f(x) p dx m({x E : f(x) y}) y p 1 dy 1 dy < +. yq p+1 Pertanto, ricordando che L p (E) è contenuto in M p (E) (come si vede utilizzando la disuguaglianza (2.25) del Capitolo 3), se m(e) < +, M p+ε (E) L p (E) M p (E), con inclusioni strette.
Esercizi 8 12 gennaio 2009
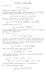 Sia α > e Esercizi 8 2 gennaio 29 f(x, y = ( + x 2 + y 2 α. Dimostrare che f appartiene a L p ( 2, con α p >. Osserviamo innanzitutto che, essendo f continua, l integrale di f p su 2 è uguale all integrale
Sia α > e Esercizi 8 2 gennaio 29 f(x, y = ( + x 2 + y 2 α. Dimostrare che f appartiene a L p ( 2, con α p >. Osserviamo innanzitutto che, essendo f continua, l integrale di f p su 2 è uguale all integrale
Analisi Reale. Anno Accademico Roberto Monti. Versione del 13 Ottobre 2014
 Analisi Reale Anno Accademico 2014-2015 Roberto Monti Versione del 13 Ottobre 2014 1 Contents Chapter 1. Introduzione alla teoria della misura 5 1. Misure esterne e misure su σ-algebre. Criterio di Carathéodory
Analisi Reale Anno Accademico 2014-2015 Roberto Monti Versione del 13 Ottobre 2014 1 Contents Chapter 1. Introduzione alla teoria della misura 5 1. Misure esterne e misure su σ-algebre. Criterio di Carathéodory
Misure e loro proprietà (appunti per il corso di Complementi di Analisi Matematica per Fisici, a.a )
 Misure e loro proprietà (appunti per il corso di Complementi di Analisi Matematica per Fisici, a.a. 2006-07 Sia Ω un insieme non vuoto e sia A una σ-algebra in Ω. Definizione 1. (Misura. Si chiama misura
Misure e loro proprietà (appunti per il corso di Complementi di Analisi Matematica per Fisici, a.a. 2006-07 Sia Ω un insieme non vuoto e sia A una σ-algebra in Ω. Definizione 1. (Misura. Si chiama misura
3. Successioni di insiemi.
 3. Successioni di insiemi. Per evitare incongruenze supponiamo, in questo capitolo, che tutti gli insiemi considerati siano sottoinsiemi di un dato insieme S (l insieme ambiente ). Quando occorrerà considerare
3. Successioni di insiemi. Per evitare incongruenze supponiamo, in questo capitolo, che tutti gli insiemi considerati siano sottoinsiemi di un dato insieme S (l insieme ambiente ). Quando occorrerà considerare
11. Misure con segno.
 11. Misure con segno. 11.1. Misure con segno. Sia Ω un insieme non vuoto e sia A una σ-algebra in Ω. Definizione 11.1.1. (Misura con segno). Si chiama misura con segno su A ogni funzione ϕ : A R verificante
11. Misure con segno. 11.1. Misure con segno. Sia Ω un insieme non vuoto e sia A una σ-algebra in Ω. Definizione 11.1.1. (Misura con segno). Si chiama misura con segno su A ogni funzione ϕ : A R verificante
Alcuni complementi di teoria dell integrazione.
 Alcuni complementi di teoria dell integrazione. In ciò che segue si suppone di avere uno spazio di misura (,, µ) 1 Sia f una funzione misurabile su un insieme di misura positiva tale che f 0. Se fdµ =
Alcuni complementi di teoria dell integrazione. In ciò che segue si suppone di avere uno spazio di misura (,, µ) 1 Sia f una funzione misurabile su un insieme di misura positiva tale che f 0. Se fdµ =
f n (x) 3 1. x Essendo g(x) = 3 1
 Secondo esonero di Analisi eale 6//9 a.a. 8-9 ) Studiare la convergenza in L p ((, )), p +, della successione di funzioni cos(nx) e nx f n (x) = 3. x Si vede facilmente che la successione f n converge
Secondo esonero di Analisi eale 6//9 a.a. 8-9 ) Studiare la convergenza in L p ((, )), p +, della successione di funzioni cos(nx) e nx f n (x) = 3. x Si vede facilmente che la successione f n converge
8. Completamento di uno spazio di misura.
 8. Completamento di uno spazio di misura. 8.1. Spazi di misura. Spazi di misura completi. Definizione 8.1.1. (Spazio misurabile). Si chiama spazio misurabile ogni coppia ordinata (Ω, A), dove Ω è un insieme
8. Completamento di uno spazio di misura. 8.1. Spazi di misura. Spazi di misura completi. Definizione 8.1.1. (Spazio misurabile). Si chiama spazio misurabile ogni coppia ordinata (Ω, A), dove Ω è un insieme
20. Prodotto di spazi di misura. I teoremi di Tonelli e di Fubini.
 20. Prodotto di spazi di misura. I teoremi di Tonelli e di Fubini. 20.1. Prodotto di σ-algebre. Definizione 20.1.1. (σ-algebra prodotto. Dati n spazi misurabili (Ω 1, A 1,..., (Ω n, A n, si chiama σ-algebra
20. Prodotto di spazi di misura. I teoremi di Tonelli e di Fubini. 20.1. Prodotto di σ-algebre. Definizione 20.1.1. (σ-algebra prodotto. Dati n spazi misurabili (Ω 1, A 1,..., (Ω n, A n, si chiama σ-algebra
Il teorema di Vitali-Lebesgue
 Il teorema di Vitali-Lebesgue Gianluca Gorni Università di Udine gennaio 0 Nel 90 Giuseppe Vitali e Henri Lebesgue, indipendentemente uno dall altro, trovarono che si possono caratterizzare in modo elegante
Il teorema di Vitali-Lebesgue Gianluca Gorni Università di Udine gennaio 0 Nel 90 Giuseppe Vitali e Henri Lebesgue, indipendentemente uno dall altro, trovarono che si possono caratterizzare in modo elegante
ELEMENTI DI TEORIA DELLA MISURA E DELL INTEGRAZIONE SECONDO LEBESGUE, versione italiana. PARTE 1: TEORIA DELLA MISURA
 ELEMENTI DI TEORIA DELLA MISURA E DELL INTEGRAZIONE SECONDO LEBESGUE, versione italiana. PARTE 1: TEORIA DELLA MISURA A. Brini October 12, 2009 Contents 1 Misura esterna e misura in R n 1 1.1 Ricoprimenti
ELEMENTI DI TEORIA DELLA MISURA E DELL INTEGRAZIONE SECONDO LEBESGUE, versione italiana. PARTE 1: TEORIA DELLA MISURA A. Brini October 12, 2009 Contents 1 Misura esterna e misura in R n 1 1.1 Ricoprimenti
Generalizzazioni del Teorema di Weierstrass
 Capitolo 2 Generalizzazioni del Teorema di Weierstrass Il principale riferimento bibliografico per questa lezione è il testo di Checcucci, Tognoli, Vesentini [1]. Introduzione Supponiamo che X = R n. È
Capitolo 2 Generalizzazioni del Teorema di Weierstrass Il principale riferimento bibliografico per questa lezione è il testo di Checcucci, Tognoli, Vesentini [1]. Introduzione Supponiamo che X = R n. È
Istituzioni di Analisi Superiore
 Istituzioni di Analisi Superiore 20 aprile 2001 2 Indice 1 Teoria della misura 7 1.1 Famiglie di insiemi.......................... 7 1.2 Misura degli insiemi piani...................... 13 1.3 Misura di
Istituzioni di Analisi Superiore 20 aprile 2001 2 Indice 1 Teoria della misura 7 1.1 Famiglie di insiemi.......................... 7 1.2 Misura degli insiemi piani...................... 13 1.3 Misura di
(2) se A A, allora A c A; (3) se {A n } A, allora +
 1. Spazi di misura In questo paragrafo accenneremo alla nozione di spazio di misura. Definizione 1. Sia X un insieme non vuoto. Una famiglia A di sottoinsiemi di X è una σ-algebra se : (1) A; (2) se A
1. Spazi di misura In questo paragrafo accenneremo alla nozione di spazio di misura. Definizione 1. Sia X un insieme non vuoto. Una famiglia A di sottoinsiemi di X è una σ-algebra se : (1) A; (2) se A
Analisi II, a.a Soluzioni 1. j j + 1 ; ( 1)j
 Analisi II, a.a. 7-8 Soluzioni Calcolare le seguenti distanze e norme: (i d (x, y dove x = {x j } e y = {y j } sono le successioni di l definite da x j = ( j, y j = j/(j + ; (ii d (f, g dove f, g sono
Analisi II, a.a. 7-8 Soluzioni Calcolare le seguenti distanze e norme: (i d (x, y dove x = {x j } e y = {y j } sono le successioni di l definite da x j = ( j, y j = j/(j + ; (ii d (f, g dove f, g sono
Analisi a più variabili: Misura di Peano - Jordan ed Integrale di Riemann
 Analisi a più variabili: Misura di Peano - Jordan ed Integrale di Riemann 1 Definizione (Algebra): T P Ω è un'algebra se: A, B T A B T, Ω T A T A C T Se A i T A i T si dice σ-algebra Definizione (Misura):
Analisi a più variabili: Misura di Peano - Jordan ed Integrale di Riemann 1 Definizione (Algebra): T P Ω è un'algebra se: A, B T A B T, Ω T A T A C T Se A i T A i T si dice σ-algebra Definizione (Misura):
Esercizi 1. 2) Sia X lo spazio delle funzioni integrabili secondo Riemann su [a, b]. Perché non è una metrica su X la funzione d(f, g) = b
![Esercizi 1. 2) Sia X lo spazio delle funzioni integrabili secondo Riemann su [a, b]. Perché non è una metrica su X la funzione d(f, g) = b Esercizi 1. 2) Sia X lo spazio delle funzioni integrabili secondo Riemann su [a, b]. Perché non è una metrica su X la funzione d(f, g) = b](/thumbs/73/69556821.jpg) sercizi ) Tutte le distanze introdotte a lezione (meno la metrica discreta) sono invarianti per traslazioni; ovvero, d(x, y) = d(x + z, y + z) per ogni x, y e z. Definire su X = una metrica non invariante
sercizi ) Tutte le distanze introdotte a lezione (meno la metrica discreta) sono invarianti per traslazioni; ovvero, d(x, y) = d(x + z, y + z) per ogni x, y e z. Definire su X = una metrica non invariante
LA TRASFORMATA DI FOURIER
 LA TASFOMATA DI FOUIE 1. Definizione della trasformata di Fourier Definizione 1.1. Sia u in L 1 ( e sia ξ in. La trasformata di Fourier di u è la funzione (1.1 F(u(ξ = e iξ x u(x dx. Ovviamente, non è
LA TASFOMATA DI FOUIE 1. Definizione della trasformata di Fourier Definizione 1.1. Sia u in L 1 ( e sia ξ in. La trasformata di Fourier di u è la funzione (1.1 F(u(ξ = e iξ x u(x dx. Ovviamente, non è
Istituzioni di Analisi Superiore, secondo modulo
 niversità degli Studi di dine Anno Accademico 997/98 Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Matematica Istituzioni di Analisi Superiore, secondo modulo Cognome e Nome: Prova
niversità degli Studi di dine Anno Accademico 997/98 Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Matematica Istituzioni di Analisi Superiore, secondo modulo Cognome e Nome: Prova
NOTE SULLE FUNZIONI CONVESSE DI UNA VARIABILE REALE
 NOTE SULLE FUNZIONI CONVESSE DI UNA VARIABILE REALE ROBERTO GIAMBÒ 1. DEFINIZIONI E PRIME PROPRIETÀ In queste note saranno presentate alcune proprietà principali delle funzioni convesse di una variabile
NOTE SULLE FUNZIONI CONVESSE DI UNA VARIABILE REALE ROBERTO GIAMBÒ 1. DEFINIZIONI E PRIME PROPRIETÀ In queste note saranno presentate alcune proprietà principali delle funzioni convesse di una variabile
Alcuni complementi sulla misura di Lebesgue in R N
 Alcuni complementi sulla misura di Lebesgue in R N Notazioni m Misura di Lebesgue in R N m e Misura esterna di Lebesgue in R N ; m e (E) = inf m(v ) V aperti V E m i Misura interna di Lebesgue in R N ;
Alcuni complementi sulla misura di Lebesgue in R N Notazioni m Misura di Lebesgue in R N m e Misura esterna di Lebesgue in R N ; m e (E) = inf m(v ) V aperti V E m i Misura interna di Lebesgue in R N ;
Teoria di Lebesgue. P n E = n=1
 Teoria di Lebesgue 1. La misura di Peano-Jordan La misura di Peano Jordan di un insieme é quasi sempre proposta per sottoinsiemi limitati E R 2 : si tratta di quanto suggerito dalla carta quadrettata,
Teoria di Lebesgue 1. La misura di Peano-Jordan La misura di Peano Jordan di un insieme é quasi sempre proposta per sottoinsiemi limitati E R 2 : si tratta di quanto suggerito dalla carta quadrettata,
2.1 La misura secondo Peano-Jordan
 Capitolo 2 Teoria della misura 2.1 La misura secondo Peano-Jordan Ricordiamo brevemente i passi necessari per definire la misura (e la misurabilità) secondo Peano-Jordan di un sottoinsieme di R. La lunghezza
Capitolo 2 Teoria della misura 2.1 La misura secondo Peano-Jordan Ricordiamo brevemente i passi necessari per definire la misura (e la misurabilità) secondo Peano-Jordan di un sottoinsieme di R. La lunghezza
c i χ Ai (x) f(x) = f(x)dx = c i m(a i ) R
 1. Integrale di Lebesgue in La differenza fondamentale tra integrale di Lebesgue e integrale di iemann consiste nella diversa scelta delle decomposizioni su cui sostanzialmente si basa ogni integrale:
1. Integrale di Lebesgue in La differenza fondamentale tra integrale di Lebesgue e integrale di iemann consiste nella diversa scelta delle decomposizioni su cui sostanzialmente si basa ogni integrale:
5.3 Alcune classi di funzioni integrabili
 3. Si verifichi che per ogni f, g : [a, b] R si ha f g = g + (f g) 0, f g = f + g f g; dedurne che se f, g R(a, b) allora f g, f g R(a, b). [Traccia: si osservi che basta verificare che f 0 R(a, b), e
3. Si verifichi che per ogni f, g : [a, b] R si ha f g = g + (f g) 0, f g = f + g f g; dedurne che se f, g R(a, b) allora f g, f g R(a, b). [Traccia: si osservi che basta verificare che f 0 R(a, b), e
12. Funzioni numeriche misurabili.
 12. Funzioni numeriche misurabili. 12.1. Funzioni numeriche misurabili. D ora in avanti, nel corso di questi appunti, adotteremo la seguente terminologia: per far riferimento ad una funzione f : Ω R, per
12. Funzioni numeriche misurabili. 12.1. Funzioni numeriche misurabili. D ora in avanti, nel corso di questi appunti, adotteremo la seguente terminologia: per far riferimento ad una funzione f : Ω R, per
Note di Teoria della Probabilità.
 Note di Teoria della Probabilità. In queste brevi note, si richiameranno alcuni risultati di Teoria della Probabilità, riguardanti le conseguenze elementari delle definizioni di probabilità e σ-algebra.
Note di Teoria della Probabilità. In queste brevi note, si richiameranno alcuni risultati di Teoria della Probabilità, riguardanti le conseguenze elementari delle definizioni di probabilità e σ-algebra.
Analisi a più variabili: Integrale di Lebesgue
 Analisi a più variabili: Integrale di Lebesgue 1 Ripasso delle definizioni di Algebre, σ-algebre, misure additive, misure σ-additive, Proprietà della misura astratta, misura esterna. Definizione (Insieme
Analisi a più variabili: Integrale di Lebesgue 1 Ripasso delle definizioni di Algebre, σ-algebre, misure additive, misure σ-additive, Proprietà della misura astratta, misura esterna. Definizione (Insieme
Limiti di successioni
 Capitolo 5 Limiti di successioni 5.1 Successioni Quando l insieme di definizione di una funzione coincide con l insieme N costituito dagli infiniti numeri naturali 1, 2, 3,... talvolta si considera anche
Capitolo 5 Limiti di successioni 5.1 Successioni Quando l insieme di definizione di una funzione coincide con l insieme N costituito dagli infiniti numeri naturali 1, 2, 3,... talvolta si considera anche
Massimo limite e minimo limite di una funzione
 Massimo limite e minimo limite di una funzione Sia f : A R una funzione, e sia p DA). Per ogni r > 0, l insieme ) E f p r) = { fx) x A I r p) \ {p} } è non vuoto; inoltre E f p r ) E f p r ) se 0 < r r.
Massimo limite e minimo limite di una funzione Sia f : A R una funzione, e sia p DA). Per ogni r > 0, l insieme ) E f p r) = { fx) x A I r p) \ {p} } è non vuoto; inoltre E f p r ) E f p r ) se 0 < r r.
( 1 π. (a n cos nt + b n sin nt) t R (3)
 7. SERIE TRIGONOMETRICHE E SERIE DI FOURIER Definizione 1. L p (R), p [1, + ), denota la classe di tutte le funzioni f : R C, misurabili secondo Lebesgue, periodiche con periodo per le quali il funzionale
7. SERIE TRIGONOMETRICHE E SERIE DI FOURIER Definizione 1. L p (R), p [1, + ), denota la classe di tutte le funzioni f : R C, misurabili secondo Lebesgue, periodiche con periodo per le quali il funzionale
CLASSE LIMITE DI UNA SUCCESSIONE DI NUMERI REALI C. MADERNA, G. MOLTENI, M. VIGNATI
 CLASSE LIMITE DI UNA SUCCESSIONE DI NUMERI REALI C. MADERNA, G. MOLTENI, M. VIGNATI Consideriamo l insieme R = R {, + } ottenuto aggiungendo all insieme dei numeri reali i simboli e +. Introduciamo in
CLASSE LIMITE DI UNA SUCCESSIONE DI NUMERI REALI C. MADERNA, G. MOLTENI, M. VIGNATI Consideriamo l insieme R = R {, + } ottenuto aggiungendo all insieme dei numeri reali i simboli e +. Introduciamo in
k=0 a k k=0 a k, quando si voglia precisare qual è l indice iniziale: si possono infatti considerare anche serie del tipo k=1 a k, k=50 a k,
 2.2 Serie Le serie numeriche sono semplicemente successioni reali o complesse di tipo particolare, che però, per la loro importanza pratica e teorica, meritano una trattazione a parte. Data una successione
2.2 Serie Le serie numeriche sono semplicemente successioni reali o complesse di tipo particolare, che però, per la loro importanza pratica e teorica, meritano una trattazione a parte. Data una successione
Appendice B ANALISI FUNZIONALE. 1 Spazi di Banach
 Appendice B ANALISI FUNZIONALE In questo capitolo si introducono gli spazi di Banach e di Hilbert, gli operatori lineari e loro spettro. Inoltre si discutono gli operatori compatti su uno spazio di Hilbert.
Appendice B ANALISI FUNZIONALE In questo capitolo si introducono gli spazi di Banach e di Hilbert, gli operatori lineari e loro spettro. Inoltre si discutono gli operatori compatti su uno spazio di Hilbert.
Esercizi del Corso di Istituzioni di Analisi Superiore, I modulo
 sercizi del Corso di Istituzioni di Analisi Superiore, I modulo 1. sercizi su massimo e minimo limite 1. lim inf a n lim sup a n 2. Se a n b n per ogni n N, allora lim inf a n lim inf b n. Vale anche lim
sercizi del Corso di Istituzioni di Analisi Superiore, I modulo 1. sercizi su massimo e minimo limite 1. lim inf a n lim sup a n 2. Se a n b n per ogni n N, allora lim inf a n lim inf b n. Vale anche lim
Si dimostri che la (*) possiede un unica soluzione (u n ) limitata.
 Scuola Normale Superiore, ammissione al IV anno del corso ordinario Prova scritta di Analisi Matematica per Fisica, Informatica, Matematica 26 Agosto 2 Esercizio. Siano (a n ) e (b n ) successioni di numeri
Scuola Normale Superiore, ammissione al IV anno del corso ordinario Prova scritta di Analisi Matematica per Fisica, Informatica, Matematica 26 Agosto 2 Esercizio. Siano (a n ) e (b n ) successioni di numeri
ANALISI 1 1 SEDICESIMA - DICIASETTESIMA LEZIONE Serie
 ANALISI 1 1 SEDICESIMA - DICIASETTESIMA LEZIONE Serie 1 prof. Claudio Saccon, Dipartimento di Matematica Applicata, Via F. Buonarroti 1/C email: saccon@mail.dm.unipi.it web: http://www2.ing.unipi.it/ d6081/index.html
ANALISI 1 1 SEDICESIMA - DICIASETTESIMA LEZIONE Serie 1 prof. Claudio Saccon, Dipartimento di Matematica Applicata, Via F. Buonarroti 1/C email: saccon@mail.dm.unipi.it web: http://www2.ing.unipi.it/ d6081/index.html
Si noti che questa definizione dice esattamente che
 DISUGUAGLIANZA INTEGRALE DI JENSEN IN DIMENSIONE FINITA LIBOR VESELY integrazione. Prima disuguaglianza integrale di Jensen.. Motivazione. Siano un insieme convesso in uno spazio vettoriale, f : (, + ]
DISUGUAGLIANZA INTEGRALE DI JENSEN IN DIMENSIONE FINITA LIBOR VESELY integrazione. Prima disuguaglianza integrale di Jensen.. Motivazione. Siano un insieme convesso in uno spazio vettoriale, f : (, + ]
1 Successioni di funzioni
 Successioni di Esercizio.. Studiare la convergenza puntuale ed uniforme della seguente successione di (.) f n (x) = n x Osserviamo che fissato x R f n(x) = + n x x R. x ( n + x ) = pertanto la successione
Successioni di Esercizio.. Studiare la convergenza puntuale ed uniforme della seguente successione di (.) f n (x) = n x Osserviamo che fissato x R f n(x) = + n x x R. x ( n + x ) = pertanto la successione
SUCCESSIONI E SERIE NUMERICHE E DI FUNZIONI
 SERIE NUMERICHE Si consideri una successione di elementi. Si definisce serie associata ad la somma Per ogni indice della successione, si definisce successione delle somme parziali associata a la somma
SERIE NUMERICHE Si consideri una successione di elementi. Si definisce serie associata ad la somma Per ogni indice della successione, si definisce successione delle somme parziali associata a la somma
INDUZIONE E NUMERI NATURALI
 INDUZIONE E NUMERI NATURALI 1. Il principio di induzione Il principio di induzione è una tecnica di dimostrazione molto usata in matematica. Lo scopo di questa sezione è di enunciare tale principio e di
INDUZIONE E NUMERI NATURALI 1. Il principio di induzione Il principio di induzione è una tecnica di dimostrazione molto usata in matematica. Lo scopo di questa sezione è di enunciare tale principio e di
Problemi di topologia metrica.
 Problemi di topologia metrica. 1.) Sia X un insieme, munito di una distanza d : X X R +. Siano x 1 ;x ;x 3 ;x 4 quattro punti qualsiasi di X. Verificare che: d (x 1 ; x 4 ) d (x 1 ; x ) + d (x ; x 3 )
Problemi di topologia metrica. 1.) Sia X un insieme, munito di una distanza d : X X R +. Siano x 1 ;x ;x 3 ;x 4 quattro punti qualsiasi di X. Verificare che: d (x 1 ; x 4 ) d (x 1 ; x ) + d (x ; x 3 )
Analisi di Fourier e alcune equazioni della fisica matematica 1. TERZA LEZIONE Serie di funzioni Serie di potenze
 Analisi di Fourier e alcune equazioni della fisica matematica 1 TERZA LEZIONE Serie di funzioni Serie di potenze 1 prof. Claudio Saccon, Dipartimento di Matematica Applicata, Via F. Buonarroti 1/C email:
Analisi di Fourier e alcune equazioni della fisica matematica 1 TERZA LEZIONE Serie di funzioni Serie di potenze 1 prof. Claudio Saccon, Dipartimento di Matematica Applicata, Via F. Buonarroti 1/C email:
Successioni numeriche (II)
 Successioni numeriche (II) Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Successioni (II) Analisi A 1 / 52 Forme indeterminate associate a funzioni razionali fratte:
Successioni numeriche (II) Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Successioni (II) Analisi A 1 / 52 Forme indeterminate associate a funzioni razionali fratte:
Topologia, continuità, limiti in R n
 Topologia, continuità, limiti in R n Ultimo aggiornamento: 18 febbraio 2017 1. Preliminari Prima di iniziare lo studio delle funzioni di più variabili, in generale funzioni di k variabili e a valori in
Topologia, continuità, limiti in R n Ultimo aggiornamento: 18 febbraio 2017 1. Preliminari Prima di iniziare lo studio delle funzioni di più variabili, in generale funzioni di k variabili e a valori in
Convergenza puntuale ed uniforme delle serie di Fourier
 Convergenza puntuale ed uniforme delle serie di Fourier 8 aprile 009 In questi appunti prendiamo in considerazione funzioni di variabile reale che possono assumere però valori complessi. Una funzione F
Convergenza puntuale ed uniforme delle serie di Fourier 8 aprile 009 In questi appunti prendiamo in considerazione funzioni di variabile reale che possono assumere però valori complessi. Una funzione F
Esercizi per il corso di Analisi 6.
 Esercizi per il corso di Analisi 6. 1. Si verifichi che uno spazio normato (X, ) è uno spazio vettoriale topologico con la topologia indotta dalla norma. Si verifichi poi che la norma è una funzione continua
Esercizi per il corso di Analisi 6. 1. Si verifichi che uno spazio normato (X, ) è uno spazio vettoriale topologico con la topologia indotta dalla norma. Si verifichi poi che la norma è una funzione continua
4. La misura di Lebesgue.
 4. La misura di Lebesgue. Nel Capitolo 2, dedicato all esposizione della teoria della misura secondo Peano- Jordan, abbiamo anche evidenziato (Esempio 2.3.1 e Osservazione 2.3.1) alcuni limiti della teoria
4. La misura di Lebesgue. Nel Capitolo 2, dedicato all esposizione della teoria della misura secondo Peano- Jordan, abbiamo anche evidenziato (Esempio 2.3.1 e Osservazione 2.3.1) alcuni limiti della teoria
Tracce di soluzioni di alcuni esercizi di matematica 1 - gruppo 76-93
 Tracce di soluzioni di alcuni esercizi di matematica 1 - gruppo 76-93 5. Funzioni continue Soluzione dell Esercizio 76. Osserviamo che possiamo scrivere p() = n (a n + u()) e q() = m (b m + v()) con lim
Tracce di soluzioni di alcuni esercizi di matematica 1 - gruppo 76-93 5. Funzioni continue Soluzione dell Esercizio 76. Osserviamo che possiamo scrivere p() = n (a n + u()) e q() = m (b m + v()) con lim
Corso di Metodi Matematici per l Ingegneria A.A. 2016/2017 Esercizi svolti su misura e integrale di Lebesgue, spazi L p, operatori lineari continui
 Corso di Metodi Matematici per l Ingegneria A.A. 26/27 Esercizi svolti su misura e integrale di Lebesgue, spazi L p, operatori lineari continui Marco Bramanti Politecnico di Milano December 4, 26 Esercizi
Corso di Metodi Matematici per l Ingegneria A.A. 26/27 Esercizi svolti su misura e integrale di Lebesgue, spazi L p, operatori lineari continui Marco Bramanti Politecnico di Milano December 4, 26 Esercizi
ANALISI MATEMATICA 4. Prova scritta del 24 gennaio 2013
 Prova scritta del 24 gennaio 2013 Esercizio 1. Sia Ω R 3 un insieme misurabile secondo Lebesgue e di misura finita. Sia {f n } n N una successione di funzioni f n : Ω R misurabili e tali che 1) f n (x)
Prova scritta del 24 gennaio 2013 Esercizio 1. Sia Ω R 3 un insieme misurabile secondo Lebesgue e di misura finita. Sia {f n } n N una successione di funzioni f n : Ω R misurabili e tali che 1) f n (x)
Analisi Matematica 3 (Fisica) Prova scritta del 27 gennaio 2012 Uno svolgimento
 Analisi Matematica 3 (Fisica) Prova scritta del 27 gennaio 22 Uno svolgimento Prima di tutto, eccovi alcuni commenti che potrebbero aiutarvi a svolgere meglio le prove scritte. Ad ogni domanda del testo
Analisi Matematica 3 (Fisica) Prova scritta del 27 gennaio 22 Uno svolgimento Prima di tutto, eccovi alcuni commenti che potrebbero aiutarvi a svolgere meglio le prove scritte. Ad ogni domanda del testo
Il teorema di Ascoli-Arzelà
 Il teorema di Ascoli-Arzelà Alcuni risultati sugli spazi metrici Spazi metrici (e topologici) compatti Richiamiamo le definizioni di compattezza negli spazi metrici. Sia (X, d) una spazio metrico e sia
Il teorema di Ascoli-Arzelà Alcuni risultati sugli spazi metrici Spazi metrici (e topologici) compatti Richiamiamo le definizioni di compattezza negli spazi metrici. Sia (X, d) una spazio metrico e sia
TOPOLOGIA - APPUNTI SETTIMANA 2/12/2013-5/11/2013
 TOPOLOGIA - APPUNTI SETTIMANA 2/12/2013-5/11/2013 KIERAN G. O GRADY - 2 DICEMBRE 2013 1. Spazi di Hausdorff Definizione 1.1. Uno spazio topologico X è di Hausdorff se dati x 1, x 2 X distinti esistono
TOPOLOGIA - APPUNTI SETTIMANA 2/12/2013-5/11/2013 KIERAN G. O GRADY - 2 DICEMBRE 2013 1. Spazi di Hausdorff Definizione 1.1. Uno spazio topologico X è di Hausdorff se dati x 1, x 2 X distinti esistono
Elementi di Algebra e Logica Esercizi 1. Insiemi, funzioni, cardinalità, induzione, funzioni ricorsive.
 Elementi di Algebra e Logica 2008 Esercizi 1 Insiemi, funzioni, cardinalità, induzione, funzioni ricorsive 1 Siano A = {0, 2, 4,, 8, 10}, B = {0, 1, 2, 3, 4, 5, } e C = {4, 5,, 7, 8, 9, 10} Determinare:
Elementi di Algebra e Logica 2008 Esercizi 1 Insiemi, funzioni, cardinalità, induzione, funzioni ricorsive 1 Siano A = {0, 2, 4,, 8, 10}, B = {0, 1, 2, 3, 4, 5, } e C = {4, 5,, 7, 8, 9, 10} Determinare:
Integrali Curvilinei
 Integrali Curvilinei Gianluca Gorni 11 gennaio 2006 1 Lunghezza di una curva Definizione 1.1. Una curva N-dimensionale è una funzione definita su un intervallo (compatto, se non specificato altrimenti)
Integrali Curvilinei Gianluca Gorni 11 gennaio 2006 1 Lunghezza di una curva Definizione 1.1. Una curva N-dimensionale è una funzione definita su un intervallo (compatto, se non specificato altrimenti)
AM2: Tracce delle lezioni- IX Settimana INSIEMI DI LIVELLO, MINIMI VINCOLATI PRINCIPIO DEI MOLTIPLICATORI DI LAGRANGE
 AM2: Tracce delle lezioni- IX Settimana INSIEMI DI LIVELLO, MINIMI VINCOLATI PRINCIPIO DEI MOLTIPLICATORI DI LAGRANGE Sia g C 1 R 2 ), c R. L insieme γ = γ c := {x, y) R 2 : gx, y) = c} si chiama insieme
AM2: Tracce delle lezioni- IX Settimana INSIEMI DI LIVELLO, MINIMI VINCOLATI PRINCIPIO DEI MOLTIPLICATORI DI LAGRANGE Sia g C 1 R 2 ), c R. L insieme γ = γ c := {x, y) R 2 : gx, y) = c} si chiama insieme
14. Confronto tra l integrale di Lebesgue e l integrale di Riemann.
 4. Confronto tra l integrale di Lebesgue e l integrale di Riemann. Lo scopo di questo capitolo è quello di mettere a confronto i vari tipi di integrale (di Riemann, generalizzato e improprio) di funzioni
4. Confronto tra l integrale di Lebesgue e l integrale di Riemann. Lo scopo di questo capitolo è quello di mettere a confronto i vari tipi di integrale (di Riemann, generalizzato e improprio) di funzioni
Le derivate parziali
 Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
COMPLEMENTI DI ANALISI MATEMATICA II. Prova scritta del 20 gennaio 2014
 Prova scritta del 2 gennaio 214 Studiare la convergenza puntuale e uniforme della serie di potenze n=1 n x 2n 2n + e n. Valutare poi la misurabilità e l integrabilità secondo Lebesgue della funzione somma
Prova scritta del 2 gennaio 214 Studiare la convergenza puntuale e uniforme della serie di potenze n=1 n x 2n 2n + e n. Valutare poi la misurabilità e l integrabilità secondo Lebesgue della funzione somma
Analisi Matematica 1. Serie numeriche. (Parte 2) Dott. Ezio Di Costanzo.
 Facoltà di Ingegneria Civile e Industriale Analisi Matematica 1 Serie numeriche (Parte 2) Dott. Ezio Di Costanzo ezio.dicostanzo@sbai.uniroma1.it Definizione Data la serie + n=0 a n si definisce resto
Facoltà di Ingegneria Civile e Industriale Analisi Matematica 1 Serie numeriche (Parte 2) Dott. Ezio Di Costanzo ezio.dicostanzo@sbai.uniroma1.it Definizione Data la serie + n=0 a n si definisce resto
Successioni numeriche
 Successioni numeriche Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Successioni Analisi Matematica 1 1 / 48 Definizione Una successione a valori reali è
Successioni numeriche Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Successioni Analisi Matematica 1 1 / 48 Definizione Una successione a valori reali è
SPAZI TOPOLOGICI. La nozione di spazio topologico è più generale di quella di spazio metrizzabile.
 SPAZI TOPOLOGICI La nozione di spazio topologico è più generale di quella di spazio metrizzabile. Definizione 1 Uno spazio topologico (X, τ) è una coppia costituita da un insieme X e da una famiglia τ
SPAZI TOPOLOGICI La nozione di spazio topologico è più generale di quella di spazio metrizzabile. Definizione 1 Uno spazio topologico (X, τ) è una coppia costituita da un insieme X e da una famiglia τ
1 - Estremo superiore ed estremo inferiore di insiemi
 - Estremo superiore ed estremo inferiore di insiemi Prima di affrontare gli esercizi su estremo superiore ed inferiore, ricordiamo alcune definizioni ed alcuni teoremi che ci verranno utili. Definizione.
- Estremo superiore ed estremo inferiore di insiemi Prima di affrontare gli esercizi su estremo superiore ed inferiore, ricordiamo alcune definizioni ed alcuni teoremi che ci verranno utili. Definizione.
Diario del Corso di Analisi Matematica II - Mod. 2
 Diario del Corso di Analisi Matematica II - Mod. 2 Corso di Laurea: Matematica Applicata Docente: Sisto Baldo ATTENZIONE: Il presente Diario del Corso vuole essere un riassunto abbastanza dettagliato di
Diario del Corso di Analisi Matematica II - Mod. 2 Corso di Laurea: Matematica Applicata Docente: Sisto Baldo ATTENZIONE: Il presente Diario del Corso vuole essere un riassunto abbastanza dettagliato di
Sviluppi e derivate delle funzioni elementari
 Sviluppi e derivate delle funzioni elementari In queste pagine dimostriamo gli sviluppi del prim ordine e le formule di derivazioni delle principali funzioni elementari. Utilizzeremo le uguaglianze lim
Sviluppi e derivate delle funzioni elementari In queste pagine dimostriamo gli sviluppi del prim ordine e le formule di derivazioni delle principali funzioni elementari. Utilizzeremo le uguaglianze lim
R. Capone Analisi Matematica Integrali multipli
 Integrali multipli Consideriamo, inizialmente il caso degli integrali doppi. Il concetto di integrale doppio è l estensione della definizione di integrale per una funzione reale di una variabile reale
Integrali multipli Consideriamo, inizialmente il caso degli integrali doppi. Il concetto di integrale doppio è l estensione della definizione di integrale per una funzione reale di una variabile reale
Spazi vettoriali topologici, spazi localmente convessi ed il teorema di Hahn-Banach: informazioni base (L.V.)
 Spazi vettoriali topologici, spazi localmente convessi ed il teorema di Hahn-Banach: informazioni base (L.V.) Questo breve testo senza dimostrazioni fornisce soltanto una prima informazione ( infarinatura
Spazi vettoriali topologici, spazi localmente convessi ed il teorema di Hahn-Banach: informazioni base (L.V.) Questo breve testo senza dimostrazioni fornisce soltanto una prima informazione ( infarinatura
COMPATTEZZA. i) X è compatto, cioè ogni ricoprimento aperto ammette un sottoricoprimento finito.
 1 COMPATTEZZA Sia X un sottoinsieme di R. Una famiglia A di sottoinsiemi aperti di R si dice ricoprimento aperto di X se X A, cioè se X è contenuto nell unione degli elementi di A. Una sottofamiglia di
1 COMPATTEZZA Sia X un sottoinsieme di R. Una famiglia A di sottoinsiemi aperti di R si dice ricoprimento aperto di X se X A, cioè se X è contenuto nell unione degli elementi di A. Una sottofamiglia di
1 Successioni di funzioni
 Analisi Matematica 2 Successioni di funzioni CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 6 SERIE DI POTENZE Supponiamo di associare ad ogni n N (rispettivamente ad ogni n p, per qualche
Analisi Matematica 2 Successioni di funzioni CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 6 SERIE DI POTENZE Supponiamo di associare ad ogni n N (rispettivamente ad ogni n p, per qualche
Integrale di Lebesgue
 Integrale di Lebesgue Retta reale ampliata R = R {, + } ottenuta aggiungendo all insieme R dei numeri reali (retta reale) i simboli e +. ordinamento completo su R ottenuto, per prolungamento dell usuale
Integrale di Lebesgue Retta reale ampliata R = R {, + } ottenuta aggiungendo all insieme R dei numeri reali (retta reale) i simboli e +. ordinamento completo su R ottenuto, per prolungamento dell usuale
Integrali doppi impropri per funzioni positive
 Integrali doppi impropri per funzioni positive Integrali doppi impropri su domini limitati Siano R 2 un insieme quadrabile (o misurabile) secondo Jordan e f(x, y) una funzione positiva a valori reali definita
Integrali doppi impropri per funzioni positive Integrali doppi impropri su domini limitati Siano R 2 un insieme quadrabile (o misurabile) secondo Jordan e f(x, y) una funzione positiva a valori reali definita
6. Boreliani di uno spazio topologico.
 6. Boreliani di uno spazio topologico. 6.1. La σ-algebra degli insiemi di Borel di uno spazio topologico. Definizione 6.1.1. (σ-algebra di Borel di uno spazio topologico). Sia S uno spazio topologico.
6. Boreliani di uno spazio topologico. 6.1. La σ-algebra degli insiemi di Borel di uno spazio topologico. Definizione 6.1.1. (σ-algebra di Borel di uno spazio topologico). Sia S uno spazio topologico.
SPAZI COMPATTI. Proposizione 2 Sia (X, d) uno spazio metrico. Se esso è sequenzialmente compatto allora è completo.
 SPAZI COMPATTI D ora in poi tutti gli spazi topologici sono di Hausdorff. Definizione 1 Uno spazio topologico (X, τ) si dice sequenzialmente compatto, o compatto per successioni, se ogni successione di
SPAZI COMPATTI D ora in poi tutti gli spazi topologici sono di Hausdorff. Definizione 1 Uno spazio topologico (X, τ) si dice sequenzialmente compatto, o compatto per successioni, se ogni successione di
Prima prova in itenere di Istituzioni di Probabilità
 Prima prova in itenere di Istituzioni di Probabilità 14 novembre 2012 Esercizio 1. Un processo di Ornstein-Uhlenbec modificato (OUM) è un processo reale, con R come insieme dei tempi, con traiettorie continue,
Prima prova in itenere di Istituzioni di Probabilità 14 novembre 2012 Esercizio 1. Un processo di Ornstein-Uhlenbec modificato (OUM) è un processo reale, con R come insieme dei tempi, con traiettorie continue,
p(ϕ) = a 0 Id + a 1 ϕ + + a n ϕ n,
 1. Autospazi e autospazi generalizzati Sia ϕ: V V un endomorfismo. Allora l assegnazione x ϕ induce un morfismo di anelli ρ: K[x] End K (V ). Più esplicitamente, al polinomio p dato da viene associato
1. Autospazi e autospazi generalizzati Sia ϕ: V V un endomorfismo. Allora l assegnazione x ϕ induce un morfismo di anelli ρ: K[x] End K (V ). Più esplicitamente, al polinomio p dato da viene associato
E, la successione di numeri {f n (x 0. n f n(x) (15.1)
 Capitolo 15 15.1 Successioni e serie di funzioni Sia {f n } una successione di funzioni, tutte definite in un certo insieme E dello spazio R n ; si dice che essa è convergente nell insieme E se, comunque
Capitolo 15 15.1 Successioni e serie di funzioni Sia {f n } una successione di funzioni, tutte definite in un certo insieme E dello spazio R n ; si dice che essa è convergente nell insieme E se, comunque
1 Funzioni reali di una variabile reale
 1 Funzioni reali di una variabile reale Qualche definizione e qualche esempio che risulteranno utili più avanti Durante tutto questo corso studieremo funzioni reali di una variabile reale, cioè Si ha f
1 Funzioni reali di una variabile reale Qualche definizione e qualche esempio che risulteranno utili più avanti Durante tutto questo corso studieremo funzioni reali di una variabile reale, cioè Si ha f
CP410: Esonero 1, 31 ottobre 2013
 Dipartimento di Matematica, Roma Tre Pietro Caputo 2013-14, I semestre 31 ottobre, 2013 CP410: Esonero 1, 31 ottobre 2013 Cognome Nome Matricola Firma 1. Fare un esempio di successione di variabili aleatorie
Dipartimento di Matematica, Roma Tre Pietro Caputo 2013-14, I semestre 31 ottobre, 2013 CP410: Esonero 1, 31 ottobre 2013 Cognome Nome Matricola Firma 1. Fare un esempio di successione di variabili aleatorie
Diario del Corso di Analisi Matematica II - Mod. 2
 Diario del Corso di Analisi Matematica II - Mod. 2 Corso di Laurea: Matematica Applicata Docente: Sisto Baldo ATTENZIONE: Il presente Diario del Corso vuole essere un riassunto abbastanza dettagliato di
Diario del Corso di Analisi Matematica II - Mod. 2 Corso di Laurea: Matematica Applicata Docente: Sisto Baldo ATTENZIONE: Il presente Diario del Corso vuole essere un riassunto abbastanza dettagliato di
Proprietà commutativa e associativa per le serie
 Analisi Matematica 1 Trentaseiesima Trentasettesimalezione Proprietà commutativa e associativa per le serie Prodotto Serie di alla potenze Cauchy prof. Claudio Saccon Dipartimento di Matematica Applicata,
Analisi Matematica 1 Trentaseiesima Trentasettesimalezione Proprietà commutativa e associativa per le serie Prodotto Serie di alla potenze Cauchy prof. Claudio Saccon Dipartimento di Matematica Applicata,
Insiemi di numeri reali
 Capitolo 1 1.1 Elementi di teoria degli insiemi Se S è una totalità di oggetti x, si dice che S è uno spazio avente gli elementi x. Se si considerano alcuni elementi di S si dice che essi costituiscono
Capitolo 1 1.1 Elementi di teoria degli insiemi Se S è una totalità di oggetti x, si dice che S è uno spazio avente gli elementi x. Se si considerano alcuni elementi di S si dice che essi costituiscono
Limiti di funzioni di una variabile
 Capitolo 6 Limiti di funzioni di una variabile 6.1 Limiti all infinito La definizione di ite data per le successioni si può immediatamente trasportare al caso di una funzione definita in un qualunque insieme
Capitolo 6 Limiti di funzioni di una variabile 6.1 Limiti all infinito La definizione di ite data per le successioni si può immediatamente trasportare al caso di una funzione definita in un qualunque insieme
! X (92) X n. P ( X n X ) =0 (94)
 Convergenza in robabilità Definizione 2 Data una successione X 1,X 2,...,X n,... di numeri aleatori e un numero aleatorio X diremo che X n tende in probabilità a X escriveremo X n! X (92) se fissati comunque
Convergenza in robabilità Definizione 2 Data una successione X 1,X 2,...,X n,... di numeri aleatori e un numero aleatorio X diremo che X n tende in probabilità a X escriveremo X n! X (92) se fissati comunque
Diario del Corso di Analisi Matematica II - Mod. 2
 Diario del Corso di Analisi Matematica II - Mod. 2 Corso di Laurea: Matematica Applicata Docente: Sisto Baldo ATTENZIONE: Il presente Diario del Corso vuole essere un riassunto abbastanza dettagliato di
Diario del Corso di Analisi Matematica II - Mod. 2 Corso di Laurea: Matematica Applicata Docente: Sisto Baldo ATTENZIONE: Il presente Diario del Corso vuole essere un riassunto abbastanza dettagliato di
Il teorema di Lagrange e la formula di Taylor
 Il teorema di Lagrange e la formula di Taylor Il teorema del valor medio di Lagrange, valido per funzioni reali di una variabile reale, si estende alle funzioni reali di più variabili. Come si vedrà, questo
Il teorema di Lagrange e la formula di Taylor Il teorema del valor medio di Lagrange, valido per funzioni reali di una variabile reale, si estende alle funzioni reali di più variabili. Come si vedrà, questo
ESERCIZI DI ANALISI FUNZIONALE. T(f) = g(x)f(x)dx
 ESERCIZI DI ANALISI FUNZIONALE.. Esercizi svolti.. Operatori lineari Esercizio.. Si consideri il funzionale T : C(,) R, dove g è la funzione g(x) = T(f) = g(x)f(x) dx, { se < x se < x < () Dimostrare che
ESERCIZI DI ANALISI FUNZIONALE.. Esercizi svolti.. Operatori lineari Esercizio.. Si consideri il funzionale T : C(,) R, dove g è la funzione g(x) = T(f) = g(x)f(x) dx, { se < x se < x < () Dimostrare che
Diario del Corso di Analisi Funzionale - Mod. I
 Diario del Corso di Analisi Funzionale - Mod. I Corso di Laurea: Matematica - Magistrale Docente: Sisto Baldo ATTENZIONE: Il presente Diario del Corso vuole essere un riassunto abbastanza dettagliato di
Diario del Corso di Analisi Funzionale - Mod. I Corso di Laurea: Matematica - Magistrale Docente: Sisto Baldo ATTENZIONE: Il presente Diario del Corso vuole essere un riassunto abbastanza dettagliato di
ANALISI 1 - Teoremi e dimostrazioni vari
 ANALISI 1 - Teoremi e dimostrazioni vari Sommario Proprietà dell estremo superiore per R... 2 Definitivamente... 2 Successioni convergenti... 2 Successioni monotone... 2 Teorema di esistenza del limite
ANALISI 1 - Teoremi e dimostrazioni vari Sommario Proprietà dell estremo superiore per R... 2 Definitivamente... 2 Successioni convergenti... 2 Successioni monotone... 2 Teorema di esistenza del limite
4 Sottoinsiemi chiusi di uno spazio metrico
 Geometria e Topologia I 16 marzo 2005 12 4 Sottoinsiemi chiusi di uno spazio metrico (4.1) Definizione. Sia A X un sottoinsieme di uno spazio metrico X. Un punto x X si dice di accumulazione (anche: punto
Geometria e Topologia I 16 marzo 2005 12 4 Sottoinsiemi chiusi di uno spazio metrico (4.1) Definizione. Sia A X un sottoinsieme di uno spazio metrico X. Un punto x X si dice di accumulazione (anche: punto
Il Teorema di Kakutani
 Il Teorema di Kakutani Abbiamo visto, precedentemente, il seguente risultato: 1 Sia X uno spazio di Banach. Se X è separabile, la palla è debolmente compatta. B X = {x X x 1} Il Teorema di Kakutani è un
Il Teorema di Kakutani Abbiamo visto, precedentemente, il seguente risultato: 1 Sia X uno spazio di Banach. Se X è separabile, la palla è debolmente compatta. B X = {x X x 1} Il Teorema di Kakutani è un
Diario del Corso di Analisi Matematica II - Mod. 2
 Diario del Corso di Analisi Matematica II - Mod. 2 Corso di Laurea: Matematica Applicata Docente: Sisto Baldo ATTENZIONE: Il presente Diario del Corso vuole essere un riassunto abbastanza dettagliato di
Diario del Corso di Analisi Matematica II - Mod. 2 Corso di Laurea: Matematica Applicata Docente: Sisto Baldo ATTENZIONE: Il presente Diario del Corso vuole essere un riassunto abbastanza dettagliato di
R = { (x, y) R 2 a x < b, c y < d } = [a, b[ [c, d[ è definita come
 5 Integrali La teoria dell integrazione in R 2 si costruisce a partire dalla nozione geometrica di area di un rettangolo Def 1 La misura (o area del rettangolo R è definita come R = (x, y R 2 a x < b,
5 Integrali La teoria dell integrazione in R 2 si costruisce a partire dalla nozione geometrica di area di un rettangolo Def 1 La misura (o area del rettangolo R è definita come R = (x, y R 2 a x < b,
Il teorema di Sard. Alessandro Ghigi. 25 ottobre 2014
 Il teorema di Sard Alessandro Ghigi 25 ottobre 2014 1 Sottoricoprimenti numerabili Esercizio 1. Sia X uno spazio topologico e sia Y X un sottospazio. Se {A i } i I è una base della topologia di X, allora
Il teorema di Sard Alessandro Ghigi 25 ottobre 2014 1 Sottoricoprimenti numerabili Esercizio 1. Sia X uno spazio topologico e sia Y X un sottospazio. Se {A i } i I è una base della topologia di X, allora
COMPLETAMENTO DI SPAZI METRICI
 COMPLETAMENTO DI SPAZI METRICI 1. Successioni di Cauchy e spazi metrici completi Definizione 1.1. Una successione x n n N a valori in uno spazio metrico X, d si dice di Cauchy se, per ogni ε > 0 esiste
COMPLETAMENTO DI SPAZI METRICI 1. Successioni di Cauchy e spazi metrici completi Definizione 1.1. Una successione x n n N a valori in uno spazio metrico X, d si dice di Cauchy se, per ogni ε > 0 esiste
TOPOLOGIA - APPUNTI SETTIMANA 2/12/2013-5/11/2013
 TOPOLOGIA - APPUNTI SETTIMANA 2/12/2013-5/11/2013 KIERAN G. O GRADY - 9 DICEMBRE 2013 1. Connessione Se X è uno spazio topologico connesso per archi vale il Teorema dei valori intermedi : dati una f :
TOPOLOGIA - APPUNTI SETTIMANA 2/12/2013-5/11/2013 KIERAN G. O GRADY - 9 DICEMBRE 2013 1. Connessione Se X è uno spazio topologico connesso per archi vale il Teorema dei valori intermedi : dati una f :
Successioni ricorsive
 Successioni ricorsive Emanuele Paolini Analisi Matematica I, 015 016 In queste note prenderemo in considerazione le successioni a n definite per ricorrenza o ricorsivamente dalle condizioni: a1 = α, (1)
Successioni ricorsive Emanuele Paolini Analisi Matematica I, 015 016 In queste note prenderemo in considerazione le successioni a n definite per ricorrenza o ricorsivamente dalle condizioni: a1 = α, (1)
