16.1. Analisi di Fourier II.
|
|
|
- Alfonso Patti
- 5 anni fa
- Visualizzazioni
Transcript
1 16.1. Analisi di Fourier II Regolarizzazione di somme e integrali. Nella dimostrazione del teorema della compltezza del sistema trigonometrico (teorema 2 della lezione 15.2) entrano in gioco due strumenti matematici di precisione che ricorrono costantemente nella fisica: la regolarizzazione di una somma o integrale e il prodotto di convoluzione. Questi due ingredienti intervengono nella formula 1 (1) f(x) = lim P r (x θ)f(θ)dθ = lim c n r n e inx. che ci ha permesso di dimostrare il teorema di completezza della base trigonometrica, usando il metodo del confronto dei limiti e il teorema della proiezione per spazi di Hilbert. Prima di continuare il nostro discorso sull analisi di Fourier, dedichiamo un po di tempo a questi metodi matematici, indipendentemente dalle loro applicazioni all analisi di Fourier. Incominciamo con la regolarizzazione di somme e integrali Il primo metodo rigoroso per sommare serie divergenti fu pubblicato dal matematico italiano Ernesto Cesaro nel L idea è semplice ed è questa: se la successione delle somme parziali S n di una serie non converge, magari ne converge la successione delle medie S 0 =S 1 S 1 = 1 2 (S 1 + S 2 ) S 2 = 1 3 (S 1 + S 2 + S 3 )... =... S N = 1 N + 1 (S 1 + S 2 + S S N+1 )... =... Una serie è detta convergente secondo Cesaro se la successione delle medie S n converge. Si può dimostrare facilmente che se una serie converge nel senso tradizionale, allora converge anche secondo Cesaro. Ma ci sono serie divergenti nel senso tradizionale che sono convergenti secondo Cesaro, per esempio, è convergente secondo Cesaro a 1/2 (esercizio). Per gli integrali, si può definire un analoga regolarizzazione che rende finiti integrali altrimenti divergenti nel senso tradizionale. Questa idea, in forma meno rigorosa, era già chiara poco meno di un secolo prima al matematico norvegese Niels Abel. 1
2 La regolarizzazione di Abel per gli integrali è (2) A- f(x)dx def = lim e λx f(x)dx λ 0 (λ positivo) e per le serie ne è l ovvia estensione. Vediamola in azione per la serie La sua regolarizzazione di Abel è A- ( 1) n = lim ( 1) n r n = lim = r = 1 2 n=0 n=0 Anche l ultimo membro della (1) è una somma secondo Abel, A- c n e inx def = lim c n r n e inx ed è la regolarizzazione di Abel della serie di Fourier. Il fisica, il metodo di Abel per regolarizzare serie e integrali è più usato di quello di Cesaro forse perché la sommabilità secondo Abel è ancora più liberale di quella secondo Cesaro. Vale infatti il teorema 1. Se a n è sommabile secondo Abel è anche sommabile secondo Cesaro. Un teorema importante, che riguarda la relazione tra sommabilità di Abel e sommabilità tradizionale, è il teorema di Tauber, anch esso, come quello di Cesaro, del 1890: 2. Se a n è sommabile secondo Abel e na n 0 quando n, allora a n è sommabile anche nel senso tradizionale. Infine, un commento sulla terminologia. Parlare di regolarizazione è, in una certa misura, fuorviante perché suggerisce che esista un modo naturale di definire somme e integrali e poi ci siano dei farmaci per curare le malattie. Niente di più sbagliato: poiché non esiste una nozione algebrica di somma infinita, qualunque somma infinita, inclusa quella tradizionale, è frutto di una definizione basata su un processo di limite. La bontà di una definizione sta solo della sua adeguatezza a cogliere un senso di limite che sia utile nella matematica o nelle applicazioni. Che un senso di limite (ad esempio, quello di limite delle somme parziali) sia più oggettivo degli altri è solo un effetto psicologico Convoluzioni. Un prodotto di convoluzione f P (x) = f(y)p (x y)dy, come quello che compare nella (1), è un operazione di allisciamento. La quintessenza della convoluzione è che il grado di liscezza del prodotto è l unione dei gradi di liscezza dei suoi fattori. In particolare, valgono i seguenti teoremi: 1. Se una funzione è continua e l altra discontinua, la loro convoluzione è continua; 2
3 2. Se una funzione è derivabile n volte e l altra m volte, la loro convoluzione è derivabile n + m volte. Questo significa che se P è una buona funzione e f non è tanto buona, il loro prodotto di convoluzione è buono. Il che vuol dire che facendo una scelta oculata di una funzione di riferimento P, possiamo trasformare una funzione brutta in una bella. Non vogliamo snaturarla, solo pulirla: vorrà dire che sceglieremo una funzione P che sia una approssimazione liscia di una delta, in modo tale che su una scala non troppo microscopica si abbia f P f, e che nella scala microscopica f venga resa liscia. Esempio 1. Per comprendere il fenomeno di allisciamento, consideriamo il prodotto di convoluzione tra un approssimante della delta n δ n (x) = π e nx2 e lo scalino unitario, cioè la funzione di Heaviside { 1 se x > 0 H(x) = 0 se x < 0 Allora n H δ n (x) = f(y)δ n (x y)dy = e n(x y)2 dy π y=0 Fatto il cambiamento di variabili u = x y, du = dy, si ha n n x H δ n (x) = e nu2 du = e nu2 du π π y=x La figura sotto mostra gli allisciamenti dello scalino per 0.8 < x < 0.8 e n = 10, 50, 100,
4 La convoluzione può essere definita per funzioni su R, su T e su R n. Può anche essere definita anche su insiemi di interi. In questo caso, l analogo di P è una matrice e il prodotto di convoluzione è un prodotto di una matrice per un vettore. Queste applicazioni (digitali) della convoluzione hanno applicazioni nell analisi numerica, nella teoria dell analisi dei segnali e, in particolare, nella progettazione e implementazione di filtri di risposta ad ingressi impulsivi. La convoluzione si applica anche allo sviluppo di filtri per l analisi di immagini e in fisica è un utile strumento per pulire una segnatura sperimentale dal rumore di fondo. Sia come sia, in tutte queste applicazioni c è qualcosa di analogo a un P tale che f P f, in una scala opportuna. Una funzione P di questo tipo è chiamato nucleo o kernel. Il nucleo di Poisson, che abbiamo incontrato nello studio del problema di Dirichlet e nell analisi di Fourier, è uno tra i tanti nuclei che sono stati utilizzati. L esercizio 15.2.(14) riguarda un altro nucleo importante dell analisi di Fourier, il nucleo di Dirichlet Una nuova notazione per le coordinate di Fourier. In vista di un balzo successivo verso l integrale di Fourier, introduciamo una notazione suggestiva per le coordinate di Fourier che è comunemente usata in matematica: f(n) def = c n = e n f = 1 Schema riassuntivo delle puntate precedenti: Se f(x) L 2 (T) allora f(x) L2 = f(n)e inx e S N (f) def = n N f(n)e inx f(x)e inx dx lim N f S N(f) L 2 = 0 f L 2 = f l L importante contributo di Fejer. Con Lipót Fejér si entra a pieno titolo nella matematica del 900. I suoi contributi all analisi di Fourier sono dei primi anni del 900 e, secondo alcuni, diedero un impronta significativa agli sviluppi dell analisi di Fourier nei cinquant anni successivi. Il problema che Fejér affronta è questo: possiamo ricuperare i valori di una funzione integrabile dalla conoscenza delle sue coordinate di Fourier? Se per
5 recuperare si intende la sintesi di Fourier tradizionale, f(x) = lim S N(f)(x) = f(n)e inx N la risposta è in generale NO. Si può avere sintesi L 2, come abbiamo appena ricordato, ma la sintesi L 2 non ci permette di concludere nulla sui valori puntuali della funzione. (Nel seguito faremo una rassegna dei risultati classici dell analisi di Fourier e vedremo che la convergenza puntuale richiede che la funzione sia molto regolare). Tuttavia, Fejér scoprì che possiamo sempre recuperare una funzione continua dalle sue coordinate di Fourier, se li sintetizziamo in una maniera diversa da quella tradizionale, cioè se utilizziamo un modo diverso di sommare le serie infinite. Fejér utilizzò il metodo che Cesaro aveva sviluppato una decina di anni prima. (Se f è solo integrabile, il metodo recupera i valori della funzione solo dove è continua.) In effetti, questo è proprio il metodo a cui abbiamo accennato alla fine della lezione scorsa, soltanto che abbiamo usato una regolarizzazione secondo Abel anziché una secondo Cesaro. Riassumendo: S (r) def N (f) = n N Se f(x) C(T) allora f(x) = lim f(n)r n e inx f(n)r n e inx lim N, f S (r) N (f) = 0 5 Si osservi che la convergenza uniforme delle somme parziali S (r) N (f) è tuttaltro che banale: l abbiamo in effetti ottenuta studiando il problema di Dirichlet nel piano seguendo le idee di Schwarz. E Schwarz fu il maestro di Fejer. E Fejer nella sua tesi di dottorato studiò il legame tra analisi di Fourier e problema di Dirichlet. Così, senza saperlo (neanche chi scrive), abbiamo già esposto molte delle idee e dei risultati di Fejér. E abbiamo anche già esposto le ragioni per cui questo metodo funziona: si tratta dell equazione (1), che qui ripetiamo, 1 f(x) = lim P r (x θ)f(θ)dθ = lim c n r n e inx e del ruolo, già discusso, che in essa svolge la convoluzione come strumento di allisciamento. L analisi di Fourier, potrebbe essere completamente sviluppata a partire dall approccio di Fejér. È comunque utile conoscere i risultati classici, che sono l oggetto dei prossimi discorsi.
6 Derivazione delle serie di Fourier. Con questa sezione incominciamo una rassegna dei risultati classici dell analisi di Fourier. Il campo è molto ampio e quella che segue è soltanto una selezione che è stata fatta avendo in mente le applicazioni alla fisica. Incominciamo con la derivazione. Sia f(x) derivabile con derivata prima continua in T. Si osservi che questo implica che la funzione ha lo stesso valore in e π e che la stesso vale per la derivata prima. Poiché f(x) è derivabile, si integri per parti Si ottiene: f(n) = 1 Dunque, = 1 [ 1 = 1 1 in f(n) = 1 f(x)e inx dx (per parti ] π Z f(x)e inx dx. Z udv = uv in e inx f(x) 1 1 in f (x)e inx dx f (x)dx = 1 in f (n) (3) f (n) = in f(n) vdu, con u = f(x), v = 1 in e inx ) Capito il gioco, con le stesse regole, si ottiene facilmente che se f(x) è derivabile due volte, con derivata prima e seconda continua, allora f (n) = n 2 f(n) Introduciamo adesso una notazione che è standard in matematica: C p (T) è l insieme delle funzioni continuamente derivabili p volte. In particolare, C 0 (T) è lo spazio C(T) dellle funzioni continue che già conosciamo; C 1 (T) è lo spazio delle funzioni continue con derivata prima continua; C 2 (T) è lo spazio delle funzioni continue derivabili due volte, con derivate prima e seconda continua, e coì via. Naturalmente, si ha C p C 2 C 1 C. La discussione sulla derivazione di una serie di Fourier è riassunta dal seguente teorema: Teorema 1. Se f C p (T), allora f (p) (n) = (in) p f(n) Dimostrazione. Analoga a quanto visto sopra per p = 1 e p = Andamento all infinito delle coordinate di Fourier. Un tema classico dell analisi di Fourier è la relazione tra le proprietà di regolarità della funzione 6
7 f(x) e l andamento all infinito delle sue coordinate di Fourier f(n). Se f C p (T) allora per il teorema 1 f(n) = 1 n f (p) (n) p = 1 1 π n p f (p) (x)e inx dx 1 ( 1 π ) f (p) (x) dx n p Poiché f (p) (x) è per ipotesi continua nell intervallo chiuso [, π], sarà limitata da una costante finita e positiva C, f(n) C n p. Risulta così dimostrato il seguente teorema: Teorema 2. Se f C p (T), allora le sue coordinate di Fourier f(n) decadono almeno come 1/ n p per n. N.B. Si faccia attenzione al fatto che l inverso del teorema 2 non vale. La funzione ottenute sintetizzando coordinate che decadono come 1/n p non solo non è necessariamente una funzione derivabile p volte, ma non è detto neanche che sia una funzione continua 1. Come esempio, si consideri la funzione f(x) che vale 1 se x [0, 1] e 0 altrimenti. La funzione è chiaramente discontinua e le sue coordinate sono f(n) = 1 f(x)e inx dx = e inx dx = 1 e in in Ne segue che f(n) 1/(πn), e dunque le coordinate di f decano come 1/n, ma la funzione non è derivabile né continua. Si osservi che come sottoprodotto del teorema 2 otteniamo, inaspettatamente, un teorema di convergenza per le serie di Fourier: Teorema 3. Se f C 2 (T), allora la sua serie di Fourier converge uniformemente in T. Dimostrazione. Se f è derivabile due volte, allora f(n) C/n 2 e quindi f(n) è assolutamente convergente. Ma allora è anche uniformente convergente (si veda la lezione 1.2) e, ovviamente, la convergenza è puntuale. Vale anche il seguente teorema: 1 La situazione è migliore di quanto sembri: per p > 1 si può dimostrare la continuità e per p > k + 1, si può dimostrare che la funzione è almeno di classe C k. Si vedano gli esercizi di riepilogo in calce alla lezione 17. 7
8 Teorema 4. Se f C 1 (T), allora la sua serie di Fourier converge uniformemente in T. Ma non possiamo dimostrare questo sulla falsa riga del teorema 3, in quanto l informazione che le coordinate di f decadono almeno come 1/n non è sufficiente a stabilire la convergenza della serie. Alla fine della sezione daremo una dimostraione della convergenza puntuale per f C 1 (T). Infine, il seguente teorema stabilisce l andamento all infinito delle coordinate per funzioni analitiche. Teorema 5. Se f è analitica, allora le sue coordinate di Fourier f(n) decadono esponenzialmente in n per n Velocità di convergenza delle somme parziali. Si può dimostrare che più liscia è f più veloce è la convergenza sue delle somme parziali di Fourier. Più precisamente, si può dimostrare che se f C p (T), per p 2, allora esiste una costante C, indipendente da x, tale che f(x) S N (f)(x) C N p 1 e se f C 1 (T), allora esiste una costante C, indipendente da x, tale che f(x) S N (f)(x) C N Questi risultati che non dimostreremo forniscono automaticamente la convergenza uniforme delle somme parziali di Fourier per funzioni C p, p 1 e, in particolare, una dimostrazione del teorema Funzioni assolutamente integrabili. Se una funzione è assolutamente integrabile, cioè se 1 π (4) f(x) dx <, si dice che f L 1 (T). Si osservi che (esercizio) 1 π 1 f(x) dx f(x) 2 dx. Quindi, se f L 2 (T), allora f L 1 (T), ma non è detto che sia vero l inverso. Se una funzione è integrabile, le sue coordinate di Fourier decadono a zero. Questo è il contenuto di un famoso lemma: Teorema 6 (Lemma di Riemann-Lebesgue). Se f L 1 (T) allora lim f(n) = 0 n 8
9 Dimostrazione. Se f L 2 (T), il teorema è immediato, poichè f è in l 2. Per la dimostrazione completa, occorre argomentare che L 2 (T) è denso in L 1 (T) nella norma definita da (4). Non intendiamo entrare nei dettagli (né ci aspettiamo che lo faccia lo studente) Integrazione delle serie di Fourier. La parola d ordine è che la derivazione peggiora la convergenza della serie di Fourier (in quando le sue coordinate sono moltiplicate per in), ma l integrazione la migliora. Se la serie è uniformemente convergente, cossiché l integrale può essere scambiato con il limite delle somme parziali, è chiaro che la serie può essere integrata termine a termine. Come effetto dell integrazione le coordinate di Fourier f(n) risultano moltiplicate per 1/(in). Ma anche se la serie f(n)e inx associata a f diverge, la serie di Fourier ottenuta per integrazione termine a termine converge, purché f L 1 (T). 9
f(n)r n e inx lim Se f(x) C(T) allora f S (r) f(x) = lim e inx
 17.1. Analisi di Fourier III. 17.1.1. Teorema di approssimazione di Weierstrass. Un polinomio trigonometrico è una qualunque funzione della forma n
17.1. Analisi di Fourier III. 17.1.1. Teorema di approssimazione di Weierstrass. Un polinomio trigonometrico è una qualunque funzione della forma n
Esercizi di riepilogo 2: soluzioni ( Verifica di analisi funzionale e serie di Fourier)
 Esercizi di riepilogo 2: soluzioni ( Verifica di analisi funzionale e serie di Fourier) Spazi Vettoriali e Funzionali 1. Risposte: (a) Spazio vettoriale complesso. (b) Spazio vettoriale reale. (c) Non
Esercizi di riepilogo 2: soluzioni ( Verifica di analisi funzionale e serie di Fourier) Spazi Vettoriali e Funzionali 1. Risposte: (a) Spazio vettoriale complesso. (b) Spazio vettoriale reale. (c) Non
Analisi di Fourier e alcune equazioni della fisica matematica 1. TERZA LEZIONE Serie di funzioni Serie di potenze
 Analisi di Fourier e alcune equazioni della fisica matematica 1 TERZA LEZIONE Serie di funzioni Serie di potenze 1 prof. Claudio Saccon, Dipartimento di Matematica Applicata, Via F. Buonarroti 1/C email:
Analisi di Fourier e alcune equazioni della fisica matematica 1 TERZA LEZIONE Serie di funzioni Serie di potenze 1 prof. Claudio Saccon, Dipartimento di Matematica Applicata, Via F. Buonarroti 1/C email:
COMPLEMENTI DI ANALISI MATEMATICA DI BASE. Prova scritta del 26 gennaio 2005
 Prova scritta del 26 gennaio 2005 Esercizio 1. Posto B = x R 2 : x 2 2}, sia f n } una successione di funzioni (misurabili e) integrabili in B tali che f n f q.o. in B e, per ogni n N, f n (x) 2 x 3 per
Prova scritta del 26 gennaio 2005 Esercizio 1. Posto B = x R 2 : x 2 2}, sia f n } una successione di funzioni (misurabili e) integrabili in B tali che f n f q.o. in B e, per ogni n N, f n (x) 2 x 3 per
Convergenza puntuale ed uniforme delle serie di Fourier
 Convergenza puntuale ed uniforme delle serie di Fourier 8 aprile 009 In questi appunti prendiamo in considerazione funzioni di variabile reale che possono assumere però valori complessi. Una funzione F
Convergenza puntuale ed uniforme delle serie di Fourier 8 aprile 009 In questi appunti prendiamo in considerazione funzioni di variabile reale che possono assumere però valori complessi. Una funzione F
Serie trigonometriche e di Fourier Ci occuperemo di serie le cui ridotte N-esime sono polinomi trigonometrici di grado (o ordine) N:
 Serie trigonometriche e di Fourier Ci occuperemo di serie le cui ridotte N-esime sono polinomi trigonometrici di grado (o ordine) N: S N (x) = N n=0 (a n cos (nx) + b n sin (nx)), a n, b n R (periodiche
Serie trigonometriche e di Fourier Ci occuperemo di serie le cui ridotte N-esime sono polinomi trigonometrici di grado (o ordine) N: S N (x) = N n=0 (a n cos (nx) + b n sin (nx)), a n, b n R (periodiche
Serie di Fourier. Hynek Kovarik. Analisi Matematica 2. Università di Brescia
 Serie di Fourier Hynek Kovarik Università di Brescia Analisi Matematica 2 Hynek Kovarik (Università di Brescia) Serie di Fourier Analisi Matematica 2 1 / 37 Polinomi trigonometrici Definizione Si dice
Serie di Fourier Hynek Kovarik Università di Brescia Analisi Matematica 2 Hynek Kovarik (Università di Brescia) Serie di Fourier Analisi Matematica 2 1 / 37 Polinomi trigonometrici Definizione Si dice
Esame di Metodi Matematici per l Ingegneria Seconda prova in itinere. Gennaio 2018 A.A. 2017/2018. Prof. M. Bramanti Tema A
 Esame di Metodi Matematici per l Ingegneria Seconda prova in itinere. Gennaio 18 A.A. 17/18. Prof. M. Bramanti Tema A Cognome: Nome N matr. o cod. persona: Dom 1 Dom Dom 3 Es 1 Es Es 3 Tot. Punti Domande
Esame di Metodi Matematici per l Ingegneria Seconda prova in itinere. Gennaio 18 A.A. 17/18. Prof. M. Bramanti Tema A Cognome: Nome N matr. o cod. persona: Dom 1 Dom Dom 3 Es 1 Es Es 3 Tot. Punti Domande
esiste. Esempio 3. La successione e x2 /n 2 è regolare. In questo caso il limite è
 9.2. Funzioni generalizzate e integrali regolarizzati. 9.2.. Funzioni generalizzate. Lasciamo per un momento da parte l analisi complessa e occupiamoci di un argomento che prima o poi spunta fuori in un
9.2. Funzioni generalizzate e integrali regolarizzati. 9.2.. Funzioni generalizzate. Lasciamo per un momento da parte l analisi complessa e occupiamoci di un argomento che prima o poi spunta fuori in un
Alcuni complementi di teoria dell integrazione.
 Alcuni complementi di teoria dell integrazione. In ciò che segue si suppone di avere uno spazio di misura (,, µ) 1 Sia f una funzione misurabile su un insieme di misura positiva tale che f 0. Se fdµ =
Alcuni complementi di teoria dell integrazione. In ciò che segue si suppone di avere uno spazio di misura (,, µ) 1 Sia f una funzione misurabile su un insieme di misura positiva tale che f 0. Se fdµ =
Serie di Fourier Richiami di teoria. Funzioni periodiche. Ci poniamo il problema dello sviluppo in serie di Fourier per funzioni f 1 : R R
 Serie di Fourier Richiami di teoria Funzioni periodiche Ci poniamo il problema dello sviluppo in serie di Fourier per funzioni f 1 : R R 2π-periodiche. Esempio 1. Consideriamo il prolungamento 2π-periodico
Serie di Fourier Richiami di teoria Funzioni periodiche Ci poniamo il problema dello sviluppo in serie di Fourier per funzioni f 1 : R R 2π-periodiche. Esempio 1. Consideriamo il prolungamento 2π-periodico
1 Successioni di funzioni
 Analisi Matematica 2 Successioni di funzioni CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 6 SERIE DI POTENZE Supponiamo di associare ad ogni n N (rispettivamente ad ogni n p, per qualche
Analisi Matematica 2 Successioni di funzioni CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 6 SERIE DI POTENZE Supponiamo di associare ad ogni n N (rispettivamente ad ogni n p, per qualche
Esercizi di riepilogo 2 ( Verifica di analisi funzionale e serie di Fourier)
 Esercizi di riepilogo 2 ( Verifica di analisi funzionale e serie di Fourier) Spazi Vettoriali e Funzionali 1. Determinare quali sei seguenti insiemi è uno spazio vettoriale rispetto alle usuali operazioni
Esercizi di riepilogo 2 ( Verifica di analisi funzionale e serie di Fourier) Spazi Vettoriali e Funzionali 1. Determinare quali sei seguenti insiemi è uno spazio vettoriale rispetto alle usuali operazioni
ANALISI DI FOURIER. 2πk. è periodica di periodo T. Più precisamente, essendo. T x + 2π = cos. s(x) = s x + T ) T +α. f(x) dx
 ANALISI DI FOURIER Sia >. Una funzione f, definita per x R, si dice periodica di periodo, se f(x + = f(x, x R. ( Se una funzione è periodica di periodo, essa è anche periodica di periodo, 3,..., k,....
ANALISI DI FOURIER Sia >. Una funzione f, definita per x R, si dice periodica di periodo, se f(x + = f(x, x R. ( Se una funzione è periodica di periodo, essa è anche periodica di periodo, 3,..., k,....
Serie e Trasformata di Fourier
 Serie e Trasformata di Fourier Corso di Analisi Funzionale Prof. Paolo Nistri Cancelli, D Angelo, Giannetti Polinomio di Fourier Si consideri la successione costituita dalle restrizioni delle funzioni
Serie e Trasformata di Fourier Corso di Analisi Funzionale Prof. Paolo Nistri Cancelli, D Angelo, Giannetti Polinomio di Fourier Si consideri la successione costituita dalle restrizioni delle funzioni
Analisi a più variabili: Integrale di Lebesgue
 Analisi a più variabili: Integrale di Lebesgue 1 Ripasso delle definizioni di Algebre, σ-algebre, misure additive, misure σ-additive, Proprietà della misura astratta, misura esterna. Definizione (Insieme
Analisi a più variabili: Integrale di Lebesgue 1 Ripasso delle definizioni di Algebre, σ-algebre, misure additive, misure σ-additive, Proprietà della misura astratta, misura esterna. Definizione (Insieme
Registro delle lezioni
 Complementi di Analisi Matematica - a.a. 2006-07 Corso di Laurea Specialistica in Ingegneria Civile (CIS) Registro delle lezioni Laura Poggiolini e Gianna Stefani 2 ottobre 2006, 2 ore, LP Il campo dei
Complementi di Analisi Matematica - a.a. 2006-07 Corso di Laurea Specialistica in Ingegneria Civile (CIS) Registro delle lezioni Laura Poggiolini e Gianna Stefani 2 ottobre 2006, 2 ore, LP Il campo dei
2. Si esponga il problema della migliore approssimazione in norma, e si dica in quali spazi esso ha certamente soluzione, e quale è questa soluzione.
 COMPLEMENTI DI MATEMATICA Corso di Laurea Magistrale in Ingegneria Elettrotecnica CM98sett.tex 6..2009 - lunedì (2 ore) Esercitazione del 6..2009 Risolvere tre esercizi per pagina, a scelta.. Si definisca
COMPLEMENTI DI MATEMATICA Corso di Laurea Magistrale in Ingegneria Elettrotecnica CM98sett.tex 6..2009 - lunedì (2 ore) Esercitazione del 6..2009 Risolvere tre esercizi per pagina, a scelta.. Si definisca
PROVE SCRITTE DI ANALISI MATEMATICA II (V.O.), ANNO 2002
 PROVE SCRITTE DI ANALISI MATEMATICA II (V.O.), ANNO 22 Prova scritta del 1/1/22 Si esamini la serie di funzioni: 1 log x (e n + n), definita per x IR. Si determini l insieme S in cui tale serie converge,
PROVE SCRITTE DI ANALISI MATEMATICA II (V.O.), ANNO 22 Prova scritta del 1/1/22 Si esamini la serie di funzioni: 1 log x (e n + n), definita per x IR. Si determini l insieme S in cui tale serie converge,
Successioni di funzioni
 Successioni di funzioni 1. Primi esempi 1, x, x 2, x 3,..., x n,..., x [0, 2] e x, e 2x, e 3x,..., e nx,..., x [ 1, 1] f n (x) = 1, n = 1, 2, 3,..., x R (n + 1) 2 + x2 f n (x) = sin(x), n = 1, 2, 3,...,
Successioni di funzioni 1. Primi esempi 1, x, x 2, x 3,..., x n,..., x [0, 2] e x, e 2x, e 3x,..., e nx,..., x [ 1, 1] f n (x) = 1, n = 1, 2, 3,..., x R (n + 1) 2 + x2 f n (x) = sin(x), n = 1, 2, 3,...,
f n (x) 3 1. x Essendo g(x) = 3 1
 Secondo esonero di Analisi eale 6//9 a.a. 8-9 ) Studiare la convergenza in L p ((, )), p +, della successione di funzioni cos(nx) e nx f n (x) = 3. x Si vede facilmente che la successione f n converge
Secondo esonero di Analisi eale 6//9 a.a. 8-9 ) Studiare la convergenza in L p ((, )), p +, della successione di funzioni cos(nx) e nx f n (x) = 3. x Si vede facilmente che la successione f n converge
ANALISI VETTORIALE COMPITO IN CLASSE DEL 8/11/2013
 ANALISI VETTORIALE COMPITO IN CLASSE DEL 8//3 Premessa (Cfr. gli Appunti di Analisi Vettoriale / del Prof. Troianiello) Nello studio degli integrali impropri il primo approccio all utilizzo del criterio
ANALISI VETTORIALE COMPITO IN CLASSE DEL 8//3 Premessa (Cfr. gli Appunti di Analisi Vettoriale / del Prof. Troianiello) Nello studio degli integrali impropri il primo approccio all utilizzo del criterio
Analisi 2. Roberto Monti. Appunti del Corso - Versione 5 Ottobre 2012
 Analisi 2 Roberto Monti Appunti del Corso - Versione 5 Ottobre 212 Indice Capitolo 1. Programma 5 Capitolo 2. Convergenza uniforme 7 1. Convergenza uniforme e continuità 7 2. Criterio di Abel Dirichlet
Analisi 2 Roberto Monti Appunti del Corso - Versione 5 Ottobre 212 Indice Capitolo 1. Programma 5 Capitolo 2. Convergenza uniforme 7 1. Convergenza uniforme e continuità 7 2. Criterio di Abel Dirichlet
Quesiti di Metodi Matematici per l Ingegneria
 Quesiti di Metodi Matematici per l Ingegneria Presentiamo una raccolta di quesiti per la preparazione alla prova orale del modulo di Metodi Matematici per l Ingegneria. Per una buona preparazione é consigliabile
Quesiti di Metodi Matematici per l Ingegneria Presentiamo una raccolta di quesiti per la preparazione alla prova orale del modulo di Metodi Matematici per l Ingegneria. Per una buona preparazione é consigliabile
Esonero di Analisi Matematica II (A)
 Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
Esame di Analisi Funzionale e Trasformate Prima prova in itinere. Aprile 2018 A.A. 2017/2018. Prof. M. Bramanti Tema A
 Esame di Analisi Funzionale e Trasformate Prima prova in itinere. Aprile 018 A.A. 017/018. Prof. M. Bramanti Tema A Cognome: Nome N matr. o cod. persona: Dom 1 Dom Dom 3 Es 1 Es Es 3 Tot. Punti Domande
Esame di Analisi Funzionale e Trasformate Prima prova in itinere. Aprile 018 A.A. 017/018. Prof. M. Bramanti Tema A Cognome: Nome N matr. o cod. persona: Dom 1 Dom Dom 3 Es 1 Es Es 3 Tot. Punti Domande
Esercizi per il corso di Analisi 6.
 Esercizi per il corso di Analisi 6. 1. Si verifichi che uno spazio normato (X, ) è uno spazio vettoriale topologico con la topologia indotta dalla norma. Si verifichi poi che la norma è una funzione continua
Esercizi per il corso di Analisi 6. 1. Si verifichi che uno spazio normato (X, ) è uno spazio vettoriale topologico con la topologia indotta dalla norma. Si verifichi poi che la norma è una funzione continua
7. Serie di Fourier Assegnata la funzione f(x) integrabile in [0, 2π] si possono determinare i suoi coefficienti di Fourier.
![7. Serie di Fourier Assegnata la funzione f(x) integrabile in [0, 2π] si possono determinare i suoi coefficienti di Fourier. 7. Serie di Fourier Assegnata la funzione f(x) integrabile in [0, 2π] si possono determinare i suoi coefficienti di Fourier.](/thumbs/98/137574113.jpg) (seguito dalla lezione precedente) 7. Serie di Fourier Assegnata la funzione f(x) tegrabile [, ] si possono determare i suoi coefficienti di Fourier f(n) = 1 si puó considerare la serie f(x)e x dx, n =,
(seguito dalla lezione precedente) 7. Serie di Fourier Assegnata la funzione f(x) tegrabile [, ] si possono determare i suoi coefficienti di Fourier f(n) = 1 si puó considerare la serie f(x)e x dx, n =,
Corso di Metodi Matematici per l Ingegneria A.A. 2016/2017 Esercizi svolti su misura e integrale di Lebesgue, spazi L p, operatori lineari continui
 Corso di Metodi Matematici per l Ingegneria A.A. 26/27 Esercizi svolti su misura e integrale di Lebesgue, spazi L p, operatori lineari continui Marco Bramanti Politecnico di Milano December 4, 26 Esercizi
Corso di Metodi Matematici per l Ingegneria A.A. 26/27 Esercizi svolti su misura e integrale di Lebesgue, spazi L p, operatori lineari continui Marco Bramanti Politecnico di Milano December 4, 26 Esercizi
Corso di Laurea in Ingegneria Edile Prova scritta dell esame di Analisi Matematica I (M-Z).C
 Analisi Matematica I (M-Z).C1 08-0-1997 1) Data la funzione h(x) = x log(x + 1 + x + x + ) + log(1 + ) determinarne il dominio D. Provare poi che h(x) > 0 x D ]0, + [, h(x) = 0 x = 0. ) Utilizzando i risultati
Analisi Matematica I (M-Z).C1 08-0-1997 1) Data la funzione h(x) = x log(x + 1 + x + x + ) + log(1 + ) determinarne il dominio D. Provare poi che h(x) > 0 x D ]0, + [, h(x) = 0 x = 0. ) Utilizzando i risultati
Corso di laurea in STM Analisi di Fourier
 Corso di laurea in STM Analisi di Fourier 2016-17 Dettaglio delle lezioni svolte e programma del corso 07/03 Ortogonalità in L 2 del sistema trigonometrico. Sviluppo di Fourier in forma reale e complessa.
Corso di laurea in STM Analisi di Fourier 2016-17 Dettaglio delle lezioni svolte e programma del corso 07/03 Ortogonalità in L 2 del sistema trigonometrico. Sviluppo di Fourier in forma reale e complessa.
12.3. Il problema di Dirichlet nel piano. In questa lezione si vuole dare risoluzione completa e rigorosa del problema di Dirichlet nel piano:
 12.3. Il problema di Dirichlet nel piano. In questa lezione si vuole dare risoluzione completa e rigorosa del problema di Dirichlet nel piano: u = 0 in R u = g in R 12.3.1. Distribuzione di temperatura
12.3. Il problema di Dirichlet nel piano. In questa lezione si vuole dare risoluzione completa e rigorosa del problema di Dirichlet nel piano: u = 0 in R u = g in R 12.3.1. Distribuzione di temperatura
Argomento della lezione N. 1. Argomento della lezione N. 2. Argomento della lezione N. 12. Argomento della lezione N. 11
 C. Presilla Modelli e Metodi Matemacici della Fisica a.a. 2011/2012 2 Argomento della lezione N. 1 Fondamenti assiomatici. L unità immaginaria Argomento della lezione N. 2 Moduli e coniugati. Disuguaglianza
C. Presilla Modelli e Metodi Matemacici della Fisica a.a. 2011/2012 2 Argomento della lezione N. 1 Fondamenti assiomatici. L unità immaginaria Argomento della lezione N. 2 Moduli e coniugati. Disuguaglianza
SUCCESSIONI E SERIE NUMERICHE E DI FUNZIONI
 SERIE NUMERICHE Si consideri una successione di elementi. Si definisce serie associata ad la somma Per ogni indice della successione, si definisce successione delle somme parziali associata a la somma
SERIE NUMERICHE Si consideri una successione di elementi. Si definisce serie associata ad la somma Per ogni indice della successione, si definisce successione delle somme parziali associata a la somma
E, la successione di numeri {f n (x 0. n f n(x) (15.1)
 Capitolo 15 15.1 Successioni e serie di funzioni Sia {f n } una successione di funzioni, tutte definite in un certo insieme E dello spazio R n ; si dice che essa è convergente nell insieme E se, comunque
Capitolo 15 15.1 Successioni e serie di funzioni Sia {f n } una successione di funzioni, tutte definite in un certo insieme E dello spazio R n ; si dice che essa è convergente nell insieme E se, comunque
c i χ Ai (x) f(x) = f(x)dx = c i m(a i ) R
 1. Integrale di Lebesgue in La differenza fondamentale tra integrale di Lebesgue e integrale di iemann consiste nella diversa scelta delle decomposizioni su cui sostanzialmente si basa ogni integrale:
1. Integrale di Lebesgue in La differenza fondamentale tra integrale di Lebesgue e integrale di iemann consiste nella diversa scelta delle decomposizioni su cui sostanzialmente si basa ogni integrale:
Soluzioni dello scritto di Analisi Matematica II - 10/07/09. C.L. in Matematica e Matematica per le Applicazioni
 Soluzioni dello scritto di Analisi Matematica II - /7/9 C.L. in Matematica e Matematica per le Applicazioni Proff. K. Payne, C. Tarsi, M. Calanchi Esercizio. a La funzione f è limitata e essendo lim fx
Soluzioni dello scritto di Analisi Matematica II - /7/9 C.L. in Matematica e Matematica per le Applicazioni Proff. K. Payne, C. Tarsi, M. Calanchi Esercizio. a La funzione f è limitata e essendo lim fx
ANALISI MATEMATICA 1 ESERCIZI ASSEGNATI IN AULA O A CASA Corso di Laurea in Matematica aa 2003/04 01/03/04
 ANALISI MATEMATICA ESERCIZI ASSEGNATI IN AULA O A CASA Corso di Laurea in Matematica aa 2003/04 0/03/04 Esercizio. Calcolare la somma della serie ( 2 k ). 3 k 2 k Esercizio 2. Scrivere sotto forma di frazione
ANALISI MATEMATICA ESERCIZI ASSEGNATI IN AULA O A CASA Corso di Laurea in Matematica aa 2003/04 0/03/04 Esercizio. Calcolare la somma della serie ( 2 k ). 3 k 2 k Esercizio 2. Scrivere sotto forma di frazione
Convergenza per funzioni tra spazi metrici. Funzioni uniformemente continue e Lipschitz continue. Esempi. somma e prodotto, il campo C dei numeri
 Argomento della Lezione N. 1 Argomento della Lezione N. 2 Argomento della Lezione N. 11 Argomento della Lezione N. 12 Fondamenti assiomatici del sistema di numeri L unita immaginaria. Convergenza per funzioni
Argomento della Lezione N. 1 Argomento della Lezione N. 2 Argomento della Lezione N. 11 Argomento della Lezione N. 12 Fondamenti assiomatici del sistema di numeri L unita immaginaria. Convergenza per funzioni
ANALISI MATEMATICA 4. Prova scritta del 24 gennaio 2013
 Prova scritta del 24 gennaio 2013 Esercizio 1. Sia Ω R 3 un insieme misurabile secondo Lebesgue e di misura finita. Sia {f n } n N una successione di funzioni f n : Ω R misurabili e tali che 1) f n (x)
Prova scritta del 24 gennaio 2013 Esercizio 1. Sia Ω R 3 un insieme misurabile secondo Lebesgue e di misura finita. Sia {f n } n N una successione di funzioni f n : Ω R misurabili e tali che 1) f n (x)
Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 2 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata, Matematica
 DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 2 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 2 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
Problemi. Problemi [101] [102] 4) Trovare tutte le soluzioni classiche dell equazione differenziale
![Problemi. Problemi [101] [102] 4) Trovare tutte le soluzioni classiche dell equazione differenziale Problemi. Problemi [101] [102] 4) Trovare tutte le soluzioni classiche dell equazione differenziale](/thumbs/97/132392447.jpg) [101] [102] Soluzioni classiche Problema di Cauchy 1) Trovare tutte le soluzioni classiche dell equazione differenziale y (x) = 0 aventi per dominio l insieme R dei numeri reali. 2) Trovare almeno una
[101] [102] Soluzioni classiche Problema di Cauchy 1) Trovare tutte le soluzioni classiche dell equazione differenziale y (x) = 0 aventi per dominio l insieme R dei numeri reali. 2) Trovare almeno una
Analisi Matematica 3/Analisi 4 - SOLUZIONI (20/01/2016)
 Corso di Laurea in Matematica Docente: Claudia Anedda Analisi Matematica 3/Analisi 4 - SOLUZIONI (//6) ) i) Dopo averla classificata, risolvere l equazione differenziale tẋ x = t cos(t), t >. ii) Scrivere
Corso di Laurea in Matematica Docente: Claudia Anedda Analisi Matematica 3/Analisi 4 - SOLUZIONI (//6) ) i) Dopo averla classificata, risolvere l equazione differenziale tẋ x = t cos(t), t >. ii) Scrivere
Soluzione dei problemi assegnati
 ANALISI MATEMATICA 3 Soluzione dei problemi assegnati anno accademico 2018/19 prof. Antonio Greco http://people.unica.it/antoniogreco Dipartimento di Matematica e Informatica Università di Cagliari 23-5-2019
ANALISI MATEMATICA 3 Soluzione dei problemi assegnati anno accademico 2018/19 prof. Antonio Greco http://people.unica.it/antoniogreco Dipartimento di Matematica e Informatica Università di Cagliari 23-5-2019
UNIVERSITÀ DEGLI STUDI DI BERGAMO. La convergenza delle serie di Fourier: proprietà classiche e moderne. Luca Brandolini
 UNIVERSITÀ DEGLI STUDI DI BERGAMO La convergenza delle serie di Fourier: proprietà classiche e moderne Luca Brandolini Analisi di Fourier Le serie (e più in generale) l analisi di Fourier sono uno strumento
UNIVERSITÀ DEGLI STUDI DI BERGAMO La convergenza delle serie di Fourier: proprietà classiche e moderne Luca Brandolini Analisi di Fourier Le serie (e più in generale) l analisi di Fourier sono uno strumento
Argomento della Lezione N. 1 Argomento della Lezione N. 2 Argomento della Lezione N. 11 Argomento della Lezione N. 12 Introduzione al corso.
 Argomento della Lezione N. 1 Argomento della Lezione N. 2 Argomento della Lezione N. 11 Argomento della Lezione N. 12 Introduzione al corso. Il campo C dei numeri complessi. Fondamenti assiomatici del
Argomento della Lezione N. 1 Argomento della Lezione N. 2 Argomento della Lezione N. 11 Argomento della Lezione N. 12 Introduzione al corso. Il campo C dei numeri complessi. Fondamenti assiomatici del
Corso di Metodi Matematici per l Ingegneria A.A. 2017/2018 Domande-tipo di teoria sulla seconda metà del corso
 Corso di Metodi Matematici per l Ingegneria A.A. 2017/2018 Domande-tipo di teoria sulla seconda metà del corso Marco Bramanti Politecnico di Milano December 20, 2017 Parte 3. Teoria della misura e dell
Corso di Metodi Matematici per l Ingegneria A.A. 2017/2018 Domande-tipo di teoria sulla seconda metà del corso Marco Bramanti Politecnico di Milano December 20, 2017 Parte 3. Teoria della misura e dell
Analisi Matematica II 6 aprile sin[π(x 2 + y 2 /5)] x 2 + y2
![Analisi Matematica II 6 aprile sin[π(x 2 + y 2 /5)] x 2 + y2 Analisi Matematica II 6 aprile sin[π(x 2 + y 2 /5)] x 2 + y2](/thumbs/98/135722489.jpg) Analisi Matematica II 6 aprile 07 Cognome: Nome: Matricola:. (0 punti) Si consideri la seguente corrispondenza tra R ed R f(x, y) = Determinare l insieme di definizione A R di f e sin[π(x + y /5)] x +
Analisi Matematica II 6 aprile 07 Cognome: Nome: Matricola:. (0 punti) Si consideri la seguente corrispondenza tra R ed R f(x, y) = Determinare l insieme di definizione A R di f e sin[π(x + y /5)] x +
USO DELL ORTOGONALITÀ E DELLE UNITÀ APPROSSIMANTI
 1. C INFINITO CI 1 USO ELL ORTOGONALITÀ E ELLE UNITÀ APPROSSIMANTI Umberto Marconi ipartimento di Matematica Pura e Applicata Padova 1 C infinito ci Consideriamo la funzione reale di variabile reale: {
1. C INFINITO CI 1 USO ELL ORTOGONALITÀ E ELLE UNITÀ APPROSSIMANTI Umberto Marconi ipartimento di Matematica Pura e Applicata Padova 1 C infinito ci Consideriamo la funzione reale di variabile reale: {
1 a Prova parziale di Analisi Matematica I (A) 16/11/2007
 Nome a Prova parziale di Analisi Matematica I (A) 6//7 ) Data la funzione ( ) = f e Calcolare il campo di esistenza e il suo comportamento agli estremi ) Definizione di derivata prima di una funzione f()
Nome a Prova parziale di Analisi Matematica I (A) 6//7 ) Data la funzione ( ) = f e Calcolare il campo di esistenza e il suo comportamento agli estremi ) Definizione di derivata prima di una funzione f()
Gli argomenti denotati con un asterisco tra parentesi (e solo quelli) sono stati dimostrati.
 Corso di laurea: Fisica ed Astronomia Programma di Analisi Matematica 2 a.a. 2018/19 Docente: Fabio Paronetto Gli argomenti denotati con un asterisco tra parentesi (e solo quelli) sono stati dimostrati.
Corso di laurea: Fisica ed Astronomia Programma di Analisi Matematica 2 a.a. 2018/19 Docente: Fabio Paronetto Gli argomenti denotati con un asterisco tra parentesi (e solo quelli) sono stati dimostrati.
Analisi Matematica 2. Michele Campiti. Prove scritte di. Ingegneria Industriale a.a
 Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
Limitiamoci dapprima a considerare una funzione f di periodo 2π. Cercheremo di approssimarla con polinomi trigonometrici di ordine n della forma
 Serie di Fourier L idea che sta alla base degli sviluppi in serie di Fourier è quella di approssimare, in qualche senso, le funzioni (integrabili periodiche per mezzo di funzioni più regolari e/o più facilmente
Serie di Fourier L idea che sta alla base degli sviluppi in serie di Fourier è quella di approssimare, in qualche senso, le funzioni (integrabili periodiche per mezzo di funzioni più regolari e/o più facilmente
Corso di Laurea in Ingegneria Informatica Prova scritta di Analisi Matematica 1
 Corso di Laurea in Ingegneria Informatica Prova scritta di Analisi Matematica 30 gennaio 207 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo.
Corso di Laurea in Ingegneria Informatica Prova scritta di Analisi Matematica 30 gennaio 207 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo.
Gli argomenti denotati con un asterisco tra parentesi (e solo quelli) sono stati dimostrati.
 Corso di laurea: Fisica ed Astronomia Programma di Analisi Matematica 2 a.a. 2017/18 Docente: Fabio Paronetto Gli argomenti denotati con un asterisco tra parentesi (e solo quelli) sono stati dimostrati.
Corso di laurea: Fisica ed Astronomia Programma di Analisi Matematica 2 a.a. 2017/18 Docente: Fabio Paronetto Gli argomenti denotati con un asterisco tra parentesi (e solo quelli) sono stati dimostrati.
Un paio di esempi su serie e successioni di funzioni
 Un paio di esempi su serie e successioni di funzioni 29 novembre 2010 1 Successione di funzioni Ricordiamo innanzitutto un po di definizioni. Definizione 1. Una successione di funzioni è una corrispondenza
Un paio di esempi su serie e successioni di funzioni 29 novembre 2010 1 Successione di funzioni Ricordiamo innanzitutto un po di definizioni. Definizione 1. Una successione di funzioni è una corrispondenza
Serie di Fourier. 1. Introduzione Le funzioni somme di funzioni trigonometriche
 Serie di Fourier. Introduzione Le funzioni somme di funzioni trigonometriche, sin(x), cos(x), sin(2x), cos(2x),...ecc. P (x) = 2 a + a cos(x) + b sin(x) +... + b n sin(x) si dicono polinomi trigonometrici:
Serie di Fourier. Introduzione Le funzioni somme di funzioni trigonometriche, sin(x), cos(x), sin(2x), cos(2x),...ecc. P (x) = 2 a + a cos(x) + b sin(x) +... + b n sin(x) si dicono polinomi trigonometrici:
Università degli Studi di Firenze Anno Accademico 2006/2007 Ingegneria per la Tutela dell Ambiente e del Territorio (Laurea Specialistica)
 Università degli Studi di Firenze Anno Accademico 2006/2007 Ingegneria per la Tutela dell Ambiente e del Territorio (Laurea Specialistica) Corso Complementi di Analisi Matematica Docente del corso: Francesca
Università degli Studi di Firenze Anno Accademico 2006/2007 Ingegneria per la Tutela dell Ambiente e del Territorio (Laurea Specialistica) Corso Complementi di Analisi Matematica Docente del corso: Francesca
( 1 π. (a n cos nt + b n sin nt) t R (3)
 7. SERIE TRIGONOMETRICHE E SERIE DI FOURIER Definizione 1. L p (R), p [1, + ), denota la classe di tutte le funzioni f : R C, misurabili secondo Lebesgue, periodiche con periodo per le quali il funzionale
7. SERIE TRIGONOMETRICHE E SERIE DI FOURIER Definizione 1. L p (R), p [1, + ), denota la classe di tutte le funzioni f : R C, misurabili secondo Lebesgue, periodiche con periodo per le quali il funzionale
Le derivate parziali
 Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
Il teorema di Ascoli-Arzelà
 Il teorema di Ascoli-Arzelà Alcuni risultati sugli spazi metrici Spazi metrici (e topologici) compatti Richiamiamo le definizioni di compattezza negli spazi metrici. Sia (X, d) una spazio metrico e sia
Il teorema di Ascoli-Arzelà Alcuni risultati sugli spazi metrici Spazi metrici (e topologici) compatti Richiamiamo le definizioni di compattezza negli spazi metrici. Sia (X, d) una spazio metrico e sia
f(x)e 2πixy dx g(y)e 2πixy dy
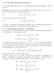 18.2. Il paradiso dell integrale di Fourier. Lo spazio delle funzioni buone è il paradiso dell integrale di Fourier. teorema: Vale il Teorema 1 (teorema di inversione di Fourier per funzioni buone). Se
18.2. Il paradiso dell integrale di Fourier. Lo spazio delle funzioni buone è il paradiso dell integrale di Fourier. teorema: Vale il Teorema 1 (teorema di inversione di Fourier per funzioni buone). Se
non solo otteniamo il valore cercato per la validità della (1.4), ma anche che tale valore non dipende da
 NOTE INTEGRATIVE PER IL CORSO DI ANALISI MATEMATICA 2 ANNO ACCADEMICO 2012/13 NOTE SULLA CONTINUITÀ UNIFORME D.BARTOLUCCI, D.GUIDO Sia f(x) = x 3, x [ 1, 1]. Si ha 1. La continuità uniforme x 3 y 3 = x
NOTE INTEGRATIVE PER IL CORSO DI ANALISI MATEMATICA 2 ANNO ACCADEMICO 2012/13 NOTE SULLA CONTINUITÀ UNIFORME D.BARTOLUCCI, D.GUIDO Sia f(x) = x 3, x [ 1, 1]. Si ha 1. La continuità uniforme x 3 y 3 = x
Politecnico di Milano Corso di Analisi e Geometria 1. Federico Lastaria Formule di Taylor Ottobre 2012
 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it Formule di Taylor Ottobre 2012 Indice 1 Formule di Taylor 1 1.1 Il polinomio di Taylor...............................
Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it Formule di Taylor Ottobre 2012 Indice 1 Formule di Taylor 1 1.1 Il polinomio di Taylor...............................
UNIVERSITÀ DEGLI STUDI DI PERUGIA Corso di Analisi Matematica III - 9 CFU C.d.S. Triennale in Matematica A.A. 2016/2017 I Esercitazione 12 Aprile 2017
 C.d.S. Triennale in Matematica A.A. 2016/2017 I Esercitazione 12 Aprile 2017 Esercizio 1. Data la successione di funzioni f n t = en1+t4 + e nt2 n 3 + e, t R, n1+t2 a determinare l insieme di convergenza
C.d.S. Triennale in Matematica A.A. 2016/2017 I Esercitazione 12 Aprile 2017 Esercizio 1. Data la successione di funzioni f n t = en1+t4 + e nt2 n 3 + e, t R, n1+t2 a determinare l insieme di convergenza
Esempi di domande tipo per l esame di Metodi Matematici per l Ingegneria A.A. 2014/2015 (prima parte)
 Esempi di domande tipo per l esame di Metodi Matematici per l Ingegneria A.A. 214/215 (prima parte) April 15, 215 1 Domande aperte 1.1 Modelli di erenziali 1. Dedurre, dalla legge di Coulomb dell elettrostatica,
Esempi di domande tipo per l esame di Metodi Matematici per l Ingegneria A.A. 214/215 (prima parte) April 15, 215 1 Domande aperte 1.1 Modelli di erenziali 1. Dedurre, dalla legge di Coulomb dell elettrostatica,
Corso di Elementi di Analisi Funzionale e Trasformate A.A. 2016/2017 Domande-tipo di teoria sulla prima metà del corso
 Corso di Elementi di Analisi Funzionale e Trasformate A.A. 2016/2017 Domande-tipo di teoria sulla prima metà del corso Marco Bramanti Politecnico di Milano April 20, 2017 Cap. 1. Elementi di analisi funzionale
Corso di Elementi di Analisi Funzionale e Trasformate A.A. 2016/2017 Domande-tipo di teoria sulla prima metà del corso Marco Bramanti Politecnico di Milano April 20, 2017 Cap. 1. Elementi di analisi funzionale
MODELLI e METODI MATEMATICI della FISICA. Programma dettagliato del corso - A.A
 MODELLI e METODI MATEMATICI della FISICA Programma dettagliato del corso - A.A. 2018-19 Lezione 1, 25 febbraio 2019: Organizzazione del corso. Introduzione ai numeri complessi. Rappresentazione cartesiana
MODELLI e METODI MATEMATICI della FISICA Programma dettagliato del corso - A.A. 2018-19 Lezione 1, 25 febbraio 2019: Organizzazione del corso. Introduzione ai numeri complessi. Rappresentazione cartesiana
ESERCIZI DI ANALISI FUNZIONALE. T(f) = g(x)f(x)dx
 ESERCIZI DI ANALISI FUNZIONALE.. Esercizi svolti.. Operatori lineari Esercizio.. Si consideri il funzionale T : C(,) R, dove g è la funzione g(x) = T(f) = g(x)f(x) dx, { se < x se < x < () Dimostrare che
ESERCIZI DI ANALISI FUNZIONALE.. Esercizi svolti.. Operatori lineari Esercizio.. Si consideri il funzionale T : C(,) R, dove g è la funzione g(x) = T(f) = g(x)f(x) dx, { se < x se < x < () Dimostrare che
e n (x) = e(x) n = e iωnx e, naturalmente,
 8.. Analisi armonica nel discreto e in un intervallo infinito. L analisi di Fourier che abbiamo visto finora può essere trasformata in due direzioni opposte: ristretta verso il discreto, cioè rivolta alle
8.. Analisi armonica nel discreto e in un intervallo infinito. L analisi di Fourier che abbiamo visto finora può essere trasformata in due direzioni opposte: ristretta verso il discreto, cioè rivolta alle
Si dimostri che la (*) possiede un unica soluzione (u n ) limitata.
 Scuola Normale Superiore, ammissione al IV anno del corso ordinario Prova scritta di Analisi Matematica per Fisica, Informatica, Matematica 26 Agosto 2 Esercizio. Siano (a n ) e (b n ) successioni di numeri
Scuola Normale Superiore, ammissione al IV anno del corso ordinario Prova scritta di Analisi Matematica per Fisica, Informatica, Matematica 26 Agosto 2 Esercizio. Siano (a n ) e (b n ) successioni di numeri
Quesiti di Analisi Matematica II
 Quesiti di Analisi Matematica II Presentiamo una raccolta di quesiti per la preparazione alla prova orale del modulo di Analisi Matematica II. Per una buona preparazione è consigliabile allenarsi a rispondere
Quesiti di Analisi Matematica II Presentiamo una raccolta di quesiti per la preparazione alla prova orale del modulo di Analisi Matematica II. Per una buona preparazione è consigliabile allenarsi a rispondere
Laurea triennale in Informatica - Corso B (M-Z) Prova scritta di Analisi Matematica Teoria
 13 giugno 2016 1. In base alla teoria studiata e giustificando la risposta, determinare (a) se la funzione f(x) = cos x è pari, dispari o nessuna delle due cose; x 5 (b) se la funzione g(x) = 2 x + x 3
13 giugno 2016 1. In base alla teoria studiata e giustificando la risposta, determinare (a) se la funzione f(x) = cos x è pari, dispari o nessuna delle due cose; x 5 (b) se la funzione g(x) = 2 x + x 3
Spazi di Hilbert: Proiezioni e Serie di Fourier
 Spazi di Hilbert: Proiezioni e Serie di Fourier Docente:Alessandra Cutrì Spazi di Hilbert Uno spazio vettoriale dotato di prodotto scalare che è completo rispetto alla norma indotta dal prodotto scalare
Spazi di Hilbert: Proiezioni e Serie di Fourier Docente:Alessandra Cutrì Spazi di Hilbert Uno spazio vettoriale dotato di prodotto scalare che è completo rispetto alla norma indotta dal prodotto scalare
Elementi di analisi matematica e complementi di calcolo delle probabilita T
 Elementi di analisi matematica e complementi di calcolo delle probabilita T Presentiamo una raccolta di quesiti per la preparazione alla prova orale di Elementi di analisi matematica e complementi di calcolo
Elementi di analisi matematica e complementi di calcolo delle probabilita T Presentiamo una raccolta di quesiti per la preparazione alla prova orale di Elementi di analisi matematica e complementi di calcolo
COMPLEMENTI DI ANALISI MATEMATICA II. Prova scritta del 20 gennaio 2014
 Prova scritta del 2 gennaio 214 Studiare la convergenza puntuale e uniforme della serie di potenze n=1 n x 2n 2n + e n. Valutare poi la misurabilità e l integrabilità secondo Lebesgue della funzione somma
Prova scritta del 2 gennaio 214 Studiare la convergenza puntuale e uniforme della serie di potenze n=1 n x 2n 2n + e n. Valutare poi la misurabilità e l integrabilità secondo Lebesgue della funzione somma
D Analisi Matematica 1 (Corso di Laurea in Informatica e Bioinformatica)
 COGNOME NOME Matr. D Firma dello studente Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
COGNOME NOME Matr. D Firma dello studente Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
Funzioni Test, Distribuzioni e Applicazioni
 Capitolo 1 Funzioni Test, Distribuzioni e Applicazioni In questo capitolo discuteremo le distribuzioni, le funzioni test e loro applicazioni principali. Il motivo principale per introdurre le distribuzioni
Capitolo 1 Funzioni Test, Distribuzioni e Applicazioni In questo capitolo discuteremo le distribuzioni, le funzioni test e loro applicazioni principali. Il motivo principale per introdurre le distribuzioni
ANALISI MATEMATICA I, Compito scritto del 5/07/2016 Corso di Laurea in Matematica. COGNOME e NOME... MATR T
 ANALISI MATEMATICA I, Compito scritto del 5/7/6 Corso di Laurea in Matematica COGNOME e NOME... MATR... 3 4 T Nelle risposte devono essere riportati anche i conti principali e le motivazioni principali.
ANALISI MATEMATICA I, Compito scritto del 5/7/6 Corso di Laurea in Matematica COGNOME e NOME... MATR... 3 4 T Nelle risposte devono essere riportati anche i conti principali e le motivazioni principali.
Correzione del secondo compitino di Analisi 1 e 2 A.A. 2014/2015
 Correzione del secondo compitino di Analisi e 2 AA 20/205 Luca Ghidelli, Giovanni Paolini, Leonardo Tolomeo febbraio 206 Esercizio Testo Dire per quali valori del parametro reale α, < α 3, la funzione
Correzione del secondo compitino di Analisi e 2 AA 20/205 Luca Ghidelli, Giovanni Paolini, Leonardo Tolomeo febbraio 206 Esercizio Testo Dire per quali valori del parametro reale α, < α 3, la funzione
3. Successioni di insiemi.
 3. Successioni di insiemi. Per evitare incongruenze supponiamo, in questo capitolo, che tutti gli insiemi considerati siano sottoinsiemi di un dato insieme S (l insieme ambiente ). Quando occorrerà considerare
3. Successioni di insiemi. Per evitare incongruenze supponiamo, in questo capitolo, che tutti gli insiemi considerati siano sottoinsiemi di un dato insieme S (l insieme ambiente ). Quando occorrerà considerare
LA TRASFORMATA DI FOURIER
 LA TASFOMATA DI FOUIE 1. Definizione della trasformata di Fourier Definizione 1.1. Sia u in L 1 ( e sia ξ in. La trasformata di Fourier di u è la funzione (1.1 F(u(ξ = e iξ x u(x dx. Ovviamente, non è
LA TASFOMATA DI FOUIE 1. Definizione della trasformata di Fourier Definizione 1.1. Sia u in L 1 ( e sia ξ in. La trasformata di Fourier di u è la funzione (1.1 F(u(ξ = e iξ x u(x dx. Ovviamente, non è
Successioni e serie di funzioni / Esercizi proposti
 M.Guida, S.Rolando, 24 Successioni e serie di funzioni / Esercizi proposti L asterisco contrassegna le richieste più difficili.. Sia f n (x) = x2 n 2 + x 4, n. a) Determinare l insieme di convergenza puntuale
M.Guida, S.Rolando, 24 Successioni e serie di funzioni / Esercizi proposti L asterisco contrassegna le richieste più difficili.. Sia f n (x) = x2 n 2 + x 4, n. a) Determinare l insieme di convergenza puntuale
Corso di Laurea in Ingegneria per l Ambiente e il Territorio - sede distaccata di Latina Corso di Analisi Matematica (1 modulo) - a.a.
 Corso di Laurea in Ingegneria per l Ambiente e il Territorio - sede distaccata di Latina Corso di Analisi Matematica ( modulo) - a.a. 00/04 APPUNTI INTEGRATIVI SUI CRITERI DI CONVERGENZA PER LE SERIE Serie
Corso di Laurea in Ingegneria per l Ambiente e il Territorio - sede distaccata di Latina Corso di Analisi Matematica ( modulo) - a.a. 00/04 APPUNTI INTEGRATIVI SUI CRITERI DI CONVERGENZA PER LE SERIE Serie
Corso di Analisi Numerica - AN410. Parte 5: formule di quadratura. Roberto Ferretti
 Corso di Analisi Numerica - AN410 Parte 5: formule di quadratura Roberto Ferretti UNIVERSITÀ DEGLI STUDI ROMA TRE Formule di quadratura interpolatorie: teoria generale Formule di Newton Cotes semplici
Corso di Analisi Numerica - AN410 Parte 5: formule di quadratura Roberto Ferretti UNIVERSITÀ DEGLI STUDI ROMA TRE Formule di quadratura interpolatorie: teoria generale Formule di Newton Cotes semplici
Gli argomenti denotati con un asterisco tra parentesi (e solo quelli) sono stati dimostrati.
 Corso di laurea: Fisica ed Astronomia Programma di Analisi Matematica 2 a.a. 2016/17 Docente: Fabio Paronetto Gli argomenti denotati con un asterisco tra parentesi (e solo quelli) sono stati dimostrati.
Corso di laurea: Fisica ed Astronomia Programma di Analisi Matematica 2 a.a. 2016/17 Docente: Fabio Paronetto Gli argomenti denotati con un asterisco tra parentesi (e solo quelli) sono stati dimostrati.
COMPLETAMENTO DI SPAZI METRICI
 COMPLETAMENTO DI SPAZI METRICI 1. Successioni di Cauchy e spazi metrici completi Definizione 1.1. Una successione x n n N a valori in uno spazio metrico X, d si dice di Cauchy se, per ogni ε > 0 esiste
COMPLETAMENTO DI SPAZI METRICI 1. Successioni di Cauchy e spazi metrici completi Definizione 1.1. Una successione x n n N a valori in uno spazio metrico X, d si dice di Cauchy se, per ogni ε > 0 esiste
Appendice B ANALISI FUNZIONALE. 1 Spazi di Banach
 Appendice B ANALISI FUNZIONALE In questo capitolo si introducono gli spazi di Banach e di Hilbert, gli operatori lineari e loro spettro. Inoltre si discutono gli operatori compatti su uno spazio di Hilbert.
Appendice B ANALISI FUNZIONALE In questo capitolo si introducono gli spazi di Banach e di Hilbert, gli operatori lineari e loro spettro. Inoltre si discutono gli operatori compatti su uno spazio di Hilbert.
A.A. 2015/16 REGISTRO ELETTRONICO DELLE LEZIONI
 A.A. 2015/16 ISTITUZIONI DI ANALISI SUPERIORE 12 crediti, I semestre Docenti: Prof. Gennaro Infante per i primi 6 crediti ed io per i rimanenti 6 crediti. REGISTRO ELETTRONICO DELLE LEZIONI IMPORTANTE:
A.A. 2015/16 ISTITUZIONI DI ANALISI SUPERIORE 12 crediti, I semestre Docenti: Prof. Gennaro Infante per i primi 6 crediti ed io per i rimanenti 6 crediti. REGISTRO ELETTRONICO DELLE LEZIONI IMPORTANTE:
PROVE SCRITTE DI ANALISI MATEMATICA I, ANNO 2009/10
 PROVE SCRITTE DI ANALISI MATEMATICA I, ANNO 9/1 Prova scritta del 13/1/1 Si determini l ordine di infinitesimo della successione a n = arctan(n + ) arctan n. Denotato poi con B il numero delle lettere
PROVE SCRITTE DI ANALISI MATEMATICA I, ANNO 9/1 Prova scritta del 13/1/1 Si determini l ordine di infinitesimo della successione a n = arctan(n + ) arctan n. Denotato poi con B il numero delle lettere
ANALISI 1 1 SEDICESIMA - DICIASETTESIMA LEZIONE Serie
 ANALISI 1 1 SEDICESIMA - DICIASETTESIMA LEZIONE Serie 1 prof. Claudio Saccon, Dipartimento di Matematica Applicata, Via F. Buonarroti 1/C email: saccon@mail.dm.unipi.it web: http://www2.ing.unipi.it/ d6081/index.html
ANALISI 1 1 SEDICESIMA - DICIASETTESIMA LEZIONE Serie 1 prof. Claudio Saccon, Dipartimento di Matematica Applicata, Via F. Buonarroti 1/C email: saccon@mail.dm.unipi.it web: http://www2.ing.unipi.it/ d6081/index.html
ANALISI MATEMATICA 4. Prova scritta del 24 gennaio 2013
 Prova scritta del 24 gennaio 2013 Esercizio 1. Sia Ω R 3 un insieme misurabile secondo Lebesgue e di misura finita. Sia {f n } n N una successione di funzioni f n : Ω R misurabili e tali che 1) f n (x)
Prova scritta del 24 gennaio 2013 Esercizio 1. Sia Ω R 3 un insieme misurabile secondo Lebesgue e di misura finita. Sia {f n } n N una successione di funzioni f n : Ω R misurabili e tali che 1) f n (x)
ANALISI MATEMATICA 1. (Ingegneria Industriale, corsi A e B) Esempi di prove scritte
 ANALISI MATEMATICA 1 (Ingegneria Industriale, corsi A e B) Esempi di prove scritte Rispondere ai quesiti a risposta multipla Qi, risolvere gli esercizi Ei, enunciare le definizioni Di e svolgere le dimostrazioni
ANALISI MATEMATICA 1 (Ingegneria Industriale, corsi A e B) Esempi di prove scritte Rispondere ai quesiti a risposta multipla Qi, risolvere gli esercizi Ei, enunciare le definizioni Di e svolgere le dimostrazioni
Elementi di analisi matematica e complementi di calcolo delle probabilita T
 Elementi di analisi matematica e complementi di calcolo delle probabilita T Presentiamo una raccolta di quesiti per la preparazione alla prova orale di Elementi di analisi matematica e complementi di calcolo
Elementi di analisi matematica e complementi di calcolo delle probabilita T Presentiamo una raccolta di quesiti per la preparazione alla prova orale di Elementi di analisi matematica e complementi di calcolo
Esercizi 8 12 gennaio 2009
 Sia α > e Esercizi 8 2 gennaio 29 f(x, y = ( + x 2 + y 2 α. Dimostrare che f appartiene a L p ( 2, con α p >. Osserviamo innanzitutto che, essendo f continua, l integrale di f p su 2 è uguale all integrale
Sia α > e Esercizi 8 2 gennaio 29 f(x, y = ( + x 2 + y 2 α. Dimostrare che f appartiene a L p ( 2, con α p >. Osserviamo innanzitutto che, essendo f continua, l integrale di f p su 2 è uguale all integrale
Serie a termini di segno non costante
 Serie a termini di segno non costante Definizione (Convergenza semplice e assoluta) Se una serie converge, cioè la sua somma esiste ed è finita, si dice anche che la serie converge semplicemente: an =
Serie a termini di segno non costante Definizione (Convergenza semplice e assoluta) Se una serie converge, cioè la sua somma esiste ed è finita, si dice anche che la serie converge semplicemente: an =
Analisi Matematica I per Ingegneria Gestionale, a.a Scritto del sesto appello, 16 luglio 2018 Testi 1
 Scritto del sesto appello, 6 luglio 208 Testi Prima parte, gruppo.. Trovare α [0, 2π) per cui vale l identità trigonometrica sin(x π/3) = cos(x + α). 2. Trovare il polinomio di Taylor (in 0) di ordine
Scritto del sesto appello, 6 luglio 208 Testi Prima parte, gruppo.. Trovare α [0, 2π) per cui vale l identità trigonometrica sin(x π/3) = cos(x + α). 2. Trovare il polinomio di Taylor (in 0) di ordine
Sviluppi e derivate delle funzioni elementari
 Sviluppi e derivate delle funzioni elementari In queste pagine dimostriamo gli sviluppi del prim ordine e le formule di derivazioni delle principali funzioni elementari. Utilizzeremo le uguaglianze lim
Sviluppi e derivate delle funzioni elementari In queste pagine dimostriamo gli sviluppi del prim ordine e le formule di derivazioni delle principali funzioni elementari. Utilizzeremo le uguaglianze lim
è un segnale periodico di periodo T0 1 equazioni di analisi e di sintesi stabiliscono
 PROPRIEA ELEMENARI Se x( t) è un segnale periodico di periodo 0 di classe C 1 -tratti e normalizzato, le equazioni di analisi e di sintesi stabiliscono una corrispondenza fra x( t) e la sequenza dei suoi
PROPRIEA ELEMENARI Se x( t) è un segnale periodico di periodo 0 di classe C 1 -tratti e normalizzato, le equazioni di analisi e di sintesi stabiliscono una corrispondenza fra x( t) e la sequenza dei suoi
Analisi a più variabili: Misura di Peano - Jordan ed Integrale di Riemann
 Analisi a più variabili: Misura di Peano - Jordan ed Integrale di Riemann 1 Definizione (Algebra): T P Ω è un'algebra se: A, B T A B T, Ω T A T A C T Se A i T A i T si dice σ-algebra Definizione (Misura):
Analisi a più variabili: Misura di Peano - Jordan ed Integrale di Riemann 1 Definizione (Algebra): T P Ω è un'algebra se: A, B T A B T, Ω T A T A C T Se A i T A i T si dice σ-algebra Definizione (Misura):
