Università degli Studi di Torino Facoltà di Scienze Matematiche, Fisiche, Naturali Corso di Laurea Specialistica in Matematica ANALISI SUPERIORE
|
|
|
- Camilla Cicci
- 5 anni fa
- Visualizzazioni
Transcript
1 Università degli Studi di Torino Facoltà di Scienze Matematiche, Fisiche, Naturali Corso di Laurea Specialistica in Matematica ANALISI SUPERIORE Prof. Elena Cordero e Luigi Rodino Appunti a cura degli studenti Anno accademico
2
3 Indice 1 Insiemi, funzioni misurabili Preliminari La misura esterna Insiemi misurabili Funzioni misurabili Integrale di Lebesgue Definizioni e proprietà dell integrale Passaggio al limite sotto il segno Gli spazi L p Prime definizioni Proprietà degli spazi L p Completezza degli spazi L p 35 5 L 2 e densità in L p Lo spazio L Densità in L p La convoluzione Operatori di traslazione Operatori di convoluzione La trasformata di Fourier La classe di Schwartz La trasformata di Fourier Il teorema di inversione Convergenza di funzioni in S(R n ) Lo spazio delle distribuzioni temperate S (R n ) Introduzione alle distribuzioni Prime definizioni ed esempi Operatori in S (R n )
4 8.4 La trasformata di Fourier in S (R n ) Convoluzione e trasformata di Fourier La trasfomata di Fourier in L La trasformata di Fourier in L p Esempi ed applicazioni Gli spazi di Sobolev Trasformate di Fourier delle funzioni in H m (R n ) Il teorema di inclusione di Sobolev Operatori Pseudo-differenziali Operatori pseudo-differenziali come operatori di convoluzione Problema di Cauchy per l equazione di Schrödinger Esistenza e unicità della soluzione di equazioni pseudo-differenziali Esempi ed esercizi Cenni sugli operatori pseudo-differenziali a coefficienti non costanti 128 4
5
6 Capitolo 1 Insiemi, funzioni misurabili 1.1 Preliminari Per poter introdurre l integrale di Lebesgue, diamo innanzitutto una motivazione per abbandonare l integrale di Riemann in favore di tale integrale. I motivi principali sono tre: 1) La classe delle funzioni Riemann integrabili R([a, b]), a, b R, non é completa rispetto alla norma f 1 = b f(x) dx. a 2) Allargare la classe delle funzioni integrabili. ESEMPIO: Un esempio di funzione che non è Riemann integrabile ma, come vedremo in seguito, è Lebesgue integrabile, è la cosiddetta funzione di Dirichlet: { 1 se x Q [0, 1] f(x) = χ Q [0,1] (x) = 0 se x Q [0, 1]. Denotiamo con P una partizione dell intervallo [0, 1]: P : x 0 = 0 < x 1 <... < x i < x i+1 <... < x n = 1. Chiamiamo i := [x i, x i+1 ), per i = 0,..., n 2 e n 1 := [x n 1, x n ]. Calcolimo l integrale superiore: S P è data da S P (f) = 1 0 n 1 i=0 f(x)dx. Innanzitutto, la somma superiore sup f(x)(x i+1 x i ). x i Siccome l insieme Q è denso in R, per ogni intervallino i esiste un r i i tale che r i Q, quindi: n 1 S P = (x i+1 x i ) = 1. i=0 1
7 Poiché questo discorso vale per ogni partizione P, si ha 1 Calcoliamo l integrale inferiore: da s P (f) = 0 n 1 i=0 f(x)dx = inf P S P (f) = f(x)dx. La somma inferiore s P è data inf f(x)(x i+1 x i ) = 0 x i quindi 1 f(x)dx = sup 0 P s P (f) = 0. Siccome l integrale superiore e l integrale inferiore sono diversi, f R([0, 1]). P, 3) Vorremmo che l ugualianza b a ( lim n f n (x))dx = lim n b a f n (x)dx (1.1) valesse sotto condizioni più deboli di quelle dell integrale di Riemann. Precisamente, per l integrale di Riemann, una condizione sufficiente per la (1.1) è la seguente: f n C([a, b]) e f n coverge ad f uniformemente su [a, b]. Tale condizione è molto forte e non sempre verificata, come mostra il seguente esempio. ESEMPIO: Sia f n (x) = x n su [0, 1]. Calcoliamo l integrale di Riemann: 1 0 x n dx = xn+1 n = 1 n + 1. La successione x n é puntualmente convergente alla funzione: { 0 se 0 x < 1 f(x) = lim f n (x) = n 1 se x = 1. Poiché f n (x) C([0, 1]), mentre f(x) C([0, 1]), non c è convergenza uniforme. Non essendo soddisfatta la condizione di convergenza uniforme non possiamo applicare (1.1). Osserviamo però che vale l ugualianza: 0 = f(x)dx = lim n n + 1. Vedremo che l integrale di Lebesgue in questo caso consente il passaggio del limite sotto il segno d integrale. 2
8 1.2 La misura esterna Definizione Sia X un insieme e sia P (X) l insieme delle parti di X. m P (X) è una σ-algebra se: 1) X m, 2) m è chiusa rispetto all operazione di complemantazione: A m CA m, 3) m è chiusa rispetto ad unioni numerabili: A i m, i N i=1a i m. La coppia (X, m) prende il nome di spazio misurabile e gli elementi di m si dicono insiemi misurabili. Ricordiamo anche la definizione di spazio topologico. Definizione Sia X un insieme e sia P (X) l insieme delle parti di X. Una famiglia τ P (X) è una topologia se: 1) X, φ τ, 2) Se A 1,.., A n τ, allora A 1.. A n τ, 3) Se {A} α A τ, allora α A A α τ. (Osserviamo che l unione potrebbe essere non numerabile). La coppia (X, τ) prende il nome di spazio topologico. Su di uno spazio misurabile (X, m), si può definire una misura µ nel modo seguente: Definizione Sia (X, m) un insieme misurabile. La funzione µ : m [0, + ] è una misura se verifica: 1) µ( ) = 0 2) Se {E i } i=1 è una successione di insiemi misurabili a 2 a 2 disgiunti, ovvero E i E j =, se i j, allora m( i=1e i ) = m(e i ). (1.2) i=1 La proprietà (1.2) è detta σ-additività della misura m. Il nostro prossimo obiettivo sarà la definizione di una misura sullo spazio R n. 3
9 Innannzitutto, fissiamo le seguenti notazioni. Sia E R n, insieme elementare, indichiamo la misura euclidea di E con E. Siano x, y R n, x = (x 1,.., x n ) e y = (y 1,.., y n ); definiamo d(x, y) = x y = n (x i y i ) 2. Vediamo ora di calcolare la misura euclidea degli insiemi elementari. Se n = 1 gli insiemi elementari sono intervalli. Se l insieme E è del tipo in tutti i casi i=1 E = [a, b], [a, b), (a, b], (a, b), E = b a, ovvero gli estremi dell insieme E non influiscono sulla misura elementare. In dimensione n = 2 gli insiemi elementari sono rettangoli, quadrati e cerchi. Studiamo i rettangoli. Se R = [a, b] [c, d], la misura euclidea di R coincide con l area di R quindi R = (b a)(d c). Tale misura si estende anche al caso n > 2, dove il rettangolo R R n è dato da R = [a 1, b 1 ].. [a n, b n ], e risulta R = Π n i=1(b i a i ). Ricordiamo che un punto x E si dice interno ad E se esiste r > 0 tale che la palla di centro x e raggio r, B r (x), è inclusa in E. Indichiamo l interno di E, ovvero l insieme dei punti interni di E, con E. La misura euclidea gode della proprietà di additività: se R = N i=1r i e Ri Rj= φ per ogni i j, allora R = N i=1 R i. Ci proponiamo ora di definire un applicazione µ, che chiameremo misura esterna, tale che: 1) Sia definita su ogni insieme E R n ; 2) Se R è il rettangolo in R n, µ (R) = R. Definizione si dice misura esterna di E R n : { } µ (E) = inf R i, E i=1r i i=1 dove R i sono rettangoli chiusi. 4
10 Proprietà La funzione µ è monotona: A B = µ (A) µ (B). (1.3) Dimostrazione. Se A B, ogni ricoprimento di B è anche ricoprimento di A. Proprietà Se R è un rettangolo chiuso, µ (R) = R. Dimostrazione. Si ha µ (R) R, perchè R è un ricoprimento rettangolare di se stesso e la disugualianza è giustificata dal significato di estremo inferiore nella definizione di µ. Resta da dimostrare che R µ (R). Consideriamo un arbitrario ricoprimento R j con j = 1,..,, risulta R j=1 R j e vogliamo provare che R j=1 R j. Sia ɛ > 0, per ogni Rj consideriamo il rettangolo aperto S j tale che S j = (1 + ɛ) R j. R j=1 R j j=1s j. Ma R è un compatto e S j è un suo ricoprimento aperto, possiamo quindi estrarre un suo sottoricoprimento finito: S j, con i = 1..N. Essendo R N j=1s j, risulta R N S j = j=1 N (1 + ɛ) R j j=1 (1 + ɛ) R j = (1 + ɛ) R j. j=1 j=1 Facendo tendere ɛ 0, si ottiene R j=1 R j. Per l arbitrarietà del ricoprimento R j, segue R µ (R). In conclusione risulta µ (R) = R. Corollario µ (x) = 0, per ogni x R n. Dimostrazione. Il punto x è un rettangolo degenere di R n, quindi il risultato segue dalla proprietà precedente. ESERCIZIO: Dimostrare che µ (R) = R per ogni rettangolo R. Soluzione. Sia R la chiusura di R, allora R R e, per la monotonia della funzione µ, si ha µ (R) µ ( R) = R = R. Proviamo il viceversa. Per ogni ɛ > 0, è possibile trovare un rettangolo chiuso R ɛ R tale che R R ɛ + ɛ. Preso un ricoprimento {R j } di R, {R j } è anche un ricoprimento di R ɛ e si ha R R ɛ + ɛ = µ (R ɛ ) + ɛ R j + ɛ. j=1 Passando al limite per ɛ 0, si ottiene R j=1 R j, da cui R µ (R) e quindi µ (R) = R. 5
11 ESERCIZIO: Si definisce contenuto esterno di Jordan di E R: { N } J (E) = inf I j, E N j=1i j, I j intervallo chiuso j=1 i) Dimostrare che J (E) = J (Ē); ii) Trovare un insieme E numerabile contenuto in [0, 1] tale che J (E) = 1 e µ (E) = 0. Soluzione. i) Dimostriamo che J (E) = J (Ē), ovvero che il contenuto esterno di Jordan di un insieme coincide col contenuto esterno di Jordan della chiusura dell insieme. Sia E R, Ē la sua chiusura quindi E Ē. Per ogni ricoprimento {I j } di Ē, {I j} è anche ricoprimento di E quindi J (E) J (Ē). Viceversa, per ogni ricoprimento {I j } di E deve essere E N j=1i j quindi, passando alla chiusura, Ē N j=1 I j = N j=1i j perchè gli I j sono chiusi e l unione è finita. Segue che J (Ē) J (E). Unendo i due risultati, J (E) = J (Ē). ii) Scegliamo l insieme: E = Q [0, 1], ovvero E = n,m { m} con n 0 e n m n. Risulta µ (E) { } m n,m = 0 perchè la misura esterna di un punto è n nulla, quindi µ (E) = 0. Usiamo ora il punto (i). Poichè Q è un sottoinsieme denso di R, risulta Ē = [0, 1] quindi J (E) = J (Ē) = 1. Proposizione La funzione µ è σ-subadditiva: E = i=ie i = µ (E) µ (E i ). i=1 Dimostrazione. Consideriamo l insieme E = i=1e i. Per ogni E i deve valere l ugualianza: { µ (E i ) = inf R i,k, E i k=1r i,k }. Per ogni ɛ > 0, deve esistere un ricoprimento {R i,k } k di E i tale che R i,k µ (E i ) + ɛ 2. i k=1 k=1 6
12 Quindi, Allora, µ (E) i=1 R i,j i=1 i=1 E = i=1e i i,k=1r i,k. Facendo tendere ɛ 0, si ottiene la tesi. (µ (E i )+ ɛ 2 ) = µ 1 (E i i )+ɛ 2 = µ (E i i )+ɛ. Proprietà Se E = E 1 E 2, con d(e 1, E 2 ) > 0, allora Dimostrazione. Ricordiamo che i=1 µ (E) = µ (E 1 ) + µ (E 2 ). d(e 1, E 2 ) = inf x 1 x 2, x 1 E 1,x 2 E 2 con x = x x 2 n. Per la subaddività di µ, si ha µ (E) µ (E 1 ) + µ (E 2 ). Proviamo la disuguaglianza opposta. Sia δ > 0, tale che d(e 1, E 2 ) > δ. Per ogni ɛ > 0, esiste un ricoprimento {R} i di E tale che R i µ (E) + ɛ. i=1 Possiamo supporre, eventualmente suddividendo ulteriormente i rettangoli, che diam(r i ) = sup x,y R1 x y < δ. Quindi, ogni R i interseca al più uno dei due insiemi E 1, E 2. Se indichiamo con J 1 (rispettivamente J 2 ) l insieme degli indici per cui R i interseca E 1 (risp. E 2 ), abbiamo Quindi E 1 = i J1 R i, E 2 = i J2 R i. µ (E 1 ) + µ (E 2 ) i J 1 R i + i J 2 R i Facendo tendere ɛ 0, si ottiene la tesi. R i i=1 µ (E) + ɛ La misura µ gode di proprietà di additività non solo nel caso precedente, ma anche quando gli insiemi in questione hanno una struttura particolare, come mostra il seguente risultato (per la dimostrazione, si rimanda a [2]). 7 i=1 i=1
13 Proprietà Se E = i=1r i, e R i R j =, se i j, allora µ (E) = E i. i=1 Tuttavia, in generale, µ non è additiva. Vediamo quindi di restringere µ ad una classe di sottoinsiemi di R n che la renda additiva. 1.3 Insiemi misurabili Definizione Sia (X, τ) uno spazio topologico, si chiama σ-algebra dei boreliani B la più piccola σ-algebra che contiene la topologia τ. Definizione Sia (X, τ) spazio topologico, se A i τ, i N, l insieme G σ è definito da G σ = A i, (1.4) mentre, presa {F i } i=1 famiglia di chiusi, definiamo F σ l insieme F σ = i=1 F i. (1.5) i=1 Consideriamo ora X = R n e costruiamo la σ-algebra di insiemi misurabili. il suo comple- Definizione Dato l insieme A R n, e indicato con A C mentare in R n, A si dice misurabile se per ogni E R n si ha µ (E) = µ (E A) + µ (E A C ). (1.6) Si presti attenzione al fatto che l equazione precedente non è verificata da ogni insieme. Introduciamo ora un criterio di misurabilità per gli insiemi. Proposizione L insieme A R n è misurabile se e solo se per ogni ɛ > 0 esiste un aperto O ɛ tale che A O ɛ e µ (O ɛ A) < ɛ. Se A è misurabile, la misura di Lebesgue µ di A si definisce come µ(a) = µ (A). (1.7) Esempio )Tutti gli aperti di R n sono misurabili, in particolare i rettangoli aperti. 2)Tutti i complementari di insiemi misurabili sono misurabili, come si vede dalla (1.6). In particolare, i chiusi sono misurabili. 8
14 Vediamo ora alcune proprietà della misura di Lebesgue. Teorema (Teorema di Caratheodory). 1) La famiglia L di insiemi misurabili è una σ-algebra. 2) La misura di Lebesgue µ è una misura σ-additiva su L. Corollario La misura di Lebesgue L è un estensione della misura elementare (euclidea). Proposizione I compatti sono misurabili ed hanno misura finita. Dimostrazione. Ricordiamo che un insieme K di R n è un compatto se e solo se è limitato e chiuso. Se K è chiuso, abbiamo visto che K è misurabile. Inoltre, in quanto compatto, esiste un quadrato n-dimensionale Q N che lo contiene, ovvero K Q N = [ N, N] [ N, N] [ N, N]. (1.8) Poiché la misura elementare di Q N è Q N = µ(q N ) = (2N) n < +, per la monotonia della misura di Lebesgue possiamo concludere che e perciò K ha misura finita. µ(k) µ(q N ) < +. (1.9) Proposizione Si ha µ(r n ) = +. Dimostrazione. R n è aperto, quindi R n misurabile. Inoltre, N N Q N R n, perciò, per la monotonia di µ, risulta Passando al limite per N +, si ottiene µ(r n ) = +. (2N) n = µ(q N ) µ(r n ). (1.10) Esempio Si può verificare che ogni semiretta [a, + ), a R, ha misura infinita. Basta mostrare che contiene tutti i chiusi del tipo [a + ɛ, N], con ɛ > 0, N N, e passando al limite per N +. Enunciamo alcune importanti proprietà della misura µ, per la dimostrazione, si veda ad esempio [2]. Proposizione (Unicità di µ). Se λ è una misura σ-additiva su L e tale che λ(r) = R, allora λ = µ. 9
15 Proposizione (σ-finitezza di µ). È possibile ricoprire R n con insiemi di misura finita (µ è σ-finita). In particolare, con Q N quadrati n-dimensionali. R n = N=1 Q N, (1.11) Proposizione (Regolarità di µ). Per ogni E L, si ha: µ(e) = inf{µ(o), O aperto e E O} (1.12) = sup{µ(k), K compatto, con K E}. (1.13) Proposizione (Invarianza di µ per traslazioni). Per ogni E L, l insieme E + h = {x + h, x E} è misurabile e risulta: µ(e + h) = µ(e). (1.14) Proposizione Sia E 1 E 2... E n... una catena ascendente infinita di sottoinsiemi appartenenti ad L. Allora: µ( i=1 E i ) = lim i + µ(e i). (1.15) Proposizione Sia E 1 E 2... E n... una catena discendente infinita di sottoinsiemi appartenenti ad L. Se esiste un k N tale che µ(e k ) < +, allora: µ( i=1 E i ) = lim i + µ(e i). (1.16) Esempio La proprietà precendente non vale con gli insiemi E n = [n, + ), perchè hanno misura infinita per ognin N. Osserviamo invece che n=1e n = e µ( ) = Funzioni misurabili Definizione Una funzione f : E R n R(C) si dice misurabile se: σ aperto di R, f 1 (σ) è misurabile. (1.17) Proposizione Se la funzione f è continua, f è anche misurabile. Dimostrazione. Una funzione f è continua se le controimmagini di suoi aperti sono ancora aperti, e tali controimmagini sono anche misurabili, perchè aperti, perciò, per la (1.17), f è misurabile. 10
16 Teorema (Criterio di misurabilità). Data f : E R n R, le seguenti condizioni sono equivalenti: 1. f misurabile. 2. f 1 ((a, + )) = {x E, f(x) > a} è misurabile, a R. 3. f 1 ([a, + )) è misurabile, a R. 4. f 1 ([, a)) è misurabile, a R. 5. f 1 ([, a]) è misurabile, a R. A partire da funzioni misurabili, possiamo ricavare altre funzioni misurabili, attraverso operazioni quali la combinazione lineare, il passaggio al limite, e così via. Vediamo allora alcune proprietà. Proposizione Sia {f n } una successione di funzioni misurabili. Allora le funzioni: sup f n, inf f n, lim sup f n, lim inf f n (1.18) n n n n sono misurabili. Proposizione Siano f, g funzioni misurabili. Allora, λ, µ C le funzioni: f λf + µg, f g, (con g 0), (1.19) g sono misurabili. Passiamo ora a definire le funzioni semplici. Definizione Sia E R n, E = j=1e j, con E j E k =, se j k. Si dice funzione semplice la funzione s : E C, s = N α j χ Ej, (1.20) j=1 dove α j C e χ Ej = { 1 se x Ej 0 se x E E j (1.21) Proposizione Le funzioni semplici sono misurabili. Dimostrazione. Sia E R n un insieme misurabile, dimostriamo dapprima che χ E : R n R è misurabile. Usiamo il criterio di misurabilità (Teorema 1.4.3): proviamo che, a R, χ 1 E {(a, + )} è misurabile. Distinguiamo i tre casi: Se a 1 allora χ 1 E (a, + ) =, che è misurabile. 11
17 Se 0 a < 1, χ 1 E (a, + ) = E, misurabile per ipotesi. Se a < 0, χ 1 E (a, + ) = R, che è misurabile. Poichè la funzione s è combinazione lineare di funzioni misurabili, per la Proposizione è misurabile. Riprendendo un esempio citato nella prima sezione del testo, è importante rilevare che attraverso l uso di funzioni semplici possiamo misurare insiemi che l integrale di Riemann non riesce a misurare, come nel caso della funzione di Dirichlet. Esempio Sia f = χ Q [0,1], la funzione di Dirichlet, definita da { 1 se x Q [0, 1] χ Q [0,1] = 0 se x / Q [0, 1] Osserviamo che Q [0, 1] = Calcoliamo la misura di Q [0, 1]: µ(q [0, 1]) = µ m,n N n>0 m n per la σ-additività della misura µ. nulla. m,n N n>0 m n { m } n = m,n { m n }. (1.22) ({ m }) µ = 0, (1.23) n Pertanto χ Q [0,1] è misurabile e ha misura Proposizione Sia f misurabile e non negativa (f 0). Allora esiste una successione monotona non decrescente {s m } m N di funzioni semplici non negative che converge puntualmente ad f: lim s m(x) = f(x). (1.24) m + Dimostrazione. Fissiamo m > 0 sull asse delle ordinate, e suddividiamo l intervallo [0, m] in una partizione di sottoinsiemi della forma m,k = ( ] k, k+1 2 m 2, con m k = 1,..., m2 m 1 e m,0 = [0, 1 ]. m Definiamo gli insiemi F m = f 1 ((m, + )) e E m,k = f 1 ( m,k ). F m è misurabile per il Teorema Inoltre, ( ( k ) ( E m,k = f 1 ( m,k ) = f 1 2, +, k + 1 ]) (1.25) m 2 m ( ( k )) ( ( = f 1, + f 1, k + 1 ]) 2m 2 m 12 (1.26)
18 ovvero E m,k è l intersezione di due insiemi misurabili (Teorema 1.4.3) ed è quindi misurabile. Introduciamo quindi la funzione semplice s m = mχ Fm + 2 m m 1 k=0 k 2 m χ E m,k. (1.27) Per costruzione, s m s m+1 ; dimostriamo che lim m + s m (x) = f(x). Fissato x E, prendiamo m N tale che f(x) < m. Allora k x E m,k e, per costruzione della s m, 0 f(x) s m (x) 1 2, m (1.28) Passando al limite per m +, si ha quindi lim f(x) s m(x) = 0. (1.29) m + Corollario Se f è una funzione misurabile definita su di un insieme E misurabile, inoltre f è non negativa e limitata, ovvero esiste M > 0 tale che 0 f M, allora s m f uniformemente. Dimostrazione. Prendiamo m > M, allora f(x) s m (x) 1 2 m, x E. Quindi: che, per m +, tende a 0. sup f(x) s m (x) 1 (1.30) x E 2 m Proposizione Sia f : E R misurabile, allora esiste una successione {s m } m N di funzioni semplici tali che lim m + s m (x) = f(x) (limite puntuale) e Dimostrazione. Definiamo la parte positiva di f: misurabile per la (1.18), e la parte negativa di f: s m s m+1 f. (1.31) f + = max{f(x), 0}, (1.32) f = max{ f(x), 0}, (1.33) anch essa misurabile per la (1.18). Si ha f = f + f. Per la Proposizione 1.4.9, esistono due successioni di funzioni semplici s (1) m e s (2) m, tali che: s (1) m f + e s (2) m f, (1.34) 13
19 puntualmente. Introduciamo la funzione semplice differenza s m := s (1) m s (2) m, allora, per costruzione, la successione s m converge ad f puntualmente. Si ha s m = s (1) m + s (2) m s (1) m+1 + s (2) m+1 = s m+1, (1.35) cioè s m è monotona nondecrescente, e che completa la dimostrazione. s m+1 = s (1) m+1 + s (2) m+1 f + + f = f, (1.36) 14
20 Capitolo 2 Integrale di Lebesgue La teoria classica dell integrazione (dovuta fra gli altri a Cauchy e Riemann), pur fornendo uno strumento analitico molto potente, si rivela insufficiente sotto vari punti di vista, soprattutto per quanto riguarda le condizioni di passaggio al limite sotto il segno di integrale. In ambito matematico si è quindi avvertita la necessità di introdurre uno strumento più forte e maneggevole. Il passo fondamentale in questo senso è stato fatto da Lebesgue che, a partire dai primissimi anni del 1900, ha introdotto una nuova nozione di integrale. La teoria dell integrale di Lebesgue ha conosciuto uno sviluppo velocissimo con il contributo di vari studiosi che, in breve tempo, hanno realizzato uno strumento versatile, il quale ha permesso di aprire nuove frontiere nella ricerca matematica. Inoltre, la nozione di integrale di Lebesgue si estende ad una classe di funzioni più grande della classe di Riemann. L esempio classico, in questo senso è rappresentato dalla funzione di Dirichlet χ [0,1] Q : { 1 se x Q χ [0,1] Q (x) = 0 se x / Q che non è Riemann integrabile, ma, come vedremo in seguito, è Lebesgue integrabile. 2.1 Definizioni e proprietà dell integrale Definizione Sia s una funzione semplice e non negativa, ovvero s = N α k χ Ek k=1 dove: 1. α k 0 15
21 2. E k insiemi misurabili di R n 3. E j Ek =, se j k. Posto E = N E k si definisce integrale di Lebesgue di s la quantità k=1 E s dµ = con µ(e k ) misura di Lebesgue di E k. N α k µ(e k ), k=1 L integrale di Lebesgue di s potrà quindi essere una quantità reale non negativa, oppure +. Definizione Una funzione s semplice e non negativa si dice Lebesgueintegrabile, se risulta: s dµ < +. Di conseguenza, se E è un insieme misurabile, χ E dµ = µ(e), E E quindi χ E è integrabile se e solo se µ(e) <. Si può provare, usando l additività della misura µ, che Proposizione L integrale di Lebesgue di funzioni s semplici e non negative non dipende dalla partizione su cui è definita s. Definizione Sia f una funzione misurabile e non negativa definita su di un insieme E R n, definiamo l integrale di Lebesgue di f: { } f dµ := sup s dµ, s semplice, 0 s f. (2.1) E E Se f dµ < +, f si dice integrabile secondo Lebesgue e il valore dell integrale E è dato da (2.1). Lemma L integrale di Lebesgue di funzioni non negative gode delle proprietà di: 1. Additività: se E = E 1 E 2, con E 1 E 2 =, insiemi misurabili, allora data f integrabile su E, f dµ = E f dµ + E 1 f dµ. E 2 16
22 2. Linearità: se f e g sono funzioni integrabili e a, b 0, allora af + bg è integrabile e: (af + bg) dµ = a f dµ + b g dµ. 3. Monotonia: se 0 f g, allora: f dµ g dµ. Introduciamo ora l integrale per le funzioni con segno. Se f è una funzione misurabile, allora possiamo scrivere: f = f + f dove parte positiva f + e parte negativa f sono definite in (1.32) e (1.33). Definizione Data f funzione misurabile su E R n, se f + e f sono funzioni Lebesgue-integrabili, allora si definisce l integrale di Lebesgue di f la quantità: f dµ := f + dµ f dµ. Osserviamo che f = f + + f, inoltre: Proposizione f è integrabile f è integrabile. Dimostrazione. Supponiamo f integrabile. Poiché: f = f + + f per la linearitá dell integrale, f dµ = f + dµ + f dµ < +. Viceversa, poiché f +, f f, per la monotonia dell integrale risulta, f + dµ, f dµ f dµ < +, da cui la tesi. L integrale si estende poi a funzioni a valori in C nel modo seguente. 17
23 Definizione Sia f : E R n C misurabile, dove f = Re(f) + i Im(f) con Re(f), Im(f) : E R, allora f è Lebesgue-integrabile se lo sono Re(f) e Im(f) e si pone f dµ := Re(f) dµ + i Im(f) dµ. Lemma L integrale di Lebesgue gode delle proprietà di: 1. Additività: se E = E 1 E 2, con E 1 E 2 =, insiemi misurabili, allora, data f integrabile su E, f dµ = E f dµ + E 1 f dµ. E 2 2. Linearità: se f e g sono funzioni integrabili e a, b C, allora af + bg è integrabile e: (af + bg) dµ = a f dµ + b g dµ. 3. Monotonia: se 0 f g e g integrabile, allora f è integrabile e f dµ g dµ. 4. Assoluta continuità: f dµ f dµ. Definizione Si dice che una proposizione p(x) è vera q.o. (quasi ovunque) se µ({x : p(x)è falsa}) = 0. Proprietà Sia f misurabile su E e f 0, allora, i) se f è integrabile f(x) < + q.o. ii) f(x) dx = 0 f = 0 q.o. Dimostrazione. i) Preso k N, sia E k = {x E : f(x) > k} = f 1 ((k, + )). Quindi E k è misurabile e E k+1 E k. Inoltre Osserviamo che kµ(e k ) E := k=1e k = {x : f(x) = + }. E χ Ek fdµ E 18 fdµ < +, k N,
24 da cui lim k µ(e k ) = 0,e, per la continuità della misura per successioni decrescenti, segue che, µ(e ) = 0. ii) La dimostrazione è simile al passo precedente. Per k N, k > 0, si definisce { F k = x E : f(x) 1 }, k e F k F k+1. Sia F = k F k = {x : f(x) > 0}. Osserviamo che 1 k µ(f k) χ Fk fdµ fdµ = 0, k N +, E quindi µ(f k ) = 0 per ogni k > 0 e µ(f ) = lim k µ(f k ) = 0. Inoltre si hanno le seguenti: Proprietà Date f, g, allora: i) se f g e g integrabile, allora f é integrabile e f g. ii) f f. Proprietà Se f R([a 1, b 1 ] [a n, b n ]), allora f è Lebesgue-integrabile. E Dunque l integrale di Lebesgue estende l integrale di Riemann. 2.2 Passaggio al limite sotto il segno Sia f n una successione di f misurabile e positiva tale che f n (x) converga puntualmente ad f(x), ci chiediamo se è vero che: f n (x) =? f(x). lim n + Il seguente esempio mostra che non è sempre vero: Esempio Si ha che: f n (x) = { n 0 < x < 1 n 0 altrove f n dx = n 1 n = 1 Inoltre, comunque fissato x R +, n 0 / 1 n 0 < x. Da cui: lim f n(x) = 0 n + 19
25 Allora: 0 = R 0 dx lim f n dx = 1. n + R Tale disuguaglianza vale in generale, come mostra il seguente risultato. Lemma (Fatou). Sia {f n } n N una successione di funzioni misurabili definite su un sottoinsieme E di R n, non negative q.o., allora: lim inf f n dµ lim inf f n dµ. n + n + Teorema (Teorema della convergenza dominata). Sia {f n } n N una successione di funzioni misurabili con lim n + f n = f q.o. e supponiamo che esista g 0 integrabile, tale che f n g q.o., allora: i) f n, f sono integrabili e f dµ = lim n + fn dµ. ii) Si ha (convergenza in media) lim n + f fn dµ = 0. Poichè f n g e g è integrabile, per la monotonia dell inte- f n dµ g dµ < + Dimostrazione. i) grale: e perciò f n è integrabile, quindi f n è integrabile. Inoltre, f n f, infatti: f n (x) f(x) f n (x) f(x) 0 q.o. Poiché f n (x) g(x) n q.o., passando al limite, f(x) = lim f n(x) g(x), n + da cui f è integrabile. Dalle ipotesi abbiamo che g f n g, n e q.o.; in particolare: g f n, (2.2) f n g. (2.3) Dalla (2.2) otteniamo che f n + g 0 q.o.; per il lemma di Fatou: lim(f n + g) lim inf (f n + g) poichè f n è convergente (lim = lim inf = lim sup). Quindi: f + g lim inf f n + g, n + 20
26 da cui f lim inf n + f n. (2.4) Analogamente, dalla (2.3), otteniamo che g f n 0 q.o.; per il lemma di Fatou: lim(g f n ) lim inf (g f n ) da cui g f g lim sup f n. Perciò, f lim sup n + Mettendo insieme la (2.4) e la (2.5) si ha f lim inf f n lim sup da cui si ha ii) f = lim n + f n. f n. (2.5) f f n f + f n 2g. Allora per quanto visto in i), lim f f n = lim f f n = 0 n + n + poiché per ipotesi, abbiamo che f f n 0 puntualmente q.o., per n +. Questo completa la dimostrazione. Teorema (Teorema della convergenza monotona). Siano {f n } n N una successione di funzioni misurabili non negative tali che f n (x) f n+1 (x) q.o.. Allora: lim f n dµ = lim f n dµ. n + n + Dimostrazione. Sia f = lim n + f n q.o. (può anche essere F (x) = +. Per il Lemma di Fatou: f lim n + perchè le due successioni sono monotone non decrescenti e quindi ammettono limite (finito o infinito). Poiché f n f q.o., per la monotonia dell integrale: f n f n N. f n f n f 21
27 Perciò: lim n + confrontando con la (2.2), si ottiene f = lim n + f n f n. f Corollario Sia {a k } k, a k 0 q.o., a k misurabili, allora: k=1 a k = Dimostrazione. Si consideri la successione delle ridotte f n (x) = k=1 a k. n a k (x), si ha f n 0 q.o. e f n f n+1 q.o.. Per il teorema della convergenza monotona: lim f n = lim f n. n + n + k=1 Allora, e per linearitá da cui la tesi. k=1 lim n + a k = n k=1 lim n + a k = n k=1 k=1 a k a k, Esempio Calcolare l integrale della Gaussiana R n e y2 dy. Per n = 2, con y = (y 1, y 2 ), si ha: e y2 = e (y2 1 +y2 2 ). Ricordando che le coordinate polari assumono la forma: { y1 = ρ cos θ y 2 = ρ sin θ Si ha dunque: R 2 e y2 dy = 2π e ρ2 ρ dρ dθ = 1 2 2π e ρ2 ρ dρ dθ = π. 22
28 Ora, R 2 e (y2 1 +y2 2 ) dy 1 dy 2 = da cui e y2 1 e y2 2 dy1 dy 2 = R 2 R e y2 dy = π = π 1/2. ( e dy1)( ) y21 e y2 2 dy2 = π, R R Lo stesso ragionamento vale per il caso n-dimensionale: ( n e (y y2 n ) dy 1... dy n = e dy) y2 = π n/2. R n R Esempio La successione f n (x) = n x e n x non soddisfa le ipotesi del teorema della convergenza monotona, ma soddisfa invece quelle del teorema della convergenza dominata. Infatti, f n (x) 0 e { 1 se x 1 f n (x) g(x) x e x se x > 1 ovunque e g è integrabile. Applicando il teorema di Lebesgue otteniamo che: n x e n x dx 0. Esempio La successione f n (x) = e x2 n soddisfa le ipotesi del teorema della convergenza monotona. Infatti, f n (x) f n+1 (x), x R e f n (x) 0, allora lim n R f n (x) dx = R 1dx = + Esempio Mostriamo un esempio in cui non vale la proprietà di passaggio al limite sotto il segno. Si consideri la successione f n (x) = e (x n)2. Tale successione non soddisfa le ipotesi dei teoremi di convergenza monotona e dominata. Si ha lim n f n (x) = 0 e l invarianza per trasaalzioni della misura di Lebesgue dà f n (x) dx = e x2 dx = π 1/2. R R 23
29 Capitolo 3 Gli spazi L p 3.1 Prime definizioni Definizione Dato (X, M, m) uno spazio di misura. proposizione P (x) è vera q.o. (quasi ovunque) se Diciamo che una m({x X : P (x) è falsa}) = 0. In esso definiamo la seguente relazione di equivalenza: f g f = g, q.o. x X. Ora prendendo 1 p < definiamo lo spazio quoziente: { } L p (X) = f : X C misurabili e tali che f p dm < /. Pertanto lo spazio L p (X) così definito non sarà uno spazio di funzioni bensì uno spazio di classi di equivalenza di funzioni. Due funzioni definiscono lo stesso elemento se l insieme su cui differiscono ha misura nulla. Se 1 p <, allora poniamo ( f p = Se p =, poniamo X X f p dm) 1/p. f = esssup X f(x) con l estremo superiore essenziale definito nel modo seguente Definizione essup X f(x) = inf {α 0 : m ({x/ f(x) > α}) = 0} 24
30 che è pertanto, come dice il nome stesso, essenzialmente l estremo superiore della funzione a meno di insiemi di misura nulla. Si vede facilmente che la definizione 1.2 è equivalente a Definiremo dunque: inf {α 0 : f(x) α q.o.}. L (X) = {f : X C/ esssup X f(x) < }. Esempio Considero la f definita nel seguente modo: e x2 se x R { 5, 3} f(x) = 5 se x = 5 se x = 3 la cui rappresentazione grafica è: In questo caso, X = R e m = µ, misura di Lebesgue su R. Per tale f risulterà pertanto: sup x R f(x) =. Questa non è la f, in questo caso avremo infatti f = 1. Definiamo ora un altra norma, strettamente legata alla precedente: Definizione Si dice norma uniforme di f f U = sup f(x). x X Osservazione 3.1. Dalle definizioni segue che: f f U. Se la f è continua, però, esse coincidono cioè vale la seguente 25
31 propo 3.1. Sia (X, M, m) uno spazio di misura. Se f è continua risulta f = f U. Dimostrazione. Si ha {x : f(x) > α} = {x : f(x) < α} {x : f(x) > α} = f 1 (, α) f 1 (α, ). L insieme, essendo unione di aperti, è aperto. Ora un aperto U di X, diverso dall insieme vuoto, ha sempre misura positiva. Infatti preso x U, ɛ > 0 tale che B(x, ɛ) U, e m(b(x, ɛ)) > 0. Per cui, in questo caso, m({x : f(x) > α}) = 0 {x : f(x) > α} =, quindi la norma infinito coincide con quella uniforme. Osservazione 3.2. f n f U 0 f n converge ad f uniformemente. f n f 0 f n converge ad f uniformemente su A X, con A insieme misurabile e tale che m(x \ A) = 0. Questo ci dice dunque che gli insiemi di misura nulla non danno contributo nemmeno in termini di convergenza. Esempio Consideriamo il caso particolare in cui X = N, M = P (N) ed m sia la misura che conta i punti. Preso E N m(e) = E (osserviamo quindi che l unico insieme di misura nulla è ) mentre le f : N C sono le successioni a = (a n ) n. Allora in questo caso particolare, per 1 p < avremo { } L p (X) = l p (X) = (a n ) n / a n p < dove n=1 ( ) 1/p a l p = a n p i=1 è una norma. Se invece p = allora si definisce a l = sup a n. n N Esempio Il seguente esempio chiarisce la differenza tra norma infinito e norma uniforme nel caso di funzioni discontinue. Sia X = R e m = µ, la misura di Lebesgue su R. Data la funzione { sin(x) se x kπ, k Z f(x) = k se x = kπ, k Z la cui rappresentazione grafica è la seguente: 26
32 ,71-12,57-9,42-6,28-3,14-0,00 3,14 6,28 9,42 12,57 15, risulta mentre f U = sup f(x) = x R f = esssup x R f(x) = 1 dato che µ(kπ/k Z) = 0, per cui i valori f(x) = k ottenuti sono trascurabili. Risulta quindi: f f U. 3.2 Proprietà degli spazi L p D ora in avanti, restringiamo la nostra attenzione al caso X R n e m = µ, misura di Lebesgue su R n. Per semplicità poniamo L p = L p (X), dµ = dx. Proposizione Sia 1 p. L p è uno spazio vettoriale. Dimostrazione. Sappiamo che L p L, spazio vettoriale delle funzioni misurabili; per cui sarà sufficiente mostrare che L p è sottospazio vettoriale utilizzando il criterio per i sottospazi, ovvero mostrando che una combinazione lineare di elementi di L p è ancora un elemento di L p. Per semplicità mostriamo solo che L p è chiuso rispetto alla somma infatti, se f L p, si verifica immediatamente che λf L p λ C (usando l omogeneità del sup nel caso p = e la linearità dell integrale nel caso 1 p < ). La domanda che ci stiamo ponendo è dunque: f, g L p f + g L p? 27
33 Caso p =. Si ha (f + g)(x) f(x) + g(x), x X. Il nostro obiettivo è dimostrare che f + g <. Si ha f = sup f(x), con µ(x \ A) = 0 x A g = sup g(x), con µ(x \ B) = 0. x B Posto E = A B si ha (X \ A) (X \ B) = X \ (A B) = X \ E e µ(x \ E) µ(x \ A) + µ(x \ B) = 0 Per cui avremo: f + g = sup f(x) + g(x) x E ( f(x) + g(x) ) sup x E sup x E perchè, per ipotesi, f, g L. Caso 1 p <. x X, si ha f(x) + sup g(x) x E g(x) sup f(x) + sup x A x B = esssup x A f(x) + essup x B g(x) = f + g <, (3.1) ( f(x) + g(x) ) p ( f(x) + g(x) ) p ( 2 max( f(x), g(x) ) x X = 2 (max p ( f(x), g(x) ) x X 2 p ( f(x) p + g(x) p ). Per la monotonia dell integrale di Lebesgue, f + g p p = f(x) + g(x) p dx X 2 p ( f(x) p + g(x) p )dx X( ) = 2 p f(x) p dx + g(x) p dx X X = 2 ( ) p f p p + g p p che, essendo la somma di due quantità finite moltiplicate per una costante, è finita. 28 ) p ) p
34 Un altra proprietà degli spazi L p è legata alla seguente Definizione Sia X uno spazio vettoriale su C. funzione : X R + tale che x, y X, λ C: Si dice norma una 1. x = 0 x = 0 2. λx = λ x (proprietà di omogeneità) 3. x + y x + y (disuguaglianza di Minkowski) In particolare uno spazio vettoriale si dice normato se è dotato di una norma. Ci domandiamo ora se lo spazio vettoriale L p sia normato. La risposta è affermativa ma, per poterlo dimostrare, sono necessarie alcune proprietà. Proposizione (Disuguaglianza di Hölder). Dato 1 p sia p il suo esponente coniugato, cioè tale che = 1. Allora, se f L p e g p p L p si ha fg L 1, con fg 1 f p g p. (3.2) Osservazione 3.3. Anche l indice p verifica 1 p e, in particolare: p = 1 p = p = p = 1 p = 2 p = 2. Dimostrazione. Caso p = e p = 1 (o viceversa). Se f = 0 f U = 0 q.o. f = 0 q.o. fg = 0 q.o. fg = 0 X fg 1 = 0 mentre f g 1 = 0 per cui la disuguaglianza cercata è soddisfatta con il segno di uguale. Se f > 0, dato che f(x) f q.o., si ha: fg 1 = f(x)g(x) dx X = f(x) g(x) dx X f g(x) dx X = f g(x) dx Caso 1 < p <. X = f g 1 29
35 Se f p = 0 X f p = 0 f p = 0 q.o. f = 0 q.o. fg = 0 q.o. fg 1 = 0 per cui, ancora una volta, la disuguaglianza si trasforma in uguaglianza. Caso analogo se g p = 0. Sia ora f p > 0 e g p > 0. Da passiamo al reciproco, ottenendo Poniamo 1 p 1 < p < 0 < 1 p < 1. = λ. Abbiamo bisogno della seguente disuguaglianza numerica Lemma Sia λ (0, 1). Allora, a, b R + risulta: a λ b 1 λ λa + (1 λ)b (3.3) Dimostrazione. Se b = 0 0 λa e la (3.3) è vera. Se b 0, dividiamo ambo i membri per b e otteniamo: a λ b 1 λ b λa + (1 λ)b b cioè a λ b λ λ a + (1 λ) b ovvero ( a ) λ a λ + (1 λ) b b Ora, posto a = t 0 e definita φ(t) = b tλ λt vogliamo dimostrare che φ(t) 1 λ. Si ha ( 1 ) ( 1 t φ (t) = λt λ 1 1 λ ) λ = λ t 1 = λ 1 λ t 1 λ φ (t) = 0 1 t 1 λ = 0 t 1 λ = 1 t = 1. Sostituendo si ricava che φ(1) = 1 λ. Vediamo che si tratta di un massimo. Infatti, φ (t) 0 1 t 1 λ 0 t 1 λ 1 t 1. Per cui la φ cresce in [0, 1], ovvero φ(t) φ(1) = 1 λ. 30
36 Applicando il lemma precedente a λ = 1 p 1 λ = 1 1 p = 1 p, ( ) p ( ) p f(x) g(x) a =, b = f p g p si ottiene f(x) g(x) 1 ( ) p f(x) + 1 ( ) p g(x). f p g p p f p p g p A questo punto, integrando ambo i membri su R n, applicando le proprietà di monotonia e di linearità otteniamo: 1 f(x) g(x) dx 1 f p g p R p + 1 = 1 p n da cui ovvero R n f(x) g(x) dx f p g p fg 1 f p g p <, poichè, per ipotesi, f L p e g L p. Questo ci dice che la moltiplicazione puntuale : L p L p L 1 è una applicazione continua. Proposizione (Disuguaglianza di Minkowski). Se f, g L p risulta f + g L p e f + g p f p + g p. (3.4) Dimostrazione. Caso 1 < p <. Utilizzando, nell ordine, il fatto che f + g f + g (cioè la disuuaglianza di Minkowski per il modulo), la monotonia e la linearità dell integrale e la disuguaglianza di Hölder appena dimostrata, abbiamo: f + g p dx = f + g f + g p 1 dx X X f f + g p 1 dx + g f + g p 1 dx dove 1 = 1 1 = p 1 p = p, quindi p p p p 1 ( ) 1/p ( f + g (p 1)p dx = X X X ( ) 1 ( f p p ( dx f + g p 1 dx ) ) 1 p p dx + X X ( ) 1 ( + g p p ( dx ) ) 1 f + g p 1 p p dx (3.5) X X X = f + g p 1 p 31 ) p 1 f + g (p 1) p p p 1 dx
37 Sostituendo quest ultima osservazione nella (3.5) abbiamo: f + g p p = f + g p dx f p f + g p 1 p + g p f + g p 1 p, X da cui, dividendo ambo i membri per f + g p 1 p, si ottiene (3.4). Se p = 1, usiamo la disuguaglianza di Minkowski per il modulo f + g (x) f(x) + g(x). Integriamo e, sfruttando la linearità dell integrale, otteniamo f + g 1 = (f + g)(x) dx X f(x) dx + g(x) dx X = f 1 + g 1. Se p =, la disuguaglianza è già stata dimostrata nella (3.1). X Siamo ora in grado di enunciare e dimostrare la seguente Proposizione (L p, p ) è uno spazio vettoriale normato. Dimostrazione. Si tratta di vedere se la p definizione di norma. verifica le tre condizioni della 1. f p = 0 f = 0 q.o. f = 0 in L p. 2. Essendo una norma, risulta λf(x) = λ f(x). Se p < integrando ambo i membri elevati alla p-esima potenza su X e applicando la linearità dell integrale si ha: λf(x) p dx = λ p f(x) p dx = λ p f(x) p dx X da cui, estraendo la radice p-esima risulta: X λf p = λ f p. Se invece p = la proprietà diventa ovvia per l omogeneità del sup. 3. La disuguaglianza di Minkowski è stata dimostrata nella Proposizione 1.4. X Vediamo infine la generalizzazione della disuguaglianza di Hölder. 32
38 Proposizione (Disuguaglianza di Hölder generalizzata). Siano 1 p j, j = 1,..., n, tali che 1 p p n = 1 r 1. Se f j L p j, j = 1,..., n, allora n j=1 f j L r e n f j r Dimostrazione. Per n = 2, considero f 1 L p 1 e f 2 L p 2 con j=1 n f j pj. (3.6) j=1 1 p p 2 = 1 r 1. Moltiplicando ambo i membri per r si ottiene r p 1 + r p 2 = 1, relazione del tipo 1 p + 1 p = 1, il che ci permette di applicare la disuguaglianza di Hölder, con esponenti p = p 1 e p = p 2 alle funzioni f r r 1 r L p 1 r e f 2 r L p 2 r. Otteniamo f 1 r f 2 r 1 f 1 r p 1 r f 2 r p 2 r. (3.7) Ma ( f 1 r p 1 r = f 1 r p 1 r ) r p 1 = f1 r p 1 e analogamente ( f 2 r p 2 r = f 1 r p 2 r ) r p 2 = f2 r p 2. Sostituendo nella (3.7) abbiamo f 1 f 2 r r f 1 r p 1 f 2 r p 2 da cui, estraendo la radice r-esima, si ottiene la tesi. Per n > 2, la dimostrazione si fa per induzione. Sappiamo che la tesi è vera nel caso n = 2; pertanto supponiamo vera la relazione per n 1 fattori e dimostriamo che vale per n fattori f j L p j, j = 1,..., n, tali che 1 p p n p n = 1 1. r Posto 1 p = p 1 p n 1 e usando l ipotesi induttiva, si ottiene n 1 f j p f j pj. n 1 j=1 33 j=1
39 Posto f = n 1 j=1 f j, applichiamo il caso n = 2 ad f L p ed f n L 1 pn, con 1 p + 1 p n = 1 r, e otteniamo ff n r f p f n pn. Infine, sostituendo il valore di f, si ottiene la tesi: n f j r j=1 n f j pj. j=1 34
40 Capitolo 4 Completezza degli spazi L p Definizione Sia X uno spazio vettoriale. Un applicazione d : X X R + si dice distanza in X, se e solo se x, y, z X sono soddisfatte le seguenti tre proprietà: 1. d(x, y) = 0 x = y 2. d(x, y) = d(y, x) (simmetria) 3. d(x, y) d(x, z) + d(z, y) (disuguaglianza triangolare). La coppia (X, d) è detta spazio metrico. Uno spazio normato (X, X ) è un caso particolare di spazio metrico con la distanza naturale: d(x, y) = x y X. In particolare, gli spazi L p sono spazi normati (e quindi spazi metrici). In uno spazio normato si ha quindi una topologia avente come base di aperti le palle aperte : B(0, r) = {x X : x X < r} e le traslate per h X B(h, r) = h + B(0, r) = {x X : x h X < r}. Definizione {x n } è una successione di Cauchy in X se: ɛ > 0, ν N : m, n > ν x n x m X < ɛ. Definizione Uno spazio metrico (X, d) si dice completo se ogni sua successione di Cauchy è convergente in X. Definizione Sia (X, X ) uno spazio normato. Se è completo si dice spazio di Banach. Dimostreremo che (L p, p ), 1 p, è di Banach. 35
41 Definizione Sia (X, X ) uno spazio normato. Una serie n x n, con x n X, si dice convergente a x X, se la successione delle ridotte N n=1 x n converge a x X, ossia: In tal caso si pone x = n=1 x n. lim N x n x X = 0. N + n=1 Definizione Una serie n x n, con x n X, si dice assolutamente convergente se è convergente la serie delle norme, ossia se x n X <. n=1 Un criterio per verificare la completezza di uno spazio normato è il seguente. Teorema Sia (X, X ) uno spazio normato. Allora X è di Banach se e solo se ogni serie assolutamente convergente è convergente in X. Dimostrazione. Sia x n, con x n X, una serie assolutamente convergente e quindi n=1 x n <. Tesi: x n converge ad un certo x X. Sia S N = N n=1 x n la ridotta N-sima della serie, proviamo che la successione delle ridotte {S N } è di Cauchy. Ovvero, dobbiamo provare che: ɛ > 0 ν > 0 / N > M > ν S N S M < ɛ. Si ha, applicando la disuguaglianza di Minkowski, S N S M = N n=m+1 x n N n=m+1 x n = N M x n x n < ɛ N > M > ν, poichè, per ipotesi, la serie delle norme x n è convergente in R e quindi è una succesione di Cauchy. Pertanto, per la completezza di X, lim N + S N = x X. Sia {x n } una successione di Cauchy in X, proviamo che è convergente in X. j N, prendiamo ɛ = 2 j e quindi n=1 n j > 0 / m, n n j x n x m < 2 j. 36 n=1
42 Possiamo sempre costruirci gli n j tali che n 1 < n 2 <... < n j < n j+1 <... Poniamo y 1 = x n1 y 2 = x n2 x n1. y j = x nj x nj 1. Consideriamo la serie telescopica j=1 y j. La ridotta k-esima della serie è k y j = x n1 + (x n2 x n1 ) (x nk x nk 1 ) = x nk. j=1 Quindi la successione delle ridotte della serie y j è una sottosuccessione di Cauchy della successione di Cauchy di partenza {x n }. La serie y j è assolutamente convergente, infatti: 1 y j = x n1 + x nj x nj 1 x n1 + <, 2j 1 j=1 j=2 poichè n j > n j 1 e, per ipotesi, m, n n j si ha x nj x nj 1 < 1. Allora, 2j 1 per ipotesi, la serie converge semplicemente Ossia: lim k + j=1 y j x X. j=1 j=2 k y j x = lim x n k x = 0, k + e quindi la sottosuccessione {x nk } è convergente a x X. Sappiamo che, se da una successione di Cauchy {x n } estraiamo una sottosuccessione {x nk } convergente, allora anche la succesione di Cauchy di partenza converge allo stesso elemento, ovvero {x n } x X e quindi X è di Banach. Usiamo il criterio precedente per provare la completezza degli spazi L p. Teorema (L p, p ), 1 p, è di Banach. Dimostrazione. Caso 1 p <. 37
43 Sia f n una serie assolutamente convergente n=1 f n p = c p <, proviamo che la serie f n converge in norma L p, allora, per il Teorema 1, L p è uno spazio di Banach. Sia g(x) = f n (x), n=1 facciamo vedere che g(x) è finita quasi ovunque. Consideriamo la ridotta N-esima g N (x) = N f n (x). n=1 Osserviamo che la successione delle ridotte è monotona crescente g N (x) g N+1 (x) q.o., e quindi g p N (x) gp N+1 (x) q.o. Proviamo che g Lp. Si ha g p p = g(x) p = ( lim g N(x)) p = lim (g N(x)) p = lim g N (x) p = N N N N ( = lim N ) p ( ) p N f n (x) p p lim f n p = lim f n p = N N N n=1 n=1 n=1 ( ) p = f n p = c p p <. n=1 Dove si è usato il Teorema di convergenza monotona, applicato alla successione {g p N (x)} monotona crescente q.o. e la disuguaglianza di Minkowski. Poichè g L p, g(x) è finita q.o. e quindi, n=1 f n(x) è assolutamente convergente q.o. e, dunque, è convergente q.o. Poniamo f(x) = n=1 f n(x) q.o. Osserviamo che f(x) = f n (x) f n (x) = g(x), n=1 e quindi f L p, in quanto f(x) p n=1 g(x) p = g p p <. Dimostriamo ora la convergenza in norma L p. p ( ) N N p ( f n (x) f(x) f n (x) + f(x) N f n (x) + f(x) n=1 n=1 n=1 (g(x) + g(x)) p (2g(x)) p = 2 p g(x) p q.o. x. ) p 38
44 Poichè g p è integrabile, possiamo applicare il Teorema di convergenza dominata e passare il limite sotto il segno di integrale: lim N p f n f p N p = lim f n (x) f(x) dx = N N n=1 n=1 p N = lim f n (x) f(x) dx = 0, N n=1 Quindi n f n converge in norma L p ad f L p. Caso p =. Proviamo che ogni successione di Cauchy in L è convergente in L. Sia {f n } una successione di Cauchy in L, ovvero, ɛ > 0 ν ɛ > 0 : n, m > ν ɛ, f n f m < ɛ. Inoltre f n (x) f m (x) f n f m x / A n,m con µ(a n,m ) = 0. Sia A = n,m A n,m. Allora, per la subadditività della misura, ( ) µ(a) = µ A n,m µ(a n,m ) = 0. n,m Quindi, n,m x / A e n, m > ν ɛ, f n (x) f m (x) f n f m < ɛ. (4.1) Allora, x / A, {f n (x)} è di Cauchy in C, che è completo f n (x) f(x) puntualmente. Poniamo f(x) = lim n f n (x), x A. Dimostriamo ora che la successione {f n } converge a f uniformemente sul complementare di A. Passando al limite in (4.1), lim f n(x) f m (x) = f n (x) f(x) ɛ, x / A, m passando al sup, sup f n (x) f(x) ɛ, n > ν ɛ. x/ A 39
45 Quindi f è il limite uniforme della {f n }. Per ipotesi f n L, dunque f L al di fuori di A (poichè il limite uniforme di una successione di funzioni limitate è limitato). Inoltre, f n f sup f n (x) f(x) < ɛ, n > ν ɛ. (4.2) x/ A Poichè la (4.2) vale ɛ > 0, ciò equivale a dire che lim f n f = 0 n e cioè che {f n } converge a f in norma L. Osservazioni. In virtù dei Teoremi 1 e 2, abbiamo: 1. Ogni serie n=1 f n assolutamente convergente in L p, converge puntualmente q.o. 2. Ogni successione di Cauchy {f n } in L p ammette una sottosuccessione {f nk } convergente puntualmente q.o. 40
46 Proposizione Se 1 p < q < r, allora L q L p + L r, ovvero f L q, g L p, h L r / f = g + h. Dimostrazione. Sia E = {x / f(x) > 1}, dove f L q. E è misurabile, poichè: E = f 1 (, 1) f 1 (1, + ) e f 1 (, 1) e f 1 (1, + ) sono due insiemi misurabili, in quanto controimmagini, mediante una funzione misurabile f, di due aperti. Possiamo quindi scrivere f come f(x) = f(x)χ E + f(x)χ E c = g(x) + h(x), dove per E c intendiamo il complementare di E. Occorre solo più verificare che g L p e h L r. Per x E, f(x) > 1 e, poichè p < q, si ha: g(x) p = f(x) p χ E f(x) q χ E f(x) q. Passando agli integrali e ricordando che f L q, g p f q <, quindi g L p. Per x E c, f(x) 1 e, siccome q < r, otteniamo: h(x) r = f(x) r χ E c f(x) q χ E c f(x) q. Passando agli integrali e ricordando che f L q, h r f q <, quindi h L r. 41
47 Proposizione Se 1 p < q < r, allora: e dove λ (0, 1) è definito da L p L r L q f q f λ p f 1 λ r, (4.3) 1 q = λ p + (1 λ)1 r. Dimostrazione. Caso r =. Dobbiamo dimostrare che se f L p L, allora f L q e che vale la (4.3), dove ci aspettiamo che λ = p/q. Si ha f q = f q p+p = f q p f p. Osserviamo che f(x) f q.o., dunque, elevando tutto alla q p si ha: f(x) q p f q p q.o. e quindi f q f q p f p q.o. Passando agli integrali f q f q p f p <, poichè per ipotesi, f L p L. Da quest ultima disuguaglianza possiamo quindi già concludere che f L q. Estraendo ora la radice q-esima: f q f 1 (p/q) ( ) 1 p f p p q = f 1 (p/q) f p/q p, che è proprio la (4.3), dove λ = p/q. Caso 1 r <. Applichiamo la disuguaglianza di Hölder generalizzata, prendendo: e al prodotto p 1 = p λ e p 2 = r 1 λ 1 q = 1 p λ + 1 r (1 λ) = 1 p p 2 f = f λ f 1 λ. 42
48 Controlliamo prima che siano verificate tutte le ipotesi. f λ p λ = ( f λ p λ ) λ/p = [ ( ) ] 1 λ f p p = f λ p <, poichè f L p, quindi f λ L p/λ. Analogamente si dimostra che f 1 λ L r/(1 λ) : ( ) [ (1 λ)/r ( ) ] 1 1 λ f 1 λ r f (1 λ) r (1 λ) = f r r = f 1 λ 1 λ r <, poichè f L r. Quindi: f q f λ p/λ f 1 λ r/(1 λ) = f λ p f 1 λ r, che è proprio ciò che volevamo dimostrare. ESERCIZIO Dimostrare che, se 1 p < r, L p L r è uno spazio di Banach con la norma f L p L r = f p + f r. Soluzione. Vogliamo provare che (L p L r, L p Lr) è uno spazio di Banach. Procediamo per gradi, provando prima che L p L r è uno spazio vettoriale normato e, in secondo luogo, che è completo. 1. (L p L r, L p Lr) è uno spazio normato poichè: L p L r è uno spazio vettoriale in quanto intersezione di due spazi vettoriali. L p L r è una norma poichè: (a) L p L r: Lp L r [0, + ). Questo è ovvio in quanto: f L p L r f L p f L r f p [0, + ) f r [0, + ) f L p L r = f p + f r [0, + ). (b) f L p Lr = 0 f = 0, infatti: poichè f L p L r = f p + f r è la somma di due quantità positive o nulle, f L p L r= 0 f p = 0 = f r f = 0, essendo p e r due norme. (c) λf L p L r = λ f L p L r, f Lp L r, λ C, infatti: λf L p L r = λf p + λf r = λ f p + λ f r = λ ( f p + f r ) = λ f L p L r, 43
(2) se A A, allora A c A; (3) se {A n } A, allora +
 1. Spazi di misura In questo paragrafo accenneremo alla nozione di spazio di misura. Definizione 1. Sia X un insieme non vuoto. Una famiglia A di sottoinsiemi di X è una σ-algebra se : (1) A; (2) se A
1. Spazi di misura In questo paragrafo accenneremo alla nozione di spazio di misura. Definizione 1. Sia X un insieme non vuoto. Una famiglia A di sottoinsiemi di X è una σ-algebra se : (1) A; (2) se A
Alcuni complementi di teoria dell integrazione.
 Alcuni complementi di teoria dell integrazione. In ciò che segue si suppone di avere uno spazio di misura (,, µ) 1 Sia f una funzione misurabile su un insieme di misura positiva tale che f 0. Se fdµ =
Alcuni complementi di teoria dell integrazione. In ciò che segue si suppone di avere uno spazio di misura (,, µ) 1 Sia f una funzione misurabile su un insieme di misura positiva tale che f 0. Se fdµ =
Il teorema di Ascoli-Arzelà
 Il teorema di Ascoli-Arzelà Alcuni risultati sugli spazi metrici Spazi metrici (e topologici) compatti Richiamiamo le definizioni di compattezza negli spazi metrici. Sia (X, d) una spazio metrico e sia
Il teorema di Ascoli-Arzelà Alcuni risultati sugli spazi metrici Spazi metrici (e topologici) compatti Richiamiamo le definizioni di compattezza negli spazi metrici. Sia (X, d) una spazio metrico e sia
Analisi Reale. Anno Accademico Roberto Monti. Versione del 13 Ottobre 2014
 Analisi Reale Anno Accademico 2014-2015 Roberto Monti Versione del 13 Ottobre 2014 1 Contents Chapter 1. Introduzione alla teoria della misura 5 1. Misure esterne e misure su σ-algebre. Criterio di Carathéodory
Analisi Reale Anno Accademico 2014-2015 Roberto Monti Versione del 13 Ottobre 2014 1 Contents Chapter 1. Introduzione alla teoria della misura 5 1. Misure esterne e misure su σ-algebre. Criterio di Carathéodory
Si noti che questa definizione dice esattamente che
 DISUGUAGLIANZA INTEGRALE DI JENSEN IN DIMENSIONE FINITA LIBOR VESELY integrazione. Prima disuguaglianza integrale di Jensen.. Motivazione. Siano un insieme convesso in uno spazio vettoriale, f : (, + ]
DISUGUAGLIANZA INTEGRALE DI JENSEN IN DIMENSIONE FINITA LIBOR VESELY integrazione. Prima disuguaglianza integrale di Jensen.. Motivazione. Siano un insieme convesso in uno spazio vettoriale, f : (, + ]
ANALISI MATEMATICA 4. Prova scritta del 24 gennaio 2013
 Prova scritta del 24 gennaio 2013 Esercizio 1. Sia Ω R 3 un insieme misurabile secondo Lebesgue e di misura finita. Sia {f n } n N una successione di funzioni f n : Ω R misurabili e tali che 1) f n (x)
Prova scritta del 24 gennaio 2013 Esercizio 1. Sia Ω R 3 un insieme misurabile secondo Lebesgue e di misura finita. Sia {f n } n N una successione di funzioni f n : Ω R misurabili e tali che 1) f n (x)
Si dimostri che la (*) possiede un unica soluzione (u n ) limitata.
 Scuola Normale Superiore, ammissione al IV anno del corso ordinario Prova scritta di Analisi Matematica per Fisica, Informatica, Matematica 26 Agosto 2 Esercizio. Siano (a n ) e (b n ) successioni di numeri
Scuola Normale Superiore, ammissione al IV anno del corso ordinario Prova scritta di Analisi Matematica per Fisica, Informatica, Matematica 26 Agosto 2 Esercizio. Siano (a n ) e (b n ) successioni di numeri
Generalizzazioni del Teorema di Weierstrass
 Capitolo 2 Generalizzazioni del Teorema di Weierstrass Il principale riferimento bibliografico per questa lezione è il testo di Checcucci, Tognoli, Vesentini [1]. Introduzione Supponiamo che X = R n. È
Capitolo 2 Generalizzazioni del Teorema di Weierstrass Il principale riferimento bibliografico per questa lezione è il testo di Checcucci, Tognoli, Vesentini [1]. Introduzione Supponiamo che X = R n. È
COMPATTEZZA. i) X è compatto, cioè ogni ricoprimento aperto ammette un sottoricoprimento finito.
 1 COMPATTEZZA Sia X un sottoinsieme di R. Una famiglia A di sottoinsiemi aperti di R si dice ricoprimento aperto di X se X A, cioè se X è contenuto nell unione degli elementi di A. Una sottofamiglia di
1 COMPATTEZZA Sia X un sottoinsieme di R. Una famiglia A di sottoinsiemi aperti di R si dice ricoprimento aperto di X se X A, cioè se X è contenuto nell unione degli elementi di A. Una sottofamiglia di
Alcuni complementi sulla misura di Lebesgue in R N
 Alcuni complementi sulla misura di Lebesgue in R N Notazioni m Misura di Lebesgue in R N m e Misura esterna di Lebesgue in R N ; m e (E) = inf m(v ) V aperti V E m i Misura interna di Lebesgue in R N ;
Alcuni complementi sulla misura di Lebesgue in R N Notazioni m Misura di Lebesgue in R N m e Misura esterna di Lebesgue in R N ; m e (E) = inf m(v ) V aperti V E m i Misura interna di Lebesgue in R N ;
Massimo limite e minimo limite di una funzione
 Massimo limite e minimo limite di una funzione Sia f : A R una funzione, e sia p DA). Per ogni r > 0, l insieme ) E f p r) = { fx) x A I r p) \ {p} } è non vuoto; inoltre E f p r ) E f p r ) se 0 < r r.
Massimo limite e minimo limite di una funzione Sia f : A R una funzione, e sia p DA). Per ogni r > 0, l insieme ) E f p r) = { fx) x A I r p) \ {p} } è non vuoto; inoltre E f p r ) E f p r ) se 0 < r r.
Esercizi per il corso di Analisi 6.
 Esercizi per il corso di Analisi 6. 1. Si verifichi che uno spazio normato (X, ) è uno spazio vettoriale topologico con la topologia indotta dalla norma. Si verifichi poi che la norma è una funzione continua
Esercizi per il corso di Analisi 6. 1. Si verifichi che uno spazio normato (X, ) è uno spazio vettoriale topologico con la topologia indotta dalla norma. Si verifichi poi che la norma è una funzione continua
Analisi a più variabili: Integrale di Lebesgue
 Analisi a più variabili: Integrale di Lebesgue 1 Ripasso delle definizioni di Algebre, σ-algebre, misure additive, misure σ-additive, Proprietà della misura astratta, misura esterna. Definizione (Insieme
Analisi a più variabili: Integrale di Lebesgue 1 Ripasso delle definizioni di Algebre, σ-algebre, misure additive, misure σ-additive, Proprietà della misura astratta, misura esterna. Definizione (Insieme
Analisi 2. Roberto Monti. Appunti del Corso - Versione 5 Ottobre 2012
 Analisi 2 Roberto Monti Appunti del Corso - Versione 5 Ottobre 212 Indice Capitolo 1. Programma 5 Capitolo 2. Convergenza uniforme 7 1. Convergenza uniforme e continuità 7 2. Criterio di Abel Dirichlet
Analisi 2 Roberto Monti Appunti del Corso - Versione 5 Ottobre 212 Indice Capitolo 1. Programma 5 Capitolo 2. Convergenza uniforme 7 1. Convergenza uniforme e continuità 7 2. Criterio di Abel Dirichlet
ANALISI 1 - Teoremi e dimostrazioni vari
 ANALISI 1 - Teoremi e dimostrazioni vari Sommario Proprietà dell estremo superiore per R... 2 Definitivamente... 2 Successioni convergenti... 2 Successioni monotone... 2 Teorema di esistenza del limite
ANALISI 1 - Teoremi e dimostrazioni vari Sommario Proprietà dell estremo superiore per R... 2 Definitivamente... 2 Successioni convergenti... 2 Successioni monotone... 2 Teorema di esistenza del limite
Corso di Metodi Matematici per l Ingegneria A.A. 2016/2017 Esercizi svolti su misura e integrale di Lebesgue, spazi L p, operatori lineari continui
 Corso di Metodi Matematici per l Ingegneria A.A. 26/27 Esercizi svolti su misura e integrale di Lebesgue, spazi L p, operatori lineari continui Marco Bramanti Politecnico di Milano December 4, 26 Esercizi
Corso di Metodi Matematici per l Ingegneria A.A. 26/27 Esercizi svolti su misura e integrale di Lebesgue, spazi L p, operatori lineari continui Marco Bramanti Politecnico di Milano December 4, 26 Esercizi
20. Prodotto di spazi di misura. I teoremi di Tonelli e di Fubini.
 20. Prodotto di spazi di misura. I teoremi di Tonelli e di Fubini. 20.1. Prodotto di σ-algebre. Definizione 20.1.1. (σ-algebra prodotto. Dati n spazi misurabili (Ω 1, A 1,..., (Ω n, A n, si chiama σ-algebra
20. Prodotto di spazi di misura. I teoremi di Tonelli e di Fubini. 20.1. Prodotto di σ-algebre. Definizione 20.1.1. (σ-algebra prodotto. Dati n spazi misurabili (Ω 1, A 1,..., (Ω n, A n, si chiama σ-algebra
Esercitazione di Analisi Matematica I Esercizi e soluzioni 19/04/2013 TOPOLOGIA
 Esercitazione di Analisi Matematica I Esercizi e soluzioni 9/04/203 TOPOLOGIA Mostrare che uno spazio infinito con la metrica discreta non può essere compatto Soluzione: Per la metrica discreta d : X X
Esercitazione di Analisi Matematica I Esercizi e soluzioni 9/04/203 TOPOLOGIA Mostrare che uno spazio infinito con la metrica discreta non può essere compatto Soluzione: Per la metrica discreta d : X X
Esercizi del Corso di Istituzioni di Analisi Superiore, I modulo
 sercizi del Corso di Istituzioni di Analisi Superiore, I modulo 1. sercizi su massimo e minimo limite 1. lim inf a n lim sup a n 2. Se a n b n per ogni n N, allora lim inf a n lim inf b n. Vale anche lim
sercizi del Corso di Istituzioni di Analisi Superiore, I modulo 1. sercizi su massimo e minimo limite 1. lim inf a n lim sup a n 2. Se a n b n per ogni n N, allora lim inf a n lim inf b n. Vale anche lim
AM2: Tracce delle lezioni- IX Settimana INSIEMI DI LIVELLO, MINIMI VINCOLATI PRINCIPIO DEI MOLTIPLICATORI DI LAGRANGE
 AM2: Tracce delle lezioni- IX Settimana INSIEMI DI LIVELLO, MINIMI VINCOLATI PRINCIPIO DEI MOLTIPLICATORI DI LAGRANGE Sia g C 1 R 2 ), c R. L insieme γ = γ c := {x, y) R 2 : gx, y) = c} si chiama insieme
AM2: Tracce delle lezioni- IX Settimana INSIEMI DI LIVELLO, MINIMI VINCOLATI PRINCIPIO DEI MOLTIPLICATORI DI LAGRANGE Sia g C 1 R 2 ), c R. L insieme γ = γ c := {x, y) R 2 : gx, y) = c} si chiama insieme
Soluzione dei problemi assegnati
 ANALISI MATEMATICA 3 Soluzione dei problemi assegnati anno accademico 2018/19 prof. Antonio Greco http://people.unica.it/antoniogreco Dipartimento di Matematica e Informatica Università di Cagliari 23-5-2019
ANALISI MATEMATICA 3 Soluzione dei problemi assegnati anno accademico 2018/19 prof. Antonio Greco http://people.unica.it/antoniogreco Dipartimento di Matematica e Informatica Università di Cagliari 23-5-2019
14. Confronto tra l integrale di Lebesgue e l integrale di Riemann.
 4. Confronto tra l integrale di Lebesgue e l integrale di Riemann. Lo scopo di questo capitolo è quello di mettere a confronto i vari tipi di integrale (di Riemann, generalizzato e improprio) di funzioni
4. Confronto tra l integrale di Lebesgue e l integrale di Riemann. Lo scopo di questo capitolo è quello di mettere a confronto i vari tipi di integrale (di Riemann, generalizzato e improprio) di funzioni
3. Successioni di insiemi.
 3. Successioni di insiemi. Per evitare incongruenze supponiamo, in questo capitolo, che tutti gli insiemi considerati siano sottoinsiemi di un dato insieme S (l insieme ambiente ). Quando occorrerà considerare
3. Successioni di insiemi. Per evitare incongruenze supponiamo, in questo capitolo, che tutti gli insiemi considerati siano sottoinsiemi di un dato insieme S (l insieme ambiente ). Quando occorrerà considerare
11. Misure con segno.
 11. Misure con segno. 11.1. Misure con segno. Sia Ω un insieme non vuoto e sia A una σ-algebra in Ω. Definizione 11.1.1. (Misura con segno). Si chiama misura con segno su A ogni funzione ϕ : A R verificante
11. Misure con segno. 11.1. Misure con segno. Sia Ω un insieme non vuoto e sia A una σ-algebra in Ω. Definizione 11.1.1. (Misura con segno). Si chiama misura con segno su A ogni funzione ϕ : A R verificante
COMPLEMENTI DI ANALISI MATEMATICA DI BASE. Prova scritta del 26 gennaio 2005
 Prova scritta del 26 gennaio 2005 Esercizio 1. Posto B = x R 2 : x 2 2}, sia f n } una successione di funzioni (misurabili e) integrabili in B tali che f n f q.o. in B e, per ogni n N, f n (x) 2 x 3 per
Prova scritta del 26 gennaio 2005 Esercizio 1. Posto B = x R 2 : x 2 2}, sia f n } una successione di funzioni (misurabili e) integrabili in B tali che f n f q.o. in B e, per ogni n N, f n (x) 2 x 3 per
Istituzioni di Analisi Superiore
 Istituzioni di Analisi Superiore 20 aprile 2001 2 Indice 1 Teoria della misura 7 1.1 Famiglie di insiemi.......................... 7 1.2 Misura degli insiemi piani...................... 13 1.3 Misura di
Istituzioni di Analisi Superiore 20 aprile 2001 2 Indice 1 Teoria della misura 7 1.1 Famiglie di insiemi.......................... 7 1.2 Misura degli insiemi piani...................... 13 1.3 Misura di
Topologia, continuità, limiti in R n
 Topologia, continuità, limiti in R n Ultimo aggiornamento: 18 febbraio 2017 1. Preliminari Prima di iniziare lo studio delle funzioni di più variabili, in generale funzioni di k variabili e a valori in
Topologia, continuità, limiti in R n Ultimo aggiornamento: 18 febbraio 2017 1. Preliminari Prima di iniziare lo studio delle funzioni di più variabili, in generale funzioni di k variabili e a valori in
Dimostrazione. Indichiamo con α e β (finiti o infiniti) gli estremi dell intervallo I. Poniamo
 C.6 Funzioni continue Pag. 114 Dimostrazione del Corollario 4.25 Corollario 4.25 Sia f continua in un intervallo I. Supponiamo che f ammetta, per x tendente a ciascuno degli estremi dell intervallo, iti
C.6 Funzioni continue Pag. 114 Dimostrazione del Corollario 4.25 Corollario 4.25 Sia f continua in un intervallo I. Supponiamo che f ammetta, per x tendente a ciascuno degli estremi dell intervallo, iti
SPAZI TOPOLOGICI COMPATTI Note informali dalle lezioni
 SPAZI TOPOLOGICI COMPATTI Note informali dalle lezioni Sia X un insieme. Un ricoprimento di X è una famiglia U = {U j } j J di sottoinsiemi di X tali che X = j J U j. Un ricoprimento U = {U j } j J si
SPAZI TOPOLOGICI COMPATTI Note informali dalle lezioni Sia X un insieme. Un ricoprimento di X è una famiglia U = {U j } j J di sottoinsiemi di X tali che X = j J U j. Un ricoprimento U = {U j } j J si
ANALISI MATEMATICA 4. Prova scritta del 24 gennaio 2013
 Prova scritta del 24 gennaio 2013 Esercizio 1. Sia Ω R 3 un insieme misurabile secondo Lebesgue e di misura finita. Sia {f n } n N una successione di funzioni f n : Ω R misurabili e tali che 1) f n (x)
Prova scritta del 24 gennaio 2013 Esercizio 1. Sia Ω R 3 un insieme misurabile secondo Lebesgue e di misura finita. Sia {f n } n N una successione di funzioni f n : Ω R misurabili e tali che 1) f n (x)
Il lemma di Baire e i teoremi di Banach-Steinhaus, della mappa aperta e del grafico chiuso.
 Il lemma di Baire e i teoremi di Banach-Steinhaus, della mappa aperta e del grafico chiuso. SEMINARIO 2 AM310 a cura di Sara Rossicone e Maria Chiara Timpone 1 Lemma di Baire Definizione 1 (Spazio di Banach).
Il lemma di Baire e i teoremi di Banach-Steinhaus, della mappa aperta e del grafico chiuso. SEMINARIO 2 AM310 a cura di Sara Rossicone e Maria Chiara Timpone 1 Lemma di Baire Definizione 1 (Spazio di Banach).
8. Completamento di uno spazio di misura.
 8. Completamento di uno spazio di misura. 8.1. Spazi di misura. Spazi di misura completi. Definizione 8.1.1. (Spazio misurabile). Si chiama spazio misurabile ogni coppia ordinata (Ω, A), dove Ω è un insieme
8. Completamento di uno spazio di misura. 8.1. Spazi di misura. Spazi di misura completi. Definizione 8.1.1. (Spazio misurabile). Si chiama spazio misurabile ogni coppia ordinata (Ω, A), dove Ω è un insieme
Teoria della misura. Tiziano Vargiolu Dipartimento di Matematica Pura ed Applicata via Belzoni, Padova
 Teoria della misura Tiziano Vargiolu Dipartimento di Matematica Pura ed Applicata via Belzoni, 7-35131 Padova email: vargiolu@galileo.math.unipd.it 8 ottobre 23 Indice Introduzione iii 1 Teoria della misura
Teoria della misura Tiziano Vargiolu Dipartimento di Matematica Pura ed Applicata via Belzoni, 7-35131 Padova email: vargiolu@galileo.math.unipd.it 8 ottobre 23 Indice Introduzione iii 1 Teoria della misura
Il teorema di Vitali-Lebesgue
 Il teorema di Vitali-Lebesgue Gianluca Gorni Università di Udine gennaio 0 Nel 90 Giuseppe Vitali e Henri Lebesgue, indipendentemente uno dall altro, trovarono che si possono caratterizzare in modo elegante
Il teorema di Vitali-Lebesgue Gianluca Gorni Università di Udine gennaio 0 Nel 90 Giuseppe Vitali e Henri Lebesgue, indipendentemente uno dall altro, trovarono che si possono caratterizzare in modo elegante
Definizione 1.1. Sia A un sottoinsieme dei numeri reali. Diciamo che A è un insieme induttivo se
 1 Numeri naturali, interi e razionali Definizione 1.1. Sia A un sottoinsieme dei numeri reali. Diciamo che A è un insieme induttivo se 1. 1 A. per ogni x A, si ha x + 1 A Definizione 1.. Chiamo insieme
1 Numeri naturali, interi e razionali Definizione 1.1. Sia A un sottoinsieme dei numeri reali. Diciamo che A è un insieme induttivo se 1. 1 A. per ogni x A, si ha x + 1 A Definizione 1.. Chiamo insieme
Spazi di Funzioni. Docente:Alessandra Cutrì. A. Cutrì e Metodi Matematici per l ingegneria Ing. Gestionale
 Spazi di Funzioni Docente:Alessandra Cutrì Spazi vettoriali normati Uno spazio Vettoriale V si dice NORMATO se è definita su V una norma, cioè una funzione che verifica: v 0 e v = 0 v = 0 λv = λ v λ R(o
Spazi di Funzioni Docente:Alessandra Cutrì Spazi vettoriali normati Uno spazio Vettoriale V si dice NORMATO se è definita su V una norma, cioè una funzione che verifica: v 0 e v = 0 v = 0 λv = λ v λ R(o
ELEMENTI DI TEORIA DELLA MISURA E DELL INTEGRAZIONE SECONDO LEBESGUE, versione italiana. PARTE 1: TEORIA DELLA MISURA
 ELEMENTI DI TEORIA DELLA MISURA E DELL INTEGRAZIONE SECONDO LEBESGUE, versione italiana. PARTE 1: TEORIA DELLA MISURA A. Brini October 12, 2009 Contents 1 Misura esterna e misura in R n 1 1.1 Ricoprimenti
ELEMENTI DI TEORIA DELLA MISURA E DELL INTEGRAZIONE SECONDO LEBESGUE, versione italiana. PARTE 1: TEORIA DELLA MISURA A. Brini October 12, 2009 Contents 1 Misura esterna e misura in R n 1 1.1 Ricoprimenti
c i χ Ai (x) f(x) = f(x)dx = c i m(a i ) R
 1. Integrale di Lebesgue in La differenza fondamentale tra integrale di Lebesgue e integrale di iemann consiste nella diversa scelta delle decomposizioni su cui sostanzialmente si basa ogni integrale:
1. Integrale di Lebesgue in La differenza fondamentale tra integrale di Lebesgue e integrale di iemann consiste nella diversa scelta delle decomposizioni su cui sostanzialmente si basa ogni integrale:
Analisi II, a.a Soluzioni 1. j j + 1 ; ( 1)j
 Analisi II, a.a. 7-8 Soluzioni Calcolare le seguenti distanze e norme: (i d (x, y dove x = {x j } e y = {y j } sono le successioni di l definite da x j = ( j, y j = j/(j + ; (ii d (f, g dove f, g sono
Analisi II, a.a. 7-8 Soluzioni Calcolare le seguenti distanze e norme: (i d (x, y dove x = {x j } e y = {y j } sono le successioni di l definite da x j = ( j, y j = j/(j + ; (ii d (f, g dove f, g sono
Appendice B ANALISI FUNZIONALE. 1 Spazi di Banach
 Appendice B ANALISI FUNZIONALE In questo capitolo si introducono gli spazi di Banach e di Hilbert, gli operatori lineari e loro spettro. Inoltre si discutono gli operatori compatti su uno spazio di Hilbert.
Appendice B ANALISI FUNZIONALE In questo capitolo si introducono gli spazi di Banach e di Hilbert, gli operatori lineari e loro spettro. Inoltre si discutono gli operatori compatti su uno spazio di Hilbert.
I teoremi della funzione inversa e della funzione implicita
 I teoremi della funzione inversa e della funzione implicita Appunti per il corso di Analisi Matematica 4 G. Mauceri Indice 1 Il teorema della funzione inversa 1 Il teorema della funzione implicita 3 1
I teoremi della funzione inversa e della funzione implicita Appunti per il corso di Analisi Matematica 4 G. Mauceri Indice 1 Il teorema della funzione inversa 1 Il teorema della funzione implicita 3 1
Misure e loro proprietà (appunti per il corso di Complementi di Analisi Matematica per Fisici, a.a )
 Misure e loro proprietà (appunti per il corso di Complementi di Analisi Matematica per Fisici, a.a. 2006-07 Sia Ω un insieme non vuoto e sia A una σ-algebra in Ω. Definizione 1. (Misura. Si chiama misura
Misure e loro proprietà (appunti per il corso di Complementi di Analisi Matematica per Fisici, a.a. 2006-07 Sia Ω un insieme non vuoto e sia A una σ-algebra in Ω. Definizione 1. (Misura. Si chiama misura
SPAZI COMPATTI. Proposizione 2 Sia (X, d) uno spazio metrico. Se esso è sequenzialmente compatto allora è completo.
 SPAZI COMPATTI D ora in poi tutti gli spazi topologici sono di Hausdorff. Definizione 1 Uno spazio topologico (X, τ) si dice sequenzialmente compatto, o compatto per successioni, se ogni successione di
SPAZI COMPATTI D ora in poi tutti gli spazi topologici sono di Hausdorff. Definizione 1 Uno spazio topologico (X, τ) si dice sequenzialmente compatto, o compatto per successioni, se ogni successione di
Esercizi 8 12 gennaio 2009
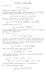 Sia α > e Esercizi 8 2 gennaio 29 f(x, y = ( + x 2 + y 2 α. Dimostrare che f appartiene a L p ( 2, con α p >. Osserviamo innanzitutto che, essendo f continua, l integrale di f p su 2 è uguale all integrale
Sia α > e Esercizi 8 2 gennaio 29 f(x, y = ( + x 2 + y 2 α. Dimostrare che f appartiene a L p ( 2, con α p >. Osserviamo innanzitutto che, essendo f continua, l integrale di f p su 2 è uguale all integrale
Teoria di Lebesgue. P n E = n=1
 Teoria di Lebesgue 1. La misura di Peano-Jordan La misura di Peano Jordan di un insieme é quasi sempre proposta per sottoinsiemi limitati E R 2 : si tratta di quanto suggerito dalla carta quadrettata,
Teoria di Lebesgue 1. La misura di Peano-Jordan La misura di Peano Jordan di un insieme é quasi sempre proposta per sottoinsiemi limitati E R 2 : si tratta di quanto suggerito dalla carta quadrettata,
TOPOLOGIA - APPUNTI SETTIMANA 2/12/2013-5/11/2013
 TOPOLOGIA - APPUNTI SETTIMANA 2/12/2013-5/11/2013 KIERAN G. O GRADY - 9 DICEMBRE 2013 1. Connessione Se X è uno spazio topologico connesso per archi vale il Teorema dei valori intermedi : dati una f :
TOPOLOGIA - APPUNTI SETTIMANA 2/12/2013-5/11/2013 KIERAN G. O GRADY - 9 DICEMBRE 2013 1. Connessione Se X è uno spazio topologico connesso per archi vale il Teorema dei valori intermedi : dati una f :
Limiti e continuità. Hynek Kovarik. Analisi A. Università di Brescia. Hynek Kovarik (Università di Brescia) Limiti e continuità Analisi A 1 / 68
 Limiti e continuità Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Limiti e continuità Analisi A 1 / 68 Cenni di topologia La nozione di intorno Sia x 0 R e r > 0.
Limiti e continuità Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Limiti e continuità Analisi A 1 / 68 Cenni di topologia La nozione di intorno Sia x 0 R e r > 0.
f n (x) 3 1. x Essendo g(x) = 3 1
 Secondo esonero di Analisi eale 6//9 a.a. 8-9 ) Studiare la convergenza in L p ((, )), p +, della successione di funzioni cos(nx) e nx f n (x) = 3. x Si vede facilmente che la successione f n converge
Secondo esonero di Analisi eale 6//9 a.a. 8-9 ) Studiare la convergenza in L p ((, )), p +, della successione di funzioni cos(nx) e nx f n (x) = 3. x Si vede facilmente che la successione f n converge
COMPLEMENTI DI ANALISI MATEMATICA II. Prova scritta del 20 gennaio 2014
 Prova scritta del 2 gennaio 214 Studiare la convergenza puntuale e uniforme della serie di potenze n=1 n x 2n 2n + e n. Valutare poi la misurabilità e l integrabilità secondo Lebesgue della funzione somma
Prova scritta del 2 gennaio 214 Studiare la convergenza puntuale e uniforme della serie di potenze n=1 n x 2n 2n + e n. Valutare poi la misurabilità e l integrabilità secondo Lebesgue della funzione somma
SPAZI METRICI COMPLETI
 Capitolo 1 SPAZI METRICI COMPLETI Sia dato uno spazio metrico (X, d). Definizione 1.1 Una successione {x n } si dice successione di Cauchy se ε > 0 n 0 n, m n 0 = d(x n x m ) < ε (1.1) Esercizio 1.1 Dimostrare
Capitolo 1 SPAZI METRICI COMPLETI Sia dato uno spazio metrico (X, d). Definizione 1.1 Una successione {x n } si dice successione di Cauchy se ε > 0 n 0 n, m n 0 = d(x n x m ) < ε (1.1) Esercizio 1.1 Dimostrare
Esame scritto di Geometria 2
 Esame scritto di Geometria Università degli Studi di Trento Corso di laurea in Matematica A.A. 013/014 Settembre 014 Esercizio 1 Sia P 3 lo spazio proiettivo reale tridimensionale dotato del riferimento
Esame scritto di Geometria Università degli Studi di Trento Corso di laurea in Matematica A.A. 013/014 Settembre 014 Esercizio 1 Sia P 3 lo spazio proiettivo reale tridimensionale dotato del riferimento
Problemi di topologia metrica.
 Problemi di topologia metrica. 1.) Sia X un insieme, munito di una distanza d : X X R +. Siano x 1 ;x ;x 3 ;x 4 quattro punti qualsiasi di X. Verificare che: d (x 1 ; x 4 ) d (x 1 ; x ) + d (x ; x 3 )
Problemi di topologia metrica. 1.) Sia X un insieme, munito di una distanza d : X X R +. Siano x 1 ;x ;x 3 ;x 4 quattro punti qualsiasi di X. Verificare che: d (x 1 ; x 4 ) d (x 1 ; x ) + d (x ; x 3 )
Note del corso di Analisi Superiore 2
 Note del corso di Analisi Superiore 2 Luca Rondi anno accademico 2017/2018 1 Teorema di convessità di Riesz Riferimento: Dunford e Schwartz, Linear Operators, Part I, Chapter VI.10 Definizione 1.1 Sia
Note del corso di Analisi Superiore 2 Luca Rondi anno accademico 2017/2018 1 Teorema di convessità di Riesz Riferimento: Dunford e Schwartz, Linear Operators, Part I, Chapter VI.10 Definizione 1.1 Sia
COMPLETAMENTO DI SPAZI METRICI
 COMPLETAMENTO DI SPAZI METRICI 1. Successioni di Cauchy e spazi metrici completi Definizione 1.1. Una successione x n n N a valori in uno spazio metrico X, d si dice di Cauchy se, per ogni ε > 0 esiste
COMPLETAMENTO DI SPAZI METRICI 1. Successioni di Cauchy e spazi metrici completi Definizione 1.1. Una successione x n n N a valori in uno spazio metrico X, d si dice di Cauchy se, per ogni ε > 0 esiste
5.3 Alcune classi di funzioni integrabili
 3. Si verifichi che per ogni f, g : [a, b] R si ha f g = g + (f g) 0, f g = f + g f g; dedurne che se f, g R(a, b) allora f g, f g R(a, b). [Traccia: si osservi che basta verificare che f 0 R(a, b), e
3. Si verifichi che per ogni f, g : [a, b] R si ha f g = g + (f g) 0, f g = f + g f g; dedurne che se f, g R(a, b) allora f g, f g R(a, b). [Traccia: si osservi che basta verificare che f 0 R(a, b), e
SERIE NUMERICHE FAUSTO FERRARI
 SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioni di Complementi di Analisi Matematica ed Elementi di Calcolo delle probabilità per il corso di Laurea in Ingegneria per la parte di Elementi
SERIE NUMERICHE FAUSTO FERRARI Materiale propedeutico alle lezioni di Complementi di Analisi Matematica ed Elementi di Calcolo delle probabilità per il corso di Laurea in Ingegneria per la parte di Elementi
x(y + z)dx dy dz y(x 2 + y 2 + z 2 )dx dy dz y 2 zdx dy dz Esempio di insieme non misurabile secondo Lebesgue.
 /3/23 Calcolare dove x(y + z)dx dy dz = {(x, y, z) R 3 : x, y, z, x + y + z }. Calcolare y(x 2 + y 2 + z 2 )dx dy dz dove = {(x, y, z) R 3 : x 2 + y 2 + z 2 z, x 2 + y 2 + z 2 3zx y }. Calcolare dove y
/3/23 Calcolare dove x(y + z)dx dy dz = {(x, y, z) R 3 : x, y, z, x + y + z }. Calcolare y(x 2 + y 2 + z 2 )dx dy dz dove = {(x, y, z) R 3 : x 2 + y 2 + z 2 z, x 2 + y 2 + z 2 3zx y }. Calcolare dove y
Spazi di Funzioni. Docente:Alessandra Cutrì. A. Cutrì e Metodi Matematici per l ingegneria Ing. Gestionale
 Spazi di Funzioni Docente:Alessandra Cutrì Spazi vettoriali normati Nel piano (R 2 ) e nello spazio ( R 3 ) sappiamo che la lunghezza di un vettore v si esprime rispettivamente come Se v = (v 1, v 2 )
Spazi di Funzioni Docente:Alessandra Cutrì Spazi vettoriali normati Nel piano (R 2 ) e nello spazio ( R 3 ) sappiamo che la lunghezza di un vettore v si esprime rispettivamente come Se v = (v 1, v 2 )
Integrale di Lebesgue
 Integrale di Lebesgue Retta reale ampliata R = R {, + } ottenuta aggiungendo all insieme R dei numeri reali (retta reale) i simboli e +. ordinamento completo su R ottenuto, per prolungamento dell usuale
Integrale di Lebesgue Retta reale ampliata R = R {, + } ottenuta aggiungendo all insieme R dei numeri reali (retta reale) i simboli e +. ordinamento completo su R ottenuto, per prolungamento dell usuale
Capitolo IV SPAZI VETTORIALI EUCLIDEI
 Capitolo IV SPAZI VETTORIALI EUCLIDEI È ben noto che in VO 3 si possono considerare strutture più ricche di quella di spazio vettoriale; si pensi in particolare all operazioni di prodotto scalare di vettori.
Capitolo IV SPAZI VETTORIALI EUCLIDEI È ben noto che in VO 3 si possono considerare strutture più ricche di quella di spazio vettoriale; si pensi in particolare all operazioni di prodotto scalare di vettori.
Il teorema di Lusin (versione )
 G.Gorni 7/8 Il teorema di Lusin versione 8-6-). Distanza da un insieme Deinizione. Dato uno spazio metrico X, d), un sottinsieme non vuoto A X e un punto x X deiniamo distanza ra x e A il numero distx,
G.Gorni 7/8 Il teorema di Lusin versione 8-6-). Distanza da un insieme Deinizione. Dato uno spazio metrico X, d), un sottinsieme non vuoto A X e un punto x X deiniamo distanza ra x e A il numero distx,
Il teorema di Sard. Alessandro Ghigi. 25 ottobre 2014
 Il teorema di Sard Alessandro Ghigi 25 ottobre 2014 1 Sottoricoprimenti numerabili Esercizio 1. Sia X uno spazio topologico e sia Y X un sottospazio. Se {A i } i I è una base della topologia di X, allora
Il teorema di Sard Alessandro Ghigi 25 ottobre 2014 1 Sottoricoprimenti numerabili Esercizio 1. Sia X uno spazio topologico e sia Y X un sottospazio. Se {A i } i I è una base della topologia di X, allora
Analisi Matematica 3 (Fisica) Prova scritta del 27 gennaio 2012 Uno svolgimento
 Analisi Matematica 3 (Fisica) Prova scritta del 27 gennaio 22 Uno svolgimento Prima di tutto, eccovi alcuni commenti che potrebbero aiutarvi a svolgere meglio le prove scritte. Ad ogni domanda del testo
Analisi Matematica 3 (Fisica) Prova scritta del 27 gennaio 22 Uno svolgimento Prima di tutto, eccovi alcuni commenti che potrebbero aiutarvi a svolgere meglio le prove scritte. Ad ogni domanda del testo
Esonero di Analisi Matematica II (A)
 Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
CORSO DI LAUREA IN MATEMATICA ANALISI MATEMATICA 6, A.A PRIMA PARTE DEL CORSO
 CORSO DI LAUREA IN MATEMATICA ANALISI MATEMATICA 6, A.A. 2009 2010 PRIMA PARTE DEL CORSO F. ZANOLIN, UNIVERSITÀ DEGLI STUDI DI UDINE, DIPARTIMENTO DI MATEMATICA E INFORMATICA, VIA DELLE SCIENZE 206, 33100
CORSO DI LAUREA IN MATEMATICA ANALISI MATEMATICA 6, A.A. 2009 2010 PRIMA PARTE DEL CORSO F. ZANOLIN, UNIVERSITÀ DEGLI STUDI DI UDINE, DIPARTIMENTO DI MATEMATICA E INFORMATICA, VIA DELLE SCIENZE 206, 33100
Soluzione della Prova Scritta di Analisi Matematica 4-25/06/13. C.L. in Matematica e Matematica per le Applicazioni. Proff. K. R. Payne e E.
 Soluzione della Prova Scritta di Analisi Matematica 4-5/6/ C.L. in Matematica e Matematica per le Applicazioni Proff. K. R. Payne e E. Terraneo Esercizio. a. Le funzioni f n (x) sono continue e quindi
Soluzione della Prova Scritta di Analisi Matematica 4-5/6/ C.L. in Matematica e Matematica per le Applicazioni Proff. K. R. Payne e E. Terraneo Esercizio. a. Le funzioni f n (x) sono continue e quindi
Esistenza ed unicità per equazioni differenziali
 Esistenza ed unicità per equazioni differenziali Per concludere queste lezioni sulle equazioni differenziali vogliamo dimostrare il teorema esistenza ed unicità per il problema di Cauchy. Faremo la dimostrazione
Esistenza ed unicità per equazioni differenziali Per concludere queste lezioni sulle equazioni differenziali vogliamo dimostrare il teorema esistenza ed unicità per il problema di Cauchy. Faremo la dimostrazione
1 Successioni di funzioni
 Analisi Matematica 2 Successioni di funzioni CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 6 SERIE DI POTENZE Supponiamo di associare ad ogni n N (rispettivamente ad ogni n p, per qualche
Analisi Matematica 2 Successioni di funzioni CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 6 SERIE DI POTENZE Supponiamo di associare ad ogni n N (rispettivamente ad ogni n p, per qualche
Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 2 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata, Matematica
 DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 2 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 2 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
Il metodo diretto del Calcolo delle Variazioni
 Capitolo 3 Il metodo diretto del Calcolo delle Variazioni Coercività Definizione 3.1 Una funzione F : X R si dice coerciva (risp. sequenzialmente coerciva) se per ogni t R esiste un sottoinsieme compatto
Capitolo 3 Il metodo diretto del Calcolo delle Variazioni Coercività Definizione 3.1 Una funzione F : X R si dice coerciva (risp. sequenzialmente coerciva) se per ogni t R esiste un sottoinsieme compatto
Istituzioni di Analisi Superiore, secondo modulo
 niversità degli Studi di dine Anno Accademico 997/98 Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Matematica Istituzioni di Analisi Superiore, secondo modulo Cognome e Nome: Prova
niversità degli Studi di dine Anno Accademico 997/98 Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Matematica Istituzioni di Analisi Superiore, secondo modulo Cognome e Nome: Prova
Equazioni differenziali del primo ordine: casi particolari e teorema di esistenza per il problema di Cauchy
 Equazioni differenziali del primo ordine: casi particolari e teorema di esistenza per il problema di Cauchy 10 maggio 2010 Supponiamo che f(x, y) sia una funzione continua definita in un rettangolo del
Equazioni differenziali del primo ordine: casi particolari e teorema di esistenza per il problema di Cauchy 10 maggio 2010 Supponiamo che f(x, y) sia una funzione continua definita in un rettangolo del
non solo otteniamo il valore cercato per la validità della (1.4), ma anche che tale valore non dipende da
 NOTE INTEGRATIVE PER IL CORSO DI ANALISI MATEMATICA 2 ANNO ACCADEMICO 2012/13 NOTE SULLA CONTINUITÀ UNIFORME D.BARTOLUCCI, D.GUIDO Sia f(x) = x 3, x [ 1, 1]. Si ha 1. La continuità uniforme x 3 y 3 = x
NOTE INTEGRATIVE PER IL CORSO DI ANALISI MATEMATICA 2 ANNO ACCADEMICO 2012/13 NOTE SULLA CONTINUITÀ UNIFORME D.BARTOLUCCI, D.GUIDO Sia f(x) = x 3, x [ 1, 1]. Si ha 1. La continuità uniforme x 3 y 3 = x
Corso di Laurea in Matematica Geometria 2. Esercizi di preparazione allo scritto a.a Topologia
 Corso di Laurea in Matematica Geometria 2 Esercizi di preparazione allo scritto a.a. 2015-16 Esercizio 1. Dimostrare che Topologia 1. d(x, y) = max 1 i n x i y i definisce una distanza su R n. 2. d(x,
Corso di Laurea in Matematica Geometria 2 Esercizi di preparazione allo scritto a.a. 2015-16 Esercizio 1. Dimostrare che Topologia 1. d(x, y) = max 1 i n x i y i definisce una distanza su R n. 2. d(x,
Successioni numeriche
 Successioni numeriche Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Successioni Analisi Matematica 1 1 / 48 Definizione Una successione a valori reali è
Successioni numeriche Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Successioni Analisi Matematica 1 1 / 48 Definizione Una successione a valori reali è
Corso di Laurea in Matematica Geometria 2. Foglio di esercizi n. 2 a.a Soluzioni
 Corso di Laurea in Matematica Geometria 2 Foglio di esercizi n. 2 a.a. 2015-16 Soluzioni Gli esercizi sono presi dal libro di Manetti. Per svolgere questi esercizi, studiare con cura i paragrafi 3.5, 3.6,
Corso di Laurea in Matematica Geometria 2 Foglio di esercizi n. 2 a.a. 2015-16 Soluzioni Gli esercizi sono presi dal libro di Manetti. Per svolgere questi esercizi, studiare con cura i paragrafi 3.5, 3.6,
Politecnico di Milano Corso di Analisi e Geometria 1. Federico Lastaria Formule di Taylor Ottobre 2012
 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it Formule di Taylor Ottobre 2012 Indice 1 Formule di Taylor 1 1.1 Il polinomio di Taylor...............................
Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@polimi.it Formule di Taylor Ottobre 2012 Indice 1 Formule di Taylor 1 1.1 Il polinomio di Taylor...............................
Un paio di esempi su serie e successioni di funzioni
 Un paio di esempi su serie e successioni di funzioni 29 novembre 2010 1 Successione di funzioni Ricordiamo innanzitutto un po di definizioni. Definizione 1. Una successione di funzioni è una corrispondenza
Un paio di esempi su serie e successioni di funzioni 29 novembre 2010 1 Successione di funzioni Ricordiamo innanzitutto un po di definizioni. Definizione 1. Una successione di funzioni è una corrispondenza
Registro delle lezioni
 Complementi di Analisi Matematica - a.a. 2006-07 Corso di Laurea Specialistica in Ingegneria Civile (CIS) Registro delle lezioni Laura Poggiolini e Gianna Stefani 2 ottobre 2006, 2 ore, LP Il campo dei
Complementi di Analisi Matematica - a.a. 2006-07 Corso di Laurea Specialistica in Ingegneria Civile (CIS) Registro delle lezioni Laura Poggiolini e Gianna Stefani 2 ottobre 2006, 2 ore, LP Il campo dei
5.1 Definizione della misura in R 2
 Capitolo 5 Misure prodotto 5.1 Definizione della misura in 2 Nell introdurre la misura secondo Lebesgue in, abbiamo definito la misura esterna di un sottoinsieme qualsiasi E come m famiglia numerabile
Capitolo 5 Misure prodotto 5.1 Definizione della misura in 2 Nell introdurre la misura secondo Lebesgue in, abbiamo definito la misura esterna di un sottoinsieme qualsiasi E come m famiglia numerabile
Università degli Studi Roma Tre - Corso di Laurea in Matematica Tutorato di GE220
 Università degli Studi Roma Tre - Corso di Laurea in Matematica Tutorato di GE220 A.A. 2010-2011 - Docente: Prof. Edoardo Sernesi Tutori: Filippo Maria Bonci, Annamaria Iezzi e Maria Chiara Timpone Tutorato
Università degli Studi Roma Tre - Corso di Laurea in Matematica Tutorato di GE220 A.A. 2010-2011 - Docente: Prof. Edoardo Sernesi Tutori: Filippo Maria Bonci, Annamaria Iezzi e Maria Chiara Timpone Tutorato
ESERCIZI DI ANALISI FUNZIONALE. T(f) = g(x)f(x)dx
 ESERCIZI DI ANALISI FUNZIONALE.. Esercizi svolti.. Operatori lineari Esercizio.. Si consideri il funzionale T : C(,) R, dove g è la funzione g(x) = T(f) = g(x)f(x) dx, { se < x se < x < () Dimostrare che
ESERCIZI DI ANALISI FUNZIONALE.. Esercizi svolti.. Operatori lineari Esercizio.. Si consideri il funzionale T : C(,) R, dove g è la funzione g(x) = T(f) = g(x)f(x) dx, { se < x se < x < () Dimostrare che
TOPOLOGIA - APPUNTI SETTIMANA 2/12/2013-5/11/2013
 TOPOLOGIA - APPUNTI SETTIMANA 2/12/2013-5/11/2013 KIERAN G. O GRADY - 2 DICEMBRE 2013 1. Spazi di Hausdorff Definizione 1.1. Uno spazio topologico X è di Hausdorff se dati x 1, x 2 X distinti esistono
TOPOLOGIA - APPUNTI SETTIMANA 2/12/2013-5/11/2013 KIERAN G. O GRADY - 2 DICEMBRE 2013 1. Spazi di Hausdorff Definizione 1.1. Uno spazio topologico X è di Hausdorff se dati x 1, x 2 X distinti esistono
Elementi di teoria della misura (incompleto)
 lementi di teoria della misura (incompleto) Marco Sandri Viale Rimembranza 2 37015 Sant Ambrogio di Valpolicella (Verona) - Italy info@msandri.it http://www.msandri.it/ 26 Maggio 1993 2 Capitolo 1 lementi
lementi di teoria della misura (incompleto) Marco Sandri Viale Rimembranza 2 37015 Sant Ambrogio di Valpolicella (Verona) - Italy info@msandri.it http://www.msandri.it/ 26 Maggio 1993 2 Capitolo 1 lementi
SPAZI TOPOLOGICI. La nozione di spazio topologico è più generale di quella di spazio metrizzabile.
 SPAZI TOPOLOGICI La nozione di spazio topologico è più generale di quella di spazio metrizzabile. Definizione 1 Uno spazio topologico (X, τ) è una coppia costituita da un insieme X e da una famiglia τ
SPAZI TOPOLOGICI La nozione di spazio topologico è più generale di quella di spazio metrizzabile. Definizione 1 Uno spazio topologico (X, τ) è una coppia costituita da un insieme X e da una famiglia τ
Analisi Matematica II
 Corso di Laurea in Matematica Analisi Matematica II Esercizi sugli spazi metrici, normati, iti e continuità Versione del 27/0/206 Esercizi di base Esercizio. (Giusti 20. Dire se le seguenti funzioni sono
Corso di Laurea in Matematica Analisi Matematica II Esercizi sugli spazi metrici, normati, iti e continuità Versione del 27/0/206 Esercizi di base Esercizio. (Giusti 20. Dire se le seguenti funzioni sono
Dispense sulla distanza di Hausdorff
 Dispense sulla distanza di Hausdorff Fabio Ferri Giada Franz Federico Glaudo 23 aprile 2014 Sommario In questo documento studieremo le proprietà della distanza di Hausdorff, la naturale distanza indotta
Dispense sulla distanza di Hausdorff Fabio Ferri Giada Franz Federico Glaudo 23 aprile 2014 Sommario In questo documento studieremo le proprietà della distanza di Hausdorff, la naturale distanza indotta
4 Sottoinsiemi chiusi di uno spazio metrico
 Geometria e Topologia I 16 marzo 2005 12 4 Sottoinsiemi chiusi di uno spazio metrico (4.1) Definizione. Sia A X un sottoinsieme di uno spazio metrico X. Un punto x X si dice di accumulazione (anche: punto
Geometria e Topologia I 16 marzo 2005 12 4 Sottoinsiemi chiusi di uno spazio metrico (4.1) Definizione. Sia A X un sottoinsieme di uno spazio metrico X. Un punto x X si dice di accumulazione (anche: punto
ANALISI C & Complementi di Analisi Matematica di Base. Prova scritta del 23 gennaio 2007
 Prova scritta del 23 gennaio 2007 Esercizio 1. Sia f : R R una funzione misurabile e non negativa; si consideri la successione di funzioni f n (x) = max3f(x) 2n, 0}, x R, n N. Provare che se f è integrabile
Prova scritta del 23 gennaio 2007 Esercizio 1. Sia f : R R una funzione misurabile e non negativa; si consideri la successione di funzioni f n (x) = max3f(x) 2n, 0}, x R, n N. Provare che se f è integrabile
I. CENNI SULL ANALISI FUNZIONALE
 I. CENNI SULL ANALISI FUNZIONALE 0 Introduzione In questo capitolo discutiamo la definizione di un operatore lineare su uno spazio di Banach e di Hilbert e alcune delle sue proprietà. Nell appendice presentiamo
I. CENNI SULL ANALISI FUNZIONALE 0 Introduzione In questo capitolo discutiamo la definizione di un operatore lineare su uno spazio di Banach e di Hilbert e alcune delle sue proprietà. Nell appendice presentiamo
Teorema di Hahn-Banach
 Teorema di Hahn-Banach Alessandra Albanese e Sara Lamboglia 12.03.2012 1 Teorema di Hahn-Banach Teorema 1.1 (Hahn-Banach). Se M é un sottospazio di uno spazio vettoriale normato X e f é un funzionale lineare
Teorema di Hahn-Banach Alessandra Albanese e Sara Lamboglia 12.03.2012 1 Teorema di Hahn-Banach Teorema 1.1 (Hahn-Banach). Se M é un sottospazio di uno spazio vettoriale normato X e f é un funzionale lineare
Complementi di Analisi Matematica Ia. Carlo Bardaro
 Complementi di Analisi Matematica Ia Carlo Bardaro Capitolo 1 Elementi di topologia della retta reale 1.1 Intorni, punti di accumulazione e insiemi chiusi Sia x 0 IR un fissato punto di IR. Chiameremo
Complementi di Analisi Matematica Ia Carlo Bardaro Capitolo 1 Elementi di topologia della retta reale 1.1 Intorni, punti di accumulazione e insiemi chiusi Sia x 0 IR un fissato punto di IR. Chiameremo
( 1 π. (a n cos nt + b n sin nt) t R (3)
 7. SERIE TRIGONOMETRICHE E SERIE DI FOURIER Definizione 1. L p (R), p [1, + ), denota la classe di tutte le funzioni f : R C, misurabili secondo Lebesgue, periodiche con periodo per le quali il funzionale
7. SERIE TRIGONOMETRICHE E SERIE DI FOURIER Definizione 1. L p (R), p [1, + ), denota la classe di tutte le funzioni f : R C, misurabili secondo Lebesgue, periodiche con periodo per le quali il funzionale
Analisi a più variabili: Misura di Peano - Jordan ed Integrale di Riemann
 Analisi a più variabili: Misura di Peano - Jordan ed Integrale di Riemann 1 Definizione (Algebra): T P Ω è un'algebra se: A, B T A B T, Ω T A T A C T Se A i T A i T si dice σ-algebra Definizione (Misura):
Analisi a più variabili: Misura di Peano - Jordan ed Integrale di Riemann 1 Definizione (Algebra): T P Ω è un'algebra se: A, B T A B T, Ω T A T A C T Se A i T A i T si dice σ-algebra Definizione (Misura):
Una semplice dimostrazione del teorema fondamentale dell algebra
 Università degli Studi di Cagliari Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Matematica Una semplice dimostrazione del teorema fondamentale dell algebra Relatore Prof. Andrea
Università degli Studi di Cagliari Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Matematica Una semplice dimostrazione del teorema fondamentale dell algebra Relatore Prof. Andrea
Il teorema di Stone Weierstrass
 APPENDICE B Il teorema di Stone Weierstrass Definizione B.1. Siano X un insieme non vuoto e A un sottospazio vettoriale dello spazio delle funzioni a valori reali (risp. complessi) su X. Si dice che A
APPENDICE B Il teorema di Stone Weierstrass Definizione B.1. Siano X un insieme non vuoto e A un sottospazio vettoriale dello spazio delle funzioni a valori reali (risp. complessi) su X. Si dice che A
Analisi Matematica 2. Michele Campiti. Prove scritte di. Ingegneria Industriale a.a
 Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
Corso di Laurea in Matematica Geometria 2. Foglio di esercizi n. 1 a.a Soluzioni
 Corso di Laurea in Matematica Geometria 2 Foglio di esercizi n. 1 a.a. 2015-16 Soluzioni Gli esercizi sono presi dal libro di Manetti. Per svolgere questi esercizi, studiare con cura i paragrafi 3.1, 3.2,
Corso di Laurea in Matematica Geometria 2 Foglio di esercizi n. 1 a.a. 2015-16 Soluzioni Gli esercizi sono presi dal libro di Manetti. Per svolgere questi esercizi, studiare con cura i paragrafi 3.1, 3.2,
Analisi funzionale. Riccarda Rossi Lezione 2. Spazi normati Definizioni topologiche Continuità Convergenza di successioni Compattezza
 Riccarda Rossi Lezione 2 Programma 1. Spazi normati; 2. Definizioni topologiche 3. Continuità di funzioni in spazi topologici in spazi metrici in spazi normati 4. Convergenza di successioni in spazi topologici
Riccarda Rossi Lezione 2 Programma 1. Spazi normati; 2. Definizioni topologiche 3. Continuità di funzioni in spazi topologici in spazi metrici in spazi normati 4. Convergenza di successioni in spazi topologici
Esame di Analisi Funzionale e Trasformate Prima prova in itinere. Maggio 2017 A.A. 2016/2017. Prof. M. Bramanti Tema A
 Esame di Analisi Funzionale e Trasformate Prima prova in itinere. Maggio 7 A.A. 6/7. Prof. M. Bramanti Tema A Cognome: Nome N matr. o cod. persona: Dom Dom Dom 3 Es Es Es 3 Tot. Punti Domande di teoria
Esame di Analisi Funzionale e Trasformate Prima prova in itinere. Maggio 7 A.A. 6/7. Prof. M. Bramanti Tema A Cognome: Nome N matr. o cod. persona: Dom Dom Dom 3 Es Es Es 3 Tot. Punti Domande di teoria
